Механизмы трансформации диванов. Как правильно выбрать?
Какие механизмы трансформации диванов бывают? В чём разница? На эти два вопроса ответит статья «Механизмы трансформации».
ЕВРОКНИЖКА
Один из самых распространённых и наиболее надежных механизмов трансформации. Трансформация диванов: уберите подушки, выкатите сиденье до упора на себя, опустите заднюю спинку. Такие модели даже со спины выглядят очень привлекательно и эстетично, поэтому ставить этот диван вы можете в любом месте помещения: и посередине, и вплотную к стене. Конструкция, как правило, дополняется ящиком для белья.
ДЕЛЬФИН
Для того чтобы разложить мебель, достаточно выдвинуть выкатную часть, затем поднять матрас спального места на себя. Как правило, такие механизмы устанавливаются на угловых моделях диванов. Все диваны оснащены вместительным бельевым ящиком.
ПУМА
Механизм Пума немного отличается от других механизмов трансформации своей простотой и удобством. Он работает бесшумно и плавно, кроме того, нет необходимости применять силу, чтобы разложить спальное место. Для трансформации диван в кровать достаточно несколько элементарных действий: плавно приподнимите и потяните сидение на себя, а далее опустите на пол.
ФРАНЦУЗСКАЯ РАСКЛАДУШКА
Опора механизма может состоять из лат, металлической или ременной сетки, поверх которой обычно натягивают тент из высокопрочной ткани, сверху кладется матрас из ППУ. Для того чтобы разложить диван, нужно снять подушки, потянуть сиденье вверх и на себя, развернуть звенья. В состоянии «кровать» подобные механизмы не способны создать идеально ровную поверхность, поэтому такой диван лучше использовать как запасное спальное место.
КНИЖКА / КЛИК-КЛЯК
«Книжка» — более простой вариант, позволяющий использовать мебель только в качестве дивана или кровати. Усовершенствованный механизм — «клик-кляк» — имеет три положения спинки: «диван», «релакс», «кровать». Отличительными преимуществами механизма «клик-кляк» являются легкость трансформации, прочность и надежность конструкции, идеально ровное положение в положении «кровать».
АККОРДЕОН
Мягкая мебель, включающая механизмы трансформации диванов «аккордеон», имеет ровное и высокое спальное место. Механизм раскладывается по принципу гармошки: нужно немного приподнять до щелчка сиденье и выдвинуть его вперед.
СУНГИРЬ
Простой в эксплуатации и надежный механизм, позволяющий разложить мебель буквально одним движением. Сиденье при трансформации дивана не выкатывается, а плавно приподнимается и устанавливается на опоры. Отсутствие роликов является огромным плюсом, если на полу в комнате лежит дорогой ковер, который вы не желаете портить.
Сиденье при трансформации дивана не выкатывается, а плавно приподнимается и устанавливается на опоры. Отсутствие роликов является огромным плюсом, если на полу в комнате лежит дорогой ковер, который вы не желаете портить.
Механизмы трансформации — Мебельная фурнитура, материалы — Статьи
Ни для кого не секрет, что большая часть населения живет в довольно-таки небольших квартирах и порой не может себе позволить даже отдельную от детей спальню. При этом, выбирая мебель, основное внимание уделяют ее эстетическим свойствам, забывая, что в приоритете должны находиться функциональные возможности. Наиболее логичным выходом в такой ситуации станет мебель с механизмами трансформации, тем более что сейчас существует огромный выбор не только диванов, но и кроватей, столов, кресел.
Что-же такое мебель трансформер? В переводе с английского языка transform — обозначает преображать, превращать, то-есть это многофункциональная мебель, у которой есть несколько функций, согласитесь это довольно удобно, особенно в условиях, так или иначе, ограниченного пространства. Свое начало мебель трансформер берет в Германии, где впервые в кроватях для прислуги, начали устраивать ящик для белья. Затем англичане, обустраивая свои небольшие дома, конструировали комоды, которые во время путешествия являлись чемоданами для вещей, а дома превращались в мебель. Дальнейшее развитие мебели с несколькими функциями, было обусловлено появлением типового и ограниченного по площади жилья. Но стала появляться и эксклюзивная, дизайнерская мебель , которая выполняла несколько функций. Расмотрим с Вами несколько таких примеров:
Свое начало мебель трансформер берет в Германии, где впервые в кроватях для прислуги, начали устраивать ящик для белья. Затем англичане, обустраивая свои небольшие дома, конструировали комоды, которые во время путешествия являлись чемоданами для вещей, а дома превращались в мебель. Дальнейшее развитие мебели с несколькими функциями, было обусловлено появлением типового и ограниченного по площади жилья. Но стала появляться и эксклюзивная, дизайнерская мебель , которая выполняла несколько функций. Расмотрим с Вами несколько таких примеров:
Механизм для подъемной кровати № 582
Описывая различные виды трансформации нельзя обойти стороной шкаф-кровать. Очень интересный и компактный выход для небольших помещений. Механизм состоит из подвижной и неподвижной частей, 2х ножек и газового упора для облегчения поднимания кровати. Механизм для подъемной кровати предназначен для опускания и поднятия ложа кровати без приложения значительных усилий, вызванных силой тяжести, действующей на ложе кровати. Комплектуется газлифтами. Для подбора газлифтов необходимо просчитать поднимаемый вес кровати. Для конструкции основания применять материал толщиной не менее 19 мм.
Комплектуется газлифтами. Для подбора газлифтов необходимо просчитать поднимаемый вес кровати. Для конструкции основания применять материал толщиной не менее 19 мм.
Механизм трансформации стола-кровати №591
Данный механизм предназначен для самостоятельной сборки трансформера типа кровать- рабочий стол школьника. Такая конструкция рабочий стол- кровать позволяет расширить свободное пространство в квартире за счет создания дополнительной функциональности одному предмету мебели.
Механизм Трансформации Дивана-Кровати №358
Принцип действия механизма «книжка»: поднимаем сидение до щелчка, затем опускается – при этом опускается и спинка. Преимущество: механизм позволяет иметь в диване емкость для белья, диван быстро и легко раскладывается, спальное место располагается вдоль стены, что важно для владельцев малогабаритных квартир.
Механизм трансформации «Дельфин» № 482
Механизм трансформации дельфин — идеальный вариант для угловых моделей диванов. Диваны с механизмом дельфин очень компактны и отлично впишутся в интерьер даже небольшой по площади комнаты.
Диваны с механизмом дельфин очень компактны и отлично впишутся в интерьер даже небольшой по площади комнаты.
Механизмы трансформации диванов дельфин просты в использовании и служат годы. Такой механизм достаточно небольшой по размеру, поэтому позволяет устроить внутри дивана большой ящик для хранения белья и спальных принадлежностей. Раскладывается этот хитроумный механизм следующим способом. Вам необходимо потянуть за специальный ремешок, спрятанный между спинкой и сиденьем дивана. При этом часть сиденья плавно выдвигается вперед и образует большое и широкое спальное место, которое вполне может сравниться с двуспальной кроватью. Максимальная нагрузка, которую способен выдержать механизм дельфин — 200 кг. Это значит, что на нем могут комфортно расположиться как минимум два человека.
Механизм трансформации № 504 (Еврокнижка)
Книжка — один из самых старых и проверенных механизмов трансформации.Спальное место образуется двумя мягкими элементами: сиденьем и задней стороной спинки. При этом нижнее сиденье выдвигается наполовину, а спинка откидывается.Преимущества: простота в использовании. Надежность механизма трансформации позволяет раскладывать диван ежедневно. Диван с таким раскладным механизмом может быть использован в квартирах с ограниченной площадью.К недостаткам можно отнести некоторое ограничение в дизайне модели, вызванное тем, что спинка и сидение должны быть приблизительно одинаковыми по высоте (ширине) и иметь ровную поверхность по отношению друг к другу, так как обе выступают в качестве спального места.
При этом нижнее сиденье выдвигается наполовину, а спинка откидывается.Преимущества: простота в использовании. Надежность механизма трансформации позволяет раскладывать диван ежедневно. Диван с таким раскладным механизмом может быть использован в квартирах с ограниченной площадью.К недостаткам можно отнести некоторое ограничение в дизайне модели, вызванное тем, что спинка и сидение должны быть приблизительно одинаковыми по высоте (ширине) и иметь ровную поверхность по отношению друг к другу, так как обе выступают в качестве спального места.
Механизм подъема матраца тахты № 509
Механизм предназначен для подъема матраца на 42°. Диван ставится вплотную к стене. Данный механизм поднимает основание, на котором лежит матрац вместе со спинкой дивана. В комплект входят 4 пружины (на левую и правую сторону по две)
Механизм № 513 (типа Дельфин большой)
Механизм трансформации дельфин — идеальный вариант для угловых моделей диванов.
Механизмы трансформации диванов дельфин просты в использовании и служат годы. Такой механизм достаточно небольшой по размеру, поэтому позволяет устроить внутри дивана большой ящик для хранения белья и спальных принадлежностей. Раскладывается этот хитроумный механизм следующим способом. Вам необходимо потянуть за специальный ремешок, спрятанный между спинкой и сиденьем дивана. При этом часть сиденья плавно выдвигается вперед и образует большое и широкое спальное место, которое вполне может сравниться с двуспальной кроватью. Максимальная нагрузка, которую способен выдержать механизм дельфин — 200 кг. Это значит, что на нем могут комфортно расположиться как минимум два человека.
Механизм трансформации № 556
Предназначен для подъема спального места в угловых диванах и тахте. Позволяет, в зависимости от установки, поднимать спальное место на угол до 70°, что обеспечивает беспрепятственный доступ к полости бельевого ящика.
Механизм трансформации № 559
Предназначен для подъема спального места в тахте. Комплектуется газлифтами немецкой фирмы с усилием 400N, 500N, 700N, 750N, 800N, 1000N или 1200N. Данный механизм позволяет поднимать мягкий элемент на угол до 36 градусов.
Механизм № 579 «Тик-так»
Недостаток трансформации «еврокнижки» (когда сиденье при выдвижении «ездит» по полу) легко устраняется установкой механизма «тик-так». Трансформация механизма осуществляется путем перемещения сиденья вперед «шагающим» способом, опоры дивана не катаются по полу, а плавно перемещаются.
Механизм трансформации стола № 587
Механизм трансформации стола № 587 предназначен для превращения журнального столика в обеденный стол. Благодаря подъемному механизму увеличивается высота ножек. Механизм прочный и надежный. Он изготовлен на точном современном оборудовании, выполнен из стали, сверху покрыт полимером – антикоррозийным покрытием.
mebelshik74.ru
Механизмы трансформации — Мебельтранс
Механизм трансформации «Тик-Так» является развитием «Еврокнижки». Диван с таким механизмом лишен недостатка, связанного с испорченным при разложении полом от передних ножек. Так же как и в традиционной «Еврокнижке» имеется вместительный ящик для белья. Подробнее »
Механизм трансформации «Венеция» используется для производства мягкой мебели, имеющей в своей конструкции принцип выкатной подъемной платформы. С помощью механизма платформа шарнирно крепится к раме, двигающейся с помощью роликов по направляющим, расположенным в коробе мебели. Таким образом при выкате рамы и подъема платформы диван трансформируется в кровать. Подробнее »
Подробнее »
Применяется для производства диванов. В комплекте 2 сабли и 2 уголка. Подробнее »
Механизм трансформации «Дельфин» используется для производства мягкой мебели, имеющей в своей конструкции принцип выкатной подъемной платформы. С помощью механизма платформа шарнирно крепится к раме, двигающейся с помощью роликов по направляющим, расположенным в коробе мебели. Таким образом при выкате рамы и подъема платформы диван трансформируется в кровать. Подробнее »
Механизмы трансформации «Подъем тахты» предназначены для подъема спальной платформы относительно короба мягкой мебели или кровати под определенным углом, удобным для извлечения из него спальных принадлежностей. При этом шарниры механизмов устроены так, чтобы платформа при открывании двигалась вперед, предотвращая задевание спинок мебели о стены. Подробнее »
Механизм трансформации ФБ-151 используется в производстве диванов типа «Книжка» и относится к группе «Книжка с полкой». Полкой называют дополнительные захваты в виде уголков. Механизм шарнирно скрепляет две половины дивана спинку и сидение, обеспечивая трансформацию мягкой мебели из положения «Диван» в положение «Кровать». Одновременно ФБ-151 шарнирно закрепляет эти половины к коробу дивана. Подробнее »
Полкой называют дополнительные захваты в виде уголков. Механизм шарнирно скрепляет две половины дивана спинку и сидение, обеспечивая трансформацию мягкой мебели из положения «Диван» в положение «Кровать». Одновременно ФБ-151 шарнирно закрепляет эти половины к коробу дивана. Подробнее »
Механизм трансформации ФА-9М используется в производстве диванов типа «Книжка» и относится к группе «Книжка с полкой». Полкой называют дополнительные захваты в виде уголков. Механизм шарнирно скрепляет две половины дивана спинку и сидение, обеспечивая трансформацию мягкой мебели из положения «Диван» в положение «Кровать». Одновременно ФА-9М шарнирно закрепляет эти половины к коробу дивана. Подробнее »
Механизмы трансформации «Подъем тахты» предназначены для подъема спальной платформы относительно короба мягкой мебели или кровати под определенным углом, удобным для извлечения из него спальных принадлежностей. При этом шарниры механизмов устроены так, чтобы платформа при открывании двигалась вперед, предотвращая задевание спинок мебели о стены. Подробнее »
Подробнее »
Диваны с механизмом трансформации «Аккордеон» очень просто и быстро раскладываются, даже у ребенка это не составит особого труда. Движение раскладывания этого механизма напоминает движение одноименного музыкального инструмента — аккордеона, будто Вы растягиваете гармошку.
Механизм трансформации «Аккордеон» прост, но очень надежен. Он позволит создать мягкую мебель для любого современного интерьера. Подробнее »
Диван … Виды, назначение диванов. Механизмы трансформации дивана
Современное производство мебели предполагает использование самых разных материалов, что позволяет получить качественный и функциональный интерьер. Большой выбор инструментов, тканей и фурнитуры привлекает многих покупателей.
Материалы
Традиционным материалом для изготовления мебели является дерево. Современная инновационная технология производства позволила создать балки с имитацией натурального дерева. Например, МДФ или ДСП часто используют для производства мебели: шкафов, стен, кухонных гарнитуров. Но и мягкой мебели не обошлось. В отделке мебели и ее бригадной части присутствует дерево или ДСП. Большой популярностью пользуется также стекло, металл, камень и керамика, но чаще всего их используют для отделки и украшения диванов.
Например, МДФ или ДСП часто используют для производства мебели: шкафов, стен, кухонных гарнитуров. Но и мягкой мебели не обошлось. В отделке мебели и ее бригадной части присутствует дерево или ДСП. Большой популярностью пользуется также стекло, металл, камень и керамика, но чаще всего их используют для отделки и украшения диванов.
Классификация
Мебель используется не только в домашних интерьерах, но и в офисах или магазинах.Условно его можно разделить на два типа.
Мебель
Состоит из отдельных жестких элементов. К ним относятся шкафы, комоды, столы, кухонные гарнитуры, полки или шкафы. Современная мебель изготавливается из разных материалов. Классический и прочный — это массив разных пород дерева, более бюджетный — ДВП и ДСП.
Стекло также очень часто используется для производства такой мебели. Такой материал может разбавить тёплую деревянную поверхность и придаст пространству воздушности.
Мебель The Right максимально функциональна, экономит пространство и создает комфорт.
Мягкая мебель
К этому типу относятся угловые и прямые диваны раскладные и не раскладные кресла, пуфики и табуреты. Производители мягкой мебели используют самые разные наполнители и обивочные материалы. Разнообразные системы трансформации позволяют использовать его во всех интерьерах. Выбирая диваны или кресла для дома и офиса, знайте о возможности такого типа мебели.
Рекомендуется
Наиболее эффективные методы проращивания семян
Несмотря на то, что метод рассады в овощеводстве является очень трудоемким процессом, его использует большинство садоводов. Посадка семян в открытый грунт — простой и удобный метод, но он эффективен только в определенных климатических зонах. I …
Светоотражающая краска. Сфера применения
Когда машины начали заполнять дороги, их популярность начала набирать светоотражающая краска.Благодаря этой краске как водителям, так и пешеходам становится намного легче избегать аварий в темноте. Назначение краски Светоотражающая краска — лакокрасочный материал, который . ..
..
Любые изменения в жилых и офисных помещениях, связанные с перепланировкой или новым ремонтом, вызывающие необходимость обновления или замены мебели. Часто хозяева дома заранее продумывают такие изменения и обращают внимание на каждый элемент, чтобы создать целостный образ.
Пожалуй, одним из самых важных предметов мебели является диван.Часто это основная часть комнаты, особенно гостиная.
Диваны: назначение
Кто-то — диван в центре комнаты как мягкий и функциональный предмет, на котором можно расслабиться после тяжелого дня перед телевизором. А кто-то видит в этом предмете мебели удобное место для ночлега. Дизайнеры и дизайнеры мягкой мебели все время стараются сделать современный диван красивым и универсальным.
Например, качественные кожаные диваны являются статусным и роскошным предметом мебели в интерьере домашних и офисных шкафов.Они подчеркивают изысканный вкус и богатство своих владельцев. Залы и рестораны в классическом стиле также преобразятся таким предметом мебели.
Современный кухонный диван украсит пространство и подарит удобство жильцам дома в самой уютной комнате квартиры. Дизайнерские варианты углов с интересными акцентами обивки в больших просторных гостиных и офисных коридорах. На пике популярности в современной мебельной индустрии находятся модульные диваны.Этот тип позволяет одновременно принимать и пуфы, и кресла, которые могут иметь угловую и линейную конструкцию.
Дизайн
Дизайн интерьера в современном стиле утомляет минимализм. Разнообразные диваны используются как в ситуационных эксклюзивных проектах, так и для украшения домашнего пространства городских квартир. Он будет уместен и для стиля хай-тек, и для более сдержанного модерна — самых популярных направлений в декоре комнат в последнее время.
Диван — это самая важная мебель в гостиной.Как правило, он подбирается под общий стиль интерьера. Но это не значит, что нельзя играть на контрастах. Даже для минималистичных дизайнов понравится изысканная мягкая мебель. Диваны для гостиной можно выбрать с учетом общего цвета или с учетом стиля комнаты.
Диваны для гостиной можно выбрать с учетом общего цвета или с учетом стиля комнаты.
Наполнитель
Качественный и хорошо набитый диван не только удобен для отдыха или сна, но и прослужит намного дольше. При производстве мягкой мебели довольно часто используется наполнитель пружинных блоков, что делает ее не только удобной, но и прочной.Многие пружины представляют собой отдельные блоки, которые, в свою очередь, расположены в отдельных ячейках. Эта система наполнения идеальна для простых путешественников и для постели. Более бюджетные варианты пружинных узлов скреплены в единую конструкцию и движутся синхронно.
Синтетические наполнители намного дешевле, но и среди них можно выбрать качественные материалы. Они не только хорошо держат форму, но и прослужат достаточно долго. Чаще всего используются пенопласт, синтепон и другие инновационные материалы.
Обивка
Выбирая обивку дивана, следует учитывать не только цвет и фактуру, но и качество материала. Самые популярные варианты — жаккард и гобелен. Эти натуральные ткани имеют высокую плотность и могут быть выполнены в любом цвете.
Самые популярные варианты — жаккард и гобелен. Эти натуральные ткани имеют высокую плотность и могут быть выполнены в любом цвете.
Особой популярностью пользуется бельгийский гобелен, напоминающий велюр. Гобелен и жаккардовая отделка идеально подходят для больших модульных конструкций, но, если правильно обыграть расцветку, их можно использовать для небольших линейных диванов. Гобелен очень приятен на ощупь и легко моется.
Не менее популярны и другие обивочные материалы: флок, велюр, синель, флок других качественных пород.Они достаточно прочные и износостойкие.
Одна из последних тенденций в производстве диванов — использование твердых тканей. Таким образом, диван (выдвижной или неразборный) становится изюминкой интерьера.
Кожа как обивка дорогая, но не менее популярный материал. У кожаных диванов есть недостатки, так как они не очень удобны для контакта с кожей при очень низких или высоких температурах. Но это легко решается с помощью мягкого текстильного покрытия. Кухонный диван с обивкой из кожзаменителя очень прост в уходе.
Кухонный диван с обивкой из кожзаменителя очень прост в уходе.
Механизмы трансформации
Для увеличения функциональности существуют различные механизмы трансформации дивана. Они позволяют изменять не только положение и форму, но и внешний вид дивана. Такие системы позволяют максимально удобно складывать и раскладывать мебель в зависимости от обстоятельств.
Диван — это необходимый предмет мебели, и благодаря трансформации системы с успехом может использоваться как кровать.
Основные виды трансформации современных диванов
- Раскладные механизмы трансформации дивана, пожалуй, самые первые и очень популярные.Особенностью является такое промежуточное полулежачье, как спинка. Раскладывание происходит в два движения. Это самая первая и простая книжка, а так же популярный в последнее время механизм «клик-кляк».
- Раскладные или выдвижные конструкции являются наиболее подходящими для мебели, которую необходимо очень часто расширять.
 Простота системы позволяет легко разместить такие диваны. Выкатные механизмы очень прочные и долговечные. Они идеально подходят для обеспечения комфортных спальных мест.К ним относятся следующие механизмы: еврокнижка, «Дельфин», «Флэш», «Пума» и другие.
Простота системы позволяет легко разместить такие диваны. Выкатные механизмы очень прочные и долговечные. Они идеально подходят для обеспечения комфортных спальных мест.К ним относятся следующие механизмы: еврокнижка, «Дельфин», «Флэш», «Пума» и другие. - Сплит-система, обеспечивающая компактность в сложенном виде. На просторном спальном месте такие диваны можно использовать для гостей. Французская и американская раскладушка — самые яркие представители этого механизма.
Совсем недавно при изготовлении мебели стали использовать конструкции, состоящие из отдельных частей. Модульные диваны позволяют разместить большое количество гостей, а также хорошо смотреться в просторных помещениях.
Диван — это не только удобный предмет мебели, но и функциональная часть интерьера.
…механизм команды — Перевод на французский — примеры английский
Эти примеры могут содержать грубые слова на основании вашего поиска.
Эти примеры могут содержать разговорные слова, основанные на вашем поиске.
Предложите пример
Другие результаты
Со временем все меры по обеспечению безопасности должны быть переданы под эгиду Организации Объединенных Наций с соответствующими механизмами командования, и контроля и подотчетности.
Le moment venu, tous les apports en matière de sécurité devront se faire sous l’égide de l’ONU, assortis des mécanismes de commandement , de contrôle et deponsabilisation qui s’imposent.Давайте подробно рассмотрим механизм выполнения команды в системе Debian.
Теперь вы немного знаете, как использовать систему Debian.Давайте подробно рассмотрим механизм выполнения команды в системе Debian. Здесь я упростил реальность для новичков.
Вы можете поддерживать определенную сенсацию в работе с системой Debian. Мы все рассматриваем и расширяем mécanisme d ‘ exécution des commandes sous le système Debian. J’ai ici, pour les débutants, simpleifié la réalité.
Мы все рассматриваем и расширяем mécanisme d ‘ exécution des commandes sous le système Debian. J’ai ici, pour les débutants, simpleifié la réalité.Каждая раздаточная вилка и селекторная заслонка могут быть независимыми и выборочно присоединяться к своему соответствующему валу или отсоединяться от него посредством соответствующих механизмов соединения под командой контроллера для координированной операции переключения.
Chaque fourche de transfert et porte sélectrice peut être couplée or découplée de manière indépendante et selective par rapport à son arbre respectif, via les mécanismes de couplage correctors, sous le contrôle dé ‘ de couplage corrects, sous le contrôle dé’ transfer de run dergés. Совместные утренние встречи директоров, еженедельные общие собрания сотрудников и общие платформы ресурсов Интранет станут ключевыми механизмами обмена информацией для поддержки единства командования и усилий.
более конкретно, варианты осуществления в данном документе предоставлены для механизма из , инкапсулирующего как команду , так и механизм привязки в одно сообщение
Позволяет регулировать , синхронный, , команду , управлять механизмами .
Контроллер работает или выполняется на компьютере, чтобы посылать команды механизма на механизм с электронным управлением.
Поскольку из — это механизм , команду не следует вызывать из одного из этих методов базы данных.
Важно понимать, что правило — это действительно команда , , механизм преобразования, , , или макрос , команда .
Он предоставляет нам механизм , чтобы указать, какую команду выполнять в случае сбоя первой.
Предлагаемые инструменты предлагают механизм для фильтрации команд , проинструктированных пользователем (клиентской программой), где они конфликтуют с протоколами приложений, определенными для конкретного типа эмулируемого устройства.
Les outils предлагает предложение mécanisme , служащее фильтру , с инструкциями données par l’utilisateur (программный клиент), которые используются для определенных протоколов приложения для специального типа устройства в процессе моделирования.
А французские будут в еще большей опасности: действительно, французская армия, которая, наряду с британской армией, является одной из тех, кто лучше всех управляет механизмами борьбы с повстанцами, хорошо справляется с задачей в Афганистане. .
Et ceux de la France le seront encore plus: l’armée française, en effet — qui, avec l’armée britannique, est l’une de celles qui domine le mieux les mécanismes de la contre insurrection — fait du bon travail ru Афганистан.Другие аспекты общей архитектуры команд пользовательского интерфейса описывают механизм активации , с помощью которого зарегистрированные команды могут быть активированы приложением.
Аспекты архитектуры позволяют использовать общий интерфейс для работы с mécanisme активировать новую архитектуру для команд , зарегистрировавшихся для участия в различных приложениях.
Игровой хост (4) состоит из вычислительного механизма , запоминающего устройства , механизма , команды поведения , генерирующей механизм , механизма выполнения игры и динамика.
Настоящий механизм позволяет командам, , введенным в строку команд в рабочей среде строки команд , возможность выполнять в первом режиме выполнения или в альтернативном режиме выполнения.
Ce mécanisme предлагает команд Entrées dans une ligne de commande d’un environment de fonctionnement de ligne de command , La capacity de s’exécuter dans un premier mode d’exécution ou dans un autre mode d казнь. На строительной площадке также проведена модернизация аппаратов связи и связи, командных, диспетчерских, , механизмов, и контактных линий.
После этого вам нужно будет настроить загрузочный механизм (обычно команда loadlin ) и файл / etc / fstab.
Добавьте модификатор mécanisme de démarrage (общий элемент с commande loadlin) и fichier / etc / fstab.Группа хотела бы отметить, что в отсутствие из такого механизма , command ответственность за нарушения прав человека гражданского населения в конечном итоге будет возложена на верховное военное командование ВСДРК.
Le Groupe tient à noter qu’en l’in l’absence d ‘ un tel mécanisme , les нарушения прав человека передают ответственность за гражданское население supérieurs hiérarchiques du haut commandement des FARDC.
датчики в каждом механизме выдают сигнал команды , который инициирует одновременную автоматическую работу обоих механизмов установки
des capteurs dans chacune des plaques de guidage génèrent un signal de command servant a lancer le fonctionnement automatique simultané des deux mécanismes d’installationСобственное время, системы координат, преобразования Лоренца
Это Приложение объясняет некоторые ключевые концепции специальной теории относительности (СТО).Он показывает, насколько предсказания СТО наиболее фундаментально отличаются от предсказаний классической механики. Это требует некоторых базовых математических знаний.
Содержание
- Собственное время
- СТО Связь между пространством, временем и собственным временем
- Системы координат
- Декартовы координаты пространства
- Выбор инерциальной системы отсчета
- Операционная спецификация систем координат для классического пространства и времени
- Операционная спецификация систем координат для СТО пространства и времени
- Операционализм
- Преобразования координат и преобразования объектов
- Допустимые преобразования
- Повышение скорости в STR и классической механике
- Преобразование системы координат Галилея
- Преобразование Лоренца системы координат
- Расширение времени и пространства
- Полная специальная теория относительности
- Ссылки и дополнительная литература
1. Надлежащее время
Надлежащее время
Суть специальной теории относительности (СТО) состоит в том, что она связывает между собой три различные величины: пространство, время и собственное время. «Время» также называется координатным временем или реальным временем , чтобы отличать его от «собственного времени». Собственное время также называется временем часов, или временем процесса , и является мерой физического процесса, которому подвергается система. Например, собственное время для обычных механических часов записывается числом оборотов стрелок часов.В качестве альтернативы мы могли бы взять гироскоп или свободно вращающееся колесо и измерить количество оборотов за заданный период. Мы также могли бы взять химический процесс с естественной скоростью, такой как горение свечи, и измерить долю свечи, которая сгорает за определенный период.
Обратите внимание, что эти процессы измеряются «абсолютными величинами»: количеством раз, когда колесо вращается вокруг своей оси, или долей свечи, которая сгорела. Они дают абсолютные физические величины и не зависят от назначения какой-либо системы координат, как и числовое представление пространства или реального времени.Используемые нами числовые системы координат в первую очередь требуют выбора единиц измерения (например, метры и секунды). Что еще более важно, измерение пространства и реального времени в STR зависит от выбора инерциальной системы отсчета. Этот выбор отчасти произвольный.
Они дают абсолютные физические величины и не зависят от назначения какой-либо системы координат, как и числовое представление пространства или реального времени.Используемые нами числовые системы координат в первую очередь требуют выбора единиц измерения (например, метры и секунды). Что еще более важно, измерение пространства и реального времени в STR зависит от выбора инерциальной системы отсчета. Этот выбор отчасти произвольный.
Наше числовое представление собственного времени также требует выбора единиц, и мы принимаем те же единицы, что и для реального времени (секунды). Но выбор системы координат, основанной на инерциальной системе отсчета, не влияет на измерение собственного времени.Вскоре мы рассмотрим понятие систем координат и единиц измерения.
Собственное время может быть определено в классической механике через циклические процессы, которые имеют естественные периоды — например, маятниковые часы основаны на подсчете количества качаний маятника. В более общем смысле, любой естественный процесс в классической системе проходит через последовательность физических состояний с определенной абсолютной скоростью, и это «надлежащая скорость» для системы.
В классической физике предсказывается, что два идентичных типа систем (с одинаковыми типами внутренней конструкции и одинаковыми начальными состояниями) будут иметь одинаковые скорости собственного времени.То есть они будут проходить через свои физические состояния в идеальной корреляции друг с другом.
Это справедливо, даже если две идентичные системы находятся в постоянном относительном движении друг относительно друга. Например, два идентичных классических часа будут работать с одинаковой скоростью, даже если одни будут оставаться неподвижными в лаборатории, а другие помещены в космический корабль, движущийся с высокой скоростью.
Этот принцип инвариантности является фундаментальным для классической физики, и это означает, что в классической физике мы можем определить: Координатное время = Собственное время для всех естественных систем.По этой причине различие между этими двумя концепциями времени едва ли признавалось в классической физике (хотя Ньютон действительно различал их концептуально, рассматривая «реальное время» как абсолютный временной поток, а «собственное время» — просто как «разумную меру» в реальном времени; см. его Scholium ).
его Scholium ).
Однако это различие приобрело реальное значение только в специальной теории относительности, которая противоречит классической физике, предсказывая, что скорость собственного времени для системы зависит от ее скорости или движения в пространстве.Связь очень проста: чем быстрее система перемещается в пространстве, тем медленнее идут ее внутренние процессы. На максимально возможной скорости, скорости света c, внутренние процессы в физической системе полностью остановятся. Действительно, для самого света скорость собственного времени равна нулю: в свете не происходит «внутреннего процесса». Как будто свет «застыл» в определенном внутреннем состоянии.
Здесь мы должны упомянуть, что концепция собственного времени сильнее проявляется в квантовой механике, чем в классической механике, из-за внутренней «волнообразной» природы квантовых частиц.В классической физике одиночные точечные частицы — простые вещи, и у них нет никакого «внутреннего состояния», которое представляет собственное время, но в квантовой механике самые фундаментальные частицы имеют собственное время, представленное внутренней частотой. Это напрямую связано с волновой природой квантовых частиц. Для радиоактивных систем скорость радиоактивного распада является мерой собственного времени. Обратите внимание, что степень распада вещества может быть измерена в абсолютном смысле. Для света, рассматриваемого как квантово-механическая частица (фотон), скорость собственного времени равна нулю, и это потому, что он не имеет массы.Но для квантово-механических частиц с массой всегда существует конечная «внутренняя» скорость собственного времени, представленная «фазой» квантовой волны. Классические частицы не имеют никакого коррелята с этой особенностью, которая отвечает за эффекты квантовой интерференции и другое неклассическое «волновое» поведение.
Это напрямую связано с волновой природой квантовых частиц. Для радиоактивных систем скорость радиоактивного распада является мерой собственного времени. Обратите внимание, что степень распада вещества может быть измерена в абсолютном смысле. Для света, рассматриваемого как квантово-механическая частица (фотон), скорость собственного времени равна нулю, и это потому, что он не имеет массы.Но для квантово-механических частиц с массой всегда существует конечная «внутренняя» скорость собственного времени, представленная «фазой» квантовой волны. Классические частицы не имеют никакого коррелята с этой особенностью, которая отвечает за эффекты квантовой интерференции и другое неклассическое «волновое» поведение.
2. Связь STR между пространством, временем и собственным временем
STR предсказывает, что движение системы в пространстве напрямую компенсируется уменьшением реальных внутренних процессов или собственных темпов времени.Таким образом, часы будут работать быстрее, когда они неподвижны. Если мы будем перемещать его в пространстве, скорость его внутренних процессов уменьшится, и он будет работать медленнее, чем стационарные часы того же типа. Взаимосвязь точно определяется самым глубоким уравнением СТО, обычно называемым метрическим уравнением (или линейным метрическим уравнением).
Если мы будем перемещать его в пространстве, скорость его внутренних процессов уменьшится, и он будет работать медленнее, чем стационарные часы того же типа. Взаимосвязь точно определяется самым глубоким уравнением СТО, обычно называемым метрическим уравнением (или линейным метрическим уравнением).
(1)
Это относится к траектории любой физической системы. Вовлеченные количества:
Dt — количество собственно времени, прошедшее между двумя точками траектории.Dt — это количество реального времени, прошедшее между двумя точками траектории.
Dr — это количество движения в пространстве между двумя точками на траектории.
c — это скорость света, она зависит от выбранных нами единиц измерения пространства и времени.
Значение этого уравнения поясняется рассмотрением простых траекторий, изображенных на пространственно-временной диаграмме.
Рис. 1. Две простые пространственно-временные траектории.
Если мы начнем с начальной точки траектории физической системы и проследим ее до более поздней точки, мы обнаружим, что система покрыла определенный объем физического пространства Dr за определенное количество реального времени Dt, и претерпел определенное количество внутренних процессов или должного времени, Dt.Пока мы используем одни и те же единицы (секунды) для представления собственного времени и реального времени, эти величины связаны соотношением (1). Соответствующие временные интервалы показаны на рисунке 1 синими точками вдоль траекторий. Если бы это были траектории движения часов, например, то синие точки представляли бы секунды, отсчитываемые часовым механизмом.
На рисунке 1 мы выбрали скорость света равной 1. Это эквивалентно использованию наших обычных единиц времени, то есть секунд, но выбору единиц измерения пространства как c метров (вместо 1 метра), где c — это скорость света в метрах в секунду.Эта система единиц часто используется физиками для удобства, и, похоже, из-за нее величина c выпадает из уравнений, поскольку c = 1. Однако важно отметить, что c — размерная константа, и даже если ее числовое значение значение устанавливается равным 1 путем выбора соответствующих единиц, но в уравнении 1 по-прежнему логически необходимо, чтобы уравнение уравновешивалось размерно. Для умножения интервала времени Dt на величину c преобразует временную величину в пространственную величину. Уравнения физики, как и обычные предложения, могут отождествлять друг с другом только объекты или количества одного и того же физического вида, и роль c как размерной константы остается решающей в уравнении 1, чтобы тождество, которое оно заявляет, имело смысл.
Однако важно отметить, что c — размерная константа, и даже если ее числовое значение значение устанавливается равным 1 путем выбора соответствующих единиц, но в уравнении 1 по-прежнему логически необходимо, чтобы уравнение уравновешивалось размерно. Для умножения интервала времени Dt на величину c преобразует временную величину в пространственную величину. Уравнения физики, как и обычные предложения, могут отождествлять друг с другом только объекты или количества одного и того же физического вида, и роль c как размерной константы остается решающей в уравнении 1, чтобы тождество, которое оно заявляет, имело смысл.
Траектории на рисунке 1
- Траектория 1 (зеленая) предназначена для неподвижной частицы, следовательно, Dr = 0 (она не движется в пространстве), и, подставив это значение в уравнение 1, мы находим, что: Dt = Dt. Для неподвижной частицы количество собственного времени равно количеству координатного времени.
- Траектория 2 (красная) — для движущейся частицы, Dr> 0.
 В этом примере мы выбрали скорость: v = c / 2, половину скорости света. Но: v = Dr / Dt (пройденное расстояние за промежуток времени).Следовательно: Dr = ½cDt. Подставляя это значение в уравнение 1, получаем: c²Dt² = c²Dt²- (½cDt) ² или: Dt = Ö (¾) Dt »0.87Dt. Следовательно, количество собственного времени составляет только около 87% координатного времени. (Несмотря на то, что эта траектория очень быстрая, собственное время все же немного замедляется.)
В этом примере мы выбрали скорость: v = c / 2, половину скорости света. Но: v = Dr / Dt (пройденное расстояние за промежуток времени).Следовательно: Dr = ½cDt. Подставляя это значение в уравнение 1, получаем: c²Dt² = c²Dt²- (½cDt) ² или: Dt = Ö (¾) Dt »0.87Dt. Следовательно, количество собственного времени составляет только около 87% координатного времени. (Несмотря на то, что эта траектория очень быстрая, собственное время все же немного замедляется.) - Траектория 3 (черная) предназначена для частицы, движущейся со скоростью света, с v = c, что дает: Dr = cDt. Подставляя это в уравнение 1, мы получаем: c²Dt² = c²Dt²- (cDt) ² = 0. Следовательно, для светоподобной частицы количество собственного времени равно 0.
Итак, с классической точки зрения уравнение (1) является неожиданностью — действительно, оно кажется странным! Ибо как может простое движение в пространстве прямо и точно влиять на скорость физических процессов, происходящих в системе? Мы привыкли к противоположной идее, что движение в пространстве само по себе не оказывает внутреннего влияния на процессы. Это лежит в основе классической галилеевой инвариантности или симметрии. Но STR нарушает это правило.
Это лежит в основе классической галилеевой инвариантности или симметрии. Но STR нарушает это правило.
Мы можем сравнить эту ситуацию с классической физикой, где (для линейных траекторий) мы имеем два независимых уравнения:
(2.а) Dt = Dt
(2.b) Dr = vDt для некоторых (действительных чисел)
- Уравнение (2.a) просто означает, что скорость собственного времени в системе неизменна — и мы измеряем ее в тех же единицах, что и координатное время, t.
- Уравнение (2.b) просто означает, что каждая частица или система имеет некоторую конечную скорость или скорость v в пространстве, где v определяется как v = Dr / Dt.
Здесь нет связи между собственным временем и пространственным движением системы.
Тот факт, что (2) заменяется в STR на (1), действительно очень своеобразен.Это означает, что скорость внутреннего процесса в такой системе, как часы (будь то механические, химические или радиоактивные часы), автоматически связана с движением часов в пространстве. Если мы ускоряем часы, движущиеся в пространстве, скорость внутреннего процесса замедляется точным образом, чтобы компенсировать движение в пространстве.
Если мы ускоряем часы, движущиеся в пространстве, скорость внутреннего процесса замедляется точным образом, чтобы компенсировать движение в пространстве.
Великая загадка состоит в том, что не существует очевидного механизма этого эффекта, называемого замедлением времени. В классической физике, чтобы замедлить часы, мы должны приложить некоторую силу, такую как трение, к их внутреннему механизму: но в СТО физический процесс в системе замедляется, просто перемещая ее.Это в равной степени относится ко всем физическим процессам. Например, радиоактивный изотоп распадается медленнее с высокой скоростью. И даже животные, в том числе люди, должны стареть медленнее, если они передвигаются с большой скоростью, что приводит к «парадоксу близнецов».
Фактически, замедление времени было уже признано Лоренцем и Пуанкаре, которые разработали большинство основных математических соотношений СТО до Эйнштейна. Но Эйнштейн сформулировал более всеобъемлющую теорию и с важным вкладом Минковского дал объяснение эффектов. Объяснение Эйнштейна-Минковского обращается к новой концепции многообразия пространства-времени и интерпретирует уравнение 1 как своего рода «геометрическую» характеристику пространства-времени. Эта точка зрения получила широкое распространение в физике ХХ века. Напротив, Лоренц отказывался верить в «геометрическое» объяснение и считал, что движение в пространстве оказывает на частицы своего рода «механический» эффект, вызывающий замедление процессов. Хотя точка зрения Лоренца отвергается большинством физиков, некоторые авторы настаивают на схожих идеях, и вопросы, связанные с объяснением уравнения 1, продолжают вызывать глубокий интерес, по крайней мере, для философов.
Объяснение Эйнштейна-Минковского обращается к новой концепции многообразия пространства-времени и интерпретирует уравнение 1 как своего рода «геометрическую» характеристику пространства-времени. Эта точка зрения получила широкое распространение в физике ХХ века. Напротив, Лоренц отказывался верить в «геометрическое» объяснение и считал, что движение в пространстве оказывает на частицы своего рода «механический» эффект, вызывающий замедление процессов. Хотя точка зрения Лоренца отвергается большинством физиков, некоторые авторы настаивают на схожих идеях, и вопросы, связанные с объяснением уравнения 1, продолжают вызывать глубокий интерес, по крайней мере, для философов.
Но прежде чем перейти к объяснению, нам нужно обсудить концепции систем координат для пространства и времени, которые мы до сих пор предполагали без объяснения.
3. Системы координат
В физике мы обычно предполагаем, что пространство — это трехмерное многообразие, а время — одномерный континуум. Система координат — это способ представления пространства и времени с помощью чисел для обозначения точек. Мы присваиваем набор из трех чисел (x, y, z), чтобы характеризовать точки в пространстве, и одно число, t, чтобы характеризовать момент времени.Объединяя их, мы получаем общие координаты пространства-времени: (x, y, z, t). Идея состоит в том, что каждое физическое событие во Вселенной имеет «пространственно-временное положение», а система координат обеспечивает численное описание системы этих возможных «местоположений».
Система координат — это способ представления пространства и времени с помощью чисел для обозначения точек. Мы присваиваем набор из трех чисел (x, y, z), чтобы характеризовать точки в пространстве, и одно число, t, чтобы характеризовать момент времени.Объединяя их, мы получаем общие координаты пространства-времени: (x, y, z, t). Идея состоит в том, что каждое физическое событие во Вселенной имеет «пространственно-временное положение», а система координат обеспечивает численное описание системы этих возможных «местоположений».
Классические системы координат использовали Декарт, Галилей, Ньютон, Лейбниц и другие классические физики для описания пространства. Под классическим пространством подразумевается трехмерное евклидово многообразие. Классические физики добавили временные координаты t в качестве дополнительного параметра для характеристики событий.Принципы, лежащие в основе систем координат, казались интуитивно понятными и естественными до начала 20 века, но с появлением STR все кардинально изменилось. Одним из первых великих достижений Эйнштейна было пересмотр концепции системы координат и предложение новой системы, подходящей для СТО, которая отличается от системы классической физики. Поступая так, Эйнштейн признал, что понятие системы координат зависит от теории. Классическая система зависит от принятия определенных физических допущений классической физики — например, что часы не изменяют свой ход при движении в пространстве.В СТО меняются некоторые законы, лежащие в основе этих классических предположений, и это меняет сами наши предположения о том, как мы можем измерять пространство и время. Чтобы успешно сформулировать СТО, Эйнштейн не мог просто предложить новый набор физических законов в рамках существующих классических рамок представлений о пространстве и времени: ему пришлось одновременно переформулировать представление пространства и времени. Он сделал это в первую очередь, переформулировав правила назначения систем координат для пространства и времени. Он дал новую систему правил, соответствующую новым физическим принципам СТО, и пересмотрел применимость старых правил классической физики в рамках этой новой системы.
Одним из первых великих достижений Эйнштейна было пересмотр концепции системы координат и предложение новой системы, подходящей для СТО, которая отличается от системы классической физики. Поступая так, Эйнштейн признал, что понятие системы координат зависит от теории. Классическая система зависит от принятия определенных физических допущений классической физики — например, что часы не изменяют свой ход при движении в пространстве.В СТО меняются некоторые законы, лежащие в основе этих классических предположений, и это меняет сами наши предположения о том, как мы можем измерять пространство и время. Чтобы успешно сформулировать СТО, Эйнштейн не мог просто предложить новый набор физических законов в рамках существующих классических рамок представлений о пространстве и времени: ему пришлось одновременно переформулировать представление пространства и времени. Он сделал это в первую очередь, переформулировав правила назначения систем координат для пространства и времени. Он дал новую систему правил, соответствующую новым физическим принципам СТО, и пересмотрел применимость старых правил классической физики в рамках этой новой системы.
Ключевой особенностью, на которой сосредоточился Эйнштейн, является то, что система координат включает в себя систему рабочих принципов, которые связывают характеристики пространства и времени с физическими процессами или «операциями», которые мы можем использовать для измерения этих характеристик. Например, теория классического пространства предполагает, что между точками пространства существует внутреннее расстояние (или длина). Мы можем принять расстояние как основную черту «пустого пространства». Геометрические линии можно определить как совокупность точек в пространстве, а сегменты линий имеют внутреннюю длину до размещения любых физических объектов в пространстве.Но, конечно, мы измеряем (или воспринимаем) основную структуру пространства только с помощью физических объектов или физических процессов для проведения измерений. Обычно мы используем «прямые жесткие линейки» для измерения расстояний между точками пространства; или мы используем «единые стандартные часы» для измерения временных интервалов между моментами времени. Линейки и часы — это особые физические объекты или процессы, и для того, чтобы они адекватно выполняли свои измерительные функции, они должны иметь соответствующие физические свойства.
Линейки и часы — это особые физические объекты или процессы, и для того, чтобы они адекватно выполняли свои измерительные функции, они должны иметь соответствующие физические свойства.
Но эти физические свойства являются предметом самих теорий физики. Классическая физика, например, предполагает, что обычные жесткие линейки сохраняют одинаковую длину (или расстояние между конечными точками) при перемещении в пространстве. Также предполагается, что существуют определенные типы систем (обеспечивающих «идеализированные часы»), которые производят циклические физические процессы и поддерживают одинаковые временные интервалы между циклами во времени, даже если мы перемещаем эти системы в пространстве.
Эти предположения внутренне согласуются с принципами измерения в классической физике. Но им противоречит СТО, и Эйнштейну пришлось переформулировать операционные принципы измерения пространства и времени таким образом, чтобы они внутренне согласовывались с новыми физическими принципами СТО.
Мы кратко опишем эти новые принципы работы в ближайшее время, но есть некоторые особенности систем координат, которые важно оценить в первую очередь.
Координаты как математический язык для времени и пространства
Назначение числовой системы координат для времени или пространства рассматривается как обеспечение математического языка (с использованием чисел в качестве имен) для представления физических вещей (времени и пространства).В некотором смысле этот язык можно «выбрать произвольно»: нет никаких законов о том, какие имена могут использоваться для обозначения вещей. Но, естественно, есть особенности, которые мы хотим, чтобы система координат отражала. В частности, мы хотим, чтобы присвоение чисел напрямую отражало концепции расстояния между точками пространства и размер интервалов между моментами времени.
Мы выполняем математические операции с числами, и мы можем вычесть два числа, чтобы найти «числовое расстояние» между ними.Ибо числа действительно определяются как определенные структуры с такими характеристиками, как непрерывность, и мы хотим использовать структуры систем счисления для представления структурных характеристик пространства и времени.
Например, в нашей фундаментальной физической теории мы предполагаем, что любые два интервала времени имеют внутренние величины, которые можно сравнивать друг с другом. «Внутреннее временное расстояние» между двумя моментами, t 1 и t 2 , может быть таким же, как и между двумя совершенно разными моментами, t 3 и t 4 .Мы, естественно, хотим присвоить числа временам, чтобы обычное числовое вычитание соответствовало «внутреннему временному расстоянию» между событиями. Для этого мы выбираем «единую» систему координат для времени.
Рис. 2. Система координат для времени дает математический язык для физических вещей.
Числа используются как имен для моментов времени.
4. Декартовы координаты пространства
Время просто, потому что оно одномерно.Трехмерное пространство намного сложнее. Поскольку пространство трехмерно, нам нужны три отдельных действительных числа для представления одной точки. Физики обычно выбирают декартову систему координат для представления пространства. Мы представляем точки в этой системе как: r = (x, y, z), где x, y и z — отдельные числовые координаты, в трех ортогональных (перпендикулярных) направлениях.
Числовая структура с точками действительного числа: (x, y, z) обозначается в математике как:. Само трехмерное пространство (физическая вещь) обозначается как:.Декартова система координат — это особый вид отображения между точками этих двух структур. Это заставляет внутреннее пространственное расстояние между двумя точками в E 3 прямо отражаться «числовым расстоянием» между их числовыми координатами в.
Числовые расстояния в определяются числовой функцией длины. Линия от начала координат: (0,0,0) до точки r = (x, y, z), которая называется вектором r, имеет длину, определяемую формулой Пифагора:
| r | = √ (x² + y² + z²).
В более общем случае для любых двух точек r 1 = (x 1 , y 1 , z 1 ) и: r 2 = (x 2 , y 2 , z 2 ) функция расстояния:
| r 2 — r 1 | = √ ((x 2 — x 1 ) ² + (y 2 — y 1 ) ² + (z 2 — z 1 ) ²)
Особенностью этой системы является то, что длины линий только в направлениях x, y или z задаются непосредственно значениями координат.Например. если: r = (x, 0,0), то вектор к r представляет собой прямую в направлении x, а его длина просто: | r | = х. Если r 1 = (x 1 , 0,0) и: r 2 = (x 2 , 0,0), то расстояние между ними равно: | r 2 — r 1 | = (x 2 — x 1 ). (Кроме того, декартова система координат обрабатывает три направления, x, y и z, симметрично: углы между любой парой этих направлений одинаковы, 90 0 .По этой причине декартова система может быть повернута, и та же самая форма функции общего расстояния сохраняется в повернутой системе.)
На самом деле, существуют пространственные многообразия, не имеющие никакой возможной декартовой системы координат — например, поверхность сферы, рассматриваемой как двумерное многообразие, не может быть представлена с помощью декартовых координат. Такие пространства впервые были изучены как геометрические системы в 19 веке и называются неклассическими или неевклидовыми геометриями.Однако классическое пространство евклидово и по определению:
- Евклидово пространство может быть представлено декартовой системой координат.
Мы можем определить альтернативные, не декартовы, системы координат для евклидова пространства; например, цилиндрическая и сферическая системы координат очень полезны в физике, и они используют смесь линейных или радиальных расстояний и углов в качестве чисел для определения точек пространства. Числовые формулы для расстояния в этих системах координат сильно отличаются от декартовой формулы.Но они определены так, чтобы давать одинаковые результаты для расстояний между физическими точками. Это самая важная особенность концепции расстояния в классической физике:
- Расстояние между точками в классическом пространстве (или между двумя событиями, происходящими в один и тот же момент времени) является физическим инвариантом. Не меняется при выборе системы координат.
Форма численного уравнения для расстояния изменяется при выборе системы координат; но это сделано намеренно, чтобы сохранить физическую концепцию расстояния.
5. Выбор инерциальной системы отсчета
Вторая важная концепция — это идея системы отсчета. Система отсчета определяет все траектории, которые считаются стационарными или покоящимися в пространстве. Это определяет свойство оставаться в одном и том же месте во времени. Но ключевая особенность как классической механики, так и СТО заключается в том, что не определяется уникальная система отсчета. Любой объект, который не ускоряется, можно рассматривать как неподвижный «в своей собственной инерциальной системе отсчета». Он определяет действительную систему отсчета для всей вселенной.Это естественная система отсчета «с точки зрения» объекта или «относительно объекта». Но, конечно, есть много возможных вариантов: потому что для любой конкретной системы отсчета любая другая система координат, определенная для придания всему постоянной скорости относительно первого кадра, также является допустимым выбором.
Объективно определяется класс возможных (физически достоверных) систем отсчета, поскольку ускорение абсолютно отличается от постоянного движения. Любой объект, который не ускоряется, можно рассматривать как определяющий действительную систему отсчета.Но конкретный выбор системы отсчета из диапазона возможностей рассматривается как произвольный или условный. Этот выбор необходимо сделать до того, как можно будет определить систему координат для представления расстояний в пространстве и времени. (Даже после того, как мы выбрали систему отсчета, остается бесчисленное множество вариантов систем координат. Но система отсчета устанавливает определение расстояний между событиями, которые должны быть определены одинаковыми в любой системе координат относительно данной системы отсчета.)
Идея условности системы отсчета отчасти очевидна уже при выборе декартовой системы координат: это произвольный вопрос, где мы выбираем начало координат или точку: 0 = (0,0,0) для таких система. Также произвольно, какие направления мы выбираем для осей x, y и z, если мы делаем их взаимно перпендикулярными. Мы можем свободно вращать данный набор осей x, y, z, чтобы создать новый набор x ’, y’ и z ’, и это дает другую декартову систему координат.Таким образом, переводы и повороты декартовых систем координат для пространства по-прежнему оставляют нам декартовы системы.
Но есть еще одна трансформация, которая является абсолютно центральной для классической физики и затрагивает как время, так и пространство. Это преобразование скорости Галилея или увеличение скорости. Существенным моментом является то, что нам нужно применить пространственную систему координат во времени. В чистой классической геометрии нам не нужно принимать во внимание время: мы просто назначаем единую систему координат в один момент времени.Но в физике нам нужно применять систему координат для пространства в разные моменты времени. Как мы узнаем, представляет ли система координат, которую мы применяем в один момент времени, ту же систему координат, которую мы используем в более поздний момент времени?
Принципы классической физики означают, что мы не можем измерить «абсолютное положение в пространстве» во времени. Причина в фундаментальном классическом принципе, согласно которому законы природы не различают две инерциальные системы отсчета, движущиеся относительно друг друга с постоянной скоростью.Это классический галилеевский принцип «относительности движения». Грубо говоря, это означает, что равномерное движение в пространстве не влияет на физические процессы. И если движение само по себе не влияет на процессы, мы не можем использовать процессы для обнаружения движения.
Ньютон считал, что классическая концепция пространства требует, тем не менее, абсолютных пространственных положений во времени, и что некоторые специальные системы координат или физические объекты действительно будут находиться в «абсолютном покое» в пространстве.Но в контексте классической физики невозможно измерить, находится ли какой-либо объект в абсолютном покое или находится в равномерном движении в пространстве. Из-за этого Лейбниц отрицал, что классическая физика требует какого-либо понятия абсолютного положения в пространстве, и утверждал, что требуется только понятие «относительного» или «относительного» пространства. С этой точки зрения реальными считаются только относительные положения объектов относительно друг друга. Для Ньютона невозможность измерения абсолютного пространства не мешает ему быть жизнеспособной концепцией и даже логически необходимой концепцией.До сих пор нет общего согласия в этом споре между «абсолютным» и «относительным» или «реляционным» концепциями пространства. Это одна из величайших исторических дискуссий в философии как классической, так и релятивистской физики. Однако общепринято считать, что классическая физика делает абсолютное пространство необнаружимым. Это означает, по крайней мере, что в контексте классической физики нет способа дать операционную процедуру для определения абсолютного положения (или абсолютного покоя) во времени.
Однако обнаруживается абсолютное ускорение. Ускорения всегда сопровождаются силами. Это означает, что мы определенно можем указать класс систем координат, которые находятся в равномерном движении или не ускоряются. Эти специальные системы называются инерциальными системами, или инерциальными системами отсчета, или системой отсчета Галилея. Существование инерциальных систем отсчета — фундаментальное предположение классической физики. Это также фундаментально в СТО, и понятие инерциальной системы отсчета очень похоже в обеих теориях.
Поэтому законы классической физики указаны для инерциальных систем координат. Они одинаково справедливы в любой инерциальной системе отсчета. То же самое и с законами СТО. Однако законы перехода от одной инерциальной системы отсчета к другой различны для этих двух теорий. Чтобы увидеть, как это работает, мы теперь рассмотрим операционную спецификацию систем координат.
6. Оперативная спецификация систем координат для классического пространства и времени
В классической физике мы можем определить «рабочую» систему измерения, которая позволяет нам присваивать координаты событиям в пространстве и времени.
Классическое время . Мы представляем себе измерение времени, создавая несколько одинаковых часов, синхронизируя их в какой-то начальный момент, проверяя, что все они работают с одинаковой скоростью (правильные скорости времени), а затем перемещая часы в разные точки пространства, где мы их держим » стационарный »в выбранной инерциальной системе отсчета. Затем мы измеряем время событий, которые происходят в разных местах, как записано разными часами в этих местах.
Конечно, мы не можем предполагать, что наша система часов действительно стационарна.Вся система часов, находящихся в равномерном движении, также будет определять действительную инерциальную систему отсчета. Но законы классической физики означают, что часы в равномерном инерционном движении идут с точно такой же скоростью, и поэтому время, записанное для конкретных событий, оказывается точно таким же, исходя из предположений классической теории, для любой такой системы часов. .
Классический космос . Мы представляем себе измерение пространства путем создания набора жестких измерительных стержней или линейок одинаковой длины, которые мы можем (по крайней мере, в воображении) создать в виде сетки в пространстве в инерциальной системе отсчета.Мы держим все линейки неподвижными относительно друг друга и используем их для измерения расстояний между различными событиями. Опять же, основная сложность состоит в том, что мы не можем определить абсолютно неподвижную систему координат для сетки линеек, и мы можем создать альтернативную систему линейок, которая находится в относительном движении. Это приводит к присвоению объектам различных «абсолютных скоростей», измеренных в двух разных кадрах. Однако, исходя из предположений классической теории, относительные расстояния между любыми двумя объектами или событиями, взятые в любой данный момент времени, измеряются одинаковыми в любой инерциальной системе отсчета.Это связано с тем, что в классической физике равномерное движение само по себе не меняет длины материальных объектов или сил между системами объектов. (Ускорения меняют длину).
7. Операционная спецификация систем координат для пространства и времени СТО
В СТО ситуация во многом очень похожа на классическую физику: все еще существует особая концепция инерциальных систем отсчета, ускорение абсолютно обнаружимо, а равномерная скорость не обнаруживается. Согласно СТО, законы физики по-прежнему инвариантны w.r.t. равномерное движение в пространстве, очень похожее на классические законы.
Мы также уточняем операционные определения инерциальных систем координат в СТО аналогично классической физике. Однако описанная выше система задания классических координат не работает, поскольку она несовместима с физическими принципами СТО. Эйнштейн был вынужден реконструировать классическую систему измерения, чтобы получить систему, внутренне совместимую с СТО.
STR Время .В STR мы по-прежнему можем создавать одинаковые часы, которые работают с одинаковой скоростью, когда они остаются неподвижными относительно друг друга. Но теперь возникла проблема с их синхронизацией в разных точках пространства. Мы можем запустить их синхронно в определенной общей точке; но перемещение их в разные точки пространства уже нарушает их синхронизацию согласно уравнению 1.
Однако, хотя синхронизация дальних часов является проблемой, они, тем не менее, работают с теми же внутренними частотами, что и друг друга, когда удерживаются в одном инерциальном кадре.И мы можем гарантировать, что два часа находятся в общей инерциальной системе отсчета, если мы можем гарантировать, что они сохраняют одинаковое расстояние друг от друга. Мы увидим, как это сделать дальше.
Учитывая, что у нас есть два часов, поддерживаемых на одинаковом расстоянии друг от друга, Эйнштейн показал, что действительно существует простая операционная процедура для установления синхронизации. Мы отправляем световой сигнал от Clock 1 к Clock 2 и отражаем его обратно к Clock 1. Мы записываем время, когда он был отправлен на Clock 1 как t 0 , а время его получения снова как более позднее время t 2 .Мы также записываем время, когда он был получен в Clock 2, как t 1 ‘на Clock 2. Теперь симметрия ситуации требует, чтобы в инерциальной системе отсчета Clock 1 мы должны предположить, что световой сигнал достиг часов 2 в момент. на полпути между t 0 и t 1 , то есть в момент времени: t 1 = ½ (t 2 — t 0 ). Это связано с тем, что из-за симметрии световой сигнал должен проходить одинаковое время в любом направлении между часами, учитывая, что они находятся на постоянном расстоянии в течение всего процесса и не ускоряются.(Если световой сигнал шел в одну сторону дольше, чем в другую, тогда свет должен был бы двигаться с разной скоростью в разных направлениях, что противоречит СТО).
Следовательно, мы должны повторно синхронизировать Clock 2, чтобы получить: t 1 ’= t 1 . Мы просто переводим стрелки часов 2 вперед на: (t 1 — t 1 ’), то есть на: ½ (t 2 — t 0 ) — t 1 ’. (Следовательно, время координат на часах 2 в t 1 ‘изменяется на: t 1 ‘ + (½ (t 2 — t 0 ) — t 1 ‘) = ½ (t 2 — t 0 ) = t 1 .)
Это иногда называют «соглашением о синхронизации часов», и некоторые философы спорят о том, оправдано ли это. Но нет никаких сомнений в том, что это успешно определяет единственную систему для назначения одновременности во времени в выбранной системе отсчета, которая согласуется с СТО.
Некоторые более глубокие вопросы возникают в связи с понятием одновременности, которое она, похоже, включает. С точки зрения часов 1 момент, записанный в: t 1 = ½ (t 2 — t 0 ), должен рассматриваться как «одновременный» с моментом, записанным в t 1 ‘на часах 2.Но в другой инерциальной системе координат естественная система координат изменит кажущуюся одновременность этих двух событий, так что одновременность сама по себе не является «объективной» в СТО, за исключением выбора инерциальной системы координат. Мы рассмотрим это позже.
STR Пространство . В СТО мы можем измерять пространство так же, как в классической физике. Мы представляем себе создание набора жестких измерительных стержней или линейок, длина которых проверяется на одинаковую длину в инерциальной системе отсчета Clock 1, и мы расширяем их в сетку в пространстве.Для начала нам нужно переместить линейки, но когда мы настроили сетку, мы сохраняем их все неподвижными в выбранной инерциальной системе координат Clock 1.
Затем мы используем эту сетку неподвижных измерительных стержней для измерения расстояний между различными событиями. Основное предположение состоит в том, что одинаковые типы измерительных стержней (которые имеют одинаковую длину, когда мы первоначально сравниваем их в состоянии покоя с часами 1) сохраняют одинаковую длину после перемещения в разные места (и снова становятся неподвижными w.r.t. Часы 1). Эта функция требуется STR.
Основная сложность, опять же, заключается в том, что мы не можем определить абсолютно стационарный каркас для сетки линеек. Мы можем создать альтернативную систему линейок, которые все находятся в относительном движении в другой инерциальной системе отсчета. Как и в классической физике, это приводит к присвоению разных «абсолютных скоростей» большинству траекторий в двух разных системах отсчета. Но в этом случае есть более глубокая разница: согласно предположениям STR, длина измерительных стержней изменяется в зависимости от их скорости.Это называется расширением пространства, и это аналог замедления времени.
Тем не менее, Эйнштейн показал, что в STR доступны вполне разумные операционные определения координатных измерений длины, а также времени. Но и одновременность, и длина становятся относительными к указанным инерциальным системам.
Именно эту запутанную концептуальную проблему, которая включает в себя теоретическую зависимость измерения, Эйнштейну впервые удалось разгадать, как прелюдию к показу, как радикально реконструировать классическую физику.
8. Операционализм
Решение этой проблемы требует от нас определения «операционных принципов» измерения, но это не требует от нас принятия операционной теории значения. Последнее является формой позитивизма, и он считает, что значение «времени» или «пространства» в физике полностью определяется путем определения процедур измерения времени или пространства. Эта теория обычно отвергается философами и логиками, и она была отвергнута самим Эйнштейном в его зрелых работах.Согласно операционализму, СТО изменяет значения концепций пространства и времени по сравнению с классической концепцией. Однако многие философы утверждали бы, что «время» и «пространство» имеют для нас значение, по сути такое же, как у Галилея и Ньютона, потому что мы отождествляем те же типы вещей, что и время и пространство; но теория относительности изменила наши научные представления об этих вещах — так же, как открытие того, что вода представляет собой h3O, изменило наше понимание природы воды, не обязательно изменив значение термина «вода».Этот семантический спор продолжается в философии науки. Прояснив эти основные идеи систем координат и инерциальных систем отсчета, мы теперь вернемся к понятию преобразований между системами координат для различных инерциальных систем отсчета.
9. Преобразования координат и преобразования объектов
Physics использует две разные концепции преобразований. Важно их тщательно различать.
- Преобразования координат: во-первых, это понятие взятия описания данного процесса (например, траектории), описанного в одной системе координат, и преобразования его описания в альтернативной системе координат.
- Преобразования объектов: Во-вторых, это понятие взятия данного процесса, описанного в данной системе координат, и преобразования его в другой процесс, описанный в той же системе координат, что и исходный процесс.
Разница проиллюстрирована на следующей диаграмме для простейшего вида преобразования, трансформации пространства.
Рис. 3. Преобразования объекта, координат и комбинированные преобразования.
- Преобразования на рисунке 3 являются простыми переводами пробелов.
- На рисунке 3 (B) показано преобразование объекта. Исходная траектория (A) перемещается в пространстве вправо на 4 единицы. Новые координаты связаны с исходными координатами следующим образом: x новая частица ® x исходная частица + 4.
- На рисунке 3 (C) показано преобразование координат: система координат сдвинута вправо на 4 единицы. Новая система координат x ’связана с исходной системой x следующим образом: x’ исходная частица = x исходная частица + 4.Результат «выглядит» так же, как (B).
- Рисунок 3 (D) показывает комбинацию преобразования объекта (B) и преобразования координат, которое является обратным преобразованию в (C) и определяется следующим образом: x » исходная частица = x исходная частица — 4 Результат этого выглядит так же, как и исходная траектория в (A), потому что преобразование координат, похоже, «отменяет» эффект преобразования объекта.
10. Допустимые преобразования
Между этими двумя видами преобразований существует тесная связь.Эта связь обеспечивает основной концептуальный аппарат современной физики через концепцию физических симметрий или принципов инвариантности и допустимых преобразований.
Самые глубокие черты законов или теорий физики отражаются в их свойствах симметрии, которые также называют инвариантами относительно преобразований симметрии. Законы или теории можно понимать как описание классов физических процессов. Физические процессы, которые соответствуют теории, являются действительными физическими процессами этой теории.Конечно, не все (логически) возможные процессы, которые мы можем себе представить, являются действительными физическими процессами данной теории. В противном случае теория охватывала бы все возможные процессы и ничего не говорила нам о том, что возможно физически, в отличие от того, что можно представить себе логически.
Симметрии теории описываются преобразованиями, которые сохраняют действительные процессы теории. Например, перевод времени — это симметрия почти всех теорий. Это означает, что если мы возьмем действительный процесс и преобразуем его без изменений в более раннее или позднее время, у нас все равно будет действующий процесс.Это эквивалентно простой установке «временного источника» процесса на более позднее или более раннее время.
Другие общие симметрии:
- Вращения в пространстве (если мы возьмем действительный процесс и повернем его в другом направлении в пространстве, мы получим другой действительный процесс).
- Переводы в пространстве (если мы возьмем действительный процесс и переместим его в другое место в пространстве, мы получим другой действительный процесс).
- Преобразования скорости (если мы возьмем действительный процесс и дадим ему равномерный прирост скорости в каком-то направлении в пространстве, мы получим другой допустимый процесс).
Эти симметрии справедливы как в классической физике, так и в СТО. В классической физике они называются галилеевыми симметриями или преобразованиями. В СТО они называются преобразованиями Лоренца. Однако, хотя симметрии в обеих теориях очень похожи, преобразования Лоренца в СТО имеют особенности, не очевидные в классической теории. Фактически, эта разница возникает только при увеличении скорости. Переводы и вращения идентичны в обеих теориях. По сути, это связано с тем, что увеличение скорости в СТО связано с преобразованием связи между собственным временем и обычным пространством и временем, чего нет в классической теории.
Концепция допустимых преобразований координат непосредственно вытекает из концепции допустимых преобразований объектов. Дело в том, что когда мы производим преобразование объекта, мы начинаем с описания процесса в системе координат и заканчиваем другим описанием другого процесса, заданного в той же системе координат. Теперь вместо преобразования задействованных процессов мы можем сделать обратное и преобразовать систему координат, так что мы получим новое описание координат исходного процесса, которое выглядит точно так же, как описание преобразованного процесса. в исходной системе координат.
Это дает альтернативный способ рассмотрения процесса и его преобразованного образа: вместо того, чтобы рассматривать их как два разных процесса, мы можем принять их как два разных координатных описания одного и того же процесса.
Это связано с идеей, что определенные аспекты системы координат произвольны или условны. Например, выбор конкретного источника для времени или пространства считается условным: мы можем перемещать исходные точки в нашем описании координат, и у нас все еще есть действующая система.Это возможно только потому, что соответствующие преобразования объекта (трансляции во времени и пространстве) являются действительными физическими преобразованиями.
Физики склонны рассматривать преобразования координат и преобразования действительных объектов как взаимозаменяемые и несколько неоднозначно, и различие между ними часто стирается в прикладной физике. Хотя это не вызывает практических проблем, при изучении концепций теории важно четко различать два вида преобразований.
11. Повышение скорости в STR и классической механике
STR и классическая механика обладают точно такой же симметрией относительно перемещений времени и пространства и вращений пространства. Они также обладают симметрией относительно увеличения скорости: обе теории утверждают, что если мы возьмем действительный физический процесс и придадим ему равномерную дополнительную скорость в каком-то направлении, мы закончим с другим действительным физическим процессом. Но преобразование координат пространства и времени, а также собственное время различны для двух теорий при повышении скорости.В классической физике это называется преобразованием Галилея, а в СТО — преобразованием Лоренца.
Чтобы увидеть, как проявляется разница, мы можем взять стационарную траекторию и рассмотреть, что происходит, когда мы применяем увеличение скорости в любой из теорий.
Рис. 4. Классическое увеличение скорости и увеличение скорости STR дают разные результаты.
На обеих диаграммах зеленая линия представляет собой исходную траекторию неподвижной частицы, и она выглядит точно так же в СТО и классической механике.Собственные временные события (отмечены синим) в обоих случаях одинаково разнесены с координатными временными интервалами.
Если мы трансформируем классическую траекторию, задав частице скорость (в этом примере v = c / 2) вправо, результат (красная линия) очень прост: события собственного времени остаются равномерно распределенными с координатными временными интервалами. Для выполнения одной и той же последовательности событий собственного времени требуется такое же количество координатного времени. Классическая частица перемещается вправо на расстояние: Dx = v.Dt, где Dt — координатная длительность исходного процесса.
Но когда мы трансформируем STR-частицу, происходит странная вещь: события собственного времени становятся более разнесенными, чем интервалы координатного времени, и для выполнения той же последовательности событий собственного времени требуется больше координатного времени. STR-частица перемещается вправо на расстояние: Dx ’= v.Dt’, где: Dt ’> Dt, и, следовательно,: Dx’> Dx.
Преобразования координат точек (собственного времени) исходных процессов показаны в следующей таблице.
Таблица 1.Пример преобразования скорости.
Мы можем разработать общую формулу для преобразования STR для t ’и x’ в этом примере, используя уравнение 1. Это требует нахождения формулы для преобразования пространственно-временных координат:
(t, 0) ® (t ’, x’)
Мы получаем это, применяя Уравнение 1 в системе координат (t ’, x’), что дает:
(1 ’)
Очень важно, чтобы это уравнение сохраняло ту же форму при уравнении Лоренца. В этом частном случае у нас есть дополнительные факты:
(i) Dt = Dt и: (ii) Dx ’= vDt’
Подставляем (i) и (ii) в (1 ’), чтобы получить:
Это переставляет, чтобы дать:
и:
Мы видим, что: Dx ’/ Dt’ = v.Это частный случай преобразования Лоренца для такого простейшего вида траектории. Обратите внимание: если мы думаем об этом как о преобразовании координат, которое создает видимость этого преобразования объекта, нам нужно переместить новую систему координат в направлении, противоположном движению объекта. Т.е. если мы определим новую систему координат (x ’, t’), перемещающуюся на –v (то есть влево) относительно. исходной системы (x, t), то исходная траектория (которая казалась неподвижной в (x, t)) будет казаться движущейся со скоростью + v (влево) в (x ’, t’).В общем, преобразования объекта соответствуют обратным преобразованиям координат.
12. Преобразования Лоренца для увеличения скорости V в направлении x
Предыдущие преобразования предназначены только для точек на специальной линии, где: x = 0. В более общем плане мы хотим разработать формулы для преобразования точек в любом месте системы координат:
(t, x) ® (t ’, x’)
Классические формулы — это преобразования Галилея, и они очень просты.
Галилеевский прирост скорости:
(t, x) ® (t, x + vt) t ’= t
x ’= x + vt
Формулы СТО являются более общими преобразованиями Лоренца.Преобразование Галилея простое, поскольку временные координаты неизменны, так что: t = t ’. Это означает, что одновременность во времени в классической физике абсолютна: она не зависит от выбора системы координат. У нас также есть это расстояние между двумя точками в данный момент времени, потому что если: x 2 -x 1 = Dx, то: x ‘ 2 -x’ 1 = (x 2 + vt) — (x 1 -vt) = Dx. Обычное расстояние в пространстве — решающая инвариантная величина в классической физике.
Но в СТО у нас сложная взаимозависимость временных и пространственных координат. Это видно, потому что формулы преобразования для t ’и x’ являются функциями как x, так и t. Т.е. есть функции f и g такие, что:
t ’= f (x, t) и: x’ = g (x, t)
Эти функции представляют преобразования Лоренца. Чтобы придать стационарным объектам скорость V в направлении x, эти общие функции оказываются равными:
Преобразования Лоренца: и:
Коэффициент: называется γ, что позволяет нам записать эти уравнения более просто как:
Преобразования Лоренца: t ’= γ (t + Vx / c 2 ) и: x’ = γ (x + Vt)
Мы также можем рассмотреть соответствующее преобразование координат, которое приведет к появлению этого преобразования объекта в новой системе координат.По сути, это то же самое, что и преобразование объекта, за исключением того, что оно должно идти в противоположном направлении. Преобразование объекта, увеличивающее скорость неподвижных частиц на скорость V в направлении x, соответствует перемещению системы координат в противоположном направлении. Т.е. если мы определим новую систему координат, назовем ее (x ‘, t’) и приведем ее в движение со скоростью –V (т.е. V в отрицательном направлении x) относительно координаты (x, t) системы, то исходные стационарные траектории в координатах (x, t) будут иметь скорость V в новых координатах (x ‘, t’).
Поскольку преобразование процессов Лоренца оставляет нам действительные процессы СТО, преобразование Лоренца в системе координат СТО оставляет нам действительную систему координат. В частности, форма уравнения 1 сохраняется преобразованием Лоренца, так что мы получаем:. Это можно проверить, подставив формулы для t ’и x’ обратно в это уравнение и упростив; полученное уравнение оказывается идентичным уравнению 1.
13. Преобразование системы координат Галилея
Один из полезных способов визуализировать эффект преобразования — создать обычную пространственно-временную диаграмму с осями пространства и времени, перпендикулярными друг другу, как обычно, а затем нарисовать новый набор координат на этой диаграмме.На этих диаграммах пространственные оси представляют точки, которые измеряются как имеющие одинаковые временные координаты, и аналогично, временные оси представляют точки, которые измеряются как имеющие одинаковые пространственные координаты. Когда мы увеличиваем скорость, эти линии одновременности и одинакового положения изменяются.
Сначала это показано для увеличения скорости Галилея, где фактически линии одновременности остаются такими же, но линии, представляющие положение, повернуты:
Рисунок 5.Повышение скорости по Галилею.
- На рисунке 5 (зеленые) горизонтальные линии — это линии абсолютной одновременности. У них одинаковые координаты в t и t ’.
- (синие) вертикальные линии — это линии с одинаковыми координатами x.
- (серые) наклонные линии — это линии с одинаковыми координатами x’.
- Расстояние между координатами x ’такое же, как и между координатами x, что означает, что относительные расстояния между точками не меняются.
- Сплошная черная стрелка представляет стационарную траекторию в (x, t).
- Преобразование объекта + V перемещает его на зеленую стрелку со скоростью: v = c / 2 в (x, t) -системе.
- Преобразование координат + V в систему (x ’, t’), движущуюся в + V относительно. (x, t), заставляет эту зеленую стрелку казаться неподвижной в системе (x ’, t’).
- Это преобразование координат создает впечатление, что черная стрелка движется в точке –V в координатах (x ’, t’).
14. Преобразование Лоренца системы координат
При повышении скорости Лоренца обе оси времени и пространства вращаются, а также изменяется интервал.
Рисунок 6 . Вращение осей пространственных и временных координат за счет повышения скорости Лоренца. Некоторые собственные временные события отмечены синим цветом.
Чтобы получить (x ‘, t’) — координаты точки, определенной в (x, t) -координатах, мы начинаем с точки и: (i) перемещаемся параллельно зеленым линиям, чтобы найти пересечение с (красный) ось t ‘, отмеченная координатами x’; и: (ii) двигайтесь параллельно красным линиям, чтобы найти пересечение с (зеленой) осью x’, которая отмечена t’-координатами.Влияние этого преобразования на твердый стержень или линейку, простирающуюся от x = 0 до x = 1 и неподвижную в (x, t), более подробно показано ниже.
Рис. 7. Повышение скорости Лоренца. Увеличенное изображение на Рисунке 6 показывает расширение времени и пространства. Серый прямоугольник представляет собой единицу пространственно-временного пути стержня (Стержень 1), неподвижного в (x, t). Темно-зеленые линии представляют преобразование Лоренца (объект) этой траектории, которое представляет собой второй стержень (стержень 2), движущийся в точке V в координатах (x, t).Это единица пространственно-временного пути неподвижного стержня в (x ’, t’).
15. Расширение времени и пространства
На рис. 7 показано, как работают эффекты расширения времени и пространства. Чтобы ясно это увидеть, нам нужно рассмотреть объемы пространства-времени, которые очерчивает объект, подобный стержню.
- (серый) прямоугольник PQRS представляет объем пространства-времени для неподвижного стержня или линейки в исходной рамке. Его длина в исходных координатах (Dx = 1) составляет 1 метр, и он отображается в течение 1 единицы собственного времени, что соответствует одной единице координатного времени (Dt = 1).
- Прямоугольник PQ’R’S ’(зеленые края) представляет второй объем пространства-времени для стержня, который кажется движущимся в исходном кадре. Так преобразуется пространственно-временной объем первого стержня при преобразовании Лоренца.
- Мы можем интерпретировать преобразование либо как: (i) увеличение лоренцевой скорости стержня на скорость + V (преобразование объекта), либо как равное: (ii) преобразование Лоренца в новую систему координат, (x ‘, t’) , двигаясь на –V относительно (х, т). Обратите внимание:
- Длина подвижного стержня, измеренная в x, теперь короче, чем у неподвижного стержня: Dx = 1 / γ.Это расширение пространства.
- Координатное время между событиями собственного времени на движущемся стержне, измеренное в t, теперь больше, чем для неподвижного стержня (Dt = γ). Это замедление времени.
Необходимость такой фиксации новой системы координат может быть решена путем рассмотрения движущегося стержня с точки зрения его собственной инерциальной системы.
- Если смотреть в его собственной инерциальной системе координат, зеленый прямоугольник PQ’R’S ’выглядит как граница пространства-времени для неподвижного стержня.В этом кадре:
- PS ’выглядит неподвижным: это линия, где: x’ = 0.
- PQ ’отображается как линия одновременности, т.е. это линия, где: t’ = 0.
- R’S ’- это также линия одновременности в t’. Точки
- на R’S ’должны иметь временную координату: t’ = 1, поскольку это время t ’, когда истекла одна единица собственного времени, а для неподвижного объекта Dt’ = Dt.
- Длина PQ ’должна составлять одну единицу в x’, поскольку движущийся стержень имеет ту же длину в своей собственной инерциальной системе отсчета, что и исходный неподвижный стержень.
Расширение времени и пространства часто называют «эффектами перспективы» при обсуждении СТО. Говорят, что объекты и процессы «выглядят» короче или длиннее, если смотреть в одной инерциальной системе отсчета, а не в другой. Обычно этот эффект рассматривается как чисто «традиционный» признак, который просто отражает традиционный выбор системы отсчета. Но это скорее вводит в заблуждение, потому что расширение времени и пространства — очень реальные физические эффекты, и они приводят к совершенно иным типам физических предсказаний, чем классическая физика.
Однако симметричные свойства преобразования Лоренца не позволяют использовать эти особенности, чтобы определить, действительно ли один кадр «движется», а другой «действительно неподвижен». Например, если объекты становятся короче, когда их приводят в движение, то почему бы нам просто не измерить длину объектов и не использовать это, чтобы определить, действительно ли они «неподвижны»? Детали на рисунке 7 показывают, почему это не работает: эффект расширения пространства меняется на противоположный, когда мы меняем системы отсчета.То есть:
- При измерении в кадре 1, т.е. в координатах (x, t), неподвижный объект (стержень 1) кажется длиннее движущегося объекта (стержень 2). Но:
- При измерении в кадре 2 с использованием координат (x ’, t’) движущийся объект (стержень 2) кажется неподвижным, в то время как первоначально неподвижный объект (стержень 1) перемещается. Но теперь эффект расширения пространства кажется обратным, и Жезл 2 кажется длиннее Жезла 1!
Причину, по которой это не настоящий парадокс или несоответствие, можно увидеть с точки зрения кадра 2, потому что теперь стержень 1 в момент времени t ‘= 0 протягивается из точки P в Q’ ‘, а не из От P до Q, как в кадре 1.Линия одновременности изменяется в новом кадре, так что мы измеряем расстояние между другой парой пространственно-временных событий. И теперь выяснилось, что PQ ’’ короче, чем PQ ’, который представляет собой длину стержня 2 в кадре 2.
В STR нет ответа на вопрос, какой стержень «действительно становится короче». Точно так же нет ответа на вопрос, какой стержень «действительно имеет более быстрое собственное время» — когда мы переключаемся на кадр 2, мы обнаруживаем, что стержень 2 имеет более высокую скорость собственного времени относительно. координировать время, обращая вспять эффект замедления времени, видимый в кадре 1.В этом смысле мы могли бы рассматривать эти эффекты как вопрос « перспективы » — хотя точнее было бы сказать, что в СТО в его обычной интерпретации просто нет фактов об абсолютной длине, абсолютном времени или абсолютной одновременности при все.
Однако это не означает, что расширение времени и пространства не являются реальными эффектами. Они отображаются в других ситуациях, где нет двусмысленности. Одним из примеров является парадокс близнецов, когда собственное время для движущихся близнецов абсолютно замедляется.И не менее реальные физические эффекты возникают в результате расширения пространства. Просто эти эффекты нельзя использовать для определения абсолютной системы покоя.

 Простота системы позволяет легко разместить такие диваны. Выкатные механизмы очень прочные и долговечные. Они идеально подходят для обеспечения комфортных спальных мест.К ним относятся следующие механизмы: еврокнижка, «Дельфин», «Флэш», «Пума» и другие.
Простота системы позволяет легко разместить такие диваны. Выкатные механизмы очень прочные и долговечные. Они идеально подходят для обеспечения комфортных спальных мест.К ним относятся следующие механизмы: еврокнижка, «Дельфин», «Флэш», «Пума» и другие. Надлежащее время
Надлежащее время 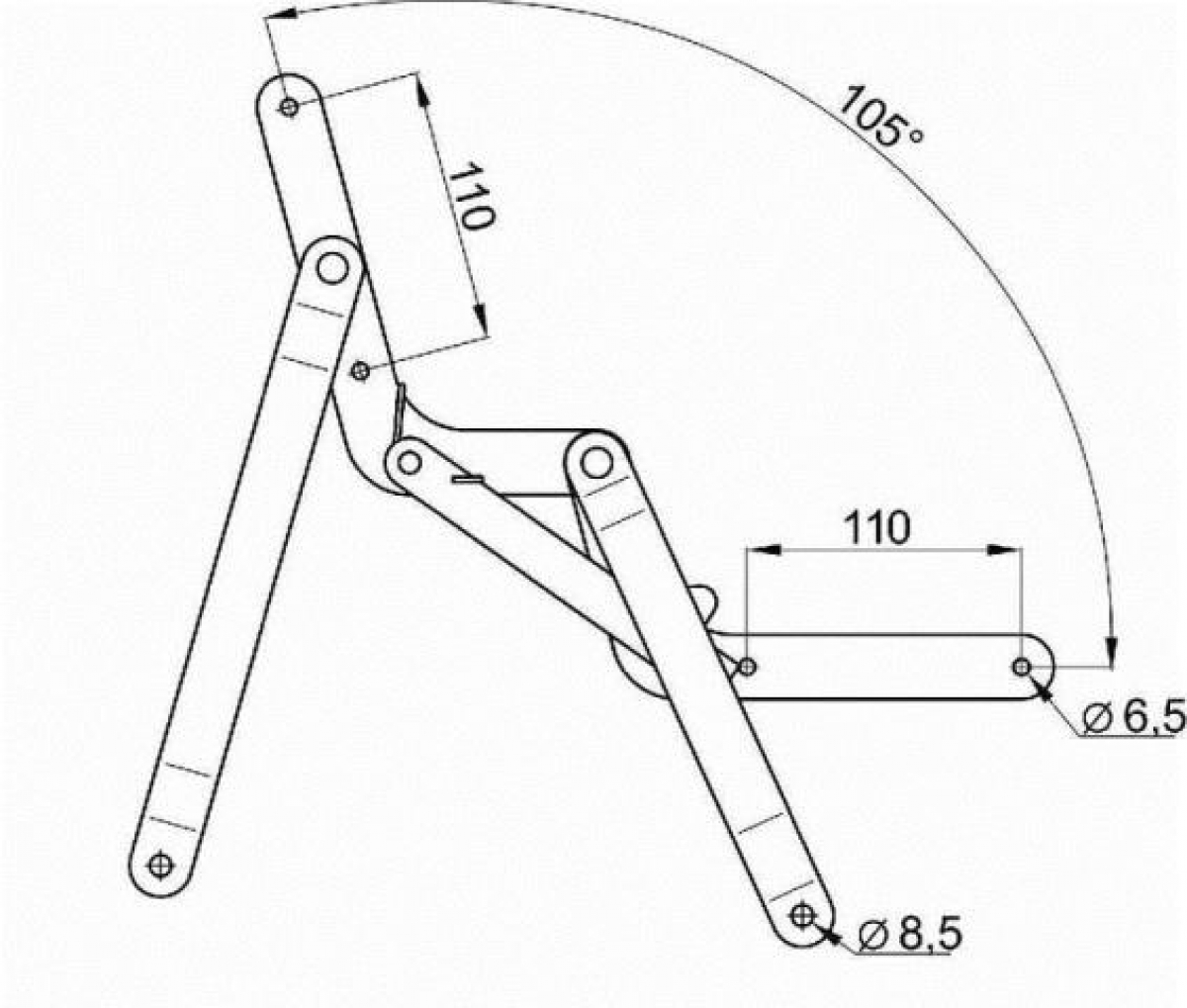 В этом примере мы выбрали скорость: v = c / 2, половину скорости света. Но: v = Dr / Dt (пройденное расстояние за промежуток времени).Следовательно: Dr = ½cDt. Подставляя это значение в уравнение 1, получаем: c²Dt² = c²Dt²- (½cDt) ² или: Dt = Ö (¾) Dt »0.87Dt. Следовательно, количество собственного времени составляет только около 87% координатного времени. (Несмотря на то, что эта траектория очень быстрая, собственное время все же немного замедляется.)
В этом примере мы выбрали скорость: v = c / 2, половину скорости света. Но: v = Dr / Dt (пройденное расстояние за промежуток времени).Следовательно: Dr = ½cDt. Подставляя это значение в уравнение 1, получаем: c²Dt² = c²Dt²- (½cDt) ² или: Dt = Ö (¾) Dt »0.87Dt. Следовательно, количество собственного времени составляет только около 87% координатного времени. (Несмотря на то, что эта траектория очень быстрая, собственное время все же немного замедляется.)