Деление окружности на равные части и построение правильных многоугольников: 3. ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ И ПОСТРОЕНИЕ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ

Деление окружности на равные части

План-конспект

Тема: Вычерчивание  в ручной  графике чертежа плоского контура  в заданном масштабе  и нанесение его размеров

Цель урока:

Ознакомление с правилами деления окружности на равное количество частей, а также приобретение ими навыков вычерчивания детали с применением деления окружности.

Ход занятия

I. Этап организационный 

Приветствие. Проверка готовности учащихся к уроку. Организация внимания учащихся.

 

II. Этап актуализации знаний

 

Проверка проведем опрос

 

В каких единицах выражают линейные размеры на машиностроительных чертежах?

Какое расстояние оставляют между контуром изображения и размерными линиями? между размерными линиями?

Как наносят размерные числа на наклонных размерных линиях?

Какие знаки и буквы наносят перед размерным числом при указании величин диаметров и радиусов?

III.

Этап мотивационный

Для точного и аккуратного построения чертежей, прежде всего, необходимо овладеть определенным объемом знаний и навыков в выполнении геометрических построений.

 

Вопрос: Какие геометрические построения вы знаете из уроков геометрии?

 

Ответ: Построение середины отрезка; построение угла, равного данному; построение биссектрисы угла; построение перпендикулярных прямых и др.

 

Сегодня на уроке мы рассмотрим, как можно выполнить деление окружности на равные части. Многие элементы детали располагаются равномерно по окружности. Поэтому и возникает необходимость делить окружность на равные части.

 

IV. Этап объяснения нового материала и первичного закрепления.

Некоторые детали машин и приборов имеют элементы, равномерно расположенные по окружности. При выполнении таких деталей необходимо знать правила деления окружности на равное количество частей.

1. Слайд

Геометрические построения

Геометрическим построением называют способ решения задачи, при котором ответ получают в основном графическим путём без каких — либо математических расчетов.

2 Слайд. Деление отрезка прямой на равные части

Из концов отрезка А и В циркулем проводят две дуги окружности радиусом R, несколько большим половины отрезка, до взаимного пересечения в точках а и в. Через полученные точки а и в проведем прямую, которая пересекает отрезок АВ в точке С, делящей отрезок на две равные части.

Проделав подобные построения для отрезков АС и СВ, получим точки D и F. Точки С, D и F делят отрезок АВ на четыре равные части.

3 Слайд. Деление отрезка прямой на произвольное число равных частей

Такое деление основано на свойстве подобных треугольников. На рис. в показано деление отрезка АВ на девять равных частей.

Через любой конец отрезка АВ под произвольным углом к нему (лучше острым) проводим вспомогательную прямую. С помощью циркуля от точки А на вспомогательной прямой прямой откладываем девять произвольных, но равных между собой отрезков. Последнюю точку 9 соединяем с точкой В, а через остальные точки 1, 2, …, 8 проводим прямые, параллельные прямой В9 до пересечения с отрезком АВ.

Точки пересечения разделят отрезок АВ на девять равных частей.

4 Слайд. Построение перпендикуляра из данной точки к прямой

Из данной точки С проводят дугу окружности произвольного радиуса так чтобы она пересекала прямую, заданную отрезком АВ, в точках D и F. Из этих точек описывают две дуги окружности радиусом R, несколько большим половины отрезка DF, до пересечения в точке Е. Точки С и Е соединяют прямой которая и будет искомым перпендикуляром.

5 Слайд. Деление угла на две равные части

Деление прямого угла АВС на три равные части выполняется в следующей последовательности:

1. Из вершины угла проводят дугу окружности произвольного радиуса R до пересечения со сторонами угла в точках D и F;

2. Из полученных точек проводят две дуги тем же радиусом R, до взаимного пересечения пересечения с дугой DF в точках К и М;

3. Точки К и М соединяют с вершиной В прямыми, которые разделят угол АВС на три равные части.

6 Слайд. Деление прямого угла на три равные части

Деление прямого угла АВС на три равные части выполняется в следующей последовательности:

1. Из вершины угла проводят дугу окружности произвольного радиуса R до пересечения со сторонами угла в точках D и F;

2. Из полученных точек проводят две дуги тем же радиусом R, до взаимного пересечения пересечения с дугой DF в точках К и М;

3. Точки К и М соединяют с вершиной В прямыми, которые разделят угол АВС на три равные части.

7 Слайд. Построение угла равного заданному

Пусть задан угол АВС. Требуется построить такой же угол, но со сторонойDE и вершиной в точке D. Для этого из вершины В данного угла проведем дугу окружности произвольного радиуса R, которая пересечет стороны угла в точках 1 и 2. Из вершины D искомого угла тем же радиусом R проведем дугу окружности, которая пересечет отрезок DE в точке 3. Из точки 3 проведем дугу радиусом r, равным отрезку 12, до пересечения с ранее проведенной дугой радиуса R в точке 4. Через полученную точку 4 и точку D проводим недостающую сторону искомого угла.

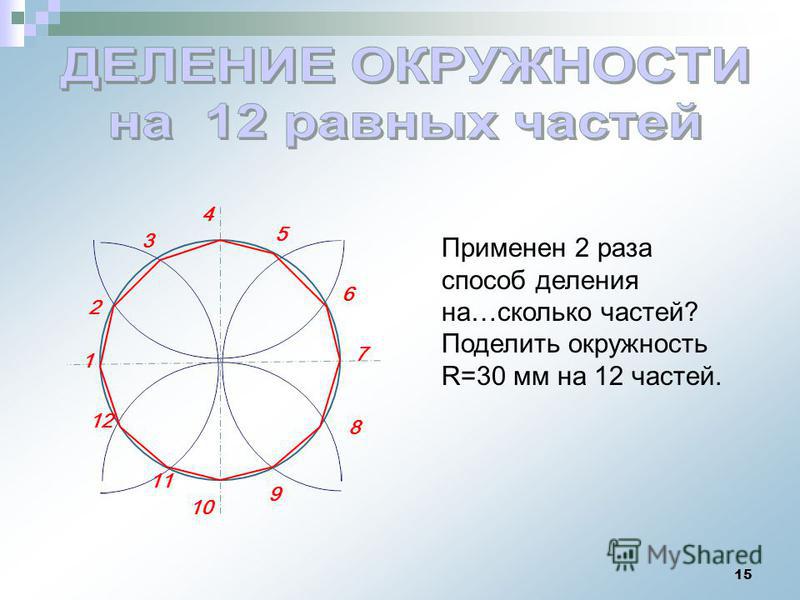
8 Слайд. Деление окружности на три, шесть и двенадцать равных частей

 Деление окружности на три, шесть и двенадцать равных частей выполняется в следующей последовательности:

1. Выбираем в качестве точки 1, точку пересечения осевой линии с окружностью;

2. Из точки 4 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 2 и 3;

3. Точки 1, 2 и 3 делят окружность на три равные части;

4. Из точки 1 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 5 и 6;

5. Точки 1 — 6 делят окружность на шесть равных частей;

6. Дуги радиусом R, проведенные из точек 7 и 8 пересекут окружность в точках 9, 10, 11 и 12;

7. Точки 1 — 12 делят окружность на двенадцать равных частей.

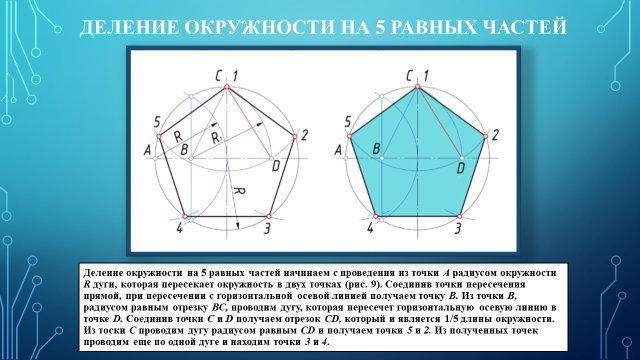
9 Слайд. Деление окружности на пять равных частей

Деление окружности на пять равных частей выполняется в следующей последовательности:

1. Из точки А радиусом, равным радиусу окружности R, проводим дугу, которая пересечет окружность в точке В;

2. Из точки В опускают перпендикуляр на горизонтальную осевую линию;

3. Из основания перпендикуляра — точки С, радиусом равным С1, проводят дугу окружности, которая пересечет горизонтальную осевую линию в точке D;

4. Из точки 1 радиусом равным D1, проводят дугу до пересечения с окружностью в точке 2, дуга 12 равна 1/5 длины окружности;

5. Точки 3, 4 и 5 находят откладывая циркулем по данной окружности хорды, равные D1.

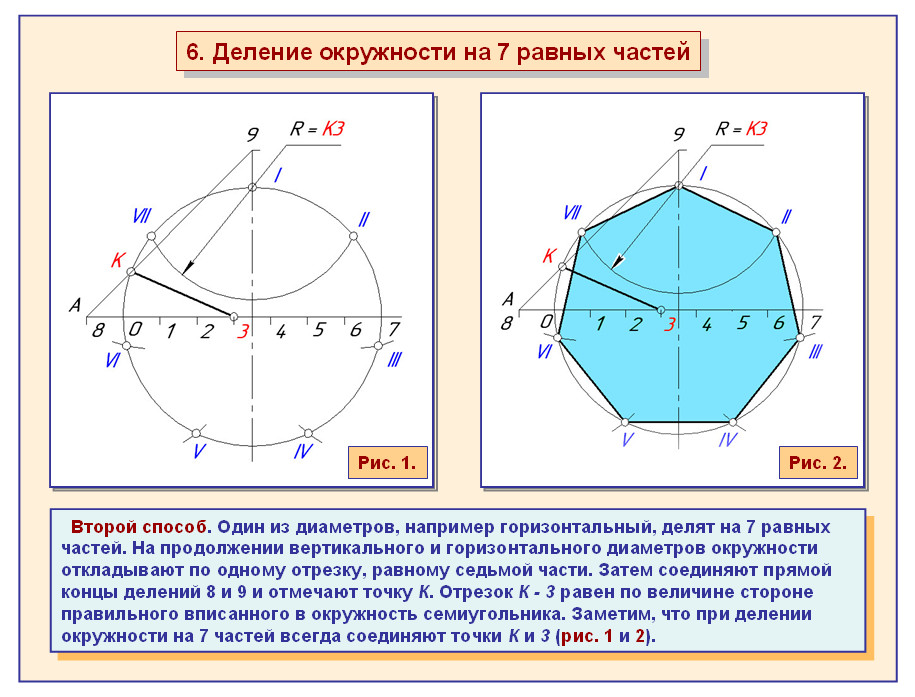
10 Слайд. Деление окружности на семь равных частей

Деление окружности на семь равных частей выполняется в следующей последовательности:

1. Из точки А радиусом, равным радиусу окружности R, проводим дугу, которая пересечет окружность в точке В;

2. Из точки В опускают перпендикуляр на горизонтальную осевую линию;

3. Длину перпендикуляра ВС откладывают от точки 1 по окружности семь раз и получают искомые точки 1 — 7.

11 Слайд. Деление окружности на восемь равных частей

Деление окружности на восемь равных частей производится в следующей последовательности:

1. Проводят две перпендикулярные оси, которые пересекая окружность в точках 1,2,3,4 делят ее на четыре равные части;

2. Применяя известный прием деления прямого угла на две равные части при помощи циркуля или угольника строят биссектрисы прямых углов, которые пересекаясь с окружностью в точках 5, 6, 7, и 8 делят каждую четвертую часть окружности пополам.

 

V. Рефлексионный этап

Домашнее задание. доработка и оформление чертежа

Итоги урока:

Что вам понравилось на сегодняшнем уроке?

Трудная – ли была работа на сегодняшнем уроке?

Добились ли вы поставленных целей?

Чему вы сегодня научились?

 

 

 

 

 

Образец расположения окружностей

 

 

 

 

 

 

 

 

 

 

 

 

 

Инструкционная карта

Практическое занятие № 6:

Графическая работа № 3 – ЧЕРТЕЖ  ДЕТАЛИ  С  ПРИМЕНЕНИЕМ ДЕЛЕНИЯ  ОКРУЖНОСТИ НА  РАВНЫЕ ЧАСТИ

1.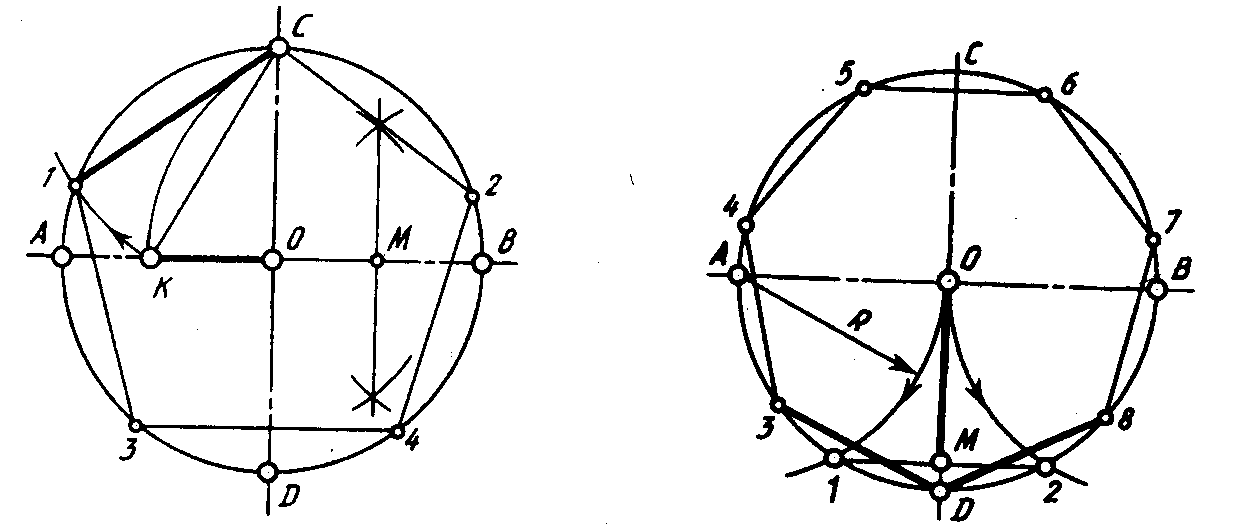 Цель работы: целью настоящей работы является ознакомление студентов с правилами деления окружности на равное количество частей, а также приобретение ими навыков вычерчивания детали с применением деления окружности.

2. Содержание работы.

Построить чертеж контуров деталей с элементами, расположенными по окружности.

Применяемые средства: чертежная бумага формата А3; набор чертежных инструментов.

4. Методические указания.

      Некоторые детали машин и приборов имеют элементы, равномерно расположенные по окружности. При выполнении таких деталей необходимо знать правила деления окружности на равное количество частей.

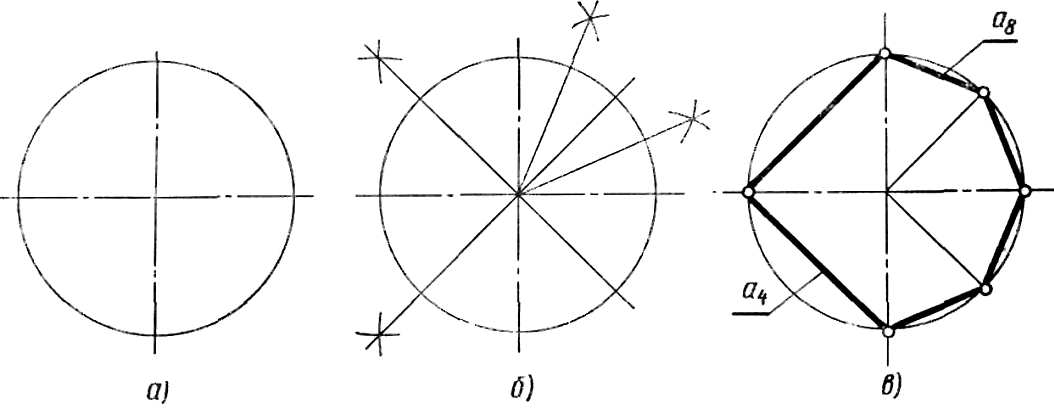
Деление окружности на четыре равные части и построение правильного вписанного четырехугольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части. Соединив точки пересечения этих линий с окружностью прямыми, получим правильный вписанный четырехугольник.

Деление окружности на восемь равных частей и построение правильного вписанного восьмиугольника.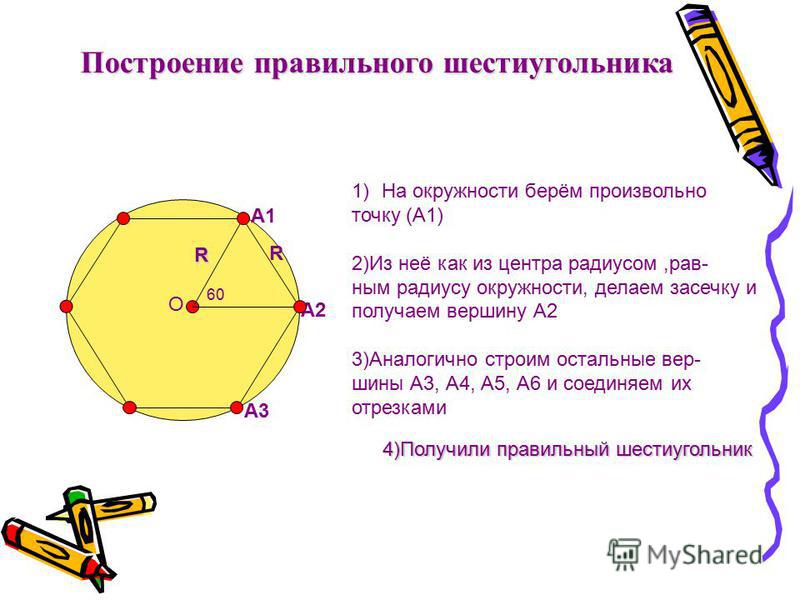 Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым линиям с помощью угольника с углами 45°, 45° и 90° и рейсшины, вместе с центровыми линиями разделять окружность на восемь равных частей.

     Деление окружности на восемь равных частей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5.

    Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.  Если полученные точки соединить последовательно прямыми линиями, то получится правильный восьмиугольник.

Деление окружности на три равные части и построение правильного вписанного треугольника. Данные построения выполняют с помощью циркуля или угольника с углами 30°, 60° и 90° и рейсшины.

     При делении окружности циркулем на три равные части из любой точки окружности, например, из точки А пересечения центровых линий с окружностью, проводят дугу радиусом R, равным радиусу данной окружности, получают точки 1 и 2.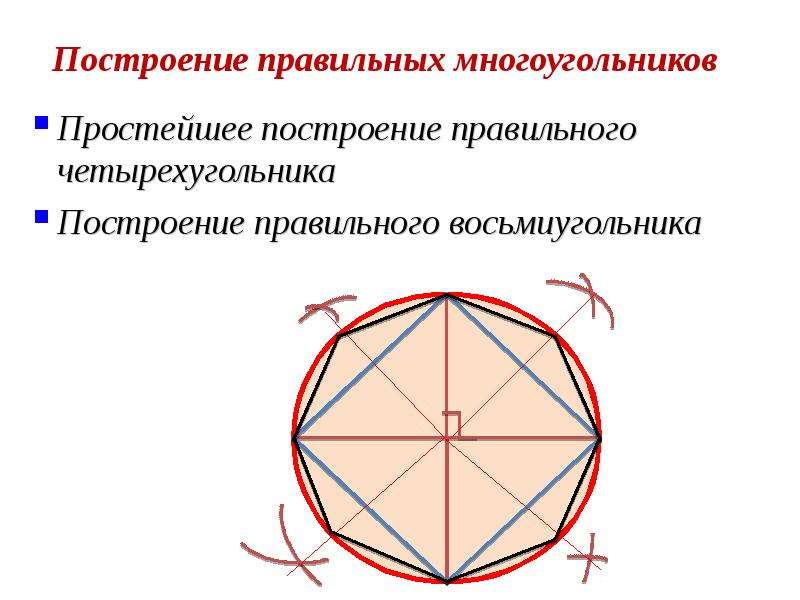 Третья точка деления (точка 3) будет находиться на противоположном конце диаметра, проходящего через точку А.

      Последовательно соединив точки 1, 2 и 3, получим правильный вписанный треугольник. При построении правильного вписанного треугольника, если задана одна из его вершин (например, точка 1), находят точку А. Для этого через заданную точку 1 проводят диаметр. Точка А будет находиться на противоположном конце этого диаметра. Затем проводят дугу радиусом R, равным радиусу данной окружности, и получают точки 2 и 3.

Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника. Данные построения выполняют с   помощью циркуля или угольника с углами 30°, 60° и 90° и рейсшины.

   При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5.    

   Последовательно соединив полученные точки, получим правильный вписанный шестиугольник:  

Деление окружности на двенадцать равных частей и построение правильного вписанного двенадцатиугольника.  Данные построения выполняют с   помощью циркуля или угольника с углами 30°, 60° и 90° и рейсшины.

    При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью. Соединив полученные точки, получают правильный вписанный двенадцатиугольник.

Деление окружности на пять и десять равных частей и построение правильных вписанных пятиугольника и десятиугольника.

   Половину любого диаметра (радиус) делят пополам, получают точку А. Из точки А, как из центра, проводят дугу радиусом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В. Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1/5 длины окружности.

     Делая засечки на окружности (рис.7, в) радиусом R, равным отрезку 1В, делят окружность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки 1 строят точки 2  и 5, затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4

Внимание!  Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок, и последняя сторона пятиугольника получается перекошенной.

      Деление окружности на десять равных частей выполняют аналогично делению окружности на пять равных частей, но сначала делят окружность на пять частей, начиная построение из точки 1, а затем из точки 6, находящейся на противоположном конце диаметра. Соединив последовательно все точки, получают правильный вписанный десятиугольник.

Деление окружности на семь равных частей и построение правильного вписанного семиугольника.

  Из любой точки, например, точки А, радиусом заданной окружности проводят дугу до пересечения с окружностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае это отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1/7 длины окружности.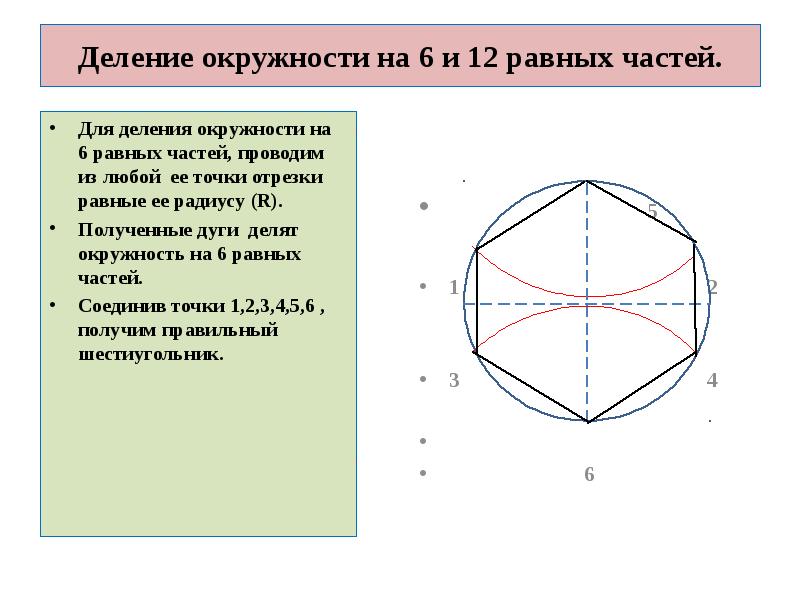 Радиусом, равным отрезку ВС, делают засечки на окружности. Соединив последовательно все точки, получают правильный вписанный семиугольник.

Деление окружности на любое число равных частей.

С достаточной точностью можно делить окружность на любое число равных частей, пользуясь таблицей коэффициентов для подсчета длины хорды.

            Таблица 1 – Коэффициенты для подсчета длины хорды

Число сторон n	Коэффициент k	Число сторон n	Коэффициент k	Число сторон n	Коэффициент k
7	0,434	17	0,184	27	0,116
8	0,383	18	0,174	28	0,112
9	0,342	19	0,165	29	0,108
10	0,309	20	0,156	30	0,104
11	0,282	21	0,149	31	0,101
12	0,259	22	0,142	32	0,098
13	0,239	23	0,136	33	0,095
14	0,223	24	0,130	34	0,092
15	0,208	25	0,125	35	0,900
16	0,195	26	0,120	36	0,087

Зная, на какое число следует разделить окружность, находят коэффициент k.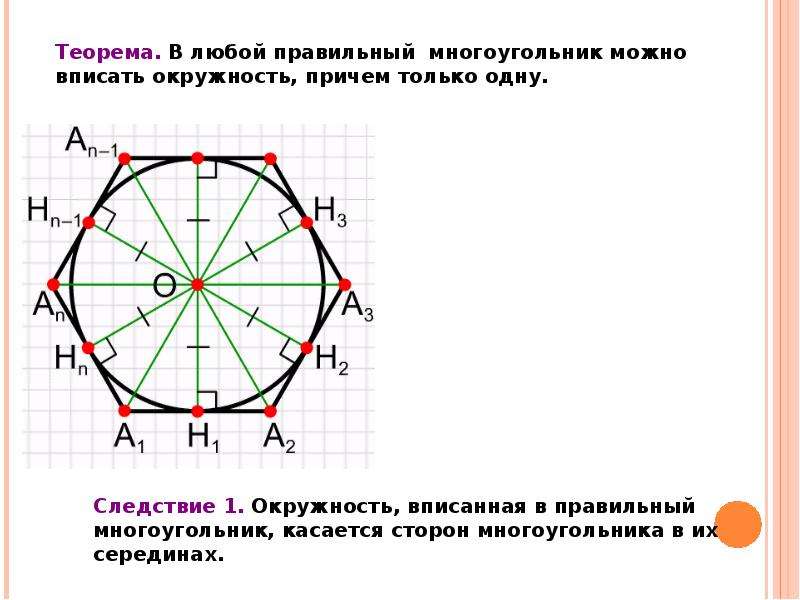 При умножении коэффициента k на диаметр D этой окружности получают длину хорды l, которую циркулем откладывают на заданной окружности n раз.

5. Последовательность выполнения задания.

На выбранном формате бумаги (А3) выполнить рамку и внизу справа основную надпись.

Определить, сколько отверстий имеется в детали.

Разделить окружность на нужное количество частей.

С помощью угольника, рейсшины и циркуля выполнить необходимые построения.

Нанести размеры на чертеж детали.

6 Контрольные вопросы:

Как с помощью угольника с углами 30°, 60° и 90° и рейсшины разделить прямой угол на три равные части?

Как найти центр дуги или окружности на чертеже и определить ее радиус?

Как разделить окружность на 14 равных частей?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок «Деление окружности на равные части», ФГОС

Деление окружности на равные части, построение правильных многоугольников

Деление окружности на 4 и 8 равных частей

Концы взаимно перпендикулярных диаметров АС и BD (рис. 1) делят окружность с центром в точке О на 4 равные части. Соединив концы этих диаметров, можно получить квадрат AВСD.

Если угол СОА между взаимно перпендикулярными диаметрами АЕ и СG (рис. 2) разделить пополам и провести взаимно перпендикулярные диаметры DH и BF, то их концы разделят окружность с центром в точке О на 8 равных частей. Соединив концы этих диаметров, можно получить правильный восьмиугольник ABCDEFGH.

Рис. 1 Рис. 2

 

Деление окружности на 3, 6 и 12 частей

Для деления окружности на 6 равных частей используют равенство сторон правильного шестиугольника радиусу описанной окружности. Если задана окружность с центром в точке О (рис. 3) и радиусом R, то из концов одного из ее диаметров (точек А и D), как из центров, проводят дуги окружностей радиусом R. Точки пересечения этих дуг с заданной окружностью разделят ее на 6 равных частей. Последовательно соединив найденные точки, получают правильный шестиугольник ABCDEF.

 Если окружность в центре с точкой О (рис.4) необходимо разделить на 3 равные части, то радиусом, равным радиусу этой окружности, следует провести дугу лишь из одного конца диаметра, например точки D. Точки В и С пересечения этой дуги с заданной окружностью, а так же точка А разделят последнюю на 3 равные части. Соединив точки А, В и С, можно получить равносторонний треугольник АВС.

Рис. 3 Рис. 4

Чтобы разделить окружность на 12 частей, деление окружности на 6 частей повторяют дважды (рис. 5), используя в качестве центров концы взаимно перпендикулярных диаметров: точки А и G, D и J. Точки пересечения проведенных дуг с заданной окружностью разделят ее на 12 частей. Соединив построенные точки, можно получить правильный двенадцати угольник.

Рис. 5

Деление окружности на 5 частей

Чтобы разделить окружность с центром в точке О (рис. 6) на 5 частей, поступают следующим образом. Один из радиусов окружности, например ОМ, делят пополам описанным ранее способом. Из середины отрезка ОМ точка N радиусом R1, равным отрезку АN, проводят дугу окружности и отмечают точку Р пересечения этой дуги с диаметром, которому принадлежит радиус ОМ. Отрезок АР равен стороне вписанного в окружность правильного пятиугольника. Поэтому из конца А диаметра, перпендикулярного к ОМ, радиусом R2, равным отрезку АР, проводят дугу окружности. Точки В и Е пересечения этой дуги с заданной окружностью позволяют отметить две вершины пятиугольника.

Еще две вершины (С и D) являются точками пересечения дуг окружностей радиусом R2 с центрами в точках В и Е с заданной окружностью с центром в точки О. Вершины правильного пятиугольника ABCDE делят заданную окружность на 5 равных частей.

Рис. 6

Деление окружности на 7 частей

Чтобы разделить окружность с центром в точке О (рис. 6) на 7 частей, необходимо из точки 1 провести вспомогательную дугу радиусом R, равным радиусу данной окружности, которая пересечет окружность в точке М.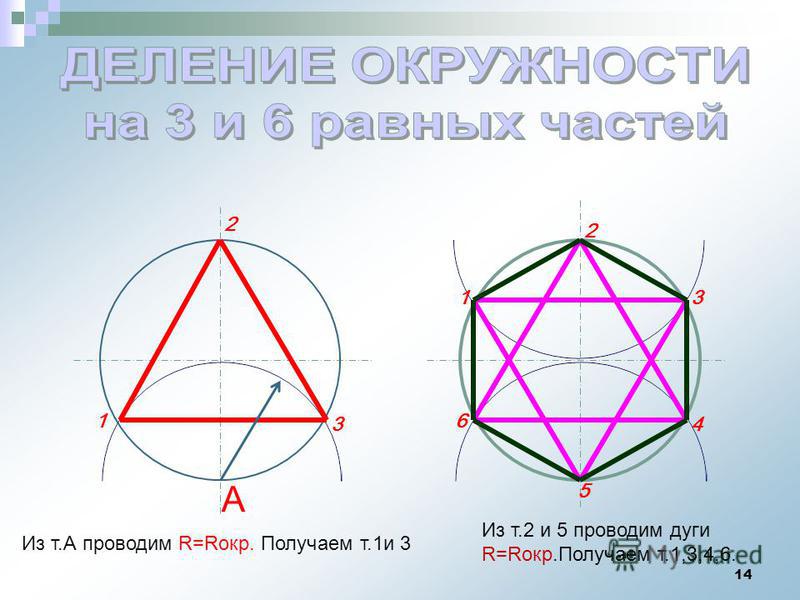 Из точки N опускаю перпендикуляр на горизонтальную осевую линию. Из точки А радиусом, равным радиусу MN, делают по окружности 7 засечек и получают семь искомых точек, соединив которые получают правильный семиугольник ABCDEFG.

Рис. 7

Деление окружности на произвольное число равных частей

Если ни в одном из рассмотренных ранее вариантов не удовлетворяет условию поставленной задачи, то используют прием, позволяющий разделить окружность на произвольное число равных частей и построить соответственно вписанные в нее правильные многоугольники с произвольным числом сторон.

Рассмотрим такое построение на примере деления окружности с центром в точке О (рис. 8а) на 7 равных частей. Сначала необходимо провести два взаимно перпендикулярных диаметра, один из которых, например проходящий через точку А, следует разделить на 7 равных частей, ограниченными точками 1…7. Из точки А, как из центра, радиусом R равным диаметру заданной окружности, надо провести дугу, пересечение которой с продолжением второго диаметра определит точки Р1 и Р2.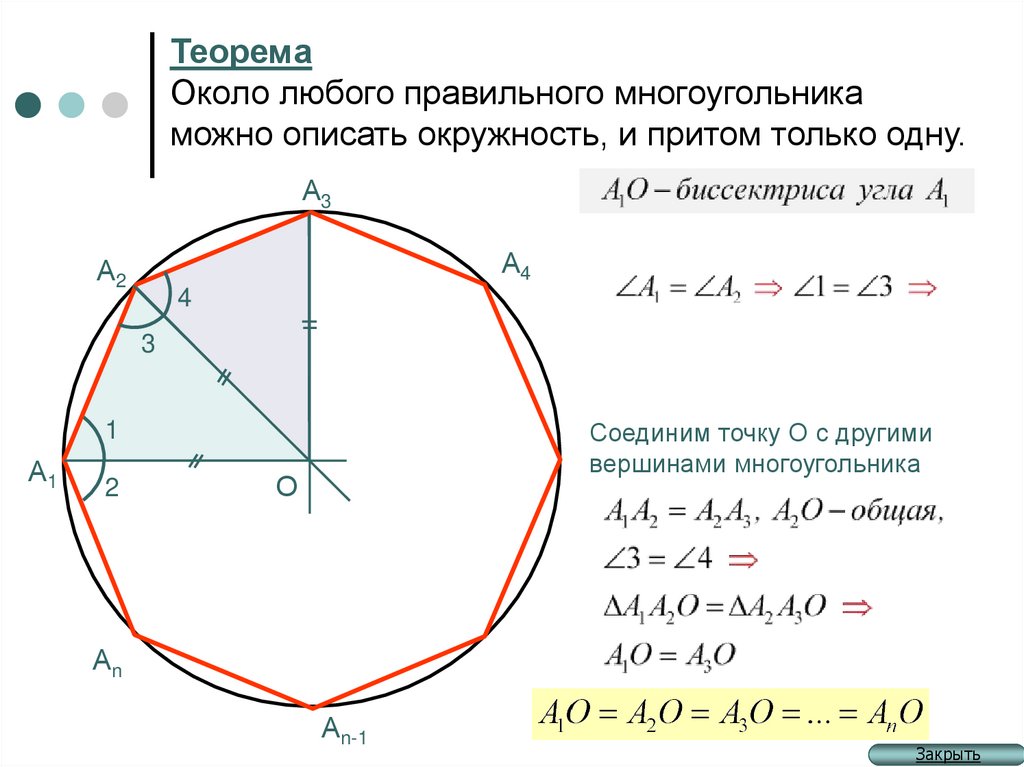 Затем через точки Р1 и Р2 (рис.8б), и четные точки, полученные при делении диаметра А7 (точки 2. 4 и 6), проводят прямые. Точки В, С, D и Е, F, G пересечения этих прямых с заданной окружностью и точка А делят окружность с центром О на 7 равных частей. Последовательно соединив построенные точки можно изобразить вписанный в окружность правильный семиугольник.

Рис. 8

 

Творческий проект для классов К-8

---

Креатив Проекты для К-12

Урок Планы

• 1869 Задача вступительного теста MIT
• Проблема «3N+1»
• Корзина, полная яиц
• Геометрическое доказательство теоремы Пифагора 9 «вырезать и вставить»0022
• Проблема для Молодые и старые ученики
• Проблема от русского Математическая олимпиада
• Доказательство Пифагора теорема с использованием подобных треугольников
• Головоломка с целыми числами от одного до шестнадцати
• Головоломка с номером 1089
• «Струнный рисунок», который мы можем нарисовать: ромб внутри шестиугольника
• Трехсторонний кот для рисования
• Путешественник на сетке 6 на 6
• Дополнительная плата
• Прибавление в детском саду и первый класс
• Арифметическое чудо из 1899 года
• Старый купец и его четверо детей
• Древний узел
• Анимации на TI
• Углы треугольника: геометрическое свойство посредством складывания бумаги
• Районы и границы
• Площадь и Периметр
• Арифметика с манипуляциями
• Средний балл за тест
• Мяч в коробке
• Банан
• Бочки, Бочки и другие фигурные контейнеры
• Большие числа АКА Зерна риса на шахматная доска
• Блочные дома
• Сборка собачьей будки в масштабе
• Создание ящика со скелетом в соответствии с к Спецификации
• Свечи
• Корзины для конфет
• Емкость
• Наутилус с камерой
• Проверка, является ли число простым номер
• Коробка с китайским календарем
• Хорды ​​по кругу
• Круг, квадрат и треугольник
• Часы и время
• Монеты
• Раскрашивание линий в шестиугольнике
• Красочный Треугольники
• Конгруэнтность Треугольники
• Подсчет
• Счетная доска для детей учащиеся
• Счет до 100
• Бумага для биговки По кривым
• Кубики
• Куб со срезанным краем
• Кухня полоски
• Вырезание прямоугольника
• Вырезание треугольника
• Разрезание треугольника на две части куски равной площади и равного периметра
• Вырезание равностороннего треугольника
• Резка многогранников
• Цилиндр и конус одинаковой высоты и диаметра основания
• Вывод формулы для площадь треугольника
• Диагональ площади
• Разделение квадрата
• Деление с остатком на ТИ-108: Два экземпляра
• Собаки, кошки и мыши
• Точка за точкой
• Удвоение и деление пополам
• Чертеж прямоугольник
• Рисование простой фигуры из устных указаний
• Рисование треугольников
• Легкие квадраты
• Яичная дилемма (Часть 1)
• Возведение в степень
• Факторинг
• фантазии Конверты
• Нахождение дроби между двумя дроби
• Пятиконечный 3D Звезда
• переворачивание монеты
• Сложенный бумажный цветок С шестью лепестками
• Четыре жука
• Четыре карты
• Четыре кубика
• От миллиарда до нуля
• От одного до одного триллиона
• Игра кругов и звезд
• Игра в десятки
• Гигантская энчилада
• Шапка для Хэллоуина
• Орел или решка?
• Шестиугольная головоломка
• Праздник Орнамент
• Лошадь на продажу
• Как работает Калькулятор Вычислить квадратный корень из числа?
• Сколько пентамино?
• Сколько клеток на шахматной доске?
• Сколько треугольников? (Части 1 и 2)
• Сколько треугольников в этом треугольнике?
• Как измерить угол без транспортира
• Как превратить прямоугольник в другой прямоугольник
• Гиперболы и Эллипсы
• Я могу угадать твой возраст!
• Я могу угадать ваш возраст и номер дома!
• Невозможный объект
• Вписанный треугольник
• Проценты
• Введение в измерения (первый класс)
• Неправильные многоугольники
• Юлекурв АКА Валентайн Корзина
• Прыжок: игра в пасьянс с десятью жетонами
• Воздушные змеи
• Умножение решетки
• Дырявая крыша
• Ушастые твари
• Волшебные бобы
• Волшебный складной кубик
• Магический квадрат
• Создание животных Режущие полигональные пазлы
• Создание блоков из четырех Кубики
• Изготовление коробок
• Изготовление эвольвенты
• Лабиринт
• Мини-слот-машина
• Луны
• Больше задач «точка-точка»
• Больше старых словесных задач
• Умножения «Готово по Адаму Рису»
• Натан подбрасывает монету 20 раз
• Игра в числа с Кости
• Головоломка с числами
• Воля старого пастыря
• Олимпийские кольца
• Одна треть
• Покраска домов (и другие «рабочие» задачи)
• Парадокс средних
• Разделение квадрата
• Пентагон Пазлы
• Алгебра телефонных номеров
• Копилка
• Игра с формами
• Powerball 55
• Красивая подарочная коробка
• Простые числа: сито Эратосфена
• Свойства коробки
• Тыквы
• Пазл с камешками
• Пирамида на четверти
• Пирамида из кубиков
• Пирамида из мрамора
• Четырехугольники
• Прямоугольники
• Правильные многоугольники с равными Районы
• Связанные проблемы
• Прямоугольный треугольник
• Последовательности составных номера: конкурс
• Фигуры цифр
• Формы чисел с использованием треугольники
• Делиться хлебом
• Овца: Старая головоломка
• Шесть пирамид
• Шестнадцать Квадратные дюймы
• Печать Соломона
• Сортировочная игра
• Спираль (марки К-4)
• Спираль (5-8 классы)
• Спираль Феодора на Калькуляторе ТИ-83/84
• Квадратные и кубические единицы
• Квадрат в треугольнике
• Соломенные многогранники
• Алгоритм вычитания
• Вычитание со счетчиками
• Сумма всех 100 чисел в таблице умножения
• Сумма первых N целых чисел
• Сумма двух квадратов
• Выживший на шестиугольном острове
• Татами
• Чайные коробки
• Преобразование температуры
• Мозаика круга
• Задача о лестнице и ящике
• Сыр «Смеющаяся корова» Клиновые контейнеры
• Практическая ценность Доказательства
• Рейнберд Зуни
• Три четверти
• Круг из трех частей Пазл
• Бросание одного кубика
• Треугольник в квадрат: A шарнирный разборный
• Превращение прямоугольника в квадрат путем вскрытия
• Двенадцать простых фигур
• Двадцать четыре кубика
• Две старые проблемы
• Два брата-пастуха
• Понимание Длинная дивизия
• Необычный Контейнеры
• Что дальше?
• Что это за прямоугольник?
• Инь Ян

Отрыв | Примечания | Кредиты | Альбом | НМСУ Курсы для учителей | Контакт США
последнее изменение: 2 февраля 2022 г.

геометрия — самый быстрый способ рисования конструируемых правильных многоугольников

спросил 7 лет, 8 месяцев назад

Изменено 4 года, 10 месяцев назад

Просмотрено 2к раз

$\begingroup$

Мы знаем из Гаусса, что правильные многоугольники порядка $3$, $4$, $5$, $6$, $8$, $10$, $12$, $15$, $16$, $17$, $20$, $24\ldots$ являются конструктивными.

• Существует ли доказуемо быстрый метод циркуля и линейки для создания каждый (или некоторые) из этих полигонов?

• Если да, то является ли минимальное количество шагов (дуг и линий) известным функция числа сторон?

Для наглядности изображение конструкции 17-угольника из Википедии, отличной от оригинальной конструкции Гаусса.

$\quad\quad\quad\quad$

• геометрия
• евклидова геометрия
• многоугольники

$\endgroup$

8

$\begingroup$

Просто чтобы сдвинуться с мёртвой точки, вот пятишаговое построение квадрата, начиная с двух точек, которые могут быть минимальными, а могут и не быть. (В комментариях под ОП я дал двухшаговое построение равностороннего треугольника, который, осмелюсь сказать, нельзя построить за один шаг.)

Начиная с точек $P$ и $Q$,

1. Нарисуйте круг с центром в $P$, проходящей через $Q$.
2. Нарисуйте окружность с центром в точке $Q$, проходящую через точку $P$. Эти две окружности пересекаются в двух точках $R$ и $S$.
3. Проведите линию через $P$ и $Q$.
4. Проведите линию через $R$ и $S$. Эти две прямые перпендикулярны и пересекаются в точке $O$.
5. Нарисуйте окружность произвольного радиуса с центром в точке $O$. Его пересечения с линиями шагов 3 и 4 являются вершинами квадрата.

Чего здесь, конечно, не хватает, так это доказательства того, что пять — это минимум. Я надеюсь, что кто-нибудь опубликует ответ, содержащий такое доказательство (или, что еще лучше, конструкцию, которая требует меньше шагов).0011

Добавлено позже : Просто чтобы не останавливаться на достигнутом (и/или потреблять дополнительные низко висящие плоды), вот четырехэтапное построение шестиугольника:

Начиная с точек $O$ и $P$,

1. Нарисуйте окружность с центром в точке $O$, проходящую через точку $P$.
2. Нарисуйте окружность с центром в точке $P$, проходящую через точку $O$. Эти две окружности пересекаются в двух точках $A$ и $D$.
3. Проведите линию через $O$ и $P$. Он пересекает окружность из шага 1 в точке $Q$.
4. Нарисуйте окружность с центром в точке $Q$, проходящую через точку $O$. Он пересекает окружность из шага 1 в двух точках $B$ и $C$. Точки $P,A,B,Q,C,D$ являются вершинами шестиугольника.

Я думаю, что это «очевидно» минимально. Но я думаю, что нам нужны некоторые явные правила для того, что составляет конструкцию, чтобы доказать ее очевидность….

$\endgroup$

6

$\begingroup$

Подсказка :

Если вы начнете с двух данных точек и позволите провести только прямую линию из двух известных точек или окружность с центром в одной известной точке и через другую, вы можете набросать все возможные построения.

В одну линию:

В две линии (получается равносторонний треугольник):

В три линии:

В четыре линии (получается шестиугольник):

Пятый построение с четырьмя линиями показывает, как получить квадрат в пять линий (с дополнительным кругом).

Я предполагаю, что разрешение рисовать через неизвестные точки не уменьшит минимальное количество линий. К сожалению, такой подход грубой силы очень быстро становится непрактичным.

---

Обновление :

Отсутствует операция: измерить расстояние между двумя известными точками с помощью компаса и нарисовать круг с этим радиусом вокруг третьей точки.

Также отсутствуют многие конструкции с большими кругами.

$\endgroup$ 92-С > n$$ Это означало бы, что количество шагов бессимптомно ограничено снизу $O\left(\sqrt{n}\right)$.

$\endgroup$

2

$\begingroup$

Чтобы не запутаться, вот быстрый способ нарисовать правильный пятиугольник.

Начните с окружности с центром $O$ и проведите два взаимно перпендикулярных диаметра $AB$ и $CD$.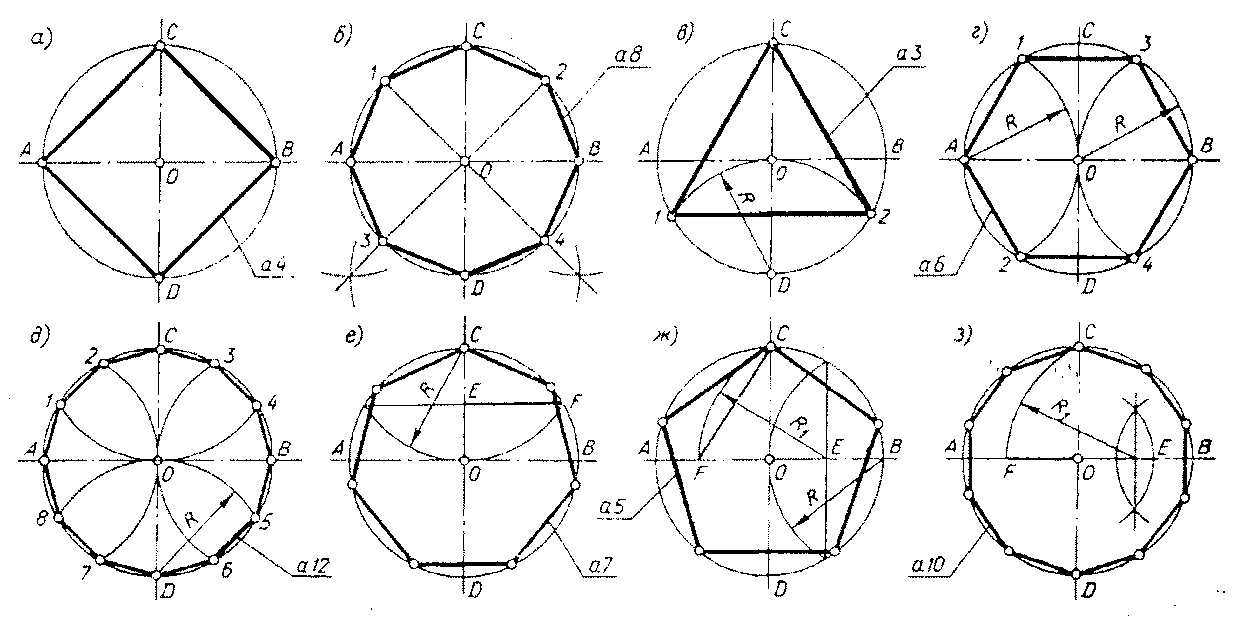

Найдите середину $OD$ и назовите ее $E$.

Проведите прямую $BE$ в продолжении и разделите угол $BEO$ пополам внутри и снаружи.

Эти биссектрисы пересекаются с $AB$ в точках $X$ и $Y$. Постройте прямые, перпендикулярные $AB$, через $X$ и $Y$.

Эти перпендикуляры пересекают окружность в четырех точках, которые вместе с $B$ образуют правильный пятиугольник.

Я не уверен, сколько это шагов по вашим правилам, но мне было бы интересно узнать, есть ли более быстрый способ. Я сомневаюсь в этом.

$\endgroup$

4

$\begingroup$

Предположим, нужно вписать правильный $n$-угольник в заданную окружность. Как только найдены вершины $P_0$ и $P_i$, где $i$ взаимно прост с $n$, остальные можно легко найти. На их построение уходит $O(n)$ шагов, поэтому эта часть задачи тем дороже, чем больше $n$.

Однако, если мы сосредоточимся на той части задачи, которая является расположением $P_i$, это может быть не сложнее для $n=2k$ или $n=4k$, чем для $n=k$. Рассмотрим, например, $n=5$ и $n=10$. Обозначим вершины пятиугольника через $P_i$, а вершины десятиугольника — через $D_i$. Если радиус описанной окружности равен $1$, сторона и диагональ пятиугольника $P_0P_2$ равны $\sqrt{\dfrac{5\mp\sqrt5}2}$. Сторона десятиугольника и диагональ $D_0D_3$ равны $\dfrac{\sqrt5\mp1}2$. Вершины десятиугольника $D_1, D_9$ можно найти из $D_0$ таким образом:

Назовите данный круг $\Omega_1$. Нарисуйте $\Omega_1$ в диаметре $D_0OD_5$. Построить радиус $OB\perp OD_0$. Разделите $OB$ пополам в точке $C$. Нарисуйте $D_0C$. Нарисуйте окружность с центром от $C$ до точки $O$, разрезав $D_0C$ в точке $D$. Нарисуйте окружность с центром от $D_0$ через $D$, разрезав $\Omega_1$ в точках $D_1$ и $D_9$.

Чтобы добраться до этого места, нужно построить 7 окружностей (3 для построения перпендикуляра, 2 для разделения отрезка пополам и еще 2). Это то же самое, что и метод Птолемея для вписания правильного пятиугольника. Действительно, правильный пятиугольник можно вписать, используя метод, аналогичный описанному выше для десятиугольника: нарисуйте $CD_5$ вместо $CD_0$, таким образом найдя $D_4, D_6$, которые равны $P_2, P_3$, где $D_0$ равно $P_0.