Построение правильных многоугольников
Оглавление
Деление окружности на шесть, три, двенадцать равных частей.
Деление окружности на четыре, восемь, шестнадцать и т.д. частей.
Деление окружности на произвольное количество частей.
1) На ШЕСТЬ ЧАСТЕЙ. Чтобы разделить окружность на шесть равных частей, от любой ее точки (1) отложим отрезки, равные радиусу окружности (R).
От одной из полученных точек (в нашем случае 2) отложим с помощью того же раствора циркуля еще один отрезок, получим точку 3, от нее отложим еще один такой же отрезок, получим точку 4, и т.д.
Полученные дуги делят окружность на шесть равных частей. Приняв точки 1, 2, 3, 4, 5, 6 за вершины шестиугольника, соединим их отрезками прямых, таким образом построим правильный шестиугольник.
2) На ТРИ ЧАСТИ. Полученные после построения шестиугольника точки соединим через одну получим правильный (равносторонний) треугольник.
3) На ДВЕНАДЦАТЬ ЧАСТЕЙ. Одну из сторон полученного при первом построении шестиугольника разделим пополам (для получения подсказки прижать CTRL и щелкнуть левой кнопкой мыши по ссылке) вместе с соответствующей дугой. Измерим циркулем полученную половину дуги, отложим данное расстояние по окружности от вершин 6-уголька. Новые точки на дуге вместе с вершинами шестиугольника – вершины двенадцатиугольника.
4) На 24 части, 48 частей и т.д. Выполнив алгоритм пункта 3 для сторон двенадцатиугольника – получим 24-угольник, выполнив этот же алгоритм со сторонами 24-угольника, получим 48-угольник и т.д.
1) На ЧЕТЫРЕ ЧАСТИ. Проведем в окружности диаметр. Построим второй диаметр, перпендикулярный первому. (для получения подсказки прижать CTRL и щелкнуть левой кнопкой мыши по ссылке) Полученные четыре точки и будут являться вершинами правильного четырехугольника (квадрата).
2) На ВОСЕМЬ ЧАСТЕЙ. Одну из сторон полученного при первом построении квадрата разделим пополам (для получения подсказки прижать CTRL и щелкнуть левой кнопкой мыши по ссылке) вместе с соответствующей дугой. Измерим циркулем полученную половину дуги, отложим данное расстояние по окружности от вершин квадрата. Новые точки на дуге вместе с вершинами квадрата – вершины 8-угольника.
Одну из сторон полученного при первом построении квадрата разделим пополам (для получения подсказки прижать CTRL и щелкнуть левой кнопкой мыши по ссылке) вместе с соответствующей дугой. Измерим циркулем полученную половину дуги, отложим данное расстояние по окружности от вершин квадрата. Новые точки на дуге вместе с вершинами квадрата – вершины 8-угольника.
3) На 16, 32 и т.д. частей. Выполнив алгоритм пункта для сторон 8-угольника – получим 16-угольник, выполнив этот же алгоритм со сторонами 16-угольника, получим 32-угольник и т.д.
Вспомним о том, что величина дуги всей окружности – 360 0 .Тогда дуги, стянутые сторонами правильного многоугольника как хордами равны 360/n, где n – количество сторон многоугольника.
| количество сторон, n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| величина угла между радиусами, соединяющими соседние вершины многоугольника, в градусах | 120 | 90 | 72 | 60 | 51,4 | 45 | 40 | 36 | 32,7 | 30 | 27,7 |
Для построения многоугольника провести произвольно радиус, отложить от него с помощью транспортира центральный угол, соответствующий значениям таблицы или вычислениям, измерить получившуюся дугу циркулем, отложить с помощью полученного раствора циркуля дуги, равные первой.
ДЕЛЕНИЕ ОТРЕЗКА ПОПОЛАМ
Из концов отрезка проведем две дуги одинакового радиуса (R – больше половины отрезка). Через точки пересечения этих дуг проведем прямую, которая разделит отрезок (а в нашем случае и соответствующую дугу) пополам.
ПОСТРОЕНИЕ ПЕРПЕНДИКУЛЯРА К ОТРЕЗКУ
Из концов отрезка проведем две дуги одинакового радиуса (R – больше половины отрезка). Через точки пересечения этих дуг проведем прямую, которая и буде перпендикуляром к данному отрезку.
⇐ Предыдущая45678910111213Следующая ⇒ Для деления окружности пополам достаточно провести любой еедиаметр. Два взаимно перпендикулярных диаметра разделят окружность на четыре равные части (рисунок 28, а).Разделив каждую четвертую часть пополам, получают восьмые части, а при дальнейшем делении – шестнадцатые, тридцать вторые части и т. Рисунок 28
Деление окружности на 3, 6, 12 и т, д. равных частей, а также построение соответствующих правильных вписанных многоугольников осуществляют следующим образом. В окружности проводят два взаимно перпендикулярных диаметра 1–2 и 3–4 (рисунок 29 а). Из точек 1 и 2 как из центров описывают дуги радиусом окружности R до пересечения с ней в точках А, В, С и D. Точки A , B, 1, С, D и 2 делят окружность на шесть равных частей. Эти же точки, взятые через одну, разделят окружность на три равные части (рисунок 29, б). Для деления окружности на 12 равных частей описывают еще две дуги радиусом окружности из точек 3 и 4 (рисунок 29, в). Для деления окружности на 12 равных частей описывают еще две дуги радиусом окружности из точек 3 и 4 (рисунок 29, в).а б в Рисунок 29
Построить правильные вписанные треугольник, шестиугольник и т. д. можно также с помощью линейки и угольника в 30 и 60°. На рисунке 30 приведено подобное построение для вписанного треугольника.
Рисунок 30
Деление окружности на семь равных частей и построение правильного вписанного семиугольника (рисунок 31) выполняют с помощью половины стороны вписанного треугольника, приблизительно равной стороне вписанного семиугольника. Рисунок 31
Для деления окружности на пять или десятьравных частей проводят два взаимно перпендикулярных диаметра (рисунок 32, а). Радиус OA делят пополам и, получив точку В, описывают из нее дугу радиусом R=BC до пересечения ее в точке D с горизонтальным диаметром. а б в Рисунок 32
На рисунке 33 приведен общий способ приближенного деления окружности на равные части. Пусть требуется разделить окружность на девять равных частей. В окружности проводят два взаимно перпендикулярных диаметра и вертикальный диаметр AB делят на девять равных частей с помощью вспомогательной прямой (рисунок 33, а). Из точки B описывают дугу радиусом R = AB, и на пересечении ее с продолжением горизонтального диаметра получают точки С и D. Рисунок 33
При построении необходимо учитывать, что такой способ деления окружности на равные части требует особенно большой точности выполнения всех операций. ⇐ Предыдущая45678910111213Следующая ⇒
|
Конструкция и основные способы использования математических инструментов
Книга I. Ч. III.
Транспортир — это полуокружность, разделенная на 180 градусов, или половину от 360, на которые предполагается разделить всю окружность, как было указано в определениях.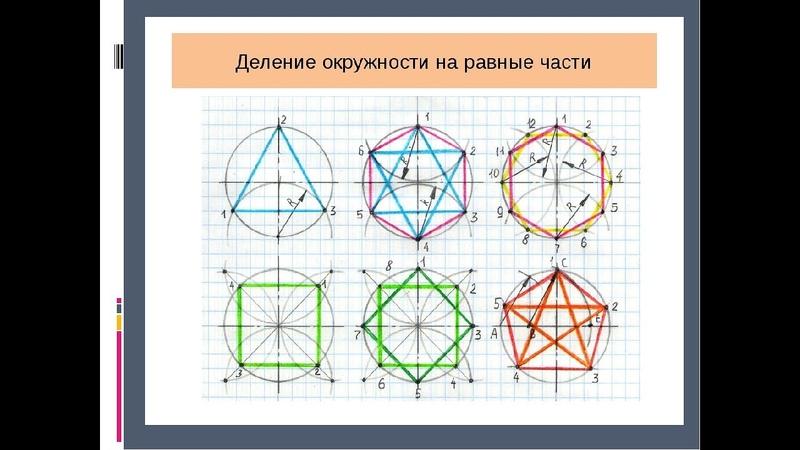
. Одна сторона этого инструмента подпилена, чтобы лучше прикладывать его к бумаге; а другая сторона наклонена; то есть утонченный к краю, на котором находятся деления: и для лучшего обнаружения точек, в которых заканчиваются углы, в центре инструмента сделана небольшая полукруглая выемка.
Как разделить конечность транспортира.
По линии AB и вокруг центра O опишите полукруг; затем проведите Радиус АО по Окружности, которая разделит Полуокружность на три равные Части, в Точках С, D, каждая из которых равна 60 Градусам. Снова разделите Дугу ВС на две равные Части, в Точке Е и Дуге ВЕ будет 30 Градусов: затем, повернув это Отверстие Циркуля вокруг Полуокружности, оно разделит его на шесть равных Частей. Более того, разделите их снова на три равные Части, и в каждой будет 10 Степеней; и разделив каждую из этих 10 градусов еще на две равные части, получим дуги из 5 градусов. И, наконец, при разделении каждой из этих пяти степеней на пять равных частей будут получены дуги в один градус.
Таким же образом весь Круг может быть разделен на 360 градусов, о которых мы поговорим ниже.
Примечание , Транспортиры иногда изготавливают из рога, которые, поскольку они прозрачны, достаточно удобны; но их следует хранить в Книге, когда они не используются, потому что Рог может сморщиться.
Рис. 46Например; чтобы сделать в точке A угол 50 градусов на линии CAB, положите центр транспортира, отмеченный полукруглой полостью, на точку A, так чтобы диаметр полукруга находился на линии AB; затем нарисуйте точку напротив 50-го градуса конечности транспортира и через нее проведите линию к точке А, которая составит угол 50 градусов с линией АВ.
Рис. 46Положите центр транспортира на точку A, а его диаметр на линию BC; затем посмотрите, в каком градусе линия AB пересекает конечность транспортира, что будет углом BAD, равным 50 градусам.
Чтобы сделать это, вы должны сначала узнать, сколько градусов содержит угол центра каждого из правильных многоугольников; который можно найти, разделив 360 градусов на число сторон предполагаемого многоугольника: например, деление 360 на 5, частное 72, показывает, что угол центра пятиугольника равен 72 градусам: опять же, в деление 360 на 8, частное 45, дает количество углов центра восьмиугольника, и так для других.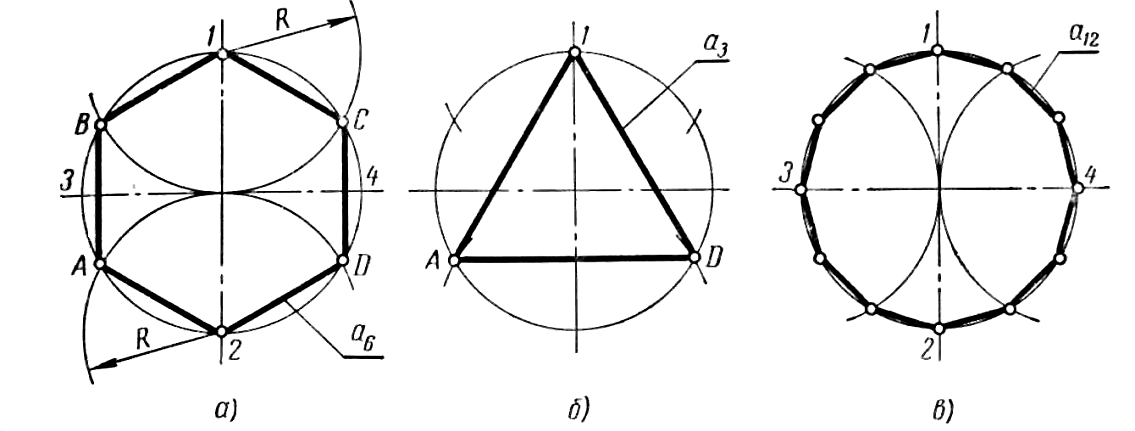
Зная Угол Центра, можно также узнать Угол, образованный Сторонами Многоугольника, если вычесть Угол Центра Многоугольника из 180 Градусов; если взять 72 градуса, угол центра пятиугольника из 180 градусов, останется 108, угол многоугольника. Более того, если взять из 180 градусов, угла центра восьмиугольника, который равен 45 градусам, останется 135 градусов, угол восьмиугольника.
Рис. 47Следовательно, чтобы вписать пятиугольник в окружность, положите центр транспортира на центр окружности и примените диаметр транспортира к диаметру окружности; затем поставьте точку против 72 d Степень конечности транспортира; и через эту точку и центр круга проведите линию, пересекающую окружность круга в точке С. Теперь возьмите между вашими компасом расстояние между точками В и С, которое разделит окружность круга на 5 равных частей и рисование 5 правильных линий, будет сделан многоугольник.
Если нужно вписать семиугольник, разделите 360 градусов на 7, и частное 51\(\frac{3}{7}\) d покажет, что центральный угол равен почти 51\(\frac{ 1}{2}\) д ; поэтому, поместив транспортир, как и прежде, обратите внимание, 51\(\frac{1}{2}\) градусов на конечность транспортира, через которые проводится линия из центра круга, и вы получите Сторона семиугольника.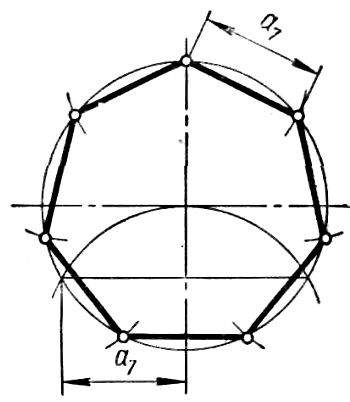
Примечание . На некоторых транспортирах нанесены числа, обозначающие правильные многоугольники, чтобы избежать проблем с делением при нахождении углов в центре: поскольку число 5 для пятиугольника установлено против 72 градусов на конечности транспортира; число 6 для шестиугольника установлено против 60 градусов, число 7 против 51\(\frac{1}{2}\) d и т. д.
Рис. 48Пусть задана линия CD, по которой требуется описать правильный пятиугольник.
Мы показали в предыдущем разделе Использование, как найти углы любого правильного многоугольника; а так как угол, образованный двумя сторонами многоугольника, равен 108 градусам, 54 градуса его половина будет полууглом многоугольника; с помощью которого вы можете описать это следующим образом:
Примените диаметр транспортира к линии CD, а его центр к концу D; затем поставьте точку на 54-м градусе конечности и проведите линию DF, образуя угол 54 9 .0027 d с линейкой CD. Кроме того, переместите центр транспортира на другой конец C и там также сделайте угол 54 градуса, начертив линию CF; затем около Точки Собрания F опишите Окружность с Расстоянием CF. Наконец, возьмите длину данной линии CD и проведите ее по окружности круга, и, проведя четыре прямые линии, получится пятиугольник.
Наконец, возьмите длину данной линии CD и проведите ее по окружности круга, и, проведя четыре прямые линии, получится пятиугольник.
Если восьмиугольник должен быть описан на заданной прямой линии, возьмите половину угла многоугольника, который составляет 67\(\frac{1}{2}\) градусов, и сделайте угол с таким же числом градусов на каждый Конец данной Линии, посредством которой будет образован Равнобедренный Треугольник, вся Вершина будет Центром Окружности, которая будет разделена на восемь равных Частей, ведя Циркуль вокруг нее с Протяженностью данной Линии.
С инструментами, о которых уже говорилось, можно производить гораздо больше Операций; но мы удовлетворимся уже упомянутыми, как наиболее распространенными и полезными.
- Предыдущий Книга I. Глава II. Квадрат
- Содержимое
- Следующий Дополнения к книге I. Глава I. Совместное правило Карпентера и ряд чисел
Документ без названия
Документ без названия
Художники, иллюстраторы и дизайнеры редко нуждаются в навыках механического рисования или специальной учености в области геометрии. Однако знание нескольких простых задач плоской геометрии часто может быть с успехом использовано в определенных классах их работы. Верные методы геометрии гораздо лучше, чем догадки в построении правильных плоских фигур, эллипсов и т. д., не говоря уже об экономии времени и труда.
Однако знание нескольких простых задач плоской геометрии часто может быть с успехом использовано в определенных классах их работы. Верные методы геометрии гораздо лучше, чем догадки в построении правильных плоских фигур, эллипсов и т. д., не говоря уже об экономии времени и труда.
Возьмем, например, деление линии на определенное количество частей. На первой диаграмме этой главы показано, как это сделать. Вам понадобится линейка и треугольник. Также доступна шкала с разметкой в сантиметры и миллиметры, так как с ее помощью очень легко вычислять деления. Вы также можете использовать Т-образный угольник с подвижной головкой, отрегулированной так, чтобы проводить параллельные косые линии. Необходимо, чтобы край чертежной доски был абсолютно прямым при проведении параллельных линий с Т-образным угольником.
Метод, как показано на схеме, отмечая радиус круга на его окружности и получая шесть точек для построения шестиугольника, может быть использован при рисовании сети линий для основы повторяющегося узора. Сделайте круг в середине бумаги и найдите шесть равноудаленных точек, затем через центр круга и шесть точек проведите два набора параллельных линий, как показано на диаграмме. Используя полученные таким образом точки и линии, а также степень наклона этих линий, вся поверхность бумаги может быть покрыта основой, на которой могут быть созданы орнаментальные или цветочные повторяющиеся узоры.
Сделайте круг в середине бумаги и найдите шесть равноудаленных точек, затем через центр круга и шесть точек проведите два набора параллельных линий, как показано на диаграмме. Используя полученные таким образом точки и линии, а также степень наклона этих линий, вся поверхность бумаги может быть покрыта основой, на которой могут быть созданы орнаментальные или цветочные повторяющиеся узоры.
Часто дизайнер хочет нарисовать многоугольник с одинаковым количеством сторон. Как мы видели, легко построить многоугольник из шести равных центров, описывающих дуги D, пересекающиеся пополам в C и D AB в E сторонах, но когда дело доходит до разметки многоугольника с нечетными сторонами, возникает трудность. деления окружности — если взять за начало окружность — на необходимое число равных частей. Диаграмма на стр. 108 в этой главе показывает, как сделать пятиугольник, вписанный в круг, а затем, если хотите, из тех же точек пятиконечную или пятиконечную звезду.
Любой правильный многоугольник можно построить с помощью окружности.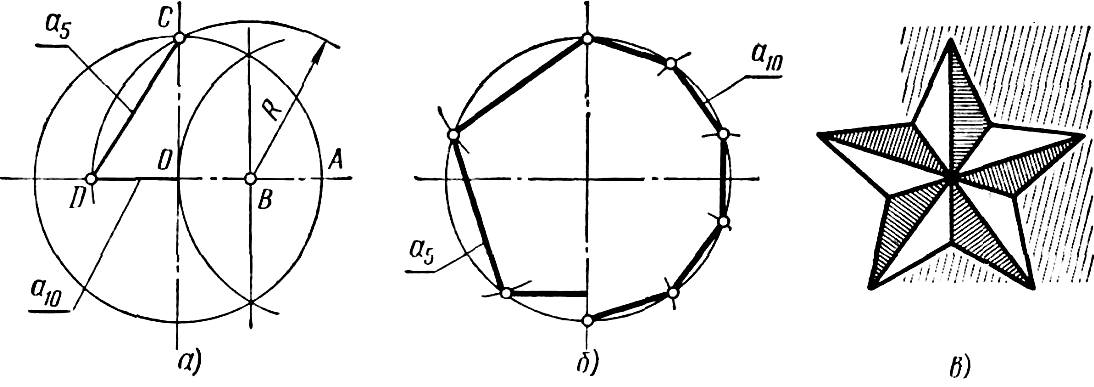 Разделите диаметр круга поровну на столько частей, сколько сторон у искомого многоугольника. Теперь от концов диаметра, как от центров, опишите дуги с радиусами, равными диаметру, и пересекающимися в точке вне круга. Затем из этой точки, где пересекаются две дуги, провести линию через второе из делений по диаметру до и пересекающую окружность окружности. Вот от этой точки до ближайшего конца диаметра у вас теперь одна сторона нужного многоугольника. Это наиболее практичный метод деления кругов или вписывания в них правильных многоугольников, когда требуемое количество сторон является нечетным числом, например 7, 9., или я 1.
Разделите диаметр круга поровну на столько частей, сколько сторон у искомого многоугольника. Теперь от концов диаметра, как от центров, опишите дуги с радиусами, равными диаметру, и пересекающимися в точке вне круга. Затем из этой точки, где пересекаются две дуги, провести линию через второе из делений по диаметру до и пересекающую окружность окружности. Вот от этой точки до ближайшего конца диаметра у вас теперь одна сторона нужного многоугольника. Это наиболее практичный метод деления кругов или вписывания в них правильных многоугольников, когда требуемое количество сторон является нечетным числом, например 7, 9., или я 1.
Важно помнить, что это всегда второе деление диаметра, через которое проводится линия из точки вне круга. Когда дизайнерам нужны овальные или эллиптические формы или части таких форм, они найдут путь через большую ось и одну через малую ось на четыре равные части; тогда как овал можно разделить на равные части только двусторонне; то есть линией, проходящей через длинную ось. Были изобретены специальные инструменты для начертания эллипсов; однако обычно художник может использовать метод, показанный здесь, с использованием булавок и ниток.
Были изобретены специальные инструменты для начертания эллипсов; однако обычно художник может использовать метод, показанный здесь, с использованием булавок и ниток.
Тень круга при определенных условиях, сечение конуса, срезанного наискось, и круг в перспективе имеют эллиптическую форму. Художники могут упростить сложную работу по рисованию колес в перспективе, грубо набросав желаемый размер, а затем построив эллипс такого же размера на другом листе бумаги, который после вырезания можно использовать для начертания четких и определенных контуров в перспективе. просмотренное колесо. Из-за простоты конструкции и того, что с помощью циркуля можно провести тонкие линии, проиллюстрирован метод создания приблизительного эллипса с помощью инструментов. Показан также способ рисования кривой, напоминающей арку моста. Часто в декоративной или промышленной работе дизайнер нуждается не только в точности, но и в точности. прочно выровненный свиток или спираль. Две схемы в этой главе показывают, как механически построить две такие формы с помощью циркуля.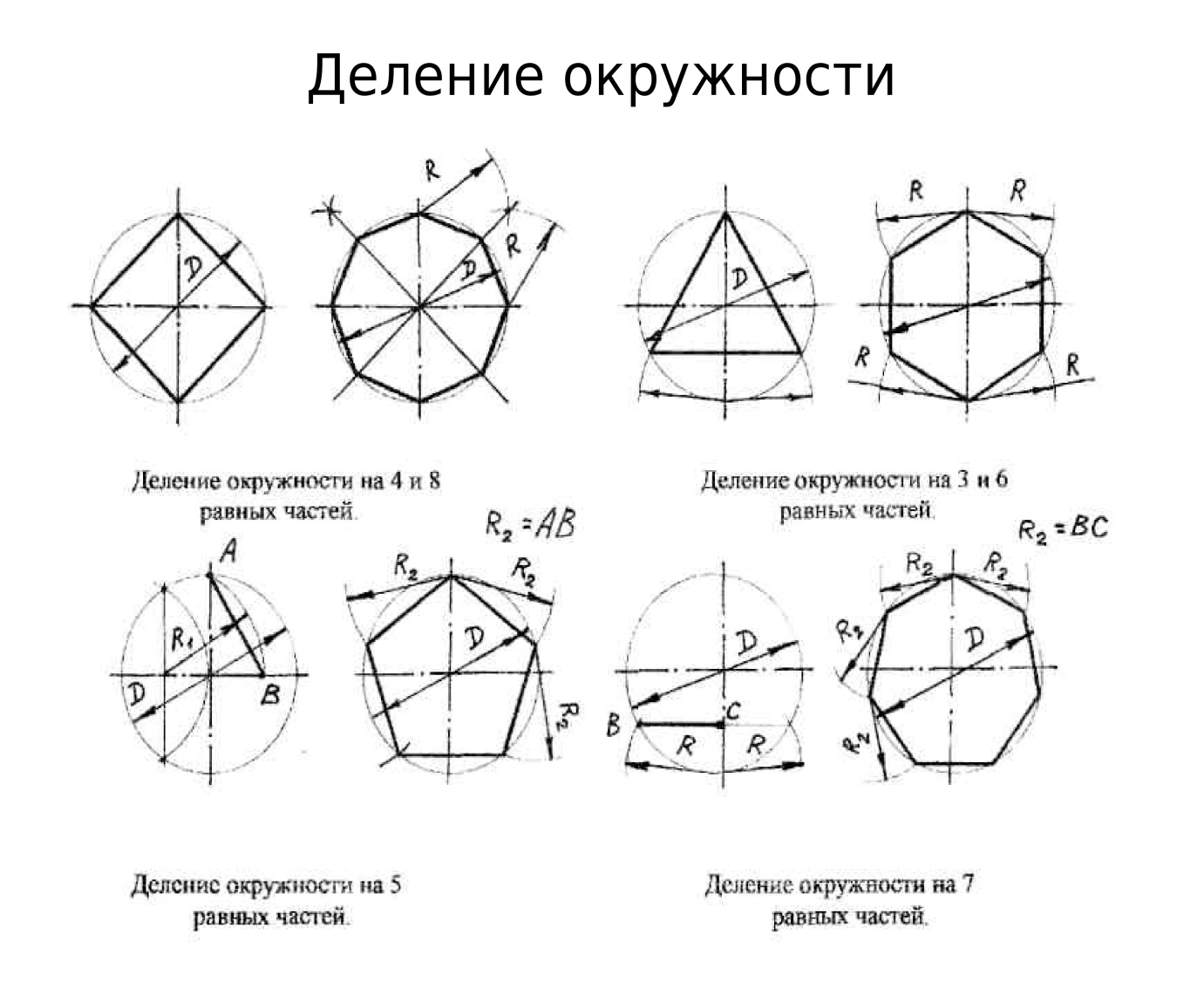
Следующая гравюра объясняет изготовление гораздо более изящного спирального орнамента, а именно ионической волюты. Чтобы нарисовать эту кривую, действуйте следующим образом: линия, представляющая высоту предполагаемой улитки, делится на восемь равных частей. В пятом делении, считая в обратном порядке, опишите круг. Это будет глаз волюты. Впишите в него. квадрат, опирающийся на один угол. Начертите его диаметры и разделите каждый на шесть равных частей; на полученных точках построить три квадрата. меньше по мере необходимости. Стороны маленьких квадратов, если их продолжить легкими вспомогательными линиями, отмечают границы квадрантов и показывают, где они соединяются друг с другом. Сложный рисунок или небольшой набросок можно увеличить, разделив его на несколько маленьких квадратов, а затем разложив большую площадь на такое же количество квадратов, но большего размера. Затем рисунок механически копируется квадрат за квадратом. Конечно, чертежи тоже можно уменьшить квадратами.
Это один из технических приемов в практическом искусстве, который так же стар, как пирамиды, поскольку он, кажется, использовался древними египтянами. Почти в каждом собрании древностей из страны фараонов экспонируется одна или несколько скульпторских копий — каменных плиток с рисунками, поверх которых прочерченными линиями прочерчены квадраты, залитые красным пигментом или мелом. Иногда рисовальщику хочется увеличить этим методом какой-нибудь рисунок, оригинал которого не должен быть изуродован карандашными пометками. Чтобы преодолеть эту трудность, возьмите лист желатина, который используют литографы и офортисты, и процарапайте на нем стальным острием ряд квадратов. Втирайте порошкообразный красный мел в нацарапанные линии, а затем покройте копию желатином. Теперь дизайн можно увидеть разделенным на квадраты красными меловыми линиями.
Когда вы отправляете на фотогравировщик большой рисунок для уменьшения до определенного размера, иногда хочется узнать точную высоту гравировки. Убедиться в этом нетрудно. Помните правило, что прямоугольники, имеющие общую диагональ, пропорциональны, и проведите по наброску легким карандашом диагональ из угла в угол. Теперь держите линейку вдоль края рядом с нижним рисунком ABCD, который должен быть уменьшен до 5 дюймов в ширину. Отметьте тонкую линию от A до D, держите линейку на расстоянии 5 дюймов от стороны AC, держите ее параллельно основанию AB и перемещайте ее вдоль до конца, пока не коснетесь диагональной линии в углу E, где проходит диагональ, затем, удерживая линейку параллельно основанию. и на необходимой ширине продвиньте его вверх, пока конец не коснется диагональной линии. От этой точки по диагонали до базовой линии будет измеряться высота гравировки. Некоторые, кажется, с трудом запоминают, с какой стороны держать дюймовую меру; но, как было сказано выше, памятование о правиле относительно общей диагонали поможет избежать всех трудностей. Когда не рекомендуется делать пометки на рисунке, даже слабо, натяжение веревки вместо диагонали, нарисованной карандашом, очень хорошо подойдет для этой цели.
Убедиться в этом нетрудно. Помните правило, что прямоугольники, имеющие общую диагональ, пропорциональны, и проведите по наброску легким карандашом диагональ из угла в угол. Теперь держите линейку вдоль края рядом с нижним рисунком ABCD, который должен быть уменьшен до 5 дюймов в ширину. Отметьте тонкую линию от A до D, держите линейку на расстоянии 5 дюймов от стороны AC, держите ее параллельно основанию AB и перемещайте ее вдоль до конца, пока не коснетесь диагональной линии в углу E, где проходит диагональ, затем, удерживая линейку параллельно основанию. и на необходимой ширине продвиньте его вверх, пока конец не коснется диагональной линии. От этой точки по диагонали до базовой линии будет измеряться высота гравировки. Некоторые, кажется, с трудом запоминают, с какой стороны держать дюймовую меру; но, как было сказано выше, памятование о правиле относительно общей диагонали поможет избежать всех трудностей. Когда не рекомендуется делать пометки на рисунке, даже слабо, натяжение веревки вместо диагонали, нарисованной карандашом, очень хорошо подойдет для этой цели.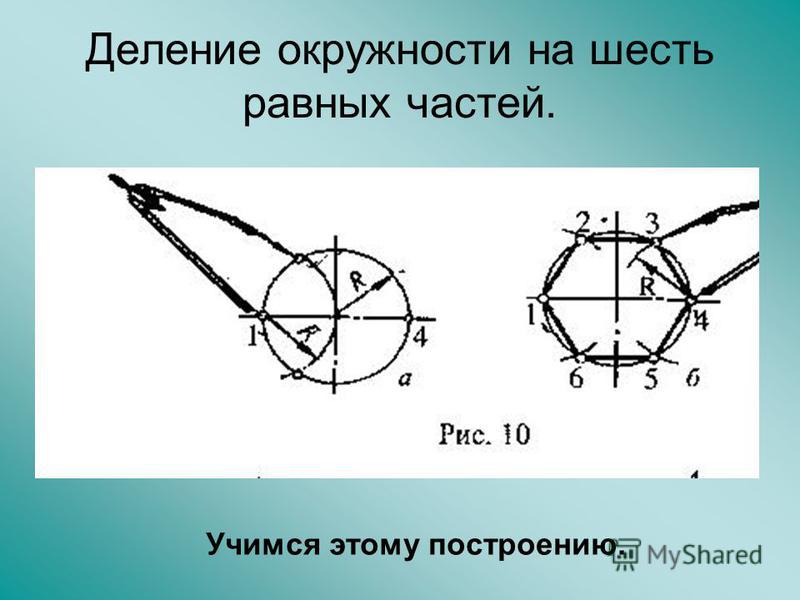


 Расстояние между точками C и D равно длине стороны правильного вписанного пятиугольника (а5), а отрезок OD равен длине стороны правильного вписанного десятиугольника (а10). Деление окружности на пять и десять равных частей, а также построение вписанных правильных пятиугольника и десятиугольника показаны на рисунке 32, б. Примером использования деления окружности на пять частей является пятиконечная звезда (рисунок 32, в).
Расстояние между точками C и D равно длине стороны правильного вписанного пятиугольника (а5), а отрезок OD равен длине стороны правильного вписанного десятиугольника (а10). Деление окружности на пять и десять равных частей, а также построение вписанных правильных пятиугольника и десятиугольника показаны на рисунке 32, б. Примером использования деления окружности на пять частей является пятиконечная звезда (рисунок 32, в). Из точек C и D через четные или нечетные точки деления диаметра
Из точек C и D через четные или нечетные точки деления диаметра 
 ..
..