Единицы длины старинные и современные: Какие Бывают Старинные Меры Длины?

Старинные русские меры длины в современной жизни человека

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа рабочего посёлка Мухен муниципального района имени Лазо Хабаровского края

Проектно-исследовательская работа

«Старинные русские меры длины

в современной жизни человека»

Руководитель работы: Кушнарь Лариса Александровна, учитель математики

Исполнитель: Караванова Алина, обучающаяся 5- а класса

Мухен 2016год

Содержание.

1.Введение………………………………………………………………. 4 стр.

2.Основная часть …………..…………………………………………………. 5 – 14 стр.

2.1. Старинные русские меры длины……………………… 5-9 стр.

2.2. Пословицы и поговорки с использованием старинных русских мер длины………..………………………………………… 10-11 стр.

1. Метрическая система мер……………………………… 12-13

2. Таблица перевода мер длины в различных единицах … 14 стр.

3.Результаты анкетирования………………………………………………….. 15 — 17стр.

4. Таблица роста одноклассников в различных единицах длины…. 18 стр.

5. Выводы……………………………………………………………………………….. 19 стр.

6. Список используемых источников ….………………………….. 20 стр.

Цель исследования: познакомиться со старинными русскими мерами длины.

Задачи:

• изучить старинные русские меры длины;

• исследовать пословицы, поговорки с упоминанием старинных мер длины;

• выяснить, когда появилась единая метрическая мера;

• установить наиболее распространённые старинные и современные меры длины, употребляемые жителями р.п. Мухен;

• составить таблицу перевода мер длины в различных единицах;

• подсчитать рост одноклассников в различных единицах длины;

Гипотеза: я предположила, что старинные русские меры длины редко используются в практической жизни современного человека и малоизвестны.

Методы исследования:

• анкетирование;

• анализ;

• систематизация;

• интервью.

Этапы работы:

• определение темы;

• определение цели и задач;

• выдвижение гипотезы;

• отбор информации из различных источников;

• проведение анкетирования населения;

• измерение роста одноклассников и перевод в различные единицы длины;

• обработка полученного материала;

• систематизация полученной информации ;

• оформление работы;

• создание буклета;

• презентация работы.

Сроки работы над исследованием: сентябрь 2015г-февраль 2016 г.

Продукт проекта: информационный буклет.

1. Введение.

Актуальность исследования.

Математику невозможно представить без подсчетов, вычислений, измерений.

Если до 18 в. людей устраивало измерение длины аршином, саженью, верстой, то уже в конце 19 века такие величины стали неприемлемыми. Это обусловлено временем: развитие экономических отношений, в том числе между странами, во — вторых, для человека стали важны точность, конкретность, четкость в расчетах.

Современным школьникам не понятны название старинных мер длины, которые они могут встретить в русских народных сказках, пословицах и поговорках, а так же в речи людей старшего поколения.

Я решила соотнести старинные единицы измерения длины с современными.

1. Основная часть

2. 1 Старинные русские меры длины

С древности, мерой длины и веса всегда был человек: на сколько он протянет руку, сколько сможет поднять на плечи и т.д. Система древнерусских мер длины включала в себя следующие основные меры: версту, сажень, аршин, локоть, пядь и вершок.

АРШИН [5.4] — старинная русская мера длины, равная, в современном исчислении 0,7112м. Аршином, так же, называли мерную линейку, на которую, обычно, наносили деления в вершках.

Есть различные версии происхождения аршинной меры длины. Возможно, первоначально, «аршин» обозначал длину человеческого шага (порядка семидесяти сантиметров, при обычной ходьбе по равнине, в среднем темпе) и являлся базовой величиной для других крупных мер определения длины, расстояний (сажень, верста). Корень «АР» в слове  а р ш и н — в древнерусском языке (и в других, у соседних народов) означает «ЗЕМЛЯ», «поверхность земли», «борозда» и указывает на то, что эта мера могла применяться при определении длины пройденного пешком пути. Было и другое название этой меры – ШАГ. Практически, счёт мог производиться парами шагов взрослого человека, нормальной комплекции («малыми саженями»;  раз-два – один,  раз-два – два,  раз-два – три …), или тройками («казёнными саженями»;  раз-два-три – один,  раз-два-три – два …), а при измерении шагами небольших расстояний, применялся пошаговый счёт. В дальнейшем, стали так же применять, под этим названием, равную величину – длину руки.

Рис.1

Купцы, продавая товар, как правило, мерили его своим аршином (линейкой) или по-быстрому – отмеряя ‘от плеча’. Чтобы исключить обмер, властями был введён, в качестве эталона – «казенный аршин», представляющий собой деревянную линейку, на концах которой клепались металлические наконечники с государственным клеймом.

ШАГ[5.4] — средняя длина человеческого шага = 71 см. Одна из древнейших мер длины.

ПЯДЬ[5.4] (пядница) — древняя русская мера длины.

МАЛАЯ ПЯДЬ[4](говорили — «пядь»; с 17-го века она называлась — «четверть» ) — расстояние между концами расставленных большого и указательного (или среднего) пальцев = 17,78 cm.

БОЛЬШАЯ ПЯДЬ[4] — расстояние между концами большого пальца и мизинца (22-23 см.).

П Я Д Ь С КУВЫРКОМ[5.2](«пядень с кувырком», по Далю — ‘п я д ь  с  кувыркой’) — пядь с прибавкой двух суставов указательного палица = 27-31 см

 ВЕРСТА[4] — старорусская путевая мера (её раннее название — »поприще»). Этим словом, первоначально называли расстояние, пройденное от одного поворота плуга до другого во время пахоты. Два названия долгое время употреблялись параллельно, как синонимы. Известны упоминания в письменных источниках 11 века. В рукописях XV в. есть запись: «поприще сажений 7 сот и 50» (длиной в 750 сажень). До царя Алексея Михайловича в 1 версте считали 1000 саженей. При Петре Первом одна верста равнялась 500 саженей, в современном исчислении — 213,36 X 500 = 1066,8 м.
«Верстой» также назывался верстовой столб на дороге.
МЕЖЕВАЯ ВЕРСТА[5.2]— старорусская единица измерения, равная двум верстам. Версту в 1000 сажен (2,16 км) употребляли широко в качестве межевой меры, обычно при определении выгонов вокруг крупных городов, а на окраинах России, особенно в Сибири — и для измерения расстояний между населенными пунктами.

Рис.2

САЖЕНЬ[5.2] — одна из наиболее распространенных на Руси мер длины. Различных по назначению (и, соответственно, величине) саженей было больше десяти.

«Маховая сажень»[5.2]–расстояние между концами средних пальцев раскинутых в стороны рук =1,76м.

» Косая сажень «[5.2] — самая длинная: расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки. (2,48м.) Наименование с а ж е н ь происходит от глагола сягать (досягать) — на сколько можно было дотянуться рукой.. Существовали саженные мерные верёвки и деревянные «складени», имевшие применение при измерении расстояний в строительстве и при межевании земли.

1 сотая сажени[5.2] = 2,134 см

По данным историков и архитекторов, саженей было более 10 и они имели свои названия, были несоизмеримы и не кратны одна другой. Сажени: городовая — 284,8 см, без названия — 258,4 см, великая — 244,0 см, греческая — 230,4 см, казённая — 217,6 см, царская — 197,4 см, церковная — 186,4 см, народная — 176,0 см, кладочная — 159,7 см, простая — 150,8 см, малая — 142,4 см и ещё одна без названия — 134,5 см (данные из одного источника), а так же — дворовая, мостовая.

 ЛОКОТЬ[5.4] равнялся длине руки от пальцев до локтя (по другим данным — «расстояние по прямой от локтевого сгиба до конца вытянутого среднего пальца руки»). Величина этой древнейшей меры длины, по разным источникам, составляла от 38 до 47 см.). Локоть широко применяли в торговле — как особенно удобную меру. В розничной торговле холстом, сукном, полотном — л о к о т ь был основной мерой. С 16-го века постепенно вытесняется аршином и в 19 веке почти не употребляется.

ЛАДОНЬ[5.4]= 1/6 локтя (локоть шестиладонный)

ПЕРСТ [5.4]= 2 см

 ВЕРШОК[5.4]равнялся 1/16 аршина, 1/4 четверти. В современном исчислении — 4,44см. Наименование «Вершок» происходит от слова «верх». В литературе XVII в. встречаются и доли вершка – пол вершки и четверть вершки.

1 дюйм[5.2] = 10 линий = 2,54 см
Название происходит от голландского — »большой палец». Равен ширине большого пальца или длине трех сухих зерен ячменя , взятых из средней части колоса.

1 линия[5.2]= 10 точек = 1/10 дюйма = 2,54 . Линия — ширина пшеничного зерна, примерно 2,54 мм.

1 точка[5.2]= 0,2540 миллиметра

1 географическая миля[5.2] (1/15 градуса земного экватора) = 7 верст = 7,42 км
(от латинского слова «милия» — тысяча двойных шагов, «тростей»)
1 морская миля[5.2](1 минута дуги земного меридиана) = 1,852 км
1 ярд[5.2] = 91,44 сантиметра

2.1 Пословицы и поговорки с использованием старинных русских мер длины

Широкое распространение среди людей старинных мер длины доказывают сложенные русским народом пословицы и поговорки .

1. Аршин да кафтан, да два на заплатки — 0,71 м да кафтан, да 1,42 м на заплатки.

2. Борода с вершок, а слов с мешок — борода с 44 см, а слов с мешок.

3. Врёт семь верст до небес, и все лесом — врёт 7,469 км до небес, и все лесом.

4. За семь верст комара искали, а комар — на носу — за 7,469 км комара искали, а комар — на носу.

5. На три аршина в землю видит — на 2,13 м в землю видит.

6. Охотник за семь верст ходит киселя хлебать — охотник за 7,469 км ходит киселя хлебать.

7. Ты от правды на пядень, а она от тебя на сажень — Ты от правды на 19 см, а она от тебя на 2,13 м.

8. Тянись верстой, да не будь простой — тянись 1,067 км, да не будь простой.

9. Два вершка (или полвершка) от горшка, а уже указчик — 0,888 м (или 0,222 м) от горшка, а уже указчик.

10. У нее суббота через пятницу на два вершка вылезла — у нее суббота через пятницу на 0,888 м вылезла.

11. Не уступишь не пяди — не уступишь не 27 см.

12. Уступишь на пядь, потеряешь сажень — уступишь 27 см, потеряешь 2,13 м.

13. Семь пядей во лбу — 189 см во лбу.

14. Сам с ноготок, а борода с локоток — сам с локоток, а борода 38—46 см.

15. Шагнул и царство покорил — на 71 см шагнул и царство покорил.

16. Ни шагу назад! — ни 71 см назад.

17. Каждый купец на свой аршин меряет — каждый купец на свои 71 см меряет.

18. На аршин борода, да ума на пядь — на 71 см борода, а ума на 27 см.

19. Косая сажень в плечах — 2,13 м в плечах.

20. Москва верстой далека, а сердцу рядом — Москва на 1,067 км далека, а сердцу рядом.

21. Любовь не верстами меряется — любовь не 1,067 км меряется.

22. От слова до дела — целая верста — от слова до дела — 1,067 км.

23. Верстой ближе, пятаком дешевле — 1,067 км ближе, пятаком дешевле.

24. Семь верст молодцу не крюк — 7,469 км молодцу не крюк.

25. .  Его за версту видно — его видно за 1,067 км.

26. .  От мысли до мысли пять тысяч верст — от мысли до мысли — 5335 км.

Метрическая система мер

Потребности практики заставили начать поиски единой системы мер. При этом было ясно, что надо отказаться от установления связей между единицами измерения и размерами человеческого тела. И шаг у людей бывает разный, и длина ступни у них неодинакова, и пальцы у них разной ширины. Поэтому надо было искать новые единицы измерения в окружающей природе.

Метрическая система мер была введена впервые во Франции в 1795 году

[1]. В 1792 году Парижская академия наук решила измерить длину земного меридиана, проходящего через Париж. Отдельные части этого меридиана были измерены. Длины других частей были вычислены на основе этих измерений. В результате большой работы была найдена длина парижского меридиана в существовавших тогда французских мерах длины – туазах (1м 95 см).

На Всемирной выставке 1867 года в Париже в организованном там международном комитете мер, весов и монет русский академик Б. С. Якоби выступал с докладом. В нём он сформулировал преимущества метрической системы как экономически самой выгодной вследствие её десятичной основы.

Основная единица системы мер должна быть определена посредством материального эталона, который наиболее точно воспроизводит длину архивного метра. Комиссия утвердила эталон метра, изготовленный из сплава платины ( 90%) и иридия ( 10%)[5.4].

К 1875 году метрическую конвенцию подписали уже 17 государств, включая Россию, где применение новой системы было разрешено, но не стало законом.

В 1889 году международные прототипы метра и килограмма были сданы в Бретейльский павильон (здание во Франции). С этого момента метр и килограмм стали определяться как длина и вес международных эталонов.

В России учёные с начала X1X века поняли значение метрической системы и пытались её широко внедрить в практику. Окончательное решение вопрос о метрической системе в России получил уже после Великой Октябрьской социалистической революции. С 1 января 1927 года, когда переход промышленности и транспорта на метрическую систему был подготовлен, метрическая система стала единственно допускаемой в СССР системой мер и весов. Большие заслуги во введении и распространении метрической системы мер в нашей стране принадлежит Дмитрию Ивановичу Менделееву, великому русскому химику.

К 1972 году метрическую конвенцию подписало уже 41 государство. Творцы этой универсальной системы мер написали на талоне метра: «На все времена всем народам!».

Для популяризации новых мер поэт В.В.Маяковский написал стихотворные тексты, посвящённые новым мерам.

2.4.Таблица перевода мер длины в различных единицах

№	Название старинной русской меры длины	СМ	М	км
1	Аршин	71,12см	0,7112м	0,0007112км
2	шаг	71см	0,71м	0,00071км
3	Малая пядь	17,78см	0,1778м	0,0001778км
4	Большая пядь	22см	0,22м	0,00022км
5	Пядь с кувырком	28см	0,28м	0,00028км
6	верста	106680см	1066,8м	1,0668км
7	Межевая верста	216000см	2160м	2,16км
8	Маховая сажень	176см	1,76м	0,00176м
9	Косая сажень	248см	2,48м	0,00248км
10	1 сотая сажени	2,134см	213,4м	0,00213км
11	локоть	47см	4,700м	0,047км
12	перст	2см	200м	0,02км
13	вершок	4,44см	444м	0,00444км
14	1дюйм	2,54см	254м	0,00254км
15	1 линия	25,4см	254м	0,00254км
16	1 точка	2,54см	254м	0,00254км
17	1 географическая миля	7,42см	742м	7,42км
18	1 морская миля	18,52см	1852м	1,852км
19	1 ярд	91,44см	9144м	0,09144км

Таблица 1

Приложение 2

1. Результаты анкетирования.

Анкетирование проведено по возрастным группам:

1 группа – с 9 -14лет;

2 группа – с15 — 18 лет;

3 группа- с 19 – по 50 лет;

4 группа – с 50 лет и старше.

Вопросы анкеты:

1. К какой возрастной группе Вы себя относите?

2. Какие современные меры длины Вы знаете?

3. Какие старинные русские меры длины Вы знаете?

Анализ анкет:

1 группа (9-14 лет)		2 группа (15-18лет)			3 группа (19-50 лет)			4группа (старше 50 лет)
мм	100%	мм	100%	см		92%	мм		100%
см	100%	см	100%	дм		92%	см		100%
м	100%	м	100%	м		77%	м		80%
км	90%	дм	78%				км		80%
аршин	50%	дюйм	67%	сажень		78%	аршин		100
Локоть	40%	верста	44%	аршин		46%	сажень		100
верста	20%			дюйм		31%	локоть		40
				Локоть		23%
Не знаю	40%	Не знаю	22%	Не знаю		8%	не знаю		0

Таблица 2

Из представленной диаграммы следует: самые популярные современные единицы длины – миллиметр и сантиметр, а также метр, чуть реже используются километр и дециметр.

Представленная диаграмма свидетельствует, что самые популярные старинные русские единицы длины среди современного населения – сажень, аршин, локоть, верста.

Сравнение популярности современных и старинных русских мер длины

Таблица 3

Сравнительный анализ позволяет сделать вывод:

• население знает и использует современные русские меры длины;

• старинные меры длины постепенно вытесняются из обихода;

• молодые люди называют старинные меры длины, но затрудняются в определении их значения.

1. Таблица роста одноклассников в различных единицах длины

Рост учащихся за 5 класс (2015 г.)

№	Фамилия , имя, учащихся	метр	аршин	маховая сажень	вершок	ярд
1	Белоусова Дарья	1,58м	2,22	0,35	0,90	0,17
2	Кузьмичева Татьяна	1,51м	2,12	0,86	0,34	0,16
3	Мелентьева Евгения	1,54м	2,17	0,87	0,35	0,17
4	Пугачев Семен	1,59м	2,24	0,90	0,36	0,17
5	Хабло Анатолий	1,61м	2,26	0,91	0,36	0,18
6	Пожидаева Диана	1,52м	2,14	0,86	0,34	0,17
7	Халилов Николай	1,60м	2,25	0,90	0,36	0,17

таблица 4

Вычисляя рост одноклассников через различные единицы длины, пришла к выводу, что это трудоемкий и неточный подсчет, что каждая из единиц длины может быть представлена через общепринятую метрическую систему мер, а следовательно, становится понятной для любого человека.

1. Выводы

Проведенное исследование показывает, что в России существовало огромное количество всевозможных единиц. В рамках своей работы, я доказала неточность старинных русских мер длины, неудобство их в применении, что и привело к созданию единой метрической системы.

В своей работе я:

• изучила старинные русские меры длины;

• изучила пословицы, поговорки со старинными мерами длины;

• составила таблицу перевода мер длины в различных единицах ;

• выразила рост учащихся 5 класса на данный момент времени в различных единицах длины;

• выразила его в метах, маховых саженях, аршинах, вершках, ярдах;

• провела анкетирование среди населения, с целью выявления популярности использования и знания русских мер длины;

• провёли сравнительный анализ по данным анкетирования;

• создала информационный буклет о старинных мерах длины.

Таким образом, гипотеза «старинные русские меры длины редко используются в практической жизни современного человека» нашла подтверждение.

Для понимания материала на уроках литературы, истории, математики , я создала информационный буклет по старинным мерам длины взаимосвязи их с современными.

1. Список используемых источников

1. Глейзер, Г.И. История математики в школе./ Г.И. Глейзер. – М.: Просвещение, 1981.

2. Марков, С.Н. Курс истории математики: Учеб.пособие./ С.Н. Марков. — Иркутск: Издательство Иркут. Ун-та, 1995.

3. Аменицкий, Н.Н. Забавная арифметика [Текст]/ Н.Н. Аменицкий – Москва «Наука», 1991. – 123 с.

4. Виленкин, Н.Я., Депман, И.Я. За страницами учебника математики [Текст]/ Н.Я. Виленкин, И.Я. Депман — М., 1981. – 217 с.

5. Интернет — ресурсы:

1. decoder. ru›list/all/topic_114/

2. mer.kakras.ru

3. traditio-ru.orgwiki/Русские_меры

4. ru.wikipedia.org›Русская система мер

5. nsportal.ru›…nauchno…starinnye—russkie—mery—dliny…

6. http://blog.kp.ua/users/muhobat/rubric/1407685/page6.html — картинка

15

Внеурочное занятие по математике «Старинные меры длины» | Дополнительное образование

Автор: Капустина Валентина Ивановна

Организация: МОУ «Останинская основная общеобразовательная школа»

Населенный пункт: Курская область, с.Останино

Цель занятия:

Познакомиться со старинными мерами длины , сопоставить их с современными мерами и научиться применять полученные знания .

Личностные УУД:

Умение ясно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл

поставленной задачи, проявлять инициативу, находчивость.

Метапредметные УУД:

Регулятивные:

Умение определять и формулировать цель занятия, проговаривать последовательность действий , работать по плану, оценивать правильность выполнения действия в соответствии с поставленной задачей.

Коммуникативные:

Умение организовывать сотрудничество и совместную деятельность с учителем и сверстниками.

Познавательные:

Умение переводить старинные меры длины в современные.

Необходимое оборудование: компьютер, проектор, экран. раздаточный материал, буквы

П,О, Б ,Е,Д,А, звездочки, шаблон салюта .

Ход занятия

1. Мотивация учебной деятельности.

Здравствуйте, ребята! Я рада встрече с вами. Сядьте удобно и повторяйте за мной: « Я хочу учиться. Я готов к работе . Я внимателен и все замечу. Я радуюсь этому».

2.Актуализация знаний и формулирование темы занятия.

Прежде, чем узнать тему занятия, мы с вами разгадаем кроссворд . (1 слайд)
 

 

1.Самая маленькая единица длины? (миллиметр) (2 слайд)
2. Единица для измерения расстояния между городами? (километр) (3 слайд)
3. 100 см одним словом называется ? (метр)

(4 слайд)
4. Эта мера в 10 раз больше миллиметра. (сантиметр) (5 слайд)
Знакомы вам эти слова ? Что объединяет все эти понятия? (Это меры длины.) Какими инструментами мы пользуемся для измерения длины? (ответы детей). Были ли эти инструменты в старину? Правильно, таких инструментов не было, но в жизни людям приходилось выполнять измерения. Как они это делали , узнаете, послушав стихотворение:

Не имели наши предки

Ни линейки, ни рулетки.

Но могли предмет любой

Измерять самим собой.

Ткани мерили локтями,

Землю мерили лаптями,

И имели пальцев пять –

Щели в доме измерять.

В общем, жили не тужили,

Не хлебали лаптем щей…

И всему на свете были

Люди – мерою вещей!

Что значит, «люди были мерою вещей» ? В давние времена, не имея измерительных приборов под рукой, люди придумали меры, используя части своего тела — пальцы, руки, ноги.

Тема занятия « Старинные меры длины». (6 слайд)

— Как вы думаете , чем мы сегодня будем заниматься ?.( мнение учащихся)

— Сегодня вы познакомитесь со старинными мерами длины , научитесь переводить их в современные единицы измерения. Чтобы советоваться, помогать друг другу , вы объединились в группы . В каждой группе есть «Историк», «Практик», «Литератор», «Математик».

Эпиграфом будут слова «Где нет знаний, там нет победы» .(7 слайд )

Как вы думаете, почему?

Учащиеся отвечают (Да, верно, каждый день, занимаясь успешно на занятии, вы одерживаете пусть маленькие, но победы).

3. Познавательная деятельность

 

Слышали ли вы о старинных мерах длины? ( ответы детей)

Что это за меры, и как их можно использовать, мы узнаем, выполнив первое задание.

 

1 задание «Старинные меры длины».

1 группа

1) («Историк» читает, «Практик» показывает наглядно) (8 слайд )

ПЯДЬ — древняя русская мера длины.

МАЛАЯ ПЯДЬ — расстояние между концами расставленных большого и указательного пальцев.

БОЛЬШАЯ ПЯДЬ — расстояние между концами большого пальца и мизинца.

Вершок – длина верхней части указательного пальца.

2) Как вы думаете, что можно измерить с помощью этих мер длины? (длину учебника, ручки, тетради, парты и т.д.)

2 группа

1) («Историк» читает, «Практик» показывает наглядно) ( 9 слайд)

— САЖЕНЬ — одна из наиболее распространенных на Руси мер длины..

Косая сажень измерялась расстоянием от пальцев левой ноги до конца пальцев поднятой правой руки.

Маховая сажень измерялась расстоянием между кончиками пальцев расставленных в стороны рук.

2) Как вы думаете, что можно измерить с помощью этих мер длины?

 

3группа

1)(«Историк» читает, «Практик» показывает наглядно) ( 10 слайд)

Аршин – это длина руки от плеча до конца среднего пальца.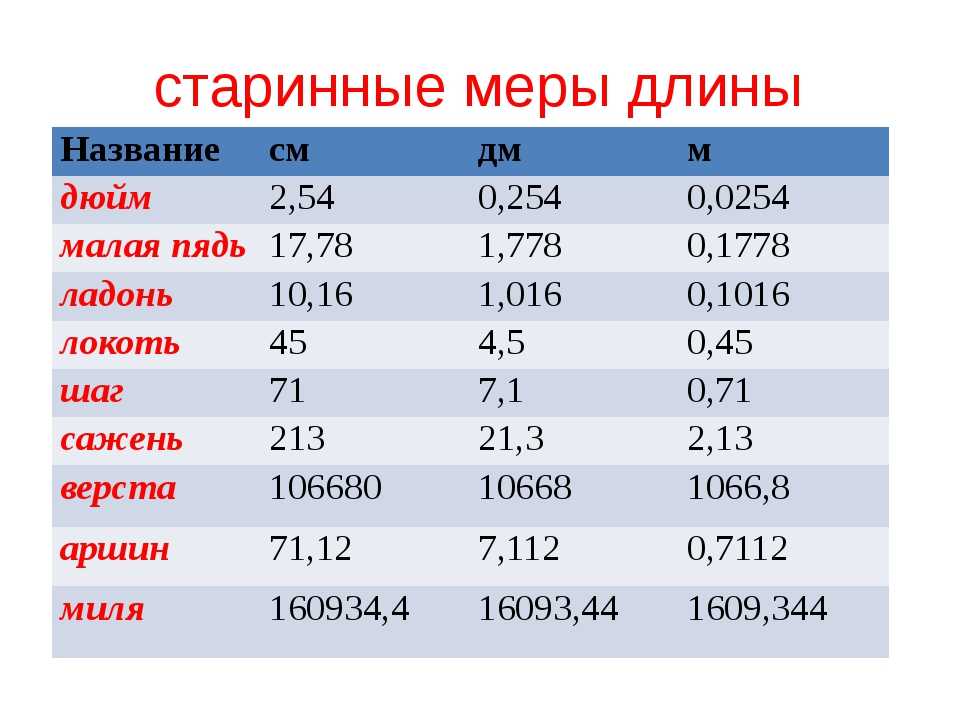

 

Локоть приблизительно равнялся длине локтевой кости человека.

 

2) Что было удобно измерять этой мерой длины? (длину нитки, веревки, ткани)

Вывод: О каких старинных мерах длины вы узнали?( ответы) (

11 слайд)

Все эти меры представляли собой измерения различных частей человеческого тела.

Ребята, а почему для нас важно знать старинные меры длины?

(Для нас важно знать их, чтобы всегда можно было прикинуть измерения. Ведь инструменты для этого всегда с человеком – руки, ноги).

Практическая работа «Удобны ли старинные меры длины в современном быту?»

Измерить длину стола малой и большой пядью.

Сравнить полученные данные с результатами взрослого человека (учителя). Они разные.

Мы убедились , что старинные меры длины не дают точного результата.

-Удобно ли пользоваться этими мерками в современной жизни ? Почему они утратили свою значимость? ( Старинные меры длины утратили свою значимость по причине своей неточности и неудобства. Они были заменены на единицы измерения , принятые во всем мире.)

Однако упоминания о них можно встретить в выражениях, пословицах и поговорках.

Задание 2 « Соотнесите выражения , пословицы и поговорки с их значением» (12 слайд)

 

Выражения, пословицы, поговорки	Значение
Семь пядей во лбу.	Говорят об очень умном, мудром человеке.
Косая сажень в плечах.	Говорят о сильном человеке, богатыре.
Общим аршином мерить.	Относиться ко всему как к обычным явлениям.
Быть на вершок от смерти.	Находиться в опасной ситуации.
От горшка два вершка, а уже указчик.	Говорят о самонадеянном человеке, не имеющем жизненного опыта.

Самопроверка

Название старинной меры длины	Перевод в современные меры длины
аршин	71см
вершок	4 см 5 мм
малая пядь	18 см
локоть	45 см
шаг	71см
косая сажень	248 см

Встречаются старинные меры длины в произведениях русских поэтов и писателей.

Чтобы понять их приблизительные значения , существует таблица перевода старинных мер длины в современные.

Задание 3 «Перевод в современные меры длины»

1 группа.

1) Прочитать отрывок из стихотворения Николая Алексеевича Некрасова

«Дедушка Мазай и зайцы» (Читает «Литератор»)

Вижу один островок небольшой –

Зайцы на нем собралися гурьбой.

С каждой минутой вода подбиралась

К бедным зверькам: уж под ними осталось

Меньше аршина земли в ширину,

Меньше сажени в длину.

2) Насколько мал был тот островок? Каковы его максимальные размеры в современных мерах длины ? Вычислите и заполните таблицу. (использовать таблицу перевода)

	Старинная мера	Перевод в современные
Ширина острова
Длина острова

(озвучивает «Математик» )

1)Ширина острова – 1 аршин * 71 см = 71 см

Длина острова – 1 сажень * 248 см = 248 см

2 Группа

1. Прочитать отрывок из стихотворения Петра Павловича Ершова

«КОНЕК ГОРБУНОК» (Читает «Литератор»)

Да игрушечку — конька

Ростом только в 3 вершка

На спине с двумя горбами
Да с аршинными ушами.

2. Вычислить рост конька , длину его ушей в современных мерах длины и заполните таблицу. (использовать таблицу перевода)

	Старинная мера	Перевод в современные
Рост Конька
Длина ушей Конька

(озвучивает «Математик» )

Рост Конька – 3 вершка * 4 см 5 мм = 13 см 5 мм

Длина ушей – 1 аршин * 71 см = 71 см

3 Группа

1. Прочитать отрывок из былины «Три поездки Ильи Муромца»

Хорош был у Ильи конь. Хвост у Бурушки двух саженей, грива до колен, а шерсть трех пядей…

2. Вычислить длину хвоста и шерсти Бурушки в современных мерах длины и заполните таблицу. (использовать таблицу перевода)

	Старинная мера	Перевод в современные
Длина хвоста Бурушки
Длина шерсти Бурушки

(озвучивает «Математик» )

Длина хвоста – 2 сажени * 248 см = 496 см =4 м 96 см

Длина шерсти – 3 пяди * 18 см = 54 см

4. Физкульминутка

 

-Жил былинный богатырь — в высоту хорош и вширь (расставить ноги на ширине плеч, руки упереть в бока).

Ильей Муромцем он звался, на рассвете просыпался (потянуться вверх).

Становился на крыльцо,

Умывал росой лицо.(движения как при умывании)

Выходил во двор босой, (шаги на месте)

Делал ловкий взмах косой (взмахнуть рукой, будто косишь траву).

И уставши от работ, вытирал со лба он пот. (движение ладонью по лбу).

После в Избу возвращался (шаги на месте)

И за завтрак принимался.

Кашу ел, да квас он пил, (движения рукой)

Набираться чтобы сил.(руку слегка согнуть в локте, и напрячь, как бы показывая мускулы)

5. Применение знаний и умений в новой ситуации

1 группа – Задание :«Старинные русские меры длины» ;

2 группа — Задание :« Старинные меры длины в пословицах и поговорках» (Собрать пословицы и поговорки .)

3. группа — Задание :« Старинные меры длины в ребусах»

6. Включение знаний в систему повторения.

 

Старинные меры длины используются при решении задач.. Решив их, вы соберете секретное слово, и узнаете, как оно связано с нашим уроком.

1. Вычислить: «семь пядей во лбу»? (Пядь = 18 см) 18*7=126 см

Г	Д	П
106	226	126


2) Купили 100 аршинов ткани. Сколько это метров ткани?
Решение:1 аршин = 71 см, 100 аршин = 71*100 = 7100 см = 71 м.

К	О	Л
710	71	701

3. Длина бревна 5 аршин. За одну минуту от этого бревна отпиливают по одному аршину. За сколько минут будет распилено все бревно?

Л	А	Б
6	5	4

 

4) Выразите в сантиметрах высоту терема , равную трем косым саженям? (248 *3=744см)

Е	Д	К
744	710	704

 

5. Выразите в сантиметрах длину отрезка полотна , равную 15 локтям?(15*45=67

Д	З	И
675	605	615

 

6. «Отдал царевич приказание и вскоре явились во дворец 12 добрых молодцев , все на одно лицо и ростом с косую сажень» Какова роста были добры молодцы?

М	А	С
208	248	218

Получилось слово : ПОБЕДА. Вернемся к эпиграфу урока. Достигли ли вы победы на уроке? Да, вы общими усилиями пришли к ней, и заслужили победный салют!( наклеивает каждый звездочку на шаблон салюта)

7. Подведение итогов занятия.

 

1) Рефлексия.

— Что вы нового узнали?

— Какое задание на ваш взгляд было самым интересным?

— Зачем современному человеку знать старинные меры длины?

— Что из услышанного на занятии вы расскажите друзьям или родителям?

2)Заключительное слово учителя: старинные русские меры неудобны, поэтому редко используются в жизни современного человека, но знать о них нужно, так как это поможет провести приблизительные измерения, если нет других инструментов. Так же, старинные меры длины часто встречаются в текстах рассказов, сказок, стихотворений, и зная, что они означают, будет проще понять смысл. Все, связанное с происходящим в давние времена, часть истории нашей страны, и нужно знать ее прошлое, чтобы создать прекрасное будущее.

3) Задание на дом. ( по желанию)

Найти информацию о старинных мерах длины , с которыми не успели познакомиться на занятии и рассказать об этом всему классу.

 

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

 

1. Виленкин, Н.Я., Депман, И.Я. За страницами учебника математики [Текст]/ Н.Я. Виленкин, И.Я. Депман — М., 1981. – 217 с.
2. История развития метрологии [Электронный ресурс]/ Режим доступа: http://www.metrologie.ru, свободный. Загл с экрана. – Яз. рус.
3. «Русские народные загадки, пословицы и поговорки» – М.: « Просвещение», 1990
4. Карпушина, Н.М. Рукотворные мерки[Текст]/ Н.М. Карпушина // Математика в школе. — 2008.- №7. –С.49-61.
5. Меры длины [Электронный ресурс]/ Режим доступа: http://www.iro.yar.ru, свободный. Загл с экрана. – Яз. рус.
6. Сравнительная таблица русских и метрических мер [Электронный ресурс]/ Режим доступа: http://trust.narod.ru, свободный. Загл с экрана. – Яз. рус.

 

Приложение

Приложения:

1. file0.docx.. 76,2 КБ
2. file1.docx.. 2,7 МБ
Опубликовано: 18.11.2021

История метрологии: 5 более древних инструментов измерения

В предыдущих сообщениях этого блога мы обсуждали инструменты метрологии, которые либо можно найти в вашей повседневной жизни, либо были древними инструментами измерения, и мы хотели бы обсудить эту тему. вернуться сюда. Хотя мы часто отслеживаем усовершенствование единиц измерения и инструментов с момента основания метрологии в 18 веке, важно помнить, что человечество не просто щелкнуло выключателем в 1700-х годах и внезапно начало заботиться о стандартизированных измерениях. Путь к стандартизации растянулся на тысячи лет и проходил по разным направлениям в цивилизациях по всему миру.

Инструменты измерения, используемые в древние времена, заложили основу для инструментов, единиц и методов, которые позже будут приняты Международной системой единиц (СИ) для формирования метрической системы. И многие из этих инструментов были усовершенствованы и усовершенствованы до такой степени, что их древние формы используются до сих пор. Ниже приведены еще 5 самых ранних и наиболее важных инструментов метрологии:

1) Солнечные часы/Обелиски

Возможно, это первая зарегистрированная попытка отслеживать ход времени в течение дня. Древние египтяне построили большие каменные башни, называемые Обелисками, в честь богов. и короли. И каждый обелиск был подношением богу солнца, сделанным на нужной высоте и расположенным так, чтобы первый и последний свет дня касался вершины. Отметки на земле могли затем отслеживать тень, которую солнце отбрасывало на башню в течение дня, и определять время. Меньшие версии того же принципа, называемые солнечными часами, стали популярными в Египте и Древнем Риме до более поздних изобретений водяных часов и песочных часов. Хотя солнечные часы по-прежнему популярны в качестве украшений или в исторических местах, в конечном итоге они не были достаточно точными для точного определения времени, поскольку изменяющийся наклон оси Земли ежегодно меняет продолжительность светового дня в течение сезона.

2) Термометры

На первый взгляд, термометр является одним из последних изобретенных инструментов измерения до метрологии, поскольку Габриэль Фаренгейт и Андерс Цельсий внесли решающий вклад в измерение температуры в начале 1700-х годов. Но концепцию термометра, пузырька воздуха, перемещаемого в жидкости в разные точки по высоте за счет расширения или сжатия жидкости из-за изменений температуры воздуха, на самом деле можно найти в Древней Греции примерно в первом веке до нашей эры. Галилею приписывают дальнейшее совершенствование конструкции флорентийского термометра, сделанного в 1650-х годах Андреа Мариани. Флорентийские термометры в основном использовали воду или вино в качестве жидкости, но в ходе испытаний Фаренгейт обнаружил, что ртуть имеет более стабильные скорости расширения и сжатия в 1714 году. шкала. И по Фаренгейту, и по Цельсию вклад в измерение температуры используется и сегодня.

3) Уровень A-Frame

Задолго до того, как появились лазерные уровни или даже пузырьковые уровни, древние египтяне должны были обеспечить горизонтальность пирамид и других сооружений с помощью аналоговых измерительных инструментов. Решением стала простая А-образная рама (вероятно, деревянная) с веревкой, свисающей из центра буквы «А». Груз, размещенный на конце струны, будет тянуть струну в одном направлении, если уровень А-образной рамы будет помещен на не идеально плоскую поверхность. На поперечной балке «А» можно было нанести маркировку, указывающую, насколько далеко от центра находилась измеряемая поверхность. Эта простая конструкция (единственным реальным ограничением которой был размер рамы) будет использоваться до тех пор, пока в Европе не будет сформирована СИ. Изобретение вулканизированной резины позволило начать массовое производство спиртового уровня, который впервые превзошел уровень с А-образной рамкой.

4) Барометр

Ранее мы упоминали Галилея как одного из отцов Термометра, но за изобретением Барометра мы фактически обращаемся к его помощнику Эванджелисте Торричелли в 1640-х годах. Изучая влияние воздуха на забор воды из глубоких колодцев, Торричелли разработал эксперимент по погружению трубки с ртутью в ртутную ванну и герметизации открытого конца. По мере того, как ртуть перемещалась по трубке от запаянного конца, Торричелли пришел к двум выводам: во-первых, вес воздуха над ванной должен поддерживать ртуть в трубке все еще над поверхностью, и во-вторых, пространство в трубке выше поэтому ртуть должна быть вакуумом. Это был один из первых экспериментов, бросивших вызов давнему убеждению, что «природа не терпит пустоты», но более поздние тексты, проведенные Блезом Паскалем и его зятем в 1646 году, подтвердили теорию Торричелли и доказали, что атмосферное давление различается в зависимости от погодных условий и на разных высотах. Изобретение барометра произвело революцию в нашем понимании погодных явлений, и они до сих пор являются основным инструментом метеорологов в прогнозировании погоды.

5) Транспортир

На протяжении веков транспортиры применялись по-разному. Простой полукруг с плоской кромкой позволяет измерять угол двух пересекающихся линий. Современный транспортир, конструкция которого практически не изменилась, был разработан Джозефом Хаддартом для морской навигации в начале 19 века. Позже этот инструмент стал полезен для строительства и помог расширить наше понимание геометрии. Но теперь считается, что гораздо более ранняя версия инструмента использовалась в Древнем Египте архитектором Кха, который помогал строить гробницы фараонов около 1400 г. до н.э. Эта конструкция представляла собой полный круг, опирающийся на плоский стержень. Когда стержень опирался на линию или поверхность, он проводил отвесную линию через угловые отметки на круге, чтобы определить угол.

Перечисленные здесь предметы — это больше, чем просто названия древних измерительных инструментов. Многие из этих инструментов все еще используются сегодня в той или иной форме, и они помогают проиллюстрировать, как еще до дисциплины метрической системы, СИ и формального изучения метрологии люди разрабатывали передовые методы измерения, которые позволяли им выполнять инженерные и строительные подвиги, изменившие саму форму нашего мира.

Источники:

https://www.worldhistory. org/Egyptian_Obelisk/ https://www.whipplemuseum.cam.ac.uk/explore-whipple-collections/meteorology/early-thermometers-and-temperature- весы

History of Thermometers

https://www.johnsonlevel.com/news/HistoryoftheLevelHowtheBu

https://www.britannica.com/technology/hand-tool /Инструменты на основе винтов#ref39230

https://www.thoughtco.com/how-barometers-measure-air-pressure-3444416

https://mtiinstruments.com/knowledge-center/history-of-measurements /

http://www.historyworld.net/wrldhis/PlainTextHistories.asp?historyid=ac07

Знаете кого-нибудь, кому тоже было бы полезно прочитать эту статью?
Почему бы не поделиться с ними!

Единицы измерения длины и скорости света в Древней Индии

Точное значение единицы измерения длины, использовавшейся в цивилизации Инда Сарасвати , было определено по точной шкале, обнаруженной Эрнестом Маккеем в 1930-х гг. 31 сезон раскопок в Мохенджо-Даро , и далее соотносится с современными единицами измерения. Затем было вычислено и показано, что скорость света, указанная в ведической литературе, при сопоставлении с этой прежней единицей измерения длины (использовавшейся в цивилизации Инда-Сарасвати) оказывается в точности равной скорости света согласно современные измерения. Настоящая статья представляет собой пошаговый процесс раскрытия этого равенства.

Точная шкала

В сезоне 1930-31 в Мохенджо-Даро Эрнест Маккей обнаружил обломок раковины с 8 делениями по 6,7056 мм каждое, с точкой и кружком, разделенными пятью делениями, что предполагает десятичную систему. Однако попытки Маккея связать такую ​​единицу измерения с измерениями в Мохенджо-Даро не увенчались успехом и поэтому были оставлены.

Единицы длины в «Артхашастре» Чанакьи

Чанакья был политическим наставником легендарного индийского монарха Чандрагупта Маурья 4 века до н. э. Он был человеком, сведущим во многих дисциплинах, и написал знаменитую книгу Артхашастра. В Артхашастра, Чанакья упоминает два типа Дхануш в качестве единиц измерения длин и расстояний. Один из них обычный Дхануша , , состоящий из 96 Ангул , , а другой Дхануша упоминается как Гархпатья Дхануша и состоит из 108 Angulas , используются для измерения дорог и расстояний. Чанакья также упоминает, что Дханурграха состоит из 4 Ангул , а Йоджана состоит из 8000 Дхануш.

Расшифровка шкалы Мохенджо-Даро

Если мы сохраним 10 делений шкалы Мохенджо-Даро равными Дханурграха или 4 Ангула, точная длина Ангула получается равной быть 16,764 мм .

Дхануша из 96 Ангул = 96 x 16,764 мм = 1,609344 м

Дхануша из 108 Ангул = 108 x 16,764 мм = 1,810512 м

Йоджана = 8000 Дхануша (по 108 Ангул каждая) = 8000 x 1,810512 м = 14,484096 км

14,484096 км = 9 миль (точно!).

1000 Дхануш по 96 Ангул каждая = 1 миля

Интересно, что когда мы изучаем историю мили, , мы обнаруживаем, что слово миля происходит от миля, , что означает тысяча.

Прочие древние шкалы

Индский дюйм

Единицей длины цивилизации Инда, широко известной как Индский дюйм , было 1,32 дюйма, что в точности равно 2 Angulas по 16,764 мм каждый.

Правило Гудеа

Правило Гудеа (2175 г. до н.э.), хранящееся в Лувре, показывает интервалы в шумерском Шуси в 0,66 дюйма, что в точности равно Индо-Сарасвати Ангула 90 055 калибра 16,764 мм.

Настенные гравюры храма

На двух гравюрах на стене храма по адресу Тирупуткали (XII век н.э.) недалеко от Канчипурама изображены две шкалы, одна из которых имеет длину 7,24 метра, с отметками, делящими шкалу на 4 равные части, а другая второй размером 5,69метров в длину и разметкой, делящей шкалу на 4 равные части. Можно заметить, что каждое деление первой шкалы в точности равно дхануше 108 Ангул по 16,764 мм каждый. Интересно, что вторая шкала точно равна 71 раз Дхануша, то есть равна окружности круга с одной Дханушей в качестве его Диаметра.

Здесь интересно отметить, что Маккей сообщает в Мохенджо-Даро о переулке и дверном проеме, имеющих ширину 1,42 м, что точно равно одному делению второй шкалы в храме Тирупуткали, указывая на то, что обе шкалы были распространены в цивилизации Инда-Сарасвати, а также в Южной Индии.

Соотношение с размерами древних построек

Большая баня Мохенджо-Даро

Высота водосточного желоба, образующего выход Великой бани Мохенджо-Даро, составляет около 1,8 м, что соответствует дхануше из 108 ангулов по 16,764 мм каждая. .

Стандартная ширина улиц

Калибангам , город в цивилизации Инда-Сарасвати (в Раджастане, Индия) имел ширину улиц 1,8 м, 3,6 м, 5,4 м и 7,2 м, т.е. построен по стандартным размерам, равным 1 Дхануша, 2 Дхануши, 3 Дхануши и 4 Дхануши соответственно. Такие ширины встречаются и на других сайтах. Большие улицы Банавали , другой город в цивилизации Инда-Сарасвати (в Харьяне, Индия), размер 5,4 м, т.е. 3 дхануши.

Великая пирамида в Гизе, Египет 3104BC

Из точных измерений основания Великой пирамиды длина ее диагонали с северо-запада на юго-восток составляет 325,87 м, что точно равно 180 Дхануш из 108 Angulas каждый, разница всего 0,02 м, что находится в пределах погрешности измерения. Ясно, что в то время в Египте преобладали единицы длины Инда Сарасвати.

Тадж-Махал

Персидская рукопись « Шах Джахан Нама » содержит очень подробное описание трех основных зданий Агры — Тадж-Махала, Моти Масджид и Джамах Масджид. В «Шах Джахан Нама» размеры этих трех зданий даны в газ. Эти размеры были измерены цв. Дж.А. Ходжсоном в декабре 1825 г., в футах и ​​дюймах. Различные размеры в футах и ​​дюймах, а также Gaz, приведены Ходжсоном в его статье в Таблице А. Средневзвешенная длина Gaz соответствует 31,7 дюймам (80,5 см) из таблицы A. Здесь уместно упомянуть, что Барро в «Полном Тадж-Махале и колоннах на берегу реки Агры» принял Gaz за 80,5 см, что точно равна половине Дхануша из 96 Ангул.

Город майя в Мексике (Северная Америка)

Дрюитт и Друкер изучили древний город Теотиуакан, принадлежащий цивилизации майя в Мексике, и выдвинули гипотезу о единице 80,5 см, которая точно равна половине Дхануша из 96 Ангулы.

Скорость света в ведической литературе

Саяна (ок. 1315-1387) был премьер-министром при дворе императоров Букка I и его преемников Империи Виджаянагар и ведический ученый. В своем комментарии к четвертому стиху гимна 1.50 Ригведы о Солнце он говорит:

татха ча смарйате йоджананам сахастрм две две шате две ча йоджане экена имишардхена крамаман намостуте.
. शते द्वे च योजने एकेन निमिषार्धेन क्रममाण नमोऽ स्तुते॥

«[О Солнце] поклон тебе, кто проходит 2,202 Йоджана в Нимишарде ».

Совершенно очевидно, что в шлоке упоминается Скорость света (или солнечных лучей). Эта шлока приписывается сыну Канвы Махарши (5-й меллениум до н.э.). Бхатта Бхаскара (вероятно, из 10 века нашей эры) сделал то же самое заявление в своем комментарии к Taittiriya Brahmana , еще одна индуистская Веда.

Говоря математическим языком, как сказано в приведенной выше шлоке, скорость света будет равна:

Скорость 0f Свет = 2202   Йоджанас/Нимишардха

Как мы подсчитали ранее, йоджана = 14,484096 км. Для значения Нимишардхи, мы ссылаемся на Вишну Парана , где указано, что:

• 15 Нимиша = 1 Каштха
• 30 Каштас = 1 кала
• 30 Калас = 1 Мухурта
• 30 Мухуртас = 1 день и ночь

Так

один день и ночь = 405, 000 Нимиши = 810, 000 Нимиши.  (Буквальное значение Нимишардха — это половина Нимиша).

В Сурья Сидхант (Глава 1, Шлока 12), утверждается, что 60 Нади составляют один Звездный День и Ночь. Также хорошо известно, что мухурты = 2 нади. Отсюда видно, что в астрономических расчетах за единицу времени принимались звездные сутки. Звездные сутки — это время, за которое созвездия совершают один оборот вокруг Земли. Звездные сутки равны 23 часам 56 минутам и 4,1 секунды или, что эквивалентно, 86 164,1 секунды.

Итак…

Нимишардха = 86164,1/810000 с = 0,1063754 с

Скорость света, указанная в ведической литературе, таким образом, получается:

, что в точности равно скорости света согласно последним современным измерениям.

Выводы

Из вышеизложенного можно сделать следующие выводы:

1. Основной единицей измерения длины в Индо-Сарасватской цивилизации была девятка.