Геометрия. Формулы en App Store
Это приложение – бесплатный справочник формул геометрии для вычисления периметра, площади и объема геометрических фигур и объемных тел.
В разделе «Периметр» приведены формулы для следующих фигур:
прямоугольник, квадрат, трапеция, параллелограмм, ромб, треугольник, круг, дуга, длина дуги по формуле Гюйгенса.
В разделе «Площадь» приведены формулы для следующих фигур:
— плоских фигур: прямоугольник, квадрат, трапеция, параллелограмм, правильный многоугольник, ромб, сектор круга, круг, сегмент круга, кольцо (по радиусам и диаметрам), сектор кольца;
— треугольник: формула площади, формула Герона, площадь через углы, прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник;
— объемных тел: сферы, куба, круглого конуса, цилиндра, прямоугольного параллелепипеда, усеченного конуса, шарового сегмента, шарового слоя, шарового сектора;
— правильных многоугольников: треугольника, четырехугольника, пятиугольника, шестиугольника, многоугольника;
— пирамид: треугольной пирамиды, четырехугольной пирамиды, шестиугольной пирамиды, площадь через высоту;
— боковой поверхности пирамид: пирамиды, усеченной пирамиды, через высоту;
— призм: треугольной призмы, четырехугольной призмы, пятиугольной призмы, шестиугольной призмы;
— боковая площадь прямых призм: прямой призмы, треугольной призмы, четырехугольной призмы, пятиугольной призмы, шестиугольной призмы. 2}$
2}$
Наклон $m$ линии, соединяющей две точки $P_1(x_1 \textrm{ , } y_1)$ и $P_2(x_2 \textrm{ , } y_2)$
$m = \frac{y_2 — y_1}{x_2 — x_1} = \textrm { tan } \theta$
Уравнение линии, соединяющей две точки $P_1(x_1 \textrm{ , } y_1)$ и $P_2(x_2 \textrm{ , } y_2)$
$\frac{y — y_1}{x — x_1} = \frac{y_2 — y_1}{x_2 — y_1} = m$
или
$y — y_1 = m(x — x_1) \\ y = mx + b$
где $b = y_1 — mx_1 = \frac{x_2y_1 — x_1y_2}{x_2 — x_1}$ пересечение на $y$ оси, т.e. $y$ пересечение.
Уравнение линии в условиях $x$ пересекает $a \ne 0$и $y$ пересекает $b \ne 0$
$\frac{x}{a} + \frac{y}{b} = 1$
Нормальная форма уравнения линии
$x \textrm{ cos } \alpha + y \textrm{ sin } \alpha = p$где $p$ = перпендикулярное расстояние от центра $O$ к линии
и α = Угол наклона перпендикуляра
с положительной $x$ осью.
Общее уравнение линии
$Ax + By + C = 0$
Расстояние от точки $(x_1 \textrm{ , } y_1)$ к линии $Ax + By + C = 0$
$\frac{Ax_1 + By_1 + C}{\pm \sqrt{A^2 + B^2}}$
где знак выбирается так, что расстояние не отрицательно.
Угол $\psi$ между двумя линиями, имеющими наклоны $m_1$ и $m_2$
$\textrm{ tan } \psi = \frac{m_2 — m_1}{1 + m_1m_2}$
Линии параллельны или совпадают тогда и только тогда, когда $m_1 = m_2$
Линии перпендикулярны тогда и только тогда, когда $m_2 = -\frac{1}{m_1}$
Площадь треугольника с вершинами в $(x_1 \textrm{ , } y_1) \textrm{ , } (x_2 \textrm{ , } y_2) \textrm{ , } (x_3 \textrm{ , } y_3)$
Площадь
$ = \pm \frac{1}{2} \left| \begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{array} \right|$
$= \pm \frac{1}{2} ( x_1y_2 + x_2y_3 + x_3y_1 — x_1y_3 — x_2y_1 — x_3y_2 )$
где знак выбран так, что площадь является неотрицательной. Если площадь равна нулю, все точки лежат на одной прямой.
Математика. Вывод формул по геометрии. | Vseznayka
Доброго времени суток. Сегодня мы познакомимся с очень необычной темой объединяющую высшую математику и школьную геометрию.Данная статья будет очень полезной для старшеклассников и студентов младших курсов. Мы постараемся разобраться с выводом формул для нахождения площади некоторый геометрических фигур, так как не все до конца понимают как их вывести, но мы это поможем исправить. Приступим.
Первая формула, которую мы будем выводить, это площадь квадрата или равностороннего четырёхугольника, что равнозначно. Зарисуем картиночку, для наглядности. Ведь нужно понимать как всё что будем находить выглядит геометрически.
Задаём уравнение прямой (y=a) и пределы интегрирования. для того чтобы получить квадрат, нужно совпадение значений по оси «y» и по «x». Иначе говоря, значение по оси «игрек» должно равняться значению по оси «икс».Задаём уравнение прямой (y=a) и пределы интегрирования. для того чтобы получить квадрат, нужно совпадение значений по оси «y» и по «x». Иначе говоря, значение по оси «игрек» должно равняться значению по оси «икс».
Часть работы выполнена. Осталось разделаться с практической частью, то есть связать нашу картинку с интегралами. Для нахождения площади могли использовать двойные интегралы. Но зачем усложнять себе работу, если в нашем случае можно использовать обычные. Составим интеграл и решим.
Осталось разделаться с практической частью, то есть связать нашу картинку с интегралами. Для нахождения площади могли использовать двойные интегралы. Но зачем усложнять себе работу, если в нашем случае можно использовать обычные. Составим интеграл и решим.
Получилось то что и ожидали.
Решение оказалось не очень сложным для большинства читающих (на это надеюсь по крайней мере). Найдя первообразную, но заменив пределы интегрирования в таком интеграле, не сложно придти к формуле площади прямоугольника. Именно этим мы сейчас и займёмся.
Нет особых различий с прошлым примером. В данном случае значение параметра «b» может принимать различные численные значения от «a».Нет особых различий с прошлым примером. В данном случае значение параметра «b» может принимать различные численные значения от «a».
Куда же без картинки. Перейдём к практической части…
Заменили предел интегрирования, получили формулу площади прямоугольника. Прям чудеса.
Прям чудеса.Заменили предел интегрирования, получили формулу площади прямоугольника. Прям чудеса.
Разобрались с прямоугольником. Напоследок оставили самую необычную геометрическую фигуру, это треугольник. Разновидностей их очень много, но мы рассмотрим только один, прямоугольный. Опираться будем на уравнение прямой (y=kx+b), но при условии что «b=0», сдвиг по оси «игрек» учитывать не будем. Нарисуем картинку.
Углы «альфа» и «бетта» могут менять своё значение в зависимости от длин сторон «a» и «b».Углы «альфа» и «бетта» могут менять своё значение в зависимости от длин сторон «a» и «b».
Как видим, мы будем находить площадь через две стороны. Используя основное тригонометрическое тождество выведем формулу Пифагора. Которая гласит, что площадь прямоугольного треугольника не зависит от углов, а лишь от длин сторон (катетов).
За «С» мы обозначили гипотенузу прямоугольного треугольника.За «С» мы обозначили гипотенузу прямоугольного треугольника.
Перейдём к вычислению площади.
k — угловой коэффициент, показывающий угол наклона прямой. К примеру: если k>1, то и отношение «a/b>1», из этого следует что значение «a>b».k — угловой коэффициент, показывающий угол наклона прямой. К примеру: если k>1, то и отношение «a/b>1», из этого следует что значение «a>b».
Запишем все полученные за сегодня формулы.
Запоминание и понимание, как мы видим, требуют разную умственную нагрузку. Чтобы понять, приходится проделать большую работу и запоминается такая информация гораздо лучше.
Не все могут подобного рода действия проделать. Но наша задача, чтобы, после прочтения этой статьи, вы могли всю написанную информацию изложить своими словами и донести до других. Заканчивая на прекрасной ноте, пришло время закругляться. В следующий раз, выведем более интересные формулы из раздела геометрии. Оставляйте свои отзывы по поводу новой тематики.Спасибо за внимание.
Другие темы:
Картинки формулы по геометрии (50 фото)
Существует множество формул по геометрии, которые находят применение среди различных областей науки. Для начала нужно изучить основные фигуры как на плоскости, так и в трехмерном пространстве. А только затем стоит приступать к освоению формул по геометрии. В итоге вы с легкостью сможете посчитать периметр треугольника, радиус окружности, объем параллелепипеда. Предлагаем тут посмотреть красивые картинки про формулы по геометрии.
Вычисляем площади простых фигур.
Квадрат, ромб, трапеция.
Формулы по геометрии для нахождения площади.
Прямоугольный треугольник, теорема Пифагора.
Уравнения с синусами и косинусами.
Картинка формул по геометрии.
Расчет площади параллелограмма.
Диагональ шестиугольника, вписанный угол.
Формулы по геометрии для объемов.
Учебник из школьного курса.
Равнобедренный треугольник.
Важные формулы геометрии на картинке.
Справочный материал студентам.
Расчет длины окружности.
Медиана, биссектриса в формулах по геометрии.
Фигуры разных форм.
Площадь прямоугольника.
Геометрические формулы в ячейках.
Свойства четырехугольников.
Памятка с большим количеством информации.
Интересная картинка формул по геометрии.
Ищем площади фигур.
Зеленый цвет квадрата.
Одни из главных формул по геометрии.
Тригонометрическое тождество.
Разнообразие форм у фигур.
Формулы по геометрии из нескольких величин.
Площадь равностороннего треугольника.
Сопоставить фигуру с равенством.
Формулы по геометрии на картинке.
Простое задание школьнику.
Полезная таблица.
Прилежащий катет в формуле по геометрии.
Функции для острого угла.
Площадь фигуры, периметр, полупериметр.
Классные формулы по геометрии с теоремами.
Правильные многоугольники.
Стороны, средняя линяя, высота.
Прямоугольный треугольник в формулах по геометрии.
Фигуры на плоскости.
Проходим формулы по геометрии.
Длина медианы.
Чертежи, подробные обозначения.
Прикольная картинка формул по геометрии.
Площадь произвольного треугольника.
Материал для заучивания наизусть.
Формулы по геометрии на зеленом фоне.
Задачи по пройденному материалу.
Тела вращения.
Формулы по геометрии для разных видов треугольников.
Понравился пост? Оцените его:
Рейтинг: 5,00/5 (голосов: 1)
Поделитесь с друзьями!
Формулы. Геометрия. (5 класс) — презентация онлайн
5 класс.Жила-была загадочная принцесса Формула.
Она была непоседа и постоянно путешествовала из государства Алгебра в государство
Геометрия. Она имела множество имён и так
часто менялась, что подданные не узнавали
её в лицо. То она Формула Пути, то Формула
для Вычисления Площади Прямоугольника.
Она очень добра и всегда готова помочь тому,
кто не только узнаёт её с первого взгляда, но
и знает наизусть все её имена.
 Потому что
Потому чтоФОРМУЛА – это…
a
Что общего в записанных
b
предложениях?
ПРАВИЛА
Как
найти
площадь
Площадь
прямоугольника
равна
прямоугольника,
известны
произведению длинесли
его сторон
его стороны?
Как
найтипрямоугольника
периметр
Периметр
равен
прямоугольника,
если известны
сумме
длин его сторон
его стороны?
Как
найти пройденный
путь, если
Пройденный
путь – это произведение
известны
скорость
скорости навремя
времяидвижения
движения?
ФОРМУЛЫ
S=a∙b
Как записать эти правила
Pна= математическом
a + a + b + b или
P =языке?
2(a + b)
s=v∙t
Правило, записанное на математическом языке,
– это формула
Формула площади
прямоугольника
ФОРМУЛЫ
S=a∙b
P = a + a + b + b или
P = 2(a + b)
s=v∙t
В дальнейшем вы узнаете
еще много новых формул…
Формулы периметра
прямоугольника
Формула пути
Формула пути.

s=v∙t
v=s:t
s = v ∙ t 90 км
12 км
t=s:v
120 км
3600м
v = s : t 15 км/ч 6 км/ч 60км/ч 6 м/с
t=s:v
6ч
2ч
2ч
10 мин
Задача.
Автомобиль движется со скоростью 60 км/ч.
За какое время он пройдёт путь в 600 км?
s=v∙t
t=s:v
Задача.
C какой скоростью должен идти человек,
чтобы пройти 24 км за 4 ч?
s=v∙t
v=s:t
Задача.
Подсказка
С одной станции в противоположных направлениях
одного поезда 50 км/ч, а другого – 70 км/ч. Какое
расстояние между ними будет через 2 часа?
s=v∙t
2ч
2ч
70 км/ч
50 км/ч
?
240 км
Задача.
Подсказка
Расстояние между двумя городами 600 км.
Навстречу друг другу из этих городов вышли
одновременно две автомашины. Одна имеет
скорость 90 км/ч, а другая – 110 км/ч. Чему будет
равно расстояние между машинами через 2 часа?
?
2ч
90 км/ч
?
2ч
s=v∙t
110 км/ч
600 км
220 км
Формула площади
прямоугольника.

a
S=a∙b
а=S:b
S
90
см2
b
b=S:a
12 км2 120 мм2
36 м2
a
15 cм
6 км
6 мм
6м
b
6 см
2 км
2 см
60 дм
Задача.
Найдите сторону прямоугольника, если его
площадь 364 см2, а длина 26см.
26 см
364 см2
S=a∙b
b=S:a
?
Подсказка
Задача.
Два прямоугольника имеют равные площади.
Длина первого прямоугольника 16 см, а его
ширина на 12 см меньше длины. Длина второго
прямоугольника 32 см. Найдите ширину
второго прямоугольника.
S1
S1 = S2
S2
a = 16 см
Дополнительно
b = 16 — 12 (см)
S1
S=a∙b
S1 = 16 (16 – 12) = 64 (см2)
a = 32 см
S2
S1 = S2
2 cм
S2 = 64 см2
b=S:a
b = 64 : 32 = 2 (см)
Чему равна сторона квадрата, имеющего такую же
площадь, что и эти прямоугольники?
8 cм
S3
а-?
S1 = S2 = S3
Sкв =
2
a
S1
S3 = 64 см2 а = 8 см
S2
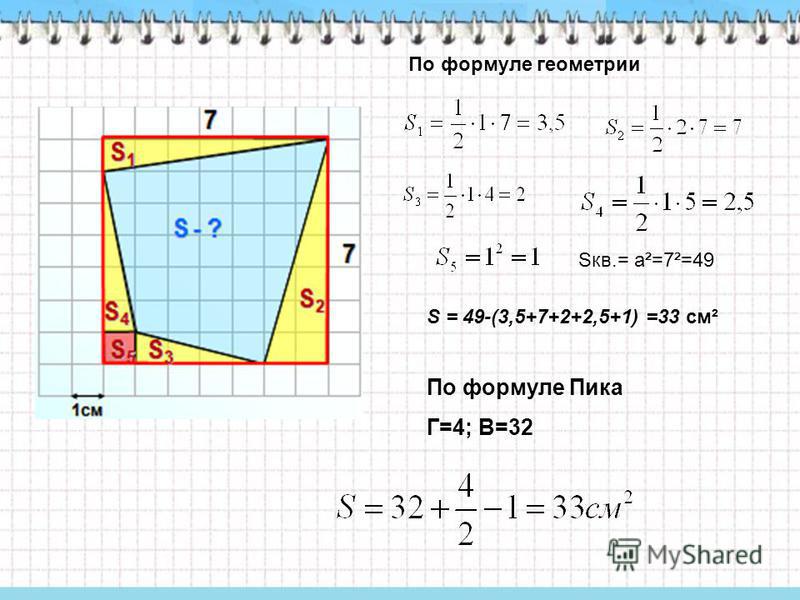
Найдите площадь фигуры, изображённой на рисунке, если
условиться, что длина стороны каждой клетки равна 1 см.
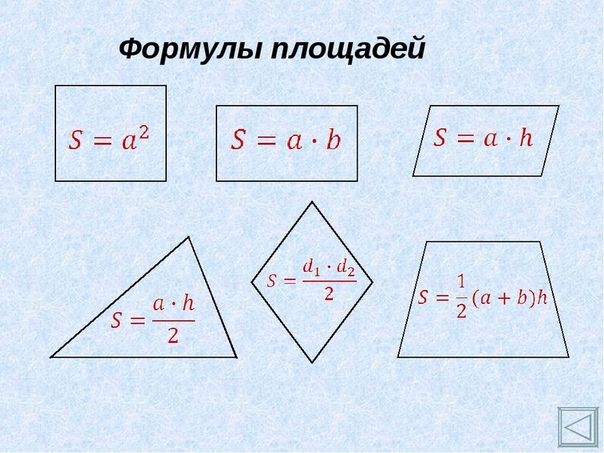
19 см2
Молодец!
16 см
15 см2
24 см2
Найдите площадь фигуры, изображённой на рисунке, если
условиться, что длина стороны каждой клетки равна 1 см.
14 см2 Молодец!
15 см2
16 см2
20 см2
Найдите площадь фигуры, изображённой на рисунке, если
условиться, что длина стороны каждой клетки равна 1 см.
40 см2
36 см2
42 см2
38 см2
Правильно!
Подсказка (3 – 1)
Задача.
Начертите прямоугольник АВСD, соедините
отрезком вершины А и С. Найдите площади
треугольников АВС и АСD, если АВ = 6 см и
ВС = 5 см.
А
6 см
В
5 см
S=a∙b
D
15
2
см
С
S2 = 6 5 = 30 (см2)
SADC = SABC
SABCD = SADC + SABC
SADC = SABC = SABCD : 2
Решение(3 – 3)
Формула периметра
прямоугольника.
P = a + a + b + b или
P = 2(a + b)
а
14
21
24
12
b
26
29
12
24
a+b
40
80
50
36
36
100
72
72
2(a + b)
Используя формулу периметра прямоугольника, найдите:
1) Периметр Р, если а = 3м 5дм, b = 1м 2дм
а = 3м 5дм = 35дм
b = 1м 2дм = 12дм
Р = 2(a + b)
Р = 2(35 + 12) = …
94 дм
Используя формулу периметра прямоугольника, найдите:
2) Сторону а, если Р = 3дм, b = 6см.

Р = 3дм = 30см
b = 6см
Р = 2(a + b)
a+b=P:2
а = 15 — b
a + b = 30 : 2 = 15 (см)
а = 15 — 6
9 cм
Математический диктант
1 вариант
2 вариант
1
Используя формулу s = vt, найдите неизвестную величину:
V (км/ч)
t (ч)
27
60
6
480
S (км)
V (км/ч)
4
t (ч)
520
S (км)
23
70
9
3
420
280
2
Используя формулу S = ab, найдите неизвестную величину :
a (м)
5
b (м)
74
S (м2)
4
3
840
a (м)
5
b (м)
94
S (м2)
4
3
92
720
Формулы объема геометрических фигур.
Объем геометрической фигуры
— количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба:
V = a3
где V — объем куба,
a — длина грани куба.

Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
V = So h
где V — объем призмы,
So — площадь основания призмы,
h — высота призмы.
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
V = So · h
где V — объем параллелепипеда,
So — площадь основания,
h — длина высоты.
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
V = a · b · h
где V — объем прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.
Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды:
где V — объем пирамиды,
So — площадь основания пирамиды,
h — длина высоты пирамиды.
Объем правильного тетраэдра
Формула объема правильного тетраэдра:
где V — объем правильного тетраэдра,
a — длина ребра правильного тетраэдра.
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Формулы объема цилиндра: где V — объем цилиндра,So — площадь основания цилиндра,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.141592.
Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса:
где V — объем конуса,
So — площадь основания конуса,
R — радиус основания конуса,
h — высота конуса,
π = 3.141592.
Объем шара
Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.
Формула объема шара:
где V — объем шара,
R — радиус шара,
π = 3.141592.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Базовая формула геометрии — Фарина Аслам
| Базовая формула геометрии |
Периметр прямоугольника = 2 (длина + ширина)
Площадь прямоугольника = длина × ширина.
Периметр квадрата = 4 × длина стороны.
Площадь квадрата = длина стороны × длина стороны.
Объем куба = длина × ширина × высота.
Прибыль = Цена продажи — себестоимость.
Убыток = Себестоимость — цена продажи.
Понятие основных математических формул
Основные математические формулы обычно используются в основной математике и используются не только в академических книгах, но и в нашей повседневной жизни. В начальном классе мы все узнали об общем правиле BODMAS. По мере приближения к старшим классам от шести до десяти человек будет сталкиваться с различными математическими формулами, основанными на различных концепциях, таких как алгебра.
В начальном классе мы все узнали об общем правиле BODMAS. По мере приближения к старшим классам от шести до десяти человек будет сталкиваться с различными математическими формулами, основанными на различных концепциях, таких как алгебра.
Практикуясь в вопросах и ответах на основе различных формул, можно выучить каждую формулу наизусть перед тем, как идти на экзамен.
Некоторые из других концепций, которые имеют формулы, приведены ниже:
Дроби
Процент
Формула для пропорции
Геометрия
Тригонометрические формулы и многое другое.
Базовая математическая формула
Основы математики показывают, как математическая задача может быть решена с помощью некоторых уравнений, таких как уравнение сил, ускорений или проделанной работы.Что еще более важно, они используются для математических решений реальных проблем в нашей повседневной жизни.
Есть много типов уравнений, и они встречаются во многих областях математики. Но методы, используемые для их изучения, различаются в зависимости от их типа. Это может быть простая формула сложения или сложная интеграция дифференцирования.
Но методы, используемые для их изучения, различаются в зависимости от их типа. Это может быть простая формула сложения или сложная интеграция дифференцирования.
Основные геометрические формулы
Периметр квадрата = P = 4a
Где ‘a’ — длина сторон квадрата
Периметр прямоугольника = P = 2 (l + b )
Где l — длина, а b — ширина
Площадь квадрата = A = a2
Где a — длина сторон квадрата
Площадь прямоугольника = A = l × b
здесь l — длина, а b — ширина
Площадь треугольника = A = ½ × b × h
Где b — это ширина основание треугольника, а ‘h’ — высота треугольника
Площадь трапеции = A = ½ × (b1 + b2) × h
Где b1 и b2 — основания Трапеции; h = высота трапеции
Площадь круга = A = π × r2
Окружность круга = A = 2πr
Где r — радиус окружности
Площадь поверхности of Cube = S = 6a2
Где ‘a’ — длина сторон куба
Площадь криволинейной поверхности цилиндра = 2πrh
Общая площадь поверхности цилиндра = 2πr (r + h)
Объем цилиндра = V = πr2h
Где r — радиус основания цилиндра, а h — высота цилиндра
Площадь криволинейной поверхности конуса = πrl
Общая площадь поверхности конуса = πr (r + l) = πr [r + √ (h3 + r2)]
Объем конуса = V = ⅓ × πr2h
Здесь ‘ r ‘- радиус основания конуса, h = высота конуса
Поверхность Ar ea сферы = S = 4πr2
Объем сферы = V = 4/3 × πr
Где, r = радиус сферы
Площадь круга | А = Π х квадрат радиуса |
Площадь равностороннего Треугольник | А = (сторона ^ 2) √3) / 4 |
Площадь н. | |
Площадь трапеции | A = ½ (Base1 + Base 2) высота |
Площадь треугольника | A = ½ База x Высота |
Базовая площадь семиугольника | Площадь основания = ½ апофемы * периметр |
Базовая площадь шестиугольника | Площадь основания = ½ апофемы * периметр |
Базовая область восьмиугольника | Площадь основания = ½ апофемы * периметр |
Базовая площадь Параллелограмм | Площадь базы = база * высота |
Базовая площадь Пентагон | Площадь основания = ½ апофемы * периметр |
Прямоугольник с площадью основания | Площадь основания = длина * ширина |
Площадь Базы | Площадь основания = квадрат стороны |
Базовая площадь трапеции | Площадь основания = ½ (высота) (основание 1 + основание 2) |
Треугольник площади основания | Площадь основания = 1/2 основания * высота |
Окружность а Круг | C = 2 x Π x радиус |
Формула расстояния | D = √ (x 2 -x 1 ) 2 + (y 2 –y 1 ) 2 |
Уравнение окружности | Общая форма (x-h) 2 + (y-k) 2 h и K — координаты круга, а r = радиус |
45 45 90 Треугольник Гипотенуза | H = нога√2 |
45 45 90 Треугольник Ноги | 1⁄2 гипотенуза √2 |
Формула Герона | s = (a + b + c) / 2, тогда A = √ (s (s-a) (s-b) (s-c)) |
Горизонтальная линия | Y = (любое число) |
Боковая часть конуса | πrsl r = радиус sl = наклонная высота |
Куб бокового сечения | 4s 2 s = сторона |
Цилиндр боковой поверхности | Окружность x Высота |
Призма боковой поверхности | Периметр x высота |
Пирамида с боковой площадью | 1 / 2P * sl sl = наклонная высота P = периметр |
Боковое пространство прямоугольное Твердый | Периметр * высота |
Боковая область справа Конус | LA = ½ Psl P = 2πr sl = высота наклона |
Боковая область справа Цилиндр | LA = 2πr * ч |
Боковая область справа Призма | LA = Ph P = сумма сторон основания h = высота |
Формула средней точки | (X1 + X2) / 2, (Y1 + Y2) / 2 |
Периметр а Параллелограмм | P = 2 (основание + сторона) |
Периметр а Прямоугольник | P = 2 (основание + высота) |
Периметр | P = количество сторон * стороны |
Периметр а Ромб | P = 4 x сторона |
Периметр квадрата | P = 4 x сторона |
Периметр а Трапеция | Base1 + Base2 + Side1 + сторона 2 |
Периметр а Треугольник | Сторона A + Сторона B + Сторона C |
Форма углового откоса | г-г 1 = м (х-х 1 ) |
Уклон | Y2-Y1 X 2 -X 1 = Rise over Run |
Форма пересечения склонов | y = mx + b M = наклон b = y перехват |
Площадь поверхности Конус | SA = π * радиус * наклонная высота + πрадиус 2 |
Площадь поверхности Куб | SA = 6сайд 2 |
Площадь поверхности Цилиндр | Боковая зона + 2πрадиус 2 |
Площадь поверхности Призма | Боковая зона + 2Base |
Площадь поверхности Пирамида | Боковая зона + 1 основание |
Площадь поверхности прямоугольника Призма | 2 (длина * ширина + длина * высота + высота * ширина) |
Площадь правого Конус | SA = 1/2 * Диаметр * π * наклон высота + основание |
Площадь поверхности права Цилиндр | 2πрадиус 2 + 2πрадиус x высота |
Площадь поверхности права Призма | SA = периметр * высота + 2 База |
Площадь поверхности Сфера | 4πрадиус 2 |
30 60 90 Треугольник короткий и длинный ноги | Короткая ветвь = ½ гипотенузы Длинная нога = 1⁄2 гипотенузы √3 |
Доказательство геометрии формулы Герона
Доказательство геометрии формулы ГеронаMATH 7200: Основы геометрии Я
Университет Джорджии, осень 2000
Доктор.
 МакКрори, инструктор
МакКрори, инструкторГеометрическое доказательство Герона Формула
Шеннон Амбергер
Примечание: Это доказательство было адаптировано из набросков пруф на странице 194 в 6-м издании
Введение в История математики Говарда Ивса.Пусть дан треугольник ABC, длина отрезка BC равна a, длина отрезка AC равна b, а длина отрезка AB равна c.
Обратите внимание на периметр p треугольника ABC = a + b + c.Половина периметр называется полупериметром, s, и поэтому для треугольника ABC, s = (a + b + c) / 2.
Пусть точка пересечения углов биссектрис углов A, B и C назовем точкой I. Постройте отрезки AI, BI и CI.
Далее пусть точка пересечения перпендикуляра
сторону AC, проходящую через точку I, назовем точкой D, точкой пересечения
перпендикуляра к стороне BC через точку I назовем
точка E и точка пересечения перпендикулярной прямой
в сторону AB, проходящую через точку I, назовем точкой F.
По определению, точка I называется центром треугольника ABC. Круг с точкой I в центре, проходящий через точки D, E и F называются вписанной окружностью треугольника ABC.
Теперь, поскольку сегмент IB является биссектрисой угла B, тогда углы IBF и IBE равны. Поскольку углы IFB и IEB прямые по построению, то они равны, а значит, углы BIF и BIE равны (так как сумма всех углов треугольника равна 180 градусам).Обратите внимание, что сегменты IF и IE равны, поскольку оба имеют радиусы тот же круг. Следовательно, треугольники BIF и BIE (красные) — это соответствует SAS.
Точно так же треугольники CID и CIE (зеленые) совпадают по SAS.
Точно так же треугольники AIF и AID (синего цвета) совпадают. пользователя SAS.
Поскольку соответствующие стороны равных треугольников равны,
отсюда следует, что отрезки BF и BE (выделены красным) равны, отрезки
CD и CE (зеленым) равны, а сегменты AD и AF (синим)
равны.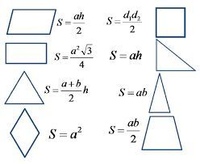
Используя формулу, которая утверждает, что площадь треугольника равна половина основания умножена на высоту, площадь треугольника AIB = (1/2) * AB * ЕСЛИ, …
… площадь треугольника BIC = (1/2) * BC * IE, …
… и площадь треугольника AIC = (1/2) * AC * ID.
Следовательно, площадь треугольника ABC равна сумме площадей. треугольников AIB, BIC и AIC.
Путем подстановки площадь треугольника ABC = (1/2) * AB * IF + (1/2) * BC * IE + (1/2) * AC * ID.Поскольку сегменты IF, IE и ID являются равны (они все радиусы одного круга), отсюда следует немного алгебры, что площадь треугольника ABC = (1/2) * ID * (AB + BC + AC). Но AB + BC + AC = a + b + c, поэтому эта сумма действительно периметр треугольника ABC; следовательно, площадь треугольника ABC = (1/2) * ID * стр. Поскольку (1/2) * p = s, полупериметр треугольника ABC, тогда площадь треугольника ABC = ID * s.
Теперь постройте точку G так, чтобы G лежала на той же прямой, что и
сегмент AC, а сегмент CG равен сегменту BE. Помните p = a +
b + c = AB + BC + AC, и поэтому путем сложения и замены сегментов
p = (BE + CE) + (CD + AD) + (AF + BF) = (BF + BE) + (CE + CD)
+ (AD + AF). Кроме того, подстановкой p = 2 * BE + 2 * CD + 2 * AD
= 2 (BE + CD + AD). Опять же, путем замены p = 2 (CG + CD + AD).
Но AG = AD + DC + CG при добавлении сегментов и, следовательно, при замене,
p = 2 * AG. Следовательно, s = AG.
Помните p = a +
b + c = AB + BC + AC, и поэтому путем сложения и замены сегментов
p = (BE + CE) + (CD + AD) + (AF + BF) = (BF + BE) + (CE + CD)
+ (AD + AF). Кроме того, подстановкой p = 2 * BE + 2 * CD + 2 * AD
= 2 (BE + CD + AD). Опять же, путем замены p = 2 (CG + CD + AD).
Но AG = AD + DC + CG при добавлении сегментов и, следовательно, при замене,
p = 2 * AG. Следовательно, s = AG.
Таким образом, подстановкой площадь треугольника ABC = ID * AG.
Постройте линию, перпендикулярную отрезку AI через точку I (розового цвета) и прямую, перпендикулярную отрезку AG через точку C (светло-голубым).Пусть точка пересечения этих двух прямых назовем точкой H. Пусть точка пересечения отрезка IH и отрезок AG назовем точкой J. Построим отрезок AH (в желтый).
Поскольку углы AIH и ACH прямые (по построению), то
треугольники AIH и ACH правы. Обратите внимание, что треугольники имеют общий
гипотенуза, отрезок AH. Следовательно, эти треугольники вписаны в
в общем круге с отрезком AH как диаметр круга.
Этот факт означает, что четырехугольник AICH является вписанным, а значит, противоположным углы AIC и AHC являются дополнительными.
Поскольку сумма углов в точке I равна 360 градусам, по углу сложение (угол BIF + угол BIE) + (угол CIE + угол CID) + (угол AID + угол AIF) = 360 градусов. Подстановкой 2 * (угол BIE) + 2 * (угол CID) + 2 * (угол AID) = 360 градусов, и поэтому угол BIE + угол CID + угол AID = 180 градусов. Но угол CID + угол AID = угол AIC путем сложения углов, таким образом, угол BIE + угол AIC = 180 градусов, поэтому углы BIE и AIC являются дополнительными.
Поскольку углы BIE и AHC являются дополнительными к одному и тому же углу, из этого следует, что угол BIE = угол AHC.
Поскольку углы BIE и AHC равны, а углы BEI и ACH равны (оба правильны по построению), то треугольники BIE и AHC похожи по сходству AA.
Путем замены AC / CG = AC / BE. Тогда по определению подобных треугольников, AC / BE = HC / IE.
Теперь, поскольку углы IJD и HJC являются вертикальными углами, они равны
равный. Кроме того, углы IDJ и HCJ равны (оба правильные по конструкции).
Следовательно, треугольники IJD и HJC подобны AA подобием.
Кроме того, углы IDJ и HCJ равны (оба правильные по конструкции).
Следовательно, треугольники IJD и HJC подобны AA подобием.
Путем подстановки HC / IE = HC / ID. Тогда по определению похожие треугольники, HC / ID = CJ / DJ.
Таким образом, по транзитивности AC / CG = CJ / DJ.
Следующие несколько шагов доказательства потребуют некоторых алгебраических приемов.
Поскольку AC / CG = CJ / DJ, то AC / CG + 1 = CJ / DJ + 1.
Итак, AC / CG + CG / CG = CJ / DJ + DJ / DJ.
Это означает, что (AC + CG) / CG = (CJ + DJ) / DJ.
Но при сложении сегментов AC + CG = AG и CJ + DJ = CD.
Следовательно, путем подстановки AG / CG = CD / DJ.
Ну, тогда AG / CG * 1 = CD / DJ * 1.
Итак, AG / CG * AG / AG = CD / DJ * AD / AD.
Затем AG 2 / CG * AG = CD * AD / DJ * AD.
Теперь, поскольку треугольник AIJ правый (по построению), а D —
точка на гипотенузе, то DJ * AD = ID 2 (по
среднее геометрическое).
Итак, подстановкой AG 2 / CG * AG = CD * AD / ID 2 .
Путем перекрестного умножения AG 2 * ID 2 = CG * AG * CD * AD.
Отсюда следует, что AG * ID = [CG * AG * CD * AD] 1/2 .
Но, площадь треугольника ABC = AG * ID.
Таким образом, по транзитивности площадь треугольника ABC = [CG * AG * CD * AD] 1 / 2 .
Наконец, помните, что сегмент AG = s.
Обратите внимание, что сегмент CG = AG — AC путем сложения сегментов, и поэтому CG = s — b подстановкой.
Также обратите внимание, что сегмент CD = AG — (AD + CG) путем добавления сегмента. Итак, CD = AG — (AF + BF) путем подстановки, и поэтому CD = s — c подстановкой.
Обратите внимание, что сегмент AD = AG — (CD + CG) путем добавления сегмента. Таким образом, AD = AG — (CE + BE) путем подстановки, и поэтому AD = s — a подстановкой.
Следовательно, подстановкой площадь треугольника ABC = [s * (s
— а) * (с — b) * (с — с)] 1/2 . QED.
QED.
Возврат на главную страницу «Формула Герона»
Трехмерная координатная геометрия — Уравнение плоскости
Когда мы знаем три точки на плоскости, мы можем найти уравнение плоскости, решив одновременные уравнения.
Пусть ax + by + cz + d = 0 ax + by + cz + d = 0ax + by + cz + d = 0 будет уравнением плоскости, на которой есть следующие три точки: A = (1,0, 2), B = (2,1,1), A = (1,0,2), B = (2,1,1), A = (1,0,2), B = (2,1, 1) и C = (- 1,2,1) .C = (- 1,2,1). С = (- 1,2,1). Тогда уравнение плоскости устанавливается следующим образом:
У нас уже есть уравнение плоскости с 4 неизвестными константами:
ax + by + cz + d = 0. (1) ax + by + cz + d = 0. \ qquad (1) ax + by + cz + d = 0. (1)
).Мы также получаем следующие 3 уравнения, подставляя координаты A, B, A, B, A, B и CCC в (1) 🙁 1) 🙁 1):
a⋅1 + b⋅0 + c⋅2 + d = 0a⋅2 + b⋅1 + c⋅1 + d = 0a⋅ (−1) + b⋅2 + c⋅1 + d = 0, \ begin {выровнено} а \ cdot 1 + b \ cdot 0 + c \ cdot 2 + d & = 0 \\ а \ cdot 2 + b \ cdot 1 + c \ cdot 1 + d & = 0 \\ а \ cdot (-1) + b \ cdot 2 + c \ cdot 1 + d & = 0, \ end {align} a⋅1 + b⋅0 + c⋅2 + da⋅2 + b⋅1 + c⋅1 + da⋅ (−1) + b⋅2 + c⋅1 + d = 0 = 0 = 0,
, что дает b = 3a, c = 4a, d = −9a.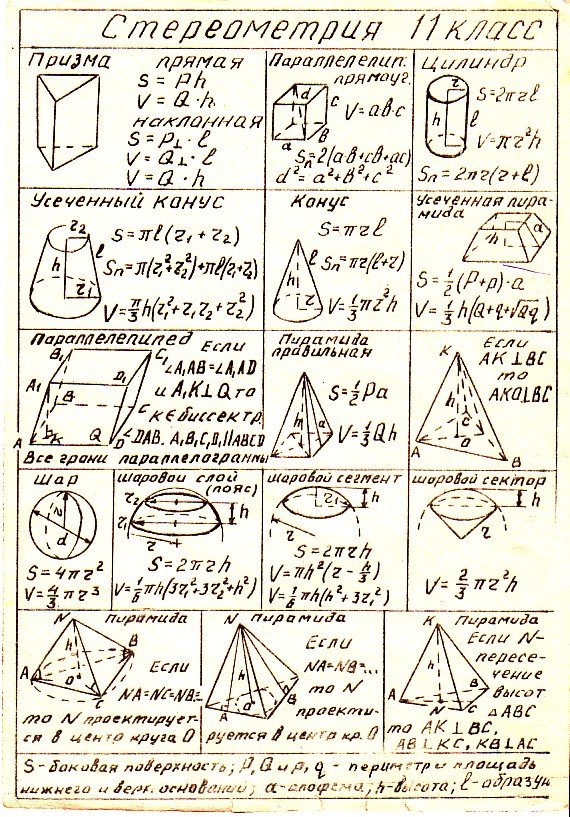 (2) b = 3a, c = 4a, d = -9a. \ qquad (2) b = 3a, c = 4a, d = −9a. (2)
(2) b = 3a, c = 4a, d = -9a. \ qquad (2) b = 3a, c = 4a, d = −9a. (2)
Подставляя (2) (2) (2) в (1), (1), (1), получаем
ax + 3ay + 4az − 9a = 0x + 3y + 4z − 9 = 0. \ begin {выровнено} ах + 3ay + 4az -9a & = 0 \\ х + 3у + 4z — 9 & = 0. \ end {align} ax + 3ay + 4az − 9ax + 3y + 4z − 9 = 0 = 0.
Следовательно, уравнение плоскости, проходящей через три точки A = (1,0,2), B = (2,1,1), A = (1,0,2), B = (2,1, 1), A = (1,0,2), B = (2,1,1) и C = (- 1,2,1) C = (- 1,2,1) C = (- 1, 2,1) — это
х + 3у + 4z − 9 = 0. х + 3у + 4z — 9 = 0.х + 3у + 4z − 9 = 0.
Используя этот метод, мы можем найти уравнение плоскости, если нам известны три точки. Вот пара примеров:
Если самолет проходит через три точки A = (0,0,2), B = (1,0,1), A = (0,0,2), B = (1,0,1), A = (0,0,2), B = (1,0,1) и C = (3,1,1), C = (3,1,1), C = (3,1,1), тогда что такое уравнение плоскости?
Пусть уравнение плоскости имеет вид ax + by + cz + d = 0. (1) ax + by + cz + d = 0.
\ qquad (1) ax + by + cz + d = 0. (1)
Тогда, поскольку эта плоскость включает три точки A = (0,0,2), B = (1,0,1), A = (0,0,2), B = (1,0,1), A = (0,0,2), B = (1,0,1) и C = (3,1,1), C = (3,1,1), C = (3,1,1), у нас есть
a⋅0 + b⋅0 + c⋅2 + d = 0a⋅1 + b⋅0 + c⋅1 + d = 0a⋅3 + b⋅1 + c⋅1 + d = 0, \ begin {выровнено} а \ cdot 0 + b \ cdot 0 + c \ cdot 2 + d & = 0 \\ а \ cdot 1 + b \ cdot 0 + c \ cdot 1 + d & = 0 \\ а \ cdot 3 + b \ cdot 1 + c \ cdot 1 + d & = 0, \ end {align} a⋅0 + b⋅0 + c⋅2 + da⋅1 + b⋅0 + c⋅1 + da⋅3 + b⋅1 + c⋅1 + d = 0 = 0 = 0,
, что дает b = −2a, c = a, d = −2a.(2) b = -2a, c = a, d = -2a. \ qquad (2) b = −2a, c = a, d = −2a. (2)
Подставляя (2) (2) (2) в (1), (1), (1), получаем
ax + −2ay + az − 2a = 0x − 2y + z − 2 = 0. \ begin {выровнено} ах + -2ay + аз -2а & = 0 \\ х -2у + г — 2 & = 0. \ end {align} ax + −2ay + az − 2ax − 2y + z − 2 = 0 = 0.
Следовательно, уравнение плоскости, проходящей через три точки A = (0,0,2), B = (1,0,1), A = (0,0,2), B = (1,0,1 ) A = (0,0,2), B = (1,0,1) и C = (3,1,1) C = (3,1,1) C = (3,1,1) равно
х-2у + г-2 знак равно 0.
□ х -2y + z — 2 = 0. \ _ \ квадрат х-2у + г-2 знак равно 0.□
Если самолет проходит через три точки A = (3,1,2), B = (6,1,2), A = (3,1,2), B = (6,1,2), A = (3,1,2), B = (6,1,2) и C = (0,2,0), C = (0,2,0), C = (0,2,0), тогда какое уравнение плоскости?
Пусть уравнение плоскости имеет вид ax + by + cz + d = 0. (1) ax + by + cz + d = 0. \ qquad (1) ax + by + cz + d = 0. (1)
Тогда, поскольку эта плоскость включает три точки A = (0,0,2), B = (1,0,1), A = (0,0,2), B = (1,0,1), A = (0,0,2), B = (1,0,1) и C = (3,1,1), C = (3,1,1), C = (3,1,1), у нас есть
a⋅3 + b⋅1 + c⋅2 + d = 0a⋅6 + b⋅1 + c⋅2 + d = 0a⋅0 + b⋅2 + c⋅0 + d = 0, \ begin {выровнено} а \ cdot 3 + b \ cdot 1 + c \ cdot 2 + d & = 0 \\ а \ cdot 6 + b \ cdot 1 + c \ cdot 2 + d & = 0 \\ а \ cdot 0 + b \ cdot 2 + c \ cdot 0 + d & = 0, \ end {align} a⋅3 + b⋅1 + c⋅2 + da⋅6 + b⋅1 + c⋅2 + da⋅0 + b⋅2 + c⋅0 + d = 0 = 0 = 0,
, что дает a = 0, c = 12b, d = −2b.(2) a = 0, c = \ frac {1} {2} b, d = -2b.
\ qquad (2) a = 0, c = 21 b, d = −2b. (2)
Подставляя (2) (2) (2) в (1), (1), (1), получаем
0x + −by + 12bz − 2b = 0x − y + 12z − 2 = 02x − 2y + z − 4 = 0. \ begin {выровнено} 0x + -by + \ frac {1} {2} bz -2b & = 0 \\ x -y + \ frac {1} {2} z — 2 & = 0 \\ 2х — 2у + г-4 & = 0. \ end {align} 0x + −by + 21 bz − 2bx − y + 21 z − 22x − 2y + z − 4 = 0 = 0 = 0.
Следовательно, уравнение плоскости, проходящей через три точки A = (0,0,2), B = (1,0,1), A = (0,0,2), B = (1,0, 1), A = (0,0,2), B = (1,0,1) и C = (3,1,1) C = (3,1,1) C = (3,1,1 ) составляет
2x − 2y + z − 4 знак равно 0.□ 2x — 2y + z-4 = 0. \ _ \ квадрат 2x − 2y + z − 4 знак равно 0. □
Попробуйте решить следующую проблему:
х = 1х = 1х = 1 х + у = 3х + у = 3х + у = 3 у-х = 1у-х = 1у-х = 1 Ни один из вышеперечисленных Найдите уравнение плоскости, проходящей через (1,2,3) (1,2,3) (1,2,3) и (1, −3,2) (1, -3,2) (1, −3,2) и параллельно оси zzz.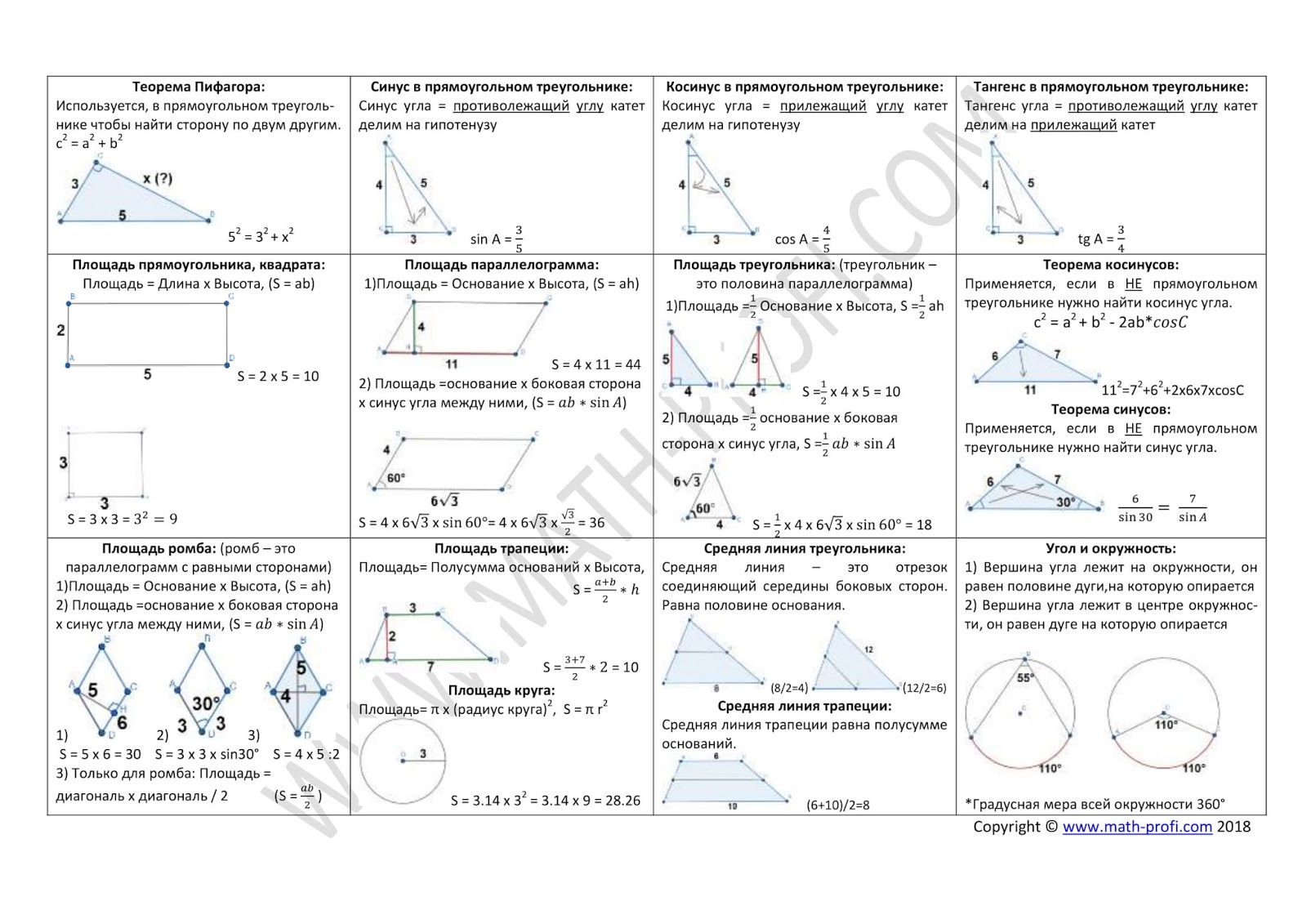
Основы координатной геометрии — Формула сечения
В этом уроке мы установим формулу для нахождения координат точки, которая разделяет отрезок прямой, соединяющий две заданные точки в заданном соотношении. Эта формула известна как формула раздела . Давайте начнем!
Рассмотрим две точки P (x 1 , y 1 ) и Q (x 2 , y 2 ) .Нам нужно найти координаты точки R , которая делит PQ в соотношении m: n , т.е. PR / RQ = m / n .
При заданном соотношении точка R может находиться либо на между P и Q , либо на за пределами линейного сегмента PQ . Взгляни.
(Обратите внимание, что на приведенном выше рисунке м и n не обозначают длины PR и QR . Они просто указывают соотношение.)
Они просто указывают соотношение.)
Давайте рассмотрим эти случаи по порядку.
Случай I — R, расположенный между P и QСначала я проиллюстрирую уродливый (но действительный) метод вычисления координат R , используя то, что мы уже знаем, — формулу расстояния. Как я упоминал ранее, существует (в общем) несколько методов решения задачи координатной геометрии. Это один из таких случаев. Идея состоит в том, чтобы развить свой уровень мышления и дать вам представление о том, какие методы хороши, а какие нет.2} \)
Я остановлюсь здесь. Вы могли догадаться, почему это не лучший метод. На самом деле, как мы увидим позже, методы, использующие формулу расстояния, обычно становятся довольно сложными и трудными для решения.
Итак, какая у нас альтернатива? Пришло время немного геометрии — давайте построим.
Я нарисовал RA и QB параллельно оси Y , а PA и RB параллельно оси X . Тогда треугольники RPA и QRB похожи, по сходству AA.
Тогда треугольники RPA и QRB похожи, по сходству AA.
Как это помогает? Нам дается PR / QR , который, исходя из сходства, равен RA / QB и PA / RB . Позвольте мне написать это лучше:
\ (\ frac {PR} {QR} = \ frac {RA} {QB} = \ frac {PA} {RB} = \ frac {m} {n} \)
Итак, PA = x — x 1 и RB = x 2 — x (я объяснил это на предыдущем уроке.)
Следовательно, мы можем написать
\ (\ frac {PA} {RB} = \ frac {x-x_1} {x_2-x} = \ frac {m} {n} \)
Решив вышеуказанное для x , мы получаем
x = \ (\ frac {mx_2 + nx_1} {m + n} \)
А как насчет y ?
Ссылаясь на рисунок выше, RA = y — y 1 и QB = y 2 — y .
Теперь мы можем использовать тот же процесс, чтобы получить
y = \ (\ frac {my_2 + ny_1} {m + n} \)
Итак, у нас есть координаты точки R , которая делит PQ в соотношении m: n .
Когда R лежит между P и Q , мы говорим, что R делит PQ в соотношении m: n внутри . Вот симуляция, которая показывает две точки A и B , а также точку C , разделяющую отрезок линии, соединяющий их в некотором соотношении.
Попробуйте изменить значения m и n и соблюдайте координаты C . Получаете ли вы те же координаты, используя формулу сечения?
Давайте посмотрим, что произойдет, если R находится за пределами PQ .
Корпус II — R, лежащий снаружи PQДанное условие такое же, т.е. PR / RQ = m / n , но цифра будет немного другой.
В этом случае мы говорим, что R делит PQ внешне на в соотношении m: n .
Я не собираюсь выводить это. Пожалуйста, попробуйте сделать это самостоятельно. Метод тот же, что и в первом случае — найти похожие треугольники, выразить данное соотношение через x 1 , x 2 , y 1 и y 2 .
Если все сделаете правильно, то должно получиться
x = \ (\ frac {mx_2-nx_1} {m-n} \)
y = \ (\ frac {my_2-ny_1} {m-n} \)
Резюме урока
- Координаты точки, разделяющей отрезок линии, соединяющий (x 1 , y 1 ) и (x 2 , y 2 ) в соотношении m: n внутри . автор \ (\ left (\ frac {mx_2 + nx_1} {m + n}, \ frac {my_2 + ny_1} {m + n} \ right) \)
- Координаты точки, разделяющей линейный сегмент, соединяющий (x 1 , y 1 ) и (x 2 , y 2 ) в соотношении m: n снаружи определяется как \ (\ left (\ frac {mx_2-nx_1} {mn}, \ frac {my_2 + ny_1} {m + n} \ right) \)
Ну вот и все. Увидимся на следующем уроке с некоторыми примерами и применением формулы раздела!
Увидимся на следующем уроке с некоторыми примерами и применением формулы раздела!
Формулы геометрии и концепции треугольников GMAT (Часть 1)
Чувствуете ли вы себя подавленным, когда изучаете множество формул и концепций GMAT Geometry [1]? Считаете ли вы, что геометрия — ваша слабая тема? Ты не одинок. Многие экзаменуемые избегают решать вопросы GMAT по геометрии, поскольку большинство из них не чувствуют себя комфортно в этой теме.В этой статье вы прочитаете-
- Слишком много формул GMAT Geometry на , чтобы запомнить .Несмотря на то, что GMAT тестирует нас на очень ограниченном количестве свойств, но поскольку эти ограниченные свойства не сопоставлены в одном месте, экзаменующемуся трудно с уверенностью сказать, что он знает все концепции.
- И скажем, даже если кому-то удастся найти и изучить все концепции , большинство из них не знают, как применить эти концепции, чтобы вывести информацию из заданного вопроса и рисунка в вопросах, проверенных на GMAT.

ПРИМЕЧАНИЕ: Это вторая статья из серии GMAT Geometry Pitfalls.Прочтите первую статью, нажмите на ссылку ниже.
Наиболее распространенные ошибки в вопросах GMAT по геометрии
Следующие 2 статьи из этой серии:
Как мы поможем вам с GMAT Geometry Prep?
В этой статье мы рассмотрим обе вышеупомянутые проблемы с помощью:
- Объединение САМЫХ важных концепций геометрии GMAT, необходимых в треугольниках .
- Сосредоточение внимания на некоторых GMAT-подобных и официальных вопросах и демонстрация применения вышеуказанных концепций в этих вопросах.
Основные свойства треугольников
В этом разделе рассматриваются следующие аспекты:
- Определение, может ли набор заданных чисел быть длиной треугольника или нет
- Диапазон значений, которые сторона треугольника может принимать с учетом значений двух других сторон, и
- Свойства углов треугольника
Концепция 1: Формулы геометрии GMAT
Геометрия GMAT Concept 1 — Сумма длин любых двух сторон треугольника> Длина третьей стороны Предположим, вам даны три длины a, b и c, и вас попросили выяснить, можем ли мы сформировать треугольник, используя эти три длины.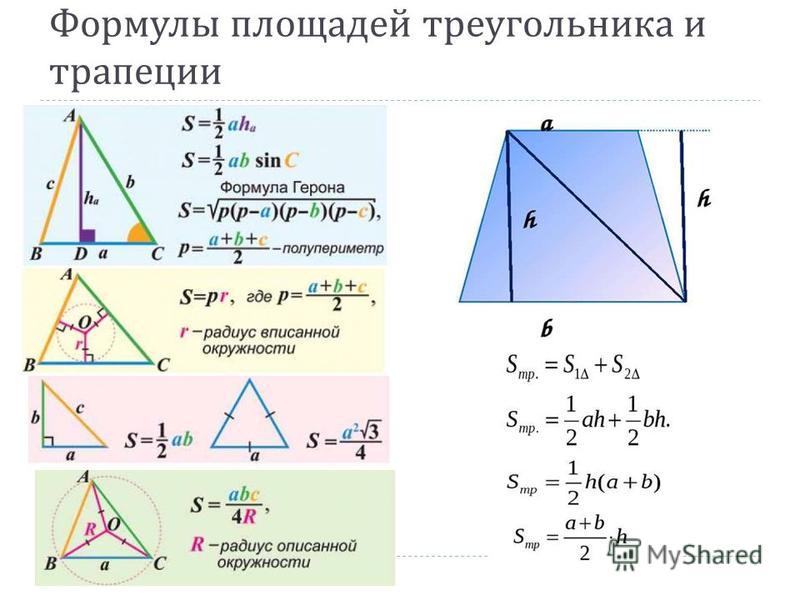
Как вы собираетесь подойти к этой проблеме?
Теория:
Чтобы определить, образуют ли три длины треугольник или нет, нам нужно знать самое основное свойство треугольника:
Сумма длин любых двух сторон треугольника> Длина третьей стороны
Это означает, что:
- a + b> c
- б + в> а
- c + a> b
Обратите внимание, что для существования треугольника все три неравенства должны удовлетворять .
Давайте разберемся с этим с помощью очень простого вопроса, похожего на GMAT:
Иллюстративный пример 1
Q. Три длины 5, 3 и x используются для образования треугольника. Что из следующего может быть значением x?
- 6
- 9
- 10
- 12
- 14
Поскольку 5, 3 и x образуют треугольник, они должны удовлетворять свойству —
Сумма длин любых двух сторон треугольника> Длина третьей стороны
Следовательно, можно написать —
I. 5 + 3> х II. 3 + x> 5 III. 5 + х> 3
5 + 3> х II. 3 + x> 5 III. 5 + х> 3
=> х <8 => х> 2 => х> -2
можно сделать вывод, что диапазон x: 2 Из указанных вариантов единственный вариант, который попадает в этот диапазон, — 6. Следовательно, вариант А — наш ответ. Следовательно, теперь мы знаем: Предположим, что после того, как вы выяснили, что заданные длины образуют треугольник, вы хотите выяснить, как длина сторон может помочь в найти связь между углами треугольника. Чтобы понять это, нам нужно знать еще два важных свойства: Обратите внимание, что указанное выше свойство справедливо для всех треугольников, независимо от их размера и формы. (Обратите внимание, я использую заглавные буквы A, B и C для обозначения углов и длины сторон треугольника a, b и c) Позвольте мне объяснить это немного подробнее: Если ABC — треугольник, в котором мы знаем, что длины AB, BC и CA следуют соотношению AB> BC> AC, то мы можем заключить, что, поскольку AB является наибольшей стороной, угол, противоположный ему i .е., угол ACB — это наибольший угол . А поскольку BC> AC, то и противоположные им углы имеют такое же соотношение, то есть угол BAC> угол ABC Отсюда можно сделать вывод, что: ∠ ACB> ∠ BAC> ∠ ABC Имейте в виду, что обратное — это , также истинное , то есть, если задано соотношение между углами, мы можем использовать это, чтобы найти соотношение между сторонами. Давайте разберемся с применением этого свойства на примере: В приведенном ниже треугольнике все обозначенные точки не перекрываются, а углы A, B и C различны.AB> AC> BC? Решение: Подъезд Нам нужно выяснить, истинно ли утверждение AB> AC> BC. Для этого достаточно получить соотношение между углами A, B и C, поскольку стороны треугольника следуют так же, как и углы, противоположные им. Анализ отчета 1 ∠ y 1 = ∠ c 1 Следовательно, в ΔBYC BY = BC Но AB = BY + YA AB> BC Однако, мы не можем вывести какую-либо связь между BC и AC (или AB и AC) из данной информации Анализ отчета 2 Дано ∠ BAC < ∠ ABC, и ни один из углов не является наибольшим. Также в формулировке вопроса упоминается, что углы BAC, ABC и ACB различны, поэтому ∠ACB должен быть наибольшим углом. Таким образом, можно сделать вывод, что ∠ BAC <∠ ABC <∠ ACB Таким образом, можно сделать вывод, что длина BC Следовательно, утверждения 2 достаточно, чтобы прийти к однозначному ответу. Правильный ответ: B На этом мы подошли к концу первой статьи из этой серии.Надеюсь, вы найдете это полезным и информативным. Прочитав это, вы легко сможете: Имея в виду эти выводы, сможете ли вы решить 2 вопроса? Начните подготовку к GMAT, подписавшись на бесплатную пробную версию и получите доступ к более чем 10 часам видеоуроков и 400+ вопросам. 1. Табличное представление: Различные типы треугольников с их НАИБОЛЕЕ важными свойствами. 2. Особые свойства: Несколько специальных свойств, которые могут быть проверены GMAT. [1] Формулы представляют собой форму множественного числа формулы , альтернативное множественное число формулы составляет формул. Многие математические теоремы настолько важны, что
неоднократно доказывались удивительно множеством различных способов.Примеры этого
включают
в
существование бесконечного числа простых чисел,
оценка
дзета (2),
основная теорема алгебры (многочлены имеют корни), квадратичные
взаимность (формула для проверки того, является ли арифметическая прогрессия
содержит квадрат) и теоремы Пифагора (которая согласно
У Уэллса не менее 367 доказательств). На этой странице приведены доказательства формулы Эйлера:
для любого выпуклого многогранника количество вершин и граней вместе
ровно на два больше, чем количество ребер.
Символически V − E + F = 2.
Например, тетраэдр имеет четыре вершины, четыре грани и шесть ребер;
4-6 + 4 = 2. Версия формулы датируется Декартом в 1630 году более чем на 100 лет раньше, чем Эйлер. Декарт дает дискретную форму теоремы Гаусса-Бонне, утверждая, что сумма углов граней многогранника равна 2π (V − 2), из чего он делает вывод, что количество плоских углов равно 2F + 2V-4.Количество плоских углов всегда в два раза больше количества ребер, поэтому это эквивалентно формуле Эйлера, но более поздние авторы, такие как Лакатос, Малькевич и Поля, не соглашаются, считая, что различие между углами лица и гранями слишком велико для этого. Формулу многогранника, конечно, можно обобщить многими важными способами:
некоторые с использованием методов, описанных ниже.
Одно важное обобщение — это планарные графы.Чтобы сформировать плоский граф из многогранника,
поместите источник света возле одной грани многогранника, а плоскость — на другую. Тени от ребер многогранника образуют плоский граф, вложенный в
таким образом, чтобы края были отрезками прямых линий.
Грани многогранника соответствуют выпуклым
многоугольники, являющиеся гранями вложения. Лицо, ближайшее к свету
источник соответствует внешней грани вложения, которая также является
выпуклый. И наоборот, любой плоский граф с определенной связностью
properties происходит от многогранника таким образом. Некоторые из приведенных ниже доказательств используют только топологию плоского графа,
некоторые используют геометрию его вложения, а некоторые используют
трехмерная геометрия исходного многогранника. Я полагаю, можно было бы построить индукции
основанный на представлении выпуклых многогранников в виде пересечений
полупространств или выпуклой оболочки точек, но необходимость
обработка входных данных в необщем положении приведет к тому, что в результате
Доказательства довольно грязные. Концепция 2: формулы геометрии GMAT

Свойство 3. В любом треугольнике наибольшая сторона всегда противоположна наибольшему углу, а наименьшая сторона всегда противоположна наименьшему углу

Иллюстративный пример 2
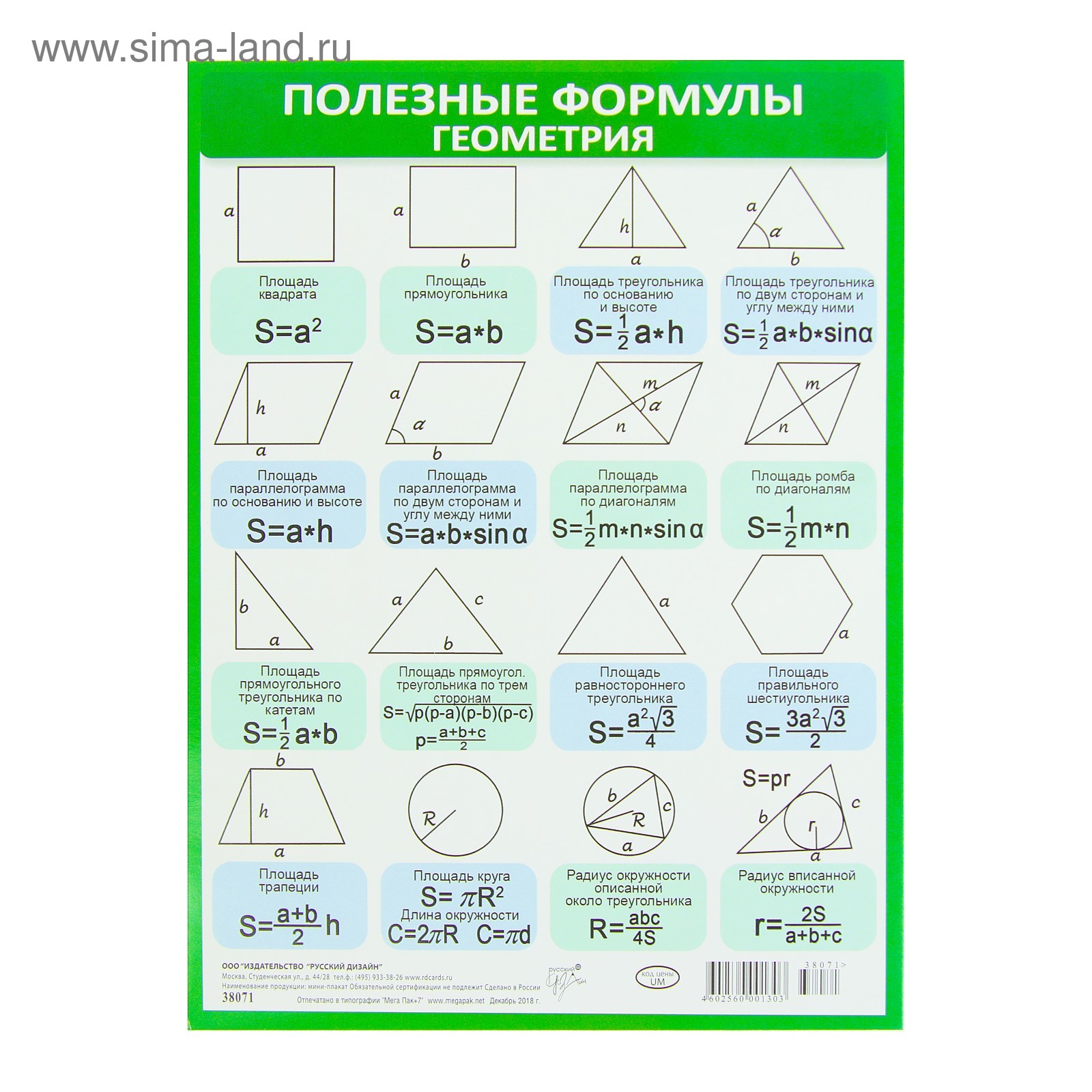
Выводы — Статья 1 — GMAT Концепции геометрического треугольника
В следующих статьях о Треугольниках читайте о .
Формула Эйлера
Формула Эйлера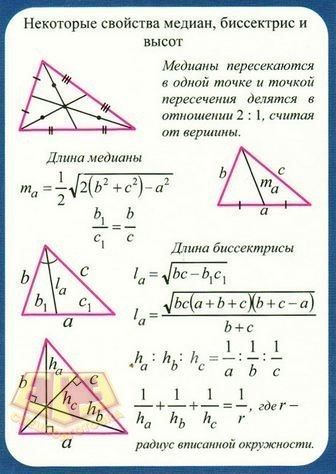 Иногда это случается и с несущественными теоремами,
например, тот факт, что в любом прямоугольнике, разрезанном на более мелкие прямоугольники,
если каждый меньший прямоугольник имеет целочисленную ширину или высоту, то же самое
большой.
Иногда это случается и с несущественными теоремами,
например, тот факт, что в любом прямоугольнике, разрезанном на более мелкие прямоугольники,
если каждый меньший прямоугольник имеет целочисленную ширину или высоту, то же самое
большой. рассматривается как та же формула. Формула V − E + F = 2 была (пере) открыта Эйлером; он писал об этом дважды в 1750 году, а в 1752 году опубликовал результат с ошибочным доказательством индукцией для триангулированных многогранников, основанных на удалении вершины и повторной триангуляции дыры, образованной ее удалением.Шаг ретриангуляции не обязательно сохраняет выпуклость или плоскостность полученной формы, поэтому индукция не проходит.
Другая ранняя попытка доказательства, выполненная Мейстером в 1784 году, по сути, является доказательством удаления треугольника, приведенным здесь, но без обоснования существования треугольника, который необходимо удалить.
В 1794 году Лежандр представил полное доказательство, используя сферические углы.
Коши вступил в акт в 1811 году, цитируя Лежандра и добавляя неполные доказательства, основанные на удалении треугольника, разложении ушей и удалении тетраэдра из тетраэдрического разбиения многогранника на более мелкие многогранники.Хилтон и Педерсон предоставляют дополнительные ссылки
а также занимательные размышления об открытии формулы Эйлером.
рассматривается как та же формула. Формула V − E + F = 2 была (пере) открыта Эйлером; он писал об этом дважды в 1750 году, а в 1752 году опубликовал результат с ошибочным доказательством индукцией для триангулированных многогранников, основанных на удалении вершины и повторной триангуляции дыры, образованной ее удалением.Шаг ретриангуляции не обязательно сохраняет выпуклость или плоскостность полученной формы, поэтому индукция не проходит.
Другая ранняя попытка доказательства, выполненная Мейстером в 1784 году, по сути, является доказательством удаления треугольника, приведенным здесь, но без обоснования существования треугольника, который необходимо удалить.
В 1794 году Лежандр представил полное доказательство, используя сферические углы.
Коши вступил в акт в 1811 году, цитируя Лежандра и добавляя неполные доказательства, основанные на удалении треугольника, разложении ушей и удалении тетраэдра из тетраэдрического разбиения многогранника на более мелкие многогранники.Хилтон и Педерсон предоставляют дополнительные ссылки
а также занимательные размышления об открытии формулы Эйлером. Как ни странно, другие уравнения, такие как e i pi = -1
и a phi ( n ) = 1 (mod n )
также называют «формулой Эйлера»; Эйлер был занятым человеком.
Как ни странно, другие уравнения, такие как e i pi = -1
и a phi ( n ) = 1 (mod n )
также называют «формулой Эйлера»; Эйлер был занятым человеком. Графики в этих доказательствах не обязательно будут простыми :
ребра могут соединять вершину с собой, а две вершины могут быть соединены
несколькими краями. Некоторые доказательства опираются на кривую Жордана.
теорема, имеющая множество доказательств; однако это не
обычно основывается на формуле Эйлера, поэтому можно использовать кривые Жордана без
боязнь циркулярных рассуждений.
Графики в этих доказательствах не обязательно будут простыми :
ребра могут соединять вершину с собой, а две вершины могут быть соединены
несколькими краями. Некоторые доказательства опираются на кривую Жордана.
теорема, имеющая множество доказательств; однако это не
обычно основывается на формуле Эйлера, поэтому можно использовать кривые Жордана без
боязнь циркулярных рассуждений.

 2
2