Радиус окружности — что такое, формула, как найти ⚪
Поможем понять и полюбить математику
Начать учиться 220.3KРешить задачу можно по-разному: посчитать на калькуляторе, взять алгоритм из похожей задачки, списать у одноклассника. Самый эффективный и радостный — запомнить формулу и прийти к ответу самому. В этой статье расскажем про способы поиска радиуса окружности.
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — часть плоскости, которая лежит внутри окружности. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать — как найти длину окружности?
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Если известна длина
, где C — длина окружности.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Если известен диаметр окружности
, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ прямоугольника.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
, где a, b — стороны вписанного прямоугольника.
Если известна сторона описанного квадрата
, где a — сторона квадрата.
Сторона описанного квадрата равна диаметру окружности.
Если известны стороны и площадь вписанного треугольника
, где a, b, с — стороны треугольника, S — площадь треугольника.
Если известна площадь и полупериметр описанного треугольника
, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
, где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
, где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
101.5KКак найти периметр квадрата
К следующей статье
555.5KТеорема Пифагора
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Все формулы окружности.
 Длина окружности формула через диаметр. Площадь круга через диаметр.
Длина окружности формула через диаметр. Площадь круга через диаметр.- Статьи
- Формулы окружности
Дарим в подарок бесплатный вводный урок!
Предметы
- Репетитор по математике
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ЕГЭ по математике (базовый уровень)
- Репетитор по химии для подготовки к ОГЭ
- Репетитор для подготовки к ЕГЭ по физике
- Репетитор по русскому языку для подготовки к ЕГЭ
- Подготовка к олимпиадам по английскому языку
- Репетитор по разговорному английскому
- ВПР по физике
- Репетитор для подготовки к ЕГЭ по обществознанию
- Репетитор по информатике для подготовки к ЕГЭ
Формулы окружности
- Длины окружности и диаметр:
\(С=\pi*D\)
- Длина окружности:
\(C = 2*\pi*R\)
- Площадь круга:
\(S=\pi*r^2\)
- Площадь через диаметр:
\(\frac{\pi*D}{4}\)
- Уравнение окружности:
\(r^2 = x^2 + y^2\)
- Выразим \(R\) из формулы \(C = 2*\pi*R\) \(—>\) \(R=\frac{c}{2*\pi}\) подставим \(R\) в формулу \(S=\pi*r^2\) \(—>\) \(S=\frac{C^2}{4*\pi}\).
 2}{4*\pi}\)
2}{4*\pi}\)Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Анжелика Салаватовна Ахметшина
Репетитор по математике
Стаж (лет)
Образование:
Астраханский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Юлия Геннадьевна Газданова
Репетитор по математике
Стаж (лет)
Образование:
Актюбинский педагогический техникум
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Ирина Анатольевна Фокина
Репетитор по математике
Стаж (лет)
Образование:
Гомельский государственный университет им Ф.
 Скорины
СкориныПроведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Похожие статьи
- Теорема Виета
- Как решать логарифмические уравнения
- ЕГЭ по математике, базовый уровень. Планиметрия. Прямоугольный треугольник (вариант 4)
- 10 полезных перекусов для ученика между уроками
- Летние идеи для занятия спортом
- На что обратить внимание при выборе репетитора
- Дети и ненормативная лексика: как объяснить ребенку, что ругаться плохо?
- Интересные факты об устройстве Вселенной
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Основы координатной геометрии — Формула раздела
В этом уроке мы установим формулу для нахождения координат точки, которая делит отрезок, соединяющий две заданные точки в заданном отношении.
 Формула известна как формула раздела . Начнем!
Формула известна как формула раздела . Начнем!Рассмотрим две точки P(x 1 , y 1 ) и Q(x 2 , y 2 ) . Нам нужно найти координаты точки R которая делит PQ в соотношении m : n , т.е. PR/RQ = m/n .
Учитывая соотношение, точка R может либо лежать между P и Q , либо вне отрезка PQ . Взгляни.
(Обратите внимание, что на приведенном выше рисунке m и n не обозначают длины PR и QR . Они просто указывают соотношение.)
Давайте рассмотреть эти случаи один за другим.
Случай I — R лежит между P и QСначала я проиллюстрирую уродливый (но действующий) метод вычисления координат R , используя то, что мы уже знаем — формулу расстояния.
 Как я упоминал ранее, существует (в общем) несколько методов решения задачи координатной геометрии. Это один из таких случаев. Идея состоит в том, чтобы развить ваш уровень мышления и дать вам представление о том, какие методы хороши, а какие нет.
Как я упоминал ранее, существует (в общем) несколько методов решения задачи координатной геометрии. Это один из таких случаев. Идея состоит в том, чтобы развить ваш уровень мышления и дать вам представление о том, какие методы хороши, а какие нет.Вот как можно подумать: «Поскольку есть два неизвестных 92}\)
На этом я остановлюсь. Возможно, вы поняли, почему это не лучший метод. На самом деле, как мы увидим позже, методы, использующие формулу расстояния, обычно становятся довольно сложными и трудными для решения.
Итак, какова наша альтернатива? Немного геометрии — давайте сделаем некоторые построения.
Я начертил RA и QB параллельно оси Y и PA и RB параллельно оси X ось. Тогда треугольники RPA и QRB подобны по АА-подобию.
Как это поможет? Нам дано PR/QR , что с помощью подобия равно RA/QB и PA/RB .
 Позвольте мне записать это лучше:
Позвольте мне записать это лучше:\(\frac{PR}{QR} = \frac{RA}{QB} = \frac{PA}{RB} = \frac{m}{n}\)
Теперь PA = x – x 1 и RB = x 900 08 2 – x (объяснение этому я дал в предыдущем уроке.)
Таким образом, мы можем написать
\(\frac{PA}{RB}=\frac{x-x_1}{x_2-x}=\frac{m}{n}\)
Решив вышеприведенное для x , мы получим
x = 9000 4 \(\frac{mx_2+nx_1}{m+n}\)
А как насчет y ?
На рисунке выше RA = y – y 1 и QB = y 2 – y .
Теперь мы можем использовать тот же процесс, чтобы получить
y = \(\frac{my_2+ny_1}{m+n}\)
Итак имеем координаты точки R , которая делит PQ в отношении м : n .
Когда R лежит между P и Q , мы говорим, что R делит PQ в отношении m : n внутренне 90 004 .
 Вот симуляция, которая показывает две точки A и B , а также точку C , разделяющую соединяющий их отрезок в некотором отношении.
Вот симуляция, которая показывает две точки A и B , а также точку C , разделяющую соединяющий их отрезок в некотором отношении.Попробуйте изменить значения м и n и посмотрите координаты C . Вы получаете те же координаты, используя формулу сечения?
Давайте посмотрим, что произойдет, когда R окажется за пределами PQ .
Случай II – R лежит вне PQДанное условие то же самое, т.е. PR / RQ = m / n , но цифра будет немного другой.
В этом случае мы говорим, что R делит PQ внешне в отношении m : n .
Я не буду его выводить. Пожалуйста, попробуйте сделать это сами. Метод тот же, что и в первом случае – найти подобные треугольники, выразить данное отношение через х 1 , х 2 , y 1 и у 2 .

Если все сделать правильно, то должно получиться
x = \( \frac{mx_2-nx_1}{m-n}\)
y = \( \frac{my_2-ny_1}{m-n}\)
- Координаты точки, разделяющей отрезок, соединяющий (x 1 , y 1 ) 90 004 и (x 2 , y 2 ) в соотношении m : n внутренне задается \(\left ( \frac{mx_2+nx_1}{m+n} , \frac{my_2+ny_1}{m+n} \right ) \)
- Координаты точки, разделяющей отрезок, соединяющий (x 1 , y 1 ) и (x 2 , y 2 ) в отношении m : n внешне задается выражением \(\left ( \frac{mx_2-nx_1}{m-n} , \frac{my_2+ny_1}{m+n} \right ) \) 902 82
Вот и все. Увидимся на следующем уроке с некоторыми примерами и применениями формулы сечения!
Геометрия статических [… формула …] идеальных жидких сфер в общей теории относительности
- Список журналов
- Открытый выбор Спрингера
- PMC
26
Являясь библиотекой, NLM предоставляет доступ к научной литературе.
 Включение в базу данных NLM не означает одобрения или согласия с
содержание NLM или Национальных институтов здравоохранения.
Узнайте больше о нашем отказе от ответственности.
Включение в базу данных NLM не означает одобрения или согласия с
содержание NLM или Национальных институтов здравоохранения.
Узнайте больше о нашем отказе от ответственности.Европейский физический журнал. C, Частицы и поля
Eur Phys J C Part Fields. 2022 г.; 82(4): 364.
Опубликовано в сети 25 апреля 2022 г. doi: 10.1140/epjc/s10052-022-10349-2
, 1 , 2 и 9032 1 3Информация об авторе Примечания к статье Информация об авторских правах и лицензиях Отказ от ответственности
- Заявление о доступности данных
Мы обсуждаем физические особенности двух последних классов аналитических решений уравнений Эйнштейна, полученных с помощью экзотической идеальной жидкости с уравнением состояния P=-ρ/5. Эти геометрии зависят от четырех параметров и являются статическими и сферически-симметричными. Они описывают компакты с голыми центральными особенностями.

Недавно Семиз [1] предложил два новых семейства статических и сферически-симметричных решений уравнений Эйнштейна (без космологической постоянной). Источником вещества является идеальная жидкость с постоянным баротропным уравнением состояния P=-ρ/5, где ρ и P — плотность энергии жидкости и давление соответственно [1]. Хотелось бы понять физическую природу этих решений и оценить, могут ли они быть полезны для моделирования областей звезд, хотя бы в качестве игрушечных моделей. Уравнение состояния P=-ρ/5 явно нефизично, так как трудно найти реалистичные ситуации, описываемые этой жидкостью, но темные энергоподобные звезды (и даже звезды фантомной энергии [2]) изучались в литературе [3–10], а также гало экзотической энергии [11]. Хотя темная энергия имеет давление P<-ρ/3 и есть все признаки того, что, если она отвечает за нынешнее ускорение нашей Вселенной, она имеет уравнение состояния P≃-ρ [12], наша ситуация с P=-ρ/5 все еще может служить игрушечной моделью для гипотетических объектов, образованных жидкостью с отрицательным давлением.
Более того, с математической точки зрения относительно сложно найти простые решения уравнений Эйнштейна, описывающих идеальные жидкости. Хотя существует более сотни аналитических решений уравнений Эйнштейна, источником которых являются идеальные (и даже несовершенные) жидкости, являющиеся потенциальными кандидатами для моделирования релятивистских звезд или, по крайней мере, звездных областей [13, 14], почти все они по тем или иным причинам оказываются нефизическими [14]. Здесь мы исследуем новые решения [1], чтобы понять их физические особенности (или их отсутствие). Эти геометрии записываются в координатах Бухдаля, но с физической точки зрения более поучительно переписать их в терминах координат Шварцшильда, что мы и делаем здесь.
Мы следуем обозначениям Ref. [15]: метрическая сигнатура -+++, и мы используем единицы, в которых скорость света в вакууме c и постоянная Ньютона G равны единице, а κ≡8πG, чтобы не отклоняться от Ref. [1].
Предложение Семиза состоит из четырехпараметрического семейства решений уравнений Эйнштейна с нулевой космологической постоянной
Rab-12gabR=κTab,
1
, где Rab — тензор Риччи метрического gab, а R — скаляр Риччи.
 Источником вещества является идеальная жидкость с тензором энергии-импульса
Источником вещества является идеальная жидкость с тензором энергии-импульсаTab=P+ρuaub+Pgab,
2
где ua – 4-скорость жидкости, а уравнение состояния P=-ρ/5 [1]. Эти геометрии сферически симметричны и статичны в соответствующем диапазоне координат. В [1] появились два новых класса решений: наиболее общее семейство параметризовано четырьмя константами C0,C1,C2,C3 и имеет линейный элемент
с C1≠0, C0+C1r≠0, и где
f(r)=3C1C2+r+C3C0+C1r3,
4
, а dΩ(2)2≡dϑ2+sin2ϑdφ2 — линейный элемент на единичной двумерной сфере. Плотность энергии равна [1]
ρ(r)=-5P(r)=-45κC13C3C0+C1r2f2(r)
5
и неотрицательна при условии, что
C1C3≤0,
6
, что мы предполагаем в дальнейшем, а предельная ситуация, заданная C3=0, соответствует вакууму. Решение для C1=0 не получается непрерывно из уравнений. (3) и (5) в пределе C1→0, но требует отдельного обсуждения [1]. Это второе семейство параметризуется оставшимися тремя константами [1]: мы начнем с анализа этого второго семейства (или «специального решения» в номенклатуре [1]) в следующем разделе.

Это трехпараметрическое семейство решений C0,C2,C3 описывается линейным элементом [1]
ds2=-C02g(r)dt2+g(r)C02dr2+g2(r)C02dΩ(2)2
7
с C0≠ 0 и где
g(r)=C0C2+C3r-r2
8
ρ(r)=-5P(r)=5κC02g2(r).
9
Для сохранения метрической сигнатуры она должна быть g(r)>0 (если g ( r ) становится отрицательным, координаты t и r меняют свою времениподобную и пространственноподобную природу, как в геометрия Шварцшильда на горизонте r=2м).
Перепишем линейный элемент (7) через площадной радиус R(r)=g(r)/|C0|. Это соотношение инвертируется путем получения
r2-C0C3r+|C0|R-C0C2=0
10
и решения для
r(R)=12C0C3±C02C32+4C0C2-|C0|R.
11
Аргумент квадратного корня в правой части должен быть неотрицательным, чтобы r оставалось действительным, что дает ограничение
0≤R
12
на диапазоне площади радиуса.
 Последняя начинается с нуля при r1=12C0C3-C02C32+4C0C2, увеличивается до максимума
Последняя начинается с нуля при r1=12C0C3-C02C32+4C0C2, увеличивается до максимумаRmax=RC0C32,
13
и затем уменьшается, пока снова не обращается в нуль при r2=12C0C3+C02C32+4C0C2. Две координатные карты r1≤r≤C0C3/2 и C0C3/2≤r≤r2 покрывают одну и ту же физическую область 0≤R≤Rmax. Ограничимся r1≤r≤C0C3/2, в котором dR/dr>0, выбрав отрицательный знак в уравнении (2.5).
Запишем
C0C3-2r=∓C02C32+4C0C2-|C0|R
14
и, подставив соотношение между дифференциалами
dr=|C0|C0C3-2rdR 90 005
15
и используя уравнение. (14), линейный элемент (7) принимает вид
ds2=-|C0|Rdt2+dR24RmaxR-1+R2dΩ(2)2.
16
Уравнение ∇cR∇cR=gRR=0, определяющее расположение кажущихся горизонтов (см., например, [16]), имеет Rmax в качестве единственного корня, который является единственным корнем, и, следовательно, при R
Плотность энергии [1]
ρ(R)=5κC02g2(r)=5κR2
17
и давление P=-ρ/5 (всегда отличные от нуля) расходятся в начале координат R=0, что соответствует r=r1, вместе с Ric ci скаляр
R=-κT=κρ-3P=8κ5ρ=8κ2R2,
18
поэтому в начале координат R=0 имеется обнаженная пространственно-временная сингулярность.

Масса Мизнера-Шарпа-Эрнандеса MMSH(R), определенная в сферической симметрии по формуле [17, 18] R)=125R-4Rmax
20
для геометрии (16) и отрицательно в области 0
Придем к максимальному значению Rmax площадного радиуса, который, несмотря на то, что является формальным корнем уравнения ∇cR∇cR=0, не описывает горизонт, а является антиподом начала координат R=0 в компактном пространстве.
 Чтобы увидеть этот факт, полезно изучить поведение радиальных нулевых геодезических в этой геометрии. Рассмотрим исходящие (+) и входящие (-) конгруэнции радиальных нулевых геодезических с касательными l(±)µ=dxµ/dλ, где λ — аффинный параметр вдоль этих кривых. Эти тангенсы имеют компоненты l(±)µ=l0,l1,0,0, и нормировка la(±)l(±)a=0 дает
Чтобы увидеть этот факт, полезно изучить поведение радиальных нулевых геодезических в этой геометрии. Рассмотрим исходящие (+) и входящие (-) конгруэнции радиальных нулевых геодезических с касательными l(±)µ=dxµ/dλ, где λ — аффинный параметр вдоль этих кривых. Эти тангенсы имеют компоненты l(±)µ=l0,l1,0,0, и нормировка la(±)l(±)a=0 даетl(±)1=±2RRmax-R|C0|l(±)0;
21
поскольку нулевой вектор может быть масштабирован функцией, мы можем выбрать l0=1 (что означает выбор координатного времени t в качестве аффинного параметра вдоль этих нулевых геодезических), получив
l(±)μ=1,±2RRmax-R|C0|,0,0.
22
Тогда имеем уравнения первого порядка 02, которые интегрируются в
t(λ)=λ-λ0,
25
Rmax-RR+2Rmax=∓3|C0|λ-λ0
26
где λ0 — постоянная интегрирования. К сожалению, это отношение нельзя инвертировать явно.
Начиная с
dRdt=dRdλ=±2|C0|Rmax-RR
27
(с верхним знаком для исходящих и нижним для входящих радиальных геодезических), вблизи начала координат R=0 dR/dt∼+∞ для исходящих и dR/dt∼-∞ для входящих геодезических.
 Кроме того, dR/dt=0 при R=Rmax. Исходящие радиальные нулевые геодезические, начинающиеся вблизи начала координат, делают это очень быстро, но замедляются по мере приближения к максимально возможному радиусу Rmax, который может быть достигнут только при нулевой скорости (см. рис. ). Нулевая геодезическая, начинающаяся точно в Rmax, делает это с нулевой скоростью dR/dλ и остается там. Входящие радиальные нуль-геодезические, начинающиеся вблизи максимального радиуса Rmax, медленны и ускоряются по мере приближения к центральной голой сингулярности, к которой они приближаются с бесконечной скоростью dR/dλ→-∞.
Кроме того, dR/dt=0 при R=Rmax. Исходящие радиальные нулевые геодезические, начинающиеся вблизи начала координат, делают это очень быстро, но замедляются по мере приближения к максимально возможному радиусу Rmax, который может быть достигнут только при нулевой скорости (см. рис. ). Нулевая геодезическая, начинающаяся точно в Rmax, делает это с нулевой скоростью dR/dλ и остается там. Входящие радиальные нуль-геодезические, начинающиеся вблизи максимального радиуса Rmax, медленны и ускоряются по мере приближения к центральной голой сингулярности, к которой они приближаются с бесконечной скоростью dR/dλ→-∞.Открыть в отдельном окне
Радиус площади R в зависимости от аффинного параметра λ вдоль радиальных нулевых геодезических геометрии (16) для значений параметров C0=C2=2, C3=3 и λ0=1. Исходящие геодезические замедляются по мере приближения к Rmax, где они останавливаются. Входящие геодезические, начинающиеся вблизи Rmax, делают это очень медленно, но ускоряются по мере приближения к R=0
.
 Мы также можем изучать радиальные времениподобные геодезические с касательными uμ=u0,u1,0,0. Нормализация ucuc=-1 дает
Мы также можем изучать радиальные времениподобные геодезические с касательными uμ=u0,u1,0,0. Нормализация ucuc=-1 даетu1=±2RRmax-R|C0|(u0)2R-1,
28
с верхним знаком для исходящих и нижним для входящих геодезических. Времяподобный вектор Киллинга ξa=∂/∂ta гарантирует сохранение энергии на единицу массы пробной частицы E вдоль этих геодезических кривых: эти кривые ориентированы на будущее, поэтому E строго положительно. Уравнение (28) дает
u1=±2RRmax-RE2R|C0|-1,
30
что говорит нам о том, что:
- Для данной энергии E определяемой начальным условием R0,R˙0, радиальное движение возможно только если
R>Rmin≡|C0|E2
31
(иначе u1 становится мнимой). Входящее радиальное движение останавливается в точке Rmin, и пробная частица не может приблизиться к началу координат, что согласуется с тем фактом, что согласно уравнению (29), u0=ER/|C0|→0 при R→0.
Исходящее радиальное движение останавливается в точке Rmax, где u1 обращается в нуль как для исходящей, так и для входящей радиальных геодезических, и частица, стартовавшая изначально в Rmax, остается там независимо от своей начальной энергии.

- Поскольку R ограничено Rmax, возможные энергии ограничены снизу,
E>|C0|Rmax=2|C0|C02C32+4C0C2≡Emin;
32
903 20 частиц с энергией ниже или равной минимальному порогу Emin не движутся.
Случай C2≠0, C3=0
В этом случае у нас остаются только два параметра C0,C2. Теперь g(r)=C0C2-r2, что требует
C0C2>0,0≤r≤C0C2.
33
Радиус площади равен
R(r)=g(r)|C0|=C0C2-r2|C0|
34
, где r=0 соответствует R=C0C2/|C0|, а r=C2sign(C0) соответствует началу R=0 физической радиальной координаты. Радиус области R ( r ) изменяется в диапазоне
0≤R≤C2sign(C0)=|C2|
35
(где в последнем равенстве использован тот факт, что C0C2>0) и является убывающей функцией от r , так как dR/dr=-2r/|C0| всегда отрицательно в допустимом диапазоне. Обращая соотношение между радиальными координатами, получаем
r(R)=C0C2-|C0|R
36
, что вместе с
dr=-|C0|dR2C0C2-|C0|R
37
дает линейный элемент
ds2=-|C0|Rdt2+dR24|C2|R-1+R2dΩ(2)2.
38
Эта геометрия такая же, как и в предыдущем случае C1=0, C3≠0, заданном линейным элементом (16), но теперь Rmax=|C2|. Опять же, плотность энергии отлична от нуля, а скаляр Риччи расходится в начале координат R=0.
Случай C2=0,C3≠0
Для этих значений параметров g(r)=rC0C3-r требует, чтобы C0C3 было положительным, и поэтому мы имеем диапазон 0≤r≤C0C3 радиуса Бухдаля. Соответственно радиус площади
R(r)=rC0C3-r|C0|
39
меняется в интервале
0≤R≤|C0|C324,
40
начиная с нуля при r=0, увеличивая до максимума
Rmax≡RC0C32=|C0|C324,
41
900 02, а затем уменьшается, пока снова не исчезнет при r=C0C3. Имеются две координатные карты 0≤r≤C0C3/2 и C0C3/2≤r≤C0C3, покрывающие одну и ту же физическую область 0≤R≤Rmax, и мы ограничимся первой, в которой dR/dr>0. Уравнение (39) даетr2-C0C3r+|C0|R=0
42
с корнями
r(R)=12C0C3±C02C32-4|C0|R,
43
где мы выбираем меньший знак для согласованности с dR/dr>0 и 0≤r≤C0C3/2. Тогда g(r)=|C0|R и
Тогда g(r)=|C0|R и
dr=|C0|C02C32-4|C0|RdR
44
дают линейный элемент
ds2=-|C0|Rdt2+dR24RmaxR-1+R2dΩ(2)2
45
, который совпадает с линейным элементом (16), но с Rmax, который теперь определяется уравнением. (41). Скаляр Риччи
R=8κ5ρ=8κ2R2=8κ2C02r2C0C3-r2,
46
расходится в начале координат R=0 (что соответствует r=0 на карте с dR/dr>0), поэтому там имеется голая пространственно-временная сингулярность.
Элемент строки для общего семейства решений Semiz равен (3) [1]. Наличие четырех параметров с относительно широкими диапазонами в настоящее время затрудняет получение определенных выводов, и мы сосредоточимся на частных случаях.
C3=0 равно Шварцшильду
Когда C3=0, плотность энергии (5) и давление P=-ρ/5 тождественно равны нулю, и это пространство-время пусто. Поскольку геометрия также сферически-симметрична и асимптотически плоская (как мы собираемся показать), она должна быть шварцшильдовской согласно теореме Джебсена-Биркгофа [15]. На самом деле имеем f(r)=3C1C2+r, радиус области равен
На самом деле имеем f(r)=3C1C2+r, радиус области равен
R=C1C2+r|C1|,
47
и
C0+C1r=C1|C1|R+C0-C12C2,
48
тогда dr=|C1 |dR, что дает линейный элемент
ds2=-C12R+C0-C12C2sign(C1)Rdt2+C12RC12R+C0-C12C2sign(C1)dR2+R2dΩ(2)2
49
≃-dt¯2+dR 2+R2dΩ(2)2asR→+∞,
50
где dt¯≡|C1|dt. Эта геометрия является асимптотически плоской: путем введения константы
м≡12C12C12C2-C0sign(C1)
51
(что не обязательно положительно) и масштабирования временной координаты в соответствии с t→t¯=|C1|t линейный элемент (49) записывается как шварцшильдовская
ds2=-1-2mRdt¯2+dR21-2m/R+R2dΩ(2)2
52
, описывающая черную дыру, если m>0, и голую центральную особенность, если m<0.
Частный случай C2=0
У нас есть три параметра C0,C1,C3, где C1C3≤0, и теперь f(r)=3r+C3C0+C1r3; радиус площади равен
R(r)=3r+C3C0+C1r33|C1|.
53
У нас есть
dRdr=1|C1|1-|C1C3|C0+C1r2,
54
, что положительно для
r+C0C1<1|C1||C1C3|.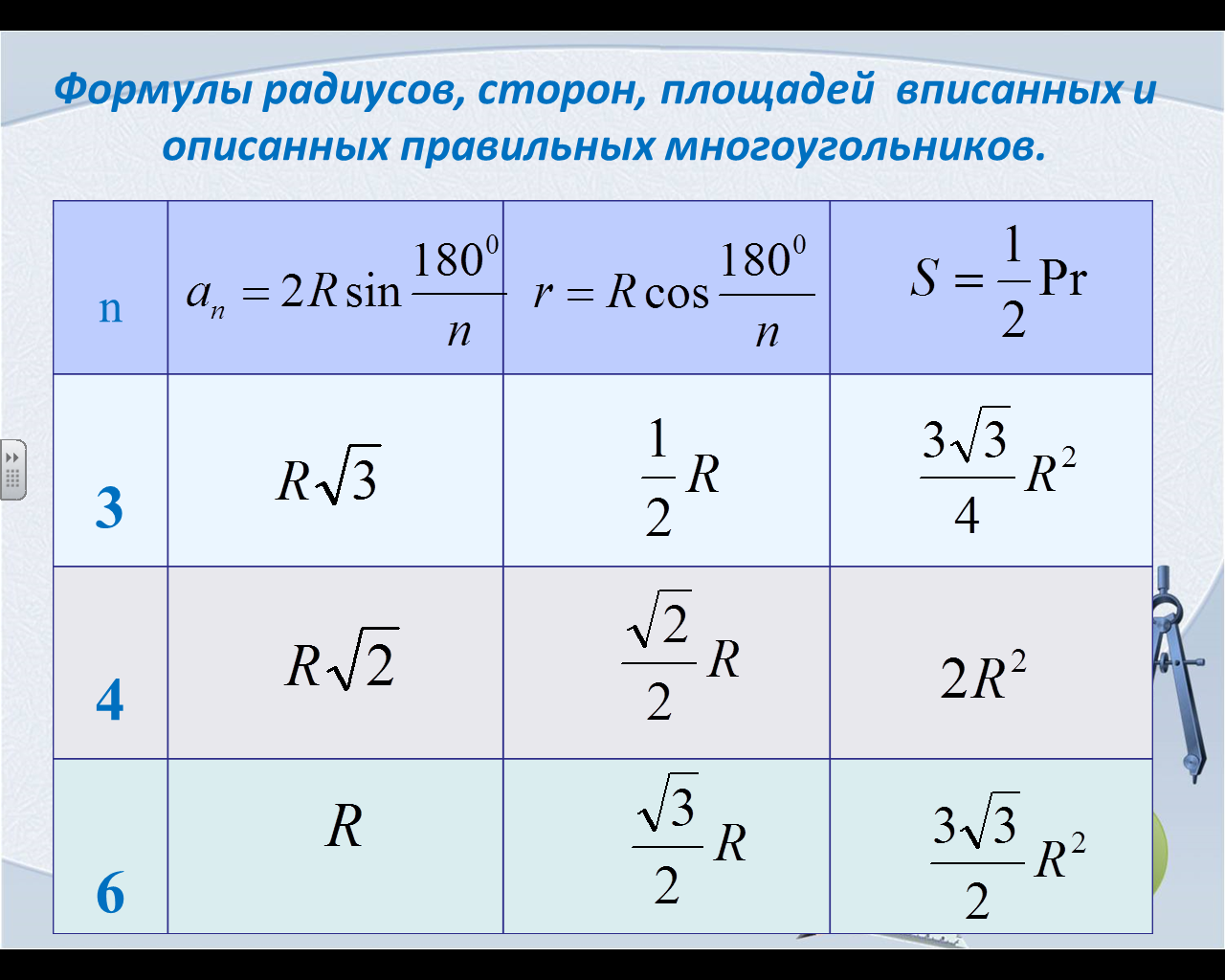
55
Для продолжения рассмотрим ситуацию r≥-C0/C1, в этом случае R возрастает в интервале
rmin≡-C0C1≤r≤1|C1||C1C3|-C0C1≡rmax
9 0002 56с Rmin≤R≤Rmax и
Rmin≡Rrmin=-C0C1|C1|
57
Rmax≡Rrmax=13|C1|3|C1||C1C3|-3C0C1+C3знак(C1)|C1C3|3=13|C1|3+знак(C1C3)|C1||C1C3|-3C0C1=13|C1|2|C1||C1C 3|-3C0C1, если C1C3<0,1C121|C1C3|-C0sign(C1), если C1C3=0.
58
У нас снова компактное пространство. Переписывая линейный элемент (3) через радиус площади, мы получаем громоздкое выражение, которое не зависит только от R , но содержит также r ( R ), поскольку отношение R ( r ) не может быть инвертировано явно.
Еще более частный случай C0=C2=0
В этом случае у нас есть только два параметра C1,C3, f(r)=r3+C13C3r2, а радиус области равен
R(r)=f(r)3|C1|=3r+C13C3r33|C1|=r3+(C1C 3)C12r23|C1|≤r|C1|,
59
где последнее неравенство следует из C1C3≤0. Так как
Так как
dRdr=1-|C1C3|C12r2|C1|≥0∀r∈0,1|C1||C1C3|,
60
радиус площади является возрастающей функцией r в интервале 0,1|C1||C1 С3| при R(0)=0, максимально при 1|C1||C1C3| а затем уменьшается, снова обращаясь в нуль при r=3|C1C3|C12. Это компактное пространство соответствует диапазону
0≤R≤Rmax=23C12|C1C3|
61
радиуса площади, где R≃r/|C1| при r→0+. Уравнение (59) инвертируется, сначала получая
C3C13r3+3r-3|C1|R=0
62
, а затем решая
r=A(R)1/32C3C12-2C1A(R)1/3
63
, где
A(R)=12|C1|C1R+49C14R2+4C12C32,
64
, а два оставшихся корня мнимые. Подставив соотношение между дифференциалами
dr=|C1|1+C3C13r2dR
65
и используя
1+C13C3r2=A(R)2/34C1C3+4C1C3A(R)2/3-1 9000 5
66
дает линейный элемент
ds2=-1|C1|RA(R)1/32C3-2C1A(R)1/3dt2+C12|C1|RB(R)dR2+R2dΩ(2)2,
67
, где
B (R)=A(R)5/332C12C33-32C13C32A(R)5/3+5A(R)1/32C3-3A(R)8C1C32+24C12C3A(R)-10C1A(R)2/3.
68
Опять же, многочисленные комбинации параметров и громоздкие метрические коэффициенты не поддаются прямому и прозрачному анализу, но ясно, что и в этом случае мы имеем компактное трехмерное пространство конечной протяженности.
Используя (3.20), плотность энергии (5) сводится к 05
как R→0+. Следовательно, ρ и P сингулярны в начале координат вместе со скаляром Риччи R и
RabRab=28κ225ρ2.
70
При R→0+ имеем асимптотику 5C12C31/3-3C1+3C3≡B0,
72
g00≈-1|C1|RC12C31/3-C1C321/3,
73
g11≈C12|C1|RB0,
74
и g00→∞, а g11→0 при R→0.
Мы изучили природу новых классов статических и сферически-симметричных решений уравнений Эйнштейна, приведенных недавно в [1]. [1] когда источником вещества является идеальная жидкость с уравнением состояния P=-ρ/5. Аналитические решения Ref. Анализируемые нами работы [1] (за исключением решения Шварцшильда, полученного при C3=0) описывают компакты с голыми центральными особенностями. «Общее» семейство решений (3) и (5) всегда сводится к шваршильдовскому, когда параметр C3 равен нулю. В большинстве других ситуаций наличие трех или четырех параметров и/или кубический характер функции R ( r ) затруднить полное описание геометрии. Однако во всех проанализированных случаях, кроме пустого пространства-времени, связанного с C3=0, мы находим компакт конечного объема (особенность, упомянутая в [1]).
«Общее» семейство решений (3) и (5) всегда сводится к шваршильдовскому, когда параметр C3 равен нулю. В большинстве других ситуаций наличие трех или четырех параметров и/или кубический характер функции R ( r ) затруднить полное описание геометрии. Однако во всех проанализированных случаях, кроме пустого пространства-времени, связанного с C3=0, мы находим компакт конечного объема (особенность, упомянутая в [1]).
Тот факт, что геометрия вместе с плотностью энергии и давлением является сингулярной при R=0, не обязательно является похоронным звоном для этих решений. Фактически считается приемлемым для флюидных решений уравнений Эйнштейна моделировать только ограниченные области релятивистских звезд, процедура, которая отражена в авторитетной работе Ref. [13] и в более специализированной литературе. Действительно, даже ньютоновские звезды редко моделируются с помощью одной жидкости, что соответствует тому факту, что разные области при разных температурах и плотностях описываются разными уравнениями состояния, если только звездный материал не хорошо перемешан, что происходит только в определенных типах звезд. Следовательно, в принципе существует (физически хорошо мотивированная) возможность удалить сингулярность и заменить ее более реалистичной геометрией, источником которой является материя с другим уравнением состояния. Однако, если кто-то хочет описать внутреннюю часть звезды с помощью этой экзотической жидкости, он должен сопоставить ее с асимптотически плоской внешностью Шварцшильда. Тот факт, что решения [1] описывают компактные пространства, указывает на возможную аналогию с моделью Оппенгеймера-Снайдера гравитационного коллапса в черную дыру [33]. В этой модели компактная, положительно искривленная вселенная Фридмана-Лемэтра-Робертсона-Уокера, коллапсирующая до Большого сжатия, сопоставляется с экстерьером Шварцшильда на поверхности 2-сферы симметрии [33], удовлетворяющим условиям соединения Дармуа-Израэля [34, 35]. Однако в модели Оппенгеймера-Снайдера совпадение возможно, поскольку коллапсирующая внутренняя Вселенная заполнена пылью с нулевым давлением повсюду. Хорошо известно, что согласование с экстерьером Шварцшильда может быть выполнено только на поверхности, на которой давление P ( R ) исчезает, иначе условия соединения нарушаются и на поверхности согласования имеется слой материала, который, конечно, не является составной частью реалистичных моделей звезд.
Следовательно, в принципе существует (физически хорошо мотивированная) возможность удалить сингулярность и заменить ее более реалистичной геометрией, источником которой является материя с другим уравнением состояния. Однако, если кто-то хочет описать внутреннюю часть звезды с помощью этой экзотической жидкости, он должен сопоставить ее с асимптотически плоской внешностью Шварцшильда. Тот факт, что решения [1] описывают компактные пространства, указывает на возможную аналогию с моделью Оппенгеймера-Снайдера гравитационного коллапса в черную дыру [33]. В этой модели компактная, положительно искривленная вселенная Фридмана-Лемэтра-Робертсона-Уокера, коллапсирующая до Большого сжатия, сопоставляется с экстерьером Шварцшильда на поверхности 2-сферы симметрии [33], удовлетворяющим условиям соединения Дармуа-Израэля [34, 35]. Однако в модели Оппенгеймера-Снайдера совпадение возможно, поскольку коллапсирующая внутренняя Вселенная заполнена пылью с нулевым давлением повсюду. Хорошо известно, что согласование с экстерьером Шварцшильда может быть выполнено только на поверхности, на которой давление P ( R ) исчезает, иначе условия соединения нарушаются и на поверхности согласования имеется слой материала, который, конечно, не является составной частью реалистичных моделей звезд. (Этот факт подчеркивается во многих исследованиях релятивистских жидких шаров [36–43] и файрболов [44].) Однако для обсуждаемых жидких растворов [1] давление P ( R ) никогда не обращается в нуль. Поэтому лучшее, что можно сделать, это смоделировать ограниченную область недр звезды с помощью решений Семиза для P=-ρ/5. Чтобы быть физической, эта область должна соответствовать положительной массе Мизнера-Шарпа-Эрнандеса MMSH и, следовательно, должна быть достаточно далеко от сингулярности при R=0. Вырезанная область, содержащая начало координат, должна быть смоделирована с помощью другого, неособого решения уравнений Эйнштейна. 1 Затем решение w=-1/5 следует непрерывно согласовывать с другим «промежуточным» решением с ненулевым давлением на поверхности постоянного радиуса, а затем давление в этом слое должно стремиться к нулю на больших радиусах, чтобы можно было согласовать его с экстерьером Шварцшильда, снова удовлетворяя условиям сопряжения Дармуа-Израэля.
(Этот факт подчеркивается во многих исследованиях релятивистских жидких шаров [36–43] и файрболов [44].) Однако для обсуждаемых жидких растворов [1] давление P ( R ) никогда не обращается в нуль. Поэтому лучшее, что можно сделать, это смоделировать ограниченную область недр звезды с помощью решений Семиза для P=-ρ/5. Чтобы быть физической, эта область должна соответствовать положительной массе Мизнера-Шарпа-Эрнандеса MMSH и, следовательно, должна быть достаточно далеко от сингулярности при R=0. Вырезанная область, содержащая начало координат, должна быть смоделирована с помощью другого, неособого решения уравнений Эйнштейна. 1 Затем решение w=-1/5 следует непрерывно согласовывать с другим «промежуточным» решением с ненулевым давлением на поверхности постоянного радиуса, а затем давление в этом слое должно стремиться к нулю на больших радиусах, чтобы можно было согласовать его с экстерьером Шварцшильда, снова удовлетворяя условиям сопряжения Дармуа-Израэля. Ввиду отсутствия в астрофизике особой потребности в такой запутанной «звездной» модели мы не будем дальше заниматься этим вопросом, ограничившись указанием ограничений для такой конструкции. Вероятно, некоторая феноменология, раскрытая здесь для геометрий, найденных в [1], применима и к другим классам идеальных флюидных решений уравнений Эйнштейна. Так ли это, будет установлено в дальнейших работах.
Ввиду отсутствия в астрофизике особой потребности в такой запутанной «звездной» модели мы не будем дальше заниматься этим вопросом, ограничившись указанием ограничений для такой конструкции. Вероятно, некоторая феноменология, раскрытая здесь для геометрий, найденных в [1], применима и к другим классам идеальных флюидных решений уравнений Эйнштейна. Так ли это, будет установлено в дальнейших работах.
Эта работа частично поддерживается Канадским советом по естественным наукам и инженерным исследованиям (грант № 2016-03803 В.Ф.).
Эта рукопись не имеет связанных данных или данные не будут депонированы. [Комментарий авторов: Данные, связанные с этой статьей, отсутствуют из-за ее теоретического и формального характера.]
1 Есть одна тонкость: согласование области Семиз с другим жидким решением в принципе возможно, поскольку геометрии Семиз решают уравнения Эйнштейна с нулевой космологической постоянной Λ. Ненулевое Λ будет присутствовать во всех областях пространства-времени, и сопоставление одной из них с экстерьером Шварцшильда невозможно [45].
Бехназ Фазлпур, электронная почта: [email protected].
Али Баниджамали, электронная почта: [email protected].
Валерио Фараони, электронная почта: ac.spohsibu@inoarafv.
1. И. Semiz, arXiv:2007.08166 [gr-qc]
2. ДеБенедиктис А., Гараттини Р., Лобо ФСН. физ. Ред. Д. 2008; 78:104003. doi: 10.1103/PhysRevD.78.104003. [CrossRef] [Google Scholar]
3. Chapline G. eConf. 2004;C041213:0205. [Google Scholar]
4. Лобо ФСН. Сорт. Квант. Грав. 2006; 23:1525–1541. дои: 10.1088/0264-9381/23/5/006. [CrossRef] [Google Scholar]
5. Bilic N, Tupper GB, Viollier RD. JCAP. 2006;02:013. doi: 10.1088/1475-7516/2006/02/013. [CrossRef] [Google Scholar]
6. Chan R, da Silva MFA, Villas da Rocha JF. Ген. отн. Гравит. 2009;41:1835–1851. doi: 10.1007/s10714-008-0755-9. [CrossRef] [Google Scholar]
7. Язаджиев С.С. физ. Ред. Д. 2011; 83:127501. doi: 10.1103/PhysRevD.83.127501. [CrossRef] [Google Scholar]
8. Rahaman F, Maulick R, Yadav AK, Ray S, Sharma R. Gen. Relativ. Гравит. 2012;44:107–124. doi: 10.1007/s10714-011-1262-y. [Перекрестная ссылка] [Академия Google]
Gen. Relativ. Гравит. 2012;44:107–124. doi: 10.1007/s10714-011-1262-y. [Перекрестная ссылка] [Академия Google]
9. Хорват Д., Марунович А. Класс. Квант. Грав. 2013;30:145006. doi: 10.1088/0264-9381/30/14/145006. [CrossRef] [Google Scholar]
10. Bhar P. Phys. Темный унив. 2021;34:100879. doi: 10.1016/j.dark.2021.100879. [CrossRef] [Google Scholar]
11. Armendariz-Picon C, Lim EA. JCAP. 2005;08:007. doi: 10.1088/1475-7516/2005/08/007. [CrossRef] [Google Scholar]
12. Амендола Л., Цудзикава С. Темная энергия: теория и наблюдения. Кембридж, Великобритания: Издательство Кембриджского университета; 2010. [Google Академия]
13. Стефани Х., Крамер Д., Маккаллум М., Хоэнселерс С., Херлт Э. Точные решения уравнений поля Эйнштейна. Кембридж: Издательство Кембриджского университета; 2003. [Google Scholar]
14. Delgaty MSR, Lake K. Comput. физ. коммун. 1998; 115: 395–415. doi: 10.1016/S0010-4655(98)00130-1. [CrossRef] [Google Scholar]
15. Уолд Р. М. Общая теория относительности. Чикаго: Издательство Чикагского университета; 1984. [Google Scholar]
М. Общая теория относительности. Чикаго: Издательство Чикагского университета; 1984. [Google Scholar]
16. В. Фараони, Космологические и видимые горизонты черных дыр , Лект. Примечания физ. 907 (Спрингер, Нью-Йорк, 2015 г.)
17. Misner CW, Sharp DH. физ. 1964; 136:B571. doi: 10.1103/PhysRev.136.B571. [CrossRef] [Google Scholar]
18. Hernandez WC, Misner CW. Астрофиз. Дж. 1966; 143:452. дои: 10.1086/148525. [CrossRef] [Google Scholar]
19. Хокинг С.В. Дж. Матем. физ. 1968; 9:598. дои: 10.1063/1.1664615. [CrossRef] [Google Scholar]
20. Hayward SA. физ. Преподобный Д. 1994; 49:831. doi: 10.1103/PhysRevD.49.831. [PubMed] [CrossRef] [Академия Google]
21. Хейворд С.А. физ. Преподобный Д. 1996; 53:1938. doi: 10.1103/PhysRevD.53.1938. [PubMed] [CrossRef] [Google Scholar]
22. Фараони В., Джусти А. Симметрия. 2020;12:1264. doi: 10.3390/sym12081264. [CrossRef] [Google Scholar]
23. В. Фараони, А. Джусти, Т. Ф. Бин, физ. Ред. Д 103 , 044026 (2021)
Ф. Бин, физ. Ред. Д 103 , 044026 (2021)
24. И.З. Фишер, Ж. Эксп, теор. Физ. 18 , 636–640 (1948)
25. Bergmann O, Leipnik R. Phys. 1957; 107:1157–1161. doi: 10.1103/PhysRev.107.1157. [Перекрестная ссылка] [Академия Google]
26. Janis AI, Newman ET, Winicour J. Phys. Преподобный Летт. 1968; 20: 878–880. doi: 10.1103/PhysRevLett.20.878. [CrossRef] [Google Scholar]
27. Buchdahl HA. Междунар. Дж. Теор. физ. 1972; 6: 407–412. doi: 10.1007/BF01258735. [CrossRef] [Google Scholar]
28. Wyman M. Phys. Преподобный Д. 1981; 24: 839–841. doi: 10.1103/PhysRevD.24.839. [CrossRef] [Google Scholar]
29. Дионисиу Д.Д. Астрофиз. Космические науки. 1982; 88:493. doi: 10.1007/BF01092715. [CrossRef] [Академия Google]
30. Agnese AG, La Camera M. Phys. Преподобный Д. 1985; 31: 1280–1286. doi: 10.1103/PhysRevD.31.1280. [PubMed] [CrossRef] [Google Scholar]
31. Вирбхадра К.С. Междунар. Дж. Мод. физ. А. 1997; 12:4831–4836. doi: 10.1142/S0217751X97002577. [CrossRef] [Google Scholar]
doi: 10.1142/S0217751X97002577. [CrossRef] [Google Scholar]
32. Фараони В., Джусти А., Фахим Б.Х. физ. Представитель 2021; 925:1–58. doi: 10.1016/j.physrep.2021.04.003. [CrossRef] [Google Scholar]
33. Оппенгеймер Дж. Р., Снайдер Дж. Р. физ. 1939; 56:455. doi: 10.1103/PhysRev.56.455. [Перекрестная ссылка] [Академия Google]
34. Darmois G. Les Equations de la Gravitation Einsteinienne. Париж: Готье-Вилларс; 1927. [Google Scholar]
35. W. Israel, Nuovo Cimento B 44 , (1966)1 Errata 48 , (1967) 463(E)
36. Вайдья ПК. физ. 1968; 174:1615. doi: 10.1103/PhysRev.174.1615. [CrossRef] [Google Scholar]
37. Машхун Б., Партови М.Х. Анна. физ. (Нью-Йорк) 1980; 130:99. doi: 10.1016/0003-4916(80)-6. [CrossRef] [Google Scholar]
38. Шривастава, округ Колумбия, Прасад С.С. Ген. отн. Гравит. 1983;15:65. doi: 10.1007/BF00755895. [CrossRef] [Google Scholar]
39. Томпсон А.Х., Уитроу В.

 2}{4*\pi}\)
2}{4*\pi}\)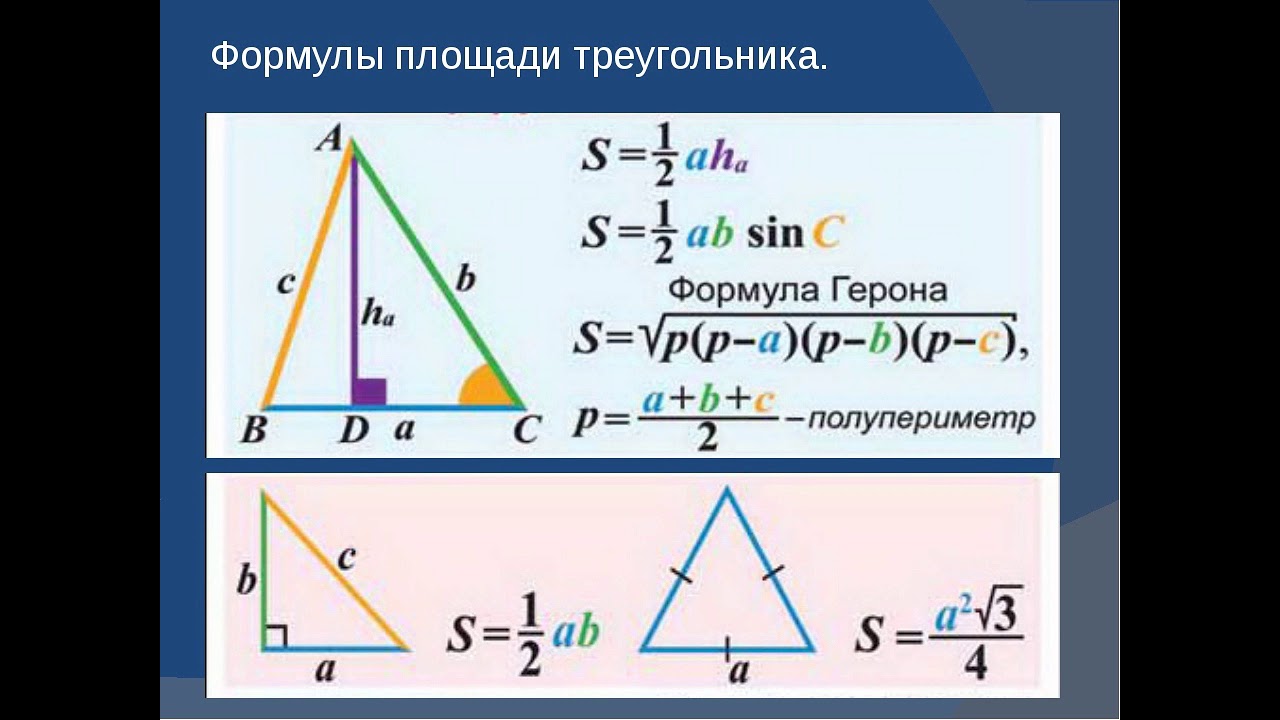 Скорины
Скорины Формула известна как формула раздела . Начнем!
Формула известна как формула раздела . Начнем! Как я упоминал ранее, существует (в общем) несколько методов решения задачи координатной геометрии. Это один из таких случаев. Идея состоит в том, чтобы развить ваш уровень мышления и дать вам представление о том, какие методы хороши, а какие нет.
Как я упоминал ранее, существует (в общем) несколько методов решения задачи координатной геометрии. Это один из таких случаев. Идея состоит в том, чтобы развить ваш уровень мышления и дать вам представление о том, какие методы хороши, а какие нет. Позвольте мне записать это лучше:
Позвольте мне записать это лучше: Вот симуляция, которая показывает две точки A и B , а также точку C , разделяющую соединяющий их отрезок в некотором отношении.
Вот симуляция, которая показывает две точки A и B , а также точку C , разделяющую соединяющий их отрезок в некотором отношении.
 Включение в базу данных NLM не означает одобрения или согласия с
содержание NLM или Национальных институтов здравоохранения.
Узнайте больше о нашем отказе от ответственности.
Включение в базу данных NLM не означает одобрения или согласия с
содержание NLM или Национальных институтов здравоохранения.
Узнайте больше о нашем отказе от ответственности.

 Источником вещества является идеальная жидкость с тензором энергии-импульса
Источником вещества является идеальная жидкость с тензором энергии-импульса
 Последняя начинается с нуля при r1=12C0C3-C02C32+4C0C2, увеличивается до максимума
Последняя начинается с нуля при r1=12C0C3-C02C32+4C0C2, увеличивается до максимума
 Чтобы увидеть этот факт, полезно изучить поведение радиальных нулевых геодезических в этой геометрии. Рассмотрим исходящие (+) и входящие (-) конгруэнции радиальных нулевых геодезических с касательными l(±)µ=dxµ/dλ, где λ — аффинный параметр вдоль этих кривых. Эти тангенсы имеют компоненты l(±)µ=l0,l1,0,0, и нормировка la(±)l(±)a=0 дает
Чтобы увидеть этот факт, полезно изучить поведение радиальных нулевых геодезических в этой геометрии. Рассмотрим исходящие (+) и входящие (-) конгруэнции радиальных нулевых геодезических с касательными l(±)µ=dxµ/dλ, где λ — аффинный параметр вдоль этих кривых. Эти тангенсы имеют компоненты l(±)µ=l0,l1,0,0, и нормировка la(±)l(±)a=0 дает Кроме того, dR/dt=0 при R=Rmax. Исходящие радиальные нулевые геодезические, начинающиеся вблизи начала координат, делают это очень быстро, но замедляются по мере приближения к максимально возможному радиусу Rmax, который может быть достигнут только при нулевой скорости (см. рис. ). Нулевая геодезическая, начинающаяся точно в Rmax, делает это с нулевой скоростью dR/dλ и остается там. Входящие радиальные нуль-геодезические, начинающиеся вблизи максимального радиуса Rmax, медленны и ускоряются по мере приближения к центральной голой сингулярности, к которой они приближаются с бесконечной скоростью dR/dλ→-∞.
Кроме того, dR/dt=0 при R=Rmax. Исходящие радиальные нулевые геодезические, начинающиеся вблизи начала координат, делают это очень быстро, но замедляются по мере приближения к максимально возможному радиусу Rmax, который может быть достигнут только при нулевой скорости (см. рис. ). Нулевая геодезическая, начинающаяся точно в Rmax, делает это с нулевой скоростью dR/dλ и остается там. Входящие радиальные нуль-геодезические, начинающиеся вблизи максимального радиуса Rmax, медленны и ускоряются по мере приближения к центральной голой сингулярности, к которой они приближаются с бесконечной скоростью dR/dλ→-∞. Мы также можем изучать радиальные времениподобные геодезические с касательными uμ=u0,u1,0,0. Нормализация ucuc=-1 дает
Мы также можем изучать радиальные времениподобные геодезические с касательными uμ=u0,u1,0,0. Нормализация ucuc=-1 дает