Быстро найти нужную формулу для расчета онлайн. Геометрия. Алгебра.
Площадь плоских фигур
Площадь треугольника
Площадь прямоугольного треугольника
Площадь треугольника формула Герона
Площадь равнобедренного треугольника
Площадь равностороннего треугольника
Площадь треугольника через две стороны и угол
Площадь треугольника через сторону и два угла
Площадь квадрата
Площадь прямоугольника
Площадь параллелограмма
Площадь ромба
Площадь произвольной трапеции
Площадь равнобедренной трапеции
Площадь правильного многоугольника
Площадь круга
Площадь сектора круга
Площадь сегмента круга
Площадь кольца
Площадь сектора кольца
Площадь эллипса
Все формулы раздела
Площадь поверхности тел
Площадь поверхности куба
Площадь поверхности параллелепипеда
Площадь поверхности сферы
Площадь поверхности шарового сегмента
Площадь поверхности шарового слоя
Площадь поверхности шарового сектора
Площадь поверхности цилиндра
Площадь поверхности конуса
Площадь поверхности усеченного конуса
Площадь поверхности правильной пирамиды
Боковая поверхность правильной усеченной пирамиды
Все формулы раздела
Объем тел
Объем куба
Объем параллелепипеда
Объем шара
Объем шарового сегмента
Объем шарового слоя
Объем шарового сектора
Объем цилиндра
Объем конуса
Объем усеченного конуса
Объем пирамиды
Объем усеченной пирамиды
Объем правильной пирамиды
Объем правильной треугольной пирамиды
Объем правильной четырехугольной пирамиды
Объем правильного тетраэдра
Все формулы раздела
Периметр фигур
Периметр круга или длина окружности
Длина дуги
Периметр треугольника
Периметр прямоугольника
Периметр квадрата
Периметр параллелограмма
Периметр ромба
Периметр трапеции
Длина дуги, формула Гюйгенса
Все формулы раздела
Радиус описанной окружности
Радиус описанной окружности треугольника
Радиус описанной окружности равностороннего треугольника
Радиус описанной окружности равнобедренного треугольника
Радиус описанной окружности прямоугольного треугольника
Радиус описанной окружности квадрата
Радиус описанной окружности прямоугольника
Радиус описанной окружности равнобокой трапеции
Радиус описанной окружности правильного шестиугольника
Радиус описанной окружности правильного многоугольника
Все формулы раздела
Радиус вписанной окружности
Радиус вписанной окружности в треугольник
Радиус вписанной окружности в равносторонний треугольник
Радиус вписанной окружности в равнобедренный треугольник
Радиус вписанной окружности в прямоугольный треугольник
Радиус вписанной окружности в квадрат
Радиус вписанной окружности в ромб
Радиус вписанной окружности в трапецию
Радиус вписанной окружности в правильный многоугольник
Радиус вписанной окружности в правильный шестиугольник
Все формулы раздела
Формулы для параллелограмма
Длина стороны параллелограмма
Длина диагоналей параллелограмма
Сумма квадратов диагоналей
Углы параллелограмма
Углы между диагоналями параллелограмма
Высота параллелограмма и угол пересечения высот
Свойства и длина биссектрисы параллелограмма
Формулы для ромба
Диагонали ромба
Сторона ромба
Углы ромба
Формулы для окружности, круга
Радиус окружности
Длина хорды окружности
Высота сегмента круга, окружности
Площадь круга
Длина окружности
Формулы для квадрата и прямоугольника
Сторона квадрата
Диагонали квадрата
Диагональ и углы прямоугольника
Формулы для треугольника
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все формулы раздела
Формулы для произвольной трапеции
Стороны трапеции
Диагональ трапеции
Средняя линия трапеции
Высота трапеции
Формулы для равнобедренной трапеции
Стороны равнобедренной трапеции
Диагональ равнобедренной трапеции
Высота равнобедренной трапеции
Средняя линия равнобедренной трапеции
Формулы для прямоугольной трапеции
Основания прямоугольной трапеции
Диагональ прямоугольной трапеции
Боковые стороны прямоугольной трапеции
Средняя линия прямоугольной трапеции
Тригонометрические тождества
sin, cos, tg, ctg
Сумма углов: sin(α+β), cos(α+β), tg(α+β), ctg(α+β)
Разность углов: sin(α-β), cos(α-β), tg(α-β), ctg(α-β)
Двойной угол: sin(2α), cos(2α), tg(2α), ctg(2α)
Тройной угол: sin(3α), cos(3α), tg(3α), ctg(3α)
Половинный угол: sin(α/2), cos(α/2), tg(α/2), ctg(α/2)
Квадрат функций: sin2(α), cos2(α), tg2(α), ctg2(α)
Куб функций: sin3(α), cos3(α), tg3(α), ctg3(α)
Сумма функций: sin(α), cos(α), tg(α), ctg(α)
Разность функций: sin(α), cos(α), tg(α), ctg(α)
Произведение функций: sin(α), cos(α), tg(α), ctg(α)
Формулы приведения функций: sin(α), cos(α), tg(α), ctg(α)
Понятие, что такое: sin(α), cos(α), tg(α), ctg(α)
Все формулы раздела
Теоремы
Теорема синусов
Теорема косинусов
Теорема Пифагора
Формулы сокращенного умножения
Квадрат суммы (a+b)2
Квадрат разности (a-b)2
Разность квадратов a2 — b2
Куб суммы (a+b)3
Куб разности (a-b)3
Сумма кубов a3 +b3
Разность кубов a3 — b3
Разность n степеней an — bn
Все формулы раздела
Производные
Производная функции Y(X)
Производная сложной функции (V, U)
Одночлены Многочлены
Правила возведения в степень
Одночлен, многочлен и действия над ними
Факториал числа
Биномиальные коэффициенты
Треугольник Паскаля
Бином Ньютона
Кинематика
Свободное падение тел
Скорость, расстояние, время и координата тела падающего вертикально вниз с нулевой начальной скоростью
Скорость, расстояние, время и координата тела падающего вертикально вниз с не нулевой начальной скоростью
Скорость, время, высота тела брошенного вертикально вверх
Скорость, время, расстояние, высота тела брошенного горизонтально
Бросок под углом к горизонту, максимальные значения
Бросок под углом к горизонту, высота
Бросок под углом к горизонту, время
На сайте, в простой и понятной форме, выложены основные формулы по геометрии, алгебре, которые вы найдете по ссылкам выше.
Формула через основание и высоту:
Любая формула в один клик с главной страницы.
Так же на основных страницах, есть боковые меню (если вы зашли с компьютера) и эти же меню, вы найдете внизу страницы (если используете мобильное устройство). Эти меню позволяет быстро перемещаться по сайту и находить необходимую информацию. Есть различные калькуляторы для расчетов необходимых значений.
Формулы регулярно добавляются
2011-08-21
- Подробности
- Автор: Сергей Кондратов
Рейтинг: 5 / 5
Пожалуйста, оцените Оценка 1Оценка 2Оценка 3Оценка 4Оценка 5Формулы.
 Геометрия. (5 класс) — презентация онлайн
Геометрия. (5 класс) — презентация онлайнПохожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
5 класс.
Жила-была загадочная принцесса Формула.
Она была непоседа и постоянно путешествовала из государства Алгебра в государство
Геометрия. Она имела множество имён и так
часто менялась, что подданные не узнавали
её в лицо. То она Формула Пути, то Формула
для Вычисления Площади Прямоугольника.
Она очень добра и всегда готова помочь тому,
кто не только узнаёт её с первого взгляда, но
и знает наизусть все её имена. Потому что
Потому что
ФОРМУЛА – это…
Что общего в записанных
b
предложениях?
ПРАВИЛА
Как
найти
площадь
Площадь
прямоугольника
равна
прямоугольника,
известны
произведению длинесли
его сторон
его стороны?
Как
найтипрямоугольника
периметр
Периметр
равен
прямоугольника,
если известны
сумме
длин его сторон
его стороны?
Как
найти пройденный
путь, если
Пройденный
путь – это произведение
известны
скорость
скорости навремя
времяидвижения
движения?
ФОРМУЛЫ
S=a∙b
Как записать эти правила
Pна= математическом
a + a + b + b или
P =языке?
2(a + b)
s=v∙t
Правило, записанное на математическом языке,
– это формула
Формула площади
прямоугольника
ФОРМУЛЫ
S=a∙b
P = a + a + b + b или
P = 2(a + b)
s=v∙t
В дальнейшем вы узнаете
еще много новых формул…
Формулы периметра
прямоугольника
Формула пути
Формула пути.

s=v∙t
v=s:t
s = v ∙ t 90 км
12 км
t=s:v
120 км
3600м
v = s : t 15 км/ч 6 км/ч 60км/ч 6 м/с
t=s:v
6ч
2ч
2ч
10 мин
Задача.
Автомобиль движется со скоростью 60 км/ч.
За какое время он пройдёт путь в 600 км?
s=v∙t
t=s:v
Задача.
C какой скоростью должен идти человек,
чтобы пройти 24 км за 4 ч?
s=v∙t
v=s:t
Задача.
Подсказка
С одной станции в противоположных направлениях
вышли два поезда в одно и то же время. Скорость
одного поезда 50 км/ч, а другого – 70 км/ч. Какое
расстояние между ними будет через 2 часа?
s=v∙t
2ч
2ч
70 км/ч
50 км/ч
?
240 км
Задача.
Подсказка
Расстояние между двумя городами 600 км.
Навстречу друг другу из этих городов вышли
одновременно две автомашины. Одна имеет
скорость 90 км/ч, а другая – 110 км/ч. Чему будет
?
2ч
90 км/ч
?
2ч
s=v∙t
110 км/ч
600 км
220 км
Формула площади
прямоугольника.

a
S=a∙b
а=S:b
S
90
см2
b
b=S:a
12 км2 120 мм2
36 м2
a
15 cм
6 км
6 мм
6м
b
6 см
2 км
2 см
60 дм
Задача.
Найдите сторону прямоугольника, если его
площадь 364 см2, а длина 26см.
26 см
364 см2
S=a∙b
b=S:a
?
Подсказка
Задача.
Два прямоугольника имеют равные площади.
Длина первого прямоугольника 16 см, а его
ширина на 12 см меньше длины. Длина второго
прямоугольника 32 см. Найдите ширину
второго прямоугольника.
S1
S1 = S2
S2
a = 16 см
Дополнительно
b = 16 — 12 (см)
S1
S=a∙b
S1 = 16 (16 – 12) = 64 (см2)
a = 32 см
S2
S1 = S2
2 cм
S2 = 64 см2
b=S:a
b = 64 : 32 = 2 (см)
Чему равна сторона квадрата, имеющего такую же
площадь, что и эти прямоугольники?
8 cм
S3
а-?
S1 = S2 = S3
Sкв =
2
a
S1
S3 = 64 см2 а = 8 см
S2
Найдите площадь фигуры, изображённой на рисунке, если
условиться, что длина стороны каждой клетки равна 1 см.

19 см2
Молодец!
2
16 см
15 см2
24 см2
Найдите площадь фигуры, изображённой на рисунке, если
условиться, что длина стороны каждой клетки равна 1 см.
14 см2 Молодец!
15 см2
16 см2
20 см2
Найдите площадь фигуры, изображённой на рисунке, если
условиться, что длина стороны каждой клетки равна 1 см.
40 см2
36 см2
42 см2
38 см2
Правильно!
Подсказка (3 – 1)
Задача.
Начертите прямоугольник АВСD, соедините
отрезком вершины А и С. Найдите площади
ВС = 5 см.
А
6 см
В
5 см
S=a∙b
D
15
2
см
С
S2 = 6 5 = 30 (см2)
SADC = SABC
SABCD = SADC + SABC
SADC = SABC = SABCD : 2
Решение(3 – 3)
Формула периметра
прямоугольника.
P = a + a + b + b или
P = 2(a + b)
а
14
21
24
12
b
26
29
12
24
a+b
40
80
50
36
36
100
72
72
2(a + b)
Используя формулу периметра прямоугольника, найдите:
1) Периметр Р, если а = 3м 5дм, b = 1м 2дм
а = 3м 5дм = 35дм
b = 1м 2дм = 12дм
Р = 2(a + b)
Р = 2(35 + 12) = …
94 дм
Используя формулу периметра прямоугольника, найдите:
2) Сторону а, если Р = 3дм, b = 6см.

Р = 3дм = 30см
b = 6см
Р = 2(a + b)
a+b=P:2
а = 15 — b
a + b = 30 : 2 = 15 (см)
а = 15 — 6
9 cм
Математический диктант
1 вариант
2 вариант
1
Используя формулу s = vt, найдите неизвестную величину:
V (км/ч)
t (ч)
27
60
6
480
S (км)
V (км/ч)
4
t (ч)
520
S (км)
23
70
9
3
420
280
2
Используя формулу S = ab, найдите неизвестную величину :
a (м)
5
b (м)
74
S (м2)
4
3
840
96
a (м)
5
b (м)
94
S (м2)
4
3
92
720
English Русский Правила
Все формулы по математике и геометрии
- Файлы
- Абитуриентам и школьникам
- Подготовка к экзамену по математике
Математика
6 класс
Алгебра
- Геометрия
Для внеклассного чтения
Домашняя работа по математике
Задачники по математике для школьников
Подготовка к экзамену по математике
Школьные математические олимпиады
- формат doc
- размер 263.
 8 КБ
8 КБ - добавлен 04 марта 2010 г.
Этот сборник для Абитуриентов, в него вошли формулы для:
Обратные тригонометрические функции.
Пределы
Производная, касательная к графику.
Свойства корня.
Свойства модуля.
Свойства степеней.
Тождественные преобразования тригонометрических выражений.
Формулы логарифмов.
Формулы сокращенного умножения.
Все формулы.
Смотрите также
Справочник
- формат doc
- размер 725 КБ
- добавлен 13 июля 2010 г.
Кафедра высшей математики СибГУТИ. Новосибирск. 2000. 19 с. Пособие содержит формулы, таблицы, графики по математике, охватывыающие основные разделы элементарной математики — алгебры и геометрии. Оно предназначено для абитуриентов при подготовке к вступительным экзаменам, а также для студентов при изучении высшей математики и других дисциплин
Оно предназначено для абитуриентов при подготовке к вступительным экзаменам, а также для студентов при изучении высшей математики и других дисциплин
- формат doc
- размер 837.59 КБ
- добавлен 16 июня 2009 г.
Справочное пособие содержит формулы, таблицы, графики по математике, охватывающие основные разделы элементарной математики — алгебры и геометрии. Оно предназначено для абитуриентов при подготовке к вступительным экзаменам, а также для студентов дневного и заочного обучения при изучении высшей математики и других дисциплин.
Билеты и вопросы
- формат doc
- размер 41.77 КБ
- добавлен 11 января 2011 г.
Стр. 10. Экзаменационные билеты по геометрии. 10 билетов. Аксиомы стереометрии. Параллелепипед, его элементы. Параллельные прямые (определение). Вывод формулы площади сферы. Прямая, параллельная плоскости (определение). Вывод формулы объема конуса. Параллельные плоскости (определение). Вывод формулы объема пирамиды. Касательная плоскость (определение). Прямая, перпендикулярная плоскости (определение). Площадь боковой поверхности пирамиды. Т…
10. Экзаменационные билеты по геометрии. 10 билетов. Аксиомы стереометрии. Параллелепипед, его элементы. Параллельные прямые (определение). Вывод формулы площади сферы. Прямая, параллельная плоскости (определение). Вывод формулы объема конуса. Параллельные плоскости (определение). Вывод формулы объема пирамиды. Касательная плоскость (определение). Прямая, перпендикулярная плоскости (определение). Площадь боковой поверхности пирамиды. Т…
- формат doc
- размер 21.76 КБ
- добавлен 17 августа 2009 г.
Шпаргалка содержит формулы по математике на следующие темы: Формулы сокращенного умножения. Свойства степеней. Геометрическая прогрессия. Модуль. Формулы cos и sin. Тригонометрические уравнения. Теоремы сложения. Правила дифференцирования. Уравнение касательной к графику функции. Площадь S фигуры, ограниченной прямыми x=a, x=b. Формула Ньютона-Лебница. Первообразная. Объемы и поверхности тел. Теорема синусов. Теорема косинусов. Неопределенные инт…
Формула Ньютона-Лебница. Первообразная. Объемы и поверхности тел. Теорема синусов. Теорема косинусов. Неопределенные инт…
Шпаргалка
- формат doc
- размер 101.5 КБ
- добавлен 04 ноября 2011 г.
2011 г. 203 формулы Содержание: Формулы сокращения умножения и разложения на множители Степени и корни Квадратное уравнение Нахождение длинны отрезка по его координатам Логарифмы Прогрессии Тригонометрия. Формулы половинного аргумента. Формулы преобразования суммы в произведение Формулы преобразования произведения в сумму Соотношение между функциями Тригонометрические уравнения Показательные уравнения. Тригонометрические неравенства Производная И…
Шпаргалка
- формат doc
- размер 156.
 5 КБ
5 КБ - добавлен 07 ноября 2011 г.
2011 г. Содержание: Алгебра формулы. Формулы сложения. Формулы двойного аргумента. Формулы половинного аргумента. Формулы преобразования суммы в произведение. Формулы преобразования произведения в сумму. Соотношения между функциями. Формулы тройного аргумента. Третья степень. Arcsin…. Производная. Прогрессии. Квадратное уравнение ax2+bx+c=0 (a?0). Первообразная. Интеграл. Логарифмы. Степени. Геометрия. Соотношение между углами и сторонами треугол…
Справочник
- формат jpg, doc
- размер 12.56 МБ
- добавлен 26 октября 2010 г.
Сборник содержит формулы элементарной и высшей математики — арифметики и алгебры, геометрии и тригонометрии, векторной и линейной алгебры, дифференциального и интегрального исчисления, рядов, теории вероятности и др. Он адресован школьникам и абитуриентам, студентам высших и средних специальных учебных заведений, преподавателям и инженерам.
Он адресован школьникам и абитуриентам, студентам высших и средних специальных учебных заведений, преподавателям и инженерам.
- формат pdf
- размер 989.08 КБ
- добавлен 02 февраля 2012 г.
Цыпкин А.Г., Цыпкин Г.Г. Математические формулы. Алгебра. Геометрия. Математический анализ: Справочник. — М.: Наука. Гл. ред. физ.-мат. литры, 1985. — 128 с. Представлены основные формулы алгебры, геометрии (включая дифференциальную гео- метрию и векторное исчисление), тригонометрии. Широко представлены формулы и основные понятия и теоремы математического анализа. Приведены таблицы основных интегралов. Для широкого круга специалистов и учащейся м…
pottee
- формат pdf
- размер 51.17 КБ
- добавлен
05 мая 2009 г.

Собраны и размещены все основные и необходимые формулы по школьному курсу математики на одном листе. Шпаргалка содержит следующие материалы: Тригонометрические тождества Свойства логарифмов Свойства интегралов Таблица интегралов Таблица производных Свойства степеней и корней Формулы сложения тригонометрических функций Формулы приведения Формулы геометрической прогрессии Формулы алгебраической прогрессии Формулы по геометрии Формулы понижения ст…
Шпаргалка
- формат doc
- размер 477.5 КБ
- добавлен 15 декабря 2010 г.
Шпаргалка по математике. все основные формулы и таблицы. Содержание: Числа, дроби, модуль: Множества. Дроби. Арифметические операции с дробями. Пропорция. Модуль числа. Определение. Свойства модуля. формулы сокращенного умножения. степени и корни: Показательные неравенства. квадратные уравнения: Корни уравнения. Формулы Виета. Разложение квадратного трехчлена на множители. Приведенное уравнение. Квадратное неравенство. прогрессии: Арифметическая…
Модуль числа. Определение. Свойства модуля. формулы сокращенного умножения. степени и корни: Показательные неравенства. квадратные уравнения: Корни уравнения. Формулы Виета. Разложение квадратного трехчлена на множители. Приведенное уравнение. Квадратное неравенство. прогрессии: Арифметическая…
App Store: Математика — геометрия алгебра
Описание
Подготовьтесь к урокам, ОГЭ и ГИА!
— Все темы школьного курса математики с 5 по 11 классы
— Все главные формулы с пояснением
— Поиск по темам
— Избранное
— Таблицы и постоянные
Версия 1.0.3
Привет! Немного улучшили интерфейс и обновили статьи!
Оценки и отзывы
Оценок: 104
Круто
Круто
Проверьте конспекты
Ошибка в разделе 9 класс §3 квадратный трёхчлен и его корни.
Квадратное уравнение имеет один корень, если дискриминант равен нулю. В вашем конспекте при дискриминанте меньше нуля.
Привет. Спасибо за отзыв. Действительно, там ошибка. Исправлю в ближайшем обновлении. Корректные шаги вычисления квадратного трёхчлена есть сейчас в разделе «Формулы». Воспользуйтесь алгоритмом оттуда, пожалуйста.
5*
Хорошее приложение, очень много формул, все подробно расписано, ясно и понятно. Есть конспекты по всем темам. Буду рекомендовать своим ученикам
Разработчик Danila Danilenko указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.
Данные, используемые для отслеживания информации
Следующие данные могут использоваться для отслеживания информации о пользователе в приложениях и на сайтах, принадлежащих другим компаниям:
- Геопозиция
- Идентификаторы
- Данные об использовании
- Диагностика
- Другие данные
Связанные с пользователем данные
Может вестись сбор следующих данных, которые связаны с личностью пользователя:
- Геопозиция
- Идентификаторы
- Данные об использовании
- Диагностика
- Другие данные
Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов. Подробнее
Подробнее
Информация
- Провайдер
- Danila Danilenko
- Размер
- 42,7 МБ
- Категория
- Образование
- Возраст
- 4+
- Copyright
- © night_coding
- Цена
- Бесплатно
- Поддержка приложения
- Политика конфиденциальности
Другие приложения этого разработчика
Вам может понравиться
Справочник репетитора по математике. Формулы, теоремы и свойства треугольников. Виртуальный онлайн репетитор.
 — Колпаков Александр Николаевич
— Колпаков Александр НиколаевичТеоретичесикие шпаргалки по элементарной геометрии для занятий с репетитором по математике. Базовый школьный уровень. Свойства элементов треугольника. В помощь для решению задач по всему курсу планиметрии. Для тренировки решения задач С4 на ЕГЭ по математике.
1) Определение тригонометрических функций острого угла в прямоугольном треугольнике и теорема Пифагора
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов, то есть
2) Формулы площади треугольника
,
где (Формула Герона)
, где r- вписанной окружности
, где R — радиус описанной окружности
3) Подобие треугольников
Определение: два треугольника называются подобными, если у них соответствующие углы равны и соответствующие стороны пропорциональны, то есть
и
Обозначение:
4) Признаки подобия двух треугольников
1-й признак: Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Коротко: если , то
2-й признак:если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами равны, то треугольники подобны
Коротко: если и , то
3-й признак:если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны, то есть
Коротко: если , то
5) Свойства подобных треугольников
если , то
, где
и — любые соответствующие медианы (проведенные к соответствующим сторонам)
и — любые соответствующие биссектрисы (проведенные к соответствующим сторонам)
и — любые соответствующие высоты (проведенные к соответствующим сторонам)
6) Подобие прямоугольных треугольников. Высота, проведенная из вершины прямого угла
Теорема: высота в прямоугольном треугольнике, поведенная из вершины прямого угла образует два треугольника, подобных исходному. Для катетов и высоты исходного треугольника верны следующие формулы:
Для катетов и высоты исходного треугольника верны следующие формулы:
7) Свойство медиан в треугольнике.
Теорема 1: Все медианы треугольника пересекаются в одной точке (центр тяжести треугольника) и делятся этой точкой в отношении 2:1, считая от вершин. То есть
Теорема 2: Каждая медиана, проведенная в треугольнике делит этот треугольник на две равновеликие части (на два треугольника с равными площадями),
То есть
Теорема 3: все три медианы делят треугольник на 6 равновеликих треугольников, то есть
8) Свойство биссектрис в треугольнике
Теорема 1: Каждая биссектриса угла в треугольнике делит его противолежащую сторону на отрезки, пропорциональные к двум другим сторонам треугольника.
То есть
Теорема 2: Все биссектрисы в треугольнике пересекаются в одной точке, которая является центром вписанной с треугольник окружности. В любой треугольник можно вписать окружность и только одну.
В любой треугольник можно вписать окружность и только одну.
9) Свойство точки пересечения серединных перпендикуляров к сторонам треугольника:
Теорема: все серединные перпендикуляры к сторонам треугольника пересекаются в одной точке и эта точка является центром описанной около треугольника окружности. Вокруг любого треугольника можно описать окружность и только одну.
10) Теорема о разделительном отрезке в треугольнике
Теорема: Отрезок, соединяющий вершину треугольника с противоположной стороной делит ее на отрезки, пропорциональные площадям образованных треугольников.
То есть
11) Средняя линия треугольника
Теорема: Средняя линия треугольника, соединяющая середины двух его сторон параллельна третьей стороне и равна ее половине.
То есть и
12) Теорема синусов и теорема косинусов
Теорема синусов: Cтороны треугольника пропорциональны синусам противолежащих углов и каждое отношение стороны к синусу равно диаметру описанной около треугольника окружности.
То есть
Теорема косинусов: Квадрат стороны треугольника равне сумме квадратов двух других сторон минус удвоенное произведение этих сторон на синус угла между ними, то есть
13) Теорема Менелая
Теорема: Произведение отношений отрезков, на которые произвольная прямая делит стороны треугольника (или их продолжения) равно единице
То есть
Комментарий репетитора по математике: несправедливо выброшенная теорема из школьного курса геометрии. Рекомендую репетиторам включить ее в подготовку, по крайней мере к вузовским олимпиадам и вступительным экзаменам по математике в МГУ. В программу ЕГЭ теорема Менелая не входит, но несколько типов задач без нее решаются очень сложно.
14) Теорема Чевы
Теорема:если через вершины треугольника и произвольную внутреннюю точку провести отрезки к противоположным сторонам (чевианы), то их точки пересечения разделят стороны на отрезки, произведение отношений которых равно единице.
То есть
Колпаков А.Н. Репетитор по математике.
Метки: Геометрия, Справочник репетитора, Ученикам
Формулы площадей всех фигур в геометрии — примеры вычислений
Площадь — это одна из наиболее важных и неотъемлемых характеристик любой замкнутой геометрической фигуры, показывающая её размер. Она может измеряться в различных единицах: квадратных миллиметрах, сантиметрах, дециметрах, метрах и так далее. Это своеобразный аналог объёма трёхмерных фигур (шара, цилиндра, конуса и других). В геометрии разработаны формулы площадей. Их доказательством являются соответствующие теоремы. Существует общепринятое обозначение площади — буква S (от англ. square).
Содержание
- Формулы для треугольников
- Площадь четырёхугольников
- Квадрат и прямоугольник
- Параллелограмм, ромб и трапеция
- Выпуклый четырёхугольник
- Круг и эллипс
Формулы для треугольников
Имеется несколько формул площади треугольника. Если в треугольнике известны две величины: во-первых, длина стороны, а во-вторых, высота, опущенная из противоположного угла перпендикулярно этой стороне, то площадь можно определить, умножив длину на высоту и разделив полученное произведение на два. Выглядит формула так: S = ½ * a * h. Буквой a обозначена длина, буквой h — высота.
Если в треугольнике известны две величины: во-первых, длина стороны, а во-вторых, высота, опущенная из противоположного угла перпендикулярно этой стороне, то площадь можно определить, умножив длину на высоту и разделив полученное произведение на два. Выглядит формула так: S = ½ * a * h. Буквой a обозначена длина, буквой h — высота.
При известности всех трёх сторон — a, b, c, широко применяется формула, названная в честь Герона — математика из Древней Греции: S = √(p*(p — a)*(p — b)*(p — c)). Величина p — это половина от периметра треугольника (полупериметр). Чтобы его рассчитать, необходимо суммировать все стороны и разделить сумму на два: (a + b + c)/2.
Для ещё одной формулы требуются следующие данные:
- длина двух соприкасающихся в одной вершине сторон — a и b;
- градус угла, который образуют эти стороны.
Тогда расчёт можно произвести таким способом: S = ½ * a * b * sin γ. Синус угла является одной из тригонометрических функций, представляющей собой результат деления (отношение) в прямоугольном треугольнике противолежащего (дальнего) катета к гипотенузе (сторона напротив прямого угла). Значение sin γ для конкретного угла можно посмотреть в специальной таблице.
Синус угла является одной из тригонометрических функций, представляющей собой результат деления (отношение) в прямоугольном треугольнике противолежащего (дальнего) катета к гипотенузе (сторона напротив прямого угла). Значение sin γ для конкретного угла можно посмотреть в специальной таблице.
Когда два треугольника являются подобными (подобие означает, что у них равны углы и стороны пропорциональны), то отношение их площадей соответствует отношению возведённых в квадрат сторон. Такое отношение сторон для них (например, AB: A (1) B (1)) именуется коэффициентом подобия (k). Поэтому отношение площадей равняется коэффициенту подобия в квадрате.
Если в треугольнике даны все стороны, тогда, кроме формулы Герона, есть возможность воспользоваться ещё одним способом. Он основан на том, что можно вписать любой треугольник в круг. Зная такую величину, радиус ® окружности и три стороны треугольника, производится расчёт: S = (a * b * c) / 4 R.
В любой треугольник: равносторонний и разносторонний, остроугольный и тупоугольный, в силу его геометрических свойств также может быть вписана окружность.
В таком случае формула нахождения площади следующая: S = p * r. Буква p обозначает ½ периметра треугольника, r — это радиус окружности.
Площадь четырёхугольников
Четырёхугольник — это одна из фигур в геометрии (многоугольник), имеющая четыре стороны, а также четыре вершины, три из которых не находятся на одной прямой. Четырёхугольник называется выпуклым, если он располагается по одну сторону относительно прямой, являющейся продолжением любой из его сторон.
К выпуклым четырёхугольникам относятся практически все известные фигуры, имеющие четыре вершины, а также четыре стороны. Основными их видами выступают: 1) ромб; 2) прямоугольник; 3) трапеция; 4) квадрат; 5) параллелограмм.
Квадрат и прямоугольник
Самый простой способ вычисления площади квадрата — умножить сторону «саму на себя», иными словами, возвести в квадрат длину любой из его сторон (S = a2 ). Такой расчёт обусловлен особым признаком квадрата — тем, что все его стороны являются абсолютно равными между собой, поэтому квадрат называется правильной фигурой.
Такой расчёт обусловлен особым признаком квадрата — тем, что все его стороны являются абсолютно равными между собой, поэтому квадрат называется правильной фигурой.
Существует вторая, более сложная, формула площади квадрата, где осуществляется расчёт через диагональ. Диагональ — это линия, соединяющая в фигуре два угла, друг другу противоположных. Для определения площади необходимо длину диагонали возвести в квадрат и полученный результат разделить на два: S = ½ d 2.
Для прямоугольника используется формула: S = a * b, где a, b — длина двух разных, имеющих общую вершину, сторон.
Параллелограмм, ромб и трапеция
Параллелограмм представляет собой четырёхугольник, в котором имеются два противоположных друг другу тупых угла и два — острых.
Применяются три формулы площади параллелограмма:
- Умножить сторону на высоту, перпендикулярную стороне: S = a * h.

- Перемножить две, выходящих из одной вершины, стороны параллелограмма, и умножить на синус угла, образованного ими: S = a * b * sin γ.
- Перемножить диагонали фигуры, затем умножить на синус угла, образованного диагоналями, и разделить результат на два: S = ½ d (1) * d (2) * sin γ.
Ромб похож на параллелограмм с одним отличием: он является равносторонним. Поэтому для вычисления площади ромба используются похожие формулы:
Трапеция является геометрической фигурой, имеющей такие элементы: два параллельных основания — верхнее и нижнее, две боковые стороны, расположенные к нижнему основанию под острым углом. Что касается боковых сторон, то они могут быть как равными по длине (так называемая равнобедренная трапеция), так и разными.
Что касается боковых сторон, то они могут быть как равными по длине (так называемая равнобедренная трапеция), так и разными.
В связи с тем, что в «составе» трапеции можно «выделить» прямоугольник и два расположенных по бокам от него треугольника, то можно определить площадь по специальной формуле Герона: S = (a + b): | a + b | * √(p — a) * (p — b) * (p — a — c) * (p — a — d).
В этой формуле имеются следующие обозначения:
- буквы a, b — это основы трапеции,
- буквы c, d — стороны,
- p — полупериметр.
Выпуклый четырёхугольник
В отношении всех иных выпуклых четырёхугольников, то есть имеющих разные по длине стороны и разные углы, разработаны свои формулы вычисления площади.
Прежде всего, можно перемножить две диагонали, а также синус образуемого ими угла, разделив общий результат на два, то есть применить формулу: S = ½ d (1) * d (2) * sin γ.
В том случае, когда внутри выпуклого четырёхугольника, так же как и внутри треугольника, может быть вписан круг, то для нахождения площади четырёхугольной фигуры, требуется определить две величины:
- r — радиус окружности;
- p — ½ периметра четырёхугольника.

После чего полупериметр умножается на радиус. Это и будет площадь четырёхугольника. Формула выглядит так: S = p * r.
Для тех случаев, когда круг может быть очерчен вокруг четырёхугольника, применяется другая формула. Для её использования все стороны фигуры должны быть известны. Они обозначаются буквами a, b, c, d. Рассчитывается половина периметра: p = (a + b + c + d)/2. Затем определяется площадь: S = √(p — a)(p — b)(p — c)(p — d).
Когда конфигурация четырёхугольника такова, что не позволяет возле него описать круг, то в связи с этим формула площади немного дополняется: S = √(p — a)(p — b)(p — c)(p — d) — abcd cos2 γ.
Коэффициент γ представляет собой половину от суммы двух противоположных углов четырёхугольной фигуры: γ = (угол (1) + угол (2)) / 2.
Круг и эллипс
Самое распространённое и широко применяемое правило определения площади круга — это умножение радиуса окружности в квадрате на число пи: S = π * r 2.
Число пи, обозначаемое греческой буквой «π» — это математическая постоянная, которая является результатом деления длины окружности на диаметр. π — иррациональное число. Для расчётов признаётся его среднее значение, равное 3,14.
Вместо радиуса можно использовать диаметр окружности: диаметр возводится в квадрат, умножается на число π, результат делится на четыре. Формула выглядит так: S = (π * d 2) / 4.
Для того чтобы посчитать площадь такой фигуры, как эллипс, необходимо провести две оси, то есть две линии, каждая из которых разделяет эллипс на две равные части, при этом сами линии перпендикулярны друг другу (образуют прямой угол). Точка пересечения разделяет каждую из осей напополам, образуя полуоси.
Площадь эллипса вычисляется как произведение трёх величин: числа π, длины большой полуоси (а) и длины малой полуоси (b): S = π * a * b. Для удобства расчёта площадей различных фигур также можно использовать специальные онлайн-калькуляторы.
youtube.com/embed/2aFhtqYi4B4″>Предыдущая
МатематикаМетод координат в геометрии — примеры решения и построения
Следующая
МатематикаСвойства и признаки диагоналей прямоугольника — формулы и примеры расчетов
Периметр квадрата — формула, определение, примеры
Периметр квадрата определяется как общая длина, которую покрывает его граница. Периметр любой замкнутой геометрической формы рассчитывается путем нахождения расстояния вокруг этой формы. Для квадрата периметр можно вычислить, найдя сумму всех сторон. Поскольку все четыре стороны равны, длина каждой стороны квадрата в четыре раза больше. Давайте узнаем о периметре квадрата подробно в этой статье.
| 1. | Что такое периметр квадрата? |
| 2. | Вычисление периметра квадрата по формуле |
3. | Как найти периметр квадрата? |
| 4. | Часто задаваемые вопросы по периметру квадрата |
Что такое периметр квадрата?
Периметр любой формы — это либо путь, который охватывает/окружает/очерчивает форму (в двух измерениях), либо ее длина (в одном измерении). Периметр квадрата можно вычислить, сложив длины всех его сторон.
Формула периметра квадрата
Формула для вычисления периметра квадрата может быть математически выражена как;
Периметр квадрата, (P) = 4 × сторона
Пример: Вычислите периметр квадрата, каждая сторона которого равна 7 единицам.
Решение: Дано: Длина стороны квадрата = 7 единиц.
Мы знаем, используя формулу периметра квадрата,
Периметр квадрата = 4 × Сторона
⇒ 4 × 7 = 28 единиц
Вычисление периметра квадрата по формуле
Периметр квадрата определяется как общая длина границы квадрата. Чтобы вычислить периметр квадрата, найдем сумму всех его сторон. Поскольку все стороны квадрата равны для квадрата, каждая сторона измеряется в единицах «s», поэтому периметр будет задан как
Чтобы вычислить периметр квадрата, найдем сумму всех его сторон. Поскольку все стороны квадрата равны для квадрата, каждая сторона измеряется в единицах «s», поэтому периметр будет задан как
Периметр квадрата = s + s + s + s
⇒ Периметр квадрата = 4s, где «s» — длина стороны квадрата.
Как найти периметр квадрата?
Периметр квадрата можно рассчитать различными способами в зависимости от известных параметров. В этом разделе рассматривается метод с использованием
- Длина стороны
- Диагональ
- Район
Периметр квадрата, используя длину стороны
В этом случае мы обычно находим периметр, умножая длину стороны на 4. Чтобы найти периметр квадрата, используя длину стороны, мы можем выполнить шаги, указанные ниже,
- Шаг 1: Запишите размер стороны.
- Шаг 2: Умножьте указанную длину на 4.
- Шаг 3: Выразите полученный результат в соответствующей единице.

Периметр квадрата с использованием диагонали
Периметр квадрата также можно вычислить, если нам известна длина его диагонали. Чтобы найти периметр квадрата по диагонали, мы можем выполнить шаги, указанные ниже:
- Шаг 1: Запишите размер диагонали квадрата.
- Шаг 2: Рассчитайте длину стороны по диагонали.
Сторона = диагональ/√2 = √2 × диагональ/2 - Шаг 3: Умножьте полученное значение длины стороны (√2 × диагональ/2) на 4 и выразите ответ в единицах.
Периметр = (√2 × диагональ/2) × 4 = (2√2 × диагональ) единиц.
Периметр квадрата с использованием площади квадрата
Мы можем найти периметр квадрата, зная его площадь. Чтобы найти периметр квадрата, используя площадь, мы можем выполнить шаги, указанные ниже:
- Шаг 1: Запишите площадь квадрата.
- Шаг 2: Рассчитайте длину стороны, используя площадь.

Сторона = √площадь - Шаг 3: Умножьте полученное значение длины стороны (√площадь) на 4 и выразите ответ в единицах.
Периметр = (√площадь) × 4 = 4√единицы площади.
Давайте посмотрим на несколько решенных примеров, чтобы лучше понять периметр квадрата.
Периметр квадрата Примеры
Пример 1: Если периметр квадрата равен 64 единицам, найдите его сторону.
Решение:
Дано: периметр квадрата = 64 единицы.
Используя формулу периметра квадрата,
Периметр = (4 × сторона) единиц
Подставляя значение периметра, получаем,
64 = 4 × сторона
⇒ Сторона = 64/4 = 16 единицОтвет: Длина стороны данного квадрата равна 16 единицам.
Пример 2: Площадь квадрата равна 225 квадратных единиц. Используя формулу периметра квадрата, вычислите его периметр.
Решение:
Дано: Площадь квадрата = 225 квадратных единиц.

Мы знаем, что площадь квадрата = (сторона) 2 квадратных единиц
⇒ 225 = (сбоку) 2
⇒ сторона = √ 225 = 15 единицТеперь, используя формулу периметра квадрата,
Периметр, P = 4 × боковые блоки
⇒ P = 4 × 15 = 60 единицОтвет: Периметр данного квадрата = 60 единиц.
Пример 3: Если диагональ квадрата равна 3√2 дюйма, каков будет периметр квадрата?
Решение:
Дано: Диагональ квадрата = 3√2 дюйма.
Поскольку мы знаем, что по диагонали периметр квадрата равен P = (2√2 × диагональ) единиц.
⇒ P = (2√2 × 3√2) дюйма
Р = 6 × 2 дюйма
p = 12 дюймовОтвет: Периметр данного квадрата = 12 дюймов.
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу в математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
Практические вопросы по периметру площади
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по периметру квадрата
Что такое периметр квадрата в математике?
Периметр квадрата в математике — это общая длина вокруг его границы. Формула периметра квадрата выражается как сумма всех сторон. Он представлен как P = 4 × боковые единицы.
☛Также проверьте:
- Формулы периметра
- Формулы площади
Что такое Формула Периметра Квадрата?
Периметр квадрата определяется как длина, которую покрывает его граница. Формула для вычисления периметра квадрата выглядит так: P = 4 × сторона.
Как рассчитать периметр квадрата?
Периметр квадрата можно вычислить, найдя общую сумму всех его сторон. Поскольку мера всех сторон квадрата одинакова, чтобы вычислить периметр квадрата, мы можем просто умножить 4 на длину его стороны.
Какова площадь и периметр квадрата?
Площадь квадрата — это пространство, занимаемое в пределах границы квадрата. Он рассчитывается по формуле: Площадь = (сторона × сторона) квадратных единиц. С другой стороны, периметр квадрата — это общая длина его границы. Его можно найти, сложив все четыре стороны квадрата или умножив любую из сторон на 4. Формула для нахождения периметра квадрата: (4 × сторона) единиц.
Как найти длину стороны квадрата, зная периметр?
Периметр квадрата определяется как P = 4 × сторона. Преобразовав приведенную выше формулу для вычисления длины стороны квадрата, когда задан периметр, мы получим сторону = P/4. Следовательно, длину стороны квадрата можно вычислить, разделив заданный периметр на 4.
Как найти периметр квадрата, зная площадь?
Площадь квадрата можно рассчитать по формуле площадь = сторона × сторона. Преобразовав эту формулу для вычисления длины стороны квадрата с использованием площади, мы получим, что сторона = √ район. Поскольку периметр квадрата задается как: 4 × сторона, мы можем вычислить периметр квадрата, когда площадь дана по формуле: 4 √ площади.
Поскольку периметр квадрата задается как: 4 × сторона, мы можем вычислить периметр квадрата, когда площадь дана по формуле: 4 √ площади.
Какова единица периметра площади?
Периметр квадрата — это общее расстояние вокруг его границы или длины его сторон, сложенные вместе. Периметр (P) измеряется в таких единицах, как дюймы (дюймы), ярды (ярды), миллиметры (мм), сантиметры (см), метры (м) и т. д.
Как пользоваться калькулятором периметра квадрата?
Калькулятор периметра квадрата используется для быстрых вычислений и быстрого получения желаемого результата периметра квадрата. Чтобы вычислить периметр квадрата с помощью калькулятора, нам нужно ввести определенные параметры, такие как длина стороны квадрата. Попробуйте калькулятор периметра квадрата Cuemath прямо сейчас и получите ответы одним щелчком мыши.
☛ Проверьте листы периметра квадратов для большей практики .
Как найти периметр квадрата по диагонали?
Диагональ квадрата определяется как √2 × сторона. Преобразовав эту формулу для вычисления стороны квадрата, мы получим: сторона = диагональ/√2 = (√2 × диагональ)/2. Таким образом, периметр квадрата можно рассчитать по формуле P = 2√2 × диагональ.
Преобразовав эту формулу для вычисления стороны квадрата, мы получим: сторона = диагональ/√2 = (√2 × диагональ)/2. Таким образом, периметр квадрата можно рассчитать по формуле P = 2√2 × диагональ.
Скачать БЕСПЛАТНЫЕ учебные материалы
Периметр квадрата Рабочий лист
Площадь трапеции — формула, примеры, определение, вывод в квадратных единицах (например, см
2 , м 2 , в 2 и т.д.). Например, если внутрь трапеции можно поместить 15 единичных квадратов длиной 1 см каждый, то ее площадь будет равна 15 см 2 . Трапеция — это тип четырехугольника с одной парой параллельных сторон (которые известны как основания). Это означает, что другая пара сторон может быть непараллельной (известной как ноги). Не всегда возможно нарисовать единичные квадраты и измерить площадь трапеции. Итак, давайте узнаем о формуле для нахождения площади трапеции на этой странице. 1. | Какова площадь трапеции? |
| 2. | Площадь трапеции Формула |
| 3. | Площадь трапеции без высоты |
| 4. | Как вывести формулу площади трапеции? |
| 5. | Калькулятор площади трапеции |
| 6. | Часто задаваемые вопросы по площади трапеции |
Какова площадь трапеции?
Площадь трапеции равна площади, занимаемой ее сторонами. Здесь следует отметить интересный момент: если мы знаем длины всех сторон, мы можем просто разделить трапецию на более мелкие многоугольники, такие как треугольники и прямоугольники, найти их площади и сложить их, чтобы получить площадь трапеции. Однако существует прямая формула, которая используется для нахождения площади трапеции, если известны определенные размеры.
Формула площади трапеции
Площадь трапеции можно вычислить, если известны длины ее параллельных сторон и расстояние (высота) между ними. Формула площади трапеции выражается следующим образом:
Формула площади трапеции выражается следующим образом:
A = ½ (a + b) h
, где (A) — площадь трапеции, а и b — основания. (параллельные стороны), а «h» — высота (перпендикулярное расстояние между a и b)
Пример:
Найдите площадь трапеции, параллельные стороны которой равны 32 см и 12 см соответственно, а высота равна 5 см.
Решение:
Основания даны как, a = 32 см; б = 12 см; высота h = 5 см.
Площадь трапеции = A = ½ (a + b) h
A = ½ (32 + 12) × (5) = ½ (44) × (5) = 110 см 2 .
Площадь трапеции без высоты
Зная все стороны трапеции и не зная высоту, можно найти площадь трапеции. В этом случае нам сначала нужно вычислить высоту трапеции. Давайте разберемся в этом с помощью примера.
Пример: Найдите площадь трапеции, у которой основания (параллельные стороны) равны 6 и 14 единицам соответственно, а непараллельные стороны (катеты) равны 5 единицам каждая.
Решение: Рассчитаем площадь трапеции, выполнив следующие действия.
- Шаг 1: Мы знаем, что площадь трапеции = ½ (a + b) h; где h — высота трапеции, которая в данном случае не приводится; a = 6 единиц, b = 14 единиц, непараллельные стороны (ножки) = по 5 единиц.
- Шаг 2: Итак, если мы найдем высоту трапеции, мы сможем вычислить площадь. Если мы начертим высоту трапеции с обеих сторон, мы увидим, что трапеция разбита на прямоугольник ABQP и 2 прямоугольных треугольника, ADP и BQC.
- Шаг 3: Поскольку прямоугольник имеет равные противоположные стороны, это означает, что AP = BQ, и известно, что стороны AD = BC = 5 единиц. Итак, высоты AP и BQ можно вычислить по теореме Пифагора.
- Шаг 4: Теперь найдем длину DP и QC. Поскольку ABQP — прямоугольник, AB = PQ и DC = 14 единиц. Это означает, что PQ = 6 единиц, а оставшуюся общую длину DP + QC можно рассчитать следующим образом.
 DC — PQ = 14 — 6 = 8. Итак, 8 ÷ 2 = 4 единицы. Следовательно, DP = QC = 4 ед.
DC — PQ = 14 — 6 = 8. Итак, 8 ÷ 2 = 4 единицы. Следовательно, DP = QC = 4 ед. - Шаг 5: Теперь можно вычислить высоту трапеции по теореме Пифагора. Взяв прямоугольный треугольник ADP, мы знаем, что AD = 5 единиц, DP = 4 единицы, поэтому AP = √(AD 2 — DP 2 ) = √(5 2 — 4 2 ) = √(25 — 16) = √9 = 3 единицы. Поскольку ABQP — прямоугольник, у которого противоположные стороны равны, AP = BQ = 3 единицы.
- Шаг 6: Теперь, когда мы знаем все размеры трапеции, включая высоту, мы можем вычислить ее площадь по формуле: площадь трапеции = ½ (a + b) h; где h = 3 ед., a = 6 ед., b = 14 ед. После подстановки значений в формулу получаем, площадь трапеции = ½ (a + b) h = ½ (6 + 14) × 3 = ½ × 20 × 3 = 30 ед. 2 .
Как вывести формулу площади трапеции?
Мы можем доказать формулу площади трапеции, используя здесь треугольник. Взяв трапецию с основаниями «а» и «b» и высотой «h», докажем формулу.
- Шаг 1: Разделите одну из ножек на две равные части и вырежьте треугольную часть трапеции, как показано на рисунке.
- Шаг 3: Прикрепите его внизу, как показано, так, чтобы получился большой треугольник.
- Шаг 4: Таким образом, трапеция преобразуется в треугольник. Даже после того, как мы присоединим его таким образом, мы знаем, что площади трапеции и нового большого треугольника остаются прежними. Мы также можем видеть, что основание нового большого треугольника равно (a + b), а высота треугольника равна h.
- Шаг 5: Итак, можно сказать, что площадь трапеции = площади треугольника
- Шаг 6: Это можно записать как площадь трапеции = ½ × основание × высота = ½ (a + b) h
Итак, мы доказали формулу нахождения площади трапеции.
Калькулятор площади трапеции
Площадь трапеции — это количество единичных квадратов, которые могут в нее поместиться.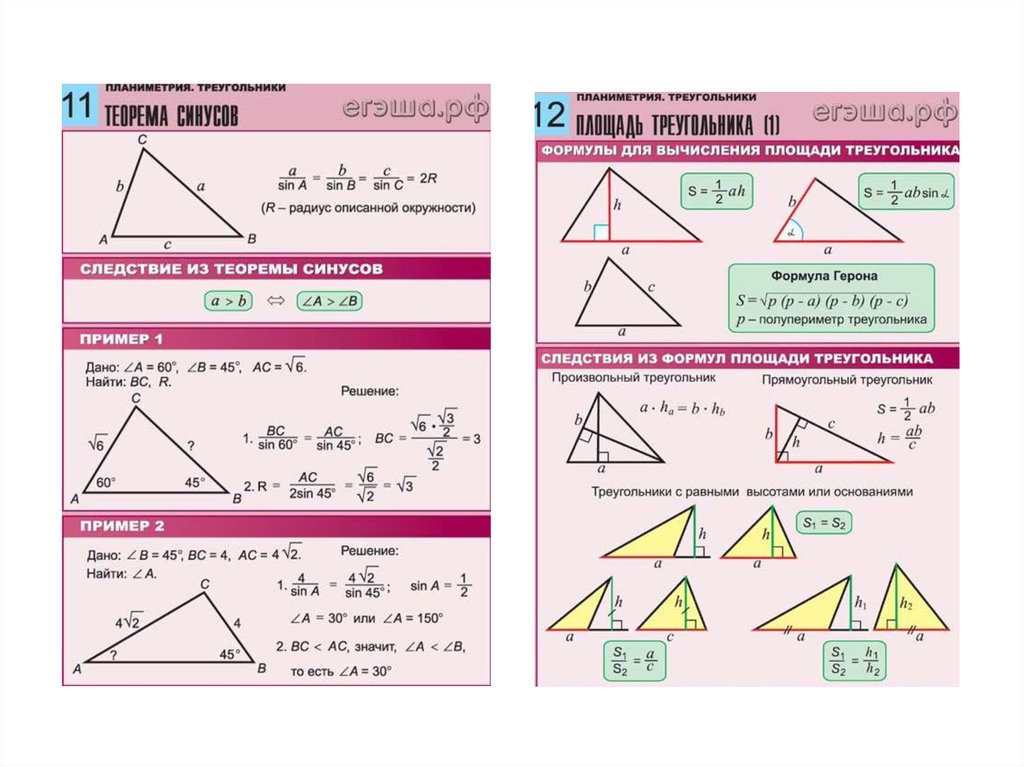 Калькулятор площади трапеции — это онлайн-инструмент, который помогает найти площадь трапеции. Если доступны определенные параметры, такие как значение основания или высоты, мы можем напрямую ввести входные данные и рассчитать площадь. Попробуйте калькулятор площади трапеции Куэмата и рассчитайте площадь трапеции за несколько секунд. Для большей практики проверьте площадь листа трапеции и решите задачи с помощью калькулятора.
Калькулятор площади трапеции — это онлайн-инструмент, который помогает найти площадь трапеции. Если доступны определенные параметры, такие как значение основания или высоты, мы можем напрямую ввести входные данные и рассчитать площадь. Попробуйте калькулятор площади трапеции Куэмата и рассчитайте площадь трапеции за несколько секунд. Для большей практики проверьте площадь листа трапеции и решите задачи с помощью калькулятора.
☛ Статьи по теме
- Площадь равностороннего треугольника
- Площадь квадрата
- Площадь параллелограмма
- Площадь прямоугольника
- Площадь ромба
- Район Пентагона
- Площадь круга
Площадь трапеции Примеры
Пример 1: Если одно из оснований трапеции равно 8 единицам, ее высота 12 единиц, а площадь 108 квадратных единиц, найдите длину другого основания.
Решение:
Одно из оснований равно «а» = 8 единиц.

Пусть другое основание будет ‘b’.
Площадь трапеции A = 108 квадратных единиц.
Его высота ‘h’ = 12 единиц.
Подставить все эти значения в область формулы трапеции,
A = ½ (a + b) h
108 = ½ (8 + b) × (12)
108 = 6 (8 + b)
Разделив обе части на 6,
18 = 8 + b
b = 10
Ответ: Длина другого основания данной трапеции = 10 единиц.
Пример 2: Найдите площадь равнобедренной трапеции, у которой длина каждого катета равна 8 единицам, а основания равны 13 единицам и 17 единицам соответственно.
Решение:
Базы a = 13 единиц и b = 17 единиц. Предположим, что его высота равна h.
Данную трапецию можно разделить на два конгруэнтных прямоугольных треугольника и прямоугольник следующим образом:
На приведенном выше рисунке
x + x + 13 = 17
2x + 13 = 17
2x = 4
x = 2
с использованием теоремы Pythagoras,
x 2 + H 333333.
 2 = 8 2
2 = 8 2 2 2 + H 2 = 64
4 + H 2 = 64
H 2 = 60
H = √ √ = = = = = = 2 = 60 0005
H = √ = = √ = № x = цин
h 2 = 60 0005
h = √ = 2 . = 2√15
Площадь данной трапеции равна,
A = ½ (a + b) h
A = ½ (13 + 17) × (2√15) = 30√15 = 116,18 квадратных единиц
Ответ: Площадь данной трапеции = 116,18 квадратных единиц.
Пример 3: Найдите площадь трапеции, у которой основания равны 7 единицам и 9 единицам, а высота равна 5 единицам.
Решение: Площадь трапеции = ½ (a + b) h; где a = 7, b = 9, h = 5.
Подставляя эти значения в формулу, получаем:
A = ½ (a + b) h
A = ½ (7 + 9) × 5
A = ½ × 16 × 5 = 40 единиц 2
Следовательно, площадь трапеции равна 40 кв. единицы.
перейти к слайдуперейти к слайдуперейти к слайду
Развивайте логическое мышление и укрепляйте его уверенность!
Благодаря гибкому учебному плану Куэмат выходит за рамки традиционных методов обучения.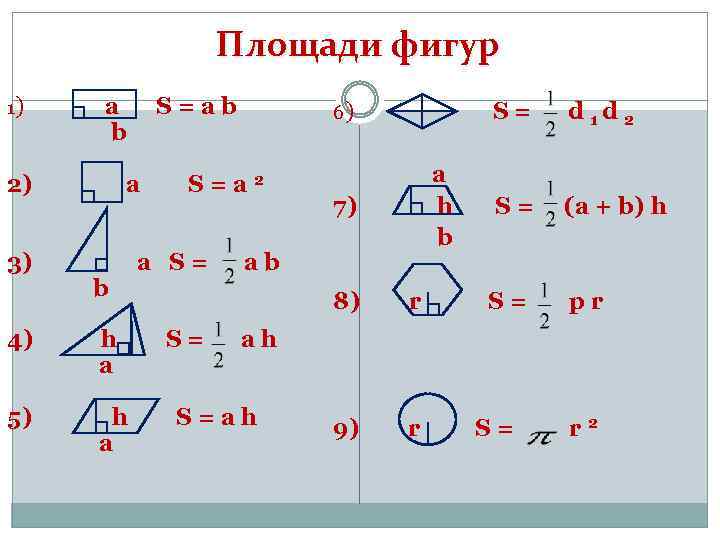 Мы делаем математику увлекательной. Проверьте, как!
Мы делаем математику увлекательной. Проверьте, как!
Забронировать бесплатный пробный урок
Практические вопросы по площади трапеции
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по площади трапеции
Что такое площадь трапеции в математике?
Площадь трапеции — это количество единичных квадратов, которые могут в нее поместиться. Мы знаем, что трапеция — это четырехугольник, у которого одна пара противоположных сторон параллельна. Площадь трапеции рассчитывается по формуле Площадь трапеции = ½ (a + b) h, где «a» и «b» — основания (параллельные стороны), а «h» — перпендикулярная высота. Он представлен в квадратных единицах.
Как найти площадь трапеции?
Площадь трапеции находится по формуле A = ½ (a + b) h, где «a» и «b» — основания (параллельные стороны), а «h» — высота (перпендикулярное расстояние между основания) трапеции.
Почему площадь трапеции равна ½ (a + b) h?
Формулу площади трапеции можно легко доказать. Рассмотрим трапецию с основаниями «а» и «b» и высотой «h». Мы можем отрезать от трапеции треугольную часть и прикрепить ее внизу, чтобы вся трапеция превратилась в треугольник. Тогда полученный треугольник имеет основание (a + b) и высоту h. Применяя формулу площади треугольника, площадь трапеции (или треугольника) = ½ (a + b) h. Для получения дополнительной информации вы можете обратиться к статье Как вывести формулу площади трапеции? раздел этой страницы.
Рассмотрим трапецию с основаниями «а» и «b» и высотой «h». Мы можем отрезать от трапеции треугольную часть и прикрепить ее внизу, чтобы вся трапеция превратилась в треугольник. Тогда полученный треугольник имеет основание (a + b) и высоту h. Применяя формулу площади треугольника, площадь трапеции (или треугольника) = ½ (a + b) h. Для получения дополнительной информации вы можете обратиться к статье Как вывести формулу площади трапеции? раздел этой страницы.
Как найти недостающее основание трапеции, если известна площадь?
Мы знаем, что площадь трапеции с основаниями а и b и высотой h равна A = ½ (a + b) h. Если одно из оснований (скажем, «а»), высота и площадь заданы, то мы просто подставим эти значения в приведенную выше формулу и решим ее для отсутствующего основания (а) следующим образом:
A = ½ (a + b) h
Умножение обеих частей на 2,
2A = (a + b) h
Деление обеих частей на h,
2A/h = a + b
Вычитание b с обеих сторон,
a = (2A/h) — b
Как найти высоту трапеции с площадью и основанием?
Если площадь и основания трапеции известны, то мы можем вычислить ее высоту по формуле Площадь трапеции = ½ (a + b) h; где «а» и «b» — основания, а «h» — высота. Другими словами, мы можем найти высоту трапеции, подставив заданные значения площади и двух оснований.
Другими словами, мы можем найти высоту трапеции, подставив заданные значения площади и двух оснований.
Как найти площадь равнобедренной трапеции без высоты?
Если высота трапеции не задана и известны все ее стороны, то мы можем разделить трапецию на два конгруэнтных прямоугольных треугольника и прямоугольник. Используя теорему Пифагора в прямоугольных треугольниках, мы можем вычислить высоту. После того, как мы получим высоту, мы можем использовать формулу A = ½ (a + b) h, чтобы получить площадь трапеции.
Какая формула площади трапеции?
Формула, используемая для нахождения площади трапеции, выражается следующим образом: Площадь трапеции = ½ (a + b) h; где а и b — основания (параллельные стороны), а h — высота трапеции.
Трапеция – свойства, формула, определение, примеры
Согласно евклидовой геометрии, четырехугольник, имеющий одну пару параллельных противоположных сторон, называется трапецией. Слово трапеция произошло от греческого слова «трапеза», что означает стол. В этом уроке мы узнаем больше о свойствах трапеции на примерах.
В этом уроке мы узнаем больше о свойствах трапеции на примерах.
| 1. | Определение трапеции |
| 2. | Типы трапеций |
| 3. | Свойства трапеции |
| 4. | Формула трапеции |
| 5. | Часто задаваемые вопросы о трапеции |
Определение трапеции
Трапеция представляет собой двумерный четырехугольник (поскольку он составлен из четырех прямых), имеющий пару параллельных противоположных сторон. Противоположные параллельные стороны называются основанием, а непараллельные стороны называются катетами трапеции. Это замкнутая плоская форма, имеющая четыре стороны и четыре угла. Форма трапеции представлена как:
На приведенном выше рисунке XY и WZ — это основания, а XW и YZ — стороны трапеции. Форму трапеции можно наблюдать в окружающих нас предметах, например:
Типы трапеций
Существуют в основном три типа трапеций, которые приведены ниже:
- Равнобедренная трапеция
- Лестничная трапеция
- Правая трапеция
Трапеции классифицируются на основе длины ножек или измерения их углов. Определение каждого типа трапеции вместе с ее формой дано ниже.
Определение каждого типа трапеции вместе с ее формой дано ниже.
Свойства трапеции
У каждого четырехугольника есть свои свойства, которые делают его узнаваемым и отличным от остальных. Эти свойства дают больше информации о геометрической конструкции формы. Свойства трапеции перечислены ниже:
- Это двумерная фигура.
- Основания трапеции параллельны друг другу.
- Длина обеих диагоналей одинакова.
- Диагонали трапеции всегда пересекаются.
- Сумма смежных внутренних углов равна 180°.
- Сумма всех внутренних углов трапеции всегда равна 360°.
Формула трапеции
Возьмем трапецию с длинами параллельных сторон a, b единиц соответственно и высотой «h».
Площадь трапеции определяется путем вычисления среднего значения оснований и умножения его результата на высоту. Следовательно, площадь трапеции = ((AB + DC)/2) × AM = ((a+b)/2) × h, где AB, CD — основания, а AM — высота.
Периметр трапеции определяется суммой всех ее сторон. Следовательно, периметра трапеции ABCD = AB + BC + CD + AD.
Темы, относящиеся к трапеции
Проверьте эти интересные статьи, связанные с концепцией формы трапеции в геометрии.
- Четырехугольники
- Трапеция
- Площадь трапеции
- Формула трапеции
- Калькулятор площади трапеции
- Равнобедренная трапеция
Примеры трапеций
Пример 1: Определите площадь трапеции, если длина ее основания соответственно 13 и 15 единиц, а высота 4 единицы.
Решение: Как мы знаем, формула площади трапеции равна ((a+b)/2) × h. Здесь a = 13 единиц, b = 15 единиц и h = 4 единицы. Следовательно, площадь = ((a+b)/2) × h = ((13+15)/2) × 4 ⇒ 14 × 4 = 56 единиц 2 . Следовательно, необходимая площадь составляет 56 единиц 2 .
Пример 2: Найдите четвертый угол прямой трапеции, если один из заданных углов равен 60°.

Решение: Как известно, в прямой трапеции прямые углы парные, а сумма всех внутренних углов трапеции всегда равна 360°. Таким образом, каждый из двух углов равен 90°. Если один из заданных углов равен 60°, пусть вычисляемый угол равен x°. Четвертый угол можно рассчитать как x° + 90° + 90° + 60° = 360°.
⇒ х° = 360° — (90° + 90° + 60°) = 120°. Следовательно, мера четвертого угла равна 120°.Пример 3: Найдите длину четвертой стороны трапеции, если остальные три стороны имеют длину 10 единиц, 12 единиц и 7 единиц, а периметр равен 40 единицам.
Решение: Как известно, периметр трапеции равен сумме всех ее сторон. Пусть длина, которую нужно найти, равна а единицам. Таким образом, периметр равен 40 = 10 + 12 + 7 + а.
⇒ а = 40 — (10 + 12 + 7) = 11 единиц. Следовательно, длина четвертой стороны равна 11 единицам.
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу в математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними.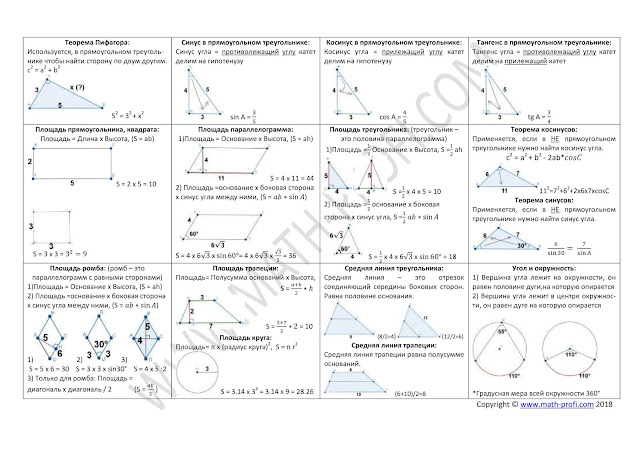 Испытайте Cuemath и приступайте к работе.
Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
Практические вопросы по трапеции
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о трапеции
Что такое форма трапеции?
Двумерный четырехугольник, имеющий пару несмежных параллельных сторон и пару непараллельных сторон, называется формой трапеции. Он выглядит как треугольник, который срезан сверху.
Как найти площадь трапеции?
Площадь трапеции можно найти, вычислив среднее значение оснований и умножив результат на высоту, то есть ((a+b)/2) × h, где a и b — длины параллельных сторон h — высота трапеции.
Является ли трапеция четырехугольником?
Да, трапеция — четырехугольник. У него четыре стороны, четыре вершины и четыре угла. Сумма всех четырех внутренних углов трапеции равна 360 градусов.
Имеет ли трапеция параллельные стороны?
Да, у трапеции есть пара параллельных сторон, которые называются основаниями.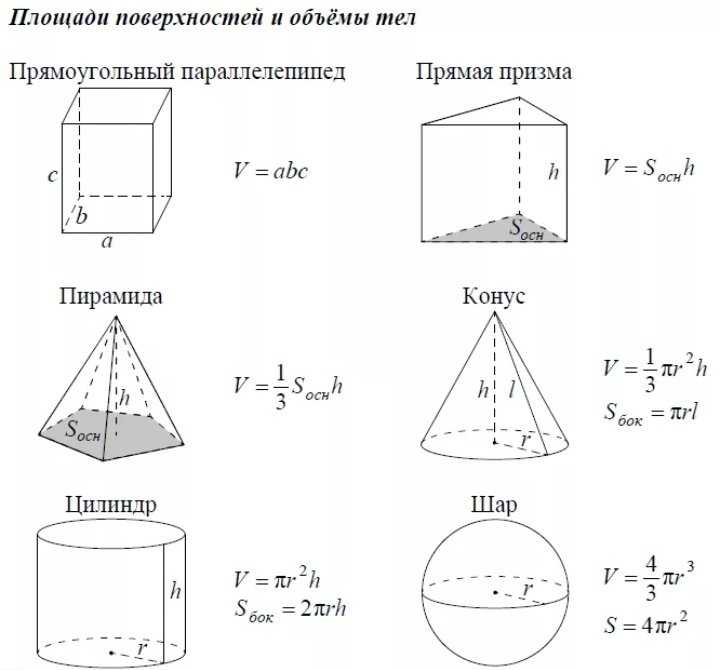
Может ли трапеция иметь прямой угол?
Да, трапеция может иметь прямой угол. Трапеция с парой прямых углов называется прямой трапецией.
Каковы свойства трапеции?
Свойства трапеции приведены ниже:
- Основания всегда параллельны друг другу.
- Обе диагонали всегда пересекаются.
- Сумма смежных внутренних углов трапеции равна 180°.
- Сумма внутренних углов трапеции всегда равна 360°.
Какая формула площади трапеции?
Если «h» — высота, а a и b — длины параллельных сторон трапеции, формула площади трапеции задается как 1/2 × (a + b) × h квадратных единиц.
Что такое равнобедренная трапеция?
Равнобедренная трапеция – это трапеция, у которой оба катета или непараллельные стороны равны друг другу. Углы, противоположные этим двум равным сторонам, также равны.
В чем разница между трапецией и трапецией?
И трапеция, и трапеция означают одно и то же. Они относятся к четырехстороннему многоугольнику, имеющему пару несмежных параллельных сторон и пару несмежных непараллельных сторон.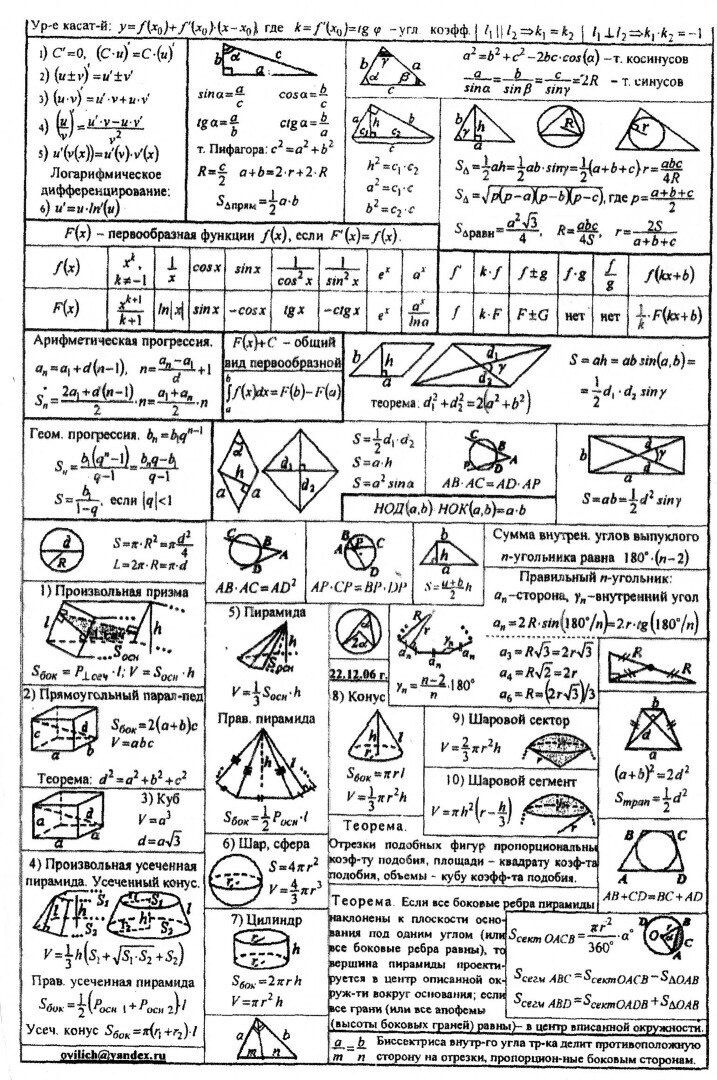 Как правило, трапеция соответствует британскому английскому языку, а трапеция является распространенным термином в американском английском.
Как правило, трапеция соответствует британскому английскому языку, а трапеция является распространенным термином в американском английском.
Сколько углов в трапеции?
Трапеция состоит из четырех сторон, четырех вершин и четырех углов.
Является ли трапеция параллелограммом?
Нет, трапеция не является параллелограммом, потому что у нее только 1 пара параллельных сторон. Тогда как параллелограмм имеет 2 пары параллельных сторон.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по трапеции
Формулы аналитической геометрии
Расстояние между двумя точками:
Расстояние между двумя точками A(x 1 , y 1 ) и B(x 2 , y 2 ) равно
(x 1 , Y 1 ) и B (x 2 , Y 2 ) IS
Секция (внутреннее дивизион):
Let A (X 1 , Y . Тогда координаты P задаются как Формула сечения (внутреннее деление) : Пусть A(x 1 , y 1 ) и B(x 2 ) есть две различные точки такие, что точка p(x, y) делит AB внешне в отношении m : n. Тогда координаты P задаются как Центр тяжести треугольника: Координаты центра тяжести (G) треугольника с вершинами A(x 1 , Y 1 ), B (x 2 , Y 2 ) и C (x 3 , Y 3 ) даны Пусть A(x 1 , y 1 ), B(x 2 , y 2 ) и C(x 3 , y 3 ) 9094 треугольника . Тогда площадь ΔABC является абсолютным значением выражения: Вершины A(x 1 , y 1 ), B(x 2 , y 2 ) и C(x 3 , y 3 ) ΔABC называются «взятыми по порядку», если A, B, C принимаются против часовой стрелки. Коллинеарность трех точек : Пусть A(x 1 , y 1 ), B(x 2 , y 2 ) и C(x 3 9 ), три отдельные точки. Если эти три точки лежат на одной прямой (на одной прямой), то ΔABC = 0,9.0005 That is, Area of a Quadrilateral : Let A(x 1 , y 1 ), B(x 2 , y 2 ), C(x 3 , y 3 ) и D(x 3 , y 3 ) — вершины четырехугольника. Тогда площадь четырехугольника ABCD равна Наклон прямой линии: по м. Следовательно, наклон прямой равен m = tanθ Наклон прямой линии при заданных двух точках: Пусть A(x 1 , y 1 , y 1 ) и B(x 2 8 , y 2 ) — две различные точки на отрезке AB. Тогда наклон отрезка AB равен Наклоны параллельных прямых: Пусть m 1 и m 2 будут наклонами двух прямых. м 1 = м 2 То есть, если две прямые параллельны, то и уклоны равны. Наклоны перпендикулярных прямых : Пусть m 1 и m 2 будут наклонами двух прямых. Если две прямые перпендикулярны, то м 1 м 2 = -1 То есть, если две прямые перпендикулярны, то произведение уклонов равно -1. Уравнение оси x: y = 0 Уравнение оси y: x = 0 Уравнение прямой линии, параллельной оси x: y = k Уравнение прямой линии, параллельной оси y: x = c Уравнение прямой в общем виде: Ax + By + C = 0 Уравнение прямой в стандартной форме: Ax + By = C Уравнение прямой в форме пересечения наклона: y = mx + b , где «m» — наклон, а «b» — точка пересечения с осью y. Уравнение прямой в форме точка-наклон: y — y 1 = m(x — x 1 ) где m — наклон и (x 1 , y 1 8 ) — точка на прямой. Уравнение линии в форме точки пересечения: , где «a» — точка пересечения по оси X, а «b» — точка пересечения по оси y. Угол между двумя прямыми: Пусть уравнения двух прямых равны y = m 1 x + b 1 y = m 2 x + b 2 Тогда угол между этими двумя прямыми равен Расстояние между точкой и прямой: 5 точка P(x 1 , y 1 ) на прямой ax + by + c = 0 is Расстояние между двумя параллельными прямыми: Пусть уравнениями двух параллельных прямых будут ax + by + с 1 = 0 топор + бай + с 2 = 0 Тогда расстояние между этими двумя параллельными прямыми равно Уравнение окружности в общем виде: x 2 + y 2 90 + 2gx = 2 + 2gx + 2f центр равен C(-g, -f), а радиус равен Уравнение окружности в стандартной форме: (x — h) 2 + (y — k) 2 = r 2 , где центр равен C(h, k), а радиус равен r. Уравнение окружности в стандартной форме с центром (0, 0) : x 2 + y 2 = r 2 Пожалуйста, присылайте свои отзывы на [email protected] Мы всегда ценим ваши отзывы. ©Все права защищены. onlinemath5all.com Некоторые люди могут сказать, что геометрия никоим образом не является «сексуальным» предметом; на самом деле, как правило, вычисление углов, объемов и площадей редко считается заманчивым или забавным. Возможно ли обратное? За последние 10 лет мы видели, как математика проникла в фильмов и телешоу ; Теория большого взрыва — яркий тому пример. Конечно, уравнения не занимают центральное место в сюжете, и, честно говоря, только первые несколько шоу были насыщены математикой. После этого алгебраическая работа всплывала лишь изредка. Тем не менее, приятно видеть, как сложные расчеты разыгрываются на популярной арене, а еще лучше, что в 9 участвуют как мужские, так и женские персонажи. Теперь ваша очередь освоить уравнения базовой геометрии , и вам нужен самый эффективный способ сделать это. Или, может быть, вы поклонник Декарта и хотите поднять декартовскую геометрию на новый уровень, но для начала вам нужен прочный фундамент. Ваш Superprof поможет вам разобраться в основных геометрических формулах; хватайте свои угольники и циркуль… мы пошли! Найдите рядом со мной репетитора по математике на Superprof. Лучшие репетиторы по математике Поехали У вас может возникнуть соблазн подумать «круг», «треугольник» или «квадрат», и вы будете абсолютно правы. Каждая из этих геометрических фигур относится к одной из следующих четырех основных категорий: Их уникальные характеристики включают в себя: Каждая из этих фигур имеет собственную формулу для вычисления периметра, площади и углов. Давайте посмотрим на них сейчас. Вам нужна помощь в изучении геометрии? Возможно, вы могли бы найти репетитора по геометрии… Начиная с форм наименьшего количества сторон (но иногда с самыми сложными формулами), мы беремся за геометрические формулы! Простейшая формула для периметра любого треугольника: a+b+c, , где каждая буква обозначает сторону. Он прекрасен в своей простоте и с ним легко работать, если вы знаете длину каждой стороны. Допустим, ваш треугольник имеет следующие размеры: a = 3 дюйма, b = 4 дюйма и c = 5 дюймов. Тогда его периметр будет 3+4+5=12 дюймов. Очевидно, что этот треугольник не является ни равносторонним, ни равнобедренным; и не прямоугольный треугольник. В таком случае мы должны опираться на теорему Пифагора : a 2 +b 2 =c 2 . Ты помнишь тот, да? Сначала проведите линию от вершины треугольника прямо к его основанию. Эта линия, h, должна быть перпендикулярной основанию, таким образом образуя два угла 90 градусов – по одному с каждой стороны линии. Теперь у вас есть два прямоугольных треугольника, один из которых имеет измерения как для a, так и для b. Отсюда очень просто подставить известные значения в теорему (не забудьте возвести их в квадрат!) и найти недостающее значение. Попробуем его с вымышленным треугольником: A = Неизвестный B = 5 C = 7 A 2 * 5 2 = 7 2 A 2 * 25 = 4 9 9 9 9 9 9 A 2 * 25 = 4 9 a 2 = 49 – 25 переместить 25 в другую сторону знака равенства, вычитая его из заданного значения c a 2 = 24 Теперь вам нужно вычислить квадратный корень из 24, чтобы найти значение ‘a’ , что равно 4,898. Поздравляем! Теперь вы знаете, как вычислить периметр любого треугольника! Выполните поиск здесь, чтобы найти некоторые из лучших эффективных онлайн-уроков по математике на суперпрофессионалах. В то время как вычисление периметра является довольно простой задачей, вычисление площади треугольника требует немного больше усилий. Если значения даны для всех трех сторон, вы можете применить Формулу Герона : площадь = квадратный корень из [s(s-a)(s-b)(s-c)], где s означает полупериметр , то есть (a+b+c)/2 Это только кажется сложным; помните, что при работе с формулой вам нужно только подставить известные значения, чтобы найти неизвестное. Теперь об уравнениях площади треугольников, где одно или несколько значений неизвестны. Если вы знаете только значение основания треугольника и его высоты , вы можете применить: площадь = (½) * b * h Если известны только длина двух сторон и степень угла, соединяющего их , вы должны использовать тригонометрию , чтобы найти пропущенные значения. Основная формула: Площадь = (½) * a * b * sin C Имейте в виду, что строчные буквы обозначают линейные измерения, а прописные буквы обозначают углы. Если бы вы знали только значения сторон a и c, вы бы подставили их и вычислили sin B . Точно так же, если вы знаете b и c, вы использовали бы sin A , чтобы получить площадь вашего треугольника. Почему бы не попрактиковаться с ними, прежде чем двигаться дальше… Лучшие репетиторы по математике Поехали Вы можете вычислить периметр квадрата или прямоугольника во сне. Эти формулы таковы: P=4a (a представляет стороны квадрата) и P=2l + 2w соответственно. Эти расчеты площадей также должны прийти к вам довольно легко. Для квадратов это A=a 2 , а для прямоугольников это A=l * w . Просто, верно? Все становится сложнее, когда мы переходим к параллелограммам и трапециям; Чтобы решить оба этих уравнения, вам нужно знать высоту форма (h) и длина основания (b) – линия внизу. Зная эти значения, выберите соответствующую формулу для фигуры: b * h = площадь параллелограмма (½)(a+b) * h = площадь трапеции, где a представляет собой сторона, противоположная букве «б». Четырехугольники могут быть самыми простыми фигурами для работы. Если вам нужна дополнительная практика, в Интернете есть множество ресурсов, где вы можете найти рабочих листа по геометрии и уравнения для решения. Столкнулись ли вы с апейрогеном (многоугольник с бесконечным числом сторон) или с более знакомым шестиугольником, вам нужно знать, как вычислить его периметр и площадь. К счастью, апейрогоны существуют только гипотетически; представьте, что у вас есть такая фигура, для которой можно вычислить площадь! Если все стороны вашего многоугольника имеют одинаковую длину, вы можете применить P=n * v , где ‘ n — количество сторон, а « v » — значение каждой стороны. Если стороны указанного многоугольника не имеют одинаковой длины, вам придется сложить эти значения , чтобы получить его периметр. Существует несколько способов определить значение площади любого многоугольника, некоторые из которых включают вычисления для треугольников. Сначала мы займемся уравнениями правильного многоугольника; такой, у которого все стороны одинаковой длины. Прежде чем мы сможем приступить к шифрованию, мы должны определить радиус полигона . Это включает в себя рисование круга внутри многоугольника таким образом, чтобы периметр круга касался периметра многоугольника. Это называется вписанной окружностью . Как только мы узнаем значение этого радиуса, мы можем применить эту формулу: A = ½ * p * r Чем больше сторон у многоугольника, тем сложнее. Допустим, количество сторон представлено ‘n’ , а количество сторон – ‘ s ’. A = ns/4 √ 4-s 2 Отсюда формулы становятся еще более сложными. Они заставляют вас бороться с основами геометрии? Вы можете обратиться к нашему полному руководству! Окружности не содержат ни углов, ни прямых, а их периметры называются «окружностями». Однако для их вычислений требуется по крайней мере отрезок прямой, который необходим для любой формулы для окружностей. Как ни странно, кажется, что формула для вычисления площадей кругов более известна, чем, возможно, для любой другой геометрической фигуры: πr 2 , или pi * r2 Наверняка вы знаете/помните, что pi (π) имеет значение 3,1415. Менее известная формула для кругов, формула для вычисления длины окружности: 2 * π * r Имейте в виду, что это формулы для вычисления площади и периметра. из двумерные фигуры ; как только они приобретают дополнительное измерение – они становятся трехмерными формами и заслуживают расчета объема, а также площади и периметра. Давайте не будем отклоняться от темы; мы будем рады предоставить формулы для этих основных геометрических построений … Но вам не нужно останавливаться на этом; зацепитесь за наше руководство для начинающих по геометрии! Базовый калькулятор Калькулятор капсул Также называется
стадион революции. Круглый конус Калькулятор Круглый цилиндр Калькулятор Conical Frustum Calculator Калькулятор куба Калькулятор полушария Калькулятор пирамиды Калькулятор прямоугольной призмы Калькулятор сферы Сферический колпачок Formulas Формулы сферического сегмента Треугольная призма Формулы Калькулятор трубки (полый цилиндр) ) и B(x 2 , y 2 ) — две различные точки, такие что точка p(x, y) делит AB внутри в отношении m : n.
) и B(x 2 , y 2 ) — две различные точки, такие что точка p(x, y) делит AB внутри в отношении m : n.. a Треугольник : 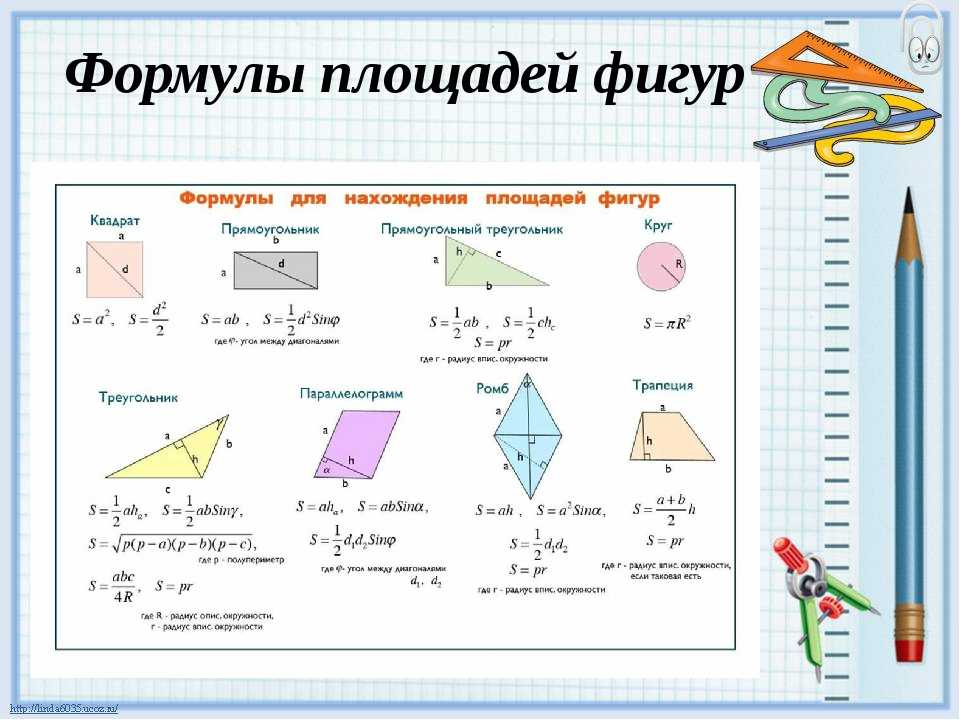 Если мы это сделаем, то площадь DABC никогда не будет отрицательной.
Если мы это сделаем, то площадь DABC никогда не будет отрицательной.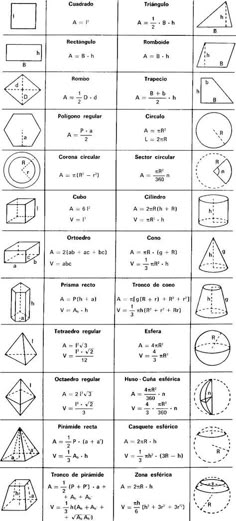 Если две прямые параллельны, то
Если две прямые параллельны, то

Базовые геометрические уравнения и примеры
 0003 корректировка уравнений ; всего 20 лет назад кинематографическими математиками могли быть только мужчины!
0003 корректировка уравнений ; всего 20 лет назад кинематографическими математиками могли быть только мужчины! Основные фигуры
Сколько геометрических фигур вы можете найти в этом узоре? Изображение от monicore с Pixabay
 С некоторыми вы, возможно, знакомы, например, с теоремой Пифагора , в то время как другие, возможно, менее запоминающиеся.
С некоторыми вы, возможно, знакомы, например, с теоремой Пифагора , в то время как другие, возможно, менее запоминающиеся. Вычисление треугольников
 Как бы мы вычислили периметр, если даны только два значения, нижняя и одна сторона?
Как бы мы вычислили периметр, если даны только два значения, нижняя и одна сторона? После того, как вы вычислили периметр одного прямоугольного треугольника, вы должны вычислить второй, чтобы получить размеры исходного треугольника.
После того, как вы вычислили периметр одного прямоугольного треугольника, вы должны вычислить второй, чтобы получить размеры исходного треугольника. Если подумать таким образом, Формула Героя , как ее еще называют, довольно проста!
Если подумать таким образом, Формула Героя , как ее еще называют, довольно проста!
Вычисление четырехугольников

Вычисление многоугольников
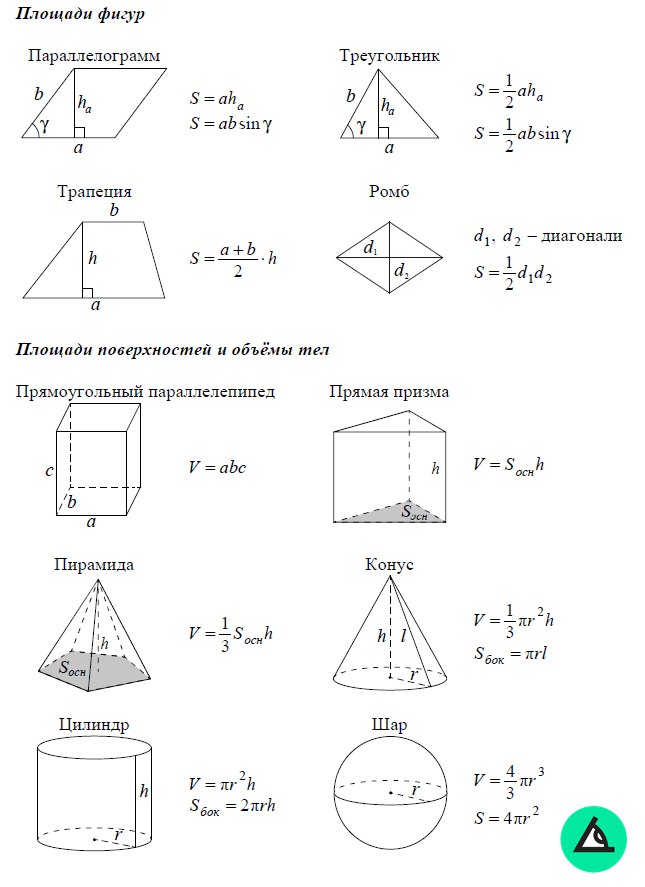
Вычисление площади многоугольника
 Радиус, также называемый апофемой , обозначается как « a ». Конечно, «A» представляет собой «площадь», что дает формулу, которая выглядит так:
Радиус, также называемый апофемой , обозначается как « a ». Конечно, «A» представляет собой «площадь», что дает формулу, которая выглядит так: Вычисление окружностей
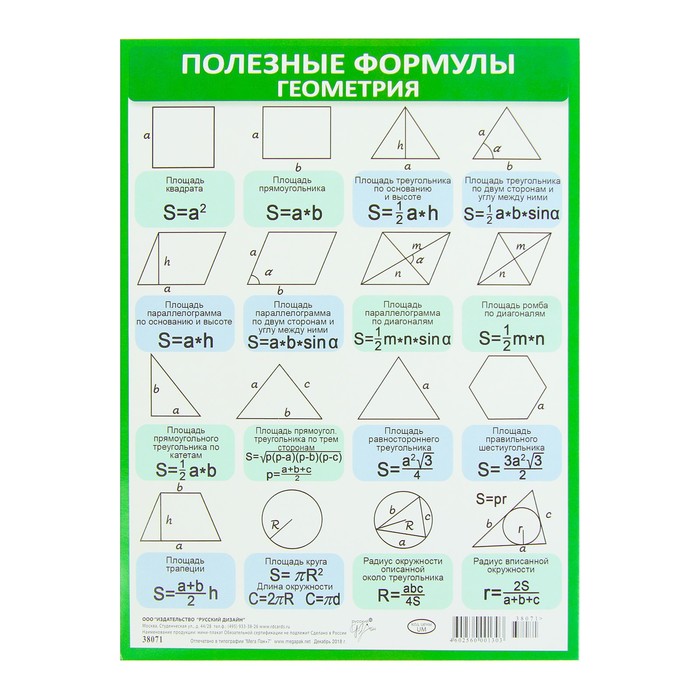 ..
.. Геометрические фигуры и формулы в объемной геометрии
Капсула

Круглый конус
= L + B = πrs + πr 2 =
πr(s + r) =
πr(r + √(r 2 + h 2 )) Круглый цилиндр
= L + T + B = 2πrh + 2(πr 2 ) = 2πr(h+r) Conical Frustum
= π(r 1 + r 2 )s =
π(r 1 + r 2 )√((r 1 — r 2 ) 2 + h 2 )
=
π(r 1 2 + r 2 2 + (r 1 + r 2 ) * s)
=
π[ r 1 2 + r 2 2 + (r 1 + r 2 ) * √((r 1 — r 2 ) 2 + h 2 ) ] Куб
Полушарие
Пирамида: Квадрат
= Л + В = 2 + а√(а 2 + 4ч 2 ))
= а(а + √(а 2 + 4h 2 )) Прямоугольная призма
Сфера
Сферический колпачок
= (1/6)πh(3a 2 + h 2 )
= (1/3)πh 2 (3R — h) Сферический сегмент
Треугольная призма
Трубка


 8 КБ
8 КБ 5 КБ
5 КБ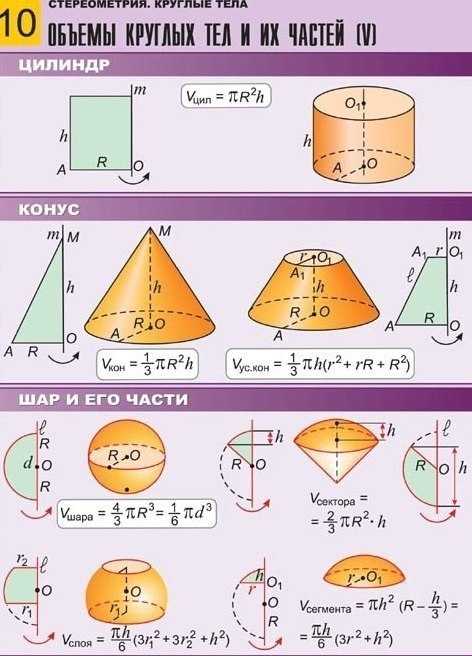
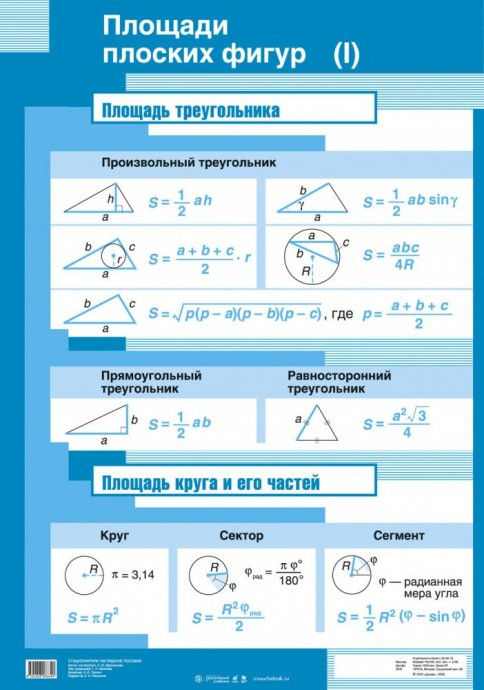 Квадратное уравнение имеет один корень, если дискриминант равен нулю. В вашем конспекте при дискриминанте меньше нуля.
Квадратное уравнение имеет один корень, если дискриминант равен нулю. В вашем конспекте при дискриминанте меньше нуля. В таком случае формула нахождения площади следующая: S = p * r. Буква p обозначает ½ периметра треугольника, r — это радиус окружности.
В таком случае формула нахождения площади следующая: S = p * r. Буква p обозначает ½ периметра треугольника, r — это радиус окружности.

/918870b1bc4a305.s.siteapi.org/img/da030ac2a7fb5c233f7bae5e5994c9ac4d7727d0.jpg)


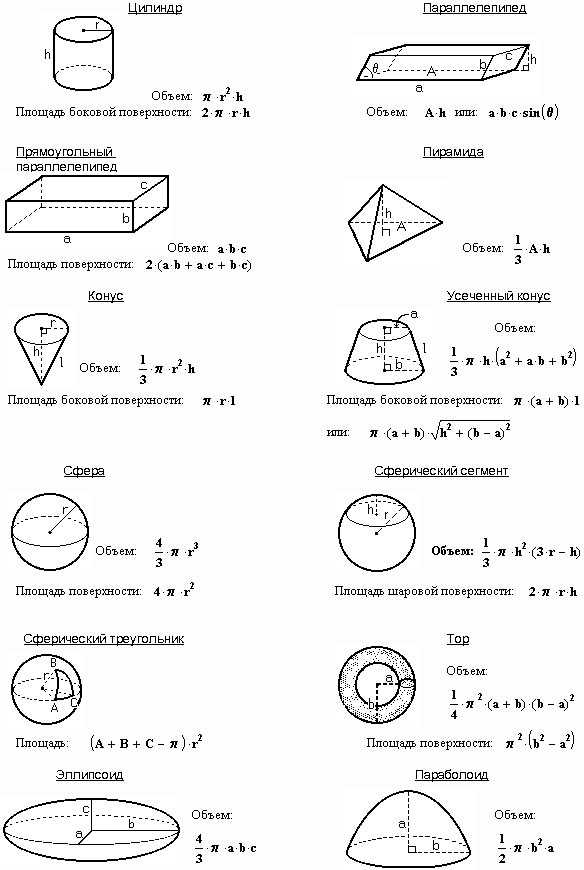 DC — PQ = 14 — 6 = 8. Итак, 8 ÷ 2 = 4 единицы. Следовательно, DP = QC = 4 ед.
DC — PQ = 14 — 6 = 8. Итак, 8 ÷ 2 = 4 единицы. Следовательно, DP = QC = 4 ед.
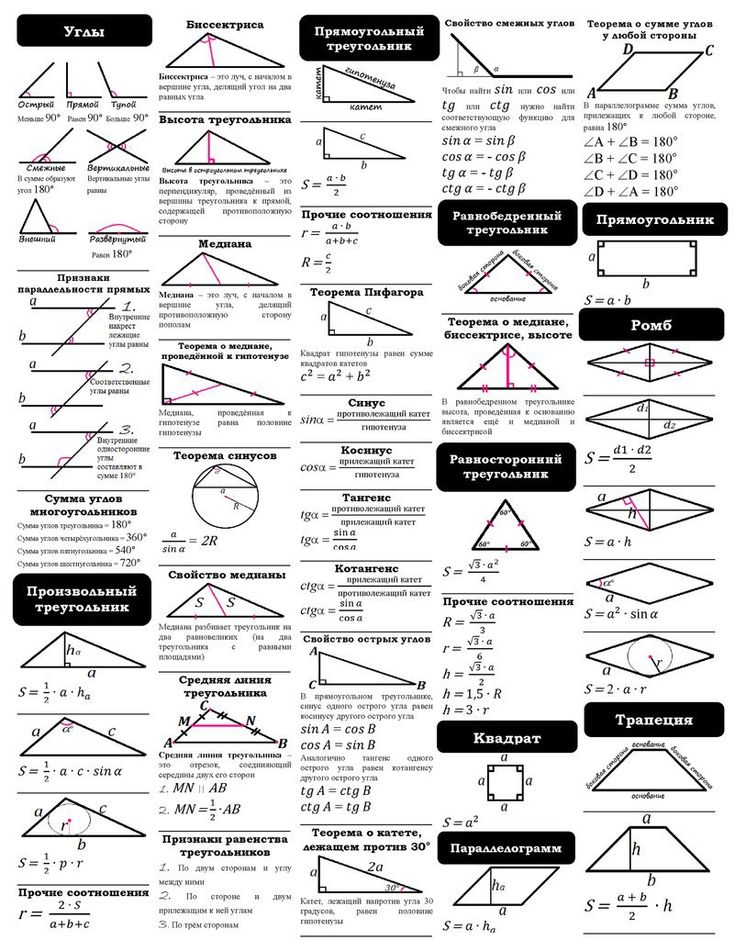 2 = 8 2
2 = 8 2 