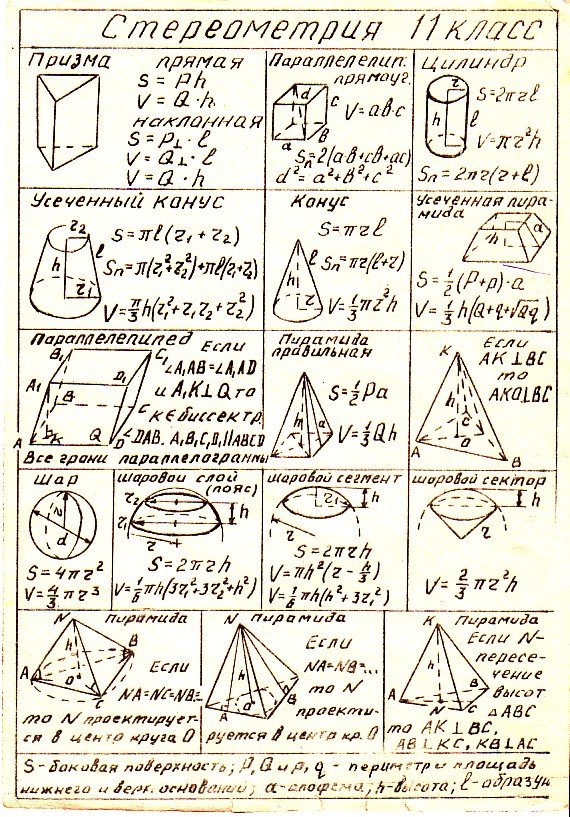
Формулы по геометрии
Формулы по геометрии
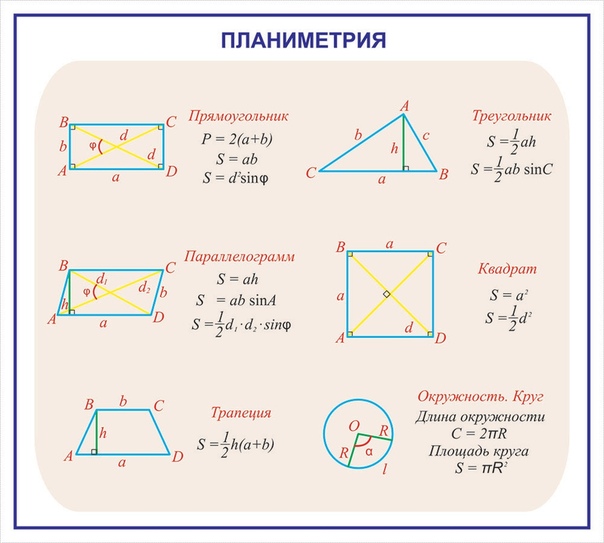
Площадь плоских фигур
Площадь треугольника
через основание и высоту
через две стороны и угол
формула Герона
через радиус вписсанной окружности
через радиус описсанной окружности
площадь прямоугольного треугольника
площадь равнобедренного треугольника
площадь равностороннего треугольника
площадь параллелограмма
площадь ромба
площадь прямоугольника
площадь квадрата
площадь трапеции
площадь правильного 6-угольника
площадь круга
площадь эллипса
площадь сектора круга
площадь сегмента круга
площадь кольца
площадь сектора кольца
Площадь поверхности тел
площадь поверхности куба
площадь поверхности параллелепипеда
площадь поверхности правильной пирамиды
боковая поверхность правильной усеченной пирамиды
площадь поверхности конуса
площадь поверхности усеченного конуса
площадь поверхности цилиндра
площадь поверхности сферы
площадь поверхности шарового сегмента
площадь поверхности шарового сектора
площадь боковой поверхности шарового слоя
Периметр фигур
периметр треугольника
периметр прямоугольника
периметр квадрата
периметр параллелограмма
периметр ромба
периметр трапеции
периметр круга или длина окружности
Радиус описанной окружности
радиус описанной окружности треугольника
радиус описанной окружности квадрата
радиус описанной окружности прямоугольника
радиус описанной окружности равнобедренной трапеции
радиус описанной окружности правильного шестиугольника
радиус описанной окружности правильного многоугольника
Объем тел
объем куба
объем параллелепипеда
объем пирамиды
объем правильной пирамиды
объем тетраэдра
объем усеченной пирамиды
объем конуса
объем усеченного конуса
объем цилиндра
объем шара
объем шарового сегмента
объем шарового сектора
объем шарового слоя
Как понять Геометрию? Основы с нуля
Поможем понять и полюбить математику
Начать учиться
105.
9K
Понять геометрию с нуля — это непросто. Но, чем дальше, тем интереснее. Новые знания можно применить везде: в школе на уроках, дома во время ремонта и даже на прогулке. В этой статье рассказали про основы геометрии для начинающих.
Идеальные объекты
Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.
Математика занимается объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Базовые геометрические объекты
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.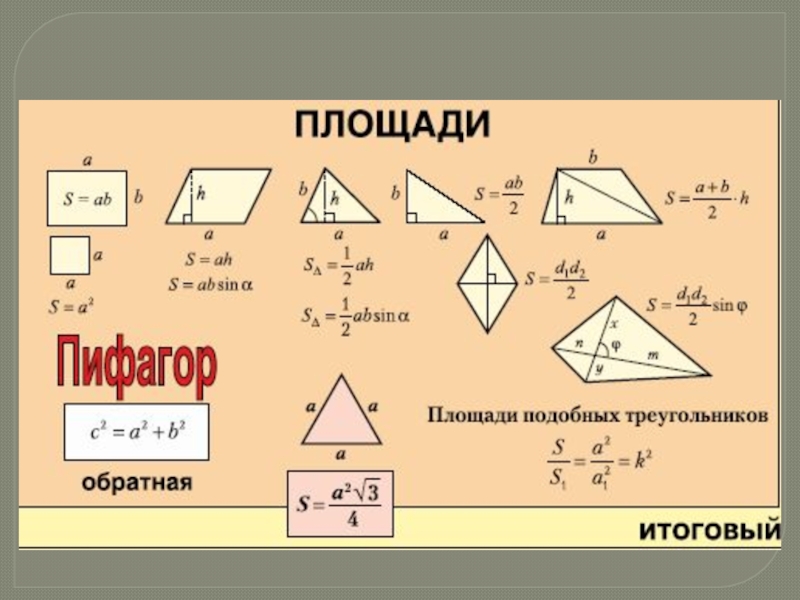
Точка — это идеальный математический объект, у которого нет длины и ширины.
Отрезок — это часть прямой, у которого есть начало и конец.
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.
Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.
Обозначать прямые принято малыми латинскими буквами (a, b, c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).
Два варианта расположения точек относительно прямой:
Точки лежат на данной прямой.
Или еще говорят, что прямая проходит через эти точки — на рисунке выше такими точками являются А и В. При решении задач для краткости используют запись A ∈ a (читается так: точка А принадлежит прямой a или точка А лежит на прямой a), аналогично будет и для точки В (B ∈ b).Точки не лежат на данной прямой. Говорят так: прямая не проходит через эти точки — на рисунке такими точками являются С и D. При решении задач для краткости используют запись C ∉ a (читается так: точка С не принадлежит прямой a или точка С не лежит на прямой a), аналогично будет и для точки D (D ∉ a).
Или еще говорят, что прямая проходит через эти точки — на рисунке выше такими точками являются А и В. При решении задач для краткости используют запись A ∈ a (читается так: точка А принадлежит прямой a или точка А лежит на прямой a), аналогично будет и для точки В (B ∈ b).Важно знать
Через любые две точки можно провести прямую и притом только одну.
Если рассмотреть две прямые, то возможны два варианта их расположения:
Прямые пересекаются, то есть имеют одну общую точку.
Для записи пересекающихся прямых используют специальный знак — ∩, то есть a∩b (читают: прямая a пересекает прямую b). Чтобы обозначить точку пересечения прямых, пишут a∩b = O (читается: прямая
- Прямые не пересекаются, то есть не имеют общих точек.
Для записи не пересекающихся прямых используют специальный знак — , то есть m n (читают: прямая m не пересекает прямую n). В дальнейшем для обозначения не пересекающихся прямых мы будем использовать знак параллельности ||.
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
На рисунке точка О разбивает прямую АВ на две части:
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.
Назовем получившиеся лучи:
Луч ОА, точка О — начало луча ОА; конца у луча ОА нет.
Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет.
Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.
Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости
Комбинации простейших объектов
Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми.
Точно так же мы изучали множества, а после — отношения между множествами, функции.
Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
Максимальный угол – это полный оборот, он составляет 360 градусов.
Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
Есть разные виды углов, выделим самые часто встречающиеся:
Если градусная мера угла меньше 90° — угол острый.
Если градусная мера угла равна 90° — угол прямой.
Если градусная мера угла больше 90°, но меньше 180° — угол тупой.
Если градусная мера угла равна 180° — угол развернутый.
Общая точка, из которой исходят лучи, называется вершиной угла, а лучи — сторонами угла.
Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.
Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.
А теперь посмотрим на взаимное расположение трех прямых.
Первый случай: все три прямые параллельны.
Второй случай: две прямые параллельны, а третья их пересекает.
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.
Треугольник
Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.
Треугольник можно использовать для измерения расстояний.
А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.
Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:
Свойства треугольников
Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.
Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.
Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.
Неравенство треугольника Сумма любых двух сторон треугольника больше его третьей стороны. |
Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.
Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.
Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.
Такой треугольник задается одним параметром — длиной стороны.
Она полностью определяет все другие значения и размеры в этом треугольнике.
От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃
Четырехугольники
Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.
Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:
площадь фигуры
периметр фигуры
площадь прямоугольника
периметр прямоугольника
площадь квадрата
периметр квадрата
параллелограмм
прямоугольный параллелепипед.
Окружность
Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Практическая сторона геометрии
Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.
Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.
А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.
Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.
Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.
Почему изучать геометрию сложно: некоторые правила придется учить наизусть.
Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
Разложение многочлена способом группировки
К следующей статье
Вынесение общего множителя за скобки
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Таблица формул геометрии
Освойте 7 столпов успеха в школе
Улучшите свои оценки и снизьте стресс
Связанные сайты Геометрические формулы 90 005
Геометрия Что нужно помнить Очень полезно высокий школьная шпаргалка по геометрии
Формулы геометрии Очень красивая страница с формулами геометрии для печати.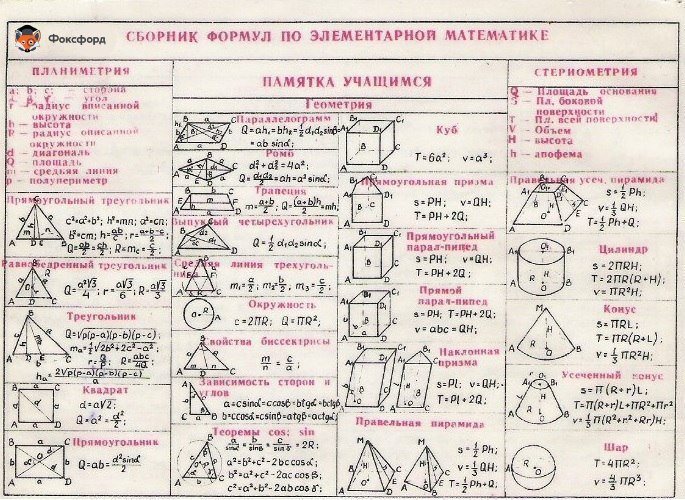
Включает в себя типичные формы плюс формулы, обычно не встречающиеся, такие как кольцо, эллипс, тор.
Страница 1 Страница 2
Скачать Полный список здесь. Таблица формул для геометрии
Страница 1 Страница 2
Площадь круга
| А = П х квадрат радиуса |
Площадь равностороннего Треугольник 92) √3)/4 | |
Площадь n Гон | А = ½ апофемы * Периметр |
Площадь Параллелограмм
| A= основание x высота |
Площадь прямоугольника | 92|
Площадь трапеции | А = ½ (основание 1 + основание 2) высота |
Площадь треугольника | А = ½ основания x Высота |
Базовая площадь Гептагона | Площадь основания = ½ апофемы * периметр |
Базовая площадь шестиугольника | Площадь основания = ½ апофемы * периметр |
Базовая зона восьмиугольника | Площадь основания = ½ апофемы * периметр |
Базовая площадь Параллелограмм | Площадь базы = база * высота |
Базовая зона Пентагона | Площадь основания = ½ апофемы * периметр |
Базовый прямоугольник | Площадь основания = длина * ширина |
Площадь базы | Площадь основания = площадь стороны |
Основание трапециевидной формы | Площадь основания = ½ (высота) (основание 1 + основание 2) |
Базовый треугольник | Площадь основания = 1/2 основания * высота |
Окружность Круг | C = 2 x Π x радиус |
Формула расстояния | D=√(х 2 -х 1 ) 2 + (у 2 –у 1 ) 2
|
Уравнение окружности | Общая форма (x-h) 2 +(y-k) 2 h и K — координаты окружности, r = радиус |
45 45 90 Треугольник Гипотенуза | Н= нога√2 |
45 45 90 Треугольник Ноги
| 1⁄2 гипотенуза√2 |
Формула Герона
| s=(a+b+c)/2, тогда A= √ (с (с-а) (с-б) (с-с)) |
Горизонтальная линия | Y = (любое число) |
Боковая часть конуса | πrsl r = радиус sl = высота наклона |
Боковой куб | 4s 2 s=сторона
|
Боковая зона цилиндра
| Окружность х Высота
|
Боковая призма | Периметр x высота
|
Боковая зона пирамиды | 1/2P * sl sl = высота наклона P=периметр
|
Прямоугольная боковая поверхность Твердый | Периметр *высота
|
Боковая область справа Конус | LA = ½ Psl P=2πr sl = высота наклона
|
Боковая область справа Цилиндр | ЛА = 2πr*ч
|
Боковая область справа Призма | LA = Ph P = сумма сторон основания h = высота |
Формула средней точки
|
(Х1 + Х2)/2, (У1 + Y2)/2 |
Периметр Параллелограмм | P= 2(основание + сторона) |
Периметр Прямоугольник | P= 2(база + высота) |
Периметр и угол | P = количество сторон * стороны |
Периметр Ромб | P= 4 стороны |
Периметр квадрата | P = 4 стороны |
Периметр Трапеция | Основание1 + Основание2 + Сторона1 + сторона 2 |
Периметр Треугольник | Сторона A + Сторона B + Сторона С |
Форма уклона точки
| г-г 1 = м(х-х 1 ) |
Склон
| Y2-Y1 Х 2 -Х 1 = Подъем над бегом |
Форма пересечения уклонов | y = mx + b M = наклон b = y перехват |
Площадь поверхности Конус | SA= π*радиус*наклонная высота+ πрадиус 2 |
Площадь поверхности Куб | СА = 6 сторона 2 |
Площадь поверхности Цилиндр | Боковая зона + 2πрадиус 2 |
Площадь поверхности Призма | Боковая зона + 2 основания |
Площадь поверхности Пирамида | Боковая зона + 1 основание |
Площадь поверхности прямоугольника Призма | 2(длина*ширина + длина*высота + высота*ширина) |
Площадь поверхности справа Конус
| SA=1/2*диаметр*π*наклон высота+база |
Площадь поверхности права Цилиндр
|
2πрадиус 2 +2πрадиус x высота |
Площадь поверхности права Призма | SA = периметр * высота + 2 База |
Площадь поверхности Сфера | 4πрадиус 2 |
30 60 90 треугольник короткий и длинный ножки
| Короткий катет = ½ гипотенузы Длинная нога = 1/2 гипотенузы√3 |
Таблица формул для геометрии.
Используйте эти формулы геометрии для расчета периметра, площади, площади основания, поперечной площади и площади поверхности для различных геометрических фигур, а также формулу расстояния и уравнение окружности. Включено более 70 формул. Таблица формул геометрии также доступна для скачивания. Надеюсь поможет
Нажмите на картинку, чтобы загрузить всю таблицу
Формула геометрии — Etsy Турция
Etsy больше не поддерживает старые версии вашего веб-браузера, чтобы обеспечить безопасность пользовательских данных. Пожалуйста, обновите до последней версии.
Воспользуйтесь всеми преимуществами нашего сайта, включив JavaScript.
Найдите что-нибудь памятное, присоединяйтесь к сообществу, делающему добро.
(
188 релевантных результатов,
с рекламой
Продавцы, желающие расширить свой бизнес и привлечь больше заинтересованных покупателей, могут использовать рекламную платформу Etsy для продвижения своих товаров.