Как заниматься математикой в пространственной геометрии
содержание
Как рассчитать пространственную геометрию?
V = π*r²*h, где r — радиус окружности основания, а h — высота.
Какие наиболее распространенные расчеты выполняются в пространственной геометрии?
Наиболее распространенные расчеты в пространственной геометрии заключаются в определении длин кривых, площадей поверхностей и объемов твердотельных областей. Другие пространственные геометрические фигуры: цилиндр, конус, сфера. «Платоновы тела» — это выпуклые многогранники, известные с античных времен.
Как работает пространственная геометрия?
Пространственная геометрия отвечает за изучение пространственных геометрических фигур, также называемых геометрическими телами, которые занимают пространство в пространстве благодаря своим трехмерным характеристикам (высоте, ширине и длине).
Como se Calcula a área?
Как правило, чтобы найти площадь фигуры, просто умножьте основание (b) на высоту (h).
Периметр – это сумма отрезков, образующих фигуру, называемых сторонами (l).
Как рассчитать призмы и пирамиды?
Даны призма и пирамида с одинаковым основанием, мы знаем, что объем призмы равен произведению площади основания на высоту, а объем пирамиды равен произведению площади основание и высота делятся на три, поэтому при одинаковой площади основания объем пирамиды будет равен 1/3 объема призмы.
Как рассчитывается объем?
Расчет объема всегда производится путем умножения высоты (h), на ширину (L), и на длину (L).
По какой формуле вычисляется объем куба?
Следовательно, объем куба зависит только от меры его ребра. Объем куба равен длине ребра, возведенного в 3, то есть V = a³.
Как рассчитать общую площадь и объем куба?
Формула площади квадрата равна мере возведения одного из его ребер в квадрат, то есть А=а².
Так как куб состоит из квадратов, то формула общей площади куба эквивалентна площади квадрата, умноженной на 6.
Что такое пространственные формы?
Фигуры, для построения которых необходимо трехмерное пространство, называются трехмерными или пространственными. Примеры пространственных фигур: пирамида, призма, куб, сфера, цилиндр и др.
Сколько в нем пространственных геометрических фигур?
Пространственные геометрические фигуры# Пространственная геометрия изучает различные геометрические тела, среди основных у нас есть: цилиндр, куб, конус, сфера, параллелепипед и пирамида.
Сколько граней у куба?
Куб представляет собой шестигранный многогранник, все грани которого квадратные. Куб, также известный как шестигранник, представляет собой геометрическое тело с шестью гранями, все они образованы квадратами.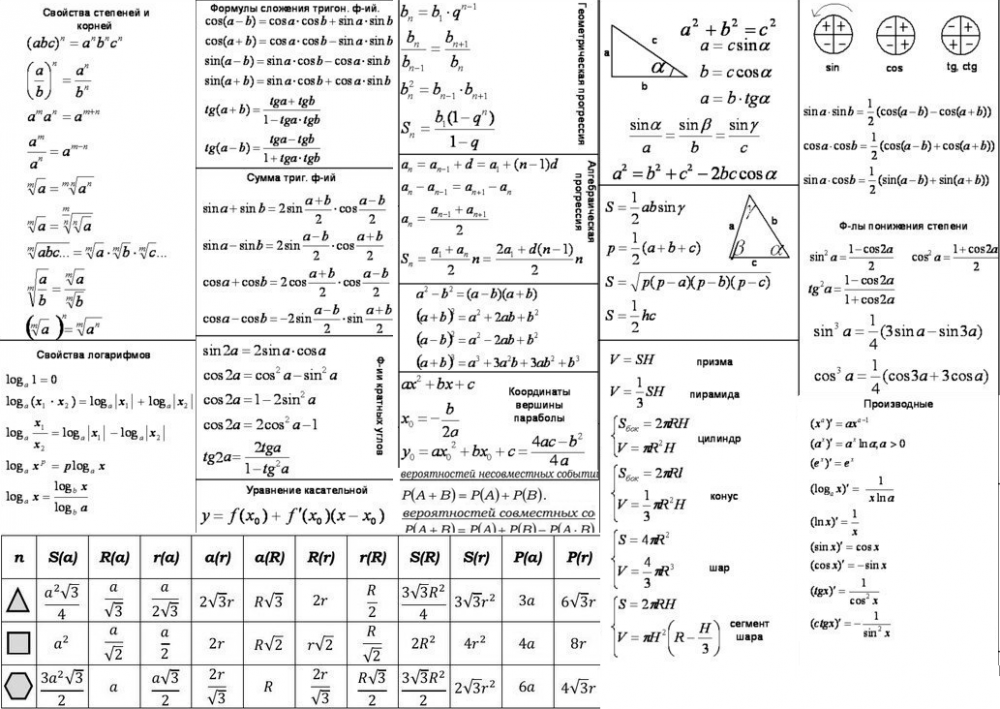
Помимо 6 граней, куб имеет 6 ребер и 12 вершин.
Как измерить периметр?
Периметр — это длина контура многоугольника (плоская и замкнутая фигура), поэтому для вычисления периметра просто добавьте меру всех сторон этого многоугольника.
Как рассчитать см2?
Значение площади квадрата всегда дается единицей измерения в квадрате. Это потому, что когда мы умножаем два значения одной и той же единицы, мы возводим квадрат (см . см = см² или м . м = м² или км.
Что такое периметр круга?
C = 2 * π * r, где: C = длина окружности или периметр.
Что такое формулы призмы?
Для проверки общей площади площади боковых граней и площади оснований необходимо сложить следующим образом: At = S1 + 2Sb, где S1 — сумма площадей боковых граней, а 2Sb — сумма площадей базы. Объем должен быть рассчитан следующим образом: V=Ab.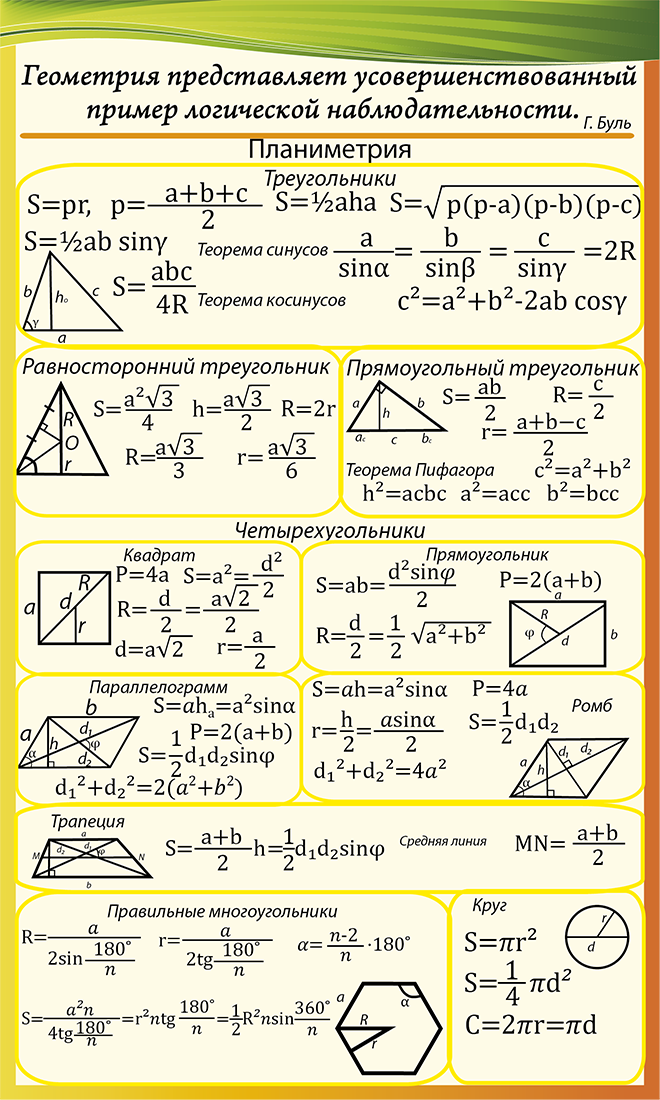
h, считая Ab площадью основания и «h» высотой.
Сколько оснований у цилиндра?
Цилиндр представляет собой геометрическое тело, состоящее из двух оснований в форме кругов и параллелей и соединяющей их боковой области.
Как рассчитать призму?
Площадь призмы можно вычислить, сложив площадь ее стороны и площади оснований. Процесс вычисления этих площадей в конечном итоге облегчается тем, что два основания призмы одинаковы, поэтому достаточно вычислить площадь основания и умножить результат на 2.
Каково число пи?
Это число является константой, и его значение приблизительно равно 3,141592653…, но наиболее часто используемое приближение для значения π равно 3,14.
Какова формула шара?
Формула объема сферы: V = 4/3 πr³. Посмотрите, как это используется в примере, где у нас есть диаметр сферы.
Как рассчитывается высота?
Как рассчитывается предполагаемая высота?
- Для девочек: к росту отца (в см) прибавляется рост матери (в см) минус 13 см. Наконец, это значение делится на два;
- Для мальчиков: рост отца (в см) прибавляется к росту матери (в см) плюс 13 см и, в конце концов, это значение делится на 2.
Какова формула цилиндра?
Площадь цилиндра, геометрического тела, образованного двумя параллельными круглыми основаниями и прямоугольной боковой площадью, равна сумме площадей двух оснований плюс сумма боковой площади цилиндра. Для вычисления общей площади цилиндра воспользуемся следующей формулой: 2πr(r + h).
Как вычислить площадь и объем?
Площадь фигуры получается умножением основания (b) на высоту (h). А объем определяется путем умножения высоты на ширину и длину.
Как вычислить площадь квадрата?
Площадь квадрата, частного случая четырехугольника, можно вычислить, возведя его сторону в квадрат. Площадь квадрата равна длине его стороны в квадрате.
Чему равна площадь сферы?
Для расчета площади поверхности шара используйте следующую формулу:SE = 4 . π . г²
Каков объем шара?
Формула объема сферы: V = 4/3 πr³.
По какой формуле вычислить площадь прямоугольника?
Прямоугольник является частным случаем четырехугольника, входящего в группу тех, у которых все углы прямые. Чтобы вычислить площадь прямоугольника, достаточно вычислить произведение между его основанием и высотой, то есть площадь дается формулой A=b⋅h. Помимо площади, еще одной важной величиной является периметр.
Где применяется пространственная геометрия?
Куб, цилиндр, конус, пирамиды и другие являются объектами изучения космической геометрии. С помощью пространственной геометрии можно обнаружить характеристики и свойства геометрических тел, а также разработать формулы для расчета объема и площади этих тел.
Кто создал геометрию?
Евклид, великий математик и писатель, жил, вероятно, в XNUMX веке до нашей эры и считается отцом геометрии. Он первым собрал всю геометрию в единое произведение под названием «Элементы». Этот математик основывал планиметрию на пяти постулатах.
Что изучает пространственная геометрия?
Пространственная геометрия — это анализ тел в пространстве, то есть геометрия для трехмерных объектов, в отличие от плоской геометрии, изучающей двумерные фигуры.
Каковы примеры космических фигур?
Поэтому любая фигура, для построения и определения которой необходимы три измерения, называется пространственной геометрической фигурой. Примеры пространственных фигур: куб, призма, параллелепипед, пирамида, конус, цилиндр, сфера и др.
Каковы элементы пространственной геометрии?
Пространственная геометрия возникает из примитивных элементов, которые называются так потому, что не имеют определения. Это: точка, линия, плоскость и пространство.
Сколько оснований у параллелепипеда?
Параллелепипед — это тип геометрического тела с тремя измерениями (высота, ширина и длина), относящийся к классу прим — многогранников, имеющих два конгруэнтных (равных) и параллельных основания в разных плоскостях.
Почему цилиндр не является многогранником?
Мы знаем как не-многогранники геометрические тела, которые не имеют граней, образованных многоугольниками. Они имеют округлые формы и поэтому называются круглыми телами или телами вращения. Это: цилиндр, сфера и конус.
По какой формуле вычисляется площадь треугольника?
Площадь треугольника – это произведение основания и высоты, деленное на 2. Площадь треугольника – это измерение его поверхности, которую можно вычислить, умножив основание на высоту и разделив на два, рассматривая любой треугольник.
Чему равна площадь квадрата со стороной 43 см?
В) 89 см2.
Добавьте метраж спереди и сзади и разделите на 2, а затем добавьте метраж сторон и разделите на 2.
Умножьте эти 2 значения, и вы получите площадь земли в квадратных футах.
Как производится расчет?
19 способов быстро считать в уме
- Используйте факторинг.
- Упрощение сложений и вычитаний.
- Оставляйте запятые в счетах последними при сложении и вычитании.
- Деление можно заменить на умножение.
- Обратите внимание на делимость чисел.
- Умножьте на два и на половину.
Какой самый сложный расчет в мире?
Гипотеза Римана
Многие математики считают эту задачу одной из самых сложных за все время. И действительно, Гипотеза Римана так и не была разрешена!
Как сделать вычисления быстрее?
Познакомьтесь с некоторыми из этих методов. Чтобы сложить число, оканчивающееся на 9, сначала округлите это число, а затем вычтите 1. Например: чтобы вычислить, сколько будет 525 + 29, выполните 525 + 30 – 1 = 554. Тот же механизм применяется для добавления числа 11: сначала вы добавляете десять, а затем добавляете 1.
Какова формула расчета объема?
Расчет объема всегда производится путем умножения высоты (h), на ширину (L), и на длину (L).
Как рассчитать общую площадь объекта?
Площадь является важной величиной в геометрии. Для заданной геометрической фигуры площадь равна площади поверхности этой фигуры. Для вычисления площади плоских фигур используем специфические формулы для каждой из них, при необходимости делим плоскую фигуру на известные плоские фигуры и складываем площади.
По какой формуле вычисляется площадь основания?
Площадь основания (АB) призмы зависит от образующего ее многоугольника. Поскольку в призме у нас есть две параллельные и конгруэнтные грани, площадь основания определяется суммой площадей параллельных многоугольников, то есть удвоенной площадью многоугольника.
Основные правила математики. Геометрия. Теоремы, определения. 7 класс
Основные правила математики. Геометрия. Теоремы, определения. 7 класс | Сайт учителя математики Косыхиной Н.
-
Репетитор по математике
Косыхина Наталья Владимировна - /whatsapp +7(908)682-97-49
Основные правила математики. Геометрия. Теоремы, определения. 7 класс
Геометрия — одна из самых древних наук, она возникла очень давно, еще до нашей эры .В переводе с греческого слово геометрия означает землемерие (гео- по-гречески земля, а метрео — мерить)
Школьный курс геометрии делится на планиметрию и стереометрию
В планиметрии рассматриваются свойства фигур на плоскости. Примерами таких фигур являются отрезки ,треугольники, прямоугольники.
В стереометрии изучаются свойства фигур в пространстве ,таких ,как параллелепипед ,шар, цилиндр.
Через любые две точки можно провести прямую и притом только одну
Взаимное расположение прямых:
- Если нет общих точек, то прямые параллельны
- Есть общая точка, то прямые пересекаются.
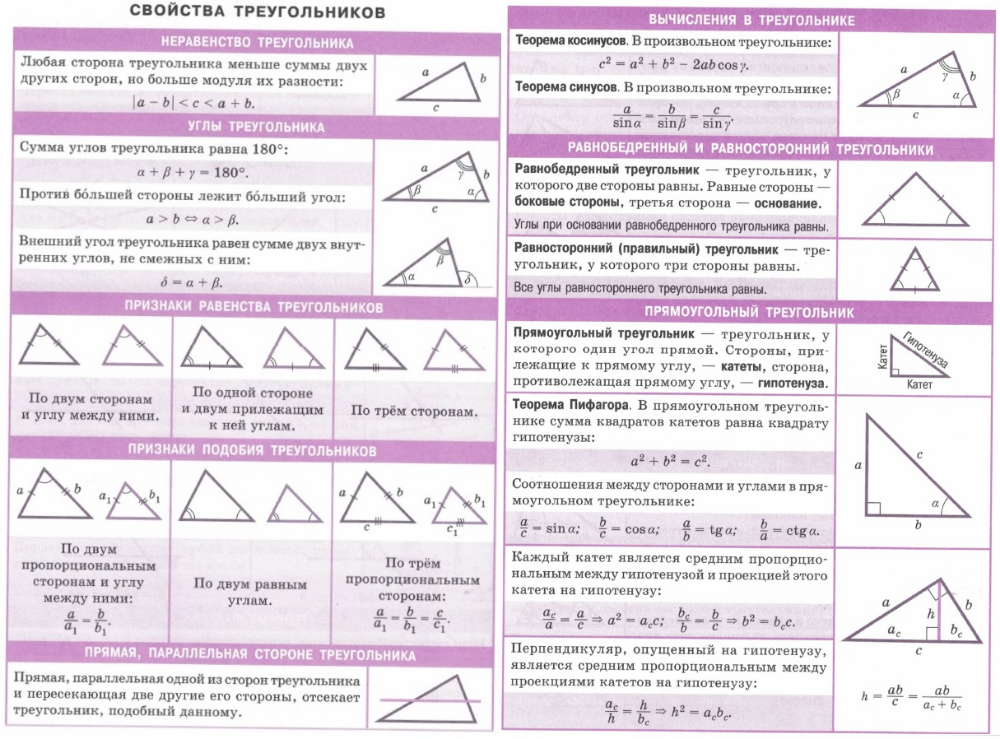
- Равные углы имеют равные градусные меры.
- Меньший угол имеет меньшую градусную меру.
- Развернутый угол равен 180 градусов.
- Неразвернутый угол — меньше 180 градусов
- Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов
- Угол называется прямым, если он равен 90 градусов.
- Острым углом называют, если он меньше 90 градусов.
- Тупым углом называют, если он больше 90 градусов.
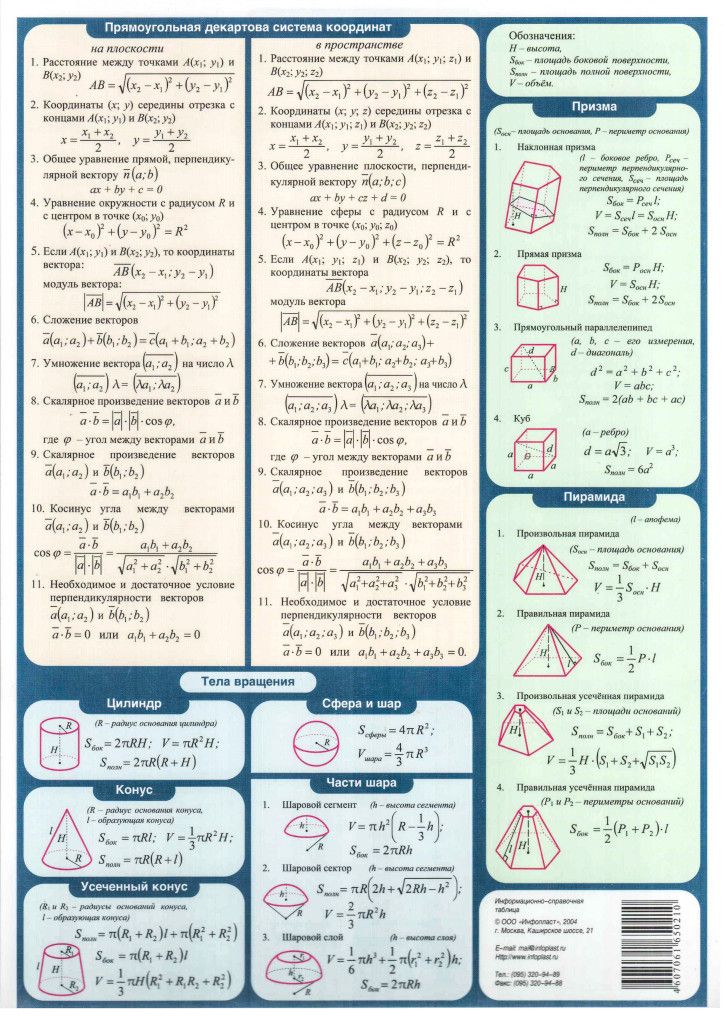
- Cмежными углами называются два угла, у которого одна сторона общая ,а две другие являются продолжениями сторон друг друга.
- Сумма смежных углов равна 180 градусов.
- Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого
- Фигура, состоящая из трех точек, не лежащих на одной прямой и трех отрезков попарно соединяющих их, называется треугольником.
- Сумма длин трех сторон треугольника называется периметром.
- Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
- Отрезок биссектрисы угла треугольника ,соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.
- Перпендикуляр ,проведенный из вершины треугольника к прямой ,содержащей противоположную сторону, называется
- Треугольник называется равнобедренным, если две его стороны равны.
- Треугольник, все стороны которого равны, называется равносторонним.
- В равнобедренном треугольнике углы при основании равны.
- В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
- В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
- В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
- Теорема 1. 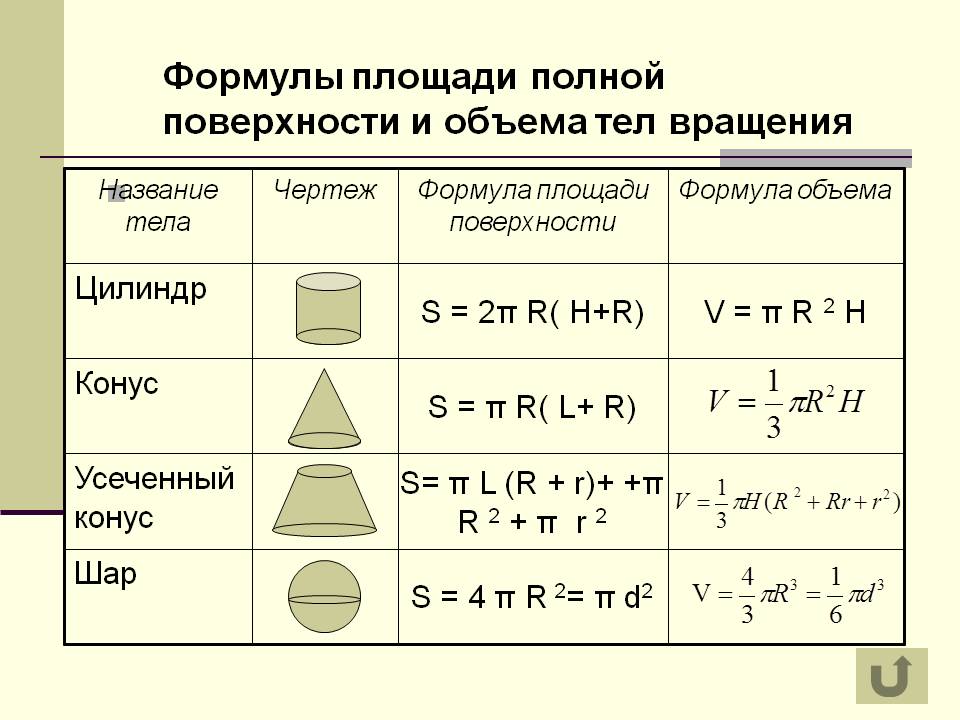Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольник, то такие треугольники равны
- Теорема 2. Если сторона и 2 прилежащих к ней угла одного треугольника равны стороне и 2 прилежащим к ней углам другого треугольник, то такие треугольники равны
- Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Отрезок, луч
Отрезком называют часть прямой, ограниченную двумя точками(концы отрезка)
Луч — это часть прямой ,имеющая начало, но не имеющая конца. Луч имеет направление.
Угол -это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла.
Угол называется развернутым, если обе его стороны лежат на одной прямой.
Любой угол разделяет плоскость на две части(полуплоскости).
Если угол неразвернутый, то одна из частей называется внутренней, а другая внешней областью
Если угол развернутый, то любую из двух частей ,на которые он разделяет плоскость ,можно считать внутренней областью угла.
Фигуру, состоящую из угла и его внутренней области также называют углом.
Если луч исходит из вершины неразвернутого угла и проходит внутри угла, то он делит этот угол на два угла.
Равные фигуры, середина отрезка, биссектриса
Равными называют две фигуры, имеющие одинаковую форму и одинаковые размеры.
Две геометрические фигуры оказываются равными, если их можно совместить наложением.
Серединой отрезка называется точка отрезка, равно удаленная от концов отрезка ,т.е. это точка разбивает исходный отрезок на два равных.
Биссектрисой угла называют луч, исходящий из вершины угла и делящий его на два равных угла.
Единицы измерения отрезков, углов
Измерение отрезков основано на сравнении их с некоторыми отрезками. Выбрав единицу измерения , можно измерить любой отрезок, т.е. выразить его длину некоторым положительным числом.
При измерении небольших расстояний, например расстояния между точками, изображенными на листе бумаги ,за единицу измерения принимают сантиметр и миллиметр.
Расстояния между отдельными объектами в реальном мире измеряются в метрах, километрах и т.д.Измерение углов аналогично измерению отрезков. Оно основано на сравнений их с углом, принятым за единицу измерения.
Обычно за единицу измерения углов применяют градус.
Градусной мерой угла называют положительное число, которое показывает, сколько раз градус и его части укладываются в данном угла.
Часть градуса называется минутой, часть минуты называется секундой.
Смежные и вертикальные углы
Перпендикулярные прямые
Две пресекающиеся прямые называются перпендикулярными, если они пересекаются под прямым углом.
Треугольник
Теоремой называют утверждение, справедливость которого устанавливается путем рассуждения.
Медиана, биссектриса, высота треугольника
Равнобедренный, равносторонний треугольники
Три признака равенства треугольников
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольник, то такие треугольники равныОкружность
Для изображении окружности на чертеже пользуются циркулем.
- Окружностью называют геометрическая фигура ,состоящая из всех точек плоскости, расположенных на заданном расстоянии от заданной точки.
- Отрезок ,соединяющий две точки окружности ,называется хордой
- Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности.
- Формула длины окружности
- Формула площади круга
2018-2023
Базовые геометрические уравнения и примеры
Некоторые люди могут сказать, что геометрия никоим образом не является «сексуальным» предметом; на самом деле, как правило, вычисление углов, объемов и площадей редко считается заманчивым или забавным.
Возможно ли обратное?
За последние 10 лет мы видели, как математика проникла в фильмов и телешоу ; Теория большого взрыва — яркий тому пример. Конечно, уравнения не занимают центральное место в сюжете, и, честно говоря, только первые несколько шоу были насыщены математикой. После этого алгебраическая работа всплывала лишь изредка.
Тем не менее, приятно видеть, как сложные расчеты разыгрываются на популярной арене, и еще лучше, что и мужские, и женские персонажи участвуют в настройке уравнений ; всего 20 лет назад кинематографическими математиками могли быть только мужчины!
Теперь ваша очередь освоить уравнения базовой геометрии , и вам нужен самый эффективный способ сделать это. Или, может быть, вы поклонник Декарта и хотите поднять декартовскую геометрию на новый уровень, но для начала вам нужен прочный фундамент.
Ваш Superprof поможет вам разобраться в основных геометрических формулах; хватайте свои угольники и циркуль… мы пошли!
Найдите рядом со мной репетитора по математике на Superprof.
Лучшие репетиторы по математике
Поехали
Основные фигуры
Ищите здесь репетитора по математике из Юты.
Сколько геометрических фигур вы можете найти в этом узоре? Изображение от monicore с PixabayУ вас может возникнуть соблазн подумать «круг», «треугольник» или «квадрат», и вы будете абсолютно правы.
Каждая из этих геометрических фигур относится к одной из следующих четырех основных категорий:
- Треугольники имеют три стороны; стороны могут быть одинаковой длины (равносторонний треугольник) или все разной длины (разносторонний треугольник).
- Четырехугольник — это любой четырехугольник. Это будут прямоугольники, квадраты, ромбы, ромбы…
- параллелограмм , фигура, имеющая 2 пары равных сторон, тоже четырехугольник
- Полигоны: буквально «много сторон». Эти формы могут быть треугольниками, шестиугольниками, пятиугольниками… все эти «угольники» являются многоугольниками. По сути, все, что имеет прямые стороны, называется многоугольником.
- Круги являются классом сами по себе, потому что они не имеют прямых линий
По сути, все, что имеет прямые стороны, называется многоугольником.Их уникальные характеристики включают:
- Квадраты имеют четыре равные стороны и четыре прямых угла
- Прямоугольники имеют две пары равных сторон
- Трапеция имеет только одну пару параллельных сторон
- Трапеция не имеет сторон одинаковой длины
- Ромбы: противоположные стороны и противоположные углы равны
- Равнобедренный треугольник имеет две равные стороны
- Прямоугольные треугольники имеют одну 90 угол, противоположный гипотенузе
Каждая из этих фигур имеет собственную формулу для вычисления периметра, площади и углов. С некоторыми вы, возможно, знакомы, например, с теоремой Пифагора 9.0004, в то время как другие, возможно, немного менее запоминающиеся.
Давайте посмотрим на них сейчас.
Вам нужна помощь в изучении геометрии? Возможно, вы могли бы найти репетитора по геометрии…
Вычисление треугольников
Начиная с форм наименьшего количества сторон (но иногда с самыми сложными формулами), мы беремся за геометрические формулы!
Простейшая формула для периметра любого треугольника: a+b+c, , где каждая буква обозначает сторону. Он прекрасен в своей простоте и с ним легко работать, если вы знаете длину каждой стороны.
Допустим, ваш треугольник имеет следующие размеры: a = 3 дюйма, b = 4 дюйма и c = 5 дюймов
Тогда его периметр будет 3+4+5=12 дюймов.
Ясно, что этот треугольник не является ни равносторонним, ни равнобедренным; и не прямоугольный треугольник. Как бы мы вычислили периметр, если даны только два значения, нижняя и одна сторона?
В таком случае мы должны опираться на теорему Пифагора : a 2 +b 2 =c 2 .
Ты помнишь тот, да?
Сначала проведите линию от вершины треугольника прямо к его основанию. Эта линия, h, должна быть перпендикулярной основанию, таким образом образуя два угла 90 градусов – по одному с каждой стороны линии.
Теперь у вас есть два прямоугольных треугольника, один из которых имеет измерения как для a, так и для b. Отсюда очень просто подставить известные значения в теорему (не забудьте возвести их в квадрат!) и найти недостающее значение.
Попробуем с воображаемым треугольником:
a = неизвестно b = 5 c = 7
a 2 * 5 2 = 7 2
a 2 * 25 = 49 неизвестное значение в уравнении должно стоять отдельно
a 2 = 49 – 25 переместите 25 в другую сторону от знака равенства, вычтя его из заданного значения c
a 2 = 24
Теперь вам нужно вычислить квадратный корень из 24, чтобы найти значение ‘a’ , которое равно 4,89.
8. После того, как вы вычислили периметр одного прямоугольного треугольника, вы должны вычислить второй, чтобы получить размеры исходного треугольника.
Поздравляем! Теперь вы знаете, как вычислить периметр любого треугольника!
Выполните поиск здесь, чтобы найти некоторые из лучших эффективных онлайн-курсов по математике на суперпрофессионале.
Этот и подобные знаки в виде треугольников используются для призыва к осторожности на дорогах. , вычисление площади треугольника немного сложнее.Если значения даны для всех трех сторон, вы можете применить Формулу Герона :
площадь = квадратный корень из [s(s-a)(s-b)(s-c)], где s — полупериметр , то есть (a+b+c)/2
Это только кажется сложным; помните, что при работе с формулой вам нужно только подставить известные значения, чтобы найти неизвестное. Если подумать таким образом, Hero’s Formula , как ее еще называют, довольно проста!
Теперь об уравнениях площади треугольников, где одно или несколько значений неизвестны.
Если вы знаете только значение основания треугольника и его высоты , вы можете применить: площадь = (½) * b * h
Если известны только длина двух сторон и степень угла, соединяющего их , вы должны использовать тригонометрию , чтобы найти пропущенные значения. Основная формула:
Площадь = (½) * a * b * sin C
Имейте в виду, что строчные буквы обозначают линейные размеры, а прописные буквы обозначают углы.
Если бы вы знали только значения сторон a и c, вы бы подставили их и вычислить грех B . Точно так же, если вы знаете b и c, вы использовали бы sin A , чтобы получить площадь вашего треугольника.
Почему бы не попрактиковаться с ними некоторое время, прежде чем двигаться дальше…
Лучшие репетиторы по математике
Поехали
Вычисление четырехугольников
Вы можете вычислить периметр квадрата или прямоугольника в своем спать.
Эти формулы таковы: P=4a (a представляет стороны квадрата) и P=2l + 2w соответственно.
Эти расчеты площадей также должны прийти к вам довольно легко. Для квадратов это A=a 2 , а для прямоугольников A=l * w . Просто, верно?
Все становится сложнее, когда мы переходим к параллелограммам и трапециям; чтобы решить оба этих уравнения, вам нужно знать высоту фигуры (h) и длину основания (b) — линия внизу.
Как только вы узнаете эти значения, выберите соответствующую формулу для формы:
b * h = площадь параллелограмма (½)(a+b) * h = площадь трапеции, где «a» представляет сторону, противоположную «b».
Четырехугольники могут быть самыми простыми фигурами для работы. Если вам нужна дополнительная практика, в Интернете есть множество ресурсов, где вы можете найти рабочих листа по геометрии и уравнения для решения.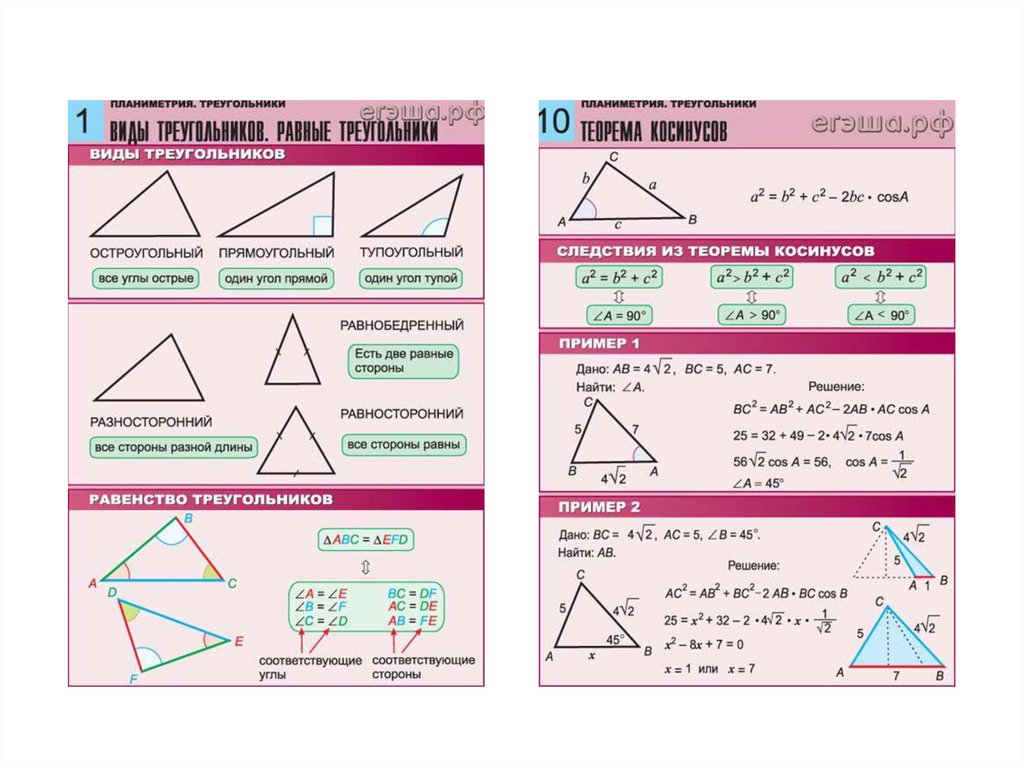
Вычисление многоугольников
Столкнулись ли вы с апейрогеном (многоугольник с бесконечным числом сторон) или с более знакомым шестиугольником, вам нужно знать, как вычислить его периметр и площадь.
К счастью, апейрогоны существуют только гипотетически; представьте, что у вас есть такая фигура, для которой можно вычислить площадь!
Если все стороны вашего многоугольника имеют одинаковую длину, вы можете применить P=n * v , где « n » — количество сторон, а « v » — значение каждой стороны.
Если стороны указанного многоугольника не имеют одинаковой длины, вам придется сложить эти значения , чтобы получить его периметр.
Знак «Стоп», пожалуй, самый известный правильный многоугольник. Изображение Уолтера Кнерра с PixabayВычисление площадей многоугольников
Существует несколько способов определения значения площади любого многоугольника, некоторые из которых включают вычисления для треугольников.
Сначала мы займемся уравнениями правильного многоугольника; такой, у которого все стороны одинаковой длины. Прежде чем мы сможем начать какое-либо шифрование, мы должны определить радиус многоугольника .
Это включает в себя рисование круга внутри многоугольника таким образом, чтобы периметр круга касался периметра многоугольника. это называется вписанный круг . Как только мы узнаем значение этого радиуса, мы можем применить эту формулу:
A = ½ * p * r
Формулы становятся более сложными, чем больше сторон у многоугольника.
Допустим, количество сторон представлено как ‘n’ , а количество сторон — как ‘ s ’. Радиус, также называемый апофемой , обозначается как « a ». Конечно, «A» представляет собой «площадь», что дает формулу, которая выглядит так:
A = ns/4 √ 4-s 2
Отсюда формулы становятся еще более сложными.
Они заставляют вас бороться с основами геометрии? Вы можете обратиться к нашему полному руководству!
Вычисление окружностей
Окружности не содержат ни углов, ни прямых, а их периметры называются «окружностями». Однако для их вычислений требуется по крайней мере отрезок прямой, который необходим для любой формулы для окружностей.
Как ни странно, формула вычисления площадей кругов известна больше, чем, возможно, любая другая геометрическая фигура: πr 2 , или pi * r2
Наверняка вы знаете/помните, что число пи (π) равно 3,1415…
Менее известная формула для вычисления окружностей равно: 2 * π * r
Имейте в виду, что это формулы для вычисления площади и периметра двумерных фигур ; как только они приобретают дополнительное измерение — они становятся трехмерными формами и заслуживают расчета объема, а также площади и периметра.
Давайте не будем отклоняться от темы; мы будем очень рады предоставить формулы для этих основных геометрических построений …
Но вам не нужно останавливаться на этом; зацепитесь за наше руководство для начинающих по геометрии!
Формулы геометрии, которые вы должны знать
Обновлено: 26 марта 2016 г. формулы, теоремы, свойства и т. д., которые вы используете для решения различных задач. Если вы зашли в тупик, работая над проблемой, и не можете придумать формулу, вам сюда.
Формулы треугольника
Сумма внутренних углов треугольника: 180°
Район:
Формула площади героя:
Площадь равностороннего треугольника:
Теорема Пифагора:
Общие пифагоровы тройки (длины сторон в прямоугольных треугольниках):
3-4-5
5-12-13
7-24-25
8-15-17
Отношения сторон в специальных прямоугольных треугольниках:
Теорема о высоте на гипотенузе:
Если высота проведена к гипотенузе прямоугольного треугольника, как показано на рисунке выше, то
Формулы полигонов
Формулы площади:
Параллелограмм:
Прямоугольник:
Воздушный змей или ромб:
Квадрат:
Трапеция:
Правильный многоугольник:
Сумма внутренних углов в n -стороннем многоугольнике:
Измерение каждого внутреннего угла правильного (или другого равноугольного) n -стороннего многоугольника:
Сумма внешних углов (по одному в каждой вершине) любого многоугольника:
Мера каждого внешнего угла правильного (или другого равноугольного) n -стороннего многоугольника:
Количество диагоналей, которые можно провести в n -стороннем многоугольнике:
Круговые формулы
Окружность:
Район:
Длина дуги:
Площадь сектора:
Мера угла .
