Формулы в геометрии основные: Формулы по геометрии, скачать основные геометрические формулы для студентов и школьников — Интернет магазин мебели "МебПилот.ру"

Разное

Содержание

Формулы по геометрии — Справочник

Формулы для геометрии

Основные формулы для решения задач с равносторонним треугольником: формулы площади и периметра равностороннего треугольника и др.

Равнобедренный треугольник формулы

Основные формулы для решения задач с равнобедренным треугольником: формулы площади и периметра равнобедренного треугольника и др.

Прямоугольный треугольник формулы

Основные формулы для решения задач с прямоугольным треугольником: формулы площади и периметра прямоугольного треугольника и др.

Треугольник формулы

Основные формулы для решения задач с треугольником: формулы площади и периметра треугольника и др.

Четырехугольник формулы

Основные формулы для решения задач с четырехугольником: формулы площади и периметра четырехугольника и др.

Трапеция формулы

Основные формулы для решения задач с трапецией: формулы площади и периметра трапеции, средней линии трапеции и др.

Параллелограмм формулы

Основные формулы для решения задач с параллелограммом: формулы площади и периметра параллелограмма и др.

Ромб формулы

Основные формулы для решения задач с ромбом: формулы площади и периметра ромба и др.

Квадрат формулы

Основные формулы для решения задач с квадратом: формулы периметра, площади и диагонали квадрата и др.

Прямоугольник формулы

Основные формулы для решения задач с прямоугольником: формулы площади, периметра и диагонали прямоугольника и др.

Куб формулы

Основные формулы для решения задач с кубом: формулы диагонали, объема и площади куба и др.

Параллелепипед формулы

Основные формулы для решения задач с параллелепипедом: формулы объема и площади параллелепипеда и др.

Шар формулы

Основные формулы для решения задач с шаром: формулы объема и площади шара и др.

Конус формулы

Основные формулы для решения задач с конусом: формулы объема и площади конуса, площади боковой поверхности и основания и др.

Цилиндр формулы

Основные формулы для решения задач с цилиндром: формулы объема и площади цилиндра, площади боковой поверхности и основания и др.

Треугольник формулы.

Worksbase. ru

15.11.2017 22:55:23

2017-11-15 22:55:23

Источники:

Http://worksbase. ru/matematika/formuly/geometriya

Формулы по геометрии, скачать основные геометрические формулы для студентов и школьников » /> » /> .keyword { color: red; }

Формулы для геометрии

В данном разделе собраны Основные формулы по геометрии, которые необходимы школьникам и студентам для подготовки к занятиям, решения задач и выполнения контрольных работ по геометрии. Геометрические формулы — это краткий теоретический материал, выучив которые вы легко сможет выполнить задания по геометрии.

Все геометрические формулы и таблицы составлены нашими специалистами и снабжены дополнительными комментариями, это идеальный материал для школьников 7, 8 и 9 классов!

Если после изучения данного теоретического материала у Вас возникнут проблемы в решении задач или появятся вопросы образовательного характера, то вы всегда можете задать их на нашем форуме.

Все геометрические формулы и таблицы составлены нашими специалистами и снабжены дополнительными комментариями, это идеальный материал для школьников 7, 8 и 9 классов.

Www. webmath. ru

15.09.2020 17:58:18

2020-09-15 17:58:18

Источники:

Https://www. webmath. ru/poleznoe/formules_main2.php

Формулы геометрии. Площади фигур — материалы для подготовки к ЕГЭ и ОГЭ по Математике » /> » /> .keyword { color: red; }

Формулы для геометрии

Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.

Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!

Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника.

О них мы обязательно расскажем.

Ты нашел то, что искал? Поделись с друзьями!

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.

1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным. Высоты этих треугольников равны и. Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга. Найдите площадь сектора круга радиуса, длина дуги которого равна.

На этом рисунке мы видим часть круга. Площадь всего круга равна, так как. Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна, следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Читайте также о задачах на тему «Координаты и векторы». Для их решения вспомните, что такое абсцисса точки (это ее координата по ) и что такое ордината (координата по ). Пригодятся также такие понятия, как координаты вектора и длина вектора (она находится по теореме Пифагора), синус и косинус угла, угловой коэффициент прямой, уравнение прямой, а также сумма, разность и скалярное произведение векторов, угол между векторами.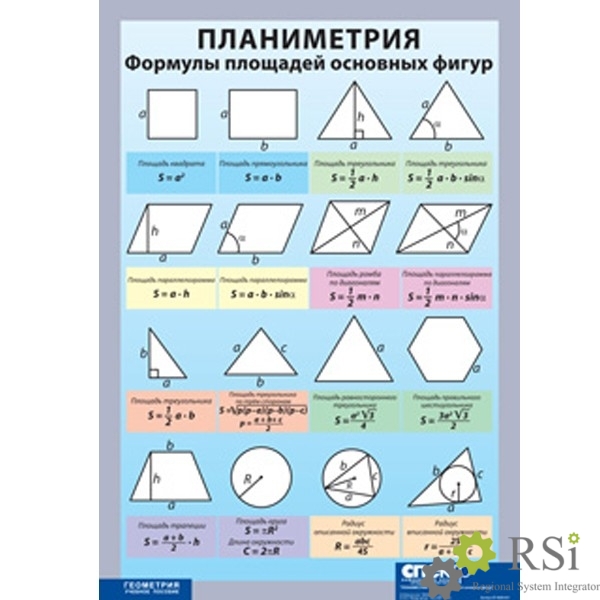

Читайте также о задачах на тему Координаты и векторы.

Ege-study. ru

13.07.2017 4:55:31

2017-07-13 04:55:31

Источники:

Https://ege-study. ru/ru/ege/materialy/matematika/formuly-geometrii/

Презентация по геометрии Основные теоремы и формулы планиметрии доклад, проект

Главная
Разное
Образование
Спорт
Естествознание
Природоведение
Религиоведение
Французский язык
Черчение
Английский язык
Астрономия
Алгебра
Биология
География
Геометрия
Детские презентации
Информатика
История
Литература
Математика
Музыка
МХК
Немецкий язык
ОБЖ
Обществознание
Окружающий мир
Педагогика
Русский язык
Технология
Физика
Философия
Химия
Шаблоны, фоны, картинки для презентаций
Экология
Экономика

Презентация на тему Презентация по геометрии Основные теоремы и формулы планиметрии, предмет презентации: Геометрия. Этот материал в формате pptx (PowerPoint) содержит 18 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.

Слайд 1Текст слайда:

Основные теоремы и формулы планиметрии

Якимчук Любовь Григорьевна,
преподаватель Технического колледжа

Слайд 2Текст слайда:

Прямоугольный треугольник

АВ – гипотенуза
АС и СВ – катеты (АС ⊥ СВ)

Теорема Пифагора
АВ2=АС2+СВ2

c2=а2+b2

Слайд 3Текст слайда:

Прямоугольный треугольник

Синус острого угла = отношению противолежащего катета к гипотенузе.

Слайд 4Текст слайда:

Прямоугольный треугольник

Косинус острого угла = отношению прилежащего катета к гипотенузе.

Слайд 5Текст слайда:

Прямоугольный треугольник

Тангенс острого угла = отношению противолежащего катета к прилежащему.

Слайд 6Текст слайда:

Прямоугольный треугольник

Свойство прямоугольного треугольника:
Катет, лежащий против угла в 30о , равен половине гипотенузы.

30о

Слайд 7Текст слайда:

Прямоугольный треугольник

Площадь прямоугольного треугольника равна половине произведения катетов.

SΔ

где а и в — катеты

Слайд 8Текст слайда:

Теорема косинусов

Слайд 9Текст слайда:

Теорема синусов

Слайд 10Текст слайда:

Площадь произвольного треугольника

h =BD –высота треугольника

Слайд 11Текст слайда:

Площадь произвольного треугольника

Слайд 12Текст слайда:

Площадь произвольного треугольника

Формула Герона:

где

полупериметр

Слайд 13Текст слайда:

Произвольный треугольник

R – радиус описанной окружности,
r – радиус вписанной окружности

Слайд 14

Текст слайда:

Равносторонний треугольник

АВ=ВС=АС=a

Площадь равностороннего треугольника:

где R – радиус описанной окружности,
r – радиус вписанной окружности

Слайд 15Текст слайда:

Прямоугольник

Слайд 16Текст слайда:

Параллелограмм

Слайд 17Текст слайда:

Ромб

где h –высота ромба

где d1 и d2 – диагонали ромба

Слайд 18Текст слайда:

Трапеция

Скачать презентацию

Что такое shareslide.

ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Топ основных именных теорем из геометрии

30 октября, 2021

2 мин

Мтмт 📈

Эта удобная шпаргалка поможет с лёгкостью запомнить все основные теоремы из геометрии для ЕГЭ по математике. В ней вы найдёте все нужные формулы и теоремы, а именно:

Теорема Фалеса;
Теорема Птолемея;
Теорема Чевы через треугольник;
Теорема Менелая через треугольник;
Теорема Чевы для линий треугольника;
Теорема Менелая для линий через треугольник;
Теорема Вариньона;
Задачи на доказательства.

Также в конце шпаргалки — видео от Эйджея с объяснениями этих теорем.

Математика — обязательный для сдачи на ЕГЭ предмет, без которого не получишь аттестат. Это также один из самых сложных экзаменов для выпускников. Рассказываем, как сдать ЕГЭ по математике на 80+ баллов и делимся лучшими ресурсами для подготовки.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!

Редакция Без Сменки

Честно. Понятно. С душой.

38 подписчиков

+ Подписаться

Редакция Без Сменки

30 декабря, 2021

1 мин

Хим 🧪

Галогены

У галогенов очень богатая химия — невозможно запомнить все реакции сразу. Но ты всегда можешь…

Редакция Без Сменки

10 июня, 2022

1 мин

Био 🦠

Кулинария в эволюции

Разберёмся в их сути на . .. кексах 🍰 Жил-был кекс. Нет, целая популяция кексов. Из-за…

Редакция Без Сменки

13 июня, 2022

1 мин

Био 🦠

Слюна и ее роль

У человека есть 3 пары крупных слюнных желез: околоушные, подчелюстные и подъязычные. И…

Редакция Без Сменки

15 июня, 2022

1 мин

Инф 💻

ВЫИГРЫШНАЯ И ПРОИГРЫШНАЯ СТРАТЕГИЯ

👉 Рассмотрим задачу: Два игрока (Петя и Ваня) играют в игру. Перед игроками лежит 1 камень. У…

Редакция Без Сменки

01 июля, 2022

1 мин

Лит 📚

Тема художественного произведения

🚂 Из пункта А в пункт Б выехал паровоз с красноречивым названием «Капитанская дочка». Прибыв на…

Редакция Без Сменки

06 июня, 2022

1 мин

Англ 🇬🇧

Разница между man/person/human

🐰 Human — это как раз один представитель человеческого рода, homo sapiens и все такое. Крутецкий…

Подпишитесь на еженедельную рассылку полезных материалов про ЕГЭ, высшее образование и вузы и получите скидку на курсы Вебиума

Плоские геометрические фигуры: свойства и основные формулы

В статье описываются геометрические фигуры: определение, основные свойства и формулы.

Плоские геометрические фигуры:

Четырехугольник (общее для всех четырехугольников)
Квадрат
Прямоугольник
Параллелограмм
Ромб
Трапеция
Треугольник
Окружность

Геометрические фигуры — это любое сочетание точек, линий и поверхностей.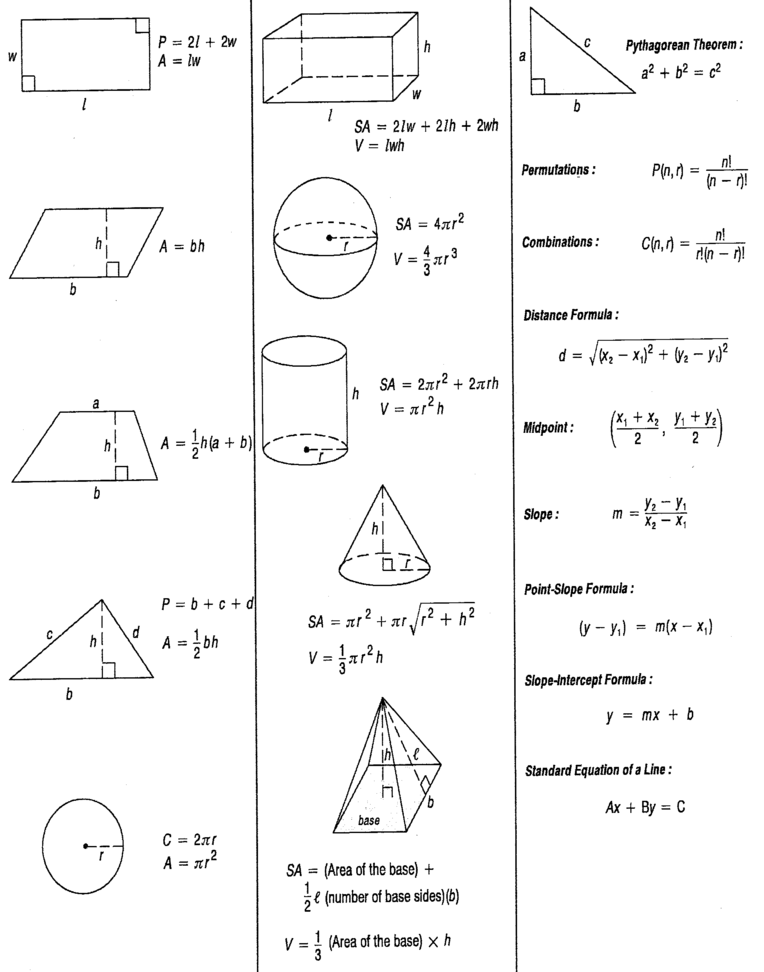 Геометрические фигуры разделяются на плоские и объемные.

Плоские геометрические фигуры — это фигуры, все точки которых лежат на одной плоскости. Объемные геометрические фигуры — это фигуры, не все точки которых лежат на одной плоскости.

Четырёхугольник

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

Сумма углов четырёхугольника равна 360°
Не существует четырёхугольников, у которых все углы острые или все углы тупые.
Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Квадрат

Квадрат — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Основные формулы:

Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a²или S=d²/2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2

где a-сторона, d-диагональ, P-периметр, S-площадь
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.

Свойства:

Все стороны равны, все углы равны и составляют 90°;
Диагонали квадрата равны и перпендикулярны;
У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
Квадрат является одновременно частным случаем ромба и прямоугольника

Калькулятор для квадрата поможет вычислить все характеристики квадрата по одной из известных величин. .

Прямоугольник

Прямоугольник — четырехугольник, у которого все углы прямые.

Основные формулы:

Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a²+b²)/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a²+b²)/2 (теорема Пифагора)

где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a²+b²) – корень квадратный из (a²+b²).

Свойства:

Диагонали прямоугольника равны и делятся точкой пересечения пополам.
Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.

Параллелограмм

Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Определения:

Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.

Основные формулы:

Стороны и диагональ связаны соотношением: (d₁)²+(d₂)²=(a²+b²)*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте: S = a*h
S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α
S (Площадь) по двум диагоналям и углу между ними: S=(d₁*d₂)/2*sin γ

где a, b — длины сторон, d₁, d₂ –диагонали, P-периметр, S-площадь,
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).

Свойства:

У параллелограмма противоположные стороны равны и противоположные углы равны.
Сумма любых двух соседних углов параллелограмма равна 180°.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Каждая диагональ делит параллелограмм на два равных треугольника.
Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Ромб

Ромб — это параллелограмм, у которого все стороны равны.

Основные формулы:

Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d₁*d₂)/2
Радиус окружности, вписанной в ромб: r=h/2 или r =(d₁*d₂)/4a
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a² · sin α

где a — длина стороны, d₁, d₂ –диагонали, P-периметр, S-площадь,
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба

Свойства:

Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d₁*d₂/4a.

Трапеция

Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.

Определения:

Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
Средняя линия (первая средняя линия) трапеции — отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
Средняя линия (вторая средняя линия) — отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.

Основные формулы:

Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2

где a,b — основания, c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d₁, d₂ –диагонали,
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне

Свойства:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

Треугольник

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Определения:

Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
Медиана треугольника — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Основные формулы:

Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь: по сторонам и углу между ними: S=(a*b)/2* sin γ
по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c²=a²+b² (Теорема Пифагора)

где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
d₁, d₂ –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ — угол между сторонами a и b
r — радиус вписанной окружности, R — радиус описанной окружности

Свойства:

В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
Сумма углов треугольника равна 180°:
Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| <c<a+b
Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
Медиана делит треугольник на два равновеликих (с равными площадями) треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников
Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник
В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
Все углы равностороннего треугольника равны 60°. Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c²=a²+b² (Теорема Пифагора). В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.

Окружность

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Определения:

Радиус — отрезок, который соединяет центр окружности с любой её точкой.
Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
Диаметр — хорда, проходящая через центр окружности(d). Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует.
Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
Секущая — прямая, которая пересекает окружность в двух различных точках.

Основные формулы:

Длина окружности: L = 2πR
Площадь круга: S = π*r² или S = π*d²/4

где π = 3,14 (3,1415926535) – величина постоянная,
где r-радиус, d –диаметр, L – длина окружности, S-площадь.

Калькулятор для окружности и круга поможет вычислить все характеристики круга по одной из известных величин.

В заключении

Весь курс начальной школы (за 1-4 классы) в краткой форме на сайте newlesson.ru. С помощью курса можно быстро повторить основные моменты и правила по предметам: русский язык, математика, окружающий мир.

Справочник по геометрии 7-9 класс

Главная
Справочники
Справочник по геометрии 7-9 класс

Точки, прямые, отрезки

Провешивание прямой на местности

Луч

Угол

Равенство геометрических фигур

Сравнение отрезков

Сравнение углов

Длина отрезка

Единицы измерения длины, расстояний

Градусная мера угла

Измерение углов на местности

Смежные углы

Вертикальные углы

Перпендикулярные прямые

Построение прямых углов на местности

Треугольник

Равенство треугольников

Первый признак равенства треугольников

Перпендикуляр к прямой

Медианы треугольника

Биссектрисы треугольника

Высоты треугольника

Равнобедренный треугольник

Свойства равнобедренного треугольника

Второй признак равенства треугольников

Третий признак равенства треугольников

Окружность

Построения циркулем и линейкой

Построение угла, равного данному

Построение биссектрисы угла

Построение перпендикулярных прямых

Построение середины отрезка

Среднее пропорциональное

Параллельные прямые

Признаки параллельности двух прямых

Практические способы построения параллельных прямых

Аксиомы геометрии

Аксиома параллельных прямых

Теорема о накрест лежащих углах

Теорема о соответственных углах

Теорема об односторонних углах

Теорема об углах с соответственно параллельными сторонами

Теорема об углах с соответственно перпендикулярными сторонами

Теорема о сумме углов треугольника

Остроугольный, прямоугольный и тупоугольный треугольники

Теорема о соотношениях между сторонами и углами треугольника

Неравенство треугольника

Некоторые свойства прямоугольных треугольников

Признаки равенства прямоугольных треугольников

Уголковый отражатель

Расстояние от точки до прямой

Расстояние между параллельными прямыми

Построение треугольника по двум сторонам и углу между ними

Построение треугольника по стороне и двум прилежащим к ней углам

Построение треугольника по трем его сторонам

Многоугольник

Выпуклый многоугольник

Четырехугольник

Параллелограмм

Признаки параллелограмма

Трапеция

Прямоугольник

Ромб и квадрат

Осевая и центральная симметрии

Понятие площади многоугольника

Площадь квадрата

Площадь прямоугольника

Площадь параллелограмма

Площадь треугольника

Площадь трапеции

Теорема Пифагора

Теорема, обратная теореме Пифагора

Формула Герона

Пропорциональные отрезки

Определение подобных треугольников

Отношение площадей подобных треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Средняя линия треугольника

Пропорциональные отрезки в прямоугольном треугольнике

Практические приложения подобия треугольников

Задачи на построение

Измерительные работы на местности

О подобии произвольных фигур

Синус, косинус и тангенс острого угла прямоугольного треугольника

Значение синуса, косинуса и тангенса для углов 30, 45 и 60

Взаимное расположение прямой и окружности

Касательная к окружности

Градусная мера дуги окружности

Теорема о вписанном угле

Свойство биссектрисы угла

Свойства серединного перпендикуляра к отрезку

Теорема о пересечении высот треугольника

Вписанная окружность

Описанная окружность

Понятие вектора

Равенство векторов

Откладывание вектора от данной точки

Сумма двух векторов

Законы сложения векторов.

Правило параллелограмма

Сумма нескольких векторов

Вычитание векторов

Произведение вектора на число

Применение векторов к решению задач

Средняя линия трапеции

Разложение вектора по двум неколлинеарным векторам

Координаты вектора

Связь между координатами вектора его начала и конца

Простейшие задачи в координатах

Уравнение линии на плоскости

Уравнение окружности

Уравнение прямой

Взаимное расположение двух окружностей

Синус, косинус, тангенс, котангенс

Основное тригонометрическое тождество.

Формулы приведения.

Формулы для вычисления координат точки

Теорема о площади треугольника

Теорема синусов

Теорема косинусов

Решение треугольников

Измерительные работы

Угол между векторами

Скалярное произведение векторов

Скалярное произведение в координатах

Свойства скалярного произведения векторов

Правильный многоугольник

Окружность, описанная около правильного многоугольника

Окружность, вписанная в правильный многоугольник

Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности

Построение правильных многоугольников

Длина окружности

Площадь круга

Площадь кругового сектора

Отображение плоскости на себя

Понятие движения

Наложения и движения

Параллельный перенос

Поворот

Предмет стереометрии

Параллельность и перпендикулярность прямых и плоскостей в пространстве

Многогранник

Призма

Параллелепипед

Объём тела

Свойства прямоугольного параллелепипеда

Пирамида

Цилиндр

Конус

Сфера и шар

Поделись с друзьями в социальных сетях:

Основные определения и теоремы по геометрии.

7 класс — Студопедия

Поделись

Геометрия – наука, занимающаяся изучением геометрических фигур (в переводе с греческого слово «геометрия» означает «землемерие»).
В планиметрии изучаются свойства фигур на плоскости. В стереометрии изучаются свойства фигур в пространстве.
Отрезок — это часть прямой, ограниченная двумя точками. Эти точки называются концами отрезка.
Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а точка — вершиной угла.
Угол называется развёрнутым, если обе его стороны лежат на одной прямой. ( Развёрнутый угол равен 180°).
Две геометрические фигуры называются равными, если их можно совместить наложением.
Середина отрезка — это точка отрезка, делящая его пополам, т. е. на два равных отрезка.
Биссектриса угла — это луч, исходящий из вершины угла и делящий его на два равных угла.
Угол называется прямым, если он равен 90°.
Угол называется острым, если он меньше 90° (т.е. меньше прямого угла).
Угол называется тупым, если он больше 90°, но меньше 180°. (т.е. больше прямого, но меньше развёрнутого).
Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. Сумма смежных углов равна 180°.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны.
Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой и трех отрезков, соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами треугольника.
Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
Теорема – утверждение, справедливость которого устанавливается путём рассуждений. Сами рассуждения называются доказательством теоремы.
(Т. Первый признак равенства треугольников) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
(Т. о перпендикуляре к прямой) Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
(Свойства медианы, биссектрисы и высоты треугольника) В любом треугольнике медианы пересекаются в одной точке; биссектрисы пересекаются в одной точке; высоты или их продолжения также пересекаются в одной точке.
Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.
Треугольник называется равносторонним, если все его стороны равны.
(Т. о свойстве равнобедренного треугольника) В равнобедренном треугольнике углы при основании равны.
(Т. о свойстве равнобедренного треугольника) В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
(Т. Второй признак равенства треугольников) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
(Т. Третий признак равенства треугольников) Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности.
Радиус окружности – отрезок, соединяющий центр окружности с какой-либо её точкой.
Отрезок, соединяющий две точки окружности, называется ее хордой.
Хорда, проходящая через центр окружности, называется диаметром.
Круг — это часть плоскости, ограниченная окружностью.
Две прямые на плоскости называются параллельными, если они не пересекаются.
При пересечении двух прямых секущей образуется восемь углов: накрест лежащие, односторонние и соответственные.
(Т. Признак параллельности двух прямых по накрест лежащим углам) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
(Т. Признак параллельности двух прямых по соответственным углам) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
(Т. Признак параллельности двух прямых по односторонним углам) Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Аксиомы – это утверждения о свойствах геометрических фигур, которые принимаются в качестве исходных положений, на основе которых доказываются теоремы и строится вся геометрия.
(Аксиома) Через любые две точки проходит прямая, и притом только одна.
(Аксиома параллельных прямых) Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Если две прямые параллельны третьей прямой, то они параллельны.
Во всякой теореме две части: условие (то, что дано) и заключение (то, что требуется доказать).
Теоремой, обратной данной,называется такая теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы.
(Т. Свойство параллельных прямых) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
(Т. Свойство параллельных прямых) Если две параллельные прямые пересечены секущей, то соответственные углы равны.
(Т. Свойство параллельных прямых) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
(Т. о сумме углов треугольника) Сумма углов треугольника равна 180°.
Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Если все три угла треугольника острые, то треугольник называется остроугольным.
Если один из углов треугольника тупой, то треугольник называется тупоугольным.
Если один из углов треугольника прямой, то треугольник называется прямоугольным.
Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две стороны, образующие прямой угол — катетами.
(Т. о соотношениях между сторонами и углами треугольника) В треугольнике против большей стороны лежит больший угол, и обратно, против большего угла лежит большая сторона.
В прямоугольном треугольнике гипотенуза больше катета.
(Признак равнобедр. треугольника) Если два угла треугольника равны, то треугольник равнобедренный.
(Т. Неравенство треугольника) Каждая сторона треугольника меньше суммы двух других сторон.
(Свойство прямоугольного треугольника) Сумма двух острых углов прямоугольного треугольника равна 90°.
(Свойство прямоугольного треугольника) Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
(Свойство прямоугольного треугольника) Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
(Признак равенства прямоугольных треугольников по двум катетам) Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
(Признак равенства прямоугольных треугольников по катету и острому углу) Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого, то такие треугольники равны.
(Т. Признак равенства прямоугольных треугольников по гипотенузе и острому углу) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
(Т. Признак равенства прямоугольных треугольников по гипотенузе и катету) Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из этой точки к прямой.
(Т. Свойство параллельных прямых) Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
Расстоянием между параллельными прямыми называется расстояние от произвольной точки одной из параллельных прямых до другой прямой.

Основные формулы геометрии — GeeksforGeeks

В математике геометрия выступает как дисциплина изучения и предмет для анализа форм и структур вместе с их свойствами. Приведенная ниже статья иллюстрирует стандартные фиксированные или производные формулы геометрии для расчета различных параметров конкретной формы. Эти формулы используются для определения неизвестных сторон, углов или других его величин.

Формула базовой геометрии

Формула представляет собой математическое правило, которое формируется путем вывода взаимосвязи между двумя или более физическими величинами или математическими отношениями. формулы обычно представляются в символической форме с помощью математических символов. Эти символические представления формул состоят из переменных, констант, операционных знаков и терминов.

Геометрические формулы являются стандартными производными формулами для расчета параметров фигур. Этими параметрами являются площадь, объем, периметр, окружность, общая площадь поверхности, площадь боковой поверхности и т. Д. Каждая форма, изучаемая в геометрии, имеет для них свою собственную формулу. Эти формулы перечислены ниже.

Квадрат

Периметр Квадрата = 4a

Площадь Квадрата = a ²

Где «a» — длина стороны квадрата

Прямоугольник

Периметр прямоугольника = 2(l + b)

Площадь прямоугольника = l2 909 × b 90 ‘l’ — это длина, а ‘b’ — это ширина

Треугольник

Площадь треугольника = A = 1/2 × b × h

Где ‘b – основание треугольника 903.
и «h» высота треугольника

Трапеция

Площадь трапеции = A =1/2 × (b1 + b2) × h

Где b1 и b2 — высота основания трапеции 9, h0030 90 of the Trapezoid

Circle

Area of Circle = A = π × r2

Circumference of Circle = A = 2πr

Where ‘r’ is the radius of a Circle

Куб

Площадь поверхности куба = 6A ²

, где ‘A’ — длина сторон куба

Цилиндер

.
Общая площадь поверхности цилиндра = 2πr(r + h)

Объем цилиндра = V = πr2h

Цилиндр

Конус

Площадь криволинейной поверхности конуса = πrl

Общая площадь поверхности конуса = πr(r + l) = πr[r + √(h 90 2 ^{2 900) )]}

Объем конуса = V =1/2× πr ² h

Здесь ‘r’ — радиус основания конуса

, а h — высота конуса

Сфера

Площадь поверхности сферы = 4πr ²

Объем сферы = 4/3 × πr ³

Где r – радиус сферы

Примеры задач

Задача 1.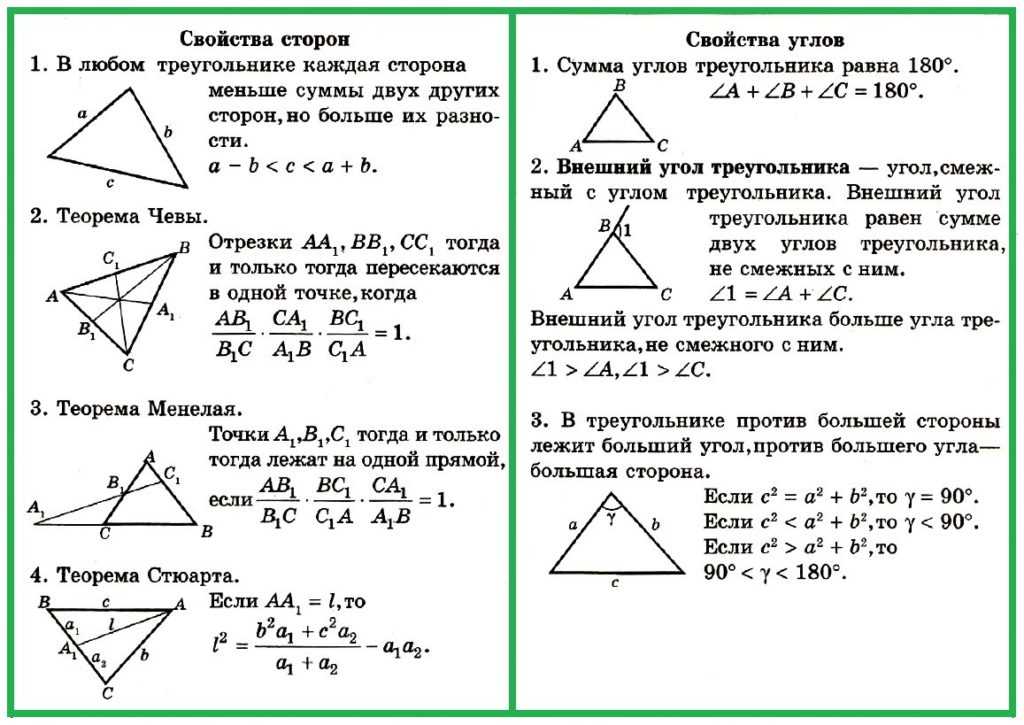 Если радиус окружности равен 14 см. Найдите площадь данного круга.

Решение:

Дано

Радиус окружности равен 14см.

Имеем,

Площадь круга (A)=πr ²

=>22/7 x 14 x 14

=>616см ²

Задача 2. Найдите площадь треугольника с основанием 12см и высотой 8см.

Решение:

Дано

Основание треугольника равно 12см.

Высота треугольника 8см.

Имеем,

Площадь треугольника(А)=1/2 x b x h

=>1/2 x 12 x 8

=>48 см ²

Задача 3. Найти периметр заданного треугольника. прямоугольник длиной 10 см и шириной 4 см.

Решение:

Дано

Длина прямоугольника 10см.

Ширина прямоугольника 4см.

Имеем,

Периметр прямоугольника(P)= 2(l+b)

=>2(10+4)

=>2 x 14

=>28см

Задача 4. Найти периметр квадрата, длина которого 5 см.

Решение:

Дано

Длина квадрата 5см.

Имеем,

Периметр квадрата(P)= 4l

=> 4 x 5

=>20см

Задача 5. Найдите объем сферы, имеющей радиус 9см.

Решение:

Дано

Радиус сферы равен 9см.

У нас есть

Объем сферы (V)=4/3 πr ³

=>4/3 x 22/7 x (9) ³

=>3054,805см
2 3

Задача 6. Вычислите площадь трапеции с основаниями 8см и 10см и высотой 12см.

Решение:

Дано

Пусть основания трапеции равны b1 и b2 со значениями 8см и 10см соответственно.

Высота трапеции 12см.

У нас есть,

Площадь трапеции = A =1/2 × (b1 + b2) × h

=>1/2 x (8 +10) x 12

=>1/2 x 18 x 12

=> 216/2

=>108см ²

Задача 7.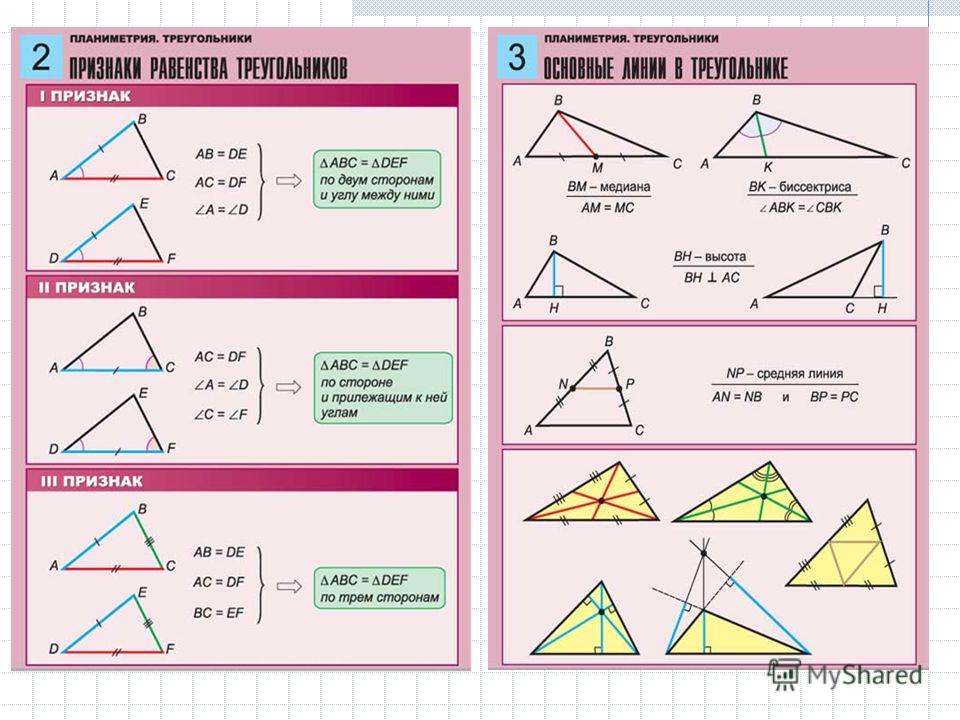 Найти объем данного конуса радиусом 6см и высотой 12см.

Решение:

Дано

Радиус конуса равен 6см.

Высота данного конуса 12см

Имеем,

Объем конуса = V =1/2× πr ² h

=>1/2 x 22/7 x (6) ² x 12

=>9504/14

=>678,85 см ³

Задача 8. Вычислить площадь криволинейной поверхности цилиндра радиусом 4см и высотой 8см.

Решение:

Дано

Радиус цилиндра равен 4см.

Высота цилиндра 8см.

Имеем,

Площадь криволинейной поверхности = 2πrh

=>2 x 22/7 x 4 x 8

=>201,14 см ²

Задача 9. Вычислите площадь куба. сторона 3 см.

Решение:

Дано

Длина стороны 3см.

У нас есть

Площадь куба (a) = 6a ²

=> 6 x 3 x3

=> 54 см ²

Основная геометрия формала 6-й.
добавить в папки.

Войти

Вы создали 2 папки. Пожалуйста, обновитесь до Cram Premium, чтобы создавать сотни папок!

Обновление

Перемешать
Включить

Выключить

В алфавитном порядке
Включить

Выключить

Передний Первый
Включить

Выключить

Обе стороны
Включить

Выключить

Читать
Включить

Выключить

Чтение. ..

Фронт

через

Кнопка воспроизведения

Кнопка воспроизведения

Прогресс

1/10

Нажмите, чтобы перевернуть

Используйте клавиши со стрелками ВЛЕВО и ВПРАВО для перемещения между карточками;

Используйте клавиши со стрелками ВВЕРХ и ВНИЗ, чтобы перевернуть карту;

H показать подсказку;

A читает текст в речь;

Делиться

Распечатать

Экспорт

Клон

10 карточек в этом наборе

Передняя часть

Спина

Длина окружности

2πr
или πd

Площадь круга

π(r*r)
или
Пи в квадрате

периметр четырехугольника

периметр квадрата

периметр любой формы

сложить все стороны вместе

площадь квадрата

с*с
или
с в квадрате

площадь прямоугольника

площадь параллелограмма

площадь треугольника

(ч)/2

объем любой формы

(площадь основания)ч

Базовые математические формулы — геометрия, вероятности, арифметика и часто задаваемые вопросы

Основная математическая формула обычно используется в базовой математике и используется не только в академических книгах, но и в нашей повседневной жизни. В начальных классах мы все узнали об общем правиле BODMAS. По мере того, как человек продолжает приближаться к более высоким классам от шести до десяти, он столкнется с различными формулами математики, основанными на различных концепциях, таких как алгебра.

Практикуя вопросы и ответы, основанные на различных формулах, можно выучить наизусть каждую формулу, прежде чем явиться на экзамены.

Некоторые из других понятий, которые имеют формулы, приведены ниже:

Основная математическая формула

Основы математики показывают, как можно решить математическую задачу с помощью некоторых уравнений, таких как уравнение сил, ускорений или работы Выполнено. Что еще более важно, они используются для предоставления математических решений реальных проблем в нашей повседневной жизни.

Существует много типов уравнений, и они встречаются во многих областях математики. Но методы, используемые для их изучения, различаются в зависимости от их типа. Это может быть простая формула сложения или сложная, например интегрирование дифференцирования.

Формулы базовой геометрии

Где «a» — длина сторон квадрата

Где «l» — длина, а «b» — ширина

Где «a» — длина сторон квадрата

здесь «l» — длина, а «b» — ширина

Где b — основание треугольника, а h — высота треугольника

Где b1 и b2 — основания трапеции; h = высота трапеции

Где r — радиус окружности

Где а — длина сторон куба

Площадь криволинейной поверхности цилиндра = 2πrh

общая площадь поверхности цилиндра = 2πr(r + h)

Объем цилиндра = V = πr ² h

Где «r» — радиус основания цилиндра, а «h» — высота цилиндра.

Площадь криволинейной поверхности конуса = πrl (r + l) = πr[r + √(h ² + r ² )]

Объем конуса = V = ⅓ × πr2h

основание конуса и h = высота конуса

Где r = радиус сферы

Базовая формула вероятности

P(A) = n(A)/n(S)

Где

P(A) — вероятность события.

n(A) — количество благоприятных исходов.

n(S) — общее количество событий в пространстве выборки.

Основные арифметические формулы

Математическая формула в простейшем виде может быть выражена как выражение, которое было получено после того, как исследователи годами изучали конкретную задачу. Эти разработанные математические формулы служат для получения правильных ответов в течение нескольких минут или даже секунд. Это позволяет быстрее решать математические задачи и повышает вашу скорость и навыки решения этих задач. Следовательно, Vedantu предоставляет полный список основных математических формул, которые помогут вам хорошо понять проблемы.

Эти формулы также пригодятся при подготовке к конкурсным экзаменам, поскольку позволяют решать вопросы всего за несколько секунд. Хотя легко просто складывать или вычитать уравнения, когда дело доходит до решения больших задач по геометрии или алгебре, это становится слишком сложным, если вы не используете эти математические формулы.

Советы по запоминанию основных математических формул — геометрия, вероятность, арифметика:

Существует более сотни формул, которые используются в жизни ученика даже во время учебы в школе, поэтому запомнить их все может быть немного сложно. но вот несколько советов по эффективному запоминанию основных математических формул:

Во-первых, вам нужно понять формулы и то, как они получены

Затем вам нужно попрактиковаться в формулах, применяя их к различным вопросам, как указано в образцах документов Веданту.

Затем сделайте контрольные листы, которые помогут вам взглянуть перед экзаменами.

Геометрия

Геометрия — это все о формах и их свойствах.

Если вы любите играть с предметами или рисовать, то геометрия для вас!

Геометрию можно разделить на:

Плоская геометрия — это плоские фигуры, такие как линии, круги и треугольники… формы, которые можно нарисовать на листе бумаги

Solid Geometry — это трехмерные объекты, такие как кубы, призмы, цилиндры и сферы.

Подсказка: попробуйте нарисовать некоторые формы и углы, когда будете учиться… это поможет.

Точка, линия, плоскость и тело

Точка не имеет размеров, только положение
Линия одномерная
Плоскость двумерная (2D)
Твердое тело трехмерное (3D)

Почему?

Почему мы занимаемся геометрией? Чтобы открывать закономерности, находить площади, объемы, длины и углы и лучше понимать окружающий мир.

Плоская геометрия

Плоская геометрия — это формы на плоской поверхности (как на бесконечном листе бумаги).

2D-фигуры

Упражнение: Сортировка фигур

Треугольники

Прямоугольные треугольники

Интерактивные треугольники

Четырехугольники (ромб, параллелограмм, и т.д.)

Прямоугольник, ромб, квадрат, параллелограмм, трапеция и воздушный змей

Интерактивные четырехугольники

Параллелограмм в любом четырехугольнике

Размеры бумаги

Фигуры Свободная игра

Периметр

Зона

Площадь плоских фигур

Инструмент расчета площади

Площадь многоугольника по чертежу

Деятельность: Сад

Общий инструмент для рисования

Калькулятор площади и калькулятор прямоугольника

Полигоны

Многоугольник — это двухмерная фигура, состоящая из прямых линий. Треугольники и прямоугольники являются многоугольниками.

Вот еще:

Пентагон

Пентаграмма

Шестигранник

Свойства правильных многоугольников
Диагонали многоугольников

Интерактивные полигоны

Круг

Круг

Пи

Площадь круга по линиям

Круговой сектор и сегмент

Площадь круга по секторам

Упражнение: Бросание монеты на сетку

Арка

Кольцо

Теоремы о кругах (дополнительная тема)

Символы

В геометрии используется много специальных символов.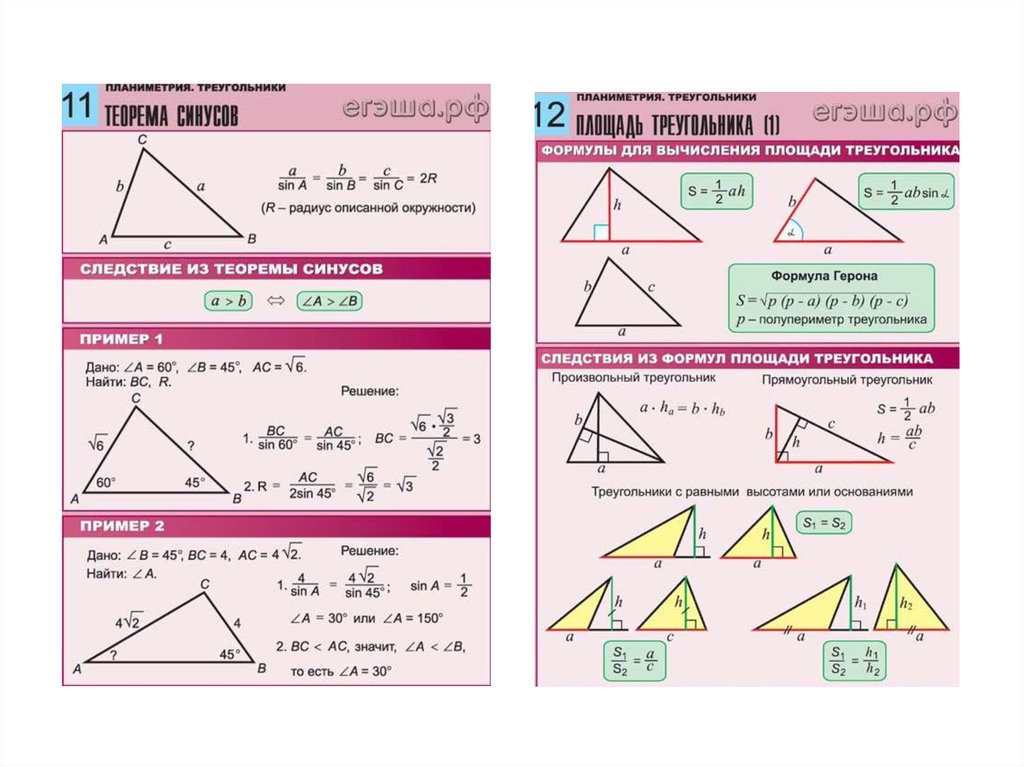 Вот краткая ссылка для вас:

Геометрические символы

Конгруэнтные и подобные

Конгруэнтные формы

Похожие формы

Уголки

Типы уголков

Острые углы Прямые углы Тупые углы Прямоугольный Рефлекторные углы Полный оборот

Градусы (угол)

радиан

Равные углы

Параллельные прямые и пары углов

Поперечный

Смежные углы

Треугольник имеет 180°

Дополнительные уголки

Дополнительные углы

Углы вокруг точки

Углы на прямой

Внутренние уголки

Наружные уголки

Внутренние углы многоугольников

Внешние углы многоугольников

Использование чертежных инструментов

Геометрические конструкции

Использование транспортира

Использование чертежного треугольника и линейки

Использование линейки и компаса

Преобразования и симметрия

Преобразования:

Вращение

Отражение

Перевод

Изменение размера

Симметрия:

Симметрия отражения

Вращательная симметрия

Точечная симметрия

Линии симметрии плоских фигур

Художник по симметрии

Упражнение: Симметрия фигур

Упражнение: Создание мандалы

Упражнение: Раскрашивание (Четыре цвета Теорема)

Мозаика

Мастер тесселяции

Координаты

Декартовы координаты

Интерактивные декартовы координаты

Игра «Найди координаты»

Дополнительные темы плоской геометрии

Пифагор

Теорема Пифагора

Пифагорейские тройки

Конические секции

Набор всех точек

Конические секции

Эксцентриситет

Эллипс

Анимация параболы и снаряда

Гипербола

Теоремы о кругах

Теоремы о кругах

Касательные и секущие линии

Пересекающиеся секущие Теорема

Теорема о пересекающихся хордах

Угол пересекающихся секущих Теорема

Треугольные центры

Тригонометрия

Тригонометрия — отдельная тема, поэтому вы можете посетить:

Введение в тригонометрию

Индекс тригонометрии

Твердотельная геометрия

Solid Geometry — это геометрия трехмерного пространства — пространства, в котором мы живем…

. .. начнем с самых простых фигур:

Общие 3D-формы

Многогранники и не-многогранники

Существует два основных типа твердых тел: «многогранники» и «не-многогранники»:

Многогранники (они должны иметь плоские грани) :

кубов и
кубоидов (объем
кубоида)

Платоновые тела

Призмы

Пирамиды

Не многогранники (когда любая поверхность не плоский) :

Сфера Тор

Цилиндр Конус

Модели многогранников

Калькулятор объема и площади сферы

Сфероид

Поперечные сечения

Вершины, грани и ребра

Конус против сферы против цилиндра

Пирамида против Конуса

Призма против цилиндра

Пирамида против куба

Объем горизонтального цилиндра

Теорема Эйлера

Пифагор в 3D

Гиперкубы

Математика строителя

Моменты площади

Геометрия Формула Диаграмма

Магистр 7 столбов школы успеха

Улучшить свои оценки и снизить стресс

Связанные сайты Геометрии. школьная шпаргалка по геометрии

Геометрические формулы Очень красивая страница с геометрическими формулами для печати. Включает в себя типичные формы плюс формулы, обычно не встречающиеся, такие как кольцо, эллипс, тор.

Страница 1 Страница 2

Скачать Полный список здесь. Таблица формул для геометрии

Страница 1 Страница 2

92

Площадь круга

92) √3)/4

Площадь n Гон

А = ½ апофемы * Периметр

Площадь Параллелограмм

A= основание x высота

Площадь прямоугольника

Площадь трапеции

А = ½ (основание 1 + основание 2) высота

Площадь треугольника

А = ½ основания x Высота

Базовая зона Гептагона

Площадь основания = ½ апофемы * периметр

Базовая площадь шестиугольника

Площадь основания = ½ апофемы * периметр

Базовая зона восьмиугольника

Площадь основания = ½ апофемы * периметр

Базовая площадь Параллелограмм

Площадь базы = база * высота

Базовая зона Пентагона

Площадь основания = ½ апофемы * периметр

Базовый прямоугольник

Площадь основания = длина * ширина

Площадь базы

Площадь основания = площадь стороны

Основание трапециевидной формы

Площадь основания = ½ (высота) (основание 1 + основание 2)

Базовый треугольник

Площадь основания = 1/2 основания * высота

Окружность Круг

C = 2 x Π x радиус

Формула расстояния

Д=√(х ₂ -х ₁ ) ² + (у ₂ –у ₁ ) ²

Уравнение окружности

Общая форма (x-h) ² +(y-k) ² h и K — координаты окружности, r = радиус

45 45 90 Треугольник Гипотенуза

Н= нога√2

45 45 90 Треугольник Ноги

1⁄2 гипотенуза√2

Формула Герона

s=(a+b+c)/2, тогда A= √ (с (с-а) (с-б) (с-с))

Горизонтальная линия

Y = (любое число)

Боковая часть конуса

πrsl r = радиус sl = высота наклона

Боковой куб

4s ² s=сторона

Боковая зона цилиндра

Окружность х Высота

Боковая призма

Периметр x высота

Пирамида боковой зоны

1/2P * sl sl = высота наклона P=периметр

Прямоугольная боковая поверхность Твердый

Периметр *высота

Боковая область справа Конус

LA = ½ Psl P=2πr sl = высота наклона

Боковая область справа Цилиндр

ЛА = 2πr*ч

Боковая область справа Призма

LA = Ph P = сумма сторон основания h = высота

Формула средней точки

(Х1 + Х2)/2, (У1 + Y2)/2

Периметр Параллелограмм

P= 2(основание + сторона)

Периметр Прямоугольник

P= 2(база + высота)

Периметр №

P = количество сторон * стороны

Периметр Ромб

P= 4 стороны

Периметр квадрата

P = 4 x сторона

Периметр Трапеция

Основание1 + Основание2 + Сторона1 + сторона 2

Периметр Треугольник

Сторона A + Сторона B + Сторона С

Форма уклона точки

г-г ₁ = м(х-х ₁ )

Склон

Y2-Y1

Х ₂ -Х _{1 =} _{Подъем над бегом}

Форма пересечения уклонов

y = mx + b M = наклон b = y перехват

Площадь поверхности Конус

SA= π*радиус*наклонная высота+ πрадиус ²

Площадь поверхности Куб

СА = 6 сторона ²

Площадь поверхности Цилиндр

Боковая зона + 2πрадиус ²

Площадь поверхности Призма

Боковая зона + 2 основания

Площадь поверхности Пирамида

Боковая зона + 1 основание

Площадь поверхности прямоугольника Призма

2(длина*ширина + длина*высота + высота*ширина)

Площадь поверхности справа Конус

SA=1/2*диаметр*π*наклон высота+база

Площадь поверхности права Цилиндр

2πрадиус ² +2πрадиус x высота

Площадь поверхности права Призма

SA = периметр * высота + 2 База

Площадь поверхности Сфера

4πрадиус ²

30 60 90 треугольник короткий и длинный ноги

Короткий катет = ½ гипотенузы

Длинная нога = 1/2 гипотенузы√3

Таблица формул для геометрии. Используйте эти формулы геометрии для расчета периметра, площади, площади основания, поперечной площади и площади поверхности для различных геометрических фигур вместе с формулой расстояния и уравнением окружности. Включено более 70 формул. Таблица формул геометрии также доступна для скачивания. Надеюсь поможет

Нажмите на картинку, чтобы загрузить всю таблицу

Таблицы формул для геометрии Скачать бесплатно PDF

21 апреля 2022 г. by quranmualim

Таблицы формул для геометрии Скачать PDF бесплатно . Формулы геометрии используются для нахождения размеров, периметра, площади, площади поверхности, объема и т. д. геометрических фигур. Геометрия — это часть математики, которая имеет дело с отношениями точек, линий, углов, поверхностей, измерением тел и свойствами.

Существует два типа геометрии: 2D или плоскостная геометрия и 3D или объемная геометрия. 2D-фигуры — это плоские фигуры, имеющие только два измерения: длину и ширину, такие как квадраты, круги, треугольники и т. д. 3D-объекты — это твердые объекты, которые имеют три измерения: длину, ширину и высоту или глубину, например куб. , прямоугольный параллелепипед, сфера, цилиндр, конус. Давайте изучим формулы геометрии вместе с несколькими решенными примерами в следующих разделах.

Что такое геометрические формулы?

Таблицы формул для геометрии . Формулы, используемые для нахождения размеров, периметра, площади, площади поверхности, объема и т. д. двумерных и трехмерных геометрических фигур, известны как формулы геометрии. 2D-формы состоят из плоских фигур, таких как квадраты, круги, треугольники и т. д., а куб, прямоугольный параллелепипед, сфера, цилиндр, конус и т. д. являются некоторыми примерами трехмерных форм. Основные формулы геометрии представлены следующим образом:

Список формул геометрии

Ниже приведен список различных формул геометрии для вас в соответствии с геометрической формой.

Периметр квадрата = 4 (сторона)

Периметр прямоугольника = 2 (длина + ширина)

Площадь квадрата = сторона2

Площадь прямоугольника = длина × ширина

Площадь треугольника = ½ × основание × высота

Площадь трапеции = ½ × (основание1+основание2)(основание1+основание2) × высота

Формулы базовой геометрии, в которых используется математическая константа π:

Площадь круга = A = π×r2

Длина окружности = 2πr

Площадь криволинейной поверхности цилиндра = 2πrh

Общая площадь поверхности цилиндра = 2πr(r + h)

Объем цилиндра = V = πr2h

Площадь криволинейной поверхности конуса = πrl

Всего площадь поверхности конуса = πr(r+l) = πr[r+√(h3+r2)]

Объем конуса = V = ⅓×πr2h

Площадь поверхности сферы = S = 4πr2

Объем a Сфера = V = 4/3×πr3

, где

r = радиус;
ч = Высота. и,

l = высота наклона

В таблице формул показаны геометрические формулы, используемые для различных 2-D и 3-D форм: c2
Площадь = ½ ab

Периметр = a + b + √(a2 + b2)

Где,

c = гипотенуза треугольника

a = 0 высота треугольника треугольника

2. Треугольник      Периметр, P = a + b + c

Площадь, A = ½ bh

Высота, h = 2(A/b)

Где,

a,b,018 arec стороны треугольника.
3. Rectangle

Perimeter = 2(l + w)

Area = lw

Diagonal, d = √(l2 + w2)

Where,

l = length of a rectangle

w = ширина прямоугольника

4. Параллелограмм

Периметр, P = 2(a + b)

Площадь, A = bh

Высота, h = A/b

Основание, b = A/h

Где,

a и b — стороны параллелограмма
h
высота параллелограмм

5. 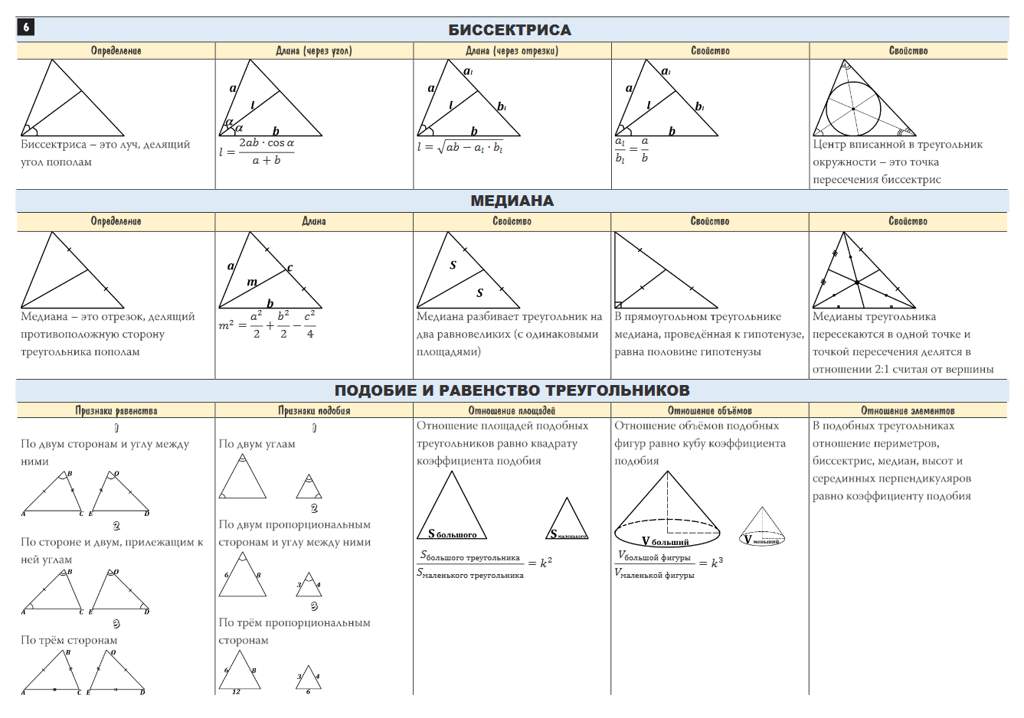Трапеция

Площадь, A = ½(a + b)h

Высота, h = 2A/(a + b)

Основание, b = 2(A/h) – a

Где,

a и b параллельные стороны

h = расстояние между двумя параллельными сторонами

6. Округа круга = 2πr

Площадь = πr2

Диаметр = 2R

, где

R = радиус круга

7. Периметр Square, P = 4A

AREA

7. ПЕРИМЕтр Square, P = 4A

a Arue

. a2

Диагональ, d = a√2

Сторона, a = √A = d/2√2

Где,

a = сторона квадрата

, L длина дуги rθ

Площадь, A = ½r2θ

Здесь θ — центральный угол в радианах.

Where,

r = radius

9. Cube            Area, A = 6a2

Volume, V = a3

Edge, a = V⅓

Space diagonal = a√3

Where ,

a = сторона куба

10. Прямоугольный параллелепипед Площадь поверхности A = 2(lb + bh + hl)

Объем V = lbh )

Где,

l= длина
b= дыхание

h= высота

11. Цилиндр Общая площадь поверхности, A = 2πrh + 2πr2

Площадь криволинейной поверхности, Ac = 2πrh

Объем, V = πr2h

Площадь основания, Ab0 , r = √(V/πh)

Где,

r= радиус цилиндра

h= высота цилиндра

12. Конус           Общая площадь поверхности, A = πr(l = πr) = πr[r+√(h3+r2)]

Площадь искривленной поверхности, Ac = πrl

Объем, V = ⅓πr2h

Высота наклона, l = √(h3+r2)

Площадь основания, Ab = πr2

Где

r= радиус конуса Высота

13. Площадь поверхности сферы, a = 4πr2

Объем, V = ⁴⁄₃πr3

Диаметр = 2R

, где

R = радиус

FAQ’s на геометрию.

	Длина окружности	2πr или πd
	Площадь круга	π(r*r) или Пи в квадрате
	периметр четырехугольника
	периметр квадрата
	периметр любой формы	сложить все стороны вместе
	площадь квадрата	с*с или с в квадрате
	площадь прямоугольника
	площадь параллелограмма
	площадь треугольника	(ч)/2
	объем любой формы	(площадь основания)ч

	кубов и кубоидов (объем кубоида)
	Платоновые тела
	Призмы
	Пирамиды

Площадь круга	92) √3)/4
Площадь n Гон	А = ½ апофемы * Периметр
Площадь Параллелограмм	A= основание x высота
Площадь прямоугольника
Площадь трапеции	А = ½ (основание 1 + основание 2) высота
Площадь треугольника	А = ½ основания x Высота
Базовая зона Гептагона	Площадь основания = ½ апофемы * периметр
Базовая площадь шестиугольника	Площадь основания = ½ апофемы * периметр
Базовая зона восьмиугольника	Площадь основания = ½ апофемы * периметр
Базовая площадь Параллелограмм	Площадь базы = база * высота
Базовая зона Пентагона	Площадь основания = ½ апофемы * периметр
Базовый прямоугольник	Площадь основания = длина * ширина
Площадь базы	Площадь основания = площадь стороны
Основание трапециевидной формы	Площадь основания = ½ (высота) (основание 1 + основание 2)
Базовый треугольник	Площадь основания = 1/2 основания * высота
Окружность Круг	C = 2 x Π x радиус
Формула расстояния	Д=√(х ₂ -х ₁ ) ² + (у ₂ –у ₁ ) ²
Уравнение окружности	Общая форма (x-h) ² +(y-k) ² h и K — координаты окружности, r = радиус
45 45 90 Треугольник Гипотенуза	Н= нога√2
45 45 90 Треугольник Ноги	1⁄2 гипотенуза√2
Формула Герона	s=(a+b+c)/2, тогда A= √ (с (с-а) (с-б) (с-с))
Горизонтальная линия	Y = (любое число)
Боковая часть конуса	πrsl r = радиус sl = высота наклона
Боковой куб	4s ² s=сторона
Боковая зона цилиндра	Окружность х Высота
Боковая призма	Периметр x высота
Пирамида боковой зоны	1/2P * sl sl = высота наклона P=периметр
Прямоугольная боковая поверхность Твердый	Периметр *высота
Боковая область справа Конус	LA = ½ Psl P=2πr sl = высота наклона
Боковая область справа Цилиндр	ЛА = 2πr*ч
Боковая область справа Призма	LA = Ph P = сумма сторон основания h = высота
Формула средней точки	(Х1 + Х2)/2, (У1 + Y2)/2
Периметр Параллелограмм	P= 2(основание + сторона)
Периметр Прямоугольник	P= 2(база + высота)
Периметр №	P = количество сторон * стороны
Периметр Ромб	P= 4 стороны
Периметр квадрата	P = 4 x сторона
Периметр Трапеция	Основание1 + Основание2 + Сторона1 + сторона 2
Периметр Треугольник	Сторона A + Сторона B + Сторона С
Форма уклона точки	г-г ₁ = м(х-х ₁ )
Склон	Y2-Y1 Х ₂ -Х _{1 =} _{Подъем над бегом}
Форма пересечения уклонов	y = mx + b M = наклон b = y перехват
Площадь поверхности Конус	SA= πрадиуснаклонная высота+ πрадиус ²
Площадь поверхности Куб	СА = 6 сторона ²
Площадь поверхности Цилиндр	Боковая зона + 2πрадиус ²
Площадь поверхности Призма	Боковая зона + 2 основания
Площадь поверхности Пирамида	Боковая зона + 1 основание
Площадь поверхности прямоугольника Призма	2(длинаширина + длинавысота + высота*ширина)
Площадь поверхности справа Конус	SA=1/2диаметрπ*наклон высота+база
Площадь поверхности права Цилиндр	2πрадиус ² +2πрадиус x высота
Площадь поверхности права Призма	SA = периметр * высота + 2 База
Площадь поверхности Сфера	4πрадиус ²
30 60 90 треугольник короткий и длинный ноги	Короткий катет = ½ гипотенузы Длинная нога = 1/2 гипотенузы√3