Геометрия формул: Основные формулы геометрия 7-11 класс

Геометрия: уроки, тесты, задания.

• Предметы

1. 1. Прямая, отрезок, точки

   2. Луч, угол, обозначение угла

   3. Сравнение отрезков и углов.

      Биссектриса

   4. Измерение отрезков и углов

   5. Перпендикулярные прямые. Смежные и вертикальные углы

2. 1. Первый признак равенства треугольников

   2. Медиана, биссектриса, высота треугольника

   3. Второй и третий признаки равенства треугольников

   4. Окружность.

      Радиус. Задачи на построение

3. 1. Признаки параллельности двух прямых. Свойства параллельных прямых. Аксиома параллельных прямых

4. 1. Сумма углов треугольника. Виды треугольников

   2. Теорема о соотношениях между сторонами и углами треугольника

   3. Прямоугольный треугольник.

      Свойства. Признаки равенства

   4. Расстояние от точки до прямой. Построение треугольника по трём элементам

1. 1. Ломаная. Виды ломаных. Многоугольники

   2. Параллелограмм.

      Свойства параллелограмма. Трапеция

   3. Прямоугольник, квадрат. Признаки прямоугольника и квадрата. Ромб

2. 1. Площадь многоугольника. Свойства площадей

   2. Формулы площадей параллелограмма, треугольника и трапеции

   3. Теорема Пифагора.

      Доказательство

3. 1. Подобные треугольники. Пропорциональные отрезки

   2. Признаки подобия треугольников

   3. Применение подобия. Решение задач

   4. Тригонометрические функции острого угла прямоугольного треугольника

4. 1. Касательная и окружность

   2. Центральные и вписанные углы.

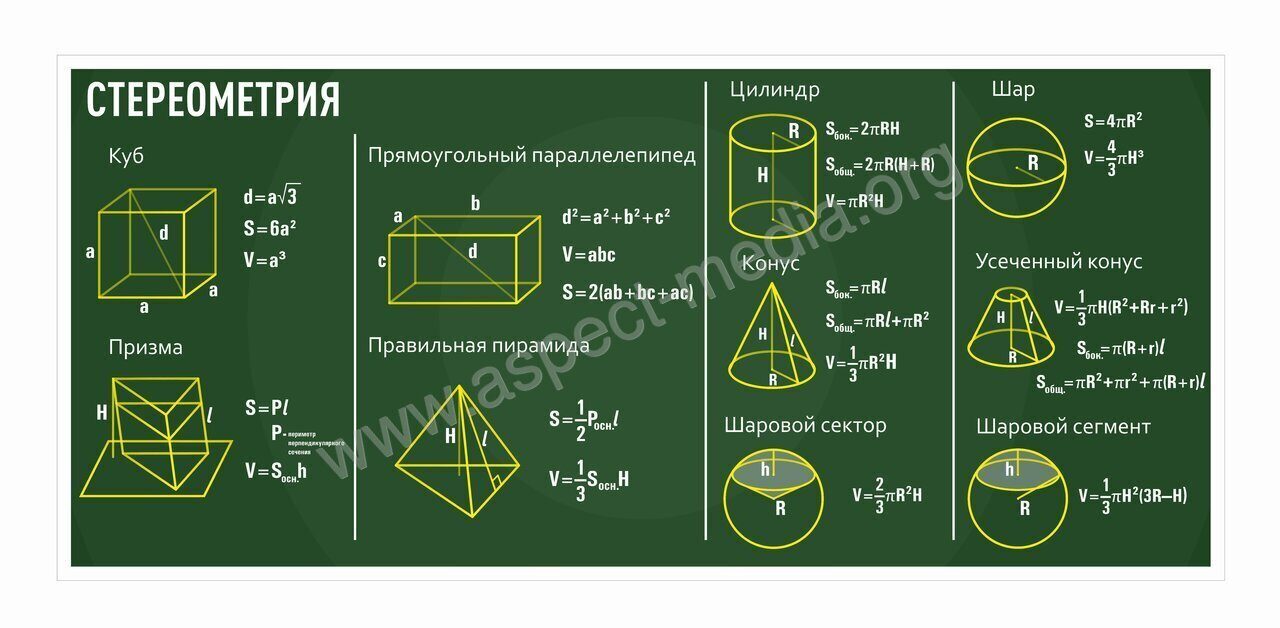      Свойство пересекающихся хорд окружности

   3. Замечательные точки треугольника

   4. Вписанная и описанная окружности

1. 1. Понятие вектора. Виды векторов

   2. Правила сложения и вычитания векторов

   3. Умножение векторов на число

   4. Проекция вектора на ось

2. 1. Вектор в системе координат

   2. Решение простейших задач в координатах

   3. Уравнение окружности.

      Уравнение прямой

3. 1. Синус, косинус, тангенс угла

   2. Соотношения между сторонами и углами треугольника

   3. Скалярное произведение векторов. Свойства

4. 1. Правильные многоугольники

   2. Длина окружности.

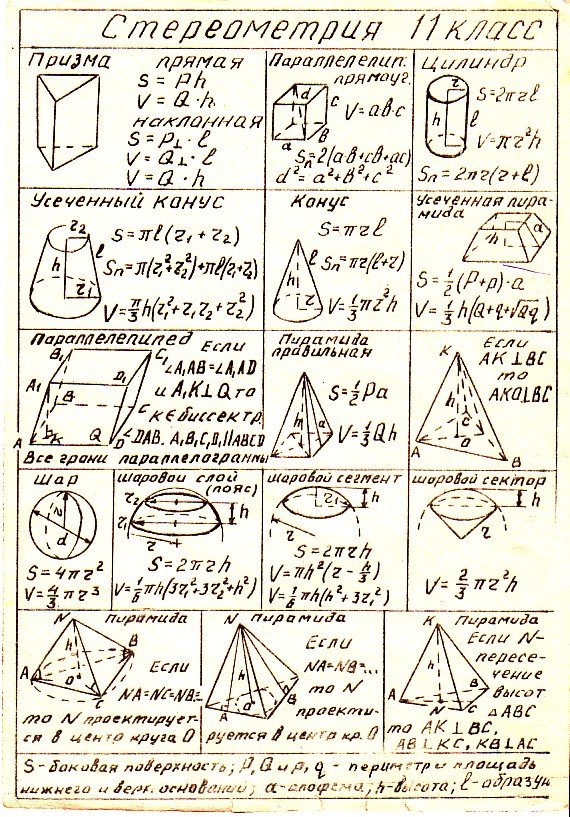      Площадь круга

5. 1. Понятие движения. Симметрия

   2. Параллельный перенос и поворот

6. 1. Многогранники. Основные формулы для расчётов

   2. Цилиндр.

      Конус. Сфера

1. 1. Аксиомы стереометрии и их простейшие следствия

2. 1. Определение и свойства параллельности прямых, прямой и плоскости

   2. Определение и свойства скрещивающихся прямых.

      Угол между прямыми

   3. Определение, признак и свойства параллельности плоскостей

   4. Элементы тетраэдра и параллелепипеда

3. 1. Определение и свойства перпендикулярности прямой и плоскости

   2. Определение перпендикуляра, наклонной.

      Теорема о трёх перпендикулярах

   3. Понятие двугранного угла. Признак перпендикулярности плоскостей

4. 1. Понятие многогранника. Призма

   2. Элементы пирамиды. Виды пирамид

   3. Определение и свойства правильных многогранников

   4. Как найти объём прямоугольного параллелепипеда

   5. Как найти объём прямой призмы

   6. Как найти объём наклонной призмы

1. 1. Определение и физический смысл вектора в пространстве

   2. Как складывать векторы и умножать вектор на число

   3. Разложение вектора.

      Понятие компланарности

2. 1. Абсцисса, ордината и аппликата точки. Простейшие задачи в координатах

   2. Угол между векторами. Скалярное произведение

   3. Отображения пространства на себя.

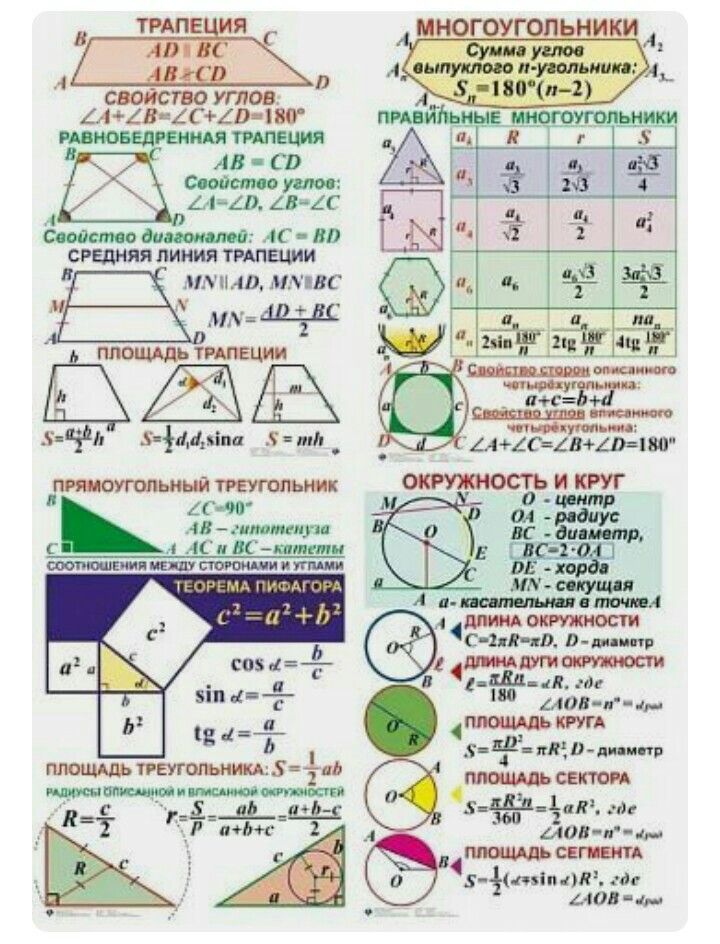      Виды движения

3. 1. Элементы цилиндра. Площадь поверхности

   2. Элементы конуса. Площадь поверхности

   3. Элементы сферы и шара. Уравнение сферы. Сечение шара плоскостью

4. 1. Как найти объём цилиндра

   2. Как найти объём конуса

   3. Как найти объём шара

1. Коллекция интерактивных моделей

Все формулы по геометрии

Все формулы по геометрии

Каталог/ Учебная литература/ Для средней и старшей школы/ Математика/Все формулы по геометрии

Аннотация к книге «Все формулы по геометрии»

Школьникам общеобразовательных школ адресован учебный материал, помогающий наглядно запомнить все формулы по геометрии.

Отзывов пока что нет

Возможно, вам понравится

• 148

  125.8 Р

• 479

  407.15 Р

• 102

  86.7 Р

• 130

  110. 5 Р

• 441

  374.85 Р

• 325

  276.25 Р

• 1095

  930.75 Р

• 184

  156. 4 Р

• 190

  161.5 Р

• 173

  147.05 Р

• 57

  48.45 Р

• 156

  132. 6 Р

• 233

  198.05 Р

• 124

  105.4 Р

• 195

  165.75 Р

• 321

  272. 85 Р

• 609

  517.65 Р

• 220

  187 Р

• 246

  209.1 Р

© 2000–2021, ООО «Гемера-Плюс»
Моя книга | Сеть книжных магазинов в Саратове

Что такое формула средней точки? Пример определения, геометрии и экономики

Руководство по формуле средней точки в геометрии и экономике с примерами

Что такое формула средней точки?

Содержимое

Определение: Формула средней точки в геометрии представляет собой уравнение, которое вычисляет расстояние между двумя известными координатами точки.

В экономике формула средней точки используется для измерения изменений кривых спроса и предложения и их относительной эластичности.

Формула средней точки

Использование

Формула средней точки часто используется для нахождения средней точки, чтобы разделить отрезок пополам. Его также можно использовать для доказательства того, что отрезок делится пополам.

Формула находит среднее или медиану двух значений. Эта формула часто используется с картами и с формулой расстояния.

Например, Найдите город, который находится между Чикаго, штат Иллинойс, и Индианаполисом, штат Индиана. Как далеко город от Чикаго?

Чтобы ответить на этот вопрос, давайте посмотрим, как найти среднюю точку ниже.

---

Что такое середина линии?

Середина — это координатная точка, которая находится посередине между двумя другими точками на отрезке.

Средние точки встречаются как в двухмерном пространстве на графике, так и в трехмерном пространстве внутри куба, сферы или другой формы.

Нахождение средней точки помогает решить географические, программные и экономические проблемы.

Давайте посмотрим, как рассчитать это уравнение.

---

Уравнение формулы расстояния и средней точки

Уравнение формулы средней точки вычисляется путем сложения двух координатных точек ( x ₁ , y ₂ ) и ( x ₂ , y ₂ ) и делением на два. Средняя точка, представленная M, , рассчитывается следующим образом:

Нижние индексы, небольшие числа в основании переменных указывают на точку, из которой исходит значение. Поскольку в формуле используется сложение, а порядок не влияет на сумму, порядок, в котором вы добавляете значения, не важен.

Важно убедиться, что вы складываете вместе координаты x- и складываете вместе координаты y-. Также обратите внимание, что ответ находится в виде координаты, так как середина является точкой, решение также должно быть в форме координат.

---

Примеры формулы средней точки в геометрии

Середина отрезка прямой Пример

Средняя точка формулы отрезка прямой вычисляет среднюю точку этого отрезка. При решении каждой переменной обязательно сложите, а затем разделите на два.

Когда отрезок прямой или горизонтальный, одна из координат не меняется.

Сначала мы пометим наши переменные индексами один или два.

Далее мы подставим значения в формулу.

Сложите значения в числителе.

Упростите дроби. Если числитель нечетный, часто результат остается в десятичной форме, но допустима и смешанная или неправильная дробь.

Обратите внимание, что для горизонтальной линии координата y средней точки совпадает с обеими конечными точками. Средняя точка вертикальной линии имеет ту же координату x , что и конечные точки.

Это может помочь сэкономить время при решении проблемы, однако, если вы склонны путать координаты x и y , то лучше выполнять каждый шаг во избежание ошибок.

---

Середина диагональной линии Пример

Давайте рассмотрим пример формулы средней точки , где отрезок расположен по диагонали.

Для начала нам нужно найти координаты точек.

Сделаем пункт A наша первая точка (индекс 1) и точка B наша вторая точка (индекс 2)

Далее мы подставим значения в формулу и упростим.

---

Формула метода средней точки в экономике

Пример формулы метода средней точки

Метод средней точки часто используется в экономике для измерения ценовой эластичности изменений кривой спроса и предложения и экономического воздействия каждого из них.

Экономика использует метод наклона по формуле средней точки и применяет его к треугольникам.

Другой тип задачи, в которой используются средние точки, — поиск второй конечной точки сегмента.

Дан отрезок с конечной точкой (-3,-5) и средней точкой (1,1), найдите другую конечную точку отрезка.

Один из способов решить эту проблему — использовать формулу средней точки. Мы можем разбить его, чтобы посмотреть на x-координаты и y -координаты отдельно.

Мы начнем с того, что пометим нашу известную конечную точку как , а наша средняя точка . Теперь мы можем подставить наши известные значения.

Начните с умножения обеих сторон на 2. Это сократит дробь.

Вычесть или, в данном случае, добавить, так как у нас отрицательное значение, чтобы изолировать переменную.

Координаты второй конечной точки (5,7).

---

Пример экономической формулы средней точки

Второй способ найти отсутствующую конечную точку в экономической формуле средней точки — использовать наклон. Мы изучим этот метод, используя те же значения.

Начнем с наброска схемы.

Найдем наклон между конечной точкой и средней точкой.

Уклон 6/4. Мы не собираемся уменьшать наклон, так как нам нужны одинаковые значения. 6 представляет вертикальное изменение или изменение координаты y .

Это означает, что мы можем добавить 6 к координате y- нашей средней точки. Цифра 4 представляет горизонтальное изменение или изменение координаты x . Мы можем добавить 4 к нашим х -координата нашей средней точки. Это дает нам координаты второй конечной точки (5,7).

Что такое формула расстояния в геометрии?

Формула геометрического расстояния используется для определения расстояния между двумя точками на плоскости. Это важная идея для студентов, изучающих геометрию, и людей, работающих в таких областях, как инженерия и физика. В этой статье рассматриваются основы формул расстояния, включая то, что они собой представляют, почему они полезны и как их использовать.

Как формула расстояния используется в геометрии?

Чтобы использовать формулы расстояний в вашей геометрии, выполните следующие действия:

1. Определите координаты двух точек.

• Эти точки могут быть представлены в системе координат, например в декартовой системе координат с осями x и y.
• Координаты точки записываются как (x, y), где координата x представляет положение точки по оси x, а координата y представляет ее положение по оси y.

2. Подставить координаты точки в формулу расстояния. Формула d = √((x2 – x1)2 + (y2 – y1)2) , где:

• d – расстояние между двумя точками и
• (x1, y1) и (x2, y2 ) — координаты

3. Вычислить расстояние между точками. Подставьте координаты точек в уравнение и найдите d. Пожалуйста, используйте правильные единицы измерения для координат и окончательного ответа.

Формулы расстояний имеют множество применений в геометрии, например, для нахождения расстояния между точками на графике, вычисления длины отрезка и нахождения расстояния между двумя линиями. Его можно использовать для многих целей, например, для поиска кратчайшего пути между двумя точками или для определения скорости движения объекта по прямой. Мы используем формулу расстояния, чтобы определить расстояние между двумя точками на единичной окружности. Если вы понимаете и знаете, как использовать формулы расстояний, вы можете использовать их для решения любой задачи геометрии.

Какая формула для вычисления расстояния в геометрии?

Следующая формула вычисляет расстояние в геометрии:

d = √((x2 – x1)2 + (y2 – y1)2)

Формула использует теорему Пифагора, которая утверждает, что квадрат гипотенуза треугольника (противоположная сторона прямого угла) равна сумме двух других его квадратов. В этом случае гипотенуза — это расстояние между двумя точками, а две другие стороны — это разница между координатами x и y соответственно.

Подставьте координаты двух точек в формулу расстояния и найдите d. Например, если две точки имеют координаты (3, 4) и (6, 8), расстояние между ними равно (3, 4).

Это эквивалентно

√((6 — 3)2 + (8 — 4)2

= √((3)2 + (4)2)

= √(9 + 16)

= √25

= 5

Другими словами, расстояние между двумя точками равно пяти единицам

В декартовой системе координат формула расстояния применяется только к точкам на двумерной плоскости. Используется трехмерное пространство, известное как формула трехмерного расстояния.0003

Почему важна формула расстояния?

Формула расстояния является важным математическим инструментом по многим причинам.

• Вы можете рассчитать точное расстояние между двумя точками на плоскости или в пространстве. Это полезно в технике, физике, навигации и других областях, где важно измерение расстояния.
• Использование Для расчета кратчайшего пути между двумя точками, расчета скорости объекта и расчета расстояния, пройденного объектом.
• Крайне важно понимать и работать с геометрией. Формула расстояния является фундаментальным понятием в геометрии, и ее базовое понимание необходимо для решения более сложных задач о расстояниях на плоскости и в пространстве. Он имеет практическое применение в повседневной жизни.
• Формула расстояния используется в повседневных приложениях, таких как навигация по карте, строительство и спорт, что делает ее ценным инструментом для решения реальных задач.

Применение формулы расстояния в реальных ситуациях

Формулы расстояний можно использовать по-разному в реальном мире, особенно в технике и физике. Вот пример использования формулы расстояния:

Навигация: Формулы расчета расстояния можно использовать для определения расстояния между двумя местами или точками на заданном маршруте или для выяснения того, до какого места потребуется наименьшее время, чтобы добраться до него. . Это особенно полезно при путешествии по воздуху или по морю, когда важны расстояние и расход топлива.

Архитектура и строительство: Для определения размеров зданий и других сооружений и организации размещения фундаментных опор и других элементов конструкций используются формулы расстояний.

Физика: Формулы расстояния используются для расчета расстояния, которое объект проходит по прямой линии, и скорости этого объекта. Он также вычисляет расстояние между двумя ее объектами в космосе, такими как планеты и спутники.

Sports: Формулы расстояния могут измерять расстояние, пройденное спортсменом, или расстояние между игроками на спортивной площадке.

Географические информационные системы (ГИС) : Формулы расстояний используются в программном обеспечении ГИС для измерения расстояния между двумя точками на карте или для нахождения кратчайшего пути между двумя точками.

Хотите начать применять математику в своей карьере? Найди пару с репетиторами по математике для взрослых!

Советы по решению задач с формулой расстояния в геометрии

Вот несколько советов по решению задач с формулой расстояния в геометрии.

1. Убедитесь, что вы понимаете суть проблемы и то, что от вас ожидается. Имея две точки и единицу измерения, определите, хотите ли вы расстояние между точками или длину отрезка, который их соединяет.
2. Определите координаты двух точек. Эти точки могут быть представлены в системе координат, такой как декартова система координат с осями x и y. Точка описывается двумя числами, где первое число x представляет расстояние от нее по оси x, а второе число y представляет расстояние по оси y.
3. Подставить координаты точки в формулу расстояния. Формулы состоят из d = √((x2 – x1)2 + (y2 – y1)2) , где d – расстояние
4. Рассчитать расстояние между точками. Подставьте координаты точек в уравнение и найдите d. Пожалуйста, используйте правильные единицы измерения для координат и окончательного ответа.
5. Проверьте свою работу. Убедитесь, что ваш окончательный ответ дан в правильных единицах и что ваше решение разумно, учитывая контекст проблемы.

Типичные ошибки, которых следует избегать при использовании формулы расстояния в геометрии две точки, в то время как формулы средней точки находят координаты точки на полпути вдоль сегмента. Убедитесь, что вы используете правильную формулу для решения проблемы.

Забыли возвести в квадрат разницу между координатами x и y. Формула расстояния требует возведения в квадрат разницы между координатами x и y перед их сложением. Игнорирование этого приведет к неправильному ответу.

Забыв про квадратный корень: Формула расстояния требует нахождения квадратного корня из суммы квадратов разностей между координатами x и y. Если вы забудете и об этом, это будет неправильно.

Использование неправильных единиц измерения: Убедитесь, что вы используете правильные координаты и окончательный ответ. Если единицы измерения не указаны, обязательно укажите единицы, которые вы используете.

Перепутаны координаты двух точек: Убедитесь, что вы используете правильные координаты для двух точек. Если вы перепутаете координаты, вы получите неправильный ответ.

Заинтересованы в изучении тригонометрии? Прочтите это

Общие заблуждения относительно формулы расстояния

Некоторые распространенные заблуждения относительно формулы расстояния могут привести к ошибкам при использовании. Вот некоторые заблуждения и пояснения к ним:

1. Формула расстояния может использоваться только для определения расстояния между двумя точками на плоскости. Он обычно используется для нахождения расстояний между двумя точками на координатной плоскости, но его также можно использовать для нахождения расстояний между любыми двумя точками, независимо от того, перекрываются ли они.
2. Формула расстояния и формула средней точки одинаковы. Формула расстояния вычисляет расстояние между двумя точками, а формула средней точки вычисляет координаты средней точки отрезка, соединяющего две точки. Хотя обе формулы не эквивалентны, их не следует путать.
3. Формулы расстояний в основном используются для нахождения расстояний между точками на плоскости. Однако их можно применять и к трехмерным пространствам. С помощью x1, y1, z1 и x2, y2, z2 идентифицируются две трехмерные точки. Последнее число представляет собой длину стороны коробки, где одно измерение пространства представляет собой бесконечную прямую линию.
4. Формула расстояния используется только в геометрии. Хотя формула расстояния обычно используется в геометрии, она также находит применение в других областях, таких как физика и инженерия.

Поняв эти распространенные заблуждения и прояснив их, вы сможете адекватно пользоваться формулой расстояния и точно рассчитывать расстояние между точками на плоскости или в пространстве.

Заинтересованы ли вы в изучении основ геометрии или вам нужен репетитор по математике

В Learner мы предлагаем лучших онлайн-репетиторов для каждого учащегося, подобранных по индивидуальному заказу с помощью нашего собственного процесса отбора и проверки. Наши преподаватели должны знать больше, чем просто предмет, который они преподают. Они также должны обладать правильными техническими и человеческими навыками, чтобы вдохновлять и мотивировать сегодняшних студентов.

Вот что мы предлагаем:

• Специально подобранный математический эксперт для решения любых задач.
• Преподаватели мирового класса, являющиеся экспертами в области педагогики, разрабатывают планы уроков в вашем собственном темпе и доводят их до вашего стиля обучения.
• Наставники учащихся выходят за рамки предмета, помогая определить траектории после проходного балла.