Геометрия формулы углов: Треугольник. Формулы и свойства треугольников.

Треугольник. Формулы и свойства треугольников.

Навигация по странице: Треугольник — определение Типы треугольников Вершины, углы и стороны треугольника    Свойства углов и сторон треугольника       Теорема синусов       Теорема косинусов Медианы треугольника Биссектрисы треугольника Высоты треугольника Вписанная окружность Описанная окружность Связь между вписанной и описанной окружностями Средняя линия треугольника Периметр треугольника Площадь треугольника Равенство треугольников Подобие треугольников

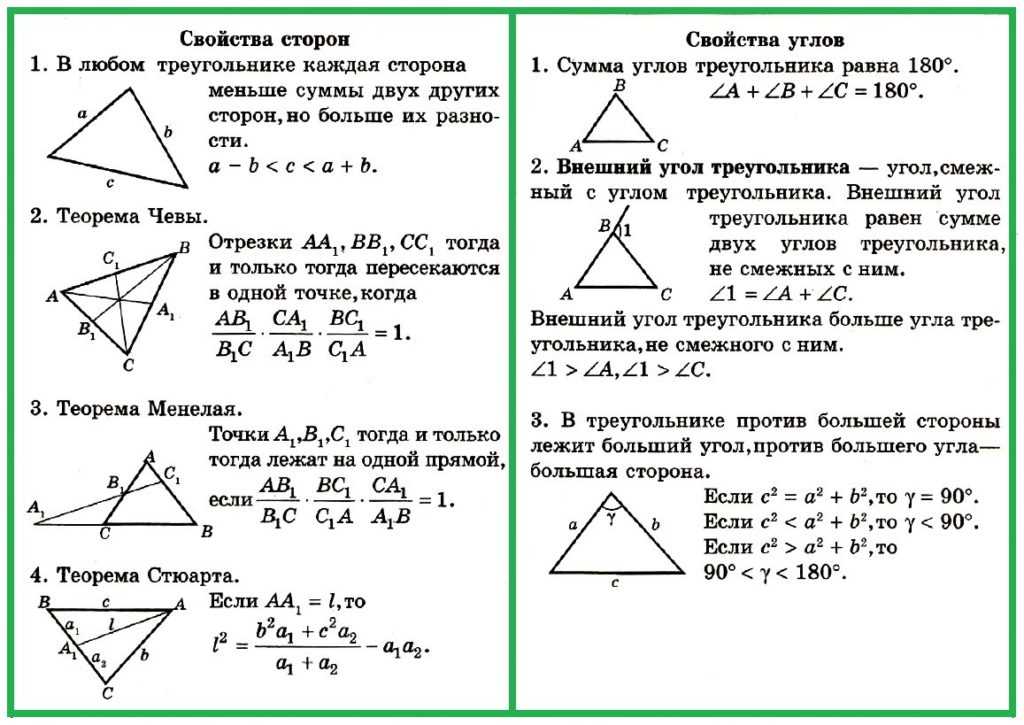
Определение. Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.

Типы треугольников

По величине углов

1. Остроугольный треугольник — все углы треугольника острые.

2. Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).

3. Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).

По числу равных сторон

1. Разносторонний треугольник — все три стороны не равны.

2. Равнобедренный треугольник — две стороны равны.

3. Равносторонним треугольник или правильный треугольник — все три стороны равны.

Вершины, углы и стороны треугольника

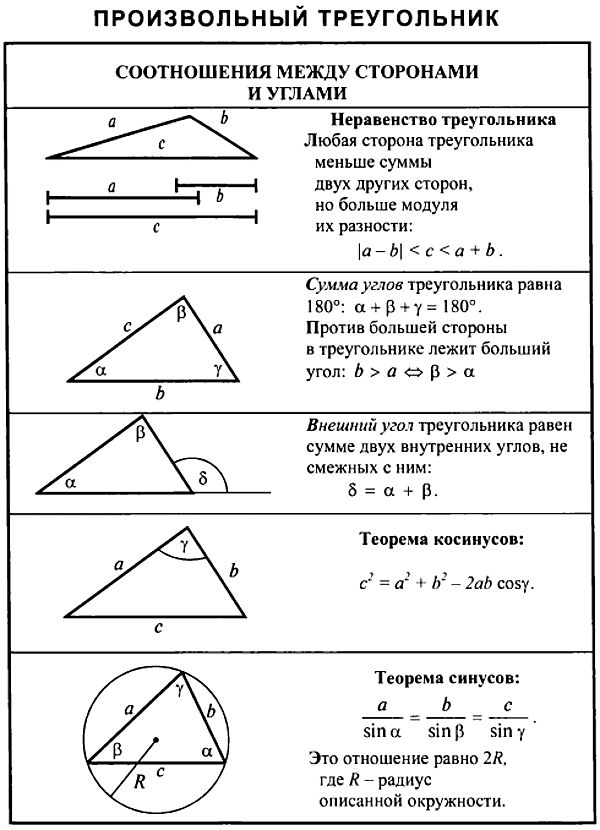
Свойства углов и сторон треугольника

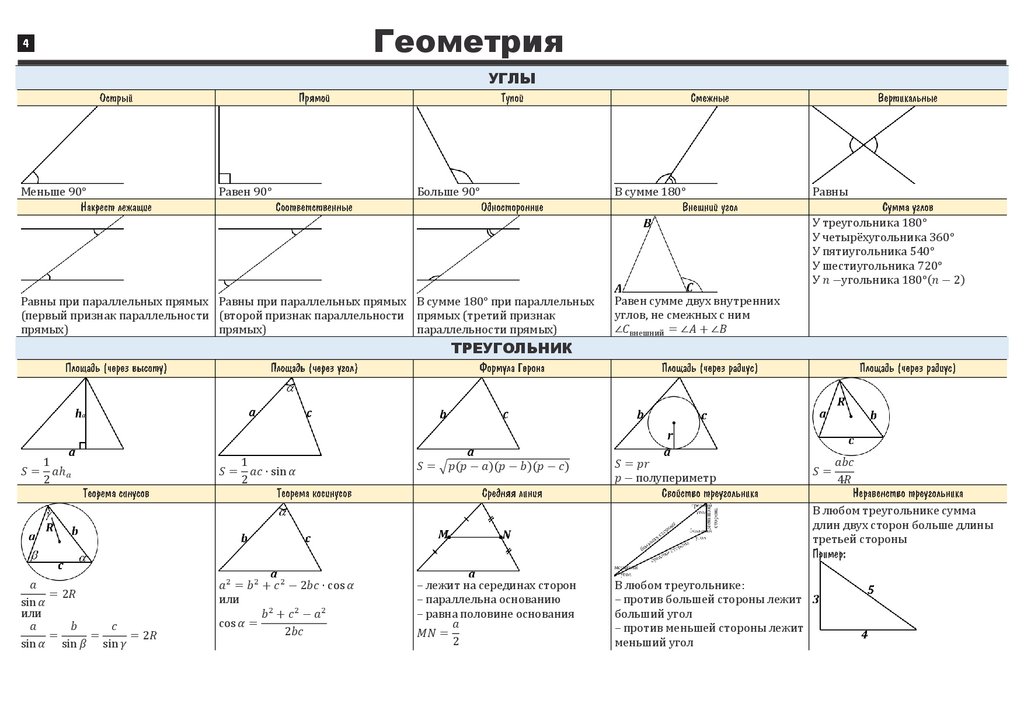
Сумма углов треугольника равна 180°:

α + β + γ = 180°

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β, тогда a > b

если α = β, тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c	= 2R
sin α		sin β		sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a² = b² + c² — 2bc·cos α

b² = a² + c² — 2ac·cos β

c² = a² + b² — 2ab·cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Формулы сторон через медианы

a = 23√2(m_b² + m_c²) — m_a²

b = 23√2(m_a² + m_c²) — m_b²

c = 23√2(m_a² + m_b²) — m_c²

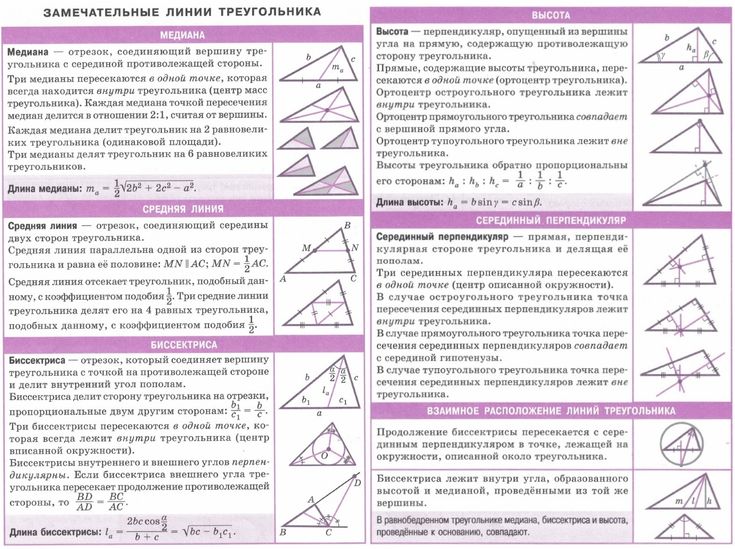
Медианы треугольника

Определение.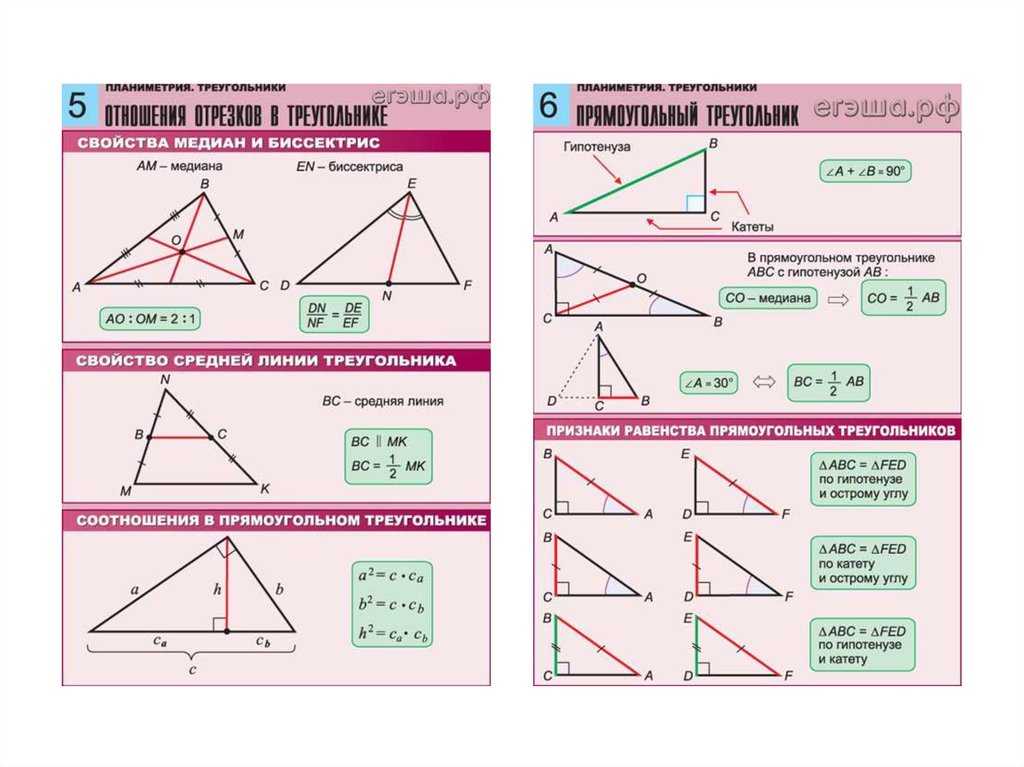 Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника:

1. Медианы треугольника пересекаются в одной точке. (Точка пересечения медиан называется центроидом)

2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

   AOOD = BOOE = COOF = 21

3. Медиана треугольника делит треугольник на две равновеликие части

   S_∆ABD = S_∆ACD

   S_∆BEA = S_∆BEC

   S_∆CBF = S_∆CAF

4. Треугольник делится тремя медианами на шесть равновеликих треугольников.

   S_∆AOF = S_∆AOE = S_∆BOF = S_∆BOD = S_∆COD = S_∆COE

5. Из векторов, образующих медианы, можно составить треугольник.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 12√2b²+2c²-a²

m_b = 12√2a²+2c²-b²

m_c = 12√2a²+2b²-c²

Биссектрисы треугольника

Определение. Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.

Свойства биссектрис треугольника:

1. Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности.

2. Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

   AEAB = ECBC

3. Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

   Угол между l_{c и lc’ = 90°}

4. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√bcp(p — a)b + c

l_b = 2√acp(p — b)a + c

l_c = 2√abp(p — c)a + b

где p = a + b + c2 — полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2bc cos α2b + c

l_b = 2ac cos β2a + c

l_c = 2ab cos γ2a + b

Высоты треугольника

Определение.

Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.

В зависимости от типа треугольника высота может содержаться

• внутри треугольника — для остроугольного треугольника;
• совпадать с его стороной — для катета прямоугольного треугольника;
• проходить вне треугольника — для острых углов тупоугольного треугольника.

Свойства высот треугольника

Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.

Если в треугольнике две высоты равны, то треугольник — равнобедренный.

h_a:h_b:h_c = 1a:1b:1c = (bc):(ac):(ab)

1h_a + 1h_b + 1h_c = 1r

Формулы высот треугольника

Формулы высот треугольника через сторону и угол:

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Формулы высот треугольника через сторону и площадь:

h_a = 2Sa

h_b = 2Sb

h_c = 2Sc

Формулы высот треугольника через две стороны и радиус описанной окружности:

h_a = bc2R

h_b = ac2R

h_c = ab2R

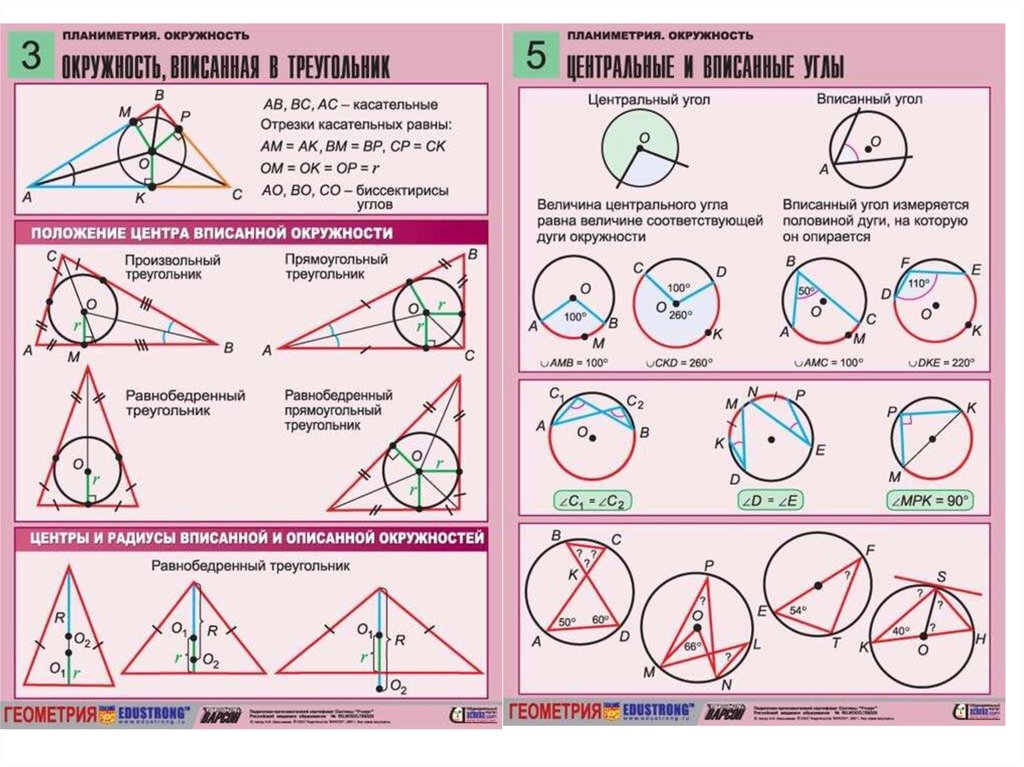
Окружность вписанная в треугольник

Определение. Окружность называется вписанной в треугольник, если она касается всех трех его сторон.

Свойства окружности вписанной в треугольник

Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.

В любой треугольник можно вписать окружность, и только одну.

Формулы радиуса окружности вписанной в треугольник

Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру:

r = Sp

Радиус вписанной в треугольник окружности через три стороны:

r = (a + b — c)(b + c — a)(c + a — b)4(a + b + c)

Радиус вписанной в треугольник окружности через три высоты:

1r = 1h_a + 1h_b + 1h_c

Окружность описанная вокруг треугольника

Определение. Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.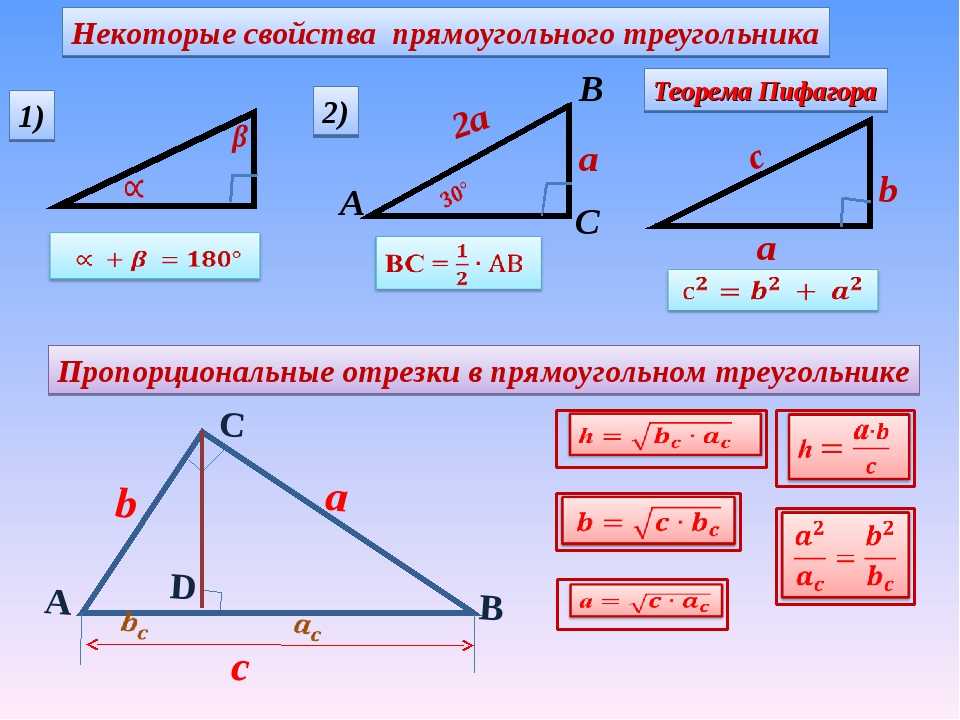

Свойства окружности описанной вокруг треугольника

Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.

Вокруг любого треугольника можно описать окружность, и только одну.

Свойства углов

Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.

Формулы радиуса окружности описанной вокруг треугольника

Радиус описанной окружности через три стороны и площадь:

R = abc4S

Радиус описанной окружности через площадь и три угла:

R = S2 sin α sin β sin γ

Радиус описанной окружности через сторону и противоположный угол (теорема синусов):

R = a2 sin α = b2 sin β = c2 sin γ

Связь между вписанной и описанной окружностями треугольника

Если d — расстояние между центрами вписанной и описанной окружностей, то.

d² = R² — 2Rr

rR = 4 sinα2 sinβ2 sinγ2 = cos α + cos β + cos γ — 1

2Rr = abca + b + c

Средняя линия треугольника

Определение. Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.

Свойства средней линии треугольника

1. Любой треугольник имеет три средних линии

2.

Средняя линия треугольника параллельна основанию и равна его половине.

MN = 12AC     KN = 12AB     KM = 12BC

MN || AC     KN || AB     KM || BC

3. Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольника

S_∆MBN = 14 S_∆ABC

S_∆MAK = 14 S_∆ABC

S_∆NCK = 14 S_∆ABC

4. При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.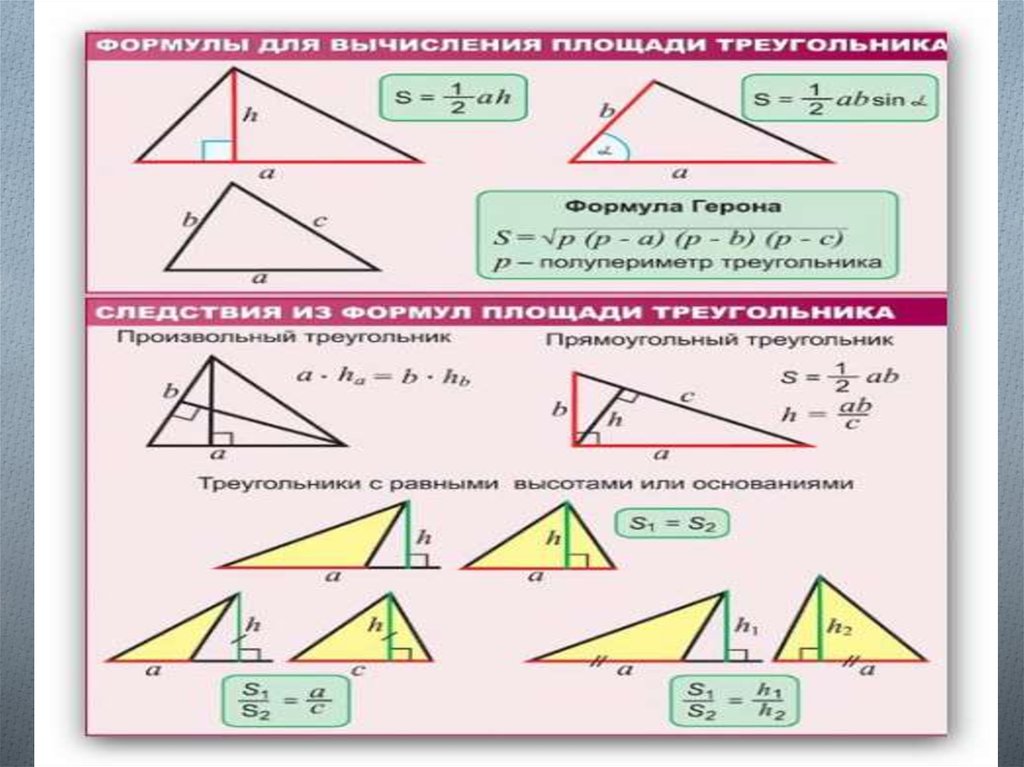

∆MBN ∼ ∆ABC

∆AMK ∼ ∆ABC

∆KNC ∼ ∆ABC

∆NKM ∼ ∆ABC

Признаки. Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.

Формулы площади треугольника

1. Формула площади треугольника по стороне и высоте
   Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

   S = 12a · h_a
   S = 12b · h_b
   S = 12c · h_c

2. Формула площади треугольника по трем сторонам

   Формула Герона

   S = √p(p — a)(p — b)(p — c)

   где p =

   a + b + c2

   — полупериметр треугльника.

3. Формула площади треугольника по двум сторонам и углу между ними
   Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.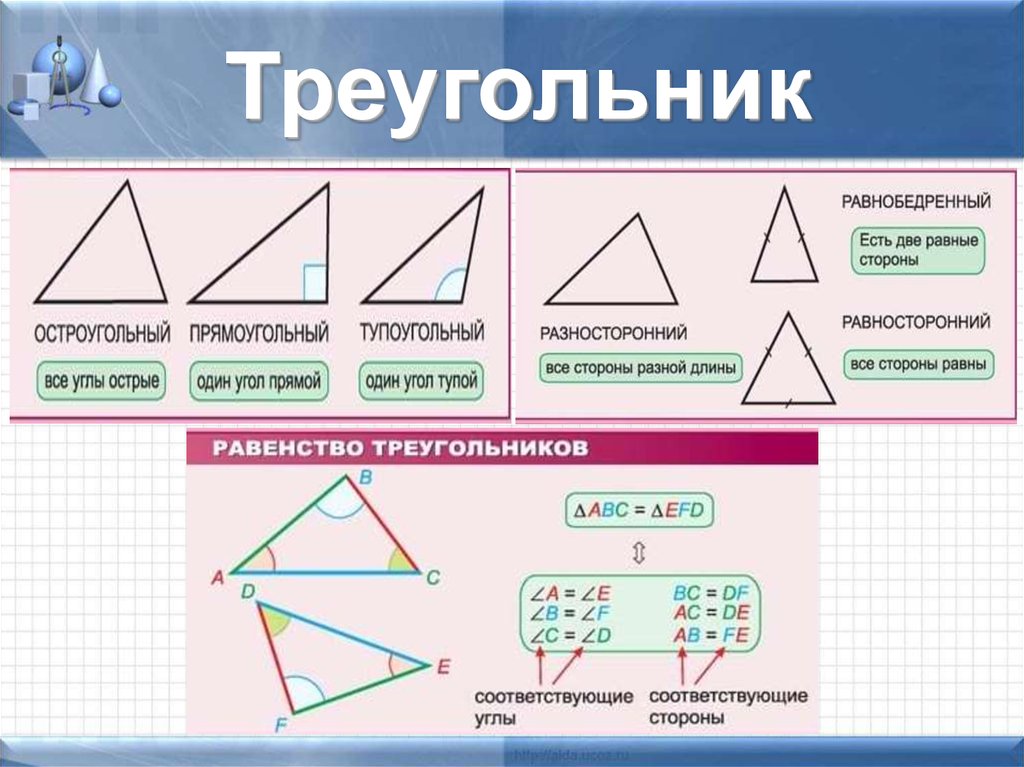

   S = 12a · b · sin γ
   S = 12b · c · sin α
   S = 12a · c · sin β

4. Формула площади треугольника по трем сторонам и радиусу описанной окружности

   S =	a · b · с
   	4R

5. Формула площади треугольника по трем сторонам и радиусу вписанной окружности
   Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

   S = p · r

Вы можете воспользоваться онлайн калькулятором для расчета площади треугольника.

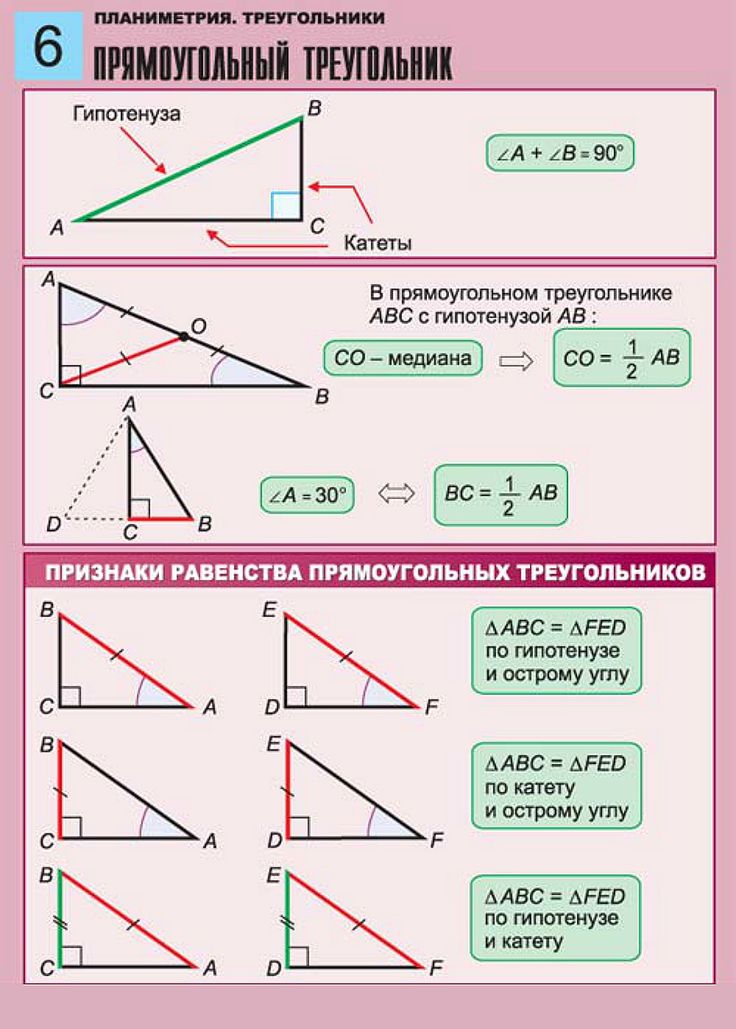
Равенство треугольников

Определение. Если два треугольника АВС и А

1В₁С₁ можно совместить наложением, то они равны.

Свойства. У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны)

Признаки равенства треугольников

Теорема 1.

Первый признак равенства треугольников — по двум сторонам и углу между ними

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Теорема 2.

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Теорема 3.

Третий признак равенства треугольников — по трем сторонам

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Подобие треугольников

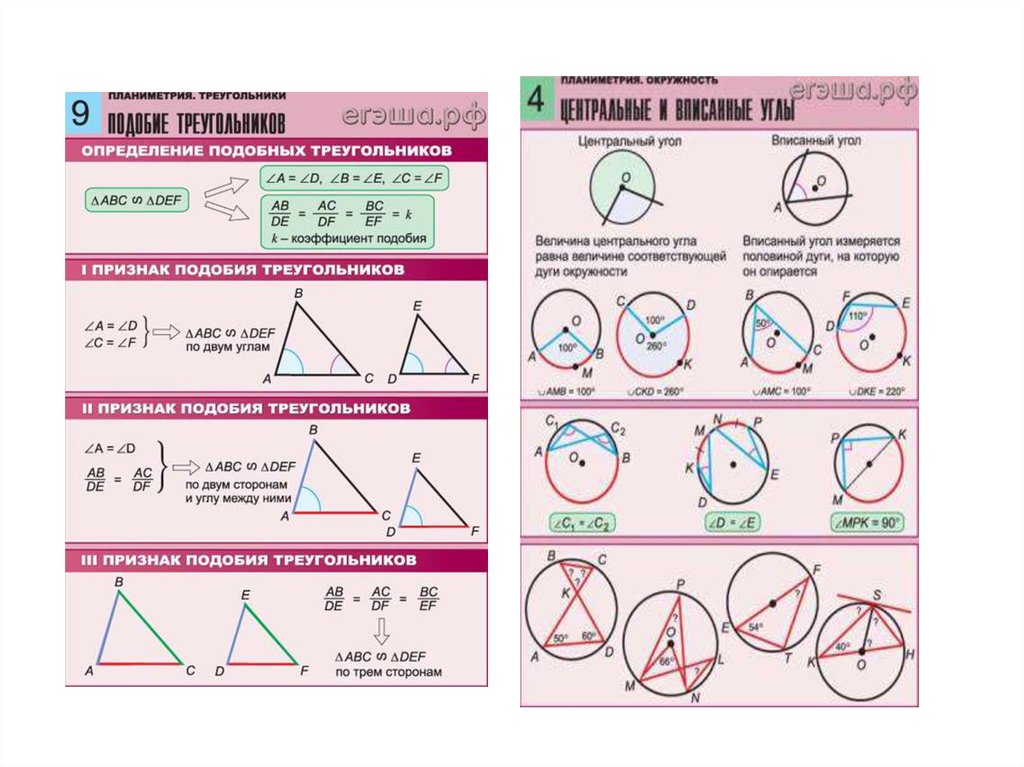
Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.

∆АВС ~ ∆MNK => α = α₁, β = β₁, γ = γ₁ и ABMN = BCNK = ACMK = k,

где k — коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Второй признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Третий признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.

Свойства. Площади подобных треугольников относятся как квадрат коэффициента подобия:

S_∆АВСS_∆MNK = k²

Все таблицы и формулы

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Справочник по математике

Геометрия (Планиметрия)

Углы

Вписанные и центральные углы

Углы, образованные хордами, касательными и секущими

Доказательства теорем об углах, связанных с окружностью

Вписанные и центральные углы

      Определение 1.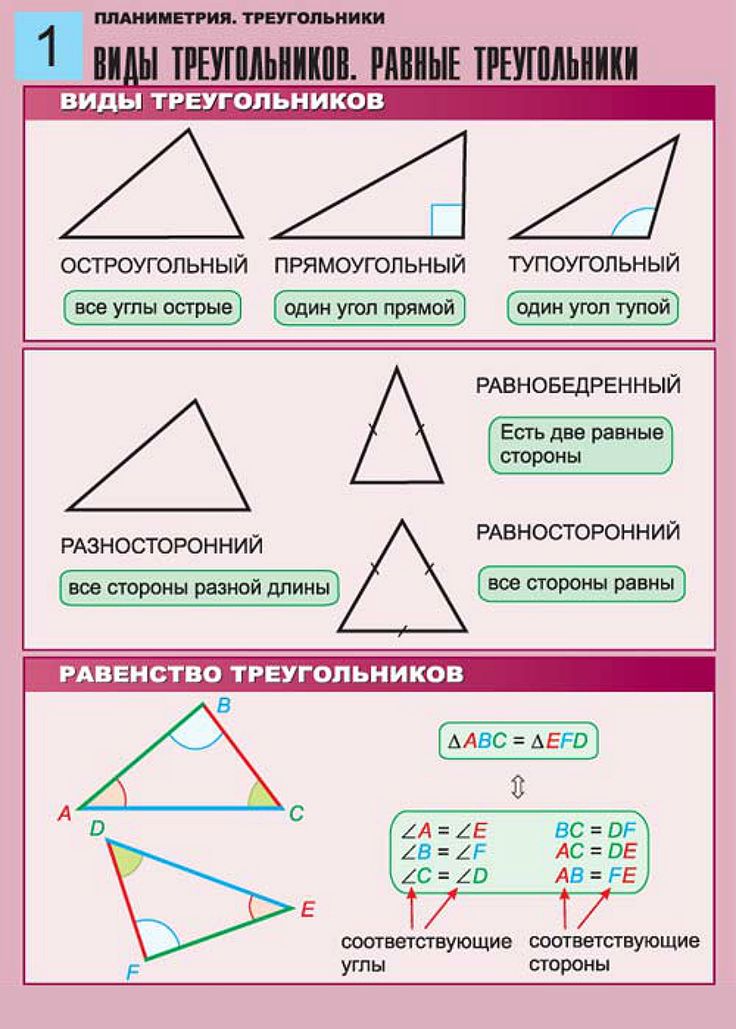 Центральным угломназывают угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).

Рис. 1

      Определение 2. Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).

Рис. 2

      Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.

      Определение 3. Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.

Теоремы о вписанных и центральных углах

Фигура	Рисунок	Теорема
Вписанный угол		Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Посмотреть доказательство
Вписанный угол		Вписанные углы, опирающиеся на одну и ту же дугу равны.
Вписанный угол		Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды
Вписанный угол		Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды
Вписанный угол		Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр
Окружность, описанная около прямоугольного треугольника		Середина гипотенузы прямоугольного треугольника является центром описанной около этого треугольника окружности. Посмотреть доказательство

Вписанный угол

Теорема: Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Посмотреть доказательство

Теорема: Вписанные углы, опирающиеся на одну и ту же дугу равны.

Теорема: Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды

Теорема: Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды

Теорема: Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр

Окружность, описанная около прямоугольного треугольника

Теорема: Середина гипотенузы прямоугольного треугольника является центром описанной около этого треугольника окружности. Посмотреть доказательство

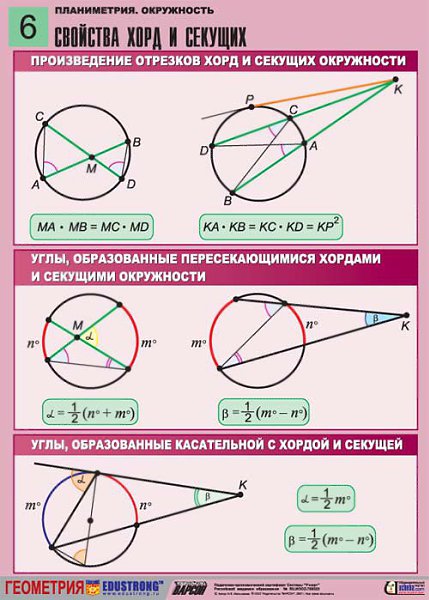
Теоремы об углах, образованных хордами, касательными и секущими

Фигура	Рисунок	Теорема	Формула
Угол, образованный пересекающимися хордами		Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Посмотреть доказательство
Угол, образованный секущими, которые пересекаются вне круга		Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство
Угол, образованный касательной и хордой, проходящей через точку касания		Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Посмотреть доказательство
Угол, образованный касательной и секущей		Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство
Угол, образованный двумя касательными к окружности		Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство

Угол, образованный пересекающимися хордами хордами

Формула:

Теорема Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Посмотреть доказательство

Угол, образованный секущими секущими, которые пересекаются вне круга

Формула:

Теорема Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство

Угол, образованный касательной и хордой хордой, проходящей через точку касания

Формула:

Теорема Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Посмотреть доказательство

Угол, образованный касательной и секущей касательной и секущей

Формула:

Теорема Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство

Угол, образованный двумя касательными касательными к окружности

Формулы:

Теорема Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство

Доказательства теорем об углах, связанных с окружностью

      Теорема 1. Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

      Доказательство. Рассмотрим сначала вписанный угол ABC, сторона BC которого является диаметром окружности диаметром окружности, и центральный угол AOC (рис. 5).

Рис. 5

      Так как отрезки AO и BO являются радиусами окружности радиусами окружности, то треугольник AOB – равнобедренный, и угол ABO равен углу OAB. Поскольку угол AOC является внешним углом треугольника AOB, то справедливы равенства

      Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.

      Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

Рис. 6

      В этом случае справедливы равенства

и теорема 1 в этом случае доказана.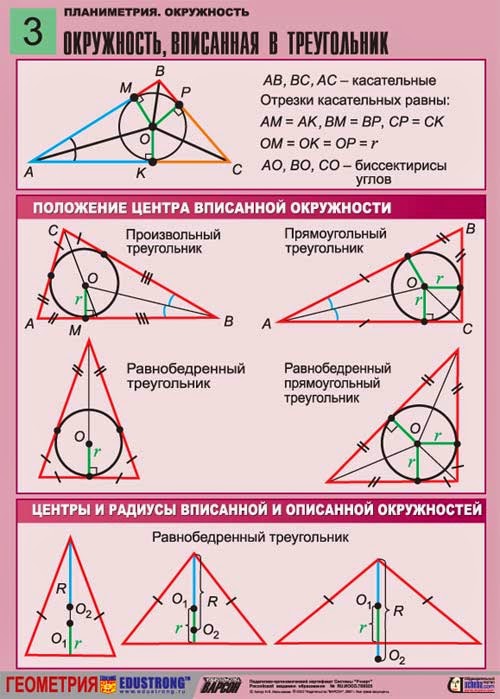

      Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

Рис. 7

      В этом случае справедливы равенства

что и завершает доказательство теоремы 1.

      Теорема 2. Величина угла, образованного пересекающимися хордами хордами, равна половине суммы величин дуг, заключённых между его сторонами.

      Доказательство. Рассмотрим рисунок 8.

Рис. 8

      Нас интересует величина угла AED, образованного пересекающимися в точке E хордами AB и CD. Поскольку угол AED – внешний угол треугольника BED, а углы CDB и ABD являются вписанными углами, то справедливы равенства

что и требовалось доказать.

      Теорема 3. Величина угла, образованного секущими секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.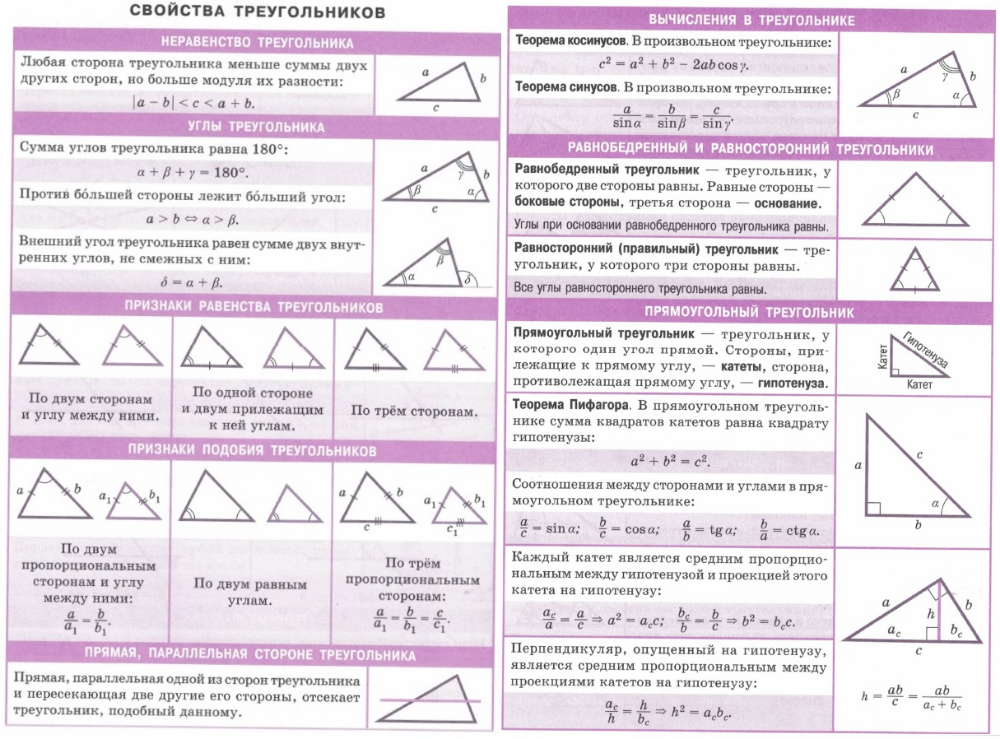

      Доказательство. Рассмотрим рисунок 9.

Рис. 9

      Нас интересует величина угла BED, образованного пересекающимися в точке E секущими AB и CD. Поскольку угол ADC – внешний угол треугольника ADE, а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства

что и требовалось доказать.

      Теорема 4. Величина угла, образованного касательной и хордой касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.

      Доказательство. Рассмотрим рисунок 10.

Рис. 10

      Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр, проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства

что и требовалось доказать

      Теорема 5.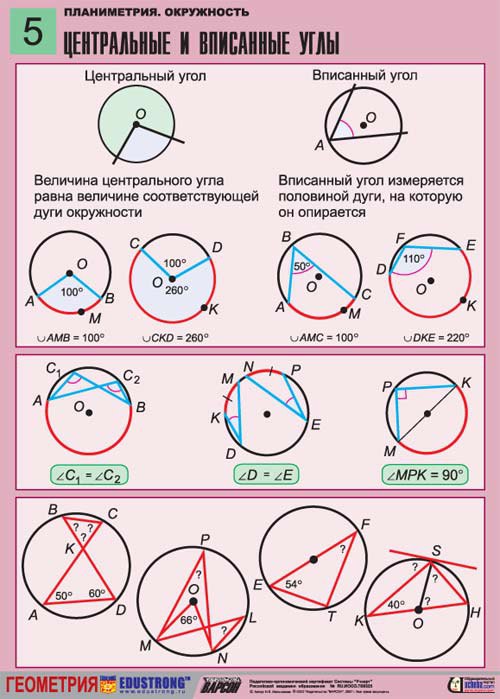 Величина угла, образованного касательной и секущей касательной и секущей, равна половине разности величин дуг, заключённых между сторонами этого угла.

      Доказательство. Рассмотрим рисунок 11.

Рис. 11

      Нас интересует величина угла BED, образованного касательной AB и секущей CD. Заметим, что угол BDC – внешний угол треугольника DBE, а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB, в силу теоремы 4, равны. Поэтому справедливы равенства

что и требовалось доказать.

      Теорема 6.Величина угла, образованного двумя касательными к окружности касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами.

      Доказательство. Рассмотрим рисунок 12.

Рис. 12

      Нас интересует величина угла BED, образованного касательными AB и CD. Заметим, что углы BOD и BED в сумме составляют   π радиан.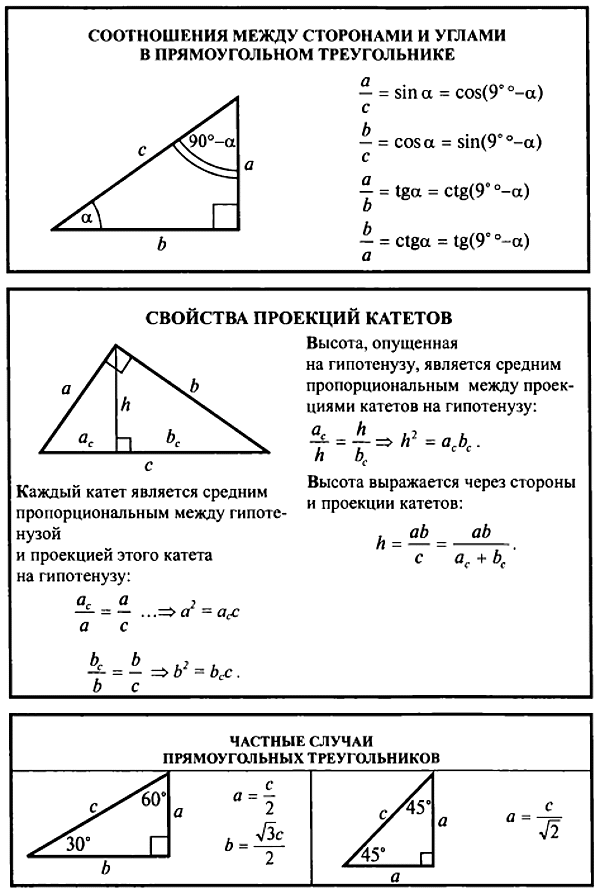 Поэтому справедливо равенство

α = π – γ .

      Далее получаем

что и требовалось доказать.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

По какой формуле находят углы? Примеры

Прежде чем изучать формулы для нахождения углов, давайте посмотрим, в каких ситуациях нам может понадобиться использовать эти формулы. Существуют разные формулы нахождения углов в зависимости от имеющихся данных. Давайте изучим формулы нахождения углов на каждом конкретном случае здесь.

• Чтобы найти недостающий угол в многоугольнике, мы используем формулу суммы внутренних углов.
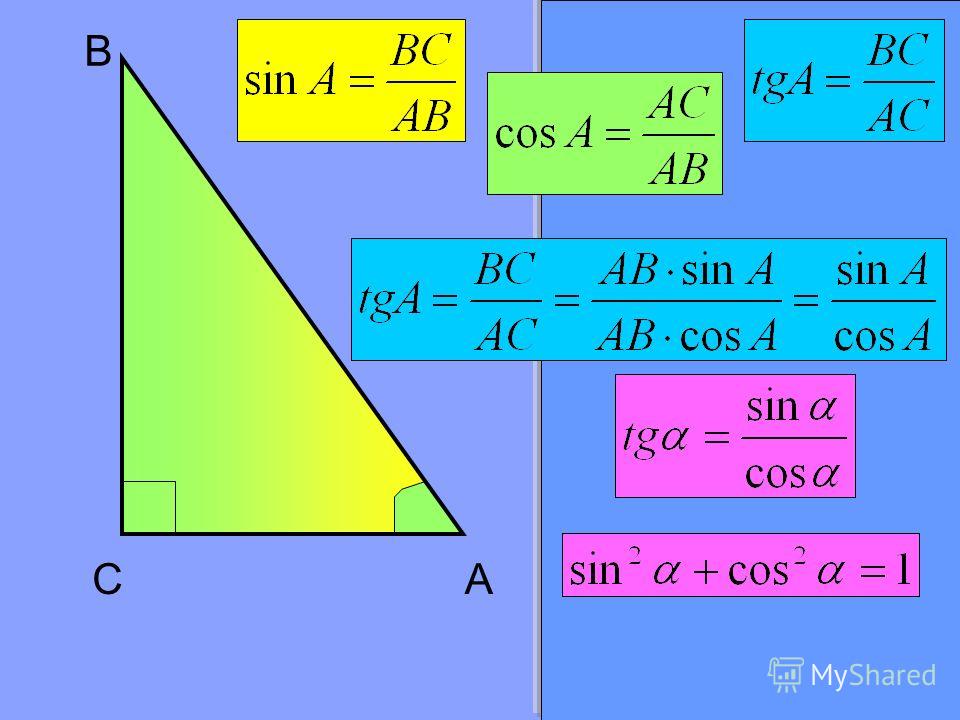
• Чтобы найти недостающий угол в прямоугольном треугольнике, мы используем тригонометрические отношения.
• Чтобы найти недостающие углы в непрямоугольном треугольнике, мы используем закон синусов и закон косинусов.

Что такое формула для нахождения углов?

Вот формулы для нахождения углов. Мы выбираем одну из этих формул, чтобы найти неизвестные углы в зависимости от данной информации.

Название формулы	Формула	Как найти неизвестные углы?
Сумма внутренних углов многоугольника с n сторонами	180 (n-2) градусов	Найдите сумму всех внутренних углов, используя эту формулу, и вычтите из нее сумму всех известных углов, чтобы найти неизвестный внутренний угол.
sin, cos и tan	sin θ = противоположность / гипотенуза cos θ = смежный / гипотенуза tan θ = напротив / рядом	Используйте одно из этих тригонометрических соотношений в зависимости от того, какие две стороны доступны для нахождения неизвестного угла.
Закон синусов	а/sin A = b/sin B = c/sin C Здесь A, B и C — углы треугольника, а a, b и c — их противоположные стороны.	Закон синусов используется для нахождения неизвестных углов, когда нам даны а) две стороны и невключенный угол (или) б) два угла и невключенная сторона.
Закон косинусов	a 2  = b 2  + c 2  — 2bc cos A b 2  = c 2  + a 2  — 2ca cos B c 2  = a 2  + b 2  — 2ab cos C Здесь A, B и C — углы треугольника, а a, b и c — их противоположные стороны.	Закон косинусов используется для нахождения неизвестных углов, когда нам дано а) с трех сторон (или) б) две стороны и угол между ними.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запись на бесплатный пробный урок

Примеры использования формулы для нахождения углов

Пример 1:  Найдите пятый внутренний угол пятиугольника, если четыре его внутренних угла равны 108°, 120°, 143° и 97°.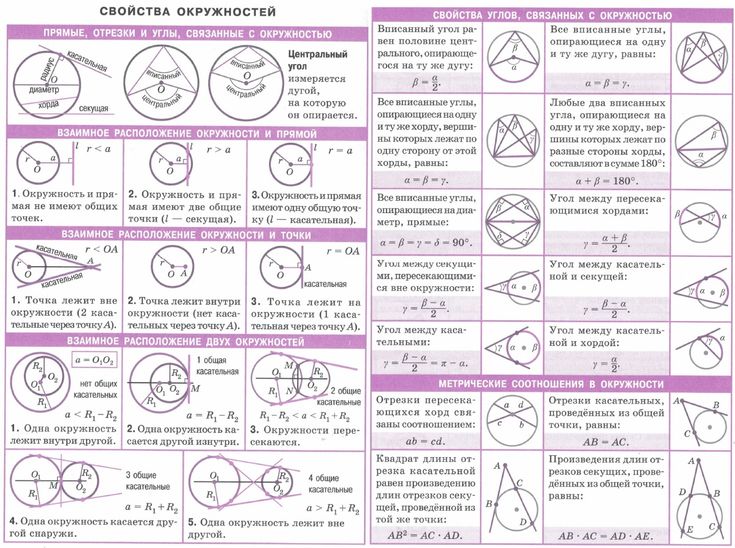

Решение:

Количество сторон пятиугольника равно, n = 5.

Сумма всех 5 внутренних углов пятиугольника = 180 (n -2)° = 180 (5 — 2)° = 540°.

Сумма данных 4 внутренних углов = 108°+ 120°+ 143°+ и 97°= 468°.

Итак, пятый внутренний угол = 540° — 468° = 72°.

Ответ: Пятый внутренний угол данного пятиугольника = 72°.

Пример 2:  Найдите угол при вершине C в следующем треугольнике, используя одну из формул для нахождения углов. Округлите ответ до ближайшего целого числа.

Решение:

Найти: угол при С, равный θ.

Дано, что AB = 6 = Противоположная сторона θ.

BC = 8 = Смежная сторона θ.

Поскольку мы знаем как противоположные, так и смежные стороны θ, мы используем формулу тангенса θ, чтобы найти θ.

тангенс θ = противоположный/прилегающий

тангенс θ = 6/8 = 0,75

θ = тангенс ^-1  (0,75) 

Используя калькулятор,

θ ≈ 7 (округлено до ближайшего целого числа).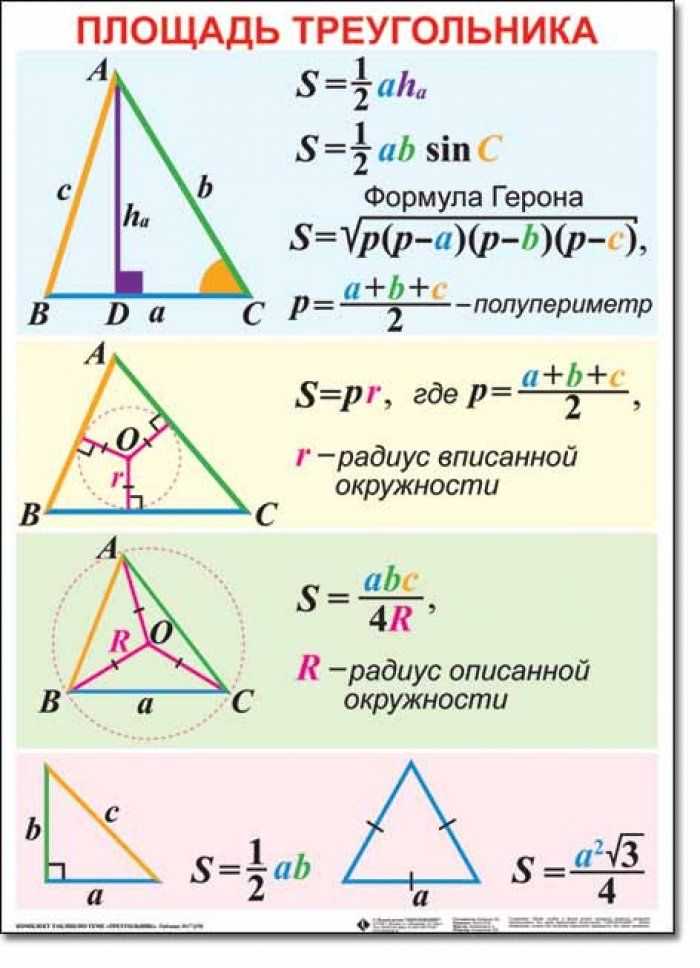

Ответ: Угол при C равен, θ = 37°

Пример 3:  Найдите угол при вершине A в следующем треугольнике, используя одну из формул для нахождения углов. Округлите ответ до ближайших десятых.

Решение:

Чтобы найти: Угол при A.

Мы знаем, что стороны, противоположные A, B и C, представлены буквами a, b и c соответственно. Итак имеем:

а = 10 дм; б = 7 дюймов; и c = 5 дюймов.

Поскольку мы знаем все три стороны, мы должны использовать закон косинусов, чтобы найти угол при A.

10 ²  = 7 ²  + 5 ²  — 2 (7)(5) cos A

100 = 49 + 25 — 70 cos A

100 = 74 — 70 cos A

70 cos A = 74 — 100

70 cos A = -26

cos A = -26 / 70

Используя калькулятор,

A ≈ 111,8° (округлено до десятых).

Ответ: Угол при A = 111,8°

По какой формуле находят углы?

В геометрии угол является важным измерением геометрической формы. Угол определяется как градус поворота вокруг точки пересечения двух линий или плоскостей, необходимый для приведения одной в соответствие с другой. Существуют различные виды углов, основанные на измерении угла. Измеряется в градусах или радианах. Угол — это фигура, образованная двумя линиями или лучами, которые расходятся из общей точки, называемой вершиной. При пересечении двух лучей, т. е. при проецировании полупрямых с общим концом, образуется угол. Теперь общие конечные точки называются вершинами, а лучи — рукавами.

 

Типы углов

 

1. Острый угол: Острый угол — это угол, который больше 0 градусов и меньше 90 градусов, т. е. он находится в диапазоне от 0° до 90° (исключая оба).
2. Прямой угол: Прямой угол называется углом, который составляет ровно 90 градусов.
3. Тупой угол: Тупой угол — это угол, который больше 90 градусов и меньше 180 градусов, т. е. находится в диапазоне от 9от 0° до 180°(исключая оба).
4. Прямой угол: Прямой угол называется углом, равным точно 180 градусам.
5. Угол рефлекса: Угол рефлекса — это угол, который больше 180 градусов и меньше 360 градусов, т. е. он находится в диапазоне от 180° до 360° (исключая оба).
6. Полный угол или Полный оборот: Полный угол называется углом, который составляет ровно 360 градусов.

Существуют и другие типы углов, такие как дополнительные углы, дополнительные углы, смежные и несмежные углы.

• Дополнительные углы: Два угла называются дополнительными, если их сумма является прямым углом, т. е. 90°.
• Дополнительные углы: Два угла называются дополнительными, если их сумма равна 180°.
• Смежные углы: Два угла называются смежными, если они имеют общую вершину и общее плечо.
• Несмежные углы: Два угла называются несмежными, если они не имеют общей вершины и общего плеча.

Формула для нахождения углов

Существуют различные типы формул для нахождения угла; некоторые из них — формула центрального угла, формула двойного угла, формула половинного угла, формула составного угла, формула внутреннего угла и т. д.

• Мы используем формулу центрального угла для определения угла сегмента, сделанного в круге.
• Мы используем формулу суммы внутренних углов, чтобы определить недостающий угол в многоугольнике.
• Мы используем тригонометрические отношения, чтобы найти недостающий угол прямоугольного треугольника.
• Мы используем закон синусов или закон косинусов, чтобы найти недостающий угол непрямоугольного треугольника.

Название формулы	Формула	Как найти неизвестный угол?
Центральный угол Формулы	θ = (S × 360 °)/2πr Здесь S — длина дуги, а r — радио0031 Подставьте значения длины дуги и радиуса окружности, чтобы определить угол сегмента, образуемого окружностью.
Сумма внутренних углов Формула	180 ° (n-2) Здесь n-число сторон полигона	. , сначала вычислите сумму всех внутренних углов, используя эту формулу, а затем вычтите из результата сумму всех известных углов.
Тригонометрические соотношения	SIN θ = противоположная сторона/Гипотенеза COS θ = Сторонняя сторона/Гипотенос TAN θ = противоположная сторона. прямоугольного треугольника, выберите одно из этих тригонометрических соотношений, чтобы найти неизвестный угол.
Закон синусов	a/sin A = b/sin B = c/sin C Здесь A, B и C — внутренние углы треугольника, а a, b и c — их противоположные стороны.	Когда мы знаем две стороны и не заключенный между ними угол (или) два угла и не заключенную между ними сторону, то закон синусов можно использовать для определения неизвестных углов треугольника.
Закон косийнсов	A 2 = B 2 + C 2 — 2BC COS A B 2 — 2BC COS A B 2 — 2BC COS A B 20081 = c 2 + a 2 – 2ca cos B c 2 = a 2 + b 2 – 2ab cos C Здесь A, B – внутренние углы a, B треугольника, а a, b и c — их противоположные стороны.	Если мы знаем три стороны (или) две стороны и угол между ними, то закон косинусов можно использовать для определения неизвестных углов треугольника.

Примеры вопросов

Вопрос 1: Найдите угол при вершине В данного треугольника, используя одну из тригонометрических формул нахождения углов.

 

Решение: 

Дано,

BC = 3 единицы = примыкающая сторона θ.

AC = 4 единицы = Противоположная сторона θ.

В этом случае мы знаем и противоположную, и прилежащую стороны θ. Следовательно, мы можем использовать формулу касательной, чтобы найти θ.

⇒ тангенс θ = противоположная сторона/прилегающая сторона

⇒ тангенс θ = 4/3

⇒ θ = tan ^-1 (4/3) ⇒ θ = 53,1°

Следовательно, угол при вершине B равен 53,1°.

Вопрос 2: Найдите углы при вершинах X и Y, если ∠Z = 35° и x = 3 дюйма, y = 8 дюймов и z = 3,5 дюйма.

 

Решение:

Дано,

∠Z = 35° и x = 6 дюймов, y = 3 дюйма и z = 3,5 дюйма

Поскольку мы знаем, все три стороны и угол, мы знаем, все три стороны и угол можно использовать формулу правила синусов.

Из формулы синусов имеем

x/sin X = y/sin Y = z/sin Z

Теперь

y/sin Y = z/sin Z

⇒ 3/sin Y = 3,5/ sin 35°

⇒ 3/sin Y = 3,5/0,574    {Так как, sin 35° = 0,574}

⇒ sin Y = 3 × (0,574/3,5) = 0,492

00 ⇒ 8 = 10002 ⇒ sin (0,492) = 29,47°

Мы знаем, что сумма трех углов треугольника равна 180°.

⇒ ∠X + ∠Y + ∠Z = 180°

⇒ ∠X + 29,47° + 35° = 180°

⇒ ∠X = 180° – 64,47° = 115,53°

Следовательно, ∠X = 115,53° и ∠Y = 29,47°.

Вопрос 3: Вычислите пятый внутренний угол пятиугольника, если четыре его внутренних угла равны 110°, 85°, 136° и 105°.

Решение:

Количество сторон пятиугольника (n) = 5.

Теперь сумма всех 5 внутренних углов пятиугольника = 180 (n -2)°  

= 180 ( 5 – 2)° = 540°.

Сумма данных 4 внутренних углов = 110°+ 85°+ 136°+ и 105°= 436°.

Итак, пятый внутренний угол = 540° – 436° = 104°

Таким образом, пятый внутренний угол пятиугольника равен 104°.

Вопрос 4: Определите значение y, а также меру углов на данной фигуре.

 

Решение:

Из данного рисунка видно, что (4y – 6)° и (3y + 5)° являются дополнительными углами, т. е. сумма (4y – 6) ° и (3y + 5)° равно 90°.

⇒ (4у – 6)° + (3у + 5)° = 90°

⇒ (7y – 1)° = 90°

⇒ 7y = 90° + 1° = 91°

⇒ y = 91°/7 = 13°

Сейчас , (4y – 6)° = (4 × 13 – 6)° = (52 – 6)° = 46°

(3y + 5)° = (3 × 13 + 5)° = (39 + 5)° = 44°

Вопрос 5. Найдите угол при вершине Q в данном треугольнике по одной из формул нахождения углов.

 

Решение:

Дано, p = QR = 6 см, q = PR = 9 см и r = PQ = 7 см.

Поскольку мы знаем все три стороны и угол, мы можем использовать формулу косинуса, чтобы найти вершину угла Q. ² = 6 ² + 7 ² – 2 (6)(7) cos Q

⇒ 81 = 36 + 49 – 84 cos Q

⇒ 81 = 85 – 8004 cos Q 90 = 81 – 85

⇒ 84 ​​cos Q = -4

⇒ cos Q = -4/84 = -1/21

⇒ ∠Q = cos ^-1 (-1/21) = 92,72°

Отсюда угол при вершине Q, ∠Q = 92,72°.

Вопрос 6: Вычислите угол отрезка, составленного из окружности, если длина дуги равна 12π, а радиус равен 9 см.