Геометрия формулы углов: Треугольник. Формулы и свойства треугольников.

Треугольник. Формулы и свойства треугольников.

Определение. Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.

Типы треугольников

По величине углов

1. Остроугольный треугольник — все углы треугольника острые.
2. Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
3. Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).

По числу равных сторон

1. Разносторонний треугольник — все три стороны не равны.
2. Равнобедренный треугольник — две стороны равны.
3. Равносторонним треугольник или правильный треугольник — все три стороны равны.

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

α + β + γ = 180°

В треугольнике против большей стороны лежит больший угол, и обратно.

Против равных сторон лежат равные углы:

если α > β, тогда a > b

если α = β, тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c	= 2R
sin α		sin β		sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a² = b² + c² — 2bc·cos α

b² = a² + c² — 2ac·cos β

c² = a² + b² — 2ab·cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Формулы сторон через медианы

a = 23√2(m_b² + m_c²) — m_a²

b = 23√2(m_a² + m_c²) — m_b²

c = 23√2(m_a² + m_b²) — m_c²

Медианы треугольника

Определение. Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника:

1. Медианы треугольника пересекаются в одной точке. (Точка пересечения медиан называется центроидом)

2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

   AOOD = BOOE = COOF = 21

3. Медиана треугольника делит треугольник на две равновеликие части

   S_∆ABD = S_∆ACD

   S_∆BEA = S_∆BEC

   S_∆CBF = S_∆CAF

4. Треугольник делится тремя медианами на шесть равновеликих треугольников.

   S_∆AOF = S_∆AOE = S_∆BOF = S_∆BOD = S_∆COD = S_∆COE

5. Из векторов, образующих медианы, можно составить треугольник.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 12√2b²+2c²-a²

m_b = 12√2a²+2c²-b²

m_c = 12√2a²+2b²-c²

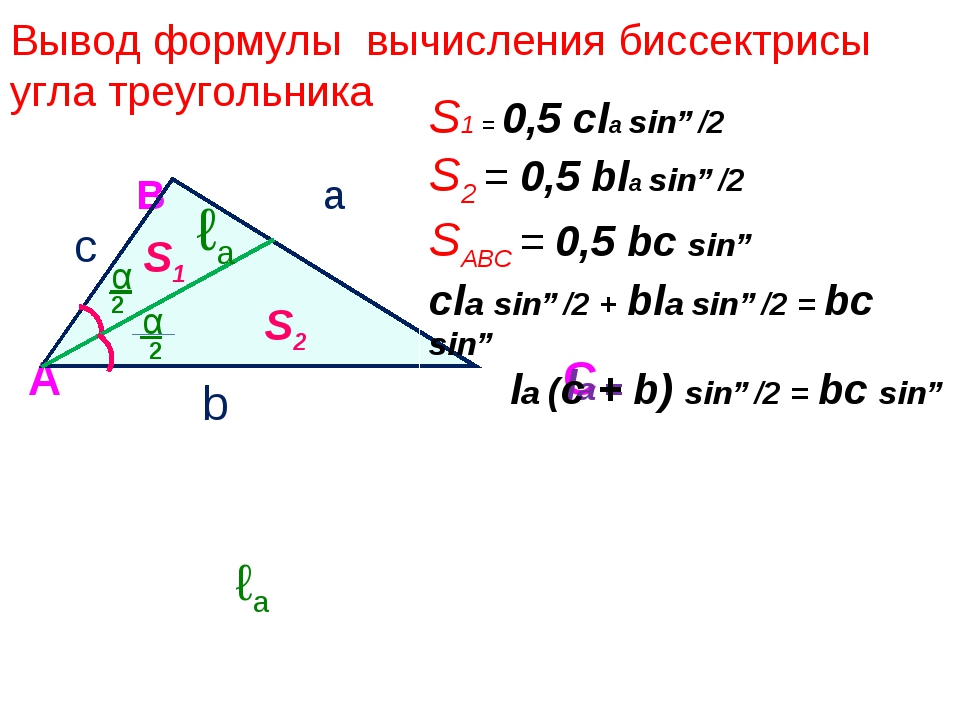
Биссектрисы треугольника

Определение. Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.

Свойства биссектрис треугольника:

1. Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности.

2. Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

   AEAB = ECBC

3. Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

   Угол между l_c и l_c‘ = 90°

4. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√bcp(p — a)b + c

l_b = 2√acp(p — b)a + c

l_c = 2√abp(p — c)a + b

где p = a + b + c2 — полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2bc cos α2b + c

l_b = 2ac cos β2a + c

l_c = 2ab cos γ2a + b

Высоты треугольника

Определение. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.

В зависимости от типа треугольника высота может содержаться

• внутри треугольника — для остроугольного треугольника;
• совпадать с его стороной — для катета прямоугольного треугольника;
• проходить вне треугольника — для острых углов тупоугольного треугольника.

Свойства высот треугольника

Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.

Если в треугольнике две высоты равны, то треугольник — равнобедренный.

h_a:h_b:h_c = 1a:1b:1c = (bc):(ac):(ab)

Формулы высот треугольника

Формулы высот треугольника через сторону и угол:

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Формулы высот треугольника через сторону и площадь:

h_a = 2Sa

h_b = 2Sb

h_c = 2Sc

Формулы высот треугольника через две стороны и радиус описанной окружности:

h_a = bc2R

h_b = ac2R

h_c = ab2R

Окружность вписанная в треугольник

Определение. Окружность называется вписанной в треугольник, если она касается всех трех его сторон.

Свойства окружности вписанной в треугольник

Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.

В любой треугольник можно вписать окружность, и только одну.

Формулы радиуса окружности вписанной в треугольник

Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру: Радиус вписанной в треугольник окружности через три стороны:

r = (a + b — c)(b + c — a)(c + a — b)4(a + b + c)

Радиус вписанной в треугольник окружности через три высоты:

Окружность описанная вокруг треугольника

Определение. Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.

Свойства окружности описанной вокруг треугольника

Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.

Вокруг любого треугольника можно описать окружность, и только одну.

Свойства углов

Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.

Формулы радиуса окружности описанной вокруг треугольника

Радиус описанной окружности через три стороны и площадь: Радиус описанной окружности через площадь и три угла:

R = S2 sin α sin β sin γ

Радиус описанной окружности через сторону и противоположный угол (теорема синусов):

R = a2 sin α = b2 sin β = c2 sin γ

Связь между вписанной и описанной окружностями треугольника

Если d — расстояние между центрами вписанной и описанной окружностей, то.

rR = 4 sinα2sinβ2sinγ2 = cos α + cos β + cos γ — 1

Средняя линия треугольника

Определение. Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.

Свойства средней линии треугольника

1. Любой треугольник имеет три средних линии

2. Средняя линия треугольника параллельна основанию и равна его половине.

MN = 12AC     KN = 12AB     KM = 12BC

MN || AC     KN || AB     KM || BC

3. Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольника

S_∆MBN = 14 S_∆ABC

S_∆MAK = 14 S_∆ABC

S_∆NCK = 14 S_∆ABC

4. При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.

∆MBN ∼ ∆ABC

∆AMK ∼ ∆ABC

∆KNC ∼ ∆ABC

∆NKM ∼ ∆ABC

Признаки. Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.

Периметр треугольника

Периметр треугольника ∆ABC равен сумме длин его сторон

P = a + b + c

Формулы площади треугольника

1. Формула площади треугольника по стороне и высоте
   
   Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

   S = 12a · h_a
   S = 12b · h_b
   S = 12c · h_c

2. Формула площади треугольника по трем сторонам
   

   Формула Герона

   S = √p(p — a)(p — b)(p — c)

   где p = a + b + c2 — полупериметр треугльника.
3. Формула площади треугольника по двум сторонам и углу между ними
   Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

   S = 12a · b · sin γ
   S = 12b · c · sin α
   S = 12a · c · sin β

4. Формула площади треугольника по трем сторонам и радиусу описанной окружности
5. Формула площади треугольника по трем сторонам и радиусу вписанной окружности
   Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

Равенство треугольников

Определение. Если два треугольника АВС и А₁В₁С₁ можно совместить наложением, то они равны.

Свойства. У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны)

Признаки равенства треугольников

Теорема 1.

Первый признак равенства треугольников — по двум сторонам и углу между ними

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Теорема 2.

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Теорема 3.

Третий признак равенства треугольников — по трем сторонам

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Подобие треугольников

Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.

∆АВС ~ ∆MNK => α = α₁, β = β₁, γ = γ₁ и ABMN = BCNK = ACMK = k,

где k — коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Второй признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Третий признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.

Свойства. Площади подобных треугольников относятся как квадрат коэффициента подобия:

S_∆АВСS_∆MNK = k²

Планиметрия (Геометрия на плоскости) — Математика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Треугольник

К оглавлению…

При решении задач по геометрии помимо всех геометрических формул и свойств, которые будут приведены ниже, нужно очень хорошо помнить основные формулы по тригонометрии. Укажем для начала несколько основных свойств различных типов углов:

• Смежные углы в сумме равны 180 градусов.
• Вертикальные углы равны между собой.

Теперь перейдем к свойствам треугольника. Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника:

Запомните также, что сумма любых двух сторон треугольника всегда больше третьей стороны. Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через сторону и высоту опущенную на неё:

Полупериметр треугольника находится по следующей формуле:

Формула Герона для площади треугольника:

Площадь треугольника через радиус описанной окружности:

Формула медианы (медиана — линия проведенная через некоторую вершину и середину противоположной стороны в треугольнике):

Свойства медиан:

• Все три медианы пересекаются в одной точке.
• Медианы  делят  треугольник  на  шесть  треугольников  одинаковой  площади.
• В точке пересечения медианы делятся в отношении 2:1, считая от вершин.

Свойство биссектрисы (биссектриса — линия, которая делит некоторый угол на два равных угла, т.е. пополам):

Важно знать: Центр вписанной в треугольник окружности лежит на пересечении биссектрис (все три биссектрисы пересекаются в этой одной точке). Формулы биссектрисы:

Основное свойство высот треугольника (высота в треугольнике — линия проходящая через некоторую вершину треугольника перпендикулярно противоположной стороне):

Все три высоты в треугольнике пересекаются в одной точке. Положение точки пересечения определяется типом треугольника:

• Если треугольник остроугольный, то точка пересечения высот находится внутри треугольника.
• В прямоугольном треугольнике высоты пересекаются в вершине прямого угла.
• Если треугольник тупоугольный, то точка пересечения высот находится за пределами треугольника.

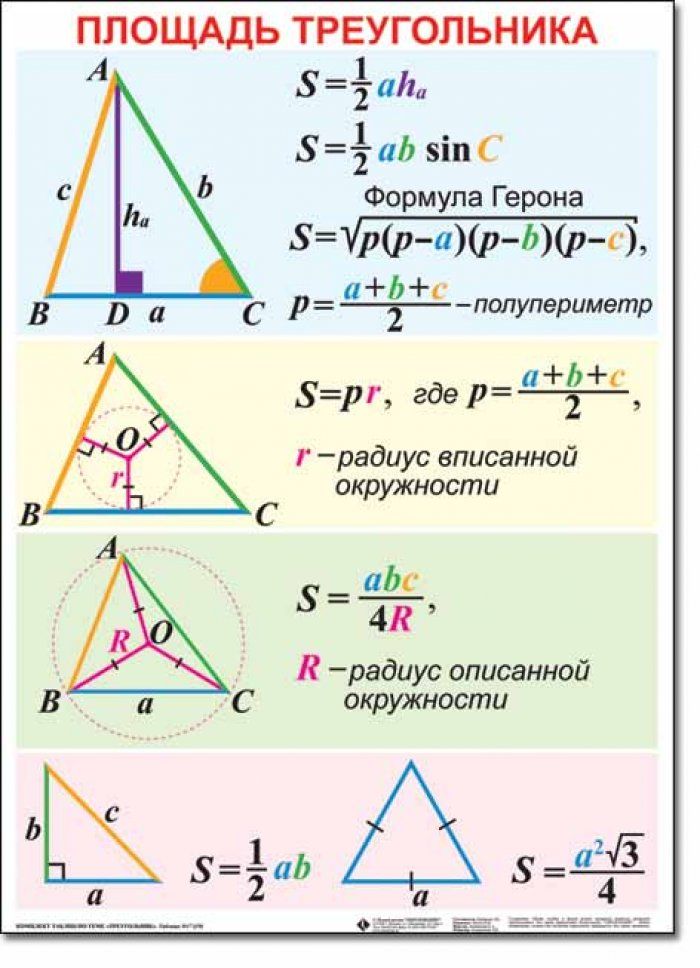
Формула высоты:

Еще одно полезное свойство высот треугольника:

Теорема косинусов:

Теорема синусов:

Центр окружности описанной около треугольника лежит на пересечении посерединных перпендикуляров. Все три посерединных перпендикуляра пересекаются в одной этой точке. Посерединный перпендикуляр — линия проведенная через середину стороны треугольника перпендикулярно ей.

Радиус окружности, вписанной в правильный треугольник:

Радиус окружности, описанной около правильного треугольника:

Площадь правильного треугольника:

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):

Радиус окружности, вписанной в прямоугольный треугольник:

Радиус окружности, описанной вокруг прямоугольного треугольника:

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого.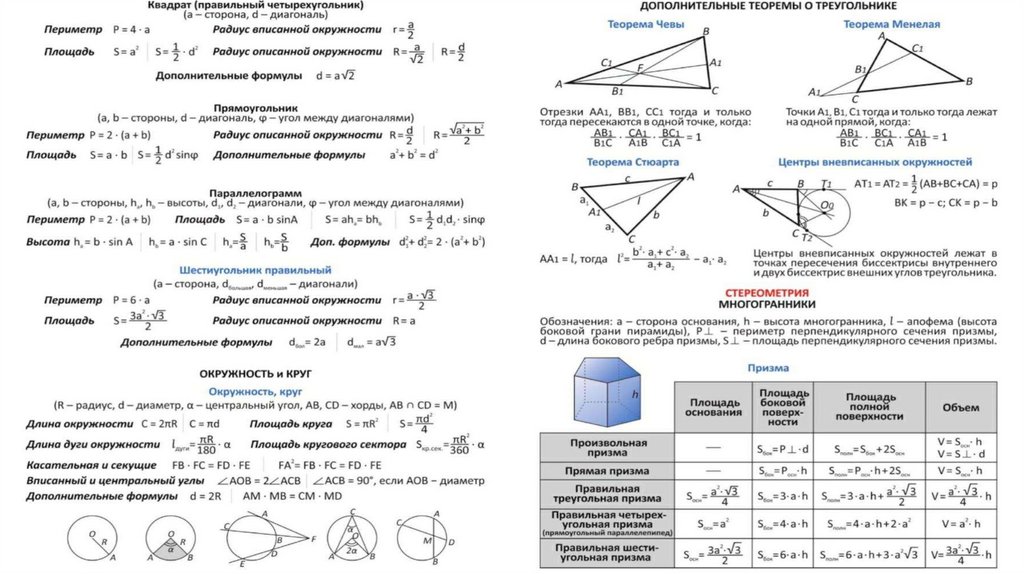 В подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т.п.) пропорциональны. Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов. Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников. Отношение периметров подобных треугольников равно коэффициенту подобия. Отношение длин биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия. Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Признаки подобия треугольников:

• По двум углам. Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
• По двум сторонам и углу между ними. Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, то треугольники подобны.
• По трём сторонам. Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны.

 

Трапеция

К оглавлению…

Трапеция — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна. Длина средней линии трапеции:

Площадь трапеции:

Некоторые свойства трапеций:

• Средняя линия трапеции параллельна основаниям.
• Отрезок,  соединяющий  середины  диагоналей  трапеции,  равен  полуразности  оснований.
• В трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон находятся на одной прямой.
• Диагонали трапеции разбивают её на четыре треугольника. Треугольники, сторонами которых являются основания — подобны, а треугольники, сторонами которых являются боковые стороны — равновелики.
• Если сумма углов при любом основании трапеции равна 90 градусов, то отрезок соединяющий середины оснований равен полуразности оснований.
• У равнобедренной трапеции углы при любом основании равны.
• У равнобедренной трапеции диагонали равны.
• В равнобедренной трапеции высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований.

 

Параллелограмм

К оглавлению…

Параллелограмм — это четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых. Площадь параллелограмма через сторону и высоту опущенную на неё:

Площадь параллелограмма через две стороны и угол между ними:

Некоторые свойства параллелограмма:

• Противоположные стороны параллелограмма равны.
• Противоположные углы параллелограмма равны.
• Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
• Сумма углов, прилежащих к одной стороне, равна 180 градусов.
• Сумма всех углов параллелограмма равна 360 градусов.
• Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.

 

Квадрат

К оглавлению…

Квадрат — четырёхугольник, у которого все стороны равны, а все углы равны по 90 градусов. Площадь квадрата через длину его стороны:

Площадь квадрата через длину его диагонали:

Свойства квадрата – это все свойства параллелограмма, ромба и прямоугольника одновременно.

 

Ромб и прямоугольник

К оглавлению…

Ромб — это параллелограмм, у которого все стороны равны. Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):

Свойства ромба:

• Ромб является параллелограммом. Его противолежащие стороны попарно параллельны.
• Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
• Диагонали ромба являются биссектрисами его углов.

Прямоугольник — это параллелограмм, у которого все углы прямые (равны 90 градусам). Площадь прямоугольника через две смежные стороны:

Свойства прямоугольника:

• Диагонали прямоугольника равны.
• Прямоугольник является параллелограммом — его противоположные стороны параллельны.
• Стороны прямоугольника являются одновременно его высотами.
• Квадрат диагонали прямоугольника равен сумме квадратов двух его не противоположных сторон (по теореме Пифагора).
• Около любого прямоугольника можно описать окружность, причем диагональ прямоугольника равна диаметру описанной окружности.

 

Произвольные фигуры

К оглавлению…

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т. е. в том числе для любых треугольников):

Обобщённая теорема Фалеса: Параллельные прямые отсекают на секущих пропорциональные отрезки.

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

 

Многоугольники

К оглавлению…

Выпуклым многоугольником называется многоугольник, обладающий тем свойством, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Сумма внутренних углов плоского выпуклого n-угольника равна:

Число диагоналей всякого многоугольника равно (где: n – число сторон):

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны. Внутренний угол правильного многоугольника равен:

Центральный угол правильного n-угольника равен:

Площадь правильного многоугольника с числом сторон n, длиной стороны a, радиусом описанной окружности R, полупериметром p и радиусом вписанной окружности r, может быть рассчитана по следующим формулам:

 

Окружность

К оглавлению. ..

Свойство касательных:

Свойство хорды:

Теорема о пропорциональных отрезках хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и секущих:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

Формулы треугольника, с примерами

Формулы площади треугольника

1. По стороне и проведенной к ней высоте

   

2. По двум сторонам и углу между ними

   

3. Формула Герона

   

где – полупериметр треугольника

4. Через радиусы вписанной и описанной окружностей

   

где – полупериметр треугольника, – радиус вписанной окружности;

   

здесь – радиус описанной окружности.

Теоремы треугольника

ТЕОРЕМА Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними

   

ТЕОРЕМА Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности:

   

ТЕОРЕМА Теорема тангенсов. Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов:

   

Равносторонний треугольник со стороной :

– радиус описанной окружности,

– радиус вписанной окружности,

– высота, совпадающая с медианой и биссектрисой,

– площадь треугольника.

Формулы прямоугольного треугольника

В прямоугольном треугольнике с , гипотенузой и катетами и

   

   

ТЕОРЕМА Теорема Пифагора. Квадрат гипотенузы равен сумме квадратов катетов.

   

Примеры решения задач

ПРИМЕР 1

Задание	В равностороннем треугольнике со стороной см найти площадь и радиусы вписанной и описанной окружностей.
Решение	Площадь равностороннего треугольника найдем по формуле , подставив :     Тогда искомые радиусы вписанной и описанной окружностей
Ответ	см см см.

ПРИМЕР 2

Задание	В треугольнике стороны см см, а . Найти все стороны и все углы треугольника .
Решение	Сделаем рисунок. Воспользуемся теоремой синусов и найдем угол :         откуда , т.е. . Следовательно, треугольник является прямоугольным. Значит,     Найдем сторону по теореме Пифагора: см
Ответ	см.

Читайте также:

Египетский треугольник

Неравенство треугольника

Виды треугольников

Тупоугольный треугольник

Остроугольный треугольник

Признаки подобия треугольников и свойства

Смежные и вертикальные углы. Треугольник. Равнобедренный треугольник. Медиана, биссектриса, высота, средняя линия

Факт 1.
\(\bullet\) Смежные углы — два угла, имеющие общую сторону, а две другие стороны являются продолжениями одна другой.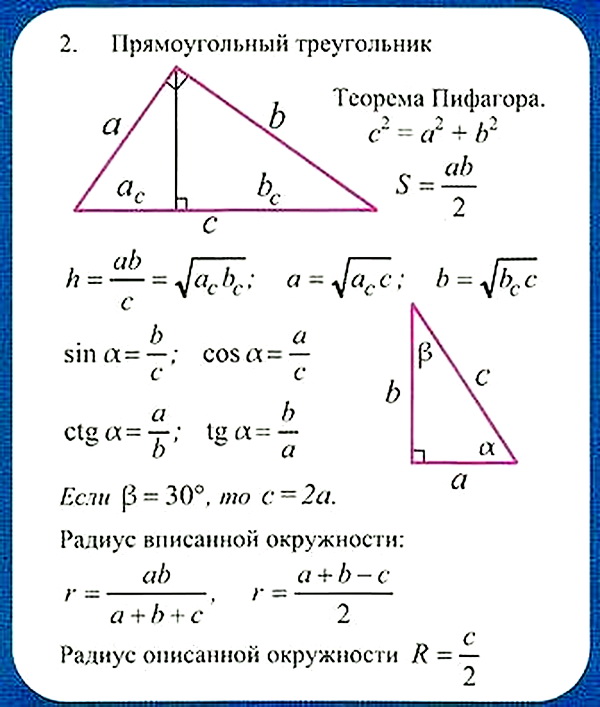 \circ\).
\(\bullet\) Внешний угол \(\angle BCD\) треугольника \(ABC\) равен сумме двух углов треугольника, не смежных с ним.

 

Факт 4.
\(\bullet\) Биссектрисы смежных углов взаимно перпендикулярны.
\(\bullet\) Биссектрисы односторонних углов при параллельных прямых взаимно перпендикулярны.

 

Факт 5.
\(\bullet\) Прямая теорема: каждая точка биссектрисы угла равноудалена от сторон угла.
\(\bullet\) Обратная теорема: если точка равноудалена от сторон угла, то она лежит на его биссектрисе.

 

Факт 6.
\(\bullet\) Равнобедренный треугольник – треугольник, у которого две стороны равны. Третья сторона треугольника называется основанием.
Первое свойство равнобедренного треугольника:

Второе свойство равнобедренного треугольника: углы при основании равны.

Первый признак равнобедренного треугольника: если у треугольника два угла равны, то он равнобедренный.
Второй признак равнобедренного треугольника: если у треугольника совпадают высота и медиана (высота и биссектриса или медиана и биссектриса), проведенные к одной и той же стороне, то этот треугольник является равнобедренным.

 

Факт 7.
\(\bullet\) Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.

 

Факт 8.
\(\bullet\) Медианы в треугольнике точкой пересечения делятся в отношении \(2:1\), считая от вершины.

 

Факт 9.
\(\bullet\) Медиана треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.

 

Факт 10.
\(\bullet\) Высота, проведенная из вершины прямого угла треугольника, делит его на два треугольника, подобных исходному.
\(\bullet\) Квадрат этой высоты равен произведению отрезков, на которые она делит гипотенузу.

 

Факт 11.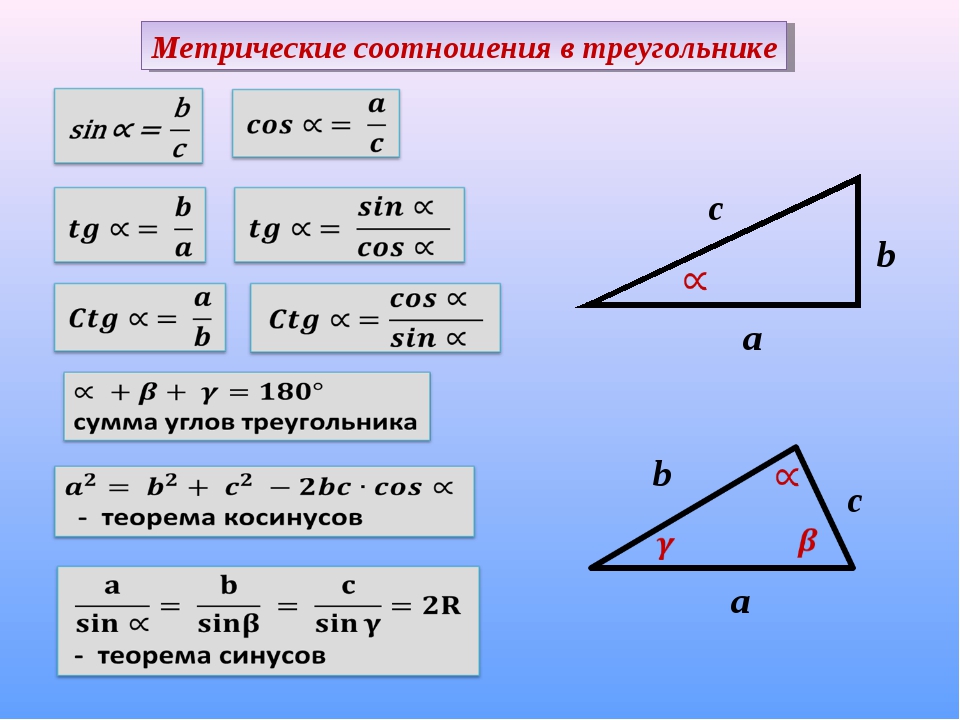 \circ\).

Вертикальные углы равны: \(\alpha=\gamma\).

 

Определения

Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой (называемых вершинами треугольника), и отрезков, соединяющих эти точки (называемых сторонами треугольника). Треугольник со своей внутренностью будем сокращенно называть также треугольником.

Угол (внутренний) треугольника – угол, образованный вершиной треугольника и двумя его сторонами.

 

Теоремы: признаки равенства треугольников

1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

 

2. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.

 

3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.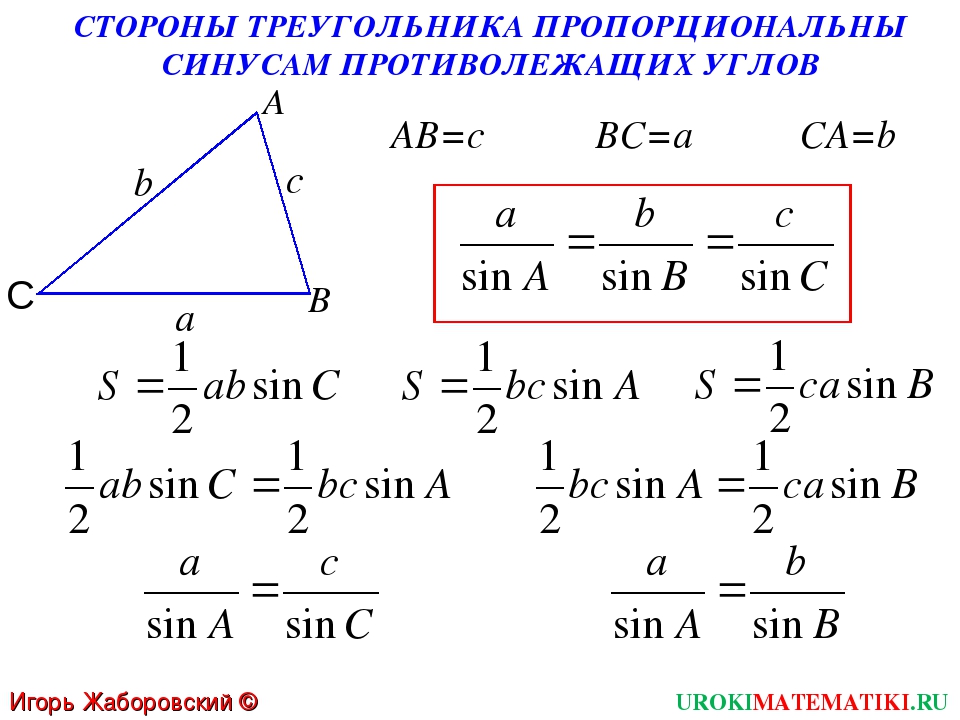 \circ\).

 

Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

 

Замечание

Если в треугольнике один угол тупой, то высоты, опущенные из вершин острых углов, упадут не на сторону, а на продолжение стороны (рис. 1).

 

Теорема

В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).

 

\[{\Large{\text{Параллельные прямые}}}\]

Определение

Две различные прямые на плоскости называются параллельными, если они не пересекаются.

 

Замечание

Заметим, что на плоскости существует три вида взаимного расположения прямых: совпадают, пересекаются и параллельны.

 

Аксиома параллельных прямых

Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.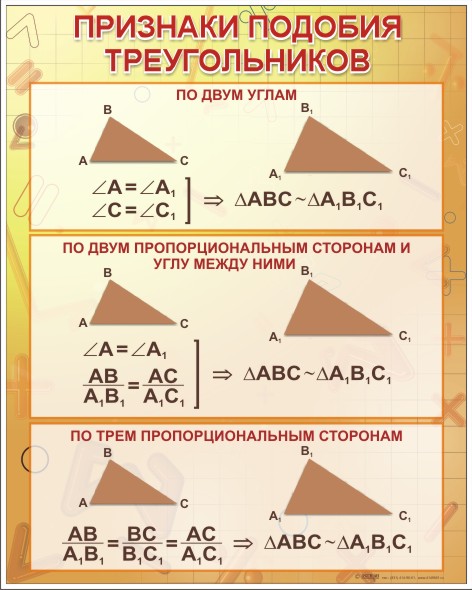 \circ\), то \(\angle 4 = \angle 1 + \angle 2\), что и требовалось доказать.  

\[{\Large{\text{Равнобедренный треугольник}}}\]

Определения

Треугольник называется равнобедренным, если две его стороны равны.
Эти стороны называются боковыми сторонами треугольника, а третья сторона — основанием.

 

Треугольник называется равносторонним, если все его стороны равны.
Равносторонний треугольник, очевидно, является и равнобедренным.

 

Теорема

В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

 

Доказательство

Пусть \(ABC\) – равнобедренный треугольник, \(AB = BC\), \(BD\) – биссектриса (проведённая к основанию).

Рассмотрим треугольники \(ABD\) и \(BCD\): \(AB = BC\), \(\angle ABD = \angle CBD\), \(BD\) – общая. Таким образом, \(\triangle ABD = \triangle BCD\) по двум сторонам и углу между ними.

Из равенства этих треугольников следует, что \(AD = DC\), следовательно, \(BD\) – медиана.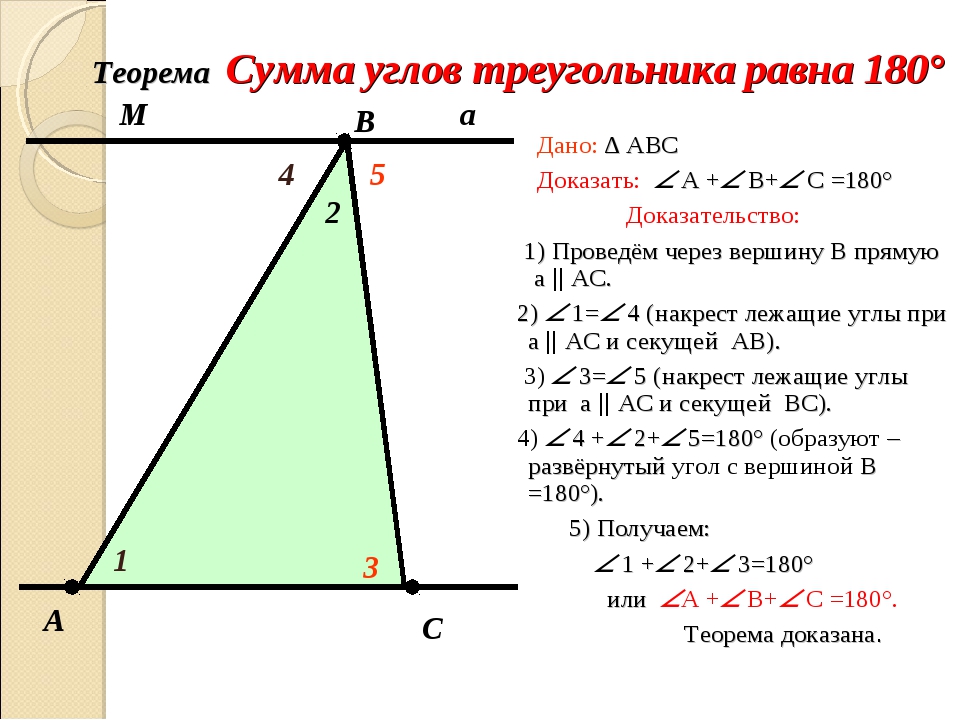 \circ = \angle CDB\), то есть \(BD\) – высота.

 

Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

 

Теорема

В равнобедренном треугольнике углы при основании равны.

 

Доказательство

Проведем биссектрису \(BD\) (см. рисунок из предыдущей теоремы). Тогда \(\triangle ABD=\triangle CBD\) по первому признаку, следовательно, \(\angle A=\angle C\).

 

Теоремы: признаки равнобедренного треугольника

1. Если в треугольнике два угла равны, то треугольник равнобедренный.

 

2. Если в треугольнике высота является медианой или биссектрисой, то треугольник равнобедренный.  

Теорема о соотношении между сторонами и углами треугольника

В треугольнике против большей стороны лежит больший угол.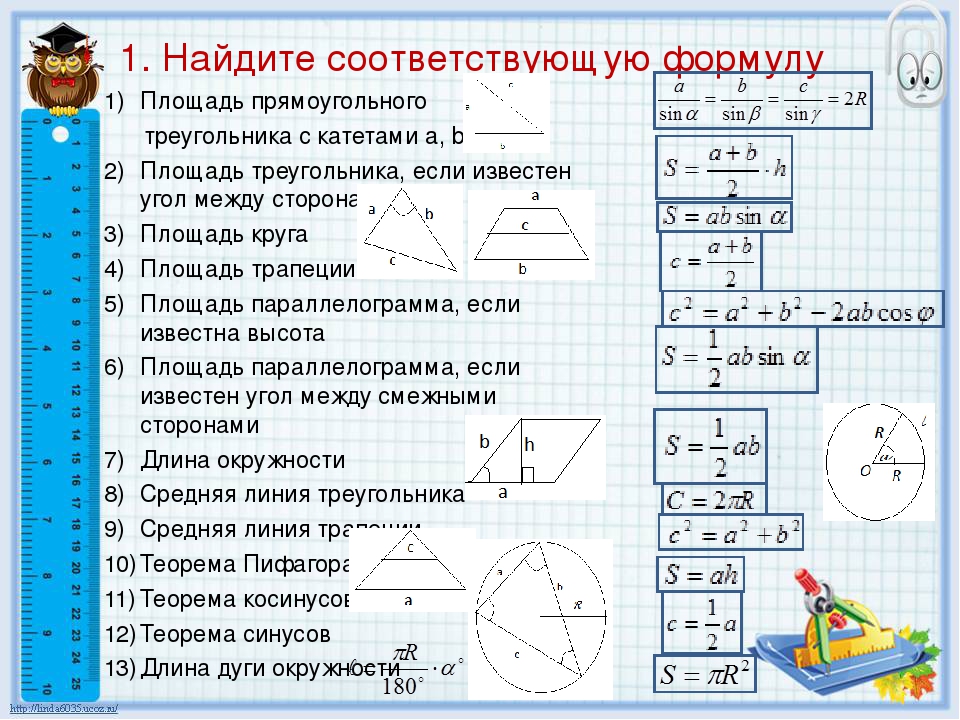 \circ\).

 

Тригонометрические и геометрические преобразования, sin(A + B), sin(A

Коэффициенты для суммы углов

Как демонстрируют различные примеры, иногда нам нужны значения углов, отличных от 0, 30, 45, 60 и 90 градусов. В этой главе вы должны научиться двум вещам:
1. sin(A + B) не является равным sinA + sinB. В этом случае не срабатывает простое раскрытие скобок, как в алгебре.
2. Формулу, по которой вычисляется sin(A + B).

Во-первых, покажем, что раскрытие скобок не «срабатывает». Пусть A = 30 градусов и B = 45 градусов. Sin30 равен 0.5. Sin45 равен 0.7071. Складывая, получим 1.2071.

Вы знаете, что ни синус, ни косинус не может быть больше 1. Почему? Потому что в дробях, по которым они вычисляются, гипотенуза выступает в качестве знаменателя. Самое большее значение мы получим, если числитель равен знаменателю. Синус или косинус не может быть больше 1, и поэтому значение 1,2071 не верно.

Нахождение синуса, косинуса или тангенса полного угла (A + B)

Нахождение sin(A + B)

Самый простой способ найти sin (A + B) — используя геометрическое построение, показанное на рисунке.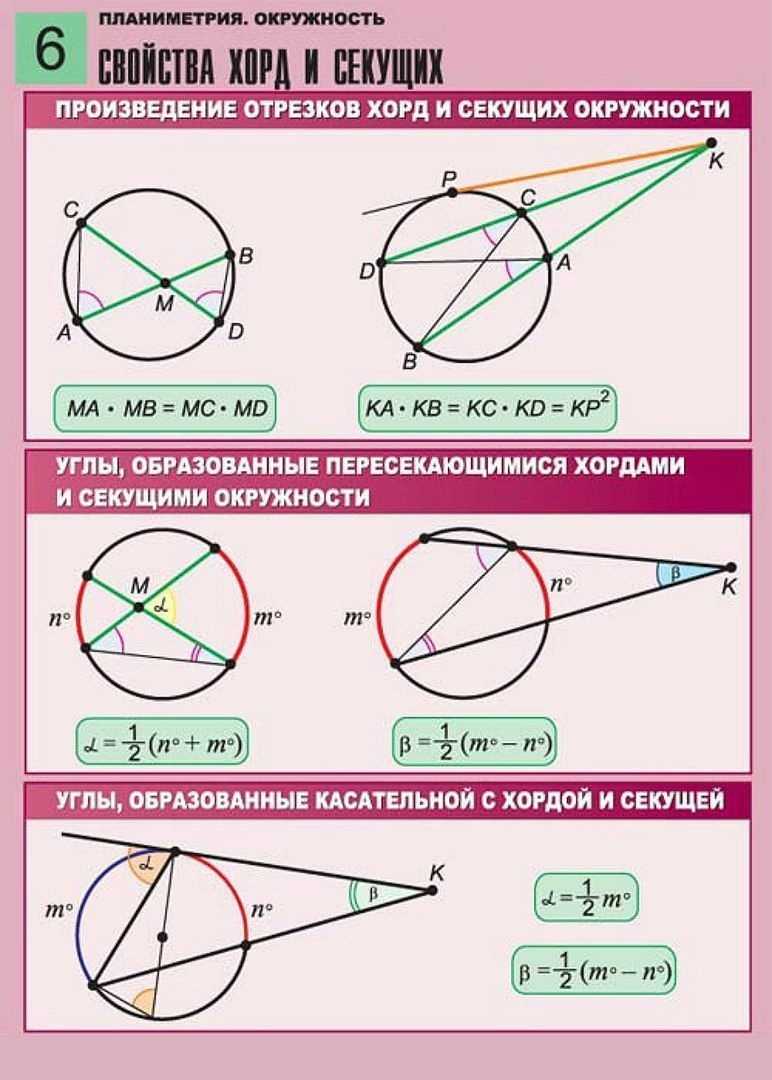 Большой угол (A + B), состоит из двух маленьких, А и В. Рисунок (1) показывает, что противоположная сторона состоит из двух частей. Нижняя часть, разделенная линией между углами (2), есть синус А. Линия между двумя углами, разделенная гипотенузой (3), есть косинус B. Умножаем их. Средняя линия и в числителе, и в знаменателе, поэтому они сокращаются, оставляя нижнюю часть противоположной стороны над гипотенузой (4).

Обратите внимание на маленький прямоугольный треугольник (5). Затененный угол есть A, потому что линия на его верхней части параллельна линии в основании. Подобные прямоугольные треугольники с углом А показывают, что верхний угол, отмеченный А также равен оригинальному углу А. Верхняя часть противоположной (6) над длинной, заштрихованный треугольник является соs А. Противоположный над основной гипотенузой (7) есть синус. Поскольку стороны с пометкой «противоположные» (7) и в числителе и знаменателе, когда cos и sin перемножаются, cosAsinB есть верхняя часть оригинального противоположного — для (A + B) — разделенные основной гипотенузой (8).

Теперь, сложим это все вместе (9). Sin(A + B) есть две части противоположного — все разделенные гипотенузой (9). Записывая это в тригонометрическую форму: sin(A + B) = sin A cos B + cos A sin B.

Нахождение cos(A + B)

Очень похожая конструкция находит формулу для косинуса угла созданного двумя углами, сложенными вместе.

Используя ту же самую конструкцию (1), обратите внимание, что смежная сторона является полной линией основания (для соs A), c частью, которая вычитается справа. Каждая часть должна использовать тот же знаменатель, гипотенузу (A + B) треугольника.

Полная линия основания, разделенная линией между углами A и E есть cosA (2). Эта разделяющая линия, деленная гипотенузой (A + B) треугольника, есть cos B (3). Поэтому, полная линия основания, деленная гипотенузой есть произведение cosAcosB (4).

Теперь, небольшая часть, которая должна быть вычтена. Заштрихованная часть (5) представляет sinA, который умножается заштрихованной частью (6) есть sin E, который есть другой частью и , которая нам нужна (7).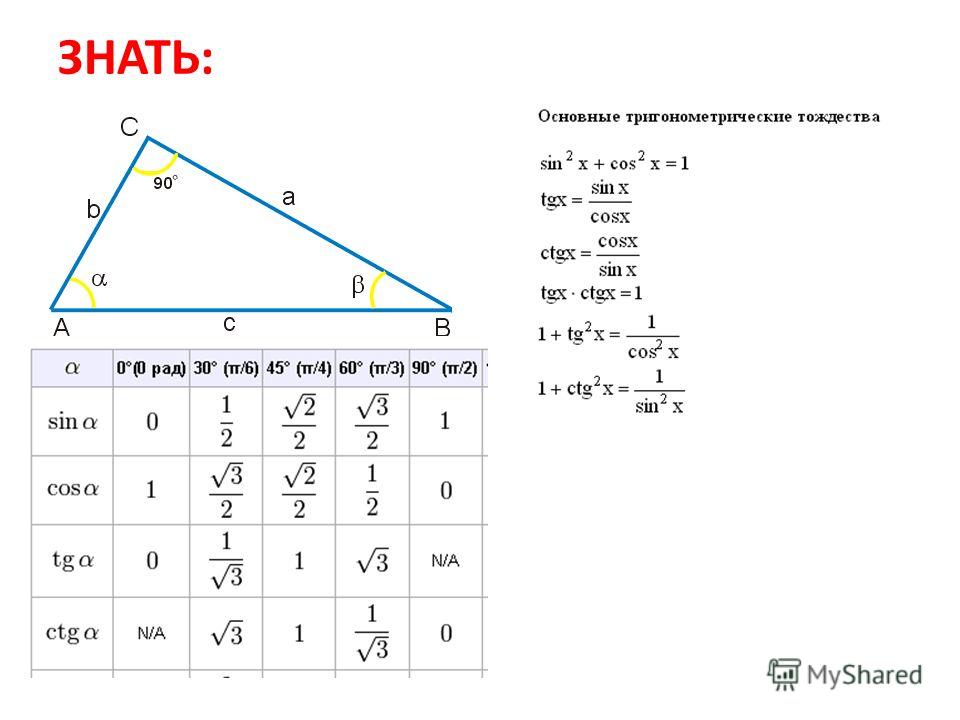 Вычитание дает соs (А + В) (8), поэтому формула, которая нам нужна:
            cos(A + B) = cos A cos B — sin A sin B

Нахождение tan(A + B)

Полный геометрический вывод формулы для tg (A + B) является сложным. Проще всего вывести его из двух формул, которые мы уже сделали. В любом угле, тангенс равен синус, деленному на косинус. Используя тот факт, tan (A + B) = sin(A + B)/соs(A + B). Это выражение можно расширить к виду:
      tan(A + B) = [sin A cos B + cos A sin B]/[cos A cos B — sin A sin B]
Разделив верхнюю и нижнюю часть на cos A cos B, что превращает все члены в тангенсы, получаем:
            tan(A + B) = [tan A + tan B]/[1 — tan A tan B]

Коэффициенты для 75 градусов

Покажем коэффициенты синуса, косинуса и тангенса, подставляя в формулу суммы, и потом упрощая результат к своей простейшей форме, прежде чем находить суммы. После внесения основных замен в каждом конкретном случае, примерная работа в заштрихованной части, чтобы показать, как результат сводится к простейшей форме для оценки.

Если вы используете ваш карманный калькулятор для оценки, скорей всего, не имеет значения или вы упрщаете выражения сначала или просто пропускаете его! Все зависит от калькулятора: некоторые вычисля.т разницу, некоторые нет!

Коэффициенты углов, больших, чем 90 градусов

До сих пор рассматривалось соотношение острых углов (между 0 и 90 градусами). Другие треугольники с тупым углом (более 90 градусов) и до 180 градусов могут появиться в последующих задачах. Для упрощения классификации углов по размеру, они делятся на сектора (квадранты).

Квадрант есть четвертой частью круга. Так как круг делится на 360 градусов, квадранты имеют по 90 градусов. 0-90 градусов это первый квадрант, 90-180 — второй, 180-270 — третий и 270-360 — четвертый.

Используя линии, обозначающие границы квадранта, 0 или 360 это горизонталь направо, 90 — вертикально вверх, 180 — горизонталь слева и 270 сверху вниз. Теперь, используем этот метод для построения графиков.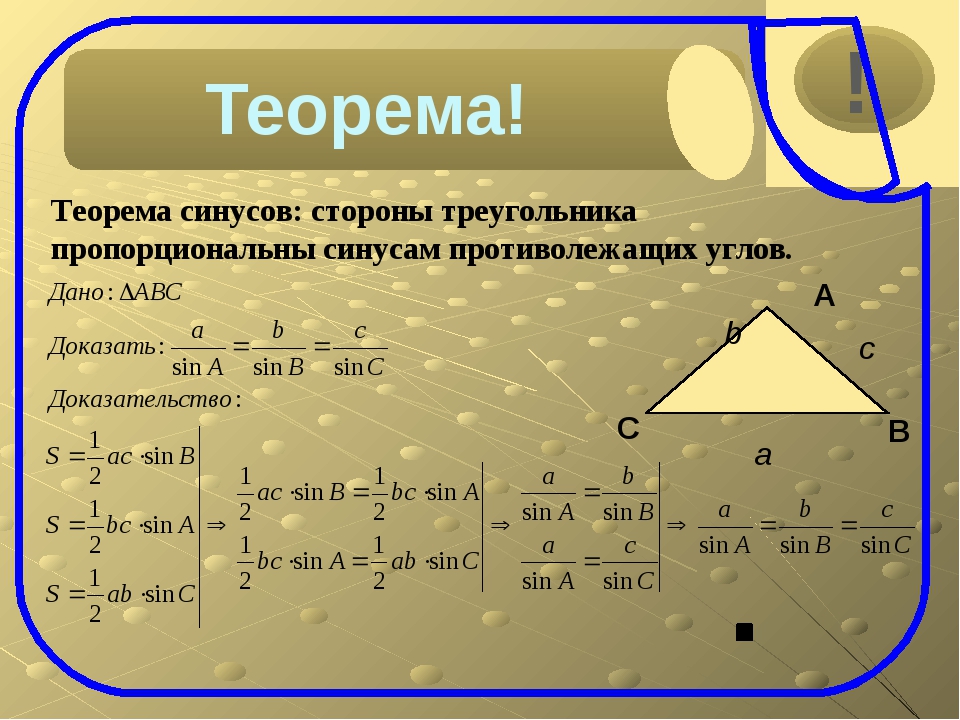

Большие углы определяется вектором вращения, начиная с нуля и вращением против часовой стрелки. Горизонтальные элементы х: положительные справа, отрицательные слева. Вертикальные элементы у: положительные вверх, отрицательные вниз. Вращающийся вектор является р. Таким образом, синус угла есть y/r, косинус х/r, и тангенс у/х. Вектор r — всегда положителен. Таким образом, знак отношения может быть вычислен для различных секторов.

Здесь приведены знаки для трех отношений в четырех квадрантах. Кроме того, как эквивалентный угол в первой четверти «переключается» когда вектор переходит из одного квадранта в другой. В первой четверти, стороны определены в соотношениях для синуса, косинуса и тангенса. При перемещении к большим углам в остальных секторах, противоположная сторона всегда есть вертикальная (у). То, что называется смежное, всегда есть горизонталью (х). Гипотенуза это всегда вращающийся вектор (r). Вы можете видеть картину как изменяются тригонометрические соотношения для углов.

Отношения в четырех квадрантах

Отношения для различных углов

Теперь у вас есть два пути получить формулы для различных углов. Во-первых, используя геометрическую конструкцию, такую, которая, например, была использована для суммы углов, реверсивную так, что (A — B) есть угол B вычитающийся из угла A.

В рассуждениях, аналогичных тем, которые были использованы для суммы углов, здесь представлены несколько сокращенные формулы для синуса и косинуса:
        sin(A — B) = sin A cos B — cos A sin B
and
        cos(A — B) = cos A cos B + sin A sin B
      Геометрическая конструкция

Формулы суммы и разницы

Второй способ нахождения формулы для разницы углов использует уже полученную формулу суммы, но делает B отрицательным. Из нашего исследования знаков для различных секторов, отрицательные углы с 1-го квадранта будут в 4 квадранте. Проводя эту подстановку, получим тот же результат, который был получен геометрически в предыдущем разделе.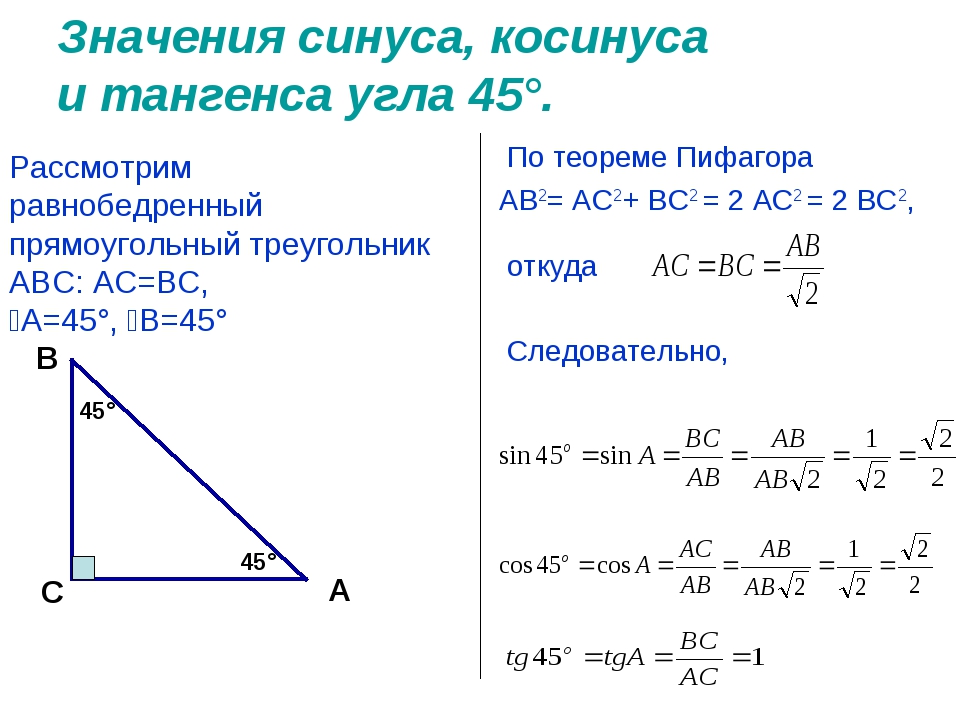

Поиск формулы тангенса проходит тем же методом, или заменой синуса и косинуса в формулах или более непосредственно, превращая tg(-B) = — tg B. В любом случае вы получите:
          tan(A — B) = [tan A — tan B]/[1 + tan A tan B]

Отношения с помощью четырех секторов

Вы можете вывести несколько отношений с формулами суммы и разности. Вы уже сделали соотношение для 75 градусов. Теперь можно выполнить то же для 15 градусов. Эти формулы дают соотношения для углов в 15 градусов интервалы через четыре квадранта. Построив их на 360 градусов, вы можете увидеть, как эти три соотношения изменяются, когда вектор проходит через четыре квадранта.

«Волна» синуса и косинуса колеблется вверх и вниз между +1 и -1. Обратите внимание, что «волны» смещены на 90 градусов друг относительно друга. Этот факт станет важным позже.

Кривая тангенса начинается, как синусоида, но вскоре она стремится достичь бесконечности на 90 градусах. Двигаясь » вне видимости» в положительном направлении, она «приходит» с отрицательного направления с другой стороны на 90 градусах. Проходя через точку в 180 градусов, функция тангенса повторяет то, что она «делала» проходя 0 или 360 градусов. На 270 градусах она повторяет то же, было на 90 градусах.

Пифагор в тригонометрии

Формула часто может быть упрощена, так как были найдены выводы формулы тангенса от формул синуса и косинуса, а также изменение ее членов одного отношения к другому отношению, использeущеuj другие члены. При этом, теорема Пифагора, выраженная в тригонометрическом соотношении, очень удобна.

Предположим, что прямоугольный треугольник имеет гипотенузу длиной 1. Тогда одна из сторон будет иметь длину sinA, а другая — cosA. Отсюда, согласно теореме Пифагора: cos² A + sin² A = 1. Это выражение всегда истинно для любого значения A.

Немного о том, как это было записано. Cos² A означает (cos A)². Если вы написали это как cos A², уравнение будет означать что-то другое. A есть число в нескольких угловых значениях, которое представляет угол. A² было бы то же самое число, возведенное в квадрат. Его значение зависело бы от использованного числового значения, поэтому это не очень хороший член для использования. Это означает квадрат синуса ли косинуса, не сам угол.

Формула Пифагора может быть выражена иначе. Например, две другие формы:
cos² A = 1 — sin² A, и sin² = 1 — cos² A.

Умножение углов

Формулы сумм, вместе с теоремой Пифагора, используются для углов, которые в 2, 3 или больше раз кратны любым оригинальным углам. Здесь приводятся формулы для 2А и 3А.

Формула суммы работает, когда оба угла одинаковые или различны: sin(A + B) или sin(A + A). Однако, sin(A + A) в действительности sin 2A. Поэтому, sin 2A есть sin A cos A + cos A sin A. Оба члена выражения есть одним и тем же произведением, записанным в разном порядке, так что это выражение может быть упрощено до sin 2A = 2 sin A cos A.

Подобным образом, cos 2A = cos A cos A — sin A sin A, что также может быть записано как: cos 2A = cos² A — sin² A. Используя теорему Пифагора, изменяем это к виду: cos 2A = 2cos² A — 1. Наконец, tg 2A = 2 tg A/[1 — tg² A].

Теперь тройной угол (3А) используется, чтобы показать, как получены следующие кратные углы. В основном, это так же просто, как запись 3A = 2 + A и повторного применения формулы суммы. Но тогда, чтобы получить в результате формулу в работающем виде, необходимо заменить часть 2А, на выражения с простым углом А.

На рисунках внизу вы можете видеть, что с каждым разом вычисления становятся сложнее.

УМНОЖЕНИЕ УГЛОВ       Производные от формул суммы

УМНОЖЕНИЕ УГЛОВ       Соотношения для 3A

Свойства равнобедренного треугольника

Вы уже видели, что прямоугольный треугольник является полезным строительным блоком для других фигур. Равнобедренный треугольник имеет несколько различных видов использования. Дело в том, что его использование основывается на том, что равнобедренный треугольник имеет две равные стороны и два равные углы между основанием и боковыми равными сторонами. Перпендикуляр из третьего угла на третью сторону делит ее пополам. Таким образом весь треугольник делится на два равных прямоугольных треугольника.

Любой треугольник, за исключением прямоугольного треугольника, можно разделить на три прилегающих равнобедренных треугольника, разделив каждую сторону на две равные части и построить перпендикуляры из точек разделения. Там, где любые два из этих перпендикуляров встречаются, если линии тянутся к углам исходного треугольника, три линии должны быть равны, потому что две из них образуют стороны равностороннего треугольника. Таким образом, перпендикуляр с третьей стороны исходного треугольника должен также встретиться в одной точке.

Это утверждение справедливо, как мы покажем здесь, независимо от того, является ли исходный треугольник острым или тупым. Разница с тупым прямоугольным треугольником в том, что место встречи перпендикуляров лежит снаружи исходного треугольника, а не внутри.

Что происходит в прямоугольном треугольнике? Перпендикуляры от средней точки гипотенузы другой стороны будут делить пополам эти две стороны — вы получаете два из трех! Место встречи находится гипотенузе.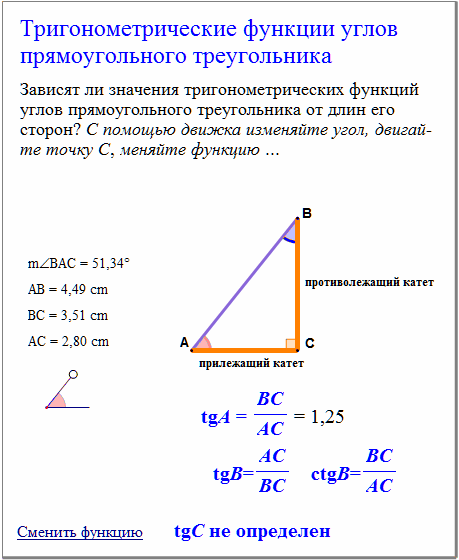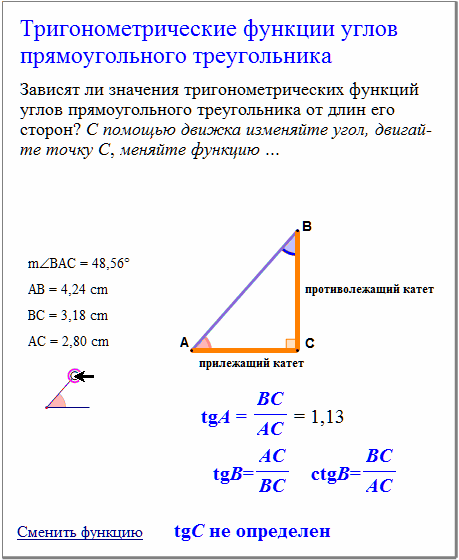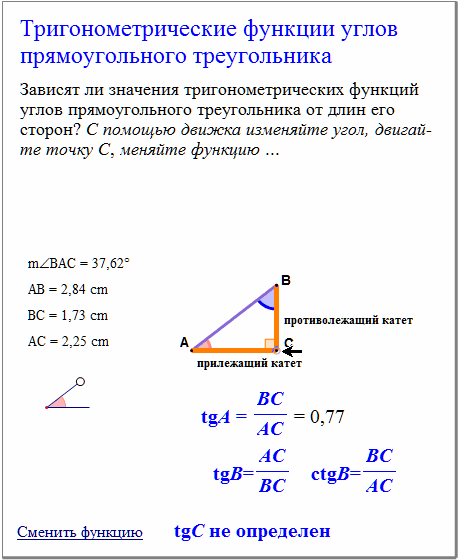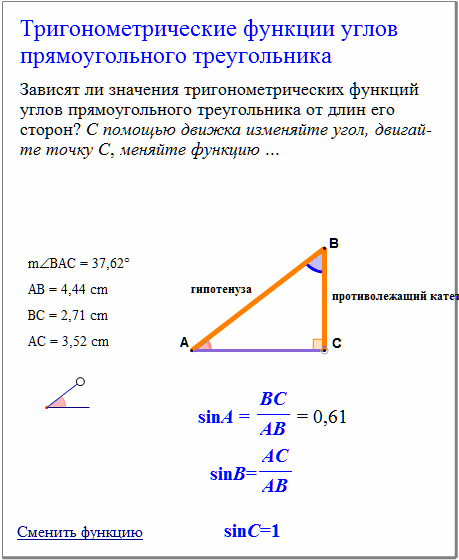

Углы в окружности

Основное свойство окружности это то, что ее центр находится на одинаковом расстоянии от любой точки окружности. Это расстояние есть радиусом окружности.

Если вы нарисуете любой треугольник внутри круга, перпендикуляры из средней точки его сторон встретятся в центре окружности а радиусы из углов треугольника делят его на три равнобедренных треугольника

Теперь, если вы назовете равные пары углов в каждом равнобедренном треугольнике A, A, B, B, C, C, вы обнаружите, что исходный треугольник имеет один угол A+B, один угол B+C, и один угол A+ C. Три угла в сумме дают 2A + 2B + 2С, а это как известно равно 180 градусов.

В любом равнобедренном треугольнике угол при вершине равен 180 градусов минус удвоенный угол при основании. Поэтому, согласно предыдущего пункта, 180 — 2A должен быть такой же, как и 2B + 2С, например.

Рассмотрим угол правый нижний угол, опирающийся на окружность. Угол в центре равен 2B + 2С. Углом, опирающийся на окружность равен B + C.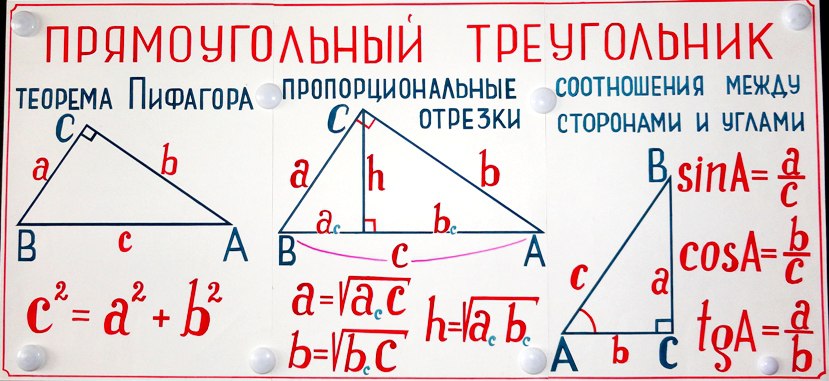 Вы видите, что для любого сегмента круга, угол в центре всегда в два раза больше угла, опирающегося на окружность.

Утверждение выше приводит к интересным фактам об углах в окружностях. Вместо определения углов со стороной треугольника, используют дугу (часть окружности) круга. Часть окружности, которая определяется углом в центре называется хордой окружности.

Угол в центре в два раза больше чем угол на окружности

Любой угол, касающийся окружности, используя хорду как ограничение угла, равен половине угла в центре. Таким образом, все углы в круге, с основанием на той же хорде, должны быть равны. Предположим, что хорда имеет угол 120 градусов. Угол на окружности будет равен 60 градусам.

Особый случай представляет собой полукруг (точный полукруг). Угол в центре представляет собой прямую линию (180 градусов). Каждый угол в полукруге равен 90 градусам (прямой угол). Любой треугольник в полукруге является прямоугольным треугольником.

Определения

Выше мы часто использовали углы, которые дополняют углы до прямого угла (90 градусов) или до двух прямых углов (180 градусов). Когда два угла образовывают угол 180 градусов (два прямых угла), они называются дополнительными. Если два угла добавить до 90 градусов (один прямой угол), их называют комплементарными

Вопросы и задачи

1. Синус угла А равен 0,8 и синус угла B равен 0.6. Из различных зависимостей, полученных до сих пор, найдите следующее: тангенс А, тангенс B, синус (A + B), косинус (A + B), синус (A — B), косинус (A — B), тангенс (А + B) и тангенс (A — B) без использования таблиц или тригонометрических клавиш калькулятора.

2.На экваторе Земля имеет радиус 4000 км. Углы вокруг экватора измеряется в меридианах долготы, с линией с севера на юг проходящей через Гринвич (Англия), в качестве нулевого отсчета. Два места используются для наблюдения за луной: первое это Кения, на экваторе 37,5 к востоку от Гринвича, а другой является Суматра, на экваторе к востоку 100,5. Как далеко друг от друга эти два места, если расстояние измерять мнимой прямой, проходящей через Землю?

3. Если бы наблюдения были сделаны горизонтально от точки наблюдения в вопросе 2 (к востоку от первой, к западу от второй), под каким углом была бы линия пересечения наблюдений?

4.В определенное время, точно синхронизированное в обоих местах, наблюдается спутник. В Кении, высота линии визирования с центром на спутнике составляет 58 градусов выше горизонтали на восток. На Суматре, высота составляет 58 градусов выше горизонтали на запад. Как далеко находится спутник? Используйте расстояние между точками рассчитанное в вопросе 2.

5. Косинус определенного угла в два раза больше синуса того же угла. Чему равен тангенс этого угла? Не используйте таблицы или калькулятор для ответа на этот вопрос.

6. Синус определенного угла равен именно 0.28. Найдите косинус и тангенс этого угла. Не используйте таблицы или калькулятор для ответа на этот вопрос.

7. Синус определенного угла равен 0.6. Найдите синус углов, больших чем заданный в два и три раза.

8. Найдите синус и косинус угла, большего ровно в два раза чем угол из вопроса 7.

9. Используя 15 градусов, как единичный угол, и формулы для отношения 2А и 3А найдите значения синусов 30 и 45 градусов.

10. Используя 30 градусов, как единичный угол, найти значения синусов 60 и 90 градусов.

11. Используя 45 градусов, как единичный угол, найдите значения тангенсов 60 и 90 градусов.

12. Используя 60 градусов, как единичный угол, найдите значения косинусов 120 и 180 градусов.

13. Используя 90 градусов, как единичный угол, найдите значения косинусов 180 и 270 градусов.

14. Используя формулы тангенса для умножения углов и таблицы, найдите тангенсы утроенных углов в 29, 31, 59 и 61 градусов. Посчитайте изменения знака между утроенным углом 29 и 31 градусов и между 59 и 61 градусов.

15. Синус угла составляет 0,96. Найдите синус и косинус удвоенного угла.

16. Задача сводится к алгебраической выражению вида 8cos² A + cos A = 3. Решите для косинуса А, и укажите, в каком квадранте будет угол, представляющий каждое решение придет.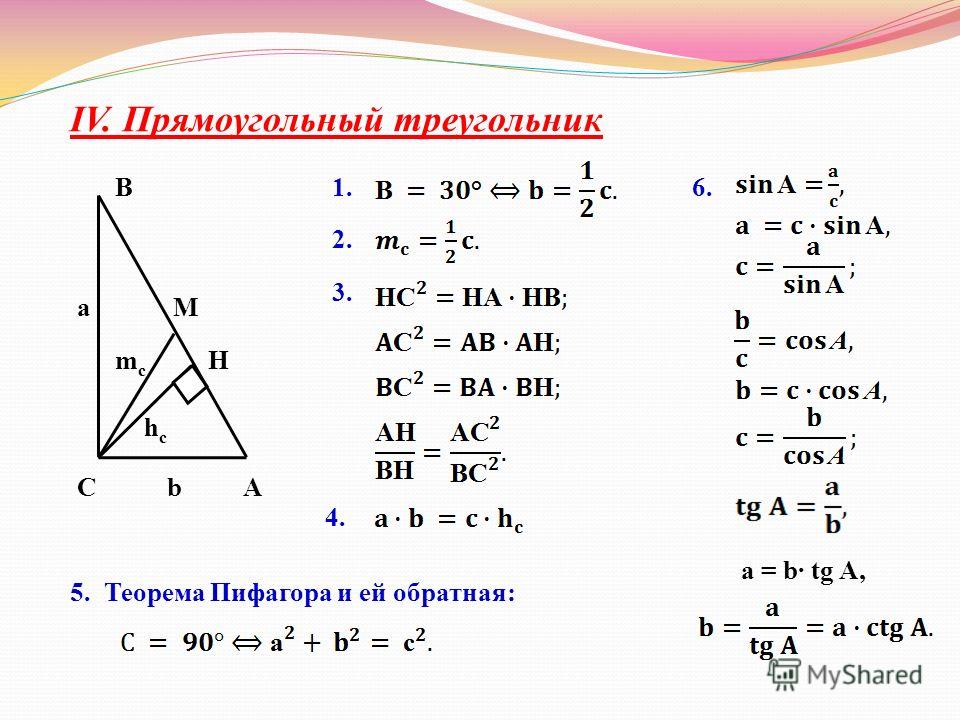 Приведите приближенные значения из таблицы или используя калькулятор.

Сумма углов треугольника — урок. Геометрия, 7 класс.

Сумма углов треугольника равна \(180°\).

 

Доказательство

 

Рассмотрим произвольный треугольник \(KLM\) и докажем, что ∡ \(K\) \(+\) ∡ \(L\) \(+\) ∡ \(M =\) 180°.

1. Через вершину \(L\) параллельно стороне \(KM\) проведём прямую \(a\).

2. При пересечении параллельных прямых \(a\) и \(KM\) секущей \(KL\), углы, которые обозначаются \(1\), будут накрест лежащими углами,  а углы, обозначенные \(2\) — это накрест лежащие углы при пересечении этих же параллельных прямых секущей \(ML\).

 

Очевидно, сумма углов \(1\), \(2\) и \(3\) равна развёрнутому углу с вершиной \(L\), т. е. 
∡ \(1\) \(+\) ∡ \(2\) \(+\) ∡ \(3 =\) 180°, или ∡ \(K\) \(+\) ∡ \(L\) \(+\) ∡ \(M =\) 180°.

 

Теорема доказана.

Следствия из теоремы о сумме углов треугольника

Следствие 1. Сумма острых углов прямоугольного треугольника равна 90°.

 

Следствие 2.  В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.

 

Следствие 3.  В равностороннем треугольнике каждый угол равен 60°.

 

Следствие 4.  В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.

 

Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

 

Доказательство

 

Из равенств ∡ \(KML\) \(+\) ∡ \(BML=\) 180° и ∡ \(K\) \(+\) ∡ \(L\) \(+\) ∡ \(KML =\) 180° получаем, что ∡ \(BML =\) ∡ \(K\) \(+\) ∡ \(L\).

Остроугольный, прямоугольный и тупоугольный треугольники

Как гласит четвёртое следствие из теоремы о сумме углов треугольника, можно выделить три вида треугольников в зависимости от углов.

 

 

У треугольника \(KLM\) все углы острые.

 

 

У треугольника \(KMN\) угол \(K = 90\)°.

У прямоугольного треугольника сторона, лежащая против прямого угла, называется гипотенузой, а две остальные стороны — катетами.

 

На рисунке \(MN\) — гипотенуза, \(MK\) и \(KN\) — катеты.

 

 

У треугольника \(KLM\) один угол тупой.

По какой формуле находят углы? Примеры

Прежде чем изучать формулы для нахождения углов, давайте посмотрим, в каких ситуациях нам может понадобиться использовать эти формулы. Существуют разные формулы нахождения углов в зависимости от имеющихся данных. Давайте изучим формулы нахождения углов на каждом конкретном случае здесь.

• Чтобы найти недостающий угол в многоугольнике, мы используем формулу суммы внутренних углов.
• Чтобы найти недостающий угол в прямоугольном треугольнике, мы используем тригонометрические соотношения.
• Чтобы найти недостающие углы в непрямоугольном треугольнике, мы используем закон синусов и закон косинусов.

Что такое формула для нахождения углов?

Вот формулы для нахождения углов. Мы выбираем одну из этих формул, чтобы найти неизвестные углы в зависимости от данной информации.

Название формулы	Формула	Как найти неизвестные углы?
Сумма внутренних углов многоугольника с n сторонами	180 (n-2) градусов	Найдите сумму всех внутренних углов, используя эту формулу, и вычтите из нее сумму всех известных углов, чтобы найти неизвестный внутренний угол.
sin, cos и tan	sin θ = противоположность / гипотенуза cos θ = смежный / гипотенуза tan θ = напротив / рядом	Используйте одно из этих тригонометрических соотношений в зависимости от того, какие две стороны доступны для нахождения неизвестного угла.
Закон синусов	а/sin A = b/sin B = c/sin C Здесь A, B и C — углы треугольника, а a, b и c — их противоположные стороны.	Закон синусов используется для нахождения неизвестных углов, когда нам дано а) две стороны и невключенный угол (или) б) два угла и невключенная сторона.
Закон косинусов	a 2  = b 2  + c 2  — 2bc cos A b 2  = c 2  + a 2  — 2ca cos B c 2  = a 2  + b 2  — 2ab cos C Здесь A, B и C — углы треугольника, а a, b и c — их противоположные стороны.	Закон косинусов используется для нахождения неизвестных углов, когда нам дано а) с трех сторон (или) б) две стороны и угол между ними.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Забронируйте бесплатный пробный урок

Примеры использования формулы для нахождения углов

Пример 1:  Найдите пятый внутренний угол пятиугольника, если четыре его внутренних угла равны 108°, 120°, 143° и 97°.

Решение:

Число сторон пятиугольника равно, n = 5.

Сумма всех 5 внутренних углов пятиугольника = 180 (n — 2)° = 180 (5 — 2)° = 540°.

Сумма данных 4 внутренних углов = 108°+ 120°+ 143°+ и 97°= 468°.

Итак, пятый внутренний угол = 540° — 468° = 72°.

Ответ: Пятый внутренний угол данного пятиугольника = 72°.

Пример 2:  Найдите угол при вершине C в следующем треугольнике, используя одну из формул для нахождения углов.Округлите ответ до ближайшего целого числа.

Решение:

Найти: Угол при С, равный θ.

Дано, что AB = 6 = Противоположная сторона θ.

до н.э. = 8 = примыкающая сторона θ.

Поскольку мы знаем как противоположные, так и смежные стороны θ, мы используем формулу тангенса θ, чтобы найти θ.

тангенс θ = напротив/смежно

тангенс θ = 6/8 = 0,75

θ = тангенс ^-1  (0,75)

Использование калькулятора,

θ ≈ 37° (округлено до ближайшего целого числа).

Ответ: Угол при вершине C равен θ = 37°

Пример 3:  Найдите угол при вершине А в следующем треугольнике, используя одну из формул для нахождения углов. Округлите ответ до ближайших десятых.

Решение:

Найти: Угол при А.

Мы знаем, что стороны, противоположные A, B и C, представлены буквами a, b и c соответственно. Итак имеем:

а = 10 дюймов; б = 7 дюймов; и с = 5 дюймов.

Поскольку мы знаем все три стороны, мы должны использовать закон косинусов, чтобы найти угол при A.

a ²  = b ²  + c ²  — 2bc cos A

10 ²  = 7 ²  + 5 ²  — 2 (7)(5) cos A

100 = 49 + 25 — 70 потому что А

100 = 74 – 70, потому что А

70 cos А = 74 — 100

70 cos A = -26

cos А = -26/70

А = cos ^-1  (-26/70)

Использование калькулятора,

А ≈ 111.8° (Округлено до десятых).

Ответ: Угол при А = 111,8°

Как найти угол прямой

Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как так как ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права. Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.

Чтобы подать уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \ достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем а ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.

Отправьте жалобу нашему назначенному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

 

Сводка тригонометрических формул

Сводка тригонометрических формул

Эти формулы связывают длины и площади определенных кругов или треугольников. На следующей странице вы найдете личности. Тождества не относятся к конкретным геометрическим фигурам, но справедливы для всех углов.

Формулы для дуг и секторов окружностей

Вы можете легко найти длину дуги и площадь сектора для угла θ в окружности радиусом r .

Длина дуги. Длина дуги равна радиусу r , умноженному на угол θ , где угол измеряется в радианах.Чтобы перевести градусы в радианы, умножьте количество градусов на π /180.
Площадь сектора. Площадь сектора равна половине квадрата радиуса, умноженного на угол, где, опять же, угол измеряется в радианах.

Формулы для прямоугольных треугольников

Наиболее важными формулами тригонометрии являются формулы прямоугольного треугольника. Если θ — один из острых углов в треугольнике, то синус теты — это отношение противолежащего катета к гипотенузе, косинус — отношение прилежащего катета к гипотенузе, а тангенс — это отношение противоположная сторона соседней стороне.

Эти три формулы вместе известны мнемоникой SohCahToa. Кроме того, есть очень важная формула Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов двух других сторон.

Зная, что два острых угла дополняют друг друга, то есть дают в сумме 90°, можно решить любой прямоугольный треугольник:

• Если известны две из трех сторон, то можно найти третью сторону и оба острых угла.
• Если вы знаете один острый угол и одну из трех сторон, вы можете найти другой острый угол и две другие стороны.

Формулы для косоугольных треугольников

Эти формулы работают для любого треугольника, острого, тупоугольного или прямоугольного. Мы будем использовать стандартные обозначения, в которых три вершины треугольника обозначаются прописными буквами A , B и C , а три стороны напротив них соответственно обозначаются строчными буквами a , б и в .

Есть две важные формулы для косых треугольников. Они называются законом косинусов и законом синусов.

Закон косинусов обобщает формулу Пифагора на все треугольники. Он говорит, что c ² , квадрат одной стороны треугольника, равен a ²  +  b ² , сумма квадратов двух других сторон минус 2. ab  cos&nbsp C , удвоенное произведение их на косинус противоположного угла.Когда угол C прямой, он становится формулой Пифагора.

Закон синусов гласит, что отношение синуса одного угла к противоположной стороне одинаково для всех трех углов.

С помощью этих двух формул вы можете решить любой треугольник:

• Если вам известны два угла и сторона, вы можете найти третий угол и две другие стороны.
• Если известны две стороны и угол между ними, то можно найти третью сторону и оба других угла.
• Если известны две стороны и угол, противолежащий одной из них, то для угла, противолежащего другой, возможны два варианта (один острый и один тупой), и для обоих вариантов можно определить оставшийся угол и оставшуюся сторону.

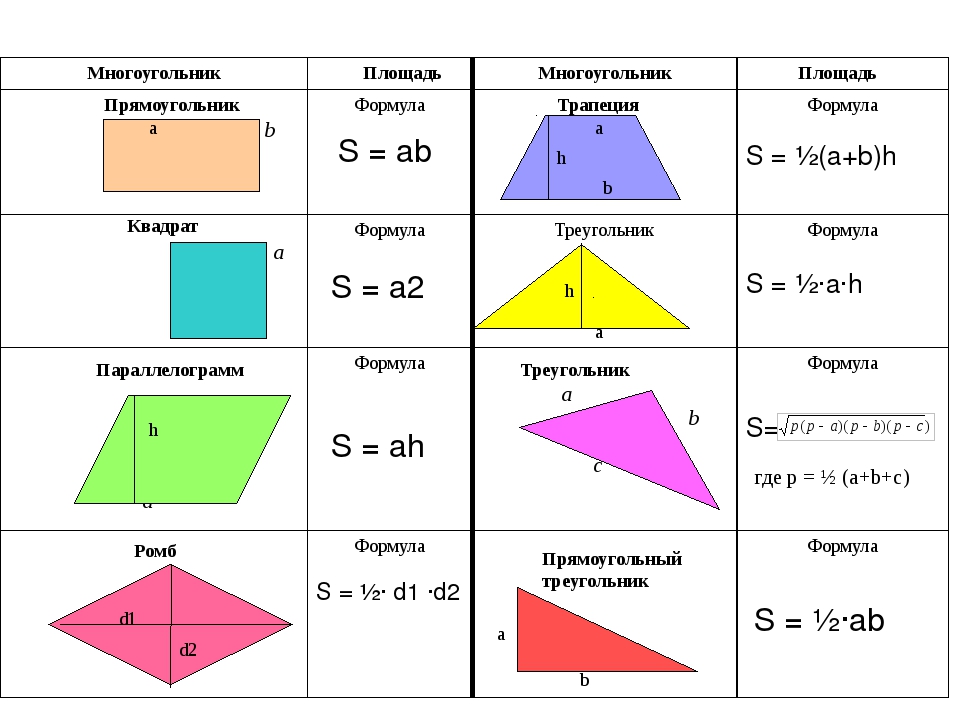
Формулы площади треугольников

Существует три различных полезных формулы площади треугольника, и какую из них использовать, зависит от имеющейся у вас информации.

Половина основания, умноженная на высоту. Это обычный способ использования, так как он самый простой, и у вас обычно есть эта информация. Выберите любую сторону для вызова базы b . Тогда, если 90 264 h 90 265 — это расстояние от противоположной вершины до 90 264 b 90 265 , то площадь равна половине 90 264 bh 90 265 .
Формула Герона. Это полезно, когда вы знаете три стороны a , b и c треугольника, и все, что вам нужно знать, это площадь.Пусть s будут половиной их суммы, называемой полупериметром . Тогда площадь равна квадратному корню из произведения s , s — a , s — b и s — c .
Формула «бок-угол-бок».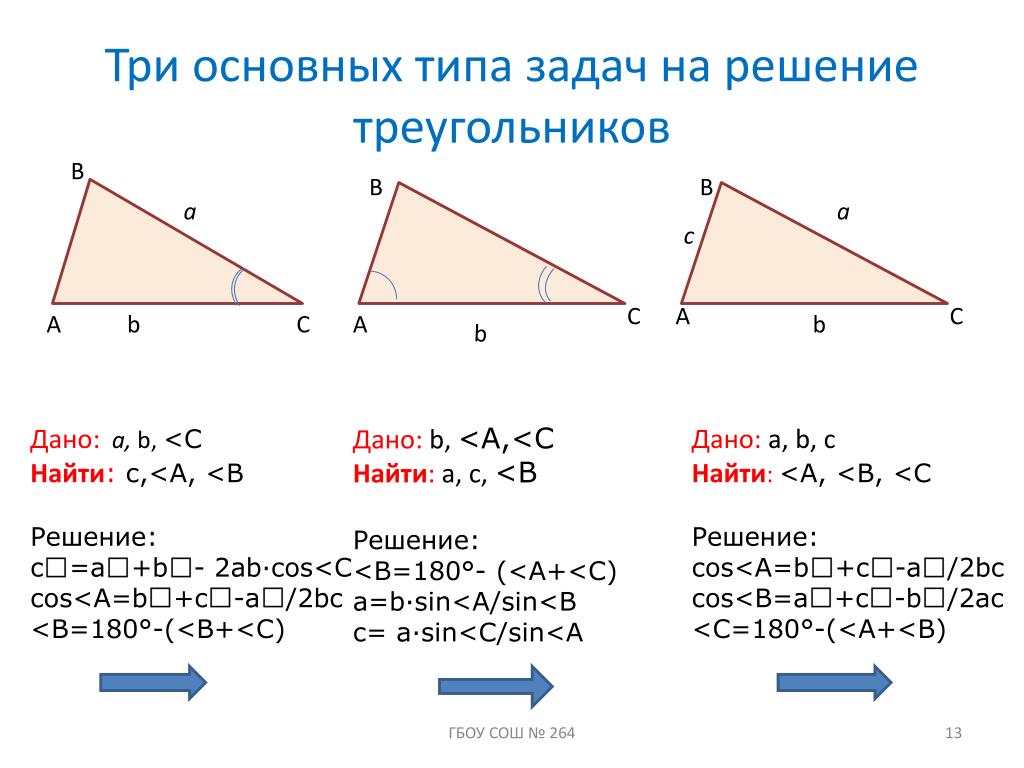 Используйте это, когда вы знаете две стороны, a и b , и прилежащий угол, C . Площадь равна половине произведения двух сторон на синус прилежащего угла.

Базовая геометрия

Базовая геометрия

Базовая геометрия

Это краткий обзор геометрических понятий и формул. которые вам понадобятся для вводного курса астрономии.

Содержимое:

1. Уголки
2. Углы и линии
3. Круги
4. Формула малого угла
5. Угловые размеры

---

Уголки

• Углы можно измерять в разных единицах.Обычно мы выражаем их в градусов :

1° = 1 градус = 60′ = 60 угловых минут 1′ = 60″ = 60 угловых секунд, так что 1° = 3600 дюймов

• Те из вас, кто занимался исчислением, также могут быть знакомы с мерой углов радиан :

2р радиан = 360° 1 радиан = 57,3°.

• Углы тоже могут называться разными способами. Например, в этом треугольнике

угол, обозначенный буквой а, также можно назвать ì BAC, а угол b также можно назвать ì ABC.

• Помните, что угол 90° прямой угол

• Всего 180° в трех углах плоского треугольника: + б + г = 180° :

• В окружности 360°:

---

Углы и линии

• Там, где две линии пересекаются, образуются 4 угла. Любые два, которые противоположные друг другу равны, а любые два соседних в сумме до 180°.

• Когда две линии параллельны (например, AB и CD на следующем рисунке) любая линия, пересекающая их обе (линия EF ) срезает равные углы двумя параллельными линиями.В сочетании с приведенным выше правилом мы видим, что все 4 угла, отмеченные в красном ниже равны.

---

Круги

Напомним определения радиуса, диаметра и длины окружности. круга:

Они связаны по

д = 2 р с = р д = 2 р р Площадь = p r ²

с конечно p = 3,14159

---

Формула малого угла

Существует очень мощная формула, связывающая с размером объект к его расстоянию и его угловому размеру .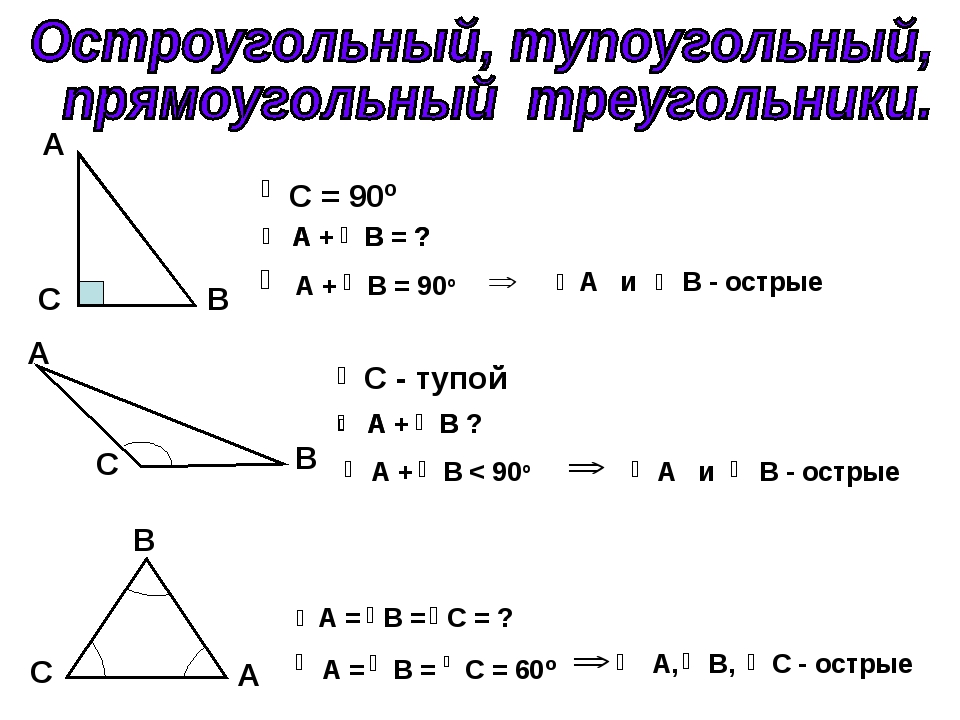 Эта формула, формула малого угла , получается из рассмотрения окружности радиусом r . Помните, что окружность c это расстояние по всему периметру круг и c=2p r . какой если нас не интересует расстояние все наоборот круг, а вместо этого хотите знать расстояние вокруг часть круга, скажем, длина дуги, отмеченной s?

Для этого мы можем установить соотношение:

так что

Это формула малого угла .

Почему эта формула так хороша? Потому что его можно использовать даже для вещи, которые не являются частью круга, пока угол небольшой! Например, когда угол мал (скажем, меньше 25), треугольник внизу очень похож на клин из круг выше.

Для этого треугольника хорошим приближением будет сказать, что s, r, и все они связаны формулой малого угла. Сейчас у нас очень действительно мощный инструмент, потому что мы можем решить множество астрономических задач в картинки с тонкими треугольниками… как вы увидите как вы читаете дальше!

---

Угловые размеры

В астрономии мы изучаем Вселенную, удобно сидя здесь, на старой доброй Terra Firma. Это означает, что мы не можем вообще измеряйте размеры предметов с помощью линеек — давайте посмотрим правде в глаза, даже если бы мы посетили Юпитер, было бы ужасно трудно найти линейка достаточно большая, чтобы измерить это….

Итак, с нашей земной точки зрения мы часто описываем размер объекта с использованием угловой меры, а не линейной (подобной линейке) один. Если нам посчастливилось узнать что-то о предмете расстояние, то мы можем связать его угловой размер с его линейным размер по формуле малого угла.Это очень способ измерения вещей в астрономии.

В качестве примера представьте, что вы смотрите на Зеленый зал. Башня с расстояния 200 метров. Вы оцениваете это по своему точки зрения, Башня покрывает угол 10°. Мы можем нарисовать следующую картину:

Обратите внимание, что это очень похоже на изображение тощего треугольника. выше — на самом деле мы можем применить формулу малого угла к треугольнику начиная с вашего глазного яблока, чтобы получить высоту Башни:

Таким образом, мы смогли измерить высоту Башни без на самом деле туда!

Угол, который охватывает объект, когда мы прослеживаем его до вашего глазное яблоко называется его угловым размером .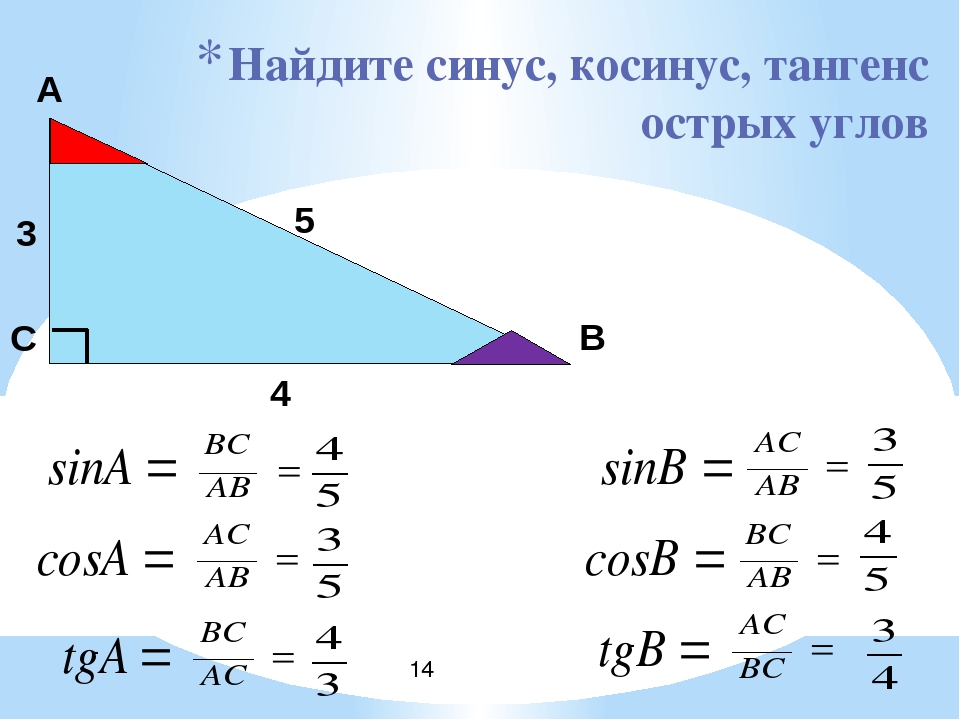 Рассмотрим следующее фотографий.

Верхний рисунок демонстрирует, что два объекта, имеющие разные линейные размеры могут иметь одинаковый угловой размер ( ), если их рассматривать с разных расстояний. Угловой размер объекта определяется по соотношению размер/расстояние. Линейный размер четверти (2,5 см) в 1,4 раза больше десятицентовика (1,8 см), поэтому его нужно поместить в 1,4 раза дальше, чтобы стянуть тот же угол. Теперь переместите четверть в два раза ближе, как на нижнем рисунке, а ее угловая размер в два раза больше (20 градусов вместо 10 градусов).

Вы можете попрактиковаться в измерении угловых размеров вещей (деревьев, созвездия, друзья) используя различные части тела! Как показано в на картинке ниже угловой размер вашего кулака, когда вы кладете ваша рука прямая перед собой примерно 10 градусов. Также с прямой рукой ваш ноготь на мизинце стягивается около 1 градуса.

Резюме

Обратите внимание, что вы должны выразить угол в градусах, чтобы заставить единицы работать должным образом. В астрономии мы часто работая с очень малыми углами, измеряемыми угловыми секундами. Мы можем изменить градусы в этом уравнении на угловые секунды, используя конвертация наших единиц измерения методы:

Формулу малого угла часто можно встретить в учебниках. в этой форме.

Упражняться

Для практики используйте формулу малого угла и понятие углового Размер для решения этих проблем:

1. Представьте, что вы наблюдаете за запуском ракеты с расстояния 3 км.Угловой размер ракеты составляет 2 градуса. Что это длина ракеты в метрах?
2. Каков угловой размер Луны и Солнца, если смотреть с Земной шар? Используйте свой учебник, чтобы найти диаметр и расстояния к Луне и Солнцу. Подсказка: ваш ответ должен быть о одинаково в обоих случаях!

Использование формул для нахождения углов окружности

Что такое центральный угол

Раньше, когда вы работали с углами в треугольнике, вы в основном работали с центральными углами. Это углы, вершины которых находятся в центре окружности. Однако в этом уроке мы не будем работать с центральными углами.

Что такое вписанный угол

Если мы не работаем с центральными углами, то на какие углы в круге мы будем ориентироваться? Мы будем решать вписанные углы.

Вписанные углы — это углы, которые могут лежать где угодно на окружности окружности. Хотя мы больше не работаем только с центральными углами, вы узнаете, что центральный угол круга по-прежнему будет играть роль, когда мы будем решать примеры задач в этом уроке.

Теорема о вписанном угле

Сегодня мы изучим несколько теорем о вписанных углах. Одним из них является угол в теореме о центре. Это говорит нам о том, что вписанный угол θ\thetaθ составляет половину центрального угла 2?. Это видно на иллюстрации ниже.

Углы, опирающиеся на одну и ту же теорему об дуге

Еще одна теорема, которую мы изучим, — это углы, образуемые одной и той же теоремой об дуге. Учитывая, что конечные точки одинаковы, вы поймете, что из приведенной ниже иллюстрации не имеет значения, где находится вписанный угол θ\thetaθ.Он останется прежним. Как вы также можете видеть, это потому, что они имеют одну и ту же дугу (оранжевая линия), отсюда и название этой теоремы.

Вопрос 1:

На следующем рисунке радиус равен 24 см, а угол НМТ равен 75°.

найти неизвестные, используя углы в окружности

а) Найдите угол ВАС.

Решение:

Угол BDC — это центральный угол, равный 75 градусам. Угол ВАС — вписанный угол. По теореме о вписанном угле угол BAC равен половине угла BDC.И наоборот, вы можете думать об отношении между углом BDC и углом BAC, поскольку центральный угол всегда удваивает угол вписанного угла.

Центральный угол = вписанный угол x 2

757575°=2θ=2\тета=2θ

θ=37,5\тета=37,5θ=37,5°

б) Найдите хорду BC

Решение:

Проведем биссектрису треугольника DBC, чтобы разрезать его пополам

Теперь посмотрите на одну из половинок, вырезанных из треугольника DBC

.

X — это половина искомой нами хорды BC.Итак, найдите x, используя sin (помните принципы SohCahToa?)

ВС=2xВС=2xВС=2x

sin⁡37,5\sin 37,5sin37,5°=x24=\frac{x}{24}=24x​

х ≅ 14,6 х 14,6 х ≅ 14,6

BC=2x=29,2 смBC=2x=29,2 смBC=2x=29,2 см

Вопрос 2:

Даны угол BAE = 44,5° и угол ADC = 64,27°.

найти недостающий угол

Найдите угол BCD.

Решение:

Угол BCD и угол BAE вписаны в одну дугу.Итак, угол BCD = BAE = 44,5°. Это основано на углах, стягиваемых той же теоремой дуги.

Все еще не уверены в теоремах? Эта онлайн-демонстрация может показать вам доказательство, когда вы перетаскиваете линии в круге, которые образуют центральный и вписанный углы.

Далее вы будете иметь дело с задачами, которые потребуют от вас нахождения дуг окружности и площади сектора в кругах. Вы также расширите изученные здесь центральные и вписанные углы, а также перейдете к доказательству вписанных углов.

Углы в круге – объяснение и примеры

Концепция углов необходима при изучении геометрии, особенно в кругах. Вы уже видели несколько теорем , связанных с окружностями , и все они включают в себя углы.

Эта статья посвящена исключительно углам окружности.

Вы также узнаете, как найти угол в окружности. Для определения углов и частей окружности вы можете обратиться к предыдущим статьям.Вы также узнаете, что влечет за собой внутренний угол и внешний угол круга.

Что такое угол окружности?

Каков угол окружности? Или, точнее, как можно образовать угол внутри фигуры, у которой нет краев?

Ответ состоит в том, что углы образуются внутри круга с радиусами, хордами и касательными. Посмотрим ниже. Угол окружности — это угол, образованный между радиусами, хордами или касательными окружности.

Мы видели разные типы углов в разделе «Углы» , но в случае с кругом, в основном, есть четыре типа углов. Это центральный, вписанный, внутренний и внешний углы. Давайте рассмотрим каждый из них по отдельности ниже.

Центральный угол образован двумя радиусами, а его вершина лежит в центре окружности.

На приведенной выше диаграмме ∠ AOB = центральный угол

, где дуга AB представляет собой дугу, на которую она опирается.

В окружности сумма центрального угла малого и большого сегментов равна 360 градусам.

С другой стороны, вписанный угол образован между двумя хордами, вершина которых лежит на окружности.

На приведенном выше рисунке ∠ AOB — это вписанный угол.

 

Как найти угол?

Как найти центральный угол:

Формула для нахождения центрального угла:

Центральный угол = (длина дуги x 360)/2πr

, где r — радиус окружности.

Как найти вписанный угол:

Формула для вписанного угла:

Вписанный угол = ½ дуги, проведенной между точками

Ранее мы изучали внутренние и внешние углы треугольников и многоугольников. Пришло время изучить их и для кругов.

Внутренний угол окружности

Внутренний угол окружности образован на пересечении двух линий, пересекающихся внутри окружности.

На диаграмме выше, если b и a являются дугами, пересекаемыми, то внутренний угол x равен половине суммы дуг.

x = ½ (b + a)

Внешний угол окружности

круг.

Величина внешнего угла равна половине разности величин образуемых дуг.

Формула для наружного угла задана

Угол внешнего вида, ∠
9 Boa = ½ (B — A)

Позвольте работать на нескольких примерах:

Пример 1

Найдите центральный угол отрезка, длина дуги которого равна 15.7 см, а радиус 6 см.

Решение

Центральный угол = (длина дуги x 360)/2πr

Центральный угол = (15,7 x 360)/2 x 3,14 x 6

= 5652/37,60

3

2 угол 150 градусов.

Пример 2

На приведенной ниже диаграмме пересекаемые дуги составляют 60 градусов и 120 градусов соответственно. Найдите градусную меру внешнего угла x?

Решение

Внешний угол, x = ½ (b – a)

x = ½ (120º – 60º)

x = 30º

x = 30º

30 градусов.

Пример 3

Найдите величину недостающего центрального угла в следующем круге.

Решение

Сумма центральных углов окружности = 360°

80° + 120° + x = 360°

Упростить.

200° + x = 360°

Вычесть по 200° с обеих сторон.

x = 160 º

Следовательно, недостающий центральный угол равен 160 градусам.

Пример 4

Какова мера ∠BOA и ∠AOE в круге, показанном ниже? 180°

2x + 60°= 180°

Вычесть 60° с обеих сторон.

2x = 120°

Разделив обе стороны на 2, мы получим

x = 60°

Теперь подставим.

(x + 50) ° = 60° + 50°

= 110°

(x + 10) ° = 60° + 10°

= 70°

Следовательно, мера ∠BOA и ∠AOE составляет 110° и 70° соответственно.

Пример 5

Найдите внутренний угол следующей окружности.

Решение

Даны длины пересекаемых дуг 150° и 100°.

Внутренний угол, x = ½ (150° + 100°)

= ½ x 250°

=125°

Таким образом, внутренний угол равен 125°.

Предыдущий урок | Главная страница | Следующий урок

Внутренние углы многоугольников

Внутренний угол — это угол внутри фигуры

Другой пример:

Треугольники

Внутренние углы треугольника в сумме дают 180°

Давайте попробуем треугольник:

90° + 60° + 30° = 180°

Работает для этого треугольника

Теперь наклоните линию на 10°:

80° + 70° + 30° = 180°

Он все еще работает!
Один угол пошел вверх на 10°,
а другой пошел вниз на 10°

Четырехугольники (квадраты и т.

д.)

(Четырехугольник имеет 4 прямые стороны)

Попробуем квадрат:

90° + 90° + 90° + 90° = 360°

Квадрат в сумме дает 360°

Теперь наклоните линию на 10°:

80° + 100° + 90° + 90° = 360°

В сумме все равно получается 360°

Внутренние углы четырехугольника в сумме дают 360°

Потому что в квадрате 2 треугольника…

Внутренние углы треугольника в сумме составляют 180° …

… и для квадрата они составляют 360° …

… ведь квадрат можно составить из двух треугольников!

Пентагон

Пятиугольник имеет 5 сторон и может быть составлен из трех треугольников , так что вы знаете что…

… его внутренние углы в сумме составляют 3 × 180° = 540°

А когда это обычный (все углы одинаковые), то каждый угол равен 540 ° /5 = 108 °

(Упражнение: убедитесь, что каждый треугольник в сумме дает 180°, а сумма внутренних углов пятиугольника равна 540°)

Внутренние углы пятиугольника в сумме дают 540°

Общее правило

Каждый раз, когда мы добавляем сторону (треугольник к четырехугольнику, четырехугольник к пятиугольнику и т. д.), мы добавляем еще 180° к сумме:

Таким образом, общее правило таково:

Сумма внутренних углов = ( n −2) × 180 °

Каждый угол (правильного многоугольника) = ( n −2) × 180 ° / n

Возможно поможет пример:

Пример: как насчет обычного десятиугольника (10 сторон)?

Сумма внутренних углов = ( n −2) × 180 °

 = ( 10 −2) × 180 °

 = 8 × 180°

 = 1440°

и для обычного десятиугольника:

Каждый внутренний угол = 1440 ° / 10 = 144°

 

Примечание. Внутренние углы иногда называют «внутренними углами».

.