Измерение углов. Транспортир
Цели:
- Образовательная: сформировать представление о градусе, как единице измерения угла, познакомить со структурой транспортира, научить измерять градусную меру угла с применением транспортира.
- Развивающая: любознательность, самостоятельность, целеустремленность, развитие креативного мышления.
- Воспитательная: интерес к предмету, уважение к одноклассникам, взаимопомощь.
Оборудование урока:
- Интерактивный комплекс.
- Презентация.
- Транспортир пластмассовый, классный.
- Учебники, письменные принадлежности, транспортиры.
Ход урока
- Организационная часть.
- Повторение материала предыдущего урока по теме «Угол. Типы углов».
- Определение темы и целей урока.
- Изучение материала по теме урока.
- Решение примеров по изученной теме урока.

- Закрепление материала.
- Домашнее задание.
1.
Повторение материала предыдущего урока по теме «Угол. Типы углов»Задание 1. На интерактивной модели построить острый угол. Назвать угол, записать обозначение угла, указать его тип (слайд 3).
Задание 2. На интерактивной модели построить тупой угол. Назвать угол, записать обозначение угла, указать его тип (слайд 3).
Задание 3. Учитель на интерактивной модели строит составные углы (слайд 3). Ученики называют углы, типы углов, записывают обозначение созданных углов, сравнивают углы.
Задание 4. На интерактивной модели построить все углы (слайд 3). Назвать углы, указать типы углов, записать обозначения углов, сравнить углы. Сколько углов построено на рисунке?
2. Запись темы в тетрадь, определение целей урока3. Изучение темы урокаУчитель: Ребята! Сегодня на уроке, мы с вами научимся применять транспортир, для определения градусной меры угла.
Обратите внимание! На слайде показаны применяемые для измерения углов три вида транспортиров: полукруговые (1, 2, 3), круговой (4), геодезический (5).
Какие транспортиры есть в вашем инструментарии, и какой имеется в классе для измерения и построения углов?
Ответы учеников.
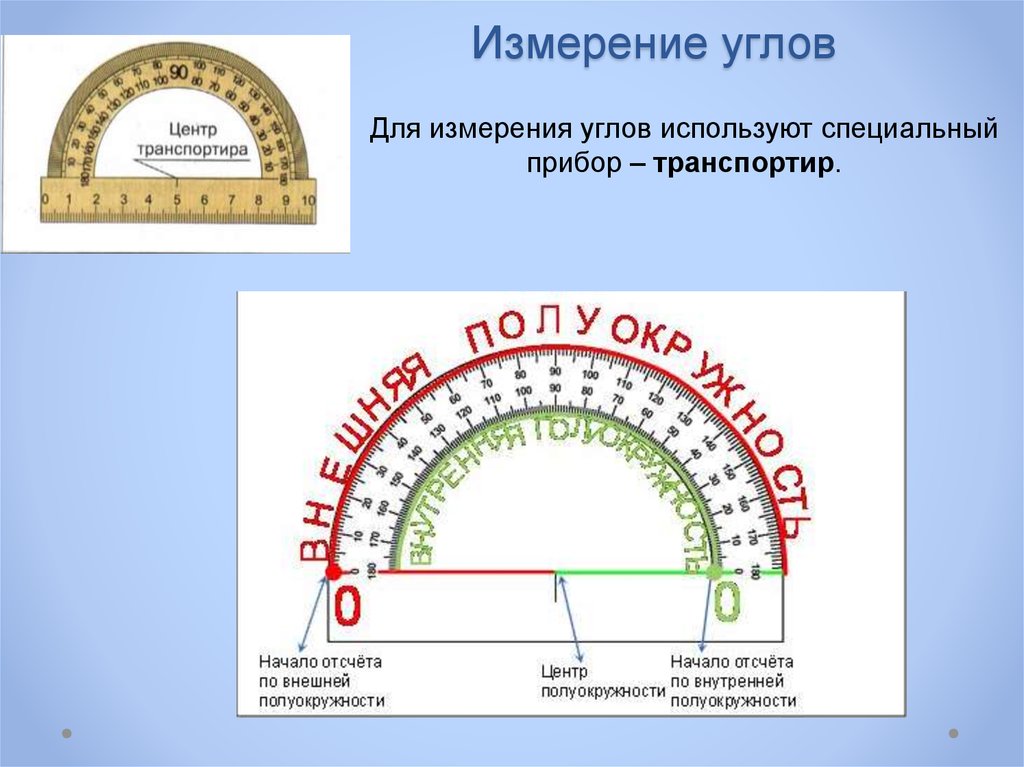
Учитель: Рассмотрим структуру транспортира, его составные части. Обратите внимание на слайд 5 нашей презентации. Анимированные стрелки показывают не только расположение двух угломерных шкал транспортира, но и направление определения градусной меры угла от начального значения – 00, внешней или внутренней шкалы, до конечного значения 1800 по каждой из угломерных шкал.
(При необходимости анимацию данного слайда можно повторить несколько раз).
Учитель: Сколько существует угломерных шкал?
Ответы учеников.
Учитель: Возьмите свои транспортиры, рассмотрите их и найдите угломерные шкалы на своих транспортирах и место расположения начального значения – нуль, каждой шкалы и конечное значение этих шкал.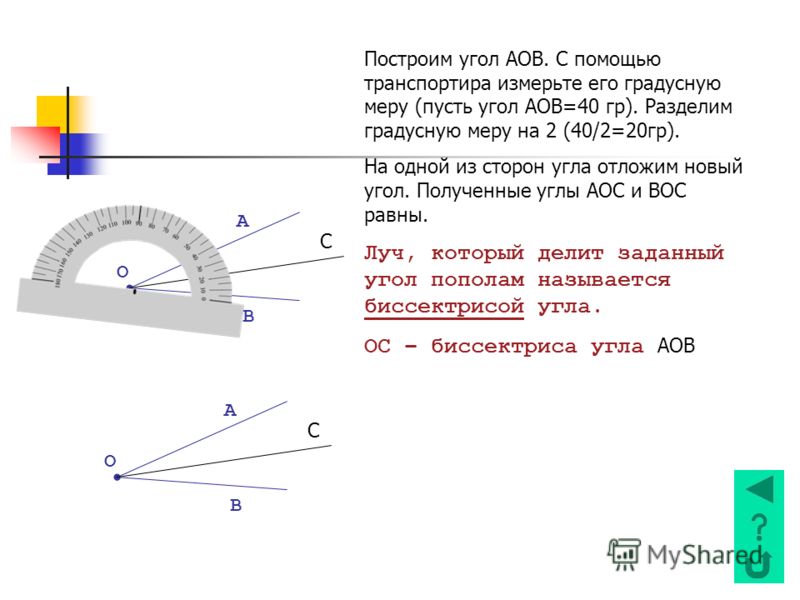
Ученики рассматривают свои транспортиры, находят и показывают учителю результат свой работы.
Учитель: На слайде № 6 презентации показано расположение центра транспортира и его обозначение. Центр транспортира может обозначаться черточкой, окружностью, концентрическими окружностями, отверстием.
Вы легко сможете найти и показать центр своих транспортиров.
Ученики показывают центр своих транспортиров.
Учитель: А сейчас познакомимся с единицей измерения углов – градусом. Обратите внимание, шкала транспортира штрихами поделена на 180 долей (слайд 7). Расстояние между двумя соседними штрихами, которые показаны анимацией и есть 1/180 доля развернутого угла. Лучи, проведенные из центра полуокружности через эти штрихи, образуют 180 углов, каждый из которых равен 1 доли от 180. Таким образом, градусом называют 1/180 долю развернутого угла. Градусная мера развернутого угла равна 180 градусам.
Учитель: Скажите, что такое градус?
Ученики отвечают.
Учитель: На сколько долей поделена шкала транспортира?
Ученики отвечают.
Учитель: Сколько углов можно провести через каждые два соседних штриха шкалы транспортира?
Ученики отвечают.
Учитель: Обратите внимание на то, каким символом обозначают градус. (слайд 8).
Учитель: А сейчас я прошу записать значения углов: 25 градусов, 107 градусов, 64 градуса (слайд 9).
Некоторые ученики делают записи на доске.
Затем, ученики называют градусные меры, которые записали на доске и те, которые представлены на слайде 8 презентации.
Учитель смотрит и проверяет записи учеников.
Учитель: На транспортире, кроме делений в 1 градус, есть деления по 5 градусов (слайд 10).
Посмотрите на свои транспортиры и найдите деления по 5 градусов.
Ученики находят и показывают эти деления.
Учитель: На транспортире есть и более крупные деления – по 10 градусов.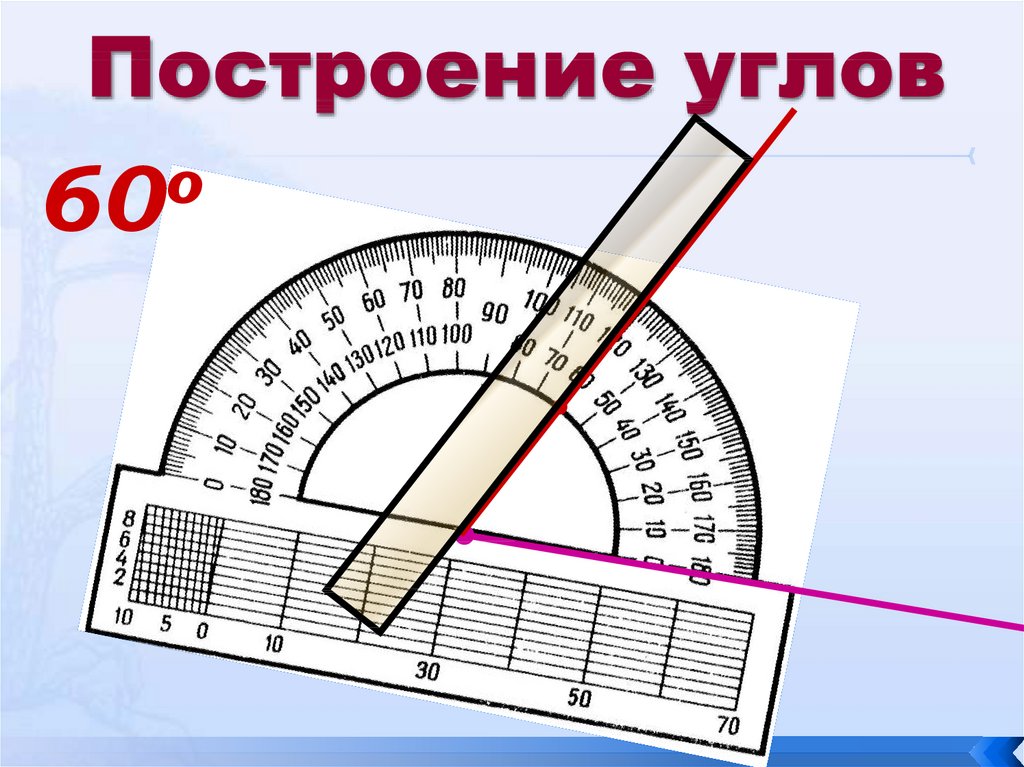 (Слайд 11).
(Слайд 11).
Найдите эти деления на своих транспортирах.
Ученики находят и показывают эти деления.
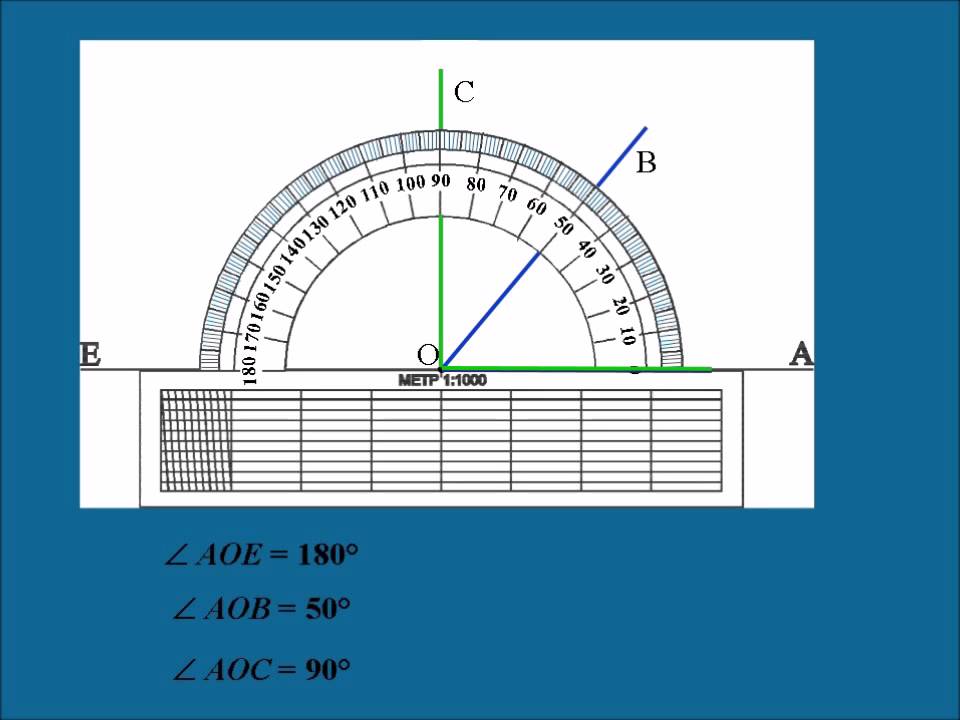
Учитель: А сейчас познакомимся с тем, как правильно записывать обозначение углов и их значение (слайд 12). Обратите внимание на то, что вершина О угла АОВ находится в центре полуокружности. Луч ОА проходит через нулевую отметку (начало отсчета), а луч ОВ проходит через отметку 110 градусов. Записывают значение угла так, как показано на слайде 12.
Обратите внимание! У вас есть карточки №K-1 – K-6. На этих карточках запишите значение каждого угла.
Ученики записывают обозначение углов с их градусной мерой. Затем показывают результаты выполненной работы.
Называют углы и их градусные меры. Во время такой работы, углы можно показать с использованием документ-камеры или со слайда презентации.
Учитель: Вспомним, что представляет собой Развернутый угол (слайд 13).
Ученики дают определение Развернутого угла.
Учитель: Обратите внимание, что градусная мера развернутого угла равна 180 градусам.
Учитель: А какой угол называют прямым? (Слайд 14).
Ученики проговаривают определение прямого угла.
Учитель: Обратите внимание на то, что градусная мера прямого угла равна 90 градусов.
Покажите те карточки, где показаны прямые углы.
Ученики показывают карточки с прямыми углами.
Учитель: Как и все геометрические фигуры, углы сравниваются с помощью наложения. Поэтому с помощью следующих слайдов презентации сравним углы и выясним, какие углы равны между собой, а какие углы не равны, а также определим градусную меру углов (слайды 15-19).
Ученики смотрят, сравнивают, определяют градусную меру углов.
Учитель: Ребята! У вас есть карточки №U-1, U-2. Измерьте транспортиром углы и найдите среди них равные между собой углы.
Ученики измеряют и находят равные углы.
Учитель: Сейчас мы применяли транспортир для измерения углов, но его можно применять и для построения углов.
Учитель по анимированному слайду объясняет алгоритм построения угла (слайд 20). При необходимости анимацию данного слайда можно повторить.
Учитель: Ребята! Расскажите алгоритм построения угла.
Ученики рассказывают алгоритм построения угла.
Учитель: Закрепим алгоритм построения угла. (Слайд 21).
Ученики рассказывают алгоритм, проверяют свои ответы с действиями, которые показаны на слайде.
Учитель: Обратите внимание на углы, которые называют острыми (слайд 22). Как вы думаете, почему эти углы называют острыми углами?
Ученики отвечают на вопрос, используя слайд презентации, на котором показано, что все острые углы меньше 90 градусов.
Учитель: За основу построений острых углов была выбрана внутренняя шкала транспортира.
Учитель: Если за основу построений углов также принять внутреннюю шкалу транспортира, то следующие углы, которые показаны на слайде 23, будут называться тупыми углами?
Ученики смотрят на слайд, отвечают на вопрос.
Учитель: Почему эти углы называют тупыми углами?
Ученики отвечают.
Учитель: А теперь познакомимся с острыми и тупыми углами, но за основу построений примем внешнюю шкалу транспортира.
Учитель: Какие углы называются острыми углами? (Слайд 24).
Ученики отвечают на вопрос.
Учитель: Обратите внимание, что сейчас мы рассматриваем углы относительно внешней шкалы транспортира.
Учитель: Как называются углы, представленные на слайде 25? Объясните, почему их так называют.
Ученики дают ответ на поставленный вопрос.
Учитель: На слайде 26 будут последовательно показаны углы. Ваша задача, записать в тетрадь градусные меры углов, назвать угол и его градусную меру, указать его тип и шкалу, относительно которой определяли градусные меры углов.
Ученики дают ответы по слайду 26 презентации, результаты ответов записывают в тетрадь.
Учитель: На слайде 27 будут последовательно показаны углы. Задача состоит в том, что вызываемый к доске ученик должен своим транспортиром измерить угол и записать на доске результат измерений, указать тип угла. Остальные ученики наблюдают за правильностью выполняемых измерений и делают записи в тетрадях.
Задача состоит в том, что вызываемый к доске ученик должен своим транспортиром измерить угол и записать на доске результат измерений, указать тип угла. Остальные ученики наблюдают за правильностью выполняемых измерений и делают записи в тетрадях.
Учитель: Разберем решение №1653 (а), которое представлено на слайде 28.
- Начнем с углов, которые равны между собой (слайд 28). ∠AOC =∠COB=90 o.
- (ЩЛКМ. Слайд 28). По условию задачи ∠AOC > ∠COB в три раза. Т.е. ∠AOC состоит из трех углов СОВ.
- (ЩЛКМ. Слайд 28). Из этого следует, что луч ОС разделит развернутый угол на два смежных угла. При этом, слева от луча ОС будет создан тупой угол, а справа – острый. На слайде 28, анимацией показано, что луч ОС создал два смежных угла: ∠AOC – тупой угол и ∠COB – острый угол.
- (ЩЛКМ. Слайд 28). Предположим, что луч ОС теперь находится там, где и должен находиться. По схеме видно, что развернутый угол состоит из суммы двух смежных углов:
∠АОВ=∠АОС + ∠СОВ = 3∠СОВ + ∠СОВ = 4∠СОВ.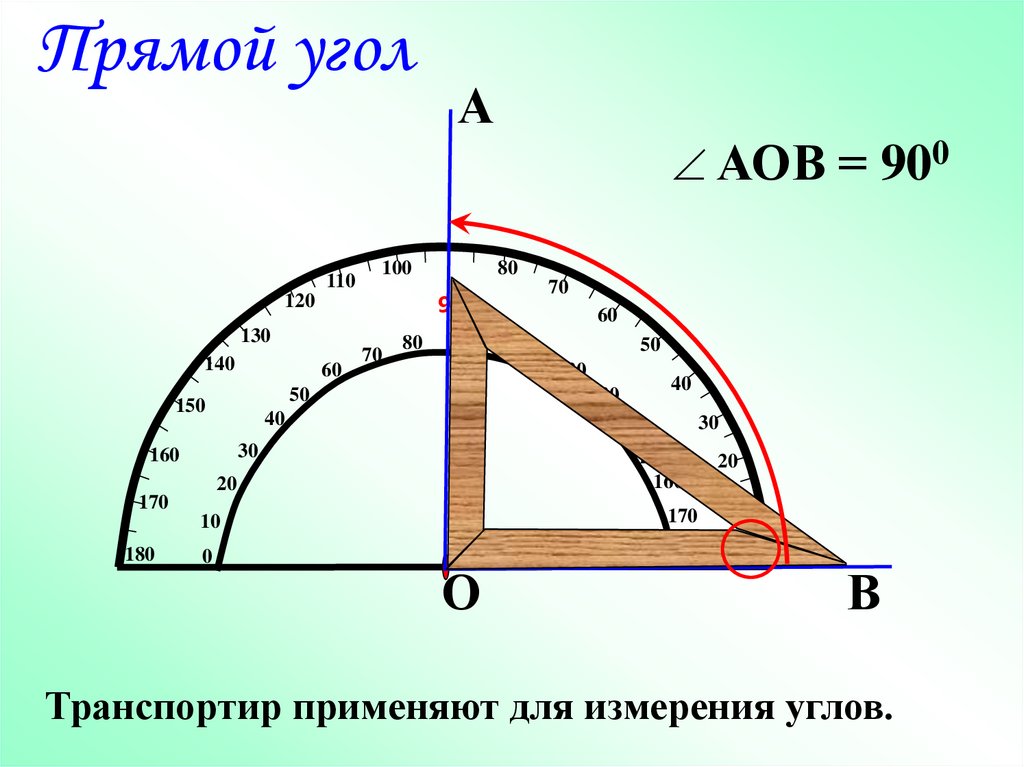
- Из этого равенства, мы можем найти градусную меру угла СОВ:
∠СОВ = ∠АОВ : 4 = 180o : 4 = 45o.
- А теперь посмотрим, через какое значение проходит луч ОС.
- (ЩЛКМ. Слайд 28). Видим, что луч ОС проходит через значение 400 по внутренней шкале, а должен проходить через значение 45o. (ЩЛКМ. Слайд 28).
- Значение угла АОВ можно вычислить, но можно значение этого угла найти на внешней шкале, т.к. луч ОС проходит через ее значение 135o. Таким образом, ∠АОС = ∠АОВ – ∠СОВ = 180o – 45o = 135o.
(Данное решение привожу с применением транспортира и анимированной схемы, т.к. это позволяет эффективно воздействовать на формирование образного мышления учащихся. Ученикам говорю и том, что вычислив одно значение, второе значение можно увидеть на противоположной шкале транспортира. Все это показано в предлагаемой презентации).
4. Решение примеров по изученной теме урока
Решение примеров по изученной теме урокаУчитель: Выполняем задание №1649 на стр.251 учебника. (Слайд 29).
Ученики выполняют задание и делают записи в тетрадях. Один из учеников работает у доски.
Чтобы ученики могли проверить свои ответы, на слайд 29 создана анимация решения данного номера. Анимация является дополнительным способом воздействия на образное мышление учеников.
Учитель: Выполняем задание №1651 на стр.251 учебника. (Слайд 30).
Ученики выполняют задание, записывают результаты измерений в тетрадь.
Проверить правильность выполнения задания можно по слайду 30.
Учитель: Выполняем №1652 на стр.251 учебника. (Слайд 31).
В случае затруднения можно показать подготовленную анимацию на слайде 30.
5. Закрепление материалаСлайд 32.
- Как называется инструмент для измерения и построения углов?
- Назовите составные части транспортира.

- Что такое градус?
- Какие углы называются острыми углами?
- Какие углы называются тупыми углами?
- Чему равна градусная мера прямого угла?
- Чему равна градусная мера развернутого угла?
- Какой из углов, представленных на слайде 32, является: прямым, острым или тупым углом? Объясните данный ответ, используя интерактивные возможности слайда.
Стр.255, №1682, 1683; стр. 256, 1692(а).
Транспортир — как правильно пользоваться инструментом для построения и измерения углов? » Kupuk.net
Транспортир — это математический инструмент, состоящий из линейки и полукруга, разделённого на градусы от 0 до 180°. Он применяется для измерения и построения углов в рисовании и математическом черчении, наряду с составлением графиков в физике. Научиться пользоваться транспортиром достаточно просто.
Люди обычно сталкиваются с транспортирами в математике, когда учатся в школе создавать точные геометрические фигуры. Возможно, у многих из них никогда больше не будет причин снова использовать эти приборы, тем не менее транспортиры имеют долгую историю применения в различных областях.
Возможно, у многих из них никогда больше не будет причин снова использовать эти приборы, тем не менее транспортиры имеют долгую историю применения в различных областях.
История изобретения
Происхождение этого математического инструмента восходит к жрецам в Египте и Вавилоне, которые установили меру углов в градусах, минутах и секундах. Однако до времён классической Греции тригонометрия не использовалась в математике.
Во втором веке до нашей эры астроном Гиппарх из Никии изобрёл тригонометрический стол, для измерения треугольников. Затем Птолемей включил в свою великую астрономическую книгу «Альмагест» таблицу, с угловыми приращениями от 0 до 180°, с погрешностью менее 1/3600 единиц. Он также объяснил метод составления этой таблицы, и на протяжении всей книги приводил много примеров того, как вычислять с помощью неё неизвестные элементы фигур.
Птолемей также был автором, так называемой теоремы Менелая для решения сферических треугольников, и на протяжении многих веков его тригонометрия была основным пособием для астрономов.
Возможно, в то же время, учёные Индии также разработали тригонометрическую систему, основанную на функции синуса, которая, в отличие от используемого в настоящее время синуса, была не пропорцией, а длиной стороны, противоположной углу в прямом треугольнике этой гипотенузы. Индийские математики использовали разные значения для этого в своих таблицах.
Томас Бландевиль рассказал о приборе специально созданном, для рисования и измерения фигур в своём «Кратком описании универсальных карт» 1589 года. Как видно из названия, он применял его, чтобы править навигационные карты для использования в высоких широтах.
Другие европейские математики также описывали подобные приборы примерно в то же время. Независимо от того, кто первым придумал этот инструмент, к началу XVII века он вошёл в стандартную практику мореплавателей и геодезистов. К XVIII веку транспортиры начали появляться в учебниках по геодезии и геометрии.
Транспортиры в современном понимании возникли во второй половине XVIII века, когда такие учёные, как Джесси Рамсден и Георг Фридрих Брандер, усовершенствовали ранее созданные устройства.
В то время предпочтительными материалами для их изготовления были:
- дерево;
- латунь;
- серебро;
- медь;
- слоновая кость.
В первой половине XX века начали применять олово и целлулоид.
Называться транспортиром (рус.) прибор стал в 1610 году. Термин произошёл от средневекового слова protractor, что означает «переносить», который, в свою очередь, произошел от латинского слова protrahere «тянуть вперёд».
Разновидности и использование
Транспортир — это простой гониометр для измерения или создания угла. Он выглядит как круглый или полукруглый диск с делением.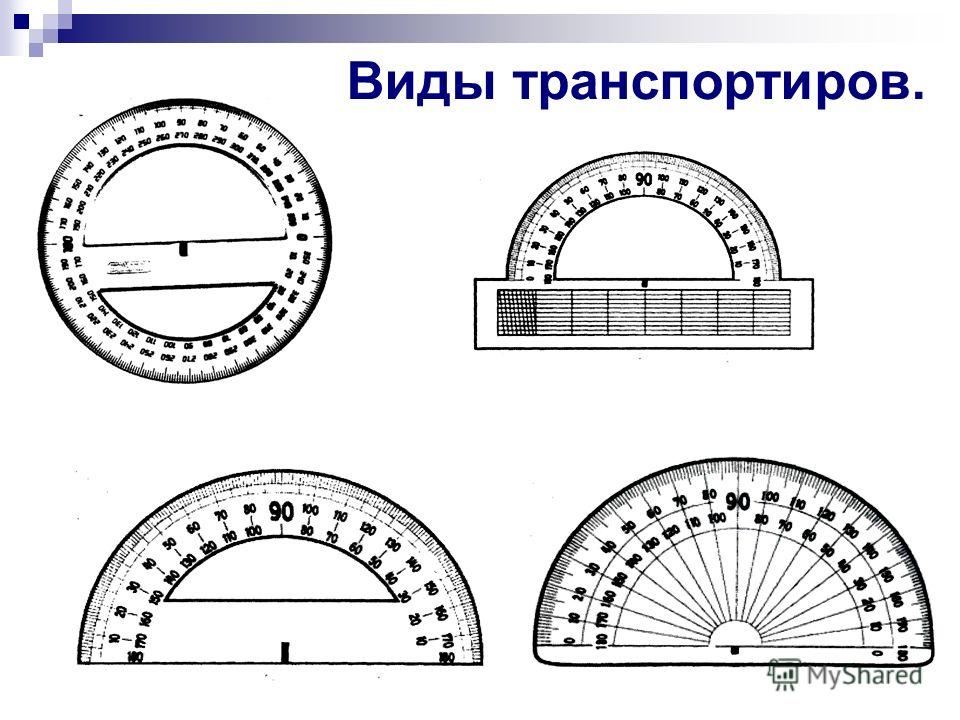 Диск может быть изготовлен из пластика, прочной бумаги или листового металла. Типичными являются диаметры от 8 до 15 см и деления на 1° и 0,5°, при измерении также 0,5 Гон (новый градус). Точность составляет от 0,1 до 0,5° в зависимости от диаметра шкалы. Более точные приборы имеют поворотную рейку со шкалой (длина до миллиметра).
Диск может быть изготовлен из пластика, прочной бумаги или листового металла. Типичными являются диаметры от 8 до 15 см и деления на 1° и 0,5°, при измерении также 0,5 Гон (новый градус). Точность составляет от 0,1 до 0,5° в зависимости от диаметра шкалы. Более точные приборы имеют поворотную рейку со шкалой (длина до миллиметра).
Частично из-за различного использования их изготавливают во многих формах: знакомый полукруг, а также круги, прямоугольники, квадраты или четверть круга (квадранты). Они также могут иметь различные диаметры. Их изготавливают из латуни, стали, дерева, слоновой кости или пластика. Самой распространённой формой является полукруг с ограничительной шкалой в 180 градусов.
Угловой транспортир — градуированный круглый инструмент с одной поворотной рукой; используется для измерения или разметки. В строительстве часто требуется отмерить угол в 90 градусов. Иногда прилагается шкала Вернье, чтобы дать более точные показания. Прибор широко применяется для изготовления архитектурных и механических чертежей, хотя его использование уменьшилось с появлением современного программного обеспечения для рисования.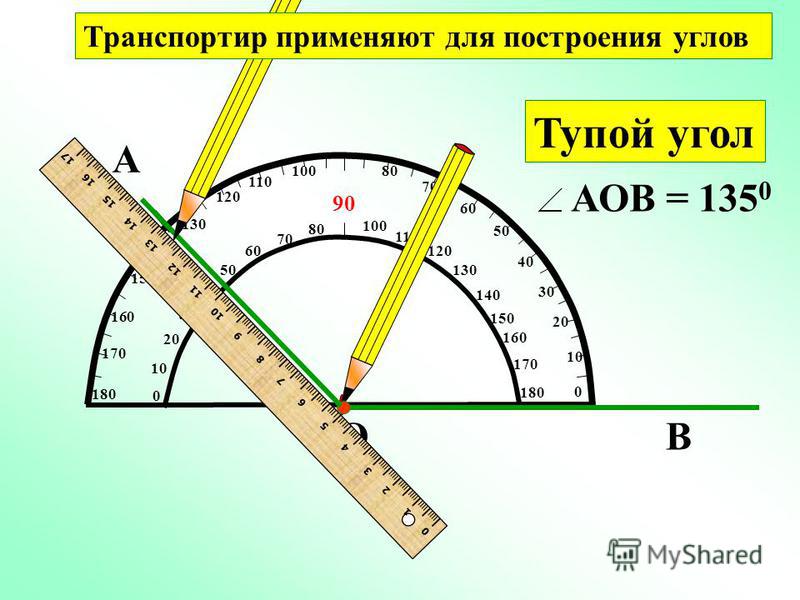
Универсальные транспортиры скоса используются изготовителями инструментов; поскольку они делают измерения посредством механического контакта с предметом, то классифицируются как механические транспортиры.
Угловой транспортир применяется для того, чтобы измерить и проверить углы с очень жёсткими допусками. Он считывает до 5 угловых минут (5 или 1/12°) и может измерять от 0 до 360°.
Сегодня также применяются электронные приборы, которые обычно работают с поворотным датчиком. Кроме того, связанными с транспортиром приборами являются:
- теодолит;
- оптический транспортир в строительной промышленности и геодезии;
- инклинометр для определения уклонов и косвенной альтиметрии;
- секстант для навигации.
Измерение градусов угла
Для того чтобы научиться пользоваться транспортиром инструкция нужна на начальном этапе. Для его освоения достаточно нескольких минут и примеров (смотреть онлайн) того, как можно измерить и построить угол с помощью этого прибора.
Для его освоения достаточно нескольких минут и примеров (смотреть онлайн) того, как можно измерить и построить угол с помощью этого прибора.
Измерить угол, значит найти его величину. Углы разделяют на три типа: острый, тупой и прямой. Прямоугольный имеет 90 градусов. Все углы что имеют больше этого значения называются тупыми, и соответственно меньше 90 градусов называются острыми. Развёрнутый угол имеет 180 градусов.
Понимание того, что углы являются частями окружностей, полезно, потому что тогда конструкция транспортира обретает смысл. Поскольку полный круг имеет 360º, отдельный угол должен быть меньше этого числа, потому что он часть круга.
Алгоритм измерения следующий: для того чтобы измерить угол транспортиром необходимо приложить его центр верхней кромки линейки к вершине измеряемого угла. Вершина — это точка, в которой две из трёх сторон треугольника пересекаются.
Нижнюю планку (основание) транспортира нужно выставить горизонтально.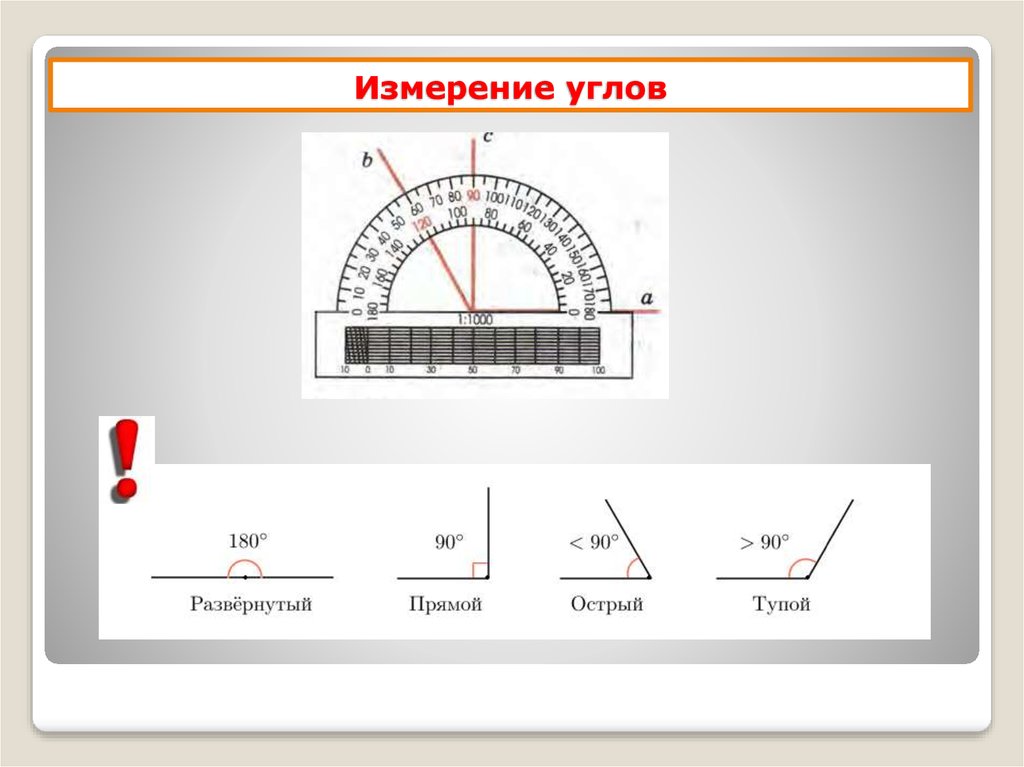 Каждый транспортир имеет точку, спроектированную в центре основания, Эта средняя точка располагается на вершине угла, который должен быть измерен или нанесён на график. Другая сторона должна пересекать транспортир в одной из точек его дуги.
Каждый транспортир имеет точку, спроектированную в центре основания, Эта средняя точка располагается на вершине угла, который должен быть измерен или нанесён на график. Другая сторона должна пересекать транспортир в одной из точек его дуги.
Если вторая сторона (линия) до дуги не доходит нужно продолжить её с помощью простой или масштабной линейки. То число, на шкале дуги, которое будет пересечено линией и есть величина угла в градусах.
Для удобства на большинстве транспортиров сделано две шкалы, внутренняя и внешняя, которые отображают числа в каждой строке.
Построение угла
Берётся чистый лист бумаги в клетку. На нём карандашом отмечается точка, от которой проводиться прямая линия, как одна из сторон будущего угла. Эта черта служит для того, чтобы задать направление второй стороне. В простых упражнениях, для приобретения навыка построения угла, линия проводится горизонтально.
Центр основы транспортира располагается на любом из концов черты, который будет вершиной угла. Эта точка отмечается на бумаге карандашом. И именно к этому месту, внутри отверстия и присоединяется вершина угла, одна из сторон которого должна совпадать в горизонтальной плоскости с внутренней стороной линейки транспортира.
Затем на шкале отмечается необходимый градус. С внутренней стороны отверстия также обозначается точка возле этого градуса. И от вершины проводится прямая линия к этой точке. Таким образом, получается необходимый угол.
Для того чтобы правильно пользоваться транспортиром очень важно его выровнять, и точно прикладывать, для получения верных измерений.
Пересечённые линии в верхней части прямой кромки линейки должны совпадать с вершиной (конечной точкой), где соединяются два луча.
«Транспортир. Измерение углов при помощи транспортира».
 Урок математики 3 класс по системе Занкова | Презентация к уроку по математике (3 класс) на тему:
Урок математики 3 класс по системе Занкова | Презентация к уроку по математике (3 класс) на тему:«Транспортир. Измерение углов при помощи транспортира».
Цель: знакомство с новым измерительным прибором — транспортиром.
Задачи урока: ознакомление с алгоритмом измерения углов при помощи транспортира; создать условия для формирования умения определять градусную меру угла;
Планируемые результаты:
Предметные:
1. Подвести обучающихся к самостоятельному открытию нового материла и решению проблемных ситуации;
2. формирование умения пользоваться составленным алгоритмом измерения углов;
3. Обучать чтению математических текстов.
4. Развивать логическое мышление;
Метапредметные:
1. Продолжить работу над развитием умения анализировать и сравнивать,
2. Выделять существенные признаки,
3. Учить аргументировать свою позицию.
Личностные:
- Способность характеризовать собственные знания по предмету
- Развитие познавательного интереса к математической науке
Тип урока:
Урок открытия нового знания.
Оборудование:
• компьютер.
• проектор.
• презентация слайдов.
• транспортир.
• карточки для работы в группах.
• учебник.
Ход урока.
Этап урока | Элементы содержания; методические приёмы | Деятельность учителя | Деятельность учащихся | Форма контроля |
1. Организационный этап | Фронтальная беседа. Проверка готовности класса. Эмоциональный настрой на урок Букет настроения | – Проверь, дружок, готов ли ты начать урок? – У каждого на парте лежат цветы. Это цветы – настроения. Если у вас сейчас хорошее настроение, то красный цветок, если не очень – тогда жёлтый, ну а если совсем плохое, тогда – синий. – Французский писатель XIX столетия Анатоль Франц однажды заметил, что: “Учиться можно только весело. Чтобы переваривать эти знания, нужно поглощать эти знания с аппетитом”. Давайте сегодня на уроке будем следовать этому совету. Будем активны, будем поглощать знания с большим желанием, потому что они пригодятся вам в дальнейшей жизни. | Приветствуют учителя. Отвечают на вопросы. Организуют рабочее место, проверяют наличие индивидуальных учебных принадлежностей. Могут проявлять эмоциональную отзывчивость. | Фронтальная. Наблюдение учителя |
2. Актуализация опорных знаний — восприятия, осмысления. | Фронтальная беседа. | – Но перед тем как двигаться дальше, приведем свои мысли в порядок. 1- МАТЕМАТИЧЕСКАЯ КАРУСЕЛЬ 2- Как называется линия, которая является границей круга? 3 – Какой угол образуют стрелки часов? | 45—5—60—24—5—40—49 Окружность центр окружности радиус угол Острый Острый , развёрнутый, острый , Прямой, тупой | |
3. | Фронтальная беседа. | — Что вы уже знаете? Что такое угол? Виды углов. Образование углов. Сравнение углов (может быть в конце урока нам удастся ответить на этот вопрос) | Геометрическая фигура Острый, прямой, тупой, развёрнутый Между лучами, исходящими из одной точки ??? | |
4. Создание проблемной ситуации. | Практическая работа | Начертите любой острый угол, назовите его АВС А сейчас — начертите еще раз точно такой же угол по величине и назовите его МКН. Ну, молодцы! — А как измерить угол? | эту работу дети выполняют в тетрадях, учитель тоже чертит угол на доске не знаете размера угла АВС (транспортир) | |
5. Работа над изучением нового материала. | Фронтальная беседа. | — Кто уже догадался, о чем мы сегодня будем говорить на уроке? — А где можно найти о нём информацию? -Откройте учебник на с. 96 Материал из истории инструментов. Найдите сведения о транспортире.
Транспортир состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы), разделенного на градусы то 0 до 180 º. В некоторых моделях – от 0 до 360 º – это круглые транспортиры. Транспортиры изготавливаются из стали, пластмассы, дерева и других материалов. | О приборе, для измерения углов – транспортире. В интернете, у взрослых, в книге (учебнике) Ученики читают « | |
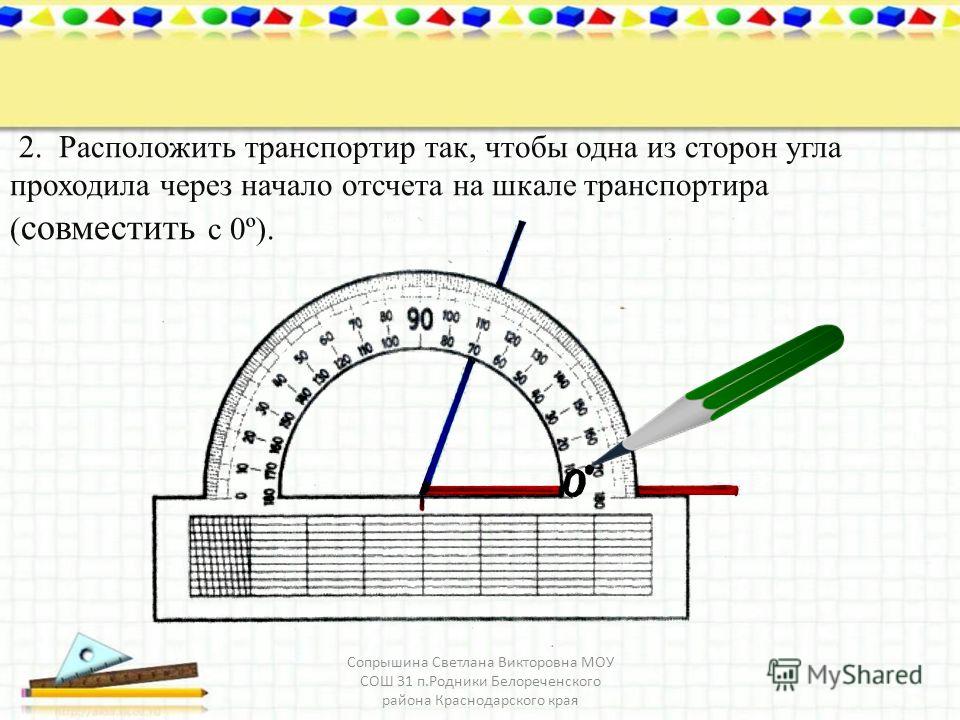
7. Работа с учебником (учебник с. 92 № 184) | Фронтальная беседа. Работа в паре | — Рассмотрите приборы. Для чего их используют? — Что общего у транспортира с теми приборами? — Вспомним, с какого деления идет измерение на шкале? — Как измерить угол при помощи транспортира? (учебник стр.93 иллюстрации помогут) Обсудить алгоритм в паре. 1. Совместить вершину угла с центром транспортира. | Шкала (0) Обсуждение алгоритма измерения угла транспортиром. | |
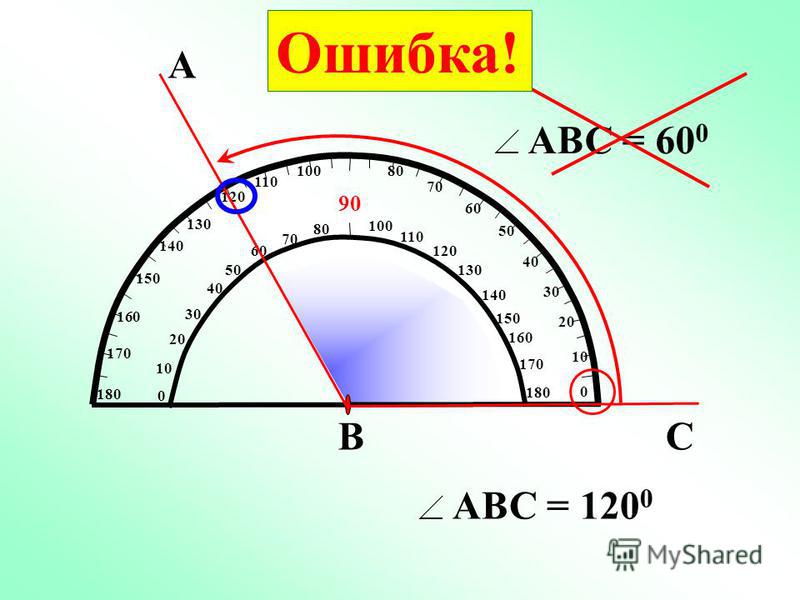
Игра «Найди ошибку» | — В чём ошибка измерения? | Ответы детей | ||
6. Физминутка | Игра «Отодвигаем стены» Уберите НЕВЕРНЫЕ ВЫСКАЗЫВАНИЯ 1) Углы измеряют с помощью линейки. 2) Углы измеряют с помощью транспортира. 3) Единицы измерения углов — килограммы. 4) Единицы измерения углов — градусы. 5) Острый угол меньше развернутого. 6) Прямой угол имеет градусную меру 90°. 7) Тупой угол больше развернутого. 8) Острый угол меньше прямого. 9) Прямой угол больше тупого. 10) Тупой угол больше прямого, но меньше развернутого. | |||
8. Использование нового материала для решения задания. | Практическая работа Работа в парах | — Откройте учебник на стр. 88 № 176 — Определите величину угла АВС, DEF, KMN Измеряем углы, проговаривая все этапы работы. — Какой из острых углов больше и на сколько? — Определите величины выделенных углов на карточках. Проверка слайд — А теперь возвращаемся к нашему заданию. У кого углы одинаковые? ( показать как подписывается величина угла) | Упр-е в определении величины угла Записывают на доске и в тетради АВС=120, DEF=80, KMN=60 Измеряют углы, записывают результаты. Проверяют АВС = МКН = | |
Как вы думаете, кому в жизни может понадобиться транспортир? | Строителю, Чертёжнику, Архитектору | |||
9. Анализ деятельности на уроке. Рефлексия. | Фронтальная беседа. | — Возвращаемся к слайду Что такое угол? Виды углов. Образование углов. Сравнение углов | Уже знаем | |
10. Подведение итогов урока и планирование дальнейших действий. | Фронтальная беседа. | — Ребята, чему мы учились на уроке? Давайте повторим алгоритм — А как вы думаете, что можно еще сделать при помощи транспортира? На доске изображена ваза. Покажите, какое у вас настроение сейчас. Если вам понравился урок, и вы узнали что-то новое, то прикрепите к вазе красный цветок, если было немного сложно – жёлтый, если не понравился и было очень тяжело – синий” | Мы учились измерять углы при помощи транспортира, измерять углы Построить углы по заданной величине. Дети выходят к доске и прикрепляют цветы |
1.15. ИЗМЕРЕНИЕ ДИРЕКЦИОННЫХ УГЛОВ ПО КАРТЕ
Книга найдена на http://www.geolink-group.com/tourclub/ — спасибо создателям
Вы можете заказать 2CD с картами Юга России
Содержание книги
1.15. ИЗМЕРЕНИЕ ДИРЕКЦИОННЫХ УГЛОВ ПО КАРТЕ
Измерение транспортиром. Тонко очиненным карандашом, аккуратно по линейке, прочерчивают линию через
главные точки условных знаков исходного пункта и ориентира. Длина
прочерченной линии должна быть больше радиуса транспортира, считая от точки
ее пересечения с вертикальной линией координатной сетки. Затем совмещают
центр транспортира с точкой пересечения и поворачивают его, сообразуясь с
величиной угла, как показано на рис. 27. Отсчет против прочерченной линии
при положении транспортира, указанном на рис. 27, а, будет соответствовать
величине дирекционного угла, а при положении транспортира, указанном на рис.
27,6, к полученному отсчету необходимо прибавить 180°.
Тонко очиненным карандашом, аккуратно по линейке, прочерчивают линию через
главные точки условных знаков исходного пункта и ориентира. Длина
прочерченной линии должна быть больше радиуса транспортира, считая от точки
ее пересечения с вертикальной линией координатной сетки. Затем совмещают
центр транспортира с точкой пересечения и поворачивают его, сообразуясь с
величиной угла, как показано на рис. 27. Отсчет против прочерченной линии
при положении транспортира, указанном на рис. 27, а, будет соответствовать
величине дирекционного угла, а при положении транспортира, указанном на рис.
27,6, к полученному отсчету необходимо прибавить 180°.
При измерении дирекционного угла необходимо помнить, что дирекционный угол отсчитывается от северного направления вертикальной линии сетки по ходу часовой стрелки.
Средняя ошибка измерения дирекционного
угла транспортиром, имеющимся на командирской линейке, примерно равна 1°. Большим транспортиром (с радиусом 8—10 см) угол на карте можно
измерить со средней ошибкой 15′.
Большим транспортиром (с радиусом 8—10 см) угол на карте можно
измерить со средней ошибкой 15′.
Рис. 27. Измерение дирекционных углов транспортиром
/
Измерение хордоугломером (рис. 28). Через главные точки условных знаков исходного пункта и ориентира проводят на карте тонкую прямую линию длиной не менее 12 см. Из точки пересечения этой линии с вертикальной линией сетки карты циркулем делают на них засечки радиусом, равным расстоянию на хордоугло-мере от 0 до 10 больших делений. Засечки делают на линиях, образующих острый угол.
Затем измеряют хорду — расстояние между
отметками отложенных радиусов. Для этого левую иглу циркуля-измерителя с
отложенной хордой передвигают по крайней левой вертикальной линии шкалы
хордоугломера до тех пор, пока правая игла циркуля не совпадет с каким-либо
пересечением наклонной и горизонтальной линии. При этом правую иглу
необходимо передвигать строго на одном уровне с левой. В таком положении
циркуля производят отсчет против его правой иглы. По верхней части шкалы
отсчитывают большие и десятки малых делений. По левой части шкалы с ценой
делений 0-01 уточняют величину угла. Пример измерения угла хордоугломером
показан на рисунке.
При этом правую иглу
необходимо передвигать строго на одном уровне с левой. В таком положении
циркуля производят отсчет против его правой иглы. По верхней части шкалы
отсчитывают большие и десятки малых делений. По левой части шкалы с ценой
делений 0-01 уточняют величину угла. Пример измерения угла хордоугломером
показан на рисунке.
С помощью хордоугломера измеряют острый угол от ближайшей вертикальной линии координатной сетки, а дирекционный угол отсчитывают от северного направления линии сетки по ходу часовой стрелки. Значение дирекционного угла определяют по изме-
Рис. 28. Измерение дирекционого угла хордоугломером
ренному углу в зависимости от четверти,
в которой расположен ориентир. Зависимость между измеренным углом а’ и дирекционным углом а показана на рис. 29.
Зависимость между измеренным углом а’ и дирекционным углом а показана на рис. 29.
Углы хордоугломером можно измерить си средней ошибкой 0-01—0-02 дел. угл. (4— 8′).
Рис. 29. Переход от угла а’, измеренного хордоугломером, к дирекционному углу а
Измерение артиллерийским кругом. Центр круга совмещают с исходным пунктом (главной точкой условного знака) и круг устанавливают так, чтобы диаметр его 0—30 был параллелен вертикальным линиям координатной сетки, а нуль направлен на север. Затем масштабную линейку совмещают с главной точкой условного знака ориентира и на пересечении ребра линейки со шкалой круга считывают величину угла.
Артиллерийским кругом можно измерить
дирекционный угол и без масштабной линейки (рис. 30). В этом случае
предварительно прочерчивают на карте линию через главные точки условных
знаков исходного пункта и ориентира. Затем артиллерийский круг
устанавливают, как указано выше, и против прочерченной линии считывают по
шкале круга величину дирекционного угла.
Затем артиллерийский круг
устанавливают, как указано выше, и против прочерченной линии считывают по
шкале круга величину дирекционного угла.
Рис. 30. Измерение дирекционного угла артиллерийским кругом
Артиллерийским кругом дирекционный угол. можно измерить со средней ошибкой 0-03 дел. угл.
Вы можете заказать 2CD с картами Юга России
Комментариев нет — Ваш будет первым!
Добавить комментарий
Ваше имя:
Текст комментария (Ссылки запрещены. Условия размещения рекламы.):
Антиспам: От пяти отминycовать тpи (ответ цифрами)
Как нарисовать углы транспортиром
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 25 человек(а).
При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 25 человек(а).
Количество источников, использованных в этой статье: 5. Вы найдете их список внизу страницы.
Транспортир — это простой и удобный инструмент для измерения и построения углов. В основном распространены транспортиры полукруглой формы, хотя существуют и круглые транспортиры, рассчитанные на 360 градусов. Если вы впервые столкнулись с транспортиром и не знаете, как им пользоваться, прочитайте эту статью! Это совсем несложно: несколько простых шагов, и вы как следует освоите этот полезный инструмент.
Люди обычно сталкиваются с транспортирами в математике, когда учатся в школе создавать точные геометрические фигуры. Возможно, у многих из них никогда больше не будет причин снова использовать эти приборы, тем не менее транспортиры имеют долгую историю применения в различных областях.
История изобретения
Происхождение этого математического инструмента восходит к жрецам в Египте и Вавилоне, которые установили меру углов в градусах, минутах и секундах. Однако до времён классической Греции тригонометрия не использовалась в математике.
Однако до времён классической Греции тригонометрия не использовалась в математике.
Во втором веке до нашей эры астроном Гиппарх из Никии изобрёл тригонометрический стол, для измерения треугольников. Затем Птолемей включил в свою великую астрономическую книгу «Альмагест» таблицу, с угловыми приращениями от 0 до 180°, с погрешностью менее 1/3600 единиц. Он также объяснил метод составления этой таблицы, и на протяжении всей книги приводил много примеров того, как вычислять с помощью неё неизвестные элементы фигур.
Птолемей также был автором, так называемой теоремы Менелая для решения сферических треугольников, и на протяжении многих веков его тригонометрия была основным пособием для астрономов.
Возможно, в то же время, учёные Индии также разработали тригонометрическую систему, основанную на функции синуса, которая, в отличие от используемого в настоящее время синуса, была не пропорцией, а длиной стороны, противоположной углу в прямом треугольнике этой гипотенузы.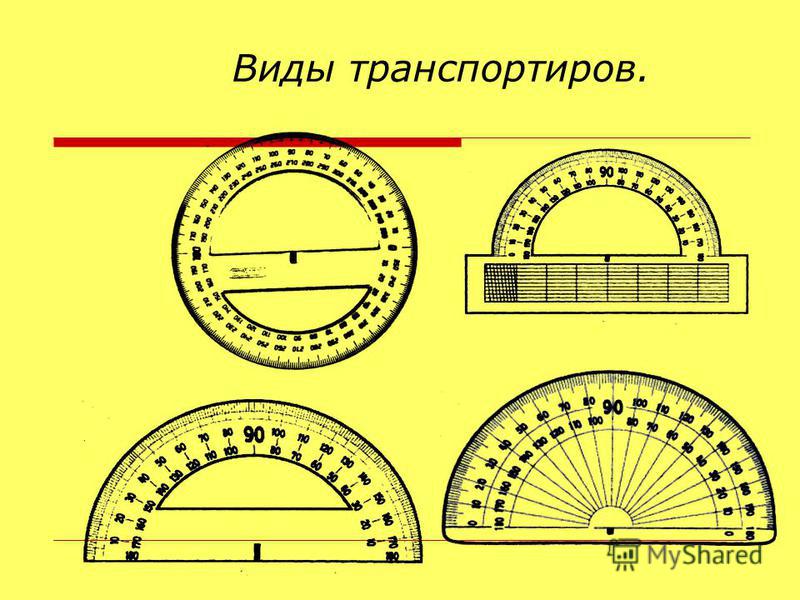 Индийские математики использовали разные значения для этого в своих таблицах.
Индийские математики использовали разные значения для этого в своих таблицах.
Томас Бландевиль рассказал о приборе специально созданном, для рисования и измерения фигур в своём «Кратком описании универсальных карт» 1589 года. Как видно из названия, он применял его, чтобы править навигационные карты для использования в высоких широтах.
Другие европейские математики также описывали подобные приборы примерно в то же время. Независимо от того, кто первым придумал этот инструмент, к началу XVII века он вошёл в стандартную практику мореплавателей и геодезистов. К XVIII веку транспортиры начали появляться в учебниках по геодезии и геометрии.
Транспортиры в современном понимании возникли во второй половине XVIII века, когда такие учёные, как Джесси Рамсден и Георг Фридрих Брандер, усовершенствовали ранее созданные устройства.
В то время предпочтительными материалами для их изготовления были:
В первой половине XX века начали применять олово и целлулоид.
Называться транспортиром (рус.) прибор стал в 1610 году. Термин произошёл от средневекового слова protractor, что означает «переносить», который, в свою очередь, произошел от латинского слова protrahere «тянуть вперёд».
Разновидности и использование
Транспортир — это простой гониометр для измерения или создания угла. Он выглядит как круглый или полукруглый диск с делением. Диск может быть изготовлен из пластика, прочной бумаги или листового металла. Типичными являются диаметры от 8 до 15 см и деления на 1° и 0,5°, при измерении также 0,5 Гон (новый градус). Точность составляет от 0,1 до 0,5° в зависимости от диаметра шкалы. Более точные приборы имеют поворотную рейку со шкалой (длина до миллиметра).
Частично из-за различного использования их изготавливают во многих формах: знакомый полукруг, а также круги, прямоугольники, квадраты или четверть круга (квадранты). Они также могут иметь различные диаметры. Их изготавливают из латуни, стали, дерева, слоновой кости или пластика. Самой распространённой формой является полукруг с ограничительной шкалой в 180 градусов.
Их изготавливают из латуни, стали, дерева, слоновой кости или пластика. Самой распространённой формой является полукруг с ограничительной шкалой в 180 градусов.
Угловой транспортир — градуированный круглый инструмент с одной поворотной рукой; используется для измерения или разметки. В строительстве часто требуется отмерить угол в 90 градусов. Иногда прилагается шкала Вернье, чтобы дать более точные показания. Прибор широко применяется для изготовления архитектурных и механических чертежей, хотя его использование уменьшилось с появлением современного программного обеспечения для рисования.
Универсальные транспортиры скоса используются изготовителями инструментов; поскольку они делают измерения посредством механического контакта с предметом, то классифицируются как механические транспортиры.
Угловой транспортир применяется для того, чтобы измерить и проверить углы с очень жёсткими допусками. Он считывает до 5 угловых минут (5 или 1/12°) и может измерять от 0 до 360°.
Сегодня также применяются электронные приборы, которые обычно работают с поворотным датчиком. Кроме того, связанными с транспортиром приборами являются:
- теодолит;
- оптический транспортир в строительной промышленности и геодезии;
- инклинометр для определения уклонов и косвенной альтиметрии;
- секстант для навигации.
Измерение градусов угла
Для того чтобы научиться пользоваться транспортиром инструкция нужна на начальном этапе. Для его освоения достаточно нескольких минут и примеров (смотреть онлайн) того, как можно измерить и построить угол с помощью этого прибора.
Измерить угол, значит найти его величину. Углы разделяют на три типа: острый, тупой и прямой. Прямоугольный имеет 90 градусов. Все углы что имеют больше этого значения называются тупыми, и соответственно меньше 90 градусов называются острыми. Развёрнутый угол имеет 180 градусов.
Понимание того, что углы являются частями окружностей, полезно, потому что тогда конструкция транспортира обретает смысл. Поскольку полный круг имеет 360º, отдельный угол должен быть меньше этого числа, потому что он часть круга.
Алгоритм измерения следующий: для того чтобы измерить угол транспортиром необходимо приложить его центр верхней кромки линейки к вершине измеряемого угла. Вершина — это точка, в которой две из трёх сторон треугольника пересекаются.
Нижнюю планку (основание) транспортира нужно выставить горизонтально. Каждый транспортир имеет точку, спроектированную в центре основания, Эта средняя точка располагается на вершине угла, который должен быть измерен или нанесён на график. Другая сторона должна пересекать транспортир в одной из точек его дуги.
Если вторая сторона (линия) до дуги не доходит нужно продолжить её с помощью простой или масштабной линейки. То число, на шкале дуги, которое будет пересечено линией и есть величина угла в градусах.
Для удобства на большинстве транспортиров сделано две шкалы, внутренняя и внешняя, которые отображают числа в каждой строке.
Построение угла
Берётся чистый лист бумаги в клетку. На нём карандашом отмечается точка, от которой проводиться прямая линия, как одна из сторон будущего угла. Эта черта служит для того, чтобы задать направление второй стороне. В простых упражнениях, для приобретения навыка построения угла, линия проводится горизонтально.
Центр основы транспортира располагается на любом из концов черты, который будет вершиной угла. Эта точка отмечается на бумаге карандашом. И именно к этому месту, внутри отверстия и присоединяется вершина угла, одна из сторон которого должна совпадать в горизонтальной плоскости с внутренней стороной линейки транспортира.
Затем на шкале отмечается необходимый градус. С внутренней стороны отверстия также обозначается точка возле этого градуса.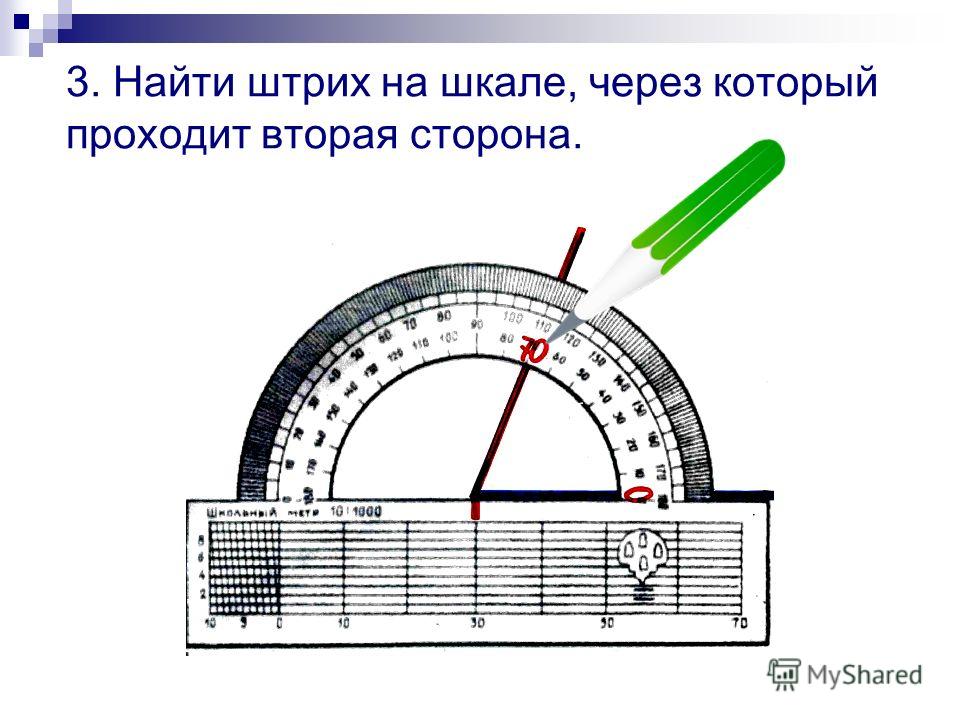 И от вершины проводится прямая линия к этой точке. Таким образом, получается необходимый угол.
И от вершины проводится прямая линия к этой точке. Таким образом, получается необходимый угол.
Для того чтобы правильно пользоваться транспортиром очень важно его выровнять, и точно прикладывать, для получения верных измерений.
Пересечённые линии в верхней части прямой кромки линейки должны совпадать с вершиной (конечной точкой), где соединяются два луча.
Это прозрачный онлайн-транспортир, также помогает измерять углы на изображении, вы можете легко измерить угол любого объекта вокруг вас, сфотографировать и загрузить его, затем перетащить среднюю точку транспортира к вершине угла.
Как пользоваться этим онлайн-транспортиром?
- Вы можете измерить угол любого реального объекта прямо на вашем экране
- Если вы хотите переместить транспортир, перетащите его середину.
- Нажмите на край снаружи транспортира, чтобы добавить к нему метку
- Размещение двух кнопок покажет градусы этого угла
- Двойной щелчок на кнопке удалит ее
Каждый раз, когда я хочу измерить угол, я всегда не могу найти транспортир. К счастью, вот онлайн-транспортир, который удобен и практичен. Теперь мы можем использовать ноутбуки, компьютеры, планшеты или смартфоны для измерения угла наклона чего угодно, вокруг нас в любое время и в любом месте.
К счастью, вот онлайн-транспортир, который удобен и практичен. Теперь мы можем использовать ноутбуки, компьютеры, планшеты или смартфоны для измерения угла наклона чего угодно, вокруг нас в любое время и в любом месте.
Если вы хотите измерить что-то маленькое, просто поместите его на экран и измерьте прямо; Если вы хотите измерить что-то большее, Вы можете сделать снимок и загрузить его, а затем переместить центральную точку транспортира, чтобы измерить его угол.
Используйте камеру или изображение для измерения угла
Вы можете сфотографировать любой объект, который вы хотели бы измерить, например, автомобиль, дорога, дом, лестница или гора, транспортир прозрачный, после того как вы загрузили изображение, оно будет отображаться в фоновом режиме. затем вы можете убрать транспортир или добавить кнопки, чтобы определить градусы углов, загрузить файл только принять файл изображения в форматах JPG, JPEG, GIF, PNG
На панели управления если цвет фона близок к транспортиру, и это не легко отличить, Вы можете изменить цвет транспортира, чтобы видеть это ясно. Также вы можете переместить его, уменьшить или увеличить размер транспортира, в соответствии с вашими потребностями.
Также вы можете переместить его, уменьшить или увеличить размер транспортира, в соответствии с вашими потребностями.
Углы и градусы
- Углы измеряются в градусах. Символом градусов является маленький кружок °
- Полный круг составляет 360 ° (360 градусов)
- Полукруг или прямой угол 180 °
- Четверть круга или прямой угол составляет 90 °
Что вы думаете об этом транспортире?
Посетите эту страницу на вашем смартфоне
Изменить текстовое описание на этой странице
Мы всегда стремимся обеспечить лучший интерфейс и пользовательский опыт, любые предложения по улучшению приветствуются. Текст этой веб-страницы автоматически генерируется Google Translate, это может быть неправильно, если вы хотите предоставить лучшее текстовое описание, пожалуйста, нажмите эту кнопку. ›››
Пожалуйста, будьте вежливы и не используйте это злонамеренно.
This transparent online protractor is 100% self-developed by us, copyright © www. ginifab.com, all rights reserved.
ginifab.com, all rights reserved.
Disclaimer:
Use of the protractor within this website is free. Whilst every effort has been made to ensure the accuracy of the protractor published within this website, you choose to use them and rely on any results at your own risk. We will not under any circumstances accept responsibility or liability for any losses that may arise from a decision that you may make as aresult of using this protractor. Similarly, we will not be requesting a share of any profits you may make as a result of using the protractor.
Измерение углов. Транспортир 5 класс онлайн-подготовка на Ростелеком Лицей
Введение
Какие-то вещи можно измерить, какие-то нельзя. Например, нельзя измерить дружбу или любовь. А расстояние, вес, температуру вполне можно. Чтобы что-то измерять, нужно всем договориться о единицах измерения.
Метр, дюйм, аршин – это и есть такие договоренности при измерении длины. Эталонный метр хранится во Франции, в Палате мер и весов.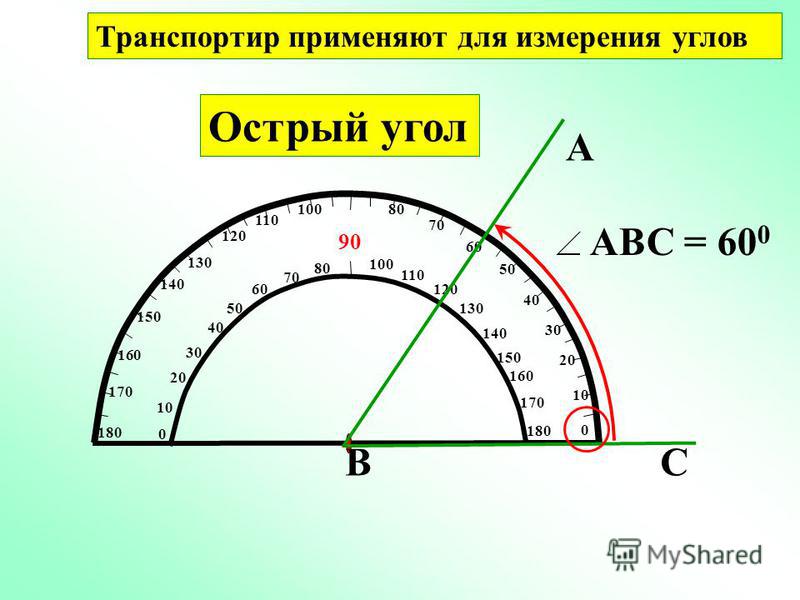 Килограмм, фунт, пуд – это договоренности для измерения массы. Эталонный килограмм тоже хранится в Палате мер и весов.
Килограмм, фунт, пуд – это договоренности для измерения массы. Эталонный килограмм тоже хранится в Палате мер и весов.
Единицы измерения придуманы для конкретных величин. В секундах не измерить вес, а в аршинах – время.
В геометрии такая же ситуация. Есть сантиметры, для измерения длин отрезков, но они не подходят для измерения углов. Для измерения углов есть свои единицы измерения. На этом уроке мы рассмотрим одну из них, а именно градусы.
Градусы
Разделим полный угол на 360 равных частей. Для этого удобно использовать окружность. Поделим ее на 360 частей и соединим каждое полученное деление с центром. Получим 360 равных углов (см. Рис. 1).
Рис. 1. Окружность, разделенная на 360 равных углов
Один такой маленький угол назовем углом в 1° (см. Рис. 2).
Рис. 2. 1 градус
Не важно, какого размера будет окружность, которую мы делим. Поделим обе окружности на 360 частей, получим равные углы в 1°, хотя стороны одного угла визуально длиннее, чем у другого (см. Рис. 3).
Рис. 3).
Рис. 3. Углы равны
Стороны углов можно продолжать бесконечно, от этого размер угла не меняется (см. Рис. 4).
Рис. 4. Более явный пример равенства углов
Полный, развернутый, прямой угол
Величина любого угла – это сколько раз в него умещается угол в 1°.
Вот мы видим угол 13° (см. Рис. 5).
Рис. 5. Угол 13°
Понятно, что полный угол состоит из 360 таких углов. То есть он равен 360° (см. Рис. 6).
Рис. 6. Полный угол
Развернутый угол – это половина полного угла. Он равен (см. Рис. 7).
Рис. 7. Развернутый угол
Прямой угол является половиной развернутого и равен 90° (см. Рис. 8).
Рис. 8. Прямой угол
Эталон градуса нет нужды где-то хранить. Если нужно, то всегда можно полный угол разделить на 360 частей, или развернутый – на 180, или прямой – на 90.
Транспортир
Линейка нужна для того, чтобы измерить имеющийся отрезок или начертить отрезок нужной длины. Чтобы измерить угол или начертить угол нужной величины, мы тоже используем линейку, только не прямую, а круглую. Она называется транспортиром (см. Рис. 9).
Чтобы измерить угол или начертить угол нужной величины, мы тоже используем линейку, только не прямую, а круглую. Она называется транспортиром (см. Рис. 9).
Рис. 9. Транспортир
Единицы измерения на ней – градусы. Шкала начинается с нуля и заканчивается 180°.То есть максимальный угол, который мы можем измерить или начертить, – это 180°, развернутый.
Транспортиры могут быть разных размеров, но это не влияет на то, какого размера углы ими измеряют. Для более крупного транспортира у углов нужно чертить стороны длиннее.
Примеры
1. Измерим пару углов.
Прямая часть транспортира совмещается с одной стороной угла, центр транспортира с вершиной угла. Смотрим, где оказалась вторая сторона угла, – 54° (см. Рис. 10, 11).
Рис. 10. Измерение угла
Проделаем то же самое со вторым углом, 137°.
Рис. 11. Измерение угла
Если сторона угла не достает до шкалы, то ее нужно сначала продлить.
2. Начертим углы 29°, 81° и 140°.
Сначала чертим одну сторону угла по линейке (см. Рис. 12).
Рис. 12. Построение одной стороны угла
Отмечаем вершину. Совмещаем с транспортиром. Отмечаем точкой нужное значение угла – 29° (см. Рис. 13).
Рис. 13. Использование транспортира для построения углов
Убираем транспортир. Соединяем полученную точку с вершиной (см. Рис. 14).
Рис. 14. Угол 29°
Точно так же строим два других угла (см. Рис. 15).
Рис. 15. Построение углов
Заключение
Итак, мы с вами обсудили, что для измерения углов люди договорились использовать градусы. Градус – это полного угла.
Инструментом для измерения и построения углов является транспортир.
Можно не использовать названия углов – полный, развернутый, прямой. Мы можем просто говорить – 360 градусов, 180 или 90 градусов.
Измерение величин «Чужими единицами»
На самом деле бывает, когда мы одни величины измеряем единицами, казалось бы, для них не предназначенными, «чужими» единицами.
Можно ли измерить расстояние в минутах? Да, мы часто используем этот способ. «От моего дома до школы 5 минут». Если быть точнее, то «5 минут пешком». Мы здесь используем известную всем величину – скорость пешехода. И величина «5 минут» на самом деле означает «расстояние, которое пешеход проходит за 5 минут». Скорость пешехода – 5 км/ч, 5 минут – это часа, умножим одно на другое. Получаем примерно 400 метров. Не очень точно, зато удобно.
Точно по такому же принципу устроена другая единица измерения расстояния – световой год. Световой год – расстояние, которое проходит свет за 1 год. С помощью этой единицы меряют расстояния между звездами.
Очень распространенный пример использования «чужой» единицы измерения – это измерять вес в килограммах. На самом деле килограмм – единица измерения массы, а вес – это другая физическая величина. Если хотите подробнее узнать, в чем разница между массой и весом, и почему измерять вес в килограммах не верно, то наберите в поисковой системе «масса и вес» и получите множество пояснений по этому поводу.
Атмосферное давление мы до сих пор измеряем в миллиметрах (миллиметрах ртутного столба).
Хотя для угла есть свои «родные» единицы измерения – градусы, которые мы и проходим на этом уроке, все-таки его можно измерять и с помощью линейных величин, например сантиметров. Если нужно измерить угол , то можно достроить его до треугольника, так чтобы один угол был прямым, и разделить длину одной стороны на другую.
Получим величину угла , которая называется тангенсом.
Если увеличить треугольник, то ничего не изменится (см. Рис. 16).
Рис. 16. Тангенс
Ведь во сколько раз увеличилась одна сторона, во столько и вторая.
То есть величины часто можно измерять «чужими» единицами, но это чуть сложнее, там нужны некоторые дополнительные договоренности.
Другие единицы измерения углов
Существуют и другие единицы измерения углов.
1. Минуты и секунды.
Как и метр можно делить на дециметры, сантиметры, миллиметры для более точных измерений, так и градусы делятся на более мелкие единицы измерения.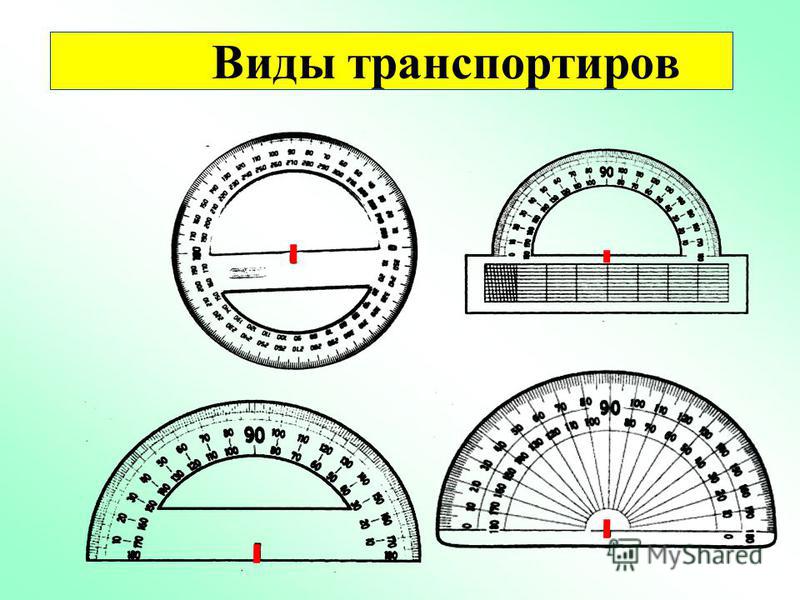
Если угол в 1° разделить на 60 равных частей, то величина полученного угла называется минута, 1′.
Если минуту поделить на 60 частей, то полученная величина называется секундой. Секунда – уже очень маленькая величина, но ее тоже можно делить дальше.
Почему вообще стали делить на 360 частей полный угол, ведь это не очень удобно? В древнем Вавилоне была шестидесятеричная система (у нас десятеричная). Им было удобно делить на 60.
2. Грады.
Чтобы сделать измерение углов ближе к нашей десятичной системе счисления, были предложены грады. Для этого прямой угол делится на 100 частей. Полученная величина называется град. Полный угол составляет тогда 400 градов. Система не прижилась, и сейчас ее не используют.
3. Радиан.
Если взять два радиуса окружности так, чтобы кусочек окружности между ними тоже был равен радиусу, то угол между радиусами мы и примем за новую единицу измерения. Он называется 1 рад (радиан). Эта мера используется наравне с градусной. У нее есть свои преимущества и свои недостатки по сравнению с градусами (см. Рис. 17).
Эта мера используется наравне с градусной. У нее есть свои преимущества и свои недостатки по сравнению с градусами (см. Рис. 17).
Рис. 17. Радианы
Например, теперь полный угол (вся окружность) состоит не из целого числа единичных углов. Полный угол состоит из 6 с лишним единичных углов. Не очень удобно, зато теперь длина дуги (части окружности) и угол хорошо связаны. Если взять окружность радиуса 1 см, то величина угла совпадает с длиной дуги. Угол 1 рад – дуга 1 см, угол 2 рад – длина дуги 2 см.
Список литературы
- Зубарева И.И., Мордкович А.Г. Математика. 5 класс. – М.: Мнемозина, 2013.
- Виленкин Н.Я. и др. Математика. 5 кл. – М.: Мнемозина, 2013.
- Ерина Т.М. Математика 5кл. Раб. тетрадь к уч. Виленкина, 2013. – М.: Мнемозина, 2013.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Shkolo.ru (Источник).
- Cleverstudents.ru (Источник).
- Festival.1september.ru (Источник).
Домашнее задание
- Зубарева И.И., Мордкович А.Г. Математика. 5 класс. – М.: Мнемозина, 2013. Стр. 144 № 522.
- Начертите углы: 23°, 167°, 84°.
- Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 5 класса (5-е изд.) – 2010. Стр. 163 № 3.
Ваше полное руководство — Mashup Math
Ключевой вопрос: Как я могу использовать транспортир для измерения углов?Узнайте, как решать подобные проблемы.
Добро пожаловать в этот бесплатный учебник, где вы научитесь читать транспортир и как использовать его для измерения углов.
Это полное руководство по использованию транспортира включает в себя несколько примеров, анимированный видео-мини-урок, а также бесплатный рабочий лист и ключ к ответу.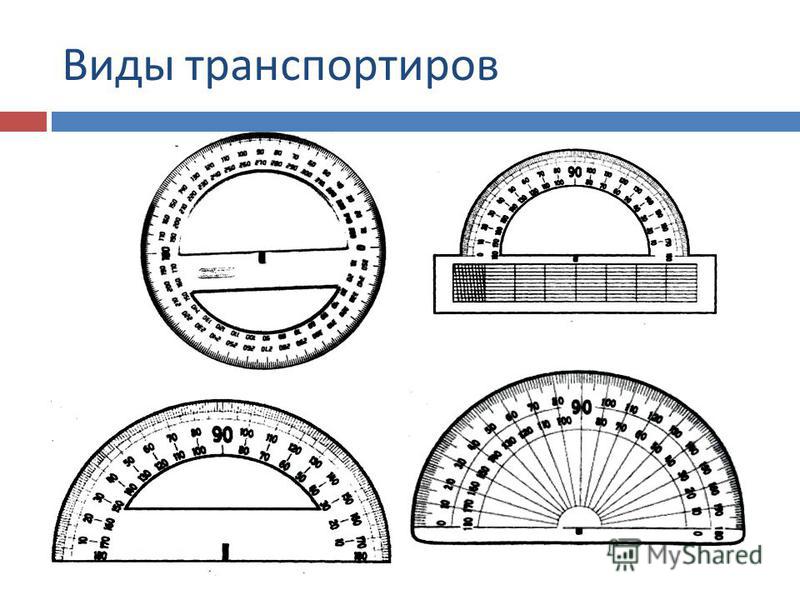
Начнем!
Прежде чем мы научимся пользоваться транспортиром для измерения углов, давайте быстро пробежимся по обозначениям углов (понимание этого важного навыка значительно облегчит обучение использованию транспортира).
Обозначение угла: В геометрии угол обозначается символом ∠ и состоит из 3 последовательных букв, обозначающих три точки, образующие угол. Обратите внимание, что средняя буква обозначает вершину угла.
Например, обратите внимание, как на диаграмме ниже оба угла ∠ABD и ∠CBD имеют точку B в качестве вершины, но имеют разные меры?
В этом примере ∠ABD=120 и ∠CBD=60. Но что происходит, когда на диаграмме не указаны меры угла? Как найти меру углов в подобных ситуациях?
Здесь пригодится транспортир!
Нужна помощь с названиями углов? Если да, посмотрите наш короткий анимационный видео-урок о том, как называть углы, прежде чем перейти к уроку транспортира.
Нажмите здесь, чтобы посмотреть видео на YouTube.
Как пользоваться транспортиромТеперь, когда вы понимаете представление углов, вы готовы научиться пользоваться транспортиром для нахождения величины угла.
Пример: Используйте транспортир, чтобы найти размер ∠MLN на диаграмме ниже.
Во-первых, убедитесь, что вы правильно определили рассматриваемый угол. ∠MLN — это угол, образованный точками M, L и N с вершиной в точке L. Обратите внимание, что ∠MLN теперь окрашен на диаграмме ниже. Если вы считаете, что цвет угла полезен, вы можете использовать маркеры или маркеры всякий раз, когда используете транспортир для измерения углов на бумаге.
Краткое примечание: прежде чем двигаться дальше, определите Маркер центра на транспортире.
Следующим шагом является совмещение маркера центра транспортира с вершиной угла (точкой L в данном примере) следующим образом:
Убедитесь, что нижний луч угла (отрезок LN в этом примере) выровнен с нижней частью транспортира, как показано на рисунке.
60 или 120?
Теперь, когда у вас есть транспортир, последний шаг — использовать его для определения меры угла.
Помните, что мы пытаемся найти меру ∠MLN. Чтобы сделать это, мы должны определить, где верхний луч угла (отрезок LM в этом примере) пересекается с транспортиром, а затем прочитать измерения.
Обратите внимание, что там, где отрезок LM пересекает транспортир, есть два значения: 60 и 120.
Так как ∠MLN острый угол (меньше 90 градусов), вы знаете, что он не может быть равен 120 градусам.
Следовательно, мера ∠MLN должна составлять 60 градусов.
Ниже приведены еще несколько примеров того, как читать транспортир.
Обратите внимание, что рассматриваемый угол тупой (>90 градусов)
Обратите внимание, что рассматриваемый угол острый (<90 градусов)
Обратите внимание, что рассматриваемый угол острый (<90 градусов)
Обратите внимание, что рассматриваемый угол тупой (>90 градусов)
В примере D , обратите внимание, что оба рассматриваемых угла ∠WYZ и ∠WYX являются прямыми углами, поэтому они не являются ни острыми, ни тупыми, и оба имеют угловую меру 90 градусов.
Вам, вероятно, не нужен транспортир, чтобы определить, что ∠WYZ и ∠WYX являются прямыми углами, но этот пример показывает, как транспортир всегда может помочь вам найти меру заданного угла.
Круто, правда?
Все еще запутались? Посмотрите анимированный видео-урок ниже:Посмотрите видеоурок ниже , чтобы узнать больше о том, как измерять углы с помощью транспортира.
Бесплатный рабочий лист!
Хотите попрактиковаться в использовании транспортира для измерения углов? Перейдите по ссылкам ниже, чтобы загрузить бесплатные рабочие листы и ключ ответа:
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ СКАЧАТЬ БЕСПЛАТНЫЙ РАБОЧИЙ ТАБЛИЦ
Продолжайте учиться:Есть мысли? Поделитесь своими мыслями в разделе комментариев ниже!
(Никогда не пропустите блог Mashup Math — нажмите здесь, чтобы получать нашу еженедельную рассылку!)
Энтони Персико Вы часто можете увидеть, как я с радостью разрабатываю анимированные уроки математики, которыми я делюсь на моем канале YouTube .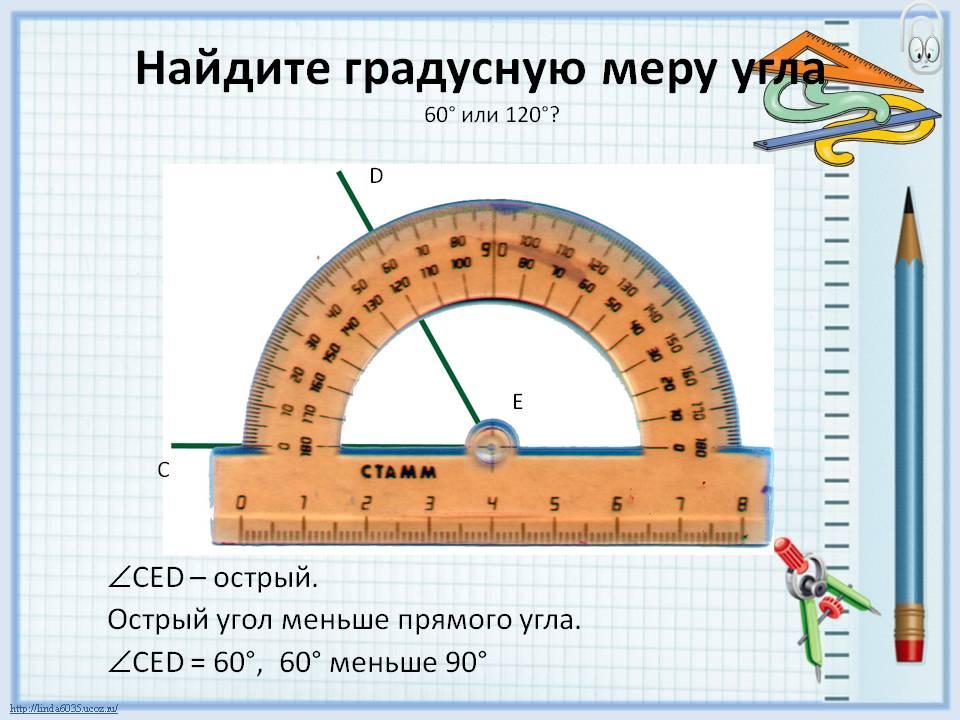 Или проводить слишком много времени в тренажерном зале или играть на своем телефоне.
Или проводить слишком много времени в тренажерном зале или играть на своем телефоне.
1 Комментарий
Измерение углов — определение, использование транспортира, примеры
Измерение углов выполняется с помощью простого геометрического инструмента, такого как транспортир. Транспортир используется чаще, чем циркуль. Измерение углов полезно для того, чтобы точно знать, в какой мере находится угол. В геометрии существуют различные типы углов, с которыми мы сталкиваемся в повседневной жизни, и с помощью этих инструментов мы можем найти 9 углов.0004 измерение углов . Давайте посмотрим, как измерить угол, необходимые шаги и решим несколько примеров.
| 1. | Что такое измерение углов? |
2. | Измерение углов с помощью транспортира |
| 3. | Построение и измерение углов с помощью транспортира |
| 4. | Единицы измерения углов |
| 5. | Часто задаваемые вопросы об измерении углов |
Что такое измерение углов?
Измерение углов выполняется с помощью основных геометрических инструментов, таких как транспортир и циркуль. Эти инструменты помогают найти точную меру угла. Транспортир помогает точно измерить угол, а циркуль помогает в построении угла. Измерение углов производится тремя способами — градусами, радианами и оборотами. Давайте посмотрим, каковы эти три способа измерения углов.
Градусы
Градус — единица измерения угла, измеряемая с помощью геометрического инструмента — транспортира. Градус обозначается символом «°». Окружность полностью вращается на 360°, и градус является частью этого вращения на 360°, поскольку он делится на 360 равных частей.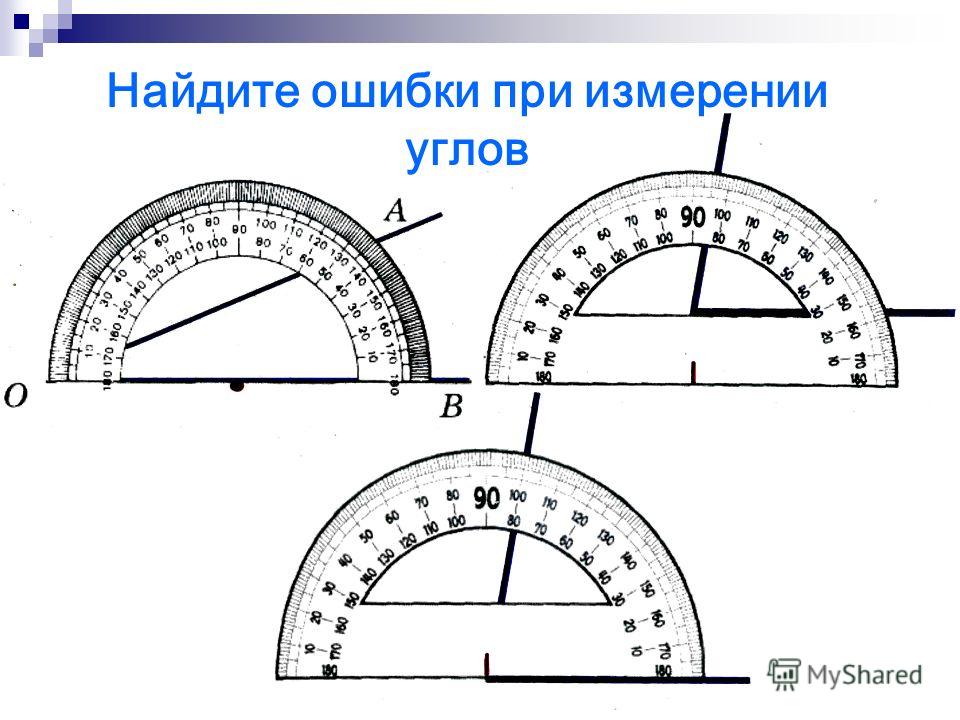 Различные углы с разными градусами составляют 30°, 45°, 90° и так далее. И читается как 30 градусов, 45 градусов, 90 градусов и т. д.
Различные углы с разными градусами составляют 30°, 45°, 90° и так далее. И читается как 30 градусов, 45 градусов, 90 градусов и т. д.
Радиан
Радиан — это еще одна единица измерения угла, которая используется вместо градусов, когда угол необходимо измерять в радианах. По определению, радиан — это отношение длины дуги, на которую опирается угол окружности, к длине радиуса той же окружности. Другими словами, радиан — это угол, образуемый дугой длины радиуса того же круга в центре, и соотношение даст радианную меру угла. Радиан обозначается как рад или c и записывается как 1,7 радиан или 1,7 рад или 1,7 c . Половина круга составляет 180°, что составляет π радиан, а один полный оборот равен 2π радианам.
Обороты
Обороты — простейшая форма измерения углов. В градусах оборот также является единицей 360 °, поскольку угол в основном является подразделением окружности, а не суммой нескольких градусов. Например, при измерении оборотов мы можем сказать, что прямой угол равен четверти окружности, а в градусах угол читается как прямой угол, равный 9. 0°.
0°.
Измерение углов с помощью транспортира
Угол измеряется с помощью двух геометрических инструментов — транспортира и циркуля. В то время как транспортир можно использовать как для построения, так и для измерения, циркуль в основном используется для построения угла. Транспортир считается одним из самых важных геометрических инструментов, поскольку он помогает измерять углы как в градусах, так и в радианах. Когда мы смотрим на транспортир, мы видим измерения от 0 до 180 слева направо по внешнему краю и от 180 до 0 справа налево по внутреннему краю. Измерения по обоим краям составляют до 180°.
При измерении с помощью транспортира измерение обычно производится в градусах. Если угол находится на левой стороне транспортира, мы используем измерение внешнего края, а если угол находится на правой стороне транспортира, мы используем измерения внутреннего края. Шаги для измерения угла:
- Шаг 1: Поместите центр транспортира в вершину угла.
- Шаг 2: Совместите одну сторону угла с нулевой линией транспортира.
- Шаг 3: Угол равен количеству градусов, пересекаемых транспортиром.
Давайте рассмотрим пример. Измерьте ∠AOB.
Шаг 1: Совместите транспортир с лучом OB, как показано ниже. Начните чтение с отметки 0 ° в правом нижнем углу транспортира.
Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на нижней дуге транспортира.
Следовательно, ∠AOB = 60°. Поскольку мера больше 0° и меньше 90°, можно сказать, что угол ∠AOB острый.
Пример: Используя тот же пример, что и выше, давайте измерим угол с другой стороны транспортира. Измерьте ∠AOC.
Шаг 1: Совместите транспортир с лучом CO, как показано ниже. Начните чтение с отметки 0 ° в левом нижнем углу транспортира.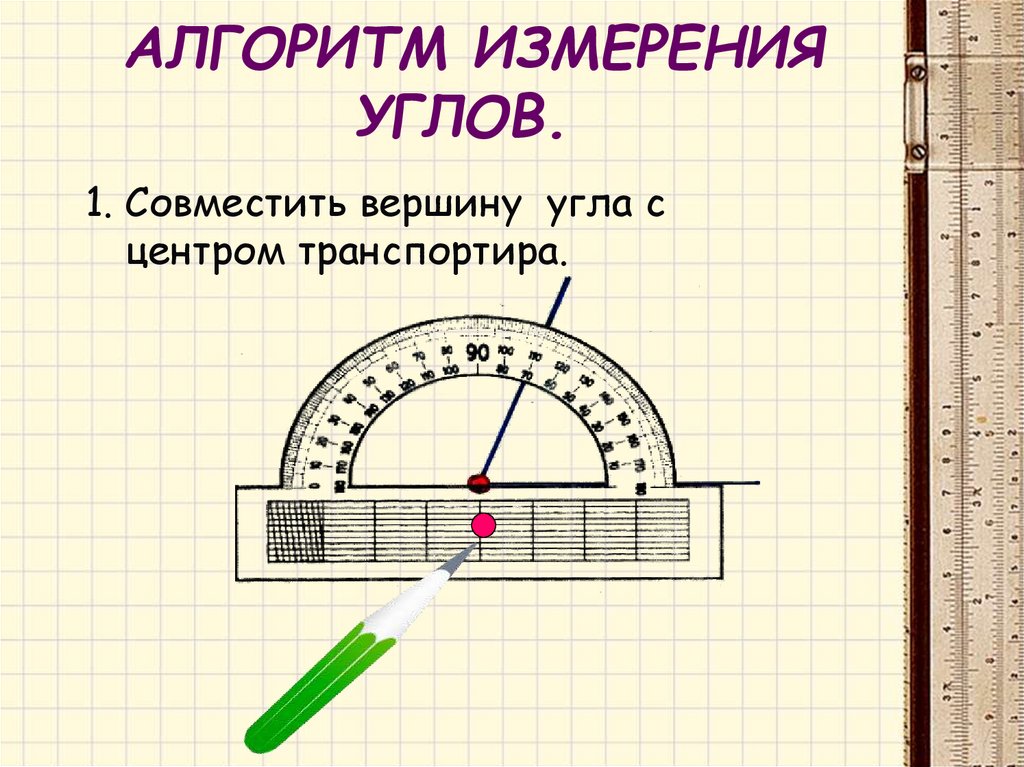
Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на верхней дуге транспортира.
Следовательно, ∠AOC = 120°. Поскольку мера больше 90° и меньше 180°, мы можем сказать, что угол ∠AOC тупой.
Построение и измерение углов с помощью транспортира
Транспортир можно использовать не только для измерения, но и для построения углов. Это помогает как точно измерить углы, так и научиться пользоваться транспортиром. Давайте посмотрим, как нарисовать 40 ° с помощью транспортира.
- Нарисуйте базовую линию AB.
- Отметьте точку O и поместите центр транспортира в точку O.
- Совместите базовую линию транспортира с линией OB.
- Во внутренних показаниях найдите угол 40º и отметьте его как точку C.
- Теперь, используя шкалу, соедините O и C.
- ∠COB = 40°
Чтобы измерить 230º, угол отражения, мы можем записать его как 180° + 50°. Мы можем просто перевернуть транспортир вдоль базовой линии и затем отметить 50°. 180° + 50° = 230°
Мы можем просто перевернуть транспортир вдоль базовой линии и затем отметить 50°. 180° + 50° = 230°
Единицы измерения углов
Углы в геометрии можно измерять, в основном, двумя единицами измерения:
- Радиан
- градусов
Радианы — это единица измерения углов в системе СИ, которая чаще всего используется в концепции тригонометрии. Другая единица, используемая для измерения углов, — градусы, обозначаемые °, — обычно используется в геометрии. Один оборот равен 360 градусам или 2π радианам.
Важные замечания по измерению углов
- Измерение углов выполняется с помощью основных геометрических инструментов, таких как транспортир и циркуль.
- Углы в геометрии можно измерять, используя в основном две единицы — радианы и градусы.
Похожие статьи
- Угол 180 градусов
- Центральный угол
- Дополнительные уголки
- Радиан в Градус
Часто задаваемые вопросы об измерении углов
Что подразумевается под измерением углов?
В геометрии процесс считывания углов или определения точного угла называется измерением углов . Лучший способ измерения углов — использование геометрического инструмента, известного как транспортир. Это полукруглый инструмент с разметкой от 0° до 180°.
Лучший способ измерения углов — использование геометрического инструмента, известного как транспортир. Это полукруглый инструмент с разметкой от 0° до 180°.
Каковы 3 способа измерения углов?
В геометрии существует 3 способа или единицы измерения углов: градусы, радианы и обороты.
- Градусы: Самый распространенный способ измерения углов — градусы. Окружность полностью вращается на 360°, и градус является частью этого вращения на 360°, поскольку он делится на 360 равных частей.
- Радиан: Радиан — это угол, образуемый дугой длины радиуса того же круга в центре, и соотношение дает радианную меру угла.
- Оборот: Оборот — это мера угла, когда он поворачивается на одну сторону, завершая 360°.
Как лучше всего измерять углы?
Углы лучше всего измерять с помощью транспортира. Шаги:
- Поместите центр транспортира в вершину угла.
- Совместите одну сторону угла с нулевой линией транспортира.
- Угол равен количеству градусов, пересекаемых транспортиром.
Как измерить угол без транспортира?
Чтобы измерить угол без транспортира, воспользуемся простой линейкой. Сначала мы соединяем два луча в точке, образуя треугольник. Вот шаги:
- Нарисуйте линию, соединяющую два луча угла.
- Измерьте длину основания треугольника с помощью линейки. Также называется бегом.
- Измерьте длину прямой стороны треугольника с помощью линейки. Также называется подъемом.
- После получения обеих длин мы используем простую формулу уклона, т. е. уклон = подъем/прогон.
- Введите значение наклона в научный калькулятор, затем нажмите кнопку обратного загара.
Каковы различные меры углов?
Различные меры или типы углов:
- Острый угол: Измерьте от 0° до 90°.
- Тупой угол: Измерьте от 90° до 180°
- Прямой угол: мера точно равна 90°.
- Прямой угол: мера точно равна 180°.
- Угол отражения: Измеряйте от 180° до 360°.

- Полный или полный угол: измерение точно равно 360°.
Какой инструмент используется для измерения углов?
Наиболее часто используемым инструментом для измерения углов является транспортир. Транспортир считается важным измерительным инструментом, имеющим форму полукруга.
Какие единицы используются для измерения углов?
Углы в геометрии можно измерять, используя в основном две единицы — радианы и градусы.
Measuring and Making Angles — dummies
By: Mark Ryan and
Updated: 12-21-2021
From The Book: Geometry For Dummies
Geometry For Dummies
Explore Book Buy On Amazon
На карте вы прокладываете свой маршрут и подходите к развилке дорог. Две расходящиеся дороги выходят из общей точки и образуют угол . Точка, в которой дороги расходятся, — это вершина . Угол отделяет область вокруг себя, известную в геометрии как 9.0422 плоскости , на две области. Точки внутри угла лежат во внутренней области угла, а точки вне угла лежат во внешней области угла.
Точка, в которой дороги расходятся, — это вершина . Угол отделяет область вокруг себя, известную в геометрии как 9.0422 плоскости , на две области. Точки внутри угла лежат во внутренней области угла, а точки вне угла лежат во внешней области угла.Как только вы узнаете типы углов и способы их измерения и создания, вы приобретете ценные навыки геометрии, которые помогут вам решить даже самые сложные геометрические головоломки.
Для выполнения обеих задач вы используете транспортир, очень полезный инструмент, который всегда под рукой (см. рис. 1).
Рис. 1. Удобный транспортир
Выбирая транспортир, постарайтесь найти его из прозрачного пластика. Вычислить меру угла проще, потому что вы можете видеть линию угла через транспортир.
Породы ангелов
Существует несколько различных угловых пород или типов. Определить, какая у вас порода угла, можно по его мерке. Наиболее распространенной мерой угла является градуса . Вот краткое введение в четыре типа углов:
Вот краткое введение в четыре типа углов:- Прямоугольный. С таким ракурсом вы никогда не ошибетесь. Прямой угол — один из самых легко узнаваемых углов. Он имеет форму буквы L и образует прямой угол (см. рис. 2). Он имеет меру 90 градусов.
Рисунок 2: Прямой угол
- Угол прямой. Знаешь что? На самом деле это прямая линия. Большинство людей даже не думают об этом типе как об угле, но это так. Прямой угол состоит из противоположных лучей или отрезков, имеющих общий конец (см. рис. 3). Этот угол имеет меру 180 градусов.
Прямые и прямые углы довольно легко определить, просто взглянув на них, но никогда не делайте поспешных выводов о величине угла. Лучше всего быть осторожным. Если информация не написана на странице, ничего не предполагайте. Мера.
Рисунок 3: Прямой уголок
- Острый угол. Это очаровательный угол .
- На самом деле, это всего лишь щепотка.
 Это любой угол, который больше 0 градусов, но меньше 90 градусов. Острый угол находится где-то между несуществующим и прямым углом (см. рис. 4).
Это любой угол, который больше 0 градусов, но меньше 90 градусов. Острый угол находится где-то между несуществующим и прямым углом (см. рис. 4).Рис. 4. Острые углы при 45° (рис. a), 60° (рис. b) и 30° (рис. c)
- Тупой угол. Этот тип просто не так захватывающий, как острый угол. Его мера находится где-то между прямым углом и прямым углом (см. рисунок 5). Это холм, на который вы должны подняться, гора, на которую вы должны взойти. Он имеет меру больше 90 градусов, но меньше 180 градусов.
Рис. 5. Тупые углы при 95° (рис. a), 125° (рис. b) и 175° (рис. c)
Измерение углов
Углы чаще всего измеряются в градусах, но те из вас, кто является приверженцем точности, могут использовать даже более мелкие единицы измерения: минуты и секунды. Такие минуты и секунды подобны часам — минута больше секунды. Так что думайте о градусе как о часе, и вы поняли: один градус равен 60 минутам. Одна минута равна 60 секундам.
Одна минута равна 60 секундам.Прежде чем измерять угол, определите его и оцените, к какому типу, по вашему мнению, он относится. Это прямой угол? Прямой угол? Острый или тупой? После того, как вы его оцените, измерьте угол. Следуй этим шагам:
- Поместите выемку или центральную точку транспортира в точку, где сходятся стороны угла (вершина).
- Поместите транспортир так, чтобы одна из линий угла, который вы хотите измерить, была равна нулю (на самом деле это 0°). Использование нулевой линии не обязательно, потому что вы можете измерить угол, получив разницу в градусах одной линии по отношению к другой. Однако проще измерить угол, когда одна его сторона находится на нулевой линии. Наличие одной линии на нулевой линии позволяет вам считывать измерения непосредственно с транспортира без необходимости выполнять дополнительные математические операции. (Но если вы готовы принять вызов, нокаутируйте себя.)
- Считайте число с транспортира там, где вторая сторона угла встречается с транспортиром.

- Убедитесь, что ваша мера близка к вашей оценке. Это говорит вам, правильно ли вы выбрали шкалу. Если вы ожидали измерения острого угла, но получили серьезно тупой угол, вам нужно переосмыслить используемую вами шкалу. Попробуйте другой.
- Если стороны вашего угла не достигают шкалы транспортира, удлините их так, чтобы они соответствовали. Это повысит точность измерения.
- Помните, что мера угла всегда является положительным числом.
Рис. 6. Углы отражения не укладываются в шкалу транспортира, поэтому для их измерения необходимо выполнить некоторые математические действия.
Об этой статье
Эта статья взята из книги:
- Геометрия для чайников,
Об авторе книги:
Марк Райан — основатель и владелец Математического центра в районе Чикаго, где он занимается репетиторством по всем математическим предметам, а также при подготовке к экзаменам. Марк является автором книг «Исчисление для чайников», рабочей тетради по математическому анализу для чайников и рабочей тетради по геометрии для чайников .
Этот артикул находится в категории:
- Геометрия,
Использование транспортира
Транспортир — удобный инструмент для измерения углов на диаграмме. Диаграмма должна быть точно нарисована и «в масштабе» для этого. работать — величина углов на быстро нарисованной схеме не будет точной. Так вы не сможете измерить углы по диаграмме, подобной этой:
Рекламные ссылки
Довольно легко сказать, что она нарисована от руки и что углы в углах нарисованы лишь приблизительно. Например, право угол, который должен быть 90°, больше похоже на 85°. Нет ничего плохого с такой диаграммой вам просто нужно помнить, что вы не сможете использовать транспортир для измерения углов на нем.
Но если у меня есть точно нарисованная схема, то Я могу использовать транспортир для измерения угла. Давайте используем вопрос о подшипниках как пример:
Подшипники вопрос |
Боб гуляет по лесу. |
Решение |
Ключом к решению большинства проблем с подшипниками является хорошая схема. Поскольку мы собираемся использовать наш транспортир для измерения некоторых углов, схема должна быть «в масштабе» и точной, иначе мы не будем возможность точного измерения любых углов. Чтобы начать рисовать схему, мы нужно нарисовать исходное местоположение Боба. Мы можем просто использовать точку: Теперь нам нужно нарисовать, где он ходит. Первый
часть его пути составляет 10 км. Поскольку мы рисуем схему «в масштабе»,
нам нужно выбрать масштаб, который соответствует для рисования диаграммы
на странице. В каком направлении рисовать? Ну, направление называется «45° к востоку от севера». Север обычно рисуется как стрелка прямо вверх по странице. Восток обычно находится справа от страницы. Итак, мы нужно начать указывать на север, повернуть на 45° на восток, а затем нарисовать линия. Мы можем использовать наш транспортир, чтобы помочь нам сделать это. Начните с рисования пунктирная линия, указывающая, где находится север: Теперь нам нужно отмерить 45° на восток от этого линия, указывающая на север. Есть две вещи, которые вам нужно сделать со своим транспортир при измерении углов: Поместите центр транспортира над точкой откуда вы измеряете угол. В данном случае мы измеряем угол от исходного положения Боба. Выровняйте угол «0» снаружи
транспортир с линией , от которой вы измеряете угол. Теперь все, что нам нужно сделать, это отмерить 45° от севера. к востоку. Посмотрите, как снаружи есть два набора чисел. транспортир? Каждый набор предназначен для измерения углов в разных направлениях. Крайний набор предназначен для измерения углов против часовой стрелки. Самый внутренний набор предназначен для измерения углов по часовой стрелке. На разные транспортиры, эти два набора углов можно поменять местами. Измерение с севера на восток — это направление по часовой стрелке, поэтому мы будем использовать внутренний набор углов. Все, что нам нужно, это сосчитать 45°, а затем поставить маленькую отметку, показывающую этот угол: Теперь нам нужно провести линию длиной 5 см от линии Боба. отправная точка, в направлении этой отметки. Эта линия представляет собой первую часть пути Боба, когда он проходит 10 км в направлении 45° к востоку от север: Обратите внимание, что линия, которую вы нарисовали, не проходит полностью. Часть 2 путешествия Боба — это 9-километровая прогулка по 22° западной долготы. юга. Нам нужно переместить транспортир так, чтобы его центр находился над последним точка в его путешествии, как на следующей диаграмме. Кроме того, нам нужно начертить угол «0» на транспортире с линией, которую мы измеряем угол от. Поскольку мы измеряем 22° западной долготы южной широты , мы измеряем угол от направления на юг, который представляет собой прямую линию вниз по странице. Измеряем угол с юга к на запад, что означает, что мы измеряем по часовой стрелке. Это означает, что мы
необходимо использовать внутренний набор углов транспортира. Теперь осталось выяснить, что такое подшипник и азимут конечного положения Боба. Мы можем провести линию, показывающую направление от его начальной позиции к его конечной позиции, как это: Подшипник от начала до конца
положение находится в «нижней» половине круга возможных пеленгов. Этот
означает, что нам нужно описать азимут относительно направления на юг.
Кроме того, азимут находится в правой половине, а это значит, что мы также будем использовать восток.
описать направление. Итак, наш последний азимут будет звучать как-то
как, «? Градусы к востоку от юга. По моим измерениям угол около 70°. Так это означает, что общий подшипник: 70 градусов к востоку от юга Теперь вопрос еще и по азимуту. Это просто угол с севера на направление, измеренный по часовой стрелке. направление. Теперь мы могли бы измерить его с помощью транспортира, или мы могли бы использовать измерение, которое мы уже сделали. Между севером и югом 180°. Мы уже измерили угол между югом и нашим направлением как около 70°. Мы можем рассчитать, какой угол между севером и нашим направлением автор:
Это означает, что у нас осталось только одно дело.
out – расстояние между стартовой и конечной позициями Боба. Мы можем
это путем измерения расстояния с помощью линейки, а затем преобразования см в
км. По моим измерениям линия от начала до финиш был около 1,96 см в длину. Чтобы преобразовать это в км, нам просто нужно сделать это:
Термин «см» — это расстояние линии в сантиметрах. это шкала, которую мы использовали – сколько километров было на сантиметр . С мы использовали 0,5 см, чтобы представить на км, это означает, что каждый целый см представляет собой два км. Таким образом, наше значение было равно 2: .
Итак, Боб оказывается в 3,92 км от того места, где он начал, в направление на 70 градусов к востоку от юга, откуда он начал. Азимут от где он начал 110º. |
Как пользоваться транспортиром для измерения и рисования углов? Facile Tips
Транспортир — это инструмент, используемый для измерения или рисования углов.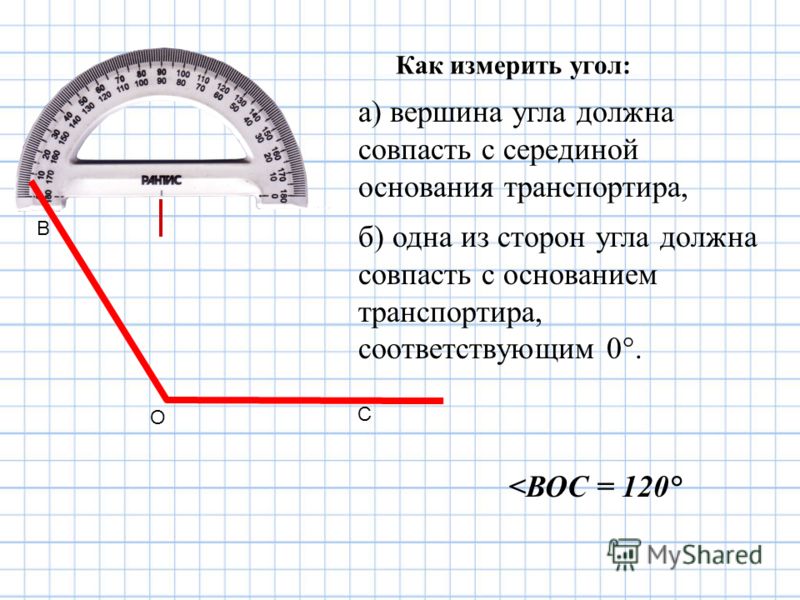 Большинство транспортиров имеют круглую или полукруглую форму и обычно изготавливаются из прозрачного пластика для большей точности. Вот несколько пошаговых инструкций, предоставленных ScienceStruck, о том, как использовать транспортир.
Большинство транспортиров имеют круглую или полукруглую форму и обычно изготавливаются из прозрачного пластика для большей точности. Вот несколько пошаговых инструкций, предоставленных ScienceStruck, о том, как использовать транспортир.
Типы углов
- Острые углы: меньше 90°
- Тупые углы: измерьте больше 90°
- Прямые углы: Измерьте ровно 90°
- Прямые углы: измерьте 180°
- Углы отражения: измерение более 180°
Большинство транспортиров измеряют углы в градусах, а некоторые также измеряют их в радианах. Последние обычно называют транспортирами в радианном масштабе; и используются для сложных механических фигур; особенно в области инженерии или архитектуры.
Транспортиры широко используются в школах для помощи учащимся в изучении геометрии. В основном они имеют полукруглую форму и могут использоваться для рисования или измерения углов до 180 °. Если полукруглые транспортиры измеряют углы до 180 °, сколько может измерять круговой транспортир? Простой! 360°. Однако полукруглый транспортир также способен измерять углы до 360 °, хотя на нем нет соответствующей маркировки.
Однако полукруглый транспортир также способен измерять углы до 360 °, хотя на нем нет соответствующей маркировки.
Начнем с того, что научимся рисовать угол с помощью транспортира, а также научимся измерять уже начерченные углы. Кроме того, мы также научим вас чертить или измерять углы более 180° с помощью обычного полукруглого транспортира. Взглянем!
Как использовать транспортир для рисования угла
Начертить угол с помощью транспортира очень просто. Все, что вам нужно, это карандаш, лист бумаги (разлинованной/неразлинованной) и линейка (по желанию). Давайте начнем.
ШАГ 1
Нарисуйте отрезок (с двумя вершинами) или луч (с одной вершиной). Не забудьте правильно отметить вершину, на которой будет нарисован предлагаемый угол. Это поможет вам легко определить его через транспортир.
ЭТАП 2
Определите градус вашего угла. Приняв решение, поместите транспортир над отмеченной вершиной так, чтобы середина транспортира и вершина совпадали (см. рисунок).
рисунок).
ШАГ 3
После выравнивания удерживайте транспортир неподвижно и отметьте требуемый угол точкой. Чтобы измерить угол, вам нужно начать с 0° (угол вашей линии) и считать вверх, пока не увидите значение желаемого угла. Большинство транспортиров имеют обратимые показания, что означает, что вы можете начать с нуля с обеих сторон.
Однако, если есть только одностороннее чтение (от 0 до 180), и вы хотите начать с большей стороны; воспринимайте 180 как 0, 170 как 10, 160 как 20, 150 как 30 и так далее.
ШАГ 4
После того, как вы отметили нужный угол, соедините вершину (используемую для рисования угла) и отмеченную точку. Этого можно добиться с помощью линейки или линейки транспортира. Вот и все! Вы успешно начертили угол с помощью транспортира.
Как пользоваться транспортиром для измерения угла
Измерить еще проще, чем нарисовать. Посмотрим, как.
ШАГ 1
Поместите транспортир на соединительную вершину ранее начерченного угла.
ШАГ 2
Совместите транспортир с базовой линией так, чтобы она совпадала с 0°. Затем отметьте угол другой линии в соответствии с показаниями транспортира. Начинайте измерение от базовой линии до линии угла, а не с другой стороны.
ШАГ 3
Измерив угол, запишите значение между двумя линиями (как показано на рисунке).
Как рисовать углы более 180° с помощью полукруглого транспортира
Хотя рисование углов более 180° с помощью обычного полукруглого транспортира может показаться сложной задачей, это не так. Вы можете узнать это в четыре простых шага. Они здесь.
ШАГ 1
Начните с рисования линии так, чтобы оставалось достаточно места сверху и снизу линии. Затем отметьте вершину и измерьте 180° с помощью транспортира.
ШАГ 2
После измерения проведите пунктирную линию от вершины до отмеченной точки.
ШАГ 3
Теперь переверните бумагу и снова удерживайте транспортир на отмеченной вершине. Принимая пунктирную линию за базовую линию, а 0° за 180°, отметьте желаемый угол. Например, если вы хотите нарисовать угол величиной 260°, начните считать со 180 до 260. Таким образом, 260° будут дополнительными 80° от 0.
Принимая пунктирную линию за базовую линию, а 0° за 180°, отметьте желаемый угол. Например, если вы хотите нарисовать угол величиной 260°, начните считать со 180 до 260. Таким образом, 260° будут дополнительными 80° от 0.
ШАГ 4
После того, как вы отметили указанный угол, проведите линию, соединяющую вершину и отмеченную точку. Затем переверните бумагу, и вы получите желаемый угол, превышающий 180 °, без использования кругового транспортира.
Как измерять углы, превышающие 180°, с помощью полукруглого транспортира
ШАГ 1
Поместите транспортир в вершину базовой линии и начертите пунктиром 180°.
ШАГ 2
Переверните бумагу, держите транспортир на вершине и измерьте расстояние от пунктирной линии до линии угла. Теперь прибавьте полученный угол к 180°. Например, если вы отсчитали 20° от пунктирной линии, угол рефлекса будет равен 180 + 20, что равно 200°.
Вот как можно использовать транспортир для измерения, а также рисования углов, быстро и легко.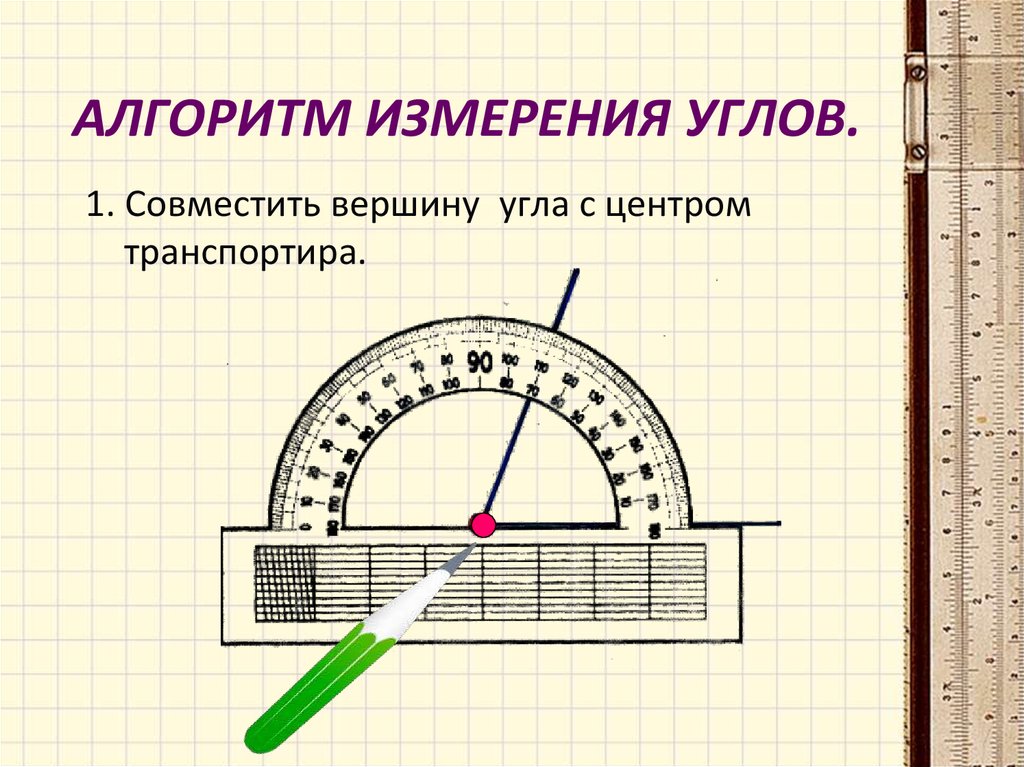 Воспользуйтесь этим руководством и получите хорошие оценки по геометрии. Удачи!
Воспользуйтесь этим руководством и получите хорошие оценки по геометрии. Удачи!
Измерение углов транспортиром в Google Drawings — журнал Digital Maestro
Alex
Алексей
В этом уроке мы создаем графику для задания углов геометрии. Изображения используются учащимися для измерения углов. Студенты используют изображение транспортира, чтобы помочь им измерить эти углы.
Углы, которые мы здесь используем, основаны на предыдущем уроке. Воспользуйтесь ссылкой ниже, чтобы просмотреть этот урок.
Я предоставляю ссылки на готовый продукт ниже. Используйте их, если не хотите создавать углы с нуля. Каждая ссылка создает копию ракурса на вашем Google Диске.
Углы можно приобрести на витрине моего магазина для учителей. Они свободны. Ссылка на витрину доступна под этим абзацем. Я призываю вас следить за ходом урока. Смысл урока в том, чтобы освоить новые навыки.
Создание основных углов с помощью Google Drawings
Рисование острого угла
Рисование тупого угла
Транспортир
Учащимся нужен транспортир для измерения углов. На Викискладе есть бесплатный ресурс изображений. Это изображение находится в общественном достоянии. Ссылка на изображение в Викимедиа доступна ниже. У меня также есть копия транспортира, доступная в Google Drawing.
Не скачивайте изображение со страницы Викимедиа. Мы будем использовать ссылку, чтобы напрямую вставить изображение в рисунок.
https://upload.wikimedia.org/wikipedia/commons/5/5b/Gradeboog1.png
Словарь
Геометрия и углы имеют свой собственный словарь. Вот термины, используемые в этом уроке.
Вершина — это точка, в которой отрезки пересекаются под углом.
Плечо — это термин, используемый для линий угла.
Угол — это место, где стороны встречаются в вершине.
Исходная сторона — это плечо, плоско лежащее на оси x.
Терминальная сторона — это плечо, противоположное начальной стороне.
Тета — это символ, используемый для обозначения углов.
Острые углы
Откройте чертеж острого угла. Используйте ссылку выше, чтобы получить копию. Сделайте копию чертежа. Нажмите «Файл» и выберите «Создать копию».
Установите имя копии под углом 15 градусов. Нажмите кнопку ОК.
Изображение на чертеже сгруппировано. Я рекомендую сгруппировать объекты, чтобы учащиеся не могли случайно сдвинуть объекты с места. Нам нужно разгруппировать объекты, чтобы создать угол.
Щелкните один раз по одной из строк. Нажмите «Упорядочить» и выберите «Разгруппировать».
Нажмите клавишу ESC на клавиатуре или щелкните один раз за пределами угла, чтобы отменить выбор объектов.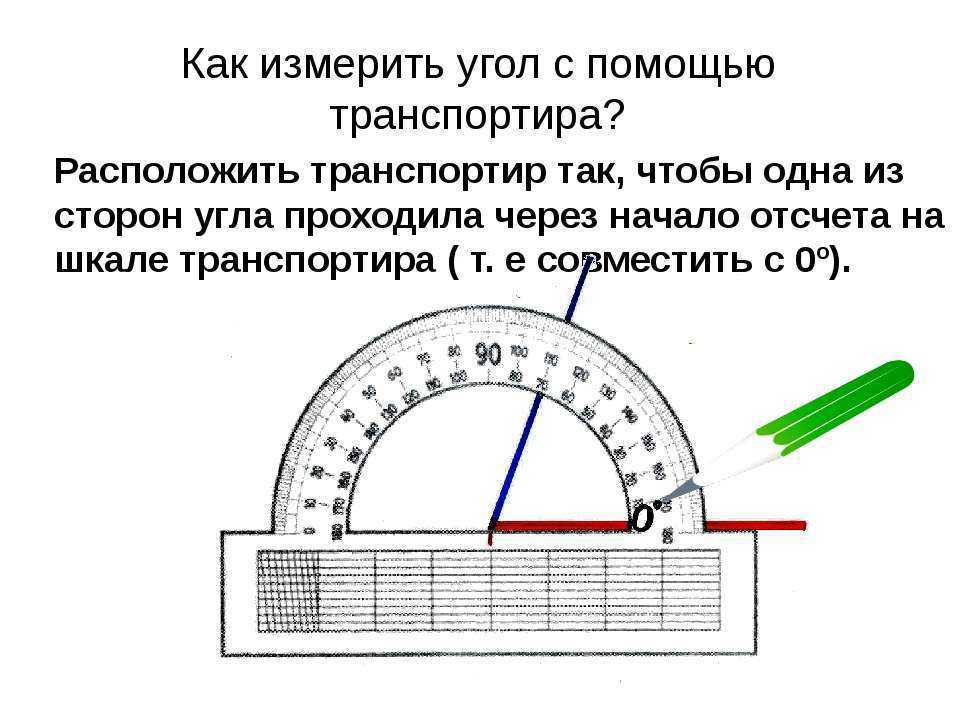 Нажмите на руку терминала.
Нажмите на руку терминала.
Мы собираемся изменить угол линии. Чтобы изменить угол, нам нужно повернуть его на 90 градусов. Нажмите и перетащите конечную точку линии терминала влево. Мы хотим, чтобы линия была прямой вверх и вниз. Удерживайте клавишу Shift, чтобы переместить конечную точку. Это переводит линию в идеально вертикальное положение.
Линия должна быть под углом 90 градусов.
Удерживая нажатой клавишу Shift, перетащите конечную точку линии вправо. Линия защелкнется, когда вы переместите ее вправо. Линия обрывается с шагом в 15 градусов.
Продолжайте перемещать конечную точку вниз. Остановитесь, когда линия защелкнется в точке до того, как она достигнет начального плеча.
Это наш угол 15 градусов. Нам нужно очистить буквы и символы. Выберите символ дуги. Переместите конечную точку верхней дуги к клеммному плечу. Используйте символ плюса, чтобы выровнять конечную точку.
Нам нужно очистить буквы и символы. Выберите символ дуги. Переместите конечную точку верхней дуги к клеммному плечу. Используйте символ плюса, чтобы выровнять конечную точку.
Переместите буквы и символ Тета.
Нарисуйте выделение вокруг всех объектов. Нажмите «Упорядочить» и выберите «Группировать».
Переместите угол к центру холста. Используйте направляющие для выравнивания, чтобы центрировать угол.
Транспортир
Нам нужно предоставить транспортир для использования учениками. Перейдите в начало этого урока и скопируйте ссылку на изображение.
Нажмите «Вставить» и перейдите к опции «Изображение». Выберите параметр для вставки изображения по URL-адресу.
Вставьте ссылку в поле URL. Изображение выписки появится в окне предварительного просмотра. Нажмите кнопку Вставить.
Измерение угла
Этим занимаются ученики. Перетащите транспортир так, чтобы отметка 90 градусов находилась в вершине. Изображение исчезает, когда мы его перетаскиваем. Поместите изображение близко к вершине. Используйте клавиши со стрелками вверх, вниз, влево и вправо, чтобы расположить изображение.
Перетащите транспортир так, чтобы отметка 90 градусов находилась в вершине. Изображение исчезает, когда мы его перетаскиваем. Поместите изображение близко к вершине. Используйте клавиши со стрелками вверх, вниз, влево и вправо, чтобы расположить изображение.
Конечная линия лежит на отметке 15 градусов.
Настройка транспортира
Транспортир и линия одного цвета. Некоторым учащимся может быть трудно определить чтение.
Выберите изображение транспортира. Нажмите кнопку Параметры формата. Выберите раздел «Перекрасить».
Щелкните селектор перекрашивания. Выберите цвет.
Цвет обеспечивает дополнительный контраст.
Есть еще вариант увеличения контраста. Откройте раздел «Настройки».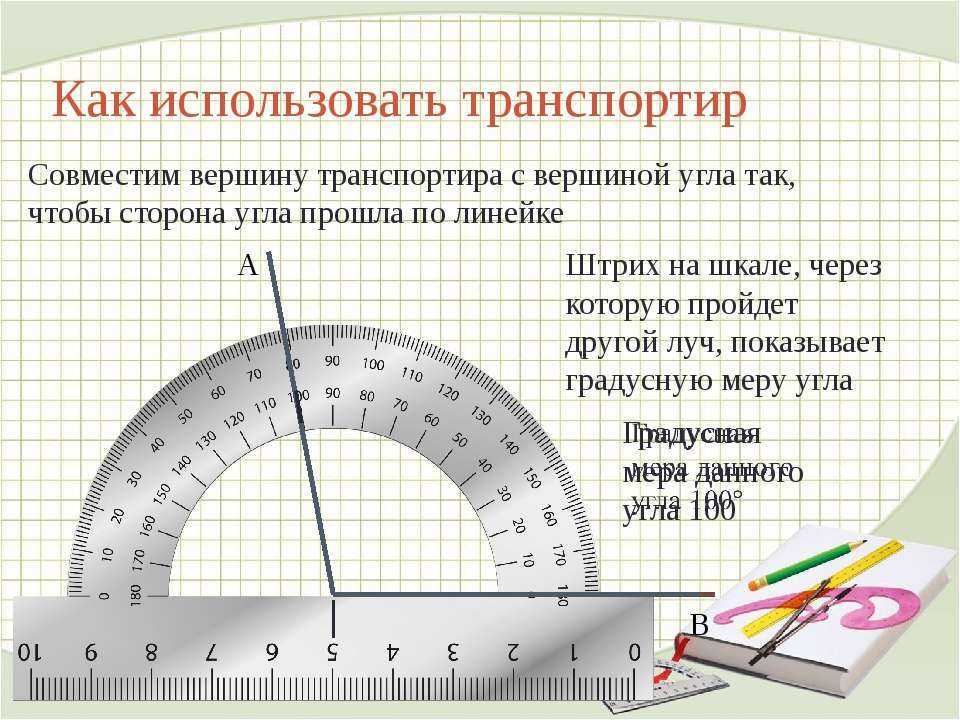 Переместите ползунок прозрачности вправо. Переместите его где-нибудь ближе к среднему положению.
Переместите ползунок прозрачности вправо. Переместите его где-нибудь ближе к среднему положению.
Конечную линию угла легче увидеть.
Поместите транспортир на одну сторону чертежа. Учащиеся перетаскивают его на рисунок.
Раздайте копию ракурса учащимся с помощью Google Classroom.
Больше углов
Есть много других вариантов углов. Сделайте копию этого рисунка. Установите имя копии под углом 30 градусов.
Выберите угол и разгруппируйте объекты. Щелкните конечную точку линии терминала. Удерживайте клавишу Shift. Переместите конечную точку вверх и влево. Он привяжется к следующей 15-градусной точке.
Настройте букву для конечной точки. Переместите конечную точку дуги так, чтобы она встретилась с конечной линией. Настройте символ тета. Выделите все объекты и сгруппируйте их. Это предотвращает случайное перемещение предметов по отдельности учащимися.
Разные углы
Мы делали углы с шагом 15 градусов. Сделаем угол 20 градусов.
Сделайте копию чертежа. Установите имя на угол 20 градусов. Выберите угол и разгруппируйте фигуры. Выберите терминальную линию. Откройте панель параметров формата. Выберите параметр «Размер и поворот».
Фигуру можно вращать только по часовой стрелке. Формы всегда устанавливаются на ноль градусов при создании. Вращение фигуры против часовой стрелки невозможно с помощью настройки вращения.
Конечная линия находится под углом 30 градусов к начальной линии. Поверните угол на 10 градусов, чтобы вернуться к 20 градусам.
Фигура вращается вокруг центра. Это приводит к тому, что конечная точка перемещается от соединения с начальной линией.
Перетащите повернутую линию вниз, пока конечная точка не совпадет с начальной линией.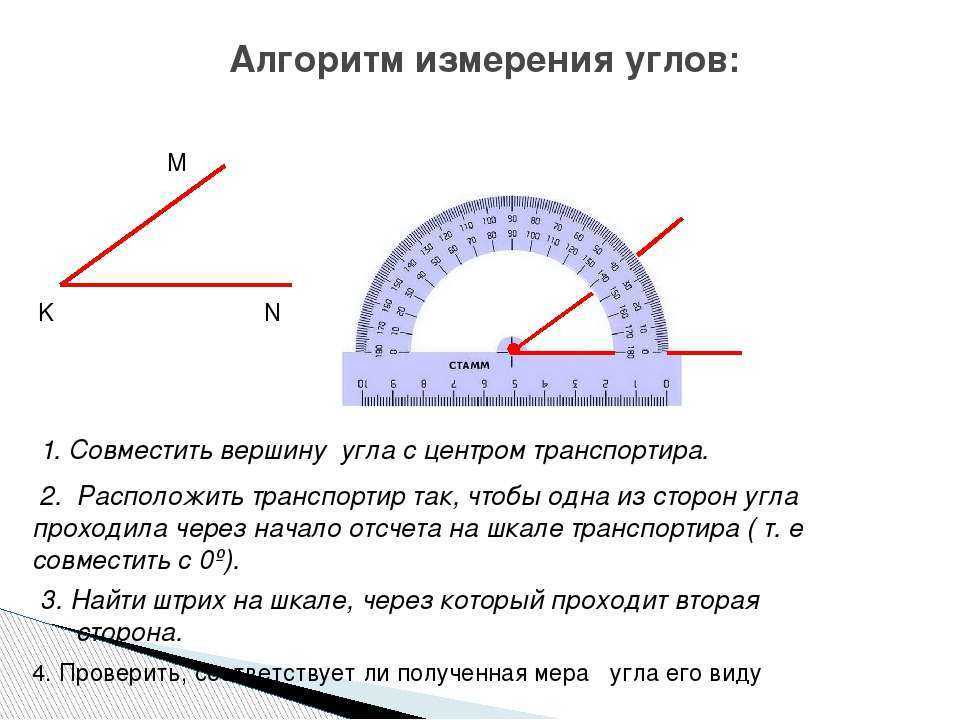
Отрегулируйте дугу и переместите символ Тета.
Переместите изображение транспортира и измерьте угол.
Верните транспортир на прежнее место.
Нарисуйте выделение вокруг объектов. Сгруппируйте объекты. Отцентрируйте угол на холсте.
Другие варианты ракурсов
Мне нравится начинать с прямого ракурса для большинства ракурсов. Сделайте копию угла, который мы создали. Назовите новый рисунок 60 градусов. Разгруппируйте угол. Выберите терминальную линию. Перетащите верхнюю конечную точку влево. Используйте клавишу Shift, чтобы сформировать вертикальную линию.
Откройте панель параметров формата. Откройте раздел «Размер и поворот». Чтобы создать угол в 60 градусов, нам нужно вычесть разницу из 90 градусов. Это дает нам 30 градусов. Введите 30 градусов в поле градусов.
Переместите конечный угол и совместите его с начальной конечной точкой линии.
Отрегулируйте дугу и переместите все текстовые поля.
Тупые углы
Мы создаем тупые углы, используя тот же процесс. Для начала нам нужен тупой угол. Воспользуйтесь ссылкой ниже, чтобы получить копию основного чертежа тупого угла.
Получить копию тупого угла.
Сделайте копию угла. Назовите копию под углом 140 градусов. Разгруппируйте объекты. Выберите терминальную линию.
Переместите верхнюю конечную точку, чтобы линия стала горизонтальной. Не забывайте использовать клавишу Shift.
Нажмите кнопку Параметры формата. Откройте раздел «Размер и поворот». Нам нужно вычесть 140 градусов из 180. Остается 40 градусов. Введите 40 градусов в поле угла. Переместите линию и совместите ее с конечной точкой горизонтальной линии.
Переставьте текстовые поля.

 Покажите, какое у вас настроение.
Покажите, какое у вас настроение. Постановка цели и задач урока. Мотивация учебной деятельности
Постановка цели и задач урока. Мотивация учебной деятельности

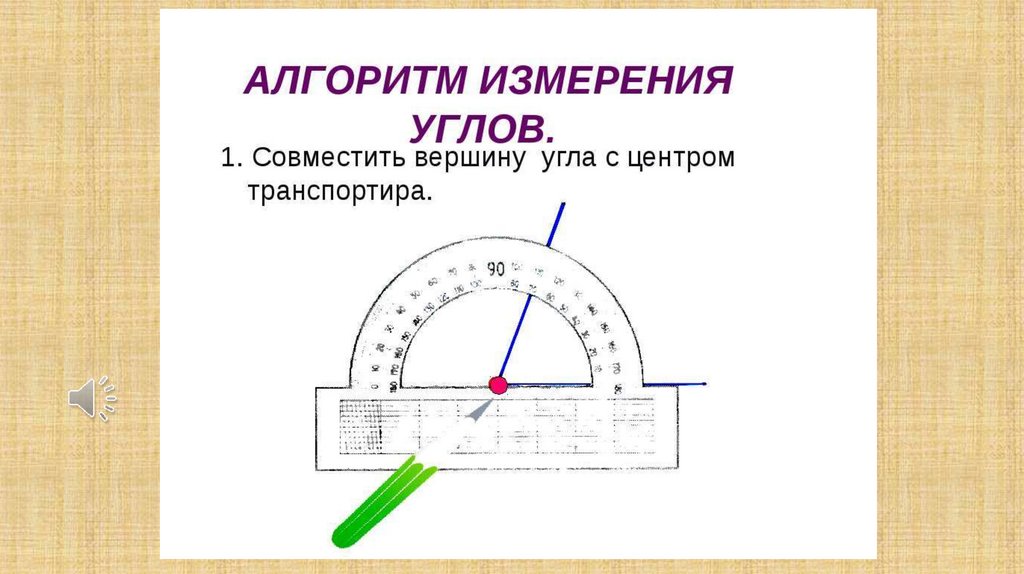 Расположить транспортир так, чтобы одна из сторон угла проходила через начало отсчета на шкале транспортира (т. е совместить с 0º).
Расположить транспортир так, чтобы одна из сторон угла проходила через начало отсчета на шкале транспортира (т. е совместить с 0º).


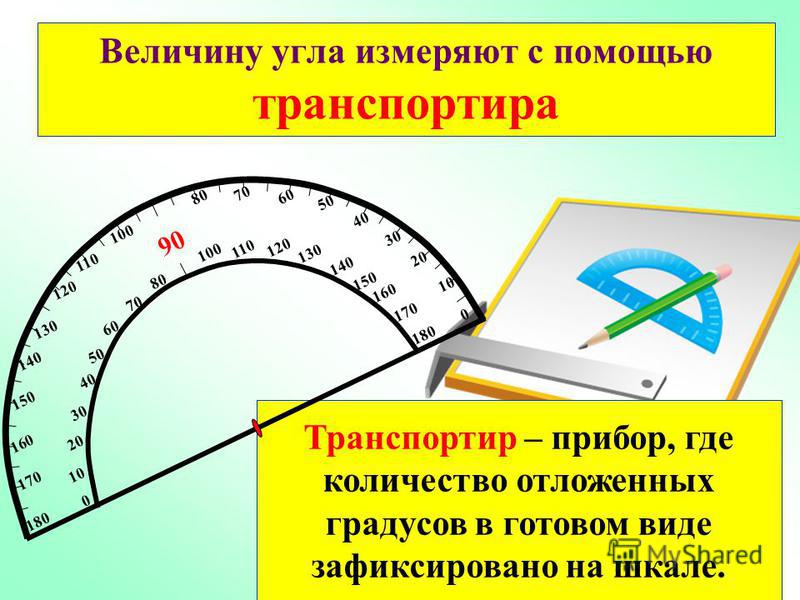 Он проходит 10 км в
направление 45° к востоку от севера. Он останавливается на некоторое время, прежде чем пройти еще 9км в направлении 22° к западу от юга. Какой подшипник откуда он
начал там, где он закончил? Выразите этот пеленг как азимут. Как далеко
он с чего начал? Решите задачу, нарисовав масштабную диаграмму
и используя свой транспортир.
Он проходит 10 км в
направление 45° к востоку от севера. Он останавливается на некоторое время, прежде чем пройти еще 9км в направлении 22° к западу от юга. Какой подшипник откуда он
начал там, где он закончил? Выразите этот пеленг как азимут. Как далеко
он с чего начал? Решите задачу, нарисовав масштабную диаграмму
и используя свой транспортир. Как насчет того, чтобы на каждый км провести линию длиной 0,5 см? Это означает
что эту 10-километровую часть его прогулки следует изобразить в виде линии длиной 5 см.
Как насчет того, чтобы на каждый км провести линию длиной 0,5 см? Это означает
что эту 10-километровую часть его прогулки следует изобразить в виде линии длиной 5 см.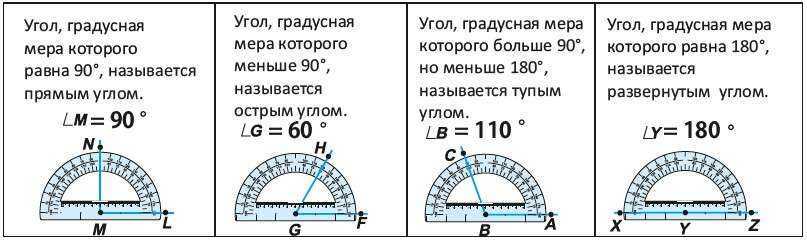 В
в этом случае мы измеряем с севера на восток, поэтому мы выстраиваемся
Угол «0» с северной линией.
В
в этом случае мы измеряем с севера на восток, поэтому мы выстраиваемся
Угол «0» с северной линией. путь к отмеченной вами точке 45°. Из-за размера
транспортир, часто точки или отметки, которые вы рисуете для угла, намного дальше
от центральной точки, то вам нужно. Но не беспокойтесь, это не
иметь значение. Просто выровняйте линейку с центральной точкой и отметкой и нарисуйте
линия настолько длинна, насколько это необходимо.
путь к отмеченной вами точке 45°. Из-за размера
транспортир, часто точки или отметки, которые вы рисуете для угла, намного дальше
от центральной точки, то вам нужно. Но не беспокойтесь, это не
иметь значение. Просто выровняйте линейку с центральной точкой и отметкой и нарисуйте
линия настолько длинна, насколько это необходимо. Нам нужно посчитать 22°
по часовой стрелке с юга и отметьте этот угол, как показано на схеме. Следующий,
мы должны решить, какой длины будет линия, которую мы рисуем. Боб проходит 9 км
в этой части похода, и мы используем 0,5 см для обозначения каждого километра. Этот
означает, что на этом участке похода должно быть 9 лотов длиной 0,5 см, или 4,5
см другими словами. Мы можем нарисовать в этой линии на нашей диаграмме:
Нам нужно посчитать 22°
по часовой стрелке с юга и отметьте этот угол, как показано на схеме. Следующий,
мы должны решить, какой длины будет линия, которую мы рисуем. Боб проходит 9 км
в этой части похода, и мы используем 0,5 см для обозначения каждого километра. Этот
означает, что на этом участке похода должно быть 9 лотов длиной 0,5 см, или 4,5
см другими словами. Мы можем нарисовать в этой линии на нашей диаграмме: Итак, как мы можем выработать этот угол? Что ж,
нам нужно измерить, насколько велик угол, начиная с юга и вращая
на восток:
Итак, как мы можем выработать этот угол? Что ж,
нам нужно измерить, насколько велик угол, начиная с юга и вращая
на восток: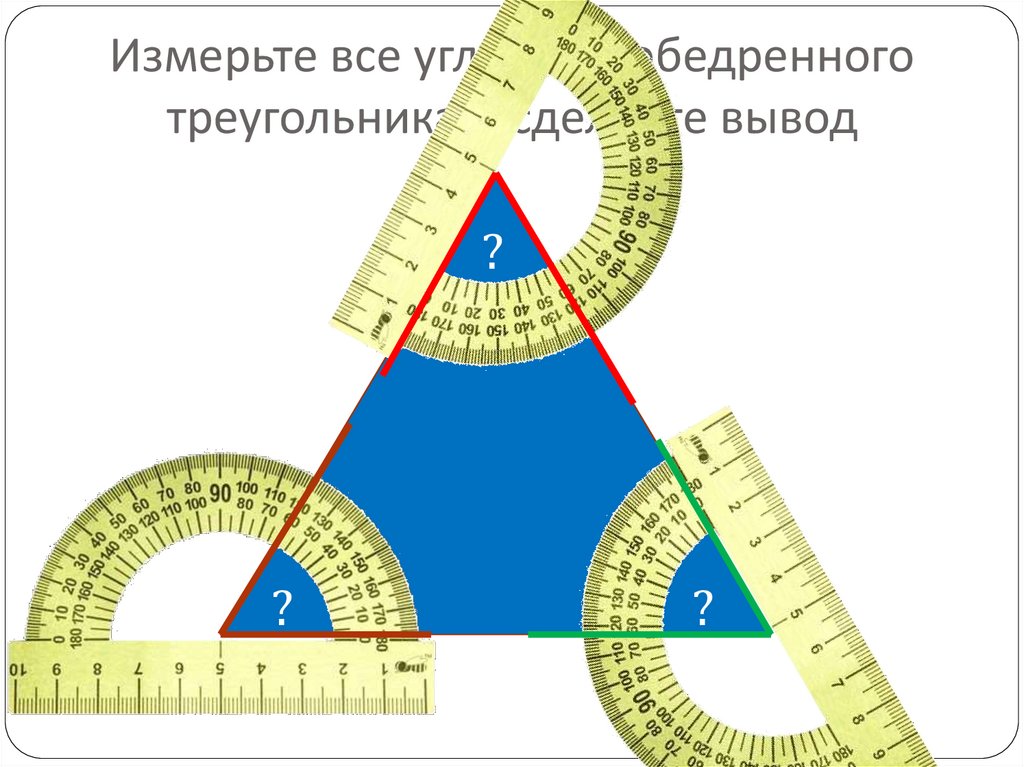 Все, что нам нужно помнить, это то, что на наших масштабных диаграммах каждый км представлен
на 0,5 см.
Все, что нам нужно помнить, это то, что на наших масштабных диаграммах каждый км представлен
на 0,5 см.