Как измеряли на руси массу и объем: Как на руси измеряли массу и объем. Древнерусские меры длины, веса, объёма. Метрическая система как наука

Меры веса разных стран. Единица измерения массы. Единая система измерений в Европе и России

единица измерения перевозок Справочник технического переводчика

Единица измерения — В физике и технике единицы измерения (единицы физических величин, единицы величин) используются для стандартизованного представления результатов измерений. Численное значение физической величины представляется как отношение измеренного… … Википедия

ЕДИНИЦА ИЗМЕРЕНИЯ ПЕРЕВОЗОК — единица, которая позволяет измерить массы перевозимых грузов и пассажиров и расстояния перевозок. Общую массу перевозимых грузов измеряют в тоннах, а для отдельных отправок грузов и в килограммах. Масса перекачиваемого по газопроводу газа… … Большой бухгалтерский словарь

ЕДИНИЦА ИЗМЕРЕНИЯ ПЕРЕВОЗОК — единица, которая позволяет измерить массы перевозимых грузов и пассажиров и расстояния перевозок. Общую массу перевозимых грузов измеряют в тоннах, а для отдельных отправок грузов и в килограммах.

Масса перекачиваемого по газопроводу газа… … Большой экономический словарь

Единицы измерения массы — Содержание 1 Единицы измерения массы 1.1 Метрическая система 1.2 Меры массы в науке … Википедия

Стоун (единица измерения) — У этого термина существуют и другие значения, см. Стоун. Стоун (англ. stone, сокр. st.; букв. «камень») британская единица измерения массы, равная 14 фунтам или 6,35029318 килограммам. В Великобритании и Ирландии используется как… … Википедия

Фунт (единица измерения) — У этого термина существуют и другие значения, см. Фунт … Википедия

Лот (единица измерения) — У этого термина существуют и другие значения, см. Лот. Лот дометрическая единица измерения массы (в России использовалась во второй половине XVIII начале XX веков), равная 1/32 фунта или 3 золотникам или 288 долям или… … Википедия

Золотник (единица измерения) — У этого термина существуют и другие значения, см. Золотник. Золотник единица измерения массы русской системы мер.

1 золотник равен 96 долям. Название «золотник», вероятно, происходит от золотой монеты золотник, имевшей хождение в Киевской Руси и… … Википедия

Доля (единица измерения) — У этого термина существуют и другие значения, см. Доля. Доля самая мелкая старорусская единица измерения массы, равная 1/96 золотника, то есть около 44,435 мг. Деление золотника на 96 частей является отголоском применявшейся в… … Википедия

ГРАН

1. Мера массы (веса) в различных странах. В английской системе мер 1 гран = 64,8 мг.
2. Аптекарская мера в различных странах. В России до введения метрической системы мер 1 гран = 62,2 мг.

ЗОЛОТНИК

Русская мера веса, употреблявшаяся до введения метрической системы мер. 1 золотник= 1/96 фунта = 4,266 г.

ДРАХМА

1. Мера массы (веса) в различных странах. В английской системе мер 1 драхма = 1,772 г. В других странах — около 3,2 г. В древних системах мер — от 3,2 до 6,5 г.
2. Аптекарская мера в различных странах. В Англии 1 драхма = 3,888 г. В России до введения метрической системы мер 1 драхма = 3,73 г.

КВАРТА

1. Мера объема жидкостей. Величина кварты различна в разных странах. В Англии кварта = 1,136 л, в США кварта = 0,946 л.
2. Мера объема сыпучих тел в США. 1 кварта = 1,01 л.
3. Прежняя русская мера жидкостей — кружка (штоф) также иногда называется квартой.

ДЮЙМ

Мера длины в английской системе мер. 1 дюйм = 1/12 фута = 2,54 см.

ФУТ

Мера длины в различных странах. Величина изменяется от 28,3 см (Нидерланды) до 32,48 см (о. Маврикия, Сейшельские острова). В английской системе мер и в России до введения метрической системы мер 1 фут = 30,48 см.

ШТОФ

Мера объема жидкостей, применявшаяся в России до введения метрической системы мер. 1 штоф = 1,23 л. Иногда вместо ШТОФА употребляют название КРУЖКА.

ФУНТ

1. Мера массы (веса) в различных странах. Величина фунта изменяется от 317,62 г (Италия) до 560,1 г (Австрия). В английской системе мер 1 фунт = 453,592 г. В России до введения метрической системы мер 1ф унт = 409,5 г.
2. Аптекарская мера в различных странах. В английской системе мер 1 фунт = 373,242 г. В России до введения метрической системы мер 1 аптекарский фунт = 358,323 г.

ПИНТА

Мера объема жидкостей и сыпучих веществ В английской системе мер 1 ПИНТА = 0,56824 л. В США 1 ПИНТА для жидкостей = 0,47317 л, для сыпучих веществ = 0,55060 л.

УНЦИЯ

1. Мера массы (веса). Величина УНЦИИ в различных странах различна В английской системе мер 1 унция = 16 ДРАХМАМ = 28,35 г.
2. Аптекарская мера в различных странах. В английской системе мер 1 унция = 8 ДРАХМАМ = 31,103 г. В России до введения метрической системы мер 1 унция = 8 ДРАХМАМ = 29,800 г.

Приветствую вас, уважаемые читатели! Очень часто в фильмах мы слышим о дюймах, ярдах, милях, акрах. Практически каждый день по новостям говорят о том, что баррель нефти подорожал на столько-то долларов. И если сколько это примерно в рублях мы представляем, то какое именно количество нефти в литрах мы понятия не имеем. Поэтому знать единицы измерения в США, Канаде и Англии необходимо не только изучающим английский, но и будет полезно для общего развития каждого, чтобы представлять, о чем говорится в новостях, литературе или в кино. Английские единицы измерения

Английские единицы и меры измерения длины, веса, объема, площади, массы и других показателей очень отличаются от подобных в им в русском языке. Многие из них, как я уже говорила, вы могли услышать из кино, телепередач или новостей, прочитать в английской литературе. Но есть в США и Англии, а также в Австралии и Канаде, такие единицы измерения, которые русскоязычным не известны вообще. Например, бушель, мил, род, перч и много других.

Порой очень непросто сориентироваться в новом материале или интересной информации на английском языке как раз именно из-за незнания значений некоторых иностранных мер. Поэтому в данной статье мы подробно разберем единицы измерения по-английски, узнаем их названия, и сколько примерно это будет, если перевести на знакомые нам единицы веса, длины, скорости, объема и расстояния.

Английская система измерений используется не только в Англии и США, но и в других англоязычных странах. Великобритания, как европейская страна, давно приняла десятичную и метрическую систему мер, однако пресса и обычные люди не спешат принимать новую систему, и пользуются старой. Самые распространенные меры длины, веса и объема в английском языке — это баррель, фут, пинта, акр, ярд, дюйм и миля.

• 1 жидкая унция (fl. oz.) = 28, 43 мл (см³)
• 1 унция = 28,6 г
• Короткая тонна = 907 кг
• Длинная тонна = 1016, 05 кг
• Баррель = 163, 6 л
• Баррель нефти = 158, 98 л
• 1 фунт = 453,5 г
• 1 акр = 0,4 га
• 1 ярд = 0,9144 м
• 1 дюйм = 2,54 см
• 1 пинта = 507 мл
• 1 гран = 64,8 мг

Это лишь малая часть единиц измерения на английском. На самом деле, их более сотни. Выучить их все вы не сможете, но с самыми популярными из них было бы неплохо ознакомиться. Ведь в газетах, по радио и телевидению регулярно встречаются эти непонятные для нас слова, символы и обозначения на английском языке или их калькой на русском языке.

Таблица самых распространенных английских мер измерения

Чтобы вам было легче сориентироваться в каждой единице меры, я распределила их по категориям, нашла их примерное значения в нашей системе, и поместила их в удобную таблицу. Эту таблицу можно скачать и сохранить себе на компьютер или распечатать и повесить на видном месте, чтоб при необходимости без проблем заглянуть в нее.

Единица на английском	На русском	Примерное значение
Длина и Площадь (Length & Areas)
mile	миля	1609 м
nautical mile	морская миля	1853 м
league	лига	4828,032 м
cable	кабельтов	185,3 м
yard	ярд	0,9144 м
pole, rod, perch	род, поль, перч	5,0292 м
furlong	фарлонг	201,16 м
mil	мил	0,025 мм
line	линия	2,116 мм
hand	хэнд	10,16 см
chain	чейн	20,116 м
point	точка	0,35 мм
inch	дюйм	2,54 см
foot	фут	0,304 м
Square mile	Квадратная миля	258,99 га
Square inch	Кв. дюйм	6,4516 с м²
Square yard	Кв. ярд	0,83 613 см²
Square foot	Кв. фут	929,03 см²
Square rod	Кв. род	25,293 см²
acre	акр	4046,86 м²
rood	руд	1011,71 м²
Вес, Масса (Weight)
long ton	тонна большая	907 кг
short ton	тонна малая	1016 кг
chaldron	челдрон	2692,5 кг
pound	фунт	453,59 г
ounce, oz	унция	28,349 г
quintal	квинтал	50,802 кг
short hundredweight	центал	45,36 кг
Hundredweight	Хандредвейт	50,8 кг
tod	тод	12,7 кг
short quarter	квартер короткий	11,34 кг
dram	драхма	1,77 г
grain	гран	64,8 мг
stone	стоун	6,35 кг
Объем (Capacity)
barrel petroleum	баррель нефтяной	158,97 л
barrel	баррель	163,6 л
pint	пинта	0,57 л
bushel	бушель	35,3 л
cubic yard	Кубический ярд	0,76 м³
cubic foot	Куб. фут	0,02 м³
cubic inch	Куб. дюйм	16,3 см³
liquid ounce	Жидкая унция	28,4 мл
quart	кварта	1,136 л
gallon	галлон	4,54 л
Melchizedek	Мелхиседек	30 л
Primat	Примат	27 л
Balthazar	Валтасар	12 л
Methuselah	Мафусаил	6 л
Melchior	Мельхиор	18 л
Jeroboam	Иеровоам	3 л
Magnum	магнум	1,5 л
Rehoboam	Ровоам	4,5 л

Попытки разобраться со средневековыми системами веса встречают те же препятствия, что и любые другие исследования в области метрологии этого периода истории.

Позднеримский фунт (327,5 г) со всевозможными местными вариациями в течение длительного времени оставался основой как весовой, так и денежной системы в раннефеодальной Европе. При Карле Великом фунт потяжелел до 367 – 491 г. Каролингский фунт делился на 20 солидов по 12 денариев в каждом. Впоследствии солиды стали называться шиллингами, а денарии – пенни, пфеннингами, пеннингами (в Скандинавии), денье (во Франции), данарами (в Италии).

Марка появилась впервые уже в IX в. в Скандинавии. На протяжении всего средневековья скандинавская марка делилась на 8 эре , причем вес эре довольна легко устанавливается благодаря найденным в захоронениях гирькам. Он оказался равным римской унции (27,3 г). Эре делилось на 3 эртуга , каждый из которых подразделялся в зависимости от местности на 10, 12, 16 или 20 пфеннингов . Итак, древняя скандинавская марка равнялась 218,3 г. В таком виде она распространилась по всей Европе.

Основной составляющей немецкой марки стал лот – 1/16 ее веса. Лоты начинают упоминаться в источниках с середины XII в. Вместе с тем, например, в Шпайере XIII в. марка по образцу римского фунта делилась на 12 составляющих, каждая из которых называлась унцией (хотя была существенно легче римской унции). В других городах Германии эти же составляющие именовались шиллингами и могли вполне в духе каролингской традиции делиться еще на 12 денариев.

Образец традиционности в сохранении средневековых систем измерения веса представляет собой Англия. В истории Англии заметное место занимают две системы веса, за которыми закрепились названия соответственно авердюпойз и трой .

В основе систем авердюпойз и трой лежат фунты: весом в 453,59 г, состоящий из 16 унций, и весом в 373,2 г, состоящий из 12 унций. Фунт «трой» применялся в основном для взвешивания драгоценных камней, металлов, лекарств и т. п. «Авердюпойз» – древний английский вес, использовался очень широко, прежде всего в торговле.

Стоит сказать также и о том, с помощью каких инструментов производилось взвешивание в средние века.

На протяжении всего средневековья использовались два основных типа весов. Первый – обыкновенные весы с двумя равными по весу чашками и равноплечим коромыслом, как правило, со стрелкой. Второй тип весов – это безмены , у которых плечи коромысла не были одинаковыми. На короткое плечо подвешивался груз, а по длинному перемещались гири. Вес вычислялся в зависимости от того, на каком расстоянии от оси вращения гиря-противовес уравновешивала груз. Существовали безмены разных конструкций, но общим у них всех была низкая точность измерений. При небольшой сноровке в обращении безмен позволял торговцу совершенно нагло обманывать покупателя.

Меры объема (сыпучих и жидких тел) в Европе долгое время представляли собой примитивные берестяные или деревянные «лукошки», выдолбленные каменные «ступы», металлические «корыта».

Пожалуй, самая известная система измерения объема, родившаяся в средневековье, – это английская, основанная на бушеле и галлоне. В «Трактате о весах и мерах» (1303 г. ) говорится: «С согласия всего королевства королевская мера была сделана так, что английский стерлинг , который весит 32 пшеничных зерна, высушенных в середине года, взятый 20 раз, дает унцию , а 12 унций составляют фунт , а 8 фунтов составляют галлон ». Дальше разъясняется, что 8 галлонов составляют бушель , а 8 бушелей – квартер .

В средневековой Западной Европе было множество особых, специфических мер и систем подсчетов, применявшихся в строго определенной области. Так, скажем, вес драгоценных камней и отчасти металлов измерялся в каратах .

Луга измеряли не в моргенах или акрах, а в стогах , которые можно на таком лугу поставить.

Много своеобразных мер и весов вызвали к жизни нужды оптовой торговли. Ясно, что перемеривать локтями или футами большие партии ткани было в высшей степени неудобно. Купцы нашли выход из положения. Во-первых, они ввели так называемый «большой локоть », равный по длине 10 обычным локтям; во-вторых, мерой длины стала сама упаковка товара. Клеймо поставщика на кипе (тюке) гарантировало, что внутри содержится строго определенное количество локтей ткани. Соответственно счет шел уже не на локти, а на кипы

Крупные корабельные грузы во всем северном торговом регионе измерялись в ластах . Слово «ласт», вероятно, древнеанглийского происхождения и означает «груз». Ласт оказывался единицей емкости, веса или штучной мерой в зависимости от того, что именно им измеряли. Так, ласт зерна в Англии представлял собой 80 бушелей, ласт перьев равнялся 1700 фунтам (771,1 кг), «ласт сельди» означал 12 тыс. штук. В восточной части Балтики, похоже, более последовательно выдерживался тот принцип, что ласт составляется из дюжины каких-либо крупных партий товара. Скажем, при перевозке соли, золы, сельдей ласт означал 12 «обычных» бочек. Для растительного масла ласт означал уже 12 «двойных» бочек. Для товаров, измерявшихся по весу, ласт составлял 12 берковцев .

Берковец (корабельный фунт) широко применялся во всем Балтийском регионе, возможно, уже с X в. Название этой единицы связывают с торговым центром Бирка в Скандинавии. Берковец, как правило, получался из 400 фунтов, принятых к употреблению в том или ином городе. В Ливонии для оптовой торговли применяли также капь и ливонский фунт . Последний считался равным 1/20 части берковца, т. е. приблизительно 8,2 кг. Восемь ливонских фунтов составляли капь.

Подобные единицы крупного веса возникали и распространялись везде, где большой размах приобретала торговля. На Средиземном море одной из самых известных был генуэзский кантаро гроссо (около 52,3 кг), на сухопутных торговых путях очень часто считали груз на «повозки» или «телеги». В Англии, например, вес «воза» предполагался равным примерно 2 тыс. фунтов, т. е. около 600 кг.

Очень часто считали на штуки , в основном десятками и дюжинами, причем «сотня» вовсе не обязательно обозначала 100 предметов. Были «сотни», составленные из дюжины десятков (120), и даже «большие сотни» из дюжины сотен (1200)

И тем не менее трудно найти в Европе страну, где удалось бы добиться до рубежа XVIII и XIX вв.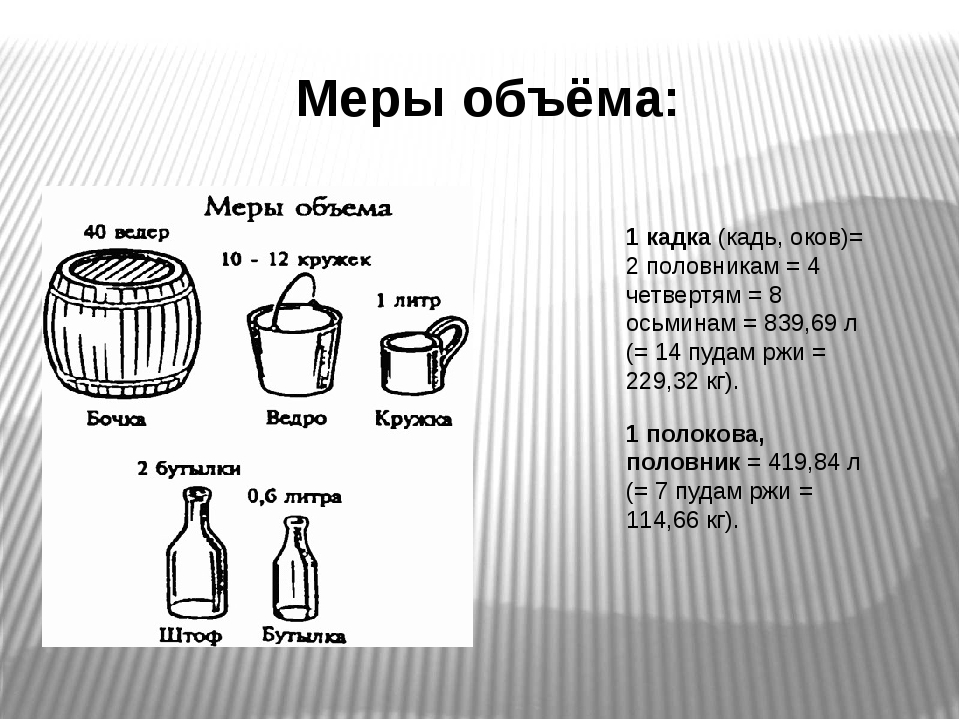 (т. е. до появления метрической системы) метрологического единообразия. Даже в Англии – стране относительно небольшой по площади, в которой рано сложилась сильная монархия, где столько усилий уделялось стандартизации мер, успехи в этой области весьма скромные.

Европейская торговля испытывала, естественно, значительные неудобства от всей этой необозримой пестроты мер и весов. И все же она находила способы вполне благополучно приспосабливаться к этому разнообразию, сохранявшемуся вплоть до XIX в. С течением времени устанавливались постоянные пропорции между мерами и весами городов и стран, находившихся в оживленных торговых отношениях. «Собственные» меры могли подгоняться к мерам «старшего партнера» если и не до полной идентичности, то по крайней мере так, что перевод из одной системы в другую происходил легко и просто. Вновь основанные города часто получали свои меры и веса вместе с городским правом от одного из старых и авторитетных городов, а затем сверялись с ним не только в судебных вопросах, но и в вопросах метрологии. Города обменивались между собой эталонами мер и весов. На крупнейших ярмарках перед зданиями ратуши выставляли образцы всевозможных футов и локтей, гирь и мер, принадлежащих близким и далеким странам, городам и местечкам со специальными клеймами их обладателей, подтверждающими идентичность этих мер.

С помощью справочников и на основе купеческой практики легко было узнать, 100 фунтов в Нюрнберге равнялся 95 пражским фунтам..

24.Древнерусские меры. Для изучения вопросов метрологии древнерусского государства используются памятники письменности и материальной культуры. Среди письменных источников следует назвать «Русскую правду», древнерусские летописи, описания путешествий, сочинения иностранных авторов.

Меры длины. Для указания самых мелких измерений длины в Древней Руси пользовались пядью. Слово «пядь» обозначает кисть руки и произошло от корня «пять». Пядь – расстояние между вытянутым большим и указательным пальцами руки. В употреблении были пяди в 19 см и в 22 (23) см.

По предположению Б.Рыбакова, существовала еще одна пядь, которая называлась пядью «с кувырком». Пядь «с кувырком» определялась путем добавления к малой пяди еще двух или трех суставов указательного пальца. В первом случае получалась пядь в 27 см, во втором случае – в 31 см.

Локоть принадлежит к числу древнейших мер длины, применявшихся у разных народов. Локтем называлось расстояние от конца вытянутого среднего пальца руки или сжатого кулака до локтевого сгиба. Размер локтя колебался от 38 до 54 см. Локоть в 38 см равнялся двум малым пядям и использовался в Московско-Владимирской системе мер, локоть в 44 (46) см – двум великим пядям и использовался в Новгородско-Псковской системе мер.

В документах периода древнерусского государства встречается упоминание о сажени как мере длины. Было несколько вариантов сажени. Есть простая (прямая) сажень, равная 152 см. Она соответствует расстоянию между размахом вытянутых рук человека от большого пальца одной руки до большого пальца другой. При последовательном делении сажени в 152 см 4 и 8 получался локоть в 38 см и пядь в 19 см.

Кроме простой сажени на основании данных памятников архитектуры можно предположить о существовании сажени, равной 176 см. Эта сажень называлась мерной, или маховой и определялась размахом рук человека от конца пальцев и до конца пальцев. При последовательном делении сажени в 176 см 4 и 8 получался локоть в 44 см и пядь в 22 см.

Самой большой из всех саженей была косая сажень. Косой саженью называлась сажень, равная 216 см. Она определялась расстоянием от пальцев ноги до конца пальцев вытянутой руки до диагонали. Также косой саженью могла называться наиболее крупная из всех саженей – сажень в 248 см.

Помимо пядей, локтей и саженей источники содержат указания на более крупные единицы измерения, которые могли применяться для определения расстояний: это верста, или поприще. Эта единица длины равнялась примерно 750 саженям (1,07 км).

Наряду с более или менее точными определениями расстояний в источниках встречаются описательные выражения: «вержение камня», «перестрел», «день пути». С.Кузнецов находит возможным считать расстояние, определяемое «вержением камня», равным 20 саженям, т. е. около 42,5 м в среднем.

На основании практики народов, еще употреблявших лук и стрелы, считается, что стрела, пущенная сильной рукой, может лететь до 100-105 м. Для стрельбы в цель считается нормальным расстояние в 50-55 м. В среднем «перестрел» можно признать равным 60-70 м.

Иногда расстояние определялось днями пути. Эта величина неопределенная. Пеший день пути едва ли может дать расстояние более 25 км, день конного пути – 50-75 км.

Меры площади .

Земля измерялась селами и плугами. Вопрос о том, равно ли село плугу или не равно, остается открытым. Есть предположение, что размер плуга нужно определять в 8 десятин, а села – в 16 десятин.

Для сенокосных угодий широко применяли «урожайные» меры – копны.

Во время феодальной раздробленности Руси как меры площади применялись «соха», «обжа» и «коробье». Но установить их точный размер сейчас не представляется возможным. Известно лишь, что соха равнялась 30 обжам, а коробье – 1 десятине (1,09 га).

Меры сыпучих тел . Древнейшей мерой сыпучих тел, употреблявшейся Древней Руси, была кадь. Кадь делилась, по системе двух, на два половника, на четыре четверти, на восемь осьмин.

В «Русской правде» упоминаются и такие меры сыпучих тел, как уборок и лукно. Точный объем уборка не известен.

Что касается лукна, то по мнению Д.Прозоровского лукно вмещало в себя 60 фунтов овса, т. е. около 24-25 кг. Меры жидких тел. Другим видом мер вместимости являются меры жидкостей. В источниках периода древнерусского государства встречаются упоминания о ведре. Например, в «Русской правде» определяется корм вирнику, причем указывается, что ему полагается по 7 ведер солода на неделю.

Встречается в летописях и бочка как мера жидких тел. Некоторые исследователи полагают, что она равнялась 40 вёдрам, соответственно 492 литрам, другие говорят, что она равнялась 10 ведрам.

В быту употреблялись разнообразные хозяйственные сосуды: бурдюки, корчаги, насадки, ушаты, коробы, ендовы.

Меры веса. В литературных источниках Древней Руси упоминаются следующие меры веса: берковец, пуд, гривна, гривенка и золотник.

Наиболее древней мерой была гривна. Половина гривны имела название гривенка. Одна гривна содержала 96 золотников. Золотник равнялся 4,266 г. В 13 веке появились ещё более мелкие единицы – почка (1/4 золотника) и пирог (1/4 почки).

Более крупными мерами веса были берковец, пуд и кап. Пуд равнялся 4 гривнам, берковец – 10 пудам, а кап – 4 пудам.

25.Меры ВКЛ и Речи Посполитой. С момента централизации ВКЛ в системе мер наблюдалось формирование единой системы измерений, чему содействовало расширение торговых связей и складывание единого рынка.

На территории Беларуси использовались определенная система мер длины.

Цаля (от немецкого фаланга пальца) была наименьшей единицей длины и равнялась 1/12 стопы, т.е. 27 мм.

Стопа была равна ступне ноги и составляла 32,4 см.

Локоть равнялся 64,96 см, что соответствовало 24 цалям. Половина локтя была равна линии – 32,48 см.

Сажень использовался в основном рижский маховый – 188,125 см. При этом следует отметить, что официально сажень был зафиксирован только в 1766 г. и был равен 3 локтям или 72 цалям (194,8 см).

Такая мера длины, как гоня (гон) – расстояние, пройденное запряженным в плуг конём в одну сторону до поворота – использовалось в быту. Равнялась гоня приблизительно 80-100 метров.

Как единица длины в ВКЛ использовалась стая (от греч. стадиум), равная приблизительно 80 м.

Верста и миля – самые крупные единицы измерения расстояний. В употреблении было 2 версты – малая (798 саженей или 1554,6 м) и большая (1000 саженей или 1948,2 м). В ВКЛ использовалась миля. Она состояла из 5 верст и равнялась 7,777 км.

Некоторые меры использовались и как меры длины, и как меры площади. К ним относятся прут и шнур. Так, прут (прент) в ВКЛ стал применяться с 16 в. (в связи с проведением валочной померы) и равнялся 4,87 м. Шнур обычно состоял из 10 прутов и равнялся 48,7 м.

Как единица площади квадратный прут равнялся 100 квадратным прутикам и соответственно 23,72 кв. м., а квадратный шнур – 100 квадратным прутам.

Кроме выше приведенных на Беларуси использовались в качестве мер площади морг, волока, реза и лан.

Волока равнялась 30 моргам или 90 квадратным шнурам или 9000 квадратным прутам и составляла 21,36 га. В соответствии с аграрной реформой 1557 г. волока должна была состоять из трёх равных полей (рез) по 10 моргов каждое, что соответствовало трехпольной системе земледелия. В одном морге было 0,71 га. При плохом качестве земли размер волоки мог доходить до 46 моргов. Лан – самая большая единица площади в ВКЛ, равная 3 волокам.

Основной мерой сыпучих и жидких веществ в ВКЛ являлась виленская бочка. Она состояла из 6 медниц, 12 чаш, 36 ведер, 72 большим гарнцам, 144 малым гарнцам, 576 квартам и равнялась 406,7 л.

В 4 раза меньше, чем бочка виленская был корец («четверть»), равный приблизительно 102 м.

Существовали также меры, которые употреблялись для измерения определенных веществ. Например, для измерения вина использовался антал, для измерения пива – вар, мёда – колдуб, лубня или колода, растительного масла – глек.

Что касается единиц массы, то самой крупной был берковец (74,964 кг). Он равнялся 5 камням и 200 фунтам. В употреблении было много иностранных единиц веса, что объясняется широкими торговыми отношениями государства. Такой единицей был, к примеру, безмен (6-10 фунтов). Пуд состоял из 40-50 фунтов. Лот составлял 1/32 часть фунта или 11,71 г.

26.Меры Беларуси в конце 18 – начале 20 века. После присоединения белорусских земель к России на территории нашего государства стали распространяться русский меры.

Ещё в 16-17 вв. в России были определены единые меры для всего государства, но в 18 в. в связи с бурным экономическим развитием, активизацией внешней торговли встал вопрос точности измерений и создания эталонов мер.

При Павле I указом от 29 апреля 1797 г. «Об учреждении повсеместно в Российской империи верных весов, питейных и хлебных мер» был начата большая работа по упорядочению мер и весов.

В 1827 г. была организована комиссия «для постановления на неизменных началах системы Российских мер и весов», которая создала единые государственные эталоны. Они были узаконены указом 1835 г. «О системе российских мер и весов».

Меры длины.

Верста = 500 сажень = 1,0668 км.

Сажень = 3 аршина = 7 футов = 213,36 см.

Аршин = 4 четверти = 16 вершков = 28 дюймов = 71,12 см.

Четверть = 4 вершка = 17,77 см.

Вершок = 4,44 см.

Фут = 12 дюймов = 30,48 см.

Дюйм = 10 линий = 2,54 см.

Линия = 10 точек = 2,54 мм.

Точка = 0,254 мм.

Меры площади.

1 квадратная верста = 1,13806 кв. км.

1 десятина = 1,09254 га.

1 квадратный аршин = 0,505805 кв. м.

1 квадратный фут = 0,092903 кв. м.

Меры сыпучих тел.

Четверть = 8 четвериков = 2,0991 гектолитров

Четверик = 8 гарнцев = 26,239 л.

Получетверик = 13,119 л.

Гарнец = 3,279 л.

Меры жидких тел.

Бочка = 40 ведер = 4 десятни = 4,9196 гектолитра.

Десятня = 10 ведер = 1,229 гектолитра.

Ведро = 12,299 л.

Штоф = 2 бутылки = 1,2299 л.

Бутылка = 2 сороковки = 0,6149 л.

Сороковка = 2,5 сотки (чарки) = 0,3047 л.

Сотка (чарка) = 2 шкалика = 0,123 л.

Шкалик = 0,0615 л.

Меры веса.

Берковец = 10 пудов = 163,9 кг.

Пуд = 40 фунтов = 16,38 кг.

Фунт = 32 лота = 96 золотников = 409,512 г.

Лот = 3 золотника = 12,797 г.

Золотник = 96 долей = 4,02657 г.

27 . Создание и введение на Беларуси метрической системы мер. С давних времен люди в разных странах мира использовали каждый свои меры веса и длины. Множественность этих мер вносили путаницу в международные торговые связи и тормозили развитие промышленности. Поэтому было решено создать единую систему для всех стран.

Такая система была разработана во второй половине XVIII в. Французской академией наук, где единица длины была названа метром, а сама система – метрической. За единицу площади приняли ар (квадрат 10 × 10 метров), за единицу массы – грамм, за единицу вместимости – литр.

По предложению комиссии из крупнейших французских ученых (Ж. Борда, Ж. Кондорсе, П. Лаплас, Г. Монж) в качестве единицы длины метра была принята одна десятимиллионная доля четверти парижского географического меридиана. Это решение было обусловлено стремлением, положить в основу новой системы мер легко воспроизводимую «естественную» единицу длины.

7 апреля 1795 года Национальным Конвентом Франции был принят Закон о введении Метрической системы мер. Позднее были изготовлены платиновые прототипы метра и килограмма. В 1799 году оба прототипа были утверждены и переданы на хранение в Национальный архив Франции.

Метрическая система мер с самого начала была задумана как международная, поэтому ее единицы не совпадали ни с какими национальными. Также важным достоинством данной системы была ее десятичность, так как дольные и кратные единицы образовывались в соответствии с десятичным счетом с помощью десятичных множителей, которым соответствуют приставки деци, санти, милли, дека, гекто и кило.

Подлинно международный характер метрическая система приобрела в 1875 году, когда 17 стран, в том числе и Россия, подписали Метрическую конвенцию, в которой метрическая система мер была признана международной, и были утверждены прототипы метра и килограмма для всех стран. Метрическая система мер была допущена к применению в России (в необязательном порядке) законом от 4 июня 1899 года, проект которого был разработан Д. И. Менделеевым, и введена в качестве обязательной декретом СНК РСФСР от 14 сентября 1918 года, а для СССР – постановлением СНК СССР от 21 июля 1925 года.

В последующие годы, в связи с развитием науки, техники и международных связей, возник целый ряд частных систем (производных от метрической). Поэтому в 1960 году на основе метрической системы мер был создан и утвержден единый, охватывающий все области измерений, стандарт – «Международная система единиц (СИ)». В настоящее время СИ уже принята в качестве обязательной или предпочтительной многими странами. Система СИ включает семь основных единиц и их производные, находящиеся в десятичных соотношениях. Основной единицей длины СИ является метр, массы – килограмм, времени – секунда, силы электрического тока – ампер, термодинамической температуры – кельвин, силы света – кандела, количества вещества – моль.

Похожая информация.

АИ 92, АИ 95, ГОСТы, в чем она измеряется и как правильно проводить замеры

Оглавление:

1. ГОСТы, регулирующие марки бензинов.
2. Как производятся расчеты.
3. Для чего нужно выполнять измерения.
4. Как измерить плотность.
5. Показатели АИ 92
6. Какие показатели соответствуют АИ 95
7. Табличные плотностные показатели бензина

Нефтепродукты отличаются по составу, области применения, физическим и химическим свойствам, методам производства. Кроме октанового числа (благодаря которому можно оценить детонационные характеристики), есть еще один определяющий показатель – плотность бензина. Удельный вес позволяет оценить физические и эксплуатационные свойства топлива, а еще – применяется для расчета объема и массы бензина, который важен при транспортировке нефтепродуктов, их хранении и проведении калибровочных работ для бензиновых двигателей и различных приборов.

Плотность измеряется в килограммах (иногда граммах) на кубический метр (предел показателя – 780). Плотность не применяется для оценки качества топлива. Она зависит от нефтепродуктов, которые использовались при производстве бензина.

1. ГОСТы, регулирующие марки бензинов.

Развитие нефтехимической отрасли и ужесточение требований к экологии привело к разработке регламентов и стандартов нефтехимической продукции. Так, с 2002 года действует ГОСТ Р 51866-2002, который определяет нормы наличия металлических соединений в бензине. Он регулирует производство высокооктановых бензинов класса «премиум» (95, 98 и их виды).

ГОСТ 32513-2013 введен после разработки стандарта ЕВРО-4 на бензин. Также в 2015 году были приняты ТУ 0251-001-12150839-2015, которые определяют нормы производства современных марок топлива.

Автомобили, нефтепродукты и топливо, которое ввозится на территорию России, соответствуют нормам ЕВРО-5. В нем регулируется более двадцати показателей топлива, включая отказ от использования веществ, которые вредят экологии (ядовитые соединения, металлосодержащие компоненты).

Стоит учитывать, что в зависимости от технологических процессов завода-изготовителя, различаются технические характеристики и плотность бензина. ГОСТы только регулируют соблюдение минимальных обязательных требований.

2. Как производятся расчеты 

Измерения плотности керосина, солярки, бензина должны производиться при определенной температуре. На данный момент ГОСТ устанавливает температуру 15ºC на бензин (ранее данное значение было на 20 градусах). Поэтому при расчете нужно учитывать информацию, которая указана в паспорте на продукт, ведь результаты будут отличаться.

При отсутствии специализированного оборудования производят теоретические расчеты, исходя из данных, которые содержатся в паспорте. Для вычисления необходимо (исходная температура принимается 20ºC):

• найти показатель плотности;

• вычислить температуру исследуемого топлива;

• определить разницу между температурными значениями;

• в таблице поправок плотностных показателей нефтепродуктов найти значение изменения на 1 градус;

• умножить поправку на температурную разницу;

• произвести окончательные расчеты – прибавить (если температура ниже 20 градусов) к паспортным показателям полученные результаты или вычесть (если выше).

Все вычисления производятся без использования лабораторного оборудования.

3. Для чего нужно выполнять измерения

Плотность помогает оценить марку бензина и его объемный вес. Данное значение необходимо при отпуске топлива и приеме продукции. 

Из-за колебаний температуры показатели топлива могут различаться, что может стать причиной разногласий при отпуске и приемке нефтепродуктов. Поэтому для стандартизации процесса измерения плотности нефтепродуктов разработаны правила пересчета количества нефтепродуктов в зависимости от средних показателей по маркам топлива.

При этом плотность помогает определять химический состав бензина и идентифицировать его. У каждой марки есть свои показатели плотности, которые варьируются в небольших пределах. Например, если при измерении получили данные, которые выше или ниже нормативных показателей, то без проведения лабораторного химического анализа нельзя убедиться в достоверности представленной марки топлива.

Также благодаря вычислению плотности бензина можно определять приблизительную массу больших объемов нефтепродуктов (например, в резервуарах), когда выполнить взвешивание невозможно. Данные методики измерений указаны в ГОСТ Р 8.595-2004.

4. Как измерить плотность

Обязательное условие при проведении измерений – организация одинаковых условий, ведь плотность представляет собой отношение массы к объему. Чтобы получить результат, нужно:

• взять любую емкость с градуированными делениями;

• взвесить емкость;

• влить в емкость 100 мл топлива;

• выполнить взвешивание жидкости и найти разницу значений измерений;

• результат разделить на объем топлива.

Удобнее будет воспользоваться ареометром. Это специализированный измерительный прибор, который выглядит как стеклянная колба. Он оснащен измерительной шкалой, встроенным термометром. Работа прибора основана на принципе Архимеда.

5. Показатели АИ 92

В большинстве автомобилей используется топливо марки 92. Данный бензин имеет высокую детонационную стойкость. При исследовании показывает октановое число АИ 91 или 82,5 (моторный метод). Плотность при 15ºC находится в интервале от 740 до 770 кг на 1 м3.

6. Какие показатели соответствуют АИ 95

Бензин марки 95 показывает при моторном методе исследования октановое число до 85, АИ показатели – до 95. Бензин отличается наличием ароматических компонентов, повышенными эксплуатационными качествами. В 95-м бензине класса «супер» отсутствует свинец. Плотность при температуре 15ºC данного бензина варьируется от 745 до 755 кг на 1 м3.

7. Табличные плотностные показатели бензина

Плотность нефтепродуктов, которые используются в автомобильной промышленности, составляет от 700 до 780 кг на 1 м3. При этом в зависимости от типа нефтепродуктов и входящих в состав соединений будут изменяться показатели плотности. Так, у ароматических соединений меньшие значения по сравнению с алифатическими.

Но данная величина – непостоянная. Она изменяется в зависимости от температуры. При ее повышении показатели снижаются, а при понижении – увеличиваются. Поэтому специалисты разработали показатели, которые отражают плотность нефтепродуктов в зависимости от температурного режима и условий его хранения. 

Приблизительные значения при 15ºC 

Марка бензина	Плотностные показатели, кг/м3
92	760
95	750
98	780
Премиум 95	725–780
Супер 98	725–780

В России и США начался дикий дефицит рабочей силы

— С начала пандемии минуло уже почти два года. Как изменилась за это время экономическая реальность и сбылись ли прогнозы экспертов относительно ее трансформации?

— В 2020-м, когда началась пандемия, ожидания были совершенно катастрофическими. Речь шла о гигантском скачке безработицы. Говорилось о том, что работу потеряют десятки миллионов человек и им будет не на что жить. Сразу скажу, что шок от пандемии не был похож на стандартный экономический кризис. Обычно кризисы вызываются неурядицами со стороны совокупного спроса. В случае с пандемией шок был со стороны совокупного предложения, так как лидеры всех стран собственными руками взяли и прикрыли значительную часть экономической активности. Сама природа этих потрясений была другой. Соответственно и далее ситуация развивалась не как при обычных кризисах и совсем не так, как ожидали на старте. С точки зрения того, что происходило в экономике, это даже не подпадает под стандартное определение экономического кризиса — рецессии. Рецессия — это отрицательные темпы экономического роста на протяжении полугода. На Западе период отрицательных темпов экономического роста составил 2 месяца. В России — чуть дольше. Да, падение было очень глубоким. Но всего через пару-тройку месяцев экономика стала восстанавливаться.

— Что этому способствовало?

— Государства начали частично снимать ограничения. По большей части кризис был рукотворным. Это «творчество» самих властей, которые директивно прихлопнули множество бизнесов. Если говорить непосредственно о кризисе, то он был беспрецедентно коротким. В США уже в апреле 2020-го экономика начала восстанавливаться. В России — в июне-июле. Другое дело, что, когда приходили новые волны COVID-19, государства частично возвращали ограничения, что тормозило процесс восстановления.

— У рынков труда получалось приспособиться к факту пандемии?

— У подавляющего большинства стран прирост безработицы был мизерный: 1–2%. В России аналогичная ситуация. Правда, есть группа государств, где безработица подпрыгнула невероятно: США, Канада, Ирландия. Но следует иметь в виду, что в этих странах есть такая специфическая форма, как временная безработица или безработица по вызову. Это когда фирма увольняет сотрудника, но с обещанием, что, если дела снова пойдут лучше, его немедленно позовут обратно. Это можно сравнить с вынужденным отпуском. Разница в том, что когда мы имеем дело с вынужденным отпуском, то юридические отношения между фирмой и работником не прерываются, а при «безработице по вызову» — наоборот. Опыт США показывает, что в 85% случаев работников, которых временно уволили, затем возвращают обратно. В обычные кризисы, например в США, показатель временно безработных почти не реагирует на спад, а весь прирост обеспечивается за счет тех, кого гонят с работы окончательно. В этот раз было все с точностью до наоборот. Если учесть эту особенность, то окажется, что практически во всем мире рост безработицы был минимальный.

Фото: tambov.gov.ru

— Что при этом происходило с занятостью?

— Она упала сильнее, чем выросла безработица. Статистика выделяет три основных состояния на рынке труда: занятость (когда у человека есть работа), безработица (когда работы нет, но ее ищут и готовы немедленно приступить), экономическая неактивность (работы нет, и люди ее и не ищут). К последней категории, например, относятся студенты очных отделений, пенсионеры, домохозяйки. Так вот, во время пандемии наблюдался активный отток из рядов рабочей силы. Люди уходили из занятости, но чаще всего становились не безработными, а экономически неактивными. Допустим, раньше человек пенсионного возраста продолжал работать, а в условиях пандемии предпочел уйти с должности, чтобы не заражаться. Другой пример: по всему свету позакрывали детские сады и школы, и многие женщины были вынуждены оставить работу, чтобы сидеть с детьми. В результате во всем мире безработица выросла совсем немного, занятость увеличилась чуть больше, но все равно не радикально.

— Почему получилось именно так?

— Потому что в ход пошли другие механизмы приспособления к экономическим шокам. Первый механизм — это сокращение заработной платы. Понятно, если работодатель понизил сотруднику в кризис зарплату на 20%, у него меньше стимулов выгонять такого сотрудника с работы: ведь он обходится дешевле. Второе — это различные формы неполной занятости: когда людей переводят на сокращенный рабочий день, отправляют в вынужденные отпуска (с сохранением зарплаты или без). Третье — переводы на дистанционный режим работы. Так вот, во всем мире такие механизмы, как неполная занятость и дистанционная работа, расцвели пышным цветом. В некоторых странах на пике кризиса 15% всех занятых могли работать в различных режимах неполного времени. Дистанционная занятость на пике вырастала до 25–30%. В результате этого сохранялись рабочие места, предотвращая падение занятости и рост безработицы. Если бы не неполная занятость и дистанционный режим, то безработица взлетела бы под небеса. Были задействованы гораздо более мягкие механизмы приспособления, что позволило пережить этот период с минимальными социальными потрясениями.

— Перечисленные вами механизмы больше относятся к странам Запада или в России все было примерно так же?

— Как раз в первую очередь такой подход характерен для России, потому что это традиционный для нашей страны механизм приспособления. Специалисты всегда говорили, что в России рынок труда какой-то неправильный. Вместо того чтобы в кризис росла безработица и падала занятость, у нашего рынка падает зарплата и сокращается продолжительность рабочего времени. «Ах, когда же российский рынок труда начнет нормально работать?» — сокрушались многие эксперты. Но когда грянул COVID-19, рынки развитых стран, грубо говоря, стали функционировать именно по такому алгоритму, по которому традиционно функционировал наш. Российский рынок труда всегда приспосабливался к негативным экономическим шокам, главным образом за счет сжатия продолжительности рабочего времени и снижения заработной платы.

— Получается, что снижение зарплаты помогло не допустить резкого роста безработицы. Но насколько в результате такого подхода сократились доходы в России и на Западе?

— В развитых странах реальная заработная плата снизилась где-то на 2–3% за 2020 год. В России в первые месяцы пандемии произошло резкое проседание, а потом заработная плата начала восстанавливаться. Если посмотреть на цифры в целом за год, то реальная заработная плата в 2020 году выросла почти на 3,8% по сравнению с 2019-м. Но такая «лобовая» статистика мало о чем говорит. Строго говоря, мы должны были бы сравнивать то, что реально получилось по итогам 2020-го, с тем, что было бы в 2020-м, если бы не пандемия. По моим прикидкам, тогда мы получим замедление темпов роста реальной заработной платы примерно на те же 3%.

— А как обстоят дела с безработицей в России?

— Есть два ее показателя. Общая безработица измеряет процент людей, не имеющих работу, но ищущих ее. Регистрируемая безработица показывает, сколько людей пошло в службы занятости и встало на учет. В России по разным причинам общая безработица всегда в несколько раз превосходила регистрируемую. Только треть или четверть безработных шли в службы занятости и регистрировались. В пандемию государство решило резко увеличить поддержку безработных: вырос минимальный и максимальный размер пособий, дополнительные категории граждан получили право на получение пособий, увеличилась длительность их выплат. Важно также, что в условиях пандемии была введена электронная регистрация потерявших работу. В результате издержки регистрации резко упали, а выгоды резко выросли. Толпы людей устремились в службы занятости. Во время пандемии регистрируемая безработица выросла раз в 5. Если безработица общая выросла на 1,9 процентного пункта, то эта увеличилась на 4–4,5. В результате разрыв между ними сильно сократился. Отмечу, что практически все эти меры были введены на временной основе. Как только дополнительные меры поддержки безработных исчерпали срок своего действия, регистрируемая безработица стремительно покатилась вниз. Сейчас регистрируемая безработица чуть выше, чем была до кризиса, а общая безработица — чуть ниже, и занятость уже превзошла докризисный уровень. Таким образом, негативные эффекты, связанные с пандемией, даже несмотря на то, что она продолжается, по большей части уже отыграны назад.

— И что же происходит на рынке труда сейчас?

— В результате рынок труда и на Западе, и в России из ледяной воды попал в кипяток. Сейчас на рынке труда США — чудовищный дефицит рабочей силы, особенно работников невысокой квалификации. Сети фастфуда не могут найти людей даже при условии, что гонят вверх зарплату. Не хватает водителей грузовиков и т.д. Такого превышения количества вакансий над численностью безработных никогда не было за всю историю США. Никогда не было и такого огромного уровня добровольных увольнений: когда люди понимают, что для них открыта более благоприятная возможность, они по собственной инициативе уходят с нынешнего места работы на новое. Нечто подобное наблюдается и в России. Это произошло по ряду причин. Сократилось предложение труда. Многие работники ушли на пенсию, либо сидят дома с детьми, либо намеренно избегают контактов с другими людьми из-за пандемии. Кроме того, выросла резервируемая заработная плата (минимальная сумма, за которую человек вообще готов идти работать). Например, американское государство за время пандемии раздало немереное количество денег людям на руки. Но если у человека есть какие-то другие источники дохода, то он, разумеется, не будет соглашаться на первую попавшуюся работу, а станет искать более привлекательное рабочее место. Он может дольше заниматься поиском на рынке труда, чем если бы у него не было подушки безопасности из денег, которые дало ему государство. Люди стали более разборчивыми и не соглашаются на низкооплачиваемую работу. Еще один момент: произошло изменение в структуре спроса на рабочую силу. Резко вырос анклав относительно неквалифицированных рабочих мест, где при этом платят приличную заработную плату. Яркий тому пример — курьеры. Лучше работать курьером и получать приличную зарплату, чем гробиться на стройке и получать в два-три раза меньше. Таких рабочих мест практически не было до пандемии. Они появились в результате переориентации спроса на рабочую силу. Появилась потребность в такого рода не очень квалифицированных работниках, которые должны получать неплохую заработную плату, так как работают в рисковой среде — в контакте с людьми. В результате у работников с невысокой квалификацией появился выбор.

— Получается, что развозить на велосипеде заказы из ресторанов стало выгодно. И как рынок отреагировал на такие изменения?

— Дело в том, что и в США, и в России резко сократилось присутствие мигрантской рабочей силы. В начале пандемии многие академические исследователи предрекали, что масса гастарбайтеров останется без работы и пойдет грабить местных жителей. Ничего этого не произошло. Подавляющая часть этих людей уехала к себе домой, а возвращаться им тяжело или даже нет желания. В результате российская экономика лишилась изрядного отряда неквалифицированной мигрантской рабочей силы. Официальное число трудовых мигрантов в России на пике кризиса снизилось в 1,5 раза. И это только официальные цифры. Сколько теневых работников покинуло страну — неизвестно. Работодатели, что в США, что в России, не могут сейчас найти никого на такие рабочие места. Вдобавок в условиях пандемии появились рабочие места с принципиально иными неденежными характеристиками. Речь о дистанционной занятости. Теперь работник может торговаться с работодателем и говорить ему «нет», если тот не может обеспечить его работой онлайн. Если человеку приходится добираться на работу, контактировать с людьми, рисковать здоровьем, то он требует повышенную зарплату. Все это дополнительно сжимает потенциал рабочей силы, готовой трудиться недистанционно. В результате действия всего этого комплекса причин зарплата резко пошла в гору. Такого большого числа вакансий в России, заявленных официально в службы занятости, вообще никогда не было (раньше было 1,5 млн, сейчас 2 млн). Рынок труда перешел в иной режим функционирования. Сейчас спрос на рабочую силу (при существующих зарплатах) намного превышает предложение. Многие что российские, что американские работодатели стонут, говоря, что никогда такого не было.

Читайте также: Как президент и премьер могут легально заработать миллион

Масса и объем: формулы, преобразование единиц измерения и практические задачи — видео и стенограмма урока

Формулы для массы и объема

Формулы о соотношениях между числами. Масса и объем связаны друг с другом через понятие, называемое плотностью. Плотность — это плотность упаковки атомов и молекул в веществе, измеряемая в килограммах на кубический метр. Если у вас много массы на небольшой площади, это высокая плотность. Если у вас есть небольшая масса, распределенная по большой площади, это низкая плотность.

Формула, связывающая плотность, массу и объем, выглядит так:

Здесь m представляет массу объекта или материала, V представляет объем, а фигурная p (греческая буква ро) представляет плотность.

Существует также множество формул для определения объема в зависимости от формы объекта. Например, способ вычисления объема сферы отличается от того, как вы вычисляете объем куба или прямоугольного параллелепипеда.Вот таблица некоторых распространенных формул объема, которые можно использовать для решения задач:

Преобразование единиц измерения

Мы уже говорили о стандартных единицах плотности (килограммы на кубический метр), массы (килограммы) и объема (кубические метры). Но иногда люди могут использовать нестандартные или ненаучные единицы измерения. Например, если кто-то использует массу в граммах, а объем в сантиметрах в кубе, то плотность выйдет в граммах на кубический сантиметр.Но иногда вам захочется быть хорошим ученым и вместо этого использовать стандартные единицы измерения. В таких ситуациях может быть полезно преобразовать единицы измерения. Возможно, вам потребуется умножить или разделить.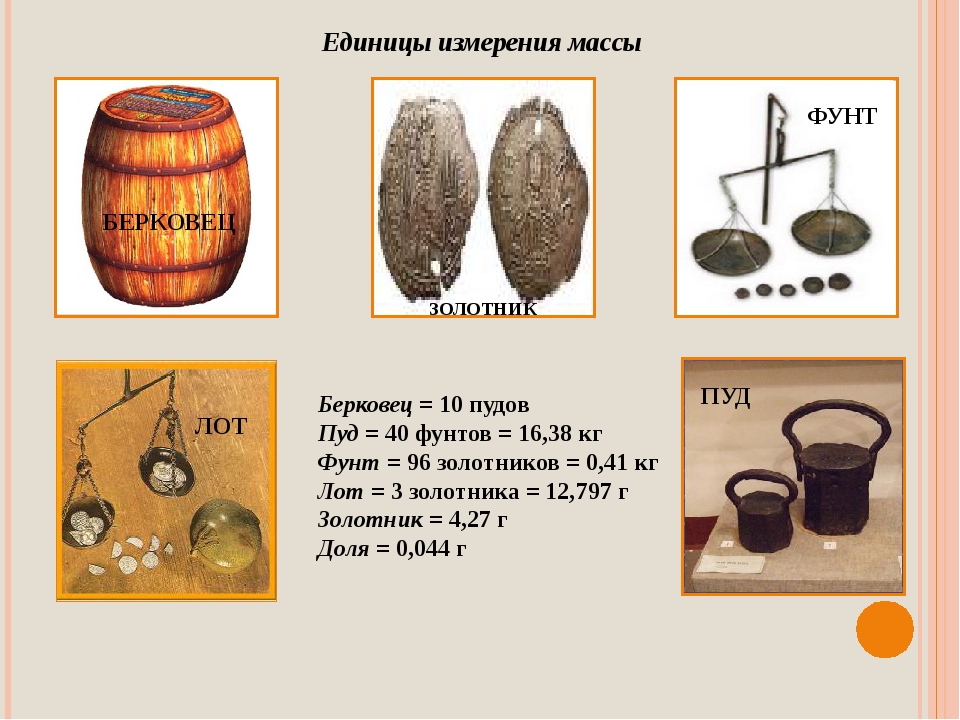

Вот некоторая информация, которая может вам понадобиться:

• В килограмме 1000 граммов
• В метре 100 сантиметров
• В килограмме примерно 2,2 фунта (или 0,45 килограмма в фунте)
• В фунте 16 унций
• Есть 0.0823 кубических метра в кубическом футе (или 5,31 кубических фута в кубическом метре)
• В кубическом литре 1000 метров
• В кубическом метре миллион кубических сантиметров

Практические задачи

Давайте рассмотрим несколько примеров!

Пример 1:

Ввозится ящик яблок, плотность необходимо указать в килограммах на кубический метр. Яблоки кладут на весы и имеют массу 15 фунтов. Коробка — это совершенный куб, длина каждой стороны которого равна 0.5 метров. Какова плотность ящика с яблоками в килограммах на кубический метр?

Придется использовать уравнение плотности и разделить массу на объем. Нам говорят, что масса 15 фунтов, но мы не знаем объема. Объем куба равен длине, умноженной на ширину, умноженной на высоту, что составляет 0,5 * 0,5 * 0,5. Это дает нам 0,125 метра в кубе.

Теперь мы можем просто разделить массу на объем, чтобы получить плотность. Но есть проблема; если мы это сделаем, наш ответ будет в фунтах на кубический метр.Нас просят дать ответ в стандартных единицах: килограммах на кубический метр. Итак, нам нужно перевести массу в фунтах в килограммы. В фунте 0,45 килограмма, поэтому умножьте 15 фунтов на 0,45, что даст нам 6,75 килограмма. Наконец, мы можем вычислить плотность, которая представляет собой массу, деленную на объем. 6,75, деленное на 0,125, дает нам 54 килограмма на кубический метр. И это все; это наш ответ!

Пример 2:

Плотность свинца составляет 11 340 кг на кубический метр.Сколько будет весить на весах свинцовый параллелепипед размером 25 х 30 х 35 см?

Если плотность равна массе, деленной на объем, то масса равна плотности, умноженной на объем. Мы уже знаем плотность (11 340), но не знаем объема.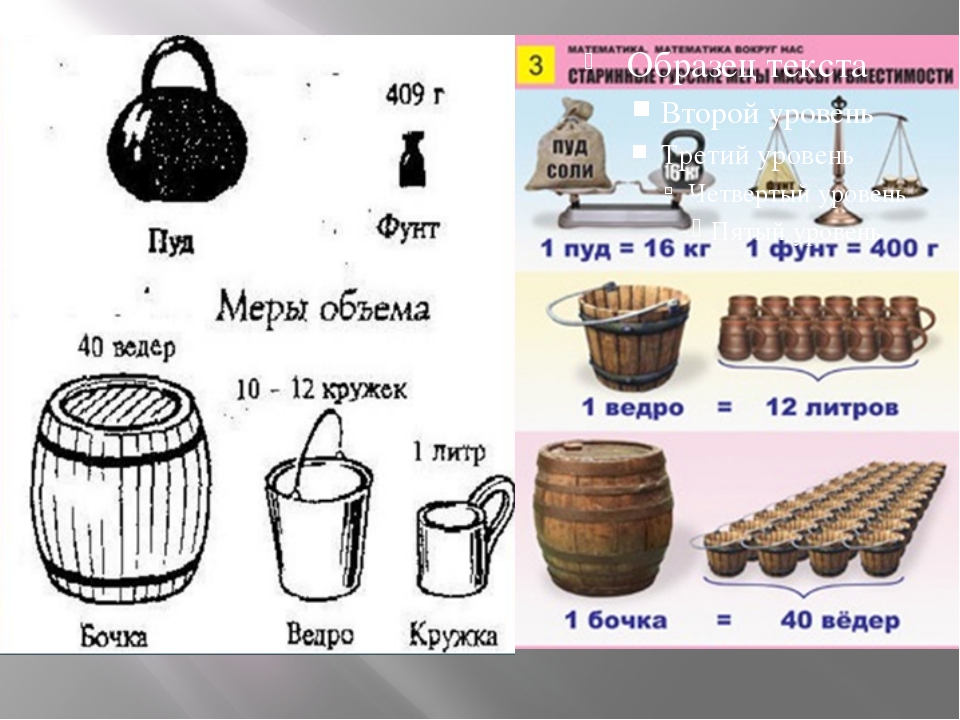 Мы можем вычислить объем прямоугольного параллелепипеда, перемножив длины его сторон. Это 25 * 30 * 35. Но поскольку наша плотность выражается в килограммах на кубический метр, мы можем упростить нашу работу, переведя сначала в метры. Таким образом, кубоид измеряет 0.25 метров на 0,3 метра, на 0,35 метра. Умножьте эти три стороны прямоугольного параллелепипеда вместе, и мы получим объем 0,0263 кубических метра.

Теперь мы наконец готовы вычислить массу прямоугольного параллелепипеда. Умножьте плотность 11 340 на объем 0,0263 кубических метра, и мы узнаем, что прямоугольный параллелепипед будет весить примерно 298 килограммов. И это наш ответ.

Краткий обзор урока

Масса — это количество «материала» внутри объекта.В науке мы предпочитаем измерять массу в килограммах, которые являются единицей массы СИ (Международный стандарт). Объем — это сколько места что-то занимает. Стандартной единицей объема являются метры в кубе (или кубические метры). Плотность — это плотность упаковки атомов и молекул в веществе, измеряемая в килограммах на кубический метр.

Формула, связывающая плотность, массу и объем, выглядит так:

Здесь m представляет массу объекта или материала, V представляет объем, а фигурная p (греческая буква ро) представляет плотность.Иногда люди могут использовать нестандартные или ненаучные единицы измерения. В таких ситуациях может быть полезно преобразовать единицы измерения.

Quick Points

Масса	Том	Плотность
*Количество вещей внутри объекта	*Количество места, которое занимает объект	*Насколько упакованы атомы и молекулы вещества (измеряется путем деления массы на объем)

Результаты обучения

Завершите урок по массе и объему, чтобы уверенно делать следующее:

• Различать массу и объем
• Напишите формулу массы и объема
• Помните, как конвертировать между единицами
• Обсудите связь между массой, объемом и плотностью

Краткое сообщение: Увеличение массы ледников в российской Арктике (2010–2017 гг.

)

Абдуллахи, С., Вессель Б., Лейхтле Т., Хубер М., Вольфарт К. и Рот A.: Исследование глубины проникновения Tandem-x над льдом Гренландии Лист в: IGARSS 2018–2018 IEEE International Geoscience and Remote Симпозиум по зондированию, IGARSS 2018–2018 IEEE International Geoscience and Симпозиум по дистанционному зондированию, Валенсия, 133–1339 гг., https://doi.org/10.1109/IGARSS.2018.8518930, 2018. 

Абдуллахи С., Вессель Б., Хубер М., Вендледер А., Рот А. и Кюнцер, C.: Оценка смещения высоты InSAR X-диапазона, связанного с проникновением: исследование закончено ледяной щит Гренландии, дистанционный датчик., 11, 2903, https://doi.org/10.3390/rs11242903, 2019. 

Бокс, Дж. Э., Колган, В. Т., Кристенсен, Т. Р., Шмидт, Н. М., Лунд, М., Парментье, Ф.-Ж. В., Браун Р., Бхатт У. С., Ойскирхен Э. С., Романовский В. Э., Уолш Дж. Э., Оверленд Дж. Э., Ван М., Корелл Р. В., Мейер, В. Н., Воутерс, Б., Мернильд, С., Морд, Дж., Павляк, Дж., и Олсен, М. С.: Ключевые индикаторы изменения климата Арктики: 1971–2017 гг. , Окружающая среда. Рез. Lett., 14, 045010, https://doi.org/10.1088/1748-9326/aafc1b, 2019. 

Браун, М.Х., Мальц П., Соммер К., Фариас-Барахона Д., Сотер Т., Касасса Г., Соруко А., Скварца П. и Зеехаус Т. К.: Ограничение изменение высоты и массы ледников в Южной Америке, Nat. Клим. Смена, 9, 130–136, https://doi.org/10.1038/s41558-018-0375-7, 2019. 

Карр, Дж. Р., Стоукс, К., и Виели, А.: Недавнее отступление крупной торговой точки ледники на Новой Земле, Российская Арктика, под влиянием геометрии фьорда и ледовые условия, J. Glaciol., 60, 155–170, https://doi.org/10.3189/2014JoG13J122, 2014 г.

Чираки Э., Великонья И. и Саттерли Т.: Массовый баланс Новой Архипелаг Земля, российская высокая Арктика, с использованием переменной силы тяжести от GRACE и данные альтиметрии от ICESat и CryoSat-2, Remote Sens., 10, 1817, https://doi.org/10.3390/rs10111817, 2018. 

Чираки, Э., Великонья, И., и Свенсон, С.: Непрерывность потери массы ледников и ледяных шапок мира из GRACE и GRACE Follow-On Миссии, Геофиз. Рез. Письма, 47, 18, https://doi.org/10.1029/2019GL086926, 2020.

Далл Дж., Мэдсен С.Н., Келлер К. и Форсберг Р.: Топография и проникновение ледяного щита Гренландии, измеренное с помощью бортового SAR Интерферометрия, Геофиз. Рез. Летт., 28, 1703–1706, https://doi.org/10.1029/2000GL011787, 2001. 

Гарднер, А.С., Мохольдт, Г., Когли, Дж.Г., Воутерс, Б., Арендт, А.А., Вар, Дж., Бертье, Э., Хок, Р., Пфеффер, В. Т., Казер, Г., Лигтенберг, С. Р. М., Болх Т., Шарп М. Дж., Хаген Дж. О., ван ден Брук М. Р. и Пол, Ф.: Согласованная оценка вклада ледников в повышение уровня моря: 2003–2009 гг., Наука, 340, 852–857, https://дои.org/10.1126/science.1234532, 2013. 

Хьюгонне, Р., Макнабб, Р., Бертье, Э., Менунос, Б., Нут, К., Жирод, Л., Фаринотти Д., Хусс М., Дюссайан И., Брун Ф. и Каэб А.: Ускоренная глобальная потеря массы ледников в начале двадцать первого века, Nature, 592, 726–731, https://doi.org/10.1038/s41586-021-03436-z, 2021. 

Huss, M.: Предположения о плотности для преобразования геодезического изменения объема ледника в изменение массы, The Cryosphere, 7, 877–887, https://doi. org/10.5194/tc-7-877-2013, 2013.

Джейкоб, Т., Вар, Дж., Пфеффер, В.Т., и Свенсон, С.: Недавние публикации ледников и ледяных шапок к повышению уровня моря, Природа, 482, 514–518, https://doi.org/10.1038/nature10847, 2012. 

Янсен Э., Кристенсен Дж. Х., Доккен Т., Нисанджиоглу К. Х., Винтер Б. М., Капрон, Э., Го, К., Дженсен, М.Ф., Ланген, П.Л., Педерсен, Р.А., Ян С., Бентсен М., Кьер Х. А., Садацки Х., Сессфорд Э. и Стендель, М.: Прошлые взгляды на нынешнюю эпоху резкого арктического климата изменить, Нат.Клим. Смена, 10, 714–721, https://doi.org/10.1038/s41558-020-0860-7, 2020. 

Li, J., Li, Z.-W., Hu, J., Wu, L.-X., Li, X., Го Л., Лю З., Мяо З.-Л., Ван, В., и Чен, Дж.-Л.: Исследование предвзятости цифрового TanDEM-X модели рельефа ледников Тибетского нагорья: воздействующие факторы и потенциальное влияние на геодезические измерения баланса массы, J. Glaciol., 67, 1–14, https://doi.org/10.1017/jog.2021.15, 2021. 

Мацуо, К. и Хеки, К.: Текущие потери льда в малых ледниковых системах Арктические острова (Исландия, Шпицберген и Российская Арктика) из Спутниковая гравиметрия, Терр. Атмос. Океан. наук, 24, 657, https://doi.org/10.3319/TAO.2013.02.22.01(TibXS), 2013. 

Мелконян А. К., Уиллис М. Дж., Притчард М. Э. и Стюарт А. Дж.: Недавние изменения скорости ледников и их истончение на Новой Земле, Удаленная Sens. Environ., 174, 244–257, https://doi.org/10.1016/j.rse.2015.11.001, 2016. 

Миллан Р., Дехек А., Трув Э., Гурмелен Н. и Бертье Э.: Изменения высоты и проникновение льда и снега в диапазоне X по данным TanDEM-X данные района Монблан, в: 2015 8-й Международный семинар по Анализ многовременных изображений дистанционного зондирования (Multi-Temp), 2015 г., 8-е место Международный семинар по анализу мультивременного дистанционного зондирования Изображения (Multi-Temp), Анси, Франция, 1–4, https://дои.org/10.1109/Multi-Temp.2015.7245753, 2015. 

Мохольдт Г., Воутерс Б. и Гарднер А.С.: Недавние массовые изменения ледники российской Арктики, Геофиз. Рез. Письма, 39, 55, https://doi.org/10.1029/2012GL051466, 2012. 

Моррис, А., Мохолдт, Г.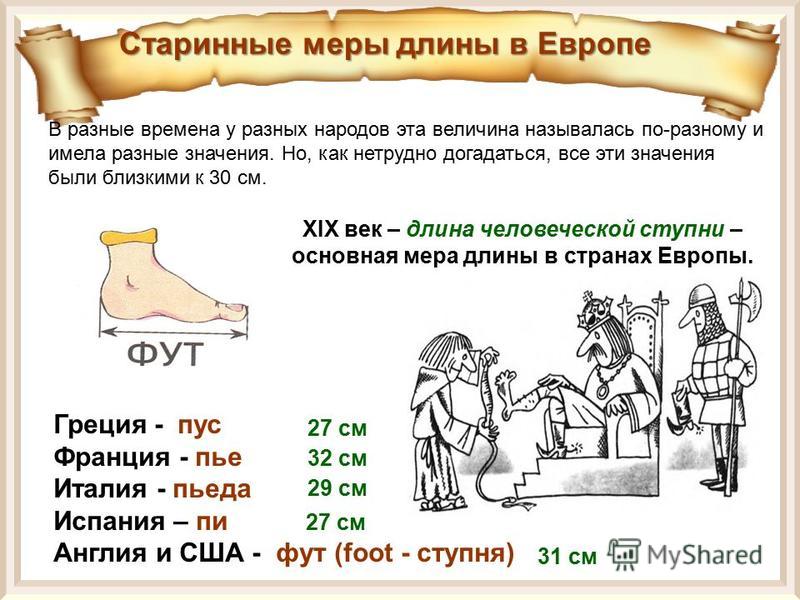 , и Грей, Л.: Распространение потери массы ледника Шпицберген. до окраин Баренцева моря, обнаруженных CryoSat-2, J. Geophys. Рез.-Прибой Земли, 125, 14, https://doi.org/10.1029/2019JF005357, 2020. 

Пфеффер, В. Т., Арендт, А. А., Блисс, А., Болч, Т., Когли, Дж. Г., Гарднер, А. С., Хаген Дж.-О., Хок Р., Касер Г., Кинхольц К., Майлз Э. С., Мохольдт Г., Мёльг Н., Пауль Ф., Радич В., Растнер П., Рауп Б. Х., Рич, Дж., Шарп, М.Дж., и Консорциум Рэндольфа: Рэндольф Glacier Inventory: глобальный полный перечень ледников, J. Glaciol., 60, 537–552. М.: Массовые изменения выводных ледников вдоль побережья Норденскёльда, север Антарктического полуострова, по спутниковым измерениям TanDEM-X: Ледники TanDEM-X Антарктического полуострова // Геофиз.Рез. Летт., 41, 8123–8129, https://doi.org/10.1002/2014GL061613, 2014 г.

Санчес-Гамес П., Наварро Ф. Дж., Бенхам Т. Дж., Глазовский А. Ф., Бассфорд, Р. П., и Даудсвелл, Дж. А.: Внутригодовая и межгодовая изменчивость в динамическом сбросе с ледяной шапки АН, Северная Земля, Российская Арктика и ее роль в модуляции баланса массы, J. Glaciol., 65, 780–797, https://doi.org/10.1017/jog.2019.58, 2019. 

Seehaus, T., Malz, P., Sommer, C., Lippl, S., Cochachin, A.и Браун, М.: Изменения тропических ледников на всей территории Перу в период с 2000 по 2016 год – баланс массы и колебания площади, Криосфера, 13, 2537–2556, https://doi.org/10.5194/tc-13-2537- 2019, 2019. 

Соммер, К., Зеехаус, Т., Глазовский, А., и Браун, М. Х.: Скорость изменения высоты поверхности большинства ледников на Земле Франца-Иосифа, Северной Земли и Новой Земли в период с 2010 по 2017 год, ПАНГЕЯ [ набор данных], https://doi.org/10.1594/PANGAEA.939836, 2022. 

Строцци, Т., Пол, Ф., Висманн, А., Шелленбергер, Т., и Каэб, A.: Циркумарктические изменения стока ледников и ледяных шапок из Спутниковые данные SAR за период с 1990-х по 2017 год, Remote Sens., 9, 947, https://doi.org/10.3390/rs

47, 2017. 

Цепеш, П., Гурмелен, Н., Ниенов, П., Цамадос, М., Шепард, А., и Вайсгербер, Ф.: Изменения высоты и массы арктических ледников и льда. колпачки, 2010–2017, Дистанционный датчик окружающей среды, 261, 112481, https://doi.org/10.1016/j.rse.2021.112481, 2021. 

Вессель, Б., Бертрам А., Грубер А., Бемм С. и Деч С.: НОВОЕ МОДЕЛЬ ВЫСОКОГО РАЗРЕШЕНИЯ ГРЕНЛАНДИИ, ПОЛУЧЕННАЯ ИЗ TANDEM-X, ISPRS Аня. фотограмм. Дистанционный сенсор Спл. Инф. наук, III-7, 9–16, https://doi.org/10.5194/isprsannals-III-7-9-2016, 2016. 

Воутерс, Б., Гарднер, А.С., и Мохольдт, Г.: Глобальная потеря массы ледника Во время спутниковой миссии GRACE (2002–2016 гг.), Front. наук о Земле, 7, 96, https://doi.org/10.3389/feart.2019.00096, 2019. 

Чжао, Дж. и Флорисиою, Д.: Влияние проникновения на возвышение TanDEM-X с использованием измерений GNSS и лазерной альтиметрии в Антарктике, ISPRS – Int.Арка фотограмм. Дистанционный сенсор Спл. Инф. наук, XLII-2/W7, 1593–1600, https://doi.org/10.5194/isprs-archives-XLII-2-W7-1593-2017, 2017. 

Чжэн, В., Притчард, М.Е., Уиллис, М.Дж., Цепеш, П., Гурмелен, Н. , Бенхэм, Т. Дж., и Даудесвелл, Дж. А.: Ускорение потери массы ледников на Земля Франца-Иосифа, Российская Арктика, ДЗЗ, 211, 357–375, https://doi.org/10.1016/j.rse.2018.04.004, 2018. 

Чжэн, В., Притчард, М.Э., Уиллис, М.Дж., и Стернс, Л.А.: Возможное Переход от ледникового нагона к ледяному течению на шапке Вавилова // Геофиз.Рез. Lett., 46, 13892–13902, https://doi.org/10.1029/2019GL084948, 2019. 

Методы измерения | Дом

Методы измерения содержит статьи, представляющие интерес для всех, кто занимается изучением и применением фундаментальных измерений.
В сферу охвата входят:

• общие проблемы метрологии;
• Единообразие результатов измерений;
• Стандарты и методы измерений;
• Новые методы измерения: линейные, механические, электромагнитные, оптические, частотно-временные, теплотехнические, ионизирующих излучений и др.

Журнал Измерительная техника является переводом рецензируемых российских журналов: Измерительная техника и избранных статей из Метрология.

Учредителями обоих российских журналов являются:

Госстандарт России, Всероссийский научно-исследовательский институт оптико-физических измерений, Метрологическая академия России, Всероссийский научно-исследовательский институт метрологии им. Всероссийский научно-исследовательский институт физико-технических и радиотехнических измерений и Уральский научно-исследовательский институт метрологии, Всероссийский научно-исследовательский институт метрологической службы (ВНИИМС) и Российский научно-технический центр информации по стандартизации, Метрология и оценка соответствия (Стандаинформ).

• Представляет интерес для всех, кто занимается изучением и применением фундаментальных измерений
• Исследует общие проблемы метрологии; Единообразие результатов измерений; стандарты и методы измерений; Новые методы измерения и многое другое
• Включает статьи из «Измерительной техники» и избранные статьи из «Метрологии»
• 100% авторов, принявших участие в опросе, сообщили, что они обязательно будут публиковаться или, вероятно, будут публиковаться в журнале снова

Информация журнала

org/CreativeWork»>

Главный редактор

Издательская модель

Подписка

Показатели журнала

35 787 (2020)

Загрузки

Веса и меры — Ресурсы

В медицине необходимы точные измерения, например, при измерении различных веществ в лабораторных тестах для оценки состояния здоровья или постановки диагноза.В зависимости от вещества могут использоваться разные единицы измерения. Обычно метрическая система, кратная 10, используется для измерения следующих величин:

• Масса: Грамм измеряет массу, количество вещества в объекте. Масса аналогична весу, но на вес влияет гравитация.

• Объем: Литры измеряют объем, количество места, которое занимает объект.

• Длина: метров длины.

Префиксы, указывающие, какое число кратно 10, могут быть добавлены к основной единице измерения, такой как метр (м), литр (л) или грамм (г). Использование префиксов помогает сделать число более читаемым. Обычно используемые префиксы включают килограмм (к), деци (д), санти (с), милли (м) и микро (μ).

Другие единицы измерения различных свойств вещества. Например, моль (моль) — это количество вещества, которое содержит такое же количество частиц (молекул или ионов), что и в 12 граммах углерода.Таким образом, независимо от вещества, 1 моль всегда содержит одинаковое количество частиц. Однако количество граммов в 1 моле сильно варьируется от вещества к веществу. Один моль равен молекулярной (атомной) массе вещества в граммах. Например, молекулярная масса натрия равна 23, поэтому 1 моль натрия равен 23 граммам. Молекула поваренной соли (хлорида натрия) состоит из одного атома натрия и одного атома хлора (имеющего молекулярную массу 35 грамм). Таким образом, один моль хлорида натрия весит 23 грамма + 35 граммов = 58 граммов.

Осмолярность — это мера количества частиц в литре жидкости, а осмоляльность — это мера количества частиц в килограмме (кг) жидкости. Поскольку 1 литр воды весит 1 кг, осмолярность и осмоляльность веществ, растворенных в воде, одинаковы. Осмол – это количество вещества, которое при растворении в жидкости образует 1 моль. Например, поскольку поваренная соль растворяется в натрии и хлориде в воде, один моль поваренной соли, растворенный в 1 литре воды, дает 1 моль натрия и 1 моль хлорида.Таким образом, его осмолярность составляет 2 осмоля на литр, а осмоляльность — 2 осмоля на кг.

Эквиваленты (экв) и миллиэквиваленты (мэкв) измеряют способность вещества соединяться с другим веществом. Миллиэквивалент примерно эквивалентен миллиосмолю.

Формулы используются для перевода измерения из одних единиц в другие. Одна и та же сумма может быть выражена в разных единицах. Например, концентрация кальция в крови обычно составляет около 10 миллиграммов на децилитр (мг/дл), 2.5 миллимолей в литре (ммоль/л) или 5 миллиэквивалентов в литре (мэкв/л).

Единицы, используемые для медицинских тестов, различаются в зависимости от измеряемого вещества. Единицы, которые традиционно используются в Соединенных Штатах, называются условными единицами. Обычные единицы обычно выражают концентрацию как массу на единицу объема, и объем может варьироваться. Международная система единиц (единицы СИ) всегда выражает концентрацию в молях на литр.

Какие страны используют метрическую систему?

Вопрос в заголовке статьи касается того, какие страны используют метрическую систему, более точно называемую Международной системой единиц, но было бы гораздо проще перечислить, какие страны ее не используют.Их всего три: Мьянма (или Бирма), Либерия и США. Все остальные страны мира приняли метрическую систему в качестве основной единицы измерения. Как эта единственная система стала настолько широко распространенной? И почему есть страны, которые сопротивляются? Мы исследуем эти вопросы ниже!

Как создаются и определяются системы измерения?

Когда люди начали создавать более сложные вещи, возникла необходимость в системе измерения. Часто эти измерения будут основаны на человеческом теле.Древние египтяне, например, использовали локти, которые составляли около 52,4 сантиметра и примерно соответствовали длине человеческого предплечья. Но измерения на основе тела могут только зайти так далеко, учитывая, что каждое тело имеет разный размер. Эту проблему можно было бы решить, создав мерные линейки и другие единицы измерения.

Британская имперская система, которая превратилась в обычную систему единиц измерения, используемую американцами сегодня, также была основана на довольно произвольных измерениях.Это происходит из измерений, проведенных римлянами, кельтами и англосаксами более тысячи лет назад. Во-первых, размер фута или дюйма изначально сильно различался в зависимости от того, где вы находились, потому что было трудно установить стандарт. Были различные королевские усилия, от саксонского короля 10-го века, держащего меру бушеля, до распространения «физических воплощений», переданных по всей Англии королевой Елизаветой I. такой же длины.

В настоящее время ученые определяют измерения, используя физические, неотъемлемые процессы, а не физические объекты. Одним из примеров этого является килограмм, который до 2019 года определялся как вес очень специфического куска платины, хранящегося во Франции. Не то чтобы кусок платины упоминался каждый раз, когда нужно было что-то взвесить, но иметь определение килограмма было важно. И проблема, которая обнаружилась, в том, что килограмм терял вес по совершенно неизвестной причине.Ученые решили, что необходимо изменить определение, чтобы оно опиралось на универсальные константы — в частности, на постоянную Планка, — чтобы килограмм никогда не мог измениться.

Почему метрическая система?

Метрическая система почти полностью восходит к одному человеку: Габриэлю Мутону. Мутон, который был викарием в Лионе, Франция, создал в 1670 году систему измерения, которая позже была названа метрической системой. Предложения, которые он сделал — например, основывать единицу на длине качания маятника — развивались и менялись по мере того, как ученые и комитеты продолжали работать над этим.Настоящим ключом к системе было определение измерений в степени 10, поэтому 10 сантиметров — это дециметр, 10 дециметров — это метр и так далее. Это значительно упрощает вычисления, чем, скажем, 12 дюймов в футе, три фута в ярде и 1760 ярдов в миле.

В 1790 году Французская академия наук назначила комитет для полной разработки логической системы измерений. «Метр» определялся как десятимиллионная часть расстояния между Северным полюсом и экватором, а «грамм» — кубический сантиметр воды.Ученые во Франции особенно поддерживали эту систему, потому что использование степеней 10 делало ее намного проще, чем другие системы.

После того, как система была полностью разработана, потребовалось несколько десятилетий, чтобы прижиться. Лишь в 1840 году метрическая система стала официальной во Франции. В 1875 году 17 стран (включая США) приняли участие в Съезде счетчиков для дальнейшей стандартизации измерений, а к 1900 году эту систему приняли 35 стран. За прошедшее столетие система была устойчиво принята большинством стран.Универсальный стандарт измерения облегчил странам участие в международной торговле, обмене информацией и более широком сотрудничестве.

Почему не метрическая система?

Учитывая, что все остальные страны мира перешли на метрическую систему, вы должны задаться вопросом, почему Либерия, Мьянма и Соединенные Штаты остаются в стороне. Однако на самом деле нет никакой причины, и оказывается, что и Либерия, и Мьянма уже проходят процесс «метрики». Таким образом, Соединенные Штаты остаются единственным противником Международной системы единиц.

Долгое время казалось, что Соединенные Штаты перейдут на метрическую систему. Страна отправила делегатов на Метрическую конвенцию в 1875 году, а в 1866 году приняла закон, разрешающий использование метрической системы в официальном качестве. После века смешанного использования Соединенные Штаты приняли Закон о преобразовании метрической системы 1975 года, который призывал к добровольному переходу на метрическую систему. Однако в акте отсутствовал какой-либо крайний срок. Американское стремление установить метрическую систему прекратилось, и обычные единицы измерения США (немного отличающиеся от имперских единиц) остались на месте.

Это не значит, что метрическая система не может быть найдена в Соединенных Штатах. Ни один физик не должен переводить метры в ярды при работе с американцами. И поскольку страна является исключением, многие отрасли, работающие на международном уровне, были вынуждены принять метрическую систему. Далеко не факт, что Соединенные Штаты когда-либо сделают окончательный шаг по переводу всего остального на метрическую систему — менять отметки на каждой миле было бы дорогостоящей задачей — но метрическая система имеет большое влияние в стране.

места, которые смешивают системы

Если вы когда-либо ездили по Соединенному Королевству (на левой стороне дороги ), вы можете быть удивлены, увидев, что «мили» часто упоминаются в стране, которая якобы использует метрическую систему. Как оказалось, есть много стран, которые не полностью привержены метрике. Причина, по-видимому, в том, что переход от одного к другому является трудным изменением для огромной группы людей, к которым нужно приспособиться.

Великобритания, которая обязалась перейти на метрическую систему в 1965 году, до сих пор во многих местах использует имперские единицы, особенно на дорогах.Ирландия тоже местами все еще использует имперскую систему; хотя трудно представить, что стакан разливного пива можно назвать чем-то иным, кроме как «пинтой». В Малайзии действует метрическая система, но местами используются и малайские измерения, особенно на традиционных рынках. Имперская система тоже имеет здесь некоторое значение. В Канаде местами есть имперские единицы (отчасти из-за ее близости к Соединенным Штатам), а Северная Корея использует свои традиционные корейские единицы в определенных условиях. Неметрические единицы можно встретить в Таиланде, Китае, Индонезии, Тайване и многих других странах.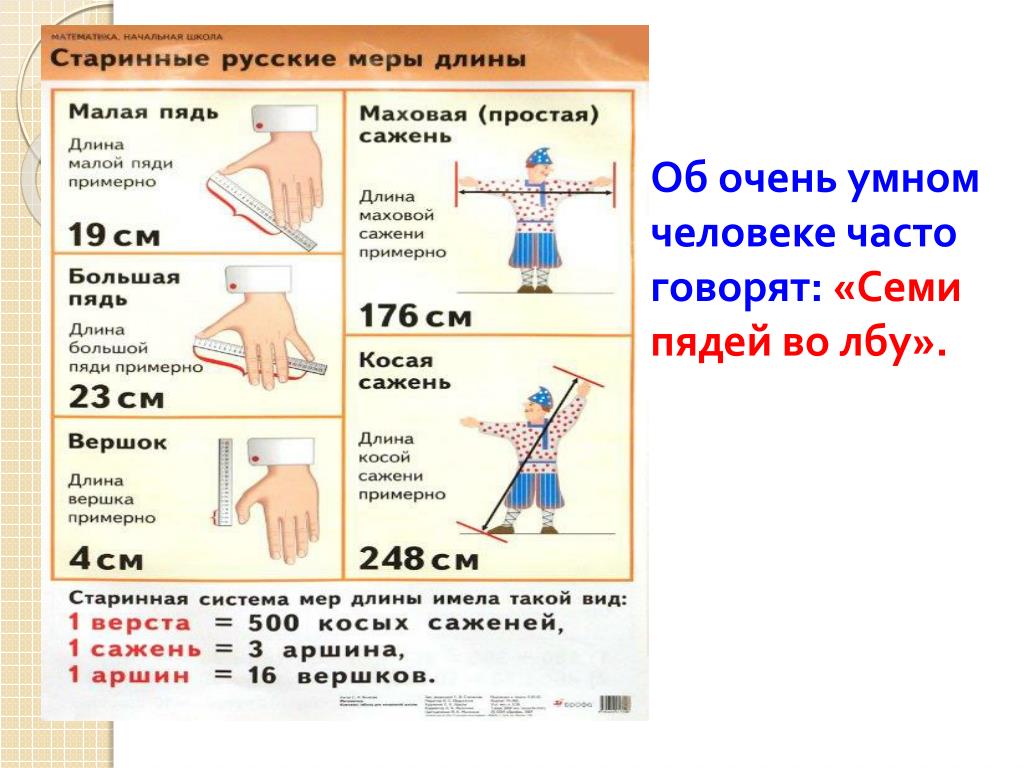

Международная Система Единиц — король измерений, но она еще не завладела всем миром. В то время как Соединенные Штаты являются наиболее очевидным примером держащейся страны, во всем мире есть места, где вы найдете другие единицы измерения.

Прецизионное измерение разности масс легких ядер и антиядер

А.И. Фонд Национальной научной лаборатории Алиханяна (Ереванский физический институт), Ереван, Армения

А.Григорян, Г. Гулканян и В. Папикян

Benemérita Autónoma Universidad de Puebla, Пуэбла, Мексика

Х. Белло Мартинес, И. Кортес Мальдонадо, А. Фернандес Телес, М. И. Мартинес, Л. Морено, М. Родригес Кауантци, Г. Техеда Муньос, А. Варгас, С. Вергара Лимон и А. Вильяторо Тельо

Институт теоретической физики им. Боголюбова, Киев, Украина

А. Алкин, В. Челноков, Б . Гринёв, Ю. Мартынов, О. Шадура, В. Трубников, В.Юрченко и Г. Зиновьев

Департамент физики и Центр астрофизики частиц и космических исследований (CAPSS), Институт Бозе, Калькутта, Индия

С. Дас, С. К. Гош, С. К. Прасад и С. Раха

Институт ядерной физики имени Будкера, Новосибирск, Россия

Ю. Пестов

Калифорнийский политехнический государственный университет, Сан-Луис-Обиспо, Калифорния, США

Дж. Л. Клэй

4 Центральный педагогический университет Китая , Ухань, Китай

П.Барталини, С. Кай, К. Гао, С. Ли, С. Рен, З. Сун, М. Ван, П. Ян, З. Инь, Х. Чжан, Ю. Чжан, Д. Чжоу, Х. Чжу, J. Zhu и X. Zhu

Centre de Calcul de l’IN2P3, Villeurbanne, France

R. Vernet

Centro de Aplicaciones Tecnológicas y Desarrollo Nuclear (CEADEN) 9004 Ceaden, 9000, Куба Санчес, Э. Лопес Торрес и К. Штейер

Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Мадрид, Испания

F.Бланко, М. А. Диас Корчеро, П. Гонсалес-Самора, Э. Монтес, А. Х. Рубио Монтеро и Э. Серрадилья

Centro de Investigacion y de Estudios Avanzados (CINVESTAV), Мехико и Мерида, Мексика

Дж. Г. Контрерас, Р. Крус Альбино, Г. Эррера Коррал, Л. Монтаньо Зетина и М. Родригес Кауантци

Centro Fermi-Storico della Fisica e Centro Studi e Ricerche ‘Enrico Fermi’, Рим, Италия

А. Алиси, Л. Чифарелли, А. Де Каро, Д.Де Груттола, Ф. Ноферини, Ж.-П. Revol & A. Zichichi

Чикагский государственный университет, Чикаго, Иллинойс, США

E. Garcia-Solis & A. Harton

Китайский институт атомной энергии, Пекин, Китай

3

X. Li

X. Li

Commissariat à l’Energie Atomique, IRFU, Saclay, France

A. Baldisseri, H. Borel, J. Castillo Castellanos, J. L. Charvet, A. Lardeux, H. Pereira Da Costa и A. Rakotozafindrabe

Институт информационных технологий COMSATS (CIIT), Исламабад, Пакистан

I.Ахмед, М. Аджаз, К. Х. Хан, М. У. Нару, М. Сулейманов и А. Заман

Департамент физики частиц и IGFAE, Университет Сантьяго-де-Компостела, Сантьяго-де-Компостела, Испания

Н. Арместо, Э. Г. Феррейро, К. Пахарес и К. А. Сальгадо

Факультет физики и технологий Бергенского университета, Берген, Норвегия

С. Алтинпинар, Ø. Джувсланд, Ø. Хааланд, М. Хуанг, П. И. Лоэнн, Дж. Нистранд, А. Рехман, Д. Рёрих, К.Уллаланд, А. Велуре, Б. Вагнер, Х. Чжан, З. Чжоу и Х. Чжу

Факультет физики, Алигархский мусульманский университет, Алигарх, Индия

М. Д. Азми, Т. Хуссейн, М. Ирфан, М. Мохисин Хан и М. Тарик

Физический факультет Университета штата Огайо, Колумбус, Огайо, США

Дж. Т. Бакстон, Т. Дж. Гуманик, А. М. Кубера, М. А , Лиза, Дж. Зальцведель и М. Штайнпрейс

Факультет физики, Седжонский университет, Сеул, Южная Корея

D.С. Хван и С. Ким

Факультет физики Университета Осло, Осло, Норвегия

И. К. Арсен, П. К. Батцинг, О. Дордич, С. Линдал, С. М. Махмуд, Дж. Милошевич, Х. Квигстад, М. Рихтер, К. Рёд, Т. Б. Скаали, Т. С. Тветер, Дж. Викне и К. Чжао

Dipartimento di Elettrotecnica ed Elettronica del Politecnico, Бари, Италия

Л. М. Минервини

Дипартименто ди Fisica dell’Università ‘La Sapienza’ и Sezione INFN Рим, Италия

F.Meddi

Dipartimento di Fisica dell’Università and Sezione INFN, Кальяри, Италия

E. A. R. Casula, A. Collu, A. De Falco, G. Puddu, V. Razazi, C. Terrevoli & G . L. Usai

Dipartimento di Fisica dell’Università и Sezione INFN, Триест, Италия

P. Camerini, R. Lea, G. Luparello, G. V. Margagliotti и R. Diparto

9004 diparto Fisica dell’Università and Sezione INFN, Турин, Италия

S.Беоле, Д. Берцано, Л. Бьянки, Э. Ботта, Ю. Корралес Моралес, А. Ферретти, М. Гальярди, М. Галлио, А. Латтука, М. Леончино, М. Маркизоне, М. Мазера, Р. Руссо , К. Штейер, С. Валлеро и Э. Верселлин

Отдел физики и астрономии Университета и отделение INFN, Болонья, Италия

С. Арчелли, М. Базиле, Ф. Беллини, Л. Чифарелли, М. . Colocci, B. Guerzoni, G. Scioli и A. Zichichi

Dipartimento di Fisica e Astronomia dell’Università и Sezione INFN, Катания, Италия

R.Барбера, П. Ла Рокка, К. Петта, Ф. Риджи и Г. Сантагати

Отдел физики и астрономии Университета и отделение INFN, Падуя, Италия

Д. Каффарри, А. Фестанти, А. Франческон , П. Джубилато, К. Йена, М. Лунардон, М. Морандо, С. Моретто, Ф. Скарлассара, Ф. Сорамель, К. Терреволи и Г. Виести

Dipartimento di Fisica ‘ER Caianiello’ dell’Università and Gruppo Collegato INFN, Салерно, Италия

A. De Caro, D. De Gruttola, S.De Pasquale, M. Fusco Girard, E. Meninno, P. Pagano и T. Virgili

Отдел науки и инноваций Технологического университета Восточной Пьемонте и Gruppo Collegato INFN, Алессандрия, Италия

P. . Ramello & M. Sitta

Dipartimento Interateneo di Fisica ‘M. Merlin’ and Sezione INFN, Бари, Италия

Ф. Бариле, Г. Э. Бруно, Ф. Коламария, Д. Колелла, Г. Д’Эразмо, Д. Ди Бари, Э. М. Фиоре, А. Мастросерио и М.А. Тангаро

Отделение экспериментальной физики высоких энергий Лундского университета, Лунд, Швеция

П. Кристиансен, Х. М. Люнггрен, А. Оскарссон, Т. Ричерт, Д. Сильвермир, К. Согаард, Э. Stenlund & V. Vislavicius

Eberhard Karls Universität Tübingen, Tübingen, Germany

B. A. Hess, H. R. Schmidt & J. Wiechula

Европейская организация ядерных исследований, Женева Швейцария

Г.Альери Ринелла, А. Аугустинус, Ф. Бальтасар Дос Сантос Педроса, Д. Берцано, Л. Бетев, С. Буфалино, П. Бунчич, Д. Каффарри, Ф. Карена, В. Карена, К. Кавиккиоли, С. Чапелэнд, В. Чибанте Баррозу, П. Чочула, Ф. Коста, Л. Кункейро, А. Ди Мауро, Р. Дивиа, Б. Эразмус, М. Флорис, А. Франческон, У. Фукс, К. Гарджуло, А. Геата, М. Геата, П. Джубеллино, А. Григорас, К. Григорас, Дж. Ф. Гроссе-Этрингхаус, Р. Гроссо, Х. Хиллеманнс, П. Христов, К. Ионита, А. Калвейт, М. Кейл, А. Клюге, М. Кофараго, К.Кузинопулос, М. Ковальски, Э. Крышен, Т. Кугатасан, И. Лакомов, Э. Лауди, И. Легран, М. Магер, В. Манзари, П. Мартиненго, М. Мартинес Педрейра, Л. Милано, А. Морш , Х. Мюллер, Л. Муса, М. Никулеску, Дж. Нидзела, А. Олсон, О. Пинацца, Р. Прегенелла, Ф. Рейдт, П. Ридлер, В. Риглер, А. Росси, К. Шафаржик, Дж. . Шукрафт, Ю. Шутц, Р. Шахоян, К. М. Силевич, Г. Симонетти, А. Щепанкевич, А. Тауро, А. Телеска, Дж. В. Ван Хорн, П. Ванде Вывре, Г. Вольпе, Б. , фон Галлер, Д. Враник, М. Вебер и М.B. Zimmermann

Excellence Cluster Universe, Мюнхенский технический университет, Мюнхен, Германия

T. Dahms, L. Fabbietti, P. Gasik и I. Vorobyev

Инженерный факультет, Бергенский университетский колледж, Норвегия, Берген

Дж. Алме, Х. Хелструп, К. Ф. Хетланд и Б. Киленг

Факультет математики, физики и информатики Университета Коменского, Братислава, Словакия

М. Мерес, М. Пикна, Б. Ситар , П.Стрмен, А. Сабо и И. Шарка

Факультет ядерных наук и физической инженерии, Чешский технический университет в Праге, Прага, Чехия

Й. Адам, Й. Бельчик, М. Броз, Й. Чепила, Й Г. Контрерас, Г. Эйюбова, М. Крелина, В. Петрачек, М. Шульц и М. Спасек

Факультет естественных наук, Университет им. Врлакова

Технологический факультет, Университетский колледж Бускеруд и Вестфолд, Вестфолл, Норвегия

R.Langoy & J. Lien

Франкфуртский институт повышения квалификации, Франкфуртский университет имени Иоганна Вольфганга Гете, Франкфурт, Германия

Т. Альт, М. Бах, Дж. де Кювелан, Д. Эшвайлер, С. Горбунов, Х. Хартманн, Д. Хаттер, С. Кирш, И. Кисель, Т. Коллеггер, М. Крец, М. Кржевицкий, И. Кулаков, В. Линденструт, Ф. Реттиг, Д. Рор и М. Зизак

Каннын — Национальный университет Вонджу, Каннын, Южная Корея

Ю. В. Бэк, Х. Юнг, Д. В.Ким, Дж. С. Ким и Мимаэ. Ким

Кафедра физики, Университет Гаухати, Гувахати, Индия

Б. Бхаттачарджи и Н. Хуссейн

Хельсинкский институт физики (HIP), Хельсинки, Финляндия

Т.Э. Хильден, М. М. Миесколайнен и С. С. Расанен

Университет Хиросимы, Хиросима, Япония

Т. Окубо, К. Шигаки, Т. Сугитате и С. Яно

Индийский технологический институт Бомбей (IIT), Мумбаи, Индия

N.Агравал, Н. К. Бехера, С. Даш, Г. Койитхата Миталевиду, Дж. Кумар, Б. К. Нанди, А. К. Пандей, Д. Пант и Р. Варма

Индийский технологический институт Индор, Indore (IITI), Индия

Н. К. Бехера, А. Н. Мишра, П. Парик, А. Рой, П. Саху и Р. Саху

Университет Инха, Инчхон, Южная Корея

М. J. Kweon

Institut de Physique Nucléaire d’Orsay (IPNO), Université Paris-Sud, CNRS-IN2P3, Orsay, France

Z.Conesa del Valle, I. Das, B. Espagnon, C. Hadjidakis, I. Lakomov, C. Suire и J. D. Tapia Takaki

Institut für Informatik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany

S. Böttger, T. Breitner, H. Engel, A. Gomez Ramirez, U. Kebschull и C. Lara

Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany

H. Appelshäuser, M. Арсландок, Р. Байлаш, Э. Барч, Х. Бек, К.Блюм, Дж. Бук, Т. А. Брокер, Х. Бюшинг, П. Дилленсегер, Б. Донигус, С. Т. Хеккель, Дж. Камин, К. Кляйн, Дж. Ленерт, П. Люттиг, М. Марквард, М. Оздемир, В. Песков, Б. Т. Рашкану, П. Райхельт, Р. Ренфордт, Б. Зальмюллер, С. Шухманн, А. Тарантола Пелони и А. Тойя

Institut für Kernphysik, Westfälische Wilhelms-Universität Мюнстер, Мюнстер, Германия

Й. Анельски, Б. Батен, Л. Фельдкамп, Р. Хааке, М. Хайде, К. Клейн-Бёзинг, Д. Мюльхейм, А. Пассфельд, Дж. П.Wessels, U. Westerhoff, M. Wilde и M. B. Zimmermann

Institut Pluridisciplinaire Hubert Curien (IPHC), Страсбургский университет, CNRS-IN2P3, Страсбург, Франция

I. Belikov, B. Hippolyte, C. Kuhn, A. Maire, L. Molnar, C. Roy & X. Sanchez Castro

Институт ядерных исследований Академии наук, Москва, Россия

Д. Финогеев, А. Фурс, Ф. Губер, О. Каравичев, Т. Каравичева, Е. Карпечев, А. Коневских, А. Курепин, А.Б. Курепин, А. Маевская, И. Пшеничнов, А. Решетин и А. Шабанов

Институт субатомной физики Утрехтского университета, Утрехт, Нидерланды

Р. А. Бертенс, К. Бьянчин, С. Белогрлич, А. Калива, А. Добрин, А. Дубла, А. Грелли, Д. Л. Д. Кейденер, Э. Леогранде, Д. Ф. Лодато, Г. Лупарелло, Дж. Маргутти, А. Мишке, Н. Мохаммади, Г. Ноорен, Т. Пайцманн, М. Райхер, Э. Рокко, Р. Дж. М. Снеллингс, Д. Томас, Дж. Ван Дер Маарель, М. ван Леувен, А. М. Вин, М.Veldhoen, H. Wang, H. Yang, Y. Zhou

Институт теоретической и экспериментальной физики, Москва, Россия

А. Акиндинов, С. Киселев, Д. Малькевич, К. Михайлов, А. Недосекин , Р. Султанов, К. Волошин и Н. Жигарева

Институт экспериментальной физики Словацкой академии наук, Кошице, Словакия

П. Калинак, И. Кралик, М. Кривда, Й. Мусинский, Л. Шандор & M. Vala

Институт физики Академии наук Чешской Республики, Прага, Чехия

J. Мареш и П. Завада

Институт физики, Бхубанешвар, Индия

Р. К. Барал, С. Саху, П. К. Саху и Н. Шарма

Институт космических наук (ИСС), Бухарест , Румыния

А. Дану, Д. Феля, М. Геата, М. Хайдук, К. М. Миту, М. Никулеску, К. Ристя, А. Шевченко, И. Стан и И. С. Згура

Instituto de Ciencias Nucleares, Национальный автономный университет Мексики, Мехико, Мексика

E. Cuautle, R.Т. Хименес Бустаманте, И. Мальдонадо Сервантес, Л. Неллен, А. Ортис Веласкес и Г. Паич

Физический институт, Национальный автономный университет Мехико, Мехико, Мексика

Р. Альфаро Молина, Э. Бельмонт — Морено, Д. М. Гомес Корал, В. Грабски, А. Менчака-Роча, А. Сандовал и Э. Серрадилья

iThemba LABS, Национальный исследовательский фонд, Сомерсет-Уэст, Южная Африка

Ф. Боссу, Z , Бутелези, С. Фёрч, С. Мюррей, К. Сеноси и Г.Стейн

Объединенный институт ядерных исследований (ОИЯИ), Дубна, Россия

Б. Батюня, С. Григорян, Л. Малинина, К. Михайлов, П. Номоконов, Е. Рогочая, А. Водопьянов, С. Запорожец

Университет Конкук, Сеул, Южная Корея

S. K. Oh & J. Seo

Корейский институт науки и технической информации, Тэджон, Южная Корея

S. U. Ahn, H. J. Jang & D. W. Kim

KTO Karatay University, Конья, Турция

A.Карасу Уйсал и А. Окатан

Laboratoire de Physique Corpusculaire (LPC), Clermont Université, Université Blaise Pascal, CNRS-IN2P3, Clermont-Ferrand, France

V. Barret, N. Bastid, A. Batista Camejo, . Crochet, P. Dupieux, S. Li, X. Lopez, F. Manso, S. Porteboeuf-Houssais, P. Rosnet, L. Valencia Palomo и B. Vulpescu

Laboratoire de Physique Subatomique et de Cosmologie, Université Гренобль-Альпы, CNRS-IN2P3, Гренобль, Франция

G.Conesa Balbastre, J. Faivre, C. Furget, R. Guernane, S. Kox, J. S. Real, C. Silvestre & A. Vauthier

Laboratori Nazionali di Frascati, INFN, Фраскати, Италия

N. Бьянки, Л. Калеро Диас, П. Ди Нецца, А. Фантони, П. Джанотти, В. Муччифора, А. Р. Реолон, Ф. Ронкетти, С. Сакаи и Э. Спирити

Laboratori Nazionali di Legnaro, INFN, Леньяро, Италия

R. A. Ricci & M. Venaruzzo

Национальная лаборатория Лоуренса в Беркли, Беркли, Калифорния, США

F.Бок, М. Фазель, Д. Р. Гангадхаран, П. М. Джейкобс, К. Лоизидес, М. Плосконь, Дж. Портер, Т. Дж. М. Саймонс, Дж. Тедер и К. Чжан

Лоуренс Ливерморская национальная лаборатория, Ливермор, Калифорния, США

Р. Сольц

Московский инженерно-физический институт, Москва, Россия

В. Беляев, А. Богданов, В. Григорьев, М. Ипполитов, В. Каплин, Н. Кондратьева, В. Логинов и Д. Пересунько

Национальный центр ядерных исследований, Варшава, Польша

А.Делофф, Т. Добровольский, И. Илькив, П. Курашвили, К. Редлих, Т. Семиарчук, Г. Стефанек и Г. Вилк

Национальный институт физики и ядерной техники, Бухарест, Румыния

К. Андрей, I. Berceanu, A. Bercuci, A. Herghelegiu, M. Petrovici, A. Pop, C. Schiaua и M.G. Tarzila

Национальный институт научного образования и исследований, Бхубанешвар, Индия

S. Biswas, Л. Кумар, Б. Моханти, К. Наяк, Р. Сингх и С. Сингха

Институт Нильса Бора, Копенгагенский университет, Копенгаген, Дания

I.Г. Берден, А. Биландзич, Х. Боггильд, М. Хойнаки, К. Х. Кристенсен, Дж. Дж. Гаардхойе, К. Гулбрандсен, А. Хансен, Б. С. Нильсен, В. Закколо и Ю. Чжоу

Nikhef, Национальный институт субатомной физики, Амстердам, Нидерланды

M. Botje, P. Christakoglou, A. Dobrin, P. G. Kuijer, C. E. Pérez Lara и A. Rodriguez Manso

Nuclear Группа физики, STFC Daresbury Laboratory, Daresbury, UK

M. Borri & R. C. Lemmon

Институт ядерной физики Академии наук Чешской Республики, Ржеж-у-Праги, Чешская Республика

D.Адамова, Дж. Бельчикова, Дж. Ференцей, Ф. Крижек, В. Кучера, С. Кушпил, Дж. Поспишил, М. Шумбера, М. Вайзер и Т. Ванат

Национальная лаборатория Ок-Ридж, Ок-Ридж, Теннесси

Ю. Бердников, В. Иванов, А. Ханзадеев, М. Малаев, В. Никулин, В. Рябов, США

Т. М. Кормье и Д. Сильвермир , Ю. Рябов, В. Самсонов и М. Жалов

Физический факультет, Крейтонский университет, Омаха, Небраска, США

М.Черни, М. Г. Погосян и Дж. Э. Сегер

Физический факультет Пенджабского университета, Чандигарх, Индия

М. М. Аггарвал, А. К. Бхати, Л. Кумар, С. Пармар и Д. Rathee

Физический факультет Афинского университета, Афины, Греция

П. Ганоти, Ф. Рукутакис, М. Спиропулу-Стассинаки и М. Василиу

Физический факультет Кейптаунского университета, Кейптаун, Юг Африка

J. Cleymans & T.Dietel

Физический факультет Университета Джамму, Джамму, Индия

Р. Бала, А. Бхасин, И. Р. Бхат, А. Гупта, Р. Гупта, М. Кур, А. Кумар, С. Махаджан , С. Раджпут, С. Самбьял, А. Шарма, М. Шарма и Р. Сингх

Факультет физики Раджастанского университета, Джайпур, Индия

Р. Ранивала и С. Ранивала

Факультет физики Мюнхенский технический университет, Мюнхен, Германия

М. Болл, Т. Дамс, Л.Фаббьетти, П. Гасик и И. Воробьев

Физический институт, Гейдельбергский университет им. Рупрехта Карла, Гейдельберг, Германия

В. Ангелов, Ф. Бок, О. Буш, А. Дайстинг, М. Г. Флек, П. Глессель, Дж. Кляйн, М. Л. Книхель, Л. Леардини, X.-G. Лу, Дж. Меркадо Перес, Х. Эшлер, К. Ояма, Ю. Пахмайер, Ф. Рейдт, К. Рейгерс, Р. Шикер, Дж. Стахель, Дж. Х. Стиллер, М. А. Фёлькль, Ю. Ван , Дж. Уилкинсон, Б. Виндельбанд, М. Винн и А. Циммерманн

Туринский политехнический университет, Турин, Италия

I.Аймо

Университет Пердью, Западный Лафайет, Индиана, США

Т. А. Браунинг, Р. П. Шаренберг и Б. К. Шривастава

Пусанский национальный университет, Пусан, Южная Корея

, К. Чой, С. У. Чунг, Дж. Сео, Дж. Сон и И.-К. Yoo

Исследовательский отдел и Институт экстремальных веществ EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Дармштадт, Германия

А. Андроник, Р. Авербек, П. Браун-Мюнцингер, А.Дайстинг, П. Фока, У. Франкенфельд, К. Гарабатос, М. Иванов, М. К. Келер, Т. Коллеггер, М. Кржевицкий, К. Липпманн, П. Мальцахер, А. Марин, Н. А. Мартин, С. Маскокки, Д. Мишковец, М. Никассио, Дж. Ондерватер, Дж. Отвиновски, В. Дж. Парк, К. Шмидт, К. Шварц, К. Шведа, И. Селюженков, Й. Тедер, Д. Враник, J. Wagner & S. G. Weber

Институт Руджера Бошковича, Загреб, Хорватия

T. Antičić

Российский федеральный ядерный центр (ВНИИЭФ), Саров, Россия

D

Будников, С. Фильчагин, Р. Илькаев, А. Курякин, А. Мамонов, С. Назаренко, В. Пунин, А. Тумкин, Ю. Виноградов, А. Вьюшин, Н. Завьялов

Российский научный центр Курчатовский институт , Москва, Россия

Александров Д., Блау Д. , Фокин С., Ипполитов М., Кучеряев Ю., Манько В., Николаев С., Никулин С., Нянин А., Пересунько Д., Рябинкин Е., Ю. Сибиряк, А. Васильев, А. Виноградов, С. Яснопольский и И. Юшманов

Институт ядерной физики Саха, Калькутта, Индия

Сукалян Чаттопадхьяй, Д.Дас, И. Дас, П. Хан, Б. Пол, П. Рой и Т. Синха

Школа физики и астрономии Бирмингемского университета, Бирмингем, Великобритания

Д. Александр, Л. С. Барнби, Д. Эванс, Л. Д. Ханратти, П. Г. Джонс, А. Юско, М. Кривда, Г. Р. Ли, Р. Лиетава и О. Вильялобос Бэйли

Departamento de Ciencias, Sección Física, Pontificia Католический университет Перу, Лима, Перу

E. Calvo Villar & A. M. Gago

Sezione INFN, Бари, Италия

G.de Cataldo, D. Elia, F. M. Fionda, V. Lenti, V. Manzari, L. M. Minervini, E. Nappi & V. Paticchio

Sezione INFN, Болонья, Италия

A. Alici, П. Антониоли, Ф. Синдоло, Д. Хацифотиаду, А. Марготти, Р. Нания, Ф. Ноферини, О. Пинацца, Р. Прегенелла, Э. Скаппарон, М. К. С. Уильямс и К. Замполли

Sezione INFN, Кальяри, Италия

C. Cicalo, A. Masoni и S. Siddhanta

Sezione INFN, Катания, Италия

A.Badalà & G. S. Pappalardo

Sezione INFN, Падуя, Италия

F. Antinori, A. Dainese, D. Fabris & R. Turrisi

M.007 M.04 Sezione

INFN

INFN 9000, Италия

, Италия Маццони

Отделение INFN, Триест, Италия

Э. Фраджакомо, Н. Грион, С. Пьяно и А. Рачевски

Отделение INFN, Турин, Италия

М. Анимелло, И. Агнимелло Алессандро, Р. Арнальди, С. Баньяско, А. М. Барбано, К. Бедда, Э.Бруна, С. Буфалино, П. Черелло, Н. Де Марко, А. Феличелло, С. Л. Ла Пуэнт, Л. Мансо, К. Оппедизано, Ф. Прино, М. Пуччо, А. Риветти, Э. Скомпарин и С. Троголо

ГНЦ ИФВЭ НИЦ Курчатовский институт, Протвино, Россия

С. Евдокимов, В. Изучеев, Ю. Харлов, Е. Кондратюк, В. Петров, Б. Полищук, С. Садовский, А. Шангараев

SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Нант, Франция

L.Афечетче, Г. Батинь, Б. Эразмус, М. Эстьен, М. Жермен, Х. Мартин Бланко, Г. Мартинес Гарсия, Л. Массакриер, Д. А. Морейра Де Годой, А. Морреале, П. Пилло, Л. Ronflette, Y. Schutz, A. Shabetai, D. Stocco, M. Wang & J. Zhu

Технологический университет Suranaree, Накхонратчасима, Таиланд

C. Kobdaj & W. Poonsawat

3 Технический университет 900 Сплит FESB, Сплит, Хорватия

С. Готовац, Э. Мудник и Л. Вицкович

Институт ядерной физики Генрика Неводничанского Польской академии наук, Краков, Польша

Й.Бартке, Дж. Фигиль, Э. Гладыш-Дзиадус, Л. Гёрлих, М. Ковальски, А. Матия, К. Майер, Дж. Отвиновски, А. Рыбицки и И. Спутовска

Физический факультет Техасского университета в Остине, Остин, Техас, США

А. Г. Кноспе, К. Маркерт и Д. Томас

Автономный университет Синалоа, Кулиакан, Мексика

И. Леон Монсон и П. Л. М. Подеста- Lerma

Universidade de São Paulo (USP), Сан-Паулу, Бразилия

C.Алвес Гарсия Прадо, М. Брегант, М. Р. Косентино, С. Де, Д. Доменисис Хименес, К. Янке, К. Лагана Фернандес, А. Мас, М. Г. Муньоз, А. К. Оливейра да Силва, Э. Перейра Де Оливейра Филью, К. С. Сидер, А. А. П. Суайде, А. Санто де Толедо и Х. Дж. К. Заноли

Universidade Estadual de Campinas (UNICAMP), Кампинас, Бразилия

Д. Д. Чинеллато, А. Даш и Дж. Такахаши

Хьюстонский университет, Хьюстон, Техас, США

Р. Беллвид, Л.Bianchi, PHSY Jayarathna, S. Jena, D. Mcdonald, F. Ng, L. Pinsky, D. B. Piyarathna, A. R. Timmins & M. Weber

Университет Ювяскюля, Ювяскюля, Финляндия

B Чанг, Д. Дж. Ким, Дж. Крал, Дж. Рак, М. Слупецки, Т. В. Снеллман, В. Х. Трзаска, М. Варгиас и Дж. Вийникайнен

Ливерпульский университет, Ливерпуль, Великобритания

М. Шартье, М. А. С. Фигередо, Дж. Норман и Р. Ромита

Университет Теннесси, Ноксвилл, Теннесси, США

A. J. Castro, I. Martashvili, J. Mazer, C. Nattrass, K. F. Read, R. Scott, N. Sharma & S. Sorensen

University of the Witwatersrand, Johannesburg, South Africa

Z. Vilakazi

University of Tokyo, Tokyo, Japan

T. Gunji, H. Hamagaki, S. Hayashi, Y. Sekiguchi, K. Terasaki, T. Tsuji & Y. Yamaguchi

University of Tsukuba, Tsukuba, Japan

J. Bhom, T. Chujo, S. Esumi, M. Inaba, T. Kobayashi, Y.Миаке, М. Сано, Н. Танака, Д. Ватанабе и Х. Йокояма

Загребский университет, Загреб, Хорватия

Ф. Эрхардт, М. Планинич, Н. Поляк, Г. Симатович и А. Утробичич

Université de Lyon, Université Lyon 1, CNRS-IN2P3, IPN-Lyon, Villeurbanne, France

C. Cheshkov, B. Cheynis, L. Ducroux, J.-Y. Grossiord, B. Teyssier, R. Tieulent, A. Uras

Физический институт им. В. Фока, Санкт-Петербургский государственный университет, Санкт-Петербург, Россия

I.Альцыбеев, Г. Феофилов, А. Колойвари, В. Кондратьев, В. Коваленко, В. Вечернин, Л. Виноградов и А. Зароченцев

Циклотронный центр переменной энергии, Калькутта, Индия

З. Ахаммед, С. Н . Алам, С. Басу, Субхасис Чаттопадхьяй, С. Чоудхури, С. Де, А. К. Дубей, П. Гош, С. Кар, С. А. Хан, Дж. Митра, Б. Моханти, С. Мухури, М. Мукерджи, Т. К. Наяк, С. К. Пал, Дж. Саини, Д. Саркар, Р. Сингараджу, С. Сингха, В. Сингхал, Б. К. Синха и Ю. П. Вийоги

Варшавский технологический университет, Варшава, Польша

L.К. Грачиковски, М. А. Яник, А. Кисиел, Дж. Оленяч, Т. Павляк, Дж. Плута, М. Шимански, А. Заборовска и Х. Зброщик

Государственный университет Уэйна, Детройт, Мичиган, США

Р. Бельмонт, К. Бьянчин, В. Р. Логгинс, Дж. Пан, К. А. Пруно, П. Пуджахари, Дж. Путчке, Р. Дж. Рид, М. А. Салех, М. Вервей, С. А. Волошин и К. Г. Ялдо

Исследовательский центр физики им. Вигнера Венгерской академии наук, Будапешт, Венгрия

Г. Г. Барнафельди, Г.Бенседи, Д. Береньи, Л. Болдисар, Э. Денес, Г. Хамар, Г. Кисс, П. Леваи, А. Лоу, Л. Олах, С. Почибова, Д. Варга и Г. Вольпе

Йельский университет Университет, Нью-Хейвен, Коннектикут, США

С. Айола, Т. Аронссон, Х. Кейнс, М. Э. Коннорс, Р. Дж. Элерс, Дж. У. Харрис, Р. Д. Майка, Дж. Д. Маллиган, С. О, М. Х. Оливер, Т. Шустер и Н. Смирнов

Университет Йонсей, Сеул, Южная Корея

Дж. Х. Кан, Б. Ким, Х. Ким, Минву Ким, Т. Ким, Ю. Квон, С.Lee & M. Song

Zentrum für Technologietransfer und Telekommunikation (ZTT), Fachhochschule Worms, Worms, Germany

R. Keidel

детекторы, написание программного обеспечения, калибровка подсистем, работа с детекторами и сбор данных и, наконец, анализ обработанных данных. Члены коллаборации ALICE обсудили и одобрили научные результаты.Рукопись была подготовлена ​​подгруппой авторов, назначенных коллаборацией, и прошла внутренний процесс рецензирования в рамках всего сотрудничества. Все авторы рассмотрели и одобрили окончательный вариант рукописи.

Как космонавты взвешиваются в космосе? | Журнал Air & Space

Астронавт Карен Найберг использует прибор для измерения массы космического линейного ускорения (SLAMMD) на борту космической станции.

Это утренний ритуал, который большинство из нас считает само собой разумеющимся.Все еще капая из душа, вы встаете на весы, чтобы оценить ущерб, причиненный тем, что вы съели большую часть орехового пирога тети Лесли во время непродуманного полуночного перекуса. Вы морщите гримасу, а затем начинаете день.

Для астронавтов, плавающих высоко над Землей, определить, вызвал ли вчерашняя еда из термостабилизированной индейки и сублимированной кукурузной заправки небольшой живот, далеко не просто. Первое препятствие состоит в том, что в условиях микрогравитации их вес практически всегда равен нулю.Но у астронавтов по-прежнему есть масса, которую они могут измерить, чтобы определить, каким будет их вес на Земле, и позволить исследователям-медикам отслеживать изменения массы тела из-за потери физической формы на орбите.

В настоящее время экипажи на борту космической станции используют два устройства для расчета своего веса. Первым из них является космическое устройство измерения массы с линейным ускорением НАСА (SLAMMD), которое основано на втором законе движения Ньютона. Как объясняют в этом видео астронавты Майкл Барретт и Коити Ваката, на астронавта действует сила двух пружин, установленных на удлинителе.Поскольку сила является известной величиной, результирующее ускорение используется (помните, 90 360 F = ma 90 361?) для определения массы члена экипажа. Точность SLAMMD составляет 0,5 фунта.

Другим устройством является российский прибор для измерения массы тела (BMMD), который Рейд Уайзман демонстрирует на этой лозе, которую он опубликовал в октябре прошлого года.

Космонавт ездит на BMMD как на пого-стике, а для измерения массы используется колебание пружины.

Оба устройства работают, но оба имеют тот недостаток, что занимают место на уже тесной космической станции. Они также требуют много энергии, еще один дефицитный ресурс на станции.

Это побудило группу европейских исследователей предложить систему измерения массы, основанную на знакомой геймерам технологии Kinect. Название «Kinect» на самом деле относится к типу устройства ввода с датчиком движения, а не просто к средству для неуклюжих танцев под песни One Direction в «Just Dance 4» после нескольких слишком больших порций напитков для взрослых. Система Kinect использует входные данные камеры для создания 3D-модели космонавта. Затем модель сопоставляется со статистической моделью почти 30 000 человек, чтобы предсказать вес космонавта.В дополнение к 97-процентной точности предлагаемое устройство является небольшим, легким и экономичным в плане энергопотребления.

В отличие от SLAMMD и BMMD, которые измеряют массу, система Kinect будет измерять объем тела, и одной из потенциальных проблем является перемещение воды внутри тела космонавта в условиях микрогравитации, что может повлиять на точность измерений.