Как измерять углы: Угол. Измерение угла — урок. Математика, 5 класс.

Измерения на местности. — Учебный центр

ЗАНЯТИЕ № 1: Тактико-строевое. Измерение на местности углов с помощью подручных предметов, линейки, компаса, приборов наблюдения и прицеливания. Определение на местности расстояний: по степени видимости и слышимости, линейным и угловым размерам предметов, соотношению скоростей света и звука, времени и скорости движения, шагами. Н-Топ.-2.

При ориентировании и целеуказании на местности горизонтальные (вертикальные) углы между направлениями на местные предметы и цели измеряют с помощью приборов наблюдения или глазомерно. Многие приборы, применяемые в войсках, имеют шкалы, оцифрованные в делениях угломера. Окружность разделена на 60 больших или 6000 малых делений угломера. Одно малое деление угломера называют тысячной. Такое название объясняется тем, что длина отрезка дуги окружности, соответствующего одному малому делению, равна тысячной доле радиуса этой окружности. Единицей измерения угла здесь служит линейный отрезок, равный тысячной доле дистанции.

Это позволяет быстро и легко посредством простейших арифметических действий переходить от угловых измерений к линейным и обратно.

При измерении углов в тысячных принято называть и записывать сначала число сотен, а затем десятков и единиц тысячных. Если при этом сотен или десятков не окажется, вместо них называют и записывают нули.

Для перехода от делений угломера к градусной мере угла пользуются соотношениями: одно малое деление (0-01) равно 3,6’, а одно большое (1-00) – 6^о.

Рассмотрим некоторые способы измерения углов.

С помощью приборов наблюдения и прицеливания. В зрительной трубе бинокля имеются две взаимно перпендикулярные шкалы (сетки) для измерения горизонтальных и вертикальных углов с ценой большого деления 0-10, а малого 0-05. Чтобы измерить угол между двумя предметами, надо совместить какой-либо штрих шкалы с одним из них и подсчитать число делений против изображения второго. Умножив число делений на цену одного деления, получим величину измеряемого угла в тысячных.

Приборы наблюдения и прицеливания имеют шкалы, подобные шкалам бинокля, поэтому углы с помощью этих приборов измеряют так же, как и с помощью бинокля.

С помощью компаса. Вначале мушку визирного устройства компаса устанавливают на нулевой отсчёт шкалы. Затем поворотом компаса в горизонтальной плоскости совмещают через целик и мушку линию визирования с направлением на левый предмет (ориентир). После этого, не меняя положения компаса, визирное устройство переводят в направление на правый предмет и снимают по шкале отсчёт, который будет соответствовать величине измеряемого угла в градусах.

При измерении угла в тысячных линию визирования совмещают сначала с направлением на правый предмет (ориентир), так как счёт тысячных возрастает против хода часовой стрелки.

С помощью линейки. С помощью линейки с миллиметровыми делениями можно измерять углы в делениях угломера и градусах. Если линейку держать перед собой на расстоянии 50 см от глаза, то один миллиметр на линейке будет соответствовать двум тысячным (0-02). При измерении угла необходимо подсчитать на линейке число миллиметров между предметами (ориентирами) и умножить на 0-02. Получаемый результат будет соответствовать величине измеряемого угла в тысячных.

Для измерения угла в градусах линейка выносится перед собой на расстояние 60 см. В этом случае 1 см на линейке будет соответствовать 1^о.

Точность измерения углов с помощью линейки зависит от точности выноса её на расстояние 50 см перед собой.

С помощью подручных предметов. Для измерения углов можно пользоваться небольшими подручными предметами (спичечная коробка, карандаш, патрон и т.п.), размеры которых в миллиметрах, а, следовательно, и в тысячных на расстоянии 50 см от глаза известны.

Для приближённого измерения углов на местности могут служить пальцы руки, вытянутой на расстояние 50 см от глаза. Угол между линиями визирования на сомкнутые указательный, средний и безымянный пальцы равен 1-00, а на разведённые до отказа большой и указательный пальцы – 2-50.

Определение направлений на местности. Направление на предмет (цель) определяется и указывается величиной горизонтального угла между начальным направлением и направлением на предмет или магнитным азимутом. При этом за начальное может быть принято направление на одну из сторон горизонта или на хорошо видимый удалённый местный предмет (ориентир).

Магнитный азимут – горизонтальный угол, измеренный по ходу часовой стрелки от северного направления магнитного меридиана до направления на предмет. Его значения могут быть от 0 до 360

0. Магнитный азимут направления определяется с помощью компаса. При этом отпускают тормоз магнитной стрелки и поворачивают компас в горизонтальной плоскости до тех пор, пока северный конец стрелки не установится против нулевого деления шкалы. Затем, не меняя положения компаса, устанавливают визирное приспособление так, чтобы линия визирования через целик и мушку совпала с направлением на предмет. Отсчёт шкалы против мушки соответствует величине определяемого магнитного азимута направления на местный предмет.

Азимут направления с точки стояния на местный предмет называется прямым магнитным азимутом. В некоторых случаях, например для отыскания обратного пути, используют обратный магнитный азимут, который отличается от прямого на 180

0. Чтобы определить обратный, нужно к прямому азимуту прибавить 180⁰, если он меньше 180⁰, или вычесть 180⁰, если он больше 180⁰.

Для определения направления на местности по заданному магнитному азимуту необходимо установить на шкале компаса против мушки отсчёт, разный значению заданного магнитного азимута. Затем, отпустив тормоз магнитной стрелки, повернуть компас в горизонтальной плоскости так, чтобы северный конец стрелки установился против нулевого деления шкалы. После этого, не меняя положения компаса, заметить на местности по линии визирования через целик и мушку какой-нибудь удалённый ориентир. Направление на ориентир и будет определяемым направлением, соответствующим заданному азимуту.

Расстояния на местности в зависимости от обстановки и характера решаемой задачи измеряют глазомерно, по угловым и линейным размерам предметов, промером шагами, по соотношению скоростей света и звука, на слух, по времени и скорости движения, геометрическими построениями на местности.

Глазомерно расстояние определяют путём сравнения с известным на местности отрезком. На точность глазомерного определения расстояния оказывают влияние освещённость, размеры объекта, его контраст с окружающим фоном, прозрачность атмосферы и другие факторы. Расстояния кажутся меньшими, чем в действительности, при наблюдении через водные пространства, лощины и долины, при наблюдении крупных и отдельно расположенных объектов. И наоборот, расстояния кажутся большими, чем в действительности при наблюдении в сумерках, против света, в туман, при пасмурной и дождливой погоде. Все эти особенности следует учитывать при глазомерном определении расстояний.

Точность глазомерного определения расстояний зависит также от натренированности наблюдателя. Опытным наблюдателем расстояния до 1000 м могут быть определены глазомерно с ошибкой 10-15%. При определении расстояния более 1000 м ошибки могут достигать 30%, а при недостаточной опытности наблюдателя 50%.

По угловым и линейным размерам предметов. С помощью линейки, расположенной на расстоянии 50 см от глаза, измеряют  в миллиметрах высоту (ширину) наблюдаемого предмета. Затем действительную высоту (ширину) предмета в сантиметрах делят на измеренную по линейке в миллиметрах, результат умножают на постоянное число 5 и получают искомую высоту предмета в метрах. Например, телеграфный столб высотой 6 м закрывает на линейке отрезок 10 мм. Следовательно, расстояние до него Д = 600/10×5 = 300 м.

Точность определения расстояний по угловым и линейным величинам составляет 5-10% длины измеряемого расстояния.

Для определения расстояний по угловым и линейным размерам предметов рекомендуется запомнить величины (ширину, высоту, длину) некоторых из них, приведённые в табл. ниже.

Обычно шаг человека среднего роста равен 0,7-0,8 м. Длину своего шага достаточно точно можно определить по формуле Д = Р/4 + 0,37,где Д – длина одного шага в метрах; Р – рост человека в метрах. Например, если рост человека 1,72 м, то длина его шага Д = 1,72/4 + 0,37 = 0,8 м.

Шагами. Этот способ применяется обычно при движении по азимуту, составлении схем местности, нанесении на карту отдельных объектов и ориентиров и в других случаях. Счёт шагов ведётся, как правило, парами. При измерении расстояний большой протяжённости шаги более удобно считать тройками попеременно под левую и правую ногу. После каждой сотни пар или троек шагов делается отметка каким-нибудь способом, и отсчёт начинается снова. При переводе измеренного расстояния шагами в метры число пар или троек шагов умножают на длину одной пары или тройки шагов. Например, между точками поворота на маршруте пройдено 254 пары шагов. Длина одной пары шагов равна 1,6 м. Тогда Д = 254×1,6 = 406,4 м.

Более точно длина шага определяется промером какого-нибудь ровного линейного участка местности, например дороги, протяжённостью 200 – 300 м, который заранее измеряется мерной рулеткой (рулеткой, дальномером и т.п.). При приближённом измерении расстояний длину пары шагов принимают равной 1,5 м.

Средняя ошибка измерения расстояний шагами в зависимости от условий движения составляет около 2 – 5% пройденного расстояния.

Счёт шагов может выполняться с помощью шагомера. Он имеет вид и размеры карманных часов. Внутри прибора помещён тяжёлый молоточек, который при встряхивании опускается, а под воздействием пружины возвращается в первоначальное положение. При этом пружина перескакивает по зубцам колёсика, вращение которого передаётся на стрелки. На большой шкале циферблата стрелка показывает число единиц и десятков шагов, на правой малой – сотни, а на левой малой – тысячи. Шагомер подвешивают отвесно к одежде. При ходьбе вследствие колебания его механизм приходит в действие и отсчитывает каждый шаг.

По времени и скорости движения. Этот способ применяется для приближённого определения величины пройденного расстояния, для чего среднюю скорость умножают на время движения. Средняя скорость пешехода около 5, а при движении на лыжах 8 – 10 км/ч. Например, если развед. дозор двигался на лыжах 3 ч, то он прошёл около 30 км.

По соотношению скоростей звука и света. Звук распространяется в воздухе со скоростью 330 м/с, т.е. округлённо 1 км за 3 с, а свет – практически мгновенно (300 000 км/ч). Таким образом, расстояние в километрах до места вспышки выстрела (взрыва) равно числу секунд, прошедших от момента вспышки до момента, когда был услышан звук выстрела (взрыва), делённому на 3. Например, наблюдатель  услышал звук взрыва через 11 с после вспышки. Расстояние до места вспышки Д = 11/3 = 3,7 км.

На слух. Натренированный слух – хороший помощник в определении расстояний ночью. Успешное применение этого способа во многом зависит от выбора места для прослушивания. Оно выбирается таким образом, чтобы ветер не попадал прямо в уши. Вокруг в радиусе нескольких метров устраняются причины шума, например сухая трава, ветки кустарника и т.п. В безветренную ночь при нормальном слухе различные источники шумов могут быть слышны на дальностях, указанных в табл. ниже.

Другой вариант. Точка С выбирается так, чтобы угол АСВ был равен 60⁰. Известно, что тангенс угла 60⁰ равен ½, следовательно, ширина реки равна удвоенному значению расстояния АС. Как в первом, так и во втором случае угол при точке А должен быть равен 90⁰.Геометрическими построениями на местности. Этот способ может применяться при определении ширины труднопроходимых или непроходимых участков местности и препятствий (рек, озёр, затопленных зон и т.п.). Например, определение ширины реки построением на местности равнобедренного треугольника. Так как в таком треугольнике катеты равны, то ширина реки АВ равна длине катета АС. Точка А выбирается на местности так, чтобы с неё был виден местный предмет (точка В) на противоположном берегу, а также вдоль берега реки можно было измерить расстояние, равное её ширине. Положение точки С находят методом приближения, измеряя угол АСВ компасом до тех пор, пока его значение не станет равным 45⁰.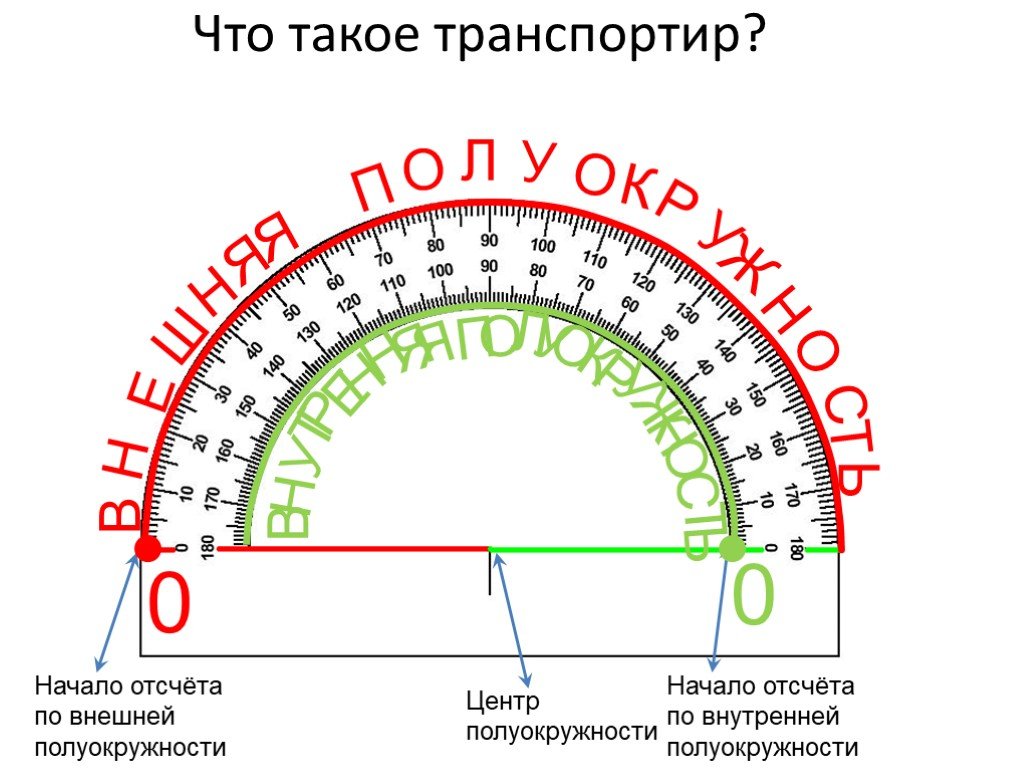

СКАЧАТЬ

Как измерить угол. Артиллерия

Как измерить угол

Цель найдена. Теперь нужно определить ее местоположение, нужно точно вычислить расстояние до цели, чтобы наша артиллерия знала, куда направить свои выстрелы.

Как же это сделать?

Местоположение цели определяется обычно по отношению к ориентиру, – именно, по отношению к тому ориентиру, который находится всего ближе к цели. Достаточно знать две координаты цели – ее дальность, то-есть расстояние от наблюдателя или от орудия до цели, и угол, на который цель видна нам правее или левее ориентира, – и тогда местоположение цели будет определено вполне точно.

Предположим, ради простоты, что цель находится от нас на том же расстоянии, что и ориентир. Расстояние до ориентира нам, конечно, известно заранее: мы потому и называем предмет ориентиром, что местоположение его нам уже известно. Пусть расстояние до ориентира равно 1000 метров. Одна координата цели, следовательно, уже определена. Остается определить другую: угол между целью и ориентиром, – насколько цель видна нам правее или левее ориентира.

Чем же и как артиллеристы измеряют углы? В обыденной жизни вам не раз приходилось измерять углы: вы измеряли их в градусах и минутах. Артиллеристам же приходится не только измерять углы, но и быстро в уме переводить полученные угловые величины в линейные и наоборот. Поэтому измерение углов градусами и минутами для артиллеристов неудобно. Артиллеристы придумали совсем иную меру углов. Мера эта – «тысячная», или, как ее называют иначе, «деление угломера». Представьте себе окружность, разделенную на 6 000 равных частей. Примем за основную меру для измерения углов одну шеститысячную долю этой окружности и попробуем определить ее величину в долях радиуса.

Рис. 174. В артиллерии углы измеряют «тысячными»

Длина любой окружности превосходит, как известно, длину ее радиуса приблизительно в шесть раз.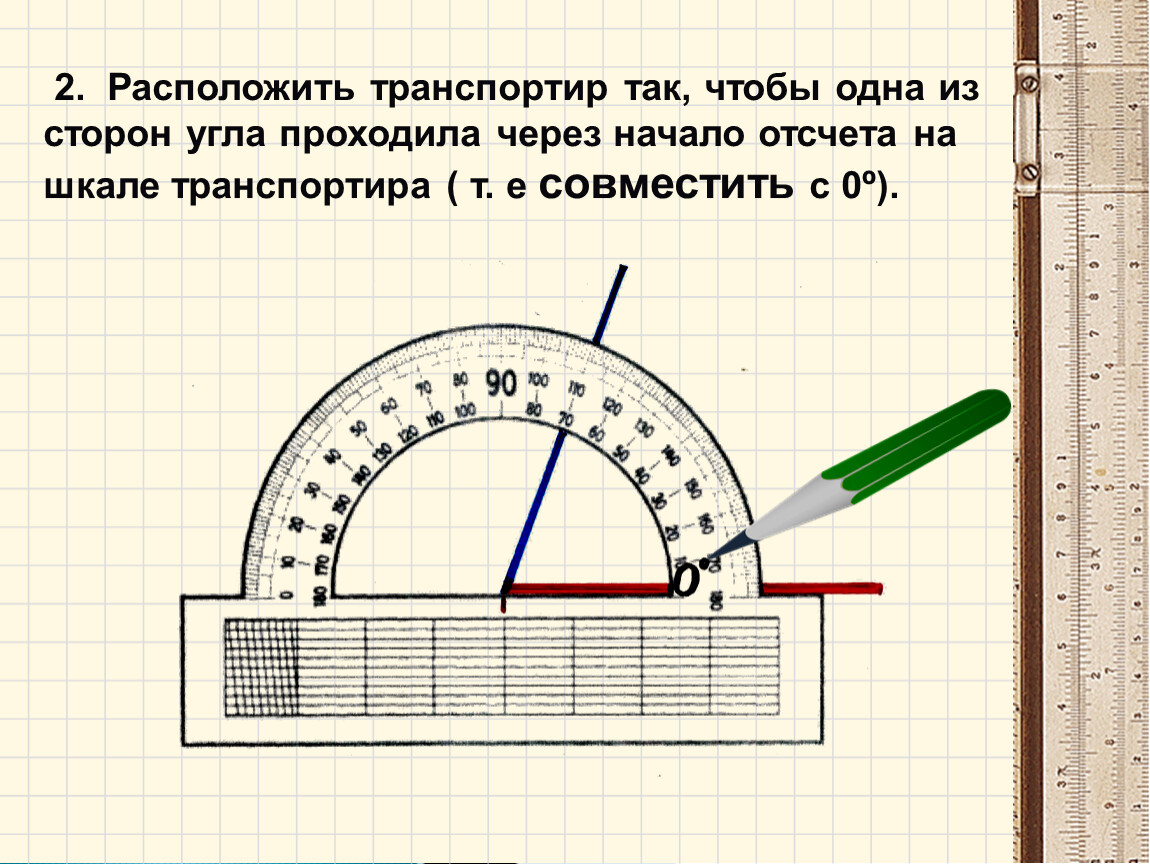 Значит, одна шеститысячная часть окружности – та мера, которой мы решили измерять углы, – будет равна примерно одной тысячной радиуса окружности… Поэтому-то артиллерийская мера углов и носит название «тысячной» (рис. 174). Этой мерой измерять углы очень удобно. Вы убедитесь в этом сами на следующих двух примерах.

Пример первый (рис. 175). Вы определяете угол, под которым видны с вашего наблюдательного пункта пулемет противника и отдельно стоящая сосна. Угол этот равен, оказывается, ста «тысячным». И пулемет, и сосна расположены на одинаковом от вас расстоянии-на расстоянии 2000 метров. Вас интересует, поразят ли осколки 152-миллиметровой гранаты людей у пулемета, если граната разорвется около сосны. Для этого, очевидно, надо прежде всего знать, как же велико расстояние от сосны до пулемета, если его измерять не в угловых, а в линейных величинах, то-есть в метрах.

Рис. 175. Как по углу определить расстояние от цели до ориентира

Задача эта решается очень просто. Надо только представить себе, что ваш наблюдательный пункт – это центр той окружности, которая описана радиусом, равным расстоянию от вас до пулемета (или до сосны). Радиус, таким образом, будет равен 2 000 метров. Углу в одну «тысячную» соответствует, как вы знаете, расстояние, равное одной тысячной радиуса, то-есть в данном случае 2 метрам. А так как угол между пулеметом и сосной равен не одной, а ста «тысячным», то, значит, расстояние между пулеметом и сосной равно не 2 метрам, а 200 метрам.

Мы знаем, что действительное поражение осколки 152-миллиметровой гранаты наносят на расстоянии до 35 метров от точки разрыва (рис. 73). Значит, в данном случае нельзя рассчитывать на поражение пулеметчиков осколками гранаты, рвущейся у сосны.

Еще один пример (рис. 176). В канаве около шоссе вы обнаружили группу стрелков, по которой и решили открыть огонь. Вам надо вычислить расстояние до стрелков или, что то же, до шоссе.

Для решения этой задачи воспользуйтесь телеграфными столбами на шоссе; высота их известна – она равна 6 метрам.

Измерьте теперь угол, которым покрывается высота телеграфного столба, и вы будете иметь все данные для решения этой задачи. Допустим, что угол этот оказался равным 3 «тысячным». Но если 6 метрам соответствует с этого расстояния угол в 3 «тысячных», то 1 «тысячной» будут соответствовать 2 метра. А всему радиусу, то-есть расстоянию от вас до шоссе, будет соответствовать величина, в 1 000 раз большая. Нетрудно сообразить, что расстояние от вас до шоссе будет равно 2 000 метров.

В действительности не все расстояния будут выражаться такими числами, как 2 000, 3 000 метров. Числа могут и не оканчиваться нулями. Но принятая в артиллерии мера для измерения углов позволяет, как в этом вы уже убедились, без всякого труда быстро находить одну «тысячную» от любого из таких чисел. Для этого надо только мысленно отделить в таком числе справа три знака, и вы получите значение одной «тысячной» этого числа. Все это проделывается очень быстро в уме.

Рис. 176. Как «тысячные» помогают определить дальность до цели

А вот что получилось бы, если бы вы за меру углов приняли не «тысячную», а обычную, применяемую в геометрии, меру углов: один градус или одну минуту. Угол в один градус был бы равен 1/60 радиуса, а угол в одну минуту 1/3600 радиуса, и, следовательно, при решении любой из приведенных задач вам приходилось бы делить числа, выражающие расстояние до целей, не на 1 000, а на 60 или на 3 600. Попробуйте проделать это деление с любым выбранным наугад числом, и вы сейчас же убедитесь, что без карандаша и бумаги вам здесь не обойтись.

Рис. 177. Сетка бинокля: маленькое деление равно пяти «тысячным», большое – десяти «тысячным»

Рис. 178. Такое приспособление имеется у стереотрубы: с его помощью измеряют углы с точностью до одной «тысячной»

Шкалы всех артиллерийских приборов приспособлены к измерению углов в «тысячных», или, иначе говоря, в делениях угломера.

Рис. 179. Ваши пальцы могут служить вам простейшим угломерным прибором

Рис. 180. «Цена» пальцев и кулака в «тысячных»

Рис. 181. «Цена» карандаша и спичечной коробки в «тысячных»

Вспомните, что в поле зрения бинокля вы всегда видели сетку с делениями (рис.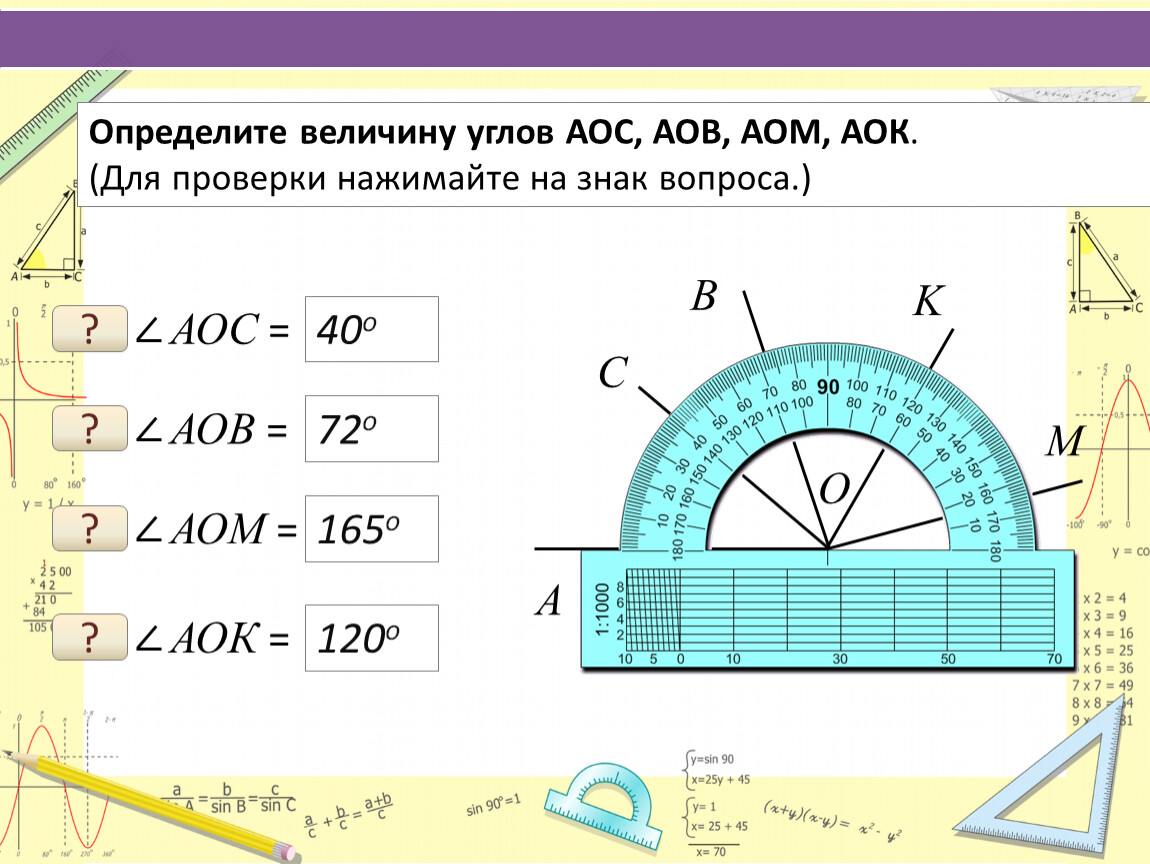 177). Эти деления и есть «тысячные». Самое маленькое деление сетки равно пяти, а большое – десяти «тысячным».

На рисунке 177 эти деления обозначены не просто числами «5» и «10», а с приставленными слева нолями – «0-05» и «0-10». Так пишут и произносят артиллеристы все величины в «тысячных», чтобы избежать ошибок в командах. Если нужно скомандовать, например, «правее 185 «тысячных», то произносят это число, как номер телефона: «один восемьдесят пять», а пишут 1-85.

Сетка с делениями, такая же, как в бинокле, имеется и в поле зрения стереотрубы. Но стереотруба имеет еще угломерную шкалу снаружи.

На рисунке 178 показаны те части стереотрубы (лимб и барабан лимба), с помощью которых можно производить более точно, чем по сетке, измерение горизонтальных углов.

Окружность лимба стереотрубы разделена на 60 частей, и поворот лимба на одно деление соответствует, таким образом, 100 «тысячным». Окружность же барабана лимба разделена на 100 частей, и полный оборот барабана заставляет передвинуться лимб трубы всего только на одно деление. Таким образом, деление барабана соответствует не 100 «тысячным», а всего одной «тысячной». Это позволяет уточнять показания лимба в сто раз и дает возможность стереотрубой измерять углы с точностью до одной «тысячной».

Но не только с помощью этих сложных приборов можно измерять углы. Ваша ладонь и ваши пальцы могут стать неплохим угломерным прибором, если только вы определите, сколько в них заключается «тысячных», какова «стоимость» их, или, как говорят артиллеристы, какова «цена» ладони и пальцев. Как это сделать, показано на рисунке 179.

Главное, о чем надо помнить при таком измерении, – это о вытягивании руки на полную ее длину.

Разные люди имеют разную длину руки и разную ширину пальцев. Поэтому каждый разведчик-наблюдатель должен заранее определить «цену» своей ладони, своих пальцев. «Цена» эта не будет сильно отличаться от указанной на рисунке 180.

Понятно, что таким простейшим «угломером» может явиться всякий предмет, «цену» которого в «тысячных» вы заблаговременно определили. На рисунке 181 показаны такие предметы и их «цена» в «тысячных».

Как найти величину угла?

Выберите область веб-сайта для поиска

MathAllУчебные пособияПомощь по домашним заданиямПланы уроков

Искать на этом сайте

Цитата страницы Начать эссе значок-вопрос Задайте вопрос Начать бесплатную пробную версию

Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой Делиться

Укажите эту страницу следующим образом:

«Как найти меру угла?» eNotes Editorial , 12 ноября 2021 г., https://www.enotes.com/homework-help/how-do-you-find-the-measure-of-an-angle-2935440. По состоянию на 17 июля 2023 г.

Ответы экспертов

Чтобы найти меру угла, вам нужно либо использовать инструмент, называемый транспортиром, либо вычислить угол на основе информации, которую вы знаете о форме, в которой он находится. -круговой инструмент с двумя рядами цифр по краю полукруга. Чтобы использовать транспортир, совместите нижнюю часть угла, который вы хотите измерить, с линией рядом с нижней частью транспортира. Затем посмотрите, где другая сторона угла совпадает с полукругом, и посмотрите на число, ближайшее к этой стороне. Это скажет вам измерение угла. Однако вы должны быть осторожны, чтобы выбрать правильное число, поскольку транспортиры предлагают две возможности. Если вы измеряете острый угол (тот, который меньше 90 градусов), затем выберите меньшее число. Если вы измеряете тупой угол (более 90 градусов), выберите большее число.

Вы можете найти меру угла, являющегося частью фигуры, используя свои знания о характеристиках этой фигуры и других углах. Например, если у вас есть квадрат или прямоугольник, вы знаете, что все его углы равны 90 градусов. Если у вас есть треугольник, вы знаете, что сумма его трех углов должна составлять 180 градусов. Если вы знаете, что один угол равен 30 градусов, а другой угол равен 90 градусов, то можно вычислить, что недостающий угол равен 60 градусам.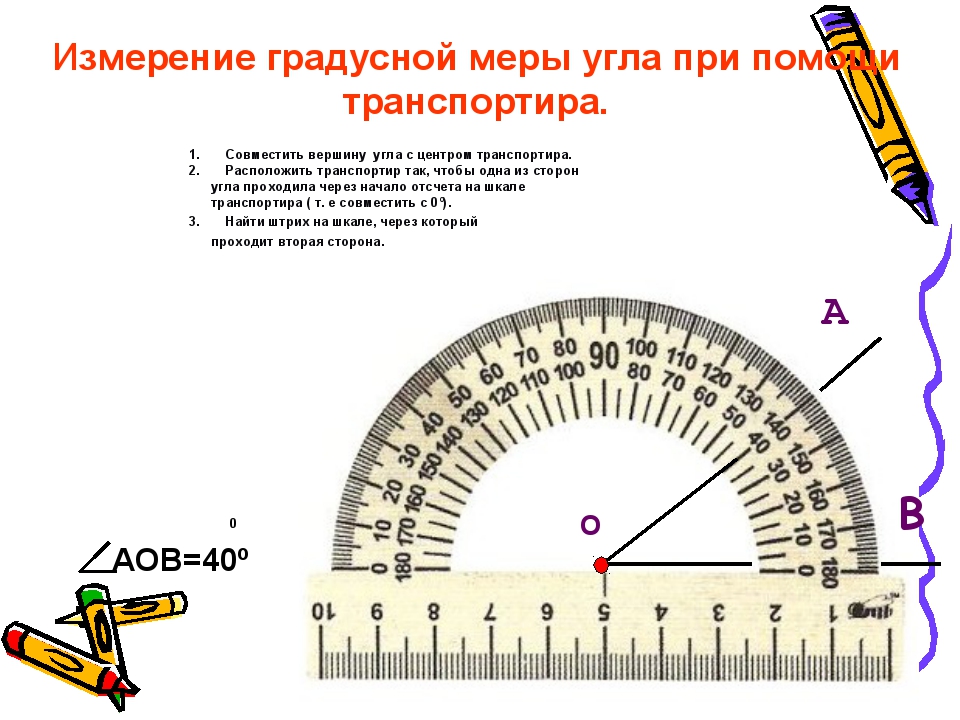

Если у вас есть параллелограмм, у которого нет углов по 90 градусов, вы знаете, что сумма всех четырех его углов должна составлять 360 градусов. Зная один угол, можно найти и другие. Если вы знаете, например, что один угол равен 45 градусам, вы сразу же знаете, что угол, противоположный этому углу, также равен 45 градусам. Чтобы найти два других, сложите 45 и 45, чтобы получить 90. Затем вычтите 90 из 360, чтобы получить 270. Разделите 270 пополам, чтобы получить измерения двух других углов, 135 градусов и 135 градусов.

См. eNotes без рекламы

Начните с 48-часовой бесплатной пробной версией , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые наши эксперты ответили.

Получите 48 часов бесплатного доступа

Уже зарегистрированы? Войдите здесь.

Утверждено редакцией eNotes

Задайте вопрос

Похожие вопросы

Просмотреть все

Математика

Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.

Что означают буквы R, Q, N и Z в математике?

14 Ответы воспитателя

Математика

Последний ответ опубликован 07 октября 2013 г. в 20:13:27.

Как определить, является ли это уравнение линейной или нелинейной функцией?

84 Ответы воспитателя

Математика

Последний ответ опубликован 28 октября 2013 г. в 2:15:05.

как найти горизонтальную асимптоту функции?

2 Ответа воспитателя

Математика

Последний ответ опубликован 09 октября 2017 г. в 00:54:39

Добавьте 1 плюс 2 плюс 3 плюс 4. . . вплоть до 100.

3 Ответа воспитателя

Математика

Последний ответ опубликован 10 мая 2010 г. в 23:45:03.

Сколько будет 11 3/4 разделить на два

3 Ответа воспитателя

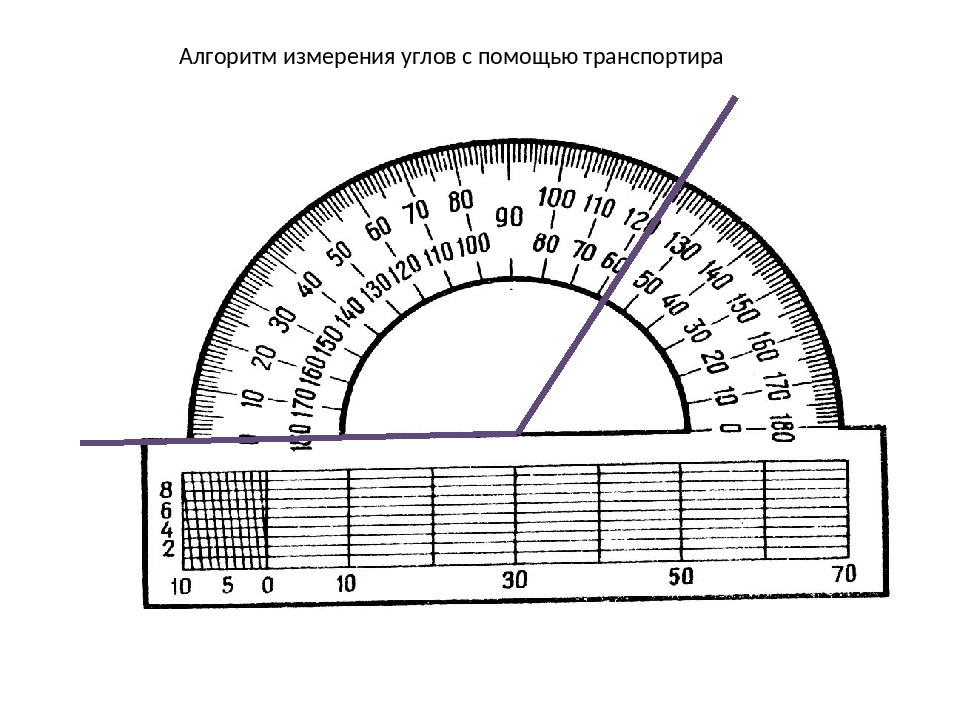
Геодезический курс: Измерение углов и направлений

Мы можем провести измерение только на основе расстояний (с помощью рулетки или EDM ) для получения карту обследуемой местности или установить БП. Такой метод называется трилатерация .

С таким оборудованием, как теодолит, мы обычно можем получить гораздо более точное описание обследуемой площади. Теодолит — это прибор для измерения горизонтали и/или вертикальные углы.

Меридиан, изображенный на горизонтальном измерении

Угол α измеряется от эталона строка , который считается равным 0 °. Такая линия называется меридиан .

Во время разговора около горизонтальных измерений только, окончательный результатом обычно будет сеть прямоугольных (декартовых) координаты.

Вертикальные углы обычно необходимы для преодоления вертикального препятствия и для тригонометрическое нивелирование (объяснено в другой главе).

Вертикальные углы

Горизонт параллелен земной поверхности, а зенит перпендикулярно горизонту. Вертикальные углы при съемке с зенита или горизонта обычно поддерживаются оба метода современными инструментами.

Зенит и горизонт

Горизонтальные углы

Измеряемый угол

• по часовой стрелке (угол вправо) или
• против часовой стрелки (угол влево).

Далее

• Внутренний угол измеряется внутри замкнутого многоугольника,
Внешний угол
• измеряется вне замкнутого многоугольника.

Сумма внутреннего и внешнего углов составляет 360°

Горизонтальные углы

Сторона измеренного угла должна быть четко отмечена в полевом журнале. Также рекомендуется

• использовать только один способ измерения, т.е. всегда берите внутренние углы;
• для проверки внутренних и внешних углов (во избежание грубых ошибок),

Азимут

Углы, полученные в поле, имеют контекст в сети точек, измерено.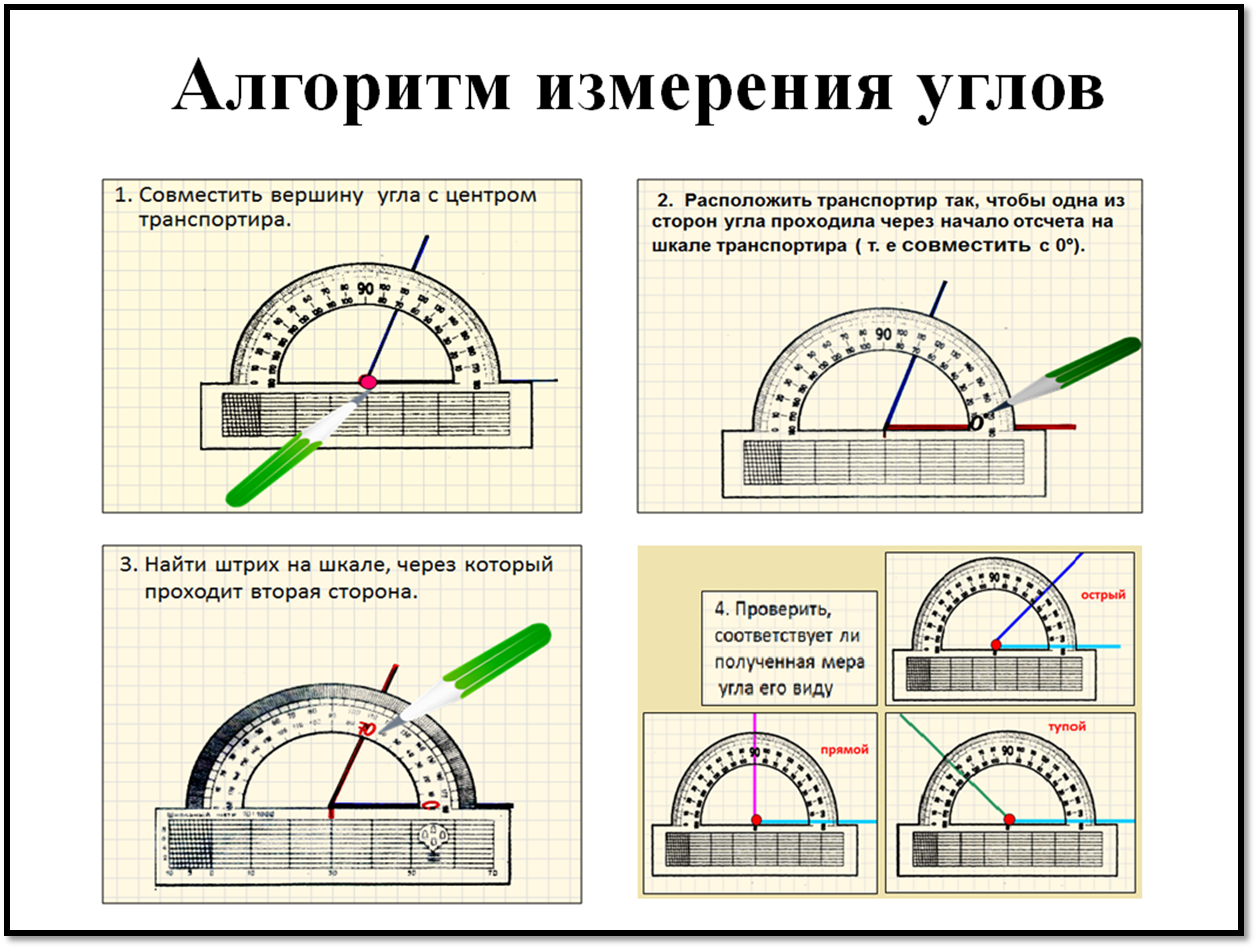 Они не имеют никакого отношения к земным координатам. Азимуты вычисляются по часовой стрелке от географического севера.

При проведении измерений аналогично выравниванию, мы движемся вперед к следующим точкам во время измерения процедура.

В контексте задней точки обратный азимут строка AB иногда упоминается.

Назад азимут берется в обратном направлении и является азимутом ВА .

1 — Азимут АВ
2 — Обратный азимут АВ

Теодолит

Теодолит — телескоп, установленный на горизонтальной и вертикальной транспортиры. Его целью является измерение вертикальных и/или горизонтальных углов.

Точность зависит от типа, а обычно составляет от

• ±0,1 секунды (теодолит хорошего качества, используемый для геодезической съемки) до
• ±0,1 минуты (т. е. 6 секунд — типичный теодолит).

Теодолит можно использовать для оценивать горизонтальные показания для нивелирования, но обычно с меньшей точностью, чем прибор уровня подойдет.

Взгляд в историю

Великий теодолит

Великий 3-х футовый теодолит 1785 года работы Рамсдена

В 1782 Джесси Рамсден начал трехлетний проект теодолита выше), позже известный как Великий теодолит . Первый Великий Теодолит был около 1 м в диаметре и весом 90 кг.

Может считывать горизонтальные углы с точностью до 1 секунды и вертикальные углов с точностью до 5 секунд с помощью приставных микроскопов. Он служил по крайней мере, несколько лет, пока легкий, Второй Великий Теодолит, не был изобретен Рамсден.

Классический механический теодолит

Классический механический теодолит от 1910 by Ertel

На изображении выше механический теодолит двойного круга 1910 года.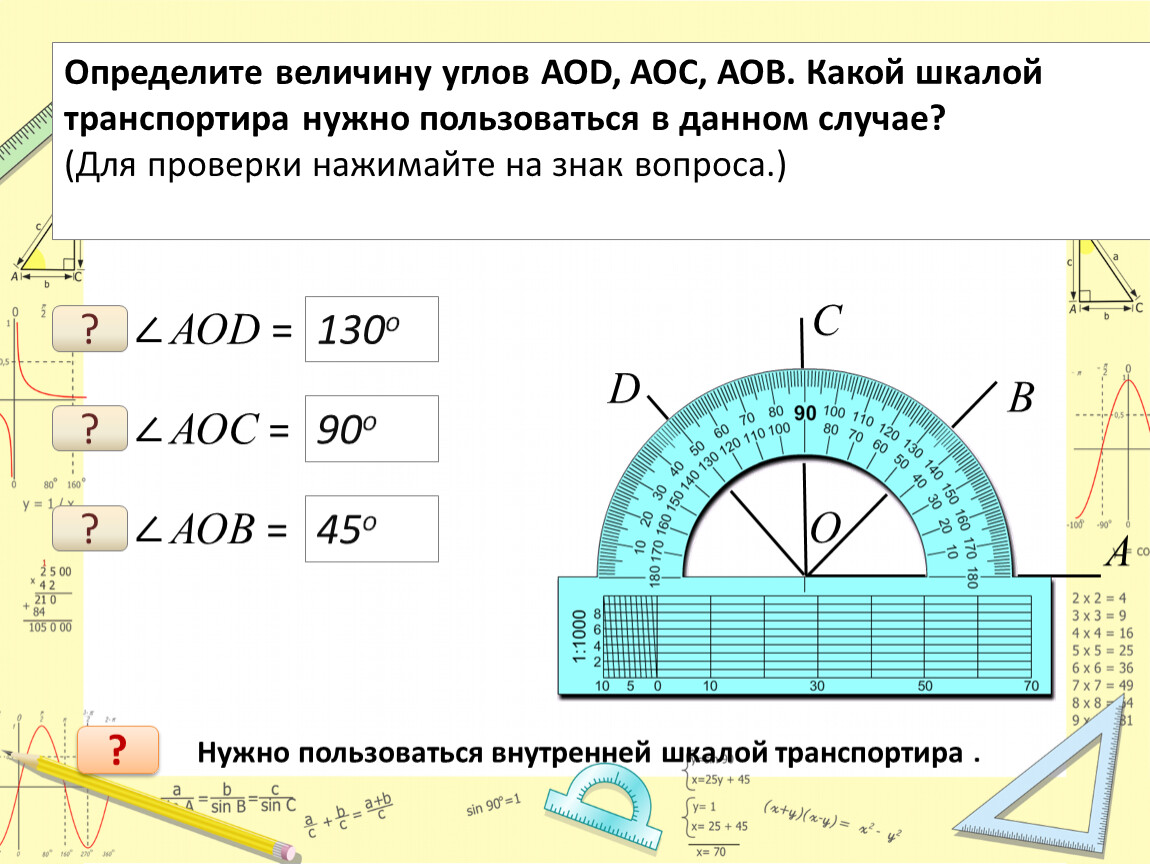 длина телескопа 29 см. В механических теодолитах используется больше кругов (нониус). для повышения точности чтения:

Нониус: шкала, используемая для повышения точности показаний. Используйте ручной уровень, установите штатив над позиционная отметка на удобная высота .

Подвесьте отвес или отпустите лазер маркировка (зависит от модели).

Повторно отрегулируйте штатив по установочной метке , переместите все три ножки штатива на одинаковую величину в одном и том же направлении.

Надежно зафиксируйте штатив . Прижмите ноги к земле.

Установка штатива (из руководства пользователя Leica T105/T110

Установка теодолита

Все части оборудования изготовлены точного качества и должны всегда принимать с повышенной осторожностью. Это особенно относится к теодолиту (но относится геодезическое оборудование в целом).

Установка штатива (из руководства пользователя Leica T105/T110

• Поместите теодолит на головку штатива , закрутите центрирующий винт, пока удерживающий инструмент. Оставьте положение свободным, чтобы теодолит все еще мог скользить вокруг головки штатива.
• Глядя через оптический отвес, сфокусируйте центрирующую метку. Сдвиньте теодолит на головку штатива до тех пор, пока контрольная метка не окажется в центре в оптический отвес.
• Полностью затяните центрирующий винт .

  Посмотрите через оптический отвес снова и отрегулируйте винты основания теодолита для совмещения с эталоном. отметка.

Выравнивание теодолита

После того, как теодолит выровнен, дважды проверьте оптический отвес, чтобы убедиться, что он по-прежнему находится в центре. Если нет, повторите шаги выше.

Измерение горизонтального угла

• Когда теодолит установлен, наведите его на заднюю точку (BS).
• Обнуление прибора. Запишите фактический ноль в полевой журнал (может быть, не точный ноль).
• Остановите движение и наведите на передний план (FS).
• Затяните движение и используйте винт для точной регулировки.
• Прочитайте угол, запишите в полевой журнал.

Целевая (измеренная) точка должна быть четко обозначена для наблюдая.

Мишень можно сделать видимой с помощью шнура (веревка) с отвесом.

Пример (точность): предположим точность теодолит 5 дюймов и цель находится на расстоянии 100 м. Тогда 5 дюймов на 100 м эквивалентно 2,5 мм (то есть 1:40 000).

Пример показывает, что теодолит является высокоточным прибором. Для измерения углах мы не можем ожидать, что удержание удилища на целевой точке (как в случае нивелирования) будет достаточным. Мы должны использовать отвес с видимой линией, чтобы обеспечить четкое чтение. мы должны заплатить внимание на точную настройку прибора над станцией.

Измеряемая цель должна быть четко отмечена отвесом и линией. В случае использования рейки для устранения ошибок наведите телескоп и сделайте отсчет близко к земле.

Измерение горизонтальных углов методом повторения (механический теодолит)

Более надежное считывание значения угла достигается путем повторения измерения. Берется первый ракурс и записывается в полевой журнал. Затем зрительная труба направлена ​​назад к БС (с заблокированным движением значения). Измерение до полной шкалы выполняется снова, затем угол накапливается. Обычно после завершения 6 циклов угол снова записано в полевой журнал. Накопленный размер угла делится на 6 до выяснить значение угла.

Телескоп направлен назад на БС (с заблокированным движением значения). Измерение до FS производится снова, затем накапливается угол .

Измерение горизонтальных углов методом повторения (цифровой теодолит)

Более надежное считывание значения угла достигается путем повторения измерение. Первый угол берется от BS до FS и записывается в полевой журнал. Затем телескоп повернут относительно оси цапфы и направлен на ПШ. Измерение обратно в BS затем выполняется снова, и результат берется как среднее обоих взятых углов..

Берется первый ракурс от БС до ПШ и записывается в полевой журнал. Затем Телескоп повернут относительно оси цапфы и направлен на ПШ. Измерение обратно в BS затем выполняется снова, и результат принято в среднем.

Станция B	BS до A	FS до C	Угол ABC
Чтение слева	0° 00′ 00″	33° 27′ 15″	33° 27′ 15″
Читать справа	180° 00′ 15″	213° 27′ 20″	33° 27′ 05″
Среднее			33 ° 27 ’10 «

Закрытие Horizon

Обычно больше уголков взяты из одной установки.