измерение углов по топографической карте
6. Измерение углов по топографической
карте
Для ориентирования линий нужно знать их расположение относительно сторон горизонта, а именно относительно меридиана. В топографии различают истинный (географический) и магнитный меридианы. Направление последнего определяется северным концом магнитной стрелки приборов (например, компаса). Угол, отсчитываемый по часовой стрелке от северного конца меридиана до направления на предмет, называют азимутом. Под направлением понимают линию на карте или на местности, имеющую начальный и конечный пункты.
Различают истинный и магнитный азимуты одного и того же направления. Эти азимуты связаны углом, называемым магнитным склонением (δ).
На
карте угол направления легче всего
измерить относительно вертикальной
линии прямоугольной (километровой)
сетки, такой угол называется дирекционным
углом α.
Угол между линией истинного
меридиана и вертикальной линией сетки
называется углом сближения меридианов
γ. Положение γ и δ относительно истинного
меридиана показано на схеме, помещенной
на поле под южной стороной рамки
топографической карты.
Рис. 1. Различные варианты расположения углов направления CD.
Задание 1. Измерить транспортиром дирекционный угол направления АВ, указанного на карте, выданной преподавателем. Результаты измерений занести в рабочую таблицу.
Направление | Дирекционный угол α | Истинный азимут Аист | Магнитный азимут | ||
измеренный | вычисленный | ||||
АВ | |||||
ВА | |||||
Методические
указания.
Рис. 2. Схема измерения транспортиром углов направления АВ по топографической карте.
Измерить транспортиром дирекционный угол направления ВА.
Измерить транспортиром истинный азимут направления АВ.
Вычислить истинный азимут АВ по формуле Аист = α + (±γ).
- Сравнить
истинный азимут Аист,
измеренный по карте и вычисленный по
формуле.
Вычислить магнитный азимут Амаг по формуле Амаг = Аист — (±δ).
Задание 2.
По известным значениям истинного азимута Аист, магнитного склонения δ и сближения меридианов γ составить схему взаимного расположения углов направления. По данным табл. 1 вычислить магнитный азимут и дирекционный угол заданного направления.
Методические
указания.
Составление схемы следует начать с
нанесения на свободном поле карты
вертикальной линии длиной 2,5 см,
обозначающей положение истинного
меридиана (на верхнем конце этой линии
поставить звездочку (рис. 1). Учитывая
знаки γ и δ и принимая во внимание закон
о взаимосвязи истинного меридиана с
линией сетки и магнитным меридианом,
расположить все линии схемы. Линия
магнитного меридиана и линия сетки
будут лежать к западу от линии истинного
меридиана, если γ и δ отрицательные, и
наоборот, восточнее истинного меридиана,
если γ и δ положительные.
Рисунок должен быть схематичным: действительные значения углов γ и δ очень малы, поэтому их величину на схеме увеличивают, считая главным сохранение ориентации линий относительно истинного меридиана и друг друга. Пользуясь схемой, можно быстро вычислить величину дирекционного угла и магнитного азимута направления, зная истинный азимут этого направления.
Вычислить истинный и магнитный азимуты можно также по формулам, учитывая знак «+» или «-» γ и δ.
Таблица 1
Задание 3. Измерить истинные азимуты Аист направлений маршрута, намеченного по топографической карте и состоящего из 5 точек. Направлением считать прямую линию между точками поворота. Результаты измерений углов всех ходовых линий занести в рабочую таблицу и вычислить по формулам угол α и азимут Амаг (см. рис. 1).
К
таблице приложить схему маршрута, на
которой в масштабе отметить выбранные
точки, и отрезки между ними, сохранив
углы поворота.
Номер линии | Истинный азимут Аист | Дирекционный угол а | Магнитный азимут Амаг | Длина по маршруту, км | Наличие видимости |
1-2 2-3 3-4 4-5 |
Методические
указания.
Точка маршрута выбирается от конкретного
объекта в указанном населенном пункте
(например, пересечение проездов,
выдающееся здание, ориентир, четко
выделяющийся среди кварталов населенного
пункта). От выбранной точки намечается
траектория маршрута и 5 точек явных
поворотов. Маршрут должен состоять из
отдельных участков (1-2, 2-3 и т. д) и
заканчиваться конкретной точкой в
населенном пункте в конце маршрута.
Маршрут прокладывают по автодорогам,
грунтовым дорогам и просекам в лесу.
Для определения истинных азимутов каждой ходовой линии маршрута нужно провести прямые линии между точками поворота. Транспортир должен располагаться вдоль по меридиану, а его центр – на пересечении линии меридиана с измеряемым направлением. Измеренный угол может иметь значение 0-360°. Для того чтобы вычислить дирекционный угол и магнитный азимут, нужно воспользоваться схемой углов направления, расположенной на полях карты.
как обозначить и измерить углы, правила
Определение
Геометрия — это раздел математики, который занимается изучением форм и их измерений.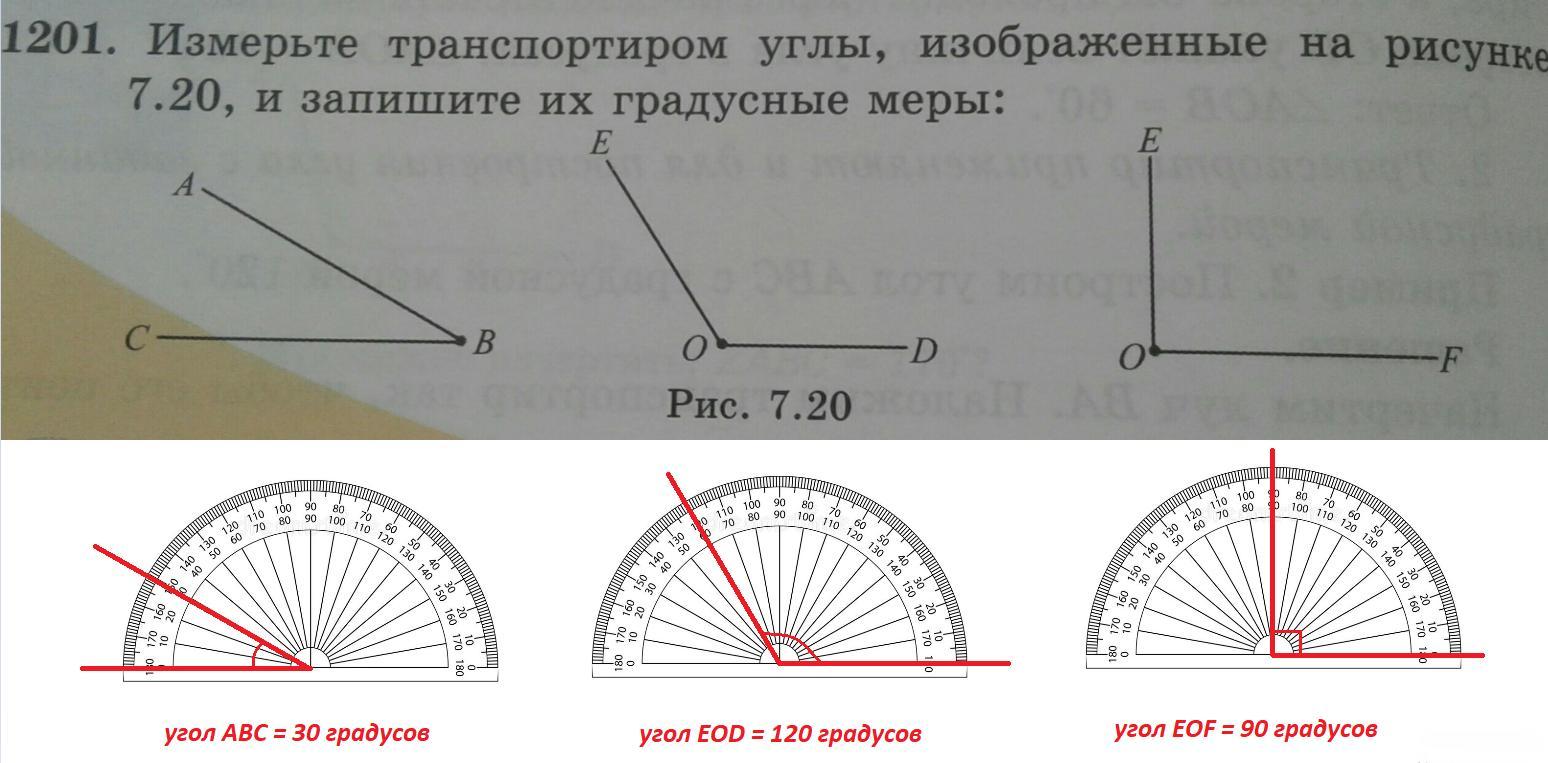
Он также фокусируется на относительной конфигурации форм и их пространственных свойствах.
Все геометрические фигуры состоят из точек, линий, лучей и плоской поверхности. Когда две линии или лучи сходятся в одной точке, измерение между двумя линиями называется углом. В этой статье мы собираемся обсудить, что такое угол, каковы различные типы углов и их значение с примерами.
Определение угла в математике
Определение
Что такое угол? Угол это — геометрическая фигура, образованная двумя лучами или линиями, имеющими общую конечную точку (вершину). Два луча называются сторонами угла, а точка, в которой пересекаются лучи, называется вершиной.
Угол, лежащий в плоскости, не обязательно должен лежать в евклидовом пространстве. В случае, если углы образованы пересечением двух плоскостей в евклидовом или другом пространстве, такие углы считаются двугранными.
Стороны угла – лучи, которые образуют угол (А, В).
Вершина угла – точка, из которой выходят лучи (О).
Угол делит плоскость на две части. Если угол не развернутый, то одна часть плоскости называется областью внутреннего угла, а другая часть называется областью внешнего угла. Ниже приведена картинка, поясняющая, какие части являются внешними, а какие внутренними.
Если углы измеряются по линии, мы можем найти два разных типа углов, например, положительный угол и отрицательный угол.
- Положительный угол: если угол идет против часовой стрелки, то он называется положительным углом.
- Отрицательный угол: если угол направлен по часовой стрелке, то он называется отрицательным углом.
Интересно
Слово «угол» произошло от латинского слова Angulus, означающего «небольшой изгиб».
Понятие угла впервые использовал Евдем, который определил угол как отклонение от прямой линии.
Как обозначить углы?
Фигура угол отмечается символом «∠». Есть два разных способа обозначения углов:
- Способ 1:
Как правило, угол обозначается строчными буквами, такими как «а», «х» и т.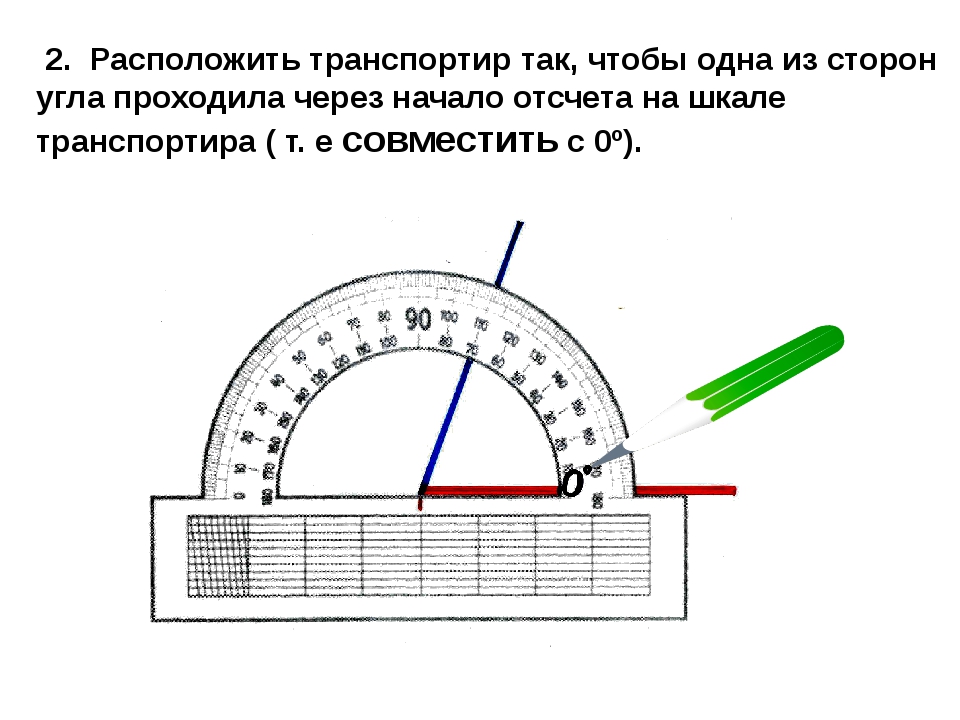 д., или греческими буквами альфа (α), бета (β), тэта (θ) и т. д. - Способ 2:
Используя три буквы на фигурах. Средняя буква должна быть вершиной (фактический угол).
Например, ABC — треугольник. Чтобы представить угол A равным 60 градусам, мы можем определить его как ∠BAC = 60 °.
д., или греческими буквами альфа (α), бета (β), тэта (θ) и т. д.Типы углов
Существует шесть типов углов. Каждый тип угла имеет уникальную идентификацию на основе измерения угла.
Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.
- Острый угол – это угол, градусная мера которого больше 0° и меньше 90°.
- Прямой угол — когда измерение угла равно 90 градусов, он известен как прямой угол.
Прямой угол можно легко наблюдать, так как он образует форму буквы L. - Тупой угол — когда измерение угла меньше 180 градусов, но больше 90 градусов,
это тупой угол. - Развернутый угол — угол, образованный прямой линией, называется прямым углом. Это
половина полного оборота круга. Размер прямого угла равен 180°. - Выпуклый угол – это угол, величина которого больше 180°, но меньше 360°.
- Полный угол — когда измерение угла равно 360 градусам, это полный угол.
ЭтоРяд углов образуется при пересечении секущей двух или более прямых. Конкретные названия даны паре углов, что зависит от расположения угла по отношению к прямым. Линии могут быть как параллельными, так и непараллельными.
Углы образованные при пересечении двух прямых
При пересечении двух прямых образуются два вида углов:
- смежные;
- вертикальные.
Смежные углы
Определение
Два угла называются смежными, если они имеют общую вершину и одну общую сторону, а две другие стороны расположены на одной прямой и образуют развернутый угол. Смежные углы между собой дополняемые, так как являются продолжением один другого.
Свойства смежных углов
- Сумма смежных углов равна 180°
- Если оба смежных угла равны между собой, то они являются прямыми. {\circ}\]
Разница между смежными и вертикальными угламиСмежные углы Вертикальные углы Два угла с общей стороной и вершиной называются смежными. Когда две прямые пересекаются друг с другом, то пары противоположных углов, образованных при вершине, называются вертикальными углами. Имеют общую сторону и общую вершину. Имеют общую вершину, но не имеют общую сторону Смежные углы не всегда равны по величине Вертикально противоположные углы равны по величине Сравнение углов
Для сравнения углов можно использовать простейший метод — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны данных углов совпадают, то углы равны. В противном случае угол, который находится внутри другого, будет меньше. Вот два наглядных примера с равными и неравными углами:
\[\angle A_{1} O_{1} B_{1}\] и \[\angle A_{2} O_{2} B_{2}\] полностью совмещаются при наложении следовательно: \[\angle A_{1} O_{1} B_{1}=\angle A_{2} O_{2} B_{2}\]
\[\angle A_{1} O_{1} B_{1}\] и \[ \angle A_{2} O_{2} B_{2}\] не совмещаются при наложении: \[\angle A_{1} O_{1} B_{1} \neq \angle A_{2} O_{2} B_{2}\]
Причем: \[\angle A_{1} O_{1} B_{1}<\angle A_{2} O_{2} B_{2}\]
При этом развернутые углы всегда являются равными.
Совмещение углов \[\angle A B C\] и \[\angle M N K\] происходит следующим образом:
- Вершину B одного угла совмещаем с вершиной N другого угла.
- Сторону BA одного угла накладываем на сторону NM другого угла так, чтобы стороны BC и NK располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠ABC = ∠MNK.
Если нет, то один угол — меньше другого: ∠ABC<∠MNK.
Некоторые важные теоремы, основанные на прямых и углах:
- Если две параллельные прямые пересечены секущей, то смежные внутренние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то противоположные внешние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то соответствующие углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то внутренние углы по одну сторону от этой секущей смежные.
- Вертикальные углы равны, когда прямая пересекает прямые. Линии могут быть как параллельными, так и непараллельными.
Измерение углов
Существует несколько единиц измерения углов. Рассмотрим наиболее часто используемые единицы измерения:
Градусная мера
Полный оборот, т. е. когда начальная и конечная стороны находятся в одном и том же положении после вращения по часовой стрелке или против часовой стрелки, делится на 360 единиц, называемых градусами. Итак, если поворот от начальной стороны к конечной стороне составляет \[\left(\frac{1}{360}\right)\] оборота, то говорят, что угол имеет меру в один градус. Обозначается как 1°.
Мы измеряем время в часах, минутах и секундах, где 1 час = 60 минут, а 1 минута = 60 секунд. Точно так же при измерении углов
- 1 градус = 60 минут, обозначаемый как 1° = 60′.
- 1 минута = 60 секунд, обозначаемая как 1 ′ = 60 ″.
Радианная мера
Радианная мера немного сложнее, чем градусная. Представьте круг с радиусом 1 единица.
Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит:Вот еще несколько примеров углов: -1 радиан, радиан, \[1 \frac{1}{2}\] радиан, \[-1 \frac{1}{2}\] радиан.
Длина окружности = \[2 \pi r \ldots\] где r — радиус окружности. Следовательно, для круга с радиусом 1 единица длины окружности равна \[2 \pi\]. Следовательно, один полный оборот начальной стороны образует в центре угол \[2 \pi\] радиан. Обобщая это, имеем:
В окружности радиуса r дуга длины r образует угол в 1 радиан в центре. Следовательно, в окружности радиуса r дуга длины l будет опираться на угол = \[\frac{l}{r}\] радиан. Обобщая это, мы имеем в окружности радиуса r, если дуга длины l образует угол θ радиан в центре, то:
\[\theta=\frac{l}{r}\]
\[l=r \theta\]
Связь между степенью и радианными мерами
По определениям степени и радиана мы знаем, что угол, образуемый окружностью в центре, равен:
- 360° – по градусной мере
- \[2 \pi\] радиан — в радианах
Следовательно, \[2 \pi\] радиан = 360° ⇒ \[\pi\] радиан = 180°.
{\prime}=\frac{\pi}{180} \times \frac{121}{3}=\frac{121 \pi}{540}\] радиан.Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Как измерить угол
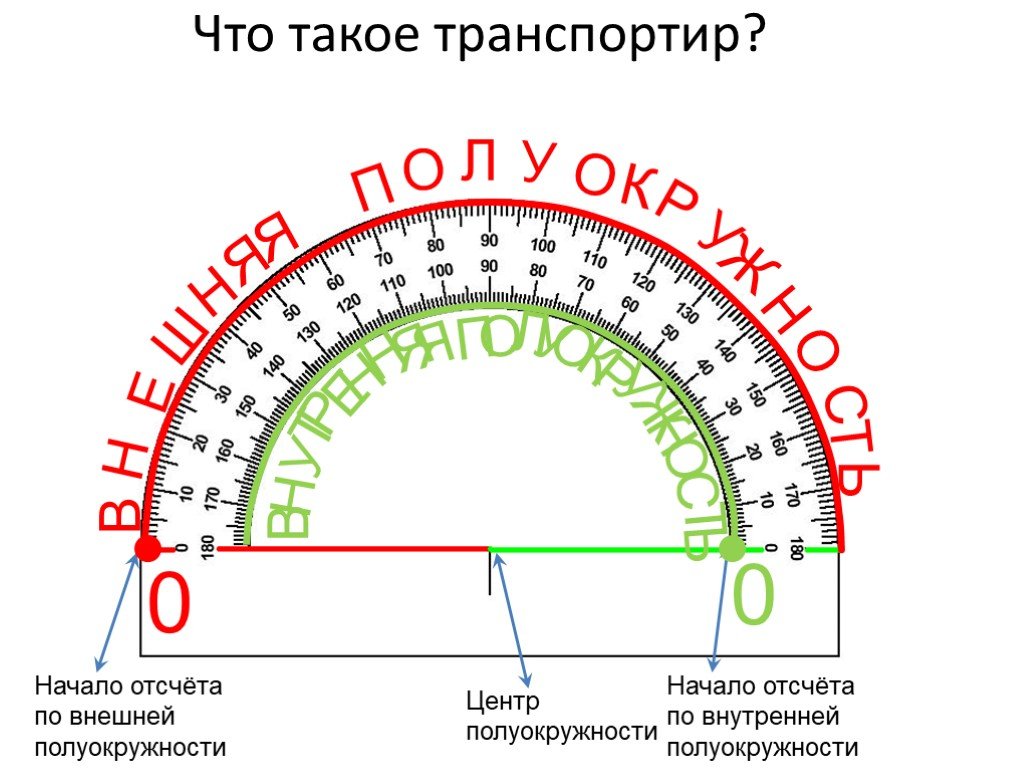
Для измерения углов используется транспортир:
ТранспортирПопробуем измерить угол \[\angle A O B\]
Шаги для измерения угла \[\angle \mathrm{AOB}\].
Шаг 1: совместите транспортир с лучом OB, как показано ниже. Начните чтение с отметки 0 ° в правом нижнем углу транспортира.
Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на «нижней дуге» транспортира. Таким образом, ∠ AOB = 37°
Далее попробуем измерить этот ∠AOC:
Шаг 1: Измерьте угол от отметки 0° в левом нижнем углу.
Шаг 2: Число на «верхней дуге» транспортира, совпадающее с OA, является мерой ∠ AOC.
Таким образом, ∠ AOC = 143°Как построить углы
Используем транспортир для построения углов. Нарисуем угол 50°.
Шаг 1: сначала нарисуйте луч OB и совместите транспортир с OB, как показано.
Шаг 2: поместите точку над отметкой на транспортире, которая соответствует 50°.
Шаг 3: Уберите транспортир и нарисуйте луч, начинающийся в точке О и проходящий через эту точку. Таким образом, ∠AOB – искомый угол, т.е. ∠AOB = 50°.
Примечание. Если луч идет в другом направлении, мы измеряем угол от отметки 0° в левом нижнем углу.
На изображении ниже показано, как нарисовать угол 50°, когда луч указывает в другом направлении.
Обозначение углов на чертеже
Для комфортного отображения дуг, углов применяют чертежи. Не всегда возможно грамотно изобразить и обозначить тот или другой угол, дугу или наименование. Равные углы имеют определение в виде идентичного числа дуг, а неравноценные в виде различного.
На чертеже запечатлено корректное обозначение острых, равных и неравных углов.
Если нужно обозначить более трех углов, то применяются специальные обозначения дуг, например, зубчатые или волнистые, но в принципе это не имеет особого значения.
Обозначение углов должно быть простым, чтобы не препятствовать иным значениям. При решении задачи рекомендовано обозначать только нужные для решения углы, чтобы не перегружать весь чертеж. Это не помешает решению задачи, а также придаст эстетичный облик чертежу.
Расчет угловых размеров. Используя транспортир, измерьте углы в целых числах градусов и начертите углы заданной величины в целых числах градусов. Докажите, что мера угла является аддитивной.
Экспорт РаспечататьСвязанные точки доступа
Альтернативная версия этого теста для учащихся с серьезными когнитивными нарушениями.
MA.
4.GR.1.AP.2: Используя инструмент с прямым углом, определите углы как острые, прямые или тупые и постройте острые, прямые или тупые углы.Связанные ресурсы
Проверенные ресурсы, которые преподаватели могут использовать для обучения концепциям и навыкам в этом эталонном тесте.
Формирующие оценки MFAS
Определение меры угла:Учащихся просят проанализировать два угла и объяснить, как определяются их величины.
Рисование и измерение углов:Учащимся предлагается нарисовать и измерить острые и тупые углы, вершины которых находятся в центре окружности.
Разбрызгиватель для газонов:Учащихся просят определить угол, исходя из количества поворотов на один градус.
Измерение углов транспортиром:Ученикам предлагается использовать транспортир для определения величины четырех углов.
Этот угол:Учащимся даются два угла с одинаковой величиной угла, но со сторонами разной длины, и их просят объяснить, какая составляющая угла определяет его величину.
Город Хэппивилль:Учеников просят нарисовать заданные углы внутри круга в контексте реальной задачи.
Использование транспортира для рисования углов:Учащиеся используют транспортир для рисования углов заданной величины.
Какова мера угла?:Учащихся просят определить меру неизвестного угла, которая является одной из составляющих большего известного угла, если известны другие составляющие.
Оригинальные учебники для учащихся по математике — классы K-5
Добавление ракурсов: Чудесные окна:Разложите и составьте различные ракурсы, изучая часы и окна в этом интерактивном руководстве.
Примечание: это руководство выходит за рамки пояснений и предназначено для улучшения навыков решения задач учащимися.
Рывок или удар: открытие углов:Узнайте, что такое угол, помогая запрограммировать робота через полосу препятствий в этом интерактивном учебном пособии.
Карта ROC: Угол измерения:Из этого интерактивного руководства вы узнаете, как измерять углы с помощью транспортира, чтобы помочь роботу преодолеть полосу препятствий.
Ресурсы для учащихся
Проверенные ресурсы, которые учащиеся могут использовать для изучения концепций и навыков в этом тесте.
Оригинальные учебные пособия для студентов
Добавление ракурсов: чудесные окна:Разложите и составьте различные ракурсы, изучая часы и окна в этом интерактивном руководстве.
Примечание: это руководство выходит за рамки пояснений и предназначено для улучшения навыков решения задач учащимися.
Тип: Оригинальное учебное пособие для учащихся
Карта ROC: Измерение углов:В этом интерактивном учебном пособии вы узнаете, как измерять углы с помощью транспортира, чтобы помочь роботу преодолеть полосу препятствий.
Тип: оригинальное учебное пособие для учащихся
Рывок или рывок: открытие углов:Узнайте, что такое угол, помогая запрограммировать робота через полосу препятствий в этом интерактивном учебном пособии.
Тип: оригинальное учебное пособие для учащихся
Руководство
Нахождение части разложенного угла:В этом обучающем видеоролике Академии Хана представлена стратегия нахождения меры одного из двух смежных углов, когда известна сумма обоих углов и мера одного из них.
Тип: Учебное пособие
Ресурсы для родителей
Проверенные ресурсы, которые воспитатели могут использовать, чтобы помочь учащимся освоить концепции и навыки в этом эталонном тесте.
Изображение/фотография
Клипарт: Геометрические фигуры:В этом уроке вы найдете картинки и различные иллюстрации многоугольников, кругов, эллипсов, звездчатых многоугольников и вписанных фигур.
Тип: изображение/фотография
Руководство по обучению углов с помощью транспортира в математике для учащихся 5 класса
Примечание редактора:
Это обновленная версия сообщения в блоге, опубликованного 16 мая 2017 г.
Ваши ученики 5-го класса борются со своими транспортирами на уроках углов? Вот удобное руководство, которое поможет им уверенно измерять углы.
Транспортиры могут выглядеть как безобидные полукруги с некоторыми числами, отмеченными снаружи. Но они сложнее, чем кажутся, и вашим учащимся может быть трудно с ними справиться.
Если вы занимаетесь угловыми уроками по математике — нет проблем! Учебник 5B, глава 9 или ищите общие советы по преподаванию углов в 5-м классе, а затем продолжайте читать.
Почему учащимся сложно измерять углы с помощью транспортира?
Мои учащиеся 5-го класса начали главу об углах, хорошо зная названия и характеристики углов. Это сослужило им хорошую службу для Урок 1: Знание типов углов .
Но мой класс наткнулся на Урок 2: Измерение углов , который был посвящен измерению углов внутри многоугольника. Темп второго урока был быстрым, и было ясно, что не все учащиеся добились «ожидаемого прогресса».
Копнув глубже, я увидел, что практические навыки, необходимые для использования транспортира для измерения углов, вызывают недоумение в моем классе. Дети, казалось, изо всех сил пытались понять разницу между «внутренней» и «внешней» шкалой транспортира, а также запутанным рефлексом и тупыми углами.
Я понял, что для решения этой проблемы мне придется разбить этапы измерения углов и замедлить процесс для учащихся, которые борются с этим аспектом темы.
Как измерять углы: пошаговое руководство
На следующем уроке я записал шаги измерения углов на доске:
- Найдите базовую линию транспортира и совместите ее с базовой линией фигуры или угла
- Поместите середину транспортир на вершине угла
- Совместите одну сторону угла с нулевой линией транспортира (там, где вы видите число 0)
- Считайте градусы, где другая сторона пересекает числовую шкалу
После прочтения этих инструкции моему классу, я решил воспользоваться своим удобным визуализатором и сказал им, что мы будем повторно измерять все многоугольники из нашей рабочей тетради, следуя пошаговым инструкциям на доске.
Мои ученики стонали, но я повторял свои инструкции, пока в конце концов все не приступили к выполнению задания и не занялись исправлением ошибок в своих рабочих тетрадях.После 20-минутного подведения итогов я почувствовал, что класс может с большей уверенностью перейти к следующему уроку (как я и планировал ранее).
Третий урок подготовил моих учеников к еще большей практике измерения углов и дал им несколько более доступных форм для измерения. Также у них была возможность измерять углы на прямой. Им это очень нравилось, и они очень хотели начать использовать свои недавно обретенные навыки работы с транспортирами.
Какие ресурсы по измерению углов вы можете использовать для обучения углам?
Ресурсы всегда полезны для моего класса, особенно если они визуальные. Чтобы помочь моим учащимся в их понимании углов, я распечатал и показал названия и характеристики различных типов углов с соответствующими картинками.
Мы также провели время, изучая наш класс и определяя, сколько прямых углов мы можем видеть.
{\circ}\]
Линии могут быть как параллельными, так и непараллельными.
Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит:
{\prime}=\frac{\pi}{180} \times \frac{121}{3}=\frac{121 \pi}{540}\] радиан.
Таким образом, ∠ AOC = 143°
4.GR.1.AP.2: Используя инструмент с прямым углом, определите углы как острые, прямые или тупые и постройте острые, прямые или тупые углы.
Мои ученики стонали, но я повторял свои инструкции, пока в конце концов все не приступили к выполнению задания и не занялись исправлением ошибок в своих рабочих тетрадях.