Семиугольник — frwiki.wiki
Для одноименной статьи см Heptagone (альбом) .
Угольник представляет собой многоугольник с семью вершинами , так семь сторон и четырнадцать диагоналей .
Сумма внутренних углов в качестве перекрещивания семиугольника является ей радиан .
Регулярный угольник является угольник со стороны все равны и все внутренние углы равны. Их три: две звездочки ( правильные гептаграммы ) и одна выпуклая . Именно о последнем мы говорим, когда говорим о «правильном семиугольнике».
Правильный семиугольник — самый маленький из правильных многоугольников, который невозможно построить с помощью линейки и циркуля . Однако можно выполнить построение с помощью линейки и циркуля, если используются другие геометрические инструменты или если линейка может быть градуированной ( построение Neusis ). Также можно нарисовать приблизительный вариант, с небольшими ошибками, с помощью циркуля и безградуированной линейки.
Резюме
- 1 Характеристики правильного семиугольника
- 2 Невозможность построения с помощью линейки и компаса
- 3 Построение пересечением коник
- 4 Строительство от neusis
- 4.1 Предварительная конструкция
- 4.2 Конструкция Neusis
- 5 Примерные конструкции
- 5.1 Использование равностороннего треугольника
- 6 Правильный семиугольник в повседневной жизни
- 7 фрагментов истории
- 8 Примечания и ссылки
- 9 См. Также
- 9.1 Статья по теме
- 9.2 Внешние ссылки
Характеристики правильного семиугольника
- Все внутренние углы равны 5π / 7 рад .
- В углы в центре все равно 2л / 7 рад .
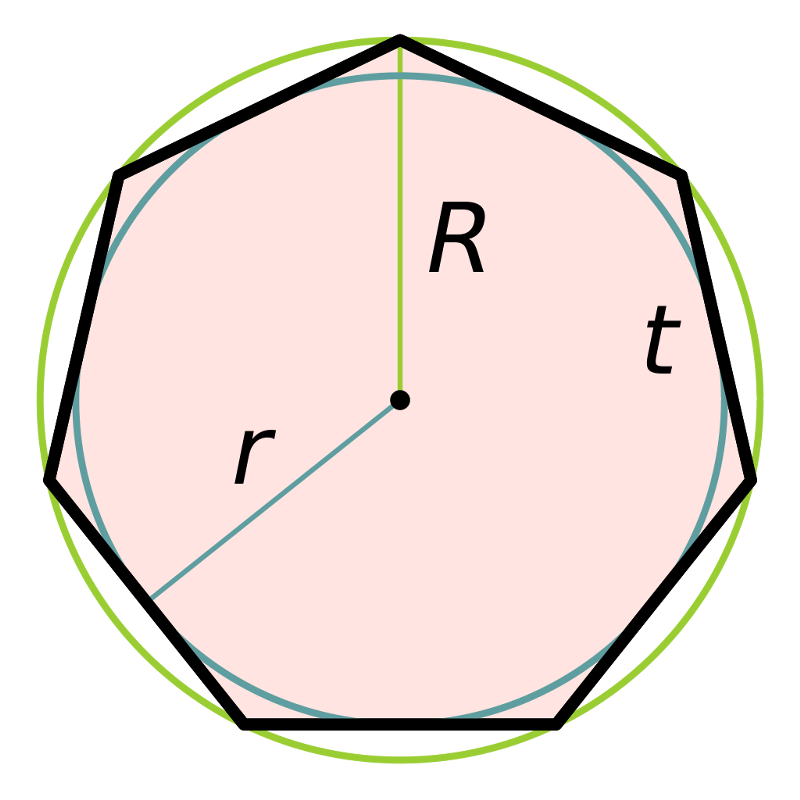
- Если сторона имеет длину а :
- радиус г по окружности равенрзнак равнов2грех(π7)≈1.
 {2} -4x-1) = 0}.
{2} -4x-1) = 0}.Для к не кратно 7, реальный х , следовательно , является корнем из 8 х 3 + 4 х 2 — 4 х — 1 , который является несократима наQ{\ displaystyle \ mathbb {Q}} и степени 3. Это находится в противоречии с результатом , установленным Wantzel , который утверждает, что минимальный многочлен конструктивного числа всегда имеет степень степени 2 . Таким образом, cos a невозможно построить, если k не делится на 7, следовательно, семиугольник не может быть построен.
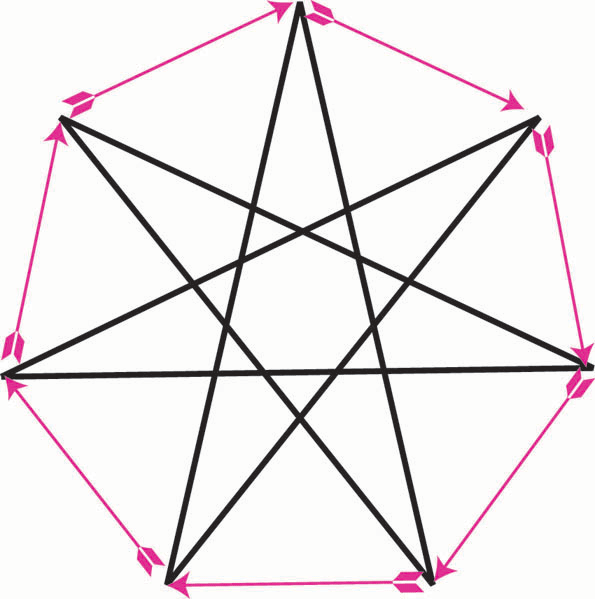
Построение пересечением коник
Построение пересечением коник.
Однако семиугольник можно построить, используя коники , поскольку 7 — простое число в форме 2 α 3 β + 1 , или еще раз: поскольку семиугольник можно построить с помощью невзиса ( см.
На прилагаемом чертеже показана конструкция семиугольника с использованием единичной окружности и прямоугольный гиперболой центр Q (1/4 √ 7 /4) и проходящей через А (1, 0) .
 {2} -2}}} {4}}}.
{2} -2}}} {4}}}.Строительство от neusis
Конструкция по neusis или путем наклона является метод строительства с помощью градуированной линейки и состоящий в построении отрезка заданной длины, концы которого лежат на двух заданных кривых. Здесь речь идет о построении угла π / 7 .
Предварительная конструкция
На прилагаемом рисунке ABCDEFGA представляет собой многоугольник, все сегменты которого имеют длину 1. ABFD и AGCE выровнены.
Докажем, что угол DAE равен π / 7 :
- обозначим этот угол a , который также является углом BAC
- треугольник ABC равнобедренный, противоположный угол ACB также имеет значение a ;
- сумма углов треугольника равна π , угол ABC равен π — 2 a, а дополнительный угол CBD равен 2 a ;
- треугольник BCD равнобедренный, противоположный угол CDB также имеет такое же значение ( 2 a ), а угол BCD равен π — 4 a ;
- сумма углов ACB (которая равна a ), BCD ( π — 4 a ) и DCE равна π , поэтому DCE равна 3 a .

- Треугольник CDE равнобедренный, противоположный угол DEC также равен 3 a ; угол DEA такой же.
- Треугольник ADE равнобедренный, это также значение угла EDA, а сумма углов равна 7 a , но также π
- поэтому a = π / 7 .
Докажем, что длина BE равна √ 2 :
- Обозначим через s и t длины BF и FD.
- Треугольник FDE равнобедренный, 2 cos (EDF) = t .
- Прямые (FC) и (DE) параллельны, угол ACF равен 3 a . Поскольку угол ACB равен a , угол BCF равен 3
- Тот же параллелизм позволяет утверждать, согласно теореме Фалеса, что
- 1+s1+s+тзнак равноs1{\ displaystyle {\ frac {1 + s} {1 + s + t}} = {\ frac {s} {1}}}
- что в результате перекрестного произведения и упрощения дает s 2 + st = 1 .
- Тогда теорема Аль-Каши в треугольнике BDE дает
- BE2знак равноBD2+DE2-2.
 {2} + st = 2}.
{2} + st = 2}.
- BE2знак равноBD2+DE2-2.
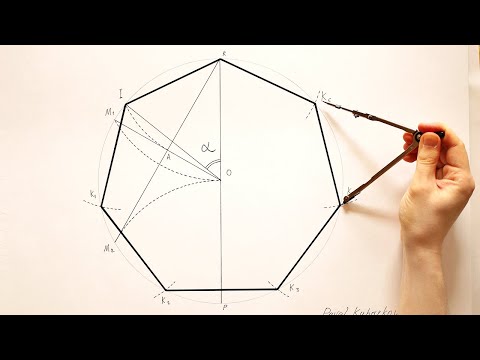
Строительство от neusis
Речь идет о построении точки A на серединном перпендикуляре отрезка [DE] и точки B на отрезке [AD], таких что AB = 1 и BE = √ 2 . Затем мы воссоздадим предыдущий треугольник.
- Строим квадрат CDEF со стороной 1, рисуем серединный перпендикуляр (d) к [DE], а также к [CF], а также окружность с центром E и радиусом EC.
- Мы помещаем начало линейки на серединный перпендикуляр, линейка опирается на точку D, мы тащим по серединному перпендикуляру начало линейки к вершине фигуры, сохраняя давление на D, пока не появится окружность (C) пересекает линейку на градуировке 1. Затем мы получаем точки B и A на градациях 0 и 1 соответственно.
- Мы строим окружность, описанную в равнобедренный треугольник ADE (методом пересечения серединных перпендикуляров двух его сторон, который определяет центр O строящейся окружности, наиболее точное позиционирование заключается в том, чтобы взять две самые длинные стороны который также должен совпадать на уже начерченном срединном перпендикуляре (d) к DE), который также является описанной окружностью основного семиугольника DEGHAIJ DE, который достаточно построить, перенеся на циркуль по описанной окружности длину его первая дуга DE, начинающаяся из точек D, E и A, уже начерчена (DE = EG = GH = HA = AI = IJ = JD).
Этот метод, позволяющий нарисовать по крайней мере один правильный семиугольник со стороной 1 (но описанного радиуса, первоначально неизвестного), затем позволяет разделить диск на 7 равных частей, перемещая центр этого контрольного семиугольника в центр круга, который будет разделить, затем с помощью линейки, опираясь на общий центр и вершины первого семиугольника, нарисуйте радиусы, разрезающие круг, который нужно разрезать на 7 равных дуг:
- Эта вторая конструкция требует только, чтобы линейка и циркуль «скользили» по уже построенному унитарному семиугольнику, чтобы центры смещенного семиугольника совпадали с центром круга, который нужно разделить.
- Достаточно просто провести первую линию, соединяющую центр первого семиугольника с центром круга, который нужно разделить, затем провести параллели, проходящие через вершины первого семиугольника, и сослаться на циркуль на этих параллелях. расстояние между двумя центрами.
- После того, как второй единичный семиугольник нарисован и выровнен с центром круга, который нужно разделить, остается только использовать его, чтобы нарисовать 7 радиусов, пересекающих круг, который нужно разделить, и проходящих через вершины перемещенного единичного семиугольника, чтобы получить вписанный в диск правильный семиугольник любого радиуса, который нужно разделить на 7 равных частей.
Примерные конструкции
Использование равностороннего треугольника
Отношение между стороной семиугольника и радиусом описанной окружности равно . Это число очень близко к, и это число очень легко получить, используя равносторонний треугольник . 2грех(π/7)≈0,8677{\ Displaystyle 2 \ грех (\ пи / 7) \ приблизительно 0 {,} 8677}32≈0,866{\ displaystyle {\ frac {\ sqrt {3}} {2}} \ приблизительно 0 {,} 866}
Отсюда следующая конструкция:
- Нарисуйте круг с радиусом 1 и центром M.
- Возьмите точку X на окружности. Окружность с центром X и радиусом XM пересекает предыдущую окружность в точках A и Y
- Прямые (AY) и (MX) пересекаются в точке H.
- Длина AH является хорошим приближением стороны семиугольника, вписанного в тот же круг.
По этому методу центральный угол составляет приблизительно 51,32 градуса вместо ожидаемых 51,43 (приблизительно) или относительной погрешности 2,15 на тысячу.
Правильный семиугольник в повседневной жизни
Семигранное розовое окно, церковь аббатства Больё-ан-Руэрг .

Семигранное окно в саду Юй в Шанхае ( Китай ).
- Огранка монеты 20 евроцентов выполнена в виде правильного семиугольника.
- В британских 20 и 50 пенсов монеты являются Рело семиугольники .
Фрагменты истории
Семиугольник — первый правильный многоугольник, который невозможно построить с помощью линейки и циркуля. Поэтому естественно, что после построения пятиугольника и шестиугольника греки, а затем арабы рассмотрели конструкцию семиугольника. Единственный текст греческого происхождения, прослеживаемый в точном построении семиугольника, приписывается Архимеду: « О делении круга на семь равных частей» . Он дошел до нас через арабский перевод Табита ибн Курры . Метод построения использует промежуточный шаг, состоящий в построении точки, уравнивающей площадь двух треугольников, но детали этого построения не приводятся. Поэтому мнения комментаторов разделились: это дыра в демонстрации? — отсутствующее сооружение требовало постройки neusis? — точка была получена пересечением коник?
Многие арабские математики , чтобы прокомментировали текст Архимеда и от
 ) , Абу Сахл аль-Кухи , Ибн Сахл , Ибн аль-Хайтам , Камаль ад-Дин ибн Юнус (умер около 1242 г.)). Связь между построением семиугольника и разрешением уравнения третьей степени изучается Абу Насром Мансуром .
) , Абу Сахл аль-Кухи , Ибн Сахл , Ибн аль-Хайтам , Камаль ад-Дин ибн Юнус (умер около 1242 г.)). Связь между построением семиугольника и разрешением уравнения третьей степени изучается Абу Насром Мансуром .Кажется, что из всех этих трактатов о семиугольнике ни один не был переведен на латынь. Тем не менее, мы находим следы строительства семиугольника со ссылкой на метод Архимеда в Де трицепсе по Иордану Nemorarius .
Примечания и ссылки
- ↑ См. Теорему 3.6, с. 195 Ж.-М. Арнодьеса и П. Делезоида, « Числа (2, 3) -конструкции », Adv. Математика. , т. 158, п о 2, стр. 169-252 ( читать онлайн ).
- ↑ См. Стр.
 373-374 по Ж.-М. Arnaudiès и П. Delezoide, « Геометрические построения на пересечениях коники », Бюллетень де л ‘ APMEP , т. 446, г., стр. 367-382 ( читать онлайн ).
373-374 по Ж.-М. Arnaudiès и П. Delezoide, « Геометрические построения на пересечениях коники », Бюллетень де л ‘ APMEP , т. 446, г., стр. 367-382 ( читать онлайн ). - ↑ Эта цифра подробно описана в книге Жана-Дени Эйдена, Le jardin d’Eiden: Une année de colles en Math Spé MP , Paris, Calvage & Mounet,, 690 с. ( ISBN 978-2-916352-27-5 ).
- ↑ (in) Январь Хогендийк , « Греческое и арабское построение правильного семиугольника » , Arch. Hist. Exact Sci. , т.
 30,, стр. 197–330, стр. 204 .
30,, стр. 197–330, стр. 204 . - ↑ (in) Генри Менделл, « Архимед и регулярный гептагон», селон Сабит ибн Курра ‘ на CSULA .
- ↑ (in) Рошди Рашед , Теория коник, геометрических конструкций и практической геометрии Ибн аль-Хайтама: История арабских наук и математики , т. 3, стр. 299 в Google Книгах .
- ↑ Hogendijk 1984 , стр. 201.
- ↑ Hogendijk 1984 , стр.
 240.
240. - ↑ Hogendijk 1984 , стр. 270.
Смотрите также
Связанная статья
Тригонометрические формулы в kπ / 7
Внешние ссылки
- Батист Горин, О правильном семиугольнике и его построении [PDF]
- Еще одна примерная конструкция ( GeoGebra с линейкой и компасом). Точность: 0,1%.
Полигоны
От 1 до 10 сторон - Хенагон (1)
- Дигон (2)
- Треугольник (3)
- Четырехугольник (4)
- Трапеция
- Описывающая трапеция
- Параллелограмм
- Алмаз
- Прямоугольник
- Квадратный
- Антипараллелограмм
- Псевдоквадрат
- воздушные змеи
- Записываемый четырехугольник
- Трапеция
- Пентагон (5)
- Правильный выпуклый пятиугольник
- Шестиугольник (6)
- Гептагон (7)
- Восьмиугольник (8)
- Эннеагон (9)
- Десятиугольник (10)
От 11 до 20 сторон Хендекагон (11) · Додекагон (12) · Трехкадр (13) · Тетрадекагон (14) · Пентадекагон (15) · Шестиугольник (16) · Гептадекагон (17) · Октадекагон (18) · Эннеадекагон (19) · Икосагон (20) Превосходство до 20 сторон Триаконтагон (30) · тетраконтагон (40) · пентаконтагон (50) · гексаконтагон (60) · гептаконтагон (70) · октаконтагон (80) · Эннеаконтагон (90) · гектогон (100) · Дигектогон (200) · Тригектогон (300) · Тетрагектогон (400) · Пентагектогон (500) · Гексагектогон (600) · Гептагектогон (700) · Октагектогон (800) · Эннеагектогон (900) · чилигон (1000) · мириагон (10000) Другие классификации, кроме количества сторон - Классификация по выпуклости
- Перекрестный многоугольник
- Простой многоугольник
- Невыпуклый многоугольник
- Звездный многоугольник
- Выпуклый многоугольник
- Невыпуклый многоугольник
- Классификация по углам и сторонам
- Равноугольный многоугольник
- Равносторонний многоугольник
- Правильный многоугольник
- Рейтинг по кругу
- Записываемый многоугольник
- Описывающий многоугольник
- Бицентрический многоугольник
Правильные звездчатые многоугольники Пентаграмма · Гексаграмма · гептаграмма · Octogramme (в) · Эннеаграмма · декаграмм (в) · Hendécagramme (в) · dodecagram Описание - Боковая сторона
- горная вершина
- Вершина
- На основе
- Внутренний угол / Внешний угол
- Периметр
- Область
- Теорема Пика
Замечательные линии и круги - Диагональ
- Апофема
- Описанный круг
- Написанный круг
Отношения между полигонами - Двойственность
- Огранка
- Звездчатость
Строительство - Теорема Гаусса-Вантцеля
- Построение правильного пятиугольника
Расслоение - Теорема Уоллеса-Больяи-Гервиена
- Равнодушие
<img src=»//fr.
 wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>Проверочные работы по математике 1 класс
Проверочная работа по теме «Подготовка к изучению чисел»
Слева от бабочки нарисуй цветок:
Считая справа налево, раскрась шестую грушу:
Одна ягода земляники зеленая, а остальные красные. Раскрась ягоды.
Нарисуй столько зернышек, сколько куриц.
___________________________________________________________________
Нарисуй 5 квадратов.
___________________________________________________________
Проверочная работа по теме “Числа от 1 до 10. ”
1 .Пересчитай кубики и запиши в рамке их число.
2.
 Сравни числа и запиши в рамке знак ,
Сравни числа и запиши в рамке знак ,8 3 6 7
3. Запиши ответы.
2
+ 7 = 9 – 2 =
5
+ 5 = 6 – 3 =
1 + 6 = 10 – 1 =
4. У Оли 4 сливы, а у Ани 2. Сколько слив у девочек?
Решение:
Ответ:
5 . Измерь длину отрезка и запиши ответ.
. .
6
. * Запиши число, которое больше 3 и меньше5.
Ответ:
7 * Сколько вершин надо отметить, чтобы начертить семиугольник?
Ответ:
8. Соедини точки так, чтобы получилась ломаная линия из двух звеньев:
Проверочная работа по теме
«Числа от 1 до 10. Сложение и вычитание»
Продолжи ряд чисел.
2, 4, …, 8,… .
9, …, 5, 3, … .
Вычисли.
4 + 2 = 2 + 3 = 4 + 1 + 2 =
5 – 3 = 8 + 2 = 7 – 1 – 1 =
7 + 1 = 6 – 4 = 9 + 1 – 2 =
3. Подчеркнуть верные записи
6+ 2 = 8 10 – 3 = 3 +3
10 – 1 8 7 -0 3+4
5+ 3
8 – 3 = 5 7 – 4 = 6 – 3
4. Прочитай задачу. Нарисуй схему, запиши решение и ответ.
В вазе лежало 4 яблока и 3 апельсина. Сколько всего фруктов было в вазе?
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
5. Начерти отрезок длиной 5 см. Ниже начерти отрезок на 2 см больше.
6. Вставить пропущенное число так , чтобы запись была верной .
2 + 4
7.* Сколько лет Юре, если через 3 года родители будут праздновать его
десятилетие?
Ответ:
8.
 Соедини точки так, чтобы получилась ломаная линия из трёх звеньев:
Соедини точки так, чтобы получилась ломаная линия из трёх звеньев:Проверочная работа по теме:
«Сложение и вычитание в пределах 10»
1. Заполни пропуски.
3 + 7 = … 4 + 5 = … 9 – 9 = … 8 – 3 + 4 = …
1 + 9 = … 8 + 2 = … 5 – 3 = … 10 – 3 + 2 = …
2. Реши задачу.
У Оли * * * * *
У Юли – на 2 больше.
Сколько звездочек у Юли?
Решение………………………………………………………………………
Ответ…………………………………………………………………………
3. Какие знаки пропущены? ( +, — )
9 … 3 … 2 = 8
4. Выполни действия, запиши конечный результат.
10 – 2 – 3 + 1 – 2 – 3 = …
9 – 3 + 2 – 3 – 3 + 2 =…
5. Нарисуй 9 треугольников, закрась их красным и синим карандашом так, чтобы красных треугольников было на один больше, чем синих.
…………………………………………………………………………………
6. Сколько звеньев у ломаной? Ответ:
Проверочная работа по теме: «Сложение и вычитание»
1.
 Выполнить действия.
Выполнить действия.7 + 2 9 – 7
4 + 4 10 – 9
1 + 0 6 – 0
2. Сравнить числа.
7 5 8 7
4 4 10 9
3. Решить задачу.
К озеру идут утки и утята: уток 5, а утят на 4 больше, чем уток. Сколько
утят?
_______________________________________________________________________
_______________________________________________________________________
4. Запиши только ответ.
Кролики сидят в клетке так, что видны только их уши. Вова насчитал
5 пар ушей. Сколько кроликов в клетке?
Ответ:__________________________________________________________
Проверочная работа по теме «Нумерация чисел от 11 до 20»
Запиши пропущенные числа:
9, 10, …, 13, !4, …, …, 17, …, …, 20.
Какое число больше в каждой паре? Обведи в кружок это число.
16 и 14; 11 и 13; 20 и 19; 19 и 17.
4. Дети вырезали из бумаги 9 больших кругов, а маленьких на 4 меньше. Сколько маленьких кругов вырезали дети?
____________________________________________________________________________________________________________________________________
5. Начерти 2 отрезка: один длиной 1дм , а другой на 1 см длиннее первого.
Уменьши на 1:
12
15
18
19
7. Нарисуй столько и , чтобы всего их было 6 и квадратов на 2 больше, чем треугольников.
Итоговая проверочная работа
1. Начерти ломаную из двух звеньев. Одно звено равно 3 см, второе 4 см.
 Найди длину этой ломаной.
Найди длину этой ломаной.2.Подчеркни числа, в записи которых есть 3 десятка:
3, 10, 30, 13, 35
3. Портниха купила ткань и сшила из нее платье и рубашку. Рассмотри таблицу. Сколько ткани осталось у портнихи?
Купила
На платье
На рубашку
Осталось
15 м
5 м
2 м
Подчеркни числовое выражение, которое поможет ответить на этот вопрос:
15 + 5 + 2 15 – 5 — 2
Запиши ответ в таблице.
4. Выпиши в первый столбик верные равенства и неравенства, а во второй столбик – неверные.
9-06+2
8-4
4+55+4
7+2=7-2
1+9
7-37-4
_________________
_________________
____________________________________
___________________
___________________5.
 ❂ На уроке чтения дети отгадывали загадки.
❂ На уроке чтения дети отгадывали загадки.Имя ребёнка.
Количество загадок.
Нина
5 загадки
Коля
2 загадки
Используя данные таблицы, ответь на вопросы:
Сколько загадок отгадал Коля? ___________
Кто из детей отгадал больше загадок? Напиши имя ребёнка. _________________
6. Начерти отрезок длиной 1дм 4 см. Поставь точку так, чтобы получилось два одинаковых отрезка.
7. Мама сварила 8 банок малинового варенья, а клубничного на 3 банки меньше. Сколько банок клубничного варенья сварила мам? Сколько всего банок варенья сварила мама?
Решение___________________________________________________________
Ответ: _____________________________________________________________
8.
 Ире надо сделать на праздник 9 цветов. 4 цветка она уже сделала. Сколько цветов осталось сделать Ире?
Ире надо сделать на праздник 9 цветов. 4 цветка она уже сделала. Сколько цветов осталось сделать Ире?Решение____________________________________________________________
Ответ: ______________________________________________________________
10. В песочнице играют 4 малыша. Мальчиков среди них меньше, чем девочек. Сколько мальчиков и сколько девочек играют в песочнице?
Ответ:______________________________________________________________
Семиугольник
СемиугольникСемиугольник
Гептагон (7-сторонний многоугольник) был формой большой загадки в геометрии. Невозможно построить семиугольник только с компасом и линейкой. Однако существует множество приближений, некоторые из которых я приведу здесь.Эта первая конструкция является самой простой. Это очень хорошее приближение к семиугольнику. Дан кружок O (желтый): - Найдите A , случайную точку на окружности.

- Найдите M , середину OA .
- Проведите перпендикуляр через M . Он пересекает окружность O в точке B .
- Нарисуйте круг в точке B (голубой) так, чтобы он пересекал M . Окружность B пересекается с окружностью O в две точки семиугольника. Вы можете использовать их, чтобы найти остальных.
Существует метод аппроксимации почти любого правильного многоугольника с помощью циркуля и линейки. Особенно полезно с странные формы, такие как семиугольники и девятиугольники. Они сложны тем, что предполагают разделение строк. - Начертить круг O . Нарисуйте AB , диаметр круга O .
- Разделить AB на n количество частей (n — количество сторон, в данном случае 7!).
- Нарисуйте два круга, один в точке A и один в точке B (голубой), каждый с радиусом AB .
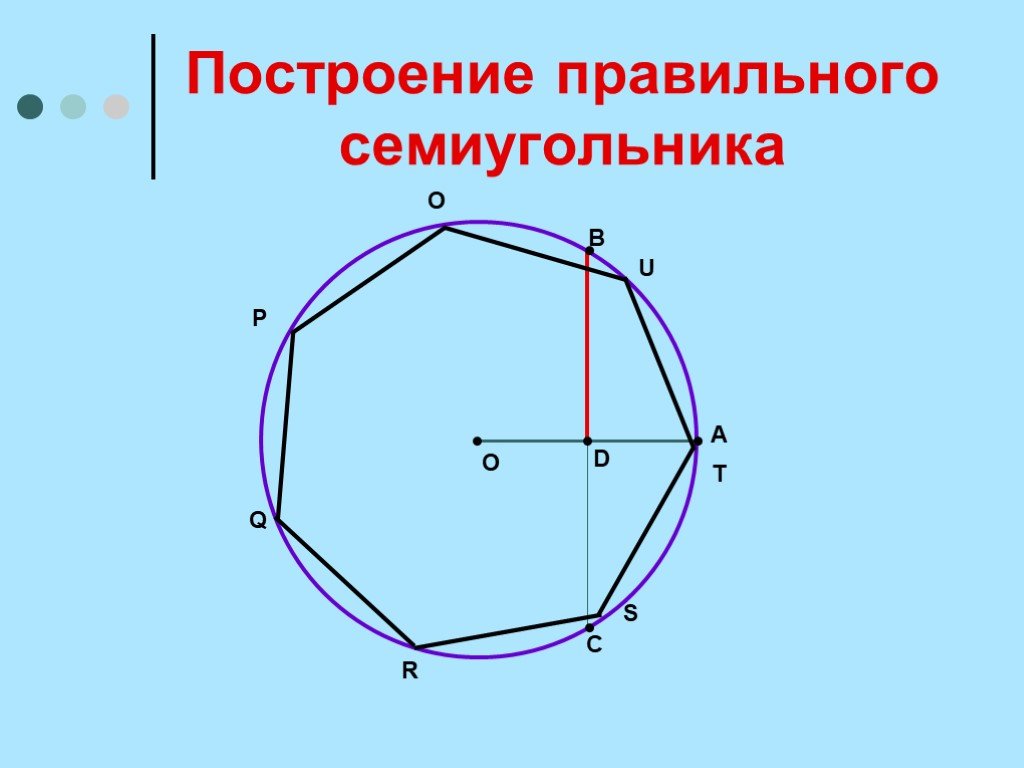 Они пересекаются в точке C .
Они пересекаются в точке C . - Точка D — вторая точка диаметра слева.
- Нарисуйте линию из C до D , продолжая его до исходного круга, где он пересекается в E .
- A и E — две точки семиугольника. Используйте их, чтобы найти остальных.
- Вы можете использовать этот приблизительный любой n-gon !
Эта следующая конструкция была сформулирована мной. Это не так точно в других, но это относительно легко. - Начертить круг O . Нарисуйте ОА и ОВ так, чтобы они были перпендикулярны друг друга и A и B находятся на круге O .
- Нарисуйте BC так, чтобы он был перпендикулярен AB (фиолетовый) и имел половину его длины.
- Проведите линию через CA (голубой).
- Нарисуйте круг в точке C так, чтобы он пересекал B (красный).
 Круг C (красный) крестики СА (голубой) по адресу D .
Круг C (красный) крестики СА (голубой) по адресу D . - В точке A нарисуйте окружность, пересекающую D . Окружность A пересекает окружность O в двух точках семиугольника.
Вот очень сложная конструкция, но очень точная. - Начертить круг O . Нарисуйте ABCDE , пятиугольник, вписанный в окружность O .
- Нарисуйте еще один круг в точке O , на этот раз внутри пятиугольника (фиолетовый). Для этого найдите середину одной из сторон пятиугольника и нарисуйте окружность, пересекающую эту точку.
- Нарисовать OA . OA пересекается с маленьким кругом (фиолетовым) в точке F .
- Нарисуйте круг в точке F (голубой), который пересекает A . Он пересекает OA в точке H . Нарисовать
круг в точке A (голубой), который пересекает H .
 Круг A (голубой) пересекает OA на G .
Круг A (голубой) пересекает OA на G . - Нарисуйте маленький круг в точке O (желтый), который пересекает H . Вписать равносторонний треугольник, ХИДЖ внутри этого круга (желтый).
- Проведите линию через точки I и J .
- Нарисуйте окружность в точке O , пересекающую точку G . Этот круг пересекает IJ в точках К и Л .
- G,K,L — 3 точки семиугольника. Используйте их, чтобы найти остальных!
Подробнее см. NexusjournalЭто новое строительство. Он предполагает использование сетки . - Найти точку (2,4) . Нарисуйте окружность с центром в начале координат, пересекающую эту точку.
- Нарисуйте линию в точке y = -1 . Эта линия пересекает окружность в двух точках семиугольника.
Здесь показана конструкция Нейзиса для семиугольника, включающая отмеченную линейку. Вы можете найти больше информации на Мир математики. - Возьмите линейку (например, лист бумаги) и отметьте на ней две точки, А и В .
- Построить сегмент CD , равный AB .
- Найдите середину CD и назовите ее M . Проведите биссектрису через точку M .
- Нарисуйте отрезок CE так, чтобы CE был перпендикулярен CD и имел одинаковую длину.
- Нарисуйте окружность с центром D и точкой пересечения E .
- Возьмите отмеченную линейку и поместите ее так, чтобы A касается дуги, B касается серединного перпендикуляра CD , и линейка касается точки C .
- Тогда угол CBM или q равен p/14. Таким образом, 4q даст вам 2p/7, чего мы и хотели!
© 7 апреля 2003 г. 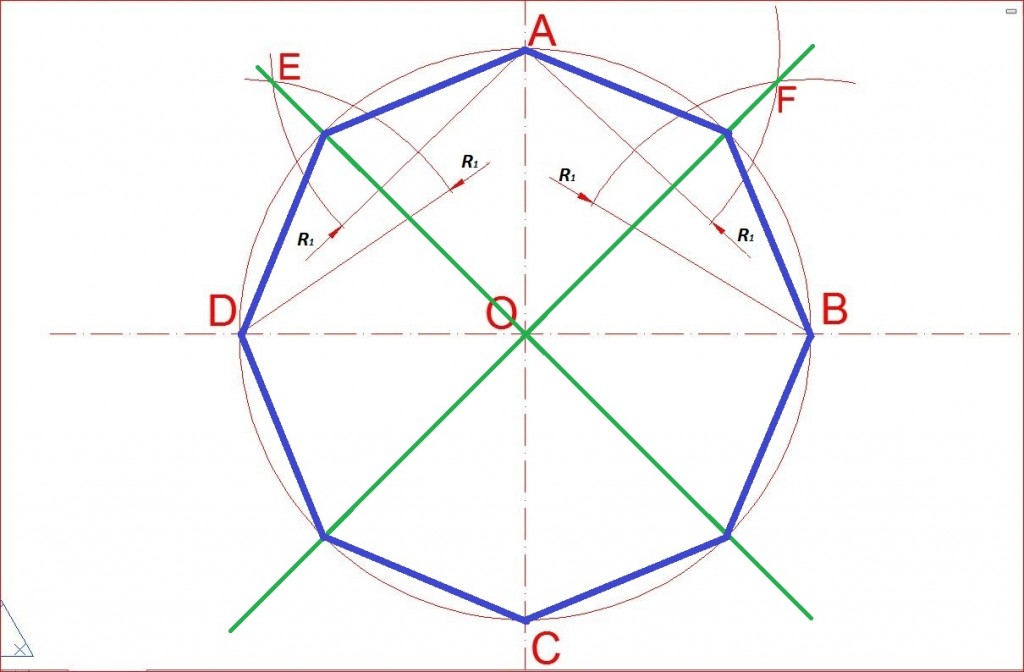 Робин Ху. Все права защищены.
Робин Ху. Все права защищены.Как с помощью tikz нарисовать семиугольник площадью 7? — ТеХ
спросил
Изменено 1 год, 1 месяц назад
Просмотрено 183 раза
Как с помощью tikz нарисовать правильный семиугольник площадью 7 кв.единиц?
- тикз-пгф
1
Быстрый поиск указывает на
shape.geometric. Я позволю вам посчитать подходящий радиус 😉\documentclass{статья} \usepackage{tikz} \usetikzlibrary{shapes.geometric} \начать{документ} {\def\PolyRadius{2см} \begin{tikzpicture} % Удалить следующую строку, чтобы убрать красный кружок \draw[red] (0,0) круг [радиус=\PolyRadius]; \node[правильный многоугольник,рисовать,стороны правильного многоугольника = 7,минимальный размер=2*\PolyRadius] at (0,0) {}; \end{tikzpicture} } \конец{документ}Для правильного многоугольника
nсторон с площадьюS, длина от центра до вершины 92\sin\left(\frac{360}{n}\right)}{2}$ \quad подразумевает\quad $r=\sqrt{\dfrac{2S}{n\sin\left(\frac{360} {n}\right)}}$}; \end{tikzpicture} \begin{tikzpicture} \def\n{7} % количество сторон семиугольника \def\S{7} % площади этого семиугольника \pgfmathsetmacro{\k}{360/\n} \pgfmathsetmacro{\r}{(sqrt(2*\S))/(\n*sin(\k))} \draw[фиолетовый] (90:\r) foreach \i[parse=true] in {1,.
- радиус г по окружности равенрзнак равнов2грех(π7)≈1.
