|
|
Деятельность учителя |
Деятельность учеников |
|
I. Самоопределение к деятельности. 1-2 мин. Цель:
|
– Французский писатель XIX столетия Анатоль Франц однажды заметил, что: «Учиться можно только весело. Чтобы переваривать эти знания, нужно поглощать эти знания с аппетитом». – Как вы понимаете этот совет? – Давайте сегодня на уроке будем следовать этому совету. Будем активны, будем поглощать знания с большим желанием. – Над какой темой вы работали на прошлом уроке? – Что вы уже узнали, чему научились, работая с углами?
– Сегодня нам предстоит узнать новое из раздела величины. |
– Угловой градус.
– Узнали виды углов, научились сравнивать углы методом наложения, единицу измерения углов, выполнять арифметические действия с углами, заданными градусными мерами. |
|
II. Актуализация знаний и фиксация затруднений в деятельности. 4-5 мин. Цель:
|
– Ребята, скажите, пожалуйста, какие величины вы знаете? – Назовите единицы измерения этих величин. – Ребята, на какие группы можно разбить эти величины углов? (на слайде) – (На столах лист) Я предлагаю вам измерить ∠ D с помощью мерки – углового градуса, который лежит у вас на столе. Какую мерку мы с вами используем при измерении угла? – Как обстоят дела? Как думаете, можно ли как-то иначе измерить этот угол? Помочь может подсказка на доске. Определите, какие величины можно измерять этими предметами?
– Кто-нибудь знает, чем можно измерить угол? – Попробуйте измерить наш ∠D с помощью транспортира. У кого какие ответы получились? Давайте сравним полученные результаты. (Запись на доске). Среди ваших ответов, есть верный. |
– Длина, площадь, объем, масса, время, скорость, градусная мера угла. – см, кв. см, л, кг, с, км/ч, °. – 1°
– Линейкой измеряют длину, палетка – площадь, часы и таймер – время; весы (безмен) – массу; емкость с делениями – объем. – Транспортиром.
|
|
III. Выявление места и причины затруднения, постановка цели деятельности. 3-4 мин. Цель:
|
– Как вы думаете, почему результаты получились разные? В чем проблема?
– Какую цель поставим на уроке?
– Значит какая будет тема нашего урока?
|
– Мы не знаем, как правильно измерять величину угла с помощью транспортира. – Научиться измерять градусную меру угла с помощью транспортира. – Транспортир.
|
|
IV. Построение проекта выхода из затруднения. 7-8 мин. Цель:
|
– Ребята, кто знает что такое транспортир? Предполагают, что это было связано с созданием первого календаря. Древние математики нарисовали круг и разделили его на столько частей, сколько дней в году. Но они думали, что в году не 365 или 366 дней, а 360. Поэтому круг, обозначающий год, они разделили на 360 равных частей. Такое изображение было очень полезным, на нем можно было отмечать каждый прошедший день, и видеть, сколько дней осталось до конца года. – Вот посмотрите, как выглядел один из первых транспортиров.
– Обратите внимание, сколько различных транспортиров бывает! Понаблюдайте, в чем различие? Транспортир состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы), разделенного на градусы то 0 до 1800. – Но в чем они все сходны? – Ребята, давайте составим алгоритм измерения градусной меры угла при помощи транспортира: Что нужно сначала сделать? Алгоритм измерения градусной меры угла при помощи транспортира:
– Пригодятся ли эти знания нам в жизни? Где можем столкнуться с измерением углов? – Вернемся к заданию, которое выполняли. |
– Транспортир (от латинского «переношу») – инструмент для построения и измерения углов.
– Они отличаются формой, размером, материалом из которого изготовлены, цветом.
– Транспортир – это специальный чертёжный прибор для измерения углов.
– Делать ремонт, на уроках изо, трудах, на черчении, постройка …
|
|
Физкультминутка Игра «Истина- ложь» истина – хлопаем, ложь – топаем 1.Острым называют угол, который больше прямого. (Нет) 2. Тупой угол всегда больше прямого и меньше развёрнутого? (да) 3. Единица измерения углов: килограмм? (нет) 4. Тупой угол меньше прямого угла. (нет) 5. Угол — фигура, образованная двумя лучами, выходящими из одной точки. 6. биссектриса — это луч, который выходит из вершины угла и делит его пополам. (да) 7. два угла можно сравнить с помощью наложения (да) 8. величина острого угла равняется 126 ( Нет) |
||
|
V. Первичное закрепление во внешней речи. 4-5 мин. Цель:
|
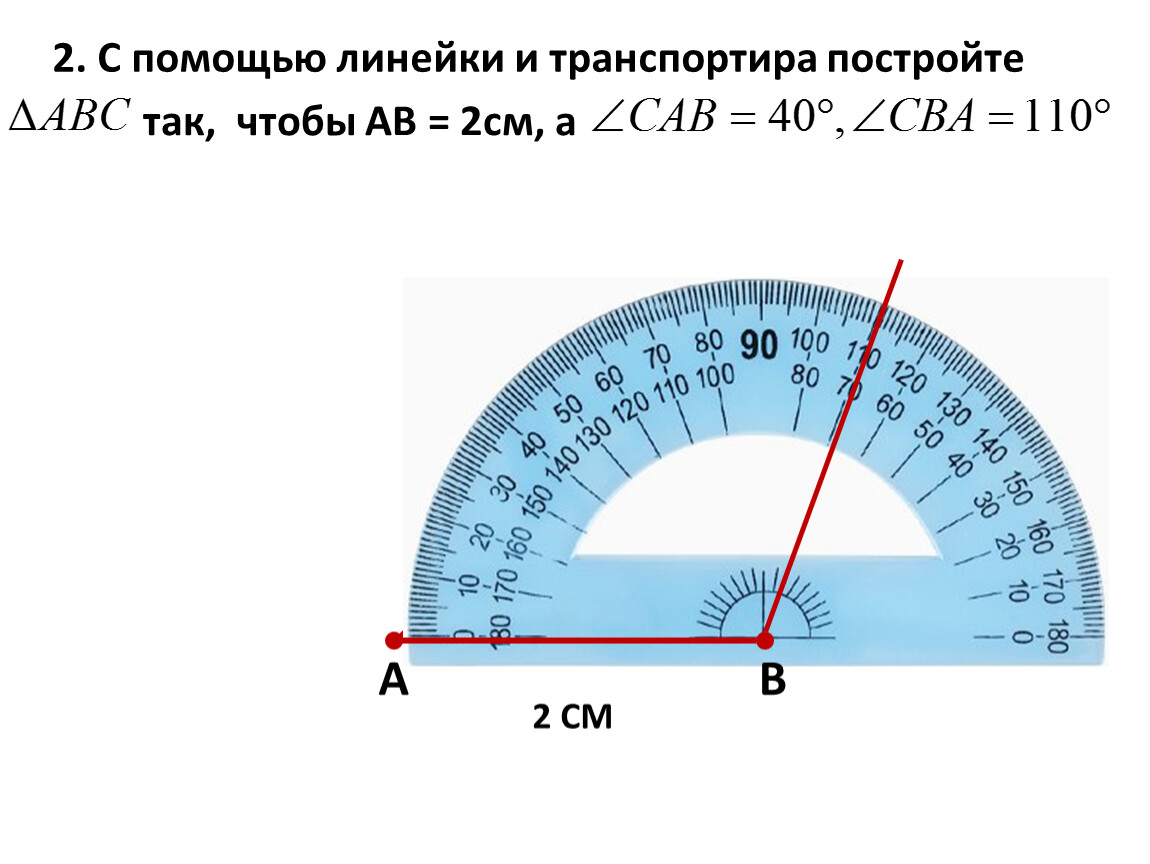
– Практическая работа (учебник с.19 №4). Прочитаем задание, Вова. – Что сначала делаем? Проговариваем алгоритм (по цепочке выполняем). – Следующее задание №8 стр.20. Катя, читай. Это задание мы будем выполнять в паре. Измеряете градусную меру каждого угла, сверяетесь с соседом. Проверьте друг у друга, все ли правильно работают по алгоритму измерения градусной меры угла. – Следующее задание (если будет время). На слайде появляются фигуры:
– У вас на столах есть карточки с изображением этих углов. Найдите градусную меру каждого из углов (по цепочке). |
|
|
VI. Самостоятельная работа с самопроверкой по эталону. 4-5 мин. Цель:
|
– Мы поработали над новой темой. Как вы думаете, что теперь нам нужно сделать? Задание на листках. Измерьте углы, изображенные на рисунках, и запишите их градусные меры.
– Итак, проверяем. Поставьте + там, где верно обведена цифра, и восклицательный знак там, где допущена ошибка. (Учащиеся сверяют свои ответы с ответами на доске. Отмечают правильные и неправильные ответы.) – Встаньте те, у кого нет ошибок. Молодцы! – У кого есть ошибки, поднимите правую руку. Вы исправили? Поняли свои ошибки? Молодцы! |
– Выполнить самостоятельную работу. – Эталон проверки на экране.
– Да. |
|
VII. Включение в систему знаний и повторение. 5-8 мин. Цель:
|
(Задача на слайде) Из двух городов навстречу друг другу выехали одновременно грузовая машина со скоростью 43 км/ч и легковая машина со скоростью 56 км/ч. Через сколько часов они встретятся, если расстояние между городами 693 км? – Прочитай задачу, Саша. – Нарисуем схему на доске, Катя. (Синтетический метод разбора задачи!) – О каких машинах идет речь в задаче? – Что известно?
– Что известно про скорости машин?
– Что мы можем найти по этим данным? Как? Каким арифметическим действием? – Егор, прочитай главный вопрос задачи. Запишите решение в тетради.
– Если останется время стр. 20 № 10, 11.
|
– О грузовой и легковой. – Что машины ехали друг другу навстречу. – Грузовая машина ехала со скоростью 43 км/ч и легковая машина со скоростью 56 км/ч. – Скорость сближения. Сложением. 56+43=99 (км/ч) – Да. Делением. 693/99=7 (ч) 1) 43 + 56 = 99 (км/ч) — скорость сближения 2) 693 /99 = 7 (ч) Ответ: через 7 часов.
|
|
VIII. Цель:
|
– В завершении нашей работы давайте ответим на вопросы: Над какой темой мы сегодня работали? – Какова была цель сегодняшнего урока?
– Удалось ли нам достигнуть нашей цели урока? Докажите. – По какому алгоритму мы измеряли величину угла при помощи транспортира? Давайте еще раз вспомним его. – Подготовьте карандаши 3 цветов (зеленый, желтый и красный). Как вы оцениваете свою работу на уроке. – Поднимите желтый карандаш те, кто допускал ошибки, но ему удалось их исправить. – Поднимите красный карандаш те, кто не успел выполнить все задания или не понимает, как измерять градусную меру угла при помощи транспортира.
– Где вы можете поработать над трудностями? – Верно, чтобы закрепить новые знания запишите домашнее задание: стр.20 № 9. Стр.21 № 15. |
– Транспортир.
– Научиться измерять градусную меру угла с помощью транспортира. – Да. Мы справились с самостоятельной работой. – Алгоритм измерения градусной меры угла при помощи транспортира:
– Дома.
|
Мерзляк 5 класс — § 12. Виды углов. Измерение углов
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
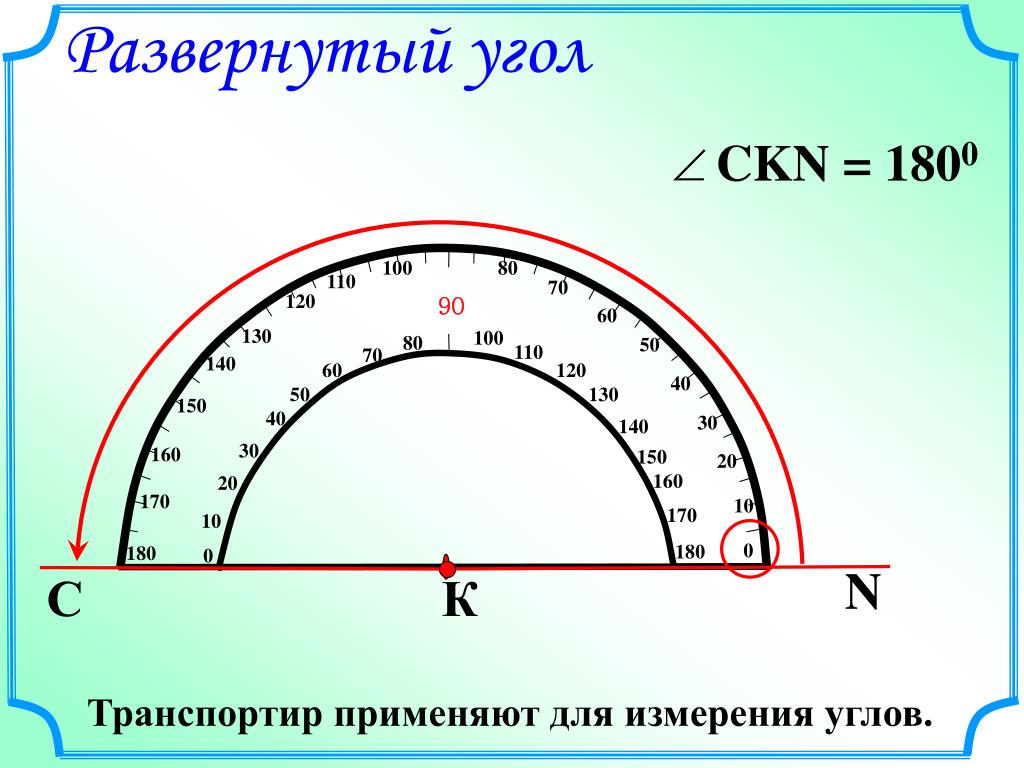
1. Какой угол называют развёрнутым? Развёрнутый угол — это угол, лучи которого образуют прямую и их начала совпадают.
2. В каких единицах измеряют углы? Углы измеряют в градусах (например ∠45° — это угол величиной 45 градусов).
3. Какова градусная мера развёрнутого угла? 180°
4. Что означает измерить угол? Измерить угол — это значит посчитать сколько единичных углов в нём помещаются.
5. Как называется прибор, который используют для измерения углов? Транспортир.
6. Расскажите, как пользоваться транспортиром. Для того, чтобы измерить угол транспортиром надо:
- приложить линейку транспортира к одной из сторон угла;
- совместить центр транспортира с вершиной угла;
- определить, какой из штрихов шкалы транспортира пересекает вторая сторона угла;
- определить градусную величину, которой соответствует пересекаемый штрих шкалы транспортира.
Важно:
- Одна из сторон транспортира должна точно лежать на линейке прибора.
- Центр транспортира должен точно совпадать с вершиной угла.
- Если вторая сторона угла не доходит до шкалы транспортира, то надо мысленно продолжить луч до пересечения с прибором, либо начертить продолжение луча до нужной длины.
7. Какие градусные меры имеют равные углы? Равные углы имеют равные градусные меры.
8.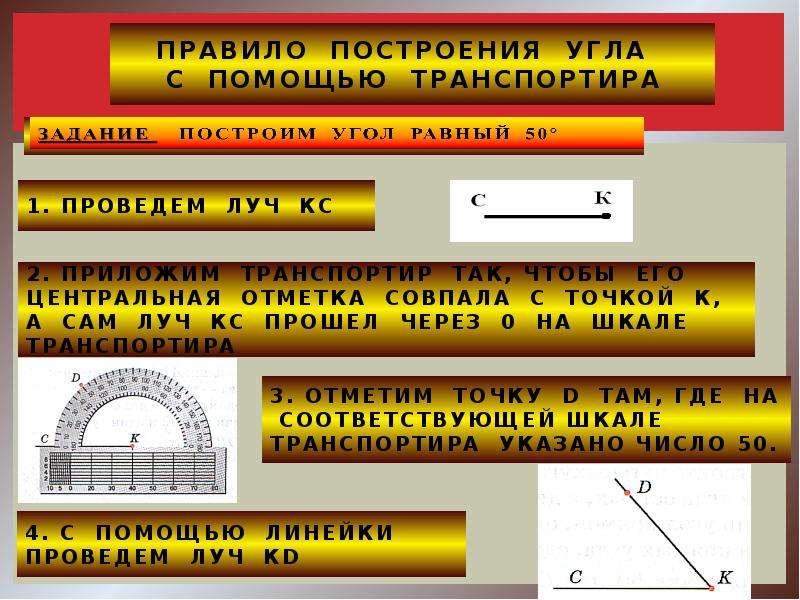 Какой из двух неравных углов считают большим? Большим считается угол, градусная мера которого больше.
Какой из двух неравных углов считают большим? Большим считается угол, градусная мера которого больше.
9. Каким свойством обладает величина угла? Если между сторонами угла АОС провести луч ОВ, то градусная мера угла АОС равна сумме градусных мер углов АОВ и ВОС:
∠АОС = ∠АОВ +∠ВОС, если луч ОВ лежит между сторонами угла АОС.
10. Какой угол называют острым? Острым углом называют угол, градусная мера которого меньше 90°.
11. Какой угол называют прямым? Прямым углом называют угол, градусная мера которого равна 90°.
12. Какой угол называют тупым? Тупым углом называют угол, градусная мера которого больше 90°, но меньше 180°.
13. На какие углы делит развёрнутый угол его биссектриса? Биссектриса делит угол на два прямых угла, то есть градусная мера каждого из этих углов равна 90°.
14. В каких случаях говорят, что от данного луча отложен данный угол? Говорят, что от данного луча отложен данный угол в том случае, если дан определённый луч, например ОА, и от него построен заданный угол, например ∠АОС = 63°, причём вершиной угла является вершина заданного луча.
Решаем устно
1. Назовите два числа, одно из которых:
- на 27 больше другого — 1 и 28 — число 28 на 27 больше числа 1.
- на 15 меньше другого — 2 и 17 — число 2 на 15 меньше числа 17.
- в 7 раз меньше другого — 3 и 21 — число 3 в 7 раз меньше исла 21.
- в 3 раза больше другого — 4 и 12 — число 12 в 3 раза больше 4.
2. Часы спешат на 10 мин и сейчас показывают время 10 ч 8 мин. Который час на самом деле?
10 ч 8 мин — 10 мин = 9 ч 58 мин
Ответ: сейчас 9 ч 58 мин.
3. Часы отстают на 7 мин и сейчас показывают время 16 ч 55 мин. Который час на самом деле?
16 ч 55 мин + 7 мин = 17 ч 2 мин.
Ответ: сейчас 17 ч. 2 мин.
4. Какие из следующих уравнений не имеют корней:
- 2х = х. Это равенство будет верным только при х = 0, значит у этого уравнения есть единственный корень — 0.

- 0х = 0. Это равенство будет верным при любом значении х, значит у этого уравнение бесконечное множество корней.
- 3 — х = 3. Это равенство будет верным только при х = 0, значит у этого уравнения есть единственный корень — 0.
- 0х = 6. Это равенство не будет верным ни при каких значениях х, значит это уравнение не имеет корней.
- х • х = х. Это равенство будет верным только при х = 0 и х = 1, значит у этого уравнения 2 корня: 0 и 1.
- х + 6 = х + 7. Это равенство не будет верным ни при каких значениях х, значит это уравнение не имеет корней.
- 8х = 0. Это равенство будет верным только при х = 0, значит у этого уравнения есть единственный корень — 0.
- 3 — х = 2. Это равенство будет верным только при х = 1, значит у этого уравнения есть единственный корень — 1.
- 1 • х = 5. Это равенство будет верным только при х = 5, значит у этого уравнения есть единственный корень — 5.
Ответ: не имеют корней уравнения под номером 4 и 6.
5. Для озеленения улицы длиной 3 км на одной из её сторон посадили деревья на расстоянии 20 м друг от друга. Первое дерево было посажено в начале улицы, а последнее — в её конце. Сколько деревьев было посажено? Чему равно расстояние между первым и пятым деревьями?
3 км = 3 000 м.
1) 3 000 : 20 + 1 = 151 (дерево) — было посажено.
2) 20 • (5 — 1) = 20 • 4 = 80 (метров) — расстояние между 1-м и 5-м деревом.
Ответ: Было посажено 151 дерево. Между первым и пятым деревом 80 метров.
Упражнения
296. Начертите:
- острый угол EFC
- прямой угол ORT
- тупой угол D
- развёрнутый угол КАР
297. Найдите на рисунке 93 острые, тупые и прямые углы.
- Острые углы: ∠C, ∠M, ∠P
- Тупые углы: ∠K, ∠Q, ∠T
- Прямые углы: ∠A, ∠O
298. Какие из данных углов острые, тупые, прямые, развёрнутые: ∠А = 96°, ∠B = 84°, ∠S= 180°, ∠D=90°, ∠R = 162°, ∠E= 60°, ∠Q = 100°, ∠M= 72°?
- Острые углы: ∠B = 84°, ∠E= 60°, ∠M= 72°
- Тупые углы: ∠А = 96°, ∠R = 162°, ∠Q = 100°
- Прямые углы: ∠D=90°
- Развёрнутые углы: ∠S= 180°
299. Найдите, пользуясь транспортиром, градусные меры углов, изображённых на рисунке 94. Определите вид каждого угла.
Найдите, пользуясь транспортиром, градусные меры углов, изображённых на рисунке 94. Определите вид каждого угла.
- ∠AMK = 28º — острый угол
- ∠CTF = 33º — острый угол
- ∠POB = 120º — тупой угол
- ∠SNE = 125º — тупой угол
300. Найдите, пользуясь транспортиром, градусные меры углов, изображённых на рисунке 95. Определите вид каждого угла.
- ∠PRT = 133º — тупой угол
- ∠EFM = 40º — острый угол
- ∠BCQ = 110º — тупой угол
- ∠AKS = 67º — острый угол
301. Начертите угол, градусная мера которого равна: 1) 38°; 2) 124°; 3) 92°; 4) 90°; 5) 87°; 6) 54°; 7) 170°; 8) 65°. Определите вид каждого угла.
- ∠A = 38º — острый угол
- ∠B = 124º — тупой угол
- ∠C = 92º — тупой угол
- ∠D = 90º — прямой угол
- ∠E = 87º — острый угол
- ∠F = 54º — острый угол
- ∠K = 170º — тупой угол
- ∠R = 65º — острый угол
302. Проведите луч. Отложите от этого луча угол, градусная мера которого равна: 1) 40°; 2) 130°; 3) 68°; 4) 164°. Определите вид каждого из построенных углов.
Проведите луч. Отложите от этого луча угол, градусная мера которого равна: 1) 40°; 2) 130°; 3) 68°; 4) 164°. Определите вид каждого из построенных углов.
Луч RE
- ∠ERD = 40º — острый угол
- ∠ERB = 130º — тупой угол
- ∠ERC = 68º — острый угол
- ∠ERA = 164º — тупой угол
303. На рисунке 96 ∠CMK = 132°, а угол АМК — развёрнутый. Вычислите величину угла АМС.
∠АМК = 180° — развёрнутый
∠АМС = ∠АМК — ∠CMK = 180° — 132° = 48°
Ответ: ∠АМС = 48°.
304. На рисунке 97 угол АОК — прямой, ∠POC — 54°, а угол СОК — развёрнутый. Вычислите величину угла АОР.
∠AOK = 90° — прямой
∠COК = 180° — развёрнутый
∠АOP = ∠COK — ∠POC — ∠AOK = 180° — 54° — 90° = 36°
Ответ: ∠АOP = 36°
305. Какой из углов, изображённых на рисунке 98, наибольший? Наименьший?
- ∠D — наименьший угол
- ∠C — наибольший угол
306.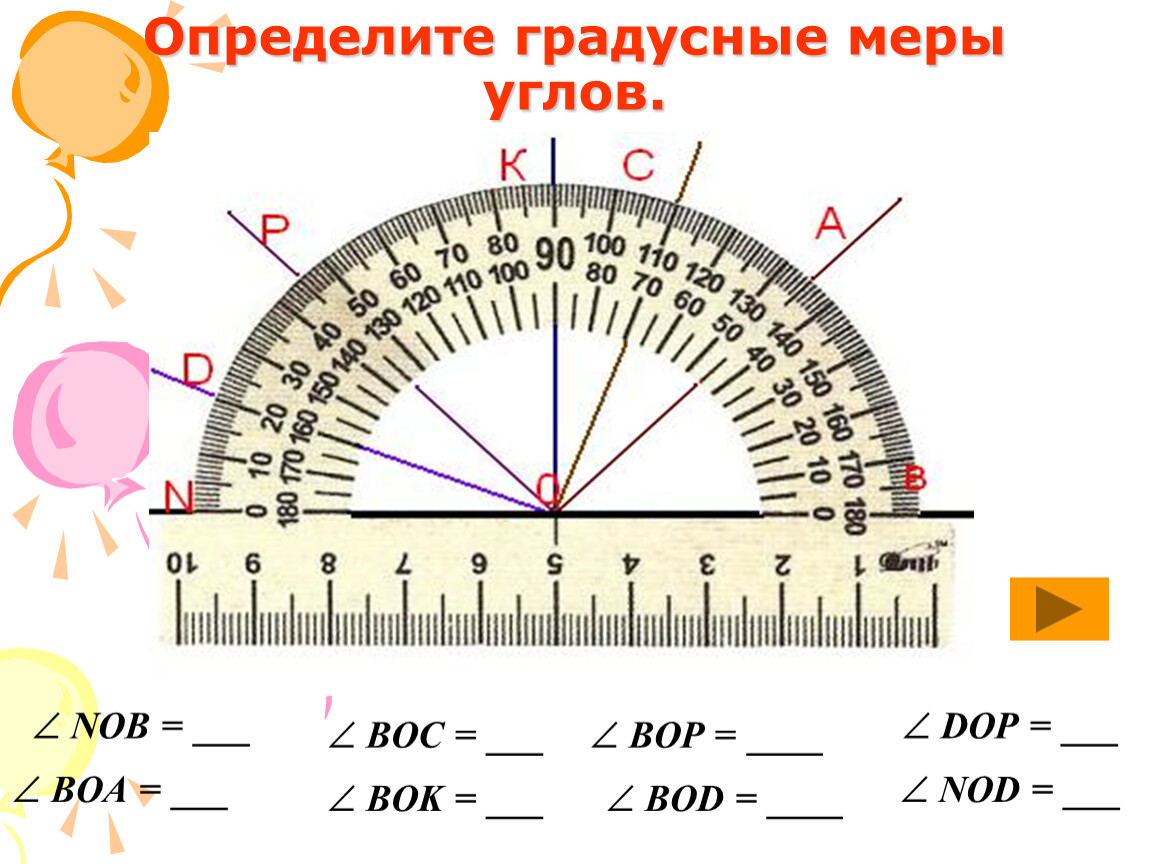 Начертите угол CDE, равный 152°. Лучом DA разделите этот угол на два угла так, чтобы ∠CDA = 98°. Вычислите величину угла ADE.
Начертите угол CDE, равный 152°. Лучом DA разделите этот угол на два угла так, чтобы ∠CDA = 98°. Вычислите величину угла ADE.
∠CDE = 152°
∠CDA = 98°
∠ADE = ∠CDE — ∠CDA = 152° — 34° = 54°
Ответ: ∠ADE = 54°.
307. Начертите угол ABC, равный 106°. Лучом BD разделите этот угол на два угла так, чтобы ∠ABD = 34°. Вычислите величину угла DBC.
∠ABC = 106°
∠ABD = 34°
∠DBC = ∠ABC — ∠ABD = 106° — 34° = 72°
Ответ: ∠DBC = 54°.
308. Из вершины прямого угла ВОМ (рис. 99) проведены два луча ОА и ОС так, что ∠BOC = 74°, ∠AOM = 62°. Вычислите величину угла АОС.
∠ВОМ = 90° — прямой
∠BOC = 74°
∠AOM = 62°
∠MOC = ∠BOM — ∠BOC = 90° — 74° = 16°
∠AOC = ∠AOM — ∠MOC = 62° — 16° = 46°
Ответ: ∠AOC = 46°.
309. Из вершины развёрнутого угла АСР (рис. 100) проведены два луча СТ и CF так, что ∠ACF = 158°, ∠TCP = 134°. Вычислите величину угла TCF.
∠ACP = 180° -развёрнутый
∠ACF = 158°
∠TCP = 134°
∠PCF = ∠ACP — ∠ACF = 180° — 158° = 22°
∠TCF = ∠TCP — ∠PCF = 134° — 22° = 112°
Ответ: ∠TCF = 112°.
310. Верно ли утверждение:
1) угол, который меньше тупого, — острый. Неверно, так как меньше тупого не только острые углы, но и прямой угол.
2) угол, который меньше развёрнутого, — тупой. Неверно, так как меньше развёрнутого угла все тупые углы, все острые углы и прямой угол.
3) половина тупого угла — острый угол. Верно, так как половина даже самого большого тупого угла будет меньше 90º.
4) сумма градусных мер двух острых углов больше 90°. Неверно, так как сумма двух острых углов может быть и меньше 90°.
5) угол, который больше прямого, — тупой. Неверно, так как больше прямого могут быть как тупые углы, так и развёрнутый угол.
311. Найдите градусную меру утла между стрелками часов, если они показывают:
- 3 ч — это угол между минутной стрелкой, указывающей на 12 часов (чёрная стрелка) и часовой стрелкой, указывающей на 3 часа (красная стрелка) — прямой угол.
 Градусная мера этого угла — 90º.
Градусная мера этого угла — 90º. - 6 ч — это угол между минутной стрелкой, указывающей на 12 часов (чёрная стрелка) и часовой стрелкой, указывающей на 6 часов (синяя стрелка) — развёрнутый угол. Градусная мера этого угла — 180º.
- 4 ч — это угол между минутной стрелкой, указывающей на 12 часов (чёрная стрелка) и часовой стрелкой, указывающей на 4 часа (зелёная стрелка) — 4/6 от развёрнутого угла. Градусная мера этого угла — 180 : 6 • 4 = 30 • 4 = 120º.
- 11 ч — это угол между минутной стрелкой, указывающей на 12 часов (чёрная стрелка) и часовой стрелкой, указывающей на 11 часов (фиолетовая стрелка) — 1/6 от развёрнутого угла. Градусная мера этого угла — 180 : 6 • 1 = 30 • 1 = 30º.
- 7 ч — это угол между минутной стрелкой, указывающей на 12 часов (чёрная стрелка) и часовой стрелкой, указывающей на 7 часов (розовая стрелка) — 5/6 от развёрнутого угла. Градусная мера этого угла — 180 : 6 • 5 = 30 • 5 = 150º.

Ответ: 1) 90º, 2) 180º, 3) 120º, 4) 30º, 5) 150º.
312. Луч BK является биссектрисой угла CBD, ∠ABK = 146° (рис. 101, a). Вычислите градусную меру угла CBD.
∠ABC = 180º — развёрнутый
∠ABK = 146º
∠KBC = ∠ABC — ∠ABK = 180º — 146º = 34º
так как луч BK — это биссектриса ∠CBD, значит луч BK делит тот угол пополам. Мы заем, что ∠KBC = 34º. Значит:
∠CBD = ∠KBC • 2 = 34º • 2 = 68º
Ответ: ∠CBD = 68º.
313. Луч ОА является биссектрисой угла СОМ, ∠СОМ = 54° (рис. 101, б). Вычислите градусную меру угла ВОА.
∠COM = 54º
так как луч OA — это биссектриса ∠COM, значит луч OA делит тот угол пополам. Мы заем, что ∠COM = 54º. Значит:
∠COA = ∠COM : 2 = 54º : 2 = 27º
∠BOC = 180º — развёрнутый
∠BOA = ∠BOC — ∠COA = 180º — 27º = 153º
Ответ: ∠BOA = 153º.
314. Проведите три прямые, пересекающиеся в одной точке. Запишите все развёрнутые углы, образовавшиеся при этом.
Каждая прямая образует по 2 развёрнутых угла. Значит образовались следующие развёрнутые углы: AOD, BOE, COF, DOA, EOB, FOC.
315. Проведите шесть прямых, пересекающихся в одной точке. Верно ли, что среди образовавшихся при этом углов есть угол, градусная мера которого меньше 31°?
Каждая прямая образует по 2 развёрнутых угла. Например, прямая MH образует развёрнутые углы MOH и HOM. Каждый из этих углов равен 180º. Значит сумма углов между соседними лучами на рисунке равна 180º • 2 = 360º.
Всего образовалось 12 углов, расположенных между соседними лучами. 360º : 12 = 30º. Значит как минимум один (а на самом деле два) угла будут иметь градусную меру менее 31º.
Ответ: верно.
Упражнения для повторениях
316. Заполните цепочку вычислений:
- 4 см • 300 = 1 200 см
- 1 200 см = 120 дм; 120 дм — 12 дм = 108 дм
- 108 дм : 9 = 12 дм
- 12 дм = 1 м 2 дм; 1 м 2 дм + 3 м = 4 м 2 дм
- 8 мин • 15 = 120 мин
- 120 мин = 2 ч; 2 ч + 2 ч = 4 ч
- 4 ч = 240 мин; 240 мин : 6 = 40 мин
- 40 мин — 54 сек = 39 мин 6 сек
317. Верно ли неравенство (а + 253) • 7 < (9 864 — а) : 4 при а = 124?
Верно ли неравенство (а + 253) • 7 < (9 864 — а) : 4 при а = 124?
Ответ: при а = 124 неравенство неверно, так как 2 639 > 2 435.
318. В четыре стакана помещается столько же молока, сколько и в банку. В стакан и банку помещается 1 кг 200 г молока. Сколько граммов молока помещается в стакан?
Так как в одной банке помещается столько же молока, сколько и в 4 стаканах, то в банке и стакане будет содержаться столько же молока сколько в 5 стаканах (4 + 1 = 5).
1 кг 200 г = 1 200 г
1 200 : 5 = 240 (г) — молока помещается в стакан.
Ответ: 240 г.
319. Длина границы России с Китаем, Монголией и Казахстаном составляет 15 293 км. Найдите длину границы России с каждым из этих государств, если длина границы с Китаем и Монголией равна 7 694 км, а с Китаем и Казахстаном — 11 808 км.
1) 15 293 — 11 808 = 3 485 (км) — граница России с Монголией.
2) 7 694 — 3 485 = 4 209 (км) — граница России с Китаем.
3) 11 808 — 4 209 = 7 599 (км) — граница России с Казахстаном.
Ответ: граница России с Китаем — 4 209 км, с Монголией — 3 485 км, с Казахстаном — 7 599 км.
Задача от мудрой совы
320. Улитка за день поднимается вверх по столбу на 3 м, а за ночь съезжает по нему на 2 м вниз. На какой день она доберётся до вершины столба, высота которого равна 20 м?
Каждые сутки улитка способна подняться по столбу на 1 м:
1) 3 метра днём — 2 метра ночью = 1 метр за сутки
Но в последний день она как обычно поднимется на 3 метра, а спускаться уже не будет. Значит, за все дни, кроме последнего, улитка поднимется на 17 м:
2) 20 — 3 = 17 (метров) — преодолеет улитка за все дни, кроме последнего.
То есть ей потребуется 17 дней для преодоления 17 метров и ещё 1 день для преодоления последних 3 метров:
3) 17 : 1 + 1 = 17 + 1 = 18 (дней) — нужно улитке для того, чтобы подняться на столб.
Ответ: улитка доберётся до вершины на 18-й день.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Формула, значение и примеры, инструменты
На вечеринке по случаю дня рождения Джона его мама Эмма хотела, чтобы у гостей были одинаковые кусочки торта. Для того, чтобы добиться этого, торт должен быть срезан под равными углами. Но как мы можем измерить эти углы?
В этой статье мы объясним концепцию меры угла.
Угол — это пространство между двумя пересекающимися лучами в месте их встречи.
Измерение угла относится к процессу определения размера, конкретного значения угла, образованного между двумя лучами в общей вершине. Это можно сделать вручную или математически с помощью расчетов.
Как измерить углы вручную с помощью инструмента?
Углы можно измерять вручную с помощью транспортира . Это делается путем размещения транспортира на одном из лучей, при этом значение 0 находится на пересечении двух лучей (общая вершина), и при этом смотрите, какое значение второго луча достигает транспортира.
Изображение правильного использования транспортира, mathbites.com
Как вы можете видеть выше, угол между двумя синими лучами составляет 40°. Транспортиром углы измеряются в градусов .
Как математически измерить углы?
Углы также могут быть математически измерены различными способами. Например, используя тот факт, что сумма всех углов вдоль прямой линии должна составлять 180°, мы можем вычислить значения недостающих углов.
Найдите значение x.
Решение
Два угла на диаграмме должны составлять в сумме 180°, так как они лежат на прямой, поэтому x=180-109=71°.
По какой формуле измерять углы?
Чтобы найти недостающие углы в многоугольниках , мы можем вычислить сумму внутренних углов, используя формулу полигон. Отсюда мы можем найти недостающий угол.
Найдите значение угла x.
Решение
Вы видите, что фигура выше имеет 6 сторон, это шестиугольник.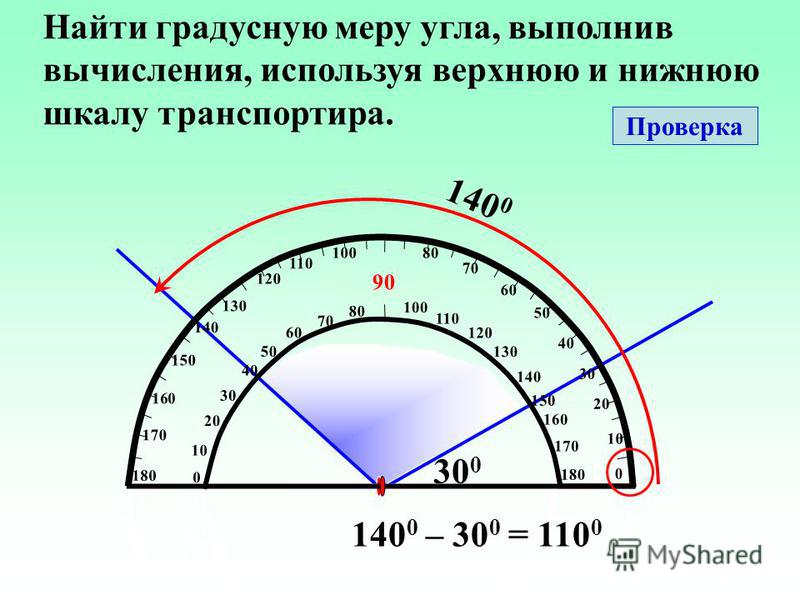
Следовательно, сумма внутренних углов равна
(6-2)×180°=720°
Зная значения всех остальных углов, мы можем вычислить x.
x=720-(138+134+100+112+125)=111°
Сумма всех внешних углов любого многоугольника всегда равна 360°. Это не зависит от количества сторон многоугольника. Следовательно, вы также можете использовать этот факт для поиска недостающих внешних углов.
Углы в треугольнике можно измерить математически с помощью тригонометрии . Тригонометрия — это область математики, которая связывает углы и стороны в треугольниках. Например, в прямоугольном треугольнике, если мы знаем длину двух сторон треугольника, мы можем вычислить любой угол θ, используя SOH CAH TOA.
Как измерить углы треугольника? Если у нас есть прямоугольный треугольник, как показано ниже, и мы обозначим один угол θ, мы должны обозначить три стороны треугольника Противоположные (для единственной стороны, которая противоположна углу θ и не соприкасается с этот угол), Гипотенуза (для самой длинной стороны, которая всегда находится напротив угла 90°) и Примыкающая (для последней стороны).
Обозначение сторон прямоугольного треугольника, StudySmarter Originals
синус, косинус и тангенс отношения относятся к отношению двух сторон в прямоугольном треугольнике к одному из углов. Чтобы запомнить, какие функции включают какие стороны треугольника, мы используем аббревиатуру SOH CAH TOA . S, C и T обозначают синус, косинус и тангенс соответственно, а O, A и H — противоположность, смежность и гипотенузу. Таким образом, отношение синуса включает в себя противоположность и гипотенузу, и так далее.
Треугольники SOH CAH TOA для запоминания тригонометрических функций, StudySmarter Originals
Все отношения синуса, косинуса и тангенса равны количеству сторон, в которые они входят, деленным друг на друга.
sinθ=противоположная гипотенуза,cosθ=прилежащая гипотенуза,tanθ=противоположноприлегающая
Найдите значение угла θ.
Решение
Из этой диаграммы видно, что гипотенуза = 9 см, а прилежащая = 4 см. Следовательно, мы можем вычислить значение cos угла θ.
Следовательно, мы можем вычислить значение cos угла θ.
cosθ=49=0,444
Чтобы теперь найти сам угол, вам нужно будет нажать кнопку cos-1 на вашем калькуляторе и ввести 0,444. Это даст ответ 63,6°.
В каких единицах измеряется угол?
Углы могут быть измерены в градусов и радиан . Градусы варьируются от 0 до 360°, а радианы — от 0 до 2π. Эта единица может быть более распространенной, но вы можете легко конвертировать между ними, используя формулу
Радианы = градусы × π180
Радианы часто выражаются в терминах π, где это возможно.
Измеренный угол треугольника равен 45°. Что это в радианах?
Решение
Используя приведенную выше формулу, находим, что
радиан=45×π180=π4
Как измерить острые углы?
Давайте вернемся к его определению.
Острый угол — это угол, величина которого меньше 90°.
Этот тип угла может быть измерен любым из упомянутых выше способов, точно так же, как тупой угол или прямой угол.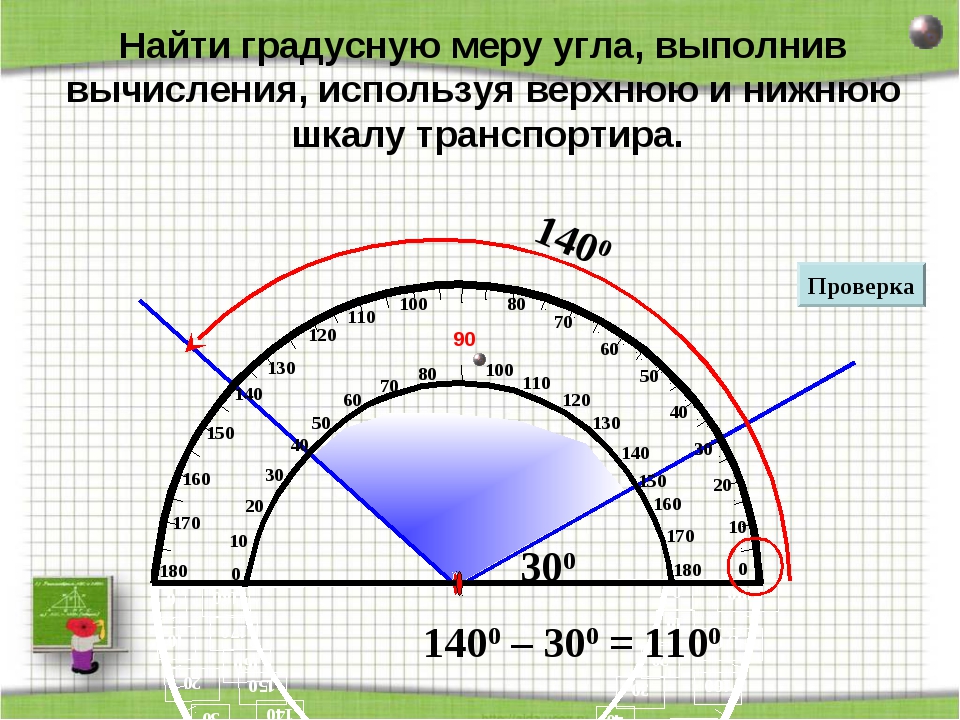
Острый угол можно измерить транспортиром, с помощью тригонометрии (SOH CAH TOA) в треугольнике или по формуле
(n-2)×180°n
для правильных многоугольников.
Измерение угла — основные выводы
- Измерение угла относится к процессу определения значения угла, образованного между двумя линиями. Это можно сделать вручную или математически.
- Вручную для измерения углов можно использовать транспортир
- В любом многоугольнике сумма внутренних углов равна (n-2)×180°, где n — количество сторон, а сумма внешних углов всегда равна 360°
- В прямоугольном треугольнике SOH CAH TOA можно использовать для вычисления значения любого угла
- Углы можно измерять в градусах или радианах, где радианы = градусы × π180
Как найти углы в столярном деле
В этом руководстве по проекту «Сделай сам» вы узнаете, как находить углы в столярных работах, используя набор различных инструментов, включая транспортиры и угловые скосы, а затем точно отметьте угол на заданном объекте, готовом к резке. Вы также узнаете, как настроить и отрезать угол с помощью торцовочной или ручной пилы.
Вы также узнаете, как настроить и отрезать угол с помощью торцовочной или ручной пилы.
Вычисление углов и резка таких элементов, как древесина, кирпичи, блоки, доски и т. д., для установки под углом — чрезвычайно распространенная работа в строительной отрасли.
Если вы когда-нибудь делали что-нибудь своими руками, скорее всего, вам нужно было отрезать кусок плинтуса или свода под заданным углом, чтобы получился стык под углом. По сути, это включает в себя разрезание двух соединительных элементов под углом 45 ° на каждом конце, где они встречаются, так что они образуют угол 90 °.
Угол под углом 90 градусов
Некоторые из наиболее распространенных работ, связанных с подрезкой уголков своими руками:
- Установка свода
- Резка и фиксация плинтуса
- Установка плинтуса и направляющих для картин
- Несущие стены и кровля
- Гипсокартон или гипсокартон
- Плитка
Как видно из вышеизложенного, почти каждая область строительства и самостоятельных работ требует некоторого расчета угла, и в конечном итоге общее качество отделки будет зависит от того, насколько точно обрезаны углы, поэтому крайне важно, чтобы вы знали, как выработать угол, а затем как его обрезать.
Как найти угол резки
Прежде чем мы сможем что-то вырезать, нужно определить точный угол, под которым вам нужно вырезать.
Практически во всех ситуациях поверхность, с которой вы работаете, не будет квадратной, хотя может показаться, что она квадратная. Например, если вы соедините два куска плинтуса вместе в углу комнаты, есть вероятность, что угол, в котором вы работаете, не будет идеально 90°
Мы получаем сотни вопросов от людей о том, как они могут заполнить большие зазоры между плинтусами из-за того, что стены комнаты расположены не точно под прямым углом.
Имея это в виду, важно сначала определить точный угол, с которым вы работаете.
Есть несколько способов и инструментов, которые вы можете использовать для этого:
Используйте старую добрую математику
Если вы хорошо разбираетесь в старой математике, то должно быть достаточно легко вычислить внутренние углы треугольника, который вы можно создать из области, в которой вы работаете.
Например, вы можете одинаково измерить каждую сторону треугольника, а затем также более длинную линию гипотенузы, которая соединяет две другие линии вместе, а затем определить все внутренние углы.
Измерение и маркировка угла комнаты для создания треугольника для определения углов
Мы не будем вдаваться в точные расчеты, необходимые ей, но отличное объяснение того, как можно решить sss треугольники (сторона, сторона, сторона) можно найти на веб-сайте Maths is Fun здесь.
Используйте специальные инструменты для определения угла
Каким бы хорошим и точным ни было приведенное выше математическое решение, иногда просто нецелесообразно тратить драгоценные минуты на выполнение вычислений, особенно если вы находитесь на месте, где время — деньги.
С этой целью существует множество ручных и цифровых угломеров, которые могут очень быстро и точно найти любой заданный угол для вас, вот некоторые распространенные:
Каждый из вышеперечисленных инструментов можно использовать для точной отметки заданного угла. практически на любой поверхности. Однако, если вы также хотите знать, с каким углом вы имеете дело, некоторые инструменты могут быть лучше, чем другие.
практически на любой поверхности. Однако, если вы также хотите знать, с каким углом вы имеете дело, некоторые инструменты могут быть лучше, чем другие.
Например, угловая фаска позволит вам устанавливать и отмечать и изменять угол, но не имеет какой-либо формы визуального датчика, чтобы указать вам, что такое угол.
Аналогичным образом, стандартный транспортир является отличным инструментом для разметки линии разреза под углом на данном объекте, но попытка использовать его для определения точного угла угла комнаты была бы практически невозможной.
Имея в виду вышеизложенное, если вы хотите приобрести инструменты для определения угла, убедитесь, что вы инвестируете в правильный инструмент, который будет соответствовать всем вашим требованиям.
Внутренние и внешние углы
Важный момент, который следует упомянуть, касается типа угла, который необходимо разметить и/или вырезать – внутренний угол или внешний угол?
Для пояснения, внутренний угол будет меньшим углом внутри объекта, с которым вы работаете, а внешний угол будет большим углом снаружи.
Чтобы точно понять, о чем мы говорим, давайте представим, что у нас есть каркасная стена, построенная по диагонали от существующей стены.
Поскольку мы отходим от существующей стены под углом, у нас будет больший угол с одной стороны стены, чем с другой, что дает нам меньший внутренний угол и больший внешний угол.
К этому моменту мы уже должны знать, с какой стороны объекта мы работаем, т.е. крепление нашего плинтуса к или установка нашей полки и т. д., и теперь, когда мы знаем наши 2 типа линейного угла, все, что нам нужно сделать, это измерить наш угол.
Совет : После того, как вы измерили один угол, т.е. внутренний угол, вы можете легко определить внешний угол.
Так как мы имеем дело с прямой линией, сколько бы углов у нас ни было, сумма их должна составлять 180°. Измерив наш внутренний угол, мы обнаружим, что он равен 35°, просто вычтите его из общей суммы 180°, и тогда мы получим наш внешний угол, в данном случае 145°
Вычисление внутренних и внешних углов вдоль линейной линии
Как рассчитать углы резания
Теперь, когда мы знаем, как вычислить угол с помощью математики или действительно измерить его с помощью специального инструмента, пришло время применить эти знания на практике. на практике и измерьте угол резания.
на практике и измерьте угол резания.
Для этого мы будем использовать один из наиболее часто используемых инструментов в строительной отрасли, особенно в столярном деле, – угловую фаску.
Для целей этого примера мы будем измерять угол между существующей стеной и стеной из стоек, чтобы можно было обрезать полку по размеру.
Установите наклонный скос на желаемый угол
Сначала возьмите скошенный скос и приложите приклад к плоской поверхности, затем ослабьте фиксирующий винт и переместите лезвие так, чтобы оно было заподлицо с наклонной поверхностью.
Убедитесь, что ложа и лезвие находятся на одном уровне с соответствующими поверхностями, а затем затяните стопорный винт, чтобы зафиксировать угол.
Угловой скос на месте и полностью затяните, чтобы зафиксировать угол
Набор для измерения угла
С нашим набором углов, следующая задача состоит в том, чтобы фактически измерить его, чтобы найти наш угол. Чтобы найти угол, заданный вашим скользящим скосом, лучше всего использовать стандартный транспортир.
Поместите фаску на плоскую поверхность прикладом к основанию.
Поместите плоскую кромку транспортира поверх инструмента для фаски и двигайте его вдоль, пока центральная точка транспортира не окажется прямо на одной линии с точкой, в которой лезвие начинает наклоняться вверх.
Наконец, посмотрите вверх и вдоль лезвия фаски и шкалы на транспортире и в точке, где лезвие останавливается над отметкой на шкале, это ваше показание угла – в данном случае рассматриваемый угол равен 135°
Измерение угла, заданного скошенным углом, с помощью транспортира
Проверка правильности измерения угла
При использовании ремня и подтяжек подход «дважды отмерь, один раз отрежь». что-либо.
Используя математический принцип, который мы изложили выше, например. угол, который мы только что измерили, и угол с другой стороны стойки, оба эти угла должны в сумме давать 180°
Поскольку мы теперь знаем наш первый угол, в данном случае 135°, мы снова можем используйте наш угловой скос и транспортир для измерения второго угла, который в данном случае должен быть равен 45°
Используйте наклонный скос, чтобы установить внутренний угол на другой стороне вашего объекта, в данном случае на нашей стене.
Использование наклонного скоса для установки противоположного угла на другой стороне стены
Как мы делали ранее, положите наклонный скос вниз так, чтобы приклад был горизонтальным, поместите транспортир сверху, а затем переверните его до точки, в которой лезвие начинает наклоняться над центральной точкой.
Как и раньше, читайте по шкале транспортира, пока не дойдете до точки, где лезвие пересекает точку шкалы, и это будет ваш угол.
Как мы и предполагали, наше показание равно 45°, а это означает, что наше начальное значение 135° для другого угла верно.
Измерение нашего противоположного угла, чтобы проверить правильность нашего первого измерения
Как точно отметить угол
Теперь, когда мы точно измерили наш угол, а также проверили правильность этого измерения, следующая задача — отметить наш под углом к поверхности, которую мы хотим разрезать.
Как уже упоминалось, в этом примере мы собираемся обрезать полку под углом, чтобы она плотно прилегала к нашей наклонной стене из стоек, когда задний край находится на одном уровне с плоской стеной позади.
Место для крепления полки, с плоской стенкой сзади и наклонной стенкой слева
Есть два решения, которые можно использовать для маркировки нашей полки:
- Используйте набор уголков на наклонном скосе
- Воспользуйтесь нашим транспортиром
Использование наклонного скоса для создания отметки для резки
Это, вероятно, самое быстрое и простое решение из всех.
На вашем объекте, в данном случае на полке, измерьте и отметьте точку, в которой должен начинаться угол. Убедитесь, что вы делаете свой знак в правильном месте!
Поскольку наш угол уже установлен на самом скосе, мы можем просто поместить скос на объект, который мы хотим отметить, так, чтобы край ложи был ровным по отношению к поверхности объекта, а точка, в которой лезвие начинает наклоняться находится непосредственно на отметке на объекте, который мы сделали выше.
С помощью ручки или карандаша просто проведите линию разреза от точки на объекте вдоль, используя лезвие в качестве линейки.
Установив угловой скос, отметьте кромку лезвия
Ваша линия реза теперь четко обозначена и готова к фактическому резанию.
Использование транспортира для отметки линии разреза
Мы также можем использовать транспортир для отметки линий и точек разреза.
Во-первых, поместите транспортир так, чтобы его центральная точка находилась прямо над отметкой, которую мы сделали выше, которая изображает начало нашего углового разреза.
Затем работайте по шкале на внешнем краю транспортира, пока не получите желаемый угол в градусах. В данном случае 135°, а затем отметьте эту точку ручкой или карандашом.
Использование транспортира для разметки наклонной линии разреза
Теперь, когда наши отметки сделаны, остается просто соединить их с помощью ручки или карандаша, и тогда у нас должна остаться четко определенная линия разреза.
Соединение меток для создания линии реза
Как уже было сказано, самый быстрый и простой способ — просто установить угол с помощью скользящего скоса, а затем нанести отметку напротив лезвия, но если вы хотите отметить точный угол, заданный транспортир, затем используйте этот метод.
Как точно вырезать угол
После того, как вы точно измерили и отметили нужный угол на объекте, следующая задача — его вырезать. Для этого у вас снова есть несколько вариантов.
Если вы достаточно опытны в использовании ручной пилы, то во что бы то ни стало используйте ручную пилу для резки.
Требуется некоторая практика, чтобы получить достойный прямой рез ручной пилой, но если вы чувствуете себя уверенно, дерзайте. Просто убедитесь, что выбранная вами пила хорошая и острая, так как это даст вам наилучшие шансы получить максимально ровный срез.
Однако, если у вас есть комбинированная торцовочная пила, торцовочная пила или аналогичная механизированная пила с плоским столом для резки, на который можно опирать объект во время резки, выберите этот вариант.
Использование электропилы в конечном счете даст вам наилучшие шансы на получение прямого и точного реза, поскольку вы можете подтолкнуть свой объект к направляющей, что позволит вам приложить к нему некоторое усилие, чтобы он не двигался во время резки.
Кроме того, поскольку лезвие, если оно зафиксировано, будет резать идеально прямую линию, не допуская никаких движений или шатких линий реза.
Чтобы установить правильный угол резки, если вы знаете точный угол, который вам нужен для резки, просто используйте угловую шкалу на столе пилы, чтобы установить угол.
Однако, если вы использовали наклонную фаску для обозначения угла, вы можете просто положить заготовку заподлицо с направляющей, а затем отрегулировать угловую шкалу так, чтобы выемка лезвия на режущем столе была выровнена и заподлицо с кромкой лезвие скошено.
Использование набора углов на наклонной фаске для установки правильного угла на торцовочной пиле
Установив правильный угол на торцовочной пиле, поместите объект на стол пилы, совместив линию реза с мертвой точкой выемки лезвия.
Линия реза выровнена на столе пилы и готова к резке
Не включая пилу, опустите диск и посмотрите, куда он упадет. Если все в порядке, он должен располагаться рядом с линией реза, но если нет или вам нужно резать немного в другом месте, переместите объект в нужное место.
Полка обрезана таким образом, чтобы идеально прилегать к плоской задней стенке и
Резка стыков болота для соответствия наклонной поверхности
Поскольку теперь мы точно знаем, как найти или измерить угол, а затем точно отметить на данном объекте, готовом к резке, чтобы он идеально подходил к наклонной поверхности, есть один еще один момент, касающийся углов резки, о котором вы должны знать.
Чтобы объяснить это в полной мере, нам нужно еще раз взглянуть на скромный сустав под углом. Как мы уже упоминали, одна из самых распространенных работ в столярном деле, а также в строительной отрасли в целом заключается в обеспечении того, чтобы два предмета, соприкасающиеся в углу, были хорошо обработаны, т.е. митред.
Чтобы гарантировать, что это произойдет, знание угла, под которым они вписываются в целом, является лишь частью. Поскольку два объекта, сходящиеся, образуют весь угол, каждый объект нужно будет разрезать на половину угла всего угла.
Чтобы немного пояснить, на изображении ниже показаны 3 стены, вдоль которых можно разместить плинтус.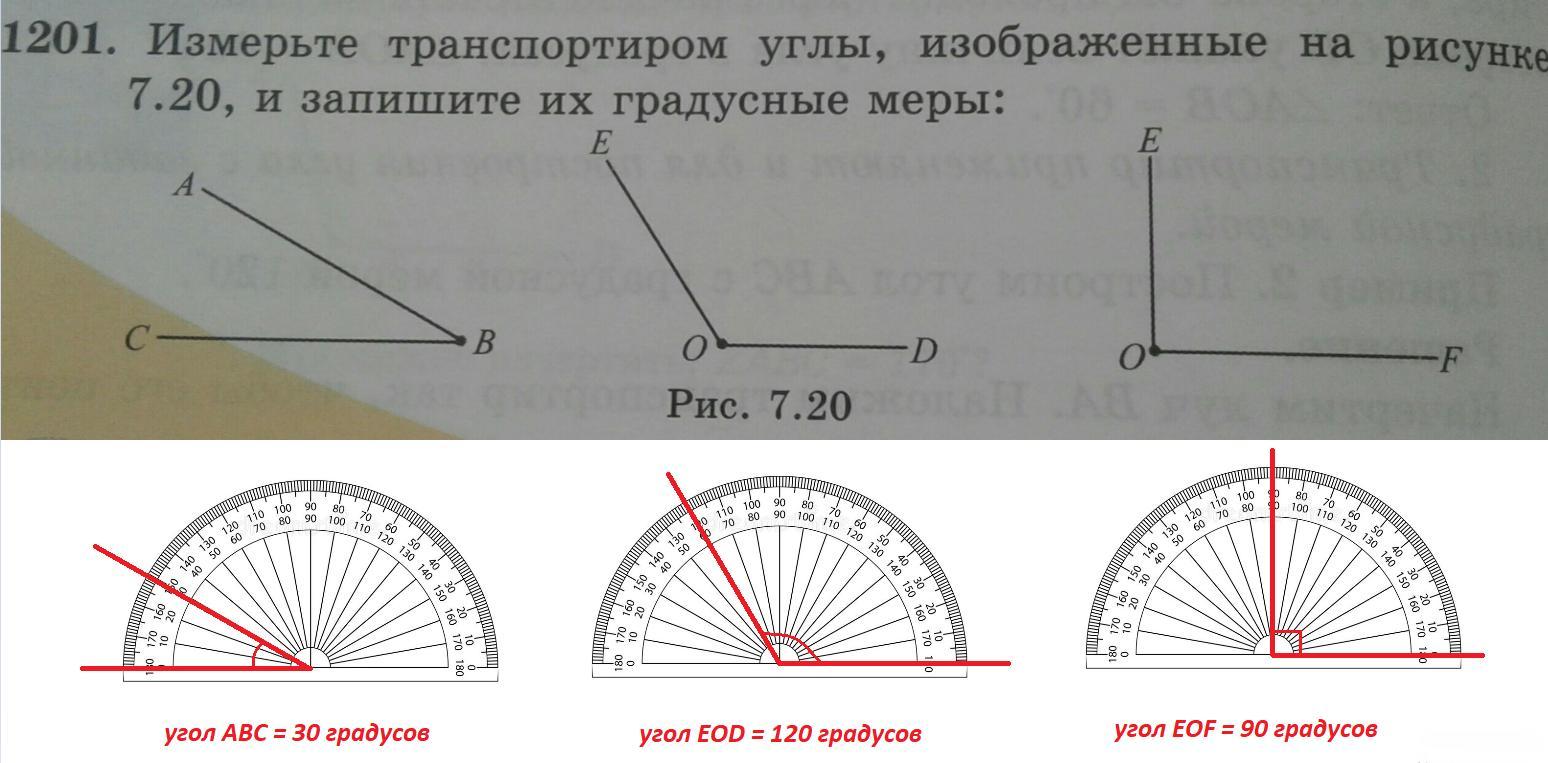


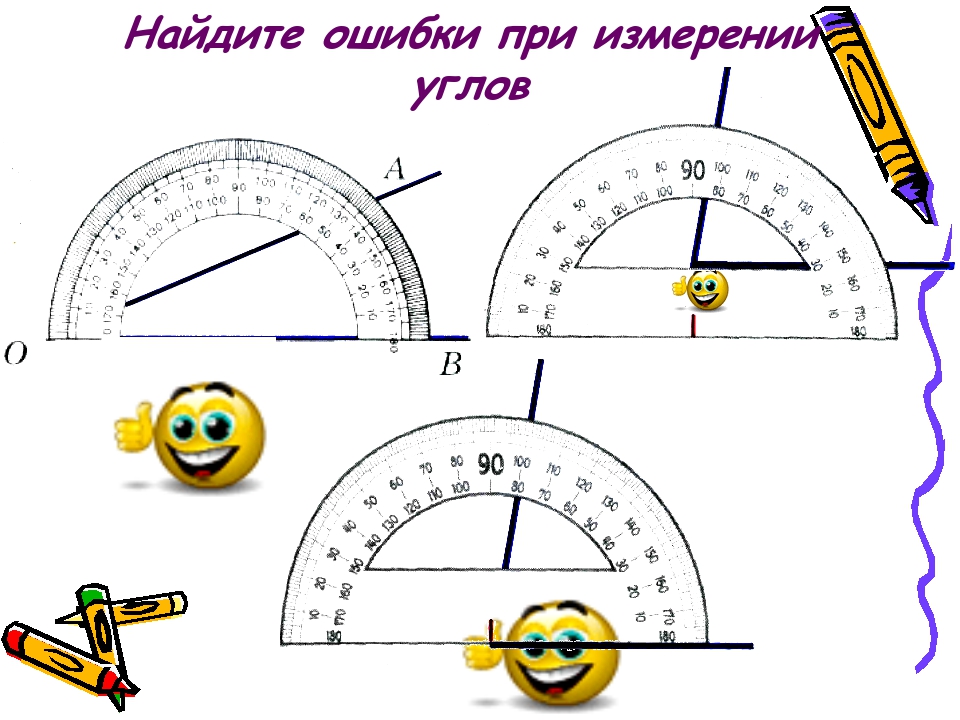



 Обратите внимание, что что нумерация идет слева направо и справа налево. В некоторых моделях – от 0 до 3600 – это круглые транспортиры. Транспортиры изготавливаются из стали, пластмассы, дерева и других материалов.
Обратите внимание, что что нумерация идет слева направо и справа налево. В некоторых моделях – от 0 до 3600 – это круглые транспортиры. Транспортиры изготавливаются из стали, пластмассы, дерева и других материалов.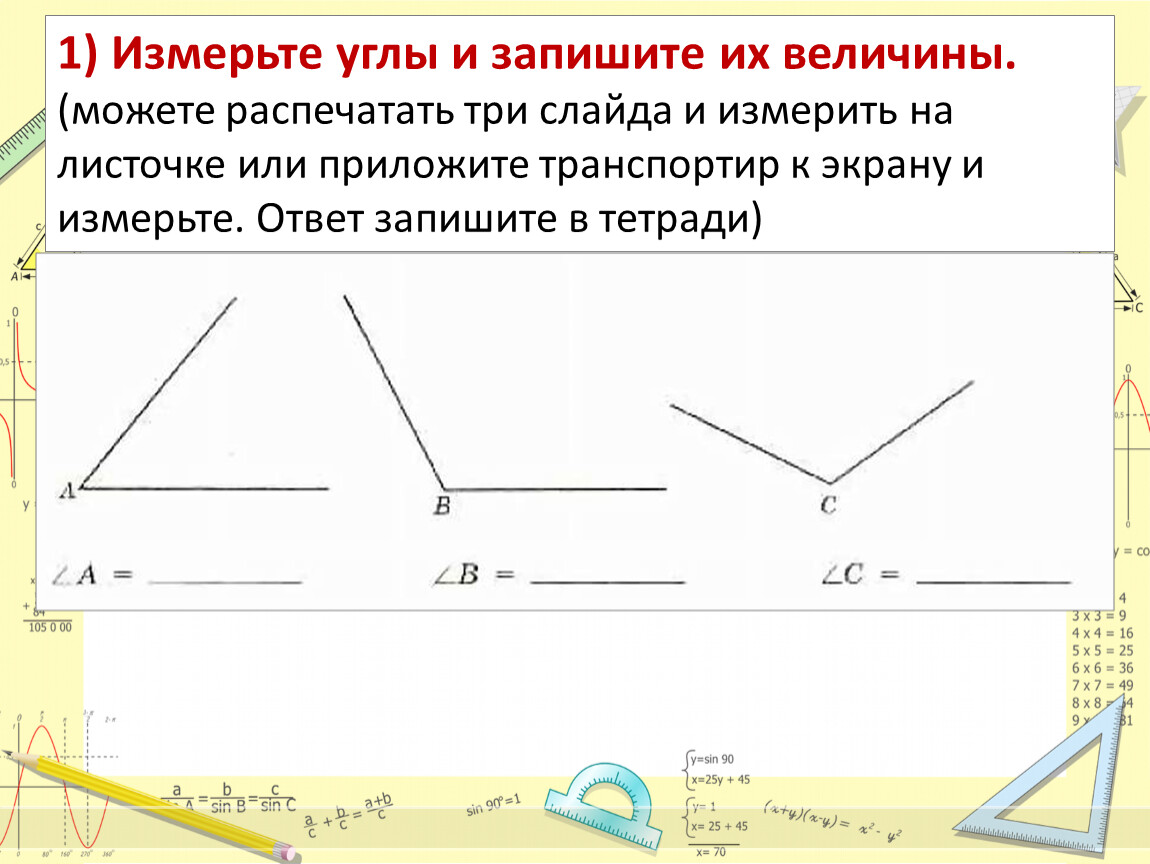 Какой ответ у нас верный? Кто правильно измерил поднимите руку.
Какой ответ у нас верный? Кто правильно измерил поднимите руку.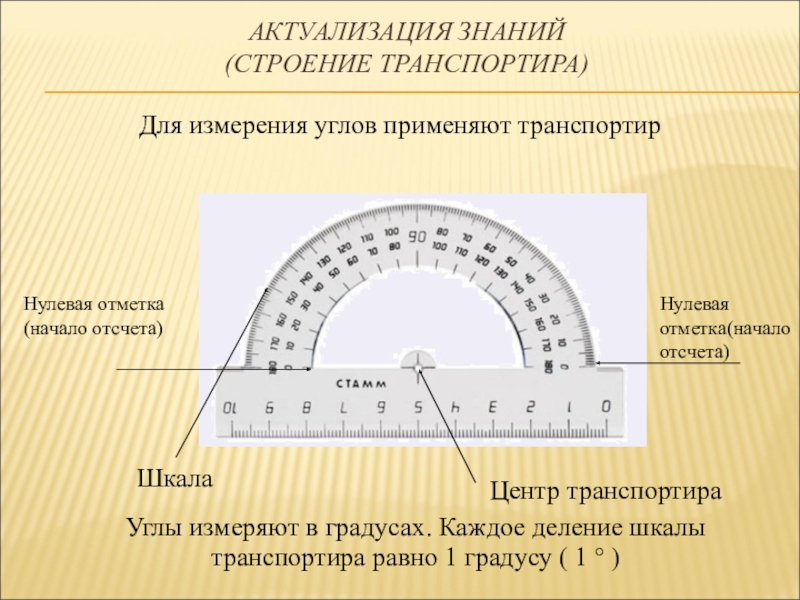

 (я в это время проверяю как дети работают). Кто закончил выполнять работу в паре, просигнализируйте (домик)
(я в это время проверяю как дети работают). Кто закончил выполнять работу в паре, просигнализируйте (домик)
 Можем ли мы ответить на него? Каким арифметическим действием?
Можем ли мы ответить на него? Каким арифметическим действием?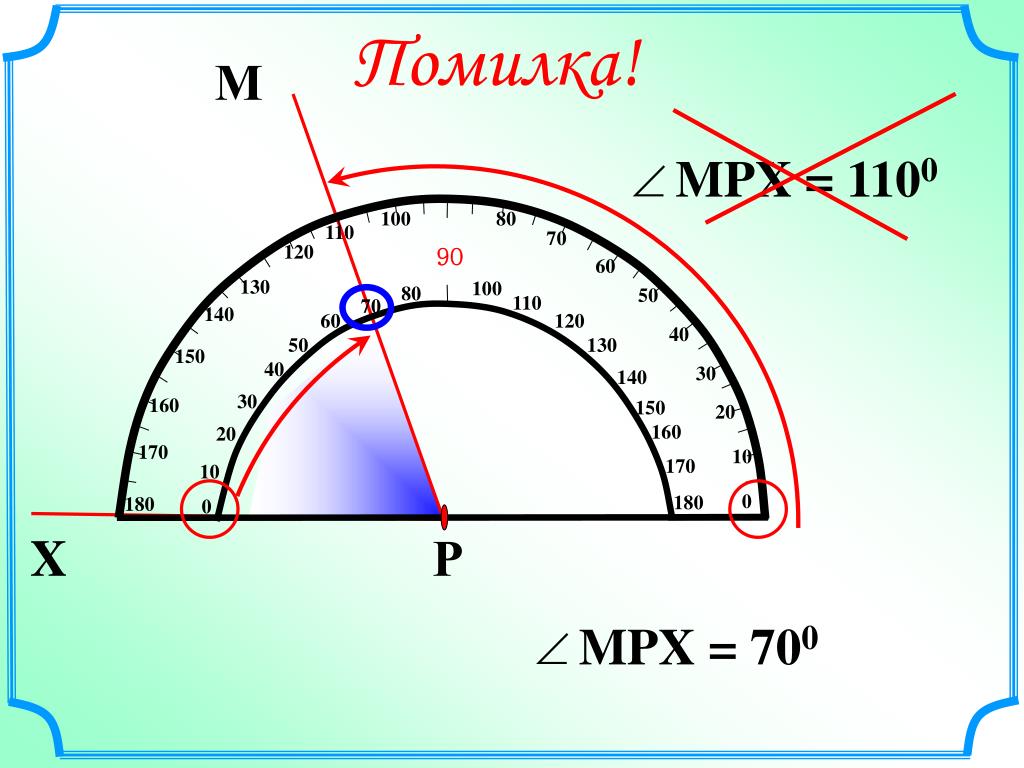 Рефлексия. 2-3 мин.
Рефлексия. 2-3 мин.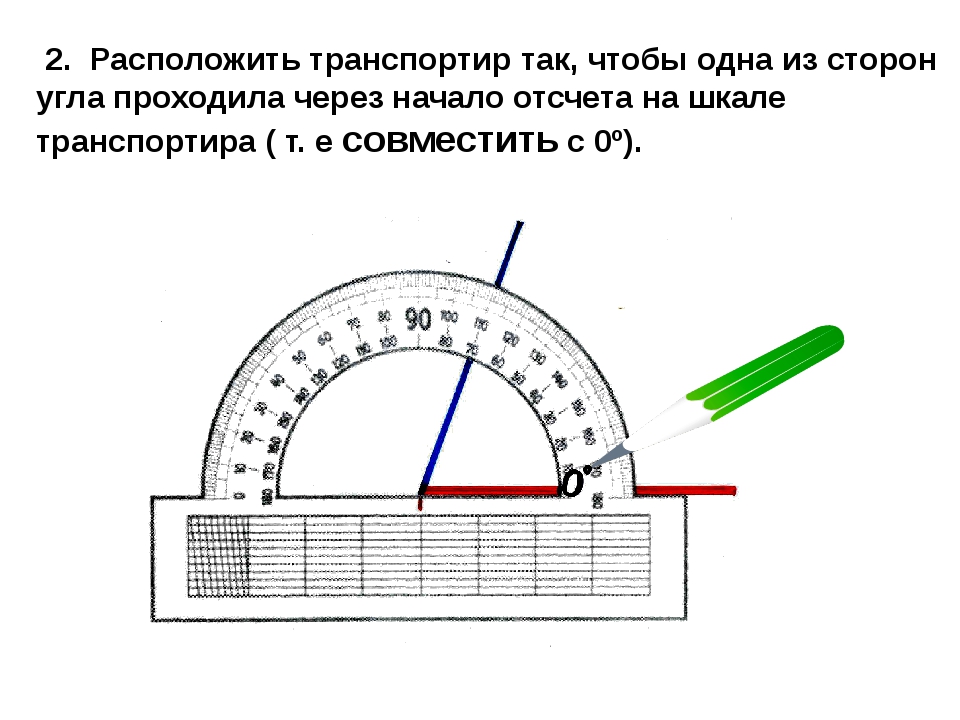 Поднимите зеленый карандаш те, кому все удалось на уроке.
Поднимите зеленый карандаш те, кому все удалось на уроке.