Как нарисовать 6 угольник: Как нарисовать правильный шестиугольник за 9 шагов

Разное

Содержание

Немного «кубизма» в CorelDRAW

4 — 2017

Один из распространенных приемов, которые используют дизайнеры при создании логотипов и стилизованных изображений, — имитация трехмерных объектов путем комбинирования простых геометрических фигур. В этой публикации мы рассмотрим один из способов выполнения подобных работ в графическом редакторе CorelDRAW, используя в качестве базового элемента квадрат.

Подготовительный этап

Для выполнения этой работы понадобится вспомогательный объект. Включите инструмент Многоугольник (Y), затем в поле Точки или стороны на панели свойств введите значение «6» (рис. 1). Удерживая нажатой клавишу Ctrl, создайте правильный шестиугольник (рис. 2).

Рис. 1. Поле ввода количества точек или сторон многоугольника на панели свойств

Рис. 2. Создание шестиугольника

Создание «кубиков»

Переключитесь на инструмент Разлинованная бумага (D) — рис. 3. В полях количества строк и столбцов на панели свойств введите значение «3» (рис. 4). Удерживая нажатой клавишу Ctrl, создайте матрицу из девяти квадратов (рис. 5).

Рис. 3. Пиктограмма выбора инструмента Разлинованная бумага на панели инструментов

Рис. 4. Поля ввода количества строк и столбцов на панели свойств

Рис. 5. Матрица из девяти квадратов, созданная при помощи инструмента Разлинованная бумага

Рис. 6. Расположение курсора над верхним левым углом группы квадратов

Рис. 7. Перемещение группы квадратов

Не снимая выделения, переключитесь на инструмент выбора. Наведите курсор на верхний левый угол созданной группы (рядом с указателем должна появиться надпись «узел» — рис. 6). Нажмите левую кнопку мыши и, удерживая ее, переместите выделенную группу таким образом, чтобы ее левый верхний угол оказался совмещен с вершиной шестиугольника (рис. 7). После того как рядом с курсором появится надпись «узел», отпустите кнопку (рис. 8).

Рис. 8. Верхний левый угол группы квадратов совмещен с вершиной шестиугольника

Рис.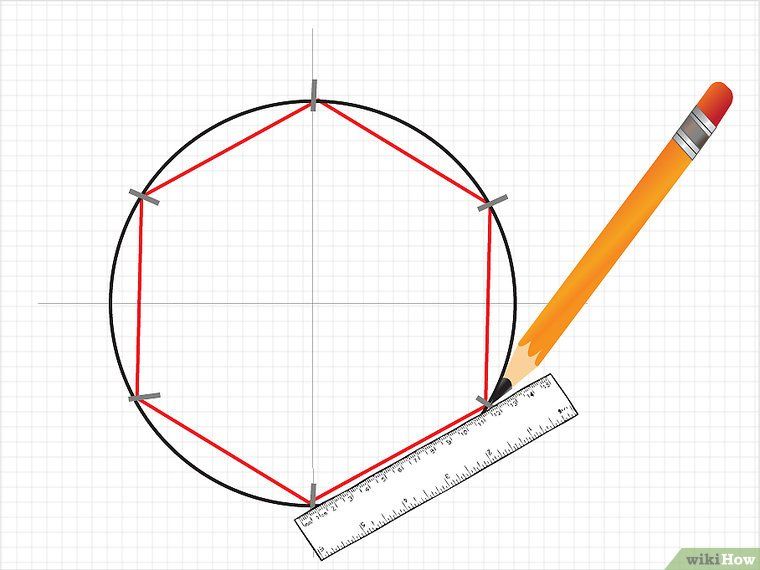 9. Установка направляющей

Установите горизонтальную направляющую таким образом, чтобы она проходила через левую нижнюю вершину шестиугольника. При выполнении этой операции ориентируйтесь по появлению надписи «узел» рядом с курсором (рис. 9). Выделите группу из девяти квадратов, затем передвиньте курсор на правый нижний маркер выделенной группы и, ориентируясь по направляющей, подгоните размер ее стороны под длину стороны шестиугольника (рис. 10).

Рис. 10. Подгонка размера группы квадратов

Рис. 11. Создание копии группы квадратов

Создайте копию выделенной группы, нажав сочетание клавиш CtrlD, и переместите ее в сторону (рис. 11).

Выделите группу квадратов, расположенную внутри шестиугольника. Наведите курсор на средний правый маркер и измените ширину группы таким образом, чтобы ее правая сторона проходила через центр шестиугольника. Ориентиром при выполнении этой операции служит появление надписи «по центру» рядом с курсором (рис. 12).

Рис.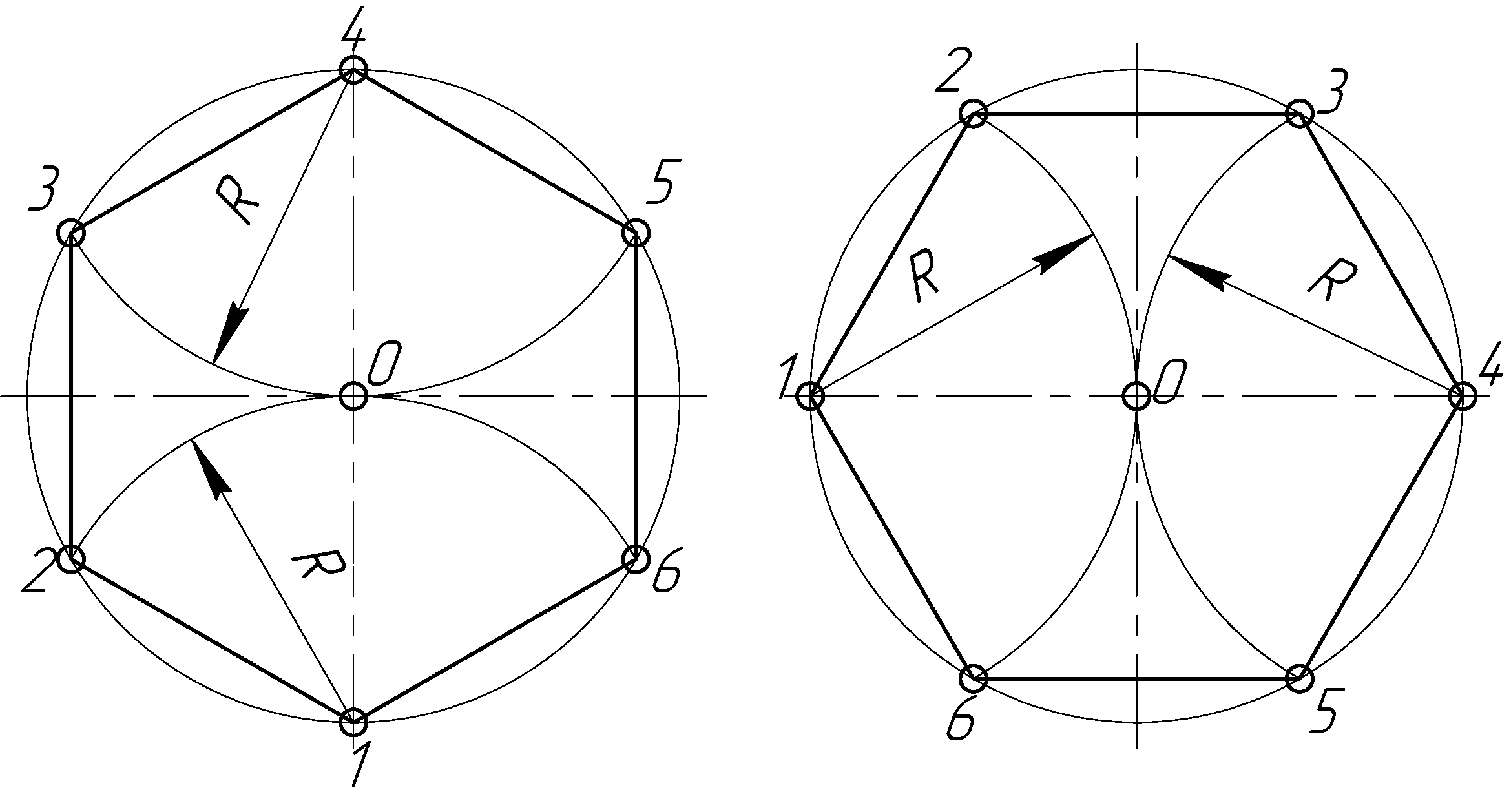 12. Изменение ширины группы квадратов

Рис. 13. Переключение в режим вращения

Рис. 14. Изменение формы группы квадратов

Щелкните по выделенной группе, чтобы переключиться на режим вращения (рис. 13). Наведите курсор на средний правый маркер и измените форму объекта, совместив его нижнюю сторону с близлежащей стороной шестиугольника (рис. 14). Щелкните по выделенной группе, чтобы переключиться на режим масштабирования (рис. 15).

Рис. 15. Переключение в режим масштабирования

Теперь необходимо создать зеркально отраженную копию выделенной группы. Откройте раздел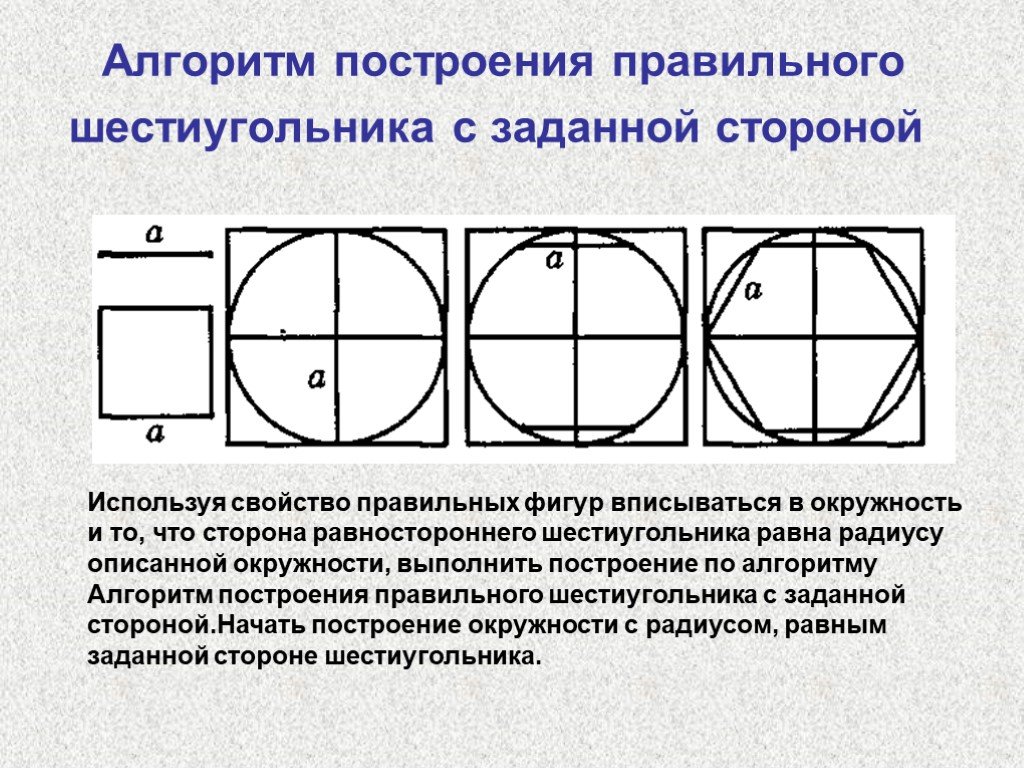

Масштаб и отражения палитры Преобразование, выбрав в меню Окно -> Окна настройки -> Преобразования -> Масштаб и отражение (рис. 16) или нажав сочетание клавиш AltF9. Нажмите кнопку Отразить по горизонтали, а в поле количества копий введите значение «1» (рис.

17). Нажмите кнопку Применить (рис. 18).

Рис. 16. Включение отображения раздела Масштаб и отражение палитры Преобразования в главном меню

Рис. 17. Кнопка Отразить по горизонтали в разделе Масштаб и отражение палитры Преобразования

Рис. 18. Кнопка Применить в палитре Преобразования

Не снимая выделения, наведите курсор на левый нижний угол созданной копии. Переместите эту группу, совместив ее на левый нижний угол с правым нижним углом исходного объекта (рис. 19 и 20). При выполнении этой операции ориентируйтесь по появлению надписи «узел» рядом с курсором.

Рис. 19. Перемещение зеркально отраженной копии группы квадратов

Рис. 20. Результат перемещения

Выделите ранее созданную копию группы квадратов, оставленную за пределами шестиугольника. Поверните ее на 45°, введя соответствующее значение в поле Угол поворота на панели свойств (рис. 21). Наведите курсор на нижнюю точку выделенной группы и переместите ее таким образом, чтобы она оказалась совмещенной с верхней точкой смежных сторон двух других групп. Ориентируйтесь по появлению надписи «узел» рядом с курсором (рис. 22).

Рис. 21. Поле ввода значения угла поворота выделенного объекта на панели свойств

Рис. 22. Перемещение группы квадратов

Переместите курсор на центральный верхний маркер и измените высоту выделенной группы таким образом, чтобы ее верхняя точка была совмещена с вершиной многоугольника (рис. 23).

Теперь установите курсор на один из средних боковых маркеров и, нажав и удерживая клавишу Shift, измените ширину выделенной группы таким образом, чтобы ее правая и левая вершины были совмещены с верхними точками двух других групп (рис. 24).

Рис. 23. Изменение высоты группы квадратов

Рис. 24. Изменение ширины группы квадратов

Шестиугольник и направляющая для выполнения дальнейших действий не потребуются, так что теперь их можно удалить. Для этого откройте палитру Диспетчер объектов, выбрав в меню Окно -> Окна настройки -> Диспетчер объектов (рис.

25). В списке объектов текущего слоя щелкните по названию Многоугольник (рис. 26) и нажмите клавишу Del. Затем выделите направляющую и удалите ее, нажав клавишу Del.

Рис. 25. Включение отображения палитры Диспетчер объектов в главном меню

Рис. 26. Выделение шестиугольника в палитре Диспетчер объектов

Раскрашиваем «кубики»

Выделите одну из групп и выберите для входящих в нее объектов однородную заливку какимлибо цветом (рис. 27). Разгруппируйте выделенный объект, выбрав в меню Объект -> Группа -> Отменить группировку (рис. 28) или нажав сочетание клавиш CtrlU. Аналогичным образом обработайте две другие группы, используя разные цвета заливки (рис. 29). Теперь у вас в распоряжении имеется заготовка, похожая на изображение кубика Рубика в изометрической проекции.

Рис. 27. Выбор заливки для одной из групп

Рис. 28. Выбор команды разгруппировки выделенных объектов в главном меню

Рис.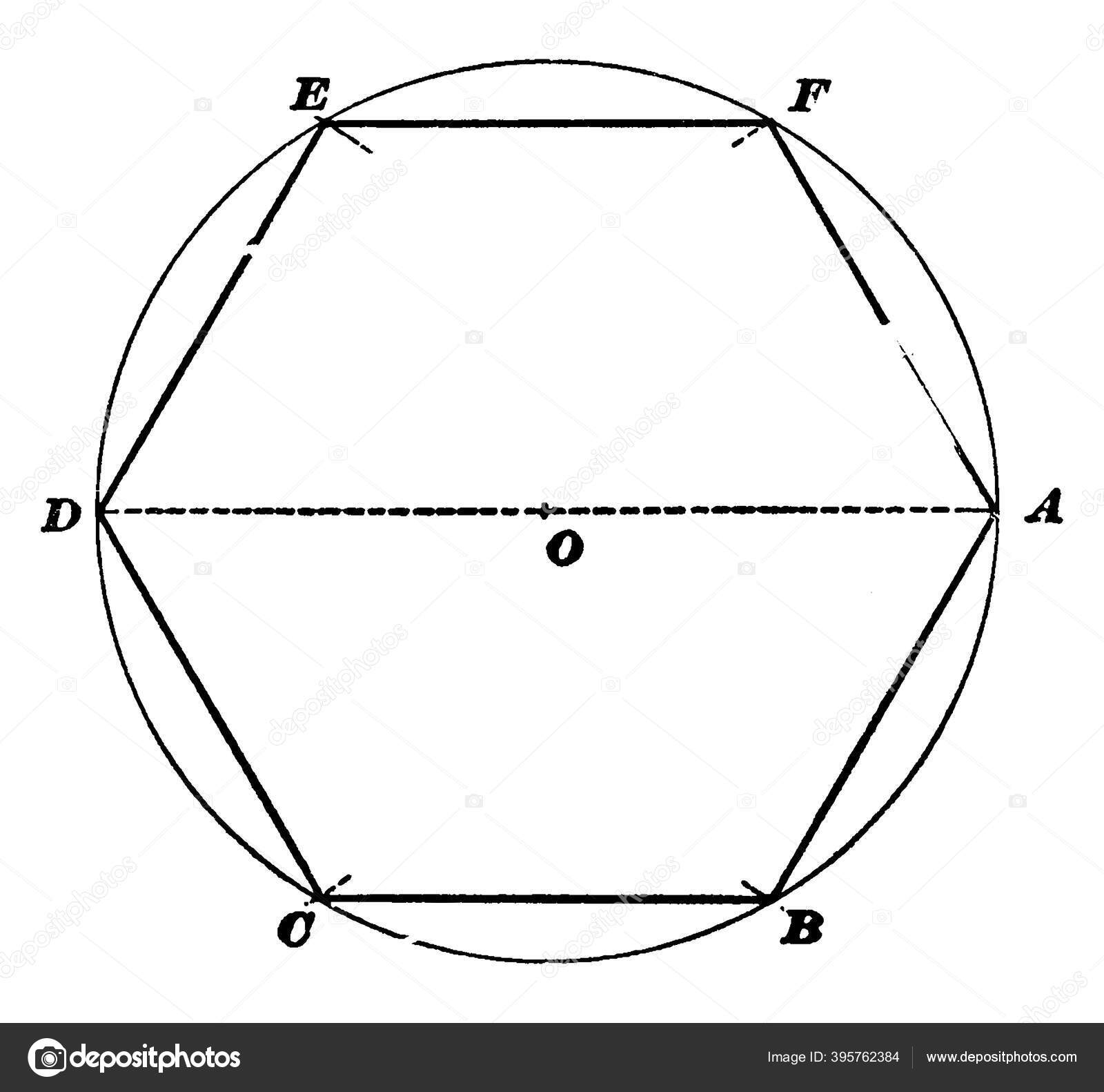 29. Объекты трех групп окрашены в разные цвета

Рис. 30. Удаление ненужных объектов

Чтобы иметь возможность экспериментировать с различными вариантами преобразования этой группы, не выполняя каждый раз всю последовательность описанных выше действий, имеет смысл сделать копию и оставить ее на полях. Для этого выделите все объекты, нажав сочетание клавиш CtrlA, а затем создайте копию нажатием сочетания клавиш CtrlD. Переместите копию за пределы страницы.

Манипуляции с «кубиками»

Теперь создадим иллюзию отсутствия угловых «кубиков». Для начала удалите по одному объекту каждого цвета, как показано на рис. 30. Теперь выделите правый, левый и нижний объекты верхней группы (на приведенных иллюстрациях они окрашены красным). Для добавления объекта к ранее выделенным удерживайте клавишу Shift. Переместите эти объекты вниз, как показано на рис. 31. Данную операцию удобно выполнять, поместив курсор на одну из узловых точек перемещаемого объекта.

Рис. 31. Перемещение трех объектов с красной заливкой

Рис. 32. Перемещение трех объектов с желтой заливкой

Выделите три оставшихся угловых объекта «желтой» группы и переместите их, как показано на рис. 32. Проделайте аналогичную операцию с угловыми объектами «зеленой» группы (рис. 33).

Рис. 33. Перемещение трех объектов с зеленой заливкой

Рис. 34. Выбор команды перемещения выделенных объектов на задний план слоя в главном меню

Выделите крайние правый и левый объекты «красной» группы, а также левый нижний из «зеленой». Переместите их на задний план слоя, выбрав в меню Объект -> Порядок -> На задний план слоя (рис. 34) или нажав сочетание клавиш ShiftPgDn. Изображение готово (рис. 35).

Рис. 35. Готовое изображение

Теперь создадим еще одну фигуру. Сделайте копию ранее оставленной на полях заготовки в виде кубика Рубика и переместите ее на страницу. Удалите средний ряд объектов из «желтой» и «зеленой» групп, как показано на рис. 36.

Рис. 36. Удаление ненужных объектов

Выделите пять объектов «красной» группы, смежных с элементами групп других цветов и переместите их, как показано на рис. 37. Затем выделите три объекта из оставшейся четверки (за исключением самого верхнего) и переместите их, как показано на рис. 38.

Рис. 37. Перемещение пяти объектов с красной заливкой

Рис. 38. Перемещение трех объектов с красной заливкой

Теперь выделите левый верхний объект «желтой» группы и переместите его, как показано на рис. 39. Аналогичным образом переместите правый верхний объект «зеленой» группы (рис. 40). Работа завершена.

Рис. 39. Перемещение объекта с желтой заливкой

Рис. 40. Перемещение объекта с зеленой заливкой

Заключение

Итак, мы рассмотрели процесс создания стилизованного изображения несложного трехмерного объекта из квадратов. Выполнение этой работы позволит освоить и закрепить на практике навыки создания и перемещения векторных объектов. Это хорошее упражнение для начинающих пользователей, которое позволит им освоиться с особенностями графического редактора CorelDRAW

Как нарисовать шестигранник без циркуля

Построение шестигранника может производиться несколькими способами. Удобнее всего использовать стандартный набор чертежных инструментов: циркуль, линейку. Однако, в отсутствие циркуля, фигура этого типа может быть начерчена с помощью рейсшины, угольника заводского изготовления с углами 90/60/30°.

Шестигранники применяются для откручивания и закручивания болтов при ремонте и сборке мебели.

В обоих случаях особенностью построения является элементарное знание основ геометрии. В правильном шестиугольнике длина его стороны всегда равна радиусу окружности, описанной вокруг него, противоположные стороны параллельны, грани сопрягаются под углом 60°.

Шестиугольник, выпуклый и невыпуклый шестиугольник:

Шестиугольник – это многоугольник с шестью углами.

Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.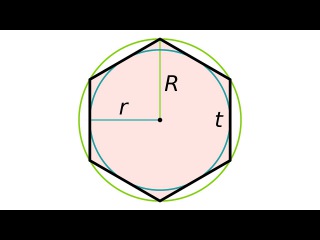

Шестиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый шестиугольник

Рис. 2. Невыпуклый шестиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 720°.

Особенности инструмента с плоским наконечником

Прямошлицевая или, по-другому, плоская отвертка обычно маркируется несколькими латинскими символами SL. Основное предназначение – это ввинчивать либо выкручивать винты, имеющие на головки одну прямую прорезь. Стоит отметить, что такие метизы не способны выдерживать большие нагрузки. Чаще всего применяют его для мелкого бытового ремонта.

Плоская отвертка не позволяет плотно ввинтить винт, так как своеобразная головка не дает возможности туго затянуть крепление. При сильном нажатии на метиз нередко срезается шлиц инструмента. Приржавевший же винт открутить плоской отверткой не всегда удается.

Правильный шестиугольник (понятие и определение):

Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.

Рис. 3. Правильный шестиугольник

Правильный шестиугольник имеет 6 сторон, 6 углов и 6 вершин.

Углы правильного шестиугольника образуют шесть равносторонних треугольников.

Правильный шестиугольник можно построить с помощью циркуля и линейки.

Модернизированные отвертки

Профессиональный инструмент отличается дополнительным набором функций.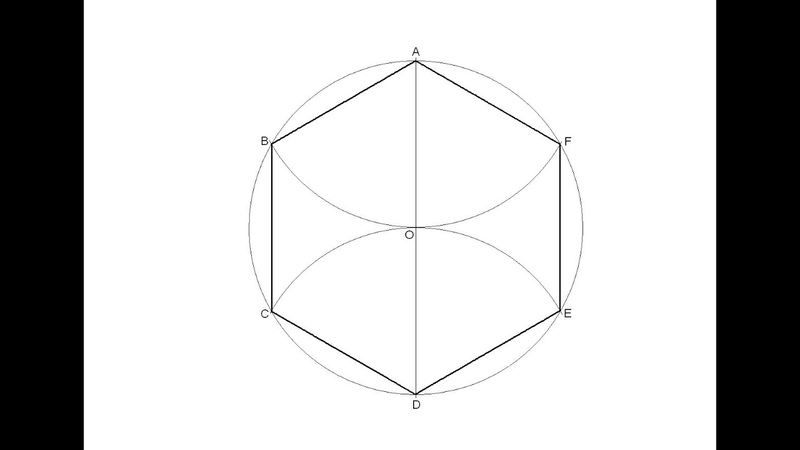

Конечно же, еще не была создана звуковая отвертка по образу и подобию универсальной модели из сериала «Доктор Кто», способная посредством кибернетических волн воздействовать на различные механизмы.

Но прогресс не стоит на месте, и кто знает, может в недалеком будущем человечество получит новые и суперсовременные девайсы.

Уже сейчас существуют модели, на фоне которых отвертка слесарная выглядит моделью инструмента из прошлого.

Но по-прежнему набор отверток усиленных цельнометаллических остается востребованным кейсом для специалистов самого разного профиля.

Так чем же примечательны модернизированные виды отверток?

Об этом подробнее.

Диэлектрические

Отвертки этого типа применяются для электромонтажных работ.

Специальная изоляция стержня отвертки защищает мастера от удара током, что позволяет использовать инструмент для откручивания деталей, находящихся под высоким напряжением.

Данный вид инструмента часто оборудуют индикатором для распознавания скрытой проводки, что позволяет «прозванивать» данные участки в целях последующего ремонта электрических сетей.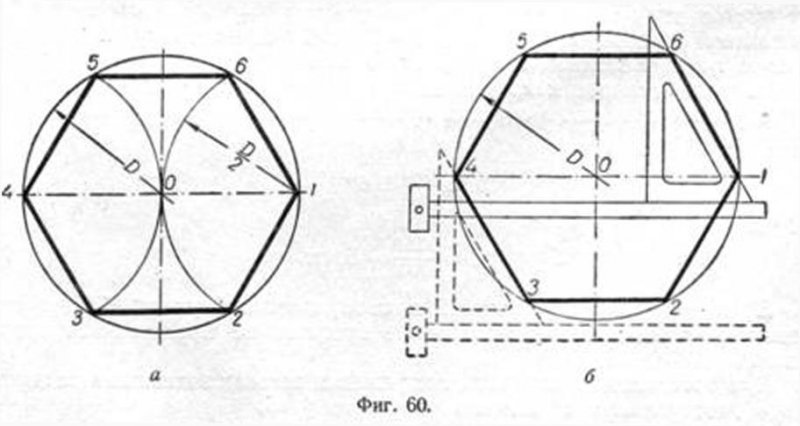

Ударные

Такой вид инструмента применяют для работы с крупными деталями, поскольку принцип его действия направлен на создание усиленного импульса.

Во время вкручивания энергия удара направляется непосредственно на винт, что позволяет утопить деталь без каких-либо особых усилий.

В наборе с ударной отверткой идут различные насадки, все они, как правило, большого размера.

Данный вид часто используют при повреждениях крепежных деталей коррозией, когда крепеж намертво врастает в поверхность.

Благодаря ударному механизму открутить такие болты можно без дополнительных физических усилий.

Реверсивные

Для длительных работ с крепежом предназначена реверсивная отвертка с храповым механизмом.

Данный вид инструмента поставляется со сменными битами разного сечения и диаметра.

Благодаря этому инструменту можно легко вкручивать, и закручивать различные детали без отрыва руки.

Изделие имеет вращающийся наконечник, который крутится за счет обратного вращения, рука мастера в этот момент остается неподвижной.

Суперсовременная механическая отвертка больше всего подходит специалистам, чей род деятельности подразумевает частую работу с деталями.

Аккумуляторные

Усовершенствованный вид, имеет встроенный аккумулятор, благодаря которому изделие может работать как шуроповерт.

С таким инструментом мастеру вообще нет необходимости прилагать какие-либо усилия на вкручивание, при этом затяжка будет более качественной с выверенным усилием, чем при ручном вкручивании с помощью другого вида инструмента.

Читать также: Как подключить кнопку с подсветкой 3 контакта

Такие модели применяется для сборки различных изделий и их ремонта.

Телескопические

Инструмент имеет особое строение стержня в виде удочки, позволяющее регулировать его длину.

С помощью специального запорного механизма установленный параметр длины можно надежно фиксировать.

Такие модели часто имеют магнитные наконечники, облегчающие работу мастера.

Например, при помощи магнита можно достать упавший винтик из труднодоступного места, или увеличить длину стержня для работы с инструментом с деталями, находящимися на большей глубине.

Динамометрические

Используют динамометрические модели инструмента в основном в высокотехнологичных отраслях, например, в авиации, кораблестроении и т.д.

В рукоятку инструмента вмонтирован специальный экран, который отображает показатели прикладываемого усилия при затяжке любой детали.

Это очень удобная и полезная функция, поскольку только так специалист может задать необходимый момент и закрепить все детали с одинаковым усилием.

Какие виды отверток нужны для работы каждому конкретному специалисту зависит от сферы деятельности человека.

На сегодняшний день существует огромное количество инструмента для выполнения самых разных видов слесарно-монтажных работ.

При выборе определенного инструмента особенно необходимо обращать внимание на маркировки изделий, только так можно обезопасить себя от покупки подделки сомнительного качества и приобрести инструмент, изготовленный в заводских условиях.

Torx

— вид шлица резьбовых крепёжных изделий в форме шестилучевой звезды. Зарегистрированный товарный знак [1] фирмы Textron Fastening Systems (ныне Acument Global Technologies). Официальное название, зафиксированное в стандарте ISO 10664 —
hexalobular internal
[2] ; в российском варианте ГОСТ Р ИСО 10664-2007 —
углубление звездообразное под ключ для болтов и винтов
. Повседневные названия — звезда, звёздочка, торкс.

Свойства правильного шестиугольника:

1. Все стороны правильного шестиугольника равны между собой.

a1 = a2 = a3 = a4= a5= a6.

2. Все углы равны между собой и составляют 120°.

α1 = α2 = α3 = α4 = α5 = α6 = 120°.

Рис. 4. Правильный шестиугольник

3. Сумма внутренних углов любого правильного шестиугольника равна 720°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.

Рис. 5. Правильный шестиугольник

5. Количество диагоналей правильного шестиугольника равно 9.

Рис. 6. Правильный шестиугольник

6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.

Рис. 7. Правильный шестиугольник

7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).

8. Радиус описанной окружности правильного шестиугольника и его сторона равны.

Рис. 8. Правильный шестиугольник

R = a

Виды шестигранников

Если вы впервые сталкиваетесь с этим шестигранным помощником, то должны знать, что они разделяются на два вида:

оснащенные стандартным наконечником;
оборудованные шаром с одного края инструмента.

Второй вид шестигранных ключей дает возможность производить работы с углом наклона почти в 30 градусов, а после полного прокручивания переставлять его не требуется, в результате чего сокращается время на производство крепежных работ.

Но обойтись одним единственным шестигранным ключом одного размера вы не сможете, поэтому хорошенько обдумайте этот вопрос и приобретите полноценный разноразмерный набор внутренних шестигранников. Это самый экономный и бюджетный вариант.

Правильный шестиугольник в природе, технике и культуре:

Пчелиные соты имеют форму правильного шестиугольника.

Графит, графен имеют гексагональную кристаллическую решетку.

Гигантский гексагон – атмосферное явление на Сатурне – имеет форму правильного шестиугольника.

Рис. 9. Гигантский гексагон на Сатурне

Сечение гайки и многих карандашей имеет вид правильного шестиугольника.

Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.

Панцирь черепахи состоит из шестиугольников.

Гексагоном иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.

Рис. 10. Материковая часть Франции

Формулы правильного шестиугольника:

Пусть a – сторона шестиугольника, r – радиус окружности, вписанной в шестиугольник, R – радиус описанной окружности шестиугольника, P – периметр шестиугольника, S – площадь шестиугольника.

Формулы периметра правильного шестиугольника:

Формулы площади правильного шестиугольника:

Формула радиуса окружности, вписанной в правильный шестиугольник:

Формула радиуса окружности, описанной вокруг правильного шестиугольника:

R = a

Страница не найдена — Фонд Наффилда

Страница, которую вы ищете, не может быть найдена. Пожалуйста, попробуйте использовать либо главное меню, либо поиск по сайту.

Поиск проектов, новостей, событий, событий

Поиск

Образование 655 Когнитивные и некогнитивные навыки 33 Учебная программа и выбор предметов 31 Ранние годы 166 Педагогические кадры 75 Оценка образования 29 Высшее образование 92 Язык и грамотность 79 Обучение на протяжении всей жизни 15Nuffield Research Placement 23Анализ математических наук 84Воспитание детей 75Педагогика 20После 16 лет образование и навыки 95Начальное образование 134Q-Step 26Эффективность школы 45Среднее образование 156Специальные образовательные потребности и инвалидность 57Системные проблемы образования 98Правосудие 236Доступ к правосудию 39Административное правосудие 26Гражданское правосудие 22Судебный опыт и доказательства 21Уголовное правосудие 25Домашнее насилие 5Равенство и права человека 17Семейное правосудие 134Частное право юридическое право 3Социальное право 12Юстиция по делам несовершеннолетних 24Социальное право 771Искусственное интеллект 3Вспомогательная смерть 1Дополненная реальность 0Преимущества 52Обязанности по уходу 27Сообщества и социальная сплоченность 63Стоимость жизни 21Страна рождения 24COVID-19327Прогнозирование преступности 2Данные для общественного блага 29Цифровой вред и дезинформация 33Цифровая интеграция и исключение 14Цифровые навыки 16Цифровое общество 48Инвалидность 14Экономика, государственные расходы и услуги 182Этническая принадлежность 48Семья и семейная динамика 117Гендер 43Глобальное неравенство в отношении здоровья 11Жилье 24Доход и богатство 116Неравенство и социальная мобильность 211Вопросы поколений 35Рынок труда 109Присмотр за детьми и нуждающиеся дети 74Психическое здоровье 91Нарушения опорно-двигательного аппарата 18Пенсии 16Физическое здоровье 50Бедность и уровень жизни 109Производительность и инновации.

когнитивные навыки 33Учебная программа и выбор предмета 31Ранние годы 166Персонал образования 75Оценка образования 29Высшее образование 92Язык и грамотность 79На протяжении всей жизни обучение 15Nuffield Research Placement 23Числа 84Воспитание детей 75Педагогика 20Образование и навыки после 16 лет 95Начальное образование 134Q-Step 26Эффективность школы 45Среднее образование 156Специальные образовательные потребности и инвалидность 57Системные проблемы образования 98Правосудие 236Доступ к правосудию 39Административное правосудие 26Гражданское правосудие 22Судебный опыт и доказательства 21Уголовное правосудие 25Домашнее насилие 5Равенство и права человека 17Семейное правосудие 134Частное право юридическое право 3Социальное право 12Юстиция по делам несовершеннолетних 24Социальное право 771Искусственное интеллект 3Вспомогательная смерть 1Дополненная реальность 0Преимущества 52Обязанности по уходу 27Сообщества и социальная сплоченность 63Стоимость жизни 21Страна рождения 24COVID-19327Прогнозирование преступности 2Данные для общественного блага 29Цифровой вред и дезинформация 33Цифровая интеграция и исключение 14Цифровые навыки 16Цифровое общество 48Инвалидность 14Экономика, государственные расходы и услуги 182Этническая принадлежность 48Семья и семейная динамика 117Гендер 43Глобальное неравенство в отношении здоровья 11Жилье 24Доход и богатство 116Неравенство и социальная мобильность 211Вопросы поколений 35Рынок труда 109Присмотр за детьми и нуждающиеся дети 74Психическое здоровье 91Нарушения опорно-двигательного аппарата 18Пенсии 16Физическое здоровье 50Бедность и уровень жизни 109Производительность и инновации 7Общественное здравоохранение 149Социальные сети 2Социоэкономика старения 25Социоэкономика раннего взросления 42Спортивная наука 1Злоупотребление психоактивными веществами 11Налоги 48Доверие к демократии 65Оценка данных 5

Ознакомьтесь с нашими проектами

В процессе

Образование | 2023 – 2025

Посмотреть проект

Правосудие | 2023 – 2023

Создание и использование более качественных данных о правосудии

Посмотреть проект

Поиск проектов, новостей, событий, событий

Поиск

Немного «кубизма» в CorelDRAW

Подготовительный этап

Создание «кубиков»

Раскрашиваем «кубики»

Манипуляции с «кубиками»

Заключение

Как нарисовать шестигранник без циркуля

Шестиугольник, выпуклый и невыпуклый шестиугольник:

Особенности инструмента с плоским наконечником

Правильный шестиугольник (понятие и определение):

Модернизированные отвертки

Диэлектрические

Ударные

Реверсивные

Аккумуляторные

Телескопические

Динамометрические

Свойства правильного шестиугольника:

Виды шестигранников

Правильный шестиугольник в природе, технике и культуре:

Формулы правильного шестиугольника:

Страница не найдена — Фонд Наффилда

Поиск проектов, новостей, событий, событий

Ознакомьтесь с нашими проектами

Целенаправленная и эффективная практическая работа по естествознанию начальных классов

Широкие плечи: повышение налогов в топ-

Подтверждение аутсорсинга оказания социальной помощи в Англии

Оптимизация и осуществимость родительской программы Triple P для дистанционного обучения

Продление трудовой жизни людям с заболеваниями опорно-двигательного аппарата

Ювенильные ревматические заболевания: образование, профессиональная подготовка и трудоустройство

Создание и использование более качественных данных о правосудии

Испытание PAW: осуществимость и приемлемость инструментария Pain-at-Work Toolkit

Приоритеты образования на следующих всеобщих выборах

Кризис стоимости жизни: влияние на школы

Широкие плечи: повышение налогов наверху

Приоритеты образования на следующих всеобщих выборах

Физические наказания и последствия для детей в Великобритании

Оптимизация и осуществимость родительской программы Triple P для дистанционного обучения

Понимание использования прав на дошкольное образование

Переосмысление особых образовательных потребностей

Артрит, работа и благополучие: исследование смешанных методов с рекомендациями по политике

Испытание PAW: осуществимость и приемлемость инструментария Pain-at-Work Toolkit

Работа или учеба? Пол и переход от учебы к работе

Региональный индекс регенерации для отслеживания социально-экономического «повышения уровня»

Пути развития после 16 лет: роль сверстников, семейное положение и ожидания

Проектирование инклюзивной удаленной и гибридной работы для поддержки работников с ограниченными возможностями

Влияние выявления потребностей в дополнительном обучении в Уэльсе

Сравнение неравенства и результатов в системе образования после 16 лет в Великобритании

Изучение расового неравенства при отвлечении от системы ювенальной юстиции

Жизнь детей в переменчивых местах

Административная справедливость в цифровом государстве всеобщего благосостояния

Дистанционное наставничество по остеоартриту для малообеспеченных людей

Ювенильные ревматические заболевания: образование, профессиональная подготовка и трудоустройство

Продление трудовой жизни людям с заболеваниями опорно-двигательного аппарата

Изменение выбора школы для более справедливого обучения в Англии

Среднесрочное влияние пандемии COVID-19 на учащихся с SEND

Личное представление свидетельских показаний адвокатами и сторонами в процессе

COVID-19 и уход за детьми: местные последствия в Англии

Когда свадьба не брак? Изучение не имеющих юридической силы церемоний

Этические принципы, лежащие в основе совместного производства с молодежью

Меры по смягчению последствий COVID-19: предоставление образования и доступ к специальным школам

Могут ли математические приложения повысить ценность обучения?

Как кризис COVID-19 влияет на продовольственную безопасность

Влияние COVID-19 на общеобразовательные школы Англии

Взросление в условиях COVID-19

Страница не найдена — Фонд Наффилда

Поиск проектов, новостей, событий, событий

Добавить комментарий Отменить ответ