Семиугольник, виды, свойства и формулы — ISaloni — студия интерьера, салон обоев
- Семиугольник, виды, свойства и формулы
- Онлайн калькулятор: Площадь многоугольника
- Выпуклый, невыпуклый и звездчатый многоугольник
- Как обрезать фотографии под разными углами — Вокруг-Дом
- Угол, виды углов и их измерение
- Многоугольники. презентация к уроку по геометрии (8 класс) на тему
- Подписи к слайдам:
- Сообщение темы урока
- Определение целей урока
- Изучение нового материала С. 42, № 1 (у.)
- Изучение нового материала
- Изучение нового материала
- Изучение нового материала
- Изучение нового материала
- Изучение нового материала
- Изучение нового материала
- Изучение нового материала
- Вывод
- Работа по учебнику С. 43, № 2
- Работа по учебнику С. 43, № 3
- Работа по учебнику С. 43, № 4
- Работа в тетради С. 16, № 1
- Работа в тетради С.

- С.44, № 7 (учебник)
- С.44, № 7 (учебник)
- С.44, № 7 (учебник)
- С.44, № 7 (учебник)
- Бывшая учительница математики предложила решение нерешаемой задачи — Российская газета
- Определение, стороны, углы (обычные и нестандартные)
- Введение, типы, формулы и решенные примеры
- Полигоны
- Периметр многоугольника — веб-формулы
- Название геометрических фигур — многоугольники, многогранники
- Как создать шестиугольник со скругленными углами в фотошопе с помощью инструмента многоугольник?
- Внутренние углы многоугольника
Семиугольник, виды, свойства и формулы
Семиугольник, виды, свойства и формулы.
Семиугольник – это многоугольник, общее количество углов (вершин) которого равно семи.
Семиугольник, выпуклый и невыпуклый семиугольник
Правильный семиугольник (понятие и определение)
Свойства правильного семиугольника
Формулы правильного семиугольника
Семиугольник в природе, технике и культуре
Шестиугольник, семиугольник, восьмиугольник
Семиугольник, выпуклый и невыпуклый семиугольник:
Семиугольник – это многоугольник с семью углами.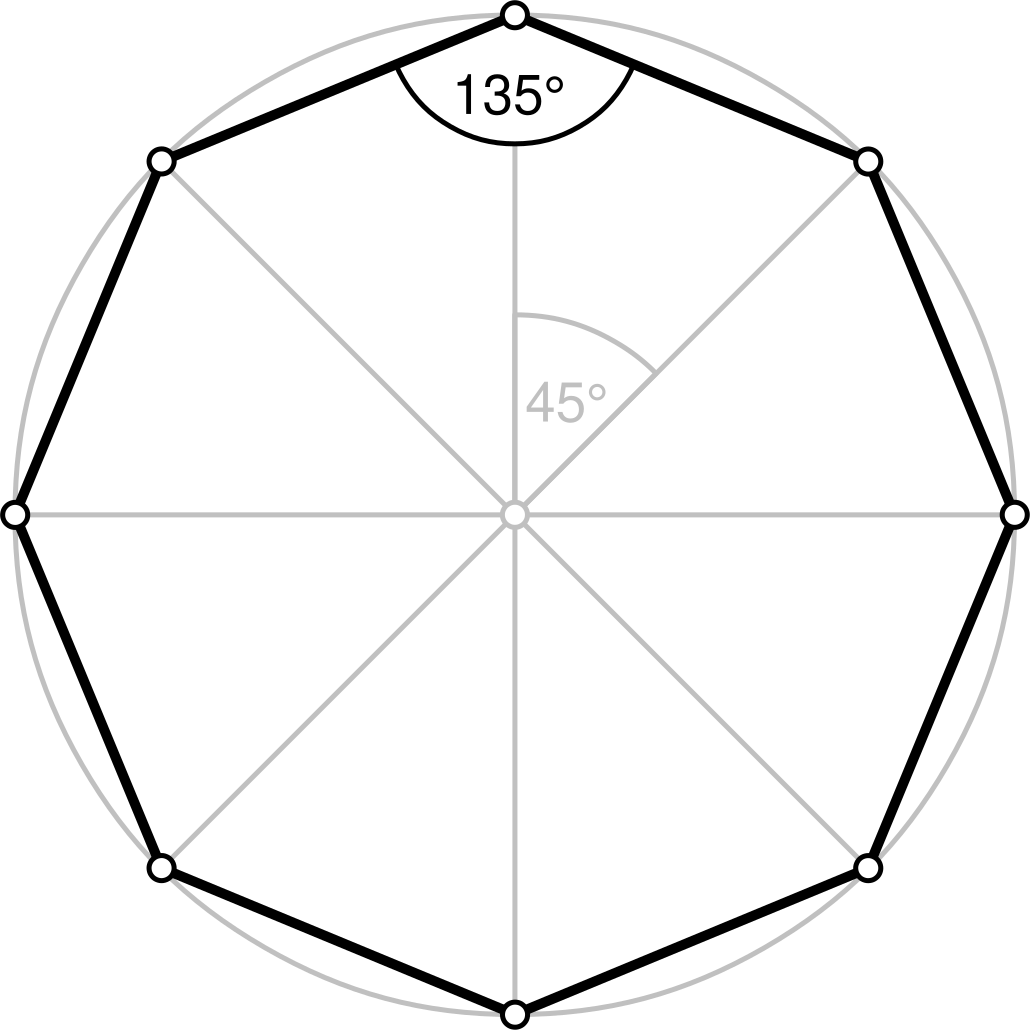
Семиугольник – это многоугольник, общее количество углов (вершин) которого равно семи.
Семиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый семиугольник – это семиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Звёздчатый семиугольник
Рис. 1. Выпуклый семиугольник
Рис. 2. Невыпуклый семиугольник
Сумма внутренних углов любого выпуклого семиугольника равна 900°.
Правильный семиугольник (понятие и определение):
Правильный семиугольник – это правильный многоугольник с семью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный семиугольник – это семиугольник, у которого все стороны равны, а все внутренние углы равны 128 4/7° ≈
128,571°.Рис. 3. Правильный семиугольник
Правильный семиугольник
имеет 7 сторон, 7 углов и 7 вершин.Углы правильного семиугольника образуют семь равнобедренных треугольников.
Правильный семиугольник можно невозможно построить с помощью циркуля и линейки, но можно построить с помощью циркуля и невсиса, то есть размеченной линейки, на которой можно делать отметки и с помощью которой можно проводить прямые, проходящие через какую-нибудь точку, причём отмеченные на линейке точки будут принадлежать данным линиям (прямым или окружностям).
Свойства правильного семиугольника:
1. Все стороны правильного семиугольника равны между собой.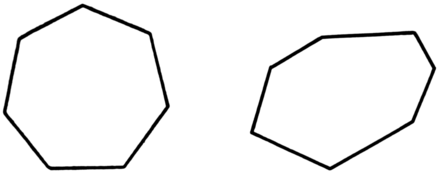
a1 = a2 = a3 = a4= a5 = a6 = a 7.
2. Все углы равны между собой и составляют 128 4/7° ≈ 128,571
α1 = α2 = α3 = α4 = α5 = α6 = α7 = 128 4/7° ≈ 128,571°.
Рис. 4. Правильный семиугольник
3. Сумма внутренних углов любого правильного семиугольника равна 900°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного семиугольника O.
Рис. 5. Правильный семиугольник
5. Количество диагоналей правильного семиугольника равно 14.
Рис. 6. Правильный семиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.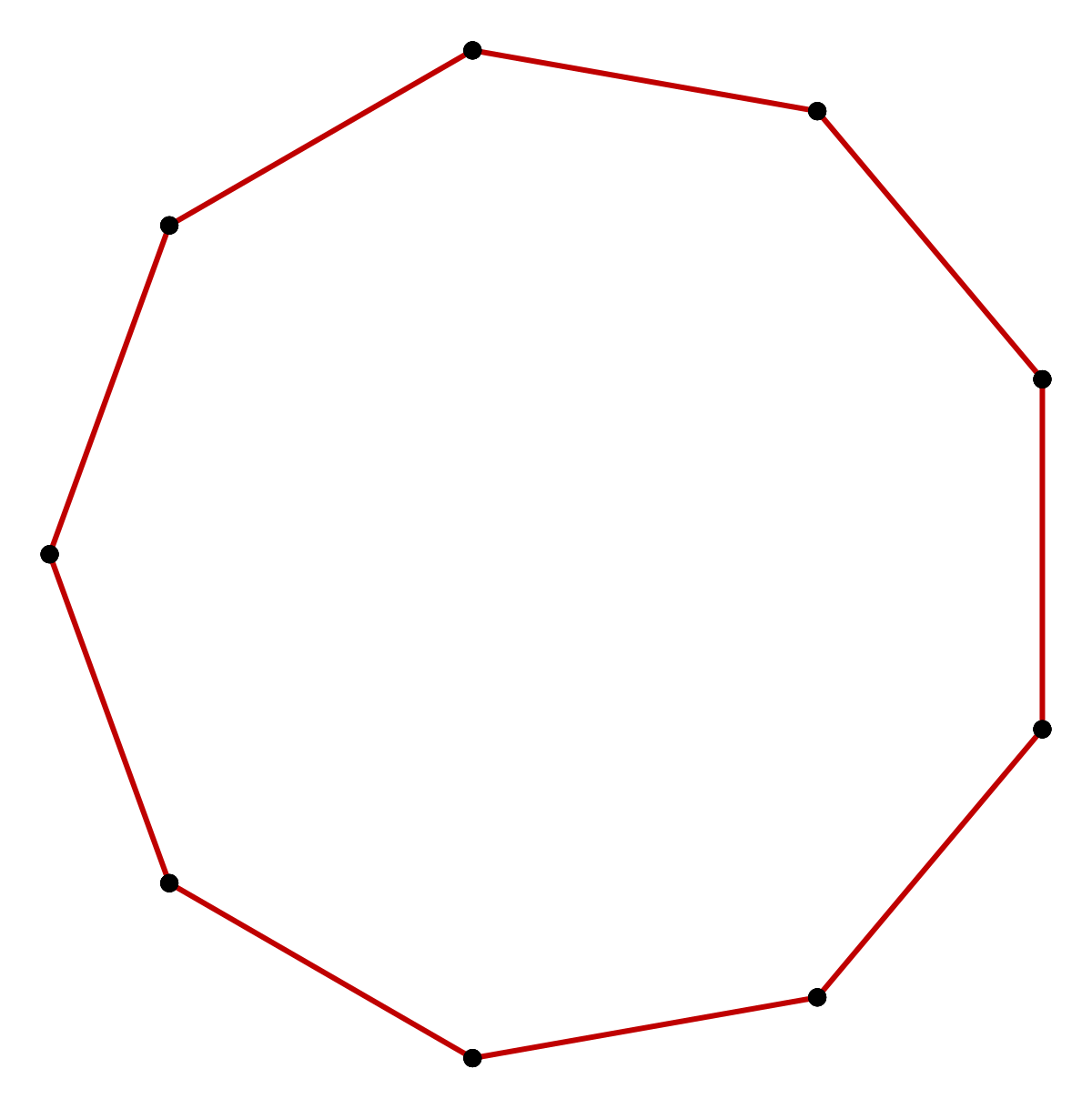
Рис. 7. Правильный семиугольник
Формулы правильного семиугольника:
Пусть a – сторона семиугольника, r – радиус окружности, вписанной в семиугольник, R – радиус описанной окружности семиугольника, P – периметр семиугольника, S – площадь семиугольника.
Формулы стороны правильного семиугольника:
Формулы периметра правильного семиугольника:
Формулы площади правильного семиугольника:
Формулы радиуса окружности, вписанной в правильный семиугольник:
Семиугольник в природе, технике и культуре:
В некоторых странах, например, в Великобритании, некоторые монеты имеют правильную криволинейную семиугольную форму.
Некоторые виды кактусовых имеют форму звездчатого семиугольника.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Восьмиугольник
Примечание: © Фото https://www.
карта сайта
Коэффициент востребованности 773
Онлайн калькулятор: Площадь многоугольника
Пример многоугольникаДанный калькулятор обсчитывает площадь многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники.
Смотрим на картинку — площадь многоугольника ABCDE можно вычислить как сумму площадей треугольников ABD, BCD и ADE. Для этого, понятно, помимо длин сторон многоугольника, надо знать еще и длины диагоналей BD и AD, но это и все что нужно — площадь любого треугольника можно вычислить только по длинам его сторон, без измерения углов.
А это довольно удобно, например, при бытовом ремонте — длины-то всяко проще померять, чем углы.
Итак, измеряем длины сторон интересующего нас многоугольника, заносим их в таблицу, мысленно разбиваем многоугольник на треугольники, измеряем нужные диагонали, также заносим их в таблицу, после чего калькулятор рассчитывает площадь всей фигуры.
По умолчанию в таблицу введены стороны и диагонали многоугольника на картинке, что легко исправить, нажав кнопку «Очистить таблицу».
Площадь многоугольника
addimport_exportmode_editdeleteСтороны и диагонали
Размер страницы: chevron_leftchevron_rightСтороны и диагонали
Сохранить ОтменитьИмпортировать данныеОшибка импорта
Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: ? EFGHIJKLMNOPQRSTUVWXYZ ?;50.5
Загрузить данные из csv файла
Импортировать Назад Отменить Точность вычисленияЗнаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Загрузить close
content_copy Ссылка save Сохранить extension Виджет
Выпуклый, невыпуклый и звездчатый многоугольник
Плоская фигура, образованная замкнутым рядом прямолинейных отрезков, называется многоугольником.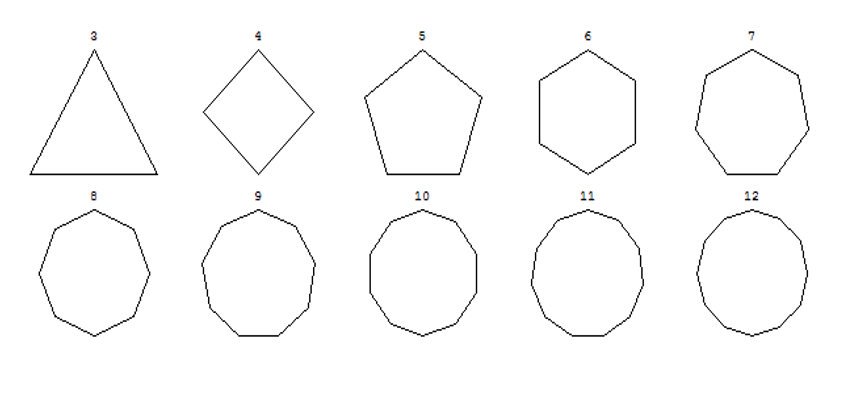 На рис.1 изображен шестиугольник ABCDEF. Точки А, В, С, D, Е, F — вершины многоугольника; углы при них (углы многоугольника) обозначаются ∠A, ∠В, ∠С, …, ∠F. Отрезки: AC, AD, BE и т.д. — диагонали, АВ; ВС, CD и т. д. — стороны многоугольника
На рис.1 изображен шестиугольник ABCDEF. Точки А, В, С, D, Е, F — вершины многоугольника; углы при них (углы многоугольника) обозначаются ∠A, ∠В, ∠С, …, ∠F. Отрезки: AC, AD, BE и т.д. — диагонали, АВ; ВС, CD и т. д. — стороны многоугольника
рис.1
В элементарной геометрии рассматриваются только простые многоугольники, т. е. такие, контур которых не имеет самопересечений.
Многоугольники, контур которых имеет самопересечения, называются звездчатыми многоугольниками. На рис.2 изображен звездчатый многоугольник ABCDE.
рис.2
Если все диагонали многоугольника лежат внутри него, многоугольник называется выпуклым.
Шестиугольник на рис.1 выпуклый; пятиугольник на рис.3 невыпуклый (диагональ ЕС лежит вне многоугольника).
рис.3
Сумма внутренних углов во всяком выпуклом многоугольнике равна 180° (n-2), где n — число сторон многоугольника*.
* В учебниках геометрии это свойство высказывается обычно только для выпуклых многоугольников. Но оно справедливо для всех простых многоугольников. Но оно справедливо для всех простых многоугольников. Нужно заметить, что в невыпуклом многоугольнике один или несколько внутренних углов превышают 180°. Так, в невыпуклом пятиугольнике, изображенном на рис.3, два угла прямые, два угла имеют по 45°, а один содержит 270°. Суммаа углов составляет 180° (5-2)=540°.
Как обрезать фотографии под разными углами — Вокруг-Дом
Типичный инструмент обрезки позволяет обрезать фотографию в квадратную или прямоугольную форму. Но иногда желательно подрезать под разными углами. Используйте инструменты маскировки и выделения для этого типа обрезки. Обратите внимание, что обрезка удаляет обрезанные области изображения, поэтому обрежьте фотографию, когда вы уверены, что хотите, чтобы она выглядела. Перед кадрированием убедитесь, что у вас есть копия оригинальной фотографии на тот случай, если вам понадобится вернуться к ней.
Обратите внимание, что обрезка удаляет обрезанные области изображения, поэтому обрежьте фотографию, когда вы уверены, что хотите, чтобы она выглядела. Перед кадрированием убедитесь, что у вас есть копия оригинальной фотографии на тот случай, если вам понадобится вернуться к ней.
Шаг 1
Нажмите синюю кнопку в верхнем левом углу окна Paint. Нажмите «Открыть» и выберите фотографию, которую хотите обрезать.
Шаг 2
Нажмите стрелку вниз под «Выбрать» в группе инструментов «Изображение».
Шаг 3
Нажмите инструмент «Прямоугольное выделение», если основная форма обрезки должна быть квадратной или прямоугольной. Нажмите на инструмент «Выбор произвольной формы», если хотите создать неправильную форму.
Шаг 4
Нажмите и перетащите указатель мыши на фотографию, чтобы создать базовую форму обрезки. Сделав выбор, нажмите «Инвертировать выделение» на панели инструментов «Рисование». Нажмите «Удалить». Это очищает инвертированный выбор, удаляя ненужные части фотографии, как если бы она была обрезана.
Шаг 5
Щелкните фигуру в группе «Фигуры», чтобы сформировать другие углы в кадрировании. Paint в Windows 7 предоставляет вам выбор из нескольких предустановленных форм, включая звезды, стрелки, облака и различные геометрические формы.
Для получения неправильной формы щелкните инструмент «Многоугольник».Шаг 6
Нарисуйте форму, где вы хотите создать другой угол обрезки. Например, нарисуйте многоугольник в одном углу фотографии, чтобы он обрезал угол под наклонным углом.
Шаг 7
Держите выбранную форму. Нажмите «Контур» в группе «Фигуры». Нажмите «Нет плана». Нажмите «Цвет 2» в группе «Цвета» и выберите белый (или любой другой цвет фона, который вы хотите использовать) в качестве цвета заливки. Форма, которую вы только что создали, должна появиться, чтобы обрезать фотографию под другим углом.
Шаг 8
Создайте больше форм, чтобы обрезать фотографию под большим углом. Убедитесь, что вы удалили контур и задали фигуру того же цвета, что и фон, обычно белый.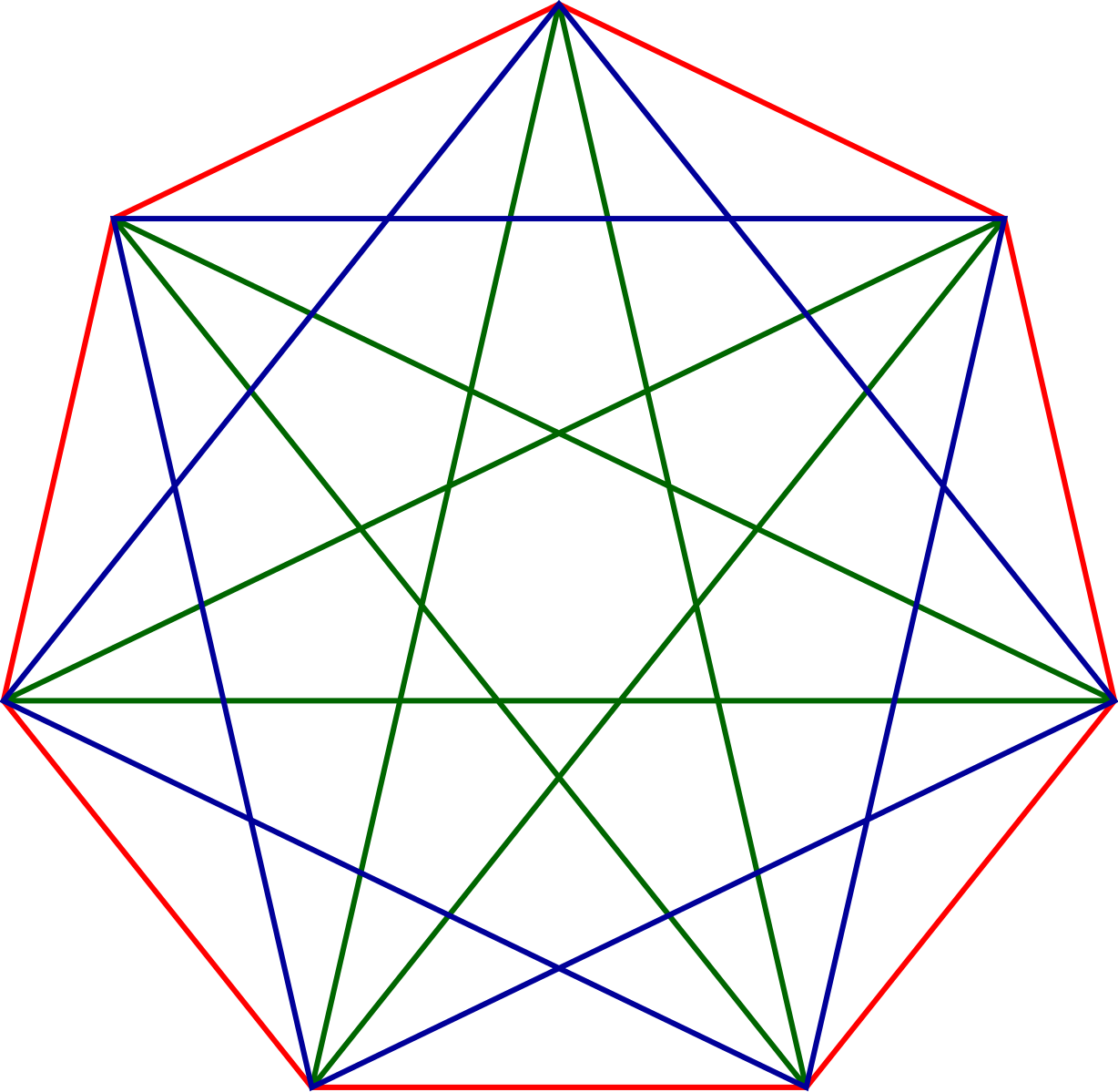
Шаг 9
Просмотрите отредактированное фото. Когда Paint очищает инвертированный выбор ранее, он должен был оставить пустые места вокруг изображения. Если вы хотите удалить эти пробелы, нажмите «Выбрать» в группе «Изображение», выберите область, которую вы хотите сохранить (оставляя пустые места), и нажмите «Обрезать» в той же группе инструментов.
Шаг 10
Нажмите синюю кнопку еще раз. Нажмите «Сохранить как». Выберите формат файла и сохраните файл под уникальным именем.
Угол, виды углов и их измерение
Определение. Угол — это часть плоскости, ограниченная двумя лучами, исходящими из одной точки, называемой вершиной угла.
Если плоскость круга разделить на 360 равных частей радиусами, то часть круга — это угловой градус, который обозначается знаком « ° » (читается — «градус»).
Следовательно, 1° = часть круга.
Круг составит * 360 = 1° * 360 = 360°.
Угол, равный плоскости круга, составляет 360° и называется полным углом.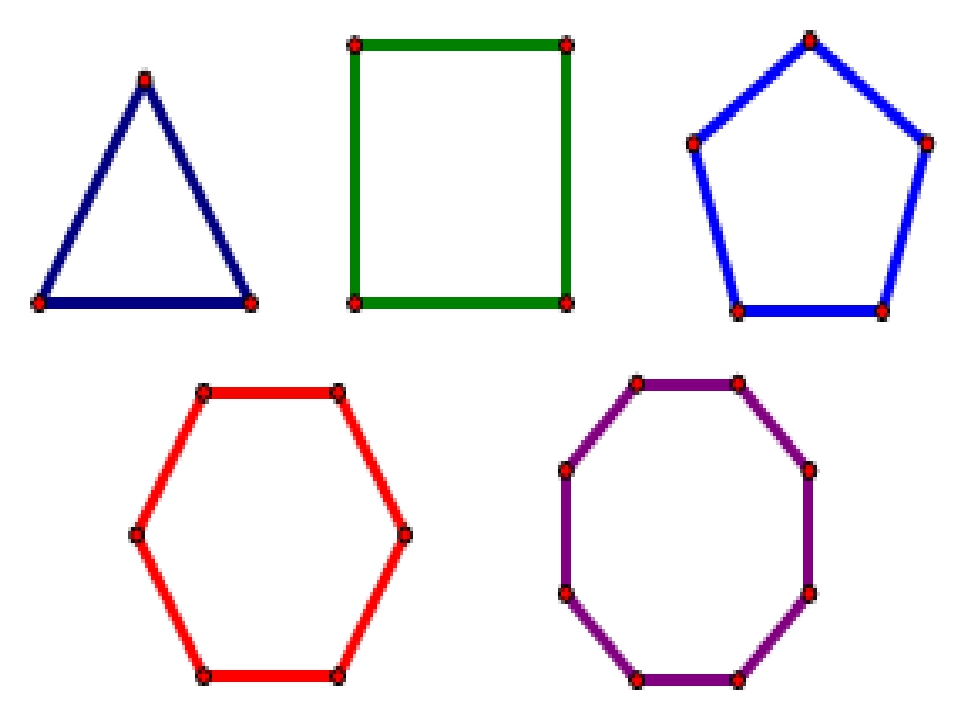
Если плоскость круга разделить диаметром (двумя радиусами, расположенными на одной прямой линии) на две равные части, то плоскость полукруга составит угол в 360′: 2 = 180°.
Угол, равный полуплоскости круга, составляет 180° и называется развернутым углом.
Если плоскость круга разделить двумя диаметрами (горизонтальной и вертикальной линиями) на четыре равные части, то плоскость одной части составит угол в 360° : 4 = 90°.
Угол, равный четвертой части круга, составляет 90° и называется прямым углом.
Отвлекаясь от плоскости, в которой расположен круг, изобразим углы таким образом:
Углы равны, если равны их градусные меры или у них при наложении одного угла на другой совпадают вершины и соответствующие стороны углов.
Например, прямой угол (рис. 1) мы трижды развернули вокруг вершины угла, при этом на двух рисунках (рис. 2 и 4) мы передвинули вершину угла по плоскости листа.
Инструментом для измерения углов служит транспортир.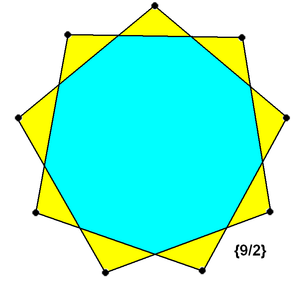
Для измерения угла следует совместить вершину угла и штрих с цифрой 0 на шкале транспортира. Одна сторона угла должна совпадать с прямой линией транспортира, на которой стоит 0, а вторая сторона угла пересекать шкалу транспортира (полуокружность с разметкой в угловых градусах).
На пересечении стороны угла и шкалы транспортира считывается градусная мера данного угла.
Мы рассмотрели полный, развернутый и прямой углы. Существует еще два типа углов: острые и тупые. Все острые углы имеют градусную меру в пределах: больше 0° и меньше 90°.
Например. острые углы:
Углы, градусная мера которых больше 90°, но меньше 180°*, называются тупыми углами.
Тупые углы (штриховой линией обозначен прямой угол в составе тупого угла) приведены на рис. 5, 6,7.
Чтобы построить заданный в градусной мере угол, необходимо иметь транспортир, линейку и карандаш.
Многоугольники. презентация к уроку по геометрии (8 класс) на тему
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Учитель математики МБОУ ООШ №14 города Темрюка Краснодарского края Боярко Ирина Геннадьевна Содержание урока
A C F G B ABCDEFG- многоугольник. Отрезки AB , BC, CD, DE, EF,FG, GA — смежные не лежат на одной прямой. Отрезки несмежные не имеют общих точек. Назовите несколько пар несмежных отрезков. D E
A C F G B A,B,C,D,E,F,G- многоугольника. D E вершины
C F G B AB , BC, CD, DE, EF, FG, GA — стороны многоугольника D E А
C F G B Сумма длин сторон AB , BC, CD, DE, EF, FG, GA — называется D E А периметром многоугольника Р= AB + BC + CD + DE + EF + FG + GA Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Многоугольник, имеющий n углов называется n -угольником. Сколько сторон имеет n –угольник? Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Сколько сторон имеет n –угольник? Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
A C F G B соседние вершины D E -две вершины, принадлежащие одной стороне Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
C F G B D E А AC, AD, AE, AF- диагонали многоугольника, проведённые из вершины А. Определение: Отрезок, соединяющий две несоседние вершины называется диагональю. Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Определение: Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону. Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Внешняя область Внутренняя область
Задача 2.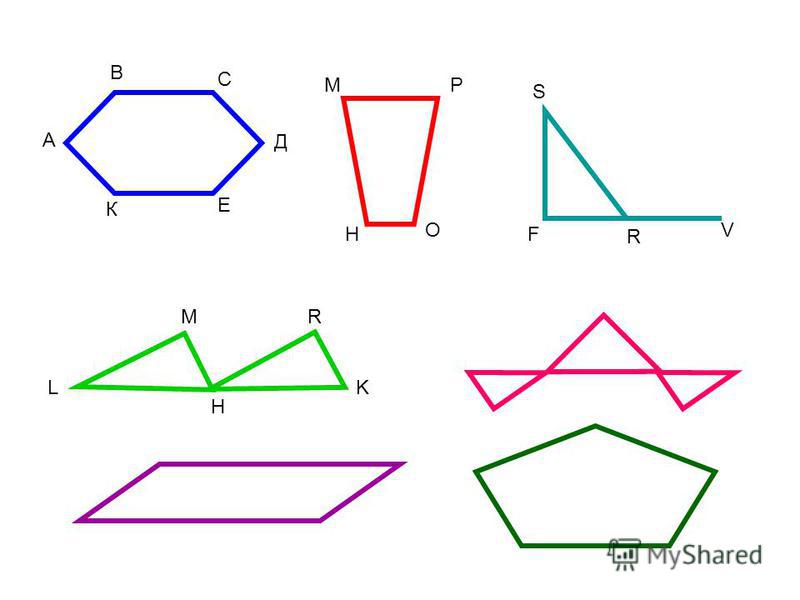 Сколько диагоналей имеет пятиугольник? Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Сколько диагоналей имеет пятиугольник? Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Задача. Сколько диагоналей имеет шестиугольник? Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
А Разделим этот многоугольник на несколько треугольников, проведя из вершины А все диагонали. Сколько получилось треугольников? Найти сумму углов многоугольника
Чему равна сумма углов треугольника? Найдите сумму всех углов этого пятиугольника. А S=180°∙ 3 =540°
Зависит ли сумма углов пятиугольника от: Размера? Формы? Цвета? От чего зависит эта сумма?
Сумма углов n -угольника равна S=180°∙(n -2)
Вариант 1 Вариант 2 1. Найти количество диагоналей прямоугольника 1. Найти количество диагоналей квадрата 2. Вычисли сумму всех углов прямоугольника 2. Вычисли сумму всех углов квадрата 3. Найти сумму углов выпуклого 12-угольника 3.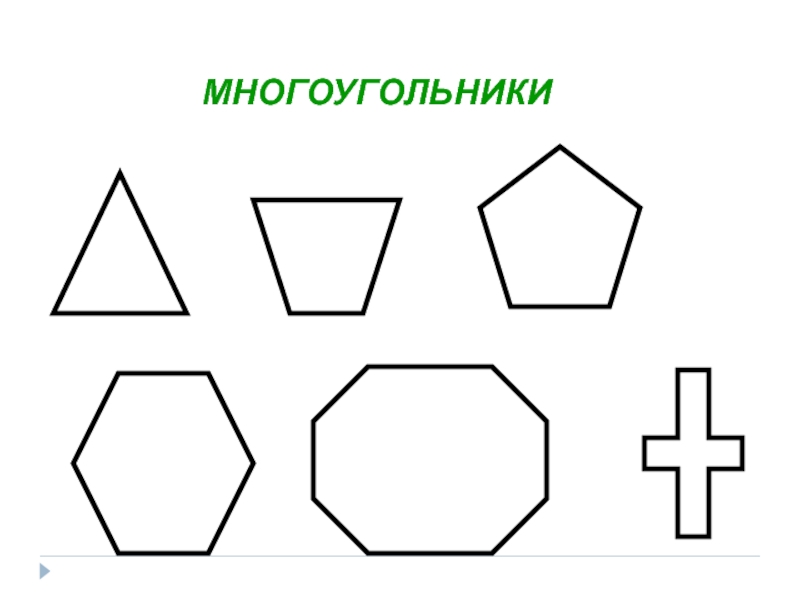 Найти сумму углов выпуклого 8-угольника 4. Укажи номера невыпуклых многоугольников 1 2 3 4 4. Укажи номера выпуклых многоугольников 1 2 3 4 5. Найти периметр прямоугольника со сторонами 4 см и 7 см 5. Найти периметр квадрата со стороной 12 см Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Найти сумму углов выпуклого 8-угольника 4. Укажи номера невыпуклых многоугольников 1 2 3 4 4. Укажи номера выпуклых многоугольников 1 2 3 4 5. Найти периметр прямоугольника со сторонами 4 см и 7 см 5. Найти периметр квадрата со стороной 12 см Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Вариант 1 Вариант 2 1. Найти количество диагоналей прямоугольника 2 1. Найти количество диагоналей квадрата 2 2. Вычисли сумму всех углов прямоугольника 360° 2. Вычисли сумму всех углов квадрата 360° 3. Найти сумму углов выпуклого 12-угольника 1800° 3. Найти сумму углов выпуклого 8-угольника 1080° 4. Укажи номера невыпуклых многоугольников 1 2 3 4 4. Укажи номера выпуклых многоугольников 1 2 3 4 5. Найти периметр прямоугольника со сторонами 4 см и 7 см 22см 5. Найти периметр квадрата со стороной 12 см 48 см
Использованная литература: Л.С. Атанасян, Геометрия 7-9 (учебник для общеобразовательных учреждений). – М.: Просвещение, 2005 Картинки: http://www.gifzona.ru/pozd_1s.htm http://images-photo.ru/photo/7-2-0-0-2 http://www.webman.ru/animation/main.htm
– М.: Просвещение, 2005 Картинки: http://www.gifzona.ru/pozd_1s.htm http://images-photo.ru/photo/7-2-0-0-2 http://www.webman.ru/animation/main.htm
1. Многоугольник 2. Выпуклый многоугольник 3. Решение задач 4. Работа лабораторий 5. Самостоятельная работа
«Площадь прямоугольника урок» — 5 см. Начертите квадрат со стороной 5 см. 3 см. А = 5 см. Постановка цели урока. 2 способ: 3+3+3+3+3 = 3 * 5 = 15 (см2). Начертите прямоугольник со сторонами 5 см и 3 см. 5 + 5 + 5 + 5 + 5 = 5 * 5 = 25 (см 2). 1 способ: 5 + 5 + 5 = 5 * 3 = 15 (см2). Как найти площадь квадрата? В = 3 см. Гребенникова Елена Викторовна, учитель начальных классов МОУ СОШ №5 г. Стрежевого.
«Прямоугольник ромб квадрат» — Ромб. D. Квадрат». Решение задач на готовых чертежах. Ответы к проверочному тесту. Решение задач на тему «Прямоугольник. Проверочный тест. C. A. Дано: АВСD – ромб. Теоретическая самостоятельная работа Заполнить таблицу, отметив знаки +(да), -(нет). Цель урока: Закрепить теоретический материал по теме «Прямоугольник.
«Площадь многоугольника» — 1. 7. В. С. Разминка з а д а н и е 1. 2. Запишите правильную последовательность цифр. Цвет (один или несколько)? Перед Вами поставлена задача, раскрасить дом! 3. ? 5. 4.
«Площади фигур геометрия» — S=AD*BH. b. А. Учитель: Ивниаминова Л.А. Фигуры имеющие равные площади называются равновеликими. S=(a?b):2. C. a. Материал к уроку геометрии в 8 классе. H. D. Площади фигур. Равные фигуры имеют равные площади. S=a?b.
«Математика прямоугольник 2 класс» — 39. 6. Чем похожи фигуры под №4 и №5 Чем отличаются? 1.Сосчитайте «цепочку» 90 — 45 -9 + 14 -12 +6 – 8 + 3 =. 60. 42. 45. 2.Увеличь каждое число на 3 до 60. Не хочется играть сегодня в прятки. Периметр прямоугольника. Геометрический материал. 57. Устный счёт. Прочитайте стихотворение.
«Урок 2 класс Площадь прямоугольника» — Формулы. Мы – отлично учимся! Ь. Л. Ключ. Мы – старательные! Д. Математика 2 класс Урок-открытие Площадь прямоугольника. Треугольник отрезок многоугольник прямоугольник четырехугольник квадрат. А. Все у нас получится! Р — ? Площадь — ? Выражения с переменной. 8: а P = (а + b) · 2 4 – х c: 3 P = a + b + a + b P = a · 2 + b · 2 14 + y.
А. Все у нас получится! Р — ? Площадь — ? Выражения с переменной. 8: а P = (а + b) · 2 4 – х c: 3 P = a + b + a + b P = a · 2 + b · 2 14 + y.
Устный счёт Сравните тексты задач. Чем они похожи и чем
отличаются?
На одной остановке из автобуса вышли 10 человек,
на другой – 20. На сколько меньше пассажиров
стало в автобусе?
На одной остановке из автобуса
вышло 10 человек, на другой – 20,
Сколько человек вышло из
автобуса?
Можно ли утверждать, что решения
задач одинаковы?
Сообщение темы урока
Рассмотрите чертежи.Какую закономерность вы обнаружили?
Название каких фигур вы знаете?
Какие затруднения у вас возникли?
Как можно назвать все фигуры одним
словом?
Об этом мы будем говорить. Прочтите.
Определение целей урока
МНОГОУГОЛЬНИК И ЕГО ЭЛЕМЕНТЫОпределите цели урока, используя опорные слова:
Мы познакомимся с …
Мы узнаем …
Мы вспомним …
Мы будем уметь …
Мы сможем поразмышлять …
Мы познакомимся с понятием
«многоугольник», научимся находить и
обозначать его вершины.
 Вы уже умеете различать и изображать на
Вы уже умеете различать и изображать набумаге такие фигуры, как треугольник,
четырёхугольник, пятиугольник. Такие
фигуры обычно называются
многоугольниками.
Посмотрите на рисунок на С. 42
учебника.
Изучение нового материала С. 42, № 1 (у.)
На кондитерской фабрике печеньеизготавливают в форме многоугольников,
изображенных в учебнике. Как можно назвать
каждый из них?
треугольник
четырёхугольник
пятиугольник
Сколько углов имеет каждая фигура?
Изучение нового материала
Рассмотрим жёлтый многоугольник.Вывод: в жёлтом многоугольнике
5 углов, 5 сторон, 5 вершин.
Сколько в нём углов?
Какой фигурой является каждая сторона?
Сколько у него сторон?
Какой фигурой является вершина?
Сколько у него вершин?
Изучение нового материала
Что вы можете сказать о количестве углов,сторон и вершин в каждом
многоугольнике?
Вывод: в любом
многоугольнике углов,
сторон и вершин поровну.
Изучение нового материала
Сколько углов в семиугольнике?Сколько вершин в десятиугольнике?
Сколько сторон в
пятнадцатиугольнике?
Изучение нового материала
Как определить название этого многоугольника?Что проще всего сосчитать?
Сосчитайте вершины многоугольника.
Как он называется?
Изучение нового материала
Бывают ли одноугольники?А двуогольники?
Какой из многоугольников имеет
наименьшее число углов?
Как называется многоугольник, у которого
100 вершин?
Изучение нового материала
Давайте научимся показывать элементымногоугольника.
Вершины – это точки.
Стороны – это отрезки.
Углы будем показывать
вращением указки.
Изучение нового материала
Вершины треугольника обозначаютсябуквами.
Читать обозначение можно
разными способами, начиная
с любой вершины
АВС, ВАС, САВ, ВСА,
АСВ, СВА.
В
А
С
Вывод
Прочитайте.Работа по учебнику С.
 43, № 2 Что изображено на рисунке?
43, № 2 Что изображено на рисунке?Как называются данные
многоугольники?
Работа по учебнику С. 43, № 3
Работа по учебнику С. 43, № 4
Работа в тетради С. 16, № 1
Работа в тетради С. 16, № 2
С.44, № 7 (учебник)
Найти сумму иразность чисел: 9 и 7.
9 + 7 = 16
9–7=2
С.44, № 7 (учебник)
Найти сумму иразность чисел: 8 и 5.
8 + 5 = 13
8–5=3
С.44, № 7 (учебник)
Найти сумму иразность чисел: 10 и 3.
10 + 3 = 13
10 – 3 = 7
С.44, № 7 (учебник)
Найти сумму иразность чисел: 7 и 7.
7 + 7 = 14
7–7=0
Презентация на тему «Выпуклый многоугольник» является интерактивным учебным пособием, целью использования которого является повышение продуктивности усвоения материала по геометрии на ранних стадиях ее изучения. Правильное и интересное преподнесение информации являются залог успеха для любого учителя, ведь учащиеся данной возрастной категории нуждаются в том, чтобы информация, которую они получают, была дана им в достаточно интересной и легкой для понимания форме.
Удачно выполненные графические изображения привлекут внимание учащихся, а у учителя не будет необходимости выполнять большое количество рисунков на доске с помощью мела, что значительно сохранит время на уроке, которое в дальнейшем можно будет потрать на изучение дополнительного интересного материала.
После слайда, содержащего название презентации, следует слайд, на котором представлены два различных многоугольника. Над изображениями вниманию учащихся представлено определение, написанное крупным шрифтом и яркими цветами, что, несомненно, привлечет внимание и хорошо запечалится в памяти учащихся.
слайды 1-2 (Тема презентации «Выпуклый многоугольник», определение выпуклого многоугольника)
Определение поясняет учащимся, что собственно является выпуклым многоугольником. Изучив данное определение, учащиеся должны понять, что фигура, изображенная справа, и является выпуклым многоугольником, что нельзя сказать о многоугольнике, изображенном слева. То, что два разных многоугольника представлены на одном слайде является очень удачным, так как учащиеся смогут провести сравнительный анализ двух фигур, что позволит еще раз закрепить в памяти изученное определение и научиться применять его на практике.
На третьем слайде презентации также имеется изображение многоугольника, который красными отрезками разбит на составляющие его треугольники. Если посчитать количество сторон многоугольника и количество треугольников, на которые он разбит, то легко можно сделать вывод о том, что представленные многоугольник состоит из треугольников, число которых на два меньше, чем сторон прямоугольника. Данные сведения необходимы для того, чтобы у учащихся была возможность посчитать сумму углов выпуклого многоугольника, содержащего любое количество вершин.
слайд 3 (сумма углов)
Исходя из знаний, полученных на более ранних сроках изучения геометрии о том, что сумма сторон треугольника всегда равна ста восьмидесяти градусам. И новой информации о том, на сколько треугольников разбивается многоугольник, учащиеся с помощью учителя могут сделать вывод о том, что сумма углов выпуклого многоугольника равна сумме сторон треугольников, на которые он разбит, умноженной на сто восемьдесят градусов.
Данная презентация на тему «Выпуклый многоугольник» на понятном и доступном уровне преподносит учащимся основную информацию, касающуюся выпуклого многоугольника. Она может использоваться не только на уроке в школе, но также является отличным материалом для самостоятельного изучения учащимися дома.
Бывшая учительница математики предложила решение нерешаемой задачи — Российская газета
В челябинскую редакцию «РГ» обратилась читательница из Миасса с очень необычной проблемой. Пенсионерка, в прошлом учительница математики, Ляля Зарипова все свободное время посвящает любимому предмету и пытается решить еще не решенные задачи — по ее собственному выражению, стереть белые пятна, существующие в математике с древних времен. Однако, сумев найти решение одной из таких задач, она уже более двух лет безуспешно старается привлечь к нему внимание общественности.
Вопреки вердикту
Одна из старейших математических загадок, доставшаяся человечеству от грека Архимеда, получила название задачи о трисекции угла. Великий мыслитель и один из отцов геометрии попытался разделить угол на три равные части с помощью циркуля и линейки. Однако найти решение не смог и завещал эту загадку ученикам и потомкам.
Великий мыслитель и один из отцов геометрии попытался разделить угол на три равные части с помощью циркуля и линейки. Однако найти решение не смог и завещал эту загадку ученикам и потомкам.
Отметим, что любой школьник сегодня легко разделит угол на две половины. Линейки и циркуля для этого вполне достаточно. Без особого труда можно разбить на три равные части прямой угол, встроив в него равносторонний треугольник. Автор этих строк справился с задачкой, потратив не более пяти минут. Однако разделить любой угол на три равные части ученые до сих пор не смогли.
Еще в 1837 году известный французский математик Пьер Ванцель, проигнорировав условия Архимеда о циркуле и линейке, попытался найти «трисекцию угла» алгебраическим путем и… потерпел фиаско. Пришел к выводу, что задача нерешаема. В дальнейшем решение искать просто перестали. А позже Французская академия наук вынесла официальный вердикт о том, что эту задачу решить невозможно, и исключила ее из всех учебников и справочников того времени.
С тех пор о головоломке, некогда занимавшей лучшие математические умы, забыли. Ляля Гиззатовна искала «ключ» несколько лет и, перепробовав множество путей, нашла простое и блестящее решение, к которому, судя по оставшимся в истории записям, шел сам Архимед, но довести его до конца не сумел.
По мнению учительницы, чтобы разделить угол на три равные части, нужно провести из его вершины окружность, отложить за ее пределами еще один радиус на биссектрисе, делящей этот угол пополам, и получить так называемый внешний угол. Он и будет в три раза меньше заданного угла, то есть станет одной из трех секций из условия задачи.
Последние три сотни лет решение даже не искали, а все это время математика шла семимильными шагами. Возможно, стоит попробовать снова?
Более того, автор геометрического подхода уверена: откладывая на биссектрисе нужное число радиусов, угол можно разделить не только на три, но и на пять, семь и девять частей — другими словами, разделить его на любое нечетное число. А это, в свою очередь, позволит найти решение еще одной математической головоломки — вписать в окружность любой правильный многоугольник. В справочниках до сих пор утверждается, что вписать правильные многоугольники, имеющие семь и девять сторон, в окружность невозможно. Ну разве это не открытие?
А это, в свою очередь, позволит найти решение еще одной математической головоломки — вписать в окружность любой правильный многоугольник. В справочниках до сих пор утверждается, что вписать правильные многоугольники, имеющие семь и девять сторон, в окружность невозможно. Ну разве это не открытие?
Однако, прежде чем понять, что решение единственно верное, Ляле Гиззатовне нужно было найти для него теоретическое обоснование. Для этого она сформулировала и доказала три теоремы, подтверждающие правильность подхода. И только после этого поделилась с миром своим открытием.
Хождение по академиям
— Однако рассказать о нем оказалось сложнее, чем сделать, — посетовала Ляля Гиззатовна. — С января 2018 года звонила, писала, умоляя чиновников от науки об одном — выслушайте! Но наталкивалась на глухую стену непонимания. Письма нераспечатанными возвращали назад. В телефонных переговорах после слов о том, что мне удалось найти трисекцию угла, обещали перезвонить и не перезванивали. Вероятно, принимали за сумасшедшую. Ведь во всех учебниках написано, что решения у этой задачи нет…
Ведь во всех учебниках написано, что решения у этой задачи нет…
Сначала учительница обратилась в Минобрнауки РФ, однако оттуда ее перенаправили в Российскую академию наук. В РАН сослались на реорганизацию и попросили написать в математический институт имени В.А. Стеклова, где объяснили, что занимаются высшей математикой, а вопросы, касающиеся элементарной математики, — компетенция специально созданного института по работе с научными открытиями.
— Директор этого учреждения, услышав голос «очередного изобретателя вечного двигателя», посоветовал получше изучить геометрию, в которой черным по белому записано, что задача о трисекции угла не имеет решения. А когда я начала его убеждать, посоветовал сначала опубликовать работу в каком-нибудь научном издании, а уж потом отнимать время у академиков, — вспоминает этот разговор учительница.
Дальше была переписка с Казанским и Новосибирским отделениями РАН, откуда Ляля Гиззатовна получила выдержку из Википедии. В итоге письмо учительницы вернулось обратно в Минобрнауки РФ, и круг замкнулся…
Эксперимент
Чтобы помочь Ляле Гиззатовне донести свои мысли до широкой общественности, предлагаем ей прямо в редакции вооружиться циркулем и линейкой. Снимаем на видео, как она делит угол на три равные части, а затем договариваемся о встрече с известным челябинским ученым, академиком РАН Сергеем Матвеевым и его коллегами-математиками из Челябинского госуниверситета.
Снимаем на видео, как она делит угол на три равные части, а затем договариваемся о встрече с известным челябинским ученым, академиком РАН Сергеем Матвеевым и его коллегами-математиками из Челябинского госуниверситета.
Сначала предложение посмотреть видео с решением задачи о трисекции угла встречает тот же отпор, с которым в течение двух лет сталкивалась педагог.
— Этой проблемой занималось не одно поколение математиков, — возмущается Сергей Матвеев. — Какое бы решение ни предложили, оно однозначно неверное. Иначе это действительно сенсация, и с ней можно претендовать на Нобелевскую премию.
— Но ведь, если верить истории, последние две сотни лет решение даже не искали, а все это время математика шла семимильными шагами, — пытаемся привести аргумент Ляли Гиззатовны. — Возможно, стоит попробовать снова? Ведь в ХIХ веке могли и ошибаться?
— Мир остался прежним, как и его законы, — отметает довод доцент кафедры математики Филипп Кораблев. — Если вы бросите камень, он на Марс не улетит. Мы, конечно, можем посмотреть видео и, возможно, даже не обнаружим в этом решении ошибку, но она там обязательно есть. Мы бы посоветовали учительнице поискать ее самой!
Мы, конечно, можем посмотреть видео и, возможно, даже не обнаружим в этом решении ошибку, но она там обязательно есть. Мы бы посоветовали учительнице поискать ее самой!
Вот как! И это экспертное мнение? Проявив немалую настойчивость, нам все-таки удается уговорить математиков потратить пять-семь минут на видео. Несмотря на высказанное недоверие, происходящее на экране вызывает у них неподдельный интерес.
Сотрудники кафедры поэтапно перематывают ролик и ищут «вкравшуюся» ошибку, обмениваясь оживленными репликами: «Если решение строится на том, что это ромб, то оно неверно, поскольку две его вершины находятся на окружности», «А действительно ли эти хорды проходят через центр окружности? Видите, как дрогнула рука, когда она их чертила?».
И, хотя явной ошибки, подрывающей все математические устои, как и предупреждал Филипп Кораблев, с ходу найти не удается, они остаются при своем мнении: решение не может быть правильным, потому что доказано обратное! Именно эту мысль и попросил как можно деликатнее донести до Ляли Гиззатовны Сергей Матвеев.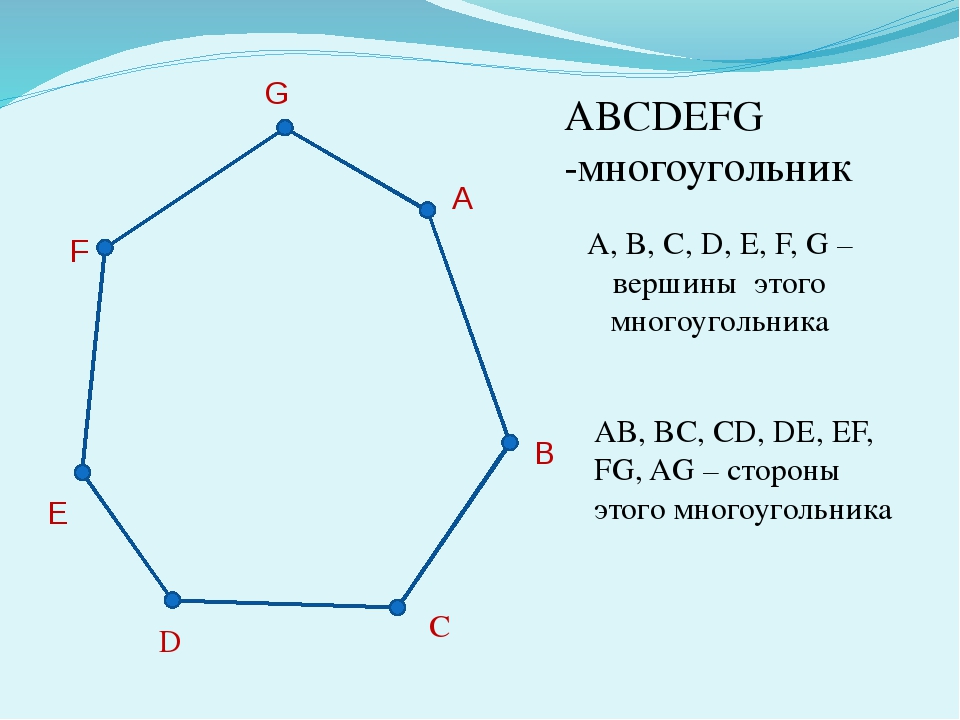 А потом добавил:
А потом добавил:
— А вообще… Было интересно…
Отложите гаджеты
Рассказывая о невозможности решить задачу Архимеда, доцент Кораблев вспомнил, как в школе ее предложила учительница математики — видимо, просто устала от класса:
— Мы пол-урока ломали головы и выдвигали свои версии, конечно, изначально неверные. И только после узнали, что она просто пошутила и водила нас за нос.
Но ведь как минимум один человек из этого класса все-таки стал математиком, разве не так?
Сегодня увлечь детей настолько, чтобы они хотя бы на пять минут отложили в сторону любимые гаджеты, — задачка не из простых. И не всякая школа способна ее решить. Интерес к естественным наукам, физике и математике, царивший в эру завоевания космоса, сильно упал. И пробудить его могли бы подвижники-учителя, такие как Архимед, преподаватель математики доцента Кораблева или скромная пенсионерка из Миасса Ляля Зарипова.
Энергии и увлеченности этого человека можно позавидовать. В 86 лет Ляля Гиззатовна продолжает увлекать любимым предметом окружающих. Наверное, поэтому к ней по-прежнему обращаются с просьбой подтянуть детей по математике. Ведь после ее уроков ученик начинает стараться понять, а не зазубрить, решить, а не списать из Интернета…
Наверное, поэтому к ней по-прежнему обращаются с просьбой подтянуть детей по математике. Ведь после ее уроков ученик начинает стараться понять, а не зазубрить, решить, а не списать из Интернета…
P. S.
Возможно, Ляля Гиззатовна и правда достойна Нобелевской премии? «РГ» обращается ко всем, кто силен в математике и геометрии: давайте найдем ошибку в решении, предложенном учительницей (свои варианты присылайте по адресу [email protected]). А может, никакой ошибки нет? Решив задачу о трисекции угла, Ляля Гиззатовна пытается разгадать загадку простых натуральных чисел…
Определение, стороны, углы (обычные и нестандартные)
Что такое семиугольник?
Гептагон — это 7-сторонний многоугольник с 7 внутренними углами, которые в сумме составляют 900 °. Название семиугольник происходит от греческих слов hepta- для семи и gon- для сторон. Семигранник также называют 7-угольником или септагоном ( септа- на латыни означает семь).
Семигранник также называют 7-угольником или септагоном ( септа- на латыни означает семь).
Форма шестиугольника
Форма семиугольника — это плоская или двумерная форма, состоящая из семи прямых сторон, семи внутренних углов и семи вершин.Форма семиугольника может быть правильной, неправильной, вогнутой или выпуклой.
Вот некоторые дополнительные свойства формы семиугольника:
- Все семиугольники имеют внутренние углы в сумме 900 °
- Все семиугольники имеют внешние углы в сумме 360 °
- Все семиугольники можно разделить на пять треугольников
- Все семиугольники имеют 14 диагоналей (отрезки прямых, соединяющие вершины)
Стороны семиугольника
Стороны семиугольника должны быть прямыми и пересекаться, чтобы образовать семь вершин, замыкающихся в пространстве.Семь сторон семиугольника встречаются, но не пересекаются и не пересекаются друг с другом.
Как и у других двумерных фигур, стороны семиугольника могут иметь разную длину, что создает неправильный семиугольник. Либо стороны могут совпадать, образуя правильный семиугольник
Либо стороны могут совпадать, образуя правильный семиугольник
семиугольник с пересекающимися сторонами называется гептаграммой.
Углы шестиугольника
У семиугольника есть семь внутренних углов в сумме 900 ° и семь внешних углов в сумме 360 °. Это верно как для правильных, так и для неправильных семиугольников.
В правильном семиугольнике каждый внутренний угол составляет примерно 128,57 °.
Ниже приведена формула для определения меры любого внутреннего угла правильного многоугольника (n = количество сторон):
Мы знаем, что все семиугольники (или септагоны) имеют 7 сторон, поэтому можем подставить это в нашу формулу:
(180 ° × 7) — 360 ° 7 =
1260 ° — 360 ° 7 =
900 ° 7 ≈ 128,5714 °
Диагонали семиугольника
семиугольника имеют 14 диагоналей.Для выпуклых семиугольников все диагонали будут внутри формы. Для вогнутых семиугольников по крайней мере одна диагональ будет за пределами формы.
Обычный семиугольник
Вот изображение правильного семиугольника . У правильного семиугольника семь совпадающих сторон, семь вершин и семь совпадающих внутренних углов:
Как указано решеткой, правильный семиугольник на картинке выше имеет равные стороны.
Выпуклый шестиугольник
Правильный семиугольник — это всегда выпуклый семиугольник.У выпуклого семиугольника внутренние углы не превышают 179 °:
Поскольку внутренний угол не превышает 179 °, диагональ не может лежать за пределами многоугольника.
Неправильный семиугольник
Вот неправильный семиугольник , что означает, что его семь сторон не совпадают, а его семь внутренних углов не идентичны:
Как и другие неправильные многоугольники, неправильные семиугольники могут быть выпуклыми или вогнутыми, как на изображении семиугольника выше.
Вогнутый семиугольник
Вогнутый семиугольник имеет как минимум один внутренний угол больше 180 °, и он имеет как минимум одну диагональ, выходящую за пределы многоугольника:
Площадь семиугольника
Площадь правильного семиугольника можно найти по формуле:
Эта формула приблизительно равна A = 3.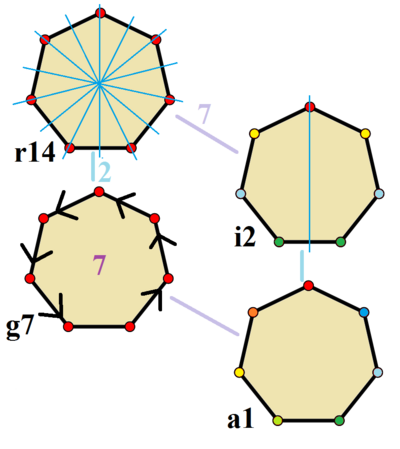 643a2
643a2
В обеих формулах a = длина стороны.
Гептагон в реальной жизни
Есть много примеров семиугольника в реальной жизни, например, на двух картинках ниже:
Подобно другим геометрическим фигурам, таким как восьмиугольник, шестиугольник и четырехугольник, семиугольные фигуры можно встретить в искусственных объектах и в природе.
Heptagon Quiz
- Для любого семиугольника какова сумма его внутренних углов?
- Сколько вершин у любого семиугольника?
- Сколько диагоналей вы можете нарисовать для любого семиугольника?
- Может ли семиугольник иметь девять сторон?
- Ниже представлены несколько полигонов.Сначала выберите все, что являются семиугольниками. Затем для каждого выбранного вами семиугольника определите, является ли он правильным или неправильным, а затем будет ли он вогнутым или выпуклым:
Пожалуйста, попробуйте работу, прежде чем искать ответы!
- Сумма внутренних углов семиугольника всегда составляет 900 °.

- У всех семиугольников семь вершин, так же как у них семь сторон и семь внутренних углов.
- У всех семиугольников будет 14 диагоналей; если диагональ лежит вне многоугольника, вы знаете, что семиугольник вогнутый.
- Нет, у семиугольников всего семь сторон. 9-сторонний многоугольник называется шестигранником.
- Из восьми фигур только пять семиугольников. Два — правильные выпуклые семиугольники. Три — неправильные вогнутые семиугольники. Бонус: одна фигура в сетке — пятиугольник.
Следующий урок:
Десятиугольник
Введение, типы, формулы и решенные примеры
Как правило, многоугольник с n сторонами имеет:
n внутренних углов.
Сумма внутренних углов = (n — 2) × 180 °
Каждый внутренний угол правильного многоугольника = \ [\ frac {(n-2) х 180⁰} {n} \]
Сумма внешних углов = 360 °
В этой статье мы подробно узнаем о семигранном многоугольнике, называемом «семиугольник», с его правильным определением, формой, количеством сторон, свойствами, его формулой периметра и площади. .
.
Определение семиугольника
(изображение скоро будет обновлено)
Семиугольник — это многоугольник, у которого семь сторон и семь углов.Слово «семиугольник» состоит из двух слов, а именно «Гепта» и «Гония», что означает семь углов.
Иногда семиугольник также называют «септагоном».
Поскольку у семиугольника 7 сторон, следовательно,
Сумма внутренних углов = (n — 2) × 180 °
= (7-2) × 180 ° = 5 × 180 °
= 900 °
Каждый внутренний угол правильного семиугольника = \ [\ frac {(n-2) х 180⁰} {n} \]
= \ [\ frac {(7-2) х 180⁰} {5 } \] = \ [\ frac {900} {5} \]
= 128.571 °
Сумма внешних углов = 360 °
Формы семиугольника
В зависимости от сторон, углов и вершин, формы семиугольника классифицируются как:
Правильные семиугольники
- Неправильные семиугольники
Обычный семиугольник
(изображение будет обновлено в ближайшее время)
Чтобы быть правильным семиугольником, семиугольник должен иметь:
семь конгруэнтных сторон (стороны равной длины)
семь конгруэнтных внутренних углов (каждый измеряет 128.
 571 °)
571 °)семь конгруэнтных внешних углов 51,428 °
Примечание: правильные семиугольники не имеют параллельных сторон.
Неправильный семиугольник
Неправильный семиугольник — это семиугольник, имеющий разные длины сторон и размеры углов. (изображение будет обновлено в ближайшее время)
Неправильные семиугольники могут быть выпуклым семиугольником или вогнутым семиугольником:
Выпуклый семиугольник — семиугольник, не имеющий внутренних углов более 180 °.
Вогнутый семиугольник — семиугольник, внутренний угол которого превышает 180 °.(изображение будет обновлено в ближайшее время)
Свойства Heptagon
У него семь сторон, семь вершин и семь внутренних углов.

Имеет 14 диагоналей.
Сумма всех внутренних углов составляет 900 °.
Сумма внешних углов составляет 360 °.
У правильного семиугольника все семь сторон равной длины.
Каждый внутренний угол правильного семиугольника равен 128.571 °.
Неправильные семиугольники имеют разную длину сторон и разную величину угла.
Все диагонали выпуклого семиугольника лежат внутри семиугольника.
некоторые диагонали вогнутого семиугольника могут лежать вне семиугольника.
Периметр семиугольника
Периметр семиугольника — это сумма длин его семи сторон.
Для правильного семиугольника, так как длины всех семи сторон равны.
Следовательно, периметр правильного семиугольника = 7 × (длина стороны) единиц.
Площадь семиугольника
Площадь семиугольника — это область, охватываемая сторонами семиугольника.
Для правильного семиугольника его площадь можно рассчитать по следующей формуле:
(изображение будет скоро обновлено)
Если заданы мера длины стороны и апофемы, то:
центр правильного многоугольника под прямым углом к любой из его сторон.)
Площадь семиугольника = \ [\ frac {7} {2} \] × (длина стороны) × (апофема) единиц 2
OR,
Площадь семиугольника = \ [\ frac {1} {2} \ ] × (периметр семиугольника) × (апофема) единиц2
Если дана только мера длины стороны, то:
Площадь семиугольника = \ [\ frac {7} {4} \] кроватка \ [ \ frac {π} {7} \] ⁰ × (длина стороны) 2 единицы 2
Где, детская кроватка \ [\ frac {π} {7} \] ⁰ = детская кроватка 25,714⁰ = 2,0765
OR,
Площадь семиугольник = 3,634 × (длина стороны) 2 единицы 2
Решенные задачи:
Q. 1. Найдите периметр и площадь правильного семиугольника со стороной 7 см?
1. Найдите периметр и площадь правильного семиугольника со стороной 7 см?
Решение: Дано, сторона семиугольника = 7 см
Периметр правильного семиугольника = 7 × (длина стороны) единиц
= 7 × 7 см
= 49 см
А,
Площадь семиугольника = 3,634 × (длина стороны) 2 шт.2
= 3.634 × (7) 2
= 178,066 см2
Следовательно, периметр и площадь правильного семиугольника со стороной 7 см составляют 40 см и 140 см2 соответственно.
Полигоны
Многоугольник — это плоская форма с прямыми сторонами.
Это многоугольник?
Многоугольники — это двумерные фигуры. Они состоят из прямых линий, а форма «замкнута» (все линии соединяются).
| Многоугольник (прямые стороны) | Не многоугольник (имеет кривую) | Не a Многоугольник (открытый, не закрытый) |
Многоугольник происходит от греческого языка. Poly- означает «много», а -угольник означает «угол».
Poly- означает «много», а -угольник означает «угол».
Типы полигонов
Обычные или нестандартные
У правильного многоугольника все углы равны и все стороны равны, в противном случае он неправильный
| Обычный | Нерегулярное |
Вогнутая или выпуклая
Выпуклый многоугольник не имеет углов, направленных внутрь.Точнее, внутренний угол не может быть больше 180 °.
Если какой-либо внутренний угол больше 180 °, тогда многоугольник вогнутый . ( Подумайте: в вогнутой части есть «пещера» )
| Выпуклый | вогнутая |
Простой или сложный
Простой многоугольник имеет только одну границу и не пересекает себя. сложный полигон пересекает сам себя! Многие правила, касающиеся многоугольников, не работают, когда они сложные.
сложный полигон пересекает сам себя! Многие правила, касающиеся многоугольников, не работают, когда они сложные.
| Простой многоугольник (это пятиугольник) | Сложный многоугольник (также пятиугольник) |
Другие примеры
| Шестигранник неправильной формы | Вогнутый восьмиугольник | Сложный многоугольник («звездообразный многоугольник», в данном случае пентаграмма) |
Играй с ними!
Попробуйте интерактивные многоугольники… сделайте их правильными, вогнутыми или сложными.
Имена полигонов
С помощью этого метода можно делать имена:
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример: 62-сторонний многоугольник — это гексаконтадигон | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
НО для многоугольников с 13 и более сторонами нормально (и проще) написать « 13-угольник », « 14-угольник » . .. « 100-угольник» и т. Д.
.. « 100-угольник» и т. Д.
Вспоминая
Четырехсторонний (4 стороны)
A Quad Велосипед с 4 колесами
Пентагон (5 сторон)
« Пентагон » в Вашингтоне, округ Колумбия, имеет 5 сторон
Шестиугольник (6 сторон)
H oneycomb имеет H эксагонов
Септагон (7 сторон)
Think Sept agon — это «Seven- agon»
Восьмиугольник (8 сторон)
Гной Octo имеет 8 щупалец
Nonagon (9 сторон)
Think Non agon is a «Nine- agon»
Десятиугольник (10 сторон)
Think Dec agon имеет 10 сторон,
точно так же, как наша Dec imal система имеет 10 цифр
Периметр многоугольника — веб-формулы
Периметр многоугольника: Многоугольник определяется как плоская фигура, заключенная в замкнутый контур или замкнутый круг.Как правило, периметр определяется как путь, окружающий область. Периметр многоугольника — это сумма длин его сторон.
Периметр многоугольника — это сумма длин его сторон.
Типы многоугольников
· Квадрат
· Прямоугольник
· Параллелограмм
· Треугольник
· Ромб
· Трапеция
Список форм многоугольника
Форма | Описание | |
Многоугольник | Замкнутая фигура, состоящая из отрезков прямой, каждый из которых пересекается ровно с двумя другими отрезками. | |
Четырехсторонний | 4-сторонний многоугольник | |
Квадрат | Четырехугольник, все стороны которого равны по длине и образуют прямые углы. | |
Треугольник | Трехсторонний многоугольник (сумма внутренних углов = 180 °) | |
Прямоугольник | Четырехсторонний многоугольник со всеми прямыми углами. | |
Параллелограмм | 4-сторонний многоугольник с двумя парами параллельных сторон. | |
Пентагон | 5-сторонний многоугольник (на рисунке показан правильный шестиугольник, где «правильный» означает, что все стороны равны по длине) | |
Шестигранник | 6-сторонний многоугольник | |
Гептагон | 7-сторонний многоугольник | |
Восьмиугольник | 8-сторонний многоугольник |
Примечания :
Периметры квадрата и ромба равны
Периметры прямоугольника и параллелограмма равны
Периметры многоугольников с более чем шестью сторонами могут быть найдены с помощью аналогичной формулы периметра.
· Гептаган (Многоугольник с семью сторонами) периметр равен сумме длин семи сторон
· Восьмиугольник (Многоугольник с восемью сторонами) периметр равен сумме длин восьми сторон
· Nenagon (Многоугольник с девятью сторонами) периметр равен сумме длин девяти сторон
· Десятиугольник (многоугольник с десятью сторонами) периметр равен сумме длин десяти сторон
Фигуры, которые не считаются многоугольниками:
Рисунок ниже не является многоугольником, так как это не замкнутая фигура:
Рисунок ниже не является многоугольником, так как он не состоит из отрезков линии:
Рисунок ниже не является многоугольником, так как его стороны не пересекаются ровно в двух местах каждый:
Правильный многоугольник :
Многоугольник, все стороны которого равны и имеют равные углы.Сумма углов многоугольника со сторонами n , где n равно 3 или более, составляет 180 ° × ( n — 2) градусов.
Примеры правильных многоугольников: Равносторонний треугольник , Квадрат и Ромб
Периметр правильного многоугольника определяется по формуле:
P = ns
Где n — количество сторон, а s — длина каждая сторона.
Неправильный многоугольник:
Многоугольник, у которого не равны стороны и разные внутренние углы, называется неправильным многоугольником.
Периметр неправильного многоугольника определяется простым сложением длины каждой стороны. На рисунках ниже показаны многоугольники, которые не считаются правильными многоугольниками:
Пример 1: Найдите периметр следующей фигуры
Решение :
AB = FE + DC = 5 + 5 = 10 см
BC = AF + ED = 4 + 4 = 8 см
P = AB + BC + CD + DE + EF + FA
P = 10 + 8 + 5 + 4 + 5 + 4
P = 36 см
Пример 2: Найдите периметр правильного десятиугольника со стороной 5 см
Решение :
Количество сторон в десятиугольнике (n) = 10 и стороне s = 5 см
Периметр десятиугольника:
P = нс
P = 10 x 5
P = 50 см
Пример 3: Найдите периметр двенадцатиугольника со стороной 7 см.
Решение :
Количество сторон в двенадцатиугольнике (n) = 12 и стороне s = 7 см
Периметр двенадцатиугольника:
P = нс
P = 12 x 7
P = 84 см
Пример 4: Каков периметр рисунка ниже, если его площадь составляет 27 футов 2 ?
Решение : Периметр фигуры = AB + BD + DE + EA
· Длина стороны AB = 2 фута
· Длина стороны DE = 4 фута
· Длина стороны EA = 5 футов
Площадь трапеции = ½ × высота × (сумма размеров параллельных сторон)
Подставляя значения, получаем:
Площадь = (12) × FC × (AE + BD)
Площадь = (12) × 3 × (5 + BD)
Так как площадь задана, мы теперь имеем:
27 футов 2 = ½ × 3 × (5 + BD)
Умножить каждую сторону на 2
54 футов 2 = 3 × (5 + BD)
Разделить каждую сторону на 3
18 ft = 5 + BD
Вычитая 5 с обеих сторон
BD = 13 ft
И теперь мы можем определить периметр трапеции:
Периметр фигуры = 2 + 13 + 4 + 5 = 24 фута.
Пример 5: Найдите периметр правильного пятиугольника, длина стороны которого равна 4 см.
Решение :
Мы знаем, что периметр правильного многоугольника определяется как: P = ns
Поскольку пятиугольник имеет 5 сторон, мы имеем: n = 5
Итак, периметр правильного пятиугольника равен 5 * 4 = 20 см.
Пример 6 : Каков периметр правильного шестиугольника с длиной стороны 3,5 см?
Решение :
Учитывая, что: s = 3.5см.
У правильного шестиугольника 6 сторон одинаковой длины.
Следовательно, периметр правильного шестиугольника равен:
P = 6 * длина
P = 6 * 3,5
P = 21 см
Онлайн-калькулятор периметра
Название геометрических фигур — многоугольники, многогранники
Поиск инструмента
Название геометрических фигур
Инструмент для поиска названия геометрических фигур. Многоугольники — это геометрические фигуры в плоскости 2D, а многогранники — это геометрические фигуры в пространстве 3D
Результаты
Название геометрических фигур — dCode
Тег (-ы): Geometry
Поделиться
dCode и др.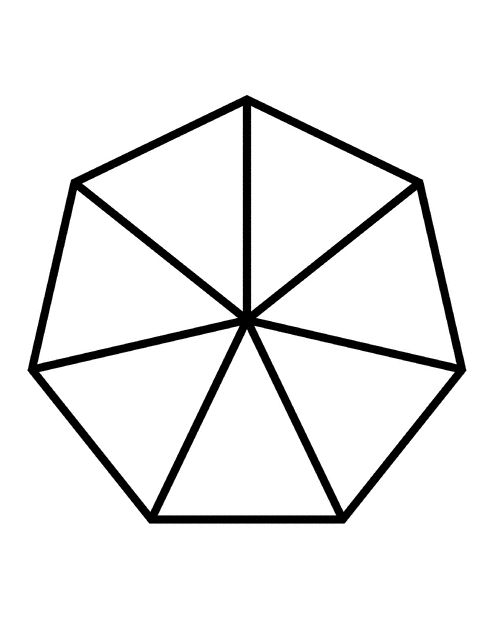
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Ответы на вопросы (FAQ)
Как называется многоугольник с…?
Укажите dCode количество сторон и он найдет имя.
Пример: 6: HEXAGON
12: DODECAGON
В более общем смысле, многоугольника записываются с префиксом, указывающим их количество сторон, и суффиксом -угольник .
Вот список в виде таблицы всех различных правильных геометрических форм 2D-плоскости (таблица имен n-сторонних многоугольников ):
Как называется многогранник с…?
Укажите количество граней, и он найдет имя трехмерной геометрической фигуры.
Пример: 6: HEXAHEDRON
Пример: 12: DODECAHEDRON
Вот таблица всех правильных геометрических форм / многогранников трехмерного пространства (таблица названий n-гранных многогранников ):
Как выучить геометрические фигуры?
Некоторые ресурсы для детей отлично подходят для изучения фигур и других геометрических фигур, например, здесь (ссылка)
Какие многоугольники обладают осевой симметрией?
Все правильные многоугольники имеют по крайней мере одну осевую симметрию.
Правильный многоугольник с таким количеством осей симметрии, сколько у него сторон.
Оси симметрии проходят через центр многоугольника и центр каждой стороны или каждой вершины / угла.
Какие многоугольники имеют центральную симметрию?
Все правильные многоугольника с четным номером стороны имеют центральную симметрию (центр многоугольника ). Многоугольники с нечетным числом сторон не имеют центральной симметрии.
Что такое многогранник?
Многогранник — это обобщение многоугольника / многогранника на все измерения.
Задайте новый вопросИсходный код
dCode сохраняет право собственности на исходный код онлайн-инструмента «Имя геометрических фигур». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любого алгоритма, апплета или фрагмента «Имя геометрических фигур» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любое другое » Имя функции геометрических фигур (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанное на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. Д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для «Имя геометрических фигур» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для «Имя геометрических фигур» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Нужна помощь?
Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!
Вопросы / комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
многоугольник, многогранник, многогранник, геометрия, евклидово, форма, префикс, геометрический, сторона, грань, форма, 2d, 3d, имя, список
Ссылки
Источник: https: // www.dcode.fr/geometric-shapes
© 2021 dCode — Лучший «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.Как создать шестиугольник со скругленными углами в фотошопе с помощью инструмента многоугольник?
Как создать шестиугольник со скругленными углами в фотошопе с помощью инструмента многоугольник? — Обмен стеками графического дизайнаСеть обмена стеков
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
- 0
- +0
- Авторизоваться Зарегистрироваться
Graphic Design Stack Exchange — это сайт вопросов и ответов для профессионалов, студентов и энтузиастов графического дизайна.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 65к раз
Как создать шестиугольник со скругленными углами в Photoshop с помощью инструмента многоугольник?
Эрик1,93311 золотых знаков99 серебряных знаков1515 бронзовых знаков
Создан 02 июл.
Ахмед Амроахмед Амро29711 золотой знак22 серебряных знака1414 бронзовых знаков
Выбрав инструмент «Многоугольник», щелкните маленький значок шестеренки на панели управления a и затем отметьте опцию Smooth Corners .
Photoshop CC или CS6:
Photoshop CS5 или CS4:
Вам также может потребоваться настроить параметры «Звездочка» ….
Создан 02 июля ’13 в 23: 352013-07-02 23:35
Скотт Скотт187k1919 золотых знаков253253 серебряных знака504504 бронзовых знака
14у меня есть идея, попробуйте это создать шестиугольник, добавить толстую границу из стиля, как показано на изображении, и следуйте инструкциям 2 и 3
Создан 19 мая ’14 в 10: 572014-05-19 10:57
1 Очень активный вопрос .Заработайте 10 репутации, чтобы ответить на этот вопрос. Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов. Graphic Design Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Внутренние углы многоугольника
Быстрые определения
Давайте пройдемся по нескольким ключевым словам, чтобы мы все оказались на одной странице.Помните, что многоугольник — это двухмерная фигура, стороны которой нарисованы прямыми линиями (без кривых), которые вместе образуют замкнутую область. Каждая точка многоугольника, где встречаются две стороны, называется вершиной . В каждой вершине есть внутренний угол многоугольника. Квадрат, например, имеет четыре внутренних угла по 90 градусов каждый. Если квадрат представляет ваш класс, внутренние углы — это четыре угла комнаты.
Сумма внутренних углов
В дальнейшем, если многоугольник имеет x сторон, сумма S мер степени этих x внутренних сторон определяется формулой S = (x — 2) (180) .
Например, треугольник имеет 3 угла, которые в сумме составляют 180 градусов. У квадрата 4 угла, которые в сумме составляют 360 градусов. Для каждой дополнительной стороны, которую вы добавляете, вы должны добавить еще 180 градусов к общей сумме.
У квадрата 4 угла, которые в сумме составляют 360 градусов. Для каждой дополнительной стороны, которую вы добавляете, вы должны добавить еще 180 градусов к общей сумме.
Давайте поговорим о диагонали минутку. Что вообще такое диагональю ? Диагональ — это отрезок линии, соединяющий две непоследовательных вершин многоугольника. Это все линии между точками в многоугольнике, если не считать те, которые также являются сторонами многоугольника.На картинке ниже BD — это диагональ. Как видите, отрезок BD делит четырехугольник ABCD на два треугольника. Сумма углов в этих треугольниках (180 + 180 = 360) равна сумме всех углов прямоугольника (360).
Пример 1
Четырехугольник ABCD, конечно, имеет четыре угла. Эти четыре угла находятся в соотношении 2: 3: 3: 4. Найдите градус наибольшего угла четырехугольника ABCD.
Что мы знаем?
У нас есть четыре неизвестных угла, но информация об их отношении друг к другу. Поскольку мы знаем, что сумма всех четырех углов должна составлять 360 градусов, нам просто нужно выражение, которое складывает наши четыре неизвестных угла и устанавливает их равными 360. Поскольку они находятся в соотношении, у них должен быть некоторый общий множитель, который нам нужен найти, называется x.
Поскольку мы знаем, что сумма всех четырех углов должна составлять 360 градусов, нам просто нужно выражение, которое складывает наши четыре неизвестных угла и устанавливает их равными 360. Поскольку они находятся в соотношении, у них должен быть некоторый общий множитель, который нам нужен найти, называется x.
Шагов:
- Добавьте условия 2x + 3x + 3x + 4x
- Приравнять сумму слагаемых к 360
- Решить для x
- Определите угол в градусах.
Решить
2x + 3x + 3x + 4x = 360
12x = 360
x = 360/12
x = 30
Несмотря на то, что мы знаем x = 30, мы еще не закончили.Умножаем 30 на 4, чтобы найти наибольший угол. Поскольку 30 умножить на 4 = 120, наибольший угол составляет 120 градусов. Аналогично, другие углы равны 3 * 30 = 90, 3 * 30 = 90 и 2 * 30 = 60.
Правильные многоугольники
Правильный многоугольник равносторонний. Все его углы имеют одинаковую меру.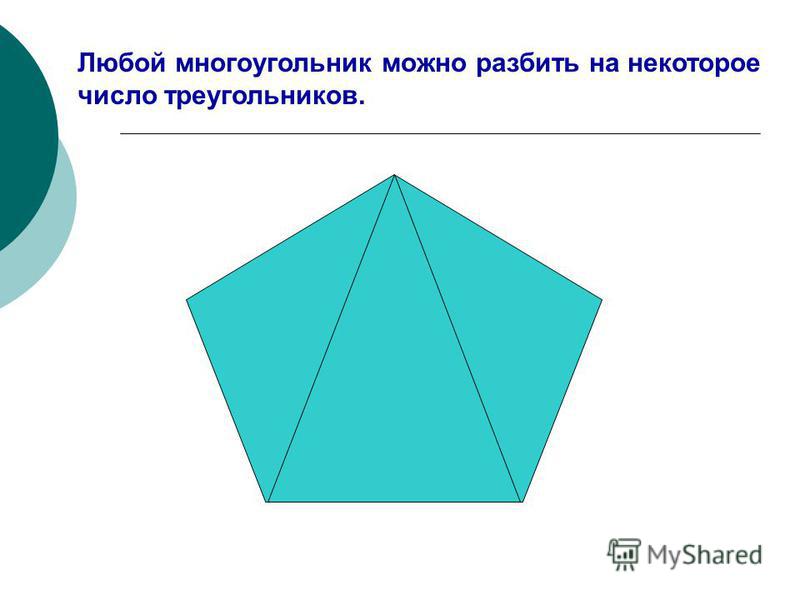 Он также равносторонний. Все его стороны имеют одинаковую длину. Квадрат — это правильный многоугольник, и хотя квадрат представляет собой тип прямоугольника, прямоугольники, которые составляют , а не квадратов, не будут правильными многоугольниками.
Он также равносторонний. Все его стороны имеют одинаковую длину. Квадрат — это правильный многоугольник, и хотя квадрат представляет собой тип прямоугольника, прямоугольники, которые составляют , а не квадратов, не будут правильными многоугольниками.
Пример 2
Найдите сумму углов шестиугольника в градусах. Предполагая, что шестиугольник равен , обычный , найдите градус каждого внутреннего угла.
Что мы знаем?
Мы можем использовать формулу S = (x — 2) (180) для суммирования степени любого многоугольника.
У шестиугольника 6 сторон, поэтому x = 6.
Решить
Пусть x = 6 в формуле и упростит:
S = (6-2) (180)
S = 4 (180)
S = 720
Правильный многоугольник — это равноугольный , что означает, что все углы имеют одинаковую величину.В случае правильного шестиугольника сумма в 720 градусов будет равномерно распределена между шестью сторонами.
Итак, 720/6 = 120.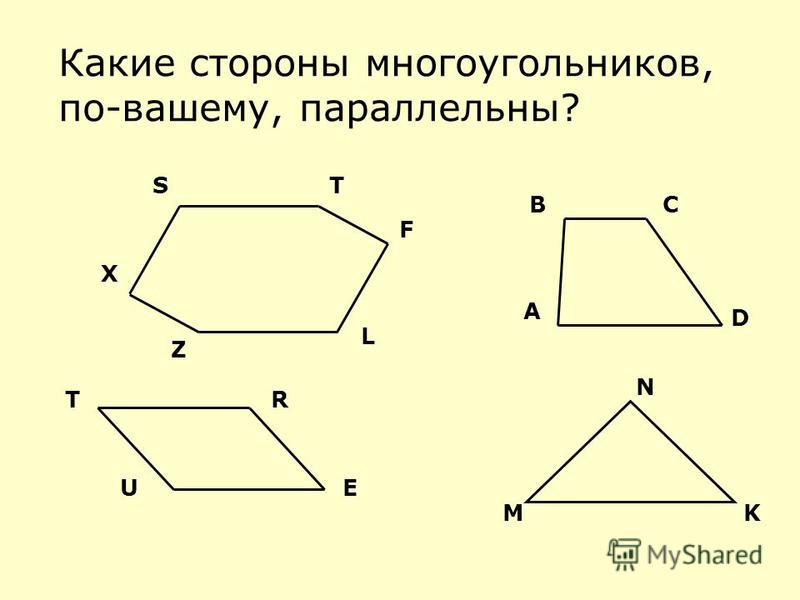 В правильном шестиугольнике шесть углов, каждый по 120 градусов.
В правильном шестиугольнике шесть углов, каждый по 120 градусов.
Пример 3
Если сумма углов многоугольника равна 3600 градусам, найдите количество сторон многоугольника.
Изменение формулы на противоположное
Опять же, мы можем использовать формулу S = (x — 2) (180), но на этот раз мы решаем для x вместо S. Ничего страшного!
Решить
В этой задаче положим S = 3600 и решим относительно x.
3600 = (x — 2) (180)
3600 = 180x — 360
3600 + 360 = 180x
3960 = 180x
3960/180 = x
22 = x
Многоугольник с 22 сторонами имеет 22 угла, сумма которых равна 3600 градусам.
Внешние углы многоугольника
В каждой вершине многоугольника может быть образован внешний угол путем удлинения одной стороны многоугольника, так что внутренний и внешний углы в этой вершине являются дополнительными (в сумме 180). На рисунке ниже углы a, b, c и d являются внешними, а сумма их градусов равна 360.
Если у правильного многоугольника x сторон, то каждый внешний угол равен 360, деленному на x.
Давайте рассмотрим два типовых вопроса.
Пример 4
Найдите градус каждого внутреннего и внешнего угла правильного шестиугольника.
Помните, что формула суммы внутренних углов S = (x-2) * 180. У шестиугольника 6 сторон. Поскольку x = 6, сумму S можно найти, используя S = (x — 2) (180)
S = (10-6) (180)
S = 4 (180)
S = 720
В шестиугольнике шесть углов, а в правильном шестиугольнике все они равны.Каждый составляет 720/6 или 120 градусов. Теперь мы знаем, что внутренние и внешние углы составляют дополнительных (в сумме 180) в каждой вершине, поэтому размер каждого внешнего угла составляет 180 — 120 = 60.
Пример 5
Если размер каждого внутреннего угла правильного многоугольника равен 150, найдите количество сторон многоугольника.
Ранее мы определили количество сторон в многоугольнике, взяв сумму углов и используя формулу S = (x-2) * 180 для решения. Но на этот раз мы знаем только размер каждого внутреннего угла.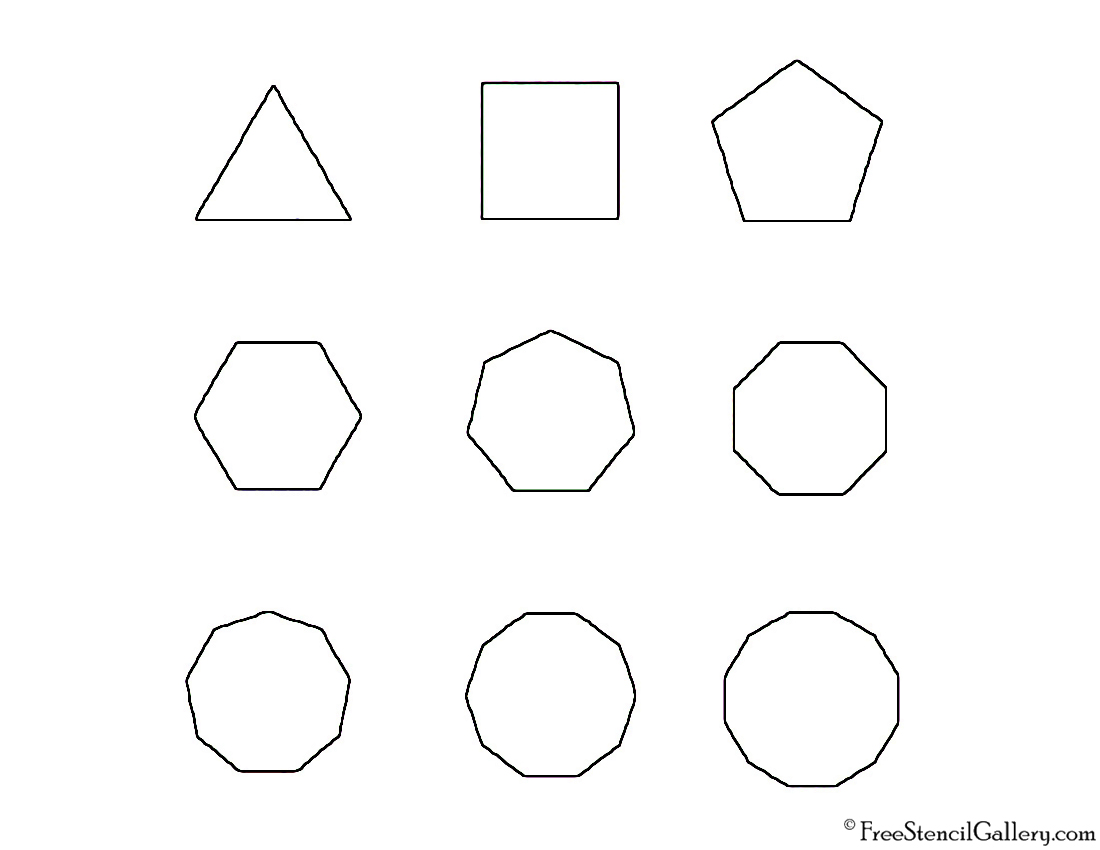 Нам пришлось бы умножить на количество углов, чтобы найти сумму … но вся проблема в том, что мы еще не знаем количество сторон ИЛИ сумму!
Нам пришлось бы умножить на количество углов, чтобы найти сумму … но вся проблема в том, что мы еще не знаем количество сторон ИЛИ сумму!
Но, поскольку размер каждого внутреннего угла равен 150, мы также знаем, что мера внешнего угла, проведенного в любой вершине в терминах этого многоугольника, равна 180 — 150 = 30. Это потому, что они образуют дополнительные пары (внутренний + внешний = 180).
До примера 4 мы узнали, что также можем вычислить величину внешнего угла в правильном многоугольнике как 360 / x, где x — количество сторон.Теперь у нас есть способ найти ответ!
30 = 360 / x
30x = 360
x = 360/30
x = 12
Наш многоугольник с внутренними углами 150 градусов (и внешними углами 30 градусов) имеет 12 сторон.
Кстати, геометрическая фигура с 12 сторонами называется двенадцатигранником.
Урок от г-на Фелиза
.Проекты
Процедура T должна начать рисование «шапочки» по текущему направлению, а закончить рисование в нижней части «ножки« с направлением по «шапочке»:
Программа должна запускаться зелёным флажком и реагировать на клавиши 1–6. Описание узоров приводится в таблице.
Для каждого из вариантов 3–6 создаём процедуру перехода (поворота), которая вместе с процедурой Т обеспечит нужный рисунок (при повторении этих двух процедур).
Примерные параметры пера:
- цвет — красный
- толщина — 4
Удобная начальная точка: (–200, 100).
Решение сохранить под именем Т узоры.
— А сможешь ли ты нарисовать лесенку? — спросили Кота.
— Легко! — ответил усатый. — Я смогу нарисовать её даже кончиком своего хвоста!
Кот сдержал обещание: нарисовал лесенку и, действительно, кончиком своего хвоста:
Лесенка начинается с точки: (−220,80)
Число ступеней: 4
Размер ступени: 90 (горизонталь), 60 (вертикаль)
Цвет: чёрный
Толщина пера: 5
Напишите и вы такую программу.
Центр спрайта сместите на кончик хвоста во встроенном графическом редакторе.
Решение сохраните под именем Лесенка.
Кот показал себя не только хорошим рисовальщиком, но и волшебником: сначала он нарисовал лесенку (как в предыдущем проекте), а затем спустился по нарисованному:
Видео выполненного проекта можно посмотреть по адресу: practical/01/unit03/
Видео проекта: practical/01/unit03/ladder. mp4
mp4
Повторите подвиг Кота в своей программе.
Решение сохраните под именем Лесенка1.
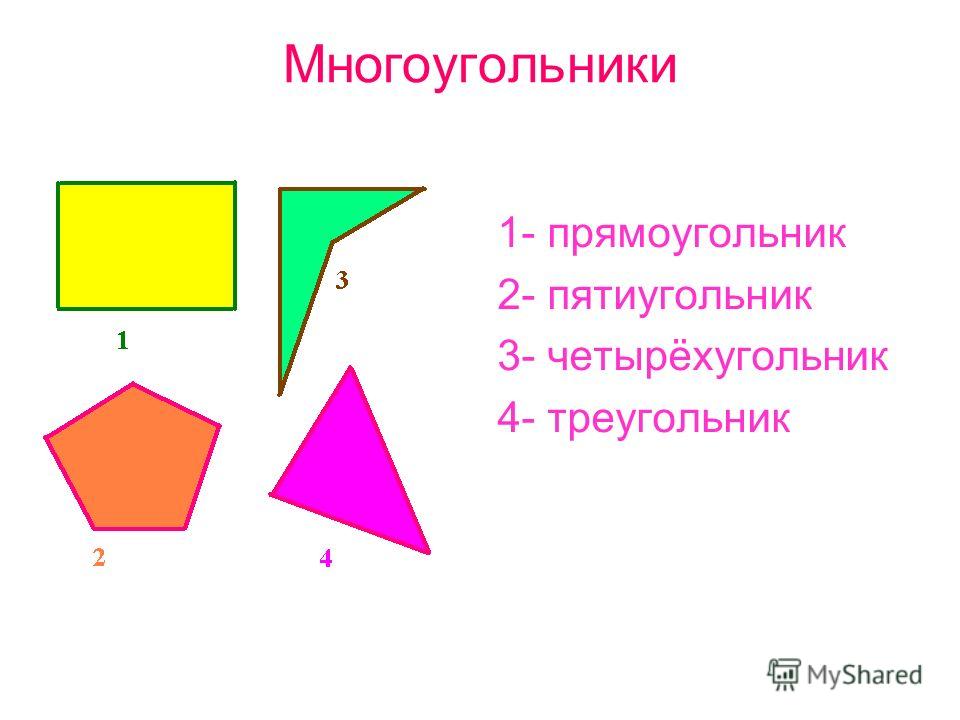
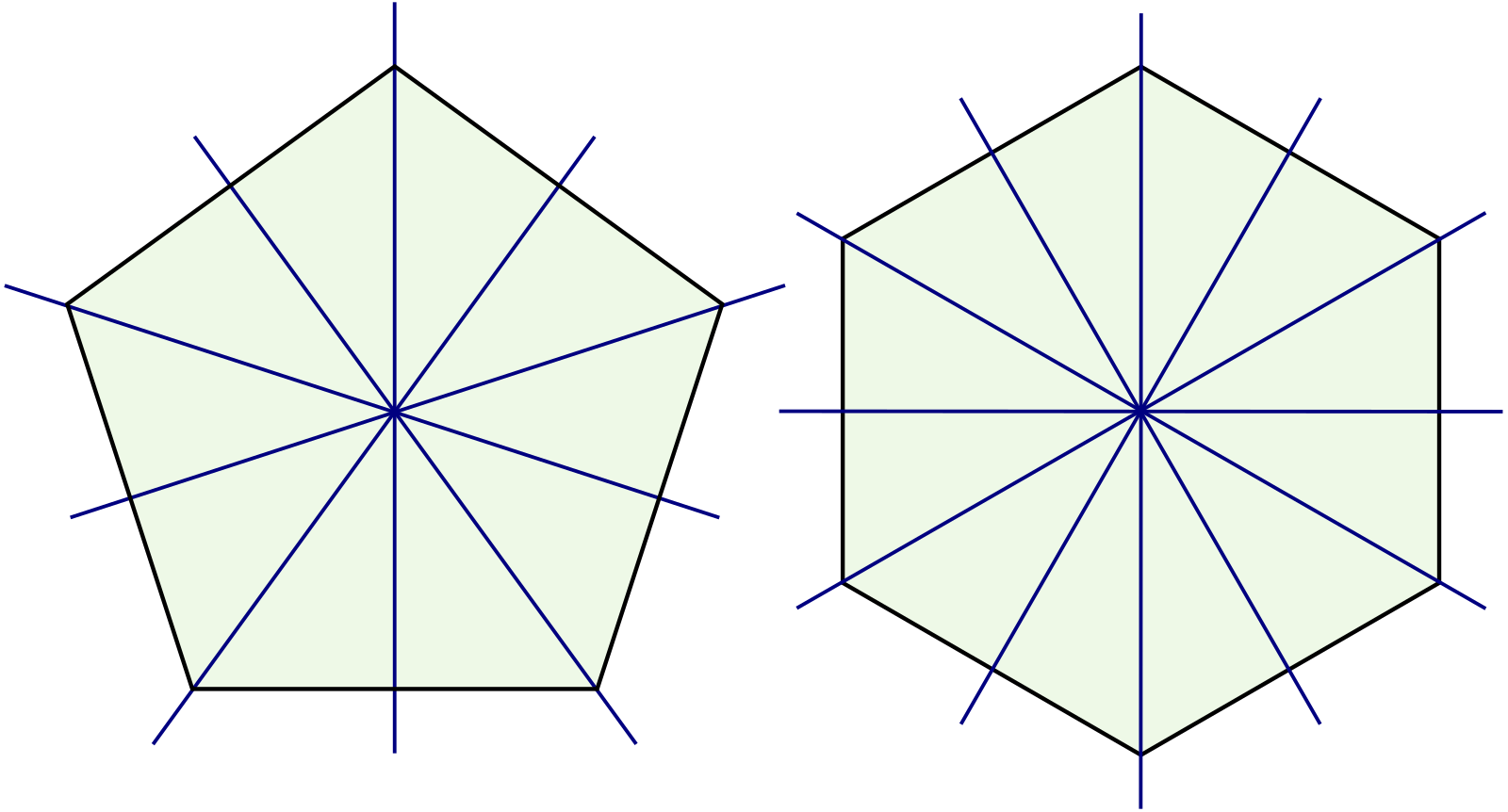
Правильным считается такой многоугольник, у которого все стороны равны между собой и все углы равны между собой. На рисунке представлены правильные: треугольник, четырёхугольник (квадрат), пятиугольник, шестиугольник, восьмиугольник и десятиугольник
Нарисовать два комплекта обозначенных выше правильных многоугольников со стороной равной 60 так, как показано на рисунке:
Размеры и положение многоугольников
Видео выполненного проекта можно посмотреть по адресу: practical/01/unit03/
Видео проекта: practical/01/unit03/Polygons. mp4
mp4
Решение сохранить под именем Многоугольники.
Анализ решения
Мы уже строили правильный треугольник и квадрат. Попробуем обобщить эти опыты на построение произвольного правильного многоугольника.
Вспомним алгоритмы построения этих фигур:
| Треугольник | Квадрат |
|---|---|
|
Повторить 3 разa:
|
Повторить 4 разa:
|
Заметим, что после всех поворотов исполнитель оказывается
установленным в прежнем направлении. Это означает, что в сумме все
повороты составляют 360°!
Это означает, что в сумме все
повороты составляют 360°!
Так как углы всех поворотов равны, то получается, что для построения N-угольника нужно после прорисовки каждой стороны поворачиваться на угол равный 360/N.
Получаем универсальный алгоритм построения правильного N-угольника:
Повторить N раз:
- Рисуем сторону
- Поворачиваемся на 360/N°
В частности, имеем:
| Пятиугольник | Шестиугольник |
|---|---|
|
Повторить 5 раз:
|
Повторить 6 раз:
|
Кукарача высказал по этому проекту два интересных замечания.
Сборку программу можно значительно ускорить, если использовать интерфейсную команду Дублировать. Команду выбираем в контекстном меню правой кнопки мыши.
Дублируем код процедуры Треугольник в процедуру Квадрат. Правим число повторений и угол поворота. Аналогично собираем процедуру Пятиугольник и все остальные N-угольники
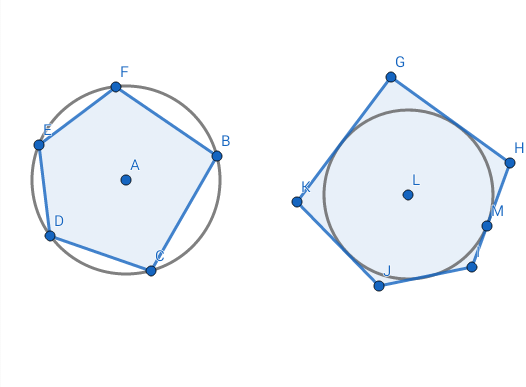
В правильных многоугольниках вершины равноудалены от центра фигуры. Значит, эти вершины лежат на одной окружности (описанной вокруг многоугольника):
Вершины правильного многоугольника лежат на окружности, описанной вокруг этого многоугольника
Как нарисовать окружность. А если вершин у правильного
многоугольника будет очень много? Тогда все точки описанной окружности будут
вершинами многоугольника, и многоугольник не будет отличаться от окружности!
Такое возможно на экране компьютера, где количество
точек-пикселей ограничено. Попробуйте нарисовать окружность при
помощи правильного многоугольника с 360 углами и стороной
равной 1.
Попробуйте нарисовать окружность при
помощи правильного многоугольника с 360 углами и стороной
равной 1.
В уроке 3 рассказано, как рисовать узоры квадратом.
— А что если вместо квадрата взять треугольник? — подумал Кот.
И у него получилось весьма неплохо!
Собрать программу, которая создавала бы узоры, приведённые ниже в таблице, при помощи процедуры, заставляющей Кота совершать поход по правильному треугольнику.
Процедура треугольник
Правильный треугольник (все стороны равны и углы равны по 60°) проходится так же, как и квадрат, но повороты выполняются на угол 120°, и сторон у треугольника три.
Начинаем с тех координат и того направления, в которые был установлен исполнитель перед входом в процедуру. Поворачиваем после прохождения каждой стороны на угол 120° против часовой стрелки. Заканчиваем в исходной точке, причём исполнитель будет установлен в том же направлении, в котором был установлен начально
Поворачиваем после прохождения каждой стороны на угол 120° против часовой стрелки. Заканчиваем в исходной точке, причём исполнитель будет установлен в том же направлении, в котором был установлен начально
Программа должна запускаться зелёным флажком и реагировать на клавиши 1–7. Описание узоров приводится в таблице.
Параметры пера:
- цвет — синий
- толщина — 1
Начальная точка: (–50, –50).
Для быстрого рисования фигур можно в меню приложения Скретч включить Турбо режим:
Решение сохранить под именем Треугольные узоры.
 Помогите роботландцам создать
макет тетрадного листа.
Помогите роботландцам создать
макет тетрадного листа.
Видео выполненного проекта можно посмотреть по адресу: practical/01/unit03/
Видео проекта: practical/01/unit03/In_line.mp4
| № | Этап ТЗ | Содержание |
|---|---|---|
| 1 | Название проекта | Тетрадь в линейку |
| 2 | Идея проекта |
Создать макет тетради в линейку согласно следующему эскизу:
Размеры и расположение линеек на тетрадном листе |
| 3 | Сценарий проекта | Установить исполнителя на начало первой линии (слева, снизу). Затем рисовать линии снизу вверх |
| 4 | Среда | Изначально белый фон |
| 5 | Спрайты |
Карандаш из библиотеки. Центр спрайта сместить на кончик карандаша
во встроенном графическом редакторе: Центр спрайта сместить на кончик карандаша
во встроенном графическом редакторе:
|
| 6 | Интерфейс | Приложение запускается по зелёному флажку, никаких взаимодействий с пользователем не предусматривается |
| 7 | Идея алгоритма | Рисовать линии в цикле. Тело цикла должно содержать: рисование линии, возврат в начальную точку, смещение вверх к началу следующей линии |
| 8 | Алгоритм | Описан отдельно за таблицей |
- Подготовка
- Повторить 15 раз:
- Линия вправо
- Возврат влево (с поднятым пером)
- На строку выше
- Линия вправо
- Возврат влево (с поднятым пером)
Скрипт, соответствующий этому алгоритму, может быть таким:
Вид главного скрипта с процедурами («самодельными» командами)
Процедура Подготовка должна сделать следующее.
- Установить исполнителя в начальное положение (на начало первой снизу линии).
- Установить стиль вращения «не вращать».
- Очистить сцену.
- Установить размер пера в 1.
- Установить синий цвет пера.
Решение сохранить под именем Тетрадь в линейку.
Видео выполненного проекта можно посмотреть по адресу: practical/01/unit03/
Видео проекта: practical/01/unit03/Pen_color_palette.mp4
В Скретч цвет Пера можно задать командой
. Число N меняется от 0 до 200.
Число N меняется от 0 до 200.
Получается, что цвет можно обозначать числом. Хотелось бы увидеть весь набор этих числовых цветов от 0 до 200!
Создайте палитру, в которой каждый цвет от 0 до 200 будет занимать полоску шириной 2 и высотой 200. При этом вся палитра будет представлять собой прямоугольник размером 400×200:
Нарисовать палитру цветов Пера в виде прямоугольника 400×200. Каждый цвет палитры занимает полоску размером 2×200
Постановка задачи порождает следующий план решения:
- Подготовить сцену и исполнитель.
- Нарисовать прямоугольник цветовыми полосками.
- Завершить работу (спрятать исполнитель).

Уточняем этот план в виде более точного алгоритма:
- Подготовка
- Повторить 200 раз:
- Рисуем прямую вниз
- Возвращаемся вверх
- Смещаемся вправо на 2
- Меняем цвет пера на 1
- Завершение
Скрипт для исполнителя, соответствующий этому алгоритму, может быть таким:
Вид главного скрипта с процедурами («самодельными» командами)
— В каких из этих процедурах нужно поднимать и опускать перо? — спросил Лисёнок.
Кукарача ответил так.
— Перо опускается перед началом рисования и поднимается
в конце рисования.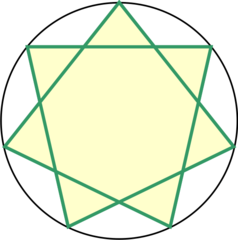 Среди всех запланированных процедур только одна
рисовальная — Рисуем прямую вниз.
Значит, опускать перо надо в начале этой процедуры, а поднимать —
в конце.
Среди всех запланированных процедур только одна
рисовальная — Рисуем прямую вниз.
Значит, опускать перо надо в начале этой процедуры, а поднимать —
в конце.
Процедура Подготовка должна сделать следующее.
- Установить исполнителя в начальное положение.
- Показать его.
- Установить стиль вращения «не вращать».
- Очистить сцену.
- Установить размер пера в 2.
- Установить цвет пера в 0.
Процедура Завершение должна:
- спрятать исполнителя.
Решение сохранить под именем Палитра цветов Пера.
 В роботландскую типографию поступил новый заказ, на этот раз
на тетради в клетку. Помогите роботландцам создать
макет тетрадного листа.
В роботландскую типографию поступил новый заказ, на этот раз
на тетради в клетку. Помогите роботландцам создать
макет тетрадного листа.
Видео выполненного проекта можно посмотреть по адресу: practical/01/unit03/
Видео проекта: practical/01/unit03/In_cell.mp4
Размеры и расположение линеек на тетрадном листе показаны на рисунке.
Размеры и расположение линеек на тетрадном листе
- Подготовка
- Горизонтали
- Вертикали
Скрипт, соответствующий этому алгоритму, может быть таким:
Вид главного скрипта с процедурами («самодельными» командами)
Рекомендация
При проектировании программы используйте скрипты, написанные
для задачи Тетрадь в линейку.
Решение сохранить под именем Тетрадь в клетку.
Вот так увидел Лео домики на крутом вираже из своего самолёта
Заставьте кота нарисовать улицу из пяти домов так, как увидел её Лео на крутом вираже.
Видео выполненного проекта можно посмотреть по адресу: practical/01/unit03/
Видео проекта: practical/01/unit03/Houses.mp4
Размеры и положение домиков показаны на рисунке.
Размеры и положение домиков
Решение сохранить под именем Домики.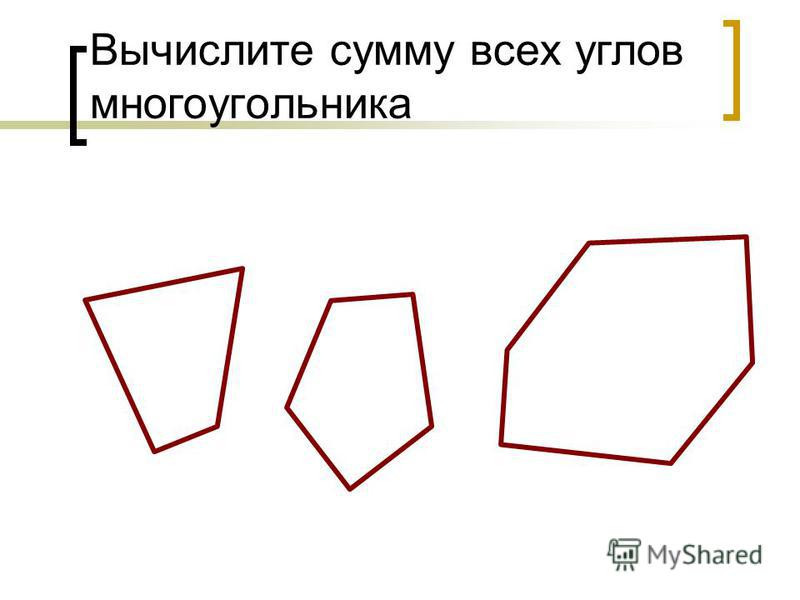
Главный скрипт
Домики удобно рисовать в цикле, повторяющего две команды:
- Рисование домика из текущего положения исполнителя.
- Переход в точку, из которой надо рисовать следующий домик.
После рисования последнего домика переходить к следующему не надо. Поэтому алгоритм решения может быть таким:
- Подготовка
- Повторить 4 разa:
- Рисуем домик
- Идём к следующему
- Рисуем домик
- Спрятать исполнителя
Скрипт, соответствующий этому алгоритму, может быть таким:
Вид главного скрипта с процедурами («самодельными» командами)
Процедура Подготовка должна сделать следующее.
- Установить исполнителя в начальное положение (на начало рисования первого домика).
- Установить исполнителя в нужном направлении.
- Показать исполнителя.
- Очистить сцену.
- Установить насыщенность цвета пера («тень» пера) в 0 (при нулевой насыщенности любой цвет становится чёрным).
- Установить размер пера в 2.
В каком направлении нужно установить исполнителя? Лео увидел домики под углом в 30° к горизонту (горизонтали). Значит, направление прямой, на которой расположены домики — 60°.
Рисуем домик
Домик состоит из сруба и крыши. Поэтому процедура рисования домика разбивается на 3 части:
- Рисуем квадрат.

- Переходим в начальную точку крыши.
- Рисуем треугольник.
Соответственно, процедура Рисуем домик может быть такой:
Определение процедуры Рисуем домик
Квадрат
Квадрат был нарисован на уроке. Ничего сложного!
Начинаем рисовать из точки A в текущем направлении, поворачиваясь после отрисовки каждой стороны на угол 90° против часовой стрелки. Заканчиваем рисование в той же точке A, причём исполнитель будет установлен в то же направление, в котором начинал рисование
Треугольник
Правильный треугольник (все стороны и углы равны) рисуется так же,
как и квадрат, но повороты выполняются на угол 120°.
Начинаем рисовать из точки B по направлению стороны квадрата, поворачиваясь после отрисовки каждой стороны на угол 120° против часовой стрелки. Заканчиваем рисование в той же точке B, причём исполнитель будет установлен в то же направление, в котором начинал рисование
Благодаря тому, что при рисовании были использованы команды поворота, а не команды направления, домики легко перестроить с любым наклоном к линии горизонта. В программе меняется только одна команда в процедуре Подготовка:
Чтобы построить домики, например, без всякого наклона, нужно изменить начальную установку исполнителя, и поставить его в направлении 90° (вправо)
Попробуйте расположить домики по горизонтали!
 По адресу practical/01/unit03/Артисты.sb2
находится программа, результат выполнения которой показан на видео.
По адресу practical/01/unit03/Артисты.sb2
находится программа, результат выполнения которой показан на видео.
Видео выполненного проекта можно посмотреть по адресу: practical/01/unit03/
Видео проекта: practical/01/unit03/Артисты.mp4
Задание. Попробуйте разобраться, как работает код и добавьте выступление 2-х новых артистов. Результат сохраните под именем Артисты-2.
Решение сохраните под своим именем.
Как нарисовать шестиугольник в линейной перспективе
Здравствуйте коллеги. В этом уроке узнаем, как нарисовать шестиугольник в перспективе.
Как вписать его фронтально в окружность мы смотрели в прошлом уроке. Заметьте ничего сложного нет. Нам удалось малыми средствами начертить равнобедренный предмет с шестью вершинами.
Его можно сделать еще проще. Например, отложить шесть радиусов на тело овала. Эта фигура не такая сложная, как с пятью или с семью углами, уроки которых мы рассмотрим в других статьях.
Я не фанат точной науки геометрии. Приходилось рисовать, но без циркуля и угольника не всегда получалось правильно создать картину.
Наша задача показать полную иллюзию пространства на двухмерной плоскости. Нарисуем многоугольник онлайн в перспективе, а для этого нужно знать правила построения.
К примеру, чтобы создать многоугольный узор на потолке, как на картине художника Премацци, нужно знать законы построения.
«Виды залов нового Эрмитажа. Галерея фламандской живописи.»
На картине Гау мы видим интерьер дворца. И все узоры выполнены в рамках законов линейной перспективы.
«Зимний дворец. Петровский зал.»
Посмотрите узор на полу в произведении Жерома Жан-Леона.
«Painting Breathes Life into Sculpture»
Задумывая сюжет в интерьере, нам придется изучать принципы построения.
Как положить шестигранник на плоскость посмотрите видео урок ниже.
Рисуем онлайн многоугольник в перспективе
Делал я его с помощью программы Photoshop, все то же самое можно сделать и на бумаге.
Для рисования нам понадобятся:
- Карандаш
- Циркуль
- Линейка
- Резинка
Такой небольшой набор инструментов необходим для черчения в живую.
Сам рисунок вы можете посмотреть на видео.
Сделаем акцент, когда шестиугольник вписанный в окружность.
Ниже на фото фигура построена. И, казалось бы, добавить нечего.
Но правильный рисунок будет если его вписать в овал. У нас есть две точки по сторонам квадрата, и появились новые четыре точки. Картинка ниже.
В таком формате он не будет деформированный, вытянутый или сплюснутый. На рисунке будет смотреться правдоподобнее.
По такому же принципу можно сделать фигуру не только горизонтально, но и вертикально.
В таком случае мы сможем выстроить призму. Для этого мы сделаем переднее и заднее основания и соединим их линиями. Эта процедура детально описана в моем платном курсе, можете перейти по этой ссылке.
Вот такой урок получился.
Творческих вам успехов.
Как сделать ровный 6 угольник. Правильный шестиугольник построение
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности.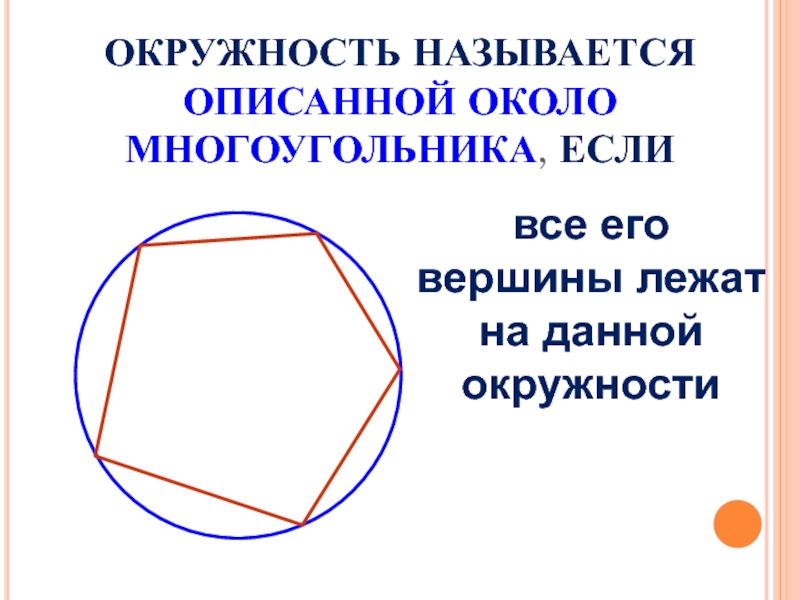 Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Правильный описанный треугольник строят следующим образом (рисунок 38). Из центра заданной окружности радиуса R 1 проводят окружность радиусом R 2 = 2R 1 и делят ее на три равные части. Точки деления А, В, С являются вершинами правильного треугольника, описанного около окружности радиуса R 1 .
Рисунок 38
Правильный описанный четырехугольник (квадрат) можно построить с помощью циркуля и линейки (рисунок 39). В заданной окружности проводят два взаимно перпендикулярных диаметра. Приняв точки пересечения диаметров с окружностью за центры, радиусом окружности R описывают дуги до взаимного их пересечения в точках А, В, С,D . Точки A , B , C , D и являются вершинами квадрата, описанного около данной окружности.
В заданной окружности проводят два взаимно перпендикулярных диаметра. Приняв точки пересечения диаметров с окружностью за центры, радиусом окружности R описывают дуги до взаимного их пересечения в точках А, В, С,D . Точки A , B , C , D и являются вершинами квадрата, описанного около данной окружности.
Рисунок 39
Для построения правильного описанного шестиугольника необходимо вначале построить вершины описанного квадрата указанным выше способом (рисунок 40, а). Одновременно с определением вершин квадрата заданную окружность радиуса R делят на шесть равных частей в точках 1, 2, 3, 4, 5, 6 и проводят вертикальные стороны квадрата. Проведя через точки деления окружности 2–5 и 3–6 прямые до пересечения их с вертикальными сторонами квадрата (рисунок 40, б), получают вершины А, В, D, Е описанного правильного шестиугольника.
Рисунок 40
Остальные вершины C и F определяют с помощью дуги окружности радиуса OA , которая проводится до пересечения ее с продолжением вертикального диаметра заданной окружности.
3 СОПРЯЖЕНИЯ
Геометрические узоры весьма популярны в последнее время. В сегодняшнем уроке мы научимся создавать один из таких узоров. Используя переход, оформление и модные цвета мы создадим паттерн, который вы сможете использовать в веб и полиграфическом дизайне.
Результат
Шаг 2
Нарисуйте еще один шестиугольник, на этот раз меньше — выберите радиус в 20pt .
2. Переход между шестиугольниками
Шаг 1
Выделите оба шестиугольника и выровняйте их по центру (вертикально и горизонтально). Используя инструмент Blend/Переход (W) , выделите оба шестиугольника и укажите им переход в 6 шагов (Steps) . Чтобы было лучше видно, измените перед переходом цвет фигур.
3. Делим на секции
Шаг 1
Инструментом Line Segment/Отрезок линии (\) нарисуйте линию, пересекающую шестиугольники по центру от самого левого угла к самому правому. Нарисуйте еще две линии, пересекающие шестиугольники по центру от противоположных углов.
Нарисуйте еще две линии, пересекающие шестиугольники по центру от противоположных углов.
4. Закрашиваем секции
Шаг 1
Перед тем как начать закрашивать секции, давайте определимся с палитрой. Вот какова палитра из примера:
- Синий: C 65 M 23 Y 35 K 0
- Бежевый: C 13 M 13 Y 30 K 0
- Персиковый: C 0 M 32 Y 54 K 0
- Светло-розовый: C 0 M 64 Y 42 K 0
- Темно-розовый: C 30 M 79 Y 36 K 4
В примере сразу использовался режим CMYK, чтобы можно было распечатать узор без изменений.
5. Последние штрихи и узор
Шаг 1
Сгруппируйте (Control-G) все секции и шестиугольники, после того как закончите с их окраской. Копируйте (Control-C) и Вставьте (Control-V) группу из шестиугольников. Назовем оригинальную группу Hexagon A, а ее копию Hexagon B . Выровняйте группы.
Выровняйте группы.
Шаг 2
Примените Linear Gradient/Линейный градиент к группе Hexagon B. В палитре Gradient/Градиент укажите заливку от фиолетового (C60 M86 Y45 K42 ) к кремовому цвету (C0 M13 Y57 K0 ).
Сетки из шестиугольников (гексагональные сетки) используются в некоторых играх, но они не так просты и распространены, как сетки прямоугольников. Я коллекционирую ресурсы о сетках шестиугольников уже почти 20 лет, и написал это руководство по самым элегантным подходам, реализуемым в простейшем коде. В статье часто используются руководства Чарльза Фу (Charles Fu) и Кларка Вербрюгге (Clark Verbrugge). Я опишу различные способы создания сеток шестиугольников, их взаимосвязь, а также самые общие алгоритмы. Многие части этой статьи интерактивны: выбор типа сетки изменяет соответствующие схемы, код и тексты. (Прим. пер.: это относится только к оригиналу, советую его изучить. В переводе вся информация оригинала сохранена, но без интерактивности. ) .
) .
Примеры кода в статье написаны псевдокодом, так их легче читать и понимать, чтобы написать свою реализацию.
Геометрия
Шестиугольники — это шестигранные многоугольники. У правильных шестиугольников все стороны (грани) имеют одинаковую длину. Мы будем работать только с правильными шестиугольниками. Обычно в сетках шестиугольников используются горизонтальная (с острым верхом) и вертикальная (с плоским верхом) ориентации.
Шестиугольники с плоским (слева) и острым (справа) верхом
У шестиугольников по 6 граней. Каждая грань общая для двух шестиугольников. У шестиугольников по 6 угловых точек. Каждая угловая точка общая для трёх шестиугольников. Подробнее о центрах, гранях и угловых точках можно прочитать в моей статье о частях сеток (квадратах, шестиугольниках и треугольниках).
Углы
В правильном шестиугольнике внутренние углы равны 120°. Есть шесть «клиньев», каждый из которых является равносторонним треугольником с внутренними углами 60°. Угловая точка i находится на расстоянии (60° * i) + 30° , на size единиц от центра center . В коде:
Угловая точка i находится на расстоянии (60° * i) + 30° , на size единиц от центра center . В коде:Function hex_corner(center, size, i):
var angle_deg = 60 * i + 30
var angle_rad = PI / 180 * angle_deg
return Point(center.x + size * cos(angle_rad), center.y + size * sin(angle_rad))
Для заполнения шестиугольника нужно получить вершины многоугольника с hex_corner(…, 0) по hex_corner(…, 5) . Для отрисовки контура шестиугольника нужно использовать эти вершины, а затем нарисовать линию снова в hex_corner(…, 0) .
Разница между двумя ориентациями в том, что x и y меняются местами, что приводит к изменению углов: углы шестиугольников с плоским верхом равны 0°, 60°, 120°, 180°, 240°, 300°, а с острым верхом — 30°, 90°, 150°, 210°, 270°, 330°.
Углы шестиугольников с плоским и острым верхом
Размер и расположение
Теперь мы хотим расположить несколько шестиугольников вместе. В горизонтальной ориентации высота шестиугольника height = size * 2 .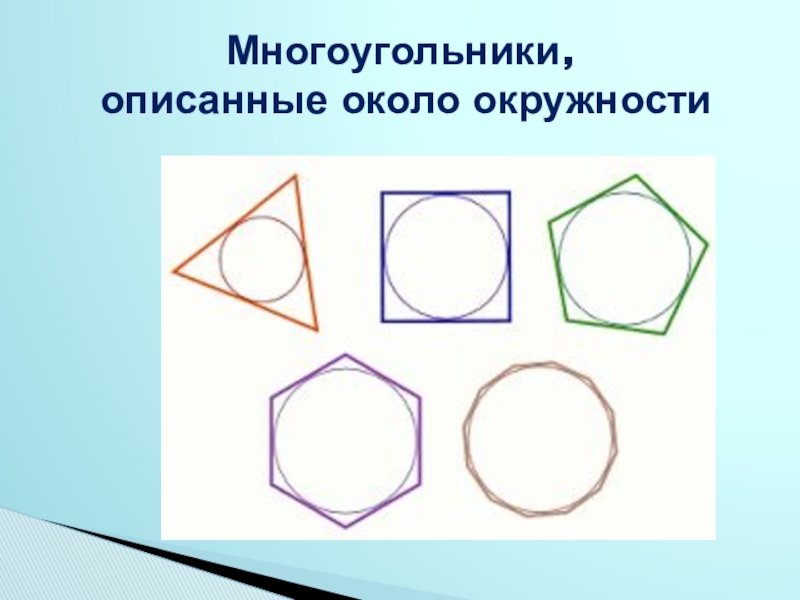 Вертикальное расстояние между соседними шестиугольниками vert = height * 3/4 .
Вертикальное расстояние между соседними шестиугольниками vert = height * 3/4 .Ширина шестиугольника width = sqrt(3)/2 * height . Горизонтальное расстояние между соседними шестиугольниками horiz = width .
В некоторых играх для шестиугольников используется пиксель-арт, который не точно соответствует правильным шестиугольникам. Формулы углов и расположений, описанные в этом разделе, не будут совпадать с размерами таких шестиугольников. Остальная часть статьи, описывающая алгоритмы сеток шестиугольников, применима даже если шестиугольники немного растянуты или сжаты.
Системы координат
Давайте приступим к сборке шестиугольников в сетку. В случае сеток квадратов существует только один очевидный способ сборки. Для шестиугольников же есть множество подходов. Я рекомендую использовать в качестве первичного представления кубические координаты. Осевые координаты или координаты смещений следует использовать для хранения карт и отображения координат для пользователя.
Координаты смещений
Наиболее частый подход — смещение каждого последующего столбца или строки. Столбцы обозначаются col или q . Строки обозначаются row или r . Можно смещать нечётные или чётные столбцы/строки, поэтому у горизонтальных и вертикальных шестиугольников есть по два варианта.
Горизонтальное расположение «нечет-r»
Горизонтальное расположение «чёт-r»
Вертикальное расположение «нечет-q»
Вертикальное расположение «чёт-q»
Кубические координаты
Ещё один способ рассмотрения сеток шестиугольников — видеть в них три основные оси, а не две , как в сетках квадратов. В них проявляется элегантная симметрия.Возьмём сетку кубов и вырежем диагональную плоскость в x + y + z = 0 . Это странная мысль, но она поможет нам упростить алгоритмы сеток шестиугольников. В частности, мы сможем воспользоваться стандартными операциями из декартовых координат: суммированием и вычитанием координат, умножением и делением на скалярную величину, а также расстояниями.
Заметьте три основные оси на сетке кубов и их соотношение с шестью диагональными направлениями сетки шестиугольников. Диагональные оси сетки соответствуют основному направлению сетки шестиугольников.
Шестиугольники
Кубы
Поскольку у нас уже есть алгоритмы для сеток квадратов и кубов, использование кубических координат позволяет нам адаптировать эти алгоритмы под сетки шестиугольников. я буду использовать эту систему для большинства алгоритмов статьи. Для использования алгоритмов с другой системой координат я преобразую кубические координаты, выполню алгоритм, а затем преобразую их обратно.
Изучите, как кубические координаты работают для сетки шестиугольников. При выборе шестиугольников выделяются кубические координаты, соответствующие трём осям.
- Каждое направление сетки кубов соответствует линии на сетке шестиугольников. Попробуйте выделить шестиугольник с z , равным 0, 1, 2, 3, чтобы увидеть связь.
 Строка отмечена синим. Попробуйте то же самое для x (зелёный) и y (сиреневый).
Строка отмечена синим. Попробуйте то же самое для x (зелёный) и y (сиреневый). - Каждое направление сетки шестиугольника — это сочетание двух направлений сетки кубов. Например, «север» сетки шестиугольников лежит между +y и -z , поэтому каждый шаг на «север» увеличивает y на 1 и уменьшает z на 1.
Существует множество различных систем координат для кубов и шестиугольников. В некоторых из них условие отличается от x + y + z = 0 . Я показал только одну из множества систем. Можно также создать кубические координаты с x-y , y-z , z-x , у которых будет свой набор интересных свойств, но я не буду их здесь рассматривать.
Но вы можете возразить, что не хотите хранить 3 числа для координат, потому что не знаете, как хранить карту в таком виде.
Осевые координаты
Осевая система координат, иногда называемая «трапецеидальной», строится на основе двух или трёх координат из кубической системы координат. Поскольку у нас есть условие x + y + z = 0 , третья координата не нужна. Осевые координаты полезны для хранения карт и отображения координат пользователю. Как и в случае с кубическими координатами, с ними можно использовать стандартные операции суммирования, вычитания, умножения и деления декартовых координат.Существует множество кубических систем координат и множество осевых. В этом руководстве я не буду рассматривать все сочетания. Я выберу две переменные, q (столбец) и r (строка). В схемах этой статьи q соответствует x , а r соответствует z , но такое соответствие произвольно, потому что можно вращать и поворачивать схемы, получая различные соответствия.
Преимущество этой системы перед сетками смещений в большей понятности алгоритмов. Недостатком системы является то, что хранение прямоугольной карты выполняется немного странно; см. раздел о сохранении карт. Некоторые алгоритмы ещё понятнее в кубических координатах, но поскольку у нас есть условие x + y + z = 0 , мы можем вычислить третью подразумеваемую координату и использовать её в этих алгоритмах. В своих проектах я называю оси q , r , s , поэтому условие выглядит как q + r + s = 0 , и я, когда нужно, могу вычислить s = -q — r .
раздел о сохранении карт. Некоторые алгоритмы ещё понятнее в кубических координатах, но поскольку у нас есть условие x + y + z = 0 , мы можем вычислить третью подразумеваемую координату и использовать её в этих алгоритмах. В своих проектах я называю оси q , r , s , поэтому условие выглядит как q + r + s = 0 , и я, когда нужно, могу вычислить s = -q — r .
Оси
Координаты смещения — это первое, о чём думает большинство людей, потому что они совпадают со стандартными декартовыми координатами, используемыми для сеток квадратов. К сожалению, одна из двух осей должна проходить «против шерсти», и это в результате всё усложняет. Кубическая и осевая система идут «по шерсти» и у них более простые алгоритмы, но хранение карт немного более сложное. Существует ещё одна система, называемая «чередуемой» или «двойной», но здесь мы не будем её рассматривать; некоторые считают, что с ней проще работать, чем с кубической или осевой.Координаты смещения, кубические и осевые
Ось — это направление, в котором соответствующая координата увеличивается.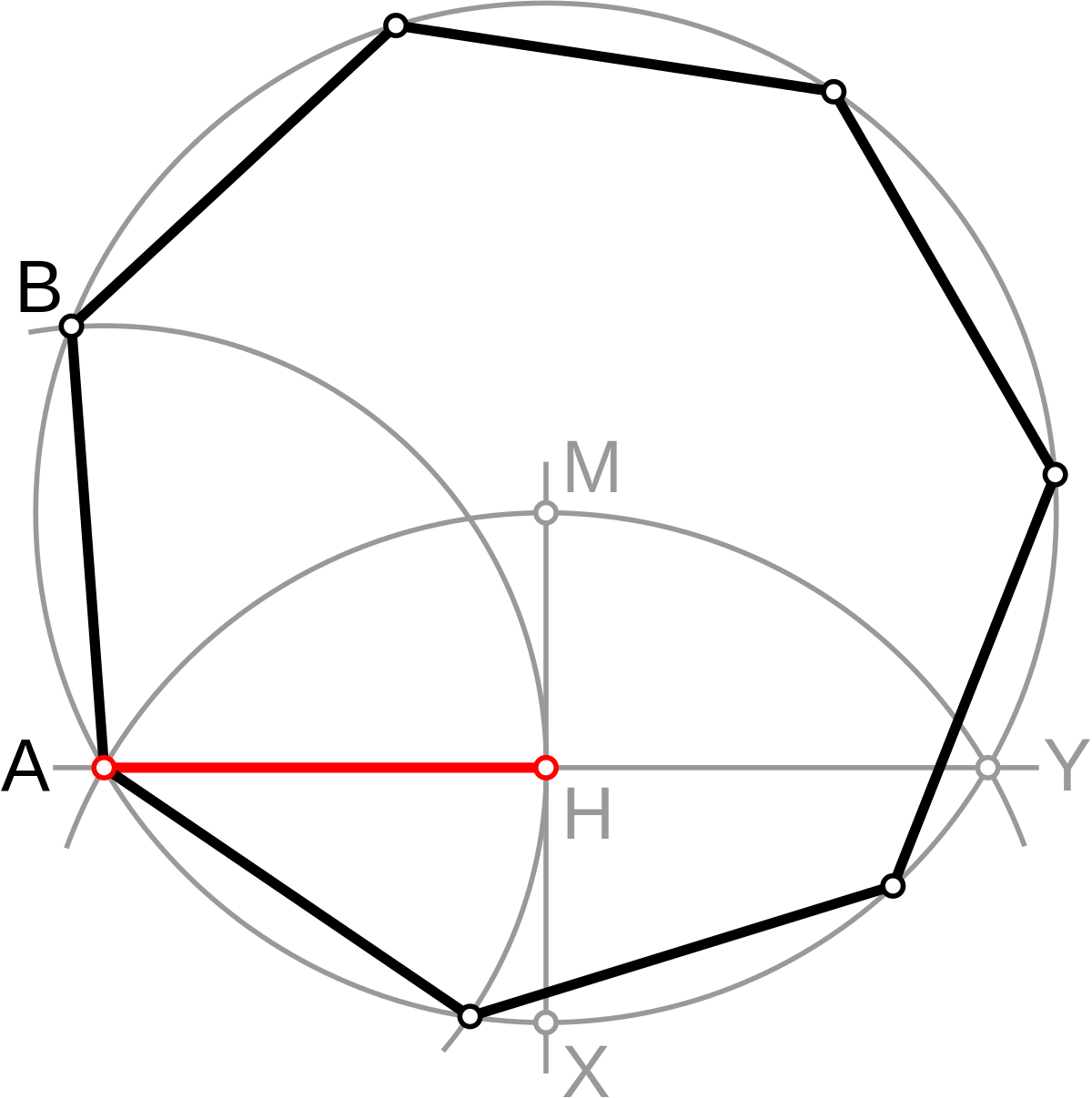 Перпендикуляр к оси — это линия, на которой координата остаётся постоянной. На схемах сеток выше показаны линии перпендикуляров.
Перпендикуляр к оси — это линия, на которой координата остаётся постоянной. На схемах сеток выше показаны линии перпендикуляров.
Преобразование координат
Вероятно, что вы будете использовать в своём проекте осевые координаты или координаты смещения, но многие алгоритмы проще выражаются в кубических координатах. Поэтому нам нужно уметь преобразовывать координаты между системами.Осевые координаты близко связаны с кубическими, поэтому преобразование делается просто:
# преобразование кубических в осевые координаты
q = x
r = z
# преобразование осевых в кубические координаты
x = q
z = r
y = -x-z
В коде эти две функции могут быть записаны следующим образом:
Function cube_to_hex(h): # осевая
var q = h.x
var r = h.z
return Hex(q, r)
function hex_to_cube(h): # кубическая
var x = h.q
var z = h.r
var y = -x-z
return Cube(x, y, z)
Координаты смещения совсем немного сложнее:
Соседние шестиугольники
Дан один шестиугольник, с какими шестью шестиугольниками он находится рядом? Как и можно ожидать, легче всего дать ответ в кубических координатах, довольно просто в осевых координатах, и немного сложнее в координатах смещения. Также может потребоваться рассчитать шесть «диагональных» шестиугольников.
Также может потребоваться рассчитать шесть «диагональных» шестиугольников.Кубические координаты
Перемещение на одно пространство в координатах шестиугольников приводит к изменению одной из трёх кубических координат на +1 и другой на -1 (сумма должна оставаться равной 0). На +1 могут изменяться три возможных координаты, а на -1 — оставшиеся две. Это даёт нам шесть возможных изменений. Каждое соответствует одному из направлений шестиугольника. Простейший и быстрейший способ — предварительно вычислить изменения и поместить их в таблицу кубических координат Cube(dx, dy, dz) во время компиляции:Var directions = [
Cube(+1, -1, 0), Cube(+1, 0, -1), Cube(0, +1, -1),
Cube(-1, +1, 0), Cube(-1, 0, +1), Cube(0, -1, +1)
]
function cube_direction(direction):
return directions
function cube_neighbor(hex, direction):
return cube_add(hex, cube_direction(direction))
Осевые координаты
Как и раньше, мы используем для начала кубическую систему. Возьмём таблицу Cube(dx, dy, dz) и преобразуем в таблицу Hex(dq, dr) :Var directions = [
Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1)
]
function hex_direction(direction):
return directions
function hex_neighbor(hex, direction):
var dir = hex_direction(direction)
return Hex(hex. q + dir.q, hex.r + dir.r)
q + dir.q, hex.r + dir.r)
Координаты смещения
В осевых координатах мы вносим изменения в зависимости от того, в каком месте сетки находимся. Если мы в столбце/строке смещения, то правило отличается от случая столбца/строки без смещения.Как и раньше, мы создаём таблицу чисел, которые нужно прибавить к col and row . Однако на этот раз у нас будет два массива, один для нечётных столбцов/строк, а другой — для чётных. Посмотрите на (1,1) на рисунке карты сетки выше и заметьте, как меняются col и row меняются при перемещении в каждом из шести направлений. Теперь повторим процесс для (2,2) . Таблицы и код будут разными для каждого из четырёх типов сеток смещений, приводим соответствующий код для каждого типа сетки.
Нечет-r
var directions = [
[ Hex(+1, 0), Hex(0, -1), Hex(-1, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ],
[ Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, 0), Hex(0, +1), Hex(+1, +1) ]
]
function offset_neighbor(hex, direction):
var parity = hex. row & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
row & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
Чёт-r
var directions = [
[ Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, 0), Hex(0, +1), Hex(+1, +1) ],
[ Hex(+1, 0), Hex(0, -1), Hex(-1, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ]
]
function offset_neighbor(hex, direction):
var parity = hex.row & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
Сетка для чётной (EVEN) и нечётной (ODD) строк
Нечет-q
var directions = [
[ Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, -1), Hex(-1, 0), Hex(0, +1) ],
[ Hex(+1, +1), Hex(+1, 0), Hex(0, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ]
]
function offset_neighbor(hex, direction):
var parity = hex.col & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
Чёт-q
var directions = [
[ Hex(+1, +1), Hex(+1, 0), Hex(0, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ],
[ Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, -1), Hex(-1, 0), Hex(0, +1) ]
]
function offset_neighbor(hex, direction):
var parity = hex. col & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
col & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
Сетка для чётного (EVEN) и нечётного (ODD) столбцов
Диагонали
Перемещение в «диагональном» пространстве в координатах шестиугольников изменяет одну из трёх кубических координат на ±2 и две другие на ∓1 (сумма должна оставаться равной 0).Var diagonals = [
Cube(+2, -1, -1), Cube(+1, +1, -2), Cube(-1, +2, -1),
Cube(-2, +1, +1), Cube(-1, -1, +2), Cube(+1, -2, +1)
]
function cube_diagonal_neighbor(hex, direction):
return cube_add(hex, diagonals)
Как и раньше, мы можем преобразовать эти координаты в осевые, откинув одну из трёх координат, или преобразовать в координаты смещения, предварительно вычислив результаты.
Расстояния
Кубические координаты
В кубической системе координат каждый шестиугольник является кубом в трёхмерном пространстве. Соседние шестиугольники находятся в сетке шестиугольников на расстоянии 1 друг от друга, но на расстоянии 2 в сетке кубов. Это делает расчёт расстояний простым. В сетке квадратов манхэттенские расстояния равны abs(dx) + abs(dy) . В сетке кубов манхэттенские расстояния равны abs(dx) + abs(dy) + abs(dz) . Расстояние в сетке шестиугольников равно их половине:
Это делает расчёт расстояний простым. В сетке квадратов манхэттенские расстояния равны abs(dx) + abs(dy) . В сетке кубов манхэттенские расстояния равны abs(dx) + abs(dy) + abs(dz) . Расстояние в сетке шестиугольников равно их половине:Function cube_distance(a, b):
return (abs(a.x — b.x) + abs(a.y — b.y) + abs(a.z — b.z)) / 2
Эквивалентом этой записи будет выражение того, что одна из трёх координат должна быть суммой двух других, а затем получение её в качестве расстояния. Можно выбрать форму деления пополам или форму максимального значения, приведённую ниже, но они дают одинаковый результат:
Function cube_distance(a, b):
return max(abs(a.x — b.x), abs(a.y — b.y), abs(a.z — b.z))
На рисунке максимальные значения выделены цветом. Заметьте также, что каждый цвет обозначает одно из шести «диагональных» направлений.
GIF
Осевые координаты
В осевой системе третья координата выражена неявно. Давайте преобразуем из осевой в кубическую систему для расчёта расстояния:Function hex_distance(a, b):
var ac = hex_to_cube(a)
var bc = hex_to_cube(b)
return cube_distance(ac, bc)
Если компилятор в вашем случае встраивает (inline) hex_to_cube и cube_distance , то он сгенерирует такой код:
Function hex_distance(a, b):
return (abs(a. q — b.q)
+ abs(a.q + a.r — b.q — b.r)
+ abs(a.r — b.r)) / 2
q — b.q)
+ abs(a.q + a.r — b.q — b.r)
+ abs(a.r — b.r)) / 2
Существует множество различных способов записи расстояний между шестиугольниками в осевых координатах, но вне зависимости от способа записи расстояние между шестиугольниками в осевой системе извлекается из манхэттенского расстояния в кубической системе . Например, описанная «разность разностей» получается из записи a.q + a.r — b.q — b.r как a.q — b.q + a.r — b.r и с использованием формы максимального значения вместо формы деления пополам cube_distance . Все они аналогичны, если увидеть связь с кубическими координатами.
Координаты смещения
Как и в случае с осевыми координатами, мы преобразуем координаты смещения в кубические координаты, а затем используем расстояние кубической системы.Function offset_distance(a, b):
var ac = offset_to_cube(a)
var bc = offset_to_cube(b)
return cube_distance(ac, bc)
Мы будем использовать тот же шаблон для многих алгоритмов: преобразуем из шестиугольников в кубы, выполняем кубическую версию алгоритма и преобразуем кубические результаты в координаты шестиугольников (осевые или координаты смещения).
Отрисовка линий
Как нарисовать линию от одного шестиугольника до другого? Я использую линейную интерполяцию для рисования линий . Линия равномерно сэмплируется в N+1 точках и вычисляется, в каких шестиугольниках находятся эти сэмплы.GIF
- Сначала мы вычисляем N , которое будет расстоянием в шестиугольниках между конечными точками.
- Затем равномерно сэмплируем N+1 точек между точками A и B. С помощью линейной интерполяции определяем, что для значений i от 0 до N , включая их, каждая точка будет A + (B — A) * 1.0/N * i . На рисунке эти контрольные точки показаны синим. В результате получаются координаты с плавающей запятой.
- Преобразуем каждую контрольную точку (float) обратно в шестиугольники (int). Алгоритм называется cube_round (см. ниже).
Function lerp(a, b, t): // для float
return a + (b — a) * t
function cube_lerp(a, b, t): // для шестиугольников
return Cube(lerp(a.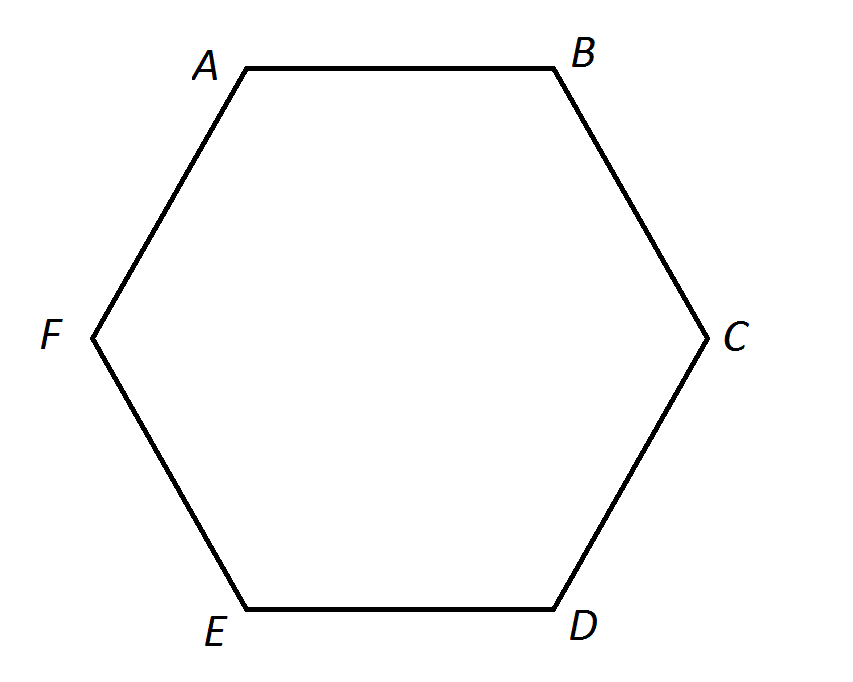 x, b.x, t),
lerp(a.y, b.y, t),
lerp(a.z, b.z, t))
function cube_linedraw(a, b):
var N = cube_distance(a, b)
var results =
for each 0 ≤ i ≤ N:
results.append(cube_round(cube_lerp(a, b, 1.0/N * i)))
return results
x, b.x, t),
lerp(a.y, b.y, t),
lerp(a.z, b.z, t))
function cube_linedraw(a, b):
var N = cube_distance(a, b)
var results =
for each 0 ≤ i ≤ N:
results.append(cube_round(cube_lerp(a, b, 1.0/N * i)))
return results
Примечания:
- Бывают случаи, когда cube_lerp возвращает точку, находящуюся точно на грани между двумя шестиугольниками. Затем cube_round сдвигает её в ту или иную сторону. Линии выглядят лучше, если их сдвигают в одном направлении. Это можно сделать, добавив «эпсилон»-шестиугольный Cube(1e-6, 1e-6, -2e-6) к одной или обеим конечным точкам перед началом цикла. Это «подтолкнёт» линию в одном направлении, чтобы она не попадала на границы граней.
- Алгоритм DDA-линии в сетках квадратов приравнивает N к максимуму расстояния по каждой из осей. Мы делаем то же самое в кубическом пространстве, что аналогично расстоянию в сетке шестиугольников.
- Функция cube_lerp должна возвращать куб с координатами в float. Если вы программируете на языке со статической типизацией, то не сможете использовать тип Cube .
 Вместо него можно определить тип FloatCube или встроить (inline) функцию в код отрисовки линий, если вы не хотите определять ещё один тип.
Вместо него можно определить тип FloatCube или встроить (inline) функцию в код отрисовки линий, если вы не хотите определять ещё один тип. - Можно оптимизировать код, встроив (inline) cube_lerp , а затем рассчитав B.x-A.x , B.x-A.y и 1.0/N за пределами цикла. Умножение можно преобразовать в повторяющееся суммирование. В результате получится что-то вроде алгоритма DDA-линии.
- Для отрисовки линий я использую осевые или кубические координаты, но если вы хотите работать с координатами смещения, то изучите .
- Существует много вариантов отрисовки линий. Иногда требуется «сверхпокрытие» . Мне прислали код отрисовки линий с сверхпокрытием в шестиугольниках, но я пока не изучал его.
Диапазон перемещения
Диапазон координат
Для заданного центра шестиугольника и диапазона N какие шестиугольники находятся в пределах N шагов от него?Мы можем произвести обратную работу из формулы расстояния между шестиугольниками distance = max(abs(dx), abs(dy), abs(dz)) . Чтобы найти все шестиугольники в пределах N , нам нужны max(abs(dx), abs(dy), abs(dz)) ≤ N . Это значит, что нужны все три значения: abs(dx) ≤ N и abs(dy) ≤ N и abs(dz) ≤ N . Убрав абсолютное значение, мы получим -N ≤ dx ≤ N и -N ≤ dy ≤ N и -N ≤ dz ≤ N . В коде это будет вложенный цикл:
Чтобы найти все шестиугольники в пределах N , нам нужны max(abs(dx), abs(dy), abs(dz)) ≤ N . Это значит, что нужны все три значения: abs(dx) ≤ N и abs(dy) ≤ N и abs(dz) ≤ N . Убрав абсолютное значение, мы получим -N ≤ dx ≤ N и -N ≤ dy ≤ N и -N ≤ dz ≤ N . В коде это будет вложенный цикл:
Var results =
for each -N ≤ dx ≤ N:
for each -N ≤ dy ≤ N:
for each -N ≤ dz ≤ N:
if dx + dy + dz = 0:
results.append(cube_add(center, Cube(dx, dy, dz)))
Этот цикл сработает, но будет довольно неэффективным. Из всех значений dz , которые мы перебираем в цикле, только одно действительно удовлетворяет условию кубов dx + dy + dz = 0 . Вместо этого мы напрямую вычислим значение dz , удовлетворяющее условию:
Var results =
for each -N ≤ dx ≤ N:
for each max(-N, -dx-N) ≤ dy ≤ min(N, -dx+N):
var dz = -dx-dy
results.append(cube_add(center, Cube(dx, dy, dz)))
Этот цикл проходит только по нужным координатам. На рисунке каждый диапазон является парой линий. Каждая линия — это неравенство. Мы берём все шестиугольники, удовлетворяющие шести неравенствам.
Мы берём все шестиугольники, удовлетворяющие шести неравенствам.
GIF
Пересекающиеся диапазоны
Если нужно найти шестиугольники, находящиеся в нескольких диапазонах, то перед генерированием списка шестиугольников можно пересечь диапазоны.Можно подойти к этой проблеме с точки зрения алгебры или геометрии. Алгебраически каждая область выражается как условия неравенств в форме -N ≤ dx ≤ N , и нам нужно найти пересечение этих условий. Геометрически каждая область является кубом в трёхмерном пространстве, и мы пересечём два куба в трёхмерном пространстве для получения прямоугольного параллелепипеда в трёхмерном пространстве. Затем мы проецируем его обратно на плоскость x + y + z = 0 , чтобы получить шестиугольники. Я буду решать эту задачу алгебраически.
Во-первых, мы перепишем условие -N ≤ dx ≤ N в более общей форме x min ≤ x ≤ x max , и примем x min = center.x — N и x max = center.x + N . Сделаем то же самое для y и z , в результате получив общий вид кода из предыдущего раздела:
Var results =
for each xmin ≤ x ≤ xmax:
for each max(ymin, -x-zmax) ≤ y ≤ min(ymax, -x-zmin):
var z = -x-y
results. append(Cube(x, y, z))
append(Cube(x, y, z))
Пересечением двух диапазонов a ≤ x ≤ b и c ≤ x ≤ d является max(a, c) ≤ x ≤ min(b, d) . Поскольку область шестиугольников выражена как диапазоны над x , y , z , мы можем отдельно пересечь каждый из диапазонов x , y , z , а затем использовать вложенный цикл для генерирования списка шестиугольников в пересечении. Для одной области шестиугольников мы принимаем x min = H.x — N and x max = H.x + N , аналогично для y и z . Для пересечения двух областей шестиугольников мы принимаем x min = max(h2.x — N, h3.x — N) и x max = min(h2.x + N, h3.x + N), аналогично для y и z . Тот же шаблон работает для пересечения трёх или более областей.
GIF
Препятствия
При наличии препятствий проще всего выполнить заливку с ограничением по расстоянию (поиск в ширину). На рисунке ниже мы ограничиваемся четырьмя ходами. В коде fringes[k] — это массив всех шестиугольников, которых можно достичь за k шагов. При каждом проходе по основному циклу мы расширяем уровень k-1 на уровень k .
Function cube_reachable(start, movement): var visited = set() add start to visited var fringes = fringes.append() for each 1
Повороты
Для заданного вектора шестиугольника (разницу между двумя шестиугольниками) нам может понадобиться повернуть его, чтобы он указывал на другой шестиугольник. Это просто сделать, имея кубические координаты, если придерживаться поворота на 1/6 окружности.Поворот на 60° вправо сдвигает каждую координату на одну позицию вправо:
[ x, y, z]
to [-z, -x, -y]
Поворот на 60° влево сдвигает каждую координату на одну позицию влево:
[ x, y, z]
to [-y, -z, -x]
«Поиграв» [в оригинале статьи] со схемой, можно заметить, что каждый поворот на 60° меняет знаки и физически «поворачивает» координаты. После поворота на 120° знаки снова становятся теми же. Поворот на 180° меняет знаки, но координаты поворачиваются в своё изначальное положение.
Вот полная последовательность поворота положения P вокруг центрального положения C, приводящего к новому положению R:
- Преобразование положений P и C в кубические координаты.
- Вычисление вектора вычитанием центра: P_from_C = P — C = Cube(P.x — C.x, P.y — C.y, P.z — C.z) .
- Поворот вектора P_from_C как описано выше и присваивание итоговому вектору обозначения R_from_C .
- Преобразование вектора обратно в положение прибавлением центра: R = R_from_C + C = Cube(R_from_C.x + C.x, R_from_C.y + C.y, R_from_C.z + C.z) .
- Преобразование кубического положения R обратно в нужную систему координат.
Кольца
Простое кольцо
Чтобы выяснить, принадлежит ли заданный шестиугольник к кольцу заданного радиуса radius , нужно вычислить расстояние от этого шестиугольника до центра, и узнать, равно ли оно radius . Для получения списка всех таких шестиугольников нужно сделать radius шагов от центра, а затем следовать за поворачиваемыми векторами по пути вдоль кольца.
Для получения списка всех таких шестиугольников нужно сделать radius шагов от центра, а затем следовать за поворачиваемыми векторами по пути вдоль кольца.Function cube_ring(center, radius): var results = # этот код не работает для radius == 0; вы понимаете, почему? var cube = cube_add(center, cube_scale(cube_direction(4), radius)) for each 0 ≤ i В этом коде cube начинается на кольце, показанном большой стрелкой от центра к углу схемы. Я выбрал для начала угол 4, потому что он соответствует пути, в котором двигаются мои числа направлений. Вам может понадобиться другой начальный угол. На каждом этапе внутреннего цикла cube двигается на один шестиугольник по кольцу. Через 6 * radius шагов он завершает там, где начал.
Спиральные кольца
Проходя по кольцам по спиральному паттерну, мы можем заполнить внутренние части колец:Function cube_spiral(center, radius):
var results =
for each 1 ≤ k ≤ radius:
results = results + cube_ring(center, k)
return results
Площадь большого шестиугольника равна сумме всех окружностей плюс 1 для центра.
 Для вычисления площади используйте эту формулу .
Для вычисления площади используйте эту формулу .Обход шестиугольников таким способом можно также использовать для вычисления диапазона перемещения (см. выше).
Область видимости
Что видимо из заданного положения с заданным расстоянием, и не перекрывается препятствиями? Простейший способ определить это — нарисовать линию к каждому шестиугольнику в заданном диапазоне. Если линия не встречается со стенами, то вы видите шестиугольник. Перемещайте мышь по шестиугольникам [на схеме в оригинале статьи], чтобы увидеть отрисовку линий к этим шестиугольникам и стены, с которыми линии встречаются.Этот алгоритм может быть медленным на больших площадях, но его легко реализовать, поэтому рекомендую начать с него.
GIF
Существует много разных определений видимости. Хотите ли вы видеть центр другого шестиугольника из центра начального? Хотите ли вы видеть любую часть другого шестиугольника из центра начального? Может быть, любую часть другого шестиугольника из любой точки начального? Мешающие взгляду препятствия меньше полного шестиугольника? Область видимости — это более хитрое и разнообразное понятие, чем кажется на первый взгляд.
 Начнём с простейшего алгоритма, но ждите, что он обязательно правильно вычислит ответ в вашем проекте. Бывают даже случаи, когда простой алгоритм даёт нелогичные результаты.
Начнём с простейшего алгоритма, но ждите, что он обязательно правильно вычислит ответ в вашем проекте. Бывают даже случаи, когда простой алгоритм даёт нелогичные результаты.Я хочу в дальнейшем расширять это руководство. У меня есть
Геометрические построения являются одной из главных частей обучения. Они формируют пространственное и логическое мышление, а также разрешают понять примитивные и натуральные геометрические обоснованности. Построения производятся на плоскости при помощи циркуля и линейки. Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.
Вам понадобится
- Циркуль, линейка, карандаш, лист бумаги.
Инструкция
1. Нарисуйте окружность. Установите некоторое расстояние между ножками циркуля. Это расстояние будет являться радиусом окружности. Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.
Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.
2. Постройте точки вершин углов верного шестиугольника. Установите ножку циркуля, в которой закреплена игла, в всякую точку окружности. Игла должна проткнуть начерченную линию. Чем вернее будет установлен циркуль, тем вернее будет построение. Проведите дугу окружности так, дабы она пересекла начерченную ранее окружность. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Начертите еще одну дугу, пересекающую окружность. Вновь переставьте иглу циркуля в точку пересечения дуги и окружности и вновь начертите дугу. Произведите данное действие еще три раза, перемещаясь в одном направлении по окружности. Каждого должно получиться шесть дуг и шесть точек пересечения.
Каждого должно получиться шесть дуг и шесть точек пересечения.
3. Постройте положительный шестиугольник. Ступенчато объедините все шесть точек пересечения дуг с изначально начерченной окружностью. Соединяйте точки прямыми, вычерчиваемыми при помощи линейки и карандаша. Позже произведенных действий будет получен верный шестиугольник, вписанный в окружность.
Шестиугольником считается многоугольник, владеющий шестью углами и шестью сторонами. Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести. Это делается в пару шагов.
Вам понадобится
- Карандаш, лист бумаги, линейка
Инструкция
1. Берется лист бумаги и на нем отмечается 6 точек приблизительно так, как это показано на рис. 1.
2. Позже того, как были подмечены точки, берется линейка, карандаш и с их подмогой ступенчато, друг за ином соединяются точки так, как это выглядит на рис. 2.
2.
Видео по теме
Обратите внимание!
Сумма всех внутренних углов шестиугольника равна 720 градусам.
Шестиугольник – это многоугольник, тот, что владеет шестью углами. Для того, дабы начертить произвольный шестиугольник, надобно проделать каждого 2 действия.
Вам понадобится
- Карандаш, линейка, лист бумаги.
Инструкция
1. Нужно взять в руку карандаш и разметить на листе 6 произвольных точек. В дальнейшем эти точки будут исполнять роль углов в шестиугольнике. (рис.1)
2. Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с ином по начерченным ранее точкам (рис.2)
Видео по теме
Обратите внимание!
Специальным типом шестиугольника является положительный шестиугольник. Он именуется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника дозволено описать либо вписать окружность.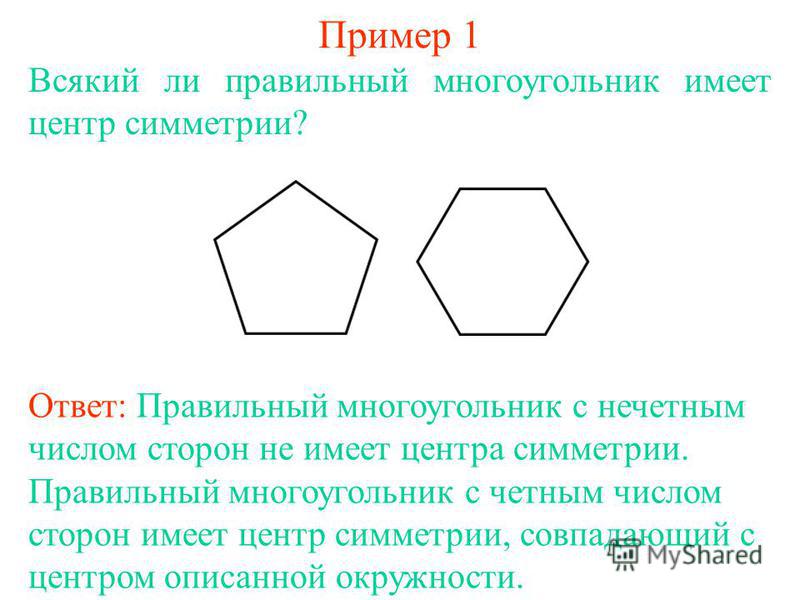 Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.
Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.
Полезный совет
В природе положительные шестиугольники владеют крупный популярностью. К примеру, вся пчелиная сота владеет положительной шестиугольной формой. Либо кристаллическая решетка графена (модификация углерода) тоже владеет формой положительного шестиугольника.
Как возвести тот либо другой угол – крупной вопрос. Но для некоторых углов задача невидимо упрощается. Одним из таких углов является угол в 30 градусов. Он равен?/6, то есть число 30 является делителем 180. Плюс к этому его синус вестим. Это и помогает при его построении.
Вам понадобится
- транспортир, угольник, циркуль, линейка
Инструкция
1. Для начала разглядим особенно примитивную обстановку, когда у вас на руках есть транспортир. Тогда прямую под углом 30 градусов к данной дозволено легко отложить с поддержкой него.
2. Помимо транспортира существуют и угол ьники, один из углов которых равен 30 градусам. Тогда иной угол угол ьника будет равен 60 градусам, то есть вам необходим визуально меньший угол для построения требуемой прямой.
3. Перейдем сейчас к нетривиальным способам построения угла 30 градусов. Как вестимо, синус угла 30 градусов равен 1/2. Для его построения нам надобно возвести прямоугол ьный треугол ьник. Возможен, мы можем возвести две перпендикулярные прямые. Но тангенс 30 градусов – иррациональное число, следственно соотношение между катетами мы можем посчитать лишь примерно (исключительно, если нет калькулятора), а, значит, и возвести угол в 30 градусов примерно.
4. В этом случае дозволено сделать и точное построение. Возведем вновь две перпендикулярные прямые, на которых будут располагаться катеты прямоугол ьного треугол ьника. Отложим по одной прямой катет BC какой-нибудь длины с поддержкой циркуля (B – прямой угол ).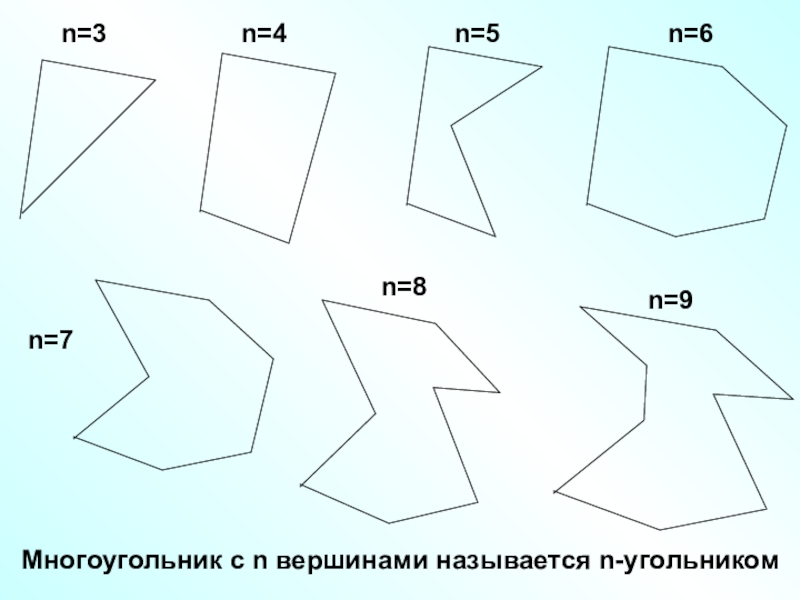 После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Проводя окружность с центром в точке C с радиусом этой длины, обнаружим точку пересечения окружности с иной прямой. Эта точка и будет точкой A прямоугол ьного треугол ьника ABC, а угол A будет равен 30 градусам.
После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Проводя окружность с центром в точке C с радиусом этой длины, обнаружим точку пересечения окружности с иной прямой. Эта точка и будет точкой A прямоугол ьного треугол ьника ABC, а угол A будет равен 30 градусам.
5. Возвести угол в 30 градусов дозволено и с поддержкой окружности, применяя то, что он равен?/6. Возведем окружность с радиусом OB. Разглядим в теории треугол ьник, где OA = OB = R – радиус окружности, где угол OAB = 30 градусов. Пускай OE – высота этого равнобедренного треугол ьника, а, следственно, и его биссектриса и медиана. Тогда угол AOE = 15 градусов, и, по формуле половинного угла, sin(15o) = (sqrt(3)-1)/(2*sqrt(2)).Следственно, AE = R*sin(15o). Отсель, AB = 2AE = 2R*sin(15o). Строя окружность радиусом BA с центром в точке B, обнаружим точку пересечения A этой окружности с начальной. Угол AOB будет равен 30 градусам.
6. Если мы можем определять длину дуг каким-нибудь образом, то, отложив дугу длиной?*R/6, мы также получим угол в 30 градусов.
Если мы можем определять длину дуг каким-нибудь образом, то, отложив дугу длиной?*R/6, мы также получим угол в 30 градусов.
Обратите внимание!
Нужно помнить, что в 5 пункте мы можем возвести угол лишь приближенно, потому что в вычислениях будут фигурировать иррациональные числа.
Шестиугольником называют частный случай полигона – фигуры, образованной большинством точек плоскости, ограниченным замкнутой полилинией. Положительный шестиугольник (гексагон), в свою очередь, также является частным случаем – это полигон с шестью равными сторонами и равными углами. Эта фигура знаменательна тем, что длина всей из ее сторон равна радиусу описанной вокруг фигуры окружности.
Вам понадобится
- – циркуль;
- – линейка;
- – карандаш;
- – лист бумаги.
Инструкция
1. Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на иной ножке, равным длине стороны вычерчиваемой фигуры. Для этого дозволено воспользоваться линейкой либо предпочесть случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая вероятность.
Для этого дозволено воспользоваться линейкой либо предпочесть случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая вероятность.
2. Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.
3. Разбейте окружность точками на шесть равных частей. Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.
4. Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна верно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, дабы она пересекла в 2-х точках окружность, начерченную первой.
5. Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с изначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в 2-х точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).
6. Сходственным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении по окружности (неизменно по либо вопреки часовой стрелки). В итоге обязаны быть выявлены шесть точек пересечения дуг с изначально построенной окружностью.
7. Нарисуйте положительный шестиугольник. Ступенчато попарно объедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В итоге будет получен верный шестиугольник. Позже осуществления построения дозволено стереть вспомогательные элементы (дуги и окружность).
Обратите внимание!
Имеет толк выбирать такое расстояние между ножками циркуля, дабы угол между ними был равен 15-30 градусов, напротив при осуществлении построений данное расстояние может легко сбиться.
При строительстве либо разработке домашних дизайн-планов зачастую требуется возвести угол , равный теснее имеющемуся. На поддержка приходят образцы и школьные умения геометрии.
На поддержка приходят образцы и школьные умения геометрии.
Инструкция
1. Угол образуют две прямые, исходящие из одной точки. Эта точка будет именоваться вершиной угла, а линии будут являться сторонами угла.
2. Для обозначения углов используйте три буквы: одна у вершины, две у сторон. Называют угол , начиная с той буквы, которая стоит у одной стороны, дальше называют букву, стоящую у вершины, и после этого букву у иной стороны. Используйте и другие методы для обозначения углов, если вам комфортнее напротив. Изредка называют только одну букву, которая стоит у вершины. А дозволено обозначать углы греческими буквами, скажем, α, β, γ.
3. Встречаются обстановки, когда нужно начертить угол , дабы он был равен теснее данному углу. Если при построении чертежа применять транспортир вероятности нет, дозволено обойтись только линейкой и циркулем. Возможен, на прямой, обозначенной на чертеже буквами MN, надобно возвести угол у точки К, так, дабы он был равен углу В. То есть из точки K нужно провести прямую, образующую с линией MN угол , тот, что будет равен углу В.
То есть из точки K нужно провести прямую, образующую с линией MN угол , тот, что будет равен углу В.
4. В начале подметьте по точке на всей стороне данного угла, скажем, точки А и С, дальше объедините точки С и А прямой линией. Получите треугол ьник АВС.
5. Теперь постройте на прямой MN такой же треугол ьник, дабы его вершина В находилась на линии в точке К. Используйте правило построения треугол ьника по трем сторонам. Отложите от точки К отрезок KL. Он должен быть равен отрезку ВС. Получите точку L.
6. Из точки K вычертите окружность радиусом равным отрезку ВА. Из L вычертите окружность радиусом СА. Полученную точку (Р) пересечения 2-х окружностей объедините с К. Получите треугол ьник КPL, тот, что будет равен треугол ьнику ABC. Так вы получите угол К. Он и будет равен углу В. Дабы это построение сделать комфортнее и стремительней, от вершины В отложите равные отрезки, применяя один раствор циркуля, не сдвигая ножек, опишите этим же радиусом из точки К окружность.
Видео по теме
Обратите внимание!
Избегайте случайного метаморфозы расстояния между ножками циркуля. В этом случае шестиугольник может получиться неправильным.
Полезный совет
Имеет толк изготавливать построения при помощи циркуля с отлично заточенным грифелем. Так построения будут особенно точны.
Построение правильных многоугольников — техническое черчение. Как построить правильный восьмиугольник Как начертить правильный 8 угольник
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг.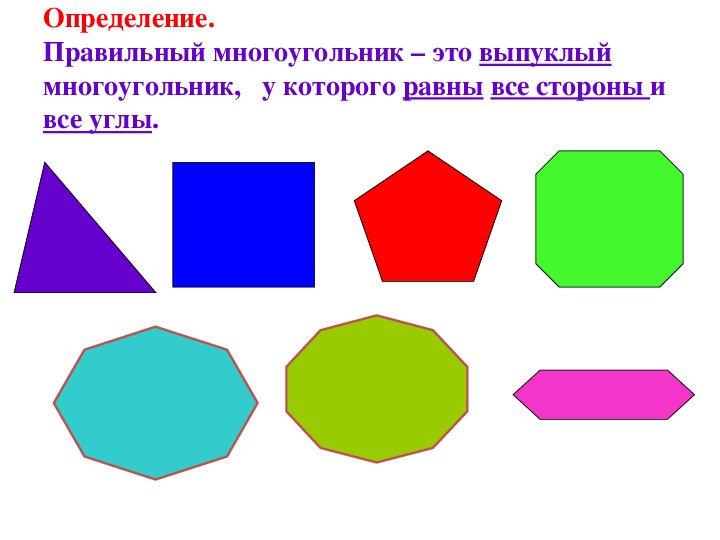 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.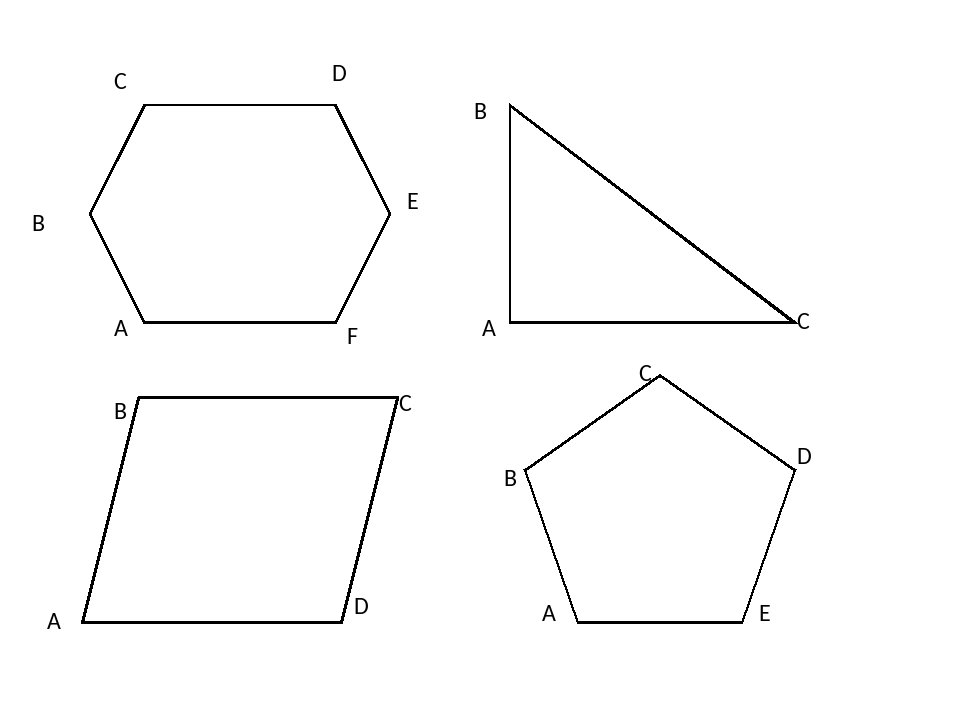
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Куклин Алексей
Работа носит реферативный характер с элементами исследовательской деятельности. В ней рассматриваются различные способы построения правильных n-угольников. В работе содержится подробный ответ на вопрос о том, что всегда ли можно построить n-угольник с помощью циркуля и линейки. К работе прилагается презентация, которую можно найти на данном мини-сайте.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Предварительный просмотр:
https://accounts.google.com
Подписи к слайдам:
Построение правильных многоугольников Работу выполнил: ученик 9 класса «В» МБОУ СОШ № 10 Куклин Алексей
Правильные многоугольники Правильным многоугольником называют выпуклый многоугольник, у которого все стороны и углы равны. Перейти к примерам Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Перейти к примерам Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Назад Правильные многоугольники
Основоположниками раздела математики о правильных многоугольниках являлись древнегреческие ученые. Одними из них были Архимед и Евклид.
Доказательство существования правильного n-угольника Если n (число углов многоугольника) больше 2, то такой многоугольник существует. Попробуем построить 8ми угольник и доказать это. Доказательство
Возьмем окружность произвольного радиуса с центром в точке О. Разделим её на некоторое число равных дуг, в нашем случае 8. Для этого проведем радиусы так, чтобы получилось 8 дуг, и угол между двумя ближайшими радиусами был равен 360°: количество сторон (в нашем случае 8), соответственно каждый угол будет равен 45°.
3. Получаем точки A1, A2, A3, A4, A5, A6, A7, A8. Поочередно соединяем их и получаем правильный восьмиугольник. Назад
Построение правильного многоугольника по стороне с использованием поворота Правильный многоугольник можно построить, зная его углы. Мы знаем, что сумма углов выпуклого n-угольника равна 180°(n — 2). Из этого можно вычислить угол многоугольника, разделив сумму на n. Углы Построение
Мы знаем, что сумма углов выпуклого n-угольника равна 180°(n — 2). Из этого можно вычислить угол многоугольника, разделив сумму на n. Углы Построение
Угол правильного: 3-угольника равен 60° 4-угольника равен 90° 5-угольника равен 108° 6-угольника равен 120° 8-угольника равен 135° 9-угольника равен 140° 10-угольника равен 144° 12-угольника равен 150° Градусная мера углов правильных треугольников Назад
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
В 1796 году одним из величайших математиков всех времён Карл Фридрих Гаусс показал возможность построения правильных n-угольников, если выполняется равенство, где n – количество углов, а k-любое натуральное число. Тем самым получилось, что в пределах 30 возможно деление окружности на 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30 равных частей. В 1836 году Ванцель доказал, что правильные многоугольники, не удовлетворяющие данному равенству при помощи линейки и циркуля построить нельзя. Теорема Гаусса
Теорема Гаусса
Построение треугольника Построим окружность с центром в точке О. Построим еще одну окружность того же радиуса проходящую через точку О.
3. Соединим центры окружностей и одну из точек их пересечения, получив правильный многоугольник. Назад Построение треугольника
Построение шестиугольника 1. Построим окружность с центром в точке О. 2. Проведем прямую линию через центр окружности. 3. Проведем дугу окружности того же радиуса с центром в точке пересечения прямой с окружностью до пересечения с окружностью.
4. Проведем прямые через центр начальной окружности и точки пересечения дуги с этой окружностью. 5. Соединяем точки пересечения всех прямых с исходной окружностью и получаем правильный шестиугольник. Построение шестиугольника
Построение четырёхугольника Построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Из точек в которых диаметры касаются окружности проводим другие окружности данного радиуса до их пересечения (окружностей).
Построение четырёхугольника 4. Проводим прямые через точки пересечения окружностей. 5. Соединяем точки пересечения прямых и окружности и получаем правильный четырехугольник.
Построение восьмиугольника Можно построить любой правильный многоугольник у которого в 2 раза больше углов, чем у данного. Построим восьмиугольник при помощи четырехугольника. Соединим противоположные вершины четырехугольника. Проведем биссектрисы углов образованных пересекающимися диагоналями.
4. Соединим точки, лежащие на окружности, получив при этом правильный восьмиугольник. Построение восьмиугольника
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Построение десятиугольника Построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Разделим радиус окружности пополам и из получившейся на нем точки проведем окружность проходящую через точку О.
Построение десятиугольника 4. Проведем отрезок из центра маленькой окружности к точки в которой большая окружность касается своего радиуса. 5. Из точки соприкосновения большой окружности и её радиуса проведем окружность так, что она будет соприкасаться с маленькой.
Построение десятиугольника 6. Из точек пересечения большой и полученной окружностей проведем окружности построенные в прошлый раз и так будем проводить до тех пор пока соседние окружности не соприкоснутся. 7. Соединим точки и получим десятиугольник.
Построение пятиугольника Для построения правильного пятиугольника нужно во время построения правильного десятиугольника соединить поочередно не все точки, а через одну.
Приблизительное построение правильного пятиугольника методом Дюрера Построим 2 окружности проходящие через центр друг друга. Соединим центры прямой, получив одну из сторон пятиугольника. Соединим точки пересечения окружностей.
Приблизительное построение правильного пятиугольника методом Дюрера 4. Проведем еще одну окружность того же радиуса с центром в точке пересечения двух других окружностей. 5. Проведем 2 отрезка как указано на рисунке.
Проведем еще одну окружность того же радиуса с центром в точке пересечения двух других окружностей. 5. Проведем 2 отрезка как указано на рисунке.
Приблизительное построение правильного пятиугольника методом Дюрера 6. Соединим точки соприкосновения этих отрезков с окружностями с концами построенной стороны пятиугольника. 7. Достроим до пятиугольника.
Приблизительное построение правильного пятиугольника методами Коваржика, Биона
В черчении зачастую требуется строить положительные многоугольники. Так, скажем, положительные восьмиугольники применяются на щитах дорожных знаков.
Вам понадобится
- – циркуль
- – линейка
- – карандаш
Инструкция
1. Пускай задан отрезок, равный длине стороны желанного восьмиугольника. Требуется возвести верный восьмиугольник. Первым шагом постройте равнобедренный треугольник на заданном отрезке, применяя отрезок, как основание. Для этого вначале постройте квадрат со стороной, равной отрезку, проведите в нем диагонали. Сейчас постройте биссектрисы углов при диагоналях (на рисунке биссектрисы указаны синим), на пересечении биссектрис образуется вершина равнобедренного треугольника, стороны которого равны радиусу окружности, описанной вокруг верного восьмиугольника.
Сейчас постройте биссектрисы углов при диагоналях (на рисунке биссектрисы указаны синим), на пересечении биссектрис образуется вершина равнобедренного треугольника, стороны которого равны радиусу окружности, описанной вокруг верного восьмиугольника.
2. Постройте окружность с центром в вершине треугольника. Радиус окружности равен стороне треугольника. Сейчас разведите циркуль на расстояние, равное величине заданного отрезка. Отложите это расстояние на окружности, начиная от всякого конца отрезка. Объедините все полученные точки в восьмиугольник.
3. Если же задана окружность, в которую должен быть вписан восьмиугольник, то построения будут еще проще. Постройте две перпендикулярные друг другу осевые линии, проходящие через центр окружности. На пересечении осевых и окружности получатся четыре вершины грядущего восьмиугольника. Осталось поделить расстояние между этими точками на дуге окружности напополам, дабы получить еще четыре вершины.
Верный треугольник – тот, у которого все стороны владеют идентичной длиной. Исходя из этого определения, построение сходственной разновидности треугольник а является нетрудной задачей.
Исходя из этого определения, построение сходственной разновидности треугольник а является нетрудной задачей.
Вам понадобится
- Линейка, лист разлинованной бумаги, карандаш
Инструкция
1. Взять лист чистой бумаги, разлинованной в клеточку, линейку и подметить на бумаге три точки так, дабы они находились на идентичном друг от друга расстоянии (рис.1)
2. С подмогой линейки объединить подмеченные на листе точки ступенчато, друг за ином так, как это показано на рисунке 2.
Обратите внимание!
В верном (равностороннем) треугольнике все углы равны 60 градусам.
Полезный совет
Равносторонний треугольник так же является и равнобедренным. Если треугольник равнобедренный, то это обозначает, что 2 из 3-х его сторон равны, а третья сторона считается основанием. Всякий положительный треугольник является равнобедренным, в то время как обратное заявление не правильно.
Восьмиугольник – это, по своей сути, два квадрата, смещенных касательно друг друга на 45° и объединенных на вершинах цельной линией.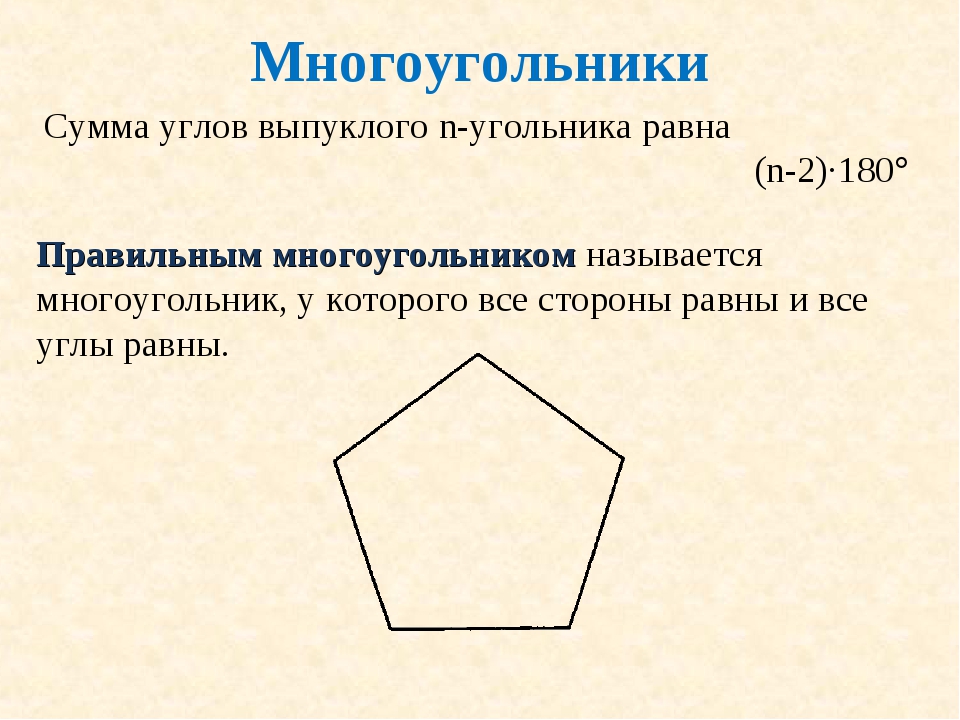 А потому, для того дабы положительно изобразить такую геометрическую фигуру, нужно твердым карандашом дюже опрятно, по правилам начертить квадрат либо круг, с которыми и проводить последующие действия. Изложение ориентировано на длину стороны, равной 20 см. А значит, при расположении чертежа рассматривайте, дабы вертикальная и горизонтальная линии длиной 20 см умещались на листе бумаги.
А потому, для того дабы положительно изобразить такую геометрическую фигуру, нужно твердым карандашом дюже опрятно, по правилам начертить квадрат либо круг, с которыми и проводить последующие действия. Изложение ориентировано на длину стороны, равной 20 см. А значит, при расположении чертежа рассматривайте, дабы вертикальная и горизонтальная линии длиной 20 см умещались на листе бумаги.
Вам понадобится
- Линейка, прямоугольный треугольник, транспортир, карандаш, циркуль, лист бумаги
Инструкция
1. Метод 1. Начертите внизу горизонтальную линию длиной 20 см. После этого с одной стороны подметьте транспортиром прямой угол, тот, что составляет 90°. То же самое дозволено сделать с поддержкой прямого треугольника. Проведите вертикальную линию и подметьте 20 см. Проделайте те же самые манипуляции с иной стороны. Объедините две полученные точки горизонтальной линией. В итоге получилась геометрическая фигура – квадрат.
2. Для того дабы возвести 2-й (смещенный) квадрат, потребуется центр фигуры.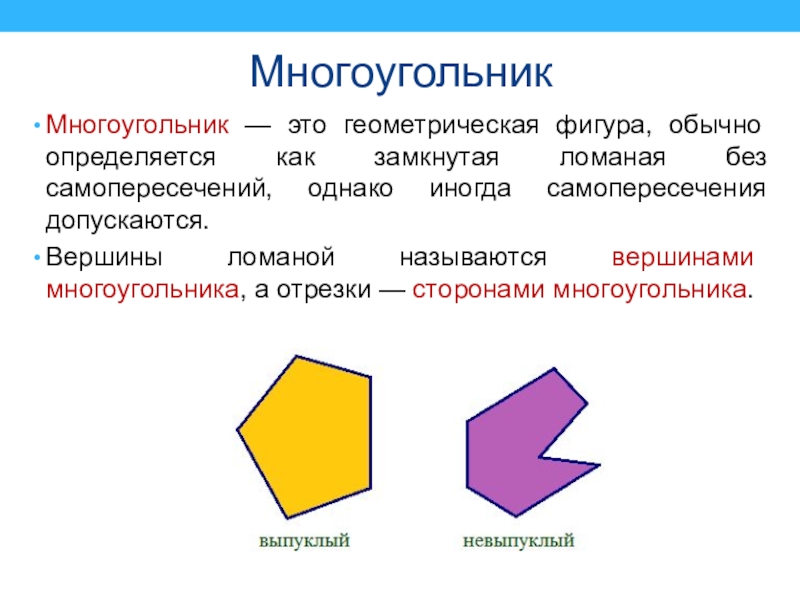 Для этого поделите всякую сторону квадрата на 2 части. Объедините вначале 2 точки параллельных верхней и нижней сторон, а потом точки боковых сторон. Проведите через центр квадрата 2 прямые линии, перпендикулярные касательно друг друга. Начиная от центра, отмерьте на новых прямых длину по 10 см, что в результате даст 4 прямые линии. Объедините 4 полученные наружные точки между собой, в итоге чего получится 2-й квадрат. Сейчас всякую точку из 8 полученных углов объедините между собой. Таким образом, будет начерчен восьмиугольник.
Для этого поделите всякую сторону квадрата на 2 части. Объедините вначале 2 точки параллельных верхней и нижней сторон, а потом точки боковых сторон. Проведите через центр квадрата 2 прямые линии, перпендикулярные касательно друг друга. Начиная от центра, отмерьте на новых прямых длину по 10 см, что в результате даст 4 прямые линии. Объедините 4 полученные наружные точки между собой, в итоге чего получится 2-й квадрат. Сейчас всякую точку из 8 полученных углов объедините между собой. Таким образом, будет начерчен восьмиугольник.
3. Метод 2. Для этого потребуется циркуль, линейка и транспортир. От центра листа с поддержкой циркуля начертите круг диаметром 20 см (радиус 10 см). Через центральную точку проведите прямую линию. После этого начертите вторую перпендикулярную ей линию. То же самое дозволено исполнить с подмогой транспортира либо прямого треугольника. В итоге круг будет поделен на 4 равные части. Дальше всякий из секций поделите еще на 2 части. Для этого также дозволено воспользоваться транспортиром, отмеряя 45° либо прямоугольным треугольником, тот, что приложите острым углом в 45° и проведите лучи. От центра на всякой прямой линии отмерьте по 10 см. В итоге получатся 8 «лучиков», которые объедините между собой. В итоге получится восьмиугольник.
От центра на всякой прямой линии отмерьте по 10 см. В итоге получатся 8 «лучиков», которые объедините между собой. В итоге получится восьмиугольник.
4. Метод 3. Для этого так же начертите круг, проведите через середину линию. После этого возьмите транспортир, поставьте его на центр и отмеряйте углы, рассматривая, что всякий секция восьмиугольника имеет в центре угол 45° . Позже этого на полученных лучах отмерьте длину в 10 см. и объедините их между собой. Восьмиугольник готов.
Полезный совет
Делайте чертеж твердым карандашом, побочные линии на котором после этого легко дозволено будет удалить
Верный восьмиугольник – это геометрическая фигура, у которой всякий угол составляет 135?, и все стороны между собою равны. Эта фигура дюже зачастую используется в архитектуре, к примеру, при постройке колон, а также при изготовлении дорожного знака STOP. Как же нарисовать положительный восьмиугольник?
Вам понадобится
- – альбомный лист;
- – карандаш;
- – линейка;
- – циркуль;
- – ластик.

Инструкция
1. Нарисуйте вначале квадрат. После этого проведите окружность так, дабы квадрат оказался внутри круга. Сейчас проведите две осевые серединные линии квадрата – горизонтальную и вертикальную до пересечения с кругом. Объедините прямыми отрезками точки пересечения осей с кругом и точки прикосновения описанной окружности с квадратом. Таким образом, получите стороны верного восьмиугольника.
2. Нарисуйте верный восьмиугольник иным методом. Вначале начертите окружность. После этого проведите горизонтальную линию через ее центр. Подметьте точку пересечения крайней правой границы окружности с горизонталью. Эта точка будет являться центром еще одной окружности, радиусом равным предыдущей фигуре.
3. Проведите вертикальную линию через точки пересечения 2-й окружности с первой. Поставьте ножку циркуля в точку пересечения вертикали с горизонталью и начертите небольшой круг радиусом, равным расстоянию от центра крошечной окружности до центра начального круга.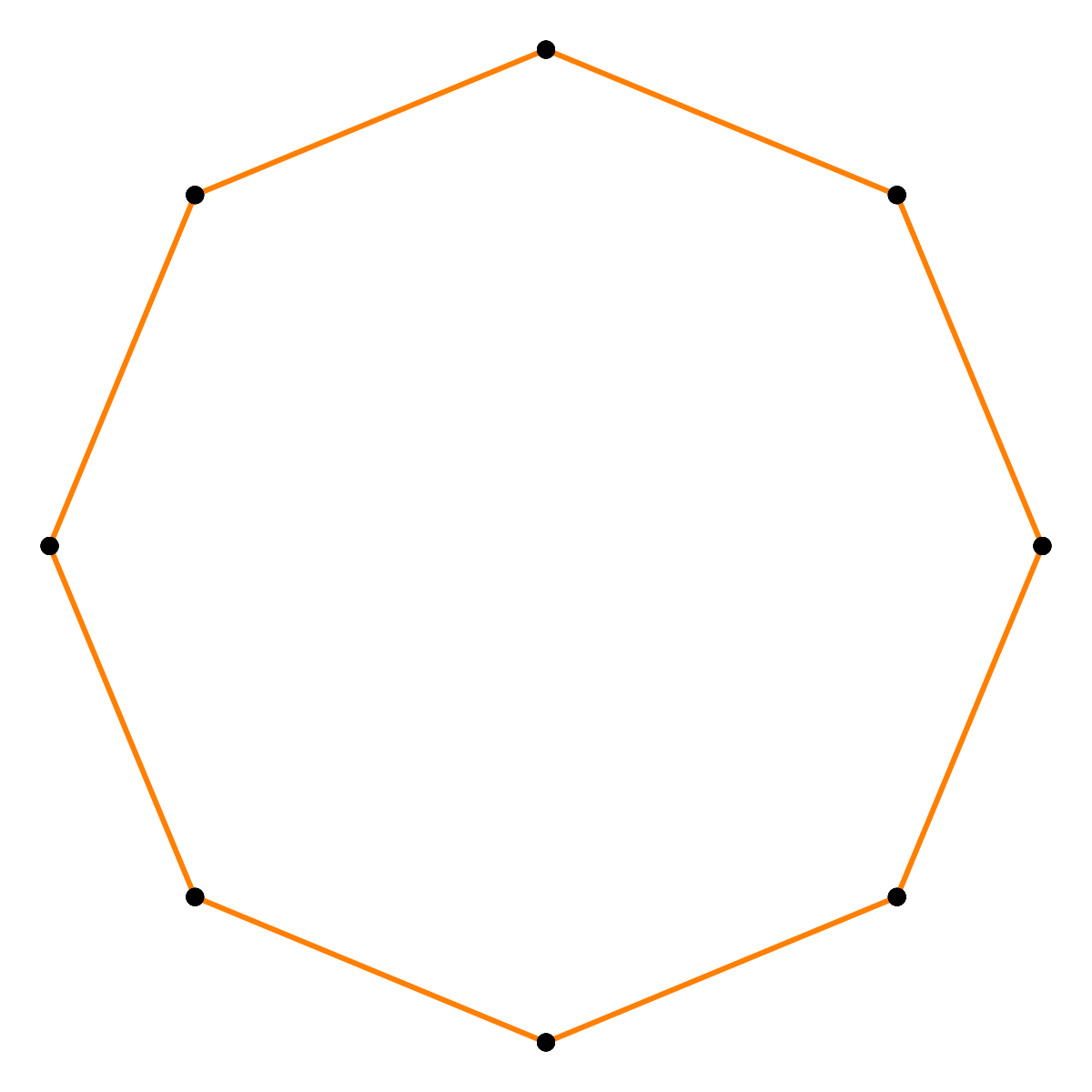
4. Начертите прямую линию через две точки – центр начального круга и точку пересечения вертикали и крошечной окружности. Продолжите ее до пересечения с рубежом изначальной фигуры. Это будет точка вершины восьмиугольника. Циркулем подметьте еще одну точку, проведя окружность с центром в точке пересечения крайней правой рубежом начального круга с горизонталью и радиусом, равным расстоянию от центра к теснее имеющейся вершине восьмиугольника.
5. Проведите прямую линию через две точки – центр начального круга и последнюю новообразованную точку. Продолжите прямую линию до пересечения с границами первоначальной фигуры.
6. Объедините прямыми отрезками ступенчато: точку пересечения горизонтали с правой рубежом начальной фигуры, после этого по часовой стрелке все образовавшиеся точки, включая точки пересечения осей с первоначальной окружностью.
Видео по теме
Урок 15. периметр многоугольника — Математика — 2 класс
Математика 2 класс.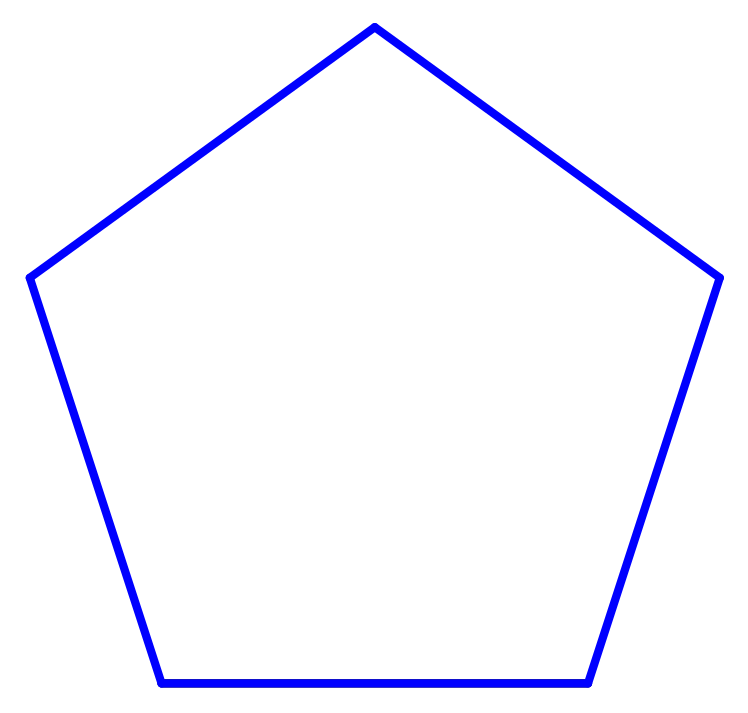 Урок №15.
Урок №15.
Периметр многоугольника
Перечень вопросов, рассматриваемых в теме:
— Что такое периметр прямоугольника?
— Как найти периметр прямоугольника?
Глоссарий по теме:
Периметр – это сумма длин сторон многоугольника.
Многоугольник – это геометрическая фигура, которая со всех сторон ограничена замкнутой ломаной линией.
Основная и дополнительная литература по теме урока
1. Моро М. И., Бантова М. А., Бельтюкова Г. В. и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/–8-е изд. – М.: Просвещение, 2017. – с. 42, 43.
2. Глаголева Ю. И., Волкова А. Д.Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, Уч. лит, 2017, с.17.
3. Волкова С. И. Математика. Проверочные работы. 2 кл.: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2017.- с.28, 29.
Теоретический материал для самостоятельного изучения
Нам уже знакомо понятие «ломаная линия». Знаем, что ломаная линия может быть незамкнутой и замкнутой.
Знаем, что ломаная линия может быть незамкнутой и замкнутой.
Замкнутая ломаная линия называется по-другому многоугольник. Многоугольники могут быть разными, их названия во многом зависят от количества углов многоугольника.
У каждого многоугольника свое число сторон. Каждая сторона имеет свою длину. Сумма длин всех сторон многоугольника называется периметром.
Кратко слово «периметр» записывается буквой «пэ» – Р.
Научимся находить периметр многоугольника двумя способами.
1 способ.
С помощью линейки измерим длину каждой стороны и найдем сумму длин
Р=2см+5см+2см+5см=14 см
Периметр четырехугольника равен четырнадцати сантиметрам.
2 способ
С помощью циркуля на прямой отложим один за другим отрезки равные по длине сторонам четырехугольника.
Далее с помощи линейки узнаем длину получившегося отрезка 14 см.
В этом случае длину каждой стороны узнавать не пришлось. Периметр четырехугольника равен четырнадцати сантиметрам.
Найдём периметр треугольника первым способом.
С помощью линейки измерим длину каждой стороны и найдем сумму длин.
Р = 5см + 5см + 3см = 13см
Вывод: Сумма длин всех сторон многоугольника называется периметром.
Тренировочные задания.
- Выберите правильный ответ
Длины сторон четырёхугольника равны 3см, 5 см, 6 см, 4 см. Чему равен периметр этой фигуры?
Варианты ответов:
1.18см
2.14см
3.17см
4.16см
Правильный ответ:
1. 18см
2.Соедините многоугольники, которые имеют одинаковый периметр
Правильный ответ:
Глава 7 – Редактор векторной графики Draw¶
Что такое Draw?
LibreOffice Draw – это векторный графический редактор, хотя он также может выполнять некоторые операции и с растровой графикой. Используя Draw, можно быстро создавать большое разнообразие графических изображений.
Векторная графика хранит и отображает изображения в виде простых геометрических элементов, таких как линии, окружности и многоугольники, а не как наборы пикселей (точек на экране), как растровая.
Векторная графика позволяет облегчить хранение и масштабирование изображения.
Draw полностью интегрирован в пакет LibreOffice и это упрощает обмен рисунками между любыми компонентами пакета. Например, если создать изображение в Draw, то повторное использование его в документе Writer будет таким же простым, как копирование и вставка изображения. Также можно работать с такой графикой непосредственно в Writer или в Impress, используя подмножество функций и инструментов из Draw.
Функциональность LibreOffice Draw обширна и, хотя он не был предназначен для конкуренции с лучшими графическими редакторами, он обладает более обширной функциональностью, чем инструменты рисования, интегрированные в большинство иных офисных пакетов.
Вот несколько примеров функций рисования в Draw: управление слоями, система привязок, отображение размеров, соединители для создания диаграмм, 3D функции, которые позволяют создавать небольшие трехмерные рисунки (с текстурированием и световыми эффектами), рисование и интеграция в стиль страницы, кривые Безье.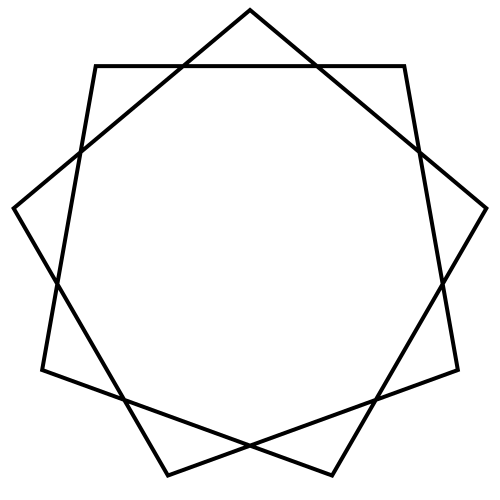
В этой главе рассматриваются только некоторые особенности Draw. Для получения дополнительной информации смотрите полное Руководство по Draw и встроенную справку в приложении.
Главное окно Draw
Основные компоненты главного окна Draw показаны на рисунке Окно программы LibreOffice Draw и перечислены ниже:
- Строка меню
- Стандартная панель инструментов
- Панель инструментов Линии и Заливки
- Панель страниц
- Рабочая область
- Строка состояния
- Панель инструментов Рисование
- Боковая панель
Рабочая область
Рабочая область – это большая область в центре окна программы, где пользователи создают свои рисунки, она может быть окружена панелями инструментов и информационными зонами. Количество и расположение видимых инструментов меняются в зависимости от поставленной задачи и пользовательских предпочтений, поэтому внешний вид программы на компьютере читателя может отличаться от показанного на рисунке Окно программы LibreOffice Draw.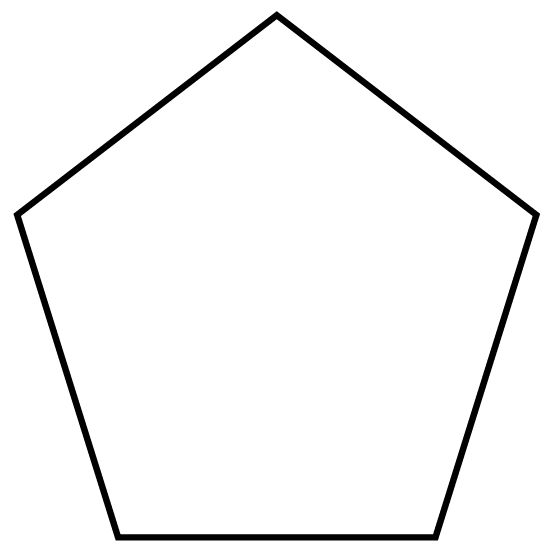 В LibreOffice Draw максимальный размер рисунка – 300х300 сантиметров.
В LibreOffice Draw максимальный размер рисунка – 300х300 сантиметров.
Окно программы LibreOffice Draw
Панель страниц
Рисунки в Draw можно разделить на несколько страниц. Многостраничные рисунки используются в основном для презентаций. На панели страниц показываются все страницы, которые были созданы в текущем документе Draw. Если панель страниц не отображается, выберите пункт меню . Чтобы внести изменения в порядок страниц, просто перетащите одну или несколько страниц на новое место.
Боковая панель
Боковая панель содержит 4 больших раздела. Чтобы развернуть раздел, который нужно использовать, нажмите на его значок или нажмите на маленький треугольник в верхней части панели и выберите раздел из выпадающего списка. Единовременно показывается только один раздел. Если боковая панель не видна, выберите пункт главного меню . Ниже описаны разделы боковой панели:
- Свойства – cодержит подразделы для свойств объекта, которые можно изменить в соответствии с требованиями пользователя.
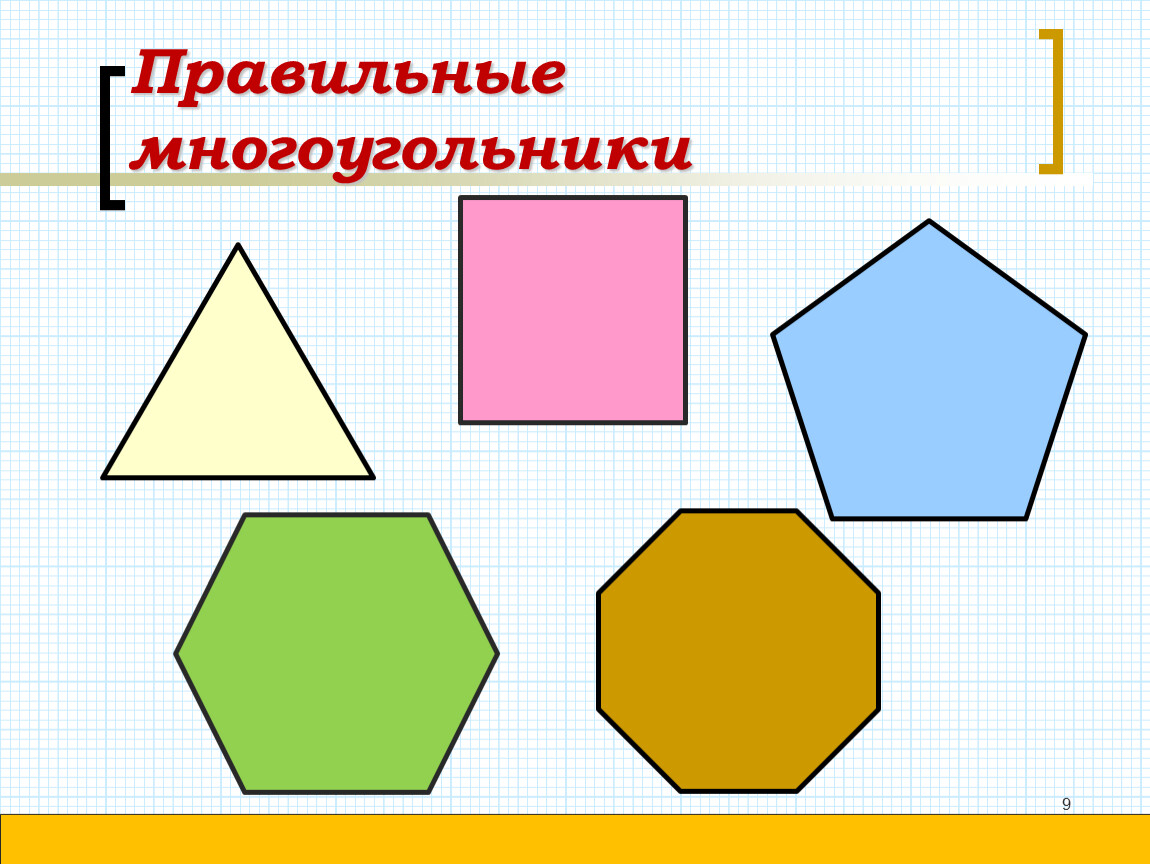 Это подразделы Символы, Абзац, Область, Линия и Положение и размер.
Это подразделы Символы, Абзац, Область, Линия и Положение и размер. - Стили и форматирование – здесь можно редактировать и применять стили изображения к объектам в рисунке. При изменении стиля, они (изменения) автоматически применятся ко всем элементам, отформатированным с этим стилем, в рисунке.
- Галерея – открывает Галерею Draw, откуда можно вставить объект в рисунок в виде копии или в виде связи. Копия объекта в рисунке не зависит от исходного объекта в Галерее. Изменения в исходном объекте в Галерее не имеют никакого влияния на их копии. Объект, вставленный в рисунок, как связь, остается зависимым от исходного объекта в Галерее. Изменения в оригинале отражаются во вставленном, как связь, объекте.
- Навигатор – открывает Навигатор Draw, в котором можно быстро перемещаться между страницами в документе Draw или выбрать объект на рисунке.
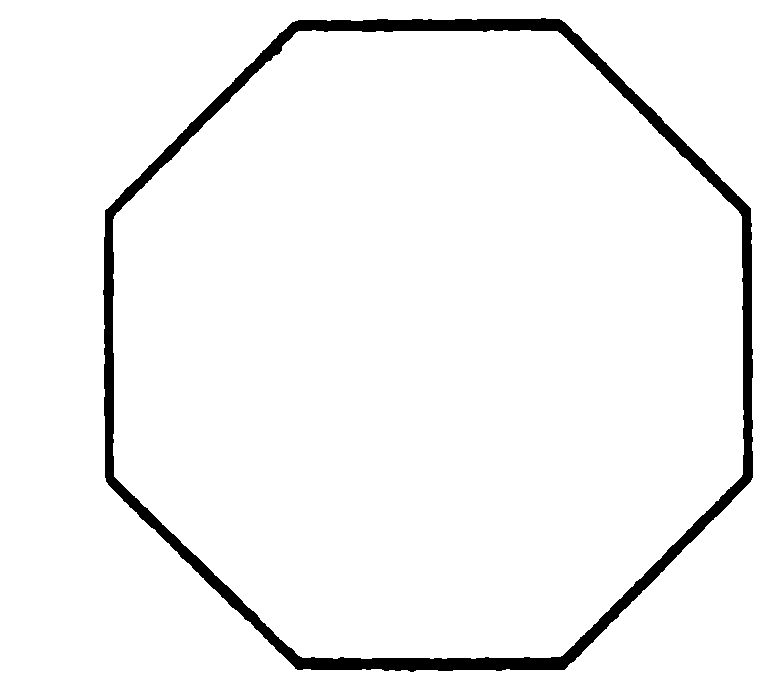 Рекомендуется давать страницам и объектам в документе осмысленные имена, что позволит легко идентифицировать их при использовании Навигатора.
Рекомендуется давать страницам и объектам в документе осмысленные имена, что позволит легко идентифицировать их при использовании Навигатора.
Линейки
Сверху и с левой стороны от рабочей области показаны линейки (полоски с числами). Если они не видны, их можно включить, выбрав пункт меню . Линейки показывают размер выбранного объекта на странице, используя двойные линии (выделены на рисунке На линейках отмечен размер выделенного объекта). Если не выбран ни один объект, то эти линии показывают местоположение курсора мыши, что позволяет позиционировать графические объекты более точно.
Также можно использовать линейки для управления объектами, двигая сдвоенные линии, упростив позиционирование объектов.
Поля страницы в области рисования также показаны на линейках. Размеры полей можно изменять непосредственно в линейках, перетаскивая их границы с помощью мыши. Область полей обозначается на линейках серым цветом, как показано на рисунке На линейках отмечен размер выделенного объекта.
Для изменения единиц измерения линейки, которые можно задать самостоятельно, щелкните правой кнопкой мыши на линейке и выберите единицы измерения из выпадающего списка, как показано на рисунке Единицы измерения линейки.
На линейках отмечен размер выделенного объекта
Единицы измерения линейки
Строка состояния
Строка состояния расположена в нижней части экрана Draw, как и во всех компонентах LibreOffice; она включает в себя некоторые специфичные для Draw поля. Для уточнения деталей по содержимому и использованию этих полей, смотрите Глава 1 – Введение в LibreOffice в этом руководстве и Главу 1. Введение в Draw в полном Руководстве по Draw.
Строка состояния Draw
Примечание
Размеры объекта даны в текущих единицах измерения, их не следует путать с единицами измерения на линейках. Единицы измерения в строке состояния определяются в меню , где также можно изменить масштаб страницы.
Панели инструментов
Чтобы показать или скрыть различные панели инструментов Draw, выберите их в меню . В появившемся меню выберите, какие панели нужно отображать. Для получения более подробной информации о работе с панелями инструментов обратитесь к Глава 1 – Введение в LibreOffice в этом руководстве.
В появившемся меню выберите, какие панели нужно отображать. Для получения более подробной информации о работе с панелями инструментов обратитесь к Глава 1 – Введение в LibreOffice в этом руководстве.
Инструменты, имеющиеся в панели инструментов Draw описаны в последующих разделах. Внешний вид панелей инструментов может различаться в зависимости от операционной системы и выбора размера и стиля значков в меню .
Стандартная панель инструментов
Стандартная панель инструментов является одинаковой для всех компонентов LibreOffice и не будет подробно описываться в этой главе .
Стандартная панель инструментов
Панель инструментов Рисование
Панель инструментов Рисование является наиболее важным инструментом в Draw. Она содержит все необходимые функции для рисования различных геометрических и произвольных форм и для размещения их на странице.
Панель инструментов Рисование
Панель инструментов Линии и заливка
Панель инструментов Линия и заливка позволяет изменять основные свойства объекта рисования. Значки и выпадающие списки варьируются, в зависимости от типа выбранного объекта. Например, чтобы изменить стиль линии, раскройте на панели выпадающий список и выберите нужный стиль.
Значки и выпадающие списки варьируются, в зависимости от типа выбранного объекта. Например, чтобы изменить стиль линии, раскройте на панели выпадающий список и выберите нужный стиль.
Панель инструментов Линия и заливка
Панель инструментов Форматирование текста
Если выбранным объектом является текст, то панель Линия и заливка заменяется панелью инструментов Форматирование текста, которая аналогична такой же панели в Writer. Для получения более подробной информации смотрите Глава 4 – Текстовый процессор Writer в этом руководстве.
Панель инструментов Форматирование текста
Панель инструментов Параметры
Используйте панель инструментов Параметры для включения или выключения различных вспомогательных функций. Панель инструментов Параметры по умолчанию не отображается. Для её отображения выберите пункт меню Вид > Панели инструментов > Параметры.
Панель инструментов Параметры
Выбор и определение цвета
Для отображения диалога Цвета (рисунок ниже) выберите пункт главного меню .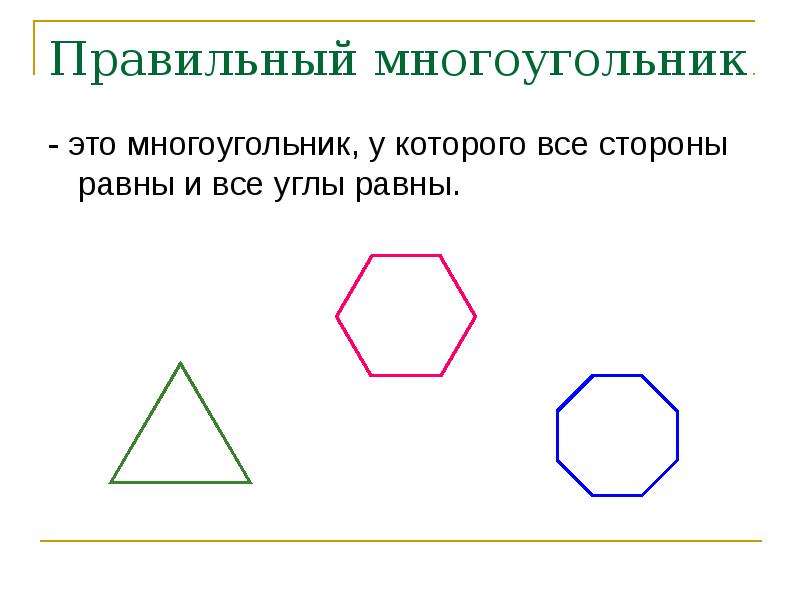 Эта панель позволяет быстро выбрать цвет различных объектов (линии, замкнутые области и 3D-эффекты). Первый квадратик (в левом верхнем углу, перечеркнут) в панели соответствует отсутствию цвета.
Эта панель позволяет быстро выбрать цвет различных объектов (линии, замкнутые области и 3D-эффекты). Первый квадратик (в левом верхнем углу, перечеркнут) в панели соответствует отсутствию цвета.
Диалог Цвета
Можно также получить доступ к нескольким специализированным цветовым палитрам в Draw, а также изменить отдельные цвета на свой вкус. Это делается с помощью диалогового окна Область, доступного после выбора пункта меню или после нажатия на на соответствующий значок Область на панели Линия и заливка, затем необходимо выбрать вкладку Цвета (рисунок ниже).
Диалог Область. Вкладка Цвета
Чтобы загрузить другие палитры нажмите на значок Загрузить список цветов. В диалоге выбора файла будет предложено выбрать одну из стандартных палитр LibreOffice (файлы с расширением .soc). Например, файл цветовой палитры web.soc, которая предназначена для создания рисунков для размещения на веб-страницах.
Окно выбора цвета также позволяет изменять любой цвет, изменяя числовые значения в соответствующих полях справа от цветовой палитры. Использовать можно известные цветовые схемы CMYK (Cyan, Magenta, Yellow, Black) или RGB (Red, Green, Blue).
Нажмите на кнопку Правка, чтобы открыть диалог Выбор цвета, где можно настроить свой индивидуальный цвет. Смотрите раздел Настройки цвета в Глава 2 – Общие параметры LibreOffice данного руководства.
Более детальное описание цветовых палитр и их настроек содержится в полном Руководстве по Draw, в Главе 10, Дополнительные возможности Draw.
Рисование основных фигур
В Draw представлен широкий выбор фигур, расположенных в палитрах, доступных из панели инструментов Рисование (рисунок Панель инструментов Рисование).
В этом разделе описываются лишь некоторые из основных фигур, в том числе текст, который в Draw рассматривается в качестве объекта. Смотрите полное Руководство по Draw для получения полного описания всех доступных фигур.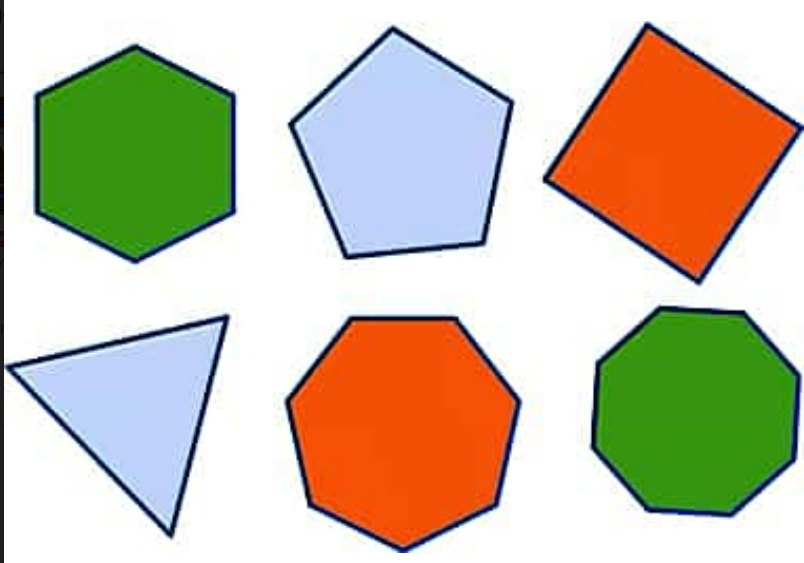
Пожалуйста, обратите внимание, что некоторые значки на панели Рисование будут изменяться в зависимости от формы, которая была выбрана. Наличие дополнительных значков в палитрах обозначено маленьким треугольником справа от значка на панели инструментов Рисование.
Примечание
При рисовании формы или выборе объекта для редактирования, поле информация на левой стороне в строке состояния отражает текущее действие: например, Линия создана, Текстовый объект XXYY выбран и так далее.
Рисование прямой линии
Нажмите левой кнопкой мыши на значок Линия и поместите курсор в место начала линии. Тащите мышку с зажатой кнопкой в нужном направлении. Отпустите кнопку мыши в точке, где линия должна закончится. На каждом конце линии будет показан маркер выделения объекта. Они показывают, что объект является выделенным в данный момент. Маркер выделения в начальной точке линии по размеру немного больше, чем маркер на конце линии.
Зажмите клавишу Shift во время рисования линии, чтобы задать угол рисования линии кратный 45 градусам (то есть 0, 45, 90, 135 и так далее).
Примечание
Такое поведение при нажатой клавише Shift задано по умолчанию. Однако, если опция При создании или перемещении объектов в разделе Применять привязку в меню будет активна, то поведение клавиши Shift изменится на противоположное и линия будет автоматически рисоваться с углом кратным 45˚ при не нажатой клавише Shift.
Держите клавишу Ctrl нажатой, рисуя линию, для того, чтобы конец линии привязать к ближайшей точке сетки.
Рисование прямой линии
Примечание
Такое поведение при нажатой клавише Ctrl задано по умолчанию. Однако, если опция Привязка к сетке в меню активна, то нажатие клавиши Ctrl временно отключает привязку к сетке.
Удерживайте клавишу Alt во время рисования линии, чтобы начать рисовать её симметрично в обе стороны от начальной точки. Это позволяет рисовать линии, начиная с середины.
Это позволяет рисовать линии, начиная с середины.
Линия рисуется с атрибутами (такими, как: толщина, стиль и цвет) по умолчанию. Чтобы изменить атрибуты уже нарисованной линии выберите её щелчком мыши, затем нажмите правую кнопку мыши и выберите пункт Линия из контекстного меню или выберите пункт меню , чтобы открыть одноименный диалог. Также можно выбрать раздел Свойства на боковой панели и открыть подраздел Линия. Стиль, толщину и цвет линии также можно выбрать, используя панель инструментов Линия и заливка.
Диалог Линия
Рисование стрелок
Стрелки рисуются так же, как и линии. Draw классифицирует стрелки, как подвид линий: линии со стрелкой на конце. Информационное поле в строке состояния показывает стрелки только, как линии. Нажмите на значок Линия со стрелкой на конце в панели инструментов Рисование, чтобы нарисовать стрелку. Стрелка появится в конечной точке линии после окончания рисования.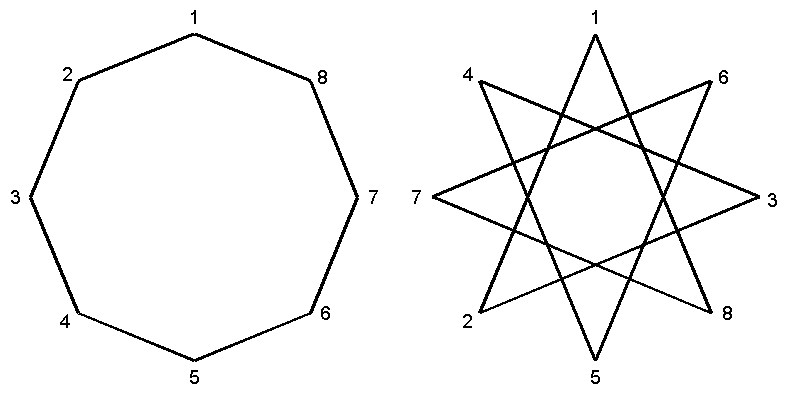
Изменение типа окончания линии (стрелки, кружки, квадратики и прочее)
В Draw доступны несколько типов окончаний линий (стрелки, кружки, квадратики и другие). Нажмите на маленький треугольник справа от значка Линии и стрелки в панели инструментов Рисование, чтобы открыть палитру, содержащую инструменты для рисования стрелок и линий. Также можно использовать пункт меню , чтобы открыть панель Стрелки в виде плавающей панели.
После того, как линия была нарисована, можно изменить стиль стрелки, нажав на значок Стиль стрелок в панели инструментов Линия и заливка, и, выбрав из выпадающего списка вид начала (слева в списке) и конца (справа в списке) линии.
Панель инструментов Стрелки и доступные инструменты
Рисование прямоугольников или квадратов
Рисование прямоугольников аналогично рисованию прямых линий. Нажмите на значок Прямоугольник на панели инструментов Рисование. Зажмите кнопку мыши и тяните курсор мыши на листе, за курсором будет вытягиваться закрашенная область прямоугольника, отпустите кнопку мыши, когда достигнете нужного размера прямоугольника.
Квадрат – это прямоугольник, у которого все стороны равны. Чтобы нарисовать квадрат, нажмите на значок Прямоугольник и удерживайте нажатой клавишу Shift во время рисования.
Примечание
Если активна опция При создании или перемещении объектов в разделе Применять привязку в меню , то нажатие клавиши Shift приведёт к обратному эффекту: при выборе инструмента Прямоугольник будет рисоваться квадрат. А чтобы нарисовать прямоугольник, нужно будет зажать клавишу Shift. Такая смена поведения клавиши Shift также применяется при рисовании эллипсов и окружностей.
Чтобы нарисовать прямоугольник или квадрат из его центра, установите курсор на чертеже, нажмите кнопку мыши и, удерживайте нажатой клавишу Alt при перетаскивании курсора. Прямоугольник или квадрат используют в качестве центра начальную точку (ту, где впервые нажата кнопка мыши).
Прямоугольник или квадрат используют в качестве центра начальную точку (ту, где впервые нажата кнопка мыши).
Рисование эллипсов и кругов
Чтобы нарисовать эллипс, нажмите на значок Эллипс на панели инструментов Рисование. Круг – это эллипс, у которого все оси равны по длине. Чтобы нарисовать круг, нажмите на значок Эллипс и, удерживая нажатой клавишу Shift, нажмите клавишу мыши в нужном месте листа и тяните курсор.
Чтобы нарисовать эллипс или круг, начиная из центра, поместите курсор на нужное место на листе, нажмите на клавишу мыши и удерживая нажатой клавишу Alt, тащите курсор. Эллипс или круг используют в качестве центра начальную точку (ту, где вы впервые нажали кнопку мыши).
Примечание
Если удерживать нажатой клавишу Ctrl, и нажать на один из значков на панели Рисование: Линия, Прямоугольник, Эллипс или Текст, то на листе будет создан объект стандартного вида: размер, форма и цвет объекта будут иметь стандартное значение. Эти атрибуты могут быть изменены позже, если это потребуется. Смотрите Руководство по Draw для получения более подробной информации.
Эти атрибуты могут быть изменены позже, если это потребуется. Смотрите Руководство по Draw для получения более подробной информации.
Рисование кривых и многоугольников
Чтобы нарисовать кривую или многоугольник нажмите на значок Кривая на панели инструментов Рисование. Нажмите на треугольник справа от значка, чтобы открыть палитру доступных инструментов (рисунок ниже). Значок принимает вид последнего использованного инструмента, что упрощает его повторное использование.
Если поместить курсор мыши на один из значков, появится всплывающая подсказка с описанием функции.
Панель Кривые (Линии) и доступные инструменты
Примечание
Если удерживать нажатой клавишу Shift при рисовании линий (кривой или многоугольника), то инструменты будут ограничены углами рисования в 45 или 90 градусов.
Кривые
Нажмите и удерживайте левую кнопку мыши, чтобы создать начальную точку кривой. Удерживая нажатой левую кнопку мыши, перетащите курсор из начальной точки в нужном направлении, чтобы нарисовать линию. Отпустите левую кнопку мыши и продолжайте двигать курсор, чтобы продолжить рисовать прямую линию в другом направлении. Каждый щелчок мыши устанавливает угловую точку и позволяет продолжить рисование другой прямой линии от угловой точки. Двойной щелчок завершает рисование всей линии.
Кривая с заполнением автоматически соединяет последнюю точку с первой точкой при завершении рисования и производит заливку получившейся фигуры стандартным цветом. Кривая без заполнения не замыкается в фигуру при окончании рисования.
Многоугольники
Нажмите и удерживайте левую кнопку мыши, тащите курсор и таким образом рисуйте первую линию из начальной точки. Как только вы отпустите кнопку мыши, появится линия между первой и второй точками. Переместите курсор, чтобы нарисовать следующую линию. Каждый щелчок мыши устанавливает угловую точку и позволяет рисовать другую линию. Двойной щелчок завершает рисование.
Многоугольник с заполнением автоматически соединит последнюю точку с первой точкой, чтобы закрыть фигуру, и зальёт её текущим стандартным цветом. Многоугольник без заполнения не будет закрыт в конце рисования.
Многоугольники 45°
Как и обычные многоугольники, они формируются из линий, но углы между линиями ограничены значением в 45 или 90 градусов.
Полилинии
Использование инструмента полилиния похоже на рисование карандашом на бумаге. Нажмите и удерживайте левую кнопку мыши и перетащите курсор по требуемой траектории. Завершать рисунок с помощью двойного щелчка мыши необязательно, просто отпустите кнопку мыши и рисунок будет завершен.
Если выбран инструмент Полилиния с заполнением, то конечная точка автоматически соединяется с начальной точкой и получившийся объект заполняется соответствующим цветом.
Добавление текста
Чтобы включить инструмент добавления горизонтального текста, нажмите на значок Текст или для вертикального текста – значок Вертикальный текст . Если значок Вертикальный текст не виден, активируйте опцию Азиатские в меню . После нажатия на значок Текст станет доступна панель инструментов Форматирование текста. На этой панели инструментов можно выбрать вид шрифта, его размер и другие свойства шрифтов перед началом ввода текста.
Примечание
Значок Вертикальный текст доступен только на панели инструментов Рисование.
После активации инструмента Текст, щелкните клавишей мыши в том месте листа, где нужно расположить текст. Появится небольшая текстовая врезка, содержащая только текстовый курсор. Эта врезка может быть перемещена в любое место на листе, как и любой другой графический объект. Текстовая врезка динамическая и изменяет свои размеры при вводе текста.
Обратите внимание на информационное поле в строке состояния: оно показывает, что в данный момент редактируется текст, а также предоставляет подробную информацию о текущем положении курсора с использованием номеров абзаца, строк и столбцов (рисунок ниже).
Информация о тексте в строке состояния
Можно вставить разрыв строки, используя комбинацию клавиш Shift+Enter, или начать новый абзац, нажав клавишу Enter. Вставка разрывов строк или новых абзацев не прекращает редактирование текста и не удаляет текстовую врезку. После окончания набора текста щелкните мышью за пределами текстовой врезки, чтобы завершить добавление или редактирование текста.
Для редактирования существующего текста, щелкните дважды мышью по тексту, чтобы открыть панель Форматирование текста и приступить к редактированию.
Атрибуты текста (вид, размер, цвет и тому подобное) могут быть изменены прямо во время ввода текста. Новые атрибуты вступят в силу для текста, введенного после изменений. Чтобы изменить атрибуты для всего текста в текстовой врезке, нужно сначала выделить весь текст во врезке.
Можно создавать стили, которые будут использоваться для других текстовых врезок. Выберите пункт меню или нажмите клавишу F11, чтобы открыть диалог Стили и форматирование. Стиль влияет на весь текст в текстовой врезке. Для форматирования только части текста используйте прямое форматирование с помощью панели Форматирование текста или подразделов Символы и Абзацы в боковой панели.
Текстовые врезки могут также иметь цвет заполнения, тени и другие атрибуты, как и любой другой объект Draw. Врезку можно вращать и писать текст под любым углом. Эти опции доступны по щелчку правой кнопкой мыши на самой текстовой врезке.
Если дважды щелкнуть кнопкой мыши по графическому объекту или нажать клавишу F2 или нажать значок Текст, когда какой-либо объект выделен, то можно будет добавить текст на графический объект. Этот текст становится частью графического объекта.
Графические объекты не являются динамическими и не ведут себя, как текстовые врезки. Чтобы вписать текст в рамки объекта, нужно использовать абзацы, разрывы строк или меньший размер текста, увеличить размер объекта или использовать все четыре метода одновременно.
Для получения более подробной информации по работе с текстом смотрите Руководство по Draw. Глава 2. Рисование основных фигур и Глава 9. Добавление и форматирование текста там же.
Точки соединений и соединительные линии
Точки соединений
Все объекты Draw имеют точки соединений, которые в нормальном состоянии не отображаются. Они становятся видимыми только, если нажат значок Соединительные линии на панели инструментов Рисование. Большинство объектов имеет четыре соединительных точки. Можете добавлять свои точки соединений или изменять существующие, используя панель инструментов Точки соединений. Используйте пункт меню , чтобы открыть эту панель.
Точки соединений
Точки соединений – это не то же самое, что точки, появляющиеся при выборе объекта. Те точки используются для перемещения или изменения формы объекта (и называются маркеры выделения). Точки соединений используются, чтобы прикрепить соединительную линию к графическому объекту таким образом, чтобы, при перемещении объекта соединительная линия осталась «приклеенной» к объекту и перемещалась вместе с ним. Для получения более подробных инструкций по использованию точек соединения прочитайте в Руководстве по Draw Главу 3. Работа с объектами и точками объекта, а также Главу 8. Соединения, блок-схемы и организационные диаграммы.
Панель инструментов Точки соединений и доступные инструменты
Соединительные линии
Соединительные линии – это линии или стрелки, концы которых автоматически присоединяются к точке соединения объекта. Соединительные линии особенно полезны при разработке организационных диаграмм и блок-схем. Когда объекты передвигаются относительно друг друга, то соединительные линии остаются прикрепленными к точке соединения. На рисунке ниже показаны для примера два объекта и соединительная линия между ними.
Соединительная линия между двух объектов
Draw предлагает широкий выбор различных соединительных линий и их вариантов. На панели инструментов Рисование щелкните треугольник справа от значка Соединительные линии, чтобы открыть палитру доступных инструментов типа Соединительная линия (рисунок ниже). Для получения более подробных инструкций по использованию соединительных линий смотрите в Руководстве по Draw Главу 8. Соединительные линии, блок-схемы и организационные диаграммы.
Панель инструментов Соединительные линии и доступные варианты линий
Рисование геометрических фигур
Значки для рисования геометрических фигур расположены на панели инструментов Рисование и каждая геометрическая фигура описывается в последующих разделах. При нажатии на треугольник справа от значка на панели инструментов Рисование открывается палитра инструментов, предоставляющая доступ к инструментам для этой геометрической фигуры.
Совет
Использование данных инструментов для рисования геометрических фигур похоже на инструменты, используемые для рисования прямоугольников и квадратов. Для получения более подробной информации смотрите раздел Рисование основных фигур в данной главе и Руководство по Draw. Глава 2. Рисование основных фигур.
Основные фигуры
Щелкните на треугольнике справа от значка Основные фигуры , чтобы открыть палитру инструментов Основные фигуры. Эта палитра включает в себя инструмент рисования прямоугольника, идентичный тому, который уже отображается на панели инструментов Рисование.
Панель инструментов Основные фигуры
Фигуры-символы
Щелкните на треугольнике справа от значка Фигуры-символы , чтобы открыть одноименную палитру инструментов.
Панель инструментов Фигуры-символы
Блочные стрелки
Щелкните на треугольнике справа от значка Блочные стрелки , чтобы открыть одноименную палитру инструментов.
Панель инструментов Блочные стрелки
Блок-схемы
Щелкните на треугольнике справа от значка Блок-схемы , чтобы открыть одноименную палитру инструментов. Создание блок-схем, организационных диаграмм, и аналогичные инструменты планирования описаны в Руководстве по Draw. Глава 8. Соединения, блок-схемы и организационные диаграммы.
Панель инструментов Блок-схемы
Выноски
Щелкните на треугольнике справа от значка Выноски , чтобы открыть одноименную палитру инструментов.
Панель инструментов Выноски
Звезды и свитки
Щелкните на треугольнике справа от значка Звезды и свитки , чтобы открыть одноименную палитру инструментов.
Панель инструментов Звезды и свитки
Примечание
Добавлять текст можно ко всем этим геометрическим фигурам. Для более подробного описания обратитесь к Руководству по Draw. Глава 2. Рисование основных фигур и Глава 10. Дополнительные возможности Draw.
Выделение объектов
Прямое выделение
Самый простой способ выделить объект, это щелкнуть мышкой прямо на нём. Для выделения объектов без заливки цветом, щелкните по контуру такого объекта. Один щелчок служит для выделения, повторный – для отмены выделения. Чтобы выделить или снять выделение более, чем одного объекта, нажмите и удерживайте кнопку Shift при щелчке мышью.
Выделение рамкой
Можно выбрать сразу несколько объектов, передвигая курсор с зажатой левой клавишей мыши. Во время движения курсора будет отображаться рамка вокруг объектов. Выделены будут только объекты, полностью расположенные внутри рамки.
Для множественного выделения объектов значок Выделение на панели инструментов Рисование должен быть нажатым.
Выделение скрытых объектов
Даже если объекты расположены за другим объектом и не видны, они всё равно могут быть выделены. Удерживая нажатой клавишу Alt, щелкните мышкой по объекту на переднем плане, под которым находится скрытый объект, а затем щелкните снова, чтобы выбрать скрытый объект. Если есть несколько скрытых объектов друг под другом, то удерживайте нажатой клавишу Alt и щелкайте по ним, пока не дойдете до объекта, который вам нужен. Для перемещения по объектам в обратном порядке, удерживайте нажатыми клавиши Alt + Shift и щелкайте мышкой по объектам.
При щелчке на выбранном объекте его контур на короткое время проявится через объекты, его скрывающие.
Примечание
Использование клавиши Alt работает на компьютерах с ОС Windows или Mac. На компьютерах под управлением Linux нужно использовать метод с клавишей Tab, описанный ниже.
Чтобы выделить объект, который скрыт другим объектом, с помощью клавиатуры, используйте клавишу Tab для перемещения по объектам, остановившись на объекте, который вам необходим. Для перемещения по объектам в обратном порядке, нажимайте сочетание клавиш Shift + Tab. Это очень быстрый способ достичь поставленной цели, но он может быть не очень удобным, если на рисунке большое количество объектов.
Расположение объектов
В сложных рисунках несколько объектов могут быть наложены друг на друга. Чтобы изменить порядок размещения объектов (передний/задний план), выделите объект, выберите пункт главного меню и выберите вариант Переместить вперед или Переместить назад. Также можно щелкнуть правой кнопкой мыши на объекте и выбрать пункт Расположить из контекстного меню, а затем вариант Переместить вперед или Переместить назад.
Настройки расположения также доступны при щелчке на треугольнике справа от значка Расположить на панели инструментов Линия и заливка. Откроется панель инструментов Положение, предоставляющая доступ к различным варианам расположения объектов (рисунок ниже).
Панель инструментов Положение и доступные инструменты
Перемещение и изменение размера объекта
При перемещении объекта или изменении его размера посмотрите на левую часть строки состояния в нижней части окна Draw (рисунок ниже). Область слева в строке состояния показывает, слева направо: какой объект выбран, его положение на рисунке в виде координат Х и Y, и размеры объекта. Единицы измерения выбираются в меню .
Левый край строки состояния при перемещении или настройке размеров объекта
Для получения более подробной информации о перемещении и о изменении размеров объектов обратитесь к Руководству по Draw. Глава 3. Работа с объектами и точками объектов.
Перемещение объекта
Чтобы переместить объект (или группу объектов), выделите его, а затем зажмите левую кнопку мыши в границах объекта и перемещайте мышь. Во время движения появляется фантомное изображение объекта, чтобы помочь с репозиционированием (рисунок ниже). Поместив объект в нужное место на листе отпустите кнопку мыши.
Перемещение объекта
Изменение размера объекта
Чтобы изменить размер выделенного объекта (или группы объектов), переместите курсор к одному из маркеров выделения по краям объекта. Курсор мыши изменит свою форму, указывая направление движения для этого маркера. Нажмите левой кнопкой мыши на одном из маркеров и, не отпускаяя её, тащите курсор в указанном направлении. При изменении размера объекта появится прозрачный контур будущего объекта (рисунок ниже). После достижения желаемого размера объекта отпустите кнопку мыши.
Изменение размера объекта
Результаты зависят от выбора используемого маркера выделения. Чтобы изменять размер объекта вдоль одной оси, используйте маркер на одной из сторон. Чтобы изменять размер по обеим осям, используйте угловой маркер.
Примечание
Если при изменении размера объекта нажать клавишу Shift, то изменение размера будет осуществляться симметрично по двум осям, так что соотношение длин сторон объекта остается таким же. Это поведение клавиши Shift работает для всех точек.
Это поведение по умолчанию клавиши Shift. Однако, если опция При создании и перемещении объектов в меню активна, то нажатие на клавишу Shift будет иметь обратное действие: соотношение сторон будет сохранено, если не нажата клавиша Shift.
Вращение и наклон объекта
Для получения более подробной информации о вращении и наклоне объектов, обратитесь к Руководству по Draw. Глава 3. Работа с объектами и точками объектов.
Вращение объекта
Чтобы вращать объект (или группу объектов), выделите объект, затем перейдите в режим вращения одним из следующих способов:
- Нажмите на треугольник справа от значка Эффекты на панели инструментов Линия и заливка и в палитре инструментов нажмите на значок Повернуть .
- Выберите пункт меню и нажмите значок Повернуть .
Маркеры выделения изменят форму и цвет: станут круглыми и красными (рисунок ниже). Также в центре объекта появится отметка центра вращения. При помещении курсора мыши над маркерами курсор меняет форму. Угловые маркеры используются для вращения объекта, а верхний, нижний и боковые маркеры наклоняют объект.
Вращение объекта
Наведите курсор мыши на один из угловых маркеров, вид курсора изменится на дугу со стрелками на каждом конце. Нажмите и удерживайте кнопку мыши, а затем перемещайте курсор, чтобы повернуть объект. Появится фантомное изображение вращающегося объекта и в строке состояния отобразится текущий угол поворота.
Примечание
Для 3D объектов вращение работает по-другому, потому что оно происходит в нескольких осях, а не в одной. Смотрите Руководство по Draw. Глава 7. 3D объекты для получения дополнительной информации .
Точка вращения, как правило, расположена в центре объекта. Чтобы изменить положение точки вращения, зажмите на объекте левую клавишу мыши и перетаскивайте объект, пока точка вращения не будет находится в нужном положении. Точка вращения может быть даже за пределами объекта.
Примечание
Если нажать клавишу Shift при вращении объекта, вращение будет производится дискретно с шагом в 15°.
Это поведение по умолчанию клавиши Shift. Однако, если опция При создании и перемещении объектов в меню активна, то нажатие на клавишу Shift будет иметь обратное действие: вращение всегда будет происходить с градацией по 15°, пока клавиша Shift не нажата.
Наклон объекта
Чтобы наклонить объект, используйте красные круглые маркеры (см.выше раздел Вращение объекта), расположенные по середине верхней, нижней и боковых сторон выделенного объекта. При наведении на любой из таких маркеров курсор мыши изменит вид на на две параллельные разнонаправленные стрелки. Ось, используемая, как основание, для наклона объекта, расположена прямо напротив маркера посередине одной из сторон. Эта ось остается неподвижной, в то время как другие стороны объекта будут наклоняться по отношению к ней на столько, насколько будет перемещён курсор мыши.
Нажмите на красную точку по середине любой из сторон объекта и, удерживая левую кнопку мыши, перетяните курсор для наклона объекта. Появится фантомное изображение наклонённого объекта (рисунок ниже), а текущий угол наклона будет показан в строке состояния.
Наклон объекта
Примечание
Если нажать клавишу Shift во время наклона объекта, то наклон будет осуществляться дискретно на величину 15°. Это поведение клавиши Shift по умолчанию. Однако, если опция При создании и перемещении объектов в меню активна, то нажатие на клавишу Shift будет иметь обратное действие: наклон всегда будет происходить дискретно по 15°, пока клавиша Shift не нажата.
Изменение объекта
Чтобы изменить объект или изменить его атрибуты, такие как цвет или толщина линии обрамления, и так далее, могут быть использованы: инструменты панели Линия и заливка, панель Форматирование текста, раздел боковой панели Свойства, либо контекстное меню. Более подробная информация по изменению объектов и изменению атрибутов объекта изложена в Руководстве по Draw. Глава 4. Изменение атрибутов объекта.
Панель инструментов
Линия и заливкаПо умолчанию панель инструментов Линия и заливка расположена в верхней части окна Draw. Однако, если панель Линия и заливка не отображается, необходимо выбрать пункт меню , чтобы отобразить панель (рисунок ниже). Используя эту панель, можно редактировать наиболее распространённые атрибуты объекта.
Панель инструментов Линия и заливка
Панель инструментов Форматирование текста
Если в Draw выделить текст, то панель Линия и заливка автоматически заменится на панель Форматирование текста (рисунок ниже). Также можно в любой момент открыть эту панель, выбрав пункт меню . Инструменты на этой панели будут неактивными, пока не будет выделен текст.
Панель инструментов Форматирование текста
Боковая панель. Раздел Свойства
Когда выделен объект на листе, в боковой панели становятся доступны подразделы раздела Свойства. Они позволяют изменять свойства или параметры объекта без необходимости открывать диалоговые окна или использовать любые из доступных инструментов на различных панелях инструментов, доступных в Draw. Чтобы развернуть подраздел, нажмите плюс (+) рядом с подзаголовком раздела.
Боковая панель. Раздел Свойства
Контекстное меню
При щелчке правой кнопкой мыши по выделенному объекту, появляется контекстное меню. Это меню предоставляет доступ к различным настройкам и позволяет изменять атрибуты объекта без необходимости открывать диалоговые окна. Пункты меню с маленькой стрелкой с правой стороны содержат подменю.
Пример контекстного меню
Форматирование линий и обрамлений
В LibreOffice термин линия может обозначать, как собственно просто отдельную линию, так и внешний край графического объекта (обрамление), а также стрелку. В большинстве случаев свойства линии, которые можно изменить – это её стиль (сплошная, пунктирная, невидимая и так далее), её толщина и цвет.
Выделите линию, которую нужно отформатировать, а затем используйте элементы управления на панели Линия и заливка, чтобы изменить её параметры (выделены на рисунке ниже).
Общие свойства линий (стиль, цвет, толщина)
Если требуется тонкая настройка внешнего вида линии, выберите пункт меню или щелкните правой кнопкой мыши на линии и выберите пункт Линия из контекстного меню, или нажмите на значок Линия на панели Линия и заливка. Все эти действия открывают диалог Линия, в котором можно установить свойства линии. Это диалоговое окно состоит из трех вкладок: линии, стили линий и стили стрелок. Можно также использовать подраздел Линия в разделе боковой панели Свойства, чтобы изменить вид линии.
Стрелки, наконечники стрелок и концы линий
Стрелки, наконечники стрелок и другие концы линий, как правило, называют просто стрелками и, при редактировании и изменении атрибутов, их можно рассматривать так же, как линии. Выделите линию и нажмите на значок Стили стрелок на панели Линия и заливка, чтобы открыть одноимённое меню.
Меню Стили стрелок
Доступны несколько типов стрелок и окончаний для линий. Каждый конец линии может иметь различные стрелки или иной вид. Наконечники применяются только к простым линиям. Не будет никакого эффекта при их назначении на линии обрамления объекта.
Форматирование области заливки
Термин область заливки относится к внутренней части объекта, которая может быть однородного цвета, градиентом, заполнена текстурой или растровым изображением. Область заливки может быть частично или полностью прозрачной. В большинстве случаев можно выбрать один из стандартных параметров заполнения, которые имеются на панели Линия и заливка или в подразделе Область в разделе боковой панели Свойства. Можно также определить свои собственные области заливки. Для получения дополнительной информации о форматировании заливки обратитесь к Руководству по Draw. Глава 4. Изменение атрибутов объекта.
Различные типы заливки области
Использование стилей
Предположим, что нужно применить одну и ту же заливку, толщину линии и тип обрамления к нескольким объектам. Этот повторяющийся процесс может быть значительно упрощен за счет использования стилей. Стили позволяют задать шаблон форматирования (собственно стиль), а затем применить этот стиль к нескольким объектам. Для получения дополнительной информации о стилях, смотрите Главу 3. Использование стилей и шаблонов в данном руководстве, полное Руководство по Writer. Глава 6. Введение в стили и полное Руководство по Draw. Глава 4. Изменение атрибутов объектов.
Позиционирование объектов
Привязка
Объекты в Draw могут быть точно и последовательно расположены на листе с использованием функции привязки. Точки сетки, вспомогательные точки и линии, области объектов, отдельные точки на объектах или края страниц, всё это может использоваться в качестве привязки.
С функцией привязки проще работать при высоких значениях приближения. Две и более различных функции привязки можно использовать одновременно: например, привязку к направляющим линиям и к краям страницы. Рекомендуется, однако, активировать только те виды привязки, которые действительно нужны для работы в настоящее время.
Для получения более подробной информации по функции привязки, смотрите полное Руководство по Draw. Глава 3. Работа с объектами и точками объектов и Глава 10. Дополнительные возможности Draw.
Привязка к сетке
Привязка к сетке позволяет позиционировать объект относительно точек сетки. Выберите пункт меню или щелкните по значку Привязка к сетке на панели инструментов Параметры, чтобы включить или отключить функцию привязки к сетке. Если панель инструментов Параметры не отображается, выберите пункт меню .
Позиционирование с использованием привязки к сетке
Отображение сетки
Чтобы отображать (или отключить отображение) сетку на листе Draw, выберите пункт меню или нажмите на значок Показать сетку на панели инструментов Параметры.
Конфигурация сетки
Разрешение, привязка и положение точек сетки и другие параметры могут быть настроены в диалоговом окне, доступном из меню .
Конфигурация сетки
- Вертикальный и горизонтальный промежуток между точками в сетке. Также можно изменить используемые единицы измерения в общих параметрах Draw, перейдя в меню .
- Разрешение – это размер квадратов или прямоугольников в сетке. Если разрешение составляет 1 см по горизонтали и 2 см по вертикали, то сетка состоит из прямоугольников высотой 2 см и шириной 1 см .
- Дополнительные узлы – это дополнительные точки, которые появляются вдоль сторон каждого прямоугольника или квадрата сетки. Объекты можно привязать к дополнительным узлам, а также к углам сетки .
- Количество пикселей в поле Область привязки определяет, насколько близко вы должны приблизить объект к точке или линии привязки, прежде, чем он будет привязываться к ним.
Цвет сетки по умолчанию светло-серый. Чтобы изменить цвет сетки, откройте меню , в списке справа найдите пункт Сетка и задайте ему новый цвет.
Вспомогательные линии
В Draw есть вспомогательные линии, которые легко позволяют позиционировать объект с помощью линеек в верхней и левой части рабочей области. Для включения или выключения вспомогательных линий, откройте диалог из меню и выберите опцию Направляющие при перемещении.
Применение специальных эффектов
Используя Draw, можно применить множество специальных эффектов к объектам и группам объектов. Этот раздел – введение в некоторые из этих эффектов. Для получения более подробной информации о специальных эффектах обратитесь к полному Руководству по Draw. Глава 4. Изменение атрибутов объектов.
Для доступа к инструментам специальных эффектов выберите пункт меню . Команды Повернуть и Отразить можно также найти в меню Изменить или, после нажатия правой кнопкой мыши на объекте, в контекстном меню.
Панель Операции и доступные инструменты
Зеркальное отражение объектов
Самые простые и быстрые способы, чтобы перевернуть объект по горизонтали или по вертикали следующие:
- Щелкните по графическому объекту, появятся маркеры выделения.
- Щелкните по объекту правой кнопкой мыши и выберите в контекстном меню пункт (или По горизонтали), или выберите пункт меню (или По горизонтали)и выбранный объект будет отражен.
Тем не менее, инструмент Отразить на панели инструментов Операции может быть использован для большего контроля над процессом отражения. Использование инструмента Отразить позволит изменять положение и угол, под которым объект зеркально отразится. Как именно это делается, описано в полном Руководстве по Draw, в Главе 4. Изменение атрибутов объекта.
Зеркальная копия
В настоящий момент такой команды в Draw нет. Однако, зеркальное отображение объекта можно эмулировать с помощью инструмента Отразить так, как это описано в полном Руководстве по Draw. Глава 4. Изменение атрибутов объекта.
Искажение объекта
Три инструмента на панели инструментов Операции позволяют перетаскивать углы и края объекта, для искажения изображения.
- Искажение – искажает объект в перспективе.
- По кругу (под наклоном) — создает псевдо трехмерный эффект.
- По кругу (в перспективе) — создает псевдо трехмерный эффект.
Во всех трех случаях Draw вначале спросит о преобразовании объекта в кривую. Этот первый шаг необходим, поэтому нажмите Да. Затем нужно перемещать маркеры объекта для получения желаемого эффекта. Смотрите полное Руководство по Draw. Глава 4. Изменение атрибутов объекта для получения дополнительной информации о том, как искажать объект.
Динамическая прозрачность градиентов
Контролировать прозрачность градиента можно таким же образом, как цвет градиента. Оба типа градиента могут быть использованы вместе. В прозрачности градиента направление и степень цвета заливки объекта измененяется от непрозрачного к прозрачному. В обычном градиенте, заливка изменяется от одного цвета к другому, но степень прозрачности остается той же.
Инструменты Прозрачность и Градиент на панели инструментов Операции динамически управляют прозрачностью и цветом градиентов. Смотрите полное Руководство по Draw. Глава 4. Изменение атрибутов объекта для получения дополнительной информации о том, как создаватьть прозрачные и градиентные заливки в объекте.
Дублирование
Дублирование создает копии объекта с применением набора изменений, таких как цвет или вращение, к дубликатам, которые создаются.
Диалог Дублирование
- Выделите объект или группу объектов и выберите пункт меню или используйте сочетание клавиш
Shift+F3, чтобы открыть одноименный диалог. - Выберите необходимые параметры из доступных вариантов. Например, когда параметры в диалоговом окне на рисунке 44, применяются к прямоугольнику, они приводят к результату, показанному на рисунке 45.
Результат дублирования
Морфинг
Морфинг преобразует объект одной формы к объекту другой формы и работает только тогда, когда выбраны два объекта:
- Выделите два объекта разной формы.
- Выберите пункт меню .
- Задайте количество шагов, чтобы определить количество форм между двумя объектами.
- Выберите опцию Атрибуты морфинга, чтобы применить постепенное изменение свойств линий и заливок между двумя объектами (если таковые разные).
- Выберите опцию Такая же ориентация, чтобы плавно перейти между двумя объектами.
Диалог Морфинг
- Нажмите на кнопку OK и в результате будет создан новый объект, начиная с первого объекта, выбранного в качестве начального, и заканчивая вторым объектом, выбранным в качестве конечного. Например, когда параметры в диалоговом окне применяются к прямоугольнику и треугольнику с активной опцией Такая же ориентация, получается результат, показанный на рисунке ниже.
Результат морфинга
Объединение нескольких объектов
Используя Draw, можно группировать объекты вместе, что позволит рассматривать несколько объектов, как один, или объединять объекты, чтобы сформировать новую фигуру. Для получения дополнительной информации смотрите полное Руководство по Draw. Глава 5. Объединение нескольких объектов.
Группировка объектов аналогична вставке объектов в контейнер. Можно перемещать объекты, как единую группу, и применять глобальные изменения ко всем объектам внутри группы одновременно. Группировка всегда может быть отменена и объектами, которые составляют группу, после отмены можно будет манипулировать по отдельности. Также объекты внутри группы сохраняют свои индивидуальные свойства.
Объединение объектов – это слияние объектов, при котором создается новый объект. Оригинальные объекты больше не будут доступны в качестве отдельных элементов и не могут быть изменены, как отдельные объекты. Любое редактирование объединенного объекта влияет на все объекты, которые были использованы при объединении.
Группировка
Временная группировка
Временная группировка происходит, когда несколько объектов выбираются с помощью значка Выделить на панели инструментов Рисование или с помощью рамки выделения. Любые изменения к параметров объекта будут применяться ко всем объектам внутри временной группы. Например, можно повернуть временную группу объектов в полном составе.
Чтобы отменить временную группировку объектов просто нажмите за пределами маркеров выделения, отображаемых вокруг группы объектов.
Постоянная группировка
Постоянная группировка объектов создается после выбора всех необходимых объектов и выбора пункта меню , или после щелчка правой кнопкой мыши по выделенным объектам и выбора пункт Сгруппировать из контекстного меню, или после выделения объектов можно нажать комбинацию клавиш Ctrl + Shift + G. После снятия выделения с объектов, они всё равно останутся сгруппированными.
Когда объекты сгруппированы, любые операции редактирования, произведенные над этой группой, применятся ко всем членам группы. Если нажать на один объект из группы, то будет выбрана вся группа.
Можно редактировать отдельные объекты в группе без разгруппировки. Выберите группу и выберите пункт меню или щелкните правой кнопкой мыши и выберите пункт Зайти в группу из контекстного меню, или используйте клавишу F3, или дважды щелкните по группе.
После окончания изменения отдельного элемента группы выберите пункт меню , или щелкните правой кнопкой мыши и выберите пункт контекстного меню Выйти из группы, или используйте сочетание клавиш Shift+F3.
Разгруппировка
Чтобы разгруппировать группу объектов, выделите группу, затем выберите пункт меню или щелкните правой кнопкой мыши и выберите пункт Разгруппировать из контекстного меню, или используйте комбинацию клавиш Ctrl + Alt + Shift + G.
Объединение объектов
Объединение объектов – это слияние объектов, при котором создается новый объект. Оригинальные объекты больше не будут доступны в качестве отдельных элементов и не могут быть изменены, как отдельные объекты. Любое редактирование объединенного объекта влияет на все объекты, которые были использованы при объединении.
Выберите несколько объектов, а затем выберите пункт меню или щелкните правой кнопкой мыши на объекте и выберите пункт Объединить из контекстного меню, или используйте сочетание клавиш Ctrl + Shift + K.
После выбора объектов станут доступны функции Сложить, Вычесть и Пересечь, с помощью которых можно создать новый объект из выбранных объектов. Смотрите полное Руководство по Draw. Глава 5. Объединение нескольких объектов для получения более подробной информации об этих функциях.
Упорядочивание, выравнивание и распределение объектов
В Draw можно упорядочить, выравнять и распределить выбранные объекты по отношению друг к другу:
- Упорядочить положение объекта, перемещая его вперед или назад по отношению к объектам .
- Выравнить объекты по отношению к друг другу, используя варианты По левому краю, По центру или По правому краю для горизонтального выравнивания и По верхнему краю, По центру или По нижнему краю для вертикального выравнивания.
- Распределить объекты таким образом, чтобы свободное пространство между ними было одинаковым.
Смотрите полное Руководство по Draw. Глава 5. Объединение нескольких объектов для получения более подробной информации по упорядочиванию и выравниванию объектов по отношению друг к другу.
Вставка и редактирование изображений
Draw содержит ряд функций для редактирования изображений или растровой графики (текстуры), например, фотографий и отсканированных изображений. Они включают в себя импорт и экспорт изображений, и преобразование из одного графического формата в другой графический формат.
Draw включает в себя широкий спектр графических фильтров, так что он может читать и отображать несколько форматов графических файлов. Он также включает в себя несколько инструментов для работы с растровой графикой, но в нём отсутствует такая обширная функциональность, как в специализированных графических программах, таких, как Gimp или Adobe Photoshop. Смотрите полное Руководство по Draw. Глава 6. Редактирование изображений для получения дополнительной информации.
Добавлять изображения можно из нескольких источников:
- Напрямую со сканера (меню )
- Изображение, созданное в другой программе, включая фотографии с цифровой камеры (меню )
- Из галереи Draw. Смотрите Главу 11. Графика, Галерея и текстовые эффекты в этом руководстве для получения более подробной информации.
Работа с 3D объектами
Хотя Draw и не соответствует по функционалу ведущим программам редактирования графики или изображений, он способен создавать и редактировать неплохие 3D рисунки.
Draw предлагает два типа 3D-объектов: 3D-тела и 3D-фигуры. В зависимости от того, какой тип выбран, существуют различные методы редактирования 3D-объекта (вращение, освещение, перспектива и так далее). 3D-фигуры проще в настройке и редактировании, чем 3D-тела. Тем не менее, 3D-тела в настоящее время имеют больше настроек.
Смотрите полное Руководство по Draw. Глава 7. Работа с 3D объектами для получения дополнительной информации.
Экспорт рисунков Draw
Draw сохраняет рисунки и изображения в формате с открытым исходным кодом и расширением .odg. Для сохранения рисунков или всего файла в другом формате, используйте пункт меню и выберите нужный формат в списке. Графические форматы, в которые Draw может экспортировать и сохранять, перечислены в Приложении B к настоящему руководству.
Также можно экспортировать файлы Draw в форматы HTML, XHTML, PDF или Flash. Экспорт в PDF для всех компонентов LibreOffice описан в Главе 10. Печать, экспорт и почтовая рассылка в этом руководстве.
При экспорте в HTML используется мастер преобразования, который создает столько веб-страниц, сколько страниц в текущем документе Draw. При желании можно выбрать страницы для отображения в навигаторе и настроить страницу index.html. Для получения более подробной информации обратитесь к Главе 12. Создание веб-страниц в данном руководстве.
Вставка примечаний в документ Draw
Вставить примечания в рисунок можно аналогично тому, как это делается в Writer и Calc:
Вставка примечаний
- Выберите пункт меню . Небольшое поле, содержащее инициалы текущего пользователя, появится в верхнем левом углу рисунка с большим текстовым полем рядом с ним. Draw автоматически добавит имя пользователя и дату в нижней части текстового поля.
- Введите или вставьте примечания в текстовое поле. Можно применять базовое форматирование к частям текста, выделив его, нажав правую кнопку мыши и выбрав нужные пункты контекстного меню. Из этого меню также можно удалить текущее примечание, все примечания одного автора или все примечания в документе.
- Также можно перемещать небольшие маркеры примечаний в любое место на листе. Обычно их помещают на объекте или вблизи объекта, к которому относится примечание.
- Чтобы отобразить или скрыть примечания используйте пункт меню Вид > Примечания.
- Используйте меню , чтобы ввести имя, которое будет отображаться в примечании в поле «Автор».
- Если более, чем один человек редактирует документ, то каждый автор автоматически выделяется другим цветом фона примечаний.
Примечание
Смотрите также статьи:
полигонов
Многоугольник — это плоская фигура с прямыми сторонами.
Это полигон?
Многоугольники — это двумерные фигуры. Они состоят из прямых линий, а форма «замкнутая» (все линии соединяются вверх).
| Многоугольник (прямые стороны) | Не Полигон (имеет кривую) | Не a Полигон (открытый, не закрытый) |
Полигон происходит от греческого. Poly- означает «много», а -gon означает «угол».
Типы полигонов
Обычные или нестандартные
У правильного многоугольника все углы равны и все стороны равны, в противном случае он неправильный
| Обычный | Нестандартный |
Вогнутая или выпуклая
Выпуклый многоугольник не имеет углов, направленных внутрь.Точнее, внутренний угол не может быть больше 180°.
Если какой-либо внутренний угол больше 180°, то многоугольник является вогнутым . ( Подумайте: в вогнутой части есть «пещера» )
| Выпуклая | Вогнутая |
Простой или сложный
Простой многоугольник имеет только одну границу и не пересекает сам себя.Сложный полигон пересекает сам себя! Многие правила о многоугольниках не работают, когда они сложные.
| Простой многоугольник (это пятиугольник) | Комплексный полигон (он же Пентагон) |
Дополнительные примеры
| Неправильный шестигранник | Вогнутый восьмиугольник | Сложный многоугольник («Звездный многоугольник», в данном случае — пентаграмма) |
Играй с ними!
Попробуйте интерактивные полигоны… сделать их правильными, вогнутыми или сложными.
Имена полигонов
Вы можете делать имена, используя этот метод:
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример: 62-сторонний многоугольник представляет собой Hexacontadigon | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
НО, для многоугольников с 13 и более сторонами можно (и проще) писать « 13-угольник «, « 14-угольник » … « 100-угольник» и т. д.
Вспоминая
Четырехугольник (4 стороны)
A Quad Четырехколесный велосипед
Пентагон (5 сторон)
« Пентагон » в Вашингтоне имеет 5 сторон
Шестигранник (6 сторон)
H Oneycomb имеет H эксагоны
Септагон (7 сторон)
Думай Сентябрь агон это «Семь- агон»
Октагон (8 сторон)
У гноя Octo 8 щупалец
Нонагон (9 сторон)
Think Не агон — это «Девять- агон»
Десятиугольник (10 сторон)
Подумай Декабрь Агон имеет 10 сторон,
так же, как наша Декабрь Имал система имеет 10 цифр
полигонов: сколько сторон?
Геометрическая фигура с тремя или более сторонами называется многоугольником или многогранником . Вот названия некоторых полигонов.
| 3 | треугольник, Trigon |
| 4 | четырехугольник, четырехугольник |
| 5 | пятиугольник |
| 6 | шестигранной |
| 7 | угольник |
| 8 | восьмиугольника |
| 9 | девятиугольника, Эннеагон |
| 10 | десятиугольник |
| 11 | одиннадцатиугольник |
| 12 | двенадцатиугольник, duodecagon |
| 13 | triskaidecagon, tridecagon |
| 14 | tetrakaidecagon, tetradecagon |
| 15 | pentadecagon |
| 16 | hexadecagon |
| 17 | правильный семнадцатиугольник |
| 18 | octadecagon |
| 19 | enneadecagon | 20 | icosagon |
Сколько углов?
Многоугольник имеет в раз больше углов, чем сторон. Например, у треугольника 3 стороны и 3 угла. У пятиугольника 5 сторон и 5 углов. Восьмиугольник имеет 18 сторон и 18 углов!
Нахождение чисел и формул периметра и длины окружности Десятичные эквиваленты обыкновенных дробей7-сторонний многоугольник | Tutorpace
Геометрическая фигура, образованная 7 прямыми линиями, соединяющимися вместе, но линии не должны пересекаться друг с другом, каждая из двух линий пересекается в точке и образует вершину. Таким образом, 7-сторонний многоугольник имеет 7 сторон и 7 вершин. 7-сторонний многоугольник известен как семиугольник .
Типы многоугольников : —
· Равносторонний многоугольник – это геометрические фигуры, состоящие из всех одинаковых сторон. Например, ромб является равносторонним многоугольником, потому что все стороны ромба равны.
· Равноугольный многоугольник – это фигура, у которой все углы равны. Например, прямоугольник является равноугольным многоугольником, потому что все углы прямоугольника равны 90 градусам.
· Правильный многоугольник – фигуры, у которых все стороны и углы равны, как равносторонний треугольник, так и квадрат являются примерами правильного многоугольника.
Формула правильного многоугольника
· Сумма внутренних углов = 180 x (n – 2)
· Каждый внутренний угол = 180 x (n – 2) / n
8
· Каждый внешний угол =360 / n
· Число диагоналей = nx (n -3) / 2
· Количество треугольников = (n – 2)
.
Вопрос : — Найдите единственный внешний угол семиугольника.
Решение : —
каждый внешний ангел = 360 / N
= 360/7
= 51,43 градуса (примерно).
Вопрос 2 : — Найдите количество диагоналей семиугольника.
Решение : —
Количество диагонали = NX (N -3) / 2
= 7 x (7 — 3) / 2
= 7×4 / 2
= 7×2
= 14
14 диагоналей в 7-стороннем многоугольнике.
Рисование базовых фигур | Справка по SketchUp
Многие модели начинаются с базовых форм. В SketchUp инструменты формы помогают рисовать прямоугольники, круги и многоугольники. Эти инструменты находятся на панели инструментов «Приступая к работе», панели инструментов «Рисование» и на панели инструментов «Большой набор инструментов».
Рисование прямоугольника или квадрата
В SketchUp вы можете рисовать прямоугольники практически где угодно:
- На земле
- На вертикальной плоскости
- На существующих гранях
- Отдельно от существующей геометрии (выровнено по плоскости осей)
- Получено из существующей геометрии
Чтобы нарисовать прямоугольник с помощью инструмента «Прямоугольник», выполните следующие действия:
- Выберите инструмент Прямоугольник () на панели инструментов или нажмите клавишу R .Курсор изменится на карандаш с прямоугольником.
Совет: Чтобы начать заново в любой момент этих шагов, нажмите Esc .
- Нажмите, чтобы установить первую угловую точку прямоугольника. .
- Нажмите, чтобы установить первую угловую точку прямоугольника. Чтобы выровнять плоскость вашего прямоугольника по определенной оси чертежа или другой геометрии, нажмите клавишу со стрелкой, которая соответствует нужному выравниванию, как описано ниже в этом разделе.
- Нажмите, чтобы установить первую угловую точку прямоугольника.Чтобы выровнять плоскость вашего прямоугольника по определенной оси чертежа или другой геометрии, нажмите клавишу со стрелкой, которая соответствует нужному выравниванию, как описано ниже в этом разделе. Если вы предпочитаете рисовать прямоугольник из центра, нажмите клавишу Ctrl (Windows) или клавишу Option (macOS).
- Переместите курсор по диагонали, чтобы найти нужный размер и форму прямоугольника. Чтобы нарисовать прямоугольник с точными размерами, используйте поле «Измерения», которое в этот момент отображает размеры вашего прямоугольника при перемещении курсора.Чтобы помочь вам разместить прямоугольник относительно осей чертежа или другой геометрии, механизм логического вывода SketchUp отображает подсказки на экране. Когда появится нужный вам вывод, перейдите к шагу 4. Выводы поля «Измерения» и инструмента «Прямоугольник» объясняются чуть позже в этом разделе.
- Щелкните еще раз, чтобы установить вторую угловую точку прямоугольника. Ваша фигура появляется с лицом, как показано на следующем рисунке.
- Щелкните еще раз, чтобы установить вторую угловую точку прямоугольника.Или, если вы рисуете прямоугольник из центра, нажмите еще раз, чтобы установить любую угловую точку. Ваша фигура появляется с лицом, как показано на следующем рисунке.
Когда вы рисуете прямоугольник, поле «Измерения» помогает вам моделировать точно следующим образом:
- Установите длину и ширину. Введите значение длины, запятую, значение ширины и нажмите . Введите . Например, введите 8’,20’ и нажмите Введите . Если вы вводите только число или числа, SketchUp использует текущую настройку единиц измерения документа.Вы также можете переопределить настройку единиц измерения документа, указав имперские (например, 1’6″ ) или метрические (например, 3,652 м ) единицы измерения.
- Укажите только длину или ширину. Если ввести значение и запятую ( 3‘, ), новое значение будет применено к первому измерению, а второе измерение не изменится. Точно так же, если вы введете запятую, а затем значение (,3′ ), изменится только второе измерение.
- Измените положение прямоугольника с помощью отрицательных чисел. Если ввести отрицательное значение ( –24, –24 ), SketchUp применяет это значение в направлении, противоположном тому, которое вы указали при рисовании.
Совет: Перед вводом значения не нужно щелкать поле «Измерения». Пока вы рисуете, окно «Измерения» ждет, пока вы введете точные измерения, если вы решите это сделать. Кроме того, пока вы не выберете другой инструмент или не нарисуете другой прямоугольник, вы можете использовать поле «Измерения», чтобы изменить размеры прямоугольника столько раз, сколько захотите.
Примечание: Если вы используете неанглийскую клавиатуру, используйте запятую для обозначения десятичного разряда и точку с запятой для разделения размеров. Например, вы можете ввести две стороны прямоугольника как: 7,6м;4,3м
При перемещении курсора с выбранным инструментом «Прямоугольник» механизм вывода SketchUp отображает следующие подсказки:
Нужно выровнять плоскость прямоугольника по оси чертежа или другой геометрии? Клавиши со стрелками могут помочь, как показано в следующей таблице.
| Ключ-модификатор | Блокирует плоскость прямоугольника, чтобы он совпадал с … | Как это выглядит на экране |
|---|---|---|
| Стрелка влево | Зеленая ось | |
| Стрелка вверх | Синяя ось | |
| Стрелка вправо | Красная ось | |
| Стрелка вниз | Выведенная геометрия |
В видео вы можете увидеть эти функции инструмента «Прямоугольник» в действии.
Рисование повернутого прямоугольника
Инструмент «Повернутый прямоугольник» может пригодиться, когда вам нужно нарисовать прямоугольник, грань которого находится под углом к красной, зеленой или синей осям SketchUp по умолчанию или к другой геометрии.
Как и инструмент «Прямоугольник», инструмент «Повернутый прямоугольник» позволяет создавать точные прямоугольники и квадраты, а также отображает выводы, которые помогут вам при рисовании. Однако, когда вы создаете прямоугольник с помощью инструмента «Повернутый прямоугольник», вы также размещаете прямоугольник под углом.На следующем рисунке показан пример прямоугольника, созданного с помощью инструмента «Повернутый прямоугольник».
Чтобы создать повернутый прямоугольник, выполните следующие действия:
- На панели инструментов в меню «Инструменты для фигур» выберите инструмент «Повернутый прямоугольник» (). Или выберите Draw > Shapes > Rotated Rectangle в строке меню.
- (Необязательно) Нажмите клавишу со стрелкой, чтобы установить плоскость для повернутого прямоугольника в соответствии с таблицей, представленной ранее в этой статье. Например, нажмите клавишу со стрелкой влево, чтобы ограничить плоскость повернутого прямоугольника зеленой плоскостью.
- Щелкните один раз, чтобы задать первый угол прямоугольника.
- Создайте первое ребро повернутого прямоугольника. Вы можете сделать это двумя способами:
- Введите точное значение и нажмите Введите .
- Или переместите курсор туда, куда вы хотите поместить вторую конечную точку этого ребра, используя механизм логического вывода SketchUp, чтобы расположить конечную точку относительно осей или другой геометрии, как показано на следующем рисунке, а затем щелкните.
Совет: Вы можете использовать несколько клавиш-модификаторов при выполнении этого шага. Удерживайте нажатой клавишу Shift , чтобы ограничить первое ребро его текущим направлением. Клавиша Alt (Windows) или Command (macOS) блокирует плоскость транспортира. Или клавиши со стрелками снова могут помочь вам выровнять первое ребро по оси. Просто нажмите клавишу со стрелкой, соответствующую желаемому выравниванию, как описано ранее в этом разделе. Например, нажмите клавишу со стрелкой вправо, чтобы совместить первое ребро с красной осью.
- На этом этапе вы устанавливаете ширину и угол вашего прямоугольника. Вы можете установить эти значения несколькими способами:
- Введите угол и ширину в поле «Измерения», следуя подсказке.
- Введите ширину и угол в поле «Измерения», следуя подсказке.
- Перемещайте транспортир, чтобы задать угол, и отодвиньте курсор от центра транспортира, чтобы задать ширину, как показано на следующем рисунке.Чтобы ограничить угол, удерживайте нажатой клавишу Shift . Нажмите, чтобы завершить создание повернутого прямоугольника.
Совет: Нажмите клавишу Alt (Windows) или Command (macOS), чтобы установить базовую линию транспортира в текущем положении курсора, а затем переместите курсор, чтобы измерить угол от установленной базовой линии. Этот метод удобен, если вы хотите измерить угол от точки, отличной от базовой линии, установленной на шаге 3. Появится пунктирная линия, чтобы вы могли видеть новую базовую линию.
Примечание. Если вы используете клавиатуру, отличную от английской, вам потребуется использовать запятую для обозначения десятичного разряда и точку с запятой для разделения значений в поле «Измерения». Например, вы можете ввести угол и ширину второго ребра как 43,2;8,2 м , чтобы получить угол 43,2 градуса и длину 8,2 метра.
Примечание. Если вы используете клавиатуру, отличную от английской, вам потребуется использовать запятую для обозначения десятичного разряда и точку с запятой для разделения значений в поле «Измерения».Например, вы можете ввести ширину и угол второго ребра как 8,2 м; 43,2 , чтобы получить ширину 8,2 метра в длину и угол 43,2 градуса.
Рисование круга или эллипса
Прежде чем рисовать круг, полезно понять, как SketchUp создает объекты круга:
- Окружности имеют радиус и соединяют несколько сегментов линий.
- Эти сегменты действуют как единая линия, поскольку они могут определять край грани и разделять грань.Кроме того, при выборе одного сегмента выделяется весь круг.
- Механизм логического вывода SketchUp по-прежнему видит сегменты в круге. Таким образом, если вы наведете указатель мыши на окружность объекта круга, вы увидите выводы конечной и средней точек.
Чтобы нарисовать круг, выполните следующие действия:
- На панели инструментов выберите инструмент Окружность () в раскрывающемся меню рядом с инструментом Прямоугольник. Или нажмите клавишу C . Курсор изменится на карандаш с кружком, а в поле «Измерения» будет указано количество сторон по умолчанию: 24, как показано на рисунке.Чтобы изменить количество сторон, вы можете ввести значение сейчас или подождать, пока вы не закончите рисовать круг.
- Щелкните, чтобы разместить центральную точку круга. В поле «Измерения» отображается радиус круга. Вы можете ввести значение радиуса сейчас или сразу после того, как нарисуете круг.
- Щелкните, чтобы разместить центральную точку круга. Чтобы выровнять плоскость вашего круга по определенной оси чертежа или другой геометрии, нажмите клавишу со стрелкой, соответствующую желаемому выравниванию.Например, стрелка вверх выравнивает плоскость круга по синей оси. Подробности см. в таблице в разделе Рисование прямоугольника или квадрата. В поле «Измерения» отображается радиус круга. Вы можете ввести значение радиуса сейчас или сразу после того, как нарисуете круг.
- Переместите курсор из центральной точки, чтобы определить радиус окружности. При перемещении курсора значение радиуса динамически отображается в поле «Измерения». Нажмите Esc в любой момент, чтобы начать заново.
- Нажмите, чтобы закончить круг. SketchUp создает круглую грань, как показано на рисунке.
- (Необязательно) Пока вы не выберете новый инструмент или не нарисуете новый круг, вы можете использовать поле «Измерения», чтобы изменить радиус круга или количество сторон следующим образом:
- Чтобы изменить количество сторон: Введите число и букву S (например, введите 5s для 5 сторон или 42s для 42 сторон).Затем нажмите Введите .
- Чтобы изменить количество сторон: Введите число и букву S (например, введите 5s для 5 сторон или 42s для 42 сторон). Затем нажмите Введите . В качестве альтернативы, вы можете удерживать нажатой клавишу Ctrl (Microsoft Windows) или клавишу Option (macOS), одновременно нажимая + или — , чтобы увеличить или уменьшить количество сторон соответственно. Если вы используете франко-канадскую клавиатуру, удерживайте нажатой клавишу Ctrl (Microsoft Windows) и клавишу +/= , чтобы увеличить сегменты.Для macOS нажмите Command и = , чтобы увеличить сегменты, или — , чтобы уменьшить сегменты.
- Чтобы изменить радиус: Введите число и единицу измерения (при желании), например, 6 дюймов , 8 футов , 34 см или 7 м . Затем нажмите Введите или Верните . Совет: Диалоговое окно «Информация об объекте» предлагает удобный способ редактирования значений сторон и радиуса в любое время. Дополнительные сведения см. в разделе Редактирование фигур далее в этой статье.
Чтобы нарисовать эллипс или овал, выполните следующие действия:
- Нарисуйте круг с помощью инструмента Circle .
- Выберите инструмент Масштаб ().
- Нажмите на кружок. Вокруг круга отображается ограничивающая рамка с восемью зелеными ручками.
- Щелкните одну из средних ручек (не угловую) и переместите мышь, чтобы превратить круг в эллипс, как показано здесь.
- Нажмите еще раз, когда закончите масштабирование круга.
Рисование многоугольника
Вы можете создавать полигональные объекты с помощью инструмента «Многоугольник». (В этом нет ничего удивительного.) Однако вот несколько фактов, которые вы можете не знать о многоугольниках, но которые полезно знать, когда вы их рисуете:
- В SketchUp многоугольник имеет радиус и 3 или более сторон. Таким образом, размер вашего многоугольника измеряется от центральной точки, а количество сторон определяет тип рисуемого вами многоугольника. Пятиугольник как 5 сторон; восьмиугольник имеет 8 сторон.
- Полигональные объекты действуют как одна линия, поскольку они могут определять край грани, а также разделять грань. При выборе одной стороны многоугольника выделяется весь многоугольник.
- Механизм вывода SketchUp интерпретирует каждую сторону многоугольника как сегмент. Когда вы наводите курсор на многоугольник, вы видите конечную точку, среднюю точку и исходную точку.
- Вы можете рисовать многоугольники на гранях или отдельно от существующей геометрии.
Чтобы нарисовать многоугольник, выполните следующие действия:
- Выберите инструмент Многоугольник () на панели инструментов.Курсор изменится на карандаш с многоугольником. В поле «Измерения» указано текущее количество сторон. Чтобы изменить количество сторон в вашем многоугольнике, вы можете ввести числовое значение сейчас или подождать, пока вы не закончите рисовать.
- Щелкните, чтобы разместить центральную точку многоугольника. Поле «Измерения» изменится, чтобы отобразить радиус. Вы можете ввести значение радиуса сейчас или сразу после того, как начертите многоугольник.
- Щелкните, чтобы разместить центральную точку многоугольника. Чтобы выровнять плоскость вашего многоугольника с определенной осью чертежа или другой геометрией, нажмите клавишу со стрелкой, соответствующую желаемому выравниванию.Например, стрелка вверх совмещает плоскость многоугольника с синей осью. Подробнее см. предыдущую таблицу в разделе Рисование прямоугольника или квадрата. В поле «Измерения» отображается радиус. Вы можете ввести значение радиуса сейчас или сразу после того, как начертите многоугольник.
- Переместите курсор из центральной точки, чтобы определить радиус многоугольника. При перемещении курсора значение радиуса динамически отображается в поле «Измерения». Чтобы задать радиус, введите значение и нажмите . Введите .Вы также можете нажать Esc , чтобы начать заново.
- Щелкните второй раз, чтобы закончить многоугольник. Здесь вы видите 5-сторонний многоугольник.
- (Необязательно) Пока вы не выберете новый инструмент или не нарисуете новый многоугольник, вы можете использовать поле «Измерения», чтобы изменить радиус или количество сторон следующим образом:
- Чтобы изменить количество сторон: Введите число и букву S (например, введите 5s для 5 сторон или 42s для 42 сторон).Затем нажмите Введите .
- Чтобы изменить количество сторон: Введите число и букву S (например, введите 5s для 5 сторон или 42s для 42 сторон). Затем нажмите Введите . В качестве альтернативы, вы можете удерживать нажатой клавишу Ctrl (Microsoft Windows) или клавишу Option (macOS), одновременно нажимая + или — , чтобы увеличить или уменьшить количество сторон соответственно. Если вы используете франко-канадскую клавиатуру, удерживайте нажатой клавишу Ctrl (Microsoft Windows) и клавишу +/= , чтобы увеличить сегменты.Для macOS нажмите Command и = , чтобы увеличить сегменты, или — , чтобы уменьшить сегменты.
- Чтобы изменить радиус: Введите число и единицу измерения (при желании), например, 6 дюймов , 8 футов , 34 см или 7 м . Затем нажмите Введите или Верните .
Совет: Хотя инструмент «Многоугольник» работает так же, как инструмент «Окружность», разница между инструментами становится очевидной, когда вы вытягиваете/вытягиваете круг или многоугольник в трехмерную фигуру.Края круга выглядят гладкими, но края многоугольника имеют четкие стороны, как показано здесь.
В этом живом видео вы можете увидеть, как инструменты «Круг» и «Многоугольник» демонстрируют все свои трюки.
Редактирование фигур
Диалоговое окно «Информация об объекте» позволяет изменить радиус или стороны круга или многоугольника в любое время после создания фигуры. Вот как:
- Щелкните в контексте ребро (не грань) круга или многоугольника, который вы хотите изменить.
- Выберите Entity Info из появившегося контекстного меню, как показано здесь.
- На панели Entity Info щелкните поле Radius или Segments , измените значение и нажмите Enter (Microsoft Windows) или Return (Mac). После того, как вы нажмете Enter или Return, ваша фигура сразу же отобразит ваши изменения.
SketchUp не позволяет изменять ширину или длину прямоугольника в любое время.Если вы уже выбрали другой инструмент или нарисовали дополнительные прямоугольники, вам нужно стереть прямоугольник, который вы хотите изменить, и перерисовать его. Дополнительные сведения см. в разделе Рисование прямоугольника. Или измените размер прямоугольника с помощью инструмента «Масштаб», если вам не нужно вводить точные размеры.
Конечно, вы можете сделать гораздо больше, чем просто изменить размер фигуры. Вы можете превратить 2D-форму в 3D-форму с помощью инструмента «Тяни/толкай». Вы можете искажать формы с помощью инструмента «Перемещение» или масштабировать всю модель или ее часть.
звезд и многоугольников — Руководство для начинающих в Inkscape 1.0 документация
Смена + F9 или *
Инструмент «Звезда/многоугольник», пожалуй, самый интересный инструмент для начинающих, и отличает Inkscape от других программ для редактирования векторов! Это предлагает многочисленные творческие варианты, которые можно легко редактировать на холсте.
Как и в случае с другими инструментами геометрической формы, перетащите мышь на холст с помощью аналогичен процессу перетаскивания рамки выбора. Звезда по умолчанию, которая имеет 5 баллов, будет отображаться с двумя ромбовидными ручками, как только как только кнопка мыши будет отпущена.
Если вам нужно повернуть звезду под определенным углом, вы можете удерживать Ctrl во время рисования. Это сделает его «щелкающим» с шагом 15°. если ты перетащите мышь вниз, кончик, на котором находится курсор мыши, будет расположен точно в 6 часов (или на юг).
Ручка, расположенная в складке между двумя концами звезды. меняется внутренний диаметр. Другая ручка изменяет длину звезды. подсказки.
Когда вы нажимаете Ctrl при перетаскивании маркеров звезды, вы можете изменить длина наконечников и внутренний радиус без вращения или скручивания звезда.
Поле с надписью «Коэффициент спиц» на панели управления инструментом также будет работать без поворота или скручивания звезды. Вы можете использовать стрелки вверх и вниз рядом с полем для изменения числа там тоже. Даже удерживая курсор мыши над полем и с помощью колеса прокрутки.
Ручка в складке между двумя наконечниками позволяет вносить изменения в внутренний диаметр звезды. Не удерживая Ctrl, можно трудно избежать скручивания звезды.Другая ручка используется для изменения длина кончиков.
Если вы предпочитаете рисовать многоугольник, щелкните значок на панели управления, который показан ниже.
В режиме «Многоугольник» фигура имеет только одну ручку: эта ручка увеличивает или уменьшает форму. Звезду можно скрутить, если не делать удерживайте клавишу Ctrl.
С помощью этих нескольких опций уже можно создавать множество различных формы, начиная с одной звезды.Но есть еще больше вариантов! К добавить больше вершин к звезде или больше сторон к многоугольнику, либо введите количество подсказок, которые вы хотите, в поле Углы в элементах управления инструментом или нажмите на стрелки вверх/вниз рядом с ним.
Чтобы скруглить вершины звезды или углы многоугольника, вы можете удерживать вниз Shift при перетаскивании любого из маркеров. Чем дальше вы перетащите их, тем больше округление вы получите (перетащите мышь горизонтально для лучших результатов). Или, как и раньше, либо используйте стрелки рядом с полем Округление на панели управления инструментом или измените его значение, введя новый.
Когда вы нажимаете Alt при перетаскивании маркера, это добавит немного случайность к звезде или многоугольнику. Или, как и раньше, используйте числовое поле с стрелки, чтобы изменить значение параметра «Случайно». Советы звезды тогда все будут разной длины, и полигон будет выглядеть искаженным.
Добавление небольшого округления. Добавим немного случайности.
Панель управления инструментом «Звезда». Крайний правый значок сбрасывается на значения по умолчанию.Очень полезно, когда не знаешь, как вернуться!
Можешь нарисовать эти звезды?
полигонов | Rhino 3-D моделирование
Полигон | Трехмерное моделирование носорога Команда «Многоугольник» рисует замкнутую полилинию с заданным количеством сторон.
шагов
- Следуйте инструкциям для выбранного параметра. Если параметр не указан, используется параметр по умолчанию.
| Параметры командной строки | |
|---|---|
Число Сторон | Указывает количество сторон многоугольника. |
Вертикальный | Рисует многоугольник перпендикулярно конструкционной плоскости. |
вокруг кривой | Рисует многоугольник перпендикулярно кривой. Для создания многоугольника вокруг кривой
|
Зарегистрировано | Рисует многоугольник, в котором углы сторон касаются воображаемой окружности заданного радиуса. Вписанные ступени
|
Описанный | Рисует многоугольник, где середины сторон касаются воображаемой окружности заданного радиуса. Описанные ступени
|
Край | Рисует многоугольник, определяя одно ребро. Краевые ступени
Флип Переворачивает многоугольник вокруг края, который вы рисуете. |
Звезда | Рисует многоугольник в форме звезды. Звездообразные ступени
АвтоматическиЕсли у многоугольника 5 или более сторон, параметр Автоматически создает звезду, у которой размеры внешней и внутренней точек равны. См.: Википедия: Правильные звездчатые многоугольники. Расстояния 1 и 2 равны. |
См. также
Рисование линий и кривых
Википедия: правильный многоугольник
Rhino 7 для Mac © 2010-2022 Robert McNeel & Associates.12 января 2022 г.
Команда AutoCAD Polygon — Javatpoint
Многоугольник — это фигура, образованная конечным числом отрезков, соединенных в замкнутую цепь.
Категории многоугольника: треугольник, четырехугольник, пятиугольники, шестиугольник, семиугольник (или септагон), восьмиугольник, и т. д. Треугольник — это фигура с тремя сторонами, а восьмиугольник — фигура с восемью сторонами.
Команда многоугольника используется для создания многоугольников в AutoCAD.Нам нужно указать количество сторон для создания многоугольника.
Максимальное количество линий, доступных для создания многоугольника, составляет 1024
Быстрая команда для создания полигона: ‘pol’ .
Типы (методы использования многоугольника)
Существует два типа многоугольника, которые приведены ниже:
1. Вписать в круг
Сформированный многоугольник будет нарисован внутри круга. Команду лучше всего использовать, когда мы хотим создать любой многоугольник, вершины или углы которого касаются окружности.
Команда быстрого доступа для записи: I .
2. Описать вокруг круга
Сформированный многоугольник будет нарисован за пределами круга. Команда быстрого доступа для описания — C .
Примечание. Многоугольник можно также нарисовать вписанным или описанным без окружности.
Давайте разберемся с вписыванием и ограничением на двух примерах.
Пример 1: Мы будем рассматривать пятиугольник как многоугольник для этого примера.
Изображение для такого примера показано ниже:
Пример 2: Мы будем рассматривать шестиугольник как многоугольник для этого примера.
Изображение для такого примера показано ниже:
Примеры создания многоугольника
Пример 1:
Шаги для создания пятиугольника (многоугольника с пятью сторонами) перечислены ниже:
1. Выберите Polygon из раскрывающегося списка Rectangle , представленного на панели ленты, как показано на рисунке ниже:
или
Введите POL в командной строке и нажмите Введите .
2. Укажите количество сторон многоугольника. Здесь мы создаем пятиугольник, поэтому введем 5 .
3. Нажмите Введите .
4. Укажите центр многоугольника на видовом экране или рабочей области.
5. Введите I или C для Inscribe или Circumscribe.
6. Нажмите Введите .
7. Укажите радиус многоугольника. Например, 4 .
8. Нажмите Введите .Многоугольник будет нарисован, как показано на изображении ниже:
Пример 2:
Шаги для создания семиугольника (многоугольника с семью сторонами) приведены ниже:
1. Выберите Polygon из раскрывающегося списка Rectangle , представленного на панели ленты, как показано на рисунке ниже:
или
Введите POL в командной строке и нажмите Enter.
2. Укажите количество сторон многоугольника. Здесь мы создаем семиугольник (также называемый Септагон ), поэтому мы введем 7 .
3. Нажмите Введите .
4. Укажите центр многоугольника на видовом экране или рабочей области.
5. Введите I или C для Inscribe или Circumscribe.
6. Нажмите Введите .
7. Укажите радиус многоугольника. Например, 5 .
8. Нажмите Введите . Многоугольник будет нарисован, как показано на изображении ниже:
Комбинированные полигоны
Мы также можем объединить два или более полигонов, указав ребро соответствующего полигона.
Давайте разберемся на примере.
Пример состоит из трех пятиугольников , соединенных вместе.
Шаги для такого примера перечислены ниже:
1. Введите POL в командной строке и нажмите Введите .
2. Укажите количество сторон. Для пятиугольника укажем 5 .
3. Нажмите Введите .
4. Укажите центр многоугольника на видовом экране или рабочей области.
5. Введите I или C для Inscribe and Circumscribe.
6. Нажмите Введите .
7. Укажите радиус многоугольника. Например, 4 .
8. Нажмите Введите . Многоугольник будет нарисован, как показано на изображении ниже:
Теперь шаги по созданию второго пятиугольника в сочетании с первым.
9. Введите POL в командной строке и нажмите Введите .
10.Укажите количество сторон, 5 .
11. Нажмите Введите .
12. Введите E (край) и нажмите Введите .
13. Укажите первую и вторую конечные точки ребра первого многоугольника через курсор, как показано на рисунке ниже:
Теперь шаги по созданию третьего пятиугольника в сочетании с первым и вторым многоугольниками.
14. Введите POL в командной строке и нажмите Введите .
15.Укажите количество сторон, 5 .
16. Нажмите Введите .
17. Введите E (Край) и нажмите Введите .
18. Укажите первую и вторую конечные точки ребра первого многоугольника через курсор, как показано на рисунке ниже:
Мы можем указать любые две конечные точки в соответствии с требованиями.
Примечание. Если мы хотим указать значимое значение для создания многоугольника, мы можем определить для него пределы.
.

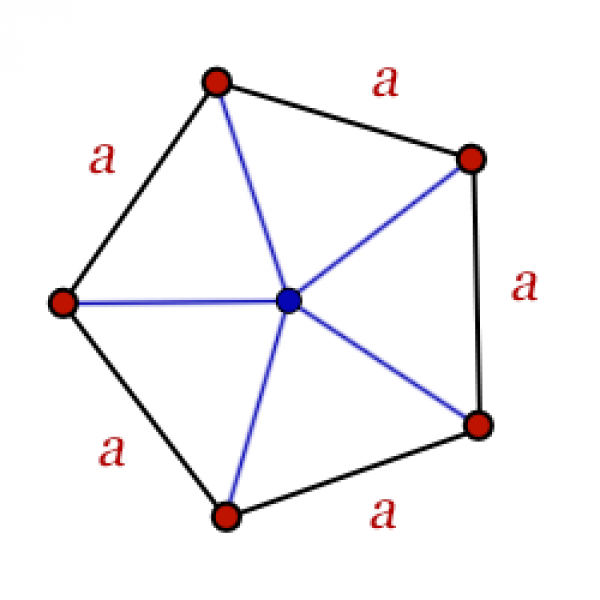 ..
..

