определение угла, измерение углов, обозначения и примеры
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Определение 1Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
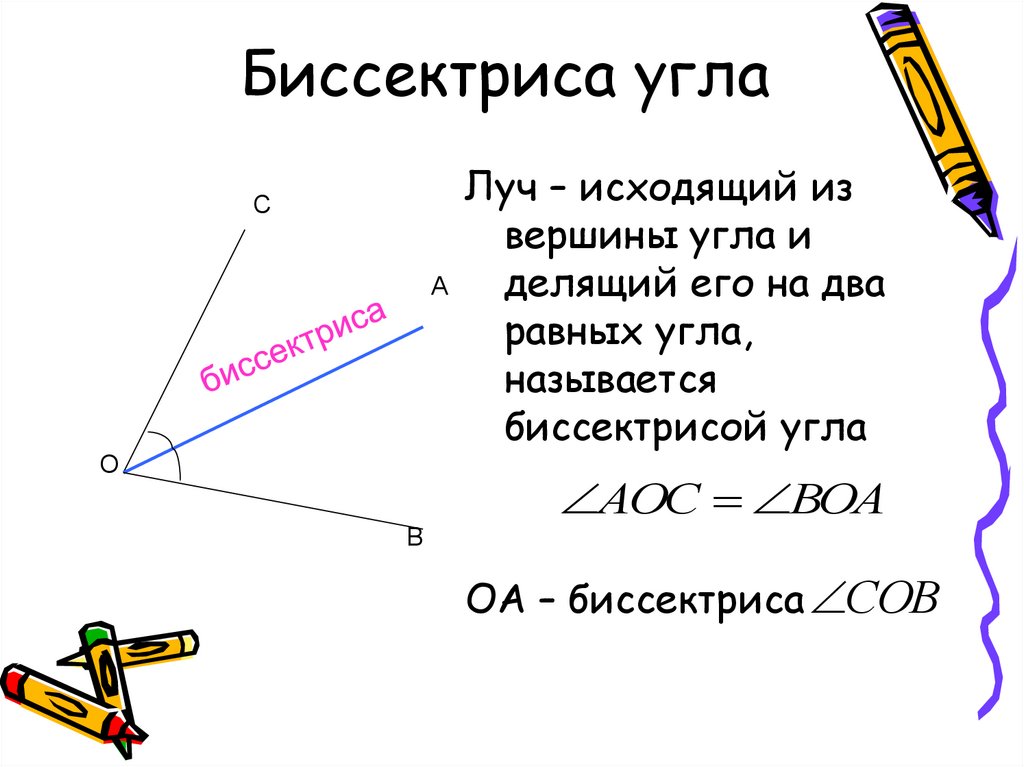
Определение 3Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.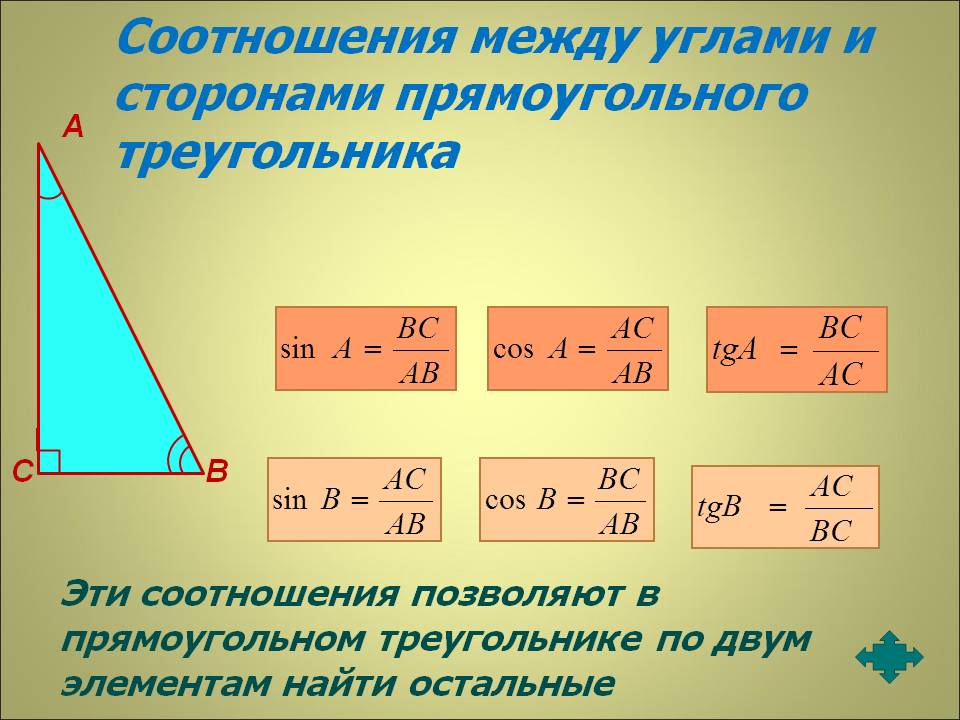
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.
Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Определение 6Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол.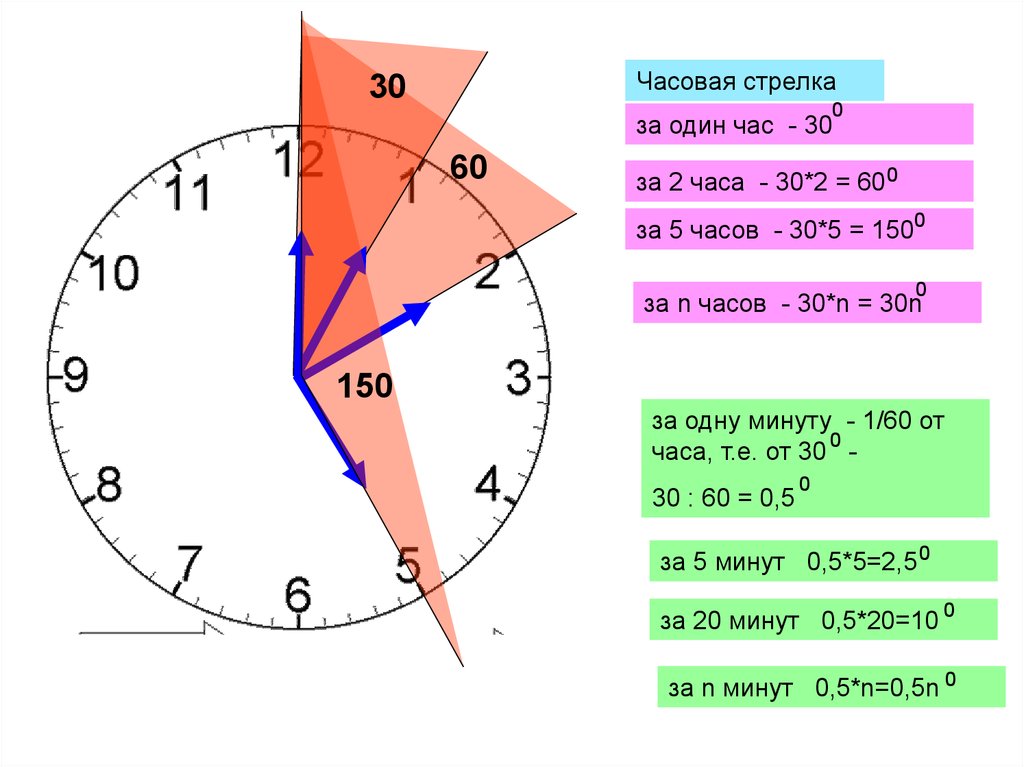 Ниже изображены неравные углы, не совмещенные при наложении.
Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Определение 9Минутой называют одну шестидесятую часть градуса.
Определение 10Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «»». Имеет место обозначение:
1°=60’=3600», 1’=(160)°, 1’=60», 1»=(160)’=(13600)° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59» .
Определение 11Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.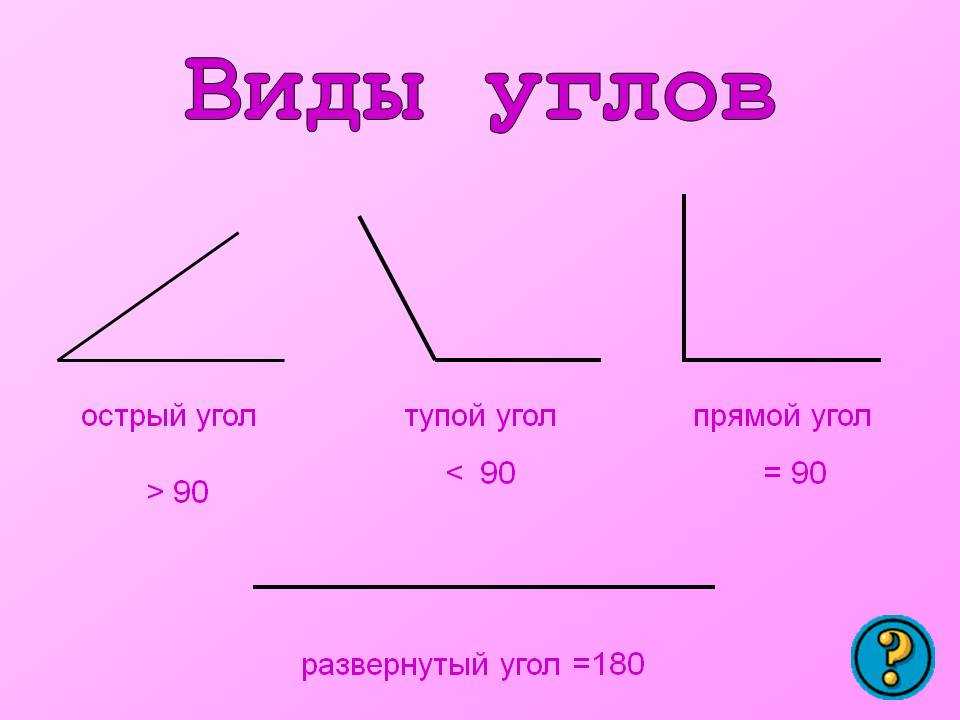
Приведем пример обозначения градусной меры угла равного 17°3’59» . Запись имеет еще один вид 17+360+593600=172393600.
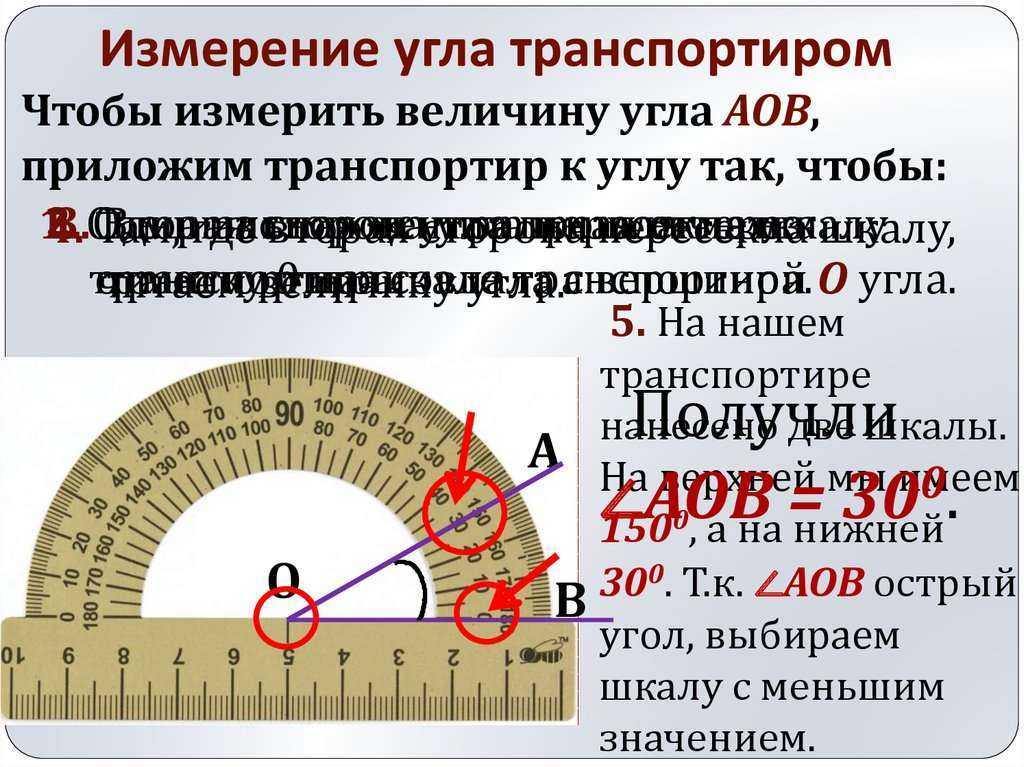
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».
В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов.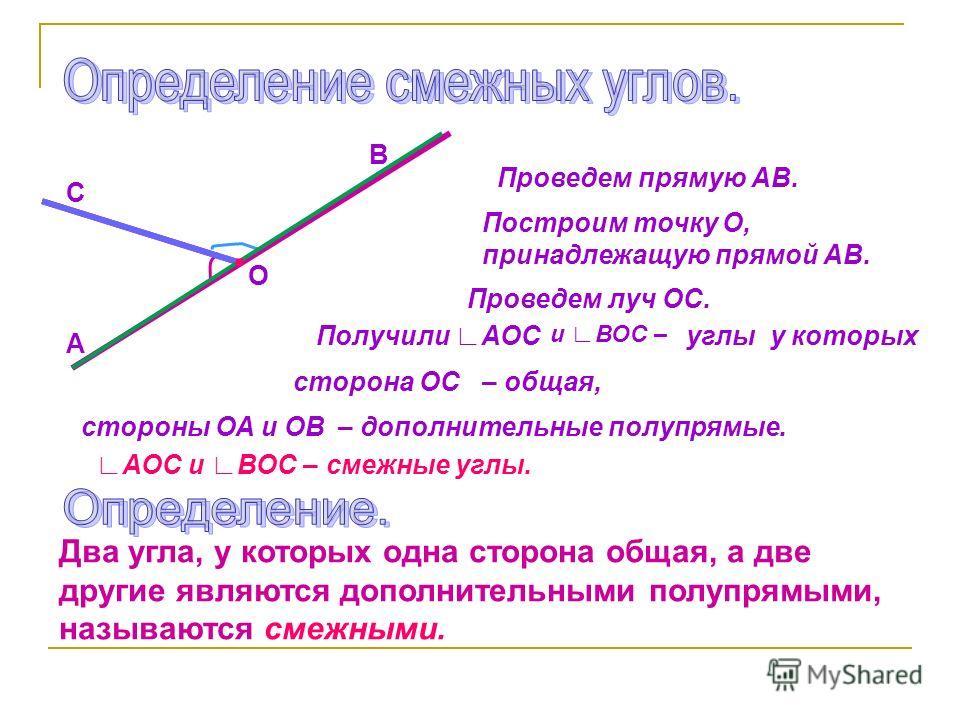 Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Исходя из этого, можно сделать вывод, что сумма
всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.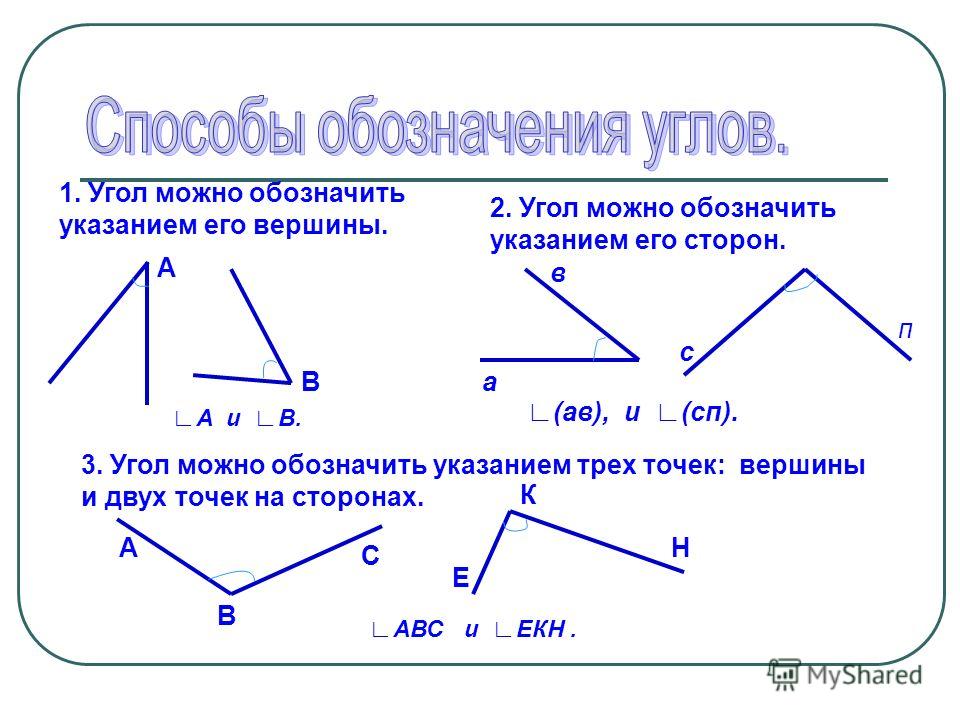
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
определение угла, измерение углов, обозначения и примеры
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы.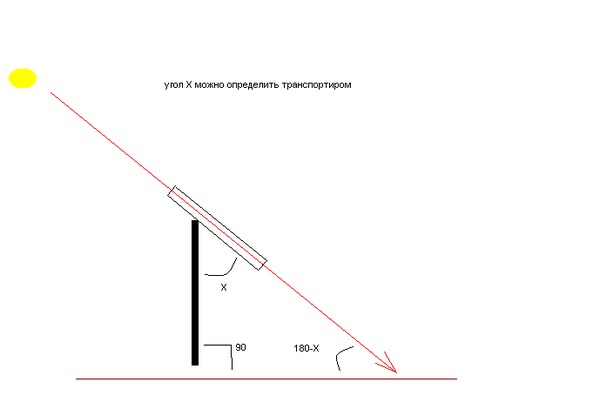 Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Определение 1Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.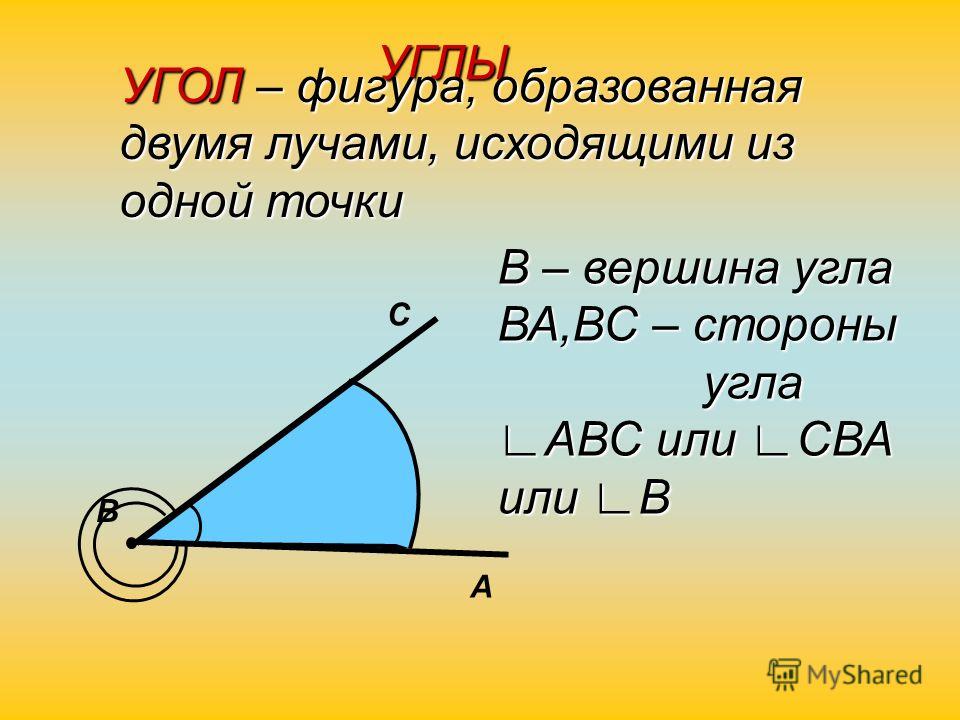
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.
Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам.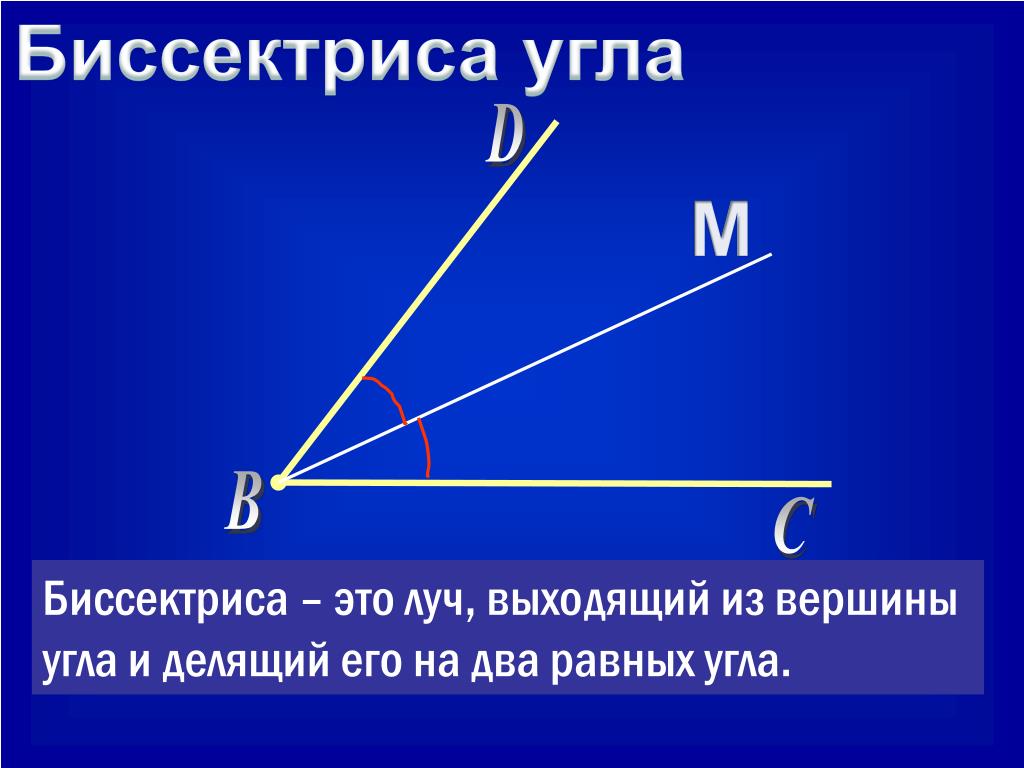 Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Определение 6Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов.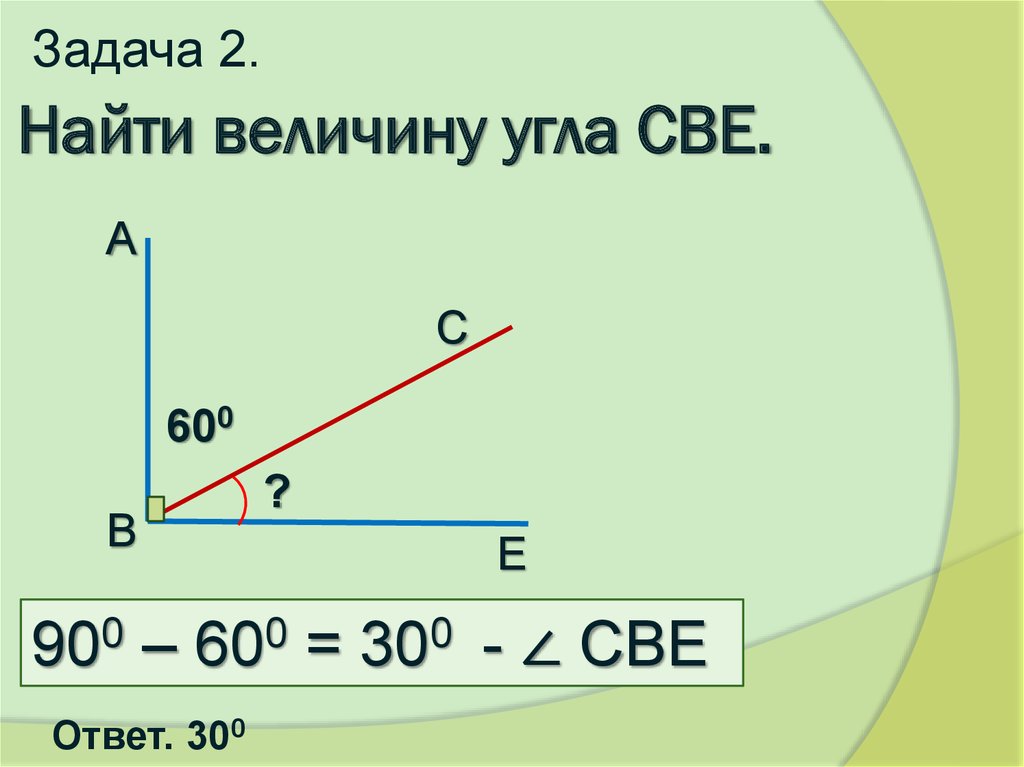 Ниже показано на рисунке.
Ниже показано на рисунке.
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Определение 8Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Определение 9Минутой называют одну шестидесятую часть градуса.
Определение 10Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «»». Имеет место обозначение:
1°=60’=3600», 1’=(160)°, 1’=60», 1»=(160)’=(13600)° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59» .
Определение 11Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Приведем пример обозначения градусной меры угла равного 17°3’59» . Запись имеет еще один вид 17+360+593600=172393600.
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».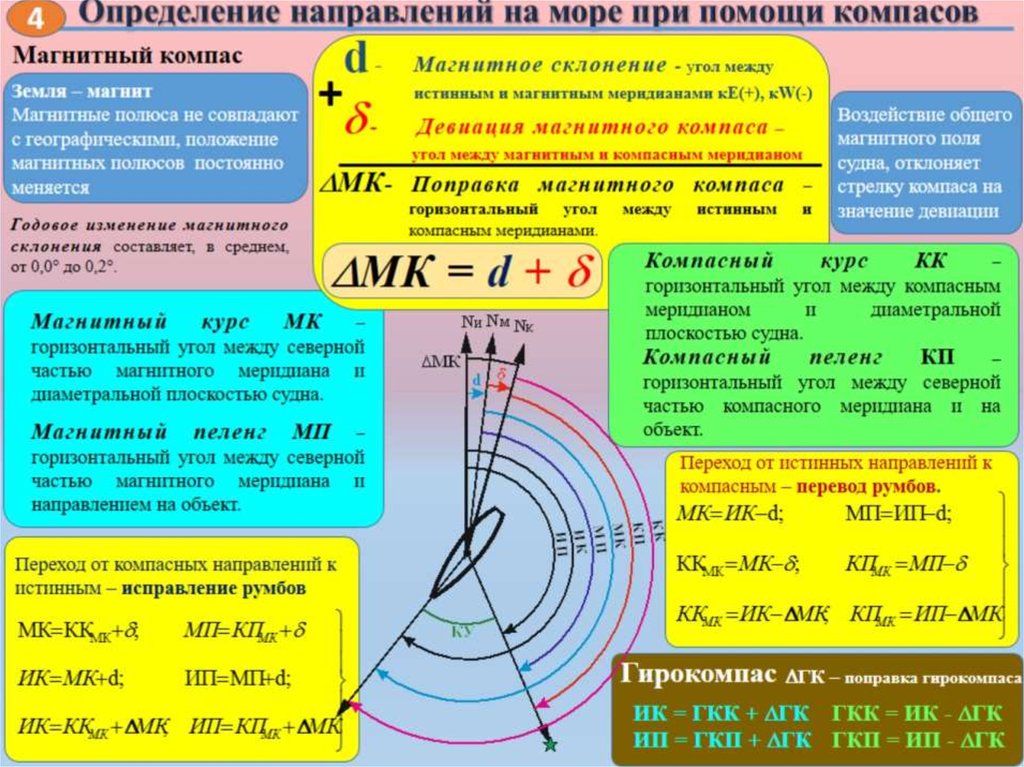
В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
определение угла, измерение углов, обозначения и примеры
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Определение 1Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.
Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений.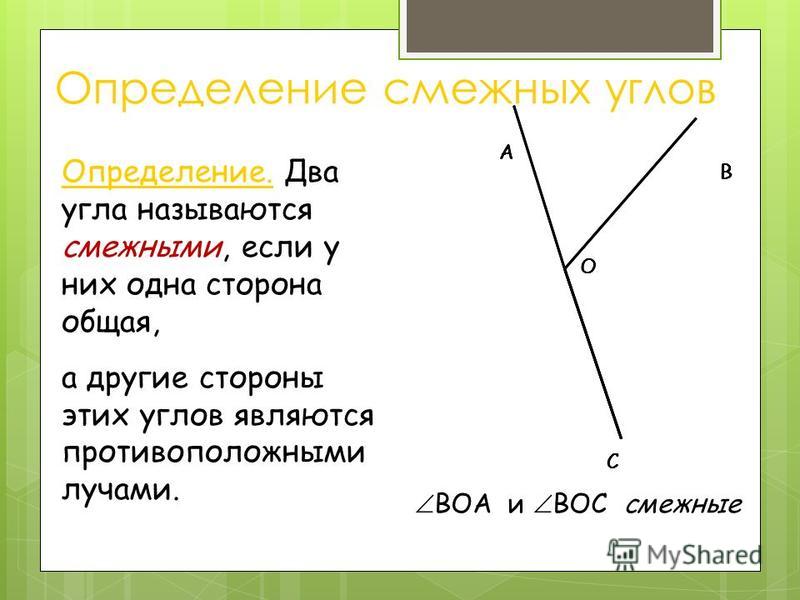 Ниже приведен рисунок, где разными способами обозначаются углы.
Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Определение 6Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Определение 8Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Определение 9Минутой называют одну шестидесятую часть градуса.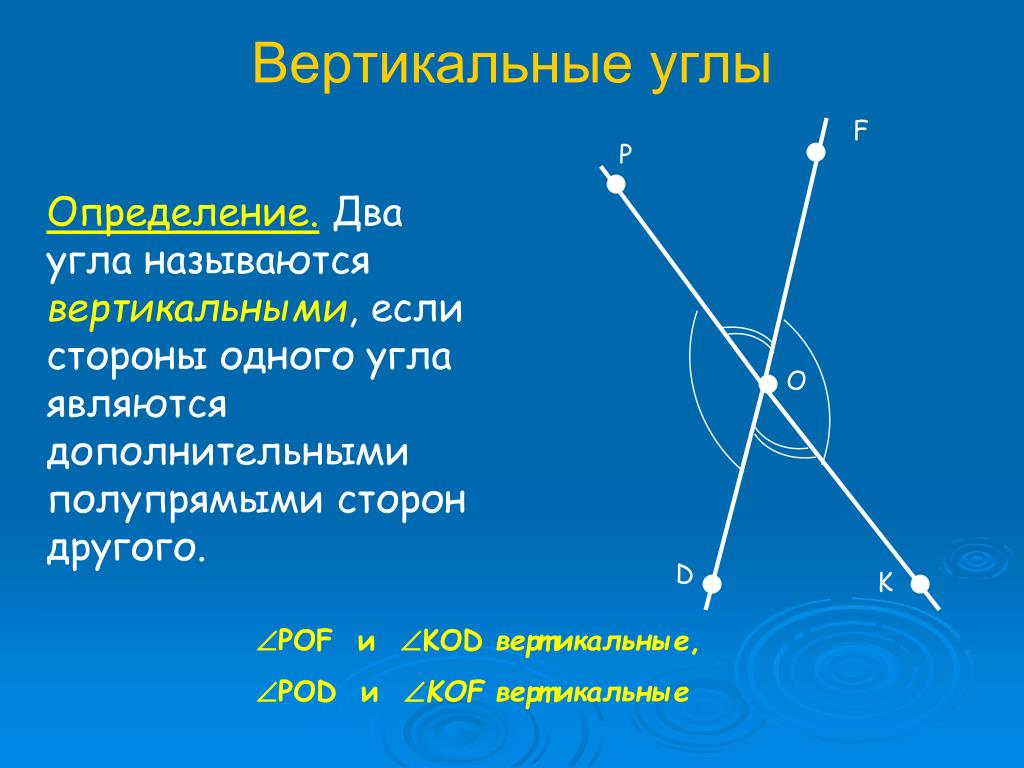
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «»». Имеет место обозначение:
1°=60’=3600», 1’=(160)°, 1’=60», 1»=(160)’=(13600)° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59» .
Определение 11Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Приведем пример обозначения градусной меры угла равного 17°3’59» . Запись имеет еще один вид 17+360+593600=172393600.
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».
В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом.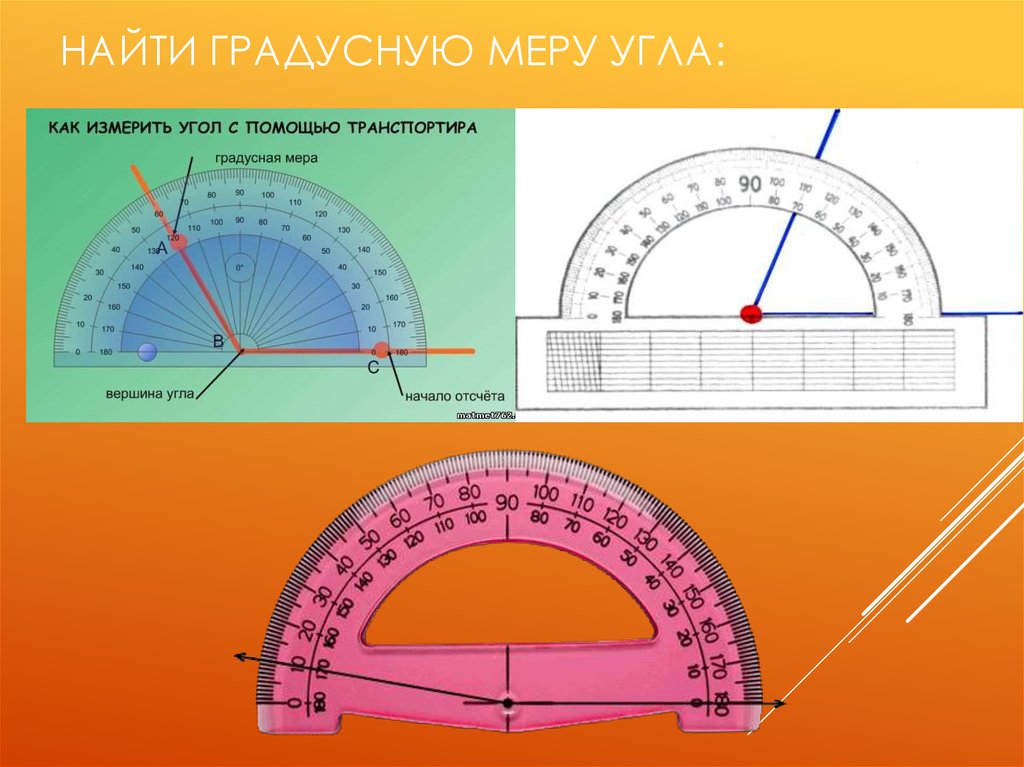 Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными.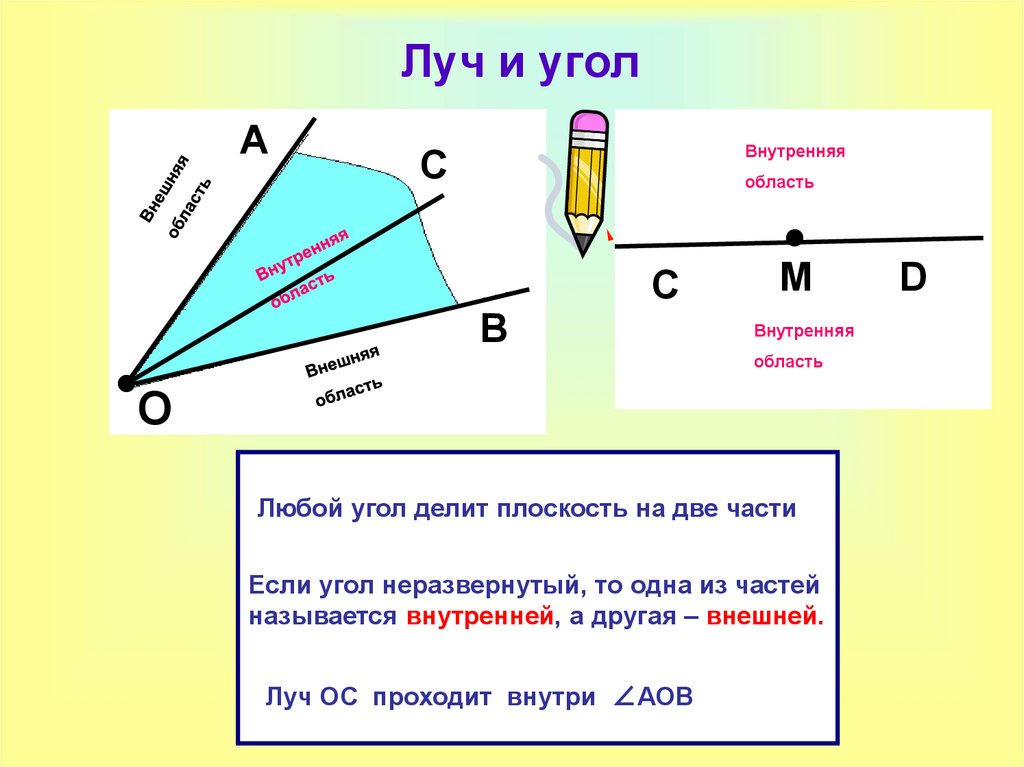 Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла.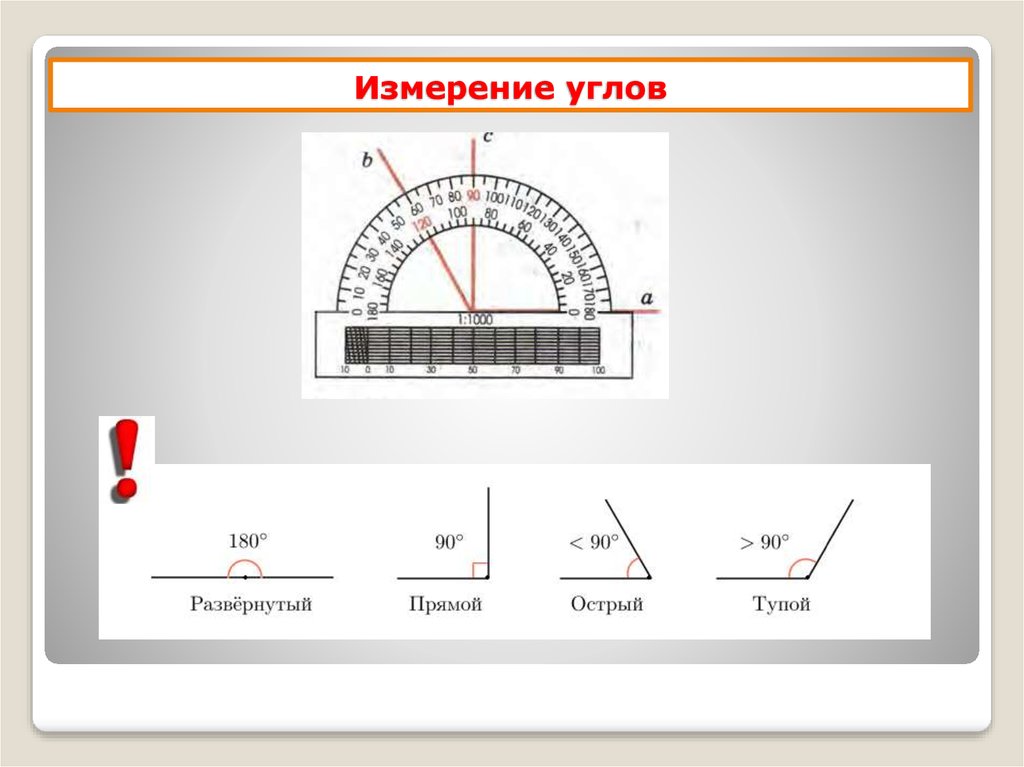 Они считаются подобными.
Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение.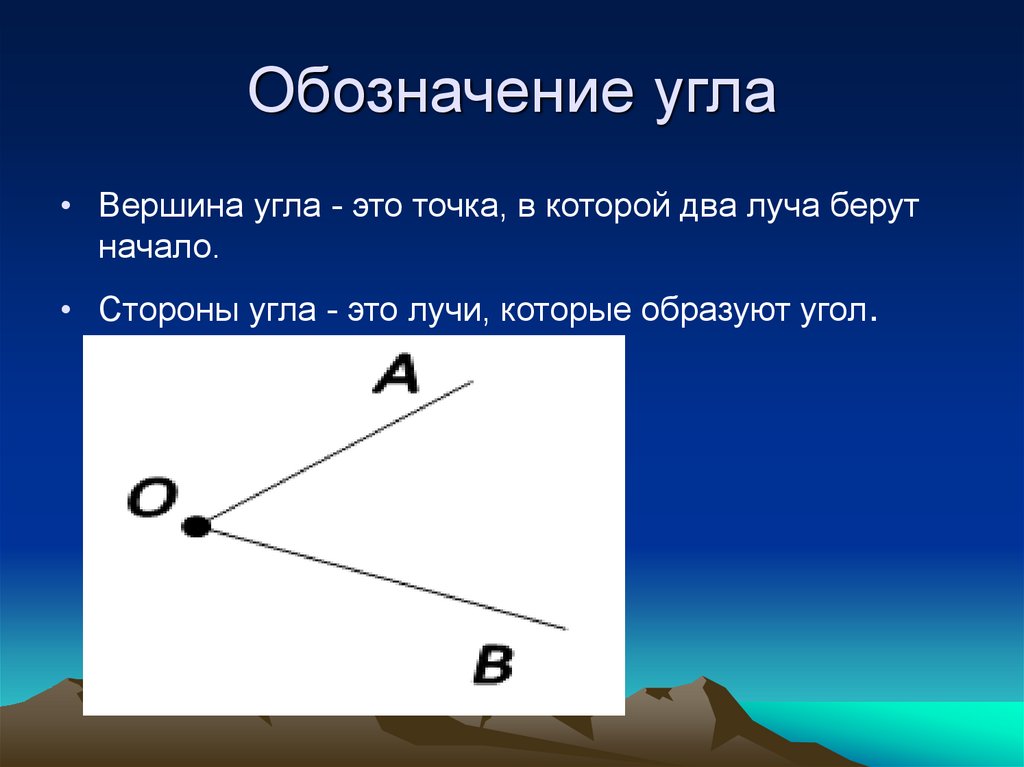 Ниже приведен рисунок, где показано их обозначение.
Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Как рассчитать угол в градусах?
Угол измеряется в градусах (°) и радианах. Он образуется между двумя соседними сторонами многоугольника. Каждый многоугольник имеет разные стороны и разное количество углов. Формула для нахождения углов в градусах полезна в геометрии и тригонометрии. Важно понимать другие понятия математики, такие как дуга, центральный угол окружности и т. д.
- Полный круг = 360°
- Прямая линия = 180°
- Полуокружность = 180°
- Четверть окружности = 90°
Вычисление углов в градусах
Существует три различных метода нахождения углов в градусах:
- Использование протектора D
- Теорема Пифагора и тригонометрическая функция в прямоугольном треугольнике
- Использование формулы суммы углов
- Центральный угол окружности
Использование протектора D
сантиметры или миллиметры. Протектор, используемый для измерения углов, имеет форму буквы «D» со значением угла, отмеченным от 0 до 180 ° в любом направлении (вправо или влево). Нам нужно выровнять ось с линией на D, чтобы измерить угол. Средняя окружность протектора совмещена с вершиной измеряемого угла. Лучи, проходящие через вершину угла, помогут найти угол в градусах.
Протектор, используемый для измерения углов, имеет форму буквы «D» со значением угла, отмеченным от 0 до 180 ° в любом направлении (вправо или влево). Нам нужно выровнять ось с линией на D, чтобы измерить угол. Средняя окружность протектора совмещена с вершиной измеряемого угла. Лучи, проходящие через вершину угла, помогут найти угол в градусах.
Использование теоремы Пифагора и тригонометрической функции в прямоугольном треугольнике
В тригонометрии есть шесть функций: синус, кос, косек, тангенс, кот, и сек. Прямоугольный треугольник имеет три стороны, основание, перпендикуляр и гипотенузу.
- Основание: Сторона, примыкающая к углу 90°.
- Перпендикуляр: Также является прилежащей стороной к углу 90°.
- Гипотенуза: Сторона, противоположная углу 90°.
Прямоугольный треугольник представлен углом 90° как одним из углов. Сумма всех углов треугольника равна 180°.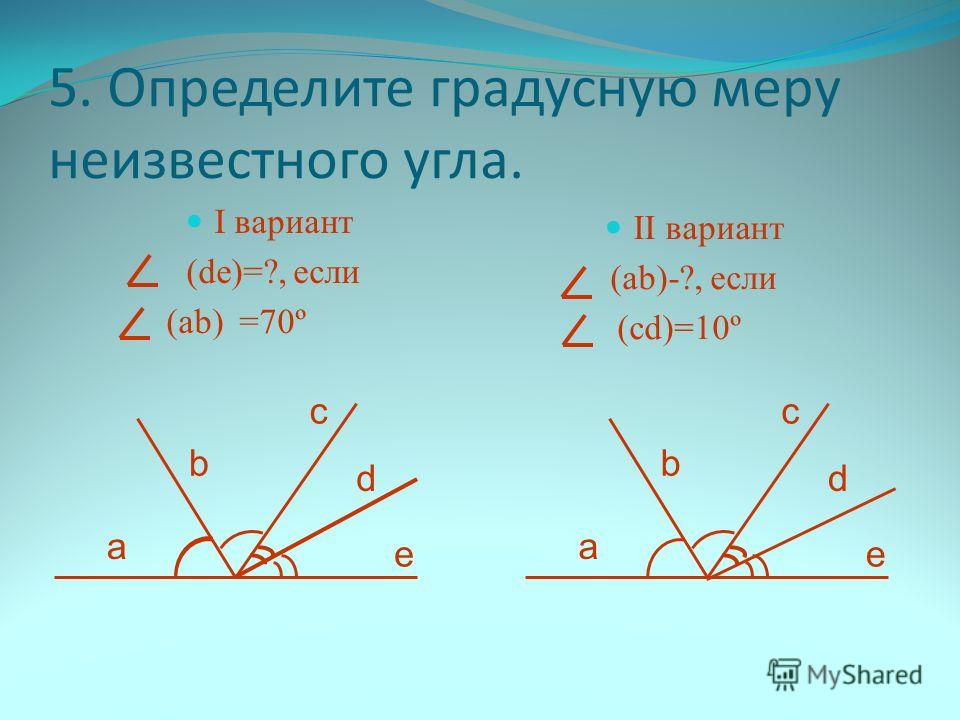
- Cosecθ: Представляется гипотенузой, деленной перпендикуляром.
Cosecθ =
- Cotθ: Представляется как основание, разделенное перпендикуляром.
Cotθ =
Остальные тригонометрические функции представлены как:
sinθ =
cosθ =
tanθ =
secθ =
cosecθ также может быть представлен как 1/ sinθ
Secθ также может быть представлен как 1/ cosθ
Cotθ также может быть представлен как 1/ tanθ
Где,
Θ угол
Теорема Пифагора
Если известны две стороны прямого угла, мы можем легко вычислить третью сторону прямоугольного треугольника. В прямоугольном треугольнике теорема Пифагора дается формулой:
(гипотенуза) 2 = (основание) 2 + (перпендикуляр) 2
Формула суммы углов, образующих сумму внутренних углов многоугольника
между двумя сторонами. Если у многоугольника шесть сторон, то и углов примерно шесть. Это помогает найти угол, если известны другие углы и сумма углов многоугольника.
Если у многоугольника шесть сторон, то и углов примерно шесть. Это помогает найти угол, если известны другие углы и сумма углов многоугольника.
Формула для нахождения суммы углов многоугольника:
Общая сумма углов = 180 (n — 2)
Где,
N — количество сторон полигона
Пример:
- , если n = 4,
- Если n = 4,
Сумма углов = 180 (4 – 2)
= 180 (2)
= 360 °
Если n = 5,
Сумма углов = 180 (5 – 2)
= 3)
= 540°
- Если n = 6
Сумма углов = 180 (6 – 2)
= 180 (4)
= 720°
Центральный угол окружности точка. Расстояние между центральной точкой и границей называется радиусом окружности. Угол, образованный двумя радиусами окружности, называется центральным углом.
 Значение центрального угла окружности лежит в пределах от 0 до 360 градусов.
Значение центрального угла окружности лежит в пределах от 0 до 360 градусов.Формула для расчета центрального угла окружности:
Длина дуги = 2πr × (θ/360)
Θ = 360L/2πr
Где
r — радиус окружности
AB — дуга
Тета — угол в градусах.
L = длина дуги
Примеры задач
Вопрос 1. Найдите центральный угол окружности радиусом 2 м с длиной дуги 4 м?
Решение :
Формула для расчета центрального угла окружности:
Θ = 360L/2πr
Где
r — радиус окружности
Тета — угол в градусах.
L = длина дуги
Θ = угол в градусах
r = 2 м
L = 4 м
Θ = 360 × 4 /2× π × 2
Θ = 190,6 центрального угла 0° окружность 114,6°.
Вопрос 2: Найдите центральный угол окружности радиусом 10см с длиной дуги 18см?
Решение :
Формула для расчета центрального угла окружности: в градусах.
L = Длина дуги
R = 10 см
L = 18 см
θ = угол в градусах
θ = 360 × 18 /2 × π × 10
θ = 103.13 °
Таким образом окружность 103,13°.
Вопрос 3: Найдите угол параллелограмма, если три других угла равны 80°, 95° и 105°?
Решение :
В параллелограмме четыре стороны с суммой углов 360°.
Формула для нахождения суммы углов = 180 (n – 2)
Где
n количество сторон многоугольника
Здесь n = 4,
Сумма углов = 180 (4 – 2)
= 180 (2)
= 360°
Общая сумма = Угол 1 + Угол 2 + Угол 3 + Угол 4
360 = 80+ 95+ 105+ Угол 4
360 = 280 + Угол 4
Угол 4 = 360 – 280
Угол 9 °
Вопрос 4: Найдите угол А на данном рисунке.
Решение :
Дано: Гипотенуза = 12
Перпендикуляр = 6
Тригонометрическая функция для вычисления угла определяется как:
2 sinA
03
A = 30°
Вопрос 5: Найдите угол A на данном рисунке.
Решение :
Дано: Гипотеновая
Вопрос 6: Найдите угол пятиугольника, если остальные четыре угла равны 115°, 100°, 105° и 100°?
Решение :
В пятиугольнике пять сторон с суммой углов 540°.
Формула для нахождения суммы углов = 180 (n – 2)
Где
n – количество сторон многоугольника
Здесь n = 5,
Сумма углов = 180 (5 – 2)
= 180 (3)
= 540°
Общая сумма = Угол 1 + Угол 2 + Угол 3 + Угол 4 + Угол 5
540 = 115° + 100° + 105°+100° + Угол 5
540 = 420 + Угол 5
Угол 5 = 540 – 420
Угол 5 = 120°
Вопрос 7: Найдите угол A на данном рисунке.
Решение :
Дано: База = √3
Перпендикуляр = 1
Функция тригонометрии для расчета угла задается:
=
Tanθ = 1/√3
A = 30°
Вопрос 8.
Найдите угол параллелограмма, если три других угла равны 100°, 70° и 80°?
Решение :
У параллелограмма четыре стороны с суммой углов 360°.
Формула для нахождения суммы углов = 180 (n – 2)
Где
n – количество сторон многоугольника
Здесь n = 4,
Сумма углов = 180 (4 – 2)
= 180 (2)
= 360°
Общая сумма = Угол 1 + Угол 2 + Угол 3 + Угол 4
360 = 100 + 70 + 80 + Угол 4
Угол 4 = 360 – 250
Угол 4 = 110°
Таким образом, второй угол равен 110°.
Вопрос 9: Найдите угол шестиугольника, если остальные пять углов равны 120°, 115°, 110°, 125° и 105°?
Решение :
В шестиугольнике шесть сторон с суммой углов 720°.
Формула для нахождения суммы углов = 180 (6 – 2)
Где,
n – количество сторон многоугольника
Здесь, n = 6,
Общая сумма углов = 180 (6 – 2)
= 180 (4)
= 720°
Общая сумма = Угол 1 + Угол 2 + Угол 3 + Угол 4 + Угол 5 + Угол 6
720 = 120 + 115 + 110 + 125 + 105 + Угол 6
720 = 575 + Угол 6
Угол 6 = 720 – 575
Угол 6 = 0002°, шестиугольника составляет 145°.
Нахождение угла в прямоугольном треугольнике
Угол с любых двух сторон
Мы можем найти неизвестный угол в прямоугольном треугольнике, если мы знаем длины двух его сторон .
Пример
Лестница прислонена к стене, как показано на рисунке.
Какой угол между лестницей и стеной?
Ответ: использовать синус, косинус или тангенс!
Но какой использовать? У нас есть специальная фраза «СОХКАТОА», которая нам помогает, и мы используем ее так:
Шаг 1 : найти имен двух сторон, которые мы знаем
- Смежный Примыкает к углу,
- Напротив находится напротив угла,
- и самая длинная сторона Гипотенуза .
Пример: в нашем примере с лестницей мы знаем длину:
- стороны противоположного угла «х», который равен 2,5
- самая длинная сторона, называемая Гипотенуза , которая равна 5
Шаг 2 : теперь используйте первые буквы этих двух сторон ( O pposite и H ypotenuse) и фразу «SOHCAHTOA», чтобы найти, какой из Sine, Cosine или Tangent использовать:
СОХ.
..
S ine: sin(θ) = O pposite / H ипотенуза
…КАХ…
C осин: cos(θ) = A djacent / H ypotenuse
…ТОА
T угол: tan(θ) = O pposite / A djacent
В нашем примере это O pposite и H ypotenuse, и это дает нам « SOH cahtoa», что говорит нам о том, что нам нужно использовать Sine .
Шаг 3 : Поместите наши значения в уравнение синуса:
S in (x) = O pposite / H ypotenuse = 2,5 / 5 = 0,5
Шаг 4 : Теперь решим это уравнение!
sin(x) = 0,5
Далее (поверьте мне на данный момент) мы можем преобразовать это в следующее:
x = sin -1 (0,5)
А затем возьмите наш калькулятор, введите 0,5 и используйте кнопку sin -1 , чтобы получить ответ:
x = 30°
И у нас есть ответ!Но что означает
sin -1 … ?скважина, синусная функция «SIN» принимает угол и дает нам соотношение «Противоположность/гипотенуза»,
Но SIN -1 SIN -1 SIN -1 SIN -1 « -1 9
». ) идет в другую сторону…
… это берет отношение «противоположное/гипотенуза» и дает нам угол.Пример:
- Функция синуса: sin( 30° ) = 0,5
- Функция обратного синуса: sin -1 ( 0,5 ) = 30°
На калькуляторе нажмите одну из следующих клавиш (в зависимости от
марки вашего калькулятора): либо «2ndF sin», либо «shift sin».Попробуйте использовать на своем калькуляторе sin и sin -1 , чтобы увидеть, какие результаты вы получите!
Также попробуйте cos и cos -1 . И тан и тан -1 .
Давай, попробуй прямо сейчас.Шаг за шагом
Вот четыре шага, которые нам нужно выполнить:
- Шаг 1 Найдите, какие две стороны мы знаем — из противоположной, смежной и гипотенузы.
- Шаг 2 Используйте SOHCAHTOA, чтобы решить, какой из синус, косинус или тангенс использовать в этом вопросе.
- Шаг 3 Для синуса вычислить противовес/гипотенузу, для косинуса вычислить соседний/гипотенузу или для тангенса вычислить противоположный/примыкающий.
- Шаг 4 Найдите угол на калькуляторе, используя один из sin -1 , cos -1 или tan -1
Примеры
Давайте посмотрим еще на пару примеров:
Пример
Найти угол места самолета из точки А на земле. Шаг 1
Шаг 2 SOHCAH TOA говорит нам, что мы должны использовать агент T . Шаг 3 Расчет Противоположный/Смежный = 300/400 = 0,75 Шаг 4 Найдите угол с помощью калькулятора, используя тангенс -1 Тангенс x° = противоположный/примыкающий = 300/400 = 0,75
тангенс -1 из 0,75 = 36,9° (с точностью до 1 знака после запятой)
Если вам не указано иное, углы обычно округляются до одного десятичного знака.
Пример
Найти величину угла a°
- Шаг 1 Две стороны, которые мы знаем, это A djacent (6750) и H ypotenuse (8100).
- Шаг 2 SOH CAH TOA говорит нам, что мы должны использовать C озин.
- Шаг 3 Вычислить смежную / гипотенузу = 6 750/8 100 = 0,8333
- Шаг 4 Найдите угол с помощью калькулятора, используя cos -1 из 0,8333:
cos a° = 6 750/8 100 = 0,8333
cos -1 из 0,8333 = 33,6° (до 1 знака после запятой)
250, 1500, 1501, 1502, 251, 1503, 2349, 2350, 2351, 3934
Калькулятор прямоугольного треугольника| Найти a, b, c и угол
Создано Ханной Памула, кандидатом наук
Отредактировано Bogna Szyk и Jack Bowater
Последнее обновление: 12 ноября 2021 г.
Содержание:
- Как найти стороны прямоугольный треугольник
- Как найти угол прямоугольного треугольника
- Как решить прямоугольный треугольник только с одной стороной?
- Как найти недостающую сторону прямоугольного треугольника? Как найти угол? Пример
- Часто задаваемые вопросы
Найти недостающую сторону или угол не может быть проще, чем с помощью нашего замечательного инструмента — калькулятора сторон и углов прямоугольного треугольника.
Выберите два заданных значения, введите их в калькулятор, и оставшиеся неизвестные будут определены в мгновение ока! Если вам интересно, как найти недостающую сторону прямоугольного треугольника, продолжайте прокручивать, и вы найдете формулы нашего калькулятора.
Как найти стороны прямоугольного треугольника
Существует несколько способов определения длины сторон прямоугольного треугольника. В зависимости от того, что дано, вы можете использовать различные отношения или законы, чтобы найти недостающую сторону:
- Даны две стороны
Если вы знаете две другие стороны прямоугольного треугольника, это самый простой вариант; все, что вам нужно сделать, это применить теорему Пифагора:
a² + b² = c²
, если нога
a— недостающая сторона, затем преобразуйте уравнение к виду, когда a находится на одной стороне, и извлеките квадратный корень:
а = √(c² - b²)если ножка
bнеизвестна, то
б = √(с² - а²)для гипотенузы c отсутствует, формула
с = √(а² + b²)
- Дан угол и гипотенуза
Примените закон синусов или тригонометрию, чтобы найти длины сторон прямоугольного треугольника:
- Данный угол и одна сторона
Найдите недостающую ногу с помощью тригонометрических функций:
а = b * тангенс (α)
б = а * тангенс (β)
- Заданная площадь и одна ножка
Как мы помним из базовой формулы площади треугольника, мы можем вычислить площадь, умножив высоту треугольника и основание и разделив результат на два.
Прямоугольный треугольник — это частный случай разностороннего треугольника, в котором одна сторона является высотой, а вторая — основанием, поэтому уравнение упрощается до:
площадь = a * b / 2Например, если мы знаем только площадь прямоугольного треугольника и длину катета
a, мы можем вывести уравнение для других сторон:
b = 2 * площадь/ас = √(а² + (2 * площадь / а)²)Как найти угол прямоугольного треугольника
Если кроме прямого угла известен еще один угол, вычисление третьего проще простого:
Дано
β:α = 90 - βДано
α:β = 90 - αОднако, если даны только две стороны треугольника, нахождение углов прямоугольного треугольника требует применения некоторых основных тригонометрические функции:
для
α
sin(α) = a/c, поэтомуα = arcsin(a/c)(обратный синус)cos(α) = b/cпоэтомуα = arccos(b/c)(арккосинус)tan(α) = a / b, поэтомуα = arctan(a / b)(арктангенс)cot(α) = b/aпоэтомуα = arccot(b/a)(арккотангенс)и для
β
sin(β) = b/cпоэтомуβ = arcsin(b/c)(обратный синус)cos(β) = a/cпоэтомуβ = arccos(a/c)(арккосинус)tan(β) = b/aпоэтомуβ = arctan(b/a)(арктангенс)cot(β) = a / bпоэтомуβ = arccot(a / b)(арккотангенс)Как решить прямоугольный треугольник только с одной стороной?
Чтобы решить треугольник с одной стороной, вам также понадобится один из непрямых углов .
Если нет, то это невозможно:
- Если у вас есть гипотенуза , умножьте ее на sin(θ) , чтобы получить длину стороны напротив угла.
- Можно также умножить гипотенузу на cos(θ), чтобы получить сторону, прилегающую к углу.
- Если у вас есть сторона , не являющаяся гипотенузой, примыкающая к углу , разделите ее на cos(θ) , чтобы получить длину гипотенузы .
- Можно также умножить эту длину на tan(θ), чтобы получить длину стороны, противоположной углу.
- Если у вас есть угол и сторона , противоположная , вы можете разделить длину стороны на sin(θ) , чтобы получить гипотенузу .
- Можно также разделить длину на tan(θ), чтобы получить длину стороны, примыкающей к углу.
Как найти недостающую сторону прямоугольного треугольника? Как найти угол? Пример
Давайте покажем, как найти стороны прямоугольного треугольника с помощью этого инструмента:
- Предположим, мы хотим найти недостающую сторону по заданной площади и одной стороне.
Выберите нужный вариант из выпадающего списка . Это третий.
- Введите указанные значения . Например, площадь прямоугольного треугольника равна 28 кв. дюймов, а b = 9 дюймов.
- Наш калькулятор сторон и углов прямоугольного треугольника показывает недостающие стороны и углы! Теперь мы знаем, что:
- а = 6,222 в
- с = 10,941 в
- α = 34,66°
- β = 55,34°
Теперь проверим, как работает нахождение углов прямоугольного треугольника:
- Обновить калькулятор. Выберите нужный вариант . Предположим, что у нас есть две стороны, и мы хотим найти все углы. Вариант по умолчанию правильный.
- Введите длину сторон . Наш прямоугольный треугольник имеет гипотенузу, равную 13 дюймам, и катет a = 5 дюймов.
- Отсутствуют стороны и углы . В нашем примере b = 12 дюймов, α = 67,38° и β = 22,62°.
Часто задаваемые вопросы
Сколько осей симметрии имеет прямоугольный треугольник?
Если прямоугольный треугольник равнобедренный (т. е. две его стороны, не лежащие в гипотенузе, имеют одинаковую длину), он имеет одну линию симметрии . В противном случае треугольник не будет иметь линий симметрии .
Может ли прямоугольный треугольник иметь равные стороны?
Нет, прямоугольный треугольник не может иметь все 3 стороны равные , так как все три угла не могут быть равными, так как один должен быть 90° по определению. Однако в прямоугольном треугольнике две стороны, не лежащие в гипотенузе, могут быть равны по длине. Это также означает, что два других угла равны 45°.
Все ли прямоугольные треугольники подобны?
Не все прямоугольные треугольники подобны , хотя некоторые могут быть. Они подобны, если все их углы имеют одинаковую длину или если отношение двух их сторон одинаково.