Описание и примеры стандартных функций SVG
Доминирующей причиной появления этого блога стало незаслуженное забвение на целых десять лет языка разметки масштабируемой векторной графики – SVG (Scalable Vector Graphics), входящего в подмножество расширяемого языка разметки XML.
Стандарт SVG 1.0 был принят в качестве спецификации Консорциумом Всемирной паутины (W3C) в сентябре 2001 г. Стандарт SVG 1.1 и его версии SVG mobile profiles (SVG Basic and SVG Tiny) были приняты консорциумом в качестве рекомендации в январе 2003 г.
Сейчас ведутся работы по созданию стандарта SVG 2.0
Основные преимущества формата SVG.
Я не буду долго распространяться о преимуществах векторной графики перед растровой в вебдизайне, замечу лишь, что, однажды созданный, файл в формате SVG одинаково хорошо выглядит без потери качества и на мобильном устройстве и на станционарном мониторе домашнего ПК.
Шапка данного сайта выполнена в формате SVG, попробуйте уменьшить окно браузера до минимальных размеров, картинка на “лету” будет также пропорционально уменьшаться.
SVG – это двухмерная графика и тем не менее это текстовый формат, который можно легко править в блокноте или просто рисовать в векторных редакторах: Incscape , Adobe illustrator, CorelDRAW
Бесконечное полотно документа svg.
Итак, как происходит формирование векторного изображения.
Документ формата SVG – это двухмерный объект, который может иметь бесконечные координаты, как в положительном, так и в отрицательном направлении по осям X и Y. Также документ SVG имеет две области просмотра: viewport – системная область просмотра и viewBox – пользовательская область просмотра, положение которой относительно начала системных координат viewport, может задаваться собственной, пользовательской системой координат. Другими словами окно просмотра viewBox, может быть перемещёно в любое место документа SVG, при этом берется фрагмент изображения под ним, который после процесса согласования между viewBox и viewport, возвращается обратно в системную область просмотра viewport, которую видит пользователь. Используя это свойство можно организовать вертикальную или горизонтальную прокрутку изображения, меняя параметры координат viewBox.
Используя это свойство можно организовать вертикальную или горизонтальную прокрутку изображения, меняя параметры координат viewBox.
При уменьшении размера пользовательского окна просмотра viewbox можно пропорционально увеличивать фрагмент изображения в системной области просмотра или уменьшать его при увеличении размера viewbox.
Таким образом реализуется эффект лупы. Более подробно эти процессы разобраны в статье: Трансформация изображений SVG при изменении параметров Viewbox.
Взаимодействие SVG, XML с HTML, CSS, Jscript
В SVG, как и в HTML можно добавлять ссылки на внешние ресурсы. Но если в HTML одна картинка может служить только для одной внешней ссылки, то в SVG документ можно добавлять сколько угодно внешних ссылок . Картинка кликабельна.
Внутрь HTML страницы легко встраивается код SVG документа или целиком подключается внешний SVG файл. Можно наоборот, внутри SVG файла разместить код HTML внутри тегов foreignObject. Получаются интересные эффекты: Внутри SVG файла находится работающий внешний HTML сайт. К SVG формату можно подключать внешние таблицы стилей CSS 2.0, что позволяет управлять сразу несколькими файлами *.svg. Также вполне допустимо подключение стилей внутри файла *.svg внутри тегов style или использовать внутренние стили непосредственно внутри командных строк фигур и путей.
К SVG формату можно подключать внешние таблицы стилей CSS 2.0, что позволяет управлять сразу несколькими файлами *.svg. Также вполне допустимо подключение стилей внутри файла *.svg внутри тегов style или использовать внутренние стили непосредственно внутри командных строк фигур и путей.
SVG, как любой основанный на XML формат, позволяет использовать для его обработки таблицы трансформации (XSLT).
Преобразуя XML-данные в SVG с помощью простого XSL, можно получить графическое представление текстовых данных, например визуализировать графики, круговые диаграммы, гистограммы и т.д.
Анимация и интерактивность SVG.
Анимация в SVG осуществляется при помощи языка SMIL (Synchronized Multimedia Integration Language). Также поддерживаются скриптовые языки на основе спецификации ECMAScript — это встраиваемый расширяемый язык программирования.
То есть всё находится в одном месте, внутри документа SVG, поэтому нет необходимости для подключения внешних библиотек.
На каждую отдельную фигуру или на целое изображение можно установить обработчик событий (клик, наведение мышки, нажатие клавиши и т.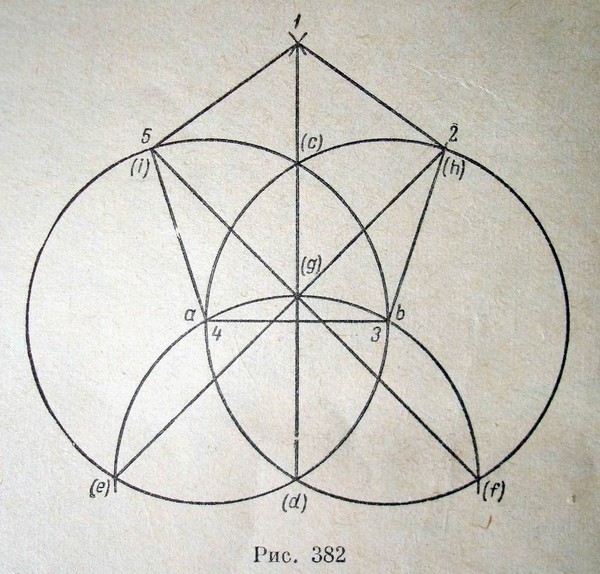 д), таким образом, пользователь может управлять рисунком. Наведите курсор мышки на кнопку“Start” на примере слева.
д), таким образом, пользователь может управлять рисунком. Наведите курсор мышки на кнопку“Start” на примере слева.
По событию mouseover на этой кнопке начнется анимация по команде begin=”startButton.mouseover” – движение цветных шариков по криволинейному пути. Закончится анимация либо через заданные в коде 16 секунд, либо в любой момент по наведению курсора мышки на цветные радиокнопки “Stop”. При этом каждая радиокнопка управляет своим объектом совпадающим по цвету. На рисунке ниже анимация начинается и заканчивается при нажатии клавиши мышки на кнопки GO и STOP. В этом случае работает событие click. Команда на запуск анимации – begin=”gO.click” и соответственно остановка – end=”stop.click”
Следующий пример анимации – плавная отрисовка картинки с нуля до полного изображения.
Уже встроенные в SVG языки программирования позволяют реализовать довольно сложные сценарии анимации. Но, в дополнение к этому есть еще более мощные средства для реализации интерактивности графики и ее анимации – это внешние библиотеки сторонних разработчиков: D3. js, BonsaiJS, Svg.js, Snapsvg.js
js, BonsaiJS, Svg.js, Snapsvg.js
Еще примеры анимации ⇛
Недостатки SVG формата
- С увеличением количества мелких деталей в изображении, быстрее растёт размер файла SVG-данных. Предельный случай — когда изображение представляет собой белый шум. В этом случае SVG не только не даёт никаких преимуществ в размере файла, но даже имеет проигрыш по отношению к растровому формату. На практике, SVG становится невыгоден уже задолго до того, как изображение дойдёт до стадии белого шума.
- Трудность использования в крупных картографических приложениях из-за того, что для правильного отображения маленькой части изображения документ необходимо прочитать целиком.
- В настоящее время SVG формат применяется в Интернете сравнительно мало, из-за недостаточной кроссбраузерности. Лучше всего обстоят дела у Mozilla Firefox со встроенным просмотрщиком SVG, так как ее разработчики находятся в рабочей группе Консорциума Всемирной паутины (W3C) по разработке и внедрению стандарта SVG.

Браузеры Apple Safari, Google Chrome намного лучше поддерживают SVG, но не полностью, так как SVG – это большая спецификация (вдвое больше HTML 4.01), именно поэтому разработчики браузеров внедряют функции постепенно, от версии к версии. Но абсолютно все разработчики современных браузеров заявляют, что за форматом SVG будущее в области графики вебдизайна.
UPD. Добавлен новый раздел онлайн генераторы SVG кода path.
следующая: Структура SVG документа ⇛
11 «а» класс МАОУ СОШ №6 с углубленным изучением отдельных предметов г.Кушва : Черчение. Урок №5
Урок №5 16.02.2015Раздел: Геометрические построения.
Тема: Деление окружности на равные части Воспитание аккуратности и точности выполнения действий при выполнении графических работ Напоминаю правило рационального использования рабочего места и проверки его в начале урока (справа все чертежные принадлежности, а слева дневник, тетрадь, папка для черчения).

Приемы деления окружности на равные части человек использовал с незапамятных времен. Например: превращение колеса из сплошного диска в обод со спицами поставило человека перед необходимостью распределить спицы в колесе равномерно. Выполняя изображение такого колеса, люди искали точные способы с помощью чертежных инструментов.
С делением окружности неразрывно связано построение правильных многоугольников, так как правильными многоугольники считаются только в том случае, если все их вершины принадлежат одной окружности и делят его на равные части.
Когда-то в построении правильных многоугольников вкладывали мистический смысл. Так, пифагорейцы, последователи религиозно-философского учения, основанного Пифагором, приняли в качестве знака своего союза звездчатый многоугольник, образованный диагоналями правильного пятиугольника.
Правила строгого геометрического построения некоторых правильных многоугольников изложены в книге “Начала” древнегреческого математика Евклида, жившего в 3 веке до н.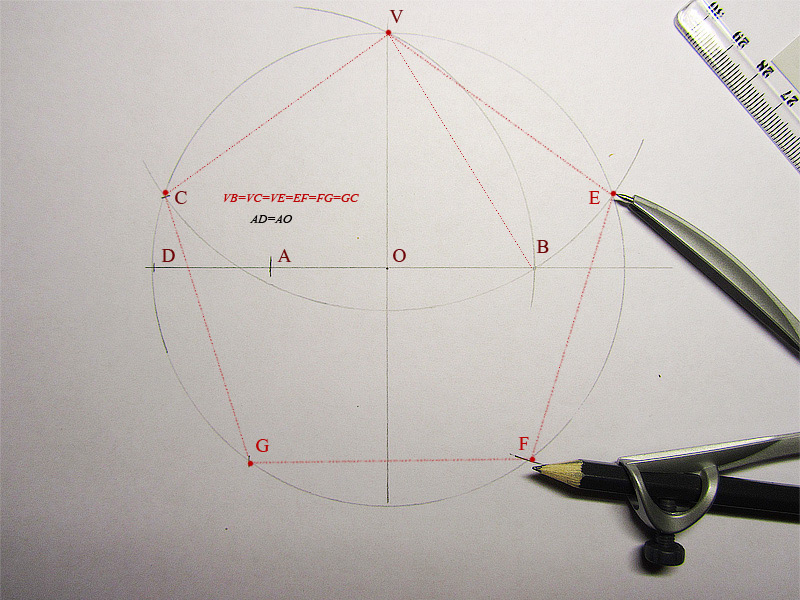 э. Для выполнения этих построений он предлагал пользоваться только линейкой и циркулем.
э. Для выполнения этих построений он предлагал пользоваться только линейкой и циркулем.
В тетради провели центровые для 6 окружностей
(штрихпунктирной тонкой линией 20 мм.-5/2 точка в клеточке по середине -20 мм.. Линии пересекаются на линии, пересечение точек
недопустимо).
В тетради будут только чертежи окружностей! (ничего писать не надо)Напоминаю правило!
Когда мы чертим в тетради или на формате все цифры, точки, знаки на чертеже мы подписываем простым карандашом
Радиус всех окружностей R = 20 мм.
1. Деление окружности на 3, 6, 12 равных частей
(выполняем вариант с циркулем)
Деление окружности на три равные части. Поставив опорную ножку циркуля в конце диаметра (рис. 126, а), описывают дугу радиусом, равным радиусу R окружности. Получают первое и второе деление. Третье деление находится на противоположном конце диаметра.
126, а), описывают дугу радиусом, равным радиусу R окружности. Получают первое и второе деление. Третье деление находится на противоположном конце диаметра.
Ту же задачу можно решить с помощью линейки и угольника с углами 30, 60 и 90°. Для этого устанавливают угольник большим катетом параллельно вертикальному диаметру. Вдоль гипотенузы из точки 1 (конца диаметра) проводят хорду, получают второе деление (рис. 126, б). Повернув угольник и проведя вторую хорду, получают третье деление (рис. 126, в).
Рис. 126. Деление окружности на три равные части: а — с помощью циркуля; б, в— с помощью угольника и линейки
Соединив точки 2 и 3 отрезком прямой, получают равносторонний треугольник.
Деление окружности на шесть равных частей. Раствор циркуля устанавливают равным радиусу R окружности, так как сторона шестиугольника равна радиусу описанной окружности. Из противоположных концов одного из диаметров окружности (например, точек 1 и 4, рис. 127, а) описывают дуги. Точки 1, 2, 3. 4, 5, 6 делят окружность на равные части. Соединив их отрезками прямых, получают правильный шестиугольник (рис. 127, б).
4, 5, 6 делят окружность на равные части. Соединив их отрезками прямых, получают правильный шестиугольник (рис. 127, б).
Рис. 127. Деление окружности на шесть равных частей с помощью циркуля
Ту же задачу можно выполнить при помощи линейки и угольника с углами 30 и 60° (рис. 128).
Рис. 128. Деление окружности на шесть равных частей с помощью угольника и линейки
2. Деление окружности на 4 и 8 равные части (выполнить на разных окружностях)
Штрихпунктирные центровые линии, проведенные перпендикулярно одна другой, делят окружность на четыре равные части. Последовательно соединив их концы, получим правильный четырехугольник (рис. 64).
Для того чтобы разделить окружность на восемь равных частей, необходимо разделить на две равные части дугу, равную 1/4 окружности.Вспомните деление отрезка на равные части. В точку 3 поставили иголку циркуля, грифель в точку 4 и провели дугу, поменяли местами иголку с грифелем и провели другую дугу. в точках их пересечений провели перпендикуляр на отрезок 34 разделив его на две равные части. Отметили точку А. Измерили циркулем отрезок 3А и отложили его от точек: 1, 2, 4. тем самым разделив окружность на 8 равных частей. Соединили все точки получив восьмиугольник.
Отметили точку А. Измерили циркулем отрезок 3А и отложили его от точек: 1, 2, 4. тем самым разделив окружность на 8 равных частей. Соединили все точки получив восьмиугольник.3. Деление окружности на 5 равных частей
Деление окружности на пять равных частей. Пятой части окружности соответствует центральный угол в 72° (360°:5 = 72°). Этот угол можно построить при помощи транспортира (рис. 129, а).
Рис. 129. Деление окружности на пять равных частей
На рисунке 129, 6 показано вычерчивание пятиконечной звезды.
Постройте с помощью линейки и угольника правильный шестиугольник, две вершины которого лежат на горизонтальной центровой линии. Выполните то же построение с помощью циркуля.
Практическая работа. Создание орнамента
В тетради создать один из примеров или придумать свой орнамент
Домашнее задание.
1. Выполнить на формате А4 Графическую работу № 3 «»Деление окружностей на равные части». Начертить 6 окружностей радиусом 20 мм. и разделить их на 3, 4, 5,
6, 8, 12 равных частей. Заполнить основную надпись по образцу из урока №2
Начертить 6 окружностей радиусом 20 мм. и разделить их на 3, 4, 5,
6, 8, 12 равных частей. Заполнить основную надпись по образцу из урока №2 5.23: Построение правильных многоугольников — K12 LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5007
Построение чертежей равносторонних треугольников, квадратов и правильных многоугольников с помощью циркуля и линейки. Создавайте полигоны с помощью Geogebra.
Построение правильных многоугольников
С помощью циркуля постройте на листе бумаги окружность, как показано ниже. Опишите, как сложить бумагу в два раза, чтобы помочь вам построить квадрат.
Рисунок \(\PageIndex{1}\)Правильные многоугольники
Правильный многоугольник — это многоугольник, который является равноугольным и равносторонним .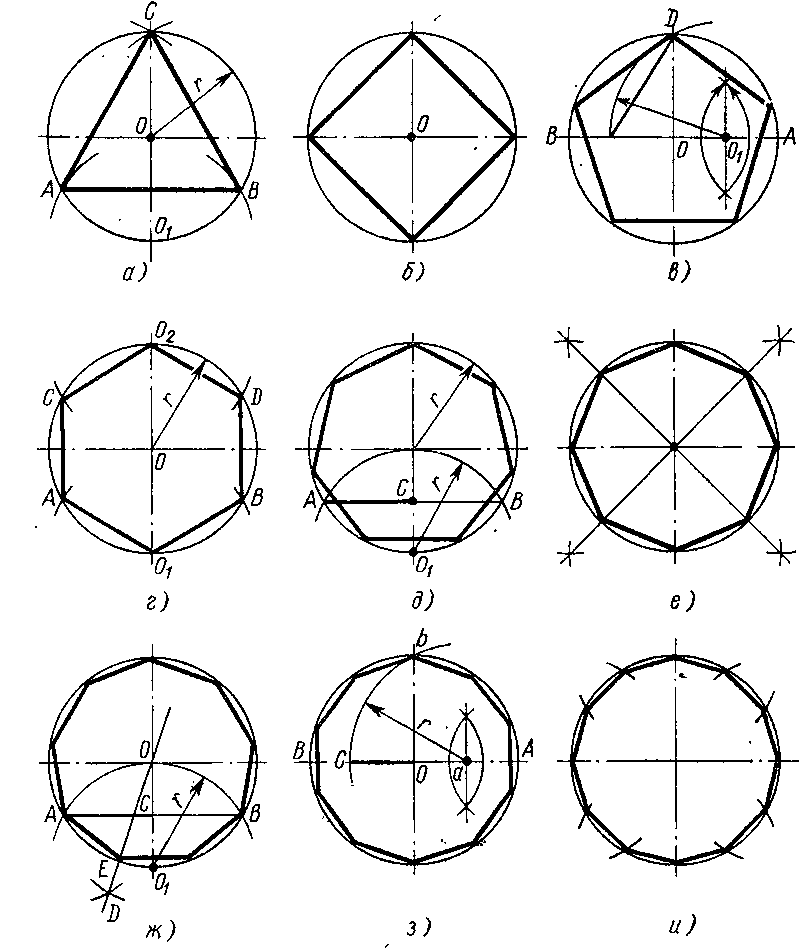
Построения — это пошаговые процессы, используемые для создания точных геометрических фигур. Для создания конструкции вручную есть несколько инструментов, которые вы можете использовать:
- Компас: Устройство, позволяющее создать окружность заданного радиуса. Компасы могут помочь вам не только создавать круги, но и копировать расстояния.
- Линейка: Все, что позволяет провести прямую линию. Линейка не должна измерять расстояния. Каталожная карточка хорошо работает как линейка. Вы также можете использовать линейку в качестве линейки, если вы используете ее только для рисования прямых линий, а не для измерения.
- Бумага: Когда на листе бумаги изображена геометрическая фигура, саму бумагу можно согнуть, чтобы построить новые линии.
Вы можете построить несколько правильных многоугольников вручную, если помните определения и свойства этих правильных многоугольников. С помощью дополнительной программы для геометрии или транспортира вы можете построить любой правильный многоугольник.
С помощью дополнительной программы для геометрии или транспортира вы можете построить любой правильный многоугольник.
Давайте рассмотрим пример задачи.
\(\overline{AB}\) — это одна сторона равностороннего треугольника \(\Delta ABC\). Вам нужно поставить точку \(C\) в правильном месте, чтобы получился равносторонний треугольник. Где должна располагаться точка \(C\) относительно точек \(A\) и \(B\)?
Пусть расстояние между \(A\) и \(B\) равно \(d\). Точка \(C\) должна быть удалена от точки \(A\), а также \(d\) от точки \(B\).
Рисунок \(\PageIndex{3}\)С помощью линейки нарисуйте отрезок \(\overline{AB}\). Используйте идеи из Примера A, чтобы построить равносторонний треугольник \(\Delta ABC\).
Рисунок \(\PageIndex{4}\) Используйте циркуль для измерения длины \(\overline{AB}\).
Создайте неполный круг из точек на расстоянии \(\overline{AB}\) от точки \(A\).
Рисунок \(\PageIndex{6}\)Создайте еще один неполный круг из точек на расстоянии \(\overline{AB}\) от точки \(B\).
Рисунок \(\PageIndex{7}\)Точкой пересечения этих двух неполных окружностей является точка \(C\).
Рисунок \(\PageIndex{8}\)Точки \(A\), \(B\), \(C\) и \(D\) лежат на окружности с центром в точке \(O\). Докажите, что \(ABCD\) — квадрат.
Рисунок \(\PageIndex{9}\) \(\overline{AO}\cong \overline{BO}\cong \overline{CO}\cong \overline{DO}\), поскольку все они имеют одинаковые радиусы круг. Поскольку \(\угол BOC\) прямой угол, \(\угол BOA\),\угол AOD\) и \(\угол COD\) также должны быть прямыми углами. Следовательно, \(\угол BOC\cong \угол BOA\cong \угол AOD\cong \угол COD\). Это означает, что \(\Delta BOC\cong \Delta AOB\cong \Delta DOA\cong \Delta COD\) by SAS\cong\). \(\overline{AB}\cong \overline{BC}\cong \overline{CD}\cong \overline{DA}\), поскольку они являются соответствующими частями конгруэнтных треугольников.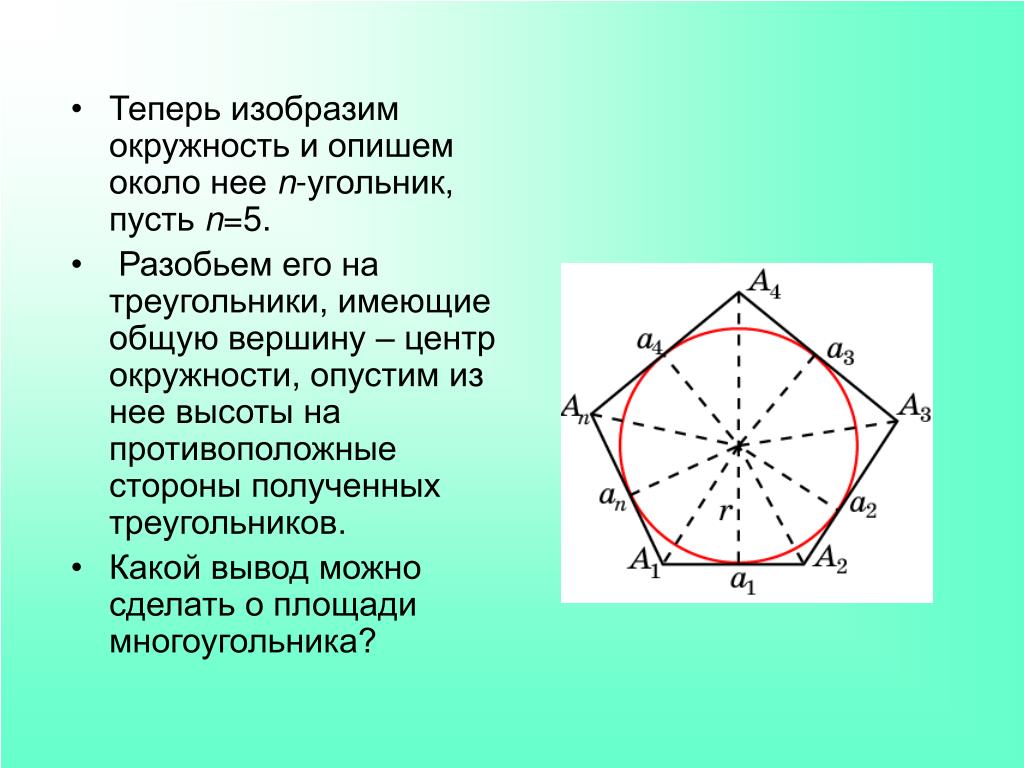 9{\circ}\) углов, это квадрат.
9{\circ}\) углов, это квадрат.
Пример \(\PageIndex{1}\)
Ранее вас попросили описать, как сложить бумагу в два раза, чтобы помочь вам построить квадрат.
Решение
Сложите круг так, чтобы две половинки перекрывали друг друга, чтобы получилась складка, равная диаметру.
Рисунок \(\PageIndex{10}\)Сложите круг еще раз пополам, чтобы получить биссектрису диаметра. Для этого согните так, чтобы две конечные точки диаметра сошлись. Вторая складка также будет диаметром.
Рисунок \(\PageIndex{11}\)Обратите внимание, что два диаметра перпендикулярны друг другу. Соедините четыре точки пересечения на круге, чтобы построить квадрат.
Рисунок \(\PageIndex{12}\)Вы можете быть уверены, что это квадрат, благодаря доказательству в Примере C.
Пример \(\PageIndex{2}\)
Правильный шестиугольник ниже разделен на шесть равных треугольников. Какие это треугольники? Объяснять.
Рисунок \(\PageIndex{13}\) Решение 9{\circ}\), поэтому все треугольники равносторонние. Пример \(\PageIndex{3}\) Шесть точек были равномерно распределены по окружности внизу. Объясните, почему при соединении этих точек получается правильный шестиугольник. Решение Поскольку шесть точек расположены на равном расстоянии друг от друга, каждый из сегментов, соединяющих шесть точек, должен иметь одинаковую длину. Следовательно, многоугольник должен быть правильным. Поскольку сторон шесть, это должен быть правильный шестиугольник. Пример \(\PageIndex{4}\) Построить правильный шестиугольник, вписанный в окружность. Решение «Вписанный в круг» означает, что все шесть вершин шестиугольника лежат на одном круге. Начните с построения окружности и точки на окружности. Вы знаете, что радиус круга равен длине каждой стороны круга (см. практику №1). Следовательно, ваша цель состоит в том, чтобы разместить вокруг круга шесть точек, которые находятся на таком же расстоянии друг от друга, как и радиус круга. Продолжайте делать новые отметки по кругу на одинаковом расстоянии друг от друга. Соедините точки пересечения, чтобы сформировать правильный шестиугольник. 1. Постройте равносторонний треугольник. 2. Постройте еще один равносторонний треугольник. 3. Объясните, почему ваш метод построения равносторонних треугольников работает. 4. Постройте квадрат, вписанный в круг, сделав две складки. 5. Обоснуйте, почему созданный вами многоугольник на самом деле является квадратом. Используйте линейку, чтобы построить \(\overline{AB}\). 6. Постройте серединный перпендикуляр к \(\overline{AB}\). 7. Построить окружность диаметром \(\overline{AB}\). 8. Постройте квадрат, вписанный в окружность, соединив четыре конца диаметров. 9. Расширьте свою конструкцию до правильного восьмиугольника, разделив пополам каждый из прямых углов в центре круга. 10. Постройте правильный шестиугольник, вписанный в окружность. 11. Объясните, почему метод построения правильного шестиугольника основан на окружности. 12. Объясните, как можно расширить построение правильного шестиугольника до построения правильного 12-угольника. 13. Построить равносторонний треугольник. Объясните, как можно построить окружность, проходящую через три точки равностороннего треугольника. 14. Учитывая равносторонний треугольник, вписанный в окружность, как можно продолжить построение, чтобы построить правильный шестиугольник? 15. Имея окружность и транспортир, объясните, как можно построить правильный пятиугольник. Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 5.4.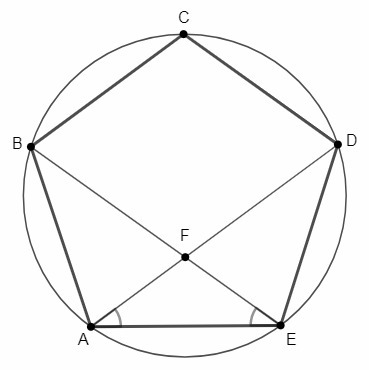
 Держите компас открытым на ту же ширину, что и радиус круга, и сделайте одну новую отметку на круге.
Держите компас открытым на ту же ширину, что и радиус круга, и сделайте одну новую отметку на круге.
Рисунок \(\PageIndex{19}\) Обзор

Обзор (ответы)
Словарь
Срок Определение Правильный многоугольник Правильный многоугольник — это многоугольник, у которого все стороны имеют одинаковую длину и все углы имеют одинаковую величину. 
Равносторонний Многоугольник является равносторонним, если все его стороны имеют одинаковую длину. Равноугольный Многоугольник является равноугольным, если все углы имеют одинаковую меру.
Эта страница под названием 5.23: Построение правильных многоугольников распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
ПОД ЛИЦЕНЗИЕЙ- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- СК12
- Лицензия
- СК-12
- Программа OER или Publisher
- СК-12
- Показать оглавление
- нет
- Теги
- правильные многоугольники
- источник@https://www.
 ck12.org/c/geometry
ck12.org/c/geometry
Многоугольные кольца
Возраст от 11 до 14 лет
Уровень испытания
Летиция из школы Бангкок Патана в Таиланде, Роуз из школы Ченнинг в Великобритании, Кэролайн, Маркос и Джейн из школы Kings’ School Al Barsha в ОАЭ и Алекс из школы Лейтон-Парк в Великобритании выяснили, сколько пятиугольников образуют кольцо.
Маркос использовал диаграмму, чтобы представить себе полное кольцо:
Что ж, если вы собираетесь думать о круге, вы можете разделить его на 4 равных размера, один из которых равен двум пятиугольникам с половиной. Если вы добавите все, получится петля, полная пятиугольников [что дает 10 пятиугольников].
Летиция и Роуз использовали интерактивность, чтобы сделать полные пятиугольные кольца. Это кольцо Роуз:
Норави из школы короля Георга V в Гонконге, и Алекс использовал углы, чтобы объяснить, почему 10 пятиугольников образуют кольцо, не перекрываясь.
Ниже приведены пояснения и схема Алекса.
Нажмите здесь, чтобы увидеть работу Норави, которая более глубока, чем работа Алекса.
Поскольку кольцо состоит из правильных пятиугольников, мы можем вычислить, что каждый из внутренних углов каждого пятиугольника равен 108* градусам. Продлив линии, которые разделяют два пятиугольника, предполагая, что все они встречаются посередине, получится треугольник.
Поскольку мы знаем, что каждый угол [правильного] пятиугольника равен 108* градусам, мы знаем, что два угла при основании треугольника равны 72**, а верхний угол равен 36 градусам.
Поскольку [сумма] углов в точке составляет 360 градусов, а 36 делится на 360, получится полное кольцо.
Также, поскольку 360 х 36 = 10, мы знаем, что кольцо будет состоять из 10 пятиугольников.
Пятиугольники выше являются правильными пятиугольниками.
*формула для расчета размера внутреннего угла многоугольника: $(n \times 180 — 360) \div n$ (где $n$ — количество сторон многоугольника).
**потому что треугольник образован продолжением линий, а углы на линии составляют $180$ градусов, $180 — 108$ (внутренний угол пятиугольника) $= 72.$
Кэролайн сказала, что 5 десятиугольников образуют кольцо , а Джейн сказала, что 10 десятиугольников образуют кольцо. Летиция сказала, что 5 десятиугольников образуют кольцо, но прислала эту картинку с 10 десятиугольниками в кольце (слева). Справа кольцо из 5 десятиугольников.
В кольце из 10 десятиугольников фигура в середине использует 3 стороны от каждого десятиугольника. В кольце из 5 десятиугольников фигура в середине использует 2 стороны от каждого десятиугольника.
Если мы заставим фигуру в середине использовать только одну сторону каждого десятиугольника (как мы сделали с пятиугольниками), тогда десятиугольники не могут образовать кольцо, потому что они перекрываются:
Какие многоугольники могут образовывать кольца вокруг фигуры который использует только 1 сторону каждого многоугольника?
Пиньо из Таиланда, Мими, Денис, Джомкван и Джессика из Международной школы Headstart на Пхукете в Таиланде и Икра из начальной школы Апхолл в Великобритании прислали ответы на этот вопрос. Вот работы Джессики:
Вот работы Джессики:
В кольце многоугольников некоторые определенные многоугольники могут образовывать кольцо с другим многоугольником внутри него. Не все полигоны могут это сделать. Единственная странность в этом заключается в том, что форма внутри кольца должна использовать только одну из внешних сторон.
Шестиугольник (6-угольник)
Мы можем видеть в шестигранном кольце то, что форма, которая сформировалась внутри кольца, представляет собой шестиугольник. На этой диаграмме одна сторона формы используется для создания внутренней формы.
Октагон (8-угольник)
В этом восьмиугольнике 4, поставленные рядом, образовали квадрат посередине. Следовательно, это соответствует моему исследованию многоугольных колец.
Додекагон (12-угольник)
В этом двенадцатиугольнике по 3 элемента каждой формы были использованы для создания многоугольника в середине. Как мы видим, фигура представляет собой треугольник и используется только 1 сторона каждой фигуры.
Икра обнаружил, что это работает и с квадратами:
Из квадратов можно сделать кольцо. Я использовал 12 квадратов, но вы можете сделать их настолько большими, насколько захотите.
Даниэль из академии Мур-Энд в Великобритании и Мими посмотрели на углы многоугольника, который образовался в середине. Это работа Даниэля:
Используются только правильные многоугольники, поэтому мы можем предположить, что внутренний угол каждого [многоугольника], используемого в диаграмме, [составляет] $\dfrac{(n-2) \times 180}n$
При соединении двух правильных [многоугольников] сумма двух внутренних углов и $x$ (где $x$ внутренний угол многоугольника в середине) , равна $360.$
Решая уравнение $2\times \dfrac{(n-2) \times 180}n + x = 360$, находим $x$.
Нам нужно найти внешний угол, чтобы найти количество сторон. Мы делаем это, вычитая [$x$] из $180$.
Если мы разделим $360$ на [внешний угол], мы получим количество сторон многоугольника в центре.
