Как построить 5 угольник в окружности: Построение пятиугольника подробно. — Чертежик

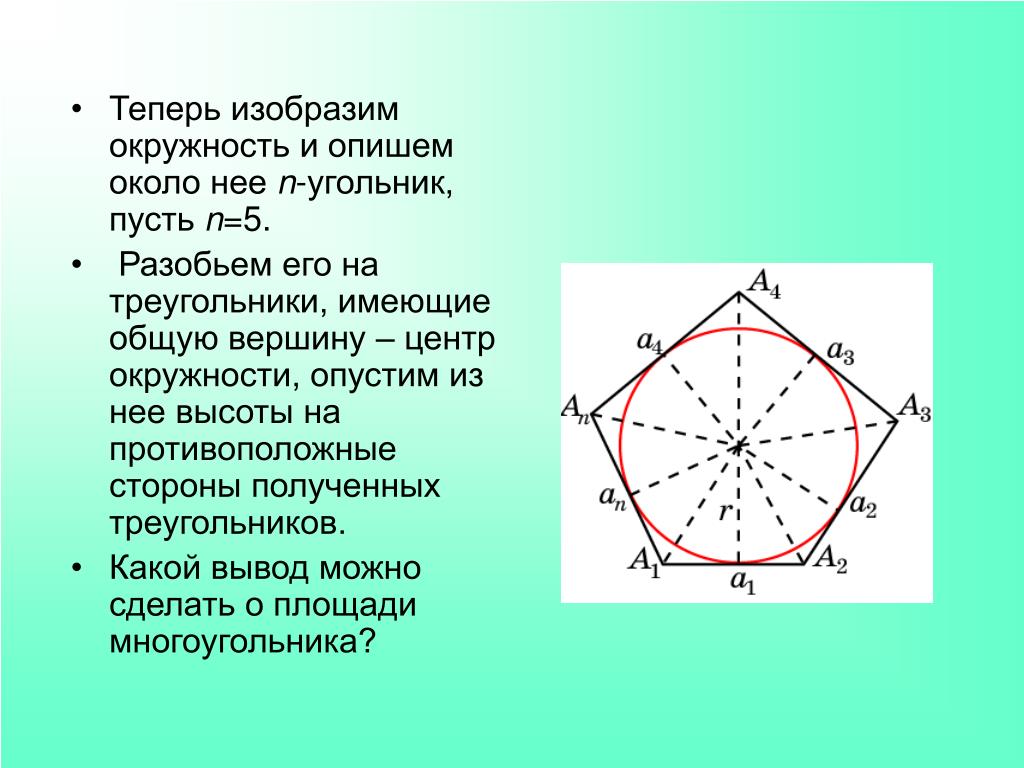
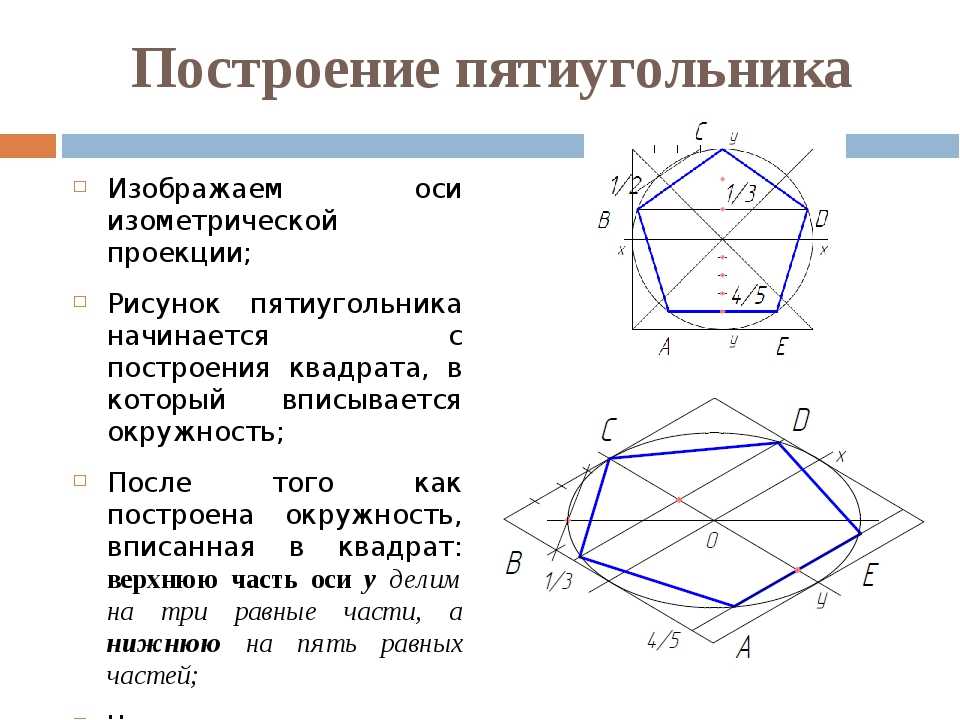
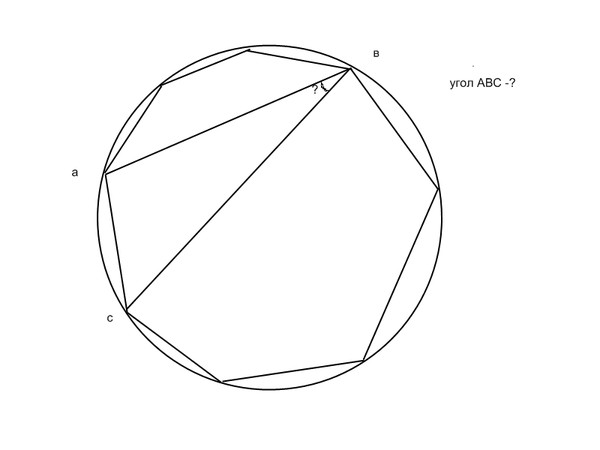
python — Питон, построить пятиугольник

Задание такое: построить правильный пятиугольник со стороной a.

Тут обязательно должна использоваться библиотека Pillow.

Вот мой код:

import PIL
from PIL import Image, ImageDraw
a=int(input("Введите размер стороны а: "))
img = Image.new("RGB",(700,700), (2555,255,255))
draw = ImageDraw.Draw(img)
draw.polygon((0.6*a,1.4*a, 1.3*a,0.9*a, 2*a,1.4*a, 1.7*a,2.2*a ,0.9*a,2.2*a), fill="lightblue",outline =(255,0,0))
img.show()

Координаты подбирал сам, и в общем то, пятиугольник похож на правильный, но доказать это не просто. Также сделали замечание, что сторона «a» должна вводиться с клавиатуры в пикселях, а у меня получается своя условная единица.. Еще каким то образом нужно на картинке подписать «Это пятиугольник».

Вот результат работы моей программы:

• python
• pillow

1

Зачем подбирать координаты, если их можно вычислить?

import math
from PIL import Image, ImageDraw, ImageFont
x=250 #центр полигона (x)
y=250 #центр полигона (y)
n=5   #число сторон полигона
r=200  #радиус окружности в которую вписываем полигон
#получаем координаты вершин
coords=[(x + r * math. cos(2 * math.pi * i / n), y + r * math.sin(2 * math.pi * i / n)) for i in range(1, n+1)]
img = Image.new("RGB",(500,500), (255,255,255))
draw = ImageDraw.Draw(img)
draw.polygon((coords), fill="lightblue",outline =(255,0,0))
unicode_font = ImageFont.truetype("arial.ttf", 22)
draw.text ((100,40), u'Это многоугольник', font=unicode_font, fill='red' )
img.show()

Ну, и поскольку изначально дается длина стороны, то радиус описываемой окружности тоже легко вычислить:

r = side/(2*math.sin(math.pi/n)) #side - длина стороны, n - количество сторон

2

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

Правильный пятиугольник — как построить, сколько осей симметрии имеет

Точное построение фигуры

Специалисты рекомендуют некоторую последовательность действий, по которым построить правильный пятиугольник очень просто.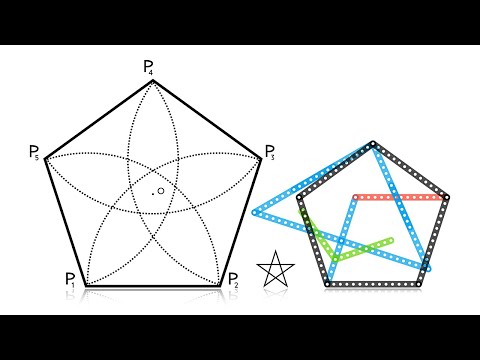 Для операции необходимы обыкновенная тетрадь в клеточку, циркуль, карандаш, резинка и линейка. Следует выполнить некоторые шаги:

1. Построить окружность с центром в некоторой точке О.
2. Провести два диаметра. Они должны пересекаться под прямым углом.
3. Поставить точку V (пересечение окружности с одним из диаметров), которая является вершиной фигуры.
4. По левой стороне поставить точку D. Это пересечение диаметра (оси симметрии) с окружностью.
5. Отметить на отрезке OD точку А, которая делит его пополам.
6. Выполнить построение вспомогательной окружности, центром которой является точка, полученная в 5 пункте. Кроме того, круг с радиусом CV должен проходить через V.
7. Точку, полученную при пересечении диаметра и окружности, нужно обозначить литерой B.
8. Нарисовать окружность с радиусом, равным CV, из точки V.
9. Отметить пересечение круга с первой окружностью, центром которой является точка О. Искомое место пересечения обозначить литерой F (вторая вершина пентагона).
10. Поставить иглу циркуля в точку F и провести окружность через Е.
11. Обозначить пересечение окружностей с центрами в F и O точкой G, которая будет вершиной пентагона.
12. Аналогичным образом проделать шаг 11, только центр выбрать не в F, а в G. Полученную точку следует обозначить литерой H (последняя вершина фигуры).
13. Соединить пять точек (СVEFG) между собой с помощью линейки.

Если все пункты алгоритма выполнены правильно, то должен получиться пентагон, изображенный на рисунке 1:

Этот способ следует применять для точных построений и чертежей деталей. Однако для решения задач, в которых необходимо схематически изобразить пятиугольник, этот вариант не подойдет.

Алгоритм Биона

Прием Биона является менее точным методом, чем первый. Он позволяет построить любой правильный многоугольник, вписанный в произвольный круг. Для операции необходимо воспользоваться алгоритмом (шаблоном) Биона, имеющим такой вид:

1. Начертить окружность с центром в точке О и радиусом R.
2. Провести в ней диаметр АD.
3. Построить правильный (равносторонний) треугольник с одной из сторон, равной диаметру.
4. Поделить диаметр на несколько равных частей (АС = СE = ED), количество которых вычисляется по формуле: (n — 2). Переменная «n» эквивалентна количеству граней правильного многоугольника, то есть n = 3. Соотношение можно записать следующей зависимостью: АС = [1 / (n — 2)] * AD = AD / 3.
5. Провести из точек С и Е прямые, перпендикулярные диаметру.
6. Точки пересечения прямых с окружностью обозначить F и G.
7. Если соединить точки, то получится пентагон ABDFG.

Погрешность построения многоугольника с 5, 7, 9 и 10 сторонами при использовании алгоритма довольно маленькая. Ее значения равно 3,2%. Однако при n>10 погрешность составляет не более 11%.

Приближенные методы

Существует несколько методов, позволяющих приближенно изобразить фигуру. Однако оптимальным является построение пентагона (рис. 2), используя две окружности (описанную и вписанную).

Метод известного математика А. Дюрера является оптимальным среди остальных, поскольку на построение затрачивается минимальное количество времени. Для его реализации следует выполнить определенные шаги алгоритма Дюрера:

1. Начертить произвольную окружность с центром в точке О.
2. Не вынимая иглу циркуля из точки О, выполнить построение другой окружности. Ее радиус нужно уменьшить таким образом, чтобы общий радиус R был равен стороне пятиугольника.
3. Отметить на окружности с большим радиусом две произвольные точки. При этом следует руководствоваться правилом: прямая, проходящая через них, должна касаться малой окружности в одной точке (касательная).
4. Отметить следующую точку, чтобы можно было соединить ее с предыдущей. Правило при этом должно соблюдаться.
5. Аналогично проделать операции с другими сторонами пентагона.

Существует еще один метод — построение пятиугольника из десятиугольника, который вписан в окружность. Для этого следует соединить его вершины через одну. Однако способ рекомендуется применять только в том случае, когда исходная фигура уже имеется. Кстати, его следует строить также методом А. Дюрера.

Математики рекомендуют еще один простой способ. Для его реализации необходимо начертить окружность с диаметром АD. После этого его нужно поделить на 3 равные части, то есть AB = BC = CD. Затем из точки С следует опустить перпендикуляры на окружность. Обозначить места пересечения точками E и F. Проделать такую же процедуру с точкой B, обозначив пересечения точками G и H. Остается лишь соединить все точки отрезками.

Признаки и свойства

Не всегда получается верно идентифицировать пятиугольник. Для этого математики предлагают признаки, которые применимы только к правильной фигуре. К ним можно отнести следующие:

1. Стороны равны между собой.
2. Любой угол правильного пятиугольника равен остальным его углам.

Следует отметить, что признаки справедливы для любого правильного многогранника. Пять осей симметрии имеет правильный пятиугольник (сколько сторон, столько и осей). Пентагон обладает некоторыми свойствами, которые будут очень полезны при решении задач. К ним можно отнести следующие:

1. Равенство сторон.
2. Углы равны по 108 градусов.
3. Центры вписанной и описанной окружностей совпадают.
4. Сумма внутренних углов равна 180 * (5 — 2) = 540 (градусов), а внешних — 360.
5. Количество диагоналей соответствует 5.
6. Значение площади кольца, которое образуется между вписанным и описанным кругами, эквивалентно произведению квадрата длины стороны на константу Pi / 4.
7. Биссектрисы, проведенные через центр, равны.
8. Диагонали — трисектрисы внутренних углов. Одна диагональ делит его на 1/3 и 2/3 части.
9. Отношение диагонали к стороне эквивалентно «золотому сечению» и равно [1 + 5^(1/2)] / 2.

Однако свойств недостаточно при решении задач, поскольку существуют некоторые формулы и соотношения для нахождения основных параметров пентагона.

Расчет параметров

С помощью соотношений можно легко найти необходимые характеристики любой фигуры. Однако в некоторых источниках не указаны условные обозначения известного параметра пентагона. Это существенно затрудняет понимание формулы, а также ее дальнейшее использование. Перед изучением следует нарисовать фигуру и обозначить некоторые величины, которыми могут быть диагонали, стороны, апофемы и радиусы.

Рекомендуется использовать различные литеры или буквенные обозначения. Недопустимо пронумеровывать вершины, поскольку при вычислениях можно ошибиться. Нельзя использовать вместо букв цифры при обозначениях. Например, пентагон ABCDE является правильной записью. Допускается применение чисел в индексах, а именно, в пятиугольнике правильного типа ABCDE при пересечении его диагоналей образовался пентагон A1B1C1D1E1.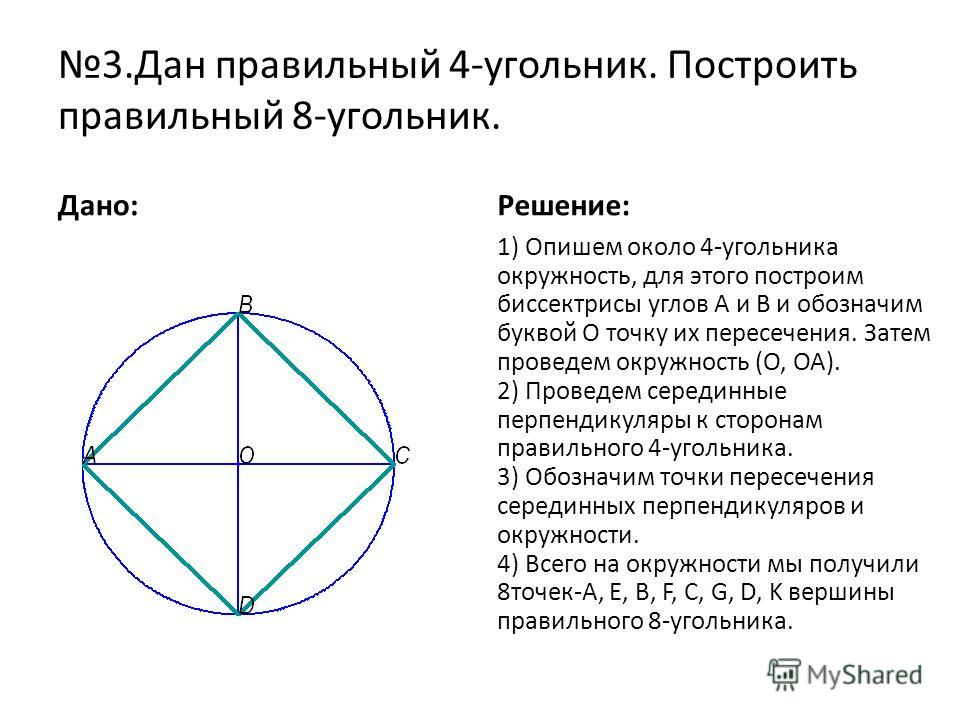

Математики рекомендуют обозначать только промежуточные фигуры или их проекции литерами с индексами. Для каждой новой фигуры следует вводить другие обозначения. Не следует использовать зарезервированные переменные. Например, центр окружности в точке P является недопустимой записью, поскольку такой буквой обозначается периметр.

Условные обозначения

Для нахождения основных величин пентагона следует обозначить некоторые его параметры. Фигура имеет следующие обозначения:

1. Сторона: a.
2. Радиус вписанной и описанной окружностей: r и R соответственно.
3. Площадь: S.
4. Периметр и полупериметр: P и p соответственно.
5. Диагональ: d.
6. Отношение золотого сечения: Ф.

Значения сторон равны между собой. Площадь правильного пятиугольника — характеристика двумерной фигуры, которая показывает ее размерность. Периметром называется сумма всех 5 сторон. Полупериметр вычисляется по следующему соотношению: p = P / 2.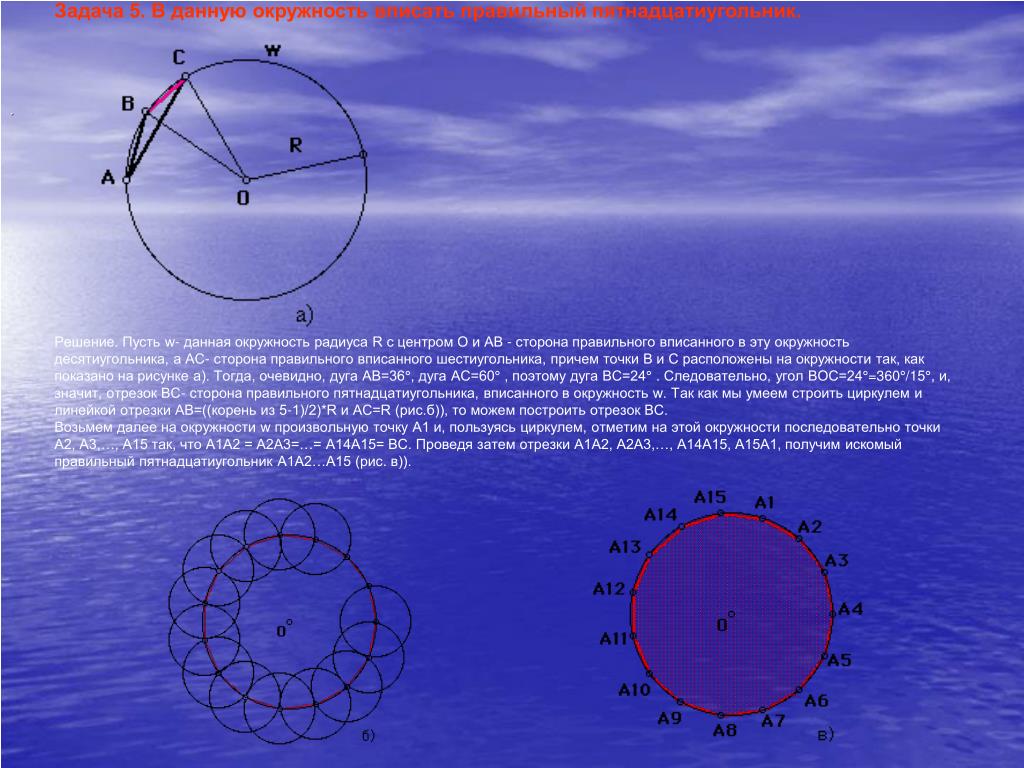 (1/2).

Таким образом, при решении задач необходимо знать основные признаки, свойства, соотношения и формулы для нахождения основных характеристик пентагона. Практика обязательна, поскольку теоретические знания без практического применения бесполезны.

Polygon Rings

Возраст от 11 до 14 лет

Уровень сложности

 
Летиция из школы Бангкок Патана в Таиланде, Роуз из школы Ченнинг в Великобритании, Кэролайн, Маркос и Джейн из школы Kings’ School Аль Барша в ОАЭ и Алекс из школы Leighton Park School в Великобритании выяснили, сколько пятиугольников образуют кольцо.

Маркос использовал диаграмму, чтобы представить полное кольцо:
Что ж, если вы собираетесь представить себе круг, вы можете разделить его на 4 равных размера, один из которых равен двум пятиугольникам с половиной. Если вы добавите все, получится петля, полная пятиугольников [что дает 10 пятиугольников].

Летиция и Роуз использовали интерактивность, чтобы сделать полные пятиугольные кольца. Это кольцо Роуз:

Норави из школы короля Георга V в Гонконге, и Алекс использовала углы, чтобы объяснить, почему 10 пятиугольников образуют кольцо, не перекрываясь.

Ниже приведены пояснения и схема Алекса.
Нажмите здесь, чтобы увидеть работу Норави, которая более глубока, чем работа Алекса.
Поскольку кольцо состоит из правильных пятиугольников, мы можем вычислить, что каждый из внутренних углов каждого пятиугольника равен 108* градусам. Продлив линии, которые разделяют два пятиугольника, предполагая, что все они встречаются посередине, получится треугольник.

Поскольку мы знаем, что каждый угол [правильного] пятиугольника равен 108* градусам, мы знаем, что два угла при основании треугольника равны 72**, а верхний угол равен 36 градусам.

Поскольку [сумма] углов в точке составляет 360 градусов, а 36 делится на 360, получится полное кольцо.
Также, поскольку 360 х 36 = 10, мы знаем, что кольцо будет состоять из 10 пятиугольников.

Пятиугольники выше являются правильными пятиугольниками.

*формула для расчета размера внутреннего угла многоугольника равна $(n \times 180 — 360) \div n$ (где $n$ — количество сторон многоугольника).

**потому что треугольник образован продолжением линий, а углы на линии составляют $180$ градусов, $180 — 108$ (внутренний угол пятиугольника) $= 72.$

Кэролайн сказала, что 5 десятиугольников образуют кольцо , а Джейн сказала, что 10 десятиугольников образуют кольцо. Летиция сказала, что 5 десятиугольников образуют кольцо, но прислала эту картинку с 10 десятиугольниками в кольце (слева). Справа кольцо из 5 десятиугольников.

        

В кольце из 10 десятиугольников фигура в середине использует 3 стороны от каждого десятиугольника. В кольце из 5 десятиугольников фигура в середине использует 2 стороны от каждого десятиугольника.

Если мы заставим фигуру в середине использовать только одну сторону каждого десятиугольника (как мы сделали с пятиугольниками), тогда десятиугольники не могут образовать кольцо, потому что они перекрываются:

Какие многоугольники могут образовывать кольца вокруг фигуры который использует только 1 сторону каждого многоугольника?
Pinyo из Таиланда, Mimi, Denis, Jomkwan и Jessica из Headstart International School Phuket в Таиланде и Iqra из начальной школы Uphall в Великобритании прислали ответы на этот вопрос. Вот работы Джессики:
В кольце многоугольников некоторые определенные многоугольники могут образовывать кольцо с другим многоугольником внутри него. Не все полигоны могут это сделать. Единственная странность в этом заключается в том, что форма внутри кольца должна использовать только одну из внешних сторон.

Шестиугольник (6-угольник)

Мы можем видеть в шестиугольном кольце то, что форма, которая сформировалась внутри кольца, является шестиугольником. На этой диаграмме одна сторона формы используется для создания внутренней формы.

Октагон (8-угольник)

В этом восьмиугольнике 4, поставленные рядом, образуют квадрат посередине. Следовательно, это соответствует моему исследованию многоугольных колец.

Додекагон (12-угольник)
 
В этом двенадцатиугольнике по 3 элемента каждой формы были использованы для создания многоугольника в середине. Как мы видим, фигура представляет собой треугольник и используется только 1 сторона каждой фигуры.

Икра обнаружил, что это также работает с квадратами:
Вы также можете использовать квадраты, чтобы сделать кольцо. Я использовал 12 квадратов, но вы можете сделать их настолько большими, насколько захотите.

Даниэль из академии Мур-Энд в Великобритании и Мими посмотрели на углы многоугольника, который образовался посередине. Это работа Даниэля:
Используются только правильные многоугольники, поэтому мы можем предположить, что внутренний угол каждого [многоугольника], используемого в диаграмме, [составляет] $\dfrac{(n-2) \times 180}n$

При соединении двух правильных [многоугольников] сумма двух внутренних углов и $x$ (где $x$ внутренний угол многоугольника в середине) равна $360.$

Решая уравнение $2\times \dfrac{(n-2) \times 180}n + x = 360$, находим $x$.

Нам нужно найти внешний угол, чтобы найти количество сторон. Мы делаем это, вычитая [$x$] из $180$.

Если мы разделим $360$ на [внешний угол], мы получим количество сторон многоугольника в центре.

Окончательное уравнение того, как сделать кольцо любой формы: $$\frac{360}{-180+\left(\frac{(n-2)\times360}n\right)}=\text {стороны или необходимое количество полигонов}$$
Знаменатель может быть записан как: $$\begin{split}-180+\left(\dfrac{(n-2)\times360}n\right)&=\dfrac{-180n}n+\dfrac{(n -2)\times360}n\\

&=\dfrac{-180n+360n-720}{n}\\
&=\dfrac{180(n-4)}{n}\end{split}$$
Это означает, что формула для количества сторон может быть переписана как: (n-2)\times360}n\right)}\\
&=\frac{360}{\frac{180(n-4)}{n}}\\
&=\frac{360n}{180 (п-4)}\\
&=\frac{2n}{n-4}\end{split}$$

Флоренс из начальной школы Уолтемстоу Холл указала, что это должно быть целое число. Этого достаточно, чтобы найти, сколько существует различных колец:
$s=\frac{2n}{n-4}\Rightarrow s(n-4)=2n$

Формула

$s$	для $n$	можно?
$3 $	$3(n-4)=2n\\ 3n-12=2n$	$n=12$ (просмотрено)
4$	$4n-16=2n\\ 2n=16$	$n=8$ (просмотрено)
$5$	$5n-20=2n\\ 3n=20$	нет
$6$	$6n-24=2n\\ 4n=24$	$n=6$ (просмотрено)
7$	$7n-28=2n\\ 5n=28$	нет
8$	$8n-32=2n\\ 6n=32$	нет
9$	$9n-36=2n\\ 7n=36$	нет
10$	$10n-40=2n\\ 8n=40$	$n=5$ (просмотрено)

• $s$ не может быть меньше $3$, поэтому двенадцатиугольники — это самые большие многоугольники, которые могут образовывать кольцо (вокруг треугольника)
• Продолжить поиск, используя $n$, начиная с суммы ниже $5$, $n=3$ или $n=4$

$n$	$s=\frac{2n}{n-4}$	комментарий
4$	деление на ноль	Это согласуется с наблюдением Икры о том, что вы можете использовать столько квадратов, сколько захотите
$3 $	отрицательный	На самом деле треугольники образуют кольцо, но в середине нет формы

Какие многоугольники могут образовывать кольца вокруг фигур, использующих более одной стороны каждого многоугольника?
Мими нашла следующие кольца многоугольников:
5 десятиугольников используют по 2 стороны каждый, 10 десятиугольников используют 3 стороны каждый, 14 семиугольников используют 3 стороны каждый, 18 нонагонов используют 3 стороны каждый, 22 десятиугольника используют 4 стороны каждый.

Построение правильных многоугольников — технический чертеж. Как нарисовать правильный восьмиугольник Как нарисовать правильный восьмиугольник

Построение правильного шестиугольника, вписанного в окружность. Построение шестиугольника основано на том, что его сторона равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (рис. 60, а).

Правильный шестиугольник можно построить из Т-угольника и квадрата 30X60°. Для выполнения этого построения за биссектрису углов 1 и 4 (рис. 60, б) берем горизонтальный диаметр окружности, строим стороны 1-6, 4-3, 4-5 и 7-2, после чего стороны розыгрыша 5-6 и 3-2.

Построение равностороннего треугольника, вписанного в окружность . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами 30 и 60° или только одного циркуля.

Рассмотрим два способа построения равностороннего треугольника, вписанного в окружность.

Первый способ (рис. 61, а) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная линия, проведенная через точку 7, является одновременно и высотой, и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то найти сторону

1-2, достаточно построить угол 30° в точке 1 и стороне 0-1. Для этого установите Т-угольник и угольник, как показано на рисунке, проведите линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, установите Т-образный квадрат в положение, показанное пунктирными линиями, и проведите прямую линию через точку 2, которая определит третью вершину треугольника.

Второй способ основан на том, что если построить правильный шестиугольник, вписанный в окружность, а затем соединить его вершины через единицу, то получится равносторонний треугольник.

Для построения треугольника (рис. 61, б) отмечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4.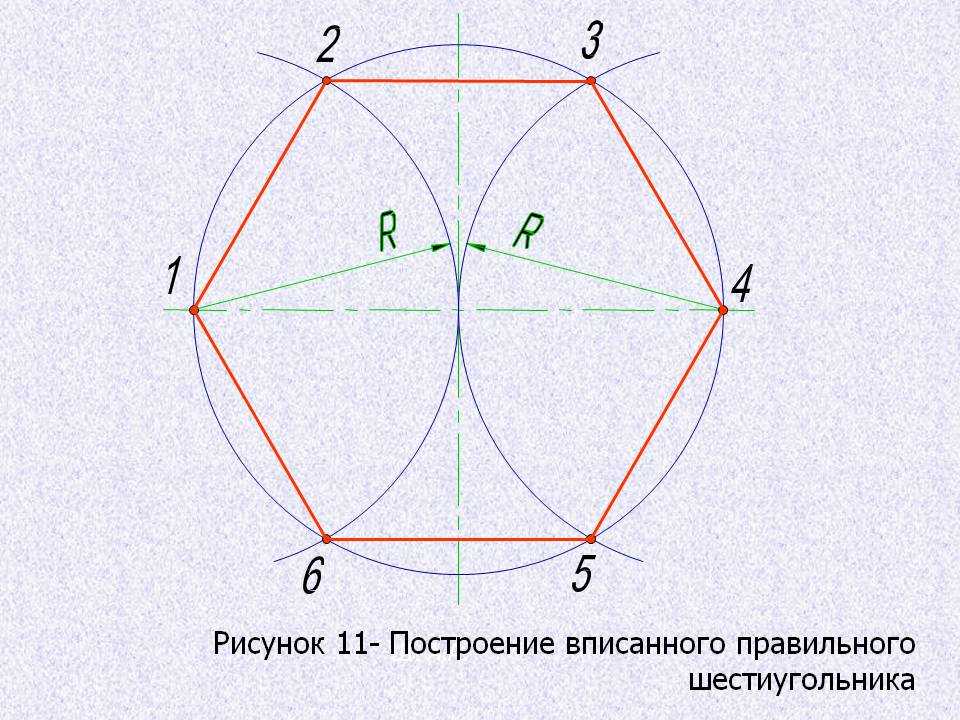 Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.

Построение квадрата, вписанного в окружность . Это построение можно сделать с помощью угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пересекаются в центре описанной окружности и наклонены к ее осям под углом 45°. Исходя из этого, устанавливаем Т-образный угольник и угольник с углами 45°, как показано на рис. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим горизонтальные стороны угольника 4- 1 и 3-2 с помощью Т-угольника. Затем с помощью Т-угольника по катету квадрата рисуем вертикальные стороны квадрата 1-2 и 4-3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключенные между концами диаметра (рис. 62, б). Отмечаем точки А, В и С на концах двух взаимно перпендикулярных диаметров и от них радиусом у описываем дуги до их пересечения.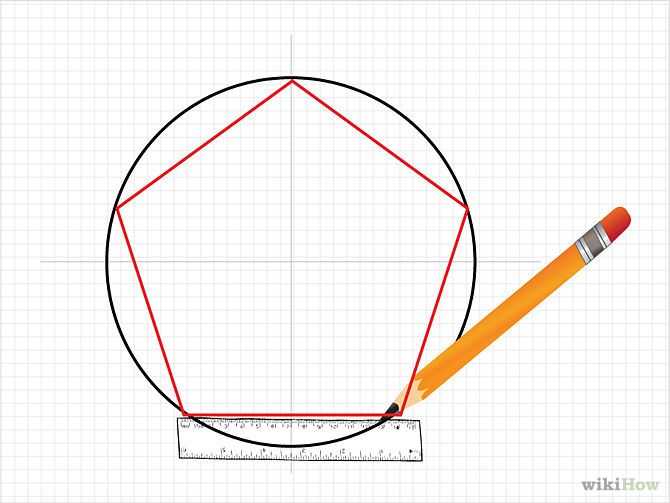

Далее через точки пересечения дуг проводим вспомогательные линии, отмеченные на рисунке сплошными линиями. Их точки пересечения с окружностью будут определять вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяются последовательно друг с другом.

Построение правильного пятиугольника, вписанного в окружность.

Для вписания правильного пятиугольника в окружность (рис. 63) проведем следующие построения.

Отмечаем на окружности точку 1 и принимаем ее за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках М и В. Соединив эти точки прямой, получим точку К, которую затем соединим с точкой 1. С радиусом, равным отрезку А7, описываем дугу от точки К до пересечения с диаметральной линией АО в точке Н. Соединив точку 1 с точкой Н, получим сторону пятиугольника. Затем при апертуре, равной отрезку 1Н, описав дугу от вершины 1 до пересечения с окружностью, находим вершины 2 и 5.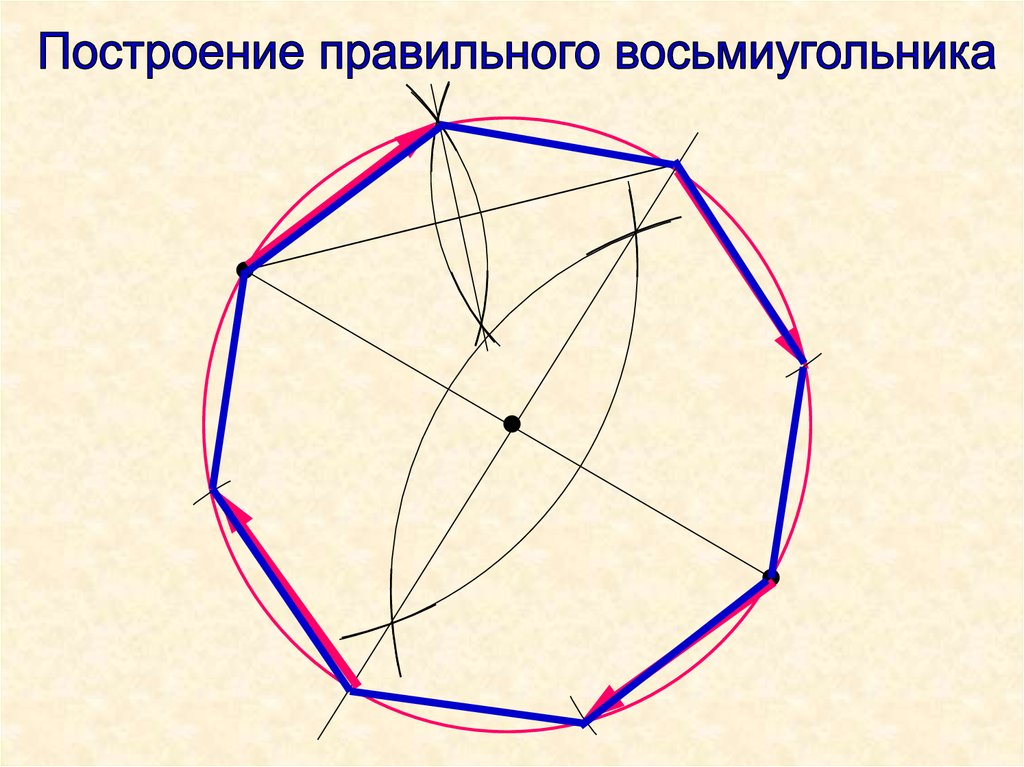 Сделав из вершин 2 и 5 засечки с тем же апертурой, получим оставшиеся вершины 3 и 4. Соединяем найденные точки последовательно друг с другом.

Построение правильного пятиугольника по стороне.

Чтобы построить правильный пятиугольник по заданной стороне (рис. 64), разделим отрезок АВ на шесть равных частей. Из точек А и В радиусом АВ описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой АВ проводим вертикальную линию.

Получаем точку 1-вершины пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, проведенными ранее из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Соединяем найденные вершины последовательно друг с другом.

Построение правильного семиугольника, вписанного в окружность.

Пусть дан круг диаметром D; в него нужно вписать правильный семиугольник (рис. 65). Разделите вертикальный диаметр круга на семь равных частей.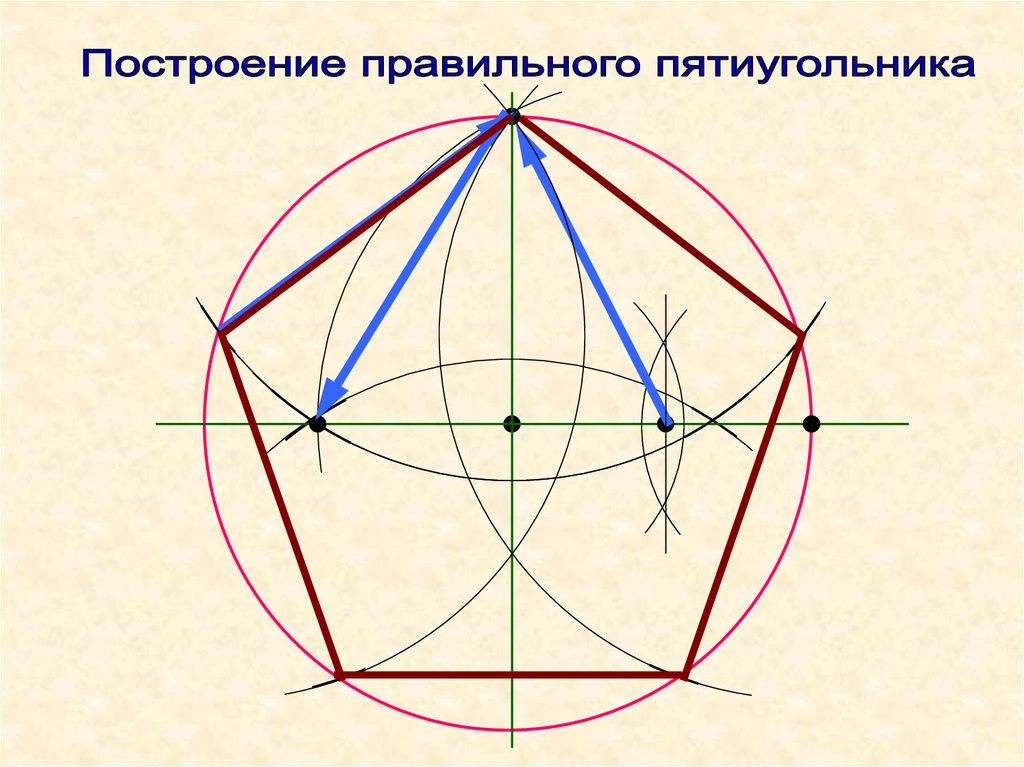 Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точка F называется полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проведем лучи от полюса F через четные деления вертикального диаметра, пересечение которых с окружностью определит вершины VI, V и IV семиугольника. Для получения вершин /-//-// из точек IV, V и VI проводим горизонтальные линии до пересечения с окружностью. Соединяем найденные вершины последовательно друг с другом. Семиугольник можно построить, проводя лучи от полюса F и через нечетные деления вертикального диаметра.

Описанный выше метод подходит для построения правильных многоугольников с любым количеством сторон.

Деление окружности на любое количество равных частей можно произвести и по данным табл. 2, где приведены коэффициенты, позволяющие определить размеры сторон правильных вписанных многоугольников.

Куклин Алексей

Работа носит реферативный характер с элементами исследовательской деятельности. В нем обсуждаются различные способы построения правильных n-угольников. В работе содержится подробный ответ на вопрос, всегда ли можно построить n-угольник с помощью циркуля и линейки. К работе прилагается презентация, которую можно найти на этом мини-сайте.

Скачать:

Предварительный просмотр:

Чтобы использовать предварительный просмотр, создайте себе учетную запись Google (аккаунт) и войдите в систему: https://accounts.google.com

Предварительный просмотр:

https://accounts.google. com

Подписи к слайдам:

Построение правильных многоугольников Работу выполнил: учащийся 9 «Б» МБОУ СОШ № 10 Куклин Алексей

Правильные многоугольники Правильным многоугольником называется выпуклый многоугольник, у которого все стороны и углы равны. Перейти к примерам Выпуклый многоугольник — это многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его смежные вершины.

Назад Правильные многоугольники

Основоположниками раздела математики о правильных многоугольниках были древнегреческие ученые. Одними из них были Архимед и Евклид.

Доказательство существования правильного n-угольника Если n (количество углов многоугольника) больше 2, то такой многоугольник существует. Попробуем построить 8-угольник и доказать это. Доказательство

Возьмем окружность произвольного радиуса с центром в точке О. Разделим ее на определенное количество равных дуг, в нашем случае 8. Для этого проведем радиусы так, чтобы получилось 8 дуг, а угол между двумя ближайшими радиусы составили 360°: количество сторон (в нашем случае случае 8), соответственно каждый угол будет равен 45°.

3. Получить очки A1, A2, A3, A4, A5, A6, A7, A8. Соединяем их по очереди и получаем правильный восьмиугольник. Назад

Построение правильного многоугольника по стороне с помощью вращения Правильный многоугольник можно построить, зная его углы. Мы знаем, что сумма углов выпуклого n-угольника равна 180°(n — 2). Отсюда можно вычислить угол многоугольника, разделив сумму на n. Angles Building

Прямой угол: 3-угольник равен 60° 4-угольник равен 90° 5-угольник равен 108° 6-угольник равен 120° 8-угольник равен 135° 9-угольник равен 140° 10-угольник равен 144° 12-угольник равен 150° Градусная мера углов правильных треугольников Назад

Предварительный просмотр:

Для использования предварительного просмотра презентаций создайте учетную запись Google (аккаунт) и войдите: https ://accounts.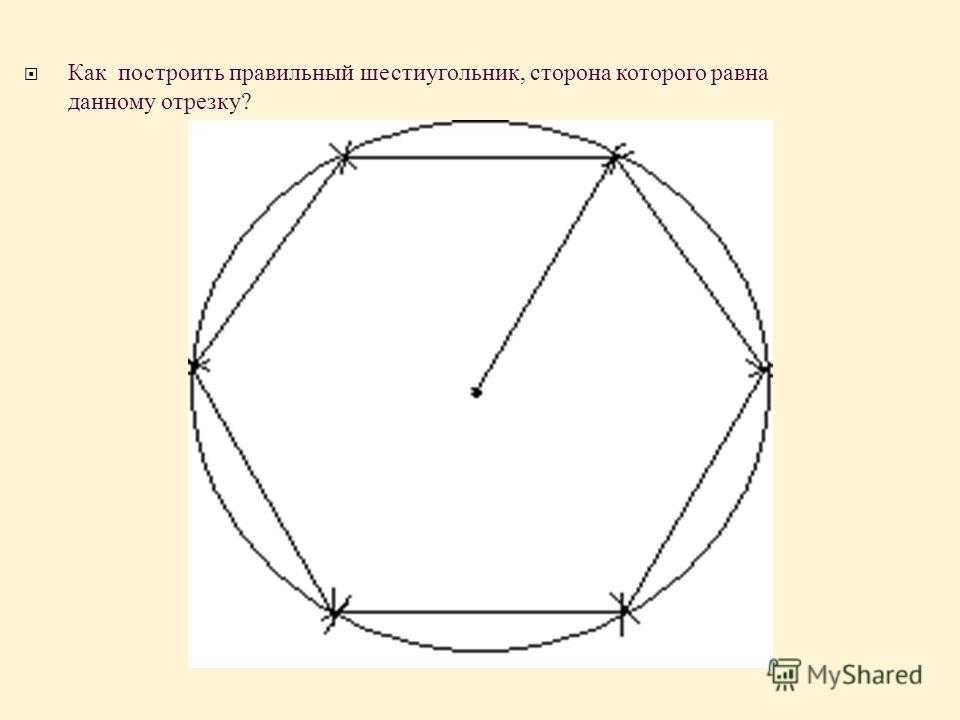 google.com

Подписи к слайдам:

В 1796 году один из величайших математиков всех времен Карл Фридрих Гаусс показал возможность построения правильных n-угольников, если выполняется равенство, где n — количество углов, а k — любое натуральное число. Таким образом, оказалось, что в пределах 30 можно разделить круг на 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30 равных частей. В 1836 году Ванзель доказал, что правильные многоугольники, не удовлетворяющие этому равенству, нельзя построить с помощью линейки и циркуля. Теорема Гаусса

Построение треугольника Построим окружность с центром в точке О. Построим еще одну окружность такого же радиуса, проходящую через точку О.

3. Соединим центры окружностей и одну из точек их пересечения, получив правильную полигон. Назад Рисуем треугольник

Построение шестиугольника 1. Построим окружность с центром в точке О. 2. Проведем прямую через центр окружности. 3. Нарисуйте дугу окружности того же радиуса с центром в точке пересечения прямой с окружностью до пересечения с окружностью.

4. Проведите прямые через центр исходной окружности и точки пересечения дуги с этой окружностью. 5. Соединяем точки пересечения всех линий с исходной окружностью и получаем правильный шестиугольник. Построение шестиугольника

Построение четырехугольника Построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Из точек, в которых диаметры касаются окружности, проводим другие окружности заданного радиуса до их пересечения (окружности).

Построение четырехугольника 4. Проведите прямые через точки пересечения окружностей. 5. Соединяем точки пересечения прямых и окружности и получаем правильный четырехугольник.

Построение восьмиугольника Можно построить любой правильный многоугольник, у которого в 2 раза больше углов, чем у заданного. Давайте построим восьмиугольник, используя четырехугольник. Соедините противоположные вершины четырехугольника. Проведем биссектрисы углов, образованных пересекающимися диагоналями.

4. Соедините точки, лежащие на окружности, получив правильный восьмиугольник. Построение восьмиугольника

Предварительный просмотр:

Чтобы использовать предварительный просмотр презентаций, создайте учетную запись Google (аккаунт) и войдите: https://accounts.google.com

Подписи к слайдам:

Построение десятиугольника Давайте построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Разделите радиус окружности пополам и из полученной точки начертите на ней окружность, проходящую через точку О.

Построение десятиугольника 4. Проведите отрезок от центра маленького круга до точки, где большой круг касается своего радиуса. 5. Из точки соприкосновения большого круга и его радиуса начертите круг так, чтобы он соприкасался с малым.

Построение десятиугольника 6. Из точек пересечения большого и получившегося кругов проводим построенные в прошлый раз круги и так будем рисовать до соприкосновения соседних кругов. 7. Соедините точки и получите десятиугольник.

Построение пятиугольника Чтобы построить правильный пятиугольник, нужно соединить не все точки по очереди, а через одну, при построении правильного десятиугольника.

Приближенное построение правильного пятиугольника методом Дюрера Построим 2 окружности, проходящие через центры друг друга. Соединим центры прямой линией, получив одну из сторон пятиугольника. Соедините точки пересечения окружностей.

Приблизительное построение правильного пятиугольника по методу Дюрера 4. Нарисуем еще одну окружность того же радиуса с центром в точке пересечения двух других окружностей. 5. Нарисуем 2 отрезка, как показано на рисунке.

Приближенное построение правильного пятиугольника по методу Дюрера 6. Соедините точки касания этих отрезков окружностями с концами построенной стороны пятиугольника. 7. Построим пятиугольник.

Приближенное построение правильного пятиугольника методами Коваржика, Биона

В черчении часто требуется строить положительные многоугольники. Итак, скажем, положительные восьмиугольников используются на дорожных знаках.

Вам понадобится

• — компасы
• — линейка
• — карандаш

Инструкция

1. Пусть задан отрезок, равный длине стороны искомого восьмиугольника. Требуется построить настоящий восьмиугольник. Первым шагом является построение равнобедренного треугольника на заданном отрезке, используя отрезок в качестве основания. Для этого сначала постройте квадрат со стороной, равной отрезку, проведите в нем диагонали. Теперь постройте биссектрисы углов по диагоналям (на рисунке биссектрисы обозначены синим цветом), на пересечении биссектрис образуется вершина равнобедренного треугольника, стороны которого равны радиусу круг, описанный вокруг правильного восьмиугольника.

2. Построить окружность с центром в вершине треугольника. Радиус окружности равен стороне треугольника. Теперь разведите компас на расстояние, равное величине данного отрезка. Отложите это расстояние по кругу, начиная с каждого конца отрезка. Объедините все полученные точки в восьмиугольник.

3. Если дана окружность, в которую следует вписать восьмиугольник, то построения будут еще проще.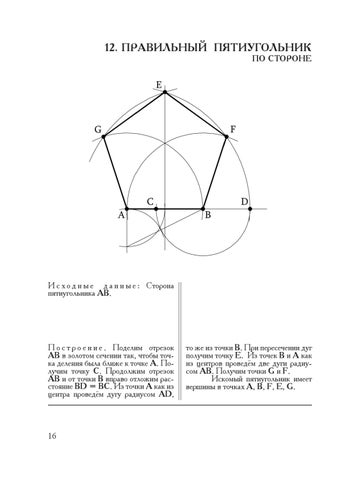 Постройте две центральные линии, перпендикулярные друг другу, проходящие через центр круга. На пересечении оси и окружности получится четыре вершины будущего восьмиугольника. Осталось разделить расстояние между этими точками на дуге окружности пополам, чтобы получить еще четыре вершины.

Верный треугольник — такой, у которого все стороны имеют одинаковую длину. Основываясь на этом определении, построение многообразия аналогичного треугольнику является простой задачей.

Вам понадобится

• Линейка, лист линованной бумаги, карандаш

Инструкция

1. Возьмите лист чистой бумаги, разлинованный в клеточку, линейку и отметьте на бумаге три точки так, чтобы они находились на одинаковом расстоянии друг от друга (рис. 1)

2. С помощью линейки совместите отмеченные на листе точки пошагово, одну за другой, как показано на рисунке 2.

Внимание!
В прямоугольном (равностороннем) треугольнике все углы равны 60 градусов.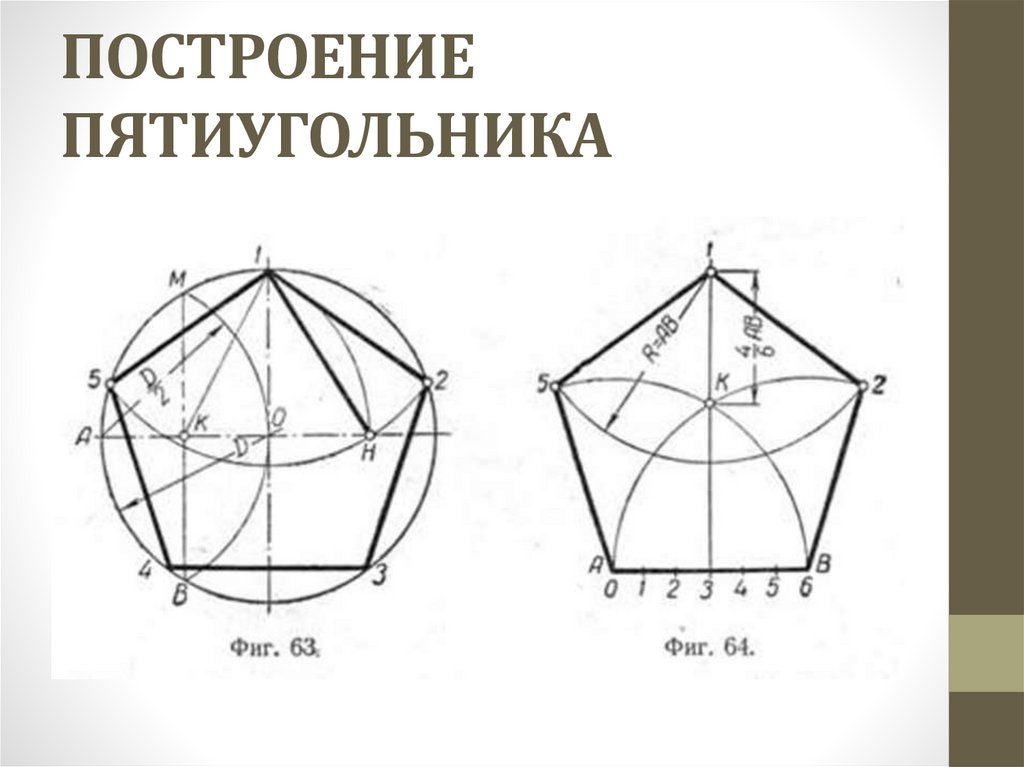

Полезный совет
Равносторонний треугольник также является равнобедренным. Если треугольник равнобедренный, то это означает, что 2 из 3 его сторон равны, а третья сторона считается основанием. Каждый положительный треугольник равнобедренный, а обратное неверно.

Октагон — это, по сути, два квадрата, смещенные друг относительно друга на 45° и объединенные в вершинах сплошной линией. И поэтому, чтобы положительно изобразить такую ​​геометрическую фигуру, нужно нарисовать квадрат или круг твердым карандашом, по правилам, с которыми выполнять последующие действия. Изложение ориентировано на длину стороны, равную 20 см. Итак, при компоновке чертежа учитывайте, чтобы вертикальные и горизонтальные линии длиной 20 см уместились на листе бумаги.

Вам понадобится

• Линейка, прямоугольный треугольник, транспортир, карандаш, циркуль, лист бумаги

Инструкция

1. Способ 1. Проведите снизу горизонтальную линию длиной 20 см. После этого с одной стороны проведите транспортиром прямой угол, тот, что равен 90°. То же самое можно сделать с опорой на прямоугольный треугольник. Проведите вертикальную линию и проведите 20 см. Те же манипуляции проделайте с другой стороны. Соедините две полученные точки горизонтальной линией. В результате получается геометрическая фигура – ​​квадрат.

2. Чтобы построить 2-й (сдвинутый) квадрат, вам нужен центр фигуры. Для этого разделите каждую сторону квадрата на 2 части. Соедините сначала 2 точки параллельных верхней и нижней сторон, а затем точки сторон. Проведите 2 прямые линии через центр квадрата перпендикулярно друг другу. Начиная от центра, отмерьте по новым прямым линиям 10 см, в результате получится 4 прямые линии. Объедините полученные 4 крайние точки друг с другом, в результате чего получится 2-й квадрат. Теперь совместите любую точку из 8 полученных углов друг с другом. Таким образом, будет нарисован восьмиугольник.

3. Способ 2. Для этого потребуются циркуль, линейка и транспортир.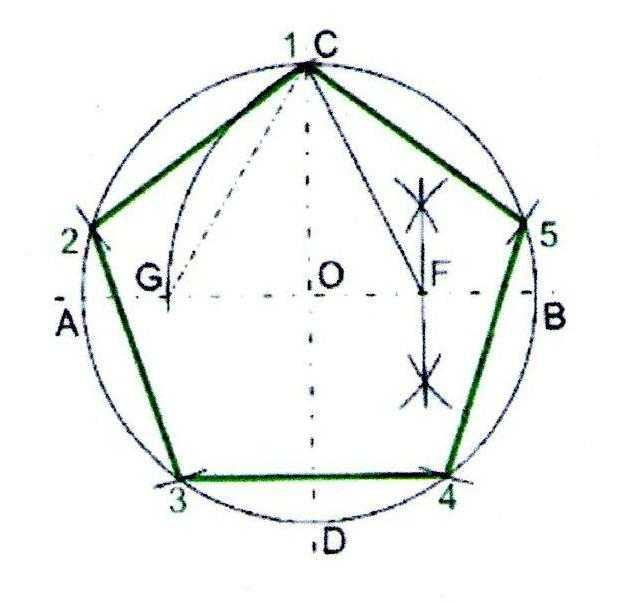 Из центра листа с помощью циркуля начертите окружность диаметром 20 см (радиус 10 см). Проведите прямую линию через центральную точку. После этого проведите вторую линию перпендикулярно ей. То же самое можно сделать с помощью транспортира или прямоугольного треугольника. В результате круг будет разделен на 4 равные части. Затем разделите каждую из секций еще на 2 части. Для этого также допускается использовать транспортир, размером 45° или с прямоугольным треугольником, тот, который присоединяет острый угол 45° и проводит лучи. Отмерьте 10 см от центра по любой прямой линии. В итоге у вас получится 8 «лучей», которые вы совместите друг с другом. В результате получается восьмиугольник.

4. Способ 3. Для этого таким же образом нарисуйте круг, проведите линию через середину. После этого возьмите транспортир, положите его в центр и измерьте углы, учитывая, что каждый участок восьмиугольника имеет в центре угол 45°. Позже на полученных лучах отмерьте длину 10 см и соедините их между собой. Октагон готов.

Полезный совет
Сделайте рисунок твердым карандашом, боковые линии на котором после этого будет легко удалить

Настоящий восьмиугольник — это геометрическая фигура, в которой каждый угол равен 135°, а все стороны равны друг другу. Эта фигура часто используется в архитектуре, например, при построении колонн, а также при изготовлении дорожного знака СТОП. Как нарисовать положительный восьмиугольник?

Вам потребуется

• — альбомный лист;
• — карандаш;
• — линейка;
• — компас;
• — ластик.

Инструкция

1. Сначала нарисуйте квадрат. После этого нарисуйте круг так, чтобы квадрат оказался внутри круга. Теперь проведите две осевые срединные линии квадрата — горизонтальную и вертикальную до пересечения с кругом. Совместите точки пересечения осей с окружностью и точки касания описанной окружности с квадратом с прямыми отрезками. Таким образом, получаются стороны настоящего восьмиугольника.

2. Нарисуйте настоящий восьмиугольник другим способом. Сначала нарисуйте круг. После этого проведите горизонтальную линию через его центр. Отметьте точку пересечения крайней правой границы круга с горизонталью. Эта точка будет центром другой окружности с радиусом, равным предыдущей фигуре.

3. Проведите вертикальную линию через точки пересечения 2-го круга с первым. Поместите ножку циркуля на пересечение вертикали и горизонтали и нарисуйте маленький круг с радиусом, равным расстоянию от центра маленького круга до центра исходного круга.

4. Проведите прямую через две точки — центр исходного круга и точку пересечения вертикали и маленького круга. Продолжайте его до пересечения с границей исходной фигуры. Это будет вершина восьмиугольника. Циркулем отметьте еще одну точку, начертив окружность с центром в точке пересечения крайней правой границы исходной окружности с горизонтальной линией и радиусом, равным расстоянию от центра до ближайшей вершины восьмиугольника.