Как разделить окружность на пять равных частей? —
Как разделить окружность на пять частей?
Рекомендуемый клип · 84 сек.
1 2 2 деление окружности на 5 равных частей — YouTube
YouTube
Начало рекомендуемого клипа
Конец рекомендуемого клипа
Как разделить окружность на 3 6 5 равных частей?
Рекомендуемый клип · 115 сек.
Деление окружности на 3; 6; 12 равных частей — YouTube
YouTube
Начало рекомендуемого клипа
Конец рекомендуемого клипа
Как разделить окружность на 10 равных частей?
Рекомендуемый клип · 104 сек.
Построение 10 угольника циркулем — YouTube
YouTube
Начало рекомендуемого клипа
Конец рекомендуемого клипа
Как разделить окружность на три равные части?
0:00
3:05
Рекомендуемый клип · 103 сек.
Как разделить круг на три равные части. — YouTube
YouTube
Начало рекомендуемого клипа
Конец рекомендуемого клипа
Как построить правильный 5 угольник с помощью циркуля?
Построение пятиугольника циркулем — YouTube
YouTube
Начало рекомендуемого клипа
Конец рекомендуемого клипа
Как разделить окружность на 6 равных частей?
Ставим на окружности точки (например, точки 2, 3, 4) Разворачиваем транспортир и делим другую часть окружности таким же способом. Бывает, что под рукой нет транспортира. Тогда окружность можно разделить на 6 равных частей с помощью циркуля. Чертим окружность, например, радиусом 5 см. (окружность красного цвета).6 дек. 2012 г.
Как разделить круг с помощью циркуля?
Деление окружности на пять равных частей выполняется в следующей последовательности:
- Из точки А радиусом, равным радиусу окружности R, проводим дугу, которая пересечет окружность в точке В;
- Из точки В опускают перпендикуляр на горизонтальную осевую линию;
Ещё
Как сделать 8 угольник?
Рекомендуемый клип · 96 сек.
Построение 8 угольника циркулем — YouTube
YouTube
Начало рекомендуемого клипа
Конец рекомендуемого клипа
Как построить правильный 7 Угольник?
Рекомендуемый клип · 98 сек.
Построение 7 угольника циркулем, приближенное — YouTube
YouTube
Начало рекомендуемого клипа
Конец рекомендуемого клипа
Как найти длину окружности круга?
Формула для вычисления длины окружности.
Длину окружности можно вычислить по двум формулам: C = 2πr или C = πd, где π – число «пи» (математическая константа, приблизительно равная 3,14), r – радиус окружности, d – диаметр окружности.
Как разделить круг на треугольник?
0:00
1:40
Рекомендуемый клип · 58 сек.
Как поделить окружность на 3 равные части. Очень просто
YouTube
Начало рекомендуемого клипа
Конец рекомендуемого клипа
Как определить длину окружности?
Запишите формулу для вычисления длины окружности через диаметр.
Как построить правильный 5 угольник?
Рекомендуемый клип · 87 сек.
Как начертить пятиугольник вписанный в круг или звезда — YouTube
YouTube
Начало рекомендуемого клипа
Конец рекомендуемого клипа
Как построить правильный 5 ти угольник?
Рекомендуемый клип · 120 сек.
Построение 5 угольника циркулем, метод с кругами Карлайла
YouTube
Начало рекомендуемого клипа
Конец рекомендуемого клипа
Как построить пятиугольник с заданной стороной?
Рекомендуемый клип · 121 сек.
Построение пятиугольника с заданной стороной циркулем
YouTube
Начало рекомендуемого клипа
Конец рекомендуемого клипа
Как разделить круг на 2 части?
Рекомендуемый клип · 84 сек.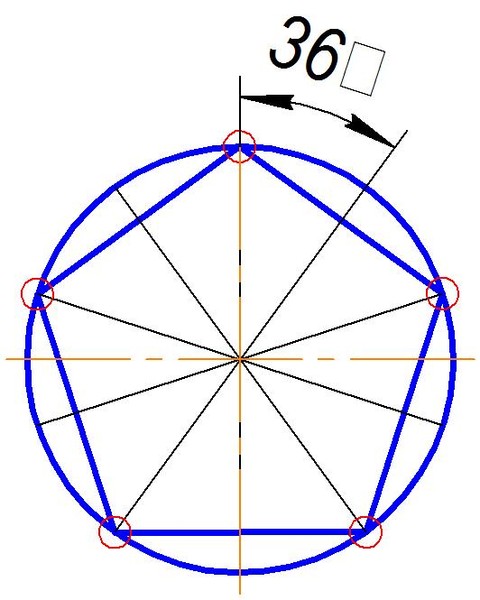
1 2 2 деление окружности на 5 равных частей — YouTube
YouTube
Начало рекомендуемого клипа
Конец рекомендуемого клипа
Как разделить круг на 9 частей без циркуля?
Рекомендуемый клип · 107 сек.
Построение девятиугольника циркулем, приближенное — YouTube
YouTube
Начало рекомендуемого клипа
Конец рекомендуемого клипа
Как разделить окружность на 7 равных частей?
Рекомендуемый клип · 47 сек.
1 2 3 деление окружности на 7 равных частей — YouTube
YouTube
Начало рекомендуемого клипа
Конец рекомендуемого клипа
Правильный 10 угольник. Построение правильных многоугольников
Десятиугольник, как и все многоугольники, можно легко построить с помощью циркуля и линейки. Существует два несложных способа для решения данной интересной и необычной задачи.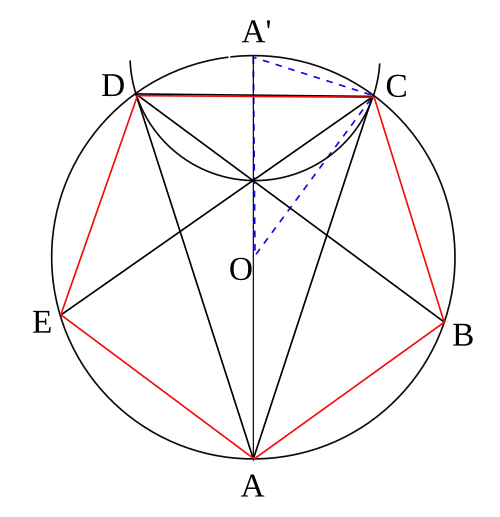
Вам понадобится
- — циркуль;
- — линейка.
Инструкция
Многоугольником называется замкнутая ломаная. Десятиугольник, соответственно, — это замкнутая ломаная, состоящая из 10 углов и 10 отрезков. Построить произвольный десятиугольник несложно. Для этого надо взять 10 любых точек, не лежащих на одной прямой, и соединить эти точки отрезками так, чтобы получилась замкнутая фигура. Причем должно выполняться условие: две любые точки внутри получившейся фигуры должны соединяться линией, не пересекающей границы фигуры. Если данное условие не выполняется, то построенная фигура не является многоугольником.
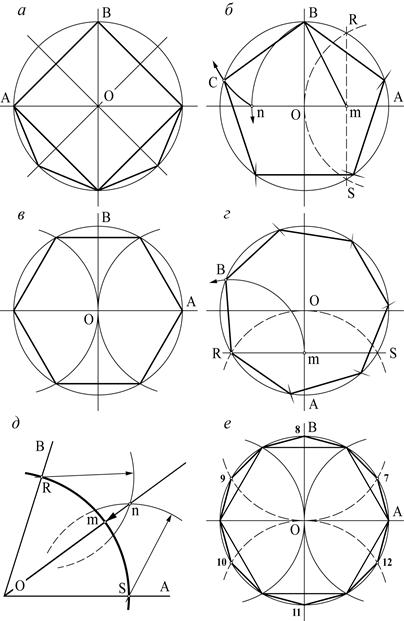
1 способ: С помощью циркуля начертите окружность. Используя транспортир, разделите ее на 10 равных секторов по 36 градусов каждый (360:10 = 36). Затем соедините последовательно все точки, отмеченные на окружности.
2 способ: Опять же, с помощью циркуля начертите окружность. Центр получившейся окружности обозначьте буквой О. Проведите два перпендикулярных диаметра данной окружности СD и АВ.
Дальше поставьте ножку циркуля в точку М и начертите окружность радиусом, равным половине радиуса первоначальной окружности. С помощью линейки соедините центр маленькой окружности М с любой из 2-х точек (А или В) на перпендикулярном диаметре. На рисунке центр маленькой окружности соединен сточкой А. Длина, получившегося отрезка АМ будет равна длине стороны десятиугольника. Осталось только сделать раствор циркуля, равный длине отрезка АМ, поставить ножку циркуля в точку А и отметить следующую точку на окружности. Далее переместите ножку циркуля в новую точку и отметьте следующую. И так до тех пор, пока на окружности не появится 10 равноудаленных друг от друга точек.
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
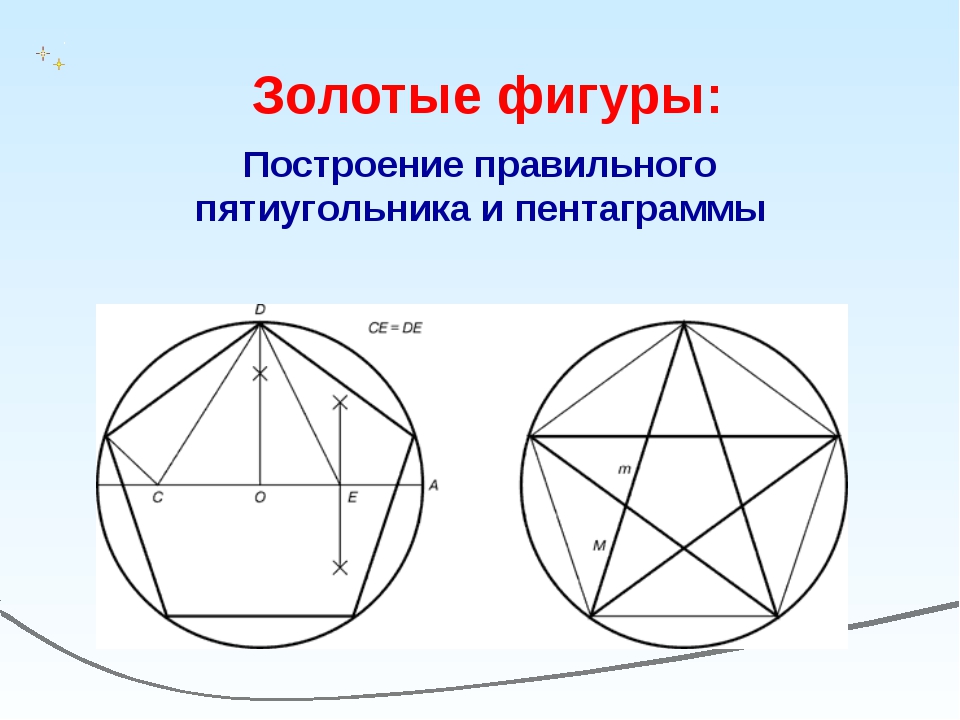
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. 2.
2.
Альтернативная формула A=2.5dt, где d — расстояние между параллельными сторонами или диаметр вписанной окружности. В тригонометрических функциях он выражается так:
d=2t\left(\cos\tfrac{3\pi}{10}+\cos\tfrac{\pi}{10}\right),
и может быть представлен в радикалах как
d=t\sqrt{5+2\sqrt{5}}.
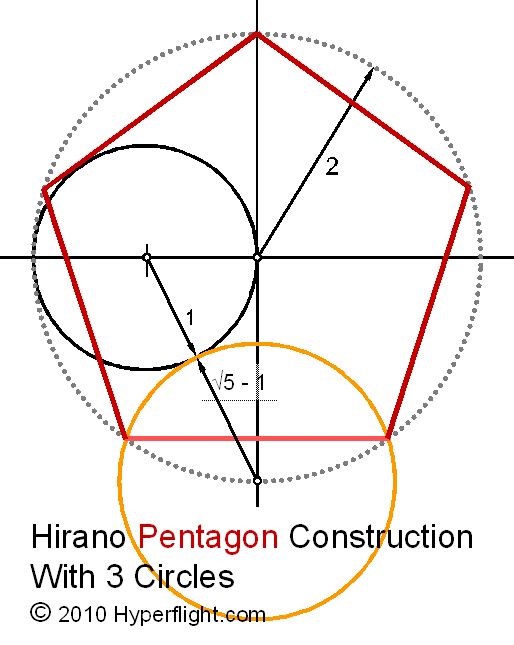
Сторона правильного десятиугольника, вписанного в единичную окружность , равна \tfrac{\sqrt{5}-1}{2}=\tfrac{1}{\varphi}, где \varphi — золотое сечение .
Радиус описанной окружности декагона равен
R=\frac{\sqrt{5}+1}{2}t,
а радиус вписанной окружности
r=\frac{\sqrt{5+2\sqrt{5}}}{2}t.
Построение
Иначе его можно построить следующим образом:
- Построить сначала правильный пятиугольник .
- Соединить все его вершины с центром описанной окружности прямыми до пересечения с этой же окружностью на противоположной стороне. В этих точках пересечения и находятся остальные пять вершин десятиугольника.
- Соединить по порядку вершины пятиугольника и пять точек, найденные шагом ранее.
 Искомый десятиугольник построен.
Искомый десятиугольник построен.
Разбиение правильного десятиугольника
Напишите отзыв о статье «Десятиугольник»
Ссылки
Отрывок, характеризующий Десятиугольник
– Ты озябла. Ты вся дрожишь. Ты бы ложилась, – сказала она.– Ложиться? Да, хорошо, я лягу. Я сейчас лягу, – сказала Наташа.
С тех пор как Наташе в нынешнее утро сказали о том, что князь Андрей тяжело ранен и едет с ними, она только в первую минуту много спрашивала о том, куда? как? опасно ли он ранен? и можно ли ей видеть его? Но после того как ей сказали, что видеть его ей нельзя, что он ранен тяжело, но что жизнь его не в опасности, она, очевидно, не поверив тому, что ей говорили, но убедившись, что сколько бы она ни говорила, ей будут отвечать одно и то же, перестала спрашивать и говорить. Всю дорогу с большими глазами, которые так знала и которых выражения так боялась графиня, Наташа сидела неподвижно в углу кареты и так же сидела теперь на лавке, на которую села. Что то она задумывала, что то она решала или уже решила в своем уме теперь, – это знала графиня, но что это такое было, она не знала, и это то страшило и мучило ее.
– Наташа, разденься, голубушка, ложись на мою постель. (Только графине одной была постелена постель на кровати; m me Schoss и обе барышни должны были спать на полу на сене.)
– Нет, мама, я лягу тут, на полу, – сердито сказала Наташа, подошла к окну и отворила его. Стон адъютанта из открытого окна послышался явственнее. Она высунула голову в сырой воздух ночи, и графиня видела, как тонкие плечи ее тряслись от рыданий и бились о раму. Наташа знала, что стонал не князь Андрей. Она знала, что князь Андрей лежал в той же связи, где они были, в другой избе через сени; но этот страшный неумолкавший стон заставил зарыдать ее. Графиня переглянулась с Соней.
– Ложись, голубушка, ложись, мой дружок, – сказала графиня, слегка дотрогиваясь рукой до плеча Наташи. – Ну, ложись же.
– Ах, да… Я сейчас, сейчас лягу, – сказала Наташа, поспешно раздеваясь и обрывая завязки юбок. Скинув платье и надев кофту, она, подвернув ноги, села на приготовленную на полу постель и, перекинув через плечо наперед свою недлинную тонкую косу, стала переплетать ее.
 Тонкие длинные привычные пальцы быстро, ловко разбирали, плели, завязывали косу. Голова Наташи привычным жестом поворачивалась то в одну, то в другую сторону, но глаза, лихорадочно открытые, неподвижно смотрели прямо. Когда ночной костюм был окончен, Наташа тихо опустилась на простыню, постланную на сено с края от двери.
Тонкие длинные привычные пальцы быстро, ловко разбирали, плели, завязывали косу. Голова Наташи привычным жестом поворачивалась то в одну, то в другую сторону, но глаза, лихорадочно открытые, неподвижно смотрели прямо. Когда ночной костюм был окончен, Наташа тихо опустилась на простыню, постланную на сено с края от двери.– Наташа, ты в середину ляг, – сказала Соня.
– Нет, я тут, – проговорила Наташа. – Да ложитесь же, – прибавила она с досадой. И она зарылась лицом в подушку.
Графиня, m me Schoss и Соня поспешно разделись и легли. Одна лампадка осталась в комнате. Но на дворе светлело от пожара Малых Мытищ за две версты, и гудели пьяные крики народа в кабаке, который разбили мамоновские казаки, на перекоске, на улице, и все слышался неумолкаемый стон адъютанта.
Долго прислушивалась Наташа к внутренним и внешним звукам, доносившимся до нее, и не шевелилась. Она слышала сначала молитву и вздохи матери, трещание под ней ее кровати, знакомый с свистом храп m me Schoss, тихое дыханье Сони.
 Потом графиня окликнула Наташу. Наташа не отвечала ей.
Потом графиня окликнула Наташу. Наташа не отвечала ей.– Кажется, спит, мама, – тихо отвечала Соня. Графиня, помолчав немного, окликнула еще раз, но уже никто ей не откликнулся.
Скоро после этого Наташа услышала ровное дыхание матери. Наташа не шевелилась, несмотря на то, что ее маленькая босая нога, выбившись из под одеяла, зябла на голом полу.
Как бы празднуя победу над всеми, в щели закричал сверчок. Пропел петух далеко, откликнулись близкие. В кабаке затихли крики, только слышался тот же стой адъютанта. Наташа приподнялась.
– Соня? ты спишь? Мама? – прошептала она. Никто не ответил. Наташа медленно и осторожно встала, перекрестилась и ступила осторожно узкой и гибкой босой ступней на грязный холодный пол. Скрипнула половица. Она, быстро перебирая ногами, пробежала, как котенок, несколько шагов и взялась за холодную скобку двери.
Ей казалось, что то тяжелое, равномерно ударяя, стучит во все стены избы: это билось ее замиравшее от страха, от ужаса и любви разрывающееся сердце.

Она отворила дверь, перешагнула порог и ступила на сырую, холодную землю сеней. Обхвативший холод освежил ее. Она ощупала босой ногой спящего человека, перешагнула через него и отворила дверь в избу, где лежал князь Андрей. В избе этой было темно. В заднем углу у кровати, на которой лежало что то, на лавке стояла нагоревшая большим грибом сальная свечка.
Приближенное построение правильных многоугольников с помощью циркуля и линейки. Учебно-методические пособие
1. Любимова Виктория Сергеевна, учитель математики ГБОУ СОШ 454 Колпинского района Санкт-Петербурга
ПРИБЛИЖЕННОЕ ПОСТРОЕНИЕправильных многоугольников
с помощью циркуля и линейки
Учебно-методические пособие
2. Пояснительная записка
• В геометрии нередко для различных целей требуетсяпостроить правильный n-угольник, но, как известно,
не все правильные n-угольники могут быть
построены с помощью циркуля и линейки абсолютно
точно.
• Тем не менее, для практических целей часто бывает
достаточно приближенного построения.
• В пособии рассматриваются некоторые способы
построения правильных n-угольников, которые без
особого труда могут освоить учащиеся.
3. Приближенное построение правильного семиугольника
Шаг 1. Построим окружность, в которую будет вписансемиугольник, и из произвольной точки этой окружности
проведем дугу тем же радиусом до пересечения с окружностью
в точках M и N:
M
N
4. Приближенное построение правильного семиугольника
Шаг 2. Половина хорды MN приблизительно равна стороневписанного семиугольника (разделить хорду пополам можно,
построив серединный перпендикуляр к отрезку MN)
M
N
5. Приближенное построение правильного семиугольника
Шаг 3. Строим дугу с центром в точке М радиуса, равногополовине хорды MN, находим точки A и B пересечения с
окружностью.
А
N
M
В
6. Приближенное построение правильного семиугольника
Шаг 4. Аналогично находим положение остальных вершинсемиугольника:
А
В
7.
 Приближенное построение правильного семиугольника Шаг 5. Соединяя найденные точки на окружности, получаем
Приближенное построение правильного семиугольника Шаг 5. Соединяя найденные точки на окружности, получаемискомый правильный семиугольник
8. Деление окружности на n равных частей
Задача о делении данной окружности на n равныхчастей равносильна задаче о построении правильного
n-угольника, вписанного в эту окружность.
Универсальный способ приблизительного построения
любого правильного n-угольника, вписанного в
окружность, особенно удобен при нечетном числе
сторон.
Величина погрешности при точном построении
не превышает 0,02d (где d – диаметр данной
окружности, описанной около многоугольника).
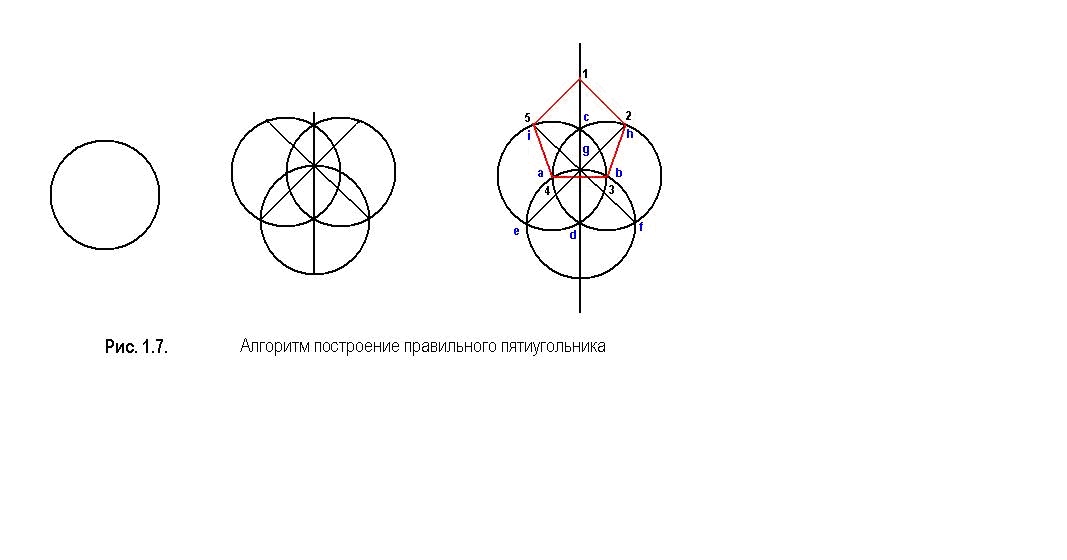
9. Последовательность действий
• Строим окружность заданного диаметра (если диаметр не задан,то выбираем такой, чтобы его удобно было разделить на
нужное число частей).
• Проводим два взаимно перпендикулярных диаметра.
• Вертикальный диаметр делим на нужное число частей.
• Из какого-либо конца вертикального диаметра, как из центра,
проводим дугу окружности радиусом, равным выбранному
диаметру, до пересечения с прямой, содержащей
горизонтальный диаметр, в двух точках справа и слева от
окружности.
• Из левой точки проводим лучи через четные деления
вертикального диаметра до пересечения с окружностью.
Аналогично проводим лучи через правую точку и те же деления
на вертикальном диаметре. В точках пересечения лучей с
окружностью получаем искомые вершины многоугольника.
• Соединяя полученные точки отрезками, строим многоугольник.
10. Приближенное построение правильного пятиугольника
Шаг 1. Строим окружность заданного диаметра, проводим двавзаимно перпендикулярных диаметра и один из диаметров
делим на нужное число частей (в данном случае – на пять
равных частей).
11. Приближенное построение правильного пятиугольника
Шаг 2. Из какого-либо конца вертикального диаметра, как изцентра, проводим дугу окружности радиусом, равным
выбранному диаметру, до пересечения с прямой, содержащей
горизонтальный диаметр, в двух точках справа и слева от
окружности.
12. Приближенное построение правильного пятиугольника
Шаг 3.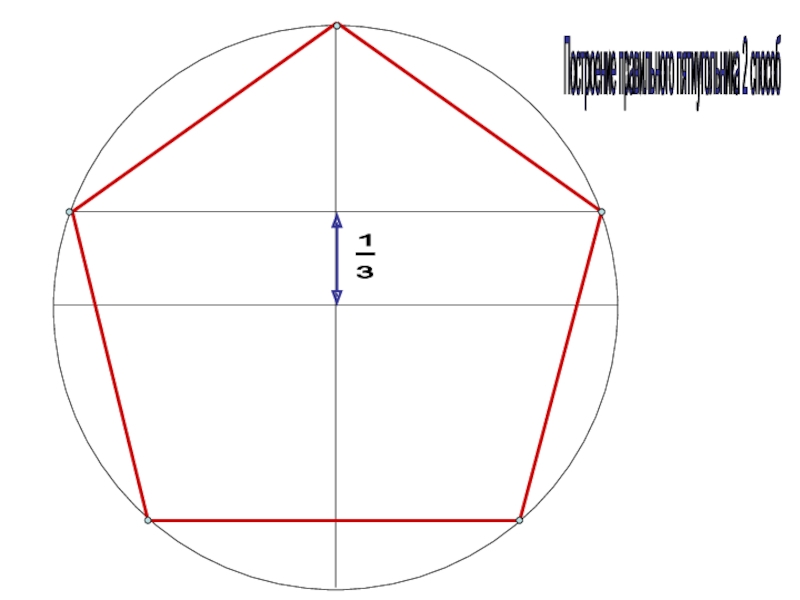 Из левой точки проводим лучи через четные деления
Из левой точки проводим лучи через четные делениявертикального диаметра до пересечения с окружностью.
Аналогично проводим лучи через правую точку и те же
деления на вертикальном диаметре.
13. Приближенное построение правильного пятиугольника
Шаг 4. В точках пересечения лучей с окружностью (дальние отначала луча точки) получаем искомые вершины
многоугольника. Соединяя полученные точки отрезками,
строим многоугольник.
14. Построение правильного восьмиугольника
15. Литература
• Годик Е. И., Хаскин А. М. Справочноеруководство по черчению. Изд. 4-е,
перераб. и доп. М., «Машиностроение»,
1974.
• Или в электронном виде
http://biblioteka.cc/index.php?newsid=86302
Построение правильного многоугольника с помощью циркуля и линейки » Аналитическая геометрия f(x)dx.Ru
п.7. Исторический экскурс к вопросу о построении правильного многоугольника с помощью циркуля и линейки.
Геометрические задачи на построение с помощью циркуля и линейки зародились еще в древней Греции во времена Евклида и Платона. Еще в те времена, математики умели строить с помощью циркуля и линейки правильные треугольники, пятиугольники и квадраты.
Еще в те времена, математики умели строить с помощью циркуля и линейки правильные треугольники, пятиугольники и квадраты.
Более того, они умели с помощью циркуля и линейки делить угол пополам, поэтому они умели строить и правильные 6-ти, 10-ти и 15-ти угольники и все правильные n-угольники, где, , и , . Очень важно, что с помощью линейки проводятся только отрезки прямых, а длины отрезков измеряются с помощью циркуля, а не делений на линейке. Так, используя эти инструменты можно построить отрезок, длина которого выражается числом, полученным из 1 с помощью четырех арифметических действий (сложения, вычитания, умножения, деления) и извлечением квадратного корня. Т.е. вначале есть только отрезок, длина которого принимается за 1. Тогда можно построить отрезок, длина которого равна рациональному числу или квадратному корню из рационального числа. Далее, если отрезок длины а уже построен с помощью циркуля и линейки, то можно построить с помощью этих инструментов отрезок длины b, если число b выражается через а с помощью арифметических действий и квадратного корня.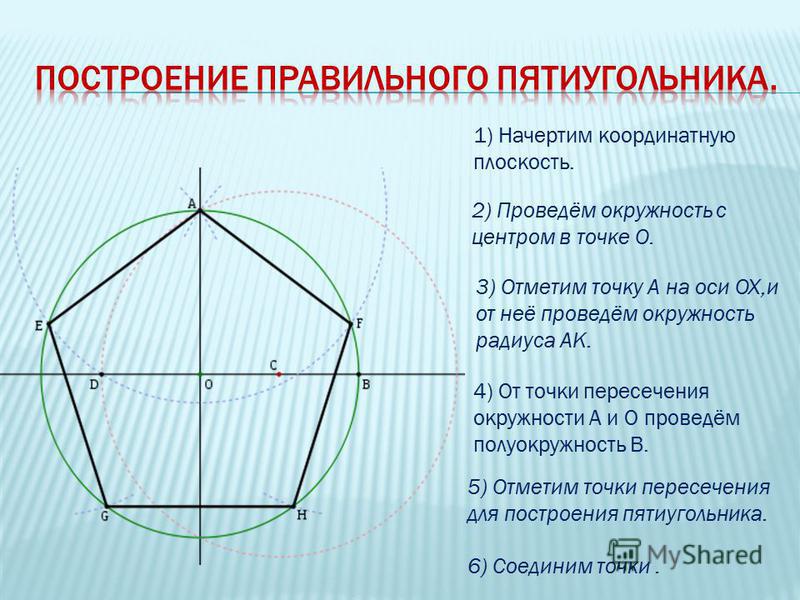 Говорят, что такое число выражается в квадратных радикалах.
Говорят, что такое число выражается в квадратных радикалах.
Таким образом, с помощью циркуля и линейки можно построить отрезок, длина которого выражается в квадратных радикалах. Все это знали еще математики древней Греции. Задачу построения других правильных многоугольников (или доказательство невозможности таких построений) не могли решить в течение двух последующих тысячелетий, а решена она была немецким студентом филологического факультета Гёттингенского университета Карлом Фридрихом Гауссом в 1796 году. В то время Гауссу было 18 лет и он разрывался между занятиями филологией и математикой и не мог сделать окончательного выбора. Решение древней задачи помогло ему сделать окончательный выбор в пользу (и на пользу) математики. Страшно даже подумать на сколько бы затормозилось развитие математики останься Гаусс филологом! До сих пор математики всего мира называют Гаусса королем математики.
Однако, вернемся к обсуждаемой задаче. Сначала Гаусс доказал, что с помощью циркуля и линейки можно построить только такие отрезки, длины которых выражаются в квадратных радикалах и только они.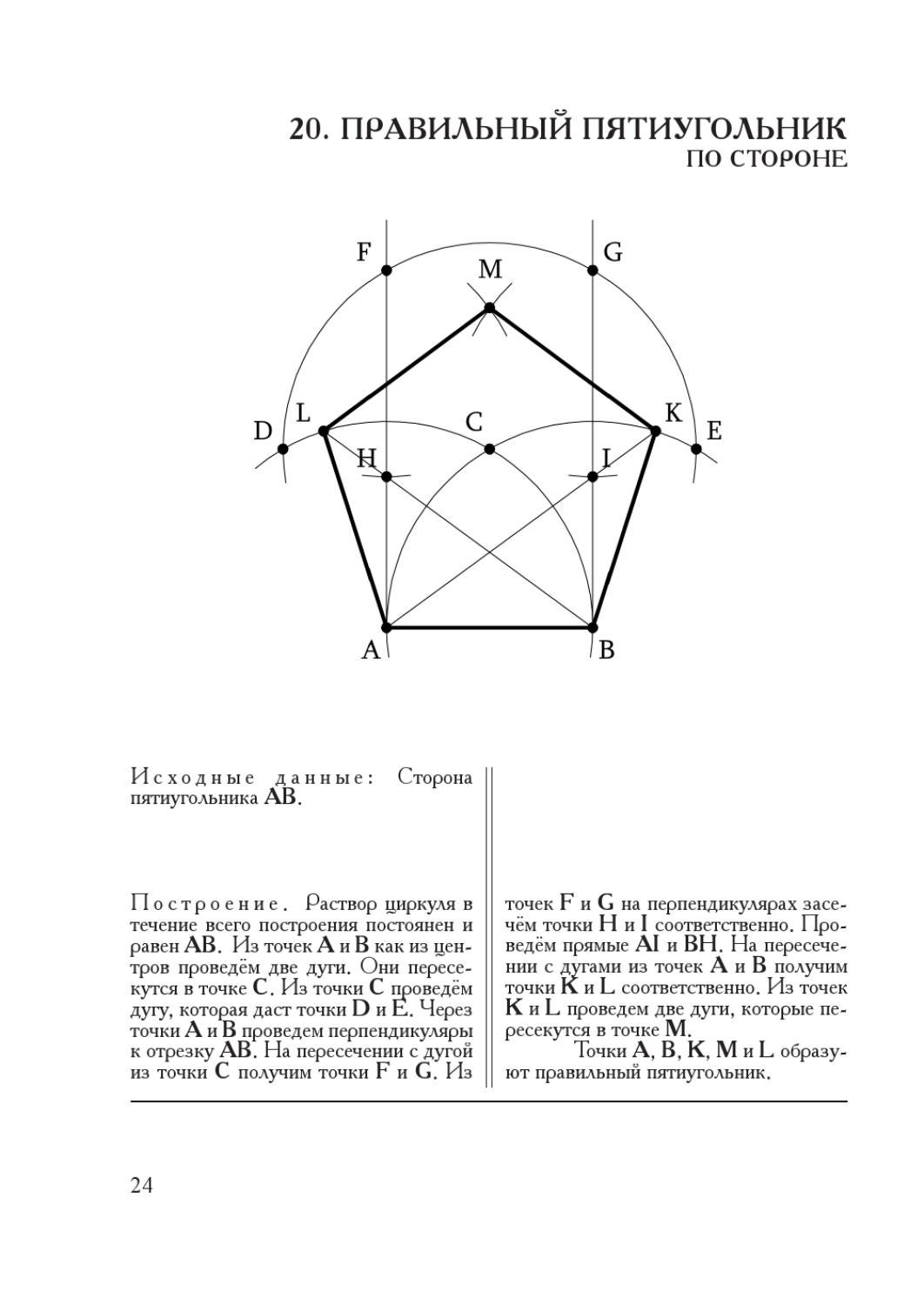 Гаусс использовал для решения задачи комплексные числа, в частности, корни из единицы. Так как корни из 1 делят окружность на равные дуги, то задача построения правильного n-угольника сводится к вопросу: при каких n корни n-й степени из 1 выражаются в квадратных радикалах. Здесь имеется ввиду их действительные и мнимые части. Таким образом, геометрическая задача была сведена к чисто алгебраической.
Гаусс использовал для решения задачи комплексные числа, в частности, корни из единицы. Так как корни из 1 делят окружность на равные дуги, то задача построения правильного n-угольника сводится к вопросу: при каких n корни n-й степени из 1 выражаются в квадратных радикалах. Здесь имеется ввиду их действительные и мнимые части. Таким образом, геометрическая задача была сведена к чисто алгебраической.
Обозначим через длину стороны правильного n-угольника. Гаусс нашел способ, с помощью которого ему удалось выразить число в квадратных радикалах и тем самым доказать, что с помощью циркуля и линейки можно построить правильный n-угольник.
Но Гаусс не был бы Гауссом, если бы он остановился на этом. Позднее он решил задачу полностью, выяснив при каких n задача построения правильного n-угольника может быть решена, а при каких нет. Чтобы понять этот результат нам понадобится одно определение.
Определение. Числа вида
,
где или , называются числами Ферма.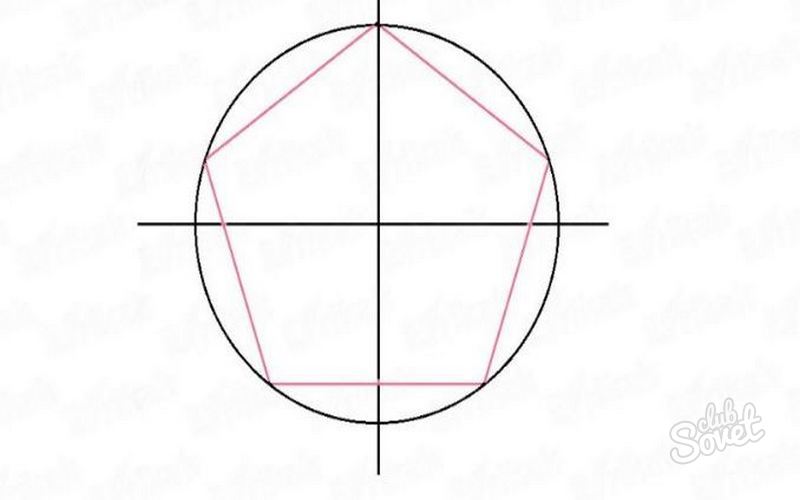
При , получаем . Далее,
, , , .
Первые пять чисел Ферма являются простыми числами, т.е. не имеют натуральных делителей, кроме 1 и самого себя. Однако, до сего момента не известно более ни одного простого числа Ферма. Более того, неизвестно, существует ли еще хотя бы одно простое число Ферма и эта проблема еще ждет своего юного гения.
Гаусс доказал следующую теорему.
Теорема. С помощью циркуля и линейки построить правильный n-угольник можно тогда и только тогда, когда
,
где или , а – различные между собой простые числа Ферма.
Замечание. Теорема утверждает только принципиальную возможность построения правильного n-угольника. Поэтому оставалась задача выразить сторону р-угольника в квадратных радикалах для оставшихся известных простых чисел Ферма и . Для числа 257 эту задачу решил немецкий математик Фридрих Ришелло. Решение занимает 80 страниц текста. Случай числа 65537 был выполнен О.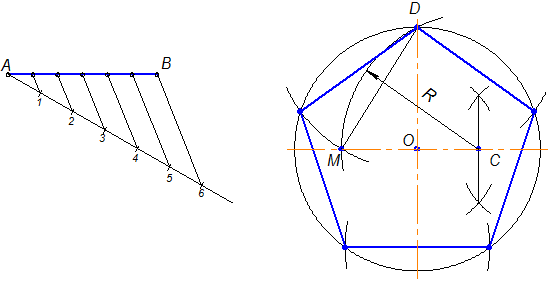 Гермесом, который потратил на вычисления 10 лет, а сама работа не опубликована ввиду ее необъятных размеров и хранится в архивах Гёттингенсного университета. Интересно, можно ли составить программу для компьютера для решения этой задачи?
Гермесом, который потратил на вычисления 10 лет, а сама работа не опубликована ввиду ее необъятных размеров и хранится в архивах Гёттингенсного университета. Интересно, можно ли составить программу для компьютера для решения этой задачи?
Гаусс очень ценил эту свою первую математическую работу и перед смертью просил высечь на своей могильной плите правильный 17-ти угольник. Увы, это не было сделано. Но в городе Брауншвейге стоит на 17-ти угольном постаменте памятник Карлу Фридриху Гауссу – королю математики.
Прошло всего 10 дней, а юный Карл Гаусс получил свой самый выдающийся результат, доказав квадратичный закон взаимности. Эту теорему многие математики считают одной из самых красивейших теорем математики.
Теорема. Для любых двух нечетных простых чисел р и q верно равенство
,
где и символы Лежандра.
Возможно найдутся ответы здесь:
Построение пятиугольника подробно. Построение пятиугольника подробно Получение с помощью полоски бумаги
Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.
Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.
Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.
Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.
Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.
Получение с помощью полоски бумаги
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°.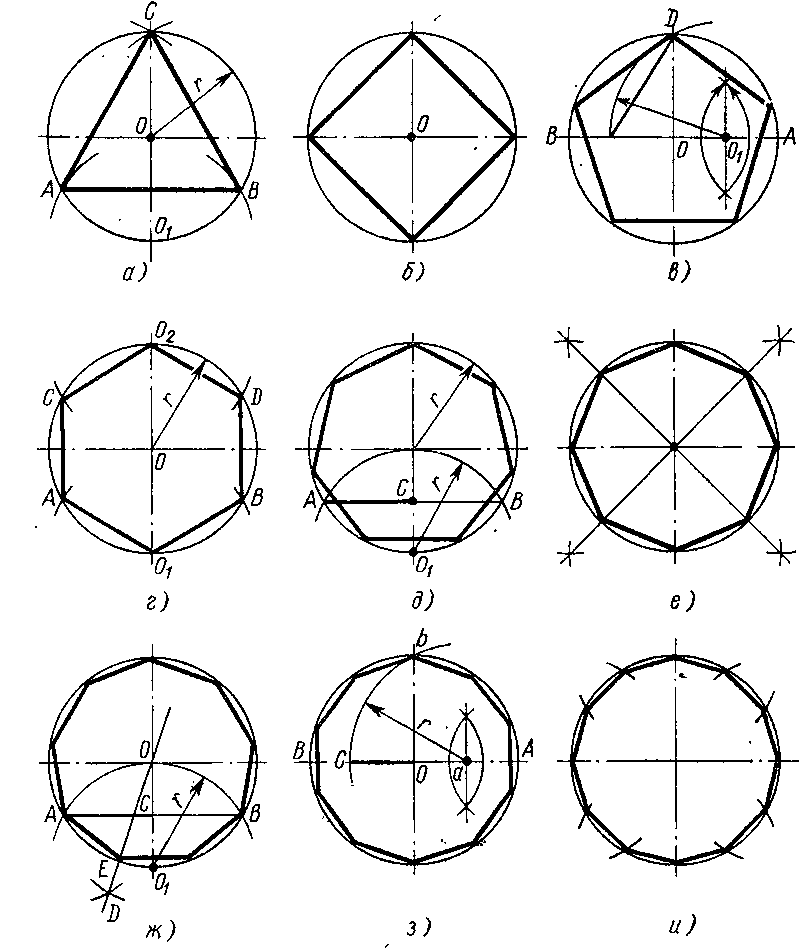 Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.
С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».
8 июня 2011Первый способ — по данной стороне S с помощью транспортира.
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.
Полученный пятиугольник — искомый.
Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N 1 , Р 1 , Q 1 , К 1 и соединяем их прямыми.
На рисунке построен шестиугольник по данной стороне.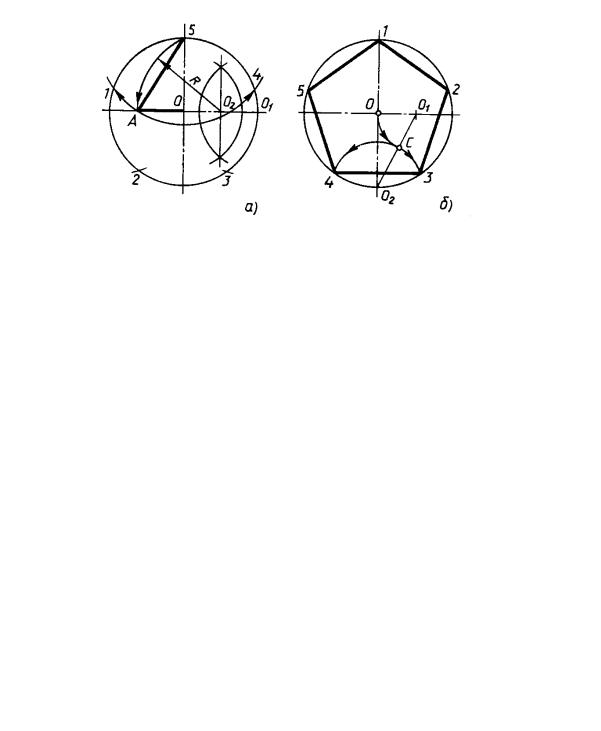
Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.
Шестиугольник ADEFGB — искомый.
«Отделка комнат при ремонте»,
Н.П.Краснов
Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц. Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…
Обмер выполненных работ, за исключением особо оговоренных случаев, производится по площади действительно обработанной поверхности с учетом ее рельефа и за вычетом необработанных мест. Для определения действительно обработанных поверхностей при малярных работах следует пользоваться переводными коэффициентами, приведенными в таблицах.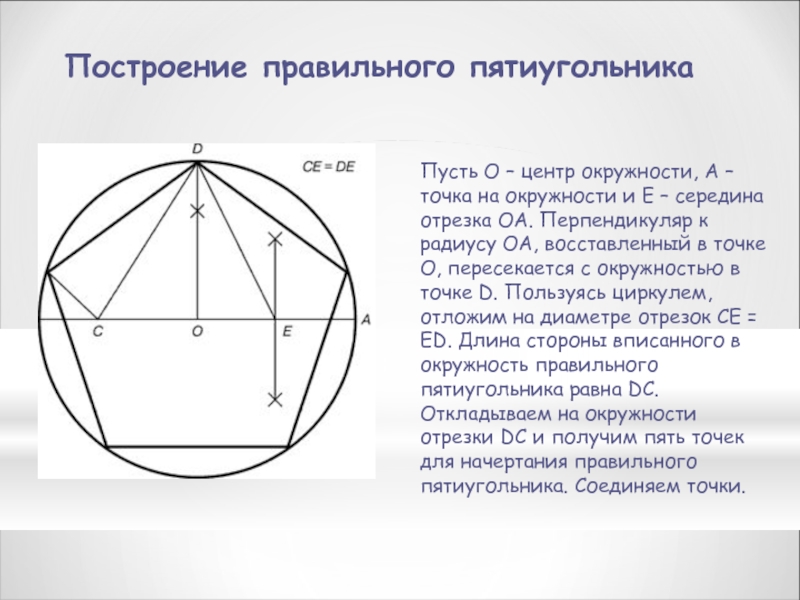 А. Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…
А. Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…
Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур. Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура. При этом надо…
Вы находитесь в категории раскраски пятиугольник. Раскраска которую вы рассматриваете описана нашими посетителями следующим образом «» Тут вы найдете множество раскрасок онлайн. Вы можете скачать раскраски пятиугольник и так же распечатать их бесплатно. Как известно творческие занятия играют огромную роль в развитии ребенка. Они активизируют умственную деятельность, формируют эстетический вкус и прививают любовь к искусству. Процесс раскрашивания картинок на тему пятиугольник развивает мелкую моторику, усидчивость и аккуратность, помогает узнать больше об окружающем мире, знакомит со всем разнообразием цветов и оттенков. Мы ежедневно добавляем на наш сайт новые бесплатные раскраски для мальчиков и девочек, которые можно раскрашивать онлайн или скачать и распечатать. Удобный каталог, составленный по категориям, облегчит поиск нужной картинки, а большой выбор раскрасок позволит каждый день находить новую интересную тему для раскрашивания.
Мы ежедневно добавляем на наш сайт новые бесплатные раскраски для мальчиков и девочек, которые можно раскрашивать онлайн или скачать и распечатать. Удобный каталог, составленный по категориям, облегчит поиск нужной картинки, а большой выбор раскрасок позволит каждый день находить новую интересную тему для раскрашивания.Как начертить правильный 8 угольник. Как построить правильный восьмиугольник
Куклин Алексей
Работа носит реферативный характер с элементами исследовательской деятельности. В ней рассматриваются различные способы построения правильных n-угольников. В работе содержится подробный ответ на вопрос о том, что всегда ли можно построить n-угольник с помощью циркуля и линейки. К работе прилагается презентация, которую можно найти на данном мини-сайте.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts. google.com
google.com
Предварительный просмотр:
https://accounts.google.com
Подписи к слайдам:
Построение правильных многоугольников Работу выполнил: ученик 9 класса «В» МБОУ СОШ № 10 Куклин Алексей
Правильные многоугольники Правильным многоугольником называют выпуклый многоугольник, у которого все стороны и углы равны. Перейти к примерам Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Назад Правильные многоугольники
Основоположниками раздела математики о правильных многоугольниках являлись древнегреческие ученые. Одними из них были Архимед и Евклид.
Доказательство существования правильного n-угольника Если n (число углов многоугольника) больше 2, то такой многоугольник существует. Попробуем построить 8ми угольник и доказать это. Доказательство
Возьмем окружность произвольного радиуса с центром в точке О. Разделим её на некоторое число равных дуг, в нашем случае 8. Для этого проведем радиусы так, чтобы получилось 8 дуг, и угол между двумя ближайшими радиусами был равен 360°: количество сторон (в нашем случае 8), соответственно каждый угол будет равен 45°.
Для этого проведем радиусы так, чтобы получилось 8 дуг, и угол между двумя ближайшими радиусами был равен 360°: количество сторон (в нашем случае 8), соответственно каждый угол будет равен 45°.
3. Получаем точки A1, A2, A3, A4, A5, A6, A7, A8. Поочередно соединяем их и получаем правильный восьмиугольник. Назад
Построение правильного многоугольника по стороне с использованием поворота Правильный многоугольник можно построить, зная его углы. Мы знаем, что сумма углов выпуклого n-угольника равна 180°(n — 2). Из этого можно вычислить угол многоугольника, разделив сумму на n. Углы Построение
Угол правильного: 3-угольника равен 60° 4-угольника равен 90° 5-угольника равен 108° 6-угольника равен 120° 8-угольника равен 135° 9-угольника равен 140° 10-угольника равен 144° 12-угольника равен 150° Градусная мера углов правильных треугольников Назад
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts. google.com
google.com
Подписи к слайдам:
В 1796 году одним из величайших математиков всех времён Карл Фридрих Гаусс показал возможность построения правильных n-угольников, если выполняется равенство, где n – количество углов, а k-любое натуральное число. Тем самым получилось, что в пределах 30 возможно деление окружности на 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30 равных частей. В 1836 году Ванцель доказал, что правильные многоугольники, не удовлетворяющие данному равенству при помощи линейки и циркуля построить нельзя. Теорема Гаусса
Построение треугольника Построим окружность с центром в точке О. Построим еще одну окружность того же радиуса проходящую через точку О.
3. Соединим центры окружностей и одну из точек их пересечения, получив правильный многоугольник. Назад Построение треугольника
Построение шестиугольника 1. Построим окружность с центром в точке О. 2. Проведем прямую линию через центр окружности. 3. Проведем дугу окружности того же радиуса с центром в точке пересечения прямой с окружностью до пересечения с окружностью.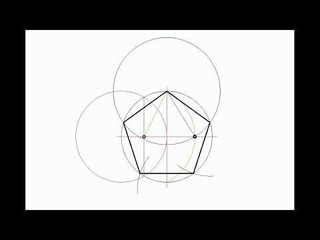
4. Проведем прямые через центр начальной окружности и точки пересечения дуги с этой окружностью. 5. Соединяем точки пересечения всех прямых с исходной окружностью и получаем правильный шестиугольник. Построение шестиугольника
Построение четырёхугольника Построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Из точек в которых диаметры касаются окружности проводим другие окружности данного радиуса до их пересечения (окружностей).
Построение четырёхугольника 4. Проводим прямые через точки пересечения окружностей. 5. Соединяем точки пересечения прямых и окружности и получаем правильный четырехугольник.
Построение восьмиугольника Можно построить любой правильный многоугольник у которого в 2 раза больше углов, чем у данного. Построим восьмиугольник при помощи четырехугольника. Соединим противоположные вершины четырехугольника. Проведем биссектрисы углов образованных пересекающимися диагоналями.
4. Соединим точки, лежащие на окружности, получив при этом правильный восьмиугольник. Построение восьмиугольника
Построение восьмиугольника
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Построение десятиугольника Построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Разделим радиус окружности пополам и из получившейся на нем точки проведем окружность проходящую через точку О.
Построение десятиугольника 4. Проведем отрезок из центра маленькой окружности к точки в которой большая окружность касается своего радиуса. 5. Из точки соприкосновения большой окружности и её радиуса проведем окружность так, что она будет соприкасаться с маленькой.
Построение десятиугольника 6. Из точек пересечения большой и полученной окружностей проведем окружности построенные в прошлый раз и так будем проводить до тех пор пока соседние окружности не соприкоснутся. 7. Соединим точки и получим десятиугольник.
Построение пятиугольника Для построения правильного пятиугольника нужно во время построения правильного десятиугольника соединить поочередно не все точки, а через одну.
Приблизительное построение правильного пятиугольника методом Дюрера Построим 2 окружности проходящие через центр друг друга. Соединим центры прямой, получив одну из сторон пятиугольника. Соединим точки пересечения окружностей.
Приблизительное построение правильного пятиугольника методом Дюрера 4. Проведем еще одну окружность того же радиуса с центром в точке пересечения двух других окружностей. 5. Проведем 2 отрезка как указано на рисунке.
Приблизительное построение правильного пятиугольника методом Дюрера 6. Соединим точки соприкосновения этих отрезков с окружностями с концами построенной стороны пятиугольника. 7. Достроим до пятиугольника.
Приблизительное построение правильного пятиугольника методами Коваржика, Биона
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.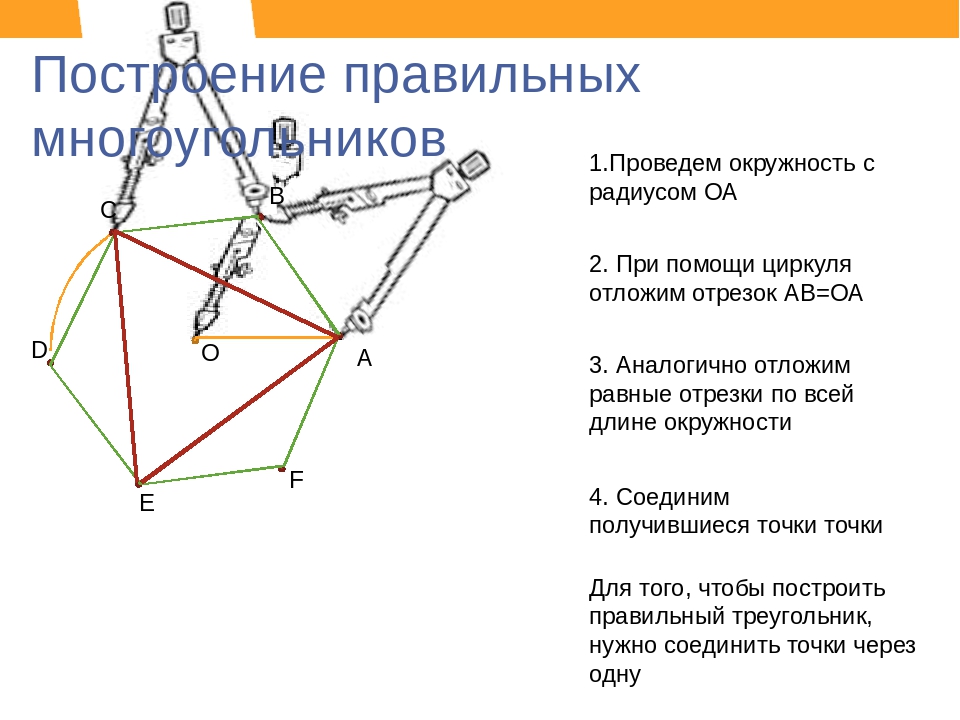
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника.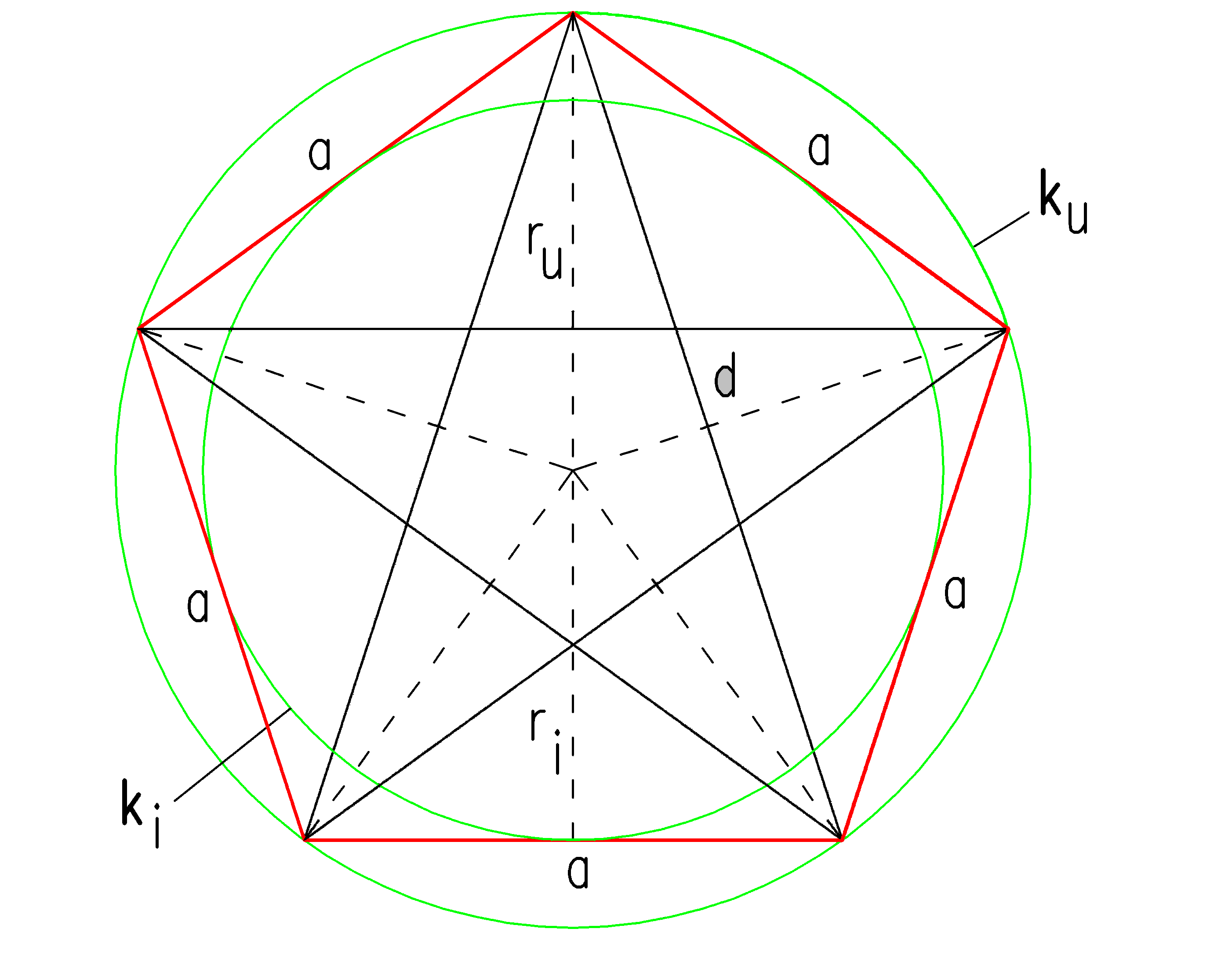 Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Построение полуправильных мозаик плоскости с помощью линейки и циркуля
После обсуждения с коллегами-геометрами возникла потребность в простом ресурсе, показывающем шаги для рисования всех восьми полуправильных мозаик плоскости с помощью линейки и циркуля , поэтому я скомпилировал представленные здесь методы. Конечно, есть много других способов приблизиться к этим плиткам в зависимости от ваших требований. Вы можете найти последовательные диаграммы ниже, однако, если вам нравятся печатные издания или вы хотите поддержать мою работу и помочь мне финансировать дальнейшие книжные проекты, вы можете приобрести печатную версию буклета (с бесплатной доставкой по Великобритании).
Вы можете найти последовательные диаграммы ниже, однако, если вам нравятся печатные издания или вы хотите поддержать мою работу и помочь мне финансировать дальнейшие книжные проекты, вы можете приобрести печатную версию буклета (с бесплатной доставкой по Великобритании).
Эти мозаики лежат в основе многих геометрических узоров и важны для понимания, если не всегда необходимы для построения. Если вам нужна помощь в построении шестиугольника и квадрата, вы можете обратиться к моему предыдущему сообщению в блоге о построении регулярных сеток с помощью линейки и компаса.
ЧТО ТАКОЕ ПОЛУПРАВИЛЬНАЯ ПЛИТКА?
Полуправильные мозаики , также известные как архимедовы мозаики , представляют собой бесконечные мозаики двумерной плоскости, состоящие из более чем одного правильного многоугольника, где каждая вершина мозаики окружена одним и тем же набором полигонов, в такой же порядок.Все это можно построить с помощью простых методов линейки и циркуля, как показано здесь.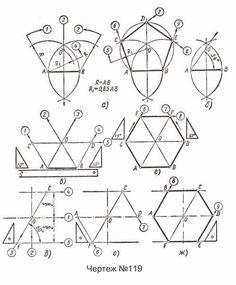
Нотация, используемая для определения каждого тайлинга, описывает последовательность полигонов вокруг каждой вершины. Следовательно, 3.4.6.4 означает, что каждая вершина имеет группу из треугольника, квадрата, шестиугольника, квадрата, расположенных вокруг каждой вершины в указанном порядке.
Унифицированные плитки — это плитки с условием одной вершины, означающим, что одна и та же группа полигонов сгруппирована вокруг каждой вершины.К ним относятся три правильных мозаики: 6.6.6 (шестиугольная или сотовая), 4.4.4.4 (квадратная) и 3.3.3.3.3.3 (треугольная или изометрическая) и еще восемь полуправильных мозаик. Они находятся в центре внимания этого поста.
Можно сгенерировать бесконечное количество мозаик с использованием правильных многоугольников, если правило вершин ослаблено. Они называются n-равномерными мозаиками , где n обозначает количество различных состояний вершин в мозаике.
ТЕССЕЛЛЯЦИЯ
Представленные здесь методы направлены на работу снаружи внутрь с максимально лаконичным построением, а не на расширение сетки из центра. Во всех случаях, кроме одного, результатом является простая воспроизводимая прямоугольная или квадратная единица.
Во всех случаях, кроме одного, результатом является простая воспроизводимая прямоугольная или квадратная единица.
Первые четыре мозаики, 3.6.3.6, 3.4.6.4, 3.12.12 и 4.6.12, все повторяются в прямоугольнике с пропорциями 1:√3 и поэтому могут быть построены из базовой компоновки на первой диаграмме.
Мозаика 3.3.3.3.6 повторяется с необычным смещением. Пунктирная линия показывает шестиугольную единицу, которую можно повторить путем переноса. Более простой вариант — построить эту мозаику на более широкой изометрической сетке.
4.8.8 и 3.3.4.3.4 повторяются в квадрате.
Финальная мозаика, 3.3.3.4.4, должна быть отражена, чтобы повторяться плавно. В качестве альтернативы можно построить еще одну вертикально отраженную плитку, чтобы создать высокий прямоугольный элемент, который можно повторить путем перемещения.
Двойные плитки
Двойные мозаики (также называемые мозаиками Catalan или Laves ) генерируются путем соединения центров каждой плитки в полуправильных мозаиках и прохождения через середину каждого края. Поскольку в полуправильных мозаиках есть только одно условие вершины, каждая двойственная мозаика состоит из одной формы.
Поскольку в полуправильных мозаиках есть только одно условие вершины, каждая двойственная мозаика состоит из одной формы.
Этот контент доступен в соответствии с лицензией Creative Commons Attribution-Non Commercial-ShareAlike CC BY-NC-SA 4.0
Дополнительное чтение
Линейка и компас – Эндрю Саттон (издание «Деревянные книги»)
Плитки и узоры – Бранко Грюнбаум и Г.К. Шепард (издано Dover Books)
http://mathworld.wolfram.com/SemiregularTessellation.html
http://mathworld.wolfram.com/DualTessellation.html
Нравится:
Нравится Загрузка…
Как нарисовать пятиугольник в круге с помощью циркуля?
Рисование пятиугольника
- Сначала нарисуйте горизонтальные и вертикальные линии.
- Затем нарисуйте круг с центром в перекрестии.
- Не регулируя компас , поместите острие компаса на окружность в том месте, где она пересекает горизонтальную линию.
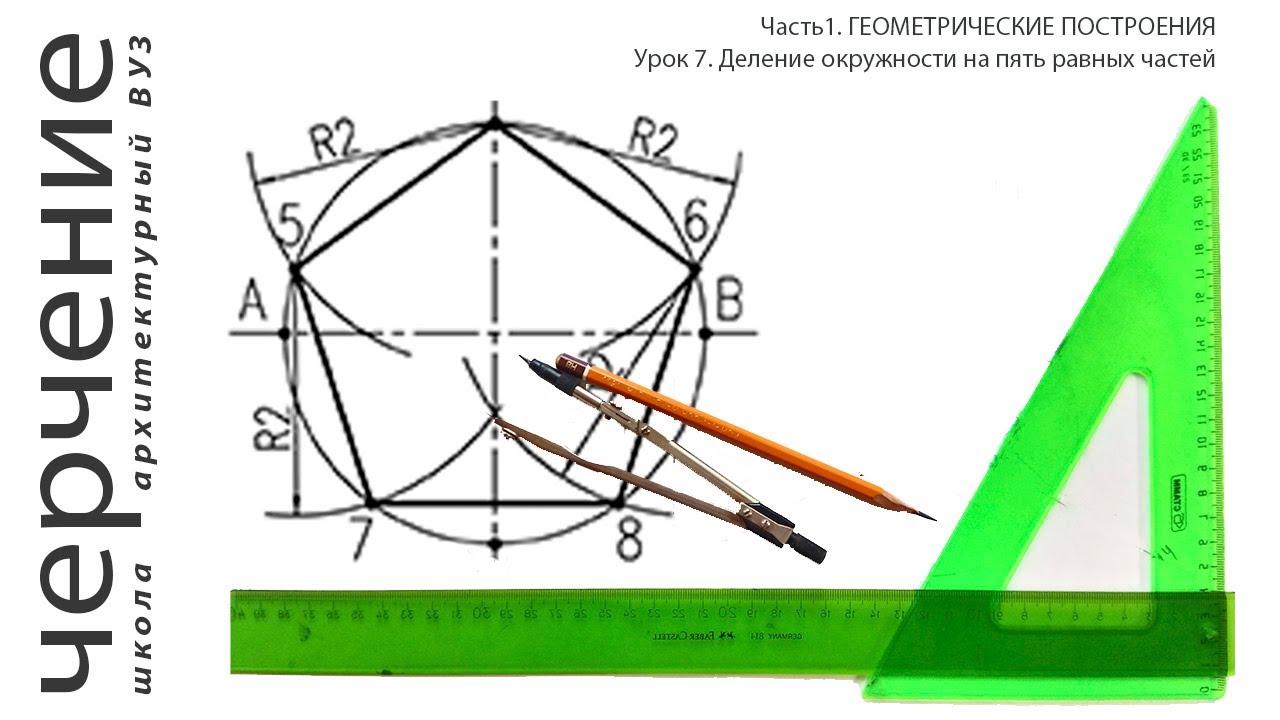
Нажмите, чтобы увидеть полный ответ
Точно так же люди спрашивают, как вы рисуете пятиугольник в круге?
Прямой метод с использованием степеней следующий:
- Нарисуйте окружность и выберите точку, которая будет пятиугольником (например, верхний центр)
- Выберите точку A на окружности, которая будет одной из вершин пятиугольника.
- Проведите направляющую через него и центр круга.
- Нарисуйте линии под углом 54° (от направляющей), пересекающие точку пятиугольника.
Кроме того, как называется шестигранная фигура? Шестигранная форма — представляет собой шестиугольник, семигранная форма представляет собой семиугольник, а восьмиугольник имеет восемь сторон … Существуют названия для многих различных типов многоугольников, и обычно число сторон составляет . важнее, чем имя формы . Правильный многоугольник имеет одинаковую длину сторон с равными углами между сторонами.
Принимая это во внимание, является ли круг многоугольником?
Полигоны .Многоугольник — это замкнутая плоская фигура с тремя или более прямыми сторонами. Следующая фигура не является многоугольником , так как это не замкнутая фигура. Круг не является многоугольником , поскольку у него нет прямых сторон.
Как называется семигранная фигура?
В геометрии семиугольником является семиугольник или 7 -угольник. Гептагон иногда называют септагоном, используя «sept-» (отказ от septua-, числового префикса латинского происхождения, а не hepta-, числового префикса греческого происхождения; оба являются родственными) вместе с греческим суффиксом «-agon» означает угол.
| ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК В ДАННЫЙ
ОПИСАННАЯ КРУГ На рис. Рис. 4-25.-правильный пятиугольник в заданной описанной круг. ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК НА ДАННОМ Вписанный круг Чтобы построить правильный пятиугольник на данном вписанный круг, определить пять равных промежутков на круг таким же образом. Однако вместо соединяя эти точки, нарисуйте каждую сторону фигура, касающаяся окружности в точке пересечения. |
Пентагон — Академические дети
От академических детей
Шаблон: Альтернативные пользователи
Отсутствует изображениеОбычный_пятиугольник.
 2<математика>
2<математика> Отсутствующее изображение
Regular_pentagram.png
Пентаграмма, заключенная в пятиугольник
Пентаграмму можно составить из правильного пятиугольника либо путем удлинения его сторон, либо путем рисования его диагоналей, и полученная фигура содержит различные длины, связанные золотым сечением, φ = (1+√5)/2.
Построение пятиугольника
Правильный пятиугольник можно построить с помощью линейки и циркуля. Этот процесс был описан Евклидом в его « элементах » около 300 г. до н.C. Карл Фридрих Гаусс сделал некоторые теоретические доказательства теории многоугольников.
- Нарисуйте горизонтальную линию с кругом размером с желаемый пятиугольник с центром на этой линии.
- Поместите стрелку циркуля там, где окружность круга пересекает горизонтальную линию, и нарисуйте полукруг через центр первого круга, пересекая окружность первого круга в двух местах. Проведите вертикальную линию через точки пересечения полукруга с первым кругом.
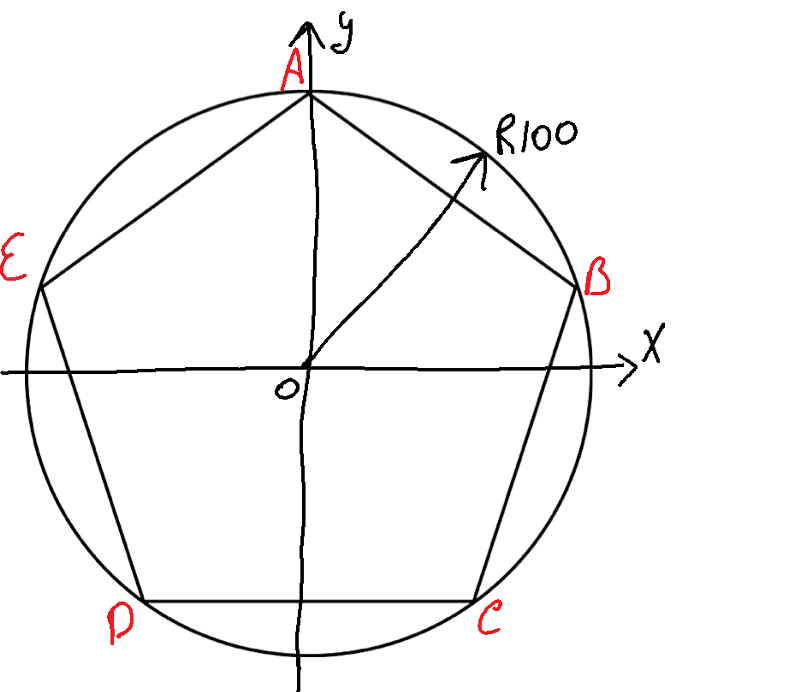 Эта линия пройдет через точку, которую мы называем (а).
Эта линия пройдет через точку, которую мы называем (а). - Откройте циркуль, чтобы можно было, поместив иглу в два пересечения между горизонтальной линией и первым кругом, нарисовать небольшой крест выше и ниже горизонтальной линии, за пределами первого круга, с одной линией креста от каждая точка. Если вы соедините эти кресты, вы получите линию, перпендикулярную горизонтальной линии, также проходящую через центр первого круга. Точку, где эта линия пересекает окружность первого круга сверху, мы называем (b).Это первый угол пятиугольника.
- Вставьте стрелку циркуля в (а) и проведите отрезок окружности, проходящий через (b) и вниз через горизонтальную линию, получив точку на этой линии, которую мы называем (с).
- Вставьте иглу в (b) и проденьте сегмент круга через (c) и первый круг. Эти точки на первой окружности являются вторым и третьим углами пятиугольника.
- Не выдвигая циркуль, вставьте его иглу во второй и третий углы и начертите отрезки окружности, проходящие через первую окружность, чтобы найти два оставшихся угла.

- Соедините каждый угол с соседними, и вы получите пятиугольник.
- Если соединить несмежные углы (проведя диагонали пятиугольника), получится пентаграмма с меньшим правильным пятиугольником в центре. Или, если вы расширите стороны до тех пор, пока не сойдутся несмежные, вы получите большую пентаграмму.
Внешние ссылки
- Пятиугольники и пентаграммы ( http://agutie.homestead.com/files/pentagram_menelaus1.htm ) новые факты о пятиугольниках и пентаграммах Антонио Гутьерреса из книги «Геометрия шаг за шагом из страны инков».Ключевая концепция: теорема Менелая. Шаблон: многоугольники.
да:Фемкант de:Фнфек фр: Пентагон он: מחומש это: Фиммхырнингур это: Pentagono (геометрия) ja:五角形 nl: Виджхук нет: Пентагон pl:Пенциоконт пт: Пентгоно СВ: Пентагон чж: 正五边形
5.23: Построение правильных многоугольников — K12 LibreTexts
Построение чертежей равносторонних треугольников, квадратов и правильных многоугольников с помощью циркуля и линейки.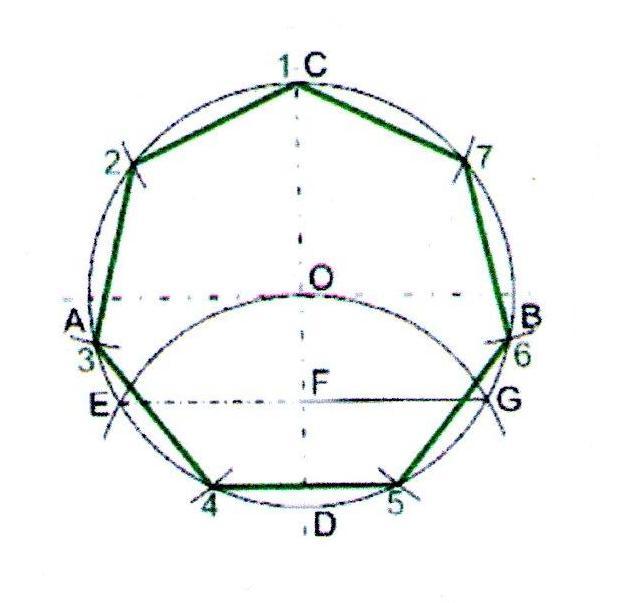 Создавайте полигоны с помощью Geogebra.
Создавайте полигоны с помощью Geogebra.
Построения правильных многоугольников
Используйте свой компас, чтобы построить круг, как показано ниже на листе бумаги.Опишите, как сложить бумагу в два раза, чтобы помочь вам построить квадрат.
Рисунок \(\PageIndex{1}\)Правильные многоугольники
Правильный многоугольник — это многоугольник, который является равноугольным и равносторонним . Это означает, что все его углы имеют одинаковую меру и все его стороны имеют одинаковую длину.
Самым простым примером правильного многоугольника является равносторонний треугольник , треугольник с тремя конгруэнтными сторонами и тремя конгруэнтными углами.{\circ}}{п}\).
Конструкции — это пошаговые процессы, используемые для создания точных геометрических фигур. Чтобы создать конструкцию вручную, есть несколько инструментов, которые вы можете использовать:
- Компас: Устройство, позволяющее построить круг заданного радиуса.
 Компасы могут помочь вам не только создавать круги, но и копировать расстояния.
Компасы могут помочь вам не только создавать круги, но и копировать расстояния. - Линейка: Все, что позволяет провести прямую линию.Линейка не должна измерять расстояния. Каталожная карточка хорошо работает как линейка. Вы также можете использовать линейку в качестве линейки, если вы используете ее только для рисования прямых линий, а не для измерения.
- Бумага: Когда на листе бумаги изображена геометрическая фигура, саму бумагу можно согнуть, чтобы построить новые линии.
Вы можете построить несколько правильных многоугольников вручную, если помните определения и свойства этих правильных многоугольников.С помощью дополнительной программы для геометрии или транспортира вы можете построить любой правильный многоугольник .
Давайте рассмотрим пример задачи.
\(\overline{AB}\) — это одна сторона того, что станет равносторонним треугольником \(\Delta ABC\).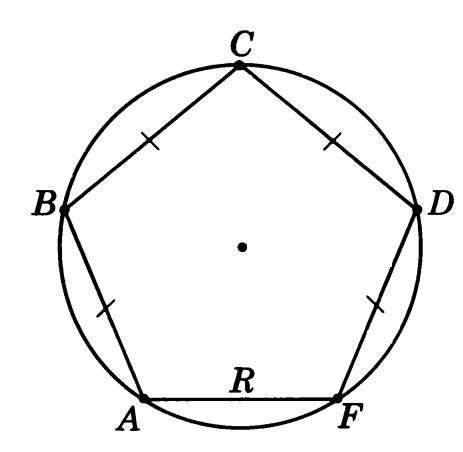 Вам нужно поставить точку \(C\) в правильном месте, чтобы получился равносторонний треугольник. Где должна располагаться точка \(C\) относительно точек \(A\) и \(B\)?
Вам нужно поставить точку \(C\) в правильном месте, чтобы получился равносторонний треугольник. Где должна располагаться точка \(C\) относительно точек \(A\) и \(B\)?
Пусть расстояние между \(A\) и \(B\) равно \(d\).Точка \(C\) должна быть удалена от точки \(A\), а также \(d\) от точки \(B\).
Рисунок \(\PageIndex{3}\)Используйте линейку, чтобы нарисовать отрезок линии \(\overline{AB}\). Используйте идеи из Примера A, чтобы построить равносторонний треугольник \(\Delta ABC\).
Рисунок \(\PageIndex{4}\)С помощью циркуля измерьте длину \(\overline{AB}\).
Рисунок \(\PageIndex{5}\)Создайте неполный круг из точек на расстоянии \(\overline{AB}\) от точки \(A\).
Рисунок \(\PageIndex{6}\)Создайте еще один неполный круг из точек на расстоянии \(\overline{AB}\) от точки \(B\).
Рисунок \(\PageIndex{7}\)Точкой пересечения этих двух неполных окружностей является точка \(C\).
Рисунок \(\PageIndex{8}\) Точки \(A\), \(B\), \(C\) и \(D\) лежат на окружности с центром в точке \(O\). Докажите, что \(ABCD\) — квадрат.
Докажите, что \(ABCD\) — квадрат.
\(\overline{AO}\cong \overline{BO}\cong \overline{CO}\cong \overline{DO}\), поскольку все они являются радиусами одного круга . Поскольку \(\угол BOC\) прямой угол, \(\угол BOA\),\угол AOD\) и \(\угол COD\) также должны быть прямыми углами.{\circ}\) углов, это квадрат.
Пример \(\PageIndex{1}\)
Ранее вас попросили описать, как сложить бумагу в два раза, чтобы помочь вам построить квадрат.
Раствор
Сложите круг так, чтобы две половинки перекрывали друг друга, чтобы получилась складка, равная диаметру.
Рисунок \(\PageIndex{10}\)Сложите круг еще раз пополам, чтобы получить серединный перпендикуляр к диаметру. Для этого согните так, чтобы две конечные точки диаметра сошлись.Вторая складка также будет диаметром.
Рисунок \(\PageIndex{11}\) Обратите внимание, что два диаметра перпендикулярны друг другу. Соедините четыре точки пересечения на круге, чтобы построить квадрат.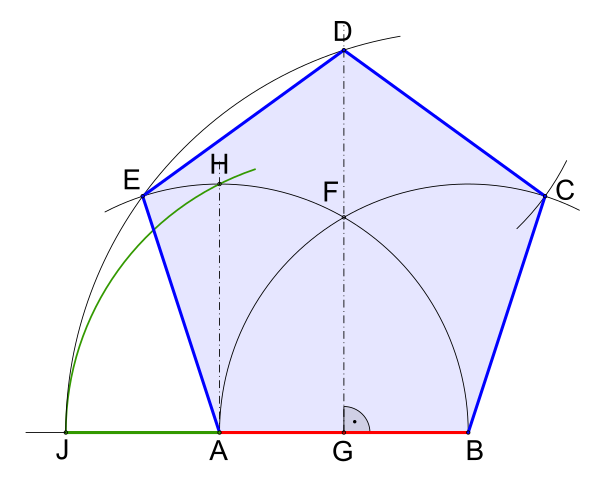
Вы можете быть уверены, что это квадрат, благодаря доказательству в примере C.
Пример \(\PageIndex{2}\)
Правильный шестиугольник ниже разделен на шесть конгруэнтных треугольников. Какие это треугольники? Объяснять.{\circ}\), поэтому все треугольники равносторонние.
Пример \(\PageIndex{3}\)
Шесть точек равномерно распределены по окружности внизу. Объясните, почему при соединении этих точек получается правильный шестиугольник.
Рисунок \(\PageIndex{14}\)Решение
Поскольку шесть точек расположены на равном расстоянии друг от друга, каждый из сегментов, соединяющих шесть точек, должен иметь одинаковую длину. Следовательно, многоугольник должен быть правильным. Поскольку сторон шесть, это должен быть правильный шестиугольник.
Пример \(\PageIndex{4}\)
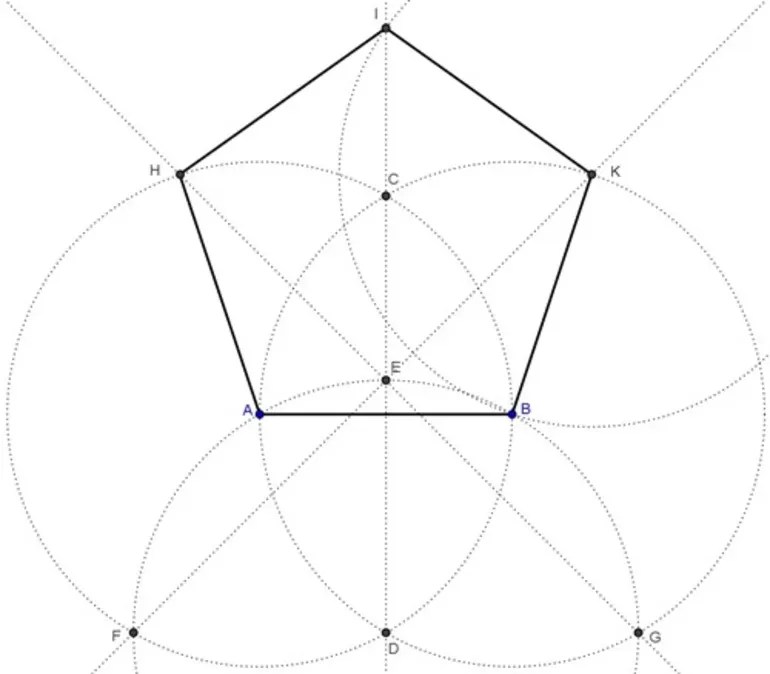
Постройте правильный шестиугольник, вписанный в окружность.
Раствор
«Вписанный в круг» означает, что все шесть вершин шестиугольника лежат на одном круге. Начните с построения окружности и точки на окружности.
Начните с построения окружности и точки на окружности.
Вы знаете, что радиус круга равен длине каждой стороны круга (см. практическое руководство №1). Таким образом, ваша цель состоит в том, чтобы разместить вокруг круга шесть точек, которые находятся на таком же расстоянии друг от друга, как и радиус круга.Держите компас открытым на ту же ширину, что и радиус круга, и сделайте одну новую отметку на круге.
Рисунок \(\PageIndex{16}\)Продолжайте делать новые метки по кругу на одинаковом расстоянии друг от друга.
Рисунок \(\PageIndex{17}\)Рисунок \(\PageIndex{18}\)Соедините точки пересечения, чтобы сформировать правильный шестиугольник.
Рисунок \(\PageIndex{19}\)
Обзор
1. Построить равносторонний треугольник.
2. Постройте еще один равносторонний треугольник.
3. Объясните, почему ваш метод построения равносторонних треугольников работает.
4. Постройте квадрат, вписанный в круг, сделав две складки.
5. Обоснуйте, почему созданный вами многоугольник на самом деле является квадратом.
Используйте линейку, чтобы построить \(\overline{AB}\).
6. Постройте серединный перпендикуляр к \(\overline{AB}\).
7. Построить окружность диаметром \(\overline{AB}\).
8. Постройте квадрат, вписанный в окружность, соединив четыре конца диаметров.
9. Расширьте свою конструкцию до правильного восьмиугольника, разделив пополам каждый из прямых углов в центре круга.
10. Постройте правильный шестиугольник, вписанный в окружность.
11. Объясните, почему метод построения правильного шестиугольника основан на окружности.
12. Объясните, как можно расширить построение правильного шестиугольника до построения правильного 12-угольника.
13. Построить равносторонний треугольник. Объясните, как можно построить окружность, проходящую через три точки равностороннего треугольника.
14. Учитывая равносторонний треугольник, вписанный в окружность, как можно продолжить построение, чтобы построить правильный шестиугольник?
15. Имея окружность и транспортир, объясните, как можно построить правильный пятиугольник.
Имея окружность и транспортир, объясните, как можно построить правильный пятиугольник.
Документ без названия
Документ без названия
ПОЛЕЗНАЯ ГЕОМЕТРИЯ
Художники, иллюстраторы и дизайнеры редко нуждаются в навыках механического рисования или специальной учености в области геометрии.Однако знание нескольких простых задач плоской геометрии часто может быть с успехом использовано в определенных классах их работы. Верные методы геометрии гораздо лучше, чем догадки в построении правильных плоских фигур, эллипсов и т. д., не говоря уже об экономии времени и труда.
Возьмем, например, деление линии на определенное количество частей. На первой диаграмме этой главы показано, как это сделать. Вам понадобится линейка и треугольник.Также доступна шкала с разметкой в сантиметры и миллиметры, так как с ее помощью очень легко вычислять деления. Вы также можете использовать Т-образный угольник с подвижной головкой, отрегулированной так, чтобы проводить параллельные косые линии. Необходимо, чтобы край чертежной доски был абсолютно прямым при проведении параллельных линий с Т-образным угольником.
Вы также можете использовать Т-образный угольник с подвижной головкой, отрегулированной так, чтобы проводить параллельные косые линии. Необходимо, чтобы край чертежной доски был абсолютно прямым при проведении параллельных линий с Т-образным угольником.
Метод, как показано на диаграмме, отмечая радиус круга на его окружности и получая шесть точек для построения шестиугольника, может быть использован при рисовании сети линий для основы повторяющегося узора.Сделайте круг в середине бумаги и найдите шесть равноудаленных точек, затем через центр круга и шесть точек проведите два набора параллельных линий, как показано на диаграмме. Используя полученные таким образом точки и линии, а также степень наклона этих линий, вся поверхность бумаги может быть покрыта основой, на которой могут быть созданы орнаментальные или цветочные повторяющиеся узоры.
Часто дизайнер хочет нарисовать многоугольник с одинаковым количеством сторон.Как мы видели, легко построить многоугольник из шести равных центров, описывающих дуги D, пересекающиеся пополам в C и D AB в E сторонах, но когда дело доходит до разметки многоугольника с нечетными сторонами, возникает трудность.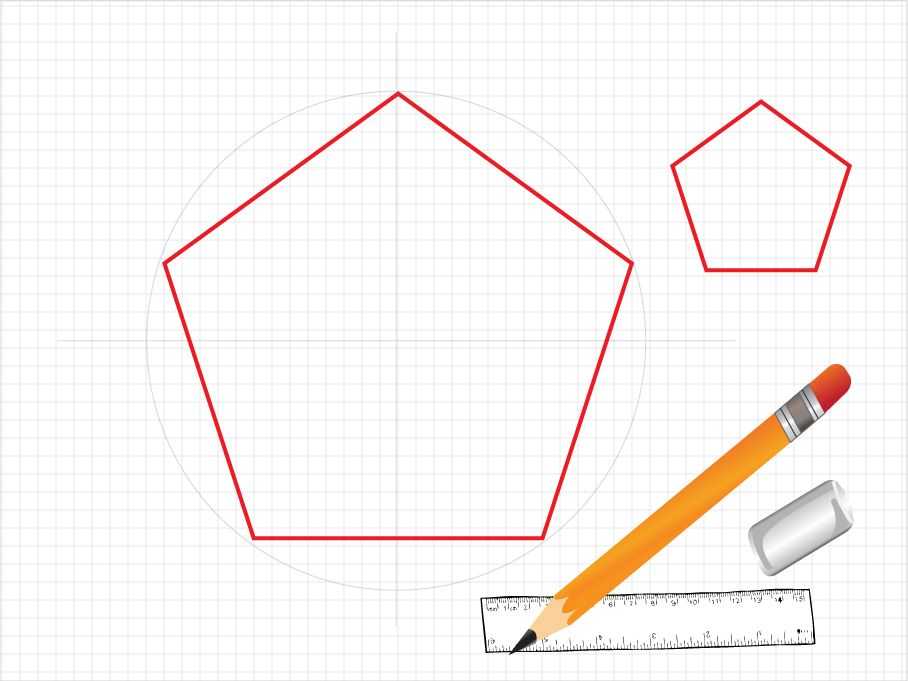 деления окружности — если взять за начало окружность — на необходимое число равных частей. Диаграмма на стр. 108 в этой главе показывает, как сделать пятиугольник, вписанный в круг, а затем, если хотите, из тех же точек пятиконечную или пятиконечную звезду.
деления окружности — если взять за начало окружность — на необходимое число равных частей. Диаграмма на стр. 108 в этой главе показывает, как сделать пятиугольник, вписанный в круг, а затем, если хотите, из тех же точек пятиконечную или пятиконечную звезду.
Любой правильный многоугольник можно построить с помощью окружности.Разделите диаметр окружности поровну на столько частей, сколько сторон у искомого многоугольника. Теперь от концов диаметра, как от центров, опишите дуги с радиусами, равными диаметру, и пересекающимися в точке вне окружности. Затем из этой точки, где пересекаются две дуги, провести линию через второе из делений по диаметру до и пересекающую окружность окружности. Вот от этой точки до ближайшего конца диаметра у вас теперь одна сторона нужного многоугольника.Это наиболее практичный метод разделения кругов или вписывания в них правильных многоугольников, когда требуемое количество сторон является нечетным числом, например 7, 9 или i 1.
Важно помнить, что это всегда второе деление диаметра, через которое проводится линия из точки вне круга. Когда дизайнерам нужны овальные или эллиптические формы или части таких форм, они найдут путь через большую ось и одну через малую ось на четыре равные части; тогда как овал можно разделить на равные части только двусторонне; то есть линией, проходящей через длинную ось.Были изобретены специальные инструменты для начертания эллипсов; однако обычно художник может использовать метод, показанный здесь, с использованием булавок и ниток.
Когда дизайнерам нужны овальные или эллиптические формы или части таких форм, они найдут путь через большую ось и одну через малую ось на четыре равные части; тогда как овал можно разделить на равные части только двусторонне; то есть линией, проходящей через длинную ось.Были изобретены специальные инструменты для начертания эллипсов; однако обычно художник может использовать метод, показанный здесь, с использованием булавок и ниток.
Тень круга при определенных условиях, сечение конуса, срезанного наискось, и круг в перспективе имеют эллиптическую форму. Художники могут упростить сложную работу по рисованию колес в перспективе, грубо набросав нужный размер, а затем построив эллипс такого же размера на другом листе бумаги, который после вырезания можно использовать для начертания четких и определенных контуров в перспективе. просмотренное колесо.Из-за простоты конструкции и того, что с помощью циркуля можно провести тонкие линии, проиллюстрирован метод создания приблизительного эллипса с помощью инструментов. Показан также способ рисования кривой, напоминающей арку моста. Часто в декоративной или промышленной работе дизайнер нуждается не только в точности, но и в точности. прочно выровненный свиток или спираль. Две схемы в этой главе показывают, как механически построить две такие формы с помощью циркуля.
Показан также способ рисования кривой, напоминающей арку моста. Часто в декоративной или промышленной работе дизайнер нуждается не только в точности, но и в точности. прочно выровненный свиток или спираль. Две схемы в этой главе показывают, как механически построить две такие формы с помощью циркуля.
Следующая гравюра объясняет изготовление гораздо более изящного спирального орнамента, а именно ионической волюты.Чтобы нарисовать эту кривую, действуйте следующим образом: линия, представляющая высоту предполагаемой улитки, делится на восемь равных частей. В пятом делении, считая в обратном порядке, опишите круг. Это будет глаз волюты. Впишите в него. квадрат, опирающийся на один угол. Начертите его диаметры и разделите каждый на шесть равных частей; на полученных точках построить три квадрата. меньше по мере необходимости. Стороны маленьких квадратов, если их продолжить легкими вспомогательными линиями, отмечают границы квадрантов и показывают, где они соединяются друг с другом. Сложный рисунок или небольшой набросок можно увеличить, разделив его на несколько маленьких квадратов, а затем разложив большую площадь на такое же количество квадратов, но большего размера. Затем рисунок механически копируется квадрат за квадратом. Конечно, чертежи тоже можно уменьшить квадратами.
Сложный рисунок или небольшой набросок можно увеличить, разделив его на несколько маленьких квадратов, а затем разложив большую площадь на такое же количество квадратов, но большего размера. Затем рисунок механически копируется квадрат за квадратом. Конечно, чертежи тоже можно уменьшить квадратами.
Это один из технических приемов в практическом искусстве, который так же стар, как пирамиды, поскольку он, кажется, использовался древними египтянами. Почти в каждом собрании древностей из страны фараонов экспонируется одна или несколько скульпторских копий — каменных плит с рисунками, поверх которых прочерченными линиями прочерчены квадраты, залитые красным пигментом или мелом.Иногда рисовальщику хочется увеличить этим методом какой-нибудь рисунок, оригинал которого не должен быть изуродован карандашными пометками. Чтобы преодолеть эту трудность, возьмите лист желатина, который используют литографы и офортисты, и процарапайте на нем стальным острием ряд квадратов. Втирайте порошкообразный красный мел в нацарапанные линии, а затем покройте копию желатином. Теперь дизайн можно увидеть разделенным на квадраты красными меловыми линиями.
Теперь дизайн можно увидеть разделенным на квадраты красными меловыми линиями.
Когда вы отправляете на фотогравировщик большой рисунок для уменьшения до определенного размера, иногда хочется узнать точную высоту гравировки.Убедиться в этом нетрудно. Помните правило, что прямоугольники, имеющие общую диагональ, пропорциональны, и проведите по наброску легким карандашом диагональ из угла в угол. Теперь держите линейку вдоль края рядом с нижним рисунком ABCD, который должен быть уменьшен до 5 дюймов в ширину. Отметьте тонкую линию от A до D, держите линейку на расстоянии 5 дюймов от стороны AC, держите ее параллельно основанию AB и перемещайте ее вдоль, пока не коснетесь диагональной линии в углу E, где проходит диагональ, затем, удерживая линейку параллельно основанию. и на необходимой ширине продвиньте его вверх, пока конец не коснется диагональной линии.От этой точки по диагонали до базовой линии будет измеряться высота гравировки. Некоторые, кажется, с трудом запоминают, с какой стороны держать дюймовую меру; но, как было сказано выше, памятование о правиле относительно общей диагонали поможет избежать всех трудностей. Когда не рекомендуется делать пометки на рисунке, даже слабо, натяжение веревки вместо диагонали, нарисованной карандашом, очень хорошо подойдет для этой цели.
Когда не рекомендуется делать пометки на рисунке, даже слабо, натяжение веревки вместо диагонали, нарисованной карандашом, очень хорошо подойдет для этой цели.
Приблизительное построение правильных многоугольников: два художника эпохи Возрождения
Альбрехт Дюрер (1471–1528), считающийся отцом современной немецкой живописи, также был большим любителем математики.Он написал книгу под названием Unterweysung der Messung …, в которой рассматриваются всевозможные геометрические задачи. В этой книге он дает точную конструкцию правильного пятиугольника, но он также дает приблизительную конструкцию, которую легко выполнить в практическом рисовании. (Его книга предназначалась для ремесленников, каменщиков и т. д., которых больше заботили простые процедуры, чем геометрическая точность.)
Эта конструкция показана ниже:
Возьмите фиксированное отверстие компаса: АВ = .Нарисуйте круги радиусом a с центрами A и B ; пусть эти окружности пересекаются в точках C и D . Тогда AB = AD = BD , как мы знаем. Нарисуйте окружность с центром D и радиусом DA . Этот круг пройдет через B ; пусть E будет точкой пересечения CD , а F и G будут точками пересечения окружностей с центрами A и B соответственно.Произведите FE , пока он не пересечет в точке H окружность с центром в точке B ; произведите GE , пока он не пересечет в точке I окружность с центром в точке A . Тогда пересечение K окружностей радиуса a с центрами H и I дает пятую вершину пятиугольника.
Тогда AB = AD = BD , как мы знаем. Нарисуйте окружность с центром D и радиусом DA . Этот круг пройдет через B ; пусть E будет точкой пересечения CD , а F и G будут точками пересечения окружностей с центрами A и B соответственно.Произведите FE , пока он не пересечет в точке H окружность с центром в точке B ; произведите GE , пока он не пересечет в точке I окружность с центром в точке A . Тогда пересечение K окружностей радиуса a с центрами H и I дает пятую вершину пятиугольника.
Насколько правильный пятиугольник? Если бы он был совершенно правильным, все стороны должны образовывать угол 360°/5 = 72° в центре пятиугольника.Следовательно все углы при вершинах пятиугольника должны быть равны 180°-72°= 108°(поскольку каждый из них есть сумма двух равных углов [180°-72°]/2).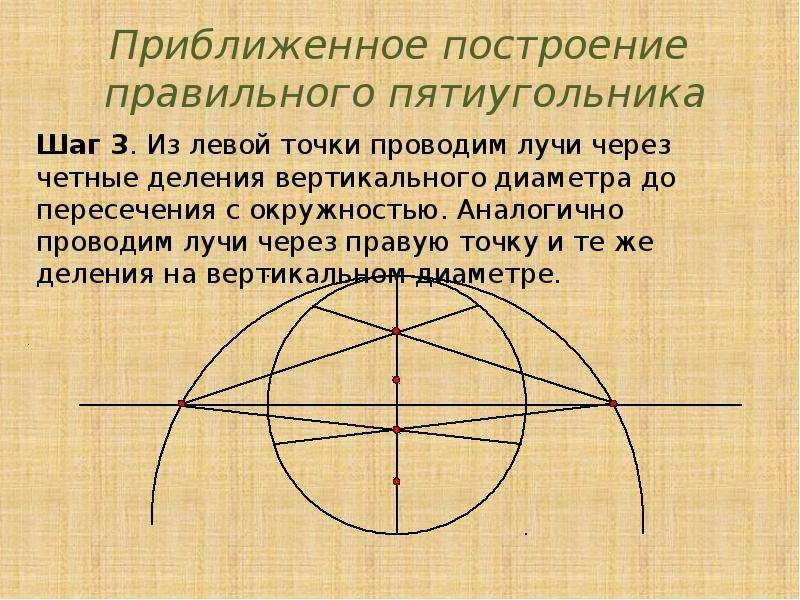 На самом деле мы увидим, что угол ABH = 108°21’58” — чуть больше 108°, так что какой-то другой угол должен быть чуть меньше 108°. Сначала обратите внимание, что угол FBG = 90°; тогда, поскольку FG = 2 a и GB = a , мы имеем FB = a √3 . Кроме того, угол DFE = 45 ° и угол DFC = угол DFA = 60 ° ( F , A , C являются коллинеарными, а также C , B , г и F , D , G ), и, следовательно, угол AFE = 15°.Поскольку угол BFE опирается на дугу окружности FABG , равную дуге, стягиваемой углом AFE , мы также имеем угол BFE = 15°.
На самом деле мы увидим, что угол ABH = 108°21’58” — чуть больше 108°, так что какой-то другой угол должен быть чуть меньше 108°. Сначала обратите внимание, что угол FBG = 90°; тогда, поскольку FG = 2 a и GB = a , мы имеем FB = a √3 . Кроме того, угол DFE = 45 ° и угол DFC = угол DFA = 60 ° ( F , A , C являются коллинеарными, а также C , B , г и F , D , G ), и, следовательно, угол AFE = 15°.Поскольку угол BFE опирается на дугу окружности FABG , равную дуге, стягиваемой углом AFE , мы также имеем угол BFE = 15°.
Теперь используем закон синусов для треугольника FBH ; это дает sin(угол BHF ) = √3 sin15° (обратите внимание, что поскольку угол BHF можно найти угол BHF , а затем угол HBF ; затем, вычитая угол ABF = 30° из угла HBF , находим, что угол ABH составляет примерно 108°22′, что близко к значению Педо [2].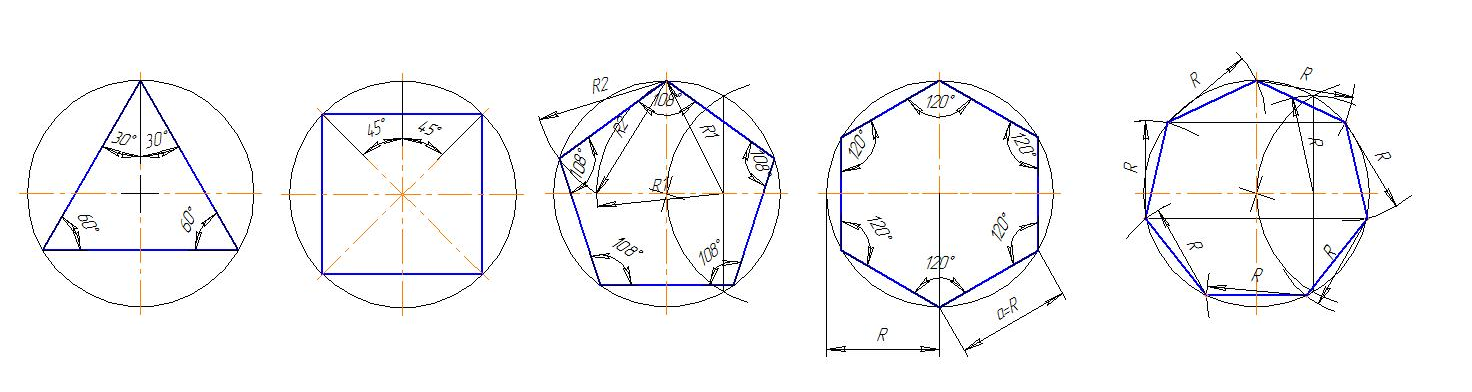
Так как угол BAI равен углу ABH , то он тоже немного больше 108°. Также каждый из углов BHK и AIK чуть больше 107°, а угол HKI чуть больше 109°… и все равно на нашем рисунке это было бы едва заметно.
Дюрер не предупреждает читателя своей книги, что это построение приближенно. (Также выполняется с «ржавым» компасом, т. е. компасом с фиксированным отверстием.) На самом деле он тоже цитирует, как мы сказали, точное построение пятиугольника.
«Интерес Дюрера к построению правильных многоугольников объясняется применением геометрии в средние века в исламском и готическом декоративном дизайне, а после изобретения пушек — в строительстве укрепленных городов. (Любопытно, что очень немногие здания в истории были построены на основе пятиугольной формы. Пентагон недалеко от Вашингтона, округ Колумбия, является заметным исключением.) [2]
Подводя итог этому обзору многоугольных конструкций эпохи Возрождения, мы можем сказать, что и Леонардо да Винчи, и Альбрехт Дюрер были большими любителями математики.

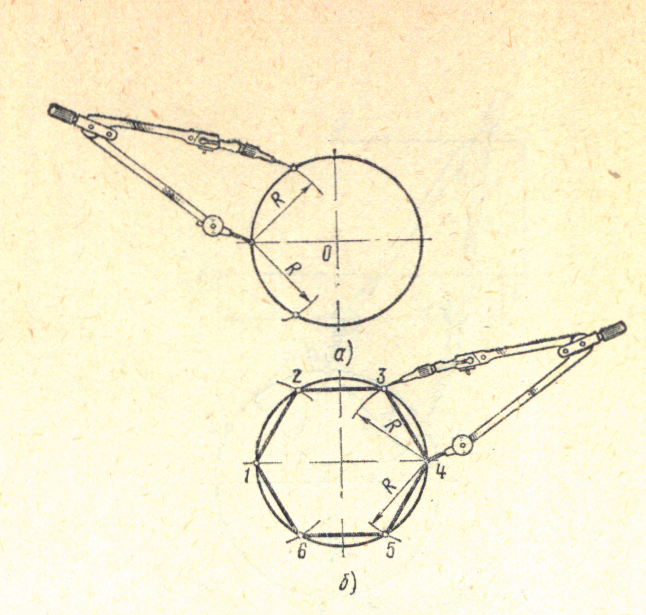 4-25 показан метод построения
а
правильный пятиугольник в данной описанной
4-25 показан метод построения
а
правильный пятиугольник в данной описанной