Как нарисовать пятиугольник (67 фото) » Рисунки для срисовки и не только
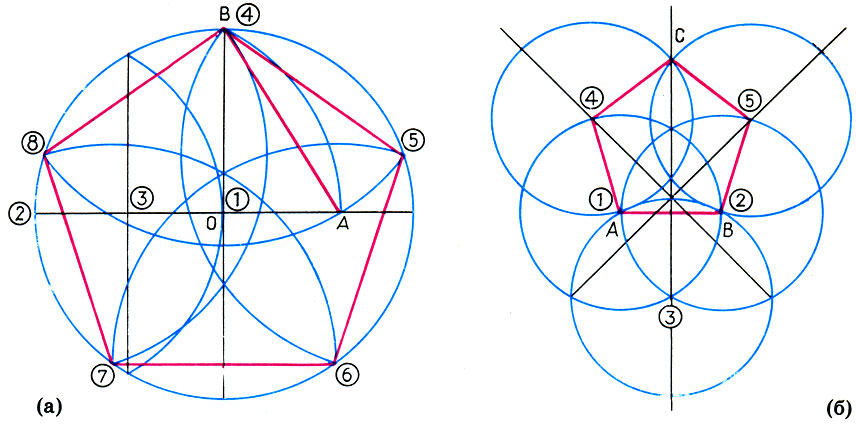
Построение правильного пятиугольника вписанного в окружность
Как начертить правильный пятиугольник в окружности
Как построить пятиугольник циркулем
Как построить пятиугольник циркулем
Как построить правильный пятиугольник
Равносторонний пятиугольник чертеж
Как построить правильный 5 угольник
Построение правильного пятиугольника с помощью циркуля
Как построить правильный 5 угольник
Пятиугольник Рело
Построение правильного пятиугольника в окружности
Как построить правильный 5 угольник
Как построить пятиугольник в окружности
Равносторонний пятиугольник чертеж
Рисование звезды циркулем
Начертить пятиугольник
Построение правильного пятиугольника в окружности
Равносторонний пятиугольник чертеж
Равносторонний пятиугольник чертеж
Построение правильных многоугольников
Равносторонний пятиугольник
Построение правильнихмногоугольников
Пятиугольник в виде домика
Восьмиугольник правильный чертеж
Правильный пятиугольник на клеточной бумаге
Геометрия построение пятиугольника
Равносторонний пятиугольник чертеж
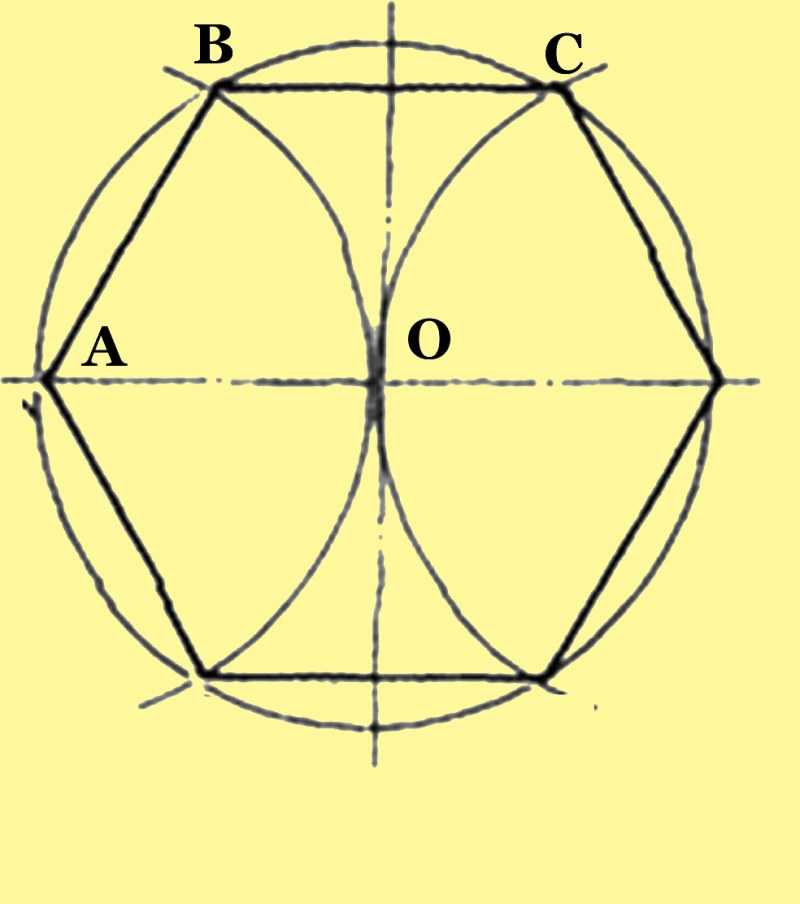
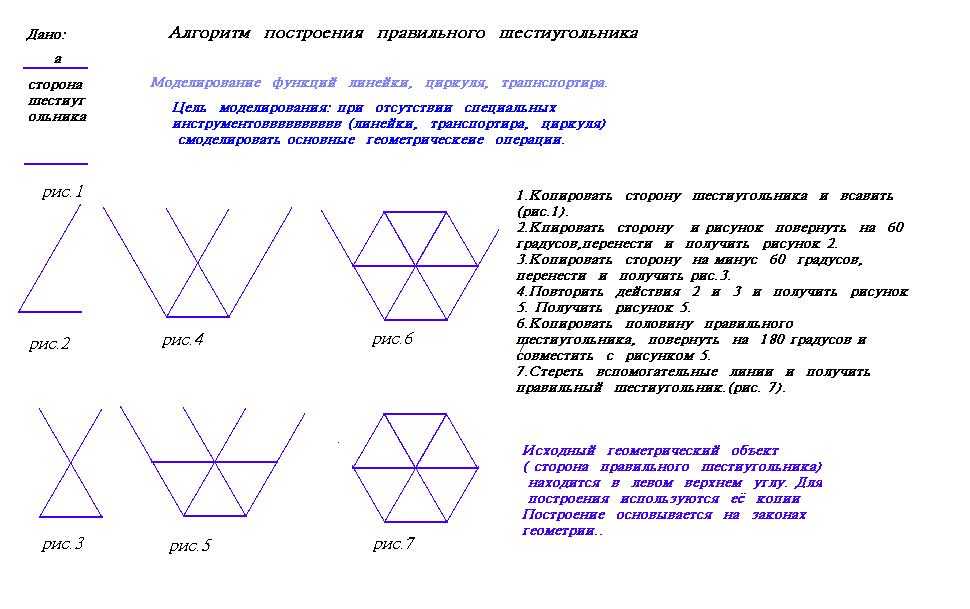
Как начертить правильный шестиугольник
Как начертить 5 угольник
Правильный шестиугольник чертеж
Регулярный пятиугольник
Пентаграмма Пифагора
Как начертить правильный шестиугольник
Построение правильных многоугольников
Многоугольники пятиугольник
Равносторонний пятиугольник
Правильный пятиугольник на клеточной бумаге
Шестиугольника начерти два 2 пятиугольника
Правильный пятиугольник внутренний пятиугольник
Шестиугольник разделить на 2 пятиугольника
Пятиугольник со стороной 4 см
Правельнвц многоугольника
Треугольник четырехугольник пятиугольник
Пятиугольник и шестиугольник
Правильный 5 угольник
Центр правильного пятиугольника
Геометрические фигуры семиугольник
Вписанный правильный восьмиугольник
Пятиугольник в круге с помощью циркуля
Гексагон Призма
Как построить пятиугольник циркулем
Осевая симметрия пятиугольника построение
Пятиугольник вписанный в окружность построение
Пентагон форма пятиугольника
Семиугольник чертеж
Пятиугольник вписанный в квадрат
Правильный 5 ти угольник
Построение пятиугольника циркулем
Пятиугольник ABCDE
Начертить правильный шестиугольник
Произвольный пятиугольник
Правильный пятиугольник построение
Пятиугольник со стороной 3 см
Равносторонний пятиугольник чертеж
Построение пятиугольника
Правильный пятиугольник вписанный в окружность
Построение треугольника по трем элементам и правильного пятиугольника
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Гнатко И. В. 1
В. 1
1МБОУ «Лицей №159»
Бутакова В.И. 1
1МБОУ «Лицей №159»
Автор работы награжден дипломом победителя III степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Гипотеза исследования построена на предположении о том, что задачи на построение правильного пятиугольника имеют достаточно широкое распространение в архитектуре, живописи и других, смежных с математикой, науках.
Методы исследования:
Поисковый;
Анализ;
Дедуктивный метод.
Объект исследования — задачи на построение с помощью циркуля и линейки.
Предмет исследования — решение задач повышенной сложности на построение треугольников по трем элементам, построение правильного пятиугольника различными способами.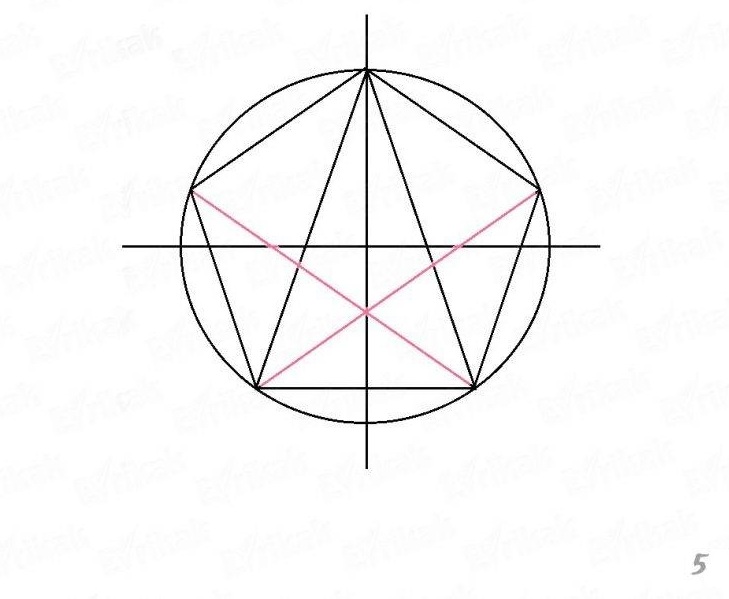
Проблема — задачи на построение правильного пятиугольника и задачи повышенной сложности на построение треугольника по трем элементам почти не изучаются в школьном курсе математики.
Цель исследования — поиск решения задач на построение правильного пятиугольника, на построение треугольников по трем элементам.
Задачи исследования:
1. Определить в математике понятие задачи на построение с помощью циркуля и линейки, изучить основную литературу по данной теме;
2. Решение задач повышенной сложности на построение треугольников по трем элементам;
3.Исследовать архитектурные сооружения, при проектировании которых использовались правильные пятиугольники;
4.Рассмотреть наиболее интересные способы построения правильных пятиугольников;
5. Создание творческих проектов.
Актуальность исследования — данная тема очень актуальна, так как, выбирая профессию инженера, ученик сталкивается с множеством вопросов, например одним из них: «Где мы можем применить знания математики?» Исследования в данной области приводят к выводу о том, что математика имеет большое практическое применение, как в архитектуре, живописи, дизайне так и в других науках.
Первые задачи на построение возникли в глубокой древности. Уже древними архитекторами и землемерами приходилось решать простейшие задачи на построение, связанные с их профессией.
Самые первые задачи на построение, по-видимому, решались непосредственно на местности и заключались в проведении прямых линий и построения прямого угла.
Древнегреческие математики еще 3000 лет назад проводили свои построения с помощью двух приборов: гладкой дощечки с ровным краем и двух заостренных палок, связанных на одном конце.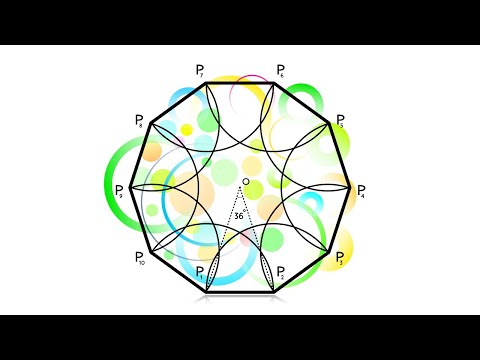
К задачам на построение прибегали древние инженеры, когда составляли рабочий чертеж того или иного сооружения. Задачи на построение помогали людям в их хозяйственной жизни, их решения формулировались в виде «практических правил», исходя из наглядных соображений.
Первым греческим ученым, который рассматривал геометрические задачи на построение, был Фалес Милетский. Это он, пользуясь построением треугольника, определил расстояние, недоступное для непосредственного измерения. Это он вычислил и высоту египетской пирамиды по отбрасываемой ею тени.
Задачи на построение интересовали и Пифагора. Пифагор и его ученики потратили много сил, чтобы отдельным геометрическим сведениям, состоящим до того времени из набора интуитивных правил, придать характер настоящей науки. Задачи на построение интересовали Платона. Платон и его ученики считали построение геометрическим, если оно выполнялось при помощи циркуля и линейки.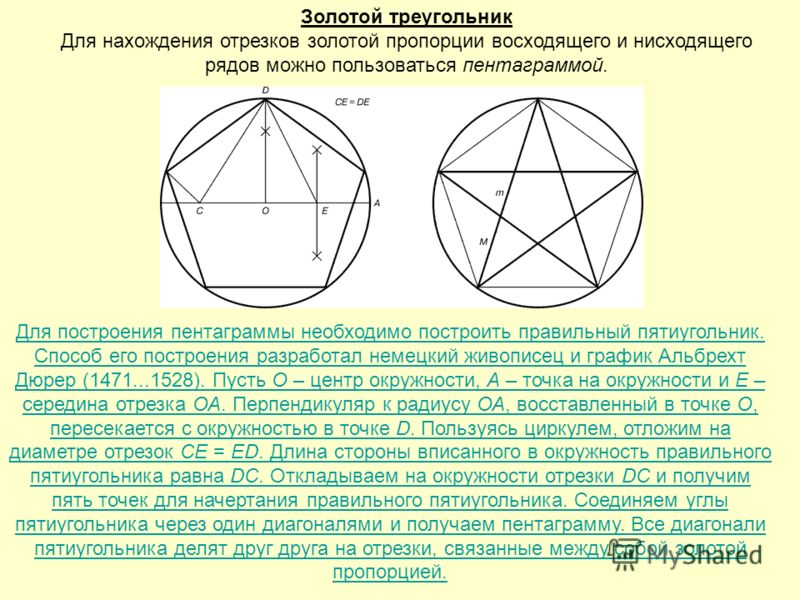 Если же в процессе построения использовались другие чертежные инструменты, то построение не считалось геометрическим. Уже в древности греческие математики встретились с тремя задачами на построение, которые не поддавались решению.
Если же в процессе построения использовались другие чертежные инструменты, то построение не считалось геометрическим. Уже в древности греческие математики встретились с тремя задачами на построение, которые не поддавались решению.
Первая задача. Задача об удвоении куба. Требуется построить ребро куба, который по объему был бы в два раза больше данного куба.
Вторая задача. Задача о трисекции угла. Требуется произвольный угол разделить на три равные части.
Третья задача. Задача о квадратуре круга. Требуется построить квадрат, площадь которого равнялась бы данному кругу. Эти три задачи на построение и носят название «знаменитых геометрических задач древности». Большую роль задачи на построение играют в «Началах» Эвклида , где существование фигур доказывается их построением при помощи циркуля и линейки. В «Началах» Эвклида находятся почти все задачи на построение, которые изучаются в настоящее время в школе.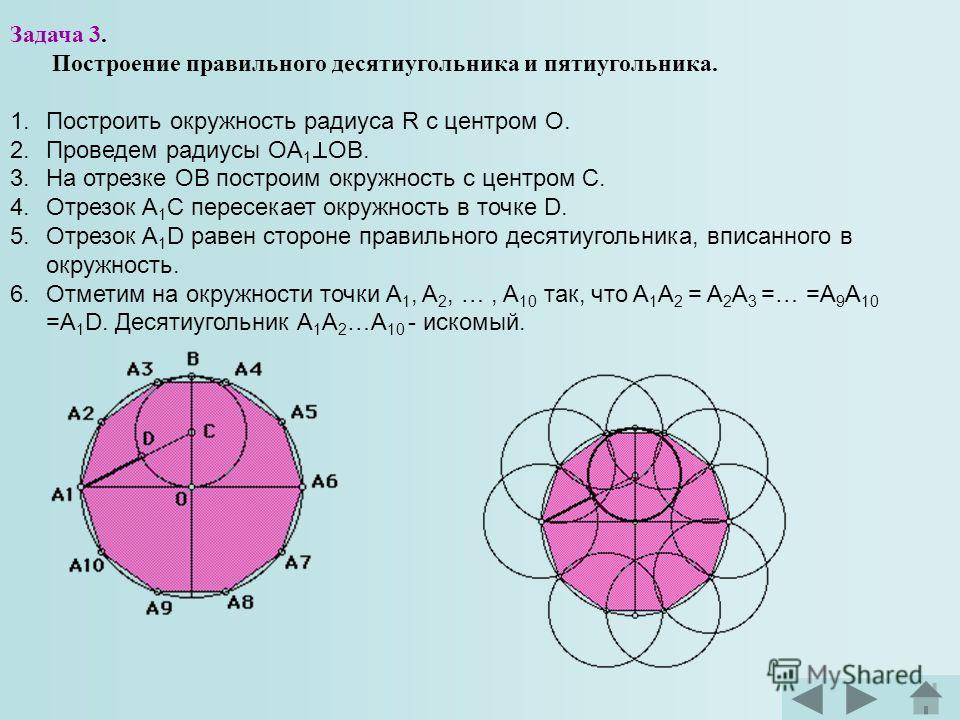
Теоретическая часть
Что такое задачи на построение?
Задача на построение — это задача, в которой требуется построить геометрический объект, пользуясь только двумя инструментами: циркулем и линейкой (односторонней и без делений). Решение задач на построение состоит не в том, чтобы проделать «руками» соответствующие построения, а в том, чтобы найти алгоритм решения, то есть описать решение задачи в виде последовательности уже известных стандартных построений, а также рассмотреть различные способы построения правильного пятиугольника. В этом и состоит цель моей работы.
К элементарным задачам на построение, которые рассматривают на начальных этапах изучения в школьном курсе геометрии, как правило, относят следующие:
1. Отложение на прямой отрезка, равного данному.
2.
3. Построение прямой, проходящей через данную точку и параллельную данной прямой.
4. Построение прямой, проходящей через данную точку и перпендикулярную к данной прямой.
5. Деление отрезка на две равные части.
6. Деление отрезка в заданном отношении.
7. Построение биссектрисы угла.
8. Построение угла, равного данному.
9. Построение треугольника по трём сторонам, по двум сторонам и углу между ними, по стороне и прилежащим к ней углам.
10. Построение прямоугольного треугольника по гипотенузе и катету, по гипотенузе и острому углу, по двум катетам.
11. Нахождение центра построенной окружности.
12. Построение касательной к окружности через заданную на ней точку. Заметим, что представленный перечень элементарных задач является условным, его можно дополнить.
Построение касательной к окружности через заданную на ней точку. Заметим, что представленный перечень элементарных задач является условным, его можно дополнить.
Сколько бывает решений для задач на построение?
Решить задачу на построение — найти все её решения. Покажем на простейших примерах возможные случаи.
З адача имеет одно решение.
Рисунок 1
Пусть требуется построить прямоугольный треугольник по катету и гипотенузе. Таких треугольников на плоскости можно построить множество, и они могут располагаться как угодно, но у всех равны соответственно две стороны два данных отрезка: гипотенуза и катет, а значит, эти треугольники равны. В этом случае говорят, что задача имеет одно решение «с точностью до равенства». Поэтому достаточно построить один треугольник.
Задача имеет конечное число решений.
Рисунок 2
Пусть требуется построить прямоугольный треугольник, катетом которого служит данный отрезок AC, а гипотенуза равна другому данному отрезку L. В этом случае условие задачи требует определённого расположения искомого треугольника относительно катета AC. Треугольник может оказаться в верхней полуплоскости и в нижней полуплоскости относительно отрезка AC. Поэтому задача имеет два решения: Δ и Δ (рис. 2), причём Δ = Δ . Важно отметить, что хотя здесь треугольники и равны, мы считаем их разными решениями (поскольку они расположены по-разному относительно отрезка AC).
Задача имеет бесконечно много решений.Такого рода задачи называют неопределёнными. Конечно, мы не можем построить все решения неопределённой задачи. Когда же считают неопределённую задачу решённой? В том случае, когда указаны:
1) приём построения одной из искомых фигур задачи;
2) приём получения других искомых фигур.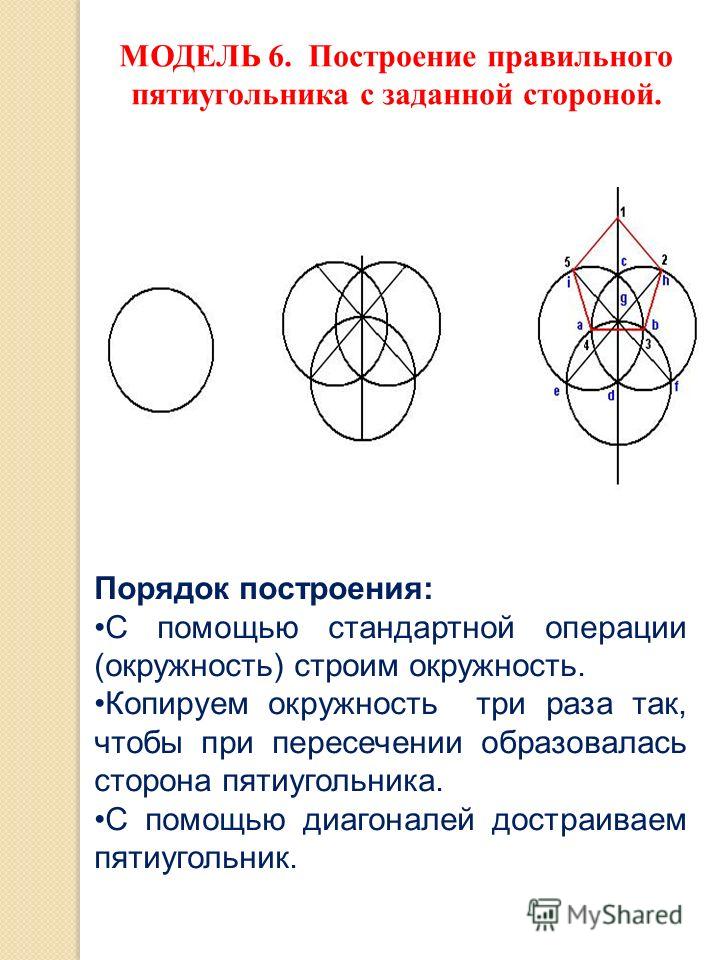
Пример. Построить окружность данного радиуса и касающуюся данной прямой.
Рисунок 3
Р ешение. Через произвольную точку B прямой L проведём прямую L1⊥L. Отложим на прямой L1 от точки B, например, в верхнюю полуплоскость отрезок BO = r. Проведём окружность ω(O;OB=r). Через точку O проведём прямую L2 параллельную L. Заметим, что при всевозможных положениях точки O на прямой L
Задача не имеет решений.
Такие задачи называют переопределёнными.
Пример. Построить окружность, проходящую через три данные точки, лежащие на одной прямой. Если точки лежат на одной прямой, то провести через них окружность нельзя. Следовательно, задача не имеет решения.
О расположении данных в задаче ничего не сказано.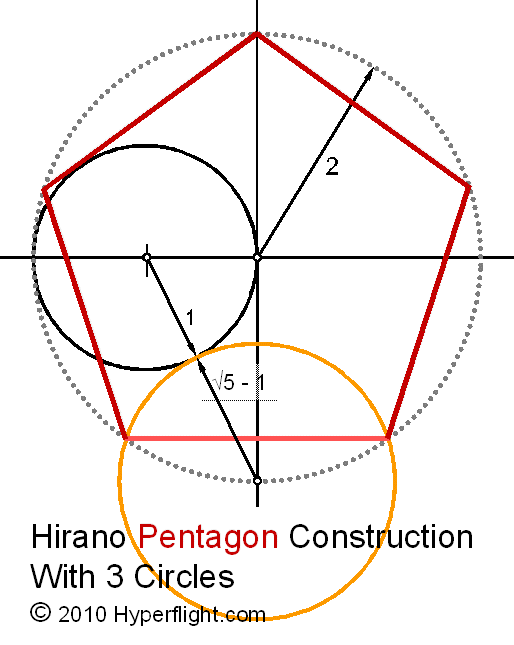 В таких случаях задачу считают решённой, если рассмотрены всевозможные случаи расположения данных.
В таких случаях задачу считают решённой, если рассмотрены всевозможные случаи расположения данных.
Пример. Провести через данную точку касательную к данной окружности.
Решение. Возможны три случая расположения данных (точки и окружности).
Случай 1. Точка находится вне окружности, но не принадлежит кругу. Здесь можно провести две касательные к окружности (рис. 4).
Случай 2. Точка находится на окружности. Здесь можно провести одну касательную (рис. 5).
Рисунок 4
Рисунок 5
Рисунок 6
С лучай 3. Точка находится вне окружности, но принадлежит кругу. Здесь касательную к окружности провести нельзя (рис. 6).
Что такое правильный пятиугольник? Правильный пятиугольник, или пентагон (от греческого πενταγωνον-пятиугольник) — выпуклая фигура, имеющая пять вершин, все стороны которой равны между собой (рис 7).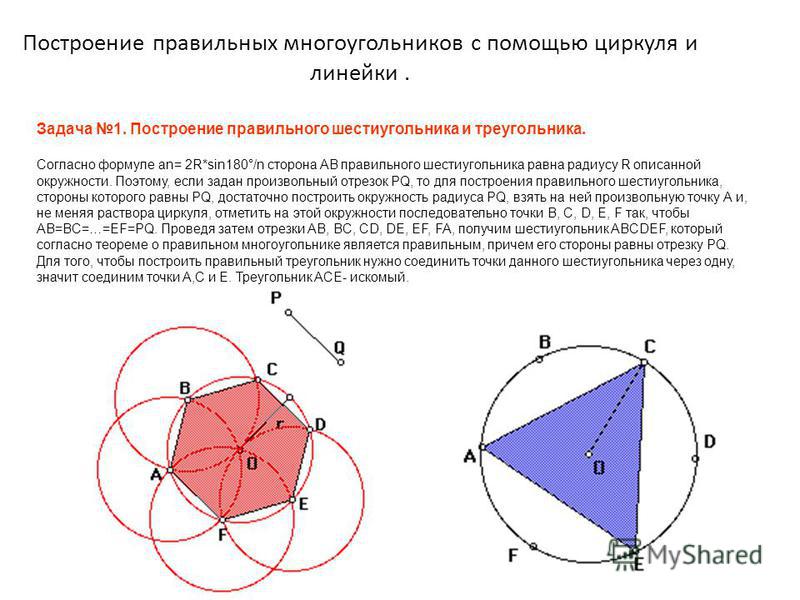
Также, можно заметить, что данная фигура делится в золотом сечении.
Рисунок 7. Правильный пятиугольник
Рисунок 8. Деление правильного пятиугольника в золотом сечении
Архитектурные сооружения, при проектировании которых использовались правильные пятиугольники
Пятиугольный храм (1475-1554) (рис. 10)
Дворец в крепости (1475-1554) (рис. 11)
Театр Советской армии (1934-1940) (рис. 12)
Цитадель в Кортрейке ( III-IV вв.) (рис. 13)
Укреплённая крепость Пиллау (начало XVIIв.) (рис. 14)
Схема типовой крепости из руководства по военному искусству(рис. 15)
Здание министерства обороны США (окончание строительства — январь 1943) (рис. 16)
Дом Советов в Махачкале (1927) (рис. 17)
План типового этажа( 2-9 этаж) 9-этажного дома башенного типа жилого комплекса Слоттсбергет в Гётеборге
Рисунок 9
Рисунок 10
Рисунок 11 Рисунок 12
Рисунок 13 Рисунок 14
Рисунок 15 Рисунок 16
Практическая часть.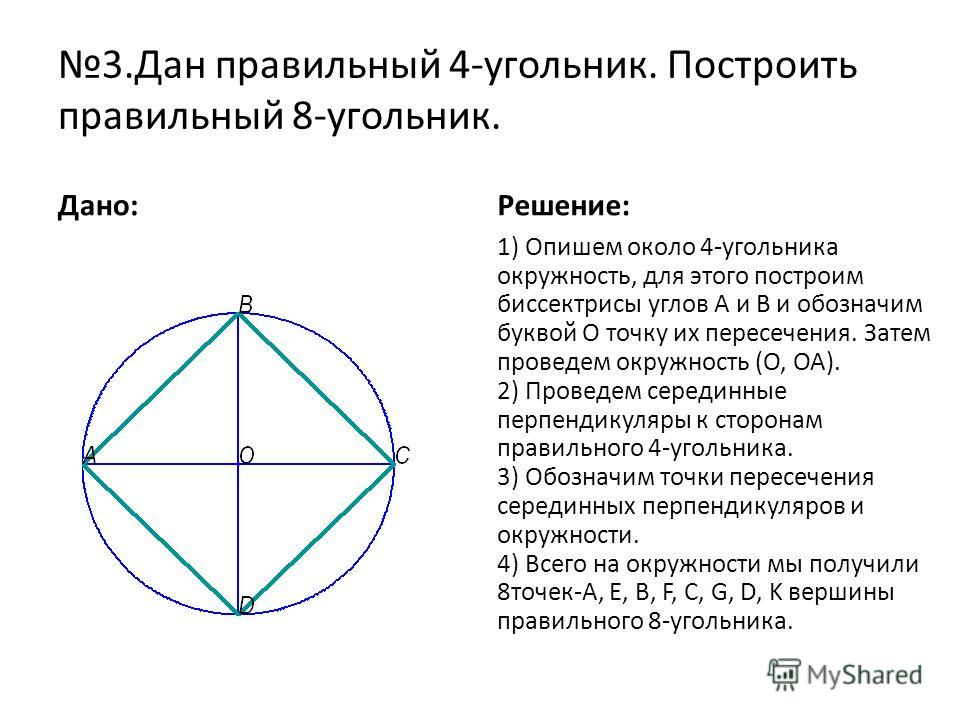 Приложение А
Приложение А
Заключение
Своеобразие геометрии,
выделяющее её среди
других разделов математики,
да и всех наук вообще,
заключается в неразрывном
органическом соединении живого
воображения со строгой логикой.
Геометрия в своей сути и есть
пространственное воображение,
пронизанное и организованное
строгой логикой.
В ходе моей работы цель исследования – поиск решений задач на построение треугольника по трем элементам и правильного пятиугольника была достигнута. В своей работе я рассмотрел архитектурные сооружения различных стилей, построенные в разные эпохи, и выявил, что при проектировании данных сооружений использовались правильные пятиугольники.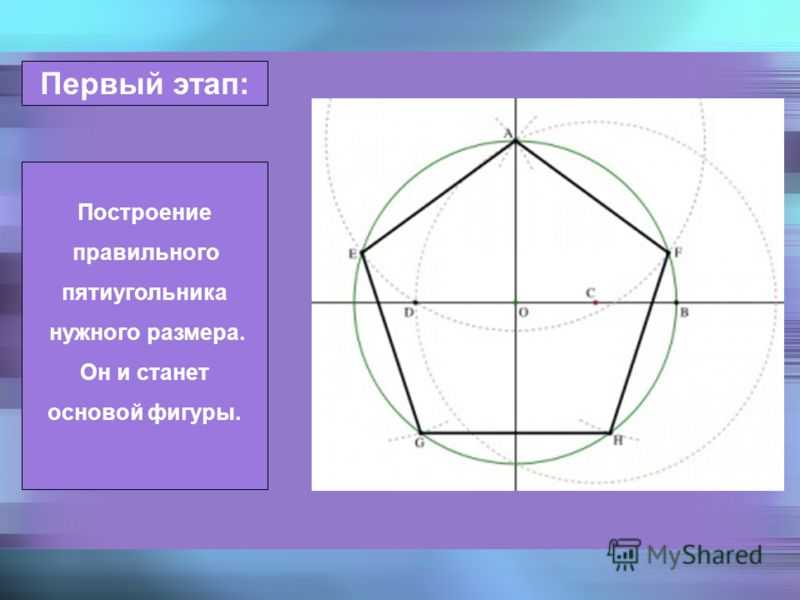 Памятники архитектуры, получившие широкую известность как образцы пропорциональности и гармонии, буквально пронизаны математикой, численными расчетами и геометрией.
Памятники архитектуры, получившие широкую известность как образцы пропорциональности и гармонии, буквально пронизаны математикой, численными расчетами и геометрией.
Практическая часть моей работы включает в себя различные задачи повышенной сложности на построение с помощью циркуля и линейки треугольника по трем элементам и правильного пятиугольника.
Я выбрал эту тему, так как она имеет большое практическое применение в нашей жизни, например, в архитектуре, геометрии, инженерной графике, проектировании.
Список использованной литературы
1.http://www.psciences.net/main/sciences/mathematics/articles/article-1.html
2.http://poisk-ru.ru/s5188t3.html
3.https://ru.wikipedia.org/wiki/Правильный_пятиугольник
4. В. Н. Литвинов «Правильный пятиугольник» 2012г.
5. Александров И.И. «Сборник геометрических задач на построение», 1950 г
Александров И.И. «Сборник геометрических задач на построение», 1950 г
Просмотров работы: 119
Построение правильных многоугольников
Построение правильных многоугольников
|
Геометрические построения – правильные многоугольники – Mathigon
Цель и обзор
концепции.
В древние времена геометрические построения фигур и длин ограничивались использованием только линейки и циркуля.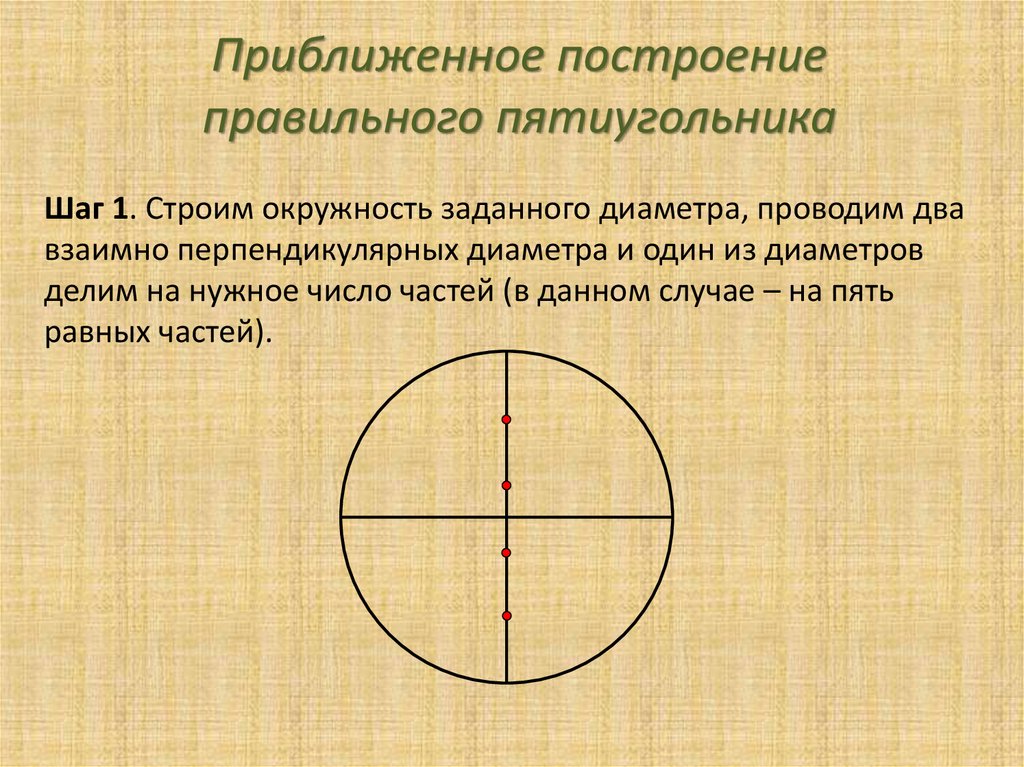 Сегодня эту традицию можно использовать для создания серии уроков-головоломок. Этот модуль посвящен геометрическим построениям правильных многоугольников:
Сегодня эту традицию можно использовать для создания серии уроков-головоломок. Этот модуль посвящен геометрическим построениям правильных многоугольников:
- ЭКВИЛАСТИЧЕСКИЙ ТРЕУГЛАНГ
- Квадрат
- Обычный Pentagon
- Обычный гексагон
- Регулярный Heptagon*
- Обычный Octagon
- Регулярный Heptagon*
- . форма. Перед началом этого занятия вы можете воспользоваться планом урока «Геометрические построения — базовый».
Попросите учащихся построить равносторонний треугольник, используя только линейку и циркуль. Напомните учащимся, что они не могут использовать линейку для измерения длины или транспортир для измерения углов. Предложите учащимся поделиться своими идеями о возможных методах. Вы также можете обсудить, как можно использовать круги для построения равностороннего треугольника. Вот два подхода:
- Если дана определенная длина, поместите компас на один конец сегмента и установите циркуль на длину данного сегмента, чтобы нарисовать дугу.

- Затем сохраните ширину циркуля постоянной и нарисуйте еще одну дугу, поместив циркуль на другой конец сегмента.
- Две дуги пересекутся где-то выше и ниже сегментов. Используйте одно из пересечений как третью вершину равностороннего треугольника.
- Соедините концы отрезка с точкой пересечения, чтобы построить равносторонний треугольник.
- Если вы повторите те же шаги, нарисовав вместо дуг полные круги, вы снова можете создать равносторонний треугольник.
Попросите учащихся измерить углы и стороны треугольников, чтобы доказать, что это равносторонний треугольник. Обсудите со студентами, почему эти методы работают после каждого построения.
Основная деятельность
Многие правильные многоугольники также можно построить с помощью линейки и циркуля.
 Предложите учащимся построить правильные многоугольники, перечисленные выше. Варианты включают представление их по одному, предоставление общего доступа к ним всем учащимся или предоставление доступа к некоторым группам. Вы можете подумать над тем, чтобы поработать над ними в течение нескольких уроков или постепенно на протяжении всей учебной единицы. Ниже приведены решения для каждого из них.
Предложите учащимся построить правильные многоугольники, перечисленные выше. Варианты включают представление их по одному, предоставление общего доступа к ним всем учащимся или предоставление доступа к некоторым группам. Вы можете подумать над тем, чтобы поработать над ними в течение нескольких уроков или постепенно на протяжении всей учебной единицы. Ниже приведены решения для каждого из них.Квадрат
Квадрат можно построить разными способами. Например, вы можете использовать свойства диагоналей квадратов, чтобы построить его.
Диагонали квадратов имеют одинаковую длину и являются биссектрисами друг друга.
- Постройте серединный перпендикуляр к отрезку AB.
- Используйте середину отрезка AB, чтобы нарисовать окружность.
- Отметьте и подпишите точки, в которых окружность пересекается с линией.
- Соедините четыре точки, чтобы построить квадрат
Вы также можете использовать нижнюю панель инструментов для прямого построения средней точки, параллели и перпендикулярных линий.

Правильный пятиугольник
Существуют различные способы построения правильного пятиугольника. Одним из них является метод построения правильного пятиугольника Хирано. В этом методе он использует тригонометрию, чтобы доказать точность построения.
- Начните с рисования окружности радиусом AB, где A — центр окружности.
- Отметьте середину радиуса AB точкой C и нарисуйте еще одну окружность с центром C.
- Проведите перпендикуляр к радиусу AB через центр A.
- Отметьте и обозначьте точку пересечения окружности с перпендикулярной линией как D.
- Соедините D и C отрезком.
- Отметьте пересечение окружности с центром C и отрезком CD и обозначьте как E.
- Нарисуйте еще одну окружность с центром D и радиусом DE.
Вы можете остановиться здесь и спросить учащихся о длине ACundefined\overlinesegment{AC}AC, CDundefined\overlinesegment{CD}CD и DEundefined\overlinesegment{DE}DE, если длина ABundefined\overlinesegment{AB}AB составляет 222 единицы.

Используя теорему Пифагора, можно найти длины сторон треугольника ACD. Поскольку ACundefined\overlinesegment{AC}AC и CEundefined\overlinesegment{CE}CE являются радиусами окружности с центром C, они конгруэнтны. Поэтому длина стороны DEundefined\overlinesegment{DE}DE составляет sqrt5-1sqrt{5}-1sqrt5-1 единиц.
- Теперь отметьте точки пересечения окружностей с центрами A и D и обозначьте их как H и G.
Вы можете продемонстрировать построение треугольника FGD с помощью пользовательского инструмента многоугольника. 9oo
Тогда мера вписанного угла HFG равна 36 градусам, что доказывает, что дуговая мера HG равна 72 градусам. Поскольку мы доказали, что делим окружность круга на 5 равных частей, мы можем продолжить и завершить правильный пятиугольник.
- Поместите циркуль на H и расположите его ширину как HG, чтобы нарисовать дуги на окружности. Повторите еще три раза, пока не отметите пять вершин пятиугольника.
Правильный шестиугольник
Правильный шестиугольник состоит из шести равносторонних треугольников.
Форма в виде цветка используется во многих областях искусства и архитектуры. Если показаны только дуги, похожие на лепестки, это называется hexafoi l. Если 19 цветков собираются вместе, его обычно называют цветком жизни.
HexafoilFlower of LifeПравильный семиугольник
*Правильный семиугольник нельзя построить с помощью циркуля и линейки, но можно построить с помощью отмеченной линейки и циркуля. Однако можно построить приближение для практического использования с погрешностью около 0,2%.
Правильный восьмиугольник
Построение правильного восьмиугольника и двенадцатиугольника (12-угольника) очень похоже.

- Начните с рисования окружности с центром A.
- Постройте перпендикулярные диаметры как CB и DE.
- Затем соедините B, C, D и E, чтобы получился квадрат. (Квадратная конструкция)
- Постройте четыре круга. Каждый угол квадрата должен быть центром одного из кругов.
- Постройте точку везде, где окружности пересекают квадрат DBEC.
- Соедините эти точки, чтобы построить правильный восьмиугольник.
- Вместо построения точек пересечения кругов с квадратом постройте точки везде, где пересекаются пять кругов.
- Соедините все точки, чтобы построить правильный додекаэдр.
Замыкание
Не все правильные многоугольники можно построить. Многоугольники с 7, 9 и 11 сторонами, например, не являются.

- Если дана определенная длина, поместите компас на один конец сегмента и установите циркуль на длину данного сегмента, чтобы нарисовать дугу.

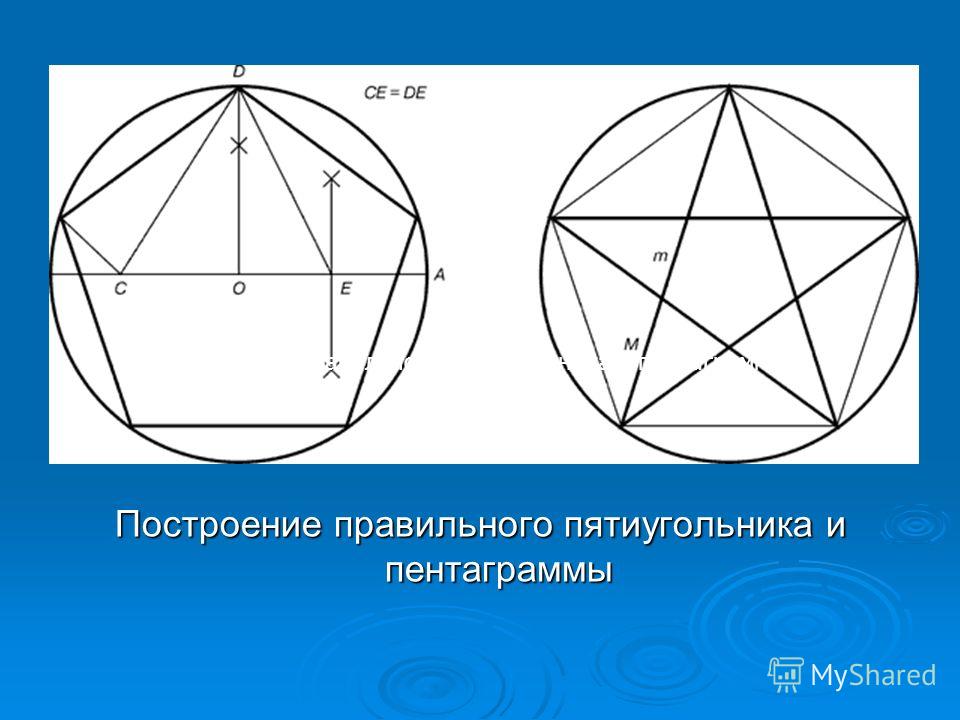 (См. рис. 2).
(См. рис. 2). 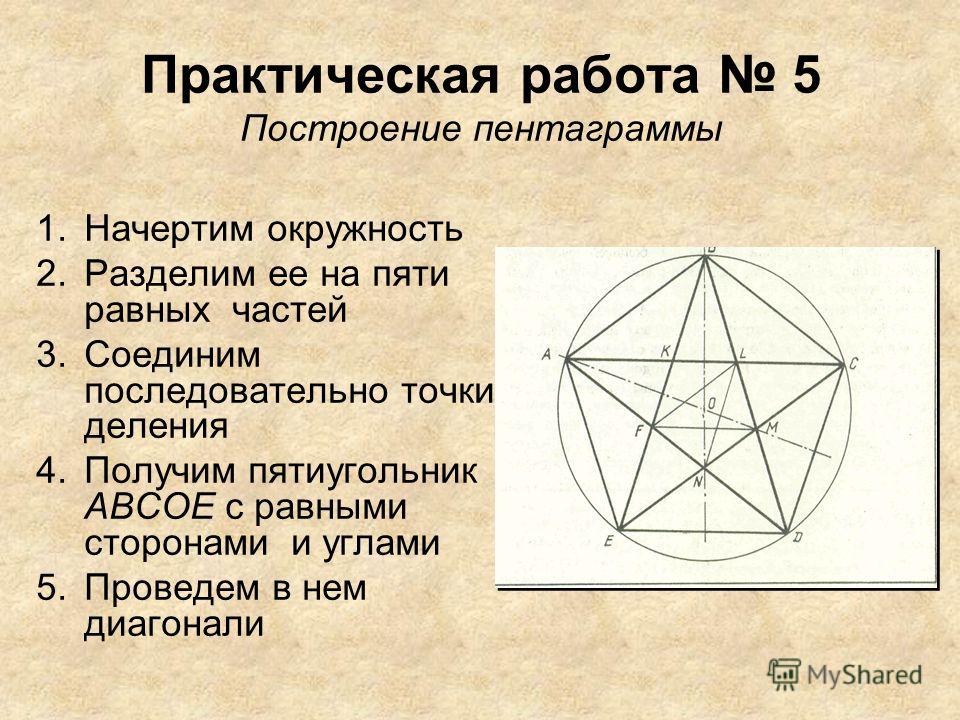 Затем, продолжая от точки В, ударить еще 4 дуги.
Затем, продолжая от точки В, ударить еще 4 дуги. , а не , см. такие ответы, как 77.3333333333333333.
, а не , см. такие ответы, как 77.3333333333333333. 
 Предложите учащимся построить правильные многоугольники, перечисленные выше. Варианты включают представление их по одному, предоставление общего доступа к ним всем учащимся или предоставление доступа к некоторым группам. Вы можете подумать над тем, чтобы поработать над ними в течение нескольких уроков или постепенно на протяжении всей учебной единицы. Ниже приведены решения для каждого из них.
Предложите учащимся построить правильные многоугольники, перечисленные выше. Варианты включают представление их по одному, предоставление общего доступа к ним всем учащимся или предоставление доступа к некоторым группам. Вы можете подумать над тем, чтобы поработать над ними в течение нескольких уроков или постепенно на протяжении всей учебной единицы. Ниже приведены решения для каждого из них.