Как построить правильный пятиугольник с помощью циркуля и линейки: Построение пятиугольника подробно. — Чертежик — Интернет магазин мебели "МебПилот.ру"

Разное

Содержание

Построение правильных многоугольников при помощи циркуля и линейки

Авторы
Руководители
Файлы работы
Наградные документы

Вагин А.С. 1

1МАОУ Школы №137 ГО г. Уфа РБ

Бикмухаметова Р.А. 1

1МАОУ Школы №137 ГО г. Уфа РБ

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

В начале прошлого столетия великий французский архитектор Корбюзье как-то воскликнул: «Все вокруг геометрия!». Сегодня уже в начале 21-го столетия мы можем повторить это восклицание с еще большим изумлением. В самом деле, посмотрите вокруг – всюду геометрия! Геометрические знания и умения, геометрическая культура и развитие являются сегодня профессионально значимыми для многих современных специальностей, для дизайнеров и конструкторов, для рабочих и ученых.

Правильные многоугольники с глубокой древности считались символом красоты и совершенства.Деление окружности на некоторое число равных частей для построения правильных многоугольников имело важное значение для пифагорейцев, которые утверждали, что числа лежат в основе всех явлений мира.

Геометрические знания и умения, геометрическая культура и развитие являются сегодня необходимыми для многих современных специальностей, для архитекторов и конструкторов, для рабочих и ученых. Со временем, человек научился использовать свойства геометрических фигур в практической жизни. Из всех многоугольников с заданным числом сторон наиболее приятен для глаза правильный многоугольник, у которого равны все стороны и равны все углы. Я увлекаюсь изобразительным искусством, и мне часто приходится рисовать различные многоугольники в своих работах. Отсюда и вытекает актуальность темы моей работы.

Цель проекта: изучить способы построения и научиться строить правильные многоугольники при помощи циркуля и линейки.

Задачи данной работы: изучить историю возникновения построений правильных многоугольников и рассмотреть известные задачи на построение геометрических фигур с помощью циркуля и линейки; научиться выполнять основные геометрические построения.

Объект исследования: алгоритмы построения правильных многоугольников.

Предмет исследования: правильные многоугольники.

Методы исследования:

– анализ источников информации;

– анализ методов построения правильных многоугольников;

– обработка полученных результатов.

Значимость работы состоит в том, что я научился строить правильные многоугольники, и в дальнейшем буду применять эти знания на других уроках и в творчестве.

Из истории геометрического построения циркулем и линейкой

Построением правильных многоугольников ученые занимались с древних времен. Искусство построения геометрических фигур было в высокой степени развито в Древней Греции.

Древнегреческие ученые стали проявлять большой интерес к правильным фигурам еще со времен Пифагора. Учение о правильных многоугольниках, начатое в школе Пифагора, продолженное и развитое в V—IV вв. до н. э., было систематизировано Евклидом и изложено в IV книге «Начал». Кроме построения правильного треугольника, четырехугольника, пятиугольника и шестиугольника, Евклид: решает и задачу построения правильного пятнадцатиугольника при помощи только циркуля и линейки.

Древнегреческие математики еще 3000 лет назад проводили свои построения с помощью двух приборов: гладкой дощечки с ровным краем – линейки и двух заостренных палок, связанных на одном конце – циркуля. Однако этих простейших инструментов оказалось достаточно для выполнения огромного множества различных построений.

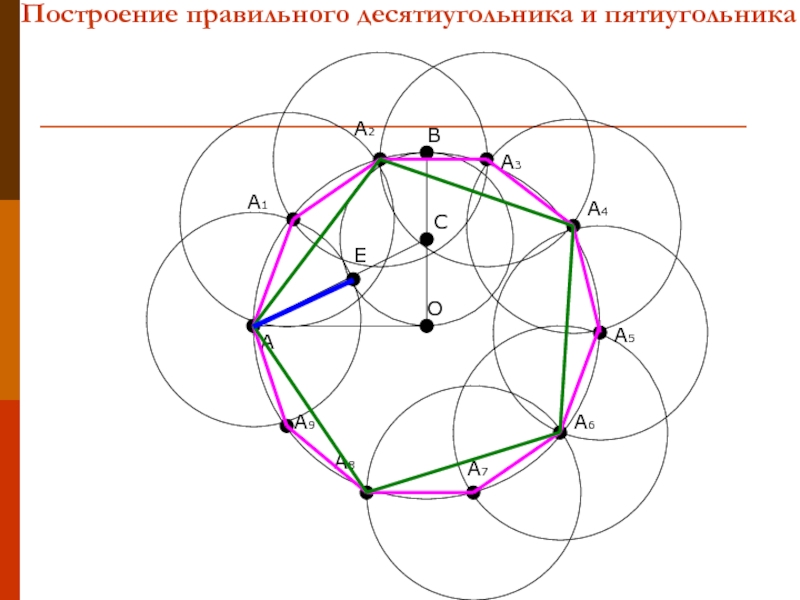
Древние греки умели строить правильный треугольник, квадрат, правильные пятиугольник и 15-угольник, а также все многоугольники, которые получаются из них путем удвоения сторон.

Долгое время математики тщетно искали способы построения правильного семиугольника, девятиугольника, одиннадцатиугольника и т. д., не зная даже, возможно ли вообще построение таких многоугольников с по мощью только циркуля и линейки. Эта проблема была решена лишь в конце ХVIII в. 19-летним К. Ф. Гауссом, великим немецким математиком, доказавшим, что с помощью циркуля и линейки можно разделить окружность на такое простое число N равных частей, которое выражается формулой

N = + 1, где n — натуральное число или нуль.

Вот несколько примеров: 1) n = 0, N = 3; 2) n = 1, N = 5; 3) n = 2, N = 17; 4) n = З, N = 257; 5) n = 4, N = 65 537 и т. д.

После открытия Гаусса стало ясно, что, помимо ранее известных правильных многоугольников с 3; 4; 5; 6; 8; 10; 12; 15; 16; 20; 24; 30; 32; 40; … сторонами, можно построить с помощью циркуля и линейки правильные многоугольники с 17; 34; 68; 126; 252; 257; 65537… сторонами.
Им было доказана невозможность циркулем и линейкой построить правильные многоугольники со следующим числом сторон: 7; 9; 11; 13; 14; 18; 19; 21; 22; 23; 25; 27; 28.

Основные построения

2.1 Построение отрезка, равного данному

Построение отрезка, равного данному отрезку АВ (приложение 1, рис. 1) выполняется с помощью циркуля таким образом: одну ножку циркуля устанавливают на один конец отрезка АВ, а другую — на другой его конец и, не меняя раствора циркуля, переносят его на некоторую прямую так, чтобы конец одной ножки отметил какую-нибудь точку N, тогда конец другой ножки циркуля отметит некоторую точку Р на этой же прямой. Отрезок NP будет равен отрезку АВ.

2.2 Деление отрезка пополам

С помощью циркуля и линейки разбить данный отрезок AB на две равные части. Одно из решений показано на рисунке (приложение 1, рис.

2): циркулем проводим окружности с центром в точках A и B радиусом AB.
Находим точки пересечения P и Q двух построенных окружностей (дуг).

По линейке проводим отрезок или линию, проходящую через точки P и Q. Находим искомую середину отрезка AB — точку пересечения AB и PQ.

2.3 Построение угла, равного данному

Проведем произвольную окружность с центром в вершине А данного угла (приложение 1, рис. 3). Пусть В и С — точки пересечения окружности со сторонами угла. Радиусом АВ проведем окружность с центром в точке О-начальной точке данной полупрямой. Точку пересечения этой окружности с данной полупрямой обозначим С₁. Опишем окружность с центром С₁ и радиусом ВС. Точка В₁ пересечения построенных окружностей в указанной полуплоскости лежит на стороне искомого угла.

2.4 Построение биссектрисы угла

Из вершины A данного угла как из центра описываем окружность произвольного радиуса r (приложение 1, рис. 4). Пусть B и С – точки ее пересечения со сторонами угла. Из точек В и С проведем окружности тем же радиусом r. Пусть точка D – точка их пересечения, отличная от A. Проведем луч AD. Проведем отрезки BD и CD. Δ ABD = Δ ACD, по третьему признаку равенства треугольников. Отсюда ∠ BAD = ∠ CAD и, следовательно, AD – биссектриса угла BAC.

2.5 Построение перпендикулярных прямых

Проводим окружность с произвольным радиусом r с центром в точке O (приложение 1, рис. 5). Окружность пересекает прямую в точках A и B. Из точек A и B проводим окружности с радиусом AB. Пусть тоска С – точка пересечения этих окружностей.Точки А и В мы получили на первом шаге, при построении окружности с произвольным радиусом.

Искомая прямая проходит через точки С и О.

Построение правильных многоугольников

Существуют различные способы построения правильных многоугольников. В данной работе рассматривается способ построения правильных многоугольников, вписанных в круг.

Для выполнения построений мы используем циркуль и линейку.

Циркуль позволяет:

– построить окружность,

– построить дугу окружности,

– отложить на прямой отрезок, равный данному.

Линейка позволяет:

– построить прямую линию,

– построить отрезок, соединяющий две точки,

– найти точку пересечения двух прямых.

Рассмотрим, каким образом можно с помощью циркуля и линейки построить правильный многоугольник, вписанный в окружность.

Построение правильного (или равностороннего) треугольника.

С помощью линейки строим две взаимоперпендикулярные прямые. Точку пересечения прямых обозначаем точку С – центр окружности. С помощью циркуля строим окружность с центром в точке С.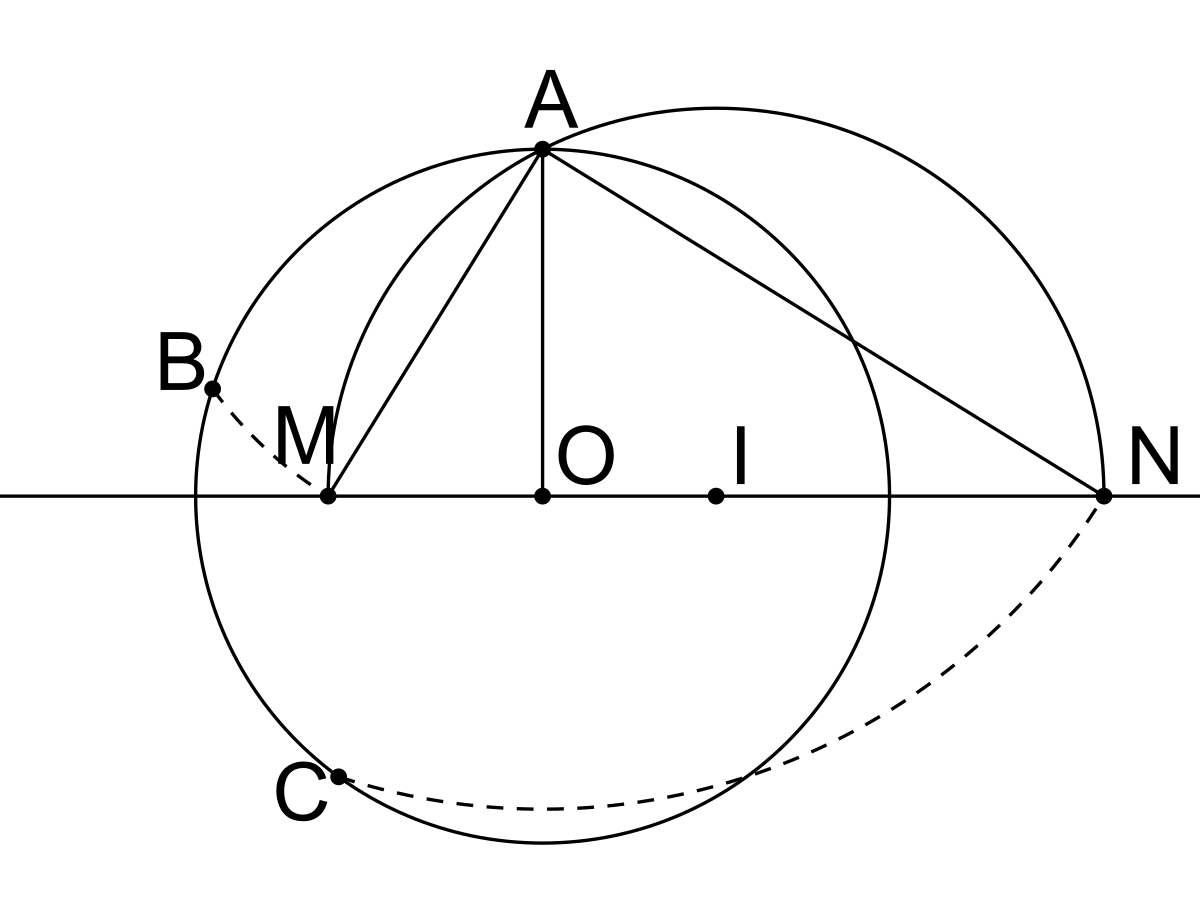 Точки пересечения вертикальной осевой линии и окружности обозначим Е и D. Раствором циркуля равным радиусу с центром в точке D, строим окружность делаем. Точки пересечения с первой окружностью обозначим F и G. Соединив линиями точки E, F,G, получим правильный или равносторонний треугольник (приложение 2, рисунок 1).

Построение правильного четырехугольника или квадрата.

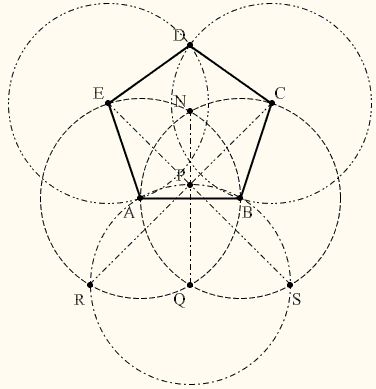
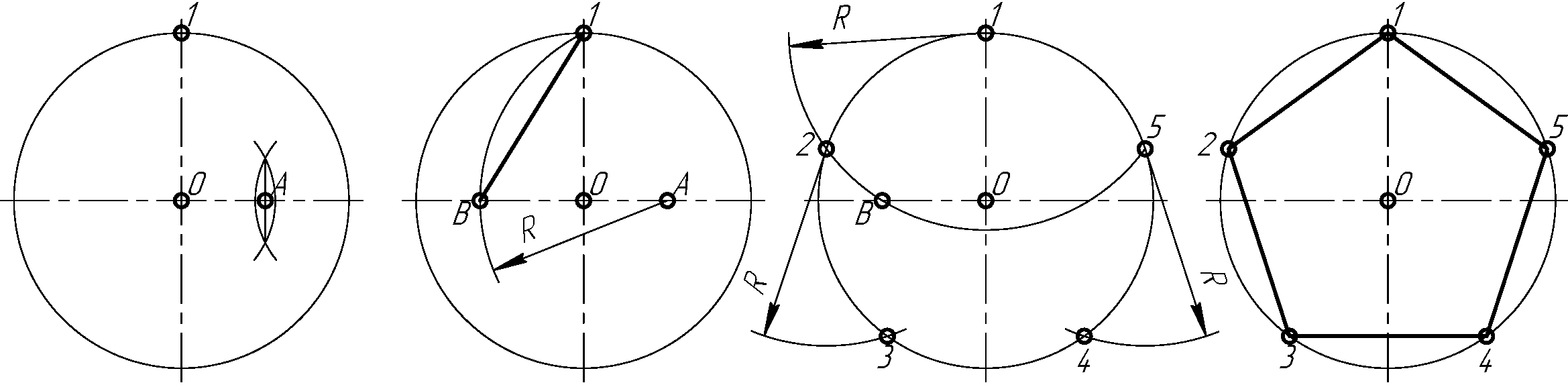
С помощью линейки строим две взаимоперпендикулярные прямые. Точку пересечения прямых обозначаем точку А – центр окружности. С помощью циркуля строим окружность с центром в точке А. Точки пересечения прямых и окружности обозначим Е, C, F и D. Эти точки делят окружность на четыре равные части. Соединяем полученные четыре точки E, C, F и D между собой отрезками и получаем правильный четырех угольник или квадрат (приложение 2, рисунок 2).

Построение правильного пятиугольника.

С помощью линейки строим две взаимоперпендикулярные осевые линии окружности. В точке пересечения линий обозначаем точку А – центр окружности. С помощью циркуля строим окружность с центром в точке А. Точки пересечения осевых линий и окружности обозначим B, Е, С D. Раствором циркуля равным радиусу построим окружность с центром в точке В. Соединим точки пересечения дуги и окружности FG. Эта линия разделит радиус BAпополам. Эту точку пересечения обозначим H. Из точки H, раствором циркуля равным длине отрезку HE, проводим окружность, которая пересекает АC в точке J. Длина отрезка EJ будет равна одной пятой длины окружности. Раствором циркуля равным длине отрезка EJ из точки Eпоследовательносделаем засечки на окружности и соединим полученные точки E, C, M, F, N, Bмежду собой отрезками и получаем правильный пятиугольник (приложение 2, рисунок 3).

Построение правильногошестиугольника.

Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура (приложение 2, рисунок 4).

Построение правильного семиугольника.

Построим окружность с центром в точке А. Проведем диаметр DB. С центром в точках B и D проведем окружность радиуса АВ. Точки пересечения окружностей обозначим С и Е. Проведем отрезки ВЕ и АС. Точку пересечения обозначим F. От точки В откладываем последовательно дуги радиуса ВF. Получим точки G, J, K, L, I, H. Соединяем точки В, G, J, K, L, I, H, В. Получим правильный семиугольник (приложение 2, рисунок 5).

Заключение

Правильные многоугольники встречаются в природе.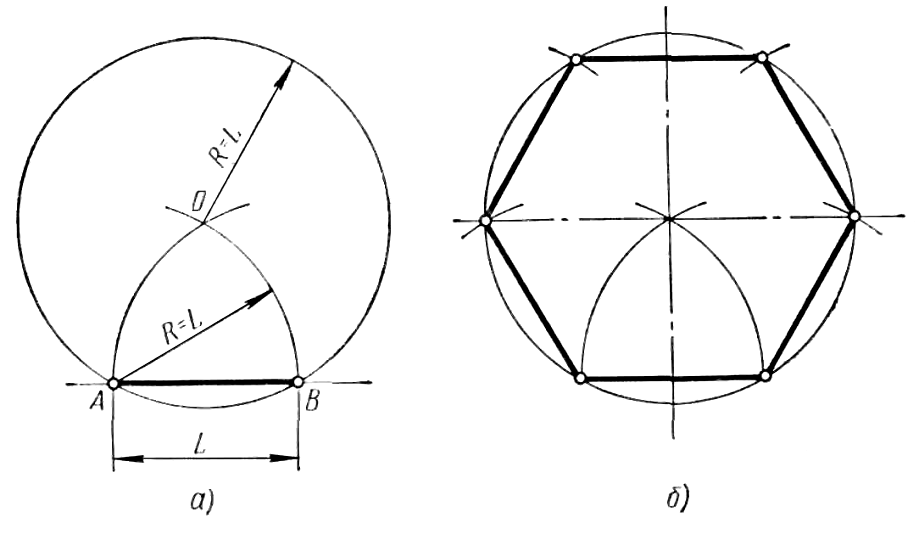 Один из примеров – пчелиные соты, которые представляют собой многоугольник, покрытый правильными шестиугольниками. Конечно, геометрию они не изучали, но природа наделила их талантом строить себе дома в форме геометрических фигур. Пчелы, не зная математики, верно «определили», что правильный шестиугольник имеет наименьший периметр среди фигур равной площади.

Красота и разнообразие геометрических форм снежинок по сей день считается уникальным природным явлением. Особенно математиков поразила найденная в середине снежинки «крошечная белая точка, точно это был след ножки циркуля, которым пользовались, чтобы очертить ее окружность».

Красивы паркеты из правильных многоугольников: треугольников, квадратов, пятиугольников, шестиугольников, восьмиугольников. Паркетный пол во все времена считался символом престижа и хорошего вкуса. Применение для производства элитного паркета ценных пород дерева и использование различных геометрических узоров придают помещению изысканности. Узоры вышивок, составленные из геометрических форм и сильно геометризированных мотивов, смотрятся прекрасно.

Этим исследованием я убедился, что геометрия очень важна для людей. Ее нужно изучать. Ее нужно применять.

А построения правильных многоугольников являются одной из важных частей геометрии. Они формируют пространственное и логическое мышление, а также позволяют осознать простые и естественные геометрические закономерности.

Знания о правильных многоугольниках применяются в разных профессиях. Например, ювелир вставляет дорогой камень в золотую оправу. Слесарь подбирает ключ для болтика формы правильного многоугольника и т.д. Решенные нами задачи также показывают, что без знаний о правильных многоугольниках нам не обойтись. Они встречаются в жизни везде. Так, например, если необходимо забором данной длины огородить четырехугольный участок наибольшей площади, то следует выбрать этот участок в виде квадрата.

Все поставленные мною задачи выполнены. Я научился строить правильные многоугольники, а способы построения правильных многоугольников начал применять в своем творчестве.

Список использованных источников и литературы

1. Гнеденко В.В. Белоусов В.Д. Энциклопедический словарь юного математика.

2. Савин А.П. Детская энциклопедия. Я познаю мир. Москва. Астрель. 2003 г.

3. http://cheloveknauka.com/uchenie-o-pravilnyh-mnogougolnikah-v-istoricheskom-razvitii

4. https://ru.wikipedia.org/wiki/%D0%90%D0%BB%D1%8C-%D0%A4%D0%B0%D1%80%D0%B0%D0%B1%D0%B8

Приложение 1

Построение отрезка равного данному.

Рисунок 1

Деление отрезка на два равных.

Рисунок 2

Построение угла равного данному.

Рисунок 3

Построение биссектрисы угла.

Рисунок 4

Построение перпендикулярных прямых.

Рисунок 5

Приложение 2

Построение правильных многоугольников.

Правильный треугольник.

Рисунок 1

Квадрат.

Рисунок 2

Пятиугольник.

Рисунок 3

Шестиугольник.

Рисунок 4

Семиугольник.

Рисунок 5

Просмотров работы: 117

Приближенное построение правильных многоугольников с помощью циркуля и линейки. Учебно-методические пособие

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас.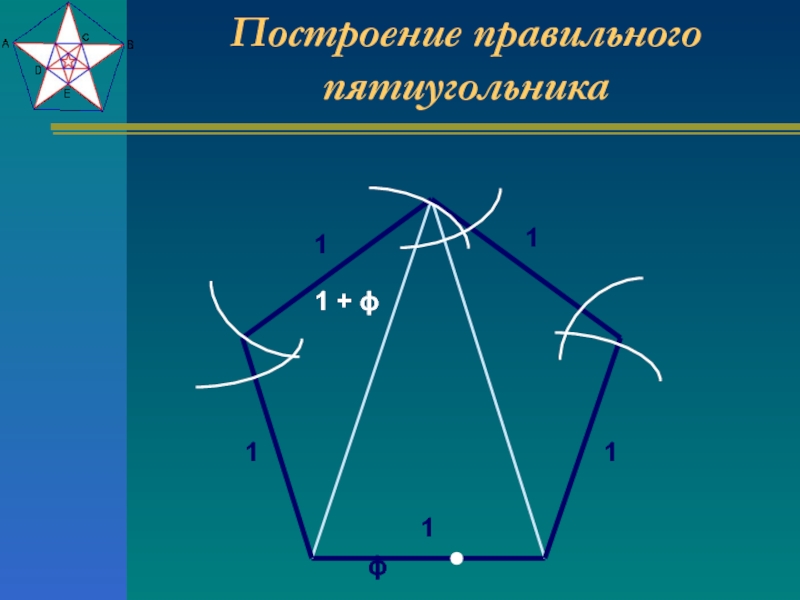 Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Любимова Виктория Сергеевна, учитель математики ГБОУ СОШ 454 Колпинского района Санкт-Петербурга

ПРИБЛИЖЕННОЕ ПОСТРОЕНИЕ
правильных многоугольников
с помощью циркуля и линейки
Учебно-методические пособие

2. Пояснительная записка

• В геометрии нередко для различных целей требуется
построить правильный n-угольник, но, как известно,
не все правильные n-угольники могут быть
построены с помощью циркуля и линейки абсолютно
точно.
• Тем не менее, для практических целей часто бывает
достаточно приближенного построения.

• В пособии рассматриваются некоторые способы
построения правильных n-угольников, которые без
особого труда могут освоить учащиеся.

3. Приближенное построение правильного семиугольника

Шаг 1. Построим окружность, в которую будет вписан
семиугольник, и из произвольной точки этой окружности
проведем дугу тем же радиусом до пересечения с окружностью
в точках M и N:
M
N

4. Приближенное построение правильного семиугольника

Шаг 2. Половина хорды MN приблизительно равна стороне
вписанного семиугольника (разделить хорду пополам можно,
построив серединный перпендикуляр к отрезку MN)
M
N

5. Приближенное построение правильного семиугольника

Шаг 3. Строим дугу с центром в точке М радиуса, равного
половине хорды MN, находим точки A и B пересечения с
окружностью.
А
N
M
В

6. Приближенное построение правильного семиугольника

Шаг 4. Аналогично находим положение остальных вершин
семиугольника:
А
В

7.

Приближенное построение правильного семиугольникаШаг 5. Соединяя найденные точки на окружности, получаем
искомый правильный семиугольник

8. Деление окружности на n равных частей

Задача о делении данной окружности на n равных
частей равносильна задаче о построении правильного
n-угольника, вписанного в эту окружность.
Универсальный способ приблизительного построения
любого правильного n-угольника, вписанного в
окружность, особенно удобен при нечетном числе
сторон.
Величина погрешности при точном построении
не превышает 0,02d (где d – диаметр данной
окружности, описанной около многоугольника).

9. Последовательность действий

• Строим окружность заданного диаметра (если диаметр не задан,
то выбираем такой, чтобы его удобно было разделить на
нужное число частей).
• Проводим два взаимно перпендикулярных диаметра.
• Вертикальный диаметр делим на нужное число частей.
• Из какого-либо конца вертикального диаметра, как из центра,
проводим дугу окружности радиусом, равным выбранному
диаметру, до пересечения с прямой, содержащей
горизонтальный диаметр, в двух точках справа и слева от
окружности.

• Из левой точки проводим лучи через четные деления
вертикального диаметра до пересечения с окружностью.
Аналогично проводим лучи через правую точку и те же деления
на вертикальном диаметре. В точках пересечения лучей с
окружностью получаем искомые вершины многоугольника.
• Соединяя полученные точки отрезками, строим многоугольник.

10. Приближенное построение правильного пятиугольника

Шаг 1. Строим окружность заданного диаметра, проводим два
взаимно перпендикулярных диаметра и один из диаметров
делим на нужное число частей (в данном случае – на пять
равных частей).

11. Приближенное построение правильного пятиугольника

Шаг 2. Из какого-либо конца вертикального диаметра, как из
центра, проводим дугу окружности радиусом, равным
выбранному диаметру, до пересечения с прямой, содержащей
горизонтальный диаметр, в двух точках справа и слева от
окружности.

12. Приближенное построение правильного пятиугольника

Шаг 3.

Из левой точки проводим лучи через четные деления
вертикального диаметра до пересечения с окружностью.
Аналогично проводим лучи через правую точку и те же
деления на вертикальном диаметре.

13. Приближенное построение правильного пятиугольника

Шаг 4. В точках пересечения лучей с окружностью (дальние от
начала луча точки) получаем искомые вершины
многоугольника. Соединяя полученные точки отрезками,
строим многоугольник.

14. Построение правильного восьмиугольника

15. Литература

• Годик Е. И., Хаскин А. М. Справочное
руководство по черчению. Изд. 4-е,
перераб. и доп. М., «Машиностроение»,
1974.
• Или в электронном виде
http://biblioteka.cc/index.php?newsid=86302

English Русский Правила

разница между построением вписанного квадрата и вписанного правильного шестиугольника

AlleBilderVideosBücherMapsNewsShopping

suchoptionen

‘В чем разница между построением квадрата и правильным шестиугольником? Диаметр круга используется для построения квадрата, а радиус круга используется для построения правильного шестиугольника.

Чем отличается построение квадрата… — Numerade

www.numerade.com › Спросите наших преподавателей › Алгебра

Hervorgehobene Фрагменты

Ähnliche Fragen

Какой шаг является одинаковым при построении вписанного квадрата и вписанного правильного шестиугольника?

При построении вписанного правильного шестиугольника по заданной точке на окружности сколько дуг будет проведено на окружности?

При построении вписанного квадрата сколько линий будет проведено в окружности 6 точек?

Опишите не менее двух отличий построения вписанного…

brainly.com › Математика › Высшая школа

Диаметр используется в квадрате, тогда как радиуса достаточно для правильного шестиугольника; Для квадрата строится биссектриса правильного …

какие 2 отличия построения вписанного правильного шестиугольника…

www.coursehero.com › репетиторы-задачи › Геометрия

При построении вписанного правильного шестиугольника мы необходимо использовать компас, чтобы получить радиус круга, а затем использовать радиус в качестве фиксированного интервала для резки . ..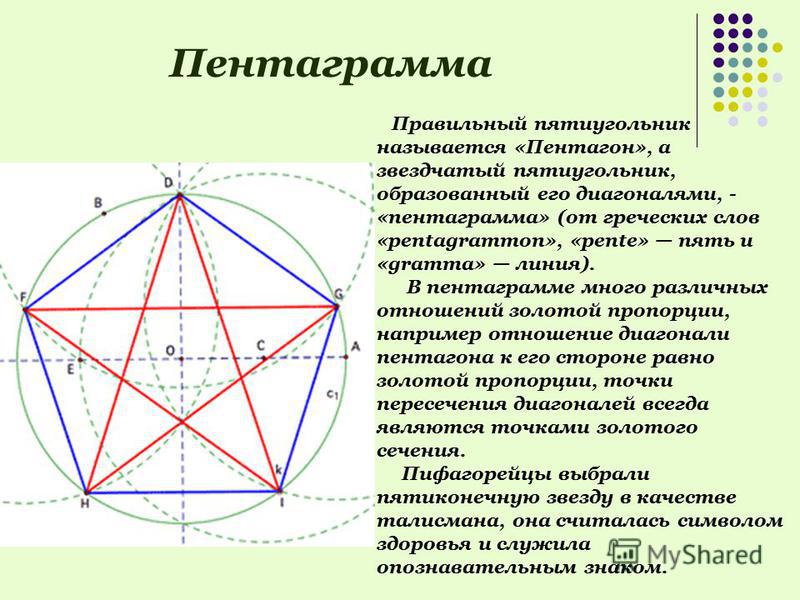

Разница между построением вписанного квадрата и вписанного …

udcsfr.swixim.es

Разница между построением вписанного квадрата и вписанного правильного шестиугольника Представим, что вписанный многоугольник в конечном итоге становится кругом.

Опишите не менее tw… — QuestionCove

questioncove.com › Вопросы › Математика

Опишите не менее двух различий между построением вписанного правильного шестиугольника и построением вписанного квадрата.

01.03 MC Опишите не менее двух отличий между — Gauthmath

www.gauthmath.com › геометрия › круги

01.03 MC Опишите не менее двух отличий между построением вписанного правильного шестиугольника и построением вписанного квадрата.

отличие построения вписанного квадрата от вписанного …

qxpvdv.bodembeheersomeren.nl

отличие построения вписанного квадрата от вписанного правильного шестиугольника

разница между построением вписанного квадрата и вписанного правильного шестиугольника.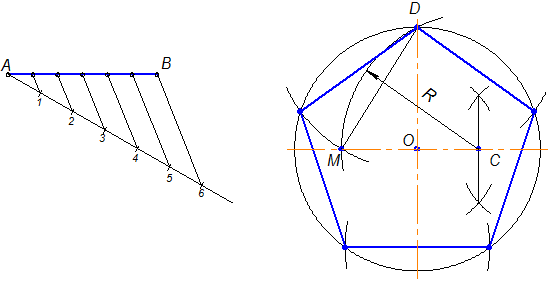

Bilder

Alle anzeigen

Школьное издание. Элементы геометрии Евклида, первые шесть …

books.google.de › books

Найдите площадь правильного шестиугольника, вписанного в круг диаметром двенадцать дюймов. В чем разница между вписанным и …

Damit du nur die relatedesten Ergebnisse erhältst, wurden einige Einträge ausgelassen, die den 8 angezeigten Treffern sehr ähnlich sind. Du kannst bei Bedarf diesuche unter Einbeziehung der übersprungenen Ergebnisse wiederholen.

Ähnlichesuchanfragen

при построении вписанного квадрата вручную, какой шаг следует за построением круга?

при построении вписанного шестиугольника вручную, какой шаг следует за построением окружности?

Какой следующий шаг в построении правильного шестиугольника

Калькулятор площади прямоугольника

Создано Bogna Szyk и Hanna Pamuła, PhD

Отзыв от Jack Bowater

Последнее обновление: 09 февраля 202 3

Таблица в комплекте:

Что такое прямоугольник?
Как найти площадь прямоугольника?
Формулы прямоугольника
Вычисление прямоугольника: найти A (площадь)
Вычисление прямоугольника: найти P (периметр)
Вычисление прямоугольника: найти D (диагональ)
Золотой прямоугольник
Свойства прямоугольника
Прямоугольник по сравнению с другим формы. Является ли квадрат прямоугольником?
Странный забавный факт: какая страна имеет самую прямоугольную форму в мире?
Прямоугольные узоры
Прямоугольники в повседневной жизни: прямоугольная форма тела, прямоугольный бассейн, прямоугольная скатерть…
Часто задаваемые вопросы

Нужно ли вам знать площадь ковра, посылки, экрана телевизора, прямоугольного бассейна или окно, этот калькулятор площади прямоугольника решит вашу проблему в мгновение ока!

Все, что вам нужно сделать, это ввести длину и ширину (или диагональ) и позволить этому прямоугольнику вычислить значения P (периметр) и A (площадь).

Продолжайте читать, если вы хотите понять, что такое прямоугольник, вас интересует определение прямоугольника, формулы и свойства прямоугольника… Или вы просто хотите узнать, как найти площадь прямоугольника.

Что такое прямоугольник?

Прямоугольник — это четырехугольник с четырьмя прямыми углами . Мы можем также определить его по-другому: параллелограмм, содержащий прямой угол — если один угол прямой, другие должны быть такими же. При этом каждая сторона прямоугольника имеет ту же длину, что и противоположная ей сторона. Он также имеет неравные смежные стороны, в отличие от квадрата, частного случая прямоугольника.

Если вы немного знаете латынь, название фигуры обычно многое объясняет. Слово прямоугольник происходит от латинского rectangulus . Это комбинация rectus (что означает «правильный, прямой») и angulus (угол), так что это может служить простым базовым определением прямоугольника.

Прямоугольник является примером четырехугольника. Вы можете использовать наш четырехугольник калькулятор, чтобы найти площадь других типов четырехугольника.

Как найти площадь прямоугольника?

На изображении выше показан типичный прямоугольник. У него четыре стороны и четыре прямых угла. Длины его сторон обозначаются a и b , а длина диагонали обозначается d .

Если все стороны прямоугольника имеют одинаковую длину, мы называем его квадратом .

Площадь прямоугольника — это пространство, ограниченное его сторонами или, другими словами, в пределах периметра прямоугольника. Чтобы найти площадь прямоугольника, достаточно умножить стороны прямоугольника на 9.0187 a и b :

Площадь = a × b

Формулы прямоугольника

В нашем калькуляторе прямоугольников реализованы следующие формулы:

Для площади прямоугольника :
A = a × b
Для периметра прямоугольника :
P = 2 × (a + b)
Для диагонали прямоугольника :
d² = a² + b²
д = √(а² + b²)

Расчет прямоугольника: найти A (площадь)

Поскольку мы знаем формулу площади прямоугольника A = a × b , покажем на примере, как можно вычислить это свойство:

Выберите длину прямоугольник – например, а = 5 см .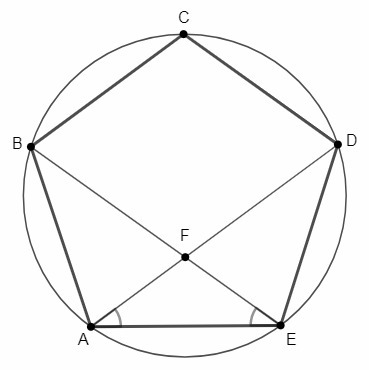
Определите ширину прямоугольника – например, b = 6 см .
Умножьте эти два значения: A = 5 см × 6 см = 30 см² .
Площадь прямоугольника 30 см².

Расчет прямоугольника: найти P (периметр)

Давайте узнаем, как найти периметр прямоугольника. Как обычно, периметр представляет собой сумму всех сторон фигуры:

P = a + b + a + b

… что можно записать как:

P = 2 × (a + b )

Возьмем для примера тот же прямоугольник:

Выберите длину прямоугольника – a = 5 см в нашем случае.
Определите ширину прямоугольника – например, b = 6 см .
Сложите эти два значения: a + b = 5 + 6 = 11 см .
Умножьте результат на 2: P = 2 × 11 = 22 см .
Вот так! Периметр нашего прямоугольника равен 22 см.

Расчет прямоугольника: найти D (диагональ)

Диагональ прямоугольника — это отрезок, соединяющий две противоположные вершины прямоугольника. Вычислим длину диагонали примерного прямоугольника:

Выберите длину прямоугольника – например, a = 5 см .
Определите ширину прямоугольника – например, b = 6 см .
Вычислите a в степени двойки: a² = 25 см² .
Вычислите b в степени двойки: b² = 36 см² .
Сложите эти два значения: a² + b² = 25 + 36 = 61 см² .
Наконец, извлеките квадратный корень из результата: d = √(a² + b²) = √61 ~ 7,81 см .
Длина диагонали 7,81 см.

Естественно, вместо того, чтобы вычислять все эти значения вручную, вы можете использовать эту область калькулятора прямоугольника. Вы также можете использовать его в обратном порядке — например, для вычисления ширины прямоугольника с известными длиной и периметром.

Золотой прямоугольник

На рисунке выше показан особый тип прямоугольника, называемый золотым прямоугольником (узнайте с помощью нашего калькулятора золотого прямоугольника). Такой прямоугольник удовлетворяет следующему условию:

(a + b) / a = a / b = ϕ

где φ — золотое сечение, равное 1,618. Узнайте больше об этом особом соотношении с помощью нашего калькулятора золотого сечения.

Как вы, наверное, помните из калькулятора отношений, отношение — это отношение между двумя величинами, часто представленное в виде дроби.

Знаете ли вы, что золотой треугольник можно построить, используя только линейку и циркуль ? Это всего несколько шагов!

Нарисуй квадрат.
Проведите линию от середины одной стороны квадрата до противоположного угла. Наш калькулятор средней точки может помочь вам с этим шагом.
Нарисуйте круг с радиусом, равным этой линии, с центром в средней точке, как показано на рисунке выше.
Точка, в которой круг встречается с расширенной стороной квадрата, является следующим углом золотого прямоугольника.
Найдите последнюю вершину и завершите золотой прямоугольник.

Таадааах! Это было не так сложно, не так ли?

Свойства прямоугольника

Прямоугольники обладают многими интересными свойствами:

Цикличность – это означает, что все углы лежат на одной окружности.
Равноугольный – все его углы равны 90 градусам.
Прямолинейный – его стороны сходятся под прямым углом.
Две линии отражательной симметрии – вертикальная и горизонтальная через центр.
Две диагонали, делящие друг друга пополам . Длину диагонали можно найти по теореме Пифагора.
Противоположные стороны прямоугольника параллельны друг другу и имеют одинаковую длину.

Другие менее известные прямоугольные свойства:

Пересечение диагоналей — это центр описанной окружности — существует окружность с центром в этой точке, которая проходит через четыре угла.
В прямоугольнике с разной длиной сторон (попросту говоря, не в квадрате) невозможно провести вписанную окружность.
Прямые, соединяющие середины сторон прямоугольника, образуют ромб, площадь которого составляет половину площади прямоугольника. Стороны фигуры параллельны диагоналям.

Можно придумать и свои собственные свойства, например, о вращении прямоугольника — по стороне или диагонали, чтобы получился цилиндр или конус соответственно.

Прямоугольник и другие формы. Является ли квадрат прямоугольником?

TL;DR:

Является ли квадрат прямоугольником? ДА .
Является ли прямоугольник параллелограммом? ДА .
Является ли прямоугольник ромбом? В целом – НЕТ. Только если это квадрат (все углы ромба 90 градусов).
Является ли ромб прямоугольником? В целом – НЕТ. Только если это квадрат (все стороны прямоугольника равны по длине).
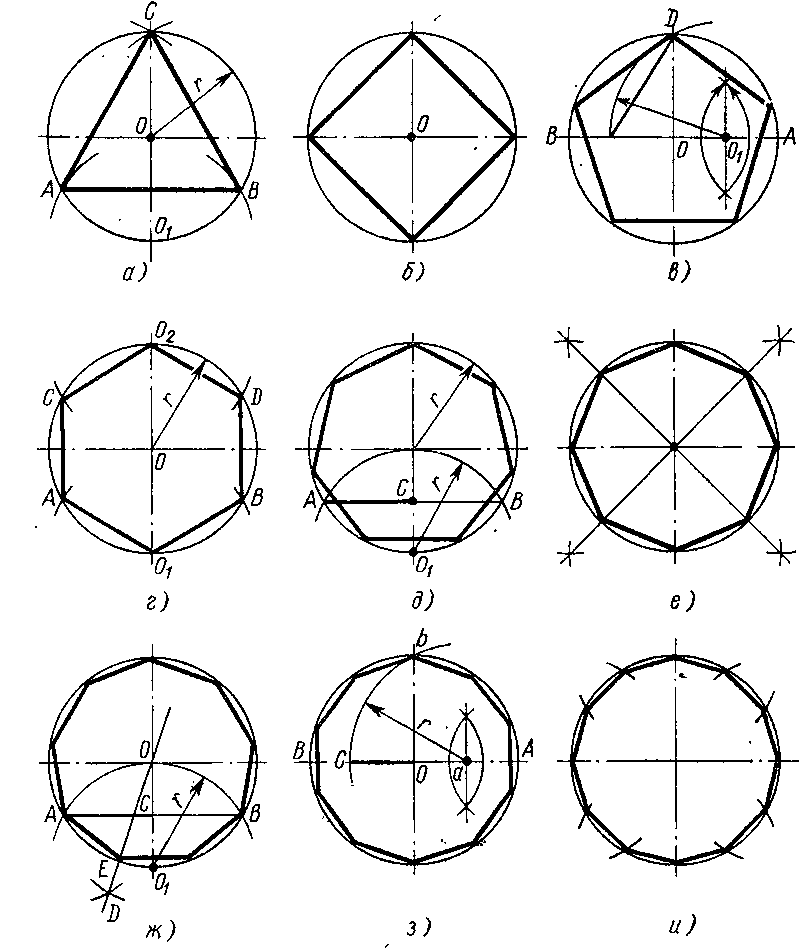
Является ли прямоугольник четырехугольником? ДА , конечно.
Является ли прямоугольник трапецией? ДА .

Хотите знать, является ли квадрат прямоугольником или прямоугольник параллелограммом? Взгляните на рисунок ниже, и у вас больше не должно быть никаких сомнений относительно отношений между четырехугольниками:

Источник: Wikimedia

Как читать эту диаграмму? Начнем с нашего прямоугольника. Непосредственно к фигуре присоединены три фигуры: квадрат, параллелограмм и равнобедренная трапеция. Итак, если фигура находится выше интересующей нас формы, например, квадрата или прямоугольника, мы можем сказать, что:

Каждый квадрат является прямоугольником и квадрат является частным случаем прямоугольника .

Для двух других фигур можно сказать аналогично:

Каждый прямоугольник является параллелограммом и прямоугольник является частным случаем параллелограмма .
Каждый прямоугольник является трапецией и прямоугольник является частным случаем трапеции .

Странный забавный факт: какая страна имеет самую прямоугольную форму в мире?

Существует множество различных рейтингов, оценивающих страны по территории, населению, уровню образования или лауреатам Нобелевской премии.

Но задумывались ли вы когда-нибудь, , кто победит в конкурсе на самую прямоугольную страну? Австралийский геостатистик Дэвид Бэрри рассчитал параметр прямоугольности для всех стран мира и составил рейтинг.

Он выяснил, что самой прямоугольной страной является Египет, тогда как титул «наименее прямоугольной страны в мире» достается Мальдивским островам (впрочем, автор допускает, что расчеты для стран, состоящих из множества мелких островов, могут быть ужасно неверными). Взгляните на таблицу ниже и проверьте первые десять стран, а также наименее прямоугольные.

9 0099 9 0099

Высшие баллы по рейтингу прямоугольности. Индекс 1 — идеальный прямоугольник, 0 — бесконечное число бесконечно малых островков. Таблица адаптирована с веб-страницы г-на Барри как изображение мира ниже.
Ранг	Страна	Округлость
1	Египет	0,955
2	Ватикан	0,948
3	Синт-Мартен	0,937
4	Лесото	0,936
5	9 0004 Йемен	0,928
6	Гана	0,924
7	Македония	0,921
8	Кот-д’Ивуар	0,919
9	9 0004 Польша	0,919
10	Науру	0,917 9009 8
. ..
169	США 9 0003	0,735
…
206 90 098	Тувалу	0,240
207	Маршалловы Острова	0,201
208	Мальдивы	0,018

Египет является лидером, но это не должно удивлять никого, кто проверяет форму этой страны на карте. USA находится в середине рейтинга, в основном из-за эксцентричности Аляски и Гавайев. Сбивает с толку то, что вторая самая прямоугольная страна — Ватикан — является в то же время четвертой самой круглой страной, и Польша , 5-е место по округлости, 9-е место по прямоугольности.

Как вообще возможно быть прямоугольным и круглым одновременно?! Как вы можете догадаться, все дело в определении прямоугольности и округлости, которое может быть неадекватным для сложных или разбросанных форм — и такими примерами обычно являются границы стран, содержащие острые края, маленькие острова или колонии где-то на другой стороне. земного шара.

Если вам интересна эта тема, вы можете ознакомиться с этим объяснением и обсуждением результатов.

Можно подумать, что мир было бы легче рисовать, если бы каждая страна была прямоугольником… Или нет?

Прямоугольные узоры

Форма прямоугольника используется во многих периодических узорах мозаики. Его можно использовать для стен из кирпича, напольной плитки, тротуара или различной мозаики. Ниже вы найдете несколько популярных рисунков:

Укладка в стопку – самый распространенный и простой узор укладки плитки, так как плитка укладывается прямыми линиями.

Текучая связка – типична для склеивания дорожных покрытий, плитки и кирпича.

Елочка – с таким рисунком хорошо смотрятся деревянные полы.

Корзиночное плетение – часто используется для коридоров или дорожек на открытом воздухе.

Конечно, плитка бывает всех форм и размеров – довольно популярны шестиугольные и восьмиугольные с квадратами. Для пятиугольника форма должна быть неправильной, чтобы образовался мозаичный узор.

Прямоугольники в повседневной жизни: прямоугольное телосложение, прямоугольный бассейн, прямоугольная скатерть…

Телосложение типа — одна из самых искомых проблем, связанных с прямоугольниками. Все, что вам нужно сделать, это измерить свой бюст, талию, бедра и высоту бедер и ввести значения в инструмент. Тогда вы получите информацию о том, какая у вас форма тела.

Например, прямоугольная фигура определяется как «мальчишеский» тип телосложения — ваши бедра, талия и бюст примерно одного размера. Ваше тело имеет правильные пропорции и спортивный вид.

Удивительно, но нас окружают прямоугольные предметы. Вот почему наш калькулятор прямоугольников может быть полезен не только на уроках математики, но и в решении повседневных задач. Конечно, идеального прямоугольника в реальности не найти, так как он всегда имеет третье измерение; но если оно мало по сравнению с двумя другими измерениями, приближение достаточно хорошее.

Прямоугольные скатерти – учитывая размер вашего стола, вы можете узнать, какая скатерть вам нужна или сколько кружева или подшивочной ленты вам нужно использовать.
Двери или оконное стекло – шторм или мяч для гольфа разбили ваше оконное стекло? Рассчитайте площадь и оцените стоимость ремонта, учитывая цену за кв.м или кв.м.
Экраны электронных устройств — планшетов, смартфонов, телевизоров — используйте этот калькулятор площади прямоугольника, чтобы оценить, сколько места на стене займет ваш экран — или насколько большой экран телефона, который вы хотите купить.
Доски, зеркала, рамы, холст, листы бумаги, блокноты, конверты, деньги, флажки, прямоугольные бассейны… Это бесконечный список!

Посмотри. Можете ли вы найти больше прямоугольных объектов вокруг вас? Что вы можете!

FAQ

Как найти периметр и площадь прямоугольника?

Чтобы найти периметр, нужно сложить все стороны прямоугольника: