Как сделать из треугольника пятиугольник: Треугольники в пятиугольнике?

детские_задачи / Правильный треугольник и правильный пятиугольник на листке в клеточку (построение от руки) / Математика

В школьные годы мы для себя только квадрат строили на математическом листке (как поле для «морского боя» на уроках). Если бы нас научили построению от руки более сложных фигур, мы предпочитали бы их квадрату, будучи настроены более возвышенно. Отчего не учат нас в школе практическому построению правильных 3-уг. и 5-уг.? от него лишь один шаг до почти точного изображения на листке всех Платоновых тел. Насколько ярче стали бы наши пространственные представления… Это была бы решительная победа над обыденностью. ||| (ответ для тех, кого тревожит современное духовное оскудение, утрата источников внутренней радости) Дети сами находят почти правильный треугольник, полуоснование которого $%4$% клеточки, а высота $%7$% клеточек. По теореме Пифагора его боковые стороны имеют длину $%\sqrt{4^2+7^2} = \sqrt{65} > 8$%, тем самым высота его чуть избыточна, но разность $%\sqrt{65} — 8 = 1/(\sqrt{65} + 8) < 1/16$% клеточки между боковой стороной и основанием почти незаметная. 2} = \sqrt{31.36+94.09} = \sqrt{125.45}$%, в то время как основание $%= 11.2 = sqrt(125.44)$%; тогда отличие $%\sqrt{125.45} — 11.2 = \frac {0.01}{\sqrt{125.45}+11.2}$% меньше чем $%1/2240$% клеточки (!). Такой треугольник будет выглядеть на тетрадном листе как безупречно правильный, исцеляя своим совершенством, настраивая душу как лиру… «Строгий» способ построения потребовал бы сначала изобразить от руки окружность — например, радиусом $%10$% клеточек, помня ее рациональные точки $%(6,8),(8,6)$% и $%(2.8,9.6),(9.6,2.8)$%; деление радиуса пополам дает точку, через которую проводится перпендикуляр — это одна из трех сторон правильного треугольника, потому что $%sin{\frac{\pi}{6}} = 1/2$%. При таком пути построения от руки точность будет меньшей, зато здесь можно будет совершить выход с плоскости в пространство: два правильных треугольника с общим центром, ориентированные противоположно, воспринимаются как две противоположные грани правильного октаэдра, и чтобы увидеть весь октаэдр (в этом простом ракурсе), останется соединить между собой его ближайшие вершины. — Для построения 5-угольника, почти не отличающегося от правильного, вновь можно применить окружность радиусом $%10$% клеточек. Очень удобны для вычисления «страшные» $%cos(2\pi/5) = (\sqrt5-1)/4 = 0.3090etc.$% и $%cos(\pi/5) = (\sqrt5+1)/4 = 0.8090etc.$%, разнящиеся на $%1/2$%. На диаметре окружности надо отложить (в противоположные стороны от ее центра) $%3.1$% и $%8.1$% клеточки соответственно, затем через получившиеся две точки провести перпендикуляры: их четыре пересечения с окружностью хорошо изобразят «нетривиальные» вершины правильного пятиугольника (все проще чем кажется: глаза боятся, а руки делают). Здесь тоже возможен выход с плоскости в пространство: два правильных пятиугольника с общим центром, ориентированные противоположно, воспринимаются как две противоположные грани додекаэдра. Проведя из всех 10-ти вершин «солнечные лучики», можно будет изобразить весь додекаэдр (помня, что диагонали его граней параллельны ребрам). И последнее построение. Два правильных пятиугольника с общим центром, ориентированные противоположно, могут создать «пояс» правильного икосаэдра — если мы соединим их ближайшие вершины. После этого останется провести ребра двух противоположных «шапочек» икосаэдра (одна из них смотрит прямо на нас), и правильный икосаэдр перед нами. — Вот геометрический кругозор рядовых людей III тысячелетия. По такому «вольному репертуару» дети очень тосковали в позднесоветской школе, что помню по себе, — а воз и ныне там((( Чтобы вырасти живым человеком, нужно дома заниматься по книгам мастеров наперекор атеистически-упрощенной школьной программе. детские_задачи задан 18 Янв 1:11 Манфред 377●1●6 0% принятых изменен 18 Янв 11:37

Свойства некоторых фигур на примере треугольника и пятиугольника на сфере и псевдосфере

Мы знаем, что фигура, у которой все углы 90 градусов и все стороны равны, квадрат.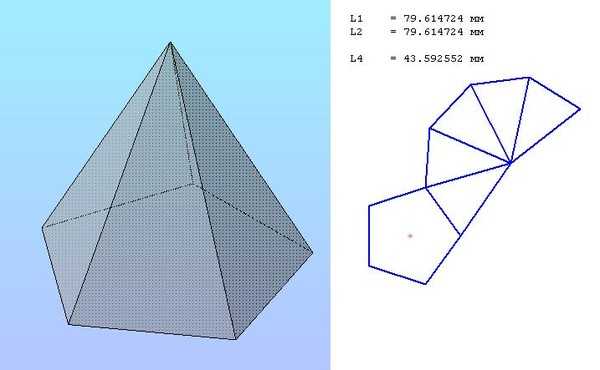

А теперь возьмем глобус. Представим себе, что мы идем по земному шару, начиная с экватора к Северному полюсу под углом 90 градусов, затем, дойдя до полюса, поворачиваемся на 90 градусов и идем вниз по долготе, которая проходит через Мексиканский Залив и полуостров Юкатан. Попадаем опять на экватор и пойдем до точки начала отсчета нашего путешествия. Можно начертить на глобусе или сфере маршрут своего движения, который будет представлять собой треугольник с углами по 90 градусов. Сумма углов у него будет больше 180 градусов. Я могу вырезать кусок бумаги, который представляет собой «трехсторонний квадрат», у которого все углы 90 градусов и все стороны равны.

Сфера (не путать с шаром) имеет постоянную кривизну Гаусса. Нарисуем на сфере 2 линии через нее и выберем максимальную и минимальную кривизну этих линий, перемножим их. Если положительное число умножить на положительное, то получится число положительное. У сферы постоянно положительная кривизна.

Возьмем псевдосферу, она противоположна сфере («фальшивая сфера», т.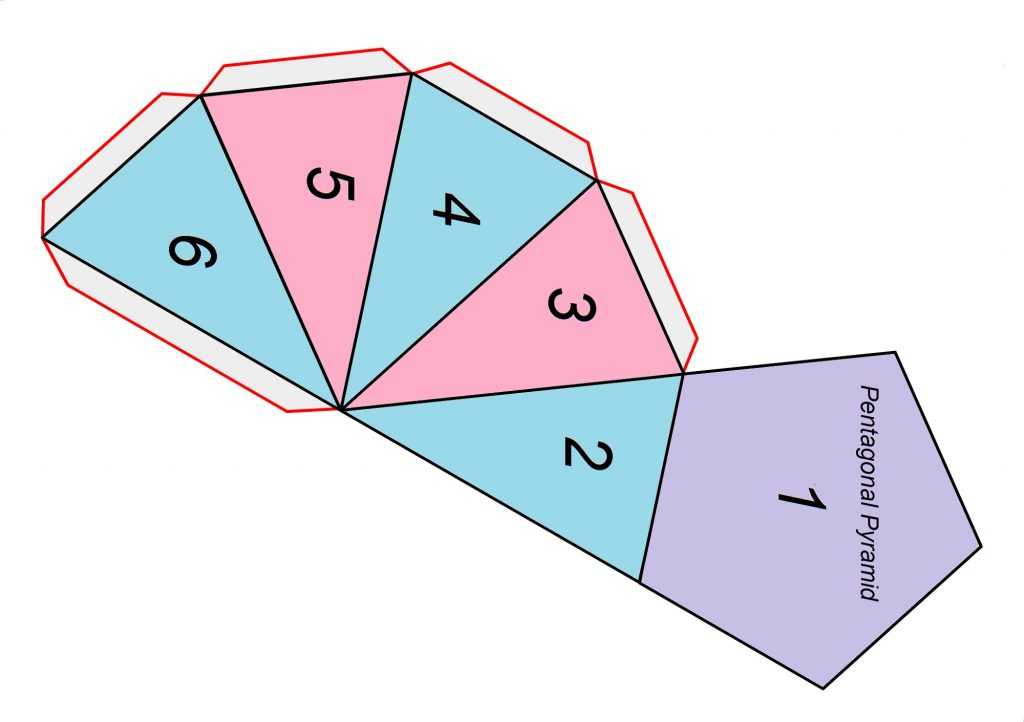

к. псевдо — кажущееся, ложное; похожее, но не настоящее). Она похожа на воронку или рог и имеет хорошее качество. Если взять на ней какую-нибудь точку, то в одном направлении она вогнутая, а в другом она выпуклая. Сделаем оговорку: надо выбрать минимум вогнутости и максимум выпуклости или одно из условий. Нужно выбрать так, чтобы в одном направлении линия выпирала, а в другом вгибалась. Оказывается, что у любой псевдосферы будет одна негативная кривизна. Это значит, что если перемножить, то в одном месте можно получить положительную кривизну не очень большую, а вот отрицательную кривизну огромную. А вот тут, где отрицательная кривизна маленькая, положительная кривизна огромна. Получается, что у псевдосферы везде отрицательная кривизна.

На обычном листе бумаге в Евклидовой геометрии каждый треугольник имеет 3 угла с сумой 180 градусов. Если же нарисовать любой треугольник на сфере, то сумма его углов будет больше 180 градусов. Это можно видеть, как на глобусе, так и на сфере. А вот на псевдосфере, неважно как как начертить треугольник, сумма его углов будет меньше 180 градусов.

Они будут заостренными и придут к слегка острой форме.

Нарисуем пятистороннюю фигуру, у которой все углы будут 90 градусов. Нужно взять лист бумаги, намочить его, обернуть его вокруг псевдосферы и у него везде будет отрицательная кривизна Гаусса. Выбрав 5 точек на ней, мы поймем, что получилась пятисторонняя фигура, каждый угол которой равен 90 градусам. Можем проверить это. Возьмем кусок бумаги с углом в 90 градусов, приложим к псевдосфере. Действительно, имеем 5 углов по 90 градусов. Вот вам «пятисторонний квадрат» !!! Вырежем его. Это пятиугольник!! Это пятиугольник, у которого все углы прямые! Так это пятиугольник или квадрат? Если это квадрат — фигура у которой все стороны равной длины и все углы равны 900, тогда я могу утверждать, что это «пятисторонний квадрат».

Что будет, если сдавить его до плоской фигуры? Топологи утверждают, что это невозможно…Ну если попытаться это сделать, то это тоже самое, если бы взять кусочек сферы, кусочек глобуса и сдавить его… Невозможно сохранить области, сохранить направление.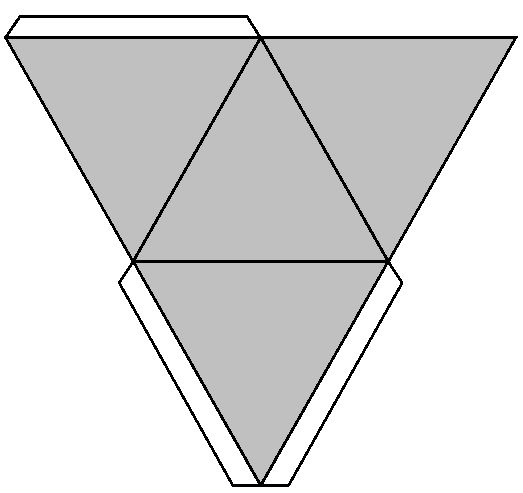 Мы сталкиваемся с проблемой конформного и неконформного отображения. Мы можем попытаться это сделать, но когда сдавливаешь одну часть, то другая часть поднимается. Не получится с точностью отобразить сферическую или псевдосферическую поверхность на Евклидовой плоскости. Эта проблема преследовала картографов долгое время.

Открытие неевклидовых пространств совершенно изменило роль геометрии. Древняя наука об «изменении форм» проникла во все области человеческого знания, она перестала быть ограниченной узкими рамками евклидова мира и теперь сама открывает безграничный простор воображению.

Ученый должен идти по непроторенным путям, несмотря на препятствия». Н.И. Лобачевский

Я убежден, что отказ от постулата о параллелях не приводит к противоречию, хотя это правда, что получаемые результаты кажутся парадоксальными.Карл Фридрих Гаусс (1777 -1875)

Треугольник и пятиугольник

ПОИСК ДОМ

Math Central Проблемы и вопросы

На этой диаграмме красная часть имеет площадь 800 квадратных сантиметров. Какова площадь зеленой части в квадратных сантиметрах? (Пожалуйста, округлите до ближайшего целого числа) Если бы у вас был ответ, я был бы так рад!! Спасибо за помощь!!

Привет, Оливия. Зеленый треугольник равнобедренный, поэтому, если известна мера угла между общими сторонами (внешняя вершина) и длина основания (сторона, общая с красным пятиугольником), то можно найти площадь треугольника. . Во-первых, угол при вершине: Напомним, что сумма углов четырехугольника составляет 360 градусов. Также следует знать, что сумма углов 5-сторонней фигуры равна 540, потому что для любого замкнутого n-угольника сумма углов равна 180(n-2) . У правильного пятиугольника, как на вашей диаграмме, все углы одинаковы, поэтому каждый внутренний угол равен 540/5 = 108 градусов. Теперь подумайте о четырехугольнике, который окрашен (не обращайте внимания на цвет и общую сторону треугольника и пятиугольника. Это четырехсторонняя фигура, поэтому сумма его углов равна 360. Но вы знаете из предыдущего, что мера трех углов по 108. Таким образом, оставшийся угол (вершина треугольника) равен 360 — 3 (108) = 360 — 324 = 36 градусов. Теперь, когда мы знаем меру угла, нам нужна длина основания треугольника, равная длине стороны правильного пятиугольника, площадь которого известна. Нарисуем центр пятиугольника и разделим его на 5 конгруэнтных треугольников, затем разделим один из этих 5 на два конгруэнтных прямоугольных треугольника: По симметрии вы должны видеть, что внутренние углы пятиугольника в 108 градусов составляют углы в 54 градуса. Также по симметрии пять треугольников равнобедренные, поэтому, когда мы разделяем один из них (зеленой линией), мы делим длину стороны пополам перпендикуляром. Таким образом, мы разделили пятиугольник на эквивалентные 10 прямоугольных треугольников с углом 54 градуса. Давайте подпишем несколько вещей на этом прямоугольном треугольнике: Какова площадь этого треугольника? Площадь любого треугольника равна половине произведения основания на высоту, поэтому площадь этого треугольника равна ½xw . Так как в пятиугольнике десять таких треугольников, площадь пятиугольника равна 10(½xw) . Но вам говорят, что это 800 см 2 , поэтому 800 = 10(½xw) , что сводится к 160 = xw . Используя тригонометрию, мы знаем, что тангенс угла в 54 градуса равен длине, противоположной прилежащей длине, поэтому tan(54) = x/w , что мы можем переписать как w tan(54) = x . Поскольку это равно x, давайте подставим его в наше предыдущее уравнение: 160 = xw = (w tan(54)) w = w 2 tan(54). Теперь мы можем найти w: 160 / тан(54) = w 2 . ш = 10,782 см. Теперь давайте разделим этот зеленый равнобедренный треугольник таким же образом: Мы разделили угол вершины пополам, так что 36/2 = 18 градусов. Таким образом, зеленый треугольник представляет собой сумму двух конгруэнтных прямоугольных треугольников. Поскольку каждый из них имеет площадь ½wy, площадь, выделенная зеленым цветом, равна wy. Снова используя тригонометрию, tan(18) = w/y , поэтому y = w/tan(18) . Это означает, что зеленая область равна wy = w 2 /tan(18) . А так как w = 10,782 см, то имеем Зеленая площадь = (10,782) 2 / загар (18) = 357,8 см 2 . Ура, Стивен Ла Рок.

Определение, форма, свойства, типы, формула и пример

Пятиугольник — это геометрическая фигура, имеющая пять сторон и пять углов. Здесь «пента» обозначает пять, а «гон» обозначает угол. Пятиугольник является одним из видов многоугольников. Сумма всех внутренних углов правильного пятиугольника равна 540 градусов.

Содержание:

• Определение
• Форма
• Правильный и неправильный пятиугольник
• Выпуклый и вогнутый пятиугольник
• Свойства
• Район
• Периметр
• Пример
• Равносторонний пятиугольник
• Циклический пятиугольник
• Часто задаваемые вопросы

В геометрии мы изучаем различные типы фигур.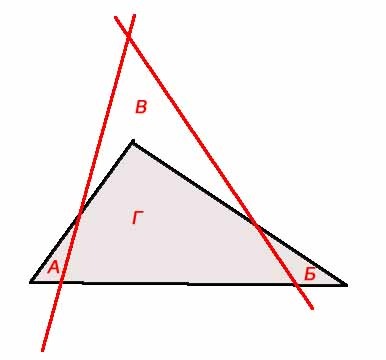 Двумерная форма, состоящая из прямых линий и внутренних углов, известна как многоугольник. Примеры полигонов:

• Треугольник (трехсторонний многоугольник)
• Четырехугольник (четырехсторонний многоугольник)
• Пятиугольник (пятиугольник)
• Шестиугольник (шестигранный многоугольник)
• Гептагон (семиугольник)
• Октагон (восьмиугольник) и так далее.

В этой статье вы можете подробно узнать о пятистороннем многоугольнике, называемом «пятиугольник», с правильным определением, формой, сторонами, свойствами, а также его периметром и площадью формулы пятиугольника.

Определение Пентагона

Пятиугольник — это многоугольник с 5 сторонами и 5 углами. Слово «пентагон» состоит из двух слов, а именно Penta и Gonia, что означает пять углов. Все стороны пятиугольника соединяются друг с другом, образуя фигуру. Следовательно,

Количество сторон пятиугольника = 5

Форма пятиугольника

Как и другие многоугольники, такие как треугольник, четырехугольник, квадрат, прямоугольник и т.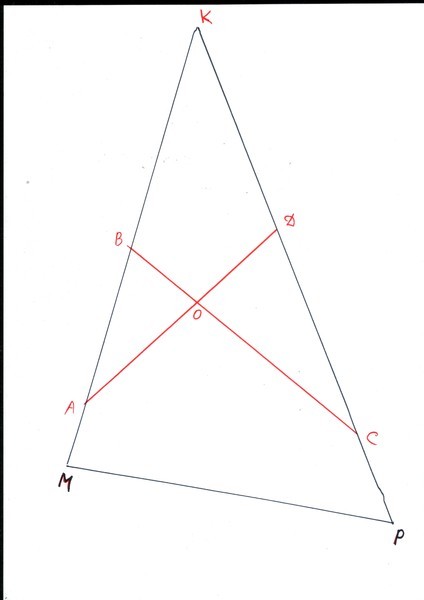 д., пятиугольник также является многоугольником, который содержит пять сторон и пять углов.

В зависимости от сторон, углов и вершин существуют различные типы пятиугольников, например

• Правильный и неправильный пятиугольник
• Выпуклый и вогнутый пятиугольник

Правильный и неправильный пятиугольник

Если пятиугольник правильный , то все стороны равны по длине и пять углов имеют одинаковую меру. Если пятиугольник не имеет одинаковой длины стороны и меры угла, то он известен как неправильный пятиугольник .

Обычный пятиугольник

Как определено выше, правильный пятиугольник содержит пять конгруэнтных сторон. Таким образом, мы можем легко найти периметр этого типа пятиугольника. Это видно из приведенного ниже рисунка.

Здесь все пять сторон равны, поэтому периметр правильного пятиугольника в пять раз больше длины любой из его сторон.

Также мы можем разделить правильный пятиугольник на пять подобных треугольников, как показано ниже.

Таким образом, мы можем сказать, что площадь правильного пятиугольника равна 5-кратной площади треугольника со сторонами, равными пятиугольнику.

Выпуклый и вогнутый пятиугольник

Если все вершины пятиугольника направлены наружу, он известен как выпуклый пятиугольник . Если пятиугольник имеет хотя бы одну вершину, указывающую внутрь, то пятиугольник известен как вогнутый пятиугольник .

Свойства Пентагона

Вот некоторые свойства пятиугольника:

• В пятиугольнике сумма внутренних углов равна 540°.
• Если все стороны равны и все углы равны, то это правильный пятиугольник. В противном случае он нерегулярен.
• В правильном пятиугольнике каждый внутренний угол равен 108°, а каждый внешний угол равен 72°.
• У равностороннего пятиугольника 5 равных сторон.
• Сумма внутренних углов прямоугольного пятиугольника равна 540°.

Площадь Пентагона

Для правильного пятиугольника со стороной и длиной апофемы формула для нахождения площади пятиугольника дается как

Площадь пятиугольника, A = (5/2) × длина стороны × квадратные единицы апофемы

Если дана только длина стороны пятиугольника, то

Площадь = 5s ² / (4 tan 36°) Квадратные блоки

Если дан только радиус пятиугольника, то

Площадь =(5/2)r ² sin 72° Квадратные единицы

Периметр Пентагона

Так как все стороны «а» правильного пятиугольника имеют одинаковую меру, то периметр или длина окружности пятиугольника записывается как

Периметр пятиугольника, P = 5a единиц

Пентагон Решенная проблема

Вопрос:  Найдите площадь и периметр правильного пятиугольника со стороной 5 см и длиной апофемы 6 см.

Решение:

Дано:

Сторона пятиугольника, а = 5 см

Длина апофемы = 6 см

Мы знаем, что

Площадь пятиугольника, A = (5/2) × длина стороны × квадратные единицы апофемы

Замещающая сторона = 5 см, Апофема = 6 см в формуле,

А = (5/2) × 5 × 6

А = 5 х 5 х 3

А = 75

Следовательно, площадь пятиугольника равна 75 см ²

Периметр пятиугольника, P = 5a единиц

Р = 5(5)

П = 25 см

Следовательно, периметр пятиугольника равен 25 см.

Основываясь на свойствах пятиугольников, в геометрии существуют и другие типы пятиугольников. Они:

1. Равносторонний пятиугольник

Многоугольник с пятью сторонами одинаковой длины называется равносторонним пятиугольником. Однако все пять внутренних углов пятиугольника могут принимать различные значения. Таким образом, они позволяют ему образовывать семейство пятиугольников. Следовательно, правильный пятиугольник уникален с точностью до подобия. Потому что это равносторонний и равноугольный (поскольку его пять углов равны) пятиугольник.

2. Циклический пятиугольник

Если все вершины пятиугольника лежат на окружности, то такой пятиугольник называется вписанным. Правильный пятиугольник — лучший пример вписанного пятиугольника. Площадь циклического пятиугольника может быть представлена ​​как одна четвертая квадратного корня из одного из корней септического уравнения. Здесь коэффициенты уравнения являются функциями сторон пятиугольника. Это относится как к правильным, так и к неправильным пятиугольникам.

Линия симметрии пятиугольника:

Что касается линейной симметрии, то каждый многоугольник имеет определенное количество линий симметрии. Например, квадрат имеет 4 оси симметрии. Точно так же правильный пятиугольник имеет 5 осей симметрии.

Оставайтесь с нами с BYJU’S — обучающим приложением, чтобы изучать все интересные понятия математики, а также просматривать видео, чтобы учиться с легкостью.

Часто задаваемые вопросы о Пентагоне – Часто задаваемые вопросы

Сколько сторон у пятиугольника?

Как указано в названии, «пента» означает 5, а «гон» означает угол. Таким образом, пятиугольник имеет 5 сторон и 5 углов.

Какие бывают пятиугольники?

Различные типы пятиугольников:
Простой пятиугольник
Сложный пятиугольник
Правильный пятиугольник
Неправильный пятиугольник
Вогнутый пятиугольник
Выпуклый пятиугольник
Равносторонний пятиугольник
Циклический пятиугольник

Что такое неправильная форма?

Если пятиугольник не имеет одинаковой длины стороны и угла, то он известен как неправильный пятиугольник.

Какие есть 12 видов многоугольников?

В геометрии 12 видов многоугольников:
Треугольник (трехсторонний многоугольник)
Четырехугольник (четырехсторонний многоугольник)
Пятиугольник (пятисторонний многоугольник)
Шестиугольник (шестисторонний многоугольник)
Семиугольник (семисторонний многоугольник)
Октагон (восьмиугольник)
Нонагон (девятиугольник)
Декагон (десятиугольник)
Икосагон (двадцатиугольник)
Триаконтагон (тридцатиугольник)
Гектагон (100-угольник)
Chiliagon (многоугольник с 1000 сторонами)

Как называется фигура с 12 сторонами?

12-сторонняя фигура или двенадцатигранный многоугольник называется додекагоном.