7 класс, простейшие задачи по геометрии
Свойства отрезков и углов
Свойства отрезков:
- Длина — основное свойство отрезка. Каждый отрезок имеет положительную отличную от нуля линейную меру.
- На данной полупрямой (луче) от начала можно отложить только один отрезок данной длины.
Свойства углов:
- Углы характеризуются градусной мерой. Градусная мера угла — положительная и отлична от нуля.
- От данной полупрямой в данной полуплоскости можно отложить только один угол данной градусной меры.
Основные построения
Построение отрезка, равного данному:
- Чтобы построить отрезок, равный данному, построим произвольный луч с началом в новой точке. Пусть AB — данный отрезок, точка C — начало луча.
- Измерим циркулем данный отрезок AB.
- Не меняя раствора циркуля, на построенном луче от его начала отложим отрезок, равный данному. Для этого установим иглу циркуля в точку C и проведем дугу, пересекающуюся с лучом.
 Назовем точку пересечения дуги с лучом точкой E. Получившийся отрезок CE равен отрезку AB.
Назовем точку пересечения дуги с лучом точкой E. Получившийся отрезок CE равен отрезку AB.
Чтобы разделить отрезок пополам, нужно найти точку, лежащую на отрезке и равноудаленную от его концов.
Деление отрезка пополам (задача на бисекцию): необходимо разделить пополам отрезок AB. Нужно найти точку C, так чтобы C AB и AC =CB. Далее:
- Раздвинем ножки циркуля на произвольное расстояние, большее половины данного отрезка AB.
- Проведем вспомогательную дугу с центром в одном конце отрезка (в точке A).
- Тем же раствором циркуля построим вторую вспомогательную дугу с центром на другом конце отрезка (в точке B) так, чтобы вторая дуга пересекалась с первой в двух местах по обе стороны отрезка. Пусть E и K — точки пересечения двух дуг.
- Построим прямую EK,EK пересекает отрезок AB в искомой середине отрезка — точке C.
Доказательство:
Треугольники AKE и BKE равны по третьему признаку равенства треугольников (по трем сторонам): KE — общая сторона, AK=BK, AE=BE. Следовательно, . При этом оба треугольника равнобедренные: AK=AEи BK=BE. Рассмотрим равнобедренный, AK = BK. KC — биссектриса , которая в равнобедренном треугольнике является одновременно медианой, то есть AC = CB.
Следовательно, . При этом оба треугольника равнобедренные: AK=AEи BK=BE. Рассмотрим равнобедренный, AK = BK. KC — биссектриса , которая в равнобедренном треугольнике является одновременно медианой, то есть AC = CB.
Построение угла, равного данному
Построим угол, равный данному углу A.
- Произвольным раствором циркуля проведем первую вспомогательную дугу с центром в вершине данного угла — точке A так, чтобы дуга пересекала обе стороны угла. Назовем точки пересечения дуги и сторон угла C и E.
- Построим произвольный луч с началом в точке B.
- Не меняя раствора циркуля, проведем вторую вспомогательную дугу в центром в точке B. Данная дуга по длине примерно равна первой вспомогательной дуге и пересекает луч B в точке K.
- Измерим циркулем расстояние CE.
- Не меняя раствора циркуля, установим иглу циркуля в точку K и проведем третью вспомогательную дугу, пересекающую вторую вспомогательную дугу. Назовем точку пересечения H.
- Проведем луч BH.
- или .
Доказательство:
по трем сторонам, так как AE=BK и AC=BH по построению (проводили одним раствором циркуля), EC=KH по построению. Поэтому .
Построение перпендикулярных прямых
Построим перпендикуляр к данной прямой в точке, лежащей на этой прямой. Пусть a — прямая, A — точка лежащая на данной прямой.
- Точка A делит прямую a на два луча, с помощью циркуля отложим на этих лучах два равных отрезка AB и AC.
- Измеряем циркулем расстояние BC.
- Не меняя раствора циркуля, построим две вспомогательные дуги с центрами в точках B и C. Дуги пересекаются по обе стороны от прямой a. Пусть E и K — точки пересечения.
- Проведем прямую EK.EK пересекается с прямой a в точке A. .
Доказательство:
Рассмотрим — равнобедренный, так как BK = KC по построению. AB=AC по построению. Следовательно, KA — медиана . По свойству равнобедренного треугольника медиана, опущенная на основание, является высотой. .
.
Построения правильных многоугольников
Построение правильного треугольника и построение равностороннего треугольника с заданной стороной, равной a.
- Построим отрезок AB, равный a.
- Измерим отрезок ABциркулем, и, не меняя раствора циркуля, построим вспомогательную дугу с центром в точке A и радиусом a.
- Построим вторую вспомогательную дугу с центром в точке B и радиусом a.
- Дуги пересекаются по обе стороны от отрезка AB Назовем точки пересечения C и E.
- Проведем отрезки AC и CB. — равносторонний.
- Построим отрезки AE и EB — равносторонний.
Доказательство:
— равносторонние по построению. Все их стороны равны а.
Построение вписанного в окружность правильного треугольника:
- Построим правильный шестиугольник, вписанный в окружность.
- Соединим вершины правильного шестиугольника через одну. Полученная фигура — правильный треугольник, вписанный в окружность.
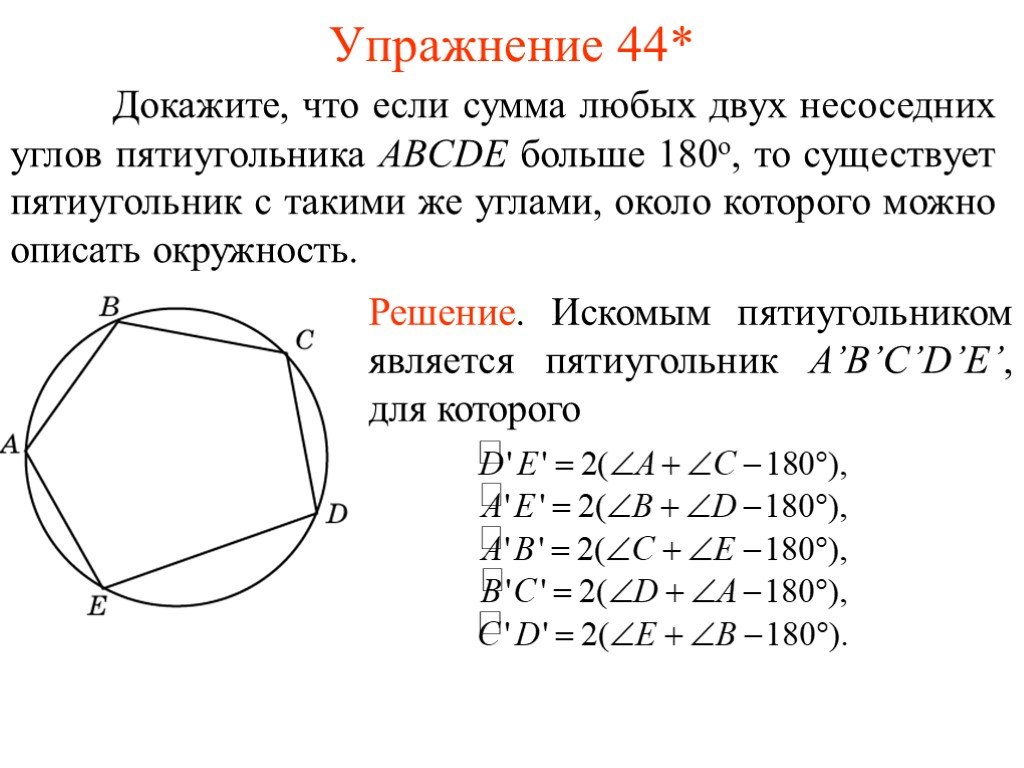
Построение правильного пятиугольника, вписанного в окружность:
- Построим окружность с центром в точке A.
 В данную окружность будет вписан правильный пятиугольник.
В данную окружность будет вписан правильный пятиугольник. - На окружности произвольно отметим точку B. Точка B будет одной из вершин правильного пятиугольника.
- Проведем прямую AB.
- Построим перпендикуляр к AB в точке A. Перпендикуляр пересекает окружность в двух точках. Пусть одна из этих точек будет C.
- Найдем точку D— середину отрезка AC.
- Измерим циркулем расстояние DB. Не меняя раствора циркуля построим дугу с центром в точке D, пересекающуюся с прямой AC внутри окружности. Назовем точку пересечения точкой E. Длина отрезка BE равна стороне правильного пятиугольника.
- Измерим циркулем расстояние BE и, не меняя раствора циркуля, проведем две дуги с центром в точке B, пересекающиеся с первоначальной окружностью в точках K и M.
- Измерим циркулем расстояние между точками M и B. Не меняя раствора циркуля проведем дугу с центром в точке M, пересекающую первоначальную окружность в двух точках, одна из которых — точка A. Обозначим вторую точку пересечения как P
- Проведем дугу с центром в точке Kчерез точку B.
 Обозначим вторую точку пересечения дуги с окружностью как Q
Обозначим вторую точку пересечения дуги с окружностью как Q - Полученные в результате построений точки B, M, P, Q, C — вершины правильного пятиугольника. Соединим вершины и построим правильный пятиугольник BMPQC .
Построение правильного шестиугольника, вписанного в окружность:
- Проведем окружность с центром в точке O.
- Отметим на окружности произвольную точку A. Точка A будет одной из вершин правильного шестиугольника.
- Поведем прямую OA. Обе точки пересечения OA с окружностью являются вершинами правильного шестиугольника. Назовем вторую точку пересечения точкой H.
- Сторона правильного шестиугольника равна радиусу описанной около него окружности. Поэтому построим две вспомогательные дуги с центром в точке A и радиусом, равным радиусу окружности или отрезку OA. Дуги пересекаются с окружностью. Назовем точки пересечения B и C, B и C — вершины правильного шестиугольника, отрезки AB и AC — стороны правильного шестиугольника, равные радиусу описанной окружности.

- Не меняя раствора циркуля, построим две дуги с центром в точке H, пересекающие окружность в точках E и K. E и K являются вершинами правильного шестиугольника.
- Соединим вершины и построим правильный шестиугольник ACKHEB.
Окружность, вписанная в правильный многоугольник 9 класс онлайн-подготовка на Ростелеком Лицей
Тема: Длина окружности и площадь круга
Урок: Окружность, вписанная в правильный многоугольник
1.Введение
Напомним определение: правильным многоугольником называется такой выпуклый многоугольник, у которого все стороны равны и все углы равны.
На Рис. 1 приведен фрагмент правильного многоугольника А1 … Аn.
Рис. 1.
Все стороны многоугольника равны между собой:
an = A1A2 = A2A3 = … = An-1An = AnA1.
Все углы фигуры также равны между собой, причем .
Вписанная окружность касается каждой стороны многоугольника, поэтому целесообразно напомнить, что называется касанием прямой и окружности.
Определение: прямая, имеющая только одну общую точку с окружностью, называется касательной к этой окружности, а их общая точка называется точкой касания прямой и окружности.
Рис. 2.
На Рис. 2 прямая m – касательная к окружности с центром в точке О. Точка А – точка касания.
Единственность точки касания доказывается теоремой, утверждающей, что m – касательная к заданной окружности тогда и только тогда, когда радиус, проведенный в точку А, перпендикулярен этой прямой.
Теория вписанных окружностей базируется на фундаментальном свойстве биссектрисы угла.
Биссектриса угла есть геометрическое место точек, равноудаленных от сторон угла.
На Рис. 3 приведен ÐА и его биссектриса – луч АО (обозначена на Рис. 3 как l). Если точка О принадлежит биссектрисе, то она равноудалена от сторон угла, т. е. ОВ = ОС (перпендикуляры, опущенные из точки О на стороны угла есть расстояния от точки до сторон угла).
3 как l). Если точка О принадлежит биссектрисе, то она равноудалена от сторон угла, т. е. ОВ = ОС (перпендикуляры, опущенные из точки О на стороны угла есть расстояния от точки до сторон угла).
Обратное утверждение: если точка О равноудалена от сторон угла, то она лежит на биссектрисе. Доказывается это утверждение очень просто, если принять во внимание равенство прямоугольных треугольников АОВ и АОС: биссектриса у них общая и меньшие катеты равны.
Рис. 3.
Еще одно следствие равенства указанных треугольников: отрезки касательных, проведенных из одной точки к окружности, равны между собой (АВ = АС).
Теперь дадим определение вписанной в многоугольник окружности и приведем примеры.
Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности.
Проиллюстрируем это определение на примере правильного треугольника АВС (Рис. A4A5.
A4A5.
Рис. 7.
Перейдем к рассмотрению правильных многоугольников.
Следующее утверждение касается свойств биссектрис углов правильного многоугольника.
Биссектрисы соседних углов правильного многоугольника пересекаются.
Это утверждение уже было доказано нами ранее, но здесь мы кратко восстановим цепочку рассуждений, используемую при этом доказательстве.
Рассмотрим фрагмент правильного многоугольника, изображенный на Рис. 7.
Предположим, что биссектрисы l1 и l2 параллельны. Тогда по свойствам параллельных прямых, сумма внутренних односторонних улов равна 180°, то есть Þ α = 180° (все обозначения показаны на рисунках). Последнее равенство говорит о том, что смежные стороны многоугольника должны лежать на одной прямой, что противоречит условию. Значит, . Отсюда следует, что если соединить точку О с остальными вершинами многоугольника, то полученные отрезки также будут биссектрисами соответствующих углов (доказать это утверждение для следующей ближайшей вершины многоугольника можно, опираясь на равенство треугольников, например ∆ОA2A1 и ∆ОA2A3, по двум сторонам и углу между ними).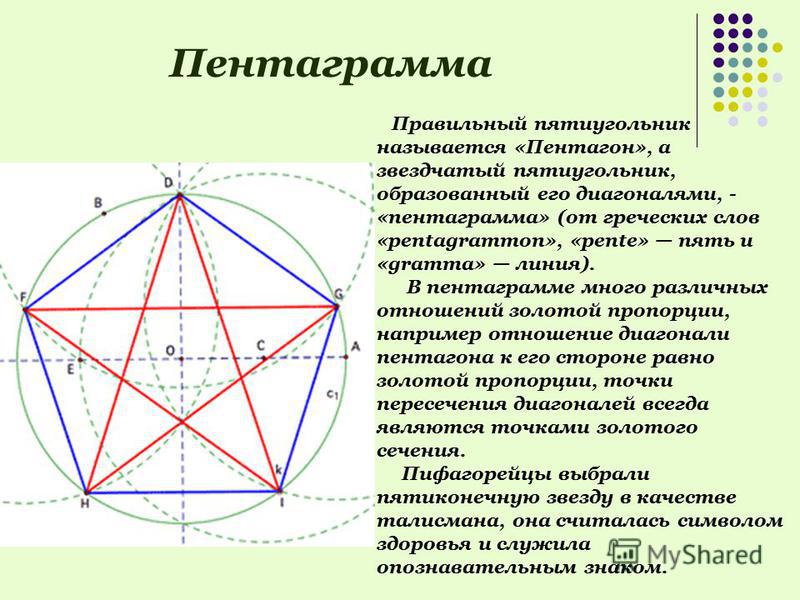
Рис. 7а.
Еще раз вернемся к свойствам точки О – точки пересечения биссектрис соседних углов правильного многоугольника.
Так как в точке О биссектрисы соседних углов пересекаются попарно, то можно утверждать, что все биссектрисы многоугольника пересекаются в этой точке, т. е. .
Основная теорема урока:
В любой правильный многоугольник можно вписать окружность, и притом только одну. На Рис. 8 дан фрагмент правильного многоугольника.
Рис. 8.
Доказательство.
1. Как было показано выше, существует точка О – точка пересечения всех биссектрис данного многоугольника.
2. Эта точка равноудалена от всех сторон многоугольника. Как мы помним, расстояние от точки до стороны – это длина перпендикуляра, опущенного из данной точки на данную сторону (перпендикуляры на Рис. 8 обозначены ОН1, ОН2, … ОНn).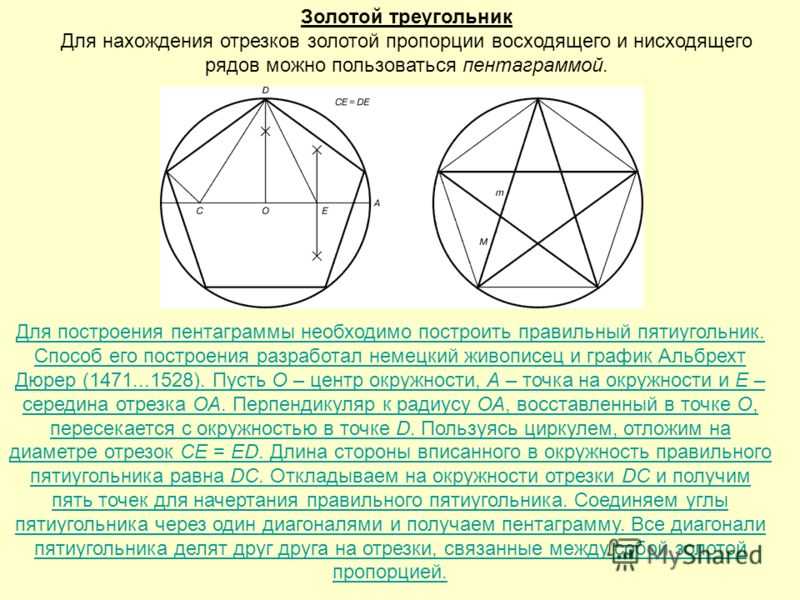 Если построить окружность радиуса ОН1 = ОН2 = … = ОНn = r с центром в точке О, то все стороны многоугольника будут касаться этой окружности (по свойствам касательной к окружности). Следовательно, в данный многоугольник можно вписать окружность.
Если построить окружность радиуса ОН1 = ОН2 = … = ОНn = r с центром в точке О, то все стороны многоугольника будут касаться этой окружности (по свойствам касательной к окружности). Следовательно, в данный многоугольник можно вписать окружность.
3. Поскольку точка О – единственная точка пересечения биссектрис, расстояние от этой точки до любой из сторон также единственно, то и вписанная в данный многоугольник окружность может быть только одна.
4. Можно привести и более подробное доказательство пункта 3, а именно: пусть существует и другая окружность, вписанная в данный многоугольник, центр ее будет располагаться в некоторой точке О1. Тогда этот центр будет равноудален от всех сторон окружности, то есть лежать на пересечении биссектрис, т. е. будет совпадать с точкой О. Раз центры окружностей (а вместе с ними и радиусы) совпадают, то и сами окружности совпадут.
Рассмотрим несколько следствий из доказанной теоремы.
Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах. А1 А2, т. е. является высотой данного треугольника, а по свойствам равнобедренного треугольника – и его медианой, опущенной на основание. Следовательно, Н1 – середина стороны А1 А2.
А1 А2, т. е. является высотой данного треугольника, а по свойствам равнобедренного треугольника – и его медианой, опущенной на основание. Следовательно, Н1 – середина стороны А1 А2.
Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в него. Эта точка называется центром правильного многоугольника.
Итак, в данном уроке мы рассмотрели окружность, вписанную в правильный многоугольник, доказали ее существование и единственность и вывели следствия из этого доказательства.
Список рекомендованной литературы
1. Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
2. Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
3. Погорелов А. В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.
Рекомендованные ссылки на интернет-ресурсы
1. Uztest.ru (Источник).
Uztest.ru (Источник).
2. Средняя математическая интернет-школа (Источник).
Рекомендованное домашнее задание
1. Учебник Погорелова (см. список литературы), стр. 211, вопросы 9–11.
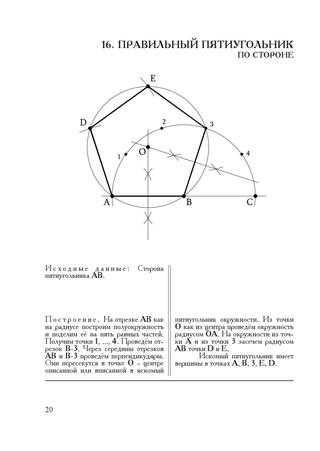
Pentagon — Интуитивная геометрия
Интуитивная геометрия — это простой метод рисования чего-либо с помощью перекрывающихся кругов. Как только вы освоите метод 8
БЫСТРЫЕ ССЫЛКИ: О, Изучите метод с пошаговыми инструкциями: Круг, Квадрат, Треугольник, Шестиугольник, Пятиугольник, Спирали, Волны, Масштабирование. Научитесь применять Метод: Пчелы, Бабочки, Цветы (3 раза), Цветы (4 раза), Цветы (5 раз), Человеческое тело, Человеческий глаз, Человеческое лицо, Снежинки, Пауки.
Интуитивная геометрия — это простой метод рисования чего-либо с помощью перекрывающихся кругов. Как только вы освоите 8 принципов метода, вы сможете применять их интуитивно и рисовать что угодно. Ниже приведены пошаговые инструкции для пятиугольника.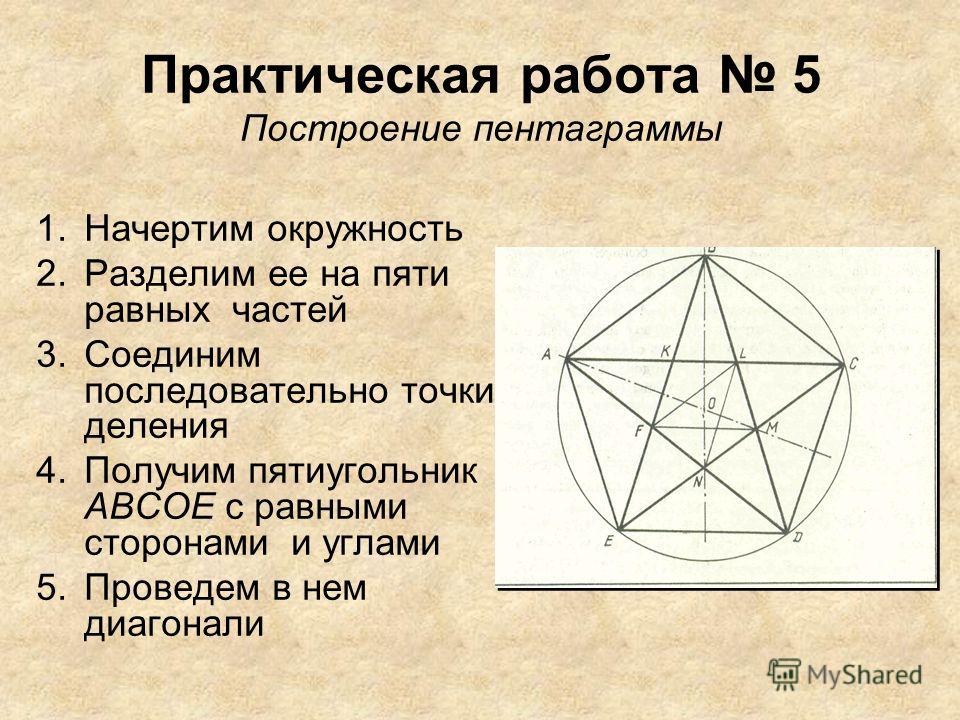
Интуитивная геометрия — это не только рисование, это развитие нашей интуиции и изучение фундаментальной структуры жизни. Практика использования перекрывающихся кругов влияет на наше сознание на всех уровнях и на нашу способность стать более могущественными творцами в этом мире. – Натали Страсбург
Купите книгу «Интуитивная геометрия» в мягкой обложке на Amazon . Купите электронную книгу по интуитивной геометрии на этом веб-сайте или на Amazon (Комиссия получена) .
Нарисуйте любую конечную линию, найдите A и B и отметьте их. Начертите окружность с центром А и радиусом АВ и центром В радиусом АВ. Найдите и соедините C и D. Нарисуйте арку с центром D и радиусом DA. Найдите E, F и G, отметьте их.
Соедините от E до G, чтобы найти H, Соедините F и G, чтобы найти I. Отметьте H, I и J. Радиусом AB нарисуйте две арки, одну с центром I, а другую с центром H. Соедините A и I, I & J, J & H и H & B.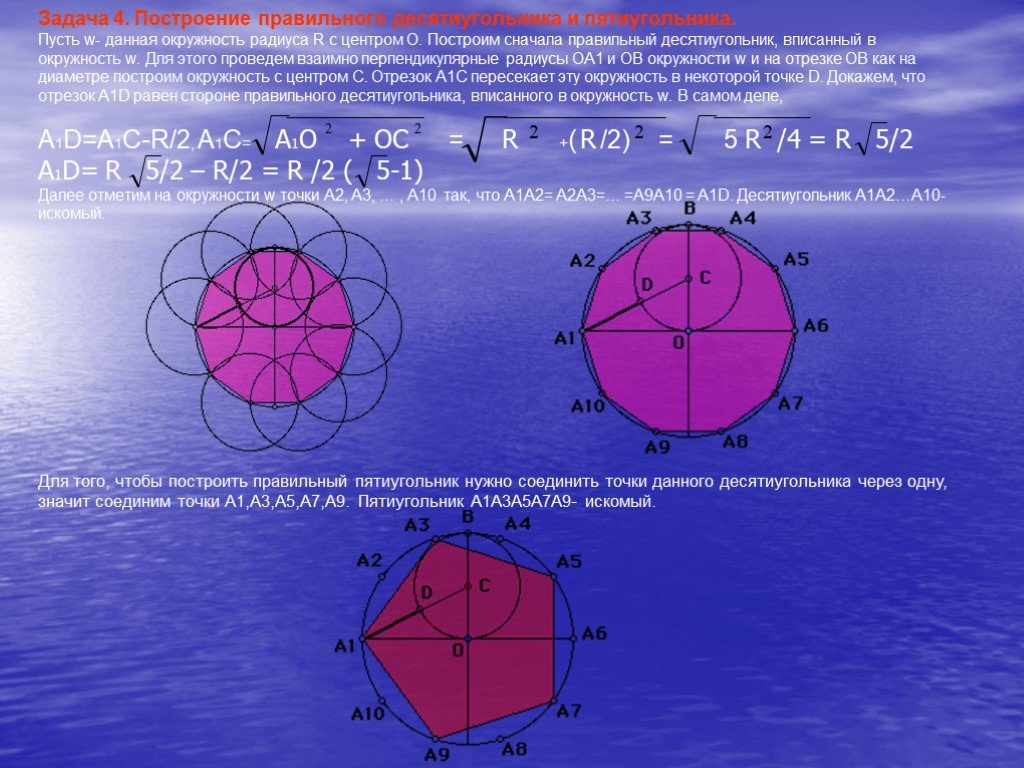 Вы нарисовали пятиугольник.
Вы нарисовали пятиугольник.
Найдите K и L, отметьте их. Соедините B через K и A через L. Найдите и отметьте M. Продлите I через M и H через M. Вы создали 10 делений.
Нарисуйте окружность с центром M и радиусом MJ. Найдите и отметьте N, O, P, Q и R.
Соедините N O P Q R, чтобы сформировать второй пятиугольник.
Найти и отметить S, T, U, V, W, X, Y , Z, Aa, Bb. Вы создали 20 дивизий. Продлите линии до окружности круга и соедините новые пятиугольники: S U W Y Aa & T V X Z Bb.
Найдите новые перекрестки Cc, Dd и т. д. и соедините их через центр M, чтобы создать в общей сложности 40 делений. Вы можете продолжить этот метод, чтобы создать 80, 160, 320 и т. д. делений.
Нарисуйте любую конечную прямую линию AB. Нарисуйте круг любого размера на линии. Используя тот же радиус, отметьте 6 делений по окружности круга. Соедините деления через середину, чтобы получились CF и DE. Используя тот же радиус, найдите и обведите G, H, I, J, K, L, M, N, O, P, Q и R.
Соедините R&I, R&J, R&M и R&N. Повторите эту схему соединения для точек G, I, L, N и P: GP, GK, GL и т.д. Найдите S&T, отметьте их и найдите остальные. Утолщайте остальные линии, чтобы показать додекаэдр.
Сеть Пентагона
Проведите линию от K до A. Используя радиус A1, найдите 2. Используя радиус AK, нарисуйте круг с центром 2. Создайте пятиугольник, используя метод 2. Повторите процесс со всех сторон, чтобы создать 5 пятиугольников, которые формируются в основании исходного.
Построить правильный пятиугольник в окружности радиусом $3.6{\text{см}}$
Ответ
Проверено
254.1k+ просмотров
Подсказка: Здесь мы сначала нарисуем окружность заданного радиуса . Теперь нарисуем правильный пятиугольник, нарисовав центральный угол пятиугольника с помощью радиусов окружности. Далее мы построим правильный пятиугольник, используя одну сторону пятиугольника, которая нарисована с использованием центрального угла.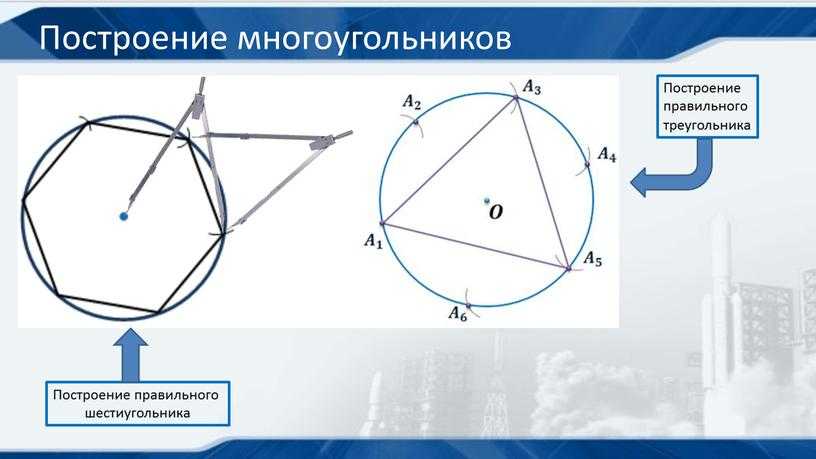

 Назовем точку пересечения дуги с лучом точкой E. Получившийся отрезок CE равен отрезку AB.
Назовем точку пересечения дуги с лучом точкой E. Получившийся отрезок CE равен отрезку AB.