геометрические построения | Справочник по математике
На отрезке ВК, равном 2а, как и на диаметре, строим (рис.1) полукруг. Этот полукруг делим на n равных частей точками C, D, E, F, G (вершинами правильного вписанного 2n-угольника; на нашем рисунке n=6). Центр А соединяем лучами со всеми полученными точками, кроме двух последних (K и G). Из точки В радиусом АВ проводим дугу ab, засекая на луче AD точку М и т.д. Точки B, L, M, N и т.д. последовательно соединяем прямыми. Многоугольник ABLMNF – искомый.
рис.1
Решить эту задачу с помощью циркуля и линейки можно не всегда; например, при n=7, n=9 этого сделать нельзя, так как полукруг с помощью циркуля и линейки на 7 или 9 точно не делится.
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, многоугольник.Отметим на окружности (рис.1) вершины A, B, …, F правильного вписанного многоугольника с тем же числом сторон (см. §33 и §36). Проведем радиусы ОА, ОВ, …, OF и продолжим их. Дугу АВ разделим пополам точкой Е (см. §15). Через Е проведем JP⊥OE. Отрезок JP, заключенный между продолжениями соседних радиусов, есть сторона искомой фигуры. На продолжении остальных радиусов откладываем отрезки ОК, OL, …, ON, равные OP. Точки J, K, L, …, N, P последовательно соединяем. Многоугольник JKLM…NP – искомый.
рис.1
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, многоугольник, окружность.Построим точку F (рис.1), как и в §33 OF есть сторона искомой фигуры. Раствором циркуля, равным OF, сделаем на окружности десять последовательных засечек. Получим вершины искомой фигуры
рис.1
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, десятиугольник, круг, многоугольник, окружность.Проводим два взаимно перпендикулярных диаметра АВ и CD (рис.1). Разделив пополам дуги AD, DB, BC, CA точками E, F, G, H (см. §15), последовательно соединяем полученные восемь точек.
рис.1
Запись опубликована автором admin в рубрике Геометрия с метками восьмиугольник, геометрические построения, круг, многоугольник, окружность. 1). Соединяя точки A, B, C, D, E, F подряд, получим правильный шестиугольник. Соединяя их через одну, получим правильный (равносторонний) треугольник.
1). Соединяя точки A, B, C, D, E, F подряд, получим правильный шестиугольник. Соединяя их через одну, получим правильный (равносторонний) треугольник.рис.1
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, многоугольник, треугольник, шестиугольник.Проводим два взаимно перпендикулярных диаметра АВ и CD (рис.1). Делим пополам радиус АО точкой Е. Из Е радиусом ЕС проводим дугу CF, пересекая ее диаметр АВ в точке F. Из С радиусом CF проводим дугу FG, пересекая ею данную окружность в точке G; CG(=CF) есть одна сторона искомой фигуры. Проводим тем же радиусом дугу mn из точки П как из центра, получаем еще одну вершину H искомой фигуры и т.д.
рис.1
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, круг, многоугольник, окружность, пятиугольник.
Проводим два взаимно перпендикулярных диаметра АВ и CD (рис.1). Из их концов, как из центров, описываем четыре полуокружности радиусами, равными ОА. Точки F, G, H и E их пересечения – вершины искомого квадрата.
рис.1
Запись опубликованаПроводим два взаимно перпендикулярных диаметра АВ и СD; ACBD – искомый квадрат (рис.1)
рис.1
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, квадрат, круг, многоугольник, окружность.Через середину АВ (рис.1) проводим к АВ перпендикуляр MN (см. п. §2). От точки О его пересечения с АВ откладываем на MN отрезки ОС и OD, равные ОА; соединяем точки С и D с точками А и В; ABCD – искомый квадрат.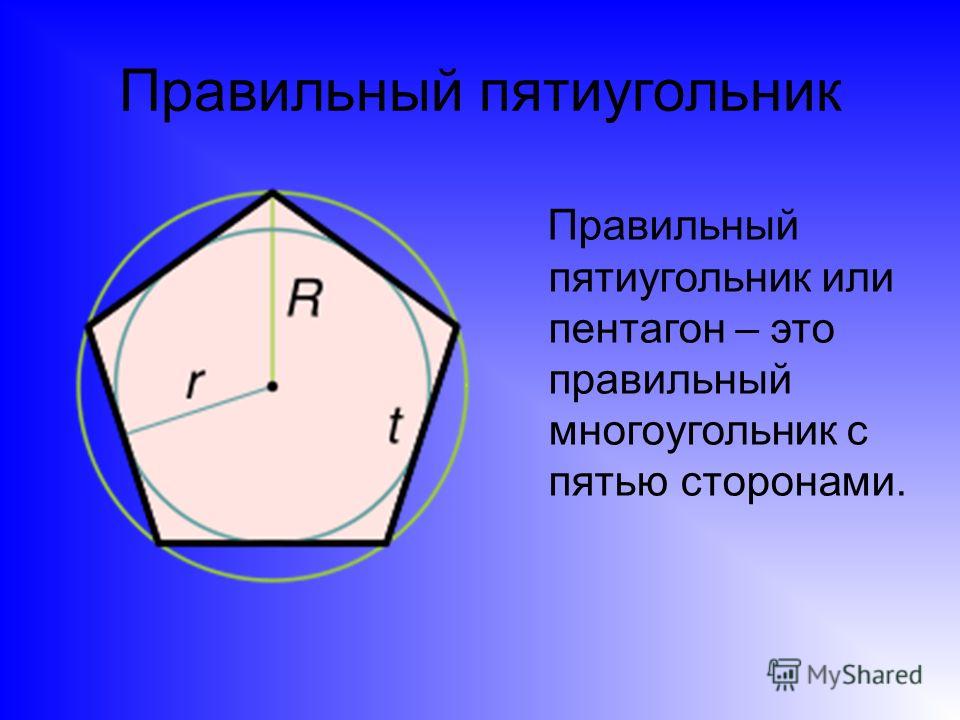
рис.1
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, квадрат, многоугольник.Поступаем как в пп. §27 и §28
Запись опубликована автором admin в рубрике Геометрия с метками геометрические построения, квадрат, многоугольник.
| ||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
Отрывок, характеризующий Правильный пятиугольник
Петя не знал, как долго это продолжалось: он наслаждался, все время удивлялся своему наслаждению и жалел, что некому сообщить его. Его разбудил ласковый голос Лихачева.
Его разбудил ласковый голос Лихачева.– Готово, ваше благородие, надвое хранцуза распластаете.
Петя очнулся.
– Уж светает, право, светает! – вскрикнул он.
Невидные прежде лошади стали видны до хвостов, и сквозь оголенные ветки виднелся водянистый свет. Петя встряхнулся, вскочил, достал из кармана целковый и дал Лихачеву, махнув, попробовал шашку и положил ее в ножны. Казаки отвязывали лошадей и подтягивали подпруги.
– Вот и командир, – сказал Лихачев. Из караулки вышел Денисов и, окликнув Петю, приказал собираться.
Быстро в полутьме разобрали лошадей, подтянули подпруги и разобрались по командам. Денисов стоял у караулки, отдавая последние приказания. Пехота партии, шлепая сотней ног, прошла вперед по дороге и быстро скрылась между деревьев в предрассветном тумане. Эсаул что то приказывал казакам. Петя держал свою лошадь в поводу, с нетерпением ожидая приказания садиться. Обмытое холодной водой, лицо его, в особенности глаза горели огнем, озноб пробегал по спине, и во всем теле что то быстро и равномерно дрожало.
– Ну, готово у вас все? – сказал Денисов. – Давай лошадей.
Лошадей подали. Денисов рассердился на казака за то, что подпруги были слабы, и, разбранив его, сел. Петя взялся за стремя. Лошадь, по привычке, хотела куснуть его за ногу, но Петя, не чувствуя своей тяжести, быстро вскочил в седло и, оглядываясь на тронувшихся сзади в темноте гусар, подъехал к Денисову.
– Василий Федорович, вы мне поручите что нибудь? Пожалуйста… ради бога… – сказал он. Денисов, казалось, забыл про существование Пети. Он оглянулся на него.
– Об одном тебя пг»ошу, – сказал он строго, – слушаться меня и никуда не соваться.
Во все время переезда Денисов ни слова не говорил больше с Петей и ехал молча. Когда подъехали к опушке леса, в поле заметно уже стало светлеть. Денисов поговорил что то шепотом с эсаулом, и казаки стали проезжать мимо Пети и Денисова. Когда они все проехали, Денисов тронул свою лошадь и поехал под гору. Садясь на зады и скользя, лошади спускались с своими седоками в лощину. Петя ехал рядом с Денисовым. Дрожь во всем его теле все усиливалась. Становилось все светлее и светлее, только туман скрывал отдаленные предметы. Съехав вниз и оглянувшись назад, Денисов кивнул головой казаку, стоявшему подле него.
Петя ехал рядом с Денисовым. Дрожь во всем его теле все усиливалась. Становилось все светлее и светлее, только туман скрывал отдаленные предметы. Съехав вниз и оглянувшись назад, Денисов кивнул головой казаку, стоявшему подле него.
– Сигнал! – проговорил он.
Казак поднял руку, раздался выстрел. И в то же мгновение послышался топот впереди поскакавших лошадей, крики с разных сторон и еще выстрелы.
В то же мгновение, как раздались первые звуки топота и крика, Петя, ударив свою лошадь и выпустив поводья, не слушая Денисова, кричавшего на него, поскакал вперед. Пете показалось, что вдруг совершенно, как середь дня, ярко рассвело в ту минуту, как послышался выстрел. Он подскакал к мосту. Впереди по дороге скакали казаки. На мосту он столкнулся с отставшим казаком и поскакал дальше. Впереди какие то люди, – должно быть, это были французы, – бежали с правой стороны дороги на левую. Один упал в грязь под ногами Петиной лошади.
У одной избы столпились казаки, что то делая. Из середины толпы послышался страшный крик. Петя подскакал к этой толпе, и первое, что он увидал, было бледное, с трясущейся нижней челюстью лицо француза, державшегося за древко направленной на него пики.
Петя подскакал к этой толпе, и первое, что он увидал, было бледное, с трясущейся нижней челюстью лицо француза, державшегося за древко направленной на него пики.
– Ура!.. Ребята… наши… – прокричал Петя и, дав поводья разгорячившейся лошади, поскакал вперед по улице.
Впереди слышны были выстрелы. Казаки, гусары и русские оборванные пленные, бежавшие с обеих сторон дороги, все громко и нескладно кричали что то. Молодцеватый, без шапки, с красным нахмуренным лицом, француз в синей шинели отбивался штыком от гусаров. Когда Петя подскакал, француз уже упал. Опять опоздал, мелькнуло в голове Пети, и он поскакал туда, откуда слышались частые выстрелы. Выстрелы раздавались на дворе того барского дома, на котором он был вчера ночью с Долоховым. Французы засели там за плетнем в густом, заросшем кустами саду и стреляли по казакам, столпившимся у ворот. Подъезжая к воротам, Петя в пороховом дыму увидал Долохова с бледным, зеленоватым лицом, кричавшего что то людям. «В объезд! Пехоту подождать!» – кричал он, в то время как Петя подъехал к нему.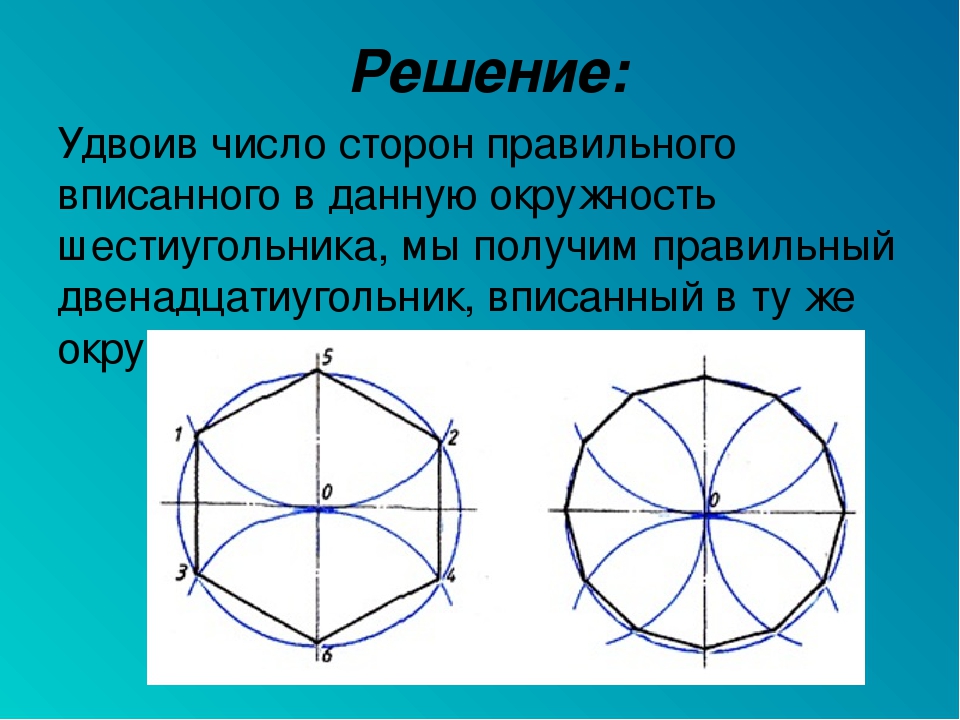
– Подождать?.. Ураааа!.. – закричал Петя и, не медля ни одной минуты, поскакал к тому месту, откуда слышались выстрелы и где гуще был пороховой дым. Послышался залп, провизжали пустые и во что то шлепнувшие пули. Казаки и Долохов вскакали вслед за Петей в ворота дома. Французы в колеблющемся густом дыме одни бросали оружие и выбегали из кустов навстречу казакам, другие бежали под гору к пруду. Петя скакал на своей лошади вдоль по барскому двору и, вместо того чтобы держать поводья, странно и быстро махал обеими руками и все дальше и дальше сбивался с седла на одну сторону. Лошадь, набежав на тлевший в утреннем свето костер, уперлась, и Петя тяжело упал на мокрую землю. Казаки видели, как быстро задергались его руки и ноги, несмотря на то, что голова его не шевелилась. Пуля пробила ему голову.
Переговоривши с старшим французским офицером, который вышел к нему из за дома с платком на шпаге и объявил, что они сдаются, Долохов слез с лошади и подошел к неподвижно, с раскинутыми руками, лежавшему Пете.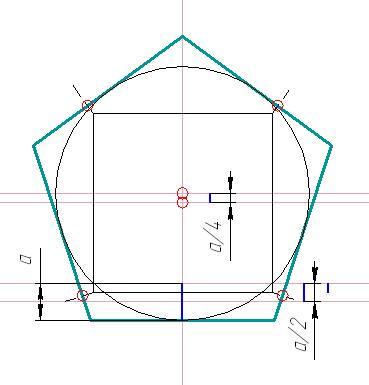
– Готов, – сказал он, нахмурившись, и пошел в ворота навстречу ехавшему к нему Денисову.
– Убит?! – вскрикнул Денисов, увидав еще издалека то знакомое ему, несомненно безжизненное положение, в котором лежало тело Пети.
– Готов, – повторил Долохов, как будто выговаривание этого слова доставляло ему удовольствие, и быстро пошел к пленным, которых окружили спешившиеся казаки. – Брать не будем! – крикнул он Денисову.
Построение вписанного в окружность правильного шестиугольника.
Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой.
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный
диаметр окружности за биссектрису углов 1 и 4, строим стороны 1 — 6, 4 — 3, 4 — 5 и 7 — 2, после чего проводим стороны 5 — 6 и 3 — 2.
Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0 — 1 — 2 равен 30°, то для нахождения стороны 1 — 2 достаточно построить по точке 1 и стороне 0 — 1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1 — 2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2 — 3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника намечаем на диаметре вершину точку 1 и проводим диаметральную линию 1 — 4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4 — 1 и 3 -2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1 — 2 и 4 — 3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра. Намечаем на концах
двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник, производим следующие построения. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А
описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным
отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем
раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из
вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Сделав тем же раствором циркуля засечки из
вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую. Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB. Получим точку 1 -вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных
частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём
полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи,
пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с
окружностью горизонтальные прямые. Найденные вершины соединяем последовательно
между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
65). Делим вертикальный диаметр окружности на семь равных
частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём
полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи,
пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с
окружностью горизонтальные прямые. Найденные вершины соединяем последовательно
между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Длины сторон правильных вписанных многоугольников.
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй — коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
Правильный пятиугольник — это многоугольник, у которого все пять сторон и все пять углов равны между собой. Вокруг него легко описать окружность. Построить пятиугольник и поможет именно эта окружность.
Инструкция
В первую очередь необходимо построить циркулем окружность. Центр окружности пусть совпадает с точкой O. Проведите оси симметрии перпендикулярные друг другу. В точке пересечения одной из этих осей с окружностью поставьте точку V. Эта точка будет вершиной будущего пятиугольник а. В точке пересечения другой оси с окружностью расположите точку D.
На отрезке OD найдите середину и отметьте в ней точку А.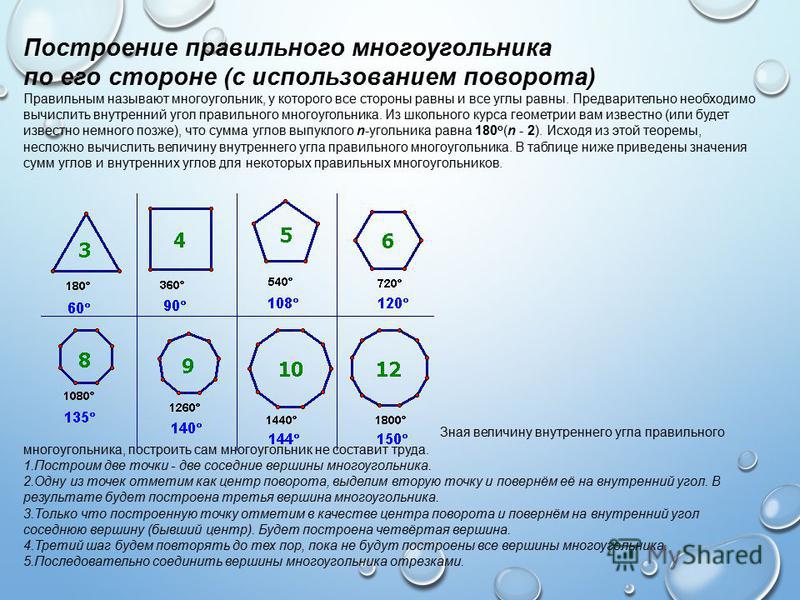 После этого нужно построить циркулем окружность с центром в этой точке. Кроме того, она должна проходить через точку V, то есть, радиусом CV. Точку пересечения оси симметрии и этой окружности обозначьте за В.
После этого нужно построить циркулем окружность с центром в этой точке. Кроме того, она должна проходить через точку V, то есть, радиусом CV. Точку пересечения оси симметрии и этой окружности обозначьте за В.
После этого при помощи циркуля проведите окружность такого же радиуса, поставив иголку в точку V. Пересечение этой окружности с первоначальной обозначьте как точку F. Эта точка станет второй вершиной будущего правильного пятиугольник а.
Теперь нужно провести такую же окружность через точку Е, но с центром в F. Пересечение только что проведенной окружности с первоначальной обозначьте как точку G. Эта точка так же станет еще одной из вершин пятиугольник а. Аналогичным образом необходимо построить еще один круг. Центр его в G. Точка пересечения его с первоначальной окружностью пусть будет H. Это последняя вершина правильного многоугольника.
У вас должно получиться пять вершин. Остается их просто соединить по линейке. В результате всех этих операций вы получите вписанный в окружность правильный пятиугольник .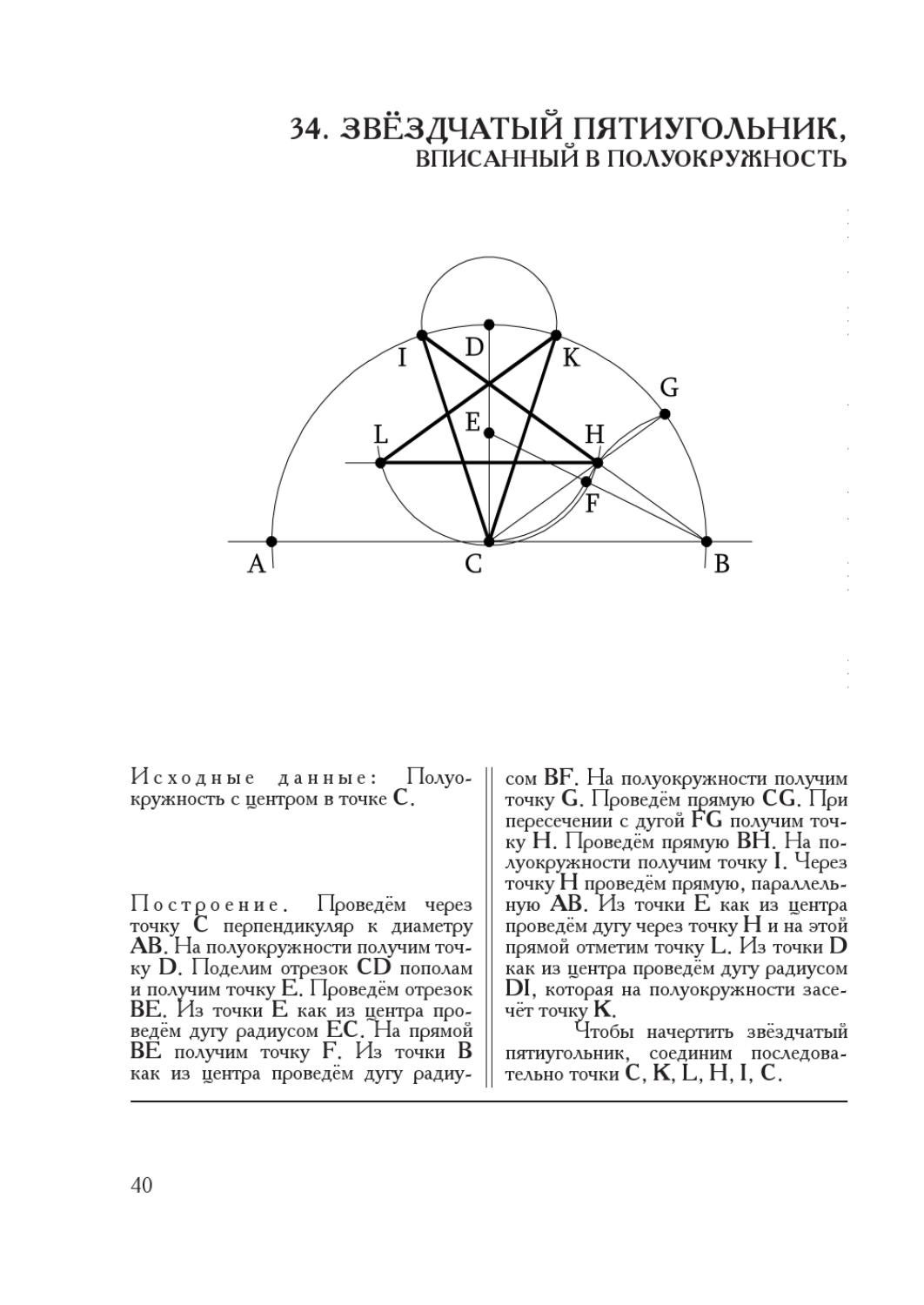
Построение правильных пятиугольников можно с помощью циркуля и линейки. Правда, процесс это достаточно длительный, как, впрочем, и построение любого правильного многоугльника с нечетным количеством сторон. Современные компьютерные программы позволяют сделать это за несколько секунд.
Вам понадобится
- — компьютер с программой AutoCAD.
Инструкция
Найдите в программе AutoCAD верхнее меню, а в нем — вкладку «Главная». Нажмите на нее левой клавишей мыши. Появится панель «Рисование». Появятся разные типы линий. Выберите замкнутую полилинию. Она и представляет собой многоугольник, остается только ввести параметры. AutoCAD. Позволяет рисовать самые разные правильне многоугольники. Число сторон может достигать 1024. Можно использовать и командную строку, в зависимости от версии набрав « _polygon» или «мн.-угол».
Вне зависимости от того, пользуетесь ли вы командной строкой или контекстными меню, на экране у вас появится окошко, в которое предлагается ввести количество сторон. Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Вбейте в появившееся окошко координаты. Можно обозначить их как (0,0), но могут быть и любые другие данные.
Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Вбейте в появившееся окошко координаты. Можно обозначить их как (0,0), но могут быть и любые другие данные.
Выберите нужный способ построения. . AutoCAD предлагает три варианта. Пятиугольник может быть описанным вокруг окружности или вписанным в нее, но можно построить его и по заданному размеру стороны. Выберите нужный вариант и нажмите на ввод. В случае необходимости задайте радиус окружности и тоже нажмите enter.
Пятиугольник по заданной стороне сначала строится точно так же. Выберите «Рисование», замкнутую полилинию и введите число сторон. Правой клавишей мыши вызовите контекстное меню. Нажмите команду «edge” или «сторона”. В командной строке наберите координаты начальной и конечной точек одной из сторон пятиугольника. После этого пятиугольник появится на экране.
Все операции можно выполнять с помощью командной строки. Например, для построения пятиугольника по стороне в русскоязычной версии программы введите букву «с». В англоязычной версии это будет «_e”. Чтобы построить вписанный или описанный пятиугольник, введите после определения количества сторон буквы «о» или «в» (либо же английские «_с» или «_i»)
В англоязычной версии это будет «_e”. Чтобы построить вписанный или описанный пятиугольник, введите после определения количества сторон буквы «о» или «в» (либо же английские «_с» или «_i»)
Таким нехитрым способом можно построить не только пятиугольник. Для того чтобы построить треугольник, необходимо разведите ножки циркуля на расстояние, равное радиусу окружности. Затем в любую точку установите иглу. Проведите тонкую вспомогательную окружность. Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины правильного треугольника.
Объект Многоугольник в Автокаде — как построить его в AutoCAD различными способами
[Уроки Автокад] Как нарисовать (начертить) многоугольник в AutoCAD
| Команда рисования в AutoCAD | |
| Многоугольник | |
| Определение | |
Многоугольник в Автокад — является замкнутой 2D-полилинией, состоящей из трех и более сегментов. Правильный многоугольник — это многоугольник у которого все стороны и углы равны. |
|
| Инструмент | |
| Инструмент Автокад Многоугольник — строит правильный многоугольник либо по конечным точкам одной стороны, либо по точке центра и радиусу вписанной или описанной окружности. | |
| Команда | |
| МН-Угол | |
| Объект | |
| Полилиния |
Команда МН-Угол в AutoCAD
За создание в Автокад правильного многоугольника отвечает команда MH-Угол.
Вызвать данную команду можно следующими способами (начать построение в AutoCAD многоугольника):
- построить многоугольник в Автокад можно из строки меню пункт Рисование — строка Многоугольник;
- начертить его можно из ленты инструментов на вкладке «Главная» — в группе Рисование кнопка Многоугольник;
- нарисовать многоугольник в Автокад можно из классической панели инструментов Рисование кнопка Многоугольник;
- либо прописать наименование команды в командной строке МН-Угол.

Построение многоугольника в Автокад вписанного в окружность
Как уже отмечалось, в вписанный в AutoCAD многоугольник в окружность задается центральной точкой и расстоянием от центра до любой из вершин. Следовательно, радиус описанной окружности — это расстояние от центра многоугольника до одной из его вершин.
Вызываем команду МН-Угол. В командной строке появляется запрос:
Число сторон <4>:
В ответ на который вы должны ввести число сторон, которое должно быть у многоугольника в AutoCAD (от 3 до 1024). Введем значение 5. Нажимаем «Enter». Появляется следующий запрос:
Введем значение 5. Нажимаем «Enter». Появляется следующий запрос:
Укажите центр многоугольника:
Зададим центр многоугольника в AutoCAD щелчком мыши. Система отобразит запрос:
Задайте параметр размещения [Вписанный в окружность/Описанный вокруг окружности] <В>:
Выбираем опцию «Вписанный в окружность». Отобразится предварительный вид многоугольника AutoCAD, который прикреплен к линии, проходящей из заданного центра до указателя. Размер его будет изменяться вместе с изменением положения указателя. В командной строке появится запрос:
Радиус окружности:
Радиус окружности можно задать, введя значение в командную строку или щелчком мыши, указав точку на чертеже. Введем значение 20 мм в командную строку и нажмем «Enter». Правильный пятиугольник (многоугольник) в Автокад с радиусом описанной окружности 20 мм построен.
Как начертить многоугольник в AutoCAD описанный вокруг окружности
Многоугольник Автокад описанный вокруг окружности задается центральной точкой и расстоянием от центра до средней точки одной из его сторон. Следовательно, радиус вписанной окружности — это расстояние от центра многоугольника до средней точки одной из его сторон.
Следовательно, радиус вписанной окружности — это расстояние от центра многоугольника до средней точки одной из его сторон.
Вызываем команду «МН-Угол». Система отобразит запрос:
Число сторон <5 — предыдущее значение>:
Соглашаемся со значением по умолчанию, нажимаем «Enter». Появляется следующий запрос:
Укажите центр многоугольника:
Указываем в Автокад центр многоугольника. Появляется запрос в командной строке:
Задайте параметр размещения [Вписанный в окружность/Описанный вокруг окружности] <В>:
Выбираем опцию «Описанный вокруг окружности» команды МН-Угол. Отобразится предварительный вид многоугольника Автокад, который прикреплен к линии, проходящей из заданного центра до указателя, соответствующего середине одной из сторон многоугольника. Размер многоугольника в Автокад будет изменяться вместе с изменением положения указателя. В командной строке появится запрос:
Радиус окружности:
Повторим ввод координат и зададим радиус описанной окружности с помощью задания относительных полярных координат. Введем в командную строку следующее значение @20<0, что означает:
Введем в командную строку следующее значение @20<0, что означает:
- «@» — отсчет координат ведется от центральной точки многоугольника Автокад;
- «20» — расстояние от центральной точки, т.е. радиус вписанной окружности;
- «<» обозначение полярности координат — возможности привязки к определенному углу;
- «0» — значение угла, т.е. 0 градусов.
Правильный многоугольник в Автокад с радиусом вписанной окружности 20 мм построен.
Совет
Задав радиус вписанной или описанной окружности в командной строке путем ввода значения радиуса, многоугольник в Автокад автоматически выравнивается так, чтобы его нижняя сторона располагалась параллельно оси X текущей ПСК. Если задать радиус при помощи мыши (различными методами задания координат), то можно повернуть многоугольник вокруг центра на нужный угол.
Если задать радиус при помощи мыши (различными методами задания координат), то можно повернуть многоугольник вокруг центра на нужный угол.Как построить многоугольник по конечным точкам одной стороны (по стороне)
Как в Автокад начертить многоугольник по стороне (алгоритм):
Вызываем команду МН-Угол в AutoCAD. В командной строке появляется запрос:
Число сторон <5 — предыдущее значение>:
Соглашаемся со значением по умолчанию, т.е. 5 сторон многоугольника Автокад. Нажимаем «Enter». Система отобразит запрос:
Укажите центр многоугольника или [Сторона]:
Выбираем опцию «Сторона», чтобы начать строить в AutoCAD многоугольник по одной из сторон. Появляется следующий запрос:
Первая конечная точка стороны:
Укажем первую конечную точку стороны многоугольника Автокад щелчком мыши. Отобразиться его предварительный вид, который прикреплен к линии, проходящей от заданной первой конечной точки стороны до второй конечной точки.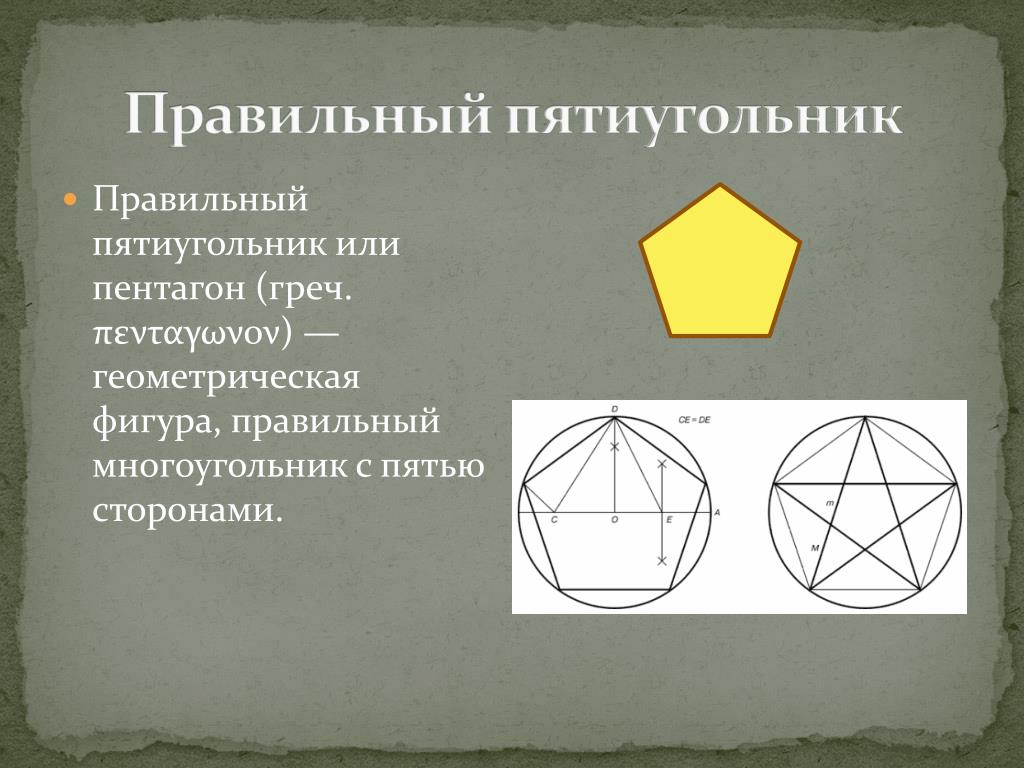 Появится запрос:
Появится запрос:
Вторая конечная точка стороны:
Вторую конечную точку стороны многоугольника в AutoCAD можете указать щелчком мыши или вводом координат в командную строку. Укажем точку щелчком мыши.
Правильный пятиугольник (многоугольник) в Автокад произвольных размеров по стороне построен.
Полезные уроки схожих тематик и рекомендации
Рекомендую ознакомиться с подобными уроками по Автокад:
Читайте и смотрите также:
Курсы, самоучители Автокад:
- 2D проектирование.
- 3D моделирование.
- Начертательная геометрия.
- Инженерная графика.
- План дома.
- Сборочный чертеж цилиндрической зубчатой передачи.
- Модель кухни 3D.
Видео «Как начертить прямоугольник и правильный многоугольник в Автокад»
Периметр пятиугольника: онлайн калькулятор, формулы, примеры решений
Пятиугольник — это многоугольник с пятью углами. Если углы и стороны такого многоугольника равны, то он считается правильным и называется пентагон. Это оригинальная фигура, которую большинство людей встречает только в учебнике по геометрии.
Если углы и стороны такого многоугольника равны, то он считается правильным и называется пентагон. Это оригинальная фигура, которую большинство людей встречает только в учебнике по геометрии.
Геометрия пятиугольника
Пятиугольник — геометрическая фигура, ограниченная пятью отрезками. Произвольный пятиугольник может иметь разные стороны, разные углы и строиться с самопересечениями, однако такая форма многоугольника крайне редко встречается в реальности. Самой распространенной формой пятиугольника считается пентагон — выпуклый многоугольник с равными сторонами и углами. Геометрическая фигура считается выпуклой, если все точки фигуры лежат с одной стороны от любой прямой, проведенной через две соседние вершины.
В отличие от треугольника, изучение которого не прерывалось на протяжении веков, все тайны пятиугольника были открыты еще в Древней Греции. В третьем веке до нашей эры Евклид описал метод построения пентагона с помощью линейки и циркуля. Пифагор изучал диагонали пентагона, которые образуют отдельную фигуру — пентаграмму, идеальную по мнению античного ученого, так как отношение сторон пентаграммы и пентагона демонстрирует золотое сечение.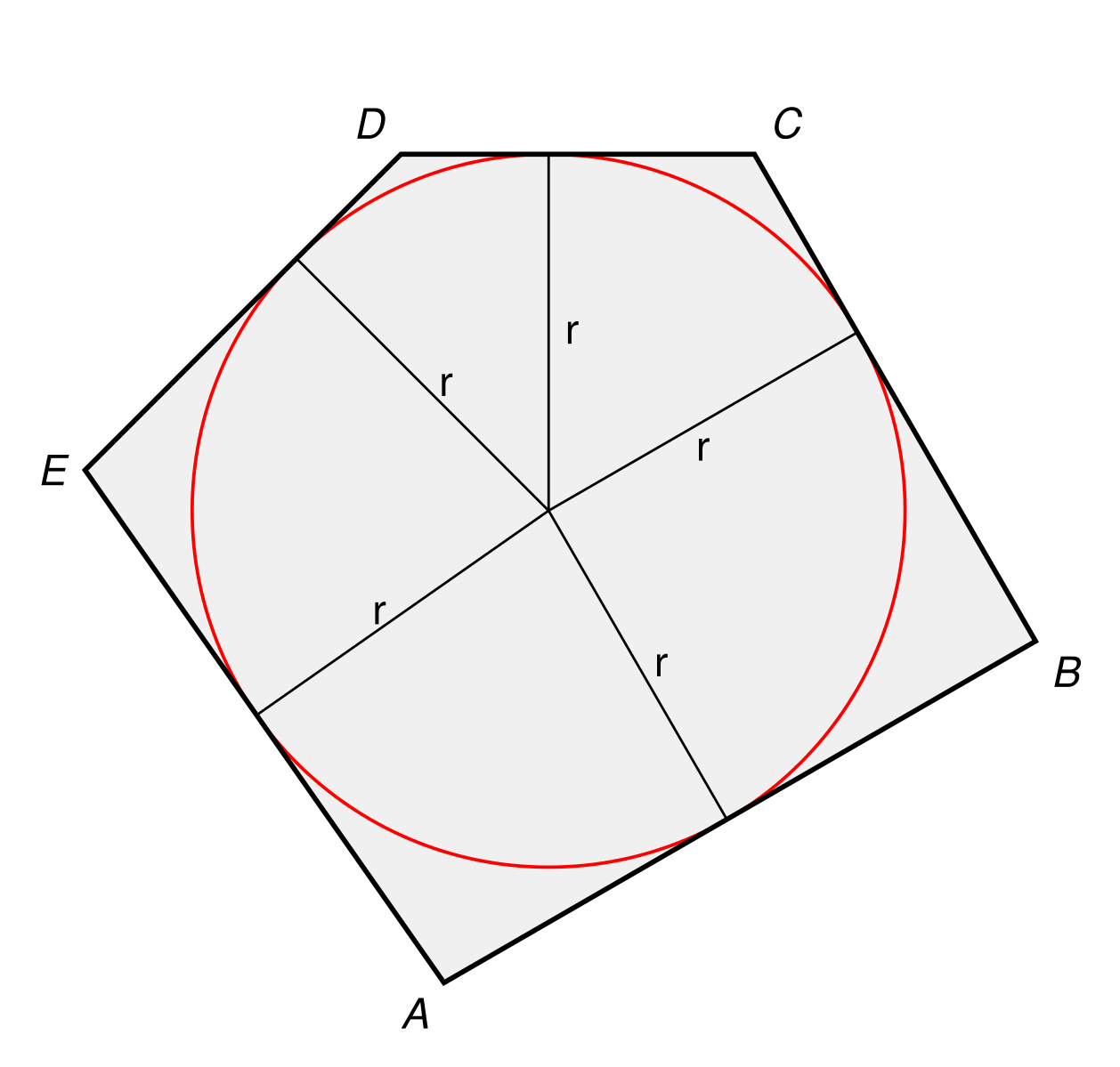
Пятиугольник в реальности
В человеческой повседневности пятиугольник встречается редко, так как пентагоном невозможно замостить плоскость без пробелов, а пентагональные призмы неудобно хранить. Форма пентагона используется обычно в архитектуре, и наиболее известным объектом, имеющим форму правильного пятиугольника, является здание министерства обороны США.
Додекаэдр – трехмерное воплощение пятиугольника, является правильным многогранником, каждая сторона которого — пентагон. В древности были распространены римские додекаэдры — бронзовые объекты, составленные из 12 пятиугольников, однако истинное назначение предметов до сих пор не выяснено. Сегодня наиболее очевидным реальным додекаэдром является игральная кость, которая выступает в качестве генератора случайных чисел для настольных ролевых игр.
В природе форма пятиугольника не встречается, однако некоторые организмы, например иглокожие, обладают пентасимметрией. Кроме того, в природе не существует кристаллов, грани которых были бы пятиугольными.
Периметр пентагона
Периметр любой геометрической фигуры — это сумма длин всех сторон. Пентагон имеет пять равных сторон, поэтому его периметр находится по простой формуле:
P = 5 a,
где a – длина одной стороны.
Сторона пятиугольника и радиусы вписанной r и описанной R окружностей приблизительно соотносятся как:
- a = 1,1756 R
- a = 1,4131 r
Таким образом, алгоритм нашего калькулятора позволяет рассчитать периметр пентагона, зная только один из трех параметров на выбор:
- сторона;
- радиус описанной окружности;
- радиус вписанной окружности.
Рассмотрим пару примеров на определение периметра правильного пятиугольника.
Примеры из жизни
Пентагон
Пентагон — всемирно известное здание, в котором располагается штаб министерства обороны США. Объект получил название благодаря своей форме, так как здание геометрически является правильным пятиугольником. Давайте посчитаем периметр Пентагона. Согласно данным из Википедии, каждая сторона здания равна 281,05 м. Зная сторону, мы можем легко вычислить периметр штаба:
Согласно данным из Википедии, каждая сторона здания равна 281,05 м. Зная сторону, мы можем легко вычислить периметр штаба:
P = 1 405,25
Таким образом, суммарная длина сторон Пентагона составляет практически полтора километра.
Школьная задача
Допустим, вам нужно определить периметр правильного пятиугольника, зная, что радиус описанной вокруг него окружности равен 5 см. Вы можете последовательно использовать приведенные выше соотношения для вычисления стороны пентагона, а затем и его периметра. Давайте сэкономим время и просто введем значение в форму калькулятора «Радиус описанной окружности R».
P = 29,38
Помимо периметра, калькулятор определил значения стороны пентагона, а также радиус вписанной в него окружности.
Заключение
Правильный пятиугольник — достаточно редкая в человеческой повседневности и природе фигура. Впрочем, вычисление параметров пентагона может понадобиться вам при решении школьных задач или рабочих вопросов. Используйте для этих целей наш онлайн-калькулятор, который определяет периметр пятиугольника, зная только один параметр фигуры.
Что нарисовать из пятиугольника. Построение правильного пятиугольника
Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.
Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.
Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.
Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр.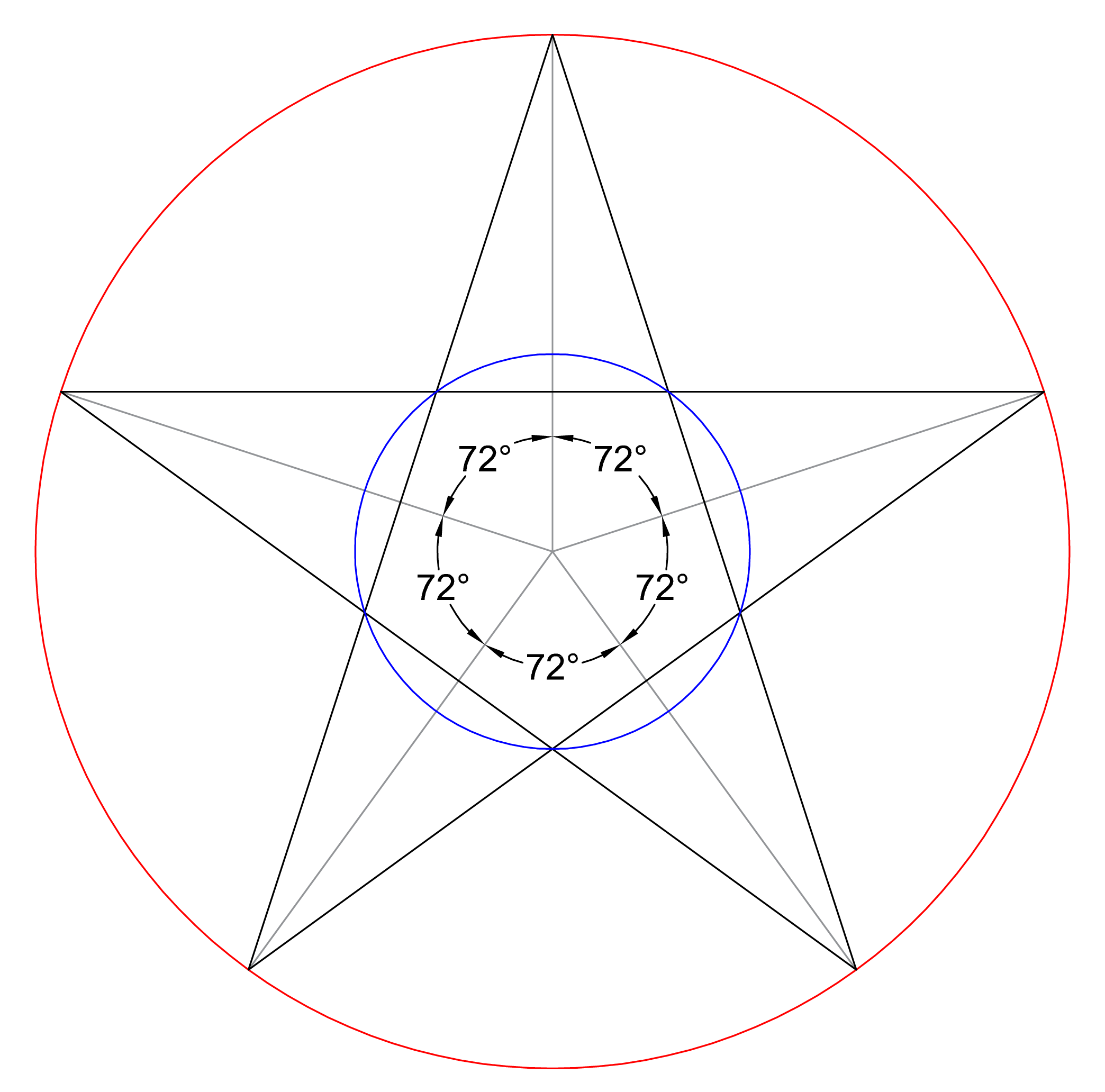 В точке сопряжения N прямой и окружности прямая является касательной к окружности.
В точке сопряжения N прямой и окружности прямая является касательной к окружности.
Получение с помощью полоски бумаги
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.
С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».
Первый способ — по данной стороне S с помощью транспортира.
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.
Полученный пятиугольник — искомый.
Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N 1 , Р 1 , Q 1 , К 1 и соединяем их прямыми.
Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N 1 , Р 1 , Q 1 , К 1 и соединяем их прямыми.
На рисунке построен шестиугольник по данной стороне.
Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.
Шестиугольник ADEFGB — искомый.
«Отделка комнат при ремонте»,
Н.П.Краснов
Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц. Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…
Только при соблюдении этого основного условия можно правильно…
Обмер выполненных работ, за исключением особо оговоренных случаев, производится по площади действительно обработанной поверхности с учетом ее рельефа и за вычетом необработанных мест. Для определения действительно обработанных поверхностей при малярных работах следует пользоваться переводными коэффициентами, приведенными в таблицах. А. Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…
Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур. Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура. При этом надо…
Правильные многоугольники
Выпуклый многоугольник называется правильным, если равны все его стороны и равны все его углы. Примерами правильных многоугольников являются равносторонний треугольник и квадрат. На рисунке 50 изображены правильные пятиугольник, шестиугольник и семиугольник. Докажем теорему об окружности, описанной около правильного многоугольника.
Примерами правильных многоугольников являются равносторонний треугольник и квадрат. На рисунке 50 изображены правильные пятиугольник, шестиугольник и семиугольник. Докажем теорему об окружности, описанной около правильного многоугольника.
Теорема. Около правильного многоугольника можно описать окружность, и притом только одну.
Доказательство. Пусть O — точка пересечения биссектрис углов A1 и A2 правильного многоугольника A1A2…An (рис. 51). Докажем сначала, что OA1 = OA2 = … = OAn.
Поскольку ∠A1 = ∠A2, то углы, прилежащие к стороне A1A2 треугольника OA1A2, равны, поэтому OA1 = OA2. Треугольники OA1A2 и OA3A2 равны по первому признаку равенства треугольников (A2A1 = A2A3, A2O — общая сторона и ∠OA2A1 = ∠OA2A3).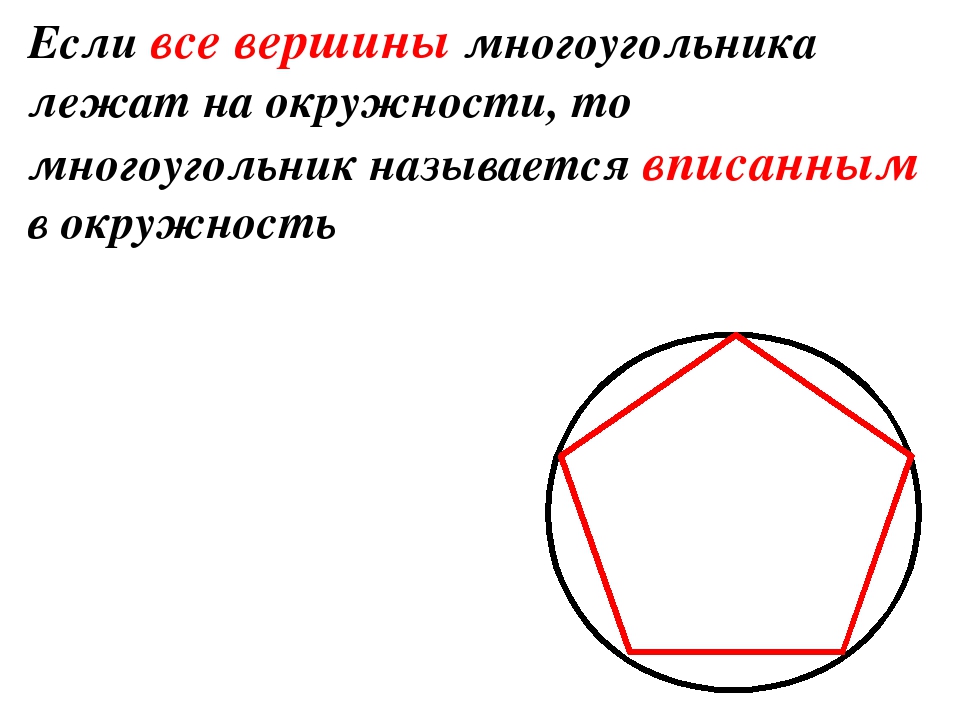 Следовательно, OA3 = OA1.
Следовательно, OA3 = OA1.
Аналогично доказывается, что ∆OA2A3 = ∆OA4A3, ∆OA3A4 = ∆OA5A4, …, поэтому OA4 = OA2, OA5 = OA3, ….
Таким образом, OA1 = OA2 = … = OAn. Из этого следует, что окружность с центром O радиуса OA1 проходит через все вершины многоугольника, т. е. является описанной около этого многоугольника.
Через точки A1, A2 и A3 проходит только одна окружность. Следовательно, около многоугольника A1A2…An можно описать только одну окружность. Теорема доказана.
Докажем теперь теорему об окружности, вписанной в правильный многоугольник.
Теорема. В правильный многоугольник можно вписать окружность, и притом только одну.
Доказательство. Пусть O — центр окружности, описанной около правильного многоугольника A1A2…An (рис. 52). Проведем высоту OH1 треугольника OA1A2. Докажем сначала, что окружность с центром O радиуса OH1 является вписанной в многоугольник A1A2…An.
52). Проведем высоту OH1 треугольника OA1A2. Докажем сначала, что окружность с центром O радиуса OH1 является вписанной в многоугольник A1A2…An.
В ходе доказательства теоремы об окружности, описанной около правильного многоугольника, мы установили, что ∆OA1A2 = ∆OA2A3 = … = ∆OAnA1, поэтому высоты OH1, OH2, …, OHn этих треугольников также равны. Следовательно, окружность с центром O радиуса OH1 проходит через точки H1, H2, …, Hn и касается сторон многоугольника в этих точках, т. е. является окружностью, вписанной в данный многоугольник.
Докажем теперь, что вписанная окружность только одна. Предположим, что имеются две окружности, вписанные в многоугольник A1A2…An. Тогда центр каждой из них равноудален от сторон многоугольника и, следовательно, совпадает с точкой O пересечения биссектрис углом многоугольника.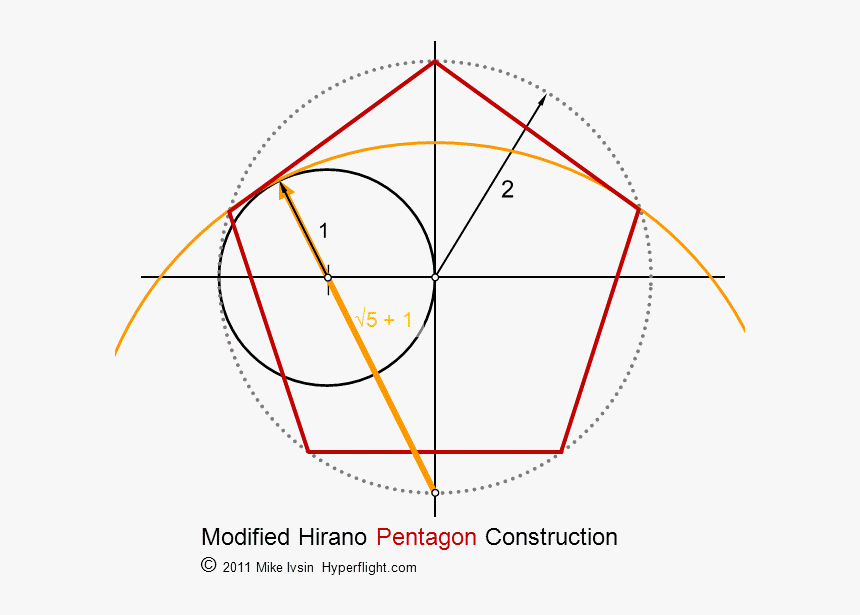
Радиус каждой окружности равен расстоянию от точки O до сторон многоугольника, т. е. равен OH1. Таким образом, центры и радиусы этих окружностей совпадают, поэтому совпадают и сами окружности. Теорема доказана.
Следствие. Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.
Центр этих окружностей называется центром правильного многоугольника.
Замечание. Многие правильные многоугольники могут быть построены с помощью циркуля и линейки. Построения правильного треугольника и правильного четырехугольника, т. е. квадрата, не вызывают затруднений.
Если уже построен какой-нибудь правильный n-угольник, то можно построить правильный 2n-угольник. В самом деле, пусть A1A2… An — построенный правильный n-угольник. Опишем около него окружность. Для этого построим биссектрисы углов A1 и A2, обозначим буквой O точку из пересечения, а затем проведем окружность с центром O радиуса OA1 (рис.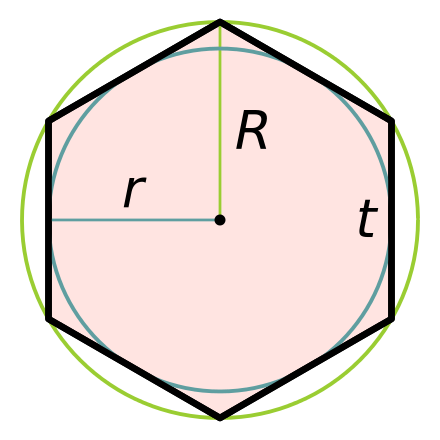 53, а). Далее проведем биссектрисы углов A1OA2, A2OA3, … до пересечения с описанной окружностью в точках B1, B2, …, Bn (рис. 53, б; на нем n = 6). Многоугольник A1B1A2B2…Bn — искомый 2n-угольник (докажите это).
53, а). Далее проведем биссектрисы углов A1OA2, A2OA3, … до пересечения с описанной окружностью в точках B1, B2, …, Bn (рис. 53, б; на нем n = 6). Многоугольник A1B1A2B2…Bn — искомый 2n-угольник (докажите это).
Применяя этот прием, можно построить целый ряд правильных многоугольников. Так, построив квадрат, можно построить правильный восьмиугольник, затем правильный шестнадцатиугольник и вообще правильный 2k-угольник, где k — любое целое число больше двух.
Оказывается, однако, что не любой правильный многоугольник допускает построение с помощью циркуля и линейки. Доказано, например, что правильный семиугольник нельзя построить с помощью циркуля и линейки, но можно построить правильный семнадцатиугольник.
Как построить восьмиугольник в окружности
Popular
Основы черчения
Строительное
Машиностроительное
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.
Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
Деление окружности на равные части и построение правильных вписанных многоугольников можно выполнить как циркулем, так и с помощью угольников и рейсшины.
Деление окружности на четыре равные части и построение правильного вписанного четырехугольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 115, а). Соединив точки пересечения этих линий с окружностью прямыми, получают правильный вписанный четырехугольник.
Деление окружности на восемь равных частей и построение правильного вписанного восьмиугольника. Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым линиям с помощью угольника с углами 45, 45 и 90° и рейсшины (рис. 115, б), вместе с центровыми линиями разделят окружность на восемь равных частей.
Деление окружности на восемь равных частей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 (рис. 115, в). Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.
Если полученные восемь точек соединить последовательно прямыми линиями, то получится правильный вписанный восьмиугольник (рис. 115, в).
Деление окружности на три равные части и построение правильного вписанного треугольника выполняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.
При делении окружности циркулем на три равные части из любой точки окружности, например из точки Л пересечения центровых линий с окружностью (рис. 116, а и б), проводят дугу радиусом R, равным радиусу данной окружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на противоположном конце диаметра, проходящего через точку Л. Последовательно соединив точки 1, 2 и 3, получают правильный вписанный треугольник. При построении правильного вписанного треугольника, если задана одна из его вершин, например точка 1, находят точку А. Для этого через заданную точку 1 проводят диаметр (рис. 116, в). Точка А будет находиться на противоположном конце этого диаметра. Затем проводят дугу радиусом R равным радиусу данной окружности, получают точки 2 и 3.
При делении окружности на три равные части с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 117, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис. 117, в).
Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5 (рис. 118). Последовательно соединив полученные точки, получают правильный вписанный шестиугольник. Деление окружности на шесть равных час-1ен и построение правильного вписанного шестиугольника с помощью угольника и рейсшины показано на рис. 119 и 120. Деление окружности на двенадцать равных частей и построение правильного вписанного двенадцатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.
При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью (рис. 121). Соединив полученные точки, получают двенадцатиугольник.
При построении двенадцатиугольника с помощью угольника и рейсшины точки деления строят, как показано на рис. 119 и 120.
Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника показано на рис. 122.
Половину любого диаметра (радиус) делят пополам (рис. 122, а), получают точку А. Из точки А, как из центра, проводят дугу радиусом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В (рис. 122, б). Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1 /5 длины окружности. Делая засечки на окружности (рис. 122, в) радиусом R, равным отрезку 1В, делят окружность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки / строят точки 2 и 5 (рис. 122, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пятиугольник (рис. 122, г).
Деление окружности на десять равных частей выполняют аналогично делению окружности на пять равных частей (рис. 122), но сначала делят окружность на пять частей, начиная построение из точки /, а затем из точки 6, находящейся на противоположном конце диаметра (рис. 123, а). Соединив последовательно все точки, получают правильный вписанный десятиугольник (рис. 123, б).
Деление окружности на семь и четырнадцать равных частей и построение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 124 и 125.
Из любой точки окружности, например точки Л, радиусом заданной окружности проводят дугу (рис. 124, а) до пересечения с окружностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1 /7 длины окружности. Радиусом, равным отрезку ВС, делают засечки на окружности в последовательности, показанной на рис. 124, б. Соединив последовательно все точки, получают правильный вписанный семиугольник (рис. 124, в).
Деление окружности на четырнадцать равных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 125, а).
Сначала окружность делится на семь равных частей от точки /, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырна-дцатиугольник (рис. 125, б).
СОПРЯЖЕНИЯ
Рассматривая детали, видим, что в их конструкции часто одна поверхность переходит в другую. Обычно эти переходы делают плавными, что повышает прочность деталей и делает их более удобными в работе. На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.
На рис. 126, а изображена деталь, в которой плавные переходы одних плоскостей в другие представляют собой цилиндрические поверхности. На чертеже (рис. 126, б) эти плоскости изображены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.
Плавный переход одной цилиндрической поверхности в другую может являться цилиндрической поверхностью (рис. 127, а). На чертеже эти цилиндрические поверхности изображены дугами окружностей, (рис. 127, б). В этом случае плавный переход одной дуги окружности в другую осуществляется дугой окружности заданного радиуса.
На рис. 126, а и 127, а рассмотрены простейшие примеры плавных переходов поверхностей. В чертежах более сложных деталей плавные переходы между поверхностями изображаются различными сочетаниями прямых, окружностей и их дуг. Вариантов таких сочетаний может быть много, но их объединяет одно — плавность перехода. Такой плавный переход одной линии (поверхности) в другую линию (поверхность) называют сопряжением. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т. е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.
Задачи на сопряжения условно можно разделить на три группы.
Первая группа задачвключает в себя задачи на построение сопряжений, где участвуют прямые линии. Это может быть непосредственное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.
Построение окружности, касательной к прямой, связано с нахождением точки касания и центра окружности.
Задана горизонтальная прямая АВ, требуется построить окружность радиусом R, касательную к данной прямой (рис. 128). Точка касания выбирается произвольно. Так как точка касания не задана, то окружность радиуса R может коснуться данной прямой в любой точке. Таких окружностей можно провести множество. Центры этих окружностей (O1, О2и т. д.) будут находиться на одинаковом расстоянии от заданной прямой, т. е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоянии R. Так как центр касательной окружности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем проводить касательную окружность, следует определить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точки О на прямую АВ. В пересечении перпендикуляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.
В детали, которая изображена на рис. 129, а, пластина плавно переходит в цилиндр. При выполнении чертежа этой детали необходимо построить плавный переход прямой в окружность.
Задача аналогична предыдущей, но дополнена условием, что точка касания задана, так как задан размер А (рис. 129, б), который определяет величину прямолинейного участка.
Отложив размер Л, находят точку касания (точку /С), затем из точки К восставляют перпендикуляр, на котором откладывают радиус R заданной окружности, и находят центр окружности (точку О). При обводке сначала от точки касания проводится дуга заданного радиуса, а потом — прямая.
Из сказанного следует:
1) центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8801 – | 7160 – или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Свойства
Правильный многоугольник – это многоугольник, у которого все стороны и углы равны между собой.2)/(4 tan〖(180°)/n〗 )
В правильный многоугольник можно вписать окружность и описать окружность вокруг него. Радиусы внутренней и внешней окружности всецело зависят от длины стороны и их количества. Чтобы найти радиус вписанной окружности правильного многоугольника, зная сторону, нужно разделить ее на два тангенса угла, полученного делением 180 градусов на количество сторон. Радиус описанной окружности, в свою очередь, равен стороне, деленной еа два синуса того же угла. r=a/(2 tan〖(180°)/n〗 ) R=a/(2 sin〖(180°)/n〗 )
Угол правильного многоугольника зависит только от количества сторон и рассчитывается как 180 градусов, деленные на количество сторон, и умноженные на разность количества сторон и двух. α=(n-2) (180°)/n
| ОБЫЧНЫЙ ПЕНТАГОН В А ДАННЫХ
ЗАПИСАННЫЙ КРУГ На рисунке 4-25 показан метод построения а правильный пятиугольник в данной описанной окружности .Нарисуйте горизонтальный диаметр AB и вертикальный диаметр CD. Найдите E, середину радиус OB. Установите компас на расстояние между E и C, и с E в центре ударьте по дуга CF. Установите компас на расстояние между C и F, и с центром C, пересекают дугу GF. Линия от G до C образует одну сторону пятиугольника. Установите компас на GC и отключите этот интервал от C по кругу. Соедините точки пересечения.Рисунок 4-25.-Правильный пятиугольник в заданном описанном круг. ОБЫЧНЫЙ ПЕНТАГОН НА ДАННОМ НАПИСАННЫЙ КРУГ Построить правильный пятиугольник на заданном вписанный круг, определить пять равных интервалов по круг таким же образом. Однако вместо этого соединения этих точек нарисуйте каждую сторону фигура, касающаяся окружности в точке пересечения. |
Круг и вписанный правильный многоугольник
Как и было обещано на прошлой неделе, давайте выясним отношения между сторонами различных вписанных правильных многоугольников и радиусом круга.
Начнем с простейшего правильного многоугольника — равностороннего треугольника. Мы будем использовать то, что мы уже знаем о треугольниках, чтобы прийти к требуемым отношениям.
Посмотрите на рисунок ниже. AB, BC и AC — стороны (длины «a») равностороннего треугольника. OA, OB и OC — это радиусы (длины r) окружности.
Внутренние углы равностороннего треугольника составляют 60 градусов каждый. Следовательно, угол OBD равен 30 градусам (поскольку ABC — равносторонний треугольник, BO делит угол ABD пополам).Итак, треугольник BOD — это треугольник 30-60-90.
Как обсуждалось в вашей книге по геометрии, соотношение сторон в треугольнике 30-60-90 равно 1:? 3: 2, следовательно, a / 2: r =? 3: 2 или a: r =? 3: 1
Сторона треугольника = sqrt (3) * Радиус окружности
Вам не нужно заучивать этот результат. Вы можете вывести его при необходимости. Обратите внимание, что вы можете получить его, используя множество других методов. Еще один метод, который легко приходит в голову, — это использование высоты AD. Высота AD равностороннего треугольника равна (sqrt (3) / 2) * a.Центр окружности находится на расстоянии 2/3 rd высоты, поэтому AO (radius) = (2/3) * (sqrt (3) / 2) * a = a / sqrt (3)
Или сторона треугольника = sqrt (3) * радиус окружности
Давайте теперь посмотрим на квадрат.
AB — сторона квадрата, а AO и BO — радиусы круга. Каждый внутренний угол квадрата равен 90 градусам, поэтому половина этого угла будет составлять 45 градусов. Следовательно, ABO представляет собой треугольник 45-45-90. Мы знаем, что соотношение сторон в треугольнике 45-45-90 равно 1: 1: sqrt (2).
r: a = 1: sqrt (2)
Сторона квадрата = sqrt (2) * Радиус круга
Опять же, результат заучивать не надо. Кроме того, есть много способов установить связь. Другой — диагональ квадрата. Диагональ квадрата равна sqrt (2), умноженному на сторону квадрата. Радиус круга равен половине диагонали. Таким образом, сторона квадрата равна sqrt (2) * радиус круга.
Случай с пятиугольником более сложен, поскольку он требует практических знаний в области тригонометрии, которые выходят за рамки GMAT, поэтому мы не будем углубляться в это.
Но мы рассмотрим шестиугольник.
Обратите внимание, что внутренний угол правильного шестиугольника составляет 120 градусов, поэтому половина этого угла будет составлять 60 градусов. Следовательно, оба угла OAB и OBA будут составлять 60 градусов каждый. Это означает, что треугольник OAB — это равносторонний треугольник со всеми углами 60 градусов и равными сторонами. Следовательно,
Сторона правильного шестиугольника = Радиус круга.
Правильные многоугольники более высокого порядка и более сложные, и мы не будем их рассматривать.На следующей неделе мы обсудим круг, вписанный в многоугольник.
Каришма, инженер-компьютерщик, проявляющий большой интерес к альтернативным математическим подходам, обучал студентов на континентах Азии, Европы и Северной Америки. Она преподает GMAT для Veritas Prep и регулярно участвует в проектах по разработке контента, таких как этот блог!
РЕШЕНИЕ: ГЕОМЕТРИЯ Найдите длины сторон…
Стенограмма видео
Хорошо, давайте начнем с наброска ситуации.Итак, я начну с наброска круга. А потом мы пошли на формирование обычного Пентагона, а у Пентагона их пять. Вергис есть. Итак, я попытаюсь сделать эти пять точек легкости Верджиса в виде пяти точек на окружности, расположенных на одинаковом расстоянии. Поэтому нам просто нужно предположить, что они расположены на одинаковом расстоянии, хотя, вероятно, на самом деле они не одинаковы. А затем давайте соединим эти точки, чтобы образовать наш Пентагон. И наша цель — найти длину одной стороны правильного Пентагона. Итак, мы пытаемся найти здесь эту длину.Итак, если мы возьмем центр круга и нарисуем немного радиоволн по радио, я смогу перейти к легкости Верджиса в Пентагоне. Мы знаем, что радиус Круга равен 25. Мы также знаем, что Пентагон имеет некоторые внутренние углы. На самом деле, вот некоторые из этих пяти углов равны 360, потому что это просто круг. Итак, когда мы разделим это на пять, каждый из этих углов будет равен 72 градусам. Итак, давайте возьмем увеличенную версию этого треугольника, где у нас здесь 25 25 72 градуса. Но я собираюсь разделиться пополам и опустить перпендикуляр, и это будет 36 градусов и 36 градусов.Мы знаем, потому что это не я видел треугольник Селеш, угол, под которым линия, которая по сексуальному углу, также по сексу, отведена в сторону офиса и перпендикулярна ему. Итак, теперь мы хотим найти длину этой стороны. Итак, я собираюсь сказать, что это длина X, а затем длина стороны будет равна двум X, чтобы мы могли установить соотношение знаков. Знак 36 градусов равен X по сравнению с 25 напротив новостей о высоких горшках, поэтому X равен 25 знаку 36, поэтому длина стороны будет в два раза больше X, так что это будет в 50 раз больше знака 36.И если вы хотите получить точный ответ, это будет ваш точный ответ. Если вы хотите приблизить это значение, вы можете ввести это в калькулятор, и вы получите 29,39, а единицы измерения —
дюймов.Видео с вопросом: вычисление длины стороны правильного окруженного пятиугольника с учетом радиуса окружности
Стенограмма видео
Правильный пятиугольник описан вокруг круга радиусом два сантиметра.Найдите длину одной стороны пятиугольника. Ответьте правильно с точностью до одного десятичного знака.
Вот круг. Во-первых, мы можем добавить центр к этому кругу. И затем у нас есть пять мест, где пятиугольник касается этой окружности. Мы знаем, что расстояние от центра до любой точки внешнего круга — это радиус. А мы знаем, что радиус составляет два сантиметра. Мы замечаем, что вершина пятиугольника — это пересечение двух касательных линий, что говорит нам о том, что каждая из этих касательных имеет одинаковую длину.Мы также должны помнить, что когда касательная пересекает радиус, пересечение составляет 90 градусов.
На данный момент может показаться, что мы больше ничего не можем добавить. Но мы знаем, что это правильный пятиугольник. А это значит, что мы можем либо запомнить каждый из этих углов, либо знать, как их вычислить. Если вы не помните, каковы внутренние углы правильного многоугольника, вы можете вычислить внутренние углы любого многоугольника по формуле 𝑠 равно 𝑛 минус два умноженных на 180 градусов.Где 𝑠 представляет собой сумму внутренних углов, а 𝑛 — количество сторон многоугольника.
У пятиугольника пять сторон. Итак, нам нужно пять минус два раза по 180 градусов. Пять минус два — три. Трижды 180 равно 540. Но помните, что это сумма всех пяти углов. Но поскольку это правильный пятиугольник, все пять углов равны. А это означает, что если мы разделим 540 на пять, мы сможем найти меру каждого из этих углов. 540, разделенное на пять, дает 108. В правильном пятиугольнике все углы составляют 108 градусов.Но это все равно нам не совсем помогает.
Но что произойдет, если мы проведем линию между одной из вершин и центром круга? Эта линия делит эти углы пополам. Вместо 108 каждый из них был бы 54 градуса. На этом этапе, вероятно, будет полезно, если мы увеличим масштаб того, о чем мы говорим.
У нас есть радиус в два сантиметра, одна часть пятиугольника и линия, которую мы только что провели от вершины пятиугольника к центру круга. Мы знаем, что радиус и касательная пересекаются под прямым углом, и что этот угол составляет 54 градуса.В любом треугольнике все углы нужно складывать до 180 градусов. Это означает, что 90 градусов плюс 54 градуса плюс некоторый угол должны равняться 180 градусам. Когда мы складываем 90 и 54, мы получаем 144. И если мы вычитаем 144 из 180, мы обнаруживаем, что наш недостающий угол составляет 36 градусов.
Помните, наша цель — найти длину одной стороны этого правильного многоугольника. Поскольку это правильный многоугольник, мы знаем, что все стороны имеют одинаковую длину. А это означает, что если мы найдем длину одной стороны, мы найдем длину всех сторон.Если мы добавим еще один радиус, мы снова увидим, что у нас есть две касательные, которые будут равной длины. А это означает, что если мы можем найти это расстояние, нам нужно умножить его на два, чтобы найти длину одной стороны пятиугольника. А это значит, что нам нужно рассмотреть этот прямоугольный треугольник. И нам нужно найти эту недостающую длину стороны.
Поскольку теперь мы имеем дело с прямоугольными треугольниками, мы можем использовать нашу тригонометрию прямоугольного треугольника. Если мы подумаем о трех тригонометрических отношениях, у нас есть синус, косинус и тангенс.Синус противоположен гипотенузе. Косинус является смежным по гипотенузе. А касательная равна противоположной по соседней. Длина желтой стороны — это гипотенуза, и мы не знаем, какова ее длина. Мы знаем радиус розовой стороны и хотим знать длину другой стороны. Нас не интересует гипотенуза. А это значит, что лучше всего использовать касательную связь.
Если мы начнем с угла в 54 градуса, мы можем сказать, что тангенс 54 градуса равен длине противоположной стороны, два сантиметра.А длина соседней стороны — это наша недостающая сторона, 𝑠. Но это не единственный вариант. Мы также можем взять тангенс 36 градусов, где противоположная сторона равна длине стороны 𝑠, а длина смежной стороны равна радиусу двух сантиметров. Любой из них будет работать. Но я собираюсь выбрать тангенс 36 градусов, поскольку математика будет немного проще, потому что длина стороны находится в числителе дроби, а не в знаменателе. Таким образом, у нас будет на один шаг меньше, чем если бы мы использовали тангенс 54 градуса.
В этом случае нам просто нужно умножить обе части уравнения на два сантиметра. И у нас получится, что два сантиметра, умноженные на тангенс 36 градусов, равны длине стороны. Когда мы умножаем тангенс 36 градусов на два раза, получаем 1.45308, продолжая. Если вы этого не понимаете, убедитесь, что на калькуляторе, который вы используете, установлены градусы, а не радианы.
Здесь нужно быть осторожным, потому что продолжение 1.45308 составляет только половину этой стороны пятиугольника. Оба эти расстояния равны 1.45308 продолжающихся сантиметров. И вместе они образуют длину одной стороны этого правильного пятиугольника. Таким образом, длина одной стороны этого пятиугольника равна двум умноженным на два сантиметра тангенсу 36 градусов, или двум умноженным на 1,45308 продолжающимся сантиметрам. Когда мы проделаем это умножение, мы получим 2,90616.
Мы округляем до первого десятичного знака. Это означает, что нам нужно смотреть вправо, на сотню. Поскольку в разряде сотен стоит ноль, мы округляем до 2.9 сантиметров.
Вся элементарная математика — Учебное пособие — Геометрия
Вписанный многоугольник. Описанный многоугольник. По окружностио многоугольнике. Ввести в многоугольник. Радиус вписанной окружности
в треугольник. Радиус описанной окружности около треугольника.
Правильный многоугольник. Центр правильного многоугольника. Apothem.
Соотношение сторон и радиусов правильного многоугольника.
Вписанный в окружность многоугольник представляет собой многоугольник, вершины которого расположены на окружности (рис.54) . Многоугольник, ограниченный вокруг Окружность представляет собой многоугольник, стороны которого касаются окружности (рис.55).
Соответственно, окружность, проходящая через вершины многоугольника (рис. 54), называется описанной окружностью вокруг многоугольника ; окружность, для стороны многоугольника являются касательными (рис.55), называется окружностью , вписанной в многоугольник. Для произвольного многоугольника невозможно вписать в него круг и описать вокруг него круг. Для треугольника всегда можно . Радиус r вписанной окружности выражается сторонами a, b, c круга a. треугольник как:
Радиус R описанной окружности выражается формулой:
Можно вписать окружность в четырехугольник , если суммы его противоположных сторон одинаковы. В случае параллелограммов это справедливо только для ромб (квадрат). Центр вписанной окружности находится в точке пересечения диагоналей.Можно описать круг вокруг четырехугольник , если сумма его противоположных углов равна 180 град. В случае параллелограммов это действительно только для прямоугольника (квадрата). Центр описанной окружности помещается в точку пересечения диагоналей. Можно описать окружность вокруг трапеции, только если это равнобедренный.
Правильный многоугольник — это многоугольник с равными сторонами и углами
На рис.56 показан правильный шестиугольник, на рис. 57 — правильный восьмиугольник. Правильный четырехугольник — это квадрат; правильный треугольник — это равносторонний треугольник. Каждый угол правильного многоугольника равен 180 ( n 2) / n градусов, , где n — количество углов. Внутри правильного многоугольника есть точка O (рис. 56), одинаково удаленная. от всех его вершин (OA = OB = OC = = OF), который называется центром правильного многоугольника. Центр также удален одинаково со всех сторон правильный многоугольник (OP = OQ = OR =).Сегменты OP, OQ, OR называются апофемами ; отрезки OA, OB, OC, радиусов правильного многоугольника. это можно вписать окружность в правильный многоугольник и описать вокруг него окружность. Центры вписанной и описанной окружностей совпадают с центром правильный многоугольник. Радиус описанной окружности — это радиус правильного многоугольника, радиус вписанной окружности — его апофема. Следующие формулы соотношение сторон и радиусов правильного многоугольника:
Для большинства правильных многоугольников невозможно выразить связь между их сторонами и радиусами алгебраической формулой.
E x a m p l e. Можно ли вырезать квадрат со стороной 30 см из круга диаметром
? 40 см?
С о л ю т и н. Самый большой квадрат, включенный в круг, представляет собой вписанный квадрат. Согласно
в приведенной выше формуле его сторона равна:
Следовательно, нельзя вырезать квадрат со стороной 30 см из круга с
диаметр 40 см.
Иллюстративная математика
Задача
Предположим, мы определяем $ \ pi $ как длину окружности, диаметр которой равен 1:
Объясните, почему длина окружности радиуса $ r \ gt 0 $ равна $ 2 \ pi r $.
Комментарий к IM
Окружность окружности радиуса $ r $ равна $ 2 \ pi r $. Эта хорошо известная формула используется здесь с точки зрения подобия. В этой задаче важно отметить, что определение для $ \ pi $ уже включает окружность круга, определенного круга.Чтобы показать, что отношение длины окружности к диаметру не зависит от размера круга, требуется аргумент подобия. Предусмотрены два разных подхода: один использует тот факт, что все круги похожи, а второй — аналогичные треугольники. Этот первый подход проще, но у второго есть то преимущество, что он приводит к аргументу для вычисления площади круга.
Старшеклассники будут знать, что окружность окружности радиуса $ r $ равна $ 2 \ pi r $, и поэтому цель этого задания — помочь им понять эту формулу с точки зрения подобия.Первое решение требует общего понимания подобия форм, а второе требует знания сходства, характерного для треугольников.
Альтернативный аргумент с использованием тригонометрических соотношений дает формулу длины окружности правильного многоугольника с $ n \ geq 3 $ сторонами, вписанными в круг. Правильный многоугольник с $ n $ сторонами можно разложить на $ n $ равнобедренных треугольников, нарисовав отрезки прямых, соединяющих центр окружности с $ n $ вершинами многоугольника.Пример такого треугольника (взятого из правильного шестиугольника) изображен ниже:
Как отмечено на рисунке, эти равнобедренные треугольники имеют две стороны длиной $ r $, радиус окружности, а третья сторона $ \ overline {AC} $ имеет длину $ b $, которая зависит от $ m (\ angle ABC ) $. Точка $ P $ на рисунке — середина $ \ overline {AC} $. Итак, у нас есть $ \ frac {| AP |} {| AB |} = \ sin {\ angle ABP} $, и отсюда мы можем вывести, что $ | AP | = r \ sin {\ angle ABP} $, а затем, используя то, что $ P $ является средней точкой $ \ overline {AC} $, $ b = 2r \ sin {\ angle ABP} $.Мы знаем, что 2n углов, конгруэнтных $ \ angle ABP $, составляют полный круг, поэтому $ m (\ angle ABP) = \ frac {360} {2n} $. Периметр правильного многоугольника с $ n $ сторонами, вписанного в круг, в $ n $ умножен на длину стороны этого многоугольника, которую мы только что вычислили: $$ n \ times 2r \ sin {\ left (\ frac {360} {2n} \ right)}. $$ Тригонометрические отношения не зависят от размера треугольника, поэтому эти формулы для $ P_n $ позволяют нам вывести, как и в решении 2, что отношение длины окружности к ее диаметру не зависит от размера окружности. .Кроме того, это обеспечивает простой количественный способ оценки $ \ pi $ путем выбора большого значения $ n $: конечно, для этого требуется знать синус угла.
Этот первый аргумент является примером MP7, Ищите и используйте структуру. Ключом к этому аргументу является определение того, что все круги похожи, а затем применение значения подобия к окружности. Второй аргумент иллюстрирует MP8, «Ищите и выражайте регулярность в повторяющихся рассуждениях». Здесь важно сравнить круг с более знакомой формой — треугольником.Особенно эффективный метод — разделить правильный многоугольник, аппроксимирующий круг, на совпадающие треугольники, что делает формулу для периметра и его связь с $ r $ особенно ясной.
Решения
Решение: 1 Сходство кругов
Ниже приведено изображение круга диаметром 1, обозначенного $ C_1 $, и диаметром $ d = 2r $, обозначенного $ C_2 $:
В изображенном случае $ d $ больше, чем $ 1 $. Все окружности похожи, и в этом случае масштабный коэффициент, идущий от окружности диаметра $ 1 $ к окружности диаметра $ 2r $, равен $ 2r $.Длина окружности — это одномерное измерение, поэтому она масштабируется так же, как и диаметры:
\ begin {align} \ frac {\ text {Окружность} (C_2)} {\ text {Окружность} (C_1)} & = \ frac {\ text {диаметр} (C_2)} {\ text {диаметр} (C_1)} \\ & = \ frac {2r} {1} \ end {align}
Поскольку окружность $ C_1 $ по определению равна $ \ pi $, из приведенного выше уравнения следует, что окружность $ C_2 $ равна $ 2 \ pi r $.
Решение: 2 Подобие треугольников
В этом решении мы аппроксимируем окружность круга с помощью многоугольников, а затем используем подобие треугольников, чтобы объяснить формулу длины окружности.Ниже показано изображение правильного восьмиугольника, вписанного в круг радиуса $ r $:
Окружность круга немного больше периметра правильного восьмиугольника, который мы можем вычислить, используя картинку ниже:
Периметр восьмиугольника равен 8 миллиардам долларов, так как он разделен на восемь равных треугольников с основанием в миллиардах долларов каждый. Мы можем вычислить углы этих восьми треугольников, используя тот факт, что восемь внутренних углов объединяются, образуя круг в 360 градусов, поэтому каждый имеет размер 45 градусов.\ circ $ похожи. Следовательно соотношение $ (b: r) $ не зависит от размера правильного восьмиугольника. Это означает, что соотношение $ (\ text {perimeter (octagon)}: r) $ также не зависит от размера правильного восьмиугольника. По мере того, как мы добавляем все больше и больше сторон, это отношение приближается к отношению длины окружности к ее радиусу. Делаем вывод, что для окружности $ C $ любого радиуса $ r $ $$ (\ text {окружность} (C): r) = \ left (\ pi: \ frac {1} {2} \ right). $$ Обратите внимание, что $ \ frac {1} {2} $ получается, если смотреть на круг диаметром 1 и окружностью $ \ pi $: радиус этого круга равен $ \ frac {1} {2} $.Это эквивалентно обычной формуле, согласно которой длина окружности радиуса $ r $ равна $ 2 \ pi r $.
Урок Решенные задачи о длине стороны правильного многоугольника
Решенные задачи о длине стороны правильного многоугольника
В этом уроке вы найдете решения некоторых типичных базовых задач о длине стороны правильного многоугольника.
Теоретической основой решения этих задач являются уроки
— Длина стороны правильного многоугольника через радиус описанной окружности и
— Длина стороны правильного многоугольника через радиус вписанной окружности.
в теме Polygons из раздела Geometry на этом сайте.
Задача 1
Найдите длину стороны и периметр правильного пятиугольника, вписанного в круг радиусом 10 см. Решение
Ответ . Длина стороны 11,7557 см. По периметру 58,7785 см (приблизительно).
Задача 2
Найдите периметр 7-стороннего правильного многоугольника, вписанного в круг радиуса 10 см.Решение
Сначала найдите длину стороны данного 7-стороннего правильного многоугольника.
Используйте формулу Теорема 1 урока Длина стороны правильного многоугольника через радиус описанной окружности
=.,
где — длина стороны правильного n-стороннего многоугольника, а — радиус окружности, описанной вокруг многоугольника.
Для данных конкретных условий длина стороны правильного 7-стороннего многоугольника равна
=. = * = см.
Теперь периметр правильного 7-стороннего многоугольника в семь раз больше длины стороны, т.е.е. 7 * 8,6777 = 60,744 см.
Ответ . По периметру 60,744 см.
Задача 3
Найдите радиус окружности, описанной около 12-стороннего правильного многоугольника с размером сторон 5 см.Решение
Используйте метрическую связь между длиной стороны правильного многоугольника и радиусом описанной окружности урока.
Длина стороны правильного многоугольника через радиус описанной окружности
=..
Дает
=.
В нашем случае
= = = = 9,659 см.
Ответ . Радиус описанной окружности 9,659 см.
Задача 4
Найдите длину стороны и периметр правильного пятиугольника, описанного вокруг круга с радиусом 10 см. Решение
Ответ . Длина стороны 14,5308 см. Периметр 72.6542 см (приблизительно).
Задача 5
Найдите периметр 7-стороннего правильного многоугольника, описанного вокруг круга радиусом 10 см.Решение
Используйте формулу Теорема 1 урока Длина стороны правильного многоугольника через радиус вписанной окружности
=.,
где — длина стороны правильного n-стороннего многоугольника, а — радиус окружности, вписанной в многоугольник.
Для данных конкретных условий длина стороны правильного 7-стороннего многоугольника равна
=. = 2 * 10 * тг (0,4488) = * = см (приблизительно).
Теперь периметр в семь раз больше длины стороны: = 7 * 9,6315 = 67,42 см.
Ответ . Длина стороны 9,6315 см. По периметру 67,42 см (примерно).
Задача 6
Найдите радиус вписанной окружности в правильный 12-сторонний многоугольник с размером сторон 8 см.Решение
Используйте метрическую связь между длиной стороны правильного многоугольника и радиусом вписанной окружности урока.
Длина стороны правильного многоугольника через радиус вписанной окружности.
= ..
Дает
=.
В нашем случае
= = = = = 14,928 см.
Ответ . Радиус вписанной окружности составляет 14,928 см (приблизительно).
Мои другие уроки по полигонам на этом сайте:
— Сумма внутренних углов многоугольника,
— Правильные многоугольники,
— Длина стороны правильного многоугольника через радиус описанной окружности,
— Длина стороны правильного многоугольника через радиус вписанной окружности,
— Разные проблемы на полигонах и
— СВОЙСТВА ПОЛИГОНОВ
в теме Polygons раздела Geometry , и
— Решенные задачи о внутренних углах многоугольника.

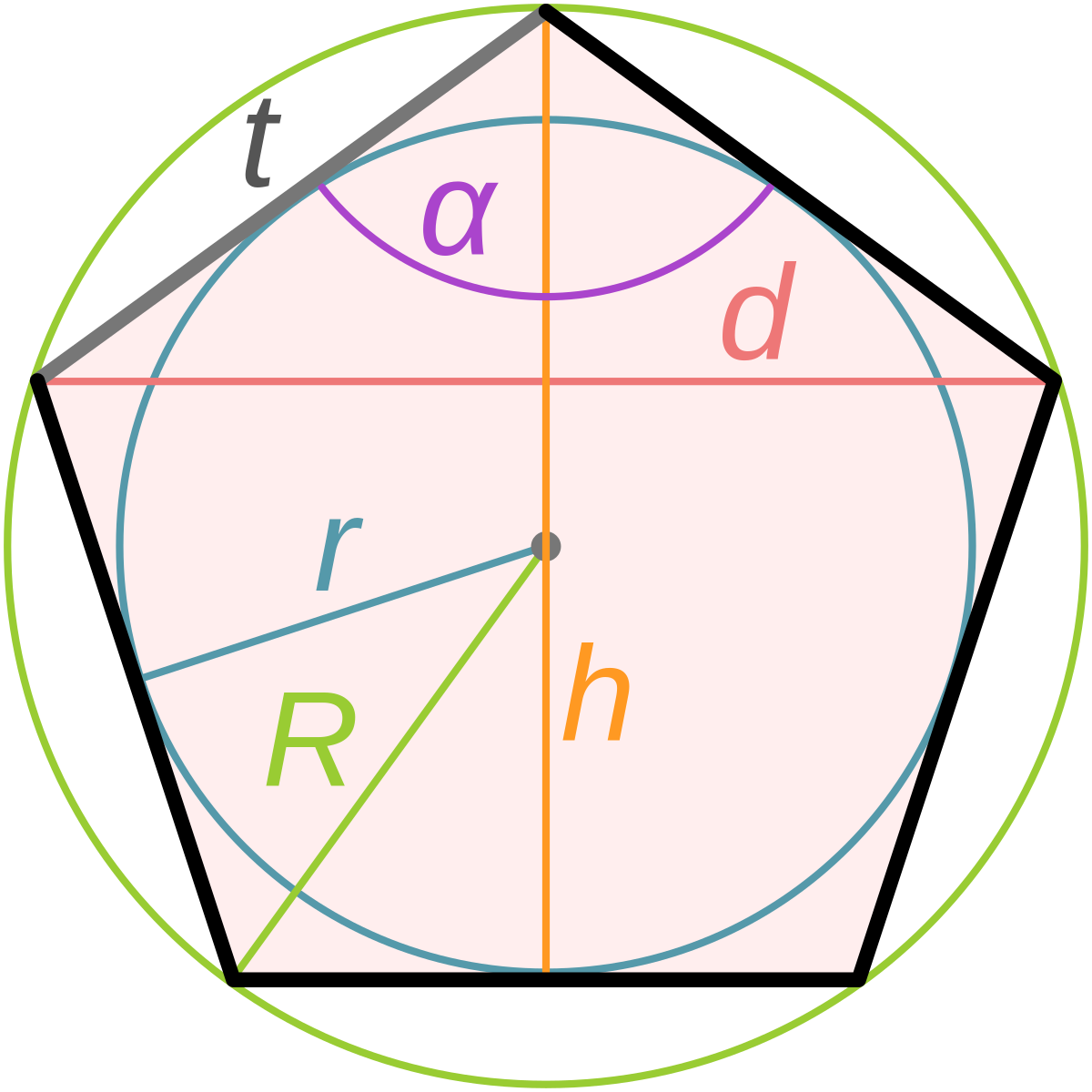 Можно, например, использовать карандаш и нитку. Отмеряем нужный диаметр на нитке. Один конец плотно зажимаем на листе бумаги, где будем чертить окружность. А на другой конец нитки устанавливаемые карандаш и одержим. Теперь действует как с циркулем: натягиваем нить и по окружности слегка надавливая карандашом чкртим окружность.
Можно, например, использовать карандаш и нитку. Отмеряем нужный диаметр на нитке. Один конец плотно зажимаем на листе бумаги, где будем чертить окружность. А на другой конец нитки устанавливаемые карандаш и одержим. Теперь действует как с циркулем: натягиваем нить и по окружности слегка надавливая карандашом чкртим окружность.

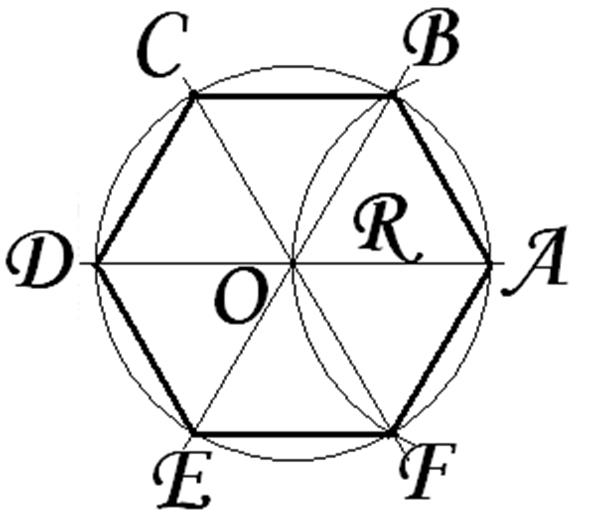 Любой другой инструмент, который позволяет провести два одинаковых, но не параллельных отрезка эквивалентен математическому циркулю.
Любой другой инструмент, который позволяет провести два одинаковых, но не параллельных отрезка эквивалентен математическому циркулю. 5 — 1 см. Как по шаблону, вырежьте по этой полосочке ещ четыре таких же полосочки, чтобы их получилось всего 5.
5 — 1 см. Как по шаблону, вырежьте по этой полосочке ещ четыре таких же полосочки, чтобы их получилось всего 5.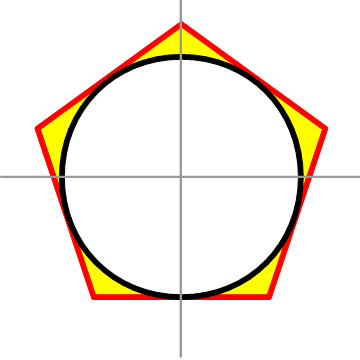 Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.
Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.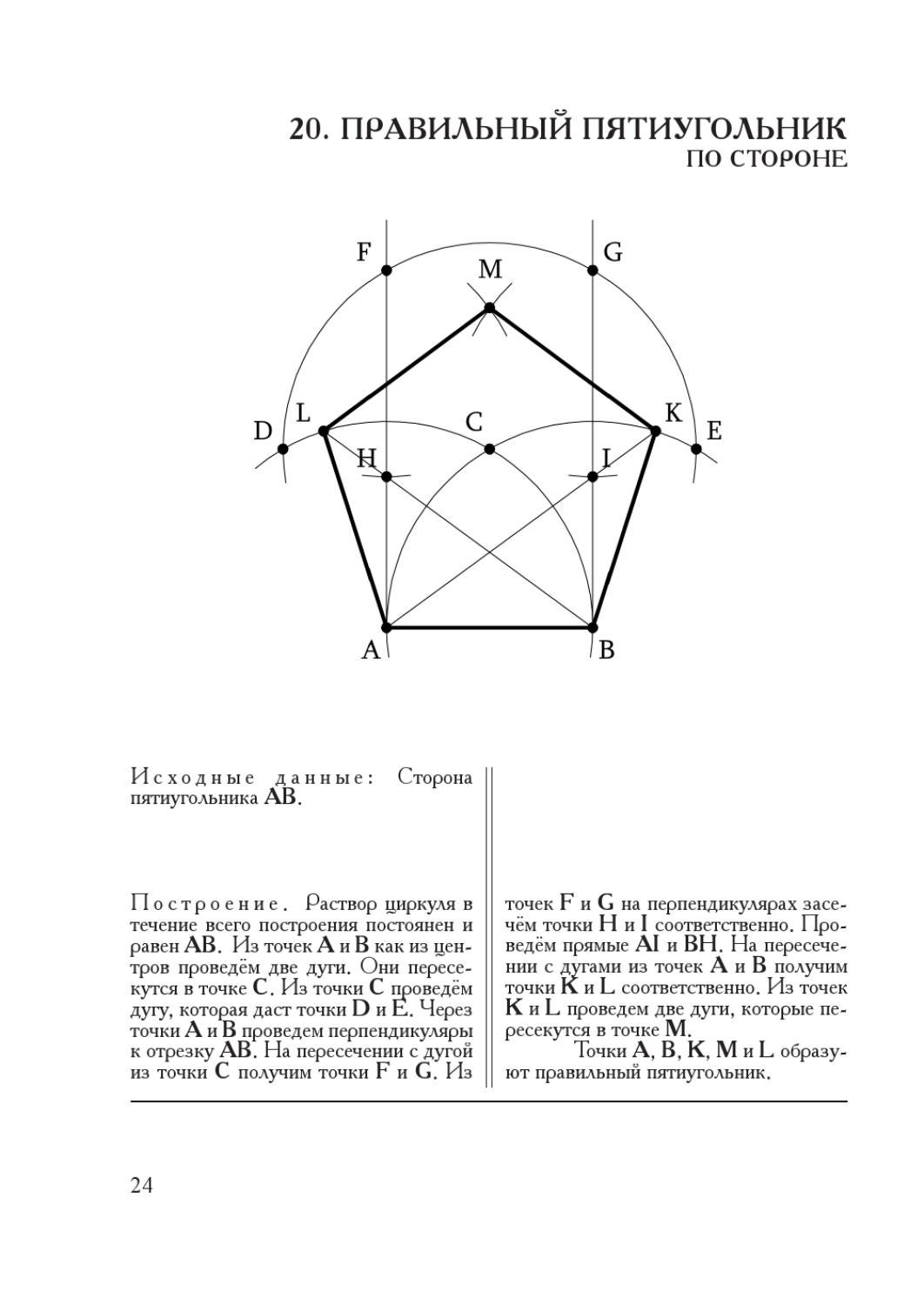 Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра. 2}{4}\sqrt{\frac{5+\sqrt{5
2}{4}\sqrt{\frac{5+\sqrt{5 также
также