Правильные многоугольники
Обобщающий урок по теме «Правильные многоугольники»
Цель урока:
- Закрепить и обобщить полученные
знания учащихся при изучении данной темы;
2. Продолжить развитие умения
учащихся решать задачи
с использованием изученного материала;
3. Наметить пути ликвидации
пробелов в усвоении данной темы.
4.Продолжить формировать навыки применения
изученного материала к решению задач модуля
«Геометрия».
«Пентагон» – правильный пятиугольник
Выпуклые и невыпуклые многоугольники
Как вы думаете, какие геометрические фигуры, показанные на рисунке, являются правильными м ногоугольниками ?
Математический диктант
- Записать формулу для вычисления угла правильного многоугольника.

2. Вычислить угол правильного шестиугольника.
3. Записать формулу для нахождения стороны правильного многоугольника.
4. Вычислить сторону квадрата, если радиус описанной около него окружности равен 4 см.
5. Записать формулу для нахождения радиуса окружности,
вписанной в правильный многоугольник.
6.Записать формулу для нахождения площади правильного многоугольника.
1.
2.
3.
4.
5.
6.
Известны углы правильных многоугольников. Сколько сторон имеет каждый из этих многоугольников.
а п =90 0
а п =135 0
а
п =60 0а п =150 0
4
12
10
3
8
Формулы для вычисления правильного треугольника, квадрата и шестиугольника
1. Дано: R = 8см.
Дано: R = 8см.
Найти: S 4 -? S 6 -?
Решение.
Правильные многоугольники в природе
Правильные многоугольники в архитектуре
Построение правильных многоугольников
- Простейшее построение правильного четырехугольника
Построение правильного шестиугольника
Построение правильного треугольника
Укажите номера верных утверждений
- Квадрат имеет две оси симметрии.
- Сумма углов n- угольника равна 180( n -2)
- Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.
- Каждая сторона треугольника больше суммы двух других.

Укажите номера верных утверждений
- Любой правильный многоугольник является выпуклым.
2. Около любого треугольника можно описать окружность.
3. Если угол меньше 90 градусов, то и смежный с ним угол также меньше 90 градусов.
4. Сторона правильного шестиугольника равна радиусу описанной окружности.
Укажите номера верных утверждений
1.Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
2. Любой выпуклый многоугольник является правильным.
3. Если диагонали четырехугольника равны, то такой четырехугольник является правильнмым.
4. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Выберите верное утверждение
- В любой прямоугольник можно вписать окружность.

- Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.
- Если в четырехугольнике две противоположные стороны равны, этот четырехугольник – параллелограмм
4. Каждый угол правильного пятиугольника равен 108.
Домашнее задание
1.Повторить тему «Центральная и осевая симметрия», п.47, с.110-111
2.Подготовить презентацию на тему «Симметрия в архитектуре, искусстве»
3.Оформить выставку рисунков на тему «Центральная и осевая симметрия».
Конспект урока «Построение правильных многоугольников» | План-конспект урока по геометрии (9 класс) на тему:
Интегрированный урок геометрия + черчение по теме: «Построение правильных многоугольников»
Гурьева Валентина Михайловна
учитель черчения и изобразительного искусства, МБОУ «Корниловская СОШ», Верхнетоемский р-н, п. Двинской, 165502, Архангельская обл. , Верхнетоемский р-н, п. Двинской.
, Верхнетоемский р-н, п. Двинской.
Стругова Нина Павловна
учитель математики, МБОУ «Корниловская СОШ», 165502, Архангельская обл., Верхнетоемский р-н, п. Двинской.
Цели:
1) Повторить способы построения многоугольников с уроков черчения и познакомить с новыми способами.
2) Воспитывать у учащихся аккуратность, чувство взаимопомощи.
3) Способствовать развитию познавательного интереса к учебным предметам геометрии и черчению.
4) Развивать мышление учащихся при решении задач, выходящих за рамки школьного курса.
5) Развивать умение анализировать, сравнивать, делать выводы.
6) Развивать память учащихся.
Оборудование:
для учителя — образцы практического применения; таблица погрешностей.
для учащихся — формат А4; чертежные инструменты.
Организационный момент.
Сегодня на уроке рассмотрим построение правильных многоугольников. Эта задача замечательна тем, что возникла в глубокой древности из практических потребностей людей в архитектуре и строительной технике.
Основная часть урока.
Учитель геометрии:
-Что надо знать для того, чтобы построить правильный многоугольник?
Ученик: Сторону и угол.
-Какую из величин можно задать произвольно?
Ученик: Сторону.
-Что можно сказать о величине угла?
Ученик: Его можно вычислить, применив теорему о сумме углов выпуклого многоугольника.
-Найдём величину угла для правильного пятиугольника.
Ученик:
S=180(n-2) n=5
S=180(5-2)=540
Т.к. углы равны, то 540/5=108
-Какой инструмент необходим для построения?
Ученик: Транспортир.
(Учащиеся строят правильный пятиугольник на доске и в тетрадях.) Рисунок 1.
-Рассмотрим построение правильного пятиугольника через центральный угол a=360/n n=5 a=360/5=72 (Учащиеся строят правильный пятиугольник на доске и в тетрадях.) Рисунок 2.
В ходе беседы учащиеся приходят к выводу, что транспортир-это инструмент небольших размеров, поэтому не обеспечивает достаточной точности и удобств в работе.
-С чем связан последний способ?
Ученик: С окружностью.
Решая эту задачу, учёные пришли к выводу, что правильные многоугольники можно построить с помощью циркуля и линейки. Хотя решения будут приближёнными (что вы и заметите), но с достаточно большой точностью. Значит, построение правильных многоугольников будет связано с окружностью.
-Следовательно какой многоугольник легче всего построить?
Ученик: Квадрат.
(У доски ученик объясняет построение квадрата. Рисунок 3.)
Ученик: Строим окружность произвольного радиуса. Проводим два перпендикулярных диаметра, затем последовательно соединяем их концы.
-Какая связь окружности и построенного правильного четырёхугольника?
Ученик: Квадрат вписан в окружность. Окружность разделили на четыре равные части.
Вывод: построить правильный многоугольник, значит разделить окружность на n равных частей.
Ученики предлагают построение правильного шестиугольника. Так как а6=R, то разделим окружность на шесть равных частей. Рисунок 4.
Рисунок 4.
В Вавилоне считали, что окружность ровно в шесть раз длиннее радиуса L=6R.Точнее L=6 2/7R.
— Нельзя ли, используя этот рисунок, построить ещё какой-нибудь правильный n – угольник?
Ученик: Треугольник соединяя через вершину.
Используя этот рисунок, ученики строят правильный треугольник. Рисунок 5.
— Существует ещё один способ построения треугольника известный вам с уроков черчения.
Учитель черчения:
Если ученики не смогли вспомнить способ построения правильного треугольника BDC, учитель напоминает им. Рисунок 6.
Для построения треугольника проводят дугу ВС из точки А. Соединяем точки В и С хордой. А точки В и C с точкой Д.
Попутно решилась другая задача – деление окружности на 7 равных частей. Соединяя точки В и С хордой и беря ее половину GC, получают длину стороны правильного семиугольника.
Если радиусом GH сделать засечку на вертикальном диаметре в точке К, то хорда КН даст величину стороны правильного пятиугольника, а катет ОК определит длину стороны правильного десятиугольника. (Рисунок 7).
(Рисунок 7).
Учитель геометрии: Нельзя ли использовать построение многоугольника правильных n – угольников с большим числом сторон? (Если ученики не смогут ответить, то познакомить их с примером в учебнике геометрии на стр. 207. рисунок 286).
Ученики самостоятельно выполняют построение 12- угольника.(Рисунок 8)
Вывод: если в окружность вписать правильный n — угольник, то легко построить правильный вписанный 2n – угольник.
Учитель геометрии: Способы построения различны, хотя есть общее в построении 3- угольника, 5- угольника, 7- угольника. Практику нужен способ достаточно простой и общий для деления окружности на любое число равных дуг.
Рассмотрим общий способ построения на примере построения 9- угольника.
Возьмем R = 45 мм., треугольник АВС — равносторонний, разделим диаметр АВ точкой Д в отношении АД:АВ = 2:9 ( в общем случае АД:АВ=2:n).
Проведем СД, получим точку Е. Дуга АЕ=1:9L окружности. Отрезок АЕ- сторона правильного 9- угольника. Разделим окружность на 9 равных частей. Рисунок 9.
Рисунок 9.
Посмотрим какова точность построения
n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 20 | 60 |
360°/n | 120° | 90° | 72° | 60° | 51°26’ | 45° | 40° | 36° | 18° | 6° |
Угол АОE | 120° | 90° | 71°57’ | 60° | 51°31’ | 45°11’ | 39°41’ | 36°21’ | 18°38’ | 6°26’ |
Погрешносность,% | 0 | 0 | 0,07 | 0 | 0,17 | 0,41 | 0,8 | 0,97 | 3,5 | 7,2 |
Как видно из таблицы, указанным способом можно разделить окружность на 5, 7, 8, 9 или10 частей с небольшой относительной погрешностью от 0,07 до 1%
(Напомнить ученикам, что такое относительная погрешность и как её рассчитать. )
)
О.П = = = 0,008 = 0,8%
Т.З-Пр.Зн.= 40°-39°41’=19’=19/60=0,32
Т.З=39°41’= 39 =39,68
Такая погрешность вполне допустима в большинстве практических работ. С увеличением числа сторон точность способа заметно падает, т.е. относительная погрешность растет, но как показали исследования, при любом n она не превышает 10%.
И всё же существует единый способ построения правильного n-угольника, в основу которого положена известная вам теорема геометрии. После знакомства с этим способом вам необходимо назвать эту теорему.
Учитель черчения: Для построения многоугольника из 11 равных сторон проведем из точки А под острым углом к отрезку (диаметру) АВ, прямую линию. На ней циркулем-измерителем откладываем нужное число равных отрезков произвольной величины, в данном случае 11. Последнюю точку соединяем с точкой В. Из нечетных точек деления с помощью линейки и угольника проводим прямые, параллельные прямой 11В. Если провести через все точки, то поделим отрезок АВ на 11 равных частей.
Сейчас проведем дугу СД радиусом ВА до пересечения с горизонтальной осью. Из точек С и Д будем проводить через точки 1’, 3’,5’ и т.д. лучи до пересечения с окружностью. Соединяем полученные точки на окружности между собой, и таким образом, мы вписали в окружность правильный многоугольник. Рисунок 10.
Учитель геометрии: Какая теорема используется?
Ученик: Теорема Фалеса.
Учитель геометрии: Ещё в XV веке великий художник Леонардо да Винчи (14521519), занимался такими построениями. В 1888 году в журнале “Вестник опытной физики и элементарной математики” появилась статья Ф. Коваржика, где он предложил общий способ построения правильных многоугольников по данной стороне. (Рисунок 11)
Пусть АВ — сторона правильного n-угольника, который требуется построить. На АВ строим равносторонний треугольник АВС, из точки С опускаем перпендикуляр СД на АВ и продолжаем его. Затем делим АВ 6 равных частей и такие части откладываем на СД по обе стороны от С. Точки деления являются центрами окружностей, описанных около искомых многоугольников. Перенумеровав эти точки, как показано на рисунке, получим, что А7-радиус, описанной около семиугольника, сторона которого равна АВ. Для шестиугольника и двенадцатиугольника такое построение дает точный результат. Для других значений n предложенное построение обладает достаточно высокой точностью.
Перенумеровав эти точки, как показано на рисунке, получим, что А7-радиус, описанной около семиугольника, сторона которого равна АВ. Для шестиугольника и двенадцатиугольника такое построение дает точный результат. Для других значений n предложенное построение обладает достаточно высокой точностью.
Ученики строят правильный 7-угольник, используя данный способ. (Рисунок 12).
Приближенные способы построения правильных многоугольников просты и удобны в практике, красивы и орнаментальны. Они применяются в архитектуре, живописи, народном творчестве, декоре, промышленности, быту; необходимые конструктору, строителю, радиолюбителю, художнику. Демонстрируем архитектурные сооружения, разделочные доски, репродукции с изображением доспехов русских воинов.
Задание по вариантам: Построить правильный 10-угольник и 12-угольник.
Итог урока.
ЛИТЕРАТУРА
А. Д. Ботвинников. Черчение 7-8 кл. Москва. Астрель. АСТ 2002.
А. В. Погорелов. Геометрия 7-11 кл. Общеобразовательных учреждений 6-е изд. Москва. Просвещение 1996.
Москва. Просвещение 1996.
Я. И. Перельман. Занимательная геометрия, — Москва АО “Столетие” 1994.
С. В. Розов. Курс черчения. Москва “Машиностроение”, 1974.
ПРИЛОЖЕНИЕ
| |||||||
| |||||||
| |||||||
Трейси, у нас есть для тебя три ответа… Привет Трейси. Площадь фигуры всегда равна сумме площадей всех ее частей. Это означает, что мы можем разрезать пятиугольник на более мелкие фигуры, площадь которых легко найти и сложить (или умножить). Если мы нарисуем радиусы всех углов зеленым цветом, пятиугольник синим цветом и круг красным цветом, мы получим диаграмму слева. Я также провел линию от центра круга до середины каждой стороны пятиугольника. Поскольку это середина, она встречается со стороной под прямым углом, поэтому образует конгруэнтные треугольники. Я думаю, вы можете видеть, что по симметрии здесь десять конгруэнтных прямоугольных треугольников. Теперь вы можете использовать теорему Пифагора, чтобы найти высоту прямоугольного треугольника. Надеюсь, это поможет,
Привет Трейси, Площадь правильного пятиугольника будет равна сумме площадей пяти одинаковых равнобедренных треугольников, которые вы можете составить, проведя радиусы к вершинам пятиугольника. Теперь вы видите, что знаете длины всех трех сторон каждого отдельного треугольника. Формулу Герона можно использовать для определения площади треугольника, если известны все три стороны:
Вы также можете определить размер центрального угла (C), который также является углом при вершине каждого образованного треугольника. а затем используйте Area=(1/2)ab*sinC. Только помните, что после того, как вы найдете площадь одного треугольника, вы должны умножить на 5, чтобы получить площадь всего пятиугольника. Это всего лишь несколько способов решения этой проблемы. Надеюсь, это поможет, Лиэнн
Трейси, Площадь равна 1/2 основания, умноженному на высоту треугольника, состоящего из одной из сторон пятиугольника и радиусов двух концов этой стороны. Вы умножаете эту площадь на 5 для площади пятиугольника. Я предполагаю, что вы можете использовать 6 как длину стороны, но сторона действительно имеет длину 10*sin (36 градусов), что равно примерно 5,8779. Высота (расстояние от центра пятиугольника до стороны) равна 5*cos (36 градусов) (что примерно равно 4,0451). (Если вы используете теорему Пифагора с треугольником, стороны которого равны 5, 5 и 6, тогда высота основания равна 4 вместо более точного 4,0451. На самом деле треугольник состоит из половины стороны, высоты и радиуса. представляет собой прямоугольный треугольник 3-4-5.) Крис | |||||||
Видео-вопрос: Вычисление длины стороны правильного описанного пятиугольника по радиусу окружности
Стенограмма видео
Правильный пятиугольник описан вокруг окружности радиусом два сантиметра. Найдите длину одной стороны пятиугольника. Дайте свой ответ правильно до одного десятичного знака.
Найдите длину одной стороны пятиугольника. Дайте свой ответ правильно до одного десятичного знака.
Здесь у нас есть круг. Во-первых, мы можем добавить центр к этой окружности. И тогда у нас есть пять мест, где пятиугольник касается этой окружности. Мы знаем, что расстояние от центра до любой точки внешней окружности есть радиус. А мы знаем, что радиус равен двум сантиметрам. Мы замечаем, что вершина пятиугольника представляет собой пересечение двух касательных линий, что говорит нам о том, что каждая из этих касательных линий имеет одинаковую длину. Мы также должны помнить, что когда касательная пересекает радиус, пересечение равно 90 градусов.
На данный момент может показаться, что нам больше нечего добавить. Но мы знаем, что это правильный пятиугольник. А это значит, что мы можем либо запомнить каждый из этих углов, либо уметь их вычислять. Если вы не помните, каковы внутренние углы правильного многоугольника, вы можете вычислить внутренние углы любого многоугольника по формуле 𝑠 равно 𝑛 минус два умноженных на 180 градусов.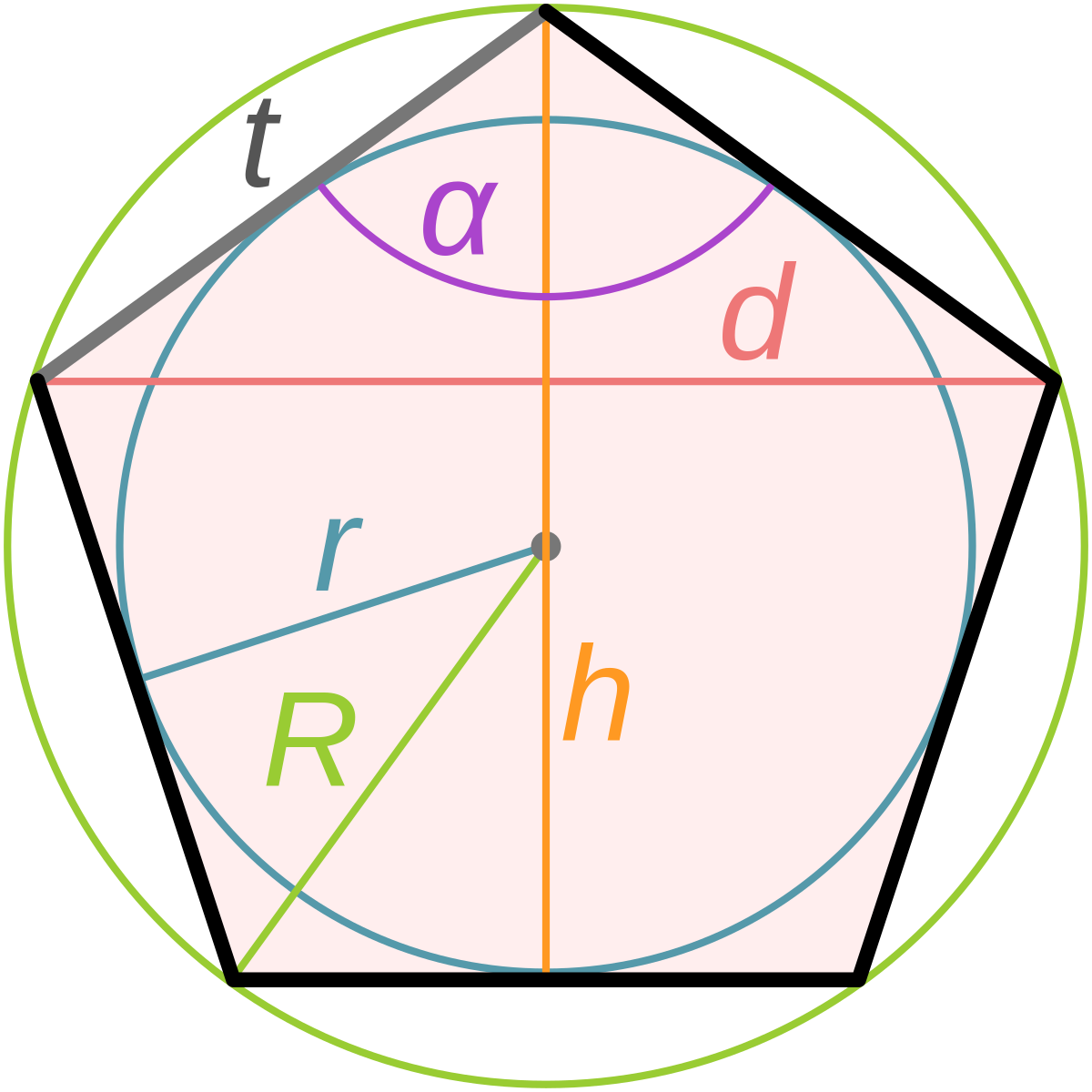
Пятиугольник имеет пять сторон. Итак, нам нужно пять минус два раза по 180 градусов. Пять минус два равно три. Три раза по 180 будет 540. Но помните, это сумма всех пяти этих углов. Но так как это правильный пятиугольник, все пять углов равны. А это значит, что если мы разделим 540 на пять, то сможем найти меру каждого из этих углов. 540 разделить на пять равно 108. В правильном пятиугольнике все углы равны 108 градусам. Но это все еще не совсем помогает нам.
Что же произойдет, если мы нарисуем линию между одной из вершин и центром круга? Эта линия делит эти углы пополам. Вместо 108 каждый из них будет по 54 градуса. На этом этапе, вероятно, будет полезно, если мы приблизимся к тому, о чем мы говорим.
У нас есть радиус в два сантиметра, одна часть пятиугольника и линия, которую мы только что провели от вершины пятиугольника к центру круга. Мы знаем, что радиус и касательная сходятся под прямым углом и этот угол равен 54 градусам. В любом треугольнике все углы должны быть в сумме равны 180 градусам. значит 90 градусов плюс 54 градуса плюс некоторый угол должны равняться 180 градусам. Если сложить 90 и 54, получится 144. А если из 180 вычесть 144, то получится, что недостающий угол равен 36 градусам.
В любом треугольнике все углы должны быть в сумме равны 180 градусам. значит 90 градусов плюс 54 градуса плюс некоторый угол должны равняться 180 градусам. Если сложить 90 и 54, получится 144. А если из 180 вычесть 144, то получится, что недостающий угол равен 36 градусам.
Помните, наша цель — найти длину одной стороны этого правильного многоугольника. Поскольку это правильный многоугольник, мы знаем, что все стороны имеют одинаковую длину. А это значит, что если мы найдем длину одной стороны, мы найдем длины всех сторон. Если мы добавим еще один радиус, мы увидим, что у нас снова есть две касательные, которые будут одинаковой длины. А это значит, что если мы сможем найти это расстояние, нам нужно умножить его на два, чтобы найти длину одной стороны пятиугольника. А это значит, что нам нужно рассмотреть этот прямоугольный треугольник. И нам нужно найти эту недостающую длину стороны.
Поскольку сейчас мы имеем дело с прямоугольными треугольниками, мы можем использовать нашу тригонометрию прямоугольного треугольника. Если мы подумаем о трех тригонометрических соотношениях, у нас есть синус, косинус и тангенс. Синус противоположен гипотенузе. Косинус — это прилежащий к гипотенузе. А тангенс равен противоположному соседнему. Длина желтой стороны — это гипотенуза, и мы не знаем, какова ее длина. Мы знаем радиус, розовую сторону и хотим узнать длину другой стороны. Нас не интересует гипотенуза. И это означает, что наш лучший вариант — использовать отношение касательной.
Если мы подумаем о трех тригонометрических соотношениях, у нас есть синус, косинус и тангенс. Синус противоположен гипотенузе. Косинус — это прилежащий к гипотенузе. А тангенс равен противоположному соседнему. Длина желтой стороны — это гипотенуза, и мы не знаем, какова ее длина. Мы знаем радиус, розовую сторону и хотим узнать длину другой стороны. Нас не интересует гипотенуза. И это означает, что наш лучший вариант — использовать отношение касательной.
Если мы начнем с угла 54 градуса, то можно сказать, что тангенс 54 градусов равен длине противоположной стороны, равной двум сантиметрам. А длина соседней стороны — это недостающая сторона, 𝑠. Но это не единственный наш вариант. Мы также можем взять тангенс 36 градусов, где противоположная сторона равна длине стороны 𝑠, а длина соседней стороны равна радиусу в два сантиметра. Любой из них будет работать. Но я выберу тангенс 36 градусов, так как математика будет немного проще, потому что длина стороны находится в числителе дроби, а не в знаменателе.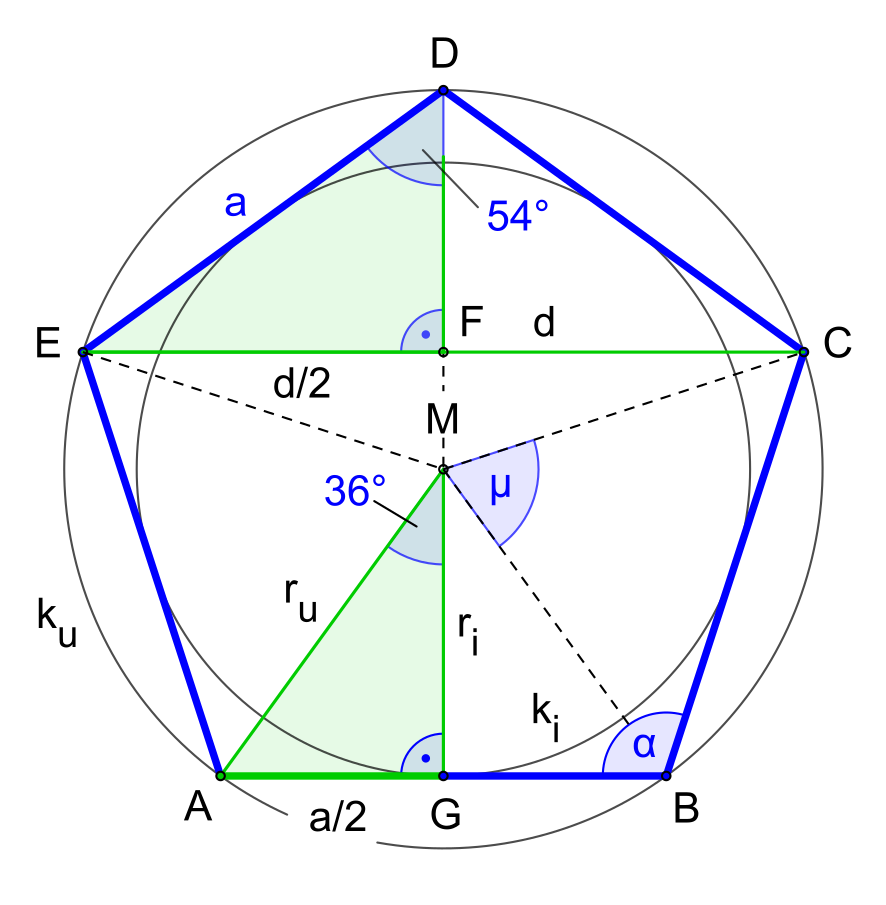


 Радиус круга равен 5 см, а каждая сторона AB = BC = CD = DE = EA = 6 см.
Радиус круга равен 5 см, а каждая сторона AB = BC = CD = DE = EA = 6 см. Затем используйте это, чтобы найти площадь прямоугольного треугольника. Наконец, умножьте на количество конгруэнтных треугольников в пятиугольнике.
Затем используйте это, чтобы найти площадь прямоугольного треугольника. Наконец, умножьте на количество конгруэнтных треугольников в пятиугольнике.