Как вписать в окружность пятиугольник с помощью циркуля: Как вписать в окружность пятиугольник 🚩 длина стороны пятиугольника вписанного в окружность 🚩 Математика — Интернет магазин мебели "МебПилот.ру"

Разное

Содержание

Метод построения двух геометрических фигур на одной модели

Авторы: Алимов Бахтияр Милибаевич, Пулатова Халима Ашраповна

Рубрика: Технические науки

Опубликовано в Молодой учёный №9 (68) июнь-2 2014 г.

Дата публикации: 20.06.2014 2014-06-20

Статья просмотрена: 556 раз

Скачать электронную версию

Скачать Часть 1 (pdf)

Библиографическое описание:

Алимов, Б.

М. Метод построения двух геометрических фигур на одной модели / Б. М. Алимов, Х. А. Пулатова. — Текст : непосредственный // Молодой ученый. — 2014. — № 9 (68). — С. 98-101. — URL: https://moluch.ru/archive/68/11417/ (дата обращения: 17.07.2023).

На кафедре «Начертательной геометрии и инженерной графики» Ташкентского института ирригации и мелиорации студентам первого курса бакалавриатуры проводится занятие по разделу «Проекции геометрических тел», где выдаются различные геометрические фигуры. На занятиях объясняется и показывается задание для выполнения графических работ по вычерчиванию геометрических фигур: призмы, пирамиды и т. д. по техническим деталям контурных их состоят из линий разного вида линий: прямых, дуг, окружностей и т. д. Поэтому для выполнения чертежей требуется знание геометрических построений — деление отрезка прямой, деление окружностей и т. п. На занятиях приводится пример деления окружностей на равные части и каждому студенту для самостоятельной графической работы выдается вариант задания с указанием числовых величин диаметра окружности и числа сторон многоугольника.

Выдаются задания: начертить на горизонтальной плоскости окружность диаметром и разделить их на три (четыре, …)

— построить на них треугольник (четырехугольник, пятиугольник, …) описанный и вписанный в данную окружность;

— выделить в горизонтальной плоскости вписанный в окружности треугольник, как пирамиду, а описанный в окружности треугольник как призму;

— спроектировать на недостающих проекциях фронтальной и профильной плоскостях пирамиду и призму с высотой .

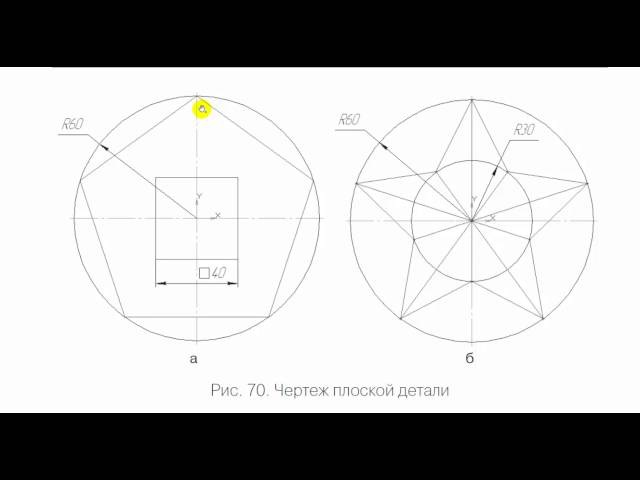
По литературным источникам [1, 2] известны методы деления окружности на равные части и построения их, как вписанных в окружность многоугольников. Разделение окружности на равные части можно несколькими способами: при помощи графических (рисунок 1, а, б) построений, с помощью таблицы хорд (таблица 1), с помощью циркуля (рисунок 2, а, б и в), с помощью транспортера и угольных линеек.

Таблица 1

Численные значения длины отрезка хорд

0,866

0,707

0,587

0,5

0,434

0,383

0,342

0,309

0,259

0,223

0,208

0,195

Примечание: n — число делений окружности;

K — коэффициент уменьшения диаметра.

а) б)

Рис. 1. Графический способ построения многоугольника.

Нами приводится методика построения описанной в окружности многоугольника, например, треугольника. Чертим осевые — горизонтальные и вертикальные линии и вычерчиваем окружность, например, диаметром (рисунок 2, а). При помощи циркуля, радиусом окружности, делим данную окружность на равные части и вершины треугольника фиксируем точками . Соединяя эти точки, получим вписанный треугольник . Для получения описанного по окружности , мы находим и определяем максимальное расстояние отрезка по сектору . Можно определить двумя способами: 1 — по вертикальной осевой линии от центра окружности на пересечения сторон отрезка и окружности фиксируем две точки: и ; 2 — радиусом , от точек и проводим засечки в двух местах и соединяя их делим отрезок пополам, место соединения этих линий будет и .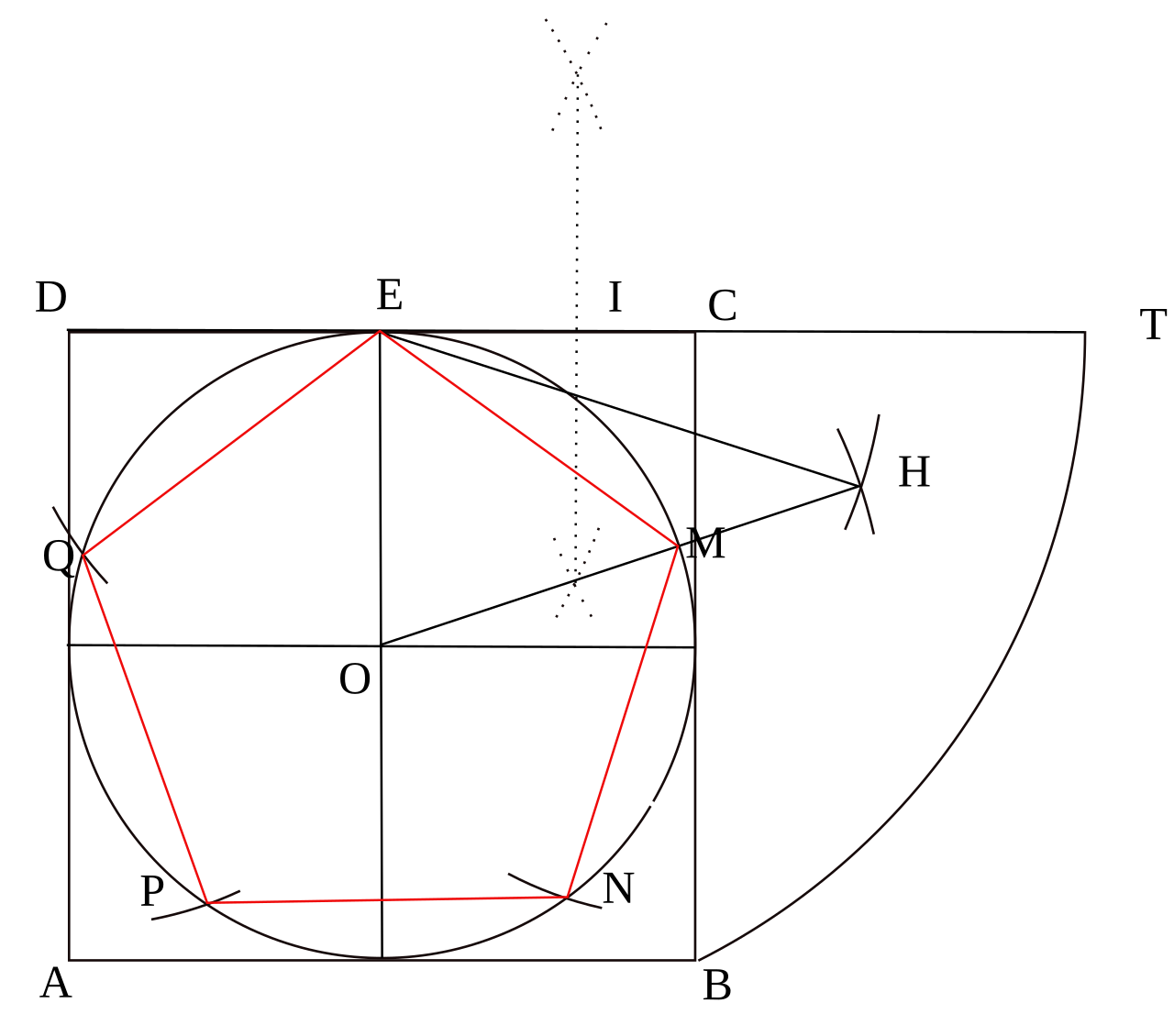

Расстояние отрезка двух точек является максимальное расстояние отрезка по сектору и фиксируем этот расстояние как радиус малой окружности, т. е. , в отличие от большой окружности.

По вершинам остроконечности треугольника вычерчиваем дуги малой окружности радиусом (рисунок 2, б). Например, по вершинам двух дуг (точка а и точка в) проводим касательную (сопряженную) линию, тогда данная линия получается как параллельная линия , т. е. отрезки . То же самое происходит и с другими линиями: от точек «» и «» проводим касательную линию, которая является параллельной линией — . Аналогично происходит и с вершинами хорд «» и «» — получаем . После полученных трех вспомогательных отрезков ; и , которые расположены вне окружности и эти вспомогательные линии доводим их до пересечения между ними (рисунок 2, в). Место пересечения их обозначим буквами

и после обведения контурными линиями — получим описанный по окружности треугольник .

а) б) в)

Рис. 2. Метод построения вписанной и описанной по окружности треугольника , где: а) — деление окружности на три части — ; б) — построение вписанной в окружности треугольника ; в) — построение описанной по окружности треугольника .

На рисунке 3 приводится построения на горизонтальной проекции описанный и вписанный в окружность треугольник. При помощи циркуля, радиусом окружности, делим данную окружность на равные части и вершины треугольника фиксируем точками . Соединяя эти точки, получим вписанный треугольник . Также по деленным точкам описанного в окружности получаем другой треугольник . В дальнейшем из горизонтальной проекции проводим во фронтальную проекцию ортогональные линии и фиксируем нижнюю часть основания призмы . Строим по выданным параметрам высоту призму и на этой полученной высоте призмы определяем ортогональную проекцию основания пирамиды . После этого, также по данной высоте строим пирамиду с вершиной . Полученная фигура состоит из двух геометрических тел — призмы и пирамиды .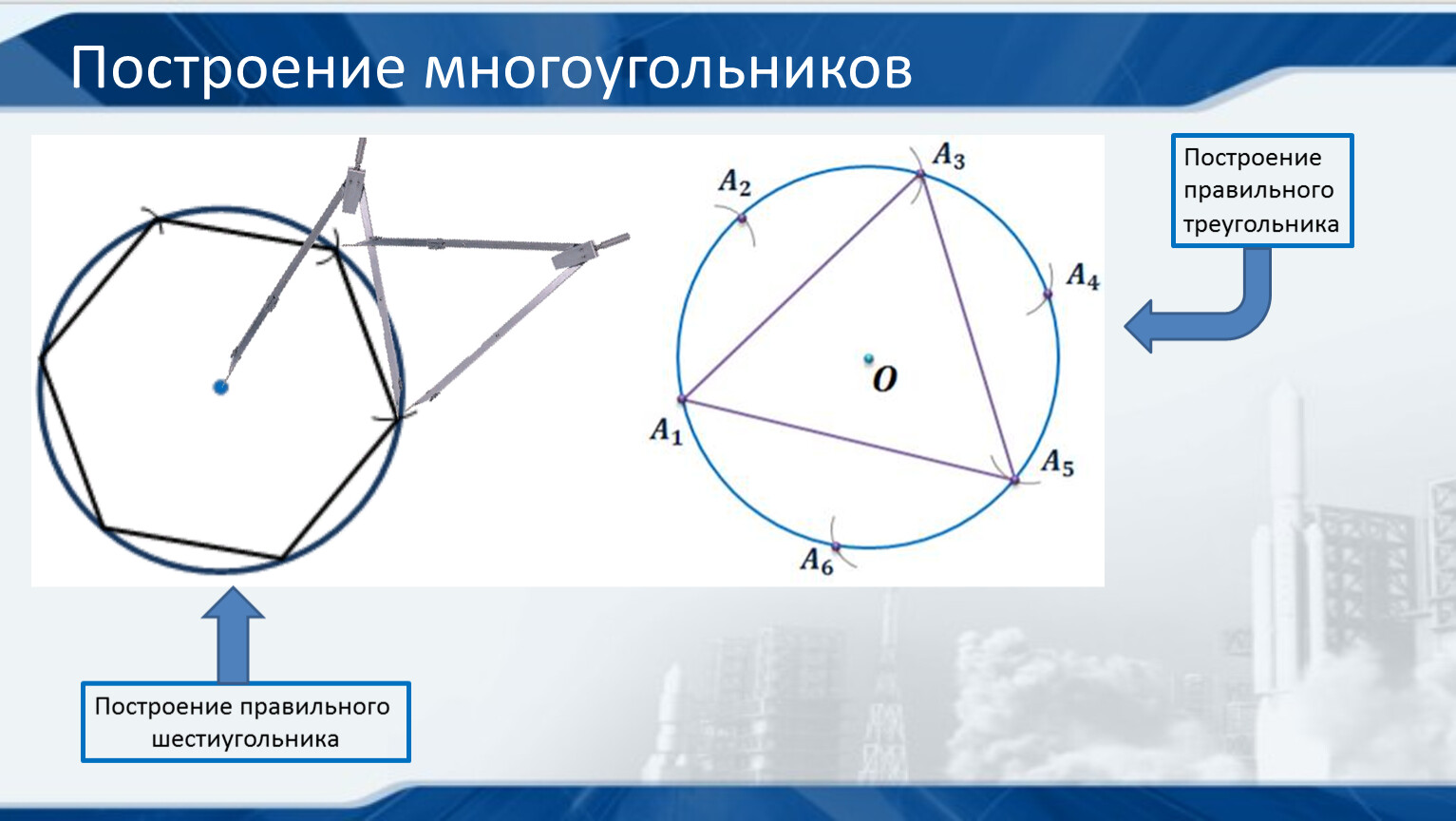

Рис. 3. Пример построения двух геометрических фигур на одной модели: призмы и пирамиды .

Далее по ортогональным проекциям строим данную фигуру в профильной проекции. Студент по своему выбору может спроектировать другой модель, т. е. вписанный треугольник выбрать как пирамиду , а описанный по окружности треугольник — призму (рисунок 4). Аналогичные построения этого примера будет как и в предыдущем построении данной модели.

Здесь в отличие от предыдущего примера, описанная по окружности треугольник является основанием усеченной, по горизонтали, пирамиды, а вписанный треугольник — призмой. Нижняя часть модели является усеченная трехгранная пирамида, а верхняя часть — трехгранная призма.

Рис. 4. Построение двух геометрических фигур на одной модели: усеченной пирамиды и призмы

Каждому студенту для самостоятельной графической работы выдается вариант задания с указанием численных величин диаметра окружности , число сторон многогранников и, варьируя двумя величинами и получим более тридцати вариантов.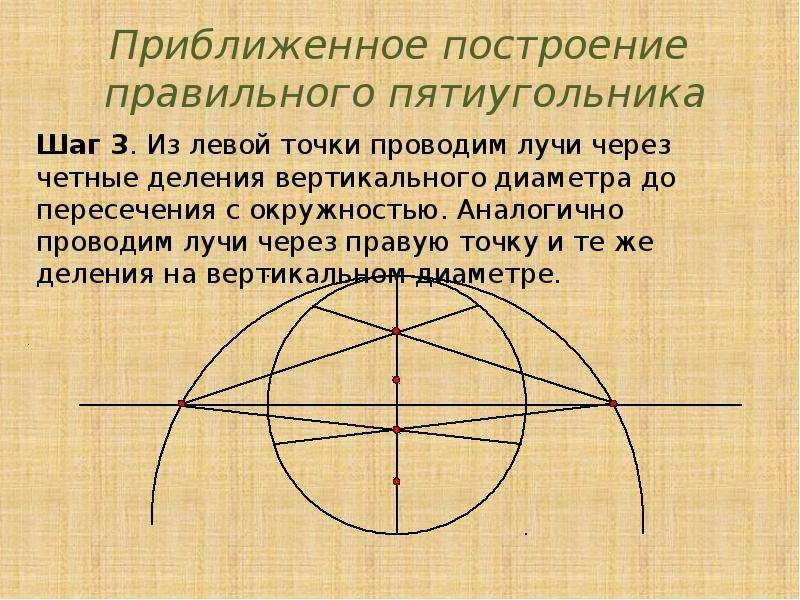 Также по такому же методу можно проделать и с четырехугольником, пятиугольником и т. д. — находим вписанный четырехугольник (пятиугольным) потом уже описанный по окружности четырехугольник.

Из выше приведенного можно сделать следующие выводы:

— при построении многоугольника надо разделить окружность на равные части (3) и построить в начале вписанный многоугольник, также следом за ним описанный по окружности многоугольник;

— при построении геометрической фигуры модели необходимо начать строить с горизонтальной проекции, затем фронтальную и профильную ;

— студент может самостоятельно спроектировать по своему выбору на одной модели две разные геометрические фигуры: призму и пирамиду;

— при построении на горизонтальной проекции из двух многоугольников необходимо сначала выбрать пирамиду, а затем уже призму.

Литература:

1. Брилинг Н. С., Евсеев Ю. П. Задания по черчению: — 2 изд, М.: Строй издат, 1984.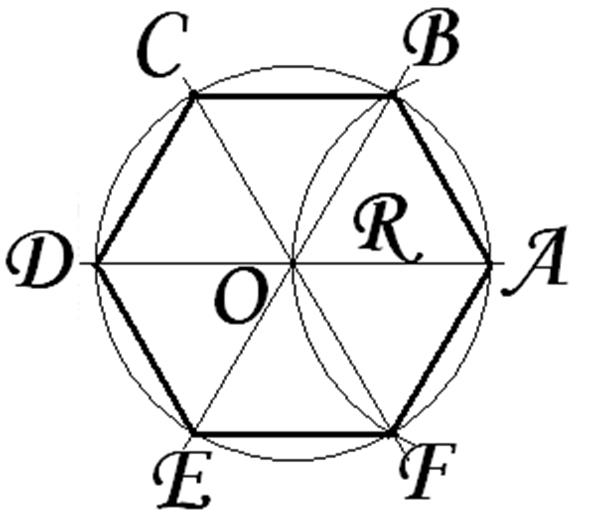 256 с.

2. Миронова Р. С., Миронов Б. Г. Сборник заданий по черчению. М.: Высш. шк., 1984.264с.

Основные термины (генерируются автоматически): окружность, вписанный треугольник, построение, призма, линия, окружность треугольника, пирамида, помощь циркуля, треугольник, горизонтальная проекция.

Построение правильных многоугольников

На этом уроке мы рассмотрим способы построения некоторых правильных многоугольников с помощью циркуля и линейки. А также изобразим правильный многоугольник графически.

Для начала давайте вспомним определение правильного многоугольника. Итак, правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.

Для выполнения построений мы используем циркуль и линейку.

Циркуль позволяет:

– построить окружность,

– построить дугу окружности,

– отложить на прямой отрезок, равный данному.

Линейка позволяет:

– построить прямую линию,

– построить отрезок, соединяющий две точки,

– найти точку пересечения двух прямых.

Ранее мы с вами уже рассматривали построения правильного треугольника и четырехугольника, т.е. квадрата.

Давайте рассмотрим, каким образом можно с помощью циркуля и линейки построить правильный треугольник и правильный четырехугольник, вписанные в окружность.

Задача 1. Вписать в заданную окружность правильный треугольник

Решение.

Первый способ.

Построение. Пусть задана окружность с центром О. Проведем произвольный диаметр BD окружности. Построим прямую l, являющуюся серединным перпендикуляром к радиусу OD. Середину радиуса ОD обозначим точкой К. Отметим точки А и C – пересечения прямой l с окружностью. И построим отрезки BA и BC. Треугольник ABC – правильный.

Доказательство.

В катет .

Тогда , .

Отсюда, .

Значит, – равносторонний – правильный.

Второй способ построения.

Пусть задана окружность с центром О. Раствором циркуля, равным радиусу, последовательно от одной точки окружности делаем на ней засечки, пока последняя засечка не совпадет с взятой первоначально точкой. Соединив полученные точки через одну, получим правильный треугольник.

Задача 2. Вписать в заданную окружность правильный четырехугольник.

Решение.

Построение. Пусть задана окружность с центром О. Построим диаметр AC. Затем построим диаметр BD перпендикулярный диаметру AC. Точки А, C и B, D – точки пересечения диаметров с окружностью. И построим отрезки АB, BC, CD и АD.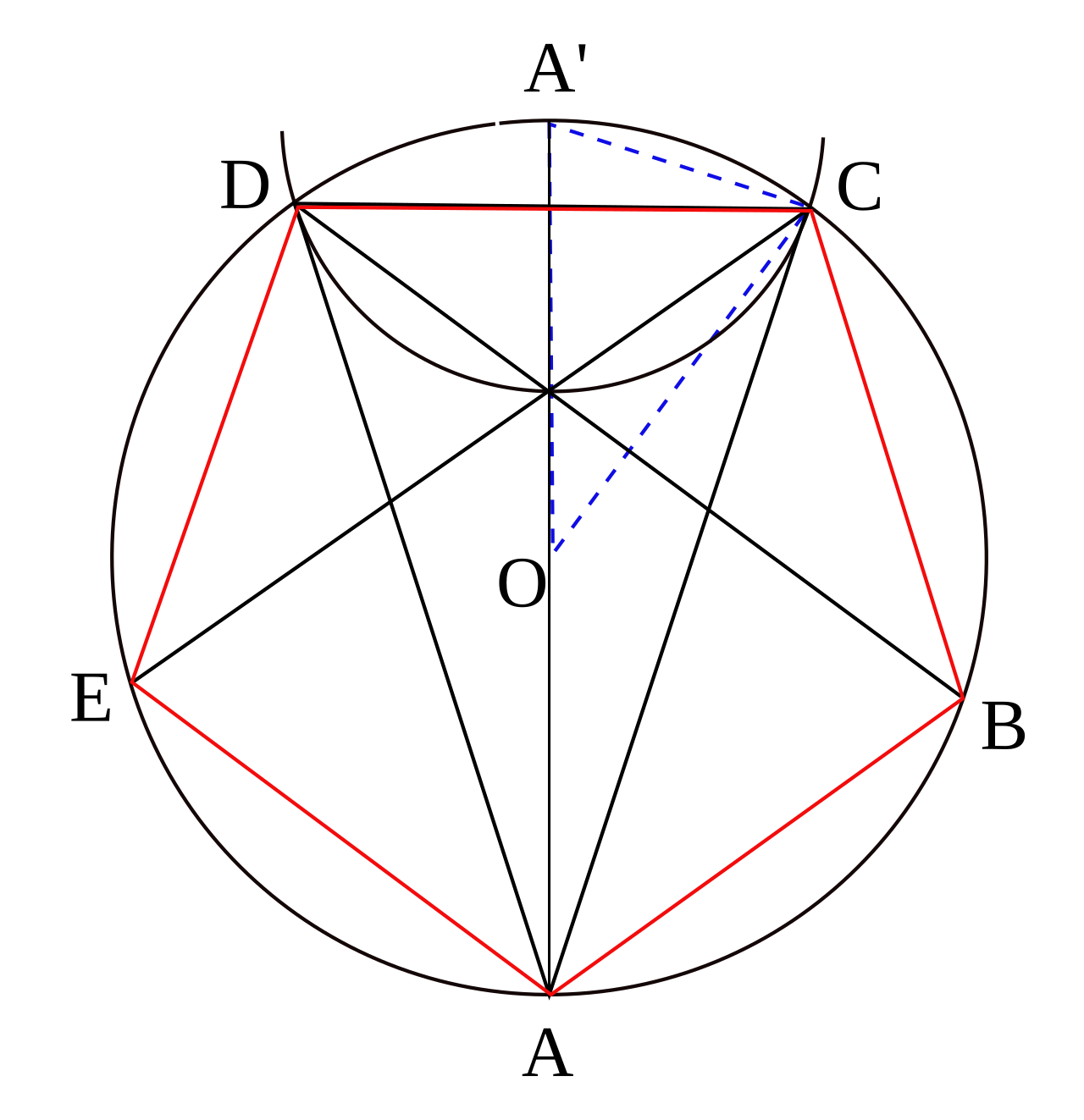 Четырехугольник ABCD – правильный.

Доказательство.

Т.к. , , то – параллелограмм.

Т.к. ,то – прямоугольник.

Т.к. ,то – ромб.

Т.к. ,то – квадрат.

Следовательно, – квадрат.

Значит, – правильный четырехугольник.

Теперь давайте рассмотрим построения правильных n-угольников при n>4. Обычно для построения таких n-угольников используется окружность, описанная около многоугольника.

Задача 3. Построить правильный шестиугольник, сторона которого равна данному отрезку.

Решение.

Построение. Так как в правильном шестиугольнике сторона а равна радиусу, то достаточно последовательно отложить от одной точки окружности 6 радиусов-хорд. Пусть МN – заданный отрезок. Построим окружность с произвольным центром О и радиуса MN. Отметим на этой окружности произвольную точку А. Затем, не меняя раствора циркуля, последовательно от этой точки А будем делать на окружности засечки, пока последняя засечка не совпадет с взятой первоначально точкой А.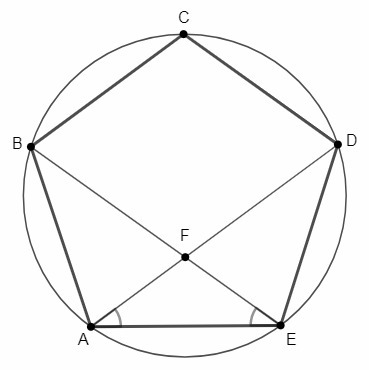 Отметим точки B, C, D, Е и F. Теперь соединим последовательно построенные точки отрезками. Получим искомый правильный шестиугольник ABCD.

Доказательство.

Равные хорды стягивают равные дуги.

Все углы шестиугольника будут равны, так как опираются на дуги, состоящие из четырех равных меньших дуг.

Для построения правильных многоугольников часто используется следующая задача: дан правильный n-угольник. Построить правильный 2n-угольник.

Задача 4. Дан правильный шестиугольник. Построить правильный двенадцатиугольник.

Решение.

Построение.

Пусть ABCDEF – данный правильный шестиугольник. Опишем около него окружность.

1. – точка пересечения биссектрис и .

2. Окружность .

3. – серединные

перпендикуляры к .

5. – правильный двенадцатиугольник.

Применяя указанный способ, можно с помощью циркуля и линейки построить целый ряд правильных многоугольников, если построен один из них. Например, построив правильный четырехугольник, т.е. квадрат, и пользуясь задачей 4, можно построить правильный восьмиугольник, затем правильный шестнадцати-угольник и вообще правильный 2^k угольник, где k – любое целое число, большее 2.

Замечание. Рассмотренные примеры показывают, что многие правильные многоугольники могут быть построены с помощью циркуля и линейки. Но важно заметить, что не все правильные многоугольники могут быть построены таким образом.

С давних времен построению правильных многоугольников математики уделяли большое внимание. Древние греки умели строить правильные треугольники, четырехугольники, пятиугольники. А также многоугольники, получаемые удвоением их сторон, шестиугольники, восьмиугольники, десятиугольники и т.д. Далее дело зашло в тупик. И только 2000 лет спустя великий немецкий математик 17 века Карл Гаусс, которого называли «королем математики», решил эту математическую проблему.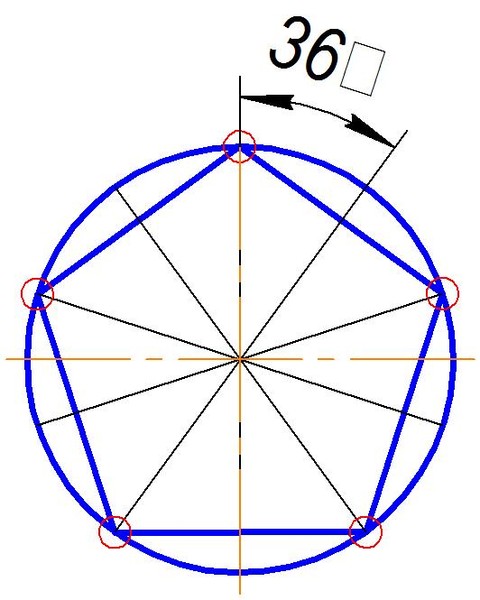 Будучи девятнадцати летним юношей, он доказал, что можно построить правильный семнадцати-угольник, а вот семиугольник, девятиугольник, одиннадцатиугольник, тринадцати-угольник циркулем и линейкой построить нельзя. Задача о построении правильного семнадцати-угольника была самым первым его научным открытием.

Подведем итоги урока.

Сегодня мы рассмотрели способы построения некоторых правильных многоугольников с помощью циркуля и линейки. Научились строить правильные треугольник и четырехугольник, вписанные в окружность. А также выполнили задачу на построение правильного многоугольника по заданному отрезку, и задачу на построение правильного 2n-угольника по заданному n-угольнику.

многоугольников, вписанных в окружность

Некоторые базовые конструкции, такие как и , были созданы с использованием нескольких инструментов и методов. Используя эти конструкции в качестве основы, этот урок расширится до более сложных конструкций, таких как построение равностороннего треугольника и правильного пятиугольника с использованием a и a .

Вот несколько рекомендуемых материалов, прежде чем приступить к этому уроку.

Джордан — начальник службы безопасности известного отеля-казино The Compazu в Лас-Вегасе. Она решила построить безопасную комнату после того, как произошло ограбление. Что касается его дизайна, безопасная комната будет , и за ней будут следить три камеры безопасности. Одна из камер будет напротив входной двери.

Джордан хочет разместить две другие камеры на одинаковом расстоянии друг от друга. Учитывая план безопасной комнаты, а и а, как она может определить положение двух других камер?

Ан можно построить несколькими способами. Один из способов заключается в использовании двух пересекающихся .

Ан с тремя сторонами.

Его можно построить с помощью a и a .

Начните с рисования точки с центром в A. Затем укажите произвольную точку B на .

Поместите циркуль в точку B и нарисуйте еще одну окружность, проходящую через точку A. Затем определите одну из окружностей как точку C.

Соедините точки с помощью линейки.

Построен равносторонний треугольник △ABC.

Обратите внимание, что точка A и точка B являются центрами ⊙A и ⊙B соответственно. Поскольку ⊙A проходит через точку B, а ⊙B проходит через точку A, окружности равны. Следовательно, АВ, ВС и АС равны. Следовательно, △ABC — равносторонний треугольник.

К сожалению, Джордану такая конструкция неудобна для размещения камер. Джордану нужно найти другой альтернативный путь. Некоторые другие методы будут найдены на протяжении всего курса.

Учитывая a и a , используйте апплет для размещения круга так, чтобы квадрат находился внутри круга. Затем нарисуйте квадрат.

Какой вывод можно сделать о связи между расположением центра круга и диагоналями квадрата?

Принимая во внимание предыдущее исследование, когда задано , построение а может быть выполнено с использованием а и .

A, который находится в a, может быть построен в несколько шагов.

Имея круг, можно выполнить эти три шага, чтобы построить квадрат, вписанный в круг.

Начните с рисования произвольного числа ⊙O с помощью файла . Определите конечные точки как A и C.

Далее к AC в точке O. Это будет другой диаметр ⊙O. Определите его конечные точки как B и D.

Наконец, соединив концы диаметров, можно нарисовать вписанный квадрат.

Обратите внимание, что квадраты являются и друг друга. Так как AC и BD равны и являются перпендикулярными биссектрисами друг к другу, ABCD является квадратом.

A может быть с использованием a и .

Для построения правильного пятиугольника можно выполнить следующие шаги.

Имея круг, начните с произвольного рисования . Затем обозначьте конечные точки диаметра как C и M.

до CM в точке O. После этого определите круг и как S.

SO и обозначьте точку пересечения как L.

Затем нарисуйте окружность с центром в точке L и длиной SL. Затем проведите прямую, проходящую через точку M и точку L, пересекающую ⊙L.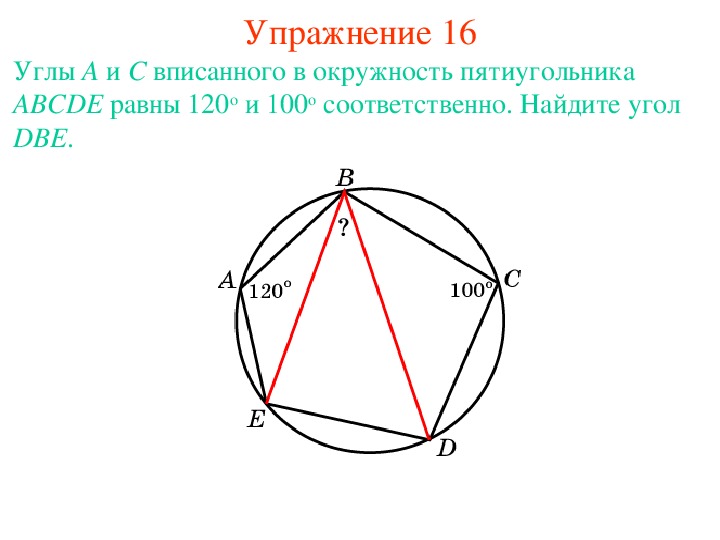 Отсюда определите точки пересечения ⊙L и сегмента как N и P.

Теперь будут нарисованы две дуги с центром в точке М. Обе дуги пересекутся с ⊙O. Одна из них пройдет через точку P, а другая — через точку N. Обозначим точки пересечения дуг и ⊙O как A, E, B и D.

Наконец, соедините точки A, B, C, D и E.

Ни одна из предыдущих построек не поможет Джордану. Наконец, используя a и a , будет построено a в надежде, что это поможет Джордану. В противном случае она может потерять работу.

Эти три шага можно выполнить, чтобы построить правильный шестиугольник в окружности.

Учитывая ⊙O, поместите компас на произвольную сторону окружности. Затем нарисуйте окружность, проходящую через центр ⊙O, и обозначьте одну из них как B.

Затем поместите циркуль в точку B и нарисуйте еще одну окружность, проходящую через центр ⊙O. Повторяйте процесс, пока ⊙O не будет перехвачен шесть раз, и обозначьте точки пересечения как C, D, E и F.

Наконец, соедините точки с помощью линейки.

Таким образом, правильный шестиугольник ABCDEF был построен.

Обратите внимание, что правильный шестиугольник состоит из шести .

Повторяя процесс несколько раз, он был найден. Следовательно, в результате получится правильный шестиугольник.

Среди всех конструкций, описанных в этом уроке, есть одна, которая поможет Джордану правильно разместить камеры — замедлит любую попытку ограбления! Напомним, что Джордан хочет определить положение трех камер, учитывая, что одна из камер будет находиться напротив входной двери.

Она пришла с , а и планом комнаты. Покажите, как она может определить положение двух других камер.

См. решение.

Следуйте процессу .

Следуя процедуре , сначала определите шесть точек на . Отправной точкой будет положение первой камеры безопасности.

По построению каждая точка окружности равноудалена друг от друга. Следовательно, можно сделать вывод, что расстояния между всеми остальными точками также равны.

Таким образом, Джордан может определить положение камер, выбрав любую вторую точку, начиная с положения первой точки — Камера 1.

С помощью этой камеры Джордан может установить три камеры наблюдения, расположенные на равном расстоянии друг от друга, и обеспечить адекватный контроль за убежищем в «Компазу».

Как нарисовать пятиугольник с равными сторонами

Содержание

Время чтения: 8 минут

Привет! В этом уроке я покажу вам, как нарисовать пятиугольник с равными сторонами. Это относительно простая форма для рисования, но есть несколько вещей, о которых следует помнить. Давайте начнем!

Во-первых, вам понадобится линейка или линейка. Поместите линейку в нижний левый угол бумаги и сделайте небольшую отметку на отметке 5 дюймов. Затем поверните линейку так, чтобы она была перпендикулярна первой отметке, и сделайте еще одну отметку на отметке 4 дюйма. Повторяйте этот процесс, пока у вас не будет пяти баллов.

Далее, соедини точки! Начиная с нижней левой метки, проведите линию к следующей метке и продолжайте, пока не соедините все пять. Теперь у вас должен получиться пятиугольник!

Если у вашего пятиугольника не равные стороны, не беспокойтесь — просто отрегулируйте расположение меток, пока оно не будет выглядеть правильно. И это все! Немного потренировавшись, вы будете рисовать идеальные пятиугольники в кратчайшие сроки.

Понимание свойств пятиугольника

В геометрии пятиугольник — это любой многоугольник с пятью сторонами. Пятиугольник со сторонами одинаковой длины называется правильным пятиугольником. Сумма внутренних углов правильного пятиугольника равна 540°.

Есть много способов нарисовать пятиугольник с равными сторонами. Один из способов — использовать циркуль и линейку. Сначала нарисуйте круг с помощью циркуля. Затем с помощью циркуля начертите пять равноотстоящих линий от центра круга до окружности. Эти линии разделят круг на пять равных частей. Наконец, соедините концы каждой линии, чтобы сформировать пятиугольник.

Другой метод заключается в построении пятиугольника с использованием только линейки и транспортира. Начните с рисования сегмента линии. С помощью транспортира разделите отрезок на пять равных частей. Затем проведите линии от конечных точек отрезка до середины остальных четырех отрезков. Наконец, соедините концы линий, чтобы сформировать пятиугольник.

Есть много других способов построить пятиугольник с равными сторонами. Некоторые методы сложнее, чем другие. В общем, чем больше сторон у многоугольника, тем сложнее построить его с равными сторонами.

Выбор правильных инструментов для рисования пятиугольника

Когда дело доходит до рисования идеального пятиугольника, очень важно иметь правильные инструменты. Традиционные методы рисования, такие как использование компаса, могут разочаровывать и часто дают далеко не идеальные результаты. линейка или другой шаблон для достижения точных результатов.

Существует несколько способов рисования пятиугольника с равными сторонами. Одним из популярных методов является использование Pentagon Tool. Это специализированная линейка, которая разработана специально для рисования идеальных пятиугольников.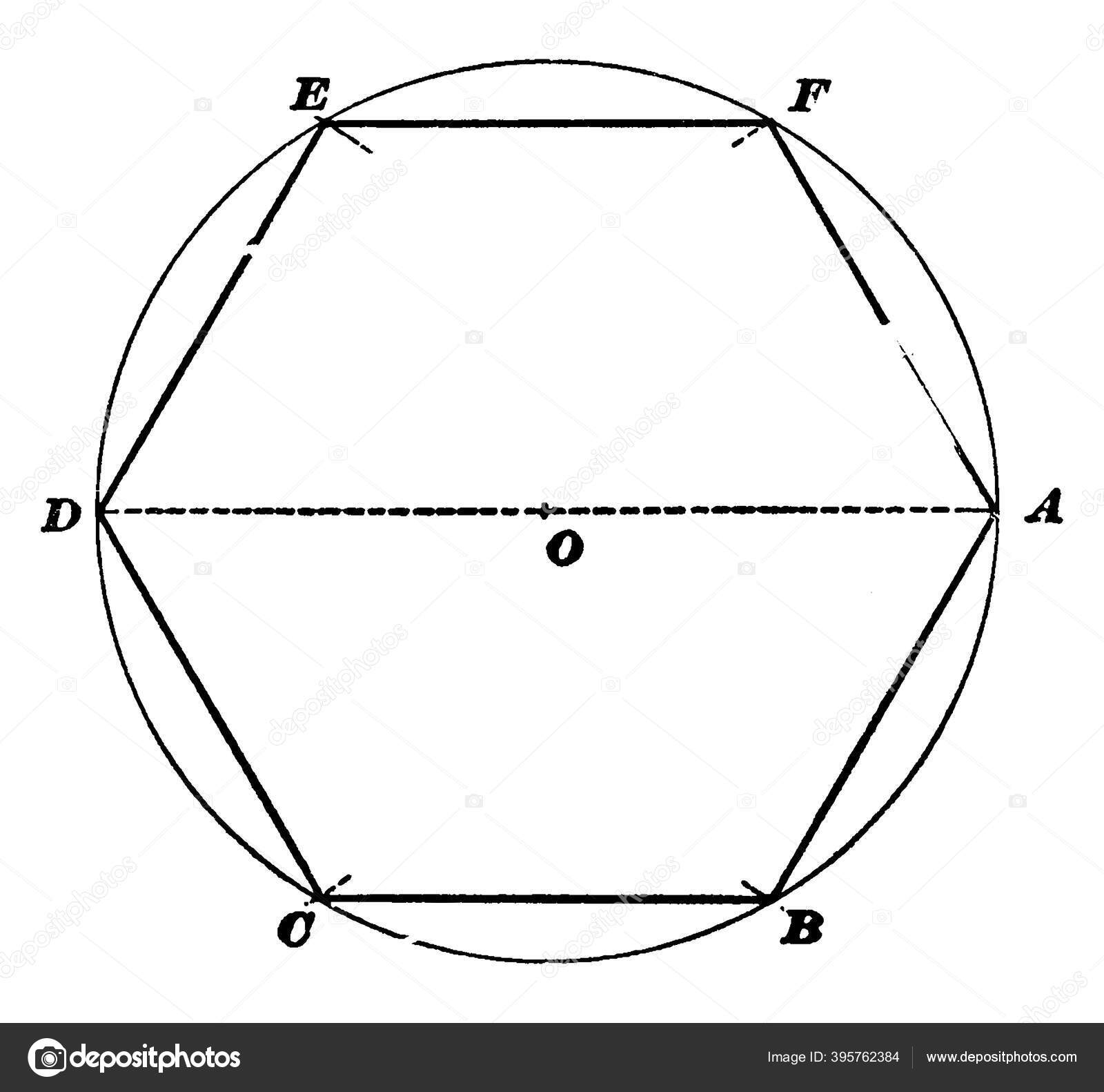 Другой метод заключается в использовании французской кривой. Это шаблон, который можно использовать для рисования различных фигур, включая пятиугольник.

Какой бы метод вы ни выбрали, ключ к успеху — не торопиться и быть точным. Немного потренировавшись, вы сможете каждый раз создавать идеальные пятиугольники!

Пошаговое руководство по рисованию пятиугольника с равными сторонами

Пятиугольник — это пятиугольник с равными сторонами. Начертить пятиугольник с равными сторонами можно разными способами. В этой статье блога мы покажем вам, как нарисовать пятиугольник с равными сторонами шаг за шагом, используя несколько различных методов.

Самый простой способ нарисовать пятиугольник с равными сторонами — использовать циркуль. Сначала найдите центр бумаги. Затем с помощью циркуля начертите окружность с радиусом, равным длине одной из сторон пятиугольника. Как только круг будет нарисован, используйте компас, чтобы провести пять линий, каждую из центра круга к краю круга. Эти пять линий будут сторонами пятиугольника.

Еще один способ нарисовать пятиугольник с равными сторонами — использовать линейку и транспортир. Сначала найдите центр бумаги. Затем используйте линейку, чтобы провести линию от центра бумаги к краю бумаги. Эта линия будет одной из сторон пятиугольника. Затем с помощью транспортира отмерьте 72 градуса (360 градусов разделить на 5, поскольку у пятиугольника пять сторон). Нарисуйте линию от центра бумаги на отметке 72 градуса. Эта линия будет другой стороной пятиугольника. Повторяйте этот процесс, пока не будут нарисованы все пять сторон пятиугольника.

Третий способ нарисовать пятиугольник с равными сторонами — использовать линейку и отрезок веревки. Сначала найдите центр бумаги. Затем используйте линейку, чтобы провести линию от центра бумаги к краю бумаги. Эта линия будет одной из сторон пятиугольника. Затем привяжите один конец веревки к центру бумаги. Отмерьте длину одной из сторон пятиугольника и привяжите другой конец нити к линейке на этой отметке. Нитью нарисуйте остальные четыре стороны пятиугольника.

Независимо от того, какой метод вы используете, нарисовать пятиугольник с равными сторонами — это простой процесс. Просто не забудьте тщательно измерить и использовать линейку, чтобы провести линии. Немного потренировавшись, вы будете рисовать идеальные пятиугольники в кратчайшие сроки!

Изучение различных способов построения пятиугольника

Существует много разных способов построения пятиугольника с равными сторонами. Самый распространенный метод — использовать циркуль и линейку для построения пятиугольника. Однако есть и другие методы, которые можно использовать. В этой статье мы рассмотрим некоторые из различных методов, которые можно использовать для построения пятиугольника с равными сторонами.

Наиболее распространенный метод построения пятиугольника с равными сторонами — это использование циркуля и линейки. Первый шаг — построить круг с помощью компаса. Затем с помощью циркуля начертите отрезок от центра круга до одной из точек на круге. Этот отрезок будет первой стороной пятиугольника. Затем с помощью циркуля начертите еще один отрезок от центра круга до другой точки на круге. Этот отрезок будет второй стороной пятиугольника. Повторяйте этот процесс, пока не будут нарисованы все пять сторон пятиугольника.

Существуют и другие методы построения пятиугольника с равными сторонами. Один из способов заключается в использовании линейки и транспортира. Во-первых, используйте линейку, чтобы нарисовать отрезок линии. Затем с помощью транспортира измерьте угол 72 градуса. Затем с помощью линейки нарисуйте еще один отрезок такой же длины, как и первый отрезок. Этот отрезок будет первой стороной пятиугольника. Повторяйте этот процесс, пока не будут нарисованы все пять сторон пятиугольника.

Другой метод построения пятиугольника с равными сторонами — использование линейки и циркуля. Во-первых, используйте линейку, чтобы нарисовать отрезок линии. Затем с помощью циркуля нарисуйте окружность с центром в конечной точке отрезка.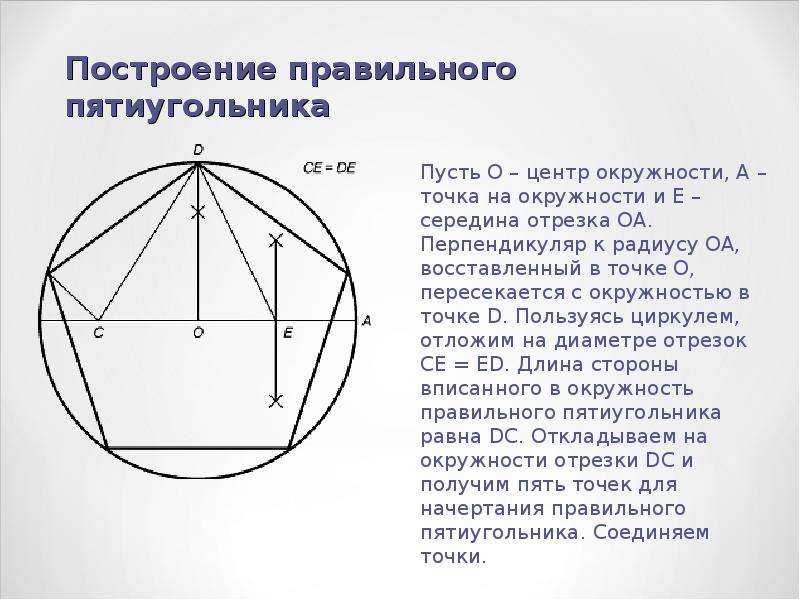 Затем с помощью циркуля начертите отрезок линии от центра круга до одной из точек на круге. Этот отрезок будет первой стороной пятиугольника. Повторяйте этот процесс, пока не будут нарисованы все пять сторон пятиугольника.

Существует множество различных методов построения пятиугольника с равными сторонами. Наиболее распространенный метод — использование циркуля и линейки. Однако есть и другие методы, которые можно использовать. В этой статье мы рассмотрели некоторые из различных методов, которые можно использовать для построения пятиугольника с равными сторонами.

Добавление деталей и симметрии к вашему рисунку пятиугольника

В этой записи блога мы рассмотрим, как нарисовать идеальный пятиугольник с равными сторонами, добавив детали и симметрию, чтобы ваш рисунок выглядел наилучшим образом.

При рисовании пятиугольника первое, что вам нужно сделать, это отметить пять углов фигуры. Когда у вас есть углы, вы можете начать рисовать стороны пятиугольника. Следите за тем, чтобы стороны были равными по длине, так как это придаст вашему пятиугольнику идеальную форму.

Когда у вас есть основная форма пятиугольника, вы можете начать добавлять детали. Например, вы можете добавить границу вокруг внешней стороны пятиугольника или добавить симметрии, нарисовав линию по центру пятиугольника.

Добавление этих деталей поможет вашему рисунку пятиугольника выглядеть наилучшим образом. Немного потренировавшись, вы сможете с легкостью рисовать идеальные пятиугольники!

Советы и рекомендации по рисованию идеального пятиугольника

Вы ищете советы и рекомендации по рисованию идеального пятиугольника с равными сторонами? Если это так, вы пришли в нужное место!

Существует несколько различных способов рисования пятиугольника с равными сторонами, но описанные ниже методы являются одними из самых простых и эффективных. Немного потренировавшись, вы сможете рисовать идеальные пятиугольники в кратчайшие сроки!

Один из самых простых способов нарисовать пятиугольник с равными сторонами — начать с квадрата. Для этого просто нарисуйте квадрат на листе бумаги. Затем используйте линейку или другую линейку, чтобы провести линии от середины каждой стороны квадрата к противоположным углам. Это разделит квадрат на пять равных частей, которые затем можно соединить, чтобы сформировать пятиугольник.

Еще один простой способ — начать с правильного пятиугольника. Для этого начертите на листе бумаги пятиугольник, следя за тем, чтобы все стороны были одинаковой длины. Затем используйте линейку или другую линейку, чтобы разделить каждую сторону пятиугольника пополам. Это разделит пятиугольник на пять равных частей, которые затем можно соединить, чтобы сформировать пятиугольник.

Если вам нужен более сложный метод, попробуйте начать с неправильного пятиугольника. Для этого начертите на листе бумаги пятиугольник, следя за тем, чтобы каждая сторона была неодинаковой длины. Затем используйте линейку или другую линейку, чтобы провести линии от середины каждой стороны пятиугольника к противоположным углам. Это разделит пятиугольник на пять неравных частей, которые затем можно соединить, чтобы сформировать пятиугольник.

Какой бы метод вы ни выбрали, немного потренировавшись, вы сможете легко рисовать идеальные пятиугольники!

Практика точности и аккуратности в рисовании пятиугольника

Вы ищете вызов своим геометрическим рисункам? Почему бы не попробовать нарисовать идеальный пятиугольник? Пятиугольник — это пятиугольник с прямыми сторонами, и нарисовать его с равными сторонами может быть немного сложно. Но немного потренировавшись, вы сможете освоить эту форму.

Вот несколько советов, как нарисовать пятиугольник с равными сторонами:

1. Начертите пятиугольник с помощью линейки или линейки. Это поможет вам добиться прямых сторон.

2. Чтобы найти центр вашего пятиугольника, проведите диагональную линию от одного угла к другому. Там, где встречаются две линии, находится центр.

3. Рисуйте пятиугольник по одной стороне за раз, начиная сверху. Убедитесь, что каждая сторона имеет ту же длину, что и предыдущая.

4. Когда вы закончите рисовать стороны, соедините последнюю сторону с первой стороной, чтобы завершить пятиугольник.

5. Сотрите все направляющие, которые вы могли использовать.

Немного потренировавшись, вы с легкостью сможете нарисовать идеальный пятиугольник!

Творческое применение рисования пятиугольника

Хотите научиться рисовать пятиугольник с равными сторонами? Если это так, вы пришли в нужное место! Эта статья в блоге научит вас всему, что вам нужно знать, чтобы создать идеальный пятиугольник.

Пятиугольник — пятиугольник, часто используемый в геометрии и архитектуре. Хотя может показаться сложным нарисовать пятиугольник с равными сторонами, на самом деле это довольно просто, если вы знаете шаги.

Для начала вам понадобится лист бумаги и карандаш. Затем выполните следующие действия:

1. Проведите горизонтальную линию по центру листа бумаги.

Метод построения двух геометрических фигур на одной модели

Похожие статьи

Наглядная геометрия | Статья в журнале «Школьная педагогика»

К вопросу

Понятия об изометрических

Методика использования нового механизма для

Математический кружок «Наглядная геометрия» для учащихся…

Способ вращения геометрической фигуры вокруг оси плоскости…

Эта загадочная пентаграмма |

Похожие статьи

Наглядная геометрия | Статья в журнале «Школьная педагогика»

К вопросу

Понятия об изометрических

Методика использования нового механизма для

Математический кружок «Наглядная геометрия» для учащихся…

Способ вращения геометрической фигуры вокруг оси плоскости…

Эта загадочная пентаграмма |

Построение правильных многоугольников

многоугольников, вписанных в окружность

Как нарисовать пятиугольник с равными сторонами

Понимание свойств пятиугольника

Выбор правильных инструментов для рисования пятиугольника

Пошаговое руководство по рисованию пятиугольника с равными сторонами

Изучение различных способов построения пятиугольника

Добавление деталей и симметрии к вашему рисунку пятиугольника

Советы и рекомендации по рисованию идеального пятиугольника

Практика точности и аккуратности в рисовании пятиугольника

Творческое применение рисования пятиугольника

Добавить комментарий Отменить ответ