Построение на плоскости | Журнал Ярмарки Мастеров
Наверняка каждому из нас приходилось сталкиваться с тем, что нужно срочно что-то начертить, точный угол или многоугольник, а транспортира как нарочно под рукой нет, или Вы вообще никогда раньше ничего не чертили. Сегодня я хочу поделиться с Вами простыми схемами построения фигур на плоскости. Думаю, этот навык пригодится всем. Продолжение статьи:
http://www.livemaster.ru/topic/383001-postroenie-na-ploskosti-chast-2?inside=1&wf=&cp=1&vr=1
Нам понадобятся: карандаш, линейка, циркуль.
Построение угла в 60
1. Проведём прямую и отметим на ней точку А.
2. Из точки А проведём дугу произвольного радиуса и получим точку В.
3. Из точки В проведём дугу радиуса АВ, чтобы она пересекла ранее начерченную дугу.
4. Проведённая через точку пересечения (С) и точку А прямая будет второй стороной требуемого угла.
Построение угла в 45
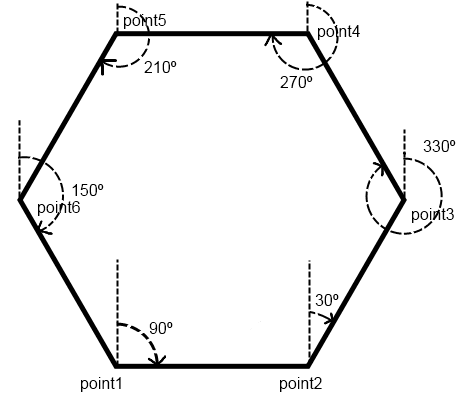 Построим угол 60, кака описано выше.
Построим угол 60, кака описано выше.
2. Разделим полученный угол пополам.
3. Угол между лучами 60 и 30 разделим пополам. В результате получим угол в 45.
Построение угла в 75
1. Построим угол в 60, как описано выше, и разделим его пополам.
2. В ходе дальнейшего деления надвое получим угол в 15.
3. Отразим угол в 15 через луч 60 и так получим угол в 75.
Построение угла в 90
1. Построим угол в 60, как описано выше, и разделим его пополам.
2. Получившийся угол в 30 через луч 60 и так получим угол точно в 90.
Разделение отрезка на равные части.
1. Проведём прямую и отметим на ней отрезок АВ.
2. Из точки А проведём вспомогательную прямую и разделим её на столько одинаковых частей, на сколько требуется разделить отрезок АВ. Делить будем при помощи циркуля. Последнюю точку обозначим буквой С.
3. Последнюю точка (С) соединим с концом отрезка АВ.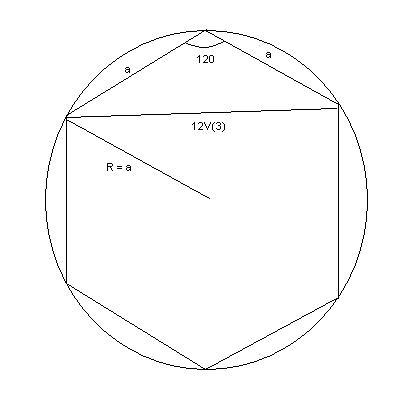 Построим рад параллельных отрезку СВ прямых по всей длине отрезка АВ. Точки пересечения параллельных прямых с отрезком АВ и будут точками раздела отрезка на несколько равных частей.
Построим рад параллельных отрезку СВ прямых по всей длине отрезка АВ. Точки пересечения параллельных прямых с отрезком АВ и будут точками раздела отрезка на несколько равных частей.
Построение правильного пятиугольника.
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
2. Разделим пополам расстояние ОВ. Разведём ножки циркуля на расстояние FC. Из точки F проведём дугу через С. Дуга пересечёт горизонтальную линию в точке G.
3. Расстояние CG будет длиной стороны пятиугольника. Из вершины С отложим пять раз расстояние CG.
Построение правильного шестиугольника.
1. Проведём окружность радиусом 50 мм.
2. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
3. Из точки А на линии окружности отложим шесть раз радиус нашей окружности. Соединив прямыми точки пересечения, получим шестиугольник.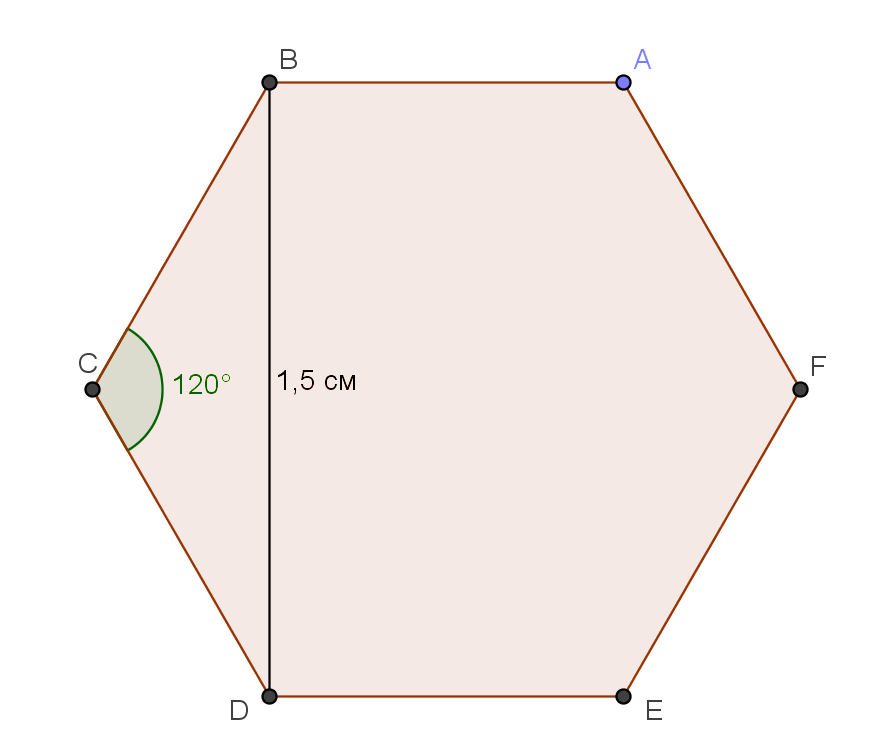
Построение правильного семиугольника.
1. Проведём окружность заданного радиуса. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
2. Из точки D проведём дугу радиусом равным радиусу окружности.
3. Дуга пересечёт окружность в точках E и G.
4. Длина отрезка EF на хорде EG равна длине стороны семиугольника. Из вершины С семь раз отложим расстояние EF.
Общий метод построения многоугольников.
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии. Продолжим горизонтальную лини. За точки А и В.
2. Из точки D проведём дугу радиусом, равным радиусу окружности так, чтобы дуга пересекла горизонтальную линию.
3. При помощи вспомогательной прямой разделим вертикальную линию на столько равных частей, сколько сторон многоугольника требуется получить. Для примера показано построение одиннадцатиугольника.
4. Из точки Е проведём прямые через нечётные точки раздела вертикальной линии так, чтобы эти прямые пересекли окружность. Такую же операцию проведём из точки G. Полученные лучи пересекают окружность в точках, соединив которые прямыми получаем одиннадцатиугольник.
Правильный шестиугольник — Карта знаний
- Правильный шестиугольник (гексагон) — правильный многоугольник с шестью сторонами.
Источник: Википедия
Связанные понятия
Правильный пятиугольник (или пентагон от греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами. Шестиугольник — многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы.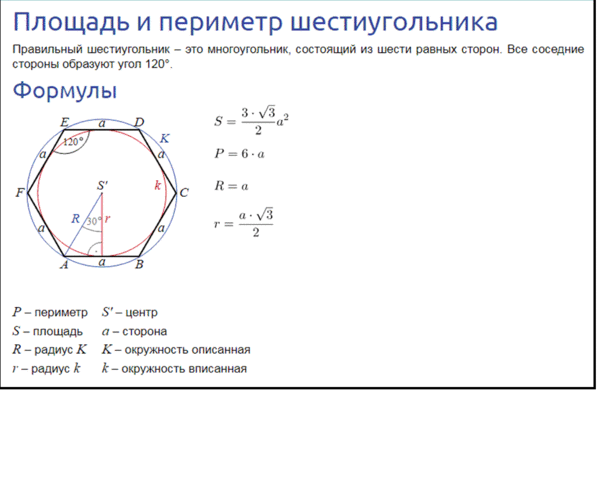 Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.
Многоугольник Петри для правильного многогранника в размерности n — это пространственный многоугольник, такой что любые (n-1) последовательных ребра (но не n) принадлежат одной (n-1)-мерной грани.
Звёздчатый многоугольник — многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника. Стороны звёздчатого многоугольника могут пересекаться между собой. Существует множество звёздчатых многоугольников или звёзд, среди них пентаграмма, гексаграмма, две гептаграммы, октограмма, декаграмма, додекаграмма. Звёздчатые многоугольники можно получить, продолжая одновременно все стороны правильного многоугольника после их пересечения в его вершинах до их…
Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.
Многоугольник Петри для правильного многогранника в размерности n — это пространственный многоугольник, такой что любые (n-1) последовательных ребра (но не n) принадлежат одной (n-1)-мерной грани.
Звёздчатый многоугольник — многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника. Стороны звёздчатого многоугольника могут пересекаться между собой. Существует множество звёздчатых многоугольников или звёзд, среди них пентаграмма, гексаграмма, две гептаграммы, октограмма, декаграмма, додекаграмма. Звёздчатые многоугольники можно получить, продолжая одновременно все стороны правильного многоугольника после их пересечения в его вершинах до их…Упоминания в литературе
Действительно, семь из 13 Архимедовых тел могут быть получены отрезанием кусочков от Платоновых тел – среди этих многогранников и классический футбольный мяч из пятиугольников и шестиугольников. Но более примечательным было открытие некоторых других форм. Оказывается, возможно объединение 30 квадратов, 20 правильных шестиугольников и 12 правильных десятиугольников в симметричную форму, которая называется ромбоусеченный икосододекаэдр (рис. 2.06).
Деление окружности на шесть равных частей. Раствор циркуля устанавливают равным радиусу R окружности. Из концов одного из диаметров окружности (из точек 1, 4) описывают дуги (рисунок 3 а, б). Точки 1, 2, 3, 4, 5, 6 делят окружность на шесть равных частей. Соединив их прямыми линиями, получают правильный шестиугольник (рисунок 3, б).
Каково соответствие между двумя предлагаемыми схемами – круглой и полукруглой? Обратимся к ценнейшим розенкрейцеровским диаграммам из книги «Магические, каббалистические и теософские сочинения Георга фон Веллинга по поводу Солей, Серы и Ртути». На рис. 6 а показана фигура, представляющая собой правильный шестиугольник с вписанными в него взаимообращёнными равносторонними треугольниками и неправильными пятиконечными звёздами, так что получается изображение спроецированного на плоскость объёмного куба.
Но более примечательным было открытие некоторых других форм. Оказывается, возможно объединение 30 квадратов, 20 правильных шестиугольников и 12 правильных десятиугольников в симметричную форму, которая называется ромбоусеченный икосододекаэдр (рис. 2.06).
Деление окружности на шесть равных частей. Раствор циркуля устанавливают равным радиусу R окружности. Из концов одного из диаметров окружности (из точек 1, 4) описывают дуги (рисунок 3 а, б). Точки 1, 2, 3, 4, 5, 6 делят окружность на шесть равных частей. Соединив их прямыми линиями, получают правильный шестиугольник (рисунок 3, б).
Каково соответствие между двумя предлагаемыми схемами – круглой и полукруглой? Обратимся к ценнейшим розенкрейцеровским диаграммам из книги «Магические, каббалистические и теософские сочинения Георга фон Веллинга по поводу Солей, Серы и Ртути». На рис. 6 а показана фигура, представляющая собой правильный шестиугольник с вписанными в него взаимообращёнными равносторонними треугольниками и неправильными пятиконечными звёздами, так что получается изображение спроецированного на плоскость объёмного куба.
Связанные понятия (продолжение)
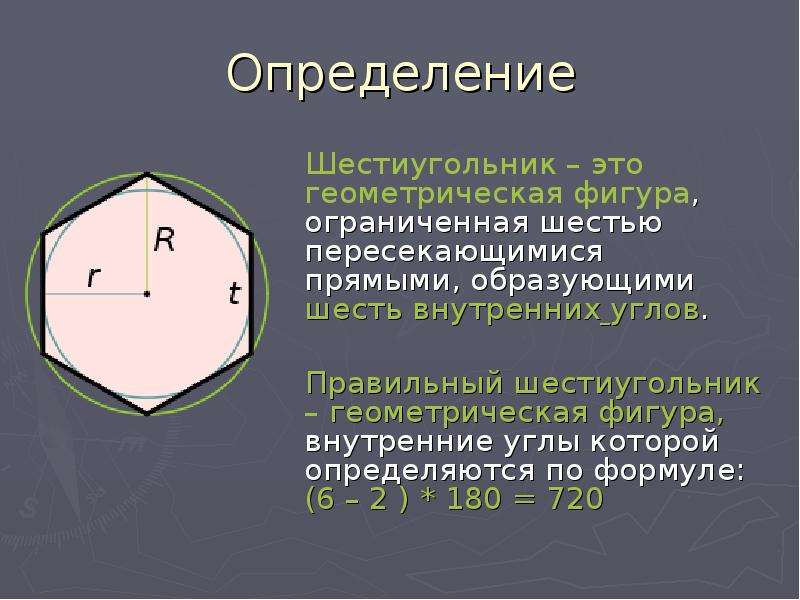
В геометрии пространственный многоугольник — это многоугольник, вершины которого не компланарны. Пространственные многоугольники должны иметь по меньшей мере 4 вершины. Внутренняя поверхность таких многоугольников однозначно не определяется. Пра́вильный многоуго́льник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны. Шестиугольник Лемуана представляет собой шестиугольник, около которого можно описать окружность.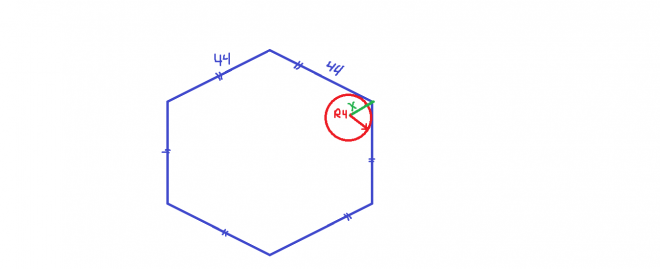
 Равносторонний четырёхугольник — это ромб, и квадрат является частным случаем ромба.
Пятиугольник Роббинса — это вписанный пятиугольник, стороны которого и площадь являются рациональными числами.
Правильный (или равносторонний) треугольник — это правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Двенадцатиуго́льник, додекаго́н (греч. δώδεκα — двенадцать и греч. γωνία — угол) — многоугольник с 12 углами и 12 сторонами. Как правило, додекагоном называют правильный многоугольник, то есть такой, у которого все стороны и все углы равны (в случае додекагона углы равны 150°). Правильный двенадцатиугольник используется в некоторых странах в качестве формы для монет.
Равносторонний четырёхугольник — это ромб, и квадрат является частным случаем ромба.
Пятиугольник Роббинса — это вписанный пятиугольник, стороны которого и площадь являются рациональными числами.
Правильный (или равносторонний) треугольник — это правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Двенадцатиуго́льник, додекаго́н (греч. δώδεκα — двенадцать и греч. γωνία — угол) — многоугольник с 12 углами и 12 сторонами. Как правило, додекагоном называют правильный многоугольник, то есть такой, у которого все стороны и все углы равны (в случае додекагона углы равны 150°). Правильный двенадцатиугольник используется в некоторых странах в качестве формы для монет.
 Многогранник является двенадцатигранником, одним из восьми дельтаэдров (выпуклых многогранников с гранями в виде правильных треугольников) и одним из 92 многогранников Джонсона (неоднородные выпуклые многогранники с правильными…
Описанный многоугольник, известный также как тангенциальный многоугольник — это выпуклый многоугольник, который содержит вписанную окружность. Это окружность, которая касательна каждой стороны многоугольника. Двойственный многоугольник описанного многоугольника — это многоугольник, который имеет описанную окружность, проходящую через все его вершины.
В геометрии гиробифастигиум или двускатный повёрнутый бикупол является 26-м многогранником Джонсона (J26). Его можно построить объединением двух треугольных призм с правильными гранями по соответствующим квадратным граням с поворотом одной призмы на 90º . Это единственное тело Джонсона, которым можно заполнить трёхмерное пространство.
Многогранник является двенадцатигранником, одним из восьми дельтаэдров (выпуклых многогранников с гранями в виде правильных треугольников) и одним из 92 многогранников Джонсона (неоднородные выпуклые многогранники с правильными…
Описанный многоугольник, известный также как тангенциальный многоугольник — это выпуклый многоугольник, который содержит вписанную окружность. Это окружность, которая касательна каждой стороны многоугольника. Двойственный многоугольник описанного многоугольника — это многоугольник, который имеет описанную окружность, проходящую через все его вершины.
В геометрии гиробифастигиум или двускатный повёрнутый бикупол является 26-м многогранником Джонсона (J26). Его можно построить объединением двух треугольных призм с правильными гранями по соответствующим квадратным граням с поворотом одной призмы на 90º . Это единственное тело Джонсона, которым можно заполнить трёхмерное пространство. В геометрии правильный косой многогранник — это обобщение множества правильных многогранников, которое включает возможность непланарных граней или вершинных фигур. Коксетер рассматривал косые вершинные фигуры, которые создавали новые четырёхмерные правильные многогранники, а много позднее Бранко Грюнбаум рассматривал правильные косые грани.
В геометрии сферический многогранник или сферическая мозаика — это тa мозаика на сфере, в которой поверхность разделена большими дугами на ограниченные области, называемые сферическими многоугольниками. Большая часть теории симметричных многогранников использует сферические многогранники.
Правильный многогранник или плато́ново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.
В геометрии японская теорема утверждает, что центры окружностей, вписанных в определённые треугольники внутри вписанного в окружность четырёхугольника, являются вершинами прямоугольника.
В геометрии правильный косой многогранник — это обобщение множества правильных многогранников, которое включает возможность непланарных граней или вершинных фигур. Коксетер рассматривал косые вершинные фигуры, которые создавали новые четырёхмерные правильные многогранники, а много позднее Бранко Грюнбаум рассматривал правильные косые грани.
В геометрии сферический многогранник или сферическая мозаика — это тa мозаика на сфере, в которой поверхность разделена большими дугами на ограниченные области, называемые сферическими многоугольниками. Большая часть теории симметричных многогранников использует сферические многогранники.
Правильный многогранник или плато́ново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.
В геометрии японская теорема утверждает, что центры окружностей, вписанных в определённые треугольники внутри вписанного в окружность четырёхугольника, являются вершинами прямоугольника.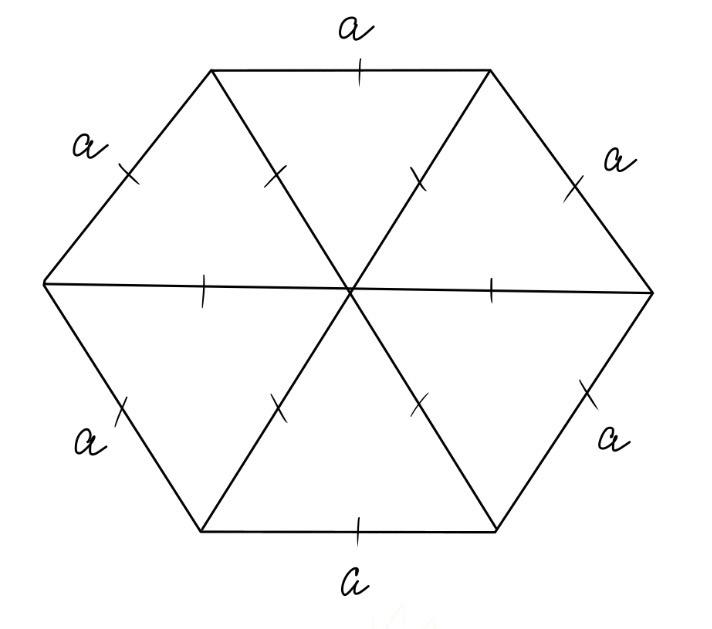 Символ Шлефли — комбинаторная характеристика правильного многогранника, применяется для описания правильных многогранников во всех размерностях. Назван в честь швейцарского математика Людвига Шлефли, который внёс значительный вклад в геометрию и другие области математики.
Пра́вильный семнадцатиуго́льник — геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Среди других правильных многоугольников с больши́м (больше пяти) простым числом сторон интересен тем, что его можно построить при помощи циркуля и линейки (так, семи-, одиннадцати- и тринадцатиугольники построить циркулем и линейкой нельзя).
Гипотеза Тёплица, также известная как гипотеза о вписанном квадрате — нерешённая проблема геометрии.
Символ Шлефли — комбинаторная характеристика правильного многогранника, применяется для описания правильных многогранников во всех размерностях. Назван в честь швейцарского математика Людвига Шлефли, который внёс значительный вклад в геометрию и другие области математики.
Пра́вильный семнадцатиуго́льник — геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Среди других правильных многоугольников с больши́м (больше пяти) простым числом сторон интересен тем, что его можно построить при помощи циркуля и линейки (так, семи-, одиннадцати- и тринадцатиугольники построить циркулем и линейкой нельзя).
Гипотеза Тёплица, также известная как гипотеза о вписанном квадрате — нерешённая проблема геометрии. Формулировка гипотезы…
Фаска или усечение рёбер в геометрии — это топологическая операция, которая преобразует многогранник в другой многогранник. Операция подобна растяжению, передвигающему грани, удаляя их от центра. Для трёхмерных многогранников операция фаски добавляет новую шестиугольную грань вместо каждого исходного ребра.
Комплексный многогранник — это обобщение многогранника в вещественном пространстве на аналогичную структуру в комплексном гильбертовом пространстве, где к каждой вещественной размерности добавляется мнимая.
В геометрии семиугольная мозаика — это правильная мозаика на гиперболической плоскости. Она представляется cимволом Шлефли {7,3} и имеет три правильных семиугольника в каждой вершине.
Апейрогон (от др.-греч. ἄπειρος — бесконечный или безграничный и др.
Формулировка гипотезы…
Фаска или усечение рёбер в геометрии — это топологическая операция, которая преобразует многогранник в другой многогранник. Операция подобна растяжению, передвигающему грани, удаляя их от центра. Для трёхмерных многогранников операция фаски добавляет новую шестиугольную грань вместо каждого исходного ребра.
Комплексный многогранник — это обобщение многогранника в вещественном пространстве на аналогичную структуру в комплексном гильбертовом пространстве, где к каждой вещественной размерности добавляется мнимая.
В геометрии семиугольная мозаика — это правильная мозаика на гиперболической плоскости. Она представляется cимволом Шлефли {7,3} и имеет три правильных семиугольника в каждой вершине.
Апейрогон (от др.-греч. ἄπειρος — бесконечный или безграничный и др. -греч. γωνία — угол) — обобщённый многоугольник со счётно-бесконечным числом сторон.
Квадратная антипризма — это второй многогранник в бесконечном ряду антипризм, образованных последовательностью треугольных граней, закрытых с обеих сторон многоугольниками. Квадратная антипризма известна также как антикуб.
Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.
Звёздчатый многогра́нник (звёздчатое тело) — это невыпуклый многогранник, грани которого пересекаются между собой. Как и у незвёздчатых многогранников, грани попарно соединяются в рёбрах (при этом внутренние линии пересечения не считаются рёбрами).
Многогранник, двойственный (или дуальный) к заданному многограннику — многогранник, у которого каждой грани исходного многогранника соответствует вершина двойственного, каждой вершине исходного — грань двойственного и каждому ребру исходного — ребро двойственного.
-греч. γωνία — угол) — обобщённый многоугольник со счётно-бесконечным числом сторон.
Квадратная антипризма — это второй многогранник в бесконечном ряду антипризм, образованных последовательностью треугольных граней, закрытых с обеих сторон многоугольниками. Квадратная антипризма известна также как антикуб.
Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.
Звёздчатый многогра́нник (звёздчатое тело) — это невыпуклый многогранник, грани которого пересекаются между собой. Как и у незвёздчатых многогранников, грани попарно соединяются в рёбрах (при этом внутренние линии пересечения не считаются рёбрами).
Многогранник, двойственный (или дуальный) к заданному многограннику — многогранник, у которого каждой грани исходного многогранника соответствует вершина двойственного, каждой вершине исходного — грань двойственного и каждому ребру исходного — ребро двойственного. Многогранник, двойственный двойственному, гомотетичен исходному.
Усечённый кубооктаэдр, усечённый кубоктаэдр — полуправильный многогранник (архимедово тело) с 12 квадратными гранями, 8 гранями в виде правильного шестиугольника, 6 гранями в виде правильного восьмиугольника, 48 вершинами и 72 рёбрами. Поскольку каждая из граней многогранника имеет центральную симметрию (что эквивалентно повороту на 180°), усечённый кубооктаэдр является зоноэдром.
В геометрии удлинённый квадратный гиробикупол или псевдоромбокубооктаэдр (по Залгаллеру — удлинённый четырёхскатный повёрнутый бикупол) — это один из многогранников Джонсона (J37 = (по Залгаллеру) М5+П8+М5). Тело, обычно, не считается архимедовым телом, хотя его грани и являются правильными многоугольниками и многоугольники вокруг каждой вершины те же самые, но, в отличие от 13 архимедовых тел, многогранник не обладает глобальной симметрией, переводящей любую вершину в любую другую (хотя Грюнбаум.
Многогранник, двойственный двойственному, гомотетичен исходному.
Усечённый кубооктаэдр, усечённый кубоктаэдр — полуправильный многогранник (архимедово тело) с 12 квадратными гранями, 8 гранями в виде правильного шестиугольника, 6 гранями в виде правильного восьмиугольника, 48 вершинами и 72 рёбрами. Поскольку каждая из граней многогранника имеет центральную симметрию (что эквивалентно повороту на 180°), усечённый кубооктаэдр является зоноэдром.
В геометрии удлинённый квадратный гиробикупол или псевдоромбокубооктаэдр (по Залгаллеру — удлинённый четырёхскатный повёрнутый бикупол) — это один из многогранников Джонсона (J37 = (по Залгаллеру) М5+П8+М5). Тело, обычно, не считается архимедовым телом, хотя его грани и являются правильными многоугольниками и многоугольники вокруг каждой вершины те же самые, но, в отличие от 13 архимедовых тел, многогранник не обладает глобальной симметрией, переводящей любую вершину в любую другую (хотя Грюнбаум. ..
Шестиуго́льный парке́т (шестиугольный паркета́ж) или шестиугольная мозаика — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.
Трисекция угла — задача о делении заданного угла на три равные части построением циркулем и линейкой.
Многогранник или полиэдр — обычно замкнутая поверхность, составленная из многоугольников, но иногда так же называют тело, ограниченное этой поверхностью.
Лемма о трезубце или теорема трилистника, или лемма Мансиона (жарг. лемма о куриной лапке) — теорема в геометрии треугольника.
При́зма (лат. prisma от др.-греч. πρίσμα «нечто отпиленное») — многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками.
..
Шестиуго́льный парке́т (шестиугольный паркета́ж) или шестиугольная мозаика — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.
Трисекция угла — задача о делении заданного угла на три равные части построением циркулем и линейкой.
Многогранник или полиэдр — обычно замкнутая поверхность, составленная из многоугольников, но иногда так же называют тело, ограниченное этой поверхностью.
Лемма о трезубце или теорема трилистника, или лемма Мансиона (жарг. лемма о куриной лапке) — теорема в геометрии треугольника.
При́зма (лат. prisma от др.-греч. πρίσμα «нечто отпиленное») — многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками.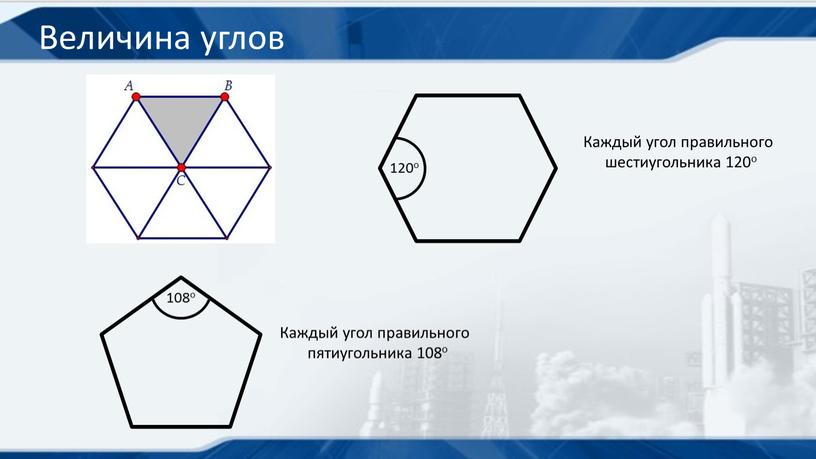 Обобщённый многоугольник — это структура инцидентности, предложенная Жаком Титсом в 1959 году. Обобщённые n-угольники вмещают в качестве частных случаев проективные плоскости (обобщённые треугольники, n=3) и обобщённые четырёхугольники (n=4). Многие обобщённые многоугольники получаются из групп типа Ли, но существуют некоторые экзотические обобщённые многоугольники, которые таким способом не получаются. Обобщённые многоугольники, удовлетворяющие условию, известному как свойство Муфанга, полностью…
Растянутый многоугольник серединных точек вписанного многоугольника P — это другой вписанный в ту же самую окружность многоугольник, вершины которого являются серединами дуг между вершинами многоугольника P. Многоугольник может быть получен из серединного многоугольника (многоугольника, вершины которого лежат в серединах сторон), если провести радиусы из центра окружности через вершины серединного многоугольника.
Обобщённый многоугольник — это структура инцидентности, предложенная Жаком Титсом в 1959 году. Обобщённые n-угольники вмещают в качестве частных случаев проективные плоскости (обобщённые треугольники, n=3) и обобщённые четырёхугольники (n=4). Многие обобщённые многоугольники получаются из групп типа Ли, но существуют некоторые экзотические обобщённые многоугольники, которые таким способом не получаются. Обобщённые многоугольники, удовлетворяющие условию, известному как свойство Муфанга, полностью…
Растянутый многоугольник серединных точек вписанного многоугольника P — это другой вписанный в ту же самую окружность многоугольник, вершины которого являются серединами дуг между вершинами многоугольника P. Многоугольник может быть получен из серединного многоугольника (многоугольника, вершины которого лежат в серединах сторон), если провести радиусы из центра окружности через вершины серединного многоугольника. В геометрии трёхскатный купол представляет собой один из многогранников Джонсона (J3 = (по Залгаллеру) М4). Купол можно рассматривать как половину кубооктаэдра.
В геометрии n-угольный осоэдр — это такая мозаика из двуугольников на сферической поверхности, что каждый такой двуугольник имеет две общие вершины (противоположные точки сферы) с другими двуугольниками.
Правильные четырёхмерные многогранники являются четырёхмерными аналогами правильных многогранников в трёхмерном пространстве и правильных многоугольников на плоскости.
В геометрии трёхскатный купол представляет собой один из многогранников Джонсона (J3 = (по Залгаллеру) М4). Купол можно рассматривать как половину кубооктаэдра.
В геометрии n-угольный осоэдр — это такая мозаика из двуугольников на сферической поверхности, что каждый такой двуугольник имеет две общие вершины (противоположные точки сферы) с другими двуугольниками.
Правильные четырёхмерные многогранники являются четырёхмерными аналогами правильных многогранников в трёхмерном пространстве и правильных многоугольников на плоскости.Подробнее: Правильный четырёхмерный многогранник
Что такое правильный шестиугольник и какие задачи с ним могут быть связаны? :: SYL.ru
Самая известная фигура, у которой больше четырех углов — это правильный шестиугольник.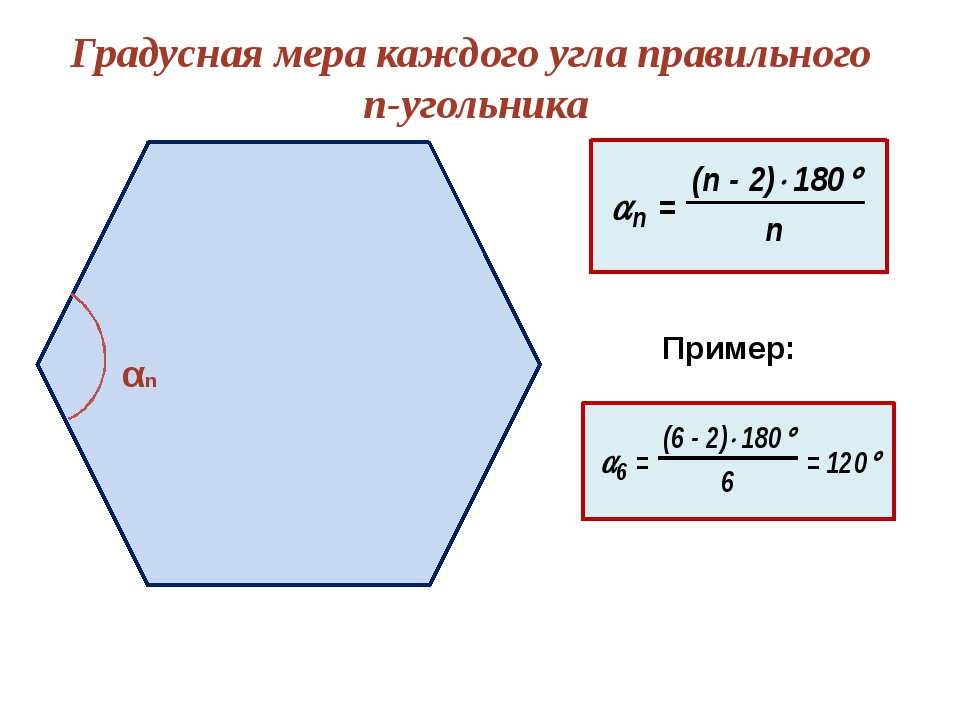 В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.
В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.
Чем он отличается от неправильного?
Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.
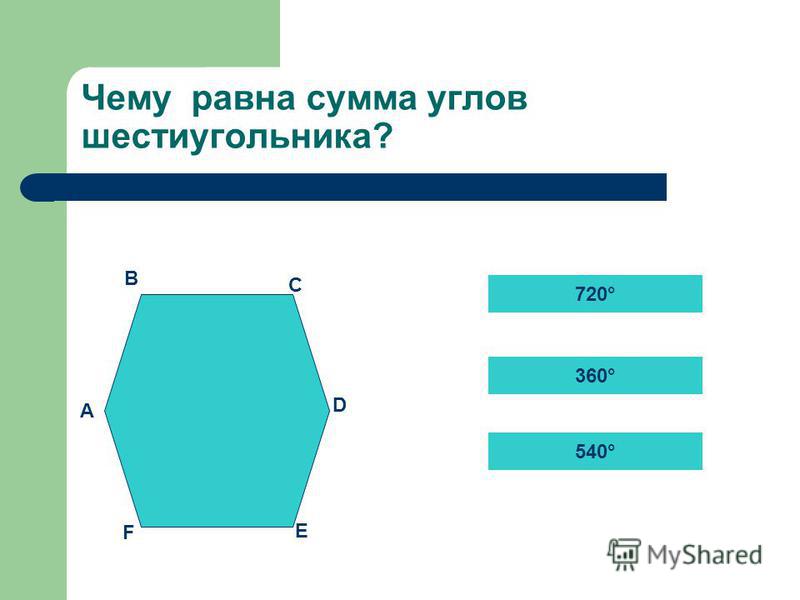
В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.
Какие свойства требуется знать при решении задач?
К тому, что указано выше, следует добавить:
- диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
- сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
- используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.
Введенные обозначения
Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника). Для них используются буквы: α, р, m.
Формулы, которые описывают фигуру
Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.
Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R.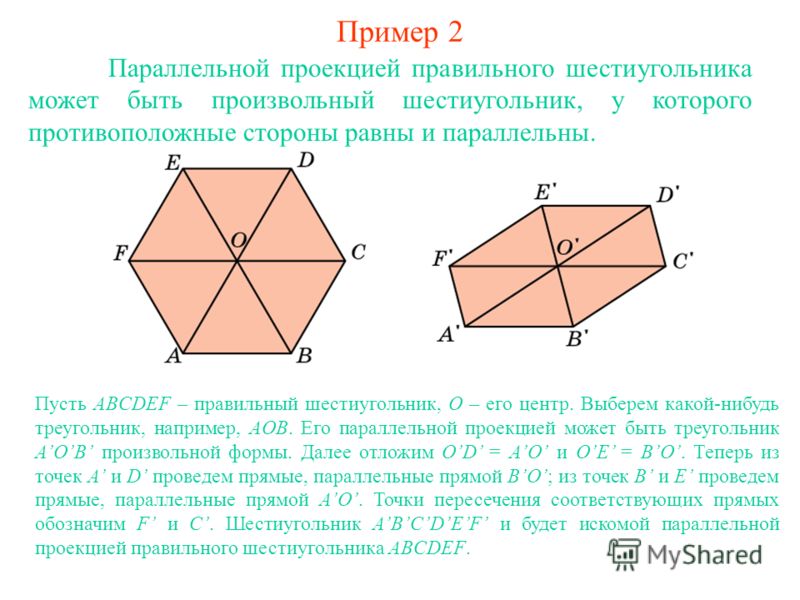 Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a2 * 3 √3) / 2.
Задачи
№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.
Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы. А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r2 = 3,14 * (2√3 )2 = 37,68 (см2).
Осталось сосчитать объем: V = 37, 68 * 4 = 150,72 (см3).
Ответ. V = 150,72 см3.
№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.
Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.
Ответ. r = 1,5 см, Р = 6√3 см.
№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?
Решение. Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Ответ. а = 4√3 см.
почему природа предпочитает шестиугольники? — T&P
При достаточной наблюдательности в живой природе легко обнаружить строгую геометрию. В особом почете оказываются гексагоны — правильные шестиугольники. Почему их так любят пчелы и архитекторы и какие у них преимущества с точки зрения физики, рассказал английский ученый и научный журналист Филип Болл. «Теории и практики» перевели отрывок из книги «Закономерности в природе: Почему живой мир выглядит так, как выглядит», опубликованный на сайте Nautilus.
Как пчелам это удается? Соты, в которых они хранят золотистый нектар, — это чудеса инженерного искусства, набор ячеек в форме призмы с правильным шестиугольником в основании. Толщина восковых стенок строго определена, ячейки немного отклоняются от горизонтали, чтобы вязкий мед не вытекал, и соты находятся в равновесии с учетом влияния магнитного поля Земли. А ведь эту конструкцию без чертежей и прогнозов строят множество пчел, которые одновременно работают и как-то координируют свои попытки сделать соты одинаковыми.
Древнегреческий философ Папп Александрийский думал, что пчелы, должно быть, наделены «геометрическим предвидением». И кто, если не Господь, мог одарить их такой мудростью? Как писал английский энтомолог Уильям Керби в середине XIX века, пчелы — «математики от Бога». Чарльз Дарвин не был в этом уверен и проводил эксперименты, чтобы установить, могут ли пчелы строить идеальные соты, используя лишь приобретенные и врожденные способности, как предполагалось в его теории эволюции. Но все же почему шестиугольник? Это чисто геометрический вопрос. Если вы хотите сложить вместе несколько одинаковых по форме и размерам ячеек таким образом, чтобы они заполняли всю плоскость, подойдут только три правильные фигуры (с равными сторонами и углами): равносторонние треугольники, квадраты и гексагоны. Если выбирать из этих вариантов, то шестиугольные соты потребуют наименьшей общей длины перегородок, в отличие от треугольников и квадратов той же площади. Поэтому в пчелиной любви к гексагонам есть смысл: на изготовление воска тратится энергия, и они стараются минимизировать расходы — точно так же, как строители пытаются сэкономить на стоимости кирпичей.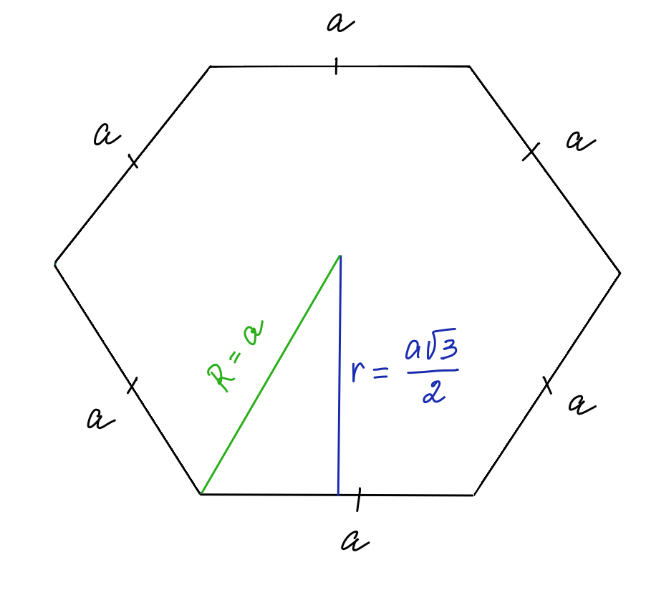 К такому выводу пришли в XVIII веке, и Дарвин объявил, что соты из правильных шестиугольников «идеальны для экономии труда и воска».
К такому выводу пришли в XVIII веке, и Дарвин объявил, что соты из правильных шестиугольников «идеальны для экономии труда и воска».
Дарвин думал, что естественный отбор наделил пчел инстинктами для строительства восковых ячеек, у которых есть весомое преимущество: на них нужно тратить меньше времени и энергии, чем на соты других форм. И хотя кажется, что пчелы действительно обладают особыми способностями в том, что касается измерения углов и толщины стен, мнения ученых по поводу того, насколько активно насекомые их используют, расходятся, поскольку скопления шестиугольников встречаются в природе довольно часто.
Если вы подуете на пузырьки на поверхности воды, чтобы согнать их вместе, то они приобретут форму шестиугольников — или, по крайней мере, приблизятся к ней. Вы никогда не увидите скопище квадратных пузырей: если даже четыре стенки соприкоснутся, они немедленно перестроятся в конструкцию с тремя сторонами, между которыми будут примерно равные углы в 120 градусов — что-то вроде центра эмблемы «Мерседеса».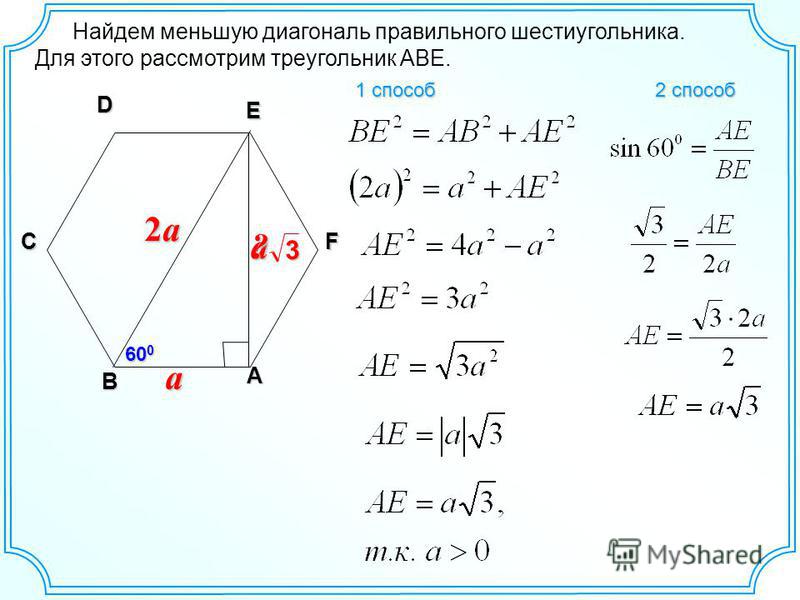
Очевидно, нет никаких организмов, которые работали бы над этими склеенными пузырями, как пчелы над сотами. Рисунок образуется исключительно благодаря законам физики. Так же очевидно, что у этих законов есть определенные предпочтения: например, склонность к трехстороннему соединению стенок пузырей. Аналогичная вещь происходит и с пеной, которая сложнее по строению. Если вы дуете через соломинку в мыльную воду и создаете «гору» пузырей в трехмерном пространстве, вы видите, что их стенки при соприкосновении всегда создают четырехсторонний союз и пересекающиеся мембраны находятся под углом около 109 градусов — это угол, который имеет непосредственное отношение к тетраэдру.
Что определяет форму пузырей и закономерности образования «развилок» мыльных стенок? Природа еще более озабочена экономией, чем пчелы. Пузыри и мыльная пленка состоят из воды (и слоя мыльных молекул), и поверхностное натяжение сжимает поверхность жидкости таким образом, чтобы она занимала наименьшую площадь. Поэтому капли дождя при падении принимают форму, близкую к сферической: у сферы наименьшая площадь поверхности по сравнению с другими фигурами того же объема. На восковом листке капли воды сжимаются в маленькие бусинки по той же причине.
Поэтому капли дождя при падении принимают форму, близкую к сферической: у сферы наименьшая площадь поверхности по сравнению с другими фигурами того же объема. На восковом листке капли воды сжимаются в маленькие бусинки по той же причине.
Поверхностное натяжение объясняет и тот узор, который образуют пузыри или пена. Пена стремится к такой конструкции, при которой общее поверхностное натяжение будет минимальным, а значит, минимальной должна быть и площадь мыльной мембраны. Но конфигурация стенок пузырей должна быть прочной и с точки зрения механики: натяжение в разных направлениях на «перекрестке» должно быть идеально сбалансировано (по тому же принципу нужен баланс при строительстве стен собора). Трехстороннее соединение в пленке из пузырьков и четырехстороннее — в пене — комбинации, которые достигают этого баланса.
Но тем, кто думает (а такие имеются), что соты — это просто застывшее обилие пузырей из теплого воска, трудно будет объяснить, как такие же множества шестиугольных ячеек получаются у бумажных ос, которые при строительстве используют не воск, а комки жеваных волокон древесины и стеблей, из которых они изготавливают подобие бумаги. Мало того, что поверхностное натяжение тут не играет особой роли, но к тому же ясно, что у разных видов ос разные врожденные инстинкты с точки зрения архитектурных решений: они могут значительно различаться.
Мало того, что поверхностное натяжение тут не играет особой роли, но к тому же ясно, что у разных видов ос разные врожденные инстинкты с точки зрения архитектурных решений: они могут значительно различаться.
Хотя геометрия стыков стенок пузырей диктуется взаимодействием механических сил, в ней бессмысленно искать намек на то, какую форму должна принять пена. Обычная пена содержит многогранные элементы различной формы и размера. Присмотритесь — и вы увидите, что их стенки не идеально прямые: они немного изогнуты. Поскольку чем меньше пузырь, тем выше в нем давление газа, стенка маленького пузыря рядом с большим будет слегка выпирать вперед. Более того, у некоторых элементов пять граней, у других — шесть, а у каких-то только четыре или всего три. При небольшой гибкости стенок все эти формы могут образовать четырехстороннее соединение, близкое по композиции к тетраэдру, что необходимо для механической устойчивости. Так что форма пузырей может изменяться. И хотя пену можно изучать с помощью правил геометрии, по своей сути она довольно хаотична.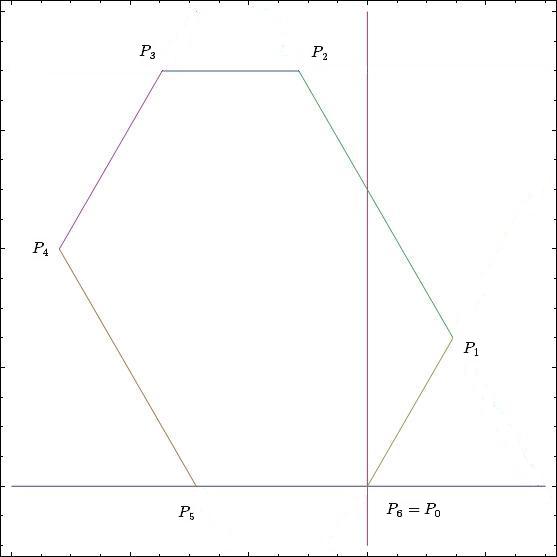
Предположим, что вы могли бы сделать «идеальную» пену, в которой все пузыри одного размера. Какой тогда должна быть их идеальная форма, чтобы общая площадь стенок была наименьшей, но требование для углов на стыке выполнялось? Этот вопрос обсуждался много лет, и долгое время считалось, что идеальной формой будет четырнадцатигранник c квадратными и шестиугольными гранями. Но в 1993 году была открыта немного более экономичная, хотя и менее упорядоченная структура, состоящая из повторяющейся группы из восьми разных форм. Этот более сложный рисунок был использован в качестве вдохновения для пеноподобного дизайна водного стадиона для Олимпиады 2008 года в Пекине.
Здание Национального плавательного комплекса в Пекине © Ben McMillan
Правила, работающие для пузырей в пене, также можно отнести и к другим узорам, которые обнаруживаются в живых организмах. Не только фасеточные глаза мухи состоят из групп шестиугольных ячеек, которые напоминают группы пузырей; еще и светочувствительные клетки в каждой из этих ячеек собираются в гроздья по четыре, что опять же напоминает мыльные пузыри.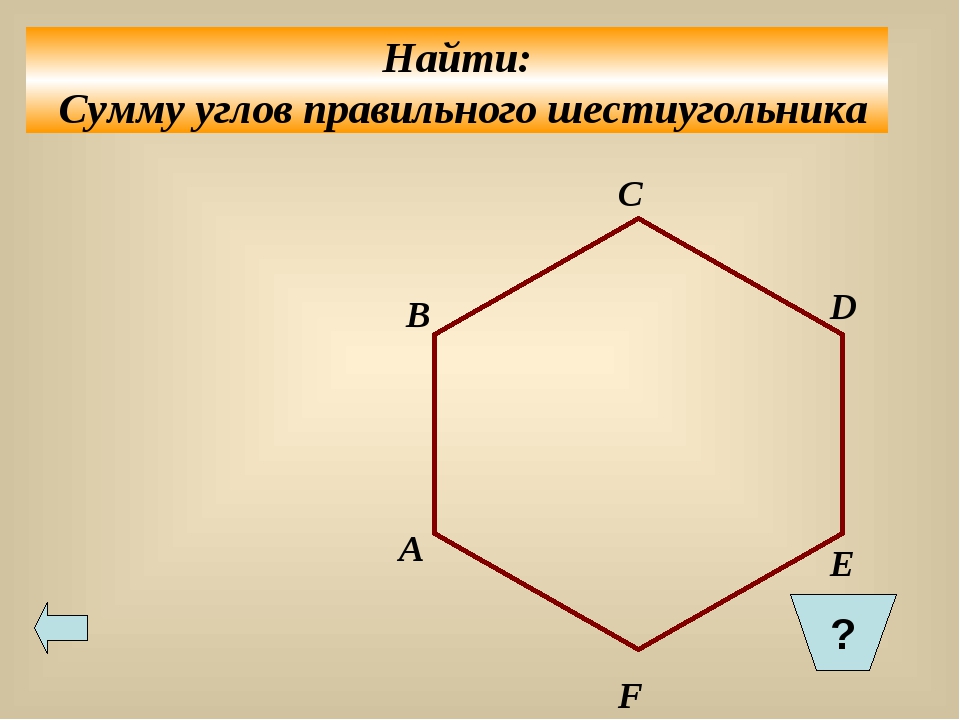 Даже в случае мух-мутантов, у которых таких клеток больше, можно говорить о том, что их организация более-менее идентична поведению пузырей.
Даже в случае мух-мутантов, у которых таких клеток больше, можно говорить о том, что их организация более-менее идентична поведению пузырей.
Из-за поверхностного натяжения мыльная пленка, охватывающая проволочную петлю, натянута ровно, как упругая сетка батута. Но если проволочный каркас погнут, то пленка также будет выгибаться элегантным контуром, который автоматически подсказывает вам наиболее экономичный с точки зрения использования материала способ покрытия пространства, огороженного каркасом. Таким образом, архитектор может увидеть, как построить крышу для здания со сложной архитектурой и потратить минимум стройматериалов. Как бы то ни было, дело не только в экономичности этих так называемых минимальных поверхностей, но и в их красоте и элегантности; вот почему такие архитекторы, как Фрай Отто, использовали их в качестве вдохновения для своих работ.
Эти поверхности минимизируют не только площадь, но и кривизну. Чем круче изгиб, тем больше кривизна. Она может быть положительной (выпуклости) или отрицательной (углубление, впадина или прогиб). Средняя кривизна изогнутой поверхности будет нулевой, если положительная и отрицательная кривизна друг друга уравновешивают. Поэтому лист может быть весь покрыт искривлениями, а средняя кривизна окажется наименьшей. Такая минимально искривленная поверхность разрезает пространство аккуратным лабиринтом коридоров и каналов — сетью.
Средняя кривизна изогнутой поверхности будет нулевой, если положительная и отрицательная кривизна друг друга уравновешивают. Поэтому лист может быть весь покрыт искривлениями, а средняя кривизна окажется наименьшей. Такая минимально искривленная поверхность разрезает пространство аккуратным лабиринтом коридоров и каналов — сетью.
Фрай Отто, Олимпийский стадион в Мюнхене © Atelier Frei Otto Warmbronn
Это явление называют периодической минимальной поверхностью («периодическая» лишь означает, что эта структура повторяется вновь и вновь; другими словами, это постоянная последовательность). Когда такие последовательности были обнаружены в XIX веке, они казались просто математическим курьезом. Но теперь мы знаем, что природа извлекает из них пользу.
Клетки организмов различных видов, от растений до миног или крыс, обладают мембранами с подобными микроскопическими структурами. Никто не знает, зачем они нужны, но они встречаются настолько часто, что логично предположить, что они выполняют какую-то полезную функцию.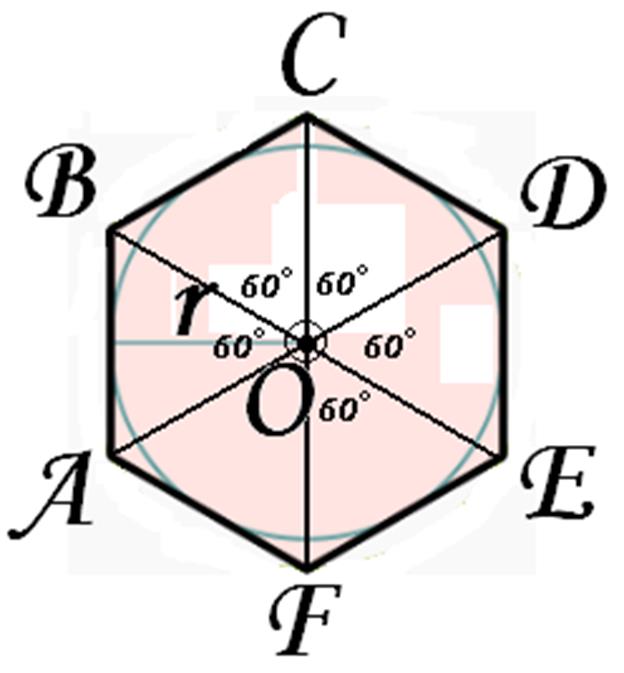 Может быть, они отделяют один биохимический процесс от другого, упраздняя их взаимное влияние друг на друга. Или, возможно, они просто эффективны в качестве «рабочей поверхности», поскольку многие биохимические процессы протекают на мембранах, где могут находиться ферменты и другие активные молекулы. Каковы бы ни были функции таких лабиринтов, вам не понадобятся сложные генетические инструкции для их строительства: законы физики сделают все за вас.
Может быть, они отделяют один биохимический процесс от другого, упраздняя их взаимное влияние друг на друга. Или, возможно, они просто эффективны в качестве «рабочей поверхности», поскольку многие биохимические процессы протекают на мембранах, где могут находиться ферменты и другие активные молекулы. Каковы бы ни были функции таких лабиринтов, вам не понадобятся сложные генетические инструкции для их строительства: законы физики сделают все за вас.
У некоторых бабочек, таких как голубянка малинная, на крыльях есть чешуйки, в которых располагается аккуратный лабиринт из жесткого материала — хитина, — сформированный в виде определенной периодической минимальной поверхности под названием гироид. Взаимодействие между неровностями на чешуйчатой поверхности крыльев приводит к тому, что волны определенной длины — то есть определенные цвета — исчезают, в то время как другие усиливают друг друга. Этот механизм влияет на окраску насекомого.
Скелет морского ежа Cidaris rugosa — пористая совокупность ячеек в форме другого вида периодической минимальной поверхности. Это экзоскелет, который расположен снаружи мягких тканей организма, защитная раковина, на которой растут кажущиеся опасными колючки из того же минерала, который входит в состав мела и мрамора. Открытая решетчатая структура указывает на то, что материал прочный, но при этом нетяжелый, — как пенометалл, который используется в авиастроительстве.
Это экзоскелет, который расположен снаружи мягких тканей организма, защитная раковина, на которой растут кажущиеся опасными колючки из того же минерала, который входит в состав мела и мрамора. Открытая решетчатая структура указывает на то, что материал прочный, но при этом нетяжелый, — как пенометалл, который используется в авиастроительстве.
Чтобы создать упорядоченную конструкцию из твердого неподатливого минерала, эти организмы, по всей видимости, делают макет из мягкой гнущейся мембраны и затем кристаллизуют твердое вещество внутри одной из взаимопроникающих сетей. Другие существа могут использовать минеральную пену для более сложных задач. Из нее они выстраивают конструкции-«трельяжи», которые, как зеркала, могут направлять свет за счет особенностей его отражения от рельефа. Сеть полых микроскопических каналов, напоминающих соты, в хитиновых щетинках необыкновенного морского червя (морской мыши) превращает эти волосоподобные структуры в природное оптическое волокно, которое может преломлять свет, благодаря чему цвет существа может измениться от красного до синевато-зеленого в зависимости от направления освещения.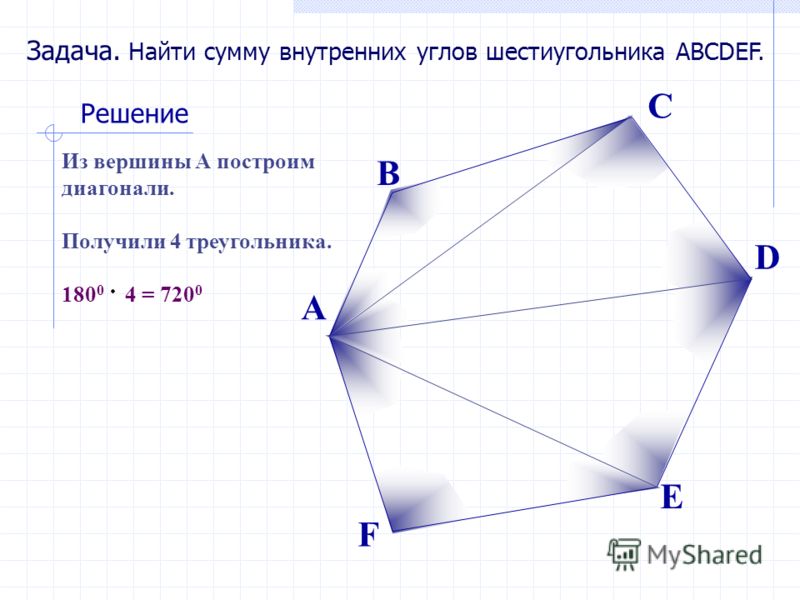 Изменение окраски помогает отпугивать хищников.
Изменение окраски помогает отпугивать хищников.
Этот принцип использования мягких тканей и мембран в качестве макета для формирования упорядоченного минерального экзоскелета широко распространен среди морских обитателей. Некоторые морские губки имеют экзоскелеты, сделанные из минеральных стержней, соединенных по принципу «паутинки» на детских площадках, и они невероятно напоминают формы, которые складываются при столкновении мыльных пузырей в пене, — и тут не может быть никаких разговоров о совпадениях, поскольку архитектуру диктует поверхностное натяжение.
Подобные процессы, известные как биоминерализация, дают впечатляющий результат в таких морских организмах, как лучевики и диатомеи. У некоторых из них встречаются аккуратно выстроенные экзоскелеты, состоящие из минеральных ячеек в виде гексагонов и пентагонов: их можно назвать морскими сотами. Когда немецкий естествоиспытатель (и талантливый художник) Эрнст Геккель впервые увидел эти формы в микроскоп в конце XIX века, он сделал их главным украшением своего собрания рисунков под названием «Красота форм в природе», которое сильно повлияло на художников начала XX века и до сих пор вызывает восхищение. Для Геккеля эти конструкции были доказательством фундаментальной креативности природы — предпочтение порядка и узоров, встроенное в сами законы естества. Даже если сегодня мы не разделяем эту теорию, что-то есть в этой убежденности Геккеля в том, что упорядоченность — это неудержимый импульс живого мира, и мы по праву можем считать его прекрасным.
Для Геккеля эти конструкции были доказательством фундаментальной креативности природы — предпочтение порядка и узоров, встроенное в сами законы естества. Даже если сегодня мы не разделяем эту теорию, что-то есть в этой убежденности Геккеля в том, что упорядоченность — это неудержимый импульс живого мира, и мы по праву можем считать его прекрасным.
Презентация по геометрии «Правильные многоугольники»
Описание презентации по отдельным слайдам:
1 слайд Описание слайда: Раздел: Многоугольники и многогранники Тема урока: Правильные многоугольники Математика, 6 класс Выполнил: учитель математики Кирилюк Светлана Александровна МБОУ СОШ №25 г. Мытищи
Мытищи
Равносторонний треугольник. Квадрат. Вы уже знакомы с такими фигурами как равносторонний треугольник и квадрат. Ответьте на вопросы: В чем отличие равностороннего треугольника от любого другого? Что можно сказать об углах равностороннего треугольника? Чем отличается квадрат от прямоугольника? Сколько градусов составляет каждый угол квадрата? Какие углы называют смежными? Как найти угол смежный данному?
3 слайд Описание слайда:Правильные многоугольники Правильный треугольник Квадрат Правильный пятиугольник Правильный шестиугольник Многоугольник, у которого равны все стороны и все углы, называют правильным. Сегодня на уроке мы познакомимся с правильными многоугольниками.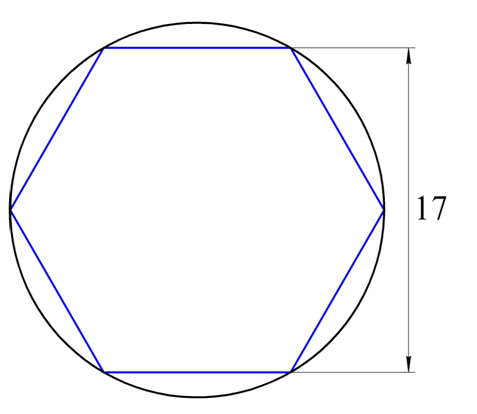 Вы уже знакомы с такими правильными многоугольниками как равносторонний треугольник и квадрат. У них все стороны и углы равны между собой. Существует пятиугольник с такими же свойствами и шестиугольник. Вообще говоря многоугольник, у которого равны все стороны и все углы называют правильным. Таким образом равносторонний треугольник – это правильный треугольник, а квадрат — это правильный четырехугольник.
Вы уже знакомы с такими правильными многоугольниками как равносторонний треугольник и квадрат. У них все стороны и углы равны между собой. Существует пятиугольник с такими же свойствами и шестиугольник. Вообще говоря многоугольник, у которого равны все стороны и все углы называют правильным. Таким образом равносторонний треугольник – это правильный треугольник, а квадрат — это правильный четырехугольник.
Величина углов 108о 120о Каждый угол правильного шестиугольника 120о Каждый угол правильного пятиугольника 108о Рассмотрим правильные пятиугольник и шестиугольник. По свойству правильного многоугольника у них все стороны и все углы будут равны. В правильном пятиугольники все углы будут равны по 108 градусов. Обратите внимание на такой интересный и важный факт: правильный шестиугольник можно составить из правильных треугольников.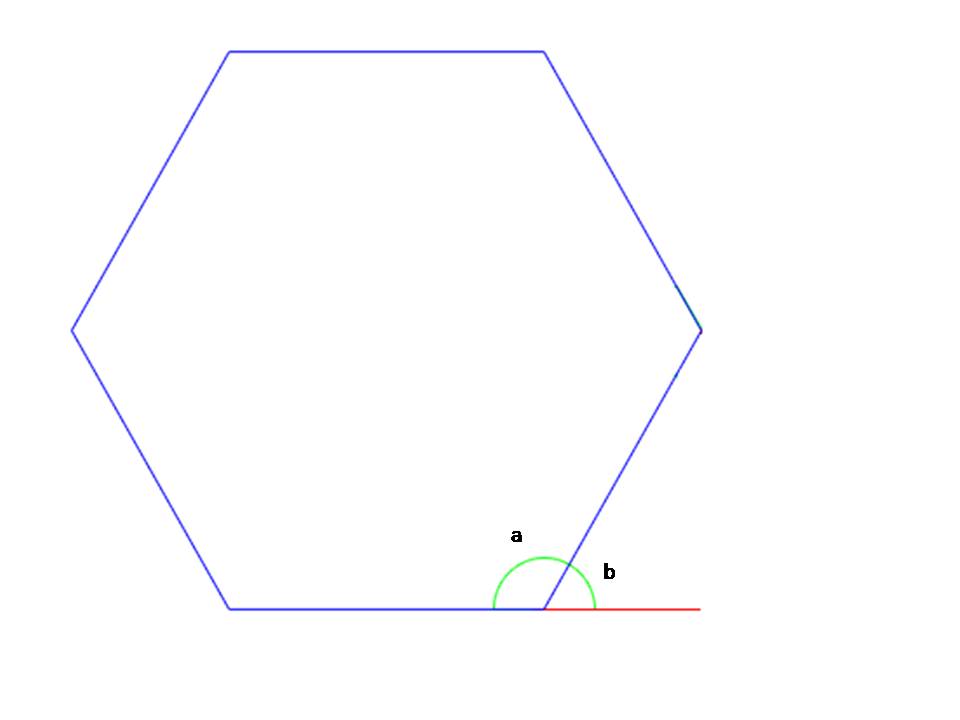 На рисунке показано как правильный шестиугольник состоит из шести правильных треугольников. Причем каждая сторона шестиугольника и каждая сторона всех треугольников равны между собой. Очевидно, что каждый угол правильного шестиугольника равен двум углам правильного треугольника и составляет 120 градусов.
На рисунке показано как правильный шестиугольник состоит из шести правильных треугольников. Причем каждая сторона шестиугольника и каждая сторона всех треугольников равны между собой. Очевидно, что каждый угол правильного шестиугольника равен двум углам правильного треугольника и составляет 120 градусов.
Многоугольники в окружности Все вершины правильного многоугольника лежат на окружности. Правильные многоугольники обладают удивительным свойством: все вершины правильного многоугольника лежат на одной окружности. На рисунке показаны правильные многоугольники, вписанные в окружность. Проведены радиусы к вершинам многоугольников.
6 слайд Описание слайда:Построение многоугольников Построение правильного треугольника Построение правильного шестиугольника Давайте рассмотрим как это свойство можно использовать для построения правильного многоугольника.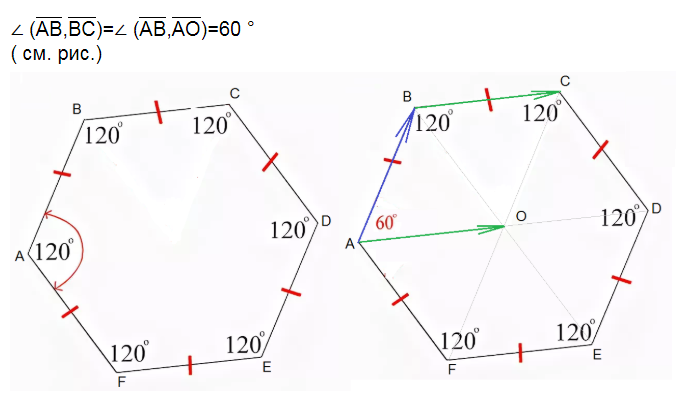 Построить правильный многоугольник можно так: разделить окружность на соответствующее число равных дуг и соединить последовательно точки деления отрезками. Давайте построим правильный шестиугольник. Чтобы разделить окружность на шесть равных частей достаточно «пройтись» по окружности циркулем с шагом, равным радиусу. Затем соединить последовательно все получившиеся точки вы получим правильный шестиугольник. Выполните построение в тетради. Подобным образом можно построить правильный треугольник. Нужно соединить шесть точек на окружности через одну. Выполните построение в тетради.
Построить правильный многоугольник можно так: разделить окружность на соответствующее число равных дуг и соединить последовательно точки деления отрезками. Давайте построим правильный шестиугольник. Чтобы разделить окружность на шесть равных частей достаточно «пройтись» по окружности циркулем с шагом, равным радиусу. Затем соединить последовательно все получившиеся точки вы получим правильный шестиугольник. Выполните построение в тетради. Подобным образом можно построить правильный треугольник. Нужно соединить шесть точек на окружности через одну. Выполните построение в тетради.
Этап исследования Мы с вами познакомились с правильными многоугольниками. Теперь переходим к практической части. Воспользуемся учебным комплектом LEGO «Лунная Одиссея».
8 слайд Описание слайда:Манипулятор LEGO Манипулятор передвигается по рабочему поле по заданной программе.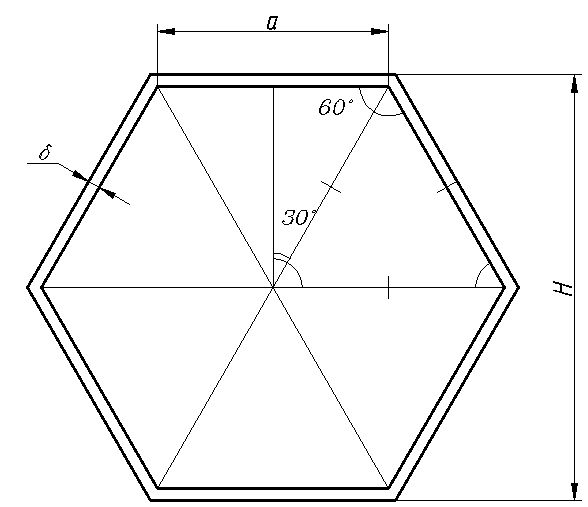 Имеется возможность установить на манипулятор гироскопический датчик. У датчика есть два режима – угол поворота и скорость поворота. Первый режим позволяет измерять угол поворота датчика, а второй – скорость изменения угла (например, при определении события столкновения).Вы умеете составлять программы, выполняя которые манипулятор перемещается на заданное расстояние и поворачивает на указанный угол. Используя эти навыки составим программы по которым манипулятор «опишет» правильные многоугольники.
Имеется возможность установить на манипулятор гироскопический датчик. У датчика есть два режима – угол поворота и скорость поворота. Первый режим позволяет измерять угол поворота датчика, а второй – скорость изменения угла (например, при определении события столкновения).Вы умеете составлять программы, выполняя которые манипулятор перемещается на заданное расстояние и поворачивает на указанный угол. Используя эти навыки составим программы по которым манипулятор «опишет» правильные многоугольники.
Угол поворота 60О 90О 108О 120О ? ? ? ? Вычислите на какой угол нужно повернуть манипулятору при «описании» правильного треугольника, четырехугольника, пятиугольника и шестиугольника. Давайте обсудим, на какой угол должен поворачивать манипулятор для описания угла правильного многоугольника. На представленном чертеже видно, что манипулятор поворачивает на угол, смежный с углом правильного многоугольника. Вычислите на какой угол нужно повернуть при «описании» правильного треугольника, четырехугольника, пятиугольника и шестиугольника.
Вычислите на какой угол нужно повернуть при «описании» правильного треугольника, четырехугольника, пятиугольника и шестиугольника.
Задания для работы в группах Задание 1. Напишите программу, исполняя которую робот опишет равносторонний треугольник. В программе используйте блок «цикл». Запустите программу на выполнение, проверьте соответствие траектории движения манипулятора равностороннему треугольнику. Задание 2. Напишите программу для движения робота по траектории «Квадрат», использующую блок «Цикл». Запустите программу на выполнение, проверьте соответствие траектории движения манипулятора квадрату. Выполните следующие задания.
11 слайд Описание слайда:Звезда Используя правильный пятиугольник можно построить звезду. Посмотрите на представленный чертеж. Давайте определим величины углов звезды. Вычислите на какие углы нужно поворачивать манипулятору для «описания» звезды.
Задания для работы в группах Задание 1. Напишите программу, исполняя которую робот опишет звезду по следующей траектории. Запустите программу на выполнение, проверьте соответствие траектории движения манипулятора. Задание 2. Составьте программу, исполняя которую робот опишет звезду по траектории приведенной на чертеже. Запустите программу на выполнение, проверьте соответствие траектории движения манипулятора. Выполните следующие задания.
13 слайд Описание слайда:Рефлексия Какие многоугольники называются правильными? Чему равны углы в правильном треугольнике, четырехугольнике, пятиугольнике, шестиугольнике? Как можно построить правильный многоугольник? Сколько существует правильных многоугольников? На какой угол поворачивал манипулятор при «обходе» правильных многоугольников? Что для вас оказалось самым сложным? Пригодятся ли в жизни полученные знания? Давайте обсудим… Пришло время подвести итоги.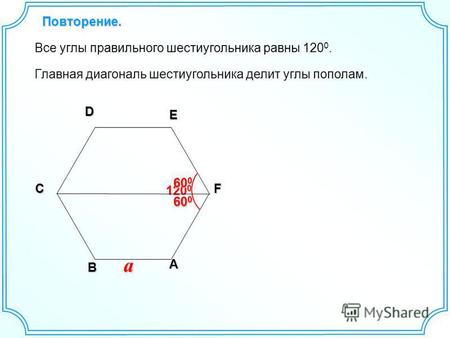 Давайте обсудим, что нового мы с вами сегодня узнали и чему научились.
Давайте обсудим, что нового мы с вами сегодня узнали и чему научились.
Спасибо за внимание! Задайте вопросы, оцените успешность своей сегодняшней работы.
Как нарисовать шестигранник без циркуля
Построение шестигранника может производиться несколькими способами. Удобнее всего использовать стандартный набор чертежных инструментов: циркуль, линейку. Однако, в отсутствие циркуля, фигура этого типа может быть начерчена с помощью рейсшины, угольника заводского изготовления с углами 90/60/30°.
Шестигранники применяются для откручивания и закручивания болтов при ремонте и сборке мебели.
В обоих случаях особенностью построения является элементарное знание основ геометрии. В правильном шестиугольнике длина его стороны всегда равна радиусу окружности, описанной вокруг него, противоположные стороны параллельны, грани сопрягаются под углом 60°.
Способ вычерчивания шестиугольника циркулем, линейкой
Чтобы построить шестигранник при наличии циркуля, достаточно вычертить окружность, найти на ее дуге 6 точек, соединив их отрезками. Для этого достаточно настроить циркуль один раз, отложив на нем значение стороны многогранника. Линейка потребуется для строительства вспомогательных, основных линий.
Метод выглядит следующим образом:
Первый способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.
- циркулем вычерчивается окружность — радиус является размером стороны;
- по линейке проводится радиус — точки пересечения этого отрезка будут углами многоугольника;
- находятся два угла многоугольника — циркуль переставляется в одну из точек пересечения отрезка (проведенный на предыдущем этапе диаметр), на дуге делаются отметки;
- находятся оставшиеся два угла — циркуль перемещается в противоположную точку пересечения отрезка с дугой окружности, создаются отметки пересечения на второй стороне окружности.
Построение правильного шестигранника завершается соединением получившихся углов по линейке. Это самый точный способ, требующий минимального количества чертежного инструмента. При значительном размере сторон (например, крой листового металла, деревянных заготовок) можно использовать шнур с карандашом. Один край шнура крепится к карандашу/маркеру, второй неподвижно фиксируется в центре окружности, затем в точках пересечения диаметра с дугой окружности.
Построение занимает минимальное количество времени, точность целиком зависит от заточки карандаша, наличия фиксатора на циркуле.
Способ вычерчивания шестиугольника без циркуля
Построение правильного шестигранника без циркуля требует обязательного наличия рейсшины — специального инструмента в виде линейки, внутри корпуса которой расположен массивный вал с резиновыми элементами, препятствующими проскальзыванию. Он создан для быстрого изготовления параллельных прямых, обеспечивая высокую точность построений. Качество вычерчивания в данном методе полностью зависит от точности угла 60° в угольнике заводского изготовления, градуирования шкалы линейки.
Способ построения выглядит следующим образом:
Второй способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.
- к одной стороне отрезка прикладывается угольник — короткая сторона совмещена с линией, угол 60° примыкает к концу отрезка изнутри, по гипотенузе угольника проводится линия произвольного размера, который корректируется впоследствии по шкале линейки;
- на листе/заготовке вычерчивается линия — длина ее равна двум размерам стороны многоугольника, края автоматически становятся центрами многогранника;
- операция повторяется при развороте угольника — угол 60° перемещается к противоположной стороне отрезка, центром вращения является длинный катет угольника;
- разворот угольника — теперь центром вращения становится короткий катет угольника, вычерчиваются еще две грани;
- уточнение размеров сторон — на четырех получившихся сторонах многоугольника по линейке откладывается их точный размер;
- строительство двух оставшихся сторон — они расположены параллельно линии, с которой было начато черчение, проводятся по линейке, затем уточняется их размер;
- контроль параллельности — шкала рейсшины совмещается с линией, от которой началось построение фигуры, затем инструмент перемещается вверх/вниз для удостоверения параллельности двух противоположных граней между собой, с этим отрезком
Шестигранник в этом случае вычерчивается дольше, чем в первом способе. Однако так можно построить необходимую фигуру, в отсутствие циркуля, угольником. Технология основана на параллельности противоположных сторон правильного шестиугольника, одинаковых внутренних углах 60°.
Промышленность выпускает угольники как с острыми углами, удобными для данного метода, так и со скругленными.
Третий способ вычерчивания шестиугольника циркулем: a — диаметр, b — сторона шестигранника.
В последнем случае удобнее несколько изменить технологию:
- после вычерчивания центрального отрезка по нему выравнивается рейсшина;
- инструмент откатывается вниз на произвольную величину;
- короткая гипотенуза угольника совмещается с линейкой рейсшины, а не с центральным отрезком;
- скругленный край инструмента не участвует в построении, линия проводится по цельной части гипотенузы.
Операция повторяется с противоположной стороны отрезка, после чего рейсшина разворачивается на 180°, опять совмещается с центральной линией, откатывается вверх для построения двух других сторон многогранника.
Это стандартные способы вычерчивания равностороннего многоугольника с шестью углами, гранями. Они удобны для кроя заготовок любых размеров из разных материалов, в стандартном черчении на ватмане. Обе методики имеют исключительно прикладное значение, так как в профессиональных графических редакторах (AutoCAD, Компас-3D) подобные фигуры создаются автоматически заданием нужных параметров.
Popular
Основы черчения
Строительное
Машиностроительное
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.
Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
Please enable cookies
This website is using a security service to protect itself from online attacks. The service requires full cookie support in order to view the website.
Please enable cookies on your browser and try again.
This website is using a security service to protect itself from online attacks.
This process is automatic, you will be redirected to the requested URL once the validation process is complete.
В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.
- Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
- Углы равны между собой, и величина каждого составляет 120°.
- Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r – радиусы описанной и вписанной окружности.
- Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон – как известно, она соответствует длине радиуса описанной окружности.
Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.
Геометрические построения являются одной из главных частей обучения. Они формируют пространственное и логическое мышление, а также разрешают понять примитивные и натуральные геометрические обоснованности. Построения производятся на плоскости при помощи циркуля и линейки. Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.
Вам понадобится
- Циркуль, линейка, карандаш, лист бумаги.
Инструкция
1. Нарисуйте окружность. Установите некоторое расстояние между ножками циркуля. Это расстояние будет являться радиусом окружности. Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.
2. Постройте точки вершин углов верного шестиугольника. Установите ножку циркуля, в которой закреплена игла, в всякую точку окружности. Игла должна проткнуть начерченную линию. Чем вернее будет установлен циркуль, тем вернее будет построение. Проведите дугу окружности так, дабы она пересекла начерченную ранее окружность. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Начертите еще одну дугу, пересекающую окружность. Вновь переставьте иглу циркуля в точку пересечения дуги и окружности и вновь начертите дугу. Произведите данное действие еще три раза, перемещаясь в одном направлении по окружности. Каждого должно получиться шесть дуг и шесть точек пересечения.
3. Постройте положительный шестиугольник. Ступенчато объедините все шесть точек пересечения дуг с изначально начерченной окружностью. Соединяйте точки прямыми, вычерчиваемыми при помощи линейки и карандаша. Позже произведенных действий будет получен верный шестиугольник, вписанный в окружность.
Шестиугольником считается многоугольник, владеющий шестью углами и шестью сторонами. Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести. Это делается в пару шагов.
Вам понадобится
- Карандаш, лист бумаги, линейка
Инструкция
1. Берется лист бумаги и на нем отмечается 6 точек приблизительно так, как это показано на рис. 1.
2. Позже того, как были подмечены точки, берется линейка, карандаш и с их подмогой ступенчато, друг за ином соединяются точки так, как это выглядит на рис. 2.
Видео по теме
Обратите внимание!
Сумма всех внутренних углов шестиугольника равна 720 градусам.
Шестиугольник – это многоугольник, тот, что владеет шестью углами. Для того, дабы начертить произвольный шестиугольник, надобно проделать каждого 2 действия.
Вам понадобится
- Карандаш, линейка, лист бумаги.
Инструкция
1. Нужно взять в руку карандаш и разметить на листе 6 произвольных точек. В дальнейшем эти точки будут исполнять роль углов в шестиугольнике. (рис.1)
2. Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с ином по начерченным ранее точкам (рис.2)
Видео по теме
Обратите внимание!
Специальным типом шестиугольника является положительный шестиугольник. Он именуется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника дозволено описать либо вписать окружность. Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.
Полезный совет
В природе положительные шестиугольники владеют крупный популярностью. К примеру, вся пчелиная сота владеет положительной шестиугольной формой. Либо кристаллическая решетка графена (модификация углерода) тоже владеет формой положительного шестиугольника.
Как возвести тот либо другой угол – крупной вопрос. Но для некоторых углов задача невидимо упрощается. Одним из таких углов является угол в 30 градусов. Он равен ?/6, то есть число 30 является делителем 180. Плюс к этому его синус вестим. Это и помогает при его построении.
Вам понадобится
- транспортир, угольник, циркуль, линейка
Инструкция
1. Для начала разглядим особенно примитивную обстановку, когда у вас на руках есть транспортир. Тогда прямую под углом 30 градусов к данной дозволено легко отложить с поддержкой него.
2. Помимо транспортира существуют и угол ьники, один из углов которых равен 30 градусам. Тогда иной угол угол ьника будет равен 60 градусам, то есть вам необходим визуально меньший угол для построения требуемой прямой.
3. Перейдем сейчас к нетривиальным способам построения угла 30 градусов. Как вестимо, синус угла 30 градусов равен 1/2. Для его построения нам надобно возвести прямоугол ьный треугол ьник. Возможен, мы можем возвести две перпендикулярные прямые. Но тангенс 30 градусов – иррациональное число, следственно соотношение между катетами мы можем посчитать лишь примерно (исключительно, если нет калькулятора), а, значит, и возвести угол в 30 градусов примерно.
4. В этом случае дозволено сделать и точное построение. Возведем вновь две перпендикулярные прямые, на которых будут располагаться катеты прямоугол ьного треугол ьника. Отложим по одной прямой катет BC какой-нибудь длины с поддержкой циркуля (B – прямой угол ). После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Проводя окружность с центром в точке C с радиусом этой длины, обнаружим точку пересечения окружности с иной прямой. Эта точка и будет точкой A прямоугол ьного треугол ьника ABC, а угол A будет равен 30 градусам.
5. Возвести угол в 30 градусов дозволено и с поддержкой окружности, применяя то, что он равен ?/6. Возведем окружность с радиусом OB. Разглядим в теории треугол ьник, где OA = OB = R – радиус окружности, где угол OAB = 30 градусов. Пускай OE – высота этого равнобедренного треугол ьника, а, следственно, и его биссектриса и медиана. Тогда угол AOE = 15 градусов, и, по формуле половинного угла, sin(15o) = (sqrt(3)-1)/(2*sqrt(2)).Следственно, AE = R*sin(15o). Отсель, AB = 2AE = 2R*sin(15o). Строя окружность радиусом BA с центром в точке B, обнаружим точку пересечения A этой окружности с начальной. Угол AOB будет равен 30 градусам.
6. Если мы можем определять длину дуг каким-нибудь образом, то, отложив дугу длиной ?*R/6, мы также получим угол в 30 градусов.
Обратите внимание!
Нужно помнить, что в 5 пункте мы можем возвести угол лишь приближенно, потому что в вычислениях будут фигурировать иррациональные числа.
Шестиугольником называют частный случай полигона – фигуры, образованной большинством точек плоскости, ограниченным замкнутой полилинией. Положительный шестиугольник (гексагон), в свою очередь, также является частным случаем – это полигон с шестью равными сторонами и равными углами. Эта фигура знаменательна тем, что длина всей из ее сторон равна радиусу описанной вокруг фигуры окружности.
Вам понадобится
Инструкция
1. Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на иной ножке, равным длине стороны вычерчиваемой фигуры. Для этого дозволено воспользоваться линейкой либо предпочесть случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая вероятность.
2. Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.
3. Разбейте окружность точками на шесть равных частей. Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.
4. Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна верно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, дабы она пересекла в 2-х точках окружность, начерченную первой.
5. Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с изначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в 2-х точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).
6. Сходственным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении по окружности (неизменно по либо вопреки часовой стрелки). В итоге обязаны быть выявлены шесть точек пересечения дуг с изначально построенной окружностью.
7. Нарисуйте положительный шестиугольник. Ступенчато попарно объедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В итоге будет получен верный шестиугольник. Позже осуществления построения дозволено стереть вспомогательные элементы (дуги и ок
Внутренние углы полигонов
Внутренний угол — это угол внутри формы
Другой пример:
Треугольники
Сумма внутренних углов треугольника составляет 180 °
Давайте попробуем треугольник:
90 ° + 60 ° + 30 ° = 180 °
Это работает для этого треугольника
Теперь наклоните линию на 10 °:
80 ° + 70 ° + 30 ° = 180 °
Еще работает!
Один угол пошел на вверх, на 10 °,
, а другой на вниз на 10 °
Четырехугольники (квадраты и т. Д.)
(У четырехугольника 4 прямые стороны)
Попробуем квадрат:
90 ° + 90 ° + 90 ° + 90 ° = 360 °
Квадрат в сумме дает 360 °
Теперь наклоните линию на 10 °:
80 ° + 100 ° + 90 ° + 90 ° = 360 °
В сумме все равно 360 °
Внутренние углы четырехугольника в сумме составляют 360 °
Потому что в квадрате 2 треугольника…
Сумма внутренних углов в треугольнике составляет 180 ° …
… а для квадрата они составляют 360 ° …
… потому что квадрат можно составить из двух треугольников!
Пентагон
У пятиугольника 5 сторон, и его можно составить из трех треугольников , так что вы знаете, что …
… его внутренние углы в сумме составляют 3 × 180 ° = 540 °
А когда это обычный (все углы одинаковые), то каждый угол будет 540 ° /5 = 108 °
(Упражнение: убедитесь, что каждый треугольник здесь составляет 180 °, и убедитесь, что внутренние углы пятиугольника составляют в сумме 540 °)
Суммарные внутренние углы пятиугольника составляют 540 °
Общие правила
Каждый раз, когда мы добавляем сторону (треугольник к четырехугольнику, четырехугольник к пятиугольнику и т. Д.), Мы добавляем еще на 180 °, к общей сумме:
Итак, общее правило:
Сумма внутренних углов = ( n −2) × 180 °
Каждый угол (правильного многоугольника) = ( n −2) × 180 ° / n
Возможно, поможет пример:
Пример: А как насчет правильного десятиугольника (10 сторон)?
Сумма внутренних углов = ( n −2) × 180 °
= ( 10 −2) × 180 °
= 8 × 180 °
= 1440 °
А для обычного десятиугольника:
Каждый внутренний угол = 1440 ° /10 = 144 °
Примечание: внутренние углы иногда называют «внутренними углами».
Нахождение угла в прямоугольном треугольнике
Угол с любых двух сторон
Мы можем найти неизвестный угол в прямоугольном треугольнике, если нам известны длины двух его сторон .
Пример
Лестница прислонена к стене, как показано.
Что такое угол между лестницей и стеной?
Ответ — использовать синус, косинус или тангенс!
Но какой использовать? У нас есть специальная фраза «SOHCAHTOA», чтобы помочь нам, и мы используем ее так:
Шаг 1 : найдите имен двух известных нам сторон
- Соседний прилегает к углу,
- Напротив , напротив угла
- , а самая длинная сторона — Гипотенуза .
Пример: в нашем примере лестницы нам известна длина:
- сторона Напротив угол «х», который равен 2,5
- самая длинная сторона, называемая Гипотенуза , что составляет 5
Шаг 2 : теперь используйте первые буквы этих двух сторон ( O pposite и H ypotenuse) и фразу «SOHCAHTOA», чтобы найти, какой из синуса, косинуса или тангенса использовать:
SOH… | S ine: sin (θ) = O pposite / H ypotenuse |
… CAH … | C осин: cos (θ) = A djacent / H ypotenuse |
… TOA | T angent: tan (θ) = O pposite / A djacent |
В нашем примере это O pposite и H ypotenuse, что дает нам « SOH cahtoa», что говорит нам, что нам нужно использовать Sine .
Шаг 3 : Поместите наши значения в уравнение синуса:
S дюйм (x) = O pposite / H ypotenuse = 2,5 / 5 = 0,5
Шаг 4 : Теперь решите это уравнение!
грех (х) = 0,5
Далее (поверьте мне на данный момент) мы можем преобразовать это в это:
х = грех -1 (0,5)
Затем возьмите наш калькулятор, введите 0,5 и используйте кнопку sin -1 , чтобы получить ответ:
х = 30 °
И у нас есть ответ!Но что означает sin -1 …?
Итак, функция синуса «sin» принимает угол и дает нам соотношение «противоположность / гипотенуза»,
Но sin -1 (так называемый «обратный синус») идет другим путем…
… это
берет отношение «противоположно / гипотенуза» и дает нам угол.
Пример:
- Функция синуса: sin ( 30 ° ) = 0,5
- Функция обратной синусоиды: sin -1 ( 0,5 ) = 30 °
| На калькуляторе нажмите одну из следующих кнопок (в зависимости от от марки вашего калькулятора): либо «2ndF sin», либо «shift sin». |
На своем калькуляторе попробуйте использовать sin и sin -1 , чтобы увидеть, какие результаты вы получите!
Также попробуйте cos и cos -1 . И загар и загар -1 .
Давай, попробуй.
Шаг за шагом
Вот четыре шага, которые нам нужно выполнить:
- Шаг 1 Определите, какие две стороны мы знаем — противоположную, смежную и гипотенузу.
- Шаг 2 Используйте SOHCAHTOA, чтобы решить, какой из синуса, косинуса или касательного использовать в этом вопросе.
- Шаг 3 Для синуса вычислить противоположное / гипотенузу, для косинуса вычислить смежное / гипотенузу или для касательного вычислить противоположное / смежное.
- Шаг 4 Найдите угол с помощью калькулятора, используя один из sin -1 , cos -1 или tan -1
Примеры
Давайте посмотрим на еще пару примеров:
Пример
Найдите угол подъема плоскости из точки А на земле.
- Шаг 1 Две известные нам стороны — это O pposite (300) и A djacent (400).
- Шаг 2 SOHCAH TOA сообщает нам, что мы должны использовать угол T .
- Шаг 3 Вычислить Напротив / Соседний = 300/400 = 0,75
- Шаг 4 Найдите угол с помощью калькулятора, используя tan -1
Tan x ° = напротив / рядом = 300/400 = 0.75
tan -1 0,75 = 36,9 ° (с точностью до 1 десятичного знака)
Если не указано иное, углы обычно округляются до одного десятичного знака.
Значение шестиугольника — Imperium ad Infinitum
Шестиугольник — это соединительный центр универсальной согласованности, который связывает все вместе и связывает все обратно. Он учит вас больше, чем больше вы смотрите на него и размышляете над ним. Это новые умопомрачительные концепции, острые ощущения и загадки для тех, кто ищет опасности, или безопасный путь домой для тех, кто ищет стабильный центр.
Универсальное геометрическое среднее
Шестиугольник обладает сверхъестественными свойствами.
Во-первых, решает проблему плитки. Шестиугольник — это форма, которую покрывает и лучше всего создает открытое пространство, минимизируя границу , как (человечески) обнаружено в 1999 году Томасом Хейлсом. Это сводит к минимуму количество материала, необходимого для построения этих границ, следовательно, пчелы используют шестиугольники.
Шестиугольник — это также компромисс между многоугольником и кругом, позволяющий строить мозаику примерно по кругу, оставаясь при этом многоугольником со сторонами и углами.Вот почему компании сотовой связи используют гексагональные «соты» для отображения и распределения своих вышек сотовой связи, устроенных аналогично планировке городов в Settlers of Catan.
Шестигранник является универсальным средним и имеет лучший крутящий момент для машиностроения.
Каждый многоугольник имеет равностороннюю форму с одинаковыми углами и равными углами, но шестиугольник отличается. Если к шестиугольнику добавить еще стороны, он будет больше круглым, чем многоугольным.Если вычесть больше сторон, получится больше многоугольника, чем круга.
Это означает, что шестигранник создает наилучший крутящий момент, поэтому его используют в гайках или соединениях труб в общественных туалетах и писсуарах. (Признаюсь, я иногда вижу какие-то восьмиугольные соединения труб общественного туалета, и это меня бесит.)
Гайка, например, с более чем шестью углами, будет легче скользить, потому что углы ее углов не будут такими жесткими. Углы квадратной гайки были бы тяжелее, но площадь поверхности, прилагающей силу / крутящий момент к гайке с четырьмя сторонами, была бы меньше, чем с шестью.
Хотя это правило технически нарушает строгое определение «многоугольника» — десятиугольная форма, десятиугольник, технически все еще является многоугольником, если вы продолжаете добавлять стороны бесконечно, он просто становится все более и более нелепым, как круг.
Круги — это форма, все точки которой одинаково удалены от центра, идеально симметричны со всех углов, наиболее симметричны нагрузка и напряжение. Таким образом, между трехсторонним многоугольником и бесконечной формой (кругом) шестигранный шестиугольник — это точный средний компромисс.
Вот почему шестиугольники структурно стабильны — их регулярность и ровность формы позволяют им повторяться, а их почти округлость обеспечивает максимально идеальное распределение нагрузки.
Нам, живущим в искусственной среде обитания человека, может показаться более очевидным, что квадраты кажутся равносторонними и достаточно симметричными. Почему они не образуются в природе? Очевидно, природа тоже спонтанно признает, что шестиугольник — это точный компромисс между равенством круга (все точки на одинаковом расстоянии от центра, идеально симметричны со всех сторон, наилучшее распределение нагрузки и напряжения) и углами многоугольника: это объяснение согласуется с теориями и иллюстрациями в этом ответе Quora, что природа стремится к энтропии и спонтанным состояниям покоя (круговое равенство), хотя ответ Quora все еще не объясняет, почему природа может выбрать шестиугольник вместо квадрата (соединяющий три вершины могли бы просто вернуться на угол в 90 градусов, возможно).
Опять же, решение проблемы плитки неявно объясняет преобладание в природе, структурную стабильность и оптимальный крутящий момент шестиугольников, не заявляя об этом сознательно или явно: шестиугольников — идеальный компромисс между округлостью и угловатостью.
(Назовите это законом Сатурна.)
Шестиугольник на Сатурне?
Возможно, вы слышали о красном пятне на Юпитере, сильном шторме. Он имеет примерно овальную форму, что подходит для шторма или погодных условий.
Однако вы, возможно, не слышали, что на северном полюсе Сатурна находится массивная шестиугольная буря, достаточно большая, чтобы соответствовать планете Земля.
Ассоциации сильны.
Сатурн — это 6 -я планета от Солнца, а его шестиугольная буря имеет 6-стороннюю форму. Странное совпадение. Также стоит отметить, что Сатурн — римский бог правопорядка, дисциплины, порядка и структуры, что также означает планета в астрологии, и примечательно, что на его поверхности появляется такая четко очерченная структура, состоящая из всего сущего. погода, воздух и газ — опять же, штормовой узор Юпитера — это просто овулярная капля, как и следовало ожидать: такая упорядоченная, структурированная форма на планете структуры и порядка.
Стоит отметить, что совсем недавно (2015 г.) был обнаружен возможный, но еще не подтвержденный и более слабый шестиугольник также на южном полюсе Нептуна (а также более слабая система колец Нептуна, такая как у Сатурна?). Хотя, с одной стороны, это может (частично) подорвать 6-стороннюю форму совпадения 6-й планеты, это также указывает на очень странное слияние шестиугольника на северном полюсе Сатурна, астрологической планеты Материи и шестиугольника на Южный полюс Нептуна, астрологическая планета Духа, действующая как дипольные врата между концептуальными противоположными полюсами.
Символ времени
Гексагональная буря на планете, римский бог Сатурн которой правил временем. Сатурн был богом сезонных сельскохозяйственных работ. Его греческого аналога буквально звали Кронос или Кронос.
Совершенный компромисс шестиугольника между полигональностью и округлостью также подразумевает нечто радикальное в природе самого времени: он по своей сути содержит ритм собственного прерывания, сегментацию времени по сравнению с течением времени.
Поскольку пространство и время тесно связаны, время необходимо для того, чтобы создать что-либо как реальное.
Но реальность — отстой. В мире идей все совместимо. В мире материи твердые объекты сталкиваются и препятствуют друг другу, а некоторые вещи просто не могут сосуществовать. Облом. Жизнь — это боль, но нам нужно быть живыми, чтобы что-то чувствовать. Вот почему реальность должна иногда отменяться посредством случайной отмены и прерывания времени.
Если время — это расстояние, конец времени означает, что все рушится в одну точку и все объединяется, что поочередно звучит как смерть, встреча с Богом, экстатический или оргиастический, в зависимости от того, как вы это интерпретируете. Каждая культура признала это, одним из самых знаковых признаний этого является праздник Сатурналии. Во время Сатурналий иерархия была приостановлена, рабы выходили на свободу весь январь, иногда их ждали хозяева, а церемониальный Владыка Сатурналий был случайно выбран, чтобы давать нелепые произвольные команды, чтобы послать их через верх.
потерять счет времениЭтот ритм встроен в времена года, колесо года. Весна и осень — как перемены и потоки, а лето и зима — как противоположные формы упразднения времени, время остановившееся.
Компромисс шестиугольника между полигональностью и округлостью символизирует этот сезонный компромисс и чередование между течением времени и самоустраняющимся временем, встроенным в природу и ритм самого времени. И все же время существует болезненными, поддающимися количественной оценке приращениями, которые по большей части абсолютно необходимы, чтобы заставить нас ценить время вечеринок, когда время упразднено.Это необходимое чередование заключения и освобождения — это природа времени. Таким образом, шестиугольник представляет время.
Шестиугольник как символ символической, значимой Вселенной
Шестиугольник — это прежде всего символ. Его обычный вид в равносторонней симметричной форме наводит на мысль о человеческом прикосновении, а его близость к округлости при сохранении углов делает его еще более символичным. Это набор линий, углов, пустого и заполненного пространства.Это эстетично, геометрически. Это связующее звено, в котором материя и сознание сходятся и пересекаются.
Все символы представляют собой комбинации некоторой материи, материала или изображения (и, следовательно, энергии), которые соответствуют идее, концепции или значению и, следовательно, буквально являются точкой соединения между материей и сознанием.
Пока сознание существует где-нибудь, вся вселенная пропитана им из-за того, что вся воспринимаемая материя интерпретируется сознанием.Всякая материя потенциально и, следовательно, неизбежно символична.
Таким образом, шестиугольник — это рекурсивный символ, символ символизма, символического порядка Вселенной. Это служит напоминанием о врожденных психических свойствах всей материи, которые допускают существование сознательных организмов, как описано в Гексагональной Доктрине.
Однако на этом не заканчивается. Символ глубоко связан с вопросом , означающим . (Что такое символ? Символ — это то, что имеет значение.Что такое значение?) Шестиугольник — это не только символ эстетической организации Вселенной, но и символ того, что сама жизнь имеет значение.
Вопрос об экзистенциальном значении (в чем смысл жизни, в чем смысл всего?), Кажется, вполне отвечает тексту или символическому определению значения : одно означает другое, одно заменяет другое, одно становится другим, все связано, мы все едины. Текстовое переходное свойство становится пресуществлением и преобразованием, а также перевоплощением.
Эта параллель пришла мне в голову совершенно естественно, когда я посмотрел на страницу значений слова «значение» в Википедии, где символическое и экзистенциальное значения перечислялись бок о бок, и поэтому стало ясно, что одно было ответом на другое … Мне неприятно думать, что все это время он смотрел нам в лицо, и мы так и не поняли этого только потому, что никогда не исследовали наши собственные определения.
, означающее , из , означающее , означает, что что-то заменяет что-то другое, то есть взаимозаменяемость: слов, понятий, вещей, людей, душ.А в чем смысл? Это бесконечная цепочка? Дело в том, что оно охватывает все, бесконечность. Да, это бесконечная цепочка, и проблема не в этом, а в решении, в этом суть.
Наконец, там, где связь и гармония между вещами еще не установлены (например, если Бог не существует и т. Д.), Шестиугольник символизирует императив, что эта связь должна быть создана наукой и силой.
Шестиугольник — символ универсальной согласованности
Единство противоположностей (как я его понимаю) — это когда две противостоящие силы или концепции находят какой-то способ не для компромисса, а для фактического дополнения друг друга или даже для синтеза и интеграции своего существования в одну связную сущность.
Универсальная когерентность — это масштабная концепция, в которой единство противоположностей применяется к каждому явлению во Вселенной, что будет более подробно описано в другом месте.
Все, что я здесь намекаю, это то, что многие специалисты по дизайну заметили двойственную природу шестиугольников — как естественных, так и искусственных, как органических, так и технологических. Таким образом, шестиугольники являются символом вездесущности сознания и значимости, распределенной по всей вселенной, и должны быть постулированы рациональными, логическими, естественными, технологическими объяснениями.Это должно быть объяснено в доктрине Универсальной Связности.
Как это:
Нравится Загрузка …
Диагоналей правильного восьмиугольника в геометрии GRE
Студенты любят пропускать основы, задавая вопросы вроде: Сколько вершин у восьмиугольника? Сколько диагоналей у восьмиугольника? В чем разница между правильным восьмиугольником и ну восьмиугольником? И геометрия GRE действительно углубляется в сложную математику полигонов.
Но прежде чем мы перейдем к этому, я начну с двух сложных математических задач GRE.
Геометрия GRE: задачи многоугольников
1) В правильном пятиугольнике P нарисованы все пять диагоналей. Каков угол между двумя из этих диагоналей в месте их пересечения в вершине пятиугольника?
(А) 12 °
(В) 36 °
(С) 54 °
(Г) 60 °
(В) 72 °
2) Сколько диагоналей у правильного 20-стороннего многоугольника?
(А) 60
(В) 120
(К) 170
(Г) 240
(R) 400
Объяснения этих практических проблем появятся в конце этой статьи блога.Забегайте вперед, нажав здесь.
Полигоны
Во-первых, немного базовой терминологии, чтобы начать это обсуждение. Многоугольник — это любая геометрическая фигура, все стороны которой являются прямыми отрезками. Любой треугольник — многоугольник. Любой четырехугольник (включая трапеции, параллелограммы, ромбы, прямоугольники и квадраты) является многоугольником. Пятиугольник — это 5-сторонний многоугольник. Шестигранник — это 6-сторонний многоугольник. Восьмиугольник — восьмиугольный многоугольник.Круг, парабола или что-либо с изогнутой стороной — это , а не многоугольник.
Точка пересечения двух сторон многоугольника называется вершиной . Количество вершин многоугольника всегда равно количеству его сторон.
Еще один важный факт о многоугольнике касается суммы углов. Возможно, вы знаете, что сумма трех углов в любом треугольнике равна 180 °. Возможно, вы даже знаете, что сумма четырех углов в любом четырехугольнике равна 360 °. Этот образец является обобщающим.Сумма всех n углов в любом n-стороннем многоугольнике:
сумма углов = (n — 2) * 180 °
Таким образом, любой пятиугольник (n = 5) будет иметь углы в сумме 3 * 180 = 540 °. У любого шестиугольника (n = 6) углы в сумме составляют 4 * 180 = 720 °. Любой восьмиугольник (n = 8) будет иметь углы в сумме 6 * 180 = 1080 °. (См. Блог о геометрических формулах GRE)
Наконец, есть это парадоксальное слово « обычный ». На обыденном языке «обычный» означает «обычный, ничем не примечательный, банальный.«В геометрии это означает прямо противоположное! Форма является правильной тогда и только тогда, когда она одновременно и равносторонняя, и равноугольная, то есть тогда и только тогда, когда все стороны имеют одинаковую длину и все углы равны. «Обычная» версия любого многоугольника — это самая элитная, наиболее симметричная возможная версия этого многоугольника. «Правильный треугольник» — это то, что мы называем равносторонним треугольником. «Правильный четырехугольник» — это квадрат. Для более высоких полигонов вы, скорее всего, увидите обычную версию на GRE, потому что тест (как и все математики) любит симметрию.
Диагонали многоугольника
Теперь мы можем поговорить о диагоналях. Диагональ — это любая линия, проходящая внутри многоугольника, которая соединяет две несмежные вершины. Что это значит? Во-первых, начиная с любой вершины, смежная вершина — это либо вершина, соединенная с начальной вершиной одной стороной многоугольника.
Рассмотрим неправильный четырехугольник:
Начнем с вершины A. Начиная с вершины A, мы соединяемся сторонами этого четырехугольника как с B, так и с D; вершины B и D — это те, которые смежны с вершиной A.Единственная вершина, не соединенная с A стороной четырехугольника, — это C. C — единственная несмежная вершина A, а A — это C. Таким образом, одна диагональ идет от A к C. Нетрудно заметить, что другая идет от B к D. Любой четырехугольник имеет только две диагонали.
Обратите внимание, что треугольников НИКОГДА не имеют диагоналей : если мы начнем с любой вершины треугольника, две другие вершины будут смежными. В треугольнике просто нет несмежных вершин, поэтому диагонали невозможны.Среди четырехугольников есть особые правила для диагоналей параллелограмма и категорий внутри параллелограммов:
Диагонали параллелограмма делят друг друга пополам: то есть точка пересечения двух диагоналей является средней точкой каждой из них.
Ромб — это параллелограмм с четырьмя равными сторонами. Диагонали ромба пересекают друг друга и перпендикулярны.
Прямоугольник — это параллелограмм с четырьмя углами 90 °. Прямоугольники ромба делят друг друга пополам и имеют одинаковую длину.Это связано со старинной уловкой плотников. Когда плотник отрезает две пары одинаковой длины, чтобы сделать стороны дверной или оконной рамы, он знает, что у него есть параллелограмм из-за одинаковой длины, но как он узнает, есть ли у него прямоугольник? Без точного оборудования очень сложно измерить разницу, скажем, между углом 89 ° или 90 °. Что ж, все, что нужно сделать плотнику, — это измерить две диагонали: если эти две легко измеряемые длины равны, то гарантировано, что у него четыре прямых угла!
Квадрат — это параллелограмм, прямоугольник и ромб.Это правильный четырехугольник с четырьмя равными сторонами и четырьмя углами 90 °. Диагонали квадрата делят друг друга пополам, имеют одинаковую длину и перпендикулярны.
Диагонали правильного пятиугольника
Пятиугольник — это любой пятиугольник, сумма углов которого равна 540 °, как мы видели выше. Единственный пятиугольник, который вы можете встретить на GRE, — это самый симметричный, правильный пятиугольник. Поскольку углы равны, мы можем разделить сумму углов на пять.
540 ° / 5 = 108 °
Это угол каждого из пяти углов пятиугольника.
Вот правильный пятиугольник с пятью диагоналями.
Сколько диагоналей у пятиугольника? У любого пятиугольника ровно пять диагоналей. Эти диагонали повторяют форму классической пятиконечной звезды, например, звезды на флаге Соединенных Штатов Америки. Длина и деления этой звезды тесно связаны с этим магическим и мистическим числом, золотым сечением; Сакральная геометрия призвана дать представление о смысле жизни, но вам не нужно знать ничего из этого для GRE!
Как нам найти углы в этой форме? Ну, мы знаем, что каждый большой угол пятиугольника составляет 108 °.Взгляните, например, на треугольник ABC. Этот треугольник — равнобедренный, потому что AB = BC, и мы знаем, что угол ABC = 108 °. Два других угла должны быть равны: назовите их x.
108 ° + х + х = 180 *
2x = 180 ° — 108 ° = 72 °
х = 36 °
Это означает, что угол BAC = угол BCA = 36 °, как и многие другие симметрично связанные углы вокруг формы. Мы могли бы вычесть (угол BAC) из (угла BAE) и получить (угол CAE)
угол CAE = (угол BAE) — (угол BAC) = 108 ° — 36 ° = 72 °
Отсюда мы можем найти много других углов внутри формы.Мы могли бы использовать аналогичные средства, чтобы найти углы, включающие диагонали любого более высокого многоугольника.
Диагонали правильного шестиугольника
Шестиугольник — это любой шестигранный многоугольник, сумма углов которого равна 720 °, как мы видели выше. В правильном шестиугольнике,
каждый угол = 720 ° / 6 = 120 °
Сколько диагоналей у шестиугольника? Начиная с одной вершины, две другие вершины являются смежными, поэтому 3 вершины не являются смежными, что делает возможными три диагонали из одной вершины.От A мы можем провести диагонали к C, D и E.
От каждой вершины по три диагонали. Поскольку существует шесть вершин, вы можете подумать, что всего будет 3 * 6 = 18 диагоналей, но этот метод подсчета учитывает все дважды. Видите ли, диагональ от A до C будет считаться один раз как диагональ от A и еще раз как диагональ от C до A. Таким образом, количество диагоналей в шестиугольнике равно 18/2 = 9. Это могут быть группы по две. виды. Шесть более коротких диагоналей вместе образуют шестигранную звезду, Маген Давид.Три более длинные диагонали образуют всего три симметрично пересекающихся сегмента, то, что в математике называется «вырожденной шестиконечной звездой».
На этих двух диаграммах показаны девять диагоналей правильного шестиугольника. Конечно, шестиконечная звезда просто состоит из двух перекрывающихся равносторонних треугольников, направленных в противоположных направлениях. (Этот геометрический факт привел к обширным мистическим рассуждениям о Звезде Давида в Каббале, но, опять же, вам не нужно понимать никакой мистики для GRE!)
Диагонали правильного семиугольника
Семигранник — это любой семигранный многоугольник (n = 7).Иногда его называют «септагон», но математическое название предпочтительнее «семиугольник». Сумма его углов будет
.(n — 2) * 180 ° = 5 * 180 ° = 900 °
Это означает, что каждый из семи углов правильного семиугольника имеет размер
.каждый угол = 900 ° / 7 = 128,5714286… °
Угловые размеры не целые! Вот почему GRE вряд ли спросит вас что-нибудь о правильном семиугольнике, и именно поэтому вы, вероятно, никогда особо не говорили о правильных семиугольниках в школьной геометрии.Вот почему большинство людей даже не знают, как назвать этого зверя! Их нецелочисленная угловая мера делает их первой «белой вороной» в семействе обычных многоугольников! Я не буду больше ничего говорить о них, потому что они почти никогда не появляются на GRE, но я покажу вам две возможные семиконечные звезды по их диагоналям: эти звезды навязчиво красивы из-за их особой симметрии.
Диагонали правильного восьмиугольника
Восьмиугольник — это любой восьмиугольный многоугольник, сумма углов которого равна 1080 °, как мы видели выше.В правильном восьмиугольнике
каждый угол = 1080 ° / 8 = 135 °
Этот угол является дополнением к углу 45 °. Правильный восьмиугольник — типичная форма знака остановки во многих частях мира.
Сколько диагоналей у восьмиугольника? Сколько вершин у восьмиугольника?
Начиная с одной вершины, две другие вершины являются смежными, поэтому пять вершин не являются смежными, что делает возможными пять диагоналей из одной вершины. От A, B и H — симметричные вершины, поэтому мы можем провести диагонали к C, D, E, F и G.
Логика аналогична шестиугольнику: пять в каждой вершине, восемь вершин, но при этом каждая диагональ считается дважды, поэтому общее число равно 5 * 8/2 = 20. AC и AG — это то, что мы могли бы назвать «3 диагоналями вершин»: их восемь, образующих звезду. AF и AD, каждая из которых параллельна двум сторонам, — это то, что мы можем назвать «четырьмя диагоналями вершин»: восемь из них образуют другую звезду. Наконец, AE подобен диаметру всего восьмиугольника, пересекающему его центр: таких линий четыре, и они образуют вырожденную восьмиконечную звезду.
Точно так же, как шестиконечная звезда состоит из двух перекрывающихся равносторонних треугольников, первая восьмиконечная звезда слева состоит из двух отдельных перекрывающихся квадратов: квадратный ACEG и квадратный BDFG. (Названия этих квадратов напоминают линии на W. 4th Street!) Между этими тремя звездами (считая вырожденный объект справа как «звезду») у нас есть все 20 диагоналей правильного восьмиугольника.
Сводка
Вперед и вверх! Методы, обсуждаемые в этом блоге, могут быть расширены для применения к шестиугольнику (n = 9), десятиугольнику (n = 10) или любому более высокому многоугольнику.Вооружившись этой информацией, вы сможете ответить на все, что вас спросит GRE о диагонали многоугольника! Если при чтении этого блога у вас были моменты «ага», возможно, вы захотите еще раз взглянуть на практические задачи в верхней части, прежде чем читать пояснения ниже.
Объяснение практических проблем
1) Давайте посмотрим на пятиугольник с пятью диагоналями.
Примером угла между двумя диагоналями в вершине может быть угол EBD, где диагонали BD и BE пересекаются в вершине B.
Мы будем следовать логике, изложенной выше.
Треугольник BCD равнобедренный, BC = CD, угол BCD = 108 °. Два других угла равны: назовите их каждый x.
108 ° + х + х = 180 *
2x = 180 ° — 108 ° = 72 °
х = 36 °
Итак, угол CBD = 36 °. Итак, треугольник ABE во всех отношениях равен треугольнику BCD, поэтому угол ABE также должен быть равен 36 °. Таким образом, мы можем вычесть из большого угла в вершине B.
(угол EBD) = (угол ABC) — (угол CBD) — (угол ABE)
(угол EBD) = 108 ° — 36 ° — 36 ° = 36 °
Ответ = (В)
2) Если мы начнем с одной вершины 20-стороннего многоугольника, то с каждой стороны будет по соседней вершине.Не считая этих трех вершин, было бы 17 несмежных вершин, поэтому из любой вершины можно было бы провести 17 возможных диагоналей. Двадцать вершин, 17 диагоналей от каждой вершины, но этот метод учитывает диагонали дважды, как указано выше.
Количество диагоналей = (17 * 20) / 2 = 17 * 10 = 170
Ответ = (C)
Примечание редактора. Этот пост был первоначально опубликован в январе 2014 года и был обновлен для обеспечения актуальности, точности и полноты.
П.С. Готовы улучшить свой GRE? Начни сегодня.
Самые популярные ресурсы
B E L L R I N G E R Четыре угла пятиугольника: 60 , 110 , 136 и 74 . Найдите размер последнего угла. Четыре угла пятиугольника 60 ,
Презентация на тему: «B E L L R I N G E R Четыре угла пятиугольника равны 60 , 110 , 136 и 74 . Найдите размер последнего угла. Четыре угла пятиугольника равны 60 » — стенограмма презентации:
1 B E L L R I N G E R Четыре угла пятиугольника: 60 , 110 , 136 и 74 .Найдите размер последнего угла. Четыре угла пятиугольника — 60 , 110 , 136 и 74 . Найдите размер последнего угла. Какова мера одного угла в правильном шестиугольнике? Какова мера одного угла в правильном шестиугольнике?
2 РЕШЕНИЯ РЕШЕНИЕ №1 У пятиугольника 5 сторон, 5 вершин и 5 углов. У пятиугольника 5 сторон, 5 вершин и 5 углов. Нам дана мера из 4 углов, которые в сумме составляют: 60 ° + 110 ° + 136 ° + 74 ° = 380 °.Нам дана мера из 4 углов, которые в сумме составляют: 60 ° + 110 ° + 136 ° + 74 ° = 380 °. Сумму всех внутренних углов пятиугольника можно найти, используя (n-2) 180. n = 5, поэтому (5-2) 180 = 3 (180) = 540 °. (См. Пример) Сумму всех внутренних углов пятиугольника можно найти, используя (n-2) 180. n = 5, поэтому (5-2) 180 = 3 (180) = 540 °. (См. Пример) пример Итак, последний угол будет 540 — 380 = 160 ° Итак, последний угол будет 540 — 380 = 160 °.
3 РЕШЕНИЯ РЕШЕНИЕ № 2 Сначала найдите сумму всех углов внутри шестиугольника.(n-2) 180 = сумма углов внутри многоугольника. Сначала найдите сумму всех углов внутри шестиугольника. (n-2) 180 = сумма углов внутри многоугольника. Итак, (6-2) 180 = (4) 180 = 720 °. Итак, (6-2) 180 = (4) 180 = 720 °. Поскольку в шестиугольнике шесть углов, и поскольку каждый из них должен быть одинаковой меры (шестиугольник правильный), мы можем разделить 720 на 6 или 720/6 = 120 °. Поскольку в шестиугольнике шесть углов, и поскольку каждый из них должен быть одинаковой меры (шестиугольник правильный), мы можем разделить 720 на 6 или 720/6 = 120 °.
4 Подробнее о ПОЛИГОНАХ: А как насчет углов ВНЕШНИХ многоугольников? НАРУЖНЫЕ углы многоугольника — это «ЛИНЕЙНЫЕ ПАРЫ» ВНУТРЕННИХ УГЛОВ. Обратите внимание на ниже: 1 2 3 4 5 6 ∠ 1, ∠ 2, ∠ 3, ∠ 4, ∠ 5 и ∠ 6 — все ВНЕШНИЕ углы шестиугольника. Каждый из них образует линейную пару с ВНУТРЕННИМИ углами фигуры.
5 Теорема о внешнем угле многоугольника Для любого многоугольника сумма измерений внешних углов будет равна 360 ° НАБЛЮДАТЬ в исследовании класса.расследование Например, 25 ° 70 ° 85 ° 155 ° 95 ° 110 ° 155 110 + 95 360 °
6 Пример. Предположим, вы наблюдаете правильный шестиугольник. Какова мера каждого внешнего угла? Мы знаем, что сумма внешних углов для любого многоугольника должна составлять 360 °. Мы знаем, что сумма внешних углов для любого многоугольника должна составлять 360 °. Нонагон правильный — все внутренние углы должны совпадать. Следовательно, все внешние углы совпадают.Нонагон правильный — все внутренние углы должны совпадать. Следовательно, все внешние углы совпадают. Имеется 9 сторон, 9 внутренних углов и 9 внешних углов. 360/9 = 40 ° Имеется 9 сторон, 9 внутренних углов и 9 внешних углов. 360/9 = 40 °
7 Как насчет этого? Предположим, у вас есть «равноугольный» 1000-угольник. Какова сумма всех углов 1000-угольника? (1000-2) 180 = 179 640 ° (1000-2) 180 = 179 640 ° А как насчет меры одного угла в 1000-угольнике? 179640/1000 = 179.64 ° Какова же мера одного внешнего угла? Поскольку внутренний угол является линейной парой, 180 — 179,64 = 0,360 °. Итак, какова мера всех внешних углов в 1000-угольнике? (.360) 1000 = 360 ° — как и любой другой когда-либо существовавший многоугольник.
8 Гипотеза о равноугольном многоугольнике В Bell Ringer мы нашли размер одного угла внутри равноугольного многоугольника, используя нашу собственную формулу — (n-2) 180 / n (то есть сумма углов в многоугольнике, деленная на количество сторон / углов в многоугольнике) Теперь мы знаем новый способ найти эту информацию.Для любого равноугольного многоугольника размер только одного угла в многоугольнике может быть найден как 180- (360 / n) Измерение одного внешнего угла. Поскольку это линейная пара с внутренним углом, просто вычтите ее из 180, и вы получите ВНУТРЕННИЙ угол!
9 А? Это означает, что: (n-2) 180 = 180 — 360 Эти двое действительно одинаковы ?? (n-2) 180 = 180 — 360 Эти двое действительно одинаковы ?? n n n n Давайте посмотрим — умножим обе части на «n».(n-2) 180 = 180n — 360 180n — 360 = 180n — 360 (распределительное свойство) Обе формулы одинаковы □
10 Попробуйте это … x x x y y 135 ° 40 ° 50 ° x =? у =? Во-первых, вы можете найти y, потому что это линейная пара с углом 50 °. y + 50 ° = 180 ° -50-50 y = 130 ° Теперь, используя сумму углов многоугольника, мы можем найти x. Один из углов этого перегородки мы можем найти, так как это линейная пара с 40 °. 180-40 = 140 ° Теперь используйте сумму углов многоугольника.У септагона 7 сторон. (7-2) 180. (5) 180 = 900 °. Итак, 130 + 130 + 135 + 140 + x + x + x = 900. 535 + 3x = 900 3x = 365 x = 365/3 = 121,7 °
11 Или Это … y x x x 116 ° 82 ° z Во-первых, y и 116 ° — LP. 180 -116 = 64 ° Все внешние углы должны составлять 360 °. Таким образом, 64 + 82 + x + x + x + 90 = 360 ° 236 + 3x = 360-236 3x = 124 x = 124/3 = 41,3 ° Теперь найдите z. Это линейная пара с x, которая, как мы обнаружили, равна 41.
