Идеи для срисовки амеба обыкновенная (90 фото) » картинки в стиле арт и не только
На этой странице размещено множество изображений из раздела ‘Картинки для срисовки’. Все изображения из подборки Идеи для срисовки амеба обыкновенная можно скачать и просмотреть бесплатно. Также вы можете поделиться содержимым с друзьями в социальных сетях и мессенджерах.
Корненожки амеба обыкновенная
СкачатьСтроение клетки амебы обыкновенной
СкачатьСтроение амебы Протей
СкачатьСтроение простейшего амёбы
СкачатьАмеба 5 класс биология
СкачатьАмёба обыкновенная строение рисунок
СкачатьАмеба и инфузория туфелька
СкачатьСтроение амебы обыкновенной
Амеба краткое описание
СкачатьПроцесс питания амебы
СкачатьПитание амебы
СкачатьСтроение амебы обыкновенной
СкачатьСтроение амебы обыкновенной
СкачатьСаркомастигофоры Саркодовые
СкачатьАмеба обыкновенная и дизентерийная
Схема питания амебы обыкновенной
СкачатьАмеба 5 класс биология
СкачатьАмёба обыкновенная
СкачатьСкачать
Пищеварительная вакуоль амебы
СкачатьСтроение амебы Протей
СкачатьАмёба обыкновенная фагоцитоз
СкачатьОдноклеточные животные строение амебы
СкачатьСтруктура клетки амебы обыкновенной
СкачатьСтроение амебы обыкновенной
СкачатьСтроение и питание амебы
СкачатьАмёба обыкновенная рисунок
СкачатьСтроение амебы 7 класс биология
СкачатьМесто обитания амебы обыкновенной
СкачатьОдноклеточные строение амебы
СкачатьВыделительная система амебы обыкновенной
СкачатьСреда обитания амебы обыкновенной
СкачатьАмёба обыкновенная кратко
СкачатьАмёба обыкновенная
Амеба одноклеточная
Амёба обыкновенная из пластилина
Корненожки амеба обыкновенная
Строение простейшего амёбы
СкачатьАппликация амебы обыкновенной
СкачатьОрганоиды амебы обыкновенной
Строение амебы Протей
СкачатьАмеба рисунок
СкачатьБиология амеба строение
СкачатьАмёба обыкновенная описание
СкачатьАмеба Протей рисунок
СкачатьАмеба царство
СкачатьДыхание амебы Протей
СкачатьМодель амебы обыкновенной
СкачатьАмёба обыкновенная 7 класс
СкачатьРазмножение амебы Протей
СкачатьЯдро амебы обыкновенной
СкачатьБудь проще амеба
СкачатьАмеба вектор
СкачатьАмеба Марина
СкачатьСаркомастигофоры Саркодовые
СкачатьСтроение амебы Протей
СкачатьСтроение амебы протея схема
СкачатьСтроение амебы Протей
СкачатьКлассификация амебы обыкновенной
Амеба Протей Amoeba Proteus
СкачатьСтроение амебы Протей
СкачатьСтроение амебы 7 класс биология
СкачатьСтроение амебы обыкновенной
СкачатьАмеба фраджилис
Амёба обыкновенная схема
СкачатьПроцессы амебы обыкновенной
СкачатьСтроение амебы Протей
СкачатьСтроение амебы 7 класс биология
СкачатьАмеба веррукоза
СкачатьАмёба обыкновенная 7 класс биология
СкачатьПитание амебы Протей
СкачатьАмеба Протей рисунок
СкачатьВнешнее строение амебы биология 7 класс
СкачатьКишечная амеба строение
СкачатьПищеварительная вакуоль амебы
СкачатьПитание амебы фагоцитоз
СкачатьАмеба 5 класс биология
Строение амебы Протей 7 класс
СкачатьСтроение амебы Протей
СкачатьАмёба обыкновенная 5 класс биология
СкачатьАмёба обыкновенная эндоплазма
СкачатьВыделение амебы обыкновенной
СкачатьСтроение амёбы обыкновенной рисунок с подписями
Питание амебы рисунок
СкачатьСтроение одноклеточной амёбы обыкновенной
СкачатьКласс Саркодовые Sarcodina
СкачатьСтроение амебы Протей Amoeba Proteus
СкачатьАмеба эвглена инфузория
СкачатьСтруктура амебы обыкновенной
СкачатьКрыло мельчайшего жука • Пётр Петров, Ирина Панина • Научная картинка дня на «Элементах» • Энтомология
Это перышко — вовсе не перышко, а целое крыло! Хотя и не птичье, а жучиное, и длина его — всего лишь около полумиллиметра.
Примерно так выглядят крылья самых маленьких жуков — представителей семейства перокрылок (Ptiliidae). В этом семействе есть и сравнительно крупные виды, имаго (взрослые особи) которых достигают 4 мм в длину, но у большинства видов длина тела имаго не превышает 1 мм. А необычное крыло на микрофотографии принадлежит мельчайшему известному науке представителю семейства — центрально- и южноамериканскому виду
Scydosella musawasensis — не только самый маленький жук, но и самое маленькое свободноживущее (непаразитическое) насекомое. Еще меньше среди взрослых насекомых бывают только некоторые наездники — перепончатокрылые паразитоиды, личинки которых развиваются внутри других насекомых (у мельчайших наездников — внутри яиц других мелких насекомых), при этом рано или поздно убивая своего хозяина (см.
картинку дня Самое маленькое насекомое). Но из насекомых, развивающихся «на свободе», никого меньше сцидозеллы найти пока не удалось.
Эти род и вид были впервые описаны в 1999 году по экземплярам из Центральной Америки, собранным еще в 1955 году. Родовое название Scydosella дано за некоторое сходство с другими мелкими жуками — сцидменинами (подсемейство Scydmaeninae семейства коротконадкрылых жуков, или стафилинид), а видовой эпитет musawasensis образован от названия деревни Мусавас (Musawás) в Никарагуа. Так что по-русски это насекомое можно назвать «сцидозелла мусавасская».
Почему же мельчайшие перокрылки обладают такими странными крыльями, похожими на птичьи перья, с крыловой пластинкой как стержень и бахромой из длинных щетинок по краю, подобным бородкам птичьего пера (см. картинку дня Стержень, бородки и крючки)? Подобные крылья независимо возникали в ходе эволюции при миниатюризации во многих группах летающих насекомых: не только у жуков, но и у мельчайших перепончатокрылых (наездников-яйцеедов из разных семейств), трипсов и некоторых других.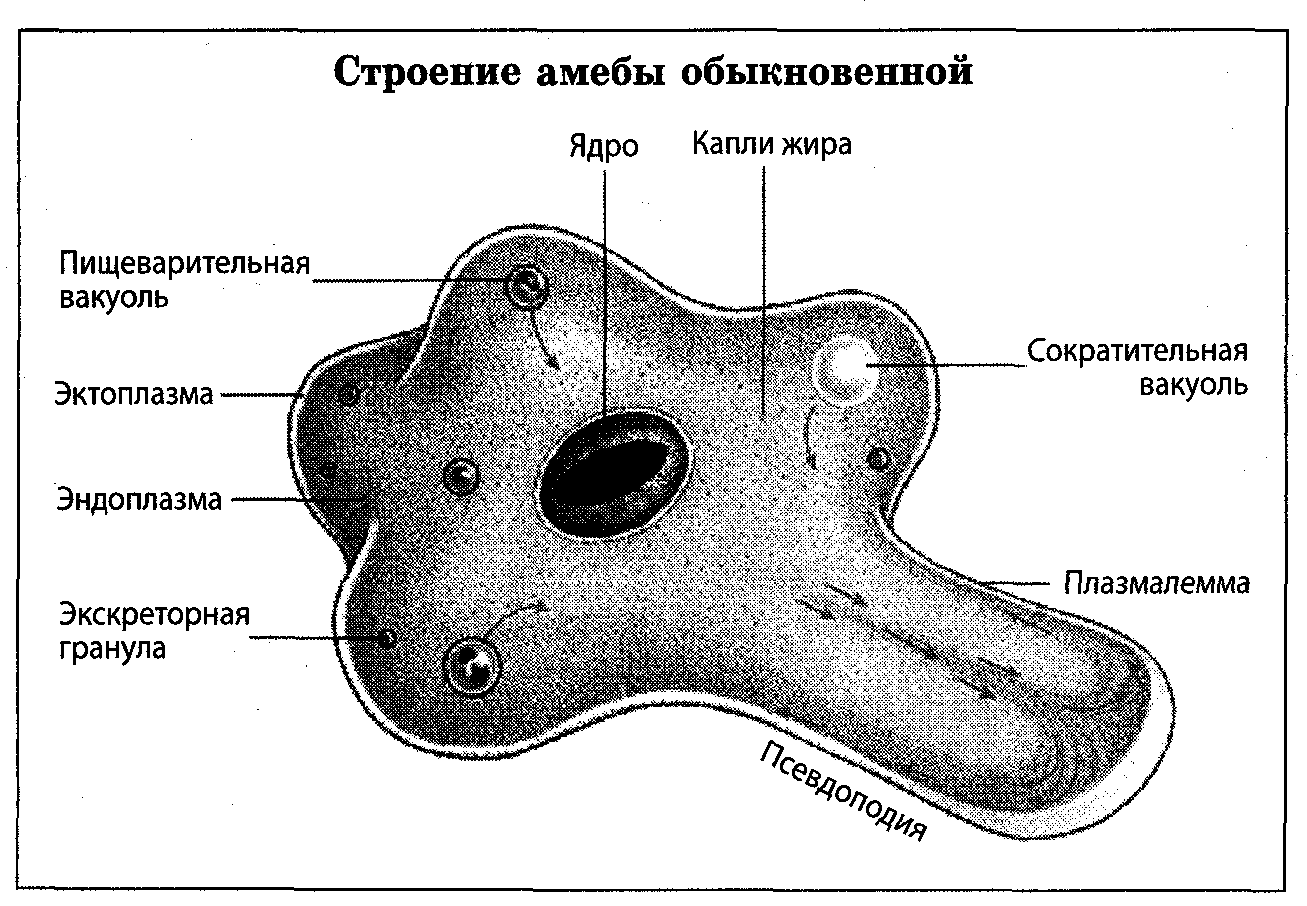
Независимое возникновение такого строения в разных группах микронасекомых — конечно, не случайность. Дело в том, что в ходе эволюции при уменьшении размеров летающих насекомых принципиально меняется соотношение сил, действующих на тело в полете. Держаться в воздухе крошечному насекомому легче, чем крупному, потому что соотношение сил вязкого трения и силы тяжести (веса тела) при уменьшении размеров смещается в пользу трения, но при этом в воздухе вокруг крыльев образуется меньше завихрений (турбулентностей), за счет которых во многом и летают обычные, более крупные насекомые. В результате полет мельчайших насекомых оказывается похож не столько на полет как мы его знаем, сколько на плавание.
Крыло мельчайшего жука испытывает в воздухе такое воздействие аэродинамических сил, какое подобное ему крыло намного больших размеров, сравнимое с крылом голубя (или одной из самых крупных бабочек, что примерно то же самое), испытывало бы не в воздухе, а в очень вязкой жидкости, например в глицерине.
Длинные периферические (окаймляющие по краю) щетинки на крыльях микронасекомых создают структуру, подобную опахалу птичьего пера, состоящему из отдельных бородок, но при этом в полете почти не пропускающему воздух. Перовидные крылья намного легче, чем могли бы быть, если бы площадь, занятая щетинками, была бы заполнена сплошной мембраной крыловой пластинки, и благодаря вязкому трению задерживают значительную часть воздуха, сквозь который движется крыло. Причем чем меньше жук, тем длиннее (относительно длины крыла) периферические щетинки его крыла и тем их меньше, а крыловая пластинка — тем ýже.
Похожие тенденции наблюдаются и среди других микронасекомых с перовидными крыльями, но у крыльев мельчайших жуков есть две уникальных особенности. Во-первых, если рассмотреть периферические щетинки их крыльев при большом увеличении, мы увидим, что сами эти щетинки, подобно бородкам первого порядка на перьях у птиц, покрыты, в свою очередь, довольно длинными выростами, отчасти напоминающими бородки второго порядка на птичьих перьях, хотя и расположенными не в одной плоскости, а по всему диаметру щетинки.
По-видимому, эти выросты еще сильнее уменьшают проницаемость бахромы из щетинок для воздуха, при этом лишь ненамного увеличивая массу крыла.
Во-вторых, из всех микронасекомых только жуки умеют складывать свои крылья под надкрыльями (видоизмененными передними крыльями, которые имеются почти у всех жуков и служат чехлами, защищающими сложенные задние крылья, когда жук не использует их для полета). Крошечные крылья микрожуков сложены под надкрыльями в несколько раз: согнуты в четырех или пяти местах, а щетинки согнуты у основания. Пока не вполне понятно, как жукам удается разворачивать свои перовидные крылья перед полетом и аккуратно прятать их под надкрылья после приземления, но ясно, что в этом процессе участвуют и неравномерно распределенные упругие участки крыла, и специальные выросты на надкрыльях и под надкрыльями, и особые движения брюшка.
Долгое время среди энтомологов было распространено мнение, что мельчайшие жуки наверняка летают намного хуже, чем их более крупные родственники (хотя никто из жуков не относится к лучшим летунам среди насекомых).
Но когда в лабораторных условиях удалось заснять полет перокрылок из числа самых миниатюрных, оказалось, что для своих размеров они летают очень неплохо: и довольно быстро, и весьма маневренно.
При этом их крылья совершают в полете движения, сильно отличающиеся от движений крыльев более крупных жуков. Самое заметное отличие — огромная амплитуда взмахов крыльев, вершины каждого из которых описывают в полете широкую восьмерку, при этом схлопываясь не только вверху, над головой (что встречается у многих летающих насекомых), но и внизу, под брюшком, что ни у каких других насекомых не наблюдалось. Кроме того, мельчайшие перокрылки с довольно большой амплитудой размахивают при полете надкрыльями, в отличие от других жуков, у которых надкрылья во время полета почти не движутся относительно тела. Участвуют ли движения надкрыльев в создании подъемной силы, или помогают уменьшить колебания тела в полете, или же их взмахи — лишь побочный эффект широких взмахов перовидных крыльев, — это нам еще предстоит выяснить.
Фото из статьи A. A. Polilov, N. I. Reshetnikova, P. N. Petrov, S. E. Farisenkov, 2019. Wing morphology in featherwing beetles (Coleoptera: Ptiliidae): Features associated with miniaturization and functional scaling analysis, с изменениями.
Петр Петров, Ирина Панина
The Arclight Photo Cinerama Dome Photograph Amoeba Music
Художественная фотография поездки по бульвару Сансет.
НАЗВАНИЕ: Amoeba and The Arclight
Голливуд, Калифорния 2007
Оригинальная художественная фотография Майана Соффиа.
➤➤➤ ОТПЕЧАТКИ НЕ МАТОВЫЕ И НЕ В РАМКИ. ЧТОБЫ ОФОРМИТЬ ЭТО ИЗОБРАЖЕНИЕ, ПОЖАЛУЙСТА, НАЖМИТЕ ЗДЕСЬ: https://etsy.me/3DHvvHr
➤ДЕТАЛИ:
Репродукции меньшего размера создаются мной в моей личной мастерской. Я выбрал красивую архивную глянцевую бумагу плотностью 300 г/м2, которую люблю за насыщенность цвета и тонкий блеск. Я также использую пигментные чернила. При правильном отображении и хранении эти отпечатки прослужат вам всю жизнь.
Подписано на обороте и будет отправлено от меня.
Крупные отпечатки печатаются в проверенной профессиональной лаборатории на высококачественной архивной глянцевой бумаге. Они доставляются прямо из лаборатории.
Все заказы тщательно упаковываются и обычно отправляются в течение 2–4 рабочих дней.
———————————————— ———
➤ Доступны холщовые накидки, отпечатки в рамках и нестандартные размеры. Напишите мне в любое время!
➤ Индивидуальные наборы со скидкой можно найти здесь: https://etsy.me/3uZuPKX
➤ ПРИНТЫ В РАМКАХ можно найти здесь: https://etsy.me/3vAk5BK
Обратите внимание:
Любое размытие или текстура на изображении являются преднамеренными. Рамки на фотографиях в листинге служат только в качестве примера. Рамка и коврик не включены в этот список. Цвета могут отображаться неточно из-за различий в калибровке монитора. Международные покупатели несут ответственность за любые таможенные сборы, налоги или сборы.
Если вы хотите, чтобы ваше изображение было преобразовано в черно-белое, пожалуйста, оставьте мне сообщение при оформлении заказа.
ПОКУПАЙТЕ БОЛЬШЕ ИЗ МОЕЙ КОЛЛЕКЦИИ ИСКУССТВ ЗДЕСЬ:
➤ Лос-Анджелес: https://etsy.me/3e89kxd
➤ Сан-Франциско: https://etsy.me/2xVu8qZ
➤ Дерево Джошуа: https://etsy.me/2VeMriY
➤ Сан-Диего: https://etsy.me/2UQVFTw
➤ Калифорния: https:/ /etsy.me/2UUvjjC
➤ Аризона, пустыня и юго-запад: https://etsy.me/34leVf3
➤ Тихоокеанский северо-запад: https://etsy.me/2RnWMry
➤ Пляжи западного побережья: https://etsy.me /3e62xDY
➤ Пляжи Восточного побережья: https://etsy.me/3c3HGQ6
➤ Новый Орлеан и Саванна: https://etsy.me/3bZKz4n
➤ Нэшвилл: https://etsy.me/39Pnf7L
➤ Природа: https://etsy.me/2xcCNoQ
➤ Кухня: https://etsy.me/3aSHvqE
➤ Черное и белое: https://etsy.me/2VfFiPg
➤ Наборы для печати: https:// etsy.me/2XkJ6S3
➤ Вернуться в мой магазин здесь: MyanSoffia.etsy.com
Instagram: @MyanSoffia и @MyanSoffiaPhotography
➤➤➤ ЗАХОДИТЕ В МОЙ ГЛАВНЫЙ МАГАЗИН, ЧТОБЫ БОЛЬШЕ О МОИХ РАБОТАХ:
InkPaperCamera.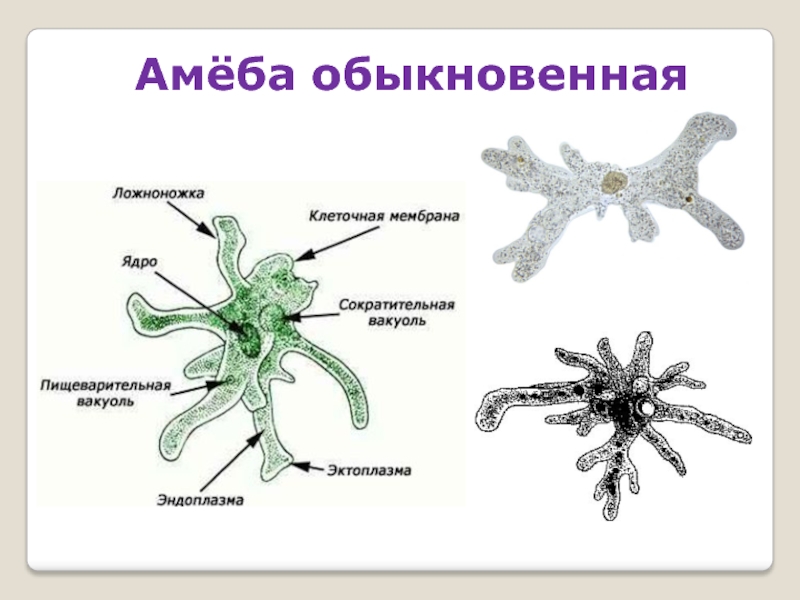
com
ПОРТФОЛИО: MyanSoffia.com
Журнал: MyanSoffia.com/InkPaperCamera
———————————- ————————
Все изображения защищены авторским правом Myan Soffia Photography. Художественные произведения нельзя воспроизводить, перепродавать, копировать, редактировать, изменять, использовать для создания производных работ или использовать в продуктах для продажи. Использование их любым способом без моего разрешения является прямым нарушением законов об авторских правах.
аг.алгебраическая геометрия — изображение трехмерной амебы.
спросил
Изменено 10 лет, 5 месяцев назад
Просмотрено 573 раза
$\begingroup$ В Википедии есть несколько изображений двумерных амеб (спасибо Олегу Александрову за изображения и код Matlab, который он дал для их построения).
Мне было интересно, есть ли где-нибудь изображения трехмерных амеб. Должен ли он выглядеть как толстые пенопластовые пузыри?
- аг.алгебраическая геометрия
- тропическая геометрия
Теперь в Википедии есть трехмерная амеба.
Добро пожаловать. Основная причина сложности изготовления таких амеб заключается в том, что это проекция 4-мерной поверхности (нулевое множество многочлена). Нахождение параметризации множества нулей произвольного многочлена от двух переменных весьма нетривиально. Случай в википедии линейный, поэтому мы можем легко его параметризовать. Теперь этот набор проецируется с помощью $Log|\cdot|$, поэтому нужно быть немного осторожным, какие точки включать, чтобы сделать изображение «красивым», поскольку нули полинома могут быть «далеко» и близко до 0,
Я нарисовал не проекцию параметризованной 4-мерной поверхности, а проекцию множества точек на поверхности, выбранных таким образом, чтобы они были распределены более или менее равномерно.
РЕДАКТИРОВАТЬ: Кроме того, ходят слухи, что у Фрэнка Соттайла есть трехмерные амебы где-то на его веб-странице, но я не смог их найти.
РЕДАКТИРОВАТЬ 2: Теперь амебы никогда не выглядят как мыльные пузыри, но связанные компоненты их комплементов. (Эти компоненты всегда выпуклые, они же мыльные пузыри)
$\endgroup$ 3Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и парольОпубликовать как гость
Электронная почтаОбязательно, но не отображается
Опубликовать как гость
Электронная почтаТребуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.