Семиугольник, виды, свойства и формулы
Семиугольник, виды, свойства и формулы.
Семиугольник – это многоугольник, общее количество углов (вершин) которого равно семи.
Семиугольник, выпуклый и невыпуклый семиугольник
Правильный семиугольник (понятие и определение)
Свойства правильного семиугольника
Формулы правильного семиугольника
Семиугольник в природе, технике и культуре
Шестиугольник, семиугольник, восьмиугольник
Семиугольник, выпуклый и невыпуклый семиугольник:
Семиугольник – это многоугольник с семью углами.
Семиугольник – это многоугольник, общее количество углов (вершин) которого равно семи.
Семиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.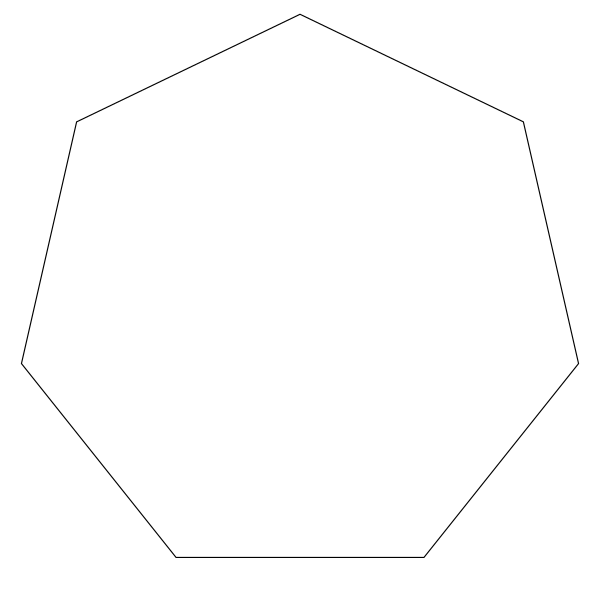
Соответственно выпуклый семиугольник – это семиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Звёздчатый семиугольник – семиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного семиугольника многоугольника. Стороны звёздчатого семиугольника могут пересекаться между собой.
Рис. 1. Выпуклый семиугольник
Рис. 2. Невыпуклый семиугольник
Сумма внутренних углов любого выпуклого семиугольника равна 900°.
Правильный семиугольник (понятие и определение):
Правильный семиугольник – это правильный многоугольник с семью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный семиугольник – это семиугольник, у которого все стороны равны, а все внутренние углы равны 128 4/7° ≈ 128,571°.
Рис. 3. Правильный семиугольник
Правильный семиугольник имеет 7 сторон, 7 углов и 7 вершин.
Углы правильного семиугольника образуют семь равнобедренных треугольников.
Правильный семиугольник можно невозможно построить с помощью циркуля и линейки, но можно построить с помощью циркуля и невсиса, то есть размеченной линейки, на которой можно делать отметки и с помощью которой можно проводить прямые, проходящие через какую-нибудь точку, причём отмеченные на линейке точки будут принадлежать данным линиям (прямым или окружностям).
Свойства правильного семиугольника:
1. Все стороны правильного семиугольника равны между собой.
a1 = a2 = a3 = a4= a5 = a6 = a7.
2. Все углы равны между собой и составляют 128 4/7° ≈ 128,571°.
α1 = α2 = α3 = α4 = α5 = α6 = α7 = 128 4/7° ≈ 128,571°.
Рис. 4. Правильный семиугольник
3. Сумма внутренних углов любого правильного семиугольника равна 900°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного семиугольника O.
Рис. 5. Правильный семиугольник
5. Количество диагоналей правильного семиугольника равно 14.
Рис. 6. Правильный семиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный семиугольник
Формулы правильного семиугольника:
Пусть a – сторона семиугольника, r – радиус окружности, вписанной в семиугольник, R – радиус описанной окружности семиугольника, P – периметр семиугольника, S – площадь семиугольника.
Формулы стороны правильного семиугольника:
Формулы периметра правильного семиугольника:
Формулы площади правильного семиугольника:
Формулы радиуса окружности, вписанной в правильный семиугольник:
Семиугольник в природе, технике и культуре:
В некоторых странах, например, в Великобритании, некоторые монеты имеют правильную криволинейную семиугольную форму.
Некоторые виды кактусовых имеют форму звездчатого семиугольника.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Восьмиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Найти что-нибудь еще?
Похожие записи:
карта сайта
Коэффициент востребованности 230
Пятиугольник, виды, свойства и формулы
Пятиугольник, виды, свойства и формулы.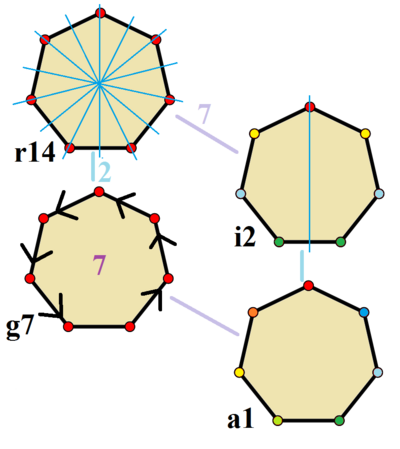
Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.
Пятиугольник, выпуклый и невыпуклый пятиугольник
Правильный многоугольник
Свойства правильного пятиугольника
Построение правильного пятиугольника
Формулы правильного пятиугольника
Правильный пятиугольник в природе, технике и культуре
Пятиугольник, шестиугольник, семиугольник, восьмиугольник
Пятиугольник, выпуклый и невыпуклый пятиугольник:
Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.
Пятиугольник – фигура, состоящая из пяти углов (вершин), которые образуются пятью отрезками (сторонами).
Пятиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.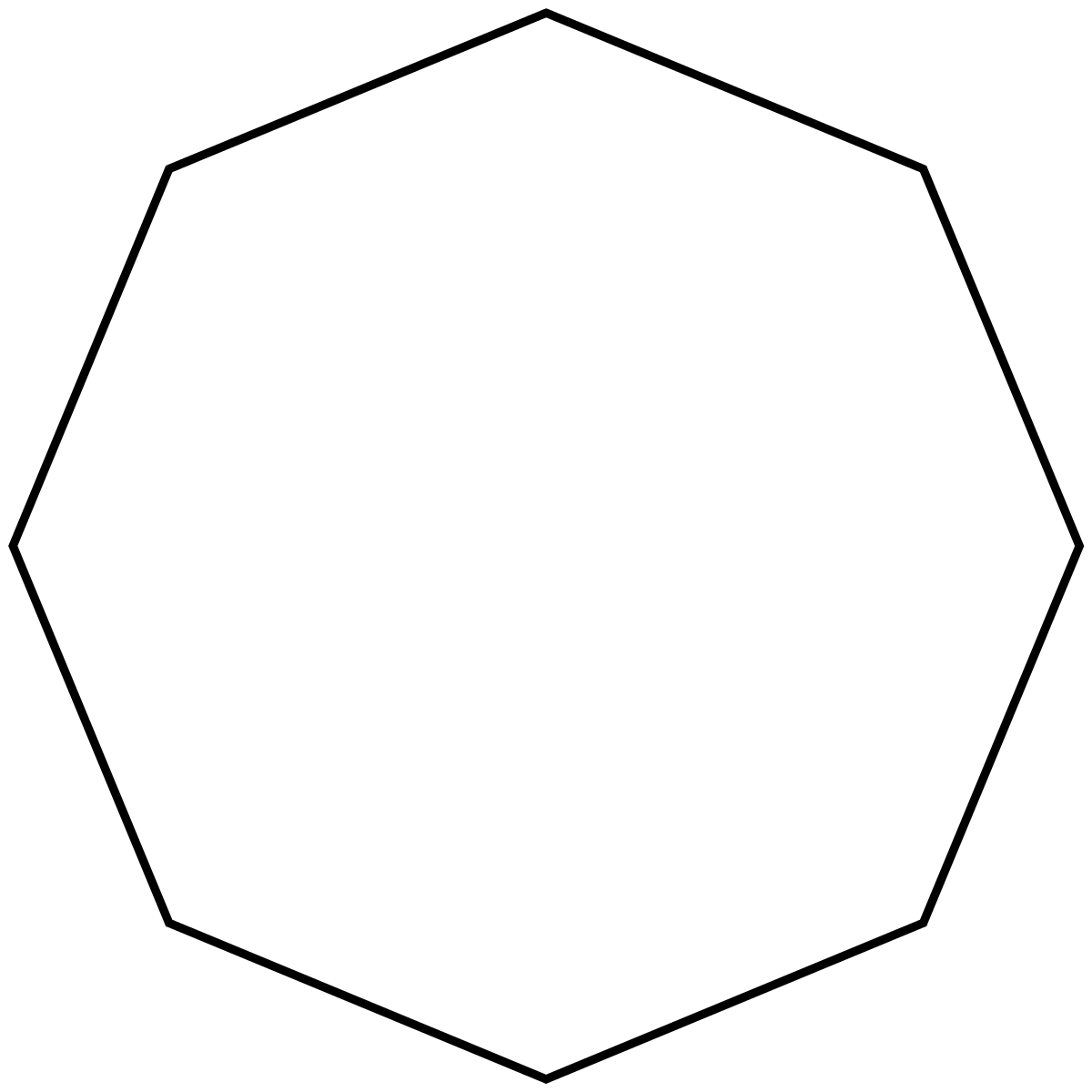
Невыпуклыми являются все остальные многоугольники.
Соответственно
Рис. 1. Выпуклый пятиугольник
Сумма внутренних углов любого выпуклого шестиугольника равна 540°.
Невыпуклый пятиугольник – это пятиугольник, у которого одна часть его точек лежат по одну сторону, а другая часть – по другую от любой прямой, проходящей через две его соседние вершины.
Рис. 2. Невыпуклый пятиугольник
Звёздчатый пятиугольник (пентаграмма) – пятиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного семиугольника многоугольника. Стороны звёздчатого пятиугольника могут пересекаться между собой.
Правильный многоугольник:
Правильный пятиугольник (пентагон) – это правильный многоугольник с пятью сторонами.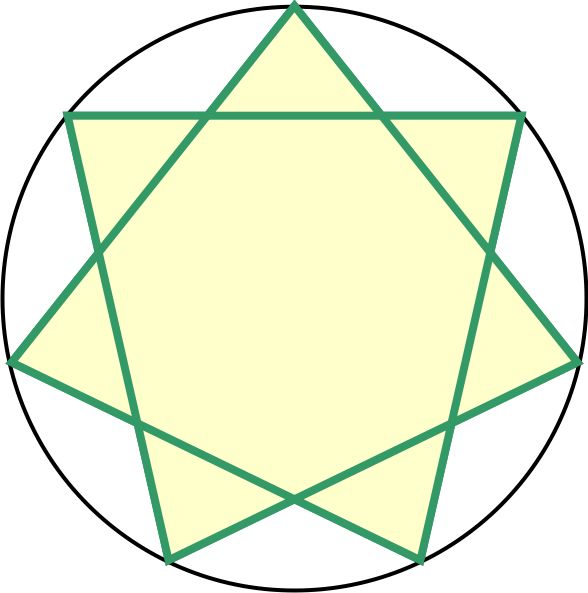
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный пятиугольник – это пятиугольник, у которого все стороны равны, а все внутренние углы равны 108°.
Рис. 3. Правильный пятиугольник
Правильный пятиугольник имеет 5 сторон, 5 углов и 5 вершин.
Углы правильного семиугольника образуют семь равнобедренных треугольников.
Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны.
Свойства правильного пятиугольника:
1. Все стороны правильного пятиугольника равны между собой.
a1 = a2 = a3 = a4= a5.
2. Все углы равны между собой и каждый угол равен 108°.
α1 = α2 = α3 = α4 = α5 = 108°.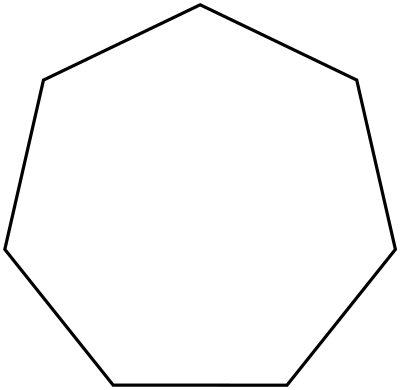
Рис. 4. Правильный пятиугольник
3. Сумма внутренних углов правильного пятиугольника равна 540°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного пятиугольника O.
Рис. 5. Правильный пятиугольник
5. Количество диагоналей правильного пятиугольника равно 5.
Рис. 6. Правильный пятиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр пятиугольника O.
Рис. 7. Правильный пятиугольник
7. Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
Рис. 8. Правильный пятиугольник
8. Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
a / c ≈ 5 / 8 ≈ 0,618.
Рис. 9. Правильный пятиугольник
Построение правильного пятиугольника:
Метод построения правильного пятиугольника вписыванием его в заданную окружность:
1. Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O.
2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
4. Постройте точку C посередине между O и B.
5. Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
9. Постройте правильный пятиугольник AEGHF.
Формулы правильного пятиугольника:
Пусть a – сторона пятиугольника, r – радиус окружности, вписанной в пятиугольник, R – радиус описанной окружности пятиугольника, S – площадь пятиугольника, h – высота пятиугольника, d – диагональ пятиугольника, Ф – отношение золотого сечения.
Формулы площади правильного пятиугольника:
Формулы высоты правильного пятиугольника:
Формулы стороны правильного пятиугольника:
Формулы диагонали правильного пятиугольника:
Формулы радиуса окружности, вписанной в правильный пятиугольник:
Формулы радиуса окружности, описанной вокруг правильного пятиугольника:
Правильный пятиугольник в природе, технике и культуре:
Пентасимметрию можно наблюдать в некоторых фруктах (например, у мушмулы германской), у иглокожих (например, у морских звёзд) и у некоторых растений.
Исследования формирования водяного льда на ровной поверхности меди при температурах 100-140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.
Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.
Паркет, тротуарная плитка, мозайки и т.п. может выкладываться элементами, которые имеют вид пятиугольников.
Государственный знак качества СССР имеет форму пятиугольника с выпуклыми сторонами.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Пятиугольник
Шестиугольник
Семиугольник
Восьмиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Найти что-нибудь еще?
Похожие записи:
карта сайта
Коэффициент востребованности 1 316
правильный семиугольник PNG, векторы, PSD и пнг для бесплатной загрузки
геометрическая форма значок вектор правильный семиугольник
1149*1149
геометрическая форма значок вектор правильный семиугольник
1149*1149
геометрическая форма значок вектор правильный семиугольник
1024*1024
геометрическая форма значок вектор правильный семиугольник
1024*1024
геометрическая форма значок вектор правильный семиугольник
1024*1024
геометрическая форма значок вектор правильный семиугольник
1024*1024
геометрическая форма значок вектор правильный семиугольник
1149*1149
геометрическая форма значок вектор правильный семиугольник
1024*1024
геометрическая форма значок вектор правильный семиугольник
1024*1024
геометрическая форма значок вектор правильный семиугольник
1149*1149
геометрическая форма значок вектор правильный семиугольник
1299*1299
геометрическая форма значок вектор правильный семиугольник
1024*1024
геометрическая форма значок вектор правильный семиугольник
1024*1024
геометрическая форма значок вектор правильный семиугольник
1024*1024
геометрическая форма значок вектор правильный семиугольник
1299*1299
геометрическая форма значок вектор правильный семиугольник
1024*1024
геометрическая форма значок вектор правильный семиугольник
1024*1024
геометрическая форма значок вектор правильный семиугольник
1024*1024
геометрическая форма значок вектор правильный семиугольник
1024*1024
геометрическая форма значок вектор правильный семиугольник
1024*1024
геометрическая форма значок вектор правильный семиугольник
1024*1024
Правильный семиугольник — это… Что такое Правильный семиугольник?
Правильный семиугольникПравильный семиугольник — это правильный многоугольник с семью сторонами.
Свойства
Построение правильного семиугольника с помощью невсисаПусть — сторона семиугольника, — радиус описанной окружности, — радиус вписанной окружности.
- ,
Периметр правильного семиугольника равен
- .
Площадь правильного семиугольника рассчитывается по формулам:
- ,
- ,
- .
Построение
Приближённое построение правильного семиугольникаТочное
Согласно теореме Гаусса — Ванцеля, правильный семиугольник невозможно построить с помощью циркуля и линейки, но можно построить с помощью циркуля и невсиса, то есть размеченной линейки, на которой можно делать отметки и с помощью которой можно проводить прямые, проходящие через какую-нибудь точку, причём отмеченные на линейке точки будут принадлежать данным линиям (прямым или окружностям).
Построим квадрат PQRO со стороной a (см. рис.). Проведём дугу окружности с центром O и радиусом OQ. Возьмём линейку невсиса с диастемой (длиной) a и используя вертикальную ось симметрии квадрата в качестве направляющей, точку P в качестве полюса и дугу окружности в качестве целевой линии, получим отрезок AB, который будет стороной правильного семиугольника, с вертикальной осью симметрии, совпадающей с осью симметрии квадрата.
Анимация приближённого построения правильного семиугольника с помощью циркуля и линейки.
Приближённое
Приближённое (но с достаточной для практики точностью ≈0,2 %) построение семиугольника показано на рисунке. Из точки на окружности радиусом, равным радиусу окружности, проводим дугу . Отрезок и даст искомое приближение.
Семиугольные звёзды
Существует два звёздчатых семиугольника (гептаграммы): 7/2 и 7/3. Методы их построения аналогичны построению обычного семиугольника, только вершины нужно соединять через одну (7/2) или через две (7/3).
Семиугольная звезда 7/2
Семиугольная звезда 7/3
Применение
Семиугольная монета в 50 пенсов (150 лет Публичной библиотеке)В Великобритании используются две монеты в форме семиугольника: 50 пенсов и 20 пенсов. Строго говоря, форма монет — криволинейный семиугольник, образующий кривую постоянной ширины, чтобы монеты плавно проходили в автоматы.
Семиугольная звезда 7/2 являлась национальным символом Грузии и применялась, как элемент герба Грузии, в том числе и в советское время. В настоящее время не применяется.
Семиугольная звезда 7/3 является эмблемой компании A.P. Moller-Maersk Group.
Правильный 65537-угольник — это… Что такое Правильный 65537-угольник?
Правильный 65537-угольник (шестѝдесятипятиты̀сячпятисо̀ттридцатисемиуго́льник) — геометрическая фигура из группы правильных многоугольников, состоящая из 65537 углов и 65537 сторон. По причине малости центрального угла в графическом изображении правильный 65537-угольник почти не отличается от окружности (см. иллюстрацию справа).
Построение
Отличительная особенность 65537-угольника — это тот факт, что его возможно построить, используя только циркуль и линейку.
Число 65537 — это самое большое известное простое число Ферма:
- .
Гауссом в 1836 году было доказано, что правильный n-угольник можно построить циркулем и линейкой, если нечётные простые делители n являются различными числами Ферма. В 1836 П. Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует. Ныне это утверждение известно как теорема Гаусса — Ванцеля.
В 1894 же году Иоганн Густав Гермес после более чем десятилетних исследований нашёл способ построения правильного 65537-угольника и описал его в рукописи размером более 200 страниц [1] (оригинал рукописи хранится в библиотеке Гёттингенского университета).
| Один слишком навязчивый аспирант довёл своего руководителя до того, что тот сказал ему: «Идите и разработайте построение правильного многоугольника с 65537 сторонами». Аспирант удалился, чтобы вернуться через 20 лет с соответствующим построением.[2] |
Пропорции
Углы
Центральный угол равен .
Внутренний угол равен .
Наглядное представление
Следующие соображения могут служить для иллюстрации пропорций практически не представимой фигуры:
- Отклонение центрального угла от 0°, а также отклонение внутреннего угла от 180° составляет всего лишь примерно 0,005°. Если приподнять за один конец лежащую на земле жердь длиной 104,3 метра только на один сантиметр, то она образует с землёй примерно этот угол.
Обоснование
Рассмотрим треугольник, одной стороной которого является указанная жердь, второй стороной — перпендикуляр, опущенный от приподнятого конца жерди на поверхность, где она лежала, а третьей стороной — отрезок от основания перпендикуляра до покоящегося конца жерди. Считая, что жердь подняли на один сантиметр, найдем какой длины она должна быть чтобы образовать с поверхностью угол , равный центральному углу правильного 65537-угольника: он будет равен отношению высоты, на которую подняли ли один край жерди к углу, который жердь образовала с поверхностью
- Если нарисовать 65537-угольник с длиной одной стороны 1 см, то его диаметр будет больше 200 м.
- Если нарисовать 65537-угольник с длиной одной стороны 1 м, то разница между радиусами его вписанной и описанной окружностей (диаметр каждой из которых будет около 10 км) составит всего лишь около 0,024 мм.
- Если нарисовать 65537-угольник диаметром 20 см, то длина одной его стороны окажется менее одной десятой толщины самого тонкого человеческого волоса.
Ссылки
- ↑ Johann Gustav Hermes (1894). «Über die Teilung des Kreises in 65537 gleiche Teile». Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse 3: 170–186. (нем.)
- ↑ Дж. Литлвуд Математическая смесь. — М.: Наука, 1990. — С. 43. — ISBN 5-02-014332-4
Многоугольники. Визуальный гид (ЕГЭ — 2021)
P.S. Последний бесценный совет 🙂
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.
Почему?
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?
Набить руку, решая задачи.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.
Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.
А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.
После регистрации ты сможешь:
Бонус: информатика и физика.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Heptagon Vector Logo Company stockvector (rechtenvrij) 1383187730
Momenteel gebruikt u een oudere browser. Uw ervaring is mogelijk niet optimaal. Обновите браузер Overweeg. Kom meer te weten.Inloggen
Registreren
Меню
Alle afbeeldingen- Alle afbeeldingen
- Foto’s
- Vectoren
- Illustraties
- Redactioneel
- Videomateriaal word
- Oziek afbeelding 9002 9239 926 926 Heptagon — математическое определение слова — Math Open Reference Определение: многоугольник с семью сторонами
также: Септагон Попробуй это Отрегулируйте семиугольник ниже, перетащив любую оранжевую точку.Нажав на верхнюю левую командную строку, вы можете переключать его между регулярные и неправильный семиугольник.Свойства правильных семиугольников
Внутренний угол 128,571 ° Как и любой правильный многоугольник, чтобы найти внутренний угол, мы используем формулу (180н – 360) / л. Для семиугольника n = 7. См. Внутренние углы многоугольника Внешний угол 51,429 ° Чтобы найти внешний угол правильного семиугольника, мы используем тот факт, что внешний угол образует линейная пара с внутренним углом, поэтому в целом он определяется формулой 180-внутренний угол.См. Внешние углы многоугольника Площадь 3,633 с 2
приблизительноГде S — длина стороны. Чтобы найти точную площадь семиугольника или любого многоугольника различными методами, см. Площадь правильного многоугольника и Площадь неправильного многоугольника Свойства всех семиугольников
Количество диагоналей 14 Количество различных диагоналей, возможных для всех вершин.(Обычно ½n (n – 3)). На рисунке выше нажмите «показать диагонали», чтобы увидеть их. См. Диагонали многоугольника Количество треугольников 5 Количество треугольников, созданных путем рисования диагоналей из заданной вершины. (В общем n – 2). На рисунке выше нажмите «показать треугольники», чтобы увидеть их. Увидеть треугольники многоугольника Сумма внутренних углов 900 ° Обычно 180 (n – 2) градусов.См. Внутренние углы многоугольника Шестиугольные монеты
Гептагоны редко встречаются в повседневной жизни, за исключением Великобритании, где есть монеты в форме семиугольника. Справа — монета в 50 пенсов. Это не строгий семиугольник, потому что стороны на самом деле представляют собой изогнутые дуги, а не прямые линии. Полученная форма известна как «семиугольник с равносторонней кривой».
У него есть одно очень любопытное свойство; несмотря на то, что это не круг, он везде имеет одинаковый диаметр! Это сделано для того, чтобы он всегда подходил в монетных автоматах, но все же ощущаются в руке иначе, чем другие круглые монеты — помощь слабовидящим.
Другие темы полигонов
Общие
Типы многоугольника
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные многоугольники
(C) Открытый справочник по математике, 2011 г.
Все права защищены.Определение выпуклого многоугольника — математическая открытая ссылка
Определение выпуклого многоугольника — математическая открытая ссылка Определение: многоугольник, в котором есть все внутренние углы менее 180 °
(Результат: все вершины направлены «наружу», от центра.)Попробуй это Отрегулируйте многоугольник ниже, перетащив любую оранжевую точку. Если какая-либо вершина направлена «внутрь» к центру многоугольника, она перестает быть выпуклым многоугольником.
Выпуклый многоугольник определяется как многоугольник со всеми его внутренними углами менее 180 °. Это означает, что все вершины многоугольник будет указывать наружу, от внутренней части фигуры. Думайте об этом как о «выпуклом» многоугольнике. Обратите внимание, что треугольник (3-угольник) всегда выпуклый.
Выпуклый многоугольник противоположен вогнутому многоугольнику.Увидеть Вогнутый многоугольник.
На рисунке выше перетащите любую из вершин с помощью мыши. Обратите внимание на то, что нужно, чтобы сделать многоугольник выпуклым или вогнутым. Также измените количество сторон.
Свойства выпуклого многоугольника
Линия, проведенная через выпуклый многоугольник , будет пересекать многоугольник ровно дважды, как это видно на рисунке слева. Вы также можете видеть, что линия разделит многоугольник ровно на две части.
Все диагонали выпуклого многоугольника целиком лежат внутри многоугольника.См. Рисунок слева. (В вогнутый многоугольник, некоторые диагонали будут лежать вне многоугольника).
Площадь неправильного выпуклого многоугольника можно найти, разделив его на треугольники и просуммировав площади треугольника. См. Площадь неправильного многоугольника
Правильные многоугольники всегда выпуклые по определению. См. Определение правильного многоугольника. На рисунке вверху страницы щелкните «Сделать регулярным», чтобы полигон всегда был правильным.Тогда вы увидите, что, что бы вы ни делали, он останется выпуклым.
Другие темы полигонов
Общие
Типы многоугольника
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные многоугольники
(C) Открытый справочник по математике, 2011 г.
Все права защищены.Полигоны
Многоугольник — это плоская форма с прямыми сторонами.Это многоугольник?
Многоугольники — это двумерные фигуры. Они состоят из прямых линий, а форма «замкнута» (все линии соединяются).
Многоугольник
(прямые стороны)Не Многоугольник
(с кривой)Не Полигон
(открытый, не закрытый)Многоугольник происходит от греческого языка. Poly- означает «много», а -угольник означает «угол».
Типы полигонов
Обычный или нестандартный
У правильного многоугольника все углы и стороны равны, в противном случае он неправильный
Обычный Нерегулярный вогнутый или выпуклый
Выпуклый многоугольник не имеет углов, направленных внутрь.Точнее, внутренний угол не может быть больше 180 °.
Если любой внутренний угол больше 180 °, то многоугольник вогнутый . ( Подумайте: в вогнутой части есть «пещера» )
выпуклая вогнутый Простой или сложный
Простой многоугольник имеет только одну границу и не пересекает себя.Сложный полигон пересекает сам себя! Многие правила, касающиеся многоугольников, не работают, когда они сложные.
Простой многоугольник
(это пятиугольник)Сложный многоугольник
(также Пентагон)Другие примеры
Шестигранник неправильной формы Вогнутый восьмиугольник
Сложный многоугольник
(«звездообразный многоугольник»,
в данном случае пентаграмма)Поиграй с ними!
Попробуйте интерактивные многоугольники… сделать их правильными, вогнутыми или сложными.
Имена полигонов
С помощью этого метода можно делать имена:
Стороны
Начать с … 20
Icosi … 30
Triaconta… 40
Тетраконта … 50
Пентаконта … 60
Hexaconta … 70
Heptaconta… 80
Octaconta … 90
Эннеаконта … 100 Гектара … и т. Д. Стороны
… закончить с +1
… шестигранник +2
… digon +3
… тригон +4
…тетрагон +5
… пятиугольник +6
… шестигранник +7
… семиугольник +8
… восьмиугольник +9
… эннеагон Пример: 62-сторонний многоугольник — это гексаконтадигон
НО, для многоугольников с 13 и более сторонами нормально (и проще) написать « 13-угольник », « 14-угольник » … « 100-угольник» и т. Д.
Вспоминая
Четырехсторонний (4 стороны)
A Quad Велосипед с 4 колесамиПентагон (5 сторон)
« Пентагон » в Вашингтоне, округ Колумбия, имеет 5 сторонШестиугольник (6 сторон)
H oneycomb имеет H эксагоновСептагон (7 сторон)
Think Sept agon — это «Seven- agon»
Восьмиугольник (8 сторон)
Гной Octo имеет 8 щупалецNonagon (9 сторон)
Heptagon PNG изображений | Векторные и PSD файлы
значок геометрической формы векторного семиугольника
1024 * 1024
значок геометрической формы векторного семиугольника
1024 * 1024
значок геометрической формы векторного семиугольника
1024 * 1024
вектор Значок геометрической формы семиугольника
1024 * 1024
Значок геометрической формы векторного семиугольника
1024 * 1024
Значок геометрической формы векторного семиугольника
1149 * 1149
c4d творческий красный семиугольник
старинная декоративная рамка
2000 * 2000Значок геометрической формы векторного семиугольника
1149 * 1149
Значок геометрической формы векторного семиугольника
1149 * 1149
Значок геометрической формы векторного семиугольника
1024 * 1024
- 0
- вектор Значок геометрической формы семиугольника
1299 * 1299
Значок геометрической формы векторного семиугольника
1249 * 1249
Значок геометрической формы векторного семиугольника
1024 * 1024
Значок геометрической формы векторного семиугольника
1299 * 1299
плавающая диаграмма семиугольника * 1200
Значок геометрической формы векторного семиугольника
1299 * 1299
Значок геометрической формы векторного семиугольника
1598 * 1598
Значок геометрической формы векторного семиугольника
1024 * 1024
- Значок геометрической формы
1998 * 1998
Значок геометрической формы векторного семиугольника
1499 * 1499
Значок геометрической формы векторного семиугольника
1399 * 1399
Значок геометрической формы векторного семиугольника
1149
вектор семиугольник значок геометрической формы 90 003
1024 * 1024
Значок геометрической формы векторного семиугольника
1024 * 1024
Значок геометрической формы векторного семиугольника
1399 * 1399
Значок геометрической формы векторного семиугольника
1024 * 10248
Значок геометрической формы векторного семиугольника
1399 * 1399
Значок геометрической формы векторного семиугольника
1299 * 1299
Значок геометрической формы
1299 * 1299
значок геометрической формы вектор семиугольника
1399 * 1399
значок геометрической формы вектор семиугольника
1998 * 1998
значок вектор геометрической формы семиугольника
1998 * 1998
- вектор Значок геометрической формы семиугольника
1024 * 1024
- 9 0002 Значок геометрической формы векторного семиугольника
1024 * 1024
Значок геометрической формы векторного семиугольника
1499 * 1499
Значок геометрической формы векторного семиугольника
1299 * 1299
-
семиугольная черепица - ↑ 1.0 1.1 Глисон, Эндрю Маттей (март 1988 г.). «Угловая секция, семиугольник и трехугольник стр. 186 (Рис.1) –187» (PDF). Американский математический ежемесячник . 95 (3): 185–194. Архивировано 31 января 2016 года из оригинального (PDF).
- ↑ G.H. Хьюз, «Полигоны Альбрехта Дюрера-1525, правильный семиугольник», рис. 11 — сторона семиугольника (7). Рис. 15, изображение слева, получено 4 декабря 2015 г.
- ↑ Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штраус, (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шафли, Типы симметрии многоугольника, стр.275-278)
Значок геометрической формы векторного семиугольника
1024 * 1024
Инфогалактическое ядро
: планетарные знанияВ геометрии семиугольник — это семигранный многоугольник или 7-угольник.
Гептагон также иногда называют септагоном , используя вместе «sept-» (элизия septua- , числовой префикс латинского происхождения, а не hepta- , числовой префикс греческого происхождения) вместе с греческим суффиксом «-agon», означающим угол.
Правильный семиугольник
Правильный семиугольник , у которого все стороны и все углы равны, имеет внутренние углы 5π / 7 радиан (128,5714286 градусов). Его символ Шлефли — {7}.
Площадь
Площадь ( A ) правильного семиугольника со стороной a определяется по формуле:
Это можно увидеть, разделив семиугольник с единичной стороной на семь треугольных «кусочков пирога» с вершинами в центре и в вершинах семиугольника, а затем разделив каждый треугольник пополам, используя апофему в качестве общей стороны. Апофема составляет половину котангенса, а площадь каждого из 14 маленьких треугольников составляет одну четвертую апофемы.
Точное алгебраическое выражение, начиная с полинома x 3 + x 2 — 2 x — 1 (один из корней) [1] дается в комплексных числах как:
, в котором мнимые части смещают друг друга, оставляя действительное выражение. Это выражение нельзя переписать алгебраически без сложных компонентов, поскольку указанная кубическая функция — это casus unducibilis .
Площадь правильного семиугольника, вписанного в круг с радиусом R , равна площади самого круга, поэтому правильный семиугольник заполняет приблизительно 0,8710 его описанной окружности.
Строительство
Поскольку 7 — простое число Пьерпона, но не простое число Ферма, правильный семиугольник нельзя построить с помощью циркуля и линейки, но можно построить с помощью отмеченной линейки и компаса. Такой тип конструкции называется конструкцией neusis. Его также можно построить с помощью циркуля, линейки и трисектора угла.Невозможность построения линейки и циркуля следует из наблюдения, которое является нулем неприводимой кубики x 3 + x 2 — 2 x — 1. Следовательно, этот многочлен является минимальным многочленом от 2cos ( 2π ⁄ 7 ), где степень минимального многочлена для конструктивного числа должна быть степенью 2.
Приблизительное значение
Приближение для практического использования с погрешностью около 0.2% показано на чертеже. Его приписывают Альбрехту Дюреру. [2] Пусть A лежит на окружности описанной окружности. Нарисуйте дугу BOC . Затем дает приближение для края семиугольника.
Пример для иллюстрации ошибки:
При радиусе описанной окружности r = 1 м абсолютная погрешность 1-й стороны будет приблизительно -1,7 мм
Более точное приближение
Правильный семиугольник со сторонами можно вписать в окружность радиуса с погрешностью менее 0.00013%.
Это следует из рационального приближения.
Для построения S и R см .: Пример деления 3 ÷ 2 на вещественной строке
и теорема о перехвате, формулировка 3-й пункт
Пример для иллюстрации ошибки:
Радиус описанной окружности R = 1 км , S = 0,867768595041322 км
и S — S должны = 0,867768595041322 км — 0,867767478235116 км
, абсолютная ошибка 1-й стороны будет примерно 1.1 мм.
«Более точное приближение», Гептагон в виде анимацииСимметрия
Симметрии правильного семиугольника. Вершины окрашены в соответствии с их положением симметрии. Синие зеркальные линии проводятся через вершины и ребра. В центре даны приказы гирации.Правильный семиугольник имеет симметрию Dih 7 , порядок 14. Поскольку 7 — простое число, имеется одна подгруппа с двугранной симметрией: Dih 1 и 2 симметрии циклических групп: Z 7 и Z 1 .
Эти 4 симметрии можно увидеть в 4 различных симметриях семиугольника. Джон Конвей помечает их буквой и групповым порядком. [3] Полная симметрия правильной формы — r14 , и никакая симметрия не помечена как a1 . Двугранные симметрии разделяются в зависимости от того, проходят ли они через вершины ( d для диагонали) или ребра ( p для перпендикуляров) и i , когда линии отражения проходят через оба ребра и вершины. Циклические симметрии в среднем столбце обозначены как g для их центральных порядков вращения.
Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только подгруппа g7 не имеет степеней свободы, но ее можно рассматривать как направленные грани.
Звездные семиугольники
Два типа звездных семиугольников могут быть построены из правильных семиугольников, помеченных символами Шлефли {7/2} и {7/3}, причем делитель представляет собой интервал соединения.
Синий, {7/2} и зеленый {7/3} семиугольник-звездочка внутри красного семиугольника.
Многие полицейские значки в США имеют контур гептаграммы 7: 2.
Использует
В настоящее время (2011 г.) Соединенное Королевство имеет две семиугольные монеты, 50 пенсов и 20 пенсов, и Барбадосский доллар также семиугольный. В монете номиналом 20 евроцентов углубления размещены аналогично. Строго говоря, форма монет представляет собой семиугольник Рело, криволинейный семиугольник, который делает их кривыми постоянной ширины: стороны изогнуты наружу, так что монета будет плавно катиться в торговых автоматах. Монеты Пула Ботсваны достоинством 2 Пула, 1 Пула, 50 Фив и 5 Фив также имеют форму семиугольника равносторонней кривой.Монеты в форме семиугольников Рило находятся в обращении на Маврикии, ОАЭ, Танзании, Самоа, Папуа-Новой Гвинее, Сан-Томе и Принсипи, Гаити, Ямайке, Либерии, Гане, Гамбии, Иордании, Джерси, Гернси, острове Мэн, Гибралтаре. , Гайана, Соломоновы острова, Фолклендские острова и остров Святой Елены. Монета Замбии в 1000 квача — это настоящий семиугольник.
На бразильской монете номиналом 25 центов нанесен семиугольник на диске. В некоторых старых версиях герба Грузии, в том числе в советские времена, в качестве элемента использовалась гептаграмма {7/2}.
В архитектуре семиугольные планы этажей встречаются очень редко. Замечательный пример — мавзолей принца Эрнста в Штадтхагене, Германия.
За исключением семиугольной призмы и семиугольной антипризмы, ни один выпуклый многогранник, полностью состоящий из правильных многоугольников, не содержит семиугольника в качестве грани.
Правильные семиугольники могут перекрывать гиперболическую плоскость, как показано на этой проекции модели диска Пуанкаре:
Графики
Полный граф K 7 часто изображается как правильный семиугольник со всеми 21 ребром, соединенным.Этот граф также представляет собой ортогональную проекцию 7 вершин и 21 ребра 6-симплекса. Правильный косой многоугольник по периметру называется многоугольником Петри.
Гептагон в природных структурах
См. Также
Список литературы
Внешние ссылки
| Найдите Heptagon в Wiktionary, бесплатном словаре. |