Математика геометрия: ГЕОМЕТРИЯ | Энциклопедия Кругосвет

Геометрия на ЕГЭ по математике. Что нужно знать?

Геометрия на профильном ЕГЭ по математике — одна из сложных тем для абитуриентов. Дело в том, что когда-то экзамен по геометрии в школе был обязательным, а сейчас — нет. В результате у большинства абитуриентов знания по геометрии близки к нулю.

Геометрия на профильном ЕГЭ — это три задачи в части 1 (сюда входит и планиметрия, и стереометрия), а также задача 14 (стереометрия) и для многих недосягаемая задача 16 (геометрия) из второй части. Как же научиться их решать?

Начнем с планиметрии. Прежде всего, выучите основные формулы геометрии.

На нашем сайте вы найдете курс геометрии с нуля — основные определения, формулы и теоремы, а также разбор множества экзаменационных задач по геометрии из части 1.

Для решения задач по геометрии из части 2 нужна более серьезная подготовка.

Первый этап — теория. Необходимый материал есть в учебнике по геометрии за 7-9 класс (автор — А. В. Погорелов или Л. С. Атанасян). Выпишите в тетрадь определения и формулировки теорем. Сделайте чертежи. Доказывать теоремы старайтесь самостоятельно.

Программа по геометрии.

1. Треугольники. Элементы треугольника. Вершины и стороны. Высоты, медианы, биссектрисы (определения).

2. Построение треугольника: практические задания.
а) Три стороны треугольника равны  и  сантиметров соответственно. Постройте треугольник с помощью циркуля и линейки.
б) В треугольнике угол  равен  градусов, сторона  равна ,  равна . Постройте треугольник .
в) В треугольнике сторона  равна , угол  равен , угол  равен . Постройте треугольник .

3. Три признака равенства треугольников. Неравенство треугольника.

4. Постройте с помощью циркуля и линейки:
а) серединный перпендикуляр к отрезку;
б) биссектрису угла.

5. Углы при параллельных прямых и секущей. Вертикальные, смежные, соответственные, односторонние и накрест лежащие углы. Их определение и свойства.

6. Теорема о сумме углов треугольника.

7. Внешний угол треугольника.

8. Постройте в одном и том же треугольнике
а) Три высоты. Рассмотрите также случаи тупоугольного и прямоугольного треугольника.
б) Три биссектрисы.
в) Три медианы.

9. Равнобедренный треугольник. Определение и свойства. Высота в равнобедренном треугольнике.

10. Средняя линия треугольника и ее свойства.

11. Прямоугольный треугольник. Теорема Пифагора.

12. Определения синуса, косинуса и тангенса:
— для острого угла прямоугольного треугольника;
— для произвольного угла.

13. Четырехугольники. Сумма углов четырехугольника.

14. Параллелограмм. Определение и свойства. Площадь параллелограмма.

15. Виды параллелограммов и их свойства (ромб, прямоугольник, квадрат).

16. Трапеция. Средняя линия трапеции. Площадь трапеции.

17. Подобные треугольники. Три признака подобия треугольников.

18. Площадь треугольника. Формулы    и  .

19. Теоремы синусов и косинусов.

20. Чему равно отношение площадей подобных фигур.

21. Свойство медианы (в каком отношении делятся медианы в точке пересечения?)

22. Свойство биссектрисы (в каком отношении биссектриса делит противоположную сторону?)

23. Окружность и круг. Длина окружности. Площадь круга. Длина дуги и площадь сектора.

24. Теорема о радиусе, проведенном в точку касания.

25. Центральный и вписанный углы. Связь между ними.

26. Теоремы о вписанных углах.

27. Теорема о пересекающихся хордах.

28. Теорема об отрезках длин касательных, проведенных из одной точки.

29. Теорема о секущей и касательной.

30. Дан треугольник . Постройте:
а) окружность, вписанную в данный треугольник;
б) окружность, описанную вокруг данного треугольника.

Где находятся центры этих окружностей?

31. Еще три формулы площади треугольника (через радиус вписанной окружности, через радиус описанной окружности и формула Герона).

32. Когда можно вписать окружность в четырехугольник? Когда — описать вокруг четырехугольника?

Программа по стереометрии

Разбирая и решая задания ЕГЭ по геометрии, вы заметите очень интересную вещь. Простые задачи из части 1, разобранные на нашем сайте, часто оказываются базовыми схемами, на которых строятся сложные задачи из части 2 профильного ЕГЭ.

Решая на ЕГЭ задачи по геометрии, обращайте особое внимание на оформление. Помните совет, который дал абитуриентам автор бестселлера «Математика — абитуриенту» В. В. Ткачук. Вот он, этот ценнейший совет:

«Подробность решения должна быть такова, чтобы его мог понять человек в 10 (десять) раз глупее вас».

Спасибо за то, что пользуйтесь нашими публикациями. Информация на странице «Геометрия на ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена: 08. 05.2023

Энциклопедия элементарной математики. Книга 4 (геометрия)

Павел Сергеевич Александров, Алексей Иванович Маркушевич, Александр Яковлевич Хинчин

М., Физматгиз, 1963. 568 с.
Тираж 20000 экз.

Загрузить (Mb) djvu (8.8) pdf (-) ps (-) html (-) tex (-)

Содержание

От редакции.

Аксиомы и основные понятия геометрии.
(Б.А.Розенфельд)

§ 1. Возникновение основных понятий геометрии.
§ 2. «Начала» Евклида.
§ 3. Появление аксиоматического метода.
§ 4. Модели.
§ 5. Непротиворечивость и полнота аксиоматики.
§ 6. Аксиоматика геометрии.
§ 7. Непротиворечивость и полнота аксиоматики евклидовой геометрии.

§ 8. Независимость аксиом.
Литература.

Геометрические преобразования.
(И.М.Яглом, Л.С.Атанасян)

§ 1. Понятие преобразования. Примеры.
§ 2. Применение преобразований к решению геометрических задач.
§ 3. Аналитическая запись геометрических преобразований.
§ 4. Произведение отображений и преобразований.
§ 5. Обратное преобразование.
§ 6. Общее определение геометрии. Группы геометрических преобразований.
§ 7. Группа проективных преобразований.
§ 8. Неточечные отображения.
§ 9. Принцип перенесения.
Литература.

Общие принципы геометрических посторений.
(Н.М.Бескин, В.Г.Болтянский, Г.Г.Маслова, Н.Ф.Четверухин, И. М.Яглом)

§ 1. Некоторые вопросы практического использования геометрических построений.
§ 2. О решении задач на построение в зависимости от принятых инртрументов.
§ 3. О построениях на ограниченном куске плоскости.
§ 4. Общие методы решения задач на построение на плоскости.
§ 5. Использование геометрических преобразований при решении задач на построение на плоскости.
§ 6. Приближенные методы геометрических построений и их значение для практики.
§ 7. Геометрические построения в пространстве.
Литература.

О разрешимости задач на построение с помощью циркуля и линейки.
(Ю.И.Манин)

Введение.
§ 1. Геометрическая часть теории.
§ 2. Перевод задачи на алгебраический язык.
§ 3. Классические задачи.
Литература.

Методы изображений.
(Н.М.Бескин)

§ 1. Постановка задачи.
§ 2. Параллельные проекции.
§ 3. Параллельная аксонометрия.
§ 4. Метод Монжа.
§ 5. Центральные проекции.
§ 6. Построения на изображении.
Литература.

Векторы и их применение в геометрии.
(В.Г.Болтянский, И.М.Яглом)

§ 1. Определение вектора.
§ 2. Сложение векторов и умножение вектора на число.
§ 3. Скалярное произведение векторов.
§ 4. Косое произведение векторов плоскости.

§ 5. Тройное произведение и векторное произведение векторов пространства.
§ 6. Применения векторного исчисления к сферической геометрии и тригонометрии.
§ 7. Понятие о векторных пространствах.
Литература.

Многоугольники и многогранники.
(В.Г.Ашкинузе)

§ 1. Основные определения. Теорема Эйлера.
§ 2. Комбинаторный (топологический) тип многогранника. Теорема Штейница.
§ 3. Развертка многогранника. Теорема Коши.
§ 4. Правильные многоугольники и многогранники и их обобщения.
Литература.

Окружности.
(И.М.Яглом)

Введение.

А. Окружность как совокупность точек.

§ 1. Обобщение понятия окружности.
§ 2. Радикальная ось и радикальный центр.
§ 3. Пучки и связки окружностей.
§ 4. Инверсия.
§ 5. Точечная геометрия окружностей.

Б. Окружность как совокупность прямых.
§ 6. Направленные окружности.
§ 7. Центр подобия и ось подобия.
§ 8. Ряды и сети окружностей.
§ 9. Осевая инверсия.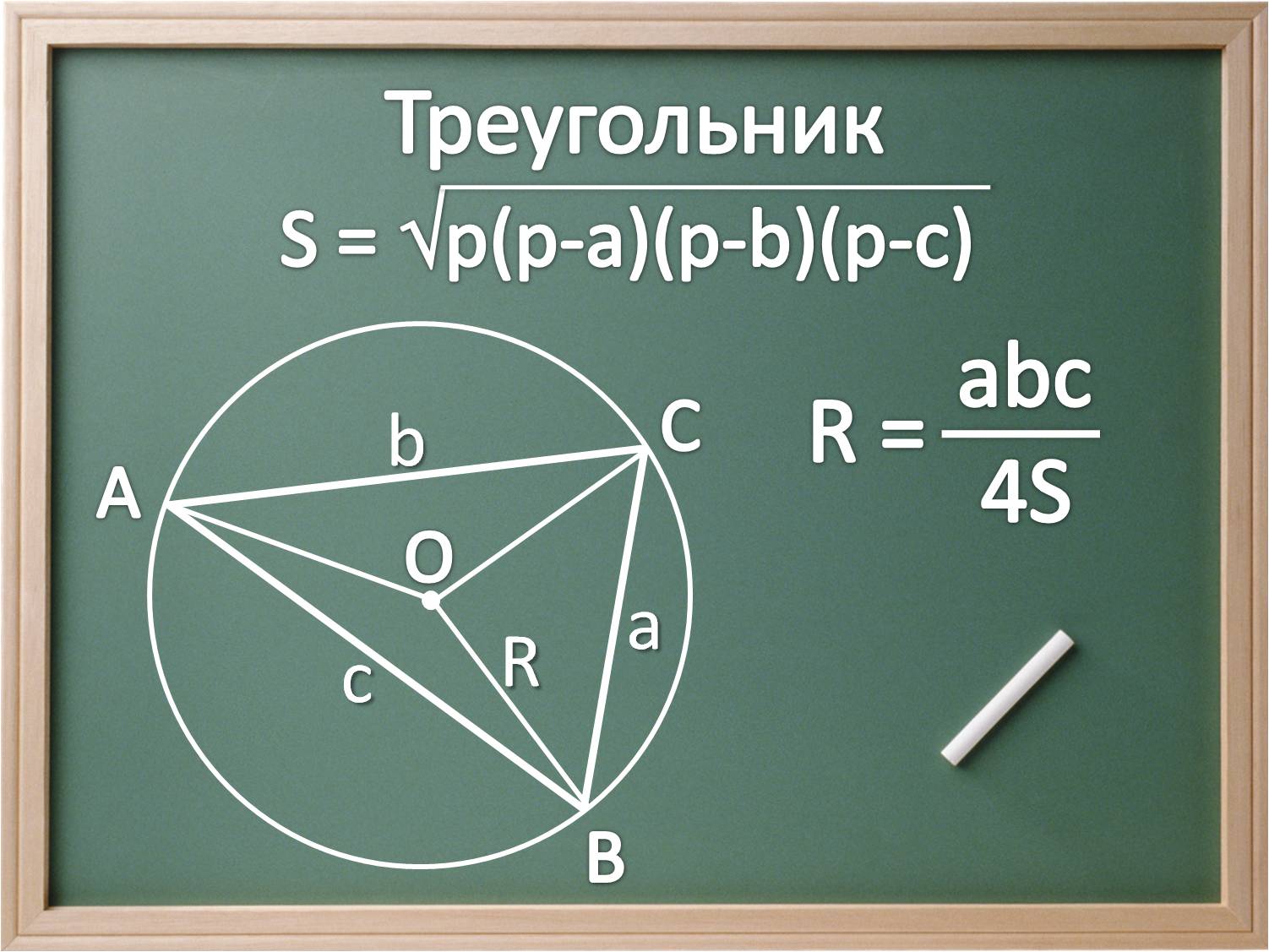
§ 10. Осевая геометрия окружностей.

В. Окружность как совокупность линейных элементов.
§ 11. Новый взгляд на окружность.
§ 12. Касательная геометрия окружностей.
Литература.

Основные понятия сферической геометрии и григонометрии.
(Б.А.Розенфельд)

§ 1. Основные понятия сферической геометрии.
§ 2. Сферические треугольники.
§ 3. Малые окружности.
§ 4. Тригонометрические соотношения в сферическом треугольнике.
Литература.

Именной указатель.

Предметный указатель.

---

Список литературы

• Книга 1. Арифметика. (1951, 448 с.)
• Книга 2. Алгебра. (1951, 424 с.)
• Книга 3. Функции и пределы, основы анализа. (1952, 559 с.)
• Книга 4. Геометрия. (1963, 568 с.)
• Книга 5. Геометрия. (1966, 624 с.)

Загрузить (Mb) djvu (8.8) pdf (-) ps (-) html (-) tex (-)

Постоянный адрес этой страницы: http://math.ru/lib/60

Геометрия

Геометрия — это все о фигурах и их свойствах.

Если вы любите играть с предметами или рисовать, то геометрия для вас!

Геометрию можно разделить на:

Плоская геометрия — это плоские фигуры, такие как линии, круги и треугольники… формы, которые можно нарисовать на листе бумаги

 

Объемная геометрия — это трехмерные объекты, такие как кубы, призмы, цилиндры и сферы.

Подсказка: попробуйте нарисовать некоторые формы и углы, когда будете учиться… это поможет.

Точка, линия, плоскость и тело

Точка не имеет размеров, только положение
Линия одномерная
Плоскость двухмерная (2D)
Твердое тело трехмерное (3D)

Почему?

Почему мы занимаемся геометрией? Чтобы открывать закономерности, находить площади, объемы, длины и углы и лучше понимать окружающий мир.

Плоская геометрия

Плоская геометрия — это формы на плоской поверхности (как на бесконечном листе бумаги).

• 2D-фигуры
• Упражнение: Сортировка фигур
• Треугольники
• Прямоугольные треугольники
• Интерактивные треугольники

 

• Четырехугольники (ромб, параллелограмм, и т. д.)
• Прямоугольник, ромб, квадрат, параллелограмм, трапеция и воздушный змей
• Интерактивные четырехугольники
• Параллелограмм в любом четырехугольнике
• Размеры бумаги
• Свободная игра фигур

• Периметр

• Зона
• Площадь плоских фигур
• Инструмент расчета площади
• Площадь многоугольника по чертежу
• Деятельность: Сад

• Общий инструмент для рисования
• Калькулятор площади и калькулятор прямоугольника

Полигоны

Многоугольник — это двухмерная фигура, состоящая из прямых линий. Треугольники и прямоугольники являются многоугольниками.

Вот еще:

Пентагон

Пентаграмма

Шестигранник

 

• Свойства правильных многоугольников
• Диагонали многоугольников
• Интерактивные полигоны

 

Круг

• Круг
• Пи
• Площадь круга по линиям
• Круговой сектор и сегмент
• Площадь круга по секторам
• Упражнение: Бросание монеты на сетку
• Арка
• Кольцо

Теоремы о кругах (расширенная тема)

 

Символы

В геометрии используется много специальных символов. Вот краткая справка для вас:

Геометрические символы

 

Конгруэнтные и аналогичные

• Конгруэнтные формы
• Похожие формы

 

Уголки

Типы уголков

Острые углы

Прямые углы

Тупые углы

Прямоугольный

Рефлекторные углы

Полный оборот

Градусы (угол) радиан Равные углы Параллельные прямые и пары углов Поперечный Смежные углы Треугольник имеет 180° Дополнительные уголки Дополнительные углы

Углы вокруг точки Углы на прямой линии Внутренние уголки Наружные уголки Внутренние углы многоугольников Внешние углы многоугольников

Использование инструментов для рисования

• Геометрические конструкции
• Использование транспортира
• Использование чертежного треугольника и линейки
• Использование линейки и компаса

 

Преобразования и симметрия

Преобразования:

• Вращение
• Отражение
• Перевод
• Изменение размера

Симметрия:

• Симметрия отражения
• Вращательная симметрия
• Точечная симметрия
• Линии симметрии плоских фигур

• Художник по симметрии

• Упражнение: Симметрия фигур
• Упражнение: Создание мандалы
• Упражнение: Раскрашивание (Четыре цвета Теорема)

• Мозаика
• Мастер тесселяции

 

Координаты

• Декартовы координаты
• Интерактивные декартовы координаты
• Игра «Найди координаты»

 

 

Дополнительные темы плоской геометрии

Пифагор

• Теорема Пифагора
• Пифагорейские тройки

 

Конические секции

• Набор всех точек
• Конические секции
• Эксцентриситет
• Эллипс
• Анимация параболы и снаряда
• Гипербола

 

Теоремы круга

• Теоремы о кругах
• Касательные и секущие линии
• Теорема о пересекающихся секущих
• Теорема о пересекающихся хордах
• Угол пересекающихся секущих Теорема

Треугольные центры

Тригонометрия

Тригонометрия — это отдельная тема, поэтому вы можете посетить:

• Введение в тригонометрию
• Индекс тригонометрии

 

Твердотельная геометрия

Solid Geometry — это геометрия трехмерного пространства, в котором мы живем…

. .. начнем с самых простых фигур:

Общие 3D-формы

Многогранники и не-многогранники

Существует два основных типа твердых тел: «многогранники» и «не-многогранники»:

Многогранники (должны иметь плоские грани) :

	кубов и кубоидов (объем кубоида)
	Платоновые тела
	Призмы
	Пирамиды

Не многогранники (когда любая поверхность не плоский) :

	Сфера			Тор
	Цилиндр			Конус

 

• Модели многогранников
• Калькулятор объема и площади сферы
• Сфероид
• Поперечные сечения
• Вершины, грани и ребра
• Конус против сферы против цилиндра
• Пирамида против Конуса
• Призма против цилиндра
• Пирамида против Куба
• Объем горизонтального цилиндра
• Теорема Эйлера
• Пифагор в 3D
• Гиперкубы
• Математика строителя
• Моменты Зоны

 

Что такое геометрия в математике? Определение, решенные примеры, факты

Что такое геометрия в математике?

Геометрия — это раздел математики, изучающий размеры, формы, положения, углы и размеры вещей.

2D-фигуры в геометрии

Плоские фигуры, такие как квадраты, круги и треугольники, являются частью плоской геометрии и называются 2D-фигурами. Эти фигуры имеют только 2 измерения: длину и ширину.

Примеры двумерных фигур в плоской геометрии показаны ниже.

2D-формы могут быть дополнительно классифицированы как открытые формы и закрытые формы. Открытые формы могут быть определены как формы или фигуры, чьи отрезки линий и/или кривые не пересекаются. Они не начинаются и не заканчиваются в одной и той же точке. Замкнутые фигуры — это геометрические фигуры, которые начинаются и заканчиваются в одной и той же точке.

Трехмерные фигуры в геометрии

В геометрии трехмерная фигура может быть определена как объемная фигура, объект или форма, имеющая три измерения: длину, ширину и высоту. В отличие от двумерных фигур трехмерные фигуры имеют толщину или глубину.

Атрибутами трехмерной фигуры являются грани, ребра и вершины. Три измерения составляют края трехмерной геометрической формы.

Куб, прямоугольная призма, сфера, конус и цилиндр — основные трехмерные формы, которые мы видим вокруг себя.

Угол

В геометрии угол можно определить как фигуру, образованную двумя лучами, сходящимися в одной точке. Угол обозначается символом ∠. Углы измеряются в градусах (°) с помощью транспортира. Например, 45 градусов представляются как 45°.

Углы классифицируются на основе их размеров как:

1. Острый угол меньше 90°.
2. Тупой угол находится в диапазоне от 90° до 180°.
3. Прямой угол точно равен 90°.
4. Угол, равный точно 180°, является прямым углом.
5. Угол рефлекса составляет от 180° до 360°.
6. Полный угол равен 360°.

Вершина фигуры, где два ребра сходятся, образуя угол. Различные фигуры в геометрии имеют разные меры угла.

Например, :

• Треугольник — это трехсторонняя фигура, сумма трех внутренних углов которого равна 180˚
• Квадрат, прямоугольник или четырехугольник — это четырехсторонние фигуры, а сумма их четырех внутренних углов равна 360˚
• Другие многоугольники, такие как пятиугольник, шестиугольник, семиугольник, восьмиугольник, имеют 5, 6, 7, 8 сторон соответственно и различные углы.

Примеры различных многоугольников с их углами и сторонами показаны ниже.

Мы изучаем различные аспекты форм, такие как измерение углов, длины сторон, площади, объема и т. д. в геометрии. Подобие и конгруэнтность — два важных аспекта геометрии.

Сходство : Сходство — это когда две формы одинаковы, но их размеры могут различаться.

Конгруэнтность : Конгруэнтность — это когда две фигуры совершенно одинаковы по форме и размеру.

Координатная плоскость:

• Координатная плоскость — это двумерная поверхность, образованная с помощью двух числовых линий, пересекающихся друг с другом под прямым углом.
• Горизонтальная числовая линия — это ось x, а вертикальная числовая линия — ось y.
• Пересечение двух осей — это координата (0,0).
• Используя координатную плоскость, мы наносим точки, линии и т. д. Соединяя различные точки на координатной плоскости, мы можем создавать формы.

Мы используем формулу и теорему для решения задач по геометрии.

Формула — это математическое уравнение для решения задачи геометрии, а теорема — это утверждение, которое доказывается с использованием ранее известных фактов.

Например, « Теорема Пифагора » доказала, что a2 + b2 = c2 для прямоугольного треугольника, где a и b — стороны прямоугольного треугольника, а c — гипотенуза.

Однако, a2 + b2 = c2 — это формула для нахождения гипотенузы прямоугольного треугольника.

Интересные факты

— Слово «геометрия» образовано от греческих слов «гео», означающих «земля», и «метрия», означающих «измерение».

Решенные примеры по геометрии

1. Является ли данная фигура примером простой замкнутой кривой, которая также является многоугольником?

Решение:

Замкнутая фигура, которая не пересекает сама себя, является простой замкнутой кривой. Многоугольники — это замкнутые формы, образованные только прямыми линиями, такие как треугольники, прямоугольники, пятиугольники и т. д.

Данная фигура изогнута и состоит не только из прямых линий, это не многоугольник.

2. В треугольнике ABC с прямым углом в точке B, если ∠C=45°, какова мера ∠A?  

Решение: △ ABC – заданный прямоугольный треугольник с ∠B=90°.

Сумма углов треугольника = 180°

∠A+∠B+∠C=180°

∠A+∠C=180°-90°=90° А =90°-45°=45°

3. Определите плоские поверхности в данной призме.  

Решение:

Плоские поверхности призмы представлены ниже:

Прямоугольник AECB, прямоугольник DCEF, прямоугольник ABDF образуют прямоугольные грани призмы.

△ BCD и △ AEF образуют треугольные грани призмы.

Практические задачи по геометрии

1

Что из следующего является простой замкнутой кривой?

A

B

C

D

Правильный ответ: B
Замкнутая фигура, которая не пересекается сама с собой, является простой замкнутой кривой. У него одинаковые начальная и конечная точки.

2

Что из перечисленного является трехмерной фигурой?

A

B

C

D

Правильный ответ: D
Данная фигура является трехмерной и называется кубом.

3

Сколько сторон и углов у данной фигуры?

10 сторон и 10 углов

12 сторон и 10 углов

5 сторон и 5 углов

18 сторон и 5 углов

Правильный ответ: 10 сторон и 10 углов
Фигура в форме звезды состоит из 10 прямых линий. Таким образом, у него 10 сторон и 10 углов.

Часто задаваемые вопросы по геометрии

Какая связь между математикой и геометрией?

Математика — это общий термин для различных дисциплин, в которых основное внимание уделяется логике и абстрактным понятиям.