«Древние меры длины» — математика, презентации
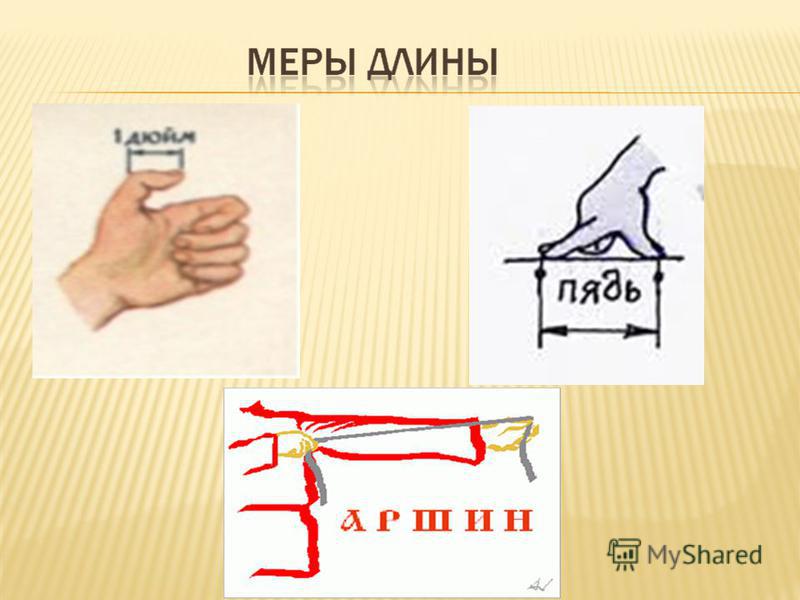
Древние меры длины
В древности человеку приходилось постепенно постигать не только искусство счета, но и измерений
Когда древний человек, уже мыслящий, попытался найти для себя пещеру, он вынужден был соразмерить длину, ширину и высоту своего будущего убежища с собственным ростом.
А ведь это и есть измерение .
Изготовляя простейшие орудия труда, строя жилища, добывая пищу, возникает необходимость измерять расстояния.
Наш предок располагал только собственным ростом, длиной рук и ног.
Если при счете человек пользовался пальцами рук и ног ,
то при измерении расстояний использовались руки и ноги .
Не было народа, который не избрал бы свои единицы измерения
а древние арабы
– волос
из ослиной морды.
Англичане до сих пор пользуются королевским футом (в переводе с английского фут означает нога),
Длина фута была уточнена с введение такой единицы длины как шток .
Это “ длина ступней 16 человек, выходящих из храма от заутрени в воскресенье”.
Деля длину штока на 16 равных частей, получали среднюю длину ступни, ибо из церкви выходили люди разного роста.
Длина фута стала равняться 30,48 см
Английский ярд тоже связан с размерами человеческого тела.
Эта мера длины была введена королем Эдгаром и равнялась расстоянию от кончика носа
его величества до кончика среднего пальца вытянутой в сторону руки .Король Генрих 1 узаконил постоянный ярд и приказал изготовить из вяза эталон. Этим ярдом в Англии пользуются до сих пор ( длина его равна 0,9144 м ).
Для измерения небольших длин употреблялась длина сустава большого пальца (в переводе с голландского дюйм означает большой палец).
Длина дюйма в Англии была уточнена и стала ровняться длине трех ячменных зерен, вынутых из средней части колоса и поставленных друг к другу своими концами.
Из английских повестей и рассказов известно, что крестьяне часто определяли высоту лошадей ладонями .
Расстояние измерялось шагами почти у всех народов, но для измерения полей и других больших расстояний шаг был слишком малой мерой, поэтому была введена мера
В морском деле трость называлась штоком .
В Англии была и такая мера, как хорошая палка пахаря, длина которой 12 – 16 футов.
В Риме вводится мера равная тысяче двойных шагов, получившая название миля (от слова милле , милиа – тысяча)
Для измерения больших расстояний в древности была введена мера, называемая поприще , а затем взамен ее появляется верста .
ВЕРСТА
Название это происходит от слова вертеть, которое в начале означало поворот плуга, а потом ряд, расстояние от одного до другого поворота плуга при пахоте. Длина версты в разное время была различной – от 500 до 750 саженей. Да и верст-то было не одна, а две: путевая – ею измеряли расстояние пути и межевая – ею мерили земельные участки
У славян была такая мера длины, как
“ вержение камня” – бросок камнем,
“ перестрел ” – расстояние, которое пролетала стрела, выпущенная из лука
Подобные меры были и у других народов – “коровий крик”, “петушиный крик”.
Эстонские моряки говорили, что до берега еще
“ три трубки”
( время затраченное на выкуривание трубок).
“ Пушечный выстрел” – тоже мера расстояния.
В Испании известна мера расстояния – сигара :
путь, который может пройти человек, куря сигару.
Древнейшими мерами длины являются локоть и сажень . Локтем являлась длина от локтя до переднего сустава среднего пальца и равнялась половине английского ярда.
В Древней Руси существовали свои измерения
Название сажень происходит от славянского слова сяг – шаг . Сначала оно означало расстояние, на которое можно шагнуть. Затем стали различать сажени – маховую, косую, казенную, мерную, большую, греческую, церковную, царскую, морскую .
Маховая или мерная сажень Это расстояние между вытянутыми пальцами раскинутых рук (176 см).
Сажень простая ( 152 см ) – расстояние между размахом вытянутых рук человека от большого пальца одной руки до большого пальца другой.
Сажень косая ( 248 см ) – расстояние между подошвой левой ноги и концом среднего пальца вытянутой вверх правой руки
Небольшие расстояния на Руси измерялись четвертями, пядями и аршинами.
Четверть – расстояние между раздвинутыми большим и указательным пальцами, пядь – расстояние от конца большого пальца до конца мизинца при наибольшем возможном их раздвижении. Четыре четверти составляли аршин, который, в свою очередь, трижды вмещался в косую сажень.
Мера длины, равная 0,1 дюйма, называлась линией (очевидно, потому, что ее можно было отложить при помощи линейки). К наиболее мелким старинным русским мерам длины относится точка , равная 0,1 линии. Возможно отсюда появилось слово точность
С развитием торговых отношений между иностранными государствами потребовалось создание эталонов.
В разные века предпринимались попытки ввести эталоны. За это время система мер протерпела множество изменений.
В 1960 собралась Генеральная конференция по мерам и весам , на которую прибыли представители 32 стран. Была принята Международная система единиц. С 1963 года ею пользуются во всех областях науки, техники и народного хозяйства.
Древние меры длины
в пословицах и поговорках
Один, как перст.
От горшка два вершка.
Семь пядей во лбу.
Косая сажень в плечах.
Семимильные шаги.
От слова до дела – целая верста.
Автор :
Белых Т.Л.
учитель начальных классов
ДОШ № 41
Какие меры длины были у древних славян?. Кто есть кто в истории России
Какие меры длины были у древних славян?. Кто есть кто в истории РоссииВикиЧтение
Кто есть кто в истории России
Ситников Виталий Павлович
Содержание
Какие меры длины были у древних славян?
Есть в русском языке выражение «семь пядей во лбу» – так говорят об очень умном человеке. А сколько это в сантиметрах? Какой высоты лоб у обладателя «семи пядей»? Пядь – это расстояние между вытянутыми большим и указательным пальцами руки, то есть примерно 19 сантиметров.
А сколько это в сантиметрах? Какой высоты лоб у обладателя «семи пядей»? Пядь – это расстояние между вытянутыми большим и указательным пальцами руки, то есть примерно 19 сантиметров.
Вы понимаете, что «семь пядей во лбу» – это конечно же преувеличение.
А вот еще одна очень образная мера. О русских богатырях говорили: «У него косая сажень в плечах». Если вытянуть вверх правую руку, то расстояние от кончиков пальцев поднятой руки до пальцев левой руки – это и есть косая сажень. Была, кстати, и сажень простая – расстояние между разведенными в стороны руками.
Ткань чаще всего мерили локтями. Локоть – расстояние от локтевого сустава до вытянутого среднего пальца.
И пядь, и локоть, и сажень – это так называемые субъективные меры, так как у каждого человека они свои и зависят от его роста. Поэтому, например, купцы, торговавшие тканями, любили нанимать невысоких продавцов: их локти были короче, а значит, и денег за отрез получалось больше. Это примерно как в мультфильме, в котором измеряли удава: если в попугаях – 38, если же в мартышках – много меньше.
Самой крупной единицей длины была верста. Она складывалась из саженей. Некоторые считают, что в версте было всего 500 саженей, другие – 750. Если при этом вспомнить, что сажень у каждого своя, станет понятно, как неудобна была такая система мер. Вот почему со временем люди перешли на метрическую систему: ведь метр, дециметр, сантиметр никак не зависят от роста человека, производящего измерения.
Данный текст является ознакомительным фрагментом.
Какие меры длины использовали в России до введения метрической системы мер?
Какие меры длины использовали в России до введения метрической системы мер? До введения метрической системы мер в России для измерения длины использовали следующие единицы: миля (7 верст) = 7,4676 километра; верста (500 саженей) = 1,0668 километра; сажень (3 аршина = 7 футов = 100 соток)
Как назывались месяцы в календаре древних славян?
 При этом одни и те же месяцы в зависимости от местного климата в разных районах получили различные
При этом одни и те же месяцы в зависимости от местного климата в разных районах получили различныеМеры длины
Меры длины До введения в 1925 году метрической системы мер и международной системы единиц в России действовали так называемые русские меры, которые постоянно встречаются в произведениях дореволюционной литературы. Нередко эти термины при чтении не вызывают у
Англо–американские меры длины и веса:
Англо–американские меры длины и веса: 1 дюйм = 2,54 см;1 фут =12 дюймов = 30,48 см;1 ярд = 3 фута = 91,44 см;1 миля = 1,760 ярдов = 1,609 км;1 кв. дюйм = 6,45 кв. см;1 кв. фут = 929,03 кв. см;1 акр = 0,4 га;1 кв. миля = 259 га;1 галлон = 4,546 л (мера ёмкости)1 галлон = 3,785 л (мера жидких и сыпучих тел)1 унция = 28,35 г;1 фунт = 453,59
Какие музыкальные инструменты были популярны у древних греков?
Какие музыкальные инструменты были популярны у древних греков?
Древние греки были очень музыкальным народом, и греческие музыканты использовали разнообразные инструменты. Среди струнных они особенно любили лиру и очень похожую на нее кифару. Под аккомпанемент звуков
Среди струнных они особенно любили лиру и очень похожую на нее кифару. Под аккомпанемент звуков
Как выглядело поселение древних славян?
Как выглядело поселение древних славян? Поселения древних славян обычно располагались на возвышенных местах, находящихся вблизи источника воды – реки, ручья или родника. Поселение, которое обычно состояло из нескольких домов, никогда не оставалось без защиты. В
Какие праздники были у древних славян?
Какие праздники были у древних славян? Так же, как и другие древние народы, славяне одновременно верили во множество богов, которых считали очень похожими на людей.Каждый день выезжает из золотого дворца в колеснице, запряженной огненными конями, бог солнца. Солнце греет
БОГИ ДРЕВНИХ СЛАВЯН
БОГИ ДРЕВНИХ СЛАВЯН
Авсень
Авсень (Баусень, Овсень, Таусень, Усень) — персонаж, связанный с началом весеннего солнечного цикла и надеждой на урожай. Иногда он воспринимался как бог смены времен года. Его атрибутами являются золотисто-рыжие кони, это позволяет
Иногда он воспринимался как бог смены времен года. Его атрибутами являются золотисто-рыжие кони, это позволяет
Мифология древних славян
Мифология древних
Как назывались месяцы в календаре древних славян?
Как назывались месяцы в календаре древних славян? У древних славян год делился на 12 месяцев, названия которых были тесно связаны с наблюдавшимися явлениями природы. При этом одни и те же месяцы в зависимости от местного климата в разных районах получили различные
Исследовательская работа «Единицы измерения длины на Руси» / Открытый урок
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №3» г. Торжка
Торжка
Тверской области
Исследовательская работа
Единицы измерения длины на Руси
Выполнила: Кудряшова Алина, 2 б класс
МБОУ СОШ №3 г. Торжка.
Руководитель: Родионова Анна Анатольевна,
учитель начальных классов
г. Торжок
2020
Оглавление
1. Введение……………………………………………………………………….3
2. Глава I. Теоретическая часть …………………………………….5
3. Глава II. Практическая часть………………………….………….7
4. Заключение……………………………………………………………………9
5. Список используемой литературы…………………………….10
6. Приложение
Введение
На летние каникулы все ученики моего класса получили список литературы для прочтения. Я люблю читать, однако, часто в литературных произведениях встречаются слова, обозначающие единицы измерения Древней Руси. В русском языке их называют устаревшими, вышедшими из активного употребления. Ведь сейчас таких слов как аршин, пядь, вершок, сажень и не услышишь. В современном языке мы их почти не используем. Лишь при чтении художественных произведений да в пословицах и поговорках сталкиваемся с этими понятиями. Какого же роста на самом деле был знаменитый Конёк – горбунок из сказки Ершова? А чему был равен шаг великана в рассказах про Гулливера? Не зная старинных единиц измерения длины нельзя понять смысл русского фольклора. Поэтому в нашей работе мы рассмотрим наиболее распространенные старинные русские единицы измерения длины.
В современном языке мы их почти не используем. Лишь при чтении художественных произведений да в пословицах и поговорках сталкиваемся с этими понятиями. Какого же роста на самом деле был знаменитый Конёк – горбунок из сказки Ершова? А чему был равен шаг великана в рассказах про Гулливера? Не зная старинных единиц измерения длины нельзя понять смысл русского фольклора. Поэтому в нашей работе мы рассмотрим наиболее распространенные старинные русские единицы измерения длины.
Проблема: в школьных учебниках, литературных произведениях часто встречаются слова, обозначающие единицы измерения Древней Руси, но мы не знаем значения этих слов, поэтому не всегда правильно понимаем смысл прочитанного.
Цель работы: исследовать возникновение старинных единиц измерения и установить их связь с современными единицами.
Предмет исследования: единицы измерений длины в древней Руси.
Объект исследования: литературные источники и Интернет-ресурсы.
Задачи работы:
1. Собрать и проанализировать литературу по данной теме, отобрать нужный материал.
2. Выбрать краткую информацию с примерами пословиц и поговорок.
3. Изучить взаимосвязь старинных единиц измерения длины с современными.
4. Провести исследовательскую работу по теме: «Удобны ли старинные меры длины в современной жизни?»
5. Оформить собранный материал.
6. Познакомить обучающихся класса, школы с результатами исследования для расширения их знаний с историей своего народа.
Гипотеза: если переход от старинных мер единиц измерения к современной международной системе единиц был оправдан, то упрощает ли производимые измерения и делает ли их наиболее точными?
Методы работы:
1. Сбор информации (работа с литературными источниками, энциклопедией, поиск информации в сети Интернет).
2. Проведение исследования.
Практическая значимость работы:Материал данной работы можно использовать как справочный материал для учителей и учащихся на уроках математики, литературного чтения, на дополнительных занятиях для расширения кругозора.
Методы исследования:
— анализ литературы;
— опрос;
— анкетирование.
Глава I. Теоретическая часть
Единицы измерения длины на Руси
«Мера – это способ определения количества по принятой единице. Погонная, линейная мера служит для означения расстояний или величины линий». В. Даль
Не было народа, который не изобрел бы свои единицы измерения. С древности, мерой длины и веса всегда был человек: на сколько он протянет руку, сколько сможет поднять на плечи и т.д.
Собрав материал и изучив литературу по данной теме, мы выяснили, что некоторые древнерусские меры длины носят названия частей тела человека, так как измерялись с их помощью.
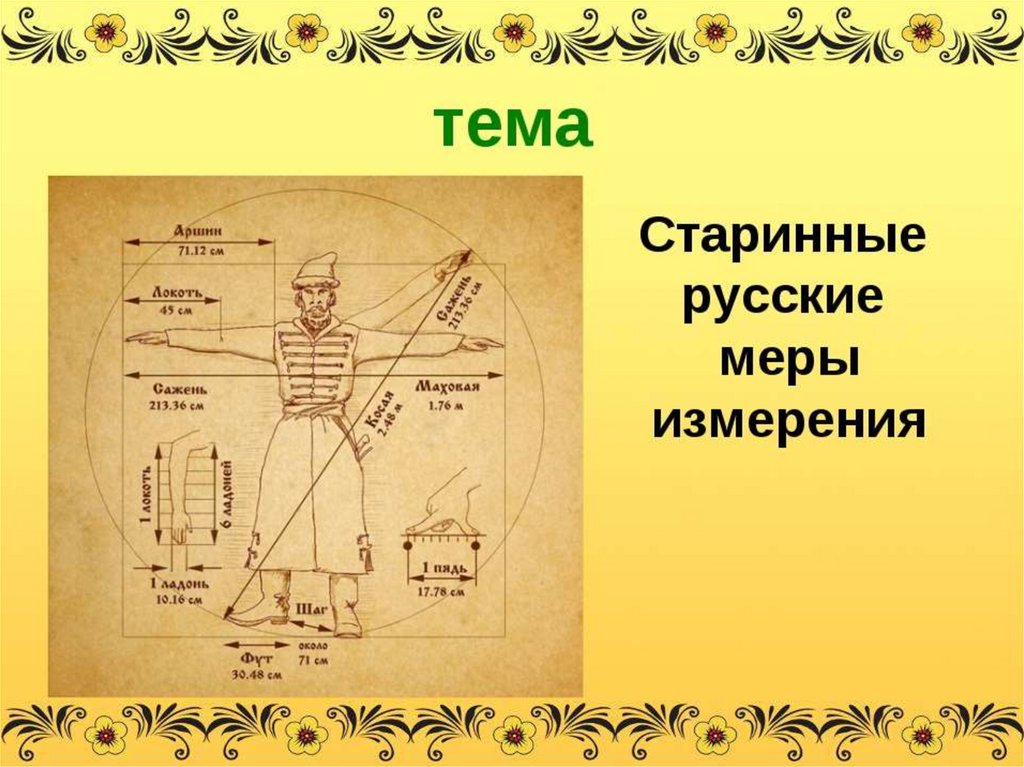
Рассмотрим подробно систему древнерусских мер длины, которая включала в себя следующие основные меры: пядь, локоть, вершок, аршин, сажень.
• Кисть руки наши предки называли словом «пядь». Малая пядь – это расстояние между раздвинутым большим и указательным пальцами и соответствует 19 см; большая или великая пядь – расстояние между большим пальцем и мизинцем – около 22 – 23 см. В качестве народной меры пядь употреблялась очень долго, ею измеряли, например, иконы (отсюда название икон, имеющих в ширину 19 или 23 см, – «пядницы») или толщину снежного покрова ещё в XVII веке. Большая часть кирпичей XII века имеют ширину также пядь в 19 см. А пословица «Семь пядей во лбу» говорит об очень умном человеке, но понятно, что это явное преувеличение.
В качестве народной меры пядь употреблялась очень долго, ею измеряли, например, иконы (отсюда название икон, имеющих в ширину 19 или 23 см, – «пядницы») или толщину снежного покрова ещё в XVII веке. Большая часть кирпичей XII века имеют ширину также пядь в 19 см. А пословица «Семь пядей во лбу» говорит об очень умном человеке, но понятно, что это явное преувеличение.
• Для измерения тканей чаще всего использовали длину «локоть». Это расстояние от локтевого сгиба до конца вытянутого среднего пальца руки. Локоть примерно равен трём пядям. Торговцы тканями хитрили и специально нанимали невысоких продавцов: их локти были короче, а значит и ткани отрезалось меньше.
• Ещё одна старинная русская мера длины – вершок. Произошло от слова «верх» («верх перста», т.е. пальца) и равнялась длине верхней части указательного пальца. В современности примерно 4,4 см. В литературе XVII в. встречаются и доли вершка «полвершка» и «четвертьвершка». Вспомните Конька – Горбунка ростом только в три вершка.
• Ах, да! Мы же забыли про аршинные уши Конька- Горбунка… Аршин пришёл на Русь вместе с купцами из далёких восточных стран. От персидского «арши» — Торговцы, отмеряя ткани, обходились без всяких метров: ткань они натягивали на свою собственную руку, до плеча. Это и называлось мерить аршинами. Он равен 71 см. Хоть и была мера очень удобной, но был у неё и большой недостаток: руки, к сожалению, у всех разные.
• А если те же самые руки развести в стороны и измерить расстояние от одного кончика среднего пальца до другого, то получится ещё одна старинная мера длины – сажень. А косая сажень – это расстояние от подошвы левой ноги до конца большого пальца вытянутой вверх правой руки. В Древней Руси о богатырях говорили: «У него косая сажень в плечах».
Глава II. Экспериментальная и практическая часть
Социологический опрос
«Знаешь ли ты старинные меры длины?»
Интересно, а как осведомлены по этому вопросу взрослые и современные дети? С этой целью был проведен опрос (Приложение 1), в котором участвовали ученики второго класса, восьмого класса, одиннадцатого класса, учителя, родители. Всего было опрошено 30 участников.
Всего было опрошено 30 участников.
Результаты опроса представлены в таблице:
|
Участвовали |
Количество |
Современные меры длины |
Старинные меры длины |
Да/Нет |
|
Одноклассники |
9 |
9 |
1 |
0/12 |
|
Ученики 8 класса |
7 |
7 |
3 |
0/4 |
|
Ученики 11 класса |
5 |
5 |
4 |
0/5 |
|
Родители |
4 |
4 |
4 |
0/4 |
|
Учителя |
5 |
5 |
5 |
0/5 |
|
Всего |
30 |
30 |
17 |
0/30 |
|
% |
100 |
100 |
57 |
0/100 |
Результаты опроса показали, что с современными мерами длины знакомы все опрошенные – 30 человек (100%).
Со старинными мерами длины оказались знакомы только 17 человек (57%).
Не знакомы со старинными мерами длины 14 человек (43%)
Старинные меры длины ни кто не использует в быту.
Так же опрос показал, что со старинными мерами длины не знакомы только одноклассники и часть учащихся 8 класса.
Исследование
«Удобны ли старинные меры длины в современной жизни?»
Задание: Измерить длину рабочего стола, используя старинные единицы измерения длины: пядь, локоть, вершок.
В исследовании участвовали: ученик 11 класса, ученица 8 класса, я.
Таблица измерений пяди, локтя и вершка в метрических мерах
|
Участники |
Пядь |
Локоть |
Вершок |
|
Ученик 11 класса |
21см |
49 см |
6 см |
|
Ученица 8 класса |
17 см |
38 см |
5 см |
|
я |
13 см |
32 см |
4 см |
Таблица измерений длины стола в русских мерах
|
Участники |
Длина стола |
||
|
в пядях |
в локтях |
в вершках |
|
|
Ученик 11 класса |
5 пядей |
2 локтя |
6,5 вершков |
|
Ученица 8 класса |
6 пядей |
2,5 локтя |
14,5 вершков |
|
я |
7,5 пядей |
3,5 локтя |
19 вершков |
Оказалось, что у нас у всех получились разные результаты. У ученика 11 класса получились самые большие единицы измерения, у ученицы 8 класса чуть меньше, а у меня самые маленькие, так как мы все разного роста и телосложения.
У ученика 11 класса получились самые большие единицы измерения, у ученицы 8 класса чуть меньше, а у меня самые маленькие, так как мы все разного роста и телосложения.
Заключение
Мною была проделана большая, интересная работа. В ходе работы я познакомилась с историей возникновения измерений в древней Руси.
В результате проведенного исследования я убедилась, что старинная система мер была разнообразной, одна мера длины могла носить множества имён, и назначений, поэтому мы пришли к выводам:
• В древней Руси меры измерения длины зависели от самого человека и видов его практической деятельности.
• Возникла необходимость отказаться от установления связей между единицами измерения и размерами человеческого тела.
• Гипотеза наша подтверждена: переход к общей для всех стран системе измерений был необходим, современные единицы и способы дают более точные результаты измерений.
Изучив много литературы и обработав ее, мы с Анной Анатольевной приготовили и провели классный час на тему: «Единицы измерения длины на Руси», который в дальнейшем может нам пригодиться на уроках математики, литературного чтения, окружающего мира и других предметах.
Единицы измерений сегодня удобны, лаконичны и понятны. Мир меняется, меняемся и мы, но знания дают нам нужную структуру для понимания духовного мира нашего народа в далёком прошлом.
Каждый человек должен знать и современные меры длины и старинные. Не зная прошлого нельзя понять настоящее!
Список использованной литературы
• В. И. Даль. Толковый словарь русского языка. М.: Астрель, 2001
• Краткий энциклопедический справочник по математике. – М., 2003
• «Русские народные загадки, пословицы и поговорки» – М.: « Просвещение», 1990
• Карпушина, Н.М. Рукотворные мерки[Текст]/ Н.М. Карпушина // Математика в школе. — 2008.- №7. –С.49-61.
• Рыбаков Б.А. Русские системы мер длины Х1-ХУ веков. Советская этнография, 1949 г., №1.
• Интернет — ресурсы
Приложение
Приложение 1
Социологический опрос «Знаешь ли ты старинные меры длины?»
1. Знакомы ли Вам современные меры длины: миллиметр, сантиметр, дециметр, метр и километр?
Знакомы ли Вам современные меры длины: миллиметр, сантиметр, дециметр, метр и километр?
2. Знакомы ли Вам старинные меры длины: пядь, локоть, вершок, аршин, сажень?
3. Используете ли вы старинные меры в быту?
Скачать публикацию
Проект меры измерения в разных странах. Единицы измерения с древности до наших дней. Всё, о чём мы не задумываемся, кажется нам простым. Вот, например, цифры
Величина — это то, что можно измерить. Такие понятия, как длина, площадь, объём, масса, время, скорость и т. д. называют величинами. Величина является результатом измерения , она определяется числом, выраженным в определённых единицах. Единицы, в которых измеряется величина, называют единицами измерения .
Для обозначения величины пишут число, а рядом название единицы, в которой она измерялась. Например, 5 см, 10 кг, 12 км, 5 мин.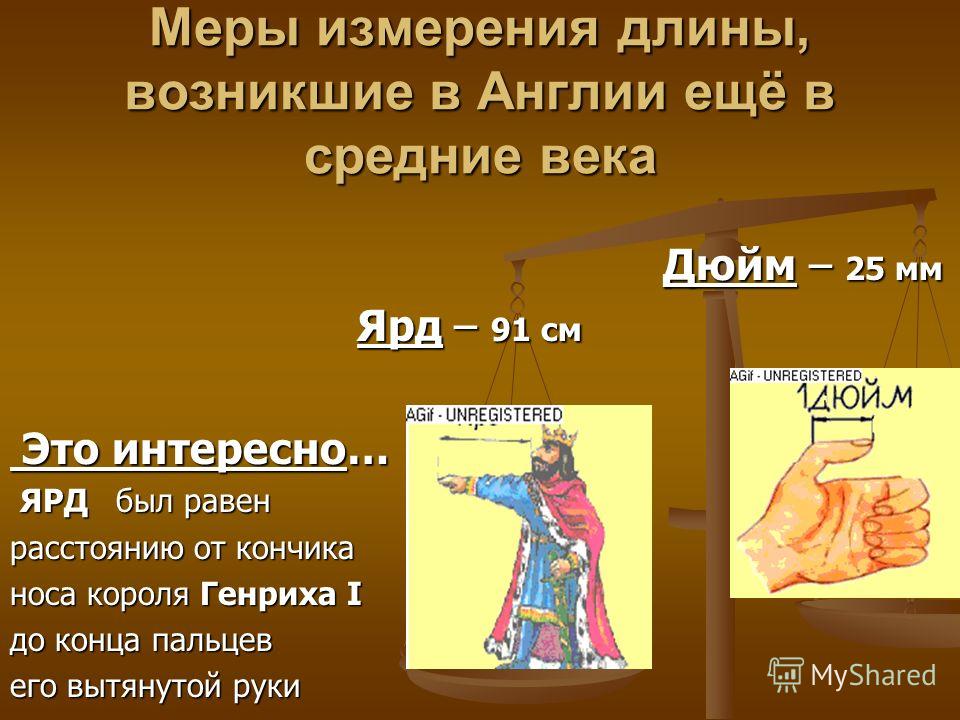 Каждая величина имеет бесчисленное множество значений, например длина может быть равна: 1 см, 2 см, 3 см и т. д.
Каждая величина имеет бесчисленное множество значений, например длина может быть равна: 1 см, 2 см, 3 см и т. д.
Одна и та же величина может быть выражена в разных единицах, например килограмм, грамм и тонна — это единицы измерения веса. Одна и та же величина в разных единицах выражается разными числами. Например, 5 см = 50 мм (длина), 1 ч = 60 мин (время), 2 кг = 2000 г (вес).
Измерить какую-нибудь величину — значит узнать, сколько раз в ней содержится другая величина того же рода, принятая за единицу измерения.
Например, мы хотим узнать точную длину какой-нибудь комнаты. Значит нам нужно измерить эту длину при помощи другой длины, которая нам хорошо известна, например при помощи метра. Для этого откладываем метр по длине комнаты столько раз, сколько можно. Если он уложится по длине комнаты ровно 7 раз, то длина её равна 7 метрам.
В результате измерения величины получается или именованное число , например 12 метров, или несколько именованных чисел, например 5 метров 7 сантиметров, совокупность которых называется составным именованным числом .
Меры
В каждом государстве правительство установило определённые единицы измерения для различных величин. Точно рассчитанная единица измерения, принятая в качестве образца, называется эталоном или образцовой единицей . Сделаны образцовые единицы метра, килограмма, сантиметра и т. п., по которым изготавливают единицы для обиходного употребления. Единицы, вошедшие в употребление и утверждённые государством, называются мерами .
Меры называются однородными , если они служат для измерения величин одного рода. Так, грамм и килограмм — меры однородные, так как они служат для измерения веса.
Единицы измерения
Ниже представлены единицы измерения различных величин, которые часто встречаются в задачах по математике:
Меры веса/массы
- 1 тонна = 10 центнеров
- 1 центнер = 100 килограмм
- 1 килограмм = 1000 грамм
- 1 грамм = 1000 миллиграмм
- 1 километр = 1000 метров
- 1 метр = 10 дециметров
- 1 дециметр = 10 сантиметров
- 1 сантиметр = 10 миллиметров
- 1 кв.
 километр = 100 гектарам
километр = 100 гектарам - 1 гектар = 10000 кв. метрам
- 1 кв. метр = 10000 кв. сантиметров
- 1 кв. сантиметр = 100 кв. миллиметрам
- 1 куб. метр = 1000 куб. дециметров
- 1 куб. дециметр = 1000 куб. сантиметров
- 1 куб. сантиметр = 1000 куб. миллиметров
Рассмотрим ещё такую величину как литр . Для измерения вместимости сосудов употребляется литр. Литр является объёмом, который равен одному кубическому дециметру (1 литр = 1 куб. дециметру).
Меры времени
- 1 век (столетие) = 100 годам
- 1 год = 12 месяцам
- 1 месяц = 30 суткам
- 1 неделя = 7 суткам
- 1 сутки = 24 часам
- 1 час = 60 минутам
- 1 минута = 60 секундам
- 1 секунда = 1000 миллисекундам
Кроме того, используют такие единицы измерения времени, как квартал и декада.
- квартал — 3 месяца
- декада — 10 суток
Месяц принимается за 30 дней, если не требуется определить число и название месяца. Январь, март, май, июль, август, октябрь и декабрь — 31 день. Февраль в простом году — 28 дней, февраль в високосном году — 29 дней. Апрель, июнь, сентябрь, ноябрь — 30 дней.
Январь, март, май, июль, август, октябрь и декабрь — 31 день. Февраль в простом году — 28 дней, февраль в високосном году — 29 дней. Апрель, июнь, сентябрь, ноябрь — 30 дней.
Год представляет собой (приблизительно) то время, в течении которого Земля совершает полный оборот вокруг Солнца. Принято считать каждые три последовательных года по 365 дней, а следующий за ними четвёртый — в 366 дней. Год, содержащий в себе 366 дней, называется високосным , а годы, содержащие по 365 дней — простыми . К четвёртому году добавляют один лишний день по следующей причине. Время обращения Земли вокруг Солнца содержит в себе не ровно 365 суток, а 365 суток и 6 часов (приблизительно). Таким образом, простой год короче истинного года на 6 часов, а 4 простых года короче 4 истинных годов на 24 часа, т. е. на одни сутки. Поэтому к каждому четвёртому году добавляют одни сутки (29 февраля).
Об остальных видах величин вы узнаете по мере дальнейшего изучения различных наук.
Сокращённые наименования мер
Сокращённые наименования мер принято записывать без точки:
| Меры веса/массы
|
Меры площади (квадратные меры)
|
|
Меры времени
| Мера вместимости сосудов
|
Измерительные приборы
Для измерения различных величин используются специальные измерительные приборы. Одни из них очень просты и предназначены для простых измерений. К таким приборам можно отнести измерительную линейку, рулетку, измерительный цилиндр и др. Другие измерительные приборы более сложные. К таким приборам можно отнести секундомеры, термометры, электронные весы и др.
Измерительные приборы, как правило, имеют измерительную шкалу (или кратко шкалу). Это значит, что на приборе нанесены штриховые деления, и рядом с каждым штриховым делением написано соответствующее значение величины. Расстояние между двумя штрихами, возле которых написано значение величины, может быть дополнительно разделено ещё на несколько более малых делений, эти деления чаще всего не обозначены числами.
Определить, какому значению величины соответствует каждое самое малое деление, не трудно. Так, например, на рисунке ниже изображена измерительная линейка:
Цифрами 1, 2, 3, 4 и т. д. обозначены расстояния между штрихами, которые разделены на 10 одинаковых делений. Следовательно, каждое деление (расстояние между ближайшими штрихами) соответствует 1 мм. Эта величина называется ценой деления шкалы измерительного прибора.
Перед тем как приступить к измерению величины, следует определить цену деления шкалы используемого прибора.
Для того чтобы определить цену деления, необходимо:
- Найти два ближайших штриха шкалы, возле которых написаны значения величины.

- Вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.
В качестве примера определим цену деления шкалы термометра, изображённого на рисунке слева.
Возьмём два штриха, около которых нанесены числовые значения измеряемой величины (температуры).
Например, штрихи с обозначениями 20 °С и 30 °С. Расстояние между этими штрихами разделено на 10 делений. Таким образом, цена каждого деления будет равна:
(30 °С — 20 °С) : 10 = 1 °С
Следовательно, термометр показывает 47 °С.
Измерять различные величины в повседневной жизни приходится постоянно каждому из нас. Например, чтобы прийти вовремя в школу или на работу, приходится измерять время, которое будет потрачено на дорогу. Метеорологи для предсказания погоды измеряют температуру, атмосферное давление, скорость ветра и т. д.
Какие меры длины существовали в древности? Каждая страна в мире пользуется своими способами измерения расстояния. Но это очень неудобно, ведь в разных странах эти системы мер не совпадают. Единицы измерения дошли до нас из глубины веков. Английский король однажды много-много лет назад вытянул вперед правую руку и заявил: «Расстояние от кончика моего носа до большого пальца руки будет служить для всего моего народа мерой длины и называться «ЯРД». Его подданные тут же приготовили бронзовый прут «от королевского носа до пальца», и ярд надолго стал для всех англичан единицей измерения длины. Длина ярда 91,44 см.Единицы измерения дошли до нас из глубины веков. Английский король однажды много-много лет назад вытянул вперед правую руку и заявил: «Расстояние от кончика моего носа до большого пальца руки будет служить для всего моего народа мерой длины и называться «ЯРД». Его подданные тут же приготовили бронзовый прут «от королевского носа до пальца», и ярд надолго стал для всех англичан единицей измерения длины. Длина ярда 91,44 см.
Единицы измерения дошли до нас из глубины веков. Английский король однажды много-много лет назад вытянул вперед правую руку и заявил: «Расстояние от кончика моего носа до большого пальца руки будет служить для всего моего народа мерой длины и называться «ЯРД». Его подданные тут же приготовили бронзовый прут «от королевского носа до пальца», и ярд надолго стал для всех англичан единицей измерения длины. Длина ярда 91,44 см.Единицы измерения дошли до нас из глубины веков. Английский король однажды много-много лет назад вытянул вперед правую руку и заявил: «Расстояние от кончика моего носа до большого пальца руки будет служить для всего моего народа мерой длины и называться «ЯРД». Его подданные тут же приготовили бронзовый прут «от королевского носа до пальца», и ярд надолго стал для всех англичан единицей измерения длины. Длина ярда 91,44 см.
В средние века в Европе придумали еще одну единицу измерения длины — ФУТ. Фут — это средняя длина ступни взрослого мужчины. По-английски это означает «ступня», «нога». Один фут равен 30,48 см. Большие расстояния измерялись в Древнем Риме шагами: 2000 шагов впос ледствии стали равняться одной миле, или 1,609 км.
Один фут равен 30,48 см. Большие расстояния измерялись в Древнем Риме шагами: 2000 шагов впос ледствии стали равняться одной миле, или 1,609 км.
В древние времена индейцы при покупке земли использовали свою единицу измерения территории. Участок, который человек обежит за день, и был такой единицей измерения. Поэтому, чтобы купить побольше земли, покупатель нанимал самого быстрого «измерителя» — бегуна например, существовали свои меры длины — вершок, пядь, локоть. Большие расстояния измеряли полетом стрелы. Однако это были приблизительные, неточные меры. Ведь у разных людей могли быть разные вершки, пяди, локти. Да и лук стрелял на разные расстояния. Поэтому с развитием торговли потребовались точные меры длины. Чтобы продавец и покупатель не обманывали друг друга… Такой мерой в России стал АРШИН. Три аршина составляли САЖЕНЬ, 500 саженей — ВЕРСТУ.В древние времена индейцы при покупке земли использовали свою единицу измерения территории. Участок, который человек обежит за день, и был такой единицей измерения. Поэтому, чтобы купить побольше земли, покупатель нанимал самого быстрого «измерителя» — бегуна. А в Древней Руси, например, существовали свои меры длины — вершок, пядь, локоть. Большие расстояния измеряли полетом стрелы. Однако это были приблизительные, неточные меры. Ведь у разных людей могли быть разные вершки, пяди, локти. Да и лук стрелял на разные расстояния. Поэтому с развитием торговли потребовались точные меры длины. Чтобы продавец и покупатель не обманывали друг друга… Такой мерой в России стал АРШИН. Три аршина составляли САЖЕНЬ, 500 саженей — ВЕРСТУ..
Поэтому, чтобы купить побольше земли, покупатель нанимал самого быстрого «измерителя» — бегуна. А в Древней Руси, например, существовали свои меры длины — вершок, пядь, локоть. Большие расстояния измеряли полетом стрелы. Однако это были приблизительные, неточные меры. Ведь у разных людей могли быть разные вершки, пяди, локти. Да и лук стрелял на разные расстояния. Поэтому с развитием торговли потребовались точные меры длины. Чтобы продавец и покупатель не обманывали друг друга… Такой мерой в России стал АРШИН. Три аршина составляли САЖЕНЬ, 500 саженей — ВЕРСТУ..
В XVIII России — достались две копии: N 11 и N 28…В XVIII веке французские ученые предложили метрическую систему мер на все времена и для всех народов. Единицей длины был выбран метр — одна сорокамиллионная часть земного меридиана, проходящего через Париж. Ученые изготовили эталон (образец) метра в виде линейки из платины. Это такой металл. Правда, все боялись, что этот эталон потеряется, и на всякий случай сделали 31 копию метра и раздали их разным странам. России — достались две копии: N 11 и N Теперь этой метрической системой пользуется большинство стран
России — достались две копии: N 11 и N Теперь этой метрической системой пользуется большинство стран
Название- перевод Древняя Греция Древний Рим Линейное значение в системе СИ (часто приблизительное)СИ Другие варианты линейных значений «палец» дактиль (др.-греч. δάκτυλος)др.-греч. дигит (лат. digitus)лат. 1,85 смсм 1,85 см ок. 1 дюймадюйма 1,997 см «1/12 целого» унцияунция (лат. un cia)лат. ок. 7 см 7,39 см 22,18 см = 3 пальма «ступня» пус (др.-греч. πούς)др.-греч. пес (лат. pes)лат. пес монеталис (лат. pes monetalis)лат. пес натуралис (лат. pes naturalis)лат. пес друзианус (лат. pes drusianus)лат. 29,62 см пес = 1 римский фут = 12 унций 29,62 см 25,00 см 33,27 см 30,80 см 29,57 см; 29,6352 см
Меры площади ГрецияГреция (Афины) Афины Римская империя На чём основывал ась мера Приблизител ьное значение iugerumюгер2523,3 м² др.- греч.др.- греч. πλεθρ ον квадратных футов 876 м² arura арура (50 квадратных футов) 43,8 м²
Древний Египет Меры длины 1 Парасанг равен 1/9 шема = 6,98 кмПарасанг 1 шем = 62,82 км Египетская система (с 5 по 1 вв. включительно до н.э.): Атур обычный = 3 милям = 5,235 км. Атур царский = 1 1/2 парасангам = 10,47 км. Парасанг = 1 1/9 шема = 6,98 км. Шем = 1 1/5 атура обычного = 6,282 км. Миля = 10 стадиям = 1,745 км. Стадий = 3 1/3 хета = 174,5 м. (употребляется также стадий = 209,4 м.) Хет (сенус) = 25 оргиям = 52,35 м. Оргия = 1 1/3 ксилона = 52,35 м. Ксилон = 3 локтям царским = 1,57 м. Локоть царский = 1 1/6 локтя малого = 1 1/5 пигона = 52,35 см. Локоть малый = 44,83 см. Пигон = 1 1/4 зерца = 43,625 см. Зерец (фут) = 1 1/3 спитама = 2 дихасам = 34,9 см. Спитам = 1 1/2 дихаса = 26,175 см. Дихас = 2 шеспам = 17,45 см. Шесп = 4 тебам = 8,725 см. Теб (палец) = 2,18 см. Канна = 5 шагам = 11 2/3 зерецам = 4,07 м. Шаг = 2 1/3 зерецам = 81,44 см.
включительно до н.э.): Атур обычный = 3 милям = 5,235 км. Атур царский = 1 1/2 парасангам = 10,47 км. Парасанг = 1 1/9 шема = 6,98 км. Шем = 1 1/5 атура обычного = 6,282 км. Миля = 10 стадиям = 1,745 км. Стадий = 3 1/3 хета = 174,5 м. (употребляется также стадий = 209,4 м.) Хет (сенус) = 25 оргиям = 52,35 м. Оргия = 1 1/3 ксилона = 52,35 м. Ксилон = 3 локтям царским = 1,57 м. Локоть царский = 1 1/6 локтя малого = 1 1/5 пигона = 52,35 см. Локоть малый = 44,83 см. Пигон = 1 1/4 зерца = 43,625 см. Зерец (фут) = 1 1/3 спитама = 2 дихасам = 34,9 см. Спитам = 1 1/2 дихаса = 26,175 см. Дихас = 2 шеспам = 17,45 см. Шесп = 4 тебам = 8,725 см. Теб (палец) = 2,18 см. Канна = 5 шагам = 11 2/3 зерецам = 4,07 м. Шаг = 2 1/3 зерецам = 81,44 см.
Английская система мер Английская система мер используется в Великобритании, США и других странах. Отдельные из этих мер в ряде стран несколько различаются по своему размеру, поэтому ниже приводятся в основном округлённые метрические эквиваленты английских мер, удобные для практических расчётов. ВеликобританииСША Постепенно меры английской системы вытесняются метрической системой мер.
ВеликобританииСША Постепенно меры английской системы вытесняются метрической системой мер.
Меры длиныдлины 1 морская миля (nautical mile, Великобритания) = 10 кабельтовым = 1,8532 кмморская миля 1 морская миля (nautical mile, США, с 1 июля 1954) = 1,852 км 1 кабельтов (cable, Великобритания) = 185,3182 мкабельтов 1 кабельтов (cable, США) = 185,3249 м 1 уставная миля (statute mile) = 8 фарлонгам = футам = 1609,344 муставная миля 1 фарлонг (furlong) = 10 чейнам = 201,168 мфарлонг 1 чейн (chain) = 4 родам = 100 линкам = 20,1168 мчейн 1 род (rod, pole, perch, поль, перч) = 5,5 ярдам = 5,0292 мродпольперч 1 ярд (yard) = 3 футам = 0,9144 мярд 1 фут (foot) = 3 хэндам = 12 дюймам = 0,3048 мфут 1 хэнд (hand) = 4 дюймам = 10,16 смхэнд 1 дюйм (inch) = 12 линиям = 72 точкам = 1000 милам = 2,54 смдюйм 1 линия (line) = 6 точкам = 2,1167 ммлиния 1 точка (point) = 0,353 ммточка 1 мил (mil) = 0,0254 мммил
Меры площадиплощади 1 миля² (square mile) = 640 акрам = 2,59 км² 1 акр (acre) = 4 рудам = 4046,86 м²акр 1 руд (rood) = 40 родам² = 1011,71 м²руд 1 род² (square rod) (поль², перч²) = 30,25 ярдам² = 25,293 м² 1 ярд² (square yard) = 9 футам² = 0,83613 м² 1 фут² (square foot) = 144 дюймам² = 929,03 см²фут² 1 дюйм² (square inch) = 6,4516 см²
 д.
д. Измерения нужны были и в строительстве, и в торговле, и в астрономии, фактически в любой сфере жизни. Очень большая точность измерений нужна была при строительстве египетских пирамид.
Рис. 0
Значение измерений возрастало по мере развития общества и, в частности, по мере развития науки. А чтобы измерять, необходимо было придумать единицы различных физических величин. Вспомним, как написано в учебнике: “Измерить какую-нибудь величину – это значит сравнить ее с однородной величиной, принятой за единицу этой величины”.
Целью моей работы было выяснить: какие существовали и существуют сейчас единицы длины и массы, каково их происхождение?
Вершок, локоть и другие единицы…
Измеряй все доступное измерению и делай не доступное измерению доступным”.
Г.Галилей
Самыми древними единицами были субъективные единицы. Так, например, моряки измеряли путь трубками, т. е. расстоянием, которое проходит судно за время, пока моряк выкурит трубку.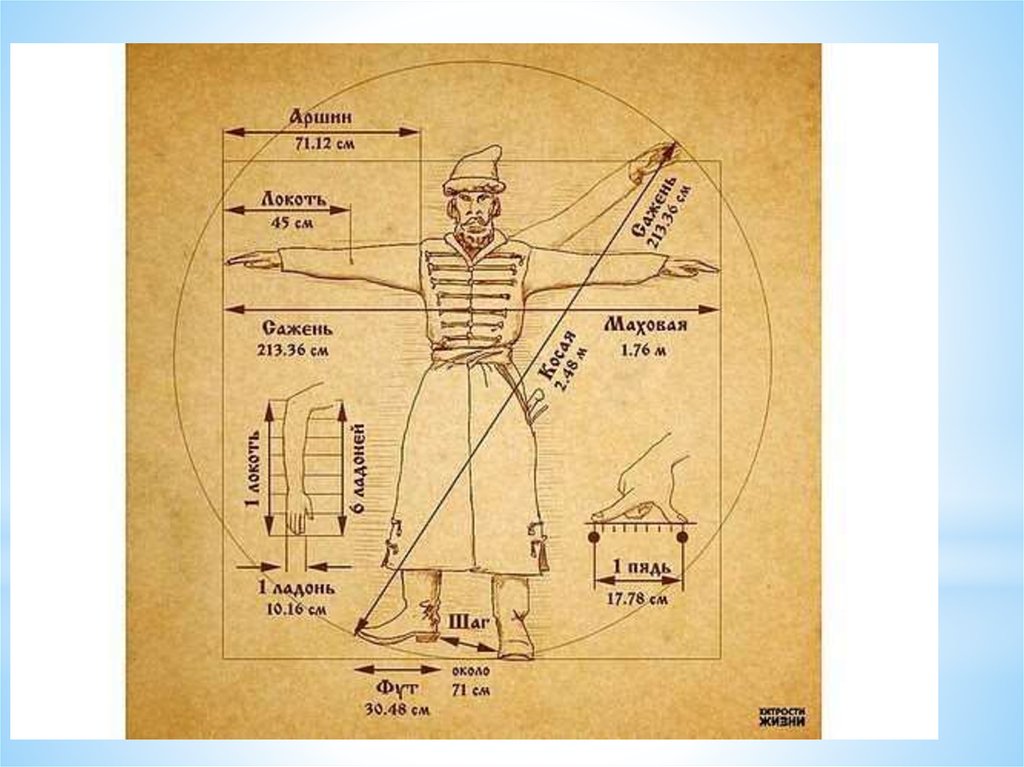 В Испании похожей единицей была сигара, в Японии – лошадиный башмак, т. е. путь, который проходила лошадь, пока не износится привязанная к ее копытам соломенная подошва, заменявшая подкову.
В Испании похожей единицей была сигара, в Японии – лошадиный башмак, т. е. путь, который проходила лошадь, пока не износится привязанная к ее копытам соломенная подошва, заменявшая подкову.
В программе Олимпийских игр Древней Эллады был бег на стадию. Установлено, что греческая стадия (или стадий) это длина стадиона в Олимпии – 192,27 м. Стадий равняется расстоянию, которое проходит человек спокойным шагом за время от появления первого луча солнца, при его восходе, до момента, когда диск солнца целиком окажется над горизонтом. Это время приблизительно равно двум минутам …
Стадий, как единица измерения расстояний, был и у римлян (185 см), и у вавилонян (около 195 см), и у египтян (195 см).
В Сибири в стародавние времена употреблялась мера расстояний – бука. Это расстояние, на котором человек перестает видеть раздельно рога быка.
У многих народов для определения расстояния использовалась единица длины стрела – дальность полета стрелы. Наши выражения “не подпускать на ружейный выстрел”, позднее “на пушечный выстрел” – напоминают о подобных единицах длины.
Древние римляне расстояния измеряли шагами или двойными шагами (шаг левой ногой, шаг правой). Тысяча двойных шагов составляла милю (лат. “милле” – тысяча).
Длину веревки или ткани неудобно измерять шагами или стадиями. Для этого оказались пригодными встречающиеся у многих народов единицы, отождествляемые с названиями частей человеческого тела. Локоть – расстояние от конца пальцев до локтевого сустава.
Рис. 1 Рис. 2
Мерой длины для тканей, веревок и т.п. наматывающихся материалов у многих народов был двойной локоть. Этой мерой мы и сейчас пользуемся для приблизительной оценки длины…
На Руси долгое время в качестве единицы длины использовали аршин (примерно 71 см). Эта мера возникла при торговле с восточными странами (перс, “арш” – локоть). Многочисленные выражения: “Словно аршин проглотил”, “Мерить на свой аршин” и другие – свидетельствуют о ее распространении.
Для измерения меньших длин применяли пядь – расстояние между концами расставленных большого и указательного пальцев.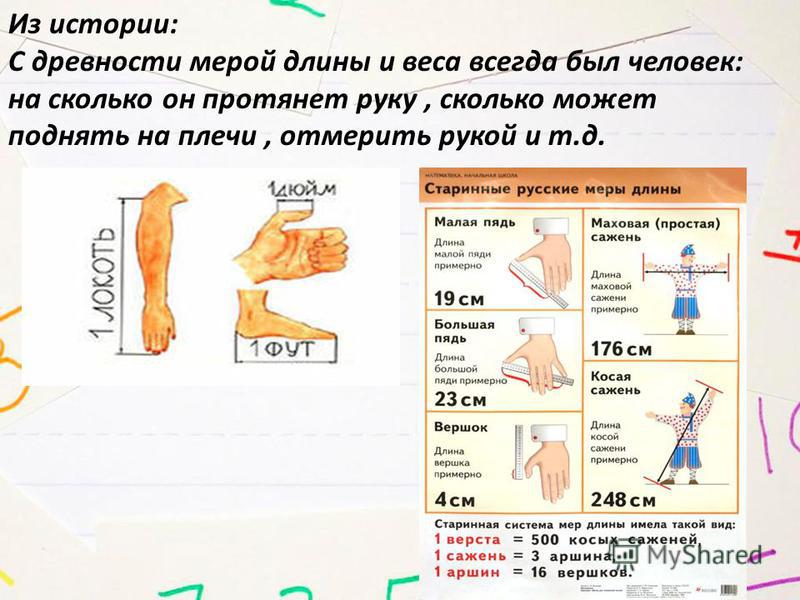
Рис. 3
Пядь или, как ее еще называли, четверть (18 см) составляла 1 / 4 аршина, а 1/ 16 аршина равнялся вершок (4,4 см).
Очень распространенной единицей длины была сажень. Впервые упоминание о ней встречается в XI в. С 1554 г. сажень устанавливают равной 3 аршинам (2,13 м) и она получает название царской (или орленой, печатной) в отличие от произвольных – маховой и косой. Маховая сажень – размах рук – равна примерно 2,5 аршинам. Рыбак, который показывает, какую большую рыбу он упустил, демонстрирует нам маховую.
Рис. 4
Косая сажень – расстояние от конца вытянутой вверх правой руки до носка левой ноги, она примерно равна 3,25 аршинам.
Рис. 5
Вспомним, как в сказках о великанах: “Косая сажень в плечах”. Удивительно совпадение древнеримской меры длины – «архитектурной трости» и древнерусской косой сажени: 248 см. Имеется в виду сажень «с ноги на руку косая, от земли и до земли». Эту сажень определяли длиной веревки, один конец которой прижимался ногой к земле, а другой перекидывался через согнутую в локте руку стоящего человека и опускался снова до земли.
При сложении упомянутой выше косой сажени вчетверо получаем «литовский локоть» (62 см).
В странах Западной Европы издавна применяли в качестве единиц дюйм (2,54 см) –длина сустава большого пальца (от голл. “дюйм” – большой палец) и фут (30 см) – средняя длина ступни человека (от англ. “фут” – ступня).
Рис. 6 Рис. 7
Локоть, вершок, пядь, сажень, дюйм, фут и т. д. очень удобны при измерениях, так как они всегда “под руками”. Но единицы длины, соответствующие частям человеческого тела, обладают большим недостатком: у различных людей пальцы, ступни и т. д. имеют разную длину. Чтобы избавиться от произвола, в XIV в. субъективные единицы начинают заменять набором объективных единиц. Так, например, в 1324 г. в Англии был установлен законный дюйм, равный длине трех приставленных друг к другу ячменных зерен, вытянутых из средней части колоса. Фут определили как среднюю длину ступни шестнадцати человек, выходящих из церкви, т. е. обмером случайных людей стремились получить более постоянное значение единицы – среднюю длину ступни.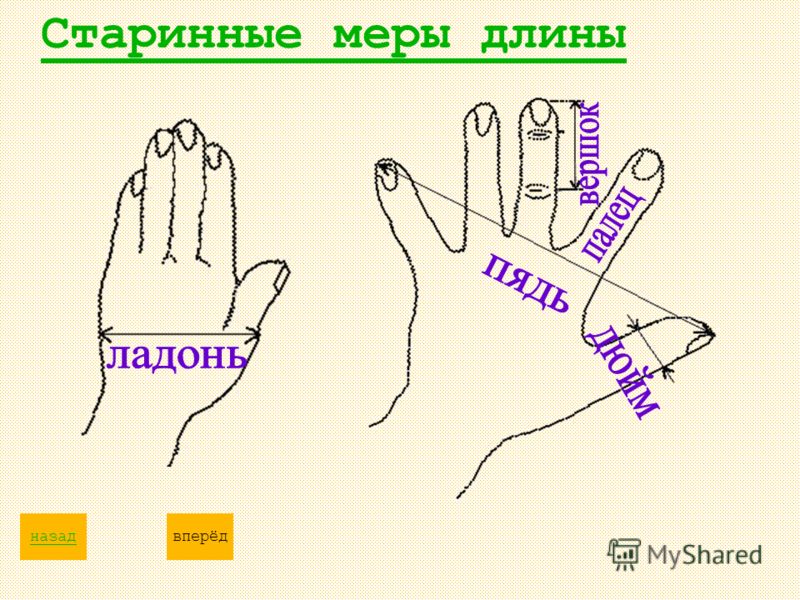
Рис. 8
Какую величину мы определяем, взвешивая тело на рычажных весах?
Какой народ и когда изобрел рычажные весы – неизвестно. Возможно, что это было сделано многими народами независимо друг от друга, а простота использования послужила причиной их широкого распространения.
Рис. 9
При взвешивании на рычажных весах на одну чашку кладут взвешиваемое тело, на другую – гири. Гири подбирают так, чтобы установить равновесие. При этом уравновешиваются массы взвешиваемого тела и гирь. Если уравновешенные весы перенести, например, на Луну, где вес тела меньше, чем на Земле, в 6 раз, равновесие не нарушится, так как вес и тела, и гирь на Луне уменьшился в одинаковое число раз, а масса осталась прежней.
Следовательно, взвешивая тело на рычажных весах, мы определяем его массу, а не вес.
Единицы массы, как и единицы длины, сначала устанавливались по природным образцам. Чаще всего по массе какого-нибудь семени. Так, например, массу драгоценных камней определяли и до сих пор определяют в каратах (0,2 г) – это масса семени одного из видов бобов.
Рис. 10
Позднее за единицу массы стали принимать массу воды, наполняющей сосуд определенной вместимости. Например, в Древнем Вавилоне за единицу массы принимали талант – массу воды, наполняющей такой сосуд, из которого вода равномерно вытекает через отверстие определенного размера в течение одного часа.
По массе зерен или воды изготовляли металлические гири разной массы. Ими пользовались при взвешивании.
Гири, служившие эталоном (образцом), хранились в храмах или правительственных учреждениях.
На Руси древнейшей единицей массы была гривна (409,5 г). Существует предположение, что эта единица ввезена к нам с Востока. Впоследствии она получила название фунта. Для определения больших масс использовался пуд (16,38 кг), а малых – золотник (12,8 г).
В 1791 г. во Франции было принято решение создать десятичную метрическую систему мер. Основными величинами в этой системе были выбраны длина и масса.
Комиссия, в которую входили крупнейшие французские ученые, предложила принять за единицу длины 1/40000000 часть длины земного меридиана, проходящего через Париж. Измерить длину меридиана было поручено астрономам Мешену и Деламберу. Работа продолжалась шесть лет. Ученые измерили часть длины меридиана, расположенную между городами Дюнкерком и Барселоной, а затем вычислили полную длину четверти меридиана от полюса до экватора.
Измерить длину меридиана было поручено астрономам Мешену и Деламберу. Работа продолжалась шесть лет. Ученые измерили часть длины меридиана, расположенную между городами Дюнкерком и Барселоной, а затем вычислили полную длину четверти меридиана от полюса до экватора.
Рис. 11
На основании их данных из платины был изготовлен эталон новой единицы. Эту единицу назвали метром – от греческого слова “метрон”, что значит “мера”.
Рис. 12
За единицу массы была принята масса одного кубического дециметра дистиллированной воды при температуре ее наибольшей плотности 4°С, определяемая взвешиванием в вакууме. Был изготовлен эталон этой единицы, названной килограммом, в виде платинового цилиндра
В 1869 г. Петербургская академия наук обратилась к научным учреждениям всего мира с призывом сделать предложенную французскими учеными десятичную метрическую систему мер международной. В этом обращении говорилось и о том, что “достижения науки привели к необходимости отказаться от прежнего определения метра как 1/40000000 доли четверти длины парижского меридиана, так как позднейшие более точные измерения меридиана давали другие результаты”. Кроме того, стало известно, что длина меридиана со временем меняется. Но так как немыслимо было после каждого измерения меридиана менять длину метра, то Петербургская академия наук предложила принять метр, хранившийся во французском архиве (архивный метр), за прототип – первый образец и изготовить с него возможно точные и устойчивые копии для разных стран, сделав этим метрическую систему мер международной.
Кроме того, стало известно, что длина меридиана со временем меняется. Но так как немыслимо было после каждого измерения меридиана менять длину метра, то Петербургская академия наук предложила принять метр, хранившийся во французском архиве (архивный метр), за прототип – первый образец и изготовить с него возможно точные и устойчивые копии для разных стран, сделав этим метрическую систему мер международной.
Когда же была введена метрическая система мер в нашей стране? Передовые русские ученые, много сделавшие для того, чтобы метрическая система мер стала международной, не смогли преодолеть сопротивления царского правительства введению метрической системы мер в нашей стране. Удалось добиться только того, что в 1899 г. был принят закон, подготовленный Д. И. Менделеевым, по которому наравне с российскими мерами “дозволялось применять в России международный метр и килограмм”, а также кратные им единицы – грамм, сантиметр и др.
Вопрос об использовании метрической системы мер в России был окончательно решен после Великой Октябрьской социалистической революции. 14 сентября 1918 г. Советом Народных Комиссаров РСФСР было издано постановление, в котором говорилось: “Положить в основу всех измерений международную метрическую систему мер и весов с десятичными подразделениями и производными”.
14 сентября 1918 г. Советом Народных Комиссаров РСФСР было издано постановление, в котором говорилось: “Положить в основу всех измерений международную метрическую систему мер и весов с десятичными подразделениями и производными”.
Единицы измерения различных стран. Каждая страна в мире пользуется своими способами измерения объема, веса и количества, то есть имеет особую систему мер. Она важна, чтобы успешно вести торговлю и обмен товарами. Но самое трудное заключается в том, что в разных странах эти системы мер не совпадают. Так, например, Соединенные Штаты заимствовали у англичан особую, «английскую» систему мер. Сегодня США практически единственная страна, которая использует ее.
Слайд 10 из презентации «Измерения» . Размер архива с презентацией 315 КБ.
Размер архива с презентацией 315 КБ.
Математика 2 класс
краткое содержание других презентаций
«Действия над числами» — Умножение и деление Кратное сравнение чисел. Буквенные выражения. 2 класс. Арифметические действия (65 часов). Деление. Таблица сложения. Выделение и сравнение частных случаев сложения и вычитания двузначных чисел. Использование таблицы умножения для выполнения табличных случаев деления.
«Переместительное свойство умножения» — Организационный момент. Актуализация знаний. Переместительное свойство умножения. Закрепление изученного. План урока. Работа над новым материалом. Итог. Устный счёт. Первичное закрепление. Постановка учебных задач.
«Действия с числами» — Закрепление. Х+14=21 35 7 9. Новый материал. 5 8=40. Математика 2 класс. Волшебный дом. Увеличить 8 на 17 Уменьшить 33 на 8 Найти сумму и разность чисел 16 и 5 Какое число больше 9 на 7? Устный счёт. «Икс» — педиция к математическому полюсу. Заменить сложение, где можно умножением. 3+3+3+3+3+3+3= 4+2+1+4= 7-7-7-7= 4+4+4+4+4=. Цель: познакомить с новым действием, раскрыть смысл действия умножения. Тема: Умножение.
3+3+3+3+3+3+3= 4+2+1+4= 7-7-7-7= 4+4+4+4+4=. Цель: познакомить с новым действием, раскрыть смысл действия умножения. Тема: Умножение.
«Петерсон математика 2 класс» — 8. С. 26. 38 + 19. 5. 4. 1м. Зрение! Тема урока: 10. 22. Молодцы! Метр. 3 м. 10 дм. В. ? На 3 дм меньше. «Метр». Древние единицы измерения: 30 — 16. Найдите периметр прямоугольника: D. 1. Пришло время отдохнуть! 3. A. 11. 100 см. =. 50. 57. Математика Л. Г. Петерсон, 2 класс. А. 14. 13. 8 м. 8 дм. Берегите. 45 – 23.
«Метр» — Сантиметр. Урок математики во 2 классе по теме «Метр». Что можно измерить с помощью метра? 100 см. Дециметр. Метр. 10 дм. Практическая работа. Древние единицы измерения: Вырази в дециметрах:
«Измерения» — Метр. 2. Метрическая система была принята во Франции, в конце 18 века. Ученика 2 «А» класса ФИРСЯНКОВА НИКИТЫ. Но постоянно ездить в Париж сверяться с эталонным метром очень неудобно. Единицы измерения различных стран. Длина фута равна 30,48 см. Эталон. «Единицы измерения». Метрическая система. Как появились единицы измерения.
Как появились единицы измерения.
Какою мерой меритеИрина Винокурова Древний мир считал, что первые системы мер возникли в Древнем Египте и Вавилоне. В их основе были определенные параметры хлебного зерна – грана. Зерно было первым эталоном, поскольку работа на земле и долгие наблюдения позволили человеку сделать вывод о том, что зерна злаковых практически идентичны по весу и размеру. Древний Шумер неизменно находится в ряду главных действующих лиц, определивших прогресс человечества. Известно, что шумеры были отличными земледельцами и выращивали большие урожаи пшеницы, полбы и ячменя. Продавая и покупая, они производили расчеты по весу в серебре или в мерах, где за основу был взят вес зерна ячменя. Малой мерой веса в Шумере был «шеум» или «ше», что означает зерно. Вес одного зерна в разных странах оценивали примерно одинаково, однако существовали различия. В зависимости от климатических условий и агротехнических представлений в качестве эталона использовали различные зерна. Это могли быть ячмень, пшеница, просо, рис, бобовые, зерна горчицы, кактусов и многое другое. У туземцев Ост – Индии минимальной единицей веса был вес 2 ячменных зерен, а в Африке – зерно боба, которое называется « куара». В Индии доступной мерой веса было зерно ячменя, а в мусульманских странах всё измеряли весом рисового зерна, которое называется «арруза». По сей день в Индии распространено использование туземной единицы, которую называют «Рутте» для золота и жемчуга – вес круглого зернышка, который равен 1/8 грамма. У многих народов древности мера веса совпадала со стоимостью продукта, поскольку деньги были слитками серебра и золота. В античном мире как меру веса и массы использовали семена рожкового дерева, которые были практически идентичны по весу, назывались они «каратами». На Руси использовались также кунные (низкопробные) серебряные и золотые гривны, а также рубль – разрубленная пополам гривна. Все древнерусские меры образовались на базе мер древнего мира. При раскопках Троицкого городища, которое датировалось примерно 4-6 веком до н.э. – 5 веком н.э., ясно обнаруживается эта преемственность. Меры веса и массы в России также связаны с зерном пшеницы, которое в старину называлось пирогом. Этимология этого слова восходит к древнерусскому названию пшеницы – пиро. В Киевской и Московской Руси были известны следующие меры веса: берковец, гривна, гривенка, золотник, и в более позднее время – почка и пирог. Эти меры соотносятся друг с другом следующим образом. Древнерусская гривна, позднее названная фунтом, оставалась неизменной на всем протяжении русской истории, хотя в отдельных русских княжествах применяли собственные меры веса. В 19 веке были узаконены как основные меры веса фунт, лот, золотник, и впоследствии вышедшие из употребления: ласт, конгарь, безмен, анасырь, либра. Лот равнялся 3 золотникам, имели хождение также ½ золотника, ¼ золотника и 1/8 золотника. В практике монетного двора использовалась такая мера, как доля, которая равнялась 1/96 золотника. В аптекарском деле применяли золотник и ползолотник, а также зерно, которое составляло приблизительно 1/68 золотника. Интересна судьба ныне забытой малой меры веса, которую называли скрупулой. По латыни ее название означало «камешек», а содержала она 20 гранов. Такой меры веса нет уже давно, но во многих языках сохранилось прилагательное «скрупулезный», что означает высшую степень точности и тщательности. На протяжении всей истории торговли и обмена людей волновал вопрос сопоставимости разных единиц измерения и точности мер. В Библии говорится о гирях – эталонах, изготовленных вначале из камня, а затем из металла. Плутоватые торговцы в специальной кожаной сумке носили два комплекта гирь, одни для продажи, другие для покупки товаров. Именно к ним обращены слова одной из притч Ветхого Завета: « Мерзость перед господом неодинаковые гири, а неверные весы — недобро». Еще в Великом Новгороде была предпринята попытка ввести эталон веса. Всем торговцам предписывалось строго соблюдать вес гирь, которыми они пользовались. В случае обмана им грозили строгие кары, вплоть до «предания казни смертию». Очевидно, что нарушителей закона было великое множество, поскольку поговорка «Всяк купец на свой аршин мерит» не теряла своей значимости долгие века. Первыми хранителями и контролерами точности мер были церковные служители, а образцы эталонных мер и весов хранились в монастырях и церквях. Сколько флейт в километре Но не только взвешивать нужно было человеку древнего мира. Построить жилище, отмерить участок для посевов, узнать расстояние между городами, отмерить полотно – это и многое другое подразумевало использование единых стандартов длины. Первыми единицами измерения длины и одновременно инструментами, которые применялись для измерений, были те, что «находились под рукой» у человека. Они были связаны с размерами и пропорциями человеческого тела. Длины мерили, прикладывая руку, ногу, используя расстояние между расставленными пальцами, по размаху разведенных рук, по шагу. У древних Египтян был свой эталон минимальной длины – волосок с ослиной морды. Большие расстояния, естественно, измерялись по-другому. В системе мер у египтян использовались ладонь, локоть, у древних евреев к ним прибавились перст, пядь, шаг, горсть. В древнеарабской системе мер длины присутствовало ячменное зерно, и его отношение к другим единицам измерения выглядело так: одна из мер длины принималась равной 24 ширинам пальца, ширина пальца принималась равной ряду ячменных зерен, которые клали бок о бок, а ширину ячменного зерна считали равной ширине 7 волосков мула. Первоосновой расчета длины в Древнем Китае было черное просо. Ученый Линь Лунь провел удивительную реформу мер, в которой, рабочим инструментом для измерений стала любимая флейта императора. В связи с тем, что зерна проса малы по размеру, флейта и была введена как более крупная мера длины. Эталонная флейта хуан-чжун равнялась длине 81 зерна, если их уложить друг за другом по длине, или 100 зернам, уложенным по толщине. Длина такой флейты равнялась 9 цуням, а средняя толщина зерен составляла 1 фэнь. Был рассчитан и объем флейты – в нее должно вмещаться 1200 зерен, суммарный вес которых исчислялся в 12 чжу, а объем флейты – как 1 юэ. В Древней Греции мера длины называлась «стадий», и представляла собой расстояние, которое можно пройти спокойным шагом за время восхода солнца, т. Древним эталоном длины в Англии являлся ярд времен короля Генриха I. История появления этой меры длины сохранилась в нескольких версиях. По первой ярд – это расстояние от кончика носа короля до конца пальцев вытянутой в сторону руки. Вторая версия говорит о том, что ярд – окружность талии монарха, а третий вариант уверенно свидетельствует о том, что это длина меча Генриха I. Король Англии Эдвард II также был озабочен стандартизацией мер длины и ввел понятие «фунт», а также уточнил длину дюйма. В 1324 г. он определил «законный дюйм» как длину трех зерен ячменя, вынутых из средней части колоса и приставленных одно к другому. В 18 веке дюйм появился в России под названием «цоль», или «палец». В феодальной Европе экономические связи были очень слабыми, а это означает, что системы мер не были унифицированы, и в них царил полный хаос. При измерении расстояний возникали парадоксальные ситуации, когда римляне и флорентийцы по-разному считали расстояние между своими городами, поскольку в Риме миля равнялась 1488м, а во Флоренции – 1633м. Во Франции каждый феодал имел право устанавливать свои единицы измерении, поэтому в них был полный разнобой. В начале 18 века в Европе использовались более 100 различных фунтов и 46 разновидностей миль. Линия была также и старинной русской мерой, которая принималась равной ширине пшеничного зерна – 2,54мм. Еще более мелкой единицей измерения была точка, которая равнялась 0,1 линии. Очевидно, слово «точность» этимологически связано с этой мельчайшей единицей. Самые первые сведения о мерах длины в Древней Руси почерпнуты из книг и «Хождение игумена Даниила в Святую Землю». В старинных грамотах о пожаловании земли можно найти такие интересные формулировки: «От погоста во все стороны на бычий рев». Этот означало расстояние, на котором слышен рев быка. Похожие меры длины были и у других народов – «петушиный крик», «коровий рев». Мерили длину и временем – «три трубки» у эстонцев означало расстояние, которое проходят или проплывают на корабле за время, пока выкуривают три трубки. В Испании расстояние измеряли временем выкуривания сигары, а в Японии – периодом, в течение которого изнашивался соломенный башмак. Понятно, что эти меры были приблизительными, ведь люди двигались, видели и слышали по-разному, а брошенный камень и выпущенная стрела пролетали у разных людей разное расстояние. Так, описывая гору Елеонскую и небольшую церковь, расположенную на ее склоне, игумен Дании пишет: «А оттуда до гроба Иосафатова вдалее, яко же человек дострелит», т. Старинная русская мера – «линия» была определенно более точной. В линиях, которые соответствовали ширине пшеничного зерна, измеряли диаметр нижней стеклянной горловины керосиновой лампы. В одном дюйме – 10 линий, и по ширине фитиля лампы, измеряемого в этих линиях, их именовали 10-линейной,15-линейной,20-линейной. Самая большая по диаметру лампа была 50-линейной. Лампы различали не только по количеству линий, существовала традиция давать им личные имена. Так, 15-линейная лампа называлась «чудо», 14-линейная – «Анна», а небольшая 10-линейная называлась почему-то «космосом». По числу линий в лампе, т.е. по ее мощности по величине фитиля судили о зажиточности хозяина. Вершок было принято определять на глаз, его ширина равнялась сложенным вместе указательному и среднему пальцу. Также называли и излишек при насыпании зерна. В России, также как и в древних странах Ближнего Востока, торговцы зерном продавали его на базаре особыми ящиками, которые назывались «мида», или «мера». До революции в России зерно также продавалось мерами. Продавец и покупатель подразумевали под мерой одну и ту же общеупотребительную единицу измерения товара. Благодаря этому купля-продажа могла проходить без споров и разногласий. Однако, мера – это еще понятие из области этики и морали. Говоря о мере в переносном смысле этого слова, мы подразумеваем либо масштаб каких-либо явлений, либо их предел или границы. Разные религии по-своему определяли границы дозволенного и недопустимого в человеческих поступках. По сути это является квинтэссенцией любых религиозных представлений, которые обозначают главные координаты в пространстве человеческой свободы. В Евангелии об этих сложных понятиях рассказывается самыми простыми словами: «И какой мерой мерите, такой и вам будут мерить». Для тех, кто прилагает этот закон только к области торговли и обмена, говорится, что этот закон намного шире: «И так во всем, как хотите, чтобы с вами поступали люди, так поступайте и вы с ними, ибо в этом закон и пророки». И дальше, еще полнее понятие меры раскрывается в отношении воздаяния за человеческие поступки: «Давайте и дастся вам: мерою доброю, утрясенною, нагнетенною и переполненной отсыплют вам в лоно ваше, ибо какой мерой мерите, такой же отмерится вам». Так чудесным образом из маленького зернышка, которое люди положили в основу мер, прорастают закономерности сложных человеческих взаимоотношений. И эти законы представляют правильную картину мира, в котором человек должен проявлять такие прекрасные качества души как честность, сострадание, милосердие и щедрость. © Все права защищены http://www.portal-slovo.ru |
Презентация по математике на тему Старинные меры длины доклад, проект
Старинные русские
меры длины
Выполнила: ученица 5б класса
МОУ СОШ № 1
Берсанова Анастасия
Наука начинается с тех пор,
как начинают измерять. Точная наука немыслима без меры.
Точная наука немыслима без меры.
Д.И. Менделеев
ЦЕЛЬ :
собрать и обобщить материал об известных старинных русских мерах длины
ЗАДАЧИ :
1.Собрать материалы о старинных русских мерах длины.
2.Выявить причины возникновения мер, их достоинства и недостатки.
3.Ответить на вопрос, необходимо ли знать старинные меры в современное время.
4.Подготовить презентацию о старинных русских мерах длины.
5.Познакомить учащихся и педагогов нашей
школы с собранным материалом.
ПРОБЛЕМНЫЕ ВОПРОСЫ :
Аршин, сажень, локоть – что это такое?
Почему возникла необходимость перехода к метрической системе мер?
Что в современном мире меряют старинными мерами?
ЧТО ТАКОЕ МЕРА?
«Мера – способ определения количества по принятой единице. Погонная, линейная мера служит для обозначения расстояний или величины линий. »
»
В.Даль
Единицы измерения
Древней Руси
С древности, мерой длины и веса всегда был человек: насколько он протянет руку, сколько сможет поднять на плечи и т.д.
Основные меры:
Перст
Вершок
Пядь
Сажень
Локоть
Аршин
Верста
ПЕРСТ
Старинное название указательного пальца руки. Русский перст равнялся приблизительно 2см. Русский перст – это толщина пальца.
ВЕРШОК
Старинная русская мера длины, равная ширине двух пальцев (указательного и среднего)
1 вершок = 1/4 пяди = 4,45 сантиметра
ПОСЛОВИЦЫ И ПОГОВОРКИ
«От горшка два вершка, а уже указчик»
(молодой человек, не имеющий жизненного опыта,
но самонадеянно поучающий всех)
«Борода с вершок, а слов с мешок».
«Сам с вершок, а ума горшок».
Задача:
Определите «рост» человека, о котором говорят «от горшка
два вершка, а уже указчик» (высоту горшка считать 25см).
Решение:
1 вершок = 4,5см
2вершка = 4,5*2 = 9 см
25+9=34см
Ответ: высота 34см
Одна из самых старинных мер длины. Название происходит от древнерусского слова «пясть» — кулак или кисть руки.
Малая пядь — расстоянием между концами растянутых большого и указательного пальцев, примерно 18 см.
Великая пядь — расстоянию между концами большого пальца и мизинца, примерно 22-23 см.
Пядь с кувырком — малая пядь с прибавкой двух суставов указательного пальца, примерно 27 -31см.
ПЯДЬ
ПОСЛОВИЦЫ И ПОГОВОРКИ
«Не уступить ни пяди»
(не отдать даже самой малости)
«Семь пядей во лбу»
(так говорят об очень умном человеке)
Задача:
Существовал ли когда-нибудь человек «семи пядей во лбу?»
Решение
1пядь = 18см,
7пядей = 18см*7 = 126см
Ответ: нет, не существовал
САЖЕНЬ
Сажень – происходит от слова «сягать», т. е. доставать до чего-либо.
е. доставать до чего-либо.
«Маховая сажень» — расстояние между концами пальцев широко расставленных рук взрослого мужчины и равнялась 1,76 м.
» Косая сажень » — самая длинная: расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки и равнялась 2,48 м.
ПОСЛОВИЦЫ И ПОГОВОРКИ
«Косая сажень в плечах»
(широкоплечий, высокого роста человек)
«Полено к полену – сажень»
(о накоплении запасов, богатства путем экономии)
ЛОКОТЬ
Расстояние от локтевого сгиба до конца вытянутого среднего пальца или сжатой в кулак кисти руки, что составляло примерно 46 см и 38 см соответственно.
Большой локоть, равен длине руки от основания плеча до большого пальца, а это приблизительно 54 см
ПОСЛОВИЦЫ И ПОГОВОРКИ
«Сам с ноготок, а борода с локоток»
«Близок локоть да не укусишь».
«Дай хоть с локоть, а ему все с ноготь»
АРШИН
Старинная мера длины, которая происходит от персидского слова «арш» — локоть.
Это длина всей вытянутой руки от плечевого сустава
до кончика вытянутого среднего пальца.
В аршине 71,12 см.
ПОСЛОВИЦЫ И ПОГОВОРКИ
«Каждый купец на свой аршин меряет»
«Сидит, ходит, словно аршин проглотил»
(о неестественно прямом человеке)
«На аршин борода, да ума на пядь»
(о взрослом, но глупом человеке)
«На три аршина в землю видит»
(о внимательном человеке, от которого ничего не утаить)
Задача
Купили 100 аршинов ткани.
Сколько это метров ткани?
Решение:
1 аршин = 71 см,
100 аршин = 71*100 = 7100 см = 71 м.
Ответ: купили 71 метр ткани.
ШАГ
Одна из древнейших мер длины, равная средней длине человеческого шага 71 см.
Сохранились сведения об использовании
шага для определения расстояния между городами в Древней Руси.
ПОСЛОВИЦЫ И ПОГОВОРКИ
«Встанешь пораньше, шагаешь подальше»
«И редко шагает, да твердо ступает»
«Семимильные шаги»
(быстрый рост, хорошее развитие чего– либо)
«Обозы идут шагом, да далеко везут»
ВЕРСТА
Русская путевая мера (её раннее название — »поприще»). Этим словом, первоначально называли расстояние, пройденное от одного поворота плуга до другого во время пахоты.
До царя Алексея Михайловича в 1 версте считали 1000 саженей. При Петре Первом одна верста равнялась 500 саженей, в современном исчислении — 213,36 * 500 = 1066,8 м.
«Верстой» также назывался верстовой столб на дороге.
ПОСЛОВИЦЫ И ПОГОВОРКИ
« Его за версту видно»,
«Коломенская верста»
( шутливое прозвище для высокого человека.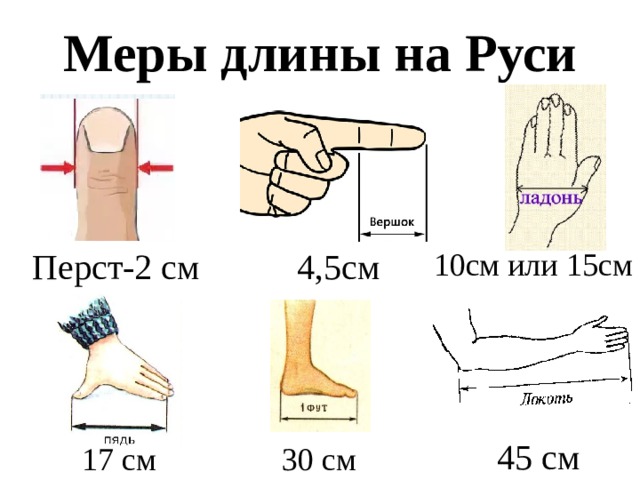 )
)
«Москва верстой далека, а сердцу рядом»
(так русские люди характеризовали свое отношение к столице)
«Любовь не верстами меряется»
«Семь верст молодцу не крюк»
«От слова до дела — целая верста»
«Верстой ближе, пятаком дешевле»
«На версту отстанешь – на десять догоняешь»
До XVIII века пользовались русским мерами длины, затем Петр I предложил воспользоваться английскими мерами длины – ярд, фут и дюйм.
Применение самых разнообразных мер длины
затрудняло развитие науки, торговли между
странами. Поэтому назрела необходимость введения единой системы мер.
Метрическая система мер была разработана во Франции в 18 в., в России допущена в 19 в. законом разработанным Д.И.Менделеевым.
Основная единица длины- 1 метр ( от греческого слова » метрон»- мера).Метр равен
1/40000000 части земного меридиана.
Эталон метра хранится в Международном
бюро мер и весов во Франции.
ИСПОЛЬЗОВАНИЕ В СОВРЕМЕННОМ МИРЕ
В настоящее время широко используется такая мера длины, как дюйм. Дюйм – ширина большого перста(пальца), примерно равен 2,54 см.
Это самая маленькая мера длины, которой измеряют внутренний диаметр труб, толщину досок и диагонали телевизоров и мониторов.
ЗАКЛЮЧЕНИЕ
Проведенная работа мне интересна. Я ближе познакомились со старинными русскими единицами измерения длины. Выявила связь между старинными единицами длины и устным народным творчеством – пословицами, поговорками. Большинство старых мер забыто, вышло из употребления, но многие из них встречаются в литературных произведениях, исторических памятниках. История мер – это история торговли, ремесел, сельского хозяйства и строительства, а в конечном итоге – это часть истории человечества. Подводя итог работы, пришла к выводу, что данная тема — актуальна.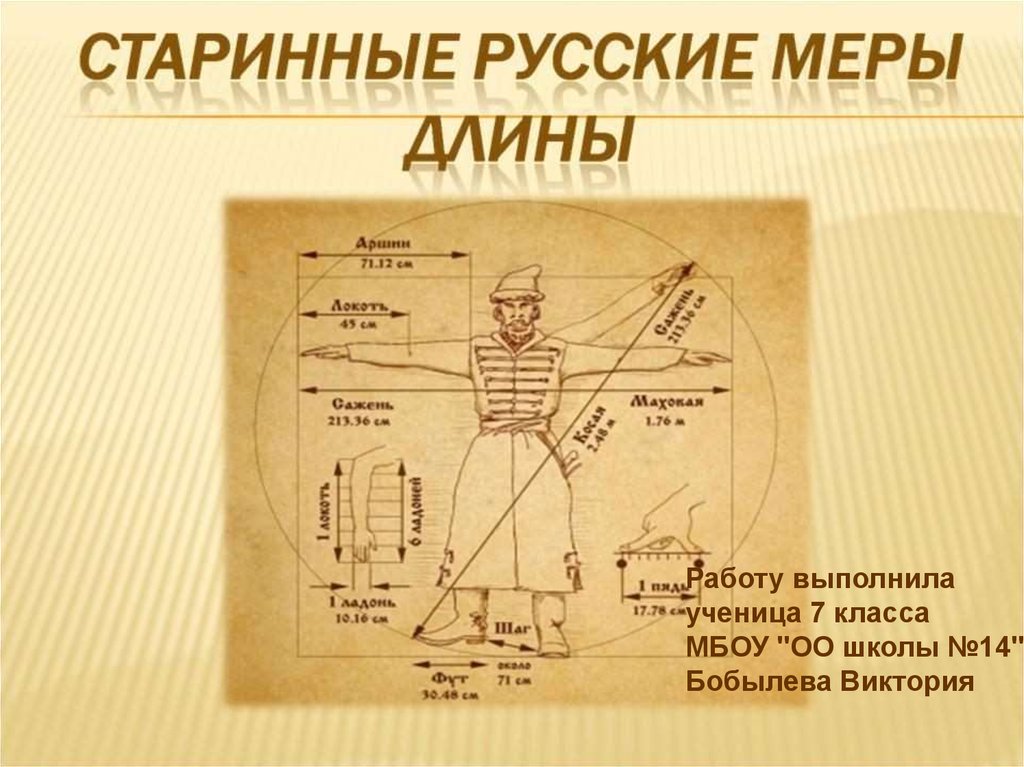 Как появились меры, как изменялись, что несли народам и как влияли на их жизнь? Это интересно и сегодня.
Как появились меры, как изменялись, что несли народам и как влияли на их жизнь? Это интересно и сегодня.
ЛИТЕРАТУРА
1.Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Щварцбурд Математика 5 класс, издательство «Мнемозина», Москва, 2015
2. Г.И. Глейзер «История математики в школе»
IV- VI классы. – Москва «Просвещение», 1981.
3.И.Я. Депман, Н.Я. Виленкин «За страницами учебника математики» Москва «Просвещение», 1989.
4. Ю.Г. Круглов, библиотека словесника «Русские народные загадки, пословицы, поговорки», Москва «Просвещение», 1980.
Эратосфен и тайна стадионов — Какова длина стадиона?
Увидев блестящее рассуждение Эратосфена о том, что длина окружности Земли составляет 250 000 стадий, естественно спросить: «Какова длина стадии?» К сожалению, на этот вопрос нет простого ответа. Без Международного бюро стандартов, обеспечивающего постоянство мер и весов во всем древнем мире, очень вероятно, что такие меры, как стадия, немного варьировались от региона к региону [2, стр. 46]. Ученые сильно расходятся во мнениях относительно степени, в которой стадия могла варьироваться в древнем мире. Исследователь греческих древностей Карл Фридрих Леманн-Гаупт утверждает существование по крайней мере шести различных стадий [2, с.43]. Напротив, астроном и историк Деннис Роулинз утверждает следующее.
46]. Ученые сильно расходятся во мнениях относительно степени, в которой стадия могла варьироваться в древнем мире. Исследователь греческих древностей Карл Фридрих Леманн-Гаупт утверждает существование по крайней мере шести различных стадий [2, с.43]. Напротив, астроном и историк Деннис Роулинз утверждает следующее.
Что 1 стадия = 185 метров ( почти точно 1/10 морской мили ) хорошо установлено. Тем не менее, некоторые ученые не хотят верить, что Эратосфен C E [ аппроксимация окружности Земли ] может быть настолько ошибочен, как 17% […] [18, с.211].
В то время как утверждения этих двух мужчин представляют противоположные крайности в этом споре, существует ряд теорий, которые лежат где-то посередине. Обычный подход к этой загадке состоит в том, чтобы исследовать связь стадии с другими древними единицами длины.
Книга вторая в В «Истории » древнего историка Геродота (480-425 гг. до н.э.) говорится, что 1 стадия равна 600 греческим футам. Как и стадия, греческий фут демонстрирует некоторые региональные различия. Однако все экземпляры греческой стопы, по-видимому, примерно соответствуют одной из трех основных длин. Чтобы различать эти разновидности, исследователь греческой архитектуры Буркхардт Везенберг называет их «аттической» (из Малой Азии и южной Италии), «дорической» (из Греции и Сицилии) и «ионической» (используемой во всей Греции). цивилизация). Каждая из этих вариаций греческой стопы, умноженная на 600, дает длину стадии, которая близко соответствует одной из шести, заявленных Леманн-Хауптом [7, стр. 359].-360]. Такое соответствие придает достоверность аргументу о том, что в древнем мире использовалось несколько стадий, и, кроме того, что один из этих стадий мог использоваться Эратосфеном.
до н.э.) говорится, что 1 стадия равна 600 греческим футам. Как и стадия, греческий фут демонстрирует некоторые региональные различия. Однако все экземпляры греческой стопы, по-видимому, примерно соответствуют одной из трех основных длин. Чтобы различать эти разновидности, исследователь греческой архитектуры Буркхардт Везенберг называет их «аттической» (из Малой Азии и южной Италии), «дорической» (из Греции и Сицилии) и «ионической» (используемой во всей Греции). цивилизация). Каждая из этих вариаций греческой стопы, умноженная на 600, дает длину стадии, которая близко соответствует одной из шести, заявленных Леманн-Хауптом [7, стр. 359].-360]. Такое соответствие придает достоверность аргументу о том, что в древнем мире использовалось несколько стадий, и, кроме того, что один из этих стадий мог использоваться Эратосфеном.
Стадия 185 метров, как утверждал Роулинз ранее, является наиболее общепринятым значением длины стадии, используемым Эратосфеном в его измерениях Земли. Это так, потому что большое количество авторов, начиная с первого века нашей эры, ссылаются на тот факт, что 1 римская миля равна 8 стадиям.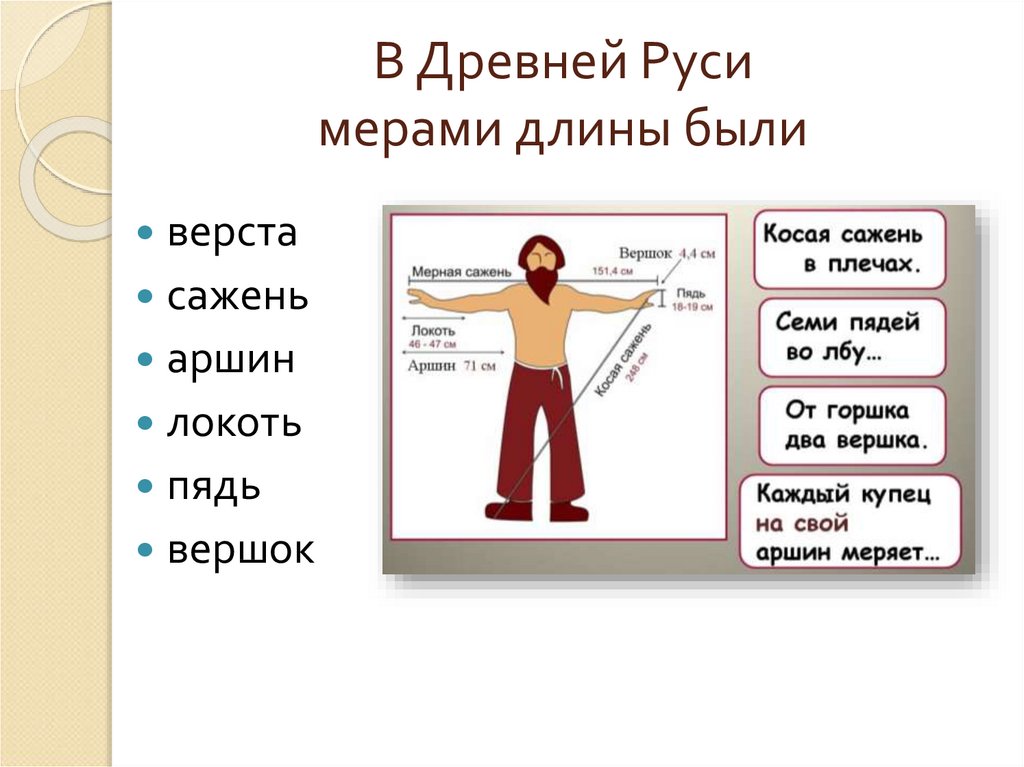 История говорит нам, что римская миля равна 5000 римским футам, каждый из которых чуть меньше знакомого нам английского фута. Точная разница между римским футом и английским футом неизвестна, но если 1 римский фут принять примерно за 11,65 английских дюймов, то одна римская миля приблизительно равна 1479.метров. Взяв 1/8 этой римской мили, мы получим длину 1 стадии примерно в 184,8 метра. Опять же, эта длина соответствует одному из шести стадий Леман-Хаупта. Он называет этот наиболее часто принятый этап «итальянским» [2, с. 42-44].
История говорит нам, что римская миля равна 5000 римским футам, каждый из которых чуть меньше знакомого нам английского фута. Точная разница между римским футом и английским футом неизвестна, но если 1 римский фут принять примерно за 11,65 английских дюймов, то одна римская миля приблизительно равна 1479.метров. Взяв 1/8 этой римской мили, мы получим длину 1 стадии примерно в 184,8 метра. Опять же, эта длина соответствует одному из шести стадий Леман-Хаупта. Он называет этот наиболее часто принятый этап «итальянским» [2, с. 42-44].
Изучая взаимосвязь между стадией, греческим футом и римской милей, можно получить четыре различных длины стадий. Используя имена, предоставленные Везенбергом и Леманн-Хауптом, каждый из четырех стадий указан в порядке возрастания вместе с соответствующей греческой стопой.
Греческая стопа | Современная эквивалентная длина стопы | Соответствующий номер | Эквивалентная современная длина стада |
Чердак | . | Олимпик | 176,4 метра |
|
| итальянский | 184,8 метра |
Дорический | .3269 метров | вавилонско-персидский | 196,1 метра |
Ионный | .3487 метров | финикийско-египетский | 209,2 метра |
Используя эти четыре стадии, можно получить современные приближения к 250 000 стадиям Эратосфена. Ниже для каждого типа стадий дан современный эквивалент 250 000 стадий. Также приведено процентное отличие от современного принятого значения экваториальной окружности Земли, равное примерно 40 075 километрам [21].
Тип стадиона | Эквивалентная современная длина стада | Стадион x 250 000 | Процентное отличие от современной окружности |
Олимпик | 176,4 метра | 44 100 километров | +10,0% |
итальянский | 184,8 метра | 46 200 километров | +15,3% |
вавилонско-персидский | 196,1 метра | 49 020 километров | +22,3% |
финикийско-египетский | 209,2 метра | 52 300 километров | +30,5% |
Ньюлин Уокап, «Эратосфен и тайна стадионов. Какова длина стадиона?», Конвергенция (август 2010 г.)
Какова длина стадиона?», Конвергенция (август 2010 г.)
Как вы измеряете расстояние между Землей и Солнцем? (Средний)
Как астрономы рассчитывают расстояние от Солнца до Земли, или реальный размер Солнца, или скорость движения Земли по орбите вокруг Солнца? Ясно, что из ответа на один из этих вопросов можно узнать ответы на остальные. Но как найти первый ответ?
Сокращенная версия: На самом деле мы измеряем расстояние от Земли до какого-то другого тела, например Венеры. Затем мы используем то, что мы знаем о соотношениях между межпланетными расстояниями, чтобы масштабировать это до расстояния Земля-Солнце. С 1961 мы смогли использовать радар для измерения межпланетных расстояний — мы передаем радиолокационный сигнал на другую планету (или луну, или астероид) и измеряем, сколько времени требуется, чтобы эхо-сигнал от радара вернулся. До появления радара астрономам приходилось полагаться на другие (менее прямые) геометрические методы.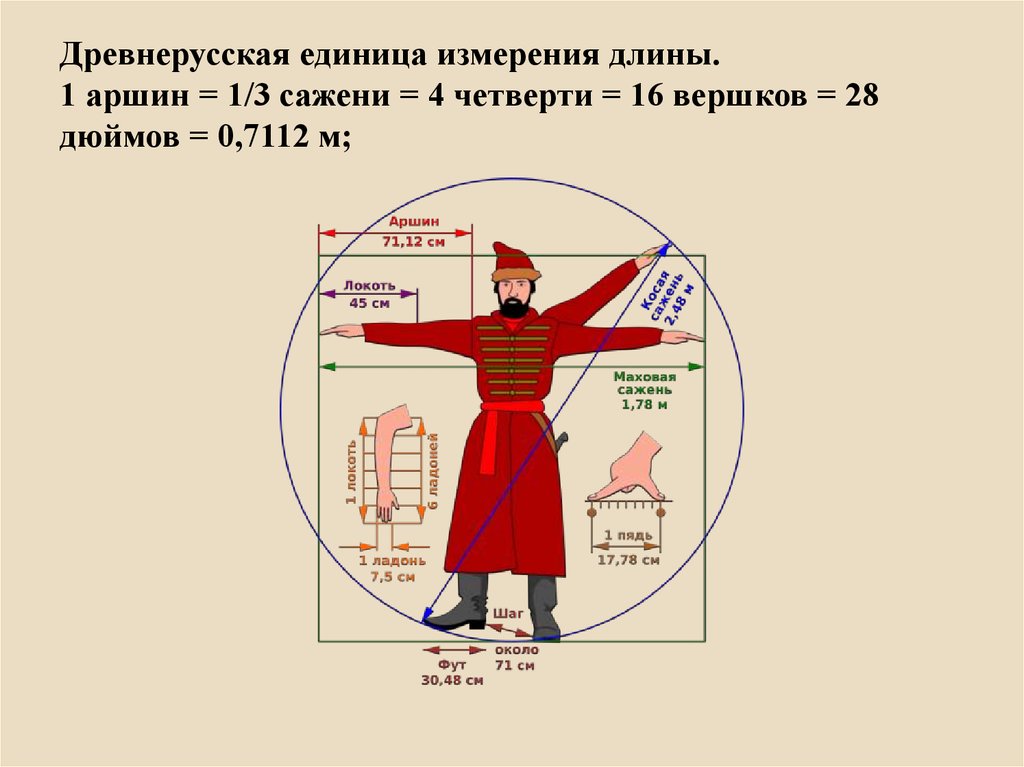
Подробнее:
Первым шагом в измерении расстояния между Землей и Солнцем является определение относительных расстояний между Землей и другими планетами. (Например, каково отношение расстояния Юпитер-Солнце к расстоянию Земля-Солнце?) Итак, скажем, что расстояние между Землей и Солнцем равно «а». Теперь рассмотрим орбиту Венеры. В первом приближении орбиты Земли и Венеры представляют собой идеальные окружности вокруг Солнца, причем орбиты лежат в одной плоскости.
Взгляните на диаграмму ниже (не в масштабе). Из изображения орбиты Венеры видно, что есть два места, где угол Солнце-Венера-Земля составляет 90 градусов. В этих точках линия, соединяющая Землю и Венеру, будет касательной к орбите Венеры. Эти две точки указывают на наибольшую -ю элонгацию Венеры и являются самыми удаленными от Солнца, на которых Венера может появиться на небе. (Формально это две точки, в которых угловое расстояние между Венерой и Солнцем, если смотреть с Земли, достигает максимально возможного значения.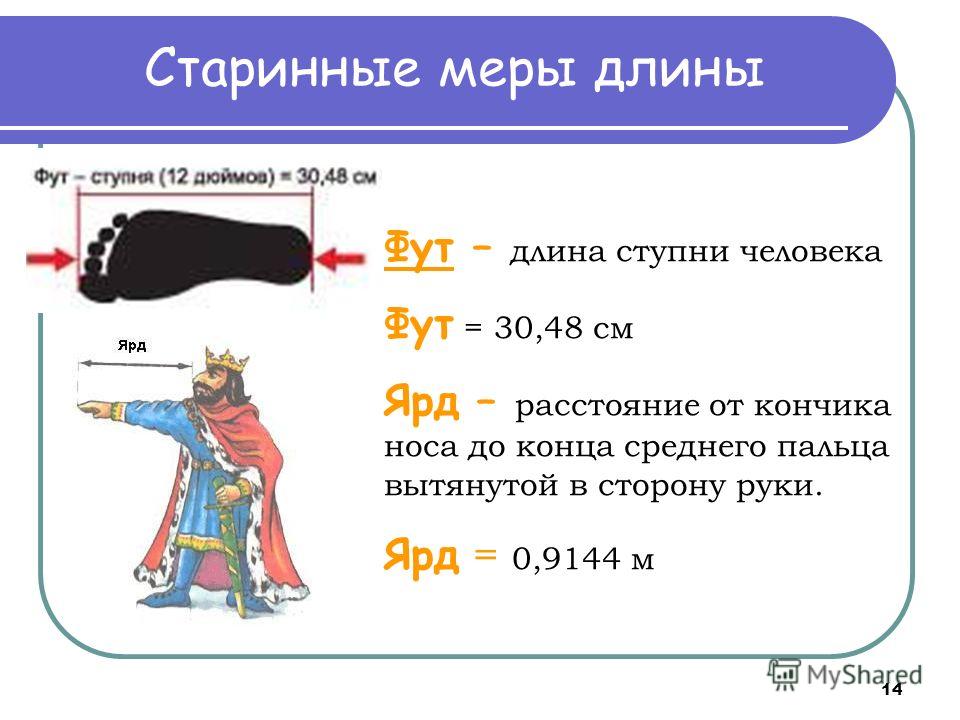 )
)
Еще один способ понять это — посмотреть на движение Венеры в небе относительно Солнца: когда Венера вращается вокруг Солнца, она удаляется от Солнца в небе, достигает максимального видимого удаления от Солнца (соответствующего до наибольшей элонгации), а затем снова начинает двигаться к Солнцу. Это, кстати, является причиной того, что Венера никогда не видна на вечернем небе более чем примерно через три часа после захода солнца или на утреннем небе более чем за три часа до восхода солнца.
Теперь, производя серию наблюдений Венеры на небе, можно определить точку наибольшего удлинения. Можно также измерить угол между Солнцем и Венерой на небе в точке наибольшего удлинения. На диаграмме этот угол будет углом Солнца-Земли-Венеры, отмеченным буквой «е» в прямоугольном треугольнике. Теперь с помощью тригонометрии можно определить расстояние между Землей и Венерой через расстояние от Земли до Солнца:
(расстояние между Землей и Венерой) = a × cos(e)
Точно так же, с немного большей тригонометрией:
(расстояние между Венерой и Солнцем) = a × sin(e)
Наибольшая элонгация Венеры составляет около 46 градусов, поэтому, исходя из этого рассуждения, расстояние между Солнцем и Венерой равно около 72% расстояния между Солнцем и Землей. Подобные наблюдения и расчеты дают относительное расстояние между Солнцем и Меркурием. (Однако с Марсом и внешними планетами дело обстоит сложнее.)
Подобные наблюдения и расчеты дают относительное расстояние между Солнцем и Меркурием. (Однако с Марсом и внешними планетами дело обстоит сложнее.)
Исторически первым известным человеком, использовавшим геометрию для оценки расстояния между Землей и Солнцем, был Аристарх (ок. 310–230 до н. э.) в Древней Греции. Он измерил угловое расстояние между Солнцем и Луной, когда Луна была освещена наполовину, чтобы определить расстояние между Землей и Солнцем с точки зрения расстояния между Землей и Луной. Его рассуждения были правильными, но его измерения — нет. Аристарх подсчитал, что Солнце примерно в девятнадцать раз дальше Луны; на самом деле около 390 раз дальше, чем Луна.
Другой древнегреческий астроном, Эратосфен (276–194 гг. до н. э.), оценил расстояние между Землей и Солнцем либо в 4 080 000 стадий, либо в 804 000 000 стадий. Существуют разногласия относительно правильного перевода значения Эратосфена, а также дальнейшие разногласия по поводу того, какую длину стадиона использовал Эратосфен.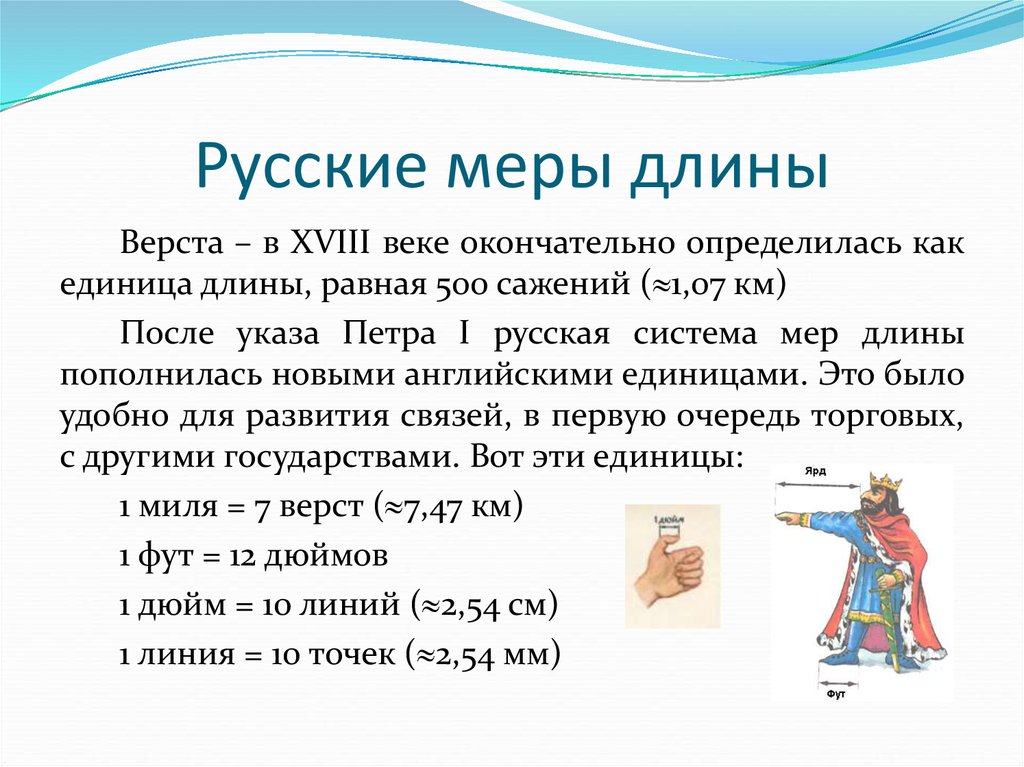 По оценкам различных источников, длина стадиона (также называемого стадионом или стадионом) в пересчете на современные единицы составляет от 157 до 209 метров.метров. Тогда 4 080 000 стадий составляют менее 1 % фактического расстояния между Землей и Солнцем, независимо от того, какое определение стадии вы выберете. Однако 804 000 000 стадий составляют от 126 миллионов до 168 миллионов километров — диапазон, который включает фактическое расстояние от Земли до Солнца (приблизительно) 150 миллионов километров. Таким образом, Эратосфен, возможно, нашел довольно точное значение расстояния между Землей и Солнцем (возможно, с некоторой удачей), но мы не можем сказать наверняка.
По оценкам различных источников, длина стадиона (также называемого стадионом или стадионом) в пересчете на современные единицы составляет от 157 до 209 метров.метров. Тогда 4 080 000 стадий составляют менее 1 % фактического расстояния между Землей и Солнцем, независимо от того, какое определение стадии вы выберете. Однако 804 000 000 стадий составляют от 126 миллионов до 168 миллионов километров — диапазон, который включает фактическое расстояние от Земли до Солнца (приблизительно) 150 миллионов километров. Таким образом, Эратосфен, возможно, нашел довольно точное значение расстояния между Землей и Солнцем (возможно, с некоторой удачей), но мы не можем сказать наверняка.
Первое строгое и точное научное измерение расстояния между Землей и Солнцем было проведено Кассини в 1672 году путем измерения параллакса Марса. Он и еще один астроном наблюдали за Марсом одновременно из двух мест. Столетие спустя серия наблюдений за прохождением Венеры дала еще более точную оценку.
С 1961 года расстояние до Венеры можно определить напрямую, с помощью радиолокационных измерений, когда серия радиоволн передается с Земли и принимается после того, как она отражается от Венеры и возвращается на Землю. Измеряя время, необходимое для возвращения радиолокационного эха, можно рассчитать расстояние, поскольку радиоволны распространяются со скоростью света. Когда известно это расстояние между Землей и Венерой, можно рассчитать расстояние между Землей и Солнцем.
Измеряя время, необходимое для возвращения радиолокационного эха, можно рассчитать расстояние, поскольку радиоволны распространяются со скоростью света. Когда известно это расстояние между Землей и Венерой, можно рассчитать расстояние между Землей и Солнцем.
Как вы указали, зная расстояние между Землей и Солнцем, можно рассчитать все остальные параметры. Мы знаем, что Солнце, если смотреть с Земли, имеет угловой диаметр около 0,5 градуса. Опять же, используя тригонометрию, радиус или диаметр Солнца можно рассчитать по расстоянию между Землей и Солнцем, а, как 2×R солнце = тангенс (0,5 градуса) × а. Кроме того, поскольку мы знаем время, затрачиваемое Землей на один оборот вокруг Солнца (P = 1 год), и расстояние, пройденное Землей в этом процессе (примерно 2πa, поскольку орбита Земли почти круговая), мы можем вычислить средняя орбитальная скорость Земли как v = (2πa)/P.
Во всяком случае, соответствующие числа таковы:
Расстояние от Земли до Солнца, a = примерно 150 миллионов км, определяемое как одна астрономическая единица (AU)
Радиус Солнца, R солнце = примерно 700 000 км
Орбитальная скорость Земли, v = примерно 30 км/с
Ссылки:
- NASA Space Place: Откуда ученые знают расстояние между планетами?
- Путеводитель по Вселенной для учителя: параллакс
- Непостоянная Венера из книги НАСА «Увидеть невидимое: История планетарной радиолокационной астрономии»
- Великие моменты в истории солнечной физики: расстояние до Солнца Книга XV, глава LIII) Евсевия Кесарийского, перевод Э.
 Х. Гиффорд. В главе LIII: «Эратосфен: расстояние от Солнца до Земли составляет четыре миллиона восемьдесят тысяч стадий»
Х. Гиффорд. В главе LIII: «Эратосфен: расстояние от Солнца до Земли составляет четыре миллиона восемьдесят тысяч стадий» - Эратосфен из Кирены биография J.J. О’Коннор и Э. Ф. Робертсон, из MacTutor History of Mathematics
- History of the Astronomical Unit, из Википедии
- Исторические попытки обнаружить астрономический параллакс (архивировано из оригинала)
А вот несколько ссылок с ответами на похожие вопросы на других сайтах «Спроси астронома»:
- Как проще всего измерить расстояние между Землей и Солнцем? из Ликской обсерватории
- Общая астрономия и астрофизика ответы на сайте Центра космических полетов имени Годдарда НАСА «Спросите астрофизика» (см. Какими способами измеряются расстояния в астрономии? и Как в древности измеряли расстояния до планет и звезд?)
- Расстояние до Солнце из блога Phil Plait’s Bad Astronomy
Последний раз эта страница обновлялась Шоном Маршаллом 30 января 2016 года. Когда люди стали цивилизованными, начали культивировать и жить в сообществах, они поняли , что нельзя делать все, и они должны быть взаимозависимыми. Это проложило путь для торговли, и тогда, вероятно, возникла необходимость в какой-то мере.
Это проложило путь для торговли, и тогда, вероятно, возникла необходимость в какой-то мере.
Были приняты различные способы измерения. С тех пор система измерения сильно изменилась.
Записанная история показывает достаточно свидетельств того, что различных частей человеческого тела использовались в качестве точки отсчета при проведении измерений. Вот некоторые из них: цифра: ширина одного пальца; стопа: длина стопы; локоть: длина руки; размах рук: расстояние между кончиком большого пальца и кончиком мизинца, когда рука полностью вытянута. Точно так же сажень означала расстояние между концами рук англосаксонского фермера, когда его руки были полностью вытянуты.
Некоторые исторические единицы были основаны на вещах вокруг нас . Например, римляне использовали единицу измерения шага, которая равнялась шагу отряда их армии, а расстояние, пройденное им за 1000 шагов, они называли равной миле. Точно так же зерно использовалось в качестве единицы массы в шестнадцатом веке и равнялось весу зерна пшеницы.
Необходимость в стандартной единице измерения
Единицы, основанные на частях человеческого тела, являются произвольными и неточными. Результаты измерений варьируются от человека к человеку, потому что размер единицы измерения у разных людей разный. Например, такие единицы, как локоть или фут, будут зависеть от человека, производящего измерение. Это создало проблемы в торговле между разными странами и, очевидно, в повседневных сделках. Чтобы преодолеть ограничения частей тела как единиц и добиться единообразия в системе измерения, возникла необходимость в точном измерении. Для этого необходимо было разработать стандарт измерений, приемлемый для всех.
Проблема точного измерения длины впервые была решена египтянами еще в 3000 году до н.э. Это было сделано путем определения стандарта локтей . Оно было определено равным расстоянию между локтем и кончиком среднего пальца фараона, правившего Египтом в то время. Были изготовлены мерные палочки, длина которых точно равнялась стандартному локтю. Таким образом они удостоверились, что длина локтя во всем Египте одинакова.
Таким образом они удостоверились, что длина локтя во всем Египте одинакова.
Подобные попытки предпринимались и другими правителями. Например, британский король Генрих I (1100-1137) постановил, что ярдов будет в точности равно расстоянию от кончика его носа до конца его большого пальца на вытянутой руке. Королева Елизавета-I объявила, что миль в точности равны восьми фарлонгам. фарлонгов (длина борозды) — это расстояние, которое пара волов может пропахать в поле, не останавливаясь на отдых. Оказалось, что это 220 метров.
Эти стандарты оказались полезными, но просуществовали недолго, так как после того, как данный правитель потерял власть или умер, система перестала соблюдаться, и возникла новая система. Далее, поскольку разные страны и разные провинции в данной стране управлялись разными правителями; они следовали разным системам единиц. Как следствие, к восемнадцатому веку большое количество единиц измерения массы, длины, площади и объема стало широко использоваться.
Индийская система измерения
Индийская система измерения также претерпела значительные изменения с древних времен.
Индийская система измерения в древний период
В древние периоды в Индии длина тени деревьев или других объектов использовалась для определения приблизительного времени суток. Продолжительность долгого времени выражалась с точки зрения лунных циклов, которые даже сейчас являются основой некоторых календарей. Доступны отличные примеры методов измерения в разные исторические периоды. Например, около 5000 лет назад, в эпоху Мохенджо-Даро, размер кирпичей во всем регионе был одинаковым. Длина, ширина и ширина кирпичей всегда находились в соотношении 4:2:1 и принимались за эталон.
Точно так же около 2400 лет назад, в период правления Чандрагупты Маурьи, существовала четко определенная система мер и весов. В то время правительство следило за тем, чтобы все пользовались одинаковыми мерами и весами. Согласно этой системе, наименьшая единица длины равнялась 1 парману . Малые длины были измерены в углов . Для дальних дистанций использовался Yojan . Один Йоджан примерно равен 10 километрам.
Малые длины были измерены в углов . Для дальних дистанций использовался Yojan . Один Йоджан примерно равен 10 километрам.
Индийская медицинская система Аюрведа также имела четко определенные единицы измерения массы и объема. Система измерения строго соблюдалась, чтобы обеспечить надлежащее количество лекарства для конкретного заболевания.
Индийская система измерения в средневековый период
В средневековый период также применялась система измерения. Как описано в Айн-и-Акбари Абул Фазл-и-Аллами, в период правления могольского императора Акбара 90 297 газов 90 298 использовались в качестве единицы измерения длины. Каждый газ был разделен на 24 равные части, и каждая часть называлась Tassuj . Эта система широко использовалась для измерения земельных участков, строительства зданий, домов, колодцев, садов и дорог.
Газ широко использовался в качестве единицы длины до тех пор, пока в 1956 году не была введена метрическая система. Даже сегодня во многих частях нашей страны, особенно в сельских районах, в качестве единицы длины используется газ.
Даже сегодня во многих частях нашей страны, особенно в сельских районах, в качестве единицы длины используется газ.
Индийская система измерения в британский период
Чтобы добиться единообразия в системе измерения и используемых весах, в британский период был предпринят ряд усилий. Британские правители хотели связать индийские меры и веса с теми, которые использовались в Великобритании в то время. В этот период дюймов, фут и ярд использовались для измерения длины, тогда как граны, унции, фунты и т. д. использовались для измерения массы. Эти единицы и веса использовались в Индии до момента обретения независимости в 1947 году.
Основные единицы массы, используемые в Индии, включали Ратти, Маша, Тола, Чхатанк, Провидец и Маунд. Раатти — это красное семя, масса которого составляет примерно 120 мг. Он широко использовался ювелирами и практиками традиционной медицины в Индии.
Современные измерительные системы
Сразу после Французской революции (1790 г. ) французские ученые взяли на себя инициативу в создании новой системы мер и весов. Они выступали за установление национальных стандартов для целей и использования десятичной арифметической системы . Это привело к рождению метрической системы, которая, как и индийско-арабская система счета, основана на кратных и подразделениях числа десять.
) французские ученые взяли на себя инициативу в создании новой системы мер и весов. Они выступали за установление национальных стандартов для целей и использования десятичной арифметической системы . Это привело к рождению метрической системы, которая, как и индийско-арабская система счета, основана на кратных и подразделениях числа десять.
После детальных обсуждений были определены основные единицы длины и массы и подготовлены их рабочие эталоны. Рабочий стандарт на метр был подготовлен путем разметки двух линий на расстоянии метра друг от друга на платиново-иридиевом стержне. Точно так же был сконструирован платино-иридиевый цилиндр, равный массе 1 кубических дециметров воды, в качестве рабочего эталона массы. Эти два стандарта сохранились в Международном бюро мер и весов при обслуживании под Парижем. Их копии были подготовлены и отправлены в разные страны. Что касается времени, концепция 90 297 часа, минуты и секунды 90 298, основанная на вращении Земли, была сохранена.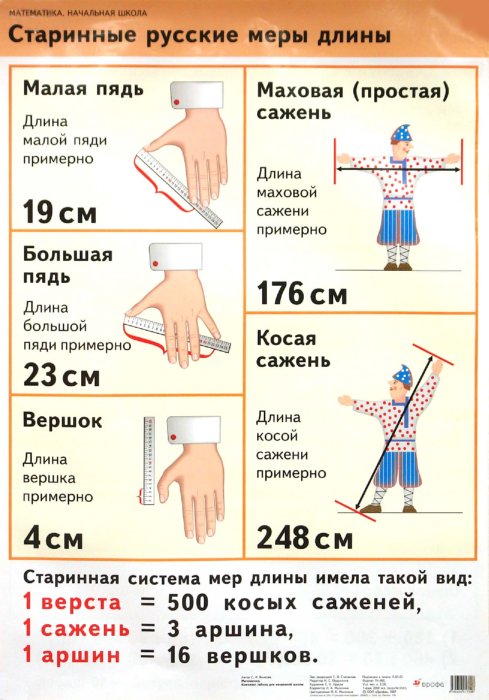
Международный договор под названием Метрическая конвенция был подписан в 1875 для соблюдения метрической системы во всем мире для торговли и коммерции.
В ходе разработки агрегатов был принят ряд систем. Широко использовались две системы: cgs и mks. Система cgs была основана на сантиметрах, граммах и секундах в качестве единиц длины, массы и времени, в то время как система mks использовала метров, килограммов и секунд 9.0298 для того же. В 1958 году стало ясно, что единицы измерения, определенные как стандартные, необходимо переопределить.
С 1983 года определяется как длина пути, пройденного светом в вакууме за 1/299 792 458 секунды. Новое определение системы единиц привело к рождению системы единиц СИ , которая в настоящее время используемая система.
Древние единицы измерения и земные измерения — Официальный сайт Грэма Хэнкока
Что касается грандиозных мегалитических сооружений древности, мы можем задаться вопросом: были ли используемые там единицы измерения пропорциональны размеру Земли? Доктор Ник Коллерстром проводит расследование.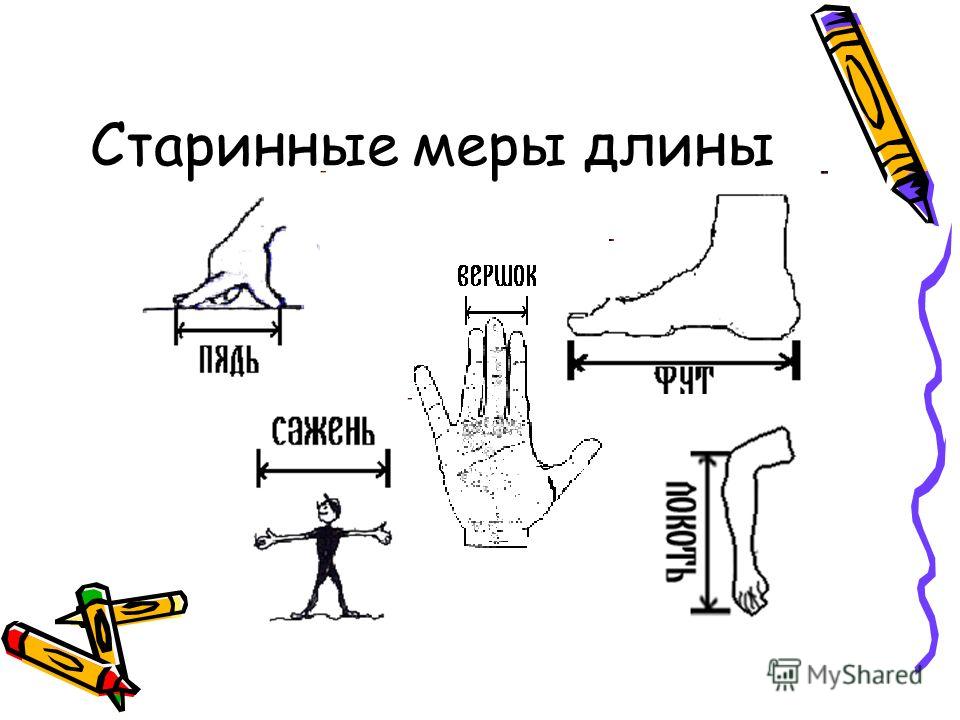
Мать-Земля явно была источником греческого состояния, хотя древнегреческие философы, кажется, не знали об этом факте. В частности, десять греческих футов, умноженные на четвертую степень числа 60, равняются средних окружностей Земли. Нашим самым точным источником греческого «олимпийского» фута был Акрополь — он назывался Гекатомпедон , что означало 100 футов, а его длина и ширина были в соотношении 4:9, 100 греческих футов на 225. Точные измерения эти две длины были получены Фрэнсисом Пенроузом, архитектором и исследователем истории архитектуры, в 1882 году; откуда мы получаем два близко согласующихся значения греческого фута, и их среднее значение составляет 12,164 дюйма.
Для сравнения, используя «геодезическое» определение греческого фута, данное выше, из самого современного значения средней окружности Земли (и не вдаваясь в то, что понимается под «средним», что довольно сложно), мы получаем то же значение , равное 12,164 дюйма, как длина 1/100 -й угловой секунды Великого круга.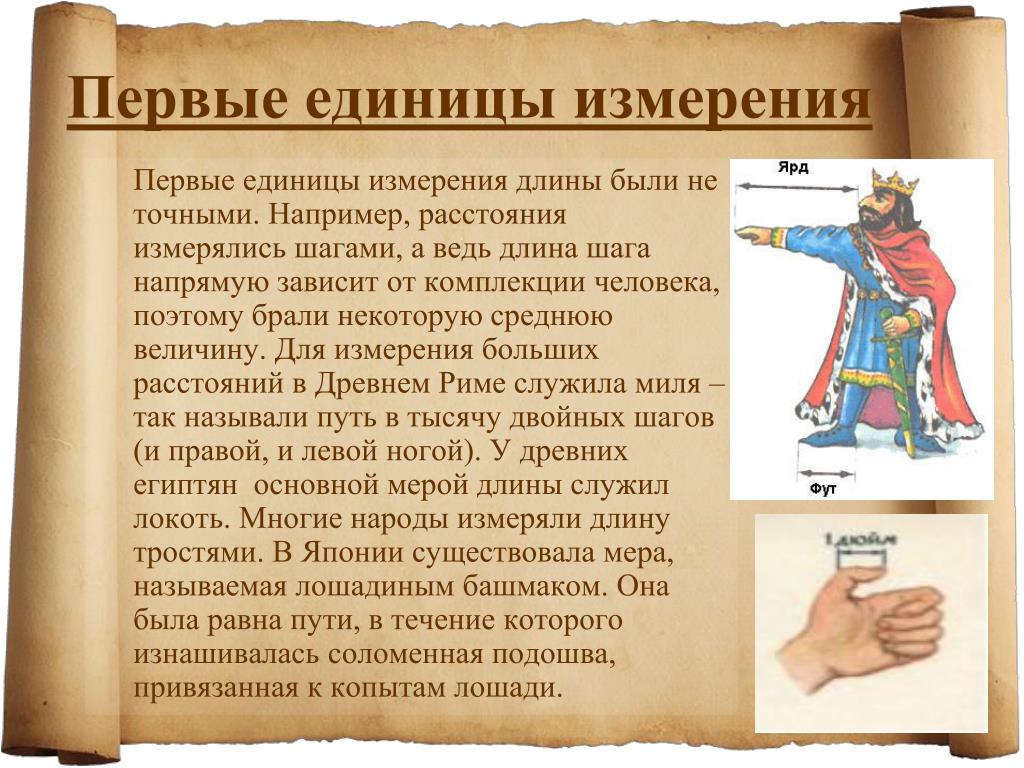 Если на лицо, то подвязка здесь работает с пятизначной точностью.
Если на лицо, то подвязка здесь работает с пятизначной точностью.
Если вы спросите, почему они хотели использовать значение «средней» окружности Земли, а не фактическую окружность, скажем, на экваторе? Ответ таков: по той же причине, что и Великобритания, определив свою морскую милю. На высоте 6080 футов морская миля равна угловой минуте 9 земных угловых минут.0006 означает окружностей. Использование этого значения для морской мили дает нам меру «греческого фута» 12,16 дюйма.
У греков была шестидесятикратная система измерения с 600 футами в стаде. Сколько длился стадий? Это была длина стадиона в Афинах — основная концепция ипподрома. В их математике не использовалось основание 60, поэтому здесь есть намек на то, что они унаследовали свою метрологию от более раннего источника.
Стадион был одинаковой длины как у греков, так и у римлян, но у них было разное количество футов. Все древние авторитеты сходятся во мнении, что греческие и римские стопы смыкались в соотношении 24:25, т. е. у римлян было 625 футов в стаде. Заметим, что 600 — это произведение 24 и 25, причем десять греческих стадий — это угловая минута средней окружности Земли. Это начало выглядеть так, как если бы дробное деление земли сначала произвело стаде, а затем оно разделилось на греческие и римские футы.
е. у римлян было 625 футов в стаде. Заметим, что 600 — это произведение 24 и 25, причем десять греческих стадий — это угловая минута средней окружности Земли. Это начало выглядеть так, как если бы дробное деление земли сначала произвело стаде, а затем оно разделилось на греческие и римские футы.
Двигаясь на юг, в Александрию, окружность земли, данная Эратосфеном, в 252 000 стадий является произведением 360 и 700, т. а не шесть, как это делали греки). Итак, что здесь происходит? Намного позже « Geographica » Клавдия Птолемея во 2 и веках нашей эры считается первым текстом, в котором указаны широта и долгота всех мест на Земле, и при этом Птолемей сообщает нам, что в одном измерении 500 стадий. степени большого круга, уверяя своих читателей, что это «измерение, которое подтверждается известными и достоверными расстояниями». Он оставляет это (с современной точки зрения) разочаровывающе расплывчатым в отношении того, определялся ли его статус путем измерения по земле или путем деления земного шара. Один — длина, другой — угловая мера!
Один — длина, другой — угловая мера!
Герой нашего рассказа — Эдме-Франсуа Жомар, французский математик и ученый-классик, который в 1798 году вместе с Наполеоном ковылял, возможно, на верблюде, чтобы вторгнуться в Египет, когда до него дошло, что разные системы измерения древность возникла просто путем деления «le Degree terrestre» на разное количество стадий. Таким образом, неотъемлемое определение стадиона было геодезическим. Земля измерялась в древности. Жомар написал все это в 1817 году. Академики никогда не вынесут этой простой истины, потому что она слишком сильно разрушила бы их представления об древности; вместо этого они бесконечно спорят о длине стадиона, но ничего не достигают.
Самая точная мера римского фута с древних времен происходит из… Стоунхенджа. Внутренний диаметр его кольца Сарсенса действительно, как заметил Флиндерс Петри, составляет сто римских футов в диаметре. Это кольцо имело размер в 100 римских футов. Взяв оценочный диаметр, опубликованный Петри в 19 -м -м веке, и диаметр, опубликованный Рональдом Аткинсоном в 20 -м -м,[1] и усреднив их (поскольку они очень близки), мы получим римский фут 11,68. дюймы. Применение к этому соотношению 24:25 дает «греческий фут» 12,165 дюйма.
дюймы. Применение к этому соотношению 24:25 дает «греческий фут» 12,165 дюйма.
Британский археолог Флиндерс Петри собрал доказательства того, что в древности использовались различные длины, и его тщательное и тщательное исследование Индуктивная метрология: восстановление древних мер из памятников (1877 г.) особенно ценно, поскольку он не поддерживал геодезическую гипотезу. , то есть его данные нельзя заподозрить в необъективности, чтобы соответствовать гипотезе земных измерений. Давайте возьмем его цитату о Стоунхендже и «римской» ноге: мера, закодированная во внутреннем круге Сарсена, равнялась 9.0003
«близко соответствует римскому футу, который, хотя и составлял 11,64 дюйма в Риме, имел среднее значение 11,68 дюйма ± 0,01 в Греции, Африке и Англии. Это не означает, что Стоунхендж был постримским, так как эта единица была великой этрурианской и циклопической единицей, первоначально полученной из Египта, и она могла быть введена в Британию в любое время».
Именно это значение в 11,68 дюйма, которое, по заключению Петри, было наиболее распространенным средним значением римского фута, как мы видели, так точно взаимосвязано с геодезической гипотезой. (Для сравнения, в 1639 г.профессор математики из Оксфорда Джон Гривз измерил римскую ногу стелы в Риме, оценив ее в 11,66 дюйма)
быть 45 мегалитических стержней (= 2,5 мегалитических ярда) [2], что дало бы значение MY в 2,717 фута, но с чем это сравнить? Мне кажется, не так много других очень заслуживающих доверия МОИХ мерок для сравнения. Все говорят, что «Том обнаружил», что MY составляет 2,72 фута, но это оказывается не очень легко оценить. Я предпочитаю лучше документированные греческие и римские меры. Заметьте, между прочим, что чудесное кольцо Сарсена было построено 46 веков назад, три века назад до внутри него была помещена (низшая технология) внутренняя подкова трилитонов.
Хотелось бы увидеть международный симпозиум по проверке гипотезы Жомара, организованный Грэмом Хэнкоком (извините! Не думаю, кто еще это сделает).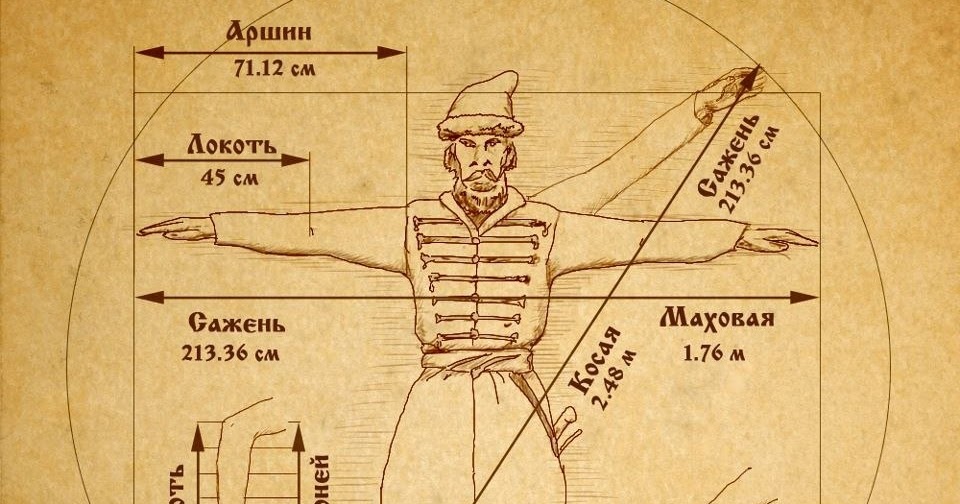 Возможно, он найдет некоторые убедительные доказательства того, что морская цивилизация, опоясывающая мир, теперь канула в глубокое забвение, которая, возможно, оставила позади свои геодезически определенные единицы. Шумеры использовали арифметику с основанием 60 в 3 – тысячелетии до н.0457-й -й или 3-й -й -й век до нашей эры, с минутами и секундами несколько веков спустя. Гипотеза действительно подразумевает, что геометрия («Земля-мера») каким-то образом выполнила это раньше, чем указывает историческая запись.
Возможно, он найдет некоторые убедительные доказательства того, что морская цивилизация, опоясывающая мир, теперь канула в глубокое забвение, которая, возможно, оставила позади свои геодезически определенные единицы. Шумеры использовали арифметику с основанием 60 в 3 – тысячелетии до н.0457-й -й или 3-й -й -й век до нашей эры, с минутами и секундами несколько веков спустя. Гипотеза действительно подразумевает, что геометрия («Земля-мера») каким-то образом выполнила это раньше, чем указывает историческая запись.
Сводка
Д-р Ник Коллерстром
Ширина Акрополя измеряется угловой секундой Большого круга, и только в последние десятилетия были достигнуты достаточно точные оценки, чтобы понять, что у привязки действительно есть пятизначная точность. В 5 -й век до н.э., когда он был построен, кто-то должен был знать об этих вещах. Для сравнения, французы в конце 18 -го -го века пытались и не смогли геодезически определить свой метр (Хотели иметь 40000 км по полярному Большому кругу, а получилось 40008 км, что никуда не годится) , и Жомар сформулировал свою гипотезу после этой неудачи.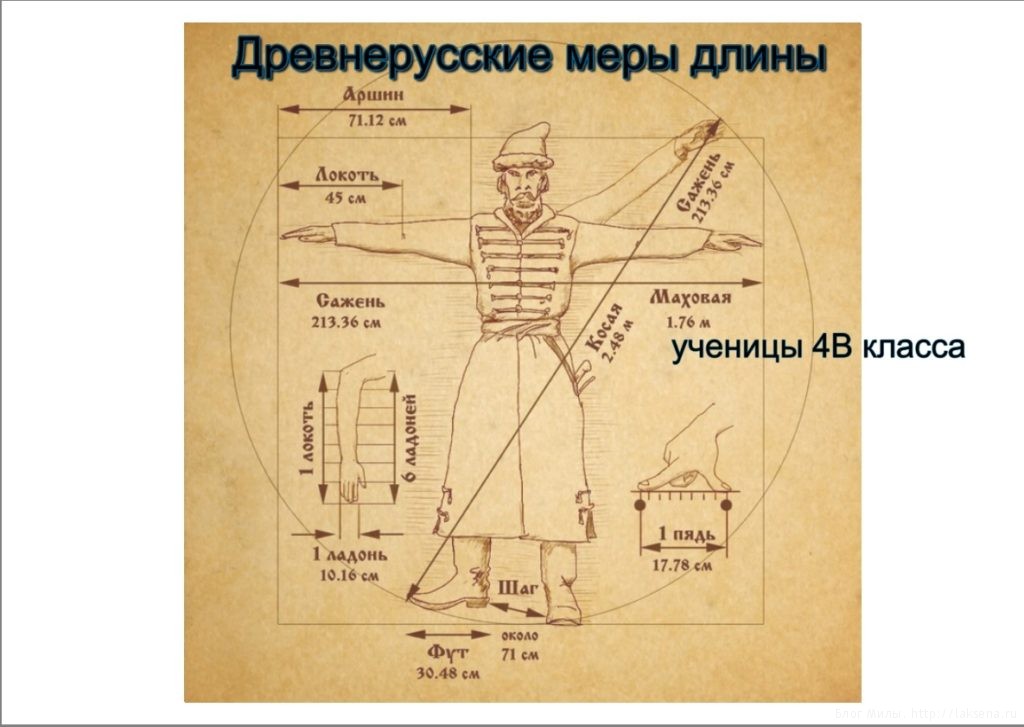
Для получения ссылок и расчетов см.
www.dioi.org/kn/stade.pdf
опубликовано в International Journal of Metrology
[1] Обри Берл Люди Стоунхенджа стр.183
[2] Юан Маки Наука и общество в доисторической Британии 1977, стр.116
Найден крупнейший каменный блок древности
2000-летний каменный блок, вероятно, был вырезан для использования в храме, но был заброшен, поскольку не подходил для транспортировки.
Росселла Лоренци
Опубликовано 01.12.2014 в 15:07
Немецкие археологи обнаружили самый большой камень, когда-либо вырезанный руками человека, возраст которого, возможно, превышает 2000 лет.
Частично погребенный монолит имеет длину 19,6 метра (64 фута), ширину 6 метров (19,6 фута) и высоту не менее 5,5 метра (18 футов). Его вес оценивается в 1650 тонн, что делает его самым большим каменным блоком древности.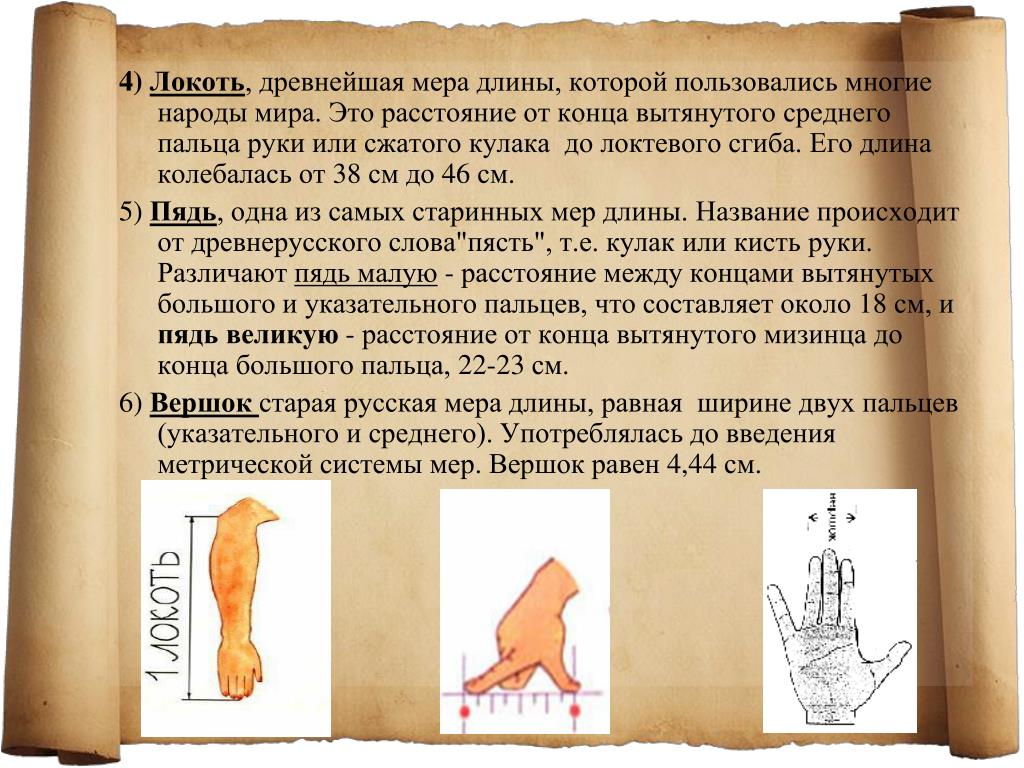
Он был найден группой из Немецкого археологического института в каменоломне в Баальбеке в Ливане. В Баальбеке, известном как Гелиополь, «город солнца», во времена римского правления находилось одно из величайших святилищ империи.
Видео: Почему мы перестали строить пирамиды?
Карьер известняка находился примерно в четверти мили от храмового комплекса и содержит два других массивных строительных блока – один весом около 1240 тонн, другой, известный как «Хаджар аль-Хибла», или «Камень беременной». Женщина, около 1000 тонн.
Рядом с полностью обнаженным камнем Хаджар аль-Хибла и под ним археологи нашли третий блок.
«Уровень гладкости указывает на то, что блок предназначался для транспортировки и использования без резки», — говорится в заявлении Немецкого археологического института.
«Таким образом, это самый большой валун, известный с древности», — добавил он.
Стоунхендж «Смайлик» и другие элементы, обнаруженные под землей
Команда работала под местным руководством Джанин Абдул Массих, долгосрочного партнера по проекту Баальбек отдела Востока Немецкого археологического института. Основная цель состояла в том, чтобы найти новую информацию о методах добычи и транспортировки мегалитов.
Археологи считают, что известняковые блоки датируются по крайней мере 27 г. до н.э., когда Баальбек был римской колонией и началось строительство трех больших и нескольких второстепенных храмов, продолжавшееся до 2 века н.э.
«Массивные каменные блоки длиной 64 фута использовались для подиума огромного Храма Юпитера в святилище», — сказали археологи.
От храма остались только части, в том числе шесть массивных колонн и 27 гигантских известняковых блоков у его основания. Три из них, весом около 1000 тонн каждая, известны как «Трилитон».
Статуи с острова Пасхи могли «ходить»
Каким образом эти монолиты транспортировались и точно располагались во время строительства храма, остается загадкой. Некоторые даже утверждают, что блок был заложен неизвестной более ранней культурой, даже предшествующей Александру Македонскому, который основал Гелиополь в 334 г. до н.э.
Недавно обнаруженный каменный блок, вероятно, был вырезан для использования в храме, но, вероятно, был заброшен, потому что его нельзя было транспортировать.
Действительно, блок Хаджар аль-Хибла поблизости дал некоторые подсказки: вероятно, он был оставлен в карьере, потому что качество камня на одном краю оказалось плохим.
«Возможно, он треснул при транспортировке», — сказали археологи.
В ходе дальнейших раскопок будет предпринята попытка установить, пострадал ли больший блок от той же проблемы.
Изображение: Самый большой каменный блок, частично закопанный. Слева находится камень Хаджар аль-Хибла. Предоставлено: Немецкий археологический институт.
Археологи в Абидосе, Египет, обнаружили гробницу и останки Восерибре Сенебкая, ранее неизвестного фараона, правившего более 3600 лет назад.
Датируется примерно 1650 г. до н.э. во Второй промежуточный период Египта гробница Сенебкая находилась рядом с большим царским саркофагом, недавно идентифицированным как принадлежащий царю Собехотепу (вероятно, Собехотепу I, ок. 1780 г. до н.э.) из 13-й династии.
Ужасно разграбленная древними грабителями гробниц, гробница Сенебкая скромна по своим размерам. Он состоит из четырех камер с украшенной известняковой погребальной камерой. никому не известный фараон, правивший более 3600 лет назад.
На картине в погребальной камере изображены богини Нейт и Нут, охраняющие святилище Сенебкая.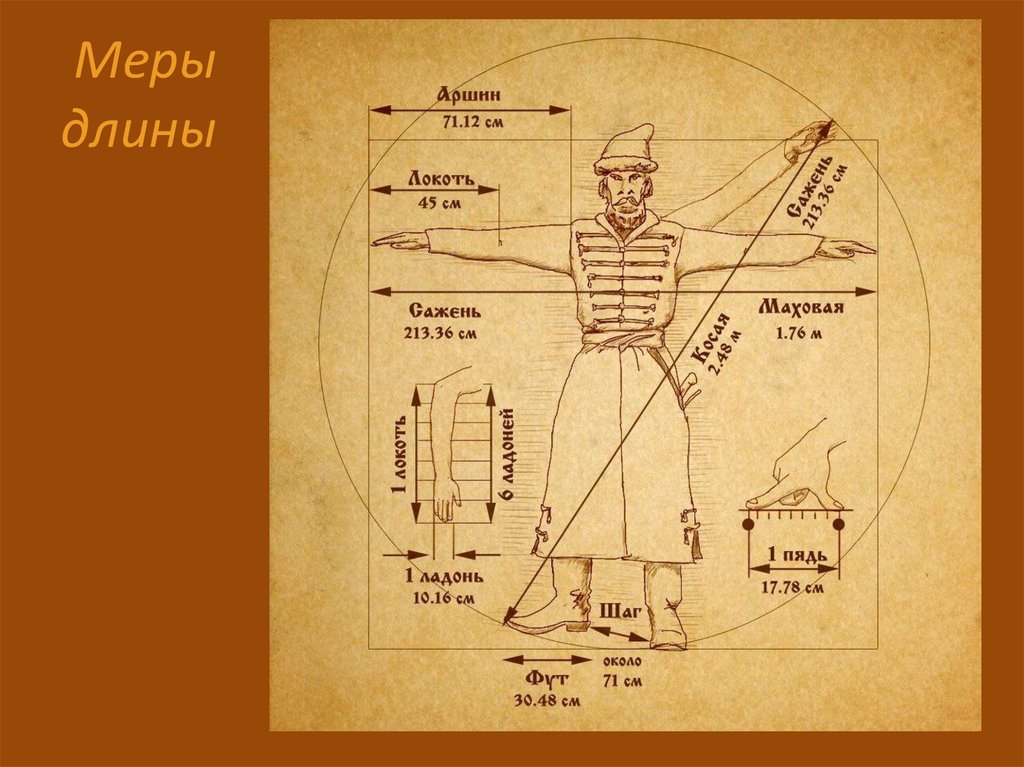
Скелет Восерибре Сенебкая, который, по-видимому, был одним из первых королей забытой династии Абидоса (1650–1600 гг. до н. э.), был найден в четырехкамерной гробнице среди обломков его фрагментов гроба, погребальной маски и канопы.
Несмотря на то, что грабители растерзали мумию Сенебкая, команда Вегнера смогла восстановить и собрать скелет фараона. Предварительное обследование показывает, что он был ростом около 1,75 м (5 футов 10 дюймов) и умер в возрасте от 40 до 40 лет. Читайте полную статью
о находке.
Календарь и Древность Бытия
Календарь и Древность Бытия
BY БИЛЛ КУПЕР, PH.D., TH.D. * |
ПОНЕДЕЛЬНИК, 1 ИЮНЯ 2009
Луна обращается вокруг Земли примерно за 29,5 дня, а год длится (примерно) 365,25 дня. Это неаккуратное расположение делает выравнивание лунного и солнечного календарей практически невозможным. 1 Насколько проще было бы, если бы Бог при сотворении постановил, что год должен быть 360 дней, а лунный месяц — 30 дней.
1 Насколько проще было бы, если бы Бог при сотворении постановил, что год должен быть 360 дней, а лунный месяц — 30 дней.
Доказательства показывают, что Бог предопределил это в начале. Лунный год состоял из 12 месяцев по 30 дней, что в точности равнялось солнечному году из 360 дней. Только после Потопа два календаря перестали соответствовать друг другу, что потребовало многочисленных реформ календаря, которые даже сегодня не решили проблему.
Но откуда можно знать, что допотопный год состоял из 12 равных месяцев по 30 дней? Сегодняшний лунный календарь не состоит из 12 равных месяцев. Нет и солнечного календаря. Сегодняшние лунные месяцы попеременно состоят из 29 и 30 дней, что делает лунный год одним из всего 354 дней, что на 11 или более дней короче нынешнего солнечного года. Есть ли доказательства того, что в лунном календаре до Потопа не было этой аберрации?
Доказательства можно найти в книге Бытия. Писатель отмечает два конкретных календарных события: точный день, когда разверзлись источники бездны и отворились окна небесные (7:11), и точный день, когда утихли воды (8:3-4).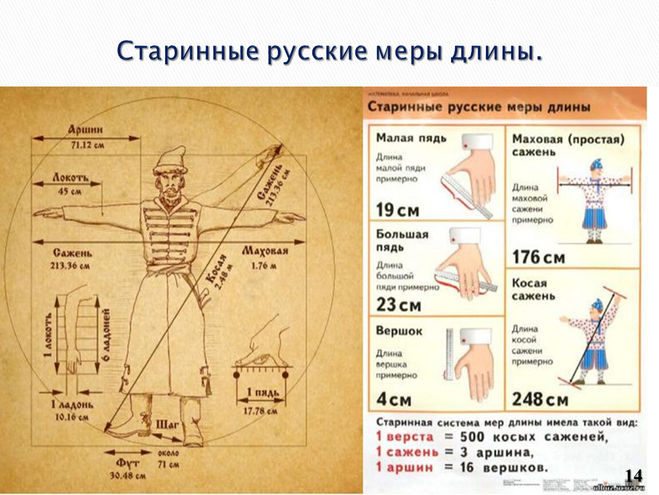 . Важность этой информации такова: Потоп начался в 17-й день 2-го месяца (7:11) и закончился к 17-му дню 7-го месяца (8:4). Это составляет 5 месяцев по 30 дней в каждом, что подчеркивается в Книге Бытия добавлением 150-дневного счета. Пять месяцев в «современном» (на самом деле древнем) еврейском календаре имели бы продолжительность либо 147, либо 148 дней, в зависимости от того, 5-месячный период начался 29-день или 30-дневный месяц.
. Важность этой информации такова: Потоп начался в 17-й день 2-го месяца (7:11) и закончился к 17-му дню 7-го месяца (8:4). Это составляет 5 месяцев по 30 дней в каждом, что подчеркивается в Книге Бытия добавлением 150-дневного счета. Пять месяцев в «современном» (на самом деле древнем) еврейском календаре имели бы продолжительность либо 147, либо 148 дней, в зависимости от того, 5-месячный период начался 29-день или 30-дневный месяц.
Тот факт, что в Книге Бытия используется -до -интеркаляционный календарь, является наиболее важным признаком его древности. Если бы Бытие было написано во время или после изгнания евреев в Вавилон или Персию (VI-V вв. до н.э.), как утверждают модернисты, в нем использовался бы интеркаляционный календарь Вавилона и Персии, который, как и еврейский календарь, определенно не измерял бы пять месяцев как 150 дней.
Кроме того, евреи после изгнания всегда называли месяцы на вавилонский манер и использовали бы эти названия в любом «отредактированном» отчете. Генезис нет. Он просто нумерует месяцы в соответствии с до Вавилонское использование. Выше показан ассирийский лунный календарь (с названиями месяцев) примерно 1800 года до н. э. Он все еще работает, но измеряет лунный год после Потопа как 354 дня. Рассказ о потопе в Книге Бытия предшествует его созданию.
Генезис нет. Он просто нумерует месяцы в соответствии с до Вавилонское использование. Выше показан ассирийский лунный календарь (с названиями месяцев) примерно 1800 года до н. э. Он все еще работает, но измеряет лунный год после Потопа как 354 дня. Рассказ о потопе в Книге Бытия предшествует его созданию.
Другими словами, эта часть Бытия была написана до того, как стали наблюдать и измерять последствия Потопа — внезапный сдвиг между лунным и солнечным временем и т. д. 2 Таким образом, календарь, изображенный в его первых главах, является еще одним свидетельством древности Книги Бытия.
Ссылки
- Даже когда мы пытаемся, расположение никогда не бывает идеальным. Лунный месяц делится на солнечный год примерно в 12,4 раза (примерно, но никогда точно, на 11 дней меньше нынешнего солнечного года). Не становится лучше, если мы сравним солнечное и лунное время со звездным временем, когда кажется, что неподвижные звезды совершают оборот вокруг Земли не раз в 24 часа, как Солнце, а каждые 23 часа 56 минут и 4 секунды, т.
 е. почти 4 минуты в день!
е. почти 4 минуты в день! - «Великий Потоп времен Ноя навсегда изменил земные системы… С фонтанами великой бездны, перемещающими огромный объем жидкости, движущимися континентами, возможной бомбардировкой астероидами и т. д., смещающей расположение большой массы, длину день, продолжительность года и наклон оси могли измениться». Моррис, Дж. 2005. На ранней Земле все месяцы были ровно по тридцать дней? Акты и факты . 34 (12).
* Доктор Купер, историк и писатель, проживает в Англии.
Процитируйте эту статью: Купер, Б. 2009. Календарь и древность Книги Бытия. Деяния и факты. 38 (6): 19.
Последние новости
НОВОСТИ АКТЫ И ФАКТЫ ПОДКАСТЫ
ПОДКАСТ CREATION
Эти животные — мастера маскировки | Подкаст Творения:…
От пятен леопарда до крыльев бабочки многие существа на нашей планете обладают способностью прятаться на виду. Откуда…
АВТОР: ШТАТНЫЙ ПИСАТЕЛЬ
НОВОСТИ
Показывают ли рыбьи черепа эволюцию?
Рыба так и не научилась ходить. Тем не менее, палеонтолог-эволюционист предложил недокументированный сценарий того, как рыба постепенно превратилась в четвероногого…
Тем не менее, палеонтолог-эволюционист предложил недокументированный сценарий того, как рыба постепенно превратилась в четвероногого…
АВТОР: FRANK SHERWIN, D.SC. (HON.)
АКТЫ И ФАКТЫ
Чествование пионеров творения
Всегда приятно встретиться со старыми друзьями. Недавно мы попросили некоторых пионеров креационного движения поделиться с нами своим…
АВТОР: ДЖЕЙМИ ДЮРАНТ
АКТЫ И ФАКТЫ
Генри М. Моррис и Дуэйн Т. Гиш: продвижение дела Христа
Следующие выдержки д-ра Генри Морриса и д-ра Дуэйна Гиша были взяты из первого выпуска журнала Creation-Science…
АВТОРЫ: РАЗЛИЧНЫЕ АВТОРЫ
АКТЫ И ФАКТЫ
Пионер сотворения Дон ДеЯнг
Впервые я встретил доктора Генри Морриса в 19 лет.73 года, когда он выступал в часовне колледжа Грейс в Вайнона-Лейк, штат Индиана. С растущим интересом к исследованиям сотворения мира,…
АВТОР: ДОНАЛЬД Б. ДЕЯНГ, PH.D.
АКТЫ И ФАКТЫ
Пионер создания Ларри Вардиман
Ларри и Жаннетт Вардиман Во время моего второго года обучения в аспирантуре Университета штата Колорадо мне позвонили.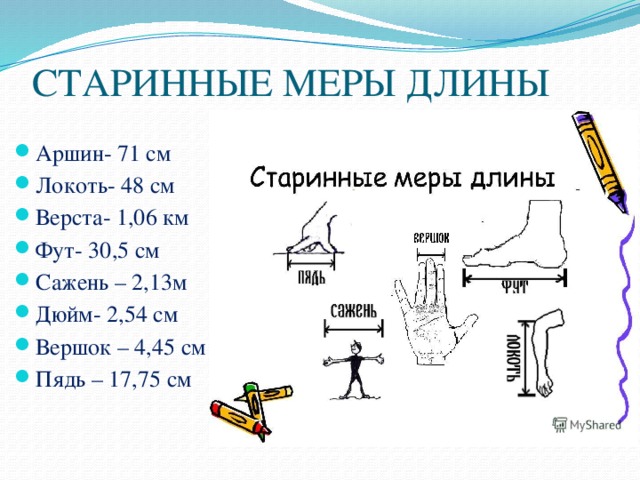

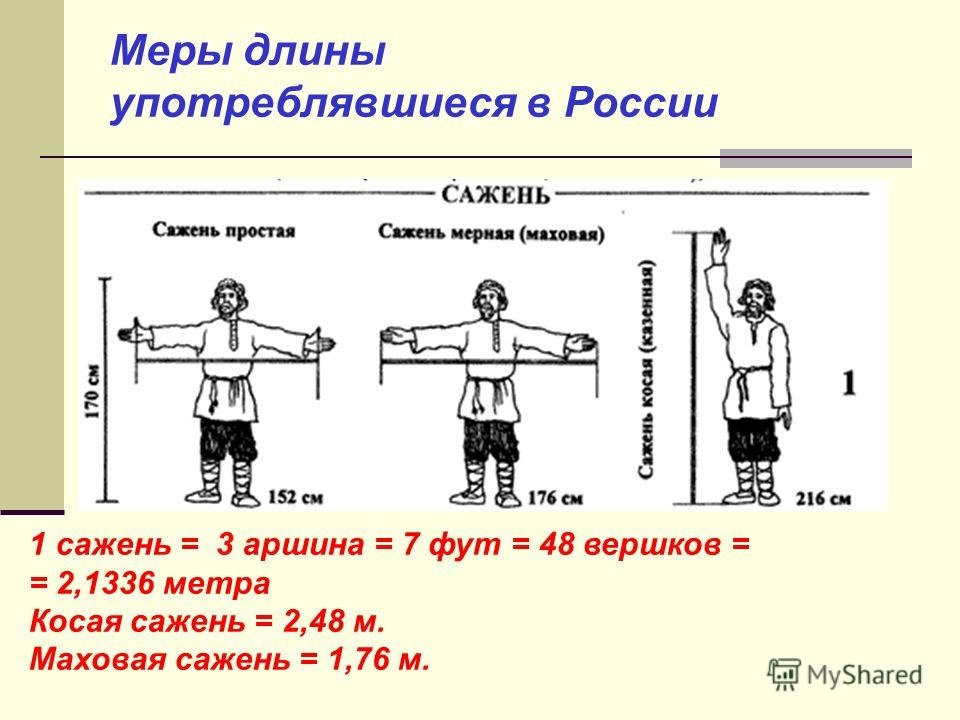 километр = 100 гектарам
километр = 100 гектарам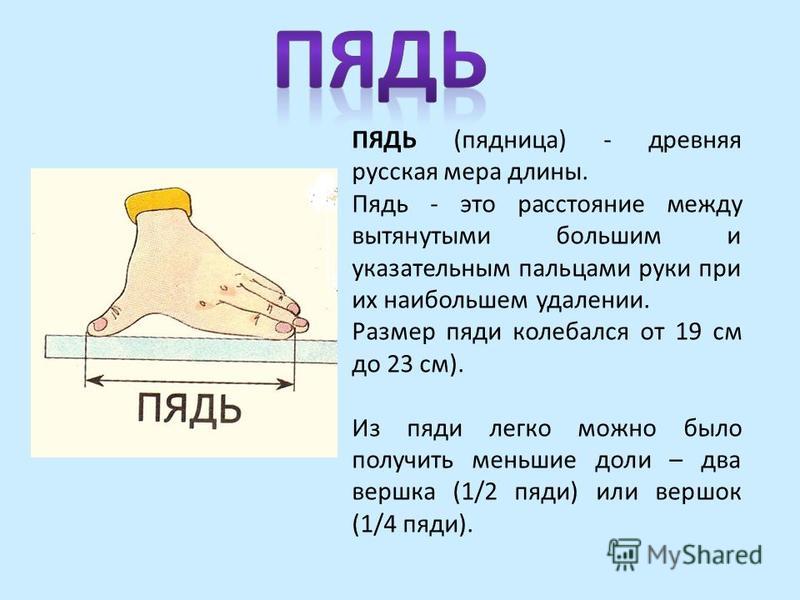 километр — км 2
километр — км 2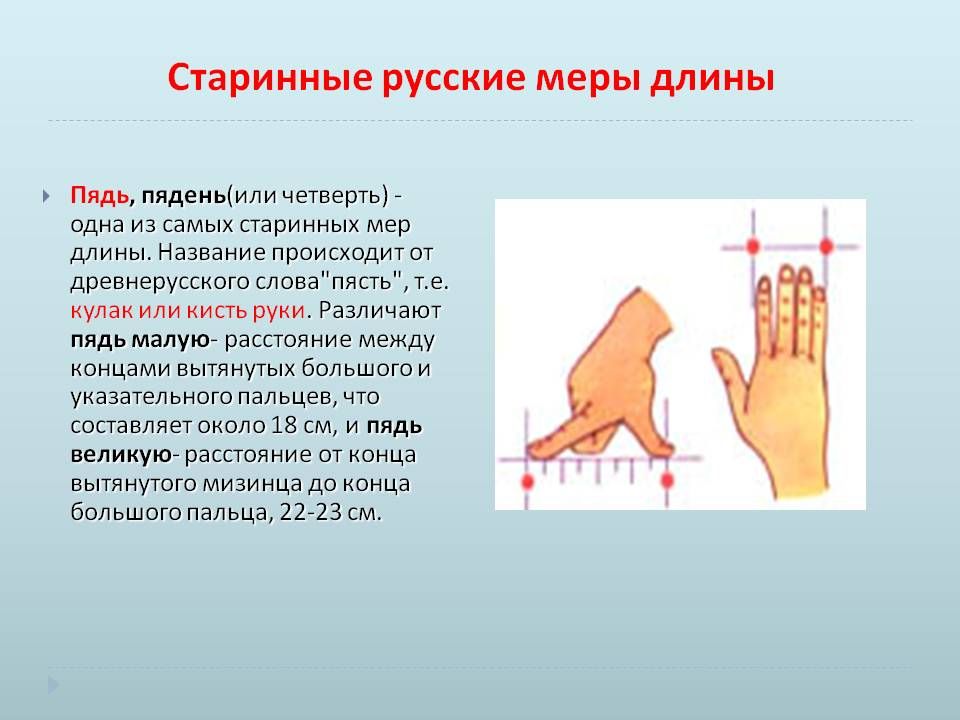
 Шеум весил примерно 0.046 г, а 180 шеумов составляли «сикль». Это слово, иначе произносящееся как «шекель» часто встречается в Ветхом Завете. Шекель также известен и по Древней Месопотамии.
Шеум весил примерно 0.046 г, а 180 шеумов составляли «сикль». Это слово, иначе произносящееся как «шекель» часто встречается в Ветхом Завете. Шекель также известен и по Древней Месопотамии. Так, в Вавилоне и Древнем Израиле денежной единицей был шекель, в Риме асс, в Англии фунт стерлингов, в России – русский фунт, состоявший из 96 золотников и т.д.
Так, в Вавилоне и Древнем Израиле денежной единицей был шекель, в Риме асс, в Англии фунт стерлингов, в России – русский фунт, состоявший из 96 золотников и т.д. Берковец = 4 пудам = 400 гривнам = 800 гривенкам. Гривенка = 2 полугривенкам = 48 золотникам =1200 почкам = 4800 пирогам.
Берковец = 4 пудам = 400 гривнам = 800 гривенкам. Гривенка = 2 полугривенкам = 48 золотникам =1200 почкам = 4800 пирогам.

 В старинных арабских книгах встречается другая модель: «…локоть же равен ширине 8 кулаков, кулак – ширине 4 пальцев, палец – толщине 6 ячменных зерен, а ячменное зерно – толщине 6 волос с ослиной морды».
В старинных арабских книгах встречается другая модель: «…локоть же равен ширине 8 кулаков, кулак – ширине 4 пальцев, палец – толщине 6 ячменных зерен, а ячменное зерно – толщине 6 волос с ослиной морды». е. за 2 минуты. Задолго до греков эта единица измерения использовалась в Вавилоне и других странах, поэтому, строго говоря, стадий не был эталоном. Ведь вавилонский, греческий, аттический, египетский, птолемеевский и римский стадий различались по длине от 194 м. в Вавилоне до 185 м. в Риме.
е. за 2 минуты. Задолго до греков эта единица измерения использовалась в Вавилоне и других странах, поэтому, строго говоря, стадий не был эталоном. Ведь вавилонский, греческий, аттический, египетский, птолемеевский и римский стадий различались по длине от 194 м. в Вавилоне до 185 м. в Риме.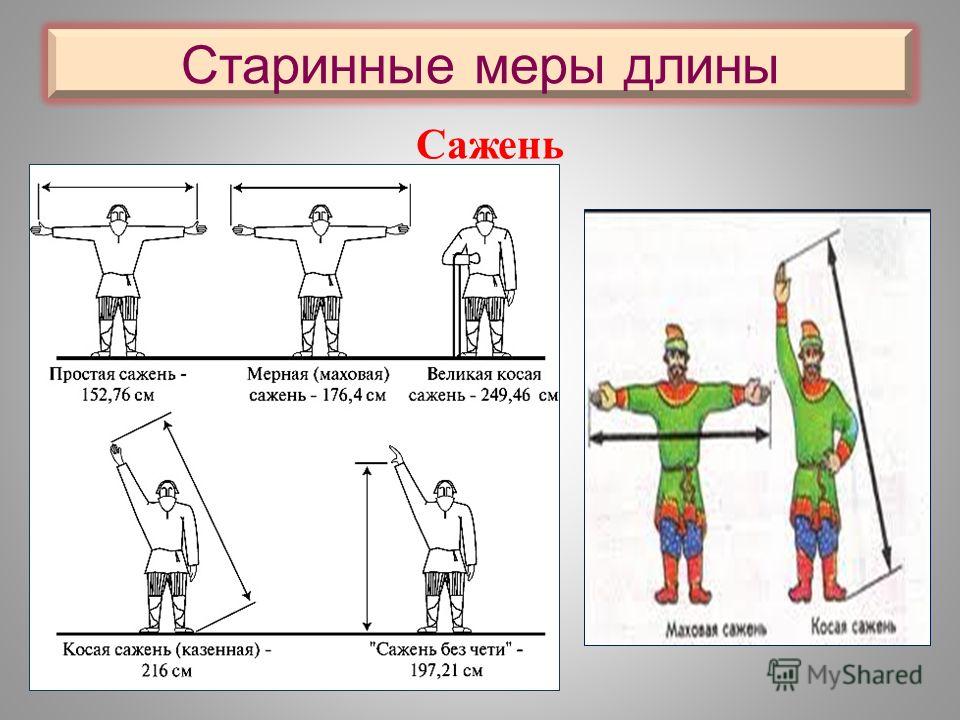 Он равнялся 2.54см и делился на 10 линий или 100 точек. Следует заметить, что линия и точка использовались только в английской, французской и русской системах мер длины.
Он равнялся 2.54см и делился на 10 линий или 100 точек. Следует заметить, что линия и точка использовались только в английской, французской и русской системах мер длины. Здесь встречаются локоть, пядь, сажень, верста и поприще, а также «вержение камня» и «перестрел». Этими мерами древние славяне пользовались для обозначения расстояния броска камня или полета выпущенной стрелы или пушечного ядра.
Здесь встречаются локоть, пядь, сажень, верста и поприще, а также «вержение камня» и «перестрел». Этими мерами древние славяне пользовались для обозначения расстояния броска камня или полета выпущенной стрелы или пушечного ядра. е. дальше, чем человек может «дострелить». Большие расстояния описывались еще более неточно – автор называет их несколькими «перестрелами».
е. дальше, чем человек может «дострелить». Большие расстояния описывались еще более неточно – автор называет их несколькими «перестрелами».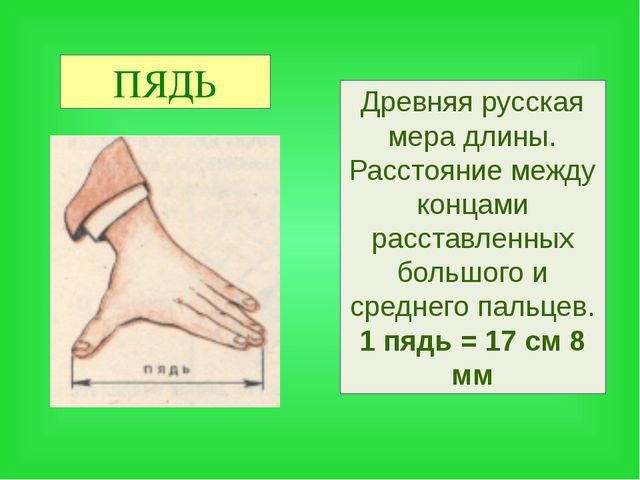 Честные продавцы, пересыпая зерно в миду из мешков, старались наполнить ее доверху, несколько раз встряхивали и разравнивали ее поверхность ладонью.
Честные продавцы, пересыпая зерно в миду из мешков, старались наполнить ее доверху, несколько раз встряхивали и разравнивали ее поверхность ладонью.
 2941 метров
2941 метров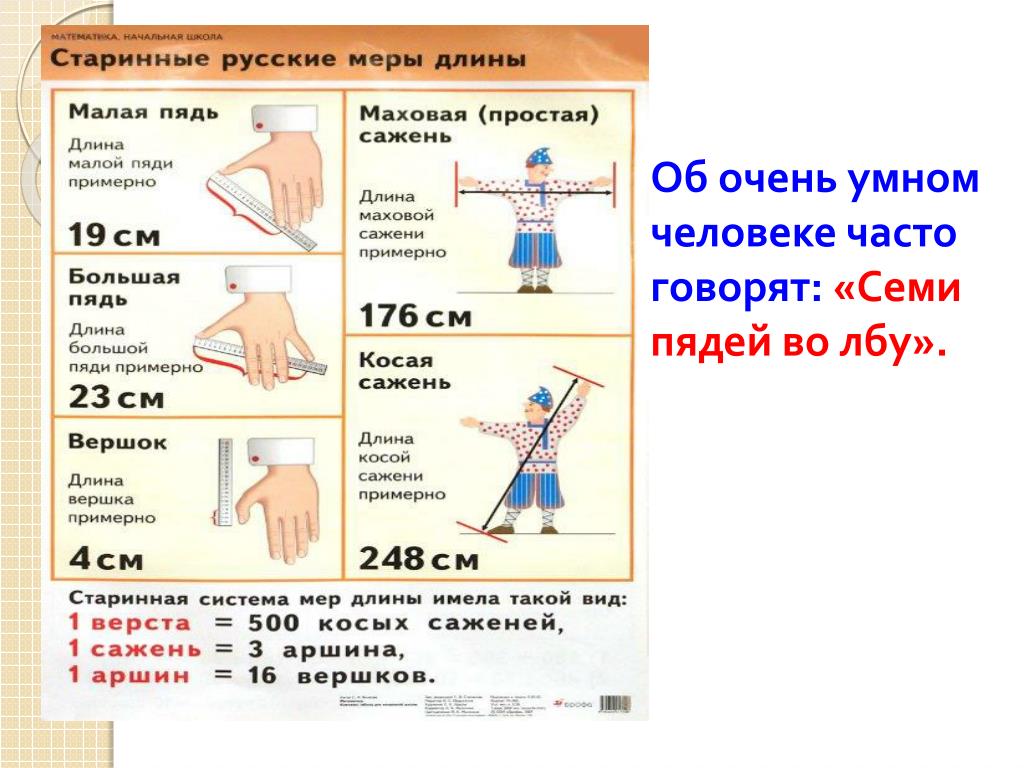 Х. Гиффорд. В главе LIII: «Эратосфен: расстояние от Солнца до Земли составляет четыре миллиона восемьдесят тысяч стадий»
Х. Гиффорд. В главе LIII: «Эратосфен: расстояние от Солнца до Земли составляет четыре миллиона восемьдесят тысяч стадий»
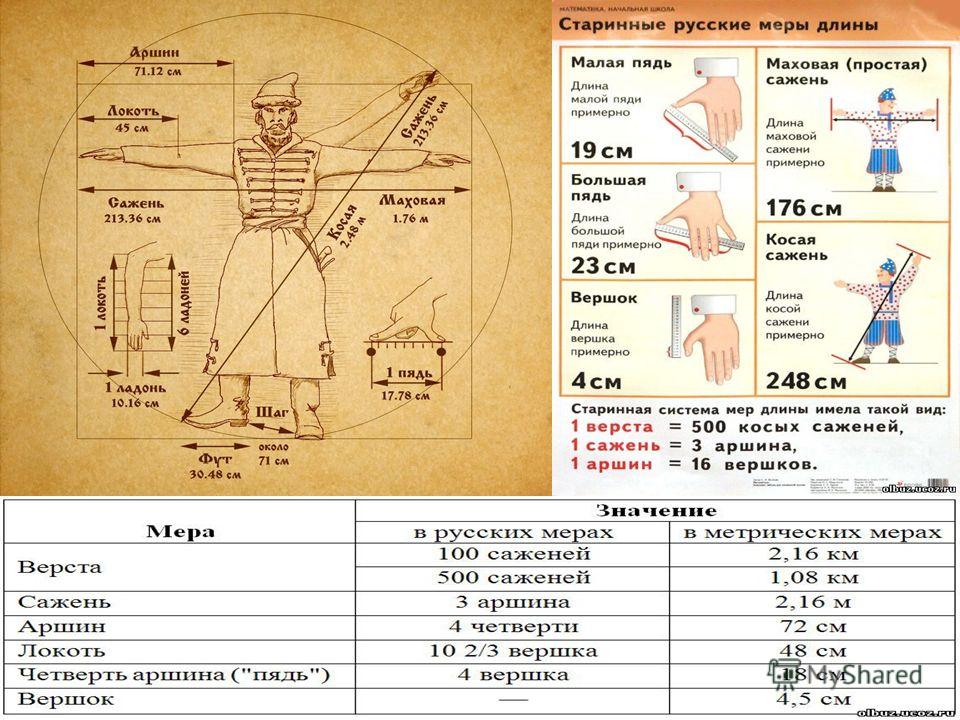 е. почти 4 минуты в день!
е. почти 4 минуты в день!