Многоугольники /qualihelpy
Многоугольником на плоскости называют фигуру, состоящую из точек и соединяющих их непересекающихся отрезков . Точки называют вершинами многоугольника, а отрезки – его сторонами.Две вершины многоугольника называются смежными, если они соединяются стороной многоугольника. Две стороны многоугольника называются смежными, если они имеют общую вершину.
Диагональю многоугольника называют отрезок, соединяющий две несмежные вершины.
Например, на рисунке 8.22 из вершины многоугольника проведены диагонали и .Многоугольник называют выпуклым, если он расположен в одной полуплоскости относительно прямой, содержащей любую его сторону.
Например, на рисунке 8.22 изображен выпуклый многоугольник, а на рисунке 8.23 – невыпуклый.
Вершины многоугольника являются вершинами его углов. Различают внутренние и внешние углы многоугольника.
Например, пятиугольник , изображенный на рисунке 8.Внешним углом многоугольника называют угол, смежный с его внутренним углом.
Например, на рисунке 8.22 угол внешний угол при вершине многоугольника .Сумму внутренних углов выпуклого многоугольника находят по формуле:
, (8.1)где n – число сторон (углов) многоугольника.
Периметром многоугольника называют сумму длин всех его сторон.
Многоугольник называют правильным, если все его стороны и все его углы равны.
Например, на рисунке 8.24 изображен правильный треугольник, на рисунке 8.25 – правильный четырехугольник, а на рисунке 8.26 – правильный шестиугольник.
Внутренние углы правильного n-угольника находят по формуле:
. (8.2) В дальнейшем мы будем рассматривать только выпуклые многоугольники.Многоугольники. Равные фигуры — презентация онлайн
Многоугольники.
Равные фигуры.
На рисунках 102 и 103 изображены три фигуры, каждая
из которых ограничена замкнутой ломаной, состоящей
из звеньев
AB,BC,CD,DA
Чем отличаются границы фигур на рисунке 102 от
границ фигуры на рисунке 103?
Фигуры, изображенные на рисунке 102 называются
четырехугольниками.
На рисунке 104 изображены треугольники ,на рисунке 105пятиугольники, на рисунке 106- шестиугольники.
Все эти фигуры являются примерами многоугольников. Фигура,
изображенная на рисунке 103, многоугольником не является.
Каждый многоугольник имеет вершины и стороны. Так, на
рисунке 102,a точки A,B,C,D-вершины четырёхугольника, отрезки
AB,BC,CD,DA-его стороны, а углы A,B,C,D-углы четырёхугольника.
этого надо последовательно записать или назвать все его вершины,
начинаю с любой.
Сумму длин всех сторон многоугольника называют его периметром.
ЗАПОМНИ!
Два многоугольника называют равными, если
она совпадают при наложении.
Две фигуры называют равными, если они
совпадают при наложении.
«Песочные часы» не являются равными
фигурами
Назовите вершины и стороны
многоугольников.
B
C
A
D
E
V
O
G
R
F
H
D
M
K
L
B
Начертите: 1) четырёхугольник,
2) пятиугольник, 3) шестиугольник,
4)семиугольник
C
C
B
D
B
A
D
E
A
B
C
A
B
D
F
C
D
A
E
E
K
F
Вычислите периметр пятиугольника, если его стороны
равны 2 см,
4 см, 5 см 5 мм,6 см, 7 см.
B
2 см
C
P=AB+BC+CD+DE+EA
5 см 5 мм
4 см
A
D
6 см
7 см
E
P= 4 см+ 2 см+ 5 см 5 мм+7 см+6 см=
24 см 5 мм
Нарисуйте в тетради фигуру, равную той, которая
нарисована на рисунке 110.
Сравните:
1) 3986 г и 4 кг
3) 60 см и 602 мм
2) 6 м и 712 см
4) 999 кг и 10 ц
Ответы:
1) 3986 г
3) 60 см
2) 6 м
4) 999 кг
Назовите равные треугольники
А
Б
В
Д
Е
Г
Ответ: А и Е ; Г и Б ; Д и В.
Как нарисовать многоугольник — Картины и живопись художников. Графика и галереи.
Здравствуйте коллеги. Как нарисовать многоугольник вопрос не сложный. Это просто — если умеешь. Для специалиста нет трудностей.
Предлагаю вам стать специалистом в этой области.
Будем рисовать фигуру с шестью вершинами. С пятью вершинами (звезда), с семью, или разделить на восемь и четыре части, на десять, а так же на двенадцать можно найти в заметках сайта.
В процессе рисования вы часто будете сталкиваться с построением. Все окружение человека состоит из геометрических фигур, большая часть «всего».
Возьмем интерьер. Сама комната — это геометрическая фигура, предметы мебели тоже геометрия, посуда, ковры, картины, окна и т. д.
На улице нас окружают дома, машины, тротуары, заборы ну и много предметов, которые нужно уметь правильно рисовать.
Первое, что приходит на ум при слове шестигранник — это колесики в часах, окно — иллюминатор, призма, алмаз. Карандаш тоже имеет шесть сторон.
Сегодня построим фигуру фронтально.
В перспективе нарисуем в следующем уроке.
Если у нас получиться сделать предмет с шестью гранями, то с тремя вершинами сделать не сложно. Рассмотрим это более подробно.
Как правильно нарисовать многоугольник
Нашу фигуру создадим в фотошопе. В этой статье я не буду разбирать, возможности программы. Кто умеет ею пользоваться, то разберется, а наша задача понять принцип. Замечу, что и простыми карандашами, линейкой, циркулем тоже получиться.
Вы можете онлайн рисовать за мной, обучение запомнится надежней. Практика всегда тесно шла с теорией. Делая руками, запоминаешь быстрее.
Берем лист бумаги и циркулем произвольно, наносим круг. Смотрим ниже.
Теперь через центр O чертим горизонтальную прямую F, F1 (зеленая линия).
Дальше ставим циркуль в точку F1, и создадим еще одну окружность через центр первой, через центр O. Картинка ниже.
Давайте обозначим пересечения. Это будут точки B, C.
Это будут точки B, C.
Теперь проведем две прямые линии через центр O. Первая это B, B1. Вторая C, C1 (они у нас синего цвета). Картинка ниже.
У нас появились шесть точек, соединив их можно получить шестигранник.
Вывод: «Сторона шестиугольника равна радиусу окружности»
Если соединить прямые, как на фото внизу, получим трехгранники. Еще такой знак называют «Звездой Давида»
Знаете другие способы построения шестигранника? Поделитесь в комментариях.
Предлагаю к просмотру статьи по построению тени от фигур.
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings. COLLECTION_DESCRIPTION}}
{{addToCollection.description.length}}/500
{{l10n_strings.TAGS}}
{{$item}}
{{l10n_strings.PRODUCTS}}
{{l10n_strings.DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}} {{l10n_strings.LANGUAGE}}
{{$select.selected.display}}
COLLECTION_DESCRIPTION}}
{{addToCollection.description.length}}/500
{{l10n_strings.TAGS}}
{{$item}}
{{l10n_strings.PRODUCTS}}
{{l10n_strings.DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}} {{l10n_strings.LANGUAGE}}
{{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}нереальная математика реального мира / Хабр
Математика даёт нам точное представление о почти точных ответах
Используя плотную бумагу и прозрачную ленту, Крэйг Каплан собирает красивый округлый объект, напоминающей творение Бакминстера Фуллера или модный новый тип футбольного мяча. Он состоит из четырёх правильных додекагонов (12-угольников с одинаковыми углами и сторонами) и 12 декагонов (10-сторонних многогранников) с 28 небольшими проёмами в виде равносторонних треугольников.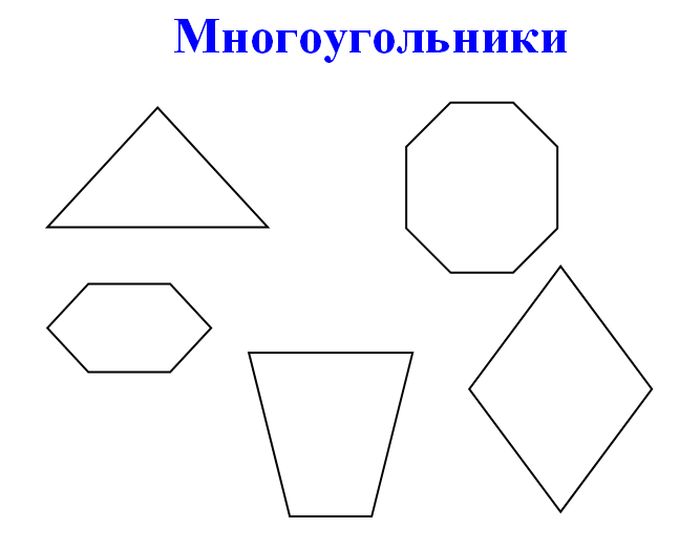 Есть только одна проблема – эта фигура не может существовать. Такой набор полигонов не совпадёт вершинами, и фигура не закроется.
Есть только одна проблема – эта фигура не может существовать. Такой набор полигонов не совпадёт вершинами, и фигура не закроется.
Модель Каплана работает лишь потому, что когда вы собираете её из бумаги, у вас есть небольшая свобода манёвра. Стороны могут почти незаметно изгибаться. «Запас на ошибку, возникающий из-за работы в реальном мире с бумагой, означает, что те вещи, которые не должны быть возможными, в реальности получаются», – говорит Каплан, специалист по информатике из Университета Ватерлоо в Канаде.
Это новый пример из класса неожиданных математических объектов, на которые в 1960-х случайно наткнулся американский математик Норман Джонсон. Джонсон работал над завершением проекта, начатого более 2000 лет назад Платоном – он создавал каталог идеальных геометрических фигур. Из всего бесконечного многообразия трёхмерных фигур только пять можно создать из одинаковых правильных многоугольников: тетраэдр, октаэдр, гексаэдр, икосаэдр, додекаэдр. Если смешать различные правильные многоугольники, можно составить ещё 13 фигур, в которых все многоугольники встречаются вершинами – архимедовы тела – а также призмы (два одинаковых многоугольника, соединённые квадратами) и «антипризмы» (два одинаковых многоугольника, соединённые равносторонними треугольниками).
В 1966 году Джонсон, работая в Университете штата Мичиган, обнаружил ещё 92 тела, состоящих только из правильных многоугольников, которые сейчас [в США] называют джонсоновыми телами. И это исчерпало все возможности, что доказал несколькими годами позже русский математик Виктор Абрамович Залгаллер, работавший тогда в Ленинградском государственном университете. Никакую другую закрытую фигуру из правильных многоугольников составить невозможно.
Но во время инвентаризации многогранников Джонсон заметил нечто странное. Он находил свои формы, составляя их модели из картона и резинок. Поскольку возможных многогранников довольно мало, он ожидал, что новые формы проявятся довольно быстро. Если начать составлять грани вместе, то фигура обязательно должна совпасть. Но этого не происходило. «При сборке кучи многоугольников было не всегда очевидно, собрал ли я допустимую фигуру», – вспоминает Джонсон.
Может казаться, что модель собралась, но «если провести подсчёты, оказывается, что это не совсем так», – говорит он. При тщательном изучении оказывалось, что то, что казалось квадратом, было не совсем квадратом, или стороны были не совсем плоскими. Можно было бы слегка подрезать грани, и они совпали бы идеально, но тогда это были бы уже не правильные многоугольники.
При тщательном изучении оказывалось, что то, что казалось квадратом, было не совсем квадратом, или стороны были не совсем плоскими. Можно было бы слегка подрезать грани, и они совпали бы идеально, но тогда это были бы уже не правильные многоугольники.
Вознамерившись подсчитать все идеальные фигуры, Джонсон не придавал значения таким «близким попаданиям». «Я отложил их, и сконцентрировался на допустимых», – говорит он. Но эти почти идеальные фигуры не только привлекли внимание Каплана и других любителей математики, они стали частью более крупного раздела почти идеальной математики.
Точного определения «почти точного» попадания не существует. Строгие правила не работают в позволяющем допуски мире. Сейчас Каплан в поиске почти правильных фигур руководствуется приближённым методом: «реальная, математическая ошибка, присущая фигуре, сравнима с практической ошибкой, возникающей из-за работы с материалами реального мира и несовершенными руками». Иначе говоря, если вам удалось собрать невозможный многогранник – если он настолько близок к возможному, что вы можете выдать его за настоящий – тогда это и будет почти точная фигура. В других разделах математики почти точные результаты оказываются так близко к реальным, что могут обмануть или удивить вас – своего рода математическая шутка.
В других разделах математики почти точные результаты оказываются так близко к реальным, что могут обмануть или удивить вас – своего рода математическая шутка.
Некоторые такие математические курьёзы нельзя назвать чем-то большим, чем простой забавой, другие же могут иметь глубинные значения в математике и физике.
Древние задачи квадратуры круга и удвоения куба попадают в категорию почти правильных решений. Они кажутся соблазнительно открытыми для нахождения правильного решения, но в итоге оказываются невозможными – как геометрическая фигура, которая выглядит закрытой, но ею не является. Некоторые конструкции, нарисованные Леонардо да Винчи и Альбрехтом Дюрером, слегка искривляли углы, выдавая почти правильные пятиугольники за настоящие.
А ещё есть загадка с пропавшим квадратом. На рисунке прямоугольный треугольник разрезан на четыре части. Если переставить их местами, в нём появляется разрыв. Откуда он взялся? Это тоже почти правильное решение. Ни один из треугольников на самом деле не треугольник. Их гипотенузы искривлены, и это почти невозможно заметить, из-за чего иллюзия настолько убедительна.
Их гипотенузы искривлены, и это почти невозможно заметить, из-за чего иллюзия настолько убедительна.
Цифровое совпадение – это одно из самых полезных в обычной жизни почти правильных решений. 27/12 почти равно 3/2. По схожей причине у фортепьяно есть 12 клавиш в октаве и в основе равномерно темперированного строя западной музыки. Это компромисс между двумя самыми важными музыкальными интервалами: октавой (частотой 2:1) и квинтой (частотой 3:2). Численно невозможно разделить октаву так, чтобы все квинты были идеальными. Но можно подойти к этому достаточно близко, разделив октаву на 12 полутонов, семь из которых дадут вам частоту в 1,498. Для большинства людей этого достаточно.
Иногда почти точные попадания возникают в математике так, будто она сама себя обманывает. В эпизоде Симпсонов «Treehouse of Horror VI» интересующиеся математикой зрители заметили нечто необычное: уравнение 178212 + 184112 = 192212. На первый взгляд может показаться, что сценаристы опровергли Великую Теорему Ферма, постулирующую, что у уравнения xn + yn = zn не существует целочисленных решений при n > 2. Если ввести эти числа в карманный калькулятор, результат покажется вам верным. Но если провести вычисления с точностью, недоступной для большинства карманных калькуляторов, окажется, что корень 12 степени от левой части уравнения равен 1921,999999955867 а не 1922, и Ферма может быть спокоен. Удивительно маленький промах – менее, чем на 10 миллионных частей.
Если ввести эти числа в карманный калькулятор, результат покажется вам верным. Но если провести вычисления с точностью, недоступной для большинства карманных калькуляторов, окажется, что корень 12 степени от левой части уравнения равен 1921,999999955867 а не 1922, и Ферма может быть спокоен. Удивительно маленький промах – менее, чем на 10 миллионных частей.
Но такие почти точные попадания – не просто шутки. «Те, что более других интригуют меня, это случаи, намекающие на наличие чего-то более значительного», – говорит Джон Баез, математик из Калифорнийского университета в Риверсайде. Таков случай величины, которую иногда называют константой Рамануджана. Это число eπ √163, равное примерно 262 537 412 640 768 743.99999999999925 – удивительно близко к целому. Мы не можем ожидать, что эти три иррациональных числа – e, π, и √163 – каким-то образом скомбинируются и дадут нам рациональное число, не говоря уже о целом. Но есть причина тому, что они так хорошо совпадают. «Это не простое совпадение, о котором мы не имеем понятия, – говорит Баез. – Это ключ к глубинам математики». Точное объяснение довольно сложное, но основывается на том, что 163 – это наибольшее из чисел Хегнера. Экспоненты, связанные с этими числами, очень близки к целым.
– Это ключ к глубинам математики». Точное объяснение довольно сложное, но основывается на том, что 163 – это наибольшее из чисел Хегнера. Экспоненты, связанные с этими числами, очень близки к целым.
Или взять математическую связь, известную как «Гипотеза монструозного вздора» (monstrous moonshine). История такая: в 1978 году математик Джон Маккей сделал насколько тривиальное, настолько же и интересное наблюдение: 196 884 = 196 883 + 1. Первое число было коэффициентом важного полинома, j-инварианта, а второе возникло в связи с огромным математическим объектом из теории групп под названием «Монстр». Многие люди пожали бы плечами и пошли дальше, но это наблюдение заинтересовало многих математиков, решивших изучить его поближе. Они обнаружили связь между двумя вроде бы несвязанными темами: теорией чисел и симметрией групп Монстр. Эта связь может обладать ещё более широкими, пока не открытыми, последствиями для других тем. Физик Эдвард Уиттен считает, что группа Монстр может быть связанной с квантовой гравитацией и структурой пространства-времени.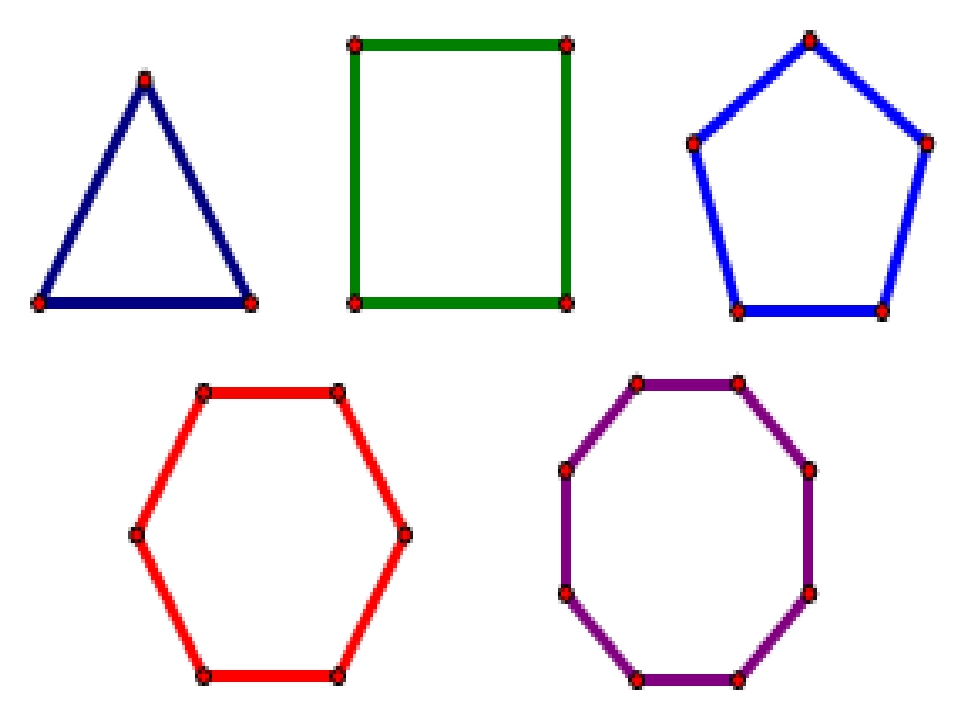
Математические почти правильные попадания показывают как игривость, так и мощь человеческого подхода к математике. Джонсон, Каплан и другие делали открытия при помощи проб и ошибок – изучая область, как биолог, продирающийся через джунгли в поисках новых видов. Но в математике проще бывает вести систематический поиск. К примеру Джим Макнил, интересующийся математикой в качестве хобби и собирающий коллекцию почти правильных попаданий на своём сайте, и Роберт Уэбб, программист, создали ПО для создания и изучения многогранников.
Почти точные попадания живут на размытой границе между идеалистической, жёсткой математикой и нашими снисходительными и практическими чувствами. Они выворачивают наизнанку логику приближения. Обычно реальный мир считается несовершенной тенью мира Платона. Совершенство лежащей в основе математики теряется при её реализации. Но в случае почти точных попаданий реальный мир – это идеальная тень неидеального мира. Аппроксимация – это «неправильное приближение правильного ответа», говорит Каплан, а «почти точное попадание – это точное представление почти точного ответа».
Таким способом почти точные ответы меняют связь математиков и математических физиков с природой. «Я благодарен за несовершенства реального мира, поскольку они позволяют мне достигать квазиидеала, работая с объектами, по сути своей неидеальными, – говорит Каплан. – Они позволяют мне преодолевать ограничения математики благодаря красоте сломанной реальности».
Что такое многоугольник? — Определение, формы и углы — Видео и стенограмма урока
Правильные многоугольники
Существует особый класс многоугольников; это происходит для многоугольников, все стороны которых имеют одинаковую длину и все углы которых одинаковы. Когда это происходит, многоугольники называются правильными многоугольниками . Знак остановки является примером правильного многоугольника с восемью сторонами. Все стороны одинаковые, и как бы вы его ни положили, он будет выглядеть одинаково. Вы не сможете сказать, какой путь был вверху, потому что все стороны одинаковы и все углы одинаковы.
Когда у треугольника все стороны и углы одинаковы, мы называем его равносторонним или правильным треугольником. Четырехугольник, у которого все стороны и углы одинаковы, называется квадратом или правильным четырехугольником. Пятиугольник, у которого все стороны и углы одинаковы, называется правильным пятиугольником. n -угольник с одинаковыми сторонами и углами называется правильным n -угольником.
Вот правильный треугольник, правильный четырехугольник и правильный пятиугольник.Видишь, все стороны одинаковые, и как ни переворачивай, все будет одинаково?
Углы правильных многоугольников
У правильных многоугольников также есть два связанных с ними угла. Первый называется внешним углом , и это измерение между фигурой и каждым сегментом линии, когда вы растягиваете его за пределы фигуры.
Сколько сторон у многоугольника, столько же и внешних углов. Итак, пятиугольник с пятью сторонами имеет пять внешних углов. Шестиугольник будет иметь шесть внешних углов и так далее. Для правильных многоугольников мы можем вычислить измерение внешнего угла, но для неправильных многоугольников мы не можем. Вот формула для правильных многоугольников:
Итак, пятиугольник с пятью сторонами имеет пять внешних углов. Шестиугольник будет иметь шесть внешних углов и так далее. Для правильных многоугольников мы можем вычислить измерение внешнего угла, но для неправильных многоугольников мы не можем. Вот формула для правильных многоугольников:
n обозначает количество сторон многоугольника. Итак, у пятиугольника внешние углы равны 360/5=72 градуса.
Второй угол называется внутренним углом , который является дополнительным углом к внешнему углу. Это означает, что внутренний угол вместе с внешним углом составит 180 градусов.
Можно также сказать, что внутренний угол — это измерение каждого угла многоугольника. Вот формула внутреннего угла:
Вторая формула такая же, как и первая, только измененная.Не беспокойтесь о том, как мы туда попали прямо сейчас; просто помните одно или другое, и все будет в порядке. Второй наиболее часто встречается в математическом мире. Давайте посмотрим на пример. Для нашего пятиугольника с пятью сторонами первое уравнение дает нам 180 — 360 / 5 = 180 — 72 = 108 градусов. Используя второе уравнение, получаем (5 — 2) * 180/5 = 3 * 180/5 = 540/5 = 108 градусов. Обе формулы дадут нам один и тот же ответ. Выберите формулу, которую вам легче запомнить.
Краткое содержание урока
Многоугольники окружают нас повсюду.Кто из нас когда-либо видел треугольник или квадрат? Многоугольник определяется как двумерная фигура с прямыми сторонами. Правильные многоугольники имеют одинаковые стороны и углы. В то время как вы можете найти размеры внешних и внутренних углов правильных многоугольников, вы не можете этого сделать с многоугольниками, которые не являются правильными.
Результаты обучения
После этого урока вы должны уметь:
- Определять многоугольник и правильный многоугольник
- Определите примеры многоугольников и правильных многоугольников
- Объясните, как найти внешний и внутренний углы правильного многоугольника
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$элемент}} {{l10n_strings.ПРОДУКТЫ}} {{l10n_strings. DRAG_TEXT}}
DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$выбрать.выбранный.дисплей}}{{article.content_lang.display}}
{{l10n_strings.АВТОР}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$выбрать. выбранный.дисплей}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}
выбранный.дисплей}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}формирующих полигонов | Справка по SketchUp
Нужен шестиугольник, чтобы продемонстрировать модель вашего пчеловодческого хозяйства? Хотите, чтобы значок пятиугольника иллюстрировал пятиэтапный план разработки? Инструмент «Многоугольник» LayOut позволяет рисовать многоугольник с любым количеством сторон.(Ну, почти любое число: у полигонов нужно как минимум три стороны.)
Вы найдете инструмент «Многоугольник» () на панели инструментов по умолчанию или выбрав «Инструменты» > «Многоугольник » в строке меню.
Чтобы нарисовать многоугольник, выполните следующие действия:
- Выберите инструмент Многоугольник .

- Щелкните в области рисования, чтобы разместить центральную точку многоугольника. Или используйте поле «Измерения», чтобы указать точную центральную точку, введя абсолютные координаты, которые относятся к верхнему левому углу области рисования.Например, чтобы поместить центральную точку на 5,5 дюймов по оси X и на 4,25 дюйма вниз по оси Y, введите [5,5″, 4,25″] и нажмите . Введите (Microsoft Windows) или Верните (Mac OS X ).
- (Необязательно) По умолчанию многоугольники имеют 5 сторон. Чтобы указать необходимое количество сторон, нажмите клавишу со стрелкой вверх или со стрелкой вниз . Или введите число и букву s . Например, если вы хотите 6 сторон, как показано на следующем рисунке, введите 6s и нажмите Введите или Верните .
- Переместите курсор внутрь или наружу от центральной точки, чтобы изменить размер многоугольника, и щелкните, чтобы закончить форму.
 Или используйте поле Измерения, чтобы указать радиус. Значение радиуса может быть единицей измерения или значением точки. Например, введите 3″ и нажмите Введите или Верните . Вы можете продолжать изменять количество сторон и радиус до тех пор, пока не нарисуете другой многоугольник или не выберете другой инструмент.
Или используйте поле Измерения, чтобы указать радиус. Значение радиуса может быть единицей измерения или значением точки. Например, введите 3″ и нажмите Введите или Верните . Вы можете продолжать изменять количество сторон и радиус до тех пор, пока не нарисуете другой многоугольник или не выберете другой инструмент.
Инструмент «Многоугольник» также может выполнять несколько других трюков:
- При рисовании многоугольника удерживайте нажатой клавишу Shift , чтобы привязать сторону многоугольника к красной или зеленой оси.
- Сразу после создания многоугольника дважды щелкните в области рисования, чтобы продублировать многоугольник. Вы можете продолжать делать двойной щелчок, чтобы создать столько копий, сколько вам нужно.
Совет: Если вы допустили ошибку при рисовании многоугольника, нажмите Esc , чтобы начать заново.
Рисование многоугольников и диагоналей многоугольников: урок для детей — видео и расшифровка урока
Как рисовать многоугольники
Треугольник
Равносторонний треугольник — это правильный многоугольник, все три стороны которого имеют одинаковую длину, а углы равны точно 60 градусам.
Чтобы нарисовать равносторонний треугольник:
- Нарисуйте первую сторону треугольника с помощью линейки.
- Поместите центр транспортира в центр стороны и сделайте отметку на уровне 60%.
- Соедините первую сторону с меткой с помощью линейки.
- Нарисуйте третью сторону треугольника с помощью линейки.
Четырехугольники
Четырехугольник представляет собой многоугольник с четырьмя сторонами и углами, сумма которых составляет 360 градусов.Типы четырехугольников включают параллелограммов , которые имеют два набора параллельных сторон, таких как прямоугольник, ромб и квадрат (правильный многоугольник). Трапеции также являются четырехугольниками.
Их можно нарисовать, выполнив аналогичные действия. Начнем с ромба, четыре стороны которого имеют одинаковую длину. Два его противоположных угла острые, а два других противоположных угла тупые. Ромб неправильный, потому что не все его углы равны.
- С помощью линейки измерьте и начертите сторону А.

- Поместите центр транспортира в конечную точку стороны А и измерьте острый угол. Сделайте отметку.
- Соедините сторону A с меткой отрезком такой же длины, как сторона A (это сторона B).
- Совместите транспортир с другой конечной точкой стороны А. Измерьте и отметьте тупой угол. (Подсказка: два угла должны быть равны 180 градусам. Если первый измеренный угол равен 50 градусам, второй угол должен быть равен 130 градусам.)
- Соедините сторону A с меткой отрезком равной длины (сторона C).
- Замкните фигуру, нарисовав сторону D.
Квадраты и прямоугольники можно рисовать одним и тем же методом. Тем не менее, каждый из углов будет измерять 90 градусов. Помните, что все четыре стороны квадрата имеют одинаковую длину. У прямоугольников противоположные стороны одинаковой длины.
Трапеции — это многоугольники только с одним набором параллельных сторон. Следуйте инструкциям по рисованию ромба, помня, что сумма первых двух углов не должна составлять 180 градусов.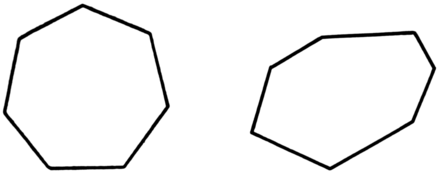
Многоугольники с пятью или более сторонами
Пятиугольник, шестиугольник и восьмиугольник можно нарисовать одинаковым образом, регулируя количество создаваемых сторон.
- Обведите верхнюю и нижнюю половины круга с помощью транспортира.
- Разделите 360 градусов на количество сторон, которые вы хотите нарисовать.
- С помощью транспортира измерьте и отметьте градусы из шага 3 по всей окружности.
- Нарисуйте отрезки, соединив каждую отметку линейкой.
- Сотрите круг, и у вас останется правильный многоугольник.
Примените те же действия при рисовании шестиугольника и восьмиугольника. Просто разделите 360 градусов на количество желаемых сторон.
Диагонали многоугольников
Вы можете нарисовать диагональ или отрезок от одной вершины к противоположной вершине, как показано на этом рисунке:
Чтобы вычислить, сколько диагоналей в каждом многоугольнике:
- Вычтите 3 из числа сторон фигуры.

- Умножьте это число на общее количество сторон.
- Разделить произведение на два.
Давайте рассмотрим пример: у пятиугольника пять сторон. Сколько у него диагоналей?
- 5 — 3 = 2
- 2 х 5 = 10
- 10/2 = 5
В пятиугольнике 5 диагоналей.
Итоги урока
Давайте повторим. Многоугольник представляет собой замкнутую форму, состоящую из отрезков прямых. Правильные многоугольники состоят из отрезков, имеющих стороны одинаковой длины и равные углы.Равносторонний треугольник — это правильный многоугольник, у которого все три стороны имеют одинаковую длину, а углы равны ровно 60 градусам. Четырехугольник — это многоугольник с четырьмя сторонами и четырьмя углами, которые в сумме составляют 360 градусов. Типы четырехугольников включают параллелограммов , которые имеют два набора параллельных сторон, таких как прямоугольник, ромб и квадрат (правильный многоугольник). Трапеции — это многоугольники только с одним набором параллельных сторон. Вы можете рисовать многоугольники с помощью транспортира и линейки.При рисовании диагонали или отрезка от одной вершины к противоположной вершине сначала определите количество диагоналей в многоугольнике.
Трапеции — это многоугольники только с одним набором параллельных сторон. Вы можете рисовать многоугольники с помощью транспортира и линейки.При рисовании диагонали или отрезка от одной вершины к противоположной вершине сначала определите количество диагоналей в многоугольнике.
фигур точечного рисования, многоугольник
Описание
Можно создать общую многоугольную форму, начиная с открытой или замкнутой кривой, определяемой сегментами. Linear , Catmull-Rom , Akima или Bezier (см. дальнейшие подробности). Исходную кривую или поверхность, называемую «базой», затем можно выдавить, перетащив предоставленные маркеры, чтобы сформировать поверхность или объемное изображение. твердые соответственно.
После создания основания (многоугольная поверхность с шестью сторонами в этом примере) перетащите зеленые маркеры, чтобы выдавить его в объемное твердое тело.
Содержимое и функциональные возможности кадров Entity Type , Grid Type , Mode и Point Placement не зависят от
тип строящейся фигуры (в данном случае Polygon ). Первые три кадра описаны в разделе Draw Shapes.
раздел; последний описан в разделе «Расстановка точек».
С другой стороны, содержимое и функциональные возможности фреймов Enclosing Parameters , Shape Parameters и Shape Options в зависимости от типа строящейся формы. Кадр Enclosing Parameters содержит команды, необходимые для определения характеристик форма в процессе создания в режиме Enclosing по отношению к набору выбранных объектов, заключенных в новую форму (см. раздел «Рисование фигур» для получения более подробной информации о доступных режимах).Параметры формы Параметры формы и кадров содержат команды, необходимые для определения общих характеристик строящейся формы. Здесь мы опишем содержимое этих трех фреймов для частный случай формы типа Polygon .
Параметры ограждения
Используйте рамку Enclosing Parameters, чтобы определить характеристики создаваемой формы относительно набора выбранных объектов, заключенных в рамки. новая форма.На этом изображении показаны команды, доступные для многоугольной формы.
новая форма.На этом изображении показаны команды, доступные для многоугольной формы.
После создания формы в режиме Enclosing ее можно масштабировать с помощью указанных коэффициентов, используя поля ввода Масштабный коэффициент . Для случая многоугольной формы есть поля ввода для масштабирования формы Ширина , Высота и Длина , отдельно. Обратите внимание, что вы можете только масштабировать фигуру до большего размера; это означает, что указанные коэффициенты должны быть больше 1.0.
Существуют также поля ввода Ширина , Высота и Длина Поля , которые позволяют указать набор полей по отношению к
набор выбранных объектов, заключенных в форму. Эти поля будут эффективно увеличивать размер фигуры на указанную величину в каждом
соответствующее направление. Обратите внимание, что вы можете только увеличить размер фигуры; это означает, что указанные поля должны быть больше 0,0.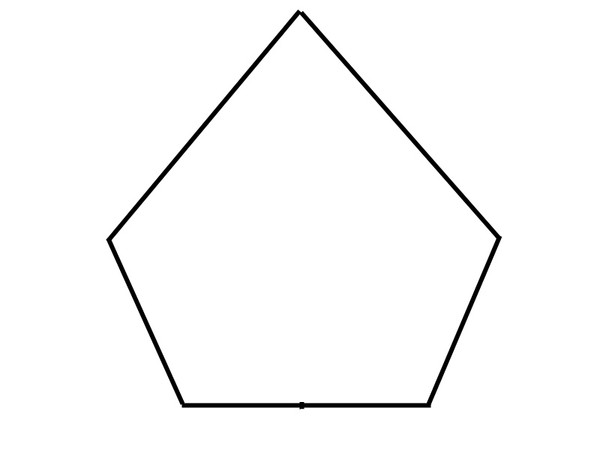
Охватывающая фигура может быть выровнена в любом из трех направлений координат с помощью соответствующей кнопки-переключателя: Ось X , Ось Y , и Ось Z .Его также можно выровнять по текущему виду, если выбран параметр To View . Обратите внимание, что последний вариант выбирается дефолт. Вы также можете выбрать, будет ли окружающая форма симметричной относительно направления X, Y или Z, выбрав соответствующую Симметрия вариант: В X , В Y , или В Z .
Последняя команда в этом фрейме: Выровнять по выбору . При нажатии этой кнопки Pointwise попытается определить основное направление вложенные сущности и выровняет вмещающую форму с этим направлением.
Параметры формы
Используйте параметры в рамке «Параметры формы», чтобы определить характеристики создаваемой формы. На этом изображении показаны команды, доступные для многоугольная форма.
В рамке Параметры формы опции Linear , Catmull-Rom , Akima и Bezier (см.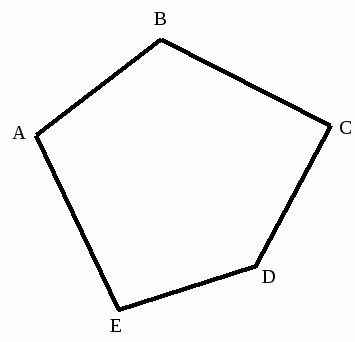 раздел «Линия» для получения дополнительной информации) позволит вам установить алгоритм управления наклоном, который будет использоваться при создании
кривые, определяющие базовую многоугольную форму.
раздел «Линия» для получения дополнительной информации) позволит вам установить алгоритм управления наклоном, который будет использоваться при создании
кривые, определяющие базовую многоугольную форму.
Команда Lock Normal To Base используется для определения направления выдавливания. Если флажок установлен (по умолчанию), направление остается нормальным по отношению к базовой форме. быть выдавленным. В противном случае направление выдавливания остается нормальным к исходной плоскости чертежа.
Опция Force Planar заставляет все контрольные точки быть в одной плоскости; плоскость, содержащая эти точки, определяется первыми тремя контрольными точками указано.
Опция Close Polygon используется для указания того, следует ли открывать или закрывать полигональное основание, определяемое указанными контрольными точками.Когда это опция включена, полигональная база будет закрыта; в противном случае он будет открыт.
Текстовое поле Длина может использоваться для установки точной длины экструзии.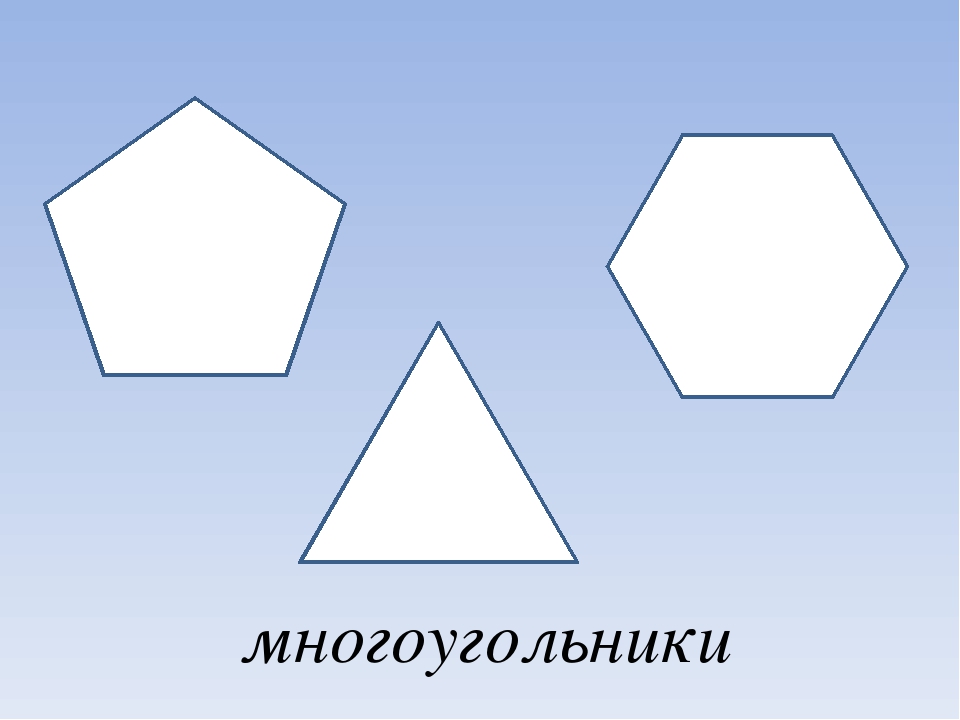
Варианты формы
Используйте параметры в рамке «Параметры формы», чтобы определить характеристики создаваемой формы. На этом изображении показаны команды, доступные для многоугольника. форма.
Для многоугольной формы во фрейме Параметры формы доступны только команды Base и Top .Эти команды используются для указания должны ли быть сохранены базовая и верхняя плоские поверхности после завершения формы. Обратите внимание, что эти команды будут отключены, если основание и верх поверхности не плоские (параметр Force Planar снят).
Персонал Полигона рисует своих мастер-чифов
Мастер Чиф — самый крутой парень из видеоигр. Он говорит достаточно, чтобы дать вам понять, какой он крутой, а затем затыкается и делает свое дело. А за последние 20 лет он стал абсолютной иконой видеоигр.
А что, если бы у него было четыре руки, а не только предплечья? Что, если бы он был не человеком в гигантском металлическом костюме, а тамагочи? Это те вопросы, которые сотрудников Полигона действительно интересуют.
К сожалению, Bungie и 343 Industries так и не предоставили нам эти версии Master Chief, поэтому мы собрались вместе, чтобы создать их собственную.
Представляем Polygon Draws: издание Master Chiefsona.
Джулия Ли Изображение: Джулия Ли«Почему бы мне не украсить свою броню милыми цветами, наклейками и аксессуарами? Я буду самым красивым Мастером Чифом на вечеринке.
Николь Карпентер Изображение: Николь Карпентер«Я начал просто рисовать шлем Мастера Чифа, а остальное само пришло в голову. Мастер Чиф — тамагочи, а теперь и я».
Касс Маршалл Изображение: Касс Маршалл «Я никогда не играл в Halo, поэтому после того, как я закончил рисовать культовый спартанский шлем, я как бы вошел в область интерпретации того, как, по моему мнению, могут выглядеть вещи из Halo. Сзади у вас Бородавочник. А потом в углу появляется Крейг, он просто вибрирует. Спасибо Крейг! Надеюсь, этого Halo достаточно для всех вас, фанатов консолей».
Сзади у вас Бородавочник. А потом в углу появляется Крейг, он просто вибрирует. Спасибо Крейг! Надеюсь, этого Halo достаточно для всех вас, фанатов консолей».
«Ее зовут Мастер Чикс, и она знает свои лучшие качества в борьбе с Ковенантом».
Пэт Гилл Изображение: Пэт Гилл«Это спартанец, который надевает верхнюю половину своих доспехов для вызова зума, но он давно не стригся и носит фланелевую шаль, потому что его домовладелец еще не включил отопление.Он также носит спортивные штаны».
Ана Диас Изображение: Ана Диас «Это вождь чиби или вождь Фанко? Как художник, я не должен указывать своим зрителям, как они должны или не должны интерпретировать мое искусство, поэтому пусть решают читатели».
«Я решил духовно создать Спартанца, которого я хотел бы видеть, когда мне было 12 лет.Итак, у нас есть тонны оружия, блочная броня, потому что это то, что я считаю крутым. Я добавил три визора, потому что, будучи взрослым, я глубоко ценю периферийное зрение. По сравнению с другими моими дерьмовыми полигональными рисунками, это особенно грубо. Но как наглядный пример того, что мои художественные навыки не улучшились со времен начальной школы? А+».
Майк Махарди, который сказал, что может «взять» Мастера Чифа Изображение: Майк Махарди«Я не хочу, чтобы люди знали, собирается ли он на пляж или в Ковчег, и я бы также нарисовал больше пресса, если бы у меня было место.
Как крупный международный издатель
академических и исследовательских журналов, Science Alert публикует
и разрабатывает игры в партнерстве с самыми
престижные научные общества и издательства. Наша цель
заключается в проведении высококачественных исследований в максимально широком
аудитория. Наша цель
заключается в проведении высококачественных исследований в максимально широком
аудитория. | ||||||
| Мы прилагаем все усилия, чтобы поддержать исследователей которые публикуются в наших журналах.Существует огромное количество информации здесь, чтобы помочь вам опубликоваться у нас, а также ценные услуги для авторов, которые уже публиковались у нас. | ||||||
Цены 2022 уже доступны. Ты
может получить личную / институциональную подписку на перечисленные
журналы непосредственно из Science Alert. В качестве альтернативы вы
возможно, вы захотите связаться с предпочитаемым агентством по подписке.Пожалуйста, направляйте заказы, платежи и запросы в службу поддержки клиентов
в службу поддержки клиентов журнала Science Alert. Ты
может получить личную / институциональную подписку на перечисленные
журналы непосредственно из Science Alert. В качестве альтернативы вы
возможно, вы захотите связаться с предпочитаемым агентством по подписке.Пожалуйста, направляйте заказы, платежи и запросы в службу поддержки клиентов
в службу поддержки клиентов журнала Science Alert. | ||||||
| Science Alert гордится своим тесные и прозрачные отношения с обществом. В виде некоммерческий издатель, мы стремимся к самому широкому возможное распространение материалов, которые мы публикуем, и на предоставление услуг самого высокого качества нашим издательские партнеры. | ||||||
Здесь вы найдете ответы на наиболее часто задаваемые вопросы (FAQ), которые мы получили по электронной почте или через контактную веб-форму. В соответствии с характером вопросов мы разделили часто задаваемые вопросы на разные категории. В соответствии с характером вопросов мы разделили часто задаваемые вопросы на разные категории. | ||||||
| Азиатский индекс научного цитирования (ASCI) обязуется предоставлять авторитетный, надежный и значимая информация путем охвата наиболее важных и влиятельные журналы для удовлетворения потребностей глобального научное сообщество.База данных ASCI также предоставляет ссылку до полнотекстовых статей до более чем 25 000 записей с ссылка на цитируемые источники. | ||||||


