Как нарисовать шестиугольник в круге
Popular
Основы черчения
Строительное
Машиностроительное
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4.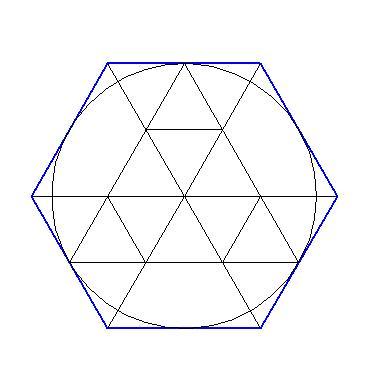
Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5.
Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг.
65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.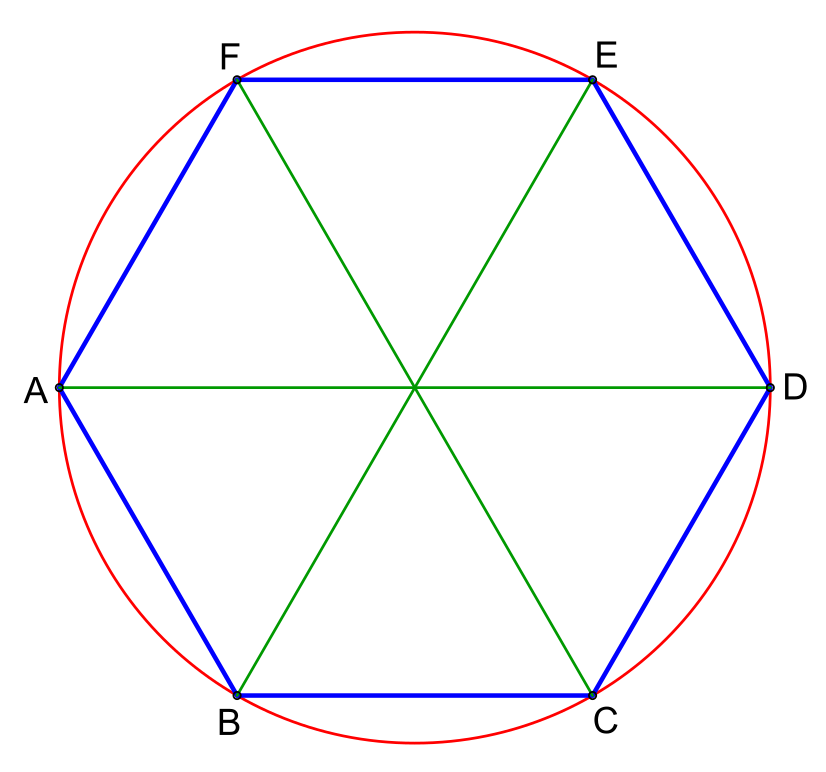
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.
Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.
Построение шестигранника может производиться несколькими способами. Удобнее всего использовать стандартный набор чертежных инструментов: циркуль, линейку. Однако, в отсутствие циркуля, фигура этого типа может быть начерчена с помощью рейсшины, угольника заводского изготовления с углами 90/60/30°.
Шестигранники применяются для откручивания и закручивания болтов при ремонте и сборке мебели.
В обоих случаях особенностью построения является элементарное знание основ геометрии. В правильном шестиугольнике длина его стороны всегда равна радиусу окружности, описанной вокруг него, противоположные стороны параллельны, грани сопрягаются под углом 60°.
Способ вычерчивания шестиугольника циркулем, линейкой
Чтобы построить шестигранник при наличии циркуля, достаточно вычертить окружность, найти на ее дуге 6 точек, соединив их отрезками. Для этого достаточно настроить циркуль один раз, отложив на нем значение стороны многогранника. Линейка потребуется для строительства вспомогательных, основных линий.
Метод выглядит следующим образом:
Первый способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.
- циркулем вычерчивается окружность — радиус является размером стороны;
- по линейке проводится радиус — точки пересечения этого отрезка будут углами многоугольника;
- находятся два угла многоугольника — циркуль переставляется в одну из точек пересечения отрезка (проведенный на предыдущем этапе диаметр), на дуге делаются отметки;
- находятся оставшиеся два угла — циркуль перемещается в противоположную точку пересечения отрезка с дугой окружности, создаются отметки пересечения на второй стороне окружности.
Построение правильного шестигранника завершается соединением получившихся углов по линейке. Это самый точный способ, требующий минимального количества чертежного инструмента. При
Заврики по математике 2020 — ответы на все задания олимпиады
На сайте Учи.ру 27 января 2020 года началась зимняя олимпиада Заврики по математике. Участвовать в основном туре могут все желающие. Результаты будут доступны сразу после окончания олимпиады. В данной статье представлены ответы на все задания основного тура Заврики по математике для 1, 2, 3 и 4 классов. Основной тур продлится до 9 февраля 2020 года включительно.
1 класс
Сосуды с водой
Кликай по вентилям, чтобы наполнить баки для полива. Необходимое количество воды указано на горшках.
Сосуды с водой — 1 класс — 1 шагСосуды с водой — 1 класс — 2 шагСосуды с водой — 1 класс — 3 шагСосуды с водой — 1 класс — 4 шагСосуды с водой — 1 класс — 5 шагСосуды с водой — 1 класс — 6 шагСосуды с водой — 1 класс — 7 шагДороги и развилки
Поменяй завриков местами, чтобы они оказались в своих домах.
Номер машинки подсказывает, к какому дому она должна приехать.
Стрелка повернётся в другую сторону после того, как машина проедет её.
Дороги и развилки — 1 класс
Решение:
Поменяем местами завриков так, как показано на картинке ниже >>
Дороги и развилки — 1 класс — ответТак они разьедутся каждый к своему дому.
Одинаковые фигуры
Собери две одинаковые по форме фигуры. Нажми на деталь, чтобы повернуть её.
Одинаковые фигуры — 1 классНачнем поворачивать детали так, чтобы получились одинаковые фигуры как на рисунке ниже.
Одинаковые фигуры — 1 класс — ответГотово!
Покорми кныша
Кнышу нужно 6 г сладостей. Перетащи миску с 8 г сладостей в прибор, который делит их пополам.
Перетащи миску с 4 г сладостей в прибор, чтобы разделить сладости пополам и получить две миски по 2 г сладостей каждая.
Перетащи в мерный стакан 6 г сладостей.
Теперь можно приступать к задаче. Сделай так, чтобы в мерном стакане Кныша оказалось 9 г сладостей.
У тебя есть миска с 24 г сладостей и прибор, который умеет делить пополам.
- Разделим 24 г на 2 миски по 12г.
- Разделим 12 г на 2 миски по 6 г
- Разделим 6 г на 2 миски по 3 г.
- Положим в мерный стакан кныша две миски. Одну с 6г и вторую с 3 г.
Снежинки
Повтори эти снежинки.
1 снежинка. Вырежи из сложенной бумаги такую же снежинку, как на картинке слева. Зеленая точка — центр будущей снежинки.
Снежинка 1 — 1 классСделаем следующие разрезы, которые позволят нам получить требуемую снежинку.
Снежинка 1 — 1 класс — ответ2 снежинка. Вырежи из сложенной бумаги такую же снежинку, как на картинке слева. Зеленая точка — центр будущей снежинки.
Снежинка 2 — 1 классСделаем следующие разрезы, чтобы получить искомую снежинку.
Снежинка 2 — 1 класс — ответРавновесие
Капитан Хрум отправляется в дальнее плавание вместе с животными. Помоги ему узнать вес животных: это нужно, чтобы корабль не повернулся.
На одном конце корабля сидит кобра (ее вес не известен), а на другом конце коробля весы, на которых сидит коала, весом 8 кг и броненосец (его вес не известен). Нужно вычислить и подписать вес животных, чтобы корабль был уравновешен.
Так как броненосец сидит на противоположном конце весов от коалы, вес которой 8 кг, значит броненосец будет также весить 8 кг.
А значит кобра будет весить 8 + 8 = 16 кг.
Сонины конфеты
На всех кусочках конфет должны стоять числа. Нажми на кнопку «Дальше», чтобы узнать, как расставить недостающие числа. Числа не должны повторяться в каждом ряду, в каждом стоблике и на каждой конфете. Заполни пропуски числами 1, 2 и 3. Числа не должны повторяться в каждом ряду, в каждом стоблике и на каждой конфете.
Сонины конфеты — 1 классРасставим цифры от 1 до 3 как требуют от нас условия задачи. Получим следующий ответ.
Сонины конфеты — 1 класс — ответКружки
Андрей, Миша и Олег — друзья. каждый занимается в двух кружках.
Каждый кружок посещают двое ребят. Андрей с ещё одним мальчиком ходит на пение. Олег любит играть в шахматы. Миша не ходит на футбол. На какие два кружка ходит Андрей?
Ответ: Андрей ходит на футбол и пение.
2 класс
Сосуды с водой (2 класс)
Кликай по вентилям, чтобы наполнить баки для полива. Необходимое количество воды указано на горшках.
Сосуды с водой 2 класс — 1 шагСосуды с водой 2 класс — 2 шагСосуды с водой 2 класс — 3 шагСосуды с водой 2 класс — 4 шагСосуды с водой 2 класс — 5 шагСосуды с водой 2 класс — 6 шагСосуды с водой 2 класс — 7 шагСосуды с водой 2 класс — 8 шагСосуды с водой 2 класс — 9 шагСосуды с водой 2 класс — 10 шагСосуды с водой 2 класс — 11 шагСосуды с водой 2 класс — 12 шагСосуды с водой 2 класс — 13 шагСосуды с водой 2 класс — 14 шагСосуды с водой 2 класс — 15 шагСосуды с водой 2 класс — 16 шагСосуды с водой 2 класс — 17 шагСосуды с водой 2 класс — 18 шагДороги и развилки
Поменяй завриков местами, чтобы они оказались в своих домах.
Номер машинки подсказывает, к какому дому она должна приехать.
Стрелка повернётся в другую сторону после того, как машина проедет её.
Дороги и развилки — 2 классРешение:
Поменяем местами завриков так, как показано на картинке ниже >>, то есть 1, потом 2, 3, 3, и 2.
Дороги и развилки — 2 класс — ответТак они разьедутся каждый к своему дому.
Ответы на остальные задания смотрите на видео ниже.
3 класс
4 класс
5 и 6 класс
У 5 и 6 класса задания и ответы абсолютно одинаковые. Так что смотрим видео!
7 класс
8 и 9 класс
У 8 и 9 класса задания и ответы одни и те же.
10 класс
11 класс
ГАУ ДО «Астраханский областной центр развития творчества»
«Яркие краски лета»
Гукасова Маргарита, Образцовый детский коллектив РФ ДСКВ «Колокольчики»
Лето в Астрахани — самое лучшее время года. Оно такое же яркое, как астраханское солнце.
И оно такое же сочное, как все летние дары природы. Вот такая чудесная вишня поспела в саду у моей бабушки в начале июня!
«Краски летних каникул»
Дормидонтова Елизавета, Образцовый коллектив Вокальный ансамбль «Настроение»
Каждый год мы с родителями летом отдыхаем в г. Кисловодск. Мы очень любим такой вид отдыха: всегда чистый воздух, спокойный размеренный ритм, природа и огромное количество зелени.
В этом году мы были просто очарованы красотой обновленного города. Преображение паркового озера, каскадной лестницы, которая стала в разы больше и современней, главного курортного фонтана не оставило никого равнодушным. Озеро стало настоящим украшением курортного г. Железноводска.
Наш визит получился очень интересным и запоминающимся для меня.
«Гигантская земляника»
Романов Илья, творческое объединение «Художественная керамика»
Видели ли вы когда-нибудь гигантскую землянику? Нет? А я «да».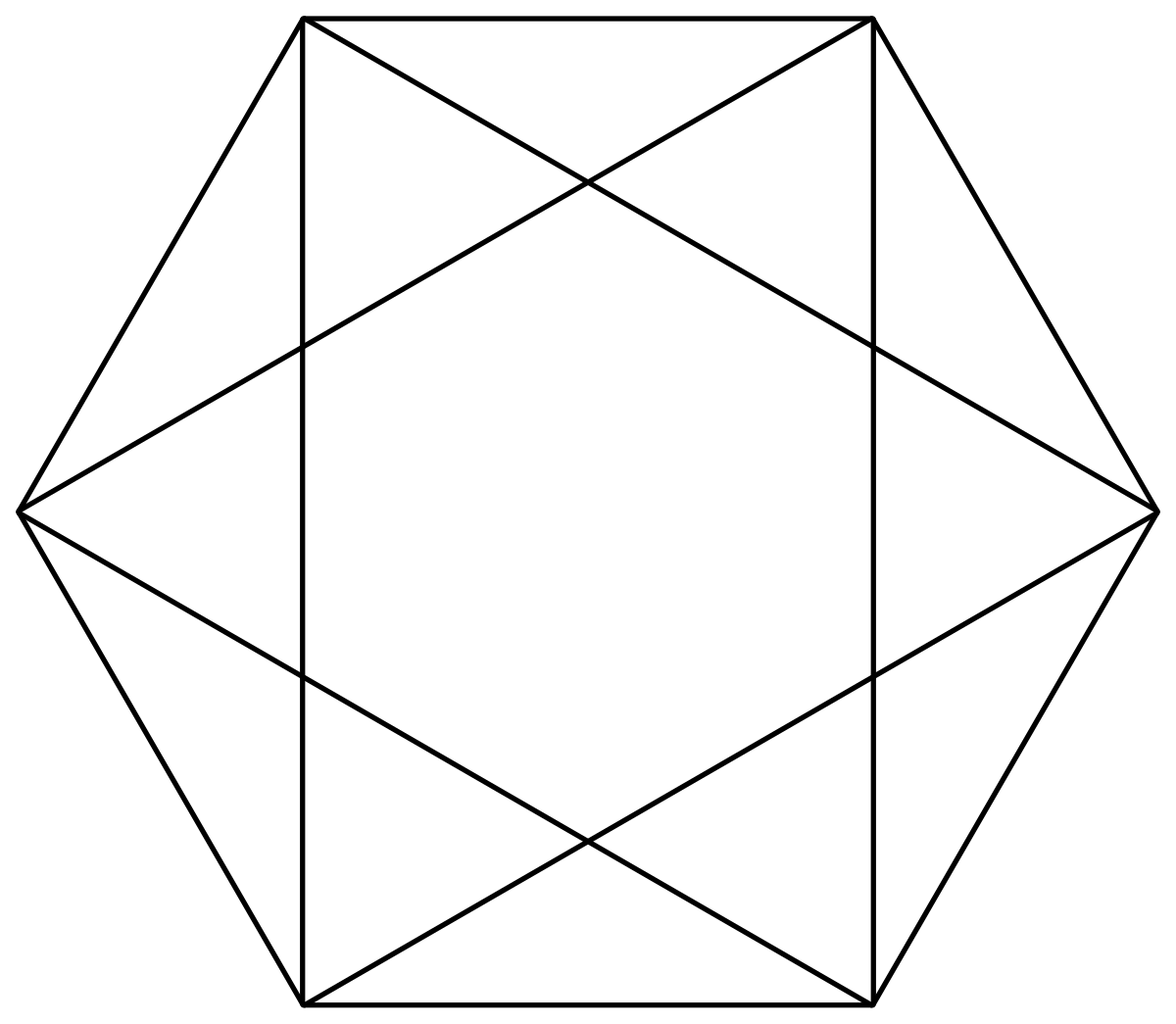
Отдыхая в одно лето в Краснодарском крае на базе отдыха «Хуторок», я увидел ее, аппетитную, сочную, сладкую… Она была настолько натуральной, что я не удержался и решил откусить кусочек. Вот было бы здорово, если такого размера земляника росла бы на грядках!
«Кроха»
Иванников Алексей, Образцовый ансамбль современного эстрадного танца «Класс-Центр»
Вот таких существ можно встретить в Астраханском крае. Наша флора и фауна крайне разнообразна. Каждое лето я открываю для себя новые вещи, среди которых и эта «кроха».
«Лотос»
Иванников Артем, Образцовый ансамбль современного эстрадного танца «Класс-центр»
В один из солнечных летних дней, мы с братом гуляли по набережной. Я увидел лотос, он был очень красив. Этот цветок олицетворял все самые яркие краски лета 2020 года. Я решил запечатлеть этот цветок, чтобы долго помнить об удивительном лете.
«Лето — это сочно»
Калмыков Эдуард, творческое объединение «Художественная керамика»
Лето, лес, пение птиц, поездки на дачу с родственниками, купание в речке с друзьями, вечерние разговоры и игры у костра — так много всего хочется вспомнить и ещё раз насладиться замечательными моментами.
«Картинг — это круто»
Кирюхин Артем, творческое объединение «Автомоделист»
«Лето-это сочно!»
Климова Ольга, Образцовый детский коллектив РФ ДСКВ «Колокольчики»
Моя бабушка очень любит цветы, сама выращивает их во дворе, я очень люблю ими любоваться и фотографировать, чтобы сохранить такую красоту.
«Краски лета»
Романов Ярослав, творческое объединение «Школа Лидера»
Лето — прекрасная пора, наполненная теплом, запахами, волшебными звуками и яркими, сочными красками. В это время года все вокруг расцветает, благоухает, заряжает положительным эмоциями и настроением. Этим летом я отдыхал у родственников в селе Енотаевка Астраханской области. Прогуливаясь как-то по двору, мое внимание привлекли яркие душистые цветы. Я не смог пройти мимо и запечатлел их красоту на фотокамеру своего телефона.
«Эльбрус»
Мартемьянова Анастасия, Образцовый коллектив Вокальный ансамбль Настроение
Этим летом я со своей семьей отдыхала в Кисловодске.
Путь на гору не близкий, надо пройти по терренкуру – так называется оздоровительный маршрут, сначала Храм воздуха, Долина Роз, потом Красно Солнышко, дальше будут Синие горы и потом вверх до горы Малое седло высота которой 1325 м.
Канатная дорога в парке в это время не работала, но мама мне сказала, что если бы даже и работала, то мы все равно пошли бы пешком, так как такую красоту надо ощущать и восхищаться ее вблизи.
Мы начали свой маршрут с веревочного парка, далее у нас была цель дойти до Долины роз, ну а потом уже к памятнику Лермонтова, ну и дальше к беседки «Семи ветров».
Проходя каждый пункт, мы останавливались и мама рассказывала нам, что это и чем примечательно данное место.
Я не смогу рассказать в своем описании красоты которые мы увидели, потому что на это потребуется гораздо больше одной страницы, а опишу мое самое главное впечатление – вид на великий двуглавый Эльбрус.
Великий Эльбрус предстал перед нами во всей своей красе в лучах утреннего солнца, он возвышается над равниной как спящий великан. Кажется, что это, что то с другой планеты приземлилось на землю и тихо спит в лучах утреннего рассвета.
«Побережье 1000 бухт»
Митченко Дарья, Образцовый детский коллектив РФ ДСКВ «Колокольчики»
Летом мы были на полуострове Крым. Он очень интересен и разнообразен. В этом году мы решили поехать на ту его часть, которая омывается Азовским морем. Называется это место «Генеральские пляжи». Это место еще называется «Побережье 1000 бухт». Там расположены живописные скалистые бухты и песчаные пляжи из ракушечника. Именно там и было сделано это фото.
«Русалочка»
Яна Михайловская, Образцовый коллектив вокальный ансамбль «Настроение»
Этим летом, три недели я провела в оздоровительный лагере «Искра», на побережье Краснодарского края. Новые друзья, тёплая атмосфера, очень активная развлекательная программа.
Впечатлений море. Два раза в день мы ходили купаться в море. Однажды мы с девчонками придумали конкурс, побеждает тот, у кого лучше получиться изобразить русалочку. Так родился этот снимок. Вечер, закат, море. Мне пришлось постараться. Сама не ожидала, что получиться так красиво.
«Мое сочное настроение»
Моргуль Каролина, Образцовый коллектив Вокальный ансамбль «Настроение»
Лето — моя любимая пора. В нашем родном городе в это время года всегда стоит очень теплая и солнечная погода. А самые яркие моменты всегда хочется оставить в памяти, чтоб в холодную пору согреваться, глядя на сочные снимки, с улыбкой вспоминая ушедшее лето. Мама любит фотографировать, а я — ее главная модель! Мы всегда стараемся придумать интересную идею, чтоб фото в семейном архиве были яркими и необычными. И конечно, как и у любого жителя Астрахани, у нас есть фото с самой большой ягодой, которой славится наш город — арбузом. Но нам стало мало арбуза в руках, и мы решили его повторить на моем лице! Получилось сочное, яркое летнее фото, которое будет дарить тепло и поднимать настроение всей семье.
«Астраханский лотос»
Мягкова Елизавета, творческое объединение «Художественная керамика»
В Астраханской области есть село Каралат, где Волга образует огромное Каспийское взморье. Можно увидеть удивительные лотосовые поля. В этом году в августе всей семьей мы ездили любоваться красивейшим лотосом. Это просто не описать, как красиво цвел лотос, а его запах после дождя – удивителен!
«Астраханское лето»
Перевалова Анна, Народный коллектив молодежный театр-студия «Мы»
Наше астраханское лето прекрасно! Яркое, жаркое, сочное. Из-за пандемии мы с семьей не поехали этим летом на море. Но и в Астрахани можно классно, весело, ярко, вкусно и интересно провести летние каникулы!
«Огонёк»
Потапова Ксения, Школа ведущих «Премиум +»
Это фото сделано мной на рынке в городе Анапа, где мы отдыхали в августе 2020года.
Фото отражает яркость лета, отдыха, сочность и вкус арбуза. А еще, глядя на него, я вспоминаю не только Анапу, но и съемки «Школы ведущих Премиум+» в передаче «Всем подъем» (канал Астрахань-24), где мы показывали номер про арбуз. И съёмка, и эфир прошли как раз перед нашим отъездом в Анапу. Благодарю это лето!
«Лето — это сочно»
Рогожкина Анастасия, Школа ведущих «Премиум +»
Летом каждые выходные я вместе с родителями проводила на даче. Я много фотографировала. Яркости лету добавляют цветы, которые цветут у нас на даче. Каких только оттенков у них нет. Цветы желтые, красные, белые, бордовые. Они такие яркие и разноцветные. Трава и листья, тоже очень яркие зеленые. Лету добавляют яркости и ягоды, фрукты и овощи. Ярко-красная спелая клубника, малиновая малина, черная и красная смородина, зеленые огурцы, красные, розовые и оранжевые помидоры, арбузы. С наступлением жарких дней мы все стараемся добавить яркие краски в свой гардероб.
Я рада, что сделала за это лето много фотографий. Но пересматривая свои фотографии, это мое самое любимое фото.
«Подготовка модели к финалу. Чемпионат России 2020 город Ростов»
Сабельников Егор, творческое объединение «Автомоделист»
«XXI Век»
Сабирова Евангелина, Образцово-художественный ансамбль народного танца «Тантана»
Летом мне удалось побывать в аквапарке в городе Волжский — «XXI век». Самое интересное место в нем, это огромный бассейн с искусственным водопадом и островом посередине. В этом бассейне я плавала на больших кругах, и решила запечатлеть его на этом фото.
«Детский лагерь Телелето»
Савельева Алиса, Образцовый детский коллектив РФ ДСКВ «Колокольчики»
Летом, во время самоизоляции, когда уже разрешили не большие послабления, меня пригласили в детский лагерь Телелето — это форум журналистики. Мы посещали его в течении недели с 8 утра до 18 часов.
Там было несколько команд, между которыми проводились различные конкурсы. У каждой команды были футболки своего цвета. Я попала в «жёлтую» команду, которая в итоге и стала победителем в этом сезоне.
«Лето – это сочно!»
Фролова Дарья, Образцовый коллектив Вокальный ансамбль «Настроение»
Лето – это сочно!
Яркими красками лета,
Я разукрашу мечты!
Вспомню, что было со мною,
Вспомни со мною и ты!
Море, песок и дельфины.
Речка палатка и пляж.
Сколько всего летом было,
Словами не передашь!
«Цветы»
Боровских Варвара, Образцово-художественный ансамбль народного танца «Тантана»
Цветы нам дарят настроение,
И пробуждают вдохновение,
Как символ чистой красоты,
Ведь очень трудно без мечты!
«Архыз»
Чабаненко Анастасия, Образцовый коллектив Вокальный ансамбль «Настроение»
Фотография сделана во время поездки в Архыз в июне 2019 года.
«Смородина»
Шилова Арина, творческое объединение «Золотой ключик»
Мне кажется, что лето любят все! Ведь краски и дары лета не сравнить ни с чем…. Я впервые в это лето собирала смородину, скажу вам честно: очень трудное дело! Хорошо, что со мной была рядом мама, мы много говорили, смеялись и сбор был весёлым и интересным! Смородина хорошо прячется за своими листочками, но мы были внимательными и бережными: осторожно снимали ягодки, не повредив веточек и листьев. Собрали с мамой целое ведро смородины, угостили всех бабушек и крёстну.
5 класс. Математика. Никольский. Учебник. Ответы к стр. 130
Измерение величин
Многоугольники
Ответы к стр. 130
580. Пчелы строят свои соты в виде правильных шестиугольников (рис. 124). Постройте на альбомном листе рисунок пчелиных сотов.
581. Из листа фанеры размером 11 см × 15 см выпилили два квадрата со стороной 5 см и три прямоугольника со сторонами 4 см и 7 см.
Определите площадь оставшейся части.
1) 11 • 15 = 165 (см2) − площадь листа фанеры
2) 5 • 5 = 25 (см2) − площадь одного выпиленного квадрата
3) 25 • 2 = 50 (см2) − общая площадь выпиленных квадратов
4) 4 • 7 = 28 (см2) − площадь одного выпиленного прямоугольника
5) 28 • 3 = 84 (см2) − общая площадь выпиленных прямоугольников
6) 50 + 84 = 134 (см2) − общая площадь выпиленной части
7) 165 – 134 = 31 (см2) − площадь оставшейся части фанеры
О т в е т: площадь оставшейся части фанеры 31 см2.
582. а) Определите периметр шестиугольника (рис. 125).
б) Определите площадь многоугольника (рис. 126).
в) Определите периметр многоугольника, изображенного на рисунке 126, a. Какое условие лишнее?
а) P = (4 + 9) • 2 = 13 • 2 = 26 (см) – периметр шестиугольника
О т в е т: периметр шестиугольника 26 см.
б) а) S = (9 • 7) – (4 • 2) = 63 – 8 = 55 (см2)
б) S = (7 • 6) : 2 = 42 : 2 = 21 (см2)
в) S = (13 • 17) + (5 • 13) : 2 + (5 • 13) : 2 • 2 = 221 + 5 • 13 = 221 + 65 = 286 (см2)
О т в е т: 55 см2, 21 м2, 286 см2.
в) P = (7 + 9) • 2 + 4 • 2 = 16 • 2 + 8 = 32 + 8 = 40 (см) – периметр многоугольника
О т в е т: периметр многоугольника 40 см, лишнее условие – 2 см.
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.
Математика. 5 класс
Понравилось? Оцени!
Разбор задачи A20 (демо ЕГЭ 2006)
Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существуют две команды:Вперед n, вызывающая передвижение Черепашки на n шагов в направлении движения.
Направо m, вызывающая изменение направления движения на m градусов по часовой стрелке.
(Вместо n и m должны стоять целые числа).
Запись:
Повтори 5 [Команда1 Команда2]
означает, что последовательность команд в квадратных скобках повторится 5 раз.
Какое число необходимо записать вместо n в следующем алгоритме:
Повтори 7 [Вперед 40 Направо n],
чтобы на экране появился правильный шестиугольник?
Решение:В задаче n определяет угол поворота исполнителя Черепашки.
1 способ.
Хотя в алгоритме написано «Повтори 7…», для построения правильного шестиугольника достаточно выполнить «Повтори 6…», т.к у шестиугольника 6 сторон. 7-й повтор просто повторяет проведенную первую сторону. Нарисуем траекторию движения робота:
На рисунке черными точками отмечены точка начала движения и точка конца, указан 7-й лишний повтор.
Чтобы нарисовать правильный шестиугольник и вернуться в ту же точку исполнитель должен выполнить алгоритм 6 раз повернуться на 360°.
Поэтому n=360°\6=60°.
2 способ.
Построим правильный шестиугольник (траектория движения исполнителя Черепашки):
Чтобы определить угол n, необходимо определить угол α.
α=Σуг.ш.\6, где
Σуг.ш. — сумма углов шестиугольника.
Сумма углов многоугольника определяется по формуле:
Σуг=180*(m-2), где
m — количество углов многоугольника.
У шестиугольника 6 углов, поэтому:
Σуг.ш.=180*(6-2)=180*4=720°.
α=Σуг.ш.\6=720\6=120°.
Определим угол n:
Как видно из рисунка выше, n=180−120=60°.
В алгоритме вместо n надо написать 60 (вариант 4).
Перейти к другим задачам.
Инженерная графика | Лекции | Технический рисунок
По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым удобным для вас способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1000 р./ак.ч.Введение
Наука, изучающая законы красоты и художественного творчества, применительно к предметам технической формы, называется технической эстетикой.
Одним из элементов технической эстетики можно считать техническое рисование.
Техническим рисунком люди пользовались давно и в самых разных его видах. Чаще всего технический рисунок используется при создании новых объектов.
Рождающаяся в сознании человека новая идея, возникший неожиданно новый образ объекта требуют немедленного закрепления, и наиболее простой, удобной и быстрой формой фиксации творческой мысли оказывается рисунок.
Инженеры — конструкторы чаще всего использовали реалистический рисунок (перспективный), примером могут служить многочисленные рисунки Леонардо да Винчи (Рисунок 8.1 и 8.2).
Рисунок 8.1 — Арбалет Леонардо да Винчи
Рисунок 8.2 — Самоходная тележка Леонардо да Винчи
Активная творческая деятельность изобретателя, инженера всегда начинается с технического рисунка. Технический рисунок позволяет сразу увидеть преимущество новых конструкционных усовершенствований и дает основание приступить к переоборудованию или замене отдельных деталей машины. Решение задач по проектированию значительно облегчается при предварительном выполнении эскизов, технических рисунков.
Несколько таких предварительно выполненных изображений позволяют выбрать лучший вариант будущей формы, или конструкции предмета. Но главное достоинство технического рисунка состоит в том, что он заставляет автора идти дальше, вносить в свой рисунок добавления и исправления, активизирует и совершенствует его творческую мысль. А это в свою очередь принуждает конструктора переходить к новым рисункам до тех пор, пока автор не приблизится к идеалу.
Дизайнеры используют рисунки как перспективные, так и построенные в аксонометрических проекциях. Чаще деятельность дизайнера ограничивается изменением лишь внешнего вида объекта — нахождением более удобных для работы и эстетически красивых форм (Рисунок 8.2).
Рисунок 8.2 — Дизайн объектов технической формы
Значение технического рисунка в работе архитектора трудно переоценить. Его рисунки разнообразны и по характеру, и по манере исполнения. Технический рисунок у архитектора уже с первых шагов проектирования играет основополагающую роль. Какой бы объект мы не взяли, касается ли это планировки города, интерьера или комплекса зданий, техническому рисунку принадлежит главенствующая роль, а иногда и решающая (Рисунок 8.3).
Рисунок 8.3 — Рисунок дизайнера интерьера
Модельеры мужской и женской одежды используют условный рисунок (Рисунок 8.4).
Рисунок 8.4 — Рисунок модельера
Наравне со словом, рисунок служит средством выражения и передачи мысли. Иногда бывает трудно, а подчас и невозможно, выразить словами то, что легко представить наброском, схемой, чертежом или эскизом.
Даже в обыденной жизни мы часто прибегаем к помощи технического рисунка, объясняя друзьям свой адрес и расположение домов. Следовательно, раскрывая понятие термина «технический рисунок», нельзя узко и односторонне трактовать его содержание и назначение.
Итак, технический рисунок — это наглядное графическое изображение объекта, выполненное от руки в глазомерном масштабе, в котором ясно раскрыта техническая идея объекта, правильно переданы его конструктивная форма и верно найдены пропорциональные соотношения.
Курс «Техническое рисование» дает основные сведения, приемы, краткие методические указания и первоначальные навыки по выполнению технических рисунков.
Курс способствует развитию:
- наблюдательности;
- зрительной памяти;
- глазомера;
- твердой руки;
- эстетического вкуса;
- пространственных представлений, что позволит быстро выполнять эскизы изделий.
Работа построена по студийному принципу.
Рисунки оформляются рамкой и упрощенной надписью (Рисунок 8.5). Чертежи оформляют основной надписью по ГОСТ 2.104-68.
Рисунок 8.5 — Пример упрощенной основной надписи
8.1. Методы проецирования
Любой предмет можно представить как совокупность простейших геометрических объектов. В качестве геометрического объекта могут быть: точка, линия, поверхность, тело.
Изображение предмета на плоскость называется проекцией его на эту плоскость (плоскость проекций), а процесс получения проекций — проецированием (Рисунок 8.6).
Рисунок 8.6 — Методы проецирования
Перспективный рисунок — наглядное изображение предмета, выполненное от руки, на основе центральных (перспективных) проекций.
8.2. Аксонометрические проекции (ГОСТ 2.317-69)
Параллельная проекция на одну аксонометрическую плоскость (плоскость проекций) координатных осей и объекта, фиксированного относительно этих осей называется аксонометрической проекцией объекта.
Объекты проецируются (за некоторым исключением) с искажением натуральной величины.
Отношение размеров изображения к действительным размерам, измеренным вдоль координатной оси, называется коэффициентом искажения по оси ( Кх, Ку, Kz ).
Для удобства пользованием коэффициентами применяют приведенные коэффициенты искажения (значения их приведены на Рисунке 8.7).
Рисунок 8.7 — Аксонометрические проекции
В аксонометрических проекциях отсутствуют перспективные искажения, вследствие чего изображение получается условным и простым.
Форму предмета можно строить точно по размерам (если нужно) и изображать ее «не как вижу, а как надо», с пониманием объективной сущности предмета. В этом заключается особенность технического рисунка и простота его выполнения, позволяющие сравнительно быстро приобрести необходимые навыки.
Для рисования используются мягкие карандаши, твердостью М, 2М, (НВ, В, 2В). Затачивают карандаш так, как показано на рисунке.
8.3. Методика рисования линий
Умение выполнять технические рисунки не требует природных способностей, а приобретается упорными систематическими упражнениями.
Техника — совокупность приемов мастерства применяемых в каком-нибудь деле: музыкальная техника, техника шахматной игры и т.д. Следовательно, выполняющий рисунок должен обладать определенной техникой исполнения.
В проведении прямой линии должна участвовать не только кисть руки, а и вся рука: это дает возможность при прямолинейном движении кисти руки, выдержать прямолинейность отрезка.
Рисунок 8.8 — Вариант работы с карандашом
Карандаш при рисовании нужно держать свободно большим и указательным пальцами и поддерживать средним; мизинец может касаться бумаги. Остро заточенный конец карандаша должен быть расположен подальше от пальцев, что облегчает проведение плавных длинных линий (Рисунок 8.8). При уточнении и прорисовке отдельных деталей на рисунке предмета в работе уже принимают участие пальцы, что сказывается на движениях карандаша. Движения получаются ограниченными, но более точными; карандаш берут ближе к острию, что позволяет проводить более четкие линии.
Начинают рисовать тонкими, едва заметными линиями. Перед проведением прямой линии необходимо предварительно определить начальную и конечную точки ее, через которые легким движением
Почти невозможно одним движением руки проводить совершенно прямую и непрерывную линию. Следует рисовать ее по частям, длинными штрихами, не упуская из вида общего ее направления (Рисунок 8.9).
Рисунок 8.9 — Рисование длинных линий
Не следует ошибочно нанесенные первоначальные штрихи стирать резинкой, а нужно исправлять неудачно проведенную линию новыми штрихами только в местах, где она неправильна.
Горизонтальные и вертикальные направления необходимо чаще проверять относительно соответственных обрезов листа бумаги.
Все вертикальные линии удобнее проводить сверху вниз, а горизонтальные — слева направо (Рисунок 8.10).
Рисунок 8.10 — Рисование линий
8.4. Деление отрезков на равные части. Построение углов
- Предположим, что заданный отрезок АВ необходимо разделить на две равные части. Для этого определяют на глаз середину отрезка и отмечают ее точкой О. Проверку точности деления осуществляют с помощью карандаша. Делается это следующим образом: конец карандаша прикладывают к точке О, а точку В отмечают на карандаше ногтем большого пальца и сравнивают полученные величины отрезков АО и ОВ. Если точка О получилась не в середине, то ее перемещают влево или вправо, пока обе части не получатся равными (Рисунок 8.11).
Рисунок 8.11 — Деление отрезка на 2 части
- При делении на 3 части, выбираем средний отрезок равный крайнему (Рисунок 8.12).
- Деление отрезка на четыре равные части.
- При делении на 5 частей, сначала делят отрезок на 3 части так, чтобы средний равнялся половине крайних, которые затем делят пополам.
- При делении на 7 частей, выбирают величину среднего отрезка такой, чтобы он укладывался три раза в крайней части отрезка.
- Для построения прямой, расположенной под углом 30° к горизонтали, надо по горизонтали отложить 5 условных единиц (клеток или сантиметров), а по вертикали — 3.
- Для построения прямой, расположенной под углом 7° к горизонтали, надо по горизонтали отложить 8 условных единиц, а по вертикали — 1.
- Для построения прямой, расположенной под углом 41° к горизонтали, надо по горизонтали отложить 8 условных единиц, а по вертикали — 7.
- Для построения прямой, расположенной под углом 45° к горизонтали, надо отложить отрезки равной длинны по горизонтали и по вертикали.
Рисунок 8.12 — Деление отрезка на разное количество частей. Проведение линии под заданным углом
При недостаточном опыте рисования или эскизирования возникают затруднения при откладывании одинаковых отрезков. В таких случаях помогает использование так называемой «бумажной линейки». На небольшом кусочке бумажки намечают нужную длину отрезка и откладывают его необходимое число раз в каких-либо направлениях. Часто прибегать к этому методу не рекомендуется, так как это задерживает развитие глазомера.
8.5. Аксонометрия плоских фигур
Построение аксонометрических изображений плоских фигур является основой построения геометрических тел и технических предметов.
Многоугольник состоит из вершин (точек) и сторон (отрезков прямых линий), следовательно, построение его аксонометрии начинается с построения вершин с последующим соединением их прямыми линиями — сторонами многоугольника.
Построение рисунка квадрата
Построим рисунок квадрата АВСD в прямоугольной изометрии при условии, что сторона АD параллельна оси X, а сторона АВ параллельна оси Y. Квадрат изобразится в виде ромба АВСD.
- Нарисуем сначала оси прямоугольной изометрии X и Y (Рисунок 8.13).
- Отложим по оси X от точки О отрезки (O-l) и (0-3), равные половине стороны квадрата.
- Отложим по оси Y от точки О отрезки (0-2) и (0-4), равные также половине стороны квадрата (так как в изометрии коэффициенты искажения по всем осям равны единице).
- Через точки 1 и 3 проведем прямые, параллельные оси Y, а через точки 2 и 4 — прямые, параллельные оси X.
- На пересечении этих прямых получим вершины параллелограмма АВСD.
Рисунок 8.13 — Построение аксонометрии квадрата
Построение рисунка правильного шестиугольника (в плоскости X0Y)
- Строим аксонометрию квадрата на осях ОХ и 0Y, проходящих через его середину (Рисунок 8.14).
- Две вершины (1-2) находятся на пересечении сторон квадрата с осью ОХ.
- Чтобы определить остальные вершины:
- отрезок (1-2) делят на 4 равные части: отрезок (0-1) делим пополам точкой М, отрезок (0-2) делим пополам точкой N;
- отрезок ОС делят на 6 частей и на одной шестой части от точки С отмечают точку К и симметрично ей точку L.
- Через М и N проводят линии, параллельные оси 0Y до пересечения с линиями, проведенными через точки L и К параллельно оси ОХ.
- Полученные точки пересечения будут искомыми вершинами.
Рисунок 8.14 — Построение аксонометрии правильного шестиугольника
Аксонометрия окружности
Окружность вначале следует рисовать вместе с квадратом, в который она вписывается. Это позволяет быстрее получить навык более правильного изображения окружностей в аксонометрических проекциях.
- Нарисуем квадрат АВСD и проведем в нем диагонали. Через середину квадрата (точку О) проведем две взаимно перпендикулярные линии — оси X, Y. Отрезки (1-3) и (2-4) будут равны диаметру окружности (Рисунок 8.15).
- Для определения промежуточных точек окружностей надо найти середину отрезка А-2 (точка Е). В свою очередь отрезок (Е-2) также разделим пополам в точке F.
- Далее отрезок (А-1) разделим на две равные части в точке G.
- Соединим точки G и F. Прямая (G-F) пересечет диагональ AC в точке 5. Точка 5 будет принадлежать окружности с центром в точке О и заданным диаметром (отрезок (1-3)).
- Для нахождения точек 6, 7, 8 проделаем те же построения, какие мы использовали при нахождении точки 5, в каждой из оставшихся трех четвертей квадрата.
- Плавно соединим последовательно все восемь точек, получив изображение окружности. Следует обратить внимание на то, что в точках 1, 2, 3 и 4 кривая (окружность или эллипс) касается сторон квадрата или параллелограмма.
- В аксонометрии окружность изобразится в виде эллипса. Для его построения нарисуем проекцию квадрата в какой-либо аксонометрии, он будет в виде параллелограмма. Точки 1,2,3 и 4 лежат на пересечении середин сторон параллелограмма с аксонометрическими осями. Определим в параллелограмме (аналогично описанному выше) промежуточные точки 5,6,7 и 8 с помощью которых нарисуем эллипс.
Рисунок 8.15 — Построение аксонометрии окружности
8.6. Понятие о пропорциях
В реалистическом рисунке объемные предметы окружающей нас действительности изображаются такими, какими они существуют в природе и как их воспринимает глаз с данной точки зрения. В процессе рисования с натуры очень важно умение подмечать главное и характерное в окружающих нас вещах и явлениях.
Чтобы правильно передать форму предмета на плоскости листа, надо научиться определять его пропорции, необходимо уяснить его конструкцию, владеть техническими приемами рисования.
Пропорции — это соотношение величин частей предмета друг к другу и его частей к целому.
Чем точнее определены пропорции предметов на рисунке, тем больше сходства имеет изображение с натурой.
При определении пропорций изображаемого предмета пользуются взаимным сравнением размеров, то есть определяют визуально (на глаз), в каком отношении находится малый размер по отношению к большому (или наоборот). Сравнивать и проверять пропорции нужно не только в натуре, но и на рисунке.
Следует отличать истинные соотношения величин частей предмета от пропорций его изображения с определенной точки зрения.
Пропорции предмета при наблюдении с различных точек зрения будут восприниматься различно, но сам предмет в реалистическом изображении должен казаться нам тем же. Например, высота вазы будет казаться сильно сокращенной по отношению к ее ширине, если смотреть на нее со значительно более высокой точки зрения (Рисунок 8.16).
Рисунок 8.16 — Пропорции. Рисунок вазы
Отмечая пропорции предмета на рисунке, надо учитывать его конструктивное строение. Так, например, ваза (на Рисунке 8.16) состоит из конусообразного горлышка, средней части яйцевидной формы и цилиндрического основания. Она представляет собой тело вращения, и поэтому в местах перехода форм четко видны окружности (с центрами на оси), которые нужно построить на рисунке.
Точность определения пропорций предмета зависит от глазомера рисующего. Глазомер развивается постепенно, благодаря систематическому рисованию с натуры.
Рассмотрим основные пропорции вазы, показанной на рисунке. Высота ее в 2 раза больше ширины. Если сравнить соотношение отдельных частей вазы по высоте, то высота горлышка составит 1/3 часть высоты вазы без подставки. Высота подставки нижней части вазы укладывается в высоте горлышка около 4 раз. Ширина подставки равна 1/2 ширины вазы в самом широком ее месте. Ширина узкой части горлышка несколько меньше 1/2 ширины верхнего края вазы и т. д.
При рисовании с натуры часто приходится решать более сложную задачу — находить пропорции предметов. Однако и в этом случае используется общий прием определения пропорций путем глазомерного сравнения величин. За единицу измерения можно взять один из предметов, входящих в группу.
Представление о масштабе следует из непосредственного глазомерного сравнения величин, что является условием правильного выполнения рисунка. Можно увеличивать и уменьшать предметы на рисунке, эскизе, чертеже — характер реальной действительности не меняется, если это увеличение тети уменьшение для всех элементов предмета делается пропорционально. Отношение размеров на рисунке должно быть равно отношению размеров в натуре.
8.7. Элементы композиции рисунка
Композиция — (compositio — (лат.)) в переводе означает составление, расположение, представляет собой средство придать единство различным частям художественного произведения.
Отдельные элементы композиции должны быть связаны между собой, а внимание зрителя сосредоточивается на главном предмете (композиционном центре), которому должно подчиняться все второстепенное (детали).
Основное требование, предъявляемое к композиции учебного рисунка, — уравновешенность расположения изображаемых предметов на листе.
Приступая к построению рисунка, нужно, прежде всего, изучить форму предмета, то есть провести внимательный анализ геометрических форм, составных элементов изображаемого предмета.
Общий путь анализа объектов сложной формы — расчленение их на более простые геометрические тела, или замена, на первых порах, построения элементов сложной формы элементами простой формы. Величину рисунка следует выбирать такой, чтобы мелкие элементы предмета были бы четко изображены. Для этого размер изображения увеличивают. Если нет необходимости детализировать мелкие элементы, или предмет имеет простую форму, то не нужно делать изображение большим. В грубом приближении рисунок должен занимать (50 — 75)% площади формата. Поэтому формат листа подбирают под планируемую величину изображения.
Деталь надо развернуть так, чтобы были видны три ее стороны (три измерения: длина, высота, ширина). Ориентация детали для различных аксонометрических проекций может меняться, принимая наиболее наглядное положение. Освещение детали, полагают, идет слева.
При компоновке рисунка, то есть расположении изображения на листе, нужно помнить, что наблюдатель, зритель, рассматривая изображение, подсознательно включает в поле изображения и некоторую часть пространства вокруг изображаемых предметов. Отсюда, если на деталь мы смотрели как бы сверху, то нужно в верхней части листа оставлять несколько больше места («больше неба»). При направлении взгляда на деталь как бы снизу изображение смещают вверх листа, оставляя больше «земли». Если главная часть детали (по содержанию) находится слева, то изображение на листе нужно сдвинуть чуть вправо, чтобы рамка не отвлекала внимание и не мешала восприятию изображения.
Композиция является одним из главных средств создания эстетических качеств изображения, она прямо связана с наглядностью и читаемостью рисунка. Поэтому, кроме названных особенностей для рисунка, очень важно выбрать такую аксонометрическую проекцию, которая наиболее полно раскрывает форму предмета.
8.8. Наглядность аксонометрических проекций
Правильный выбор аксонометрической проекции обеспечивает большую наглядность изображения и простоту построения рисунка. Под наглядностью следует понимать наиболее отчетливую видимость на рисунке основных частей детали и наименьшее искажение ее форм.
Выбор аксонометрической проекции зависит также от формы детали. Главной задачей при этом является обеспечение видимости всех основных элементов изображаемой детали. Кроме того, отдельные части детали не должны закрывать друг друга.
Чтобы лучше представить, насколько важна наглядность изображения, сравним несколько рисунков таких предметов, как куб, цилиндр, деталь «фланец», выполненных в прямоугольных и косоугольных проекциях.
На Рисунке 8.17 эти предметы показаны в прямоугольной изометрической проекции. Грани куба получились мало выразительными, поскольку по всем трем направлениям координатных осей X, Y, Z они имеют одинаковые искажения.
| Рисунок 8.17 — Прямоугольная изометрия | Рисунок 8.18 — Прямоугольная диметрия |
Прямоугольную изометрию применяют в тех случаях, когда три стороны предмета имеют одинаковое количество элементов, необходимых для характеристики изображаемого предмета, но куб получается мало выразительным.
Наибольшей наглядностью отличается изображение в прямоугольной диметрии как изображение, сходное с перспективным.
В прямоугольной диметрической проекции (Рисунок 8.18) благодаря большему сокращению размеров по одной из координатных осей рисунки куба и цилиндра получились более наглядными. Рисунок же детали «фланец» в прямоугольной диметрии менее выразителен, чем в прямоугольной изометрии.
На Рисунке 8.19 куб, цилиндр и фланец выполнены в косоугольной фронтальной изометрической проекции. Куб и цилиндр в этой проекции получились маловыразительными и с большим искажением формы. При изображении фланца потребовалось рисовать несколько окружностей, а нарисовать окружность сложнее, чем эллипс. Поэтому такой рисунок уступает в простоте построения. К тому же он нисколько не наглядней двух предшествующих рисунков.
| Рисунок 8.19 — Косоугольная фронтальная изометрия | Рисунок 8.20 — Косоугольная горизонтальная изометрия |
Косоугольную фронтальную аксонометрию используют в случаях, когда обтекаемые формы предметов в виде кривых поверхностей можно расположить параллельно фронтальной плоскости проекций, тогда они изображаются в неискаженном виде и их проще рисовать.
В косоугольной горизонтальной изометрической проекции (Рисунок 8.20) все рисунки обладают меньшей наглядностью и строить их несколько сложнее.
Рисунки, выполненные в косоугольной фронтальной диметрической проекции, выглядят по-разному (Рисунок 8.21).
| Рисунок 8.21 — Косоугольная фронтальная диметрия |
Цилиндр в косоугольной фронтальной диметрии получается мало выразительным и с большим искажением формы. Рисунки куба и фланца, наоборот, обладают хорошей наглядностью.
Таким образом, рисунок куба лучше всего выполнять в косоугольной фронтальной диметрии, рисунок цилиндра — в прямоугольной диметрии, а рисунок фланца — в прямоугольной изометрии.
В некоторых случаях сразу трудно определить, какой вид аксонометрии дает более наглядное изображение изделия (особенно, если у него имеются наклонные элементы — ребра, спицы, стенки…).
В таких случаях рекомендуется выполнять технические рисунки в различных аксонометрических проекциях и из них выбрать наиболее наглядный.
8.9. Плоскостной рисунок
Плоскостное рисование (орнамент, фронтальные изображения фасадов зданий, планы сооружений) развивалось значительно быстрее рельефного изображения, хотя возникли они одновременно.
Зрительный подход к натуре может быть двоякий:
- плоскостное восприятие натуры;
- объемное восприятие.
При плоскостном восприятии натура целиком, во всей своей пространственной сложности, изображается спроектированной на плоскости в ортогональной проекции.
Целью плоскостного рисования является развитие чувства пропорции и глазомера, восприятия и передачи на рисунке отношения размеров изображаемой фигуры; научиться «видеть» натуру. (Смотреть не значит видеть).
Чтобы «увидеть» надо внимательно рассмотреть, то есть изучить форму натуры. Разбивка контура предмета на более простые геометрические формы позволит легко и правильно его изобразить.
Даже дети дошкольного возраста с успехом нарисуют сидящего котенка после указания, что форма его составлена из двух эллипсов (овалов) разной величины и двух треугольников.
Рисунок 8.22 — Плоскостной рисунок
Умению «видеть» при рисовании помогает знание законов математики, физики и других наук. Физиологи говорят: человек глядит не глазами, а мозгом. Убедимся в этом на примере рисунка чайника.
На Рисунке 8.22 чайник построен не правильно, так как учащийся недостаточно вдумчиво рисовал:
- особенности усеченного конуса — очерковые образующие надо было нарисовать сходящимися на оси вращения в одной точке;
- Закон сообщающихся сосудов должен был подсказать, что носик чайника должен быть поднят выше.
Итак, приступая к изучению изображаемого предмета, необходимо установить:
- из каких главных простейших составляющих элементов (шар, цилиндр, призма, пирамида, конус и др.) составлена натура;
- взаимное расположение выявленных фигур относительно друг друга;
- пропорциональные соотношения размеров фигур, а также расстояние между ними.
8.10. Рисунок детали и сборочной единицы
Переход от рисования плоскостных форм к рисованию объемных тел, в аксонометрической проекции осуществляется с помощью введения высотных размеров на основе построений аксонометрии плана (вида сверху) (Рисунок 8.23).
Рисунок 8.23 — Плоскостной рисунок и аксонометрия
Такой прием дает возможность непосредственно переходить от прямоугольного чертежа к наглядному изображению предмета.
а) Рисование детали с натуры
Прежде чем приступить к рисованию детали с натуры, рисующий должен проанализировать деталь, а именно:
- Определить название и назначение детали.
- Рассмотреть деталь со всех сторон и определить ее рабочее положение. Иногда для большей выразительности деталь рисуют и не в рабочем положении.
- Установить на глаз общие пропорции детали и определить пропорциональную зависимость всех ее частей.
- Мысленно расчленить деталь на простые геометрические тела, то есть выявить конструктивную форму детали.
- Определить, какие необходимо выполнить разрезы.
- Выбрать вид аксонометрической проекции.
- Определить композицию рисунка.
б) Рисование детали по чертежу
Выполнение рисунка по чертежу требует от рисующего умения читать чертеж, то есть представлять форму детали в целом и отдельных ее частей. В процессе чтения необходимо тщательно изучить чертеж, сопоставить на глаз габаритные размеры предмета и соотношение его частей. Рисунок позволяет лучше понять конструктивную форму предмета.
При рисовании деталей по чертежу не следует делать никаких замеров при помощи циркуля или линейки. Все размеры надо брать в пропорциональном отношении на глаз. Рисунок можно выполнять либо увеличенным, либо уменьшенным в зависимости от его композиции. Так же как и при рисовании детали с натуры, вначале определяют на глаз отношения между крайними точками всей детали, а потом намечают размеры каждой отдельной ее части, сравнивая их величины. Таким образом, правила выполнения рисунка детали по чертежу точно такие же, как и при рисовании с натуры.
в) Рисование сборочной единицы с натуры
Сборочной единицей называется изделие, составные части которого подлежат соединению между собой на предприятии — изготовителе с помощью сборочных операций: свинчивания, пайки, опрессовки, развальцовки, склеивания и др.
Рисование сборочной единицы с натуры основано на тех же принципах, что и рисование с натуры отдельных деталей, а именно:
- Определяют название и назначение изделия.
- Разбирают и уясняют взаимосвязь отдельных деталей между собой.
- Определяют назначение каждой детали и запоминают последовательность их соединения между собой.
- Продумывают, какой целесообразнее сделать вырез, с тем чтобы получить более ясное представление о внутреннем расположении деталей и их взаимодействии.
- Выбирают аксонометрическую проекцию, в которой сборочная единица будет изображена наиболее наглядно.
- Продумывают композицию рисунка.
- Приступают к построению рисунка.
г) Рисование сборочной единицы по чертежу
Сборочный чертеж — документ, содержащий изображение сборочной единицы и другие данные, необходимые для ее сборки и контроля. Прежде чем приступить к построению рисунка сборочной единицы, надо ознакомиться со спецификацией и сборочным чертежом.
Спецификация — текстовый документ, определяющий состав изделия, состоящего из двух и более частей. По спецификации изучают последовательность соединения всех деталей между собой.
Выполнение рисунка сборочной единицы по чертежу требует от рисующего обязательного умения читать чертеж. Вначале надо изучить чертеж: выявить на глаз соотношение габаритных размеров и сопоставить отдельные части между собой и со всей сборкой в целом. Изучив характерные особенности формы каждой детали в механизме и расположение деталей относительно друг друга, приступают к построению рисунка, используя те же правила, что и при рисовании сборочной единицы с натуры.
8.11. Разрезы на аксонометрических изображениях
В аксонометрических изображениях изделий разрезы, как правило, получают путем сечения плоскостями, параллельными плоскостям проекций, и условного удаления отсекаемой части. Разрезы следует применять в тех случаях, когда они действительно необходимы и при этом не теряется наглядность конструктивных форм.
Для отличия рассеченной части изделия от частей, не попавших в разрез, применяют штриховку. Линии штриховки сечений наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям с учетом коэффициента искажения по осям (Рисунок 8.24).
Рисунок 8.24 — Правила штриховки в аксонометрии
8.12. Методика рисования
Характерно для рисования группы тел (когда натура состоит из нескольких геометрических элементов) то, что тела рисуются все сразу, а не каждый в отдельности.
«Художник должен работать как деревообделочник. Сначала он грубо обтесывает топором, потом строгает рубанком, и все дальше и дальше инструменты его тоньше, заканчивает он шкуркой, полировкой и лаком,» – слова известного художника И.Е.Репина.
В целях упрощения построения рисунка следует располагать изображение так, чтобы его основные измерения были параллельны аксонометрическим осям. Это позволяет строить изображение, откладывая размеры (или координаты) по направлениям соответствующих осей с учетом коэффициентов искажения. Изображая симметричные предметы, целесообразно одну из аксонометрических осей совмещать с осью симметрии предмета.
В процессе выполнения рисунка переводят объемную форму предмета в плоскостное изображение. При этом необходимо определить, как преобразуется видимая форма предмета при плоскостном изображении, какие части и элементы предмета изменяются, какие будут видимыми и т.д. Правильность решения этой задачи зависит от умения наблюдать и знания законов построения аксонометрии.
Необходимо разобраться в общей форме предмета и правильно понять ее. Для облегчения этой задачи можно применить способ обобщения (упрощения формы). Суть его заключается в том, что любую сложную форму рассматривают как простейшую геометрическую. Такой способ построения помогает правильно понять и изобразить трехмерный объемный предмет, развивает пространственное представление и облегчает работу.
Работу над рисунком необходимо начинать с больших обобщений, с решения общей задачи, постепенно переходя к решению частных второстепенных задач, которые в конечном результате не должны нарушать впечатления целого. Главному в предмете сначала нужно уделять больше внимания, чем второстепенному, являющемуся дополнением к целому.
Сначала определяют пропорции всей натуры, то есть отношение высоты к ширине всей группы тел, а затем определяют отношение отдельных тел друг к другу.
На следующем этапе на листе отмечают местоположение каждого элемента и его габариты, учитывая выявленные пропорции, тем самым строим как бы «скелет» натуры (Рисунок 8.25).
Рисунок 8.25 — Последовательность построения
Начинают рисунок легкими, едва заметными линиями, а затем, когда правильно решена композиция рисунка и найдены пропорции элементов и натуры в целом, постепенно уточняют линии и усиливают тон.
Все второстепенные, не характерные для изображаемого предмета детали не рисуют, а, прежде всего, устанавливают схематично, набросочными линиями общую форму натуры.
После этого начинают построение каждого элемента. Сложные элементы (тела вращения, многогранники) на первоначальном этапе можно заменять параллелепипедами, не вырисовывая мелкие особенности этих элементов.
Когда общая форма натуры будет найдена, можно приступить к размещению мелких элементов, также начиная с более крупных из них. Набросок натуры уточняется проверкой пропорционального соотношения геометрических элементов и симметрии.
Если линия проведена не правильно, то ее не стирают, а проводят рядом другую, более точную. Первоначальные неточные линии, проведенные при построении, зрительно на рисунке почти не воспринимаются. В стадии Завершения они поглощаются общим тоном рисунка.
Далее сотрем ненужные линии построения и проверим точность выполнения рисунка, после чего обведем рисунок более четким контуром.
8.13. Оттенение поверхностей
Каждый предмет находится в конкретной световой среде и освещен не только основным источником света, но и светом, отраженным от окружающих его других предметов, которые, будучи сами также освещены, являются источником отраженного света. Светлые и хорошо освещенные предметы отражают много света, а темные и плохо освещенные — мало. Форма предметов ограничивается различными поверхностями, поэтому лучи света, падая на эти поверхности, распределяются на них неравномерно. Одни части поверхности получают больше света, другие меньше, а третьи почти совсем не получают световых лучей.
Для придания рисунку большей наглядности и выразительности в техническом рисовании применяются условные средства передачи объема с помощью светотеней — оттенения.
Светотенью называется распределение света на поверхности предмета. Она играет главную роль при восприятии объема предмета.
Освещенность предмета зависит от угла наклона световых лучей. В техническом рисовании условно принято считать, что источник света находится сверху и сзади рисующего, таким образом, свет всегда будет слева, а тень — справа.
Отображение выпуклости предмета достигается путем градации света и тени: наиболее освещенные поверхности оттеняются светлее, чем поверхности, удаленные от света.
Светотень состоит из следующих элементов: собственной тени, рефлекса, полутона, света и блика.
Освещенную часть поверхности предмета называют светом.
Собственная тень образуется на части поверхности тела, на которую не падают световые лучи основного источника света. Освещенная поверхность, отражая свет, ослабляет силу собственной тени.
Такое высветление собственной тени отраженным светом называется рефлексом. Рефлекс всегда бывает темнее поверхностей света и полутени.
Слабо освещенные места на поверхности предмета называются полутонами. При помощи полутонов осуществляется постепенный переход от тени к свету.
Блик — самое светлое пятно на предмете.
Для правильной передачи на изображении объема и формы предмета необходимо ясно представлять его конструкцию и расположение отдельных частей в пространстве по отношению к источнику света.
Самую большую освещенность получает поверхность в том случае, если лучи падают на нее перпендикулярно. Чем меньше угол наклона лучей по отношению к поверхности, тем меньше падает на нее лучей и тем слабее она освещена. Освещенность зависит также от расстояния поверхности до источника света.
Светотень на изображении выявляют тоном. Тон (tonos — греческое слово, означающее качество, оттенок) наносится различными способами и должен соответствовать отношению света и тени, наблюдаемому в натуре. Выдержать рисунок в тоне — значит передать на нем световую гамму от темного тона через оттенки серого к светлому, сведенные в гармонию тональных отношений. Самым светлым тоном на рисунке будет цвет бумаги, а самым темным — линия, проведенная графитом карандаша с полным нажимом.
Аксонометрические чертежи и технические рисунки, на которых использована светотень, бывают штриховые и тоновые. На штриховых рисунках тон передают условно — точками или штрихами, карандашом или тушью с помощью ручки с пером или рейсфедера (Рисунок 8.26, 8.27). На тоновых рисунках тон наносят карандашом, тушью, акварельными красками и пр. (Рисунок 8.28).
Рисунок 8.26 — Штриховка
Рисунок 8.27 — Шрафировка
Тон должен плавно переходить от белого до темного без заметных границ элементов светотени.
Технику работы карандашом при нанесении светотени на тоновом рисунке называют тушевкой.
Рисунок 8.28 — Тушевка
Явление освещенности лучше всего наблюдается на примере куба и цилиндра, помещенных рядом. Анализируя эти тела с точки зрения распределения элементов светотени, можно установить, что характер освещенности грани куба и поверхности цилиндра различен. Переход от света к тени на гранях куба резкий и определенный, тогда как переход освещенной поверхности цилиндра к теневой мягкий и постепенный.
Свет на поверхности предмета распределяется неодинаково: одни части поверхности освещаются больше, другие меньше. Существует два правила, которыми следует руководствоваться при нанесении светотеней на изображение:
- Освещенные части предметов с удалением от наблюдателя становятся темнее, затемненные — высветляются;
- Контраст тени и света на предметах, расположенных ближе к источнику света, резче, чем на предметах, удаленных от него.
Рассмотрим эти правила на примере куба (Рисунок 8.29).
Нанесение светотени на поверхности многогранников
Рисунок 8.29 — Распределение светотени на параллелепипеде
Горизонтальная грань куба освещена равномерно, но зона 6 вследствие того, что удалена от наблюдателя изображена более затемненной. Самым светлым местом на передней грани кажется зона 1. Однако зоны 1, 2, 3 освещены одинаково, но из — за контраста с находящейся рядом собственной тенью на правой грани куба зона 1 кажется более светлой, а зоны 2, 3 — менее светлыми. В зоне 4 освещение усиливается. Это рефлекс, полученный кубом от плоскости, на которой он находится. Из всех зон зоны 7 и 8 самые темные. Не следует опасаться перетемнить их. Эта ошибка вполне допустима, так как усиливается рельефность куба. В зоне 9 и особенно в зоне 10 наблюдается ярко выраженный рефлекс от горизонтальной плоскости проекций.
Штриховку наносят в зависимости от положения изображаемой многогранной поверхности. Вертикальные поверхности штрихуют в вертикальном направлении, горизонтальные — в горизонтальном (параллельно аксонометрическим осям), наклонные — в направлении, параллельном углу наклона плоскости.
Нанесение светотени на поверхности вращения
Нанесение светотени на поверхности полого цилиндра показано на Рисунке 8.30.
Наружную и внутреннюю поверхности цилиндра можно разделить условно на семь равных зон. Эти зоны соответствуют следующим элементам светотени: 1 — полутень (полутон), 2 — свет, 3 — блик, 4 — свет, 5 — полутень (полутон), 6 — тень, 7 — рефлекс.
Рисунок 8.30 — Распределение светотени на цилиндре
Штриховку основания цилиндра наносят по тем же правилам, что и штриховку граней куба. На внешней и внутренней поверхностях цилиндра линии штриховки наносят параллельно образующим. Внутреннюю поверхность цилиндра Заштриховывают по такому же принципу, что и внешнюю, но блик, полутона, собственную тень и рефлекс соответственно перемещают на противолежащие зоны поверхности.
Нанесение тона на изображение рекомендуется выполнять от более темного к более светлому. Переходы от тени к свету должны быть незаметными. Необходимо сверять тональную взаимосвязь, сравнивая полученный тон с крайними тонами (темным и светлым).
Перед нанесением тушевки построенное изображение обводят с небольшим нажимом карандаша. Затем все стирают и на листе остаются «вмятины» от грифеля (они нам дают информацию о контуре изображения), после этого начинают затушевывать поверхности.
Шестиугольник: шестигранный многоугольник.
Произношение: /ˈhɛk.səˌgɒn/ Объяснить
| Шестигранник — это шестигранник. многоугольник. Стороны шестиугольника — это отрезки прямых линий. Шестиугольник — это плоский фигура, фигура, существующая в самолет. Шестиугольник может быть вогнутый или выпуклый.Если выпуклый шестиугольник равносторонний (стороны одинаковой длины), то шестиугольник — правильный шестиугольник. |
Список статей
ШестиугольникПравильный шестиугольник
Части правильного шестиугольника
Формулы правильного шестиугольника
Как построить правильный шестиугольник из его окружности
Как построить центр, вписанную и окружность правильного шестиугольника
Тесселяции правильного шестиугольника
и изготовленные шестиугольники
Правильный шестиугольник
Правильный шестиугольник — это шестигранник, равносторонний, выпуклый многоугольник.У равностороннего многоугольника все стороны одинаковой длины. Между любые две точки выпуклой фигуры покидают фигуру.
| Нажмите на синие точки и перетащите их, чтобы изменить фигуру. Когда длина стороны отличается от радиуса описанной окружности? |
| Manipulative 1 — Regular Hexagon, созданный с помощью GeoGebra. |
Части правильного шестигранника
- сторона или край : одна из отрезок что составляет шестиугольник.Длина стороны правильного шестиугольника в этой статье мы будем обозначать s .
- вершина: Где встречаются две стороны шестиугольника.
- интерьер: Площадь внутри шестиугольника.
- Внешний вид: Площадь за пределами шестиугольника. Граница
- : Стороны и вершины шестиугольника.
- центр: Точка в середине шестиугольника.Центр правильного шестиугольника можно найти на пересечении серединных перпендикуляров любого две стороны. См. Как построить центр, Вписанная и кольцевая окружность правильного шестиугольника. Центр правильный шестиугольник — это также его центр тяжести .
- вписанный круг: Круг, центр которого находится в центре правильного шестиугольника, который касается каждую сторону шестиугольника один раз.В этой статье радиус Вписанную окружность обозначим r 1 .
- описанной окружности: Круг, центр которого находится в центре правильного шестиугольника, который пересекает каждую из вершин правильного шестиугольника. В этой статье, Радиус описанной окружности обозначим r 2 .
- апофема: Отрезок от центра правильного шестиугольника до середины одной из сторон.Длина апофемы такая же, как и радиус вписанной окружности и обозначается ( r 1 ).
- сагитта: Отрезок от центра стороны до края описанная окружность правильного шестиугольника, лежащего на одной прямой с апофемой.
- центральный угол: : угол между двумя отрезками прямой от центра правильного шестиугольника до двух соседних вершин.В центральный угол правильного шестиугольника всегда 72 °.
- внутренний угол: Угол между двумя соседними сторонами. Внутренние углы обычного шестиугольник всегда измеряйте 120 °. Сумма мер внутренних углов любого выпуклого шестиугольника составляет 720 °.
- внешний угол: Угол между удлиненной стороной правильного шестиугольника и соседняя сторона. Внешние углы правильного шестиугольника всегда Измерьте 60 °.
Формулы правильного шестиугольника
Как построить правильный шестиугольник из его окружности
| Шаг | Иллюстрация | Описание и обоснование |
|---|---|---|
| 1 | Нарисуйте круг. Обозначьте центр круга a . Это дано. | |
| 2 | Нарисуйте круг с центром на окружности a это тот же радиус, что и у окружности и .Обозначьте центр этого круга б . | |
| 3 | Обозначьте пересечения окружностей c и d . | |
| 4 | Построение отрезков линии ab , ac , ad , bc и bd . Обратите внимание, что все эти отрезки являются радиусами конгруэнтных круги.Это означает, что все они одинаковой длины. Итак, треугольники Δabc и Δabd — равносторонние треугольники, треугольники, стороны которых имеют одинаковую меру. Углы равносторонних треугольников тоже есть такая же мера. Следовательно, треугольники Δabc и Δabd конгруэнтны Теорема сравнения SAS. | |
| 5 | Нарисуйте еще один круг с тем же радиусом, что и a , с центром в с .Обозначьте новое пересечение круга c и круга a как e . | |
| 6 | Нарисуйте еще один круг с тем же радиусом, что и a , с центром в и . Обозначьте новое пересечение окружности e и окружности. a как f . Обратите внимание, что с помощью тех же аргументов, которые использовались в шаг 5, треугольники Δabc и Δace составляют конгруэнтные равносторонние треугольники. | |
| 7 | Продолжайте узор до кругов с центрами в b , c , d , e , f и g нарисованы. Мы знаем это
правильный шестиугольник, потому что
| |
| Таблица 2: Как построить правильный шестиугольник от его описанной окружности. | ||
Как построить центр, окружность и окружность правильного шестиугольника
Мозаика шестиугольника
Тесселяция одного или нескольких многоугольников — это расположение тех многоугольников, которые заполняет самолет. Это ряд мозаик, в которых используются шестиугольники. В большинстве представленных здесь мозаик используются правильные шестиугольники.
| Обычная мозаика шестиугольника.Вокруг три шестиугольника каждая вершина. | Трехгранник. Каждая вершина имеет правильный шестиугольник, равносторонний треугольник, правильный шестиугольник и равносторонний треугольник. |
| Таблица 4: мозаика шестиугольника | |
Природные и изготовленные шестиугольники
Список литературы
- МакАдамс, Дэвид Э .. All Math Dictionary Dictionary, шестиугольник . 2-е классное издание 20150108-4799968.стр. 90. ООО «Жизнь — это история проблемы». 8 января 2015 года. Купить книгу
Дополнительная информация
- МакАдамс, Дэвид Э. Многоугольник . allmathwords.org. ООО «Жизнь — это история проблемы». 22.10.2010.
Цитируйте эту статью как:
Макадамс, Дэвид Э. Шестиугольник . 22.04.2019. Энциклопедия всех математических слов. ООО «Жизнь — это история проблемы». http://www.allmathwords.org/en/h/hexagon.html.Изображение кредита
История изменений
22.04.2019: Обновите уравнения и выражения в новом формате.(Макадамс, Дэвид Э.)21.12.2018: Пересмотрено и исправлено произношение IPA. (Макадамс, Дэвид Э.)
16.07.2018: Удалены неработающие ссылки, обновлена лицензия, введена новая разметка, реализован новый протокол Geogebra. (Макадамс, Дэвид Э.)
22.10.2010: Начальная версия. (Макадамс, Дэвид Э.)
Angles — Mathematics GCSE Revision — Revision Maths
Углы измеряются в градусах, записываются в °. Максимальный угол 360 °. Это угол вокруг точки.Половина этого угла составляет 180 ° на прямой.
В видеоролике ниже объясняется, как рассчитать связанные углы, смежные углы, внутренние углы и дополнительные углы.
Связанные углы
Линии AB и CD параллельны друг другу (отсюда »на линиях).
a и d известны как , вертикально противоположные углам . Вертикально противоположные углы равны. (b и c, e и h, f и g также противоположны по вертикали).
g и c — это соответствующих углов . Соответствующие углы равны. (h и d, f и b, e и a также соответствуют).
d и e — это альтернативных углов . Альтернативные углы равны. (c и f также чередуются). Альтернативные углы образуют Z-образную форму и иногда называются Z-углами.
a и b — это смежных углов . Смежные углы в сумме составляют 180 градусов. (d и c, c и a, d и b, f и e, e и g, h и g, h и f также смежны).
d и f — это внутренние углы . В сумме они составляют 180 градусов (е и с также являются внутренними).
Любые два угла, которые в сумме составляют 180 градусов, называются дополнительными углами .
Сумма углов треугольника
Используя некоторые из приведенных выше результатов, мы можем доказать, что сумма трех углов внутри любого треугольника всегда в сумме составляет 180 градусов.
Если у нас есть треугольник, вы всегда можете провести две параллельные линии следующим образом:
Теперь мы знаем, что альтернативных углов равны.Следовательно, два угла, обозначенные x, равны. Кроме того, два угла, обозначенные буквой y, равны.
Мы знаем, что x, y и z вместе составляют 180 градусов, потому что вместе они представляют собой просто угол вокруг прямой линии. Таким образом, сумма трех углов треугольника должна составлять 180 градусов.
Сумма углов четырехугольника
Четырехугольник — это фигура с 4 сторонами.
Теперь, когда мы знаем сумму углов в треугольнике, мы можем вычислить сумму углов в четырехугольнике.
Для любого четырехугольника мы можем провести диагональную линию, чтобы разделить его на два треугольника. Каждый треугольник имеет сумму углов 180 градусов. Следовательно, общая сумма углов четырехугольника составляет 360 градусов.
Наружные углы
Внешние углы формы — это углы, которые вы получите, если удлинить стороны. Показаны внешние углы шестиугольника:
Многоугольник — это фигура с прямыми сторонами.Все внешние углы многоугольника составляют в сумме 360 °. потому что, если вы сложите их все вместе, они образуют угол на всем протяжении точки:
Следовательно, если у вас есть правильный многоугольник (другими словами, у которого все стороны имеют одинаковую длину и все углы одинаковы), каждый из внешних углов будет иметь размер 360 ÷ количество сторон. Так, например, каждый из внешних углов шестиугольника составляет 360/6 = 60 °.
Внутренние углы
Внутренние углы формы — это углы внутри нее.Если вы знаете размер внешнего угла, вы можете определить размер внутреннего угла рядом с ним, потому что в сумме они составляют 180 ° (поскольку вместе они составляют угол на прямой).
Внешний угол треугольника
Угол x — это внешний угол треугольника:
Внешний угол треугольника равен сумме внутренних углов в двух других вершинах. Другими словами, x = a + b на диаграмме.
Проба:
- Сумма углов в треугольнике составляет 180 градусов.Итак, a + b + y = 180.
- Сумма углов прямой линии составляет 180 градусов. Итак, x + y = 180.
- Следовательно, y = 180 — x. Помещение этого в первое уравнение дает нам: a + b + 180 — x = 180. Следовательно, a + b = x после перестановки. Это то, что мы хотели доказать.
Правильные многоугольники
Обзор
Многоугольник (от греческих слов poly, означающих «много» и «gon», что означает «угол») — это замкнутая двумерная фигура с множеством (т.е.е. три и более) прямых сторон. Правильный многоугольник — это такой многоугольник, у которого все стороны имеют одинаковую длину (т. Е. Фигура равносторонняя ), и все внутренние углы (и, следовательно, все внешние углы) имеют одинаковую величину (т. Е. Фигура равносторонний ). Когда мы говорим, что фигура замкнута , мы имеем в виду, что ровно две стороны встречаются в каждой вершине фигуры. Правильный многоугольник может быть простым или сложным .Простой правильный многоугольник — это выпуклая фигура, стороны которой образуют границу вокруг единого замкнутого пространства, а внутренний угол не превышает ста восьмидесяти градусов. Сложный правильный многоугольник будет иметь форму звезды, а его стороны будут пересекаться друг с другом в разных точках. Ниже мы приводим некоторые из наиболее часто встречающихся выпуклых правильных многоугольников.
- Равносторонний треугольник — трехсторонняя фигура с внутренними углами шестьдесят градусов (60 °)
Равносторонний треугольник
- Квадрат — четырехсторонняя фигура, в которой все внутренние углы прямые (90 °)
Площадь
- Пентагон — пятиугольная фигура с внутренними углами сто восемь градусов (108 °)
Пятиугольник
- Шестиугольник — шестигранная фигура с внутренними углами сто двадцать градусов (120 °)
Шестиугольник
По мере увеличения количества сторон ему соответствует количество вершин.Величина внутреннего угла в каждой вершине будет одинаковой и будет увеличиваться по мере увеличения количества сторон. Сумма внутренних углов будет просто внутренним углом в любой вершине, умноженным на количество сторон. Если у многоугольника n сторон, соотношение между количеством сторон и внутренним углом в любой вершине (в градусах) можно найти по следующей формуле:
| Внутренний угол = ( n -2) × | 180 ° |
| n |
В качестве альтернативы мы можем выразить внутренний угол в радианах:
| Внутренний угол = ( n -2) × | π |
| n |
Внешний угол в каждой вершине выпуклого правильного многоугольника будет одинаковым и будет разницей между внутренним углом в этой вершине и ста восемьюдесятью градусами, так как внутренний и внешний углы выпуклого многоугольника всегда равны дополнительный (в сумме дает сто восемьдесят градусов).Чем больше сторон имеет выпуклый правильный многоугольник, тем меньше будет внешний угол в каждой вершине, потому что внутренний угол будет больше. Сумма внешних углов выпуклого многоугольника всегда будет составлять триста шестьдесят градусов (360 °), поэтому, если многоугольник имеет n сторон, соотношение между количеством сторон и внешним углом в любой вершине ( в градусах) можно выразить следующей формулой:
| Внешний угол = | 360 ° |
| n |
Мы также можем выразить внешний угол в радианах:
| Внешний угол = | 2π радиан |
| n |
На схеме ниже показано соотношение между внутренними и внешними углами выпуклого многоугольника.Показанная здесь фигура представляет собой шестиугольник, что означает, что у него шесть сторон, что дает внутренний угол в сто двадцать градусов (120 °) и внешний угол в шестьдесят градусов (60 °) в каждой вершине.
Внутренний и внешний углы выпуклого правильного многоугольника являются дополнительными.
Выше мы упоминали, что сумму внутренних углов можно вычислить, умножив внутренний угол в любой вершине на количество сторон.Следующая формула также работает для выпуклого правильного многоугольника со сторонами n и не требует, чтобы вы сначала находили внутренний угол в одной вершине:
Сумма внутренних углов = ( n -2) × 180 °
Детали других выпуклых правильных многоугольников приведены в таблице ниже. Обратите внимание, что теоретически нет ограничений на количество возможных выпуклых правильных многоугольников, хотя по мере увеличения количества сторон и вершин форма будет все больше и больше походить на круг.
Анатомия выпуклого правильного многоугольника
Внутри любого выпуклого правильного многоугольника есть точка, которая равноудалена от вершин многоугольника. Эта точка, которая называется центром многоугольника, также находится на одинаковом расстоянии от середин сторон многоугольника. Отрезок линии, проведенный от центра к любой вершине выпуклого правильного многоугольника, известен как радиус многоугольника.Это также радиус круга, который полностью охватывает многоугольник и проходит через все вершины. Этот круг называется описанным кругом или описанным кругом . Второй отрезок линии, проведенный от центра к середине любой стороны выпуклого правильного многоугольника, известен как апофема многоугольника. Он также образует радиус круга, в данном случае тот, который полностью заключен в многоугольник и касается каждой стороны многоугольника в его средней точке.Этот круг известен как вписанный круг или вписанный круг .
Связь между радиусом ( r ), апофемой ( a ) и стороной ( s ) восьмиугольника
Восьмиугольник с описанной и вписанной окружностями
Из рисунка выше вы должны увидеть, что размер области восьмиугольника будет где-то между размером вписанной и описанной окружностей.По мере увеличения количества сторон в выпуклом правильном многоугольнике он будет становиться все более и более похожим на круг, а разница в длине между радиусом и апофемой будет становиться все менее и менее значительной. Области многоугольника, вписанной и описанной окружности также сойдутся.
Вращательная симметрия
Линия симметрии , проведенная через двумерную фигуру, — это линия, которая делит фигуру на две половины, являющиеся зеркальным отображением друг друга.У правильных многоугольников может быть много линий симметрии, что позволяет им поворачиваться вокруг своего центра на некоторый угол (кроме трехсот шестидесяти градусов) без изменения их внешнего вида. Количество линий симметрии напрямую связано с количеством сторон многоугольника, так что равносторонний треугольник имеет три линий симметрии, пятиугольник имеет пять линий симметрии, восьмиугольник имеет восемь линий симметрии , и так далее. Линии симметрии этих форм показаны ниже.Обратите внимание, что для правильных многоугольников с числом сторон и вершин и даже линии симметрии будут проходить как через пары противоположных вершин, так и через середины противоположных сторон. Для правильных многоугольников с нечетным числом сторон и вершин каждая линия симметрии будет проходить через одну вершину и среднюю точку стороны, противоположной этой вершине.
Правильный многоугольник с n сторонами имеет n линий симметрии.
Диагонали
Диагональ в правильном многоугольнике — это любой отрезок линии, отличный от стороны , которая соединяет одну вершину с другой.Другими словами, это любой отрезок линии, соединяющий две непоследовательных вершины . Любой правильный многоугольник с более чем тремя сторонами имеет две или более диагоналей. Количество диагоналей увеличивается с количеством сторон n и связано с n следующей формулой:
| Количество диагоналей = | n ( n — 3) |
| 2 |
Давайте рассмотрим те же самые правильные многоугольники, которые мы использовали для демонстрации вращательной симметрии, но на этот раз со ссылкой на их диагонали.Равносторонний треугольник имеет нулевые диагонали, потому что все три отрезка, соединяющие вершины, являются сторонами треугольника. Пентагон имеет пять сторон и вершин, и из рисунка ниже видно, что он также имеет пять диагоналей (использование приведенной выше формулы для определения количества диагоналей для пятиугольника также даст результат пять). Последний правильный многоугольник, показанный здесь, — это восьмиугольник, восьмиугольная фигура. Теперь вы можете начать испытывать некоторые трудности с подсчетом числа диагоналей, но формула говорит нам, что на самом деле их двадцать (20).Квадратный член в формуле говорит нам, что количество диагоналей увеличивается на экспоненциально по мере увеличения количества сторон.
Количество диагоналей увеличивается экспоненциально с n
Помимо количества диагоналей, принадлежащих конкретному правильному многоугольнику, математиков также интересует количество пересечений между диагоналями (включая вершины многоугольника), количество отрезков линии , которые они пересекают друг друга. в (это включает стороны многоугольника), и количество областей (замкнутые области), которые создают пересечения внутри многоугольника.Взяв в качестве примера пятиугольник, у нас есть десять (10) пересечений, двадцать (20) отрезков прямых и одиннадцать (11) областей. В восемнадцатом веке нашей эры швейцарский математик Леонард Эйлер разработал формулу, связывающую количество пересечений, отрезков прямых и областей. Формула Эйлера представляет особый интерес в связи с изучением теории графов . Кстати, обратите внимание, что рисование всех диагоналей из одной вершины только правильного многоугольника разделит многоугольник на n — 2 треугольника, где n — количество сторон.
Диагонали одной вершины образуют n — 2 треугольника
Нахождение площади выпуклого правильного многоугольника
Определение периметра правильного многоугольника — относительно тривиальное упражнение. Как только вы знаете длину одной стороны, вы просто умножаете ее на количество сторон, чтобы получить периметр.Найти площадь правильного многоугольника не так-то просто. Самый простой правильный многоугольник — это равносторонний треугольник. Если мы знаем длину каждой стороны, мы можем относительно легко найти площадь, потому что площадь треугольника определяется путем умножения длины основания треугольника на его высоту и деления на два. Если мы возьмем одну сторону в качестве основания треугольника, мы сможем использовать теорему Пифагора, чтобы найти высоту. Рассмотрим следующий равносторонний треугольник:
Треугольник ABC — равносторонний треугольник
В равностороннем треугольнике ABC длина каждой стороны треугольника равна s .Высота треугольника h — это длина перпендикуляра от средней точки D основания треугольника до вершины B. Поскольку треугольник ABD является прямоугольным, теорема Пифагора говорит нам, что длина перпендикуляра BD и, следовательно, высота треугольника h , может быть найдена по следующей формуле:
ч = √ ( с 2 — ( 1 / 2 с ) 2 )
Следовательно, если мы знаем значение s , мы можем найти высоту ( BD ) треугольника и, следовательно, площадь треугольника (площадь равна половине длины основания, умноженной на высоту).Если у нас есть значение для s из шесть (6), мы получим следующее:
ч = √ (6 2 — 3 2 ) = √ (36 — 9) = √27 = 5,196
Теперь мы можем вычислить площадь треугольника:
| Площадь треугольника = | 6 × 5,196 | = 15,588 |
| 2 |
В качестве альтернативы мы могли бы использовать следующую формулу, которая позволяет нам найти площадь равностороннего треугольника без предварительного определения высоты треугольника, при условии, что мы знаем длину s каждой стороны:
| Площадь треугольника = | с 2 × √3 |
| 4 |
С помощью этой формулы, если мы снова используем значение для s из шести, мы получим следующее:
| Площадь треугольника = | 36 × 1.732 | = 15.588 |
| 4 |
Нахождение площади квадрата — тривиальное упражнение, так как площадь будет просто длиной одной стороны, умноженной на себя (то есть в квадрате). Найти площадь правильного выпуклого многоугольника с более чем четырьмя сторонами не так просто, хотя есть простая формула, которую можно применить, если мы знаем длину каждой стороны и длину апофемы (отрезок линии соединяет центр многоугольника со средней точкой любой стороны).Длину апофемы для данного правильного многоугольника с n сторонами и длиной s можно найти с помощью ряда различных формул, но поскольку все эти формулы используют тригонометрические функции, мы не будем их здесь обсуждать. Предположим вместо этого, что для целей этого упражнения мы нашли апофему путем измерения. Мы можем использовать следующую формулу, чтобы найти площадь:
| Площадь выпуклого правильного многоугольника = | ap |
| 2 |
где:
- a = длина апофемы
- p = длина периметра
Рассмотрим следующий восьмиугольник:
У восьмиугольника длина стороны 6 и апофема 7.