Исследовательская работа «Старинные русские меры»
Частное
общеобразовательное учреждение «Школа-интернат № 24
среднего общего образования открытого акционерного общества
«Российские железные дороги»
Старинные
меры длины
в творчестве поэтов и писателей
СОДЕРЖАНИЕ
Введение …………………………………………………………………………………………….. | 3 | |
1. | Исторический обзор …………………………………………………….. | 5 |
| 1. 1. Зачем человеку нужны измерения ………………………………. | 5 |
| 1. 2. Единицы измерения Древней Руси ……………………………….. | 6 |
| 1. 3. Метрическая система измерений …………………………………. | 13 |
2. | Старые русские меры длины в литературе ……………………………. | 14 |
| 2. 1. В устном народном творчестве …………………………………… | 14 |
|
| 2. | 17 |
3. | Практическая часть ……………………………………………………… | 20 |
Заключение ………………………………………………………………………………………… | 24 | |
Литература …………………………………………………………………………………………. | ||
Приложения …………………………………………………………………. | 27 | |
Введение
Сегодня
мы повсюду используем современные термины, обозначающие меры длины, и это
является нормой жизни.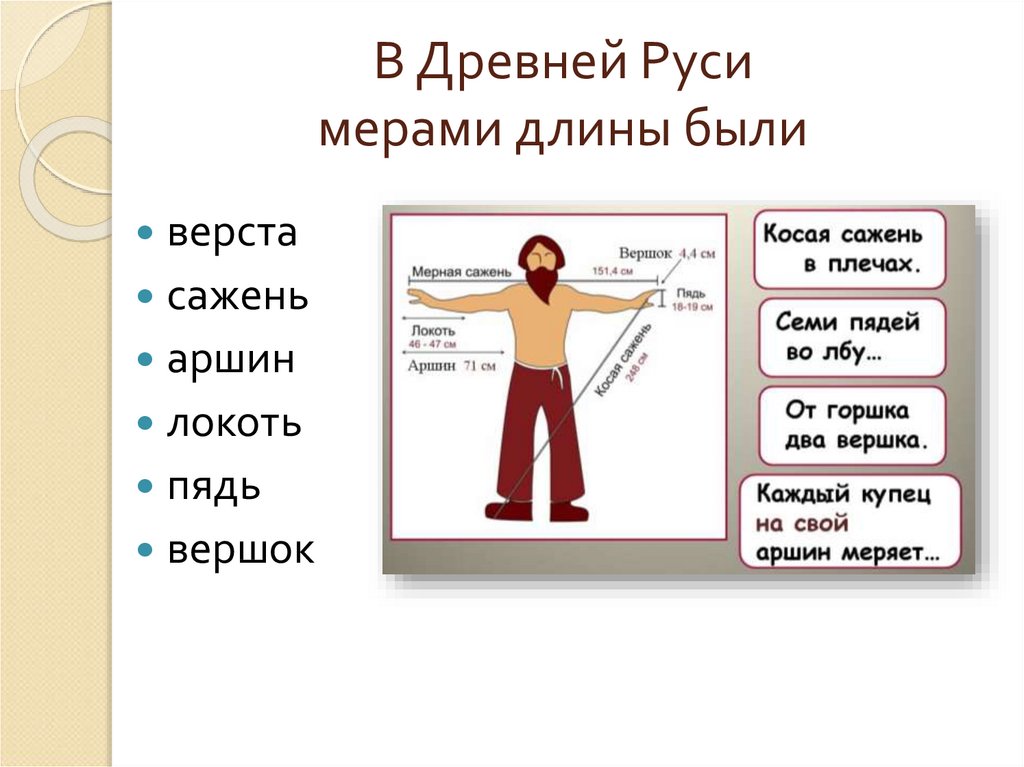 Однако в литературе и истории нередко встречаются нам
«локти», «аршины», «ладони», «пяди», и это тоже нормально. Все эти понятия,
употребляемые нами в повседневной жизни, обогащают не только язык
художественных произведений, но и наш внутренний мир. Ведь мы часто в своей
речи используем их в поговорках, пословицах, пришедших к нам из древней
старины, порой даже не замечая этого. Все это является частью культуры нашей
великой страны, частью истории России. Я считаю, что мы не просто должны, мы
обязаны знать и понимать выражения, которые давно вышли из обихода,
терминологию прошлых веков. Это культурно нас обогащает, повышает
интеллектуальный уровень, помогает окунуться в славное прошлое Руси, лучше
понимать ценности наших предков, познавать историю родной страны.
Однако в литературе и истории нередко встречаются нам
«локти», «аршины», «ладони», «пяди», и это тоже нормально. Все эти понятия,
употребляемые нами в повседневной жизни, обогащают не только язык
художественных произведений, но и наш внутренний мир. Ведь мы часто в своей
речи используем их в поговорках, пословицах, пришедших к нам из древней
старины, порой даже не замечая этого. Все это является частью культуры нашей
великой страны, частью истории России. Я считаю, что мы не просто должны, мы
обязаны знать и понимать выражения, которые давно вышли из обихода,
терминологию прошлых веков. Это культурно нас обогащает, повышает
интеллектуальный уровень, помогает окунуться в славное прошлое Руси, лучше
понимать ценности наших предков, познавать историю родной страны.
Актуальность: Вопрос о значимости единиц измерения всегда актуален, так как метрология всегда находится в центре внимания человеческой деятельности.
Цель
исследования: установить старинные меры длины,
сравнить их с новой измерительной системой и найти отражение этих мер в русских
пословицах и поговорках, в литературных произведениях.
В рамках достижения данной цели мною были поставлены следующие задачи:
· Познакомиться с измерительной системой, которая существовала ранее.
· Проследить отражение старых мер в русском фольклоре.
· Выяснить, что означают пословицы и поговорки, в которых встречаются названия старинных мер длины. Перевести старинные меры в пословицах и поговорках в современные.
· Познакомить учащихся школы с результатами исследования, с целью расширения их знаний и кругозора в целом.
Методы исследования:
Изучение познавательной и художественной литературы.
Практическая работа.
1. Исторический обзор
Исторический обзор
1.1. Зачем человеку нужны измерения
На первых этапах развития человечества измерения были связаны с производством предметов быта. Отмерялось необходимое количество материала для производства орудий, одежды, сооружений. С развитием человеческого общества стали возникать новые потребности в измерениях. Торговля и развитие ремесел требовали точного определения весов и длин. Сбор налогов требовал определения площадей земельных участков. С развитием мореплавания появилась необходимость астрономических измерений для определения местоположения корабля по звездам.
В настоящее время развитие науки и техники привело к тому, что человек может проводить самые высокоточные измерения не только длины и веса, но и многих других параметров. В повседневной жизни, производстве или науке большинство дел начинается с измерений и расчетов. Меряют расстояние, вес, температуру, давление, скорость и многое другое.
Врачи
начинают осмотр больных с измерения температуры тела, роста, веса и кровяного
давления.
Идет время. Меняются инструменты и способы измерений, но цели остаются прежними – описывать окружающий нас мир, проектировать, моделировать и контролировать процессы в производстве и научной деятельности
1. 2. Единицы измерения Древней Руси
С
давних пор у разных народов для измерения малых предметов и расстояния
использовались мелкие единицы длины «естественного» происхождения. Первыми
эталонами служили отдельные части человеческого тела. Как и при счёте,
использовались те «измерительные инструменты», которые всегда были при себе —
рука и её части. Очень удобными для замеров оказались длина и ширина
указательного пальца, а также ширина ладони. Для определения величины предметов
более крупных подошло расстояние от локтя до кончика среднего пальца, которое к
тому же хорошо согласовывалось с размерами пальца и ладони.
Первые единицы для измерения величин были не слишком точными. Например, расстояния измерялись шагами. Так как у разных людей величина шага различна, то брали некоторую среднюю величину. Для измерения больших расстояний шаг был слишком мелкой единицей, поэтому большие расстояния измеряли переходами или днями передвижения.
Система древнерусских мер длины включала в себя следующие основные меры: версту, сажень, аршин, локоть, пядь и вершок.
Для мелких мер длины, базовой величиной была «пядь» (c XVII века — длину равную пяди называли уже иначе – «четверть аршина», «четверть» или «четь»), из которой легко можно было получить меньшие доли – два вершка (1/2 пяди) или вершок (1/4 пяди).
Купцы,
продавая товар, мерили его каждый своим аршином (линейкой) или по-быстрому –
отмеряя «от плеча». Чтобы исключить обмер, властями был введён эталон –
«казенный аршин», представляющий собой деревянную линейку, на концах
которой клепались металлические наконечники с государственным клеймом.
Вершо́к — старорусская единица измерения, первоначально равнялась длине двух фаланг указательного пальца, приблизительно 4,5 см. Наименование «вершок» происходит как раз от слова «верх» (верх перста, т. е. пальца).
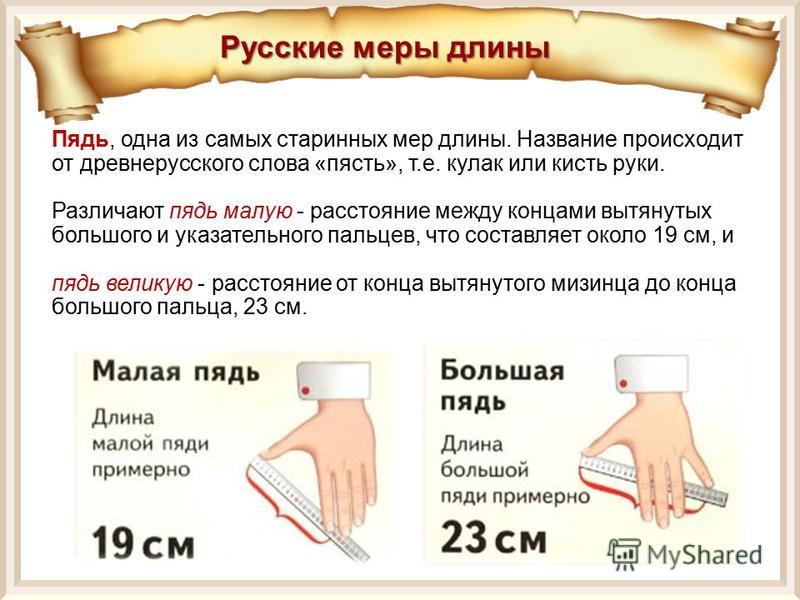
Пядь — древнерусская мера длины, изначально равная расстоянию между концами растянутых пальцев руки — большого и указательного. Различали три древнерусские пяди. Малая пядь определялась расстоянием между концами растянутых большого и указательного пальцев и равнялась примерно 19см. Великая пядь равнялась расстоянию между концами большого пальца и мизинца – 23см. Пядь с кувырком получалась при добавлении к малой пяди две длины сустава указательного (по некоторым источникам – среднего) пальца и равнялась 27 см.
Локоть равнялся длине руки от пальцев до локтя (по другим данным — расстояние по
прямой от локтевого сгиба до конца вытянутого среднего пальца руки или сжатой в
кулак кисти руки). Величина этой древнейшей меры длины, по разным источникам,
составляла от 38 до 47 см.
Величина этой древнейшей меры длины, по разным источникам,
составляла от 38 до 47 см.
Локоть широко использовался (наряду с пядью и саженью) в строительном деле. Особое значение он приобрел в торговле: при розничной продаже тканей считался основной единицей длины, а при оптовых закупках играл роль контрольной мерки.
С конца XII в. локоть начал вытесняться более крупной единицей длины – аршином, использование которого началось с торговых отношений с Востоком. Длительное время локоть и аршин применялись одновременно друг с другом: первым измеряли ткани русского производства, вторым – иностранного. Однако со временем аршин стал доминировать, проник в различные отрасли производства и в XVII в. был признан официальной мерой длины в государстве.
Возможно, слово «аршин» происходит от персидского «арш» — локоть, которое было заимствованно в тюркских языках.
Аршин — старинная русская мера длины, равная, в современном исчислении 72см. Аршином,
так же, называли мерную линейку, на которую, обычно, наносили деления в
вершках.
Сажень — одна из наиболее распространенных на Руси мер длины. «Маховая сажень» — расстояние между концами пальцев широко расставленных рук взрослого мужчины (Рис. 1). «Косая сажень» — самая длинная: расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки. Наименование сажень происходит от глагола сягать — насколько можно было дотянуться рукой. Существовали саженные мерные верёвки и деревянные «складени», применявшиеся при измерении в строительстве и при межевании (разделении) земли.
По данным историков, саженей было более 10, они имели свои названия, были разного размера и не кратны одна другой. Сажени: Городовая сажень = 2, 85 м
Великая сажень = 2, 44 м
Греческая сажень = 2, 30 м
Казённая сажень = 2, 17 м
Царская сажень = 1, 97 м
Церковная сажень = 1, 86 м
Народная сажень = 1, 76 м
Кладочная сажень = 1, 59 м
Простая сажень = 1, 50 м
Малая сажень = 1, 42 м
Дворовая (мостовая) сажень = 1, 34 м
Маховая сажень = 1,76 м
Косая сажень (первоначально «косовая») =2,48 м
Сажени
употреблялись до введения метрической системы мер.
Рис. 1. Иллюстрация старорусских мер длины.
Верста — старорусская путевая мера (её раннее название — »поприще»). Этим словом, первоначально называли расстояние, пройденное от одного поворота плуга до другого во время пахоты. Два названия долгое время употреблялись параллельно, как синонимы. Известны упоминания в письменных источниках XI века. В рукописях XV в. есть запись: «поприще сажений 7 сот и 50» (длиной в 750 сажень). До царя Алексея Михайловича в 1 версте считали 1000 саженей. При Петре Первом одна верста равнялась 500 саженей, в современном исчислении = 1066,8м.
«Верстой»
также назывался верстовой столб на дороге.
Величина версты неоднократно менялась в зависимости от числа сажен, входивших в
неё, и величины сажени. Уложением 1649 года была установлена «межевая
верста» в 1 тысячу саженей. Позже, в XVIII веке наряду с ней стала
использоваться и «путевая верста» в 500 саженей («пятисотная
верста»).
Межевая
Верста — старорусская единица измерения, равная
двум верстам. Версту в 1000 сажен (2,16
км) употребляли широко в качестве межевой меры, обычно при определении выгонов
вокруг крупных городов, а на окраинах России, особенно в Сибири — и для
измерения расстояний между населенными пунктами. Большие расстояния, особенно в
Восточной Сибири, определялись в днях пути. В XVIII в. межевые вёрсты
постепенно вытесняются путевыми, и единственной верстой в XIX в. остается
верста «путевая», равная 500 саженям.
Версту в 1000 сажен (2,16
км) употребляли широко в качестве межевой меры, обычно при определении выгонов
вокруг крупных городов, а на окраинах России, особенно в Сибири — и для
измерения расстояний между населенными пунктами. Большие расстояния, особенно в
Восточной Сибири, определялись в днях пути. В XVIII в. межевые вёрсты
постепенно вытесняются путевыми, и единственной верстой в XIX в. остается
верста «путевая», равная 500 саженям.
Наряду с основными мерами длины существовали единицы измерений, получившие менее широкое распространение.
Перст – равен ширине указательного и среднего пальцев. Перст = 2 см.
Коршок – равен ширине кулака, происходит от слова корх (кулак). Коршок = 9 см
Шаг — Одна из древнейших мер длины, средняя длина человеческого шага = 71 см.
Бадог (батог) – ходовая мера, использовалась при строительных работах,
½ часть сажени. Бадог = 1, 06 м.
Ладонь = 1/6 локтя (локоть шестиладонный) и многие другие. (см.Приложение 1)
(см.Приложение 1)
К XVIII веку насчитывалось до 400 различных по величине единиц мер, употребляемых в разных странах. Разнообразие мер затрудняло торговые операции. Поэтому каждое государство стремилось установить единообразные меры для своей страны.
В XVIII в. в связи с экономическим развитием и необходимостью строгого учета при внешней торговлей, в России встал вопрос точности измерений, создании эталонов, на основе некоторых можно было бы организовать проверочное дело («метрологию»).
Россия стала больше торговать с Западной Европой. Нужны были меры, которые было бы легче сравнить с западными мерами. Названия старых мер сохранили, но поменяли их длину. Для этого Петр I предложил воспользоваться английскими мерами, которые не менялись уже несколько столетий, и ими часто пользовались в торговле.
В 1835 году Указом Петра I были установлены общие и введены новые меры длины, употреблявшиеся до введения метрической системы.
Географическая
миля – равнялась 1/15 части градуса земного экватора. Географическая миля = 7, 42
км
Географическая миля = 7, 42
км
Морская миля – равнялась 1 минуте дуги земного меридиана.
Морская миля = 1,85 км
Английская миля = 1, 61 км
1
верста = 500 саженей = 1,0668 км
1 сажень = 3 аршина = 7
фут = 48 вершков = 2,1336 м
Косая сажень = 2,48 м
Маховая сажень = 1,76 м
Ярд = 91,44 см
1
аршин = 4 четверти (пяди) = 16 вершков = 28
дюймов = 71,12 см
1 локоть = 44 см (по разным источникам от 38 до 47
см)
1 фут = 1/7 сажени = 12 дюймов = 30,479 см (Фут и дюйм были равны по величине английским мерам).
Большая пядь = 1/2 локтя = 22 — 23 см
1четверть (пядь, малая пядь, пядень, пядка) = 4 вершка = 17,78 см Синоним «четверти» — «четь».
1 вершок = 1/4 пяди = 1/16 аршина = 4,445см (равен ширине указательного и среднего пальцев).
1 дюйм = 2,54 см (равен ширине большого пальца или длине трех сухих зерен ячменя).
1 перст = 2 см
Линия – равнялась 1/10 дюйма = 2,54 мм
Точка
= 0,25 мм.
Со второй половины XVIII века подразделения вершка были заменены мелкими английскими мерами: дюймом, линией и точкой, но прижился только дюйм. Линии и точки применялись сравнительно мало. В линиях выражались калибры ружей. Точки применялись только для определения размеров золотой и серебряной монеты.
Несмотря на царский указ, повсюду применялись самые разные меры длины, объема и площади. Только переход к метрической системе мер положил конец этой неразберихе.
1. 3. Метрическая система измерений
Потребности практики заставили начать поиски единой системы мер. При этом было ясно, что надо отказаться от установления связей между единицами измерения и размерами человеческого тела. Тогда были созданы определённые общегосударственные единицы измерения, для чего были изготовлены образцы единиц измерения – эталоны.
Была создана метрическая система мер во Франции в конце ХVIII – начале ХIХ вв.
В её основу положена единица длины метр – одна сорокамиллионная доля земного
меридиана. В нашей стране метрическая система мер была введена в 1918
г.
В нашей стране метрическая система мер была введена в 1918
г.
Метрическая система мер была допущена к применению в России (в необязательном порядке) законом от 4 июня 1899 года, проект которого был разработан Д. И. Менделеевым, и введена в качестве обязательной в 1918 году.
На основе метрической системы была разработана и принята в 1960 году XI Генеральной конференцией по мерам и весам Международная система единиц (СИ). В течение второй половины XX века большинство стран мира перешло на систему СИ.
2. Старые русские меры длины в литературе
2.1. В устном народном творчестве
В нашем современном языке старые единицы измерения и слова, их обозначающие сохранились, как правило, в виде пословиц и поговорок.
& Один, как перст. – Одинокий человек
& Пять
верст до небес, и все лесом. – Очень далеко и неудобно добираться.
– Очень далеко и неудобно добираться.
& Любовь не верстами меряется. – Чувство не материально, поэтому нельзя измерить.
& Не указывай на людей перстом! Не указали бы на тебя шестом! – Не суди о других предвзято, можешь и сам попасть под суд
& От горшка два вершка, а уже указчик. – Молодой человек, не имеющий своего жизненного опыта, но поучающий всех.
& Не уступить ни пяди. – Не отдать даже самой малости.
& Сам с ноготок, а борода с локоток – Сам маленький (или слишком молод), а умный.
& Каждый купец на свой аршин меряет. – Каждый судит о любом деле односторонне, исходя из собственных интересов.
& Сидит, ходит, словно аршин проглотил. – Говорят о человеке с неестественно прямой осанкой.
& На аршин борода, да ума на пядь. – О взрослом, но глупом человеке.
& Косая сажень в плечах. – Статный, широкоплечий, высокого роста человек.
& На
три аршина в землю видит. – О прозорливом человеке, от которого ничего
невозможно утаить.
& Коломенская верста – шутливое прозвище для высокого человека.
& Семь пядей во лбу – Об очень умном человеке.
& Москва верстой далека, а сердцу рядом. – Так русские люди характеризовали свою любовь к столице.
& От слова до дела – целая верста. — Каждый может сказать, но не каждый выполнит обещанное.
& Верстой ближе — пятаком дешевле. – Об экономии.
& На версту отстанешь — на десять догоняешь. – Даже небольшое отставание очень трудно преодолевать.
& Семимильные шаги – быстрый рост, хорошее развитие чего-либо.
& Семь футов воды под килем. — Пожелание доброго пути судну или человеку, уходящему в море.
& Сам с вершок, а слово с горшок. — Сам маленький, а умный (большая голова).
& Пишешь аршинными буквами. – Крупно
& Борода с локоть, а сам с ноготь. – Невысокий человек с длинной, густой бородой.
& Ехать
за семь верст киселя хлебать. — Необдуманно стремиться куда-либо, имея
возможность достичь желаемого на месте.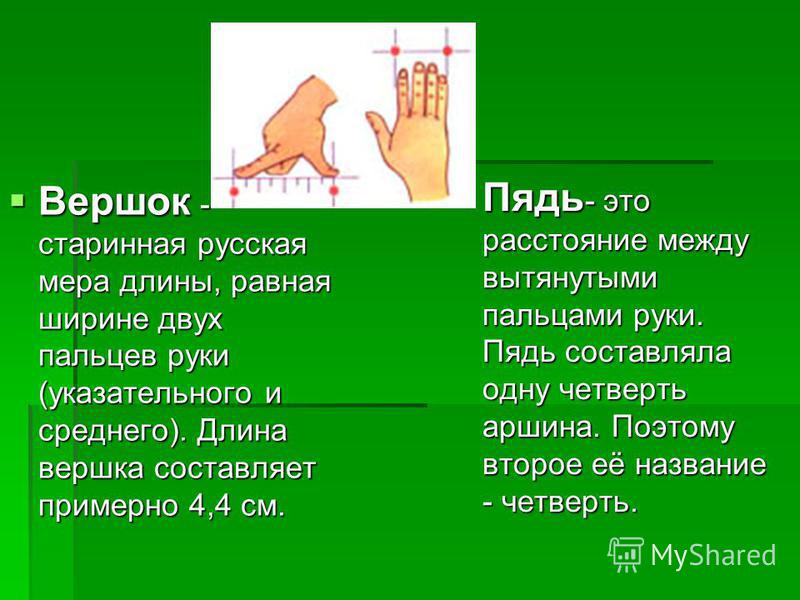
& Родная сторона верстою далека, а сердцу рядом. – О любви к Родине.
& Сто верст молодцу не крюк. — Даже такое молодому человеку не по чём.
& Для друга семь верст не околица. — Ради близкого человека и длинный, окольный путь кажется коротким.
& На аршин голова, да ума на пядь. – Голова большая, но глупая.
& Нос с локоть, а ум с ноготь. – Вырос большим, а ума не нажил.
& Старичок с кувшин, борода с аршин. – О невысоком бородатом человеке.
& Тянись верстой, да не будь простой.
& За семь верст комара искали, а комар на носу. – О чем-то очевидном.
& Ты от правды на пядень, а она от тебя на сажень. – Ответ ближе, чем пытаешься его найти.
& Жили с локоть, а жизнь с ноготь — т.е. жили долго, а жизнь оказалась короткой.
& В чужих руках ноготок с локоток. – О зависти
& Семь аршин говядины да три фунта лент. – Говорят о чём-то бессмысленном.
& Аршин
на кафтан, два на заплаты. – Ремонт вещи обойдется дороже ее стоимости.
– Ремонт вещи обойдется дороже ее стоимости.
& Полено к полену – сажень. – О накоплении запасов, богатства путём экономии.
& Чужой земли не надо нам ни пяди, но и своей вершка не отдадим.
& По утру с сажень, в полдень – пядень, а к вечеру через поле хватает. Ответ: (тень)
В былинах встречаем много устаревших слов и измерений. Так читая книгу Русские богатыри, в которой И.В.Карнаухова собрала былины и сказки о героях Руси, я встретил много таких упоминаний, вот некоторые из них:
& «Илья избавляет Царьград от Идолища»: Он ростом больше двух саженей, сам толстый, как столетний дуб, нос у него – что локоть торчит…
& «Первый бой Ильи Муромца»: Поезжай ты, Илья, дорогой окольной. Правда, прямо до Киева триста верст, а окольной дорогой – целая тысяча.
& «Три поездки Ильи Муромца»: Хорош был у старого добрый конь, его Бурушка Косматушка. Хвост у Бурушки трех саженей, грива до колен, а шерсть трех пядей…
& «Былина об Илье Муромце»:
Да отъехал-де ведь старый за три поприща,
Да по-русски
то сказать да за три верстоньки.
2. 2. В прозе и поэзии
Названия старинных единиц измерения длины мы также встречаем в произведениях поэтов и прозаиков.
& А. С. Пушкин
«Зимняя дорога»
Ни огня, ни чёрной хаты,
Глушь и снег… навстречу мне
Только вёрсты полосаты
Попадаются одни…
& А. С. Пушкин
«Сказка о царе Салтане…»
Сына бог им дал в аршин,
И царица над ребенком,
Как орлица над орленком;
Шлет с письмом она гонца,
Чтоб обрадовать отца.
& П. П. Ершов
«Конёк-горбунок»
Ростом только в три вершка,
На спине с двумя горбами
Да с аршинными ушами.
& Н. А. Некрасов
«Дедушка Мазай и зайцы»
С каждой минутой вода подбиралась
К бедным зверькам; уж под ними осталось
Меньше аршина земли в ширину,
Меньше сажени в длину.
& С. Я. Маршак
« Сказка про козла »
Эй, не плачьте, баба с дедом!
Накормлю я вас обедом,
Испеку пирог грибной
В
два аршина шириной.
& Н. А. Некрасов
«Крестьянские дети»
И, шествуя важно, в спокойствии чинном,
Лошадку ведет под уздцы мужичок
В больших сапогах, в полушубке овчинном,
В больших рукавицах…, а сам с ноготок!
& А.Погорельский
«Чёрная курица, или подземные жители»
«…отворилась боковая дверь… и вошло множество маленьких людей, ростом не более как с пол-аршина»
& Д. Мамин-Сибиряк
«Серая Шейка»
«Свободного места, где можно было плавать, оставалось не больше пятнадцати сажен»
& И. С. Тургенев
«Муму»
«Из всей ее челяди самым замечательным лицом был дворник Герасим, мужчина двенадцати вершков роста, сложенный богатырем и глухонемой от рождения».
«Но Герасим только закивал головою и так сильно принялся грести, хотя и против течения реки, что в одно мгновение умчался саженей на сто. »
& К.М.Станюкович.
Вокруг света на «Коршуне»
«Это было небольшое, стройное и изящное судно 240 футов длины и 35 футов ширины в своей середине…»
& Л. Н.Толстой
Н.Толстой
«Кавказский пленник»
«Ехать было 25 верст. Обоз шел тихо…»
«Где брод был, там на три аршина вода пошла, камни ворочает».
3. Практическая часть
3.1. Анкетирование учащихся в 5б классе
Провели анкетирование учащихся 5б класса в количестве 22 человек. Вопросы анкеты были неизменны для всех опрашиваемых. С вопросами можно ознакомиться в Приложении 2.
Проведенное в 5 классе анкетирование (Рис.3) выявило, что учащиеся зачастую встречались со старинными мерами длины при чтении различной литературы, в повседневной жизни, слышали поговорки и пословицы, однако не все знают соотношения старинных мер с современными. Опрошены 22 человек.
Рис. 1. Результаты анкетирования 5 класса.
3.2. Практическая работа
Была
проведена практическая работа по пересчету старинных мер длины, встретившихся
нам в литературных произведениях, в современную систему измерений. Писатели в своих произведениях часто используют
старинные меры длины. Вот некоторые из них, которые встретились на
страницах прочитанных мною книг:
Писатели в своих произведениях часто используют
старинные меры длины. Вот некоторые из них, которые встретились на
страницах прочитанных мною книг:
Автор | Произведение | Упоминание меры длины | Преобразование |
Д. Мамин-Сибиряк | «Свободного места, где можно было плавать, оставалось не больше пятнадцати сажен» |
15 сажень = 32 м 55см | |
Г.Х.Андерсен | «…в
чашечке цветка сидела хорошенькая крошечная девочка ростом не больше дюйма». |
1дюйм = 2 см 54 мм | |
П.П.Ершов
| «Да игрушечку-конька Ростом только в три вершка, На спине с двумя горбами Да с аршинными ушами» |
3 вершка =13см 3мм 1 аршин = 71см | |
Н.Н.Некрасов | «С каждой минутой вода подбиралась К бедным зверькам; уж под ними осталось Меньше аршина земли в ширину, Меньше сажени в длину» |
1 аршин = 71см 1 сажень = 2 м 17 см | |
А. | «…отворилась боковая дверь… и вошло множество маленьких людей, ростом не более как с пол-аршина» |
1/2 аршина = 35,5см | |
А.С.Пушкин | «…Сына Бог ей дал в аршин» |
1 аршин = 71см | |
В.М.Гаршин | «..тащить хотя и лёгкую лягушку три тысячи верст, не бог знает какое удовольствие…» |
3000 вёрст = 3198 км | |
И.С.Тургенев | «Но Герасим только
закивал головою и так сильно принялся грести, хотя и против течения реки, что
в одно мгновение умчался саженей на сто. |
100 саженей = 217 м
| |
Устное народное творчество | «…Хвост у Бурушки трех саженей, грива до колен, а шерсть трех пядей…»
|
3 сажени = 6 м 51см 3 пяди = 53см 34мм | |
Устное народное творчество | Дразнилка | Молодиченька – невеличенька, сама с вершок, голова с горшок |
1 вершок = 4 см 4 мм |
Устное народное творчество | Поговорка | Ты от правды на пядень, а она от тебя на сажень | 1 пядень = 17 см 78 мм 1 сажень = 2 м 17 см |
Устное народное творчество | Поговорка | За семь верст комара искали, а комар на носу | 7 верст = 7,4676 км |
|
|
|
|
Проведя повторное исследование в своем классе, у меня получились следующие результаты
Результат
улучшился.
Заключение
Проведя
свое исследование, я выяснила, что современные дети мало знакомы со старинными единицами
измерения – это показали анкетные данные. Я уверена, что проведенная мною
работа интересна во многих отношениях. Я ближе познакомилась со старинными
русскими единицами измерения, выявили взаимосвязь между ними и устным народным
творчеством. Старинные русские пословицы и поговорки метки и выразительны, а
найденные мною стихотворения, в которых точно и ярко упоминаются старинные
единицы измерения, тоже подтверждают, как много для нас значит наследие наших
предков. Конечно, большинство старых мер забыто, вышло из употребления, но
многие из них и сегодня живут не только в старинных постройках, в древних
рецептах лекарств и всевозможных кушаний, но и фигурируют в современных
литературных произведениях, исторических памятниках. Меры эти жили всегда, иногда
старились и умирали, но всегда возрождались к новой жизни, так же, как и наш
русский дух, который не сломить никакими трудностями.
История мер – это история торговли, ремесел, сельского хозяйства и строительства в Древней Руси, а в конечном итоге – это часть истории всего человечества. Сведения из истории мер длины, в том числе исконно русских, раскрывают связь математики с жизнью. Они показывают, что единицы измерения люди не придумали, а принимали вначале в качестве мер части своего тела, которые постепенно превращались в общепринятые образцы. Изучая появление математических понятий, я проник в образ мыслей древнерусского человека и тем самым углубил познания и по истории России и по литературе.
Подводя итог работы, я пришла к выводу о большой ее значимости, поскольку знать и понимать, как появились меры, как изменялись, что несли народам и как влияли на их жизнь — это интересно и сегодня. Большинство старых мер забыто, вышло из употребления, но они хоть используются редко, все же, применяются в современной жизни, например, сажень используется до сих пор в сельском хозяйстве.
Мне
кажется, что материалы данной работы можно использовать как
информационно-справочный материал для учителей и учащихся на классных часах, на
уроках математики, истории, литературы, технологии.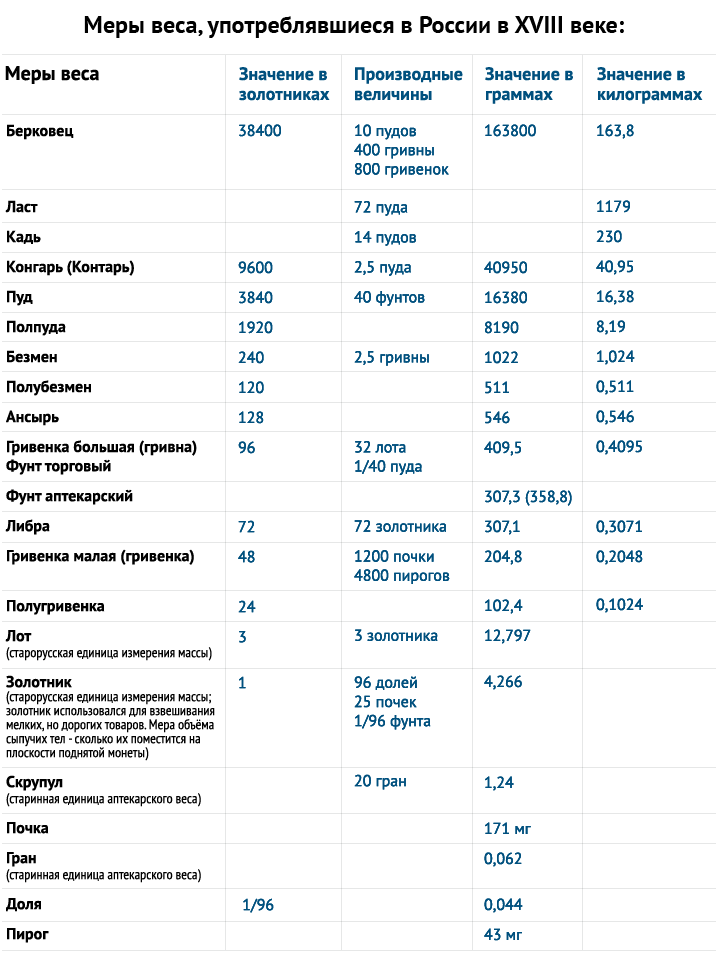
Можете верить или не верить,
Но всё на свете можно измерить:
Время помогут измерить часы,
Размеры – линейка, тяжесть – весы.
Есть масса приборов – для измеренья
Скорости, шума, объёма, давленья.
Море измерит до дна эхолот,
Температуру – градусник.
И – при желании – каждый найдёт
Величину своей радости…
Вы думаете, это – бред?
А мы откроем секрет:
Простой линейкой – без ошибки –
Измерьте ширину улыбки!
Литература
1. А.С.Пушкин. Избранные сочинения. В 2-х т. Т.1. – 1980. 814 с. – Б-ка классики. Русская лит-ра.
2. В.И. Даль. Толковый словарь живого великорусского языка. — М., 1955.
3. И.В.Карнаухова. Русские богатыри. – М.:Дет.лит., 2006. – 238 с.:ил. – (Школьная б-ка).
4. К.М.Станюкович. Вокруг света на «Коршуне»: Сцены из морской жизни в двух частях. – Одесса: Маяк, 1980. – 392 с., ил. – (Морская б-ка. Кн.21-я)
5. Литература.
5 класс. Учеб. Для общеобразоват. Организаций с прил. На электрон. носителе. В
2 ч. Ч. 1 / В.Я. Коровина, В.П. Журавлев, В.И.Коровин. – 3-е изд. – М.: Просвещение,
2014. – 303с.: ил.
Литература.
5 класс. Учеб. Для общеобразоват. Организаций с прил. На электрон. носителе. В
2 ч. Ч. 1 / В.Я. Коровина, В.П. Журавлев, В.И.Коровин. – 3-е изд. – М.: Просвещение,
2014. – 303с.: ил.
6. Фразеологический словарь русского языка / под ред. А.И. Молоткова. – М.: Советская энциклопедия, 1986.
«Старинные русские меры длины, веса, объёма», http://mer.kakras.ru
Приложение 1.
Приложение 2.
Анкета
- Знакомы ли Вам старинные меры длины: аршин, верста, пядь, сажень, вершок?
- Знаете ли Вы приблизительное значение этих мер в современной
системе измерений?
Аршин =
Верста =
Пядь =
Сажень =
Вершок =
- Знаете ли Вы пословицы и поговорки с этими словами?
- Расставьте в порядке увеличения:
Перст
Вершок
Пядь
Аршин
Сажень
Верста
Шаг
Линия
Старинные русские меры длины, веса, объёма.
 презентация, доклад
презентация, докладСтаринные русские меры длины, веса, объёма.
Работу выполнила Галкина Юля
«в» класс
МОУ «Кишертская средняя школа»
С глубокой древности наши предки измеряли расстояние собой, своим телом. Это и удобно, и руки с ногами всегда при тебе, их нельзя «забыть дома».Система древнерусских мер длины включала в себя следующие основные меры: версту, сажень, аршин, локоть, пядь и вершок.
Аршин
АРШИН — старинная русская мера длины, равная, в современном исчислении 0,7112м.
Есть различные версии происхождения аршинной меры длины. Возможно, первоначально, «аршин» обозначал длину человеческого шага (порядка семидесяти сантиметров, при ходьбе по равнине, в среднем темпе) и являлся базовой величиной для других крупных мер определения длины, расстояний (сажень, верста).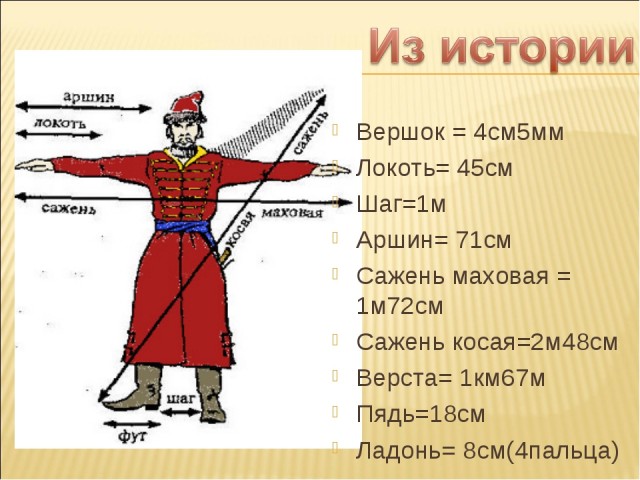 Корень «АР» в слове а р ш и н — в древнерусском языке (и в других, соседних) означает «ЗЕМЛЯ», «поверхность земли», и указывает на то, что эта мера могла применяться при определении длины пройденного пешком пути. Было и другое название этой меры – ШАГ. Практически, счёт мог производиться парами шагов взрослого человека («малыми саженями»; раз-два – один, раз-два – два, раз-два – три …), или тройками («казёнными саженями»; раз-два-три – один, раз-два-три – два …), а при измерении шагами небольших расстояний, применялся пошаговый счёт. В дальнейшем, стали так же применять, под этим названием, равную величину – длину руки.
Корень «АР» в слове а р ш и н — в древнерусском языке (и в других, соседних) означает «ЗЕМЛЯ», «поверхность земли», и указывает на то, что эта мера могла применяться при определении длины пройденного пешком пути. Было и другое название этой меры – ШАГ. Практически, счёт мог производиться парами шагов взрослого человека («малыми саженями»; раз-два – один, раз-два – два, раз-два – три …), или тройками («казёнными саженями»; раз-два-три – один, раз-два-три – два …), а при измерении шагами небольших расстояний, применялся пошаговый счёт. В дальнейшем, стали так же применять, под этим названием, равную величину – длину руки.
Пядь
. Для мелких мер длины базовой величиной была, применяемая испокон на Руси мера — «пядь», из которой глазомерно, легко можно было получить меньшие доли – два вершка (1/2 пяди) или вершок (1/4 пяди). ПЯДЬ (пядница) — древняя русская мера длины.
МАЛАЯ ПЯДЬ — расстояние между концами расставленных большого и указательного (или среднего) пальцев = 17,78 см.
БОЛЬШАЯ ПЯДЬ — расстояние между концами большого пальца и мизинца (22-23 см.).
ПЯДЬ С КУВЫРКОМ («пядень с кувырком», по Далю — ‘пядь с кувыркой’) — пядь с прибавкой двух суставов указательного палица = 27-31 см
Верста
ВЕРСТА — старорусская путевая мера (её раннее название — »поприще»). Этим словом, первоначально называли расстояние, пройденное от одного поворота плуга до другого во время пахоты. Два названия долгое время употреблялись параллельно, как синонимы. «Верстой» также назывался верстовой столб на дороге.
Величина версты неоднократно менялась в зависимости от числа сажен, входивших в неё, и величины сажени. До царя Алексея Михайловича в 1 версте считали 1000 саженей.
Сажень
САЖЕНЬ — одна из наиболее распространенных на Руси мер длины..
Наименование с а ж е н ь происходит от глагола сягать (досягать) — на сколько можно было дотянуться рукой. Для определения значения древнерусской сажени большую роль сыграла находка камня, на котором была высечена славянскими буквами надпись: «В лето 6576 (1068 г.) индикта 6 дня, Глеб князь мерил … 10000 и 4000 сажен». Из сравнения этого результата с измерениями топографов получено значение сажени 151,4 см. С этим значением совпали результаты измерений храмов и значение русских народных мер. Существовали саженные мерные веревки и деревянные «складени», имевшие применение при измерении расстояний и в строительстве.
Для определения значения древнерусской сажени большую роль сыграла находка камня, на котором была высечена славянскими буквами надпись: «В лето 6576 (1068 г.) индикта 6 дня, Глеб князь мерил … 10000 и 4000 сажен». Из сравнения этого результата с измерениями топографов получено значение сажени 151,4 см. С этим значением совпали результаты измерений храмов и значение русских народных мер. Существовали саженные мерные веревки и деревянные «складени», имевшие применение при измерении расстояний и в строительстве.
«Маховая сажень» — 1,76м, расстояние между концами пальцев широко расставленных рук взрослого мужчины.
» Косая сажень » — 2,48м ,самая длинная: расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки
По данным историков и архитекторов, саженей было более 10 и они имели свои названия, были несоизмеримы и не кратны одна другой. Сажени: городовая — 284,8 см, без названия — 258,4 см, великая — 244,0 см, греческая — 230,4 см, казённая — 217,6 см, царская — 197,4 см, церковная — 186,4 см, народная — 176,0 см, кладочная — 159,7 см, простая — 150,8 см, малая — 142,4 см и ещё одна без названия — 134,5 см (данные из одного источника), а так же — дворовая, мостовая.
Сажени: городовая — 284,8 см, без названия — 258,4 см, великая — 244,0 см, греческая — 230,4 см, казённая — 217,6 см, царская — 197,4 см, церковная — 186,4 см, народная — 176,0 см, кладочная — 159,7 см, простая — 150,8 см, малая — 142,4 см и ещё одна без названия — 134,5 см (данные из одного источника), а так же — дворовая, мостовая.
Локоть
ЛОКОТЬ равнялся длине руки от пальцев до локтя (по другим данным — «расстояние по прямой от локтевого сгиба до конца вытянутого среднего пальца руки»). Величина этой древнейшей меры длины, по разным источникам, составляла от 38 до 47 см. С 16-го века постепенно вытесняется аршином и в 19 веке почти не употребляется.
Локоть — исконно древнерусская мера длины, известная уже в 11 веке. Значение древнерусского локтя в 10.25-10.5 вершков (в среднем приблизительно 46-47 см) было получено из сравнения измерений в Иерусалимском храме
Вершок
ВЕРШОК — мера длины , равная ширине двух пальцев (указательного и среднего). Равнялся 1/16 аршина, 1/4 четверти. В современном исчислении — 4,44см. На
Равнялся 1/16 аршина, 1/4 четверти. В современном исчислении — 4,44см. На
именование «Вершок» происходит от слова «верх»
Меры объема.
Ведро.
Ведро = 1/40 бочки = 10 кружек = 30 фунтов воды = 100 чарок = 200 шкаликов = 12 литров. Это железная, деревянная или кожаная посуда, преимущественно цилиндрической формы, с ушками или дужкой для ношения. В обиходе, два ведра на коромысле должны быть в «подъём женщине». Деление на более мелкие меры проводилось по двоичному принципу: ведро делили на 2 полуведра или на 4 четверти ведра или на 8 получетвертей, а также на кружки и чарки. Древнейшая «международная» мера объёма — «горсть».
До середины XVII в. в ведре содержалось 12 кружек, во второй половине XVIIв. так называемое казённое ведро содержало 10 кружек, а в кружке — 10 чарок, так что в ведро входило 100 чарок. Затем, по указу 1652 года чарки сделали втрое больше по сравнению с прежними («чарки в три чарки»). В торговое ведро вмещалось 8 кружек. Значение ведра было переменным, а значение кружки неизменным, в 3 фунта воды (1228,5 грамма). Объем ведра был равен 134,297 кубических вершков.
Затем, по указу 1652 года чарки сделали втрое больше по сравнению с прежними («чарки в три чарки»). В торговое ведро вмещалось 8 кружек. Значение ведра было переменным, а значение кружки неизменным, в 3 фунта воды (1228,5 грамма). Объем ведра был равен 134,297 кубических вершков.
Бочка.
Бочка, как мера жидкостей применялась в основном в процессе торговли с иностранцами, которым запрещалось вести розничную торговлю вином на малые меры. Равнялась 40 ведрам (492 л)
Чаще всего в крестьянском быту использовались небольшие бочки и бочонки от 5-и до 120-и литров. Большие бочки вмещали до сорока вёдер (сороковки)
В XV в. еще были распространены старинные меры — голважня, лукно и уборок. В XVI-XVII вв. наряду с довольно распространенными коробьей и пузом часто встречается вятская хлебная мера куница, пермская сапца (мера соли и хлеба), старорусские луб и пошев.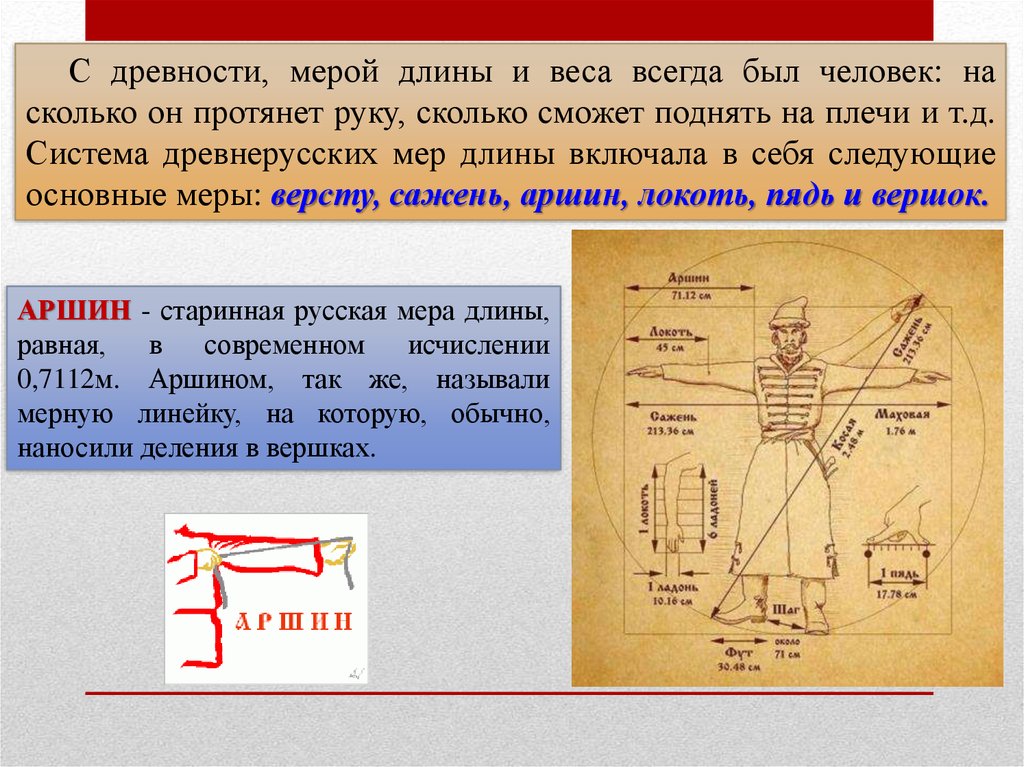 «.
«.
В житейском обиходе и в торговле употребляли разнообразные хозяйственные сосуды: котлы, жбаны, корчаги, братины, ендовы. Значение таких бытовых мер в разных местах было различно: например, емкость котлов колебалась от полуведра до 20 ведер. В XVII в. была введена система кубических единиц на основе 7-футовой сажени, а также введён термин кубический (или «кубичный»). Кубическая сажень содержала 27 кубических аршин или 343 кубических фута; кубический аршин — 4096 кубических вершков или 21952 кубических дюймов.
Кружка.Чарка.
Кружка (слово означает — ‘для пития по кругу’) = 10 чаркам = 1,23 л.
Современный граненый стакан раньше назывался «досканом» («строганые доски»), состоящим из обвязанных верёвкой ладов-дощечек, вокруг деревянного донца.
Чарка (рус. мера жидкости) = 1/10 штофа = 2 шкаликам = 0,123 л.
Ендова.Бурдюк.Корчага. Насадка.Ушат.Короб.Балакирь.
Насадка.Ушат.Короб.Балакирь.
Ендова- деревянная или металлическая утварь (часто, украшенная орнаментом), используемая для подачи к столу напитков. Представляла собой невысокую чашу с носиком. Металлическая ендова изготавливалась из меди или латуни. Деревянные ендовы изготавливали из осины, липы или берёзы.
Кожаный мешок (бурдюк) – до 60 л
Корчага — 12 л
Насадка — 2,5 ведра (Ногородская мера жидкости, XV век)
Ушат – высота посудины – 30-35 сантиметров, диаметр – 40 сантиметров, объем – 2 ведра или 22-25 л.
Короб — из цельных кусков луба, сшитых полосами лыка. Донце и верхняя крышка — из досок. Размеры – от небольших коробушек до больших «комодов»
Балакирь — долбленая деревянная посудина, объемом в 1/4—1/5, ведра.
Как правило, в центральной и западной частях России мерные емкости для хранения молока были пропорциональны суточным потребностям семьи и представляли собой разнообразные глиняные горшки, корчаги, подойники, крынки, кувшины, горланы, дойницы, берестяные бурачки с крышками, туеса, вместимость которых составляла примерно 1/4— 1/2 ведра (около 3—5 л). Емкости же махоток, ставцов, туесков, в которых держали кисломолочную продукцию— сметану, простоквашу и сливки, примерно соответствовали 1/8 ведра.
Емкости же махоток, ставцов, туесков, в которых держали кисломолочную продукцию— сметану, простоквашу и сливки, примерно соответствовали 1/8 ведра.
В старорусских мерах и в посуде, используемой для питья, заложен принцип соотношения объемов – 1:2:4:8:16.
Старинные меры объема:
1 куб. сажень = 9,713 куб. метра
1 куб. аршин = 0,3597 куб. метра
1 куб. вершок = 87,82 куб. см
1 куб. фут = 28,32 куб. дециметра (литра)
1 куб. дюйм = 16,39 куб. см
1 куб. линия = 16,39 куб. мм
1 Кварта — немногим больше литра.
:
.
Меры объема жидких и сыпучих тел:
1 четверть = 2,099 гектолитра = 209,9 л
1 четверик («мера») = 2,624 декалитра = 26,24 л
1 гарнец = 3,280 литра
Меры веса.
На Руси использовались в торговле следующие меры веса :
• берковец = 10 пудов
• пуд = 40 фунтов = 16,38 кг
• фунт (гривна) = 96 золотников = 0,41 кг
• лот = 3 золотника = 12,797 г
• золотник = 4,27 г
• доля = 0,044 г
Берковец.
БЕРКОВЕЦ — эта большая мера веса, употреблялась в оптовой торговле преимущественно для взвешивания воска, меда и т.д.
Берковец — от названия острова Бьерк. Так на Руси называлась мера веса в 10 пудов, как раз стандартная бочка с воском, которую один человек мог закатить на купеческую ладью, плывущую на этот самый остров. (163,8 кг).Известно упоминание берковца в XII веке в уставной грамоте князя Всеволода Гавриила Мстиславича новгородскому купечеству.
Золотник,куль,гарнец.
ЗОЛОТНИК равнялся 4,26 г. Про него говорили: «мал золотник да дорог». Это слово, первоначально обозначало зoлотую монету.
КУЛЬ (ранее Мехъ БЕРКОВЕЦ — эта большая мера веса, употреблялась в оптовой торговле преимущественно для взвешивания воска, меда и т.д.
ГАРНЕЦ («горшок» по-древнерусски). В Царстве Польском употреблялся до 1849г., разделялся на 4 кварты = 4 литра. В Галиции употреблялся до 1857г. = 3,85 литра (по Южакову). Общевосточнославянская мера сыпучих тел. «Найдется купец и на дырявый гарнец!»
Общевосточнославянская мера сыпучих тел. «Найдется купец и на дырявый гарнец!»
Четверик,осьмина,уборок.
ЧЕТВЕРИК = 26,25 литра. Мера емкости в России. В одном четверике 8 гарнцев, 1/8 четверти.
ОСЬМИНА (осьминка). Мера сыпучих тел равная половине четверти (105 – 125 литра). (по «Библиотеке Фольклора»)
УБОРОК — старинная русская мера небольшой вместимости – около ежедневной порции зерна (по «Русской Правде»).
Меры площади.
Основной мерой измерения площадей считалась десятина, а так же, доли десятины: полдесятины, четверть (четь — составляла 40 саженъ длины и 30 широты) и так далее. Землемеры применяли (особенно после «Соборного уложения» 1649 г.) преимущественно, казённую трехаршинную сажень, равную 2.1336 м., таким образом, десятина в 2400 квадратных сажен равнялась, приблизительно, 1. 093 гектара.
093 гектара.
Масштабы использования десятины и четверти росли в соответствии с освоением угодий и увеличением территории государства. Однако уже в первой половине XVI века выяснилось, что при измерении земель в четвертях общая опись земель затянется на много лет. И тогда в 40-х годах XVI века один из просвещеннейших людей Ермолай Еразм предложил пользоваться более крупной единицей — четверогранным поприщем, под которым подразумевалась квадратная площадь со стороной в 1000-саженную версту. Это предложение не было принято, но сыграло определенную роль в процессе введения большой сохи. Ермолай Еразм — один из первых метрологов-теоретиков, к тому же стремившийся сочетать решение метрологических и социальных вопросов. При определении площадей сенокосных угодий десятина внедрялась с большим трудом т.к. угодия из-за их расположения и неправильных форм были неудобны для измерения. Чаще применялась урожайная мера — копна. Постепенно эта мера получила значение, увязанное с десятиной, и подразделялась на 2 полукопны, на 4 четверти копны, на 8 полчетвертей копны и т. д. С течением времени копна, как мера площади, была приравнена 0,1 десятины (т.е. считали, что с десятины снимали в среднем 10 копен сена). Трудовые и посевные меры выражались через геометрическую меру — десятину.
д. С течением времени копна, как мера площади, была приравнена 0,1 десятины (т.е. считали, что с десятины снимали в среднем 10 копен сена). Трудовые и посевные меры выражались через геометрическую меру — десятину.
Меры площади поверхности:
1 кв. верста = 250000 квадратных саженей = 1,138 кв. километра
1 десятина = 2400 квадратных саженей = 1,093 гектара
1 копна = 0,1 десятины
1 кв. сажень = 16 квадратных аршинов = 4,552 кв. метра
1 кв. аршин=0,5058 кв. метра
1 кв. вершок=19,76 кв. см
1 кв. фут=9,29 кв. дюйма=0,0929 кв. м
1 кв. дюйм=6,452 кв. сантиметра
1 кв. линия=6,452 кв. миллиметра
Спасибо за внимание!
Скачать презентацию
Физические величины. Измерение физических величин. Школьный курс физики
Главная | Физика 7 класс | Физические величины. Измерение физических величин
Измерение физических величин
В быту, технике, при изучении физических явлений часто приходится выполнять различные измерения. Так, например, изучая падение тела, необходимо измерить высоту, с которой падает тело, массу тела, его скорость, время падения. Высота, масса, скорость, время ит. д. являются физическими величинами. Физическую величину можно измерить.
Измерить какую-нибудь величину — это значит сравнить её с однородной величиной, принятой за единицу.
Так, например, измерить длину стола — значит сравнить её с другой длиной, которая принята за единицу длины, например с метром.
Для каждой физической величины приняты свои единицы.
Для удобства все страны мира стремятся пользоваться одинаковыми единицами физических величин. С 1963 г. в России и других странах применяется Международная система единиц — СИ (система интернациональная). В этой системе основной единицей длины является метр (1 м), единицей времени — секунда (1 с), единицей массы — килограмм (1 кг).
Часто применяют единицы, которые в 10, 100, 1000 и т. д. раз больше принятых единиц (кратные). Эти единицы получили наименования с соответствующими приставками, взятыми из греческого языка. «Дека» — 10, «гек- то» — 100, «кило» — 1000 и др.
Если используются единицы, которые в 10, 100 и 1000 и т. д. раз меньше принятых единиц (дольные), то применяют приставки, взятые из латинского языка. «Деци» — 0,1, «санти» — 0,01, «милли» — 0,001 и др.
Приставки к названиям единиц
| Кратные | Обозначение | Название | Множитель |
| г | гекто | 100 (или 102) | |
| к | кило | 1000 (или 103) | |
| M | мега | 1 000 000 (или 106) | |
| Дольные | Обозначение | Название | Множитель |
| д | деци | 0,1 (или 10-1) | |
| с | санти | 0,01 (или 10-2) | |
| м | милли | 0,001 (или 10-3) |
Пример. Длина теннисной ракетки 60 см. Выразите её длину в метрах (м).
Длина теннисной ракетки 60 см. Выразите её длину в метрах (м).
60 см = 0,6 м или 6 • 10-1 м.
Для проведения опытов необходимы приборы. Одни из них очень просты и предназначены для простых измерений. К таким приборам можно отнести: измерительную линейку, рулетку (рис. 6), измерительный цилиндр (рис. 7) и др.
Рис. 6. Приборы для измерения длины: а — линейка; б — рулетка
Рис. 7. Измерительный цилиндр
По мере развития физики приборы усложнялись и совершенствовались. Появились амперметры (рис. 8), вольтметры (рис. 9), секундомеры (рис. 10), термометры (рис. 11), электронные весы, шагомеры (рис. 12).
Рис. 8. Амперметр
Рис. 9. Вольтметр
Рис. 10. Секундомер
Рис. 11. Термометры: а — электронный; б — спиртовой
Рис. 12. Электронные приборы: весы, шагомер
Измерительные приборы, как правило, имеют шкалу. Это значит, что на приборе нанесены штриховые деления, а рядом написаны значения величин, соответствующие делениям.
Расстояния между двумя штрихами, возле которых написаны значения физической величины, могут быть дополнительно разделены ещё на несколько делений. Эти деления иногда не обозначены числами.
Определить, какому значению величины соответствует каждое самое малое деление, нетрудно. Так, например, на рисунке 6, а изображена измерительная линейка. Цифрами 1, 2, 3, 4 и т. д. обозначены расстояния между штрихами, которые разделены на 10 одинаковых делений. Следовательно, каждое деление (расстояние между ближайшими штрихами) соответствует 1 мм. Эта величина называется ценой деления шкалы прибора.
Перед тем как приступить к измерению физической величины, следует определить цену деления шкалы используемого прибора.
Для того чтобы определить цену деления, необходимо:
— найти два ближайших штриха шкалы, возле которых написаны значения величины;
— вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.
Определим цену деления шкалы термометра, изображённого на рисунке 11, б.
Возьмём два штриха, около которых нанесены значения измеряемой величины (температуры).
Например, штрихи с обозначениями 10 °С и 20 °С. Расстояния между этими штрихами разделены на 10 делений. Таким образом, цена каждого деления будет равна
Следовательно, термометр показывает 29 °С. Измерять физические величины в повседневной жизни приходится каждому из вас. Например, чтобы вовремя прийти в школу, приходится измерять время, которое вы тратите на дорогу.
Метеорологи для предсказания погоды измеряют температуру, атмосферное давление, скорость ветра. Врачи при исследовании пациентов измеряют его артериальное давление, температуру, вес. Модельеры, разрабатывая модели одежды, измеряют рост человека, длину рук и пр. Астрономы, изучая планеты, должны знать их температуру, расстояние, на которое они удалены от Земли, и др.
Вопросы:
1. Что значит измерить какую-либо величину?
Что значит измерить какую-либо величину?
2. Каковы единицы длины, времени, массы в СИ?
3. Как определяется цена деления шкалы измерительного прибора?
Упражнения:
Упражнение № 1
1. Определите цену деления секундомера (см. рис. 10).
2. По рисункам 8 и 9 определите цену деления амперметра и вольтметра.
Задания:
1. По Интернету найдите прибор для измерения артериального давления — тонометр механический. Определите цену деления шкалы. В каких единицах измеряют артериальное давление?
2. На сайте http://mer.kakras.ru найдите старинные меры объёма, используемые в Древней Руси.
3. Выразите свой вес в пудах, а рост в аршинах.
4. Запишите 2—3 пословицы, поговорки или образных выражения, в которых упоминаются старинные меры длины, массы, объёма и т. п.
Это любопытно…
Старинные меры
С давних времен человеку приходилось проводить измерения.
В русской системе мер, которая традиционно применялась на Руси, мерой длины, например, мог быть сам человек (рис. 13). Так, косая сажень — это расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки. Пядь или четверть — расстояние между концами расставленных большого и указательного пальцев руки.
Рис. 13. В старину мерой длины был сам человек
В 1899 году наряду с русской системой мер к использованию была разрешена метрическая система.
Сегодня в России применяется Международная система единиц, а старинные меры сохранились лишь в пословицах и поговорках.
Русские меры
Меры длины
1 аршин =71,12 см
1 вершок = 4,44 см
1 косая сажень =2,48 м
1 пядь (четверть) =17,78 см
1 верста = 1,0668 км
Меры веса
1 пуд = 16,38 кг
1 фунт = 0,41 кг
1 унция = 29,86 г
Иностранные меры
Меры длины
1 миля (англ.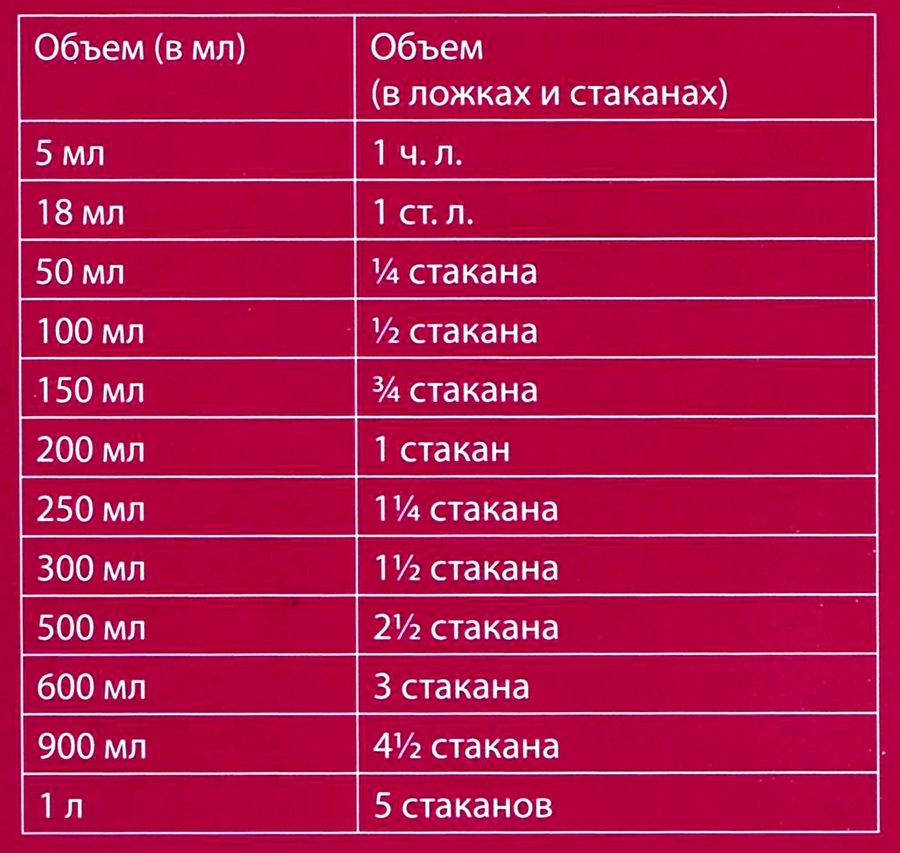 ) = 1,609 км.
) = 1,609 км.
1 ярд = 91,44 см
Меры веса
1 фунт (англ.) = 0,45359 кг
1 унция = 28,35 г.
Меры объёма
1 пинта (фр) = 0,9 л
1 пинта (англ., США) = 0,57 л
1 галлон = 4,546 л 1 баррель = 159 л
Единица измерения температуры
1 градус Фаренгейта = 5/9 градуса Цельсия
Предыдущая страницаСледующая страница
дм — мера длины. Единицы длины
Линейные меры длины, меры площади, меры объема, меры массы. Три варианта таблицы умножения. Десятичная система счисления
Таблица умножения. Вариант 1
Таблица умножения от 1 (одного) до 10 (десяти). Десятичная система
Таблица умножения. Вариант 2
Таблица умножения, сокращенная от 2 (двух) до 9 (девяти). Десятичная система
2 x 1 = 2 | 3 x 1 = 3 | 4 x 1 = 4 | 5 x 1 = 5 |
6 x 1 = 6 6 х 9 = 54 6 х 10 = 60 | 7 x 1 = 7 | 8 x 1 = 8 | 9 x 1 = 9 |
Таблица умножения.
 Вариант 3
Вариант 3Таблица умножения от 1 (одного) до 20 (двадцати). Десятичная система
Значение можно измерить. Такие понятия, как длина, площадь, объем, масса, время, скорость и т. д., называются величинами. Значение результат измерения , определяется числом, выраженным в определенных единицах. Единицы, в которых измеряется величина, называются 9.0131 единиц измерения .
Для обозначения величины пишется число, а рядом название единицы, в которой оно измерялось. Например, 5 см, 10 кг, 12 км, 5 мин. Каждое значение имеет бесконечное количество значений, например, длина может быть равна: 1 см, 2 см, 3 см и т.д.
Одно и то же значение может быть выражено в разных единицах, например, килограмм, грамм и тонна являются единицами веса. Одна и та же величина в разных единицах выражается разными числами. Например, 5 см = 50 мм (длина), 1 час = 60 минут (время), 2 кг = 2000 г (вес).
Измерить величину означает выяснить, сколько раз она содержит другую величину того же рода, взятую за единицу измерения.
Например, мы хотим знать точную длину комнаты. Значит, нам нужно измерить эту длину, используя другую хорошо известную нам длину, например, с помощью метра. Для этого отложите по метру по длине комнаты максимальное количество раз. Если он уместится ровно 7 раз по длине комнаты, то ее длина составит 7 метров.
В результате измерения величины получают либо именное число , например 12 метров, либо несколько именованных чисел, например 5 метров 7 сантиметров, совокупность которых называется составное именное число .
Меры
В каждом штате правительство установило определенные единицы измерения для различных величин. Точно рассчитанная единица измерения, взятая за образец, называется эталонной или образцовой единицей . Были изготовлены модельные единицы метра, килограмма, сантиметра и др., по которым изготавливаются единицы повседневного обихода. Единицы, вошедшие в обиход и утвержденные государством, называются мерами .
Меры называются однородными , если они служат для измерения величин одного и того же вида. Итак, граммы и килограммы являются однородными мерами, так как служат для измерения веса.
Единицы
Ниже приведены единицы измерения различных величин, которые часто встречаются в математических задачах:
Меры веса/массы
- 1 тонна = 10 центнеров
- 1 центнер = 100 килограммов
- 1 килограмм = 1000 грамм
- 1 грамм = 1000 миллиграммов
- 1 километр = 1000 метров
- 1 метр = 10 дециметров
- 1 дециметр = 10 сантиметров
- 1 сантиметр = 10 миллиметров
- 1 кв. км = 100 га
- 1 га = 10000 кв. метров
- 1 кв. метр = 10000 кв. сантиметров
- 1 кв. сантиметр = 100 кв. миллиметров
- 1 куб. метр = 1000 кубических метров дециметров
- 1 куб. дециметр = 1000 куб. сантиметры
- 1 куб.
 сантиметр = 1000 куб. миллиметры
сантиметр = 1000 куб. миллиметры
Рассмотрим другое значение, например литр . Литр используется для измерения вместимости сосудов. Литр – это объем, равный одному кубическому дециметру (1 литр = 1 кубический дециметр).
Меры времени
- 1 столетие = 100 лет
- 1 год = 12 месяцев
- 1 месяц = 30 дней
- 1 неделя = 7 дней
- 1 день = 24 часа
- 1 час = 60 минут
- 1 минута = 60 секунд
- 1 секунда = 1000 миллисекунд
Кроме того, используются такие единицы измерения времени, как четверть и декада.
- квартал — 3 месяца
- декада — 10 дней
Месяц принимается равным 30 дням, если не требуется указывать число и название месяца. Январь, март, май, июль, август, октябрь и декабрь — 31 день. В феврале простого года 28 дней, в феврале високосного 29.дней. Апрель, июнь, сентябрь, ноябрь — 30 дней.
Год — это (приблизительно) время, за которое Земля совершает один оборот вокруг Солнца. Принято считать каждые три года подряд по 365 дней, а следующий за ними четвертый – по 366 дней. Год с 366 днями называется високосным годом , а год, содержащий 365 дней — простым . К четвертому году добавляется один дополнительный день по следующей причине. Время обращения Земли вокруг Солнца содержит не ровно 365 дней, а 365 дней и 6 часов (приблизительно). Таким образом, простой год короче истинного года на 6 часов, а 4 простых года короче 4-х истинных лет на 24 часа, то есть на один день. Поэтому в один прекрасный день (29 февраля) добавляется к каждому четвертому году.
Принято считать каждые три года подряд по 365 дней, а следующий за ними четвертый – по 366 дней. Год с 366 днями называется високосным годом , а год, содержащий 365 дней — простым . К четвертому году добавляется один дополнительный день по следующей причине. Время обращения Земли вокруг Солнца содержит не ровно 365 дней, а 365 дней и 6 часов (приблизительно). Таким образом, простой год короче истинного года на 6 часов, а 4 простых года короче 4-х истинных лет на 24 часа, то есть на один день. Поэтому в один прекрасный день (29 февраля) добавляется к каждому четвертому году.
О других типах величин вы узнаете по мере дальнейшего изучения различных наук.
Сокращения мер
Сокращенные наименования мер обычно пишут без точки:
| Меры веса/массы
|
Меры площади (квадратные меры)
|
|
Меры времени
| Мера вместимости судов
|
Измерительные приборы
Для измерения различных величин используются специальные измерительные приборы. Некоторые из них очень просты и предназначены для простых измерений. К таким приспособлениям относятся мерная линейка, рулетка, мерный цилиндр и др. Другие измерительные приспособления более сложны. К таким приборам относятся секундомеры, термометры, электронные весы и др.
Другие измерительные приспособления более сложны. К таким приборам относятся секундомеры, термометры, электронные весы и др.
Средства измерений, как правило, имеют мерную шкалу (или короткую шкалу). Это означает, что на приборе отмечены деления тире, и рядом с каждым делением тире написано соответствующее значение количества. Расстояние между двумя штрихами, рядом с которым пишется значение значения, может быть дополнительно разделено еще на несколько более мелких делений, эти деления чаще всего цифрами не обозначаются.
Несложно определить, какое значение значения соответствует каждому наименьшему делению. Так, например, на рисунке ниже изображена измерительная линейка:
Цифры 1, 2, 3, 4 и т. д. обозначают расстояния между штрихами, которые разбиты на 10 равных делений. Следовательно, каждое деление (расстояние между ближайшими штрихами) соответствует 1 мм. Это значение называется делением шкалы измерительным прибором.
Прежде чем приступить к измерению величины, следует определить значение деления шкалы используемого прибора.
Для того, чтобы определить цену деления, необходимо:
- Найти два ближайших штриха шкалы, рядом с которыми написаны значения величины.
- Вычесть меньшее значение из большего и разделить полученное число на количество промежуточных делений.
В качестве примера определим значение деления шкалы термометра, показанного на рисунке слева.
Возьмем два штриха, возле которых нанесены числовые значения измеряемой величины (температуры).
Например, штрихи с символами 20 °С и 30 °С. Расстояние между этими штрихами делится на 10 делений. Таким образом, цена каждого деления будет равна:
(30 °С — 20 °С) : 10 = 1 °С
Следовательно, термометр показывает 47 °С.
Каждому из нас в повседневной жизни постоянно приходится измерять различные величины. Например, чтобы прийти в школу или на работу вовремя, нужно измерять время, которое будет потрачено на дорогу. Метеорологи измеряют температуру, атмосферное давление, скорость ветра и т. д., чтобы предсказать погоду.
д., чтобы предсказать погоду.
Этот урок не будет новым для новичков. Все мы слышали из школы такие понятия, как сантиметр, метр, километр. А когда дело касалось массы, обычно говорили граммы, килограммы, тонны.
Сантиметры, метры и километры; граммы, килограммы и тонны имеют одно общее название — единицы измерения физических величин .
В этом уроке мы рассмотрим самые популярные единицы измерения, но не будем углубляться в эту тему, так как единицы измерения уходят в область физики. Сегодня мы вынуждены изучать часть физики, так как она нам нужна для дальнейшего изучения математики.
Содержание урока
Единицы длиныДля измерения длины используются следующие единицы измерения:
- миллиметра;
- сантиметра;
- дециметра;
- метра;
- км.
миллиметр (мм). Даже миллиметры можно увидеть своими глазами, если взять линейку, которой мы пользовались в школе каждый день.
Маленькие линии, идущие подряд друг за другом, составляют миллиметры. Точнее, расстояние между этими линиями составляет один миллиметр (1 мм):
сантиметр (см). На линейке каждый сантиметр обозначен цифрой. Например, наша линейка, которая была на первом рисунке, имела длину 15 сантиметров. Последний сантиметр на этой линейке отмечен цифрой 15.
В одном сантиметре 10 миллиметров. Вы можете поставить знак равенства между одним сантиметром и десятью миллиметрами, так как они обозначают одинаковую длину:
1 см=10 мм
Вы можете убедиться сами, если посчитаете количество миллиметров на предыдущем рисунке. Вы обнаружите, что число миллиметров (расстояние между линиями) равно 10.
Следующая единица длины дециметр (дм). В одном дециметре десять сантиметров. Между одним дециметром и десятью сантиметрами можно поставить знак равенства, так как они обозначают одну и ту же длину:
1 дм = 10 см
В этом можно убедиться, если посчитать количество сантиметров на следующем рисунке:
Вы обнаружите, что количество сантиметров равно 10.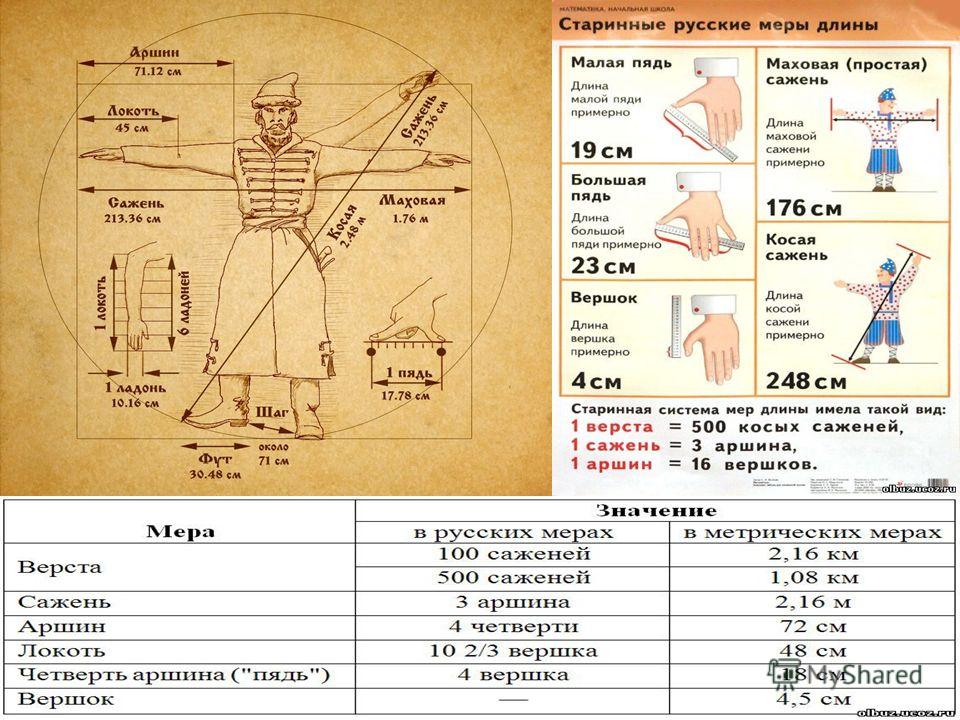
Следующая единица измерения метр (м). В одном метре десять дециметров. Между одним метром и десятью дециметрами можно поставить знак равенства, так как они обозначают одинаковую длину:
1 м = 10 дм
К сожалению, метр не может быть проиллюстрирован на рисунке, так как он довольно большой. Если вы хотите увидеть счетчик вживую, возьмите рулетку. У каждого есть в доме. На рулетке один метр будет обозначаться как 100 см. Это потому, что в одном метре десять дециметров, а в десяти дециметрах — сто сантиметров:
1 м = 10 дм = 100 см
100 получается путем перевода одного метра в сантиметры. Это отдельная тема, которую мы рассмотрим чуть позже. А пока перейдем к следующей единице длины, которая называется километр.
Километр считается наибольшей единицей измерения длины. Конечно, есть и другие более старые единицы, такие как мегаметр, гигаметр, тераметр, но мы их рассматривать не будем, так как километра нам достаточно для дальнейшего изучения математики.
В одном километре тысяча метров. Между одним километром и тысячей метров можно поставить знак равенства, так как они обозначают одинаковую длину:
1 км = 1000 м
Расстояния между городами и странами измеряются в километрах. Например, расстояние от Москвы до Санкт-Петербурга составляет около 714 километров.
Международная система единиц СИМеждународная система единиц СИ представляет собой определенный набор общепринятых физических величин.
Основной целью международной системы единиц СИ является достижение соглашений между странами.
Мы знаем, что языки и традиции стран мира разные. Ничего не поделаешь. Но законы математики и физики везде работают одинаково. Если в одной стране «дважды два четыре», то в другой стране «дважды два четыре».
Основная проблема заключалась в том, что для каждой физической величины существует несколько единиц измерения. Например, мы только что узнали, что для измерения длины существуют миллиметры, сантиметры, дециметры, метры и километры. Если несколько ученых, говорящих на разных языках, собираются в одном месте для решения какой-то задачи, то такое большое разнообразие единиц длины может породить противоречия между этими учеными.
Если несколько ученых, говорящих на разных языках, собираются в одном месте для решения какой-то задачи, то такое большое разнообразие единиц длины может породить противоречия между этими учеными.
Один ученый скажет, что в их стране длина измеряется в метрах. Второй может сказать, что в их стране длина измеряется в километрах. Третий может предложить свою единицу измерения.
Поэтому была создана международная система единиц СИ. СИ — это сокращение от французского словосочетания Le Système International d’Unités, SI (что в переводе на русский означает — международная система единиц СИ).
В СИ перечислены наиболее популярные физические величины и каждая из них имеет свою общепринятую единицу измерения. Например, во всех странах при решении задач было оговорено, что длина будет измеряться в метрах. Поэтому при решении задач, если длина дана в другой единице измерения (например, в километрах), то ее необходимо перевести в метры. О том, как перевести одну единицу измерения в другую, мы поговорим чуть позже. А пока нарисуем нашу международную систему единиц СИ.
А пока нарисуем нашу международную систему единиц СИ.
Нашим рисунком будет таблица физических величин. Каждую изучаемую физическую величину мы включим в нашу таблицу и укажем единицу измерения, принятую во всех странах. Теперь мы изучили единицы измерения длины и узнали, что в системе СИ для измерения длины определены метры. Итак, наша таблица будет выглядеть так:
Единицы массыМасса – это мера количества вещества в теле. В народе массу тела называют весом. Обычно, когда что-то взвешивают, говорят «весит столько-то килограммов» , хотя речь идет не о весе, а о массе этого тела.
Однако масса и вес — разные понятия. Вес – это сила, с которой тело действует на горизонтальную опору. Вес измеряется в ньютонах. А масса – это величина, показывающая количество материи в этом теле.
Но нет ничего плохого в том, чтобы назвать массу тела весом. Даже в медицине говорят «вес человека» , хотя речь идет о массе человека. Главное, осознавать, что это разные понятия.
Главное, осознавать, что это разные понятия.
Для измерения массы используются следующие единицы измерения:
- миллиграмм;
- грамма;
- килограмма;
- центнера;
- тонны.
Наименьшая единица измерения – миллиграмм (мг). Миллиграмм скорее всего вы никогда не будете применять на практике. Их используют химики и другие ученые, работающие с небольшими веществами. Вам достаточно знать, что такая единица измерения массы существует.
Следующая единица измерения грамм (Г). В граммах принято измерять количество продукта при составлении рецепта.
В одном грамме тысяча миллиграммов. Между граммом и тысячей миллиграммов можно поставить знак равенства, так как они обозначают одну и ту же массу:
1 г = 1000 мг
Следующая единица измерения килограмм (кг). Килограмм является общепринятой единицей измерения. Он измеряет все. Килограмм входит в систему СИ. Давайте также включим в нашу таблицу СИ еще одну физическую величину. Назовем его «массовым»:
Назовем его «массовым»:
В одном килограмме тысяча граммов. Между одним килограммом и тысячей граммов можно поставить знак равенства, так как они обозначают одну и ту же массу:
1 кг = 1000 г
Следующая единица измерения центнер (с). В центнерах удобно измерять массу урожая, собранного с небольшого участка или массу какого-либо груза.
В одном центнере сто килограммов. Между одним центнером и ста килограммами можно поставить знак равенства, так как они обозначают одну и ту же массу:
1 q = 100 кг
Следующая единица измерения тонна (т). В тоннах обычно измеряют большие нагрузки и массы крупных тел. Например, масса космического корабля или автомобиля.
В одной тонне тысяча килограммов. Между тонной и тысячей килограммов можно поставить знак равенства, так как они обозначают одну и ту же массу:
1 т = 1000 кг
Единицы времени Нам не нужно объяснять, что такое время. Все знают, что такое время и зачем оно нужно. Если мы откроем дискуссию о том, что такое время, и попытаемся дать ему определение, то мы начнем углубляться в философию, а это не то, что нам сейчас нужно. Начнем с единиц времени.
Все знают, что такое время и зачем оно нужно. Если мы откроем дискуссию о том, что такое время, и попытаемся дать ему определение, то мы начнем углубляться в философию, а это не то, что нам сейчас нужно. Начнем с единиц времени.
Для измерения времени используются следующие единицы измерения:
- секунды;
- минуты; часы
- ;
- день.
Наименьшая единица измерения секунд (С). Конечно, есть и более мелкие единицы, такие как миллисекунды, микросекунды, наносекунды, но мы их рассматривать не будем, так как на данный момент в этом нет смысла.
В секундах измеряются различные показатели. Например, сколько секунд требуется спортсмену, чтобы пробежать 100 метров. Секунда входит в международную систему единиц измерения времени СИ и обозначается как «с». Давайте также включим в нашу таблицу СИ еще одну физическую величину. Назовем его «время»:
минута (м). В одной минуте 60 секунд. Вы можете поставить знак равенства между минутой и шестьюдесятью секундами, поскольку они представляют одно и то же время:
1 м = 60 с
Следующая единица измерения — час (ч). В одном часе 60 минут. Вы можете поставить знак равенства между одним часом и шестьюдесятью минутами, так как они представляют одно и то же время:
В одном часе 60 минут. Вы можете поставить знак равенства между одним часом и шестьюдесятью минутами, так как они представляют одно и то же время:
1 ч = 60 м
Например, если мы изучали этот урок один час и нас спрашивают, сколько времени мы потратили на его изучение, мы можем ответить двумя способами: «мы изучали урок один час» или около того «мы изучали урок шестьдесят минут» . В обоих случаях мы ответим правильно.
Следующая единица времени день . В сутках 24 часа. Между сутками и сутками можно поставить знак равенства, так как они обозначают одно и то же время:
1 день = 24 часа
Понравился урок?
Присоединяйтесь к нашей новой группе Вконтакте и начните получать уведомления о новых уроках
В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория «Ахиллес и черепаха». Вот как это звучит:
Вот как это звучит:
Допустим, Ахиллес бежит в десять раз быстрее черепахи и отстает от нее на тысячу шагов. За время, за которое Ахилл пробегает это расстояние, черепаха проползает сто шагов в том же направлении. Когда Ахиллес пробежит сто шагов, черепаха проползет еще десять шагов и так далее. Процесс будет продолжаться бесконечно, Ахиллес никогда не догонит черепаху.
Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они, так или иначе, считали апории Зенона. Потрясение было настолько сильным, что «… дискуссии продолжаются и в настоящее время, научное сообщество еще не успело прийти к единому мнению о сущности парадоксов… математический анализ, теория множеств, новые физические и философские подходы занимались изучением вопроса, ни одно из них не стало общепринятым решением проблемы… » [Википедия, «Апории Зенона»]. Все понимают, что их дурят, но никто не понимает, в чем состоит обман.
С точки зрения математики Зенон в своих апориях наглядно продемонстрировал переход от значения к «Этот переход подразумевает применение вместо констант. Насколько я понимаю, математический аппарат для применения переменных единиц измерения либо еще не разработан, либо он не применялся к апориям Зенона. Применение нашей обычной логики приводит нас к ловушка. Мы по инерции мышления применяем постоянные единицы времени к обратным. С физической точки зрения это выглядит как замедление времени до полной остановки в тот момент, когда Ахиллес догоняет черепаху. Если время останавливается, Ахиллес уже не может догнать черепаху.0003
Если включить привычную нам логику, все встанет на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно время, затраченное на его преодоление, в десять раз меньше предыдущего. Если применить к этой ситуации понятие «бесконечность», то правильно будет сказать «Ахиллес бесконечно быстро догонит черепаху».
Как избежать этой логической ловушки? Оставайтесь в постоянных единицах времени и не переходите на обратные величины. На языке Зенона это выглядит так:
За время, необходимое Ахиллу, чтобы пробежать тысячу шагов, черепаха проползет сто шагов в том же направлении. За следующий промежуток времени, равный первому, Ахиллес пробежит еще тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес опережает черепаху на восемьсот шагов.
Такой подход адекватно описывает реальность без каких-либо логических парадоксов. Но это не полное решение проблемы. Утверждение Эйнштейна о непреодолимости скорости света очень похоже на апорию Зенона «Ахиллес и черепаха». Нам еще предстоит изучить, переосмыслить и решить эту проблему. И решение надо искать не в бесконечно больших числах, а в единицах измерения.
Еще одна интересная апория Зенона повествует о летящей стреле:
Летящая стрела неподвижна, так как в каждый момент времени она покоится, а так как она покоится в каждый момент времени, то она всегда покоится .
В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и есть движение. Здесь следует отметить еще один момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но их нельзя использовать для определения расстояния. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в одно и то же время, но по ним нельзя определить факт движения (естественно, для расчетов еще нужны дополнительные данные, в этом вам поможет тригонометрия). В частности, я хочу отметить, что две точки во времени и две точки в пространстве — это две разные вещи, которые не следует путать, поскольку они предоставляют разные возможности для исследования.
Среда, 4 июля 2018 г.
Очень хорошо различия между набором и мультимножеством описаны в Википедии. Мы смотрим.
Как видите, «в множестве не может быть двух одинаковых элементов», но если в множестве есть одинаковые элементы, такое множество называется «мультимножеством». Разумные существа никогда не поймут такой логики абсурда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных тренеров, проповедуя нам свои абсурдные идеи.
Когда-то инженеры, строившие мост, находились в лодке под мостом во время испытаний моста. Если мост рухнул, бездарный инженер погиб под обломками своего творения. Если мост выдерживал нагрузку, талантливый инженер строил другие мосты.
Как бы математики ни прикрывались фразой «заметьте, я в доме», а точнее «математика изучает абстрактные понятия», есть одна пуповина, которая неразрывно связывает их с реальностью. Эта пуповина — деньги. Применим математическую теорию множеств к самим математикам.
Мы очень хорошо изучили математику и сейчас сидим за кассой, платим зарплату. Вот математик приходит к нам за своими деньгами. Пересчитываем ему всю сумму и раскладываем у себя на столе в разные стопки, в которые кладем купюры одного номинала. Затем берем по одной банкноте из каждой стопки и отдаем математику его «математический набор зарплаты». Объясняем математикой, что остальные купюры он получит только тогда, когда докажет, что набор без одинаковых элементов не равен набору с одинаковыми элементами. Здесь начинается самое интересное.
Во-первых, сработает депутатская логика: «Вы можете применить это к другим, но не ко мне!» Далее начнутся заверения, что на банкнотах одного достоинства разные номера банкнот, а значит, их нельзя считать идентичными элементами. Что ж, считаем зарплату в монетах — цифр на монетах нет. Тут математик судорожно вспомнит физику: разные монеты имеют разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально. ..
..
А теперь у меня самый интересный вопрос: где та граница, за которой элементы мультимножества превращаются в элементы множества и наоборот? Такой линии не существует — все решают шаманы, наука здесь и близко не стоит.
Смотри сюда. Мы подбираем футбольные стадионы с одинаковой площадью поля. Площадь полей одинаковая, значит у нас мультисет. Но если рассматривать названия одних и тех же стадионов, то получается много, потому что названия разные. Как видите, один и тот же набор элементов является одновременно и набором, и мультимножеством. Как правильно? И тут математик-шаман-шуллер достает из рукава козырного туза и начинает нам рассказывать то ли о множестве, то ли о мультимножестве. В любом случае он убедит нас в своей правоте.
Чтобы понять, как современные шаманы оперируют теорией множеств, привязывая ее к реальности, достаточно ответить на один вопрос: чем элементы одного множества отличаются от элементов другого множества? Я вам покажу, без всяких «мыслимых как не единое целое» или «не мыслимых как единое целое».
Воскресенье, 18 марта 2018 г.
Сумма цифр числа — это танец шаманов с бубном, не имеющий никакого отношения к математике. Да, на уроках математики нас учат находить сумму цифр числа и пользоваться ею, но они для этого и шаманы, чтобы учить потомков своим навыкам и мудрости, иначе шаманы просто вымрут.
Вам нужны доказательства? Откройте Википедию и попробуйте найти страницу «Сумма цифр числа». Она не существует. В математике нет формулы, по которой можно найти сумму цифр любого числа. Ведь числа — это графические символы, которыми мы пишем числа, а на языке математики задача звучит так: «Найди сумму графических символов, представляющих какое-либо число». Математики не могут решить эту задачу, а вот шаманы элементарно могут.
Давайте разберемся, что и как мы делаем, чтобы найти сумму цифр заданного числа. И так, допустим, у нас есть число 12345. Что нужно сделать, чтобы найти сумму цифр этого числа? Рассмотрим все шаги по порядку.
1. Запишите номер на листе бумаги. Что мы наделали? Мы преобразовали число в числовой графический символ. Это не математическая операция.
Запишите номер на листе бумаги. Что мы наделали? Мы преобразовали число в числовой графический символ. Это не математическая операция.
2. Разрезаем одну полученную картинку на несколько картинок, содержащих отдельные номера. Вырезание изображения — это не математическая операция.
3. Преобразование отдельных графических символов в числа. Это не математическая операция.
4. Сложите полученные числа. Теперь это математика.
Сумма цифр числа 12345 равна 15. Это «курсы кройки и шитья» от шаманов, используемые математиками. Но это не все.
С точки зрения математики не имеет значения, в какой системе счисления мы пишем число. Так, в разных системах счисления сумма цифр одного и того же числа будет разной. В математике система счисления обозначается индексом справа от числа. С большим числом 12345 голову морочить не хочется, считайте число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, мы это уже сделали. Посмотрим на результат.
Посмотрим на результат.
Как видите, в разных системах счисления сумма цифр одного и того же числа разная. Этот результат не имеет ничего общего с математикой. Это все равно, как если бы вы получили совсем другие результаты при определении площади прямоугольника в метрах и сантиметрах.
Ноль во всех системах счисления выглядит одинаково и не имеет суммы цифр. Это еще один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего кроме чисел не существует? Для шаманов я могу это допустить, а для ученых — нет. Реальность — это не только цифры.
Полученный результат следует рассматривать как доказательство того, что системы счисления являются единицами измерения чисел. Ведь мы не можем сравнивать числа с разными единицами измерения. Если одни и те же действия с разными единицами измерения одной и той же величины приводят к разным результатам после их сравнения, то это не имеет никакого отношения к математике.
Что такое настоящая математика? Это когда результат математического действия не зависит от значения числа, используемой единицы измерения и от того, кто выполняет это действие.
Открывает дверь и говорит:
Ой! Это не женский туалет?
— Молодая женщина! Это лаборатория для изучения беспредельной святости душ при вознесении на небо! Нимб сверху и стрелка вверх. Какой еще туалет?
Женщина… Ореол сверху и стрелка вниз — мужчина.
Если у вас такое произведение дизайнерского искусства мелькает перед глазами несколько раз в день,
Тогда неудивительно, что вы вдруг обнаруживаете странный значок в своей машине:
Лично я делаю над собой усилие, чтобы увидеть у какающего человека минус четыре градуса (одна картинка) (композиция из нескольких картинок: знак минус, цифра четыре, обозначение градусов). И я не считаю эту девушку дурой, не знающей физики. Просто у нее дуговой стереотип восприятия графических образов. И математики учат нас этому все время. Вот пример.
И математики учат нас этому все время. Вот пример.
1А не «минус четыре градуса» или «один а». Это «какающий человечек» или число «двадцать шесть» в шестнадцатеричной системе счисления. Те люди, которые постоянно работают в этой системе счисления, автоматически воспринимают цифру и букву как один графический символ.
В этом уроке мы рассмотрим единицы длины, площади и таблицу единиц площади. Рассмотрите различные единицы измерения длины и площади, выясните, в каких случаях они используются. Систематизируем наши знания с помощью таблицы. Решим ряд примеров перевода одной единицы измерения в другую.
Вы знакомы с различными единицами длины. Какими единицами длины удобно пользоваться при измерении толщины спички или длины тела божьей коровки? Я думаю, вы сказали миллиметры.
Какой единицей длины удобно пользоваться при измерении длины карандаша? Разумеется, в сантиметрах (см. рис. 1).
Рис. 1. Измерение длины
Какие единицы длины удобно использовать при измерении ширины или длины окна? Удобно мерить в дециметрах.
А длина коридора или длина забора? Воспользуемся метрами (см. рис. 2).
Рис. 2. Измерение длины
Для измерения больших расстояний, например, расстояний между городами, используется более крупная, чем метр, единица длины — километр (см. рис. 3).
Рис. 3. Измерение длины
В 1 километре 1000 метров.
Выразите расстояние в километрах.
1 километр — это тысяча метров, поэтому число тысяч будет означать километры.
8000 м = 8 км
385007 м = 385 км 7 м
34125 м = 34 км 125 м
В числе сотен, десятков и единиц указываются метры.
Можно рассуждать иначе: 1 км в тысячу раз больше 1 метра, значит, количество километров должно быть в 1000 раз меньше количества метров. Следовательно, 8000:1000=8, цифра 8 означает количество километров.
385007: 1000 = 385 (остальные 7). Число 385 обозначает километры, остаток – количество метров.
34125:1000 = 34 (ост. 125), то есть 34 километра 125 метров.
Прочитать таблицу единиц длины (см. рис. 4). Постарайтесь запомнить это.
Рис. 4. Таблица единиц длины
Для измерения площадей используются различные единицы измерения. Квадратный сантиметр – это квадрат со стороной 1 см (см. рис. 5), квадратный дециметр – это квадрат со стороной 1 дм (см. рис. 6), квадратный метр – это квадрат со стороной 1 м (см. рис. .7).
Рис.5. квадратный сантиметр
Рис. 6. Квадратный дециметр
Рис. 7. Квадратный метр
Для измерения больших площадей используется квадратный километр – это квадрат, сторона которого равна 1 км (см. рис. 8).
Рис. 8. Квадратный километр
Слова «квадратный километр» сокращают цифрой следующим образом – 1 км 2 , 3 км 2 , 12 км 2 . В квадратных километрах, например, измеряют площади городов, площадь Москва S = 1091 км 2 .
Вычислите, сколько квадратных метров в одном квадратном километре. Чтобы найти площадь квадрата, умножьте длину на ширину. Дан квадрат со стороной 1 км. Мы знаем, что 1 км = 1000 м, поэтому чтобы найти площадь такого квадрата, умножаем 1000 м на 1000 м, получаем 1 000 000 м 2 = 1 км 2.
Дан квадрат со стороной 1 км. Мы знаем, что 1 км = 1000 м, поэтому чтобы найти площадь такого квадрата, умножаем 1000 м на 1000 м, получаем 1 000 000 м 2 = 1 км 2.
Выразим в квадратных метрах 2 км 2 . Будем рассуждать так: так как 1 км 2 равен 1 000 000 м 2 , то есть количество квадратных метров в миллион раз больше количества квадратных километров, значит 2 умножаем на 1 000 000, мы получаем 2 000 000 м. 2.
56 км 2: умножьте 56 на 1 000 000, мы получаем 56 000 000 м. 2.
202 км 2 15 М 2: 202 ∙ 1 000 000 + 15 = 202 000 000 М 2 + 15 М = 202 000,015 М. 2.
Для измерения небольших площадей используется квадратный миллиметр (мм 2). Это квадрат со стороной 1 мм. Слова «квадратный миллиметр» с цифрой записываются так: 1 мм 2, 7 мм 2, 31 мм 2.
Подсчитайте, сколько квадратных миллиметров в одном квадратном сантиметре. Чтобы найти площадь квадрата, умножьте длину на ширину. Нам дан квадрат со стороной 1 см. Мы знаем, что 1 см = 10 мм. Итак, чтобы найти площадь такого квадрата, умножаем 10 мм на 10 мм, получаем 100 мм 2 .
Выразим в квадратных миллиметрах 4 см 2 . Будем рассуждать так: так как 1 см 2 равен 100 мм 2 , то есть число мм 2 в 100 раз больше числа см 2, поэтому умножаем 4 на 100, получаем 400 мм 2.
16 см 2 : 16 умножить на 100 = 1600 мм 2 . площади, как ар и гектар часто используются. Ар представляет собой квадрат со стороной 10 м (см. рис. 9). С цифрами ар пишут короче: 1 а, 5 а, 12 а.
Рис. 9. 1 ар
1 а = 100 м 2 , поэтому его часто называют сотней.
Гектар – это квадрат со стороной 100 м (см. рис. 10). Слово «га» с цифрами сокращается так: 1 га, 6 га, 23 га. 1 га = 10000 м 2 .
Рис. 10. 1 га
Подсчитайте, сколько соток в 1 га.
1 га = 10000 м 2
1 а = 100 м 2 , тогда 10000: 100 = 100 а
Теперь внимательно рассмотрите таблицу единиц площади (см. рис. 11), постарайтесь ее запомнить.
Рис. 11. Таблица единиц площади
На уроке мы познакомились с новой единицей длины — км и единицами площади — м 2 , км 2 , а, га.
- Башмаков М.И. Нефедова М.Г. Математика. 4 класс. М.: Астрель, 2009..
- М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и другие. Математика. 4 класс. Часть 1 из 2, 2011.
- Демидова Т. Е. Козлова С. А. Тонких А. П. Математика. 4 класс 2 изд., исправлен. — М.: Баласс, 2013.
- School.xvatit.com().
- Мер.какрас.ру ().
- dpva.info().
Домашнее задание
- Найдите площадь квадрата со стороной 15 см.
- Express: в квадратных метрах: 5 га; 3 га 18 а; 247 акров; 16 а;
- в га: 420 000 м 2 ; 45 км 2 19 га;
- в акрах: 43 га; 4 га 5 а; 30 700 м 2 ; 5 км2 13 га;
- в гектарах и акрах: 930 а; 45 700 м2.
Сантиметр и миллиметр Но сначала давайте рассмотрим основной инструмент, которым пользуются ученики — линейку . Взгляните на картинку. Сантиметр делится пополам, на пять миллиметров, меньшим делением. Сантиметр обозначается как: см. Для измерения отрезка линейка прикладывается с нулем деления к началу измеряемого отрезка, как показано на рисунке. Деление, на котором заканчивается отрезок, является длиной этого отрезка. Длина отрезка на рисунке равна 5 см или 50 мм. На следующем рисунке показана линия длиной 5 см 6 мм или 56 мм. Давайте рассмотрим несколько примеров перевода различных единиц длины: Например, нам нужно перевести 1 м 30 см в сантиметры. Мы знаем, что 1 метр — 100 сантиметров… Получается: 100 см + 30 см = 130 см Для обратного перевода отделяем сто сантиметров — это 1м и осталось еще 30см. Ответ: 1 м 30 см. Если мы хотим выразить сантиметры в миллиметрах, то помним, что в 1 сантиметре — 10 миллиметров. Например, переведем 28 см в миллиметры: 28 × 10 = 280 Это означает 28 см — 280 мм. СчетчикОсновная единица длины метр … Остальные единицы образованы от метра с использованием латинских префиксов. Например, в слове сантиметр латинская приставка санти означает сто, а значит, один метр равен ста сантиметрам. В слове миллиметр приставка миллиметр тысяча, что означает, что в одном метре тысяча миллиметров. Десять сантиметров это 1 дециметр … Обозначается: дм. 1 метр — 10 дециметров Выразите в сантиметрах: 1 дм = 10 см 4 дм = 40 см 3 дм 4 см = 30 см + 4 см = 34 см 1 м 2 дм 5 см = 100 см + 20 см + 5 см = 125 см Теперь выразим в дециметрах: 1 м = 10 дм 4 м 8 дм = 48 дм 20 см = 2 дм Столько разных видов измерений и как можно сравнивать длину разных отрезков, если первый отрезок 5 см длиной 10 мм, а второй 10 дм. Для сравнения результатов измерений необходимо выразить их в одних и тех же единицах измерения. Итак, переведем длину наших отрезков в сантиметры: 5 см 10 мм = 51 см 10 дм = 100 см 51 см Это означает, что второй сегмент длиннее первого. кмБольшие расстояния измеряются в километрах. V 1 километр — 1000 метров . Слово километр образовано с греческой приставкой кило — 1000. Выразим километры в метрах: 3 км = 3000 м 23 км = 23000 м И обратно: 2400 м = 2 км 400 м 7650 м = 7 км 650 м Итак, сведем все единицы измерения в одну таблицу: Таблица измерений.
Таблица преобразования единиц измерения.
| ||||
Азбука измерения объемов внутримозгового кровоизлияния
Сохранить цитату в файл
Формат: Резюме (текст) PubMedPMIDAbstract (текст) CSV
Добавить в коллекции
- Создать новую коллекцию
- Добавить в существующую коллекцию
Назовите свою коллекцию:
Имя должно содержать менее 100 символов
Выберите коллекцию:
Невозможно загрузить вашу коллекцию из-за ошибки
Повторите попытку
Добавить в мою библиографию
- Моя библиография
Не удалось загрузить делегатов из-за ошибки
Повторите попытку
Ваш сохраненный поиск
Название сохраненного поиска:
Условия поиска:
Тестовые условия поиска
Эл. адрес:
(изменить)
адрес:
(изменить)
Который день? Первое воскресеньеПервый понедельникПервый вторникПервая средаПервый четвергПервая пятницаПервая субботаПервый деньПервый будний день
Который день? воскресеньепонедельниквторниксредачетвергпятницасуббота
Формат отчета: SummarySummary (text)AbstractAbstract (text)PubMed
Отправить максимум: 1 шт. 5 шт. 10 шт. 20 шт. 50 шт. 100 шт. 200 шт.
Отправить, даже если нет новых результатов
Необязательный текст в электронном письме:
Создайте файл для внешнего программного обеспечения для управления цитированием
Полнотекстовые ссылки
Атыпон
Полнотекстовые ссылки
. 1996 авг; 27 (8): 1304-5.
1996 авг; 27 (8): 1304-5.
doi: 10.1161/01.стр.27.8.1304.
Р У Котари 1 , Т. Бротт, Дж. П. Бродерик, В. Г. Барсан, Л. Р. Зауэрбек, М. Зуккарелло, Дж. Хури
Принадлежности
принадлежность
- 1 Отделение неотложной медицины, Университет Цинциннати, Огайо 45267-0769, США. [email protected]
- PMID: 8711791
- DOI: 10.1161/01.стр.27.8.1304
R U Котари и др. Инсульт. 1996 авг.
. 1996 авг; 27 (8): 1304-5.
1996 авг; 27 (8): 1304-5.
doi: 10.1161/01.стр.27.8.1304.
Авторы
Р У Котари 1 , Т. Бротт, Дж. П. Бродерик, В. Г. Барсан, Л. Р. Зауэрбек, М. Зуккарелло, Дж. Хури
принадлежность
- 1 Отделение неотложной медицины, Университет Цинциннати, Огайо 45267-0769, США. [email protected]
- PMID: 8711791
- DOI: 10.1161/01.стр.27.8.1304
Абстрактный
г.
Предыстория и цель: Объем кровоизлияния является мощным предиктором 30-дневной смертности после спонтанного внутримозгового кровоизлияния (ВМК). Мы сравнили прикроватный метод измерения объема КТ ВМК с измерениями, выполненными с помощью компьютерного планиметрического анализа изображений.
Мы сравнили прикроватный метод измерения объема КТ ВМК с измерениями, выполненными с помощью компьютерного планиметрического анализа изображений.
Методы: Использовалась формула ABC/2, где А — наибольший диаметр кровоизлияния по данным КТ, В — диаметр под углом 90 градусов к А, С — приблизительное количество КТ-срезов с кровоизлиянием, умноженное на толщину среза.
Полученные результаты: Объемы ICH для 118 пациентов оценивались в среднем за 38 секунд и коррелировали с планиметрическими измерениями (R2 = 9,6). Межэкспертная и внутриэкспертная надежность была превосходной, с внутриклассовой корреляцией 0,99 для обоих.
Выводы: Мы пришли к выводу, что объем ICH можно точно оценить менее чем за 1 минуту с помощью простой формулы ABC/2.
Похожие статьи
ABC/XYZ оценивает объем внутримозгового кровоизлияния в процентах от общего объема головного мозга у детей.

Beslow LA, Ichord RN, Kasner SE, Mullen MT, Licht DJ, Smith SE, Storm PB, Jordan LC, Messé SR. Беслоу Л.А. и соавт. Инсульт. 2010 г., апрель; 41 (4): 691-4. doi: 10.1161/STROKEAHA.109.566430. Epub 2010 24 февраля. Инсульт. 2010. PMID: 20181678 Бесплатная статья ЧВК.
Сравнение методов расчета объема внутримозгового кровоизлияния и их влияние на инструменты оценки.
Хан М., Бэрд Г.Л., Элиас Р., Родригес-Средницки Дж., Яги С., Ян С., Коллинз С., Томпсон Б.Б., Венделл Л.С., Поттер Н.С., Фенел С., Саад А., Сильвер Б. Хан М. и др. J Нейровизуализация. 2017 янв; 27(1):144-148. дои: 10.1111/jon.12370. Epub 2016 14 июня. J Нейровизуализация. 2017. PMID: 27300754
Объемы гематомы при спонтанном внутримозговом кровоизлиянии: метод эллипса (ABC/2) дает меньшие объемы, чем объемы, измеренные планиметрическим методом.

Маэда А.К., Агияр Л.Р., Мартинс С., Бичиньо Г.Л., Гариба М.А. Маэда А.К. и др. Арк Нейропсиквиатр. 2013 авг; 71 (8): 540-4. doi: 10.1590/0004-282X20130084. Арк Нейропсиквиатр. 2013. PMID: 23982013
Сравнение метода оценки ABC/2 с компьютерным планиметрическим анализом внутримозгового паренхиматозного кровоизлияния, связанного с варфарином.
Huttner HB, Steiner T, Hartmann M, Köhrmann M, Juettler E, Mueller S, Wikner J, Meyding-Lamade U, Schramm P, Schwab S, Schellinger PD. Хаттнер Х.Б. и соавт. Инсульт. 2006 г., февраль; 37(2):404-8. doi: 10.1161/01.STR.0000198806.67472.5c. Epub 2005, 22 декабря. Инсульт. 2006. PMID: 16373654
Величина ошибки измерения объема гематомы при внутримозговом кровоизлиянии.

Родригес-Луна Д., Бойко М., Субраманиам С., Клоурфельд Э., Джо П., Дидерихс Б.Дж., Косиор Дж.С., Довлатшахи Д., Авив Р.И., Молина К.А., Хилл М.Д., Демчук А.М.; Исследовательская группа PREDICT/Sunnybrook ICH CTA. Родригес-Луна Д. и соавт. Инсульт. 2016 Апрель; 47 (4): 1124-6. doi: 10.1161/STROKEAHA.115.012170. Epub 2016 18 февраля. Инсульт. 2016. PMID: 26892283
Посмотреть все похожие статьи
Цитируется
Связь между субпопуляциями лейкоцитов и расширением гематомы после спонтанного внутримозгового кровоизлияния: ретроспективное когортное исследование.
Цинь Дж., Вэй Х., Лю Ю., Ду Л., Ся Дж. Цинь Дж. и др. Фронт Нейрол. 2022 6 сент.; 13:992851. doi: 10.3389/fneur.2022.992851. Электронная коллекция 2022. Фронт Нейрол. 2022. PMID: 36147038 Бесплатная статья ЧВК.

Фиброз печени связан с клиническими исходами у пациентов с внутримозговым кровоизлиянием.
Ван Дж., Бянь Л., Ван А., Чжан С., Ван Д., Цзян Р., Ван В., Ю. Ю., Лу Дж., Чжао Х. Ван Дж. и др. Нейропсихиатр Dis Treat. 2022 8 сентября; 18:2021-2030. дои: 10.2147/NDT.S375532. Электронная коллекция 2022. Нейропсихиатр Dis Treat. 2022. PMID: 36105249 Бесплатная статья ЧВК.
Расходы на лечение пациентов со спонтанным внутримозговым кровоизлиянием в течение одного года в отделении интенсивной терапии.
Смедс М., Скриварс М.Б., Рейникайнен М., Бендель С., Хоппу С., Лаитио Р., Ала-Кокко Т., Куртце С., Сибольт Г., Мартинес-Маяндер Н., Радж Р. Смедс М. и соавт. Eur Stroke J. 2022 Sep;7(3):267-279. дои: 10.1177/23969873221094705.
 Epub 2022 29 апр.
Евро Инсульт Дж. 2022.
PMID: 36082247
Бесплатная статья ЧВК.
Epub 2022 29 апр.
Евро Инсульт Дж. 2022.
PMID: 36082247
Бесплатная статья ЧВК.Маркеры внутримозгового кровоизлияния на бесконтрастной компьютерной томографии как предикторы признака динамического пятна на КТ перфузии и ассоциации с расширением гематомы и исходом.
Truong MQ, Metcalfe AV, Ovenden CD, Kleinig TJ, Barras CD. Truong MQ и др. Нейрорадиология. 9 сентября 2022 г. doi: 10.1007/s00234-022-03032-6. Онлайн перед печатью. Нейрорадиология. 2022. PMID: 36076088
Прогностическое значение отношения нейтрофилов к лимфоцитам на 30-дневные исходы у пациентов со спонтанным внутримозговым кровоизлиянием после хирургического лечения: ретроспективный анализ 128 пациентов.
Чжао И, Се И, Ли С, Ху М. Чжао Ю и др.



 2. В прозе и поэзии ……………………………………………………
2. В прозе и поэзии ……………………………………………………
 Погорель-ский
Погорель-ский »
»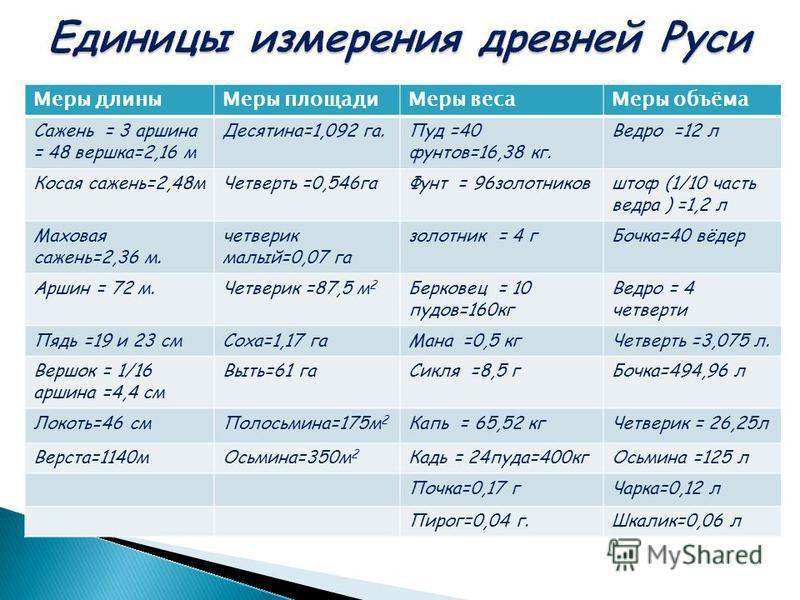 км — км 2
км — км 2 Минимальная цена деления линейки миллиметр … Обозначается: мм. Крупные деления обозначают сантиметр. В одном сантиметре 10 миллиметров.
Минимальная цена деления линейки миллиметр … Обозначается: мм. Крупные деления обозначают сантиметр. В одном сантиметре 10 миллиметров.
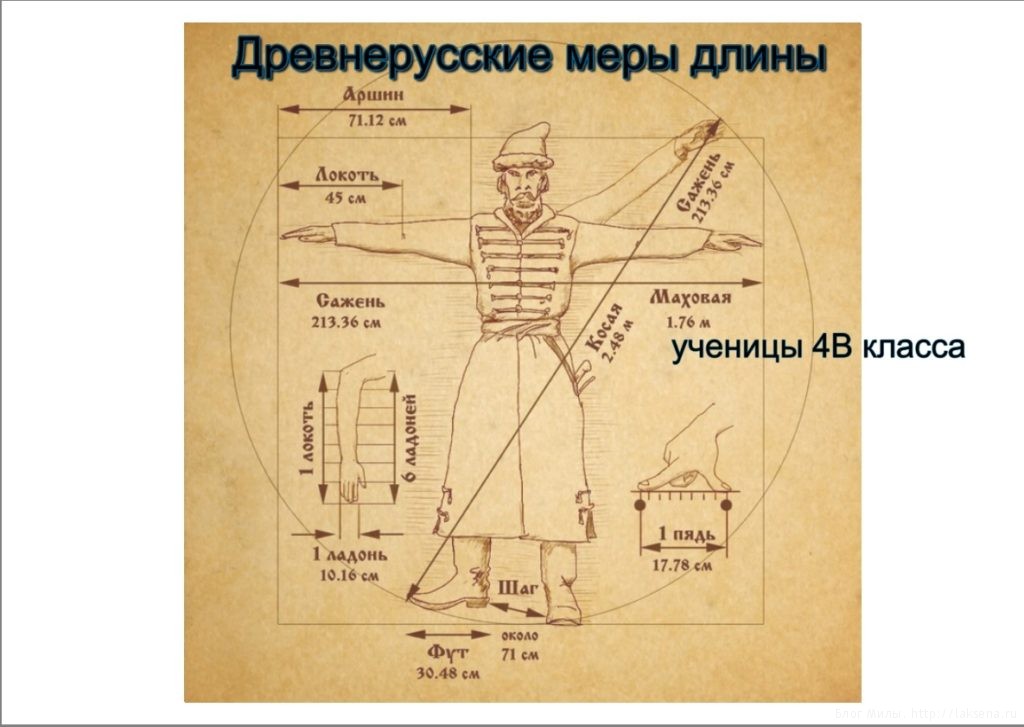 Разобраться в нашей задаче поможет главное правило сравнения значений:
Разобраться в нашей задаче поможет главное правило сравнения значений: м = 1 000 000 кв.м
м = 1 000 000 кв.м  ед. Преобразователь магнитодвижущей силы Преобразователь напряженности магнитного поля Преобразователь магнитного потока Преобразователь магнитной индукции Излучение. Конвертер мощности поглощенной дозы ионизирующего излучения Радиоактивность. Преобразователь излучения радиоактивного распада. Конвертер экспозиционной дозы Радиация. Конвертер поглощенной дозы Конвертер десятичной приставки Передача данных Конвертер единиц типографии и обработки изображений Конвертер единиц объема древесины Расчет молярной массы Периодическая таблица химических элементов Д. И. Менделеев
ед. Преобразователь магнитодвижущей силы Преобразователь напряженности магнитного поля Преобразователь магнитного потока Преобразователь магнитной индукции Излучение. Конвертер мощности поглощенной дозы ионизирующего излучения Радиоактивность. Преобразователь излучения радиоактивного распада. Конвертер экспозиционной дозы Радиация. Конвертер поглощенной дозы Конвертер десятичной приставки Передача данных Конвертер единиц типографии и обработки изображений Конвертер единиц объема древесины Расчет молярной массы Периодическая таблица химических элементов Д. И. Менделеев ) локоть (Великобритания) размах руки ноготь пальца дюйм (США, геодез.) ячменное зерно (англ. barleycorn) тысячная микродюйм ангстрем атомная единица длины x-единица Ферми Арпан пайка типографская точка твип локоть (шведский) сажень (шведский) калибр сантидюйм кен аршин актус (др. рим) вара де тареа вара кону кера вара кастеллана локоть (греч.) длинный тростник длинный локоть ладонь «палец» планковская длина классический электронный радиус боровский радиус экваториальный радиус Земли полярный радиус Земли расстояние от Земли до Солнца радиус Солнца световой наносекундный световой микросекундный световой миллисекундный световой час световой день световой день световая неделя Миллиард световых лет Расстояние от Земли до Луны кабельный (международный) кабельный (британский) кабельный (США ) морская миля (США) свет минута стеллаж единица горизонтальный шаг цицерон пиксель линия дюйм (русский) дюймы пролет фут сажень косая сажень верста граничная верста
) локоть (Великобритания) размах руки ноготь пальца дюйм (США, геодез.) ячменное зерно (англ. barleycorn) тысячная микродюйм ангстрем атомная единица длины x-единица Ферми Арпан пайка типографская точка твип локоть (шведский) сажень (шведский) калибр сантидюйм кен аршин актус (др. рим) вара де тареа вара кону кера вара кастеллана локоть (греч.) длинный тростник длинный локоть ладонь «палец» планковская длина классический электронный радиус боровский радиус экваториальный радиус Земли полярный радиус Земли расстояние от Земли до Солнца радиус Солнца световой наносекундный световой микросекундный световой миллисекундный световой час световой день световой день световая неделя Миллиард световых лет Расстояние от Земли до Луны кабельный (международный) кабельный (британский) кабельный (США ) морская миля (США) свет минута стеллаж единица горизонтальный шаг цицерон пиксель линия дюйм (русский) дюймы пролет фут сажень косая сажень верста граничная верста
 0003
0003 Это значение используется в научно-популярной литературе чаще, чем в физике и астрономии.
Это значение используется в научно-популярной литературе чаще, чем в физике и астрономии. Длина каждого из отрезков E1S и E2S равна одной астрономической единице. Если отложить отрезок через точку S, перпендикулярный Е1Е2, то он пройдет через точку пересечения отрезков Е1А2 и Е2А1, I. Расстояние от Солнца до точки I есть отрезок SI, он равен одному парсеку при угле между сегментами A1I и A2I составляет две угловые секунды.
Длина каждого из отрезков E1S и E2S равна одной астрономической единице. Если отложить отрезок через точку S, перпендикулярный Е1Е2, то он пройдет через точку пересечения отрезков Е1А2 и Е2А1, I. Расстояние от Солнца до точки I есть отрезок SI, он равен одному парсеку при угле между сегментами A1I и A2I составляет две угловые секунды. По-английски и лиги, и лиги называются одинаково, лига. В литературе le иногда встречается в названиях книг, например, «20 000 лье под водой» — знаменитый роман Жюля Верна.
По-английски и лиги, и лиги называются одинаково, лига. В литературе le иногда встречается в названиях книг, например, «20 000 лье под водой» — знаменитый роман Жюля Верна. Сегодня метр определяется как расстояние, пройденное светом в вакууме за 1/299 792 458 секунд.
Сегодня метр определяется как расстояние, пройденное светом в вакууме за 1/299 792 458 секунд.
 Дома мы используем метры для измерения длины комнаты. Когда мы едем куда-то, например, в другой город или на дачу, мы пользуемся единицей длины — километром.
Дома мы используем метры для измерения длины комнаты. Когда мы едем куда-то, например, в другой город или на дачу, мы пользуемся единицей длины — километром. расстояние до соседнего города;
расстояние до соседнего города; 
 Это очень удобно и практично. Если необходимо использовать более крупные меры массы, например, для измерения веса автомобиля, то применяют такие меры массы, как тонна или центнер.
Это очень удобно и практично. Если необходимо использовать более крупные меры массы, например, для измерения веса автомобиля, то применяют такие меры массы, как тонна или центнер. 


 Чтобы найти площадь квадрата, нужно длину умножить на ширину. Дан квадрат со стороной 1 км. Мы знаем, что 1 км = 1000 м, поэтому чтобы найти площадь такого квадрата, умножаем 1000 м на 1000 м, получаем 1 000 000 м 2 = 1 км 2.
Чтобы найти площадь квадрата, нужно длину умножить на ширину. Дан квадрат со стороной 1 км. Мы знаем, что 1 км = 1000 м, поэтому чтобы найти площадь такого квадрата, умножаем 1000 м на 1000 м, получаем 1 000 000 м 2 = 1 км 2.
 11. Таблица единиц площади
11. Таблица единиц площади