Расчет нагрузки на балку перекрытия. Красивые интерьеры и дизайн
Существуют специальные таблицы, позволяющие рассчитать предельно допустимую нагрузку на балку в зависимости от длины бревна и размера его поперечного сечения. Однако все приведенные величины являются лишь примерными. Для более точных расчетов необходимо учитывать дополнительные факторы, речь о которых пойдет ниже.
Восемь важных факторов при расчете нагрузки на балку перекрытия
Основой надежности крыши, стропил или любой другой несущей конструкции является несущая способность ее элементов, которая зависит от следующих факторов:
- сечение балки
- длина балки
- вид древесины
- расстояние между соединениями балок
- напряжение балки при изгибе
- напряжение на срез
- прогиб балки
- устойчивость балки
В качестве основы расчетов берется предельно допустимая нагрузка на 1 кв.м. площади. Средняя норма нагрузки в обычном жилом здании составляет минимум 200 килоньютонов (кН).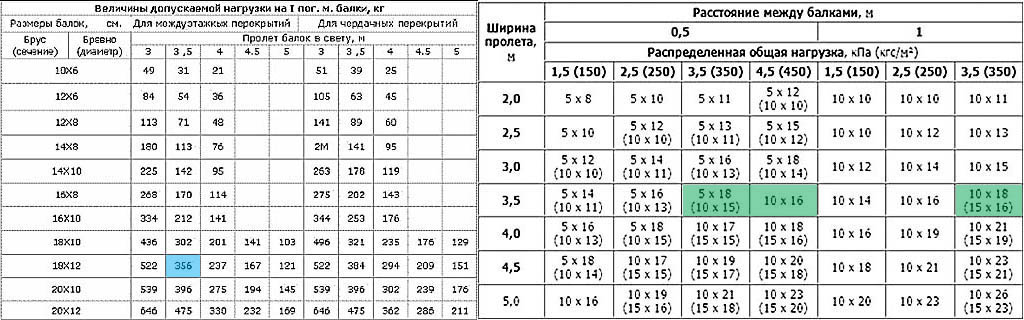
Один килоньютон — это чуть больше ста килограмм
Так как один килоньютон приблизительно равен ста килограммам, можно проводить и грубые расчеты «один к одному». Хотя если говорить точно, то 1 кН равен 101,97 кг. В таблице ниже вы найдете приблизительные значения предельно допустимой нагрузки на балку, выраженные в килограммах на метр:
| Сечение (см) | Длина балки (м) | Нагрузка (кг/м) |
|---|---|---|
| 6/10 | 3 | 1,63 |
| 6/10 | 10 | 0,73 |
| 6/20 | 3 | 3,26 |
| 6/20 | 10 | 1,47 |
| 8/10 | 3 | 1,80 |
| 8/10 | 10 | 0,98 |
| 8/20 | 3 | 3,59 |
| 8/20 | 10 | 1,96 |
| 10/10 | 3 | 1,94 |
| 10/10 | 10 | 1,17 |
| 10/20 | 3 | 3,87 |
| 10/20 | 10 | 2,33 |
Крепления часто бывают самым слабым местом
На безопасность влияют не только характеристики самих балок, но и допустимая предельная нагрузка всей конструкции. Потенциально слабыми местами могут быть:
Потенциально слабыми местами могут быть:
- удлинения балок
- места соединений
- внешние крепления
- выравнивающая балка
Если вес или длина балок в конструкции превышает допустимую норму, используйте опорные балки или раскосы под балки, которые примут на себя лишний вес. Кроме того, таким образом вы можете использовать имеющиеся под рукой балки малого сечения
Источник: diybook.de
Построение эпюр балки | buildingbook.ru
Эпюра — это вид графика, показывающий распределение нагрузки по стержню. Эпюра необходима, чтобы вычислить максимальные напряжения в стержне и на основе этих данных подобрать сечение для конструкции. Как построить эпюру подробно расписано в курсе сопротивления материалов, мы же остановимся на самых необходимых эпюрах для проектирования балок.
Из эпюры балки нам необходимо будет вычислить максимальный изгибающий момент, поперечную силу, опорные реакции стержня. Эти данные нам понадобятся для подбора сечения и проверочного расчета элемента конструкции.
Рассмотрим самые распространенные эпюры балки:
1) Балка имеет шарнирное закрепление по двум сторонам и равномерно-распределенную нагрузку.
Здесь и далее Q — Это поперечная сила, M — изгибающий момент.
Как видим максимальная поперечная нагрузка на балку находится в опорах балки, а максимальный момент в центре балки.
К полезной нагрузке можно прибавить и вес балки т.к. он, как правило, также равномерно распределен по длине балки.
2) Балка имеет шарнирное закрепление по двум сторонам и сосредоточенную нагрузку.
Этот вариант загрузки можно применить к подкрановой балке, хотя чаще всего подкрановая балка имеет несколько пролетов.
Максимальная поперечная сила возникает по всей длине участка от точки приложения силы до ближайшей опоры, причем чем ближе к опоре, тем больше поперечная сила. В расчетах этот показатель необходим чтобы рассчитать стенку балки на устойчивость и подобрать ребра жесткости в случае необходимости.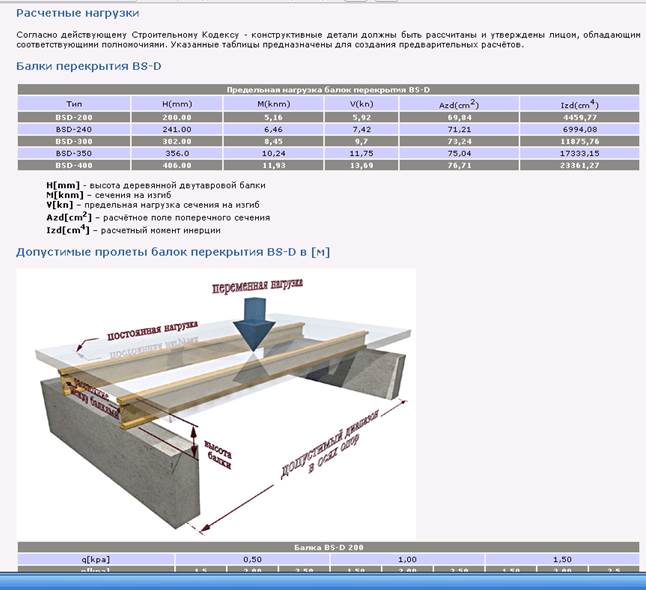
Максимальный момент возникает в точке приложения силы. Чем ближе точка приложения силы к центру балки, тем выше момент, поэтому если точка приложения нагрузки движется по балке, то подбор сечения необходимо сделать для приложения нагрузки по центру балки.
Эта эпюра не учитывает вес балки, но ее вес также необходимо считать. Для этого можно отдельно построить эпюру моментов для веса балки и сложить показатели в одинаковых точках.
3) Балка защемлена в опорах и равномерно-нагружена по всей длине
При защемлении в узлах максимальный момент в балке в 2-а раза ниже, чем в балке с равномерно-распределённой, однако необходимо сделать жесткий узел с колонной, что создает некоторые сложности. Кроме того момент от балки будет передаваться на колонны, как и момент с колонн будет передаваться на балку.
В расчетных программах необходимо быть внимательным и контролировать закрепление балок т.к. если расчет балки и подбор сечения будет произведен для жестко закрепленной балки, а в реальности узлы будут шарнирными, то балка будет посчитана не правильно и запас прочности может быть не достаточен.
4) Двухпролетная балка с шарнирными опорами и равномерно-распределенной нагрузкой
В данной схеме мы видим, что максимальный момент находиться на средней опоре, причем больше растянута верхняя часть балки.
Максимальная поперечная сила также находится в точке «В».
При расчете многопролетных балок необходимо учитывать то, что все пролеты могут быть не загружены равномерно, в этом случае эпюра 2-х пролетной балки выглядит следующим образом:
Как видим момент в пролете увеличился, все остальные параметры уменьшились, поэтому момент в пролете для расчета надо брать по этому варианту загружения.
_____________________________________________________________________
Как подобрать сечение стальной балки читайте в статье Расчет балки
Как правильно закрепить балку на колонне читайте в статье Опорные узлы балки
Расчет балки | Стеллажи
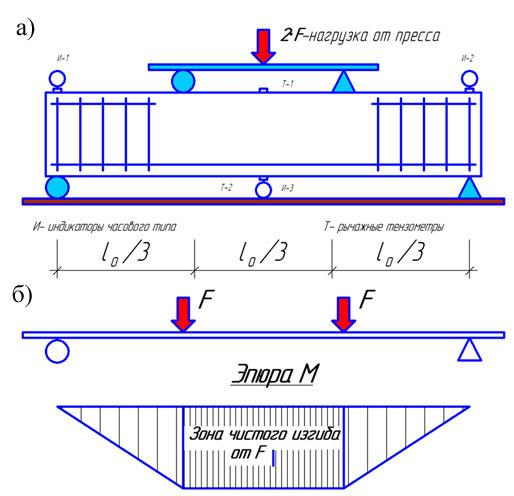
Груз опирается на балки.
При максимальной расчетной нагрузке прогиб балки не должен превышать 1/180 расстояния между опорами. Так, если длина балки 180 дюйм (4,57 м), то 1/180 длины составит 1 дюйм (25,4 мм), другими словами, допускается прогиб не более 1 дюйма. Если длина балки 90 дюймов (2,28 м), то прогиб не может превышать 1/2 дюйма (12,7 мм). Величина прогиба балки не связана с ее прочностью. Однако если балка сильно деформируется, то сокращается просвет под балкой, что может повлиять на несущую способность всей пространственной конструкции. Новое требование, в противоположность сложившейся практике, сводится к тому, что деформация величиной в 1/180 длины балки, включает любое смещение в месте соединения балки со стойкой.
 В этом заключается новизна требования. Ранее все таблицы прогибов основывались на величине прогиба самой балки без учета деформации соединения.
В этом заключается новизна требования. Ранее все таблицы прогибов основывались на величине прогиба самой балки без учета деформации соединения.Если изготовитель может воспользоваться обычными методами расчета, чтобы определить несущую способность балки, то нет необходимости прибегать к испытаниям. Однако, если поперечное сечение балки, в силу своей сложности, не позволяет рассчитать нагрузку и величину де формации, следует провести испытания по методике, разработанной институтом. В методике описывается как и в течение какого времени следует нагружать балку, как определить деформацию и допустимые нагрузки.
Условия испытания максимально приближены к реальным: силы, действующие на балку, распределены вдоль балки и направлены перпендикулярно к ее оси.
Допустимая для балки нагрузка определяется следующим образом: 1) как 1/2 от предельной разрушающей нагрузки; 2) как 2/3 нагрузки, при которой соединение между балкой и стойкой начинает терять первоначальную форму; 3) как нагрузка, при которой вертикальный прогиб балки составляет 1/180 расстояния между опорами.

Расчет нагрузки двутавровой балки – максимальные значения + Видео
Расчет нагрузки двутавровой балки проводится для определения номера из списка сортамента при проектировании несущих конструкций зданий и сооружений. Расчет производится согласно формулам и таблицам, а полученные параметры влияют на процесс проектирования и строительства, а также дальнейшие эксплуатационные характеристики конструкции.
1 Применение двутавровой балки и основные параметры
Основная функция двутавра при проектировании различных зданий и сооружений – создание надежной и эффективной несущей конструкции. В отличии от бетонных вариантов несущих конструкций, использование двутавровой балки позволяет добиться увеличения ширины пролетов жилых или коммерческих зданий и уменьшить массу основных несущих конструкций. Таким образом, существенно повышается рентабельность строительства.
Двутавровое балки
Двутавровый швеллер выбирается, исходя из длины и веса. Балки могут быть горячекатаными стандартными или специальными и иметь параллельные или наклонные грани полок. Они изготавливаются из низкоуглеродистой стали различных марок и используются в разных сферах строительства. Согласно нормам ГОСТ 823989, длина двутаврового швеллера может быть от 3 до 12 метров. По типу использования такие балки могут быть балочными, колонными, широкополочными или монорельсными, которые используются для строительства подвесных мостов. Определить тип балки можно по буквенной маркировке в таблице сортамента.
Балки могут быть горячекатаными стандартными или специальными и иметь параллельные или наклонные грани полок. Они изготавливаются из низкоуглеродистой стали различных марок и используются в разных сферах строительства. Согласно нормам ГОСТ 823989, длина двутаврового швеллера может быть от 3 до 12 метров. По типу использования такие балки могут быть балочными, колонными, широкополочными или монорельсными, которые используются для строительства подвесных мостов. Определить тип балки можно по буквенной маркировке в таблице сортамента.
Масса двутавра рассчитывается согласно таблице сортамента, в которой указан конкретный номер и маркировка двутавровой балки, а также показатели ширины, высоты, толщины полок и средняя толщина стенок профиля. Таким образом, для определения массы, согласно таблице, необходимо знать нормативный вес одного погонного метра. Например, балка с номером 45, при весе погонного метра 66,5 кг, имеет длину 15,05 метров.
Помимо расчета массы, который можно провести, используя простой калькулятор, в процессе проектирования необходимо рассчитать максимальную и минимальную нагрузку на изгиб и прогиб (деформацию), чтобы выбрать подходящую под конкретные цели строительства двутавровую балку. Данные расчеты основаны на таких параметрах металлического профиля, как:
Данные расчеты основаны на таких параметрах металлического профиля, как:
- минимальное и максимальное расстояние между полками (стенками) балки с учетом их толщины;
- максимальная нагрузка на будущую конструкцию перекрытия;
- тип и форма конструкции, метод крепления;
- площадь поперечного сечения.
В некоторых случаях для проведения расчетов может понадобиться и шаг укладки, то есть расстояние, через которое балки укладываются параллельно друг другу.
Расчет двутавровой балки, как правило, производится на прочность и прогиб. Для максимально точных расчетов в таблице сортамента и нормах ГОСТ прописаны и такие необходимые параметры, как момент сопротивления, который делится на статистический и осевые моменты. Помимо этого, иногда необходимо знать величину расчетного сопротивления, которая зависит от типа и марки стали, из которой изготовлена двутавровая балка, а также от типа производства (сварная или прокатная). В случае сварного профиля при расчете прочности прибавляется до 30 процентов к вычисленной несущей нагрузке профиля.
2 Выбор металлической балки по номеру и примеры расчета
В таблице сортамента все номера металлического двутавра указаны согласно нормам ГОСТ 823989. Таким образом, выбор номера должен осуществляться с учетом предполагаемой нагрузки на балку, длины пролетов, веса. Например, если максимальная нагрузка на двутавровую балку равна 300 кг/м.п, из таблицы выбирается балка номер 16, при этом пролет будет равен 6 метрам при шаге укладки от 1 до 1,2 метров. При выборе 20-го профиля максимальная нагрузка увеличивается до 500 кг/ м.п, а шаг может быть увеличен до 1,2 метра. Профиль с номерами 10 или 12 означает максимально допустимую нагрузку до 300 кг/м.п и сокращение пролета до 3-4 метров.
Применение балок в строительстве
Таким образом, расчет того, какую нагрузку выдерживает балка, производится так:
- определяется величина нагрузки, которая давит на перекрытие с учетом веса самого профиля (из таблицы), которая рассчитывается на 1 погонный метр профиля;
- полученная нагрузка, согласно формуле, умножается на показатель коэффициента надежности и упругости стали, который прописан в ГОСТ 823989;
- используя таблицу расчетных значений по ГОСТ, необходимо определить величину момента сопротивления;
- исходя из момента сопротивления, выбираем соответствующий номер из таблицы сортамента.

Рассчитывая несущую нагрузку при выборе профиля, рекомендуем выбирать номера балки на 1-2 пункта выше полученных расчетных значений. Несущая способность профиля также рассчитывается при определении нагрузки двутавровой балки на изгиб.
3 Как марки стали влияют на расчеты?
При расчете прочности несущей балки в обязательном порядке учитывается марка стали, которая использовалась в процессе производства, и тип производственного проката. Для сложных конструкций и возведения перекрытий жилых зданий, коммерческих помещений, мостов необходимо выбирать балки из максимально прочных марок стали. Изделия с более высокой прочностью обладают меньшими габаритными размерами, но при этом способны выдерживать большие нагрузки.
Балки на производстве
Таким образом, расчет на прочность рекомендуется проводить несколькими способами, а полученные данные сравнить для получения максимально точных результатов вычислений. При определении прочности необходимо знать нормативные и расчетные напряжения и учитывать такие параметры, как поперечные и продольные силы, а также крутящие моменты. Существует несколько вариантов расчетных калькуляторов, с помощью которых определяется максимально и минимально допустимая нагрузка на прочность.
4 Как вычислить нагрузку на деформацию?
Для определения нагрузки балки на деформацию необходимо учитывать такие параметры, как:
- расчетная и нормативная нагрузка;
- длина и вес перекрытия;
- нормативное сопротивление.
Двутавровые балки для строительства
При этом для некоторых типов балок невозможно рассчитать нагрузку на прогиб, ввиду их формы и видов крепления при строительстве. Следует также понимать, что деформация балки (прогиб) возникает в поворотных углах. Поэтому она сильно зависит от габаритов конструкции, ее назначения, марки стали и других свойств и показателей. Существует несколько формул и вариантов для расчета балки на прогиб, использование которых зависит от расчета деформации внизу и вверху балки. Чаще всего для того, чтобы вычислить максимальную нагрузку на прогиб, специалисты используют универсальную формулу. Величину нагрузки на будущую конструкцию необходимо умножить на ширину пролета в кубическом объеме. Полученный параметр разделите на произведение модуля упругости и величины инерционного момента.
Модуль упругости вычисляется, исходя из конкретной марки стали, момент инерции прописан в ГОСТе по номеру выбранной балки. Полученное число необходимо умножить на коэффициент, равный 0,013. В том случае, если рассчитанный относительный коэффициент деформации больше или меньше, чем прописано в нормативе, то в строительной конструкции необходимо использовать двутавры большего или меньшего типоразмера из таблицы.
Следует понимать, что двутавровая балка, ввиду своей формы, конструкции и веса, довольно редко используется в частном строительстве. Обычно вместо балок применяются более легкие швеллеры или стальные уголки. Но если вы все же используете балку для строительства небольшого частного дома, дачи, то необязательно проводить сложные расчеты по всем видам деформации и нагрузок. Для небольшой конструкции перекрытия достаточно рассчитать максимальную и минимальную нагрузку на изгиб.
Расчет балки на прочность онлайн калькулятор
Балка длиной L загружена равномерно распределенной нагрузкой q либо сосредоточенной силой P, которые необходимо будет задать
(как собрать нагрузки на балку можно получить тут Сбор нагрузок (калькулятор).
Все геометрические размеры сечения можно задать самому, поэтому в калькуляторе реализован огромный выбор самых различных балок: труба,
швеллер, профильная труба, двутавр, уголок, пластина и др.
Расчет проходит по нормальным и касательным напряжениям, которые возникают из-за поперечной силы.
Касательные напряжения получаем по формуле Журавского и производим проверку с использованием главных напряжений по 3-ей теории прочности.
В онлайн расчет входят такие материалы, как сталь нескольких классов (С235, С245, С255, С345) и дерево трех сортов.
Для расчета вам необходимо:
1. Выбрать форму поперечного сечения (труба, швеллер, профильная труба, двутавр, уголок, пластина и др.)
2. Выбрать материал (сталь, дерево)
3. Выбрать необходимую расчетную схему
4. Выбрать вид нагрузки (распределенная по длине балки либо сосредоточенная)
5. Указать геометрические размеры, указанные на картинках
6. Задать нагрузку (нагрузку можно рассчитать онлайн здесь)
Также есть возможность выбора расчетной схемы: шарнир-шарнир, заделка-шарнир, заделка-заделка, свободный конец балки.
Коэффициенты поправки расчетного сопротивления дерева на изгиб приняты следующие:
Mдл = 0.66 — совместное действие постоянной и кратковременной снеговой нагрузок
Mв = 0.9 — нормальные условия эксплуатации дерева (влажность менее 12%)
Mт = 0.8 — эксплуатация дерева при температуре 50 градусов
Mсс = 0.9 — срок эксплуатации конструкции 75 лет
При расчете уже учитывается собственный вес конструкции.
Последние изменения
1. Добавлена возможность расчета балки при сосредоточенной нагрузке
— Добавлена проверка устойчивости стенки и полки двутавра, швеллера, уголка, профильной трубы
— Исправлено расчетное сопротивление дерева на изгиб согласно СП 64.13330.2017 «Деревянные конструкции»
— Исправлены расчетные сопротивления стали
— Исправлено допустимое эквивалентное напряжение при действии нормальных и касательных напряжений
— Добавлена возможность поворота швеллера
Если данный калькулятор оказался Вам полезен – не забывайте делиться им с друзьями и коллегами ссылкой в соц.сети, а также посмотреть другие строительные калькуляторы онлайн, они простые, но здорово облегчают жизнь строителям и тем, кто решил сам строить свой дом с нуля.
Нагрузка на главную балку | Домострой
Балку проектируем переменного по длине сечения и рассчитываем без учёта развития пластических деформаций. Главная балка воспринимает нагрузку от балок настила, расположенных с шагом 1408 мм. При таком частом расположении этих балок можно считать, что главная балка нагружена равномерно распределённой нагрузкой.
Вес настила и балок настила:
,где
– собственный вес настила, ;– линейная плотность балок настила, ;– шаг балок настила, .Вес главной балки принимаем в пределах (1..2)% от нагрузки на балку:
,где
– шаг колонн в поперечном направлении, .Нормативная нагрузка на главную балку:
.Расчётная нагрузка на главную балку:
Компоновка сечения главной балки.Максимальный расчётный изгибающий момент в середине пролёта:
.Максимальная поперечная сила на опоре:
.Требуемый момент сопротивления сечения главной балки в упругой стадии работы:
,где
– расчётное сопротивление стали С345 для листового, широкополосного универсального проката по ГОСТ 27772-88 при толщине от 20 до 40 мм (т. 2.3 [1]).Определяем ориентировочную высоту главной балки:
.При расчёте по эмпирической формуле толщина стенки главной балки:
.Толщина стенки главной балки из условий среза:
,где
– расчётное сопротивление стали срезу, .Толщина стенки главной балки из условия местной устойчивости:
.Принимаем толщину стенки главной балки
по ГОСТ 82-70* (т. 7.14 [1]).Определяем оптимальную высоту главной балки при
:,где
– коэффициент, зависящий от соотношения конструктивных коэффициентов поясов и стенки балки.Минимальная высота главной балки:
,где
– величина, характеризующая допустимый прогиб, при длине главной балки по т. 1.5 [1] интерполяцией определяем ;– расчётное сопротивление стали С345 для листового, широкополосного универсального проката по ГОСТ 27772-88 при толщине свыше 20 до 40 мм (т. 2.3 [1]).Принимаем высоту главной балки
.Принимаем толщину полки главной балки
(т. 7.14 [1]), тогда высота стенки:.Высота по осям поясов:
.Требуемый момент инерции сечения главной балки:
.Требуемый момент инерции стенки главной балки:
.Требуемый момент инерции полки главной балки:
.Определяем требуемую площадь полки главной балки:
.Определяем требуемую ширину полки главной балки:
.Ширина полки главной балки принимается в пределах
, но не менее 180 мм.Принимаем ширину полки главной балки
из универсальной широкополосной стали по ГОСТ 82-70 * (т. 7.14 [1])..Из условия свариваемости отношение толщины полки
к толщине стенки не должно превышать 3:.Проверяем принятую ширину (свес) поясов
, исходя из обеспечения их местной устойчивости:Рис. 2.2 Сечение главной балки
Уточняем нагрузку на главную балку с учётом собственного веса главной балки.
Площадь поперечного сечения главной балки:
.Вес главной балки:
.Нормативная нагрузка на главную балку:
.Расчётная нагрузка на главную балку:
Максимальный расчётный изгибающий момент в середине пролёта:
.Максимальная поперечная сила на опоре:
.Проверяем толщину стенки главной балки из условия среза:
,где
– расчётное сопротивление стали срезу, .Проверяем условие, при соблюдении которого не требуется постановка продольных ребер в стенке:
.Расчётные геометрические характеристики сечения главной балки.
Момент инерции сечения главной балки:
Момент сопротивления сечения главной балки:.Дата добавления: 2016-10-22 ; просмотров: 882 | Нарушение авторских прав
Требуется собрать нагрузки на монолитную балку перекрытия жилого дома (балка по оси «2» в осях «Б-В» на рис.1). Размеры сечения балки: h = 0,5 м, b = 0,4 м. Конструкцию пола принять по рисунку в Пример 1.1 Сбор нагрузок на плиту перекрытия жилого здания.
Решение
Данный тип здания относится ко II классу ответственности. Коэффициент надежности по ответственности γн = 1,0.
Состав пола и значения постоянных нагрузок примем из примера 1.1.
Нагрузки, действующие на балку, принимаются линейно распределенными (кН/м). Для этого равномерно распределенные нагрузки на перекрытие умножаются на ширину грузового участка, равному для средних балок шагу рам. В нашем примере см. рис. 1 ширина грузового участка составляет В = 6,6 м. Остается умножить постоянную нагрузку, вычисленную в примере 1.1, на данную величину и записать в таблицу 1:
q1 = 5,89*В = 5,89*6,6 = 38,87 кН/м;
q1p = 6,63*В = 6,63*6,6 = 43,76 кН/м.
Таблица 1
Сбор нагрузок на балку перекрытия
Вид нагрузки
Норм. кН/м
Коэф. γt
Расч. кН/м
Постоянная нагрузка
1. Ж.б. плита + пол
2. Собственный вес балки
Всего:
Временная нагрузка
1. Полезная нагрузка:
кратковременная ν1
длительная р1
2. Перегородки (длительная) р2
Вычислим нагрузку от собственного веса балки.
Объемный вес железобетона равен 2500 кг/м3 (25 кН/м3). При высоте балки h = 0,5 м и ее ширине b = 0,4 м нормативное значение нагрузки от собственного веса составляет
q2 = 25*h*b*γн =25*0,5*0,4*1,0 =5,0 кН/м.
Коэффициент надежности по нагрузке γt = 1,1, тогда расчетное значение составит:
q2р = q2*γt =5*1,1 =5,5 кН/м.
Суммарная нормативная постоянная нагрузка составляет
q = q1 + q2 = 38,87 + 5,0 = 43,87 кН/м;
qр = q1р + q2р = 43,76 + 5,5 = 49,26 кН/м.
Понижающие коэффициенты φ1, φ2, φ3 или φ4, при расчете балок нормативные значения нагрузок, допускается снижать в зависимости от грузовой площади А, м2, рассчитываемого элемента умножением на коэффициент сочетания φ. При грузовой площади А = 6,6*7,2 = 47,52 м2 и при А = 47,52 м2 > А1 = 9,0 м2 для помещений коэффициент сочетания φ1 определяется по формуле:
φ1 = 0,4 + 0,6/ √(А/А1) = 0,4 + 0,6/√(47,52/9,0) = 0,66.
Полное (кратковременное) нормативное значение нагрузки от людей и мебели для квартир жилых зданий составляет 1,5 кПа (1,5 кН/м2). Учитывая коэффициент надежности по ответственности здания γн = 1,0 и коэффициент сочетания φ1 = 0,66, итоговая нормативная кратковременная полезная нагрузка составляет:
ν1 = 1,5*В*γн*φ1 = 1,5*6,6*1,0*0,66 = 6,53 кН/м.
При нормативном значении временной нагрузки менее 2,0 кПа коэффициент надежности по нагрузке γt принимается равным γt = 1,3. Тогда расчетное значение составляет:
ν1р = ν1*γt = 6,53*1,3 = 8,49 кН/м.
Длительную полезную нагрузку получаем путем умножения ее полного значения на коэффициент 0,35 т.е:
р1 = 0,35*ν1 = 0,35*6,53 = 2,29 кН/м;
р1р = р1*γt = 2,29*1,3 = 2,98 кН/м.
Нормативное значение равномерно распределенной нагрузки от перегородок составляет не менее 0,5 кН/м2. Приводим ее к линейно распределенной нагрузке на балку путем умножения на ширину грузового участка В=6,6 м:
р2 = 0,5*В*γн = 0,5*6,6*1,0 = 3,3 кН/м.
Расчетное значение нагрузки тогда:
р2р = р2*γt = 3,3*1,3 = 4,29 кН/м.
I сочетание: постоянная нагрузка (собственный вес перекрытия и балки) + полезная (кратковременная).
При учете основных сочетаний, включающих постоянные нагрузки и одну временную нагрузку (длительную или кратковременную), коэффициент Ψl, Ψt вводить не следует.
q1 = q + ν1 = 43,87 + 6,53 = 50,4 кН/м;
q1р = qр + ν1р = 49,26 + 8,49 = 57,75 кН/м.
II сочетание: постоянная нагрузка (собственный вес перекрытия и балки) + полезная (кратковременная) + нагрузка от перегородок (длительная).
Для основных сочетаний коэффициент сочетаний длительных нагрузок Ψ1 принимается: для первой (по степени влияния) длительной нагрузки — 1,0, для остальных — 0,95. Коэффициент Ψ2 для кратковременных нагрузок принимается: для первой (по степени влияния) кратковременной нагрузки — 1,0, для второй — 0,9, для остальных — 0,7.
Поскольку во II сочетании присутствует одна кратковременная и одна длительная нагрузка, то коэффициент Ψl и Ψt = 1,0.
qII = q + ν1 + р2 = 43,87 + 6,53 + 3,3 = 53,7 кН/м;
qIIр = qр+ ν1р + р2р = 49,26 + 8,49 + 4,29 = 62,04 кН/м.
Определение нагрузки на главную балку
Нагрузка на главную балку складывается из полезной нагрузки и от собственной массы настила, вспомогательных и главных балок. Нормативная равномерно-распределенная нагрузка на главную балку определяем как:
где нормативная полезная равномерно-распределенная нагрузка, кПа;
— приведенная масса настила и вспомогательных балок, кг/мІ;
- — коэффициент перегрузки для полезной нагрузки, принимаем ;
- — коэффициент надежности по нагрузке;
- — пролет вспомогательной балки, м;
- 1,03- коэффициент, который учитывает собственную массу главной балки (3%).
Определение размеров сечения главной балки
Определение высоты главной балки
Для определения высоты главной балки предварительно вычисляем расчетный изгибающий момент и требуемый момент сопротивления:
где МПа — расчетное сопротивление стали по пределу текучести;
Оптимальная высота главной балки, обеспечивающая минимальный расход стали:
где К — коэффициент, зависящий от соотношения конструктивных коэффициентов поясов и стенки балки, принимаемый равным 1,10-1,15.
Для балок высотой до 2м толщина стенки может назначаться по эмпирической формуле: (мм),
- — толщина стенки, мм;
- (м)- высота балки, принимаем предварительно равной 1/10 пролета балки.
Минимальная высота главной балки, обеспечивающая жесткость балки:
допустимый относительный прогиб главной балки, принимаемый равным ;
расчет нагрузки, несущая способность, прочность
Двутавр – это металлопрофильная конструкция перекрытия, наклонная или горизонтальная, рассчитанная в первую очередь на изгиб. Прежде всего она находится под воздействием весовой нагрузки, направленной по вертикали. Фактически это первичное воздействие, которому должен противостоять прокатный профиль из металла.
Технические характеристики металлического профиля необходимы, чтобы их правильно применять в строительстве, ведь несмотря на большое разнообразие сфер применения, суть остается одна – создать надежную несущую конструкцию. Она позволяет преобразовывать архитектуру сооружений:
- увеличивает ширину пролетов зданий;
- значительно, примерно на 35%, уменьшить массу несущих конструкций;
- существенно увеличить рентабельность проектов.
Говоря о достоинствах конструкции, нельзя не отметить и минусы, хотя их немного. Основные из них – это
- необходимость применять при создании ребер жесткости дополнительную арматуру;
- достаточно существенные трудозатраты, которые нужны для ее изготовления.
Однако, следует отметить, что с другой стороны дополнительные ребра жесткости дают возможность:
- уменьшить общую металлоемкость сварной металлоконструкции, так как ощутимо уменьшают толщину стенок. Таким образом удается понизить ее стоимость, но целиком сохранить механические характеристики;
- помимо этого облегченная конструкция экономична и с точки зрения устройства фундамента, поскольку после снижения общей массы можно использовать фундамент под БМЗ (быстровозводимые здания).
Чтобы найти двутавр, подходящий для конкретного случая, требуется произвести некоторые расчеты. Обычно для этого используют таблицы или онлайн калькуляторы. В их основе лежат заданные два параметра: расстояние от одной стены до другой и будущая нагрузка на строительную конструкцию.
Прочность двутавровой балки определяется такими параметрами, как:
- длина,
- метод закрепления,
- форма,
- площадь поперечного сечения.
Большее распространение получили изделия с буквой «Н» в сечении.
На заметку
Жесткость металлической конструкции двутавра в 30 раз превышает жесткость квадратного профиля, а прочность, соответственно, в 7 раз.
Длина данной металлоконструкции бывает разной, к примеру, в случае ГОСТ 8239-89 это 4 –12 метров, то есть в зависимости от сортамента размеры и вес балки двутавровой отличаются. Помимо длины величина веса определяется толщиной металла и размерами граней. Поэтому для выполнения различных расчетов было введено понятие «вес метра балки двутавровой».
При покупке сварной конструкции обязательно требуется расчет на прочность, а для конкретного использования еще и расчет на прогиб. Грамотный расчет нагрузки на двутавровую балку позволит обеспечить устойчивость конструкции к проектным воздействиям, то есть способность воспринимать их без разрушения.
Нагрузка собственного веса ↑
Чтобы определить в случае необходимости вес двутавровой балки пользуются специальными таблицами, где расписаны ее характеристики, к примеру, габариты, марка стали и т. д. В таблице представлена теоретическая масса 1 м профиля.
балка двутавровая размеры и вес (ГОСТ 8239-89)
Пример расчета двутавра ↑
Предположим необходимо рассчитать вес двутавра № 12 длиной в 3 метра. Согласно таблице условная масса погонного метра данного профиля равна 11,50 кг. Если перемножить полученные значения, то получим величину общей массы – 34,5 кг.
Точнее значение веса сварной металлоконструкции можно посчитать, используя специальные онлайн калькуляторы, один из которых предоставлен на нашем сайте в рубрике “Калькуляторы”.
В калькуляторе выбирают соответствующий номер двутавра и вводят необходимый метраж. Как видите, полученное значение больше рассчитанного нами на 0,12 кг.
Несущая способность ↑
Среди всех типов балок двутавровая имеет наибольшую прочность, более того, она устойчива к температурным перепадам. Допустимая нагрузка на двутавр бывает указана на маркировке, как размер. Чем больше число, указанное в его наименовании, тем большую нагрузку может воспринимать балка.
Любой расчет предполагает изначальное знание размеров прокатного или сварного профиля, его длины и ширины. Проясним смысл значения ширины на примере самой популярной балочной опоры – колонны.
Пример расчета
Предположим, что в сечении колонны лежит квадрат со стороной 510 мм, тогда на нее можно будет опереть профиль, для которого ширина не может превышать 460 мм. Это связано с тем, что двутавр придется приваривать к железобетонной подушке, а для сварочных швов понадобится запас, по крайней мере, в 40 мм.
После определения ширины переходят к выбору профиля и расчету нагрузки, воздействующей на профиль. Она представляет собой совокупность воздействий от перекрытия, а также воздействий временного и постоянного характера.
На заметку
Нагрузку, выражающую величину нормативной нагрузки, собирают на длину 1 м профиля.
Но, расчет несущей способности двутавровой балки предполагает учет другого воздействия. Чтобы получить расчетную нагрузку, рассчитанное нормативное воздействие умножается на так называемый коэффициент прочности по нагрузке. Остается к результату прибавить уже подсчитанную массу изделия и найти его момент сопротивления.
Полученных данных достаточно, чтобы из сортамента подобрать профиль, необходимый для изготовления сварного профиля. Как правило, с учетом прогиба конструкции рекомендуется выбирать профиль выше на два порядка.
Важно
Сварная металлическая конструкция должна использовать примерно 70–80% от максимально допустимого прогиба.
Усиление ↑
Если несущая способность двутавра оказывается недостаточной, то возникает необходимость ее усиления. Для различных элементов сварной конструкции этот вопрос решается по-разному.
К примеру, для элементов, воспринимающих нагрузки типа растяжения, сжатия или изгиба, используют такой вариант усиления: увеличивают сечение, иначе говоря, повышают жесткость, скажем, приварив дополнительные детали.
Теоретически – это один из лучших вариантов усиления, однако, при его реализации не всегда удается получить требуемый результат. Дело в том, что элементы в процессе сварочных работ нагреваются, а это несет за собой уменьшение несущей способности.
В какой степени можно ожидать такого понижения зависит от размеров двутавра и режима и направления сварочных работ. Если для продольных швов максимальное понижение оказывается в пределах 15%, то для швов в поперечном направлении оно может достичь и 40%.
Внимание
Поэтому при усилении двутавра под нагрузкой категорически запрещено накладывать швы в направлении, поперечном к элементу.
Расчетно и экспериментально было доказано, что оптимального результата усиления под нагрузкой можно получить при максимальном напряжении в 0,8 Ry, то есть 80% расчетного сопротивления стали, которая была использована для изготовления двутавра.
© 2021 stylekrov.ru
Калькулятор нагрузки на балку
Этот калькулятор нагрузки на балку поможет вам определить реакции на опоры балки с простой опорой из-за вертикальных точечных нагрузок или сил. С помощью этого калькулятора вы узнаете, что такое реакция опоры , и научитесь основам расчета несущей способности балки.
Знание того, как найти опорные реакции, — отличное место для начала при анализе балок, например, при определении отклонения балки. Продолжайте читать, чтобы узнать больше.
Что такое реакция поддержки?
Согласно третьему закону движения Ньютона , каждая сила, действующая на объект, имеет равную и противоположную реакцию. Если вы пытаетесь надавить на что-то, скажем, стену, вам кажется, что стена тоже отталкивает вас. Именно это и описывает третий закон движения Ньютона.
В машиностроении элементы конструкции, такие как балки и колонны, взаимодействуют друг с другом в точках, где они встречаются. Представьте себе балку, которая опирается на двумя колоннами.Вес балки давит на колонны, и, благодаря третьему закону движения Ньютона, мы можем также сказать, что колонны оказывают на балку эквивалентную противоположную силу реакции. Мы называем эти силы реакции реакциями опоры .
На балке с простой опорой реакции опоры на каждом конце балки могут быть одинаковыми или иметь разные значения. Их значения зависят от приложенных нагрузок на балку. Если на более близком расстоянии к одной опоре находится больше нагрузок, эта опора испытывает большую силу и, следовательно, испытывает большую реакцию.
Как рассчитать опорные реакции в балке?
Поскольку опорные реакции действуют в направлении, противоположном силе, мы можем сказать, что вся система находится в равновесии. Это означает, что балка не движется, а сумма сил и моментов дает ноль. Приравнивая моментов от нагрузки к моментам из-за опорных реакций , мы можем затем определить реакции на опорах.
Так же, как при расчете крутящего момента, мы также можем выполнить суммирование моментов на каждой опоре, чтобы найти реакции.Ниже мы выражаем сумму, Σ , моментов на опоре A, чтобы найти реакцию на опоре B, обозначенную как R B , как показано ниже:
Σ (F * x) - (R B * диапазон) = 0
(F 1 * x 1 ) + (F 2 * x 2 ) + (F 3 * x 3 ) + ... + (F n * x n ) - (R B * пролет) = 0
где:
-
F,F 1,F 2,F 3иF n— точечные нагрузки на балку на расстоянияхx,x 1,х 2;x 3иx nот опоры A; соответственно -
R B— реакция на опоре B, а -
пролет— длина балки между опорой A и опорой B.
Переставив уравнение, мы можем выделить R B следующим образом:
R B * диапазон = (F 1 * x 1 ) + (F 2 * x 2 ) + (F 3 * x 3 ) + ... + ( F n * x n )
R B = ((F 1 * x 1 ) + (F 2 * x 2 ) + (F 3 * x 3 ) +... + (F n * x n )) / пролет ✔
Теперь, когда у нас есть выражение для нахождения R B , и поскольку мы знаем, что общие приложенные силы равны сумме реакций, теперь мы также можем найти реакцию на опоре A R A , используя следующие уравнения:
Σ (F) = Rᴀ + Rʙ
R A = Σ (F) - Rʙ ✔
Пример расчета реакции опоры
Предположим, у нас есть 4.0-метровая балка с простой опорой длиной с приложенной точечной нагрузкой 10,0 килоньютон (кН) на расстоянии 2,0 метра от опоры A и прикладываемой другой точечной нагрузкой 3,5 кН на расстоянии 1,5 метра от опоры B , как показано ниже:
Для расчета R B сформулируем уравнение моментного равновесия следующим образом:
R B = (F 1 * x 1 + F 2 * x 2 ) / пролет
R B = (10 кН * 2.0 м + 3,5 кН * (4,0 м - 1,5 м)) / 4,0 м
R B = (20 кН-м + 3,5 кН * 2,5 м) / 4,0 м
R B = (20 кН-м + 8,75 кН-м) / 4,0 м
R B = 7,1875 кН
Суммируя силы, получаем:
Σ (F n ) = 0
Факс 1 + Факс 2 + (-Rᴀ) + (-Rʙ) = 0
10 кН + 3.5 кН + (-Rᴀ) + (-7,1875 кН) = 0
R A = 10 кН + 3,5 кН - 7,1875 кН
R A = 6,3125 кН
Обратите внимание, что для этого суммирования , мы рассмотрели все нисходящих сил как положительные и все восходящих сил как отрицательные . Основываясь на наших расчетах выше, мы теперь получили реакции на опорах A и B, которые составляют 6,3125 кН и 7,1875 кН , соответственно.
Также обратите внимание, что в этом примере и в калькуляторе нагрузки на балку мы предположили, что балка невесома. Однако, если указан вес балки, вы можете рассматривать ее как еще одну направленную вниз точечную нагрузку в центре или центроиде балки.
Использование нашего калькулятора нагрузки на балку
Наш калькулятор легок и прост в использовании. Все, что вам нужно сделать, это ввести пролет балки , величину точечных нагрузок и их расстояние от опоры A .Сначала вы увидите поля только для двух нагрузок (Нагрузка 1 и Нагрузка 2), но как только вы введете значение для x 2 , появятся поля для Нагрузки 3 и так далее.
Если вы хотите ввести восходящую нагрузку, просто введите отрицательное значение для величины нагрузки. Всего в наш калькулятор нагрузки на балку можно ввести до 11 точечных нагрузок.
Хотите узнать больше?
Теперь, когда вы узнали, как рассчитать допустимую нагрузку на балку, определив реакции на опорах, возможно, вы также захотите узнать больше о том, что такое прогиб балки и изгиб балки.
StructX — Формулы расчета балок
Формулы расчета балок
Просто выберите изображение, которое больше всего соответствует конфигурации балки и условиям нагрузки, которые вас интересуют, чтобы получить подробный обзор всех структурных свойств. Уравнения балки для результирующих сил, поперечных сил, изгибающих моментов и прогиба можно найти для каждого показанного случая балки. Для проектирования и оценки балок в метрических и дюймовых единицах предусмотрены удобные калькуляторы.
Сборник электронных таблиц по проектированию конструкций для расчета балок с использованием Excel доступен для покупки и может быть найден под каждым типом балки.
Дополнительную информацию о теории проектирования балок и сделанных допущениях можно найти здесь.
Простая балка с UDL
Простая балка с UIL
Простая балка с центральной УИЛ
Простая балка с PDUL
Простая балка с PDUL на одном конце
Простая балка с PDUL на каждом конце
Простая балка с PL в центре
Простая балка с PL в любой точке
Простая балка с одинаково расположенными PL
Балка с неравномерно разнесенными пластинами
Балка с неравномерно разнесенными ВИП
Простая балка с UDL и EM
Простая балка с PL и EM
Фиксированная торцевая балка с UDL
Фиксированная торцевая балка с центральным PL
Фиксированная торцевая балка.PL в любой точке
Неподвижная балка с UDL
Фиксированная балка с центральным PL
Неподвижная балка с PL в любой точке
Консольная балка с UIL
Консольная балка с UDL
Консольная балка с UDL и EM
Консольная балка. PL в любой точке
Консольная балка с PL на свободном конце
Консольная балка с PL и EM
Балка навесная с UDL
Свесная балка с UDL на конце
Балка навесная с PL на конце
Балка навесная с деталью UDL
Свисающая балка PL в любой точке
Балка с двумя свесами и UDL
Двухпролетная балка с частичным UDL
Двухпролетная балка с PL
Двухпролетная балка.PL в любой точке
Двухпролетная балка с UDL
Двухпролетная балка с двумя PL
Два неравных пролета с UDL
Два неравных пролета с PL
Трехпролетная балка с частичным UDL
Трехпролетная балка с концевыми UDL
Трехпролетная балка с UDL
Четырехпролетная балка. Незагруженный пролет
Четырехпролетная балка.Разгрузочные пролеты
Четырехпролетная балка с UDL
Как делать расчеты балочной нагрузки
Достаточно взглянуть вокруг, чтобы понять тот простой, но интересный факт, что каждый объект, живой или неживой, постоянно прикладывает определенную нагрузку к определенной базе, а также одновременно подвергается воздействию подвергается воздействию равной и противоположной силы со стороны поддерживаемого основания.
Автомобиль, припаркованный над местом, оказывает на землю силу или предлагает нагрузку на землю, которая может быть равна его весу; однако земля также оказывает на машину равную, но противоположную силу, поэтому она остается на месте в целости и сохранности.Поскольку автомобиль удерживается в одном постоянном положении, это означает, что две силы должны быть равны и действовать в противоположных направлениях.
В основном следующие две силы обычно действуют на любой объект, который в основном составляет нагрузку:
- Вес объекта, действующий по направлению к земле
- Реакция земли или основания, действующая вверх над объектом
Перед тем, как мы Если перейти к деталям расчета нагрузки на балку, важно сначала узнать о типах нагрузок, которые могут действовать на балку, поддерживаемую на ее концах.
Нагрузку можно разделить на следующие важные типы:
- Точечная нагрузка, резко ограниченная одной точкой,
- Равномерно или равномерно распределенная нагрузка и,
- Равномерно изменяющаяся нагрузка.
Давайте разберемся с ними по очереди.
Точечная нагрузка: Нагрузка или груз, воздействующий на точечную область, называется точечной нагрузкой . Однако математически точечная нагрузка не представляется возможной просто потому, что любая нагрузка должна иметь определенную область воздействия и не может балансировать по точке, но если площадь удара слишком мала по сравнению с длиной балки, может приниматься как определено.
Равномерно распределенная нагрузка: как следует из названия, нагрузка, равномерно выровненная по всей балке, называется равномерно распределенной нагрузкой .
Равномерно изменяющаяся нагрузка: Нагрузки, распределенные по балке, которые создают равномерно увеличивающийся градиент нагрузки по всей балке от конца до конца, называется равномерно изменяющейся нагрузкой .
Балка может подвергаться одной из вышеуказанных нагрузок или их сочетаниям.
Реакции балки
Следующая простая иллюстрация проведет нас по формулам, относящимся к расчету нагрузки на балку или, точнее, к реакциям балки:
Ссылаясь на диаграмму рядом, давайте рассмотрим балку, поддерживаемую на ее концах (слева и справа), обозначаемые буквами A и B соответственно.
Пусть на балку действуют точечные нагрузки в положениях, обозначенных как W1, W2 и W3.
Также пусть,
RA = Реакция на конце A балки.
RB = Реакция на конце B балки.
Итак, в первую очередь существует пара сил (эффект поворота), которые действуют на концы балки A и B, а именно. по часовой стрелке и против часовой стрелки момент силы.
Поскольку момент силы , действующий на опорную балку, равен произведению Силы (здесь вес) и ее расстояния от опоры или оси, общий момент по часовой стрелке, действующий в точке A, может быть задан как:
W1.a + W2.b + W3.c,
Кроме того, против часовой стрелки момент силы, действующей на точку B, должен быть:
RB.l
Теперь, поскольку балка находится в равновесии, подразумевается, что указанные выше два момента силы должны быть равны по величине, поэтому приравнивание двух выражений дает:
W1.a + W2.b + W3.c = RB.l
RB = W1.a + W2.b + W3.c / l
Равновесие с балкой также подразумевает, что:
RA + RB = W1.a + W2.b + W3.c
RA = (W1.a + W2.b + W3.c) — RB
Теперь, согласно условиям равновесия, алгебраическая сумма всех горизонтальных составляющих в приведенном выше выражении становится несущественной и может быть обнулена (ƩH = 0.)
Следовательно, Окончательное уравнение принимает вид
RA = (W1 + W2 + W3) — RB
Вышеупомянутая формула может использоваться для определения реакции нагруженной балки на ее концевые опоры.
Расчет поперечной силы и изгибающего момента
Двумя важными параметрами, также участвующими в расчетах нагрузки на балку, являются поперечная сила (SF) и изгибающий момент (BM).
Выведем их с помощью следующей простой иллюстрации:
Ссылаясь на рисунок рядом, рассмотрим балку, нагруженную равномерно распределенной нагрузкой Вт на единицу длины. Также рассмотрим определенное сечение балки RS длиной δx на расстоянии x от левой опоры балки.
Нагрузка, действующая на сечение RS балки, будет равна Вт. δx ( момент Силы).
Теперь предположим, что поперечная сила в точке R = F,
Тогда в точке S она будет F + δF .
Также, если изгибающий момент в R = M , то в S он становится M + δM.
Так как балка находится в равновесии, задействованный момент также должен подчиняться законам равновесия, поэтому приравняв два неуравновешенных выражения в S, мы получаем:
_F + W._ δx = F + δF
Или δF / δx = W,
Приведенные выше выражения показывают, что скорость изменения поперечной силы равна давлению нагрузки или интенсивности.
Точно так же моменты в S могут быть приравнены как:
M — F.δx — Wδx2 / 2 = M + δM
Или δM = — F.δx, (игнорируя тривиальную величину δx2)
Получаем , δM / δx = — F
Приведенное выше соотношение показывает, что скорость изменения изгибающего момента равна поперечной силе сечения RS.
Данные (формула реакции, соотношение силы сдвига и изгибающего момента), описанные в этой статье, могут быть использованы при расчетах нагрузки на балку для дальнейшего определения качества и типа материала, который будет использоваться для безопасной нагрузки на балку.
Измерение изгибающего момента консольных балок
Балка, закрепленная на одном конце и свободно свисающая на другом, называется консольной балкой.
Глядя на рисунок, показанный в этом разделе, рассмотрим консольную балку длиной l и несущую нагрузку W над своим свободным концом _._ Осмотр секции _X_, которая находится на расстоянии _x_ от свободного конца мы находим, что поперечная сила равна общей неуравновешенной силе (весу), действующей вертикально на балку, т.е.например:
Fx = –W (знак минус означает, что правая сторона идет вниз)
А изгибающий момент можно выразить как:
Mx = –Wx (знак минус указывает противоположный изгиб)
Сила сдвига постоянна по всему сечению AB и равна –W . Изгибающий момент равен нулю в точке B, потому что x = 0 там, и увеличивается до –Wl по закону прямой линии в точке A , где x = l.
.
Ссылка
Книга: Прикладная механика и сопротивление материалов.
Автор: Хурми Р.С.
Издатель: S.Chand and Company Ltd. (Индия)
Заголовки и балки: таблицы выбора размеров
Таблицы с выбором размеров для различных пролетов балок и комбинаций нагрузок для размерной пиломатериала Southern Pine и клееного бруса Southern Pine доступны для следующих областей применения:
- Заглушки для окон, дверей и гаражных ворот — только несущие нагрузки на крышу
- Заглушки для окон, дверей и гаражных ворот — Несущие нагрузки на крышу, стены и пол
- Балки перекрытия
- Торцевые балки перекрытия
- Коньковая балка
Условия нагрузки подробно описаны ниже.Для каждого приложения доступна загрузка в формате PDF.
См. Также Допущения для разработки таблиц. См. Публикацию SFPA Southern Pine Headers и Beams (загрузите в Publications) , которая включает все таблицы выбора размеров и допустимых нагрузок.
| Номер таблицы | Класс | Снеговая нагрузка в реальном времени или на грунт (psf) | Статическая нагрузка (psf) | Коэффициент продолжительности нагрузки, C D |
|---|---|---|---|---|
| Заглушки для окон, дверей и гаражных ворот — только поддержка нагрузки на крышу | ||||
| 1 2 3 4 5 6 | Все Все Все Все Все Все | 30 40 50 70 20 20 | 10 909 10 10 20 | 1.15 1,15 1,15 1,15 1,25 1,25 |
| Скачать PDF, таблицы 1 — 6 | ||||
| Заглушки для окон, дверей и гаражных ворот — Несущие нагрузки на крышу, стены и пол | ||||
| 7 8 9 10 11 12 | Все Все Все Все Все Все | 30 40 50 70 20 20 | 10 909 10 10 20 | 1.15 1,15 1,15 1,15 1,25 1,25 |
| Скачать PDF, таблицы 7–12 | ||||
| Балки перекрытия | ||||
| 13 | Все | 40 | 10 | 1,00 |
| Торцевые балки перекрытия | ||||
| 14 | Все | 40 | 10 | 1,00 |
| Скачать PDF, таблицы 13–14 | ||||
| Балки конька крыши | ||||
| 15 16 17 18 19 20 | Все Все Все Все Все Все | 30 40 50 70 20 20 | 10 909 10 10 20 | 1.15 1,15 1,15 1,15 1,25 1,25 |
| Скачать PDF, таблицы 15-20 | ||||
Влияние нагрузки и размеров балки на конструктивное поведение железобетонных балок при пожаре и после пожара | Международный журнал бетонных конструкций и материалов
Результаты испытаний на огнестойкость
Результаты экспериментов показывают, что температуры, полученные с помощью термопар, находятся в диапазоне от 100 до 600 ° C в зависимости от местоположения внутри секции балки.График зависимости температуры от времени для P1-120 на рис. 10 показывает, что температура быстро увеличивается до 20 мин испытания на огнестойкость. Однако через 20 мин повышение температуры замедляется. Кривые время-температура у других образцов имеют тенденцию быть похожими. Самые высокие температуры достигаются термопарами среди CON1, 3 и 4 балок серии S и CON1, 4 и 5 балок серии M и L. Все эти температуры находятся на расстоянии 40 мм от поверхности, подверженной воздействию огня. Самая высокая температура увеличивается с увеличением нагрузки, как показано в Таблице 4, потому что балка, нагруженная с высоким коэффициентом номинального момента, вызывает больше трещин, и через трещины легче передается тепло.Однако различия в максимальной температуре между балками с разными размерами поперечного сечения незначительны.
Рис. 10График зависимости температуры от времени для P1-120, нагруженного 40% номинального момента под огнем.
Таблица 4 Максимальные температуры и максимальный прогиб во время огневого испытания.Максимальный прогиб балок во время испытания на огнестойкость увеличивается с увеличением уровня нагрузки. Однако максимальный прогиб во время испытания на огнестойкость уменьшается по мере увеличения размера поперечного сечения, и степень уменьшения не является линейно пропорциональной размерам поперечного сечения.Это связано с тем, что существует комбинированное влияние размеров поперечного сечения и распределения температуры на прогиб балок под огнем. Рисунок 11 показывает, что прогиб всех образцов быстро увеличивается до 20 мин. Через 60 мин разница в прогибе между образцами больше. Максимальный прогиб балок достигается примерно на 90 мм в центре P3-120, нагруженного 80% номинального момента, что в три раза больше, чем у P1-120, нагруженного 40% номинального момента.Максимальные отклонения для P1-60 и MP1-60 аналогичны. Причина наличия аналогичных прогибов между MP1-60 и P1-60 может быть из-за комбинированного влияния размеров поперечного сечения и распределения температуры. Несмотря на то, что MP1-60 имеет больший размер поперечного сечения, он также показывает более высокие распределения температуры, чем P1-60. Максимальный прогиб LP1-60 достигается примерно на 9,14 мм в центре балки, что вдвое меньше, чем у P1-60.
Рис. 11Прогиб образцов при огневых испытаниях. a по сравнению с другим уровнем нагрузки и b по сравнению с другим размером поперечного сечения.
Результаты испытания на остаточную прочность
Несущая способность
Кривые нагрузка-прогиб всех образцов, полученных в результате испытания на остаточную прочность, показаны на рис. 12. Различия в максимальных нагрузках между всеми образцами невелики, поскольку температуры арматурные стержни не достигают температуры 500 ° C, в то время как прочность стали значительно снижается до 50% от исходной прочности.Для образцов, нагретых в течение 120 мин, максимальная нагрузка P1-120, P2-120 и P3-120 составляет 169,88, 172,96 и 161,58 кН соответственно. Разница между максимальными нагрузками на управляющую балку и другую балку находится в пределах 10%, так что разница между максимальными нагрузками на управляющую балку и P3-120 является наибольшей и составляет 6,6%. Разница между максимальной нагрузкой управляющих балок и балок, поврежденных огнем, уменьшается с увеличением размера поперечного сечения (рис. 12).
Рис. 12Кривые нагрузки-прогиба для образцов. a Образцы серии S, нагруженные 40% номинального момента, b образцы серии S, нагруженные 60% номинального момента, c образцы серии S, нагруженные 80% номинального момента, d образцы серии M , и экз. серии L.
Начальная жесткость
Как показано на кривых нагрузка-прогиб для образцов, не может быть обнаружено значительных различий в остаточной прочности образцов. Однако уклоны для балок, поврежденных огнем, существенно различаются.Таким образом, начальная жесткость балок сравнивается с уровнем нагрузки, размером поперечного сечения и временем (Sullivan et al. 2004). Жесткость уменьшается по мере увеличения уровня нагрузки или времени, как указано в Таблице 5. Жесткость поврежденных огнем балок уменьшается из-за деградации материала бетона и стали с повышением температуры, например уменьшения модуля упругости. Степень уменьшения жесткости поврежденной огнем балки, нагретой в течение 1 часа, является наибольшей, а степень снижения жесткости со временем уменьшается.Жесткость P1-60, P1-90 и P1-120 на 31, 42 и 44% меньше, чем у контрольной балки соответственно.
Таблица 5 Температура и прогиб во время огневого испытания.Как указано в Таблице 5, жесткость линейно уменьшается с увеличением уровня нагрузки. Жесткость балок P1-60, P2-60 и P3-60 соответственно на 31, 37 и 43% меньше, чем у управляющих балок.
Скорость уменьшения не пропорциональна размеру поперечного сечения. Жесткость P1-60, MP1-60 и LP1-60 на 31, 31 и 23% меньше, чем у контрольной балки соответственно.Жесткость серии S аналогична серии M, но отличается от серии L, поскольку отношение площади, подверженной воздействию высокой температуры, ко всей площади поперечного сечения невелико. Поскольку P1-60 и MP1-60 показывают схожие отклонения друг от друга, жесткость P1-60 и MP1-60 аналогична из-за комбинированного влияния размеров поперечного сечения и распределения температуры. Несмотря на то, что MP1-60 имеет больший размер поперечного сечения, он также показывает более высокие распределения температуры, чем P1-60.Результаты показывают, что на жесткость балок сильно влияет температура.
Пластичность
Поврежденные огнем балки демонстрируют хрупкое поведение по сравнению с контрольным пучком, как показано в Таблице 6. Пластичность уменьшается с увеличением нагрузки или времени воздействия огня, и скорость уменьшения не пропорциональна времени воздействия огня. период. Разница в пластичности между контрольной балкой и балкой, нагретой в течение 1 часа, больше, чем разница между балками, нагретыми в течение 1 и 2 часов.Для балки, нагруженной 40% номинального момента, показатели пластичности для P1-60, P1-90 и P1-120 на 34,11, 45,44 и 50,59% меньше, чем у контрольной балки, соответственно. Для балки, нагруженной 60% номинального момента, показатели пластичности P2-60 и P2-120 на 44,75 и 55,88% меньше, чем у управляющей балки, соответственно. Для балки, нагруженной 80% номинального момента, показатели пластичности P3-60 и P3-120 на 49,65 и 65,18% меньше, чем у управляющей балки, соответственно.Кроме того, пластичность уменьшается с увеличением уровня нагрузки, поскольку распределение температуры внутри балки увеличивается с увеличением уровня нагрузки. Для балок, нагретых в течение 2 ч, пластичность П1-120, П2-120 и П3-120 на 50,59, 55,88 и 65,18% меньше, чем у контрольной балки, соответственно.
Таблица 6 Показатель пластичности балок на прогиб.Пластичность увеличивается с увеличением размера поперечного сечения. Как показано в Таблице 6, снижение пластичности управляющих балок происходит по мере увеличения размера поперечного сечения.Однако коэффициент уменьшения пластичности уменьшается с увеличением размера поперечного сечения. Показатели пластичности P1-60, MP1-60 и LP1-60 соответственно на 34,11, 33,28 и 16,33% меньше, чем у контрольной балки. Можно заметить, что балка с большим размером поперечного сечения более устойчива к возгоранию с точки зрения максимальной нагрузки, а также пластичности.
Результаты показывают, что пластичность балок сильно зависит от пламени, хотя балки имеют небольшие различия в максимальной нагрузке, поскольку модуль упругости бетона и стали, снижающийся в зависимости от температуры, в большей степени влияет на пластичность, а предел прочности на растяжение уменьшение для арматурных стержней, связанное с максимальной нагрузкой, незначительно до 500 ° С.
На основе анализа КЭ можно предсказать пластичность балок, поврежденных огнем, и прогнозируемые индексы пластичности показывают разумную тенденцию по сравнению с коэффициентами жесткости.
Определения, различия и дизайн »Компании Mazzella
Распределительные балки и подъемные балки — понимаете ли вы разницу и какой подъемник следует использовать для следующего подвесного подъемника?
Распорка и подъемная балка — это два разных типа подъемных устройств под крюком, используемых для стабилизации и поддержки груза во время подъема над головой.Оба типа устройств используются для удержания подъемных строп под устройством под углом 90 ° или около него (перпендикулярно горизонту). Это помогает избежать повреждения груза, повреждения такелажного оборудования и подъемных строп, а также помогает удерживать стропы от соскальзывания с груза во время подъема.
В то время как распорные балки и подъемные балки являются наиболее популярными типами подъемных устройств ниже крюка, существует большая путаница в отношении различий между ними в том, как они сконструированы и для чего используются.Основное различие между двумя типами подъемных устройств — это типы сил, которые прилагаются к балке.
Эта статья отлично объясняет различные силы, применяемые к каждому типу балки, и то, как они влияют на балку. Автор также дает простые определения каждого типа подъемного устройства, основанные исключительно на типе силы, прилагаемой к балке:
- Подъемная балка — Любая балка, на которую поднимается груз, создает изгибающее напряжение в балке.
- Распорная балка — Любая балка, на которую поднимается груз, в основном создает сжимающее напряжение в балке.
Компания Mazzella предлагает широкий выбор подъемных устройств «ниже крюка» стандартных размеров и конфигураций, а также у нас есть программа, полностью посвященная подъемным устройствам, изготовленным по индивидуальному заказу.
Наша цель в этой статье — предоставить простую и понятную разбивку распорных балок и подъемных балок на основе их конструкции, а также преимуществ и недостатков использования каждого устройства.
Распорка
Распорные балки преобразуют подъемные нагрузки в сжимающие силы в балке и растягивающие усилия в стропах.
Распределительная балка — это простое устройство, состоящее из длинной перекладины, которая удерживает две стропы друг от друга. Он разработан для преобразования подъемных нагрузок в чистые сжимающие силы, а также для раздвигания ног стропа.
Две подъемные проушины в верхней части балки прикрепляются к опорам цепной стропы или синтетической стропы под определенным углом, предназначенным для обеспечения чистого сжатия.Это равномерно распределяет вес груза между двумя стропами, которые затем соединяются с краном, подъемником или другой подъемной машиной. Две проушины внизу (по одной на каждом конце) соединяются с стропой или крюком, которые затем присоединяются к нагрузке.
Преимущества использования распорной балкиРаспорные балки преобразуют подъемные нагрузки в сжимающие силы стержня и растягивающие усилия в стропах. Из-за этого распорные балки высокоэффективны в использовании материала, поэтому они, как правило, меньше, легче и дешевле в разработке и производстве, чем подъемная балка.
Поскольку они используют две точки подъема вместо одной точки подъема, вес груза равномерно распределяется по балке, что устраняет нагрузку на одну точку подъема. Распорные балки идеально подходят для подъема очень широких или тяжелых грузов.
Распорные балки также помогают контролировать нагрузку и при правильной установке могут снизить вероятность:
- Опрокидывание, скольжение или изгиб груза
- Сдавливание или повреждение груза из-за того, что вы можете контролировать угол наклона стропы
Они также могут иметь фиксированные размеры или могут быть спроектированы с возможностью постепенной регулировки угла стропы, и длина самой балки для регулировки нагрузки вне центра.
Недостатки использования распорной балки Распоркаимеет верхний такелаж, состоящий из троса, цепных строп или синтетических строп, поэтому они не идеальны в ситуациях, когда пространство над головой может быть ограничено.
Для распорных балок требуется больше места над головой, чем для подъемной балки, чтобы можно было разместить подвесные стропы.
Для длинных балок или неравномерных нагрузок может потребоваться трос, чтобы держать нагрузку под контролем и снизить вероятность вращения.
Если груз необходимо поддерживать по всей его длине, то подъемная балка может быть более выгодной, поскольку у нее будет больше точек подъема на нижней стороне, чтобы поддерживать центр груза, а также точки подъема на обоих концах. балки.
Подъемные балки
Подъемные балки преобразуют подъемные нагрузки в изгибающие силы на балке.
Подъемная балка имеет простую конструкцию, состоящую из балки с единственной точкой крепления с центром на верхней стороне балки для подсоединения к крану, лебедке или другой подъемной машине.Некоторые подъемные балки могут иметь две скобы для зацепления двух крановых или подъемных крюков. Обычно на нижней стороне балки есть две или более равномерно расположенных подъемных проушины, которые прикрепляют и поддерживают груз с помощью крюка или стропы.
Преимущества использования подъемной балки Подъемные балкиидеально подходят для подъемников с более легкими и короткими пролетами, для которых не требуется много места над головой. Поскольку наверху имеется единственная скоба для крепления крана, для него не требуется такое же пространство над головой, как для распорной балки.
Подъемные балки идеально подходят для ситуаций, когда возникает проблема с верхним пространством, поскольку они соединяются с краном или подъемником с помощью дужки.
Подъемные балки также имеют несколько точек подъема внизу и могут быть выполнены с регулируемыми или фиксированными подъемными проушинами. Этот тип регулируемости означает, что подъемные балки можно использовать во многих различных приложениях и для многих различных типов грузов. Эта регулируемая конструкция позволяет подъемным балкам:
- Работа с несбалансированными грузами
- Управление внутренними силами дробления
- Использование специальных приспособлений для крепления груза
Жесткая и прочная конструкция подъемной балки идеально подходит для грузов, которые слишком слабые или гибкие, чтобы их можно было поднимать без опора — например, длинные или тонкие листы металла или стальные пластины.
Недостатки использования подъемной балкиПодъемные балки более жесткие, используют больше материала и тяжелее, чем эквивалентная распорная балка, чтобы противодействовать изгибающим силам, прилагаемым к балке. Поэтому они не так эффективно используют материал, как распорная балка, и, как правило, стоят дороже.
Даже для легкого груза с широким пролетом потребуется довольно большая и жесткая подъемная балка, поэтому в этом типе разгрузочная балка может быть более выгодной и рентабельной.
При использовании подъемной балки может потребоваться метка для удержания груза на одном уровне и предотвращения опрокидывания или вращения груза во время подъема.
Какие факторы влияют на использование распорной балки или подъемной балки?
Распорка или подъемная балка могут быть сконфигурированы или настроены для несбалансированных нагрузок и могут быть отрегулированы для нецентральных нагрузок.
Мы надеемся, что теперь вы лучше понимаете различия между распорной балкой и подъемной балкой.Принимая решение об использовании распорной балки или подъемной балки, учитывайте следующее:
- Что поднимают?
- Как поднимается?
- Каков вес и размер груза?
- Где его поднимают?
Вес груза и длина груза являются основными факторами. Если это тяжелый груз или груз с большим пролетом, то, вероятно, лучшим вариантом будет распорная балка. Если это груз, который необходимо поддерживать по всему пролету, в том числе в центре груза, то лучшим вариантом будет подъемная балка.
Особое внимание следует уделить месту подъема. Если у вас есть ограничения по высоте или низкая высота над головой, то подъемная балка может быть лучшим выбором. Особое внимание следует уделить тому, используется ли он с мостовым краном с верхним или нижним ходом. Из-за двух подъемных строп, прикрепленных к верхним перекладинам, для распорной балки требуется больше места над головой, чем для подъемной балки.
В Mazzella мы решаем каждую задачу подъема одинаково — делаем ли мы обычную подъемную балку на 150 фунтов.груз, либо специально сконструированный 330-тонный подъемник электропечи. У нас есть полностью укомплектованный инженерно-технический отдел, менеджеры проектов и сметчики, которые помогут решить ваши проблемы с подъемом и разработать идеальное решение для вашего уникального подъемного оборудования.
Мы приветствуем возможность удовлетворить ваши потребности в накладных расходах на погрузочно-разгрузочные работы. Если вы хотите узнать больше о том, как подъемное устройство, расположенное ниже крюка, может повысить эффективность и безопасность ваших подвесных подъемников, или хотите назначить консультацию, свяжитесь с нами, чтобы поговорить со специалистом.
Подъемные устройства под крюком
Мы обладаем более чем 65-летним опытом проектирования и разработки изделий по индивидуальному заказу, подъемных устройств под крюком и подъемного оборудования для использования со всеми типами кранов.
Персональный инжиниринг и наша приверженность ISO 9001: 2015 ведет нас к постоянному успеху в создании качественных продуктов и процессов.
Мы можем спроектировать и изготовить все типы подъемных устройств «ниже крюка» для любого применения — все наши работы выполняются в соответствии с ASME B30.20 и ASME BTH-1. Наша продукция варьируется от обычной подъемной балки до специально спроектированного подъемника линии двигателя на 150 фунтов и подъемника для электропечи на 330 тонн.
Позвоните нам по номеру 800.362.4601 или щелкните здесь, чтобы указать свой следующий проект, который будет ниже крючка!
Наряду с проектированием и изготовлением, мы обеспечиваем ремонт или переаттестацию подъемных устройств под крюк.
Щелкните здесь, если вам требуется ремонт или повторная сертификация подъемного устройства.
Лучевые реакции и диаграммы — Приложение «Сопротивление материалов для энергетики»
Диаграммы
Цели обученияВ конце этой главы вы должны уметь:
- Определение реакции свободно опертых, выступающих и консольных балок
- Рассчитайте и начертите диаграммы силы сдвига и изгибающего момента балок, подверженных сосредоточенным нагрузкам, равномерно распределенным нагрузкам и их комбинациям.
Балки обзор
Балки — это конструкционные элементы для различных инженерных применений, таких как крыши, мосты, механические узлы и т. Д. В целом балки являются тонкими, прямыми, жесткими, изготовлены из изотропных материалов и, что наиболее важно, подвергаются нагрузкам, перпендикулярным их продольной оси. Если вместо перпендикулярных нагрузок тот же элемент конструкции будет подвергаться продольным нагрузкам, он будет называться колонной или стойкой. Если тот же самый элемент будет подвергаться крутящему моменту, он будет называться и рассматриваться как вал.Следовательно, при определении механических или конструктивных компонентов очень важно учитывать способ нагрузки.
Обратите внимание, что когда дело доходит до ориентации, балки могут быть горизонтальными, вертикальными или с любым наклоном между ними (например, погруженные пластины, анализируемые в гидромеханике)… при условии, что нагрузка перпендикулярна их главной оси.
Опоры балок:
Нагрузки на балку :
| Нагрузки | Символ | Примеры | Покрытый |
| Точка, также называемая |
| Есть | |
| Равномерное распределенное |
| Есть | |
| Переменная Распределенная |
| Есть | |
| Концентрированные моменты | № |
Типы балок:
Решение для лучевых реакций
При решении для реакций рекомендуются следующие шаги:
- Нарисуйте диаграмму тела без балки
- Замените равномерно распределенную нагрузку (если есть) эквивалентной точечной нагрузкой
- Решите ΣM A = 0 (сумма моментов относительно опоры A).Это даст вам B R (реакция на поддержке B).
- Решите ΣM B = 0. Это даст вам R A .
- Используя R A и R B , найденные на шагах 3 и 4, проверьте, удовлетворяется ли ΣV = 0 (сумма всех вертикальных сил).
- Обратите внимание, что шаги 4 и 5 можно поменять местами.
- Для консольной балки используйте ΣV = 0, чтобы найти вертикальную реакцию на стене, и ΣM wall = 0, чтобы найти моментную реакцию на стене. Другого уравнения для подтверждения ваших результатов нет.
Диаграммы поперечных сил и изгибающих моментов
Обратите внимание:«Сдвиговые силы — это внутренние силы, развивающиеся в материале балки для уравновешивания приложенных извне сил для обеспечения равновесия всех частей балки.
Изгибающие моменты — это внутренние моменты, возникающие в материале балки для уравновешивания тенденции внешних сил вызывать вращение любой части балки ». [3]
Сила сдвига в любом сечении балки может быть найдена путем суммирования всех вертикальных сил слева или справа от рассматриваемого сечения.
Аналогичным образом изгибающий момент в любом сечении балки может быть найден путем сложения моментов слева или справа от рассматриваемого сечения. Опорной точкой момента является рассматриваемое местоположение.
По соглашению внутренние сдвигающие силы, действующие вниз, считаются положительными. Они противодействуют восходящим внешним силам. Следовательно, при представлении поперечных сил вы можете нарисовать их в направлении внешних сил. Это визуально проще, чем следовать условным обозначениям.
Моменты по часовой стрелке обычно считаются отрицательными, а моменты против часовой стрелки — положительными. При представлении изменения изгибающего момента обратитесь к следующей таблице, в которой показаны качественные кривые изгибающего момента в зависимости от формы графиков поперечной силы.
.
При построении диаграмм поперечных сил и изгибающих моментов важны условные обозначения, но решающее значение имеет согласованность. Например, рассмотрим простую балку, нагруженную точечной нагрузкой, приложенной к нагрузке UD.Запуск диаграмм на опоре A, глядя на страницу, выдаст следующее:
Теперь переверните луч горизонтально на 180º (или измените точку наблюдения, глядя на луч с противоположной стороны) и начертите диаграммы, начиная с той же точки A. Диаграммы будут выглядеть следующим образом:
Обратите внимание, что, хотя диаграммы поперечных сил выглядят как зеркальные изображения (перевернутые по горизонтали), на диаграмму изгибающего момента это не влияет. Кроме того, наиболее важный результат этого анализа показывает, что значения максимальной силы сдвига и изгибающего момента всегда будут одинаковыми.
КПП КПППри построении схем балок необходимо учитывать следующее:
Диаграммы поперечных сил:
- На концах свободно опертой балки поперечная сила равна нулю.
- У стены консольной балки поперечная сила равна вертикальной реакции у стены. На свободном конце балки поперечная сила равна нулю.
- На любом сегменте балки, где отсутствуют нагрузки, поперечная сила остается постоянной (горизонтальная линия).
- Точечная нагрузка или реакция на диаграмме поперечных сил вызывает резкое изменение графика в направлении приложенной нагрузки.
- Равномерно распределенная нагрузка, действующая на балку, представлена прямой поперечной силой с отрицательным или положительным наклоном, равной нагрузке на единицу длины.
Диаграмма изгибающих моментов:
- На концах свободно опертой балки изгибающие моменты равны нулю.
- У стенки консольной балки изгибающий момент равен моменту реакции.На свободном конце изгибающий момент равен нулю.
- В том месте, где поперечная сила пересекает нулевую ось, соответствующий изгибающий момент имеет максимальное значение.
- Форма кривой изгибающего момента между двумя точками балки показана в двух таблицах выше.
- Изменение изгибающего момента между двумя точками балки равно площади под диаграммой поперечных сил между теми же двумя точками.
Приведенные выше рекомендации помогут вам в построении диаграмм направленности; они также служат проверкой.
Назначенные задачиРассчитайте реакции балки и нарисуйте диаграммы поперечной силы и изгибающего момента для следующих балок.
При составлении диаграмм пучка в классе и дома вы можете проверить свои ответы с помощью бесплатного онлайн-калькулятора пучка: SkyCiv Cloud Engineering Software
Задача 1: Укажите максимальные значения поперечной силы и изгибающего момента.
Задача 2: Укажите максимальные значения поперечной силы и изгибающего момента.
Проблема 3: Балка длиной 24 метра просто опирается на 3 метра с каждого конца. Балка несет точечную нагрузку 18 кН на левом конце и 22 кН на правом конце балки. Балка весит 400 кг / м. Нарисуйте схемы балок и определите место на балке, где изгибающий момент равен нулю.
Задача 4: Простая свисающая балка длиной 112 футов выступает над левой опорой на 14 футов. Балка несет сосредоточенную нагрузку в 90 тысяч фунтов на 12 футов от правого конца и равномерно распределенную нагрузку в 12 тысяч фунтов / фут на 40 футов. раздел с левого конца.Нарисуйте схемы балок и определите поперечную силу и изгибающий момент на участке в 50 футах от левого конца.
Задача 5: Предложите улучшение для этой главы.
.