Нагрузка на брус: Какие нагрузки выдержит брус?

Какие нагрузки выдержит брус?

Дата публикации: 03.03.2018 00:00

Брус и бревно издавна использовали на Руси для строительства домов. Деревянные строения имеют целый ряд преимуществ:

• Простота возведения здания.
• Высокая скорость постройки;
• Низкая стоимость.
• Уникальный микроклимат. Деревянный дом «дышит», в нем воздух намного легче и приятнее;
• Отличные эксплуатационные характеристики;
• Деревянный дом хорошо держит тепло. Он теплее кирпичных зданий в 6 раз, а строений из пенобетона в 1, 5 раза;
• Различные виды и размеры этого пиломатериала позволяют воплотить в жизнь самые разнообразные проекты и дизайнерские идеи.

Брус

Этот вид строительного материала представляет из себябревно прямоугольного сечения. Он считается самым дешевым пиломатериалом и в то же время очень удобным для строительства.

Изготавливают брус из пиловочных бревен, хвойных пород.

Виды бруса:

• Двухкантный — обработаны (срезаны у бревна) только две противоположные стороны, а другие две оставлены закругленными.
• Трёхкантный. Здесь срезаны три стороны.
• Четырёхкантный–срезаны 4-истороны.

Размеры:

Стандартная длина бруса – 6 метров. Клееный брус – это сборная конструкция, поэтому здесь длина может достигать 18 метров.

Размеры сечения

• Толщина от 100 до 250 мм. Размер шага сечения 25 мм, то есть толщина равняется 100, 125.
• Ширина от 100 мм до 275 мм.

К выбору сечения бруса нужно подходить с особой тщательностью. Ведь от того какую нагрузку сможет выдержать этот строительный материал будет зависеть безопасность здания.

Для правильного подсчета нагрузки существуют особые формулы и программы.

Виды нагрузок

1. Постоянные. Это те нагрузки на брус, которые оказывает вся конструкция здания, вес утеплителя, отделочных материалов и кровли.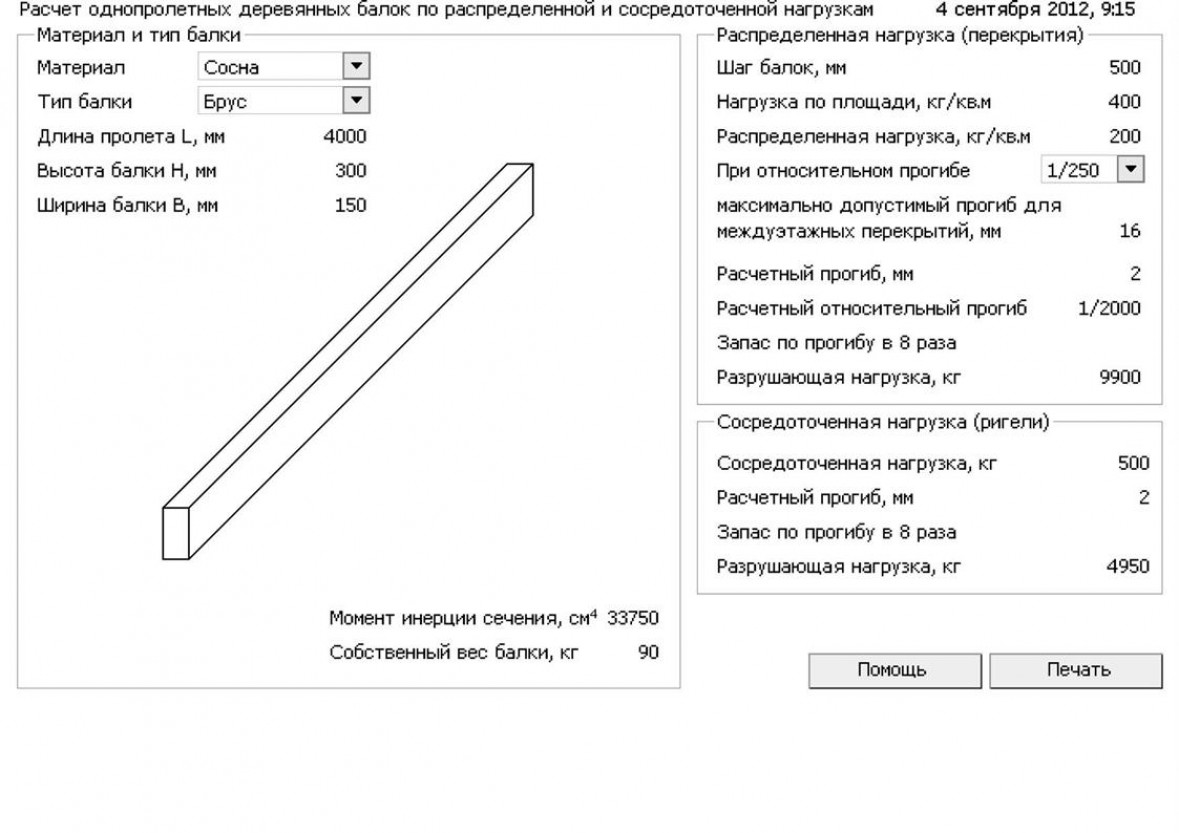

2. Временные. Эти нагрузки могут быть кратковременными, редкими и длительными. Сюда относятся движения грунта и эрозия, ветровые, снеговые нагрузки, вес людей при строительных работах. Снеговые нагрузки разные, они зависят от региона возведения строения. На севере снежный покров больше, поэтому нагрузка на брус будет выше.

Чтобы расчет нагрузки оказался верным в формулу (ее можно найти в интернете) надо вводить оба типа нагрузок, характеристику строительного материала, его качество, влажность. Особенно тщательно нужно высчитать нагрузку на брус при возведении стропиловки.

Какую нагрузку выдерживает брус 150х150Брус сечением 15 на 15 см широко используют при возведении зданий. Его применяют для изготовления подпорок, опалубка и для возведения стен, так как он выдерживает большие нагрузки. Но размер 15 на 15 лучше использовать для строительства домов в южных районах, на севере понадобиться дополнительное утепление стен, так как этот пиломатериал хранит тепло только при температуре воздуха –15 градусов.

Но если использовать клееный брус этого размера, то он по своим теплосберегающим свойствам будет равняться брусу сечением 25 на 20 см.

Какую нагрузку выдерживает брус 100 на 100 мм

Этот брус уже не такой надежный, он выдерживает нагрузку меньше, поэтому его основное применение– изготовление стропиловки и перекрытия между этажами. Необходим он и при сооружении лестниц, изготовления подпорок, арок, оформления мансард, потолка дома. Можно из него сделать и каркас панельного одноэтажного дома.

Какую нагрузку выдерживает брус 50 на 50 мм 

Брус 50х50 мм очень востребован. Без этого размера не обойтись при строительстве домов из бруса, та как он является вспомогательным материалом. Он, конечно, не подойдет для возведения стен, так как он выдерживает малую нагрузку, но для возведения обрешеток для внешней отделки стен, каркасов, перегородок необходим именно этот размер. Из бруса 50 на 50 делается каркас стены, на который потом прикрепляется гипсокартон.

Здесь можно использовать самые разнообразные крепления от гвоздей до скоб или проволоки.

видео-инструкция по монтажу своими руками, особенности букового материала, 50х20, 50х25, 50х30, 50х40, 50х50, 50х60, 50х70, 50х200, 50х3000, 50х6000, какой вес, нагрузку выдерживает, технические данные, ГОСТ, цена, фото

Статьи

Брус сечением 50х50 мм является достаточно распространенным в строительстве материалом, область применения которого очень обширна. Причем в продаже можно встретить несколько его разновидностей, которые обладают разными эксплуатационными качествами. Далее мы подробней рассмотрим особенности и некоторые технические данные бруса 50 на 50 мм, ознакомимся с его видами и областями применения материала.

Брусья сечением 50х50 мм

Общие сведения

Брус является природным пиломатериалом, который получают путем распиловки сырья, т.е. бревна.

Большая его популярность связана с некоторыми его достоинствами, такими как:

• доступная цена;
• простота обработки;
• хорошая прочность, благодаря чему можно использовать его в качестве конструкционного материала;
• хорошая долговечность при правильной обработке.

Конечно, наряду с достоинствами этот материал имеет и некоторые недостатки:

• небольшое сечение, в результате чего не может выдерживать большие нагрузки. Соответственно, его нельзя использовать в качестве балок и прочих несущих элементов. К примеру, брусья сечением 50 на 70, установленные на ребро, способны выдержать гораздо большую нагрузку на изгиб;
• по этим же причинам его не используют для возведения стен, где требуется сечение 200 на 200 или хотя бы 150 на 150 мм;
• имеется склонность к деформации и растрескиванию, поэтому использовать можно только высушенное дерево (оптимальный уровень влажность 8-12 процентов).

Таким образом, прежде чем использовать в строительстве брус 50х50 мм, следует рассчитать, какую нагрузку выдерживает этот пиломатериал, и какая нагрузка будет на него оказываться в конструкции. Кроме того, необходимо убедиться, что влажность материала не превышает 15 процентов.

Строганый брусок 50х50 мм

Виды

Особенности изготовления

В зависимости от типа обработки и технологии изготовления, согласно ГОСТ на брус 50х50 № 8486-86 и 20850-84, в продаже можно встретить следующие его виды:

Тип	Особенности
Не строганый	Получают путем распиловки бревна или бруса большего сечения. В продаже можно встретить этот материал как высушенным, так и сырым. Последний является наиболее дешевым видом этого пиломатериала.
Строганый	Обладает гладкой поверхностью, так как дополнительно подвергается механической обработке. Этот пиломатериал в продаже чаще встречается высушенным.
Клееный	В отличие от всех вышеперечисленных материалов изготавливается не из цельной древесины, а отдельных, склеенных между собой ламелей (состыкованных в длину досок). Клееный брус имеет много преимуществ перед цельным: в результате роспуска пиломатериалов на тонкие доски снимается внутреннее напряжение, соответственно, исключается возможность деформации и растрескивания; дерево подвергается сушке в печах, в результате чего имеет оптимальную влажность; обладает большей прочностью, чем цельное дерево; не содержит сучков и прочих дефектов, так как в процессе изготовления они обрезаются. Правда, следует отметить, что данная технология содержит и некоторые недостатки – в результате использования клея снижается экологичность материала. Кроме того, ограничено минимальное сечение – клееный брусок 40 на 40 мм в продаже уже не найти.

На фото — клееные бруски 50х50 мм

Совет!
При выборе следует обращать внимание не только на технологию изготовления, но и длину бруса.
Чаще всего он имеет размеры 50 на 50 на 3000 мм, реже можно встретить его длиной 4000 и 6000 мм.

Выбор типа материала во многом зависит от области его применения. К примеру, если его планируется использовать для сборки несущей конструкции, то лучше использовать клееные брусья.

Породы древесины

Помимо технологии изготовления данный пиломатериал может различаться породой древесины, из которой выполнен.

Чаще всего для данных целей используют следующие породы:

• ель и сосну – являются наиболее дешевым видом древесины, среди достоинств можно выделить хорошую прочность и устойчивость к влаге благодаря наличию большого количества смолы;

Брусок из сосны

• кедр – мягкий материал, благодаря чему его легко обрабатывать своими руками, но в то же время он достаточно прочный. Следует отметить, что кедр известен своими бактерицидными свойствами;
• бук – представляет собой тяжелую и прочную древесину, напоминающую по своим характеристикам дуб. Однако, при покупке следует учитывать, что буковый брус 50х50 мм сильно подвержен короблению в процессе высыхания;

Строганый брусок из лиственницы

• лиственница – главной особенностью этой древесины является устойчивость к гниению и заражению грибками;
• дуб – является наиболее дорогим, но в то же время наиболее прочным материалом. Поэтому дубовое дерево можно использовать для несущих конструкций.

Обратите внимание!
От породы древесины зависит не только стоимость пиломатериала и его эксплуатационные качества, но и вес.
Приблизительные параметры можно узнать из справочной литературы.
Единственное, для этого нужно посчитать количество бруса 50 на 50 на 6000 или на 3000 мм в одном кубе.

Теплица из брусков 50х50 мм

Область применения

Как уже было сказано выше, область применения этого материала довольно обширна.

Чаще всего брус используют в следующих целях:

• для сооружения каркаса небольших строений – деревянных беседок, летних душей, навесов, теплиц и пр.
• в качестве материала для обрешеток, правда, если на конструкцию не будут оказываться большие нагрузки, целесообразней использовать для этих целей рейки 20 на 20 или 30х30 мм;

Бруски для обрешетки 50 на 30 мм

• в качестве лаг для укладки полов;
• для обустройства каркасов для вентилируемых фасадов;
• в качестве стропил крыши небольших строений. Единственное, для этого нужно рассчитать какой вес выдерживает брус 50х50 в той или иной конструкции.
  Зачастую целесообразней в качестве стропил использовать пиломатериал 50 на 60 или на 70 мм. На нашем портале вы можете найти подробную информацию о том, как рассчитать прочность пиломатериала;
• в качестве столбиков для ограждений, единственное, в этом случае должна строго соблюдаться инструкция по вкапыванию деревянных столбов, в противном случае они быстро сгниют.

Совет!
При обустройстве ограждений между столбами можно расположить рейки 50 на 25 мм в виде косой решетки.
Такое ограждение смотрится красиво и оригинально.

Вывод

Как мы выяснили, эксплуатационные свойства бруса 50х50 мм во много зависят от технологии его изготовления и породы древесины. Поэтому прежде чем закупить пиломатериал, следует определиться с областью его применения, и в соответствии с этим выбрать наиболее подходящий тип бруса.

Получить дополнительную полезную информацию по озвученной теме можно из видео в этой статье.

Калькулятор нагрузки на балку

Калькулятор нагрузки на балку поможет вам определить реакции на опоры свободно опертой балки, вызванные вертикальными точечными нагрузками или силами. В этом калькуляторе мы рассмотрим:

• Что такое реакция поддержки;
• Как рассчитать опорные реакции в балке;
• Пример расчета по нахождению опорных реакций; и
• Как рассчитать допустимую нагрузку на балку с помощью этого калькулятора нагрузки на балку.

Знание того, как найти опорные реакции, является отличным началом при анализе балок, например, при определении прогиба балки. Продолжайте читать, чтобы узнать больше.

🙋 Если вам интересно, как рассчитать прогиб балки, у нас есть наш калькулятор прогиба балки, который вы можете проверить, или наш многофункциональный калькулятор пролета деревянной балки для углубленного расчета конструкции деревянной балки.

Что такое реакция поддержки?

Согласно третьему закону движения Ньютона , каждая сила, действующая на объект, имеет равную и противоположную реакцию. Если вы пытаетесь на что-то надавить, скажем, на стену, вам кажется, что стена тоже отталкивает вас. Именно это явление описывает третий закон движения Ньютона.

В машиностроении элементы конструкции, такие как балки и колонны, взаимодействуют друг с другом в точках, где они встречаются. Представьте себе балку, которая поддерживается двумя колоннами. Вес балки давит на колонны, и из-за третьего закона движения Ньютона мы можем также сказать, что колонны воздействуют на балку эквивалентной противоположной реактивной силой. Мы называем эти силы реакции реакции поддержки .

Вы можете представить дверной потолок в виде балки, показанной выше, и две домкратные стойки (вертикальные стойки, на которые опирается дверной потолок) в качестве двух опорных конструкций дверного потолка. Узнайте больше о размерах дверных перемычек, воспользовавшись нашим калькулятором размеров дверных перемычек.

На свободно опертой балке опорные реакции на каждом конце балки могут быть либо равны друг другу, либо иметь разные значения. Их значения зависят от приложенных к балке нагрузок. Если на более близком расстоянии от одной опоры находится больше нагрузок, эта опорная конструкция испытывает большую силу и, следовательно, испытывает большую реакцию.

Как рассчитать опорные реакции в балке?

Поскольку опорные реакции действуют в направлении, противоположном силе, можно сказать, что вся система находится в равновесии. Это означает, что балка не движется, а сумма сил и моментов равна нулю. Приравняв момента от нагрузки к моментам от опорных реакций , мы можем определить реакции на опорах.

Как и при расчете крутящего момента, мы также можем выполнить суммирование моментов на каждой опоре для расчета реакций. Ниже мы выражаем сумму ∑\small \sum∑ моментов на опоре A, чтобы найти реакцию на опоре B, обозначенную как RB\small R_\text{B}RB​, как показано ниже: 9n(F_i\times x_i) — (R_\text{B}\times\text{span}) = 0 i=1∑n​(Fi​×xi​)−(RB​×span)=0

или

(F1×x1) ⁣+ ⁣(F2×x2) ⁣+ ⁣(F3×x3) ⁣+ … ⁣+ ⁣(Fn×xn) ⁣− ⁣(RB×span)=0,\small (F_1\x_1 раз)\! +\! (F_2\x_2 раз)\! +\! (F_3\x_3 раз)\! +\\ …\! +\!(F_n\times x_n)\! -\! (R_\text{B}\times \text{span}) = 0,(F1​×x1​)+(F2​×x2​)+(F3​×x3​)+…+(Fn​× xn​)−(RB​×span)=0,

, где:

• F1F_1F1​, F2F_2F2​, F3F_3F3​ и FnF_nFn​ — точечные нагрузки на балку на расстояниях x1x_1x1​, x2x_2x2​, x3x_3x3​, и xnx_nxn от опоры A соответственно;
• RBR_\text{B}RB​ – Реакция на поддержке B; и
• span\text{span}span – Длина балки между опорой A и опорой B.

Преобразовав уравнение, мы можем изолировать RBR_\text{B}RB​ следующим образом: +… ⁣+ ⁣(Fn×xn)\маленький \начать{выравнивать*} R_\text{B} \times \text{span}\! =& (F_1\x_1 раз)\! +\! (F_2\x_2 раз)\! +\! (F_3\x_3 раз)\! +\\ & …\! +\!(F_n\times x_n)\\ \end{align*}RB​×span=​(F1​×x1​)+(F2​×x2​)+(F3​×x3​)+…+(Fn​×xn​)​

RB=[(F1×x1) ⁣+ ⁣(F2×x2) ⁣+ ⁣(F3×x3) ⁣+… ⁣+ ⁣(Fn×xn)]÷span ✔\small \начать{выравнивать*} R_\text{B} =&[(F_1\times x_1)\! +\! (F_2\x_2 раз)\! +\! (F_3\x_3 раз)\! +\\ & …\! +\!(F_n\times x_n)] \div \text{span}\ \text{✔} \end{align*}RB​=​[(F1​×x1​)+(F2​×x2​)+(F3​×x3​)+…+(Fn​×xn​)]÷span ✔​

Теперь, когда у нас есть выражение для нахождения RB\small R_\text{B}RB​, и поскольку мы знаем, что общие приложенные силы равны сумме реакций, теперь мы можем также найти реакцию на опоре A , RA\small R_\text{A}RA​, используя следующие уравнения: 9n F_i — R_\text{B}\ \text{✔}RA​=i=1∑n​Fi​−RB​ ✔

Теперь, когда мы знаем, как рассчитать опорные реакции в балках, давайте теперь рассмотрим пример расчет, чтобы укрепить наши знания об этом. 🙂

Пример расчета по нахождению опорных реакций

Предположим, что у нас есть 4,0-метровая свободно опертая балка с приложенной точечной нагрузкой 10,0 килоньютонов (кН) в 2,0 метрах от опоры A и другой приложенной 3,5 кН точечная нагрузка 1,5 метра от опоры B , как показано ниже:

Для расчета RB\small R_\text{B}RB​ сформулируем уравнение моментного равновесия следующим образом:

RB=(F1×x1)+(F2×x2)span= (10 кН×2,0 м)+(3,5 кН×(4,0 м−1,5 м))4,0 м=20 кН-м+8,75 кН-м4,0 м=7,1875 кН\scriptsize \начать{выравнивать*} R_\text{B} &= \frac{(F_1\times x_1)\! +\! (F_2\times x_2)}{\text{span}}\\[1.2em] &= \frac{(10\ \text{kN}\!\times\! 2.0\ \text{m})\! +\! (3,5\ \text{кН}\!\times\! (4,0\ \text{м}\! -\! 1,5\ \text{м}))}{4,0\ \text{м}}\\[1,2 Эм] &= \frac{20\ \text{кН-м} + 8,75\ \text{кН-м}}{4,0\ \text{м}}\\[1,2см] &= 7,1875\ \text{кН} \end{align*}RB​=span(F1​×x1​)+(F2​×x2​)​=4,0 м(10 кН×2,0 м)+(3,5 кН×(4,0 м−1,5 м)) ​=4,0 м20 кН-м+8,75 кН-м​=7,1875 кН​

Выполняя суммирование сил, получаем:

∑F=0F1+F2+(−RA)+(−RB)=010+3,5+(−RA)+(−7,1875)=0RA=10+3,5− 7,1875RA=6,3125 кН\размер сценария \начать{выравнивать*} \сумма F\! &= 0\\ Ф_1\! +\! Ф_2\! +\! (-R_\текст{А})\! +\! (-R_\текст{B})\! &= 0\\ 10\! +\! 3,5\! +\! (-R_\текст{А})\! +\! (-7. 1875)\! &= 0\\ Р_\текст{А}\! &= 10\! +\! 3,5\! -7.1875\\ Р_\текст{А}\! &= 6,3125\ \text{кН} \end{align*}∑FF1​+F2​+(-RA​)+(-RB​)10+3.5+(-RA​)+(-7.1875)RA​RA​=0=0=0= 10+3,5−7,1875=6,3125 кН​

Обратите внимание , что для этого суммирования , мы рассмотрели все нисходящие силы как положительные и все направленные вверх силы как отрицательные . Основываясь на наших расчетах, приведенных выше, мы получили, что реакции на опорах A и B равны 6,3125 кН и 7,1875 кН соответственно.

Также обратите внимание, что в этом примере расчета опорных реакций и в калькуляторе нагрузки на балку мы предполагали, что балка невесома. Однако, если указан вес балки, вы можете рассматривать вес балки как еще одну направленную вниз нагрузку в центре или центроиде балки.

Использование нашего калькулятора нагрузки на балку

Наш калькулятор прост и удобен в использовании. Все, что вам нужно сделать, это ввести пролет балки , величину точечных нагрузок и их расстояния от опоры A . Сначала вы увидите только поля для двух загрузок (Загрузка 1 и Загрузка 2), но как только вы введете значение для x2\small x_2x2​, появятся поля для Загрузки 3 и так далее.

Если вы хотите ввести восходящую нагрузку, просто введите отрицательное значение для величины нагрузки. Всего в наш калькулятор нагрузки на балку можно ввести до 11 точечных нагрузок.

4.2 Общие типы нагрузки для балок и рам

>>Когда вы закончите читать этот раздел, проверьте свое понимание с помощью интерактивного теста внизу страницы.

Ряд распространенных типов нагрузки на балки и рамы показан на рисунке 4.1. Это не исчерпывающий список, но он показывает все типы нагрузок, с которыми мы будем иметь дело в этой книге. Из них, безусловно, наиболее распространенными являются два верхних: 90 125 точечной нагрузки 90 126 и 90 125 равномерно распределенной нагрузки 9.0126 . Точечная нагрузка — это всего лишь одна сила, действующая на одну точку балки или элемента рамы. Равномерно распределенная нагрузка, также называемая равномерной нагрузкой , представляет собой нагрузку, равномерно распределенную по некоторой длине балки или элемента рамы. В конструкциях эти равномерные нагрузки обычно исходят от площадных нагрузок, действующих на поверхность пола или стены, которым должна сопротивляться соединенная балка или колонна. Эта нагрузка на площадь умножается на ширину ответвления , обычно на расстояние между соседними балками или колоннами, чтобы преобразовать нагрузку на площадь в равномерную линейную нагрузку, как показано на рисунке. Эти равномерные нагрузки даны в единицах силы на единицу расстояния (например, кН/м). В дополнение к равномерной нагрузке, нагрузка на элементы конструкции может распределяться другими способами, такими как треугольная или трапециевидная распределенная нагрузка, показанная на рисунке 4.1 (среди прочего). Мы также столкнемся с точечными моментами, как показано на рисунке. Эти точечные моменты часто могут быть вызваны другими элементами или элементами, соединенными с балкой или элементом рамы, которые не включены непосредственно в схему свободного тела. Чаще всего вы будете сталкиваться с точечными моментами в фиксированных местах конечной реакции.

Рисунок 4.1: Общие типы нагрузки

Как мы можем работать с этими типами равномерной или другой распределенной нагрузки при выполнении расчетов равновесия? Способ сделать это состоит в том, чтобы рассмотреть эквивалентную общую нагрузку или эффективную силу , вызванную распределенной нагрузкой, которая действует в центре тяжести распределения. Расположение этого центроида зависит от типа распределения нагрузки, как показано в правой части рисунка 4.1. Для равномерной нагрузки действующая сила равна общей нагрузке, определяемой нагрузкой на единицу длины, умноженной на общую длину (или $wL$). Это также равно площади под диаграммой распределенной нагрузки, в данном случае прямоугольника. Для равномерной нагрузки центроид находится в центре распределения ($L/2$). Это то место, куда вы бы поместили действующую силу, чтобы использовать ее в расчетах равновесия. Для треугольной нагрузки эффективной нагрузкой снова является общая нагрузка, равная площади под распределением, в данном случае $wL/2$ ($\frac{1}{2}bh$), и она действует в центре тяжести треугольника, расположенного на одной трети длины от высокой стороны.