Напомним некоторые старинные меры длины решение: Напомним некоторые старинные меры длины: 1 вершок равен примерно 44 мм; 1 аршин равен 16 вершкам; 1 сажень равна 3 аршинам;

«Старинные русские меры длины, их роль в современном мире»

Государственное бюджетное общеобразовательное учреждение лицей

имени Героя Советского Союза П.И. Викулова

городского округа Сызрань Самарской области

Тема исследовательской работы:

«Старинные русские меры длины, их роль в современном мире»

Выполнил:

Куракин Ярослав

учащийся 4″Б» класса

ГБОУ лицей г. Сызрани.

Руководитель работы:

Гордеева Наталья Викторовна,

учитель начальных классов

г. Сызрань, 2022г.

Оглавление

Введение…………………………………………………………………………………3

1. Единицы измерения Древней Руси………………………………………………….5

2. Задачи, в которых используются старинные меры длины………………………. 11

4. Пословицы и поговорки с упоминанием старинных мер длины…………………13

5. Анкетирование……………………………………………………………………….16

6. Введение в России единой метрической системы мер……………………………19

Заключение……………………………………………………………………………..20

Список литературы…………………………………………………………………….22

Приложения………………………………………………………………………….…23

Введение.

Нельзя представить себе жизнь человека, который не производил бы какие-нибудь, хотя бы самые простые, измерения. Даже для первобытного человека, строившего себе жилище, изготовлявшего простейшие орудия и посуду, применение мер длины, веса и объемов было необходимостью. Без измерений невозможно узнать, что находится рядом с нами, а что — вдали, какой предмет больше, а какой меньше.

В древности люди упорно и настойчиво пытались найти точный ответ на вопрос «сколько?». Чтобы это сделать, им нужно было научиться измерять расстояние, время, вес, то есть научиться видеть особое свойство у предметов и явлений – количество. «Инструментами» для измерения количества сначала был сам человек и его ближайшее окружение. Предметы измерялись руками (толщина пальца, размах рук), ногами (длина стопы, длина шага).

Старинные меры длины встречаются в учебных пособиях, литературных и исторических произведениях, пословицах, поговорках, математических задачах. И чтобы правильно понимать текст, мы должны иметь представление о том, какие мерные единицы были в древности и в каком отношении они находились друг с другом.

Например, загадка:

Поутру в сажень, в полдень с пядень,

а к вечеру через поле хватает?

(Ответ: тень)

Старинные меры длины и по величинам, и по названиям непривычны для человека, живущего в XXI веке, но мы обязаны их знать хотя бы потому, что это часть нашего прошлого.

Тема моей исследовательской работы звучит так: «Старинные русские меры длины, их узнаваемость и используемость в современности.»

Целью моей исследовательской работы будет изучение материалов о мерах длины, используемых в древности на Руси, исследование пословиц и поговорок с упоминанием старинных мер длины, выяснение насколько современные люди знают и используют старинные меры длины.

Задачи:

1. Изучить информацию о мерах длины, используемых в древности на Руси.

2. Познакомиться с примерами задач, в которых используются старинные меры длины.

3. Исследовать пословицы, поговорки с упоминанием старинных мер длины.

4. Выявить, знают ли современные люди старинные меры длины.

5. Выяснить, когда появилась единая метрическая мера.

Методы исследования:

1. Изучение литературных и электронных источников информации.

2. Систематизирование и обобщение найденного материала.

3. Анкетирование.

4. Анализ полученных результатов.

Старинные русские меры длины.

Линия — очень маленькая старинная мера длины, равная 2,54 мм (0,1 дюйма) или ширине пшеничного зерна.

Перст — старинное название указательного пальца руки, ширина которого равна приблизительно 2 см.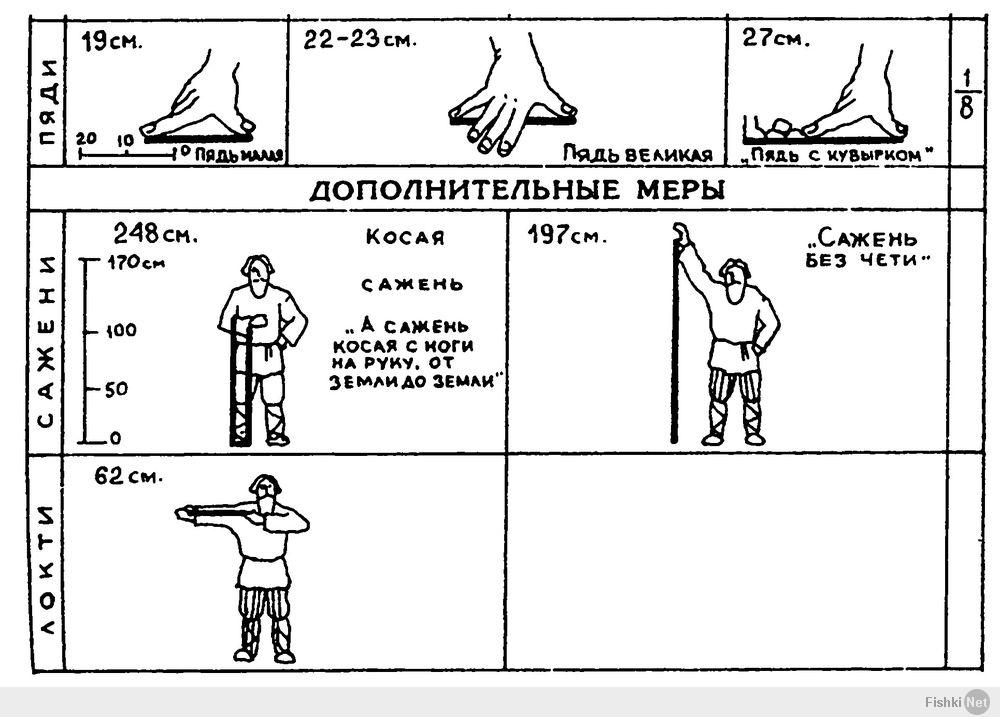 Отсюда происходит анатомический термин «двенадцатиперстная кишка». Длина этого человеческого органа составляет 24-25 см. Перст использовался в качестве меры длины или толщины предмета.

Вершок — старинная русская мера длины, равная ширине двух пальцев руки (указательного и среднего). Длина вершка составляет примерно 4,4 см.

Ладонь – ширина кисти руки, равная четырём пальцам.

Пядь, пядень (или четверть) — одна из самых старых мер длины, название которой происходит от древнерусского слова пясть — кулак или пять — кисть руки. Данная мера длины удобна тем, что каждый всегда носит её с собой. Ведь пядь — это расстояние между  вытянутыми пальцами руки. Пядь составляла одну четверть аршина. Поэтому второе её название — четверть.

Пядь малая — расстояние между концами вытянутых большого и указательного пальцев руки. Длина малой пяди равна примерно 19 см.

Пядь великая — расстояние от конца вытянутого мизинца до конца большого пальца, равное 22-23 см.

Пядь с кувырком. В старину эту меру получали прибавлением к малой пяди длины двух или трёх суставов указательного пальца. Длина такой пяди равна, соответственно, 27 и 31 см или 5 вершков.

Локоть — древнейшая мера длины, которой пользовались многие народы мира. Это расстояние от конца вытянутого среднего пальца или сжатого кулака до локтевого сгиба. Эта длина колебалась от 38 до 47 см или 11-16 вершков. Как мера длины на Руси встречается с XI века. Её применяли в крестьянском хозяйстве, когда нужно было измерить длину изготовленной в домашних условиях шерстяной пряжи или пеньковой верёвки (такую продукцию наматывали на локоть).

Аршин — одна из основных русских мер длины, которая использовалась с XVI века. Пришёл аршин на Русь вместе с купцами из далёких восточных стран. Купцы привозили невиданные ткани, например, тончайшие китайские шелка или сделанную из настоящих золотых и серебреных нитей тяжёлую индийскую парчу. А также бархат и тафту, затканную цветами и драконами, — из Персии. Купцы привозили ткани и их приходилось отмерять. Восточные купцы обходились без всяких метров: ткань они натягивали на собственную руку до плеча. Это и называлось мерить аршинами. Название аршин происходит от персидского слова «арш» — локоть. Это длина всей вытянутой руки от плечевого сустава до конца фаланги среднего пальца. Длина аршина составляет 71 см.

Мера была очень удобной — руки всегда при себе, — но был у неё существенный недостаток: руки, к сожалению, у всех разные. У одних они длинные, у других — короче. Хитрые купцы стали искать приказчиков с руками покороче. Но однажды э тому пришёл конец. Продавать «на свой аршин» властями было строжайше запрещено. Употреблять разрешалось только «казённый аршин». Это эталон аршина, представляющий собой металлическую линейку изготовили в Москве. Деревянные когти такой линейки рассылались по всей территории России. Чтобы деревянный аршин нельзя было укоротить, концы оковывали железом и помечали государственным клеймом.
Длина казённого аршина составляла 71 см 12 мм, что равно 16 вершкам или 28 дюймам.

Шаг — это расстояние между пятками или носками шагающего человека. Средняя длина шага равна 71 см. Шаг является одной из древнейших мер длины, дошедшей до нашего времени. Сохранились сведения об использовании «шага» для определения расстояния между городами в Древнем Риме, Египте, Персии. В Древней Греции расстояние в «шагах» указывалось на придорожных столбах. В России в «шагах» определяли длину сторон земельных участков, расстояние между населёнными пунктами. Шаг, как мера длины, используется и в настоящее время. Существует также специальный прибор — шагомер, который автоматически отсчитывает число пройденных шагов.

Сажень — мера длины, которая упоминается ещё в летописи XI века (1017г,) составленной киевским монахом Нестором. Её размер связан с человеком: наименование «сажень» происходит от глагола сягать (досягать) — на сколько можно было дотянуться рукой (размах рук). По данным историков и архитекторов, саженей было более 10 и они имели свои названия. Сажень — это три аршина, или 213,36 см.

Маховая сажень — расстояние между концами средних пальцев раскинутых в стороны рук человека среднего роста или 176 см.

Косая сажень — расстояние от пальцев левой (правой) ноги стоящего человека до конца пальцев вытянутой по диагонали правой (левой) руки, около 248 см.

Существовали саженные мерные верёвки и деревянные «складени», имевшие применение при измерении расстояний в строительстве и при межевании земли.

В завершение рекомендую обратить внимание на иллюстрацию, которая поможет наглядно понять и запомнить некоторые старинные малые меры длины:

Верста — от слова вертеть. Первоначально — расстояние от одного поворота плуга до другого во время пахоты. Длина версты составляет 1060 м. Верста, как мера длины, на Руси встречается с XI века. Коломенская верста — «верзила» — шутливое название очень высокого человека. Оно берёт своё начало со времён царя Алексея Михайловича, царствовавшего с 1645 по 1676 г. Он повелел расставить вдоль дороги, проложенной от Калужской заставы Москвы до летнего дворца в селе Коломенском, столбы с орлами наверху на расстоянии 700 саженей друг от друга. Высота каждого из них была равна приблизительно двум саженям.

Межевая верста — существовала на Руси до XVIII века для определения расстояния между населёнными пунктами и для межевания (от слова межа — граница земельных владений в виде узкой полосы). Длина такой версты составляет 1000 саженей или 2,13 км.

Задачи, в которых используются старинные меры длины.

В старинных учебниках и книгах часто встречаются задачи с использованием старинных единиц измерения. Попробуем решить некоторые из них.

1. Собака и заяц.

Собака усмотрела зайца в 150 саженях от себя. Заяц пробегает за 2 минуты 500 саженей, а собака – за 5 минут 1300 саженей.

За какое время собака догонит зайца?

Решение:

За одну минуту заяц пробегает 250 саженей (500 : 2 = 250), а собака 260 саженей (1300 : 5 = 260). Следовательно, за одну минуту расстояние между собакой и зайцем уменьшится на 10 саженей (260 – 250 = 10). Поскольку между собакой и зайцем, когда собака увидала зайца, было 150 саженей, то собака догонит зайца через 15 минут.

150*10=15 минут.

1. Через сколько дней путники встретятся?

Идет один человек в другой город и проходит в день 40 верст, а другой человек идет навстречу ему из другого города и в день проходит по 30 верст. Расстояние между городами 700 верст.

Через сколько дней путники встретятся?

Решение:

За один день путники сближаются на 70 верст (40 + 30 = 70). Поскольку расстояние между городами равно 700 верст, то встретятся они через 10 дней.

700:70=10 дней.

1. Н.А.Некрасов «Дедушка Мазай и зайцы».




Вижу один островок небольшой –
Зайцы на нем собралися гурьбой.
С каждой минутой вода подбиралась
К бедным зверькам: уж под ними осталось
Меньше аршина земли в ширину,
Меньше сажени в длину.


Какова приблизительно площадь острова?

Решение:

71 * 213 = 15 123 (кв. см.) = 1,5 (кв. м.)

1. П. П. Ершов «Конёк-горбунок».

П о исходе же трех дней,
Двух рожу тебе коней –
Да таких, каких поныне
Не бывало и в помине,
Да еще рожу конька,
Ростом только в три вершка
На спине с двумя горбами,
Да с аршинными ушами


Во сколько раз (приблизительно) рост конька – горбунка больше длины ушей?

Решение:

В старину при определении роста человека или животного счет велся после двух аршин. Если говорилось три вершка, то это означало 2 аршина + 3 вершка.


Рост конька три вершка – это значит 2 аршина и 3 вершка.
2 аршина = 2*71,12 = 142,24 (см.)
3 вершка = 4,45*3=13,35 (см.)
Итого 142,24 + 13,35 = 155,59 (см.)
Длина ушей – аршин = 71,12см.
Определим во сколько раз рост конька больше длины ушей: 155,59 : 71,12=2,18. Приблизительно в 2 раза.

Пословицы и поговорки с упоминанием старинных мер длины и их толкование.

Несмотря на отсутствие практического применения, старые единицы измерения сохранились в современном русском языке, в основном, в виде пословиц и поговорок.

1.«Не указывай на людей перстом! Не указали бы на тебя шестом!» — Если будешь кого-то обвинять (показывать на него пальцем), то тебя могут обвинять в чем-то худшем или сделать это в еще более грубой манере.


2.«От горшка два вершка, а уже указчик» — молодой человек, не имеющий жизненного опыта, но самонадеянно поучающий всех.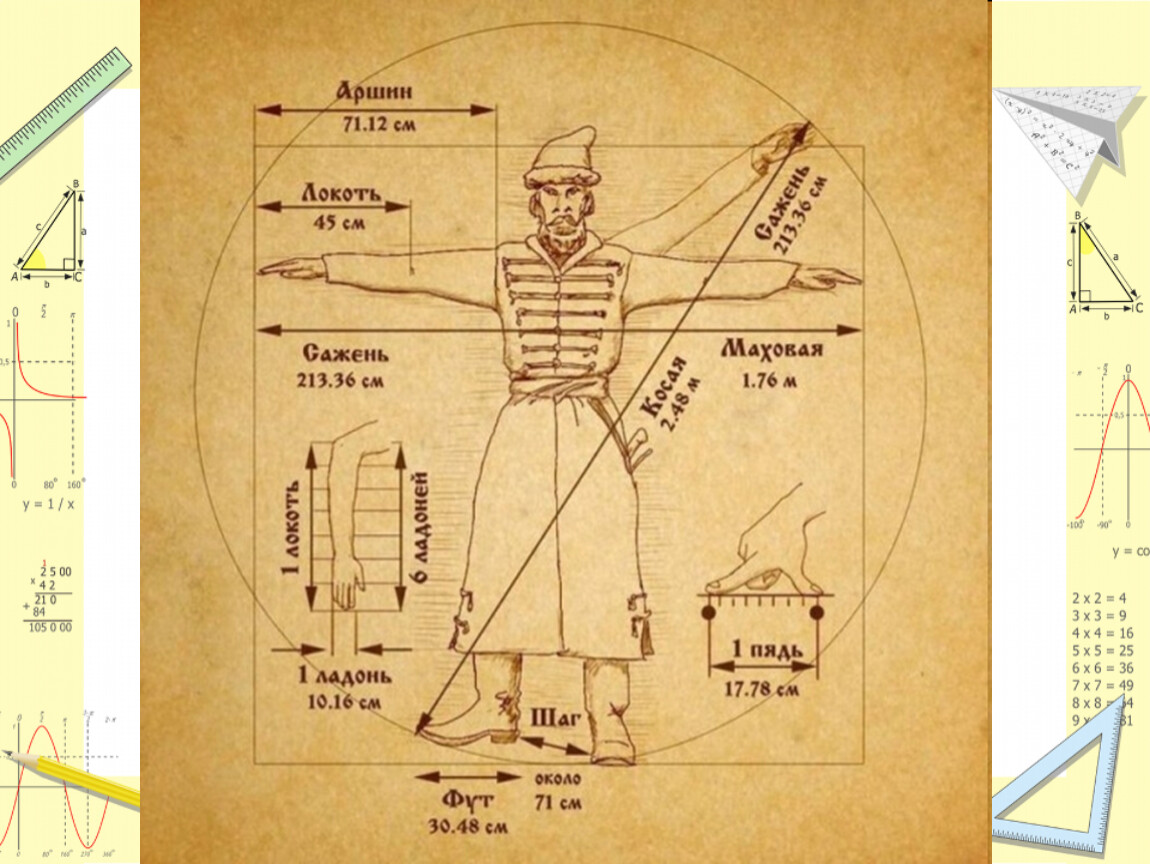

3.«Ни пяди» (не отдать, не уступить) — даже самой малой части; («чужой земли — не надо, но и своей не отдадим ни пяди»).

4.«Семи пядей во лбу» (разг.) — когда хотят сказать об очень умном человеке.

5.«Косая сажень в плечах» – говорят о широкоплечем человеке.

6. «Видеть на сажень сквозь землю» — об очень проницательном человеке.
7.Когда хотят сказать о человеке, который обо всём судит по себе, употребляют выражение: «Меряет на свой аршин», « На свой аршин не меряй».

8.«Ходит, словно аршин проглотил» — т. е. прямо, синонимы стоять по струнке, вытянуться во весь рост.

9. «Пишешь аршинными буквами» – крупно.

10. «Близок локоть да не укусишь» — о каком-нибудь простом, но невыполнимом деле.

11.« Нос с локоть, а ум с ноготь» — говорили о глупом человеке.

12.«Сам с ноготок, а борода с локоток» — о человеке незавидной внешности, но пользующемся авторитетом благодаря своему уму, социальному положению или жизненному опыту. Петра 1 борода, особенно у бояр, служила признаком знатности рода и происхождения.

13.« Ни шагу назад», т. е. не отступать.

14.« Семимильными шагами» (т.е. гигантскими) – когда хотят сказать о достижении крупного успеха в течение короткого времени.

15.«За семь верст киселя хлебать». Ехать, идти далеко без особой надобности.

16.«Мерить версты» — ходить на большое расстояние. Для друга семь верст – не околица.

17.«Бешеной собаке семь верст не крюк» — о ситуации, когда собственная глупость вынуждает тратить куда больше усилий, чем требуется.

18. «Аршин на кафтан, два на заплаты» — починка дороже вещи.

Анкетирование.

В процессе работы над проектом было проведено анкетирование среди учащихся четвертых классов (20 человек) и взрослых людей в возрасте от 25 до 50 лет, имеющих высшее образование (30человек).

При обработке данных были сделаны следующие выводы:

1. Ученики 4 класса знают старинные меры длины, но не понимают, что они обозначают, слышали термины. Наиболее известными меры длины среди детей – верста, шаг, локоть.

Взрослые знаю названия практически всех старорусских мер длины, но затрудняются перевести их в современные, многие выбирали правильные ответы интуитивно, так как знают, сколько составляет та или иная мера длины приблизительно. (Рис. 1).

Рис. 1.

1. На вопрос: «Знаете ли вы пословицы и поговорки, в которых употребляются старинные меры длины?» утвердительно ответили 24 человека из 50 опрошенных, но привести примеры таких пословиц и поговорок смогли только 19 взрослых, некоторые вспомнили по несколько пословиц. (Рис. 2.)

Рис. 2.

1. Вопрос анкеты: как вы понимаете пословицу «Мерить на свой аршин»?

На данный вопрос смогли ответить 25 взрослых и 6 детей. Таким образом, можно сделать вывод, что взрослые используют данную пословицы в повседневной жизни и знают ее значение. (Рис. 3.)

Рис. 3.

Анкетирование показало, что учащиеся зачастую встречались со старинными мерами длины при чтении различной литературы, в повседневной жизни, слышали поговорки и пословицы, однако не знают соотношения старинных мер длины с современными. Проведя исследование, я выяснил, что современные дети мало знакомы со старинными единицами измерения. Именно поэтому я решил познакомить со своей работой учащихся и выступить на школьной научной конференции.

Введение в России единой метрической системы мер.

К XVIII веку насчитывалось до 400 различных по величине единиц мер, употребляемых в разных странах.

Отсутствие единой для всех системы мер вызывало затруднения и в торговых делах, и при взимании налогов, и в развитии промышленности. Особенно обострилась проблема в XVII-XVIII веках. Так, когда Германия оказалась раздробленной на множество государств, в ней насчитывалось 40 различных футов и локтей, 30 различных центнеров, 24 различных мили. Во Франции было 18 единиц длины. В этом было трудно разобраться и многоопытному купцу, а что уж говорить о неграмотном крестьянине. Это заставило начать поиски единой системы мер.

Метрической, или десятичной, системой мер называют совокупность единиц физических величин, в основу которой положена единица длины – метр.

Декрет о введении метрической системы мер был принят 7 апреля 1795 года во Франции. Для удобства решили принять за единицу длины одну сорокамиллионную часть земного меридиана. Это решение было обусловлено стремлением положить в основу метрической системы мер легко воспроизводимую «естественную» единицу длины, связанную с практически неизменным объектом природы, не носила национального характера и могла быть принята всеми странами.

В 1799 году был изготовлен и утвержден платиновый прототип метра. Подлинно международный характер метрическая система мер приобрела в 1875 году, когда 17 стран, в том числе Россия, подписали Метрическую конвенцию для обеспечения международного единства и усовершенствования метрической системы.

19 ноября 1892 года всемирно известный ученый Дмитрий Иванович Менделеев был назначен главным хранителем Депо образцовых мер и весов. Менделеев выступил инициатором создания системы национальных эталонов, благодаря ученому были установлены верные соотношения между метрическими и старинными российскими мерами. Это позволило подготовить страну к последовательному введению международной метрической системы.

Метрическая система мер была допущена к применению в России (в необязательном порядке) законом от 4 июня 1899 года, проект которого был разработан Менделеевым, и введена в качестве обязательной декретом СНК РСФСР от 14 сентября 1918 года, а для СССР — постановлением СНК СССР от 21 июля 1925 года. Переход на метрическую систему мер в СССР завершился к 1927 году.

Заключение.

Сейчас старинные меры длины забыты и практически не используются. Но если под рукой нет измерительных предметов для определения длины, то мы можем измерить длину с помощью старинных русских мер, используя руки и ноги. Хороши эти меры тем, что они всегда при себе и воспользоваться ими можно в любых условиях, но они неточные, так как у разных людей эти единицы различные. Даже играя с друзьями и родителями в разные игры, я часто использую такую единицу измерения как шаг.

В ходе проделанной работы я ближе познакомился со старинными русскими единицами измерения, изучил значение слов, связанных со старинными мерами длины, научился правильно понимать смысл пословиц, поговорок и литературных произведений, в которых они употребляются.

Анкетирование показало, что подрастающее поколение плохо знакомо со старинными единицами измерения. Большинство старых мер забыто, вышло из употребления, но мы можем встретить их в рассказах, повестях, стихотворениях, в книгах по истории, в устном народном творчестве, в исторических памятниках, в древних рецептах лекарств и всевозможных кушаний. Некоторые же из старых мер длины актуальны и по сей день. Например, размер экрана телевизора или размер трубок для водопроводного  крана измеряют в дюймах, сажень до сих пор используется в сельском хозяйстве.

При подготовке материала для проекта, я поговорил со своими бабушками. Они рассказали, что даже в своем детстве уже пользовались современными единицами измерения, но так же они вспомнили инструмент измерения «сажень». Им измеряли земельные участки, которые выделялись работникам предприятий для посадки картофеля.

Проанализировав весь собранный материал, я понял, как важна информация о появлении старинных мер измерения, их изменении и влиянии на жизнь людей. Это очень интересно и в современности, ведь история мер – это история торговли, ремесел, строительства, развития математики, а в конечном итоге – это часть истории человечества. Необходимо сохранять эти знания, чтобы передать их следующему поколению.

Список литературы.

1. С.Н. Олехник, Ю.В. Нестеренко, М.К. Потапов, Старинные занимательные задачи./ Илл. Попова С.И. – Москва.: АО «Столетие», 1994. — 192 с.

1. Маш Л., Граник Г. Моя самая первая книжка по м атематике. – М.: Дрофа, 1995. – 160 с.

1. Рослова Л.О., Шарыгин И.Ф. Измерения: Учеб. пособие/Художник В.В. Иванюк. – М.: Изд-во гимназии «Открытый мир», 1995. – 64 с.: ил. – (Учеб. сер. «Шаг за шагом»: Математика).

1. Я познаю мир: Детская энциклопедия: Математика / Сост. А. П. Савин, В. В. Станцо, А. Ю. Котова: Под общ. ред. О. Г. Хинн; Худож. А. В. Кардашук, А. Е. Шабельник, А. О. Хоменко. – М.: ООО «Издательство АСТ-ЛТД», 1998.- 480с.

1. Ермаков, Н. Я. Пословицы русского народа / Н. Я. Ермаков. – Санкт-Петербург : Типография С. А. Корнатовского, 1894. – 48 с.

Интернет ресурсы:

1. http://tmel.ru/drevnie-mery-dliny/

1. https://mer.kakras.ru/

1. https://ru.wikipedia.org/wiki/

1. https://www.infouroki.net/issledovatelskaya-rabota—ot-el-do-sistemy-si-9084.html

1. https://xn--80acgfbsl1azdqr.xn--p1ai/news/6009-istoriya-112-let-nazad-na-rynkakh-i-v-torgovykh-lavkakh-ekaterinburga-vpervye-nachali-ispolzovat-metricheskuyu-sistemu-mer-i-vesov

1. https://info. wikireading.ru/645

1. https://sprint-olympic.ru/uroki/matematika-uroki/92807-starinnye-mery-dliny-tablicy-i-primery-ispolzovaniia-v-sovremennoi-sisteme.html

1. https://ucthat-v-skole.ru/biblioteka/poslovitsy/854-poslovitsy-v-kotorykh-upominayutsya-starinnye-mery-dliny#:~:text

1. https://ru.wiktionary.org/wiki

1. https://kopilkaurokov.ru/matematika/prochee/proiektno-issliedovatiel-skaia-rabota-starinnyie-russkiie-miery-dliny-v-sovriemiennoi-zhizni-chielovieka

Приложение.

Уважаемый участник опроса, просим вас ответить на несколько вопросов. Ваши ответы помогут выяснить, знакомы ли современным детям старинные русские меры длины. Опрос имеет анонимный характер.

1. Какие из перечисленных ниже старинные русские меры длины вам знакомы?

	перст		ладонь		аршин		сажень
	вершок		локоть		шаг		верста

1. Как вы думаете, если перевести аршин в сантиметры, сколько это будет?

	51 см.			72 см.
	85 см.			104 см.

1. Как вы считаете, сколько примерно метров в 1 сажени?

	1 метр			3 метра
	2 метра			4 метра

1. Знаете ли вы пословицы и поговорки, в которых употребляются старинные меры длины?

да

нет

Если можете, приведите пример:

________________________________________________________________________

1. Как вы понимаете пословицу: «Мерить на свой аршин».

________________________________________________________________________________________________________________________________________________

единиц измерения США | Математика для гуманитарных наук

Результаты обучения

• Дайте определение единицам длины и преобразуйте их из одних в другие.
• Выполнять арифметические вычисления с единицами длины.
• Решите прикладные задачи, связанные с единицами длины.
• Определение единиц веса и преобразование из одной в другую.
• Выполнять арифметические вычисления единиц веса.
• Решите прикладные задачи, связанные с единицами веса.
• Опишите общую взаимосвязь между обычными единицами измерения США и метрическими единицами длины, веса/массы и объема.
• Определите префиксы метрических единиц и используйте их для выполнения основных преобразований между метрическими единицами.
• Решение прикладных задач, связанных с метрическими единицами длины, массы и объема.
• Укажите точки замерзания и кипения воды по шкале Цельсия и Фаренгейта.
• Преобразование из одной температурной шкалы в другую с использованием формул преобразования.

Измерение — это число, описывающее размер или количество чего-либо. Вы можете измерять многие вещи, такие как длина, площадь, емкость, вес, температура и время. В Соединенных Штатах используются две основные системы измерения: метрическая система и обычная система измерения США .

В этом разделе мы рассмотрим единицы измерения длины, веса и вместимости, а также решим задачи, связанные с преобразованием различных единиц длины, веса или вместимости.

Единицы длины

В этом разделе рассматривается измерение длины с использованием традиционной системы измерения США.

Предположим, вы хотите купить трубы для проекта и видите две вывески в хозяйственном магазине: 1,88 доллара за 2 фута труб и 5,49 долларов за 3 ярда труб.

Если оба типа трубок одинаково хорошо подходят для вашего проекта, какая цена будет лучше? Вам нужно знать о двух единицах измерения , ярдах и футах, чтобы определить ответ.

Длина — это расстояние от одного конца объекта до другого конца или от одного объекта до другого. Например, длина листа бумаги размером с письмо составляет 11 дюймов. Система измерения длины в Соединенных Штатах основана на четырех общепринятых единицах длины: дюймов , футов , ярдов и миль . Ниже приведены примеры, показывающие измерение в каждой из этих единиц.

Коврики

Блок	Описание	Изображение
Дюймы/дюймы	Некоторые люди жертвуют свои волосы на парики для больных раком, потерявших волосы в результате лечения. Одна компания требует, чтобы пожертвованные волосы были не менее 8 дюймов в длину.
	Размер рамы велосипеда: расстояние от центра кривошипа до верха подседельной трубы. Размер рамы обычно измеряется в дюймах. Эта рама 16 дюймов.
Футы/футы	обычно продаются стандартной длины. Один типичный размер — это ковер шириной 8 футов и длиной 11 футов. Его часто называют ковриком 8 на 11.
Двор/Ярды	Футбольные поля несколько различаются по размеру. Официальное поле может быть любой длины от 100 до 130 ярдов.
Миля/Мили	Длина марафона составляет 26,2 мили. Один маршрут марафона показан на карте справа.

Вы можете использовать любую из этих четырех единиц измерения, принятых в США, для описания длины чего-либо, но более разумно использовать определенные единицы для определенных целей. Например, имеет смысл описывать длину ковра в футах, а не в милях, и описывать марафон в милях, а не в дюймах.

Возможно, вам потребуется преобразовать единицы измерения. Например, вы можете указать свой рост в футах и ​​дюймах (5 футов 4 дюйма) или только в дюймах (64 дюйма). Вам нужно знать эквиваленты единиц, чтобы сделать эти преобразования между единицами.

В таблице ниже показаны эквиваленты и коэффициенты пересчета для четырех общепринятых единиц измерения длины.

Эквиваленты единиц измерения	Коэффициенты пересчета (от более длинных к более коротким единицам измерения)	Коэффициенты пересчета (от коротких до длинных единиц измерения)
1 фут = 12 дюймов	[латекс] \displaystyle \frac{12\ \text{дюймы}}{1\ \text{фут}}[/латекс]	[латекс] \displaystyle \frac{1\text{ фут}}{12\text{ дюймов}}[/latex]
1 ярд = 3 фута	[латекс] \displaystyle \frac{3\text{ футов}}{1\text{ярд}}[/latex]	[латекс] \displaystyle \frac{\text{1 ярд}}{\text{3 фута}}[/latex]
1 миля = 5280 футов	[латекс] \displaystyle \frac{5,280\text{ футов}}{1\text{миля}}[/latex]	[латекс] \displaystyle \frac{\text{1 миля}}{\text{5280 футов}}[/latex]

Обратите внимание, что каждый из этих коэффициентов преобразования представляет собой отношение равных значений, поэтому каждый коэффициент преобразования равен 1. Умножение измерения на коэффициент преобразования вообще не меняет размер измерения, поскольку это то же самое, что умножение на 1; он просто изменяет единицы, которые вы используете для измерения.

Преобразование различных единиц длины

Коэффициенты преобразования можно использовать для преобразования измерения, например футов, в другой тип измерения, например дюймы.

Обратите внимание, что количество дюймов для измерения намного больше, чем футов для того же измерения, поскольку футы являются более длинной единицей измерения. Вы можете использовать коэффициент преобразования [латекс] \displaystyle \frac{\text{12 дюймов}}{\text{1 фут}}[/latex].

Если длина измеряется в футах, и вы хотите перевести длину в ярды, вы можете подумать: «Я перевожу более короткую единицу измерения в более длинную, так что длина в ярдах будет меньше, чем длина в футах. Вы можете использовать коэффициент преобразования [латекс] \displaystyle \frac{\text{1 ярд}}{\text{3 фута}}[/latex].

Если расстояние измеряется в милях, и вы хотите узнать, сколько в нем футов, вы можете подумать: «Я перевожу более длинную единицу измерения в более короткую, так что количество футов будет больше, чем количество миль. Вы можете использовать коэффициент преобразования [латекс] \displaystyle \frac{5,280\text{ футов}}{1\text{ миля}}[/latex].

Вы можете использовать коэффициент метку метод (также известный как размерный анализ ) для преобразования длины из одной единицы измерения в другую с использованием коэффициентов преобразования. В методе метки фактора вы умножаете на доли единицы измерения, чтобы преобразовать измерение из одной единицы в другую. Изучите приведенный ниже пример, чтобы увидеть, как можно использовать метод метки фактора для преобразования [латексных] \displaystyle 3\frac{1}{2}[/latex] футов в эквивалентное количество дюймов.

Пример

Сколько дюймов в [латексных] \displaystyle 3\frac{1}{2}[/latex] футах?

Показать решение

Обратите внимание, что, используя метод метки фактора, вы можете исключить единицы измерения из задачи, как если бы они были числами. Вы можете отменить только в том случае, если отменяемая единица находится как в числителе, так и в знаменателе дробей, которую вы умножаете.

В приведенной выше задаче вы отменили фута и фута , оставив вам дюйма , это то, что вы пытались найти.

[латекс]\frac{7}{2}\cancel{\text{футы}}\cdot\frac{12\text{дюймы}}{\cancel{1\text{фут}}}=\text{ ? дюймы}[/latex]

Что, если вы использовали неправильный коэффициент преобразования?

[латекс]\frac{7}{2}\text{футы}\cdot\frac{1\text{foor}}{12\text{дюймы}}=\text{? дюймов}[/латекс]?

Вы не можете отменить футы, потому что единицы не совпадают как в числителе, так и в знаменателе. Таким образом, если вы завершите вычисление, в ответе останутся и футы, и дюймы, и никакого преобразования не произойдет.

Вот еще один пример преобразования длины с использованием метода метки фактора.

Пример

Сколько ярдов составляют 7 футов?

Показать решение

Попробуйте

Применить преобразование единиц измерения длины

Бывают случаи, когда вам нужно выполнить вычисления для измерений, которые даны в разных единицах. Например, рассмотрим задачу о трубке, заданную ранее. Вы должны решить, какой из двух вариантов является лучшей ценой, и вы должны сравнить цены, указанные в различных единицах измерения.

Для того, чтобы сравнить, вам нужно преобразовать измерения в одну единую общепринятую единицу измерения. Чтобы быть уверенным, что вы произвели вычисления точно, подумайте, больше или меньше единицы, в которые вы конвертируете, чем число, которое у вас есть. Его относительный размер скажет вам, является ли число, которое вы пытаетесь найти, больше или меньше заданного числа.

Пример

Художнику по интерьеру нужна отделка бордюра для дома, который она оклеивает обоями. Ей нужно 15 футов бордюра для гостиной, 30 футов бордюра для спальни и 26 футов бордюра для столовой. Сколько ярдов бордюра ей нужно?

Показать решение

Попробуйте

В следующем примере используется метод метки фактора для решения задачи, требующей преобразования миль в футы.

Пример

Два бегуна сравнивали, сколько они тренировались ранее в тот день. Джо сказал: «Согласно моему шагомеру, я пробежал 8,3 мили». Алекс сказал: «Это немного больше, чем я пробежал. Я пробежал 8,1 мили. На сколько футов больше пробежала Джо, чем Алекс?

Показать решение

В следующем примере мы покажем, как сравнить цены на два разных вида трубок для вашего проекта. Для одного типа трубок указана стоимость за ярды, а для другого — за футы. Сравнивать легче, когда единицы одинаковы, поэтому мы конвертируем одну цену в те же единицы, что и другую. Для таких проблем не имеет значения, какую стоимость вы конвертируете, любая из них будет работать.

Пример

Вы идете по строительному магазину и замечаете две распродажи труб.

3 ярда трубки А стоят 5,49 доллара.

Трубка B продается по цене 1,88 доллара США за 2 фута.

Любая трубка подходит для вашего проекта. Какая трубка дешевле?

Показать решение

В приведенной выше задаче вы также могли бы найти цену за фут для каждого типа труб и сравнить цены за единицу каждого из них за фут.

Вам необходимо преобразовать одну единицу измерения в другую, если вы решаете задачи, включающие измерения, включающие более одного типа измерения. Каждая из единиц может быть преобразована в одну из других единиц с помощью таблицы эквивалентов, коэффициентов преобразования и/или метода метки коэффициента, показанного в этом разделе. Четыре основные единицы измерения, которые используются в традиционной системе измерения США. являются: дюйм, фут, ярд и миля. Обычно люди используют ярды, мили, а иногда и футы для описания больших расстояний. Измерение в дюймах обычно используется для более коротких объектов или длин.

Единицы веса

Когда вы упоминаете, насколько тяжелым или легким является объект, вы имеете в виду его вес. В принятой в США системе измерения вес измеряется в унциях, фунтах и ​​тоннах. Эти измерения на самом деле относятся к тому, насколько гравитационная сила Земли притягивает объект. Как и другие единицы измерения, вы можете конвертировать между этими единицами, и иногда вам нужно это делать для решения проблем.

Продуктовый магазин продает канистру молотого кофе на 36 унций за 14 долларов и продает кофе на развес за 9 долларов.за фунт. Какая сделка лучше? Чтобы ответить на этот вопрос, вам нужно понять взаимосвязь между унциями и фунтами.

Вы часто используете слово вес , чтобы описать, насколько тяжелым или легким является объект или человек. Вес измеряется в принятой в США системе с использованием трех единиц: унций, фунтов и тонн. унций — наименьшая единица измерения веса, фунтов — большая единица, а тонн — самая большая единица.

Киты — одни из самых крупных животных в мире. Некоторые виды могут достигать веса до 200 тонн, что равно 400 000 фунтов.
Мясо — это продукт, который обычно продается на вес. Из одного фунта говяжьего фарша получается около четырех котлет для гамбургеров.
Унции используются для измерения более легких предметов. Пачка из 11 пенни равна примерно одной унции.

Вы можете использовать любую из обычных единиц измерения для описания веса чего-либо, но более разумно использовать определенные единицы для определенных целей. Например, имеет смысл описывать вес человека в фунтах, а не в тоннах. Имеет смысл описывать вес автомобиля в тоннах, а не в унциях.

1 фунт = 16 унций

[латекс]\frac{16\text{ унций}}{1\text{ фунт}}[/латекс]

Преобразование единиц веса

Четыре унции — типичный размер порции мяса. Поскольку мясо продается по фунтам, вы можете преобразовать вес упаковки мяса из фунтов в унции, чтобы определить, сколько порций содержится в упаковке мяса.

Грузоподъемность грузового автомобиля часто указывается в тоннах. Вам может понадобиться преобразовать фунты в тонны, если вы пытаетесь определить, может ли грузовик безопасно перевозить большую партию тяжелых материалов.

В таблице ниже показаны единицы преобразования и коэффициенты преобразования, которые используются для преобразования между обычными единицами веса.

Эквиваленты единиц измерения	Коэффициенты пересчета (из более тяжелых единиц измерения в более легкие)	Коэффициенты пересчета (из более легких единиц измерения в более тяжелые)
1 фунт = 16 унций	[латекс]\фракция{16\текст{унций}}{1\текст{фунт}}[/латекс]	[латекс] \displaystyle \frac{\text{1 фунт}}{\text{16 унций}}[/latex]
1 тонна = 2000 фунтов	[латекс]\фракция{2000\текст{фунты}}{1\текст{тонна}}[/латекс]	[латекс] \displaystyle \frac{\text{1 тонна}}{\text{2000 фунтов}}[/latex]

Вы можете использовать метод метки фактора , чтобы преобразовать одну обычную единицу веса в другую обычную единицу веса. В этом методе используются коэффициенты преобразования, которые позволяют вам «отменить» единицы измерения, чтобы получить желаемую единицу измерения.

Каждый из этих коэффициентов пересчета представляет собой отношение равных значений, поэтому каждый коэффициент пересчета равен 1. Умножение измерения на коэффициент пересчета вообще не меняет размер измерения, поскольку это то же самое, что умножение на 1. Это просто измените единицы измерения, которые вы используете для его измерения.

Два примера, иллюстрирующие метод метки фактора, показаны ниже.

Упражнения

Сколько унций в [латексе] \displaystyle 2\frac{1}{4}[/latex] фунтов?

Показать решение

ПОПРОБУЙТЕ СЕЙЧАС

Пример

Сколько тонн составляет 6500 фунтов?

Показать решение

ПОПРОБУЙТЕ СЕЙЧАС

 

Применение преобразования единиц измерения с весом

Бывают случаи, когда вам нужно выполнить вычисления для измерений, которые даны в разных единицах. Чтобы решить эти проблемы, вам нужно преобразовать одно из измерений в ту же единицу измерения, что и другое измерение.

Подумайте, больше или меньше единицы, в которые вы конвертируете, чем единицы, из которых вы конвертируете. Это поможет вам быть уверенным, что вы делаете правильные вычисления. Вы можете использовать метод метки коэффициента для преобразования одной единицы измерения в другую.

Вот пример задачи, требующей преобразования единиц измерения.

Пример

Муниципальный мусоропровод позволяет человеку выбрасывать максимум 30 фунтов мусора в неделю. На прошлой неделе максимально допустимый мусор выбросили 140 человек. Скольким тоннам мусора это равнялось?

Показать решение

ПОПРОБУЙТЕ СЕЙЧАС

 

Давайте вернемся к проблеме цены на кофе, которая была поставлена ​​ранее. Мы можем использовать преобразование единиц измерения, чтобы решить эту проблему.

Пример

Продуктовый магазин продает канистру молотого кофе на 36 унций по 14 долларов, а кофе в развес — по 7 долларов за фунт. Какая сделка лучше?

Показать решение

 

ПОПРОБУЙТЕ СЕЙЧАС

Средний вес северного голубого тунца составляет 1800 фунтов. Средний вес большой белой акулы составляет [латекс] \displaystyle 2\frac{1}{2}[/latex] тонны. В среднем, насколько большая белая акула весит в фунтах больше, чем северный голубой тунец?

Показать решение

Резюме

В принятой в США системе измерения вес измеряется в трех единицах: унциях, фунтах и ​​тоннах. Фунт равен 16 унциям, а тонна равна 2000 фунтам. В то время как вес объекта можно описать с помощью любой из этих единиц, обычно очень тяжелые объекты описывают с помощью тонн, а очень легкие — с помощью унций. Фунты используются для описания веса многих предметов и людей.

Часто, чтобы сравнить вес двух предметов или людей или решить задачи, связанные с весом, необходимо преобразовать одну единицу измерения в другую единицу измерения. Использование коэффициентов преобразования с методом меток факторов является эффективной стратегией преобразования единиц и решения проблем.

Единицы вместимости

Вместимость — это количество жидкости (или другого текучего вещества), которое может вместить объект, когда он наполнен. Когда жидкость, такая как молоко, описывается в галлонах или квартах, это мера емкости.

Понимание единиц вместимости может помочь вам решить такие задачи: Свен и Джоанна устроили общий обед. Они не просили своих гостей сказать им, что они принесут, и в итоге три человека принесли суп. Эрин принесла 1 литр, Ричард — 3 пинты, а ЛеВар — 9.чашки. Сколько чашек супа они съели все вместе?

В традиционной системе измерения США существует пять основных единиц измерения емкости. Наименьшая единица измерения — жидких унций . «Унция» также используется как мера веса, поэтому важно использовать слово «жидкость» вместе с унцией, когда вы говорите о емкости. Иногда приставку «флюид» не используют, когда из контекста ясно, что измеряется вместимость, а не вес.

Другими единицами мощности в обычной системе являются чашка , пинта , кварт и галлон . В приведенной ниже таблице описывается каждая единица емкости и приводится пример, иллюстрирующий размер единицы измерения.

Унция жидкости Единица вместимости, равная [латекс] \displaystyle \frac{1}{8}[/латекс] чашки. Одна жидкая унция воды при температуре 62°F весит около одной унции. Количество жидкого лекарства часто измеряется в жидких унциях.
Чашка Единица, равная 8 жидким унциям. Вместимость стандартного мерного стакана – одна чашка.
Пинта Единица, равная 16 жидким унциям или 2 чашкам. Емкость коробки мороженого часто измеряется в пинтах.
Кварта Единица, равная 32 жидким унциям или 4 чашкам. Вы часто видите, что молоко продается в супермаркетах литрами.
Галлон Единица, равная 4 квартам или 128 жидким унциям. Когда вы заправляете машину бензином, цена бензина часто указывается в долларах за галлон.

Вы можете использовать любую из этих пяти единиц измерения для описания емкости объекта, но более целесообразно использовать определенные единицы для определенных целей. Например, вместимость плавательного бассейна имеет смысл указывать в галлонах, а вместимость дорогих духов — в жидких унциях.

Попробуйте

 

Иногда вам потребуется конвертировать единицы измерения. Например, вы можете захотеть выразить 5 галлонов лимонада в чашках, если вы пытаетесь определить, сколько порций по 8 жидких унций получится из этого количества лимонада.

В таблице ниже показаны некоторые из наиболее распространенных эквивалентов и коэффициентов пересчета для пяти общепринятых единиц измерения мощности.

Аналоги блока	Коэффициенты пересчета (из более тяжелых единиц измерения в более легкие)	Коэффициенты пересчета (от легких к более тяжелым единицам измерения)
1 чашка = 8 жидких унций	[латекс] \displaystyle \frac{\text{1 чашка}}{\text{8 жидких унций}}[/latex]	[латекс] \displaystyle \frac{\text{8 жидких унций}}{\text{1 чашка}}[/latex]
1 пинта = 2 чашки	[латекс] \displaystyle \frac{\text{1 пинта}}{2\text{чашки}}[/latex]	[латекс] \displaystyle \frac{2\text{чашки}}{1\text{пинта}}[/latex]
1 кварта = 2 пинты	[латекс] \displaystyle \frac{\text{1 кварта}}{2\text{пинты}}[/latex]	[латекс] \displaystyle \frac{2\text{ пинты}}{\text{1 кварта}}[/latex]
1 кварта = 4 чашки	[латекс] \displaystyle \frac{\text{1 кварта}}{4\text{чашки}}[/latex]	[латекс] \displaystyle \frac{4\text{ чашки}}{\text{1 кварта}}[/latex]
1 галлон = 4 кварты	[латекс] \displaystyle \frac{\text{1 галлон}}{4\text{кварты}}[/latex]	[латекс] \displaystyle \frac{4\text{кварт}}{\text{1 галлон}}[/latex]
1 галлон = 16 чашек	[латекс] \displaystyle \frac{1\text{ галлон}}{\text{16 чашек}}[/latex]	[латекс] \displaystyle \frac{\text{16 чашек}}{1\text{галлон}}[/latex]

Преобразование единиц мощности

Как и при преобразовании единиц длины и веса, вы можете использовать метод метки коэффициента для преобразования одной единицы мощности в другую.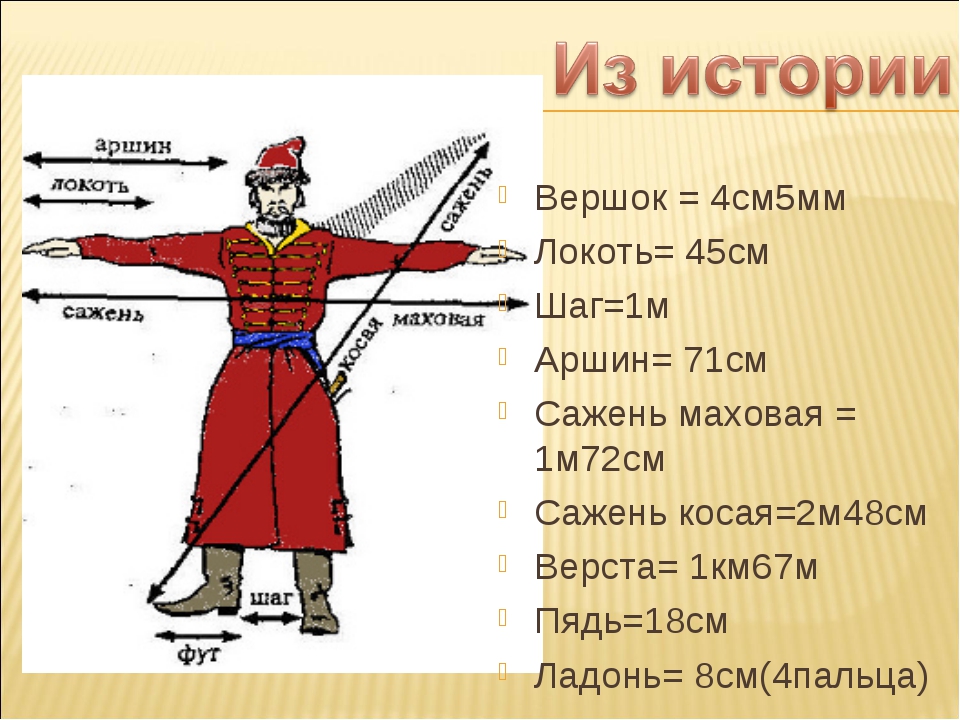 Пример этого метода показан ниже.

Пример

Сколько пинт составляет [латекс] \displaystyle 2\frac{3}{4}[/latex] галлонов?

Показать решение

Пример

Сколько галлонов составляют 32 унции жидкости?

Показать решение

Попробуйте

Найдите сумму 4 галлона и 2 пинты. Выразите ответ в чашках.

Показать решение

Применение преобразования единиц измерения

Бывают случаи, когда вам нужно объединить измерения, данные в разных единицах. Для этого вам нужно сначала преобразовать, чтобы единицы были одинаковыми.

Рассмотрим ситуацию, описанную ранее в этом разделе.

Упражнения

Свен и Джоанна устроили общий обед. Они не просили своих гостей сказать им, что они принесут, и в итоге три человека принесли суп. Эрин принесла 1 литр, Ричард — 3 пинты, а ЛеВар — 9 чашек. Сколько всего супа у них было?

Показать решение

Упражнения

Наташа делает лимонад для пляжа. У нее два контейнера. Один вмещает один галлон, а другой вмещает 2 кварты. Если она наполнит оба контейнера, сколько чашек лимонада у нее будет?

Показать решение

Еще один способ решить описанную выше проблему — сначала заменить 1 галлон на 16 чашек, а затем заменить 2 кварты на 8 чашек. Затем добавьте: [латекс]16+8=24[/латекс] чашек.

В следующем видео мы приводим еще один пример использования преобразования единиц измерения для решения проблемы. Мы покажем, как найти количество лимонов, необходимое для приготовления пирога, учитывая, что каждый лимон дает около 4 столовых ложек сока.

Попробуйте

Алан готовит чили. Он использует рецепт, из которого получается 24 чашки чили. У него есть горшок на 5 кварт и горшок на 2 галлона, и он пытается определить, поместятся ли все чили в один из этих горшочков. В какой из горшков поместится перец чили?

Показать решение

В следующем примерно 10-минутном видеоролике мы представляем мини-урок, в котором рассказывается об измерениях США длины, веса и емкости, а также о том, как преобразовать большие и меньшие единицы для каждого типа. Это хороший обзор концепций, рассмотренных в разделе «Единицы измерения США» этого модуля.

 

Резюме

В традиционной системе измерения США существует пять основных единиц измерения емкости. Это жидкая унция, чашка, пинта, кварта и галлон. Эти единицы измерения связаны друг с другом, и мощность может быть описана с использованием любой из единиц. Как правило, люди используют галлоны для описания больших количеств и жидкие унции, чашки, пинты или кварты для описания меньших количеств. Часто для сравнения или решения задач, связанных с количеством жидкости в таре, необходимо перевести одну единицу измерения в другую.

9.1 Воспоминания как типы и стадии – Введение в психологию – 1-е канадское издание

Глава 9. Воспоминания и суждения

Цели обучения

1. Сравните явную и имплицитную память, определяя характеристики, определяющие каждую из них.
2. Объясните функцию и продолжительность эйдетических и эхоических воспоминаний.
3. Обобщите возможности кратковременной памяти и объясните, как рабочая память используется для обработки содержащейся в ней информации.

Как видно из Таблицы 9.1 «Концептуализация памяти в терминах типов, стадий и процессов», психологи концептуализируют память в терминах типов , стадий и процессов . В этом разделе мы рассмотрим два типа памяти , явную память и неявную память , а затем три основных этапа памяти : сенсорную , кратковременную и долгосрочный (Аткинсон и Шиффрин, 1968). Затем, в следующем разделе, мы рассмотрим природу долговременной памяти, уделяя особое внимание когнитивным методам, которые мы можем использовать для улучшения нашей памяти. Наше обсуждение будет сосредоточено на трех процессах, которые являются центральными для долговременной памяти : кодирование , хранение и извлечение .

Таблица 9.1 Память, концептуализированная с точки зрения типов, стадий и процессов.

Как типы	Явная память Неявная память
В качестве ступеней	Сенсорная память Кратковременная память Долговременная память
Как процессы	Кодировка Хранение Поиск

Явная память

Когда мы оцениваем память, прося человека сознательно помнить вещи, мы измеряем явная память . Явная память  относится к знаниям или опыту, которые можно сознательно запомнить . Как вы можете видеть на рисунке 9.2, «Типы памяти», существует два типа явной памяти: эпизодическая и семантическая . Эпизодическая память относится к личному опыту, который у нас был (например, воспоминания о дне окончания средней школы или о фантастическом ужине, который мы устроили в Нью-Йорке в прошлом году). Семантическая память относится к нашему знанию фактов и понятий о мире (например, что абсолютное значение -90 больше, чем абсолютное значение 9, и что одно из определений слова «аффект» — это «переживание чувства или эмоции»). »).

Рисунок 9.2 Типы памяти.

Эксплицитная память оценивается с помощью показателей, при которых испытуемый должен сознательно пытаться запомнить информацию. Тест вспоминания памяти  – это мера эксплицитной памяти, которая включает извлечение из памяти информации, которая ранее была запомнена . Мы полагаемся на нашу память припоминания, когда сдаем тест на эссе, потому что тест требует от нас генерировать ранее запомненную информацию. Тест множественного выбора является примером теста памяти распознавания, меры явной памяти, которая включает определение того, была ли информация видна или изучена до .

Ваш собственный опыт прохождения тестов, вероятно, приведет вас к согласию с выводами научных исследований о том, что вспомнить сложнее, чем распознать. Припоминание, как это требуется в тестах на сочинение, включает в себя два этапа: сначала создание ответа, а затем определение того, кажется ли он правильным. Распознавание, как и в тесте с множественным выбором, включает только определение того, какой пункт из списка кажется наиболее правильным (Haist, Shimamura, & Squire, 19).92). Хотя они включают разные процессы, показатели памяти припоминания и узнавания, как правило, коррелируют. Учащиеся, которые лучше справляются с экзаменом с несколькими вариантами ответов, также в целом будут лучше сдавать экзамен по эссе (Bridgeman & Morgan, 1996).

Третий способ измерения памяти известен как переобучение (Нельсон, 1985). Показатели повторного обучения (или накопления) оценивают, насколько быстрее обрабатывается или усваивается информация, когда она изучается снова после того, как она уже была усвоена, но затем забыта . Например, если вы посещали курсы французского языка в прошлом, вы могли забыть большую часть выученной лексики. Но если бы вам снова пришлось работать над своим французским языком, во второй раз вы выучили бы словарный запас намного быстрее. Повторное обучение может быть более чувствительной мерой памяти, чем припоминание или узнавание, потому что оно позволяет оценивать память с точки зрения «сколько» или «как быстро», а не просто «правильные» и «неправильные» ответы. Повторное обучение также позволяет нам измерять память на такие действия, как вождение автомобиля или игра на фортепиано, а также память на факты и цифры.

Неявная память

В то время как эксплицитная память состоит из вещей, о которых мы можем сознательно сообщить, что мы знаем, имплицитная память относится к знанию, к которому мы не можем сознательно получить доступ. Тем не менее имплицитная память чрезвычайно важна для нас, поскольку она оказывает прямое влияние на наше поведение. Имплицитная память относится к влиянию опыта на поведение, даже если человек не осознает эти влияния . Как вы можете видеть на рисунке 9.2, «Типы памяти», существует три основных типа имплицитной памяти: процедурная память, классические условные эффекты и прайминг.

Процедурная память относится к нашим часто необъяснимым знаниям о том, как что-то делать . Когда мы идем из одного места в другое, говорим с другим человеком на английском языке, набираем номер мобильного телефона или играем в видеоигру, мы используем процедурную память. Процедурная память позволяет нам выполнять сложные задачи, даже если мы не можем объяснить другим, как мы их делаем. Невозможно рассказать кому-то, как ездить на велосипеде; человек должен учиться, делая это. Идея имплицитной памяти помогает объяснить, как младенцы способны учиться. Способность ползать, ходить и говорить — это процедуры, и эти навыки легко и эффективно развиваются в детстве, несмотря на то, что во взрослом возрасте мы не помним о том, что научились им.

Второй тип имплицитной памяти — это классические обусловливающие эффекты , при которых мы учимся, часто без усилий или осознания, ассоциировать нейтральные стимулы (например, звук или свет) с другим стимулом (например, едой), что создает естественная реакция, такая как удовольствие или слюноотделение . Память на ассоциацию проявляется, когда условный раздражитель (звук) начинает вызывать такую ​​же реакцию, как безусловный раздражитель (еда) до обучения.

Последний тип имплицитной памяти известен как прайминг или изменения в поведении в результате событий, которые происходили часто или недавно . Прайминг относится как к активации знания (например, мы можем активировать понятие доброты, предъявляя людям слова, связанные с добротой), так и к влиянию этой активации на поведение (люди, которые настроены на понятие доброты, могут действовать более доброжелательно). ).

Одним из показателей влияния прайминга на имплицитную память является Тест фрагмента слова , в котором человека просят заполнить пропущенные буквы, чтобы составить слова. Вы можете попробовать сами: сначала попробуйте закончить следующие фрагменты слов, но работайте над каждым всего три-четыре секунды. Какие слова быстро приходят на ум?

_ я б _ а _ г

_ ч _ с _ _ и _ п

_ о _ к

_ ч _ и с _

Теперь внимательно прочитайте следующее предложение:

«Он взял свои материалы с полок, проверил их и вышел из здания».

Затем попробуйте снова составить слова из фрагментов слов.

Думаю, вы обнаружите, что фрагменты 1 и 3 легче завершить как «библиотека» и «книга» соответственно после того, как вы прочитали предложение, чем до того, как вы его прочитали. Однако чтение предложения не очень помогло вам завершить фрагменты 2 и 4 как «врач» и «фаэтон». Это различие в имплицитной памяти, вероятно, произошло потому, что, когда вы читали предложение, понятие «библиотека» (и, возможно, «книга») было подготовлено, хотя они никогда не упоминались явно. После того, как понятие введено в действие, оно влияет на наше поведение, например, в тестах на фрагменты слов.

На наше повседневное поведение влияет прайминг в самых разных ситуациях. Увидев рекламу сигарет, мы можем начать курить, увидев флаг своей страны, мы можем пробудить в себе патриотизм, а увидев ученика из конкурирующей школы, мы можем пробудить в себе дух соперничества. И эти влияния на наше поведение могут происходить без нашего ведома.

Направление исследования: подготовка внешнего осознания влияет на поведение

Одной из наиболее важных характеристик имплицитных воспоминаний является то, что они часто формируются и используются автоматически без особых усилий или осознания с нашей стороны. Для демонстрации автоматизма и влияния эффектов прайминга Джон Барг и его коллеги (Bargh, Chen, & Burrows, 1996) провели исследование, в котором они показали студентам бакалавриата списки из пяти зашифрованных слов, каждое из которых они должны были преобразовать в предложение. Кроме того, для половины участников исследования слова были связаны со стереотипами пожилых людей. Эти участники видели такие слова, как следующие:

в Виктории пенсионеры живые люди

человек в бинго забывчивый играет

Другая половина участников исследования тоже составляла предложения, но из слов, которые не имели ничего общего со старческими стереотипами. Цель этого задания заключалась в том, чтобы у одних участников закрепить в памяти стереотипы о пожилых людях, а у других — нет.

Затем экспериментаторы оценили, повлияет ли прайминг на стереотипы пожилых людей на поведение студентов, и они действительно повлияли. Когда участник исследования собрал все свои вещи, думая, что эксперимент окончен, экспериментатор благодарил его или ее за участие и указывал дорогу к ближайшему лифту. Затем, без ведома участников, экспериментаторы зафиксировали количество времени, которое участник провел, идя от дверного проема экспериментальной комнаты к лифту. Как вы можете видеть на рисунке 9. 3, «Результаты исследований». участники, которые составили предложения, используя слова, связанные со стереотипами пожилых людей, переняли поведение пожилых людей — они шли значительно медленнее, когда покидали экспериментальную комнату.

Рисунок 9.3 Результаты исследования. Барг, Чен и Берроуз обнаружили, что начальные слова, связанные с пожилыми людьми, заставляют людей ходить медленнее (1996).

Чтобы определить, возникли ли эти предварительные эффекты вне сознания участников, Барг и его коллеги попросили еще одну группу студентов выполнить предварительное задание, а затем указать, считают ли они, что слова, которые они использовали для составления предложений, имеют какую-либо связь друг другу или, возможно, каким-либо образом повлияли на их поведение. Эти студенты не знали о возможности того, что слова могли быть связаны с пожилыми людьми или могли повлиять на их поведение.

Стадии памяти: сенсорная, кратковременная и долговременная память

Еще один способ понять память — рассматривать ее с точки зрения стадий, описывающих продолжительность времени, в течение которого информация остается доступной для нас. В соответствии с этим подходом (см. рис. 9.4, «Длительность памяти») информация начинается в сенсорной памяти , перемещается в кратковременную память и, в конце концов, перемещается в долговременную память . Но не вся информация проходит все три стадии; большая часть забыта. Переместится ли информация из кратковременной памяти в долговременную или же она будет потеряна из памяти, полностью зависит от того, как эта информация воспринимается и обрабатывается.

Рисунок 9.4 Продолжительность памяти. Память можно охарактеризовать с точки зрения стадий — промежутка времени, в течение которого информация остается доступной для нас.

Сенсорная память

Сенсорная память  относится к кратковременному хранению сенсорной информации . Сенсорная память — это буфер памяти, который длится очень недолго, а затем, если на него не обращают внимание и не передают для дальнейшей обработки, он забывается. Цель сенсорной памяти — дать мозгу время на обработку поступающих ощущений и позволить нам видеть мир как непрерывный поток событий, а не как отдельные его части.

Зрительная сенсорная память известна как иконическая память . Знаковая память была впервые изучена психологом Джорджем Сперлингом (1960). В своем исследовании Сперлинг показал участникам отображение букв в ряды, подобное показанному на рис. 9.5 «Измерение иконической памяти». Однако отображение длилось всего около 50 миллисекунд (1/20 секунды). Затем Сперлинг дал своим участникам тест на запоминание, в котором их попросили назвать все буквы, которые они могли вспомнить. В среднем участники смогли вспомнить только около четверти букв, которые они видели.

Рисунок 9.5. Измерение иконической памяти. Сперлинг показал своим участникам такие изображения всего за 1/20 секунды. Он обнаружил, что, когда он предлагал участникам сообщить об одном из трех рядов букв, они могли это сделать, даже если сигнал был дан вскоре после того, как дисплей был удален. Исследование продемонстрировало существование иконической памяти.

Сперлинг пришел к выводу, что участники видели все письма, но могли вспомнить их очень кратко, что не позволяло им сообщить о них все. Чтобы проверить эту идею, в своем следующем эксперименте он сначала показывал те же буквы, но затем, после того, как дисплей был удален, он давал участникам сигнал сообщать о буквах из первого, второго или третьего ряда. В этом состоянии участники сообщали почти все буквы в этом ряду. Это открытие подтвердило догадку Сперлинга: участники имели доступ ко всем буквам в своих знаковых воспоминаниях, и если задание было достаточно коротким, они могли сообщить о той части дисплея, о которой он их просил. «Достаточно короткий» — это длина иконической памяти, которая составляет около 250 миллисекунд (¼ секунды).

Слуховая сенсорная память известна как эхоическая память . В отличие от иконических воспоминаний, которые распадаются очень быстро, эхоические воспоминания могут длиться до четырех секунд (Cowan, Lichty, & Grove, 1990). Это удобно, так как позволяет вам, среди прочего, помнить слова, которые вы сказали в начале длинного предложения, когда вы дойдете до его конца, и делать заметки о последнем заявлении вашего профессора психологии даже после того, как он или она закончила говорить это.

У некоторых людей иконическая память сохраняется дольше, явление, известное как эйдетические образы (или фотографическая память ), когда люди могут сообщать детали изображения в течение длительных периодов времени . Эти люди, которые часто страдают психологическими расстройствами, такими как аутизм, утверждают, что они могут «видеть» образ спустя долгое время после того, как он был представлен, и часто могут точно описать этот образ. Есть также некоторые свидетельства эйдетических воспоминаний в слухе; некоторые люди сообщают, что их эхо-воспоминания сохраняются необычно долго. Композитор Вольфганг Амадей Моцарт, возможно, обладал эйдетической памятью на музыку, потому что, даже когда он был очень молод и еще не имел большого музыкального образования, он мог слушать длинные произведения, а затем воспроизводить их почти идеально (Соломон, 19).95).

Кратковременная память

Большая часть информации, попадающей в сенсорную память, забывается, но информация, на которую мы обращаем внимание с целью ее запоминания, может переходить в кратковременную память . Кратковременная память (STM) — это место, где небольшие объемы информации могут временно храниться более нескольких секунд, но обычно менее одной минуты (Baddeley, Vallar, & Shallice, 1990). Информация в кратковременной памяти не хранится постоянно, а становится доступной для обработки, и процессы, которые мы используем для осмысления, модификации, интерпретации и хранения информации в STM , известны как рабочая память .

Хотя рабочая память называется памятью, она не является хранилищем памяти, как STM, а представляет собой набор процедур или операций с памятью. Представьте, например, что вас просят принять участие в таком задании, как это, которое является мерой рабочей памяти (Unsworth & Engle, 2007). Каждый из следующих вопросов появляется отдельно на экране компьютера, а затем исчезает после того, как вы ответите на вопрос:

Является ли 10 × 2 − 5 = 15? (Ответьте ДА ИЛИ НЕТ) Тогда запомните «S»

Является ли 12 ÷ 6 − 2 = 1? (Ответьте ДА ИЛИ НЕТ) Тогда запомните «R»

Является ли 10 × 2 = 5? (Ответьте ДА ИЛИ НЕТ) Тогда запомните «P»

Является ли 8 ÷ 2 − 1 = 1? (Ответьте ДА ИЛИ НЕТ) Тогда запомните «Т»

Является ли 6 × 2 − 1 = 8? (Ответьте ДА ИЛИ НЕТ) Тогда запомните «У»

Является ли 2 × 3 − 3 = 0? (Ответьте ДА ИЛИ НЕТ) Тогда запомните «В»

Чтобы успешно выполнить задание, вы должны правильно ответить на каждую из математических задач и при этом запомнить букву, которая следует за задачей. Затем, после шести вопросов, вы должны перечислить буквы, встречавшиеся в каждом из испытаний, в правильном порядке (в данном случае S, R, P, T, U, Q).

Чтобы выполнить эту непростую задачу, вам нужно использовать различные навыки. Вам явно нужно использовать STM, так как вы должны хранить письма в хранилище, пока вас не попросят перечислить их. Но вам также нужен способ наилучшим образом использовать имеющиеся у вас внимание и обработку информации. Например, вы можете решить использовать стратегию повторения букв дважды, затем быстро решить следующую задачу, а затем снова повторить буквы дважды, включая новую. Поддержание этой стратегии (или других подобных ей) — задача рабочей памяти.0029 центральный исполнительный орган — часть рабочей памяти, которая направляет внимание и обрабатывает . Центральный исполнитель будет использовать любые стратегии, которые кажутся лучшими для данной задачи. Например, центральный исполнительный орган будет направлять процесс репетиции и в то же время направлять зрительную кору на формирование образа списка букв в памяти. Вы можете видеть, что, хотя STM задействован, процессы, которые мы используем для работы с материалом в памяти, также имеют решающее значение.

Кратковременная память ограничена как по длине, так и по количеству информации, которую она может хранить. Петерсон и Петерсон (1959) обнаружили, что, когда людей просили запомнить список строк из трех букв, а затем сразу же просили выполнить отвлекающую задачу (счет в обратном порядке до трех), материал быстро забывался (см. рис. 9.6, «СТМ»). Decay»), так что к 18 секундам его практически не было.

Рисунок 9.6 Распад СТМ. Исследователи обнаружили, что информация, которая не была отрепетирована, быстро улетучивалась из памяти.

Один из способов предотвратить разрушение информации из кратковременной памяти — использовать рабочую память для ее повторения. Репетиция технического обслуживания  – это процесс повторения информации в уме или вслух с целью сохранения ее в памяти . Мы занимаемся поддерживающей репетицией, чтобы удержать в памяти что-то, что мы хотим запомнить (например, имя человека, адрес электронной почты или номер телефона), достаточно долго, чтобы записать это, использовать или, возможно, перенести в долговременную память.

Если мы продолжим репетировать информацию, она останется в STM до тех пор, пока мы не прекратим ее репетировать, но у STM также есть предел емкости. Попробуйте прочитать каждый из следующих рядов чисел, по одному ряду за раз, со скоростью примерно одно число в секунду. Затем, когда вы закончите каждый ряд, закройте глаза и запишите столько цифр, сколько сможете вспомнить.

019

3586

10295

861059

1029384

75674834

657874104

6550423897

Если вы похожи на обычного человека, вы обнаружите, что в этом тесте оперативной памяти, известном как тест на диапазон цифр , вы довольно хорошо справлялись примерно до четвертой строки, а затем у вас начались проблемы. Бьюсь об заклад, вы пропустили некоторые числа в последних трех рядах и довольно плохо справились с последним.

Размах цифр у большинства взрослых составляет от пяти до девяти цифр, в среднем около семи. Когнитивный психолог Джордж Миллер (1956) называл «семь плюс-минус два» фрагментов информации магическим числом в кратковременной памяти. Но если мы можем удерживать в кратковременной памяти максимум около девяти цифр, то как мы можем запомнить большее количество информации, чем это? Например, как мы можем запомнить 10-значный телефонный номер достаточно долго, чтобы набрать его?

Один из способов, которым мы можем расширить нашу способность запоминать вещи в STM, — это использовать метод запоминания, называемый фрагментация . Разделение на фрагменты  – это процесс организации информации в более мелкие группы (фрагменты), в результате чего увеличивается количество элементов, которые могут храниться в STM . Например, попробуйте запомнить эту строку из 12 букв:

.

XOFCBANNCVTM

Вероятно, у вас это не получится, потому что количество букв больше, чем магическое число семь.

Теперь попробуйте еще раз с этим:

CTVCBCTSNHBO

Вам поможет, если я укажу, что материал в этой строке можно разбить на четыре набора по три буквы в каждом? Я думаю, да, потому что тогда вместо того, чтобы запоминать 12 букв, вам нужно было бы запомнить только названия четырех телевизионных станций. В этом случае разбиение на фрагменты изменяет количество элементов, которые вы должны запомнить, с 12 до четырех.

Эксперты полагаются на фрагментацию, чтобы помочь им обрабатывать сложную информацию. Герберт Саймон и Уильям Чейз (1973) показывали шахматным мастерам и новичкам различные положения фигур на шахматной доске в течение нескольких секунд каждое. Эксперты запоминали позиции намного лучше, чем новички, потому что они могли видеть «картину в целом». Им не нужно было запоминать положение каждой из частей по отдельности, они разделили части на несколько более крупных макетов. Но когда исследователи показали обеим группам случайные шахматные позиции — позиции, которые очень маловероятны в реальной игре, — обе группы выступили одинаково плохо, потому что в этой ситуации эксперты потеряли способность организовывать раскладки (см. рис. 9)..7, «Возможные и невозможные шахматные позиции»). То же самое происходит и с баскетболом. Баскетболисты гораздо лучше помнят реальные баскетбольные позиции, чем неигроки, но только тогда, когда позиции имеют смысл с точки зрения того, что происходит на площадке или что может произойти в ближайшем будущем, и, таким образом, могут быть разбиты на более крупные единицы (Дидьержан). и Мармеш, 2005).

Рисунок 9.7 Возможные и невозможные шахматные позиции. Опыт имеет значение: опытные шахматисты гораздо лучше запоминают позиции партии справа, чем новички. Но эксперты не лучше новичков запоминают позиции слева, чего не может быть в реальной игре.

Если информация выходит за пределы кратковременной памяти, она может попасть в долговременную память (LTM) , хранилище памяти, которое может хранить информацию в течение дней, месяцев и лет . Емкость долговременной памяти велика, и нет известного предела тому, что мы можем запомнить (Wang, Liu, & Wang, 2003). Хотя мы можем забыть какую-то информацию после того, как узнаем ее, другие вещи останутся с нами навсегда. В следующем разделе мы обсудим принципы долговременной памяти.

Key Takeaways

• Память относится к способности сохранять и извлекать информацию с течением времени.
• Для некоторых вещей наша память очень хороша, но наша активная когнитивная обработка информации гарантирует, что память никогда не будет точной копией того, что мы испытали.
• Эксплицитная память относится к переживаниям, которые можно намеренно и сознательно запомнить, и она измеряется с помощью припоминания, узнавания и повторного обучения. Эксплицитная память включает эпизодические и семантические воспоминания.
• Показатели повторного обучения (также известные как «сбережения») оценивают, насколько быстрее усваивается информация, когда она изучается снова после того, как она уже была усвоена, но затем забыта.
• Имплицитная память относится к влиянию опыта на поведение, даже если человек не осознает эти влияния. Три типа имплицитной памяти — это процедурная память, классическая обусловленность и прайминг.
• Обработка информации начинается в сенсорной памяти, перемещается в кратковременную память и в конечном итоге переходит в долговременную память.
• Репетиция технического обслуживания и фрагментация используются для хранения информации в кратковременной памяти.
• Емкость долговременной памяти велика, и нет известного предела тому, что мы можем запомнить.

Ссылки

Аткинсон, Р. К., и Шиффрин, Р. М. (1968). Человеческая память: предлагаемая система и процессы управления ею. В К. Спенсе (ред.), Психология обучения и мотивация  (Том 2). Оксфорд, Англия: Academic Press.

Баддели, А. Д., Валлар, Г., и Шаллис, Т. (1990). Развитие концепции рабочей памяти: последствия и вклад нейропсихологии. В G. Vallar & T. Shallice (Eds.), Нейропсихологические нарушения кратковременной памяти (стр. 54–73). Нью-Йорк, штат Нью-Йорк: Издательство Кембриджского университета.

Барг, Дж. А., Чен, М., и Берроуз, Л. (1996). Автоматизм социального поведения: прямое влияние конструкции черты и активации стереотипа на действие. Журнал личности и социальной психологии, 71 , 230–244.

Бриджмен, Б., и Морган, Р. (1996). Успешная учеба в колледже для учащихся с расхождениями в результатах тестов с несколькими вариантами ответов и тестов сочинений. Журнал педагогической психологии, 88 (2), 333–340.

Коуэн, Н., Лихти, В., и Гроув, Т. Р. (1990). Свойства памяти на произносимые без присмотра слоги. Журнал экспериментальной психологии: обучение, память и познание, 16 (2), 258–268.

Дидьежан, А., и Мармеш, Э. (2005). Упреждающее представление визуальных сцен баскетбола новичками и опытными игроками. Визуальное познание, 12 (2), 265–283.

Хейст, Ф., Шимамура, А.П., и Сквайр, Л.Р. (1992). О связи припоминания и узнавания памяти. Журнал экспериментальной психологии: обучение, память и познание, 18 (4), 691–702.

Миллер, Джорджия (1956). Волшебное число семь плюс-минус два: некоторые ограничения нашей способности обрабатывать информацию. Психологический обзор, 63 (2), 81–97.

Нельсон, Т.О. (1985). Вклад Эббингауза в измерение удержания: экономия во время повторного обучения. Журнал экспериментальной психологии: обучение, память и познание, 11 (3), 472–478.

Петерсон, Л., и Петерсон, М.Дж. (1959).