Окружности черчение: Чертеж круга, построение окружности в изометрии, формулы

Чертеж круга, построение окружности в изометрии, формулы

Чертеж круга, построение окружности в изометрии прямоугольной по всем трем осевым направлениям X, Y, Z уменьшаются на восемнадцать процентов. По ГОСТу рекомендуют строить изометрическую проекцию по осям без сокращения. При таком построении происходит увеличение изображений в одну целую двадцать две сотых раза.

Посмотрим на 1-ый рисунок, как правильно располагать оси координат и наносить штриховку в прямоугольной изометрии.

На 2-ом рисунке посмотрим как правильно построить изометрическую проекцию окружности.

Если строим проекцию без искажения по трем осям X, Y, Z, значит большая ось эллипсов будет равняться 1,22, а малая – 0,71. Если строим проекцию с искажениями по трем осям X, Y, Z, значит большая ось эллипсов будет равняться диаметру (D), а малая – 0,58D.

На 3-ем рисунке показано как правильно располагать окружность на чертеже.

Чертеж круга и окружности.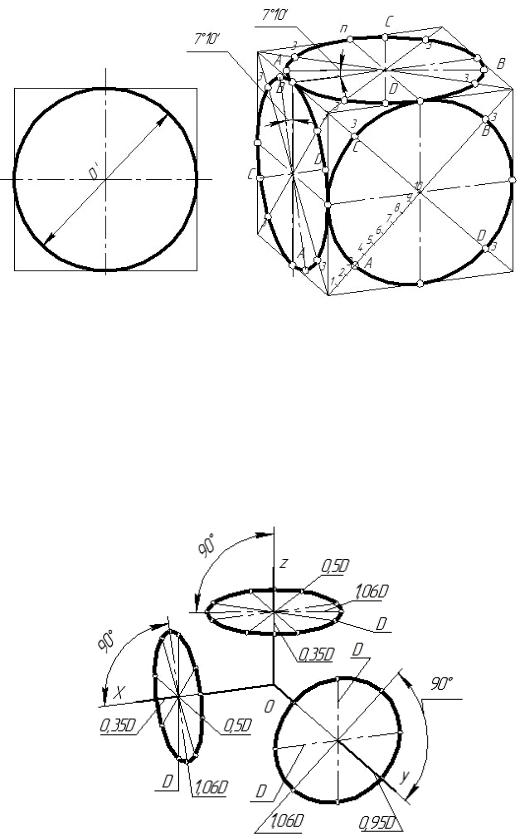

Основным геометрическим размер окружности является прямой отрезок, который соединяет ее центр с точкой.

Условное обозначение R. Название радиус.

Смотрим 4-ый рисунок.

Множество точек, одинаково удаленных от центра на расстояние R описывают замкнутую плоскую кривую, которая и называется окружность.

Диаметр окружности обозначается D
D = 2R

Длина окружности обозначается С
С = 2πR = πD

π=С/D=3,141 592 653 589 793 … (трансцендентное число)

Множество точек, удаленных от центра на расстояние не превышающее R, называется кругом.

Площадь круга обозначается S
S = πR² = πD²/4

Вспомогательные формулы
С = 2√πS ≈ 3,545√S ≈ 3,142D
S = CD/4 ≈ 3,142 R² ≈ 0,785 D² ≈ 0,25CD
R = C/2π ≈ 0,159C
D = 2√S/π ≈ 1,128√S

Дополнительную информацию по геометрии смотрим на страницах сайта

Заказать чертеж

Поделитесь с друзьями!

ЧЕРЧЕНИЕ.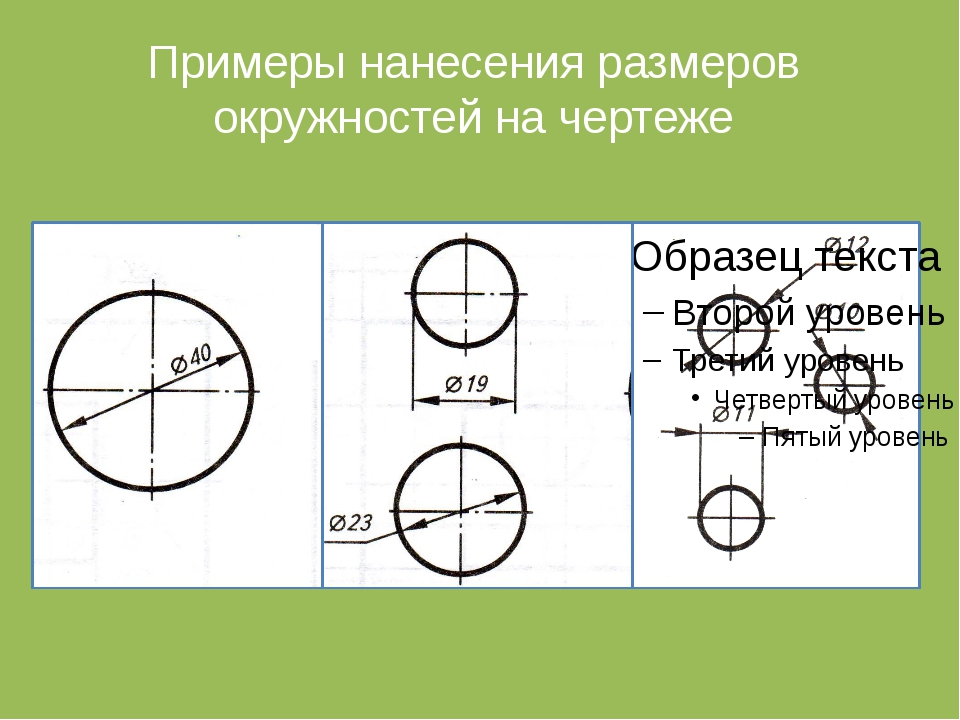 Школьный интернет-учебник — Чтение чертежей 3-1

При выполнении графических работ приходится решать многие задачи на построение. Наиболее встречающиеся при этом задачи — деление отрезков прямой, углов и окружностей на равные части, построение различных сопряжений.

 

Деление окружности на равные части с помощью циркуля

Пользуясь радиусом, нетрудно разделить окружность и на 3, 5, 6, 7, 8, 12  равных участков.

Деление окружности на четыре равные части.

Штрихпунктирные центровые линии, проведенные перпендикулярно одна другой, делят окружность на четыре равные части. Последовательно соединив их концы, получим правильный четырехугольник (рис. 1).

Рис.1 Деление окружности на 4 равные части.

Деление окружности на восемь равных частей.

Чтобы разделить окружность на восемь равных частей, дуги, равные четвертой части окружности, делят пополам.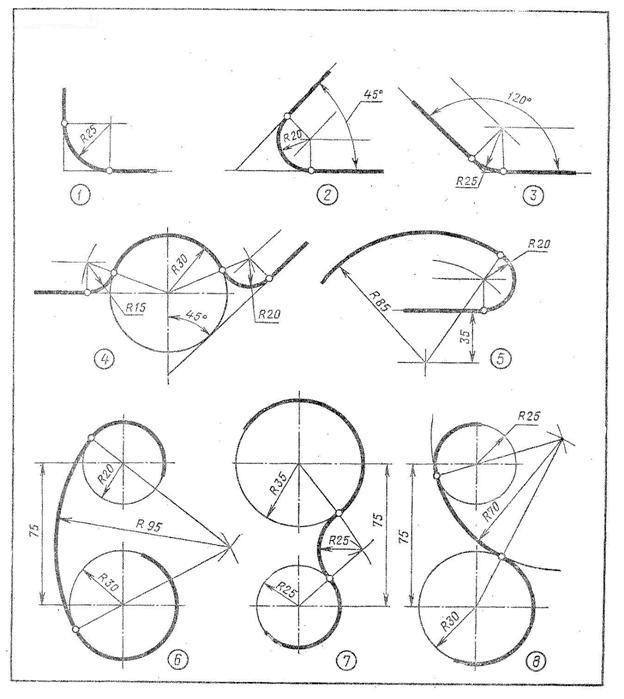

Для этого из двух точек, ограничивающих четверть дуги, как из центров радиусов окружности выполняют засечки за ее пределами. Полученные точки соединяют с центром окружностей и на пересечении их с линией окружности получают точки, делящие четвертные участки пополам, т. е. получают восемь равных участков окружности (рис. 2).

Рис.2. Деление окружности на 8 равных частей.

Деление окружности на шестнадцать равных частей.

Разделив циркулем дугу, равную 1/8, на две равные части, нанесём засечки на окружность. Соединив все засечки, отрезками прямых, получим правильный шестнадцатиугольник.

Рис.3. Деление окружности на 16 равных частей.

Деление окружности на три равные части.

Чтобы разделить окружность радиуса R на 3 равные части, из точки пересечения центровой линии с окружностью (например, из точки А) описывают как из центра дополнительную дугу радиусом R. Получают точки 2 и 3. Точки 1, 2, 3 делят окружность на три равные части.

Рис. 4. Деление окружности на 3 равные части.

Деление окружности на шесть равных частей. Сторона правильного шестиугольника, вписанного в окружность, равна радиусу окружности (рис. 5.).

Для деления окружности на шесть равных частей надо из точек 1 и 4 пересечения центровой линии с окружностью сделать на окружности по две засечки радиусом R, равным радиусу окружности. Соединив полученные точки отрезками прямых, получим правильный шестиугольник.

Рис. 5. Деление окружности на 6 равных частей

Деление окружности на двенадцать равных частей.

Чтобы разделить окружность на двенадцать равных частей, надо окружность поделить на четыре части взаимно перпендикулярными диаметрами. Приняв точки пересечения диаметров с окружностью А, В, С, D за центры, величиной радиуса проводят четыре дуги до пересечения с окружностью.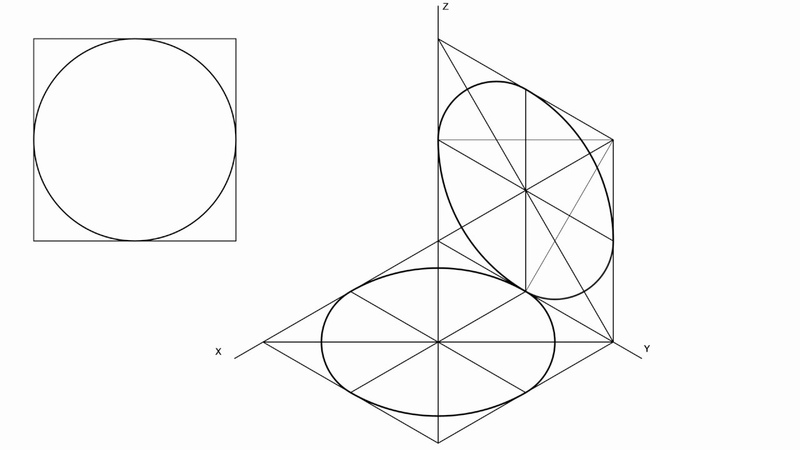 Полученные точки 1, 2, 3, 4, 5, 6, 7, 8 и точки А, В, С, D разделяют окружность на двенадцать равных частей (рис. 6).

Рис. 6. Деление окружности на 12 равных частей

 

Деление окружности на пять равных частей

Из точки А проведем дугу тем же радиусом, что и радиус окружности до пересечения с окружностью – получим точку В

. Опустив перпендикуляр с этой точки – получим точку С.   Из точки С – середины радиуса окружности, как из центра, дугой радиуса СD сделаем засечку на диаметре, получим точку Е. Отрезок DЕ равен длине стороны вписанного правильного пятиугольника. Сделав радиусом DЕ засечки на окружности, получим точки деления окружности на пять равных частей.

Рис. 7. Деление окружности на 5 равных частей

 Деление окружности на десять равных частей

Разделив окружность на пять равных частей, легко можно разделить окружность и на 10 равных частей. Проведя прямые от получившихся точек через центр окружности до противоположных сторон окружности – получим ещё 5 точек.

Рис. 8. Деление окружности на 10 равных частей

Деление окружности на семь равных частей

Чтобы разделить окружность радиуса R на 7 равных частей, из точки пересечения центровой линии с окружностью (например, из точки А) описывают как из центра дополнительную дугу этим же радиусом R – получают точку В.  Опустив перпендикуляр с точки В – получим точку С.   Отрезок ВС равен длине стороны вписанного правильного семиугольника.

Рис. 9. Деление окружности на 7 равных частей

 

 

 

Мастер-класс смотреть онлайн: Деление окружности, или Геометрия для чайников

Приветствую всех мастеров и мастериц!

Очень многие из нас, учась в школе, думали, что очень многие предметы школьной программы в жизни нам никогда не понадобятся.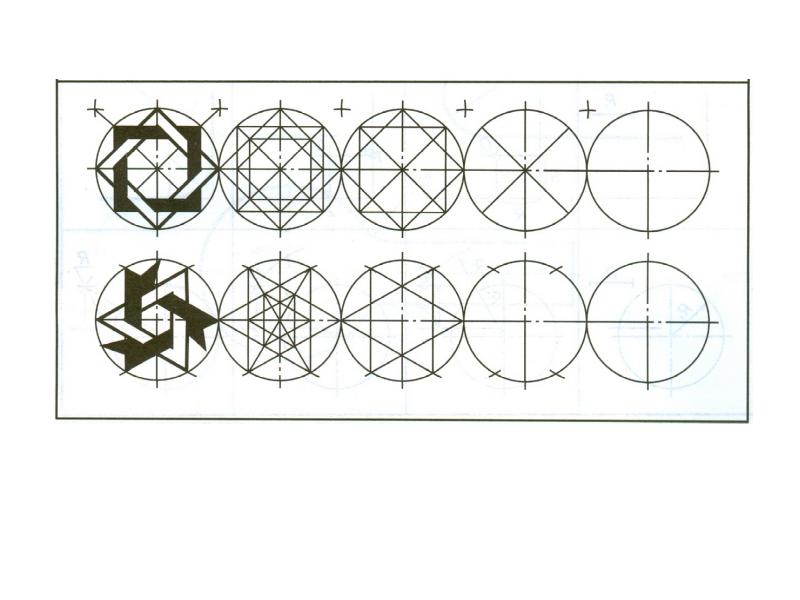 Я так думала про геометрию. Однако жизнь сложилась так, что именно геометрия мне оказалась и нужна.

Одной из основных сложностей при создании круглого орнаменты является его симметричность. Иногда хочется, чтобу у нас был точный 8-ми гранник, иногда 5-ти конечная звезда, а иногда нужен 7-ми конечный цветок.

Эту глобальную проблему симметричного деления окружности на равное количество частей можно решить просто при помощи циркуля, линейки, листа бумаги и геометрии.

Деление окружности на 3 равных сектора.

Для начала нам понадобиться сама окружность. Рисуем ее при помощи циркуля

Выбираем на поверхности окружности любую точку, отмечаем ее карандашиком. Далее циркулем отмеряем радиус нашей окружности (кто забыл — это расстояние от центра окружности до любой ее точки)

Ставим наш циркуль с набранным радиусом в точку, которую мы на окружности отметили и проводим дугу до пересечения с нашей основной окружностью.

Через точку на окружности и центр окружность проводим линию до пересечения с гранью.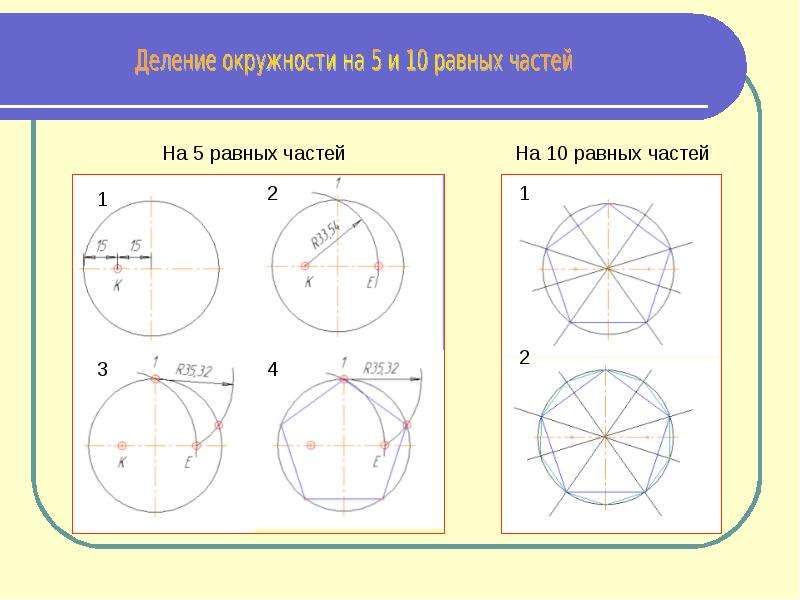

Таким образом мы получили 3 точки на нашей окружности.

Теперь из центра проводим линии, соединяя центр с этими точками и у нас образовались 3 одинаковых сектора.

Деление окружности на 4 равных сектора.

Начинаем опять с окружности, необходимого нам диаметра. Назову ее окружность 1.

Через центр окружности 1 проводим линию до пересечения с обеими сторонами окружности 1.

Из центра окружность 1 при помощи циркуля рисуем окружность больше диаметра — окружность 2.

Ставим ножку циркуля в точку на пересечении наше прямой линии и окружности 2 и из нее проводим дугу. Расстояние от точки на окружности до дуги равно диаметру окружности 1. (диаметр = 2 радиусам). Ту же процедуру повторяем с точкой на другой стороны окружности.

У нас есть 2 новые точки, появившиеся на пересечении дуг. Соединяем их и получаем окружность, разбитую на 4 ровных сектора.

Деление окружности на 5 равных секторов.

Начало работы с делением окружности на 5 частей очень схожа с делением окружности на 4 части, поэтому я начну уже с разделенного круга на 4 части.

Циркулем набираем радиус нашей окружности и ставим ножку в одну из имеющихся у нас точек. В моем случае это левая точка. Проводим дугу до пересечения ее с основной линии окружности.

Соединяем получившиеся точки при помощи линейки и находим новую точку пересечения (точка Н)

Циркулем набираем расстояние от верхний точки на окружности до точки Н. Ставим ножку в точку Н и проводим дугу и получаем еще одну точку (точка М)

Ставим ножку циркуля в верхнюю точку окружности и набираем расстояние до точки М.

Ставим ножку циркуля в верхнюю точку и откладываем набранное нами расстояние на нашей окружности.

Ставим циркуль в получившуюся точку и еще раз откладываем это расстояние. Таким же образом ставим еще 2 точки.

У нас получилось 4 отложенных точки и 1 верхняя точка окружности.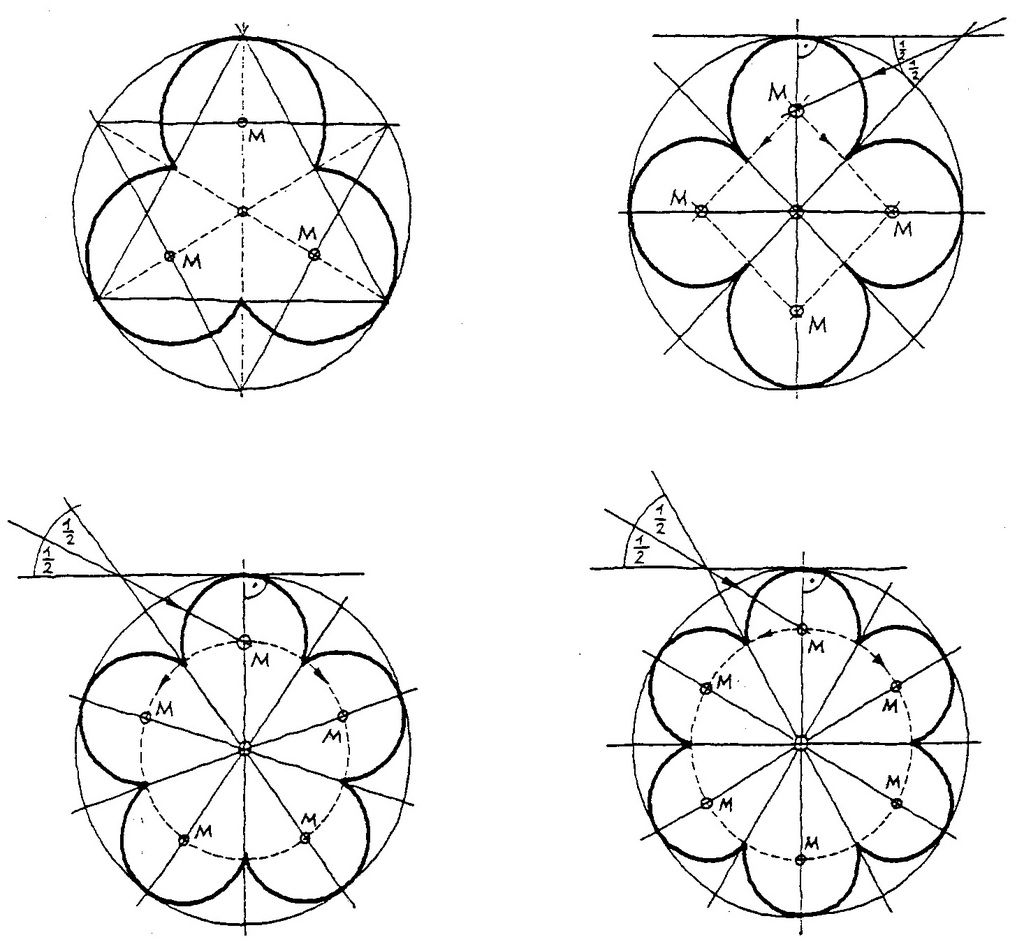 Соединяем центр окружности с этими точками и получаем 5 равных секторов.

Деление окружности на 6 равных секторов.

Нам снова нужна окружность.

Берем любую точку на этой окружности, ставим в нее ножку циркуля с набранным расстоянием радиуса и проводим дугу до пересечения с нашей окружностью.

Далее соединяем выбранную нами точку с центром окружности и находим еще одну точку с противоположной стороны.

Из этой точки таким же расстоянием проводим еще одну дугу.

Мы получили 6 точек — 2 мы шали при помощи дуг, 1- наша выбранная и 1 найденная при помощи линейки. Соединяем их с центром и получаем 6 равных секторов.

Деление окружности на 7 равных секторов.

Чтобы не повторяться и не описывать уже знакомые алгоритмы, берем за основу момент нахождения точки Н для разбития окружности на 5 частей.

Отмеряем циркулем расстояние от точки Н до точки на окружности.

Ставим ножку циркуля в верхнюю точку и набранным на циркуле расстоянием откладываем точки, аналогично как мы делали в случае разбивки окружности на 5 частей

Соединяем наши новые точки с центром и получаем 7 равных секторов.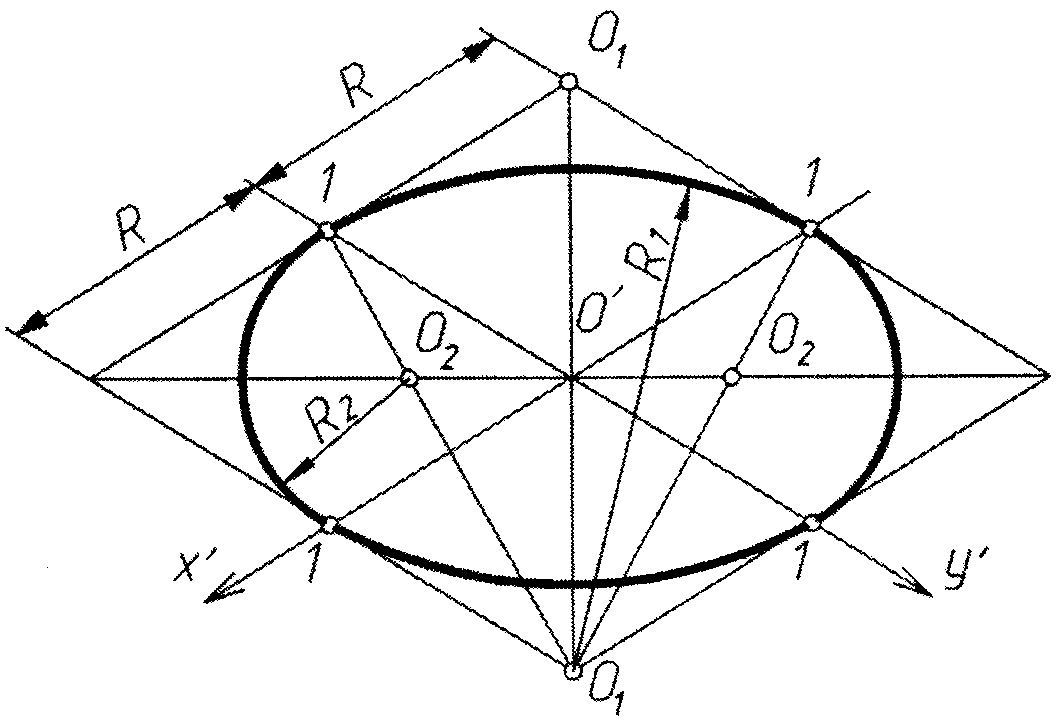

Используя эти простые приемы можно создавать геометрические орнаменты различной сложности

Надеюсь мой МК окажется кому-то полезным.

Удачи в создании шедеворов.

Ваша Velimira

Сопряжения — Сопряжение окружностей, сопряжение углов, сопряжение линий, сопряжение дуг

В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.

Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.

Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

Ниже будут рассмотрены основные типы сопряжений.

Сопряжение углов (Сопряжение пересекающихся прямых)

Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)

В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R.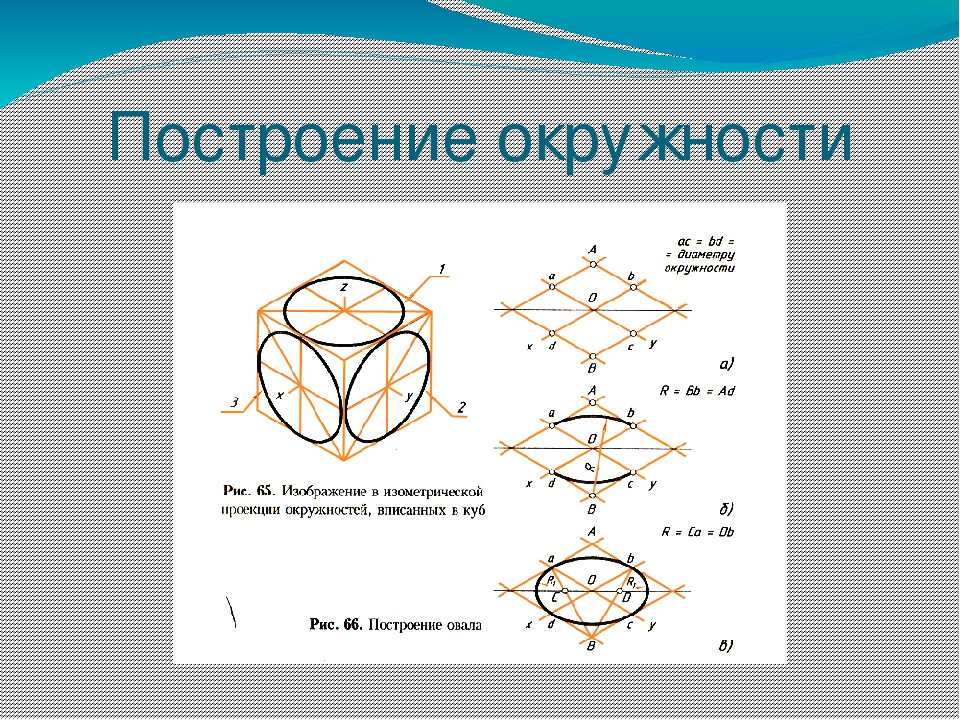 Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)

Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.

Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)

Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.

Сопряжение параллельных прямых линий

Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.

Сопряжение окружностей(дуг) с прямой линией

Внешнее сопряжение дуги и прямой линии

В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.

Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности OR радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой Оr.

Из центра сопряжения, точки Оr, опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности ОR и центр сопряжения Оr линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.

Внутреннее сопряжение прямой линии с дугой

По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности OR радиусом R-r. Точка Оr, полученная на пересечении прямой и дуги, и будет центром сопряжения.

Из центра сопряжения(точка Оr) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.

Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности ОR прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки Оr, центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.

Сопряжение окружностей (дуг)

Внешнее сопряжение дуг окружностей

Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

Внутреннее сопряжение дуг окружностей

Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

Смешанное сопряжение дуг окружностей

Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

Определение центра окружности и центра дуги окружности

Взаимное пересечение перпендикуляров, восставленных в середине каждой хорды, определяет центр окружности (точку О). На фиг. 9,6 показано нахождение центра дуги окружности (построение аналогично предыдущему).

Выпрямление дуги окружности

Определение длины 1 дуги АВ окружности (приближенный способ, фиг. 10).

Через хорду АВ проводят перпендикуляр (фиг. 10,а), пересекающий дугу в точке К. Из точек С и D, как из центров, радиусами г, равными d— диаметру окружности, проводят две дуги до взаимного их  пересечения в точке 01.

Расстояние между точками пересечения лучей 01А и O1B с касательной, проведенной к окружности в точке К, определяет приближенное значение спрямленной дуги (отрезок А1В1).

Расстояние между точками С1 и D1 определяет приближенную длину полуокружности. При отсутствии центра окружности

длина дуги АВ (фиг. 10,6) может быть определена следующим путем: хорду А В делят на четыре равные части; одну четвертую часть откладывают от точки В на дуге АВ; полученную точку С соединяют с точкой деления 1. Отрезок 1—С равен половине длины дуги АВ; CD — приближенное значение длины всей дуги АВ.

Определение  длины  окружности. Длину окружности определяют по формуле l=П*D, где l — длина окружности, П = 3,14159, a D—диаметр окружности. На фиг. 11,а показана длина l окружности диаметра D.

Графически длина окружности приближенно может быть определена путем суммирования длины двух сторон аз равностороннего треугольника и двух сторон а\ квадрата, вписанных в окружность, как это показано на фиг. 11,6 (2аз + 2а4). Точность определения — 0,01. На фиг. 11,в длина окружности определена следующим способом: из центра О под углом 30° проводят прямую до пересечения ее в точке А с касательной к окружности; от точки А откладывают отрезок АВ, равный трем радиусам R; из точки В, как из центра, радиусом ВМ проводят дугу окружности до пересечения с касательной прямой в точках С и D. Отрезок CD будет равен длине окружности. Точность определения — 0,0001.

Определение приближенной длины очерка эллипса (фиг.  12). Для определения длины очерка эллипса ACBD соединяют точки А  и С и из центра О радиусом, равным АС, засекают на осях эллипса точки М и N. Измерив длину отрезка MN, умножают ее на 3,14 и получают приближенную длину  очерка  эллипса   (l = 3,14*MN).

Размеры на чертеже — Тема Нанесение размеров — Уроки черчения — Каталог статей

Как наносят размеры на чертеже.

Чертежи должны содержать размеры, чтобы можно было судить по ним о величине изображенного предмета и его частей. Размеры на чертежах наносят в миллиметрах, но наименование измерений не указывают. Как наносят эти размеры?

1. Вначале проводят выносные линии перпендикулярно тому отрезку, размер которого указывают (рис. 28, а). Затем на расстоянии 6…10 мм от контура детали проводят параллельно ему размерную линию. Размерная линия ограничивается с двух сторон стрелками. Какой должна быть стрелка и в какой последовательности ее вычерчивать, показано на рис. 29. Выносные

линии выходят за концы стрелок размерной линии нa 1…5 мм. Выносные и размерные линии — сплошные тонкие. Над размерной линией, ближе к ее середине, наносят размерное число.

2. Для обозначения диаметра перед размерным числом наносят специальный знак — кружок, перечеркнутый прямой линией (рис. 28, б и 30). Если внутри окружности размерное число не помещается, его выносят за пределы окружности, как показано на рис. 28, в. Аналогично поступают при нанесении размера прямолинейного отрезка.

3. Для обозначения радиуса перед размерным числом всегда пишут латинскую букву R (рис. 28, г). Размерную линию при нанесении радиуса проводят из центра дуги. Она оканчивается стрелкой с одной стороны.

4. Обратите внимание, как нанесено размерное число 30 на рис.28, а. Размерная линия расположена вертикально, поэтому размерное число пишут так, чтобы его можно было читать справа. При наклонных размерных линиях цифры располагают, как показано на рис. 28, б и г.

5. Если на чертеже несколько размерных линий, параллельных друг другу, то вначале наносят меньший размер. Так, на рис. 28, а сначала нанесен размер 10, а затем 30. В этом случае выносные и размерные линии на чертеже не пересекаются. Расстояние между параллельными размерными линиями равно от 6 до 10 мм.

6. Величину углов указывают в градусах с обозначением единицы измерения (значок 0). Размерную линию при этом проводят в виде дуги окружности с центром в вершине угла (рис. 28, д).

7. Если в детали имеется несколько одинаковых элементов, то на чертеже рекомендуется наносить размер лишь одного из них с указанием количества. Например, запись на чертеже «3 отв. 0 10» означает, что в детали имеется три одинаковых отверстия диаметра 10 мм

Применение масштаба в черчении

В практике приходится вычерчивать очень крупные детали, как, например, детали самолета, корабля, автомашины, и очень мелкие: детали часового механизма, некоторых приборов и т.д. Крупные детали не поместятся на чертеже стандартного формата, если не уменьшить их изображение. Мелкие детали, которые порой еле заметны простым глазом, невозможно вычертить в натуральную, т. е. истинную, величину имеющимися чертежными инструментами. Поэтому в черчении изображения

больших деталей уменьшают, а малых увеличивают по сравнению с действительными размерами.

Число, которое показывает, во сколько раз размеры изображения больше или меньше действительных размеров детали, называется масштабом.

Говоря иными словами, масштаб— это отношение линейных размеров изображения к линейным размерам самой детали.

Масштабы, применяемые при выполнении чертежей, стандартизованы. Стандарт разрешает выбирать следующие масштабы:

а) для уменьшения: 1:2; 1:2,5; 1:4; 1:5; 1:10 и др.,

б) для увеличения: 2:1; 2,5:1: 4:1; 5:1; 10:1 и др.

Наиболее желателен масштаб 1:1. В этом случае при выполнении чертежа не нужно пересчитывать размеры детали (рис. 31, в).

Масштабы записывают так: М 1:2, М5:1, М1:1 и т.д. Если масштаб указывают на чертеже в специально назначенной графе Основной надписи, то перед обозначением масштаба букву М не пишут (см. рис. 22, о).

Следует помнить, что, в каким бы масштабе ни выполнялось изображение. размеры на чертеже проставляют действительные, т.е. те, которые имеет деталь в натуре (рис. 31, в и г).

Круг

Круг сделать легко: Нарисуйте кривую на расстоянии от центральной точки. А так: Все точки находятся на одинаковом расстоянии от центра.

Самостоятельно нарисовать

Вставьте булавку в доску, оберните вокруг нее петлю и вставьте в петлю карандаш.Держите веревку натянутой и нарисуйте круг!

Поиграй с ним

Попробуйте перетащить точку, чтобы увидеть, как меняются радиус и окружность.

(Посмотрите, сможете ли вы сохранить постоянный радиус!)

Радиус, диаметр и окружность

Радиус — это расстояние от центра наружу.

Диаметр проходит прямо по окружности через центр.

Окружность — это расстояние один раз по окружности.

А вот и действительно крутая вещь:

Когда мы разделим длину окружности на диаметр, мы получим 3,141592654 …
, что является числом π (Pi)

Таким образом, когда диаметр равен 1, длина окружности равна 3,14 1592654 …

Можно сказать:

Окружность = π × Диаметр

Пример: вы ходите по кругу диаметром 100 м. Как далеко вы прошли?

Пройденное расстояние = Окружность = π × 100 м

= 314м (с точностью до метра)

Также обратите внимание, что диаметр в два раза больше радиуса:

Диаметр = 2 × Радиус

Так же верно и то:

Окружность = 2 × π × Радиус

Вкратце:

× 2	× π

Радиус

Диаметр

Окружность

Вспоминая

Длина слов может помочь вам запомнить:

• Радиус — кратчайшее слово и кратчайшая мера
• Диаметр длиннее
• Окружность самая длинная

Определение

Окружность плоская (двумерная), поэтому:

Площадь

Площадь круга в π в раз больше квадрата радиуса, что записывается:

A = π r ²

Где

• A — это Площадь
• r — радиус

Чтобы помочь вам запомнить, подумайте «Пирог в квадрате» (хотя пироги обычно круглые):

Пример: Какова площадь круга с радиусом 1.2 м?

Площадь = πr ²

= π × 1,2 ²

= 3,14159 … × (1,2 × 1,2)

= 4,52 (до 2 десятичных знаков)

Или, используя диаметр:

A = ( π /4) × D ²

Площадь

по сравнению с площадью

окружности составляет около 80% площади квадрата такой же ширины.
Фактическое значение (π / 4) = 0.785398 … = 78,5398 …%

И кое-что интересное для вас:

Посмотреть площадь круга по линиям

Имена

Так как люди изучали круги в течение тысяч лет, у них появились особые имена.

Никто не хочет говорить «линия, которая начинается на одной стороне круга, проходит через центр и заканчивается на другой стороне» , когда они могут просто сказать «Диаметр».

Итак, вот самые распространенные специальные имена:

линий

Линия, которая «просто касается» круга, когда проходит мимо, называется касательной .

Линия, разрезающая круг в двух точках, называется секущей .

Отрезок линии, который идет от одной точки к другой на окружности круга, называется хордой .

Если он проходит через центр, он называется диаметром .

А часть окружности называется Дуга .

Ломтики

Есть два основных «кусочка» круга.

Кусочек «пиццы» называется сектором.

А отрезок, образованный аккордом, называется отрезком.

Общие сектора

Квадрант и Полукруг — это два особых типа сектора:

Четверть круга называется квадрантом .

Полукруг называется Полукруг.

Внутри и снаружи

У круга есть внутренняя и внешняя стороны (конечно же!).Но у него также есть «включено», потому что мы можем оказаться прямо на круге.

Пример: «A» находится за пределами круга, «B» внутри круга, а «C» находится на круге.

Эллипс

Круг — это «частный случай» эллипса.

Как нарисовать круг с помощью этих уроков и руководств по рисованию и идеальных кругов от руки

Рисование кругов и овалов в перспективе

Узнайте, как рисовать овалы и круги в перспективе, чтобы ваши рисунки выглядели более реалистично.

Как рисовать объекты и фигуры с помощью кругов и овалов

Узнайте, как рисовать фигуры и объекты с кругами, овалами и эллипсами, с помощью следующих руководств по рисованию.

Рисование кругов в перспективе

Используя клетчатые квадраты, легко нарисовать идеальный круг … даже в перспективе. Это простой прием для идеального рисования кругов в перспективе.

Рисование кругов в ракурсе: как рисовать круги под углами, которые потом выглядят как эллипсы / овалы

Рисование круга при его повороте влево или вправо или при наклоне вперед или назад

Рисование сфер, кругов и эллипсов

Как рисовать и закрашивать сферы, а также как рисовать круги и эллипсы.

Рисование круга в 1-точечной перспективе

Чтобы нарисовать круг в линейной перспективе, лучше всего начать с квадрата. На схеме показан вид сверху и вид в перспективе круга, нарисованного в одноточечной перспективе. После того, как вы установили линию горизонта, создайте квадрат, ограничивающий края круга, который вы хотите создать. Следуйте этой пошаговой процедуре, чтобы создать убедительные круги в перспективе.

Рисование окружности через 3 точки

Построение геометрии с помощью циркуля и линейки

Как нарисовать круг

Если вы когда-нибудь захотите начертить круг и у вас под рукой нет циркуля, или если вы захотите нарисовать круг большего размера, чем вы можете с помощью циркуля, привяжите к булавке немного прочной нити, сделайте петлю на веревке любой длины. хочу, чтобы радиус, равный половине диаметра круга, был.

Как нарисовать круг и его центр, не поднимая карандаша

Если вы хотите повеселиться, поставьте это задание перед друзьями, а затем покажите им, как это делается. Покажите им фигуру, похожую на ту, что справа. Легко, правда? Задача такая: нарисовать его, не отрывая карандаш от бумаги. Если вы думаете, что это невозможно, читайте дальше, чтобы узнать, как это сделать.

Как нарисовать круг

Хотя есть много способов нарисовать идеальный круг, некоторые из них работают лучше, чем другие в определенных ситуациях. Вот несколько приемов; вы выбираете свою любимую!

Как нарисовать идеальный круг — Даже для самых талантливых художников одной из самых сложных вещей в рисовании является круг. В рассказе Вазари художник Джотто однажды нарисовал идеальный круг, чтобы подарить Папе Римскому.Есть несколько методов, которые помогут нарисовать круг как можно лучше.

Как нарисовать круговой трекер (пошаговое руководство)

Раскрытие информации: некоторые из приведенных ниже ссылок являются партнерскими ссылками, что означает, что без дополнительных затрат для вас я получу комиссию, если вы перейдете и сделаете покупка. Пожалуйста, ознакомьтесь с нашим раскрытием для получения дополнительной информации. Круговые трекеры

сейчас невероятно популярны. И это неудивительно, ведь они простые, функциональные и есть бесконечные способы их украсить.Эта статья покажет вам, как шаг за шагом создать круговой трекер. Просто читайте!

На самом деле я веду пулевое ведение журнала более двух лет и никогда не пробовал использовать круговой разворот до этого месяца. Меня всегда это немного пугало. Я перфекционист, и мысль о создании менее чем идеального круга всегда была препятствием. Тем более, что до недавнего времени у меня не было компаса или «компаса безопасности».

Итак, несколько месяцев назад я купил Helix Angle and Circle Maker на Amazon.И он так и остался, мысль о круге все еще пугала меня, хотя у меня был идеальный инструмент! Но я увидела этот потрясающий пост в Instagram Эрин с сайта thepetiteplanner.com и знала, что мне нужно попробовать. Вот как я это сделал…

Перед тем, как начать

Сначала вам нужно решить, для чего будет использоваться ваш круговой трекер. Вот несколько примеров того, как можно использовать круговой разворот.

Круговой трекер привычек

Это вариант вашего стандартного средства отслеживания привычек в виде графика, вместо того, чтобы отображать дни и привычки по осям x и y, все они находятся внутри круга.Здесь @journalbymir назначил каждую строку внутри круга разной привычке, а дни месяца написаны по окружности круга. Каждый «квадрат» будет заполнен, когда привычка будет завершена.

Вам нужно будет решить, сколько привычек вы хотите отслеживать, чтобы вы знали, сколько кругов вам нужно нарисовать для вашего трекера.

Источник: @journalbymir
Принадлежности: Tombow Dual Brush Pens

Циркулярный трекер настроения

Этот простой трекер настроения даст вам краткий обзор того, как вы себя чувствовали в течение месяца.Вам нужно будет создать цветовой ключ для вашего настроения и также добавить его на страницу. Вот красивый трекер настроения по частично заполненному кругу от @bujo_nina

Источник: @bujo_nina Принадлежности: Ручки с двумя кистями Tombow

Ежемесячный журнал (календарное колесо)

Изначально он был создан Ди с сайта Decemberthirty.com и действует как ежемесячный журнал. Задачи и встречи связаны с соответствующей датой прямой линией.

Источник: @decadethirty

Циркулярный календарь дней рождения

Этот разворот разбивает круг на месяцы. Вы можете добавить важные даты рождения по кругу рядом с соответствующим месяцем.Этот красивый был создан @bumblebujo (Pssst — если вы действительно хотите, чтобы именно он был в своем журнале пуль, она действительно продает эти наклейки в своем магазине Etsy)

Источник: @bumblebujo Принадлежности: Zebra Mildliners

Circular Future Log

Вариант календарного колеса, вместо круга, представляющего один месяц, круг представляет целый год и, как и выше, разделен на месяцы. Важные даты добавлены снаружи. Этот красивый разворот в виде круга был создан Erin @the.petite.planner

Источник: @ the.petite.planner Расходные материалы: Nuuna Notebook

Приступим….

Использованных расходных материалов:

1. Dingbats * Notebook (Я также настоятельно рекомендую Scribbles That Matter и Leuchtturm)
2. Карандаш
3. Ластик
4. Пигментный лайнер Black Staedtler
5. Конструктор спиральных углов и кругов

Как нарисовать круговой трекер

В следующем примере я собираюсь создать комбинацию примеров выше.Мой круговой разворот будет одновременно и круговым трекером настроения, и календарным колесом.

Разместите создатель круга в центре страницы. Карандашом нарисуйте круг с внешней стороны создателя круга. Этот круг на самом деле НЕ будет частью вашего трекера, но будет просто руководством на тот случай, если вам понадобится переставить создатель круга обратно на страницу позже. Поверьте, вы меня за это поблагодарите. Также отметьте, где находится центр круга.

Используя первое отверстие, ближайшее к краю создателя круга, нарисуйте первый круг.Затем пропустите отверстие и нарисуйте еще один круг. Продолжайте, пока у вас не появится 4 круга друг в друге.

Затем вырежьте кружки по дням месяца. Для этого сделайте отметку через каждые 10 градусов по кругу.

Теперь вы можете присоединить каждую из этих меток к центральной точке круга.

Отсчитайте количество разделов, чтобы их хватило на каждый день месяца, затем сотрите строки, которые вам больше не нужны. Если вы не хотите, чтобы непрерывный кружок был, сотрите и этот раздел.(Я всегда стираю ненужные линии перед тем, как рисовать пером, чтобы не запутать себя. Много раз я просто бездумно обводил карандашными отметками пером, чтобы понять, что я не должен делать это!)

Переместите создатель кругов и нанесите черную ручку на карандашные отметки.

Обозначьте свои круги и добавьте дни и даты. Здесь я решил, что хочу, чтобы день и свидания происходили во внутреннем кругу с настроением снаружи. Затем украсьте надписью и своими любимыми каракулями.

Мои надписи от руки были выполнены желтой двойной кистью, затем я обрисовал их оранжевой гелевой ручкой muji. Наконец, я использовал светло-серую ручку с двойной кистью, чтобы создать эффект тени.

Я нарисовал цветы внизу с помощью пигментного карандаша Staedtler и раскрасил круг и вокруг него желтым акварельным карандашом. Я провел по нему влажной кистью, чтобы сделать цвет более ярким и распределить цвет за пределами круга.

Я добавил в угол маленькую цветовую кнопку для обозначения своего настроения.А потом добавил свои задачи и встречи (в этом месяце у меня почти НИЧЕГО нет!)

ВЫ МОЖЕТЕ НАЙТИ ПОЛЕЗНЫЕ СООБЩЕНИЯ:

Как видите, с помощью Helix Angle и Circle Maker невероятно легко собрать круговой разворот. Мне очень нравится этот инструмент, я очень рекомендую его, к тому же он действительно доступен по цене. Однако, если вы не можете достать один, вы можете просто использовать стандартный циркуль, чтобы нарисовать круг, и транспортир, чтобы отметить свои участки.

Надеюсь, вы попробуете и расскажете, как у вас дела.Мне бы хотелось увидеть, какие развороты вы придумываете!

Если вам понравилась эта статья, поделитесь ею в Pinterest!

Python OpenCV: рисование кругов — techtutorialsx

В этом уроке мы проверим, как рисовать круги на изображении с помощью OpenCV и Python.

Введение

В этом уроке мы проверим, как рисовать круги на изображении с помощью OpenCV и Python.

Одна из частых задач при использовании OpenCV — обнаружение интересующих областей с помощью компьютерного алгоритма зрения. Таким образом, для программиста имеет смысл иметь возможность каким-то образом выделить интересующие области.

Таким образом, OpenCV предлагает приличное количество функций рисования, которые мы можем использовать для рисования форм на изображениях. Итак, как уже упоминалось, в этом уроке мы проверим, как рисовать круги на изображениях.

Важно подчеркнуть, что при рисовании изображения справочные координаты работают, как показано на рисунке 1.Начало координат находится в верхнем левом углу изображения, и мы указываем координату x слева направо и координату y сверху вниз. Также координаты указаны в пикселях.

Рисунок 1 — Ссылка при рисовании в OpenCV.

Это руководство было протестировано на версии 3.2.0 OpenCV.

Код

Как обычно, мы начинаем с импорта модуля cv2 , поэтому у нас есть доступ ко всем функциям OpenCV, которые нам понадобятся.

импорт cv2
 

Затем нам нужно прочитать изображение, на котором мы хотим нарисовать круги. Для этого нам просто нужно использовать функцию imread , передавая в качестве входных данных путь к изображению в файловой системе.

изображение = cv2.imread ('C: /Users/N/Desktop/Test.jpg')
 

Теперь, чтобы нарисовать круг на изображении, нам просто нужно вызвать функцию круга модуля cv2 . Обратите внимание, что эта функция не возвращает новое изображение, а рисует круг на изображении, которое мы передадим в качестве входных данных.

Но пока мы не сохраняем это отредактированное изображение, круг будет нарисован на изображении, которое у нас есть в памяти, а не в исходном файле, который мы прочитали, поэтому эти функции можно использовать безопасно.

В качестве первого ввода функция circle получает изображение, на котором мы хотим нарисовать круг. Во-вторых, он получает кортеж с координатами x и y центра круга.

В качестве третьего аргумента нам нужно передать радиус круга, а в качестве четвертого нам нужно указать другой кортеж с цветом круга в формате BGR (синий, зеленый и красный).

Это обязательные параметры, которые нам нужно передать, чтобы нарисовать круг, но есть несколько дополнительных, которые принимают значения по умолчанию, если не указаны.

Итак, сначала мы нарисуем зеленый круг с координатами x = 100 и y = 0 и с радиусом 25 пикселей.

cv2.circle (изображение, (100, 0), 25, (0,255,0))
 

Затем мы нарисуем круг с координатами x = 0 и y = 100, также с радиусом 25 пикселей. Его цвет будет красным.

cv2.circle (изображение, (0, 100), 25, (0,0,255))
 

Обратите внимание, что в предыдущих вызовах мы не указали, какой будет толщина контура круга.Но это значение на самом деле является одним из дополнительных параметров, которые мы можем передать функции circle , которая по умолчанию равна 1 пикселю. Итак, предыдущие два круга будут иметь толщину 1 пиксель.

Чтобы проиллюстрировать использование этого параметра, мы нарисуем круг с координатами x = 100 и y = 100, радиусом 50 и синим цветом. Кроме того, мы передадим пятый параметр, который будет соответствовать толщине контура круга со значением 3 пикселя.

cv2.круг (изображение, (100, 100), 50, (255,0,0), 3)
 

Наконец, мы отобразим изображение с нарисованными кружками и дождемся ключевого события. Когда это событие произойдет, мы уничтожим окно, в котором отображалось изображение, и завершим выполнение. Окончательный исходный код показан ниже и уже включает эти последние вызовы.

импорт cv2

изображение = cv2.imread ('C: /Users/N/Desktop/Test.jpg')

cv2.circle (изображение, (100, 0), 25, (0,255,0))
cv2.circle (изображение, (0, 100), 25, (0,0,255))

cv2.circle (изображение, (100, 100), 50, (255,0,0), 3)

cv2.imshow ('Тестовое изображение', изображение)
cv2.waitKey (0)
cv2.destroyAllWindows ()
 

Проверка кода

Чтобы протестировать код, просто запустите предыдущую программу в выбранной среде Python и укажите на существующий образ в файловой системе.