- Площадь правильного пятиугольника рассчитывается по любой из формул:
S = 5 4 t 2 c t g π 5 = 5 5 + 2 5 4 t 2 = 5 12 R d = 5 2 R 2 sin 2 π 5 = 5 r 2 t g π 5 {displaystyle S={frac {5}{4}}t^{2}mathop {mathrm {ctg} } ,{frac {pi }{5}}={frac {{sqrt {5}}{sqrt {5+2{sqrt {5}}}}}{4}}t^{2}={frac {5}{12}}Rd={frac {5}{2}}R^{2}sin {frac {2pi }{5}}=5r^{2}mathop {mathrm {tg} } ,{frac {pi }{5}}} , где R {displaystyle R} — радиус описанной окружности, r {displaystyle r} — радиус вписанной окружности, d {displaystyle d} — диагональ, t {displaystyle t} — сторона.
- Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу 1 + 5 2 {displaystyle {frac {1+{sqrt {5}}}{2}}} .
Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:
- Сторона:
t = R 5 − 5 2 ≈ 1,175 57 R {displaystyle t=R{sqrt {frac {5-{sqrt {5}}}{2}}}approx 1{,}17557~R}
- Радиус вписанной окружности:
r = 5 5 + 2 5 10 t ≈ 0,688 191 t {displaystyle r={frac {{sqrt {5}}{sqrt {5+2{sqrt {5}}}}}{10}}tapprox 0{,}688191~t}
- Радиус описанной окружности:
R = 1 0 5 + 5 10 t = ( 5 − 1 ) r ≈ 0,850 651 t ≈ 1,236 07 r {displaystyle R={frac {{sqrt {1}}0{sqrt {5+{sqrt {5}}}}}{10}}t=({sqrt {5}}-1)~rapprox 0{,}850651~tapprox 1{,}23607~r}
- Диагональ:
d = Φ 5 R = 5 + 1 2 t ≈ 1,902 R ≈ 1,618 t {displaystyle d={sqrt {Phi {sqrt {5}}}}R={frac {{sqrt {5}}+1}{2}}tapprox 1{,}902~Rapprox 1{,}618~t}
- Площадь:
S = 5 5 + 2 5 4 t 2 ≈ 1,720 48 t 2 {displaystyle S={frac {{sqrt {5}}{sqrt {5+2{sqrt {5}}}}}{4}}t^{2}approx 1{,}72048~t^{2}}
- Правильным пятиугольником невозможно заполнить плоскость без промежутков (см.
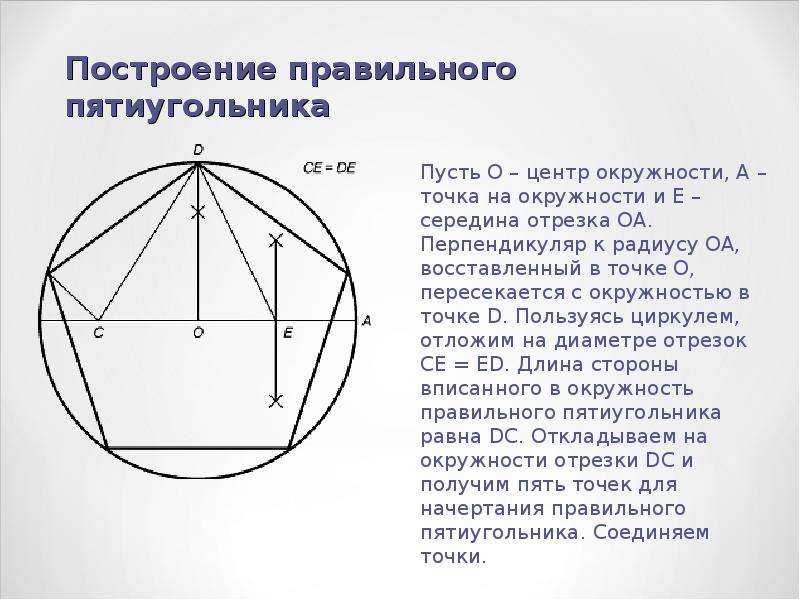 {4}=3Phi +2={frac {3{sqrt {5}}+7}{2}}approx 6{,}8541} где Φ {displaystyle Phi } — отношение золотого сечения.
{4}=3Phi +2={frac {3{sqrt {5}}+7}{2}}approx 6{,}8541} где Φ {displaystyle Phi } — отношение золотого сечения.Построение
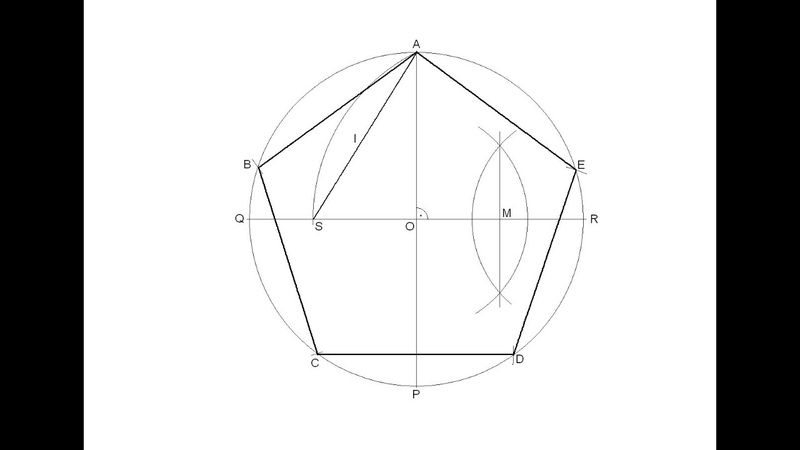
Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.
Вот один из методов построения правильного пятиугольника в заданной окружности:
- Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
- Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
- Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
- Постройте точку C посередине между O и B.

- Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
- Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
- Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
- Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
- Постройте правильный пятиугольник AEGHF.
- Воспроизвести медиафайл
Построение правильного пятиугольника
Построение правильного пятиугольника
Построение правильного пятиугольника
Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля
Пятиугольный узел на полоске бумаги
Иглокожие, например морские звёзды, обладают пентасимметрией
Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как мушмула германская
Пентагон — здание Министерства обороны США
- Додекаэдр — единственный из правильных многогранников, грани которого представляют собой правильные пятиугольники.
- Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.
- Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
- В природе не существует кристаллов с гранями в форме правильного пятиугольника.
- Правильный пятиугольник со всеми его диагоналями является проекцией правильного пятиячейника (4-симплекса).
- Алексеенко, Валентина Харитоновна
- Биллевич, Леон
- Брохвайл Искитрог
- Димитрий (Устимович)
- Шумахер, Генрих Христиан
- Все стороны равны. .
- Все углы равны. .
- Центр вписанной окружности совпадает с центром описанной окружности. Центр вписанной и описанной окружностей является центром многоугольника.
- Сумму всех углов правильного многоугольника можно найти по формуле: . Где n — количество вершин правильного многоугольника, — внутренние углы многоугольника.

- Сумма внешних углов правильного многоугольника равна 360°. . Где n — количество вершин правильного многоугольника, — внешние углы многоугольника.
- Количество диагоналей правильного многоугольника равно произведения количества вершин многоугольника на количество диагоналей, которые можно провести из одной вершины. Из одной вершины n-угольника можно провести n-3 диагонали, так как нельзя провести диагонали в две соседние вершины (они будут совпадать со сторонами) и в эту же вершину. . Где — количество диагоналей правильного многоугольника, n — количество вершин правильного многоугольника.
- Биссектрисы всех углов многоугольника равны и проходят через центр вписанной и описанной окружностей.
- Чтобы построить правильный треугольник с заданной стороной а, построим отрезок АВ, равный а. Точки А и В — две вершины правильного треугольника.
- Затем построим две дуги с радиусом а и центрами в точках А и В. Точка пересечения С равноудалена от точек А и В и является третьей вершиной треугольника.
- Соединим вершины. ΔАВС построен.
- Построим отрезок АВ произвольной или заданной длины. Точки А и В — вершины правильного треугольника.
- С помощью транспортира из точки А от отрезка АВ отложим угол 60° и проведем луч.
- Отложим угол 60° и проведем луч из точки В.
- Два луча пересекаются в точке С — третьей вершине правильного треугольника.
- Соединим вершины А и С, В и С. Правильный ΔАВС построен.
- Построим одну из сторон квадрата — отрезок АВ.

- Построим перпендикуляры к АВ в точках А и В, лежащие по одну сторону от отрезка АВ.
- На построенных перпендикулярах отложим отрезки АD и ВС, равные отрезку АВ.
- Соединим точки С и D. Квадрат АВСD построен.
- Построим окружность произвольного радиуса с центром в точке А.
- Произвольно отметим точку В, лежащую на окружности.
- Проведем прямую АВ.
- Построим перпендикуляр к прямой АВ в точке А. Назовем одно из пересечений данного перпендикуляра и окружности точкой С.
- Найдем середину отрезка АС — точку D.
- Измерим циркулем расстояние DВ. Не меняя раствора циркуля, проведем вспомогательную дугу с центром в точке D, пересекающую прямую АС внутри окружности. Назовем точку пересечения точкой Е.
- Расстояние между точками В и Е равно стороне правильного пятиугольника. Измерим циркулем ВЕ и, не меняя раствора циркуля, построим две вспомогательные дуги с центром в точке В, пересекающие окружность.
 Пусть М и К — точки пересечения. Точки М и К — вершины правильного пятиугольника.
Пусть М и К — точки пересечения. Точки М и К — вершины правильного пятиугольника. - Тем же раствором циркуля проведем вспомогательную дугу с центром в точке М. Дуга пересекается с окружностью в точке Р — одной из вершин правильного пятиугольника.
- Не меняя раствора циркуля построим дугу с центром в точке К. Точка пересечения данной дуги и окружности — точка Q. Q — вершина пятиугольника.
- Проведем отрезки ВК, КQ, QР, РМ, МВ. Правильный пятиугольник ВКQРМ построен.
- Построим окружность с произвольным или заданным радиусом а, равным стороне будущего правильного шестиугольника. Точка С — центр данной окружности.
- На окружности отметим произвольную точку D и проведем прямую DС. Назовем вторую точку пересечения с окружностью точкой G. Точки D и G — вершины правильного шестиугольника.
- Тем же раствором циркуля построим вспомогательную дугу с радиусом а и центром в точке D. Дуга пересекает окружность в двух точках.
 Назовем точки пересечения Е и В. Данные точки являются вершинами шестиугольника.
Назовем точки пересечения Е и В. Данные точки являются вершинами шестиугольника. - Не меняя раствора циркуля, проведем вспомогательную дугу с центром в точке G и найдем точки пересечения дуги с окружностью — две вершины шестиугольника. Назовем точки пересечения А и F.
- Проведем отрезки АВ, ВD, DE, EF, FG, GA. АВDEFGA — правильный шестиугольник, все стороны которого равны по построению.
Знаменитое здание Министерства обороны США в Вашингтоне, округ Колумбия (здание Пентагона)
Домашняя табличка на бейсбольном поле
Знаки перехода через школу
9018 1
Получение с помощью полоски бумаги
Правильный пятиугольник можно получить, завязав узлом полоску бумаги.
В природе
Исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры. Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская. Пентасимметрией обладают иглокожие (например морские звёзды) и некоторые растения. См. также Закономерности в природе.
Интересные факты
Построение ⭐ правильных многоугольников: формулы геометрии
Что такое правильный многоугольник
Определение 1Правильный многоугольник — это выпуклый многоугольник, у которого все стороны и все углы равны.
Ниже перечислены некоторые правильные многоугольники
Правильный треугольник: все углы правильного треугольника равны 60°.
Правильный четырехугольник (квадрат): все углы квадрата равны 90°.
Правильный пятиугольник: все углы правильного пятиугольника равны 108°.
Правильный шестиугольник: все углы правильного шестиугольника равны 120°.
Правильный семиугольник: все углы правильного семиугольника равны 128,57°.
Правильный восьмиугольник: все углы правильного восьмиугольника равны 135°.
Признак правильного многоугольника: многоугольник будет правильным, если все его стороны равны и все его углы равны .
Свойства правильного многоугольника
Вписанная и описанная окружности правильного многоугольника
Определение 2Вписанная окружность — это окружность, лежащая внутри многоугольника и касающаяся всех его сторон.
Радиус вписанной в правильный многоугольник окружности равен:
Формула 4
где r — радиус окружности, описанной около правильного многоугольника,
n — количество вершин многоугольника,
— сторона многоугольника.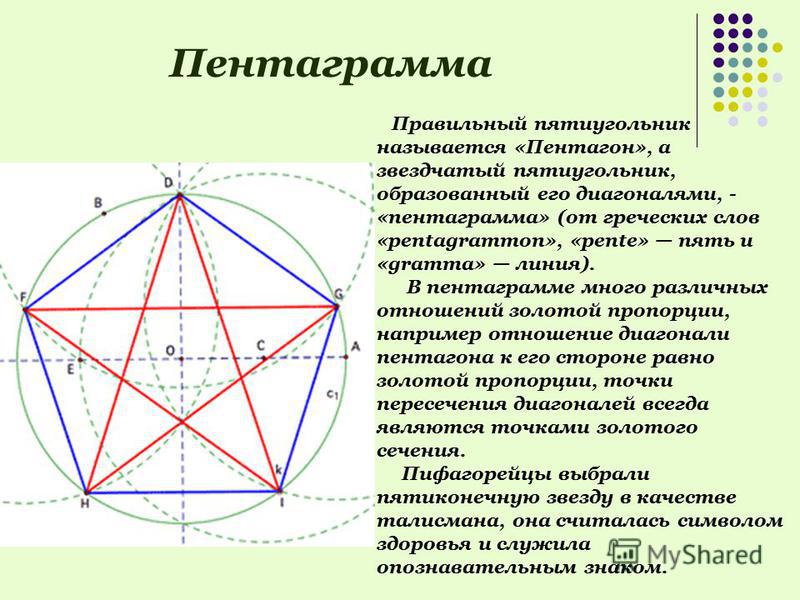
Описанная окружность — это окружность, лежащая снаружи многоугольника и проходящая через все его вершины.
Радиус описанной около правильного многоугольника окружности равен:
Формула 5где R — радиус окружности, описанной около правильного многоугольника,
n — количество вершин многоугольника,
— сторона многоугольника.
На рисунке изображены вписанная и описанная окружности правильного шестиугольника. R — радиус описанной окружности, r — радиус вписанной окружности. Точка О — центр вписанной и описанной окружностей.
Формулы для правильного многоугольника
Сторона правильного многоугольника через радиус описанной окружности:
Формула 6где R — радиус окружности, описанной около правильного многоугольника,
n — количество вершин многоугольника,
— сторона многоугольника.
Сторона правильного многоугольника через радиус вписанной окружности:
Формула 7где r — радиус вписанной в правильный многоугольник окружности,
n — количество вершин многоугольника,
— сторона многоугольника.
Площадь правильного многоугольника, если известна его сторона:
Формула 8где — площадь правильного многоугольника,
n — количество вершин многоугольника,
— сторона многоугольника.
Площадь правильного многоугольника, если известны его сторона и радиус вписанной окружности:
Формула 9где — площадь правильного многоугольника,
r — радиус вписанной окружности многоугольника,
P — периметр правильного многоугольника,
Площадь правильного многоугольника, если известен радиус описанной окружности:
Формула 10где — площадь правильного многоугольника,
R — радиус вписанной окружности многоугольника,
n — количество вершин правильного многоугольника.
Построение правильных многоугольников
Построение правильного треугольника с помощью циркуля и линейки:
Правильный треугольник можно построить с помощью транспортира, так как известна величина его углов.
Построение квадрата с помощью линейки и циркуля:
Построение правильного пятиугольника:
Построение правильного шестиугольника:
Приблизительное построение правильных многоугольников: два художника эпохи Возрождения — Альбрехт Дюрер
Альбрехт Дюрер (1471-1528), считающийся отцом современной немецкой живописи, был также большим любителем математики. Он написал книгу под названием Unterweysung der Messung …, в которой рассматриваются всевозможные геометрические задачи. В этой книге он дает точную конструкцию правильного пятиугольника, но он также дает приблизительную конструкцию, которую легко выполнить в практическом рисовании. (Его книга была адресована ремесленникам, каменщикам и т.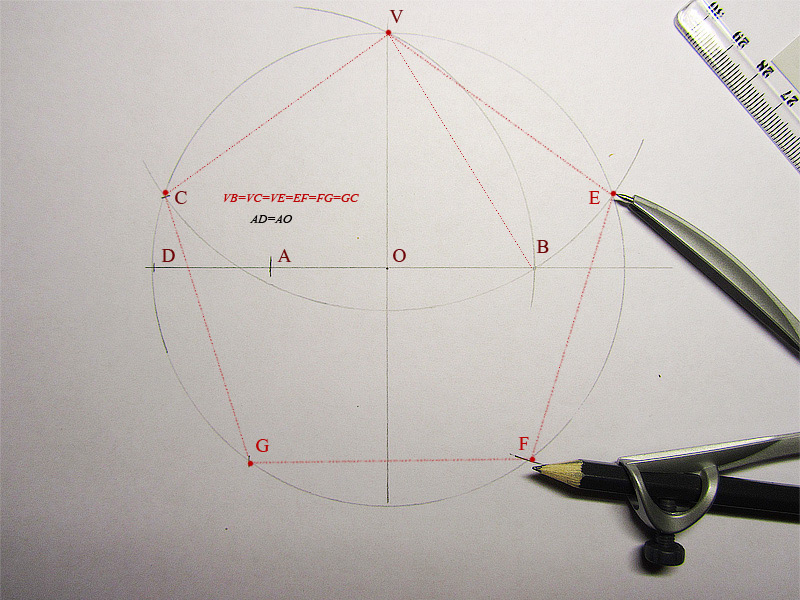 д., которые больше заботились о простых процедурах, чем о геометрической точности.)
д., которые больше заботились о простых процедурах, чем о геометрической точности.)
Это построение показано ниже:
Возьмите фиксированное отверстие компаса: AB = a . Нарисуйте круги радиусом a с центрами A и B ; пусть эти окружности пересекаются в точках C и D . Тогда AB = AD = BD , как мы знаем. Нарисуйте окружность с центром D и радиусом DA . Этот круг пройдет через B ; пусть E будет точкой пересечения CD , и пусть F и G будут точками пересечения окружностей с центрами A и B соответственно. Произведите FE , пока он не пересечет в точке H окружность с центром в точке B ; произведите GE , пока он не пересечет в точке I окружность с центром в точке A . Тогда пересечение K окружностей радиуса a с центрами H и I дает пятую вершину пятиугольника.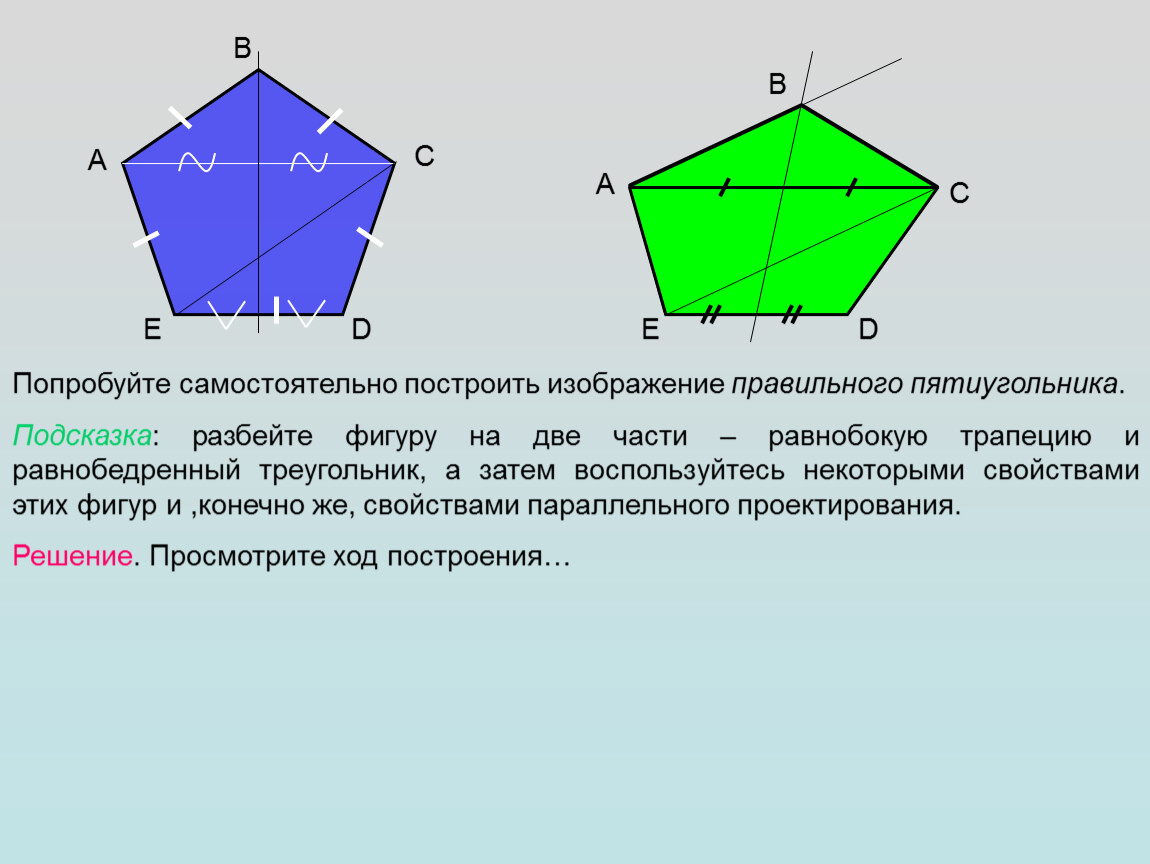
Насколько правильный пятиугольник? Если бы он был совершенно правильным, все стороны должны образовывать угол 360°/5 = 72° в центре пятиугольника. Следовательно все углы при вершинах пятиугольника должны быть равны 180°-72°= 108°(поскольку каждый из них есть сумма двух равных углов [180°-72°]/2). На самом деле мы увидим, что угол ABH = 108°21’58” — чуть больше 108°, так что какой-то другой угол должен быть чуть меньше 108°. Сначала обратите внимание, что угол FBG = 90°; тогда, поскольку FG = 2 a и GB = a , мы имеем FB = a √3 . Кроме того, угол DFE = 45° и угол DFC = угол DFA = 60° ( F , A , C лежат на одной прямой, как и C 90 004, Б , Г и F , D , G ), и, следовательно, угол AFE = 15°. Поскольку угол BFE стягивает дугу окружности FABG равен углу AFE , также имеем угол BFE = 15°.
Теперь используем закон синусов для треугольника FBH ; это дает sin(угол BHF ) = √3 sin15° (обратите внимание, что, поскольку можно найти угол BHF BHF, а затем угол HBF ; затем, вычитая угол ABF = 30° из угла HBF , мы находим, что угол ABH составляет примерно 108°22′, что близко к значению Педо [2].0005
Так как угол BAI равен углу ABH , то он тоже чуть больше 108°. Также каждый из углов BHK и AIK чуть больше 107°, а угол HKI чуть больше 109°… и все равно на нашем рисунке это будет едва заметно.
Дюрер не предупреждает читателя своей книги, что эта конструкция приблизительна. (Он же выполнен «ржавым» циркулем, т. е. циркулем с фиксированным отверстием.) На самом деле он тоже приводит, как мы сказали, точное построение пятиугольника.
«Интерес Дюрера к построению правильных многоугольников объясняется применением геометрии в средние века в исламском и готическом декоративном дизайне, а после изобретения пушек — в строительстве укрепленных городов. (Любопытно, что очень немногие здания в истории были построены на основе пятиугольной формы. Пентагон недалеко от Вашингтона, округ Колумбия, является заметным исключением.)» [2]
(Любопытно, что очень немногие здания в истории были построены на основе пятиугольной формы. Пентагон недалеко от Вашингтона, округ Колумбия, является заметным исключением.)» [2]
Подводя итог этому обзору многоугольных конструкций эпохи Возрождения, мы можем сказать что и Леонардо да Винчи, и Альбрехт Дюрер были большими любителями математики. «Леонардо много писал о полигонах; но именно Дюрер, а не Леонардо, передал нам популярные средневековые конструкции». [2]
Рауль А. Саймон, «Приблизительное построение правильных многоугольников: два художника эпохи Возрождения — Альбрехт Дюрер», Convergence (август 2010 г.)
Что такое пятиугольник? — Определение, свойства и типы
Автор:
Malcolm McKinsey
Свойства правильного пятиугольника
Как и любой правильный многоугольник, обход пятиугольника завершает один полный круг, поэтому внешние углы находятся путем деления 360° на количество сторон, в данном случае 360°5=72°\frac {360°}{5}=72° 5360°=72°.
Неправильные пятиугольники
Неправильные пятиугольники могут быть выпуклыми или вогнутыми пятиугольниками, но они должны иметь пять сторон разной длины.
Типы и свойства неправильных пятиугольниковТипичным примером выпуклого неправильного пятиугольника является базовая пластина на бейсбольном поле.
Все пятиугольники (правильные и неправильные) пятиугольники с пятью внутренними и пятью внешними углами.
Примеры пятиугольников
Если вы будете искать вокруг себя форму пятиугольника, вы обязательно ее найдете. Будь то неправильный пятиугольник с разной длиной сторон или правильный пятиугольник с равными сторонами и равными углами, существует множество реальных примеров пятиугольников:
Секции футбольного мяча
Когда вы найдете пятигранную форму, вы можете описать ее как пятиугольную форму.
