Правильный 6 угольник: Шестиугольник и его свойства — Интернет магазин мебели "МебПилот.ру"

Разное

Содержание

Как нарисовать правильный 6 угольник. Правильный шестиугольник и его свойства. Последние штрихи и узор

Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.

Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.

Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.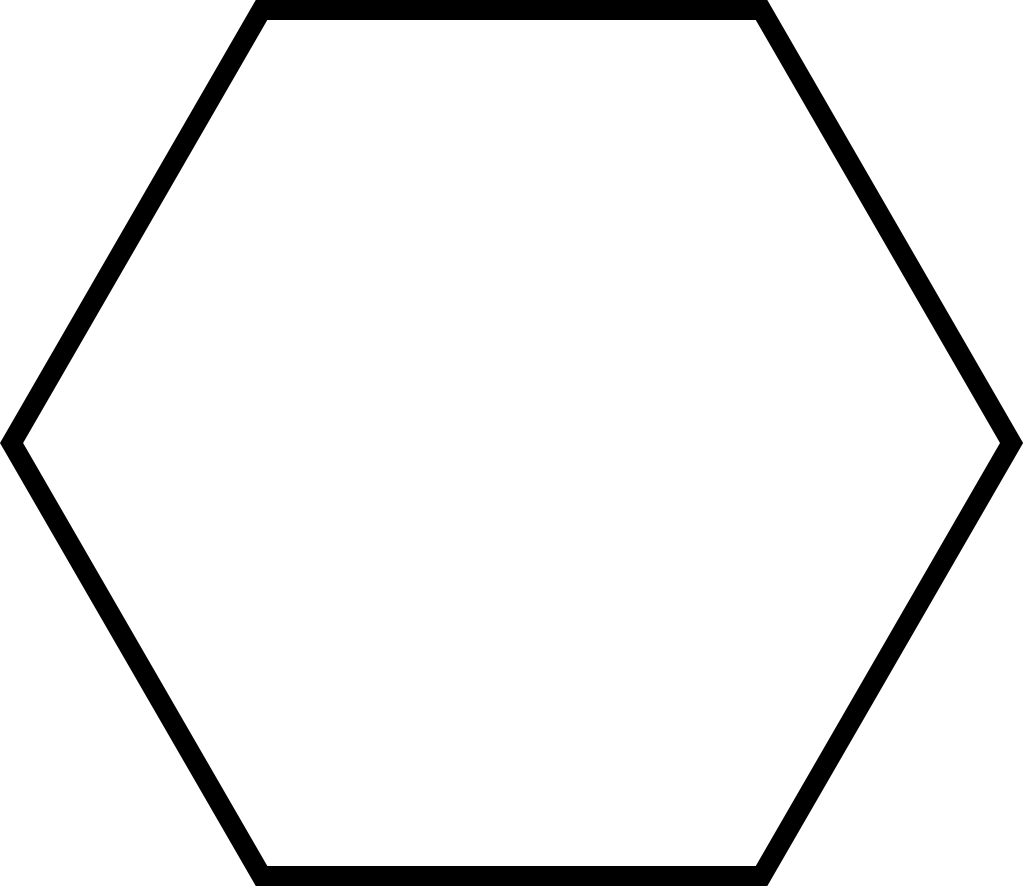

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны

1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2.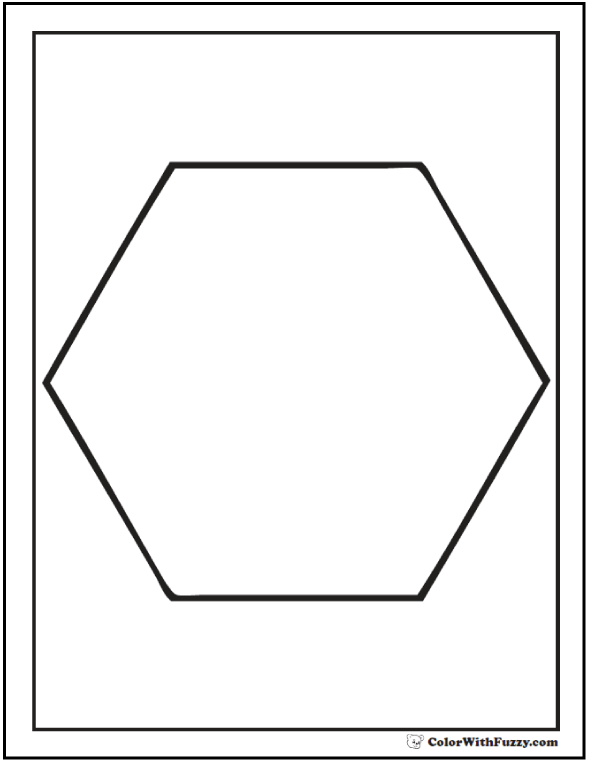

Полученные точки будут двумя другими вершинами искомого треугольника.

Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4.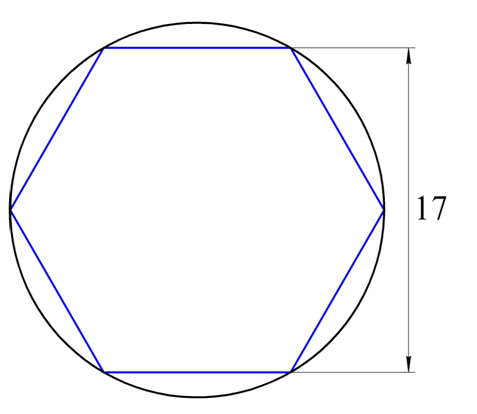

Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.

Определение и построение

Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.

Если вспомнить формулу суммы углов многоугольника

то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.

Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.

Пошаговая инструкция будет выглядеть так:

При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.

Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.

Свойства простые и интересные

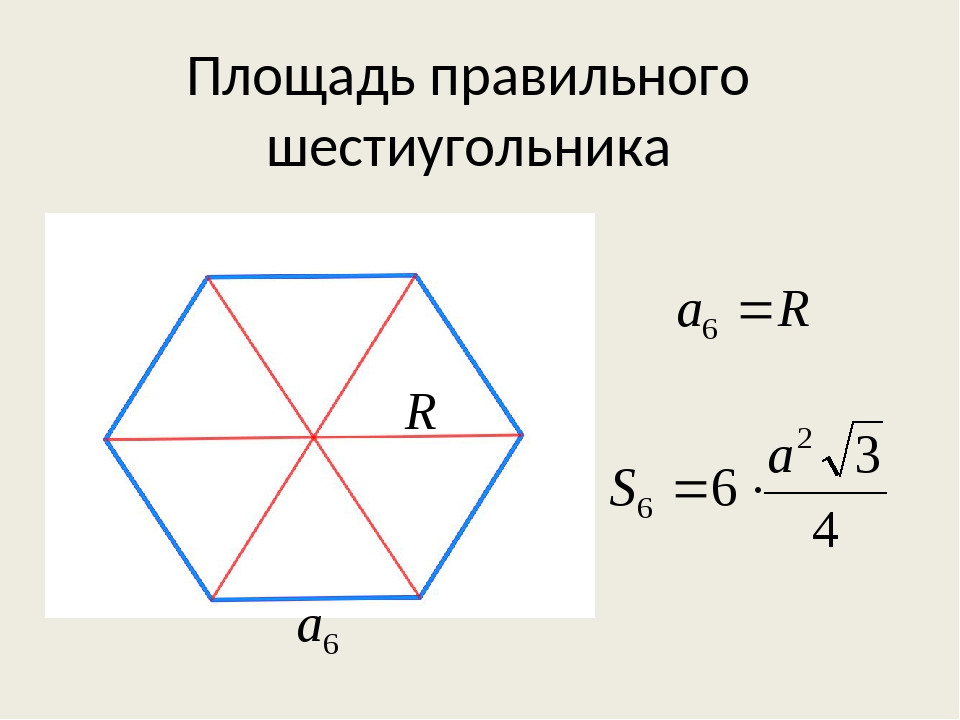
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:

Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:

диаметр описанной окружности;
диаметр вписанной окружности;
площадь;
периметр.

Описанная окружность и возможность построения

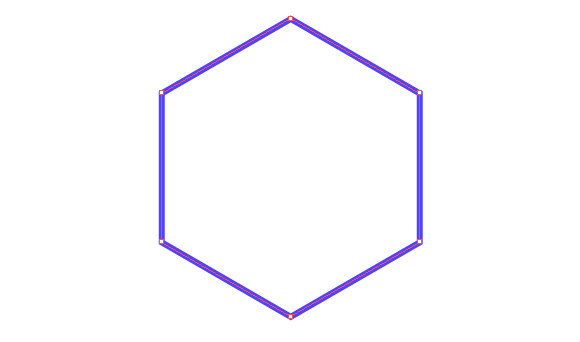
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.

Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.

После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:

Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.

Ну а площадь этой окружности будет стандартная:

Вписанная окружность

Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.

Высота равностороннего треугольника вычисляется просто:

h²=а²-(а/2)²= а²3/4, h=а(√3)/2

А поскольку R=a и r=h, то получается, что

r=R(√3)/2 .

Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.

Ее площадь будет составлять:

S=3πa²/4 ,

то есть три четверти от описанной.

Периметр и площадь

С периметром все ясно, это сумма длин сторон:

P=6а , или P=6R

А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:

S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или

S=3R²(√3)/2

Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:

S=3(2r/√3)²(√3)/2=r²(2√3)

Занимательные построения

В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:

Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:

Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.

Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:

Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:

d=а(√3)/3

Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:

r₂=а/2

S=(3(√3)/2)(а(√3)/3)²=а(√3)/2

Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.

От теории к практике

Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.

Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:

Выпускается и бетонная плитка для мощения.

Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.

Правильный описанный треугольник строят следующим образом (рисунок 38).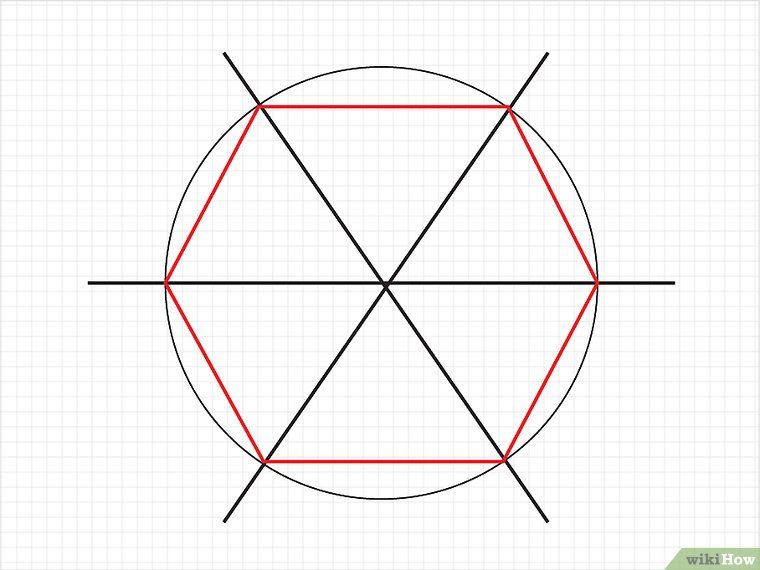 Из центра заданной окружности радиуса R 1 проводят окружность радиусом R 2 = 2R 1 и делят ее на три равные части. Точки деления А, В, С являются вершинами правильного треугольника, описанного около окружности радиуса R 1 .

Рисунок 38

Правильный описанный четырехугольник (квадрат) можно построить с помощью циркуля и линейки (рисунок 39). В заданной окружности проводят два взаимно перпендикулярных диаметра. Приняв точки пересечения диаметров с окружностью за центры, радиусом окружности R описывают дуги до взаимного их пересечения в точках А, В, С,D . Точки A , B , C , D и являются вершинами квадрата, описанного около данной окружности.

Рисунок 39

Для построения правильного описанного шестиугольника необходимо вначале построить вершины описанного квадрата указанным выше способом (рисунок 40, а). Одновременно с определением вершин квадрата заданную окружность радиуса R делят на шесть равных частей в точках 1, 2, 3, 4, 5, 6 и проводят вертикальные стороны квадрата. Проведя через точки деления окружности 2–5 и 3–6 прямые до пересечения их с вертикальными сторонами квадрата (рисунок 40, б), получают вершины А, В, D, Е описанного правильного шестиугольника.

Рисунок 40

Остальные вершины C и F определяют с помощью дуги окружности радиуса OA , которая проводится до пересечения ее с продолжением вертикального диаметра заданной окружности.
3 СОПРЯЖЕНИЯ

Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.

Правильный шестиугольник представляет собой многоугольник с шестью одинаковыми сторонами и равными углами. Из школьного курса нам известно, что он обладает следующими свойствами:

Длина его сторон соответствует радиусу описанной окружности. Из всех это свойство имеет лишь правильный шестиугольник.
Углы равны между собой, и величина каждого составляет 120°.
Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r — радиусы описанной и вписанной окружности.
Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2)/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.

У правильного шестиугольника есть одна интересная особенность, благодаря которой он получил в природе такое широкое распространение, — он способен заполнить любую поверхность плоскости без наложений и пробелов. Существует даже так называемая лемма Пала, согласно которой правильный гексагон, сторона которого равна 1/√(3), представляет собой универсальную покрышку, то есть может покрыть любое множество с диаметром в одну единицу.

Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.

На практике бывают случаи, когда требуется нарисовать шестиугольник большого размера. Например, на двухуровневом гипсокартонном потолке, вокруг места крепления центральной люстры, нужно установить на нижнем уровне шесть небольших светильников. Циркуль таких размеров найти будет очень и очень сложно. Как поступить в этом случае? Как вообще нарисовать большую окружность? Очень просто. Нужно взять крепкую нить нужной длины и обвязать один из ее концов напротив карандаша. Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.

Научимся изображать шестигранную призму в различных положениях.

Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольников постройте шестигранные призмы.

Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.53. В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — одинаковые прямоугольники. Для того, чтобы правильно изобразить шестигранник в перспективе, необходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести. Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5 — 2 на четыре равных отрезка (эти отрезки обозначены дугами). Противоположные стороны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (например, стороны 6 — 1 и 4 — 3 параллельны прямой 5 — 2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения. Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.

На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольника принадлежат описанной окружности, радиус которой равен стороне шестиугольника.

Горизонтальный шестиугольник. Изобразите горизонтальный эллипс произвольного раскрытия, т. е. описанную окружность в перспективе. Теперь необходимо найти на ней шесть точек, являющихся вершинами шестиугольника. Проведите любой диаметр данной окружности через ее центр (рис. 3.57). Крайние точки диаметра — 5 и 2, лежащие на эллипсе, являются вершинами шестиугольника. Для нахождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диаметр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус пополам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5 — 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5 — 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5 — 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).

Проверьте правильность вашего построения разными способами. Если построение верно, то линии, соединяющие противоположные вершины шестиугольника, пересекаются в центре окружности (рис. 3.62), а противоположные стороны шестиугольника параллельны соответствующим диаметрам (рис. 3.63). Еще один способ проверки показан на рис. 3.64.

Вертикальный шестиугольник. В таком шестиугольнике прямые, соединяющие точки 7 и 3, б и 4, а также касательные к описанной окружности в точках 5 и 2, имеют вертикальное направление и сохраняют его на перспективном рисунке. Таким образом, проведя две вертикальные касательные к эллипсу, найдем точки 5 и 2 (точки касания). Соедините их прямой линией, а затем разделите полученный диаметр 5 — 2 на 4 равных отрезка, учитывая их перспективные сокращения (рис. 3.65). Проведите вертикальные прямые через точки А и Б, а на их пересечении с эллипсом найдите точки 1,3,6л4. Затем последовательно соедините точки 1 — 6 прямыми (рис. 3.66). Правильность построения шестиугольника проверьте аналогично предыдущему примеру.

Описанный способ построения шестиугольника позволяет получить эту фигуру на основе окружности, изобразить которую в перспективе проще, чем квадрат заданных пропорций. Поэтому данный способ построения шестиугольника представляется наиболее точным и универсальным. Способ построения на основе квадрата позволяет легко изобразить шестигранник в том случае, когда на рисунке уже есть куб, иными словами, когда пропорции квадрата и направление его сторон определены.

На основе квадрата. Рассмотрите рис. 3.67. Вписанный в квадрат шестиугольник по горизонтальному направлению 5 — 2 равен стороне квадрата, а по вертикали — меньше ее длины.

Вертикальный шестиугольник. Нарисуйте вертикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5 — 2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис. 3.68). Линии, ограничивающие шестиугольник сверху и снизу, не совпадают со сторонами квадрата. Изобразите их на некотором расстоянии (1114 а) от горизонтальных сторон квадрата и параллельно им. Соединив найденные таким образом точки 1 и 3 с точкой 2, а точки 6 и 4 — с точкой 5, получим шестиугольник (рис. 3.69).

Горизонтальный шестиугольник строится в той же последовательности (рис. 3.70 и 3.71).

Этот способ построения уместен только для шестиугольников с достаточным раскрытием. В случае, если раскрытие шестиугольника незначительно, лучше воспользоваться способом на основе описанной окружности. Для проверки шестиугольника, построенного через квадрат, можно использовать уже известные вам методы.

Кроме того существует еще один — описать вокруг полученного шестиугольника окружность (на вашем рисунке — эллипс). Все вершины шестиугольника должны принадлежать этому эллипсу.

Овладев навыками изображения шестиугольника, вы свободно перейдете к изображению шестигранной призмы. Внимательно рассмотрите схему на рис. 3.72, а также схемы построения шестигранных призм на основе описанной окружности (рис. 3.73; 3.74 и 3.75) и на основе квадрата (рис. 3.76; 3.77 и 3.78). Изобразите вертикальные и горизонтальные шестигранники различными способами. На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке горизонтального шестигранника длинные стороны боковых граней будут сходиться в точке схода на горизонте, а раскрытие шестиугольника основания будет тем больше, чем дальше от зрителя он находится. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).

Правильный шестиугольник — это… Что такое Правильный шестиугольник?

Шестиугольник — Правильный шестиугольник Шестиугольник многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы. Сумма внутренних углов выпуклого шестиугольника р … Википедия

Шестиугольник Сатурна — Гексагональное устойчивое атмосферное образование на северном полюсе Сатурна, открытое аппаратом Вояджер 1 и наблюдаемое снова в 2006 году а … Википедия

Правильный многоугольник — Правильный семиугольник Правильный многоугольник это выпуклый многоугольник, у которого все стороны и углы равны . Определение правильного многоугольника может зависеть от определения … Википедия

Правильный семиугольник — Правильный семиугольник это правильный многоугольник с семью сторонами. Содержание … Википедия

Правильный треугольник — Правильный треугольник. Правильный (или равносторонний) треугольник это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны … Википедия

Правильный девятиугольник — это правильный многоугольник с девятью сторонами. Свойства Правиль … Википедия

Правильный 17-угольник — Правильный семнадцатиугольник геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Содержание 1… … Википедия

Правильный семнадцатиугольник — геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Содержание … Википедия

Правильный восьмиугольник — (октагон) геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов и все углы и стороны равны между собой … Википедия

Правильный 65537-угольник — 65537 угольник или окружность? Правильный 65537 угольник (шестѝдесятипятиты̀сячпятисо̀ттридцатисемиугольник) геометрическая фигура из группы правильных многоугольников, состоящая из 65537 … Википедия

Построение правильных многоугольников / Длина окружности и площадь круга / Справочник по геометрии 7-9 класс

Задача 1

Построить правильный шестиугольник, сторона которого равна данному отрезку.

Дано: отрезок DC.

Построить: правильный шестиугольник, сторона которого равна DC.

Решение:

Для решения задачи воспользуемся тем, что сторона шестиугольника равна радиусу описанной около него окружности, т.е. (смотри формулу для вычисления стороны правильного многоугольника), где — радиус окружности описанной около правильного многоугольника. Нам нужно построить правильный шестиугольник со стороной DC, поэтому с помощью циркуля измеряем отрезок DC и строим окружность радиуса DC, и отмечаем на ней произвольную точку А₁, центр окружности обозначаем буквой О.

Затем не меняя раствора циркуля, построим на этой окружности точки А₂, А₃, А₄, А₅, А₆, так, чтобы выполнялись равенства

А₁А₂ = А₂А₃ = А₃А₄ = А₄А₅ = А₅А₆ = DC (т.е. сначала строим окружность радиуса DC с центром в точке А₁(всю окружность строить необязательно, смотри выделенное красным), данная окружность пересечет окружность с центром О в точке А₂, далее аналогично строим окружность радиуса DC с центром в точке А₂, она пересечет окружность с центром О в точке А₃ и т.д.).

Теперь соединяя последовательно построенные точки отрезками, получим искомый правильный шестиугольник А₁А₂А₃А₄А₅А₆.

Задача 2

Дан правильный -угольник. Построить правильный 2-угольник.

Дано: правильный -угольник А₁А₂А₃…А_n.

Построить: правильный 2-угольник.

Решение:

Пусть, например, нам дан шестиугольник А₁А₂А₃А₄А₅А₆, значит, построить нужно двенадцатиугольник.

Сначала опишем около данного шестиугольника А₁А₂А₃А₄А₅А₆ окружность. Для этого построим биссектрисы углов А₁и А₂. Чтобы построить биссектрису угла А₁, строим окружность произвольного радиуса с центром в точке А₁ (полностью окружность строить необязательно, смотри выделенное красным цветом), данная окружность пересечет стороны А₁А₂ и А₁А₆ угла А₁ в точках Е и К. Затем строим две окружности с центрами в точках Е и К радиуса ЕК (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом), данные окружности пересекутся в точке Р. Далее проводим луч А₁Р, который и будет биссектрисой угла А₁.

Аналогично строим биссектрису угла А₂.

Точку пересечения биссектрис углов А₁и А₂ обозначаем буквой О и строим окружность радиуса ОА₁ с центром О (окружность описанная около А₁А₂А₃А₄А₅А₆).

Далее нужно каждую из дуг А₁А₂, А₂А₃, А₃А₄, А₄А₅, А₅А₆, А₆А₁ разделить пополам. Чтобы разделить дугу А₁А₂пополам, построим серединный перпендикуляр к отрезку А₁А₂. Для этого строим две окружности с центрами в точках А₁и А₂ радиуса А₁А₂ (полностью окружность строить необязательно, смотри выделенное красным цветом). Данные окружности пересекутся в двух точках, одну обозначим буквой М, а другая совпадет с точкой О, т.к. у шестиугольника сторона равна радиусу (с другими многоугольниками совпадения с точкой О не будет) . Затем проводим прямую МО, данная прямая пересечет дугу А₁А₂ в точке В₁, которая и разделит дугу А₁А₂пополам. Далее точку В₁ соединяем с концами А₁и А₂ дуги А₁А₂.

Аналогично находим точки В₂, В₃. Точки В₄, В₅, В₆ в данном случае строить необязательно, они получаются автоматически при построении точек В₁, В₂, В₃, т.к. шестиугольник симметричная фигура.

Получили двенадцатиугольник А₁В₁А₂В₂А₃В₃А₄В₄А₅В₅А₆В₆ (смотри выделенное красным).

Мы выполняли построения на примере правильного шестиугольника, если мы имеем произвольный правильный -угольник, то все построения выполняются аналогично.

Применяя указанный способ, можно с помощью циркуля и линейки построить целый ряд правильных многоугольников, если построен один из них. Например, построив правильный треугольник и пользуясь результатом задачи 2, можно построить правильный шестиугольник, затем правильный двенадцатиугольник и вообще 2^k-угольник, где — любое целое число, больше двух.

Замечание

Не все правильные многоугольники можно построить с помощью циркуля и линейки. Доказано, например, что правильный семиугольник не может быть построен при помощи циркуля и линейки.

Правильный шестиугольник углы равны — Морской флот

Самая известная фигура, у которой больше четырех углов – это правильный шестиугольник. В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.

Чем он отличается от неправильного?

Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.

В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.

В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.

Какие свойства требуется знать при решении задач?

К тому, что указано выше, следует добавить:

диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.

Введенные обозначения

Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.

В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника). Для них используются буквы: α, р, m.

Формулы, которые описывают фигуру

Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.

Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R. Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.

Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a 2 * 3 √3) / 2.

Задачи

№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.

Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы. А она равна стороне правильного шестиугольника. То есть высота цилиндра – тоже 4 см.

Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r 2 = 3,14 * (2√3 ) 2 = 37,68 (см 2 ).

Осталось сосчитать объем: V = 37, 68 * 4 = 150,72 (см 3 ).

Ответ. V = 150,72 см 3 .

№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?

Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.

Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.

Ответ. r = 1,5 см, Р = 6√3 см.

№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?

Решение. Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.

Правильным шестиугольником называется шестиугольник, у которого все стороны и углы равны. Правильный шестиугольник обладает следующими свойствами.

– Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.

– Большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам.

– Меньшая диагональ правильного шестиугольника в раз больше его стороны.

– Угол между сторонами правильного шестиугольника равен 120°.

– Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.

– Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.

Главная ≫ Инфотека ≫ Математика ≫ Правильный шестиугольник

Комментарии: 0

Правильный шестиугольник (гексагон) — это правильный многоугольник с шестью сторонами.

Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности , поскольку

Все углы равны 120°.

Радиус вписанной окружности равен:

Периметр правильного шестиугольника равен:

Площадь правильного шестиугольника рассчитывается по формулам:

Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет.

Шестиугольный паркет (шестиугольный паркетаж) — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.

Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж. Символ Шлефли шестиугольного паркета — <6,3>, что означает, что в каждой вершине паркета сходятся три шестиугольника.

Шестиугольный паркет является наиболее плотной упаковкой кругов на плоскости. В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки равна . В 1940 году было доказано, что данная упаковка является самой плотной.

Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной (лемма Пала).

Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.

Пчелиные соты показывают разбиение плоскости на правильные шестиугольники. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.

Некоторые сложные кристаллы и молекулы , например графит, имеют гексагональную кристаллическую решётку.

Снежинки образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.

Гигантский гексагон — атмосферное явление на Сатурне.

Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.

Дорога гигантов — памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана. Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса.

Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов.circ>) .

Правильный шестиугольник — это такой шестиугольник у которого все шесть сторон равны и его шесть углов равны.

Центр правильного шестиугольника — на рисунке точка O равноудалена от вершин.

Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.

Отрезки OA , OB — радиусы правильного шестиугольника.

Обозначения на рисунке для правильного шестиугольника

n=6	число сторон и вершин правильного шестиугольника,	шт
α	центральный угол правильного шестиугольника,	радианы, °
β	половина внутреннего угла правильного шестиугольника,	радианы, °
γ	внутренний угол правильного шестиугольника,	радианы, °
a	сторона правильного шестиугольника,	м
R	радиусы правильного шестиугольника,	м
p	полупериметр правильного шестиугольника,	м
L	периметр правильного шестиугольника,	м
h	апофемы правильного шестиугольника,	м

Основные формулы для правильного шестиугольника

Периметр правильного шестиугольника

Полупериметр правильного шестиугольника

Центральный угол правильного шестиугольника в радианах

Центральный угол правильного шестиугольника в градусах

Половина внутреннего угла правильного шестиугольника в радианах

Половина внутреннего угла правильного шестиугольника в градусах

Внутренний угол правильного шестиугольника в радианах

Внутренний угол правильного шестиугольника в градусах

Площадь правильного шестиугольника

Отсюда получим апофему правильного шестиугольника

Как сделать ровный 6 угольник. Правильный шестиугольник построение

Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.

Построение правильного пятиугольника по данной его стороне.

Построение вписанного в окружность правильного семиугольника.

Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

Рисунок 38

Рисунок 39

Рисунок 40

Геометрические узоры весьма популярны в последнее время. В сегодняшнем уроке мы научимся создавать один из таких узоров. Используя переход, оформление и модные цвета мы создадим паттерн, который вы сможете использовать в веб и полиграфическом дизайне.

Результат

Шаг 2
Нарисуйте еще один шестиугольник, на этот раз меньше — выберите радиус в 20pt .

2. Переход между шестиугольниками

Шаг 1
Выделите оба шестиугольника и выровняйте их по центру (вертикально и горизонтально). Используя инструмент Blend/Переход (W) , выделите оба шестиугольника и укажите им переход в 6 шагов (Steps) . Чтобы было лучше видно, измените перед переходом цвет фигур.

3. Делим на секции

Шаг 1
Инструментом Line Segment/Отрезок линии (\) нарисуйте линию, пересекающую шестиугольники по центру от самого левого угла к самому правому. Нарисуйте еще две линии, пересекающие шестиугольники по центру от противоположных углов.

4. Закрашиваем секции

Шаг 1
Перед тем как начать закрашивать секции, давайте определимся с палитрой. Вот какова палитра из примера:

Синий: C 65 M 23 Y 35 K 0
Бежевый: C 13 M 13 Y 30 K 0
Персиковый: C 0 M 32 Y 54 K 0
Светло-розовый: C 0 M 64 Y 42 K 0
Темно-розовый: C 30 M 79 Y 36 K 4

В примере сразу использовался режим CMYK, чтобы можно было распечатать узор без изменений.

5. Последние штрихи и узор

Шаг 1
Сгруппируйте (Control-G) все секции и шестиугольники, после того как закончите с их окраской. Копируйте (Control-C) и Вставьте (Control-V) группу из шестиугольников. Назовем оригинальную группу Hexagon A, а ее копию Hexagon B . Выровняйте группы.

Шаг 2
Примените Linear Gradient/Линейный градиент к группе Hexagon B. В палитре Gradient/Градиент укажите заливку от фиолетового (C60 M86 Y45 K42 ) к кремовому цвету (C0 M13 Y57 K0 ).

Сетки из шестиугольников (гексагональные сетки) используются в некоторых играх, но они не так просты и распространены, как сетки прямоугольников. Я коллекционирую ресурсы о сетках шестиугольников уже почти 20 лет, и написал это руководство по самым элегантным подходам, реализуемым в простейшем коде. В статье часто используются руководства Чарльза Фу (Charles Fu) и Кларка Вербрюгге (Clark Verbrugge). Я опишу различные способы создания сеток шестиугольников, их взаимосвязь, а также самые общие алгоритмы. Многие части этой статьи интерактивны: выбор типа сетки изменяет соответствующие схемы, код и тексты. (Прим. пер.: это относится только к оригиналу, советую его изучить. В переводе вся информация оригинала сохранена, но без интерактивности.) .

Примеры кода в статье написаны псевдокодом, так их легче читать и понимать, чтобы написать свою реализацию.

Геометрия

Шестиугольники — это шестигранные многоугольники. У правильных шестиугольников все стороны (грани) имеют одинаковую длину. Мы будем работать только с правильными шестиугольниками. Обычно в сетках шестиугольников используются горизонтальная (с острым верхом) и вертикальная (с плоским верхом) ориентации.

Шестиугольники с плоским (слева) и острым (справа) верхом

У шестиугольников по 6 граней. Каждая грань общая для двух шестиугольников. У шестиугольников по 6 угловых точек. Каждая угловая точка общая для трёх шестиугольников. Подробнее о центрах, гранях и угловых точках можно прочитать в моей статье о частях сеток (квадратах, шестиугольниках и треугольниках).

Углы

В правильном шестиугольнике внутренние углы равны 120°. Есть шесть «клиньев», каждый из которых является равносторонним треугольником с внутренними углами 60°. Угловая точка i находится на расстоянии (60° * i) + 30° , на size единиц от центра center . В коде:

Function hex_corner(center, size, i): var angle_deg = 60 * i + 30 var angle_rad = PI / 180 * angle_deg return Point(center.x + size * cos(angle_rad), center.y + size * sin(angle_rad))
Для заполнения шестиугольника нужно получить вершины многоугольника с hex_corner(…, 0) по hex_corner(…, 5) . Для отрисовки контура шестиугольника нужно использовать эти вершины, а затем нарисовать линию снова в hex_corner(…, 0) .

Разница между двумя ориентациями в том, что x и y меняются местами, что приводит к изменению углов: углы шестиугольников с плоским верхом равны 0°, 60°, 120°, 180°, 240°, 300°, а с острым верхом — 30°, 90°, 150°, 210°, 270°, 330°.

Углы шестиугольников с плоским и острым верхом

Размер и расположение

Теперь мы хотим расположить несколько шестиугольников вместе. В горизонтальной ориентации высота шестиугольника height = size * 2 . Вертикальное расстояние между соседними шестиугольниками vert = height * 3/4 .

Ширина шестиугольника width = sqrt(3)/2 * height . Горизонтальное расстояние между соседними шестиугольниками horiz = width .

В некоторых играх для шестиугольников используется пиксель-арт, который не точно соответствует правильным шестиугольникам. Формулы углов и расположений, описанные в этом разделе, не будут совпадать с размерами таких шестиугольников. Остальная часть статьи, описывающая алгоритмы сеток шестиугольников, применима даже если шестиугольники немного растянуты или сжаты.

Системы координат

Давайте приступим к сборке шестиугольников в сетку. В случае сеток квадратов существует только один очевидный способ сборки. Для шестиугольников же есть множество подходов. Я рекомендую использовать в качестве первичного представления кубические координаты. Осевые координаты или координаты смещений следует использовать для хранения карт и отображения координат для пользователя.

Координаты смещений

Наиболее частый подход — смещение каждого последующего столбца или строки. Столбцы обозначаются col или q . Строки обозначаются row или r . Можно смещать нечётные или чётные столбцы/строки, поэтому у горизонтальных и вертикальных шестиугольников есть по два варианта.

Горизонтальное расположение «нечет-r»

Горизонтальное расположение «чёт-r»

Вертикальное расположение «нечет-q»

Вертикальное расположение «чёт-q»

Кубические координаты

Ещё один способ рассмотрения сеток шестиугольников — видеть в них три основные оси, а не две , как в сетках квадратов. В них проявляется элегантная симметрия.

Возьмём сетку кубов и вырежем диагональную плоскость в x + y + z = 0 . Это странная мысль, но она поможет нам упростить алгоритмы сеток шестиугольников. В частности, мы сможем воспользоваться стандартными операциями из декартовых координат: суммированием и вычитанием координат, умножением и делением на скалярную величину, а также расстояниями.

Заметьте три основные оси на сетке кубов и их соотношение с шестью диагональными направлениями сетки шестиугольников. Диагональные оси сетки соответствуют основному направлению сетки шестиугольников.

Шестиугольники

Кубы

Поскольку у нас уже есть алгоритмы для сеток квадратов и кубов, использование кубических координат позволяет нам адаптировать эти алгоритмы под сетки шестиугольников. я буду использовать эту систему для большинства алгоритмов статьи. Для использования алгоритмов с другой системой координат я преобразую кубические координаты, выполню алгоритм, а затем преобразую их обратно.

Изучите, как кубические координаты работают для сетки шестиугольников. При выборе шестиугольников выделяются кубические координаты, соответствующие трём осям.

Каждое направление сетки кубов соответствует линии на сетке шестиугольников. Попробуйте выделить шестиугольник с z , равным 0, 1, 2, 3, чтобы увидеть связь. Строка отмечена синим. Попробуйте то же самое для x (зелёный) и y (сиреневый).
Каждое направление сетки шестиугольника — это сочетание двух направлений сетки кубов. Например, «север» сетки шестиугольников лежит между +y и -z , поэтому каждый шаг на «север» увеличивает y на 1 и уменьшает z на 1.

Кубические координаты — разумный выбор для системы координат сетки шестиугольников. Условием является x + y + z = 0 , поэтому в алгоритмах оно должно сохраняться. Условие также гарантирует, что для каждого шестиугольника всегда будет каноническая координата.

Существует множество различных систем координат для кубов и шестиугольников. В некоторых из них условие отличается от x + y + z = 0 . Я показал только одну из множества систем. Можно также создать кубические координаты с x-y , y-z , z-x , у которых будет свой набор интересных свойств, но я не буду их здесь рассматривать.

Но вы можете возразить, что не хотите хранить 3 числа для координат, потому что не знаете, как хранить карту в таком виде.

Осевые координаты

Осевая система координат, иногда называемая «трапецеидальной», строится на основе двух или трёх координат из кубической системы координат. Поскольку у нас есть условие x + y + z = 0 , третья координата не нужна. Осевые координаты полезны для хранения карт и отображения координат пользователю. Как и в случае с кубическими координатами, с ними можно использовать стандартные операции суммирования, вычитания, умножения и деления декартовых координат.

Существует множество кубических систем координат и множество осевых. В этом руководстве я не буду рассматривать все сочетания. Я выберу две переменные, q (столбец) и r (строка). В схемах этой статьи q соответствует x , а r соответствует z , но такое соответствие произвольно, потому что можно вращать и поворачивать схемы, получая различные соответствия.

Преимущество этой системы перед сетками смещений в большей понятности алгоритмов. Недостатком системы является то, что хранение прямоугольной карты выполняется немного странно; см. раздел о сохранении карт. Некоторые алгоритмы ещё понятнее в кубических координатах, но поскольку у нас есть условие x + y + z = 0 , мы можем вычислить третью подразумеваемую координату и использовать её в этих алгоритмах. В своих проектах я называю оси q , r , s , поэтому условие выглядит как q + r + s = 0 , и я, когда нужно, могу вычислить s = -q — r .

Оси

Координаты смещения — это первое, о чём думает большинство людей, потому что они совпадают со стандартными декартовыми координатами, используемыми для сеток квадратов. К сожалению, одна из двух осей должна проходить «против шерсти», и это в результате всё усложняет. Кубическая и осевая система идут «по шерсти» и у них более простые алгоритмы, но хранение карт немного более сложное. Существует ещё одна система, называемая «чередуемой» или «двойной», но здесь мы не будем её рассматривать; некоторые считают, что с ней проще работать, чем с кубической или осевой.

Координаты смещения, кубические и осевые

Ось — это направление, в котором соответствующая координата увеличивается. Перпендикуляр к оси — это линия, на которой координата остаётся постоянной. На схемах сеток выше показаны линии перпендикуляров.

Преобразование координат

Вероятно, что вы будете использовать в своём проекте осевые координаты или координаты смещения, но многие алгоритмы проще выражаются в кубических координатах. Поэтому нам нужно уметь преобразовывать координаты между системами.

Осевые координаты близко связаны с кубическими, поэтому преобразование делается просто:

# преобразование кубических в осевые координаты q = x r = z # преобразование осевых в кубические координаты x = q z = r y = -x-z
В коде эти две функции могут быть записаны следующим образом:

Function cube_to_hex(h): # осевая var q = h.x var r = h.z return Hex(q, r) function hex_to_cube(h): # кубическая var x = h.q var z = h.r var y = -x-z return Cube(x, y, z)
Координаты смещения совсем немного сложнее:

Соседние шестиугольники

Дан один шестиугольник, с какими шестью шестиугольниками он находится рядом? Как и можно ожидать, легче всего дать ответ в кубических координатах, довольно просто в осевых координатах, и немного сложнее в координатах смещения. Также может потребоваться рассчитать шесть «диагональных» шестиугольников.

Кубические координаты

Перемещение на одно пространство в координатах шестиугольников приводит к изменению одной из трёх кубических координат на +1 и другой на -1 (сумма должна оставаться равной 0). На +1 могут изменяться три возможных координаты, а на -1 — оставшиеся две. Это даёт нам шесть возможных изменений. Каждое соответствует одному из направлений шестиугольника. Простейший и быстрейший способ — предварительно вычислить изменения и поместить их в таблицу кубических координат Cube(dx, dy, dz) во время компиляции:

Var directions = [ Cube(+1, -1, 0), Cube(+1, 0, -1), Cube(0, +1, -1), Cube(-1, +1, 0), Cube(-1, 0, +1), Cube(0, -1, +1) ] function cube_direction(direction): return directions function cube_neighbor(hex, direction): return cube_add(hex, cube_direction(direction))

Осевые координаты

Как и раньше, мы используем для начала кубическую систему. Возьмём таблицу Cube(dx, dy, dz) и преобразуем в таблицу Hex(dq, dr) :

Var directions = [ Hex(+1, 0), Hex(+1, -1), Hex(0, -1), Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ] function hex_direction(direction): return directions function hex_neighbor(hex, direction): var dir = hex_direction(direction) return Hex(hex.q + dir.q, hex.r + dir.r)

Координаты смещения

В осевых координатах мы вносим изменения в зависимости от того, в каком месте сетки находимся. Если мы в столбце/строке смещения, то правило отличается от случая столбца/строки без смещения.

Как и раньше, мы создаём таблицу чисел, которые нужно прибавить к col and row . Однако на этот раз у нас будет два массива, один для нечётных столбцов/строк, а другой — для чётных. Посмотрите на (1,1) на рисунке карты сетки выше и заметьте, как меняются col и row меняются при перемещении в каждом из шести направлений. Теперь повторим процесс для (2,2) . Таблицы и код будут разными для каждого из четырёх типов сеток смещений, приводим соответствующий код для каждого типа сетки.

Нечет-r
var directions = [ [ Hex(+1, 0), Hex(0, -1), Hex(-1, -1), Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ], [ Hex(+1, 0), Hex(+1, -1), Hex(0, -1), Hex(-1, 0), Hex(0, +1), Hex(+1, +1) ] ] function offset_neighbor(hex, direction): var parity = hex.row & 1 var dir = directions return Hex(hex.col + dir.col, hex.row + dir.row)

Чёт-r
var directions = [ [ Hex(+1, 0), Hex(+1, -1), Hex(0, -1), Hex(-1, 0), Hex(0, +1), Hex(+1, +1) ], [ Hex(+1, 0), Hex(0, -1), Hex(-1, -1), Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ] ] function offset_neighbor(hex, direction): var parity = hex.row & 1 var dir = directions return Hex(hex.col + dir.col, hex.row + dir.row)

Сетка для чётной (EVEN) и нечётной (ODD) строк

Нечет-q
var directions = [ [ Hex(+1, 0), Hex(+1, -1), Hex(0, -1), Hex(-1, -1), Hex(-1, 0), Hex(0, +1) ], [ Hex(+1, +1), Hex(+1, 0), Hex(0, -1), Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ] ] function offset_neighbor(hex, direction): var parity = hex.col & 1 var dir = directions return Hex(hex.col + dir.col, hex.row + dir.row)

Чёт-q
var directions = [ [ Hex(+1, +1), Hex(+1, 0), Hex(0, -1), Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ], [ Hex(+1, 0), Hex(+1, -1), Hex(0, -1), Hex(-1, -1), Hex(-1, 0), Hex(0, +1) ] ] function offset_neighbor(hex, direction): var parity = hex.col & 1 var dir = directions return Hex(hex.col + dir.col, hex.row + dir.row)

Сетка для чётного (EVEN) и нечётного (ODD) столбцов

Диагонали

Перемещение в «диагональном» пространстве в координатах шестиугольников изменяет одну из трёх кубических координат на ±2 и две другие на ∓1 (сумма должна оставаться равной 0).
Var diagonals = [ Cube(+2, -1, -1), Cube(+1, +1, -2), Cube(-1, +2, -1), Cube(-2, +1, +1), Cube(-1, -1, +2), Cube(+1, -2, +1) ] function cube_diagonal_neighbor(hex, direction): return cube_add(hex, diagonals)
Как и раньше, мы можем преобразовать эти координаты в осевые, откинув одну из трёх координат, или преобразовать в координаты смещения, предварительно вычислив результаты.

Расстояния
Кубические координаты
В кубической системе координат каждый шестиугольник является кубом в трёхмерном пространстве. Соседние шестиугольники находятся в сетке шестиугольников на расстоянии 1 друг от друга, но на расстоянии 2 в сетке кубов. Это делает расчёт расстояний простым. В сетке квадратов манхэттенские расстояния равны abs(dx) + abs(dy) . В сетке кубов манхэттенские расстояния равны abs(dx) + abs(dy) + abs(dz) . Расстояние в сетке шестиугольников равно их половине:
Function cube_distance(a, b): return (abs(a.x — b.x) + abs(a.y — b.y) + abs(a.z — b.z)) / 2
Эквивалентом этой записи будет выражение того, что одна из трёх координат должна быть суммой двух других, а затем получение её в качестве расстояния. Можно выбрать форму деления пополам или форму максимального значения, приведённую ниже, но они дают одинаковый результат:
Function cube_distance(a, b): return max(abs(a.x — b.x), abs(a.y — b.y), abs(a.z — b.z))
На рисунке максимальные значения выделены цветом. Заметьте также, что каждый цвет обозначает одно из шести «диагональных» направлений.
GIF

Осевые координаты
В осевой системе третья координата выражена неявно. Давайте преобразуем из осевой в кубическую систему для расчёта расстояния:
Function hex_distance(a, b): var ac = hex_to_cube(a) var bc = hex_to_cube(b) return cube_distance(ac, bc)
Если компилятор в вашем случае встраивает (inline) hex_to_cube и cube_distance , то он сгенерирует такой код:
Function hex_distance(a, b): return (abs(a.q — b.q) + abs(a.q + a.r — b.q — b.r) + abs(a.r — b.r)) / 2
Существует множество различных способов записи расстояний между шестиугольниками в осевых координатах, но вне зависимости от способа записи расстояние между шестиугольниками в осевой системе извлекается из манхэттенского расстояния в кубической системе . Например, описанная «разность разностей» получается из записи a.q + a.r — b.q — b.r как a.q — b.q + a.r — b.r и с использованием формы максимального значения вместо формы деления пополам cube_distance . Все они аналогичны, если увидеть связь с кубическими координатами.
Координаты смещения
Как и в случае с осевыми координатами, мы преобразуем координаты смещения в кубические координаты, а затем используем расстояние кубической системы.
Function offset_distance(a, b): var ac = offset_to_cube(a) var bc = offset_to_cube(b) return cube_distance(ac, bc)
Мы будем использовать тот же шаблон для многих алгоритмов: преобразуем из шестиугольников в кубы, выполняем кубическую версию алгоритма и преобразуем кубические результаты в координаты шестиугольников (осевые или координаты смещения).
Отрисовка линий
Как нарисовать линию от одного шестиугольника до другого? Я использую линейную интерполяцию для рисования линий . Линия равномерно сэмплируется в N+1 точках и вычисляется, в каких шестиугольниках находятся эти сэмплы.
GIF

Сначала мы вычисляем N , которое будет расстоянием в шестиугольниках между конечными точками.
Затем равномерно сэмплируем N+1 точек между точками A и B. С помощью линейной интерполяции определяем, что для значений i от 0 до N , включая их, каждая точка будет A + (B — A) * 1.0/N * i . На рисунке эти контрольные точки показаны синим. В результате получаются координаты с плавающей запятой.
Преобразуем каждую контрольную точку (float) обратно в шестиугольники (int). Алгоритм называется cube_round (см. ниже).
Соединяем всё вместе для отрисовки линии от A до B:
Function lerp(a, b, t): // для float return a + (b — a) * t function cube_lerp(a, b, t): // для шестиугольников return Cube(lerp(a.x, b.x, t), lerp(a.y, b.y, t), lerp(a.z, b.z, t)) function cube_linedraw(a, b): var N = cube_distance(a, b) var results = for each 0 ≤ i ≤ N: results.append(cube_round(cube_lerp(a, b, 1.0/N * i))) return results
Примечания:
Бывают случаи, когда cube_lerp возвращает точку, находящуюся точно на грани между двумя шестиугольниками. Затем cube_round сдвигает её в ту или иную сторону. Линии выглядят лучше, если их сдвигают в одном направлении. Это можно сделать, добавив «эпсилон»-шестиугольный Cube(1e-6, 1e-6, -2e-6) к одной или обеим конечным точкам перед началом цикла. Это «подтолкнёт» линию в одном направлении, чтобы она не попадала на границы граней.
Алгоритм DDA-линии в сетках квадратов приравнивает N к максимуму расстояния по каждой из осей. Мы делаем то же самое в кубическом пространстве, что аналогично расстоянию в сетке шестиугольников.
Функция cube_lerp должна возвращать куб с координатами в float. Если вы программируете на языке со статической типизацией, то не сможете использовать тип Cube . Вместо него можно определить тип FloatCube или встроить (inline) функцию в код отрисовки линий, если вы не хотите определять ещё один тип.
Можно оптимизировать код, встроив (inline) cube_lerp , а затем рассчитав B.x-A.x , B.x-A.y и 1.0/N за пределами цикла. Умножение можно преобразовать в повторяющееся суммирование. В результате получится что-то вроде алгоритма DDA-линии.
Для отрисовки линий я использую осевые или кубические координаты, но если вы хотите работать с координатами смещения, то изучите .
Существует много вариантов отрисовки линий. Иногда требуется «сверхпокрытие» . Мне прислали код отрисовки линий с сверхпокрытием в шестиугольниках, но я пока не изучал его.
Диапазон перемещения
Диапазон координат
Для заданного центра шестиугольника и диапазона N какие шестиугольники находятся в пределах N шагов от него?
Мы можем произвести обратную работу из формулы расстояния между шестиугольниками distance = max(abs(dx), abs(dy), abs(dz)) . Чтобы найти все шестиугольники в пределах N , нам нужны max(abs(dx), abs(dy), abs(dz)) ≤ N . Это значит, что нужны все три значения: abs(dx) ≤ N и abs(dy) ≤ N и abs(dz) ≤ N . Убрав абсолютное значение, мы получим -N ≤ dx ≤ N и -N ≤ dy ≤ N и -N ≤ dz ≤ N . В коде это будет вложенный цикл:
Var results = for each -N ≤ dx ≤ N: for each -N ≤ dy ≤ N: for each -N ≤ dz ≤ N: if dx + dy + dz = 0: results.append(cube_add(center, Cube(dx, dy, dz)))
Этот цикл сработает, но будет довольно неэффективным. Из всех значений dz , которые мы перебираем в цикле, только одно действительно удовлетворяет условию кубов dx + dy + dz = 0 . Вместо этого мы напрямую вычислим значение dz , удовлетворяющее условию:
Var results = for each -N ≤ dx ≤ N: for each max(-N, -dx-N) ≤ dy ≤ min(N, -dx+N): var dz = -dx-dy results.append(cube_add(center, Cube(dx, dy, dz)))
Этот цикл проходит только по нужным координатам. На рисунке каждый диапазон является парой линий. Каждая линия — это неравенство. Мы берём все шестиугольники, удовлетворяющие шести неравенствам.
GIF

Пересекающиеся диапазоны
Если нужно найти шестиугольники, находящиеся в нескольких диапазонах, то перед генерированием списка шестиугольников можно пересечь диапазоны.
Можно подойти к этой проблеме с точки зрения алгебры или геометрии. Алгебраически каждая область выражается как условия неравенств в форме -N ≤ dx ≤ N , и нам нужно найти пересечение этих условий. Геометрически каждая область является кубом в трёхмерном пространстве, и мы пересечём два куба в трёхмерном пространстве для получения прямоугольного параллелепипеда в трёхмерном пространстве. Затем мы проецируем его обратно на плоскость x + y + z = 0 , чтобы получить шестиугольники. Я буду решать эту задачу алгебраически.
Во-первых, мы перепишем условие -N ≤ dx ≤ N в более общей форме x min ≤ x ≤ x max , и примем x min = center.x — N и x max = center.x + N . Сделаем то же самое для y и z , в результате получив общий вид кода из предыдущего раздела:
Var results = for each xmin ≤ x ≤ xmax: for each max(ymin, -x-zmax) ≤ y ≤ min(ymax, -x-zmin): var z = -x-y results.append(Cube(x, y, z))
Пересечением двух диапазонов a ≤ x ≤ b и c ≤ x ≤ d является max(a, c) ≤ x ≤ min(b, d) . Поскольку область шестиугольников выражена как диапазоны над x , y , z , мы можем отдельно пересечь каждый из диапазонов x , y , z , а затем использовать вложенный цикл для генерирования списка шестиугольников в пересечении. Для одной области шестиугольников мы принимаем x min = H.x — N and x max = H.x + N , аналогично для y и z . Для пересечения двух областей шестиугольников мы принимаем x min = max(h2.x — N, h3.x — N) и x max = min(h2.x + N, h3.x + N), аналогично для y и z . Тот же шаблон работает для пересечения трёх или более областей.
GIF

Препятствия
При наличии препятствий проще всего выполнить заливку с ограничением по расстоянию (поиск в ширину). На рисунке ниже мы ограничиваемся четырьмя ходами. В коде fringes[k] — это массив всех шестиугольников, которых можно достичь за k шагов. При каждом проходе по основному циклу мы расширяем уровень k-1 на уровень k .
Function cube_reachable(start, movement): var visited = set() add start to visited var fringes = fringes.append() for each 1
Повороты
Для заданного вектора шестиугольника (разницу между двумя шестиугольниками) нам может понадобиться повернуть его, чтобы он указывал на другой шестиугольник. Это просто сделать, имея кубические координаты, если придерживаться поворота на 1/6 окружности.
Поворот на 60° вправо сдвигает каждую координату на одну позицию вправо:
[ x, y, z] to [-z, -x, -y]
Поворот на 60° влево сдвигает каждую координату на одну позицию влево:
[ x, y, z] to [-y, -z, -x]

«Поиграв» [в оригинале статьи] со схемой, можно заметить, что каждый поворот на 60° меняет знаки и физически «поворачивает» координаты. После поворота на 120° знаки снова становятся теми же. Поворот на 180° меняет знаки, но координаты поворачиваются в своё изначальное положение.
Вот полная последовательность поворота положения P вокруг центрального положения C, приводящего к новому положению R:
Преобразование положений P и C в кубические координаты.
Вычисление вектора вычитанием центра: P_from_C = P — C = Cube(P.x — C.x, P.y — C.y, P.z — C.z) .
Поворот вектора P_from_C как описано выше и присваивание итоговому вектору обозначения R_from_C .
Преобразование вектора обратно в положение прибавлением центра: R = R_from_C + C = Cube(R_from_C.x + C.x, R_from_C.y + C.y, R_from_C.z + C.z) .
Преобразование кубического положения R обратно в нужную систему координат.
Здесь несколько этапов преобразований, но каждый из них довольно прост. Можно сократить некоторые из этих этапов, определив поворот непосредственно в осевых координатах, но векторы шестиугольников не работают с координатами смещения, и я не знаю, как сократить этапы для координат смещения. См. также обсуждение других способов вычисления поворота на stackexchange.
Кольца
Простое кольцо
Чтобы выяснить, принадлежит ли заданный шестиугольник к кольцу заданного радиуса radius , нужно вычислить расстояние от этого шестиугольника до центра, и узнать, равно ли оно radius . Для получения списка всех таких шестиугольников нужно сделать radius шагов от центра, а затем следовать за поворачиваемыми векторами по пути вдоль кольца.
Function cube_ring(center, radius): var results = # этот код не работает для radius == 0; вы понимаете, почему? var cube = cube_add(center, cube_scale(cube_direction(4), radius)) for each 0 ≤ i В этом коде cube начинается на кольце, показанном большой стрелкой от центра к углу схемы. Я выбрал для начала угол 4, потому что он соответствует пути, в котором двигаются мои числа направлений. Вам может понадобиться другой начальный угол. На каждом этапе внутреннего цикла cube двигается на один шестиугольник по кольцу. Через 6 * radius шагов он завершает там, где начал.
Спиральные кольца
Проходя по кольцам по спиральному паттерну, мы можем заполнить внутренние части колец:
Function cube_spiral(center, radius): var results = for each 1 ≤ k ≤ radius: results = results + cube_ring(center, k) return results

Площадь большого шестиугольника равна сумме всех окружностей плюс 1 для центра. Для вычисления площади используйте эту формулу .
Обход шестиугольников таким способом можно также использовать для вычисления диапазона перемещения (см. выше).
Область видимости
Что видимо из заданного положения с заданным расстоянием, и не перекрывается препятствиями? Простейший способ определить это — нарисовать линию к каждому шестиугольнику в заданном диапазоне. Если линия не встречается со стенами, то вы видите шестиугольник. Перемещайте мышь по шестиугольникам [на схеме в оригинале статьи], чтобы увидеть отрисовку линий к этим шестиугольникам и стены, с которыми линии встречаются.
Этот алгоритм может быть медленным на больших площадях, но его легко реализовать, поэтому рекомендую начать с него.
GIF

Существует много разных определений видимости. Хотите ли вы видеть центр другого шестиугольника из центра начального? Хотите ли вы видеть любую часть другого шестиугольника из центра начального? Может быть, любую часть другого шестиугольника из любой точки начального? Мешающие взгляду препятствия меньше полного шестиугольника? Область видимости — это более хитрое и разнообразное понятие, чем кажется на первый взгляд. Начнём с простейшего алгоритма, но ждите, что он обязательно правильно вычислит ответ в вашем проекте. Бывают даже случаи, когда простой алгоритм даёт нелогичные результаты.
Я хочу в дальнейшем расширять это руководство. У меня есть
Геометрические построения являются одной из главных частей обучения. Они формируют пространственное и логическое мышление, а также разрешают понять примитивные и натуральные геометрические обоснованности. Построения производятся на плоскости при помощи циркуля и линейки. Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.
Вам понадобится
Циркуль, линейка, карандаш, лист бумаги.
Инструкция
1. Нарисуйте окружность. Установите некоторое расстояние между ножками циркуля. Это расстояние будет являться радиусом окружности. Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.
2. Постройте точки вершин углов верного шестиугольника. Установите ножку циркуля, в которой закреплена игла, в всякую точку окружности. Игла должна проткнуть начерченную линию. Чем вернее будет установлен циркуль, тем вернее будет построение. Проведите дугу окружности так, дабы она пересекла начерченную ранее окружность. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Начертите еще одну дугу, пересекающую окружность. Вновь переставьте иглу циркуля в точку пересечения дуги и окружности и вновь начертите дугу. Произведите данное действие еще три раза, перемещаясь в одном направлении по окружности. Каждого должно получиться шесть дуг и шесть точек пересечения.
3. Постройте положительный шестиугольник. Ступенчато объедините все шесть точек пересечения дуг с изначально начерченной окружностью. Соединяйте точки прямыми, вычерчиваемыми при помощи линейки и карандаша. Позже произведенных действий будет получен верный шестиугольник, вписанный в окружность.
Шестиугольником считается многоугольник, владеющий шестью углами и шестью сторонами. Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести. Это делается в пару шагов.
Вам понадобится
Карандаш, лист бумаги, линейка
Инструкция
1. Берется лист бумаги и на нем отмечается 6 точек приблизительно так, как это показано на рис. 1.
2. Позже того, как были подмечены точки, берется линейка, карандаш и с их подмогой ступенчато, друг за ином соединяются точки так, как это выглядит на рис. 2.
Видео по теме
Обратите внимание!
Сумма всех внутренних углов шестиугольника равна 720 градусам.
Шестиугольник – это многоугольник, тот, что владеет шестью углами. Для того, дабы начертить произвольный шестиугольник, надобно проделать каждого 2 действия.
Вам понадобится
Карандаш, линейка, лист бумаги.
Инструкция
1. Нужно взять в руку карандаш и разметить на листе 6 произвольных точек. В дальнейшем эти точки будут исполнять роль углов в шестиугольнике. (рис.1)
2. Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с ином по начерченным ранее точкам (рис.2)
Видео по теме
Обратите внимание!
Специальным типом шестиугольника является положительный шестиугольник. Он именуется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника дозволено описать либо вписать окружность. Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.
Полезный совет
В природе положительные шестиугольники владеют крупный популярностью. К примеру, вся пчелиная сота владеет положительной шестиугольной формой. Либо кристаллическая решетка графена (модификация углерода) тоже владеет формой положительного шестиугольника.
Как возвести тот либо другой угол – крупной вопрос. Но для некоторых углов задача невидимо упрощается. Одним из таких углов является угол в 30 градусов. Он равен?/6, то есть число 30 является делителем 180. Плюс к этому его синус вестим. Это и помогает при его построении.
Вам понадобится
транспортир, угольник, циркуль, линейка
Инструкция
1. Для начала разглядим особенно примитивную обстановку, когда у вас на руках есть транспортир. Тогда прямую под углом 30 градусов к данной дозволено легко отложить с поддержкой него.
2. Помимо транспортира существуют и угол ьники, один из углов которых равен 30 градусам. Тогда иной угол угол ьника будет равен 60 градусам, то есть вам необходим визуально меньший угол для построения требуемой прямой.
3. Перейдем сейчас к нетривиальным способам построения угла 30 градусов. Как вестимо, синус угла 30 градусов равен 1/2. Для его построения нам надобно возвести прямоугол ьный треугол ьник. Возможен, мы можем возвести две перпендикулярные прямые. Но тангенс 30 градусов – иррациональное число, следственно соотношение между катетами мы можем посчитать лишь примерно (исключительно, если нет калькулятора), а, значит, и возвести угол в 30 градусов примерно.
4. В этом случае дозволено сделать и точное построение. Возведем вновь две перпендикулярные прямые, на которых будут располагаться катеты прямоугол ьного треугол ьника. Отложим по одной прямой катет BC какой-нибудь длины с поддержкой циркуля (B – прямой угол ). После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Проводя окружность с центром в точке C с радиусом этой длины, обнаружим точку пересечения окружности с иной прямой. Эта точка и будет точкой A прямоугол ьного треугол ьника ABC, а угол A будет равен 30 градусам.
5. Возвести угол в 30 градусов дозволено и с поддержкой окружности, применяя то, что он равен?/6. Возведем окружность с радиусом OB. Разглядим в теории треугол ьник, где OA = OB = R – радиус окружности, где угол OAB = 30 градусов. Пускай OE – высота этого равнобедренного треугол ьника, а, следственно, и его биссектриса и медиана. Тогда угол AOE = 15 градусов, и, по формуле половинного угла, sin(15o) = (sqrt(3)-1)/(2*sqrt(2)).Следственно, AE = R*sin(15o). Отсель, AB = 2AE = 2R*sin(15o). Строя окружность радиусом BA с центром в точке B, обнаружим точку пересечения A этой окружности с начальной. Угол AOB будет равен 30 градусам.
6. Если мы можем определять длину дуг каким-нибудь образом, то, отложив дугу длиной?*R/6, мы также получим угол в 30 градусов.
Обратите внимание!
Нужно помнить, что в 5 пункте мы можем возвести угол лишь приближенно, потому что в вычислениях будут фигурировать иррациональные числа.
Шестиугольником называют частный случай полигона – фигуры, образованной большинством точек плоскости, ограниченным замкнутой полилинией. Положительный шестиугольник (гексагон), в свою очередь, также является частным случаем – это полигон с шестью равными сторонами и равными углами. Эта фигура знаменательна тем, что длина всей из ее сторон равна радиусу описанной вокруг фигуры окружности.
Вам понадобится
– циркуль;
– линейка;
– карандаш;
– лист бумаги.
Инструкция
1. Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на иной ножке, равным длине стороны вычерчиваемой фигуры. Для этого дозволено воспользоваться линейкой либо предпочесть случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая вероятность.
2. Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.
3. Разбейте окружность точками на шесть равных частей. Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.
4. Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна верно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, дабы она пересекла в 2-х точках окружность, начерченную первой.
5. Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с изначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в 2-х точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).
6. Сходственным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении по окружности (неизменно по либо вопреки часовой стрелки). В итоге обязаны быть выявлены шесть точек пересечения дуг с изначально построенной окружностью.
7. Нарисуйте положительный шестиугольник. Ступенчато попарно объедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В итоге будет получен верный шестиугольник. Позже осуществления построения дозволено стереть вспомогательные элементы (дуги и окружность).
Обратите внимание!
Имеет толк выбирать такое расстояние между ножками циркуля, дабы угол между ними был равен 15-30 градусов, напротив при осуществлении построений данное расстояние может легко сбиться.
При строительстве либо разработке домашних дизайн-планов зачастую требуется возвести угол , равный теснее имеющемуся. На поддержка приходят образцы и школьные умения геометрии.
Инструкция
1. Угол образуют две прямые, исходящие из одной точки. Эта точка будет именоваться вершиной угла, а линии будут являться сторонами угла.
2. Для обозначения углов используйте три буквы: одна у вершины, две у сторон. Называют угол , начиная с той буквы, которая стоит у одной стороны, дальше называют букву, стоящую у вершины, и после этого букву у иной стороны. Используйте и другие методы для обозначения углов, если вам комфортнее напротив. Изредка называют только одну букву, которая стоит у вершины. А дозволено обозначать углы греческими буквами, скажем, α, β, γ.
3. Встречаются обстановки, когда нужно начертить угол , дабы он был равен теснее данному углу. Если при построении чертежа применять транспортир вероятности нет, дозволено обойтись только линейкой и циркулем. Возможен, на прямой, обозначенной на чертеже буквами MN, надобно возвести угол у точки К, так, дабы он был равен углу В. То есть из точки K нужно провести прямую, образующую с линией MN угол , тот, что будет равен углу В.
4. В начале подметьте по точке на всей стороне данного угла, скажем, точки А и С, дальше объедините точки С и А прямой линией. Получите треугол ьник АВС.
5. Теперь постройте на прямой MN такой же треугол ьник, дабы его вершина В находилась на линии в точке К. Используйте правило построения треугол ьника по трем сторонам. Отложите от точки К отрезок KL. Он должен быть равен отрезку ВС. Получите точку L.
6. Из точки K вычертите окружность радиусом равным отрезку ВА. Из L вычертите окружность радиусом СА. Полученную точку (Р) пересечения 2-х окружностей объедините с К. Получите треугол ьник КPL, тот, что будет равен треугол ьнику ABC. Так вы получите угол К. Он и будет равен углу В. Дабы это построение сделать комфортнее и стремительней, от вершины В отложите равные отрезки, применяя один раствор циркуля, не сдвигая ножек, опишите этим же радиусом из точки К окружность.
Видео по теме
Обратите внимание!
Избегайте случайного метаморфозы расстояния между ножками циркуля. В этом случае шестиугольник может получиться неправильным.
Полезный совет
Имеет толк изготавливать построения при помощи циркуля с отлично заточенным грифелем. Так построения будут особенно точны.
%d0%bf%d1%80%d0%b0%d0%b2%d0%b8%d0%bb%d1%8c%d0%bd%d1%8b%d0%b9 %d1%88%d0%b5%d1%81%d1%82%d0%b8%d1%83%d0%b3%d0%be%d0%bb%d1%8c%d0%bd%d0%b8%d0%ba пнг образ | Векторы и PSD-файлы
Мемфис дизайн геометрические фигуры узоры мода 80 90 х годов
4167*4167
день независимости бангладеш
1500*1500
аудиокассета изолированные вектор старая музыка ретро плеер ретро музыка аудиокассета 80 х пустой микс
5000*5000
Элемент мазка кистью флаг Бангладеш
5000*5000
80 основных форм силуэта
5000*5000
80 е брызги краски дизайн текста
1200*1200
80 летний юбилей дизайн шаблона векторные иллюстрации
4083*4083
ba угол звезда голографическая радуга лазерная наклейка
1200*1200
Шаблон элементов инфографики 81
1200*1200
3d визуализация текста 80 процентов от большой продажи
1200*1200
число 80
2000*2000
3d Изометрические номера 76 80
1200*1200
Минимализм Супер Продажа до 80 ramadan label
2000*2000
al ba ith 99 ИМЯ АЛЛАХ
1200*1200
Диско вечеринка в стиле ретро 80 х art word design
1200*1200
green environmental protection pattern garbage can be recycled green clean
2000*2000
День независимости Бангладеш надписи с флагом Бангладеши
2500*2500
микс ленты ретро кассеты
1200*1200
но логотип компании вектор дизайн шаблона иллюстрация
4083*4083
Мать горилла очков векторные иллюстрации
5000*5000
ретро восьмидесятых бумбокс
1200*1200
Природа ретро наклейки векторные иллюстрации
5000*5000
облака комиксов
5042*5042
бумбокс с разноцветными музыкальными нотами
1200*1200
аудио кассета плоский дизайн
1200*1200
Бигфут бегущий ретро векторные иллюстрации
5000*5000
iftar party ramadhan kareem 82
1300*1300
3d счетное число 81 с прозрачным фоном и редактируемым
1200*1200
скачать букву т серебро 80 х
1200*1200
Скидка 80 процентов на 3d золото
3000*3000
любовь речи пузырь клипарт векторный элемент png
5000*5000
Номер 80 процентов от 3d золотой
5000*5000
iftar party ramadhan kareem 81
1300*1300
я выбираю быть геймером потому что в реальной жизни ничего эпического не происходит
1200*1200
значок кассеты мультяшном стиле
5000*5000
Ручная роспись борода ба zihu большая борода
1200*1200
голова льва ретро очки векторная иллюстрация король лев
5000*5000
витамины и минеральные сложных трехмерных знамя пищевой добавки и лекарства
1200*1200
схема бд электронный компонент технологии принципиальная схема технологическая линия
2000*2000
ретро аудио кассета вектор
5000*5000
Искусство selamat hari raya idul adha с абстрактными ka ba vectir иллюстрация
1200*1200
ретро стиль текста
1200*1200
скачать буквы алфавита в классическом стиле 80 х
1200*1200
Мемфис бесшовные модели 80 х 90 х стилей
4167*4167
Мемфис шаблон 80 х 90 х годов стилей фона векторные иллюстрации
4167*4167
губы жвачки
1200*1200
милая ретро девушка 80 х 90 х годов
800*800
естественный цвет bb крем цвета
1200*1200
рисованной радио 80 х
1200*1200
yeti играет на сноуборд векторные иллюстрации
5000*5000
Полигоны
Многоугольник — это замкнутая плоская фигура, образованная соединением трех или более прямые линии. Правильный многоугольник — это многоугольник с равными сторонами и равными внутренние углы.
Правильные многоугольники
Стороны
Имя Интерьер
Угол Внешний вид
Уголки
3
Треугольник
60.00 °
120,00 °
4
Четырехугольник
90,00 °
90,00 °
5
Пентагон
108,00 °
72,00 °
6
Шестиугольник
120.00 °
60,00 °
7
Гептагон
128,57 °
51,43 °
8
Восьмиугольник
135,00 °
45,00 °
9
Nonagon
140.00 °
40,00 °
10
Десятиугольник
144,00 °
36,00 °
11
Hendecagon
147,27 °
32,73 °
12
Додекагон
150.00 °
30,00 °
13
Triskaidecagon
152,31 °
27,69 °
14
Tetrakaidecagon
154,29 °
25,71 °
15
Pendecagon
156.00 °
24,00 °
16
Шестигранник
157,50 °
22,50 °
17
Heptdecagon
158,82 °
21,18 °
18
Восьмиугольник
160.00 °
20,00 °
19
Enneadecagon
161,05 °
18.95 °
20
Икосагон
162,00 °
18,00 °
30
Триаконтагон
168.00 °
12,00 °
40
Тетрактагон
171,00 °
9,00 °
50
Пентаконтагон
172,80 °
7.20 °
60
Шестигранник
174.00 °
6,00 °
70
Гептаконтагон
174,86 °
5,14 °
80
Octacontagon
175,50 °
4,50 °
90
Эннеаконтагон
176.00 °
4,00 °
100
Гектогон
176,40 °
3,60 °
1,000
Чилигон
179.64 °
0,36 °
10 000
Мириагон
179.96 °
0,04 °
Примечание: примерно через 6 сторон математики обычно ссылаются на эти многоугольники как
n-угольник, поэтому 23-сторонний многоугольник будет называться 23-угольником.
Сумма углов выпуклого многоугольника со сторонами n равна ( n — 2) 180.

% PDF-1.5 % 43 0 obj> эндобдж xref 43 212 0000000016 00000 н. 0000004974 00000 н. 0000004536 00000 н. 0000005036 00000 н. 0000005215 00000 н. 0000005569 00000 н. 0000005743 00000 н. 0000005912 00000 н. 0000005946 00000 н. 0000006164 00000 н. 0000006545 00000 н. 0000006758 00000 н. 0000007655 00000 н. 0000008757 00000 н. 0000009813 00000 н. 0000010839 00000 п. 0000011978 00000 п. 0000013099 00000 н. 0000014162 00000 п. 0000015281 00000 п. 0000016343 00000 п. 0000017141 00000 п. 0000054032 00000 п. 0000078448 00000 п. 0000078607 00000 п. 0000078916 00000 п. 0000085105 00000 п. 0000085317 00000 п. 0000085346 00000 п. 00000
00000 п. 00000
00000 п. 00000
00000 н. 00000
00000 п. 0000093246 00000 п. 0000093440 00000 п. 0000093461 00000 п. 0000093618 00000 п. 0000094669 00000 п. 0000094862 00000 п. 0000094883 00000 п. 0000095014 00000 п. 0000095132 00000 п. 0000095497 00000 п. 0000096563 00000 п. 0000096757 00000 п. 0000096778 00000 п. 0000096935 00000 п. 0000102097 00000 н. 0000102288 00000 н. 0000103185 00000 п. 0000103348 00000 п. 0000104521 00000 н. 0000104716 00000 н. 0000104741 00000 н. 0000104872 00000 н. 0000104990 00000 п. 0000105530 00000 н. 0000106752 00000 н. 0000106946 00000 н. 0000106968 00000 н. 0000107102 00000 п. 0000111518 00000 н. 0000111710 00000 н. 0000112552 00000 н. 0000112718 00000 н. 0000112825 00000 н. 0000113178 00000 н. 0000114244 00000 н. 0000114440 00000 н. 0000114462 00000 н. 0000114622 00000 н. 0000119746 00000 н. 0000119939 00000 н. 0000120805 00000 н. 0000120971 00000 н. 0000122092 00000 н. 0000122287 00000 н. 0000122313 00000 н. 0000122447 00000 н. 0000122569 00000 н. 0000123036 00000 н. 0000124167 00000 н. 0000124364 00000 н. 0000124386 00000 н. 0000124520 00000 н. 0000130201 00000 н. 0000130393 00000 п. 0000131291 00000 н. 0000131457 00000 н. 0000132579 00000 н. 0000132775 00000 н. 0000132797 00000 н. 0000132959 00000 н. 0000133081 00000 н. 0000133454 00000 н. 0000138913 00000 н. 0000139106 00000 н. 0000139948 00000 н. 0000140114 00000 п. 0000141392 00000 н. 0000141587 00000 н. 0000141613 00000 н. 0000141747 00000 н. 0000141854 00000 н. 0000142272 00000 н. 0000143338 00000 п. 0000143534 00000 н. 0000143556 00000 н. 0000143716 00000 н. 0000147390 00000 н. 0000147587 00000 н. 0000147609 00000 н. 0000147777 00000 н. 0000149241 00000 н. 0000149438 00000 н. 0000149472 00000 н. 0000149606 00000 н. 0000154907 00000 н. 0000155099 00000 н. 0000155457 00000 н. 0000155623 00000 н. 0000155760 00000 н. 0000156310 00000 н. 0000157362 00000 н. 0000157557 00000 н. 0000157579 00000 п. 0000157713 00000 н. 0000158779 00000 н. 0000158975 00000 н. 0000158997 00000 н. 0000159157 00000 н. 0000163776 00000 н. 0000163968 00000 н. 0000164810 00000 н. 0000164976 00000 н. 0000165098 00000 н. 0000165445 00000 н. 0000166733 00000 н. 0000166928 00000 н. 0000166954 00000 н. 0000167088 00000 н. 0000171885 00000 н. 0000172078 00000 н. 0000172436 00000 н. 0000172602 00000 н. 0000172709 00000 н. 0000173131 00000 н. 0000174249 00000 н. 0000174445 00000 н. 0000174467 00000 н. 0000174627 00000 н. 0000175688 00000 н. 0000175883 00000 н. 0000175905 00000 н. 0000176039 00000 н. 0000179857 00000 н. 0000180049 00000 н. 0000180303 00000 н. 0000180469 00000 н. 0000180591 00000 н. 0000180993 00000 н. 0000186050 00000 н. 0000186242 00000 н. 0000186544 00000 н. 0000186710 00000 н. 0000187998 00000 н. 0000188193 00000 н. 0000188219 00000 н. 0000188353 00000 н. 0000188460 00000 н. 0000188807 00000 н. 0000188829 00000 н. 0000188989 00000 н. 00001
00000 н. 00001 00000 н. 00001
00000 н. 00001 00000 н. 0000195903 00000 н. 0000196095 00000 н. 0000196993 00000 н. 0000197159 00000 н. 0000197281 00000 н. 0000197776 00000 н. 0000198842 00000 н. 0000199038 00000 н. 0000199060 00000 н. 0000199220 00000 н. 0000204365 00000 н. 0000204558 00000 н. 0000205424 00000 н. 0000205590 00000 н. 0000206857 00000 н. 0000207052 00000 н. 0000207078 00000 н. 0000207212 00000 н. 0000207334 00000 н. 0000207856 00000 н. 0000212874 00000 н. 0000213067 00000 н. 0000213933 00000 н. 0000214099 00000 н. 0000215204 00000 н. 0000215399 00000 н. 0000215425 00000 н. 0000215559 00000 н. 0000216625 00000 н. 0000216821 00000 н. 0000216843 00000 н. 0000217003 00000 н. 0000217125 00000 н. 0000217543 00000 н. 0000217584 00000 н. трейлер ] >> startxref 0 %% EOF 45 0 obj> поток xt = KP ۜ ii $ Tppsp5NjC + U JĢ.
Правильные многоугольники (видео) Определение, примеры и свойства
Содержание
Мы уже говорили о многоугольниках, но сами по себе правильные многоугольники не рассматривали. Это крем-де-ла-крем многоугольников, класс сам по себе!
Что такое многоугольник?
Что такое правильный многоугольник?
Свойства правильных многоугольников
Имена правильных многоугольников
Части правильных многоугольников
Углы правильного многоугольника
Формула правильного многоугольника
Многоугольники — это прямые плоские формы, закрывающиеся в пространстве.Это означает, что каждый многоугольник:
Двумерный
Использует только линейные сегменты для создания сторон
Имеет интерьер и экстерьер
Слово «многоугольник» происходит от греческого языка и означает «много углов», , потому что все простые многоугольники имеют столько же сторон, сколько и углов. Самый простой многоугольник, треугольник, имеет три внутренних угла (и три внешних!), Поэтому у него также есть три стороны.
У многоугольников может быть так много сторон, что они кажутся кругами, даже если это не так.Как только вы получите более 10 сторон, большинство студентов-математиков просто скажут « n -угольник», где n — это количество сторон или внутренних углов, как в «18-угольнике» или «25-угольнике». вместо того, чтобы пытаться вспомнить имя греческого происхождения.
Что такое правильный многоугольник?
Чтобы быть правильным многоугольником , плоская, замкнутая, прямолинейная форма должна иметь еще одно свойство. Каждый внутренний и внешний угол в правильном многоугольнике равен любому другому внутреннему и внешнему углу, и каждая сторона равна по длине любой другой стороне.
У правильного многоугольника:
Два измерения
Борта прямые
Конгруэнтные стороны (равной длины)
Интерьер и экстерьер
Внутренние равные углы
Равные внешние углы
Примеры правильных многоугольников
Несколько примеров правильных многоугольников: треугольник, четырехугольник, пятиугольник, шестиугольник, семиугольник и десятиугольник.
Обычный Vs. Неправильные многоугольники
Если хотя бы один из этих объектов отсутствует, у вас нет правильного многоугольника .У вас может быть три объекта (два измерения; прямые стороны; внутреннее и внешнее), но при этом не будет правильного многоугольника. У вас будет неправильный многоугольник .
Прямоугольник, длина которого превышает высоту, является примером неправильного многоугольника. Разносторонний треугольник, домашняя тарелка на поле для бейсбола или софтбола и воздушный змей также являются примерами неправильных многоугольников.
Свойства правильных многоугольников
Только при соблюдении всех шести условий, описанных выше, у вас будет правильный многоугольник.Рассмотрим подозрительную фигуру и увидим:
Здесь у нас есть △ CAT, нарисованный черными линиями. Так что наша черная КОШКА действительно подозрительна.
Просмотрите шесть свойств правильных многоугольников:
Это двумерное изображение?
Сделано с прямыми сторонами?
Конгруэнтны ли его стороны?
Замыкается ли он в пространстве, создавая интерьер и экстерьер?
У него одинаковые внутренние углы?
У него одинаковые внешние углы?
Результаты нашего исследования с использованием шести идентифицирующих свойств правильных многоугольников: △ CAT — это правильный многоугольник, самый простой вид.Это равносторонний треугольник с внутренними углами 60 ° и внешними углами 120 °.
Имена правильных многоугольников
Представьте, что вы распаковываете партию полигонов. Вы должны поместить все неправильные многоугольники на полку со скидками, а все правильные многоугольники на полку с полной ценой. Используя свои знания об отличительных свойствах правильных многоугольников, вы можете легко увидеть, что только несколько типичных многоугольников являются правильными:
Правильный многоугольник Количество сторон Внутренний угол Уголки внешние
Равносторонний треугольник 3-х сторонний 3 внутренних угла по 60 ° 3 внешних угла по 120 °
Квадрат 4 стороны 4 внутренних угла по 90 ° 4 внешних угла по 90 °
Правильный пятиугольник 5 сторон 5 внутренних углов 108 ° 5 внешних углов 72 °
Правильный шестигранник 6 сторон 6 внутренних углов по 120 ° 6 внешних углов по 60 °
Правильный семиугольник 7 сторон 7 внутренних углов ≅ 128.57 ° 7 внешних углов ≅ 51,43 °
Правильный восьмиугольник 8 сторон 8 внутренних углов 135 ° 8 внешних углов по 45 °
Сколько сторон у правильного многоугольника?
Вы можете создать правильных многоугольников с любым количеством сторон и внутренними углами , но обычно вы не называете их ничем, кроме количества их сторон или внутренних углов, а затем -gon:
Правильный многоугольник Количество сторон Внутренний угол Уголки внешние
Обычный четырехугольник или 9-угольник 9 сторон 9 внутренних углов 140 ° 9 внешних углов 40 °
Обычный десятиугольник или 10-угольник 10 сторон 10 внутренних углов 144 ° 10 внешних углов 36 °
Обычный гектогон или 100-угольник 100 сторон 100 внутренних углов 176.4 ° 100 внешние углы 3,6 °
Любой многоугольник, у которого стороны не равной длины с одинаковыми внутренними и внешними углами, является неправильным многоугольником; идет на дисконтную полку!
Части правильных многоугольников
Какими бы простыми ни были правильные многоугольники, они по-прежнему состоят из шести частей:
Стороны
Интерьер и экстерьер
Уголки внутренние
Уголки внешние
Вершины
Диагонали
Мы проиллюстрируем это на примере обычного правильного многоугольника — шестиугольника.Это знакомая форма (представьте клетки пчелиного улья):
У нашего шестиугольника шесть равных сторон . Он имеет шесть равных внутренних угла , каждый по 120 °. Он также имеет шесть равных внешних углов. Внешний угол создается путем расширения одной стороны и измерения угла между этим расширением и соседней стороной.
Углы правильного многоугольника
Внешние углы правильного многоугольника
Внешние углы каждого простого многоугольника в сумме составляют 360 °, потому что обход многоугольника завершает поворот или возвращает в исходное место.В местах пересечения сторон они образуют вершины, поэтому у нашего шестиугольника также есть шесть вершин.
Внутренние углы правильного многоугольника
Внутри сторон шестиугольника, где находятся внутренние углы, находится внутренняя часть шестиугольника . С внешней стороны шестиугольник , внешний . Это становится важным, когда вы рассматриваете сложные многоугольники, такие как форма звезды (например, пентаграмма).
Диагональ многоугольника
Соедините все несмежные вершины внутри шестиугольника, чтобы получилось диагонали .Все простые многоугольники можно разделить на треугольники с помощью диагоналей. Минимальное количество треугольников, созданных в нашем шестиугольнике путем рисования трех диагоналей, равно четырем; каждый треугольник имеет внутренние углы в сумме 180 °, поэтому сумма внутренних углов правильного шестиугольника составляет 4 × 180 ° или 720 °.
Формула правильного многоугольника
Формула для вычисления суммы внутренних углов любого правильного многоугольника с n сторонами:
Чтобы найти какой-либо единственный внутренний угол, разделите ответ на n.
∠A = (n — 2) × 180 ° n
Резюме урока
Теперь у вас есть все инструменты, необходимые для идентификации многоугольников, отличия правильных от неправильных, именования правильных многоугольников и распознавания их по их свойствам, составления списка частей правильных многоугольников (стороны, внутренние, внутренние углы, вершины, диагонали, внешние углы). ) и вычислим суммы внутренних углов многоугольников.
Следующий урок:
Диагональная формула
углов в многоугольниках — объяснения и примеры
Многоугольник касается не только сторон.Возможны сценарии, когда у вас есть несколько фигур с одинаковым количеством сторон.
Как же тогда их различать?
УГЛЫ!
Самый простой пример — прямоугольник и параллелограмм имеют 4 стороны каждая, причем противоположные стороны параллельны и равны по длине. Разница заключается в углах, где прямоугольник имеет углы 90 градусов на всех 4 сторонах, а параллелограмм имеет противоположные углы равной меры.
Из этой статьи вы узнаете:
Как найти угол многоугольника?
Внутренние углы многоугольника.
Внешние углы многоугольника.
Как рассчитать размер каждого внутреннего и внешнего угла правильного многоугольника.

Как найти углы многоугольника?
Мы знаем, что многоугольник — это двумерная многосторонняя фигура, составленная из отрезков прямой линии . Сумма углов многоугольника — это сумма всех внутренних углов многоугольника.
Так как все углы внутри многоугольников одинаковые.Таким образом, формула для определения углов правильного многоугольника имеет вид;
Сумма внутренних углов = 180 ° * (n — 2)
Где n = количество сторон многоугольника.
Примеры
треугольник имеет 3 стороны, поэтому
n = 3
Подставьте n = 3 в формулу нахождения углов многоугольника.
Сумма внутренних углов = 180 ° * (n — 2)
= 180 ° * (3 — 2)
= 180 ° * 1
= 180 °
Углы четырехугольника:
A четырехугольник — это четырехугольник, поэтому
n = 4.
Путем подстановки
сумма углов = 180 ° * (n — 2)
= 180 ° * (4-2)
= 180 ° * 2
= 360 °
Пятиугольник равен 5 — двусторонний многоугольник.
n = 5
Заменитель.
Сумма внутренних углов = 180 ° * (n — 2)
= 180 ° * (5-2)
= 180 ° * 3
= 540 °
Восьмиугольник — это 8-сторонний многоугольник
n = 8
При подстановке
Сумма внутренних углов = 180 ° * (n — 2)
= 180 ° * (8-2)
= 180 ° * 6
= 1080 °
Углы a Hectagon:
a Hectagon — это 100-сторонний многоугольник.
n = 100.
Заменитель.
Сумма внутренних углов = 180 ° * (n — 2)
= 180 ° * (100-2)
= 180 ° * 98
= 17640 °
Внутренний угол многоугольников
Внутренний угол равен угол, образованный внутри многоугольника, между двумя сторонами многоугольника.
Количество сторон в многоугольнике равно количеству углов, образованных в конкретном многоугольнике. Размер каждого внутреннего угла многоугольника определяется выражением;
Измерение каждого внутреннего угла = 180 ° * (n — 2) / n
, где n = количество сторон.
Примеры
Размер внутреннего угла десятиугольника.
Десятиугольник — это 10-сторонний многоугольник.
n = 10
Измерение каждого внутреннего угла = 180 ° * (n — 2) / n
Замена.
= 180 ° * (10-2) / 10
= 180 ° * 8/10
= 18 ° * 8
= 144 °
Внутренний угол шестигранника.
Шестигранник имеет 6 сторон. Следовательно, n = 6
Заменитель.
Измерение каждого внутреннего угла = 180 ° * (n — 2) / n
= 180 ° * (6-2) / 6
= 180 ° * 4/6
= 60 ° * 2
= 120 °
Внутренний угол прямоугольника
Прямоугольник является примером четырехугольника (4 стороны)
n = 4
Измерение каждого внутреннего угла = 180 ° * (n — 2) / n
= 180 ° * (4-2) / 4
= 180 ° * 1/2
= 90 °
Внутренний угол пятиугольника.
Пятиугольник состоит из 5 сторон.
n = 5
Размер каждого внутреннего угла = 180 ° * (5-2) / 5
= 180 ° * 3/5
= 108 °
Внешний угол многоугольников
Внешний угол равен угол, образованный вне многоугольника между одной стороной и расширенной стороной. Мера каждого внешнего угла правильного многоугольника определяется выражением;
Размер каждого внешнего угла = 360 ° / n, где n = количество сторон многоугольника.
Одним из важных свойств внешних углов правильного многоугольника является то, что сумма размеров внешних углов многоугольника всегда равна 360 °.
Примеры
Внешний угол треугольника:
Для треугольника n = 3
Заменить.
Измерение каждого внешнего угла = 360 ° / n
= 360 ° / 3
= 120 °
Внешний угол пятиугольника:
n = 5
Измерение каждого внешнего угла = 360 ° / n
= 360 ° / 5
= 72 °
ПРИМЕЧАНИЕ: Формулы внутреннего и внешнего углов работают только для правильных многоугольников.Неправильные многоугольники имеют разные внутренние и внешние размеры углов.
Давайте рассмотрим другие примеры задач о внутренних и внешних углах многоугольников.
Пример 1
Внутренние углы неправильного 6-стороннего многоугольника равны; 80 °, 130 °, 102 °, 36 °, x ° и 146 °.
Вычислить размер угла x в многоугольнике.
Решение
Для многоугольника с 6 сторонами n = 6
сумма внутренних углов = 180 ° * (n — 2)
= 180 ° * (6-2)
= 180 ° * 4
= 720 °
Следовательно, 80 ° + 130 ° + 102 ° + 36 ° + x ° + 146 ° = 720 °
Упростить.
494 ° + x = 720 °
Вычтем 494 ° с обеих сторон.
494 ° — 494 ° + x = 720 ° — 494 °
x = 226 °
Пример 2
Найдите внешний угол правильного многоугольника с 11 сторонами.
Решение
n = 11
Измерение каждого внешнего угла = 360 ° / n
= 360 ° / 11
≈ 32,73 °
Пример 3:
Внешние углы многоугольник; 7x °, 5x °, x °, 4x ° и x °.Определите значение x.
Решение
Сумма внешнего вида = 360 °
7x ° + 5x ° + x ° + 4x ° + x ° = 360 °
Упростите.
18x = 360 °
Разделите обе стороны на 18.
x = 360 ° / 18
x = 20 °
Следовательно, значение x равно 20 °.
Пример 4
Как называется многоугольник, каждый внутренний угол которого равен 140 °?
Решение
Размер каждого внутреннего угла = 180 ° * (n — 2) / n
Следовательно, 140 ° = 180 ° * (n — 2) / n
Умножьте обе стороны на n
140 ° n = 180 ° (n — 2)
140 ° n = 180 ° n — 360 °
Вычтем обе стороны на 180 ° n.
140 ° n — 180 ° n = 180 ° n — 180 ° n — 360 °
-40 ° n = -360 °
Разделите обе стороны на -40 °
n = -360 ° / -40 °
= 9.
Следовательно, количество сторон равно 9 (неугольник).
Практические вопросы
Первые четыре внутренних угла пятиугольника — это все, а пятый угол равен 140 °. Найдите размер четырех углов.
Найдите размер восьми углов многоугольника, если первые семь углов равны 132 ° каждый.
Вычислить углы многоугольника, которые задаются как; (x — 70) °, x °, (x — 5) °, (3x — 44) ° и (x + 15) °.
Отношение углов шестиугольника равно; 1: 2: 3: 4: 6: 8. Вычислите величину углов.
Как называется многоугольник, каждый внутренний угол которого равен 135 °?

Предыдущий урок | Главная страница | Следующий урок
Угловая сумма многоугольников
Когда вы начинаете с многоугольника с четырьмя или более сторонами и рисуете все возможные диагонали из одной вершины, многоугольник затем делится на несколько неперекрывающихся треугольников.Рисунок иллюстрирует это деление с помощью семигранного многоугольника. Сумма внутренних углов этого многоугольника теперь может быть найдена умножением количества треугольников на 180 °. При исследовании обнаруживается, что количество треугольников всегда на два меньше, чем количество сторон. Этот факт утверждается в виде теоремы.

Рисунок 1 Триангуляция семистороннего многоугольника для нахождения суммы внутренних углов.
Теорема 39: Если у выпуклого многоугольника n сторон, то сумма его внутренних углов определяется следующим уравнением: S = ( n −2) × 180 °.
Многоугольник на рисунке 1 имеет семь сторон, поэтому, используя теорему , дает:
Внешний угол многоугольника образован продолжением только одной из его сторон. Непрямым углом, примыкающим к внутреннему углу, является внешний угол. Рисунок может предложить следующую теорему:
Рисунок 2 Внешние (непрямые) углы многоугольника.
Теорема 40: Если многоугольник выпуклый, то сумма степеней внешних углов, по одному в каждой вершине, равна 360 °.
Пример 1: Найдите сумму внутренних углов десятиугольника.
У десятиугольника 10 сторон, поэтому:
Пример 2: Найдите сумму внешних углов, по одному внешнему углу в каждой вершине, выпуклого шестиугольника.
Сумма внешних углов любого выпуклого многоугольника равна 360 °.
Пример 3: Найдите размер каждого внутреннего угла правильного шестиугольника (рисунок 3).
Рисунок 3 Внутренний угол правильного шестиугольника.
Метод 1: Поскольку многоугольник правильный, все внутренние углы равны, поэтому вам нужно только найти сумму внутренних углов и разделить их на количество углов.
Есть шесть углов, поэтому 720 ÷ 6 = 120 °.
Каждый внутренний угол правильного шестиугольника имеет размер 120 °.
Метод 2: Поскольку многоугольник правильный и все его внутренние углы равны, все его внешние углы также равны. Посмотрите на рисунок 2.Это означает, что
Поскольку сумма этих углов всегда будет 360 °, каждый внешний угол будет 60 ° (360 ° ÷ 6 = 60 °). Если каждый внешний угол равен 60 °, то каждый внутренний угол равен 120 ° (180 ° — 60 ° = 120 °).
методов построения правильных многоугольников, подходящих для вводных занятий
Охочуку Н. Стивен
Кафедра химии, факультет естественных и прикладных наук, Педагогический университет Игнатия Аджуру, Порт-Харкорт, Нигерия
Адрес для корреспонденции: Охочуку Н.Стивен, кафедра химии, факультет естественных и прикладных наук, Педагогический университет Игнатиуса Аджуру, Порт-Харкорт, Нигерия.
Электронная почта:
Авторские права © 2016 Научно-академическое издательство. Все права защищены.
Эта работа находится под лицензией Creative Commons Attribution International License (CC BY).
http: // creativecommons.org / licenses / by / 4.0 /
Аннотация
Введение правильных многоугольников и их построение всегда включало правильные шестиугольники и правильные восьмиугольники. Вводные конструкции правильных шестиугольников представляют собой использование кругов, разделенных на шесть равных секторов с использованием радиуса круга, в то время как в случае восьмиугольников используется разбиение кругов на восемь равных секторов.После этого конструкции различных классов правильных многоугольников исследуются с использованием либо базового угла, либо внешнего угла, либо другого сложного метода, свойственного конкретному семейству многоугольников. В этой статье представлены новые методы построения каждого семейства правильных многоугольников от 3-угольника до 9-угольника (от трехугольника до девятиугольника), которые подходят для вводных классов. Методы, перечисленные для каждого семейства правильных многоугольников, настолько просты, что вызывают интерес к построению многоугольников другими методами.Методы, представленные здесь для использования во вводных уроках, хотя и простые, также проходят как стандартные методы для построения конкретного семейства правильных многоугольников.
Ключевые слова: Вводные способы построения многоугольника
Цитируйте эту статью: Охочуку Н.Стивен, Методы построения правильных многоугольников, подходящие для вводных уроков, Американский журнал математики и статистики , Vol. 6 No. 6, 2016, pp. 242-250. DOI: 10.5923 / j.ajms.20160606.04.
Краткое содержание статьи
1. Введение
2. Методология
2.2. Построение правильного «треугольника» (равностороннего треугольника) стороны AB
2.2.1. Построение правильного «треугольника» (равностороннего треугольника) стороны AB прямым методом, рисунок 2
2.2.2. Построение правильного треугольника (равностороннего треугольника) методом сектора круга, рисунок 3
2.2.3. Построение правильного треугольника (равностороннего треугольника) методом пересекающихся окружностей, рисунок 4
2.3. Строительство правильного Тетрагона (Квадрата)
2.3.1. Построение правильного тетрагона (квадрата) стороны AB методом пересекающихся кругов, рис. 5а
2.3.2. Построение квадрата квадрантным методом, рис. 6
2.3.3. Тетрагон через данный равнобедренный прямоугольный треугольник ABC, рис. 7
2.4. Строительство регулярного Пентагона
2.4.1. Из равностороннего треугольника с той же стороны. Метод треугольника / круга, рисунок 8
2.4.2. Правильный Пентагон из трех пересекающихся коллинеарных окружностей, рис. 8a
2.5. Построение правильного шестиугольника известной стороны AB
2.5.1. Шестиугольник от любого равностороннего треугольника через перпендикулярную сторону или биссектрису угла, рисунок 9
2.5.2. Шестиугольник из равностороннего треугольника с той же стороной AB с помощью процедуры увеличения, рисунок 10
2.5.3. Создание шестиугольника из пересекающихся кругов с центрами в вершинах равностороннего треугольника, рис. 11
2.6. Обычный семиугольник
2.6.1. Развертка из треугольника с помощью процедуры множественного круга, рисунок 12
2.6.2. Правильный семиугольник из треугольника с помощью процедуры создания нескольких кругов, альтернативная процедура, рисунок 13
2.7. Октагон. Развитие правильного восьмиугольника из квадрата той же стороны AB
2.7.1. Создание правильного восьмиугольника из квадрата той же стороны через изготовленные стороны, рис. 14
2.7.2. Создание правильного восьмиугольника из квадрата той же стороны через полученные биссектрисы сторон и внутренних углов, рис. 15
2.7.3. Обычный восьмиугольник из обычного треугольника, рисунок 16
2.8. Обычный Нонагон
3. Результаты и обсуждение
3.1. Конструкции Треугольника
3.2. Конструкция Tetragon
3.3. Пентагоны
3.4. Шестиугольники
3.5. Гептагон
3.6. Октагоны
3.7. Нонагоны.
3.8. Общие комментарии к методам
3.8.1. Важность равностороннего треугольника в построении многоугольника
3.8.2. Дополнительные наблюдения
3.8.3. Угловые конструкции
4. Выводы
1.Введение
Как общее определение, многоугольник определяется как любая геометрическая фигура, ограниченная тремя или более сторонами; а правильный многоугольник — это многоугольник с равными сторонами и равными углами основания / внешнего основания [1-3]. Равносторонние треугольники и квадраты квалифицируются как правильные многоугольники не только по приведенному выше определению, но и потому, что они также подчиняются правилам, регулирующим правильные многоугольники. В некоторых учебниках [1] правильные многоугольники начинаются с пятиугольников, но в этой статье, как и в других работах [2-5], правильные многоугольники начинаются с равносторонних треугольников и квадратов.Эти два семейства (равносторонние треугольники и квадраты) играют важную роль в этой работе. По определению, геометрические плоские фигуры, ограниченные замкнутыми прямыми линиями в качестве сторон, являются многоугольниками; треугольники и четырехугольники образуют младшие семьи.
Вводные уроки по правильным многоугольникам и их построению обычно демонстрируются в основном с правильными шестиугольниками [2], потому что правильные шестиугольники можно легко построить простыми методами, которые находятся в пределах элементарной геометрии плоскости, рис. 1.Правильный восьмиугольник иногда также используется, потому что его внешний базовый угол легко построить путем деления круга на восемь равных секторов, как в случае правильного шестиугольника, который построен с помощью правильных многоугольников, которые проиллюстрированы с использованием их деления круга на шесть. равные сектора, рисунок 1. Другие обычные методы строительства, включающие угловые конструкции и перенос углов. Более того, у многих правильных многоугольников есть основания / внешние углы, которые трудно построить; хотя сейчас есть простые и легкие методы [6] построения любого угла.Даже при этом использование новых методов требует построения углов и копирования их в нужное место в качестве средства разгрузки рабочего пространства. Все это может внушить страх учащемуся. Поэтому необходимо искать другие способы введения построения семейств многоугольников, особенно нижних семейств, которые всегда используются на уроках, с помощью простых методов, которые также могут вызвать интерес к построениям в плоской геометрии.
Рисунок 1. Иллюстрации построения многоугольника
Разработанные таким образом методы должны также быть аутентичными процедурами для построения проиллюстрированных правильных многоугольников и требовать только базовых знаний в области геометрии плоскости. Это основная цель данной статьи. Предлагаемые здесь методы могут вызвать у новичка интерес к построению правильных многоугольников до уровня, на котором необходимо использование передовых практик. Эти простые методы, лишенные специальных конструкций и копирования углов, которые загромождают рабочее пространство вспомогательными линиями, описаны ниже.
2. Методология
2.1. Как указано выше, правильные многоугольники начинаются с равностороннего треугольника, проходящего через квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник и заканчивая более высокими элементами. Любой метод построения правильного многоугольника приемлем, но более полезен, когда метод строит правильный многоугольник с известной длиной стороны с самого начала. Методы, описанные здесь, достигают цели. Круги играют важную роль в последующих построениях; поэтому, чтобы упростить наименование кругов, круг, обозначенный как круг A, является кругом с центром A.С этого момента именованный многоугольник или многоугольник означает обычный тип.
2.2. Построение правильного «треугольника» (равностороннего треугольника) стороны AB
2.2.1. Построение правильного «треугольника» (равностороннего треугольника) стороны AB прямым методом, рис. 2
Рис. 2. Построение правильного треугольника (равностороннего треугольника) прямым методом
(a ). Рядом с центром прямой PQ отметьте расстояние AB, рисунок 2.
(б). А как центр и радиус AB поворачивают дугу над AB.
(в). B как центр и тот же радиус пересекает дугу в C. Соедините AC и BC. Фигура ABC — это треугольник (равносторонний треугольник).
2.2.2. Построение правильного треугольника (равностороннего треугольника) Метод кругового сектора, рисунок 3
Рисунок 3. Построение правильного треугольника (равносторонний треугольник): метод кругового сектора
(a) .На прямой PQ отметьте точку A. Центр A радиусом AB нарисуйте окружность A, которая пересекает PQ в точках D и E.
(b). Центр E и радиус AB отсекают окружность A в точках B и F; центр D того же радиуса, разрезать окружность A в точках C и E. Соедините AB, BC и AC, чтобы получить треугольник ABC.
2.2.3. Построение правильного треугольника (равностороннего треугольника) Метод пересекающихся окружностей, рисунок 4
Рисунок 4. Построение правильного треугольника (равносторонний треугольник) Метод пересекающихся окружностей
(a ).Нарисуйте сторону AB треугольника ABC, фигура 4. Центр A радиусом AB нарисуйте окружность A; центр B того же радиуса нарисуйте окружность B, чтобы пересечься с окружностью A в точках C и D. Соедините AC и BC, чтобы получить треугольник ABC.
2.3. Строительство правильного Тетрагона (Квадрата)
2.3.1. Построение правильного четырехугольника (квадрата) стороны AB методом пересекающихся кругов, рис. 5a
Рис. 5. Построение квадрата стороны AB: метод пересекающихся кругов
(a ).Рядом с центром PQ отметьте AB. Центр A, радиус AB, нарисуйте окружность A; центр B, такого же радиуса нарисуйте окружность B, пересекающуюся с окружностью A в точке E над AB; центр E того же радиуса нарисуйте окружность E, отсекающую окружность A в точке F и окружность B в точке G.
(b). Центр F с тем же радиусом вырезания окружности E в H; центр G и такой же радиус разрезают окружность E в точке K. Соедините AH, чтобы разрезать окружность A в точке D; присоединитесь к BK, чтобы разрезать круг B в C. Присоединитесь к DC. ABCD — четырехугольник (квадрат). В качестве альтернативы , на прямой линии XY отметка PQ = QR. PQ = AB, рисунок 5b.
(а). Центр P, радиус PQ начертить окружность P; центр R, тот же радиус, нарисуйте окружность R; центр Q, тот же радиус нарисуйте окружность Q, которая разрезает окружность P в точках E и F и окружность R в точках G и H. Соедините FE и HG, образуя каждую линию вверх и пересекающуюся с XY в точках A и B соответственно.
(б). Центр A, резка FE с таким же радиусом, полученная в D, центр B, резка HG с таким же радиусом, полученная в C. Соедините CD. ABCD — это квадрат.
2.3.2. Построение квадрата квадрантным методом, рисунок 6
Рисунок 6.Построение квадрата методом квадранта
(а). В точке A на прямой PQ постройте ∠RAQ = 45 °, рис. 6.
(b). Центр A и удобный радиус AB разрезают AR в точке D. Проведите вниз перпендикуляр от D к O на PQ.
(в). Центр O и радиус AO начертите окружность O, которая разрезает PQ в точке C и DO, полученную в точке B. Соедините AB, BC и CD. ABCD — четырехугольник.
2.3.3. Тетрагон через данный равнобедренный прямоугольный треугольник ABC, рисунок 7
Рисунок 7. Построение квадрата с помощью метода конгруэнтных прямоугольных равнобедренных треугольников
(a). Нарисуйте равнобедренный прямоугольный треугольник ACB с горизонтальным основанием (длинной стороной AC).
(б). Центр Радиус AB отклоняет дугу ниже AC; центр C того же радиуса разрезает дугу в точке D. Соедините AD и DC, чтобы получить квадрат ABCD.
2.4. Строительство Правильного Пентагона
2.4.1. Из равностороннего треугольника с той же стороны. Метод треугольника / круга, рисунок 8
Рисунок 8. Строительство Пентагона. Метод треугольника / круга
(а). Нарисуйте равносторонний треугольник ABF с вершиной F вертикально под AB, рис. 8. Центр A и радиус AB нарисуйте окружность A; центр B того же радиуса, нарисуйте круг B, который пересекается с кругом A в точках F и G; присоединяйтесь к FG, производящему вверх. Центр F, тот же радиус нарисуйте окружность F, которая пересекает окружность A в точке H, FG в точке J и окружность B в точке K.
(b). Присоединитесь к KJ, чтобы разрезать круг A в точке E; присоединиться к HJ, производя разрезание круга B в точке C.Присоединяйтесь к AE и BC.
(в). Центр C, вырез FG того же радиуса, полученный в D; присоединяйтесь к CD и DE. Пятиугольник — это ABCDE.
2.4.2. Правильный пятиугольник из пересекающихся трех коллинеарных кругов, рисунок 8a
Рисунок 8a. Правильный пятиугольник от пересечения трех коллинеарных окружностей
(a). На отметке XY равные точки пересечения PQ = QR.
(б). Центр P, радиус PQ начертите окружность P; центр R того же радиуса начертить окружность R; центр Q того же радиуса нарисуйте окружность Q, которая разрезает окружность A в точках F и G и окружность R в точках H и J.
(в). Пусть общая хорда FG (не нарисована) окружностей P и Q разрезает XY в точке A, а общая хорда HJ (не нарисована) окружностей Q и R разрезает XY в точке B; центр. Тот же радиус PQ вырезать окружность P в точке E; центр B тот же радиус разрезает окружность R в точке C. Соедините AE и BC.
(d) Центр C дуги поворота того же радиуса над окружностью Q. Центр E того же радиуса пересекает эту дугу над окружностью Q в точке D. Соедините CD и DE. ABCDE — правильный пятиугольник.
2,5. Построение правильного шестиугольника известной стороны AB
2.5.1. Шестиугольник от любого равностороннего треугольника через перпендикулярную сторону или биссектрису угла, рисунок 9
Рисунок 9. Шестиугольник от любого треугольника через угол или перпендикулярную биссектрису стороны Метод
(a). Нарисуйте любой равносторонний треугольник PQR, цифра 9; пусть перпендикулярные (или угловые) биссектрисы PQ и QR (или ∠P и ∠Q) пересекаются в точке O. Соедините RO, создавая все три биссектрисы в обе стороны.
(б). Центр O и радиус AB (сторона шестиугольника) нарисуйте окружность O, которая пересекает биссектрисы в точках A, (A находится на OP), B, C, D, E и F в направлении против часовой стрелки.Присоединяйтесь к ABCDEF как к правильному шестиугольнику.
2.5.2. Шестиугольник из равностороннего треугольника той же стороны AB с помощью процедуры увеличения, рисунок 10
Рисунок 10. Шестиугольник из треугольника той же стороны с помощью процедуры увеличения
(a). Нарисуйте данный равносторонний треугольник PFE (ΔPFE = ΔABC), продолжая PF до M и PE до N, рисунок 10.
(b). Центр F, радиус PF срез PM в точке A; центр A, срез PM того же радиуса в точке Q; центр E, такой же радиус резания PN в точке D; центр D, такой же радиус резания PN в точке R.Присоединяйтесь к QR. Центр Отрезок QR с таким же радиусом в точке B и центр D срез с таким же радиусом RQ в точке C.
(c). Присоединяйтесь к AB и CD. ABCDEF — правильный шестиугольник.
2.5.3. Рис. 11
Рис. 11. Создание шестиугольника из пересекающихся кругов с центрами в вершинах равностороннего треугольника
(а). Нарисуйте равносторонний (треугольник) ABG, рисунок 11.Центр A радиус AB нарисуйте окружность A; центр B того же радиуса нарисуйте круг B и центр G того же радиуса нарисуйте круг G, который разрезает круг A в точке F и круг B в точке C.
(b). Центр F такой же разрез радиуса G в E и центр C, такой же радиус разрезания G в D. Соедините BC, CD, DE, EF и FA. ABCDEF — шестиугольник.
2.6. Обычный семиугольник
2.6.1. Развертка из треугольника с помощью процедуры множественного круга, рисунок 12
Рисунок 12. Обычный семиугольник через треугольник
(а). Около середины прямой XY нарисуйте треугольник ABM, рисунок 12, с вершиной M вертикально ниже AB. Центр A, радиус AB нарисуйте окружность A, которая разрезает XY в точке H; центр B того же радиуса нарисуйте круг B, который разрезает XY в точке J, а также окружность A в точках M и N, соедините MN, производя движение вверх.
(б). Центр M, такого же радиуса нарисуйте круг M, который пересекает круг A в точке P; обведите B в R и MN в O.
(c). Центр H того же радиуса нарисуйте окружность H; центр P тот же радиус разрезает окружность H в точке Q.
(д). Центр J того же радиуса нарисуйте окружность J; центр R того же радиуса вырезать окружность J в точке S.
(e). Присоединитесь к QO, чтобы разрезать круг B в точке C; присоединитесь к SO, чтобы разрезать круг A в точке G. Присоединитесь к BC и AG.
(ж). Центр O срез MN с таким же радиусом выполнен в точке T, разрез по центру T и срез MN с таким же радиусом снова выполнен в точке E.
(g). Центр E тот же радиус начертания окружности E. Центр G такой же радиус вырезания окружности E в F, центр C и такой же радиус вырезания окружности E в D. Соедините GF, FE, ED и DC. ABCDEFG — это сторона AB правильного семиугольника, через процедуру треугольника с множеством пересекающихся окружностей, рисунок 11.
2.6.2. Правильный семиугольник из треугольника с помощью процедуры создания нескольких кругов, альтернативная процедура, рисунок 13
Рисунок 13. Гептагон из треугольника; Альтернативная процедура
(а). Нарисуйте треугольник ABH, образующий AB в обоих направлениях к X и Y. Центр A, радиус AB нарисуйте окружность A; центр B, тот же радиус нарисуйте круг B, который разрезает окружность A в точках H и J. Присоединитесь к HJ, производя движение вверх.
(б). Центр H, разрез HJ с таким же радиусом, полученный в K; центр K, одинаковый радиус срезан с равными пересечениями вдоль HJ, полученными в L и E.Соедините AE и EB, которые разрезают окружность A в точке M и окружность B в точке N соответственно.
(в). Центр E, тот же радиус, нарисуйте окружность E, которая разрезает AE в точке O и BE в точке P соответственно. Центр O, окружность A с таким же радиусом в точке G; центр P, тот же радиус, вырезать окружность B в точке C.
(d). Центр M, окружность сечения E с таким же радиусом в точке F; центр N, окружность E с одинаковым радиусом в точке D. Соедините BC, CD, DE, EF, FG и GA, чтобы сформировать правильный 7-угольник.
2.7. Октагон. Развитие правильного восьмиугольника из квадрата той же стороны AB
2.7.1. Рис. 14
Рис. 14. Развитие правильного восьмиугольника той же стороны AB, что и данный квадрат, с помощью созданных сторон
( а). Нарисуйте квадрат PQRS с PQ, равным AB (дано), образуя стороны в обе стороны, рис. 14. Пусть O будет пересечением диагоналей.
(б). Центр P радиус PO вырез SP, произведенный в A. Центр радиуса O OA начертите окружность O, которая разрезает полученные стороны в точках A, B, C, D, E, F, G и H (в направлении против часовой стрелки).Соедините соседние точки, чтобы получился правильный восьмиугольник со стороной AB.
2.7.2. Рис. 15
Рис. 15. Развитие правильного восьмиугольника той же стороны AB, что и данный квадрат, через полученные биссектрисы внутренние углы и стороны
(а). Нарисуйте квадрат PQRS, где PQ равно AB (дано), рис. 15.
Нарисуйте серединные перпендикулярные стороны сторон и биссектрисы углов, образующие каждую биссектрису в обоих направлениях.Пусть O — пересечение этих биссектрис. Производим SP и QP.
(б). Центр P радиус PO вырез SP, произведенный в J. Центр радиуса O OJ начертите окружность O, которая разрезает RP, полученный в A, и полученные линии в точках J, B, C, D, E, F, G, H и K (против часовой стрелки) . Соедините соседние точки (исключая K и J), чтобы получить правильный восьмиугольник ABCDEFG стороны AB.
2.7.3. Правильный восьмиугольник из обычного треугольника, рисунок 16
Рисунок 16. Правильный восьмиугольник из треугольника
Правильный восьмиугольник можно построить из правильного треугольника следующим образом.
(а). Нарисуйте правильный треугольник ABJ с горизонтальным основанием AB и вершиной J вертикально над AB. Произведите AB в обоих направлениях к XY соответственно. Обратите внимание, что точки A, B и J обозначают треугольник.
Центр A, радиус AB, нарисуйте круг A, который разрезает XY в точке K рядом с X. Центр B, тот же радиус нарисуйте круг B, который разрезает XY в L и окружность A в M и J.
Центр J, тот же радиус, нарисуйте круг J, который разрезает окружность A в точке N и окружность B в точке O.
Центр N того же радиуса, нарисуйте окружность N, которая разрезает окружность J в точке P.Присоединитесь к AP, которая разрезает круг A в точке Q; производите AP вверх.
Центр O, тот же радиус, нарисуйте круг O, разрезающий круг J в точке R. Присоединитесь к BR, разрезающему круг B в точке S; производят BR вверх.
(б). С точками K и P в качестве центров и одинакового радиуса разделите ∠PAK пополам и пусть биссектриса пересекает окружность A в точке H. Соедините AH.
С точками S и L в качестве центров и одинаковым радиусом разделите пополам ∠SBL и пусть биссектриса пересекает окружность B в точке C. Соедините BC.
(в). Центр H, тот же радиус, поверните дугу над H; центр Q, тот же радиус, дуга разреза в G.Присоединяйтесь к HG.
Центр C, тот же радиус, поверните дугу над C; центр S, тот же радиус, дуга разреза в D. Соедините CD.
Центр G, тот же радиус, разрез AP произведен на F; присоединиться к FG.
Центр D, тот же радиус, вырез BR произведен в точке E; присоединиться к DE. ABCDEFGH — правильный восьмиугольник.
2,8. Обычный нонагон
Рисунок 17. Обычный нонагон
(a) Нарисуйте прямую линию XY и отметьте указанную AB, рисунок 17.
(b).Центр A и радиус AB начертить окружность A; Центр B, тот же радиус, нарисуйте круг B, который разрезает окружность A в точках K и L. Соедините KL, производя движение вверх. Центр L, разрез LK с таким же радиусом на M.
(c). Центр M, радиус 3AB, разрез KL, полученный в F. Центр F, радиус AB, начертите окружность F. Присоединитесь к FA, которая разрезает окружность F в N и окружность A в O. Присоединитесь к FB, которая разрезает окружность F в точке P и окружность B в точке Q.
(г). Центр N, радиус AB, отрезок окружности F в точке G, соединение FG; центр O, такой же радиус разрезает окружность A в точке J. Присоединитесь к AJ.
Центр P, тот же радиус AB, отрезок окружности F в точке E, соединение EF; центр Q, такая же окружность, разрезанная adius, B в C, соединяется с BC.
(е). Центр G, тот же радиус AB, поверните дугу ниже G, центр J, тот же радиус пересекает дугу в H. Соедините GH и HJ. Центр E с таким же радиусом поверните дугу ниже E, центр C, тот же радиус пересекает эту дугу в D. Соедините DC и DE. ABCDEFGHJ — правильный шестиугольник.
3. Результаты и обсуждение
3.1. Конструкции треугольника
Построение треугольника в разделе 2.2.1, рис. 2 является обычным модным методом. Стороны равны, потому что они имеют одинаковый радиус, а внутренние углы равны 60 °.Примечание: любые смежные точки на окружности можно соединить, а также с центром круга, чтобы получить треугольник.
Метод кругового сектора (раздел 2.2.2, рисунок 3) основан на том факте, что радиус круга делит круг на шесть равных секторов. У каждого сектора прямые стороны равны радиусу круга. Хорда сектора равна радиусу окружности.
В методе пересекающихся окружностей, раздел 2.2.3 рис. 4, который используется как вводное построение правильного треугольника [5].два круга имеют общие радиусы. Остальные стороны — такие же равные радиусы равных кругов. Итак, треугольник равносторонний. Примечание: процедура такая же, как и при прямом методе; в прямом методе показаны только соответствующие дуги окружностей раздела 2.2.3.
3.2. Конструкция тетрагона
В разделе 2.3.1, конструкция тетрагона путем пересечения окружностей, рис. 5a, окружности F, E и G имеют одинаковый радиус и коллинеарны, а окружность E пересекается с окружностями F и G в точках H и K соответственно, и они находятся на расстоянии друг от друга, HA параллельно KB, оба перпендикулярны AB и разнесены по радиусу (поскольку AB является общим радиусом для всех окружностей).AD равен и параллелен BC, поэтому DC касается окружностей A и B, а также равен и параллелен AB. Таким образом, AB = BC = AD = DC и внутренние углы равны 90 ° каждый, следовательно, ABCD — квадрат. На рисунке 5b A и B являются серединами PQ и QR, поэтому AB = PQ. AD ǁ BC оба перпендикулярны XY и AD = DC (одинаковый радиус). Итак, ABCD — квадрат. Вышеупомянутый метод, особенно рисунок 5b, — это быстрый и удобный способ построить квадрат без ошибок.
В разделе 2.3.2 рис. 6 каждый квадрант имеет прямоугольный равнобедренный треугольник e.грамм. ΔAOD и любые два соседних квадранта, образующие полукруг, составляют прямоугольный равнобедренный треугольник, например Δ ACD под прямым углом к D, с AC (диаметром) в качестве длинной стороны и с равными хордами, как у двух других сторон. Комбинация ΔADC с его конгруэнтным треугольником ΔABC (в другом полукруге) с общим основанием AC с помощью процесса, описанного в разделе 2.3.2, дает квадрат ABCD. Построение квадрата ABCD можно было бы укоротить после шага (а), используя центр A с радиусом AD для поворота дуги, которая разрезает AR в точке D и продолжается ниже PQ; центр D с тем же радиусом выреза PQ в точке C; центр C, тот же радиус пересекает дугу ниже PQ в B.Соединение AB, BC и CD даст требуемый квадрат. Первая процедура принята для ясности на уроке по использованию квадранта для построения квадрата, а также для исключения путаницы с процедурой в разделе 2.3.3, которая аналогична.
В разделе 2.3.3, рисунок 7, равнобедренный прямоугольный треугольник имеет две равные стороны с включенным прямым углом. Два таких равных треугольника, имеющих общее более длинное основание, образуют квадрат.
3.3. Пентагоны
Есть два метода построения правильных пятиугольников: с помощью внешнего / внутреннего угла основания или путем развития правильного треугольника [4] (равносторонний треугольник).Эти методы не просты, чтобы их можно было использовать в качестве демонстрационных. С введением раздела 2.4.2 можно продемонстрировать построение правильного пятиугольника. Конструкция использует круги одинакового радиуса для построения правильного пятиугольника из равностороннего треугольника с той же стороной, так что стороны построенного пятиугольника равны сторонам треугольника. Построение внутреннего угла CBA (правильного пятиугольника) с использованием линии HJC не является ортодоксальным методом, но дает ожидаемый результат.На рис. 8а в разделе 2.4.2 показана новая простая конструкция пятиугольника. Точки A и B являются серединами PQ и QR соответственно, поэтому AB равен радиусу любого из кругов. Процедура регулярного треугольника и круга представляет собой интересную практику. Заслуживает упоминания построение правильного пятиугольника с помощью процедуры, полученной путем применения продвинутой алгебры к построению многоугольника [5]. Процедура, хотя и простая, не позволяет построить правильный пятиугольник с заданной длиной стороны, поэтому здесь не сообщается и не включается.
3.4. Шестиугольники
У правильного шестиугольника есть много простых и удобных методов, подходящих для вводных уроков, кроме метода деления окружности круга на его радиус (рис. 1). Правильные шестиугольники могут быть построены любым из методов, использующих равносторонний треугольник, как показано выше в разделах с 2.5.1 по 2.5.3, включая разделение круга на шесть равных частей с использованием радиуса круга для получения шестиугольника на рисунке 1.
Шестиугольник из угловой или перпендикулярной стороны биссектрисы треугольника (сечение 2.5.1) имеет ту же сторону, что и секторный треугольник; OA = OB (радиусы одного круга), каждый угол при O равен 60 °, поэтому каждый базовый угол в треугольнике OAB равен 60 °, поэтому ∠ABO равносторонний, а OA = OB = AB = сторона равностороннего треугольника сектора. Радиус окружности O (как в случае метода равномерного разбиения окружности на шесть частей на рис. 1) определяет длину стороны шестиугольника.
В увеличенном равностороннем треугольнике, раздел 2.5.2, каждый из маленьких треугольников, скажем, PFE, является равносторонним.По построению FE = FA, поэтому ABCDEF — правильный шестиугольник с заданной стороной. Этот метод и разделение круга на шесть равных секторов подходят для правильных шестиугольников с очень короткими сторонами.
В разделе 2.5.3 использование системы трех кругов с равносторонним треугольником аналогично иллюстрации, показанной на рисунке 1; вершина G равностороннего треугольника на рисунке 11 определяет центр окружности на рисунке 1, точки пересечения A, B, C и F на окружности G являются вершинами шестиугольника, а AB — длина каждой стороны шестиугольника. шестиугольник на рисунке 11.AB (сторона треугольника) — это радиус каждой из окружностей на рисунке 11.
3.5. Гептагон
Раньше правильный семиугольник не демонстрировался из-за сложности его построения из внешнего или внутреннего угла. Метод, описанный в разделе 2.6.2, рисунок 13, является новым и может использоваться в качестве демонстрационной конструкции. Опять же, построение внешнего угла CBY (правильного семиугольника) с использованием линии QOC, рис. 12, не является ортодоксальным методом, хотя и дает ожидаемый результат.Однако оказывается, что точка J (рис. 8), которая совпадает с точкой O на рис. 12, является полезной точкой при построении правильных многоугольников с нечетными номерами с помощью процедуры «треугольник-круг». Эта точка, К рис. 13 в разделе 2.6.2, используется в альтернативной процедуре построения семиугольника. Процедура правильного треугольника и круга здесь представляет интересную практику, как и в случае с пятиугольником.
3,6. Октагоны
Помимо метода разделения круга на восемь равных частей, показанного на рисунке 1, существуют другие методы, которые можно использовать для обучения построению правильных восьмиугольников.Эти методы включают построение под разными углами, которые в этой статье мы пытаемся найти минимально. В связи с этим метод приведения квадрата к правильному восьмиугольнику по Блейки [7] путем отсечения вычисленных равных длин от каждой вершины квадрата исключен из этого отчета, как и другие в той же категории, поскольку сторона многоугольника длина должна быть измерена или рассчитана. Введение этих других новых методов упрощает дело.
В разделе 2.7.1 рисунок 14 (восьмиугольник от четырехугольника через образованные стороны четырехугольника), OP = PA = PH по конструкции; AB ² = PQ ² = 2OP ² = 2PH ² = HA ². Следовательно, AB = HA = PQ.
В разделе 2.7.2 (рис. 15) используются диагонали и перпендикулярные биссектрисы для построения правильного восьмиугольника. Квадрат разделен биссектрисой на восемь равных частей (секторов); круг с центром O и радиусом OJ разделен на восемь равных секторов, как в четырехугольнике.Круг O разрезает QP, полученный при K, PJ = PK, сектор KOJ (линии OK и OJ не показаны) = сектор AOB (те же радиусы и угол сектора 45 °). Итак, KJ = AB. Но AB = PQ (по построению или ΔKPJ ≡ ΔPOQ SAS). Следовательно, KJ = PQ = AB. Примечание: если квадраты на рисунках 14 и 15 одинаковы, построенные восьмиугольники одинаковы.
В разделе 2.7.3, рис. 16 восьмиугольник построен в виде треугольника с процедурой с использованием окружности. В этом методе много кругов, поэтому он может сбивать с толку, но он показывает, что n-угольники от n = 3 до 9, которые здесь рассматриваются, могут быть построены с помощью обычного метода с помощью тригона / круга.
3,7. Нонагоны.
Раздел 2.8, рис. 17, строит правильный 9-угольник (нонагон) с помощью процедуры треугольника / окружности, метода, обычно используемого в этой работе. Этот новый метод построения многоугольника включен, потому что несколько иллюстративных примеров построения многоугольников обычно заканчиваются восьмиугольником, последним наиболее легко построенным многоугольником. Процедура проста и может быть использована.
3.8. Общие комментарии к методам
Цель этой статьи — представить простые методы построения нижних членов многоугольников во вводных классах инструкций.Такие методы должны быть лишены построения и / или копирования углов, которые загромождают рабочую плоскость, а также должны давать многоугольник с известной длиной стороны. Представленные здесь методы удовлетворяют этим целям.
3.8.1. Важность равностороннего треугольника в построении многоугольника
Ранее во введении было сказано, что равносторонний треугольник играет важную роль в построении многоугольника. Используя метод, представленный здесь для каждого семейства многоугольников, все они могут быть получены из правильных треугольников с помощью построений с использованием окружностей.Одно очевидное наблюдение состоит в том, что многоугольник с четным числом сторон, треугольник, используемый в процедуре триагома и круга, — это тот, вершина которого находится вертикально над горизонтальным основанием, в то время как у многоугольников с нечетным числом сторон вершина используемого треугольника находится вертикально ниже горизонтальное основание. На самом деле есть два правильных треугольника с общей базой (основание строящегося многоугольника), образованных двумя пересекающимися окружностями (константа для всех построений этим методом), вертикально противоположные вершины этих двух треугольников с общим основанием являются точкой пересечения двух кругов.
Получается, что равносторонний треугольник является основным элементом при построении любого правильного многоугольника, когда он соединен с кругами того же радиуса. Правильный четырехугольник (квадрат) также является важным элементом при построении правильного 8-угольника, сечения 2.7.1 на рис. 14 и сечения 2.7.2 на рис. 15. Правильный 6-угольник также может быть получен из правильного четырехугольника (квадрата). такой же длины стороны. Нарисован квадрат. Нарисуется середина диагонали O как центр и сторона квадрата как радиус окружности O.Равное разбиение окружности окружности O на сектора и ее радиуса дает точки вдоль окружности в виде вершин правильного 6-угольника. Этот метод аналогичен равному разделению круга на шесть секторов, показанных на рисунке 1 во вводной части, с квадратом, представляющим центр и радиус круга и, следовательно, сторону шестиугольника.
Другим аспектом процедуры треугольник-окружность является использование постоянного радиуса (стороны треугольника) на протяжении всей конструкции. Это упрощает конструкцию после правильного определения необходимых центров.
3.8.2. Дополнительные наблюдения
Дополнительные наблюдения, полезные для учащегося, включают следующее: линия, проходящая через точки пересечения двух окружностей, перпендикулярна линии центров; если два круга имеют общий радиус, линия, проходящая через точки пересечения, является серединным перпендикуляром линии центров, например. линия GF в разделе 2.4.1 на рисунке 8 и может использоваться в разделе 2.5.1, рисунок 9, чтобы получить угол или боковые биссектрисы треугольника; но для перегруженности рабочего пространства показаны только соответствующие дуги.В общем, любая дуга, нарисованная в конструкции, является частью круга (общая рабочая лошадка / помощник в плоских геометрических конструкциях) с известным центром.
3.8.3. Конструкции углов
Одной из основных трудностей при построении правильных многоугольников является невозможность построить большую часть основания или внешнего угла основания. До сих пор такие углы копируются с транспортира до появления методов равнораспределения углов на любое количество частей [6]. Разделы 2.4.1 и 2.4.2 представляют два соответствующих метода построения 72 (внешний угол правильного пятиугольника), а в разделе 2.5.3 на рисунке 12 показана модификация раздела 2.4.1 для построения 51 ³/₇ ^o (внешний угол правильного семиугольника). Эти методы предполагают существование других методов построения углов некоторых из этих многоугольников, которые не исследовались.
4. Выводы
Для вводного обучения правильным многоугольникам достаточно простых построений.Эти новые методы подробно описаны в разделах 2.2.2, 2.3.1, 2.3.2, 2.3.3, 2.4.2, 2.5.1, 2.5.2, 2.5.3, 2.6.1, 2.6.2, 2.7.1. , 2.7.2, 2.7.3 и 2.8 — это новые методы, которые могут быть добавлены к любым существующим процедурам, используемым для иллюстративных построений. Инструктор может выбрать любой из перечисленных методов. Эти методы, хотя и просты, в равной степени являются стандартными процедурами, применимыми к каждому классу полигонов. Для новичков, имеющих предварительные навыки геометрического построения, эти конструкции не только будут легко усвоены, но также вызовут больший интерес, чтобы побудить их к более высоким методам построения в этой области.
Каталожные номера

[1] Бамиро О. А., Элеква И., Околи Оньединма А. С. Б, Окори О. О. и Аньяболу И. С. 1985. Вводная технология для школ и колледжей. Evans Brothers (Nigeria Publishers) Ltd, Джерико Роуд, Ибадан, Нигерия, стр. 14.
[2] Макреа М. Ф., Каледжайе А. О., Чима З. И., Гарба Г. У, Ченнон Дж. Б., Маклиш Смит А. и Хед Х. С.2008. Новая общая математика для старших классов средней школы UBE Edition. Pearson Educational Ltd, Edinburh Gate, Harlow, Essex CM 20 2EJ, England, p9.
[3] Бейли, Дэй, ФРЕЙ, Ховард, Хатченс, Маклейн, Мур-Харрис, Олт, Пелфри, При, Вильхабер и Уиллард. Математика: приложения и курс концепций 2. Флоридское издание, fl.msmaths.net McGraw Hill Glencoe. Нью-Йорк. Глава 10-7 с. 446-447.
[4] Центр сравнительного обучения и адаптации, CESAC.1986. Вводная технология для младших классов средней школы Учебник 2, стр. 16.
[5] Динамика Polygons.org Построение правильных многоугольников.
[6] Охочуку Н. С. 2015. Равнораспределение плоских геометрических углов на любое количество частей. Журнал прикладной математики, 5 (4). Pp84 — 87. http://journal.sapub.org/am.
[7] Блейки Дж. Математика среднего уровня. Кливер-Хьюм Пресс Лтд.Кесингтон Лондон. 1960, 2 ^{-е издание}, стр.186.
правильных многоугольников | Блестящая вики по математике и науке
Площадь правильного многоугольника может быть найдена разными способами в зависимости от заданных переменных. Обычно задается длина стороны ss s, апофема aaa (расстояние от центра до стороны — это также радиус тангенциальной окружности , вписанной в , часто обозначаемый как rrr), или радиус RRR (расстояние от центра до вершины — это также радиус описанной окружности ).\ circ} {n} \ right) = \ frac {n a s} {2}. \ _ \ square na2tan (n180∘) = 4ns2 кроватка (n180∘) = 2nR2 sin (n360∘) = 2nas. □
Доказательство следует из использования переменной для вычисления площади равнобедренного треугольника и последующего умножения на nnn треугольников. Вот доказательство или вывод приведенной выше формулы площади правильного многоугольника.
На рисунке ниже показан один из равнобедренных треугольников nnn, образующих правильный многоугольник.
Длина стороны обозначена как sss, радиус обозначен как RRR, а половина центрального угла обозначена как θ \ theta θ.{2} \ big). \ _\квадратный \ end {align} Ap = 45 (62) cot6180∘ = 45⋅cot30∘≈77,9 (см2). □
Апофема правильного шестиугольника имеет размер 6. Найдите площадь шестиугольника.
Пусть CCC будет центром правильного шестиугольника, а ABABAB — одной из его сторон. Нарисуйте CA, CB, CA, CB, CA, CB и апофему CDCDCD (((которая, как вы должны помнить, перпендикулярна ABABAB в точке D) .D) .D). Тогда, поскольку CA≅CBCA \ cong CBCA≅CB, △ ABC \ треугольник ABC △ ABC равнобедренный, и, в частности, для правильного шестиугольника ABC \ треугольник ABC △ ABC равносторонний.
Длина CDCDCD (((которая в данном случае также является высотой равностороннего △ ABC) \ треугольник ABC) △ ABC) составляет 32 \ frac {\ sqrt {3}} {2} в 23 раза больше длины одной стороны (((здесь AB) .AB) .AB). Таким образом, CD = 32AB ⟹ AB = 23CD = 233 (6) = 43. CD = \ frac {\ sqrt {3}} {2} {AB} \ подразумевает AB = \ frac {2} {\ sqrt {3}} {CD } = \ frac {2 \ sqrt {3}} {3} (6) = 4 \ sqrt {3}. CD = 23 AB⟹AB = 3 2 CD = 323 (6) = 43 . Теперь, когда мы нашли длину одной стороны, приступаем к поиску площади. Для этого есть (как минимум) 3 способа:
Первый метод: Используйте формулу периметра-апофемы .2} {2} \ sqrt {3} = 72 \ sqrt {3}. \ _ \ SquareA = 4ns2 cotn180∘ = 46s2 cot6180∘ = 23s2 cot30∘ = 23s2 3 = 723. □
Отправьте свой ответ
Какова площадь красной области, если площадь синей области равна 5?

Примечание: Шестигранник правильный.

Стороны	Имя	Интерьер Угол	Внешний вид Уголки
Правильные многоугольники
3	Треугольник	60.00 °	120,00 °
4	Четырехугольник	90,00 °	90,00 °
5	Пентагон	108,00 °	72,00 °
6	Шестиугольник	120.00 °	60,00 °
7	Гептагон	128,57 °	51,43 °
8	Восьмиугольник	135,00 °	45,00 °
9	Nonagon	140.00 °	40,00 °
10	Десятиугольник	144,00 °	36,00 °
11	Hendecagon	147,27 °	32,73 °
12	Додекагон	150.00 °	30,00 °
13	Triskaidecagon	152,31 °	27,69 °
14	Tetrakaidecagon	154,29 °	25,71 °
15	Pendecagon	156.00 °	24,00 °
16	Шестигранник	157,50 °	22,50 °
17	Heptdecagon	158,82 °	21,18 °
18	Восьмиугольник	160.00 °	20,00 °
19	Enneadecagon	161,05 °	18.95 °
20	Икосагон	162,00 °	18,00 °
30	Триаконтагон	168.00 °	12,00 °
40	Тетрактагон	171,00 °	9,00 °
50	Пентаконтагон	172,80 °	7.20 °
60	Шестигранник	174.00 °	6,00 °
70	Гептаконтагон	174,86 °	5,14 °
80	Octacontagon	175,50 °	4,50 °
90	Эннеаконтагон	176.00 °	4,00 °
100	Гектогон	176,40 °	3,60 °
1,000	Чилигон	179.64 °	0,36 °
10 000	Мириагон	179.96 °	0,04 °

Правильный многоугольник	Количество сторон	Внутренний угол	Уголки внешние
Равносторонний треугольник	3-х сторонний	3 внутренних угла по 60 °	3 внешних угла по 120 °
Квадрат	4 стороны	4 внутренних угла по 90 °	4 внешних угла по 90 °
Правильный пятиугольник	5 сторон	5 внутренних углов 108 °	5 внешних углов 72 °
Правильный шестигранник	6 сторон	6 внутренних углов по 120 °	6 внешних углов по 60 °
Правильный семиугольник	7 сторон	7 внутренних углов ≅ 128.57 °	7 внешних углов ≅ 51,43 °
Правильный восьмиугольник	8 сторон	8 внутренних углов 135 °	8 внешних углов по 45 °

Правильный многоугольник	Количество сторон	Внутренний угол	Уголки внешние
Обычный четырехугольник или 9-угольник	9 сторон	9 внутренних углов 140 °	9 внешних углов 40 °
Обычный десятиугольник или 10-угольник	10 сторон	10 внутренних углов 144 °	10 внешних углов 36 °
Обычный гектогон или 100-угольник	100 сторон	100 внутренних углов 176.4 °	100 внешние углы 3,6 °

[1]	Бамиро О. А., Элеква И., Околи Оньединма А. С. Б, Окори О. О. и Аньяболу И. С. 1985. Вводная технология для школ и колледжей. Evans Brothers (Nigeria Publishers) Ltd, Джерико Роуд, Ибадан, Нигерия, стр. 14.
[2]	Макреа М. Ф., Каледжайе А. О., Чима З. И., Гарба Г. У, Ченнон Дж. Б., Маклиш Смит А. и Хед Х. С.2008. Новая общая математика для старших классов средней школы UBE Edition. Pearson Educational Ltd, Edinburh Gate, Harlow, Essex CM 20 2EJ, England, p9.
[3]	Бейли, Дэй, ФРЕЙ, Ховард, Хатченс, Маклейн, Мур-Харрис, Олт, Пелфри, При, Вильхабер и Уиллард. Математика: приложения и курс концепций 2. Флоридское издание, fl.msmaths.net McGraw Hill Glencoe. Нью-Йорк. Глава 10-7 с. 446-447.
[4]	Центр сравнительного обучения и адаптации, CESAC.1986. Вводная технология для младших классов средней школы Учебник 2, стр. 16.
[5]	Динамика Polygons.org Построение правильных многоугольников.
[6]	Охочуку Н. С. 2015. Равнораспределение плоских геометрических углов на любое количество частей. Журнал прикладной математики, 5 (4). Pp84 — 87. http://journal.sapub.org/am.
[7]	Блейки Дж. Математика среднего уровня. Кливер-Хьюм Пресс Лтд.Кесингтон Лондон. 1960, 2 ^{-е издание}, стр.186.