Правильный н угольник: Правильные многоугольники — урок. Геометрия, 9 класс.

что значит, сколько видов существует, формула нахождения угла

Содержание:

• Правильный многоугольник — что значит
• Признаки и свойства правильного многоугольника
• Основные свойства, определение правильного n-угольника
• Формула угла правильного многоугольника

Содержание

• Правильный многоугольник — что значит
• Признаки и свойства правильного многоугольника
• Основные свойства, определение правильного n-угольника
• Формула угла правильного многоугольника

Правильный многоугольник — что значит

Многоугольник представляет собой часть площади, ограниченную замкнутой ломаной линией, которая не пересекает сама себя.

Многоугольники различают по количеству сторон и углов.

Примечание

Правильный многоугольник обладает одинаковыми сторонами и углами.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Существует несколько разновидностей правильных многоугольников. К наиболее известным относят равносторонний треугольник, который обладает тремя одинаковыми сторонами и углами, равными 60 градусов. В связи с этим данную геометрическую фигуру называют правильным треугольником.

Квадрат обладает четырьмя одинаковыми сторонами и углами по 90 градусов. Такую геометрическую фигуру называют правильным четырехугольником.

Источник: 100urokov.ru

Примечание

В геометрии можно встретить фигуры с одинаковыми сторонами и разными углами, к примеру, ромб. Существуют фигуры, углы которых равны, но стороны различны по длине. К данному типу относится прямоугольник. Важно отметить, что прямоугольник и ромб не являются правильными многоугольниками.

При каком-либо заданном числе n, начиная с n=3, можно построить правильный n-угольник. Примеры таких многоугольников изображены на рисунке:

Источник: 100urokov.ru

Признаки и свойства правильного многоугольника

Многоугольник можно считать правильным в том случае, когда все его стороны и углы одинаковы. Таким образом, должно выполняться правило:

\(a_{1} = a_{2} = a_{3} = … = a_{n-1} = a_{n}\)

\(\alpha _{1} = \alpha _{2} = \alpha _{3} = … = \alpha _{n-1} = \alpha _{n}\)

Существуют основные свойства, характерные для правильных многоугольников.

Источник: ru.onlinemschool.com Источник: ru.onlinemschool.com

1. Все стороны правильного многоугольника равны, то есть: \(a_{1} = a_{2} = a_{3} = … = a_{n-1} = a_{n}\)
2. Углы правильного многоугольника равны, то есть: \(\alpha _{1} = \alpha _{2} = \alpha _{3} = … = \alpha _{n-1} = \alpha _{n}\)
3. Центр вписанной в правильный многоугольник окружности \(O _{B}\) соответствует центру описанной вокруг этого многоугольника окружности \(O _{O}\), что в результате образует центр многоугольника О
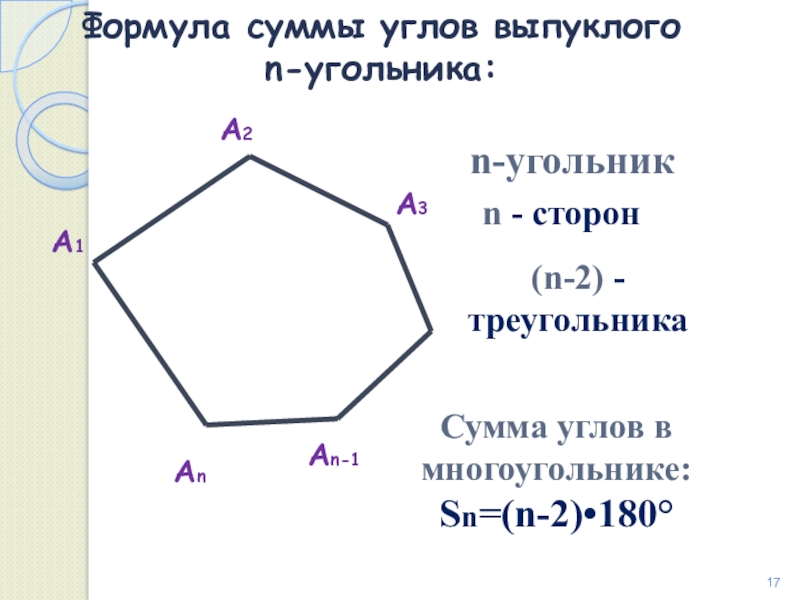
4. Сумма всех углов n-угольника составляет: \(180^{0}*(n-2)\)
5. Внешние углы n-угольника в сумме равны 360^{0} или \(\beta _{1} + \beta _{2} + \beta _{3} + … + \beta _{n-1} + \beta _{n} = 360^{0}\)
6. Число диагоналей \(D _{n}\), которыми обладает n-угольник, соответствует половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины, то есть: \(\beta _{1}=\frac{n*(n-3)}{2}\)
7. В правильный многоугольник можно вписать окружность и описать круг. {0}\)

   Известно, что треугольник можно задать с помощью длин трех его сторон. Однако в случае правильного треугольника необходимо знать только одну длину стороны, так как все правильные треугольники подобны. Таким образом, при отсутствии данных о масштабе или метрики, правильные треугольники эквивалентны друг другу.

   Источник: static-interneturok.cdnvideo.ru

   Такими же свойствами обладает квадрат, то есть правильный четырехугольник.

   Источник: static-interneturok.cdnvideo.ru

   В качестве примеров таких геометрических фигур можно рассмотреть правильные пяти, шести и сколь угодно большие n-угольники. Предельным случаем при бесконечно увеличивающемся n является окружность. Для всех таких многоугольников характерны следующие свойства:

   • геометрические фигуры задают с помощью одного параметра, то есть длиной элемента;
   • рассматриваемые многоугольники подобны всем многоугольникам своего класса.

   В геометрии можно встретить разные виды правильных n-угольников. 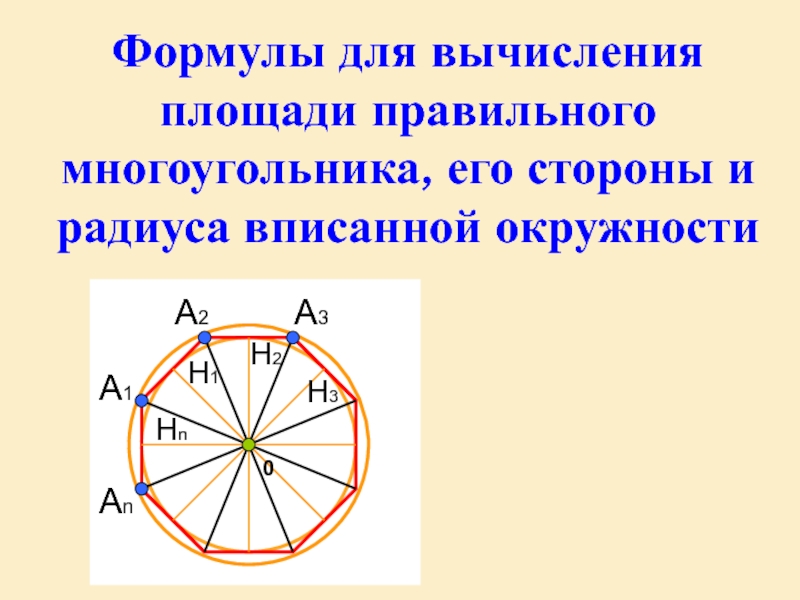Все они обладают не только одним параметром, с помощью которого задаются, но и характеризуются осями и центром симметрии. Правильный треугольник возможно три раза повернуть вокруг центра. При этом разница между данными положениями отсутствует.

   Квадрат можно повернуть таким же способом четыре раза. Предельным случаем является окружность, которую можно повернуть бесконечное число раз, но результат при этом не изменится, то есть данная геометрическая фигура обладает бесконечным количеством осей симметрии.

   В природе невозможно найти идеальную окружность или любой другой правильный n-угольник. В реальности предметы рассматривают лишь в качестве их приближений. Однако многие практические задачи характеризуются достаточно точным приближением, что позволяет применять правильные многоугольники в их решении, как полезный инструмент. Свойства таких геометрических фигур изучают и фиксируют.

   В дальнейшем при рассмотрении окружности в качестве предельного случая правильных n-угольников эти свойства переносят на нее для получения полезных утверждений не для ломаной, а для гладкой кривой.

   Известно, что равносторонний треугольник представляет собой правильный треугольник. Необходимо выяснить, является ли любой равносторонний многоугольник также правильным многоугольником.

   В качестве примера можно рассмотреть ромб, имеющий равные стороны. Таким образом, ромб является равносторонним четырехугольником, но не относится к правильным n-угольникам. К данной категории справедливо отнести только квадрат, так как он обладает не только равными сторонами, но и углами, что отличает его от ромба.

   Источник: static-interneturok.cdnvideo.ru

   Напомним, что правильными многоугольниками являются те, которые имеют равные стороны и равные углы.

   Источник: static-interneturok.cdnvideo.ru

   В случае треугольника достаточным условием является равенство сторон. Так как из этого следует равенство его углов. При рассмотрении других n-угольников это утверждение не верно.

   Формула угла правильного многоугольника

   Существует закономерность, согласно которой можно рассчитать угол правильного многоугольника. 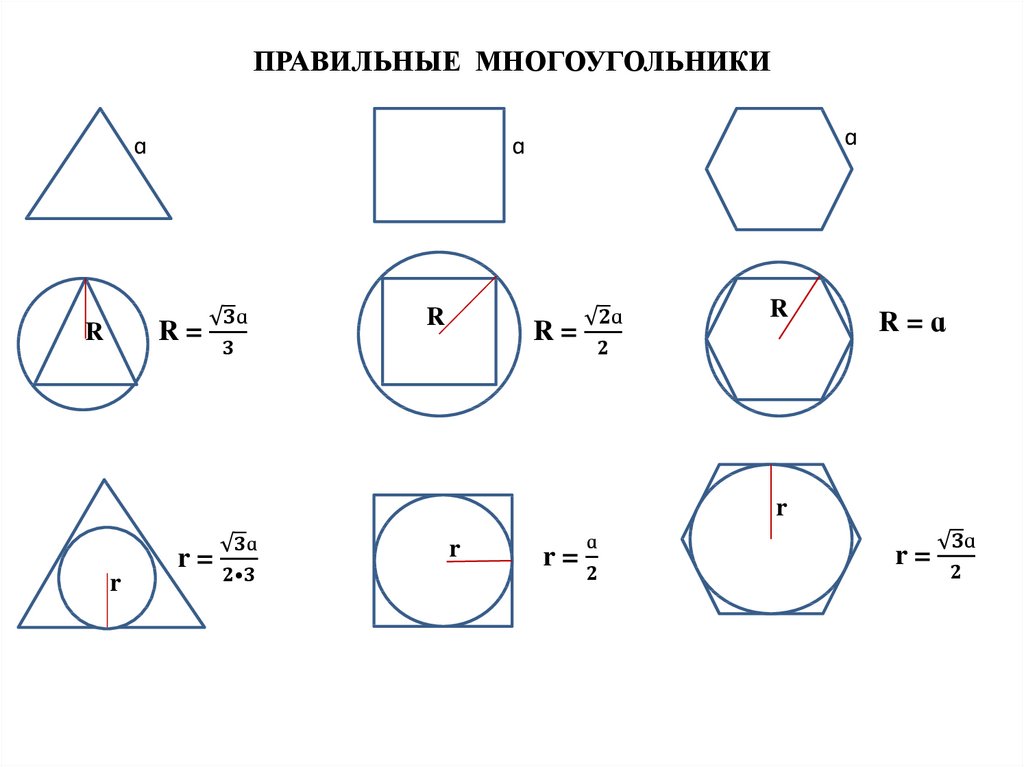{0}(n-2)}{n}\)

   \(145=\frac{180(n-2)}{n}\)

   \(145n=180(n-2)\)

   \(145n=180n-360\)

   \(145n-180n=-360\)

   \(-35n=-360\)

   \(n=\frac{360}{35}=\frac{72}{7}=10\frac{2}{7}\)

   Исходя из того, что число сторон является не целым, а дробным, можно сделать вывод о невозможности существования такого многоугольника.

   Насколько полезной была для вас статья?

   У этой статьи пока нет оценок.

   Поиск по содержимому

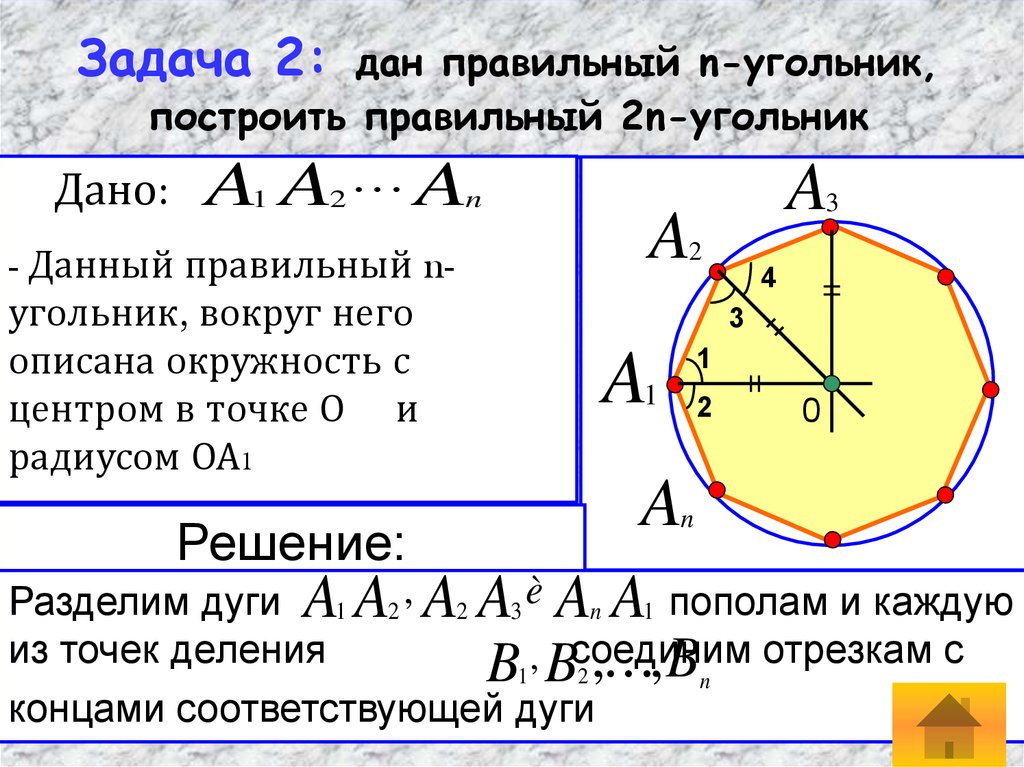
   Окружность, описанная около правильного многоугольника и вписанная в правильный многоугольник 9 класс онлайн-подготовка

   Тема 33

   Окружность, описанная около правильного многоугольника и вписанная в правильный многоугольник.

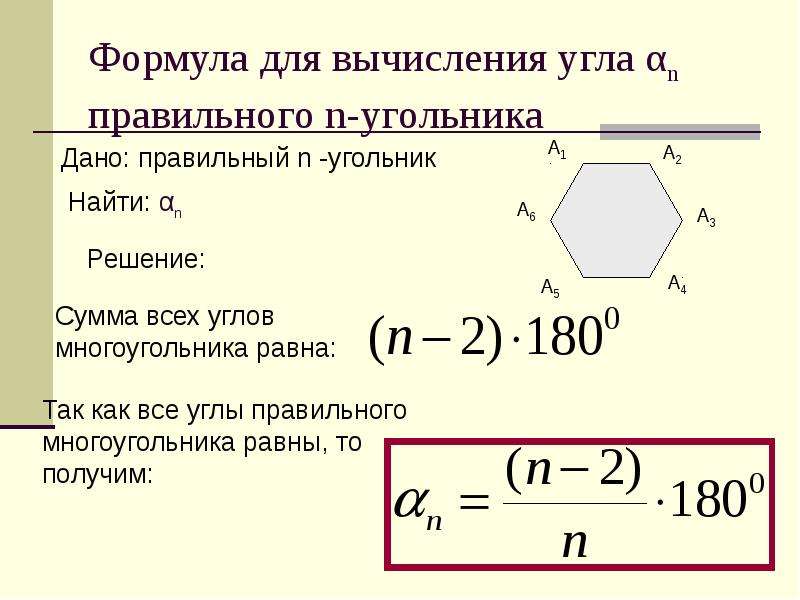
   Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.

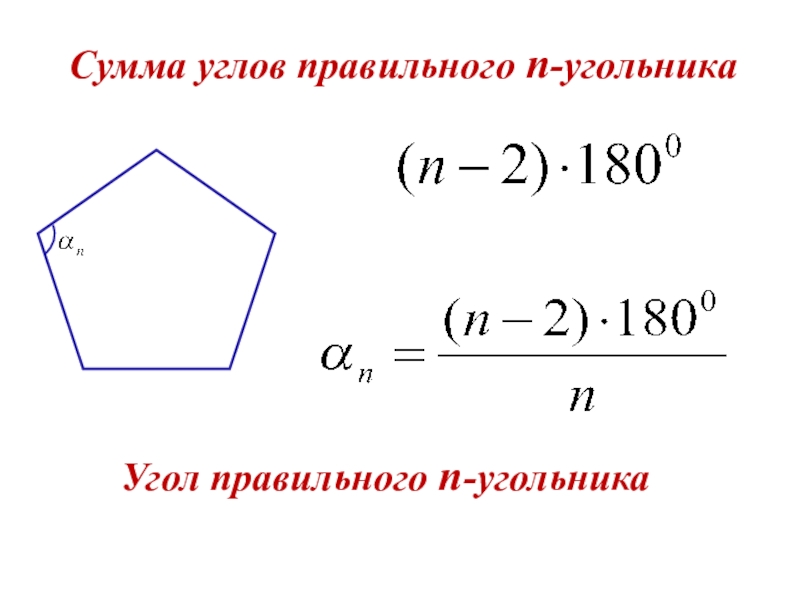
   Выведем формулу для вычисления угла α_n правильного n — угольника.

   Сумма всех углов такого n — угольника равна (n — 2) ⋅ 180°, причем все стороны и углы равны, поэтому

   αn=n-2n⋅180°

   Окружность называется описанной около многоугольника, если все его вершины многоугольника лежат на этой окружности.

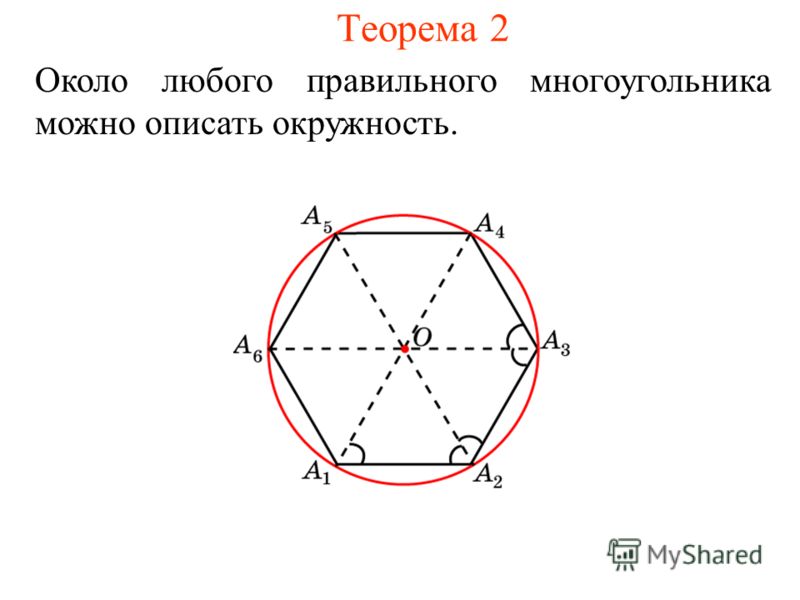
   Теорема

   Около любого правильного многоугольника можно описать окружность, и притом только одну.

   Доказательство

   Пусть A₁A₂A₃…A_n — правильный многоугольник, О — точка пересечения биссектрис углов A₁ и A₂

   Докажем, что OA₁ = OA₂ =…= OA_n

   Так как OA₁ и OA₂ – биссектрисы углов A

   1 и A₂, ∠A₁ = ∠A₂, то ∠1 = ∠2 = ∠3 = ∠4, значит, ∆A₁OA₂ равнобедренный, следовательно, OA₁ = OA₂.

   ∆A₁OA₂ = ∆A₂OA₃ по двум сторонам и углу между ними

   1. A₁A₂ = A₃A₂
   2. A₂O — общая сторона
   3. ∠3 = ∠4

   Следовательно, OA₃ = OA₁.

   Аналогично можно доказать, что OA₄ = OA₂, OA₅ = OA₃и т.д.

   Итак, OA₁ = OA₂ =…= OA_n, т.е. точка O равноудалена от всех вершин многоугольника. Значит, окружность с центром O и радиусом OA₁ является описанной около многоугольника.

   Докажем теперь, что описанная окружность только одна. 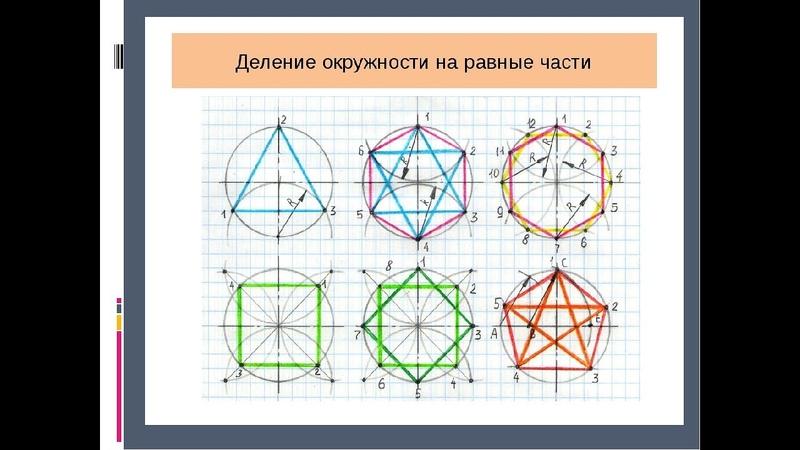Рассмотрим какие-нибудь три вершины многоугольника, например A₁, A₂, A₂. Так как через три точки проходит только одна окружность, то около многоугольника A₁A₂…A_n можно описать только одну окружность.

   Ч.т.д

   Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности

   Теорема

   В любой правильный многоугольник можно вписать окружность, и притом только одну.

   Следствие 1

   Окружность, вписанная в правильный многоугольник, касается всех сторон многоугольника в их серединах.

   Следствие 2

   Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник

   Эта точка называется центром правильного многоугольника.

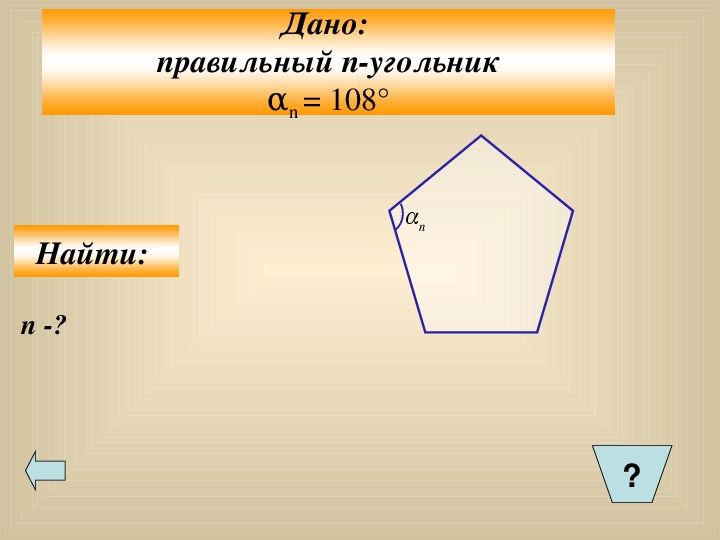
   Сколько сторон имеет правильный многоугольник, если каждый его угол равен 150°

   Воспользуемся формулой αn=n-2n⋅180°

   150°=n-2n∙180°

   150n=180n-360

   30n=360

   n=12

   Значит, правильный многоугольник имеет 12 сторон.

   find A, A_l, V, A_F

   Автор: Kenneth Alambra

   Отзыв от Dominik Czernia, PhD

   Последнее обновление: 02 февраля 2023 г.

   Содержание:
   • 010
   • Что прямоугольная пирамида и как найти A_l
   • Прямоугольная пирамида вычислить: Найти A_f
   • Общая площадь поверхности прямоугольной пирамиды
   • Формула для вычисления объема прямоугольной пирамиды
   • Другие связанные калькуляторы
   • FAQ

   В этом калькуляторе прямоугольной пирамиды вы сможете узнать:

   • как найти объем прямоугольной пирамиды,
   • как рассчитать площадь поверхности прямоугольной пирамиды и
   • различные формулы для прямоугольных пирамид.

   Что еще замечательно, вы можете найти их все, просто зная любые два измерения вашей пирамиды: ребро основания (a)

   , высота пирамиды (H) , высота наклона (s) или боковая кромка (d) , как показано на рисунке ниже:

   У вас есть проект правильной квадратной пирамиды? Вы хотите узнать различные формулы для расчета правильной квадратной пирамиды? Тогда этот калькулятор правильной квадратной пирамиды для вас! 🙂

   Если вы готовы использовать наш расчет правильной квадратной пирамиды, чтобы найти:

   • A_f — площадь боковой грани,
   • А_л — общая боковая площадь,
   • A — общая площадь поверхности, а
   • В — объем,

   тогда продолжайте чтение 051 , очень просто, а ты нужно всего лишь любых двух известных размеров вашей правильной квадратной пирамиды , чтобы найти все, что вам нужно!

   Путем ввода значений базовой кромки a длина и высота пирамиды H , вы можете мгновенно найти другие размеры вашей пирамиды, то есть высоту наклона

   s и боковую грань d длину, или наоборот. Вы также можете ввести значения для a и d , чтобы получить H и s . Вы поняли. После ввода как минимум двух измерений вычисление прямоугольной пирамиды одновременно находит объем V и общую площадь поверхности A вместе с другими площадями поверхности вашей пирамиды.

   В расширенном режиме этого калькулятора вы обнаружите, что вы также можете ввести значение для базовой диагонали длины вместе в качестве другого измерения, чтобы увидеть окончательные результаты. У нас есть отдельная диагональ квадратного калькулятора, если вы хотите узнать об этом подробнее 🙂.

   Если вам интересно узнать формулы правильной квадратной пирамиды, которые мы используем в этом калькуляторе, вы узнаете их все в следующих разделах этого текста. Читайте дальше, чтобы узнать, как рассчитать общую площадь поверхности прямоугольной пирамиды и ее объем.

   Что такое прямоугольная пирамида и как ее найти A_l

   Говоря о пирамидах, квадратные пирамиды, безусловно, являются наиболее распространенными пирамидами, о которых мы можем думать в первую очередь. Возможно, вы уже слышали и видели изображения Великих пирамид в Гизе. Это пример правильной квадратной пирамиды (по крайней мере приблизительно).

   Мы называем квадратную пирамиду «правильной» (или «правильной») всякий раз, когда ее вершина совпадает непосредственно с центром ее квадратного основания (отсюда и название «квадратная» пирамида). Термин «правильный» произошел от прямого угла, образованного воображаемой линией, соединяющей центр квадратного основания пирамиды и вершину пирамиды. Эта характеристика прямоугольной пирамиды приводит к тому, что ее боковые грани равны . Мы также можем наблюдать это с другими правильными пирамидами с правильными многоугольными основаниями.

   При этом при определении общей боковой площади прямоугольной пирамиды (показанной на анимированном изображении выше) мы обозначаем как A_l , мы можем рассчитать его, найдя площадь боковой поверхности A_f и умножив ее на 4, как показано в уравнении ниже:

   A_l = 4 * A_f

   это то, что нам нужно; скажем, если мы хотим нарисовать видимые стороны пирамиды.

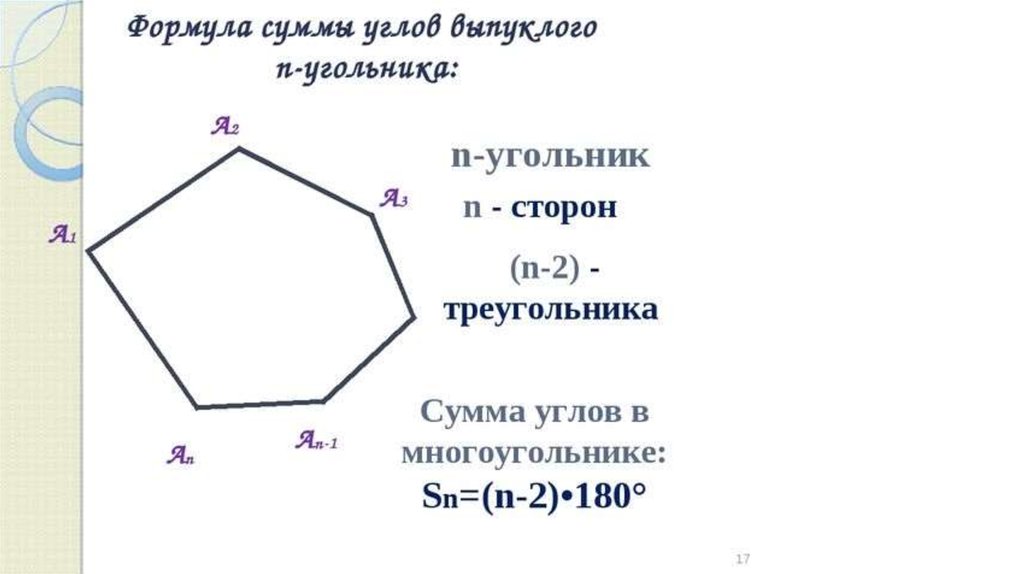
   Расчет прямоугольной пирамиды: найти A_f

   Поскольку мы не можем найти A_l, не зная A_f (показано на рисунке ниже), в этом разделе мы обсудим, как вычислить A_f.

   Чтобы найти A_f , возьмем одну боковую грань пирамиды, представляющую собой равнобедренный треугольник, и вычислим ее площадь по формуле:

   A_f = (a * s) / 2

   где:

   • a — Размер стороны квадратного основания пирамиды; и
   • s — Наклонная высота пирамиды.

   Наклонная высота также является гипотенузой внутреннего воображаемого прямоугольного треугольника (выделено розовым цветом), образованного внутри пирамиды, как показано на рисунке ниже:

   С помощью теоремы Пифагора мы можем найти наклонную высоту по следующей формуле:

   s² = H² + (a / 2)² ,

   , где H — высота квадратной пирамиды.

   💡 Пока мы здесь, мы также можем найти боковое ребро, d , рассмотрев прямоугольный треугольник, образованный делением боковой грани пополам, и используя теорему Пифагора следующим образом:
   d² = s² + (a / 2)²

   Выразив наклонную высоту через H и a , у нас может быть упрощенная формула для нахождения d , как показано ниже:

   d² = H² + a² / 2

   Мы также можем найти высоту прямоугольной пирамиды, H , измерив его боковую кромку ( d ) и преобразовав приведенную выше формулу в следующее уравнение:

   H² = d² - a² / 2

   🙋 Вопреки тому, что мы обсуждали ранее, на самом деле мы можем найти A_l без A_f . Но только если мы знаем s . Итак, теперь, если мы заменим формулу A_F в формулу A_L , и упростите ее, мы можем получить это более простое уравнение для A_L :

   A_L = 2 * A * S

   Общая область поверхности. прямоугольной пирамиды

   Возвращаясь к площади поверхности прямоугольной пирамиды, если мы хотим рассчитать ее общую площадь поверхности , A , нам нужно добавить площадь основания , A_b , к площади боковой поверхности, A_l как показано ниже:

   A = A_l + A_b

   Поскольку мы имеем дело с пирамидой с квадратным основанием, площадь ее основания будет равна площадь квадрата, которая будет равна:

   A_b = a² ,

   где a , опять же, является измерением стороны квадратного основания пирамиды.

   Площадь основания правильной квадратной пирамиды нужна не только для нахождения общей площади поверхности вашей пирамиды. Вы тоже обязательно используйте площадь основания для нахождения объема вашей пирамиды . Узнайте, как это сделать, в следующем разделе этого текста 🙂

   Формула для объема прямоугольной пирамиды

   Нахождение объема прямоугольной пирамиды основано на той же концепции, что и нахождение объема конуса. Умножив площадь основания пирамиды на высоту пирамиды и разделив ее на 3, мы получим объем нашего твердого тела, как показано в этом уравнении:

   V = A_b * H / 3

   0035 квадрат также технически является прямоугольником (но не наоборот), вы также можете использовать наш прямоугольный калькулятор пирамиды для получения результатов в этом калькуляторе. Тем не менее, вам придется дважды ввести размер основания.

   Знание того, как рассчитать объем правильной квадратной пирамиды, может быть очень полезным, скажем, для проектов по формованию и литью. Чтобы количественно определить, сколько нужно залить в прямоугольную форму в форме пирамиды, вы можете легко рассчитать объем вашей формы после измерения, скажем, внутренней стороны вашей формы (9). 0050 a ), и возможно высота ( H ) или боковая кромка ( d ).

   Если вы найдете этот калькулятор информативным и интересным, возможно, вам также пригодятся следующие:

   • Калькулятор прямоугольной пирамиды
   • Калькулятор объема пирамиды
   • Калькулятор квадратной пирамиды
   • Калькулятор объема квадратной пирамиды
   • Калькулятор высоты квадратной пирамиды
   • Калькулятор площади поверхности квадратной пирамиды
   • Калькулятор объема прямоугольной пирамиды
   • Калькулятор площади поверхности прямоугольной пирамиды

   Часто задаваемые вопросы

   Какой объем прямоугольной пирамиды может поместиться в 12-дюймовый куб?

   Так как наша правильная квадратная пирамида умещается в 12-дюймовом кубе, ребро основания нашей пирамиды имеет длину 12 дюймов, а ее высота равна 12 дюймам. Чтобы получить его объем:

   1. Получите площадь основания, возведя длину основания в квадрат, 12 дюймов * 12 дюймов = 144 дюйма² .
   2. Затем умножьте эту площадь на высоту пирамиды, 144 дюйма² * 12 дюймов = 1728 дюймов³ .
   3. Наконец, разделите это на 3, 1728 дюймов³ / 3 = 576 дюймов³ .

   Какова площадь поверхности прямоугольной пирамиды?

   Допустим, его основание имеет размеры 6 дюймов, его высота 4 дюйма, а наклонная высота 5 дюймов:

   1. Сначала вычислите площадь его боковой поверхности, 6 дюймов * 5 дюймов / 2 = 15 дюймов² .
   2. После этого умножьте боковую площадь лица на 4, чтобы найти общую боковую площадь (A_l), 15 дюймов² * 4 = 60 дюймов² .
   3. Затем найдите площадь основания пирамиды (A_b), 6 дюймов * 6 дюймов = 36 дюймов² .
   4. Наконец, сложите A_l и A_b, чтобы получить общую площадь поверхности, 60 дюймов² + 36 дюймов² = 96 дюймов²

   Сколько прямых углов у пирамиды с квадратным основанием?

   Прямоугольная пирамида имеет только четыре прямых угла , и вы можете найти их в четырех углах ее квадратного основания. Все остальные углы прямоугольной пирамиды острые. Однако другие квадратные пирамиды, которые не являются «правильными», могут иметь на один до 3 (очень частный случай) прямых углов больше.

   Кеннет Аламбра

   Этот калькулятор может найти площадь поверхности и объем любой прямоугольной пирамиды . Начните вычисления, введя любых двух измерений вашей пирамиды.

   Базовая кромка (a)

   Высота пирамиды (H)

   Наклонная высота (s)

   Боковая кромка (d)

   Предварительные результаты

   Площадь боковой поверхности (A_ f)

   Базовая зона (A_b)

   Результаты

   Общая боковая площадь (A_l)

   Общая площадь поверхности (A)

   Объем (V)

   Посмотреть 23 похожих калькулятора 3d геометрии 📦

   Площадь полушарияCubeCube Рассчитать: найти v, a, d… Еще 20

   Объем прямоугольной пирамиды 9 0001

   LearnPracticeDownload

   Объем прямоугольной пирамиды – это пространство, занимаемое прямоугольной пирамидой. Прямоугольная пирамида представляет собой трехмерную геометрическую фигуру, имеющую прямоугольное основание и четыре треугольные грани, соединенные в вершине. Давайте узнаем, как найти объем прямоугольной пирамиды с помощью нескольких решенных примеров и практических вопросов.

   1.	Каков объем прямоугольной пирамиды?
   2.	Формула объема прямоугольной пирамиды
   3.	Как найти объем прямоугольной пирамиды?
   4.	Часто задаваемые вопросы о пирамиде Right Square Volume

   Каков объем прямоугольной пирамиды?

   Объем прямоугольной пирамиды — это количество единичных кубов, которые могут в нее поместиться. Прямоугольная пирамида представляет собой трехмерную фигуру, имеющую прямоугольное основание и четыре треугольные грани, соединенные в вершине. Прямоугольная пирамида представляет собой многогранник (пятигранник) с пятью гранями. Единицей объема являются «кубические единицы». Например, это может быть выражено как m ³ , cm ³ , in ³ и т. д. в зависимости от заданных единиц.

   Прямоугольная пирамида состоит из трех компонентов.

   • Верхняя точка пирамиды называется вершиной.
   • Нижний правый квадрат называется основанием.
   • Стороны треугольника называются гранями.

   Формула объема прямоугольной пирамиды

   Формула для определения объема прямоугольной пирамиды: V = 1/3 × b ² × h, где «b» — длина основания, а « h» — высота перпендикуляра. Связь между наклонной высотой, перпендикулярной высотой и основанием определяется с помощью теоремы Пифагора s ² = h ² + (b/2) ² , где «s», «h» и «b» — наклон. высота, высота перпендикуляра и длина основания правильной квадратной пирамиды соответственно. Таким образом, объем правильной квадратной пирамиды получается путем замены данных размеров в формуле V = 1/3 × b ² × h.

   Как найти объем прямоугольной пирамиды? 92 \раз \text{ч}\). Таким образом, мы следуем приведенным ниже шагам, чтобы найти объем правильной квадратной пирамиды.

   • Шаг 1: Определите площадь основания (b ² ) и высоту (h) пирамиды.
   • Шаг 2: Найдите объем по формуле 1/3 × b ² × h
   • Шаг 3: Представьте окончательный ответ в кубических единицах.

   Пример: Найдите объем правильной квадратной пирамиды, высота и длина основания которой равны 9ед. и 5 ед. соответственно.

   Решение: Учитывая, что h = 9 единиц и b = 5 единиц.

   Тогда объем правильной квадратной пирамиды равен V = 1/3 × b ² × h
   ⇒ V = 1/3 × 5 ² × 9
   ⇒ V = 5 ² × 3 = 75 кубических единиц

   Ответ: Объем правильной квадратной пирамиды равен 75 кубических единиц.

    

   Решенные примеры на объем прямоугольной пирамиды

   1. Пример 1: У Юлии есть сосуд в виде перевернутой правильной прямоугольной пирамиды, который нужно наполнить водой. Высота сосуда 10 дюймов, а длина кромки основания 7 дюймов. Какой объем воды Юля может налить в сосуд?

      Решение: Дано h = 10 дюймов и b = 7 дюймов

      Объем сосуда равен V = 1/3 × b ² × h
      ⇒ V = 1/3 × 7 ² × 10
      ⇒ V = 490/3
      ⇒ V = 163,33 кубических дюйма

      Ответ: Таким образом, объем сосуда равен 163,33 в ³ .

   2. Пример 2: Каков будет объем правильной квадратной пирамиды со стороной основания 10 см и высотой 18 см?

      Решение: Учитывая, что b = 10 см и h = 18 см

      Формула объема квадратной пирамиды определяется как V = 1/3 × b ² × h

      Площадь основания = Квадрат длины основания = 10 ² или 100  см ² .
      Подставив в формулу значения b ² = 100 и h = 18.

      V = 1/3 × 100 × 18 = 600 см ³ .

      Ответ: Объем правильной квадратной пирамиды равен 600 см ³ .

   перейти к слайдуперейти к слайду

   Разбивайте сложные концепции с помощью простых визуальных средств.

   Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

   Записаться на бесплатный пробный урок

   Практические вопросы по объему прямоугольной пирамиды

    

   перейти к слайдуперейти к слайду

   Часто задаваемые вопросы об объеме прямоугольной пирамиды

   Каков объем прямоугольной пирамиды?

   Объем прямоугольной пирамиды определяется как количество единичных кубов, которые могут поместиться в прямоугольную пирамиду. Прямоугольная пирамида представляет собой трехмерную геометрическую фигуру, имеющую прямоугольное основание и четыре треугольные грани, соединенные в вершине.

   В каких единицах измеряется объем правильной квадратной пирамиды?

   Единица измерения объема правильной квадратной пирамиды указывается в кубических единицах. Например, м ³ , см ³ , ин ³ и т. д. в зависимости от заданных единиц.

   Какова формула объема прямоугольной пирамиды?

   Формула объема правильной квадратной пирамиды представлена ​​в виде V = 1/3 × Площадь основания × Высота = 1/3 × b ² × h, где b ² показывает площадь основания, а h показывает высоту правильной квадратной пирамиды.

   Как найти объем прямоугольной пирамиды?

   Объем (V) прямоугольной пирамиды можно найти, выполнив следующие шаги:

   • Шаг 1: Найдите площадь основания (b ² ) и высоту (h) пирамиды.
   • Шаг 2: Определите объем по формуле 1/3 × b ² × h
   • Шаг 3: Теперь запишите окончательный ответ в кубических единицах.

   Как найти объем прямоугольной пирамиды с наклонной высотой?

   Объем (V) прямоугольной пирамиды можно найти, выполнив следующие шаги:

   • Шаг 1: Определите заданные размеры правильной квадратной пирамиды.
   • Шаг 2: Найдите недостающий размер по формуле s ² = h ² + (b/2) ² где «s», «h» и «b» — наклонная высота, высота длины перпендикуляра и длины основания правильной квадратной пирамиды соответственно.
   • Шаг 2: Определите объем по формуле V = 1/3 × b ² × h
   • Шаг 3: Теперь запишите окончательный ответ в кубических единицах.

   Что произойдет с объемом прямоугольной пирамиды, если высоту пирамиды увеличить вдвое?

   Объем правильной квадратной пирамиды удваивается, если высота пирамиды удваивается как «h». В формуле V = 1/3 × b ² × h, высота подстановки = 2h, V = 1/3 × b ² × (2h) = 2 × (1/3 × b ² × h), что дает удвоенный объем исходного объема правильной квадратной пирамиды.