Презентация на тему: «Построение правильного пятиугольника «Геометрия обладает двумя великими сокровищами. Первое — это теорема Пифагора, второе
1 Построение правильного пятиугольника «Геометрия обладает двумя великими сокровищами. Первое — это теорема Пифагора, второе — деления отрезка в крайнем и среднем отношении» Иоганн Кеплер
2
Правильные многоугольники привлекали внимание древнегреческих учёных ещё задолго да Архимеда.
Это я и вознамерился сделать». Живописец подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица – ртом и т.д. Известен пропорциональный циркуль Дюрера. 4
Леонардо да Винчи также много писал о многоугольниках, но именно Дюрер, а не Леонардо, передал средневековые способы построения потомкам.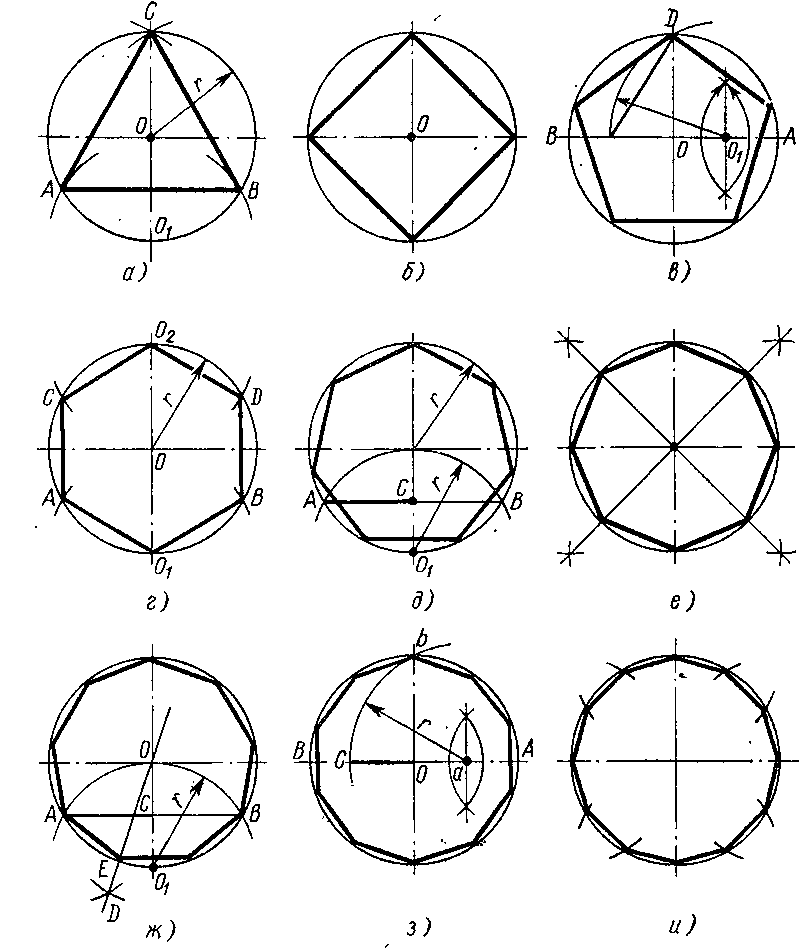
Дюрер, конечно, был знаком с » Началами» Евклида, но не привел в своем «Руководстве к измерению» (о построениях при помощи циркуля и линейки) предложенный Евклидом теоретически точный способ построения правильного пятиугольника.
5
Предложенное Евклидом построение правильного пятиугольника включает в себя деление отрезка прямой в среднем и крайнем отношении, названное впоследствии золотым сечением и привлекавшим к себе внимание художников и архитекторов на протяжении нескольких столетий.
6 Способы построение пятиугольника По Дюреру По Евклиду
7
Пентагональная симметрия встречается только в живой природе и является отличительной чертой саморегулирующихся систем.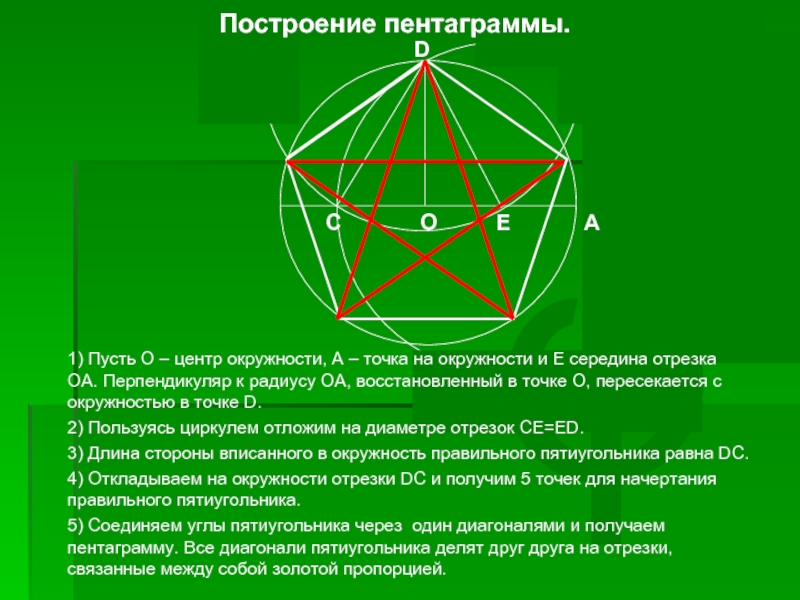
8
Приближенное построение правильного пятиугольника представляет собой интерес.
» Построение по Дюреру9 AB C D E F G H J K Вернуться Попробуем выполнить построение Дюрера самостоятельно: Тест
10
1.
11 Следующий вопрос
12 Вернуться к вопросу!
13
2.
Кто из перечисленных ученых не исследовал пятиугольники? Коперник Евклид Дюрер
14 Следующий вопрос
15 Вернуться к вопросу!
16
3.
Как называется великий труд Евклида? «Основы геометрии» «Пентаграммы» «Начала»
17 Следующий вопрос
18 Вернуться к вопросу!
19
4.
Где встречается пентагональная симметрия? В неживой природе В живой природе В учебнике геометрии
20 Выйти из теста
21 Вернуться к вопросу!
22
Выполнила Бурова Елена ученица 9Б класса МОУ «Лицей 43» Проверила Лобанова О.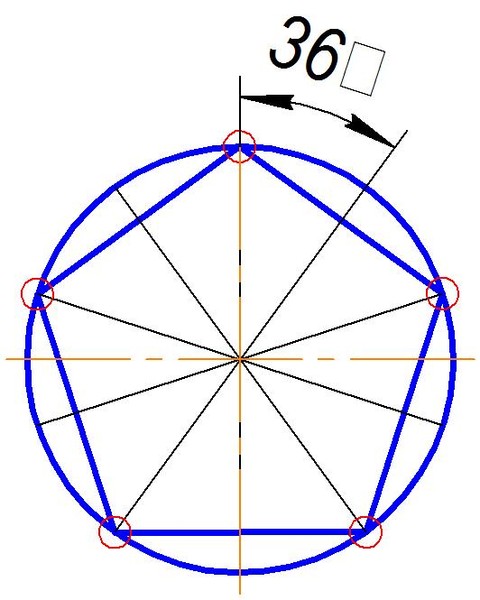
Е. учитель алгебры и геометрии МОУ «Лицей 43» Саранск 2007
23 Выход
Все страницы — Юнионпедия
Все страницы — ЮнионпедияНовый! Скачать Юнионпедия на вашем Android™ устройстве!
УстановитьБолее быстрый доступ, чем браузер!Все страницы · Предыдущая («Торонто Блю Джейс» в сезоне 2004) · Следующий (Ɐ (звук))
Из:
| ⬠ | ⬡ | ⬣ |
| ⬤ | ⬥ | ⬦ |
| ⬧ | ⬨ | ⬩ |
| ⬪ | ⬫ | ⬬ |
| ⬭ | ⬮ | ⬯ |
| ⬰ | ⬱ | ⬲ |
| ⬳ | ⬴ | ⬶ |
| ⬷ | ⬸ | ⬹ |
| ⬺ | ⬻ | ⬼ |
| ⬽ | ⬾ | ⬿ |
| ⬌ | ⬜ | ⬃ |
| ⬈ | ⬵ | ⬑ |
| ⬂ | ⬄ | ⬆ |
| ⬇ | ⬅ | ⬉ |
| ⬋ | ⬛ | ⬀ |
| ⭊ | ⭚ | ⭟ |
| ⭎ | ⭞ | ⭁ |
| ⭍ | ⭏ | 子 |
| ⭝ | ⭠ | ⭡ |
| ⭢ | ⭣ | ⭤ |
| ⭥ | ⭦ | ⭧ |
| ⭨ | ⭩ | ⭪ |
| ⭫ | 孫大文 | ⭬ |
| ⭭ | ⭮ | ⭯ |
| ⭰ | ⭱ | ⭲ |
| ⭳ | ⭶ | ⭷ |
| ⭸ | ⭹ | ⭺ |
| ⭻ | ⭼ | ⭽ |
| ⭾ | ⭿ | ⭌ |
| ⭜ | ⭃ | ⭈ |
| ⭘ | 字母词 Lettered-words | ⭂ |
| ⭓ | ⭔ | ⭄ |
| ⭆ | ⭇ | ⭕ |
| ⭅ | ⭉ | ⭋ |
| ⭛ | ⭀ | 孙大文 |
| ® | Į | ஊ |
| ச | ⮊ | ⮚ |
| சங்கர் மகாதேவன் | ச் | ட |
| ⮟ | ட் | எ |
| ஞ | ⮎ | ⮞ |
| ஞ் | ⮁ | ⮍ |
| ஏ | ⮏ | ஐ |
| ⮐ | ⮝ | ⮠ |
| ⮡ | ⮢ | ண |
| ⮣ | ண் | த |
| ⮤ | த் | ⮥ |
| ⮦ | ⮧ | ந |
| ⮨ | ந் | ன |
| ⮩ | ப | ⮪ |
| ப் | ⮫ | ⮬ |
| ⮭ | ம | ⮮ |
| ய | ⮯ | ர |
| ⮰ | ற | ⮱ |
| ல | ⮲ | ள |
| ⮳ | ழ | ⮴ |
| ⮶ | ⮷ | ஸ |
| ⮸ | ஸ் | ⮹ |
| ⮌ | ⮜ | ஃ |
| ⮃ | ஈ | ⮈ |
| ஈ (எழுத்து) | ⮘ | வ |
| ⮵ | ⮑ | ஒ |
| ⮒ | ⮂ | ஓ |
| ⮓ | ஔ | ⮔ |
| ⮄ | ஆ | ⮆ |
| இ | ⮇ | இலங்கைத் துடுப்பாட்ட அணி |
| க | ⮕ | க் |
| அ | ⮅ | உ |
| ⮉ | ⮋ | ⮛ |
| ⮀ | 宀 | ங |
| ⮙ | ங் | ¯ |
| ⯊ | ⯁ | ⯬ |
| ⯭ | ⯮ | ⯯ |
| ௹ | 寺沢 徹 | ⯃ |
| ⯈ | ⯂ | ⯆ |
| ⯇ | ⯅ | ⯋ |
| ⯀ | ° | İ |
| Ű | İ (латиница) | İ с точкой |
| İş Bankası | İşbank Tower 1 | °C |
| °C-ute | İctimai Televiziya | İctimai Televiziya və Radio Yayımları Şirkəti |
| °F | İhlas Haber Ajansı | İhlas Holding |
| İlham Tanui Özbilen | İlkay Gündoğan | °Ra |
| İrem Karamete | చ | İstanbul Deniz Otobüsleri |
| ట | ఞ | 小宮山清 |
| 小谷 欣矢 | 小澤 征爾 | ఝ |
| ఠ | డ | ఢ |
| ణ | త | థ |
| ద | ధ | న |
| ప | Ⱚ | ఫ |
| బ | భ | య |
| ర | ల | శ |
| ష | స | హ |
| 尾崎 好美 | 尾方 剛 | °С |
| జ | ఘ | ఖ |
| గ | ఔ | క |
| అ | ఛ | Ⰰ |
| ఙ | ± | Ⱡ |
| ⱡ | Ɫ | Ɽ |
| Ɑ | Ɑ (звук) | Ɑ́ |
| Ɑ̌ | Ɑ̂ | Ɑ̀ |
| Ɱ | Ɱ (звук) | Ɐ |
правильный пятиугольник
правильный пятиугольник
Введение В данной статье описывается построение правильного пятиугольника. Также объясняется, почему эта конструкция является правильной. Строительство
Строительство включает в себя следующие этапы:
2. конструктивный центр М CD 3. построить линию перпендикулярно CD и через D 4. Нарисуйте N, так что DN = DM 5. продлить линию CN 6. нарисуйте окружность с центром N и радиусом DN, P пересечение с продолженной линией от 5.  7. Продлить биссектрису CD 8. Нарисуйте окружность с центром C и радиусом CP, A пересечет биссектрису CD 9. Нарисуйте окружности с радиусом CD и центрами A, C и D. Точки B и E — другие углы пятиугольника. Почему это правильно? Посмотрите на рисунок 2:
Каждый угол пятиугольника равен 108 градусам.
Все углы треугольников вместе составляют 5 * 180 = 900 градусов. Вычесть углы в центре: 900 — 360 = 540 град. Каждый угол пятиугольника равен 540/5=108 градусов. L ECD = L CED так Каждый угол отмечен + 36 градусов. CS — биссектриса L ACD L CSD = L SDC = 72 градуса, поэтому
.
частей. отношение которых равно сторонам угла
х 2 — х — 1 = 0
Расчет предоставляется читателю. | ||||||||||||
./images/bmCT.gif»/>
Применим эту лемму:Евклидово построение правильного пятиугольника с заданной длиной ребра
Наиболее известный метод построения правильного пятиугольника заключается в том, что его вписывают в заданную окружность с известным центром. Его легко найти в Интернете или в учебниках, и я не буду воспроизводить здесь эту конструкцию.
Поскольку диагонали и стороны правильного пятиугольника находятся в золотом сечении, также несложно построить золотой прямоугольник, а затем использовать его для построения правильного пятиугольника. Однако, учитывая легкость поиска инструкций по построению золотого прямоугольника в другом месте, я также не публикую это построение здесь. Этот начинается с двух различных точек, А и В, и отрезка, который их соединяет. Цель здесь состоит в том, чтобы начать только с этого, а затем построить правильный пятиугольник со сторонами длины AB, используя только методы, разрешенные для евклидовых построений.
После того, как отрезок AB был нарисован, следующим шагом будет продолжение его в обоих направлениях, чтобы сформировать линию AB. Затем постройте две окружности, каждая с радиусом AB: одна с центром в A, а другая с центром в B. Эти окружности должны пересекаться в двух точках, обозначенных C и D, как показано выше. Следующим шагом является построение линии CD и обозначение точкой E пересечения линий AB и CD.
Это хорошо известная процедура построения серединного перпендикуляра к отрезку, поэтому Е — середина отрезка АВ, а все четыре угла с вершинами в Е — прямые.
Затем постройте окружность с центром в точке E и радиусом AE. Обозначьте точкой F точку пересечения этой окружности с отрезком СЕ. После этого постройте окружность с центром в B и радиусом BE. Эта окружность пересекает линию AB в двух точках, одна из которых уже помечена как E. Обозначьте как точку G другую такую точку пересечения. В настоящее время, поскольку все они являются радиусами кругов одинакового размера, следующие длины равны: AE, BE, BG и EF. Однако отрезок EG в два раза длиннее любого из этих более коротких и равных по длине отрезков, поскольку он представляет собой прямой отрезок, образованный объединением непересекающихся отрезков BE и BG. Поскольку то же самое можно сказать и об отрезке AB — его длина равна AE + BE, или 2AE подстановкой и сложением, — то AB = EG. Следующим шагом является построение линии FG, в которую обязательно входит отрезок FG.
Так как отрезок FG является гипотенузой прямоугольного треугольника EFG, у которого один катет (отрезок EG) вдвое длиннее другого катета (отрезок EF), то из теоремы Пифагора следует, что расстояние FG равно расстоянию EF умножить на квадратный корень из пяти. Затем постройте окружность с центром в точке F и радиусом отрезка EF. Обозначьте точки пересечения линии FG и этой окружности точками H и K, как показано выше, где K ближе к точке G. Теперь есть два новых сегмента, FH и FK, которые, поскольку они являются радиусами той же окружности, что и отрезок EF, равны по длине отрезку EF, а также отрезкам AE, BE и GB, каждый из которых, как уже было показано, равен EF по длине и вдвое короче любого из отрезки EG и AB равной длины.
Следующим шагом будет построение окружности с центром в G и радиусом EG. После этого рассмотрим коллинеарные и смежные отрезки FH и FG, которые вместе составляют отрезок GH. FH — один из нескольких отрезков, которые, как известно, в два раза длиннее AB, а длина FG, как уже известно, равна этой более короткой длине (длине отрезков EF, FH, AE и т.
д.), умноженной на квадратный корень из пяти. Таким образом, согласно постулату сложения сегментов, длина сегмента GH равна длине одного из более коротких сегментов AE, EF и т. д., умноженной на сумму единицы и квадратного корня из пяти. Эта длина, GH, будет использоваться как длина диагонали правильного пятиугольника, поскольку длина GH и исходная длина ребра (AB) находятся в золотом сечении, поскольку отрезок AB в два раза длиннее отрезка EF, и GH равно EF, умноженному на сумму единицы и квадратного корня из пяти. GH — радиус следующего круга, который нужно построить, и этот круг должен быть с центром в H. Этот круг, самый большой из построенных, пересекает круг радиуса EG с центром в G в двух точках. Одну из этих точек пересечения, на той же стороне от линии AB, что и прямоугольный треугольник EFG, не нужно помечать, а другую, по другую сторону от линии AB, следует помечать как точку J, как показано выше. Следовательно, отрезки GJ и EG имеют одинаковую длину, поскольку они являются радиусами одной и той же окружности, а расстояние EG, как уже было показано, равно расстоянию AB, поэтому GJ также = AB.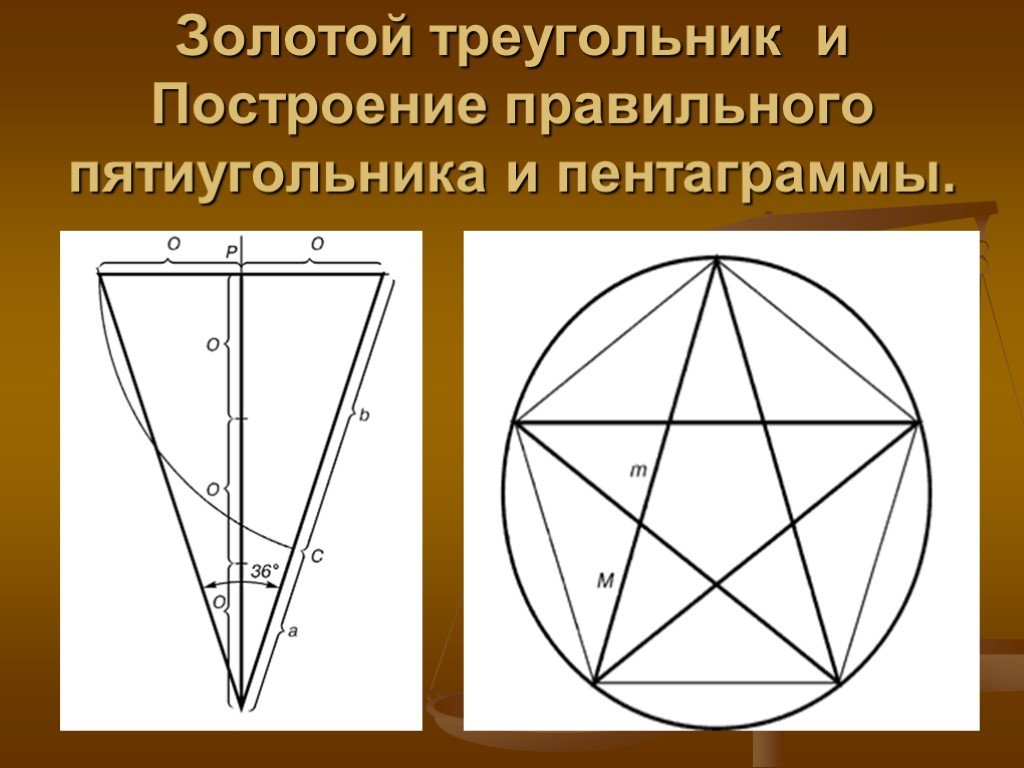
Отрезки GJ и AB выделены розовым цветом на приведенной выше диаграмме с указанием их длин, чтобы обеспечить дополнительное доказательство того, что их длины равны.
На приведенной выше диаграмме отрезок GJ выделен жирным шрифтом, поскольку он является стороной строящегося пятиугольника. Затем строится отрезок HJ, который также выделен жирным шрифтом, поскольку он является диагональю того же самого пятиугольника и имеет правильную длину в силу того, что он является радиусом той же окружности, что и отрезок GH, который, как уже было показано, имеет правильную длину. для диагонали пятиугольника. Следующим шагом будет определение точки L, которая будет вершиной пятиугольника. Для этого постройте окружность радиуса HK с центром в H. Поскольку отрезок HK образован непересекающимися, смежными и коллинеарными отрезками FH и FK, каждый из которых имеет ту же длину, что и AE или AB, отсюда следует, что HK, радиус последней построенной окружности, равен по длине как AB, так и GJ, причем это расстояние равно длине стороны строящегося пятиугольника.
Затем постройте окружность радиусом GH (длина диагонали пятиугольника) с центром в точке G. Эта окружность и уже построенная окружность радиусом HK с центром в точке H пересекаются в двух точках. Обозначьте одну из этих точек пересечения (ту, что на той же стороне от линии AB, что и точка J) как точку L, как показано выше, а затем постройте стороны пятиугольника HL и JL, также выделенные жирным шрифтом на рисунке выше. (Также показаны: измеренные длины всех сегментов, выделенных до сих пор жирным шрифтом, а также AB.) Из этих двух последних точек пересечения окружностей одна теперь помечена как точка L. Следующим шагом является пометка другого такого пересечения как точка М, как показано на рисунке ниже.
Как только точка M будет найдена, оставшиеся стороны и диагонали правильного пятиугольника GJLHM можно построить, как показано выше, выделенным жирным шрифтом, просто соединив каждую оставшуюся несоединенную пару пятиугольников-вершин отрезком. Длины всех сегментов, выделенных жирным шрифтом, плюс исходный сегмент AB также показаны выше.
Как видите, все пять сторон имеют длину, равную длине отрезка АВ, а все пять диагоналей имеют длину большую, чем длина АВ, но постоянную на всем наборе диагоналей.
На приведенной выше диаграмме новые объекты не были построены с помощью инструментов Евклида, но пятиугольнику был присвоен цвет, и была выполнена проверка отношения длины диагонали к длине стороны. Как видите, в самом верхнем вычислении десятичное приближение для этого отношения расстояний дается как 1,61803. Тот же результат получается во втором показанном вычислении, когда сумма одного и квадратного корня из пяти делится на два, и, поскольку это определение золотого сечения, получается один и тот же результат для обоих из эти расчеты, обеспечивают подтверждающие доказательства правильности этой конструкции.
Чтобы выполнить еще один тест этой конструкции — он возможен только с виртуальным компасом и линейкой, такой как Geometer’s Sketchpad , который я использовал здесь — точки A и/или B можно перемещать.