Расчет балок онлайн. Примеры расчета
Расчет балки различается в зависимости от того, является она статически определимой, либо статически неопределимой. На сайте производится расчет любых балок, но подробное решение расписывается только для статически определимых балок, не имеющих промежуточных шарниров.
Балка на двух опорах. Построение эпюр
Для этого типа балок сервис позволяет определить и подробно расписывает:
- реакции опор
- эпюры поперечных сил и изгибающих моментов (эпюры Q и M)
- подбор сечений — двутавр, прямоугольник, круг, квадрат, труба
- строятся эпюры нормальных и касательных напряжений
- по уравнениям метода начальных параметров вычисляются прогибы и углы поворота.

Посмотреть пример »
Консольная балка. Построение эпюр.
Для этого типа балок сервис позволяет определить и подробно расписывает:
- построение эпюр поперечных сил и изгибающих моментов
- подбор сечений — двутавр, прямоугольник, круг, квадрат, труба
- строятся эпюры нормальных и касательных напряжений
- вычисляются прогибы и углы поворота.
Посмотреть пример »
Статически неопределимая балка. Подбор сечения.
Для такого типа балок Вы можете получить
- только результаты расчета — (эпюры Q и M).
Естественно, по этим эпюрам можно легко найти реакции опор. Подробный ход расчета не расписывается,
но, имея результаты, Вы легко можете проверить все промежуточные итоги своего расчета.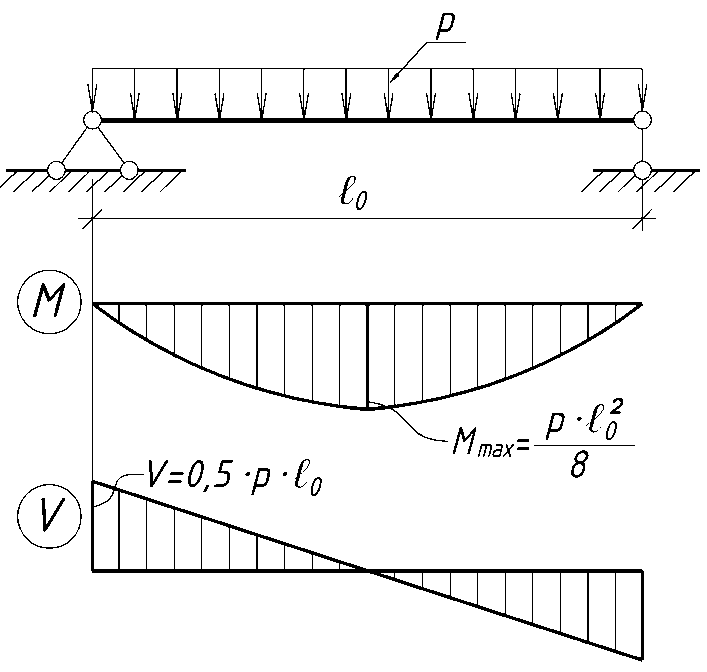
Посмотреть пример »
Балка с промежуточными шарнирами
Расчет балки с промежуточными шарнирами Вы должны производить, скорее всего, методом построения поэтажной схемы. Сервис, опять же, дает только конечный результат, но его наличие, естественно, очень упрощает проверку промежуточных этапов решения заданий.
Посмотреть пример »
Меню сайтаРасчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. + Полное расписанное решение! Теперь и для статически неопределимых балок! Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции — теория, практика, задачи… Примеры решения задач Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Форум сопромата и механики Книги — разная литература по теме. Заказать задачу Друзья сайта (ссылки) WIKIbetta Разработчикам (сотрудничество) Веб-мастерам (партнёрка) О проекте, контакты Подпроекты |
Пример №1. Расчет статически определимой балки, подбор сечения. Расчет статически определимой балки, подбор сечения.Необходимо определить минимальный диаметр круглого сечения d балки в точке С. Решение.откуда: Проверка показала, что реакции опор найдены верно. 1) Участок 1 (от A до B) Mx = Ra · z; z = 0; Mx = 0; z = l; Mx = Fl; 2) Участок 2 (от B до C) Mx = Ra z = 0; Mx = 5Fl; z = l; Mx = 6Fl; 3) Участок 3 (от D до C, подчеркиваю от D до С, т.к. балку на этом участке рассматривает справа налево): Mx = 3F · z; z = 0; Mx = 0; z = 2L; Mx = 6Fl; где Мс – момент на эпюре моментов в точке С Все. Автор решения Алексей Большаков (The Боль). Копирование материалов допускается при наличии ссылки на первоисточник (на эту страницу). Полезные ресурсы1. Он-лайн программа (версия 2004 года), которая выдаст расписанное решение любой балки. Пример результата. 2. Он-лайн программа (версия 2008 года), которая строит 4 вида эпюр и рассчитывает реакции для любых балок (даже для статически неопределимых). |
СообществоВходРешение задачРасчет редукторовДля Android (рекомендую)NEW Mobile Beam 2.0 Программа для расчета балок на прочность на Вашем Android устройстве… Java 2 ME |
Расчет балки на действие равномерно распределенной нагрузки
Дано:
1. Однопролетная балка постоянного по длине сечения на двух шарнирных опорах А и В, без консолей, длиной l = 4.6 м. Балка расположена горизонтально.
Однопролетная балка постоянного по длине сечения на двух шарнирных опорах А и В, без консолей, длиной l = 4.6 м. Балка расположена горизонтально.
2. Равномерно распределенная нагрузка q = 3.2 кН приложена перпендикулярно к нейтральной оси балки по всей длине балки.
Вот собственно и все, что следует знать на первом этапе расчета — определении максимальных напряжений в поперечном сечении балки. И да, длина балки может измеряться кроме метров в сантиметрах, миллиметрах, дюймах, футах и т.д. Нагрузка может также обозначаться другими литерами, измеряться в килограммах, грамах, тоннах пудах, фунтах и т.д. — принципиального значения это не имеет и на методику расчета никак не влияет.
Если теоретические основы расчета вас не интересуют, а вы просто хотите рассчитать свою балку, то можете воспользоваться калькулятором для данной расчетной схемы (в части определения требуемых параметров сечения этот калькулятор только для деревянных балок, со временем будет и для стальных, а может и для железобетонных).
Далее возможны 2 варианта расчета:
1. Упрощенный, по готовым формулам, которые приводятся буквально в каждом справочнике по сопромату. Для человека, занимающегося частным строительством и желающего просчитать ту или иную балку, такой расчет, самое то.
2. Классический, основанный на уравнениях равновесия системы и методе начальных параметров. Такой расчет чаще всего требуется от студентов. Но и людям, желающим узнать, откуда взялись те или иные формулы, пример такого расчета также будет полезен.
Рассмотрим эти варианты более подробно.
1. Упрощенный расчет (по готовым формулам)
Расчет производится по формулам расчетной схемы 2.1 для шарнирной балки.
1.1 Определение опорных реакций:
А = B = ql/2 = 3.2·4.6/2 = 7.36 кН (671.1)
Соответственно максимальная поперечная сила, действующая в поперечных сечениях балки будет «Q» = 7.36 кН. Действовать эта поперечная сила будет на опорах балки
1.
 2. Определение максимального изгибающего момента:
2. Определение максимального изгибающего момента:
Максимальный изгибающий момент будет действовать посредине пролета балки и он составит:
М = ql2/8 = 3.2·4.62/8 = 8,464 кНм (671.2)
1.3. Подбор сечения балки:
3.1 Для деревянной балки с расчетным сопротивлением R = 13 МПа (13000 кПа) требуемый момент сопротивления составит:
Wтр = M/R = 8.464/13000 = 0.000651077 м3 (651.077 см3) (671.3.1)
Как правило поперечные сечения деревянных балок имеют прямоугольную форму. Момент сопротивления прямоугольного сечения определяется по следующей формуле:
W = bh2/6 (671.3.2)
Дальше возможны различные варианты, например при высоте сечения балки h = 20 см требуемая ширина сечения составит не менее:
b = 6W/h2 = 6·651.77/202 = 9.77 см (671.3.3)
По сортаменту таким требованиям удовлетворяет балка с сечением 20х10 см.
Если поперечное сечение деревянной балки имеет форму, отличную от прямоугольной или квадратной, то для определения момента сопротивления можно воспользоваться одной из следующих формул, а при особо сложной форме сечения сначала определить момент инерции, а потом уже момент сопротивления.
3.2 Для стальной балки с расчетным сопротивлением R = 245 Мпа (245000) кПа) требуемый момент сопротивления составляет:
Wтр = M/R = 8.464/245000 = 3.45·10-5 м3 (34.5 см3) (658.3.7)
Далее требуемое сечение подбирается по одному из сортаментов.
Ну а подбор сечения ж/б балки — это отдельная большая тема.
1.4. Проверка по касательным напряжениям (для деревянной балки):
Расчетное сопротивление скалыванию вдоль волокон (для древесины второго сорта) Rск = 1.6 МПа.
Для прямоугольного сечения максимальные касательные напряжения определяются по следующей формуле:
т = 1.
Требование по касательным напряжениям соблюдено.
Для сечений другой формы значение касательных напряжений определяется по формуле Журавского.
Стандартные стальные профили в дополнительной проверке по касательным напряжениям как правило не нуждаются.
1.5. Определение прогиба:
Для деревянной балки сечением 20х10 см момент инерции составит:
I = Wh/2 = 666.66·20/2 = 6666.6 см4 (0.00006666 м4) (671.5.1)
Модуль упругости древесины составляет Е = 1·104 МПа (107 кПа)
f = 5Ql4/(384EI) = 0.02798 м (2.798 см) (671.5.2)
В данном случае прогиб составляет 1/164 от длины пролета балки.
Вот собственно и весь упрощенный расчет.
2. Классический расчет
Ну а теперь перейдем к классическому расчету. Но сразу скажу, от упрощенного он отличается только первыми двумя пунктами — определением опорных реакций и максимальных напряжений, принципы подбора сечения такие же, как и изложенные выше. Ну и добавится определение начального и конечного углов поворота, эпюры поперечных сил, изгибающих моментов, углов поворота и прогиба, куда ж без этого в классическом-то расчете.
Но сразу скажу, от упрощенного он отличается только первыми двумя пунктами — определением опорных реакций и максимальных напряжений, принципы подбора сечения такие же, как и изложенные выше. Ну и добавится определение начального и конечного углов поворота, эпюры поперечных сил, изгибающих моментов, углов поворота и прогиба, куда ж без этого в классическом-то расчете.
2.1. Определение опорных реакций
Для определения опорной реакции А воспользуемся третьим уравнением статического равновесия системы (уравнением моментов относительно точки В):
ΣМВ = Al — ql2/2 = 0 (671.6.1)
тогда
Аl = ql2/2; (671.6.2)
A = ql2/2l = 4.6·3.2/2 = 7.36 кН (671.1)
Для определения опорной реакции В также воспользуемся третьим уравнением статического равновесия системы (уравнением моментов относительно точки А):
ΣМА = Вl — ql2/2 = 0 (671. 6.3)
6.3)
тогда
Вl = ql2/2; (671.6.4)
В = ql2/2= 4.6·3.2/2 = 7.36 кН (671.1.2)
Для проверки воспользуемся вторым уравнением статического равновесия системы:
∑у = ql — А — В = 0 (671.6.5)
4.6·3.2 — 7.36 — 7.36 = 0 (671.6.6)
Условие выполняется.
В точке А поперечные силы условно равны нулю.
Уравнение поперечных сил будет иметь следующий вид:
«Q» = А — qx (671.6.7)
где х — расстояние от начала координат (точки А) до рассматриваемого сечения балки.
Соответственно на расстоянии 0 м от точки А поперечные силы будут равны:
«Q»А = 7.36 — 3.2·0 = 7.36 кН (671.6.8)
в точке В:
«Q» = А — ql + В = 7.36 — 3.2·4.6 + 7.36 = 0 (671.6.9)
Этих данных достаточно для построения эпюр поперечных сил.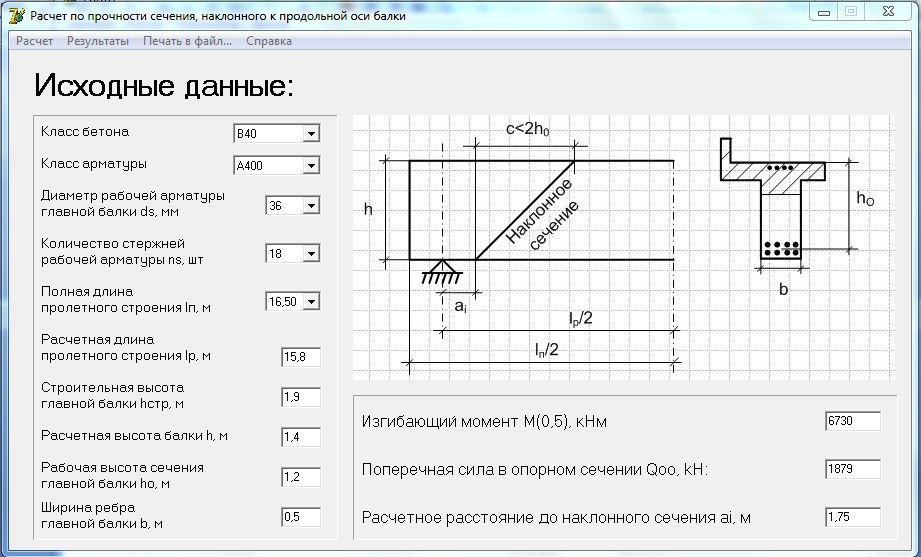
2.2. Определение изгибающих моментов:
Для определения изгибающих моментов, действующих в поперечных сечениях балки, используется метод сечений, согласно которому уравнение моментов будет иметь следующий вид:
М = Ах — qx2/2 (671.7.1)
тогда
МА = А·0 — q02/2 = 0 (671.7.2)
в середине пролета:
М = Аl/2 -q(l/2)2/2 = 8.464 кНм (671.2.1)
в точке В (в конце балки):
М = Al — ql2/2 = ql·l/2 — ql2/2 = 0 (671.7.3)
Примечание: эпюра изгибающих моментов — квадратная парабола. Если есть необходимость определить значение изгибающего момента для любого другого поперечного сечения, то для этого нужно воспользоваться формулой (671.7.1). Но как правило в таких простых случаях загружения в этом нет необходимости. Опять же варианты использования балок переменного сечения, когда требуется знать различные значения моментов, здесь не рассматриваются.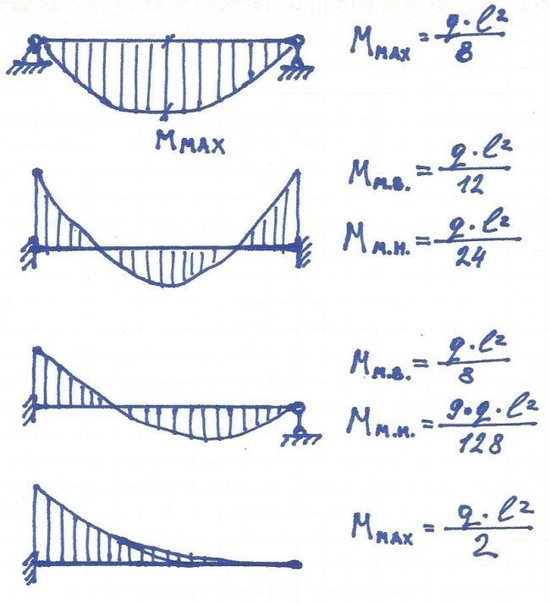
2.3 Определение углов поворота и прогибов поперечного сечения.
Уравнение углов поворота — результат интегрирования уравнения моментов. А как известно, при интегрировании появляется постоянная интегрирования, в данном случае начальный угол поворота ΘА, который в данном случае не равен нулю. Кроме того на значение углов поворота и прогибов влияет жесткость рассматриваемой балки, выражаемая через ЕI, т.е. чем больше жесткость балки (модуль упругости и момент инерции) тем меньше в итоге углы поворота и прогибы.
Уравнение углов поворота для нашей балки будет выглядеть так:
θx = ∫Mdx/EI = — ΘА + Ax2/2EI — qx3/6EI (671.8.1)
Уравнение прогибов — это в свою очередь результат интегрирования уравнения углов поворота на рассматриваемом участке:
fх = ∫ΘАdx = — θAx + Ax3/6EI- qx4/24EI (671. 8.2)
8.2)
Как видим, в данном случае постоянная интегрирования — начальный прогиб — равна нулю и это логично — на опорах прогиба быть не может (во всяком случае в теории). Это позволяет составить дополнительное уравнение прогиба для одной из опор, например для точки В уравнение прогиба будет иметь вид:
fВ = — θAl + Al3/6EI — ql4/24EI = 0 (671.8.3)
тогда
θAl = Al3/6EI — ql4/24EI (671.8.4)
θA = ql3/(2·6EI) — ql4/(l·24EI) (671.8.5)
θA = ql3/24EI = 12.978/EI (671.8.6)
Так как у нас симметричны и балка и нагрузка, что мы уже заметили раньше, то конечный угол поворота поперечного сечения (на опоре В) будет равен начальному углу поворота.
Проверяем правильность вычислений:
θB = — ΘА + Al2/2EI — ql3/6EI = (-12. 978 + 77.8688 — 51.9125)/EI = 12.977/EI (671.8.7)
978 + 77.8688 — 51.9125)/EI = 12.977/EI (671.8.7)
Надеюсь разница в третьем знаке после запятой в значениях начального и конечного угла поворота не будет вас сильно пугать, хотя подобные вопросы иногда возникают. Сразу скажу, тут дело только в калькуляторе — чем более точный результат вы хотите получить, тем больше знаков после запятой следует него забивать.
Так как у нас симметричные и балка и нагрузка, то нет необходимости определять точку, где прогиб максимальный. Это сечение будет посредине балки. Впрочем есть формула (671.8.3) и с помощью ее можно определить прогиб в любом рассматриваемом сечении, но нас в данном случае интересует только максимальный прогиб:
fmax = — θВ2.3 + В·2.33/6EI — q2.34/24EI = — 18.6561/ЕI (671.8.8)
Ну или:
fmax = — θА2.3 + А·2.33/6EI — q2.34/24EI = — 18.6561/ЕI (671.8.9)
Чтобы эпюры углов поворота и прогибов были универсальными и подходили и для деревянных и для стальных и для железобетонных и для каких угодно других балок, на эпюрах показываются не абсолютные значения, а относительные. Т.е. обе части уравнения умножаются на ЕI.
Т.е. обе части уравнения умножаются на ЕI.
2.4. Построение эпюр поперечных сил и изгибающих моментов:
На основании полученных ранее данных строим эпюры:
Рисунок 671.1. Расчетная схема (а), замена опор на реактивные силы (б), эпюра поперечных сил (в), эпюра изгибающих моментов (г), эпюра углов поворота (д), эпюра прогибов (е).
На эпюре поперечных сил в начале координат (в точке А) откладываем вверх значение опорной реакции А, согласно направлению действия реактивной силы (опорной реакции. В точке В откладываем значение опорной реакции вниз. Соединяем полученные точки прямой.
Тут может возникнуть вопрос: а почему на опоре В мы откладываем значение вниз, когда значение опорной реакции у нас положительное? Отвечаю: дело в том, что мы не просто рисуем картинку, а вообще то строим график функции, описываемой уравнением (671.6.7) и согласно этому уравнению в сечении максимально близком к опоре В (х→l) значение этого уравнения будет:
«Q»х→l = Аl — ql = — 7. 36 кН (671.9)
36 кН (671.9)
А в точке В, где приложена реактивная сила (опорная реакция В) на эпюре происходит скачок (как впрочем и в точке А) т.е. формально мы все-таки откладываем опорную реакцию вверх и таким образом все, как положено.
Так как у нас балка на шарнирных опорах, на которую действует только равномерно распределенная нагрузка, то значения моментов на опорах равны нулю, что мы и определили ранее. На эпюре моментов посредине пролета (на расстоянии 2.3 м от начала координат) откладываем вниз значение максимального момента. Соединяем эти точки кривой линией, как показано на рисунке. В общем-то как уже говорилось, эта кривая линия — квадратичная парабола и формально для ее построения можно определить сколь угодно много значений моментов для различных сечений. Но как правило необходимости в этом нет: никакой, даже очень придирчивый преподаватель не сможет отличить квадратичную параболу от кубической, особенно если вы большими способностями в рисовании не отличаетесь.
Примечание: откладывать значение момента можно и вверх, как это принято у конструкторов машин и механизмов, принципиального значения это не имеет. Просто у строителей принято строить эпюры моментов на растянутой стороне сечения.
На эпюре углов поворота в точке А откладываем значение начального угла поворота, в точке В — значение конечного угла поворота. Соединяем эти точки кубической параболой так, чтобы она проходила через середину пролета.
На эпюре углов поворота откладываем значение максимального прогиба на расстоянии 2.3 м от начала координат (середина пролета). Проводим параболу четвертой степени через точку А, точку максимального прогиба и точку В. Если с этим возникают проблемы, то можно вычислить значения и прогибов и углов поворота для любых других поперечных сечений балки.
Вот собственно и весь расчет.
Пример расчет балки на изгиб — Студопедия
Для заданной балки двутаврового сечения ( = 210 МПа, Е = 2 х 105 МПа) и нагрузок требуется;
1. Построить эпюры поперечных сил и изгибающих моментов;
Построить эпюры поперечных сил и изгибающих моментов;
2. Определить нормальные и касательные напряжения в сечениях с наибольшим моментом и поперечной силой на расстоянии h/4 от нейтральной оси;
3. Определить прогиб конца балки точки В.
При построении эпюр Q и М необходимо соблюдать правило знаков. Положительное направление сил показано на схеме.
РЕШЕНИЕ.
1. Определяем опорные реакции
2. Методом сечений определяем ординаты поперечной силы в характерных сечениях. Для этого балку разбиваем на два участка. Границы участков — места изменения нагрузки. Построение эпюры начинаем с правого свободного конца балки.
Максимум изгибавшего момента находится в сечении, где поперечная сила равна нулю. Положение этого сечения определяем из условия:
3. Методом сечений определяем изгибающие моменты в характерных сечениях и строим эпюру моментов. Экстремум в т. х = 2 м.
х = 2 м.
Наиболее нагруженным сечением в балке является сечение А у заделки, где Мmax = 120 кН м, Qmах = — 80 кН.
4. Из условий прочности по нормальным напряжениям определяем требуемый момент сопротивления сечения.
По сортаменту ГОСТ 8509-72 принимаем двутавр № 33.
Максимальные напряжения в опасном сечении будут равны
5. Определяем нормальное напряжение в точке Е сечения на расстоянии h/4 = 8,25 см от нейтральной оси (рис. 4.9.).
Для определения касательного напряжения в точке Е вычислим статический момент отсеченной выше точки Е площади относительно центральной оси Х.
6. Определяем прогиб балки в точке В, используя универсальное уравнение прогибов
Для заданной консольной балки граничные условия будут: угол поворота сечения А ; прогиб сечения А
Пример расчета балки с концентрированной нагрузкой — Sulde’ — блог
Расчет на жесткость
Допустим мы хотим соорудить гаражный кран
Грузоподъёмность 1т при максимальном вылете 2метра и прогибом стрелы под нагрузкой не более 5мм, при этом ось цилиндра закреплена на расстоянии 250мм от оси крепления консоли
Полистаем справочник Анурьева до страницы 56 по моему схема 8 то что нам надо 🙂
В третьей колонке мы видим знакомую нам букву Mmax а вот в четвертой есть не знакомая нам буква «зю» хотя правильно говорить Дзета http://ru.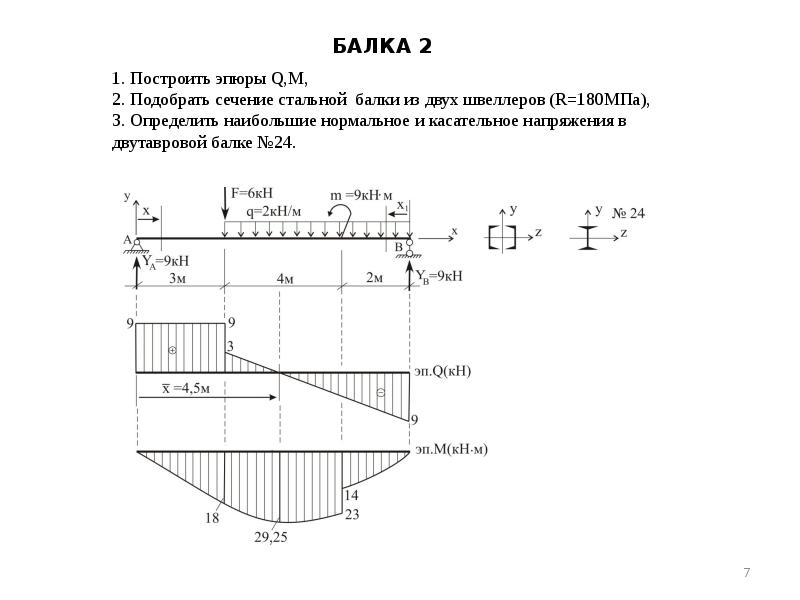 3)/25))=-2856,3058см4
3)/25))=-2856,3058см4
Во избежание ошибок при вбивании длинных формул в таблицу рекомендую разбивать её на несколько ячеек как показано на рисунке
Поверьте набить длинную формулу в одну ячейку без ошибки не так и просто. При этом таблица выдаст безупречный с точки зрения арифметики результат, но вот цена этой ошибки может быть чрезвычайно высока…. Поэтому внимательность и еще раз внимательность.
Ну будем надеяться мы ввели формулу верно
И минимально допустимый момент инерции нашего сечения Jдоп.=2856,31см4
Будет это двутавр, или круглая труба, или уголок не суть важно главное чтобы момент инерции этого профиля (J) был не меньше рассчитанного нами.
Для ориентировки по размерам сечения можно пролистать справочник до страницы 153 или 154 и увидеть что по условию жесткости нам вполне подходит швеллер или двутавр №24.
Мы пока не будем вдаваться в свойства геометрических сечений скажем только, что два швеллера сваренные коробкой «[ ]» позволяют суммировать их момент , следовательно нашим условиям вполне удовлетворит балка из двух швеллеров №20П даже двух двутавров 18а.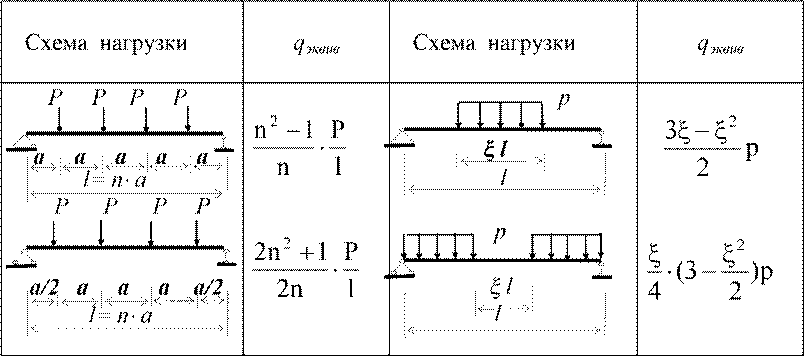
Перейдем к расчету на прочность
Формула приведенная в столбце три позволяет рассчитать момент реакции опоры M
Однако нас с вами интересует не он, а не превысят ли напряжения в материале балки некую критическую величину называемую допустимыми напряжениями.
В литературе для обозначения напряжения используется прописная греческая буква сигма http://ru.wikipedia….%BA%D0%B2%D0%B0) по начертанию она похожа на русскую «б» поэтому в написании формул я буду использовать её (извините но мне лень подставлять греческий символ)
Чтобы узнать значения допустимых напряжений для стали, нам придется прогуляться до страницы 61 нашего справочника . На страницах следующих за ней даны значения для более продвинутых марок сталей, чугунов, и пластмасс. Если же вы решили построить кран чего то более экзотического например из фанеры или титана вам придется поискать эти значения, на страницах посвященным соответствующим материалам.
В любом случае для создания надежной конструкции расчетные напряжения не должны превышать пределов текучести материала.
Как вы могли заметить допустимые напряжения для стали (бдоп) указанные в таблице Анурьева в 2 а то и в 3раза меньше пределов текучести (бт) соответствующих марок, связано это с явлениям усталости метала.
Итак по условию прочности напряжения в материале балки (бм) должны быть меньше или равны допустимым напряжениям (бдоп)
За способность сечения воспринимать нагрузки отвечает «момент сопротивления изгибу» или просто «момент сопротивления» обозначают его латинской буквой W, как и момент инерции (J) его указывают в сортаменте для основных осей Wx или Wy соответственно. Исключением из этого правила является квадратные и круглые сечения моменты которых по главным осям равны между собой. По сути W является производной величиной от J но об этом чуть ниже.
Для того чтобы определить напряжения материала в сечении (бм) нам достаточно разделить момент в этом сечении (М) на момент сопротивления этого сечения (W)
Считаем :
Mмах=P*a=1000*200=200000кгс/см
Допустим мы собираемся использовать для нашей балки сталь 3, очевидно работает она на изгиб и режим нагрузки стрелы крана пульсирующий, следовательно бдоп=110Мпа=110*10,19716213=1121,68кгс/см2
Поскольку бм=M/W следовательно:
Wдоп=Mмах/бдоп=200000/1121,68=178,3см3
Теперь мы знаем что сечение нашей балки должно иметь момент инерции не менее Jдоп. =2856,31см4 и момент сопротивления не меньше Wдоп=178,3см3
=2856,31см4 и момент сопротивления не меньше Wдоп=178,3см3
Пойдем смотреть сортамент (страница 137 и далее)
В принципе нашим требованием вполне удовлетворяет выбранный нами ранее двутавр №24
Однако качество нашего крана нисколько не пострадает если под нагрузкой стрела будет прогибаться, не на 5мм а на 10мм, так или иначе нам хватит хода чтобы выдернуть движок из автомобиля. Следовательно нас вполне удовлетворит и №20 который на целых 6,3кг легче и скорее всего на 20% дешевле. Пересчитав значение прогиба V мы можем обнаружить что фактический прогиб составит не более 7,8мм.
Если же мы хотим повторить конструкцию крана показанную на картинке то нам скорее всего потребуется профильная труба сортамента на которую мы в справочнике не имеем.
Не беда поищем в интернет … например вот http://www.b2bmetal.eu/ru/pages/index/index/id/111/
Но не спешите радоваться интернет в отличие от справочника не надежный источник информации.
Поэтому прежде чем листать таблицу в поисках нужных цифр попробуем оценить её достоверность.
Читаем «I — Момент инерции сечения»
Да называйте его какой угодно буквой хоть «Ы» лишь бы цифра правильная была…
Как вы уже заметили чем выше момент инерции сечения тем оно жестче, на практике это удобно показывать на стальной линейке, положенная плашмя она прогибается даже от легкого нажатия пальцем, но стоит поставить её на ребро и нажатие пальцем не вызовет видимых изменений.
Связано это с тем что Jx работающий когда линейка стоит на ребре на несколько порядков выше Jy работающего когда линейка уложена плашмя.
Мы легко можем в этом убедиться рассчитав момент инерции прямоугольника который из себя представляет сечение линейки.
В справочнике Анурьева масса полезной информации в частотности формулы расчета характеристик сечения простых фигур на странице 35, и далее …
На странице 42 мы без труда обнаружим прямоугольник и убедимся что у линейки шириной 3см и толщиной 1мм Jх=(0,1*3^3)/12=0.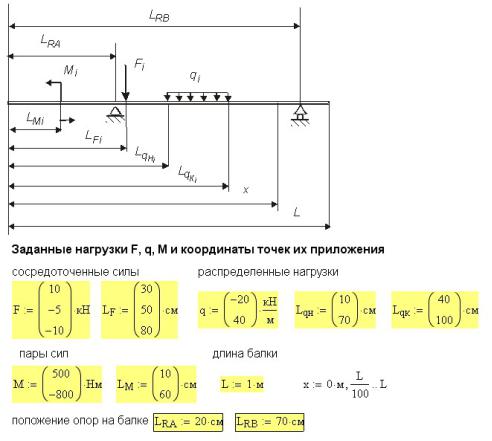 3)/12=0,00025см4
3)/12=0,00025см4
Теперь мы можем вернуться к сортаменту и обнаружить, что ребята малость перепутали местами X и Y, весьма распространённая ошибка должен заметить.
Вот например труба 50х30х2,5 Iyy=11.8см4 Ixx=5.22см4, сами то цифры похожи на верные но читать следует Jx=11.8см4 Jy=5.22см4, принцип тот же что и с линейкой, ставим сечение на ребро получаем больше жесткости.
Вы также можете проверить верность самих приведенных моментов воспользовавшись формулами со страницы 43 справочника Анурьева. Если ваш ответ чуть больше приведенного в сортаменте значит всё хорошо, если он меньше или равен то вероятно вас дурачат. (ну или вы ошиблись в расчетах)
Проверяем значения W. На самом деле это не самостоятельная величина а производная от J и для симметричных сечений типа прямоугольника или двутавра имеющая зависимость Wх=Jх/(A*0.5), Wy=Jy/(B*0.5) где А и B высота и ширина сечения соответственно.
Вернемся к нашей трубе 50*30 считаем Wх=Jх/(А*0,5)=11,8/(5*0,5)= 4,72см3 странно откуда у них Welxx=4,73см3 впрочем 0,01см4 можно простить списав на погрешность вычислений и округлений.
Однако следует помнить, такого рода «опечатки» довольно популярны в каталогах нестандартных профилей недобросовестных производителей где они могут достигать десятков процентов в плюс к фактическому моменту, поэтому проверка и еще раз проверка.
Конечно стрела гаражного крана не самая ответственная балка… в худшем случае она просто сломается оставив двигатель на прежнем месте … при совсем печальном раскладе прищемит чью-нибудь шаловливую ручонку грубо нарушающую ТБ … .
А вот обрушения балок перекрытия может иметь совсем другие последствия…
Очень важно понимать
Формулы приведенные у Анурьева верны на 100%
Арифметика вычисления таблиц безупречна.
Поэтому у вас есть только два способа получить неверный результат при решении задач.
1) Ошибиться при составлении формулы в ячейке
2) Скормить правильной формуле не верное значение переменной
Если вы смогли этого избежать то полученный ответ верен!
И воплощенный в материале он будет на 100% безопасен для вас и окружающих.
Для полного спокойствия при расчетах в водят коэффициент запаса в строительстве их минимальные значения регламентированы СНиП, в случае поделки типа нашего крана это кровавая борьба паранойи и жадности конструктора.
По моему разумению в нашем примере изначально заложен большой запас , не много найдется двигателей массой больше 900кг, да и вылет в 2 метра скорее всего избыточен.
Итак ищем оптимальную трубу
Минимальной массы (М) при соблюдении условий Welxx>=Wдоп, и Iyy>=Jдоп
Конечно можно и в рукопашную таблицу просмотреть прямо на сайте , но я рекомендую перенести эту таблицу в «Эксель» и изучить возможности вашей программы на предмет логических функций, поверьте это сделает вашу жизнь гораздо проще и занимательнее.
Ну или как минимум научитесь пользоваться сортировкой и фильтрами если вы этого еще не умеете….
У меня получается: оптимальной будет труба 260*140*4 массой 24,6кг/м и имеющая момент инерции Jx=2888cм4 откуда фактический прогиб нашей стрелы V=4. 94мм как мы и хотели в начале
94мм как мы и хотели в начале
При этом труба имеет момент сопротивления Wx=222см3 что даёт нам запас по прочности около 25% по моему весьма достойно….
Помимо выше изложенных соображений про достаточный момент и минимальную массу не следует забывать о других моментах.
Так например стенка у нашей трубы всего 4мм что вероятно потребует усиления в местах устройства шарниров и сочленения.. поэтому возможно имеет смысл поискать более толстостенный вариант трубы пусть он и не будет оптимальным по массе.
Так или иначе расчетную часть данной балки можно считать закрытой .
1.5. Пример расчета прокатной балки
1.5.1. Материалы для прокатной балки
Согласно табл. 50
[4] ригель многоэтажного промышленного
здания относится ко второй группе
конструкций. По табл. 53 [4] для конструкций
второй группы может быть использована
сталь марки С235.
Расчетное сопротивление для первой группы предельных состояний для фасонного проката при толщине полок от 11 до 20 мм Ry = 230 МПа. Модуль упругости для всех строительных сталей одинаковый Е = 2,1 ∙ 105 МПа.
1.5.2 Предварительный подбор сечения прокатной балки
Расчетная схема конструкции – разрезная балка (рис. ), загруженная равномерно распределенной нагрузкой от плит перекрытия.
Расчетный пролет балки при опирании ее на консоли колонн
lo = l – hcol – с/2 = 7,2 – 0,4 – 0,475/2 = 6,56 м
где l – шаг колонн в поперечном направлении;
hcol – размер поперечного сечения колонн;
0,04 – зазор на свободную укладку ригеля на консоли колонн.
Вычисляем расчетную нагрузку на 1м длины ригеля. Подсчет нагрузок на 1м2 перекрытия приведен в табл.1.
Ширина
грузовой полосы, с которой нагрузка
передается от плит на ригель, равна шагу
колонн в продольном направлении здания
5,6 м.
Расчетные нагрузки на ригель для расчета по первой группе предельных состояний (табл.1):
– постоянная нагрузка
q = 4,5 ∙ 5,6 = 25,2 кН/м
– временная нагрузка
ν = 9,0 ∙ 5,6 = 50,4 кН/м
Итого, с учетом коэффициента надежности по назначению здания γn = 1,0:
– расчетная нагрузка для расчета по второй группе предельных состояний
q = (25,2 + 50,4) ∙ 1,0 = 75,6 кН/м
Расчетные усилия:
– изгибающий момент для расчетов по первой группе:
кН ∙ м
14
1.5.2.1. Расчет прочности ригеля.
Требуемый момент сопротивления
где γc = 1 – коэффициент условий работы металлических конструкций в промышленных зданиях [4, табл.6].
По сортаменту [1,
приложение 10] подбираем требуемый номер
двутавра (№55), Wх = 2035 см3 > Wmp = 1768 см3 , момент инерции Iх = 55962 см4,
масса единицы длины прокатного двутавра
– 926 Н/м.
1.5.2.2. Расчет ригеля по второй группе предельных состояний.
Расчётные нарузки на ригель для расчёта по второй группе предельных состояий:
Нагрузка от веса панели и пола 4,0 ∙ 5,6 =22,4 кН/м.
Нагрузка от собственного веса ригеля 0,926 кН/м.
— постоянная нагрузка gn =22,4 + 0,926 = 23,326 кН/м;
— временная нагрузка νn=7,5 · 5,6 = 42,0 кН/м.
q = (23,326 + 42,0)∙1 = 65,326кН/м.
Расчетный изгибающий момент для расчетов по второй группе:
Проверяем достаточность высоты подобранной балки по формуле 7.1 [6].
Для балок междуэтажных перекрытий отношение допустимого прогиба fu к пролету балки lо не должно превышать fu =
Следовательно, fu = 16,4 мм.
Расчетный прогиб балки в середине пролета будет равен
13,4 мм < 16,4мм
Следовательно, высота подобранной балки достаточна.
15
Шишкин В.Е. Примеры расчета конструкций из дерева и пластмасс. М., 1974
%PDF-1.6 % 1 0 obj > endobj 554 0 obj >stream 2013-04-02T11:20:072017-02-21T15:05:28+05:002017-02-21T15:05:28+05:00libtiff / tiff2pdf — 20060323 / dШишкин В.Е. Примеры расчета конструкций из дерева и пластмасс. М., 1974application/pdf
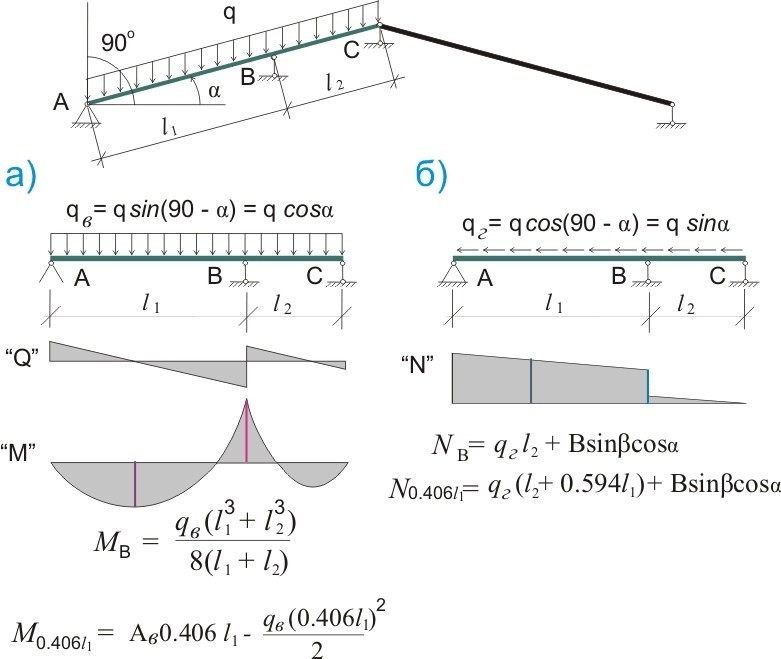 М.
М.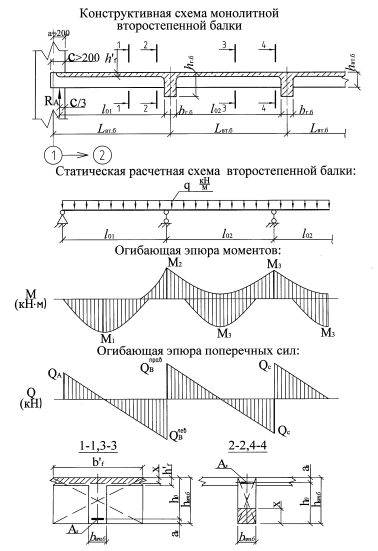 0400 0.0000 0.0000 842.4000 0.0000 0.0000 cm /Im110 Do Q
endstream
endobj
552 0 obj
>/Filter/CCITTFaxDecode/Height 1755/Length 20055/Name/Im110/Subtype/Image/Type/XObject/Width 1248>>stream
&~\-p1K’2MrlJG»24(Fpld̑F\2;
ч3@d(3G»jHbQ@[Q,2dIj*ڒZIS\_7″
0400 0.0000 0.0000 842.4000 0.0000 0.0000 cm /Im110 Do Q
endstream
endobj
552 0 obj
>/Filter/CCITTFaxDecode/Height 1755/Length 20055/Name/Im110/Subtype/Image/Type/XObject/Width 1248>>stream
&~\-p1K’2MrlJG»24(Fpld̑F\2;
ч3@d(3G»jHbQ@[Q,2dIj*ڒZIS\_7″1дA
5GH:;_gZB}URঝk#ƏeGKX>G__.
U3;]&g-=Q`ze*nPH
/kh#dtCȢ`xgY»»hL]N!0IQ B,e)ANWGDE2c,/b*tGDxʈ+q»ɦSƆu1hlFh#=VdDF»P[cgr «»»»$!G#+jgnXv5dڼ 莔8″$-kepDv]8#hN@eDGGp
u%
o.»‘f_#dD|[2» xeA7G_3\5 xISx04\d08;Y|ÐFTÄ
!ѠKp5p!l&8LB]Yۧ(#- e_3/6/@~d?u;_d~wT0űb»0?)YeP>963Fda|2CPA|.q
2CL’$2
Расчет напряжения изгиба секции балки
Как рассчитать напряжение изгиба в балках? В этом руководстве мы рассмотрим, как рассчитать изгибающее напряжение балки, используя формулу изгибающего напряжения, которая связывает распределение продольных напряжений в балке с внутренним изгибающим моментом, действующим на поперечное сечение балки.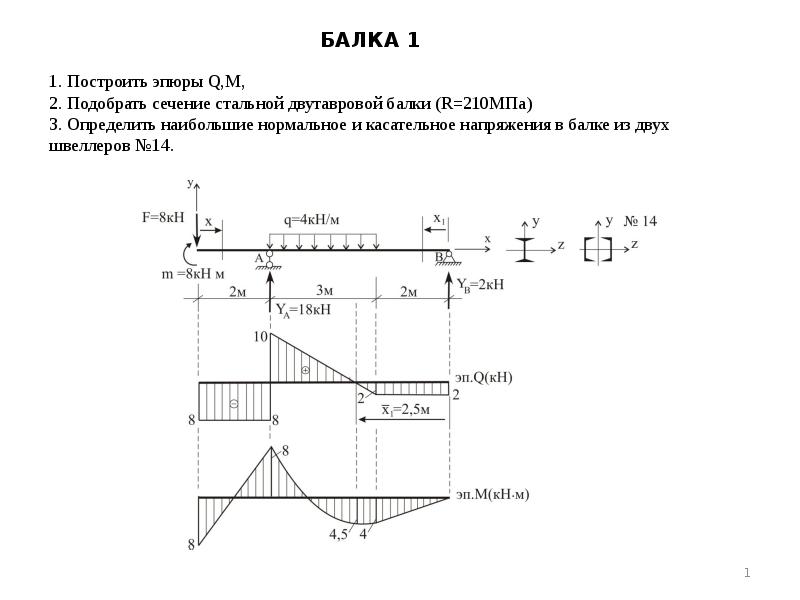 Мы предполагаем, что материал балки линейно-упругий (т.е. применим закон Гука). Напряжение изгиба важно, и, поскольку изгиб балки часто является определяющим результатом при проектировании балки, это важно понимать.
Мы предполагаем, что материал балки линейно-упругий (т.е. применим закон Гука). Напряжение изгиба важно, и, поскольку изгиб балки часто является определяющим результатом при проектировании балки, это важно понимать.
Давайте посмотрим на пример. Рассмотрим двутавровую балку, показанную ниже:
На некотором расстоянии по длине балки (ось x) она испытывает внутренний изгибающий момент (M), который обычно можно найти на диаграмме изгибающего момента. Общая формула для изгиба или нормального напряжения в сечении:
Для конкретного сечения балки очевидно, что напряжение изгиба будет максимальным на расстоянии от нейтральной оси (y).Таким образом, максимальное напряжение изгиба будет возникать либо в ВЕРХНЕ, либо в НИЖНЕЙ части секции балки, в зависимости от того, какое расстояние больше:
Давайте рассмотрим реальный пример нашей двутавровой балки, показанной выше.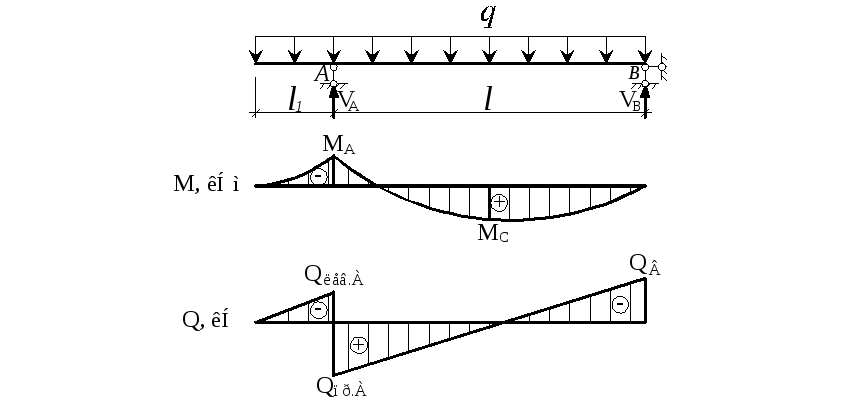 В нашем предыдущем уроке по моменту инерции мы уже обнаружили, что момент инерции относительно нейтральной оси равен I = 4,74 × 10 8 мм 4 . Кроме того, в учебнике по центроиду мы обнаружили, что центроид и, следовательно, расположение нейтральной оси находятся на расстоянии 216,29 мм от нижней части секции.Это показано ниже:
В нашем предыдущем уроке по моменту инерции мы уже обнаружили, что момент инерции относительно нейтральной оси равен I = 4,74 × 10 8 мм 4 . Кроме того, в учебнике по центроиду мы обнаружили, что центроид и, следовательно, расположение нейтральной оси находятся на расстоянии 216,29 мм от нижней части секции.Это показано ниже:
Очевидно, что очень часто требуется МАКСИМАЛЬНОЕ напряжение изгиба, которое испытывает секция. Например, предположим, что мы знаем из нашей диаграммы изгибающего момента, что балка испытывает максимальный изгибающий момент 50 кН-м или 50 000 Нм (преобразование единиц изгибающего момента).
Затем нам нужно определить, находится ли верх или низ секции дальше всего от нейтральной оси. Ясно, что нижняя часть секции дальше на расстояние c = 216.29 мм. Теперь у нас достаточно информации, чтобы найти максимальное напряжение, используя приведенную выше формулу напряжения изгиба:
Точно так же мы можем найти напряжение изгиба в верхней части секции, поскольку мы знаем, что оно составляет y = 159,71 мм от нейтральной оси (NA):
Последнее, о чем следует беспокоиться, это то, вызывает ли напряжение сжатие или растяжение волокон секции. Если балка прогибается в форме буквы «U», то верхние волокна испытывают сжатие (отрицательное напряжение), а нижние волокна — растяжение (положительное напряжение).Если балка провисает, как перевернутая буква «U», то все наоборот: нижние волокна сжимаются, а верхние — растягиваются.
Если балка прогибается в форме буквы «U», то верхние волокна испытывают сжатие (отрицательное напряжение), а нижние волокна — растяжение (положительное напряжение).Если балка провисает, как перевернутая буква «U», то все наоборот: нижние волокна сжимаются, а верхние — растягиваются.
Конечно, вам не нужно выполнять эти расчеты вручную, потому что вы можете использовать SkyCiv Beam — калькулятор напряжения изгиба, чтобы определить напряжение сдвига и изгиба в балке! Просто начните с моделирования балки с опорами и приложения нагрузок. Как только вы нажмете «Решить», программа покажет максимальные напряжения из этого калькулятора напряжения изгиба.На изображении ниже показан пример двутавровой балки, испытывающей напряжение изгиба:
Начните расчет напряжения изгиба с помощью SkyCiv Beam Calculator:Бесплатный калькулятор луча
Пример разработки стальной балки[Универсальная балка]
Рабочий пример конструкции стальной балки представляет собой конструкцию балки с простой опорой, имеющей равномерно распределенную нагрузку. Балка считается просто поддерживаемой, и расчетные данные для расчета изгибающего момента и поперечных сил приведены ниже.
Кроме того, свойства раздела, которые необходимо учитывать, также задаются на каждом этапе проверки раздела.
Теоретические аспекты и процедуры проектирования кодов обсуждаются в проекте изделия стальной балки согласно BS 5950 .
Расчетные данные- Нагрузка UDL 20 кН / м
- Пролет балки 6 м
- Балка с простой опорой
- Расчетная прочность стали, Py = 275 Н / мм 2
Максимальный изгибающий момент
= wl 2 /8 = 20 x 6 2 /8 = 90 кНм
Максимальное поперечное усилие
= wl / 2 = 20 x 6/2 = 60 кН
Рассмотрим универсальную балку 500x200x89.7 кг / м (P y = 275 Н / мм 2 )
Данные профиля- D = 500 мм
- T = 16 мм
- t = 10 мм
- B = 200 мм
- b = 100 мм
- r 1 = 20 мм
- d = 500 — 16 x 2 — 2 x 20 = 428 мм
- S x = 2175 × 10 3 мм 3
- Z x = 1914 × 10 3 мм 3
- r y = 43,3 мм
Начнем расчет конструкции стальной балки.В рамках этого расчета конструкции стальной балки выполняются следующие проверки.
- Классификация сечений
- Расчет на сдвиг
- Расчет на изгиб
- Проверка бокового изгиба при кручении
- Проверка прогиба
- Проверка продольного изгиба перемычки
Классификация профиля
Первым этапом проектирования стальной балки является классификация профиля, чтобы определить, является ли он пластичным, полупластичным, компактным или тонким.
T = 16 мм, P y = 275 Н / мм 2
ε = (275 / P y ) 0,5 = 1
Контрольный фланец
b / T = 100/16 = 6,25 <9ε = 9 - Фланец пластиковый
Проверить полотно
d / t = 428/10 = 42,8 <80ε = 80 - полотно пластик
Кроме того, d / t <70ε = 70 - Следовательно, нет необходимости проверять коробление при сдвиге
Следовательно, сечение является пластиковым
Расчетное усилие сдвига
Расчетное усилие сдвига, F v = 60 кН
P v = 0.6 P y A v = 0,6 P y tD = 0,6 x 275 x 10 x 500 x 10 -3 = 825 кН
F v
v Усилие сдвига в норме
В зависимости от силы сдвига решается, будет ли секция подвергаться низкому или высокому сдвигу в конструкции стальной балки.
Расчет на изгиб
Проверить, подвергается ли секция низкому или высокому сдвигу
60% x P v = 0,6 x 825 = 495 кН
F v <0.6 P v Сечение, подверженное низкому сдвигу
M c должно быть меньше 1,2 P y Z x или P y S x согласно кл. 4.2.5.1 и кл. 4.2.5.2
M c ≤ 1.2P y Z x = 1,2 x 275 x 1914 x10 3 x 10 -6 = 613,62 кНм
M c = P y S x = 275 x 2175 x 10 3 x 10 -6 = 598,125 кНм
Следовательно,
M c = 598.125 кНм> 90 кНм
Изгиб в норме
Проверка бокового продольного изгиба при кручении
M x
В этом примере промежуточные ограничения не учитывались
м LT , Таблица 18, BS 5950
M b = P b S x Cl. 4.3.6.4
Существует два метода проверки продольного изгиба при кручении, как описано в статье , конструкция стальной балки в соответствии с BS 5950 .Это строгий метод и упрощенный метод.
В этом примере конструкции стальной балки мы обсудили оба метода, чтобы подробно описать процедуры, которым необходимо следовать при использовании любого из этих методов.
Кроме того, основное различие между этими двумя методами заключается в оценке прочности на изгиб .
Строгий метод
M b = P b S x
P b зависит от λ LT и P y
λ LT = uv8λ√ (β 9010 w )
λ = L E / r y
L E — берется из таблицы 13 согласно кл.4.3.5.1 и рассмотрим L LT = L — пролет
L E = 1,0 L LT = 1 x 6 = 6 м
λ = L E / r y = 6000 / 43,3 = 138,568
Для катаных двутавровых и двутавровых профилей, кл. 4.3.6.8
x = D / T используется с u = 0,9
x = D / T = 500/10 = 50
β w должно быть получено из класса 4.3.6.9
β w = 1 для пластиковых секций класса 1 или компактных секций класса 2
v — коэффициент гибкости должен быть получен из таблицы 19 на основе λ / x и η
λ / x = 138.568/50 = 2,771
η = 0,5 для равных фланцев
v = 0,919 из таблицы 19
λ LT = uvλ√ (β w ) = 0,9 x 0,919 x 138,568 x √ (1) = 114,6
λ LO можно получить из таблицы 16 (см. Нижнюю часть таблицы)
Если λ LO ≥ λ LT ; P b = P y или в противном случае P b следует брать из таблицы 16 для сортового проката.
Если λ LO ≥ λ LT не нужно делать припуск на продольный изгиб при кручении, и в противном случае проверьте наличие продольного изгиба при кручении.
P y = 275 Н / мм 2 ; λ LO = 37,3
λ LO <λ LT Поэтому проверьте наличие бокового продольного изгиба при кручении
Из таблицы 16, для λ LT = 114,6; P b = 102 Н / мм 2
M b = P b S x = 102 x 2175 x 10 3 x 10 -6 = 221,85 кНм
M b / m LT = 221.85 / 0,925 = 239,838 кНм
Следовательно, M x = 90 кНм
Раздел соответствует .
Упрощенный метод
Примечание. При проектировании балки применять оба метода не требуется. Достаточно следовать упрощенному или строгому методу.
M b = P b S x : кл. 4.3.7
В этом методе определение P b отличается от предыдущего метода.Этот метод дает консервативные ответы. P b может быть получен из Таблицы 20 BS 5950 на основе √ (β w ) (L E / r y ) и D / T
β w = 1; предыдущий расчет
L E / r y = 138,568; предыдущий расчет
√ (β w ) (L E / r y ) = 1 0,5 x 135,568 = 138,568
D / T = 500/16 = 31,25
P b = 116 .646 Н / мм 2 Из таблицы 20
M b = P b S x = 116,646 x 2175 x 10 3 x 10 -6 = 253,705 кНм
M b / м LT = 253,705 / 0,925 = 274,3 кНм
Следовательно, M x = 90 кНм
Сечение соответствует Отклонение 9 Максимальный прогиб (δ) для равномерно распределенной балки с свободно опертой опорой можно оценить по следующему уравнению. δ = 5W e L 4 / (384EI) Это уравнение можно упростить следующим образом. δ = 0,104M max L 2 / (EI) Поскольку мы оцениваем прогиб из-за приложенных нагрузок, в этом расчете учитываем приложенную нагрузку как 10 кН / м. δ = 0,104 x 90 x 10 6 6000 2 / (205 x 10 3 x 478 x 10 6 ) = 1,7 мм При условии использования хрупкой отделки Пролет / 360 = 6000 / 360 = 16.7 мм δ Различные методы расчета отклонений обсуждаются в статье Википедии отклонение (инженерное дело) . Необходимо проверить несущую способность стенки в конструкции стальной балки. В этой категории выполняются подшипники и изгибы стенки. P bw = (b 1 + nk) tP yw t = 10 мм T = 10 мм r = 10 мм g = 5 мм b e = 5 мм b 1 = t + T + 0.8r — g = 10 + 10 + 0,8 x 10-5 = 23 мм k = T + r = 16 + 20 = 36 мм (для сортового проката) на конце, n = (2 + 0,6b e / k), но ≤ 5 n = (2 + 0,6 x 5/36) = 2,083 <5 P yw = 275 Н / мм 2 из таблицы 9 P bw = (b 1 + nk) tP yw = (23 +2,083 x 36) x 10 x 275 x 10 -3 = 269,5 кН Отношение опоры составляет 60 кН. Подшипник перемычки в порядке, ребра жесткости не требуются. Когда F x > P bw , нам необходимо предусмотреть ребра жесткости для обеспечения баланса сил (F x — P bw ). Допустимая нагрузка ребер жесткости должна быть получена из P s = A s.net P y . Где A s.net — площадь поперечного сечения жесткости. Если стенка и жесткость имеют разные значения прочности, меньшее значение следует использовать для расчета P s и P bw . Когда e ≥ 0.7d P x = 25εt P bw / √ [(b 1 + nk) d] Когда e <0,7d P x = [(a e + 0,7d) / 1,4d] {25εt P bw / √ [(b 1 + nk) d]} Где a e = 0,7d = 23/2 = 11,5 мм <0,7 x 428 = 300 мм P x = [(a e + 0.7d) /1.4d] {25εt P bw / √ [(b 1 + nk) d]} P x = [(11.5 + 0,7 × 428) / 1,4 × 428] {25x1x10x275 / √ [(23 + 2,083 × 36) 428]} = 174,3 кН F x x Ребра жесткости не требуются. Луч удовлетворяет всем проверкам. Этот калькулятор отклонения балки поможет вам определить максимальное отклонение балки для балок с простой опорой и консольных балок, несущих простых конфигураций нагрузки . Вы можете выбрать один из нескольких типов нагрузки, которые могут воздействовать на балку любой длины по вашему желанию.Величина и расположение этих нагрузок влияют на то, насколько балка изгибается. В этом калькуляторе отклонения балки вы узнаете о различных формулах отклонения балки , используемых для расчета отклонений балок с жесткой опорой и балок консольных балок. Вы также узнаете, как модуль упругости балки и момент инерции ее поперечного сечения влияют на расчетный максимальный прогиб балки. В строительстве мы обычно используем каркасных конструкций , которые удерживаются фундаментом в земле.Эти каркасные конструкции подобны каркасам зданий, домов и даже мостов. В кадре мы называем вертикальное обрамление колонн , а горизонтальные балки . Балки — это длинные элементы конструкции, которые несут нагрузки, создаваемые горизонтальными плитами конструкций, включая перекрытия и крыши. Когда балки несут слишком тяжелые для них нагрузки, они начинают гнуться. Мы называем величину изгиба балки , прогиб балки . Отклонение балки — это вертикальное смещение точки вдоль центра тяжести балки.Мы также можем рассматривать поверхность балки как опорную точку, если нет изменений в высоте или глубине балки во время изгиба. Мы снабдили наш калькулятор прогиба балки формулами, которые инженеры и студенты-инженеры используют для быстрого определения максимального прогиба, который будет испытывать конкретная балка из-за нагрузки, которую она несет. Однако эти формулы могут решать только простые нагрузки и их комбинацию.Мы составили для вас таблицы этих формул, как показано ниже: Формулы отклонения балок с простой опорой Формулы прогиба консольной балки Для расчета максимального прогиба балки с комбинацией нагрузок мы можем использовать метод наложения . Метод наложения утверждает, что мы можем приблизительно оценить полное отклонение балки, сложив вместе все отклонения, вызванные каждой конфигурацией нагрузки.Однако этот метод дает нам лишь приблизительное значение фактического максимального прогиба. Расчет сложных нагрузок потребует от нас использования так называемого метода двойного интегрирования . Для расчета прогиба балки необходимо знать жесткость балки и величину силы или нагрузки, которые могут повлиять на изгиб балки. Мы можем определить жесткость балки, умножив модуль упругости балки , E , на ее момент инерции , I .Модуль упругости зависит от материала балки. Чем выше модуль упругости материала, тем больше прогиб может выдержать огромные нагрузки, прежде чем достигнет предела разрушения. Модуль упругости бетона составляет 15-50 ГПа (гигапаскалей), а у стали — около 200 ГПа и выше. Эта разница в значениях модуля упругости показывает, что бетон может выдерживать лишь небольшой прогиб и трескается быстрее, чем сталь. Вы можете узнать больше о модуле упругости, воспользовавшись нашим калькулятором напряжений.С другой стороны, чтобы определить момент инерции для определенного поперечного сечения балки, вы можете воспользоваться нашим калькулятором момента инерции. Момент инерции представляет собой величину сопротивления материала вращательному движению. Момент инерции зависит от размеров поперечного сечения материала. Момент инерции также зависит от оси вращения материала. Чтобы лучше понять эту концепцию, давайте рассмотрим поперечное сечение прямоугольной балки шириной 20 см и высотой 30 см.Используя формулы, которые вы также можете увидеть в нашем калькуляторе момента инерции, мы можем вычислить значения момента инерции этого поперечного сечения следующим образом: Обратите внимание на два значения момента инерции. Это потому, что мы можем рассматривать изгиб балки по вертикали (по оси x, то есть Iₓ) или по горизонтали (по оси y, то есть Iᵧ).Поскольку мы учитываем отклонение балки при вертикальном изгибе, для наших расчетов всегда нужно использовать Iₓ . Полученные нами значения говорят нам о том, что балку труднее изгибать при вертикальной нагрузке и легче изгибать при горизонтальной нагрузке. Эта разница в значениях момента инерции является причиной того, что мы видим балки в этой конфигурации, в которой ее высота больше, чем ее ширина. Теперь, когда мы знаем концепции модуля упругости и момента инерции, мы можем теперь понять, почему эти переменные являются знаменателями в наших формулах отклонения балки.Формулы показывают, что чем жестче балка, тем меньше будет ее прогиб. Однако, изучив наши формулы, мы также можем сказать, что длина балки также напрямую влияет на прогиб балки. Чем длиннее балка, тем больше она может изгибаться и тем больше может быть прогиб. влияют на отклонение балки двумя способами: направление отклонения и величина отклонения . Нисходящие нагрузки склонны отклонять балку вниз.Нагрузки могут быть в виде точечной нагрузки, линейного давления или моментной нагрузки. Формулы в этом калькуляторе ориентированы только на нисходящие или восходящие направления для точечной нагрузки и распределенных нагрузок. Распределенные нагрузки аналогичны давлению, но учитывают только длину балки, а не ширину балки. Формулы в этом калькуляторе также учитывают момент или крутящий момент нагрузки как по часовой стрелке, так и против часовой стрелки. Просто проконсультируйтесь по направлениям стрелок на соответствующем изображении формулы, чтобы выяснить, в каком направлении имеется положительное значение нагрузки. Для примера расчета прогиба балки рассмотрим простую деревянную скамью с ножками на расстоянии 1,5 метра друг от друга в их центрах. Допустим, у нас есть доска из восточной белой сосны толщиной 4 см и шириной 30 см, которая служит сиденьем для этой скамейки. Мы можем рассматривать это сиденье как балку, которая отклоняется, когда кто-то садится на скамейку. Зная размеры этого сиденья, мы можем вычислить его момент инерции, как в нашем примере выше.Поскольку нам нужно рассчитать Iₓ, его момент инерции будет: Сосна белая восточная имеет модуль упругости Это означает, что многоместное сиденье прогнется примерно на 2.6 миллиметров от исходного положения, когда ребенок сидит посередине скамейки. Если вы нашли эту тему интересной и хотели бы узнать больше о прочности материалов, вам также может понравиться наш калькулятор запаса прочности. Вы также можете воспользоваться нашим конвертером силы, если хотите изучить различные единицы измерения точечных нагрузок и расчета сил. Обратите внимание: Эта старая статья нашего бывшего преподавателя остается доступной на нашем сайте в архивных целях.Некоторая информация, содержащаяся в нем, может быть устаревшей. Понимание того, как нагрузки передаются через конструкцию и воздействуют на элементы конструкции, является первым шагом к определению размеров коллекторов и балок Пол Физетт — © 2005 Большинство строителей автоматически выбирают двойные заголовки -2 x 8 или -2 x 10 для обрамления окон и дверей в каждом доме, который они строят. Эти коллекторы работают для поддержки большинства жилых помещений и по совпадению удерживают верхние части окон на одинаковой высоте.Замечательное решение, но эффективно ли это и экономично ли использование материала? То же самое верно и для балок, таких как конструкционные коньковые балки и центральные балки. Слишком часто строители собирают брус размером 2 дюйма, чтобы выдержать нагрузки на крышу и пол, не рассматривая другие варианты. Вы не сможете превзойти пиломатериалы для большинства небольших оконных коллекторов, но по мере увеличения пролётов и нагрузок более прочные материалы становятся лучшим выбором. Пиломатериалы ограничивают возможности дизайна и в некоторых случаях просто не работают. Parallam, Timberstrand, клееный брус и Anthony Power Beam — примеры альтернативных материалов, которые предоставляют строителям захватывающий выбор. В этой серии из двух частей мы рассмотрим, как пиломатериалы и эти инженерные материалы подходят для использования в качестве коллекторов и балок. Часть I покажет вам, как отследить структурные нагрузки до коллекторов и балок. В части II будут рассмотрены процедуры определения размеров, характеристики и стоимость этих материалов для нескольких приложений (см. «Определение размеров проектируемых балок и коллекторов» для части 2). Работа коллекторов и балок проста. Они передают нагрузки сверху на фундамент снизу через сеть конструктивных элементов.Идея определения размеров коллекторов и балок проста: сложите все временные и статические нагрузки, действующие на элемент, а затем выберите материал, который будет выдерживать нагрузку. Балка должна быть достаточно прочной, чтобы не сломаться (значение Fb), и достаточно жесткой, чтобы она не прогибалась чрезмерно под нагрузкой (значение E). Однако процесс определения размеров этих структурных элементов может быть сложным, если вы не инженер. Вот упрощенный подход, который поможет вам указать подходящий материал для многих приложений. Первый шаг такой же для пиломатериалов и конструкционных древесных материалов: сложите все нагрузки, действующие на жатку или балку, и затем преобразуйте эту нагрузку в , какую нагрузку будет ощущать каждая прямая опора жатки или балки . Говоря лучевым языком, вы говорите: этот заголовок должен нести X-фунтов на линейный фут. Этот перевод является ключом к любой проблеме определения размеров конструкции. Вооружившись этой информацией, вы можете определить минимальный размер, пролет или силу балки (кредит джулио). Размеры инженерных деревянных компонентов определяются с помощью таблиц пролетов, которые соответствуют различным пролетам и фунтам на фут балки.Для пиломатериалов необходимо произвести математические расчеты. считаются либо распределенных , либо точек нагрузок. Слой песка, равномерно распределенный по поверхности, является примером чистой распределенной нагрузки. Каждый квадратный фут поверхности испытывает одинаковую нагрузку. Текущие и статические нагрузки, указанные в строительных нормах и правилах для крыш и полов, являются приблизительными значениями распределенных нагрузок. Точечные нагрузки возникают, когда груз накладывается на одно место в конструкции, например на колонну.Нагрузка на опорную конструкцию распределяется неравномерно. Анализ точечной нагрузки лучше доверить инженерам. Мы будем рассматривать только распределенные нагрузки. Это позволит нам определять размеры балок для наиболее распространенных приложений. Давайте проследим распределенные нагрузки для нескольких разных домов. Предположим, что все они расположены в одном климате, но имеют разные пути загрузки из-за конструкции. Эти примеры показывают, как распределенные нагрузки распределяются между элементами конструкции.Наши образцы домов находятся в районе, где снеговая нагрузка составляет 50 фунтов на квадратный фут площади крыши (снег рассматривается как временная нагрузка). Само собой разумеется, что в более теплом климате снеговая нагрузка, вероятно, была бы меньше, поэтому вам необходимо проверить свою кодовую книгу на предмет временных и статических нагрузок в вашем регионе. Все нагрузки указаны в фунтах на квадратный фут горизонтальной проекции (площадь пятна контакта). (СМ. РИСУНОК 1) Здесь каждый квадратный фут кровельной системы обеспечивает 50 фунтов динамической нагрузки и 15 фунтов статической нагрузки (всего 65 фунтов на квадратный фут) на систему несущей конструкции.Помните, что эти нагрузки равномерно распределяются по всей поверхности крыши. Наружная стена (и коллекторы внутри) будут нести все нагрузки от средней точки дома (между опорными стенами) к внешней стороне дома (включая свес крыши). Расстояние в этом случае составляет 12 футов + 2 фута = 14 футов. Таким образом, каждый линейный фут стены должен выдерживать нагрузки, создаваемые полосой шириной 1 фут в этом районе 14 футов. С технической точки зрения стена имеет ширину притока 14 футов. Отсюда мы легко можем видеть, что каждая линейная опора стены поддерживает: Условия: живая нагрузка (снег): 50 фунтов на квадратный фут x 14 футов = 700 фунтов на линейный фут Собственная нагрузка на крышу: 15 фунтов на квадратный фут x 14 футов = 210 фунтов на линейный фут общая нагрузка: = 910 фунтов на линейный фут Важно перечислить временную нагрузку, постоянную нагрузку и общую нагрузку отдельно, поскольку временная нагрузка используется для расчета жесткости, а общая нагрузка используется для расчета прочности. Этот дом идентичен нашему первому примеру, за исключением того, что он построен из палки. В результате временная нагрузка, статическая нагрузка и распределение сил различны. В отличие от стропильной крыши, временная нагрузка и собственная нагрузка на стропила и балки перекрытия должны учитываться как отдельные системы. Поскольку чердак можно использовать для хранения, временная нагрузка на чердак в соответствии с нормами составляет 20 фунтов на квадратный фут. Условия: живая нагрузка (снег): 50 фунтов на квадратный фут x 14 футов = 700 фунтов на линейный фут Собственная нагрузка на крышу: 10 фунтов на квадратный фут x 14 футов = 140 фунтов на линейный фут перегрузка потолка: 20 фунтов на фут x 6 футов = 120 фунтов на линейный фут статическая нагрузка потолка: 10 фунтов на квадратный фут x 6 футов = 60 фунтов на линейный фут общая нагрузка: = 1020 фунтов на линейный фут Опять же, у этого дома такая же ширина, но у него 2 уровня.Нагрузки на нижний коллектор создают крыша, верхние стены и система 2-го этажа. В Стандартах архитектурной графики вес внешней стены размером 2 × 6 составляет 16 фунтов на фут 2 . Таким образом, стена высотой 8 футов весит 8 футов x 16 фунтов / фут 2 = 128 фунтов на линейный фут. На жатку доставлено: Условия: живая нагрузка (снег): 50 фунтов на квадратный фут x 14 футов = 700 фунтов на линейный фут Собственная нагрузка на крышу: 15 фунтов на квадратный фут x 14 футов = 210 фунтов на линейный фут стена верхнего уровня: = 128 фунтов на линейный фут Живая нагрузка 2-го этажа: 30 фунтов на фут x 6 футов = 180 фунтов на линейный фут Собственная нагрузка 2-го этажа: 10 фунтов на фут x 6 футов = 60 фунтов на линейный фут общая нагрузка: = 1278 фунтов на линейный фут Условия коньковой балки живая нагрузка (снег): 50 фунтов на фут x 12 футов = 600 фунтов на линейный фут Собственная нагрузка на крышу: 10 фунтов на фут x 12 футов = 120 фунтов на линейный фут общая нагрузка: = 720 фунтов на линейный фут Пример фермы Центральная балка несет половину нагрузки на пол, нагрузку на перегородку и половину нагрузки на второй этаж.Текущие и статические нагрузки указаны в строительных нормах и правилах. Вес перегородки указан в Стандартах архитектурной графики как 10 фунтов на квадратный фут. B) Состояние балок первого этажа Живая нагрузка 1-го этажа: 40 фунтов на фут x 12 футов = 480 фунтов на линейный фут Статическая нагрузка 1-го этажа: 10 фунтов на фут x 12 футов = 120 фунтов на линейный фут Перегородка высотой 8 футов: = 80 фунтов на линейный фут Живая нагрузка 2-го этажа: 30 фунтов на фут x 12 футов = 360 фунтов на линейный фут Собственная нагрузка 2-го этажа: 10 фунтов на фут x 12 футов = 120 фунтов на линейный фут общая нагрузка: = 1160 фунтов на линейный фут Эти примеры являются типичными для типов вычислений, которые вам необходимо выполнить для определения равномерной нагрузки, которая распределяется на балку или коллектор.Вы должны установить, какую нагрузку принимает каждая прямая опора жатки или балки. Следующим шагом является использование технической литературы любой из компаний, производящих деревянные компоненты, для определения пролета и размера балки. Все они соотносят допустимые пролеты с нагрузкой на фут балки. Списки пролетов основаны на допустимом прогибе, динамической нагрузке и статической нагрузке, которые перечислены в вашей книге строительных норм. В части 2 «Определение размеров инженерных коллекторов и балок» мы сравниваем стоимость и характеристики некоторых деревянных изделий с пиломатериалами. Все иллюстрации любезно предоставлены Journal of Light Construction. Некоторые эксперты говорят, что инженерия — это на 80% логика и на 20% приложение. Некоторые могут
обсудите это, но здесь мы предоставим вам основную инженерную информацию
и приложения, которые не всегда доступны. При этом балки нагружаются по-разному. Балка с простой опорой — это
обычно используемая балка (как показано выше). Ниже вам будет показано, как все это работает, и как спроектировать и выбрать балку (дерево или
стали). Мы также коснемся выбора бетонной балки. В приведенных ниже примерах представлены шаги, необходимые для выбора и проектирования деревянного
Луч. Если вы хотите выбрать и спроектировать стальную балку, шаги будут
одно и тоже. Отличаются только свойства материала, например, напряжение изгиба в
Материал (fb), момент инерции (I), модуль упругости (E) и сечение
Модуль (S). Все остальные уравнения были бы такими же, если бы у вас были такие же
нагрузка (W) и пролет (L). Обычные шаги для проектирования балки: Пример простой опорной балки с равномерно распределенной нагрузкой Точечная сосредоточенная нагрузка (600 фунтов) на 2 x 12 Пример простой опорной балки с сосредоточенной нагрузкой Точечная сосредоточенная нагрузка (1200 фунтов) на 4 x 12 Пример простой опорной балки с сосредоточенной нагрузкой Для среднего домовладельца, который хочет построить дом или построить пристройку, наиболее распространенной используемой бетонной балкой является сборная балка или сборная перемычка. Эти балки или перемычки обычно производятся на фабрике с контролируемым качеством. У этих компаний обычно есть в наличии
Руководства, в которых указана грузоподъемность и пролет балок или перемычек, которые они изготавливают. Это очень полезно и удобно, поскольку вам не нужно проводить фактические расчетные операции. Если вам нужна специальная балка с особыми условиями нагрузки, рекомендуется обратиться к инженеру для проектирования балки. Деревянная балка АВ пролетом 3 м, шириной 200 мм и высотой 100 мм предназначена для поддержки трех
сосредоточенные нагрузки показаны на рисунке. Модуль упругости выбранного класса древесины составляет 8 ГПа, а плотность
бруса 600 кг / м 3 Рассчитайте макс. прогиб, макс. усилие сдвига, макс. изгибающий момент, средний пролет
силы прогиба / наклона и конечной реакции деревянной прямоугольной балки для следующих
условия загрузки. Шаг 1: Запишите входные параметры (включая свойства материала), которые
определено в образце примера. Шаг 2: Перейдите в «Калькулятор свойств сечения твердого прямоугольного стержня»
страница для расчета второго момента площади вокруг оси x (I xx ) Шаг 3: Перейдите на страницу «Калькулятор напряжения и прогиба простой опоры балки», чтобы рассчитать максимальный сдвиг.
сила, изгибающий момент и прогиб древесины.Введите три точечные нагрузки, указанные на рисунке, и одну распределенную нагрузку (из-за нагрузки на деревянную балку).
собственный вес). Распределенная нагрузка равна
(М * г) / L = 36 * 9,81 / 3 = 117,7 Н / м. На деревянную балку не действует момент, поэтому установите значения момента на 0. Шаг 4: Результаты вычислений на шаге 3 следующие. Макс. прогиб, макс. усилие сдвига, макс. изгибающий момент, прогиб / наклон в середине пролета и силы реакции конца деревянной прямоугольной балки были рассчитаны с помощью
использование следующих калькуляторов. Пример 6: Для консольной балки и нагрузки
показано, определить реакции на опоре. Решение: Мы начнем наш анализ с рисования диаграммы свободного тела балки. После определения неизвестных реакционных нагрузок мы решаем их, используя уравнения равновесия. Схема балки со свободным телом: Балка закреплена в точке А. Следовательно, в этой точке действуют две силы реакции и один момент реакции, как показано ниже. Мы предполагаем направление для каждой реактивной нагрузки. Также для упрощения расчетов распределенная сила представлена ее равнодействующей, действующей в ее центре тяжести., Реакционные нагрузки: Как показано на диаграмме свободного тела, существуют три неизвестные реакции, которые необходимо решить для использования условия равновесия.Поскольку это двумерная система сил, мы можем использовать только три уравнения равновесия. Мы начинаем решение с использования равновесия моментов с точкой A в качестве
центр момента. Мы выбираем точку A, так как она устранит вклады
двух неизвестных сил реакции. Отрицательный знак указывает, что направление QA противоположно тому, которое показано на
диаграмма свободного тела. Теперь приступим к решению двух сил реакции.Использование равновесия сил в направлении x дает Горизонтальная сила реакции в точке A равна нулю, поскольку другой горизонтальной
сила, действующая на балку. Проверка результатов: Мы можем проверить решение
суммируя моменты относительно D или любой другой точки, чтобы увидеть, равно ли оно нулю. Если e равно нулю, мы уверены, что в решении нет ошибок. В отличие от примеров 4 и 5, вся нагрузка поддерживается в точке А. Фиксированная опора также развивает моментную реакцию, поскольку балка удерживается от вращения. Этот элемент является важным фактором при проектировании балок. Несущая способность стенки
Устойчивость к паутине
Калькулятор отклонения балки
Что такое прогиб балки и изгиб балки
Как рассчитать максимальный прогиб балки
Метод наложения
Жесткость балки
Iₓ = ширина * высота³ / 12
= 20 * (30³) / 12
= 45000 см⁴ Iᵧ = высота * ширина³ / 12
= 30 * (20³) / 12
= 20,000 см⁴ Понимание формул прогиба балки
Пример расчета прогиба балки
Iₓ = ширина * высота³ / 12
= 30 * (4³) / 12
= 160,0 см⁴ или 1,6x10⁻⁶ м⁴ 6800 МПа (6,8x10⁹ Па) , что является значением, которое мы получили из Справочника по древесине. Вы также можете легко получить значение модуля упругости для других материалов, таких как сталь и бетон, в Интернете или в местной библиотеке.Теперь, когда мы знаем эти значения, давайте рассмотрим нагрузку, которую будет нести этот стенд. Предположим, что ребенок 400 N сидит в центре скамейки. Теперь мы можем рассчитать прогиб сиденья скамейки из-за точечной нагрузки в его центре: δₘₐₓ = P * L³ / (48 * E * I)
δₘₐₓ = (400 Н) * (1,5 м) ³ / (48 * 6,8x10⁹ Па * 1,6x10⁻⁶ м⁴)
δₘₐₓ = 0,002585 m = 2,5850 мм Расчет нагрузок на коллекторы и балки | Строительство и строительные технологии
Делаю работу
Рисунок 1
Рисунок 2
Рисунок 3
Рисунок 4 Балки
Пример коньковой балки
Рисунок 5 — На этом рисунке показаны 2 конструктивных элемента: конструкционная коньковая балка и центральная балка.У обоих есть приток площадью 12’0 ″. Нагрузка на фут балки определяется так же, как и для жаток. Резюме
(Балки — TotalConstructionHelp)
Все это может показаться ошеломляющим, но это не так.
Получите момент (Mmax).
Мы хотим, чтобы балка была разработана для максимальной безопасности. Для балки с простой опорой и
Равномерно распределенная нагрузка Максимальный момент вычисляется с использованием уравнения M = WL 2 /8.
Теперь нам нужно знать
будет ли Луч будет деревянным или стальным.Если балка деревянная, то в зависимости от
для древесины типичное значение fb (напряжение изгиба) может варьироваться от 1000 фунтов на квадратный дюйм.
(фунт на квадратный дюйм) до 1200 фунтов на квадратный дюйм, ниже или выше.
Как правило, консервативное значение будет
около 1000 фунтов на квадратный дюйм, если вы используете пихту или болиголов, это также можно получить
из Строительного кодекса для различных пород дерева.
Точно так же, если вы намерены
для использования стали значение Fy = 36000 Steel будет fb = 24000 psi (где,
fb = 0.66 x Fy). Как видно, Сталь — 24000, а Дерево — 1000, что
указывает на то, что сталь примерно в 24 раза прочнее древесины при изгибе.
Что также указывало на то, что стальная балка будет меньше деревянной балки.
Если у вас ограниченное пространство, стальная балка может быть лучшим выбором.
Как видно из примера, мы вычислили максимальное значение
Прогиб в центре Луча.
В этом примере максимальное отклонение
разрешено контролируется Кодексом. Некоторые из допустимых отклонений показаны на
пример. Чтобы вычислить отклонение, нам нужна дополнительная информация,
что составляет E (модуль упругости) материала и I (момент
Инерция) для выбранного элемента. (См. Раздел о вычислении момента инерции.
на этом веб-сайте)
Модуль упругости (E) древесины колеблется в районе 11, для этих
в примерах использовалось значение 11
.Если используется сталь, то значение E
будет около 2
00, как показано в примерах.
Момент инерции (I) может быть либо вычислен, либо выбран из таблиц.
при условии. (См. Раздел о вычислении момента инерции)
Допустимые отклонения для элементов, поддерживающих:
L = пролеты, например: 12 футов, умножьте 12 футов на 12 дюймов = 144 дюйма, разделенные на 360, 240 или 180, в зависимости от того, что применимо.
Ниже приведены практические примеры нагрузок и расчетов, применяемых к прямоугольным стержням. Равномерно распределенная нагрузка (100 фунтов на фут) на 2 x 10
с уравнениями и решениями:
с уравнениями и решениями:
с уравнениями и решениями:
Бетонные балки: Пример простого поддерживаемого отклонения луча
Решение:
ВХОДНЫЕ СВОЙСТВА Параметр Значение Ширина бруса [b] 100 мм Высота бруса [H] 200 мм Длина бруса [L] 3000 мм Расстояние x (средний пролет) [x] 1500 мм Модуль упругости древесины [E] 8 ГПа Тип балки Балка с простой опорой
с многоточечными нагрузками ВХОДНЫЕ ПАРАМЕТРЫ Параметр Значение Высота [H] 200 мм Ширина [B] 100 Длина [L] 3000 Плотность [p] 600 кг / м 3 ВЫХОДНЫЕ ПАРАМЕТРЫ Параметр Значение Площадь поперечного сечения [A] 20000 мм ^ 2 Масса [M] 36 кг Второй момент площади [I xx ] 66666668 мм ^ 4 Второй момент площади [I yy ] 16666667 Модуль упругости [S xx ] 666666.3 Модуль упругости сечения [S yy ] 333333.344 Радиус вращения [r x ] 57,735 мм Радиус вращения [r y ] 28.868 Расстояние CoG в направлении x [x cog ] 50 мм Расстояние CoG в направлении y [y cog ] 100 ВХОДНЫЕ ПАРАМЕТРЫ ТОЧЕЧНЫЕ НАГРУЗКИ Параметр Символ Величина Расстояние кН м Нагрузка 1 ** Т 1 10 0.5 Нагрузка 2 ** П 2 5 1,5 Нагрузка 3 ** П 3 10 2.5 Нагрузка 4 ** П 4 0 0 Нагрузка 5 ** П 5 0 0 КОНЦЕНТРИРОВАННЫЕ МОМЕНТЫ Параметр Символ Величина Расстояние Н * м м Момент 1 ** П 1 0 0 Момент 2 ** П 2 0 0 Момент 3 ** П 3 0 0 Момент 4 ** П 4 0 0 Момент 5 ** П 5 0 0 РАСПРЕДЕЛЕННЫЕ НАГРУЗКИ Параметр Символ Величина Расстояние Н / м м wa wb b Распределенная нагрузка 1 ** w 1 117.7 117,7 0 3 Распределенная нагрузка 2 ** w 2 0 0 0 0 Распределенная нагрузка 3 ** w 3 0 0 0 0 Распределенная нагрузка 4 ** ш 4 0 0 0 0 Распределенная нагрузка 5 ** w 5 0 0 0 0 КОНСТРУКТИВНАЯ СВОЙСТВА БАЛКИ Параметр Символ Значение Длина балки L 3 м Расстояние x х 1.5 Модуль упругости E 8 ГПа Расстояние от нейтральной оси до крайних волокон с 50 мм Второй момент области Я 66666668 мм ^ 4 ВХОДНАЯ НАГРУЗКА НА ПРОСТО ОПОРНУЮ БАЛКУ ТОЧЕЧНЫЕ НАГРУЗКИ № Расположение Величина 1 0.5 м 10 кН 2 1,5 м 5 кН 3 2,5 м 10 кН КОНЦЕНТРИРОВАННЫЕ МОМЕНТЫ РАСПРЕДЕЛЕННЫЕ НАГРУЗКИ Нет. Начальная точка Величина Конечное местоположение Величина 1 0 м 117.7 Н / м 3 м 117,7 Н / м РЕЗУЛЬТАТЫ Параметр Значение Сила реакции 1 [R 1 ] 12676.5 N Сила реакции 2 [R 2 ] 12676,5 Поперечное поперечное усилие на расстоянии x [V x ] 2500,0 Максимальное поперечное усилие сдвига [V max ] 12676.5 Момент на расстоянии x [M x ] 8882,4 Н * м Максимальный момент [M max ] 8882,4 Наклон 1 [θ 1 ] -0.988 степень Наклон 2 [θ 2 ] 0,988 Наклон на расстоянии x [θ x ] 0,000 Максимальный наклон [θ макс ] -0.988 Прогиб на расстоянии x [y x ] -15,662 мм Максимальный прогиб [y max ] -15,662 Напряжение изгиба на расстоянии x [σ x ] 6.7 МПа Максимальное напряжение изгиба [σ макс ] 6,7 Сводка
Дополнения:
Пример 6
=>