Примеры хищник жертва: Приведите примеры : отношения хищник-жертва отношения паразит-хозяин взаимовыгодные отношения конкурентные отношения

Отношения Хищник-жертва: определение и примеры

Определение отношений хищник-жертва

Отношения между хищником и добычей состоят из взаимодействия двух вид и их последующее влияние друг на друга. В отношениях жертвы хищника один вид питается другим видом. Вид добычи – это животное, которым кормят, а хищник – животное, которого кормят. Отношения между хищником и добычей развиваются с течением времени, когда взаимодействуют многие поколения каждого вида. При этом они влияют на успех и выживание видов друг друга. Процесс эволюции выбирает для адаптаций, которые повышают пригодность каждого Население, Ученые, изучающие динамику популяции или изменения в популяции с течением времени, заметили, что отношения между хищниками и жертвами сильно влияют на популяции каждого вида, и что из-за взаимосвязей между хищниками и жертвами эти колебания популяций связаны между собой.

Отношения между хищниками и добычей и динамика населения

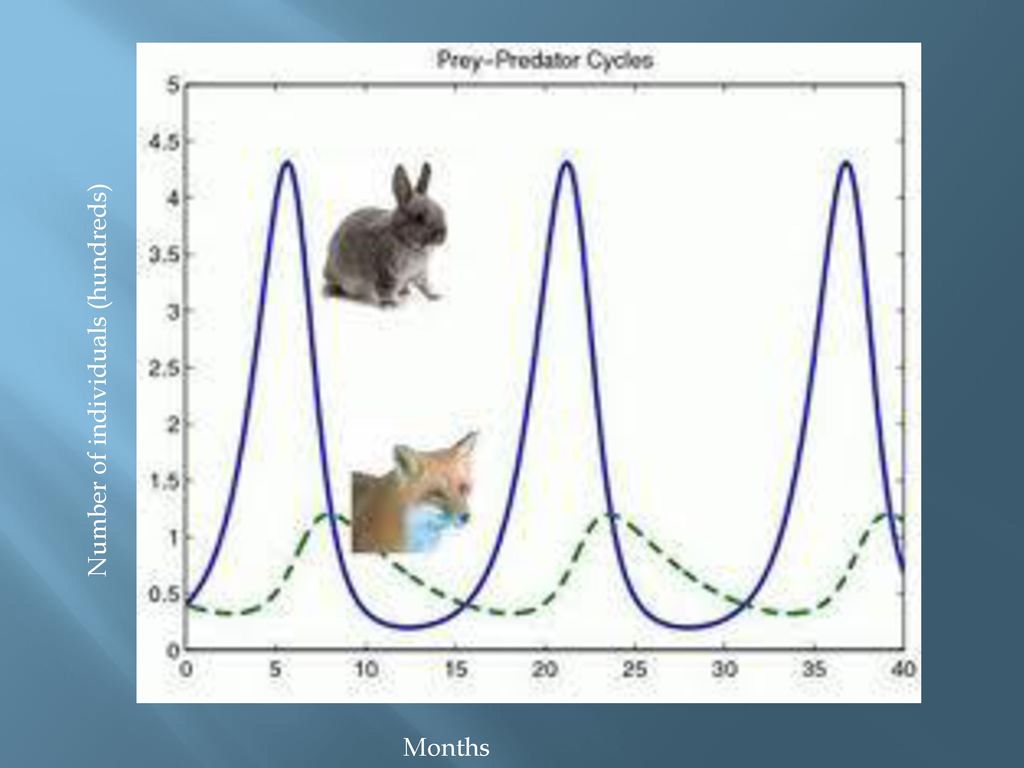
В некоторых примерах отношений с хищником у хищника действительно есть только один предмет. В этих сценариях легко увидеть, как отношение добычи хищника влияет на динамику популяции каждого вида. Простым примером являются взаимоотношения хищников с рысой и зайцем на снегоступах. Заяц образует большой продукт в рационе рыси. Без зайца рысь будет голодать. Однако, когда рысь ест зайца или многих зайцев, он может размножаться. Таким образом, популяция рыси увеличивается. С увеличением охоты на рысь популяция зайцев быстро сокращается. Посмотрите на график ниже.

Синим цветом показана популяция рыси, а красным – популяция зайцев. В начале графика популяция рыси была очень высокой, а популяция зайцев была относительно низкой. Когда рысь начала мигрировать или отмирать, популяция зайцев восстановилась. С 1845 года эта 10-летняя закономерность продолжала повторяться, и сразу же после отмирания зайца отмирала рысь. Отношения хищника и жертвы между зайцем и рысью помогают управлять этим паттерном. Однако, если вы усредните пики популяции, обе популяции останутся стабильными или покажут лишь незначительное увеличение или уменьшение во времени.

Помните также, что у зайца также есть связь добычи хищника с организмами, которыми он питается, которые, как оказалось, являются растениями. Когда зайцы взрываются, они едят больше, чем может выдержать растительность, и они загнаны в голод. Это, а также их связь между добычей и хищниками и рысью, приводят к очень изменчивым изменениям в популяции.

Хищническая добыча Отношения и эволюция

Поскольку эти популяции продолжают воспроизводиться с течением времени, действия естественный отбор также может изменить вид, чтобы сделать их лучшими хищниками или более оборонительной добычей. В любом случае, это приспособление изменяет динамику всей добычи хищника. Если один вид не сможет приспособить соответствующую защиту, он может исчезнуть. Таким образом, отношения между хищником и добычей часто образуют «эволюционную гонку вооружений», в которой быстро эволюционируют пищевые виды, чтобы противостоять другим.

В то время как многочисленные примеры были замечены относительно развития черт через отношения добычи хищника, некоторые из самых интересных примеров происходят, когда отношения приостановлены.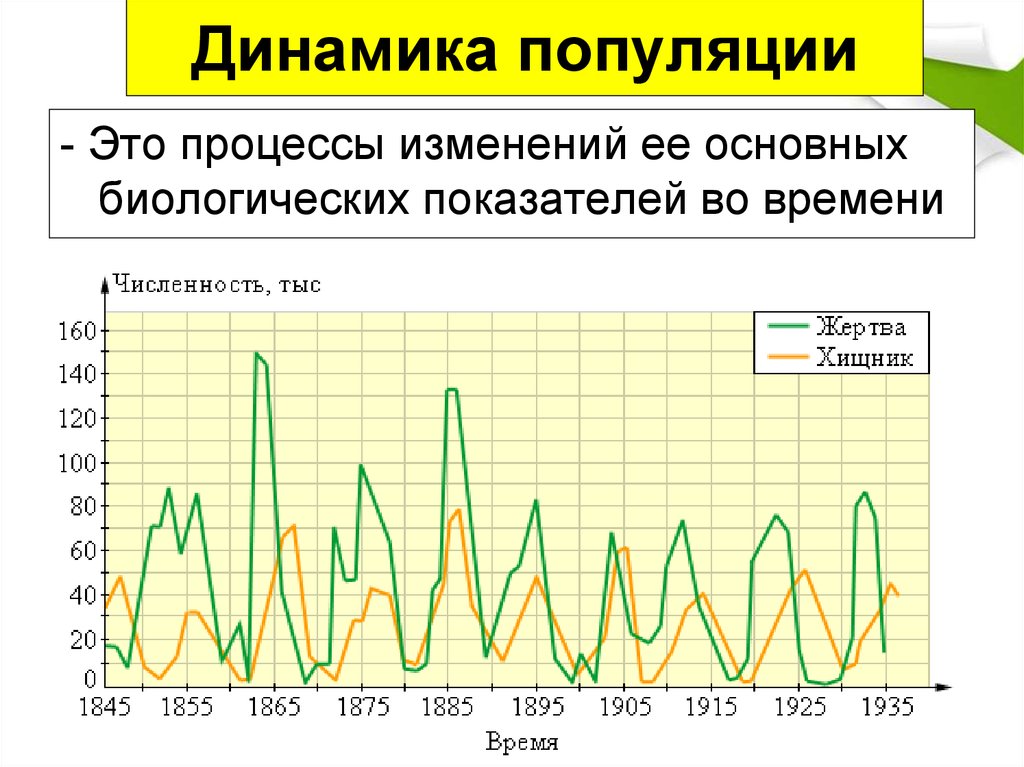 В тестах на гуппи ученые показали, что большое, красочное пятно является сексуально подобранной чертой. Самцы предпочитают самцов гуппи с яркими пятнами. Тем не менее, хищники могут легко определить эти цвета и съесть самых ярких самцов.

В ручьях, где нет хищников, самцы становятся ярко окрашенными. Сексуальный отбор быстро превращает мужчин в ярко окрашенных, а их новизна и яркость способствуют их эволюционному успеху. В ручьях с хищниками мужчины, которые преуспевают, делают это не обязательно, потому что они были самыми привлекательными, но потому что они жили дольше всего. В этом случае отношения между хищниками и жертвами преодолели давление, связанное с сексуальным отбором. Это хороший пример того, как взаимоотношения хищников и жертв могут значительно повлиять на путь эволюции.

Примеры отношений Хищник-жертва

Обычный Хищник

Как правило, у вида есть более чем одно отношение жертвы хищника. Рассмотрим, например, ягуара. Ягуар – одинокий хищник, предпочитающий охотиться и жить один. Ягуар является хищником многих разных животных, от диких свиней до каймана. С каждым из этих видов он поддерживает связь с добычей хищника. Тем не менее, ягуар также является предметом добычи для определенных видов. Маленькие ягуары остаются со своими матерями в течение года или более, прежде чем смогут полностью защитить себя. Анаконды, крупные птицы и другие кошачьи – это лишь некоторые из опасностей для молодого ягуара.

Ягуар, как и выше, представляет собой обычного хищника. Он охотится, убивает и ест другие организмы. В то время как ягуары – одиночные хищники, есть и социальные хищники, которые охотятся группами. К ним относятся такие виды, как волки, косатки и львы. Различия в этих социальных структурах представляют разные эволюционные ниши, которые выделяют виды, а также прошлые отношения с хищниками, которые сформировали животных, какими они являются сегодня.

Нетрадиционные Хищники

Помимо обычных хищников, многие организмы соответствуют определению хищника за пределами типичных границ. Мусорщики, как тип хищника, имеют отношение к добыче хищника с каждым видом, которым они питаются. Например, падальщик, такой как стервятник, подвергается воздействию, когда популяция буйволов падает. С меньшим количеством буйволов, львы отмирают и делают меньше убийств, а затем затрагивается сам стервятник. Хотя это может быть однобокое отношение жертвы хищника, потому что стервятник не убивает напрямую буйвола, он все еще подвержен влиянию популяции бизонов. К счастью для стервятников, они убирают много видов и не зависят только от популяции буйволов. Это не верно для всех падальщиков.

Другие нетрадиционные хищники включают паразитов, которые питаются от хозяина организм, но не обязательно убить его. Хотя хищник может быть намного меньше, чем жертва, у них все еще есть отношения. Например, отношения между хищниками и жертвами между оленями и клещами очень похожи на отношения между хищниками и жертвами рыси и зайца. Когда олени отмирают, клещам нужно меньше питаться, особенно клещам, которые специализируются на оленях. Снижение вызвано частично самими клещами, которые добавляют паразитическую нагрузку на оленей и переносят болезни в популяции. Клещи тогда уменьшатся в количестве, позволяя оленю процветать.

Почти 10% всех известных насекомых проявляют особую форму паразитизм, Эти паразитоиды, как они известны, разработали особые отношения с хищниками, в которых они откладывают яйца внутри другого вида. Личинка выводится и съедает свой выход, когда хозяин медленно умирает. В то время как взрослый не потребляет другие виды непосредственно, личинки делают. Ниже приведена фотография осы-паразитоида с тарантулом, которого она парализовала. Оса будет откладывать яйца в живой тарантул, который будет выводить и пожирать его изнутри.

Растения как жертвы и хищники

Растения часто игнорируются как жертвы и хищники, потому что они кажутся безразличными к действиям вокруг них. Однако многие эксперименты и наблюдения показали, что растения являются активными участниками отношений. Потрясающим примером является растение общение в ответ на хищников. Было показано, что некоторые виды растений выработали особую защиту от чрезмерного выпаса скота. После того, как умеренный уровень выпаса будет превышен, и растение находится в опасности, оно начнет выпускать гормон газ этилен в воздух. Другие растения получают этот гормональный сигнал и начинают производить токсичные вещества в своих листьях. Животные, которые питаются этими растениями, заболевают и умирают. Таким образом, эволюционные отношения битвы и добычи хищника развивались между растениями и травоядными с тех пор, как они впервые сосуществовали.

Кроме того, растения могут быть прямыми хищниками и развивать сложные характеристики взаимоотношений с хищниками и с этой стороны. Рассмотрите Ловушку Мухи Венеры, изображенную ниже. Это растение развилось непосредственно как хищник многих летающих насекомых. У растения не только есть особые волоски на листьях, которые могут чувствовать движение насекомых и большие шипы, чтобы захватить их, но они также активно выделяют вещества, чтобы привлечь насекомых. Другие растения разработали различные формы ловушек для насекомых, и они обеспечивают растения дополнительными питательными веществами. Эти отношения между хищниками и жертвами мало чем отличаются от змей, ожидающих, когда мышь пересечет их путь.

викторина

Ссылки

• Blumstein, D.T. & Fernandez-Juricic, E. (2010). Учебник по сохранению поведения. Сандерленд: Sinauer Associates, Inc. Издатели.
• Feldhamer, G.A., Drickamer, L.C., Vessey, S.H., Merritt, J.F. & Krajewski, C. (2007). Маммология: адаптация, разнообразие, экология (3-е изд.). Балтимор: издательство Университета Джонса Хопкинса.
• Kaiser, M.J., Attrill, M.J., Jennings, S., Thomas, D.N., Barnes, D.K., Brierley, A.S. & Hiddink, J.G. (2011). Экология моря: процессы, системы и воздействия. Нью-Йорк: издательство Оксфордского университета.

Математическая модель хищник-жертва на линейном ареале

Поставлена математическая задача о двух взаимодействующих на линейном ареале популяциях по принципу хищник-жертва (модель Вольтерра). Математическая модель представляет собой краевую задачу для системы двух нелинейных дифференциальных уравнений в частных производных. Исследуется устойчивость стационарных состояний. Для построения численного решения используется вариационный метод с представлением решений в виде тригонометрических рядов. Дана оценка зависимости амплитуды и частоты затухающих колебаний от параметров, характеризующих подвижность особей. Теоретические результаты сопоставляются с результатами численных экспериментов.

Ключевые слова: популяция, краевые задачи, математическое моделирование.

Введение. Математическому моделированию системы «хищник-жертва» посвящено большое число работ [1–3, 6–8, 32, 44, 50, 57–59, 62–68, 70]. Как правило, математическая часть моделей представлена задачей Коши для системы обыкновенных дифференциальных уравнений. В таких моделях не учитывается пространственное распределение особей. Реальные популяции живут на ограниченных территориях с различными свойствами среды обитания в разных ее частях [5, 11, 16, 34, 41, 45, 51, 60, 68]. Часть особей по различным причинам (например, в поисках пищи или свободных мест обитания) склонна к перемещению по территории. Как показывает анализ результатов полевых наблюдений [16, 45, 51, 59, 60] перемещение особей происходит случайным образом. В моделях с распределенными параметрами, в которых учитывается пространственное распределение особей популяции, вводится плотность популяции на единицу длины, площади или объема, и считается, что особи распределены в пространстве. Среда обитания считается сплошной, что позволяет использовать аппарат дифференциальных уравнений в частных производных, широко применяемый при разработке математических моделей сплошных сред с нелинейными свойствами [17, 20, 27, 37–40, 47–49, 56, 61, 68, 69].

В природных условиях изменение численности популяции носит колебательный характер. Колебания численности связаны с реакцией популяции на внешние воздействия и внутренние изменения в биоценозе. Период и амплитуда колебаний зависят от механизмов регуляции численности популяции, особенностей вида и от условий его существования. Существенное влияние на биоценозы оказывает и производственная деятельность человека, приводящая к изменению условий существования флоры и фауны. Для учета негативных последствий, вносимых человеком нарушений в ход эволюционных процессов, в модели популяционной биологии необходимо подключать модели математической экономики [14, 15, 35, 36, 43].

Точечная модель хищник-жертва. Математическая модель, описывающая динамику численности двух популяций, взаимодействующих по принципу хищник-жертва, была предложена Лотка и Вольтерра [7].

                                                                                                         (1)

В этих уравнениях  и  — численности популяций жертвы и хищника соответственно, –удельнаяскорость роста популяции жертвы в отсутствие хищника,  — константа, характеризующая скорость потребления популяцией хищника особей популяции жертвы, – удельная скорость смертности хищника, –константа, характеризующая скорость увеличения численности хищника за счет уничтожении им жертвы. Стационарной точкой системы уравнений (1) является , . Эта стационарная точка устойчива, является центром, в ее окрестности происходят гармонические колебания численности обеих популяций с частотой  [3].

Модель Вольтерра объясняет одну из причин колебаний в системе «хищник-жертва», но она, как правило, плохо согласуется с экспериментальными данными. Так, например, в работах [33, 41, 45, 51] приводятся данные по численности различных видов хищников и жертв. Авторы отмечают, что в динамике экстремумы численности жертв и хищников совпадают — модель Вольтерра такой результат не дает. Не удается с высокой степенью точности описать и динамику изменения численности популяций в системе «хищник-жертва», поскольку одновременно оценить значения всех констант, входящих в (1), для реальных популяций не просто [21–25]. Наиболее точно можно оценить удельные скорости рождения  и смертности  и, соответственно период колебаний [3, 5]. По данным статистического учета особей по площадям или индивидуальным участкам [16, 41, 51, 59, 60] можно оценить значения  и  и, соответственно, значения констант  и .

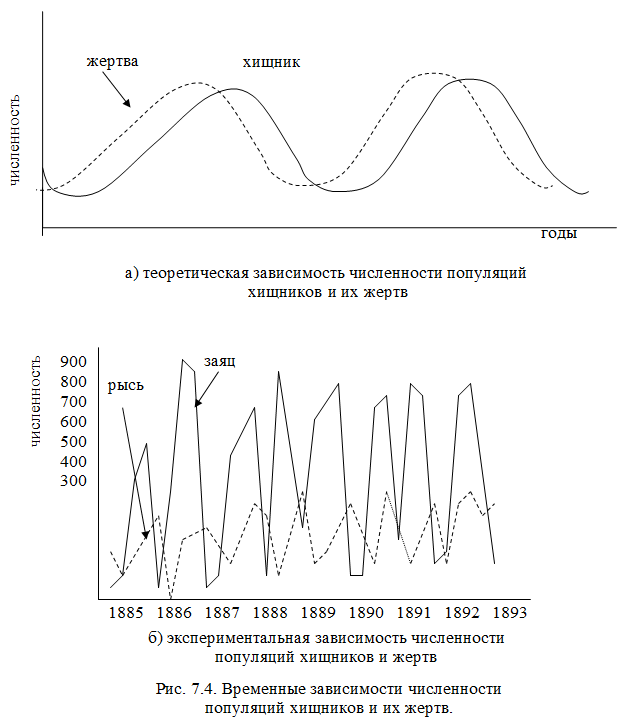
Результаты сопоставления расчетных (, , , ) и экспериментальных данных, приведенных в [45], представлены на рис. 1 для жертвы, а на рис. 2 для хищника. Символом  отмечены экспериментальные данные, сплошными линиями — расчетные. Как следует из анализа этих результатов, теоретические результаты в лучшем случае могут предсказать лишь период колебаний . Но вместе с этим понятно, что модель Вольтерра не учитывает многочисленные факторы, влияющие на численность популяций, одним из которых является неоднородность среды обитания.

Рис. 1. Изменение численности жертвы во времени

Рис. 2. Изменение численности хищника во времени

Модель хищник-жертва на линейном ареале. Примерами линейных ареалов служат трубопроводы, обочины дорог, лесные просеки [3, 5, 11, 16, 34, 45, 51, 52, 58, 59 60, 68]. Математическая модель «хищник-жертва» (1) на отрезке с учетом замены переменных [3]

, ,

представляется системой двух эволюционных уравнений [4, 12, 18, 19, 56, 58,59, 62, 68]

                                                                                           (2)

В этих уравнениях  — координата,  — время,  и  — линейные плотности популяций,  и  — параметры, характеризующие подвижности особей.

В качестве начальных условий задается значение функций  и  в начальный момент времени: при  , .

В качестве граничных условий для случая отрезка длиной  рассматриваются два варианта:

,                                                                     (3)

и

, .                                                           (4)

Условие обращения в ноль функций  и  на границе отрезка соответствует невозможности существования популяции в этой точке, а условие обращения в ноль производных  и  (условие наполнения среды [13, 29, 30, 31, 44, 50, 58, 59, 68]) допускает свободный рост численности популяций.

Общие численности жертвы () и хищника () на отрезке в момент времени  подсчитываются по формулам

, .

Устойчивость решений. Встационарном случае системе уравнений (2) при граничных условиях (3) или (4) удовлетворяет тривиальное решение , . Возмущение этого равновесного состояния представляется в виде [9, 10, 26, 29–31, 53] , , где  и  малые по сравнению с единицей величины: , . Тогда уравнения (2) с точностью до величин второго порядка малости [19, 26, 30] приводятся к виду

                                                                                               (5)

Решение первого уравнения, удовлетворяющее граничным условиям (3), представляется в виде тригонометрического ряда

.

При этом коэффициенты разложения должны удовлетворять уравнениям [56]

,         .

Из первого уравнения находится, что  будет возрастающей функцией времени. То есть решение  будет неустойчивым.

Решение первого уравнения в (5), удовлетворяющее граничным условиям (4), представляется в виде тригонометрического ряда

.

При этом коэффициенты разложения должны удовлетворять уравнениям

 .

Отсюда следует, что при выполнении неравенства  все коэффициенты  будут убывающими функциями времени и, соответственно, решение  будет устойчивым. Последнее означает, что при высокой подвижности особей жертвы малочисленная популяция в рассматриваемой модели погибает. Аналогичный результат получен в [13, 31] для одиночной популяции.

Для случая граничных условий (3) в стационарном случае уравнениям (2) удовлетворяют , . В окрестности этого решения решение уравнений (2) представляется в виде [26]

, ,

где  и  малые по сравнению с единицей величины: , . Тогда уравнения (2) с точностью до величин второго порядка малости приводятся к виду

Решение этих уравнений представляется в виде тригонометрических рядов [56]

, .

Коэффициенты разложения  и  должны удовлетворять системе обыкновенных дифференциальных уравнений ()

Собственные значения матрицы Якоби правой части этих уравнений удовлетворяют квадратному уравнению

.

При   будут иметь отрицательные вещественные части, а . То есть все коэффициенты  и  при  будут убывающими функциями времени, а коэффициенты  и  будут изменяться по гармоническому закону. То есть при малых отклонениях от стационарного решения ,  возникнут периодические по времени колебания, а решение со временем стремится к гомогенному по пространственной переменной.

Численное решение. Построить аналитическое решение нелинейных уравнений (2) не представляется возможным. Поэтому используются различные методы аппроксимаций уравнений (2) или их решений. Наибольшее распространение получили конечно-разностная аппроксимация уравнений и вариационные методы, основанные на представлении решения в виде линейной комбинации аналитических функций [13, 19, 20, 28, 31, 32, 42, 44, 46, 54, 55]. Численное решение уравнений (2), удовлетворяющее граничным условиям (4) на отрезке ищется в виде суммы тригонометрических функций [42, 44, 56]

,                                                                                                                                             .                                                                                                                                                  (6)

Система функций  () удовлетворяет граничным условиям (4), является полной и ортогональной на отрезке . После подстановки выражений (6) в уравнения (2), умножения последних на  () и последующего интегрирования по промежутку  будет получена система обыкновенных дифференциальных уравнений для коэффициентов  и  ()

                          (7)

Начальные условия для функций  и  () определяются из соотношений

,

.

Для одного члена разложения () в (5) для случая отрезка единичной длины () коэффициенты  и  удовлетворяют уравнениям

Нетривиальная стационарная точка этих уравнений со значениями

 и (8)

реализуется, если выполняется неравенство .

Собственными значениями матрицы Якоби

в этой стационарной точке будут

,       .

Как следует из этих соотношений в первом приближении в системе возникают колебания с частой . Частота колебаний растет с увеличением подвижности хищника (параметр ) и уменьшается, если растет подвижность жертвы (параметр ). При этом, как это следует из (8), увеличение подвижности хищника приводит и к увеличению амплитуды колебаний у жертвы. Амплитуда колебаний хищника от его подвижности в первом приближении не зависит.

Анализ поведения решения при большем числе слагаемых в представлениях (6) не представляется возможным без использования численных методов. Решение задачи Коши для системы уравнений (7) осуществлялось с применением численных методов типа Рунге-Кутты [46]. Некоторые из результатов численных экспериментов приведены на рис. 3–7.

Рис. 3. Значения коэффициентов  () в момент времени

Рис. 4. Значения коэффициентов  () в момент времени

Рис. 5. Зависимость функций  и  от времени

Рис. 6. Зависимость функций  и  от координаты в момент времени

Рис. 7. Зависимость функции  от координаты в момент времени  при ,  и

На рис. 3 отражены значения коэффициентов  (, ), а на рис. 4 — , в момент времени  при  и  (подвижности хищников и жертв одинаковы). Из анализа этого результата следует, что при решении уравнений вариационным методом с высокой степенью точности можно ограничиться 4–5 членами в представлении (6). На рис. 5 отражено изменение функций  и  (общей численности популяции жертвы и популяции хищника на отрезке) во времени при , ,  (подвижности хищника значительно больше подвижности жертвы), а на рис.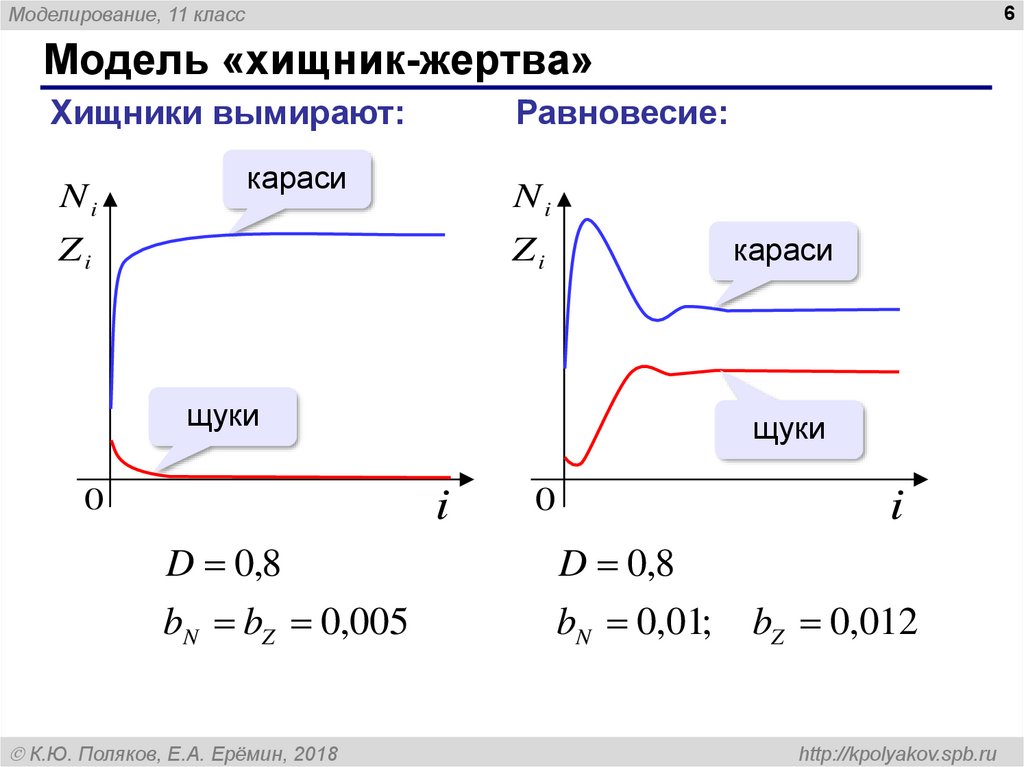 6 — изменение функций  и  от координаты в момент времени . Влияние подвижности хищника (параметра ) на распределение плотности популяции жертвы отражено на рис. 7 (, ,  ). Как следует из полученных результатов при высокой подвижности хищника в системе возникают затухающие колебания (рис. 5), в отличие от результатов, полученных для одного слагаемого в (6). Плотность популяции жертвы в окрестности точки  растет с ростом подвижности хищников (рис. 7) и одновременно растет и общая численность популяции жертвы.

Заключение. Учет неоднородности среды в математической модели хищник-жертва Вольтерра приводит к результатам, которые не дает точечная модель. Основной из них: от подвижности особей, как хищника, так и жертвы может зависеть общая численность популяций. При высокой подвижности особей популяция жертвы может погибнуть. Рост подвижности особей популяции хищника приводит к уменьшению периода возникающих колебаний и к увеличению численности жертвы.

Литература:

1.              Апонин Ю.  М., Апонина Е. А. Математическая модель сообщества хищник — жертва с нижним порогом численности жертвы // Компьютерные исследования и моделирование. — 2009. — Т. 1. — № 1. — С. 51–56.

2.              Апонин Ю. М., Апонина Е. А. Принцип инвариантности Ла-Салля и математические модели эволюции микробных популяций // Компьютерные исследования и моделирование. — 2011. — Т. 3. — № 2. — С. 177–190.

3.              Базыкин А. Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: Институт компьютерных технологий, 2003. — 368 с.

4.              Балыкина Ю. Е., Колпак Е. П. Математические модели функционирования фолликула щитовидной железы // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2013. — № 3. — С. 20–31.

5.              Бигон М., Харпер Дж., Таунсенд К. Экология. Особи, популяции и сообщества: в двух томах. М.: Мир, 1989. Т. 1. — 667 с. Т. 2. — 477с.

6.              Будянский А. В. , Цибулин В. Г. Моделирование пространственно-временной миграции близкородственных популяций // Компьютерные исследования и моделирование. — 2011. — Т. 3. — № 4. — С. 477–488.

7.              Вольтерра В. Математическая теория борьбы за существование. Москва-Ижевск:, Институт компьютерных технологий, 2004. — 288 с.

8.              Гайко В. А. Глобальный бифуркационный анализ квартичной модели «хищник–жертва» // Компьютерные исследования и моделирование. — 2011. — Т. 3. — № 2. — С. 125–134.

9.              Гасратова Н. А. Напряженно-деформированное состояние упругого пространства со сферическим жестким включением // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 1. — С. 14–18.

10.          Гасратова Н. А., Шамина В. А. Решение в напряжениях линейной осесимметричной задачи для сферы и упругого пространства со сферической полостью // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2008. — № 2. — С. 122–128.

11.          Гилев А. В. Закономерности пространственного распределения и научные основы охраны рыжих лесных муравьев // Зоологический журнал. — 2010. — Т. 89. — № 12. — С. 1413–1420.

12.          Глызин С. Д. Разностная аппроксимация уравнения «реакция — диффузия» на отрезке // Моделирование и анализ информационных систем. — 2009. — Т. 16. — № 3. — С. 96–116.

13.          Горбунова Е. А., Колпак Е. П. Математические модели одиночной популяции // Вест. С.-Петерб. ун-та. Сер. 10. — 2012. — Вып. 4. — С. 18–30.

14.          Григорьева К. В., Иванов А. С., Малафеев О. А Статическая коалиционная модель инвестирования инновационных проектов // Экономическое возрождение России. — 2011. — № 4. — С. 90–98.

15.          Григорьева К. В., Малафеев О. А. Динамический процесс кооперативного взаимодействия в многокритериальной (многоагентной) задаче почтальона // Вестник гражданских инженеров. — 2011 — № 1. — С. 150–156.

16.          Громов В. С. Пространственно-этологическая структура популяций грызунов. М.: Т-во научн. изданий КМК, 2008. — 581 с.

17.          Даль Ю. М., Пронина Ю. Г. Деформация шаровой поры в нелинейно-упругом теле // Известия Российской академии наук. Серия физическая. — 2006. — Т. 70. — № 9. — С. 1341–1343.

18.          Жукова И. В., Колпак Е. П. Математическая модель солидной опухоли // Естественные и математические науки в современном мире. — 2013. — № 13. — С. 18–25.

19.          Жукова И. В., Колпак Е. П. Математические модели злокачественной опухоли // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 3. — С. 5–18.

20.          Кабриц С. А. Мальков В. М., Мансурова С. Е. Математическое моделирование нелинейной деформации эластомерного слоя // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 3. — С. 56–63.

21.          Карелин В. В Один подход к задаче оценки параметров динамической системы в условиях неопределенности // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2012. — № 4. — С. 31–36.

22.          Карелин В. В Точные штрафы в задаче наблюдения // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2008. — № 4. — С. 3–8.

23.          Карелин В. В. Точные штрафы в задаче оценки координат динамической системы в условиях неопределенности // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 4. — С. 40–46.

24.          Карелин В. В. Штрафные функции в задаче управления процессом наблюдения // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2010. — № 4. — С. 109–114.

25.          Колокольцов В. Н., Малафеев О.  А. Динамические конкурентные системы многоагентного взаимодействия и их асимптотическое поведение (часть I) // Вестник гражданских инженеров. — 2010 — № 4 — С. 144–153.

26.          Колпак Е. П. Устойчивость и закритические состояния безмоментных оболочек при больших деформациях // диссертация на соискание ученой степени доктора физико-математических наук / Санкт-Петербург, 2000.

27.          Колпак Е. П. Введение в механику сплошных сред учебное пособие / Е. П. Колпак; С.-Петерб. гос. ун-т. СПб. 2004.

28.          Колпак Е. П., Балыкина Ю. Е., Котина Е. Д., Жукова И. В. Математическая модель нарушений функционирования щитовидной железы // Молодой Ученый. — 2014. — № 2(61). — С. 19–24.

29.          Колпак Е. П., Горбунова Е. А., Балыкина Ю. Е., Гасратова Н. А. Математическая модель одиночной популяции на билокальном ареале // Молодой ученый. — 2014. — № 1 (6). — С. 28–33.

30.          Колпак Е. П., Горбунова Е. А., Жукова И. В. Математическая модель популяционной волны // Естественные и математические науки в современном мире.  — 2014. — № 16. — С. 25–41.

31.          Колпак Е. П., Горбунова Е. А., Столбовая М. В., Балыкина Ю. Е Математическая модель логистической популяции на линейном ареале // Молодой ученый. — 2014. — № 3 (62). — С. 6–14.

32.          Колпак Е. П., Жукова И. В., Степанова Д. С., Крицкая А. В. О численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва» // Молодой ученый. — 2014. — № 4. — С. 20–30.

33.          Колпак Е. П., Столбовая М. В. Математическая модель кинетики роста растений // Журнал научных публикаций аспирантов и докторантов. — 2013. — № 12 (90). — С. 230–232.

34.          Коробченко М. А. Расширение ареала крота европейского (talpa europaea) в долине реки Северный Донец // Зоологический журнал. — 2009. — Т. 88. — № 4. — С. 465–472.

35.          Малафеев О. А., Пахар О. В. Динамическая нестационарная задача инвестирования проектов в условиях конкуренции // Проблемы механики и управления: Нелинейные динамические системы.  — 2009. — № 41. — С. 103–108.

36.          Малафеев О. А., Соснина В. В. Модель управления процессом кооперативного трехагентного взаимодействия // Проблемы механики и управления: Нелинейные динамические системы. — 2007. — № 39. — С. 131–144.

37.          Мальков В. М., Малькова Ю. В. Исследование нелинейной задачи Фламана // Известия Российской академии наук. Механика твердого тела. — 2006. — № 5. — С. 68–78.

38.          Мальков В. М., Малькова Ю. В., Иванов В. А. Бесконечная плоскость с круговым включением, имеющим отслоение на части границы // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 4. — С. 152–165.

39.          Мальков В. М., Малькова Ю. В.Плоская задача нелинейной упругости для гармонического материала // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2008. — № 3. — С. 114–126.

40.          Мальков В. М., Малькова Ю. В. Нелинейная задача Фламана для несжимаемого материала // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2004. — № 4. — С. 73–82.

41.          Мамонтов С. Н. Распределение по стволу дерева короеда-типографа (ips typographus, coleoptera, scolyniddae) и его энтомогафов // Зоологический журнал. — 2009. — Т. 88. — № 9. — С. 1139–1145.

42.          Матросов А. В. Сходимость степенных рядов в методе начальных функций // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2012. — № 1. — С. 41–51.

43.          Миндлин Ю. Б., Колпак Е. П., Балыкина Ю. Е Проблемы использования кластеров в Российской Федерации // Вестник НГУЭУ. — 2014. — № 1. — С. 22–32.

44.          Мятлев В. Д., Панченко Л. А., Ризниченко Г. Ю., Терехин А. Т. Теория вероятностей и математическая статистика. Математические модели. М.: Издательский центр «Акадкмия», 2009. — 320 с.

45.          Окулова Н. М., Катаев Г. Д. Взаимосвязи «хищник-красно-серая полевка» в сообществах позвоночных животных Лапландского заповедника // Зоологический журнал.  — 2007. — Т. 86. — № 8. — С. 989–998.

46.          Олемской И. В. Модификация алгоритма выделения структурных особенностей // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2006. — № 2. — С. 55–64.

47.          Пронина Ю. Г. Периодическая задача о точечных воздействиях в упругой полуплоскости с отверстиями // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 3. — С. 118–128.

48.          Пронина Ю. Г. Сосредоточенные силы и моменты в упругой полуплоскости с отверстием // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 2. — С. 104–114.

49.          Пронина Ю. Г. Центры расширения-сжатия в упругой полуплоскости // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2007. — № 2. — С. 140–149.

50.          Ризниченко Г.  Ю., Рубин А. Б. Биофизическая динамика продукционных процессов. Москва — Ижевск: Институт компьютерных технологий, 2004. — 464 с.

51.          Садыков О. Ф., Бененсон И. Е. Динамика численности мелких млекопитающих: Концепции, гипотезы, модели. М.: Наука, 1992. — 191 с.

52.          Свирежев Ю. М. Нелинейные волны, диссипативные структуры и катастрофы в экологии. М: Наука, 1987. — 368 с.

53.          Старков В. Н., Степенко Н. А. Исследование динамики маятниковых систем с переменными параметрами // Естественные и математические науки в современном мире. — 2014. — № 15. — С. 20–36.

54.          Тамасян Г. Ш. Градиентные методы в вариационной задаче со свободными концами // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2012. — № 4. — С. 77–84.

55.          Тамасян Г. Ш. Градиентные методы решения задачи Коши // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 4. — С. 224–230.

56.          Тихонов А. Н., Самарский А. А. Уравнение математической физики. М.: Наука, 1972. — 735 с.

57.          Трубецков Д. И. Феномен математической модели Лотки-Вольтерры и сходных с ней // Известия высших учебных заведений. Прикладная нелинейная динамика. — 2011. — Т. 19. — № 2. — С. 69–88.

58.          Тютюнов Ю. В. Пространственная модель развития устойчивости насекомых-вредителей к трансгенной инсектицидной сельскохозяйственной культуре // Биофизика. — 2007. — Т. 52. — № 1. — С. 95–113.

59.          Тютюнов Ю. В., Загребнева А. Д., Сурков Ф. А., Азовский А. И. Микромасштабная пятнистость распределения веслоногих рачков как результат трофически обусловленных миграций // Биофизика. — 2009. — Т. 54. — Вып. 3. — С. 508–514.

60.          Уморин П. П. Роль хищников в устойчивом существовании нескольких видов водорослей // Биология внутренних вод. — 2009. — № 1. — С. 3–7.

61.          Черных К. Ф. , Кабриц С. А., Колпак Е. П., Слепнева Л. В. Точные решения краевых задач нелинейной теории упругости // отчет о НИР № 96–01–00739 (Российский фонд фундаментальных исследований).

62.          Чеснокова О. И., Мелких А. В. Имитационное моделирование направленного движения в условиях градиента освещенности // Компьютерные исследования и моделирование. — 2012. — Т. 4. — № 2. — С. 401–406.

63.          Abrams P. A., Chad E., Brassil C. E., Robert D., Holt R. D. Dynamics and responses to mortality rates ofcompeting predators undergoing predator–prey cycles // Theoretical Population Biology. — 2003. — V. 64. — P. 163–176.

64.          Garvie M. R. Finite-difference schemes for reaction–diffusion equations modeling predator–prey interactions in Matlab // Bulletin of Mathematical Biology. — 2007. — V. 69. — P. 931–956.

65.          Ge w., Gui z. The effect of harvesting on a predator–prey system with stage structure // Ecological Modelling. — 2005. — V. 187. — P. 329–340.

66.          Jones L. E., Ellner S. P Evolutionary Tradeoff and Equilibrium in an Aquatic Predator–Prey System // Bulletin of Mathematical Biology. — 2004. — V. 66. — P. 1547–1573.

67.          Lopez-Sanchez J. F., Alhama F., Gonzalez-Fernandez C.F Introduction and permanence of species in a diffusive Lotka-Volterra system with time-dependent coefficients // Ecological Modelling. — 2005. — V. 183. P. 1–9.

68.          Murray D. D. Mathematical biology. N. Y. Springer. 2002. — 551 p.

69.          Pronina Y. G. Estimation of the life of an elastic tube under the action of a longitudinal force and pressure under uniform surface corrosion conditions // Russian metallurgy (Metally). — 2010. — Т. 2010. — № 4. — С. 361–364.

70.          Wang W., Takeuchi Y.Adaptation of prey and predators between patches // Journal of Theoretical Biology. — 2009. — V. 258. — P. 603–613.

Основные термины (генерируются автоматически): момент времени, уравнение, математическая модель, вид, значение коэффициентов, коэффициент разложения, Модель, система, система уравнений, вариационный метод.

Система «хищник-жертва» | это… Что такое Система «хищник-жертва»?

Система «хищник-жертва» — сложная экосистема, для которой реализованы долговременные отношения между видами хищника и жертвы, типичный пример коэволюции.

Отношения между хищниками и их жертвами развиваются циклически, являясь иллюстрацией нейтрального равновесия^[1].

Содержание 1 Биологическая система 2 Математическая модель 2.1 Поведение модели 2.2 История 3 См. также 4 Примечания 5 Литература 6 Ссылки

Биологическая система

Приспособления, вырабатываемые жертвами для противодействия хищникам, способствуют выработке у хищников механизмов преодоления этих приспособлений. Длительное совместное существование хищников и жертв приводит к формированию системы взаимодействия, при которой обе группы устойчиво сохраняются на изучаемой территории. Нарушение такой системы часто приводит к отрицательным экологическим последствиям.

Негативное влияние нарушения коэволюционных связей наблюдается при интродукции видов. В частности, козы и кролики, интродуцированные в Австралии, не имеют на этом материке эффективных механизмов регуляции численности, что приводит к разрушению природных экосистем.

Математическая модель

Основная статья: Модель Лотки — Вольтерра

Допустим, что на некоторой территории обитают два вида животных: кролики (питающиеся растениями) и лисы (питающиеся кроликами). Пусть число кроликов , число лис . Используя Модель Мальтуса с необходимыми поправками, учитывающими поедание кроликов лисами, приходим к следующей системе, носящей имя модели Вольтерра — Лотки:

Эта система имеет равновесное состояние, когда число кроликов и лис постоянно. Отклонение от этого состояния приводит к колебаниям численности кроликов и лис, аналогичным колебаниям гармонического осциллятора.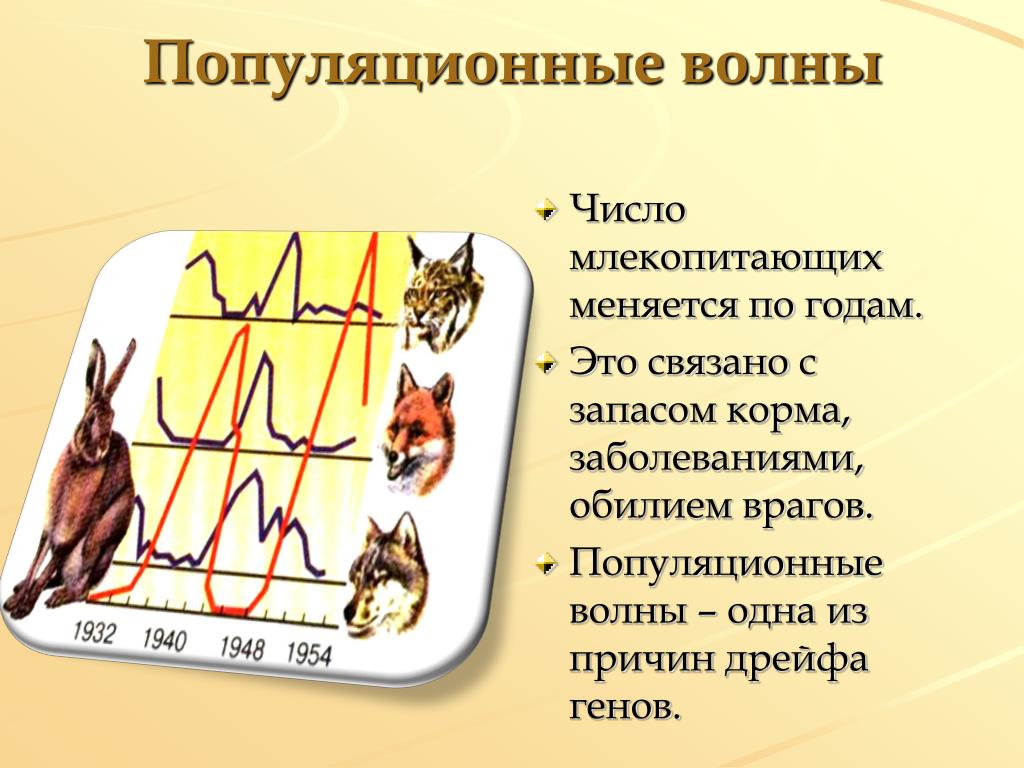 Как и в случае гармонического осциллятора, это поведение не является структурно устойчивым: малое изменение модели (например, учитывающее ограниченность ресурсов, необходимых кроликам) может привести к качественному изменению поведения. Например, равновесное состояние может стать устойчивым, и колебания численности будут затухать. Возможна и противоположная ситуация, когда любое малое отклонение от положения равновесия приведет к катастрофическим последствиям, вплоть до полного вымирания одного из видов. На вопрос о том, какой из этих сценариев реализуется, модель Вольтерра — Лотки ответа не даёт: здесь требуются дополнительные исследования.

С точки зрения теории колебаний модель Вольтерра — Лотки является консервативной системой, обладающей первым интегралом движения. Эта система не является грубой, поскольку малейшие изменения правой части уравнений приводят к качественным её изменениям динамического поведения. Однако, возможно «слегка» модифицировать правую часть уравнений таким образом, что система станет автоколебательной. Наличие устойчивого предельного цикла, свойственного грубым динамическим системам, способствует значительному расширению области применимости модели^[2].

Поведение модели

Групповой образ жизни хищников и их жертв радикально меняет поведение модели, придает ей повышенную устойчивость.

Обоснование: при групповом образе жизни снижается частота случайных встреч хищников с потенциальными жертвами, что подтверждается наблюдениями за динамикой численности львов и антилоп гну в парке Серенгети^[3].

История

Модель совместного существования двух биологических видов (популяций) типа «хищник — жертва» называется также моделью Вольтерра — Лотки.

Была впервые получена А. Лоткой в 1925 году (использовал для описания динамики взаимодействующих биологических популяций).

В 1926 году (независимо от Лотки) аналогичные (и более сложные) модели были разработаны итальянским математиком В. Вольтерра. Его глубокие исследования в области экологических проблем создали основу математической теории биологических сообществ (математической экологии)^[4].

См. также

• Принцип конкурентного исключения
• Теория оптимального фуражирования
• Дифференциальное использование ресурсов
• Теорема о маргинальных значениях
• Цепь Маркова
• Экспоненциальный рост
• Основные законы эволюции живого вещества в биосфере
• Пищевая цепь
• Экологическая система

Примечания

1. ↑ Элементы: Отношения хищник—жертва
2. ↑ Неймарк Ю. И. Математические модели естествознания и техники (лекции). Изд. ННГУ, Н. Новгород, части 1, 2, 3, издания 1994, 1996 и 1997 гг.
3. ↑ Общественный образ жизни повышает стабильность системы «хищник-жертва» (John M. Fryxell, Anna Mosser, Anthony R. E. Sinclair, Craig Packer. Group formation stabilizes predator-prey dynamics // Nature. 2007. V. 449. P. 1041—1043)
4. ↑ Простейшая модель «хищник-жертва»

Литература

• В. Вольтерра, Математическая теория борьбы за существование. Пер. с франц. О. Н. Бондаренко. Под ред и послесловием Ю. М. Свирежева. М.: Наука, 1976. 287 c. ISBN 5-93972-312-8
• А. Д. Базыкин, Математическая биофизика взаимодействующих популяций. М.: Наука, 1985. 181 с.
• А. Д. Базыкин, Ю. А. Кузнецов, А. И. Хибник, Портреты бифуркаций (Бифуркационные диаграммы- динамических систем на плоскости) /Серия «Новое в жизни, науке, технике. Математика, кибернетика» — М.: Знание, 1989. 48 с.
• П. В. Турчин, Популяционная динамика

Ссылки

• Выставка-триллер под названием «Хищник — жертва»

10 ошеломляющих примеров взаимоотношений хищник-жертва

И хищник, и жертва играют решающую роль в нормальном функционировании экосистемы. Изучая эти примеры отношений хищник-жертва, вы получите лучшее представление об этой концепции, а также о ее важности для окружающей среды.

Странны пути природы!

Когда хищник истощает популяцию жертв в своей среде обитания, возникающая в результате нехватка пищи автоматически замедляет популяцию хищников, тем самым давая популяции жертв шанс возродиться.

Что будет, если вымрут львы, гепарды, гиены и другие хищники африканской саванны? Поскольку на них не будет хищников, популяция антилоп гну, газелей и других травоядных увеличится, и они устроят бунт в саванне, уничтожая растительный покров. А что, если антилопы гну и газели вымрут? Без еды хищники либо умрут от голода, либо в конечном итоге перебьют друг друга. Хотя гипотетические, такие сценарии нельзя исключать. На самом деле отношения между хищником и жертвой более сложны, чем показано в этом примере.

Что такое отношения хищник-жертва?

Почти все виды в данной экосистеме взаимозависимы до такой степени, что потеря одного вида может иметь неблагоприятные последствия для других. В широком смысле зависимость можно разделить на симбиотические отношения и отношения хищник-жертва. Неудивительно, что отношения между хищником и добычей играют решающую роль, когда речь идет об экологическом балансе. Наклон в любую сторону может вызвать эффект домино для окружающей среды в целом. Если, например, запасы пищи изменятся из-за отсутствия добычи, это отразится на популяции хищных видов, поскольку им будет трудно размножаться во времена нехватки пищи. И, как мы уже говорили ранее, если популяция хищников сократится, травоядные устроят бунт в экосистеме.

В африканской саванне самым известным примером дуэта хищник-жертва будут отношения между гепардом — самым быстрым наземным животным в мире — и газелью. Не имея места, чтобы спрятаться в открытых лугах, у газели нет другого выбора, кроме как убежать от гепарда, и газель, зная, что гепард быстрее всего движется по прямой, делает это, бегая зигзагом. заг узор. Это классический пример выживания сильнейших.

Отношения между гепардом и газелью резко контрастируют с отношениями между африканскими дикими собаками и зебрами. Дикие собаки могут быть маленькими, но они компенсируют это поведением стаи и своей замечательной выносливостью. Стратегия проста: скоординировать атаку, изолировать особь, утомить ее и сбить, схватив за хвост и нос. Что касается зебр, то их камуфляж работает в их пользу, мешая их хищникам изолировать и атаковать особь.

Проанализировав количество шкур рысей и зайцев, добытых охотниками, канадский биолог Чарльз Гордон Хьюитт пришел к выводу, что эти два вида сильно зависят друг от друга, так что популяция канадской рыси растет и падает с взлеты и падения популяции зайцев-беляков. Дальнейшие исследования показали, что именно нехватка пищи в результате сокращения популяции зайцев повлияла на скорость размножения этого вида рысей.

В то время как антилопы гну и капские буйволы составляют основную часть их рациона, известно, что африканские львы также охотятся на бородавочников, особенно когда они легко доступны. Однако бородавочники с глазами на макушке и бивнями не обязательно становятся легкой добычей для льва, особенно если последнему требуется время, чтобы убить.

С точки зрения исследователей, отношения между волками и лосями на острове Рояль дают наилучшую картину взаимоотношений хищник-жертва, так как лоси являются почти единственной добычей волков на этом изолированном острове. Изучая их отношения в течение десятилетий, исследователи поняли, что нехватка пищи, вызванная тем, что волки едят слишком много лосей, также сдерживает волчью популяцию.

В морском биоме большая белая акула является высшим хищником. Обычно он охотится на морских слонов. Для тюленей лучшая линия защиты — оставаться на суше. Для большой белой акулы ее исключительные слуховые способности помогают найти тюленя. Тюленю не всегда удается оставаться вне воды, чтобы не умереть с голоду. В тот момент, когда он попадает в воду, он находится на радаре большой белой акулы. Все зависит от того, кто моргнет первым.

В пресноводном биоме скопа, ловящая рыбу, будет прекрасным примером взаимодействия хищника и добычи. Эта птица встречается почти везде, где она может найти рыбу для добычи. Обладая исключительным зрением, скопа может видеть любое движение в воде. Он атакует с молниеносной скоростью и вытаскивает рыбу из воды благодаря противостоящим когтям и острым колючим чешуям на пальцах ног. Что касается рыб, то их лучшая защита — избегать мелководья.

В биоме тундры у нас есть интересный пример в виде отношений между песцом и леммингами; интересен тем, что популяция леммингов циклична, т. е. колеблется каждые три-пять лет. Популяция песцов в определенных регионах обусловлена ​​популяцией леммингов, и, таким образом, мы видим прямую зависимость между количеством и размером помета песца и доступностью леммингов.

В некоторых отношениях хищник-жертва жертва практически не имеет защиты от хищника. Отношения медведя гризли и лосося — хороший тому пример. Плохой ход лосося может иметь эффект домино на здоровье и популяцию медведей гризли, и исследователи обеспокоены тем, что плохой ход лосося со временем станет частым; вежливость, чрезмерный вылов рыбы и изменение климата.

На самом базовом уровне одним из самых простых примеров отношений хищник-жертва будет отношения кошки и мыши, и маловероятно, что вы никогда не слышали об этом дуэте. Тем не менее, есть вероятность, что кошка может не охотиться на мышь в поисках пищи, особенно если она привыкла к среде, в которой ей время от времени подают еду в миске.

И хищник, и жертва эволюционируют с течением времени; хищник эволюционирует, чтобы охотиться, а жертва эволюционирует, чтобы избежать охоты. Оба прибегают к поведенческой и физической адаптации, чтобы превзойти друг друга. У хищника, плохо подготовленного к охоте из-за старости или инвалидности, безрадостное будущее. Так же поступает и жертва, которая плохо подготовлена ​​к тому, чтобы избежать охоты.

Отношения между хищником и добычей — Молодой натуралист

 

---

Будь то бегун, проглатывающий ящерицу, синий краб, поедающий рыбу, американская белая цапля, ловящая окуня, акула, исследующая возмущение поверхности, которое может быть едой, или человек, собирающий корову на убой, хищник убивает, чтобы обеспечить себя или свою семью пищей.

В плане Природы нет такого понятия, как хорошее или плохое животное. Есть только те животные, которые убивают, чтобы поесть (хищники) и те, которых убивают и съеден (добыча). Нам несправедливо судить об их естественных действиях по выживанию. нашими собственными представлениями о том, что хорошо и что плохо, или решить, что все хищники злодеи.

Когда койот гонится, ловит, убивает и ест милый пушистый кролик, это не намеренно жестокий. это только встреча его физическая потребность в еда с чем угодно доступны в то время. Его еда могла так же легко был мышью, крыса или другое мелкое существо если один из этих других животные были ближе или легче поймать.

Есть ли разница между голодной горой лев преследует, убивает, и съесть оленя и выслеживание охотников, стрельба, и взять оленя домой для его семья, чтобы поесть? Оба горный лев и человек-охотник — хищник, использование оленей в пищу. Вы можете подумать, что с тех пор ты не охотник, ты не хищник. Как про говядину, свинину, баранину, рыба или курица, которую вы едите каждый день? Просто потому, что ты не убивайте животное самостоятельно не делает тебя меньше хищник. Ты все еще животное, поедающее мясо другого животного, чтобы удовлетворить твой голод.

Люди обычно думают о хищниках как о плотоядных млекопитающих (плотоядных), но у семейств птиц, рептилий, амфибий, рыб и насекомых также есть свои хищники. Орлы, ястребы, соколы и совы, пожалуй, самые известные хищники птичий мир. Всем известно, как один из них может налететь, поймать и убить маленькое существо, а затем используйте остроконечный крючковатый клюв, чтобы разорвать кусочки мяса животного. Потому что они питаются мелкими млекопитающими, эти птицы более жестокие, чем рыбоядные пеликаны, чайки, крачки, цапли, белые цапли, и зимородки или насекомоядные дятлы, мухоловки, славки, ласточки, стрижи и синицы? Хотя их предпочтения в еде различны, они все хищные птицы убивают, чтобы утолить голод.

Вероятно, у вас не возникнет проблем с узнаванием члена аллигатора семейство рептилий как хищник, потому что он ест все, что может поймать, либо в воде или на суше. Змеи также известны тем, что ловят и глотают самых разных существ, но многие ли из вас остановились, чтобы понять, что ящерица тот, кто ест насекомых, тоже хищник? Пара других хищников с острыми языками, лягушка и жаба принадлежат к семейству земноводных. Ты бы поставил ящерицу, лягушка и жаба в одной категории с аллигатором? Вам следует. Все хищники, убивающие и поедающие, чтобы выжить.

Акулы, пожалуй, самые опасные морские хищники, но их пищевые привычки, хотя и порочные, не более хищные, чем у пресноводных бас? С тех пор, как он стал достаточно большим, чтобы съесть некоторых из своих собратьев и сестер до того времени, когда он может проглотить лягушку или утёнка, плавающего по воде. поверхность, черный окунь проводит время в поисках вещей в водном мире есть. Если бы не его хищные повадки, мы бы не смогли поймать окуня со всеми видами приманок и приманок, которые мы используем. Эта рыбообразная приманка выглядит как настоящая рыба, а этот пластиковый червь выглядит как настоящий червь или маленькая змея к голодному окуню.

Хотя многие насекомые питаются друг другом, т. один ты, наверное, наиболее знакомым является паук. Он сидит в своей паутине и терпеливо ждет насекомое, которое нужно поймать в своей липкой ловушке. Когда такое бывает, паук выбегает, убивает или парализует насекомое, заворачивает его в шелк, а затем высасывает жидкости его тела.

Вы можете подумать в этот момент, что хищник лучше всех жизнь, ни к чему беспокоиться о том, кроме как поймать свой следующий прием пищи. Но сделал ты знаешь, что много животных являются одновременно хищниками и добыча?

Когда паук сидит в паутине в ожидании еды из насекомых, это хищник. Однако, если язык ящерицы высунется и поймает паука, паук становится добычей ящерицы. Затем хищную ящерицу можно проглотить. дорожным бегуном, которого позже может поймать и съесть койот. Блуждающий койот может стать жертвой величайшего хищника из всех, человека.

Хищничество, поедание одного животного другим, является одним из способов, которым природа держит популяцию животных под контролем. Огромные стаи насекомых вскоре покрывают землю, создавая угрозу всему живому, если бы не пауки, лягушки, рыбы, ящерицы, змеи, птицы и млекопитающие, которые их едят. Животные, питающиеся растениями, такие как мыши, крысы и кролики, вскоре лишатся растительности. земля голая без контролирующего воздействия хищников. Места, где обитают крупные хищники были сокращены за счет отлова, отстрела и других методов борьбы с хищниками. часто развиваются большие популяции мышей, крыс и кроликов, которые могут уничтожить растения, необходимые другим видам диких животных как для еды, так и для убежища. Если хищникам было позволено остаться, виды добычи, вероятно, держали под контролем.

Хищничество также обеспечивает «выживание наиболее приспособленных», основной закон. Старые, больные или раненые животные — легкая добыча для хищников.

Молодые животные также находятся в опасности, поскольку они не такие сильные, быстрые или мудрые. как взрослые животные. Те, у кого сильные инстинкты выживания, узнают, как чтобы избежать их хищников. Естественное хищничество занимает определенное место в балансе природы, так что в следующий раз поймаете себя на мысли, насколько опасен хищник для убийства милого маленького кролика, помните, что хищник только убивает для продуктов питания.

Модель «хищник-жертва» — Scholarpedia

Фрэнк Хоппенстедт (2006), Scholarpedia, 1(10):1563.

doi:10.4249/scholarpedia.1563

, редакция #91667 [ссылка/цитирование этой статьи]

Постпубликационная деятельность

Куратор: Фрэнк Хоппенстедт

Авторы:

 

0. 38 —

Евгений Михайлович Ижикевич

0,12 —

Настоящее имя WikiSysop

0,12 —

Тобиас Деннингер

Бенджамин Броннер

• Д-р Фрэнк Хоппенстедт, Институт математических наук Куранта, Нью-Йоркский университет, Нью-Йорк, штат Нью-Йорк

Рисунок 1: Периодическая активность, генерируемая моделью Predator-Prey.

Модели «хищник-жертва» , возможно, являются строительными блоками био- и экосистем, поскольку биомассы выращены

из массы их ресурсов. Виды конкурируют, развиваются и рассредоточиться просто с целью поиска ресурсов для поддержания своей борьбы за само существование. В зависимости от конкретных настроек приложений они могут принимать формы взаимодействий «ресурс-потребитель», «растение-травоядное животное», «паразит-хозяин», «опухолевые клетки (вирус)-иммунная система», «восприимчивый-инфекционный» и т. д. взаимодействия и, следовательно, могут иметь приложения вне экосистем. Когда кажущиеся конкурентными взаимодействия тщательно изучаются, они часто на самом деле являются замаскированными формами взаимодействия хищник-жертва.

Содержимое 1 Модель General Predator-Prey 2 Лотка-Вольтерра Модель 3 Кермак-МакКендрик Модель 4 Модель Jacob-Monod 5 Логистическое уравнение 6 Хищничество с временными задержками: хаос в уравнении воспроизведения Рикера 7 Каталожные номера 8 внешних ссылок 9 См. также

Модель General Predator-Prey

Рассмотрим две популяции, размеры которых в контрольный момент времени \(t\) равны обозначаются через \(x(t)\ ,\) \(y(t)\ ,\) соответственно. Функции \(x\) и \(y\) могут обозначать численность или концентрацию населения (количество на площадь) или какой-либо другой шкалы размера популяции, но принимаются к быть непрерывными функциями. Изменения численности популяции со временем описывается производными по времени \(\dot x \equiv dx/dt\) и \(\dot y \equiv dy/dt\ ,\) соответственно и общую модель взаимодействующих популяций записывается в виде двух автономных дифференциальных уравнений \[ \точка x = x f(x,y) \] \[ \точка у = у г(х,у)\] (т. е. время \(t\) не фигурирует явно в функции \(x f(x,y)\) и \(y g(x,y)\)). Функции \(f\) и \(g\) обозначают соответствующие темпы роста на душу населения из двух видов. Предполагается, что \( df(x, y)/dy<0 \) и \( dg(x, y)/dx>0. \) Эту общую модель часто называют колмогоровской моделью «хищник-жертва» (Freedman 1980, Brauer and Castillo-Chavez 2000).

Лотка-Вольтерра Модель

В 1926 году известный итальянский математик Вито Вольтерра предложил дифференциальное уравнение модели для объяснения наблюдаемого увеличения хищной рыбы (и соответствующего уменьшение добычи рыбы) в Адриатическом море во время Первой мировой войны. В то же время в США уравнения, изученные Вольтеррой, были выведен независимо Альфредом Лоткой (1925) для описания гипотетической химической реакции, в которой химические концентрации колеблются. Модель Лотки-Вольтерры — простейшая модель взаимодействия хищника и жертвы. Он основан на линейном росте на душу населения. ставки, которые записываются как \[f= b-p y\] и \(g=r x-d\ .\)

• Параметр \(b\) — скорость роста вида \(x\) (жертвы) при отсутствии взаимодействия с видом \(y\) (хищники). Количество жертв уменьшается в результате этих взаимодействий: скорость роста на душу населения уменьшается (здесь линейно) с увеличением \(y\,\), возможно, становящимся отрицательным.
• Параметр \(p\) измеряет воздействие хищничества на \(\dot x/x\ .\)
• Параметр \(d\) — скорость гибели (или эмиграции) видов \(y\) при отсутствии взаимодействия с видами \(x\ .\)
• Термин \(r x\) обозначает чистую скорость роста (или иммиграции) популяции хищников в ответ на размер популяции добычи.

Модель «Добыча-Хищник» с линейными темпами роста на душу населения \[\dot x = (b — p y) x\] (Добыча) \[\dot y = (r x — d) y\] (Хищники) Эта система называется 9.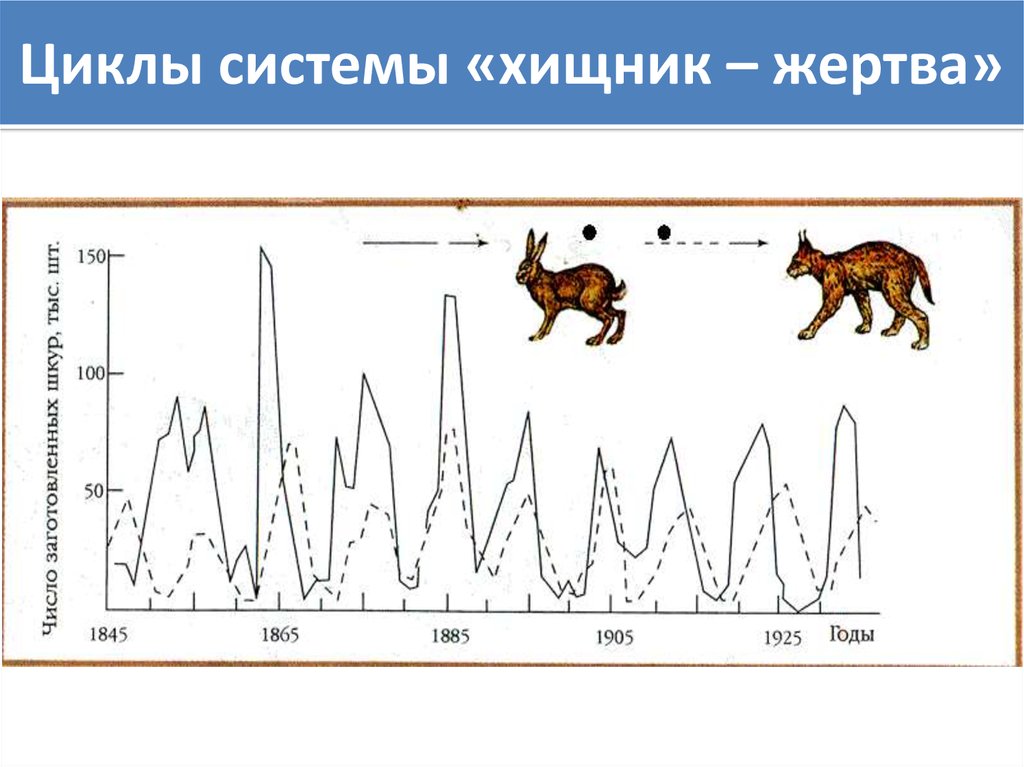 0081 Модель Лотки-Вольтерры : представляет собой одну из самых ранних моделей в математической экологии.

Рисунок 2: Динамика «жертва-хищник», описываемая кривыми уровня сохраняющейся величины. Стрелки описывают скорость и направление решений. В этом моделировании данные \(d=r=b=d=1\ .\) Существуют равновесия в точках \(x=1, y=1\) и в точках \(x=0, y=0\). \)

Система может быть интегрирована напрямую. В частности, любое решение \((x(t),y(t))\) системы удовлетворяет тождеству \[ C = b \ln y(t) — p y(t) — r x(t) + d \ln x(t) \] для всех \(t\ ,\), где константа \(C= b \ln y(0) — p y(0) — r x(0) + d \ln x(0)\) определяется начальными условиями и параметрами системы. (Здесь \(\ln x\) обозначает натуральный логарифм \(x\ ,\) и т. д.) количество в правой части тождества выше относится к как закон сохранения , так как он постоянен вдоль любой решение. Сохраняющееся количество облегчает визуализацию решения. На рисунке проводим нивелирные контуры поверхность \[z = b \ln y — p y — r x + d \ln x\] в первом квадранте \(xy\)-плоскости. Контуры описывают решения системы определяются своими начальными данными, а так как они являются замкнутыми кривыми, то решения представляют собой периодические колебания.

Если \(b>0\ ,\) есть два равновесия, \(x=0, y=0\) (угасание) и \(x=d/r, y=b/p\) (сосуществование), а поверхность \[z = b \ln y — p y — r x + d \ln x\] имеет единственный пик в последнем равновесии. контурные линии на рисунке описывают классический циклы жертва-хищник, наблюдаемые в экологических системах.

Приведенная выше модель была получена независимо в следующих областях:

• эпидемии (Кермак и МакКендрик 1927, 1932, 1933) (\(b=0\))
  • \(x\) являются восприимчивыми лицами и
  • \(y\) — заразные лица,
• экология (Лотка 1925, Вольтерра 1926)
  • \(x\) являются добычей и
  • \(у\) хищники,
• теория горения (Семенов 1935)
  • \(x\) и \(y\) — химические радикалы, образующиеся при H ₂ O ₂ горение,
• экономика (Гэлбрейт 2006)
  • \(x\) это население и
  • \(y\) является хищническим учреждением,

и многие другие исследования из различных дисциплин.

Альфред Джеймс Лотка (1880 — 1949, США, химик, демограф, эколог и математик) родился во Львове (Лемберг), в то время находившемся в Австрии, ныне на Украине. Он приехал в Соединенные Штаты в 1902 и написал ряд теоретических статей о химических колебаниях в первые десятилетия двадцатого века, а также написал книгу по теоретической биологии (1925). Затем он оставил (академическую) науку и провел большую часть своей трудовой жизни в страховой компании (Metropolitan Life). В этом качестве он стал президентом PAA (Американской ассоциации народонаселения).

Вито Вольтерра (3 мая 1860 — 11 октября 1940, итальянский математик и физик, наиболее известный своим вкладом в математическую биологию) родился в Анконе, в очень бедной семье. Вольтерра рано подавал надежды в математике еще до поступления в Пизанский университет. Его работа подытожена в его книге «Теория функционалов и интегральных и интегро-дифференциальных уравнений» (19).30). После Первой мировой войны Вольтерра обратил внимание на применение своих математических идей в биологии, в основном повторяя и развивая работу Пьера Франсуа Ферхюльста. Наиболее известным результатом этого периода является модель Лотки-Вольтерры. В 1922 году он присоединился к оппозиции фашистскому режиму Бенито Муссолини, а в 1931 году отказался принести обязательную присягу на верность. Он был вынужден оставить свою университетскую должность и членство в научных академиях, и в последующие годы он жил в основном за границей, вернувшись в Рим незадолго до своей смерти.

Модель Kermack-McKendrick

Коллективный иммунитет возникает при хищничестве и эпидемиях. это удобно сформулировать это с точки зрения эпидемиологии, где мы сейчас к жертве как к восприимчивой, а к хищнику как к заразные. Динамика заражения представлена ​​на графике \(x\to y\to \,\), что указывает на то, что восприимчивые люди могут стать заразными и что инфекционные агенты могут быть удалены из процесса (например, через смерть, карантин или прививка). Рассмотрим временной интервал, который является коротким по сравнению с воспроизводством восприимчивой популяции, т. е. пусть \(b=0\ .\) Если начальная восприимчивая популяция настолько велика, что \(x(0)> d/r\ ,\) то из второго уравнения в модели хищник-жертва мы видим, что изначально \(\dot y>0\ ,\), что указывает на то, что заразные изначально будут более чем заменить себя, передав инфекцию. Однако, если это условие не выполняется, заразная популяция снижаться. Критическое значение \(R\equiv rx(0)/d=1\) называется быть эпидемическим порогом или переломным моментом для процесса.

Рисунок 3: Модель Кермака-МакКендрика распространения инфекционного заболевания. Переломный момент находится в точке \(x = 1,0\ .\). Если \(x(0)\) выше этого значения, наступит эпидемия. Серьезность можно оценить, проследив кривую, исходящую от \(x(0)\), пока она не сходится к горизонтальной оси. Это указывает на размер восприимчивой популяции, которая избегает инфекции. Обратите внимание, что горизонтальная ось, как показано здесь, начинается с x = 0,1, чтобы избежать логарифмической сингулярности.

Краткий расчет показывает, что \(x(t)\) сходится к константе, скажем \(x(t)\to x^*,\), где \(x^*\) можно найти, решив уравнение \(C=r x^* — d \ln x^*\ ,\), как показано на рисунке.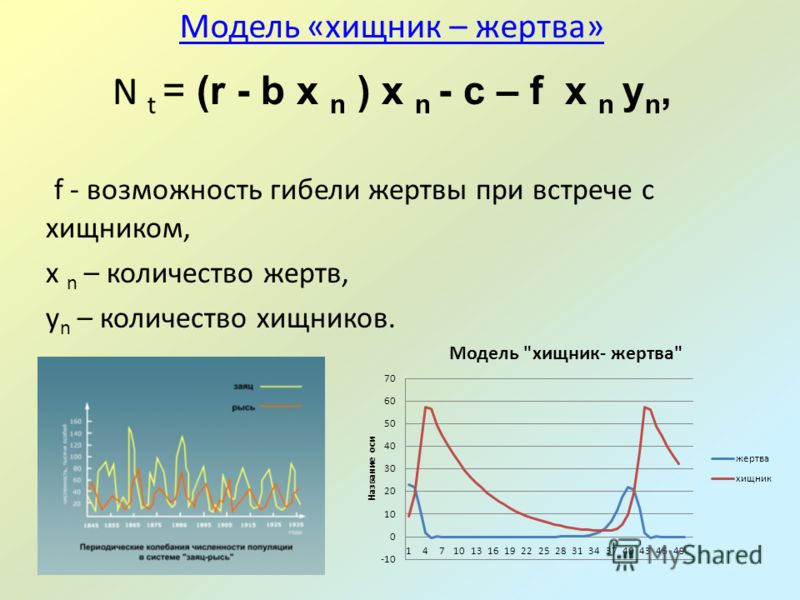 Удивительно, но это число всегда больше нуля, что показывает, что некоторые восприимчивые всегда выживут!

Это явление, которое упоминается к as коллективный иммунитет наблюдается на практике; на самом деле, номер \(R\) регулярно публикуется для различных заболеваний и регионов. в качестве меры борьбы с эпидемией. Он отражает тот факт, что восприимчивое население может быть снижено до уровня, ниже которого Инфекционизм не увеличится. Модель в данном случае называется как модель Кермака-МакКендрика взаимодействий между восприимчивыми и инфекционными агентами в эпидемиологии.

Якоб-Моно Модель

Другой подход к моделированию взаимодействия между добычей и хищников был разработан для учета организмов (таких как бактерии), поглощающие питательные вещества. Существует ограниченная скорость поглощения, которая такие организмы способны, и следующая модель объясняет ограниченные скорости поглощения. Предположим теперь, что \(x\) обозначает размер популяции кормушек и что они питаются химическим виды концентрации \(y\ . \). Обычно они представляют концентрация кормов и питательных веществ в растворе, а не «счет голов». Якоб-Моно модель есть \[\dot x = \frac{V y}{K+y}x\] \[\dot y = -\frac 1Y \frac{V y}{K+y}x\] куда

• \(V\) — скорость захвата,
• \(K\) — константа насыщения, а
• \(Y\) — выход \(x\) на единицу \(y\) использованного товара.

Обратите внимание, что при \(y=K\ ,\) скорость поглощения составляет \(V/2\ ,\) половину максимальной; на практике \(y=K\) принимается за точку невозврата: Если \(y Он служит одним из важных строительные блоки в исследованиях сложных биохимических реакций и в экология (Смит и Уолтман 1997).

Величина \(C=x +Y y\) сохраняется (поскольку производная с по времени правая часть равна нулю), где \(C=x(0)+Yy(0)\ .\) Подстановка этого в первое уравнение дает \[\dot x =\frac{V (Cx)}{Y K+(Cx)}x\ .\] Решения можно найти в квадратурах, и они показывают, что если \(x(0)>0\,\), затем \(x(t)\to C\) как \(t\to\infty\,\), после чего питательные вещества были истощены.

Типичное использование этой модели для описания роста с непрерывным потоком устройство, такое как хемостат, где происходит непрерывное удаление питательных веществ и кормушек и непрерывное снабжение свежими питательными веществами. Модель Джейкоба-Моно используется для описания такого устройства для роста бактерий, например, для определения условий существования устойчивого динамического равновесия путем уравновешивания роста за счет поглощения питательных веществ с вымыванием кормушек.

В некоторых моделях «хищник-жертва» используются термины, аналогичные тем, которые появляются в модели Джейкоба-Моно, для описания скорости, с которой хищники поедают добычу. В более общем плане любые данные в модели Лотки-Вольтерры можно рассматривать как зависящие от плотности добычи, что соответствует изучаемой системе. Это называется функциональной реакцией, идея, которую вводит и обсуждает К. С. Холлинг (1959). В популяционных моделях использовалось несколько различных форм функционального ответа, но форма Джейкоба-Монода, также называемая экологами формой Холлинга типа 2, является одной из наиболее распространенных. Многие другие исследования моделей хищник-жертва включали функциональные реакции. Например, \(r\) заменяется на \(r \ln(K/x)\) (Gompertz, 1825), \(r(K-x)/(K+\epsilon x),\) (Smith, 19g-1\right)\) с \(0< g \le 1\ ,\) (Rosenzweig, 1971). Эти и другие функциональные реакции также обсуждаются в May (1974). Такие механизмы в модели Лотки-Вольтерры могут стабилизировать или дестабилизировать систему, например, приводя к исчезновению хищников или к сосуществованию жертвы и хищника. Это контрастирует с множеством циклов, предсказанных исходной моделью Лотки-Вольтерры.

Логистическое уравнение

Интересный случай для \[\ точка х =\ гидроразрыва {V (С-х)} {Y К + (С-х)} х \] когда \(V\) и \(YK\) очень велики по сравнению с другими данными в модели, но с их отношение имеет умеренную величину, скажем \(V/(YK)\приблизительно r\ .\). Тогда мы можно игнорировать второй член в знаменателе и получить \[\точка х = г(С-х)х\ .\] Это называется логистическое уравнение . Оно тоже возникло в различных дисциплин, но одно из первых его появления связано с Verhulst в середине 19 века, который использовал его для исправления некоторых отклонения модели Мальтуса (\(\dot x = r x\)) от определенных человеческих данные о населении. Число \(C\) теперь называют числом грузоподъемность для населения; это соответствует в модели Якоба-Моно не осталось питательных веществ.

Логистическое уравнение можно решить в замкнутая форма квадратурами. Это показывает, что \(x(t)\to C\) как \(t\to\infty\ ,\), если \(x(0)> 0\ . \)

Хищничество с временными задержками: хаос в уравнении воспроизводства Рикера

Временные задержки происходят в биологических системах, и они могут производить сложная динамика. Для моделирования возрастной структуры (и других временных задержек) в системе мы используем подход, который был введен Эйлером в 18 век. Пусть \(x(t)\) обозначает число родившихся в момент времени \(t\ .\) Тогда \(x(t-a)\) обозначает число родившихся \(a\) единиц назад. Предположим, что существует нелинейный эффект, такой, что количество новорожденных \(a\) единиц назад, способных участвовать в размножении в момент времени \(t\) есть \(h(x(t-a))\), где функция \(h\) называется 9t m(a) h(x(t-a))\, da\ ,\] где \(x_0(t)\) обозначает затяжной вклад в более поздние рождения начальной популяции. В случае, когда \(h(x)=x\) — линейная функция, это уравнение называют Уравнение восстановления , которое широко используется в демографии. Его решение можно найти с помощью преобразований Лапласа (Keyfitz and Flieger, 1971). n x_0\ .\) Однако, если \(h\) равно в случае Ферхюльста, где \(h(x) = x (C — x)_+ \equiv \max(C-x,0),\) рекурсия становится \[x_{n+1}=r x_n(C-x_n)_+\,\] чьи итерации могут демонстрировать довольно дикое поведение. Это было первым заметил эколог В.Е. Рикер в 1950-х годов, которые использовали функция \(h(x)=x\exp{(-x)}\) в исследованиях динамики промысла, хотя в то время его работа в значительной степени игнорировалась. Это воспроизведение функция объясняет каннибализм (самохищничество) в том, что если населения мало, модель похожа на мальтусовскую, но для больших популяции, размножение сильно подавлено. Работа была позже заново открыт Робертом Мэем, который стимулировал нынешнее заметная область хаоса (Gleick 1987).

Рисунок 4: Динамика популяции Рикера. 9{-x_n}\ .\] Начиная с \(x_1=1\ ,\), мы определяем последовательность \(\{x_{50},x_{51},x_{52},x_{53},\dots,x_{300}\}\) и запишите в массив, скажем \(D(r,x)\ ,\) количество элементов последовательности, которые находятся в каждый бункер. Мы начинаем считать только после 50 начальных повторяется, чтобы избежать переходных процессов. Результатом является поверхность \(D(r,x)\), которая описывает динамику. Построим эту запись, глядя сверху, как показано на рисунке (Hoppensteadt and Hyman 1977). Решение всегда укладывается в какую-то структуру, которая может быть очень сложной. Сначала существует единственное устойчивое состояние. Около \(r=8\) этого состояния бифуркация в колебание периода 2. Вблизи \(r=12\) периода 2 решение разветвляется на решение периода 4 и т. д. По \(r=18\) набор решений довольно сложен. Это в пределах хаотичного динамика. Когда функция плодородия \(m\) имеет более широкую поддержку, решение набор еще сложнее.

Ссылки

• Ф. Брауэр и К. Кастильо-Чавес, Математические модели в популяционной биологии и эпидемиологии, Springer-Verlag, Heidelberg, 2000.
• Х. И. Фридман, Детерминированные математические модели в популяционной экологии. Нью-Йорк: Марсель Деккер, 1980.
• Дж. К. Гэлбрейт, Государство Хищников, Мать Джонс, май/июнь 2006 г.
• Дж. Глейк, Хаос: Создание новой науки, Viking Press, Нью-Йорк, 1987.
• К. С. Холлинг, Характеристики простого типа хищничества и паразитизма, Канадский энтомолог 91 (1959), 385-398.
• Ф.К. Хоппенстедт, Дж. М. Хайман, Периодические решения разностного уравнения логистики, SIAM J. Appl. Мат. 58 (1977) 73-81.
• О. Кермак, А. Г. МакКендрик, Proc. Рой. соц. А, 115(1927)700-721, 138(1932)55-83, 141(1933)94-122.
• Н. Кейфиц, В. Флигер, Население: факты и методы демографии, У. Х. Фримен, Сан-Франциско, 1971.
• М. Кот, Элементы математической экологии, издательство Кембриджского университета, 2001 г.
• А.Дж. Лотка, Элементы физической биологии. Уильямс и Уилкинс, Балтимор, 19 лет.25.
• Р. М. Мэй, Стабильность и сложность модельных экосистем, Princeton U. Press, NJ, 1974.
• Н.Н. Семенов, Химическая кинетика и цепные реакции, Кларендон, Оксфорд, 1935.